my homework lesson seven solve problems with angles

• Texas Go Math
• Big Ideas Math
• Engageny Math
• McGraw Hill My Math
• enVision Math
• 180 Days of Math
• Math in Focus Answer Key
• Math Expressions Answer Key
• Privacy Policy

McGraw Hill My Math Grade 4 Chapter 14 Lesson 7 Answer Key Solve Problems with Angles

All the solutions provided in  McGraw Hill My Math Grade 4 Answer Key PDF Chapter 14 Lesson 7 Solve Problems with Angles will give you a clear idea of the concepts.

McGraw-Hill My Math Grade 4 Answer Key Chapter 14 Lesson 7 Solve Problems with Angles

An angle can be decomposed, or broken, into non-overlapping parts. The angle measure of the whole is the sum of the angle measures of the parts.

Math in My World

Guided Practice

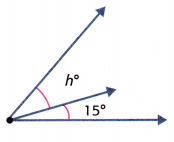
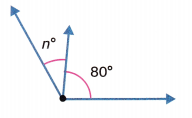
Algebra Find each unknown.

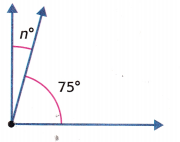
Independent Practice

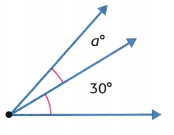
Problem Solving

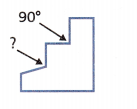
HOT Problems

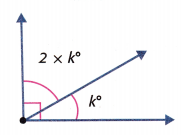
Question 13. Building on the Essential Question How is addition related to angle measurement? Answer: Two angles that are next to each other without overlapping are called Adjacent angles. These angles can be added together to make a larger angle. Adding angles is the same as adding numbers. We can add two or more angles as long as they are not overlapping.

McGraw Hill My Math Grade 4 Chapter 14 Lesson 7 My Homework Answer Key

Question 7. Mathematical PRACTICE Make a Plan Suppose you draw a line from the center of a clock face to the number 12. When the minute hand gets to 3 on the clock face, the line and minute hand form a 90° angle. What angle does the line and the minute hand make when the minute hand is on 2? Answer: 55 degrees When hour and minute hand are at 12 and 2, then the time showing is 12:10 A clock is shaped like a circle and is composed of 360 degrees. There are 60 minutes in an hour, and 360 degrees divided by 60 minutes is 6. Therefore, the minute hand moves 6 degrees per minute. It takes 720 minutes for the hour hand to move around the clock. 360 degrees divided by 720 minutes is 0.5. Therefore, the hour hand moves 0.5 degrees per minute. At 12:10, the hour hand has moved 10 out of 720 possible times from the top of the clock. 10 times 0.5 degrees is 5 degrees. At 12:10, the minute hand has moved 10 out of 60 possible times from the top of the clock. 10 times 6 degrees is 60 degrees. 60-5 = 55 degrees

Test Practice

Leave a Comment Cancel Reply

You must be logged in to post a comment.

Angles and Equations

Our Angles and Equations lesson plan teaches students different ways that angles can be used to find missing angles in equations. Students also learn how to use addition and subtraction to find the measure of an unknown angle.

Included with this lesson are some adjustments or additions that you can make if you’d like, found in the “Options for Lesson” section of the Classroom Procedure page. One of the optional additions to this lesson is to have groups of students make their own angle problems using a protractor and various shapes; they can then swap them with another group’s problems and solve them.

Description

Additional information, what our angles and equations lesson plan includes.

Lesson Objectives and Overview: Angles and Equations explores different ways angles can be used in equations to find missing angle measurements. The lesson focuses specifically on adding and subtracting angles. At the end of this lesson, students will be able to use addition and subtraction to find the measure of an unknown angle. This lesson is for students in 4th grade and 5th grade.

Classroom Procedure

Every lesson plan provides you with a classroom procedure page that outlines a step-by-step guide to follow. You do not have to follow the guide exactly. The guide helps you organize the lesson and details when to hand out worksheets. It also lists information in the orange box that you might find useful. You will find the lesson objectives, state standards, and number of class sessions the lesson should take to complete in this area. In addition, it describes the supplies you will need as well as what and how you need to prepare beforehand. The only supplies you will need for this lesson are charts of angles for the activity worksheet. To prepare for this lesson ahead of time, you can copy all of the materials and handouts and copy the shapes for the activity worksheet and draw in angles.

Options for Lesson

Included with this lesson is an “Options for Lesson” section that lists a number of suggestions for activities to add to the lesson or substitutions for the ones already in the lesson. For this lesson, one optional addition is to have groups of students make their own angle problems using a protractor and various shapes; they can then swap them with another group’s problems and solve them. You can also have older or more advanced students learn about the sum of interior angles and have them add up the sum of the interior angles for all of the shapes used during this lesson. Finally, you can have students solve more challenging problems alongside you where you add and subtract using three angles.

Teacher Notes

The teacher notes page includes lines that you can use to add your own notes as you’re preparing for this lesson.

ANGLES AND EQUATIONS LESSON PLAN CONTENT PAGES

The Angles and Equations lesson plan includes two content pages. The lesson begins with a quick review of some information students will have already learned from a previous lesson about angles. It reiterates that a circle has 360 degrees but can be broken up into many different angles of different sizes. All of these angles added together equal 360. You can add angles together to make larger angles or divided to make smaller ones. You could also use addition and subtraction to find missing angles. You can find angle measurements using mathematical equations. We can use a variable to represent the missing angle.

Students next learn about how they can use addition to find the total number of degrees in an angle. The lesson includes some helpful diagrams and figures of angles to illustrate this concept. You can add together adjacent angles, or angles that are next to each other but don’t overlap, to make a larger angle. You can also add adjacent angles together to find the sum of the larger angle. Additionally, you can add two or more angles together for the sum of the largest angle. You can add angles if they’re independent from one another or adjacent. The lesson also notes that geometry actually uses the additive properties of angles a lot!

Subtraction

Students finally learn about subtraction in relation to angles. You can subtract the measurement of a smaller angle from the measurement of a larger angle in order to find the missing measurement. The lesson includes two helpful examples to illustrate this along with diagrams of shapes and angles. One of the examples shows how to solve for a missing angle in a shape. In the example, a square is shown with a line running diagonally through it. The angle on one side is marked 45°, and the angle on the other side is marked x. 45°plus x is the total measurement of the larger angle, a square has four right angles, and a right angle is equal to 90 degrees. Therefore, you can come up with the right equation to solve for x, which equals 45°!

ANGLES AND EQUATIONS LESSON PLAN WORKSHEETS

The Angles and Equations lesson plan includes four worksheets: an activity worksheet, a practice worksheet, a homework assignment, and a quiz. You can refer to the guide on the classroom procedure page to determine when to hand out each worksheet.

SHAPES AND ANGLES ACTIVITY WORKSHEET

Students can work either alone or in groups for this activity. For the activity worksheet, you will need to either provide each student with a copy of the chart showing shapes and the measurements of a single side angle of that shape or display it at the front of the room. You will also print out the shapes, draw angles with measurements, and give them to the students. They will then determine the missing angles. Students will identify the shape, find the angle measurement on the chart, and then solve for the missing measurement.

ANGLES AND EQUATIONS PRACTICE WORKSHEET

For the practice worksheet, students determine the value of x in ten different problems.

MISSING ANGLES HOMEWORK ASSIGNMENT

The homework assignment asks students to look at figures and both write the equation and find the missing angles.

VALUE OF X QUIZ

This lesson plan also includes a quiz to test the students’ knowledge and understanding of the lesson material. For the quiz, students solve two problems where they have to determine the value of x.

Worksheet Answer Keys

This lesson plan includes answer keys for the practice worksheet, the homework assignment, and the quiz. No answer key is provided for the activity worksheet. If you choose to administer the lesson pages to your students via PDF, you will need to save a new file that omits these pages. Otherwise, you can simply print out the applicable pages and keep these as reference for yourself when grading assignments.

Thank you for submitting a review!

Your input is very much appreciated. Share it with your friends so they can enjoy it too!

Nice product

A very good product that helps your kids learn about angles and equation.

Related products

Sports: Disc Golf

Sports: Professional Wrestling

Sports: Ice Hockey

Make Your Life Easier With Our Lesson Plans

Stay up-to-date with new lessons.

• Lesson Plans
• For Teachers

© 2024 Learn Bright. All rights reserved. Terms and Conditions. Privacy Policy.

• Sign Up for Free

Solve Angle Problems and Equations

Related Topics: Lesson Plans and Worksheets for Grade 7 Lesson Plans and Worksheets for all Grades More Lessons for Grade 7 Common Core For Grade 7

Examples, videos, and solutions to help Grade 7 students learn how to use facts about supplementary, complementary, vertical, and adjacent angles in a multi-step problem, write and solve simple equations for an unknown angle in a figure.

New York State Common Core Math Grade 7, Module 3, Lesson 10

Download worksheets for Grade 7  

Lesson 10 Student Outcomes

• Students use vertical and adjacent angles and angles on a line and angles at a point in a multi-step problem to write and solve simple equations for an unknown angle in a figure.

Relevant Vocabulary Adjacent Angles: Two angles ∠BAC and ∠CAD with a common side AC are adjacent angles if C belongs to the interior of ∠BAD. Vertical Angles: Two angles are vertical angles (or vertically opposite angles) if their sides form two pairs of opposite rays. Angles on a Line: The sum of the measures of adjacent angles on a line is 180°. Angles at a Point: The sum of the measures of adjacent angles at a point is 360°.

Classwork We can name an angle by naming the arc, by the vertex or three points.

Example 1 Estimate the measurement of x. In a complete sentence, describe the angle relationship in the diagram. Write an equation for the angle relationship shown in the figure and solve for x. Then find the measures of ∠BAC and confirm your answers by measuring the angle with a protractor.

Exercise 1 In a complete sentence, describe the angle relationship in the diagram. Find the measurements of ∠BAC and ∠DAE.

Example 2 In a complete sentence, describe the angle relationship in the diagram. Write an equation for the angle relationship shown in the figure and solve for x and y. Find the measurements of ∠LEB and ∠KEB.

Example 3 In a complete sentence, describe the angle relationships in the diagram. Write an equation for the angle relationship shown in the figure and solve for x. Find the measurement of ∠EKF and confirm your answers by measuring the angle with a protractor.

Exercise 3 In a complete sentence, describe the angle relationships in the diagram. Find the measurement of ∠GAH.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Lesson 7: Solve for Unknown Angles—Transversals

Related documents

Add this document to collection(s)

You can add this document to your study collection(s)

Add this document to saved

You can add this document to your saved list

Suggest us how to improve StudyLib

(For complaints, use another form )

Input it if you want to receive answer

Please log in to save materials. Log in

• Classroom Supplies

Constructions and Angles

Unit overview.

Type of Unit: Concept

Prior Knowledge

Students should be able to:

• Use a protractor and ruler.
• Identify different types of triangles and quadrilaterals and their characteristics.

Lesson Flow

After an initial exploratory lesson involving a paper folding activity that gets students thinking in general about angles and figures in a context, the unit is divided into two concept development sections. The first section focuses on types of angles—adjacent, supplementary, complementary, and vertical—and how they are manifested in quadrilaterals. The second section looks at triangles and their properties, including the angle sum, and how this affects other figures.

In the first set of conceptual lessons, students explore different types of angles and where the types of angles appear in quadrilaterals. Students fold paper and observe the angles formed, draw given angles, and explore interactive sketches that test many cases. Students use a protractor and ruler to draw parallelograms with given properties. They explore sketches of parallelograms with specific properties, such as perpendicular diagonals. After concluding the investigation of the angle types, students move on to the next set.

In the second set of conceptual development lessons, students focus on triangles. Students again fold paper to create figures and certain angles, such as complementary angles.

Students draw, using a protractor and ruler, other triangles with given properties. Students then explore triangles with certain known and unknown elements, such as the number of given sides and angles. This process starts with paper folding and drawing and continues with exploration of interactive sketches. Students draw conclusions about which cases allow 0, 1, 2, or an infinite number of triangles. In the course of the exploration, students discover that the sum of the measure of the interior angles of a triangle is 180°. They also learn that the sum of the measures of the interior angles of a quadrilateral is 360°. They explore other polygons to find their angle sum and determine if there is a relationship to angle sum of triangles. The exploration concludes with finding the measure of the interior angles of regular polygons and speculating about how this relates to a circle.

Lastly, students solve equations to find unknown angle measures. Using their previous experience, students find the remaining angle measures in a parallelogram when only one angle measure is given. Students also play a game similar to 20 Questions to identify types of triangles and quadrilaterals. Having completed the remaining lessons, students have a four-day Gallery to explore a variety of problems.

The unit ends with a unit assessment.

• Paper Folding

8½ in. x 11 in. sheets of blank paper or origami paper (1 sheet for each student)

8½ in. x 11 in. sheets of paper (1 sheet for each student)

Protractors (1 for each student)

8½ in. x 11 in. sheets of paper (3 sheets for each student)

Rulers (1 for each student)

8½ in. x 11 in. sheets of paper (2 sheets for each student)

Compasses (available as needed)

Protractors and paper (available as needed)

8½ in. x 11 in. sheets of blank paper (1 sheet for each student)

• Resource Library

Education Standards

Maryland college and career ready math standards.

Learning Domain: Geometry

Standard: Draw (freehand, with ruler and protractor, and with technology) geometric shapes with given conditions. Focus on constructing triangles from three measures of angles or sides, noticing when the conditions determine a unique triangle, more than one triangle, or no triangle.

Standard: Use facts about supplementary, complementary, vertical, and adjacent angles in a multi-step problem to write and solve simple equations for an unknown angle in a figure.

Learning Domain: Mathematical Practices

Standard: Make sense of problems and persevere in solving them. Mathematically proficient students start by explaining to themselves the meaning of a problem and looking for entry points to its solution. They analyze givens, constraints, relationships, and goals. They make conjectures about the form and meaning of the solution and plan a solution pathway rather than simply jumping into a solution attempt. They consider analogous problems, and try special cases and simpler forms of the original problem in order to gain insight into its solution. They monitor and evaluate their progress and change course if necessary. Older students might, depending on the context of the problem, transform algebraic expressions or change the viewing window on their graphing calculator to get the information they need. Mathematically proficient students can explain correspondences between equations, verbal descriptions, tables, and graphs or draw diagrams of important features and relationships, graph data, and search for regularity or trends. Younger students might rely on using concrete objects or pictures to help conceptualize and solve a problem. Mathematically proficient students check their answers to problems using a different method, and they continually ask themselves, "Does this make sense?"ť They can understand the approaches of others to solving complex problems and identify correspondences between different approaches.

Standard: Reason abstractly and quantitatively. Mathematically proficient students make sense of the quantities and their relationships in problem situations. Students bring two complementary abilities to bear on problems involving quantitative relationships: the ability to decontextualize"Óto abstract a given situation and represent it symbolically and manipulate the representing symbols as if they have a life of their own, without necessarily attending to their referents"Óand the ability to contextualize, to pause as needed during the manipulation process in order to probe into the referents for the symbols involved. Quantitative reasoning entails habits of creating a coherent representation of the problem at hand; considering the units involved; attending to the meaning of quantities, not just how to compute them; and knowing and flexibly using different properties of operations and objects.

Standard: Construct viable arguments and critique the reasoning of others. Mathematically proficient students understand and use stated assumptions, definitions, and previously established results in constructing arguments. They make conjectures and build a logical progression of statements to explore the truth of their conjectures. They are able to analyze situations by breaking them into cases, and can recognize and use counterexamples. They justify their conclusions, communicate them to others, and respond to the arguments of others. They reason inductively about data, making plausible arguments that take into account the context from which the data arose. Mathematically proficient students are also able to compare the effectiveness of two plausible arguments, distinguish correct logic or reasoning from that which is flawed, and"Óif there is a flaw in an argument"Óexplain what it is. Elementary students can construct arguments using concrete referents such as objects, drawings, diagrams, and actions. Such arguments can make sense and be correct, even though they are not generalized or made formal until later grades. Later, students learn to determine domains to which an argument applies. Students at all grades can listen or read the arguments of others, decide whether they make sense, and ask useful questions to clarify or improve the arguments.

Standard: Model with mathematics. Mathematically proficient students can apply the mathematics they know to solve problems arising in everyday life, society, and the workplace. In early grades, this might be as simple as writing an addition equation to describe a situation. In middle grades, a student might apply proportional reasoning to plan a school event or analyze a problem in the community. By high school, a student might use geometry to solve a design problem or use a function to describe how one quantity of interest depends on another. Mathematically proficient students who can apply what they know are comfortable making assumptions and approximations to simplify a complicated situation, realizing that these may need revision later. They are able to identify important quantities in a practical situation and map their relationships using such tools as diagrams, two-way tables, graphs, flowcharts and formulas. They can analyze those relationships mathematically to draw conclusions. They routinely interpret their mathematical results in the context of the situation and reflect on whether the results make sense, possibly improving the model if it has not served its purpose.

Standard: Use appropriate tools strategically. Mathematically proficient students consider the available tools when solving a mathematical problem. These tools might include pencil and paper, concrete models, a ruler, a protractor, a calculator, a spreadsheet, a computer algebra system, a statistical package, or dynamic geometry software. Proficient students are sufficiently familiar with tools appropriate for their grade or course to make sound decisions about when each of these tools might be helpful, recognizing both the insight to be gained and their limitations. For example, mathematically proficient high school students analyze graphs of functions and solutions generated using a graphing calculator. They detect possible errors by strategically using estimation and other mathematical knowledge. When making mathematical models, they know that technology can enable them to visualize the results of varying assumptions, explore consequences, and compare predictions with data. Mathematically proficient students at various grade levels are able to identify relevant external mathematical resources, such as digital content located on a website, and use them to pose or solve problems. They are able to use technological tools to explore and deepen their understanding of concepts.

Standard: Attend to precision. Mathematically proficient students try to communicate precisely to others. They try to use clear definitions in discussion with others and in their own reasoning. They state the meaning of the symbols they choose, including using the equal sign consistently and appropriately. They are careful about specifying units of measure, and labeling axes to clarify the correspondence with quantities in a problem. They calculate accurately and efficiently, express numerical answers with a degree of precision appropriate for the problem context. In the elementary grades, students give carefully formulated explanations to each other. By the time they reach high school they have learned to examine claims and make explicit use of definitions.

Standard: Look for and make use of structure. Mathematically proficient students look closely to discern a pattern or structure. Young students, for example, might notice that three and seven more is the same amount as seven and three more, or they may sort a collection of shapes according to how many sides the shapes have. Later, students will see 7 x 8 equals the well remembered 7 x 5 + 7 x 3, in preparation for learning about the distributive property. In the expression x^2 + 9x + 14, older students can see the 14 as 2 x 7 and the 9 as 2 + 7. They recognize the significance of an existing line in a geometric figure and can use the strategy of drawing an auxiliary line for solving problems. They also can step back for an overview and shift perspective. They can see complicated things, such as some algebraic expressions, as single objects or as being composed of several objects. For example, they can see 5 - 3(x - y)^2 as 5 minus a positive number times a square and use that to realize that its value cannot be more than 5 for any real numbers x and y.

Standard: Look for and express regularity in repeated reasoning. Mathematically proficient students notice if calculations are repeated, and look both for general methods and for shortcuts. Upper elementary students might notice when dividing 25 by 11 that they are repeating the same calculations over and over again, and conclude they have a repeating decimal. By paying attention to the calculation of slope as they repeatedly check whether points are on the line through (1, 2) with slope 3, middle school students might abstract the equation (y - 2)/(x -1) = 3. Noticing the regularity in the way terms cancel when expanding (x - 1)(x + 1), (x - 1)(x^2 + x + 1), and (x - 1)(x^3 + x^2 + x + 1) might lead them to the general formula for the sum of a geometric series. As they work to solve a problem, mathematically proficient students maintain oversight of the process, while attending to the details. They continually evaluate the reasonableness of their intermediate results.

Common Core State Standards Math

Cluster: Draw, construct, and describe geometrical figures and describe the relationships between them.

Cluster: Solve real-life and mathematical problems involving angle measure, area, surface area, and volume

Cluster: Mathematical practices

Standard: Make sense of problems and persevere in solving them. Mathematically proficient students start by explaining to themselves the meaning of a problem and looking for entry points to its solution. They analyze givens, constraints, relationships, and goals. They make conjectures about the form and meaning of the solution and plan a solution pathway rather than simply jumping into a solution attempt. They consider analogous problems, and try special cases and simpler forms of the original problem in order to gain insight into its solution. They monitor and evaluate their progress and change course if necessary. Older students might, depending on the context of the problem, transform algebraic expressions or change the viewing window on their graphing calculator to get the information they need. Mathematically proficient students can explain correspondences between equations, verbal descriptions, tables, and graphs or draw diagrams of important features and relationships, graph data, and search for regularity or trends. Younger students might rely on using concrete objects or pictures to help conceptualize and solve a problem. Mathematically proficient students check their answers to problems using a different method, and they continually ask themselves, “Does this make sense?” They can understand the approaches of others to solving complex problems and identify correspondences between different approaches.

Standard: Reason abstractly and quantitatively. Mathematically proficient students make sense of the quantities and their relationships in problem situations. Students bring two complementary abilities to bear on problems involving quantitative relationships: the ability to decontextualize—to abstract a given situation and represent it symbolically and manipulate the representing symbols as if they have a life of their own, without necessarily attending to their referents—and the ability to contextualize, to pause as needed during the manipulation process in order to probe into the referents for the symbols involved. Quantitative reasoning entails habits of creating a coherent representation of the problem at hand; considering the units involved; attending to the meaning of quantities, not just how to compute them; and knowing and flexibly using different properties of operations and objects.

Standard: Construct viable arguments and critique the reasoning of others. Mathematically proficient students understand and use stated assumptions, definitions, and previously established results in constructing arguments. They make conjectures and build a logical progression of statements to explore the truth of their conjectures. They are able to analyze situations by breaking them into cases, and can recognize and use counterexamples. They justify their conclusions, communicate them to others, and respond to the arguments of others. They reason inductively about data, making plausible arguments that take into account the context from which the data arose. Mathematically proficient students are also able to compare the effectiveness of two plausible arguments, distinguish correct logic or reasoning from that which is flawed, and—if there is a flaw in an argument—explain what it is. Elementary students can construct arguments using concrete referents such as objects, drawings, diagrams, and actions. Such arguments can make sense and be correct, even though they are not generalized or made formal until later grades. Later, students learn to determine domains to which an argument applies. Students at all grades can listen or read the arguments of others, decide whether they make sense, and ask useful questions to clarify or improve the arguments.

Standard: Look for and make use of structure. Mathematically proficient students look closely to discern a pattern or structure. Young students, for example, might notice that three and seven more is the same amount as seven and three more, or they may sort a collection of shapes according to how many sides the shapes have. Later, students will see 7 × 8 equals the well remembered 7 × 5 + 7 × 3, in preparation for learning about the distributive property. In the expression x^2 + 9x + 14, older students can see the 14 as 2 × 7 and the 9 as 2 + 7. They recognize the significance of an existing line in a geometric figure and can use the strategy of drawing an auxiliary line for solving problems. They also can step back for an overview and shift perspective. They can see complicated things, such as some algebraic expressions, as single objects or as being composed of several objects. For example, they can see 5 – 3(x – y)^2 as 5 minus a positive number times a square and use that to realize that its value cannot be more than 5 for any real numbers x and y.

Standard: Look for and express regularity in repeated reasoning. Mathematically proficient students notice if calculations are repeated, and look both for general methods and for shortcuts. Upper elementary students might notice when dividing 25 by 11 that they are repeating the same calculations over and over again, and conclude they have a repeating decimal. By paying attention to the calculation of slope as they repeatedly check whether points are on the line through (1, 2) with slope 3, middle school students might abstract the equation (y – 2)/(x –1) = 3. Noticing the regularity in the way terms cancel when expanding (x – 1)(x + 1), (x – 1)(x^2 + x + 1), and (x – 1)(x^3 + x^2 + x + 1) might lead them to the general formula for the sum of a geometric series. As they work to solve a problem, mathematically proficient students maintain oversight of the process, while attending to the details. They continually evaluate the reasonableness of their intermediate results.

Constructions and Angles Exercises  

File size 1.0 MB

You are using an outdated browser and it's not supported. Please upgrade your browser to improve your experience.

• LOGIN FOR PROGRAM PARTICIPANTS
• PROGRAM SUPPORT

Angle Problems and Solving Equations

Description.

Students use vertical angles, adjacent angles, angles on a line, and angles at a point in a multistep problem to write and solve simple equations

There may be cases when our downloadable resources contain hyperlinks to other websites. These hyperlinks lead to websites published or operated by third parties. UnboundEd and EngageNY are not responsible for the content, availability, or privacy policies of these websites.

• Grade 7 Mathematics Module 3, Topic B, Lesson 10: Student Version
• Grade 7 Mathematics Module 3, Topic B, Lesson 10: Teacher Version

Prerequisites

• CCSS Standard:

Related Guides and Multimedia

Our professional learning resources include teaching guides, videos, and podcasts that build educators' knowledge of content related to the standards and their application in the classroom.

There are no related guides or videos. To see all our guides, please visit the Enhance Instruction section here .

Curriculum  /  Math  /  7th Grade  /  Unit 6: Geometry  /  Lesson 2

Lesson 2 of 21

Criteria for Success

Tips for teachers, anchor problems, problem set, target task, additional practice.

Use vertical, complementary, and supplementary angle relationships to find missing angles. 

Common Core Standards

Core standards.

The core standards covered in this lesson

7.G.B.5 — Use facts about supplementary, complementary, vertical, and adjacent angles in a multi-step problem to write and solve simple equations for an unknown angle in a figure.

Foundational Standards

The foundational standards covered in this lesson

Measurement and Data

4.MD.C.5 — Recognize angles as geometric shapes that are formed wherever two rays share a common endpoint, and understand concepts of angle measurement:

4.MD.C.6 — Measure angles in whole-number degrees using a protractor. Sketch angles of specified measure.

4.MD.C.7 — Recognize angle measure as additive. When an angle is decomposed into non-overlapping parts, the angle measure of the whole is the sum of the angle measures of the parts. Solve addition and subtraction problems to find unknown angles on a diagram in real world and mathematical problems, e.g., by using an equation with a symbol for the unknown angle measure.

The essential concepts students need to demonstrate or understand to achieve the lesson objective

• Understand that vertical angles are the pair of angles formed across from one another when two lines intersect, and that the measurements of vertical angles are congruent. 
• Identify pairs of vertical angles in angle diagrams.
• Find the values of angles using vertical, complementary, and supplementary angle relationships and equations.

Suggestions for teachers to help them teach this lesson

Lesson Materials

• 180° Protractor (1 per student)
• Ruler (1 per student)

Unlock features to optimize your prep time, plan engaging lessons, and monitor student progress.

Problems designed to teach key points of the lesson and guiding questions to help draw out student understanding

In small groups, with a ruler, draw two intersecting lines on a piece of paper. 

• Label the angles formed by the two lines as 1–4, in a clockwise direction. 
• Measure each angle with a protractor and record the information.
• Compile your results as a class.

Vertical angles are a pair of angles formed across from one another when two lines intersect. Based on the data from your class, what can you conclude about the measurements of vertical angles? 

Guiding Questions

In the diagram below, line  $${CD}$$  intersects line  $${AB}$$  through point $$E$$ . Ray  $$EF$$  extends from point $$E$$ .

Callie says that $$\angle CEB$$  is vertical to $$\angle AEF$$ . Explain why her reasoning is incorrect and name the angle that is vertical to $$\angle CEB$$ .

Three lines meet at a point, as shown below.

a.   Describe the angle relationships you see in the diagram.

b.   Set up and solve an equation to find the value of $$z$$ .

Grade 7 Mathematics > Module 6 > Topic A > Lesson 2 of the New York State Common Core Mathematics Curriculum from EngageNY and Great Minds . © 2015 Great Minds. Licensed by EngageNY of the New York State Education Department under the CC BY-NC-SA 3.0 US  license. Accessed Dec. 2, 2016, 5:15 p.m..

A set of suggested resources or problem types that teachers can turn into a problem set

Give your students more opportunities to practice the skills in this lesson with a downloadable problem set aligned to the daily objective.

A task that represents the peak thinking of the lesson - mastery will indicate whether or not objective was achieved

Three lines intersect at a common point, as shown in the diagram below. 

Write and solve an equation to determine the value of $$x$$ .

Student Response

An example response to the Target Task at the level of detail expected of the students.

The following resources include problems and activities aligned to the objective of the lesson that can be used for additional practice or to create your own problem set.

• Kuta Software Free Pre-Algebra Worksheets Angle Relationships — #1–6, 11, 13, 14, 15 only
• Open Up Resources Grade 7 Unit 7 Practice Problems — Lesson 3
• Smarter Balanced Assessment Consortium: Sample Items Item MAT.07.ER.3.0000G.B.160
• EngageNY Mathematics Grade 7 Mathematics > Module 6 > Topic A > Lesson 2 — Problem Set #1–6

Topic A: Angle Relationships

Identify and determine values of angles in complementary and supplementary relationships.

Use equations to solve for unknown angles. (Part 1)

Use equations to solve for unknown angles. (Part 2)

Create a free account to access thousands of lesson plans.

Already have an account? Sign In

Topic B: Circles

Define circle and identify the measurements radius, diameter, and circumference. 

Determine the relationship between the circumference and diameter of a circle and use it to solve problems. 

Solve real-world and mathematical problems using the relationship between the circumference of a circle and its diameter. 

Determine the relationship between the area and radius of a circle and use it to solve problems.

Solve real-world and mathematical problems using the relationship between the area of a circle and its radius.

Solve problems involving area and circumference of two-dimensional figures (Part 1).

7.G.B.4 7.G.B.6

Solve problems involving area and circumference of two-dimensional figures (Part 2).

Topic C: Building Polygons and Triangles

Draw two-dimensional geometric shapes using rulers, protractors, and compasses. 

7.G.A.2 7.G.B.5

Determine if three side lengths will create a unique triangle or no triangle. 

Identify unique and identical triangles. 

Determine if conditions describe a unique triangle, no triangle, or more than one triangle.

Topic D: Solid Figures

Identify and describe two-dimensional figures that result from slicing three-dimensional figures.

Find the surface area of right prisms.

 Find the surface area of right pyramids.

Find the volume of right prisms and pyramids.

Solve real-world and mathematical problems involving volume.

Distinguish between and solve real-world problems involving volume and surface area.

Request a Demo

See all of the features of Fishtank in action and begin the conversation about adoption.

Learn more about Fishtank Learning School Adoption.

Contact Information

School information, what courses are you interested in, are you interested in onboarding professional learning for your teachers and instructional leaders, any other information you would like to provide about your school.