explain assignment problem with example

Assignment Problem: Meaning, Methods and Variations | Operations Research

After reading this article you will learn about:- 1. Meaning of Assignment Problem 2. Definition of Assignment Problem 3. Mathematical Formulation 4. Hungarian Method 5. Variations.

Meaning of Assignment Problem:

An assignment problem is a particular case of transportation problem where the objective is to assign a number of resources to an equal number of activities so as to minimise total cost or maximize total profit of allocation.

The problem of assignment arises because available resources such as men, machines etc. have varying degrees of efficiency for performing different activities, therefore, cost, profit or loss of performing the different activities is different.

Thus, the problem is “How should the assignments be made so as to optimize the given objective”. Some of the problem where the assignment technique may be useful are assignment of workers to machines, salesman to different sales areas.

Definition of Assignment Problem:

ADVERTISEMENTS:

Suppose there are n jobs to be performed and n persons are available for doing these jobs. Assume that each person can do each job at a term, though with varying degree of efficiency, let c ij be the cost if the i-th person is assigned to the j-th job. The problem is to find an assignment (which job should be assigned to which person one on-one basis) So that the total cost of performing all jobs is minimum, problem of this kind are known as assignment problem.

The assignment problem can be stated in the form of n x n cost matrix C real members as given in the following table:

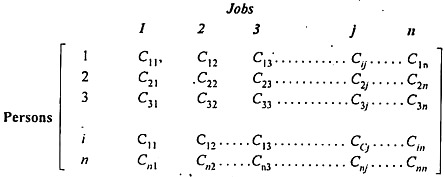
www.springer.com The European Mathematical Society

• StatProb Collection
• Recent changes
• Current events
• Random page
• Project talk
• Request account
• What links here
• Related changes
• Special pages
• Printable version
• Permanent link
• Page information
• View source

Assignment problem

The problem of optimally assigning $ m $ individuals to $ m $ jobs. It can be formulated as a linear programming problem that is a special case of the transport problem :

maximize $ \sum _ {i,j } c _ {ij } x _ {ij } $

$$ \sum _ { j } x _ {ij } = a _ {i} , i = 1 \dots m $$

(origins or supply),

$$ \sum _ { i } x _ {ij } = b _ {j} , j = 1 \dots n $$

(destinations or demand), where $ x _ {ij } \geq 0 $ and $ \sum a _ {i} = \sum b _ {j} $, which is called the balance condition. The assignment problem arises when $ m = n $ and all $ a _ {i} $ and $ b _ {j} $ are $ 1 $.

If all $ a _ {i} $ and $ b _ {j} $ in the transposed problem are integers, then there is an optimal solution for which all $ x _ {ij } $ are integers (Dantzig's theorem on integral solutions of the transport problem).

In the assignment problem, for such a solution $ x _ {ij } $ is either zero or one; $ x _ {ij } = 1 $ means that person $ i $ is assigned to job $ j $; the weight $ c _ {ij } $ is the utility of person $ i $ assigned to job $ j $.

The special structure of the transport problem and the assignment problem makes it possible to use algorithms that are more efficient than the simplex method . Some of these use the Hungarian method (see, e.g., [a5] , [a1] , Chapt. 7), which is based on the König–Egervary theorem (see König theorem ), the method of potentials (see [a1] , [a2] ), the out-of-kilter algorithm (see, e.g., [a3] ) or the transportation simplex method.

In turn, the transportation problem is a special case of the network optimization problem.

A totally different assignment problem is the pole assignment problem in control theory.

• This page was last edited on 5 April 2020, at 18:48.
• Privacy policy
• About Encyclopedia of Mathematics
• Disclaimers
• Impressum-Legal

• Google OR-Tools
• Español – América Latina
• Português – Brasil
• Tiếng Việt

Solving an Assignment Problem

This section presents an example that shows how to solve an assignment problem using both the MIP solver and the CP-SAT solver.

In the example there are five workers (numbered 0-4) and four tasks (numbered 0-3). Note that there is one more worker than in the example in the Overview .

The costs of assigning workers to tasks are shown in the following table.

The problem is to assign each worker to at most one task, with no two workers performing the same task, while minimizing the total cost. Since there are more workers than tasks, one worker will not be assigned a task.

MIP solution

The following sections describe how to solve the problem using the MPSolver wrapper .

Import the libraries

The following code imports the required libraries.

Create the data

The following code creates the data for the problem.

The costs array corresponds to the table of costs for assigning workers to tasks, shown above.

Declare the MIP solver

The following code declares the MIP solver.

Create the variables

The following code creates binary integer variables for the problem.

Create the constraints

Create the objective function.

The following code creates the objective function for the problem.

The value of the objective function is the total cost over all variables that are assigned the value 1 by the solver.

Invoke the solver

The following code invokes the solver.

Print the solution

The following code prints the solution to the problem.

Here is the output of the program.

Complete programs

Here are the complete programs for the MIP solution.

CP SAT solution

The following sections describe how to solve the problem using the CP-SAT solver.

Declare the model

The following code declares the CP-SAT model.

The following code sets up the data for the problem.

The following code creates the constraints for the problem.

Here are the complete programs for the CP-SAT solution.

Except as otherwise noted, the content of this page is licensed under the Creative Commons Attribution 4.0 License , and code samples are licensed under the Apache 2.0 License . For details, see the Google Developers Site Policies . Java is a registered trademark of Oracle and/or its affiliates.

Last updated 2023-01-02 UTC.

Quadratic assignment problem

Author: Thomas Kueny, Eric Miller, Natasha Rice, Joseph Szczerba, David Wittmann (SysEn 5800 Fall 2020)

• 1 Introduction
• 2.1 Koopmans-Beckman Mathematical Formulation
• 2.2.1 Parameters
• 2.3.1 Optimization Problem
• 2.4 Computational Complexity
• 2.5 Algorithmic Discussions
• 2.6 Branch and Bound Procedures
• 2.7 Linearizations
• 3.1 QAP with 3 Facilities
• 4.1 Inter-plant Transportation Problem
• 4.2 The Backboard Wiring Problem
• 4.3 Hospital Layout
• 4.4 Exam Scheduling System
• 5 Conclusion
• 6 References

Introduction

The Quadratic Assignment Problem (QAP), discovered by Koopmans and Beckmann in 1957 [1] , is a mathematical optimization module created to describe the location of invisible economic activities. An NP-Complete problem, this model can be applied to many other optimization problems outside of the field of economics. It has been used to optimize backboards, inter-plant transportation, hospital transportation, exam scheduling, along with many other applications not described within this page.

Theory, Methodology, and/or Algorithmic Discussions

Koopmans-beckman mathematical formulation.

Economists Koopmans and Beckman began their investigation of the QAP to ascertain the optimal method of locating important economic resources in a given area. The Koopmans-Beckman formulation of the QAP aims to achieve the objective of assigning facilities to locations in order to minimize the overall cost. Below is the Koopmans-Beckman formulation of the QAP as described by neos-guide.org.

Quadratic Assignment Problem Formulation

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F = (F_{ij})} is an n x n matrix where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_{ij}} the required flow between facilities Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} . Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D = (D_{ij})} is an n x n matrix where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_{ij}} the distance between facilities Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} [2] . Intuitively, the product of distance and flow represents cost, and the objective is to minimize this cost. Ideally, two facilities with lots of flow (more product or supplies) between the two should be placed closer together than two facilities that rarely interact (low flow).

Consider the set of numbers Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N = \big\{1, 2, ...n\big\} } . The group of bijections between Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N } and itself is defined as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{n} = \{\phi: N \rightarrow N \}} . Each member Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi \in S_n} represents a particular arrangement of the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} elements. As an example, the permutation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi=(3 2 1)} represents facility 3 being placed at location 1, facility 1 at location 3 and facility 2 at location 2. Each permutation can be assigned a permutation matrix. The permutation matrix of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi } can be written as [3]

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_{\phi} = \begin{bmatrix} 0 & 0 & 1 \\ 0 & 1 &0 \\ 1 & 0 & 0 \end{bmatrix}}

The operation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_{\phi}DX_{\phi}^{T} } permutes the values of the distance matrix Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D} so that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (X_{\phi}DX_{\phi}^{T})_{i,j} } represents the distance between facilities Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} if the facilities are arranged according to the permutation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} . The cost function between facilities Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} , after being permuted to their location, is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_{i,j}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (X_{\phi}DX_{\phi}^{T})_{i,j} } [3] . To find the total cost, sum over each Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} for the facilities arranged according to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} .

Inner Product

The inner product of two matrices Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A,B} is defined as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle A,B \rangle= \sum_{i=1}^{n}\sum_{j=1}^{n}a_{i,j}b_{i,j}} . The inner product

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle F,X_{\phi}DX_{\phi}^{T} \rangle = \sum_{i=1}^{n}\sum_{j=1}^{n}F_{i,j}(X_{\phi}DX_{\phi}^{T})_{i,j}}

thus describes the total cost of assigning facilities [3] to locations according to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} . The objective function to minimize cost can be written as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle F,XDX^{T} \rangle } .

Note: The true objective cost function only requires summing entries above the diagonal in the matrix comprised of elements

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_{i,j}(X_{\phi}DX_{\phi}^{T})_{i,j} } .

Since this matrix is symmetric with zeroes on the diagonal, dividing by 2 removes the double count of each element to give the correct cost value. See the Numerical Example section for an example of this note.

Optimization Problem

With all of this information, the QAP can be summarized as:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \min_{X \in P} \langle F,XDX^{T} \rangle } .

Computational Complexity

QAP belongs to the classification of problems known as NP-complete, thus being a computationally complex problem. QAP’s NP-completeness was proven by Sahni and Gonzalez in 1976, who states that of all combinatorial optimization problems, QAP is the “hardest of the hard”. [2]

Algorithmic Discussions

While an algorithm that can solve QAP in polynomial time is unlikely to exist, there are three primary methods for acquiring the optimal solution to a QAP problem:

• Dynamic Program
• Cutting Plane

Branch and Bound Procedures

The third method has been proven to be the most effective in solving QAP, although when n > 15, QAP begins to become virtually unsolvable.

The Branch and Bound method was first proposed by Ailsa Land and Alison Doig in 1960 and is the most commonly used tool for solving NP-hard optimization problems.

A branch-and-bound algorithm consists of a systematic enumeration of candidate solutions by means of state space search: the set of candidate solutions is thought of as forming a rooted tree with the full set at the root. The algorithm explores branches of this tree, which represent subsets of the solution set. Before one lists all of the candidate solutions of a branch, the branch is checked against upper and lower estimated bounds on the optimal solution, and the branch is eliminated if it cannot produce a better solution than the best one found so far by the algorithm.

Linearizations

The first attempts to solve the QAP eliminated the quadratic term in the objective function of

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle min \sum_{i=1}^{n}\sum_{j=1}^{n}c{_{\phi(i)\phi(j)}} + \sum_{i=1}^{n}b{_{\phi(i)}}}

in order to transform the problem into a (mixed) 0-1 linear program. The objective function is usually linearized by introducing new variables and new linear (and binary) constraints. Then existing methods for (mixed) linear integer programming (MILP) can be applied. The very large number of new variables and constraints, however, usually poses an obstacle for efficiently solving the resulting linear integer programs. MILP formulations provide LP relaxations of the problem which can be used to compute lower bounds.

Numerical Example

Qap with 3 facilities.

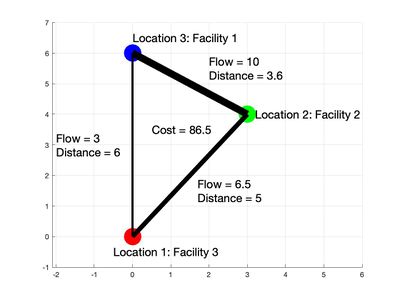
Consider the QAP of placing 3 facilities in 3 locations. Let the distance and flow matrices be defined respectively as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\begin{bmatrix} 0 & 5 & 6 \\ 5 & 0 & 3.6 \\ 6 & 3.6 & 0 \end{bmatrix} } , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle F=\begin{bmatrix} 0 & 10 & 3 \\ 10 & 0 & 6.5\\ 3 & 6.5 & 0 \end{bmatrix} } .

Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P} be the set of permutation matrices for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_3 } . The problem can be stated as follows:

The table lists the resulting cost function to place the facilities according to each permutation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi \in S_3 } . Note that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi = (123) } is the identity mapping where the number of the facility matches the location number. Based on these results, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_4=(321)} is the arrangement of facilities that minimizes the cost function with a value of 86.5. Facility 1 should be placed at location 3, Facility 2 remains at location 2 and Facility 3 is placed at location 1.

For the optimal solution Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_4=(13)} , the calculation is as follows:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle XDX^T = \begin{bmatrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \end{bmatrix}\begin{bmatrix} 0 & 5 & 6 \\ 5 & 0 & 3.6 \\ 6 & 3.6 & 0 \end{bmatrix}\begin{bmatrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \end{bmatrix} = \begin{bmatrix} 0 & 3.6 & 6 \\ 3.6 & 0 & 5 \\ 6 & 5 & 0 \end{bmatrix} }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_{i,j}(X_{\phi}DX_{\phi}^{T})_{i,j} = \begin{bmatrix} 0 & 36 & 18 \\ 36 & 0 & 32.5\\ 18 & 32.5 & 0 \end{bmatrix} }

Looking at the figure of the optimal solution, the flow Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \times} distance values are repeated in this matrix which is why the sum of all elements must be divided by 2. This gives Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle F,X_{\phi}DX_{\phi}^{T} \rangle = 173} so the minimum cost is 86.5.

Applications

Inter-plant transportation problem.

The QAP was first introduced by Koopmans and Beckmann to address how economic decisions could be made to optimize the transportation costs of goods between both manufacturing plants and locations. [1] Factoring in the location of each of the manufacturing plants as well as the volume of goods between locations to maximize revenue is what distinguishes this from other linear programming assignment problems like the Knapsack Problem.

The Backboard Wiring Problem

As the QAP is focused on minimizing the cost of traveling from one location to another, it is an ideal approach to determining the placement of components in many modern electronics. Leon Steinberg proposed a QAP solution to optimize the layout of elements on a blackboard by minimizing the total amount of wiring required. [4]

When defining the problem Steinberg states that we have a set of n elements

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E = \left \{ E_{1}, E_{2}, ... , E_{n}\right \}}

as well as a set of r points

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{1}, P_{2}, ... , P_{r}} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r \geq n}

In his paper he derives the below formula:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle min \sum_{1\leq i \leq j \leq n }^{} C_{ij}(d_{s(i)s(j))})}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{ij}} represents the number of wires connecting components Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{i}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{i}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_{s(i)s(j))}} is the length of wire needed to connect tow components if one is placed at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{\alpha}} and the other is placed at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{\beta}} . If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{\alpha}} has coordinates Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (x_{\alpha}, y_{\alpha}, z_{\alpha})} then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_{s(i)s(j))}} can be calculated by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_{s(i)s(j))} = \surd(\bigl(x_{\alpha} - x_{\beta}\bigr)^{2} + \bigl(y_{\alpha} - y_{\beta}\bigr)^{2} + \bigl(z_{\alpha} - z_{\beta}\bigr)^{2}) }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s(x)} represents a particular placement of a component.

In his paper Steinberg a backboard with a 9 by 4 array, allowing for 36 potential positions for the 34 components that needed to be placed on the backboard. For the calculation, he selected a random initial placement of s1 and chose a random family of 25 unconnected sets.

The initial placement of components is shown below:

After the initial placement of elements, it took an additional 35 iterations to get us to our final optimized backboard layout. Leading to a total of 59 iterations and a final wire length of 4,969.440.

Hospital Layout

Building new hospitals was a common event in 1977 when Alealid N Elshafei wrote his paper on "Hospital Layouts as a Quadratic Assignment Problem". [5] With the high initial cost to construct the hospital and to staff it, it is important to ensure that it is operating as efficiently as possible. Elshafei's paper was commissioned to create an optimization formula to locate clinics within a building in such a way that minimizes the total distance that a patient travels within the hospital throughout the year. When doing a study of a major hospital in Cairo he determined that the Outpatient ward was acting as a bottleneck in the hospital and focused his efforts on optimizing the 17 departments there.

Elshafei identified the following QAP to determine where clinics should be placed:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle min \sum_{i,j } \sum_{k,q } f_{ik}d_{jq}y_{ij}y_{kq} }

Such that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{j \epsilon J }y_{ij} = 1 \forall i \epsilon I }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i \epsilon I }y_{ij} = 1 \forall j \epsilon J }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_{ij} = \begin{Bmatrix} 1 \mbox{, if facility i is located at j} \\ 0\mbox{, otherwise} \end{Bmatrix} }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_{ik} } is the yearly flow between facilities i and k

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_{jq} } is the distance between the possible facility locations j and q

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I } is the initial set of facilities

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J } is the initial set of all locations

It can take a large amount of computational power to calculate the solution to a QAP problem, necessitating the use of a heuristic solution rather than using an optimizing algorithm. This approach is composed of two parts(Parts A and Part B). Part A develops the initial layout of the hospital, this is done by the following two strategies. Strategy 1 where we use a rank Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_{i} } that designates the number of interactions facility Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i } has with with the other facilities. As well as ranking them in terms of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{j} } , which designates the sum of distances from j to all other locations. then we go through the list and find the facility with the greatest Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_{i} } and the least Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{j} } . Strategy 2 says that at any step in the process we next place an unassigned facility that has the largest number of interactions with the most recently placed facility. Part B covers improving the initial solution developed in Part A, here at any step in the process we test whether the assignment is best for all of the facilities that are involved and make swaps where necessary until there are no more swaps to be made.

For the Cairo hospital with 17 clinics, and one receiving and recording room bringing us to a total of 18 facilities. By running the above optimization Elshafei was able to get the total distance per year down to 11,281,887 from a distance of 13,973,298 based on the original hospital layout.

Exam Scheduling System

The scheduling system uses matrices for Exams, Time Slots, and Rooms with the goal of reducing the rate of schedule conflicts. To accomplish this goal, the “examination with the highest cross faculty student is been prioritized in the schedule after which the examination with the highest number of cross-program is considered and finally with the highest number of repeating student, at each stage group with the highest number of student are prioritized.” [6]

Optimization of the QAP is easily stated but requires significant computational power. The number of potential facility/location combinations grows as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n!} . Thus for a QAP of just Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n=6 } facilities and location, there are Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 720} facility/location pairings. The QAP can be used in applications beyond just the location of economic activities that it was originally developed for by Koopmans and Beckmann. [1] The QAP has been used to optimize backboard wiring [4] , hospital layouts [5] , and to schedule exams [6] , along with other applications not defined on this page.

• ↑ 1.0 1.1 1.2 Koopmans, T., & Beckmann, M. (1957). Assignment Problems and the Location of Economic Activities. Econometrica, 25(1), 53-76. doi:10.2307/1907742
• ↑ 2.0 2.1 Quadratic Assignment Problem. (2020). Retrieved December 14, 2020, from https://neos-guide.org/content/quadratic-assignment-problem
• ↑ 3.0 3.1 3.2 Burkard, R. E., Çela, E., Pardalos, P. M., & Pitsoulis, L. S. (2013). The Quadratic Assignment Problem. https://www.opt.math.tugraz.at/~cela/papers/qap_bericht.pdf .
• ↑ 4.0 4.1 Leon Steinberg. The Backboard Wiring Problem: A Placement Algorithm. SIAM Review . 1961;3(1):37.
• ↑ 5.0 5.1 Alwalid N. Elshafei. Hospital Layout as a Quadratic Assignment Problem. Operational Research Quarterly (1970-1977) . 1977;28(1):167. doi:10.2307/300878
• ↑ 6.0 6.1 Muktar, D., & Ahmad, Z.M. (2014). Examination Scheduling System Based On Quadratic Assignment.
• Pages with math errors
• Pages with math render errors

Navigation menu

Quantitative Techniques: Theory and Problems by P. C. Tulsian, Vishal Pandey

Get full access to Quantitative Techniques: Theory and Problems and 60K+ other titles, with a free 10-day trial of O'Reilly.

There are also live events, courses curated by job role, and more.

WHAT IS ASSIGNMENT PROBLEM

Assignment Problem is a special type of linear programming problem where the objective is to minimise the cost or time of completing a number of jobs by a number of persons.

The assignment problem in the general form can be stated as follows:

“Given n facilities, n jobs and the effectiveness of each facility for each job, the problem is to assign each facility to one and only one job in such a way that the measure of effectiveness is optimised (Maximised or Minimised).”

Several problems of management has a structure identical with the assignment problem.

Example I A manager has four persons (i.e. facilities) available for four separate jobs (i.e. jobs) and the cost of assigning (i.e. effectiveness) each job to each ...

Get Quantitative Techniques: Theory and Problems now with the O’Reilly learning platform.

O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

Don’t leave empty-handed

Get Mark Richards’s Software Architecture Patterns ebook to better understand how to design components—and how they should interact.

It’s yours, free.

Check it out now on O’Reilly

Dive in for free with a 10-day trial of the O’Reilly learning platform—then explore all the other resources our members count on to build skills and solve problems every day.

Unbalanced Assignment Problem: Definition, Formulation, and Solution Methods

Table of Contents

Are you familiar with the assignment problem in Operations Research (OR)? This problem deals with assigning tasks to workers in a way that minimizes the total cost or time needed to complete the tasks. But what if the number of tasks and workers is not equal? In this case, we face the Unbalanced Assignment Problem (UAP). This blog will help you understand what the UAP is, how to formulate it, and how to solve it.

What is the Unbalanced Assignment Problem?

The Unbalanced Assignment Problem is an extension of the Assignment Problem in OR, where the number of tasks and workers is not equal. In the UAP, some tasks may remain unassigned, while some workers may not be assigned any task. The objective is still to minimize the total cost or time required to complete the assigned tasks, but the UAP has additional constraints that make it more complex than the traditional assignment problem.

Formulation of the Unbalanced Assignment Problem

To formulate the UAP, we start with a matrix that represents the cost or time required to assign each task to each worker. If the matrix is square, we can use the Hungarian algorithm to solve the problem. But when the matrix is not square, we need to add dummy tasks or workers to balance the matrix. These dummy tasks or workers have zero costs and are used to make the matrix square.

Once we have a square matrix, we can apply the Hungarian algorithm to find the optimal assignment. However, we need to be careful in interpreting the results, as the assignment may include dummy tasks or workers that are not actually assigned to anything.

Solutions for the Unbalanced Assignment Problem

Besides the Hungarian algorithm, there are other methods to solve the UAP, such as the transportation algorithm and the auction algorithm. The transportation algorithm is based on transforming the UAP into a transportation problem, which can be solved with the transportation simplex method. The auction algorithm is an iterative method that simulates a bidding process between the tasks and workers to find the optimal assignment.

In summary, the Unbalanced Assignment Problem is a variant of the traditional Assignment Problem in OR that deals with assigning tasks to workers when the number of tasks and workers is not equal. To solve the UAP, we need to balance the matrix by adding dummy tasks or workers and then apply algorithms such as the Hungarian algorithm, the transportation algorithm, or the auction algorithm. Understanding the UAP can help businesses and organizations optimize their resource allocation and improve their operational efficiency.

How useful was this post?

Click on a star to rate it!

Average rating 1.5 / 5. Vote count: 2

No votes so far! Be the first to rate this post.

We are sorry that this post was not useful for you! 😔

Let us improve this post!

Tell us how we can improve this post?

Operations Research

1 Operations Research-An Overview

• History of O.R.
• Approach, Techniques and Tools
• Phases and Processes of O.R. Study
• Typical Applications of O.R
• Limitations of Operations Research
• Models in Operations Research
• O.R. in real world

2 Linear Programming: Formulation and Graphical Method

• General formulation of Linear Programming Problem
• Optimisation Models
• Basics of Graphic Method
• Important steps to draw graph
• Multiple, Unbounded Solution and Infeasible Problems
• Solving Linear Programming Graphically Using Computer
• Application of Linear Programming in Business and Industry

3 Linear Programming-Simplex Method

• Principle of Simplex Method
• Computational aspect of Simplex Method
• Simplex Method with several Decision Variables
• Two Phase and M-method
• Multiple Solution, Unbounded Solution and Infeasible Problem
• Sensitivity Analysis
• Dual Linear Programming Problem

4 Transportation Problem

• Basic Feasible Solution of a Transportation Problem
• Modified Distribution Method
• Stepping Stone Method
• Unbalanced Transportation Problem
• Degenerate Transportation Problem
• Transhipment Problem
• Maximisation in a Transportation Problem

5 Assignment Problem

• Solution of the Assignment Problem
• Unbalanced Assignment Problem
• Problem with some Infeasible Assignments
• Maximisation in an Assignment Problem
• Crew Assignment Problem

6 Application of Excel Solver to Solve LPP

• Building Excel model for solving LP: An Illustrative Example

7 Goal Programming

• Concepts of goal programming
• Goal programming model formulation
• Graphical method of goal programming
• The simplex method of goal programming
• Using Excel Solver to Solve Goal Programming Models
• Application areas of goal programming

8 Integer Programming

• Some Integer Programming Formulation Techniques
• Binary Representation of General Integer Variables
• Unimodularity
• Cutting Plane Method
• Branch and Bound Method
• Solver Solution

9 Dynamic Programming

• Dynamic Programming Methodology: An Example
• Definitions and Notations
• Dynamic Programming Applications

10 Non-Linear Programming

• Solution of a Non-linear Programming Problem
• Convex and Concave Functions
• Kuhn-Tucker Conditions for Constrained Optimisation
• Quadratic Programming
• Separable Programming
• NLP Models with Solver

11 Introduction to game theory and its Applications

• Important terms in Game Theory
• Saddle points
• Mixed strategies: Games without saddle points
• 2 x n games
• Exploiting an opponent’s mistakes

12 Monte Carlo Simulation

• Reasons for using simulation
• Monte Carlo simulation
• Limitations of simulation
• Steps in the simulation process
• Some practical applications of simulation
• Two typical examples of hand-computed simulation
• Computer simulation

13 Queueing Models

• Characteristics of a queueing model
• Notations and Symbols
• Statistical methods in queueing
• The M/M/I System
• The M/M/C System
• The M/Ek/I System
• Decision problems in queueing

Hungarian Method Examples

Now we will examine a few highly simplified illustrations of Hungarian Method for solving an assignment problem .

Later in the chapter, you will find more practical versions of assignment models like Crew assignment problem , Travelling salesman problem , etc.

Example-1, Example-2

Example 1: Hungarian Method

The Funny Toys Company has four men available for work on four separate jobs. Only one man can work on any one job. The cost of assigning each man to each job is given in the following table. The objective is to assign men to jobs in such a way that the total cost of assignment is minimum.

This is a minimization example of assignment problem . We will use the Hungarian Algorithm to solve this problem.

Identify the minimum element in each row and subtract it from every element of that row. The result is shown in the following table.

"A man has one hundred dollars and you leave him with two dollars, that's subtraction." -Mae West

On small screens, scroll horizontally to view full calculation

Identify the minimum element in each column and subtract it from every element of that column.

Make the assignments for the reduced matrix obtained from steps 1 and 2 in the following way:

• For every zero that becomes assigned, cross out (X) all other zeros in the same row and the same column.
• If for a row and a column, there are two or more zeros and one cannot be chosen by inspection, choose the cell arbitrarily for assignment.

An optimal assignment is found, if the number of assigned cells equals the number of rows (and columns). In case you have chosen a zero cell arbitrarily, there may be alternate optimal solutions. If no optimal solution is found, go to step 5.

Use Horizontal Scrollbar to View Full Table Calculation

Draw the minimum number of vertical and horizontal lines necessary to cover all the zeros in the reduced matrix obtained from step 3 by adopting the following procedure:

• Mark all the rows that do not have assignments.
• Mark all the columns (not already marked) which have zeros in the marked rows.
• Mark all the rows (not already marked) that have assignments in marked columns.
• Repeat steps 5 (ii) and (iii) until no more rows or columns can be marked.
• Draw straight lines through all unmarked rows and marked columns.

You can also draw the minimum number of lines by inspection.

Select the smallest element (i.e., 1) from all the uncovered elements. Subtract this smallest element from all the uncovered elements and add it to the elements, which lie at the intersection of two lines. Thus, we obtain another reduced matrix for fresh assignment.

Now again make the assignments for the reduced matrix.

Final Table: Hungarian Method

Since the number of assignments is equal to the number of rows (& columns), this is the optimal solution.

The total cost of assignment = A1 + B4 + C2 + D3

Substituting values from original table: 20 + 17 + 17 + 24 = Rs. 78.

Share This Article

Operations Research Simplified Back Next

Goal programming Linear programming Simplex Method Transportation Problem

• Branch and Bound Tutorial
• Backtracking Vs Branch-N-Bound
• 0/1 Knapsack
• 8 Puzzle Problem
• Job Assignment Problem
• N-Queen Problem
• Travelling Salesman Problem
• Branch and Bound Algorithm
• Introduction to Branch and Bound - Data Structures and Algorithms Tutorial
• 0/1 Knapsack using Branch and Bound
• Implementation of 0/1 Knapsack using Branch and Bound
• 8 puzzle Problem using Branch And Bound

Job Assignment Problem using Branch And Bound

• N Queen Problem using Branch And Bound
• Traveling Salesman Problem using Branch And Bound

Let there be N workers and N jobs. Any worker can be assigned to perform any job, incurring some cost that may vary depending on the work-job assignment. It is required to perform all jobs by assigning exactly one worker to each job and exactly one job to each agent in such a way that the total cost of the assignment is minimized.

Let us explore all approaches for this problem.

Solution 1: Brute Force  

We generate n! possible job assignments and for each such assignment, we compute its total cost and return the less expensive assignment. Since the solution is a permutation of the n jobs, its complexity is O(n!).

Solution 2: Hungarian Algorithm  

The optimal assignment can be found using the Hungarian algorithm. The Hungarian algorithm has worst case run-time complexity of O(n^3).

Solution 3: DFS/BFS on state space tree  

A state space tree is a N-ary tree with property that any path from root to leaf node holds one of many solutions to given problem. We can perform depth-first search on state space tree and but successive moves can take us away from the goal rather than bringing closer. The search of state space tree follows leftmost path from the root regardless of initial state. An answer node may never be found in this approach. We can also perform a Breadth-first search on state space tree. But no matter what the initial state is, the algorithm attempts the same sequence of moves like DFS.

Solution 4: Finding Optimal Solution using Branch and Bound  

The selection rule for the next node in BFS and DFS is “blind”. i.e. the selection rule does not give any preference to a node that has a very good chance of getting the search to an answer node quickly. The search for an optimal solution can often be speeded by using an “intelligent” ranking function, also called an approximate cost function to avoid searching in sub-trees that do not contain an optimal solution. It is similar to BFS-like search but with one major optimization. Instead of following FIFO order, we choose a live node with least cost. We may not get optimal solution by following node with least promising cost, but it will provide very good chance of getting the search to an answer node quickly.

There are two approaches to calculate the cost function:  

• For each worker, we choose job with minimum cost from list of unassigned jobs (take minimum entry from each row).
• For each job, we choose a worker with lowest cost for that job from list of unassigned workers (take minimum entry from each column).

In this article, the first approach is followed.

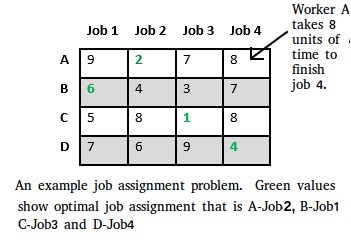
Let’s take below example and try to calculate promising cost when Job 2 is assigned to worker A. 

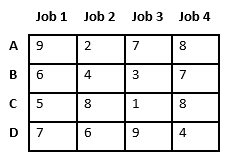
Since Job 2 is assigned to worker A (marked in green), cost becomes 2 and Job 2 and worker A becomes unavailable (marked in red). 

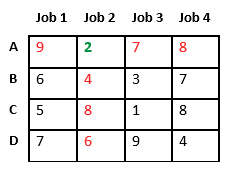
Now we assign job 3 to worker B as it has minimum cost from list of unassigned jobs. Cost becomes 2 + 3 = 5 and Job 3 and worker B also becomes unavailable. 

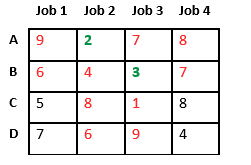
Finally, job 1 gets assigned to worker C as it has minimum cost among unassigned jobs and job 4 gets assigned to worker D as it is only Job left. Total cost becomes 2 + 3 + 5 + 4 = 14. 

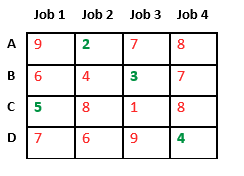
Below diagram shows complete search space diagram showing optimal solution path in green. 

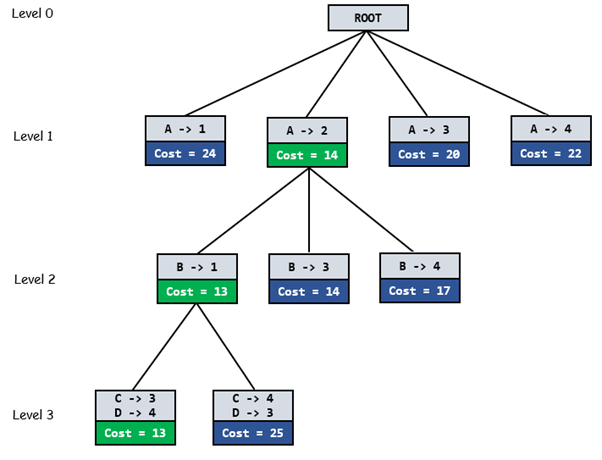
Complete Algorithm:  

Below is the implementation of the above approach:

Time Complexity: O(M*N). This is because the algorithm uses a double for loop to iterate through the M x N matrix.  Auxiliary Space: O(M+N). This is because it uses two arrays of size M and N to track the applicants and jobs.

Please Login to comment...

Similar reads.

• Branch and Bound

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Procedure, Example Solved Problem | Operations Research - Solution of assignment problems (Hungarian Method) | 12th Business Maths and Statistics : Chapter 10 : Operations Research

Chapter: 12th business maths and statistics : chapter 10 : operations research.

Solution of assignment problems (Hungarian Method)

First check whether the number of rows is equal to the numbers of columns, if it is so, the assignment problem is said to be balanced.

Step :1 Choose the least element in each row and subtract it from all the elements of that row.

Step :2 Choose the least element in each column and subtract it from all the elements of that column. Step 2 has to be performed from the table obtained in step 1.

Step:3 Check whether there is atleast one zero in each row and each column and make an assignment as follows.

Step :4 If each row and each column contains exactly one assignment, then the solution is optimal.

Example 10.7

Solve the following assignment problem. Cell values represent cost of assigning job A, B, C and D to the machines I, II, III and IV.

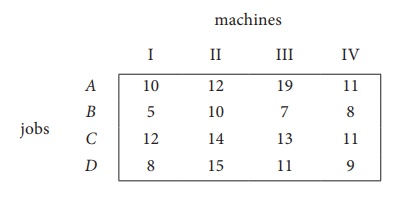
Here the number of rows and columns are equal.

∴ The given assignment problem is balanced. Now let us find the solution.

Step 1: Select a smallest element in each row and subtract this from all the elements in its row.

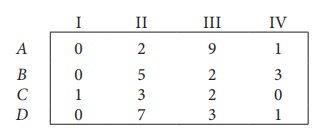
Look for atleast one zero in each row and each column.Otherwise go to step 2.

Step 2: Select the smallest element in each column and subtract this from all the elements in its column.

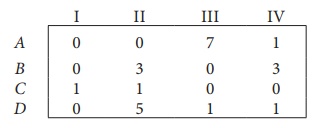
Since each row and column contains atleast one zero, assignments can be made.

Step 3 (Assignment):

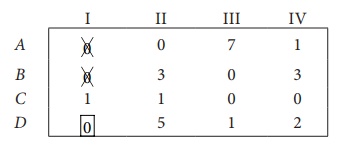
Thus all the four assignments have been made. The optimal assignment schedule and total cost is

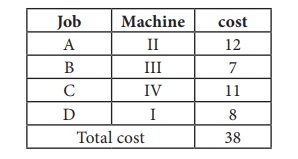
The optimal assignment (minimum) cost

Example 10.8

Consider the problem of assigning five jobs to five persons. The assignment costs are given as follows. Determine the optimum assignment schedule.

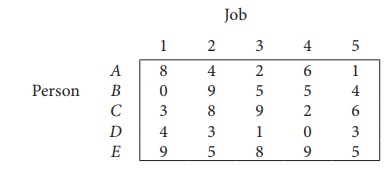
∴ The given assignment problem is balanced.

Now let us find the solution.

The cost matrix of the given assignment problem is

Column 3 contains no zero. Go to Step 2.

Thus all the five assignments have been made. The Optimal assignment schedule and total cost is

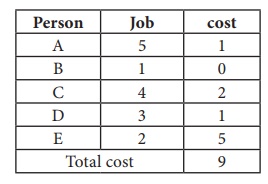
The optimal assignment (minimum) cost = ` 9

Example 10.9

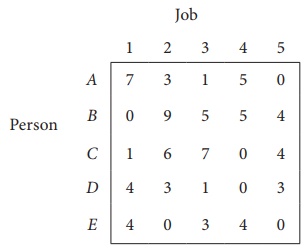
Solve the following assignment problem.

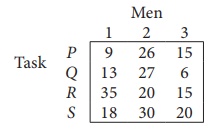
Since the number of columns is less than the number of rows, given assignment problem is unbalanced one. To balance it , introduce a dummy column with all the entries zero. The revised assignment problem is

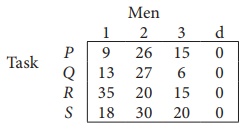
Here only 3 tasks can be assigned to 3 men.

Step 1: is not necessary, since each row contains zero entry. Go to Step 2.

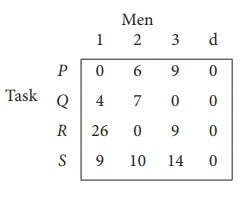
Step 3 (Assignment) :

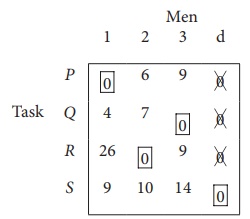
Since each row and each columncontains exactly one assignment,all the three men have been assigned a task. But task S is not assigned to any Man. The optimal assignment schedule and total cost is

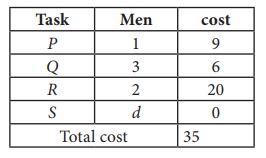
The optimal assignment (minimum) cost = ₹ 35

Related Topics

Privacy Policy , Terms and Conditions , DMCA Policy and Compliant

Copyright © 2018-2024 BrainKart.com; All Rights Reserved. Developed by Therithal info, Chennai.