special products problem solving

6.4 Special Products

Learning objectives.

By the end of this section, you will be able to:

• Square a binomial using the Binomial Squares Pattern
• Multiply conjugates using the Product of Conjugates Pattern
• Recognize and use the appropriate special product pattern

Be Prepared 6.8

Before you get started, take this readiness quiz.

Simplify: ⓐ 9 2 9 2 ⓑ ( −9 ) 2 ( −9 ) 2 ⓒ − 9 2 . − 9 2 . If you missed this problem, review Example 1.50 .

Square a Binomial Using the Binomial Squares Pattern

Mathematicians like to look for patterns that will make their work easier. A good example of this is squaring binomials. While you can always get the product by writing the binomial twice and using the methods of the last section, there is less work to do if you learn to use a pattern.

Look at these results. Do you see any patterns?

What about the number of terms? In each example we squared a binomial and the result was a trinomial .

Now look at the first term in each result. Where did it come from?

The first term is the product of the first terms of each binomial. Since the binomials are identical, it is just the square of the first term!

To get the first term of the product, square the first term .

Where did the last term come from? Look at the examples and find the pattern.

The last term is the product of the last terms, which is the square of the last term.

To get the last term of the product, square the last term .

Finally, look at the middle term . Notice it came from adding the “outer” and the “inner” terms—which are both the same! So the middle term is double the product of the two terms of the binomial.

To get the middle term of the product, multiply the terms and double their product .

Putting it all together:

Binomial Squares Pattern

If a and b a and b are real numbers,

To square a binomial:

• square the first term
• square the last term
• double their product

A number example helps verify the pattern.

To multiply ( 10 + 4 ) 2 ( 10 + 4 ) 2 usually you’d follow the Order of Operations.

The pattern works!

Example 6.47

Multiply: ( x + 5 ) 2 . ( x + 5 ) 2 .

Try It 6.93

Multiply: ( x + 9 ) 2 . ( x + 9 ) 2 .

Try It 6.94

Multiply: ( y + 11 ) 2 . ( y + 11 ) 2 .

Example 6.48

Multiply: ( y − 3 ) 2 . ( y − 3 ) 2 .

Try It 6.95

Multiply: ( x − 9 ) 2 . ( x − 9 ) 2 .

Try It 6.96

Multiply: ( p − 13 ) 2 . ( p − 13 ) 2 .

Example 6.49

Multiply: ( 4 x + 6 ) 2 . ( 4 x + 6 ) 2 .

Try It 6.97

Multiply: ( 6 x + 3 ) 2 . ( 6 x + 3 ) 2 .

Try It 6.98

Multiply: ( 4 x + 9 ) 2 . ( 4 x + 9 ) 2 .

Example 6.50

Multiply: ( 2 x − 3 y ) 2 . ( 2 x − 3 y ) 2 .

Try It 6.99

Multiply: ( 2 c − d ) 2 . ( 2 c − d ) 2 .

Try It 6.100

Multiply: ( 4 x − 5 y ) 2 . ( 4 x − 5 y ) 2 .

Example 6.51

Multiply: ( 4 u 3 + 1 ) 2 . ( 4 u 3 + 1 ) 2 .

Try It 6.101

Multiply: ( 2 x 2 + 1 ) 2 . ( 2 x 2 + 1 ) 2 .

Try It 6.102

Multiply: ( 3 y 3 + 2 ) 2 . ( 3 y 3 + 2 ) 2 .

Multiply Conjugates Using the Product of Conjugates Pattern

We just saw a pattern for squaring binomials that we can use to make multiplying some binomials easier. Similarly, there is a pattern for another product of binomials. But before we get to it, we need to introduce some vocabulary.

What do you notice about these pairs of binomials?

Look at the first term of each binomial in each pair.

Notice the first terms are the same in each pair.

Look at the last terms of each binomial in each pair.

Notice the last terms are the same in each pair.

Notice how each pair has one sum and one difference.

A pair of binomials that each have the same first term and the same last term, but one is a sum and one is a difference has a special name. It is called a conjugate pair and is of the form ( a − b ) , ( a + b ) ( a − b ) , ( a + b ) .

Conjugate Pair

A conjugate pair is two binomials of the form

The pair of binomials each have the same first term and the same last term, but one binomial is a sum and the other is a difference.

There is a nice pattern for finding the product of conjugates. You could, of course, simply FOIL to get the product, but using the pattern makes your work easier.

Let’s look for the pattern by using FOIL to multiply some conjugate pairs.

Each first term is the product of the first terms of the binomials, and since they are identical it is the square of the first term.

The last term came from multiplying the last terms, the square of the last term.

What do you observe about the products?

The product of the two binomials is also a binomial! Most of the products resulting from FOIL have been trinomials.

Why is there no middle term? Notice the two middle terms you get from FOIL combine to 0 in every case, the result of one addition and one subtraction.

The product of conjugates is always of the form a 2 − b 2 a 2 − b 2 . This is called a difference of squares.

This leads to the pattern:

Product of Conjugates Pattern

The product is called a difference of squares.

To multiply conjugates, square the first term, square the last term, and write the product as a difference of squares.

Let’s test this pattern with a numerical example.

Notice, the result is the same!

Example 6.52

Multiply: ( x − 8 ) ( x + 8 ) . ( x − 8 ) ( x + 8 ) .

First, recognize this as a product of conjugates. The binomials have the same first terms, and the same last terms, and one binomial is a sum and the other is a difference.

Try It 6.103

Multiply: ( x − 5 ) ( x + 5 ) . ( x − 5 ) ( x + 5 ) .

Try It 6.104

Multiply: ( w − 3 ) ( w + 3 ) . ( w − 3 ) ( w + 3 ) .

Example 6.53

Multiply: ( 2 x + 5 ) ( 2 x − 5 ) . ( 2 x + 5 ) ( 2 x − 5 ) .

Are the binomials conjugates?

Try It 6.105

Multiply: ( 6 x + 5 ) ( 6 x − 5 ) . ( 6 x + 5 ) ( 6 x − 5 ) .

Try It 6.106

Multiply: ( 2 x + 7 ) ( 2 x − 7 ) . ( 2 x + 7 ) ( 2 x − 7 ) .

The binomials in the next example may look backwards – the variable is in the second term. But the two binomials are still conjugates, so we use the same pattern to multiply them.

Example 6.54

Find the product: ( 3 + 5 x ) ( 3 − 5 x ) . ( 3 + 5 x ) ( 3 − 5 x ) .

Try It 6.107

Multiply: ( 7 + 4 x ) ( 7 − 4 x ) . ( 7 + 4 x ) ( 7 − 4 x ) .

Try It 6.108

Multiply: ( 9 − 2 y ) ( 9 + 2 y ) . ( 9 − 2 y ) ( 9 + 2 y ) .

Now we’ll multiply conjugates that have two variables.

Example 6.55

Find the product: ( 5 m − 9 n ) ( 5 m + 9 n ) . ( 5 m − 9 n ) ( 5 m + 9 n ) .

Try It 6.109

Find the product: ( 4 p − 7 q ) ( 4 p + 7 q ) . ( 4 p − 7 q ) ( 4 p + 7 q ) .

Try It 6.110

Find the product: ( 3 x − y ) ( 3 x + y ) . ( 3 x − y ) ( 3 x + y ) .

Example 6.56

Find the product: ( c d − 8 ) ( c d + 8 ) . ( c d − 8 ) ( c d + 8 ) .

Try It 6.111

Find the product: ( x y − 6 ) ( x y + 6 ) . ( x y − 6 ) ( x y + 6 ) .

Try It 6.112

Find the product: ( a b − 9 ) ( a b + 9 ) . ( a b − 9 ) ( a b + 9 ) .

Example 6.57

Find the product: ( 6 u 2 − 11 v 5 ) ( 6 u 2 + 11 v 5 ) . ( 6 u 2 − 11 v 5 ) ( 6 u 2 + 11 v 5 ) .

Try It 6.113

Find the product: ( 3 x 2 − 4 y 3 ) ( 3 x 2 + 4 y 3 ) . ( 3 x 2 − 4 y 3 ) ( 3 x 2 + 4 y 3 ) .

Try It 6.114

Find the product: ( 2 m 2 − 5 n 3 ) ( 2 m 2 + 5 n 3 ) . ( 2 m 2 − 5 n 3 ) ( 2 m 2 + 5 n 3 ) .

Recognize and Use the Appropriate Special Product Pattern

We just developed special product patterns for Binomial Squares and for the Product of Conjugates. The products look similar, so it is important to recognize when it is appropriate to use each of these patterns and to notice how they differ. Look at the two patterns together and note their similarities and differences.

Comparing the Special Product Patterns

Example 6.58.

Choose the appropriate pattern and use it to find the product:

ⓐ ( 2 x − 3 ) ( 2 x + 3 ) ( 2 x − 3 ) ( 2 x + 3 ) ⓑ ( 8 x − 5 ) 2 ( 8 x − 5 ) 2 ⓒ ( 6 m + 7 ) 2 ( 6 m + 7 ) 2 ⓓ ( 5 x − 6 ) ( 6 x + 5 ) ( 5 x − 6 ) ( 6 x + 5 )

Try It 6.115

ⓐ ( 9 b − 2 ) ( 2 b + 9 ) ( 9 b − 2 ) ( 2 b + 9 ) ⓑ ( 9 p − 4 ) 2 ( 9 p − 4 ) 2 ⓒ ( 7 y + 1 ) 2 ( 7 y + 1 ) 2 ⓓ ( 4 r − 3 ) ( 4 r + 3 ) ( 4 r − 3 ) ( 4 r + 3 )

Try It 6.116

ⓐ ( 6 x + 7 ) 2 ( 6 x + 7 ) 2 ⓑ ( 3 x − 4 ) ( 3 x + 4 ) ( 3 x − 4 ) ( 3 x + 4 ) ⓒ ( 2 x − 5 ) ( 5 x − 2 ) ( 2 x − 5 ) ( 5 x − 2 ) ⓓ ( 6 n − 1 ) 2 ( 6 n − 1 ) 2

Access these online resources for additional instruction and practice with special products:

• Special Products

Section 6.4 Exercises

Practice makes perfect.

In the following exercises, square each binomial using the Binomial Squares Pattern.

( w + 4 ) 2 ( w + 4 ) 2

( q + 12 ) 2 ( q + 12 ) 2

( y + 1 4 ) 2 ( y + 1 4 ) 2

( x + 2 3 ) 2 ( x + 2 3 ) 2

( b − 7 ) 2 ( b − 7 ) 2

( y − 6 ) 2 ( y − 6 ) 2

( m − 15 ) 2 ( m − 15 ) 2

( p − 13 ) 2 ( p − 13 ) 2

( 3 d + 1 ) 2 ( 3 d + 1 ) 2

( 4 a + 10 ) 2 ( 4 a + 10 ) 2

( 2 q + 1 3 ) 2 ( 2 q + 1 3 ) 2

( 3 z + 1 5 ) 2 ( 3 z + 1 5 ) 2

( 3 x − y ) 2 ( 3 x − y ) 2

( 2 y − 3 z ) 2 ( 2 y − 3 z ) 2

( 1 5 x − 1 7 y ) 2 ( 1 5 x − 1 7 y ) 2

( 1 8 x − 1 9 y ) 2 ( 1 8 x − 1 9 y ) 2

( 3 x 2 + 2 ) 2 ( 3 x 2 + 2 ) 2

( 5 u 2 + 9 ) 2 ( 5 u 2 + 9 ) 2

( 4 y 3 − 2 ) 2 ( 4 y 3 − 2 ) 2

( 8 p 3 − 3 ) 2 ( 8 p 3 − 3 ) 2

In the following exercises, multiply each pair of conjugates using the Product of Conjugates Pattern.

( m − 7 ) ( m + 7 ) ( m − 7 ) ( m + 7 )

( c − 5 ) ( c + 5 ) ( c − 5 ) ( c + 5 )

( x + 3 4 ) ( x − 3 4 ) ( x + 3 4 ) ( x − 3 4 )

( b + 6 7 ) ( b − 6 7 ) ( b + 6 7 ) ( b − 6 7 )

( 5 k + 6 ) ( 5 k − 6 ) ( 5 k + 6 ) ( 5 k − 6 )

( 8 j + 4 ) ( 8 j − 4 ) ( 8 j + 4 ) ( 8 j − 4 )

( 11 k + 4 ) ( 11 k − 4 ) ( 11 k + 4 ) ( 11 k − 4 )

( 9 c + 5 ) ( 9 c − 5 ) ( 9 c + 5 ) ( 9 c − 5 )

( 11 − b ) ( 11 + b ) ( 11 − b ) ( 11 + b )

( 13 − q ) ( 13 + q ) ( 13 − q ) ( 13 + q )

( 5 − 3 x ) ( 5 + 3 x ) ( 5 − 3 x ) ( 5 + 3 x )

( 4 − 6 y ) ( 4 + 6 y ) ( 4 − 6 y ) ( 4 + 6 y )

( 9 c − 2 d ) ( 9 c + 2 d ) ( 9 c − 2 d ) ( 9 c + 2 d )

( 7 w + 10 x ) ( 7 w − 10 x ) ( 7 w + 10 x ) ( 7 w − 10 x )

( m + 2 3 n ) ( m − 2 3 n ) ( m + 2 3 n ) ( m − 2 3 n )

( p + 4 5 q ) ( p − 4 5 q ) ( p + 4 5 q ) ( p − 4 5 q )

( a b − 4 ) ( a b + 4 ) ( a b − 4 ) ( a b + 4 )

( x y − 9 ) ( x y + 9 ) ( x y − 9 ) ( x y + 9 )

( u v − 3 5 ) ( u v + 3 5 ) ( u v − 3 5 ) ( u v + 3 5 )

( r s − 2 7 ) ( r s + 2 7 ) ( r s − 2 7 ) ( r s + 2 7 )

( 2 x 2 − 3 y 4 ) ( 2 x 2 + 3 y 4 ) ( 2 x 2 − 3 y 4 ) ( 2 x 2 + 3 y 4 )

( 6 m 3 − 4 n 5 ) ( 6 m 3 + 4 n 5 ) ( 6 m 3 − 4 n 5 ) ( 6 m 3 + 4 n 5 )

( 12 p 3 − 11 q 2 ) ( 12 p 3 + 11 q 2 ) ( 12 p 3 − 11 q 2 ) ( 12 p 3 + 11 q 2 )

( 15 m 2 − 8 n 4 ) ( 15 m 2 + 8 n 4 ) ( 15 m 2 − 8 n 4 ) ( 15 m 2 + 8 n 4 )

In the following exercises, find each product.

ⓐ ( p − 3 ) ( p + 3 ) ( p − 3 ) ( p + 3 ) ⓑ ( t − 9 ) 2 ( t − 9 ) 2 ⓒ ( m + n ) 2 ( m + n ) 2 ⓓ ( 2 x + y ) ( x − 2 y ) ( 2 x + y ) ( x − 2 y )

ⓐ ( 2 r + 12 ) 2 ( 2 r + 12 ) 2 ⓑ ( 3 p + 8 ) ( 3 p − 8 ) ( 3 p + 8 ) ( 3 p − 8 ) ⓒ ( 7 a + b ) ( a − 7 b ) ( 7 a + b ) ( a − 7 b ) ⓓ ( k − 6 ) 2 ( k − 6 ) 2

ⓐ ( a 5 − 7 b ) 2 ( a 5 − 7 b ) 2 ⓑ ( x 2 + 8 y ) ( 8 x − y 2 ) ( x 2 + 8 y ) ( 8 x − y 2 ) ⓒ ( r 6 + s 6 ) ( r 6 − s 6 ) ( r 6 + s 6 ) ( r 6 − s 6 ) ⓓ ( y 4 + 2 z ) 2 ( y 4 + 2 z ) 2

ⓐ ( x 5 + y 5 ) ( x 5 − y 5 ) ( x 5 + y 5 ) ( x 5 − y 5 ) ⓑ ( m 3 − 8 n ) 2 ( m 3 − 8 n ) 2 ⓒ ( 9 p + 8 q ) 2 ( 9 p + 8 q ) 2 ⓓ ( r 2 − s 3 ) ( r 3 + s 2 ) ( r 2 − s 3 ) ( r 3 + s 2 )

Everyday Math

Mental math You can use the product of conjugates pattern to multiply numbers without a calculator. Say you need to multiply 47 times 53. Think of 47 as 50 − 3 50 − 3 and 53 as 50 + 3 50 + 3 .

• ⓐ Multiply ( 50 − 3 ) ( 50 + 3 ) ( 50 − 3 ) ( 50 + 3 ) by using the product of conjugates pattern, ( a − b ) ( a + b ) = a 2 − b 2 ( a − b ) ( a + b ) = a 2 − b 2 .
• ⓑ Multiply 47 · 53 47 · 53 without using a calculator.
• ⓒ Which way is easier for you? Why?

Mental math You can use the binomial squares pattern to multiply numbers without a calculator. Say you need to square 65. Think of 65 as 60 + 5 60 + 5 .

• ⓐ Multiply ( 60 + 5 ) 2 ( 60 + 5 ) 2 by using the binomial squares pattern, ( a + b ) 2 = a 2 + 2 a b + b 2 ( a + b ) 2 = a 2 + 2 a b + b 2 .
• ⓑ Square 65 without using a calculator.

Writing Exercises

How do you decide which pattern to use?

Why does ( a + b ) 2 ( a + b ) 2 result in a trinomial, but ( a − b ) ( a + b ) ( a − b ) ( a + b ) result in a binomial?

Marta did the following work on her homework paper:

Explain what is wrong with Marta’s work.

Use the order of operations to show that ( 3 + 5 ) 2 ( 3 + 5 ) 2 is 64, and then use that numerical example to explain why ( a + b ) 2 ≠ a 2 + b 2 ( a + b ) 2 ≠ a 2 + b 2 .

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ On a scale of 1-10, how would you rate your mastery of this section in light of your responses on the checklist? How can you improve this?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/elementary-algebra-2e/pages/1-introduction

• Authors: Lynn Marecek, MaryAnne Anthony-Smith, Andrea Honeycutt Mathis
• Publisher/website: OpenStax
• Book title: Elementary Algebra 2e
• Publication date: Apr 22, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/elementary-algebra-2e/pages/1-introduction
• Section URL: https://openstax.org/books/elementary-algebra-2e/pages/6-4-special-products

© Jan 23, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Drag image here or click to upload

Recap on the FOIL Method

Sum and difference formula, special product patterns, advanced applications, special products in algebra: patterns, applications, and examples.

Special Products in algebra are certain types of polynomial multiplications that follow specific patterns, allowing for quicker simplification and solution without the need for long multiplication methods.

Understanding these patterns is not just a shortcut to solving problems faster; it deepens comprehension of algebraic structures, enhances problem-solving skills, and lays a foundation for more advanced mathematical concepts.

In this blog, we'll explore the key special product patterns, each illustrated with geometrical representations and worked examples to cater to a variety of learning styles.

Before delving into special products, it's essential to revisit the FOIL method, a foundational technique in algebra used to multiply two binomials.

FOIL stands for First, Outside, Inside, Last, representing the order in which you multiply terms in each binomial before summing them up.

Given two binomials \((a + b)\) and \((c + d)\), their product can be expressed as:

\[ (a + b)(c + d) = a \cdot c + a \cdot d + b \cdot c + b \cdot d \]

This process is straightforward but becomes cumbersome with more complex or higher degree polynomials. That's where special products come in handy, streamlining the multiplication process. Let's explore some of these special products and their significance.

Special products follow specific patterns that, once mastered, make it easier to multiply polynomials and recognize these patterns in various algebraic expressions.

One of the first special product patterns you'll encounter is the sum and difference formula, expressed as:

\[ (a + b)(a - b) = a^2 - b^2 \]

This pattern tells us that the product of a sum and a difference is the difference of two squares. It's a direct application of the FOIL method, illustrating how the middle terms cancel each other out.

Geometrical Representation

A geometric representation can help visualize this formula. Imagine a square with side \(a + b\) and another square with side \(a - b\). The area of the larger square minus the smaller one visually demonstrates the difference of two squares.

Worked Examples

Find the product of \( (3x + 4) \) and\( (3x - 4) \).

Applying the formula:

\[ (3x + 4)(3x - 4) = (3x)^2 - (4)^2 = 9x^2 - 16 \]

This shows how quickly we can arrive at the solution using the sum and difference formula.

After revisiting the FOIL method, we dive into the essence of this article—special product patterns. These patterns not only make polynomial multiplication more efficient but also deepen our understanding of algebraic operations. Let's explore these patterns in detail.

Square of a Binomial Pattern

The square of a binomial pattern applies when squaring a binomial expression. This pattern can be expressed as:

\[ (a + b)^2 = a^2 + 2ab + b^2 \]

Similarly, for the square of a binomial with a subtraction sign, we have:

\[ (a - b)^2 = a^2 - 2ab + b^2 \]

To understand the square of a binomial geometrically, imagine a square with side length \(a + b\). This square can be divided into four parts: two squares of areas \(a^2\) and \(b^2\), and two rectangles, each with area \(ab\). The total area, \(a^2 + 2ab + b^2\), represents the expanded form of \((a + b)^2\).

Calculate the square of \( (x + 5) \).

Using the formula, we get:

\[ (x + 5)^2 = x^2 + 2 \cdot x \cdot 5 + 5^2 = x^2 + 10x + 25 \]

Calculate the square of \( (3x - 2) \).

Applying the pattern:

\[ (3x - 2)^2 = (3x)^2 - 2 \cdot 3x \cdot 2 + (2)^2 = 9x^2 - 12x + 4 \]

Sum and Difference of Two Cubes

Another interesting pattern emerges when dealing with the sum and difference of cubes. These can be expressed as:

\[ a^3 + b^3 = (a + b)(a^2 - ab + b^2) \]

\[ a^3 - b^3 = (a - b)(a^2 + ab + b^2) \]

Note on Connection to Advanced Concepts

Understanding these cubic formulas is crucial for solving polynomial equations of higher degrees. While these directly lead to cubic solutions, they lay the groundwork for techniques used in solving quadratic equations and beyond, facilitating a smoother transition to more complex algebraic concepts.

Simplify \( x^3 + 27 \).

Recognize \(27\) as \(3^3\), then apply the sum of cubes formula:

\[ x^3 + 27 = x^3 + 3^3 = (x + 3)(x^2 - 3x + 9) \]

Simplify \( 8x^3 - 125 \).

Recognizing \(8x^3\) as \((2x)^3\) and \(125\) as \(5^3\), apply the difference of cubes formula:

\[ 8x^3 - 125 = (2x)^3 - 5^3 = (2x - 5)((2x)^2 + 2x \cdot 5 + 5^2) = (2x - 5)(4x^2 + 10x + 25) \]

The beauty of special product patterns extends beyond their simplicity and efficiency—they pave the way for advanced applications in mathematics.

Understanding these patterns is not merely about speeding up polynomial multiplication; it's about building a foundational understanding that is crucial for higher-level math. Here are some areas where special products play a significant role:

Algebraic Manipulation and Simplification

Special products allow for the quick manipulation and simplification of algebraic expressions, making it easier to solve equations, particularly those involving quadratic and cubic terms.

Solving Polynomial Equations

Recognizing special product patterns can simplify the process of factoring and solving polynomial equations, including higher-degree polynomials that might otherwise seem daunting.

In calculus, special product patterns assist in the simplification of functions for differentiation and integration. For instance, recognizing a binomial square can simplify the process of finding a derivative using the chain rule.

Geometry and Trigonometry

Geometrical proofs and trigonometric identities often involve algebraic expressions that can be simplified using special product patterns. This simplification can unveil elegant solutions and deeper insights into geometric relationships and trigonometric functions.

Mastering the art of special products in algebra is more than just a mathematical exercise; it's a journey towards developing a deeper and more intuitive understanding of the language of mathematics.

These patterns serve as essential tools in the toolbox of students, educators, and professionals, enabling them to tackle a wide array of mathematical challenges with greater ease and confidence.

As we explored the square of a binomial pattern, the sum and difference of two cubes, and their geometrical representations, we've seen how abstract algebraic concepts can be made tangible and accessible.

These patterns are not just shortcuts; they are insights into the structural beauty of algebra that echoes across various branches of mathematics.

Related Posts

Understanding the radius of convergence in power series.

Explore the concept of radius of convergence in power series, including definitions, examples, and applications with a focus on geometric series, sin(x), and the Ratio Test for clarity and insight.

Parametric Integration (Equations, Differentiation & Examples)

Discover the concept of Parametric Integration in mathematics, including equations, differentiation techniques, and a variety of examples.

Quantitative Variables: Definition, Types, & Examples

In this article, we are going to study deeper into quantitative variables and how they compare to another type of variable, the qualitative variables.

The Power Function: Definition, Examples and Solutions

Explore power functions's definition, discover real-life examples, and learn effective problem-solving solutions. Enhance your understanding of this fundamental mathematical concept and its applications through this in-depth resource.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Chapter 6: Polynomials

6.6 Special Products

There are a few shortcuts available when multiplying polynomials. When recognized, they help arrive at the solution much quicker.

The first is called a difference of squares. A difference of squares is easily recognized because the numbers and variables in its two factors are exactly the same, but the sign in each factor is different (one plus sign, one minus sign). To illustrate this, consider the following example.

Example 6.6.1

Multiply the following pair of binomials: [latex](a+b)(a-b).[/latex]

[latex]\begin{array}{rrrrr} a&+&b&& \\ a&-&b&& \\ \hline a^2&+&ab&& \\ &-&ab&-&b^2 \\ \hline a^2&-&b^2&& \end{array}[/latex]

Notice the middle term cancels out and [latex](a+b)(a-b) = a^2 - b^2[/latex]. Cancelling the middle term during multiplication is the same for any difference of squares.

Example 6.6.2

Multiply the following pair of binomials: [latex](x - 5)(x + 5).[/latex]

Recognize a difference of squares. The solution is [latex]x^2 - 25.[/latex]

Example 6.6.3

Multiply the following pair of binomials: [latex](3x + 7)(3x - 7).[/latex]

Recognize a difference of squares. The solution is [latex]9x^2 - 49.[/latex]

Example 6.6.4

Multiply the following pair of binomials: [latex](2x - 6y)(2x + 6y).[/latex]

Recognize a difference of squares. The solution is [latex]4x^2 - 36y^2.[/latex]

Another pair of binomial multiplications useful to know are perfect squares. These have the form of [latex](a + b)^2[/latex] or [latex](a - b)^2[/latex].

Example 6.6.5

Multiply the following pair of binomials: [latex](a + b)^2[/latex] and [latex](a - b)^2.[/latex]

[latex]\begin{array}{rr} \begin{array}{rrrrrr} &(a&+&b)&& \\ \times &(a&+&b)&& \\ \hline &a^2&+&ab&& \\ &&+&ab&+&b^2 \\ \hline &a^2&+&2ab&+&b^2 \end{array}\hspace{0.5in} & \begin{array}{rrrrrr} &(a&-&b)&& \\ \times &(a&-&b)&& \\ \hline &a^2&-&ab&& \\ &&-&ab&+&b^2 \\ \hline &a^2&-&2ab&+&b^2 \end{array} \end{array}[/latex]

The pattern of multiplication for any perfect square is the same. The first term in the answer is the square of the first term in the problem. The middle term is 2 times the first term times the second term. The last term is the square of the last term.

[latex](a + b)^2 = a^2 + 2ab + b^2 \text{ and }(a - b)^2 = a^2 - 2ab + b^2[/latex]

Example 6.6.6

Multiply out the following expression: [latex](x - 5)^2.[/latex]

Recognize a perfect square. Square the first term, subtract twice the product of the first and last terms, and square the last term.

[latex](x - 5)^2 = x^2 - 10x + 25[/latex]

Example 6.6.7

Multiply out the following expression: [latex](3x - 7y)^2.[/latex]

[latex](3x - 7y)^2 = 9x^2 - 42xy + 49y^2[/latex]

Example 6.6.8

Multiply out the following expression: [latex](5a + 9b)^2.[/latex]

Recognize a perfect square. Square the first term, add twice the product of the first and last terms, and square the last term.

[latex](5a + 9b)^2 = 25a^2 + 90ab + 81b^2[/latex]

Find each product.

• [latex](x + 8)(x - 8)[/latex]
• [latex](a - 4)(a + 4)[/latex]
• [latex](1 + 3p)(1 - 3p)[/latex]
• [latex](x - 3)(x + 3)[/latex]
• [latex](1 - 7n)(1 + 7n)[/latex]
• [latex](8m + 5)(8m - 5)[/latex]
• [latex](4y - x)(4y + x)[/latex]
• [latex](7a + 7b)(7a - 7b)[/latex]
• [latex](4m - 8n)(4m + 8n)[/latex]
• [latex](3y - 3x)(3y + 3x)[/latex]
• [latex](6x - 2y)(6x + 2y)[/latex]
• [latex](1 + 5n)^2[/latex]
• [latex](a + 5)^2[/latex]
• [latex](x - 8)^2[/latex]
• [latex](1 - 6n)^2[/latex]
• [latex](4x - 5)^2[/latex]
• [latex](5m - 8)^2[/latex]
• [latex](3a + 3b)^2[/latex]
• [latex](5x + 7y)^2[/latex]
• [latex](4m - n)^2[/latex]
• [latex](5 + 2r)^2[/latex]
• [latex](m - 7)^2[/latex]
• [latex](4v - 7)(4v + 7)[/latex]
• [latex](b + 4)(b - 4)[/latex]

Answer Key 6.6

Intermediate Algebra Copyright © 2020 by Terrance Berg is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

Want Better Math Grades?

✅ Unlimited Solutions

✅ Step-by-Step Answers

✅ Available 24/7

➕ Free Bonuses ($1085 value!)

On this page

• Factoring and Fractions

1. Special Products

• 2. Common Factor and Difference of Squares
• 3. Factoring Trinomials
• 4. The Sum and Difference of Cubes
• 5. Equivalent Fractions
• 6. Multiplication and Division of Fractions
• 7. Addition and Subtraction of Fractions
• 8. Equations Involving Fractions

Related Sections

Math Tutoring

Need help? Chat with a tutor anytime, 24/7.

Online Algebra Solver

Solve your algebra problem step by step!

IntMath Forum

Get help with your math queries:

What makes these products "special"?

The algebraic products on this page are used all the time later in this chapter, and in a lot of the math you will come across later. They are "special" because they are very common, and they're worth knowing.

If you can recognize these products easily, it makes your life easier later on.

Special Products involving Squares

The following special products come from multiplying out the brackets. You'll need these often, so it's worth knowing them well.

a ( x + y ) = ax + ay (Distributive Law) ( x + y )( x − y ) = x 2 − y 2 (Difference of 2 squares) ( x + y ) 2 = x 2 + 2 xy + y 2 (Square of a sum) ( x − y ) 2 = x 2 − 2 xy + y 2 (Square of a difference)

Examples using the special products

Example 1: Multiply out 2 x ( a − 3)

This one uses the first product above. We just multiply the term outside the bracket (the "2 x ") with the terms inside the brackets (the " a " and the "−3").

2 x ( a − 3) = 2 ax − 6 x

Example 2: Multiply (7 s + 2 t )(7 s − 2 t )

We recognize this one involves the Difference of 2 squares :

(7 s + 2 t )(7 s − 2 t )

= (7 s ) 2 − (2 t ) 2 = 49 s 2 − 4 t 2

Example 3: Multiply (12 + 5 ab )(12 − 5 ab )

(12 + 5 ab )(12 − 5 ab )

= (12 ) 2 − (5 ab ) 2 = 144 − 25 a 2 b 2

The answer is a difference of 2 squares.

Example 4: Expand (5 a + 2 b ) 2

This one is the square of a sum of 2 terms .

(5 a + 2 b ) 2

= (5 a ) 2 + 2(5 a )(2 b ) + (2 b ) 2 = 25 a 2 + 20 a b + 4 b 2

Example 5: Expand ( q − 6) 2

( q − 6) 2

= ( q ) 2 − 2( q )(6) + (6) 2 = q 2 − 12 q + 36

This example involved the square of a difference of 2 terms.

Example 6: Expand (8 x − y )(3 x + 4 y )

This question is not in any of the formats we have above. So we just need to multiply out the brackets, term-by-term.

It's important to recognize when we have a Special Product and when our question is something else.

(8 x − y )(3 x + 4 y )

= 8 x (3 x + 4 y ) − y (3 x + 4 y ) = 8 x (3 x ) + 8 x (4 y ) − y (3 x ) − y (4 y ) = 24 x 2 + 32 x y −3 xy − 4 y 2 = 24 x 2 + 29 x y − 4 y 2

Example 7: Expand ( x + 2 + 3 y ) 2

To expand this, we put it in the form ( a + b ) 2 and expand it using the third rule above, which says:

( a + b ) 2 = a 2 + 2 ab + b 2

a = x + 2 b = 3 y

This gives me:

( x + 2 + 3 y ) 2

[This is the ( a + b ) 2 step.]

= ([ x + 2] + 3 y ) 2

= [ x + 2] 2 + 2[ x + 2](3 y ) + (3 y ) 2

[Here I apply: ( a + b ) 2 = a 2 + 2 ab + b 2 ]

= [ x 2 + 4 x + 4] + (2 x + 4)(3 y ) + 9 y 2

[In this row I just expand out the brackets.]

= x 2 + 4 x + 4 + 6 xy + 12 y + 9 y 2

[This is a "tidy up" step.]

I could have chosen the following and obtained the same answer:

a = x b = 2 + 3 y

Special Products involving Cubes

The following products are just the result of multiplying out the brackets.

( x + y ) 3 = x 3 + 3 x 2 y + 3 xy 2 + y 3 (Cube of a sum) ( x − y ) 3 = x 3 − 3 x 2 y + 3 xy 2 − y 3 (Cube of a difference) ( x + y )( x 2 − xy + y 2 ) = x 3 + y 3 (Sum of 2 cubes) ( x − y )( x 2 + xy + y 2 ) = x 3 − y 3 (Difference of 2 cubes)

These are also worth knowing well enough so you recognize the form, and the differences between each of them. (Why? Because it's easier than multiplying out the brackets and it helps us solve more complex algebra problems later.)

Example 8: Expand (2 s + 3) 3

This involves the Cube of a Sum:

(2 s + 3) 3

= (2 s ) 3 + 3(2 s ) 2 (3) + 3(2 s )(3) 2 + (3) 3

= 8 s 3 + 36 s 2 + 54 s + 27

(1) ( s + 2 t )( s − 2 t )

Using the Difference of 2 Squares formula

( x + y )( x − y ) = x 2 − y 2 ,

( s + 2 t )( s − 2 t )

= ( s ) 2 − (2 t ) 2 = s 2 − 4t 2

(2) ( i 1 + 3) 2

Using the Square of a Sum formula

( x + y ) 2 = x 2 + 2 xy + y 2 ,

( i 1 + 3) 2

= ( i 1 ) 2 + 2( i 1 )(3) + (3) 2 = i 1 2 + 6 i 1 + 9

(3) (3 x + 10 y ) 2

(3 x + 10 y ) 2

= (3 x ) 2 + (2)(3 x )(10 y ) + (10 y ) 2 = 9 x 2 + 60 xy + 100 y 2

(4) (3 p − 4 q ) 2

Using the Square of a Difference formula

( x − y ) 2 = x 2 − 2 xy + y 2 ,

(3 p − 4 q ) 2

= (3 p ) 2 − (2)(3 p )(4 q ) + (4 q ) 2 = 9 p 2 − 24 pq + 16 q 2

Tips, tricks, lessons, and tutoring to help reduce test anxiety and move to the top of the class.

Email Address Sign Up

Special products: Step by step tutorial. Resolved examples.

If you never remember to apply the special product formulas and when you remember, then you don’t know how to apply it, keep reading because in less than 5 minutes your doubts will be solved.

Multiplying two polynomials together, if they have more than three terms and in their terms have several variables, can be very tedious and you can invest a lot of time in multiplying.

Fortunately, if the polynomials to be multiplied are of two terms (binomials) and their terms are equal, you can apply the formulas of notable products, which will allow you to carry out the multiplication directly.

Would you like to know how to identify when you have a special product and how to apply its formula?

In this post I will explain to you step by step the different special product formulas , with examples resolved step by step, so that you learn how to apply them in your exercises.

Índice de Contenidos

Definition os special products

What are special products ?

Special products,  are polynomials of two terms (binomials) elevated to the square, or the product of two binomials, as we will see later, whose development always follows the same rules .

Therefore, at the moment you identify them, you directly have to apply their formulas to develop them, without having to multiply term by term, to save you time and complications.

The special product formulas more important are: the square of sum , the square of difference and the sum by difference or difference of squares .

Let’s see every one of them.

Special product formulas

Square of sum formula.

The way to read this special product is: Square of the first, plus double of the first by the second, plus the square of the second:

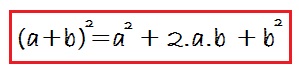
The first i s «a» (the first term of the polynomial) and the second is «b» (the second term of the polynomial).

To apply this formula you only have to replace the terms of the polynomial with a and b. For example:

The first is x and the second is 1. So then:

• Square of the first: x
• Double of the first by the second: 2. x. 1
• Square of the second: 1

So far you’ve applied the formula. Now we have to operate within each term to simplify, multiplying numbers and solving powers:

A serious mistake is not realizing that the above expression is a special product and squaring each term incorrectly:

Square of difference formula

This formula is very similar to the square of sum formula, with the difference of the minus sign in the second term.

It reads as follows: Square of the first, minus twice the first by the second, plus the square of the second:

As in the previous case, the first is «a» (the first term of the polynomial) and the second is «b» (the second term of the polynomial). To apply this formula you only have to replace the terms of the polynomial with a and b.

For example:

• Square of the first: 2²
• Double of the first by the second: 2.2.x
• Square of the second: x²

Both the square of a sum and the square of a difference can be used to factor polynomials , applied in reverse, that is, from the development, obtaining the special products.

Difference of squares formula

This formula is very useful for factoring polynomials and simplifying algebraic fractions when we have the subtraction of two squared terms:

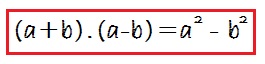
Usually the difference of squares is «camouflaged» and is not directly visible, so it is very important to know how to identify it .

For example: x²-25 is apparently not a difference of squares, because we don’t see the second term elevated to the square, but since we know that 25 is 5² then we can apply the formula:

To be taken into account with the special product formulas

I’ve just shown you the three formulas of the most important special products.

There are other special productssuch as the cube of a sum, the cube of a difference, trinomial squared… that are not at all practical or most complicated to memorize.

In such cases, it is preferable to develop the multiplication of polynomials rather than memorize a formula.

Another thing you have to keep in mind is that the first and second terms don’t have to be made up of a single factor. Each term can consist of several factors, such as:

In that case, be very careful and do not forget to elevate the whole term to the square, with the application of the property of the corresponding power.

Deja un comentario Cancelar la respuesta

Este sitio usa Akismet para reducir el spam. Aprende cómo se procesan los datos de tus comentarios .

• Engineering Economy
• Derivation of Formulas
• General Engineering
• Spherical Trigonometry
• Solid Geometry
• Analytic Geometry
• Integral Calculus
• Differential Equations
• Advance Engineering Mathematics
• Strength of Materials
• Theory of Structures
• CE Board: Math
• CE Board: Hydro Geo
• CE Board: Design
• Reinforced Concrete Design
• Timber Design
• Geotechnical Engineering
• Problem 10 | Special Products and Factoring

Problem 10 Given that $x + y + xy = 1$, where $x$ and $y$ are nonzero real numbers,find the value of $xy + \dfrac{1}{xy} - \dfrac{y}{x} - \dfrac{x}{y}$.  

    $= \dfrac{x^2y^2 + 1 - y^2 - x^2}{xy}$

    $= \dfrac{(x^2y^2 - y^2) - (x^2 - 1)}{xy}$

    $= \dfrac{y^2(x^2 - 1) - (x^2 - 1)}{xy}$

    $= \dfrac{(x^2 - 1)(y^2 - 1)}{xy}$

    $= \dfrac{(x - 1)(x + 1)(y - 1)(y + 1)}{xy}$

    $= \dfrac{(x - 1)(y - 1) \times (x + 1)(y + 1)}{xy}$

    $= \dfrac{(xy - x - y + 1) \times (xy + x + y + 1)}{xy}$

    $= \dfrac{[ \, xy + (1 - x - y) \, ] \times [ \, (x + y + xy) + 1 \, ]}{xy}$  

From the given: $x + y + xy = 1$ and

$1 - x - y = xy$  

Thus, $xy + \dfrac{1}{xy} - \dfrac{y}{x} - \dfrac{x}{y}$

    $= \dfrac{[ \, xy + xy \, ] \times [ \, 1 + 1 \, ]}{xy}$

    $= \dfrac{2xy \times 2}{xy}$

    $= \dfrac{4xy}{xy}$

    $= 4$           answer

• Log in to post comments
• 13433 reads

More Reviewers

• Laws of Exponents and Radicals
• Logarithm and Other Important Properties in Algebra
• Quadratic Equations in One Variable
• Arithmetic, geometric, and harmonic progressions
• Binomial Theorem
• System of Equations
• Variation / Proportional
• Verbal Problems in Algebra
• Probability and Statistics

Follow @iMATHalino

Special Binomial Products

See what happens when we multiply some binomials ...

A binomial is a polynomial with two terms

Product means the result we get after multiplying.

In Algebra xy means x multiplied by y

And (a+b)(a−b) means (a+b) multiplied by (a−b) . We use that a lot here!

So when we multiply binomials we get ... Binomial Products!

And we will look at three special cases of multiplying binomials ... so they are Special Binomial Products .

1. Multiplying a Binomial by Itself

What happens when we square a binomial (in other words, multiply it by itself) .. ?

(a+b) 2 = (a+b)(a+b) = ... ?

The result:

(a+b) 2 = a 2 + 2ab + b 2

This illustration shows why it works:

2. Subtract Times Subtract

And what happens when we square a binomial with a minus inside?

(a−b) 2 = (a−b)(a−b) = ... ?

(a−b) 2 = a 2 − 2ab + b 2

If you want to see why, then look at how the (a−b) 2 square is equal to  the big a 2 square minus the other rectangles:

3. Add Times Subtract

And then there is one more special case ... what about (a+b) times (a−b) ?

(a+b)(a−b) = ... ?

(a+b)(a−b) = a 2 − b 2

That was interesting! It ended up very simple.

And it is called the " difference of two squares " (the two squares are a 2 and b 2 ).

Note: (a−b) can swap places with (a+b):

(a−b)(a+b) = a 2 − b 2

The Three Cases

Here are the three results we just got:

The first two are the "perfect square trinomials" and the last is the "difference of squares"

Remember those patterns, they will save you time and help you solve many algebra puzzles.

So far we have just used "a" and "b", but they could be anything.

Example: (y+1) 2

We can use the (a+b) 2 case where "a" is y, and "b" is 1:

(y+1) 2 = (y) 2 + 2(y)(1) + (1) 2 = y 2 + 2y + 1

Example: (3x−4) 2

We can use the (a-b) 2 case where "a" is 3x, and "b" is 4:

(3x−4) 2 = (3x) 2 − 2(3x)(4) + (4) 2 = 9x 2 − 24x + 16

Example: (4y+2)(4y−2)

We know the result is the difference of two squares, because:

(4y+2)(4y−2) = (4y) 2 − (2) 2 = 16y 2 − 4

Sometimes we can see the pattern of the answer:

Example: which binomials multiply to get 4x 2 − 9

Hmmm... is that the difference of two squares?

4x 2 is (2x) 2 , and 9 is (3) 2 , so we have:

4x 2 − 9 = (2x) 2 − (3) 2

And that can be produced by the difference of squares formula:

Like this ("a" is 2x, and "b" is 3):

(2x+3)(2x−3) = (2x) 2 − (3) 2 = 4x 2 − 9

So the answer is that we can multiply (2x+3) and (2x−3) to get 4x 2 − 9

Elementary Algebra

Katherine Yoshiwara

Section 7.4 Special Products and Factors

Subsection squares of monomials.

A few special binomial products occur so frequently that it is useful to recognize their forms. This will enable you to write their factored forms directly, without trial and error. To prepare for these special products, we first consider the squares of monomials.

Study the squares of monomials in Example 7.30 . Do you see a quick way to find the product?

Example 7.30 .

\(\displaystyle (w^5)^2 = w^5 \cdot w^5 = w^{10}\)

\(\displaystyle (4x^3)^2 = 4x^3 \cdot 4x^3 = 4 \cdot 4 \cdot x^3 \cdot x^3 = 16x^6\)

Look Closer.

In Example 7.30 a, we doubled the exponent and kept the same base. In Example 7.30 b, we squared the numerical coefficient and doubled the exponent.

Reading Questions Reading Questions

Why do we double the exponent when we square a power?

Because when we multiply powers with the same base, we add the exponents.

Example 7.31 .

Find a monomial whose square is \(36t^8\text{.}\)

When we square a power, we double the exponent, so \(t^8\) is the square of \(t^4\text{.}\) Because 36 is the square of 6, the monomial we want is \(6t^4\text{.}\) To check our result, we square \(6t^4\) to see that \((6t^4)^2=36t^8\text{.}\)

Subsection Squares of Binomials

You can use the distributive law to verify each of the following special products.

Squares of Binomials.

\(\displaystyle \blert{(a+b)^2=a^2+2ab+b^2}\)

\(\displaystyle \blert{(a-b)^2=a^2-2ab+b^2}\)

Explain why it is NOT true that \((a+b)^2=a^2+b^2\text{.}\)

Because we must square \((a+b)\) using FOIL.

We can use these results as formulas to compute the square of any binomial.

Example 7.32 .

Expand \(~(2x+3)^2~\) as a polynomial.

The formula for the square of a sum says to square the first term, add twice the product of the two terms, then add the square of the second term. We replace \(a\) by \(2x\) and \(b\) by \(3\) in the formula.

Of course, you can verify that you will get the same answer for Example 7.32 if you compute the square by multiplying \((2x+3)(2x+3)\text{.}\)

Caution 7.33 .

We cannot square a binomial by squaring each term separately! For example, it is NOT true that

We must use the distributive law to multiply the binomial times itself.

How do we compute \((a+b)^2\text{?}\)

\(a^2+2ab+b^2\)

Subsection Difference of Two Squares

Now consider the product

In this product, the two middle terms cancel each other, and we are left with a difference of two squares.

Difference of Two Squares.

Example 7.34 ..

Multiply \(~(2y+9w)(2y-9w)~\)

The product has the form \((a+b)(a-b)\text{,}\) with \(a\) replaced by \(2y\) and \(b\) replaced by \(9w\text{.}\) We use the difference of squares formula to write the product as a polynomial.

Explain the difference between \((a-b)^2\) and \(a^2-b^2\text{.}\)

To simplify \((a-b)^2\text{,}\) we must square the binomial.

Subsection Factoring Special Products

The three special products we have just studied are useful as patterns for factoring certain polynomials. For factoring, we view the formulas from right to left.

Special Factorizations.

\(\displaystyle \blert{a^2+2ab+b^2=(a+b)^2}\)

\(\displaystyle \blert{a^2-2ab+b^2=(a-b)^2}\)

\(\displaystyle \blert{a^2-b^2=(a+b)(a-b)}\)

If we recognize one of the special forms, we can use the formula to factor it. Notice that all three special products involve two squared terms, \(a^2\) and \(b^2\text{,}\) so we first look for two squared terms in our trinomial.

Example 7.35 .

Factor \(~x^2+24x+144\)

This trinomial has two squared terms, \(x^2\) and \(144\text{.}\) These terms are \(a^2\) and \(b^2\text{,}\) so \(a=x\) and \(b=12\text{.}\) We check whether the middle term is equal to \(2ab\text{.}\)

This is the correct middle term, so our trinomial has the form (1), with \(a=x\) and \(b=12\text{.}\) Thus,

How can we factor \(a^2- 2ab + b^2\text{?}\)

\((a-b)^2\)

How can we factor \(a^2- b^2\text{?}\)

\((a+b)(a-b)\)

Caution 7.36 .

The sum of two squares, \(a^2+b^2\text{,}\) cannot be factored! For example,

cannot be factored. You can check, for instance, that \(x^2+16 \not= (x+4)(x+4)\text{.}\)

Sum of Two Squares.

The sum of two squares, \(~a^2+b^2~\text{,}\) cannot be factored.

As always when factoring, we should check first for common factors.

Example 7.37 .

Factor completely \(~98-28x^4+2x^8\)

Each term has a factor of 2, so we begin by factoring out 2.

The polynomial in parentheses has the form \((a-b)^2\text{,}\) with \(a=7\) and \(b=x^4\text{.}\) The middle term is

We use equation (2) to write

What expression involving squares cannot be factored??

\(a^2+b^2\)

Subsection Skills Warm-Up

Exercises exercises, exercise group..

Express each product as a polynomial.

Subsubsection Answers to Skills Warm-Up

\(\displaystyle z^2-6z+9\)

\(\displaystyle x^2+8x+16\)

\(\displaystyle 9a^2+30a+25\)

\(\displaystyle 4b^2-28b+49\)

\(\displaystyle 4n^2-25\)

\(\displaystyle 16m^2-81\)

Subsection Lesson

Subsubsection activity 1: special products.

Simplify each square.

\(\displaystyle (-6h^6)^2\)

\(\displaystyle (12st^8)^2\)

Find a monomial whose square is given.

\(\displaystyle 64b^6\)

\(\displaystyle 169a^4b^{16}\)

Use a formula to expand each product.

\(\displaystyle (4-3t)^2\)

\(\displaystyle (6s+2t)^2\)

\(\displaystyle (5x^4+4)(5x^4-4)\)

Subsubsection Activity 2: Special Factorizations

Use one of the three formulas to factor each polynomial.

\(\displaystyle 25y^2-w^2\)

\(\displaystyle m^6-18m^3+81\)

\(\displaystyle 4h^2+36hk+81k^2\)

Factor completely.

\(\displaystyle x^6-16x^2\)

\(\displaystyle 3b^9+18b^6+27b^3\)

\(\displaystyle 2x^5y-20x^3y^3+50xy^3\)

Subsubsection Wrap-Up

Objectives..

In this Lesson we practiced the following skills:

Identifying squares of monomials

Using the fromulas for squares of binomials and difference of squares

Factoring squares of binomials and difference of squares

Knowing that the sum of squares cannot be factored

Explain the difference between squaring \(3b^3\) and squaring \(3+b^3\text{.}\)

How can you check whether a trinomial might be the square of a binomial?

Explain why we can factor the difference of two squares, but we cannot factor the sum of two squares.

Subsection Homework Preview

Expand each product.

\((4a-5b)^2\)

\((4a+5b)^2\)

\((4a+5b)(4a-5b)\)

\(36x^2+96x+64\)

\(36x^2-96x+64\)

\(36x^2-64\)

Subsubsection Answers to Homework Preview

\(\displaystyle 16a^2-40ab+25b^2\)

\(\displaystyle 16a^2+40ab+25b^2\)

\(\displaystyle 16a^2-25b^2\)

\(\displaystyle 4(3x+4)^2\)

\(\displaystyle 4(3x-4)^2\)

\(\displaystyle 4(3x+4)(3x-4)\)

Exercises Homework 7.4

Square each monomial.

\(\displaystyle (8t^4)^2\)

\(\displaystyle (-12a^2)^2\)

\(\displaystyle (10h^2k)^2\)

\(\displaystyle 16b^{16}\)

\(\displaystyle 121z^{22}\)

\(\displaystyle 36p^6q^{24}\)

For Problems 3–4, write the area of the square in two different ways:

as the sum of four smaller areas,

as one large square, using the formula Area = (length)\(^2\text{.}\)

For Problems 5–7, compute the product.

For Problems 8–13, compute the product.

For Problems 14–19, use the formula for difference of two squares to multiply.

For Problems 20–22, multiply. Write your answer as a polynomial.

For Problems 23–25, factor the squares of binomials.

For Problems 26–31, factor.

For Problems 32–40, factor completely.

Is \(x-3)^2\) equivalent to \(x^2-3^2\text{?}\) Explain why or why not, and give a numerical example to justify your answer.

Use areas to explain why the figure illustrates the product \((a+b)^2 = a^2+2ab+b^2.\)

Use evaluation to decide whether the two expressions \((a+b)^2\) and \(a^2+b^2\) are equivalent.

Explain why you can factor \(x^2-4\text{,}\) but you cannot factor \(x^2+4\text{.}\)

Expand \((a-b)^3\) by multiplying.

Use your formula from part (a) to expand \((2x-3)^3\)

Substitute \(a=5\) and \(b=2\) to show that \((a-b)^3\) is not equivalent to \(a^3-b^3\text{.}\)

Multiply \((a+b)(a^2-ab+b^2)\text{.}\)

Factor \(a^3+b^3\)

Factor \(x^3+8\text{.}\)

• Kindergarten
• Greater Than Less Than
• Measurement
• Multiplication
• Place Value
• Subtraction
• Punctuation
• 1st Grade Reading
• 2nd Grade Reading
• 3rd Grade Reading
• Cursive Writing

Problem Solving Using Special Products

Problem Solving Using Special Products - Displaying top 8 worksheets found for this concept.

Some of the worksheets for this concept are Factoring solvingequations and problem solving 5, Factoring, Word problem practice workbook, Hands on activities for innovative problem solving, X lesson 21 problem solving process, Problem solving and critical thinking, Multiplying binomials using special products, When im at work solving problems.

Found worksheet you are looking for? To download/print, click on pop-out icon or print icon to worksheet to print or download. Worksheet will open in a new window. You can & download or print using the browser document reader options.

1. Factoring, SolvingEquations, and Problem Solving 5

2. factoring, 3. word problem practice workbook, 4. hands-on activities for innovative problem solving*, 5. xxx lesson 21 problem-solving process, 6. problem solving and critical thinking, 7. multiplying binomials using special products, 8. when im at work: solving problems.

Special Products Calculator

Get detailed solutions to your math problems with our special products step-by-step calculator . practice your math skills and learn step by step with our math solver. check out all of our online calculators here .,  example,  solved problems,  difficult problems, are you struggling with math.

Access detailed step by step solutions to thousands of problems, growing every day!

 Related Calculators

 popular problems.

Most popular problems solved with this calculator:

• Spencer Greenberg
• 14 min read

Problem-Solving Techniques That Work For All Types of Challenges

Essay by Spencer Greenberg, Clearer Thinking founder

A lot of people don’t realize that there are general purpose problem solving techniques that cut across domains. They can help you deal with thorny challenges in work, your personal life, startups, or even if you’re trying to prove a new theorem in math.

Below are the 26 general purpose problem solving techniques that I like best, along with a one-word name I picked for each, and hypothetical examples to illustrate what sort of strategy I’m referring to.

Consider opening up this list whenever you’re stuck solving a challenging problem. It’s likely that one or more of these techniques can help!

1. Clarifying

Try to define the problem you are facing as precisely as you can, maybe by writing down a detailed description of exactly what the problem is and what constraints exist for a solution, or by describing it in detail to another person. This may lead to you realizing the problem is not quite what you had thought, or that it has a more obvious solution than you thought.

Life Example

“I thought that I needed to find a new job, but when I thought really carefully about what I don’t like about my current job, I realized that I could likely fix those things by talking to my boss or even, potentially, just by thinking about them differently.”

Startup Example

“we thought we had a problem with users not wanting to sign up for the product, but when we carefully investigated what the problem really was, we discovered it was actually more of a problem of users wanting the product but then growing frustrated because of bad interface design.”

2. Subdividing

Break the problem down into smaller problems in such a way that if you solve each of the small problems, you will have solved the entire problem. Once a problem is subdivided it can also sometimes be parallelized (e.g., by involving different people to work on the different components).

“My goal is to get company Z to become a partner with my company, and that seems hard, so let me break that goal into the steps of (a) listing the ways that company Z would benefit from becoming a partner with us, (b) finding an employee at company Z who would be responsive to hearing about these benefits, and (c) tracking down someone who can introduce me to that employee.”

Math Example

“I want to prove that a certain property applies to all functions of a specific type, so I start by (a) showing that every function of that type can be written as a sum of a more specific type of function, then I show that (b) the property applies to each function of the more specific type, and finally I show that (c) if the property applies to each function in a set of functions then it applies to arbitrary sums of those functions as well.”

3. Simplifying

Think of the simplest variation of the problem that you expect you can solve that shares important features in common with your problem, and see if solving this simpler problem gives you ideas for how to solve the more difficult version.

“I don’t know how to hire a CTO, but I do know how to hire a software engineer because I’ve done it many times, and good CTOs will often themselves be good software engineers, so how can I tweak my software engineer hiring to make it appropriate for hiring a CTO?”

“I don’t know how to calculate this integral as it is, but if I remove one of the free parameters, I actually do know how to calculate it, and maybe doing that calculation will give me insight into the solution of the more complex integral.”

4. Crowd-sourcing 

Use suggestions from multiple people to gain insight into how to solve the problem, for instance by posting on Facebook or Twitter requesting people’s help, or by posting to a Q&A site like Quora, or by sending emails to 10 people you know explaining the problem and requesting assistance.

Business Example

“Do you have experience outsourcing manufacturing to China? If so, I’d appreciate hearing your thoughts about how to approach choosing a vendor.”

Health Example

“I have trouble getting myself to stick to doing exercise daily. If you also used to have trouble getting yourself to exercise but don’t anymore, I’d love to know what worked to make it easier for you.”

5. Splintering

If the problem you are trying to solve has special cases that a solution to the general problem would also apply to, consider just one or two of these special cases as examples and solve the problem just for those cases first. Then see if a solution to one of those special cases helps you solve the problem in general.

“I want to figure out how to improve employee retention in general, let me examine how I could have improved retention in the case of the last three people that quit.”

“I want to figure out how to convince a large number of people to become customers, let me first figure out how to convince just Bill and John to become customers since they seem like the sort of customer I want to attract, and see what general lessons I learn from doing that.”

Read the books or textbooks that seem most related to the topic, and see whether they provide a solution to the problem, or teach you enough related information that you can now solve it yourself.

Economics Example

“Economists probably have already figured out reasonable ways to estimate demand elasticity, let’s see what an econometrics textbook says rather than trying to invent a technique from scratch.”

Mental Health Example

“I’ve been feeling depressed for a long time, maybe I should read some well-liked books about depression.”

7. Searching

Think of a similar problem that you think practitioners, bloggers or academics might have already solved and search online (e.g., via google, Q&A sites, or google scholar academic paper search) to see if anyone has done a write-up about how they solved it.

Advertising Example

“I’m having trouble figuring out the right advertising keywords to bid on for my specific product, I bet someone has a blog post describing how to approach choosing keywords for other related products.”

Machine Learning Example

“I can’t get this neural network to train properly in my specific case, I wonder if someone has written a tutorial about how to apply neural networks to related problems.”

8. Unconstraining

List all the constraints of the problem, then temporarily ignore one or more of the constraints that make the problem especially hard, and try to solve it without those constraints. If you can, then see if you can modify that unconstrained solution until it becomes a solution for the fully constrained problem.

“I need to hire someone who can do work at the intersection of machine learning and cryptography, let me drop the constraint of having cryptography experience and recruit machine learning people, then pick from among them a person that seems both generally capable and well positioned to learn the necessary cryptography.”

Computer Science Example

“I need to implement a certain algorithm, and it needs to be efficient, but that seems very difficult, so let me first figure out how to implement an inefficient version of the algorithm (i.e., drop the efficiency constraint), then at the end I will try to figure out how to optimize that algorithm for efficiency.”

9. Distracting

Fill your mind with everything you know about the problem, including facts, constraints, challenges, considerations, etc. and then stop thinking about the problem, and go and do a relaxing activity that requires little focus, such as walking, swimming, cooking, napping or taking a bath to see if new ideas or potential solutions pop into your mind unexpectedly as your subconscious continues to work on the problem without your attention.

“For three days, I’ve been trying to solve this problem at work, but the solution only came to me when I was strolling in the woods and not even thinking about it.”

Example from mathematician Henri Poincaré

“The incidents of the travel made me forget my mathematical work. Having reached Coutances, we entered an omnibus to go someplace or other. At the moment when I put my foot on the step, the idea came to me, without anything in my former thoughts seeming to have paved the way for it, that the transformations I had used to define the Fuchsian functions were identical with those of non-Euclidean geometry.”

10. Reexamining

Write down all the assumptions you’ve been making about the problem or about what a solution should I look like (yes – make an actual list). Then start challenging them one by one to see if they are actually needed or whether some may be unnecessary or mistaken.

Psychology Example

“We were assuming in our lab experiments that when people get angry they have some underlying reason behind it, but there may be some anger that is better modeled as a chemical fluctuation that is only loosely related to what happens in the lab, such as when people are quick to anger because they are hungry.”

“I need to construct a function that has this strange property, and so far I’ve assumed that the function must be smooth, but if it doesn’t actually need to be then perhaps I can construct just such a function out of simple linear pieces that are glued together.”

11. Reframing

Try to see the problem differently. For instance, by flipping the default, analyzing the inverse of the problem instead, thinking about how you would achieve the opposite of what you want, or shifting to an opposing perspective.

If we were building this company over again completely from scratch, what would we do differently in the design of our product, and can we pivot the product in that direction right now?”

“Should move to New York to take a job that pays $20,000 more per year? Well, if I already lived in New York, the decision to stay there rather than taking a $20,000 pay cut to move here would be an easy one. So maybe I’m overly focused on the current default of not being in New York and the short term unpleasantness of relocating.”

Marketing Example

“If I were one of our typical potential customers, what would I do to try to find a product like ours?”

12. Brainstorming

Set a timer for at least 5 minutes, and generate as many plausible solutions or ideas that you can without worrying about quality at all. Evaluate the ideas only at the end after the timer goes off.

“I’m going to set a timer for 5 minutes and come up with at least three new ways I could go about looking for a co-founder.”

“I’m going to set a timer for 20 minutes and come up with at least five possible explanations for why I’ve been feeling so anxious lately.”

13. Experting

Find an expert (or someone highly knowledgeable) in the topic area and ask their opinion about the best way to solve the problem.

“Why do you think most attempts at creating digital medical records failed, and what would someone have to do differently to have a reasonable chance at success?”

“What sort of optimization algorithm would be most efficient for minimizing the objective functions of this type?”

14. Eggheading

Ask the smartest person you know how they would solve the problem. Be sure to send an email in advance, describing the details so that this person has time to deeply consider the problem before you discuss it.

“Given the information I sent you about our competitors and the interviews we’ve done with potential customers, in which direction would you pivot our product if you were me (and why)?”

Research Example

“Given the information I sent you about our goals and the fact that our previous research attempts have gotten nowhere, how would you approach researching this topic to find the answer we need?”

15. Guessing

Start with a guess for what the solution could be, now check if it actually works and if not, start tweaking that guess to see if you can morph it into something that could work.

“I don’t know what price to use for the product we’re selling, so let me start with an initial guess and then begin trying to sell the thing, and tweak the price down if it seems to be a sticking point for customers, and tweak the price up if the customers don’t seem to pay much attention to the price.”

“My off the cuff intuition says that this differential equation might have a solution of the form x^a * e^(b x)for some a or b, let me plug it into the equation to see if indeed it satisfies the equation for any choice of a and b, and if not, let me see if I can tweak it to make something similar work.”

“I don’t know what the most effective diet for me would be, so I’ll just use my intuition to ban from my diet some foods that seem both unhealthy and addictive, and see if that helps.”

16. Comparing

Think of similar domains you already understand or similar problems you have already solved in the past, and see whether your knowledge of those domains or solutions to those similar problems may work as a complete or partial solution here.

“I don’t know how to find someone to fix things in my apartment, but I have found a good house cleaner before by asking a few friends who they use, so maybe I can simply use the same approach for finding a person to fix things.”

“This equation I’m trying to simplify reminds me of work I’m familiar with related to Kullback-Leibler divergence, I wonder if results from information theory could be applied in this case.”

17. Outsourcing

Consider whether you can hire someone to solve this problem, instead of figuring out how to solve it yourself.

“I don’t really understand how to get media attention for my company, so let me hire a public relations firm and let them handle the process.”

“I have no fashion sense, but I’d like to look better. Maybe I should hire someone fashionable who works in apparel to go shopping with me and help me choose what I should wear.”

18. Experimenting

Rapidly develop possible solutions and test them out (in sequence, or in parallel) by applying cheap and fast experiments. Discard those that don’t work, or iterate on them to improve them based on what you learn from the experiments.

“We don’t know if people will like a product like the one we have in mind, but we can put together a functioning prototype quickly, show five people that seem like they could be potential users, and iterate or create an entirely new design based on how they respond.”

“I don’t know if cutting out sugar will help improve my energy levels, but I can try it for two weeks and see if I notice any differences.”

19. Generalizing

Consider the more general case of the specific problem you are trying to solve, and then work on solving the general version instead. Paradoxically, it is sometimes easier to make progress on the general case rather than a specific one because it increases your focus on the structure of the problem rather than unimportant details.

“I want to figure out how to get this particular key employee more motivated to do good work, let me construct a model of what makes employees motivated to do good work in general, then I’ll apply it to this case.”

“I want to solve this specific differential equation, but it’s clearly a special case of a more general class of differential equations, let me study the general class and see what I can learn about them first and then apply what I learn to the specific case.”

20. Approximating

Consider whether a partial or approximate solution would be acceptable and, if so, aim for that instead of a full or exact solution.

“Our goal is to figure out which truck to send out for which delivery, which theoretically depends on many factors such as current location, traffic conditions, truck capacity, fuel efficiency, how many hours the driver has been on duty, the number of people manning each truck, the hourly rate we pay each driver, etc. etc. Maybe if we focus on just the three variables that we think are most important, we can find a good enough solution.”

“Finding a solution to this equation seems difficult, but if I approximate one of the terms linearly it becomes much easier, and maybe for the range of values we’re interested in, that’s close enough to an exact solution!”

21. Annihilating

Try to prove that the problem you are attempting to solve is actually impossible. If you succeed, you may save yourself a lot of time working on something impossible. Furthermore, in attempting to prove that the problem is impossible, you may gain insight into what makes it actually possible to solve, or if it turns out to truly be impossible, figure out how you could tweak the problem to make it solvable.

“I’m struggling to find a design for a theoretical voting system that has properties X, Y, and Z, let me see if I can instead prove that no such voting system with these three properties could possibly exist.”

“My goal has been to prove that this property always applies to this class of functions, let me see if I can generate a counterexample to prove that this goal is actually impossible.”

Physics Example

“I was trying to design a physical system with certain properties, but I now realize that if such a system could be realized, then it would allow for perpetual motion, and therefore it is impossible to build the sort of system I had in mind.”

22. Modeling

Try to build an explicit model of the situation, including what elements there are and how they related to each other. For instance, try drawing a diagram or flow chart that encapsulates your understanding of all the important information that relates to the problem.

“I’ve noticed that there are certain situations that cause me to freak out that would not bother other people. So what are the common elements when this happens, and how do they seem to relate to each other and to the way I end up feeling? Let me see if I can draw a diagram of this on paper.”

“What are all the different groups (e.g., providers, payers, patients) involved in the healthcare system, and if we diagram how they interact with each other, will that give us ideas for how we can sell our healthcare product?”

23. Brute forcing

One-by-one, consider every possible solution to the problem until you’ve found a good one or exhausted them all.

Startup example

“We’re not sure the order that these four parts of the user registration process should go in, so let’s make a list of all 24 possible orderings, and examine them one by one to see which makes the most sense.”

“It’s not clear how to pick which of these machine learning methods to use on this problem, but since we have lots of data, we can just try each of the algorithms and see which makes the most accurate predictions on data we’ve held to the side for testing.”

24. Refocusing

Forget about trying to solve the problem, and instead consider why you are trying to solve it. Then consider if there is a different problem you can work on that is aimed at producing the same sort of value in a different way.

Startup Example 1

“Maybe instead of trying increasingly hard to figure out how to get this type of consumer to buy, we need to switch our focus to the problem of how to sell to businesses, since what we actually care about is selling it, not selling it to one particular group.”

Startup Example 2

“I’ve been banging my head against the wall trying to implement this extremely complex feature, but there are lots of features that users would find just as valuable that are much easier to implement, maybe I should focus on those instead.”

25. Sidestepping

Consider whether you really want to spend more time trying to solve this problem and whether you can avoid the problem by instead working on totally different problems that you also care about.

“We’ve tried selling our solution to replace Excel for 12 months without much success, maybe we should go back to the drawing board and consider designing a totally new product. Our assumptions about customer needs seem to simply have been wrong.”

“I’ve spent six months on this math problem with little progress, but there are two other math problems I’m equally excited about, so maybe I should spend some time investigating whether one of those may be more tractable.”

26. Aggregating

Consider whether multiple problems you’re now experiencing might, in fact, be caused by the same source of difficulty, rather than being independent problems.

“I seem to be having conflict with a few different friends right now – could it be that I’m doing something without realizing it that is increasing my chance of conflict with all of them?”

“Three employees have quit in the last month. Perhaps the primary problem isn’t really about convincing this one important employee to stay, which is how I was framing it, but rather, about identifying why people keep leaving more generally.”

Recent Posts

We're launching a scientific test of astrology, and anyone can participate!

Remembering Daniel Kahneman: 7 theories that can help you understand how you think

Test how well you understand human psychology with our new quiz

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

6.7: Special Products

• Last updated
• Save as PDF
• Page ID 61423

• David Arnold
• College of the Redwoods

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

This section is dedicated to explaining a number of important shortcuts for multiplying binomials. These are extremely important patterns that will produce the same products computed in previous sections. It is essential that readers practice until they become proficient using each of the patterns presented in this section.

The FOIL Method

Consider the product of two binomials \((x + 3)(x + 6)\). We already know how to find the product of these two binomials; we multiply \(x\) times both terms of \(x + 6\), then we multiply \(3\) times both terms of \(x + 6\).

\[(x+3)(x+6)=x^{2}+6 x+3 x+18 \nonumber \]

Normally we combine like terms, but we halt the process at this point so as to introduce the pattern called the FOIL method. The letters in the word FOIL stand for “First,” “Outer,” “Inner,” and “Last.”

Let’s see how we can connect these terms to the product \((x+3)(x+6)\).

• The arrows indicate the terms in the “First” positions in each binomial. If you multiply the terms in the “First” position, you get \(x^2\).\[{\color {Red}\underbrace{\color {Black}(x+3)(x}_{F}}+6) \nonumber \]
• The arrows indicate the terms in the “Outer” positions in each binomial. If you multiply the terms in the “Outer” positions, you get \(6x\).\[{\color {Red}\underbrace {\color {Black}(x+3)(x+6}_{O}}) \nonumber \]
• The arrows indicate the terms in the “Inner” positions in each binomial. If you multiply the terms in the “Inner” positions, you get \(3x\).\[(x+{\color {Red}\underbrace{\color {Black}{3)(x}}_{I}}+6) \nonumber \]
• The arrows indicate the terms in the “Last” positions in each binomial. If you multiply the terms in the “Last” positions, you get \(18\).\[(x+{\color {Red}\underbrace{\color {Black}{3)(x+6}}_{L}}) \nonumber \]

The following diagram shows the connection between “First,” “Outer,” “Inner,” “Last,” and the answer.

\[(x+3)(x+6)=\begin{array}{ccccccc} \color {Red}{F} & {} & \color {Red}{O} & {} & \color {Red}{I} & {} & \color {Red}{L}\\ x^{2}&+&6x&+&3x&+&18\end{array} \nonumber \]

Example \(\PageIndex{1}\)

Use the FOIL method to simplify: \((x + 5)(x + 7)\)

Multiply the “First” positions: \(x^2\). Multiply the “Outer” positions: \(7x\). Multiply the “Inner” positions: \(5x\). Multiply the “Last” positions: \(35\).

\[(x+5)(x+7)=\begin{array}{ccccccc} \color {Red}{F} & {} & \color {Red}{O} & {} & \color {Red}{I} & {} & \color {Red}{L}\\ x^{2}&+&7x&+&5x&+&35\end{array} \nonumber \]

Combining like terms, \((x+5)(x+7)=x^{2}+12 x+35\)

Exercise \(\PageIndex{1}\)

Simplify: \((x + 2)(x + 11)\)

\(x^{2}+13 x+22\)

Example \(\PageIndex{2}\)

Use the FOIL method to simplify: \((2x−7)(x−4)\)

Multiply the “First” positions: \(2x^2\). Multiply the “Outer” positions: \(−8x\). Multiply the “Inner” positions: \(−7x\). Multiply the “Last” positions: \(28\).

\[(2x-7)(x-4)=\begin{array}{ccccccc} \color {Red}{F} & {} & \color {Red}{O} & {} & \color {Red}{I} & {} & \color {Red}{L}\\ 2x^{2}&-&8x&-&7x&+&28\end{array} \nonumber \]

Combining like terms, \((2 x-7)(x-4)=2 x^{2}-15 x+28\)

Exercise \(\PageIndex{2}\)

Simplify: \((x−1)(4x + 5)\)

\(4 x^{2}+x-5\)

At first glance, the FOIL method doesn’t look like much of a shortcut. After all, if we simply use the distributive property on the product of Example \(\PageIndex{2}\), we get the same quick result.

\[\begin{aligned}(2 x-7)(x-4) &=2 x(x-4)-7(x-4) \\ &=2 x^{2}-8 x-7 x+28 \\ &=2 x^{2}-15 x+28 \end{aligned} \nonumber \]

The FOIL method becomes a true shortcut when we add the “Outer” and “Inner” results in our head.

FOIL Shortcut

To multiply two binomials, follow these steps:

• Multiply the terms in the “First” positions.
• Multiply the terms in the “Outer” and “Inner” positions and combine the results mentally (if they are like terms).
• Multiply the terms in the “Last” positions.

Example \(\PageIndex{3}\)

Use the FOIL shortcut to simplify: \((3x + 8)(2x−1)\)

Each of the following steps is performed mentally.

• Multiply the terms in the “First” positions: \(6x^2\)
• Multiply the terms in the “Outer” and “Inner” positions and add the results mentally: \(−3x + 16x = 13x\)
• Multiply the terms in the “Last” positions: \(−8\)

Write the answer with no intermediate steps: \((3 x+8)(2 x-1)=6 x^{2}+13 x-8\)

Exercise \(\PageIndex{3}\)

Simplify: \((2z−3)(5z−1)\)

\(10 z^{2}-17 z+3\)

Example \(\PageIndex{4}\)

Use the FOIL shortcut to simplify: \((4y−3)(5y + 2)\)

• Multiply the terms in the “First” positions: \(20y^2\)
• Multiply the terms in the “Outer” and “Inner” positions and add the results mentally: \(8y−15y = −7y\)
• Multiply the terms in the “Last” positions: \(−6\)

Write the answer with no intermediate steps: \((4 y-3)(5 y+2)=20 y^{2}-7 y-6\)

Exercise \(\PageIndex{4}\)

Simplify: \((7 x+2)(2 x-3)\)

\(14 x^{2}-17 x-6\)

The Difference of Squares

We can use the FOIL shortcut to multiply \((a + b)(a−b)\).

• Multiply the terms in the “First” positions: \(a^2\)
• Multiply the terms in the “Outer” and “Inner” positions and add the results mentally: \(ab−ab =0\)
• Multiply the terms in the “Last” positions: \(−b^2\)

Thus, \((a+b)(a-b)=a^{2}-b^{2}\). Note how the right-hand side \(a^2 −b^2\) is the difference of two squares. This leads to the following shortcut.

The difference of squares

If you have identical terms in the “First” positions and identical terms in the “Last” positions, but one set is separated with a plus sign while the other is separated by a minus sign, then proceed as follows:

• Square the “First” term.
• Square the “Last” term.
• Place a minus sign between the results

\[(a+b)(a-b)=a^{2}-b^{2} \nonumber \]

If you don’t have identical terms in the “First” and “Last” positions, with one set separated with a plus sign and the other with a minus sign, then you do not have the difference of squares pattern and you must find some other way to multiply. For example, \((x+3)(x−3)\) is an example of the difference of squares pattern, but \((2y + 3)(2y−5)\) is not.

Example \(\PageIndex{5}\)

Use the difference of squares shortcut to simplify: \((x+3)(x− 3)\)

Note how the terms in the “First” position are identical, as are the terms in the “Last” position, with one set separated by a plus sign and the other with a minus sign. Hence, this is the difference of squares pattern and we proceed as follows:

• Square the term in the “First” position: \(x^2\)
• Square the term in the “Last” position: \((−3)^2 =9\)
• Separate the squares with a minus sign.

\[\begin{aligned}(x+3)(x-3) &=x^{2}-(3)^{2} \\ &=x^{2}-9 \end{aligned} \nonumber \]

You should practice this pattern until you can go straight from the problem statement to the answer without writing down any intermediate work, as in \((x + 3)(x−3) = x^2 −9\).

Exercise \(\PageIndex{5}\)

Simplify: \((x + 5)(x−5)\)

\(x^{2}-25\)

Example \(\PageIndex{6}\)

Use the difference of squares shortcut to simplify: \((8y +7z)(8y−7z)\)

• Square the term in the “First” position: \((8y)^2 = 64 y^2\)
• Square the term in the “Last” position: \((7z)^2 = 49 z^2\)

\[\begin{aligned}(8 y+7 z)(8 y-7 z) &=(8 y)^{2}-(7 z)^{2} \\ &=64 y^{2}-49 z^{2} \end{aligned} \nonumber \]

You should practice this pattern until you can go straight from the problem statement to the answer without writing down any intermediate work, as in \((8 y+7 z)(8 y-7 z)=64 y^{2}-49 z^{2}\)

Exercise \(\PageIndex{6}\)

Simplify: \((3a−6b)(3a +6b)\)

\(9 a^{2}-36 b^{2}\)

Example \(\PageIndex{7}\)

Use the difference of squares shortcut to simplify: \(\left(x^{3}-5 y^{2}\right)\left(x^{3}+5 y^{2}\right)\)

• Square the term in the “First” position: \((x^3)^2 = x^6\)
• Square the term in the “Last” position: \((5y^2)^2 = 25 y^4\)

\[\begin{aligned}\left(x^{3}-5 y^{2}\right)\left(x^{3}+5 y^{2}\right) &=\left(x^{3}\right)^{2}-\left(5 y^{2}\right)^{2} \\ &=x^{6}-25 y^{4} \end{aligned} \nonumber \]

You should practice this pattern until you can go straight from the problem statement to the answer without writing down any intermediate work, as in \(\left(x^{3}-5 y^{2}\right)\left(x^{3}+5 y^{2}\right)=x^{6}-25 y^{4}\)

Exercise \(\PageIndex{7}\)

Simplify: \(\left(2 y^{4}+z^{3}\right)\left(2 y^{4}-z^{3}\right)\)

\(4 y^{8}-z^{6}\)

Squaring a Binomial

Before demonstrating the correct procedure for squaring a binomial, we will first share one of the most common mistakes made in algebra.

Warning! This is incorrect!

One of the most common mistakes made in algebra is the assumption that:

\[(a+b)^{2}=a^{2}+b^{2} \nonumber \]

The fact that this is incorrect is easily checked. Substitute \(3\) for \(a\) and \(4\) for \(b\).

\[\begin{aligned}(3+4)^{2} &=3^{2}+4^{2} \\ 7^{2} &=3^{2}+4^{2} \\ 49 &=9+16 \end{aligned} \nonumber \]

Clearly this is incorrect!

So what is the correct answer? First, \((a+b)^{2}=(a+b)(a+b)\). We can now use the FOIL shortcut.

• Multiply the terms in the “Outer” and “Inner” positions and add the results mentally: \(ab + ab =2ab\)
• Multiply the terms in the “Last” positions: \(b^2\)

Hence, the correct answer is \((a+b)^{2}=a^{2}+2 a b+b^{2}\). This leads us to the following shortcut for squaring a binomial.

Squaring a binomial

To square a binomial, such as \((a + b)^2\), perform the following steps:

• Square the “First” term: \(a^2\)
• Multiply the “First” and “Last” terms and double the result: \(2ab\)
• Square the “Last” term: \(b^2\)

\[(a+b)^{2}=a^{2}+2 a b+b^{2} \nonumber \]

Example \(\PageIndex{8}\)

Use the squaring a binomial shortcut to expand: \((x+5)^{2}\)

Follow these steps:

• Square the first term: \(x^2\)
• Multiply the “First” and “Last” terms and double the result: \(2(x)(5) = 10x\)
• Square the “Last” term: \(5^2 = 25\)

\[\begin{aligned}(x+5)^{2} &=x^{2}+2(x)(5)+(5)^{2} \\ &=x^{2}+10 x+25 \end{aligned} \nonumber \]

You should practice this pattern until you can go straight from the problem statement to the answer without writing down any intermediate work, as in \((x+5)^{2}=x^{2}+10 x+25\)

Exercise \(\PageIndex{8}\)

Simplify: \((x+3)^{2}\)

\(x^{2}+6 x+9\)

Students often refuse to learn the “squaring a binomial” shortcut, noting that they can just as easily use the FOIL technique or a simple application of the distributive property to arrive at the same result. Unfortunately, failure to learn the “squaring a binomial” shortcut will severely handicap students, as this pattern is an important component of many procedures in future mathematics courses.

Example \(\PageIndex{9}\)

Use the squaring a binomial shortcut to expand: \((3 x+7 y)^{2}\)

• Square the first term: \((3x)^2 =9x^2\)
• Multiply the “First” and “Last” terms and double the result: \(2(3x)(7y)= 42xy\)
• Square the “Last” term: \((7y)^2 = 49 y^2\)

\[\begin{aligned}(3 x+7 y)^{2} &=(3 x)^{2}+2(3 x)(7 y)+(7 y)^{2} \\ &=9 x^{2}+42 x y+49 y^{2} \end{aligned} \nonumber \]

You should practice this pattern until you can go straight from the problem statement to the answer without writing down any intermediate work, as in \((3 x+7 y)^{2}=9 x^{2}+42 x y+49 y^{2}\)

Exercise \(\PageIndex{9}\)

Simplify: \((2 y+3 z)^{2}\)

\(4 y^{2}+12 y z+9 z^{2}\)

In the next example, when squaring a binomial with a minus sign, we take care of the minus sign by “adding the opposite.”

Example \(\PageIndex{10}\)

Use the squaring a binomial shortcut to expand: \(\left(4 a^{2}-5 b^{3}\right)^{2}\)

Add the opposite: \((4a^2−5b^3)^2 = (4 a^2+(−5b^3))^2\). Now follow these steps:

• Square the first term: \((4a^2)^2 = 16 a^4\)
• Multiply the “First” and “Last” terms and double the result: \(2(4a^2)(−5b^3)= −40a^2b^3\)
• Square the “Last” term: \((−5b^3)^2 = 25 b^6\)

\[\begin{aligned}\left(4 a^{2}-5 b^{3}\right)^{2} &=\left(4 a^{2}+\left(-5 b^{3}\right)\right)^{2} \\ &=\left(4 a^{2}\right)^{2}+2\left(4 a^{2}\right)\left(-5 b^{3}\right)+\left(-5 b^{3}\right)^{2} \\ &=16 a^{4}-40 a^{2} b^{3}+25 b^{6} \end{aligned} \nonumber \]

You should practice this pattern until you can go straight from the problem statement to the answer without writing down any intermediate work, as in \[\left(4 a^{2}-5 b^{3}\right)^{2}=16 a^{4}-40 a^{2} b^{3}+25 b^{6} \nonumber \]

Exercise \(\PageIndex{10}\)

Simplify: \(\left(3 x^{4}-5 z^{2}\right)^{2}\)

\(9 x^{8}-30 x^{4} z^{2}+25 z^{4}\)

Example \(\PageIndex{10}\) shows us that if we are squaring a difference, the middle term will be minus. That is, the only difference between \((a+b)^2\) and \((a−b)^2\) is the sign of the middle term.

The shortcuts for squaring a binomial are:

\[(a-b)^{2}=a^{2}-2 a b+b^{2} \nonumber \]

Example \(\PageIndex{11}\)

Use the squaring a binomial shortcut to expand: \(\left(x^{3}-y^{3}\right)^{2}\)

Use the pattern \((a−b)^2 = a^2 −2ab+ b^2\). Square the “First” term, multiply the “First” and “Last” terms and double the result, then square the “Last” term. Because of the minus sign, the middle term will be minus, but all other terms are plus.

\[\begin{aligned}\left(x^{3}-y^{3}\right)^{2} &=\left(x^{3}\right)^{2}-2\left(x^{3}\right)\left(y^{3}\right)+\left(y^{3}\right)^{2} \\ &=x^{6}-2 x^{3} y^{3}+y^{6} \end{aligned} \nonumber \]

Exercise \(\PageIndex{11}\)

Simplify: \(\left(a^{2}-3 b^{5}\right)^{2}\)

\(a^{4}-6 a^{2} b^{5}+9 b^{10}\)

An Application

In Example \(\PageIndex{7}\), we found the area of the outer square by summing the areas of its parts (see Figure \(\PageIndex{1}\)). Recall that the answer was \(A = x^2 + 6x + 9\).

Now that we have the squaring a binomial shortcut, we can simplify the process of finding the area of the outer square by squaring its side. That is:

\[A=(x+3)^{2} \nonumber \]

Now we can use the squaring the binomial technique to expand.

\[\begin{array}{l}{=x^{2}+2(x)(3)+(3)^{2}} \\ {=x^{2}+6 x+9}\end{array} \nonumber \]

Note that this is the same as the answer found by summing the four parts of the square in Example \(\PageIndex{7}\).

• lol Badge Feed
• win Badge Feed
• trending Badge Feed

Browse links

• © 2024 BuzzFeed, Inc
• Consent Preferences
• Accessibility Statement

Beauty + Personal Care

Sports + Fitness

• Trending badge Trending

We hope you love our recommendations! Some may have been sent as samples, but all were independently selected by our editors. Just FYI, BuzzFeed and its publishing partners may collect a share of sales and/or other compensation from the links on this page.

30 Products To Help Solve The Common (Yet Kinda Embarrassing) Problems You're Dealing With

Gonna let you in on a little secret here: everyone deals with a handful of these problems at some point or another.

BuzzFeed Staff

1. A set of  cold sore healing patches  that are SUPER discreet and help to reduce the pain and blistering that can come with those pesky guys while aiming to prevent post-sore scabbing in the process.  

Promising review:  "I wish I had found these sooner!! These cold sores were probably the worst I've had and wouldn't clear up or stop itching/hurting. I googled cold sore remedies, and these happened to pop up. After reading the reviews, I immediately ordered them. They came right on time, and I put them on before bed last night.  It's been less than 36 hours, and these cold sores are already healing beautifully. I plan to order another pack or three, so I can keep one at home, one in my purse, and one in my locker at work so if I ever feel the warning tingle/itching of a new breakout, I can slap one of these bad boys on and get rid of it quickly! Highly recommend for my fellow cold sore sufferers." — Jessica Hill

Get a pack of 15 from Amazon for $13.98+  (also available in a two-pack).

2. A patio crack weeder tool if your unkempt driveway/patio is something you're constantly finding yourself apologizing for when you have guests visiting. This thing makes it easy to pull those little suckers. Now, you'll be able to accept compliments on how clean and polished it looks instead!

Promising review: " I've been searching for something to remove the weeds for a while and came across this amazing tool. Since I refuse to use chemicals in my yard, I've been left with scraped knuckles every time I attempt to remove weeds. The weeds have grown so tightly in the concrete cracks that I pretty much gave up; even weed-whacking it didn't help much. Yes, you do have to use a little bit of effort, but the end result was so worth it!" — Shelley Arakaki

Get it from Amazon for $19.94 .

3. Schick Silk touch-up tools  perfect for painless, precise eyebrow shaping, cleaning up peach fuzz hairs on your face, and even clearing away dead skin. These little guys go a long way.

Promising review: "I suppose it's my hearty German peasant ancestry, but I've always been a hairy girl. Plucking the more egregious of the thick black hairs is required at least two to three times a week. I'd been eying these razors for a while and finally took the plunge. I could not believe how easy and quick it was. After a couple of swipes down my cheek, I noticed that it was done. I thought it was going to take a lot more skill and time. So much easier than tweezers and depilatories!! Wow." — Tara D.

Get a pack of three from Amazon for $5.94 .

4. A set of  antimicrobial toothbrushes  featuring "floss" bristles that are designed to reach between your teeth (bye bye little food bits hiding in there) and are formulated with  nano-silver , which may help kill off microbes left on the bristles. Your other toothbrushes simply cannot relate!!!

Mouthwatchers  is a small business established by Ronald Plotka, DDS. It specializes in antimicrobial toothbrushes designed for deeper cleans.

Here's what BuzzFeed Shopping writer  Emma Lord  has to say: "I love it just after the first few days of use! I use an electric toothbrush usually, but I feel like I'm getting a much more satisfying clean from these?? Especially because I tend to get yellow stains between my teeth no matter *how* much I floss, and these bristles seem to actually target that a lot more effectively." 

Promising review: "I'm amazed at how well this toothbrush cleans my teeth — it definitely gets between the teeth and also, more importantly for me, gets in the small, deep crevices in my molars where I always have food stuck, and regular toothbrushes couldn't get stuff out. I brush more often (after meals/snacks) because of how effective it is. As stated, definitely go easy around the gums. The bristles feel soft but will cause your gums to bleed if you use regular pressure. Nice and easy does the trick, SO WELL!" — Jason A.

Get a pair from Amazon for $9.90 .

5. A  mold and mildew spray  because let's be real, it's not exactly the most sightly thing to see on your shower walls. 

This can also be used on mold and mildew stains outside of your home!

Promising review: "We've been struggling with mold/mildew stains in our shower and front load washer for quite some time. Nothing bought at the grocery store or hardware store would work. We found this product and used it as directed, and wow, what a difference! This is the only product that has helped remove those stains. Highly recommended!" — David B. Neely

Get a gallon from Amazon for $29.99  (available in smaller and larger sizes and multi-packs).

6. A set of  acne patches  you can apply over a popped whitehead. Simply put the patch over a zit, let it sit overnight or throughout the day, peel it off, and watch it take all the pore-clogging gunk with it. 

I suffer from hormonal acne — it's just something that I have come to terms with and will have to deal with for many more years to come, and while it's not fun, these acne patches make it sooo much easier. When I have a pimple about to come to a head, I pop one of these babies on it before bed and then peel it off along with all the gunk it pulls out. It definitely helps speed up the process, and they're gentle on my sensitive skin!

Promising review: "These patches are the only reliable way to shrink an existing pimple. I always get pimples that swell up but won't come to a head. I've tried all the lotions, creams, salves, hot compresses, etc. Nothing worked on existing pimples. But these patches take the swelling right down. For really bad ones, it sometimes takes a couple of days of wearing the patches, but it will go away (much faster than the one to two weeks it always takes if I just do nothing). Plus, the patch keeps you from touching or picking at it.” — snowmentality

Get 72 stickers from Amazon for $21.99  (also available in a pack of 36 ).

Read our  Hero Cosmetics Mighty Patch review !

7. A  butt acne-clearing lotion  because, yes, acne on the derriere *is* a thing, and if you're reading this thinking you were alone in this struggle, we're here to remind you, you're not. Enter this product, made with pure plant extracts like Australian tea oil, to help target the root of this annoyance on your booty and help kick it in the ~behind~.

Promising review: "I've battled painful acne on my rear end for years, and no dermatologist, cream, scrub, antibiotics, or ointment has ever been able to keep it under control. I bought this cream on a whim based solely on the reviews, and I'm so glad I did! After just one week of treatment, the acne was gone! No more painful days sitting at my desk or nights wondering if sitting on the couch too long was going to make my butt sweaty and cause another breakout. It's been almost two months, and just following the recommendations on the bottle, the acne hasn't returned. The scars from previous breakouts are even starting to fade. This cream is amazing, and I wouldn't hesitate to recommend it. You won't regret this purchase." — deirdreD

Get it from Amazon for $24.99 . 

8. Bio-Oil , a skincare oil for aiding in reducing the appearance of scars left behind by acne, pregnancy, injuries, or surgeries thanks to a powerful (but gentle) combo of vitamin A oil, vitamin E oil, sunflower oil, lavender oil, and chamomile oil.

Promising reviews: "I love everything about it, especially applying it at night after a relaxing bath, right before going to bed. It smells wonderful, and my skin feels like baby skin." — Derek Schmiedl

Get it from Amazon for $11.12+ (available in two sizes).

9. An  oven cleaning spray  so next time you open the oven door and pop in dinner, you're not tempted to puke all over it because of the yucky buildup you've let your oven accumulate.

Promising review: "I am amazed at this stuff. I've lived in my house for three years, and I have never cleaned my oven. I doubt the previous owners ever did, either. It was a blackened, grody mess. I sprayed a heavy coat of this stuff all over the inside and let it sit for a while. Then I got to scraping and wiping. I couldn't believe how much rock-hard soot came off. I gave some stubborn spots a second coat and eventually had the entire thing looking new. It's a miracle spray." — GinHum

Get it from Amazon for $8.98 .

10. A pack of  extra strength Gas-X chewable tablets  to keep on hand in case you're seeking relief from bloating and gas — both of which we all deal with at some point, but if it happens at an inopportune time, well, you might want to see if these work for you. 

Promising review: "Sometimes you eat something that is too rich on an empty stomach and wham — the pain, the bloating, the weird weird noises start. And then if you have this, within minutes it helps relieve the gas, bloating, and discomfort . Taking this is nothing to be ashamed about; it happens to everyone whether they like to admit it or not." — MusicLover

Get a pack of 72 chewable tablets from Amazon for $14.20 .

11. A  pumice toilet bowl ring remover  so you can easily scratch away at those yucky stains without leaving behind scratch marks in the bowl. 

Promising review: "I have a 19-year-old primary bathroom toilet that had accumulated some nasty stains over time, and regular toilet brushes and cleaning products just would not remove them. I decided to try this pumice stone, and it worked like a charm! Given the nature and severity of the stains, some elbow grease was required. But 10 minutes later, I have a new-looking bowl, and I see no signs of scratching. " — Happy Retiree

Get it from Amazon for $13.99 .

12. A  tonsil stone removal kit  to assist in seamlessly saying goodbye to those little annoyances hiding out in the back of your throat. It's gonna be so gross seeing them come out, but oh so satisfying!

If you suspect you have  tonsil stones  (also called tonsilloliths), talk to your dentist or doctor! They can perform a physical exam or imaging scan and deliver a diagnosis.

These also come with an LED light to get right to the source of the problem.

Promising review: "I'm in my early 30s and just started getting tonsil stones. Until a few months ago, I never even knew what these things were! Anyway, I've been struggling with cotton buds to fully remove the stones, but I couldn't get rid of them, and they would just come back within the week. I received this and OMFG...best investment ever. No struggle holding my phone as a flashlight while awkwardly poking myself in front of my badly lit bathroom mirror. I sat comfortably at my vanity, used one hand, and removed the whole stone in less than a minute. Why did I not know this was a thing? Why have I been struggling? Get it! Stop struggling, suffering, and awkwardly dealing with this ridiculous condition...trust me." — Wren

Get it from Amazon for $9.98+ (available in two colors and a multipack).

13. A  callus-removal gel  so you can experience the baby-soft feet you not only want but truly deserve. Soak your feet for two to three minutes in hot water, dry them, and apply a generous layer of the gel to your calloused feet. Then let it sit for three minutes, wipe it off, use a foot scrubber of your choice, and bam — dead skin be gone.

If you're looking for recs for a good foot file, we adore this one that you can get from Amazon for  $9.99 !

Promising review:  "Best foot callus remover I have ever used! I read a lot of the reviews before purchasing this product. Most callus removers I have purchased in the past were not very effective. So, I was encouraged by the reviews. I saw that a lot of reviewers mentioned being very careful not to leave it on longer than three or four minutes. My feet were the softest they had ever been. Love love love." — Cheri whisker

Get it from Amazon for $14.99 .

14. Compound W One Step Pads  for applying to plantar warts — they look like bandages, but they're working hard to remove those stubborn little guys.

Promising review: "This stuff works! I'd never had a wart in my life! At first, I thought it was a small callus, but as months went by, it was getting larger. I started to google and realized I had a plantar wart on my thumb! So I got the Freeze Off and thought, 'This has to work!' Nope! I tried the Freeze Off three times, and nothing! I then realized the same thing was happening on my other thumb: a small callus. I knew that the wart had spread! Now I was desperate to get rid of them and knew I had waited too long! Bought the invisible strips, and it removed my small wart in four days and my big wart in eight!! I couldn't believe it. I left strips on for two days, then pulled back the dead skin with a cuticle clipper and reapplied! My bigger wart was a little tougher to remove, and I had irritated my skin trying to cut it out, so I left it alone for a few days before reapplying a strip, and by the second 48-hour treatment, it was gone! I thought my skin would be damaged, but it looks like nothing was ever there!" — Audrey N.

Get 14 pads from Amazon for $7.29+  (available in two styles).

15. O'Keefe's Working Hands Cream  that will make dry, cracked hands feel as if they were just treated to a five-star manicure (without having to change out of your pajamas and leave the house).

Promising review: "I have suffered from splitting and cracking fingers every fall and winter for years. I tried Eucerin, Lubriderm, and Gold Bond creams, but none seemed to relieve the splitting from reoccurring. I tried O'Keeffe's Working Hand Cream, and within two and a half days, the splitting and cracking were no longer a factor. Since using the cream, I have not suffered any more cracking or splitting. I am on a busy schedule and only use it at night when I go to bed. It says it's non-greasy, but you can definitely feel a slick texture on your hands once it is applied. That's why I use it at night before bed when I don't have to open door knobs, touch smartphones, or shake hands. It has the texture of cake icing, goes on smooth, and works into the skin quickly. It has no smell I can detect. I am so glad I found this cream; it has ended years of splitting and cracked fingers/hands. " — T.H.

Get it from Amazon for $9.99 .

Our  O'Keeffe's Working Hands Cream deep dive goes into more details, so be sure to check it out.

16. A  hairbrush cleaning tool  because in the long run, it'll be a heck of a lot cheaper to get rid of the combo of hair, dust, and fluff residing between the bristles than it will be to keep buying new hairbrushes. 

Promising review:  " I cannot believe I have lived my whole life and never had such a unique tool to clean long, thick hair out of my brushes! It is inexpensive yet well-made. I will mostly buy a few more as gifts for my long-hair friends. Highly recommend this product." — Piper

Get it from Amazon for $11.95 .

17. A bottle of  nail and cuticle care oil  to help make your nails look fresh and healthy with consistent use over time — just apply a coat and let it wow you!

Promising review: "After my acrylics came off during quarantine, I wanted to make my natural nails stronger as they had had acrylics on them constantly for the better part of two years. I searched around Amazon and gave this product a try. I'm glad I did. I started using it twice a day, once in the morning and once toward the end of my workday. I'm down to once every few days now and my nails are much stronger after the past two months. I'll continue to use it until I can get back to the salon." — Alice B.

Get it from Amazon for $9.90+  (available in three sizes).

18. Cleaning tablets  that'll make you realize the important task of sanitizing your retainer, dentures, night guard, or any other dental appliances you use can be quick and easy. Simply drop a tablet and your dental appliance into warm water and let it soak! 

Promising review: "I really loved this product. I am currently waiting for a new Invisalign set. My old Invisalign needed to be cleaned. I read the reviews and decided to purchase. OMG, it worked! They had a fresh taste and were clean. I wish I had found this product sooner. I did let them soak overnight only because I had been wearing them for the last four months. Nothing happened to Invisalign; there was no weakness or anything. Just very clean and fresh. If I could have given the product 10 stars, I would have. " — Lisa R.

Get 120 tablets from Amazon for $17.69 .

19. A twice-daily  antiperspirant hand lotion  made with eucalyptus oil and absorbing powders to help provide relief to sweat-prone hands. 

Read more about the use of antiperspirants to manage symptoms of hyperhidrosis at  Cleveland Clinic .  

Promising review: "I used this product on my 10-year-old son. He sweats A LOT on his hands. He would tell me that he was embarrassed at school and he had problems making friends. My son told me he had never shaken a hand outside of mine ever before in his life...it broke me. As a father, I knew I had to fix this. I set an appointment with his doctor and got nowhere. The doctor said it's normal and should go away in the coming years. I asked about surgery, and they said it would cost around $10,000, so I started saving. A couple of weeks went by, and I came across this product. I asked my son if he was OK with trying it, and he desperately said yes. We put it on, and his hands are completely dry now. When it worked, he started practicing shaking hands and high-fives with his brother. It's been two weeks now, and it is working. AMAZING." — Hector Lorenzo

Get it from Amazon for $19.95+  (also available in packs of two and three).

20. A  scalp shampoo brush  that'll not only aid in giving you a deeper clean when shampooing your hair, but will also feel so relaxing and soothing on your scalp.

Promising review: "I love everything about this product! I have had a dry scalp since I was a kid, and I remember my grandmother using something similar to scrub my scalp as a kid. This product is much softer yet gets the job done! It feels like a mini massage! My scalp and hair feel so much cleaner now! It's easy to hold and clean after each use!" — Leah Heimbach

Get it from Amazon for $6.98+ (available in three colors).

21. A  KP body scrub  for buffing away red bumps. Use it one to two times a week for smoother skin — it's like a microdermabrasion treatment at a fraction of the cost and without leaving the house.

Promising review:  "Amazing! I am so happy to say this product is a game-changer! I have always been so embarrassed by the extremely red and bumpy skin on my arms above my elbow. I've tried tons of products with zero sign of improvement. I always moisturize daily, and nothing has ever helped. I have used this product two times, and the skin on my arms is almost all the same color, and the bumps are gone! I could cry. I am so grateful for this product. It doesn't have any kind of smell, which is perfect cause I can pair it with any moisturizer I like." — Lynn

Get it from Amazon for $11.97+  (available in four sizes and a two-pack).

22. A  Squatty Potty  that'll help make squatting while using the restroom more seamless and comfortable. It's actually better for your body to squat than sit, just FYI.

Read more about constipation relief at home, including using a squatting position, at Cleveland Clinic .

If you want more Squatty Potty content before making the best purchase of your life, check out our Squatty Potty review .

Promising review: "I'll do you all the courtesy of NOT adding a photo or video (You're welcome). This works. Whoever invented the toilet had their heart in the right place, but not their knees. This device mimics proper positioning, and you should get one. That is all. Thank you for coming to my TedTalk." — P.W.

Get it from Amazon for $24.99  (get the acrylic version for $79.99  or the teak wood version for $55.99 ). 

23. A  FlexiSnake  for unclogging your hair-filled drain. Simply ~snake~ this tool down there, let it grab the hair, pull it back up, and then decide whether you should marvel at its abilities or gag.

This pack contains a reusable handle and five single-use heads that you just remove and dispose of after handling your clogged pipes.

Promising review: "Wow. Best thing ever. Seriously. I have had tweezers and sticks and plumbers and chemicals trying to get my master sink to drain. The plumber even said I needed an entirely new faucet to get the drain plug part because they don't sell those separately. Well, I have two sinks, a tub, and a shower that all match, so that was not a valid solution. Doubt I can find the same model. So I bought this thing, stuffed it down, and pulled up hair and black muck. Did it about eight times quickly, ran the water, and went right down the drain. Seriously. This is the best tool ever and the best $20 I have ever spent. Everyone with a sink needs this tool. Seriously." — juliejules

Get a five-pack from Amazon for $19.99 .

24. A  portable carpet and upholstery cleaner  that boasts strong spray and suction so cleaning stubborn stains will feel effortless. Messes left behind by pets shouldn't mean permanently ruined carpets, furniture, or car interiors.

Promising review : "Went ahead and purchased after reading the glowing reviews, crossed my fingers that this product was as great as everyone claimed. Sure enough, it's A MIRACLE! I had tried so many upholstery cleaners, and they just made the stains more prominent, but this adorable little robot cured my couch of its stains. I could have spent more time and diligence cleaning and probably gotten the couch even more sparkly, but I am so satisfied with these results that I don't even care. Go ahead and purchase this bad boy." — Hannah Arst

Get it from Amazon for  $98.59 .

25. An  ingrown hair oil  whose combo of jojoba, grapeseed, and tea tree oils may help reduce the appearance and soften the skin around post-shaving and waxing bumps, ingrown hairs, and redness. 

Bushbalm is an Ottawa-based small skincare brand creating products for our most sensitive areas.

Promising review: "I've bought this product numerous times, and it never fails. I have no more ingrowns and it also helps so much with irritation after shaving!" — Pris

Get it from  Amazon  and  Bushbalm  for $26.

26. An  ultra-hydrating lip balm  rich in antioxidants, vitamin E, and green tea that your dry-as-heck lips are gonna be sure to savor. 

Promising reviews:  "This is truly a miracle product that provides intense moisture every time that I wear it." — Elizabeth W

"My lips were fried from the Florida sun, and I tried many different brands. Finally found one that works. Try it, you'll be glad you did." — Grammy

Get it from Amazon for $10  (available in six scents).

27. A set of  Kegel exercise weights  for strengthening your pelvic floor muscles a little bit with each exercise (they recommend doing it for 15 minutes a day). Some benefits reviewers love from these are a decrease in incontinence and an increase in more pleasurable sex. 

Read more about kegel exercises at  Cleveland Clinic .

Intimate Rose  is a small biz! 

Promising review: "Since starting, my bladder control has significantly improved. I am now able to sneeze or cough without peeing myself. Yes, that's right. I am able to hold my pee longer, which means I can actually make it to the bathroom without dribbling on myself. The best part is that just a few short weeks into the program you will have results you can feel. I think every woman who has ever had kids should try this out. The overall quality of my life has improved. Ditch your panty liners, stop the embarrassing dribbles, and no more mad dashes to the restroom because of a weak bladder. Even my sex life has improved; I have control of those pelvic muscles now. Just remember to wash the weights before and after each use with an antibacterial spray, and allow time to air dry before putting them away. I say air dry because if you wipe them dry with a cloth you run the risk of giving yourself a bladder infection or urinary tract infection, and those are no laughing matter. Easy to use, easy to clean, stores away quickly." — Lady Tauber

Get a set of six weights from Amazon for $49.99  (also available in a two-pack option).

28. A  stainless-steel odor-absorbing soap bar  because garlic, onion, and fish may taste delicious in your meal, but their smell is pretty yucky, ESPECIALLY when it lingers on your hands hours after cooking. 

Promising review:  "Works wonders. I was very impressed. Tried using it after cutting meats, fish, and onions, and it really works well. No smelly hands at all. If you're in the kitchen a lot, get yourself one. You won't regret it." — Sweety mum

Get it from Amazon for $8.59 . 

29. Sweat-absorbing bra liners  for those who get as sweaty during their morning commute as they would have if they went to the gym before work. We get the struggle and we're here to help.

Promising review: "This is one of those things that I wish I'd found years earlier. I've suffered from mortifying stress-induced under-boob sweat for most of my adult life. Also, I'm a lifelong Seattle girl who gets upset when it's warmer than 65° outside. So when I stumbled upon this product, I was curious enough to buy a small pack. And yes, I've come back for MORE! For real, I won't put on a bra without one of these liners now. It absorbs all the moisture from heat and stress. And because it's a really soft bamboo/cotton mix, my skin is finally not feeling tortured under there! To the makers of this ingenious life-changing product: thank you, thank you, thank you! Sincerely, all the grateful ta-tas you've helped to care for" — Niko

Get a three-pack from Amazon for $14.99+ (available in women's sizes M–XXL and several color combos). 

30. A  liquid drain clog dissolver  to help save the day from showers, sinks, and toilets clogged from hair, toilet paper, soap scum, or anything else. It's a lot better than having to explain to your house guests that the toilet may or may not flush before they use it.

Promising review:  "I tried this product as a plumber told me it would not harm your pipes. My toilet was clogged, and I poured it in and let it sit overnight, and voilà; today, it was cleared. I have used many products over the years, and this one guarantees that it works, and it really did." — Jill Goodman

Get a pack of two from Amazon for $23.68 .

The reviews for this post have been edited for length and clarity.

Share This Article