basics of transformations answer key homework 1

Child Login

• Kindergarten
• Number charts
• Skip Counting
• Place Value
• Number Lines
• Subtraction
• Multiplication
• Word Problems
• Comparing Numbers
• Ordering Numbers
• Odd and Even
• Prime and Composite
• Roman Numerals
• Ordinal Numbers
• In and Out Boxes
• Number System Conversions
• More Number Sense Worksheets
• Size Comparison
• Measuring Length
• Metric Unit Conversion
• Customary Unit Conversion
• Temperature
• More Measurement Worksheets
• Writing Checks
• Profit and Loss
• Simple Interest
• Compound Interest
• Tally Marks
• Mean, Median, Mode, Range
• Mean Absolute Deviation
• Stem-and-leaf Plot
• Box-and-whisker Plot
• Permutation and Combination
• Probability
• Venn Diagram
• More Statistics Worksheets
• Shapes - 2D
• Shapes - 3D
• Lines, Rays and Line Segments
• Points, Lines and Planes
• Transformation
• Quadrilateral
• Ordered Pairs
• Midpoint Formula
• Distance Formula
• Parallel, Perpendicular and Intersecting Lines
• Scale Factor
• Surface Area
• Pythagorean Theorem
• More Geometry Worksheets
• Converting between Fractions and Decimals
• Significant Figures
• Convert between Fractions, Decimals, and Percents
• Proportions
• Direct and Inverse Variation
• Order of Operations
• Squaring Numbers
• Square Roots
• Scientific Notations
• Speed, Distance, and Time
• Absolute Value
• More Pre-Algebra Worksheets
• Translating Algebraic Phrases
• Evaluating Algebraic Expressions
• Simplifying Algebraic Expressions
• Algebraic Identities
• Quadratic Equations
• Systems of Equations
• Polynomials
• Inequalities
• Sequence and Series
• Complex Numbers
• More Algebra Worksheets
• Trigonometry
• Math Workbooks
• English Language Arts
• Summer Review Packets
• Social Studies
• Holidays and Events
• Worksheets >
• Geometry >

Transformation Worksheets: Translation, Reflection and Rotation

Exercise this myriad collection of printable transformation worksheets to explore how a point or a two-dimensional figure changes when it is moved along a distance, turned around a point, or mirrored across a line. Encompassing basic transformation practice on slides, flips, and turns, and advanced topics like translation, rotation, reflection, and dilation of figures on coordinate grids, these pdf worksheets on transformation of shapes help students of grade 1 through high school sail smoothly through the concept of rigid motion and resizing. Access some of these worksheets for free!

Printing Help - Please do not print transformation worksheets directly from the browser. Kindly download them and print.

» Slide, Flip and Turn

» Rotation

» Translation

» Reflection

» Dilation with Center at Origin

» Dilation with Center not at Origin

Identify the Transformation

In these worksheets identify the image which best describes the transformation (translation, reflection or rotation) of the given figure. Ideal for grade 5 and grade 6 children.

• Download the set

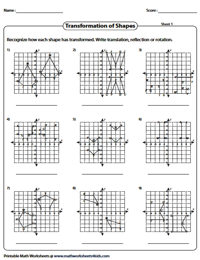
Write the Type of Transformation

Each grid has the figure and the image obtained after transformation. Write, in each case the type of transformation undergone. Recommended for 6th grade and 7th grade students.

Transformation of Points: Multiple Choices

Rotate, reflect and translate each point following the given rules. Grade 7 students should choose the correct image of the transformed point.

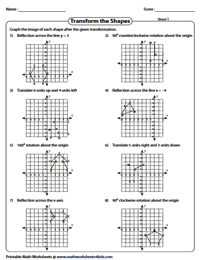
Multiple Choices: Transformation

The coordinates of a point are given. Perform the required transformation and check mark the correct choice.

Transformation of Shapes

Translate, reflect or rotate the shapes and draw the transformed image on the grid. Each printable worksheet has eight practice problems.

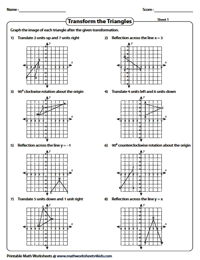
Transformation of Triangles

Draw the transformed image of each triangle. The type of transformation to be performed is described above each question.

Transformation of Quadrilaterals

Let the high school students translate each quadrilateral and graph the image on the grid. Label the quadrilateral after transformation.

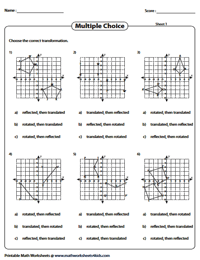
Transformation: Any Two of Three

Two types of transformation have been performed to each figure. Middle school children should choose the correct transformations undergone.

Write the Rules

Identify the transformation undergone by the figure and write a rule to describe each of them.

Writing Coordinates: With Graph

Perform the required transformation for each figure and graph it. Also write the coordinates of the image obtained. Suitable for 8th graders.

Writing New Coordinates

The coordinates of the figure are given. Write down the coordinates of the vertices of the image after transformation.

Add-On Practice Worksheets

Become a Member

Membership Information

Privacy Policy

What's New?

Printing Help

Testimonial

Copyright © 2024 - Math Worksheets 4 Kids

This is a members-only feature!

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.7E: Exercises

• Last updated
• Save as PDF
• Page ID 120121

• Roy Simpson
• Cosumnes River College

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Suppose \((2,-3)\) is on the graph of \(y = f(x)\). In Exercises 1 - 8, use Theorem 1.7.7 to find a point on the graph of the given transformed function.

• \(y = f(x)+3\)
• \(y = f(x+3)\)
• \(y = f(x)-1\)
• \(y = f(x-1)\)
• \(y = 3f(x)\)
• \(y = f(3x)\)
• \(y = -f(x)\)
• \(y = f(-x)\)
• \(y = f(x-3)+1\)
• \(y = 2f(x+1)\)
• \(y = 10 - f(x)\)
• \(y = 3f(2x) - 1\)
• \(y = \frac{1}{2} f(4-x)\)
• \(y = 5f(2x+1) + 3\)
• \(y = 2f(1-x) -1\)
• \(y =f\left(\dfrac{7-2x}{4}\right)\)
• \(y = \dfrac{f(3x) - 1}{2}\)
• \(y = \dfrac{4-f(3x-1)}{7}\)

The complete graph of \(y = f(x)\) is given below. In Exercises 19 - 27, use it and Theorem 1.7.7 to graph the given transformed function.

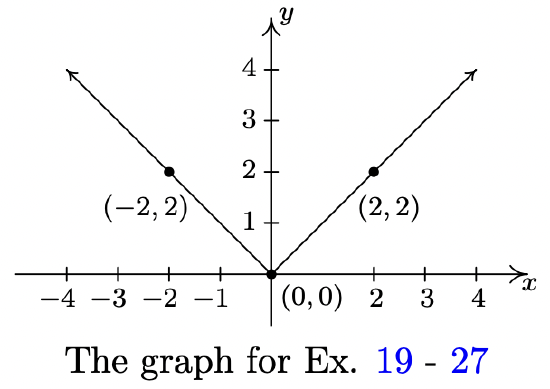
• \(y = f(x) + 1\)
• \(y = f(x) - 2\)
• \(y = f(x+1)\)
• \(y = f(x - 2)\)
• \(y = 2f(x)\)
• \(y = f(2x)\)
• \(y = 2 - f(x)\)
• \(y = f(2-x)\)
• \(y = 2-f(2-x)\)
• Some of the answers to Exercises 19 - 27 above should be the same. Which ones match up? What properties of the graph of \(y=f(x)\) contribute to the duplication?

The complete graph of \(y = f(x)\) is given below. In Exercises 29 - 37, use it and Theorem 1.7.7 to graph the given transformed function.

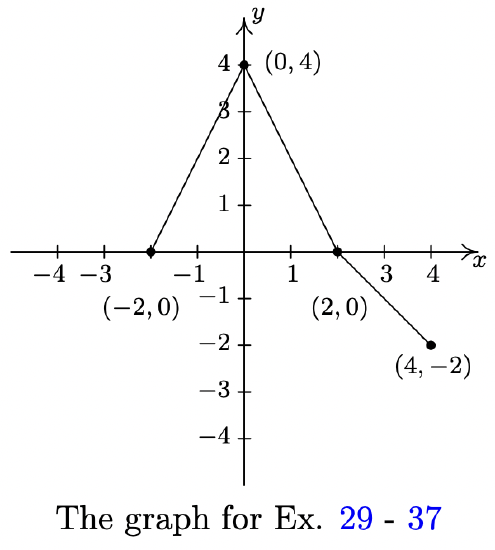
• \(y = f(x) - 1\)
• \(y = f(x + 1)\)
• \(y = \frac{1}{2} f(x)\)
• \(y = - f(x)\)
• \(y = f(x+1) - 1\)
• \(y = 1 - f(x)\)
• \(y = \frac{1}{2}f(x+1)-1\)

The complete graph of \(y = f(x)\) is given below. In Exercises 38 - 49, use it and Theorem 1.7.7 to graph the given transformed function.

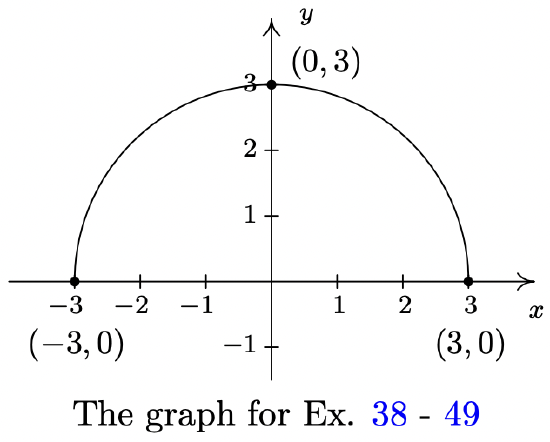
• \(g(x) = f(x) + 3\)
• \(h(x) = f(x) - \frac{1}{2}\)
• \(j(x) = f\left(x - \frac{2}{3}\right)\)
• \(a(x) = f(x + 4)\)
• \(b(x) = f(x + 1) - 1\)
• \(c(x) = \frac{3}{5}f(x)\)
• \(d(x) = -2f(x)\)
• \(k(x) = f\left(\frac{2}{3}x\right)\)
• \(m(x) = -\frac{1}{4}f(3x)\)
• \(n(x) = 4f(x - 3) - 6\)
• \(p(x) = 4 + f(1 - 2x)\)
• \(q(x) = -\frac{1}{2}f\left(\frac{x + 4}{2}\right) - 3\)

The complete graph of \(y = S(x)\) is given below.

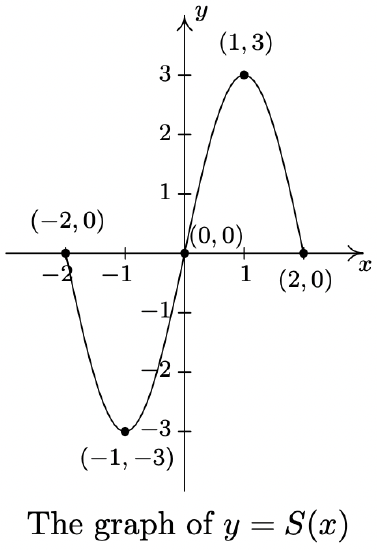
The purpose of Exercises 50 - 53 is to graph \(y = \frac{1}{2}S(-x+1) + 1\) by graphing each transformation, one step at a time.

• \(\ y=S_{1}(x)=S(x+1)\)
• \(\ y=S_{2}(x)=S_{1}(-x)=S(-x+1)\)
• \(\ y=S_{3}(x)=\frac{1}{2} S_{2}(x)=\frac{1}{2} S(-x+1)\)
• \(\ y=S_{4}(x)=S_{3}(x)+1=\frac{1}{2} S(-x+1)+1\)

Let \(f(x) = \sqrt{x}\). Find a formula for a function \(g\) whose graph is obtained from \(f\) from the given sequence of transformations.

• (1) shift right 2 units; (2) shift down 3 units
• (1) shift down 3 units; (2) shift right 2 units
• (1) reflect across the \(x\)-axis; (2) shift up 1 unit
• (1) shift up 1 unit; (2) reflect across the \(x\)-axis
• (1) shift left 1 unit; (2) reflect across the \(y\)-axis; (3) shift up 2 units
• (1) reflect across the \(y\)-axis; (2) shift left 1 unit; (3) shift up 2 units
• (1) shift left 3 units; (2) vertical stretch by a factor of 2; (3) shift down 4 units
• (1) shift left 3 units; (2) shift down 4 units; (3) vertical stretch by a factor of 2
• (1) shift right 3 units; (2) horizontal shrink by a factor of 2; (3) shift up 1 unit
• (1) horizontal shrink by a factor of 2; (2) shift right 3 units; (3) shift up 1 unit

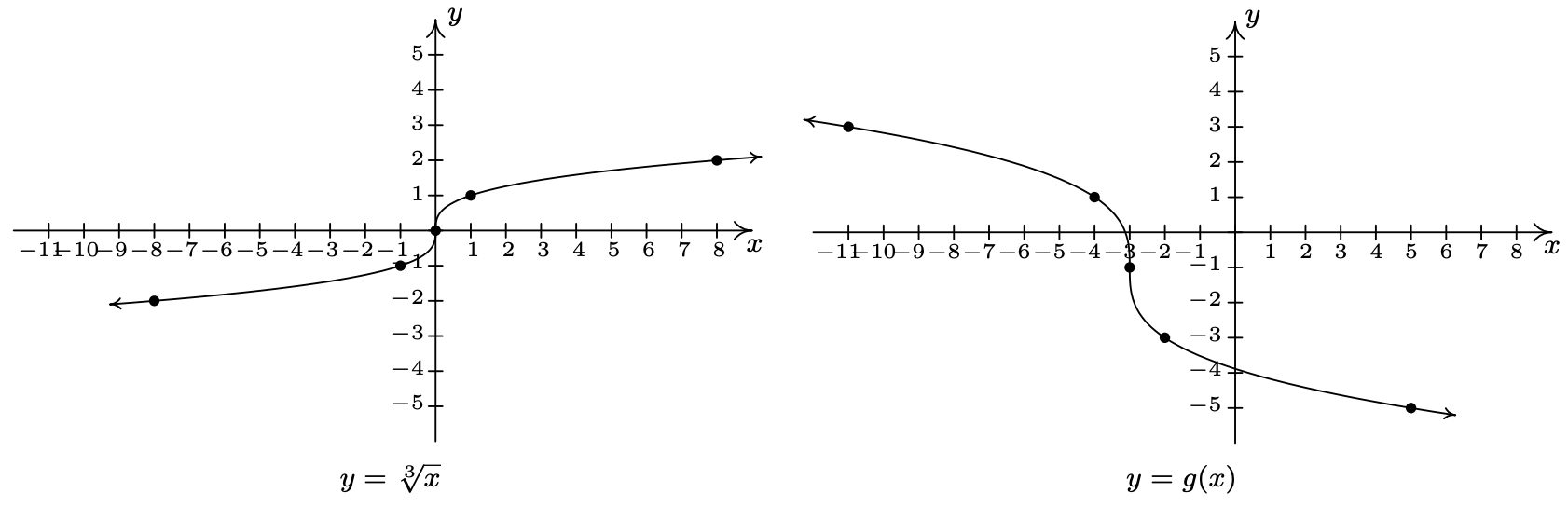
• For many common functions, the properties of Algebra make a horizontal scaling the same as a vertical scaling by (possibly) a different factor. For example, we stated earlier that \(\sqrt{9x} = 3\sqrt{x}\). With the help of your classmates, find the equivalent vertical scaling produced by the horizontal scalings \(y = (2x)^{3}, \, y = |5x|, \, y = \sqrt[3]{27x} \,\) and \(\, y = \left(\frac{1}{2} x\right)^{2}\). What about \(y = (-2x)^{3}, \, y = |-5x|, \, y = \sqrt[3]{-27x}\,\) and \(\, y = \left(-\frac{1}{2} x\right)^{2}\)?
• We mentioned earlier in the section that, in general, the order in which transformations are applied matters, yet in our first example with two transformations the order did not matter. (You could perform the shift to the left followed by the shift down or you could shift down and then left to achieve the same result.) With the help of your classmates, determine the situations in which order does matter and those in which it does not.
• What happens if you reflect an even function across the \(y\)-axis?
• What happens if you reflect an odd function across the \(y\)-axis?
• What happens if you reflect an even function across the \(x\)-axis?
• What happens if you reflect an odd function across the \(x\)-axis?
• How would you describe symmetry about the origin in terms of reflections?
• As we saw in Example 1.7.5, the viewing window on the graphing calculator affects how we see the transformations done to a graph. Using two different calculators, find viewing windows so that \(f(x) = x^{2}\) on the one calculator looks like \(g(x) = 3x^{2}\) on the other.
• \((-1,-3)\)
• \(\left(\frac{2}{3}, -3\right)\)
• \((-2,-3)\)
• \(y = (1,-10)\)
• \(\left(2, -\frac{3}{2}\right)\)
• \(\left(\frac{1}{2}, -12 \right)\)
• \((-1,-7)\)
• \(\left(-\frac{1}{2}, -3\right)\)
• \(\left(\frac{2}{3}, -2 \right)\)

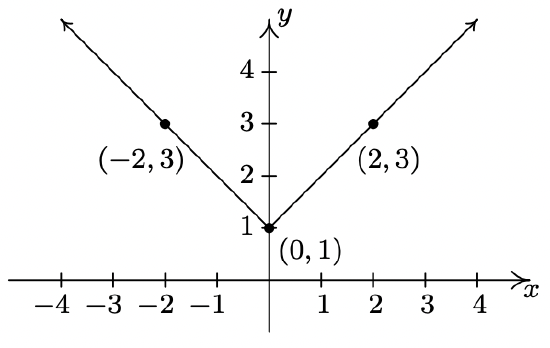
• \(g(x) = \sqrt{x-2} - 3\)
• \(g(x) = -\sqrt{x} + 1\)
• \(g(x) = -(\sqrt{x} + 1) = -\sqrt{x} - 1\)
• \(g(x) = \sqrt{-x+1} + 2\)
• \(g(x) = \sqrt{-(x+1)} + 2 = \sqrt{-x-1} + 2\)
• \(g(x) = 2\sqrt{x+3} - 4\)
• \(g(x) = 2\left(\sqrt{x+3} - 4\right) = 2\sqrt{x+3} - 8\)
• \(g(x) = \sqrt{2x-3} + 1\)
• \(g(x) = \sqrt{2(x-3)} + 1 = \sqrt{2x-6}+1\)
• \(g(x) = -2\sqrt[3]{x + 3} - 1\) or \(g(x) = 2\sqrt[3]{-x - 3} - 1\)

• Skip to main content

Maneuvering the Middle

Student-Centered Math Lessons

• All Products

Transformations Unit 8th Grade TEKS

Description, additional information.

• Reviews (0)

An 11-day Transformations TEKS-Aligned complete unit including: transformations on the coordinate plane (translations, reflections, rotations and dilations) and the effect of dilations and scale factor on the measurements of figures.

Students will practice with both skill-based problems, real-world application questions, and error analysis to support higher level thinking skills.  You can reach your students and teach the standards without all of the prep and stress of creating materials!

Standards:   TEKS: 8.3A, 8.3B, 8.3C, 8.10A, 8.10B, 8.10C, 8.10D;  Looking for CCSS-Aligned Resources?  Grab the Transformations CCSS-Aligned Unit.  Please don’t purchase both as there is overlapping content.

Learning Focus:

• generalize the properties of orientation and congruence of transformations
• use algebraic representations to explain the effect of transformations
• describe the effect of dilations on linear and area measurements

What is included in the 8th grade TEKS Transformations Unit?

1. Unit Overviews

• Streamline planning with unit overviews that include essential questions, big ideas, vertical alignment, vocabulary, and common misconceptions.
• A pacing guide and tips for teaching each topic are included to help you be more efficient in your planning.

2. Student Handouts

• Student-friendly guided notes are scaffolded to support student learning.
• Available as a PDF and the student handouts/homework/study guides have been converted to Google Slides™ for your convenience.

3. Independent Practice

• Daily homework is aligned directly to the student handouts and is versatile for both in class or at home practice.

4. Assessments

• 1-2 quizzes, a unit study guide, and a unit test allow you to easily assess and meet the needs of your students.
• The Unit Test is available as an editable PPT, so that you can modify and adjust questions as needed.

5. Answer Keys

• All answer keys are included.

***Please download a preview to see sample pages and more information.***

How to use this resource:

• Use as a whole group, guided notes setting
• Use in a small group, math workshop setting
• Chunk each student handout to incorporate whole group instruction, small group practice, and independent practice.
• Incorporate our  Transformations Activity Bundle  for hands-on activities as additional and engaging practice opportunities.

Time to Complete:

• Each student handout is designed for a single class period. However, feel free to review the problems and select specific ones to meet your student needs. There are multiple problems to practice the same concepts, so you can adjust as needed.

Is this resource editable?

• The unit test is editable with Microsoft PPT. The remainder of the file is a PDF and not editable.

Looking for more 6th Grade Math Material? Join our All Access Membership Community! You can reach your students without the “I still have to prep for tomorrow” stress, the constant overwhelm of teaching multiple preps, and the hamster wheel demands of creating your own teaching materials.

• Grade Level Curriculum
• Supplemental Digital Components
• Complete and Comprehensive Student Video Library 

Click here to learn more about All Access by Maneuvering the Middle®!

Licensing: This file is a license for ONE teacher and their students. Please purchase the appropriate number of licenses if you plan to use this resource with your team. Thank you!

Customer Service: If you have any questions, please feel free to reach out for assistance .  We aim to provide quality resources to help teachers and students alike, so please reach out if you have any questions or concerns. 

Maneuvering the Middle ® Terms of Use: Products by Maneuvering the Middle®, LLC may be used by the purchaser for their classroom use only. This is a single classroom license only. All rights reserved. Resources may only be posted online in an LMS such as Google Classroom, Canvas, or Schoology. Students should be the only ones able to access the resources.  It is a copyright violation to upload the files to school/district servers or shared Google Drives. See more information on our terms of use here . 

If you are interested in a personalized quote for campus and district licenses, please click here . 

©Maneuvering the Middle® LLC, 2012-present

This file is a license for one teacher and their students. Please purchase the appropriate number of licenses if you plan to use this resource with your team. Thank you!

Customer Service

We strive to provide quality products to help teachers and students alike, so contact us with any questions.

Maneuvering the Middle® Terms of Use

Products by Maneuvering the Middle, LLC may be used by the purchaser for their classroom use only. This is a single classroom license only. All rights reserved. Resources may only be posted online if they are behind a password-protected site.

Campus and district licensing is available please contact us for pricing.

©Maneuvering the Middle LLC, 2012-present

There are no reviews yet.

Only logged in customers who have purchased this product may leave a review.

This resource is often paired with:

Transformations Unit 8th Grade CCSS

Transformations Activity Bundle 8th Grade

Digital Math Activity Bundle 8th Grade