case study class 8 probability

Gurukul of Excellence

Classes for Physics, Chemistry and Mathematics by IITians

Join our Telegram Channel for Free PDF Download

Case Study Questions for Class 8 Maths Chapter 5 Data Handling

• Last modified on: 8 months ago
• Reading Time: 6 Minutes

Table of Contents

Here we are providing Case Study questions for Class 8 Maths Chapter 5 Data Handling.

Case Study Questions

Related posts, cbse class 8 maths chapter 5 data handling, learning outcomes.

• Circle Graph or Pie Chart
• Chance and Probability

Important Keywords

• Data: Numerical observations collected by an observer is called data (raw data).
• Frequency: The number of times an observation occurs in the given data is called the frequency of the observation.
• Frequency Distribution: A way of presenting data that exhibits the values of the variable and corresponding frequencies is called a frequency distribution.
• Range: The difference between the highest and the lowest values of observation is called range. i.e., Range = Highest observation – Lowest observation
• Class-mark: The mid-point of a class-interval is called class-mark.
• Histogram: Grouped data can be presented using the histogram. A histogram is a type of bar diagram, where the class intervals are shown on the horizontal axis and the height of the bars show the frequency of the class interval. Also, there is no gap between the bars as there is no gap between the class intervals.
• Pie-chart or Pie-diagram: A pie-chart is a pictorial representation of the numerical data by non-intersecting adjacent sectors of the circle such that area of each sector is proportional to the magnitude of the data represented by the sector.
• Probability: Probability is the possibility and impossibility of an event (E).

Important Facts

• Data mostly available to us in an unorganized form is called raw data.
• In order to draw meaningful inferences from any data, we need to organise the data systematically.
• Frequency gives the number of times that a particular entry occurs.
• Raw data can be ‘grouped’ and presented systematically through ‘grouped frequency distribution’.
• Grouped data can be presented using histogram. Histogram is a type of bar diagram, where the class intervals are shown on the horizontal axis and the heights of the bars show the frequency of the class interval. Also, there is no gap between the bars as there is no gap between the class intervals.
• Data can also presented using circle graph or pie chart. A circle graph shows the relationship between a whole and its part.

Download CBSE Books

Exam Special Series:

• Sample Question Paper for CBSE Class 10 Science (for 2024)
• Sample Question Paper for CBSE Class 10 Maths (for 2024)
• CBSE Most Repeated Questions for Class 10 Science Board Exams
• CBSE Important Diagram Based Questions Class 10 Physics Board Exams
• CBSE Important Numericals Class 10 Physics Board Exams
• CBSE Practical Based Questions for Class 10 Science Board Exams
• CBSE Important “Differentiate Between” Based Questions Class 10 Social Science
• Sample Question Papers for CBSE Class 12 Physics (for 2024)
• Sample Question Papers for CBSE Class 12 Chemistry (for 2024)
• Sample Question Papers for CBSE Class 12 Maths (for 2024)
• Sample Question Papers for CBSE Class 12 Biology (for 2024)
• CBSE Important Diagrams & Graphs Asked in Board Exams Class 12 Physics
• Master Organic Conversions CBSE Class 12 Chemistry Board Exams
• CBSE Important Numericals Class 12 Physics Board Exams
• CBSE Important Definitions Class 12 Physics Board Exams
• CBSE Important Laws & Principles Class 12 Physics Board Exams
• 10 Years CBSE Class 12 Chemistry Previous Year-Wise Solved Papers (2023-2024)
• 10 Years CBSE Class 12 Physics Previous Year-Wise Solved Papers (2023-2024)
• 10 Years CBSE Class 12 Maths Previous Year-Wise Solved Papers (2023-2024)
• 10 Years CBSE Class 12 Biology Previous Year-Wise Solved Papers (2023-2024)
• ICSE Important Numericals Class 10 Physics BOARD Exams (215 Numericals)
• ICSE Important Figure Based Questions Class 10 Physics BOARD Exams (230 Questions)
• ICSE Mole Concept and Stoichiometry Numericals Class 10 Chemistry (65 Numericals)
• ICSE Reasoning Based Questions Class 10 Chemistry BOARD Exams (150 Qs)
• ICSE Important Functions and Locations Based Questions Class 10 Biology
• ICSE Reasoning Based Questions Class 10 Biology BOARD Exams (100 Qs)

✨ Join our Online JEE Test Series for 499/- Only (Web + App) for 1 Year

✨ Join our Online NEET Test Series for 499/- Only for 1 Year

2 thoughts on “ Case Study Questions for Class 8 Maths Chapter 5 Data Handling ”

Not opening

Please refresh the page.

Leave a Reply Cancel reply

Join our Online Test Series for CBSE, ICSE, JEE, NEET and Other Exams

Editable Study Materials for Your Institute - CBSE, ICSE, State Boards (Maharashtra & Karnataka), JEE, NEET, FOUNDATION, OLYMPIADS, PPTs

Discover more from Gurukul of Excellence

Subscribe now to keep reading and get access to the full archive.

Type your email…

Continue reading

Talk to our experts

1800-120-456-456

• RD Sharma Class 8 Solutions Chapter 26 - Data Handling Probability (Ex 26.1) Exercise 26.1
• RD Sharma Solutions

Data Handling Probability - Free PDF RD Sharma Solutions

Probability is the chance of a particular event occurring expressed in numbers. It determines the likeliness of an event to happen. Students need to start Data Handling Probability from earlier classes if they envision a career in science and mathematics since these are the basic concepts on which science and technology development develops.  

This is an important chapter in the Class 8 curriculum as well as in later classes syllabus will be built on it. Students need to have a conceptual understanding of this chapter to be able to perform well. They also need to practice extensively to develop a deep understanding of the foundation which will be built upon in higher classes.The chapter deals with the pictorial representation of data as pie charts or circle graphs.

Method to Calculate The Probability of Any Event

Divide the number of events by the number of possible outcomes.

Determine a single event with a single outcome. 

Identify the total number of outcomes that can occur. 

Divide the number of events by the number of possible outcomes. 

Determine each event you will calculate. 

Calculate the probability of each event

Information on RD Sharma Class 8 Solutions Chapter 26 - Data Handling Probability (Ex 26.1) Exercise 26.1 - Free PDF

Students should start with NCERT for learning the basic concepts. Every NCERT Solution is provided to make the study simple and interesting on Vedantu.  Students need to practice RD Sharma to build deep-rooted concepts that can help them in their higher classes. Students can get Free PDF download of RD Sharma Class 8 Solutions Chapter 26 - Data Handling Probability Exercise 26.1 solved by Expert Mathematics Teachers on Vedantu.com. 

All Chapter 26 - Data Handling Probability Ex 26.1 Questions with Solutions for RD Sharma Class 8 Maths will to help you to revise the complete Syllabus and Score More marks. Register for online coaching for IIT JEE (Mains & Advanced) and other engineering entrance exams.

FAQs on RD Sharma Class 8 Solutions Chapter 26 - Data Handling Probability (Ex 26.1) Exercise 26.1

1. What is the importance of Data Handling Probability for Class 8 students?

There are some important topics in Mathematics that are the pillars of advanced Science and Maths. Studying and revising those topics are extremely important at the school level for future studies at both school level and college. A good grasp on this subject will help them understand the increased level of complexity of the topics in higher classes. The same is applicable for Data Handling Probability. If they want to understand probability at a deeper level in college then one should start before their school classes. This will help them to develop a stronger foundation and own concepts to take a load of complexity in higher classes and competitive exams.

2. What is the significance of Data Handling Probability?

Data handling Probability is quite significant with both theoretical and experimental models. The most important outcome of the theoretical models is making charts, simple and complex counting procedures, making tree diagrams for other science subjects as well. Experimental models help in preparing a dish like cookies with choco chip toppings. Only Data Handling Probability can help you to understand how many choco chips each cookie will get.  Practical experiments in day-to-day life also depend upon Data Handling Probability. It helps one to make decisions on a matter of daily issues like which brand in cosmetics, battery or whatever, even whether to go to a certain place is risky or not, whether to take the umbrella depending upon the chance of rain. All these practical experiments depend upon Data Handling Probability.

3. How important is probability in school and real-world life?

Data Handling Probability sharpens the skill of reasoning, questioning, and solving real-world problems. We can in no way avoid them while living in a world of probability. To live and function, we need to nurture our probability skills. In the modern world and society, probability plays the role in both public and professional life, medicine, technology. The in-school curriculum also makes graphs, charts, tables, counting, and mapping all developed with the learning of Data Handling Probability. Even to learn other mathematical chapters like fractions etc knowledge of Data Handling Probability helps a lot.

4. How can the students develop a good knowledge in Data Handling Probability?

It is now well established that to function in a society full of probabilities one needs to sharpen their probability skills. Students also have to take this path to be successful in this world of probability. Hence extra effort has to be taken to understand this topic. Students need to first clear their basic concepts from NCERT books which are scientifically designed for the betterment of their knowledge. NCERT textbook for learning and NCERT Exemplar for solving purposes are both much needed. However to further develop sound concepts they need to solve RD Sharma Data Handling Probability. 

Vedantu provides solutions to the chapters with detailed explanations which helps the students a lot. They can even sharpen their knowledge by taking the help of reference books. Good reference books like HC Verma solutions and TS Grewal solutions should be of help to the students. Subject experts in the Vedantu can also help in clearing the rising doubts in the mind of the students at any class level.

5. How to score high in Class 8 Data Handling Probability in exams and discuss some properties of probability?

Data Handling Probability is an easy topic and if studied with the right approach the students can score high in this section. Proper concepts on this topic will also help them to score high in other topics and even subjects of their level. They should remember the following key points when preparing for Data Handling Probability.

The probability of zero means an event cannot occur

The probability of one means an event is certain to occur

Probabilities are always between zero and one

The probability of different outcomes always sums up to 1.

Probability Rules

Determining an event with a single outcome

Identifying the total number of outcomes to occur

Dividing the single outcome by the total number of possible outcomes

Determine the Probability

• New QB365-SLMS
• NEET Materials
• JEE Materials
• Banking first yr Materials
• TNPSC Materials
• DIPLOMA COURSE Materials
• 5th Standard Materials
• 12th Standard Materials
• 11th Standard Materials
• 10th Standard Materials
• 9th Standard Materials
• 8th Standard Materials
• 7th Standard Materials
• 6th Standard Materials
• 12th Standard CBSE Materials
• 11th Standard CBSE Materials
• 10th Standard CBSE Materials
• 9th Standard CBSE Materials
• 8th Standard CBSE Materials
• 7th Standard CBSE Materials
• 6th Standard CBSE Materials
• Tamilnadu Stateboard
• Scholarship Exams
• Scholarships

CBSE 8th Standard CBSE all question papers, important notes , study materials , Previuous Year questions, Syllabus and exam patterns. Free 8th Standard CBSE all books and syllabus online. Practice Online test for free in QB365 Study Material. Important keywords, Case Study Questions and Solutions. Updates about latest education news and Scholorships in one place.

8th Standard CBSE Subjects

8th standard cbse study materials.

Class VI to XII

Tn state board / cbse, 3000+ q&a's per subject, score high marks.

Latest CBSE 8th Standard CBSE Study Material Updates

+91-9148737576

Free counselling, request a demo.

Chance and Probability

CBSE Class 8 Mathematics- Chapter 5- Data Handling- Chance and Probability Notes. The chance of happening of an event is known as probability.

CBSE Class 8 Mathematics Notes

Read More related topics…..

Introduction to Data Handling

• CBSE Syllabus for all class
• Class 8th Study Material
• Previous Year Paper
• NCERT Solutions

LATEST OFFERS & PROMOTIONS

Ask for discount

50,00,000 +

Questions Attempted

Assesments Taken

Hours of Video Content

What our students and parents say about us!

Choose edusaksham, embrace better learning.

• Data Handling-Probability Statistics

NCERT curriculum (for CBSE/ICSE) Class 8 - Data Handling-Probability Statistics

Unlimited worksheets.

Every time you click the New Worksheet button, you will get a brand new printable PDF worksheet on Data Handling-Probability Statistics . You can choose to include answers and step-by-step solutions.

Unlimited Online Practice

Unlimited adaptive online practice on Data Handling-Probability Statistics . Practice that feels like play! Get shields, trophies, certificates and scores. Master Data Handling-Probability Statistics as you play.

Unlimited Online Tests

Take unlimited online tests on Data Handling-Probability Statistics . Get instant scores and step-by-step solutions on submission. Make sure you always get your answers right in Data Handling-Probability Statistics .

Contents: Data Handling-Probability Statistics

Data Handling-Probability Statistics - Introduction to probability.

• Home keyboard_arrow_right

RS Aggarwal Class 8 Solutions Exercise 25A Chapter 25 Probability

Get the Latest Edition of RS Aggarwal Solutions Class 8 Chapter 25 Probability Exercise 25A. Probability RS Aggarwal Class 8 Maths Solutions helps you to revise the complete syllabus and score excellent marks.

RS Aggarwal Solutions Class 8 Chapter 25 Ex 25A

Also, check the solutions of other exercises from below.

• Chapter 25 Probability Exercise 25B

Leave a Comment Cancel Reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

Computational Probability and Statistics

7 case study, 7.1 objectives.

• Use R to simulate a probabilistic model.
• Use basic counting methods.

7.2 Introduction to probability models

In this second block of material we will focus on probability models. We will take two approaches, one is mathematical and the other is computational. In some cases we can use both methods on a problem and in others only the computational approach is feasible. The mathematical approach to probability modeling allows us insight into the problem and the ability to understand the process. Simulation has a much greater ability to generalize but can be time intensive to run and often requires the writing of custom functions.

This case study is extensive and may seem overwhelming, do not worry we will discuss these ideas again in the many lessons we have coming up this block.

7.3 Probability models

Probability models are an important tool for data analysts. They are used to explain variation in outcomes that cannot be explained by other variables. We will use these ideas later in this text to help us make decisions about our statistical models.

Often probability models are used to answer a question of the form “What is the chance that …..?” This means that we typically have an experiment or trial where multiple outcomes are possible and we only have an idea of the frequency of those outcomes. We use this frequency as a measure of the probability of a particular outcome.

For this block we will focus just on probability models. To apply a probability model we will need to

• Select the experiment and its possible outcomes.
• Have probability values for the outcomes which may include parameters that determine the probabilities.
• Understand the assumptions behind the model.

7.4 Case study

There is a famous example of a probability question that we will attack in this case study. The question we want to answer is “In a room of \(n\) people what is the chance that at least two people have the same birthday?”

Exercise : The typical classroom at USAFA has 18 students in it. What do you think the chance that at least two students have the same birthday? 62

7.4.1 Break down the question

The first action we should take is to understand what is being asked.

• What is the experiment or trial?
• What does it mean to have the same birthday?
• What about leap years?
• What about the frequency of births? Are some days less likely than others?

Exercise : Discuss these questions and others that you think are relevant. 63

The best first step is to make a simple model, often these are the only ones that will have a mathematical solution. For our problem this means we answer the above questions.

• We have a room of 18 people and we look at their birthdays. We either have two or more birthdays matching or not; thus there are two outcomes.
• We don’t care about the year, only the day and month. Thus two people born on May 16th are a match.
• We will ignore leap years.
• We will assume that a person has equal probability of being born on any of the 365 days of the year.
• At least two means we could have multiple matches on the same day or several different days where multiple people have matching birthdays.

7.4.2 Simulate (computational)

Now that we have an idea about the structure of the problem, we next need to think about how we would simulate a single classroom. We have 18 students in the classroom and they all could have any of the 365 days of the year as a birthday. What we need to do is sample birthdays for each of the 18 students. But how do we code the days of the year?

An easy solution is to just label the days from 1 to 365. The function seq() does this for us.

Next we need to pick one of the days using the sample function. Note that we set the seed to get repeatable results, this is not required.

The first person was born on the 228th day of the year.

Since R works on vectors, we don’t have to write a loop to select 18 days, we just have sample() do it for us.

What do we want R to do? Sample from the numbers 1 to 365 with replacement, which means a number can be picked more than once.

Notice in our sample we have at least one match, although it is difficult to look at this list and see the match. Let’s sort them to make it easier for us to see.

The next step is to find a way in R for the code to detect that there is a match.

Exercise : What idea(s) can we use to determine if a match exists?

We could sort the data and look at differences in sequential values and then check if the set of differences contains a zero. This seems to be computationally expensive. Instead we will use the function unique() which gives a vector of unique values in an object. The function length() gives the number of elements in the vector.

Since we only have 17 unique values in a vector of size 18, we have a match. Now let’s put this all together to generate another classroom of size 18.

The next problem that needs to be solved is how to repeat the classrooms and keep track of those that have a match. There are several functions we could use to include replicate() but we will use do() from the mosaic package because it returns a data frame so we can use tidyverse verbs to wrangle the data.

The do() function allows us to repeat an operation many times. The following template

where {stuff to do} is typically a single R command, but may be something more complicated.

Load the libraries.

Let’s repeat for a larger number of simulated classroom, remember you should be asking yourself:

What do I want R to do? What does R need to do this?

This is within 2 decimal places of the mathematical solution we develop shortly.

How many classrooms do we need to simulate to get an accurate estimate of the probability of a match? That is a statistical modeling question and it depends on how much variability we can accept. We will discuss these ideas later in the semester. For now, you can run the code multiple times and see how the estimate varies. If computational power is cheap, you can increase the number of simulations.

7.4.3 Plotting

By the way, the method we have used to create the data allows us to summarize the number of unique birthdays using a table or bar chart. Let’s do that now. Note that since the first argument in tally() is not data then the pipe operator will not work without some extra effort. We must tell R that the data is the previous argument in the pipeline and thus use the symbol . to denote this.

Figure 7.1 is a plot of the number of unique birthdays in our sample.

Figure 7.1: Bar chart of the number of unique birthdays in the sample.

Exercise : What does it mean if the length of unique birthdays is 16, in terms of matches? 64

7.4.4 Mathematical solution

To solve this problem mathematically, we will step through the logic one step at a time. One of the key ideas that we will see many times is the idea of the multiplication rule. This idea is the foundation for permutation and combinations which are counting methods frequently used in probability calculations.

The first step that we take is to understand the idea of 2 or more people with the same birthday. With 18 people, there are a great deal of possibilities for 2 or more birthdays. We could have exactly 2 people with the same birthday. We could have 18 people with the same birthday, We could have 3 people with the same birthday and another 2 people with the same birthday but different from the other 3. Accounting for all these possibilities is too large a counting process. Instead, we will take the approach of finding the probability of no one having a matching birthday. Then the probability of at least 2 people having a matching birthday is 1 minus the probability that no one has a matching birthday. This is known as a complementary probability. A simpler example is to think about rolling a single die. The probability of rolling a 6 is equivalent to 1 minus the probability of not rolling a 6.

We first need to think about all the different ways we could get 18 birthdays. This is going to be our denominator in the probability calculation. First let’s just look at 2 people. The first person could have 365 different days for their birthday. The second person could also have 365 different birthdays. So for each birthday of the first person there could be 365 birthdays for the second. Thus for 2 people there are \(365^2\) possible sets of birthdays. This is an example of the multiplication rule . For 18 people there are \(365^{18}\) sets of birthdays. That is a large number. Again, this will be our denominator in calculating the probability.

The numerator is the number of sets of birthdays with no matches. Again, let’s consider 2 people. The first person can have a birthday on any day of the year, so 365 possibilities. Since we don’t want a match, the second person can only have 364 possibilities for a birthday. Thus we have \(365 \times 364\) possibilities for two people to have different birthdays.

Exercise: What is the number of possibilities for 18 people so that no one has the same birthday.

The answer for 18 people is \(365 \times 364 \times 363 ... \times 349 \times 348\) . This looks like a truncated factorial. Remember a factorial, written as \(n!\) with an explanation point, is the product of successive positive integers. As an example \(3!\) is \(3 \times 2 \times 1\) or 6. We could write the multiplication for the numerator as \[\frac{365!}{(365-n)!}\] As we will learn, the multiplication rule for the numerator is known as a permutation .

We are ready to put it all together. For 18 people, the probability of 2 or more people with the same birthday is 1 minus the probability that no one has the same birthday, which is

\[1 - \frac{\frac{365!}{(365-18)!}}{365^{18}}\] or

\[1 - \frac{\frac{365!}{347!}}{365^{18}}\]

In R there is a function called factorial() but factorials get large fast and we will overflow the memory. Try factorial(365) in R to see what happens.

It is returning infinity because the number is too large for the buffer. As is often the case we will have when using a computational method, we must be clever about our approach. Instead of using factorials we can make use of R s ability to work on vectors. If we provide R with a vector of values, the prod() will perform a product of all the elements.

7.4.5 General solution

We now have the mathematics to understand the problem. We can easily generalize this to any number of people. To do this, we have to write a function in R . As with everything in R , we save a function as an object. The general format for creating a function is

For this problem we will call the function birthday_prob() . The only parameter we need is the number of people in the room, n . Let’s write this function.

Notice we assigned the function to the name birthday_prob , we told R to expect one argument to the function, which we are calling n , and then we provide R with the code to find the probability. We set a default value for n in case one is not provided to prevent an error when the function is run. We will learn more about writing functions over this and the next semester.

Test the code with a know answer.

Now we can determine the probability for any size room. You may have heard that it only takes about 23 people in a room to have a 50% probability of at least 2 people matching birthdays.

Let’s create a plot of the probability versus number of people in the room. To do this, we need to apply the function to a vector of values. The function sapply() will work or we can also use Vectorize() to alter our existing function. We choose the latter option.

First notice what happens if we input a vector into our function.

It only uses the first value. There are several ways to solve this problem. We can use the map() function in the purrr package. This idea of mapping a function to a vector is important in data science. It is used in scenarios where there is a lot of data. In this case the idea of map-reduce is used to make the analysis amenable to parallel computing.

We could also just vectorize the function.

Now notice what happens.

We are good to go. Let’s create our line plot, Figure 7.2 .

Figure 7.2: The probability of at least 2 people having mathcing birthdays

Is this what you expected the curve to look like? We, the authors, did not expect this. It has a sigmodial shape with a large increase in the middle range and flatten in the tails.

7.4.6 Data science approach

The final approach we will take is one based on data, a data science approach. In the mosaicData package is a data set called Births that contains the number of births in the US from 1969 to 1988. This data will allow us to estimate the number of births on any day of the year. This allows us to eliminate the reliance on the assumption that each day is equally likely. Let’s first inspect() the data object.

It could be argued that we could randomly pick one year and use it. Let’s see what happens if we just used 1969. Figure 7.3 is a scatter plot of the number of births in 1969 for each day of the year.

Figure 7.3: The number of births for each day of the year in 1969

Exercise : What patterns do you see in Figure 7.3 ? What might explain them?

There are definitely bands appearing in the data which could be the day of the week; there are less birthdays on the weekend. There is also seasonality with more birthdays in the summer and fall. There is also probably an impact from holidays.

Quickly, let’s look at the impact of day of the week by using color for day of the week. Figure 7.4 makes it clear that the weekends have less number of births as compared to the work week.

Figure 7.4: The number of births for each day of the year in 1969 broken down by day of the week

By only using one year, this data might give poor results since holidays will fall on certain days of the week and the weekends will also be impacted. Note that we also still have the problem of leap years.

The years 1972, 1976, 1980, 1984, and 1988 are all leap years. At this point, to make the analysis easier, we will drop those years.

Notice in filter() we used the %in% argument. This is a logical argument checking if year is one of the values. The ! at the front negates this in a sense requiring year not to be one of those values.`

We are almost ready to simulate. We need to get the count of births on each day of the year for the non-leap years.

Let’s look at a plot of the number of births versus day of the year. We combined years in Figure 7.5 .

Figure 7.5: Number of births by day of the year for all years.

This curve has the seasonal cycling we would expect. The smaller scale cycling is unexpected. Maybe because we are dropping the leap years, we are getting some days appearing in our time interval more frequently on weekends. We leave it to you to investigate this phenomenon.

We use these counts as weights in a sampling process. Days with more births will have a higher probability of being selected. Days such as Christmas and Christmas Eve have a lower probability of being selected. Let’s save the weights in an object to use in the sample() function.

The pull() function pulls the vectors of values out of the data frame format into a vector format which the sample() needs.

Now let’s simulate the problem. The probability of a match should change slightly, maybe go down slightly?, but not much since most of the days have about the same probability or number of occurrences.

We could not solve this problem of varying frequency of birth days using mathematics, at least as far as we know.

Cool stuff, let’s get to learning more about probability models in the next chapters.

7.5 Homework Problems

• Exactly 2 people with the same birthday - Simulation . Complete a similar analysis for case where exactly 2 people in a room of 23 people have the same birthday. In this exercise you will use a computational simulation.
• Create a new R Markdown file and create a report. Yes, we know you could use this file but we want you to practice generating your own report.
• Simulate having 23 people in the class with each day of the year equally likely. Find the cases where exactly 2 people have the same birthday, you will have to alter the code from the Notes more than changing 18 to 23.
• Plot the frequency of occurrences as a bar chart.
• Estimate the probability of exactly two people having the same birthday.
• Exactly 2 people with the same birthday - Mathematical . Repeat problem 1 but do it mathematically. As a big hint, you will need to use the choose() function. The idea is that with 23 people we need to choose 2 of them to match. We thus need to multiply, the multiplication rule again, by choose(23,2) . If you are having trouble, work with a total of 3 people in the room first.
• Find a formula to determine the exact probability of exactly 2 people in a room of 23 having the same birthday.
• Generalize your solution to any number n people in the room and create a function.
• Vectorize the function.
• Plot the probability of exactly 2 people having the same birthday versus number of people in the room.
• Comment on the shape of the curve and explain it.

• RD Sharma Solutions
• Chapter 25 Pictorial Representation Of Data As Pie Charts Or Circle Graphs

RD Sharma Solutions for Class 8 Maths Chapter 25 Data Handling - III (Pictorial Representation of Data as Pie Charts or Circle Graphs)

In previous chapters, we have learnt about the classification and tabulation of data and their graphical representation by using histograms. In this chapter, we will learn about the diagrammatic representation of data. There are a very large variety of diagrams in use, and we mainly focus on pie diagrams or pie charts or circle graphs to represent the given data. By referring to RD Sharma Class 8 textbook, students can get all the references required to solve the problems. Our experts have solved the problems using shortcut methods to help students understand the concepts clearly. RD Sharma Solutions Class 8 Maths Chapter 25 are available in the PDF, which can be downloaded easily from the links provided below.

Chapter 25 Data Handling – III (Pictorial Representation of Data as Pie Charts or Circle Graphs) contains two exercises, and the RD Sharma Class 8 Solutions available on this page provide solutions to the questions present in each exercise. Now, let us have a look at the concepts discussed in this chapter.

• Pie Diagrams
• Construction of Pie Diagrams
• Reading of Pie Charts
• RD Sharma Solutions for Class 8 Maths Chapter 1 Rational Numbers
• RD Sharma Solutions for Class 8 Maths Chapter 2 Powers
• RD Sharma Solutions for Class 8 Maths Chapter 3 Squares and Square Roots
• RD Sharma Solutions for Class 8 Maths Chapter 4 Cubes and Cube Roots
• RD Sharma Solutions for Class 8 Maths Chapter 5 Playing with Numbers
• RD Sharma Solutions for Class 8 Maths Chapter 6 Algebraic Expressions and Identities
• RD Sharma Solutions for Class 8 Maths Chapter 7 Factorization
• RD Sharma Solutions for Class 8 Maths Chapter 8 Division of Algebraic Expressions
• RD Sharma Solutions for Class 8 Maths Chapter 9 Linear Equations in One Variable
• RD Sharma Solutions for Class 8 Maths Chapter 10 Direct and Inverse Variations
• RD Sharma Solutions for Class 8 Maths Chapter 11 Time and Work
• RD Sharma Solutions for Class 8 Maths Chapter 12 Percentage
• RD Sharma Solutions for Class 8 Maths Chapter 13 Profit, Loss, Discount and Value Added Tax (VAT)
• RD Sharma Solutions for Class 8 Maths Chapter 14 Compound Interest
• RD Sharma Solutions for Class 8 Maths Chapter 15 Understanding Shapes – I (Polygons)
• RD Sharma Solutions for Class 8 Maths Chapter 16 Understanding Shapes – II (Quadrilaterals)
• RD Sharma Solutions for Class 8 Maths Chapter 17 Understanding Shapes – II (Special Types of Quadrilaterals)
• RD Sharma Solutions for Class 8 Maths Chapter 18 Practical Geometry (Constructions)
• RD Sharma Solutions for Class 8 Maths Chapter 19 Visualising Shapes
• RD Sharma Solutions for Class 8 Maths Chapter 20 Mensuration – I (Area of a Trapezium and a Polygon)
• RD Sharma Solutions for Class 8 Maths Chapter 21 Mensuration – II (Volumes and Surface Areas of a Cuboid and a Cube)
• RD Sharma Solutions for Class 8 Maths Chapter 22 Mensuration – III (Surface Area and Volume of a Right Circular Cylinder)
• RD Sharma Solutions for Class 8 Maths Chapter 23 Data Handling – I (Classification and Tabulation of Data)
• RD Sharma Solutions for Class 8 Maths Chapter 24 Data Handling – II (Graphical Representation of Data as Histograms)
• RD Sharma Solutions for Class 8 Maths Chapter 25 Data Handling – III (Pictorial Representation of Data as Pie Charts)
• RD Sharma Solutions for Class 8 Maths Chapter 26 Data Handling – IV (Probability)
• RD Sharma Solutions for Class 8 Maths Chapter 27 Introduction to Graphs
• Exercise 25.1 Chapter 25 Data Handling – III
• Exercise 25.2 Chapter 25 Data Handling – III

RD Sharma Solutions for Class 8 Maths Chapter 25 Data Handling – III (Pictorial Representation of Data as Pie Charts or Circle Graphs)

carouselExampleControls111

Previous Next

Access Answers to RD Sharma Solutions for Class 8 Maths Chapter 25 Data Handling – III (Pictorial Representation of Data as Pie Charts or Circle Graphs)

EXERCISE 25.1 PAGE NO: 25.12

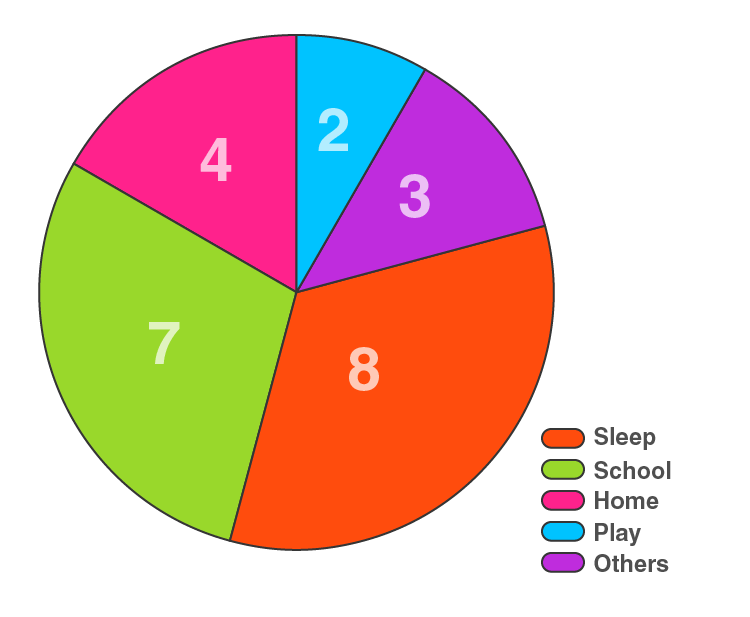
1. The number of hours spent by a schoolboy on different activities in a working day is given below:

Present the information in the form of a pie chart.

Here, the total number of hours = 24

The central angle = (component value/24) × 360°

The central angle for each activity will be calculated as follows:

Now, the pie chart can be constructed by using the given data.

Steps to construct:

Step 1: Draw the circle of an appropriate radius.

Step 2: Draw a vertical radius anywhere inside the circle.

Step 3: Choose the largest central angle. Here, it is 120 o . Construct a sector of central angle 120 o whose one radius coincides with the radius drawn in step 2, and the other radius is in a clockwise direction to the vertical radius.

Step 4: Construct other sectors representing other values in a clockwise direction in descending order of magnitudes of their central angles.

Step 5: Shade the sectors so obtained by different colours and label them as shown in the below figure.

2. Employees of a company have been categorised according to their religions as given below:

Draw a pie chart to represent the above information.

Here, the total number of workers = 1080

The central angle = (component value/1080) × 360°

Step 3: Choose the largest central angle. Construct a sector of a central angle, whose one radius coincides with the radius drawn in step 2, and the other radius is in a clockwise direction to the vertical radius.

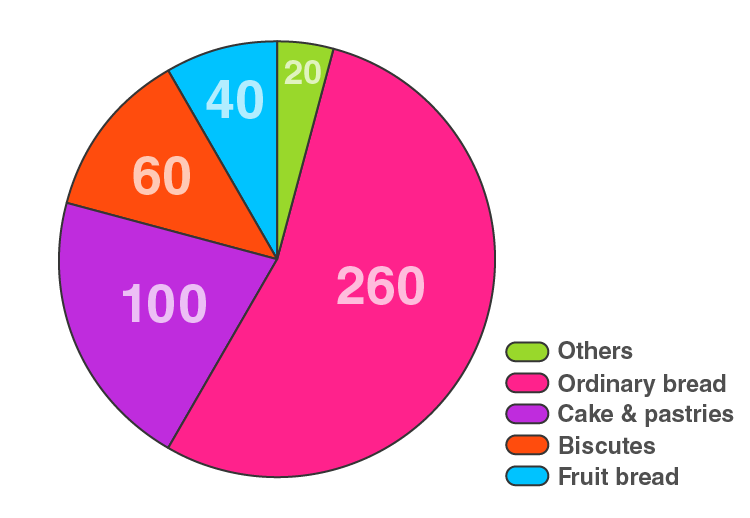
3. In one day, the sales (in rupees) of different items of a baker’s shop are given below:

Here, total sales = 480

The central angle = (component value/480) × 360°

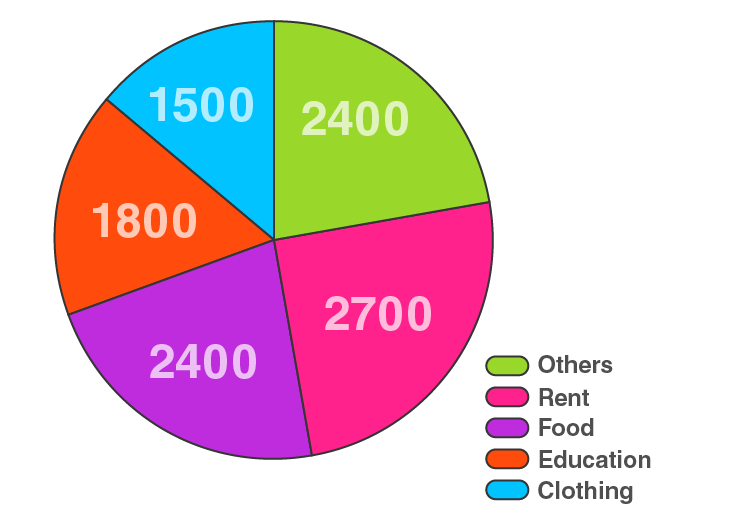
4. The following data shows the expenditure of a person on different items during a month. Represent the data in a pie chart.

Here, total amount = Rs 10800

The central angle = (component value/10800) × 360°

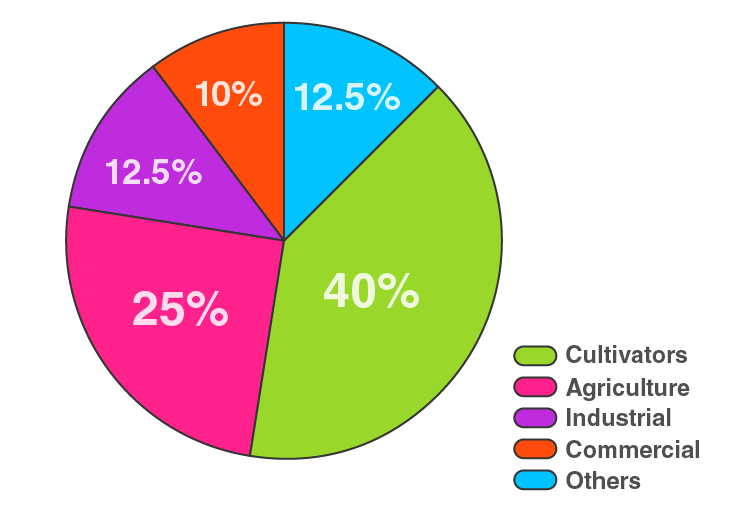
5. The percentages of various categories of workers in a state are given in the following table.

Here, total % of workers = 100%

The central angle = (component value/100) × 360°

6. The following table shows the expenditure incurred by a publisher in publishing a book:

Present the above data in the form of a pie chart.

Here, total expenditure (in %) = 100%

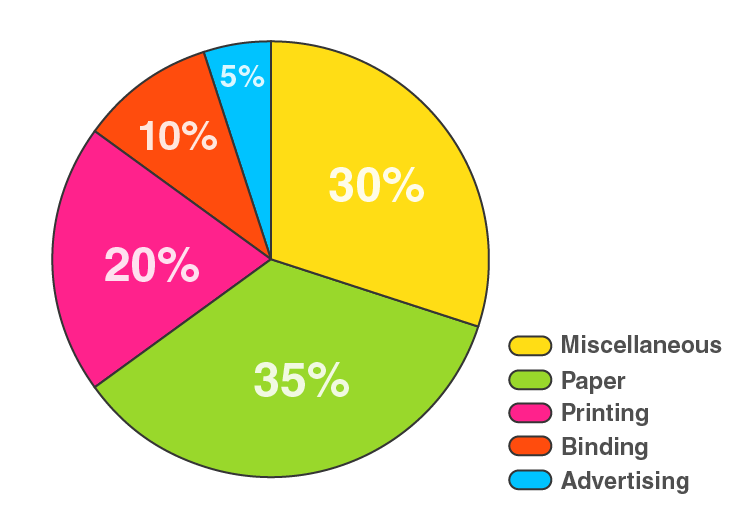
7. The percentage of the different products of a village in a particular district is given below. Draw a pie chart representing this information.

Here, total % = 100%

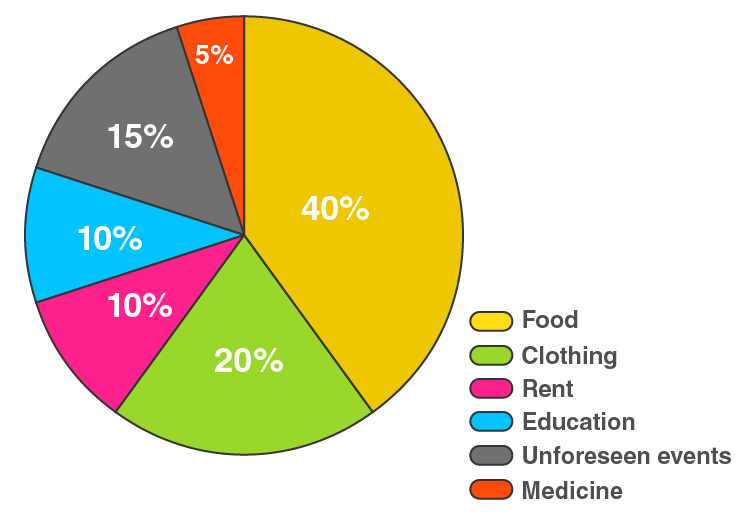
8. Draw a pie diagram for the following data of expenditure pattern in a family:

Step 3: Choose the largest central angle. Construct a sector of a central angle, whose one radius coincides with the radius drawn in step 2, and the other radius is in clockwise direction to the vertical radius.

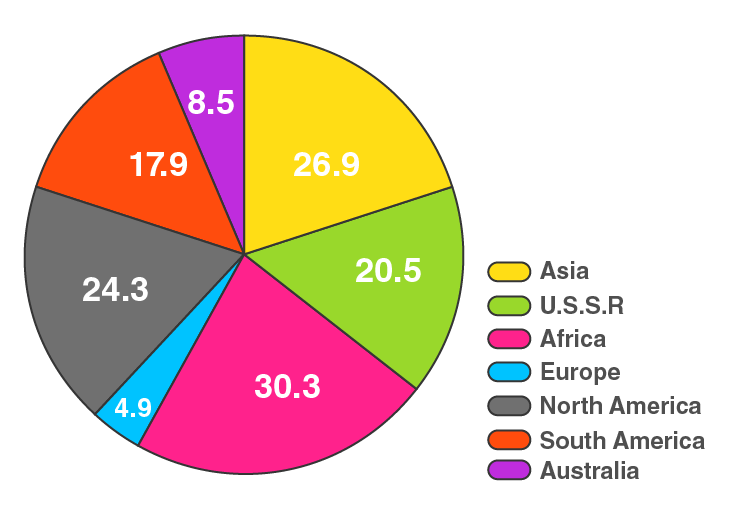
9. Draw a pie diagram of the areas of continents of the world given in the following table:

Here, total Area = 133.3 million sq.km

The central angle = (component value/133.3) × 360°

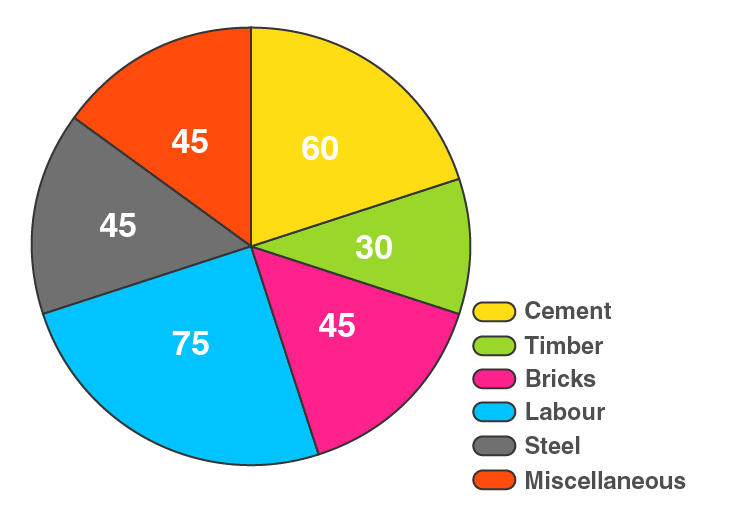
10. The following data gives the amount spent on the construction of a house. Draw a pie diagram.

Here, total Expenditure = 300 thousand rupees

The central angle = (component value/300) × 360°

11. The following table shows how a student spends his pocket money during the course of a month. Represent it by a pie diagram.

Here, total Expenditure = 100%

Step 3: Choose the largest central angle. Construct a sector of central angle, whose one radius coincides with the radius drawn in step 2, and the other radius is in a clockwise direction to the vertical radius.

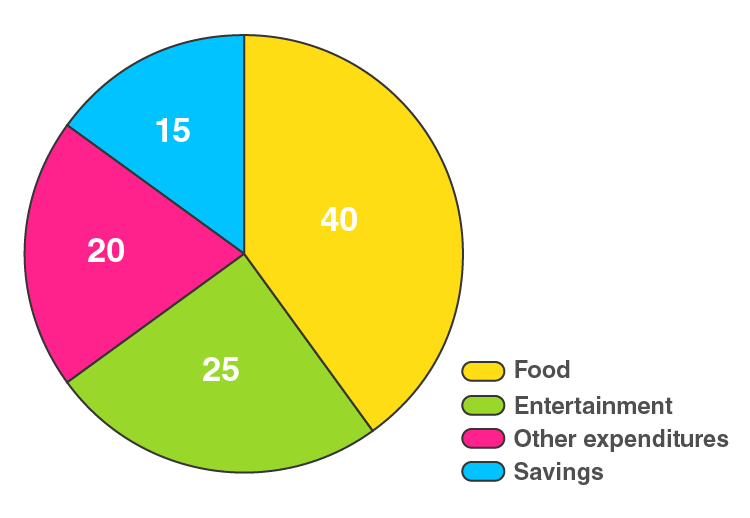
12. Represent the following data by a pie diagram:

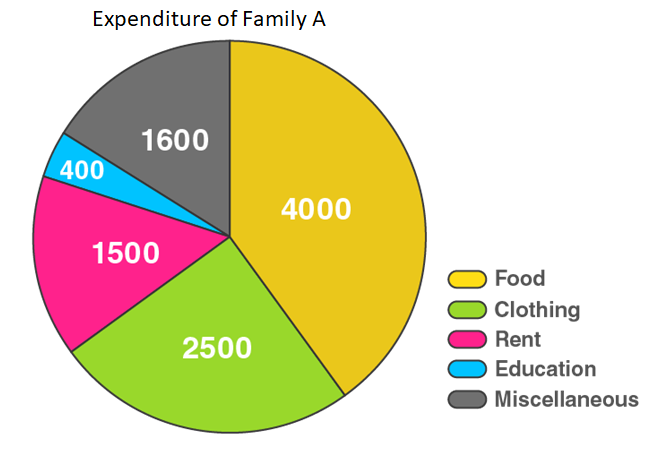
Here, the total expenditure of family A = 10000 and family B = 11680

The central angle for family A = (component value/10000) × 360°

The central angle for family B = (component value/11680) × 360°

Hence, the central angle for each activity will be calculated as follows:

Now, the pie chart for Family A and Family B can be constructed by using the given data.

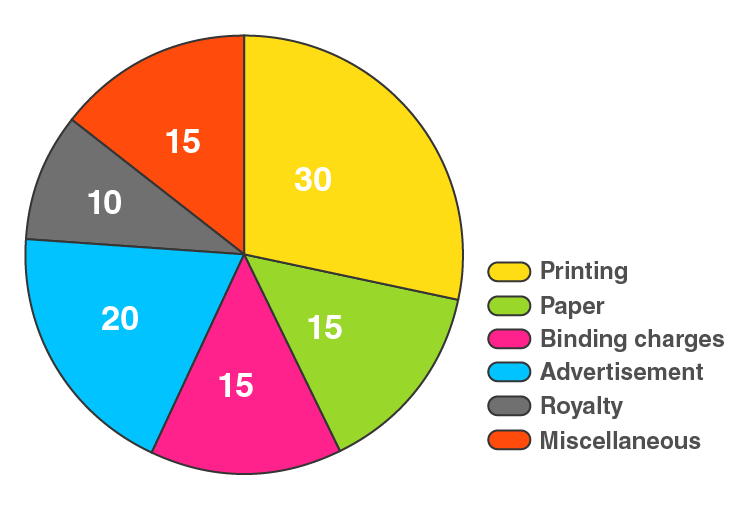
13. Following data gives a break up of the cost of production of a book:

Draw a pie diagram depicting the above information.

Here, the total cost of production of the book = 105%

The central angle = (component value/105) × 360°

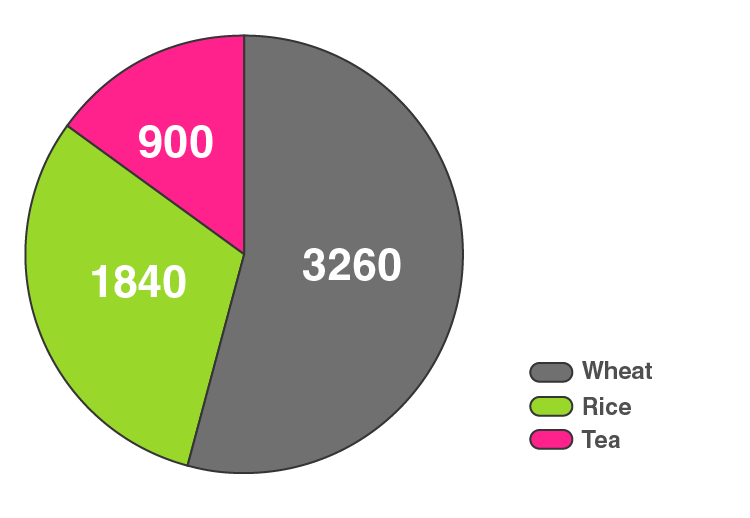
14. Represent the following data with the help of a pie diagram:

Here, the total cost of production = 6000 metric tons

The central angle = (component value/6000) × 360°

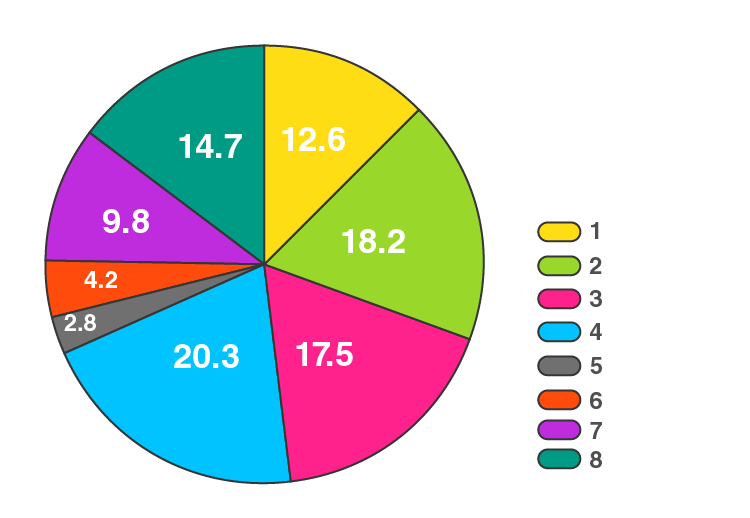
15. Draw a pie diagram representing the relative frequencies (expressed as percentages) of the eight classes as given below: 12.6, 18.2, 17.5, 20.3, 2.8, 4.2, 9.8, 14.7

Here, total amount = 100.1%

The central angle = (component value/100.1) × 360°

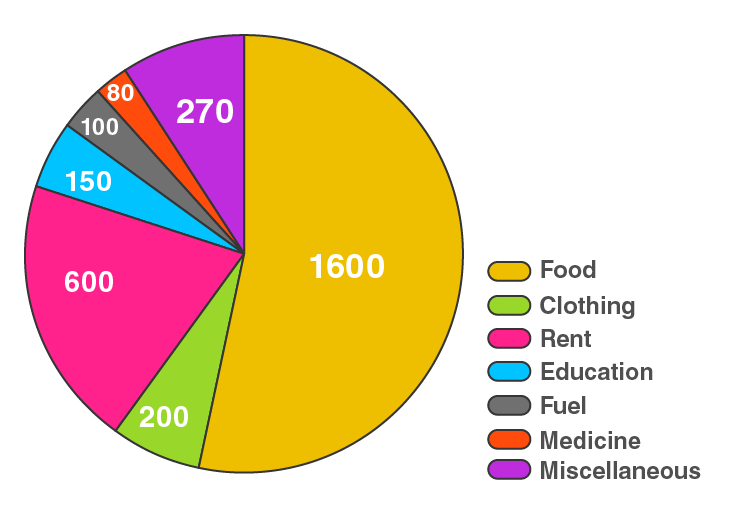
16. Following is the break up of the expenditure of a family on different items of consumption:

Draw a pie diagram to represent the above data.

Here, total expenditure = Rs. 3000

The central angle = (component value/3000) × 360°

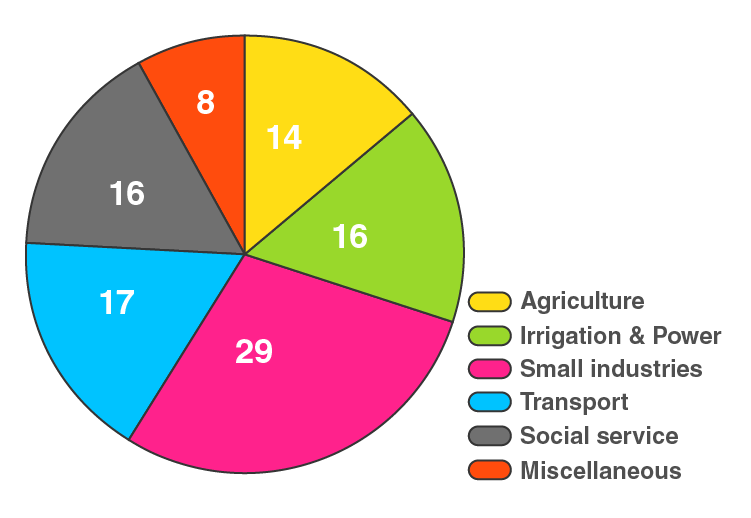
17. Draw a pie diagram for the following data of the investment pattern in a five years plan:

Here, total investment = 100%

EXERCISE 25.2 PAGE NO: 25.21

1. The pie chart given in Fig. 25.17 represents the expenditure on different items in constructing a flat in Delhi. If the expenditure incurred on cement is Rs. 112500, find the following:

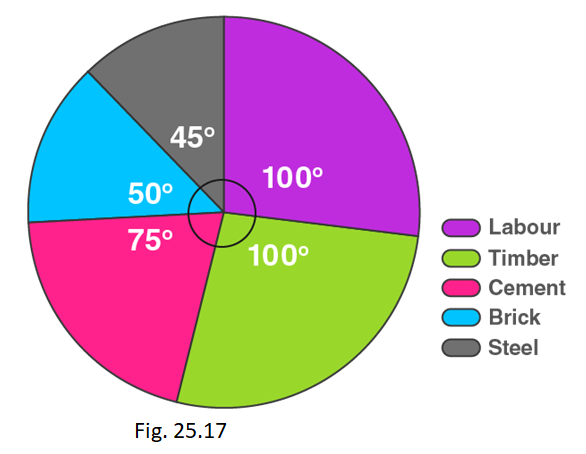
(i) Total cost of the flat. (ii) Expenditure incurred on labour.

(i)  By using the formula,

Expenditure incurred on cement = (central angle × Total cost) / 360°

Total cost of the flat = (360° × 112500) / 75 o = Rs. 540000

(ii)  By using the formula,

Expenditure incurred on labour = (central angle × Total cost) / 360°

= (100° × 540000) / 360 o = Rs. 150000

2. The pie chart given in Fig. 25.18 shows the annual agricultural production of an Indian state. If the total production of all the commodities is 81000 tonnes, find the production (in tonnes) of

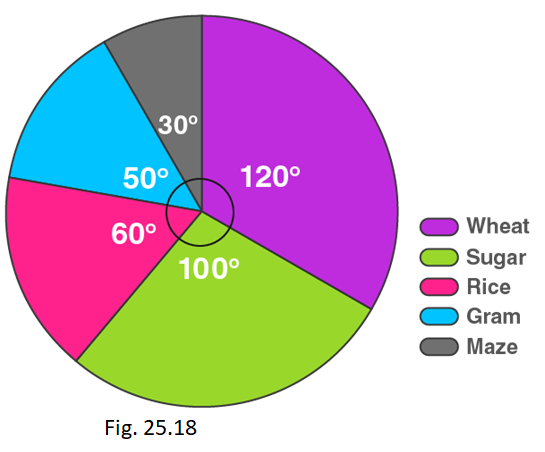
(i) Wheat (ii) Sugar (iii) Rice (iv) Maize (v) Gram

We know that,

Total Production = 81000 Tonnes.

(i)  Production of wheat = (central angle of wheat × Total production) / 360°

= (120 o × 81000) / 360 o = 27000 tonnes

(ii)  Production of sugar = (central angle of sugar × Total production) / 360°

= (100 o × 81000) / 360 o = 22500 tonnes

(iii) Production of rice = (central angle of rice × Total production) / 360°

= (60 o × 81000) / 360 o = 13500 tonnes

(iv) Production of maize = (central angle of maize × Total production) / 360°

= (30 o × 81000) / 360 o = 6750 tonnes

(v)  Production of gram = (central angle of gram × Total production) / 360°

= (50 o × 81000) / 360 o = 11250 tonnes

3. The following pie chart shows the number of students admitted in different faculties of a college. If 1000 students are admitted in Science, answer the following :

(i) What is the total number of students? (ii) What is the ratio of students in science and arts?

Students in science = (central angle × Total students) / 360°

1000 = (100 o × Total students) / 360 o

Total students = (1000 × 360 o )/100 o

= 3600 students

∴ The total number of students is 3600.

(ii)  Students in arts = (central angle of arts × Total students) / 360°

= (120 o × 3600) / 360 o = 1200 students

∴ The ratio of students in science and arts is 1000:1200 = 5:6

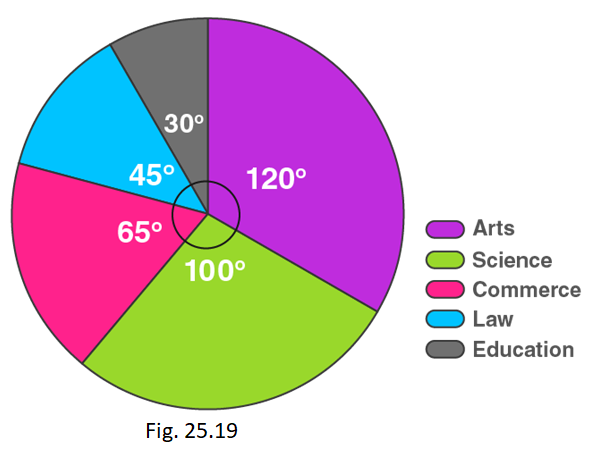
4. In Fig. 25.20, the pie chart shows the marks obtained by a student in an examination. If the student secures 440 marks in all, calculate his marks in each of the given subjects.

Marks secured in Mathematics = (central angle of maths × Total score secured) / 360°

= (108 × 440) / 360 o = 132 marks

Marks secured in Science = (central angle of science × Total score secured) / 360°

= (81 × 440) / 360 o = 99 marks

Marks secured in English = (central angle of English × Total score secured) / 360°

= (72 × 440) / 360 o = 88 marks

Marks secured in Hindi = (central angle of Hindi × Total score secured) / 360°

= (54 × 440) / 360 o = 66 marks

Marks secured in Social Science = (central angle of social science × Total score secured) / 360°

= (45 × 440) / 360 o = 55 marks

5. In Fig. 25.21, the pie chart shows the marks obtained by a student in various subjects. If the student scored 135 marks in Mathematics, find the total marks in all the subjects. Also, find his score in individual subjects.

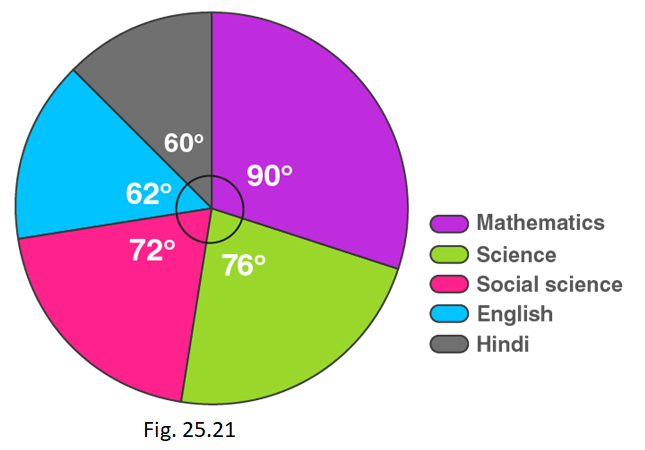
Let us calculate the total marks.

Marks scored in Mathematics = (central angle of Maths × Total marks) / 360°

135 = (90 × Total marks) / 360 o

Total marks = (135 × 360)/90

= 540 marks

Marks scored in Hindi = (central angle of Hindi × Total marks) / 360°

= (60 × 540) / 360 o

Marks scored in Science = (central angle of Science × Total marks) / 360°

= (76 × 540) / 360 o

= 114 marks

Marks scored in Social Science = (central angle of Social Science × Total marks) / 360°

= (72 × 540) / 360 o

= 108 marks

Marks scored in English = (central angle of English × Total marks) / 360°

= (62 × 540) / 360 o

6. The following pie chart shows the monthly expenditure of Shikha on various items. If she spends Rs. 16000 per month, answer the following questions:

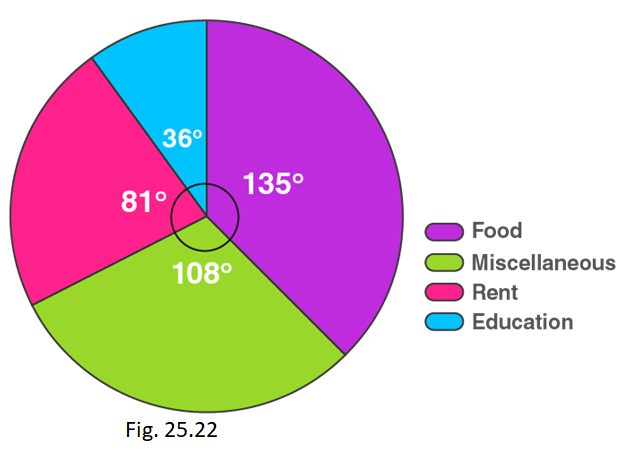
(i) How much does she spend on rent?

(ii) How much does she spend on education?

(iii) What is the ratio of expenses on food and rent?

(i) Money spent on rent = (central angle of rent × total money spent) / 360°

= (81 × 16000) / 360 o

(ii) Money spent on education = (central angle of education × total money spent) / 360°

= (36 × 16000) / 360 o

(iii) Money spent on food = (central angle of food × total money spent) / 360°

= (135 × 16000) / 360 o

The ratio of expenses on food and rent is Rs. 6000/Rs. 3600 = 5/3

Ratio = 5:3

7. The pie chart (as shown in figure 25.23) represents the amount spent on different sports by a sports club in a year. If the total money spent by the club on sports is Rs. 108000, find the amount spent on each sport.

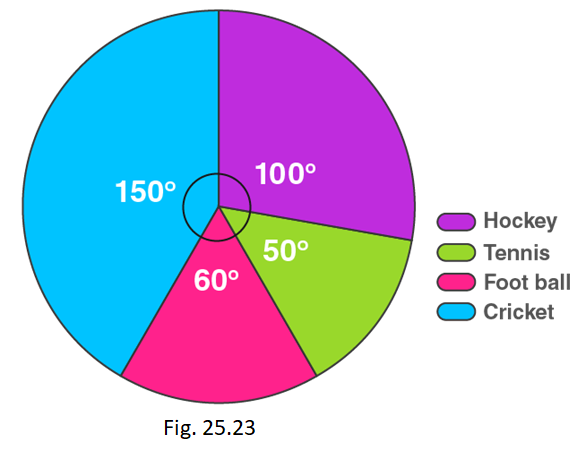
Money spent on cricket = (central angle of cricket × Total money spent) / 360°

= (150 × 108000) / 360 o

= Rs. 45000

Money spent on football = (central angle of football × Total money spent) / 360°

= (60 × 108000) / 360 o

= Rs. 18000

Money spent on tennis = (central angle of tennis × Total money spent) / 360°

= (50 × 108000) / 360 o

= Rs. 15000

Money spent on hockey = (central angle of cricket × Total money spent) / 360°

= (100 × 108000) / 360 o

= Rs. 30000

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.