problem solving linear equations pdf

• Number Charts
• Multiplication
• Long division
• Basic operations
• Telling time
• Place value
• Roman numerals
• Fractions & related
• Add, subtract, multiply,   and divide fractions
• Mixed numbers vs. fractions
• Equivalent fractions
• Prime factorization & factors
• Fraction Calculator
• Decimals & Percent
• Add, subtract, multiply,   and divide decimals
• Fractions to decimals
• Percents to decimals
• Percentage of a number
• Percent word problems
• Classify triangles
• Classify quadrilaterals
• Circle worksheets
• Area & perimeter of rectangles
• Area of triangles & polygons
• Coordinate grid, including   moves & reflections
• Volume & surface area
• Pre-algebra
• Square Roots
• Order of operations
• Scientific notation
• Proportions
• Ratio word problems
• Write expressions
• Evaluate expressions
• Simplify expressions
• Linear equations
• Linear inequalities
• Graphing & slope
• Equation calculator
• Equation editor
• Elementary Math Games
• Addition and subtraction
• Math facts practice
• The four operations
• Factoring and number theory
• Geometry topics
• Middle/High School
• Statistics & Graphs
• Probability
• Trigonometry
• Logic and proof
• For all levels
• Favorite math puzzles
• Favorite challenging puzzles
• Math in real world
• Problem solving & projects
• For gifted children
• Math history
• Math games and fun websites
• Interactive math tutorials
• Math help & online tutoring
• Assessment, review & test prep
• Online math curricula

Worksheets for simplifying expressions

Worksheets for evaluating expressions with variables

Worksheets for writing expressions with variables from verbal expressions

Worksheets for linear inequalities

Key to Algebra Workbooks

Key to Algebra offers a unique, proven way to introduce algebra to your students. New concepts are explained in simple language, and examples are easy to follow. Word problems relate algebra to familiar situations, helping students to understand abstract concepts. Students develop understanding by solving equations and inequalities intuitively before formal solutions are introduced. Students begin their study of algebra in Books 1-4 using only integers. Books 5-7 introduce rational numbers and expressions. Books 8-10 extend coverage to the real number system.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

8.E: Solving Linear Equations (Exercises)

• Last updated
• Save as PDF
• Page ID 5024

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

8.1 - Solve Equations using the Subtraction and Addition Properties of Equality

In the following exercises, determine whether the given number is a solution to the equation.

• x + 16 = 31, x = 15
• w − 8 = 5, w = 3
• −9n = 45, n = 54
• 4a = 72, a = 18

In the following exercises, solve the equation using the Subtraction Property of Equality.

• y + 2 = −6
• a + \(\dfrac{1}{3} = \dfrac{5}{3}\)
• n + 3.6 = 5.1

In the following exercises, solve the equation using the Addition Property of Equality.

• u − 7 = 10
• x − 9 = −4
• c − \(\dfrac{3}{11} = \dfrac{9}{11}\)
• p − 4.8 = 14

In the following exercises, solve the equation.

• n − 12 = 32
• y + 16 = −9
• f + \(\dfrac{2}{3}\) = 4
• d − 3.9 = 8.2
• y + 8 − 15 = −3
• 7x + 10 − 6x + 3 = 5
• 6(n − 1) − 5n = −14
• 8(3p + 5) − 23(p − 1) = 35

In the following exercises, translate each English sentence into an algebraic equation and then solve it.

• The sum of −6 and m is 25.
• Four less than n is 13.

In the following exercises, translate into an algebraic equation and solve.

• Rochelle’s daughter is 11 years old. Her son is 3 years younger. How old is her son?
• Tan weighs 146 pounds. Minh weighs 15 pounds more than Tan. How much does Minh weigh?
• Peter paid $9.75 to go to the movies, which was $46.25 less than he paid to go to a concert. How much did he pay for the concert?
• Elissa earned $152.84 this week, which was $21.65 more than she earned last week. How much did she earn last week?

8.2 - Solve Equations using the Division and Multiplication Properties of Equality

In the following exercises, solve each equation using the Division Property of Equality.

• 13a = −65
• 0.25p = 5.25
• −y = 4

In the following exercises, solve each equation using the Multiplication Property of Equality.

• \(\dfrac{n}{6}\) = 18
• y −10 = 30
• 36 = \(\dfrac{3}{4}\)x
• \(\dfrac{5}{8} u = \dfrac{15}{16}\)

In the following exercises, solve each equation.

• −18m = −72
• \(\dfrac{c}{9}\) = 36
• 0.45x = 6.75
• \(\dfrac{11}{12} = \dfrac{2}{3} y\)
• 5r − 3r + 9r = 35 − 2
• 24x + 8x − 11x = −7−14

8.3 - Solve Equations with Variables and Constants on Both Sides

In the following exercises, solve the equations with constants on both sides.

• 8p + 7 = 47
• 10w − 5 = 65
• 3x + 19 = −47
• 32 = −4 − 9n

In the following exercises, solve the equations with variables on both sides.

• 7y = 6y − 13
• 5a + 21 = 2a
• k = −6k − 35
• 4x − \(\dfrac{3}{8}\) = 3x

In the following exercises, solve the equations with constants and variables on both sides.

• 12x − 9 = 3x + 45
• 5n − 20 = −7n − 80
• 4u + 16 = −19 − u
• \(\dfrac{5}{8} c\) − 4 = \(\dfrac{3}{8} c\) + 4

In the following exercises, solve each linear equation using the general strategy.

• 6(x + 6) = 24
• 9(2p − 5) = 72
• −(s + 4) = 18
• 8 + 3(n − 9) = 17
• 23 − 3(y − 7) = 8
• \(\dfrac{1}{3}\)(6m + 21) = m − 7
• 8(r − 2) = 6(r + 10)
• 5 + 7(2 − 5x) = 2(9x + 1) − (13x − 57)
• 4(3.5y + 0.25) = 365
• 0.25(q − 8) = 0.1(q + 7)

8.4 - Solve Equations with Fraction or Decimal Coefficients

In the following exercises, solve each equation by clearing the fractions.

• \(\dfrac{2}{5} n − \dfrac{1}{10} = \dfrac{7}{10}\)
• \(\dfrac{1}{3} x + \dfrac{1}{5} x = 8\)
• \(\dfrac{3}{4} a − \dfrac{1}{3} = \dfrac{1}{2} a + \dfrac{5}{6}\)
• \(\dfrac{1}{2}\)(k + 3) = \(\dfrac{1}{3}\)(k + 16)

In the following exercises, solve each equation by clearing the decimals.

• 0.8x − 0.3 = 0.7x + 0.2
• 0.36u + 2.55 = 0.41u + 6.8
• 0.6p − 1.9 = 0.78p + 1.7
• 0.10d + 0.05(d − 4) = 2.05

PRACTICE TEST

• \(\dfrac{23}{5}\)
• n − 18 = 31
• 4y − 8 = 16
• −8x − 15 + 9x − 1 = −21
• −15a = 120
• \(\dfrac{2}{3}\)x = 6
• x + 3.8 = 8.2
• 10y = −5y + 60
• 8n + 2 = 6n + 12
• 9m − 2 − 4m + m = 42 − 8
• −5(2x + 1) = 45
• −(d + 9) = 23
• 2(6x + 5) − 8 = −22
• 8(3a + 5) − 7(4a − 3) = 20 − 3a
• \(\dfrac{1}{4} p + \dfrac{1}{3} = \dfrac{1}{2}\)
• 0.1d + 0.25(d + 8) = 4.1
• Translate and solve: The difference of twice x and 4 is 16.
• Samuel paid $25.82 for gas this week, which was $3.47 less than he paid last week. How much did he pay last week?

Contributors and Attributions

Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/[email protected] ."

A zeroing feedback gradient-based neural dynamics model for solving dynamic quadratic programming problems with linear equation constraints in finite time

• Original Article
• Published: 27 May 2024

Cite this article

• Shangfeng Du 1 ,
• Dongyang Fu   ORCID: orcid.org/0000-0003-0426-4356 1 ,
• Long Jin 2 ,
• Yang Si 1 &
• Yongze Li 1  

30 Accesses

Explore all metrics

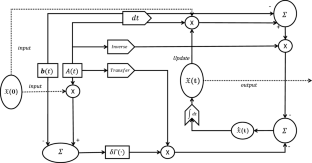
Gradient-based neural dynamics (GND) models are a classical algorithm for solving optimization problems, but it has non-negligible flaws in solving dynamic problems. In this study, a novel GND model, namely the zeroing feedback gradient-based neural dynamics (ZF-GND) models, is proposed based on the original GND model for tracking down the exact solution of dynamic quadratic programming problem (DQP). Further, a nonlinear projection function is designed to accelerate the convergence of the model. An upper bound on the convergence time of the ZF-GND model is rigorously defined through theoretical analysis. The superior effect of the ZF-GND model in terms of convergence is verified through comparison experiments. Finally, an application of robot motion planning is introduced to verify the practicality of the ZF-GND model.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Data availability

The data that support the findings this study are available from the corresponding author upon reasonable request.

Mattingley J, Boyd S (2010) Real-Time convex optimization in signal processing. IEEE Signal Process Mag 27(3):50–61

Article   Google Scholar  

Jiang C, Xiao X, Liu D, Huang H, Xiao H, Lu H (2021) Nonconvex and bound constraint zeroing neural network for solving time-varying complex-valued quadratic programming problem. IEEE Trans Ind Informat 17(10):6864–6874

Liao-McPherson D, Huang M, Kolmanovsky I (2019) A regularized and smoothed fischer-burmeister method for quadratic programming with applications to model predictive control. IEEE Trans Autom Control 64(7):2937–2944

Article   MathSciNet   Google Scholar  

Wang G, Hao Z, Huang H, Zhang B (2023) A proportional-integral iterative algorithm for time-variant equality-constrained quadratic programming problem with applications. Artif Intell Rev 56:4535–4556

Fu D, Huang H, Xiao X, Xia L, Jin L (2022) A generalized complex-valued constrained energy minimization scheme for the arctic sea ice extraction aided with neural algorithm. IEEE Trans Geosci Remote Sens 60(4303017):1–17

Google Scholar  

Minet J, Taboury J, Goudail F, Pèalat M, Roux N, Lonnoy J, Ferrec Y (2011) Influence of band selection and target estimation error on the performance of the matched filter in hyperspectral imaging. Appl Opt 50(22):4276–4285

Manolakis D, Lockwood R, Cooley T, Jacobson J (2009) Hyperspectral detection algorithms: use covariances or subspaces? Proc. SPIE 7457, Imaging Spectrometry XIV, Aug

Si Y, Wang D, Chou Y, Fu D (2023) Non-convex activated zeroing neural network model for solving time-varying nonlinear minimization problems with finite-time convergence, Knowl.-Based Syst., vol. 274, Aug

Yaǧmur N, Alagöz BB (2019) Comparision of solutions of numerical gradient descent method and continous time gradient descent dynamics and lyapunov stability. In: Proceedings on 2019 27th signal processing and communications applications conference (SIU), pp. 1–4

Li W, Swetits J (1993) A Newton method for convex regression, data smoothing, and quadratic programming with bounded constraints. SIAM J Optim 3(3):466–488

Liu M, Chen L, Du X, Jin L, Shang M (2023) Activated gradients for deep neural networks. IEEE Trans Neural Netw Learn Syst 34(4):2156–2168

Plevris V, Papadrakakis M (2010) A hybrid particle swarm?gradient algorithm for global structural optimization. Comput-Aided Civ Infrastruct Eng 26(1):48–68

Andrei N (2014) An accelerated subspace minimization three-term conjugate gradient algorithm for unconstrained optimization. Numer. Algor. 65:859–874

Wang F, Jian J, Wang C (2014) A model-hybrid approach for unconstrained optimization problems. Numer Algor 66:741–759

Mathews JH, Fink KD (2004) Numerical Methods using MATLAB., Englewood Cliffs, NJ, USA: Prentice-Hall

Zhang Y, Jiang D, Wang J (2002) A recurrent neural network for solving sylvester equation with time-varying coefficients. IEEE Trans Neural Netw 13(5):1053–1063

Sun B, Cao Y, Guo Z, Yan Z, Wen S (2020) Synchronization of discrete-time recurrent neural networks with time-varying delays via quantized sliding mode control. Appl Math Comput 375:125093

MathSciNet   Google Scholar  

Zhang X, Chen L, Li S, Stanimirović P, Zhang J, Jin L (2021) Design and analysis of recurrent neural network models with non-linear activation functions for solving time-varying quadratic programming problems. CAAI Trans Intell Technol 6(4):394–404

Jia C, Kong D, Du L (2022) Recursive terminal Sliding-Mode control method for nonlinear system based on double hidden layer fuzzy emotional recurrent neural network. IEEE Access 10:118012–118023

Zhang Z, Zheng L, Yu J, Li Y, Yu Z (2017) Three recurrent neural networks and three numerical methods for solving a repetitive motion planning scheme of redundant robot manipulators. IEEE / ASME Trans Mechatr 22(3):1423–1434

Zhang Y, Wang J (2001) Recurrent neural networks for nonlinear output regulation. Automatica 37:1161–1173

Chen D, Zhang Y (2018) Robust zeroing neural-dynamics and its time-varying disturbances suppression model applied to mobile robot manipulators. IEEE Trans Neural Netw Learn Syst 29(9):4385–4397

Wang G, Li Q, Liu S, Xiao H, Zhang B (2022) New zeroing neural network with finite-time convergence for dynamic complex-value linear equation and its applications. Chaos Soliton Fractal 164:112674

Chen D, Li S, Wu Q (2021) A novel supertwisting zeroing neural network with application to mobile robot manipulators. IEEE Trans Neural Netw Learn Syst 32(4):1776–1787

Shi Y, Sheng W, Li S, Li B, Sun X (2023) Neurodynamics for equality-constrained time-variant nonlinear optimization using discretization. IEEE Trans Ind Inf. https://doi.org/10.1109/TII.2023.3290187

Shi Y, Wang J, Li S, Li B, Sun X (2023) Tracking control of cable-driven planar robot based on discrete-time recurrent neural network with immediate discretization method. IEEE Trans Ind Inf 19(6):7414–7423

Shi Y, Zhao W, Li S, Li B, Sun X (2023) Novel discrete-time recurrent neural network for robot manipulator: a direct discretization technical route. IEEE Trans Neural Netw Learn Syst 34(6):2781–2790

Shi Y, Jin L, Li S, Li J, Qiang J, Gerontitis DK (2022) Novel discrete-time recurrent neural networks handling discrete-form time-variant multi-augmented Sylvester matrix problems and manipulator application. IEEE Trans. Neural Netw. Learn. Syst. 33(2):587–599

Liao B, Zhang Y, Jin L (2016) Taylor \(O(h^{3})\) discretization of ZNN models for dynamic equality-constrained quadratic programming with application to manipulators. IEEE Trans Neural Netw Learn Syst 27(2):225–237

Liao S, Liu J, Qi Y, Huang H, Zheng R, Xiao X (2022) An adaptive gradient neural network to solve dynamic linear matrix equations. IEEE Trans, Syst, Man, Cybern, Syst 52(9):5913–5924

Liao S, Liu J, Xiao X, Fu D, Wang G, Jin L (2020) Modified gradient neural networks for solving the time-varying sylvester equation with adaptive coefficients and elimination of matrix inversion. Neurocomputing 379:1–11

Wang G, Hao Z, Li H, Zhang B (2023) An activated variable parameter gradient-based neural network for time-variant constrained quadratic programming and its applications. CAAI Trans Intell Technol, pp. 1–10, Feb

Li W, Han L, Xiao X et al (2022) A gradient-based neural network accelerated for vision-based control of an RCM-constrained surgical endoscope robot. Neural Comput Appl 34:1329–1343

Liufu Y, Jin L, Xu J, Xiao X, Fu D (2022) Reformative noise-immune neural network for equality-constrained optimization applied to image target detection. IEEE Trans Emerg Top Comput 10(2):973–984

Liu B, Fu D, Qi Y, Huang H, Jin L (2021) Noise-tolerant gradient-oriented neurodynamic model for solving the sylvester equation. Appl Soft Comput J, vol. 109

Jin L, Li S, Wang H, Zhang Z (2018) Nonconvex projection activated zeroing neurodynamic models for time-varying matrix pseudoinversion with accelerated finite-time convergence. Appl Soft Comput J 62:840–850

Jin L, Li S, Liao B, Zhang Z (2017) Zeroing neural networks: a survey. Neurocomputing 267:597–604

Zhang Y, Chen K, Tan H-Z (2009) Performance analysis of gradient neural network exploited for online Time-Varying matrix inversion. IEEE Trans Autom Control 54(8):1940–1945

Jin L, Wei L, Li S (2023) Gradient-based differential neural-solution to time-dependent nonlinear optimization. IEEE Trans Autom Control 68(1):620–627

Jarlebring E, Poloni F (2019) Iterative methods for the delay Lyapunov equation with T-Sylvester preconditioning. Appl Numer Math 135(1):173–185

Hunger R (2005) Floating point operations in matrix-vector calculus[M]. Munich, Germany: Munich University of Technology, Inst. for Circuit Theory and Signal Processing

Zuo Q, Li K, Xiao L, Wang Y, Li K (2021) On generalized zeroing neural network under discrete and distributed time delays and its application to dynamic Lyapunov equation. IEEE Trans Syst, Man, Cybern, Syst 52:5114–5126

Xiao L, Song W, Jia L, Li X (2022) ZNN for time-variant nonlinear inequality systems: A finite-time solution. Neurocomputing 500:319–328

Zhang Y, Li Z, Guo D, Chen K, Chen P (2013) Superior robustness of using power-sigmoid activation functions in Z-type models for time-varying problems solving. ICMLC., pp. 759–764

Zuo Q, Li K, Xiao L, Wang Y, Li K (2022) On generalized zeroing neural network under discrete and distributed time delays and its application to dynamic Lyapunov Equation. IEEE Trans Syst, Man, Cybernet: Syst 52(8):5114–5126. https://doi.org/10.1109/TSMC.2021.3115555

Download references

Acknowledgements

This research was funded in part by the National Key Research and Development Program of China under Grant No. 2022YFC3103101, Key Special Project for Introduced Talents Team of Southern Marine Science and Engineering Guangdong Laboratory under Contract GML2021GD0809, National Natural Science Foundation of China under Contract 42206187, Key projects of the Guangdong Education Department under Grant No. 2023ZDZX4009.

Author information

Authors and affiliations.

School of Electronic and Information Engineering, Guangdong Ocean University, Zhanjiang, 524088, China

Shangfeng Du, Dongyang Fu, Yang Si & Yongze Li

School of Information Science and Engineering, Lanzhou University, Lanzhou, 730000, China

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Dongyang Fu .

Ethics declarations

Ethical approval.

We confirm that the manuscript has been read and approved by all named authors and that there are no other persons who satisfied the criteria for authorship but are not listed. We further confirm that the other of authors listed in the manuscript has been approved by all of us. We confirm that we have given due consideration to the protection of intellectual property associated with this work and that there are no impediments to publication, including the timing of publication, with respect to intellectual property. In so doing we confirm that we have followed the regulations of our institutions concerning intellectual property. We understand that the Corresponding Author is the sole contact for the Editorial process (including Editorial Manager and direct communications with the office). He is responsible for communicating with the other authors about progress, submissions of revision, and final approval of proof. We confirm that we have provided a current email address, which is accessible by the corresponding author, which has been configured to accept email from the Neural Computing and Applications Editorial Office.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Du, S., Fu, D., Jin, L. et al. A zeroing feedback gradient-based neural dynamics model for solving dynamic quadratic programming problems with linear equation constraints in finite time. Neural Comput & Applic (2024). https://doi.org/10.1007/s00521-024-09762-3

Download citation

Received : 27 July 2023

Accepted : 25 March 2024

Published : 27 May 2024

DOI : https://doi.org/10.1007/s00521-024-09762-3

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Zeroing feedback gradient-based neural dynamic (ZF-GND) model
• Nonlinear projection function
• Robotic motion planning
• Find a journal
• Publish with us
• Track your research