research paper on number theory

Help | Advanced Search

Number Theory

Authors and titles for recent submissions.

• Fri, 17 May 2024
• Thu, 16 May 2024
• Wed, 15 May 2024
• Tue, 14 May 2024
• Mon, 13 May 2024

Fri, 17 May 2024 (showing 8 of 8 entries )

Thu, 16 may 2024 (showing 5 of 5 entries ), wed, 15 may 2024 (showing 11 of 11 entries ), tue, 14 may 2024 (showing first 1 of 15 entries ).

Number Theory

The research of the UCLA Number Theory Group is concerned with the arithmetic of modular forms, automorphic forms, Galois representations, Selmer groups, and classical and p-adic L-functions. The group has 5 permanent faculty: Don Blasius, William Duke, Haruzo Hida, Chandrashekhar Khare, and Romyar Sharifi.  Each works broadly in number theory and has settled conjectures and introduced new topics of study. As a case in point, Hida’s theory of ordinary p-adic families, and the theories to which it gave rise constitute an area of research that is broadly studied by mathematicians around the world. His theory also provides a powerful tool for applications to Galois representations and p-adic L-functions. Likewise, Khare and his collaborator Wintenberger proved Serre’s Conjecture on modular forms, which was widely viewed as one of the most important conjectures in the field of arithmetic geometry.  Since that proof, the extension of this conjecture to automorphic forms has taken hold and stimulated a great deal of research. Duke is a leading analytic number theorist, known for many basic contributions, including the settling, using modular forms, of a well-known equidistribution problem dating back to Gauss. Blasius has made basic contributions to the special values of L-functions, and pioneered, with J. Rogawski, the use of endoscopy in the study of Galois representations. Sharifi formulated a conjecture which provides a explicit refinement to the Iwasawa main conjecture. This has opened up an exciting new avenue of research concerned with the description of arithmetic objects in terms of higher-dimensional geometry.

At any given time, the Number Theory Group has two or more postdocs, and up to 10 graduate students. There is a weekly number theory seminar and typically several ongoing instructional seminars devoted to the study of current research papers or topics, and the presentation of research of group members at all levels.  

Don Blasius

William duke, chandrashekhar khare, romyar sharifi, visiting faculty, yesim demiroglu, kim tuan do, graduate students, ethan alwaise, rohan joshi, timothy smits, jacob swenberg, frederick vu, emeriti faculty, alfred hales, haruzo hida, murray schacher.

Research in Number Theory

Subject Area and Category

• Algebra and Number Theory

SpringerOpen

Publication type

Information.

How to publish in this journal

The set of journals have been ranked according to their SJR and divided into four equal groups, four quartiles. Q1 (green) comprises the quarter of the journals with the highest values, Q2 (yellow) the second highest values, Q3 (orange) the third highest values and Q4 (red) the lowest values.

The SJR is a size-independent prestige indicator that ranks journals by their 'average prestige per article'. It is based on the idea that 'all citations are not created equal'. SJR is a measure of scientific influence of journals that accounts for both the number of citations received by a journal and the importance or prestige of the journals where such citations come from It measures the scientific influence of the average article in a journal, it expresses how central to the global scientific discussion an average article of the journal is.

Evolution of the number of published documents. All types of documents are considered, including citable and non citable documents.

This indicator counts the number of citations received by documents from a journal and divides them by the total number of documents published in that journal. The chart shows the evolution of the average number of times documents published in a journal in the past two, three and four years have been cited in the current year. The two years line is equivalent to journal impact factor ™ (Thomson Reuters) metric.

Evolution of the total number of citations and journal's self-citations received by a journal's published documents during the three previous years. Journal Self-citation is defined as the number of citation from a journal citing article to articles published by the same journal.

Evolution of the number of total citation per document and external citation per document (i.e. journal self-citations removed) received by a journal's published documents during the three previous years. External citations are calculated by subtracting the number of self-citations from the total number of citations received by the journal’s documents.

International Collaboration accounts for the articles that have been produced by researchers from several countries. The chart shows the ratio of a journal's documents signed by researchers from more than one country; that is including more than one country address.

Not every article in a journal is considered primary research and therefore "citable", this chart shows the ratio of a journal's articles including substantial research (research articles, conference papers and reviews) in three year windows vs. those documents other than research articles, reviews and conference papers.

Ratio of a journal's items, grouped in three years windows, that have been cited at least once vs. those not cited during the following year.

Evolution of the percentage of female authors.

Evolution of the number of documents cited by public policy documents according to Overton database.

Evoution of the number of documents related to Sustainable Development Goals defined by United Nations. Available from 2018 onwards.

Leave a comment

Name * Required

Email (will not be published) * Required

* Required Cancel

The users of Scimago Journal & Country Rank have the possibility to dialogue through comments linked to a specific journal. The purpose is to have a forum in which general doubts about the processes of publication in the journal, experiences and other issues derived from the publication of papers are resolved. For topics on particular articles, maintain the dialogue through the usual channels with your editor.

Follow us on @ScimagoJR Scimago Lab , Copyright 2007-2024. Data Source: Scopus®

Cookie settings

Cookie Policy

Legal Notice

Privacy Policy

Research Publications

Book chapter.

Academia.edu no longer supports Internet Explorer.

To browse Academia.edu and the wider internet faster and more securely, please take a few seconds to  upgrade your browser .

•  We're Hiring!
•  Help Center

Number Theory

• Most Cited Papers
• Most Downloaded Papers
• Newest Papers
• Save to Library
• Last »
• Mathematics Follow Following
• Algebraic Number Theory Follow Following
• Analytic Number Theory Follow Following
• Elementary Number Theory Follow Following
• Applied Mathematics Follow Following
• Algebra Follow Following
• Graph Theory Follow Following
• Combinatorics Follow Following
• Algebraic Geometry Follow Following
• Pure Mathematics Follow Following

Enter the email address you signed up with and we'll email you a reset link.

• Academia.edu Publishing
•   We're Hiring!
•   Help Center
• Find new research papers in:
• Health Sciences
• Earth Sciences
• Cognitive Science
• Mathematics
• Computer Science
• Academia ©2024

Secondary Menu

• Math Intranet
• Number Theory

Number theory is the study of the integers (e.g. whole numbers) and related objects. Topics studied by number theorists include the problem of determining the distribution of prime numbers within the integers and the structure and number of solutions of systems of polynomial equations with integer coefficients. Many problems in number theory, while simple to state, have proofs that involve apparently unrelated areas of mathematics. A beautiful illustration is given by the use of complex analysis to prove the “Prime Number Theorem,” which gives an asymptotic formula for the distribution of prime numbers. Yet other problems currently studied in number theory call upon deep methods from harmonic analysis.

In addition, conjectures in number theory have had an impressive track record of stimulating major advances even outside the subject. For example, attempts to prove “Fermat’s Last Theorem” resulted in the development of large areas of algebra over the course of three centuries, and its recent proof involved a profound unifying force in modern mathematics known as the Langlands program.

Our specialties include analytic number theory, the Langlands program, the geometry of locally symmetric spaces, arithmetic geometry and the study of algebraic cycles.

Master's of Science in Labor Studies

Many labor studies graduate programs are a mix of employer- and worker-viewpoint courses and experiences. That's not the case here at the UMass Labor Center.

We are the premier labor-side Master's Degree in Labor Studies in the United States.

This is not the program you come to if you want to specialize in HR and work for the boss. This is the program where you study and train-up to become one of the next generation of labor leaders at the forefront of organizing, building labor power, and bargaining big wins for workers. Our programs have a distinct focus on inclusively building worker power with an eye always toward the greater good.

Theory, Politics, and Practice

The UMass Labor Center offers Master's Degrees in Labor Studies with a focus at the intersection of Theory, Politics and Practice. Our program combines rigorous study of labor history and current issues.  Our students dig in to real data and learn research techniques to inform any campaign. Our professors seat current labor struggles in an intersectional historical context inseparable from race, gender, and class politics.

For over fifty years, we have built one of the premiere graduate programs in labor studies in the United States. With a near 100% placement record, our graduates are in high demand to join our over 1,000 alumni in key position in the labor movement and social justice organizations.

Organized Labor is surging in a way we haven't seen in a generation. New units are certifying every week and we want you to have the degree that offers the skills to fuel this movement. These new units have also combined efforts with a wide variety of alt-labor organizations, building strong connections with new social movements in broad-based coalitions for justice. Become one of our graduates who are at the forefront of many of these new and exciting developments to build justice and dignity in the workplace and the community, here and abroad.

Three Graduate Degree Options

• Fall 2024 Admissions Deadline - March 1, 2024
• July 2024 Admissions Deadline - April 1, 2024
• January 2025 Admissions Deadline - October 7, 2024

Undergraduate Courses

In addition to our graduate offerings, we offer limited undergraduate opportunities cross-listed with the Sociology Department.

In the news

UMass Amherst Labor Center Thompson Hall, 200 Hicks Way Amherst, MA 01003-9277

tel: (413) 545-4875

Cultural Relativity and Acceptance of Embryonic Stem Cell Research

Article sidebar.

Main Article Content

There is a debate about the ethical implications of using human embryos in stem cell research, which can be influenced by cultural, moral, and social values. This paper argues for an adaptable framework to accommodate diverse cultural and religious perspectives. By using an adaptive ethics model, research protections can reflect various populations and foster growth in stem cell research possibilities.

INTRODUCTION

Stem cell research combines biology, medicine, and technology, promising to alter health care and the understanding of human development. Yet, ethical contention exists because of individuals’ perceptions of using human embryos based on their various cultural, moral, and social values. While these disagreements concerning policy, use, and general acceptance have prompted the development of an international ethics policy, such a uniform approach can overlook the nuanced ethical landscapes between cultures. With diverse viewpoints in public health, a single global policy, especially one reflecting Western ethics or the ethics prevalent in high-income countries, is impractical. This paper argues for a culturally sensitive, adaptable framework for the use of embryonic stem cells. Stem cell policy should accommodate varying ethical viewpoints and promote an effective global dialogue. With an extension of an ethics model that can adapt to various cultures, we recommend localized guidelines that reflect the moral views of the people those guidelines serve.

Stem cells, characterized by their unique ability to differentiate into various cell types, enable the repair or replacement of damaged tissues. Two primary types of stem cells are somatic stem cells (adult stem cells) and embryonic stem cells. Adult stem cells exist in developed tissues and maintain the body’s repair processes. [1] Embryonic stem cells (ESC) are remarkably pluripotent or versatile, making them valuable in research. [2] However, the use of ESCs has sparked ethics debates. Considering the potential of embryonic stem cells, research guidelines are essential. The International Society for Stem Cell Research (ISSCR) provides international stem cell research guidelines. They call for “public conversations touching on the scientific significance as well as the societal and ethical issues raised by ESC research.” [3] The ISSCR also publishes updates about culturing human embryos 14 days post fertilization, suggesting local policies and regulations should continue to evolve as ESC research develops. [4]  Like the ISSCR, which calls for local law and policy to adapt to developing stem cell research given cultural acceptance, this paper highlights the importance of local social factors such as religion and culture.

I.     Global Cultural Perspective of Embryonic Stem Cells

Views on ESCs vary throughout the world. Some countries readily embrace stem cell research and therapies, while others have stricter regulations due to ethical concerns surrounding embryonic stem cells and when an embryo becomes entitled to moral consideration. The philosophical issue of when the “someone” begins to be a human after fertilization, in the morally relevant sense, [5] impacts when an embryo becomes not just worthy of protection but morally entitled to it. The process of creating embryonic stem cell lines involves the destruction of the embryos for research. [6] Consequently, global engagement in ESC research depends on social-cultural acceptability.

a.     US and Rights-Based Cultures

In the United States, attitudes toward stem cell therapies are diverse. The ethics and social approaches, which value individualism, [7] trigger debates regarding the destruction of human embryos, creating a complex regulatory environment. For example, the 1996 Dickey-Wicker Amendment prohibited federal funding for the creation of embryos for research and the destruction of embryos for “more than allowed for research on fetuses in utero.” [8] Following suit, in 2001, the Bush Administration heavily restricted stem cell lines for research. However, the Stem Cell Research Enhancement Act of 2005 was proposed to help develop ESC research but was ultimately vetoed. [9] Under the Obama administration, in 2009, an executive order lifted restrictions allowing for more development in this field. [10] The flux of research capacity and funding parallels the different cultural perceptions of human dignity of the embryo and how it is socially presented within the country’s research culture. [11]

b.     Ubuntu and Collective Cultures

African bioethics differs from Western individualism because of the different traditions and values. African traditions, as described by individuals from South Africa and supported by some studies in other African countries, including Ghana and Kenya, follow the African moral philosophies of Ubuntu or Botho and Ukama , which “advocates for a form of wholeness that comes through one’s relationship and connectedness with other people in the society,” [12] making autonomy a socially collective concept. In this context, for the community to act autonomously, individuals would come together to decide what is best for the collective. Thus, stem cell research would require examining the value of the research to society as a whole and the use of the embryos as a collective societal resource. If society views the source as part of the collective whole, and opposes using stem cells, compromising the cultural values to pursue research may cause social detachment and stunt research growth. [13] Based on local culture and moral philosophy, the permissibility of stem cell research depends on how embryo, stem cell, and cell line therapies relate to the community as a whole. Ubuntu is the expression of humanness, with the person’s identity drawn from the “’I am because we are’” value. [14] The decision in a collectivistic culture becomes one born of cultural context, and individual decisions give deference to others in the society.

Consent differs in cultures where thought and moral philosophy are based on a collective paradigm. So, applying Western bioethical concepts is unrealistic. For one, Africa is a diverse continent with many countries with different belief systems, access to health care, and reliance on traditional or Western medicines. Where traditional medicine is the primary treatment, the “’restrictive focus on biomedically-related bioethics’” [is] problematic in African contexts because it neglects bioethical issues raised by traditional systems.” [15] No single approach applies in all areas or contexts. Rather than evaluating the permissibility of ESC research according to Western concepts such as the four principles approach, different ethics approaches should prevail.

Another consideration is the socio-economic standing of countries. In parts of South Africa, researchers have not focused heavily on contributing to the stem cell discourse, either because it is not considered health care or a health science priority or because resources are unavailable. [16] Each country’s priorities differ given different social, political, and economic factors. In South Africa, for instance, areas such as maternal mortality, non-communicable diseases, telemedicine, and the strength of health systems need improvement and require more focus. [17] Stem cell research could benefit the population, but it also could divert resources from basic medical care. Researchers in South Africa adhere to the National Health Act and Medicines Control Act in South Africa and international guidelines; however, the Act is not strictly enforced, and there is no clear legislation for research conduct or ethical guidelines. [18]

Some parts of Africa condemn stem cell research. For example, 98.2 percent of the Tunisian population is Muslim. [19] Tunisia does not permit stem cell research because of moral conflict with a Fatwa. Religion heavily saturates the regulation and direction of research. [20] Stem cell use became permissible for reproductive purposes only recently, with tight restrictions preventing cells from being used in any research other than procedures concerning ART/IVF.  Their use is conditioned on consent, and available only to married couples. [21] The community's receptiveness to stem cell research depends on including communitarian African ethics.

c.     Asia

Some Asian countries also have a collective model of ethics and decision making. [22] In China, the ethics model promotes a sincere respect for life or human dignity, [23] based on protective medicine. This model, influenced by Traditional Chinese Medicine (TCM), [24] recognizes Qi as the vital energy delivered via the meridians of the body; it connects illness to body systems, the body’s entire constitution, and the universe for a holistic bond of nature, health, and quality of life. [25] Following a protective ethics model, and traditional customs of wholeness, investment in stem cell research is heavily desired for its applications in regenerative therapies, disease modeling, and protective medicines. In a survey of medical students and healthcare practitioners, 30.8 percent considered stem cell research morally unacceptable while 63.5 percent accepted medical research using human embryonic stem cells. Of these individuals, 89.9 percent supported increased funding for stem cell research. [26] The scientific community might not reflect the overall population. From 1997 to 2019, China spent a total of $576 million (USD) on stem cell research at 8,050 stem cell programs, increased published presence from 0.6 percent to 14.01 percent of total global stem cell publications as of 2014, and made significant strides in cell-based therapies for various medical conditions. [27] However, while China has made substantial investments in stem cell research and achieved notable progress in clinical applications, concerns linger regarding ethical oversight and transparency. [28] For example, the China Biosecurity Law, promoted by the National Health Commission and China Hospital Association, attempted to mitigate risks by introducing an institutional review board (IRB) in the regulatory bodies. 5800 IRBs registered with the Chinese Clinical Trial Registry since 2021. [29] However, issues still need to be addressed in implementing effective IRB review and approval procedures.

The substantial government funding and focus on scientific advancement have sometimes overshadowed considerations of regional cultures, ethnic minorities, and individual perspectives, particularly evident during the one-child policy era. As government policy adapts to promote public stability, such as the change from the one-child to the two-child policy, [30] research ethics should also adapt to ensure respect for the values of its represented peoples.

Japan is also relatively supportive of stem cell research and therapies. Japan has a more transparent regulatory framework, allowing for faster approval of regenerative medicine products, which has led to several advanced clinical trials and therapies. [31] South Korea is also actively engaged in stem cell research and has a history of breakthroughs in cloning and embryonic stem cells. [32] However, the field is controversial, and there are issues of scientific integrity. For example, the Korean FDA fast-tracked products for approval, [33] and in another instance, the oocyte source was unclear and possibly violated ethical standards. [34] Trust is important in research, as it builds collaborative foundations between colleagues, trial participant comfort, open-mindedness for complicated and sensitive discussions, and supports regulatory procedures for stakeholders. There is a need to respect the culture’s interest, engagement, and for research and clinical trials to be transparent and have ethical oversight to promote global research discourse and trust.

d.     Middle East

Countries in the Middle East have varying degrees of acceptance of or restrictions to policies related to using embryonic stem cells due to cultural and religious influences. Saudi Arabia has made significant contributions to stem cell research, and conducts research based on international guidelines for ethical conduct and under strict adherence to guidelines in accordance with Islamic principles. Specifically, the Saudi government and people require ESC research to adhere to Sharia law. In addition to umbilical and placental stem cells, [35] Saudi Arabia permits the use of embryonic stem cells as long as they come from miscarriages, therapeutic abortions permissible by Sharia law, or are left over from in vitro fertilization and donated to research. [36] Laws and ethical guidelines for stem cell research allow the development of research institutions such as the King Abdullah International Medical Research Center, which has a cord blood bank and a stem cell registry with nearly 10,000 donors. [37] Such volume and acceptance are due to the ethical ‘permissibility’ of the donor sources, which do not conflict with religious pillars. However, some researchers err on the side of caution, choosing not to use embryos or fetal tissue as they feel it is unethical to do so. [38]

Jordan has a positive research ethics culture. [39] However, there is a significant issue of lack of trust in researchers, with 45.23 percent (38.66 percent agreeing and 6.57 percent strongly agreeing) of Jordanians holding a low level of trust in researchers, compared to 81.34 percent of Jordanians agreeing that they feel safe to participate in a research trial. [40] Safety testifies to the feeling of confidence that adequate measures are in place to protect participants from harm, whereas trust in researchers could represent the confidence in researchers to act in the participants’ best interests, adhere to ethical guidelines, provide accurate information, and respect participants’ rights and dignity. One method to improve trust would be to address communication issues relevant to ESC. Legislation surrounding stem cell research has adopted specific language, especially concerning clarification “between ‘stem cells’ and ‘embryonic stem cells’” in translation. [41] Furthermore, legislation “mandates the creation of a national committee… laying out specific regulations for stem-cell banking in accordance with international standards.” [42] This broad regulation opens the door for future global engagement and maintains transparency. However, these regulations may also constrain the influence of research direction, pace, and accessibility of research outcomes.

e.     Europe

In the European Union (EU), ethics is also principle-based, but the principles of autonomy, dignity, integrity, and vulnerability are interconnected. [43] As such, the opportunity for cohesion and concessions between individuals’ thoughts and ideals allows for a more adaptable ethics model due to the flexible principles that relate to the human experience The EU has put forth a framework in its Convention for the Protection of Human Rights and Dignity of the Human Being allowing member states to take different approaches. Each European state applies these principles to its specific conventions, leading to or reflecting different acceptance levels of stem cell research. [44]

For example, in Germany, Lebenzusammenhang , or the coherence of life, references integrity in the unity of human culture. Namely, the personal sphere “should not be subject to external intervention.” [45]  Stem cell interventions could affect this concept of bodily completeness, leading to heavy restrictions. Under the Grundgesetz, human dignity and the right to life with physical integrity are paramount. [46] The Embryo Protection Act of 1991 made producing cell lines illegal. Cell lines can be imported if approved by the Central Ethics Commission for Stem Cell Research only if they were derived before May 2007. [47] Stem cell research respects the integrity of life for the embryo with heavy specifications and intense oversight. This is vastly different in Finland, where the regulatory bodies find research more permissible in IVF excess, but only up to 14 days after fertilization. [48] Spain’s approach differs still, with a comprehensive regulatory framework. [49] Thus, research regulation can be culture-specific due to variations in applied principles. Diverse cultures call for various approaches to ethical permissibility. [50] Only an adaptive-deliberative model can address the cultural constructions of self and achieve positive, culturally sensitive stem cell research practices. [51]

II.     Religious Perspectives on ESC

Embryonic stem cell sources are the main consideration within religious contexts. While individuals may not regard their own religious texts as authoritative or factual, religion can shape their foundations or perspectives.

The Qur'an states:

“And indeed We created man from a quintessence of clay. Then We placed within him a small quantity of nutfa (sperm to fertilize) in a safe place. Then We have fashioned the nutfa into an ‘alaqa (clinging clot or cell cluster), then We developed the ‘alaqa into mudgha (a lump of flesh), and We made mudgha into bones, and clothed the bones with flesh, then We brought it into being as a new creation. So Blessed is Allah, the Best of Creators.” [52]

Many scholars of Islam estimate the time of soul installment, marked by the angel breathing in the soul to bring the individual into creation, as 120 days from conception. [53] Personhood begins at this point, and the value of life would prohibit research or experimentation that could harm the individual. If the fetus is more than 120 days old, the time ensoulment is interpreted to occur according to Islamic law, abortion is no longer permissible. [54] There are a few opposing opinions about early embryos in Islamic traditions. According to some Islamic theologians, there is no ensoulment of the early embryo, which is the source of stem cells for ESC research. [55]

In Buddhism, the stance on stem cell research is not settled. The main tenets, the prohibition against harming or destroying others (ahimsa) and the pursuit of knowledge (prajña) and compassion (karuna), leave Buddhist scholars and communities divided. [56] Some scholars argue stem cell research is in accordance with the Buddhist tenet of seeking knowledge and ending human suffering. Others feel it violates the principle of not harming others. Finding the balance between these two points relies on the karmic burden of Buddhist morality. In trying to prevent ahimsa towards the embryo, Buddhist scholars suggest that to comply with Buddhist tenets, research cannot be done as the embryo has personhood at the moment of conception and would reincarnate immediately, harming the individual's ability to build their karmic burden. [57] On the other hand, the Bodhisattvas, those considered to be on the path to enlightenment or Nirvana, have given organs and flesh to others to help alleviate grieving and to benefit all. [58] Acceptance varies on applied beliefs and interpretations.

Catholicism does not support embryonic stem cell research, as it entails creation or destruction of human embryos. This destruction conflicts with the belief in the sanctity of life. For example, in the Old Testament, Genesis describes humanity as being created in God’s image and multiplying on the Earth, referencing the sacred rights to human conception and the purpose of development and life. In the Ten Commandments, the tenet that one should not kill has numerous interpretations where killing could mean murder or shedding of the sanctity of life, demonstrating the high value of human personhood. In other books, the theological conception of when life begins is interpreted as in utero, [59] highlighting the inviolability of life and its formation in vivo to make a religious point for accepting such research as relatively limited, if at all. [60] The Vatican has released ethical directives to help apply a theological basis to modern-day conflicts. The Magisterium of the Church states that “unless there is a moral certainty of not causing harm,” experimentation on fetuses, fertilized cells, stem cells, or embryos constitutes a crime. [61] Such procedures would not respect the human person who exists at these stages, according to Catholicism. Damages to the embryo are considered gravely immoral and illicit. [62] Although the Catholic Church officially opposes abortion, surveys demonstrate that many Catholic people hold pro-choice views, whether due to the context of conception, stage of pregnancy, threat to the mother’s life, or for other reasons, demonstrating that practicing members can also accept some but not all tenets. [63]

Some major Jewish denominations, such as the Reform, Conservative, and Reconstructionist movements, are open to supporting ESC use or research as long as it is for saving a life. [64] Within Judaism, the Talmud, or study, gives personhood to the child at birth and emphasizes that life does not begin at conception: [65]

“If she is found pregnant, until the fortieth day it is mere fluid,” [66]

Whereas most religions prioritize the status of human embryos, the Halakah (Jewish religious law) states that to save one life, most other religious laws can be ignored because it is in pursuit of preservation. [67] Stem cell research is accepted due to application of these religious laws.

We recognize that all religions contain subsets and sects. The variety of environmental and cultural differences within religious groups requires further analysis to respect the flexibility of religious thoughts and practices. We make no presumptions that all cultures require notions of autonomy or morality as under the common morality theory , which asserts a set of universal moral norms that all individuals share provides moral reasoning and guides ethical decisions. [68] We only wish to show that the interaction with morality varies between cultures and countries.

III.     A Flexible Ethical Approach

The plurality of different moral approaches described above demonstrates that there can be no universally acceptable uniform law for ESC on a global scale. Instead of developing one standard, flexible ethical applications must be continued. We recommend local guidelines that incorporate important cultural and ethical priorities.

While the Declaration of Helsinki is more relevant to people in clinical trials receiving ESC products, in keeping with the tradition of protections for research subjects, consent of the donor is an ethical requirement for ESC donation in many jurisdictions including the US, Canada, and Europe. [69] The Declaration of Helsinki provides a reference point for regulatory standards and could potentially be used as a universal baseline for obtaining consent prior to gamete or embryo donation.

For instance, in Columbia University’s egg donor program for stem cell research, donors followed standard screening protocols and “underwent counseling sessions that included information as to the purpose of oocyte donation for research, what the oocytes would be used for, the risks and benefits of donation, and process of oocyte stimulation” to ensure transparency for consent. [70] The program helped advance stem cell research and provided clear and safe research methods with paid participants. Though paid participation or covering costs of incidental expenses may not be socially acceptable in every culture or context, [71] and creating embryos for ESC research is illegal in many jurisdictions, Columbia’s program was effective because of the clear and honest communications with donors, IRBs, and related stakeholders.  This example demonstrates that cultural acceptance of scientific research and of the idea that an egg or embryo does not have personhood is likely behind societal acceptance of donating eggs for ESC research. As noted, many countries do not permit the creation of embryos for research.

Proper communication and education regarding the process and purpose of stem cell research may bolster comprehension and garner more acceptance. “Given the sensitive subject material, a complete consent process can support voluntary participation through trust, understanding, and ethical norms from the cultures and morals participants value. This can be hard for researchers entering countries of different socioeconomic stability, with different languages and different societal values. [72]

An adequate moral foundation in medical ethics is derived from the cultural and religious basis that informs knowledge and actions. [73] Understanding local cultural and religious values and their impact on research could help researchers develop humility and promote inclusion.

IV.     Concerns

Some may argue that if researchers all adhere to one ethics standard, protection will be satisfied across all borders, and the global public will trust researchers. However, defining what needs to be protected and how to define such research standards is very specific to the people to which standards are applied. We suggest that applying one uniform guide cannot accurately protect each individual because we all possess our own perceptions and interpretations of social values. [74] Therefore, the issue of not adjusting to the moral pluralism between peoples in applying one standard of ethics can be resolved by building out ethics models that can be adapted to different cultures and religions.

Other concerns include medical tourism, which may promote health inequities. [75] Some countries may develop and approve products derived from ESC research before others, compromising research ethics or drug approval processes. There are also concerns about the sale of unauthorized stem cell treatments, for example, those without FDA approval in the United States. Countries with robust research infrastructures may be tempted to attract medical tourists, and some customers will have false hopes based on aggressive publicity of unproven treatments. [76]

For example, in China, stem cell clinics can market to foreign clients who are not protected under the regulatory regimes. Companies employ a marketing strategy of “ethically friendly” therapies. Specifically, in the case of Beike, China’s leading stem cell tourism company and sprouting network, ethical oversight of administrators or health bureaus at one site has “the unintended consequence of shifting questionable activities to another node in Beike's diffuse network.” [77] In contrast, Jordan is aware of stem cell research’s potential abuse and its own status as a “health-care hub.” Jordan’s expanded regulations include preserving the interests of individuals in clinical trials and banning private companies from ESC research to preserve transparency and the integrity of research practices. [78]

The social priorities of the community are also a concern. The ISSCR explicitly states that guidelines “should be periodically revised to accommodate scientific advances, new challenges, and evolving social priorities.” [79] The adaptable ethics model extends this consideration further by addressing whether research is warranted given the varying degrees of socioeconomic conditions, political stability, and healthcare accessibilities and limitations. An ethical approach would require discussion about resource allocation and appropriate distribution of funds. [80]

While some religions emphasize the sanctity of life from conception, which may lead to public opposition to ESC research, others encourage ESC research due to its potential for healing and alleviating human pain. Many countries have special regulations that balance local views on embryonic personhood, the benefits of research as individual or societal goods, and the protection of human research subjects. To foster understanding and constructive dialogue, global policy frameworks should prioritize the protection of universal human rights, transparency, and informed consent. In addition to these foundational global policies, we recommend tailoring local guidelines to reflect the diverse cultural and religious perspectives of the populations they govern. Ethics models should be adapted to local populations to effectively establish research protections, growth, and possibilities of stem cell research.

For example, in countries with strong beliefs in the moral sanctity of embryos or heavy religious restrictions, an adaptive model can allow for discussion instead of immediate rejection. In countries with limited individual rights and voice in science policy, an adaptive model ensures cultural, moral, and religious views are taken into consideration, thereby building social inclusion. While this ethical consideration by the government may not give a complete voice to every individual, it will help balance policies and maintain the diverse perspectives of those it affects. Embracing an adaptive ethics model of ESC research promotes open-minded dialogue and respect for the importance of human belief and tradition. By actively engaging with cultural and religious values, researchers can better handle disagreements and promote ethical research practices that benefit each society.

This brief exploration of the religious and cultural differences that impact ESC research reveals the nuances of relative ethics and highlights a need for local policymakers to apply a more intense adaptive model.

[1] Poliwoda, S., Noor, N., Downs, E., Schaaf, A., Cantwell, A., Ganti, L., Kaye, A. D., Mosel, L. I., Carroll, C. B., Viswanath, O., & Urits, I. (2022). Stem cells: a comprehensive review of origins and emerging clinical roles in medical practice.  Orthopedic reviews ,  14 (3), 37498. https://doi.org/10.52965/001c.37498

[2] Poliwoda, S., Noor, N., Downs, E., Schaaf, A., Cantwell, A., Ganti, L., Kaye, A. D., Mosel, L. I., Carroll, C. B., Viswanath, O., & Urits, I. (2022). Stem cells: a comprehensive review of origins and emerging clinical roles in medical practice.  Orthopedic reviews ,  14 (3), 37498. https://doi.org/10.52965/001c.37498

[3] International Society for Stem Cell Research. (2023). Laboratory-based human embryonic stem cell research, embryo research, and related research activities . International Society for Stem Cell Research. https://www.isscr.org/guidelines/blog-post-title-one-ed2td-6fcdk ; Kimmelman, J., Hyun, I., Benvenisty, N.  et al.  Policy: Global standards for stem-cell research.  Nature   533 , 311–313 (2016). https://doi.org/10.1038/533311a

[4] International Society for Stem Cell Research. (2023). Laboratory-based human embryonic stem cell research, embryo research, and related research activities . International Society for Stem Cell Research. https://www.isscr.org/guidelines/blog-post-title-one-ed2td-6fcdk

[5] Concerning the moral philosophies of stem cell research, our paper does not posit a personal moral stance nor delve into the “when” of human life begins. To read further about the philosophical debate, consider the following sources:

Sandel M. J. (2004). Embryo ethics--the moral logic of stem-cell research.  The New England journal of medicine ,  351 (3), 207–209. https://doi.org/10.1056/NEJMp048145 ; George, R. P., & Lee, P. (2020, September 26). Acorns and Embryos . The New Atlantis. https://www.thenewatlantis.com/publications/acorns-and-embryos ; Sagan, A., & Singer, P. (2007). The moral status of stem cells. Metaphilosophy , 38 (2/3), 264–284. http://www.jstor.org/stable/24439776 ; McHugh P. R. (2004). Zygote and "clonote"--the ethical use of embryonic stem cells.  The New England journal of medicine ,  351 (3), 209–211. https://doi.org/10.1056/NEJMp048147 ; Kurjak, A., & Tripalo, A. (2004). The facts and doubts about beginning of the human life and personality.  Bosnian journal of basic medical sciences ,  4 (1), 5–14. https://doi.org/10.17305/bjbms.2004.3453

[6] Vazin, T., & Freed, W. J. (2010). Human embryonic stem cells: derivation, culture, and differentiation: a review.  Restorative neurology and neuroscience ,  28 (4), 589–603. https://doi.org/10.3233/RNN-2010-0543

[7] Socially, at its core, the Western approach to ethics is widely principle-based, autonomy being one of the key factors to ensure a fundamental respect for persons within research. For information regarding autonomy in research, see: Department of Health, Education, and Welfare, & National Commission for the Protection of Human Subjects of Biomedical and Behavioral Research (1978). The Belmont Report. Ethical principles and guidelines for the protection of human subjects of research.; For a more in-depth review of autonomy within the US, see: Beauchamp, T. L., & Childress, J. F. (1994). Principles of Biomedical Ethics . Oxford University Press.

[8] Sherley v. Sebelius , 644 F.3d 388 (D.C. Cir. 2011), citing 45 C.F.R. 46.204(b) and [42 U.S.C. § 289g(b)]. https://www.cadc.uscourts.gov/internet/opinions.nsf/6c690438a9b43dd685257a64004ebf99/$file/11-5241-1391178.pdf

[9] Stem Cell Research Enhancement Act of 2005, H. R. 810, 109 th Cong. (2001). https://www.govtrack.us/congress/bills/109/hr810/text ; Bush, G. W. (2006, July 19). Message to the House of Representatives . National Archives and Records Administration. https://georgewbush-whitehouse.archives.gov/news/releases/2006/07/20060719-5.html

[10] National Archives and Records Administration. (2009, March 9). Executive order 13505 -- removing barriers to responsible scientific research involving human stem cells . National Archives and Records Administration. https://obamawhitehouse.archives.gov/the-press-office/removing-barriers-responsible-scientific-research-involving-human-stem-cells

[11] Hurlbut, W. B. (2006). Science, Religion, and the Politics of Stem Cells.  Social Research ,  73 (3), 819–834. http://www.jstor.org/stable/40971854

[12] Akpa-Inyang, Francis & Chima, Sylvester. (2021). South African traditional values and beliefs regarding informed consent and limitations of the principle of respect for autonomy in African communities: a cross-cultural qualitative study. BMC Medical Ethics . 22. 10.1186/s12910-021-00678-4.

[13] Source for further reading: Tangwa G. B. (2007). Moral status of embryonic stem cells: perspective of an African villager. Bioethics , 21(8), 449–457. https://doi.org/10.1111/j.1467-8519.2007.00582.x , see also Mnisi, F. M. (2020). An African analysis based on ethics of Ubuntu - are human embryonic stem cell patents morally justifiable? African Insight , 49 (4).

[14] Jecker, N. S., & Atuire, C. (2021). Bioethics in Africa: A contextually enlightened analysis of three cases. Developing World Bioethics , 22 (2), 112–122. https://doi.org/10.1111/dewb.12324

[15] Jecker, N. S., & Atuire, C. (2021). Bioethics in Africa: A contextually enlightened analysis of three cases. Developing World Bioethics, 22(2), 112–122. https://doi.org/10.1111/dewb.12324

[16] Jackson, C.S., Pepper, M.S. Opportunities and barriers to establishing a cell therapy programme in South Africa.  Stem Cell Res Ther   4 , 54 (2013). https://doi.org/10.1186/scrt204 ; Pew Research Center. (2014, May 1). Public health a major priority in African nations . Pew Research Center’s Global Attitudes Project. https://www.pewresearch.org/global/2014/05/01/public-health-a-major-priority-in-african-nations/

[17] Department of Health Republic of South Africa. (2021). Health Research Priorities (revised) for South Africa 2021-2024 . National Health Research Strategy. https://www.health.gov.za/wp-content/uploads/2022/05/National-Health-Research-Priorities-2021-2024.pdf

[18] Oosthuizen, H. (2013). Legal and Ethical Issues in Stem Cell Research in South Africa. In: Beran, R. (eds) Legal and Forensic Medicine. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-32338-6_80 , see also: Gaobotse G (2018) Stem Cell Research in Africa: Legislation and Challenges. J Regen Med 7:1. doi: 10.4172/2325-9620.1000142

[19] United States Bureau of Citizenship and Immigration Services. (1998). Tunisia: Information on the status of Christian conversions in Tunisia . UNHCR Web Archive. https://webarchive.archive.unhcr.org/20230522142618/https://www.refworld.org/docid/3df0be9a2.html

[20] Gaobotse, G. (2018) Stem Cell Research in Africa: Legislation and Challenges. J Regen Med 7:1. doi: 10.4172/2325-9620.1000142

[21] Kooli, C. Review of assisted reproduction techniques, laws, and regulations in Muslim countries.  Middle East Fertil Soc J   24 , 8 (2020). https://doi.org/10.1186/s43043-019-0011-0 ; Gaobotse, G. (2018) Stem Cell Research in Africa: Legislation and Challenges. J Regen Med 7:1. doi: 10.4172/2325-9620.1000142

[22] Pang M. C. (1999). Protective truthfulness: the Chinese way of safeguarding patients in informed treatment decisions. Journal of medical ethics , 25(3), 247–253. https://doi.org/10.1136/jme.25.3.247

[23] Wang, L., Wang, F., & Zhang, W. (2021). Bioethics in China’s biosecurity law: Forms, effects, and unsettled issues. Journal of law and the biosciences , 8(1).  https://doi.org/10.1093/jlb/lsab019 https://academic.oup.com/jlb/article/8/1/lsab019/6299199

[24] Wang, Y., Xue, Y., & Guo, H. D. (2022). Intervention effects of traditional Chinese medicine on stem cell therapy of myocardial infarction.  Frontiers in pharmacology ,  13 , 1013740. https://doi.org/10.3389/fphar.2022.1013740

[25] Li, X.-T., & Zhao, J. (2012). Chapter 4: An Approach to the Nature of Qi in TCM- Qi and Bioenergy. In Recent Advances in Theories and Practice of Chinese Medicine (p. 79). InTech.

[26] Luo, D., Xu, Z., Wang, Z., & Ran, W. (2021). China's Stem Cell Research and Knowledge Levels of Medical Practitioners and Students.  Stem cells international ,  2021 , 6667743. https://doi.org/10.1155/2021/6667743

[27] Luo, D., Xu, Z., Wang, Z., & Ran, W. (2021). China's Stem Cell Research and Knowledge Levels of Medical Practitioners and Students.  Stem cells international ,  2021 , 6667743. https://doi.org/10.1155/2021/6667743

[28] Zhang, J. Y. (2017). Lost in translation? accountability and governance of Clinical Stem Cell Research in China. Regenerative Medicine , 12 (6), 647–656. https://doi.org/10.2217/rme-2017-0035

[29] Wang, L., Wang, F., & Zhang, W. (2021). Bioethics in China’s biosecurity law: Forms, effects, and unsettled issues. Journal of law and the biosciences , 8(1).  https://doi.org/10.1093/jlb/lsab019 https://academic.oup.com/jlb/article/8/1/lsab019/6299199

[30] Chen, H., Wei, T., Wang, H.  et al.  Association of China’s two-child policy with changes in number of births and birth defects rate, 2008–2017.  BMC Public Health   22 , 434 (2022). https://doi.org/10.1186/s12889-022-12839-0

[31] Azuma, K. Regulatory Landscape of Regenerative Medicine in Japan.  Curr Stem Cell Rep   1 , 118–128 (2015). https://doi.org/10.1007/s40778-015-0012-6

[32] Harris, R. (2005, May 19). Researchers Report Advance in Stem Cell Production . NPR. https://www.npr.org/2005/05/19/4658967/researchers-report-advance-in-stem-cell-production

[33] Park, S. (2012). South Korea steps up stem-cell work.  Nature . https://doi.org/10.1038/nature.2012.10565

[34] Resnik, D. B., Shamoo, A. E., & Krimsky, S. (2006). Fraudulent human embryonic stem cell research in South Korea: lessons learned.  Accountability in research ,  13 (1), 101–109. https://doi.org/10.1080/08989620600634193 .

[35] Alahmad, G., Aljohani, S., & Najjar, M. F. (2020). Ethical challenges regarding the use of stem cells: interviews with researchers from Saudi Arabia. BMC medical ethics, 21(1), 35. https://doi.org/10.1186/s12910-020-00482-6

[36] Association for the Advancement of Blood and Biotherapies.  https://www.aabb.org/regulatory-and-advocacy/regulatory-affairs/regulatory-for-cellular-therapies/international-competent-authorities/saudi-arabia

[37] Alahmad, G., Aljohani, S., & Najjar, M. F. (2020). Ethical challenges regarding the use of stem cells: Interviews with researchers from Saudi Arabia.  BMC medical ethics ,  21 (1), 35. https://doi.org/10.1186/s12910-020-00482-6

[38] Alahmad, G., Aljohani, S., & Najjar, M. F. (2020). Ethical challenges regarding the use of stem cells: Interviews with researchers from Saudi Arabia. BMC medical ethics , 21(1), 35. https://doi.org/10.1186/s12910-020-00482-6

Culturally, autonomy practices follow a relational autonomy approach based on a paternalistic deontological health care model. The adherence to strict international research policies and religious pillars within the regulatory environment is a great foundation for research ethics. However, there is a need to develop locally targeted ethics approaches for research (as called for in Alahmad, G., Aljohani, S., & Najjar, M. F. (2020). Ethical challenges regarding the use of stem cells: interviews with researchers from Saudi Arabia. BMC medical ethics, 21(1), 35. https://doi.org/10.1186/s12910-020-00482-6), this decision-making approach may help advise a research decision model. For more on the clinical cultural autonomy approaches, see: Alabdullah, Y. Y., Alzaid, E., Alsaad, S., Alamri, T., Alolayan, S. W., Bah, S., & Aljoudi, A. S. (2022). Autonomy and paternalism in Shared decision‐making in a Saudi Arabian tertiary hospital: A cross‐sectional study. Developing World Bioethics , 23 (3), 260–268. https://doi.org/10.1111/dewb.12355 ; Bukhari, A. A. (2017). Universal Principles of Bioethics and Patient Rights in Saudi Arabia (Doctoral dissertation, Duquesne University). https://dsc.duq.edu/etd/124; Ladha, S., Nakshawani, S. A., Alzaidy, A., & Tarab, B. (2023, October 26). Islam and Bioethics: What We All Need to Know . Columbia University School of Professional Studies. https://sps.columbia.edu/events/islam-and-bioethics-what-we-all-need-know

[39] Ababneh, M. A., Al-Azzam, S. I., Alzoubi, K., Rababa’h, A., & Al Demour, S. (2021). Understanding and attitudes of the Jordanian public about clinical research ethics.  Research Ethics ,  17 (2), 228-241.  https://doi.org/10.1177/1747016120966779

[40] Ababneh, M. A., Al-Azzam, S. I., Alzoubi, K., Rababa’h, A., & Al Demour, S. (2021). Understanding and attitudes of the Jordanian public about clinical research ethics.  Research Ethics ,  17 (2), 228-241.  https://doi.org/10.1177/1747016120966779

[41] Dajani, R. (2014). Jordan’s stem-cell law can guide the Middle East.  Nature  510, 189. https://doi.org/10.1038/510189a

[42] Dajani, R. (2014). Jordan’s stem-cell law can guide the Middle East.  Nature  510, 189. https://doi.org/10.1038/510189a

[43] The EU’s definition of autonomy relates to the capacity for creating ideas, moral insight, decisions, and actions without constraint, personal responsibility, and informed consent. However, the EU views autonomy as not completely able to protect individuals and depends on other principles, such as dignity, which “expresses the intrinsic worth and fundamental equality of all human beings.” Rendtorff, J.D., Kemp, P. (2019). Four Ethical Principles in European Bioethics and Biolaw: Autonomy, Dignity, Integrity and Vulnerability. In: Valdés, E., Lecaros, J. (eds) Biolaw and Policy in the Twenty-First Century. International Library of Ethics, Law, and the New Medicine, vol 78. Springer, Cham. https://doi.org/10.1007/978-3-030-05903-3_3

[44] Council of Europe. Convention for the protection of Human Rights and Dignity of the Human Being with regard to the Application of Biology and Medicine: Convention on Human Rights and Biomedicine (ETS No. 164) https://www.coe.int/en/web/conventions/full-list?module=treaty-detail&treatynum=164 (forbidding the creation of embryos for research purposes only, and suggests embryos in vitro have protections.); Also see Drabiak-Syed B. K. (2013). New President, New Human Embryonic Stem Cell Research Policy: Comparative International Perspectives and Embryonic Stem Cell Research Laws in France.  Biotechnology Law Report ,  32 (6), 349–356. https://doi.org/10.1089/blr.2013.9865

[45] Rendtorff, J.D., Kemp, P. (2019). Four Ethical Principles in European Bioethics and Biolaw: Autonomy, Dignity, Integrity and Vulnerability. In: Valdés, E., Lecaros, J. (eds) Biolaw and Policy in the Twenty-First Century. International Library of Ethics, Law, and the New Medicine, vol 78. Springer, Cham. https://doi.org/10.1007/978-3-030-05903-3_3

[46] Tomuschat, C., Currie, D. P., Kommers, D. P., & Kerr, R. (Trans.). (1949, May 23). Basic law for the Federal Republic of Germany. https://www.btg-bestellservice.de/pdf/80201000.pdf

[47] Regulation of Stem Cell Research in Germany . Eurostemcell. (2017, April 26). https://www.eurostemcell.org/regulation-stem-cell-research-germany

[48] Regulation of Stem Cell Research in Finland . Eurostemcell. (2017, April 26). https://www.eurostemcell.org/regulation-stem-cell-research-finland

[49] Regulation of Stem Cell Research in Spain . Eurostemcell. (2017, April 26). https://www.eurostemcell.org/regulation-stem-cell-research-spain

[50] Some sources to consider regarding ethics models or regulatory oversights of other cultures not covered:

Kara MA. Applicability of the principle of respect for autonomy: the perspective of Turkey. J Med Ethics. 2007 Nov;33(11):627-30. doi: 10.1136/jme.2006.017400. PMID: 17971462; PMCID: PMC2598110.

Ugarte, O. N., & Acioly, M. A. (2014). The principle of autonomy in Brazil: one needs to discuss it ...  Revista do Colegio Brasileiro de Cirurgioes ,  41 (5), 374–377. https://doi.org/10.1590/0100-69912014005013

Bharadwaj, A., & Glasner, P. E. (2012). Local cells, global science: The rise of embryonic stem cell research in India . Routledge.

For further research on specific European countries regarding ethical and regulatory framework, we recommend this database: Regulation of Stem Cell Research in Europe . Eurostemcell. (2017, April 26). https://www.eurostemcell.org/regulation-stem-cell-research-europe   

[51] Klitzman, R. (2006). Complications of culture in obtaining informed consent. The American Journal of Bioethics, 6(1), 20–21. https://doi.org/10.1080/15265160500394671 see also: Ekmekci, P. E., & Arda, B. (2017). Interculturalism and Informed Consent: Respecting Cultural Differences without Breaching Human Rights.  Cultura (Iasi, Romania) ,  14 (2), 159–172.; For why trust is important in research, see also: Gray, B., Hilder, J., Macdonald, L., Tester, R., Dowell, A., & Stubbe, M. (2017). Are research ethics guidelines culturally competent?  Research Ethics ,  13 (1), 23-41.  https://doi.org/10.1177/1747016116650235

[52] The Qur'an  (M. Khattab, Trans.). (1965). Al-Mu’minun, 23: 12-14. https://quran.com/23

[53] Lenfest, Y. (2017, December 8). Islam and the beginning of human life . Bill of Health. https://blog.petrieflom.law.harvard.edu/2017/12/08/islam-and-the-beginning-of-human-life/

[54] Aksoy, S. (2005). Making regulations and drawing up legislation in Islamic countries under conditions of uncertainty, with special reference to embryonic stem cell research. Journal of Medical Ethics , 31: 399-403.; see also: Mahmoud, Azza. "Islamic Bioethics: National Regulations and Guidelines of Human Stem Cell Research in the Muslim World." Master's thesis, Chapman University, 2022. https://doi.org/10.36837/ chapman.000386

[55] Rashid, R. (2022). When does Ensoulment occur in the Human Foetus. Journal of the British Islamic Medical Association , 12 (4). ISSN 2634 8071. https://www.jbima.com/wp-content/uploads/2023/01/2-Ethics-3_-Ensoulment_Rafaqat.pdf.

[56] Sivaraman, M. & Noor, S. (2017). Ethics of embryonic stem cell research according to Buddhist, Hindu, Catholic, and Islamic religions: perspective from Malaysia. Asian Biomedicine,8(1) 43-52.  https://doi.org/10.5372/1905-7415.0801.260

[57] Jafari, M., Elahi, F., Ozyurt, S. & Wrigley, T. (2007). 4. Religious Perspectives on Embryonic Stem Cell Research. In K. Monroe, R. Miller & J. Tobis (Ed.),  Fundamentals of the Stem Cell Debate: The Scientific, Religious, Ethical, and Political Issues  (pp. 79-94). Berkeley: University of California Press.  https://escholarship.org/content/qt9rj0k7s3/qt9rj0k7s3_noSplash_f9aca2e02c3777c7fb76ea768ba458f0.pdf https://doi.org/10.1525/9780520940994-005

[58] Lecso, P. A. (1991). The Bodhisattva Ideal and Organ Transplantation.  Journal of Religion and Health ,  30 (1), 35–41. http://www.jstor.org/stable/27510629 ; Bodhisattva, S. (n.d.). The Key of Becoming a Bodhisattva . A Guide to the Bodhisattva Way of Life. http://www.buddhism.org/Sutras/2/BodhisattvaWay.htm

[59] There is no explicit religious reference to when life begins or how to conduct research that interacts with the concept of life. However, these are relevant verses pertaining to how the fetus is viewed. (( King James Bible . (1999). Oxford University Press. (original work published 1769))

Jerimiah 1: 5 “Before I formed thee in the belly I knew thee; and before thou camest forth out of the womb I sanctified thee…”

In prophet Jerimiah’s insight, God set him apart as a person known before childbirth, a theme carried within the Psalm of David.

Psalm 139: 13-14 “…Thou hast covered me in my mother's womb. I will praise thee; for I am fearfully and wonderfully made…”

These verses demonstrate David’s respect for God as an entity that would know of all man’s thoughts and doings even before birth.

[60] It should be noted that abortion is not supported as well.

[61] The Vatican. (1987, February 22). Instruction on Respect for Human Life in Its Origin and on the Dignity of Procreation Replies to Certain Questions of the Day . Congregation For the Doctrine of the Faith. https://www.vatican.va/roman_curia/congregations/cfaith/documents/rc_con_cfaith_doc_19870222_respect-for-human-life_en.html

[62] The Vatican. (2000, August 25). Declaration On the Production and the Scientific and Therapeutic Use of Human Embryonic Stem Cells . Pontifical Academy for Life. https://www.vatican.va/roman_curia/pontifical_academies/acdlife/documents/rc_pa_acdlife_doc_20000824_cellule-staminali_en.html ; Ohara, N. (2003). Ethical Consideration of Experimentation Using Living Human Embryos: The Catholic Church’s Position on Human Embryonic Stem Cell Research and Human Cloning. Department of Obstetrics and Gynecology . Retrieved from https://article.imrpress.com/journal/CEOG/30/2-3/pii/2003018/77-81.pdf.

[63] Smith, G. A. (2022, May 23). Like Americans overall, Catholics vary in their abortion views, with regular mass attenders most opposed . Pew Research Center. https://www.pewresearch.org/short-reads/2022/05/23/like-americans-overall-catholics-vary-in-their-abortion-views-with-regular-mass-attenders-most-opposed/

[64] Rosner, F., & Reichman, E. (2002). Embryonic stem cell research in Jewish law. Journal of halacha and contemporary society , (43), 49–68.; Jafari, M., Elahi, F., Ozyurt, S. & Wrigley, T. (2007). 4. Religious Perspectives on Embryonic Stem Cell Research. In K. Monroe, R. Miller & J. Tobis (Ed.),  Fundamentals of the Stem Cell Debate: The Scientific, Religious, Ethical, and Political Issues  (pp. 79-94). Berkeley: University of California Press.  https://escholarship.org/content/qt9rj0k7s3/qt9rj0k7s3_noSplash_f9aca2e02c3777c7fb76ea768ba458f0.pdf https://doi.org/10.1525/9780520940994-005

[65] Schenker J. G. (2008). The beginning of human life: status of embryo. Perspectives in Halakha (Jewish Religious Law).  Journal of assisted reproduction and genetics ,  25 (6), 271–276. https://doi.org/10.1007/s10815-008-9221-6

[66] Ruttenberg, D. (2020, May 5). The Torah of Abortion Justice (annotated source sheet) . Sefaria. https://www.sefaria.org/sheets/234926.7?lang=bi&with=all&lang2=en

[67] Jafari, M., Elahi, F., Ozyurt, S. & Wrigley, T. (2007). 4. Religious Perspectives on Embryonic Stem Cell Research. In K. Monroe, R. Miller & J. Tobis (Ed.),  Fundamentals of the Stem Cell Debate: The Scientific, Religious, Ethical, and Political Issues  (pp. 79-94). Berkeley: University of California Press.  https://escholarship.org/content/qt9rj0k7s3/qt9rj0k7s3_noSplash_f9aca2e02c3777c7fb76ea768ba458f0.pdf https://doi.org/10.1525/9780520940994-005

[68] Gert, B. (2007). Common morality: Deciding what to do . Oxford Univ. Press.

[69] World Medical Association (2013). World Medical Association Declaration of Helsinki: ethical principles for medical research involving human subjects. JAMA , 310(20), 2191–2194. https://doi.org/10.1001/jama.2013.281053 Declaration of Helsinki – WMA – The World Medical Association .; see also: National Commission for the Protection of Human Subjects of Biomedical and Behavioral Research. (1979).  The Belmont report: Ethical principles and guidelines for the protection of human subjects of research . U.S. Department of Health and Human Services.  https://www.hhs.gov/ohrp/regulations-and-policy/belmont-report/read-the-belmont-report/index.html

[70] Zakarin Safier, L., Gumer, A., Kline, M., Egli, D., & Sauer, M. V. (2018). Compensating human subjects providing oocytes for stem cell research: 9-year experience and outcomes.  Journal of assisted reproduction and genetics ,  35 (7), 1219–1225. https://doi.org/10.1007/s10815-018-1171-z https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6063839/ see also: Riordan, N. H., & Paz Rodríguez, J. (2021). Addressing concerns regarding associated costs, transparency, and integrity of research in recent stem cell trial. Stem Cells Translational Medicine , 10 (12), 1715–1716. https://doi.org/10.1002/sctm.21-0234

[71] Klitzman, R., & Sauer, M. V. (2009). Payment of egg donors in stem cell research in the USA.  Reproductive biomedicine online ,  18 (5), 603–608. https://doi.org/10.1016/s1472-6483(10)60002-8

[72] Krosin, M. T., Klitzman, R., Levin, B., Cheng, J., & Ranney, M. L. (2006). Problems in comprehension of informed consent in rural and peri-urban Mali, West Africa.  Clinical trials (London, England) ,  3 (3), 306–313. https://doi.org/10.1191/1740774506cn150oa

[73] Veatch, Robert M.  Hippocratic, Religious, and Secular Medical Ethics: The Points of Conflict . Georgetown University Press, 2012.

[74] Msoroka, M. S., & Amundsen, D. (2018). One size fits not quite all: Universal research ethics with diversity.  Research Ethics ,  14 (3), 1-17.  https://doi.org/10.1177/1747016117739939

[75] Pirzada, N. (2022). The Expansion of Turkey’s Medical Tourism Industry.  Voices in Bioethics ,  8 . https://doi.org/10.52214/vib.v8i.9894

[76] Stem Cell Tourism: False Hope for Real Money . Harvard Stem Cell Institute (HSCI). (2023). https://hsci.harvard.edu/stem-cell-tourism , See also: Bissassar, M. (2017). Transnational Stem Cell Tourism: An ethical analysis.  Voices in Bioethics ,  3 . https://doi.org/10.7916/vib.v3i.6027

[77] Song, P. (2011) The proliferation of stem cell therapies in post-Mao China: problematizing ethical regulation,  New Genetics and Society , 30:2, 141-153, DOI:  10.1080/14636778.2011.574375

[78] Dajani, R. (2014). Jordan’s stem-cell law can guide the Middle East.  Nature  510, 189. https://doi.org/10.1038/510189a

[79] International Society for Stem Cell Research. (2024). Standards in stem cell research . International Society for Stem Cell Research. https://www.isscr.org/guidelines/5-standards-in-stem-cell-research

[80] Benjamin, R. (2013). People’s science bodies and rights on the Stem Cell Frontier . Stanford University Press.

Mifrah Hayath

SM Candidate Harvard Medical School, MS Biotechnology Johns Hopkins University

Olivia Bowers

MS Bioethics Columbia University (Disclosure: affiliated with Voices in Bioethics)

Article Details

This work is licensed under a Creative Commons Attribution 4.0 International License .

On Pillai’s Problem involving Lucas sequences of the second kind

• Open access
• Published: 13 May 2024
• Volume 10 , article number  51 , ( 2024 )

Cite this article

You have full access to this open access article

• Sebastian Heintze 1 &
• Volker Ziegler   ORCID: orcid.org/0000-0002-6744-586X 2  

32 Accesses

Explore all metrics

In this paper, we consider the Diophantine equation \( V_n - b^m = c \) for given integers b ,  c with \( b \ge 2 \) , whereas \( V_n \) varies among Lucas-Lehmer sequences of the second kind. We prove under some technical conditions that if the considered equation has at least three solutions ( n ,  m ) , then there is an upper bound on the size of the solutions as well as on the size of the coefficients in the characteristic polynomial of \( V_n \) .

Similar content being viewed by others

On the exponential Diophantine equation related to powers of two consecutive terms of Lucas sequences

Curious properties of generalized lucas numbers, on members of lucas sequences which are products of factorials.

Avoid common mistakes on your manuscript.

1 Introduction

In recent times, many authors considered Pillai-type problems involving linear recurrence sequences. For an overview we refer to [ 5 ]. Let us note that these problems are inspired by a result due to S. S. Pillai [ 9 , 10 ] who proved that for given, coprime integers a and b , there exists a constant \(c_0(a,b)\) , depending on a and b , such that for any \(c>c_0(a,b)\) the equation

has at most one solution \((n,m)\in \mathbb {Z}_{>0}^2\) .

Replacing the powers \(a^n\) and \(b^m\) by other linear recurrence sequences seems to be a challenging task which was supposedly picked up first by Ddamulira, Luca and Rakotomalala [ 4 ], where it was shown that

has at most one solution \((n,m)\in \mathbb {Z}_{>0}^2\) provided that

More generally, Chim, Pink and Ziegler [ 3 ] proved that for two fixed linear recurrence sequences \((U_n)_{n\in \mathbb {N}}\) , \((V_n)_{n\in \mathbb {N}}\) (with some restrictions) the equation

has at most one solution \((n,m)\in \mathbb {Z}_{>0}^2\) for all \(c\in \mathbb {Z}\) , except if c is in a finite and effectively computable set \(\mathcal {C} \subset \mathbb {Z}\) that depends on \((U_n)_{n\in \mathbb {N}}\) and \((V_n)_{n\in \mathbb {N}}\) .

In more recent years, several attempts were made to obtain uniform results, i.e. to allow to vary the recurrence sequences \((U_n)_{n\in \mathbb {N}}\) and \((V_n)_{n\in \mathbb {N}}\) in the result of Chim, Pink and Ziegler [ 3 ]. In particular, Batte, Ddamulira, Kasozi and Luca [ 1 ] showed that for all pairs \((p,c)\in \mathbb {P} \times \mathbb {Z}\) with p a prime, the Diophantine equation

has at most four solutions \((n,m)\in \mathbb {N}^2\) with \(n\ge 2\) . This result was generalized by Heintze, Tichy, Vukusic and Ziegler [ 5 ]. They proved that for a given linear recurrence sequence \((U_n)_{n\in \mathbb {N}}\) (with irrational simple dominant root \( \alpha > 1 \) having a positive Binet coefficient a , such that \( \alpha \) and a are multiplicatively independent and such that the equation \( \alpha ^z-1=a^x \alpha ^y \) has no solutions with \( z \in \mathbb {N}\) , \( x,y \in \mathbb {Q}\) and \( -1<x<0 \) ), there exist an effectively computable bound \( B\ge 2 \) such that for an integer \( b > B \) the Diophantine equation

has at most two solutions \((n,m)\in \mathbb {N}^2\) with \(n\ge N_0\) . Here \(N_0\) is an effectively computable constant depending only on \((U_n)_{n\in \mathbb {N}}\) .

In this paper, we want to fix b in ( 2 ) and let \((U_n)_{n\in \mathbb {N}}\) vary over a given family of recurrence sequences. In particular, we consider the case where \((U_n)_{n\in \mathbb {N}}\) varies over the family of Lucas-Lehmer sequences of the second kind.

2 Notations and statement of the main results

In this paper, we consider Lucas-Lehmer sequences of the second kind, that is we consider binary recurrence sequences of the form

where \(\alpha \) and \(\beta \) are the roots of the quadratic polynomial

with \(A^2\ne 4B\) and \(\gcd (A,B)=1\) . In the following, we will assume that \(V_n\) is non-degenerate, i.e. that \( \alpha /\beta \) is not a root of unity. More precisely, we assume \(A^2-4B>0\) and \(A\ne 0\) , since this implies that \(\alpha \) and \(\beta \) are distinct real numbers with \(|\alpha |\ne |\beta |\) . We will also assume that \(A>0\) , which results in \(V_n>0\) for all \(n\in \mathbb {N}\) . Then we consider the Diophantine equation

where \(b,c\in \mathbb {Z}\) with \(b>1\) are fixed.

Let \(0<\epsilon <1\) be a fixed real number and A ,  B coprime integers satisfying \( A^2-4B>0 \) . Assume that \(|B|<A^{2-\epsilon }\) as well as that the polynomial \(X^2-AX+B\) is irreducible and \(A \ge 32^{1/\epsilon }\) . Furthermore, assume that \(b\ge 2\) if \(c\ge 0\) and \(b\ge 3\) if \(c<0\) . Assume that Eq. ( 3 ) has three solutions \((n_1,m_1),(n_2,m_2),(n_3,m_3)\in \mathbb {N}^2\) with \(n_1>n_2>n_3\ge N_0(\epsilon )\) for the bound \(N_0(\epsilon )=\frac{3}{2\epsilon }\) . Then there exists an effectively computable constant \(C_1=C_1(\epsilon ,b)\) , depending only on \(\epsilon \) and b , such that \(n_1<C_1\) . In particular, we can choose

Let us note that the bound \(N_0=N_0(\epsilon )\) in Theorem 1 ensures that \(V_n\) is strictly increasing for \(n\ge N_0\) (see Lemma 9 below). Let us also mention that it is essential to exclude the case that \(V_{n_2}=V_{n_3}\) .

Although we can bound \(n_1\) in terms of b and \(\epsilon \) , our method does not provide upper bounds for A and | B |. However, in the case that we are more restrictive in the possible choice of B , we can prove also upper bounds for A and | B |.

Let \(\kappa \ge 1\) be a fixed real number and A ,  B coprime integers satisfying \( A^2-4B>0 \) . Assume that \(|B|<\kappa A\) as well as that the polynomial \(X^2-AX+B\) is irreducible. Furthermore, assume that \(b\ge 2\) if \(c\ge 0\) and \(b\ge 3\) if \(c<0\) . Assume that Eq. ( 3 ) has three solutions \((n_1,m_1),(n_2,m_2),(n_3,m_3)\in \mathbb {N}^2\) with \(n_1>n_2>n_3\ge 1\) . Then there exist effectively computable constants \(C_2=C_2(\kappa ,b)\) , depending only on \(\kappa \) and b , and \(C_3=C_3(b)\) , depending only on b , such that \(\log A<\max \{C_2,C_3\}\) . We can choose

A straight forward application of our bounds yields:

Corollary 3

Assume that \(|B|<A\) . If the Diophantine equation

with \(c\ge 0\) has three solutions \((n_1,m_1),(n_2,m_2),(n_3,m_3)\in \mathbb {N}^2\) with \(n_1>n_2>n_3\ge 1\) , then either

\( A<1024 \) or

\(n_1<2.3\cdot 10^{40}\) and \(\log A<4.48\cdot 10^{13}\) .

Another consequence of Theorem 2 together with the results of Chim, Pink and Ziegler [ 3 ] is that there exist only finitely many Diophantine equations of the form of ( 3 ) that admit more than two solutions, provided that \(|B|<\kappa A\) . The following corollary gives a precise statement.

Corollary 4

Let \(\kappa \ge 1\) be a fixed real number and \(b\ge 2\) a fixed integer. Then there exist at most finitely many, effectively computable 9-tuples \((A,B,c,n_1,m_1,n_2,m_2\) , \(n_3,m_3)\in \mathbb {Z}^9\) such that

A and B are coprime;

\(A \ge \max \{\kappa ^2,1024\}\) , \(|B|< \kappa A\) and \(A^2-4B>0\) ;

\(X^2-AX+B\) is irreducible;

if \(b=2\) , then \(c\ge 0\) ;

\(n_1>n_2>n_3\ge 1\) and \(m_1,m_2,m_3\ge 1\) ;

\(V_{n_i}(A,B)-b^{m_i}=c\) for \(i=1,2,3\) .

For any fixed value of c , we apply Theorem 2 and get an upper bound for A , independent of c . So there remain only finitely many, effectively computable possibilities for A and B . Thus we have finitely many possibilities for the recurrence \( V_n \) . Chim, Pink and Ziegler [ 3 ] proved that, for two in absolute values strictly increasing linear recurrences \( (X_n)_{n\ge N_0} \) and \( (Y_m)_{m\ge M_0} \) with multiplicatively independent dominant roots, there exists only finitely many, effectively computable integers c such that \( X_n - Y_m = c \) has more than one solution. First, we have to ensure that \(\alpha \) and b are multiplicatively independent. However, \(\alpha \) and b are multiplicatively dependent if and only if there exist integers x ,  y not both zero such that \(\alpha ^x=b^y\) . But \(\alpha ^x\) cannot be a rational number, unless \(x=0\) , since by our earlier assumptions \( A>0 \) and \( A^2-4B > 0 \) is not a perfect square. Second, we note that \( V_n \) is strictly increasing for \( n \ge 1 \) by Lemma 10 since \(A \ge \max \{\kappa ^2,1024\}\) implies \( A \ge 4\kappa +4 \) . Therefore we can apply their result in our situation and obtain that there are only finitely many, effectively computable values for c . Finally, we use Theorem 1 with \( \epsilon =\frac{1}{2} \) to bound the \( n_i \) . Clearly, the \( m_i \) can now be calculated. \(\square \)

Let us give a quick outline for the rest of the paper. In the next section we establish several lemmas concerning properties of Lucas sequences \(V_n\) under the restrictions that \(|B|<A^{2-\epsilon }\) and \(|B|<\kappa A\) , respectively, that we will frequently use throughout the paper. The main tool for the proofs of the main theorems are lower bounds for linear forms in logarithms of algebraic numbers. In Sect. 6 we establish bounds for \(n_1\) , which still depend on \(\log \alpha \) , following the usual approach (cf. [ 3 ]). In Sect. 7 , under the assumption that three solution exist, we obtain a system of inequalities involving linear forms in logarithms which contain \(\log \alpha \) . Combining these inequalities we obtain a linear form in logarithms which does no longer contain \(\log \alpha \) . Thus we obtain that Theorems 1 and 2 hold or one of the following two cases occurs:

\(n_1m_2-n_2m_1=0\) ;

\(m_2-m_3\ll \log n_1\) .

That each of these cases implies Theorems 1 and 2 is shown in the subsequent Sects. 8 and 9 .

3 Auxiliary results on Lucas sequences

Let \(\alpha \) and \(\beta \) be the roots of \(X^2-AX+B\) . By our assumptions, \(\alpha \) and \(\beta \) are distinct real numbers \(\notin \mathbb {Q}\) . Throughout the rest of the paper, we will assume that \( \alpha \) is the larger one, i.e. \(|\alpha |>|\beta |\) , which we can do since, by our assumptions, we have \(A > 0\) . Therefore we obtain

First, note that \(\alpha >1\) can be bounded in terms of A :

Assuming that \(|B|<A^2\) , we have \(\frac{A}{2}<\alpha <2A\) .

At some point in our proofs of Theorems 1 and 2 , we will use that \(\beta \) cannot be to close to 1. In particular, the following lemma will be needed.

Let \( A, B, \alpha , \beta \) be as above, in particular \( X^2-AX+B \) irreducible with real roots. Assume that \(A\ge 4\) . Then we have

First, let us note that the function \(f(x)=\frac{A-\sqrt{A^2-4x}}{2}\) is strictly increasing for all \(x<A^2/4\) . Moreover, we have \(f(A-1)=1\) and \(f(-A-1)=-1\) . By our assumption that \(X^2-AX+B\) is irreducible, a choice for B such that \(|\beta |=1\) is not admissible. Therefore we have

provided that \(A^2-2A+1\ge A^2-4A+8\) , which certainly holds for \(A\ge 7/2\) . Similar computations yield

provided that \(A\ge 4\) . \(\square \)

Next, we show that under our assumptions \(|\beta |\) is not to large.

Assume that \(|B|<A^{2-\epsilon }\) and that \(A^{\epsilon } \ge 8\) . Then we have \(\frac{\alpha }{|\beta |}>\frac{1}{2}A^{\epsilon }\) .

First we note that

From the observation

then it follows

\(\square \)

Assume that \(|B|<\kappa A\) and that \(A \ge 4 \kappa \) . Then we have \(|\beta |<2\kappa \) .

Let us now consider the function \(f(x)=\frac{2x}{A+\sqrt{A^2-4x}}\) . This function is strictly increasing with x since obviously the numerator is strictly increasing with x while the denominator is strictly decreasing with x . Therefore we obtain

since \(A\ge 4\kappa \) . \(\square \)

Now let us take a look at the recurrence sequence \( V_n \) .

Assume that \(|B|<A^{2-\epsilon }\) and \( A^{\epsilon } \ge 8 \) . Then \(V_n\) is strictly increasing for \(n\ge \frac{3}{2\epsilon }\) .

First, we note that

certainly holds if

Note that \(\frac{\alpha }{|\beta |}>\frac{1}{2}A^\epsilon \) , by Lemma 7 , and, by Lemma 5 ,

Moreover, note that the smallest possible value for \( \alpha \) is \(\frac{1+\sqrt{5}}{2}\) . Therefore ( 5 ) is certainly fulfilled if

Thus \(V_n\) is increasing if

or equivalently

Since the rational function \(f(x)=\frac{ax+b}{cx+d}\) is strictly increasing if \(ad-bc>0\) , strictly decreasing if \(ad-bc<0\) , and constant if \(ad-bc=0\) , we obtain that for

the Lucas sequence is strictly increasing. \(\square \)

Assume that \(|B|<\kappa A\) and \( A \ge 4\kappa + 4 \) . Then \(V_n\) is strictly increasing for \(n\ge 0\) .

By ( 5 ) we know that \(V_n\) is increasing for all \(n\ge 0\) if \(1>\frac{|\beta |+1}{\alpha -1}\) . By Lemma  5 , we have \(\alpha>\frac{A}{2} \ge 2\kappa +2>2\) and, using Lemma 8 , also \(|\beta |<2\kappa \) . Therefore we get

Note that assuming \(|B|<\kappa A\) and \(A\ge \kappa ^2\) implies \(|B|<A^{3/2}=A^{2-\epsilon }\) with \(\epsilon =1/2\) . Therefore all results that are proven under the assumption \(|B|<A^{2-\epsilon }\) with \(\epsilon =1/2\) also hold under the assumption \(|B|<\kappa A\) and \(A\ge \kappa ^2\) .

In view of this remark and in view of the proofs of the following lemmas, we will assume for the rest of the paper that one of the following two assumptions holds:

\(|B|<A^{2-\epsilon }\) , \(A^{\epsilon }\ge 32\) and \(N_0= \frac{3}{2\epsilon }\) ,

\(|B|<\kappa A\) , \(A\ge \max \{\kappa ^2,16\kappa +12,1024\}\) and \(N_0=1\) .

Let us note that the bound \(A\ge \kappa ^2\) and \(A\ge 1024\) in assumption A2 results in the useful fact that assumption A2 implies assumption A1 with \(\epsilon =\frac{1}{2}\) , but with \(N_0=1\) instead of \(\frac{3}{2\epsilon }\) . The assumption \(A\ge 16\kappa +12\) is mainly used in the proofs of the Lemmas 12 and 13 . Moreover, assumptions A1 and A2 both imply \( |B| < A^2 \) .

In view of the assumptions stated above, an important consequence of Lemmas  9 and 10 is the following:

Corollary 11

Let assumption A1 or A2 be in force and let us assume that ( 3 ) has two solutions \((n_1,m_1)\) and \((n_2,m_2)\) with \(n_1>n_2\ge N_0\) . Then \(m_1>m_2\) .

Let assumption A1 or A2 be in force and \(n\ge N_0\) . Then we have \(\frac{5}{4} \alpha ^n>V_n>\frac{3}{4} \alpha ^n\) .

Assume that A1 holds. Then, by Lemma 7 , we have

If A2 holds, by Lemma 8 , we have

Therefore in any case we get

Another lemma that will be used frequently is the following:

Let assumption A1 or A2 be in force and assume that Eq. ( 3 ) has two solutions \((n_1,m_1)\) and \((n_2,m_2)\) with \(n_1>n_2\ge N_0\) . Then we have

Assuming the existence of two different solutions implies by an application of Lemma  12 the inequality

which proves the first inequality.

For the second inequality, we apply again Lemma 12 to obtain

Since we assume in any case that \(\alpha>\frac{A}{2}>4\) , we get \(V_{n_1}-V_{n_2}> \frac{3}{8} \alpha ^{n_1}\) and thus

which yields the second inequality. \(\square \)

Finally, let us remind Carmichael’s theorem [ 2 , Theorem XXIV]:

Let A ,  B be coprime integers with \( A>0 \) and \( A^2-4B>0 \) . For any \(n\ne 1,3\) there exists a prime Footnote 1 p such that \(p\mid V_n\) , but \(p\not \mid V_m\) for all \(1 \le m<n\) , except for the case that \(n=6\) and \((A,B)=(1,-1)\) .

This lemma can be used to prove the following result:

Assume that \(c=0\) and \(A>1\) . Then the Diophantine Eq. ( 3 ) has at most one solution ( n ,  m ) with \(n\ge 1\) .

Assume that ( 3 ) has two solutions \((n_1,m_1), (n_2,m_2)\) with \(n_1>n_2\ge 1\) . Then by Carmichael’s primitive divisor theorem (Lemma 14 ) we deduce that \(n_1=3\) and \(n_2=1\) . Since \(V_1=A\) and \(V_3=A^3-3AB\) we obtain the system of equations

which yields

That is \(b\mid 3B\) . Since we assume that \(\gcd (A,B)=1\) and \( A>1 \) , we deduce \(b\mid 3\) and \(b=3\) . We also conclude that \(3\not \mid B\) . By considering 3-adic valuations, this yields \(m_1-m_2=1\) since \(m_2=0\) would imply \(A=1\) . Hence we have \(B=3^{2m_2-1}-1\) .

Note that we also assume \(A^2-4B>0\) which implies that

holds. But this is only possible for \(m_2=1\) and we conclude that \(A=3\) and \(B=2\) . Since \(X^2-3X+2=(X-2)(X-1)\) is not irreducible, this is not an admissible case. Therefore there exists at most one solution to ( 3 ). \(\square \)

4 Lower bounds for linear forms in logarithms

The main tool in proving our main theorems are lower bounds for linear forms in logarithms of algebraic numbers. In particular, we will use Matveev’s lower bound proven in [ 7 ]. Therefore let \(\eta \ne 0\) be an algebraic number of degree d and let

be the minimal polynomial of \(\eta \) . Then the absolute logarithmic Weil height is defined by

With this notation, the following result due to Matveev [ 7 ] holds:

(Theorem 2.2 with \(r=1\) in [ 7 ]) Denote by \(\eta _1, \ldots , \eta _N\) algebraic numbers, neither 0 nor 1, by \(\log \eta _1, \ldots , \log \eta _N\) determinations of their logarithms, by D the degree over \(\mathbb {Q}\) of the number field \(K = \mathbb {Q}(\eta _1,\ldots ,\eta _N)\) , and by \(b_1, \ldots , b_N\) rational integers with \(b_N\ne 0\) . Furthermore let \(\kappa =1\) if K is real and \(\kappa =2\) otherwise. For all integers j with \(1\le j\le N\) choose

Assume that

In our applications, we will be in the situation \(N \in \{2,3\}\) and \(K=\mathbb {Q}(\alpha )\subseteq \mathbb {R}\) , i.e. we have \(D=2\) and \( \kappa =1 \) . In this special case Matveev’s lower bounds take the following form:

Corollary 17

Let the notations and assumptions of Theorem 16 be in force. Furthermore, assume that K is a real quadratic number field and that \( \Lambda \ne 0 \) . Then we have

Let us note that the form of E is essential in our proof to obtain an absolute bound for \(n_1\) in Theorem 1 . Let us also note that in the case of \(N=2\) one could use the results of Laurent [ 6 ] to obtain numerically better values but with an \(\log (E)^2\) term instead. This would lead to numerically smaller upper bounds for concrete applications of our theorems. However, we refrain from the application of these results to keep our long and technical proof more concise.

In order to apply Matveev’s lower bounds, we provide some height computations. First, we note the following well known properties of the absolute logarithmic height (see for example [ 12 , Chapter 3] for a detailed reference):

For any \(\eta , \gamma \in \overline{\mathbb {Q}}\) and \(l \in \mathbb {Q}\) we have

Note that for a positive integer b we have \(h(b)=\log b\) and, with \( \alpha \) and \( \beta \) from Sect. 3 , we have

This together with the above mentioned properties yields for \( t\in \mathbb {Z}_{>0} \) the bound

One other important aspect in applying Matveev’s result (Theorem 16 ) is that the linear form \(\Lambda \) should not vanish. We will resolve this issue with the following lemma:

Assume that the Diophantine Eq. ( 3 ) has three solutions \((n_1,m_1)\) , \((n_2,m_2)\) , \((n_3,m_3)\in \mathbb {N}^2\) with \(n_1>n_2>n_3>0\) . Then we have

Assume that \(\Lambda _i=n_i\log \alpha -m_i\log b=0\) for some \(i\in \{1,2,3\}\) . But \(\Lambda _i=0\) implies \(\alpha ^{n_i}-b^{m_i}=0\) which results in view of ( 3 ) in

Since \(X^2-AX+B\) is irreducible, \(\alpha \) and \(\beta \) are Galois conjugates. Therefore, by applying the non-trivial automorphism of \(K=\mathbb {Q}(\alpha )\) to the equation \(\beta ^{n_i}=c\) , we obtain \(\alpha ^{n_i}=c\) since \(c\in \mathbb {Q}\) . But this implies \(\beta ^{n_i}=\alpha ^{n_i}\) , hence \(|\alpha |=|\beta |\) , a contradiction to our assumptions.

Now, let us assume that

This implies \(\alpha ^{n_1}-\alpha ^{n_2}=b^{m_1}-b^{m_2}\) which results in view of ( 3 ) in \(\beta ^{n_1}=\beta ^{n_2}\) . But then \(\beta =0\) or \( \beta \) is a root of unity. Both cases contradict our assumption that \(X^2-AX+B\) is irreducible and \(\beta \in \mathbb {R}\) . \(\square \)

Finally, we want to record three further elementary lemmas that will be helpful. The first lemma is a standard fact from real analysis.

If \(|x|\le \frac{1}{2}\) , then we have \( \left| \log (1+x)\right| \le 2|x| \) and

A direct application of Taylor’s theorem with a Cauchy and Lagrange remainder, respectively. \(\square \)

Next, we want to state another estimate from real analysis:

Let \(x\in \mathbb {R}\) and \( n \in \mathbb {N}\) such that \(|2nx|<\frac{1}{2}\) and \(n\ge 1\) . Then we have

Since the case \( x=0 \) is trivial, we may assume \( x \ne 0 \) . From the mean value theorem, we then get

The third lemma is due to Pethő and de Weger [ 8 ].

Let \(a,b \ge 0\) , \(h \ge 1\) and \(x\in \mathbb {R}\) be the largest solution of \(x=a + b(\log x)^h\) . If \(b > (e^2/h)^h\) , then

and if \(b\le (e^2/h)^h\) , then

A proof of this lemma can be found in [ 11 , Appendix B].

5 A lower bound for | c | in terms of \(n_1\) and \(\alpha \)

The purpose of this section is to prove a lower bound for | c |. In particular, we prove the following proposition:

Proposition 23

Assume that assumption A1 or A2 holds and assume that Diophantine Eq. ( 3 ) has two solutions \((n_1,m_1)\) and \((n_2,m_2)\) with \(n_1>n_2\ge N_0\) . Then we have

with \(K_0=2.69 \cdot 10^9 \log b\) .

Let us first take a look at the case

Here we get immediately

and are done. Now we can assume

We consider equation

The goal is to apply Matveev’s theorem (Theorem 16 ) with \(N=2\) . Note that with \(\eta _1=b\) and \(\eta _2=\alpha \) we choose \(A_1=2\log b\) and \(A_2=2\log \alpha \) , in view of Remark  4 , and obtain

Due to Lemma 13 we have

Therefore we obtain by Corollary 17 that

which implies the content of the proposition. \(\square \)

6 Bounds for \(n_1\) in terms of \(\log \alpha \)

In this section, we will assume that assumption A1 or A2 holds. However, in the proofs we will mainly consider the case that assumption A1 holds. Note that this is not a real restriction since assumption A2 implies assumption A1 with \(\epsilon =\frac{1}{2}\) and \(N_0=1\) instead of \(N_0=\frac{3}{2\epsilon }\) (cf. Remark 2 ). Also assume that Diophantine Eq. ( 3 ) has three solutions \((n_1,m_1)\) , \((n_2,m_2)\) , \((n_3,m_3)\) with \(n_1>n_2>n_3\ge N_0\) . In this section we follow the approach of Chim et al. [ 3 ] and prove upper bounds for \(n_1\) in terms of \(\alpha \) . To obtain explicit bounds and to keep track of the dependence on \(\log b\) and \(\log \alpha \) of the bounds we repeat their proof. This section also delivers the set up for the later sections which provide proofs of our main theorems. Moreover, note that the assumption that three solutions exist, simplifies the proof of Chim et al. [ 3 ].

The main result of this section is the following statement:

Proposition 24

Assume that assumption A1 or A2 holds and that Diophantine Eq. ( 3 ) has three solutions \((n_1,m_1)\) , \((n_2,m_2)\) , \((n_3,m_3)\) with \(n_1>n_2>n_3\ge N_0\) . Then we have

where we choose \(\epsilon =1/2\) in case that assumption A2 holds.

Since we assume the existence of two solutions, we have

and therefore obtain

Let us write \(\gamma :=\min \{\alpha ,\alpha /|\beta |\}\) . Note that we have \(\gamma>\frac{1}{2} A^\epsilon >\frac{1}{4} \alpha ^\epsilon \) , by Lemma  7 and Lemma  5 . With this notation we get the inequality

Note that, depending on whether \(|\beta |>1\) or \(|\beta |\le 1\) , we have

Therefore, using Lemma 13 , we obtain

First, let us assume that the maximum in ( 8 ) is \(\gamma ^{-n_1}\) . Under our assumptions, we have \(A^{\epsilon }\ge 32\) and \(n_1\ge 3\) , which implies \(7\gamma ^{-n_1}<\frac{1}{2}\) . Thus taking logarithms and applying Lemma 20 yields

We apply Matveev’s theorem (Theorem 16 ) with \(N=2\) . Note that with \(\eta _1=b\) and \(\eta _2=\alpha \) we choose \(A_1=2\log b\) and \(A_2=2\log \alpha \) , in view of Remark 4 , to obtain

Note that, due to Lemma 13 ,

Therefore we obtain from Corollary 17 that

where for the last inequality we used \( A^{\epsilon } \ge 32 \) . Thus we have

which, using Lemma 22 , proves Proposition 24 in this case. Note that this also proves, in this specific case, Theorem 1 .

Now we assume that the maximum in ( 8 ) is \(\alpha ^{n_2-n_1}\) . By our assumptions on A we have \(7\alpha ^{n_2-n_1}<\frac{1}{2}\) and obtain, by Lemma 20 ,

As computed before, an application of Matveev’s theorem yields

and therefore

For the rest of the proof of Proposition 24 , we will assume that ( 9 ) holds. Since we assume that a third solution exists, the statement of Lemma 13 also holds for \(m_2\) and \(n_2\) instead of \(m_1\) and \(n_1\) . In particular we have

Let us rewrite Eq. ( 7 ) again to obtain the inequality

As previously noted we have \(4\gamma ^{-n_1}<\frac{1}{2}\) and therefore we obtain

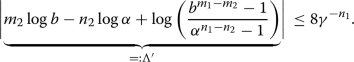
We aim to apply Matveev’s theorem to \(\Lambda '\) with \(\eta _3=\frac{b^{m_1-m_2}-1}{\alpha ^{n_1-n_2}-1}\) . Note that, due to Remark 4 and the properties of heights, we obtain

Thus we obtain \(E\le 2n_1\) as before, and from Matveev’s theorem

If we put \(n'=27.62 n_1\) and apply Lemma 22 to ( 11 ), then we end up with

which yields the content of Proposition 24 .

7 Combining linear forms of logarithms

As done before, let us assume that Diophantine Eq. ( 3 ) has three solutions \((n_1,m_1)\) , \((n_2,m_2)\) , \((n_3,m_3)\) with \(n_1>n_2>n_3\ge N_0\) . Again we assume that assumption A1 or A2 holds.

Let us reconsider inequality ( 8 ) with \(n_1,m_1,n_2,m_2\) replaced by \(n_2,m_2,n_3,m_3\) , respectively. Then we obtain

Let us assume for the next paragraphs that

Then, by applying Lemma 20 to ( 8 ) and ( 12 ), we obtain the system of inequalities

We eliminate the term \(\log \alpha \) from these inequalities by considering \(\Lambda _0=n_2\Lambda _1-n_1\Lambda _2\) and obtain the inequality

Let us write M for the maximum on the right hand side of ( 14 ). If \(n_2m_1-n_1m_2\ne 0\) , we obtain the inequality \(\log b \le M\) . Since we will study the case that \(n_2m_1-n_1m_2=0\) in Sect. 8 , we will assume for the rest of this section that \(n_2m_1-n_1m_2\ne 0\) , i.e. we have \(\log b \le M\) . Therefore we have to consider five different cases. In each case we want to find an upper bound for \(\log \alpha \) if possible:

The case \(M=12n_1 \alpha ^{n_3-n_2}\!\!:\) In this case we get

since we assume \(b\ge 2\) .

The case \(M=30 n_1 b^{m_3-m_2}\!\!:\) In this case we obtain

To obtain from this inequality a bound for \(\log \alpha \) is not straight forward and we will deal with this case in Sect. 9 .

The case \(M=24 n_1 \gamma ^{-n_2}\!\!:\) This case implies

and we obtain

The case \(M=28 n_2\alpha ^{n_2-n_1}\!\!\!:\) By a similar computation as in the first case, we obtain in this case the inequality

The case \(M=16 n_2\gamma ^{-n_1}\!\!\!:\) Almost the same computations as in the case that \(M=24 n_1 \gamma ^{-n_2}\) lead to

In the case that ( 13 ) does not hold, i.e. that \(M_0\ge 1/2\) , we obtain by similar computations in each of the five possibilities the following inequalities:

The case \(M_0=3 \alpha ^{n_3-n_2}\!\!:\) \(\log \alpha \le \log 6\) ;

The case \(M_0=\frac{15}{2} b^{m_3-m_2}\!\!:\) \(m_2-m_3\le 3\) ;

The case \(M_0=6 \gamma ^{-n_2}\!\!:\) \(\log \alpha \le \frac{\log 144}{\epsilon }\) ;

The case \(M_0=7 \alpha ^{n_2-n_1}\!\!:\) \(\log \alpha \le \log 14\) ;

The case \(M_0=4 \gamma ^{-n_1}\!\!:\) \(\log \alpha \le \frac{\log 64}{\epsilon }\) .

Let us recap what we have proven so far in the following lemma:

Assume that assumption A1 or A2 holds and assume that Diophantine Eq. ( 3 ) has three solutions \((n_1,m_1)\) , \((n_2,m_2)\) , \((n_3,m_3)\) with \(n_1>n_2>n_3\ge N_0\) . Then one of the following three possibilities holds:

\(n_2m_1-n_1m_2=0\) ;

\(m_2-m_3 < 1.45 \log (43.3 n_1)\) ;

\(\log \alpha <\frac{2\log (34.7 n_1)}{\epsilon }.\)

Since we will deal with the first and second possiblity in the next sections, we close this section by proving that the last possibility implies Theorems 1 and 2 . Therefore let us plug in the upper bound for \(\log \alpha \) into inequality ( 11 ) to obtain

Writing \(n'=34.7 n_1\) , this inequality turns into

and an application of Lemma 22 implies

Thus Theorem 1 is proven in this case.

Now let us assume that assumption A2 holds. By Remark 2 we get the bound

If we insert our upper bound for \(n_1\) into the upper bound for \(\log \alpha \) , we obtain

This proves Theorem 2 in the current case.

8 The case \(n_1m_2-n_2m_1=0\)

We distinguish between the cases \(c\ge 0\) and \(c<0\) .

8.1 The case \( c \ge 0 \) – bound for \( n_1 \)

In this case we have

Furthermore it holds

holds under our assumptions, we may apply Lemma 20 to get the two inequalities

Multiplying the first inequality by \(n_2\) and the second one by \(n_1\) as well as forming the difference afterwards yields

Let us note that \((a+b)^2\le 4\max \{|a|^2,|b|^2\}\) , and therefore we obtain

Together with the estimate

this implies

Let us assume for the moment that the maximum is \(\frac{c^2}{\alpha ^{n_2}}\) . Then we obtain

which implies \(\alpha <24\) and thus Theorem 2 . Plugging in \(\alpha <24\) in Proposition  24 yields the content of Theorem 1 in this case.

Therefore we assume now \(c<12|\beta |^{n_2}\) . By Proposition 23 we obtain

Note that, due to our assumptions, we have the bound

which implies \((1-\frac{\epsilon }{4}) \log \alpha > \log |\beta |\) . Thus we get

As previously, solving this inequality with the help of Lemma 22 yields

which proves Theorem 1 in this case.

So we may now assume that assumption A2 holds and the bound for \(n_1\) with \(\epsilon =\frac{1}{2}\) is valid. This yields

8.2 The case \( c \ge 0 \) \( - \) bound for \( \log A \)

For \( c \ge 0 \) it remains to prove the bound for \( \log A \) stated in our second theorem. We can already use the above proven bound ( 19 ) for \( n_1 \) since we assume assumption A2. Note that under assumption A2 we have \(|\beta |<2\kappa \) , by Lemma 8 . Hence the quantities \(|c|,|\beta |^{n_1},|\beta |^{n_2}\) are bounded by effectively computable constants depending only on \( \kappa \) and b .

Let us consider the case \(|c-\beta ^{n_2}|\ge 2(|c|+|\beta |^{n_1})\alpha ^{n_2-n_1}\) . Note that \( \beta ^{n_2} \ne c \) by the usual Galois conjugation argument. If \( c > \beta ^{n_2} \) , then ( 16 ) gives us

As \(c<2\alpha ^{n_3}\) (see inequality ( 15 )) we obtain

which yields \(\alpha < 20 \kappa \) .

If \( c < \beta ^{n_2} \) , then ( 16 ) gives us

which implies

and hence \( \alpha < 104\kappa \) .

Thus we may now assume \(|c-\beta ^{n_2}|< 2(|c|+|\beta |^{n_1})\alpha ^{n_2-n_1}\) . Let us note that under the assumption \(\alpha >4(|c|+\max \{1,|\beta |\}^{n_1})\) we can deduce

and otherwise we would get the constant \( C_2 \) in Theorem 2 (cf. the calculations below). Then, by Lemma 20 , we get

Recalling from the beginning of Sect. 7 the bound

we can again eliminate the term \(\log \alpha \) from these inequalities by considering the form \(\Lambda _0'=n_3\Lambda _1-n_1\Lambda _3\) and obtain the inequality

If \( n_3m_1-n_1m_3 \ne 0 \) , then we have

which yields \( \log \alpha \le 5 + \log n_1 + n_1 \log (4\kappa ) \) , and together with the bound ( 19 ) this gives us constant \( C_2 \) in Theorem 2 .

Hence we can assume \( n_3m_1-n_1m_3 = 0 \) and replace in the discussion above \(m_2\) by \(m_3\) as well as \(n_2\) by \(n_3\) . Since by ( 20 ) we have

we may apply Lemma 20 also to this expression and get an analogous version of ( 16 ) with \(n_2\) replaced by \(n_3\) . The consideration of \(|c-\beta ^{n_3}| \ge 2(|c|+|\beta |^{n_1})\alpha ^{n_3-n_1}\) yields in the case \( c > \beta ^{n_3} \) , in the same way as above, \( \alpha < 20\kappa \) , and in the case \( c < \beta ^{n_3} \) we apply the analogous version of ( 16 ), as done above, with the conclusion

a contradiction stating that this case is not possible. For this reason we may now assume \(|c-\beta ^{n_3}|< 2(|c|+|\beta |^{n_1})\alpha ^{n_3-n_1}\) . Thus altogether we obtain

From ( 22 ) we deduce that one of the two factors of the left hand side is smaller than \(2\alpha ^{\frac{n_2-n_1}{2}}\sqrt{|c|+|\beta |^{n_1}}\) . By thinking of constant \( C_2 \) in Theorem 2 , we may assume \(\alpha >64(|c| +|\beta |^{n_1})\) . So we have \(2\alpha ^{\frac{n_2-n_1}{2}}\sqrt{|c|+|\beta |^{n_1}} < \frac{1}{4}\) . Let us first assume that

This implies \(|\beta |^{n_3}< \frac{1}{4}\) and further

Therefore we have \(c=0\) . But Lemma 15 states that there cannot be three solutions for \( c=0 \) .

Now we may assume

Here we get the further bound

Assuming \(\alpha >64n_2^2(|c|+|\beta |^{n_1})\) , we obtain by an application of Lemma 21 that

This together with our assumption \( ||c|-|\beta |^{n_2}| \le |c-\beta ^{n_2}|< 2(|c|+|\beta |^{n_1})\alpha ^{n_2-n_1}\) gives us

provided that

Thus we may assume \(c=1\) provided that \(\alpha \) is large enough. But this also implies

If \(\beta ^{n_3}<0\) , we get

Therefore we may assume \(\beta ^{n_3}=|\beta |^{n_3}\) is positive. Since for any real numbers \(x>0\) and \(n\ge 1\) we have \(|1-x| \le |1-x^n|\) , we obtain from Lemma 6 together with Lemma 5

Hence we get

in this case.

So it remains to consider the situation

With ( 19 ) and Lemma 5 this implies

and Theorem 2 is proven in that case.

8.3 The case \(c< 0\)

The case \(c<0\) can be treated with similar arguments. Therefore we will only point out the differences.

We start with the observation

and write again

Note that, using Lemma 13 ,

holds under our assumptions if in addition \( m_2-m_3 \ge 2 \) . The case \( m_2-m_3 =1 \) is included in the next section. Thus we get again the inequality chain ( 16 ) and furthermore the bound

If the maximum is \( \frac{|c|^2}{\alpha ^{n_2}} \) , then we have

which implies \( m_2-m_3 \le 3 \) . This will be handled in Sect. 9 . Therefore we may now again assume \( |c| < 12|\beta |^{n_2} \) . In the same way as in the case \( c \ge 0 \) we obtain again the upper bound ( 18 ) proving Theorem 1 also in the case \(c<0\) . Moreover, we get under assumption A2 the same upper bound ( 19 ) for \(n_1\) . In particular, the quantities \(|c|,|\beta |^{n_1},|\beta |^{n_2}\) are bounded by effectively computable constants depending only on \( \kappa \) and b .

The reader might already have noticed that, in the case \( c \ge 0 \) , we sometimes have written | c | and sometimes c . We did this in order to reuse these calculations now for the case \( c<0 \) . The only adaptions we need for \( c<0 \) when going through the previous subsection are the following: First, the special case

now, by Lemma 13 , yields

and thus \( \alpha < 60 \kappa \) . Second, we have to consider \( c=-1 \) instead of \( c=1 \) , which implies

If \(\beta ^{n_3}>0\) , we get

and if \(\beta ^{n_3}=-|\beta |^{n_3}\) is negative, we obtain from Lemma 6 together with Lemma 5

The other steps work as above. Hence Theorem  2 is proven in this case as well.

Let us summarize what we have proven so far:

Assume that assumption A1 or A2 holds and assume that Diophantine Eq. ( 3 ) has three solutions \((n_1,m_1)\) , \((n_2,m_2)\) , \((n_3,m_3)\) with \(n_1>n_2>n_3\ge N_0\) . Then at least one of the following three possibilities holds:

assumption A1 holds and

assumption A2 holds and

\(m_2-m_3<1.45 \log (43.3 n_1)\) .

9 The case \(m_2-m_3\ll \log n_1\)

In view of Theorems 1 and 2 and Lemma 26 we may assume that assumption A1 or A2 holds and that \(m_2-m_3<1.45 \log (43.3 n_1)\) .

First, we reconsider inequality ( 8 ) and note that \(7\max \left\{ \alpha ^{n_2-n_1},\gamma ^{-n_1}\right\} \ge \frac{1}{2}\) implies either \(\alpha \le 14\) or \(A^{\epsilon } \le 28\) . In the first cases we have an upper bound for \(\alpha \) and by Proposition 24 also an upper bound for \(n_1\) ; the second case contradicts assumption A1 and A2 respectively. Thus Theorems 1 and 2 are shown in those situations. Now we may apply Lemma 20 and obtain, as in Sect. 6 , the inequality

Next, let us consider the inequality

In particular, note that \(b^{m_2}-b^{m_3}\ge \frac{1}{2} b^{m_2} > \frac{3}{16} \alpha ^{n_2}\) by Lemma 13 . Assuming that \(18\alpha ^{n_3-n_2} \ge \frac{1}{2}\) yields \(\alpha \le 36\) which implies by Proposition 24 Theorems 1 and 2 . Similarly, using \( n_2\ge 2 \) , the assumption \(18\gamma ^{-n_2} \ge \frac{1}{2}\) gives us either \( \alpha \le 6 \) or \(A^{\epsilon } \le 12\) and we are done as well. Thus we may apply Lemma 20 and obtain

Eliminating the term \(\log \alpha \) from the linear forms \(\Lambda _1\) and \(\Lambda _2\) by considering \(\Lambda =n_1\Lambda _2-n_2\Lambda _1\) yields together with ( 23 ) and ( 24 ) the bound

Now we have to distinguish between the cases \(\Lambda =0\) and \(\Lambda \ne 0\) .

9.1 The case \(\Lambda = 0\)

Since \(n_1\ne 0\) this case can only occur if b and \(b^{m_2-m_3}-1\) are multiplicatively dependent. This is only possible if \(b=2\) and \(m_2-m_3=1\) , i.e. if \(b^{m_2-m_3}-1=1\) . Note that our assumptions imply \(c\ge 0\) if \(b=2\) . Therefore we obtain

which implies \(b^{m_3}\le 2\alpha ^{n_3}\) .

From Lemma 13 we know that \(b^{m_2}>\frac{3}{8} \alpha ^{n_2}\) . Hence, using the facts \(b=2\) and \(m_2=m_3+1\) , we get the inequality

which implies \(\alpha ^{n_2-n_3}<11\) and thus \(\alpha <11\) . An application of Proposition  24 yields Theorems 1 and 2 .

Let us note that in the case \(c<0\) the argument above does not work. This is the reason why we exclude \(b=2\) if \(c<0\) .

9.2 The case \(\Lambda \ne 0\)

Here we may apply Matveev’s theorem, Theorem 16 , to \(\Lambda \) . Note that the case \(b^{m_2-m_3}-1=1\) can be excluded by the previous subsection.

First, let us find an upper bound for \(|m_1n_2-m_3n_1|\) . We deduce from ( 25 ) the bound

Furthermore, using Lemma 18 , we have

Therefore we may choose \(E=52 n_1\) in Theorem 16 .

Now we obtain by Matveev’s theorem

Together with the upper bound for \(|\Lambda |\) this yields

Similar as in Sect. 7 we plug in this upper bound for \(\log \alpha \) into ( 11 ) and obtain the inequality

Writing \(n'=719 n_1\) and applying Lemma 22 gives us an upper bound for \(n'\) and in the sequel for \(n_1\) , namely

This concludes the proof of Theorem 1 .

Now let us assume that assumption A2 holds. Then we put \(\epsilon =\frac{1}{2}\) and get

in particular \(n_1 < 2.3\cdot 10^{40}\) for \(b=2\) (cf. Corollary 3 ). If we insert this upper bound into ( 26 ) with \(\epsilon =\frac{1}{2}\) , then we obtain

which finally proves Theorem 2 .

Data availability

This manuscript has no associated data.

This prime p is called a primitive divisor.

Batte, H., Ddamulira, M., Kasozi, J., Luca, F.: On the multiplicity in Pillai’s problem with Fibonacci numbers and powers of a fixed prime. Glas. Mat. Ser. III 57(77) (2), 185–201 (2022)

Carmichael, R.D.: On the numerical factors of the arithmetic forms \(\alpha ^n\pm \beta ^n\) . Ann. Math. 2 (15), 49–70 (1913)

Article   MathSciNet   Google Scholar  

Chim, K.C., Pink, I., Ziegler, V.: On a variant of Pillai’s problem II. J. Number Theory 183 , 269–290 (2018)

Ddamulira, M., Luca, F., Rakotomalala, M.: On a problem of Pillai with Fibonacci numbers and powers of 2. Proc. Indian Acad. Sci. Math. Sci. 127 (3), 411–421 (2017)

Heintze, S., Tichy, R., Vukusic, I., Ziegler, V.: On the Diophantine equation \(U_n-b^m=c\) . Math. Comput. 92 (344), 2825–2859 (2023)

Laurent, M.: Linear forms in two logarithms and interpolation determinants II. Acta Arith. 133 (4), 325–348 (2008)

Matveev, E.M.: An explicit lower bound for a homogeneous rational linear form in logarithms of algebraic numbers II. Izv. Ross. Akad. Nauk Ser. Mat. 64 (6), 125–180 (2000)

MathSciNet   Google Scholar  

Pethő, A., de Weger, B.M.M.: Products of prime powers in binary recurrence sequences. I. The hyperbolic case, with an application to the generalized Ramanujan-Nagell equation. Math. Comp. 47 (176), 713–727 (1986)

Pillai, S.S.: On \(a^x-b^y=c\) . J. Indian Math. Soc. New Ser. 2 , 119–122 (1936)

Google Scholar  

Pillai, S.S.: A correction to the paper “On \(a^x - b^y=c\) .” J. Indian Math. Soc. New Ser. 2 , 215 (1937)

Smart, N.P.: The algorithmic resolution of Diophantine equations, London Mathematical Society Student Texts, vol. 41. Cambridge University Press, Cambridge (1998)

Book   Google Scholar  

Zannier, U.: Lecture notes on Diophantine analysis, volume 8 of Appunti. Scuola Normale Superiore di Pisa (Nuova Serie) [Lecture Notes. Scuola Normale Superiore di Pisa (New Series)]. Edizioni della Normale, Pisa, With an appendix by Francesco Amoroso (2009)

Download references

Acknowledgements

We want to thank the anonymous referees for carefully reading our manuscript and their many helpful suggestions which improved the quality of the paper significantly. This research was funded in whole or in part by the Austrian Science Fund (FWF) [10.55776/I4406]. For open access purposes, the author has applied a CC BY public copyright license to any author accepted manuscript version arising from this submission.

Open Access funding provided by the Paris Lodron University of Salzburg.

Author information

Authors and affiliations.

Institute of Analysis and Number Theory, Graz University of Technology, Steyrergasse 30/II, A-8010, Graz, Austria

Sebastian Heintze

University of Salzburg, Hellbrunnerstrasse 34/I, A-5020, Salzburg, Austria

Volker Ziegler

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Volker Ziegler .

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This work was supported by the Austrian Science Fund (FWF) under the project I4406

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Heintze, S., Ziegler, V. On Pillai’s Problem involving Lucas sequences of the second kind. Res. number theory 10 , 51 (2024). https://doi.org/10.1007/s40993-024-00534-5

Download citation

Received : 25 September 2023

Accepted : 02 April 2024

Published : 13 May 2024

DOI : https://doi.org/10.1007/s40993-024-00534-5

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Diophantine equations
• Pillai’s Problem
• Lucas sequences

Mathematics Subject Classification

• Find a journal
• Publish with us
• Track your research