test statistic formula hypothesis testing

If you could change one thing about college, what would it be?

Graduate faster

Better quality online classes

Flexible schedule

Access to top-rated instructors

Test Statistics: Definition, Formulas & Examples

03.17.2022 • 10 min read

Sarah Thomas

Subject Matter Expert

This article explains what a test statistic is, how to complete one with formulas, and how to find the value for t-tests.

In This Article

What is a Standardized Test Statistic?

The general formula for calculating test statistics, types of test statistics with formulas, difference between t-tests and z-tests and when to use each, how to interpret a test statistic, don't overpay for college statistics.

Take Intro to Statistics Online with Outlier.org

From the co-founder of MasterClass, earn transferable college credits from the University of Pittsburgh (a top 50 global school). The world's best online college courses for 50% less than a traditional college.

A test statistic is a standardized score used in hypothesis testing. It tells you how likely the results obtained from your sample data are under the assumption that the null hypothesis is true. The more unlikely your results are under this assumption, the easier it becomes to reject the null hypothesis in favor of an alternative hypothesis. The more likely your results are, the harder it becomes to reject the null hypothesis.

There are different kinds of test statistics, but they all work the same way. A test statistic maps the value of a particular sample statistic (such as a sample mean or a sample proportion) to a value on a standardized distribution, such as the Standard Normal Distribution or the t-distribution. This allows you to determine how likely or unlikely it is to observe the particular value of the statistic you obtained.

Olanrewaju Michael Akande reviews normal distribution in the following lesson clip:

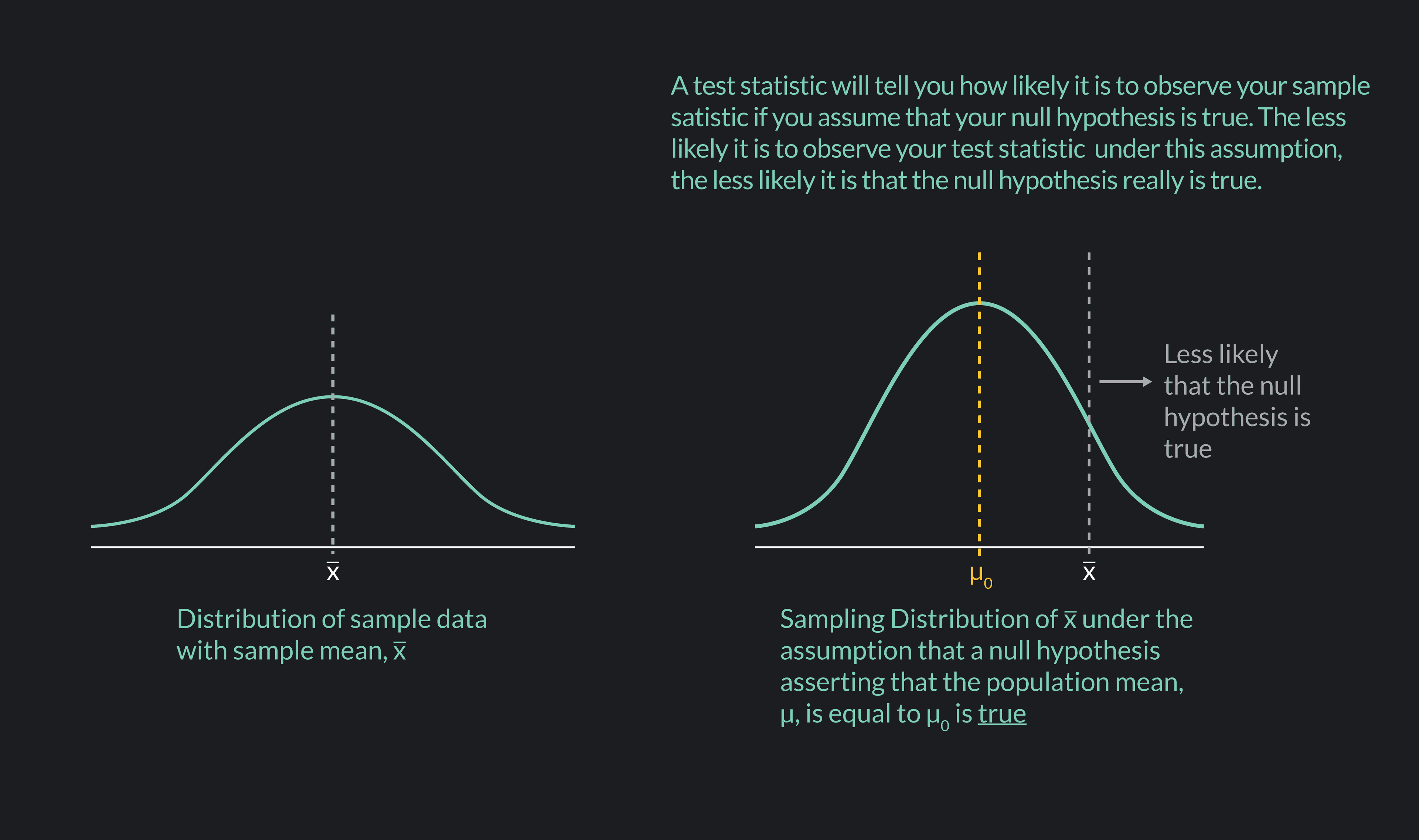
As a quick example, say you have a null hypothesis that the average wait time to get seated at your favorite restaurant—at a table for two without a reservation on a Friday night—is 45 minutes. You select a random sample of 100 parties that got seated under these conditions and ask them what their wait times were. You find that the average wait time for your sample is 55 minutes ( x ˉ \bar{x} x ˉ = 55 minutes). A test statistic will convert this sample statistic x ˉ \bar{x} x ˉ into a standardized number that helps you answer this question:

“Assuming that my null hypothesis is true—assuming that the average wait time at the restaurant actually is 45 minutes—what is the likelihood that I found an average wait time of 55 minutes for my randomly drawn sample?”

Remember, the lower the likelihood of observing your sample statistic, the more confident you can be rejecting the null hypothesis.

The type of test statistic you use in a hypothesis test depends on several factors including:

The type of statistic you are using in the test

The size of your sample

Assumptions you can make about the distribution of your data

Assumptions you can make about the distribution of the statistic used in the test

The formula for calculating test statistics takes the following general form:

Remember, a statistic is a measure calculated from a single sample or many samples. Examples include the sample mean x ˉ \bar{x} x ˉ , the difference between two sample means x 1 ˉ − x 2 ˉ \bar{x_{1}} - \bar{x_{2}} x 1 ​ ˉ ​ − x 2 ​ ˉ ​ , or a sample proportion p ^ \hat{p} p ^ ​ .

A parameter is a measure calculated from a single population or many populations. Examples include the population mean μ \mu μ , the difference between two population means μ 1 − μ 2 \mu_{1}-\mu_{2} μ 1 ​ − μ 2 ​ , or a population proportion p p p .

In the denominator of the equation, you have the standard deviation—or the approximated standard deviation—of the statistic used in the numerator. If you use the sample mean x ˉ \bar{x} x ˉ , in the numerator, you should use the standard deviation of x ˉ \bar{x} x ˉ or an approximation of it in the denominator.

The test statistics you are most likely to encounter in an introductory statistics class are:

The Z-test statistic for a single sample mean

The Z-test statistic for population proportions

The t-test statistic for a single sample mean

The t-test statistic for two sample means

Z-test for a Sample Mean

We use the Z-test statistic (or Z-statistic) for a sample mean in hypothesis tests involving a sample mean x ˉ \bar{x} x ˉ , calculated for a single sample.

You use this test statistic when:

Your sample size is greater than or equal to 30 (n ≥ \geq ≥ 30)

The sampling distribution of the sample mean is assumed to be normal

The standard deviation of the population parameter σ \sigma σ is known.

The formula for this type of Z-test statistic is:

Z Z Z is the symbol for the Z-test statistic

x ˉ \bar{x} x ˉ is the sample mean

μ 0 \mu_{0} μ 0 ​ is the hypothesized value of the population mean according to the null hypothesis

σ \sigma σ is the population standard deviation

n n n is the sample size

σ n \frac{\sigma}{\sqrt{n}} n ​ σ ​ is the standard error of x ˉ \bar{x} x ˉ . The standard error is just the standard deviation of the sampling distribution of the sample mean.

You may notice that a Z-test statistic is just a z-score for a particular value of a normally distributed statistic. There are many variations of the Z-test statistic. We can use these in hypothesis tests, where the sample statistic is being used in the test is approximately normally distributed. One such variation of the Z-test statistic is the Z-test for proportions.

Z-test for Proportions

We use the Z-test statistic for proportions in hypothesis tests where a sample proportion p ^ \hat{p} p ^ ​ is being tested against the hypothesized value of the population proportion, p 0 p_{0} p 0 ​ . We use the Z-test for proportions when your sample size is greater than or equal to 30 (n ≥ \geq ≥ 30), and the distribution of the sample statistic is assumed to be normal. The formula for the Z-test statistic for population proportions is:

Z is the symbol for the Z-test statistic for population proportions

p ^ \hat{p} p ^ ​ is the sample proportion

p 0 p_{0} p 0 ​ is the hypothesized value of the population proportion according to the null hypothesis

When your sample size is smaller than 30 (n<30)—or when you cannot assume that the distribution of your sample statistic is normally distributed—you’ll often use a t-test statistic rather than a Z-test.

T-test for a Single Sample Mean

We use the t-test statistic (or t-statistic) for a sample mean in hypothesis tests involving a sample mean calculated for a single sample drawn from a population. Unlike the Z-test for a single sample mean, you use the t-test when:

Your sample size is less than 30 (n<30)

The distribution of the sample statistic is not approximated by a normal distribution

The standard deviation of the population parameter σ \sigma σ is unknown

A t-test statistic maps your statistics to a t-distribution as opposed to the normal distribution with a Z-test. A t-distribution is like a standard normal distribution, but it has thicker tails and changes depending on your sample size n n n . When n n n is large, the t-distribution is closer to the normal distribution; and as the sample size gets larger and larger, a t-distribution will converge to the normal distribution. As n n n gets smaller, the t-distribution gets flatter with thicker tails.

The formula for the t-test statistic for a sample mean is:

t t t is the symbol for the t-test statistic

μ 0 \mu_0 μ 0 ​ is the value of the population mean according to the null hypothesis

s s s is the sample standard deviation

s n \frac{s}{\sqrt{n}} n ​ s ​ is an approximation of the standard error of x ˉ \bar{x} x ˉ . In a t-test, because you do not know the value of the population standard deviation, you need to approximate the standard error of x ˉ \bar{x} x ˉ using the sample standard deviation s s s .

T-test for Two Sample Means

We can also use t-test statistics in hypothesis tests where the values of two sample means ( x 1 x_{1} x 1 ​ and x 2 x_{2} x 2 ​ ) are being compared. You do this to test the null hypothesis that the two samples are drawn from the same underlying population. If the null hypothesis is true, then any difference between the sample means is due to random variations in the data. Rejecting the null hypothesis suggests that the samples were drawn from two distinct populations and that the difference in the sample means reflects actual differences in the characteristics of subjects in one population compared to the other.

Like the t-test for a single sample mean, you use the t-test for two sample means when:

Your sample sizes are less than 30 (n<30)

The distribution of the sample statistics are not approximated by a normal distribution

The formula for the t-test statistic for two sample means is‌:

x 1 ˉ \bar{x_1} x 1 ​ ˉ ​ is the sample mean of sample 1

x 2 ˉ \bar{x_2} x 2 ​ ˉ ​ is the sample mean of sample 2

μ 1 \mu_1 μ 1 ​ is the mean of the population from which sample 1 was drawn

μ 2 \mu_2 μ 2 ​ is the mean of the population from which sample 2 was drawn

s 1 2 s_1^2 s 1 2 ​ is the variance of sample 1

s 2 2 s_2^2 s 2 2 ​ is the variance of sample 2

n 1 n_{1} n 1 ​ is the sample size for sample 1

n 2 n_{2} n 2 ​ is the sample size for sample 2

T-tests are generally used in place of Z-tests when one or more of the following conditions hold: The sample size is less than 30 (n \sigma is unknown

If you know the population standard deviation σ \sigma σ and you are confident that the statistic used in your hypothesis test is normally distributed, then you can use a Z-test.

As with all test statistics, you should only use a Z-test or a t-test when your data is from a randomly and independently drawn sample.

We use test statistics together with critical values, p-values, and significance levels to determine whether to reject or not a null hypothesis.

A critical value is a value of a test statistic that marks a cutoff point. If a test statistic is more extreme than the critical value—greater than the critical value in the right tail of a distribution or less than the critical value in the left tail of a distribution—the null hypothesis is rejected.

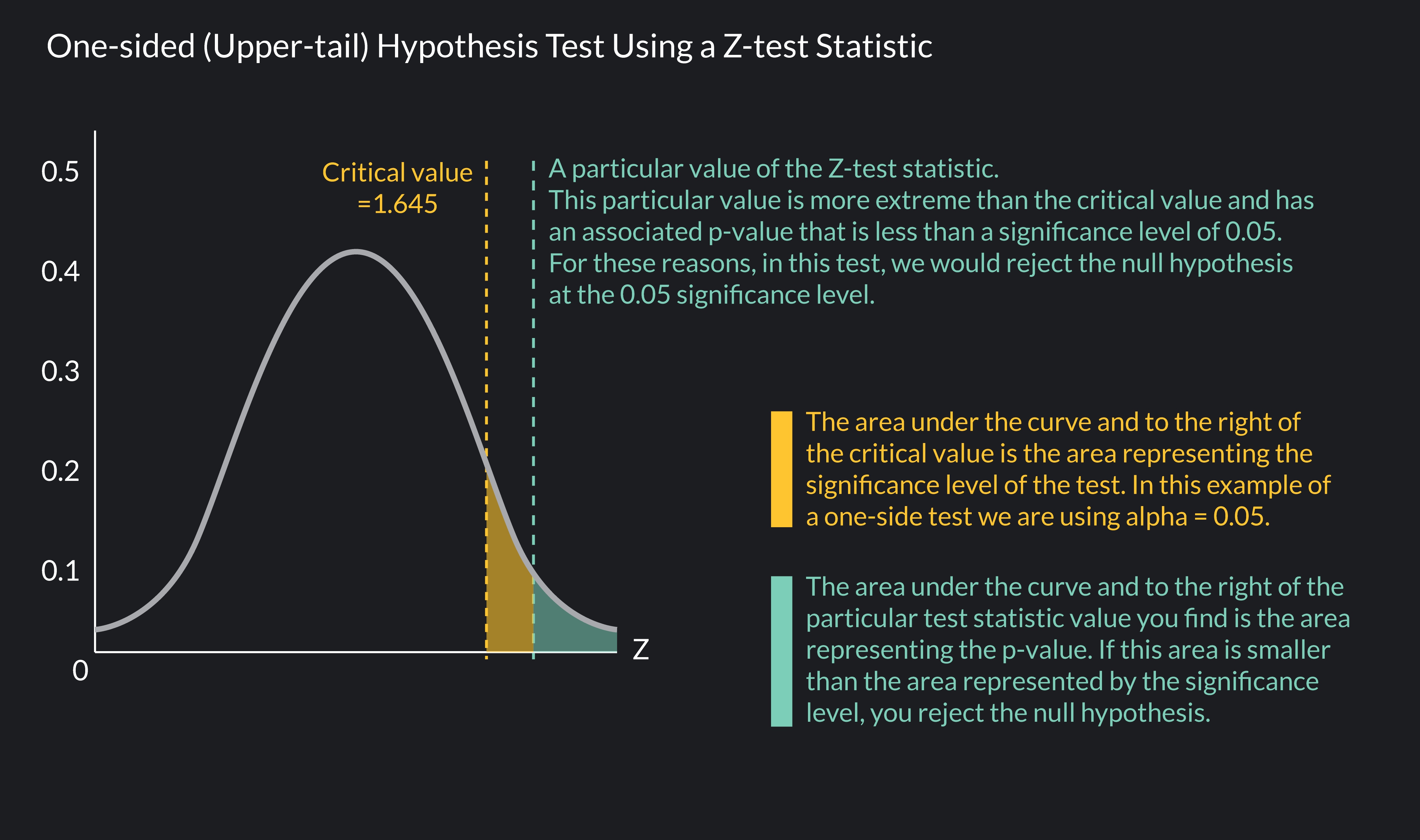
Critical values are determined by the significance level (or alpha level) of a hypothesis test. The significance level you use is up to you, but the most commonly used significance level is 0.05 ( α \alpha α =0.05).

A significance level of 0.05 means that if the probability of observing a sample statistic at least as extreme as the one you observed is less than 0.05 (or 5%), you should reject your null hypothesis. In a one-sided hypothesis test that uses a Z-test statistic, a significance level of 0.05 is associated with a critical value of 1.645 when you conduct the test in the right tail and a value of -1.645 when you conduct the test in the left tail.

A p-value is the probability associated with your test statistic’s value. Let’s say you calculate a Z-test statistic that maps to the standard normal distribution. You find that the test statistic is equal to 1.75. For this ‌value of a Z-test statistic, the associated p-value is 0.04 or 4%—you can find p-values using tables or statistical software.

A p-value of 0.04 means that the probability of observing a sample statistic at least as extreme as the one you found from your sample data is 4%. If you choose a significance level of 0.05 for your test, we would reject the null hypothesis, since the p-value of 0.04 is less than the significance level of 0.05.

It can be easy to confuse test statistics, critical values, significance levels, and p-values. Remember, these are all different measures involved in determining whether to reject or fail to reject a null hypothesis.

Critical values and significance levels provide cut-offs for your test. The difference between a critical value and a significance level is that the critical value is a point on the distribution, and the significance level is a probability represented by an area under the distribution.

You can compare the test statistic and the p-value against the critical value and the significance level.

If the test statistic is more extreme than the critical value, you reject the null hypothesis.

If the p-value is less than the significance level, you reject the null hypothesis.

If the test statistic is less extreme than the critical value, you fail to reject the null hypothesis.

If the p-value is greater than the significance level, you reject the null hypothesis.

Explore Outlier's Award-Winning For-Credit Courses

Outlier (from the co-founder of MasterClass) has brought together some of the world's best instructors, game designers, and filmmakers to create the future of online college.

Check out these related courses:

Intro to Statistics

How data describes our world.

Intro to Microeconomics

Why small choices have big impact.

Intro to Macroeconomics

How money moves our world.

Intro to Psychology

The science of the mind.

Related Articles

What Do Subsets Mean in Statistics?

This article explains what subsets are in statistics and why they are important. You’ll learn about different types of subsets with formulas and examples for each.

Set Operations: Formulas, Properties, Examples & Exercises

Here is an overview of set operations, what they are, properties, examples, and exercises.

Definite Integrals: What Are They and How to Calculate Them

Knowing how to find definite integrals is an essential skill in calculus. In this article, we’ll learn the definition of definite integrals, how to evaluate definite integrals, and practice with some examples.

Rachel McLean

Further reading, understanding math probability - definition, formula & how to find it, calculate outlier formula: a step-by-step guide, z-score: formula, examples & how to interpret it, a step-by-step guide on how to calculate standard deviation, mean absolute deviation (mad) - meaning & formula.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 12: Significance tests (hypothesis testing)

About this unit.

Significance tests give us a formal process for using sample data to evaluate the likelihood of some claim about a population value. Learn how to conduct significance tests and calculate p-values to see how likely a sample result is to occur by random chance. You'll also see how we use p-values to make conclusions about hypotheses.

The idea of significance tests

• Simple hypothesis testing (Opens a modal)
• Idea behind hypothesis testing (Opens a modal)
• Examples of null and alternative hypotheses (Opens a modal)
• P-values and significance tests (Opens a modal)
• Comparing P-values to different significance levels (Opens a modal)
• Estimating a P-value from a simulation (Opens a modal)
• Using P-values to make conclusions (Opens a modal)
• Simple hypothesis testing Get 3 of 4 questions to level up!
• Writing null and alternative hypotheses Get 3 of 4 questions to level up!
• Estimating P-values from simulations Get 3 of 4 questions to level up!

Error probabilities and power

• Introduction to Type I and Type II errors (Opens a modal)
• Type 1 errors (Opens a modal)
• Examples identifying Type I and Type II errors (Opens a modal)
• Introduction to power in significance tests (Opens a modal)
• Examples thinking about power in significance tests (Opens a modal)
• Consequences of errors and significance (Opens a modal)
• Type I vs Type II error Get 3 of 4 questions to level up!
• Error probabilities and power Get 3 of 4 questions to level up!

Tests about a population proportion

• Constructing hypotheses for a significance test about a proportion (Opens a modal)
• Conditions for a z test about a proportion (Opens a modal)
• Reference: Conditions for inference on a proportion (Opens a modal)
• Calculating a z statistic in a test about a proportion (Opens a modal)
• Calculating a P-value given a z statistic (Opens a modal)
• Making conclusions in a test about a proportion (Opens a modal)
• Writing hypotheses for a test about a proportion Get 3 of 4 questions to level up!
• Conditions for a z test about a proportion Get 3 of 4 questions to level up!
• Calculating the test statistic in a z test for a proportion Get 3 of 4 questions to level up!
• Calculating the P-value in a z test for a proportion Get 3 of 4 questions to level up!
• Making conclusions in a z test for a proportion Get 3 of 4 questions to level up!

Tests about a population mean

• Writing hypotheses for a significance test about a mean (Opens a modal)
• Conditions for a t test about a mean (Opens a modal)
• Reference: Conditions for inference on a mean (Opens a modal)
• When to use z or t statistics in significance tests (Opens a modal)
• Example calculating t statistic for a test about a mean (Opens a modal)
• Using TI calculator for P-value from t statistic (Opens a modal)
• Using a table to estimate P-value from t statistic (Opens a modal)
• Comparing P-value from t statistic to significance level (Opens a modal)
• Free response example: Significance test for a mean (Opens a modal)
• Writing hypotheses for a test about a mean Get 3 of 4 questions to level up!
• Conditions for a t test about a mean Get 3 of 4 questions to level up!
• Calculating the test statistic in a t test for a mean Get 3 of 4 questions to level up!
• Calculating the P-value in a t test for a mean Get 3 of 4 questions to level up!
• Making conclusions in a t test for a mean Get 3 of 4 questions to level up!

More significance testing videos

• Hypothesis testing and p-values (Opens a modal)
• One-tailed and two-tailed tests (Opens a modal)
• Z-statistics vs. T-statistics (Opens a modal)
• Small sample hypothesis test (Opens a modal)
• Large sample proportion hypothesis testing (Opens a modal)

Hypothesis Testing

Hypothesis testing is a tool for making statistical inferences about the population data. It is an analysis tool that tests assumptions and determines how likely something is within a given standard of accuracy. Hypothesis testing provides a way to verify whether the results of an experiment are valid.

A null hypothesis and an alternative hypothesis are set up before performing the hypothesis testing. This helps to arrive at a conclusion regarding the sample obtained from the population. In this article, we will learn more about hypothesis testing, its types, steps to perform the testing, and associated examples.

What is Hypothesis Testing in Statistics?

Hypothesis testing uses sample data from the population to draw useful conclusions regarding the population probability distribution . It tests an assumption made about the data using different types of hypothesis testing methodologies. The hypothesis testing results in either rejecting or not rejecting the null hypothesis.

Hypothesis Testing Definition

Hypothesis testing can be defined as a statistical tool that is used to identify if the results of an experiment are meaningful or not. It involves setting up a null hypothesis and an alternative hypothesis. These two hypotheses will always be mutually exclusive. This means that if the null hypothesis is true then the alternative hypothesis is false and vice versa. An example of hypothesis testing is setting up a test to check if a new medicine works on a disease in a more efficient manner.

Null Hypothesis

The null hypothesis is a concise mathematical statement that is used to indicate that there is no difference between two possibilities. In other words, there is no difference between certain characteristics of data. This hypothesis assumes that the outcomes of an experiment are based on chance alone. It is denoted as \(H_{0}\). Hypothesis testing is used to conclude if the null hypothesis can be rejected or not. Suppose an experiment is conducted to check if girls are shorter than boys at the age of 5. The null hypothesis will say that they are the same height.

Alternative Hypothesis

The alternative hypothesis is an alternative to the null hypothesis. It is used to show that the observations of an experiment are due to some real effect. It indicates that there is a statistical significance between two possible outcomes and can be denoted as \(H_{1}\) or \(H_{a}\). For the above-mentioned example, the alternative hypothesis would be that girls are shorter than boys at the age of 5.

Hypothesis Testing P Value

In hypothesis testing, the p value is used to indicate whether the results obtained after conducting a test are statistically significant or not. It also indicates the probability of making an error in rejecting or not rejecting the null hypothesis.This value is always a number between 0 and 1. The p value is compared to an alpha level, \(\alpha\) or significance level. The alpha level can be defined as the acceptable risk of incorrectly rejecting the null hypothesis. The alpha level is usually chosen between 1% to 5%.

Hypothesis Testing Critical region

All sets of values that lead to rejecting the null hypothesis lie in the critical region. Furthermore, the value that separates the critical region from the non-critical region is known as the critical value.

Hypothesis Testing Formula

Depending upon the type of data available and the size, different types of hypothesis testing are used to determine whether the null hypothesis can be rejected or not. The hypothesis testing formula for some important test statistics are given below:

• z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\). \(\overline{x}\) is the sample mean, \(\mu\) is the population mean, \(\sigma\) is the population standard deviation and n is the size of the sample.
• t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\). s is the sample standard deviation.
• \(\chi ^{2} = \sum \frac{(O_{i}-E_{i})^{2}}{E_{i}}\). \(O_{i}\) is the observed value and \(E_{i}\) is the expected value.

We will learn more about these test statistics in the upcoming section.

Types of Hypothesis Testing

Selecting the correct test for performing hypothesis testing can be confusing. These tests are used to determine a test statistic on the basis of which the null hypothesis can either be rejected or not rejected. Some of the important tests used for hypothesis testing are given below.

Hypothesis Testing Z Test

A z test is a way of hypothesis testing that is used for a large sample size (n ≥ 30). It is used to determine whether there is a difference between the population mean and the sample mean when the population standard deviation is known. It can also be used to compare the mean of two samples. It is used to compute the z test statistic. The formulas are given as follows:

• One sample: z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\).
• Two samples: z = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\).

Hypothesis Testing t Test

The t test is another method of hypothesis testing that is used for a small sample size (n < 30). It is also used to compare the sample mean and population mean. However, the population standard deviation is not known. Instead, the sample standard deviation is known. The mean of two samples can also be compared using the t test.

• One sample: t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\).
• Two samples: t = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{s_{1}^{2}}{n_{1}}+\frac{s_{2}^{2}}{n_{2}}}}\).

Hypothesis Testing Chi Square

The Chi square test is a hypothesis testing method that is used to check whether the variables in a population are independent or not. It is used when the test statistic is chi-squared distributed.

One Tailed Hypothesis Testing

One tailed hypothesis testing is done when the rejection region is only in one direction. It can also be known as directional hypothesis testing because the effects can be tested in one direction only. This type of testing is further classified into the right tailed test and left tailed test.

Right Tailed Hypothesis Testing

The right tail test is also known as the upper tail test. This test is used to check whether the population parameter is greater than some value. The null and alternative hypotheses for this test are given as follows:

\(H_{0}\): The population parameter is ≤ some value

\(H_{1}\): The population parameter is > some value.

If the test statistic has a greater value than the critical value then the null hypothesis is rejected

Left Tailed Hypothesis Testing

The left tail test is also known as the lower tail test. It is used to check whether the population parameter is less than some value. The hypotheses for this hypothesis testing can be written as follows:

\(H_{0}\): The population parameter is ≥ some value

\(H_{1}\): The population parameter is < some value.

The null hypothesis is rejected if the test statistic has a value lesser than the critical value.

Two Tailed Hypothesis Testing

In this hypothesis testing method, the critical region lies on both sides of the sampling distribution. It is also known as a non - directional hypothesis testing method. The two-tailed test is used when it needs to be determined if the population parameter is assumed to be different than some value. The hypotheses can be set up as follows:

\(H_{0}\): the population parameter = some value

\(H_{1}\): the population parameter ≠ some value

The null hypothesis is rejected if the test statistic has a value that is not equal to the critical value.

Hypothesis Testing Steps

Hypothesis testing can be easily performed in five simple steps. The most important step is to correctly set up the hypotheses and identify the right method for hypothesis testing. The basic steps to perform hypothesis testing are as follows:

• Step 1: Set up the null hypothesis by correctly identifying whether it is the left-tailed, right-tailed, or two-tailed hypothesis testing.
• Step 2: Set up the alternative hypothesis.
• Step 3: Choose the correct significance level, \(\alpha\), and find the critical value.
• Step 4: Calculate the correct test statistic (z, t or \(\chi\)) and p-value.
• Step 5: Compare the test statistic with the critical value or compare the p-value with \(\alpha\) to arrive at a conclusion. In other words, decide if the null hypothesis is to be rejected or not.

Hypothesis Testing Example

The best way to solve a problem on hypothesis testing is by applying the 5 steps mentioned in the previous section. Suppose a researcher claims that the mean average weight of men is greater than 100kgs with a standard deviation of 15kgs. 30 men are chosen with an average weight of 112.5 Kgs. Using hypothesis testing, check if there is enough evidence to support the researcher's claim. The confidence interval is given as 95%.

Step 1: This is an example of a right-tailed test. Set up the null hypothesis as \(H_{0}\): \(\mu\) = 100.

Step 2: The alternative hypothesis is given by \(H_{1}\): \(\mu\) > 100.

Step 3: As this is a one-tailed test, \(\alpha\) = 100% - 95% = 5%. This can be used to determine the critical value.

1 - \(\alpha\) = 1 - 0.05 = 0.95

0.95 gives the required area under the curve. Now using a normal distribution table, the area 0.95 is at z = 1.645. A similar process can be followed for a t-test. The only additional requirement is to calculate the degrees of freedom given by n - 1.

Step 4: Calculate the z test statistic. This is because the sample size is 30. Furthermore, the sample and population means are known along with the standard deviation.

z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\).

\(\mu\) = 100, \(\overline{x}\) = 112.5, n = 30, \(\sigma\) = 15

z = \(\frac{112.5-100}{\frac{15}{\sqrt{30}}}\) = 4.56

Step 5: Conclusion. As 4.56 > 1.645 thus, the null hypothesis can be rejected.

Hypothesis Testing and Confidence Intervals

Confidence intervals form an important part of hypothesis testing. This is because the alpha level can be determined from a given confidence interval. Suppose a confidence interval is given as 95%. Subtract the confidence interval from 100%. This gives 100 - 95 = 5% or 0.05. This is the alpha value of a one-tailed hypothesis testing. To obtain the alpha value for a two-tailed hypothesis testing, divide this value by 2. This gives 0.05 / 2 = 0.025.

Related Articles:

• Probability and Statistics
• Data Handling

Important Notes on Hypothesis Testing

• Hypothesis testing is a technique that is used to verify whether the results of an experiment are statistically significant.
• It involves the setting up of a null hypothesis and an alternate hypothesis.
• There are three types of tests that can be conducted under hypothesis testing - z test, t test, and chi square test.
• Hypothesis testing can be classified as right tail, left tail, and two tail tests.

Examples on Hypothesis Testing

• Example 1: The average weight of a dumbbell in a gym is 90lbs. However, a physical trainer believes that the average weight might be higher. A random sample of 5 dumbbells with an average weight of 110lbs and a standard deviation of 18lbs. Using hypothesis testing check if the physical trainer's claim can be supported for a 95% confidence level. Solution: As the sample size is lesser than 30, the t-test is used. \(H_{0}\): \(\mu\) = 90, \(H_{1}\): \(\mu\) > 90 \(\overline{x}\) = 110, \(\mu\) = 90, n = 5, s = 18. \(\alpha\) = 0.05 Using the t-distribution table, the critical value is 2.132 t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\) t = 2.484 As 2.484 > 2.132, the null hypothesis is rejected. Answer: The average weight of the dumbbells may be greater than 90lbs
• Example 2: The average score on a test is 80 with a standard deviation of 10. With a new teaching curriculum introduced it is believed that this score will change. On random testing, the score of 38 students, the mean was found to be 88. With a 0.05 significance level, is there any evidence to support this claim? Solution: This is an example of two-tail hypothesis testing. The z test will be used. \(H_{0}\): \(\mu\) = 80, \(H_{1}\): \(\mu\) ≠ 80 \(\overline{x}\) = 88, \(\mu\) = 80, n = 36, \(\sigma\) = 10. \(\alpha\) = 0.05 / 2 = 0.025 The critical value using the normal distribution table is 1.96 z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\) z = \(\frac{88-80}{\frac{10}{\sqrt{36}}}\) = 4.8 As 4.8 > 1.96, the null hypothesis is rejected. Answer: There is a difference in the scores after the new curriculum was introduced.
• Example 3: The average score of a class is 90. However, a teacher believes that the average score might be lower. The scores of 6 students were randomly measured. The mean was 82 with a standard deviation of 18. With a 0.05 significance level use hypothesis testing to check if this claim is true. Solution: The t test will be used. \(H_{0}\): \(\mu\) = 90, \(H_{1}\): \(\mu\) < 90 \(\overline{x}\) = 110, \(\mu\) = 90, n = 6, s = 18 The critical value from the t table is -2.015 t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\) t = \(\frac{82-90}{\frac{18}{\sqrt{6}}}\) t = -1.088 As -1.088 > -2.015, we fail to reject the null hypothesis. Answer: There is not enough evidence to support the claim.

go to slide go to slide go to slide

Book a Free Trial Class

FAQs on Hypothesis Testing

What is hypothesis testing.

Hypothesis testing in statistics is a tool that is used to make inferences about the population data. It is also used to check if the results of an experiment are valid.

What is the z Test in Hypothesis Testing?

The z test in hypothesis testing is used to find the z test statistic for normally distributed data . The z test is used when the standard deviation of the population is known and the sample size is greater than or equal to 30.

What is the t Test in Hypothesis Testing?

The t test in hypothesis testing is used when the data follows a student t distribution . It is used when the sample size is less than 30 and standard deviation of the population is not known.

What is the formula for z test in Hypothesis Testing?

The formula for a one sample z test in hypothesis testing is z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\) and for two samples is z = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\).

What is the p Value in Hypothesis Testing?

The p value helps to determine if the test results are statistically significant or not. In hypothesis testing, the null hypothesis can either be rejected or not rejected based on the comparison between the p value and the alpha level.

What is One Tail Hypothesis Testing?

When the rejection region is only on one side of the distribution curve then it is known as one tail hypothesis testing. The right tail test and the left tail test are two types of directional hypothesis testing.

What is the Alpha Level in Two Tail Hypothesis Testing?

To get the alpha level in a two tail hypothesis testing divide \(\alpha\) by 2. This is done as there are two rejection regions in the curve.

Statistics Made Easy

5 Tips for Interpreting P-Values Correctly in Hypothesis Testing

Hypothesis testing is a critical part of statistical analysis and is often the endpoint where conclusions are drawn about larger populations based on a sample or experimental dataset. Central to this process is the p-value. Broadly, the p-value quantifies the strength of evidence against the null hypothesis. Given the importance of the p-value, it is essential to ensure its interpretation is correct. Here are five essential tips for ensuring the p-value from a hypothesis test is understood correctly. 

1. Know What the P-value Represents

First, it is essential to understand what a p-value is. In hypothesis testing, the p-value is defined as the probability of observing your data, or data more extreme, if the null hypothesis is true. As a reminder, the null hypothesis states no difference between your data and the expected population. 

For example, in a hypothesis test to see if changing a company’s logo drives more traffic to the website, a null hypothesis would state that the new traffic numbers are equal to the old traffic numbers. In this context, the p-value would be the probability that the data you observed, or data more extreme, would occur if this null hypothesis were true. 

Therefore, a smaller p-value indicates that what you observed is unlikely to have occurred if the null were true, offering evidence to reject the null hypothesis. Typically, a cut-off value of 0.05 is used where any p-value below this is considered significant evidence against the null. 

2. Understand the Directionality of Your Hypothesis

Based on the research question under exploration, there are two types of hypotheses: one-sided and two-sided. A one-sided test specifies a particular direction of effect, such as traffic to a website increasing after a design change. On the other hand, a two-sided test allows the change to be in either direction and is effective when the researcher wants to see any effect of the change. 

Either way, determining the statistical significance of a p-value is the same: if the p-value is below a threshold value, it is statistically significant. However, when calculating the p-value, it is important to ensure the correct sided calculations have been completed. 

Additionally, the interpretation of the meaning of a p-value will differ based on the directionality of the hypothesis. If a one-sided test is significant, the researchers can use the p-value to support a statistically significant increase or decrease based on the direction of the test. If a two-sided test is significant, the p-value can only be used to say that the two groups are different, but not that one is necessarily greater. 

3. Avoid Threshold Thinking

A common pitfall in interpreting p-values is falling into the threshold thinking trap. The most commonly used cut-off value for whether a calculated p-value is statistically significant is 0.05. Typically, a p-value of less than 0.05 is considered statistically significant evidence against the null hypothesis. 

However, this is just an arbitrary value. Rigid adherence to this or any other predefined cut-off value can obscure business-relevant effect sizes. For example, a hypothesis test looking at changes in traffic after a website design may find that an increase of 10,000 views is not statistically significant with a p-value of 0.055 since that value is above 0.05. However, the actual increase of 10,000 may be important to the growth of the business. 

Therefore, a p-value can be practically significant while not being statistically significant. Both types of significance and the broader context of the hypothesis test should be considered when making a final interpretation. 

4. Consider the Power of Your Study

Similarly, some study conditions can result in a non-significant p-value even if practical significance exists. Statistical power is the ability of a study to detect an effect when it truly exists. In other words, it is the probability that the null hypothesis will be rejected when it is false. 

Power is impacted by a lot of factors. These include sample size, the effect size you are looking for, and variability within the data. In the example of website traffic after a design change, if the number of visits overall is too small, there may not be enough views to have enough power to detect a difference. 

Simple ways to increase the power of a hypothesis test and increase the chances of detecting an effect are increasing the sample size, looking for a smaller effect size, changing the experiment design to control for variables that can increase variability, or adjusting the type of statistical test being run.

5. Be Aware of Multiple Comparisons

Whenever multiple p-values are calculated in a single study due to multiple comparisons, there is an increased risk of false positives. This is because each individual comparison introduces random fluctuations, and each additional comparison compounds these fluctuations. 

For example, in a hypothesis test looking at traffic before and after a website redesign, the team may be interested in making more than one comparison. This can include total visits, page views, and average time spent on the website. Since multiple comparisons are being made, there must be a correction made when interpreting the p-value. 

The Bonferroni correction is one of the most commonly used methods to account for this increased probability of false positives. In this method, the significance cut-off value, typically 0.05, is divided by the number of comparisons made. The result is used as the new significance cut-off value.  Applying this correction mitigates the risk of false positives and improves the reliability of findings from a hypothesis test. 

In conclusion, interpreting p-values requires a nuanced understanding of many statistical concepts and careful consideration of the hypothesis test’s context. By following these five tips, the interpretation of the p-value from a hypothesis test can be more accurate and reliable, leading to better data-driven decision-making.

Featured Posts

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

8.2: Hypothesis Testing of Single Proportion

• Last updated
• Save as PDF
• Page ID 25674

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• To learn how to apply the five-step critical value test procedure for test of hypotheses concerning a population proportion.
• To learn how to apply the five-step \(p\)-value test procedure for test of hypotheses concerning a population proportion.

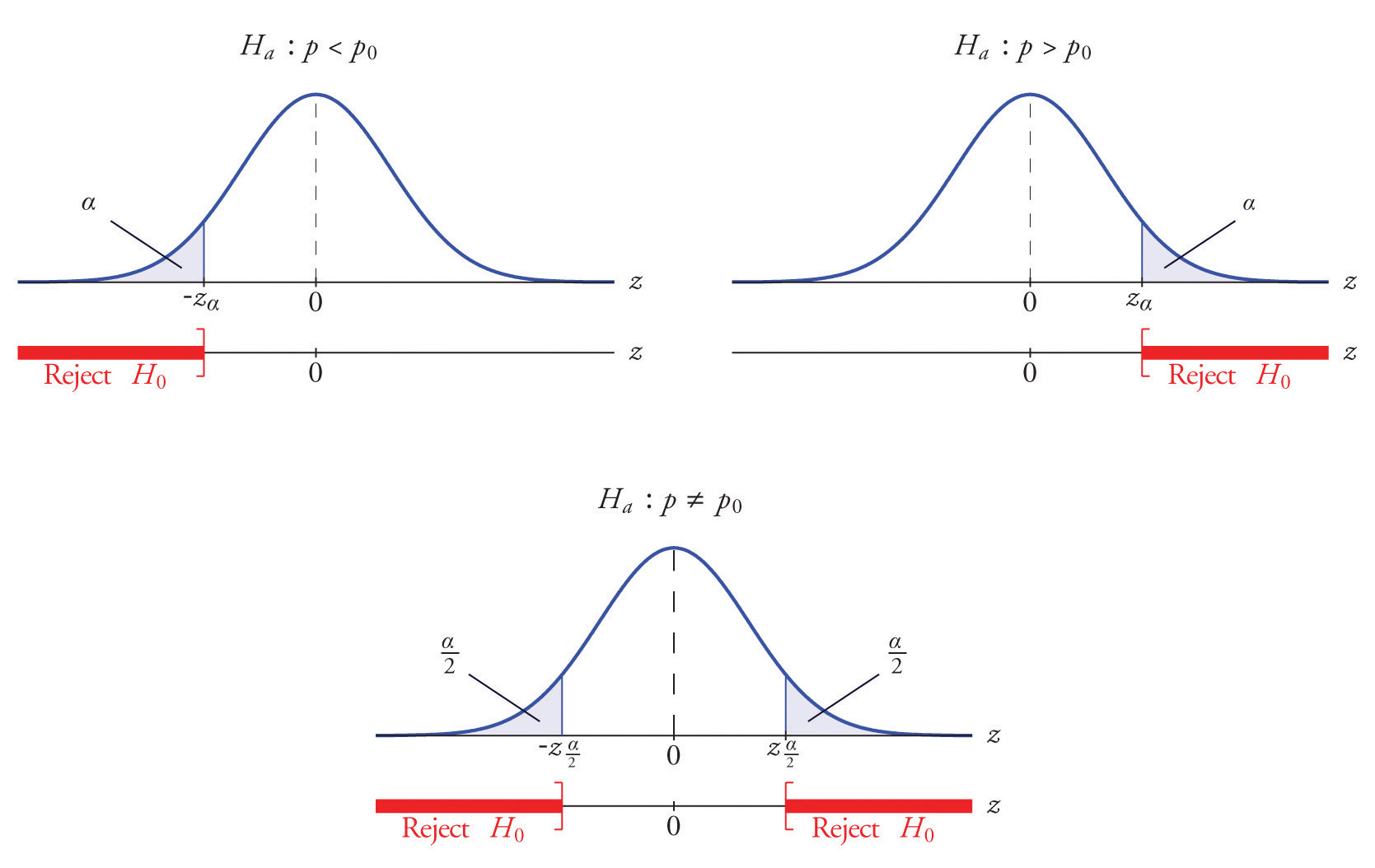
Both the critical value approach and the p-value approach can be applied to test hypotheses about a population proportion p. The null hypothesis will have the form \(H_0 : p = p_0\) for some specific number \(p_0\) between \(0\) and \(1\). The alternative hypothesis will be one of the three inequalities

• \(p <p_0\),
• \(p>p_0\), or
• \(p≠p_0\)

for the same number \(p_0\) that appears in the null hypothesis.

The information in Section 6.3 gives the following formula for the test statistic and its distribution. In the formula \(p_0\) is the numerical value of \(p\) that appears in the two hypotheses, \(q_0=1−p_0, \hat{p}\) is the sample proportion, and \(n\) is the sample size. Remember that the condition that the sample be large is not that \(n\) be at least 30 but that the interval

\[ \left[ \hat{p} −3 \sqrt{ \dfrac{\hat{p} (1−\hat{p} )}{n}} , \hat{p} + 3 \sqrt{ \dfrac{\hat{p} (1−\hat{p} )}{n}} \right] \nonumber \]

lie wholly within the interval \([0,1]\).

Standardized Test Statistic for Large Sample Hypothesis Tests Concerning a Single Population Proportion

\[ Z = \dfrac{\hat{p} - p_0}{\sqrt{\dfrac{p_0q_o}{n}}} \label{eq2} \]

The test statistic has the standard normal distribution.

The distribution of the standardized test statistic and the corresponding rejection region for each form of the alternative hypothesis (left-tailed, right-tailed, or two-tailed), is shown in Figure \(\PageIndex{1}\).

Example \(\PageIndex{1}\)

A soft drink maker claims that a majority of adults prefer its leading beverage over that of its main competitor’s. To test this claim \(500\) randomly selected people were given the two beverages in random order to taste. Among them, \(270\) preferred the soft drink maker’s brand, \(211\) preferred the competitor’s brand, and \(19\) could not make up their minds. Determine whether there is sufficient evidence, at the \(5\%\) level of significance, to support the soft drink maker’s claim against the default that the population is evenly split in its preference.

We will use the critical value approach to perform the test. The same test will be performed using the \(p\)-value approach in Example \(\PageIndex{3}\).

We must check that the sample is sufficiently large to validly perform the test. Since \(\hat{p} =270/500=0.54\),

\[\begin{align} & \left[ \hat{p} −3\sqrt{ \dfrac{\hat{p} (1−\hat{p} )}{n}} ,\hat{p} +3\sqrt{ \dfrac{\hat{p} (1−\hat{p} )}{n}} \right] \\ &=[0.54−(3)(0.02),0.54+(3)(0.02)] \\ &=[0.48, 0.60] ⊂[0,1] \end{align} \nonumber \]

so the sample is sufficiently large.

• Step 1. The relevant test is

\[H_0 : p = 0.50  \nonumber \]

\[vs. \nonumber \]

\[H_a : p > 0.50\, @ \,\alpha =0.05 \nonumber \]

where \(p\) denotes the proportion of all adults who prefer the company’s beverage over that of its competitor’s beverage.

• Step 2. The test statistic (Equation \ref{eq2}) is

\[Z=\dfrac{\hat{p} −p_0}{\sqrt{ \dfrac{p_0q_0}{n}}} \nonumber \]

and has the standard normal distribution.

• Step 3. The value of the test statistic is

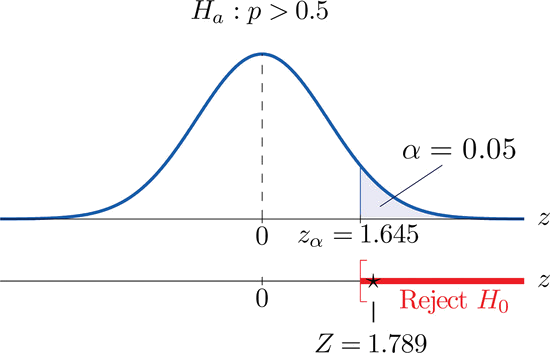
\[ \begin{align} Z &=\dfrac{\hat{p} −p_0}{\sqrt{ \dfrac{p_0q_0}{n}}} \\[6pt] &= \dfrac{0.54−0.50}{\sqrt{\dfrac{(0.50)(0.50)}{500}}} \\[6pt] &=1.789 \end{align} \nonumber \]

• Step 4. Since the symbol in \(H_a\) is “\(>\)” this is a right-tailed test, so there is a single critical value, \(z_{α}=z_{0.05}\). Reading from the last line in Figure 7.1.6 its value is \(1.645\). The rejection region is \([1.645,∞)\).
• Step 5. As shown in Figure \(\PageIndex{2}\) the test statistic falls in the rejection region. The decision is to reject \(H_0\). In the context of the problem our conclusion is:

The data provide sufficient evidence, at the \(5\%\) level of significance, to conclude that a majority of adults prefer the company’s beverage to that of their competitor’s.

Example \(\PageIndex{2}\)

Globally the long-term proportion of newborns who are male is \(51.46\%\). A researcher believes that the proportion of boys at birth changes under severe economic conditions. To test this belief randomly selected birth records of \(5,000\) babies born during a period of economic recession were examined. It was found in the sample that \(52.55\%\) of the newborns were boys. Determine whether there is sufficient evidence, at the \(10\%\) level of significance, to support the researcher’s belief.

We will use the critical value approach to perform the test. The same test will be performed using the \(p\)-value approach in Example \(\PageIndex{1}\).

The sample is sufficiently large to validly perform the test since

\[\sqrt{ \dfrac{\hat{p} (1−\hat{p} )}{n}} =\sqrt{ \dfrac{(0.5255)(0.4745)}{5000}} ≈0.01 \nonumber \]

\[\begin{align} & \left[ \hat{p} −3\sqrt{ \dfrac{\hat{p} (1−\hat{p} )}{n}} ,\hat{p} +3\sqrt{ \dfrac{\hat{p} (1−\hat{p} )}{n}} \right] \\ &=[0.5255−0.03,0.5255+0.03] \\ &=[0.4955,0.5555] ⊂[0,1] \end{align} \nonumber \]

• Step 1 . Let \(p\) be the true proportion of boys among all newborns during the recession period. The burden of proof is to show that severe economic conditions change it from the historic long-term value of \(0.5146\) rather than to show that it stays the same, so the hypothesis test is

\[H_0 : p = 0.5146  \nonumber \]

\[H_a : p \neq 0.5146\, @ \,\alpha =0.10 \nonumber \]

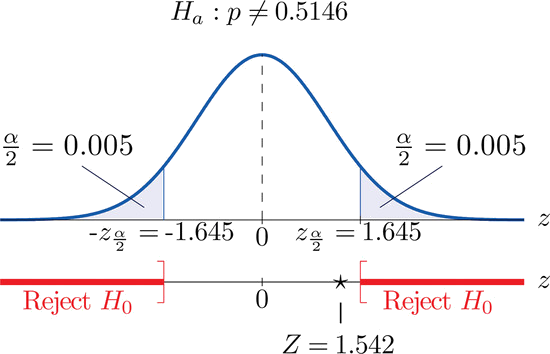
\[ \begin{align} Z &=\dfrac{\hat{p} −p_0}{\sqrt{ \dfrac{p_0q_0}{n}}} \\[6pt] &= \dfrac{0.5255−0.5146}{\sqrt{\dfrac{(0.5146)(0.4854)}{5000}}} \\[6pt] &=1.542 \end{align} \nonumber \]

• Step 4. Since the symbol in \(H_a\) is “\(\neq\)” this is a two-tailed test, so there are a pair of critical values, \(\pm z_{\alpha /2}=\pm z_{0.05}=\pm 1.645\). The rejection region is \((-\infty ,-1.645]\cup [1.645,\infty )\).
• Step 5. As shown in Figure \(\PageIndex{3}\) the test statistic does not fall in the rejection region. The decision is not to reject \(H_0\). In the context of the problem our conclusion is:

The data do not provide sufficient evidence, at the \(10\%\) level of significance, to conclude that the proportion of newborns who are male differs from the historic proportion in times of economic recession.

Example \(\PageIndex{3}\)

Perform the test of Example \(\PageIndex{1}\) using the \(p\)-value approach.

We already know that the sample size is sufficiently large to validly perform the test.

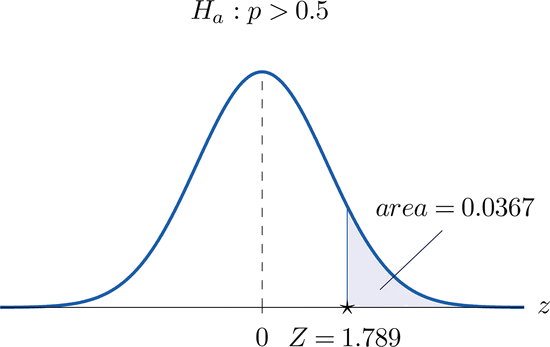
• Steps 1–3 of the five-step procedure described in Section 8.3 have already been done in Example \(\PageIndex{1}\) so we will not repeat them here, but only say that we know that the test is right-tailed and that value of the test statistic is \(Z = 1.789\).
• Step 4. Since the test is right-tailed the p-value is the area under the standard normal curve cut off by the observed test statistic, \(Z = 1.789\), as illustrated in Figure \(\PageIndex{4}\). By Figure 7.1.5 that area and therefore the p-value is \(1−0.9633=0.0367\).
• Step 5. Since the \(p\)-value is less than \(α=0.05\) the decision is to reject \(H_0\).

Example \(\PageIndex{4}\)

Perform the test of Example \(\PageIndex{2}\) using the \(p\)-value approach.

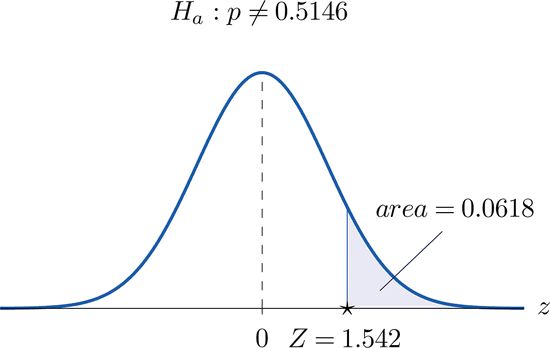
• Steps 1–3 of the five-step procedure described in Section 8.3 have already been done in Example \(\PageIndex{2}\). They tell us that the test is two-tailed and that value of the test statistic is \(Z = 1.542\).
• Step 4. Since the test is two-tailed the \(p\)-value is the double of the area under the standard normal curve cut off by the observed test statistic, \(Z = 1.542\). By Figure 7.1.5 that area is \(1-0.9382=0.0618\), as illustrated in Figure \(\PageIndex{5}\), hence the \(p\)-value is \(2\times 0.0618=0.1236\).
• Step 5. Since the \(p\)-value is greater than \(\alpha =0.10\) the decision is not to reject \(H_0\).

Key Takeaway

• There is one formula for the test statistic in testing hypotheses about a population proportion. The test statistic follows the standard normal distribution.
• Either five-step procedure, critical value or \(p\)-value approach, can be used.