biography of ramanujan in 300 words

Srinivasa Ramanujan

(1887-1920)

Who Was Srinivasa Ramanujan?

After demonstrating an intuitive grasp of mathematics at a young age, Srinivasa Ramanujan began to develop his own theories and in 1911, he published his first paper in India. Two years later Ramanujan began a correspondence with British mathematician G. H. Hardy that resulted in a five-year-long mentorship for Ramanujan at Cambridge, where he published numerous papers on his work and received a B.S. for research. His early work focused on infinite series and integrals, which extended into the remainder of his career. After contracting tuberculosis, Ramanujan returned to India, where he died in 1920 at 32 years of age.

Srinivasa Ramanujan was born on December 22, 1887, in Erode, India, a small village in the southern part of the country. Shortly after this birth, his family moved to Kumbakonam, where his father worked as a clerk in a cloth shop. Ramanujan attended the local grammar school and high school and early on demonstrated an affinity for mathematics.

When he was 15, he obtained an out-of-date book called A Synopsis of Elementary Results in Pure and Applied Mathematics , Ramanujan set about feverishly and obsessively studying its thousands of theorems before moving on to formulate many of his own. At the end of high school, the strength of his schoolwork was such that he obtained a scholarship to the Government College in Kumbakonam.

A Blessing and a Curse

However, Ramanujan’s greatest asset proved also to be his Achilles heel. He lost his scholarship to both the Government College and later at the University of Madras because his devotion to math caused him to let his other courses fall by the wayside. With little in the way of prospects, in 1909 he sought government unemployment benefits.

Yet despite these setbacks, Ramanujan continued to make strides in his mathematical work, and in 1911, published a 17-page paper on Bernoulli numbers in the Journal of the Indian Mathematical Society . Seeking the help of members of the society, in 1912 Ramanujan was able to secure a low-level post as a shipping clerk with the Madras Port Trust, where he was able to make a living while building a reputation for himself as a gifted mathematician.

Around this time, Ramanujan had become aware of the work of British mathematician G. H. Hardy — who himself had been something of a young genius — with whom he began a correspondence in 1913 and shared some of his work. After initially thinking his letters a hoax, Hardy became convinced of Ramanujan’s brilliance and was able to secure him both a research scholarship at the University of Madras as well as a grant from Cambridge.

The following year, Hardy convinced Ramanujan to come study with him at Cambridge. During their subsequent five-year mentorship, Hardy provided the formal framework in which Ramanujan’s innate grasp of numbers could thrive, with Ramanujan publishing upwards of 20 papers on his own and more in collaboration with Hardy. Ramanujan was awarded a bachelor of science degree for research from Cambridge in 1916 and became a member of the Royal Society of London in 1918.

Doing the Math

"[Ramanujan] made many momentous contributions to mathematics especially number theory," states George E. Andrews, an Evan Pugh Professor of Mathematics at Pennsylvania State University. "Much of his work was done jointly with his benefactor and mentor, G. H. Hardy. Together they began the powerful "circle method" to provide an exact formula for p(n), the number of integer partitions of n. (e.g. p(5)=7 where the seven partitions are 5, 4+1, 3+2, 3+1+1, 2+2+1, 2+1+1+1, 1+1+1+1+1). The circle method has played a major role in subsequent developments in analytic number theory. Ramanujan also discovered and proved that 5 always divides p(5n+4), 7 always divides p(7n+5) and 11 always divides p(11n+6). This discovery led to extensive advances in the theory of modular forms."

But years of hard work, a growing sense of isolation and exposure to the cold, wet English climate soon took their toll on Ramanujan and in 1917 he contracted tuberculosis. After a brief period of recovery, his health worsened and in 1919 he returned to India.

The Man Who Knew Infinity

Ramanujan died of his illness on April 26, 1920, at the age of 32. Even on his deathbed, he had been consumed by math, writing down a group of theorems that he said had come to him in a dream. These and many of his earlier theorems are so complex that the full scope of Ramanujan’s legacy has yet to be completely revealed and his work remains the focus of much mathematical research. His collected papers were published by Cambridge University Press in 1927.

Of Ramanujan's published papers — 37 in total — Berndt reveals that "a huge portion of his work was left behind in three notebooks and a 'lost' notebook. These notebooks contain approximately 4,000 claims, all without proofs. Most of these claims have now been proved, and like his published work, continue to inspire modern-day mathematics."

A biography of Ramanujan titled The Man Who Knew Infinity was published in 1991, and a movie of the same name starring Dev Patel as Ramanujan and Jeremy Irons as Hardy, premiered in September 2015 at the Toronto Film Festival.

QUICK FACTS

Name: Srinivasa Ramanujan
Birth Year: 1887
Birth date: December 22, 1887
Birth City: Erode
Birth Country: India
Gender: Male
Best Known For: Srinivasa Ramanujan was a mathematical genius who made numerous contributions in the field, namely in number theory. The importance of his research continues to be studied and inspires mathematicians today.
Education and Academia
Astrological Sign: Sagittarius
University of Madras
Cambridge University
Nacionalities
Death Year: 1920
Death date: April 26, 1920
Death City: Kumbakonam
Death Country: India

We strive for accuracy and fairness.If you see something that doesn't look right, contact us !

CITATION INFORMATION

Article Title: Srinivasa Ramanujan Biography
Author: Biography.com Editors
Website Name: The Biography.com website
Url: https://www.biography.com/scientists/srinivasa-ramanujan
Access Date:
Publisher: A&E; Television Networks
Last Updated: September 10, 2019
Original Published Date: September 10, 2015

Famous Mathematicians

albert einstein sitting in front of a bookcase with his arms folded

Archimedes: The Mathematician Who Discovered Pi

Benjamin Banneker

stephen hawking smiles at the camera while sitting in his wheelchair in front of a green chalkboard with written equations, he wears a dark suit jacket and blue collared shirt with white pinstripes

22 Famous Scientists You Should Know

Charles Babbage

Blaise Pascal

Leonhard Euler

Ada Lovelace

Valerie Thomas

Mary Jackson

CBSE Class 10th
CBSE Class 12th
UP Board 10th
UP Board 12th
Bihar Board 10th
Bihar Board 12th
Top Schools in India
Top Schools in Delhi
Top Schools in Mumbai
Top Schools in Chennai
Top Schools in Hyderabad
Top Schools in Kolkata
Top Schools in Pune
Top Schools in Bangalore

Products & Resources

JEE Main Knockout April
Free Sample Papers
Free Ebooks
NCERT Notes
NCERT Syllabus
NCERT Books
RD Sharma Solutions
Navodaya Vidyalaya Admission 2024-25
NCERT Solutions
NCERT Solutions for Class 12
NCERT Solutions for Class 11
NCERT solutions for Class 10
NCERT solutions for Class 9
NCERT solutions for Class 8
NCERT Solutions for Class 7
JEE Main 2024
MHT CET 2024
JEE Advanced 2024
BITSAT 2024
View All Engineering Exams
Colleges Accepting B.Tech Applications
Top Engineering Colleges in India
Engineering Colleges in India
Engineering Colleges in Tamil Nadu
Engineering Colleges Accepting JEE Main
Top IITs in India
Top NITs in India
Top IIITs in India
JEE Main College Predictor
JEE Main Rank Predictor
MHT CET College Predictor
AP EAMCET College Predictor
GATE College Predictor
KCET College Predictor
JEE Advanced College Predictor
View All College Predictors
JEE Advanced Cutoff
JEE Main Cutoff
JEE Main Advanced Answer Key
JEE Advanced Result
Download E-Books and Sample Papers
Compare Colleges
B.Tech College Applications
KCET Result
MAH MBA CET Exam
View All Management Exams

Colleges & Courses

MBA College Admissions
MBA Colleges in India
Top IIMs Colleges in India
Top Online MBA Colleges in India
MBA Colleges Accepting XAT Score
BBA Colleges in India
XAT College Predictor 2024
SNAP College Predictor
NMAT College Predictor
MAT College Predictor 2024
CMAT College Predictor 2024
CAT Percentile Predictor 2023
CAT 2023 College Predictor
CMAT 2024 Answer Key
TS ICET 2024 Hall Ticket
CMAT Result 2024
MAH MBA CET Cutoff 2024
Download Helpful Ebooks
List of Popular Branches
QnA - Get answers to your doubts
IIM Fees Structure
AIIMS Nursing
Top Medical Colleges in India
Top Medical Colleges in India accepting NEET Score
Medical Colleges accepting NEET
List of Medical Colleges in India
List of AIIMS Colleges In India
Medical Colleges in Maharashtra
Medical Colleges in India Accepting NEET PG
NEET College Predictor
NEET PG College Predictor
NEET MDS College Predictor
NEET Rank Predictor
DNB PDCET College Predictor
NEET Result 2024
NEET Asnwer Key 2024
NEET Cut off
NEET Online Preparation
Download Helpful E-books
Colleges Accepting Admissions
Top Law Colleges in India
Law College Accepting CLAT Score
List of Law Colleges in India
Top Law Colleges in Delhi
Top NLUs Colleges in India
Top Law Colleges in Chandigarh
Top Law Collages in Lucknow

Predictors & E-Books

CLAT College Predictor
MHCET Law ( 5 Year L.L.B) College Predictor
AILET College Predictor
Sample Papers
Compare Law Collages
Careers360 Youtube Channel
CLAT Syllabus 2025
CLAT Previous Year Question Paper
NID DAT Exam
Pearl Academy Exam

Predictors & Articles

NIFT College Predictor
UCEED College Predictor
NID DAT College Predictor
NID DAT Syllabus 2025
NID DAT 2025
Design Colleges in India
Top NIFT Colleges in India
Fashion Design Colleges in India
Top Interior Design Colleges in India
Top Graphic Designing Colleges in India
Fashion Design Colleges in Delhi
Fashion Design Colleges in Mumbai
Top Interior Design Colleges in Bangalore
NIFT Result 2024
NIFT Fees Structure
NIFT Syllabus 2025
Free Design E-books
List of Branches
Careers360 Youtube channel
IPU CET BJMC
JMI Mass Communication Entrance Exam
IIMC Entrance Exam
Media & Journalism colleges in Delhi
Media & Journalism colleges in Bangalore
Media & Journalism colleges in Mumbai
List of Media & Journalism Colleges in India
CA Intermediate
CA Foundation
CS Executive
CS Professional
Difference between CA and CS
Difference between CA and CMA
CA Full form
CMA Full form
CS Full form
CA Salary In India

Top Courses & Careers

Bachelor of Commerce (B.Com)
Master of Commerce (M.Com)
Company Secretary
Cost Accountant
Charted Accountant
Credit Manager
Financial Advisor
Top Commerce Colleges in India
Top Government Commerce Colleges in India
Top Private Commerce Colleges in India
Top M.Com Colleges in Mumbai
Top B.Com Colleges in India
IT Colleges in Tamil Nadu
IT Colleges in Uttar Pradesh
MCA Colleges in India
BCA Colleges in India

Diploma Colleges

Top Diploma Colleges in Maharashtra
UPSC IAS 2024
SSC CGL 2024
IBPS RRB 2024
Previous Year Sample Papers
Free Competition E-books
Sarkari Result
QnA- Get your doubts answered
UPSC Previous Year Sample Papers
CTET Previous Year Sample Papers
SBI Clerk Previous Year Sample Papers
NDA Previous Year Sample Papers

Upcoming Events

NDA Application Form 2024
UPSC IAS Application Form 2024
CDS Application Form 2024
CTET Admit card 2024
HP TET Result 2023
SSC GD Constable Admit Card 2024
UPTET Notification 2024
SBI Clerk Result 2024

Other Exams

SSC CHSL 2024
UP PCS 2024
UGC NET 2024
RRB NTPC 2024
IBPS PO 2024
IBPS Clerk 2024
IBPS SO 2024
Top University in USA
Top University in Canada
Top University in Ireland
Top Universities in UK
Top Universities in Australia
Best MBA Colleges in Abroad
Business Management Studies Colleges

Top Countries

Study in USA
Study in UK
Study in Canada
Study in Australia
Study in Ireland
Study in Germany
Study in China
Study in Europe

Student Visas

Student Visa Canada
Student Visa UK
Student Visa USA
Student Visa Australia
Student Visa Germany
Student Visa New Zealand
Student Visa Ireland
CUET PG 2024
IGNOU B.Ed Admission 2024
DU Admission 2024
UP B.Ed JEE 2024
LPU NEST 2024
IIT JAM 2024
IGNOU Online Admission 2024
Universities in India
Top Universities in India 2024
Top Colleges in India
Top Universities in Uttar Pradesh 2024
Top Universities in Bihar
Top Universities in Madhya Pradesh 2024
Top Universities in Tamil Nadu 2024
Central Universities in India
CUET DU Cut off 2024
IGNOU Date Sheet
CUET Mock Test 2024
CUET Admit card 2024
CUET Result 2024
CUET Participating Universities 2024
CUET Previous Year Question Paper
CUET Syllabus 2024 for Science Students
E-Books and Sample Papers
CUET Exam Pattern 2024
CUET Exam Date 2024
CUET Cut Off 2024
CUET Exam Analysis 2024
IGNOU Exam Form 2024
CUET PG Counselling 2024
CUET Answer Key 2024

Engineering Preparation

Knockout JEE Main 2024
Test Series JEE Main 2024
JEE Main 2024 Rank Booster

Medical Preparation

Knockout NEET 2024
Test Series NEET 2024
Rank Booster NEET 2024

Online Courses

JEE Main One Month Course
NEET One Month Course
IBSAT Free Mock Tests
IIT JEE Foundation Course
Knockout BITSAT 2024
Career Guidance Tool

Top Streams

IT & Software Certification Courses
Engineering and Architecture Certification Courses
Programming And Development Certification Courses
Business and Management Certification Courses
Marketing Certification Courses
Health and Fitness Certification Courses
Design Certification Courses

Specializations

Digital Marketing Certification Courses
Cyber Security Certification Courses
Artificial Intelligence Certification Courses
Business Analytics Certification Courses
Data Science Certification Courses
Cloud Computing Certification Courses
Machine Learning Certification Courses
View All Certification Courses
UG Degree Courses
PG Degree Courses
Short Term Courses
Free Courses
Online Degrees and Diplomas
Compare Courses

Top Providers

Coursera Courses
Udemy Courses
Edx Courses
Swayam Courses
upGrad Courses
Simplilearn Courses
Great Learning Courses

Essay on Srinivasa Ramanujan in English - 100, 200, 500 Words

Srinivasa Ramanujan was the greatest mathematician of all time. He is still remembered for his contributions to the field of mathematics. Theorems formulated by him are to date studied by students across the world and within very few years of his lifespan, he made some exceptional discoveries in mathematics. Here are a few sample essays on Srinivasa Ramanujan.

100 Words Essay on Srinivasa Ramanujan

200 words essay on srinivasa ramanujan, 500 words essay on srinivasa ramanujan.

Srinivasa Ramanujan was a renowned mathematician of India. He was born on 22 December 1887 in Madras during the British Raj. Since childhood, he was drawn towards maths and took a particular interest in learning the subject. He did not receive formal education in mathematics but had mastered maths in various sections. During his time in Cambridge, he grew close to the great mathematician named Hardy. Together they invented the Hardy-Ramanujan number 1729. He got married at the age of 22 to Janakiammal on 14th July 1904. He wrote several books based on his theories and formulas. He even received the K. Ranganatha Rao prize for mathematics. On 26 April 1920, he departed at the age of 32.

Srinivasa Ramanujan was a well-known Indian Mathematician who was born on 22 December 1887 during British rule. He was born in a poor Indian village, Erode, belonging to a Tamil family. His father’s name was Kuppuswamy Srinivas Aiyangar who worked as a clerk in a saree shop, and his mother was a religious housewife. They lived in Erode only for a year and then moved to Kumbakonam.

In this small town, Ramanujan attended many primary schools and achieved a distinction in his primary education. At the age of thirteen, he focused his attention on the sum of geometric and arithmetic series and in 1902, he created a method to solve quadratic equations and even explored Euler’s Constant. In the same year, he received a scholarship for his outstanding performance in his studies, and therefore he was admitted at Kumbakonam’s Government college.

His passion for mathematics grew more robust, and hence he excelled in maths but failed in other subjects. The failure caused him depression, and he fled to Visakhapatnam without telling his parents. One year later, he returned to study and passed the First Art examination but again failed in all and passed in maths.

He published his first paper based on Bernoulli numbers in the Journal of the Indian Mathematical Society and received recognition and achievement. His hard work paid off, and he was appointed as a clerk at Madras Port Trust. At this time, he became famous throughout Madras and caught the attention of C.L.T Griffith who helped Ramanujan. Later, Ramanujan graduated from London and held a degree in Science for research on highly composite numbers.

Ramanujan is referred to as an Indian Mathematician who lived during the British period and who contributed substantially to mathematics analysis, number theory, infinite series and continued fractions. He has been described by many as a simple person with pleasant manners.

He was well-versed in the Brahmin culture and followed particular eating habits. Just before turning 10 years old, he passed his primary education in English, Tamil, geography and arithmetic. His scores were the best in the district. In the same year, he encountered formal mathematics for the first time.

At the age of sixteen, he acquired a library copy of ‘A Synopsis of Elementary Results in Pure and Applied Mathematics’ from a friend. He studied the contents of the book thoroughly. The next year, he developed and investigated the Bernoulli numbers and calculated Euler’s constant up to 15 decimals. His peers could hardly understand his nature, and were always in awe because of his brilliance. Due to his extraordinary mind, he received a scholarship to study at Government Arts College, Kumbakonam. But he lost this scholarship because of his firm determination towards studying only maths and ignoring other subjects.

Later, too he failed in subjects like English, Sanskrit and physiology. In 1906, he flunked his Fellow of Arts exam in December. Without a FA degree, he left college and decided to study independently in mathematics through research and referring books. Such a condition caused him extreme poverty, and he reached the brink of starvation.

Ramanujan met deputy collector V. Ramaswamy Aiyer in 1910, who was the founder of the Mathematical society and wished to work in the revenue department. When Ramanujan showed his mathematics book to him, he stated that he was struck by the extraordinary mathematical results contained in Ramanujan’s books. As he advanced further in maths, he even wrote his formal paper on the properties of Bernoulli numbers.

A journal editor M.T. Narayana Iyengar noted that Ramanujan’s methods and presentation was terse and lacked precision and clearness. An ordinary person could hardly follow him. In England, he was awarded a Bachelor of Arts by Research degree. He was also elected to the London Mathematical Society. Ramanujan was the first Indian to be elected a Fellow of Trinity College, Cambridge.

Achievements of Srinivasa Ramanujan

At the age of 12, he had completely read Loney’s book on Plane Trigonometry and A Synopsis of Elementary Results in Pure and Applied Mathematics, which were way beyond the standard of a high school student

In 1916, he was granted a Bachelor of Science degree “by research” at the Cambridge University

In 1918, he became the first Indian to be honoured as a Fellow of the Royal Society

In 1997, The Ramanujan Journal was launched to publish work “in areas of mathematics influenced by Ramanujan”

The year 2012 was declared as the National Mathematical Year as it marked the 125th birth year of one of the greatest Indian mathematicians

Since 2021, his birth anniversary, December 22, is observed as the National Mathematicians Day every year in India.

Applications for Admissions are open.

Aakash iACST Scholarship Test 2024

Get up to 90% scholarship on NEET, JEE & Foundation courses

ALLEN Digital Scholarship Admission Test (ADSAT)

JEE Main Important Physics formulas

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

PW JEE Coaching

Enrol in PW Vidyapeeth center for JEE coaching

PW NEET Coaching

Enrol in PW Vidyapeeth center for NEET coaching

JEE Main Important Chemistry formulas

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

Download Careers360 App's

Regular exam updates, QnA, Predictors, College Applications & E-books now on your Mobile

Certifications

We Appeared in

Biography of Srinivasa Ramanujan, Mathematical Genius

Public Domain

Famous Inventors
Famous Inventions
Patents & Trademarks
Invention Timelines
Computers & The Internet
American History
African American History
African History
Ancient History and Culture
Asian History
European History
Latin American History
Medieval & Renaissance History
Military History
The 20th Century
Women's History
Ph.D., Materials Science and Engineering, Northwestern University
B.A., Chemistry, Johns Hopkins University
B.A., Cognitive Science, Johns Hopkins University

Srinivasa Ramanujan (born December 22, 1887 in Erode, India) was an Indian mathematician who made substantial contributions to mathematics—including results in number theory, analysis, and infinite series—despite having little formal training in math.

Fast Facts: Srinivasa Ramanujan

Full Name: Srinivasa Aiyangar Ramanujan
Known For: Prolific mathematician
Parents’ Names: K. Srinivasa Aiyangar, Komalatammal
Born: December 22, 1887 in Erode, India
Died: April 26, 1920 at age 32 in Kumbakonam, India
Spouse: Janakiammal
Interesting Fact: Ramanujan's life is depicted in a book published in 1991 and a 2015 biographical film, both titled "The Man Who Knew Infinity."

Early Life and Education

Ramanujan was born on December 22, 1887, in Erode, a city in southern India. His father, K. Srinivasa Aiyangar, was an accountant, and his mother Komalatammal was the daughter of a city official. Though Ramanujan’s family was of the Brahmin caste , the highest social class in India, they lived in poverty.

Ramanujan began attending school at the age of 5. In 1898, he transferred to Town High School in Kumbakonam. Even at a young age, Ramanujan demonstrated extraordinary proficiency in math, impressing his teachers and upperclassmen.

However, it was G.S. Carr’s book, "A Synopsis of Elementary Results in Pure Mathematics," which reportedly spurred Ramanujan to become obsessed with the subject. Having no access to other books, Ramanujan taught himself mathematics using Carr’s book, whose topics included integral calculus and power series calculations. This concise book would have an unfortunate impact on the way Ramanujan wrote down his mathematical results later, as his writings included too few details for many people to understand how he arrived at his results.

Ramanujan was so interested in studying mathematics that his formal education effectively came to a standstill. At the age of 16, Ramanujan matriculated at the Government College in Kumbakonam on a scholarship, but lost his scholarship the next year because he had neglected his other studies. He then failed the First Arts examination in 1906, which would have allowed him to matriculate at the University of Madras, passing math but failing his other subjects.

For the next few years, Ramanujan worked independently on mathematics, writing down results in two notebooks. In 1909, he began publishing work in the Journal of the Indian Mathematical Society, which gained him recognition for his work despite lacking a university education. Needing employment, Ramanujan became a clerk in 1912 but continued his mathematics research and gained even more recognition.

Receiving encouragement from a number of people, including the mathematician Seshu Iyer, Ramanujan sent over a letter along with about 120 mathematical theorems to G. H. Hardy, a lecturer in mathematics at Cambridge University in England. Hardy, thinking that the writer could either be a mathematician who was playing a prank or a previously undiscovered genius, asked another mathematician J.E. Littlewood, to help him look at Ramanujan’s work.

The two concluded that Ramanujan was indeed a genius. Hardy wrote back, noting that Ramanujan’s theorems fell into roughly three categories: results that were already known (or which could easily be deduced with known mathematical theorems); results that were new, and that were interesting but not necessarily important; and results that were both new and important.

Hardy immediately began to arrange for Ramanujan to come to England, but Ramanujan refused to go at first because of religious scruples about going overseas. However, his mother dreamed that the Goddess of Namakkal commanded her to not prevent Ramanujan from fulfilling his purpose. Ramanujan arrived in England in 1914 and began his collaboration with Hardy.

In 1916, Ramanujan obtained a Bachelor of Science by Research (later called a Ph.D.) from Cambridge University. His thesis was based on highly composite numbers, which are integers that have more divisors (or numbers that they can be divided by) than do integers of smaller value.

In 1917, however, Ramanujan became seriously ill, possibly from tuberculosis, and was admitted to a nursing home at Cambridge, moving to different nursing homes as he tried to regain his health.

In 1919, he showed some recovery and decided to move back to India. There, his health deteriorated again and he died there the following year.

Personal Life

On July 14, 1909, Ramanujan married Janakiammal, a girl whom his mother had selected for him. Because she was 10 at the time of marriage, Ramanujan did not live together with her until she reached puberty at the age of 12, as was common at the time.

Honors and Awards

1918, Fellow of the Royal Society
1918, Fellow of Trinity College, Cambridge University

In recognition of Ramanujan’s achievements, India also celebrates Mathematics Day on December 22, Ramanjan’s birthday.

Ramanujan died on April 26, 1920 in Kumbakonam, India, at the age of 32. His death was likely caused by an intestinal disease called hepatic amoebiasis.

Legacy and Impact

Ramanujan proposed many formulas and theorems during his lifetime. These results, which include solutions of problems that were previously considered to be unsolvable, would be investigated in more detail by other mathematicians, as Ramanujan relied more on his intuition rather than writing out mathematical proofs.

His results include:

An infinite series for π, which calculates the number based on the summation of other numbers. Ramanujan’s infinite series serves as the basis for many algorithms used to calculate π.
The Hardy-Ramanujan asymptotic formula, which provided a formula for calculating the partition of numbers—numbers that can be written as the sum of other numbers. For example, 5 can be written as 1 + 4, 2 + 3, or other combinations.
The Hardy-Ramanujan number, which Ramanujan stated was the smallest number that can be expressed as the sum of cubed numbers in two different ways. Mathematically, 1729 = 1 3 + 12 3 = 9 3 + 10 3 . Ramanujan did not actually discover this result, which was actually published by the French mathematician Frénicle de Bessy in 1657. However, Ramanujan made the number 1729 well known. 1729 is an example of a “taxicab number,” which is the smallest number that can be expressed as the sum of cubed numbers in n different ways. The name derives from a conversation between Hardy and Ramanujan, in which Ramanujan asked Hardy the number of the taxi he had arrived in. Hardy replied that it was a boring number, 1729, to which Ramanujan replied that it was actually a very interesting number for the reasons above.
Kanigel, Robert. The Man Who Knew Infinity: A Life of the Genius Ramanujan . Scribner, 1991.
Krishnamurthy, Mangala. “The Life and Lasting Influence of Srinivasa Ramanujan.” Science & Technology Libraries , vol. 31, 2012, pp. 230–241.
Miller, Julius. “Srinivasa Ramanujan: A Biographical Sketch.” School Science and Mathematics , vol. 51, no. 8, Nov. 1951, pp. 637–645.
Newman, James. “Srinivasa Ramanujan.” Scientific American , vol. 178, no. 6, June 1948, pp. 54–57.
O'Connor, John, and Edmund Robertson. “Srinivasa Aiyangar Ramanujan.” MacTutor History of Mathematics Archive , University of St. Andrews, Scotland, June 1998, www-groups.dcs.st-and.ac.uk/history/Biographies/Ramanujan.html.
Singh, Dharminder, et al. “Srinvasa Ramanujan's Contributions in Mathematics.” IOSR Journal of Mathematics , vol. 12, no. 3, 2016, pp. 137–139.
“Srinivasa Aiyangar Ramanujan.” Ramanujan Museum & Math Education Centre , M.A.T Educational Trust, www.ramanujanmuseum.org/aboutramamujan.htm.
Popular Math Terms and Definitions
What Is the Hardy-Weinberg Principle?
Biography of Ada Lovelace, First Computer Programmer
Biography of Johannes Kepler, Pioneering German Astronomer
The History of Algebra
5 Conditions for Hardy-Weinberg Equilibrium
Life and Work of Gustav Kirchhoff, Physicist
What Does Unity Mean in Mathematics?
Biography of John Napier, Scottish Mathematician
Biography of Lewis Carroll, Author of Children's Books and Mathematician
Biography of Subrahmanyan Chandrasekhar
Euclid of Alexandria and His Contributions to Geometry
Biography of J.B.S. Haldane
Biography of Blaise Pascal, 17th Century Inventor of the Calculator
The Life of Pythagoras
Biography of Joseph Louis Lagrange, Mathematician

Essay on Srinivasa Ramanujan

500 words essay on srinivasa ramanujan.

Srinivasa Ramanujan is one of the world’s greatest mathematicians of all time. Furthermore, this man, from a poor Indian family, rose to prominence in the field of mathematics. This essay on Srinivasa Ramanujan will throw more light on the life of this great personality.

Essay On Srinivasa Ramanujan

Early Life of Srinivasa Ramanujan

Ramanujan was born in Erode on December 22, 1887, in his grandmother’s house. Furthermore, he went to primary school in Kumbakonamwas when he was five years old. Moreover, he would attend several different primary schools before his entry took place to the Town High School in Kumbakonam in January 1898.

At the Town High School, Ramanujan proved himself as a talented student and did well in all of his school subjects. In 1900, he became involved with mathematics and began summing geometric and arithmetic series on his own.

In the Town High School, Ramanujan began reading a mathematics book called ‘Synopsis of Elementary Results in Pure Mathematics’. Furthermore, this book was by G. S. Carr.

With the help of this book, Ramanujan began to teach himself mathematics . Furthermore, the book contained theorems, formulas and short proofs. It also contained an index to papers on pure mathematics.

His Contribution to Mathematics

By 1904, Ramanujan’s focus was on deep research. Moreover, an investigation took place by him of the series (1/n). Moreover, calculation took place by him of Euler’s constant to 15 decimal places. This was entirely his own independent discovery.

Ramanujan gained a scholarship because of his outstanding performance in his studies. Consequently, he was a brilliant student at Kumbakonam’s Government College. Moreover, his fascination and passion for mathematics kept on growing.

In the spring of 1913, there was the presentation of Ramanujan’s work to British mathematicians by Narayana Iyer, Ramachandra Rao and E. W. Middlemast. Afterwards, M.J.M Hill did not made an offer to take Ramanujan on as a student, rather, he provided professional advice to him. With the help of friends, Ramanujan sent letters to leading mathematicians at Cambridge University and was ultimately selected.

Ramanujan spent a significant time period of five years at Cambridge. At Cambridge, collaboration took place of Ramanujan with Hardy and Littlewood. Most noteworthy, the publishing of his findings took place there.

Ramanujan received the honour of a Bachelor of Arts by Research degree in March 1916. This honour was due to his work on highly composite numbers, sections of the first part whose publishing had taken place the preceding year. Moreover, the paper’s size was more than fifty pages long.

Get the huge list of more than 500 Essay Topics and Ideas

Conclusion of the Essay on Srinivasa Ramanujan

Srinivasa Ramanujan is a man whose contributions to the field of mathematics are unmatchable. Furthermore, experts in mathematics worldwide all recognize his tremendous worth. Most noteworthy, Srinivasa Ramanujan made his country proud at a time when India was still under British occupation.

FAQs For Essay on Srinivasa Ramanujan

Question 1: What is Srinivasa Ramanujan famous for?

Answer 1: Srinivas Ramanujan is famous for his discoveries that have influenced several areas of mathematics. Furthermore, he is famous for his contributions to number theory and infinite series. Moreover, he came up with fascinating formulas that facilitate in the calculation of the digits of pi in unusual ways.

Question 2: What is the special quality of number 1729 discovered by Srinivasa Ramanujan?

Answer 2: Srinivas Ramanujan discovered that the number 1729 had a special characteristic. Furthermore, this quality is that the number 1729 is the only number whose expression can take place as the sum of the cubes of two different sets of numbers. Consequently, people call 1729 the magic number.

Customize your course in 30 seconds

Which class are you in.

Travelling Essay
Picnic Essay
Our Country Essay
My Parents Essay
Essay on Favourite Personality
Essay on Memorable Day of My Life
Essay on Knowledge is Power
Essay on Gurpurab
Essay on My Favourite Season
Essay on Types of Sports

Download the App

MacTutor

Srinivasa aiyangar ramanujan.

A short uncouth figure, stout, unshaven, not over clean, with one conspicuous feature-shining eyes- walked in with a frayed notebook under his arm. He was miserably poor. ... He opened his book and began to explain some of his discoveries. I saw quite at once that there was something out of the way; but my knowledge did not permit me to judge whether he talked sense or nonsense. ... I asked him what he wanted. He said he wanted a pittance to live on so that he might pursue his researches.

I have passed the Matriculation Examination and studied up to the First Arts but was prevented from pursuing my studies further owing to several untoward circumstances. I have, however, been devoting all my time to Mathematics and developing the subject.

I can strongly recommend the applicant. He is a young man of quite exceptional capacity in mathematics and especially in work relating to numbers. He has a natural aptitude for computation and is very quick at figure work.

I have had no university education but I have undergone the ordinary school course. After leaving school I have been employing the spare time at my disposal to work at mathematics. I have not trodden through the conventional regular course which is followed in a university course, but I am striking out a new path for myself. I have made a special investigation of divergent series in general and the results I get are termed by the local mathematicians as 'startling'.

I was exceedingly interested by your letter and by the theorems which you state. You will however understand that, before I can judge properly of the value of what you have done, it is essential that I should see proofs of some of your assertions. Your results seem to me to fall into roughly three classes: (1) there are a number of results that are already known, or easily deducible from known theorems; (2) there are results which, so far as I know, are new and interesting, but interesting rather from their curiosity and apparent difficulty than their importance; (3) there are results which appear to be new and important...

I have found a friend in you who views my labours sympathetically. ... I am already a half starving man. To preserve my brains I want food and this is my first consideration. Any sympathetic letter from you will be helpful to me here to get a scholarship either from the university of from the government.

What was to be done in the way of teaching him modern mathematics? The limitations of his knowledge were as startling as its profundity.

... that it was extremely difficult because every time some matter, which it was thought that Ramanujan needed to know, was mentioned, Ramanujan's response was an avalanche of original ideas which made it almost impossible for Littlewood to persist in his original intention.

Batty Shaw found out, what other doctors did not know, that he had undergone an operation about four years ago. His worst theory was that this had really been for the removal of a malignant growth, wrongly diagnosed. In view of the fact that Ramanujan is no worse than six months ago, he has now abandoned this theory - the other doctors never gave it any support. Tubercle has been the provisionally accepted theory, apart from this, since the original idea of gastric ulcer was given up. ... Like all Indians he is fatalistic, and it is terribly hard to get him to take care of himself.

I think we may now hope that he has turned to corner, and is on the road to a real recovery. His temperature has ceased to be irregular, and he has gained nearly a stone in weight. ... There has never been any sign of any diminuation in his extraordinary mathematical talents. He has produced less, naturally, during his illness but the quality has been the same. .... He will return to India with a scientific standing and reputation such as no Indian has enjoyed before, and I am confident that India will regard him as the treasure he is. His natural simplicity and modesty has never been affected in the least by success - indeed all that is wanted is to get him to realise that he really is a success.

References ( show )

O Ore, Biography in Dictionary of Scientific Biography ( New York 1970 - 1990) . See THIS LINK .
Biography in Encyclopaedia Britannica. http://www.britannica.com/biography/Srinivasa-Ramanujan
B C Berndt and R A Rankin, Ramanujan : Letters and commentary ( Providence, Rhode Island, 1995) .
G H Hardy, Ramanujan ( Cambridge, 1940) .
R Kanigel, The man who knew infinity : A life of the genius Ramanujan ( New York, 1991) .
J N Kapur ( ed. ) , Some eminent Indian mathematicians of the twentieth century ( Kapur, 1989) .
S Ram, Srinivasa Ramanujan ( New Delhi, 1979) .
S Ramanujan, Collected Papers ( Cambridge, 1927) .
S R Ranganathan, Ramanujan : the man and the mathematician ( London, 1967) .
P K Srinivasan, Ramanujan : Am inspiration 2 Vols. ( Madras, 1968) .
P V Seshu Aiyar, The late Mr S Ramanujan, B.A., F.R.S., J. Indian Math. Soc. 12 (1920) , 81 - 86 .
G E Andrews, An introduction to Ramanujan's 'lost' notebook, Amer. Math. Monthly 86 (1979) , 89 - 108 .
B Berndt, Srinivasa Ramanujan, The American Scholar 58 (1989) , 234 - 244 .
B Berndt and S Bhargava, Ramanujan - For lowbrows, Amer. Math. Monthly 100 (1993) , 644 - 656 .
B Bollobas, Ramanujan - a glimpse of his life and his mathematics, The Cambridge Review (1988) , 76 - 80 .
B Bollobas, Ramanujan - a glimpse of his life and his mathematics, Eureka 48 (1988) , 81 - 98 .
J M Borwein and P B Borwein, Ramanujan and pi, Scientific American 258 (2) (1988) , 66 - 73 .
S Chandrasekhar, On Ramanujan, in Ramanujan Revisited ( Boston, 1988) , 1 - 6 .
L Debnath, Srinivasa Ramanujan (1887 - 1920) : a centennial tribute, International journal of mathematical education in science and technology 18 (1987) , 821 - 861 .
G H Hardy, The Indian mathematician Ramanujan, Amer. Math. Monthly 44 (3) (1937) , 137 - 155 .
G H Hardy, Srinivasa Ramanujan, Proc. London Math, Soc. 19 (1921) , xl-lviii.
E H Neville, Srinivasa Ramanujan, Nature 149 (1942) , 292 - 294 .
C T Rajagopal, Stray thoughts on Srinivasa Ramanujan, Math. Teacher ( India ) 11 A (1975) , 119 - 122 , and 12 (1976) , 138 - 139 .
K Ramachandra, Srinivasa Ramanujan ( the inventor of the circle method ) , J. Math. Phys. Sci. 21 (1987) , 545 - 564 .
K Ramachandra, Srinivasa Ramanujan ( the inventor of the circle method ) , Hardy-Ramanujan J. 10 (1987) , 9 - 24 .
R A Rankin, Ramanujan's manuscripts and notebooks, Bull. London Math. Soc. 14 (1982) , 81 - 97 .
R A Rankin, Ramanujan's manuscripts and notebooks II, Bull. London Math. Soc. 21 (1989) , 351 - 365 .
R A Rankin, Srinivasa Ramanujan (1887 - 1920) , International journal of mathematical education in science and technology 18 (1987) , 861 -.
R A Rankin, Ramanujan as a patient, Proc. Indian Ac. Sci. 93 (1984) , 79 - 100 .
R Ramachandra Rao, In memoriam S Ramanujan, B.A., F.R.S., J. Indian Math. Soc. 12 (1920) , 87 - 90 .
E Shils, Reflections on tradition, centre and periphery and the universal validity of science : the significance of the life of S Ramanujan, Minerva 29 (1991) , 393 - 419 .
D A B Young, Ramanujan's illness, Notes and Records of the Royal Society of London 48 (1994) , 107 - 119 .

Additional Resources ( show )

Other pages about Srinivasa Ramanujan:

Multiple entries in The Mathematical Gazetteer of the British Isles ,
Miller's postage stamps
Heinz Klaus Strick biography

Other websites about Srinivasa Ramanujan:

Dictionary of Scientific Biography
Dictionary of National Biography
Encyclopaedia Britannica
Ramanujan's last letter
Srinivasa Rao
Plus Magazine
A Sen ( An article about the influence of Carr's book on Ramanujan )
Kevin Brown ( Something else about 1729)
The mathematician and his legacy ( YouTube video )
Sci Hi blog
Google doodle
Mathematical Genealogy Project
MathSciNet Author profile
zbMATH entry

Honours ( show )

Honours awarded to Srinivasa Ramanujan

Fellow of the Royal Society 1918
Popular biographies list Number 1
Google doodle 2012

Cross-references ( show )

History Topics: Squaring the circle
Famous Curves: Ellipse
Societies: Indian Academy of Sciences
Societies: Indian Mathematical Society
Societies: Ramanujan Mathematical Society
Other: 16th March
Other: 1st April
Other: 2009 Most popular biographies
Other: 22nd December
Other: 27th February
Other: 8th February
Other: Cambridge Colleges
Other: Cambridge Individuals
Other: Earliest Known Uses of Some of the Words of Mathematics (D)
Other: Earliest Known Uses of Some of the Words of Mathematics (H)
Other: Jeff Miller's postage stamps
Other: London Learned Societies
Other: London individuals N-R
Other: Most popular biographies – 2024
Other: Oxford individuals
Other: Popular biographies 2018

Reset password New user? Sign up

Existing user? Log in

Srinivasa Ramanujan

Already have an account? Log in here.

Srinivasa Ramanujan (1887-1920) was an Indian mathematician who made great and original contributions to many mathematical fields, including complex analysis , number theory , infinite series , and continued fractions . He was "discovered" by G. H. Hardy and J. E. Littlewood, two world-class mathematicians at Cambridge, and enjoyed an extremely fruitful period of collaboration with them from 1914 to 1919. Unfortunately, his mathematical career was curtailed by health problems; he returned to India and died when he was only 32 years old.

Hardy, who was a great mathematician in his own right, recognized Ramanujan's genius from a series of letters that Ramanujan sent to mathematicians at Cambridge in 1913. Like much of his writing, the letters contained a dizzying array of unique and difficult results, stated without much explanation or proof. The contrast between Hardy, who was above all concerned with mathematical rigor and purity, and Ramanujan, whose writing was difficult to read and peppered with mistakes but bespoke an almost supernatural insight, produced a rich partnership.

Since his death, Ramanujan's writings (many contained in his famous notebooks) have been studied extensively. Some of his conjectures and assertions have led to the creation of new fields of study. Some of his formulas are believed to be true but as yet unproven.

There are many existing biographies of Ramanujan. The Man Who Knew Infinity , by Robert Kanigel, is an accessible and well-researched historical account of his life. The rest of this wiki will give a brief and light summary of the mathematical life of Ramanujan. As an appetizer, here is an anecdote from Kanigel's book.

In 1914, Ramanujan's friend P. C. Mahalanobis gave him a problem he had read in the English magazine Strand . The problem was to determine the number \( x \) of a particular house on a street where the houses were numbered \( 1,2,3,\ldots,n \). The house with number \( x \) had the property that the sum of the house numbers to the left of it equaled the sum of the house numbers to the right of it. The problem specified that \( 50 < n < 500 \).

Ramanujan quickly dictated a continued fraction for Mahalanobis to write down. The numerators and denominators of the convergents to that continued fraction gave all solutions \( (n,x) \) to the problem \((\)not just the particular one where \( 50 < n < 500). \) Mahalanobis was astonished, and asked Ramanujan how he had found the solution.

Ramanujan responded, "...It was clear that the solution should obviously be a continued fraction; I then thought, which continued fraction? And the answer came to my mind."

This is not the most illuminating answer! If we cannot duplicate the genius of Ramanujan, let us at least find the solution to the original problem. What is \( x \)?

\(\) Bonus: Which continued fraction did Ramanujan give Mahalanobis?

This anecdote and problem is taken from The Man Who Knew Infinity , a biography of Ramanujan by Robert Kanigel.

Taxicab numbers, nested radicals and continued fractions, ramanujan primes, ramanujan sums, the ramanujan \( \tau \) function and ramanujan's conjecture.

Many of Ramanujan's mathematical formulas are difficult to understand, let alone prove. For instance, an identity such as

\[\frac1{\pi} = \frac{2\sqrt{2}}{9801}\sum_{k=0}^{\infty} \frac{(4k)!(1103+26390k)}{(k!)^4 396^{4k}}\]

is not particularly easy to get a handle on. Perhaps this is why the most famous mathematical fact about Ramanujan is trivial and uninteresting, compared to the many brilliant theorems he proved.

The story goes that Hardy was visiting Ramanujan in the hospital, and remarked offhandedly that the taxi he had taken had a "dull number," 1729. Instantly Ramanujan replied, "No, it is a very interesting number! It is the smallest positive integer expressible as the sum of two positive cubes in two different ways."

That is, \( 1729 = 1^3+12^3 = 9^3+10^3 \).

Hardy and Wright proved in 1938 that for every \( n \), there is a positive integer \( \text{Ta}(n) \) that is expressible as the sum of two positive cubes in \( n \) different ways. So \( \text{Ta}(2) = 1729 \). \((\)The value of \( \text{Ta}(2) \) had been known since the \(17^\text{th}\) century, which is in some sense characteristic of Ramanujan as well: as he was largely self-taught, he was often rediscovering theorems that were already well-known at the same time as he was constructing entirely new ones.\()\) The numbers \( \text{Ta}(n) \) are called taxicab numbers in honor of Hardy and Ramanujan.

Ramanujan developed several formulas that allowed him to evaluate nested radicals such as \[ 3 = \sqrt{1+2\sqrt{1+3\sqrt{1+4\sqrt{\cdots}}}}. \] This is a special case of a result from his notebooks, which is proved in the wiki on nested functions .

He also contributed greatly to the theory of continued fractions . One of the identities in his letter to Hardy was \[ 1+\frac{e^{-2\pi}}{1+\frac{e^{-4\pi}}{1+\frac{e^{-6\pi}}{\cdots}}} = \left( \sqrt{\frac{5+\sqrt{5}}2} - \frac{1+\sqrt{5}}2 \right)e^{2\pi/5}. \] This and several others along these lines were among the results that convinced Hardy that Ramanujan was a brilliant mathematician. This result is in fact a special case of the Rogers-Ramanujan continued fraction , which is of the form \[ R(q) = \frac{q^{1/5}}{1+\frac{q}{1+\frac{q^2}{1+\frac{q^3}{\cdots}}}} \] and is related to the theory of modular forms, a deep branch of modern number theory.

Ramanujan's work with modular forms produced the following celebrated divisibility results involving the partition function \( p(n) \): \[ \begin{align} p(5k+4) &\equiv 0 \pmod 5 \\ p(7k+5) &\equiv 0 \pmod 7 \\ p(11k+6) &\equiv 0 \pmod{11}. \end{align} \] Ramanujan commented in the paper in which he proved these results that there did not appear to be any other simple results of the same type. But in fact there are similar congruences of the form \( p(ak+b) \equiv 0 \pmod n \) for any \( n \) relatively prime to \( 6\); this is due to Ken Ono (2000). (Even for small \( n\), the values of \( a \) and \( b \) in the congruences are quite large.) The topic remains the subject of much contemporary research.

Ramanujan proved a generalization of Bertrand's postulate , as follows: Let \( \pi(x) \) be the number of positive prime numbers \( \le x \); then for every positive integer \( n \), there exists a prime number \( R_n \) such that \[ \pi(x)-\pi(x/2) \ge n \text{ for all } x \ge R_n. \] \((\)The case \( n = 1 \), \( R_n = 2 \) is Bertrand's postulate.\()\)

The \( R_n \) are called Ramanujan primes .

The sum \( c_q(n) \) of the \(n^\text{th}\) powers of the primitive \( q^\text{th}\) roots of unity is called a Ramanujan sum . It can be shown that these are multiplicative arithmetic functions , and in fact that \[c_q(n) = \frac{\mu\left(\frac qd\right)\phi(q)}{\phi\left(\frac qd\right)},\] where \( d = \text{gcd}(q,n)\), and \( \mu \) and \( \phi \) are the Mobius function and Euler's totient function , respectively.

Let \(c_{2015}(n)\) be the sum of the \(n^\text{th}\) powers of all the primitive \(2015^\text{th}\) roots of unity, \(\omega.\) Find the minimal value of \(c_{2015}(n)\) for all positive integers \(n\).

This year's problem

Ramanujan found nice infinite sums of the form \( \sum a_n c_q(n) \) or \( \sum a_q c_q(n) \) representing the standard arithmetic functions that are important in number theory. For instance, \[ d(n) = -\frac1{2\gamma+\ln(n)} \sum_{q=1}^{\infty} \frac{\ln(q)^2}{q} c_q(n), \] where \( \gamma \) is the Euler-Mascheroni constant .

Another example: the identity \[ \sum_{q=1}^{\infty} \frac{c_q(n)}{q} = 0 \] turns out to be equivalent to the prime number theorem .

Sums involving \( c_q(n) \) are known as Ramanujan sums ; these were also used in applications including the proof of Vinogradov's theorem that every sufficiently large odd positive integer is the sum of three primes.

Ramanujan's \( \tau \) function is defined by the formula \[ \sum_{n=1}^{\infty} \tau(n) q^n = q\prod_{n=1}^{\infty} (1-q^n)^{24} \] and is related to the theory of modular forms.

Ramanujan conjectured several properties of the \( \tau \) function, including \[ |\tau(p)| \le 2p^{11/2} \text{ for all primes } p. \] This turned out to be an extremely important and deep result, which was proved in 1974 by Pierre Deligne in his Fields-medal-winning proofs of the Weil conjectures on points on algebraic varieties over finite fields.

Problem Loading...

Note Loading...

Set Loading...

Subscriber Services
For Authors
Publications
Archaeology
Art & Architecture
Bilingual dictionaries
Classical studies
Encyclopedias
English Dictionaries and Thesauri
Language reference
Linguistics
Media studies
Medicine and health
Names studies
Performing arts
Science and technology
Social sciences
Society and culture
Overview Pages
Subject Reference
English Dictionaries
Bilingual Dictionaries

Srinivasa Ramanujan

(1887—1920) mathematician

Quick Reference

(1887–1920) Indian mathematician

Ramanujan, the son of a clerk, was born into a poor Brahmin family in Erode near Madras, India. Sometime in 1903, while a student at Kumbakonam High School, he acquired a copy of G. S. Carr's Synopsis of Elementary Results in Pure Mathematics. Carr is an unusual work, normally of use as a reference work for a professional mathematician: it consists of about 6000 theorems presented without comment, explanation, or proof. Ramanujan set himself the task of demonstrating all the formulas, a task only a natural-born mathematician would contemplate, let alone pursue. Indifferent to other subjects, Ramanujan failed every exam he entered. For a time he was supported by Ramachandra Rao, a senior civil servant and secretary of the Indian Mathematical Society (IMS). In 1912 he took a clerical position with the Madras Port Trust. At the same time it was suggested that he should seek the advice of a number of British mathematicians about his work and career.

In January 1913 Ramanujan sent a letter to a number of British mathematicians containing a number of formulas. The only one to respond was the Cambridge mathematician G. H. Hardy. Hardy noted that, while some of the formulas were familiar, others “seemed scarcely possible to believe.” Some he thought he could, with difficulty, prove himself; others, he had never seen anything like before, and they defeated Hardy completely. Despite this, it was obvious to Hardy that the formulas must be true and could only come from a mathematician of the very highest class. With Hardy's backing, Ramanujan was awarded a scholarship by the University of Madras and invited to visit Cambridge.

There were, however, religious problems facing the devout Ramanujan but these were resolved when the goddess Namagiri appeared in a dream to Ramanujan's mother absolving him from his traditional obligations. By June 1913 Ramanujan was in Cambridge working with Hardy. They collaborated on five important papers. Ramanujan was elected to the Royal Society in 1918, the first Indian to be honored in this way, and was made a fellow of Trinity College, Cambridge, in 1919. By this time his health had begun to fail. He returned to India in 1919 and died soon after from TB.

Part of Ramanujan's mathematical ability came from his ability to do mental calculations extremely quickly. It is said that he was traveling in a cab with Hardy when Hardy observed that the number of the cab in front, 1729, was a dull number. “No,” replied Ramanujan, “it is a very interesting number; it is the smallest number expressible as a sum of two cubes in two different ways.” (1729 = 1 3 +12 3 and 9 3 +10 3 .)

From: Ramanujan, Srinivasa Iyengar in A Dictionary of Scientists »

Subjects: Science and technology — Mathematics and Computer Science

Ramanujan: The Man Who Knew Infinity

Srinivasa Ramanujan (1887-1920), the man who reshaped twentieth-century mathematics with his various contributions in several mathematical domains, including mathematical analysis, infinite series, continued fractions, number theory, and game theory is recognized as one of history's greatest mathematicians. Leaving this world at the youthful age of 32, Ramanujan made significant contributions to mathematics that only a few others could match in their lifetime. Surprisingly, he never received any formal mathematics training. Most of his mathematical discoveries were based only on intuition and were ultimately proven correct. With its humble and sometimes difficult start, his life story is just as fascinating as his incredible work. Every year, Ramanujan’s birth anniversary on December 22 is observed as National Mathematics Day.

Born in Erode, Tamil Nadu, India, Ramanujan demonstrated an exceptional intuitive grasp of mathematics at a young age. Despite being a mathematical prodigy, Ramanujan's career did not begin well. He received a college scholarship in 1904, but he quickly lost it by failing in nonmathematical subjects. Another attempt at college in Madras (now Chennai) ended in failure when he failed his First Arts exam. It was around this time that he began his famous notebooks. He drifted through poverty until 1910 when he was interviewed by R. Ramachandra Rao, secretary of the Indian Mathematical Society. Rao was initially sceptical of Ramanujan, but he eventually recognised his abilities and supported him financially.

Srinivasa Ramanujan began developing his theories in mathematics and published his first paper in 1911. He was mentored at Cambridge by GH Hardy, a well-known British mathematician who encouraged him to publish his findings in a number of papers. In 1918, Ramanujan became the second Indian to be included as a Fellow of the Royal Society.

Ramanujan’s major contributions to mathematics:

Ramanujan's contribution extends to mathematical fields such as complex analysis, number theory, infinite series, and continued fractions.

Infinite series for pi: In 1914, Ramanujan found a formula for infinite series for pi, which forms the basis of many algorithms used today. Finding an accurate approximation of π (pi) has been one of the most important challenges in the history of mathematics.

Game theory: Ramanujan discovered a long list of new ideas for solving many challenging mathematical problems that have given great impetus to the development of game theory. His contribution to game theory is purely based on intuition and natural talent and is unmatched to this day.

Mock theta function: He elaborated on the mock theta function, a concept in the field of modular forms of mathematics.

Ramanujan number: 1729 is known as the Ramanujan number which is the sum of the cubes of two numbers 10 and 9.

Circle Method: Ramanujan, along with GH Hardy, invented the circle method which gave the first approximations of the partition of numbers beyond 200. This method contributed significantly to solving the notorious complex problems of the 20th century, such as Waring's conjecture and other additional questions.

Theta Function: Theta function is a special function of several complex variables. German mathematician Carl Gustav Jacob Jacobi invented several closely related theta functions known as Jacobi theta functions. Theta function was studied by extensively Ramanujan who came up with the Ramanujan theta function, that generalizes the form of Jacobi theta functions and also captures general properties. Ramanujan theta function is used to determine the critical dimensions in Bosonic string theory, superstring theory, and M-theory.

Other notable contributions by Ramanujan include hypergeometric series, the Riemann series, the elliptic integrals, the theory of divergent series, and the functional equations of the zeta function.

Ramanujan‘s achievements were all about elegance, depth, and surprise beautifully intertwined. Unfortunately, Ramanujan contracted a fatal illness in England in 1918. He convalesced there for more than a year and returned to India in 1919. His condition then worsened, and he died on 26 April 1920. One might expect that a dying man would stop working and await his fate. However, Ramanujan spent his last year producing some of his most profound mathematics.

It has been more than a century, however, his mathematical discoveries are still alive and flourishing. "Ramanujan is important not just as a mathematician but because of what he tells us that the human mind can do”. "Someone with his ability is so rare and so precious that we can't afford to lose them. A genius can arise anywhere in the world. It is our good fortune that he was one of us. It is unfortunate that too little of Ramanujan’s life and work, esoteric though the latter is, seems to be known to most of us".

More Resources:

1 . The Awardees of Ramanujan Fellowships

2. Awardees of Ramanujan Fellowship for 2019-20 & 2020-21

3 . Recipients of The Ramanujan Prize

4 . Ramanujan Fellowship

5 . India and Mathematics

6 . India celebrates National Mathematics Day

7 . Mathematical Organisations

8 . Statistical Organisations

9 . Centre of Excellence in Science and Mathematics Education

10. Ramanujan's legacy: Another cryptic clue of Ramanujan solved

Subodh Kumar

Essay On Ramanujan

Essay on Ramanujan

500+ words essay on ramanujan.

Srinivasa Ramanujan Aiyangar, who is also known as Ramanujan, is one of the greatest mathematicians of all time. The genius mathematician made a significant contribution to several areas of mathematics though he had no formal training in pre-mathematics. His contributions to the theory of numbers, mathematical analysis, number theory, infinite series, and continued fractions are considered to be extraordinary. The Indian mathematician is also known for his ability to solve mathematical problems that were previously considered impossible to solve.

About Srinivasa Ramanujan

Srinivasa Ramanujan, who is often referred to as ‘The World’s Greatest Mathematician’, was born in Erode on 22nd December 1887. His parents were Kuppuswamy Srinivasa Iyengar and Komalatammal. As a young boy, Srinivasa Ramanujan did not like going to school, and his parents had to enlist a constable’s help to ensure he attended school. But by the age of 11, Ramanujan was a child prodigy who developed his own sophisticated theorems to master trigonometry.

By the age of 17, the young mathematical genius had received several awards and merit certificates. Upon graduating high school, S. Ramanujan was awarded a scholarship to study at Government Arts College, Kumbakonam. But since he was intent only on studying mathematics, he failed all other subjects. He later enrolled at Pachaiyappa’s College, Madras, where he failed all other subjects and passed only in mathematics. Ramanujan continued to pursue independent research in mathematics and was eventually included as a researcher at the University of Madras.

His work and intellect were recognized by British mathematicians too. He was elected to the London Mathematical Society in 1917, and in 1918, he was elected to the Royal Society of London. He was the second Indian to be elected to the Royal Society and one of the youngest fellows elected in the history of the society. In 1918, he became the first Indian to be elected to the Fellow of Trinity College, Cambridge.

Ramanujan was a deeply religious person who believed there was a link between mathematics and spirituality. He thought that zero represented absolute reality. He credited his mathematical genius and acumen to his family deity, Goddess Namagiri Thayar. He drew inspiration from her for his work and he claimed to have visions that gave him knowledge of complex mathematical content.

Ramanujan found theorems and formulae as the best manifestation of reality. He compiled around 4000 results, which included theorems, equations and identities in number theory, combinatorics and algebra. He focused on several areas, from hypergeometric and infinite series to highly composite numbers. However, the two central regions Ramanujan felt he had a relationship with are ‘number theory’ and ‘modular functions’. He wrote and published several papers of great mathematical significance with his mentor Professor Hardy during his stay at Cambridge University.

But the mathematical genius did not live a long life. Ramanujan fell sick in 1919, which compelled him to return to India from Cambridge. The genius mathematician died on 26th April 1920 after a brief illness at the young age of 32. His last letters to his mentor, English mathematician G. H. Hardy revealed that he continued working on mathematical ideas before his death. His work was so intricate that it opened up new directions for mathematical research.

Posthumous Awards and Recognition

Srinivasa Ramanujan’s mathematical genius, his work and his achievements were recognized posthumously. The Government of India 2011 declared his birthday National Mathematics Day to commemorate his valuable contribution. The former Prime Minister, Dr Manmohan Singh, proclaimed that 2012 would be celebrated as the National Mathematics Year.

Tamil Nadu, which is Ramanujan’s home state, recognizes his birthday (22nd December) as “State IT Day.” The Government of India also introduced several stamps picturing Ramanujan in 1962, 2011, 2012 and 2016. Several universities and institutions have introduced prizes and awards in his name to students making outstanding contributions to the field of mathematics.

In conclusion, Ramanujan has been compared to notable names, including some masters of mathematics like Euler and Jacobi. He has inspired a whole generation of mathematicians, and his legacy lives on. Ramanujan died at the young age of 37, leaving us a rich legacy of mathematical discoveries.

Download and register with BYJU’S to find more CBSE Essays on different topics. You can also find study materials like textbooks and solutions to prepare for the exams.

Register with BYJU'S & Download Free PDFs

The man who taught infinity: how GH Hardy tamed Srinivasa Ramanujan’s genius

Professor of Pure Mathematics, University of Cambridge

Disclosure statement

Béla Bollobás is a Fellow of Trinity College Cambridge

University of Cambridge provides funding as a member of The Conversation UK.

View all partners

Throughout the history of mathematics, there has been no one remotely like Srinivasa Ramanujan. There is no doubt that he was a great mathematician, but had he had simply a good university education and been taught by a good professor in his field, we wouldn’t have a film about him .

As the years pass, I admire more and more the astonishing body of work Ramanujan produced in India before he made contact with any top mathematicians. Not because the results he got at the time changed the face of mathematics, far from it, but because, working by himself, he fearlessly attacked many important and some not so important problems in analysis and, especially, number theory – simply for the love of mathematics.

It cannot be understated, however, the role played by Ramanujan’s tutor Godfrey Harold Hardy in his life story. The Cambridge mathematician worked tirelessly with the Indian genius, to tame his creativity within the then current understanding of the field. It was only with Hardy’s care and mentoring that Ramanujan became the scholar we know him as today.

Determined and obsessed

In December 1903, at the age of 16, Ramanujan passed the matriculation exam for the University of Madras. But as he concentrated on mathematics to the exclusion of all other subjects, he did not progress beyond the second year. In 1909 he married a nine-year-old girl, but failed to secure any steady income until the beginning of 1912, when he became a clerk in the Madras Port Trust office on a meagre salary.

All this time, Ramanujan remained obsessed with mathematics and kept working on continued fractions, divergent series, elliptic integrals, hypergeometric series and the distribution of primes. By 1911, Ramanujan was desperate to gain recognition from leading mathematicians, especially those in England. So, at the beginning of 1913, when he was just past 25, he dispatched a letter to Hardy in Cambridge with a long list of his discoveries –- a letter which changed both their lives.

Although only 36 when he received Ramanujan’s letter, Hardy was already the leading mathematician in England . The mathematical scene in England in the first half of the 20th century was dominated by Hardy and another titan of Trinity College, J.E. Littlewood . The two formed a legendary partnership, unique to this day, writing an astounding 100 joint papers. They were instrumental in turning England into a superpower in mathematics, especially in number theory and analysis.

Hardy was not the first mathematician to whom Ramanujan had sent his results, however the first two to whom he had written judged him to be a crank. But Hardy was not only an outstanding mathematician, he was also a wonderful teacher, eager to nurture talent.

Genius unknown

After dinner in Trinity one evening, some of the fellows adjourned to the combination room. Over their claret and port Hardy mentioned to Littlewood some of the claims he had received in the mail from an unknown Indian. Some assertions they knew well, others they could prove, others they could disprove, but many they found not only fascinating and unusual but also impossible to resolve.

This toing and froing between Hardy and Littlewood continued the next day and beyond, and soon they were convinced that their correspondent was a genius. So Hardy sent an encouraging reply to Ramanujan, which led to a frequent exchange of letters.

It was clear to Hardy that Ramanujan was totally exceptional: however, in spite of his amazing feats in mathematics, he lacked the basic tools of the trade of a professional mathematician. Hardy knew that if Ramanujan was to fulfil his potential, he had to have a solid foundation in mathematics, at least as much as the best Cambridge graduates.

It was for Ramanujan’s good that Hardy invited him to Cambridge, then, and he was taken aback when, due to caste prejudices, Ramanujan did not jump at the chance. As a Brahmin , Ramanujan was not allowed to cross the ocean and his mother was totally opposed to the idea of the voyage. When, in early 1914, Ramanujan gained his mother’s consent, Hardy swang into action. He asked E.H Neville, another fellow of Trinity College , who was on a serendipitous trip to Madras, to secure Ramanujan a scholarship from the University of Madras. Neville’s wrote in a letter to the university that “the discovery of the genius of S. Ramanujan of Madras promises to be the most interesting event of our time in the mathematical world …”

Ramanujan sailed for England in the company of Neville, and arrived in Cambridge in April 1914.

Fearless mentoring

I cannot but admire Hardy for his care in mentoring Ramanujan. His main worry was how to teach this astounding talent much mathematics without destroying his confidence. The last thing Hardy wanted was to dent Ramanujan’s fearless approach to the most difficult problems. To quote Hardy:

The limitations of his knowledge were as startling as its profundity. Here was a man who could work out modular equations, and theorems of complex multiplication, to orders unheard of, whose mastery of continued fractions was, on the formal side at any rate, beyond that of any mathematician in the world … It was impossible to ask such a man to submit to systematic instruction, to try to learn mathematics from the beginning once more. On the other hand there were things of which it was impossible that he would remain in ignorance … so I had to try to teach him, and in a measure I succeeded, though I obviously learnt from him much more than he learnt from me.

For almost three years, things went extremely well. In 1916 Ramanujan got his BA from Cambridge and his research went from strength to strength. He published one excellent paper after another, with a great deal of Hardy’s help in the proofs and presentation. They also collaborated on several great projects, and published wonderful joint papers. Sadly, in the spring of 1917 Ramanujan fell ill, and was in and out of sanatoria for the rest of his stay in Cambridge.

By early 1919 Ramanujan seemed to have recovered sufficiently, and decided to travel back to India. Hardy was alarmed not to have heard from him for a considerable time, but a letter in February 1920 made it clear that Ramanujan was very active in research.

Ramanujan’s letter contained some examples of his latest discovery, mock theta functions , which have turned out to be very important. A main conjecture about them was solved 80 years later , and these functions are now seen as interesting examples of a much larger class of mock modular forms in mathematics, which have applications to elliptic curves, Borcherds products , Eichler cohomology and Galois representations – and the nature of black holes.

Sadly, Ramanujan’s recovery was short-lived. His illness returned and killed him, aged just 32, on April 26 1920, leaving him only a short time to benefit from his fellowship of the Royal Society and fellowship of Trinity.

Ramanujan’s death at the height of his powers was a tremendous blow to mathematics. His like may never be seen again, and certainly such a partnership as that which Hardy and Ramanujan built will not either.

Mathematics
Cambridge University

Head, School of Psychology

Senior Lecturer (ED) Ballarat

Senior Research Fellow - Women's Health Services

Lecturer / Senior Lecturer - Marketing

Assistant Editor - 1 year cadetship

Verbal Ability

Interview Q

Send your Feedback to [email protected]

Help Others, Please Share

Learn Latest Tutorials

Transact-SQL

Reinforcement Learning

R Programming

React Native

Python Design Patterns

Python Pillow

Python Turtle

Preparation

Interview Questions

Company Questions

Trending Technologies

Artificial Intelligence

Cloud Computing

Data Science

Machine Learning

B.Tech / MCA

Data Structures

Operating System

Computer Network

Compiler Design

Computer Organization

Discrete Mathematics

Ethical Hacking

Computer Graphics

Software Engineering

Web Technology

Cyber Security

C Programming

Control System

Data Mining

Data Warehouse

India’s Largest Career Transformation Portal

Essay on Srinivasa Ramanujan for Students | 500+ Words Essay

December 10, 2020 by Sandeep

Essay on Srinivasa Ramanujan: Srinivasa Ramanujan was a renowned mathematician of India. He was born on 22nd December 1887 in Madras during the British Raj. Since childhood, he was drawn towards maths and took a particular interest in learning the subject. He did not receive formal education in mathematics but had mastered maths in various sections. During his time in Cambridge, he grew close to the great mathematician named Hardy. Together they invented the Hardy-Ramanujan number 1729. He got married at the age of 22 to Janakiammal on 14th July 1904. Several books were written by him based on his theories and formulas. He even received the K. Ranganatha Rao prize for mathematics. On 26th April 1920, he departed at the age of 32.

Below we have provided an essay on Srinivasa Ramanujan in English, written in easy and simple words for class 4, 5, 6, 7, 8, 9 and 10 school students.

Essay on Srinivasa Ramanujan 500 Words in English

Below we have provided extended essay on Srinivasa Ramanujan, suitable for classes 7, 8, 9 and 10 students.

Ramanujan was the maths genius who said that “An equation for me has no meaning unless it expresses a thought of God.” He always had a vision of scrolls of complicated maths unfolding before him. He is referred to as an Indian Mathematician who lived during the British period and who contributed substantially to mathematics analysis, number theory, infinite series and continued fractions. He has been described by many as a simple person with pleasant manners.

Ramanujan was born on 22nd December 1887 into a Tamil Brahmin family in Erode, Madras. His father, Kuppuswamy Srinivasa Iyengar hailed from Thanjavur district and worked as a clerk in a saree shop. His mother, Komalatammal, was a housewife and used to sing at a local temple. They lived in a small traditional home. When Ramanujan was only a year and a half old, his mother was blessed with a son named Sadagopan but unfortunately died less than three months later.

In 1889, Ramanujan contracted smallpox but recovered, unlike many others who faced the death. Then, in 1891 and 1894, his mother again gave birth to two more children, but both of them died before their first birthdays. Since his father was at work most of the day, his mother took care of him, and their bond grew stronger. From his mother he learnt about the tradition and Puranas, to sing religious songs and to attend puja at a temple.

He became well versed with the Brahmin culture and followed particular eating habits. Just before turning ten, he passed his primary education in English, Tamil, geography and arithmetic. His scores were the best in the district. In the same year, he encountered formal mathematics for the first time. At the age of sixteen, he acquired a library copy of A Synopsis of Elementary Results in Pure and Applied Mathematics from a friend.

He studied the contents of the book thoroughly. The next year, he developed and investigated the Bernoulli numbers and calculate Euler’s constant up to 15 decimals. His peers could hardly understand his nature, and we’re always in awe because of his brilliance. Due to his extraordinary mind, he received a scholarship to study at Government Arts College, Kumbakonam. But he lost this scholarship because of his firm determination towards studying only maths and ignoring other subjects.

Later, too he failed in subjects like English, Sanskrit and physiology. In 1906, he flunked in his Fellow of Arts exam in December. Without a FA degree, he left college and decided to study independently in mathematics through research and referring books. Such a condition caused him extreme poverty, and he reached on the brink of starvation. He married Janakiammal on 14th July 1909 and took a job as a tutor at Presidency College.

Ramanujan met deputy collector V. Ramaswamy Aiyer in 1910, who was the founder of Mathematical society and wished to work in the revenue department. When Ramanujan showed his mathematics book to him, he stated that- “I was struck by the extraordinary mathematical results contained in Ramanujan’s books.” As he advanced further in maths, he even wrote his formal paper on the properties of Bernoulli numbers.

A journal editor M.T. Narayana Iyengar noted that Mr Ramanujan’s methods and presentation was terse and lacked precision and clearness. An ordinary person could hardly follow him. In England, he was awarded a Bachelor of Arts by Research degree. He was also elected to the London Mathematical Society. Ramanujan was the first Indian to be elected a Fellow of Trinity College, Cambridge.

In 1994, he died due to Tuberculosis and left the world. In the words of Hardy, Ramanujan had produced groundbreaking theorems and defeated him many times. He had never seen such theories in his life before. In his obituary, it was written that his insight into the subject was terrific and what he did was outstanding and remarkable.

The government of India in 2011, declared his birthday as National Mathematics Day to commemorate his valuable contribution and efforts. The former President even proclaimed that 2012 would be celebrated as National Mathematics Year.

Also Read – Republic Day Speech 2022 in English

Short Essay on Srinivasa Ramanujan in 250 Words

Below we have provided a short essay on Srinivasa Ramanujan, suitable for class 3, 4, 5 & 6 students.

Srinivasa Ramanujan was a well-known Indian Mathematician who was born on 22nd December 1887 during the British rule. He was born in a poor Indian village, Erode belonging to a Tamil family. His father’s name was Kuppuswamy Srinivas Aiyangar who worked as a clerk in a saree shop, and his mother was a religious housewife. They lived in Erode only for a year and then moved to Kumbakonam.

In this small town, Ramanujan attended many primary schools and achieved a distinction in his primary education. At the age of thirteen, he focused his attention on the sum of geometric an arithmetic series and in 1902, he created a method to solve quadratic equations and even explored Euler’s Constant. In the same year, he received a scholarship for his outstanding performance in his studies, and therefore he got admission at Kumbakonam’s Government college.

His passion for mathematics grew more robust, and hence he excelled in maths but failed in other subjects. The failure caused him depression, and he fled to Vizagapatnam without telling his parents. One year later, he returned to study and pass at First Art’s examination but again failed in all and passed in maths. Ramanujan got married to his old distant relative Janaki Ammal.

Furthermore, he published his first paper based on Bernoulli numbers in Journal of the Indian Mathematical Society and received recognition and achievement. His hard work got paid off, and he was appointed as a clerk at Madras Port Trust. At this time, he became famous throughout Madras and caught the attention of C.L.T Griffith who helped Ramanujan. Later, Ramanujan graduated from London and held a degree of Science for research on highly composite numbers.

Ramanujan | 10 Major Contributions And Achievements

Srinivasa Ramanujan FRS (1887 – 1920) was a self-taught Indian mathematical genius who made numerous contributions in several mathematical fields including mathematical analysis, infinite series, continued fractions, number theory and game theory . Ramanujan provided solutions to mathematical problems that were then considered unsolvable. Moreover, some of his work was so ahead of his time that mathematicians are still understanding its relevance . In 1914, Ramanujan found a formula for computing π (pi) that is currently the basis for the fastest algorithms used to calculate π. The circle method , which he developed with G. H. Hardy , constitute a large area of current mathematical research. Moreover, Ramanujan discovered K3 surfaces which play key roles today in string theory and quantum physics; while his mock modular forms are being used in an effort to unlock the secret of black holes. Know more about the achievements of Srinivasa Ramanujan through his 10 major contributions to mathematics.

#1 HE WAS THE SECOND INDIAN TO BE ELECTED A FELLOW OF THE ROYAL SOCIETY

A self-taught genius, Ramanujan moved to England in March 1914 after his talent was recognized by British mathematician G. H. Hardy . In 1916, Ramanujan was awarded a Bachelor of Science by Research degree (later named Ph.D.) by Cambridge even though he was not an undergraduate. The Ph.D. was awarded in recognition of his work on ‘Highly composite numbers’ . In 1918, Ramanujan became one of the youngest Fellows of the Royal Society and only the second Indian member . The same year he was elected a Fellow of Trinity College, Cambridge , the first Indian to be so honored . During his short lifespan of 32 years, Ramanujan independently compiled around 3,900 results . Apart from the below mentioned achievements his contributions include developing the relationship between partial sums and hyper-geometric series ; independently discovering Bernoulli numbers and using these numbers to formulated the value of Euler’s constant up to 15 decimal places ; discovering the Ramanujan prime number and the Landau–Ramanujan constant ; and coming up with Ramanujan’s sum and the Ramanujan’s master theorem.

#2 THE FASTEST ALGORITHMS FOR CALCULATION OF PI ARE BASED ON HIS SERIES

Finding an accurate approximation of π (pi) has been one of the most important challenges in the history of mathematics. In 1914, Srinivasa Ramanujan found a formula for computing pi that converges rapidly . His formula computes a further eight decimal places of π with each term in the series . It was in 1989, that Chudnovsky brothers computed π to over 1 billion decimal places on a supercomputer using a variation of Ramanujan’s infinite series of π. This was a world record for computing the most digits of pi . Moreover, the Ramanujan series is currently the basis for the fastest algorithms used to calculate π.

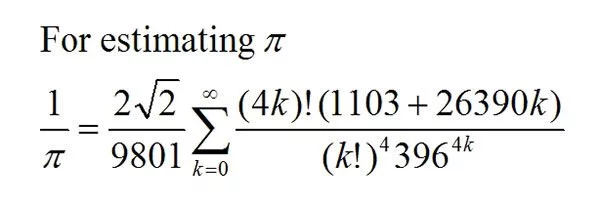
#3 RAMANUJAN CONJECTURE PLAYED A KEY ROLE IN THE FAMOUS LANGLANDS PROGRAM

In 1916 , Ramanujan published his paper titled “On certain arithmetical functions” . In the paper, Ramanujan investigated the properties of Fourier coefficients of modular forms . Though the theory of modular forms was not even developed then , he came up with three fundamental conjectures that served as a guiding force for its development . His first two conjectures helped develop the Hecke theory , which was formulated 20 years after his paper, in 1936, by German mathematician Erich Hecke . However, it was his last conjecture, known as the Ramanujan conjecture , that created a sensation in in 20th century mathematics . It played a pivotal role in the Langlands program , which began in 1970 through the proposal of American-Canadian mathematician Robert Langlands . The Langlands program aims to relate representation theory and algebraic number theory , two seemingly different fields of mathematics . It is widely viewed as the single biggest project in modern mathematical research . “On certain arithmetical functions” by Ramanujan thus effectively changed the course of 20th century mathematics .

#4 HE DEVELOPED THE INFLUENTIAL CIRCLE METHOD IN PARTITION NUMBER THEORY

A partition for a positive integer n is the number of ways the integer can be expressed as a sum of positive integers . For example p(4) = 5 . That means 4 can be expressed as a sum of positive integers in 5 ways: 4, 3+1, 2+2, 2+1+1 and 1+1+1 +1. Ramanujan, along with G. H. Hardy, invented the circle method which gave the first approximations of the partition of numbers beyond 200 . This method was largely responsible for major advances in the 20th century of notoriously difficult problems such as Waring’s conjecture and other additive questions. The circle method is now one of the central tools of analytic number theory . Moreover, circle method and its refinements constitute a large area of current mathematical research.

#5 HE DISCOVERED THE THREE RAMANUJAN’S CONGRUENCES

Related to the Partition Theory of Numbers, Ramanujan also came up with three remarkable congruences for the partition function p(n) . They are p(5n+4) = 0(mod 5); p(7n+4) = 0(mod 7); p(11n+6) = 0(mod 11) . For example, the first congruence means that if an integer is 4 more than a multiple of 5, then number of its partitions is a multiple of 5 . The study of Ramanujan type congruence is a popular research topic of number theory. It was in 2011, that a conceptual explanation for Ramanujan’s congruences was finally discovered . Ramanujan’s work on partition theory has applications in a number of areas including particle physics (particularly quantum field theory) and probability .

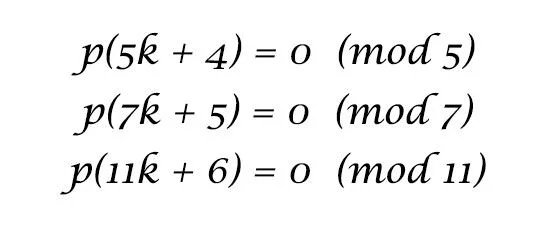
#6 NUMBER 1729 IS NAMED HARDY–RAMANUJAN NUMBER

In a famous incident British mathematician G. H. Hardy while visiting Ramanujan had ridden in a taxi cab with the number 1729 . He remarked to Ramanujan that the number “seemed to me rather a dull one, and that I hoped it was not an unfavorable omen” . “No,” Ramanujan replied, “it is a very interesting number; it is the smallest number expressible as the sum of two cubes in two different ways.” The two different ways are: 1729 = 1 3 + 12 3 = 9 3 + 10 3 . 1729 is now known as the Hardy–Ramanujan number . Moreover, numbers that are the smallest number that can be expressed as the sum of two cubes in n distinct ways are now referred to as taxicab numbers due to the incident. The relevance of 1729 has recently come to light as it was part of a much larger theory that Ramanujan was developing . Theorems have been established in theory of elliptic curves that involve this fascinating number.

#7 HE DID GROUNDBREAKING RESEARCH RELATED TO FERMAT’S LAST THEOREM

In 2013 famous Japanese American Mathematician Ken Ono , along with Sarah Trebat-Leder , found an equation by Ramanujan had clearly showed that he had been working on Fermat’s last theorem, one of the most notable and difficult to prove theorems in the history of mathematics. In 1637, French mathematician Pierre de Fermat had asserted that: if n is a whole number greater than 2 , then there are no positive whole number triples x, y and z , such that x n + y n = z n . This means that there are no numbers which satisfy the equations: x 3 + y 3 = z 3 ; x 4 + y 4 = z 4 ; and so on . The equation of Ramanujan illustrates that he had found an infinite family of positive whole number triples x, y and z that very nearly, but not quite, satisfy Fermat’s equation for n=3 . They are off only by plus or minus one . Among them is 1729 , which misses the mark by 1 for x=9, y=10 and z=12 . Moving forward, Ramanujan also considered the equations of the form: y 2 =x 3 + ax + b . If you plot the points (x,y) for this equation you get an elliptic curve . Elliptic curves played a key role when English mathematician Sir Andrew Wiles finally proved Fermat’s last theorem in 1994, a feat described as a “stunning advance” in mathematics.

#8 RAMANUJAN WAS THE FIRST TO DISCOVER K3 SURFACES

Ken Ono also found that Ramanujan went on to discover an object more complicated than elliptic curves. When it was re-discovered in 1958 by Andre Weil , it was named K3 surface . Thus it has come to light that Ramanujan was using 1729 and elliptic curves to develop formulas for a K3 surface. “Elliptic curves and K3 surfaces form an important next frontier in mathematics and Ramanujan gave remarkable examples illustrating some of their features that we didn’t know before.” Moreover, K3 surfaces play key roles today in string theory and quantum physics . Like, string theory suggests that the world consists of more than the three dimensions that we can see . These extra dimensions are rolled up tightly in tiny little spaces too small for us to perceive . These tiny spaces have a particular geometric structure. Calabi–Yau manifold is a class of geometric objects that have similar structure and one of the simplest classes of Calabi-Yau manifolds comes from K3 surfaces.

#9 HIS THETA FUNCTION LIES AT THE HEART OF STRING THEORY IN PHYSICS

In mathematics, theta functions are special functions of several complex variables . German Mathematician Carl Gustav Jacob Jacobi came up with several closely related theta functions known as Jacobi theta functions . Theta functions were studied extensively by Ramanujan. He came up with the Ramanujan theta function , which generalizes the form of Jacobi theta functions while also capturing their general properties . In particular, the Jacobi triple product takes on an elegant form when written in terms of the Ramanujan theta function . Ramanujan theta function has several important applications. It is used to determine the critical dimensions in Bosonic string theory, superstring theory and M-theory .

#10 HIS MOCK MODULAR FORMS MAY UNLOCK THE SECRET OF BLACK HOLES

In a 1920 letter to Hardy, Ramanujan described several new functions that behaved differently from known theta functions , or modular forms , and yet closely mimicked them. These were the first ever examples of mock modular forms . More than 80 years later, in 2002 , a description for these functions was provided by Sander Zwegers . Further, Ramanujan predicted that his mock modular forms corresponded to ordinary modular forms producing similar outputs for roots of 1 . Ken Ono ultimately showed that a mock modular form could be computed just as Ramanujan predicted . It was found as the output of mock modular forms shoot off to enormous numbers, the corresponding ordinary modular form expand at a similar rate and thus their difference is a relatively small number. Expansion of mock modular forms is now used to compute the entropy, or level of disorder, of black holes. Thus even through black holes were virtually unknown during his time, Ramanujan was able to do mathematics which may unlock their secret.

4 thoughts on “Ramanujan | 10 Major Contributions And Achievements”

A major method for computation of Feynman integrals is the bracket integration method, a direct result from his Master Theorem ( https://en.wikipedia.org/wiki/Ramanujan%27s_master_theorem )

What is plus and minus infinity, he used in his theta function? Infinity in two opposite directions?

very useful information but no that much recognition

awesome pic. loved it

Srinivasa Ramanujan and his contribution to mathematics

Bi india bureau .

Ramanujan compiled around 3,900 results consisting of equations and identities. One of his most treasured findings was his infinite series for pi. This series forms the basis of many algorithms we use today. He gave several fascinating formulas to calculate the digits of pi in many unconventional ways.
He discovered a long list of new ideas to solve many challenging mathematical problems, which gave a significant impetus to the development of game theory. His contribution to game theory is purely based on intuition and natural talent and remains unrivalled to this day.
He elaborately described the mock theta function, which is a concept in the realm of modular form in mathematics. Considered an enigma till sometime back, it is now recognized as holomorphic parts of mass forms.
One of Ramanujan’s notebooks was discovered by George Andrews in 1976 in the library at Trinity College. Later the contents of this notebook were published as a book.
1729 is known as the Ramanujan number. It is the sum of the cubes of two numbers 10 and 9. For instance, 1729 results from adding 1000 (the cube of 10) and 729 (the cube of 9). This is the smallest number that can be expressed in two different ways as it is the sum of these two cubes. Interestingly, 1729 is a natural number following 1728 and preceding 1730.
Ramanujan’s contributions stretch across mathematics fields, including complex analysis, number theory, infinite series, and continued fractions.

biography of ramanujan in 300 words

IMAGES

VIDEO

COMMENTS

Srinivasa Ramanujan

Who Was Srinivasa Ramanujan?

A Blessing and a Curse

Doing the Math

The Man Who Knew Infinity

QUICK FACTS

CITATION INFORMATION

Famous Mathematicians

Products & Resources

Colleges & Courses

Predictors & E-Books

Predictors & Articles

Top Courses & Careers

Quick Links

Diploma Colleges

Upcoming Events

Other Exams

Top Countries

Student Visas

Engineering Preparation

Medical Preparation

Online Courses

Top Streams

Specializations

Top Providers

Essay on Srinivasa Ramanujan in English - 100, 200, 500 Words

100 Words Essay on Srinivasa Ramanujan

Achievements of Srinivasa Ramanujan

Applications for Admissions are open.

Aakash iACST Scholarship Test 2024

ALLEN Digital Scholarship Admission Test (ADSAT)

JEE Main Important Physics formulas

PW JEE Coaching

PW NEET Coaching

JEE Main Important Chemistry formulas

Download Careers360 App's

We Appeared in

Biography of Srinivasa Ramanujan, Mathematical Genius

Fast Facts: Srinivasa Ramanujan

Early Life and Education

Personal Life

Honors and Awards

Legacy and Impact

Essay on Srinivasa Ramanujan

Early Life of Srinivasa Ramanujan

His Contribution to Mathematics

Conclusion of the Essay on Srinivasa Ramanujan

FAQs For Essay on Srinivasa Ramanujan

Customize your course in 30 seconds

Leave a Reply Cancel reply

Download the App

MacTutor

References ( show )

Additional Resources ( show )

Honours ( show )

Cross-references ( show )

Srinivasa Ramanujan

This anecdote and problem is taken from The Man Who Knew Infinity , a biography of Ramanujan by Robert Kanigel.

Recently viewed (0)

Related Content

More Like This

Srinivasa Ramanujan

Quick Reference

Related content in Oxford Reference

Ramanujan: The Man Who Knew Infinity

Essay on Ramanujan

About Srinivasa Ramanujan

Posthumous Awards and Recognition

Register with BYJU'S & Download Free PDFs

The man who taught infinity: how GH Hardy tamed Srinivasa Ramanujan’s genius

Disclosure statement

Determined and obsessed

Genius unknown

Fearless mentoring

Head, School of Psychology

Senior Lecturer (ED) Ballarat

Senior Research Fellow - Women's Health Services

Lecturer / Senior Lecturer - Marketing

Assistant Editor - 1 year cadetship

Help Others, Please Share