case study questions on quadrilaterals class 8

Gurukul of Excellence

Classes for Physics, Chemistry and Mathematics by IITians

Join our Telegram Channel for Free PDF Download

Case Study Questions for Class 8 Maths Chapter 3 Understanding Quadrilaterals

• Last modified on: 8 months ago
• Reading Time: 3 Minutes

Here we are providing Case Study questions for Class 8 Maths Chapter 3 Understanding Quadrilaterals.

Case Study Questions

Related posts, learning outcomes.

• Convex and Concave Polygons.
• Regular and Irregular Polygons.
• Sum of Measures of the Exterior Angles of a Polygon.
• Kinds of QuadrilateralTrapezium; Kite; Parallelogram.
• Some Special ParallelogramsRhombus; Rectangle; Square.

Important Keywords

• Convex Polygon: Polygons that have any line segment joining any two different points in the interior and have no portions of their diagonals in their exteriors are called convex polygons.
• Concave Polygon: Polygons that have one diagonal outside it are called concave polygons.
• Regular Polygon: A polygon whose all sides, all angles are equal that is which is both equiangular and equilateral are called regular polygon. Example: Square; Equilateral triangle
• Irregular Polygon: Polygon whose all sides are not equal are called Irregular polygon. Example: Rectangle.

Fundamental Facts

• Convex Polygon has each angle either acute or obtuse.
• Concave Polygon has one angle as reflex angle.

Download CBSE Books

Exam Special Series:

• Sample Question Paper for CBSE Class 10 Science (for 2024)
• Sample Question Paper for CBSE Class 10 Maths (for 2024)
• CBSE Most Repeated Questions for Class 10 Science Board Exams
• CBSE Important Diagram Based Questions Class 10 Physics Board Exams
• CBSE Important Numericals Class 10 Physics Board Exams
• CBSE Practical Based Questions for Class 10 Science Board Exams
• CBSE Important “Differentiate Between” Based Questions Class 10 Social Science
• Sample Question Papers for CBSE Class 12 Physics (for 2024)
• Sample Question Papers for CBSE Class 12 Chemistry (for 2024)
• Sample Question Papers for CBSE Class 12 Maths (for 2024)
• Sample Question Papers for CBSE Class 12 Biology (for 2024)
• CBSE Important Diagrams & Graphs Asked in Board Exams Class 12 Physics
• Master Organic Conversions CBSE Class 12 Chemistry Board Exams
• CBSE Important Numericals Class 12 Physics Board Exams
• CBSE Important Definitions Class 12 Physics Board Exams
• CBSE Important Laws & Principles Class 12 Physics Board Exams
• 10 Years CBSE Class 12 Chemistry Previous Year-Wise Solved Papers (2023-2024)
• 10 Years CBSE Class 12 Physics Previous Year-Wise Solved Papers (2023-2024)
• 10 Years CBSE Class 12 Maths Previous Year-Wise Solved Papers (2023-2024)
• 10 Years CBSE Class 12 Biology Previous Year-Wise Solved Papers (2023-2024)
• ICSE Important Numericals Class 10 Physics BOARD Exams (215 Numericals)
• ICSE Important Figure Based Questions Class 10 Physics BOARD Exams (230 Questions)
• ICSE Mole Concept and Stoichiometry Numericals Class 10 Chemistry (65 Numericals)
• ICSE Reasoning Based Questions Class 10 Chemistry BOARD Exams (150 Qs)
• ICSE Important Functions and Locations Based Questions Class 10 Biology
• ICSE Reasoning Based Questions Class 10 Biology BOARD Exams (100 Qs)

✨ Join our Online JEE Test Series for 499/- Only (Web + App) for 1 Year

✨ Join our Online NEET Test Series for 499/- Only for 1 Year

Leave a Reply Cancel reply

Join our Online Test Series for CBSE, ICSE, JEE, NEET and Other Exams

Editable Study Materials for Your Institute - CBSE, ICSE, State Boards (Maharashtra & Karnataka), JEE, NEET, FOUNDATION, OLYMPIADS, PPTs

Discover more from Gurukul of Excellence

Subscribe now to keep reading and get access to the full archive.

Type your email…

Continue reading

NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals

NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals are provided below. Our solutions covered each questions of the chapter and explains every concept with a clarified explanation. To score good marks in Class 8 Mathematics examination, it is advised to solve questions provided at the end of each chapter in the NCERT book.

NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals are prepared based on Class 8 NCERT syllabus, taking the types of questions asked in the NCERT textbook into consideration. Further, all the CBSE Class 8 Solutions Maths Chapter 3 are in accordance with the latest CBSE guidelines and marking schemes.

Class 8 Maths Chapter 3 Exercise 3.1 Solutions

Class 8 Maths Chapter 3 Exercise 3.2 Solutions

Class 8 Maths Chapter 3 Exercise 3.3 Solutions

Class 8 Maths Chapter 3 Exercise 3.4 Solutions

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

• CBSE-Understanding Quadrilaterals
• Sample Questions

Understanding Quadrilaterals-Sample Questions

• STUDY MATERIAL FOR CBSE CLASS 8 MATH
• Chapter 1 - Algebraic Expressions and Identities
• Chapter 2 - Comparing Quantities
• Chapter 3 - Cubes and Cube Roots
• Chapter 4 - Data handling
• Chapter 5 - Direct and Inverse Proportions
• Chapter 6 - Exponents and Powers
• Chapter 7 - Factorization
• Chapter 8 - Introduction to Graphs
• Chapter 9 - Mensuration
• Chapter 10 - Playing with Numbers
• Chapter 11 - Practical Geometry
• Chapter 12 - Squares and Square Roots
• Chapter 13 - Visualizing Solid Shapes
• Chapter 14 - Linear Equations in One Variable
• Chapter 15 - Rational Numbers
• Chapter 16 - Understanding Quadrilaterals

NCERT Solutions Class 8 Maths Chapter 3 Understanding Quadrilaterals

NCERT solutions for class 8 maths chapter 3 understanding quadrilaterals define a polygon as a simple closed curve that is made up of straight lines. Thus, a quadrilateral can be defined as a polygon that has four sides, four angles, and four vertices. This chapter starts by introducing children to some very important concepts that they need to learn before moving on to studying quadrilaterals . These topics include the classification of polygons on the basis of sides, examining diagonals , concave, convex, regular, and irregular polygons as well as the angle sum property. The scope of NCERT solutions class 8 maths chapter 3 is very vast as there are several properties and types of quadrilaterals available. However, the explanation given in these solutions helps to simplify the learning process ensuring that students can build a strong geometrical foundation. 

Class 8 maths NCERT solutions chapter 3 elaborates on special quadrilaterals such as squares , rectangles , parallelograms , kites , and rhombuses . They show kids how to solve problems based on these figures and intelligently utilize the associated properties to remove the complexities from such questions. In the NCERT solutions Chapter 3 Understanding Quadrilaterals we will take an in-depth look at the basic elements and theories of these four-sided polygons and also you can find some of these in the exercises given below.

• NCERT Solutions Class 8 Maths Chapter 3 Ex 3.1
• NCERT Solutions Class 8 Maths Chapter 3 Ex 3.2
• NCERT Solutions Class 8 Maths Chapter 3 Ex 3.3
• NCERT Solutions Class 8 Maths Chapter 3 Ex 3.4

NCERT Solutions for Class 8 Maths Chapter 3 PDF

Using the NCERT solutions class 8 maths children can solidify several concepts of quadrilaterals. They understand the conditions under which a special quadrilateral such as a parallelogram becomes a square, how to find the measure of an interior or exterior angle , and so on. The links to all these brief and precise solutions are given below and kids can use them to improve their mathematical acumen.

☛ Download Class 8 Maths NCERT Solutions Chapter 3 Understanding Quadrilaterals

NCERT Class 8 Maths Chapter 3   Download PDF

NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals

Quadrilaterals form a vital shape contributing to geometrical studies. Thus, children need to develop a robust conceptual foundation as they will require it in higher classes for solving more complicated problems and constructing this figure. They can do this by revising the solutions given above regularly. The following sections deal with an exercise-wise detailed analysis of NCERT Solutions Class 8 Maths Chapter 3 understanding quadrilaterals.

• Class 8 Maths Chapter 3 Ex 3.1 - 7 Questions
• Class 8 Maths Chapter 3 Ex 3.2 - 6 Questions
• Class 8 Maths Chapter 3 Ex 3.3 - 12 Questions
• Class 8 Maths Chapter 3 Ex 3.4 - 6 Questions

☛ Download Class 8 Maths Chapter 3 NCERT Book

Topics Covered: Identifying the polygon, finding the measure of angles, and verifying the exterior angles of a polygon are topics under class 8 maths NCERT solutions chapter 3. Apart from this, there are many sections dealing with the various elements of trapeziums , parallelograms, rectangles, squares, etc.

Total Questions: There are a total of 31 fantastic sums in Class 8 maths chapter 3 Understanding Quadrilaterals. 7 are simple theory-based problems, 16 are in-between and 8 are higher-order thinking sums.

List of Formulas in NCERT Solutions Class 8 Maths Chapter 3

The questions in the NCERT solutions class 8 maths chapter 3 are not only based on some formulas but also see the use of various vital properties. The sum of interior and exterior angles , along with theorems give the keys to attempting these sums. The angle sum property states that the sum of all the interior angles of a polygon is a multiple of the number of triangles that make up that polygon. Such pointers covered in NCERT solutions for class 8 maths chapter 3 make up the crux of this lesson and are given below.

• Angle Sum Property of a Quadrilateral: a + b + c + d = 360°. (a, b, c, d are the interior angles).
• The opposite sides and opposite angles of a parallelogram are equal in length.
• The adjacent angles in a parallelogram are supplementary.
• The diagonals of a parallelogram bisect each other.
• The diagonals of a rhombus are perpendicular bisectors of one another.

Important Questions for Class 8 Maths NCERT Solutions Chapter 3

Ncert solutions for class 8 maths video chapter 3, faqs on ncert solutions class 8 maths chapter 3, do i need to practice all questions provided in ncert solutions class 8 maths understanding quadrilaterals.

All the sums in the NCERT Solutions Class 8 Maths Understanding Quadrilaterals cover different subtopics of the lesson. These sums also pave a foundation for the geometrical topics in grades that are to follow. Thus, it is crucial for kids to practice all questions so as to get a clear idea of all the components in a quadrilateral.

What are the Important Topics Covered in Class 8 Maths NCERT Solutions Chapter 3?

Each exercise is based on a different topic such as angles of a polygon, rhombus, square, and rectangles; thus, each section that falls under the NCERT Solutions Class 8 Maths Chapter 3 must be given equal importance. Kids need to strategize their studies to focus more on learning properties and then applying them to questions.

How Many Questions are there in NCERT Solutions Class 8 Maths Chapter 3 Understanding Quadrilaterals?

There are a total of 31 questions in the NCERT Solutions Class 8 Maths Chapter 3 Understanding Quadrilaterals that are distributed among 4 exercises. There are different types of questions such as true and false sums, identifying the type of shape based on certain properties, and finding the measure of a particular angle using formulas.

What are the Important Formulas in Class 8 Maths NCERT Solutions Chapter 3?

Formulas such as the angle sum property of a quadrilateral, exterior angle property of a polygon, and other associated theories form the foundation of the NCERT Solutions Class 8 Maths Chapter 3. Students must spend a good amount of time practicing questions so as to get a good understanding of their application.

How CBSE Students can utilize NCERT Solutions Class 8 Maths Chapter 3 effectively?

To effectively utilize NCERT Solutions Class 8 Maths Chapter 3 it is advised that students go through the theory and solved examples associated with each exercise. They should then try to attempt the problem on their own. Finally, to get the best out of these solutions kids should cross-check their answers and go through the steps so that they can organize their answers in a well-structured manner.

Why Should I Practice NCERT Solutions Class 8 Maths Understanding Quadrilaterals Chapter 3?

The only way to ensure that a student has perfected his knowledge of a chapter is by practicing the questions periodically. The NCERT Solutions Class 8 Maths Understanding Quadrilaterals Chapter 3 has been given by experts with certain tips included to simplify the problems. By regular revision, kids will be confident with the topic and can get an amazing score in their examination.

Talk to our experts

1800-120-456-456

NCERT Solutions for Class 8 Maths Chapter 3 - Understanding Quadrilaterals

• Ncert solutions
• Chapter 3 Understanding Quadrilaterals

NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals - Free PDF

Students can easily download the free PDF available of NCERT Solutions for Class 8 Maths chapter 3 understanding quadrilaterals from the website. All questions are discussed by the experts of maths teachers and according to the guidelines of NCERT (CBSE). While answering the exercise questions, students will understand the topic in a more comfortable and better way. We try to keep all the answers exciting and straightforward so that students can easily understand. Other than this, you can also download the NCERT Solutions for Class 8 Science . It will help to improve the syllabus and secure good marks in the examinations. NCERT Solutions for all classes and subjects are also available on Vedantu.

Access NCERT Solutions for Class 8 Mathematics Chapter 3– Understanding Quadrilaterals

Exercise 3.1.

1. Given here are some figures.

Classify each of them on the basis of following.

Simple Curve

Ans: Given: the figures $(1)$to $(8)$

We need to classify the given figures as simple curves.

We know that a curve that does not cross itself is referred to as a simple curve.

Therefore, simple curves are $1,2,5,6,7$.

Simple Closed Curve

We need to classify the given figures as simple closed curves.

We know that a simple closed curve is one that begins and ends at the same point without crossing itself.

Therefore, simple closed curves are $1,2,5,6,7$.

We need to classify the given figures as polygon.

We know that any closed curve consisting of a set of sides joined in such a way that no two segments

cross is known as a polygon.

Therefore, the polygons are $1,2$.

Convex Polygon

We need to classify the given figures as convex polygon.

We know that a closed shape with no vertices pointing inward is called a convex polygon.

Therefore, the convex polygon is $2$.

Concave Polygon

We need to classify the given figures as concave polygon.

We know that a polygon with at least one interior angle greater than 180 degrees is called a concave

Therefore, the concave polygon is $1$.

2. How many diagonals does each of the following have? 

A Convex Quadrilateral

Ans: Given: a convex quadrilateral

We need to find the number of diagonals in the given quadrilateral

We know that a four-sided closed shape with no vertices pointing inward is called a convex quadrilateral.

Consider, a convex quadrilateral

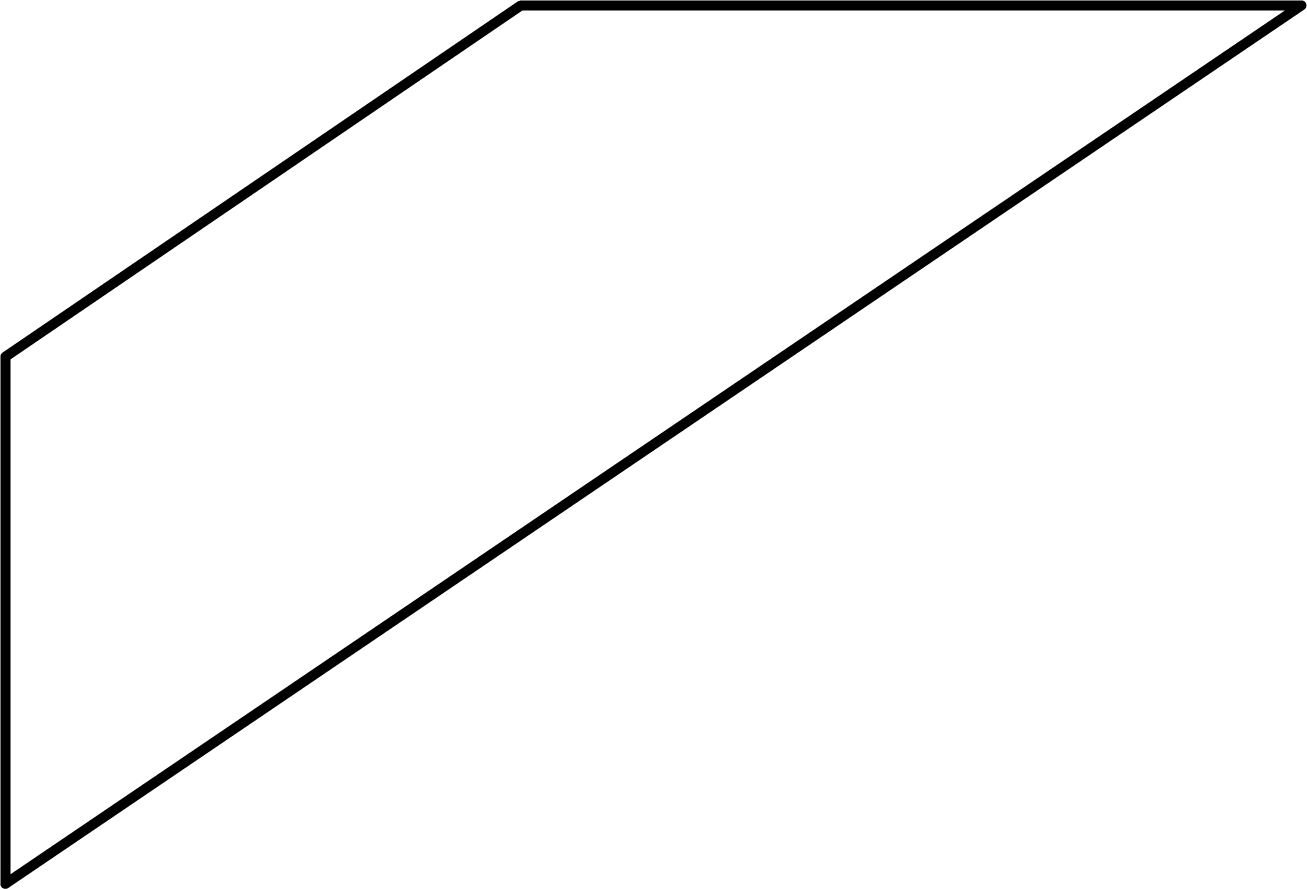
Now, make diagonals

Therefore, a convex quadrilateral has 2 diagonals.

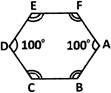
A Regular Hexagon

Ans: Given: A regular hexagon

We need to find the number of diagonals of a regular hexagon.

We know that a regular hexagon is a closed curve with six equal sides.

Consider, a regular hexagon

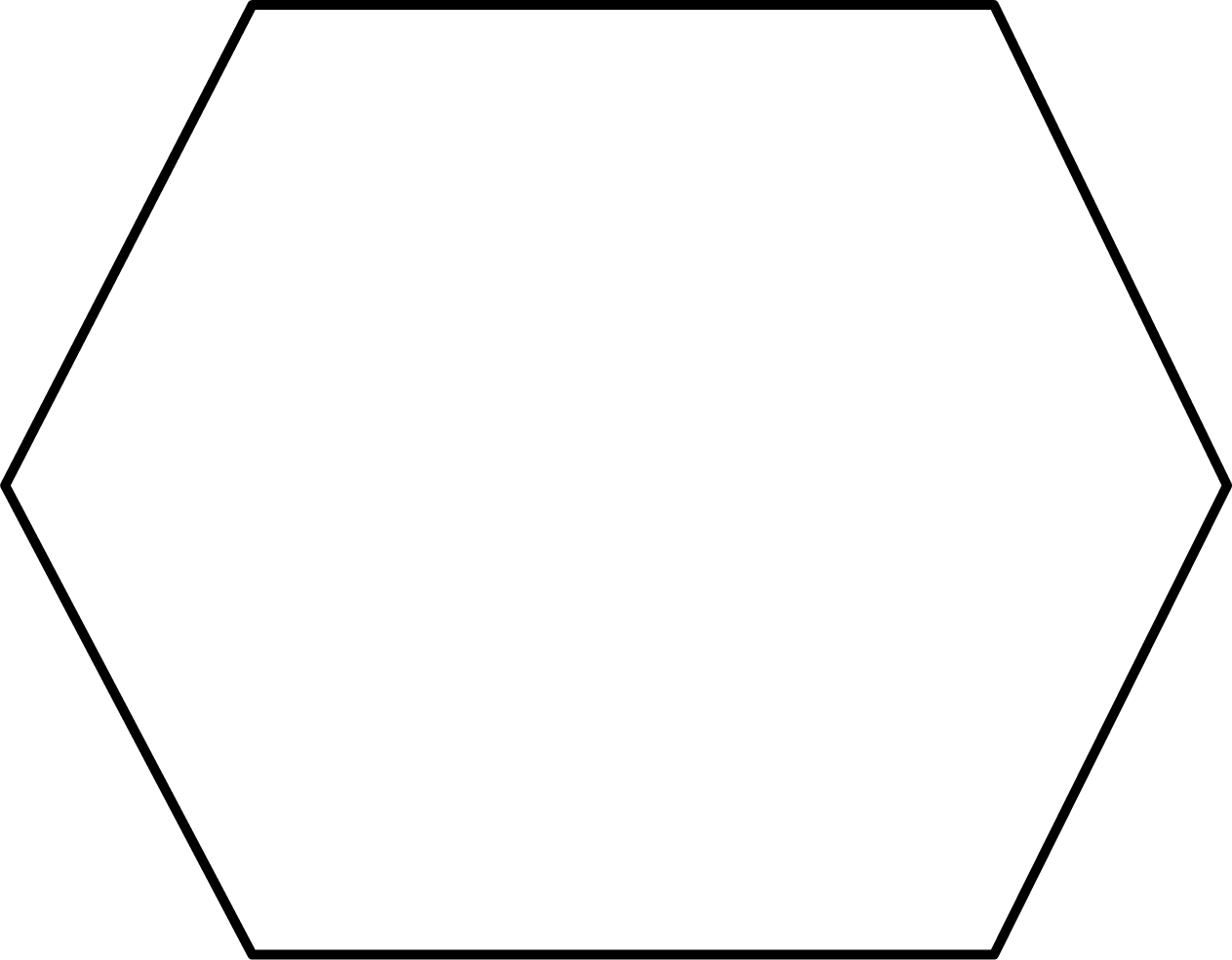
Therefore, a regular hexagon has $9$ diagonals.

Ans:  Given: A triangle

We need to find the number of diagonals of a triangle.

We know that a triangle is a closed curve having three sides.

Consider, a triangle

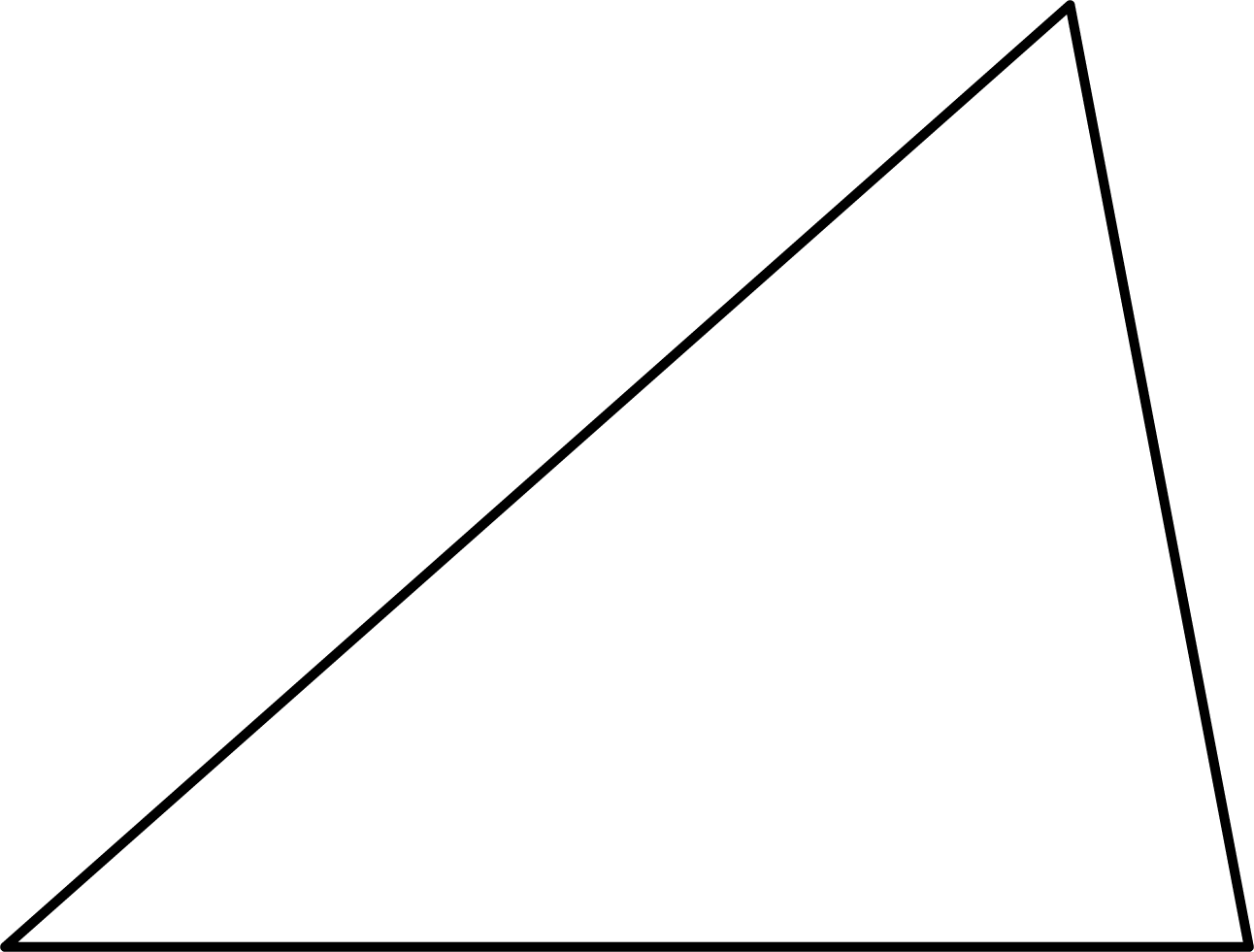
Therefore, a triangle does not have any diagonal.

3. What is the sum of the measures of the angles of a convex quadrilateral? Will this property hold if the quadrilateral is not convex? (Make a non-convex quadrilateral and try!)

Ans: Given: A convex quadrilateral

We need to find the sum of the measures of the angles of a convex quadrilateral. Will this property hold if the quadrilateral is not convex?

Consider, a convex quadrilateral ABCD and then make a diagonal AD.

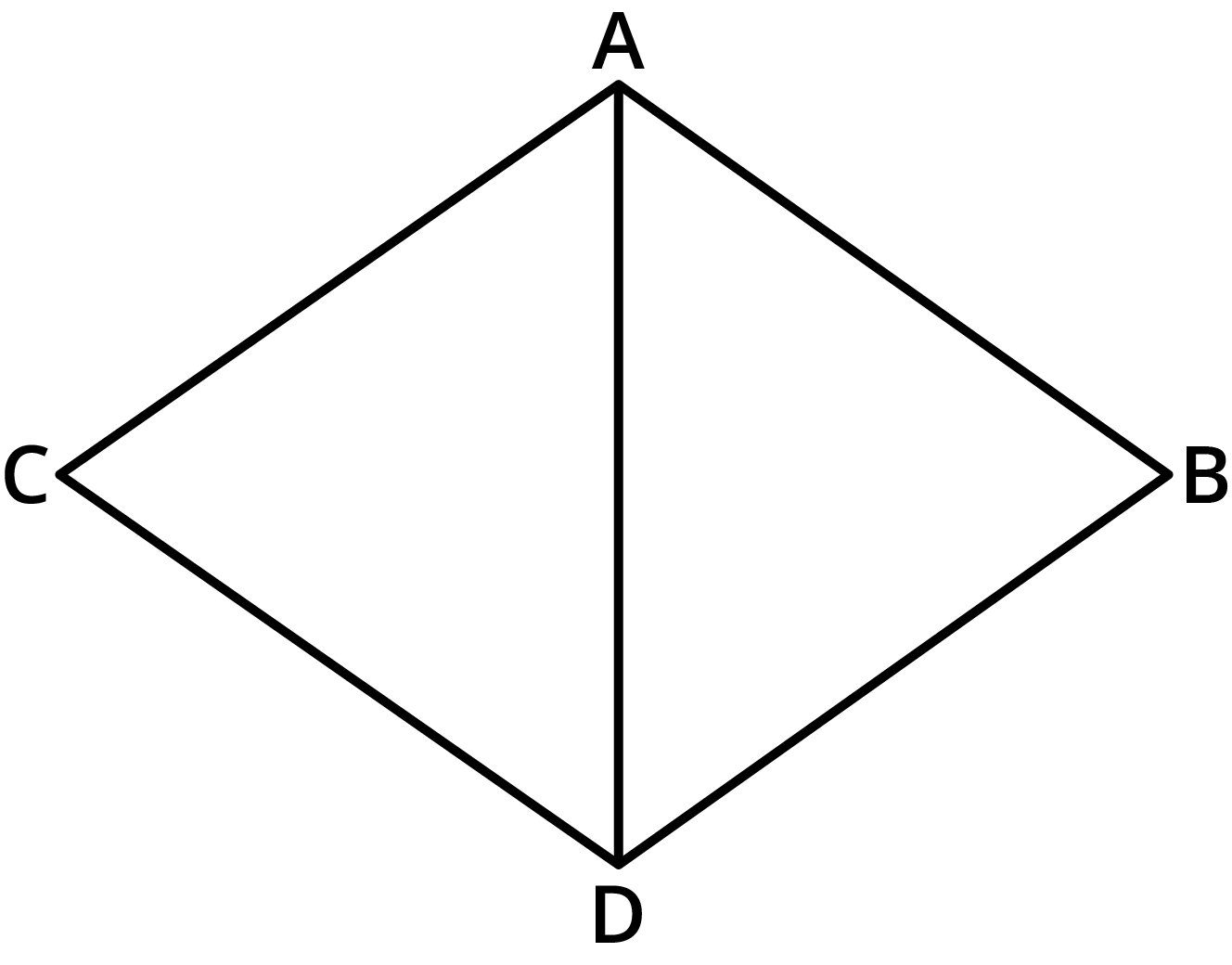
We know that the sum of angles of a triangle is ${180^ \circ }$.

So, In $\vartriangle {\text{ACD}}$

Sum of angles of $\vartriangle {\text{ACD}}$ is ${180^ \circ }$

Now, In $\vartriangle {\text{ABD}}$ 

Sum of angles of $\vartriangle {\text{ABD}}$ is ${180^ \circ }$.

Therefore, sum of angles of a convex quadrilateral will be sum of angles of $\vartriangle {\text{ACD}}$ and $\vartriangle {\text{ABD}}$

$= {180^ \circ } + {180^ \circ } $

$= {360^ \circ } $ 

Now, consider a concave quadrilateral ABCD, and then make a diagonal AC. The quadrilateral ABCD is made of two triangles, $\vartriangle {\text{ACD}}$ and $\vartriangle {\text{ABC}}$.

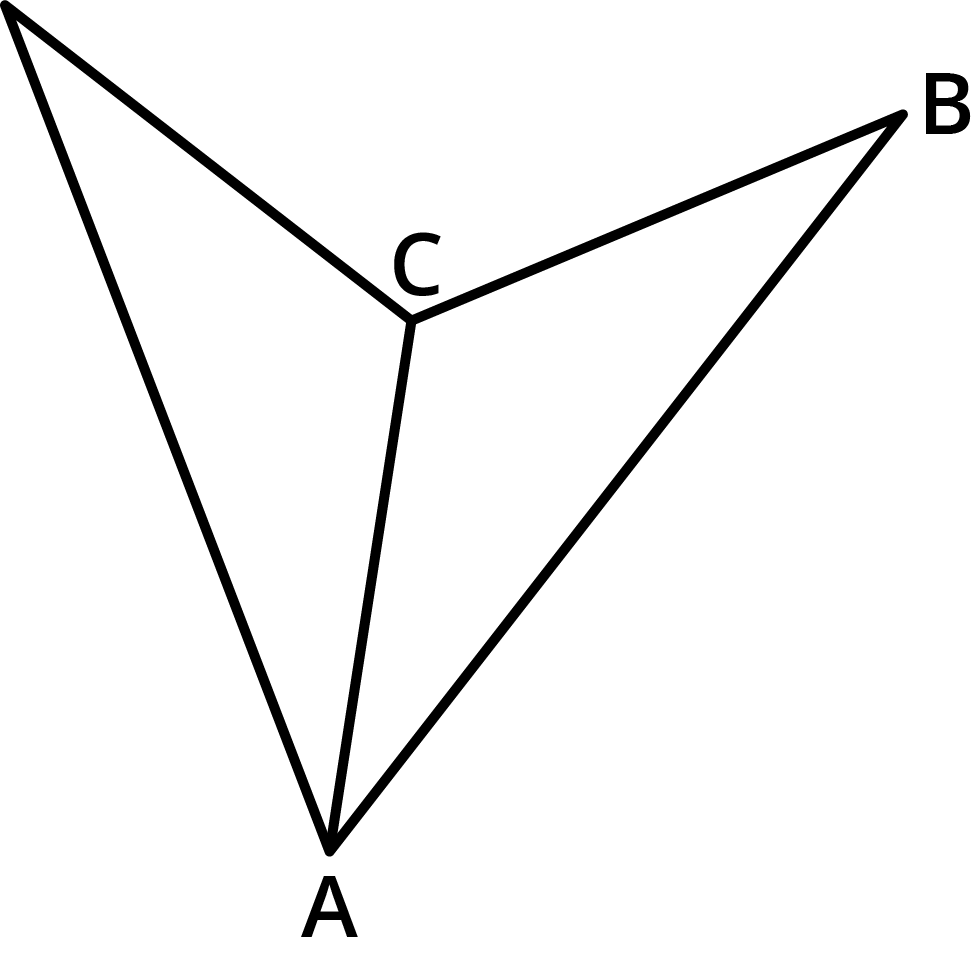
Consider, $\vartriangle {\text{ACD}}$

The sum of angles of the triangle are ${180^ \circ }$.

Now, consider $\vartriangle {\text{ABC}}$

The sum of the angles of triangle are ${180^ \circ }$.

Therefore, sum of the angles of quadrilateral ABCD will be

$ = {180^ \circ } + {180^ \circ } $

$   = {360^ \circ } $ 

Thus, we can say that the property hold true for a quadrilateral which is not convex because a quadrilateral can be divided into two triangles.

4. Examine the table. (Each figure is divided into triangles and the sum of the angles deduced from that.)

What can you say about the angle sum of a convex polygon with number of sides?

Given: the table

We need to observe table and make a statement about the angle sum of a convex polygon with number of sides.

From table, we can observe that the angle sum of a convex polygon with ${\text{n}}$sides is $({\text{n}} - 2) \times {180^ \circ }.$

Therefore, the angle sum of a convex polygon with $7$ number of sides will be

$   = (7 - 2) \times {180^ \circ } $

$   = 5 \times {180^ \circ } $

$ = {900^ \circ } $ 

Ans: Given: the table

Therefore, the angle sum of a convex polygon with $8$ number of sides will be

$   = (8 - 2) \times {180^ \circ } $

$   = 6 \times {180^ \circ } $

$   = {1080^ \circ } $ 

Therefore, the angle sum of a convex polygon with $10$ number of sides will be

$ = (10 - 2) \times {180^ \circ } $

$   = 8 \times {180^ \circ } $

$   = {1440^ \circ } $ 

From table, we can observe that the angle sum of a convex polygon with ${\text{n}}$sides will be

$ = ({\text{n}} - 2) \times {180^ \circ }$

5. What is a regular polygon? State the name of a regular polygon of 

Given: $3$ sides

We need to write the statement of a regular polygon and then state the name of the regular polygon with given number of sides.

A regular polygon is a polygon having all angles equal and all sides equal.

We know that a polygon with three equal sides and each ${60^ \circ }$ angle is a triangle.

So, it will be an equilateral triangle. The diagram will be

Ans: Given: $4$ sides

We know that a polygon with four equal sides and each ${90^ \circ }$ angle is called a square.

So, the diagram will be

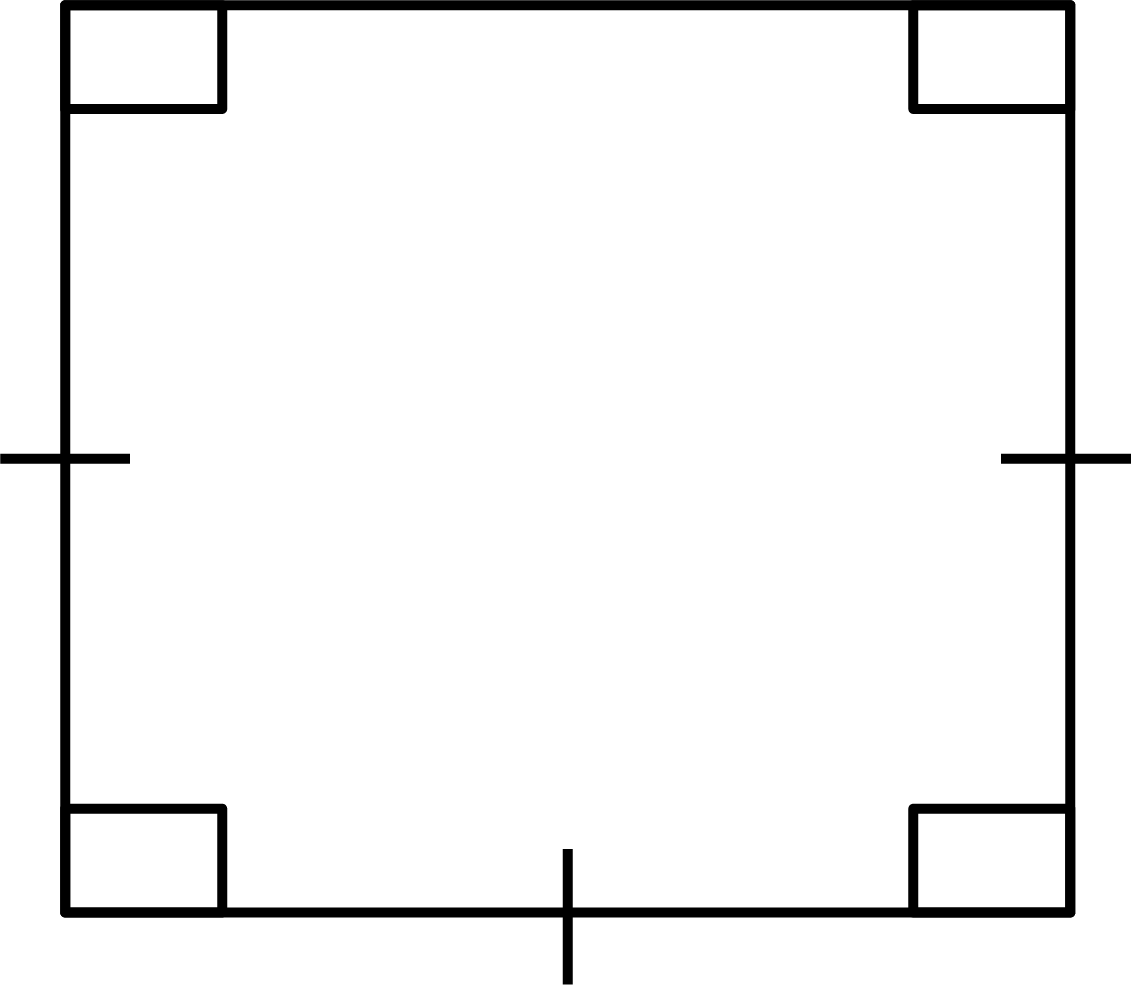
Ans: Given: $6$ sides

We know that a polygon with six equal sides and each ${120^ \circ }$ angle is called a regular hexagon.

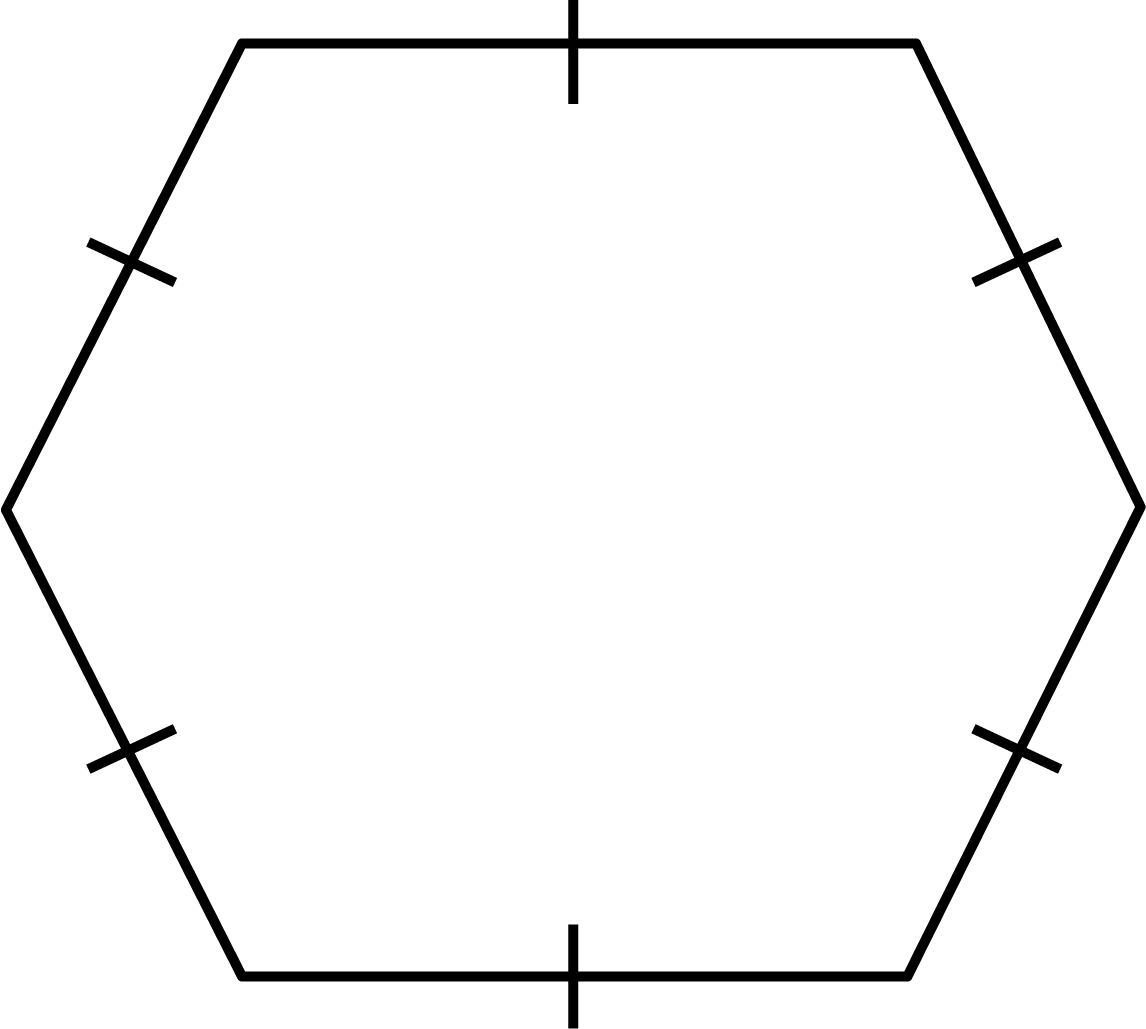
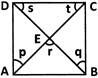
6.  Find the angle measure ${\text{'x'}}$in the following figures.

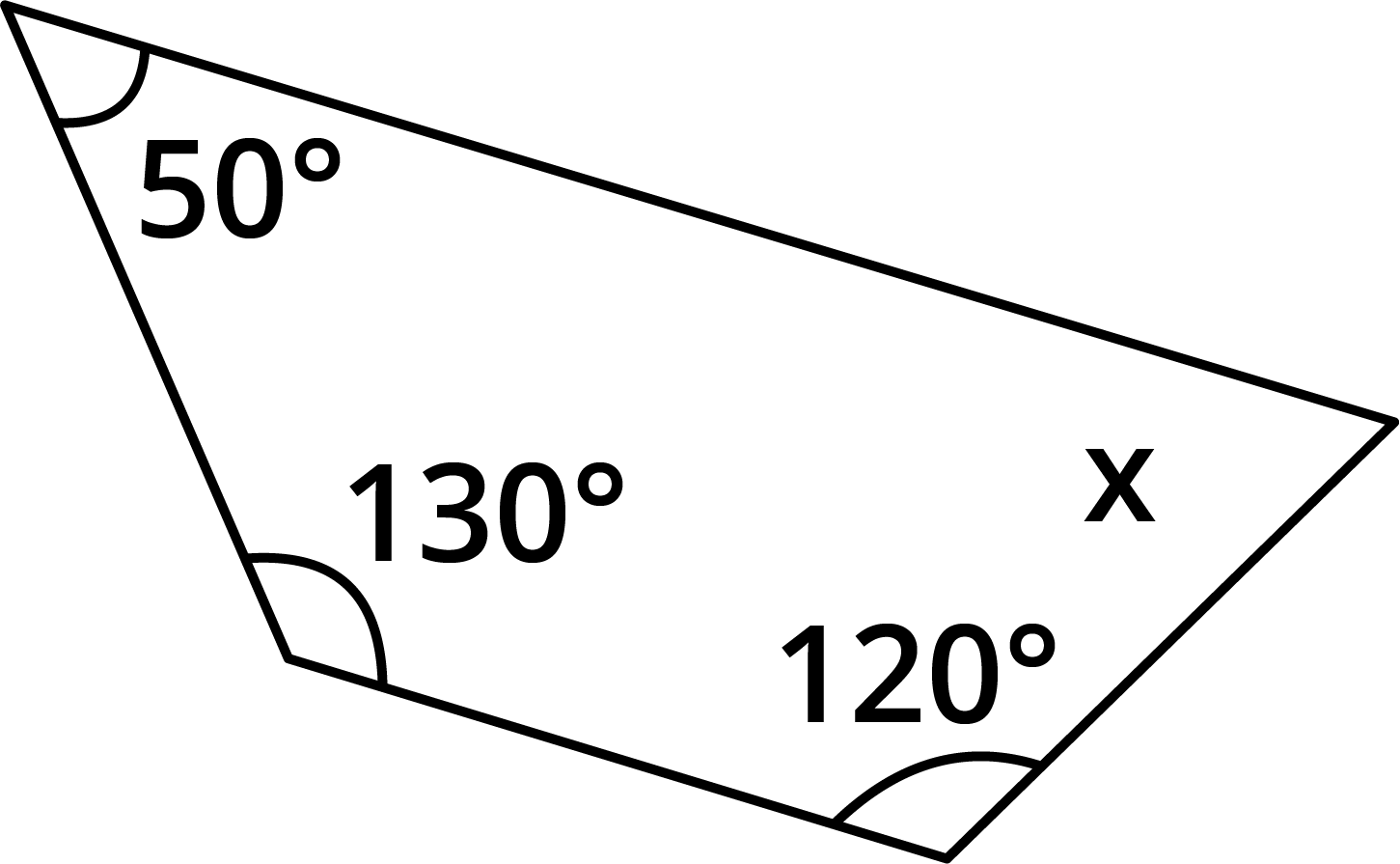
Given: A quadrilateral with angles ${50^ \circ },{130^ \circ },{120^ \circ },{\text{x}}$

We need to find the value of ${\text{x}}{\text{.}}$

We know that the sum of all interior angles of a quadrilateral is ${360^ \circ }.$

${50^ \circ } + {130^ \circ } + {120^ \circ }{\text{ + x}} = {360^ \circ } $

 $  \Rightarrow {300^ \circ } + {\text{x}} = {360^ \circ } $

 $  \Rightarrow {\text{x}} = {360^ \circ } - {300^ \circ } $

 $  \Rightarrow {\text{x}} = {60^ \circ } $ 

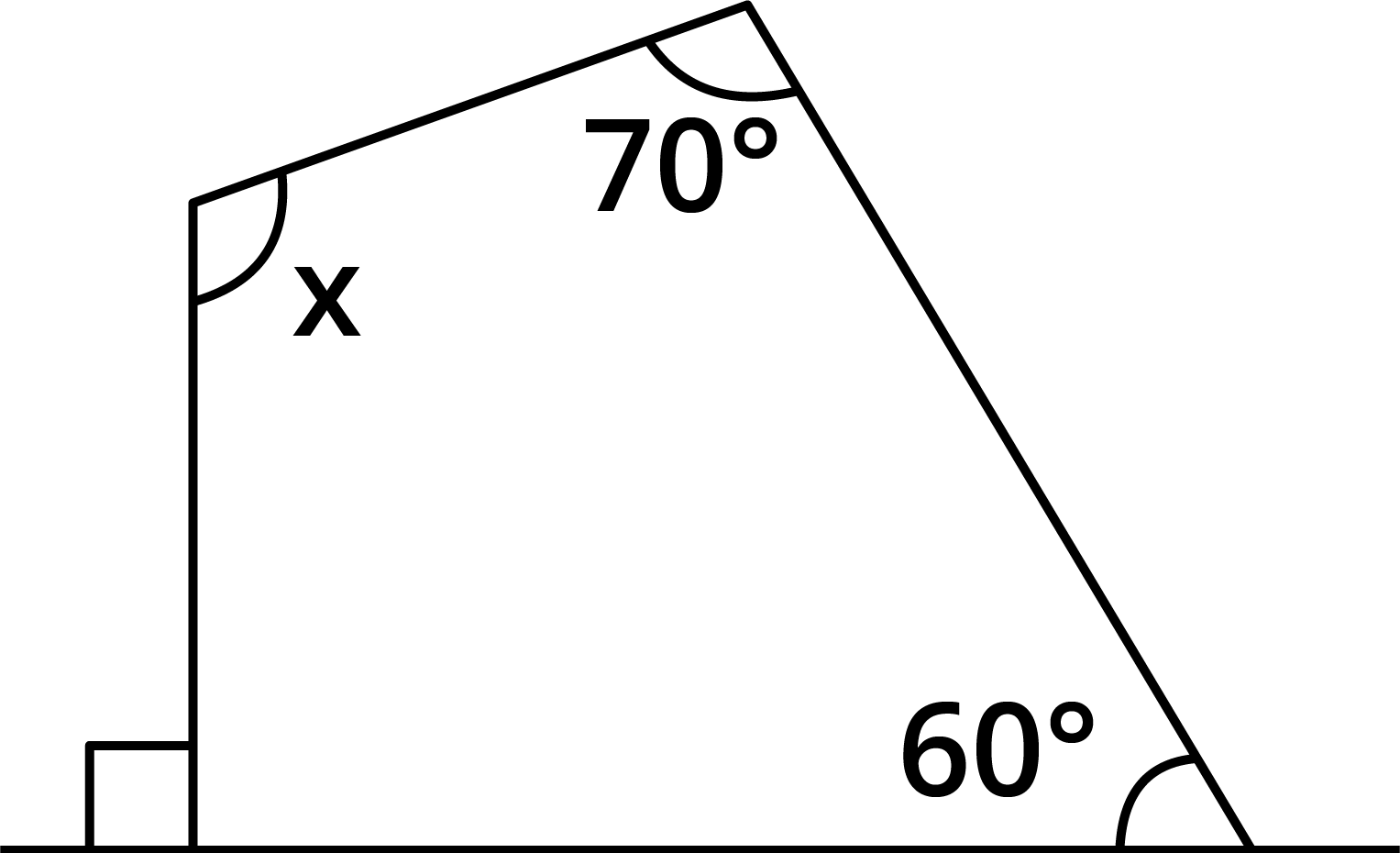
Given: A quadrilateral with angles ${70^ \circ },{60^ \circ },{\text{x}}$

From given figure, 

$  {90^ \circ } + y = {180^ \circ } $

 $  \Rightarrow y = {180^ \circ } - {90^ \circ } $

 $  \Rightarrow y = {90^ \circ } $ 

Now, the quadrilateral has angles, ${70^ \circ },{60^ \circ },{90^ \circ }{\text{,x}}$

We know that sum of all interior angles of a quadrilateral is ${360^ \circ }.$

Thus, 

$  {70^ \circ } + {60^ \circ } + {90^ \circ }{\text{ + x}} = {360^ \circ } $

$   \Rightarrow {220^ \circ } + {\text{x}} = {360^ \circ } $

 $  \Rightarrow {\text{x}} = {360^ \circ } - {220^ \circ } $

$   \Rightarrow {\text{x}} = {140^ \circ } $ 

Ans: We need to find the value of ${\text{x}}{\text{.}}$

From given figure,

$  {70^ \circ } + {\text{a}} = {180^ \circ } $

 $ \Rightarrow {\text{a}} = {180^ \circ } - {70^ \circ } $

$   \Rightarrow {\text{a}} = {110^ \circ } $ 

$  {60^ \circ } + {\text{b}} = {180^ \circ } $

$   \Rightarrow {\text{b}} = {180^ \circ } - {60^ \circ } $

 $  \Rightarrow {\text{b}} = {120^ \circ } $ 

Therefore, the angles of the pentagon are ${30^ \circ }{\text{,x,}}{110^ \circ },{120^ \circ }{\text{,x}}$

We know that the sum of all interior angles of a pentagon is ${540^ \circ }.$

  ${30^ \circ } + {\text{x}} + {110^ \circ } + {120^ \circ } + {\text{x}} = {540^ \circ } $

  $ \Rightarrow {260^ \circ } + 2{\text{x}} = {540^ \circ } $

  $ \Rightarrow 2{\text{x}} = {540^ \circ } - {260^ \circ } $

 $  \Rightarrow 2{\text{x}} = {280^ \circ } $

  $ \Rightarrow {\text{x}} = \dfrac{{{{280}^ \circ }}}{2} $

 $  \Rightarrow {\text{x}} = {140^ \circ } $ 

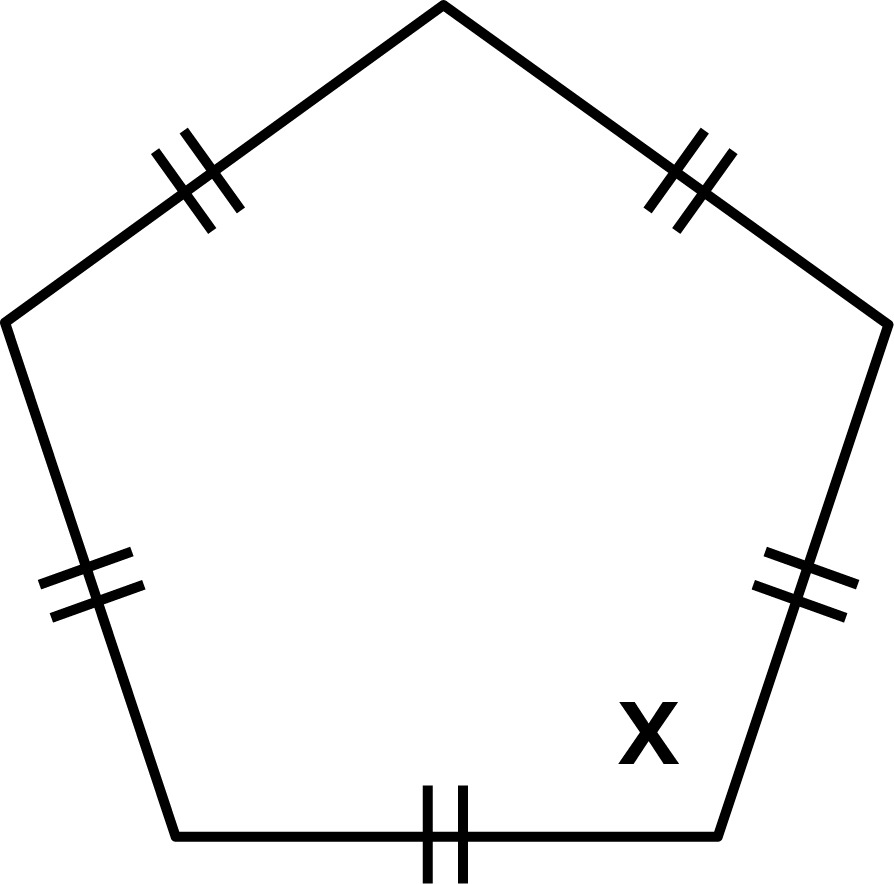
Ans: Given: a regular pentagon with angle ${\text{x}}{\text{.}}$

$ 5{\text{x}} = {540^ \circ } $

 $  \Rightarrow {\text{x}} = \dfrac{{{{540}^ \circ }}}{5} $

$   \Rightarrow {\text{x}} = {108^ \circ } $ 

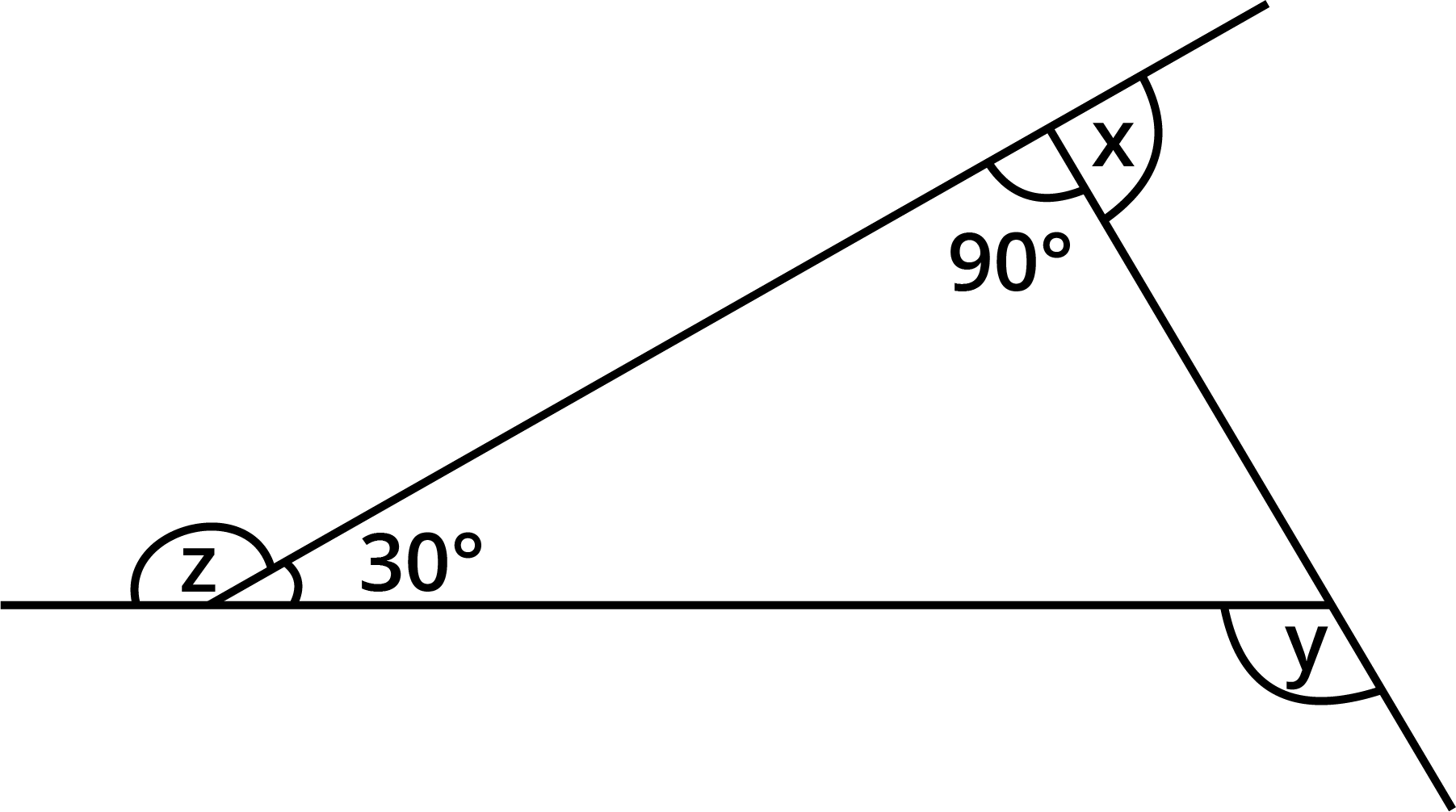
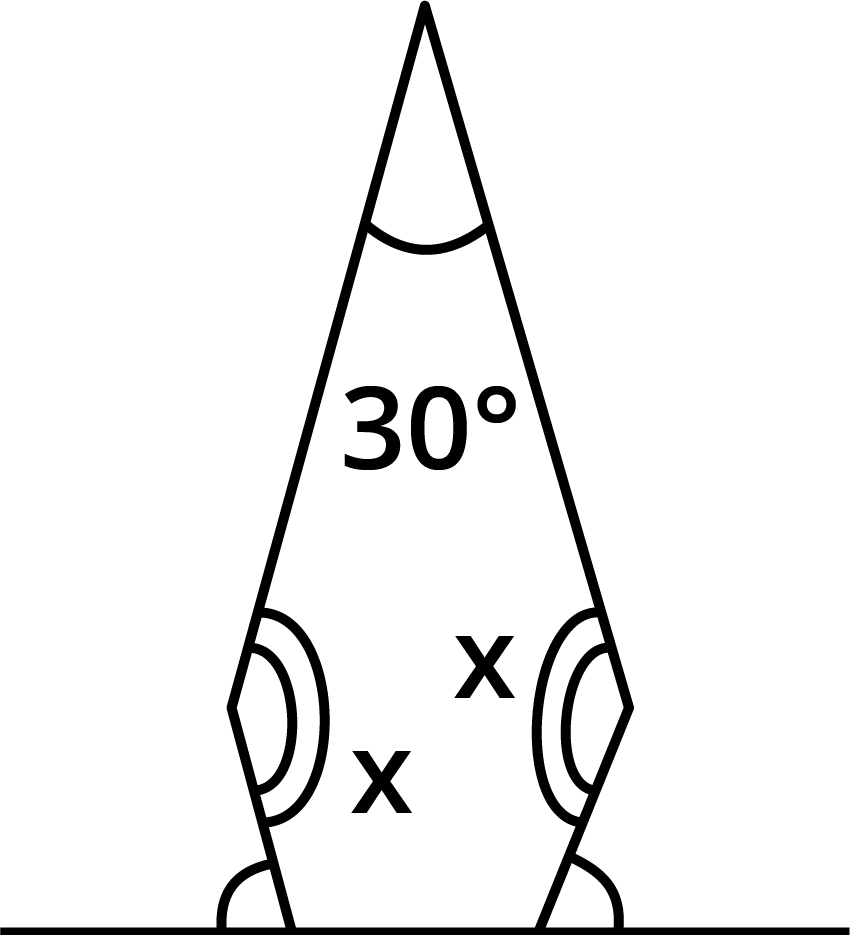
Find ${\text{x}} + {\text{y}} + {\text{z}}$

Given: 

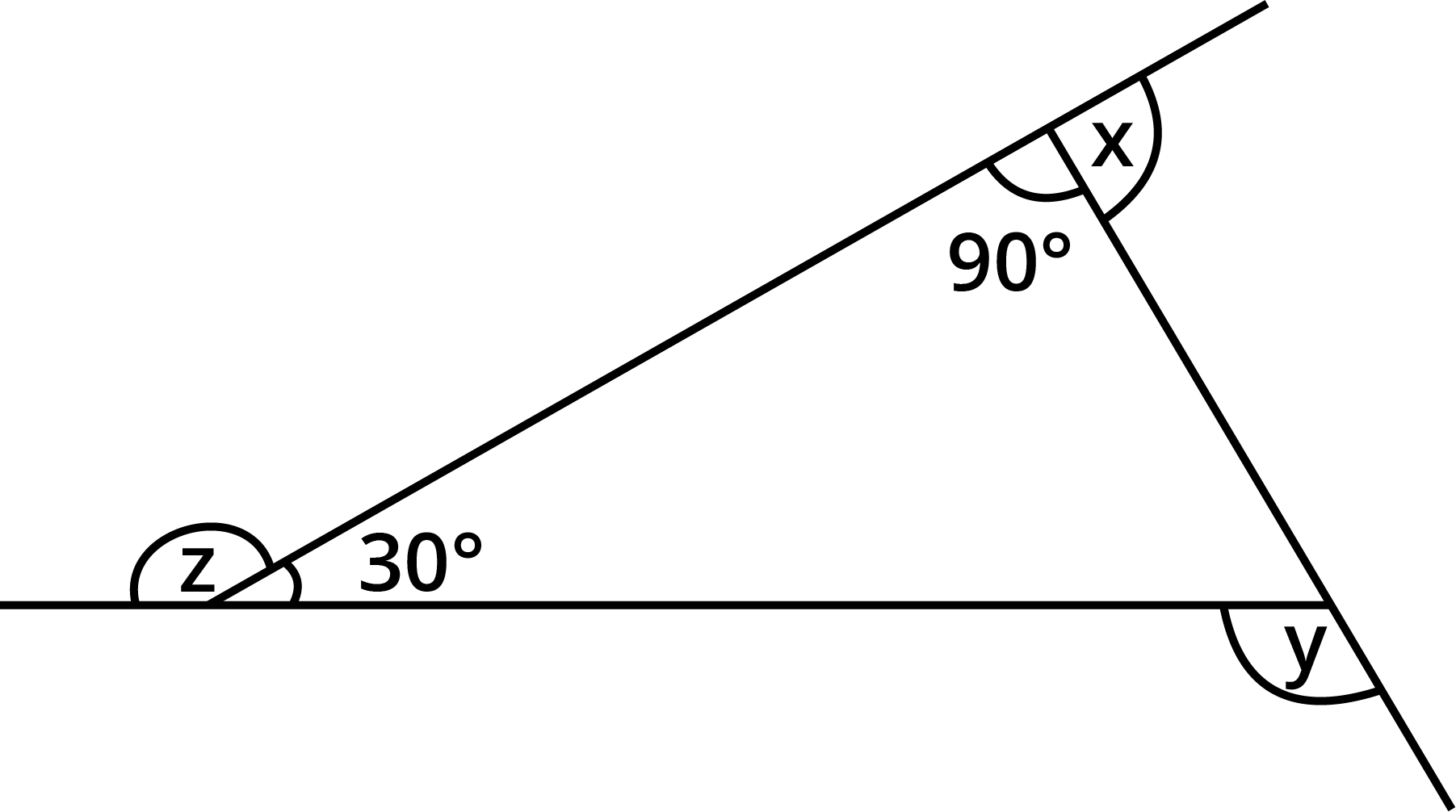
We need to find the value of ${\text{x}} + {\text{y}} + {\text{z}}$.

Property Used:

A linear pair can be defined as two adjacent angles that add up to ${180^ \circ },$ or two angles that combine to form a line or right angle.

Exterior angle theorem: If a polygon is convex, the total of the exterior angle measures, one at each vertex, equals${360^ \circ }$.

Using Linear pair,

$  {\text{z}} + {30^ \circ } = {180^ \circ } $

$   \Rightarrow {\text{z}} = {180^ \circ } - {30^ \circ } $

 $  \Rightarrow {\text{z}} = {150^ \circ } $ 

Again, using Linear pair

$  {\text{x}} + {90^ \circ } = {180^ \circ } $

 $  \Rightarrow {\text{x}} = {180^ \circ } - {90^ \circ } $

$   \Rightarrow {\text{x}} = {90^ \circ } $ 

Using Exterior Angle Theorem,

$  {\text{y}} = {90^ \circ } + {30^ \circ } $

$   \Rightarrow {\text{y}} = {120^ \circ } $ 

$  {\text{x}} + {\text{y}} + {\text{z}} = {90^ \circ } + {120^ \circ } + {150^ \circ } $

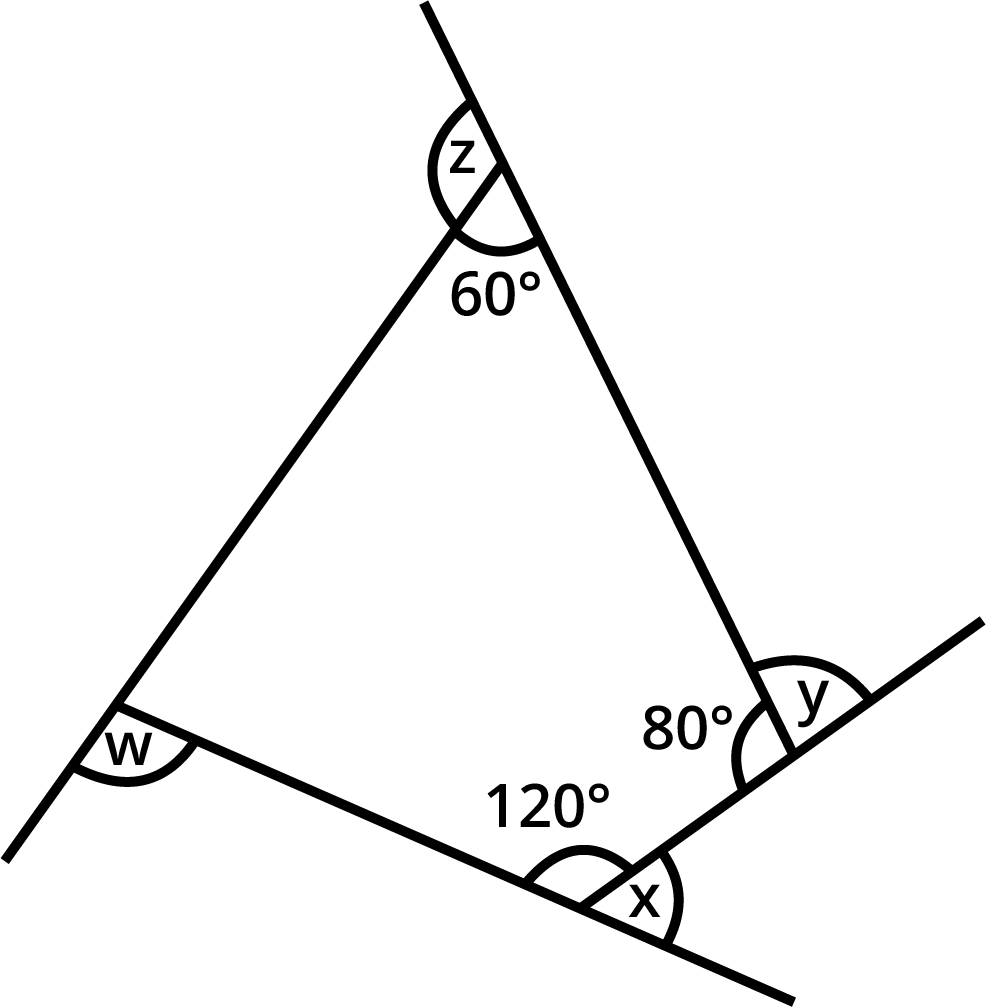
Find ${\text{x}} + {\text{y}} + {\text{z}} + {\text{w}}$

We need to find the measure of ${\text{x + y + z + w}}$.

Sum of all the interior angles of a quadrilateral is ${360^ \circ }$.

$  {\text{a}} + {60^ \circ } + {80^ \circ } + {120^ \circ } = {360^ \circ } $

$   \Rightarrow {\text{a}} + {260^ \circ } = {360^ \circ } $

$   \Rightarrow {\text{a}} = {360^ \circ } - {260^ \circ } $

$   \Rightarrow {\text{a}} = {100^ \circ } $ 

$  {\text{a}} + {\text{w}} = {180^ \circ } $

 $  \Rightarrow {100^ \circ } + {\text{w}} = {180^ \circ } $

 $  \Rightarrow {\text{w}} = {180^ \circ } - {100^ \circ } $

$   \Rightarrow {\text{w}} = {80^ \circ } $ 

$  {\text{x}} + {120^ \circ } = {180^ \circ } $

$   \Rightarrow {\text{x}} = {180^ \circ } - {120^ \circ } $

$   \Rightarrow {\text{x}} = {60^ \circ } $ 

$  {\text{y}} + {80^ \circ } = {180^ \circ } $

$   \Rightarrow {\text{y}} = {180^ \circ } - {80^ \circ } $

 $  \Rightarrow {\text{y}} = {100^ \circ } $ 

$  {\text{z}} + {60^ \circ } = {180^ \circ } $

 $  \Rightarrow {\text{z}} = {180^ \circ } - {60^ \circ } $

  $ \Rightarrow {\text{z}} = {120^ \circ } $ 

$  {\text{x}} + {\text{y}} + {\text{z}} + {\text{w}} = {60^ \circ } + {100^ \circ } + {120^ \circ } + {80^ \circ } $

Exercise-3.2

1. Find ${\text{x}}$in the following figures.

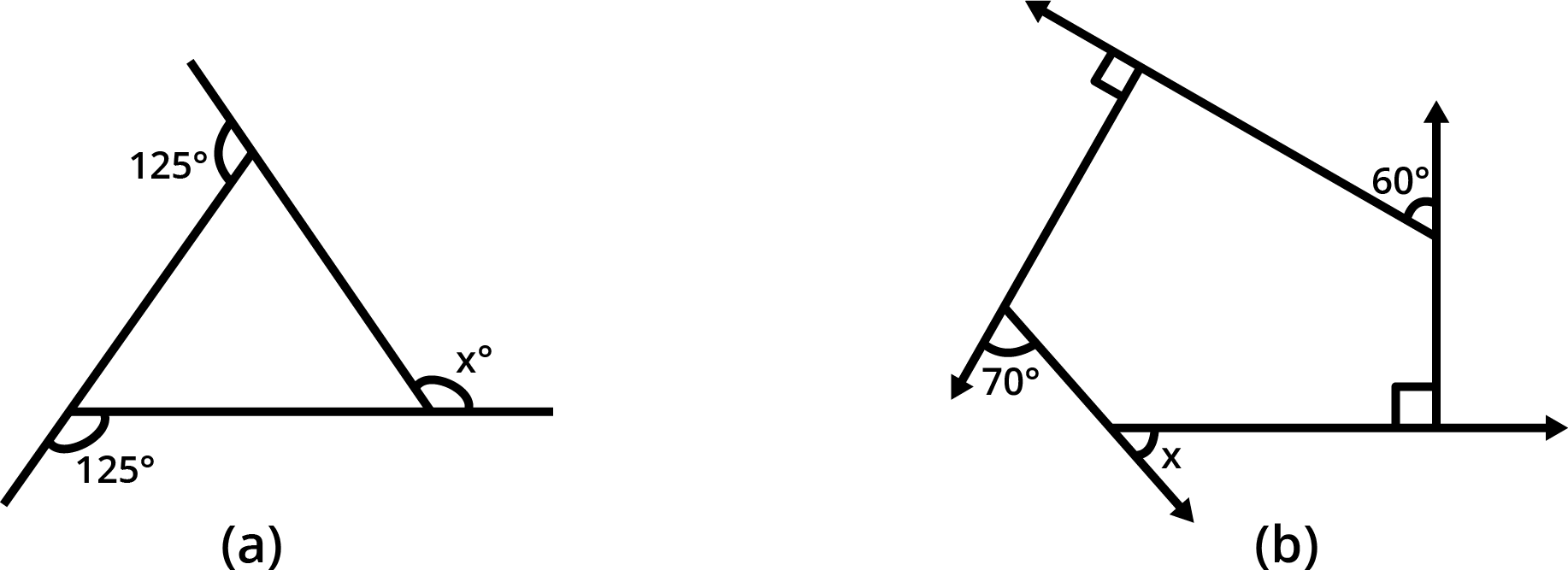
We know that the sum of all exterior angles of a polygon is ${360^ \circ }.$

$  {\text{x}} + {125^ \circ } + {125^ \circ } = {360^ \circ } $

$   \Rightarrow {\text{x}} + {250^ \circ } = {360^ \circ } $

$   \Rightarrow {\text{x}} = {360^ \circ } - {250^ \circ } $

$   \Rightarrow {\text{x}} = {110^ \circ } $ 

$  {\text{x}} + {90^ \circ } + {60^ \circ } + {90^ \circ } + {70^ \circ } = {360^ \circ } $

$  \Rightarrow {\text{x}} + {310^ \circ } = {360^ \circ } $

$   \Rightarrow {\text{x}} = {360^ \circ } - {310^ \circ } $

 $  \Rightarrow {\text{x}} = {50^ \circ } $ 

2. Find the measure of each exterior angle of a regular polygon of 

Given: a regular polygon with $9$ sides

We need to find the measure of each exterior angle of the given polygon.

We know that all the exterior angles of a regular polygon are equal.

The sum of all exterior angle of a polygon is ${360^ \circ }$.

Formula Used: ${\text{Exterior}}\;{\text{angle}} = \dfrac{{{{360}^ \circ }}}{{{\text{Number}}\;{\text{of}}\;{\text{sides}}}}$

Sum of all angles of given regular polygon $ = {360^ \circ }$

Number of sides $ = 9$

Therefore, measure of each exterior angle will be

$   = \dfrac{{{{360}^ \circ }}}{9} $

 $  = {40^ \circ } $ 

Given: a regular polygon with $15$ sides

Number of sides $ = 15$

$   = \dfrac{{{{360}^ \circ }}}{{15}} $

$ = {24^ \circ } $ 

3. How many sides does a regular polygon have if the measure of an exterior angle is ${24^ \circ }$?

Ans: Given: A regular polygon with each exterior angle ${24^ \circ }$

We need to find the number of sides of given polygon.

We know that sum of all exterior angle of a polygon is ${360^ \circ }$.

Formula Used: ${\text{Number}}\;{\text{of}}\;{\text{sides}} = \dfrac{{{{360}^ \circ }}}{{{\text{Exterior}}\;{\text{angle}}}}$

Each angle measure $ = {24^ \circ }$

Therefore, number of sides of given polygon will be

$   = \dfrac{{{{360}^ \circ }}}{{{{24}^ \circ }}} $

 $  = 15 $ 

4. How many sides does a regular polygon have if each of its interior angles is ${165^ \circ }$?

Ans: Given: A regular polygon with each interior angle ${165^ \circ }$

We need to find the sides of the given regular polygon.

${\text{Exterior}}\;{\text{angle}} = {180^ \circ } - {\text{Interior}}\;{\text{angle}}$

Each interior angle $ = {165^ \circ }$

So, measure of each exterior angle will be

$   = {180^ \circ } - {165^ \circ } $

$   = {15^ \circ } $ 

Therefore, number of sides of polygon will be

$   = \dfrac{{{{360}^ \circ }}}{{{{15}^ \circ }}} $

$   = 24 $ 

Is it possible to have a regular polygon with measure of each exterior angle as ${22^ \circ }$?

Given: A regular polygon with each exterior angle ${22^ \circ }$

We need to find if it is possible to have a regular polygon with given angle measure.

We know that sum of all exterior angle of a polygon is ${360^ \circ }$. The polygon will be possible if ${360^ \circ }$ is a perfect multiple of exterior angle.

$\dfrac{{{{360}^ \circ }}}{{{{22}^ \circ }}}$ does not give a perfect quotient. 

Thus, ${360^ \circ }$ is not a perfect multiple of exterior angle. So, the polygon will not be possible.

Can it be an interior angle of a regular polygon? Why?

Ans: Given: Interior angle of a regular polygon $ = {22^ \circ }$

We need to state if it can be the interior angle of a regular polygon.

And, ${\text{Exterior}}\;{\text{angle}} = {180^ \circ } - {\text{Interior}}\;{\text{angle}}$

Thus, Exterior angle will be

$   = {180^ \circ } - {22^ \circ } $

 $  = {158^ \circ } $ 

$\dfrac{{{{158}^ \circ }}}{{{{22}^ \circ }}}$ does not give a perfect quotient. 

Thus, ${158^ \circ }$ is not a perfect multiple of exterior angle. So, the polygon will not be possible.

What is the minimum interior angle possible for a regular polygon?

Ans:   Given: A regular polygon

We need to find the minimum interior angle possible for a regular polygon.

A polygon with minimum number of sides is an equilateral triangle.

So, number of sides $ = 3$

${\text{Exterior}}\;{\text{angle}} = \dfrac{{{{360}^ \circ }}}{{{\text{Number}}\;{\text{of}}\;{\text{sides}}}}$

Thus, Maximum Exterior angle will be

$   = \dfrac{{{{360}^ \circ }}}{3} $

$   = {120^ \circ } $ 

We know, ${\text{Interior}}\;{\text{angle}} = {180^ \circ } - {\text{Exterior}}\;{\text{angle}}$

Therefore, minimum interior angle will be

$   = {180^ \circ } - {120^ \circ } $

$   = {60^ \circ } $ 

What is the maximum exterior angel possible for a regular polygon?

Ans: Given: A regular polygon

We need to find the maximum exterior angle possible for a regular polygon.

Therefore, Maximum Exterior angle possible will be

$ = {120^ \circ } $

 Exercise 3.3

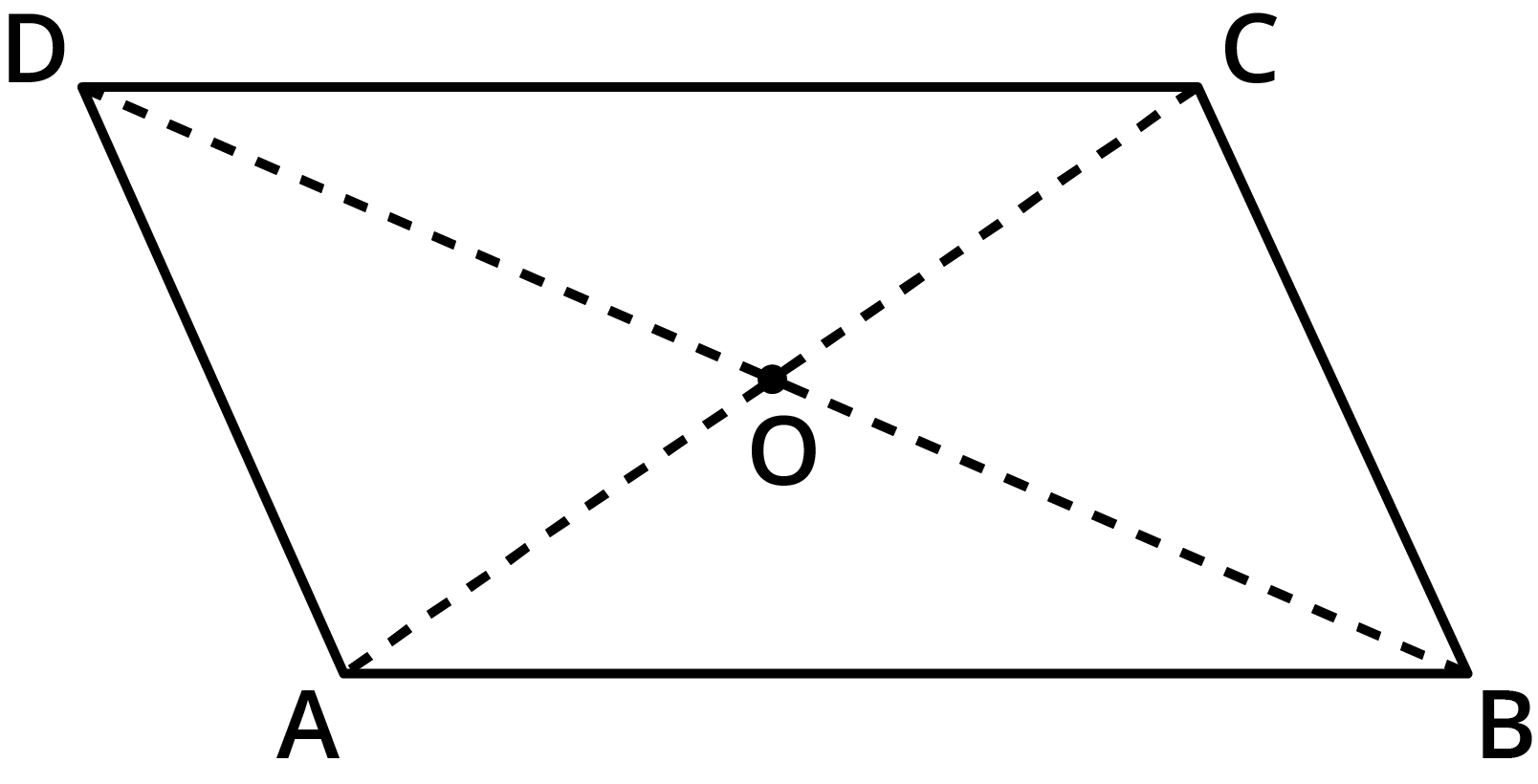
1. Given a parallelogram ABCD. Complete each statement along with the definition or property used.

$\;{\text{AD}}$ = $...$

Given: A parallelogram ${\text{ABCD}}$ 

We need to complete each statement along with the definition or property used.

We know that opposite sides of a parallelogram are equal.

Hence, ${\text{AD}}$ = ${\text{BC}}$ 

$\;\angle {\text{DCB }} = $ $...$

Given: A parallelogram ${\text{ABCD}}$.

${\text{ABCD}}$ is a parallelogram, and we know that opposite angles of a parallelogram are equal.

Hence, $\angle {\text{DCB   =  }}\angle {\text{DAB}}$

${\text{OC}} = ...$ 

${\text{ABCD}}$ is a parallelogram, and we know that diagonals of parallelogram bisect each other.

Hence, ${\text{OC  =  OA}}$

$m\angle DAB\; + \;m\angle CDA\; = \;...$

Given : A parallelogram ${\text{ABCD}}$.

${\text{ABCD}}$ is a parallelogram, and we know that adjacent angles of a parallelogram are supplementary to each other.

Hence, $m\angle DAB\; + \;m\angle CDA\; = \;180^\circ $

 2. Consider the following parallelograms. Find the values of the unknowns x, y, z.

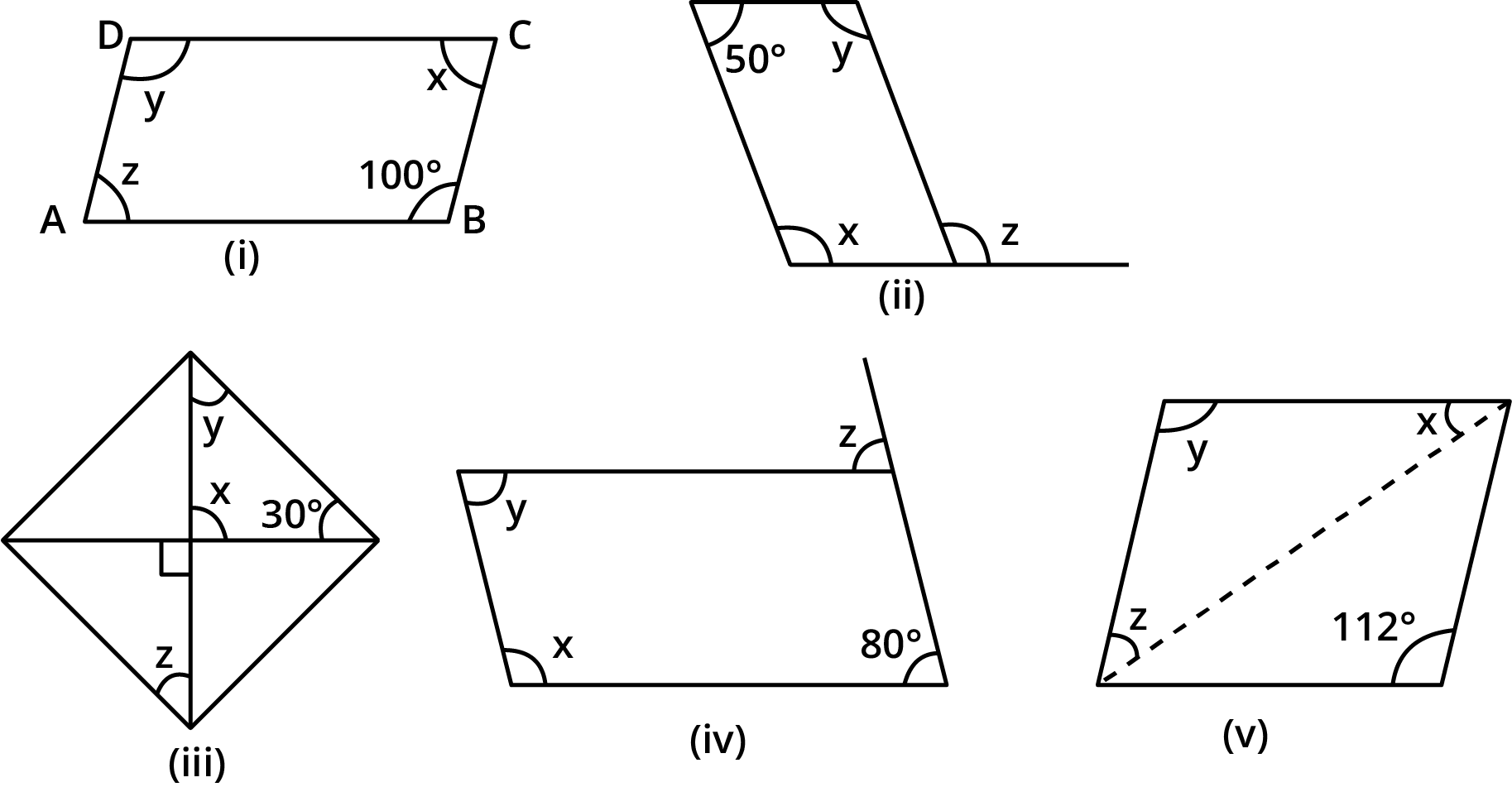
Given: A parallelogram ${\text{ABCD}}$

We need to find the unknowns ${\text{x,y,z}}$

The adjacent angles of a parallelogram are supplementary.

Therefore, ${\text{x} + 100^\circ  = 180^\circ }$

${\text{x} = 80^\circ }$ 

Also, the opposite angles of a parallelogram are equal.

Hence, ${\text{z}} = {\text{x}} = 80^\circ $ and ${\text{y}} = 100^\circ $

Given: A parallelogram.

We need to find the values of ${\text{x,y,z}}$

The adjacent pairs of a parallelogram are supplementary.

Hence, $50^\circ  + {\text{y}} = 180^\circ $

${\text{y}} = 130^\circ $

Also, ${\text{x}} = {\text{y}} = 130^\circ $(opposite angles of a parallelogram are equal)

And, ${\text{z}} = {\text{x}} = 130^\circ $ (corresponding angles)

(iii)  

Given: A parallelogram 

${\text{x}} = 90^\circ $(Vertically opposite angles)

Also, by angle sum property of triangles

${\text{x}} + {\text{y}} + 30^\circ  = 180^\circ $

${\text{y}} = 60^\circ $

Also,${\text{z}} = {\text{y}} = 60^\circ $(alternate interior angles)

Given: A parallelogram

Corresponding angles between two parallel lines are equal.

Hence, ${\text{z}} = 80^\circ $ Also,${\text{y}} = 80^\circ $ (opposite angles of parallelogram are equal)

In a parallelogram, adjacent angles are supplementary

Hence,${\text{x}} + {\text{y}} = 180^\circ $

$  {\text{x}} = 180^\circ  - 80^\circ  $

$  {\text{x}} = 100^\circ  $ 

As the opposite angles of a parallelogram are equal, therefore,${\text{y}} = 112^\circ $ 

Also, by using angle sum property of triangles

$  {\text{x}} + {\text{y}} + 40^\circ  = 180^\circ  $

$  {\text{x}} + 152^\circ  = 180^\circ  $

$  {\text{x}} = 28^\circ  $ 

And ${\text{z}} = {\text{x}} = 28^\circ $(alternate interior angles)

3. Can a quadrilateral ${\text{ABCD}}$be a parallelogram if 

(i) $\angle {\text{D}}\;{\text{ + }}\angle {\text{B}} = 180^\circ ?$

Given: A quadrilateral ${\text{ABCD}}$

We need to find whether the given quadrilateral is a parallelogram.

For the given condition, quadrilateral ${\text{ABCD}}$ may or may not be a parallelogram.

For a quadrilateral to be parallelogram, the sum of measures of adjacent angles should be $180^\circ $ and the opposite angles should be of same measures.

(ii) ${\text{AB}} = {\text{DC}} = 8\;{\text{cm}},\;{\text{AD}} = 4\;{\text{cm}}\;$and ${\text{BC}} = 4.4\;{\text{cm}}$

As, the opposite sides ${\text{AD}}$and ${\text{BC}}$are of different lengths, hence the given quadrilateral is not a parallelogram.

(iii) $\angle {\text{A}} = 70^\circ $and $\angle {\text{C}} = 65^\circ $

As, the opposite angles have different measures, hence, the given quadrilateral is a parallelogram.

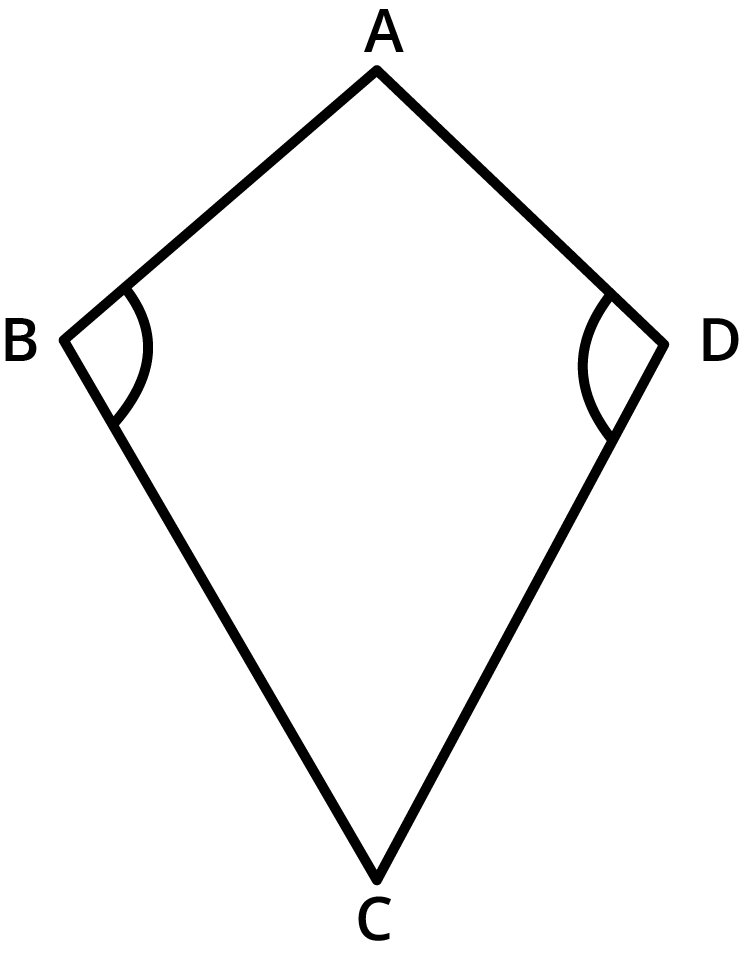
4. Draw a rough figure of a quadrilateral that is not a parallelogram but has exactly two opposite angles of equal measure.

Given: A quadrilateral.

We need to draw a rough figure of a quadrilateral that is not a paralleloghram but has exactly two opposite angles of equal measure.

A kite is a figure which has two of its interior angles, $\angle {\text{B}}$and $\angle {\text{D}}$of same measures. But the quadrilateral ${\text{ABCD}}$is not a parallelogram as the measures of the remaining pair of opposite angles are not equal.

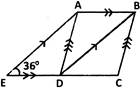
5. The measures of two adjacent angles of a parallelogram are in the ratio 3:2. Find the measure of each of the angles of the parallelogram.

Ans: Given: A parallelogram with adjacent angles in the ratio $3:2$

We need to find the measure of each of the angles of the parallelogram.

Let the angles be $\angle {\text{A}} = 3{\text{x}}$and $\angle {\text{B}} = 2{\text{x}}$

As the sum of measures of adjacent angles is $180^\circ $ for a parallelogram.

$  \angle {\text{A}} + \angle {\text{B}} = 180^\circ  $

 $ 3{\text{x}} + 2{\text{x}} = 180^\circ  $

 $ 5{\text{x}} = 180^\circ  $

 $ {\text{x}} = 36^\circ  $ 

$~\angle A=$ $\angle {\text{C}}$ $= 3{\text{x}} = 108^\circ$and $~\angle B=$ $\angle {\text{D}}$ $= 2{\text{x}} = 72^\circ$(Opposite angles of a parallelogram are equal).

Hence, the angles of a parallelogram are $108^\circ ,72^\circ ,108^\circ $and $72^\circ $.

6. Two adjacent angles of a parallelogram have equal measure. Find the measure of each of the angles of the parallelogram.

Given: A parallelogram with two equal adjacent angles.

The sum of adjacent angles of a parallelogram are supplementary.

$  \angle {\text{A}} + \;\angle {\text{B}} = 180^\circ  $

$  2\angle {\text{A}}\;{\text{ =  180}}^\circ  $

$  \angle {\text{A}}\;{\text{ = }}\;{\text{90}}^\circ  $

$  \angle {\text{B}}\;{\text{ = }}\angle {\text{A}}\;{\text{ = }}\;{\text{90}}^\circ  $

Also, opposite angles of a parallelogram are equal

$  \angle {\text{C}} = \angle {\text{A}} = 90^\circ  $

$  \angle {\text{D}} = \angle {\text{B}} = 90^\circ  $ 

Hence, each angle of the parallelogram measures $90^\circ $.

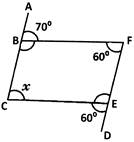
7. The adjacent figure ${\text{HOPE}}$is a parallelogram. Find the angle measures x, y and z. State the properties you use to find them.

Given: A parallelogram ${\text{HOPE}}$.

We need to find the measures of angles ${\text{x,y,z}}$and also state the properties used to find these angles.

$\angle {\text{y}} = 40^\circ $(Alternate interior angles)

And $\angle {\text{z}} + 40^\circ  = 70^\circ $(corresponding angles are equal)

$\angle {\text{z}} = 30^\circ $

Also, ${\text{x}} + {\text{z}} + 40^\circ  = 180^\circ $(adjacent pair of angles)

${\text{x}} = 110^\circ $

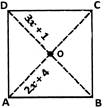
8. The following figures ${\text{GUNS}}$and ${\text{RUNS}}$are parallelograms. Find ${\text{x}}$and${\text{y}}$. (Lengths are in cm).

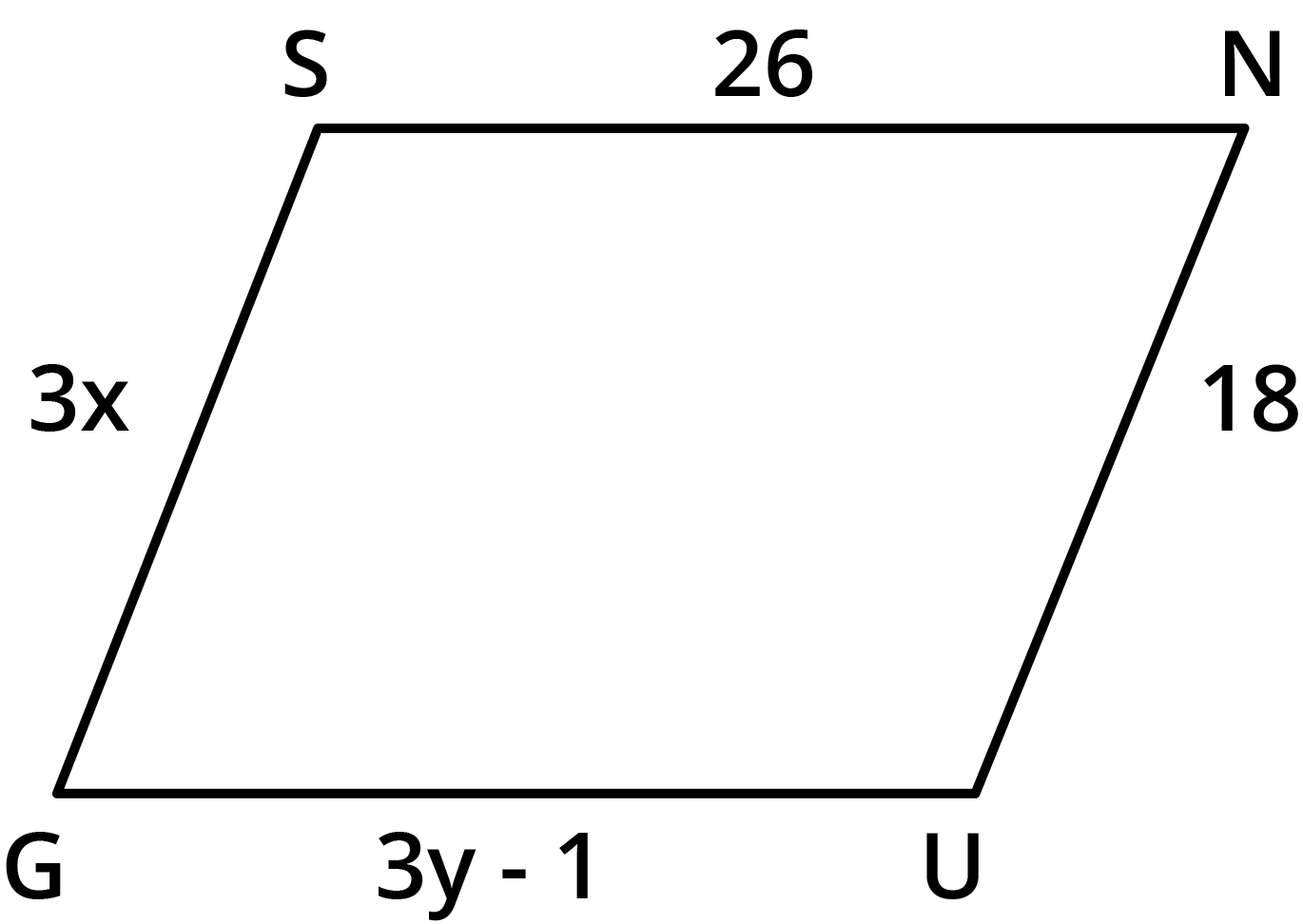
Given: Parallelogram ${\text{GUNS}}$.

We need to find the measures of ${\text{x}}$and ${\text{y}}$.

${\text{GU = SN}}$(Opposite sides of a parallelogram are equal).

$  3{\text{y }} - {\text{ }}1{\text{ }} = {\text{ }}26{\text{ }} $

$  3{\text{y }} = {\text{ }}27{\text{ }} $

$  {\text{y }} = {\text{ }}9{\text{ }} $ 

Also,${\text{SG = NU}}$

Therefore, 

$  3{\text{x}} = 18 $

$  {\text{x}} = 3 $ 

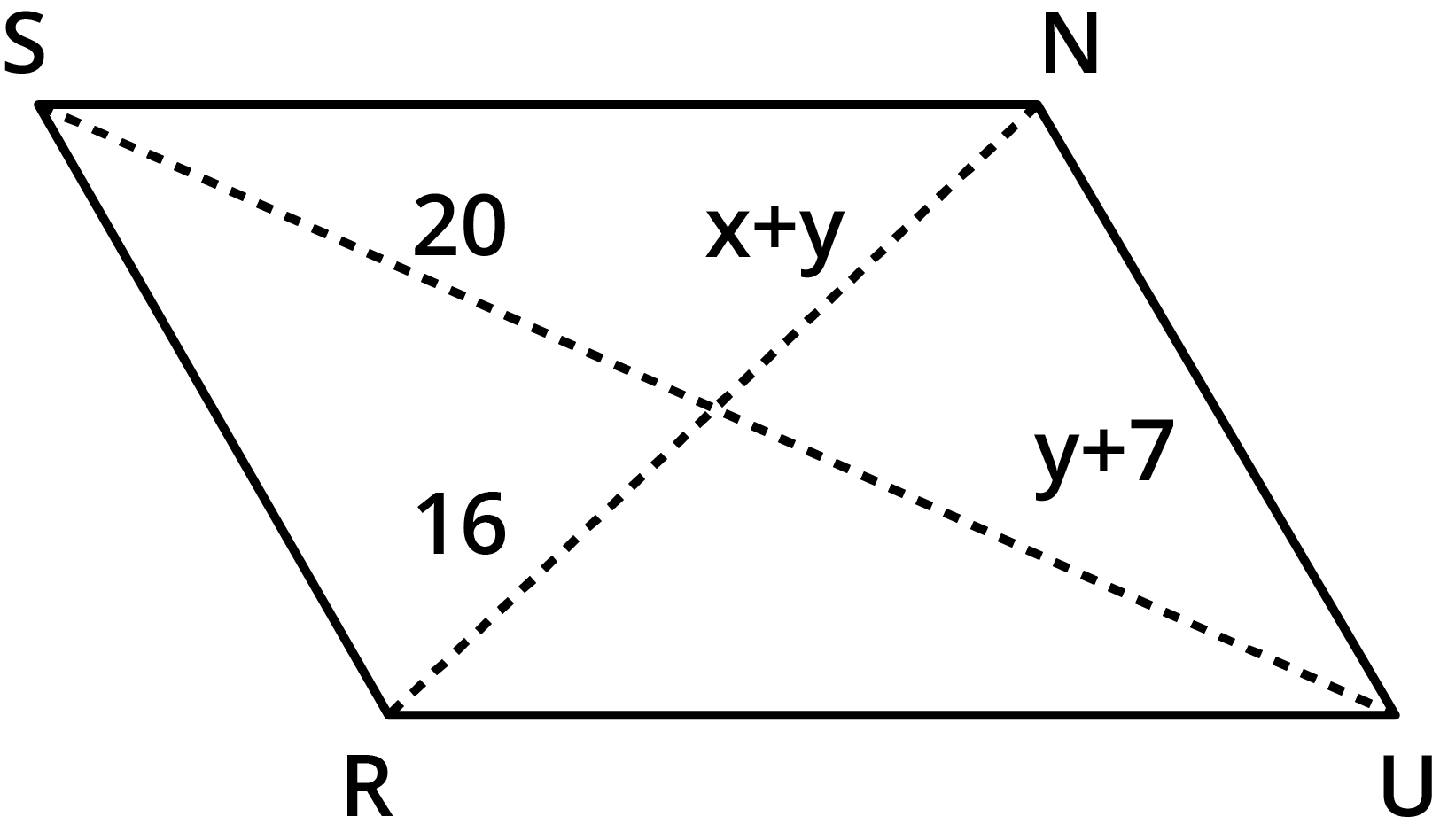
Given: Parallelogram ${\text{RUNS}}$

We need to find the value of ${\text{x}}$and ${\text{y}}{\text{.}}$

The diagonals of a parallelogram bisect each other, therefore, 

$  {\text{y }} + {\text{ }}7{\text{ }} = {\text{ }}20{\text{ }} $

$  {\text{y }} = {\text{ }}13 $

 $ {\text{x }} + {\text{ y }} = {\text{ }}16 $

$  {\text{x }} + {\text{ }}13{\text{ }} = {\text{ }}16 $

 $ {\text{x }} = {\text{ }}3{\text{ }} $ 

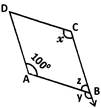
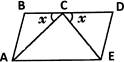
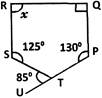
9. In the above figure both ${\text{RISK}}$and ${\text{CLUE}}$are parallelograms. Find the value of ${\text{x}}{\text{.}}$

Given: Parallelograms ${\text{RISK}}$and ${\text{CLUE}}$

As we know that the adjacent angles of a parallelogram are supplementary, therefore, 

In parallelogram ${\text{RISK}}$

$  \angle {\text{RKS  + }}\angle {\text{ISK}} = 180^\circ  $

 $ 120^\circ  + \angle {\text{ISK}} = 180^\circ  $ 

As the opposite angles of a parallelogram are equal, therefore,

In parallelogram ${\text{CLUE}}$,

$\angle {\text{ULC}} = \angle {\text{CEU}} = 70^\circ $

Also, the sum of all the interior angles of a triangle is $180^\circ $

$  {\text{x }} + {\text{ }}60^\circ {\text{ }} + {\text{ }}70^\circ {\text{ }} = {\text{ }}180^\circ  $

$  {\text{x }} = {\text{ }}50^\circ  $ 

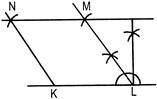
10. Explain how this figure is a trapezium. Which of its two sides are parallel?

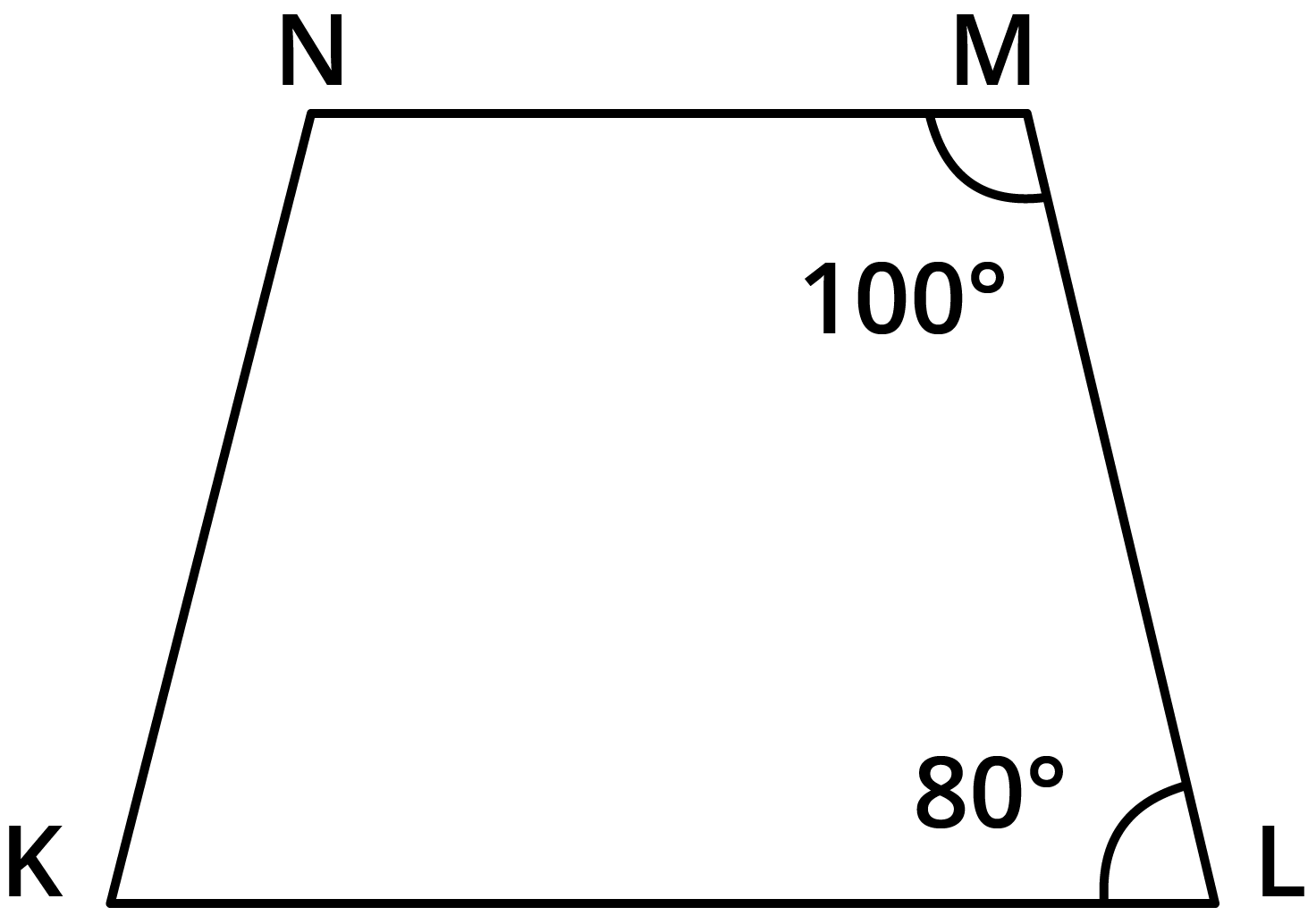
We need to explain how the given figure is a trapezium and find its two sides that are parallel.

If a transversal line intersects two specified lines in such a way that the sum of the angles on the same side of the transversal equals $180^\circ $, the two lines will be parallel to each other.

Here, $\angle {\text{NML}} = \angle {\text{MLK}} = 180^\circ $

Hence, ${\text{NM}}||{\text{LK}}$

Hence, the given figure is a trapezium.

11. Find ${\text{m}}\angle {\text{C}}$in the following figure if ${\text{AB}}\parallel {\text{CD}}$${\text{AB}}\parallel {\text{CD}}$.

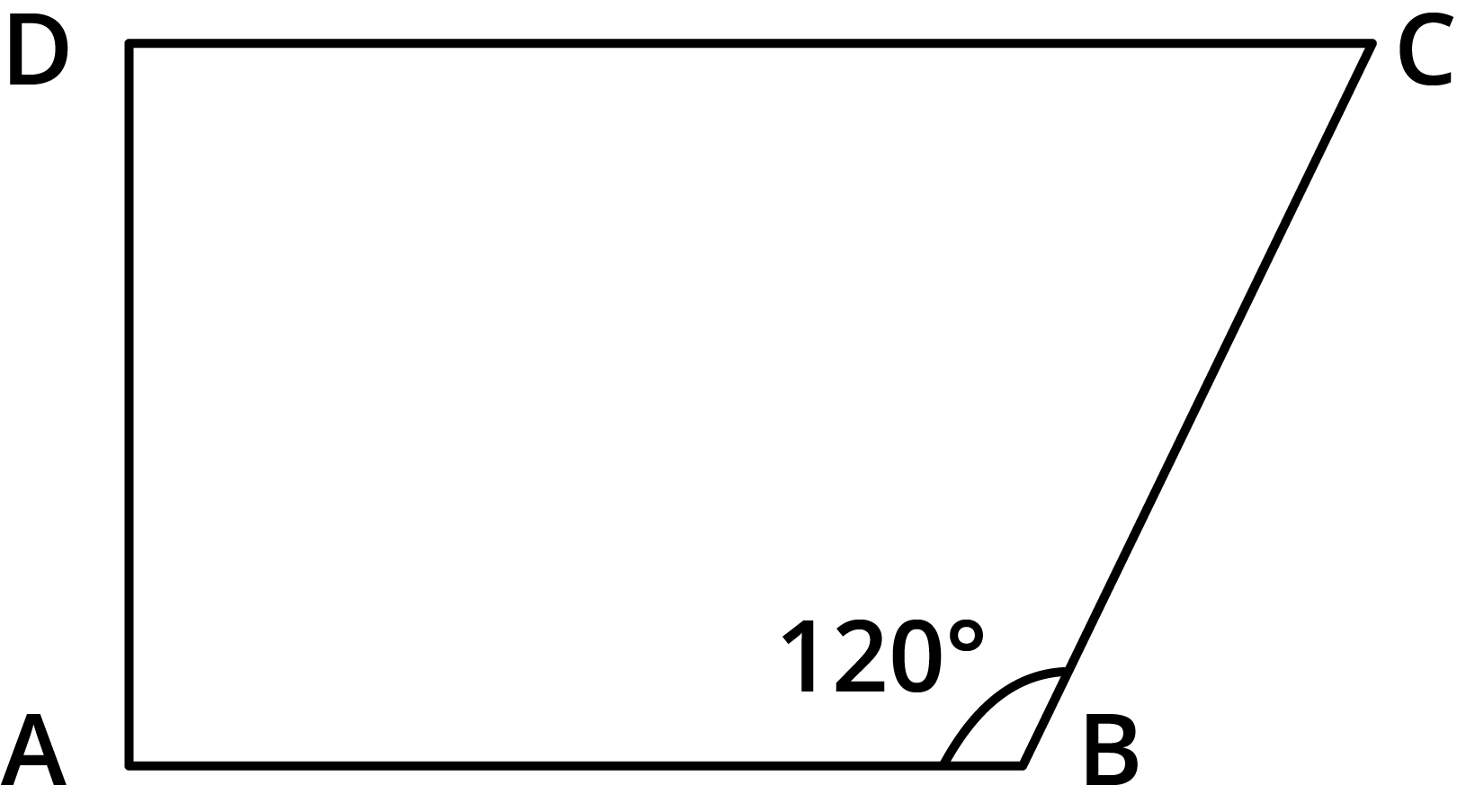
Given: ${\text{AB}}\parallel {\text{CD}}$ and quadrilateral

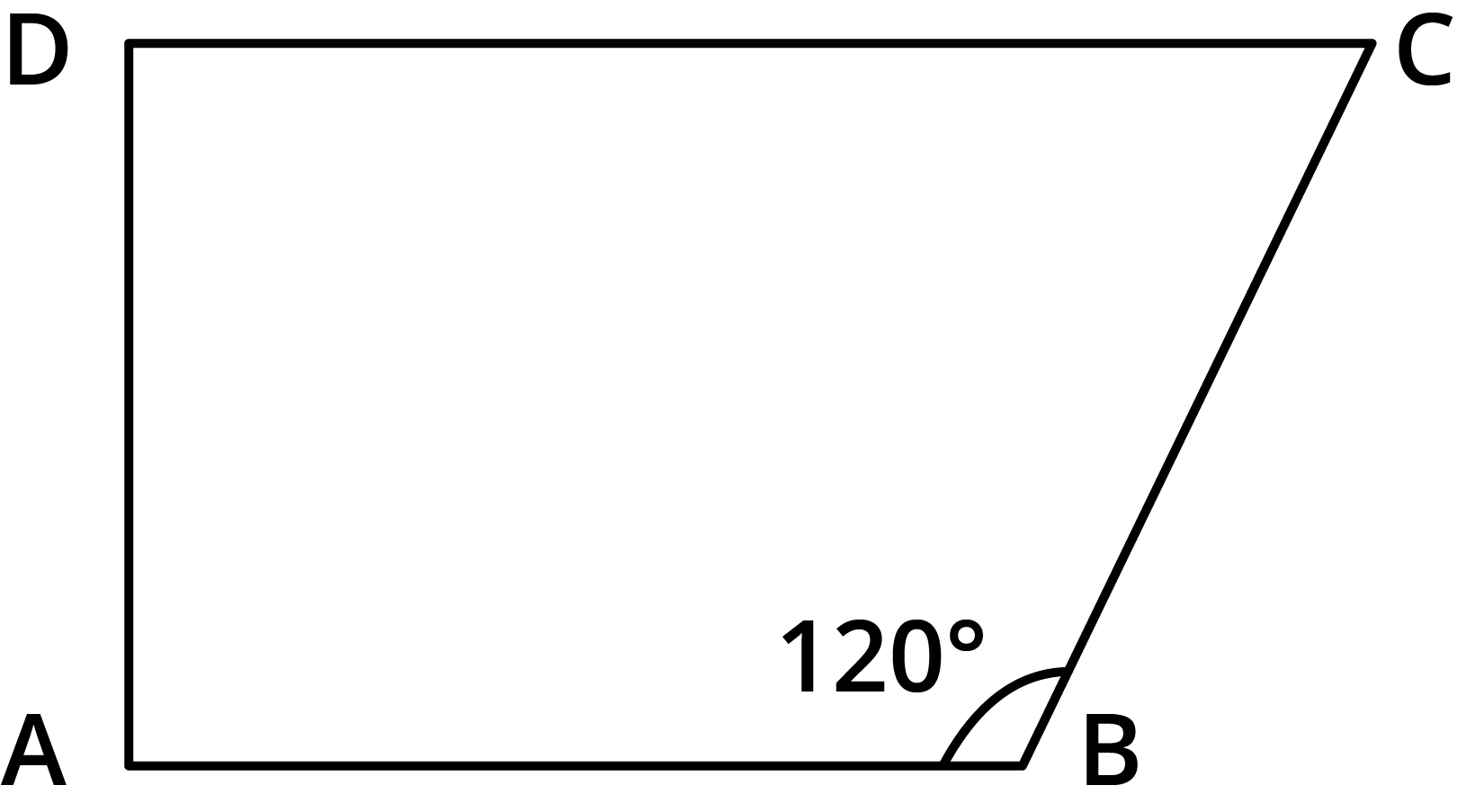
We need to find the measure of $\angle {\text{C}}$

$\angle {\text{B}} + \angle {\text{C}} = 180^\circ $(Angles on the same side of transversal).

$  120^\circ  + \angle {\text{C}} = 180^\circ  $

$  \angle {\text{C}} = 60^\circ  $ 

12. Find the measure of $\angle {\text{P}}$and$\angle {\text{S}}$, if ${\text{SP}}\parallel {\text{RQ}}$in the following figure. (If you find${\text{m}}\angle {\text{R}}$, is there more than one method to find${\text{m}}\angle {\text{P}}$?)

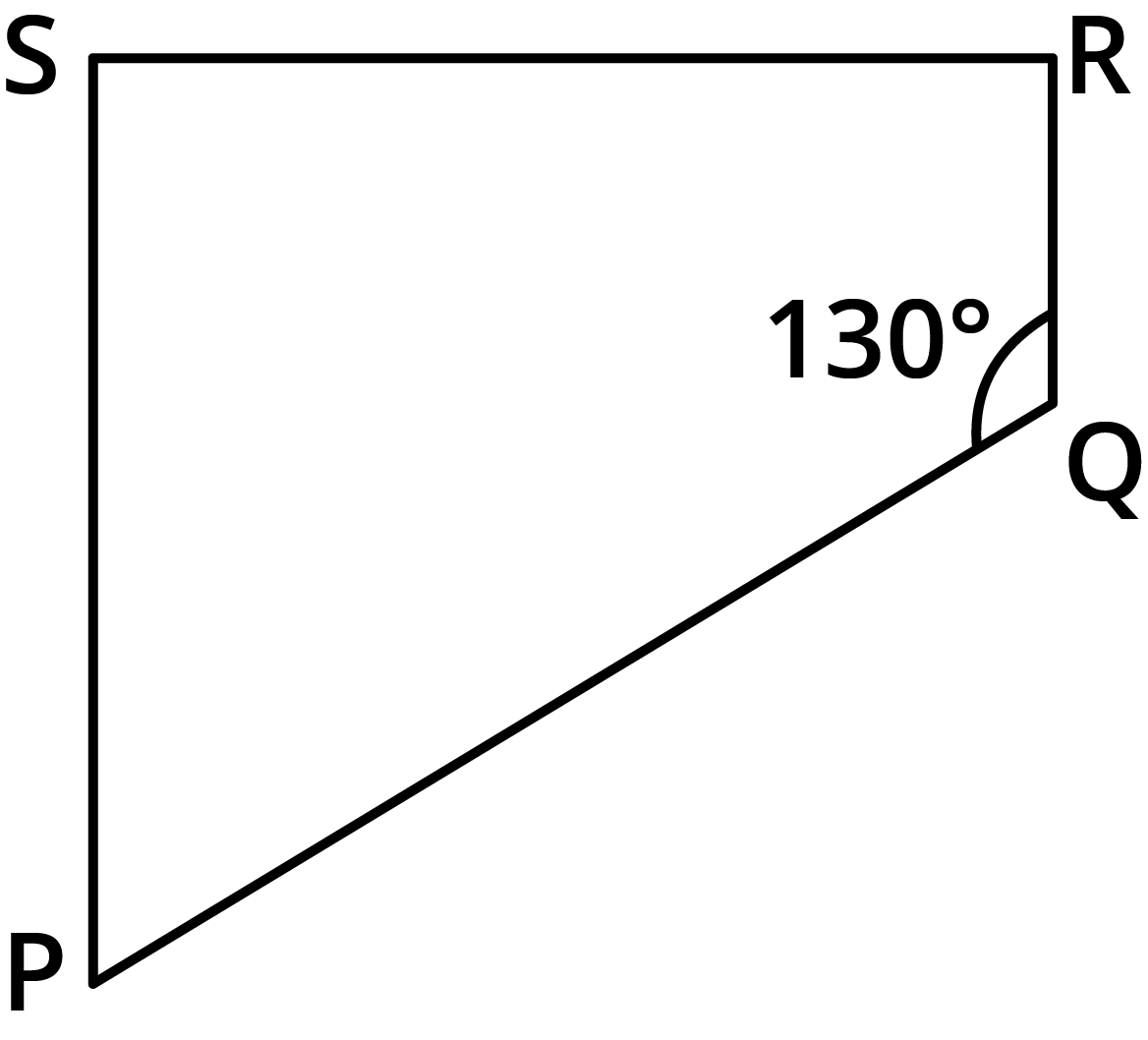
Given: ${\text{SP}}\parallel {\text{RQ}}$and 

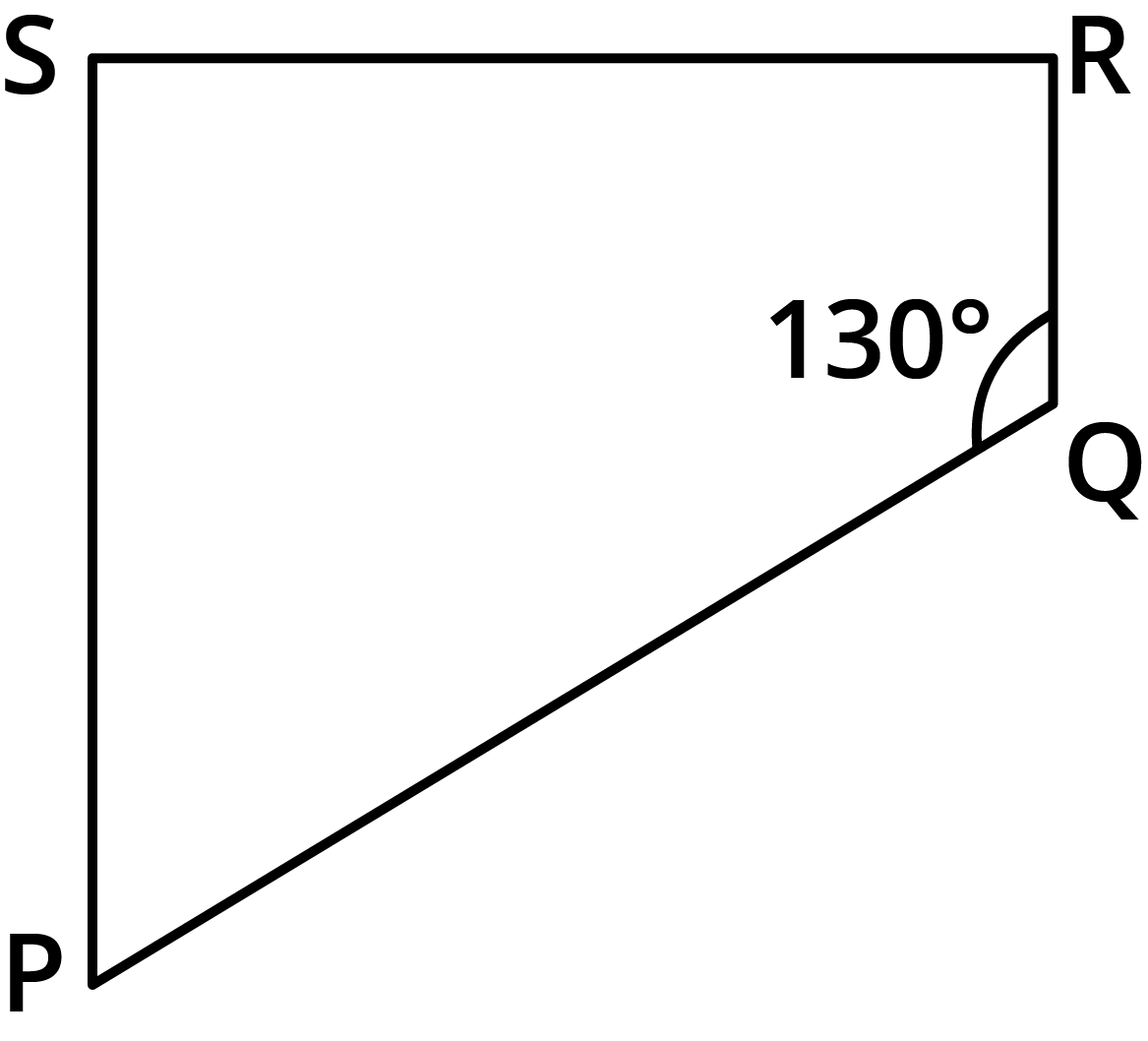
We need to find the measure of $\angle {\text{P}}$and $\angle {\text{S}}$.

The sum of angles on the same side of transversal is $180^\circ .$

$\angle {\text{P}} + \angle {\text{Q}} = 180^\circ $

$  \angle {\text{P}} + 130^\circ  = 180^\circ  $

$  \angle {\text{P}} = 50^\circ  

 $\angle {\text{R }} + {\text{ }}\angle {\text{S }} = {\text{ }}180^\circ {\text{ }} $

$  {\text{ }}90^\circ {\text{ }} + {\text{ }}\angle {\text{S }} = {\text{ }}180^\circ  $

  ${\text{ }}\angle {\text{S }} = {\text{ }}90^\circ {\text{ }} $ 

Yes, we can find the measure of ${\text{m}}\angle {\text{P}}$ by using one more method.

In the question,${\text{m}}\angle {\text{R}}$and ${\text{m}}\angle {\text{Q}}$are given. After finding ${\text{m}}\angle {\text{S}}$ we can find ${\text{m}}\angle {\text{P}}$ by using angle sum property.

Different Types of Polygons, Their Sides, and Angle Sum

Polygons are closed figures having at least or more than three sides. They are made of line segments only. Polygons are classified according to the number of sides they have. Some of the most common polygons and their properties are given in the table below.

Understanding Quadrilaterals Class 8

According to geometry, a quadrilateral is a covered, two-dimensional shape that has four straight sides. The polygon has four vertices or corners. Quadrilaterals will typically imply approved forms with four sides like rectangle, square, Trapezoid, kite, or uneven and uncharacterized. From the polygon formula, we can also derive the Sum of interior angles, i.e. (n - 2) × 180, where n stands for the polygon's number of sides. However, squares, rectangles, etc., are particular types of quadrilaterals with some of their sides and equal angles.

Different Types of Quadrilaterals

There are five types of quadrilaterals based on their shape:

Parallelogram

A rectangle is a kind of quadrilateral having four right angles. Hence, every angle in a rectangle is equal (360°/4 = 90°). Moreover, the opposite planes of a rectangle are parallel and similar. Diagonals bisect each other. Letting the length of the rectangle L and breadth B then,

Area of a Rectangle = Length(L) × Breadth(B).

Perimeter = 2 × (L + B).

Properties:

Every angle of a rectangle are 90°.

Opposite sides are equal and Parallel.

Diagonals of a rectangle bisect each other.

Square is another quadrilateral having four equal sides and angles. It's also a normal quadrilateral as both its sides and angles are equal. Accurately like a rectangle, a square has four angles of 90 degrees each. We can also call it a rectangle whose two adjacent sides are equal. Letting the side of a square 'a' then,

Area = a × a = a².

Perimeter = 2 × (a + a) = 4a.

All the angles are 90°.

Each and every side is parallel and also equal to each other.

Diagonals bisect each other perpendicularly.

A parallelogram is a simple quadrilateral whose opposite sides are parallel, as we can understand by the name itself. Thus, it consists of two pairs of parallel sides. Besides, the opposite angles in a parallelogram are alike, and its diagonals divide each other.

Opposite angles are equal.

Opposite sides are equal and parallel.

Diagonals bisect each other.

The summation of any two adjacent angles is 180 degrees.

A rhombus is also a quadrilateral whose all four sides are identical in length and opposite sides parallel. However, the angles are not similar to 90°. A rhombus with right angles would match a square. We often call rhombus a diamond' as it looks similar to the diamond suit in playing cards. Letting the side of a rhombus is 'a' then, the perimeter = 4a.

Considering the length of two diagonals of the rhombus are d1 and d2, then the rhombus area = ½ × d1 × d2.

All planes are equal, and opposite planes are parallel.

The diagonals bisect each other at 90°.

A trapezium is also a quadrilateral having one parallel side pair. The parallel sides are known as 'bases,' and the rest are known as 'legs' or lateral sides. Letting the height of a trapezium 'h' then:

Perimeter = Sum of lengths of all the sides = AB + BC + CD + DA.

Area = ½ × (Sum of lengths of parallel sides) × h = ½ × (AB + CD) × h.

A trapezium is another type of quadrilateral in which it follows a single property where only one pair of opposite sides of trapezium should be parallel to each other.

Kite: A Special Quadrilateral

Kite is a quadrilateral that has the following properties.

It has two pairs of consecutive sides that are equal in size.

Diagonals intersect each other at 90°, therefore the diagonals of a kite are perpendicular to each other.

When diagonals intersect each other, only one of them will be bisected.

NCERT Solutions for Class 8 Maths - Chapterwise Solutions

Chapter 1 - Rational Numbers

Chapter 2 - Linear Equations in One Variable

Chapter 4 - Practical Geometry

Chapter 5 - Data Handling

Chapter 6 - Squares and Square Roots

Chapter 7 - Cubes and Cube Roots

Chapter 8 - Comparing Quantities

Chapter 9 - Algebraic Expressions and Identities

Chapter 10 - Visualising Solid Shapes

Chapter 11 - Mensuration

Chapter 12 - Exponents and Powers

Chapter 13 - Direct and Inverse Proportions

Chapter 14 - Factorisation

Chapter 15 - Introduction to Graphs

Chapter 16 - Playing with Numbers

We Cover all the Given Exercises of Chapter 3 Understanding Quadrilaterals:-

Benefits of ncert solutions for class 8 maths chapter 3 understanding quadrilaterals.

Our subject specialists worked hard to make the solutions to NCERT Answers for Class 8 Mathematics Chapter 3 Understanding Quadrilaterals easier to comprehend for students. We have answered all of the questions from the chapter in the NCERT textbook. Students will be able to recognise the problems and solve them correctly in the test if they refer to these solutions.

Quick Revision 

Quadrilaterals are majorly of 6 types - Squares, Rectangles, Parallelograms, Trapeziums, Rhombuses, and Kites. It is important that students learn the formulas of area and perimeter for these quadrilaterals. It is also imperative that they revise the same so that they can use these to solve sums from this chapter quickly and efficiently.

List of Formulas

There are two major kinds of formulas related to quadrilaterals - Area and Perimeter. The following tables depict the formulas related to the areas and perimeters of different kinds of quadrilaterals.

Area of Quadrilaterals

Perimeter of quadrilaterals.

Perimeter of any quadrilateral is equal to the sum of all its sides, that is, AB + BC + CD + AD.

In conclusion, NCERT Solutions for Class 8 Maths Chapter 3 - Understanding Quadrilaterals provide a comprehensive and detailed understanding of the properties and characteristics of various types of quadrilaterals. By studying this chapter and using the NCERT solutions, students can enhance their knowledge of quadrilaterals and develop their problem-solving abilities.

The chapter begins by introducing the concept of a quadrilateral and its different types, such as parallelograms, rectangles, squares, rhombuses, and trapeziums. Each type is explained in terms of its defining properties, including sides, angles, diagonals, and symmetry.

FAQs on NCERT Solutions for Class 8 Maths Chapter 3 - Understanding Quadrilaterals

1. What is the Area of a Field in the Shape of a Rectangle with Dimensions of 20 Meters and 40 Meters?

We know that the field is rectangular. Hence, we can apply the area of a rectangle to find the field area.

Length of the field = 40 Metre

Width of the field = 20 Metre

Area of the rectangular field = Length × Width = 40 × 20 = 800 Sq. Meters.

We know if the length of the rectangle is L and breadth is B then,

Area of a rectangle = Length × Breadth or L × B

Perimeter = 2 × (L + B)

So, the properties and formulas of quadrilaterals that are used in this question:

Area of the Rectangle = Length × Width

So, we used only a specific property to find the answer.

2. Find the Rest of the Angles of a Parallelogram if one Angle is 80°?

For a parallelogram ABCD, as we know the properties:

The summation of any two adjacent angles = 180 degrees.

So, the angles opposite to the provided 80° angle will likewise be 80°.

Like we know, know that the Sum of angles of any quadrilateral = 360°.

So, if ∠A = ∠C = 80° then,

Sum of ∠A, ∠B, ∠C, ∠D = 360°

Also, ∠B = ∠D

Sum of 80°, ∠B, 80°, ∠D = 360°

Or, ∠B +∠ D = 200°

Hence, ∠B = ∠D = 100°

Now, we found all the angles of the quadrilateral, which are:

3. Why are the NCERT Solutions for Class 8 Maths Chapter 3 important?

The questions included in NCERT Solutions for Chapter 3 of Class 8 Maths are important not only for the exams but also for the overall understanding of quadrilaterals. These questions have been answered by expert teachers in the subject as per the NCERT (CBSE) guidelines. As the students answer the exercises, they will grasp the topic more comfortably and in a better manner.

4. What are the main topics covered in NCERT Solutions for Class 8 Maths Chapter 3?

All the topics of the syllabus of Class 8 Maths Chapter 3 have been dealt with in detail in the NCERT Solutions by Vedantu. The chapter is Understanding Quadrilaterals and has four exercises. All the important topics in Quadrilaterals have also been carefully covered. Students can also refer to the important questions section to get a good idea about the kind of questions usually asked in the exam.

5. Do I need to practice all the questions provided in the NCERT Solutions Class 8 Maths “Understanding Quadrilaterals”?

It helps to solve as many questions as possible because Mathematics is all about practice. If you solve all the practice questions and exercises given in NCERT Solutions for Class 8 Maths, you will be able to score very well in your exams comfortably. This will also help you understand the concepts clearly and allow you to apply them logically in the questions.

6. What are the most important concepts that I need to remember in Class 8 Maths Chapter 3?

For Class 8 Maths Chapter 3, you must remember the definition, characteristics and properties of all the quadrilaterals prescribed in the syllabus, namely, parallelogram, rhombus, rectangle, square, kite, and trapezium. Also know the properties of their angles and diagonals. Regular practise will help students learn the chapter easily.

7. Is Class 8 Maths Chapter 3 Easy?

Class 8 chapter 3 of Maths is a really interesting but critical topic. It's important not only for the Class 8 exams but also for understanding future concepts in higher classes. So, to stay focused and get a good grip of all concepts, it is advisable to download the NCERT Solutions for Class 8 Maths from the Vedantu website or from the Vedantu app at free of cost. This will help the students to clear out any doubts and allow them to excel in the exams. 

NCERT Solutions for Class 8 Maths

Ncert solutions for class 8.

• Class 6 Maths
• Class 6 Science
• Class 6 Social Science
• Class 6 English
• Class 7 Maths
• Class 7 Science
• Class 7 Social Science
• Class 7 English
• Class 8 Maths
• Class 8 Science
• Class 8 Social Science
• Class 8 English
• Class 9 Maths
• Class 9 Science
• Class 9 Social Science
• Class 9 English
• Class 10 Maths
• Class 10 Science
• Class 10 Social Science
• Class 10 English
• Class 11 Maths
• Class 11 Computer Science (Python)
• Class 11 English
• Class 12 Maths
• Class 12 English
• Class 12 Economics
• Class 12 Accountancy
• Class 12 Physics
• Class 12 Chemistry
• Class 12 Biology
• Class 12 Computer Science (Python)
• Class 12 Physical Education
• GST and Accounting Course
• Excel Course
• Tally Course
• Finance and CMA Data Course
• Payroll Course

Interesting

• Learn English
• Learn Excel
• Learn Tally
• Learn GST (Goods and Services Tax)
• Learn Accounting and Finance
• GST Tax Invoice Format
• Accounts Tax Practical
• Tally Ledger List
• GSTR 2A - JSON to Excel

Are you in school ? Do you love Teachoo?

We would love to talk to you! Please fill this form so that we can contact you

You are learning...

Chapter 3 Class 8 Understanding Quadrilaterals

Click on any of the links below to start learning from Teachoo ...

Updated for new NCERT Book .

Get NCERT Solutions of Chapter 3 Class 8 Understanding Quadrilaterals free at teachoo. Answers to all exercise questions and examples have been solved, with concepts of the chapter explained.

In this chapter, we will learn

• What are curves , open curves, closed curves, simple curves
• What are polygons , Different Types of Polygons
• Diagonal of a Polygon
• Convex and Concave Polygons
• Regular and Irregular Polygons
• Angle Sum Property of Polygons
• Sum of Exterior Angles of a Polygon
• Exterior Angles of a Regular Polygon
• What is a Quadrilateral
• Parallelogram
• Parallelogram propertie s - Opposite Angles are equal, Opposite sides are equal, Adjacent Angles are supplementary, Diagonals Bisect Each other
• Rhombus, Rectangle, Square are all parallelograms with additional properties

To learn from the NCERT, click on an exercise or example link below to get started.

To learn the Teachoo (टीचू) way, click on a concept below Concept Wise. In Concept Wise, first the concept is explained, and then the questions of that concept is solved - from easy to difficult

Note : When you click on a link, the first question or topic will open. To see other questions, there is a list with all the questions and concepts (it has arrows). You can refer to the list for other questions.

Click on a link now to begin.

Serial order wise

Concept wise.

What's in it?

Hi, it looks like you're using AdBlock :(

Please login to view more pages. it's free :), solve all your doubts with teachoo black.

The Site is down as we are performing important server maintenance, during which time the server will be unavailable for approximately 24 hours. Please hold off on any critical actions until we are finished. As always your feedback is appreciated.

• Study Packages
• NCERT Solutions
• Sample Papers
• Online Test

• Questions Bank
• Mathematics
• Understanding Quadrilaterals
• Test Series
• Ncert Solutions
• Solved Papers
• Current Affairs
• JEE Main & Advanced
• Pre-Primary
• MP State Exams
• UP State Exams
• Rajasthan State Exams
• Jharkhand State Exams
• Chhattisgarh State Exams
• Bihar State Exams
• Haryana State Exams
• Gujarat State Exams
• MH State Exams
• Himachal State Exams
• Delhi State Exams
• Uttarakhand State Exams
• Punjab State Exams
• J&K State Exams

8th Class Mathematics Understanding Quadrilaterals Question Bank

Done understanding quadrilaterals total questions - 44.

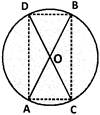
question_answer 1) ABCD is a quadrilateral. If AC and BD bisect each other, what is ABCD?

A)  A square      done clear

B)                         A parallelogram done clear

C)                         A rectangle    done clear

D)                         All the above done clear

question_answer 2) ABCD is a parallelogram. The angle bisectors of \[\angle A\] and \[\angle D\] meet at O. What is the measure of \[\angle AOD\]?

A)  \[{{45}^{o}}\]                    done clear

B)                         \[{{90}^{o}}\]                    done clear

C)                         \[{{75}^{o}}\]                                    done clear

D)                         \[{{180}^{o}}\]                 done clear

question_answer 3) The diagonal of a rectangle is \[10\text{ }cm\] and its breadth is\[6\text{ }cm\]. What is its length?

A)  \[6\text{ }cm\] done clear

B)                                                        \[5\,\,cm\]                         done clear

C)                         \[8\,\,cm\]                         done clear

D)                         \[4\,\,cm\] done clear

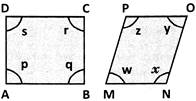
A)   \[p+q+r+s=w+x+y+z\] done clear

B)                         \[p+q+r+s<w+x+y+z\] done clear

C)                         \[p+q+r+s>w+x+y+z\]       done clear

D)                         Either (B) or (C) done clear

question_answer 5) What do you call a parallelogram which has equal diagonals?

A)  A trapezium   done clear

B)                         A rectangle done clear

C)                         A rhombus    done clear

D)                         A kite done clear

question_answer 6) In a square ABCD, the diagonals bisect at O. What type of a triangle is AOB?

A)  An equilateral triangle. done clear

B)                         An isosceles but not a right angled triangle. done clear

C)                         A right angled but not an isosceles triangle. done clear

D)                         An isosceles right angled triangle. done clear

question_answer 7) The perimeter of a parallelogram is\[180\text{ }cm\]. If one side exceeds the other by \[10\text{ }cm,\] what are the sides of the parallelogram?

A)  \[40\text{ }cm,\text{ }50\text{ }cm~\] done clear

B)                         \[45\text{ }cm\] each done clear

C)                         \[50\text{ }cm\] each    done clear

D)                         \[45\text{ }cm,\text{ }50\text{ }cm\] done clear

question_answer 8) In the quadrilateral ABCD, the diagonals   AC and BD are equal and perpendicular to each other. What type of a quadrilateral is ABCD?

D)                         A trapezium done clear

A)  \[{{90}^{o}}\]                    done clear

B)                         \[{{60}^{o}}\]    done clear

C)                         \[{{45}^{o}}\]                    done clear

D)                         \[{{135}^{o}}\] done clear

question_answer 10) In a parallelogram ABCD, if \[AB=2x+5,\]\[CD~=y+1,\] \[AD=y+5~\] and \[BC=3x-4,\]what is the ratio of AB and BC?

A)  \[71:21\]                             done clear

B)                         \[12:11\]                                             done clear

C)                         \[31:35\]                             done clear

D)                         \[4:7\]  done clear

question_answer 11) If ABCD is an isosceles trapezium, what is the measure of \[\angle C\]?

A)  \[\angle B\]                                       done clear

B)                         \[\angle A\]                       done clear

C)                         \[\angle D\]                                       done clear

D)                         \[{{90}^{o}}\] done clear

question_answer 12) A diagonal of a rectangle is inclined to one side of the rectangle at \[{{25}^{o}}\]. What is the measure of the acute angle between the diagonals?

A)  \[{{25}^{o}}\]                    done clear

B)                         \[{{40}^{o}}\]  done clear

C)                         \[{{50}^{o}}\]                    done clear

D)                         \[{{55}^{o}}\] done clear

question_answer 13) If angles P, Q, R and S of the quadrilateral PQRS, taken in order, are in the ratio \[3:7:6:4,\]what is PQRS?

A)  A rhombus                         done clear

B)                         A parallelogram               done clear

C)                         A trapezium                      done clear

A)  A square done clear

B)                         A trapezium done clear

C)                         An isosceles trapezium done clear

D)                         A rectangle done clear

question_answer 15) If two adjacent angles of a parallelogram are in the ratio \[3:2,\]what are their measures?

A)  \[{{108}^{o}},{{72}^{o}}\]      done clear

B)                         \[{{72}^{o}},{{36}^{o}}\] done clear

C)                         \[{{100}^{o}},{{80}^{o}}\]      done clear

D)                         \[{{144}^{o}},{{36}^{o}}\] done clear

A)  \[{{60}^{o}}\]                                    done clear

B)                         \[{{70}^{o}}\]                    done clear

C)                         \[{{80}^{o}}\]                                    done clear

D)                         \[{{85}^{o}}\]                    done clear

A)  \[2\]     done clear

B)                                                         \[3\]                     done clear

C)                         \[-3\]                    done clear

D)                         \[-2\] done clear

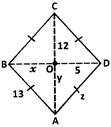
A)  \[12,5,13\]                         done clear

B)                         \[5,12,13\]         done clear

C)                         \[5,13,5\]                            done clear

D)                         \[12,13,5\] done clear

A)  \[{{100}^{o}},\text{ }{{80}^{o}},\text{ }{{100}^{o}}\] done clear

B)                         \[{{100}^{o}},\text{ }{{100}^{o}},\text{ }{{80}^{ol}},\] done clear

C)                         \[{{80}^{o}},{{100}^{o}},{{100}^{o}}\] done clear

D)                         \[{{80}^{o}},{{80}^{o}},{{100}^{o}}\] done clear

A)  \[{{36}^{o}}\]                    done clear

B)                         \[{{72}^{o}}\]    done clear

C)                         \[{{108}^{o}}\]                 done clear

D)                         \[{{120}^{o}}\] done clear

A)  \[{{210}^{o}}\]                 done clear

B)                         \[{{110}^{o}}\] done clear

C)                         \[{{540}^{o}}\]                 done clear

D)                         \[{{105}^{o}}\] done clear

question_answer 22) Each interior angle of a regular polygon is \[{{150}^{o}}\] How many sides has the polygon?

A)  \[8\]                                     done clear

B)                         \[12\]                   done clear

C)                         \[9\]                                     done clear

D)                         \[10\] done clear

A)  \[{{30}^{o}}\]                    done clear

B)                         \[{{40}^{o}}\]    done clear

C)                         \[{{60}^{o}}\]                                    done clear

D)                         \[{{50}^{o}}\] done clear

A)  \[{{100}^{o}}\]                 done clear

C)                         \[{{130}^{o}}\]                 done clear

D)                         \[{{120}^{o}}\]                 done clear

question_answer 25) Each interior angle of a regular polygon is \[{{162}^{o}}\] How many sides has the polygon?

A)  \[12\]                   done clear

B)                                                         \[20\]                   done clear

C)                         \[16\]                                                   done clear

question_answer 26) ABCD is a quadrilateral such that \[AB=BC,\] \[AD=\frac{1}{2}CD\] and \[AD=\frac{1}{4}AB\]. If \[BC=12\text{ }cm,\]what is the measure of AD?

A)  \[6\,cm\]                            done clear

B)                         \[4\,cm\]            done clear

C)                         \[12\,cm\]                          done clear

D)                         \[3\,cm\]                            done clear

A)  \[4\]                     done clear

B)                         \[3\sqrt{3}\]      done clear

C)                         \[3\]                                     done clear

D)                         \[5\] done clear

question_answer 28) How many measurements are required to construct a quadrilateral?

A)  \[5\]                                     done clear

B)                         \[4\]    done clear

D)                         \[2\]                     done clear

question_answer 29) How many unique measurements are needed to construct a parallelogram?

A)  \[2\]                                     done clear

B)                         \[3\]    done clear

C)                         \[4\]                                     done clear

D)                         \[1\] done clear

question_answer 30) What is the minimum number of dimensions needed to construct a rectangle?

A)  \[1\]                                     done clear

B)                         \[2\]                     done clear

C)                        \[3\]                                      done clear

D)                         \[4\]                     done clear

question_answer 31) What is the minimum number of measurements needed to construct a square?

B)                         \[2\]      done clear

D)                         \[4\] done clear

A) \[{{15}^{o}}\]                     done clear

B)                        \[{{30}^{o}}\]                     done clear

C)                        \[{{45}^{o}}\]                     done clear

D)                        \[{{60}^{o}}\] done clear

A)  A trapezium      done clear

B)                         A rhombus done clear

C)                         A rectangle   done clear

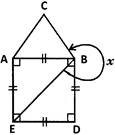
A)  \[{{200}^{o}}\]                 done clear

B)                         \[{{270}^{o}}\]                 done clear

C)                         \[{{360}^{o}}\]                 done clear

D)                         \[{{540}^{o}}\] done clear

question_answer 35) In a trapezium ABCD, AB is parallel to CD and the diagonals intersect each other at O. What is the ratio of OA and OC?

A)  \[\frac{OB}{OD}\]                                           done clear

B)                         \[\frac{BC}{CD}\]                            done clear

C)                         \[\frac{AD}{AB}\]                                            done clear

D)                         \[\frac{AC}{BD}\] done clear

question_answer 36) In \[\Delta ABC,\] P and Q are the midpoints of AB and AC. If PQ is produced to R such that \[PQ=QR,\]what is PRCB?

A)  A rectangle   done clear

B)                         A square done clear

C)                         A rhombus   done clear

D)                         A parallelogram done clear

question_answer 37) Three angles of a quadrilateral are equal and the measure of the fourth angle is \[{{120}^{o}}\]. Find the measure of each of these equal angles.

A)  \[{{80}^{o}}\]                    done clear

B)                         \[{{120}^{o}}\]                 done clear

C)                         \[{{60}^{o}}\]                    done clear

D)                         \[{{140}^{o}}\]                 done clear

question_answer 38) A quadrilateral has three acute angles, each measuring \[{{75}^{o}}\] Find the measure of the fourth angle.

A)  \[{{65}^{o}}\]                    done clear

B)                         \[{{135}^{o}}\]                 done clear

C)                         \[{{140}^{o}}\]                 done clear

D)                        \[{{225}^{o}}\] done clear

B)                         \[{{110}^{o}}\]                 done clear

C)                         \[{{120}^{o}}\]                 done clear

D)                         \[{{130}^{o}}\]                 done clear

A)  \[{{45}^{o}}\]                    done clear

C)                         \[{{255}^{o}}\]                 done clear

D)                         \[{{225}^{o}}\] done clear

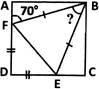
A)  \[{{28}^{o}}\]                    done clear

B)                         \[{{33}^{o}}\]                    done clear

C)                         \[{{55}^{o}}\]                    done clear

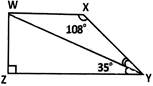
D)                         \[{{37}^{o}}\]                    done clear

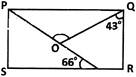
A)  \[{{47}^{o}}\]                    done clear

B)                         \[{{24}^{o}}\]                    done clear

C)                         \[{{67}^{o}}\]                    done clear

D)                         \[{{58}^{o}}\] done clear

A)  \[{{105}^{o}}\]                 done clear

B)                         \[{{95}^{o}}\]                    done clear

C)                         \[{{135}^{o}}\]                 done clear

A)  \[{{85}^{o}}\]                    done clear

B)                         \[{{65}^{o}}\]                    done clear

C)                         \[{{50}^{o}}\]                    done clear

D)                         \[{{130}^{o}}\] done clear

Study Package

Question - Understanding Quadrilaterals

Related question.

Reset Password.

OTP has been sent to your mobile number and is valid for one hour

Mobile Number Verified

Your mobile number is verified.

CBSE Class 8 Maths Understanding Quadrilaterals Worksheets

Table of Contents

Access free PDF worksheets for CBSE Class 8 Understanding Quadrilaterals , featuring essential chapter-wise and topic-wise questions. Regular practice of these CBSE NCERT worksheets, question banks, workbooks, and exercises with solutions is crucial for reinforcing learning and revising key concepts in Class 8 Understanding Quadrilaterals. Aligned with the latest CBSE syllabus from NCERT, and CBSE , these resources cover chapters from the NCERT book , ensuring comprehensive preparation for school exams.

Fill Out the Form for Expert Academic Guidance!

Please indicate your interest Live Classes Books Test Series Self Learning

Verify OTP Code (required)

I agree to the terms and conditions and privacy policy .

Fill complete details

Target Exam ---

Understanding Quadrilaterals Class 8 Worksheet

Download PDFs of test papers covering important topics to excel in your school exams. Explore CBSE Class 8 Understanding Quadrilaterals worksheets , including vital questions, solutions, and solved test papers. These resources offer topic-wise practice and solutions, aiding in a deeper understanding of Class 8 Understanding Quadrilaterals concepts.

Understanding Quadrilaterals Class 8 Worksheet PDF

Download PDF for Free. Study without Internet (Offline)

Grade --- Class 1 Class 2 Class 3 Class 4 Class 5 Class 6 Class 7 Class 8 Class 9 Class 10 Class 11 Class 12

Target Exam JEE NEET CBSE

Preferred time slot for the call --- 9 am 10 am 11 am 12 pm 1 pm 2 pm 3 pm 4 pm 5 pm 6 pm 7 pm 8pm 9 pm 10pm

Language --- English Hindi Marathi Tamil Telugu Malayalam

Are you a Sri Chaitanya student? No Yes

Understanding Quadrilaterals Class 8 Worksheet with Answers

Ques. In a parallelogram, if the length of one side is 8 cm, and the length of the adjacent side is 12 cm, what is the length of the opposite side?

Ans. 12 cm (since opposite sides are equal in length).

Ques. If the sum of the interior angles of a quadrilateral is 360 degrees, and one angle is 120 degrees, what is the measure of the adjacent angle?

Ans. 240 degrees (since the sum of the interior angles is 360 degrees).

Ques. In a rhombus, if the length of one diagonal is 10 cm, and the length of the other diagonal is 8 cm, what is the length of the side?

Ans. 5 cm (since diagonals bisect each other, and the length of each half is the length of the side).

Ques. If a quadrilateral has two pairs of opposite angles as 90 degrees each, what type of quadrilateral is it?

Ans. It is a rectangle.

Ques. In a trapezium, if the length of one base is 6 cm, and the length of the other base is 8 cm, what is the length of the height?

Ans. 4 cm (since the area of a trapezium is half the product of the sum of the bases and the height).

Ques. If the diagonals of a quadrilateral are perpendicular, what type of quadrilateral is it?

Ques. In a parallelogram, if the length of one side is 10 cm, and the length of the adjacent side is 12 cm, what is the length of the diagonal?

Ans. 14 cm (since diagonals bisect each other, and the length of each half is the length of the side).

Ques. If the sum of the interior angles of a quadrilateral is 360 degrees, and one angle is 150 degrees, what is the measure of the adjacent angle?

Ans. 210 degrees (since the sum of the interior angles is 360 degrees).

Ques. In a rhombus, if the length of one side is 8 cm, and the length of the adjacent side is 12 cm, what is the length of the diagonal?

Ans. 10 cm (since diagonals bisect each other, and the length of each half is the length of the side).

Ques. If a quadrilateral has one pair of opposite angles as 90 degrees each, and one angle is 60 degrees, what is the measure of the adjacent angle?

Ans. 30 degrees (since opposite angles are equal in a parallelogram).

Ques. In a trapezium, if the length of one base is 8 cm, and the length of the other base is 10 cm, what is the length of the height?

Ans. 6 cm (since the area of a trapezium is half the product of the sum of the bases and the height).

Ques. If the diagonals of a quadrilateral are equal in length, what type of quadrilateral is it?

Ans. It is a square.

Ques. In a parallelogram, if the length of one side is 10 cm, and the length of the adjacent side is 12 cm, what is the length of the height?

Ans. 2 cm (since the area of a parallelogram is the product of the base and the height).

Ques. If the sum of the interior angles of a quadrilateral is 360 degrees, and one angle is 90 degrees, what is the measure of the adjacent angle?

Ans. 270 degrees (since the sum of the interior angles is 360 degrees).

Maximize Your Performance with Expertly Crafted Worksheets

Benefit from expertly crafted CBSE printable worksheets for Class 8 Understanding Quadrilaterals , designed by experienced teachers to align with the latest CBSE Class 8 syllabus . By utilizing these worksheets with answers and solutions, students can enhance their performance in class tests and school examinations, ultimately securing higher marks.

Effective Preparation Strategies for Class 8 Mathematics Understanding Quadrilaterals

Follow these expert-recommended steps from Infinity Learn to optimize your preparation for final exams:

• Establish a Study Schedule: Organize your study time by prioritizing topics based on their importance and mark distribution.
• Access Comprehensive Worksheets: Utilize high-quality worksheets covering all aspects of Class 8 Mathematics Understanding Quadrilaterals to enhance your preparation.
• Thorough Revision: Before attempting worksheets, revise the entire syllabus to ensure a thorough understanding of the concepts.
• Focus on High-Weightage Topics: Begin with topics carrying higher marks weight-age to maximize your preparation efficiency.
• Time-Based Evaluation: Evaluate your performance by timing yourself while solving worksheets to improve time management skills.

Unlock the Benefits of Understanding Quadrilaterals Worksheets for Class 8

By engaging with CBSE Class 8 Understanding Quadrilaterals worksheet s, students can strengthen their conceptual clarity, boost exam scores, and enhance problem-solving abilities. These resources, meticulously crafted by Infinity Learn teachers, offer a valuable tool for Class 8 students seeking academic improvement.

Experience the Advantages of Class 8 Understanding Quadrilaterals Worksheets

Empower yourself with CBSE Class 8 Understanding Quadrilaterals Worksheets to solidify your understanding, enhance analytical skills, and elevate your exam performance. These free printable worksheets, curated by educators at Infinity Learn, cater to students of all levels, providing a valuable resource for comprehensive study and revision. Make the most of your study sessions by incorporating daily practice of CBSE Class 8 Understanding Quadrilaterals Worksheets to excel in your examinations.

Improve Your Understanding of Quadrilaterals in Class 8 with Free Study Materials

Get helpful resources like sample papers, past question papers, NCERT books , and NCERT solutions for Understanding Quadrilaterals in Class 8 . These materials are created by experienced teachers and are available for free in PDF format to help you prepare for your exams.

Practice Worksheets: A Great Way to Learn Quadrilaterals

Explore our Worksheet on Understanding Quadrilaterals class 8 that cover important topics from your NCERT book . These worksheets have lots of multiple-choice questions to help you practice and understand the subject better. By using these worksheets, you can improve your performance in exams as many questions may come from them.

Worksheets with Answers: Clearing Doubts and Improving Understanding

Our worksheets come with answers to help you understand and solve questions easily. By practicing these worksheets regularly, you can enhance your overall understanding of the subject.

Benefits of Using Worksheets for Class 8 Understanding Quadrilaterals

Regularly practicing these worksheets is important for improving your knowledge and understanding of Understanding Quadrilaterals in Class 8. Parents can encourage their children to use these worksheets for daily practice and check answers to identify areas for improvement.

Covering All Topics and Exam Patterns

Our worksheets cover all topics from your NCERT book and are designed by experienced teachers to match the latest exam patterns. They include different types of questions like short answers, fill-in-the-blanks, and more to help you prepare effectively.

Easy-to-Use PDF Worksheets

All our worksheets are in PDF format, making it easy for you to download and print them. You can access and solve these worksheets whenever you want to study and revise.

Free Worksheets for Class 8 Understanding Quadrilaterals

Infinity Learn offers free downloadable worksheets for all subjects in Class 8, including Understanding Quadrilaterals. These resources are designed to help you improve your knowledge and are available in PDF format for easy access.

Class 8 Maths Understanding Quadrilaterals Worksheets FAQs

What are the benefits of using cbse class 8 maths understanding quadrilaterals worksheets.

Using CBSE Class 8 Maths Understanding Quadrilaterals Worksheets can help students in several ways. These worksheets provide practice and reinforcement of concepts, help in identifying areas of improvement, and enhance problem-solving skills. They also help students to develop a deeper understanding of the subject and improve their performance in exams.

How do I access the CBSE Class 8 Maths Understanding Quadrilaterals Worksheets?

ou can access the CBSE Class 8 Maths Understanding Quadrilaterals Worksheets by visiting the official website of Infinity Learn or by downloading the Infinity Learn app. You can also search for the worksheets on various online platforms or Infinity Learnwebsites.

Are the CBSE Class 8 Maths Understanding Quadrilaterals Worksheets free?

Yes, the CBSE Class 8 Maths Understanding Quadrilaterals Worksheets are available for free download on the Infinity Learn website and app. You can access and use them without any cost or subscription.

Are the CBSE Class 8 Maths Understanding Quadrilaterals Worksheets aligned with the CBSE syllabus?

Yes, the CBSE Class 8 Maths Understanding Quadrilaterals Worksheets are designed to align with the CBSE syllabus and curriculum. They cover all the important topics and concepts as per the CBSE guidelines, ensuring that students are well-prepared for their exams.

Can I use the CBSE Class 8 Maths Understanding Quadrilaterals Worksheets for self-assessment?

Yes, the CBSE Class 8 Maths Understanding Quadrilaterals Worksheets can be used for self-assessment. Students can use these worksheets to assess their understanding of the subject, identify areas of improvement, and track their progress over time.

Related content

Talk to our academic expert!

Get access to free Mock Test and Master Class

Register to Get Free Mock Test and Study Material

Offer Ends in 5:00

NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals

Ncert solutions for class 8 maths chapter 3 understanding quadrilaterals| pdf download.

• Exercise 3.1 Chapter 3 Class 8 Maths NCERT Solutions
• Exercise 3.2 Chapter 3 Class 8 Maths NCERT Solutions
• Exercise 3.3 Chapter 3 Class 8 Maths NCERT Solutions
• Exercise 3.4 Chapter 3 Class 8 Maths NCERT Solutions

NCERT Solutions for Class 8 Maths Chapters:

How many exercises in chapter 3 understanding quadrilaterals, what is equilateral triangle, in a quadrilateral abcd, the angles a, b, c and d are in the ratio 1 : 2 : 3 : 4. find the measure of each angle of the quadrilateral., the interior angle of a regular is 108°. find the number of sides of the polygon., contact form.

• NCERT Solutions
• NCERT Class 8
• NCERT 8 Maths
• Chapter 3: Understanding Quadrilaterals

NCERT Solutions for Class 8 Maths Chapter 3 - Understanding Quadrilaterals

NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals are provided here, which can be downloaded for free in PDF format. The NCERT Solutions for the chapter Understanding Quadrilaterals are prepared by the mathematics experts at BYJU’S, from an examination point of view. These solutions explain the accurate method of solving problems. By understanding the concepts used in NCERT Solutions for Class 8, students will be able to clear all their doubts related to Understanding Quadrilaterals.

Download Exclusively Curated Chapter Notes for Class 8 Maths Chapter – 3 Understanding Quadrilaterals

Download most important questions for class 8 maths chapter – 3 understanding quadrilaterals.

NCERT Solutions for Class 8 Maths Chapter 3 – Understanding Quadrilaterals

carouselExampleControls111

Previous Next

Access Answers of Maths NCERT Class 8 Chapter 3 – Understanding Quadrilaterals

Exercise 3.1 page: 41.

1. Given here are some figures.

Classify each of them on the basis of the following.

Simple curve (b) Simple closed curve (c) Polygon

(d) Convex polygon (e) Concave polygon

a) Simple curve: 1, 2, 5, 6 and 7

b) Simple closed curve: 1, 2, 5, 6 and 7

c) Polygon: 1 and 2

d) Convex polygon: 2

e) Concave polygon: 1

2. How many diagonals does each of the following have?

a) A convex quadrilateral (b) A regular hexagon (c) A triangle

a) A convex quadrilateral: 2.

b) A regular hexagon: 9.

c) A triangle: 0

3. What is the sum of the measures of the angles of a convex quadrilateral? Will this property hold if the quadrilateral is not convex? (Make a non-convex quadrilateral and try!)

Let ABCD be a convex quadrilateral.

From the figure, we infer that the quadrilateral ABCD is formed by two triangles,

i.e. ΔADC and ΔABC.

Since we know that sum of the interior angles of a triangle is 180°,

the sum of the measures of the angles is 180° + 180° = 360°

Let us take another quadrilateral ABCD which is not convex .

Join BC, such that it divides ABCD into two triangles ΔABC and ΔBCD. In ΔABC,

∠1 + ∠2 + ∠3 = 180° (angle sum property of triangle)

∠4 + ∠5 + ∠6 = 180° (angle sum property of triangle)

∴, ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 = 180° + 180°

⇒ ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 = 360°

⇒ ∠A + ∠B + ∠C + ∠D = 360°

Thus, this property holds if the quadrilateral is not convex.

4. Examine the table. (Each figure is divided into triangles and the sum of the angles deduced from that.)

What can you say about the angle sum of a convex polygon with number of sides? (a) 7 (b) 8 (c) 10 (d) n

The angle sum of a polygon having side n = (n-2)×180°

Here, n = 7

Thus, angle sum = (7-2)×180° = 5×180° = 900°

Here, n = 8

Thus, angle sum = (8-2)×180° = 6×180° = 1080°

Here, n = 10

Thus, angle sum = (10-2)×180° = 8×180° = 1440°

Here, n = n

Thus, angle sum = (n-2)×180°

5. What is a regular polygon?

State the name of a regular polygon of

(i) 3 sides (ii) 4 sides (iii) 6 sides

Regular polygon: A polygon having sides of equal length and angles of equal measures is called a regular polygon. A regular polygon is both equilateral and equiangular.

(i) A regular polygon of 3 sides is called an equilateral triangle.

(ii) A regular polygon of 4 sides is called a square.

(iii) A regular polygon of 6 sides is called a regular hexagon.

6. Find the angle measure of x in the following figures.

a) The figure has 4 sides. Hence, it is a quadrilateral. Sum of angles of the quadrilateral = 360°

⇒ 50° + 130° + 120° + x = 360°

⇒ 300° + x = 360°

⇒ x = 360° – 300° = 60°

b) The figure has 4 sides. Hence, it is a quadrilateral. Also, one side is perpendicular forming a right angle.

Sum of angles of the quadrilateral = 360°

⇒ 90° + 70° + 60° + x = 360°

⇒ 220° + x = 360°

⇒ x = 360° – 220° = 140°

c) The figure has 5 sides. Hence, it is a pentagon.

Sum of angles of the pentagon = 540° Two angles at the bottom are a linear pair.

∴, 180° – 70° = 110°

180° – 60° = 120°

⇒ 30° + 110° + 120° + x + x = 540°

⇒ 260° + 2x = 540°

⇒ 2x = 540° – 260° = 280°

⇒ 2x = 280°

d) The figure has 5 equal sides. Hence, it is a regular pentagon. Thus, all its angles are equal.

⇒ x = 540°/5

a) Sum of all angles of triangle = 180°

One side of triangle = 180°- (90° + 30°) = 60°

x + 90° = 180° ⇒ x = 180° – 90° = 90°

y + 60° = 180° ⇒ y = 180° – 60° = 120°

z + 30° = 180° ⇒ z = 180° – 30° = 150°

x + y + z = 90° + 120° + 150° = 360°

b) Sum of all angles of quadrilateral = 360°

One side of quadrilateral = 360°- (60° + 80° + 120°) = 360° – 260° = 100°

x + 120° = 180° ⇒ x = 180° – 120° = 60°

y + 80° = 180° ⇒ y = 180° – 80° = 100°

z + 60° = 180° ⇒ z = 180° – 60° = 120°

w + 100° = 180° ⇒ w = 180° – 100° = 80°

x + y + z + w = 60° + 100° + 120° + 80° = 360°

Exercise 3.2 Page: 44

1. Find x in the following figures.

125° + m = 180° ⇒ m = 180° – 125° = 55° (Linear pair)

125° + n = 180° ⇒ n = 180° – 125° = 55° (Linear pair)

x = m + n (The exterior angle of a triangle is equal to the sum of the two opposite interior angles)

⇒ x = 55° + 55° = 110°

Two interior angles are right angles = 90°

70° + m = 180° ⇒ m = 180° – 70° = 110° (Linear pair)

60° + n = 180° ⇒ n = 180° – 60° = 120° (Linear pair) The figure is having five sides and is a pentagon.

Thus, sum of the angles of a pentagon = 540°

⇒ 90° + 90° + 110° + 120° + y = 540°

⇒ 410° + y = 540° ⇒ y = 540° – 410° = 130°

x + y = 180° (Linear pair)

⇒ x + 130° = 180°

⇒ x = 180° – 130° = 50°

2. Find the measure of each exterior angle of a regular polygon of

(i) 9 sides (ii) 15 sides

Sum of the angles of a regular polygon having side n = (n-2)×180°

(i) Sum of the angles of a regular polygon having 9 sides = (9-2)×180°= 7×180° = 1260°

Each interior angle=1260/9 = 140°

Each exterior angle = 180° – 140° = 40°

Each exterior angle = Sum of exterior angles/Number of angles = 360/9 = 40°

(ii) Sum of angles of a regular polygon having side 15 = (15-2)×180°

= 13×180° = 2340°

Each interior angle = 2340/15 = 156°

Each exterior angle = 180° – 156° = 24°

Each exterior angle = sum of exterior angles/Number of angles = 360/15 = 24°

3. How many sides does a regular polygon have if the measure of an exterior angle is 24°?

Each exterior angle = sum of exterior angles/Number of angles

24°= 360/ Number of sides

⇒ Number of sides = 360/24 = 15

Thus, the regular polygon has 15 sides.

4. How many sides does a regular polygon have if each of its interior angles is 165°?

Interior angle = 165°

Exterior angle = 180° – 165° = 15°

Number of sides = sum of exterior angles/exterior angles

⇒ Number of sides = 360/15 = 24

Thus, the regular polygon has 24 sides.

5. a) Is it possible to have a regular polygon with measure of each exterior angle as 22°?

    b) Can it be an interior angle of a regular polygon? Why?

a) Exterior angle = 22°

Number of sides = sum of exterior angles/ exterior angle

⇒ Number of sides = 360/22 = 16.36

No, we can’t have a regular polygon with each exterior angle as 22° as it is not a divisor of 360.

b) Interior angle = 22°

Exterior angle = 180° – 22°= 158°

No, we can’t have a regular polygon with each exterior angle as 158° as it is not a divisor of 360.

6.  a) What is the minimum interior angle possible for a regular polygon? Why?

     b) What is the maximum exterior angle possible for a regular polygon?

a) An equilateral triangle is the regular polygon (with 3 sides) having the least possible minimum interior angle because a regular polygon can be constructed with minimum 3 sides.

Since the sum of interior angles of a triangle = 180°

Each interior angle = 180/3 = 60°

b) An equilateral triangle is the regular polygon (with 3 sides) having the maximum exterior angle because the regular polygon with the least number of sides has the maximum exterior angle possible. Maximum exterior possible = 180 – 60° = 120°

Exercise 3.3 Page: 50

1. Given a parallelogram ABCD. Complete each statement along with the definition or property used.

(i) AD = …… (ii) ∠DCB = ……

(iii) OC = …… (iv) m ∠DAB + m ∠CDA = ……

(i) AD = BC (Opposite sides of a parallelogram are equal)

(ii) ∠DCB = ∠DAB (Opposite angles of a parallelogram are equal)

(iii) OC = OA (Diagonals of a parallelogram are equal)

(iv) m ∠DAB + m ∠CDA = 180°

2. Consider the following parallelograms. Find the values of the unknown x, y, z

y = 100° (opposite angles of a parallelogram)

x + 100° = 180° (adjacent angles of a parallelogram)

⇒ x = 180° – 100° = 80°

x = z = 80° (opposite angles of a parallelogram)

∴, x = 80°, y = 100° and z = 80°

50° + x = 180° ⇒ x = 180° – 50° = 130° (adjacent angles of a parallelogram) x = y = 130° (opposite angles of a parallelogram)

x = z = 130° (corresponding angle)

x = 90° (vertical opposite angles)

x + y + 30° = 180° (angle sum property of a triangle)

⇒ 90° + y + 30° = 180°

⇒ y = 180° – 120° = 60°

also, y = z = 60° (alternate angles)

z = 80° (corresponding angle) z = y = 80° (alternate angles) x + y = 180° (adjacent angles)

⇒ x + 80° = 180° ⇒ x = 180° – 80° = 100°

y = 112o z = 28o

3. Can a quadrilateral ABCD be a parallelogram if (i) ∠D + ∠B = 180°?

(ii) AB = DC = 8 cm, AD = 4 cm and BC = 4.4 cm?

(iii)∠A = 70° and ∠C = 65°?

(i) Yes, a quadrilateral ABCD can be a parallelogram if ∠D + ∠B = 180° but it should also fulfil some conditions, which are:

(a) The sum of the adjacent angles should be 180°.

(b) Opposite angles must be equal.

(ii) No, opposite sides should be of the same length. Here, AD ≠ BC

(iii) No, opposite angles should be of the same measures. ∠A ≠ ∠C

4. Draw a rough figure of a quadrilateral that is not a parallelogram but has exactly two opposite angles of equal measure.

ABCD is a figure of quadrilateral that is not a parallelogram but has exactly two opposite angles, that is, ∠B = ∠D of equal measure. It is not a parallelogram because ∠A ≠ ∠C.

5. The measures of two adjacent angles of a parallelogram are in the ratio 3 : 2. Find the measure of each of the angles of the parallelogram.

Let the measures of two adjacent angles ∠A and ∠B be 3x and 2x, respectively in

parallelogram ABCD.

∠A + ∠B = 180°

⇒ 3x + 2x = 180°

⇒ 5x = 180°

We know that opposite sides of a parallelogram are equal.

∠A = ∠C = 3x = 3 × 36° = 108°

∠B = ∠D = 2x = 2 × 36° = 72°

6. Two adjacent angles of a parallelogram have equal measure. Find the measure of each of the angles of the parallelogram.

Let ABCD be a parallelogram.

Sum of adjacent angles of a parallelogram = 180°

⇒ 2∠A = 180°

also, 90° + ∠B = 180°

⇒ ∠B = 180° – 90° = 90°

∠A = ∠C = 90°

∠B = ∠D = 90

7. The adjacent figure HOPE is a parallelogram. Find the angle measures x, y and z. State the properties you use to find them.

y = 40° (alternate interior angle)

∠P = 70° (alternate interior angle)

∠P = ∠H = 70° (opposite angles of a parallelogram)

z = ∠H – 40°= 70° – 40° = 30°

∠H + x = 180°

⇒ 70° + x = 180°

⇒ x = 180° – 70° = 110°

8. The following figures GUNS and RUNS are parallelograms. Find x and y. (Lengths are in cm)

(i) SG = NU and SN = GU (opposite sides of a parallelogram are equal) 3x = 18

3y – 1 = 26

⇒ 3y = 26 + 1

⇒ y = 27/3=9

x = 6 and y = 9

(ii) 20 = y + 7 and 16 = x + y (diagonals of a parallelogram bisect each other) y + 7 = 20

⇒ y = 20 – 7 = 13 and,

⇒ x + 13 = 16

⇒ x = 16 – 13 = 3

x = 3 and y = 13

9. In the above figure both RISK and CLUE are parallelograms. Find the value of x.

∠K + ∠R = 180° (adjacent angles of a parallelogram are supplementary)

⇒ 120° + ∠R = 180°

⇒ ∠R = 180° – 120° = 60°

also, ∠R = ∠SIL (corresponding angles)

⇒ ∠SIL = 60°

also, ∠ECR = ∠L = 70° (corresponding angles) x + 60° + 70° = 180° (angle sum of a triangle)

10. Explain how this figure is a trapezium. Which of its two sides are parallel? (Fig 3.32)

When a transversal line intersects two lines in such a way that the sum of the adjacent angles on the same side of transversal is 180°, then the lines are parallel to each other. Here, ∠M + ∠L = 100° + 80° = 180°

Thus, MN || LK

As the quadrilateral KLMN has one pair of parallel lines, it is a trapezium. MN and LK are parallel lines.

11. Find m∠C in Fig 3.33 if AB || DC.

m∠C + m∠B = 180° (angles on the same side of transversal)

⇒ m∠C + 120° = 180°

⇒ m∠C = 180°- 120° = 60°

12. Find the measure of ∠P and ∠S if SP || RQ ? in Fig 3.34. (If you find m∠R, is there more than one method to find m∠P?)

∠P + ∠Q = 180° (angles on the same side of transversal)

⇒ ∠P + 130° = 180°

⇒ ∠P = 180° – 130° = 50°

also, ∠R + ∠S = 180° (angles on the same side of transversal)

⇒ 90° + ∠S = 180°

⇒ ∠S = 180° – 90° = 90°

Thus, ∠P = 50° and ∠S = 90°

Yes, there are more than one method to find m∠P.

PQRS is a quadrilateral. Sum of measures of all angles is 360°.

Since, we know the measurement of ∠Q, ∠R and ∠S.

∠Q = 130°, ∠R = 90° and ∠S = 90°

∠P + 130° + 90° + 90° = 360°

⇒ ∠P + 310° = 360°

⇒ ∠P = 360° – 310° = 50°

Exercise 3.4 Page: 55

1. State whether True or False.

(a) All rectangles are squares.

(b) All rhombuses are parallelograms.

(c) All squares are rhombuses and also rectangles.

(d) All squares are not parallelograms.

(e) All kites are rhombuses.

(f) All rhombuses are kites.

(g) All parallelograms are trapeziums.

(h) All squares are trapeziums.

Because all squares are rectangles but all rectangles are not squares.

Because all squares are parallelograms as opposite sides are parallel and opposite angles are equal.

Because, for example, the length of the sides of a kite are not of the same length.

2. Identify all the quadrilaterals that have.

(a) four sides of equal length (b) four right angles

(a) Rhombus and square have all four sides of equal length.

(b) Square and rectangle have four right angles.

3. Explain how a square is

(i) a quadrilateral (ii) a parallelogram (iii) a rhombus (iv) a rectangle

(i) Square is a quadrilateral because it has four sides.

(ii) Square is a parallelogram because it’s opposite sides are parallel and opposite angles are equal.

(iii) Square is a rhombus because all the four sides are of equal length and diagonals bisect at right angles.

(iv)Square is a rectangle because each interior angle, of the square, is 90°

4. Name the quadrilaterals whose diagonals.

(i) bisect each other (ii) are perpendicular bisectors of each other (iii) are equal

(i) Parallelogram, Rhombus, Square and Rectangle

(ii) Rhombus and Square

(iii)Rectangle and Square

5. Explain why a rectangle is a convex quadrilateral.

A rectangle is a convex quadrilateral because both of its diagonals lie inside the rectangle.

6. ABC is a right-angled triangle and O is the mid-point of the side opposite to the right angle. Explain why O is equidistant from A, B and C. (The dotted lines are drawn additionally to help you).

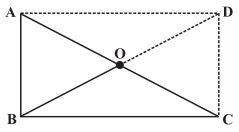
AD and DC are drawn so that AD || BC and AB || DC

AD = BC and AB = DC

ABCD is a rectangle as opposite sides are equal and parallel to each other and all the interior angles are of 90°.

In a rectangle, diagonals are of equal length and also bisect each other.

Hence, AO = OC = BO = OD

Thus, O is equidistant from A, B and C.

The major concepts covered in this chapter include: 3.1 Introduction 3.2 Polygons 3.2.1 Classification of Polygons 3.2.2 Diagonals 3.2.3 Convex and Concave Polygons 3.2.4 Regular and Irregular Polygons 3.2.5 Angle sum property 3.3 Sum of the Measures of the Exterior Angles of a Polygon 3.4 Kinds of Quadrilaterals 3.4.1 Trapezium 3.4.2 Kite 3.4.3 Parallelogram 3.4.4 Elements of a parallelogram 3.4.5 Angles of parallelogram 3.4.6 Diagonals of a parallelogram 3.5 Some special parallelograms 3.5.1 Rhombus 3.5.2 A rectangle 3.5.3 A square Exercise 3.1 Solutions 7 Questions (1 Long Answer Question, 6 Short Answer Questions) Exercise 3.2 Solutions 6 Questions (6 Short Answer Questions) Exercise 3.3 Solutions 12 Questions (6 Long Answer Questions, 6 Short Answer Questions) Exercise 3.4 Solutions 6 Questions (1 Long Answer Question, 5 Short Answer Questions)

Chapter 3 of NCERT Solutions for Class 8 Maths helps you understand the fundamental concepts related to quadrilaterals. From explanations of quadrilaterals to different types of quadrilaterals, the chapter mainly discusses the following concepts: 1. Parallelogram: A quadrilateral with each pair of opposite sides parallel. Properties: Opposite sides are equal. Opposite angles are equal. Diagonals bisect one another 2. Rhombus: A parallelogram with sides of equal length. Properties: All the properties of a parallelogram. Diagonals are perpendicular to each other 3. Rectangle: A parallelogram with a right angle. Properties: All the properties of a parallelogram. Each of the angles is a right angle. Diagonals are equal. 4. Square: A rectangle with sides of equal length. Properties: All the properties of a parallelogram, rhombus and a rectangle. 5. Kite: A quadrilateral with exactly two pairs of equal consecutive sides Properties: The diagonals are perpendicular to one another. One of the diagonals bisects the other.

Learning the chapter Understanding Quadrilaterals enables the students to understand the following:

• Properties of quadrilaterals: Sum of angles of a quadrilateral is equal to 360 o
• Properties of parallelogram: Opposite sides of a parallelogram are equal. Opposite angles of a parallelogram are equal.
• Diagonals of a parallelogram bisect each other.
• Diagonals of a rectangle are equal and bisect each other.
• Diagonals of a rhombus bisect each other at right angles.
• Diagonals of a square are equal and bisect each other at right angles.

Disclaimer:

Dropped Topics – 3.1 Introduction, 3.2 Polygons, 3.2.1 Classification of polygons, 3.2.2 Diagonals and 3.2.5 Angle sum property.

Frequently Asked Questions on NCERT Solutions for Class 8 Maths Chapter 3

What kind of questions are there in ncert solutions for class 8 maths chapter 3, what is the meaning of quadrilaterals according to ncert solutions for class 8 maths chapter 3, what are the main topics covered in ncert solutions for class 8 maths chapter 3, leave a comment cancel reply.

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

it was so helpful for all

This is a very good app

It’s really very helpful app 👍👍

I like this app This app help me so much Thanks byjus for help to all students

Thank you for this app It is so helpful for me and my father to explain me

This is a very helpful I loved it it’s good app

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Class 9 Maths Case Study Questions of Chapter 8 Quadrilaterals PDF Download

• Post author: studyrate
• Post published:
• Post category: class 9th
• Post comments: 0 Comments

Class 9 Maths Case Study Questions Chapter 8  are very important to solve for your exam. Class 9 Maths Chapter 8 Case Study Questions have been prepared for the latest exam pattern. You can check your knowledge by solving case study-based questions for Class 9 Maths Chapter 8 Quadrilaterals

Join our Telegram Channel, there you will get various e-books for CBSE 2024 Boards exams for Class 9th, 10th, 11th, and 12th.

These case study questions challenge students to apply their knowledge of quadrilaterals in practical scenarios, enhancing their problem-solving abilities. This article provides the Class 9 Maths Case Study Questions of Chapter 8: Quadrilaterals, enabling students to practice and excel in their examinations.

Quadrilaterals Case Study Questions With Answers

Here, we have provided case-based/passage-based questions for Class 9 Maths Chapter 8 Quadrilaterals

Case Study/Passage-Based Questions

Case Study 1: Laveena’s class teacher gave students some colorful papers in the shape of quadrilaterals. She asked students to make a parallelogram from it using paper folding. Laveena made the following parallelogram.

How can a parallelogram be formed by using paper folding? (a) Joining the sides of a quadrilateral (b) Joining the mid-points of sides of a quadrilateral (c) Joining the various quadrilaterals (d) None of these

Answer: (b) Joining the mid-points of sides of quadrilateral

Which of the following is true? (a) PQ = BD (b) PQ = 1/2 BD (c) 3PQ = BD (d) PQ = 2BD

Answer: (b) PQ = 1/2 BD

Which of the following is correct combination? (a) 2RS = BD (b) RS = 1/3 BD (c) RS = BD (d) RS = 2BD

Answer: (a) 2RS = BD

Which of the following is correct? (a) SR = 2PQ (b) PQ = SR (c) SR = 3PQ (d) SR = 4PQ

Answer: (b) PQ = SR

Case Study/Passage Based Questions

Case Study 2: Anjali and Meena were trying to prove mid-point theorem. They draw a triangle ABC, where D and E are found to be the midpoints of AB and AC respectively. DE was joined and extended to F such that DE = EF and FC is also joined.

▲ADE and ▲CFE are congruent by which criterion? (a) SSS (b) SAS (c) RHS (d) ASA

Answer: (b) SAS

∠EFC is equal to which angle? (a) ∠DAE (b) ∠EDA (c) ∠AED (d) ∠DBC

Answer: (b)∠EDA

∠ECF is equal to which angle? (a) ∠EAD (b) ∠ADE (c) ∠AED (d) ∠B

Answer: (a) ∠EAD

CF is equal to (a) EC (b) BE (c) BC (d) AD

Answer: (d) AD

CF is parallel to (a) AE (b) CE (c) BD (d) AC

Answer: (c) BD

Case Study 3. A group of students is exploring different types of quadrilaterals. They encountered the following scenario:

Four friends, Aryan, Bhavana, Chetan, and Divya, participated in a geometry project. They constructed a figure with four sides and made the following observations:

• The opposite sides of the figure are parallel.
• The opposite angles of the figure are congruent.
• The figure has two pairs of congruent adjacent sides.
• The sum of the measures of the interior angles of the figure is 360 degrees.

Based on this information, the students were asked to analyze the properties of the quadrilateral they constructed. Let’s see if you can answer the questions correctly:

MCQ Questions:

Q1. The type of quadrilateral formed by their figure is: (a) Parallelogram (b) Rhombus (c) Rectangle (d) Square

Answer: (a) Parallelogram

Q2. The measure of each angle in the figure is: (a) 90 degrees (b) 120 degrees (c) 135 degrees (d) 180 degrees

Answer: (d) 180 degrees

Q3. The figure is an example of a quadrilateral that satisfies the: (a) Opposite sides are equal condition (b) Opposite angles are congruent condition (c) Diagonals bisect each other condition (d) None of the above

Answer: (b) Opposite angles are congruent condition

Q4. The sum of the measures of the exterior angles of the figure is: (a) 90 degrees (b) 180 degrees (c) 270 degrees (d) 360 degrees

Answer: (d) 360 degrees

Q5. The figure has rotational symmetry of: (a) Order 1 (b) Order 2 (c) Order 3 (d) Order 4

Answer: (a) Order 1

Hope the information shed above regarding Case Study and Passage Based Questions for Class 9 Mathematics Chapter 8 Quadrilaterals with Answers Pdf free download has been useful to an extent. If you have any other queries about CBSE Class 9 Maths Quadrilaterals Case Study and Passage Based Questions with Answers, feel free to comment below so that we can revert back to us at the earliest possible By Team Study Rate

You Might Also Like

Class 9 mcq questions for chapter 4 structure of the atom with answers, class 9 science mcq questions for chapter 13 why do we fall ill with answers, class 9 geography case study questions chapter 5 natural vegetation and wildlife, leave a reply cancel reply.

Save my name, email, and website in this browser for the next time I comment.

• Education News

SSC CHSL exam 2024: Check Tier 1 exam pattern, important topics for Math section and more

SSC CHSL Tier 1 exam pattern

Ssc chsl mathematics syllabus 2024, important topics for ssc chsl math section.

• Data Interpretation
• Profit, Loss & Discount
• Trigonometry

Visual Stories