problem solving involving scientific notation

Module 7: Exponents

Problem solving with scientific notation, learning outcome.

• Solve application problems involving scientific notation

A water molecule.

Solve Application Problems

Learning rules for exponents seems pointless without context, so let us explore some examples of using scientific notation that involve real problems. First, let us look at an example of how scientific notation can be used to describe real measurements.

Think About It

Match each length in the table with the appropriate number of meters described in scientific notation below. Write your ideas in the textboxes provided before you look at the solution.

Several red blood cells.

One of the most important parts of solving a “real-world” problem is translating the words into appropriate mathematical terms and recognizing when a well known formula may help. Here is an example that requires you to find the density of a cell given its mass and volume. Cells are not visible to the naked eye, so their measurements, as described with scientific notation, involve negative exponents.

Human cells come in a wide variety of shapes and sizes. The mass of an average human cell is about [latex]2\times10^{-11}[/latex] grams. [1] Red blood cells are one of the smallest types of cells [2] , clocking in at a volume of approximately [latex]10^{-6}\text{ meters }^3[/latex]. [3] Biologists have recently discovered how to use the density of some types of cells to indicate the presence of disorders such as sickle cell anemia or leukemia. [4]  Density is calculated as [latex]\frac{\text{ mass }}{\text{ volume }}[/latex]. Calculate the density of an average human cell.

Read and Understand:  We are given an average cellular mass and volume as well as the formula for density. We are looking for the density of an average human cell.

Define and Translate:   [latex]m=\text{mass}=2\times10^{-11}[/latex], [latex]v=\text{volume}=10^{-6}\text{ meters}^3[/latex], [latex]\text{density}=\frac{\text{ mass }}{\text{ volume }}[/latex]

Write and Solve:  Use the quotient rule to simplify the ratio.

[latex]\begin{array}{c}\text{ density }=\frac{2\times10^{-11}\text{ grams }}{10^{-6}\text{ meter }^3}\\\text{ }\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=2\times10^{-11-\left(-6\right)}\frac{\text{ grams }}{\text{ meter }^3}\\\text{ }\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=2\times10^{-5}\frac{\text{ grams }}{\text{ meter }^3}\\\end{array}[/latex]

If scientists know the density of healthy cells, they can compare the density of a sick person’s cells to that to rule out or test for disorders or diseases that may affect cellular density.

The average density of a human cell is [latex]2\times10^{-5}\frac{\text{ grams }}{\text{ meter }^3}[/latex]

The following video provides an example of how to find the number of operations a computer can perform in a very short amount of time.

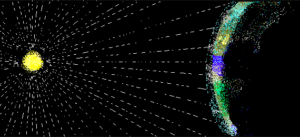
Light traveling from the sun to the earth.

In the next example, you will use another well known formula, [latex]d=r\cdot{t}[/latex], to find how long it takes light to travel from the sun to Earth. Unlike the previous example, the distance between the earth and the sun is massive, so the numbers you will work with have positive exponents.

The speed of light is [latex]3\times10^{8}\frac{\text{ meters }}{\text{ second }}[/latex]. If the sun is [latex]1.5\times10^{11}[/latex] meters from earth, how many seconds does it take for sunlight to reach the earth?  Write your answer in scientific notation.

Read and Understand:  We are looking for how long—an amount of time. We are given a rate which has units of meters per second and a distance in meters. This is a [latex]d=r\cdot{t}[/latex] problem.

Define and Translate: 

[latex]\begin{array}{l}d=1.5\times10^{11}\\r=3\times10^{8}\frac{\text{ meters }}{\text{ second }}\\t=\text{ ? }\end{array}[/latex]

Write and Solve:  Substitute the values we are given into the [latex]d=r\cdot{t}[/latex] equation. We will work without units to make it easier. Often, scientists will work with units to make sure they have made correct calculations.

[latex]\begin{array}{c}d=r\cdot{t}\\1.5\times10^{11}=3\times10^{8}\cdot{t}\end{array}[/latex]

Divide both sides of the equation by [latex]3\times10^{8}[/latex] to isolate  t.

[latex]\begin{array}{c}\frac{1.5\times10^{11}}{3\times10^{8}}=\frac{3\times10^{8}}{3\times10^{8}}\cdot{t}\end{array}[/latex]

On the left side, you will need to use the quotient rule of exponents to simplify, and on the right, you are left with  t. 

[latex]\begin{array}{c}\text{ }\\\left(\frac{1.5}{3}\right)\times\left(\frac{10^{11}}{10^{8}}\right)=t\\\text{ }\\\left(0.5\right)\times\left(10^{11-8}\right)=t\\0.5\times10^3=t\end{array}[/latex]

This answer is not in scientific notation, so we will move the decimal to the right, which means we need to subtract one factor of [latex]10[/latex].

[latex]0.5\times10^3=5.0\times10^2=t[/latex]

The time it takes light to travel from the sun to Earth is [latex]5.0\times10^2[/latex] seconds, or in standard notation, [latex]500[/latex] seconds.  That is not bad considering how far it has to travel!

Scientific notation was developed to assist mathematicians, scientists, and others when expressing and working with very large and very small numbers. Scientific notation follows a very specific format in which a number is expressed as the product of a number greater than or equal to one and less than ten times a power of [latex]10[/latex]. The format is written [latex]a\times10^{n}[/latex], where [latex]1\leq{a}<10[/latex] and n is an integer. To multiply or divide numbers in scientific notation, you can use the commutative and associative properties to group the exponential terms together and apply the rules of exponents.

• Orders of magnitude (mass). (n.d.). Retrieved May 26, 2016, from https://en.wikipedia.org/wiki/Orders_of_magnitude_(mass) ↵
• How Big is a Human Cell? ↵
• How big is a human cell? - Weizmann Institute of Science. (n.d.). Retrieved May [latex]26, 2016[/latex], from http://www.weizmann.ac.il/plants/Milo/images/humanCellSize120116Clean.pdf ↵
• Grover, W. H., Bryan, A. K., Diez-Silva, M., Suresh, S., Higgins, J. M., & Manalis, S. R. (2011). Measuring single-cell density. Proceedings of the National Academy of Sciences, 108(27), 10992-10996. doi:10.1073/pnas.1104651108 ↵
• Revision and Adaptation. Provided by : Lumen Learning. License : CC BY: Attribution
• Application of Scientific Notation - Quotient 1 (Number of Times Around the Earth). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/san2avgwu6k . License : CC BY: Attribution
• Application of Scientific Notation - Quotient 2 (Time for Computer Operations). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/Cbm6ejEbu-o . License : CC BY: Attribution
• Unit 11: Exponents and Polynomials, from Developmental Math: An Open Program. Provided by : Monterey Institute of Technology and Education. Located at : http://nrocnetwork.org/dm-opentext . License : CC BY: Attribution

The Math You Need, When You Need It

math tutorials for students majoring in the earth sciences

Scientific Notation - Practice Problems

Solving earth science problems with scientific notation, × div[id^='image-'] {position:static}div[id^='image-'] div.hover{position:static} introductory problems.

These problems cover the fundamentals of writing scientific notation and using it to understand relative size of values and scientific prefixes.

Problem 1: The distance to the moon is 238,900 miles. Write this value in scientific notation.

Problem 2: One mile is 1609.34 meters. What is the distance to the moon in meters using scientific notation?

`1609.34 m/(mi) xx 238","900 mi` = 384,400,000 m

Notice in the above unit conversion the 'mi' units cancel each other out because 'mi' is in the denominator for the first term and the numerator for the second term

Problem 4: The atomic radius of a magnesium atom is approximately 1.6 angstroms, which is equal to 1.6 x 10 -10 meters (m). How do you write this length in standard form?

 0.00000000016 m  

Fissure A = 40,0000 m Fissure B = 5,0000 m

This shows fissure A is larger (by almost 10 times!). The shortcut to answer a question like this is to look at the exponent. If both coefficients are between 1-10, then the value with the larger exponent is the larger number.

Problem 6: The amount of carbon in the atmosphere is 750 petagrams (pg). One petagram equals 1 x 10 15 grams (g). Write out the amount of carbon in the atmosphere in (i) scientific notation and (ii) standard decimal format.

The exponent is a positive number, so the decimal will move to the right in the next step.

750,000,000,000,000,000 g

Advanced Problems

Scientific notation is used in solving these earth and space science problems and they are provided to you as an example. Be forewarned that these problems move beyond this module and require some facility with unit conversions, rearranging equations, and algebraic rules for multiplying and dividing exponents. If you can solve these, you've mastered scientific notation!

Problem 7: Calculate the volume of water (in cubic meters and in liters) falling on a 10,000 km 2 watershed from 5 cm of rainfall.

`10,000  km^2 = 1 xx 10^4  km^2`

5 cm of rainfall = `5 xx 10^0 cm`

Let's start with meters as the common unit and convert to liters later. There are 1 x 10 3 m in a km and area is km x km (km 2 ), therefore you need to convert from km to m twice:

`1 xx 10^3 m/(km) * 1 xx 10^3 m/(km) = 1 xx 10^6 m^2/(km)^2` `1 xx 10 m^2/(km)^2 * 1 xx 10^4 km^2 = 1 xx 10^10 m^2` for the area of the watershed.

For the amount of rainfall, you should convert from centimeters to meters:

`5 cm * (1 m)/(100 cm)= 5 xx 10^-2 m`

`V = A * d`

When multiplying terms with exponents, you can multiply the coefficients and add the exponents:

`V = 1 xx 10^10 m^2 * 5.08 xx 10^(-2) m = 5.08 xx 10^8 m^3`

Given that there are 1 x 10 3 liters in a cubic meter we can make the following conversion:

`1 xx 10^3 L * 5.08 xx 10^8 m^3 = 5.08 xx 10^11 L`

Step 5. Check your units and your answer - do they make sense?           

`V = 4/3 pi r^3`

Using this equation, plug in the radius (r) of the dust grains.

`V = 4/3 pi (2 xx10^(-6))^3m^3`

Notice the (-6) exponent is cubed. When you take an exponent to an exponent, you need to multiply the two terms

`V = 4/3 pi (8 xx10^(-18)m^3)`

Then, multiple the cubed radius times pi and 4/3

`V = 3.35 xx 10^(-17) m^3`

`m = 3.35 xx 10^(-17) m^3 * 3300 (kg)/m^3`

Notice in the equation above that the m 3 terms cancel each other out and you are left with kg

`m = 1.1 xx 10^(-13) kg`

`V = 4/3 pi (2.325 xx10^(15) m)^3`

`V = 5.26 xx10^(46) m^3`

Number of dust grains = `5.26 xx10^(46) m^3 xx 0.001` grains/m 3

Number of dust grains = `5.26xx10^43 "grains"`

Total mass = `1.1xx10^(-13) (kg)/("grains") * 5.26xx10^43 "grains"`

Notice in the equation above the 'grains' terms cancel each other out and you are left with kg

Total mass = `5.79xx10^30 kg`

If you feel comfortable with this topic, you can go on to the assessment . Or you can go back to the Scientific Notation explanation page .

« Previous Page       Next Page »

• Pre-algebra lessons
• Pre-algebra word problems
• Algebra lessons
• Algebra word problems
• Algebra proofs
• Advanced algebra
• Geometry lessons
• Geometry word problems
• Geometry proofs
• Trigonometry lessons
• Consumer math
• Baseball math
• Math for nurses
• Statistics made easy
• High school physics
• Basic mathematics store
• SAT Math Prep
• Math skills by grade level
• Ask an expert
• Other websites
• K-12 worksheets
• Worksheets generator
• Algebra worksheets
• Geometry worksheets
• Free math problem solver
• Pre-algebra calculators
• Algebra Calculators
• Geometry Calculators
• Math puzzles
• Math tricks
• Member login

Scientific Notation Word Problems

This lesson is about six carefully chosen scientific notation word problems along with their solutions.

Example #1:

Jupiter is the largest planet in our solar system and its mass in scientific notation is about 1.9 × 10 27 . Write the mass in standard notation.

1.9 × 10 27 =  1.9 × 10 × 10 26 = 19 × 10 26 = 1900000000000000000000000000

The mass of Jupiter in standard notation is 1900000000000000000000000000

Example #2:

It is predicted that the world population in 2025 may reach eight billion. Write eight billion in scientific notation.

Eight billion = 8000000000 = 8 × 10 9

Example #3:

The oxygen atom has a mass of about 0.00000000000000000000000003 kg. Write the mass of the oxygen atom in scientific notation.

0.00000000000000000000000003 = 3 × 10 -26 kg

Example #4:

The following masses which are parts of an atom are measured in grams. Order the parts of an atom from greatest to least mass. 

electron: 9.1096 × 10 -28 , neutron: 1.6749 × 10 -24 , proton: 1.6726 × 10 -24

The smallest mass is since 9.1096 × 10 -28  since -28 will create more zeros after the decimal point.

1.6749 × 10 -24  and 1.6726 × 10 -24 have the same exponent. So we just need to compare 1.6749 to 1.6726.

Since 1.6726 is smaller than 1.6749, 1.6726 × 10 -24   is smaller than 1.6749 × 10 -24

From greatest to least mass, we get: 1.6749 × 10 -24 > 1.6726 × 10 -24 > 9.1096 × 10 -28 

Example #5:

The weight of an adult male elephant is about 5600 kg. What is the weight in scientific notation?

Solution: In scientific notation the weight of an adult male elephant is 5.6 × 10 3

Example #6:

A computer can perform about 5 × 10 8 instructions per second. How many instructions is that per hour? Express the answer in scientific notation.

1 hour is equal to 3600 seconds. Therefore, we need to multiply 5 × 10 8  by 3600

3600 × 5 × 10 8 = 36 × 10 2 × 5 × 10 8

3600 × 5 × 10 8  = 36 × 5 × 10 2  × 10 8

3600 × 5 × 10 8  = 180 × 10 10

3600 × 5 × 10 8  = 1.80 × 10 12

3600 × 5 × 10 8  = 1.8 × 10 12

The computer can perform about 1.8 × 10 12  instructions per hour

Scientific notation

Recent Articles

How to divide any number by 5 in 2 seconds.

Feb 28, 24 11:07 AM

Math Trick to Square Numbers from 50 to 59

Feb 23, 24 04:46 AM

Sum of Consecutive Odd Numbers

Feb 22, 24 10:07 AM

100 Tough Algebra Word Problems. If you can solve these problems with no help, you must be a genius!

 Recommended

About me :: Privacy policy :: Disclaimer :: Donate   Careers in mathematics  

Copyright © 2008-2021. Basic-mathematics.com. All right reserved

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

3.8: Scientific Notation

• Last updated
• Save as PDF
• Page ID 58348

• Denny Burzynski & Wade Ellis, Jr.
• College of Southern Nevada via OpenStax CNX

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Standard Form to Scientific Form

Very large numbers such as \(43,000,000,000,000,000,000\) (the number of different possible configurations of Rubik’s cube) and very small numbers such as \(0.000000000000000000000340\) (the mass of the amino acid tryptophan) are extremely inconvenient to write and read. Such numbers can be expressed more conveniently by writing them as part of a power of 10.

To see how this is done, let us start with a somewhat smaller number such as \(2480\). Notice that

\(\begin{aligned} \underbrace{2480}_{\text {Standard form }} &=248.0 \times 10^{1} \\ &=24.80 \times 10^{2} \\ &=\underbrace{2.480 \times 10^{3}}_{\text {Scientific form }} \end{aligned}\)

Scientific Form

The last form is called the scientific form of the number. There is one nonzero digit to the left of the decimal point and the absolute value of the exponent on 10 records the number of places the original decimal point was moved to the left .

\(\begin{aligned} 0.00059 &=\dfrac{0.0059}{10}=\dfrac{0.0059}{10^{1}}=0.0059 \times 10^{-1} \\ &=\dfrac{0.059}{100}=\dfrac{0.059}{10^{2}}=0.059 \times 10^{-2} \\ &=\dfrac{0.59}{1000}=\dfrac{0.59}{10^{3}}=0.59 \times 10^{-3} \\ &=\dfrac{5.9}{10,000}=\dfrac{5.9}{10^{4}}=5.9 \times 10^{-4} \end{aligned}\)

There is one nonzero digit to the left of the decimal point and the absolute value of the exponent of 10 records the number of places the original decimal point was moved to the right .

Scientific Notation

Numbers written in scientific form are also said to be written using scientific notation. In scientific notation , a number is written as the product of a number between and including 1 and 10 (1 is included,10 is not) and some power of 10.

Writing a Number in Scientific Notation

To write a number in scientific notation:

1. Move the decimal point so that there is one nonzero digit to its left. 2. Multiply the result by a power of 10 using an exponent whose absolute value is the number of places the decimal point was moved. Make the exponent positive if the decimal point was moved to the left and negative if the decimal point was moved to the right.

Sample Set A

Write the numbers in scientific notation.

Example \(\PageIndex{1}\)

The number \(981\) is actually \(981.\), and it is followed by a decimal point. In integers, the decimal point at the end is usually omitted.

\(981 = 981. = 9.81 \times 10^2\)

The decimal point is now two places to the left of its original position, and the power of \(10\) is \(2\).

Example \(\PageIndex{2}\)

\(54.066 = 5.4066 \times 10^1 = 5.4066 \times 10\)

The decimal point is one place to the left of its original position, and the power of \(10\) is \(1\)

Example \(\PageIndex{3}\)

\(0.000000000004632 = 4.632 \times 10^{-12}\)

The decimal point is twelve places to the right of its original position, and the power of \(10\) is \(−12\).

Example \(\PageIndex{4}\)

\(0.027 = 2.7 \times 10^{-2}\)

The decimal point is two places to the right of its original position, and the power of \(10\) is \(-2\)

Practice Set A

Write the following numbers in scientific notation.

Practice Problem \(\PageIndex{1}\)

\(3.46 \times 10^2\)

Practice Problem \(\PageIndex{2}\)

\(7.233 \times 10\)

Practice Problem \(\PageIndex{3}\)

\(5387.7965\)

\(5.3877965 \times 10^3\)

Practice Problem \(\PageIndex{4}\)

\(87,000,000\)

\(8.7 \times 10^7\)

Practice Problem \(\PageIndex{5}\)

\(179,000,000,000,000,000,000\)

\(1.79 \times 10^{20}\)

Practice Problem \(\PageIndex{6}\)

\(100,000\)

\(1.0 \times 10^5\)

Practice Problem \(\PageIndex{7}\)

\(1,000,000\)

\(1.0 \times 10^6\)

Practice Problem \(\PageIndex{8}\)

\(8.6 \times 10^{-3}\)

Practice Problem \(\PageIndex{9}\)

\(0.000098001\)

\(9.8001 \times 10^{-5}\)

Practice Problem \(\PageIndex{10}\)

\(0.000000000000000054\)

\(5.4 \times 10^{-17}\)

Practice Problem \(\PageIndex{11}\)

\(0.0000001\)

\(1.0 \times 10^{-7}\)

Practice Problem \(\PageIndex{12}\)

\(0.00000001\)

\(1.0 \times 10^{-8}\)

Scientific Form to Standard Form

A number written in scientific notation can be converted to standard form by reversing the process shown in Sample Set A.

Converting from Scientific Notation

To convert a number written in scientific notation to a number in standard form, move the decimal point the number of places prescribed by the exponent on the 10.

Positive Exponent Negative Exponent

Move the decimal point to the right when you have a positive exponent, and move the decimal point to the left when you have a negative exponent.

Sample Set B

Example \(\pageindex{5}\).

\(4.63 \times 10^4\)

The exponent of \(10\) is \(4\) so we must move the decimal point to the right \(4\) places (adding 0's if necessary).

\(4.6730 \times 10^4 = 46730\)

\(2.9 \times 10^7\)

The exponent of \(10\) is \(7\) so we must move the decimal point to the right \(7\) places (adding 0's if necessary).

\(2.9 \times 10^7 = 29000000\)

Example \(\PageIndex{6}\)

\(1 \times 10^{27}\)

The exponent of \(10\) is \(27\) so we must move the decimal point to the right \(27\) places (adding 0's if necessary).

\(1 \times 10^{27}= 1,000,000,000,000,000,000,000,000,000\)

Example \(\PageIndex{7}\)

\(4.21 \times 10^{-5}\)

The exponent of \(10\) is \(-5\) so we must move the decimal point to the left \(5\) places (adding 0's if necessary).

\(4.21 \times 10^{-5} = 0.0000421\)

Example \(\PageIndex{8}\)

\(1.006 \times 10^{-18}\)

The exponent of \(10\) is \(-18\) so we must move the decimal point to the left \(18\) places (adding 0's if necessary).

\(1.006 \times 10^{-18} = 0.000000000000000001006\)

Practice Set B

Convert the following numbers to standard form.

Practice Problem \(\PageIndex{13}\)

\(9.25 \times 10^2\)

Practice Problem \(\PageIndex{14}\)

\(4.01 \times 10^5\)

Practice Problem \(\PageIndex{15}\)

\(1.2 \times 10^{-1}\)

Practice Problem \(\PageIndex{16}\)

\(8.88 \times 10^{-5}\)

\(0.0000888\)

Working with Numbers in Scientific Notation

Multiplying Numbers Using Scientific Notation

There are many occasions (particularly in the sciences) when it is necessary to find the product of two numbers written in scientific notation. This is accomplished by using two of the basic rules of algebra.

Suppose we wish to find \((a \times 10^n)(b \times 10^m). Since the only operation is multiplication, we can use the commutative property of multiplication to rearrange the numbers.

\((a \times 10^n)(b \times 10^m) = (a \times b)(10^n \times 10^m)

Then, by the rules of exponents, \(10^n \times 10^m = 10^{n+m}\). Thus,

\((a \times 10^n)(b \times 10^m) = (a \times b) \times 10^{n+m}\)

The product of \((a \times b)\) may not be between \(1\) and \(10\), so \((a \times b) \times 10^{n+m}\) may not be in scientific form. The decimal point in \((a \times b)\) may have to be moved. An example of this situation is in Sample Set C, example 3.8.10.

Sample Set C

Example \(\pageindex{9}\).

\(\begin{aligned} \left(2 \times 10^{3}\right)\left(4 \times 10^{8}\right) &=(2 \times 4)\left(10^{3} \times 10^{8}\right) \\ &=8 \times 10^{3+8} \\ &=8 \times 10^{11} \end{aligned}\)

Example \(\PageIndex{10}\)

\( \begin{aligned} \left(5 \times 10^{17}\right)\left(8.1 \times 10^{-22}\right) &=(5 \times 8.1)\left(10^{17} \times 10^{-22}\right) \\ &=40.5 \times 10^{17-22} \\ &=40.5 \times 10^{-5} \end{aligned} \)

We need to move the decimal point one place to the left to put this number in scientific notation. Thus, we must also change the exponent of \(10\).

\( \begin{array}{l} 40.5 \times 10^{-5} \\ 4.05 \times 10^{1} \times 10^{-5} \\ 4.05 \times\left(10^{1} \times 10^{-5}\right) \\ 4.05 \times\left(10^{1-5}\right) \\ 4.05 \times 10^{-4} \end{array} \)

Thus, \( \left(5 \times 10^{17}\right)\left(8.1 \times 10^{-22}\right)=4.05 \times 10^{-4} \)

Practice Set C

Perform each multiplication.

Practice Problem \(\PageIndex{17}\)

\((3 \times 10^5)(2 \times 10^{12})\)

\(6 \times 10^{17}\)

Practice Problem \(\PageIndex{18}\)

\((1 \times 10^{-4})(6 \times 10^{24}\)

\(6 \times 10^{20}\)

Practice Problem \(\PageIndex{19}\)

\((5 \times 10^{18})(3 \times 10^6)\)

\(1.5 \times 10^{25}\)

Practice Problem \(\PageIndex{20}\)

\((2.1 \times 10^{-9})(3 \times 10^{-11})\)

\(6.3 \times 10^{-20}\)

Convert the numbers used in the following problems to scientific notation.

Exercise \(\PageIndex{1}\)

Mount Kilimanjaro is the highest mountain in Africa. It is 5890 meters high.

\(5.89 \times 10^3\)

Exercise \(\PageIndex{2}\)

The planet Mars is about 222,900,000,000 meters from the sun.

Exercise \(\PageIndex{3}\)

There is an irregularly shaped galaxy, named NGC 4449, that is about 250,000,000,000,000,000,000,000 meters from earth.

\(2.5 \times 10^{23}\)

Exercise \(\PageIndex{4}\)

The farthest object astronomers have been able to see (as of 1981) is a quasar named 3C427. There seems to be a haze beyond this quasar that appears to mark the visual boundary of the universe. Quasar 3C427 is at a distance of 110,000,000,000,000,000,000,000,000 meters from the earth.

Exercise \(\PageIndex{5}\)

The smallest known insects are about the size of a typical grain of sand. They are about 0.0002 meters in length (2 ten-thousandths of a meter).

\(2 \times 10^{-4}\)

Exercise \(\PageIndex{6}\)

Atoms such as hydrogen, carbon, nitrogen, and oxygen are about 0.0000000001 meter across.

Exercise \(\PageIndex{7}\)

The island of Manhattan, in New York, is about 57,000 square meters in area.

\(5.7 \times 10^4\)

Exercise \(\PageIndex{8}\)

The second largest moon of Saturn is Rhea. Rhea has a surface area of about 735,000 square meters, roughly the same surface area as Australia.

Exercise \(\PageIndex{9}\)

A star, named Epsilon Aurigae B, has a diameter (distance across) of 2,800,000,000,000 meters. This diameter produces a surface area of about 24,630,000,000,000,000,000,000,000 square meters. This star is what astronomers call a red giant and it is the largest red giant known. If Epsilon Aurigae were placed at the sun’s position, its surface would extend out to the planet Uranus.

\(2.8 \times 10^{12}\), \(2.463 \times 10^{25}\)

Exercise \(\PageIndex{10}\)

The volume of the planet Venus is 927,590,000,000,000,000,000 cubic meters.

Exercise \(\PageIndex{11}\)

The average mass of a newborn American female is about 3360 grams.

\(3.36 \times 10^3\)

Exercise \(\PageIndex{12}\)

The largest brain ever measured was that of a sperm whale. It had a mass of 9200 grams.

Exercise \(\PageIndex{13}\)

The mass of the Eiffel tower in Paris, France, is 8,000,000 grams.

\(8 \times 10^6\)

Exercise \(\PageIndex{14}\)

In 1981, a Japanese company built the largest oil tanker to date. The ship has a mass of about 510,000,000,000 grams. This oil tanker is more than 6 times as massive as the U.S. aircraft carrier, U.S.S. Nimitz.

Exercise \(\PageIndex{15}\)

In the constellation of Virgo, there is a cluster of about 2500 galaxies. The combined mass of these galaxies is 150,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000 grams.

\(1.5 \times 10^{62}\)

Exercise \(\PageIndex{16}\)

The mass of an amoeba is about 0.000004 gram.

Exercise \(\PageIndex{17}\)

Cells in the human liver have masses of about 0.000000008 gram.

\(8 \times 10^{-9}\)

Exercise \(\PageIndex{18}\)

The human sperm cell has a mass of about 0.000000000017 gram.

Exercise \(\PageIndex{19}\)

The principal protein of muscle is myosin. Myosin has a mass of 0.00000000000000000103 gram.

\(1.03 \times 10^{-18}\)

Exercise \(\PageIndex{20}\)

Amino acids are molecules that combine to make up protein molecules. The amino acid tryptophan has a mass of 0.000000000000000000000340 gram.

Exercise \(\PageIndex{21}\)

An atom of the chemical element bromine has 35 electrons. The mass of a bromine atom is 0.000000000000000000000000031 gram.

\(3.1 \times 10^{-26}\)

Exercise \(\PageIndex{22}\)

Physicists are performing experiments that they hope will determine the mass of a small particle called a neutrino. It is suspected that neutrinos have masses of about 0.0000000000000000000000000000001 gram.

Exercise \(\PageIndex{23}\)

The approximate time it takes for a human being to die of asphyxiation is 316 seconds.

\(3.16 \times 10^2\)

Exercise \(\PageIndex{24}\)

On the average, the male housefly lives 1,468,800 seconds (17 days).

Exercise \(\PageIndex{25}\)

Aluminum-26 has a half-life of 740,000 years.

\(7.4 \times 10^5\)

Exercise \(\PageIndex{26}\)

Manganese-53 has a half-life of 59,918,000,000,000 seconds (1,900,000 years).

Exercise \(\PageIndex{27}\)

In its orbit around the sun, the earth moves a distance one and one half feet in about 0.0000316 second.

\(3.16 \times 10^{-5}\)

Exercise \(\PageIndex{28}\)

A pi-meson is a subatomic particle that has a half-life of about 0.0000000261 second.

Exercise \(\PageIndex{29}\)

A subatomic particle called a neutral pion has a half-life of about 0.0000000000000001 second.

\(1 \times 10^{-16}\)

Exercise \(\PageIndex{30}\)

Near the surface of the earth, the speed of sound is 1195 feet per second.

For the following problems, convert the numbers from scientific notation to standard decimal form.

Exercise \(\PageIndex{31}\)

The sun is about \(1 \times 10^8\) meteres from earth.

100,000,000

Exercise \(\PageIndex{32}\)

The mass of the earth is about \(5.98 \times 10^{27}\) grams.

Exercise \(\PageIndex{33}\)

Light travels about \(5.866 \times 10^{12}\) miles in one year.

5,866,000,000,000

Exercise \(\PageIndex{34}\)

One year is about \(3 \times 10^7\) seconds.

Exercise \(\PageIndex{35}\)

Rubik’s cube has about \(4.3 \times 10^{19}\) different configurations.

43,000,000,000,000,000,000

Exercise \(\PageIndex{36}\)

A photon is a particle of light. A 100-watt light bulb emits \(1 \times 10^{20}\) photons every second.

Exercise \(\PageIndex{37}\)

There are about \(6 \times 10^7\) cells in the retina of the human eye.

Exercise \(\PageIndex{38}\)

A car traveling at an average speed will travel a distance about equal to the length of the smallest fingernail in \(3.16 \times 10^{-4}\) seconds.

Exercise \(\PageIndex{39}\)

A ribosome of E. coli has a mass of about \(4.7 \times 10^{-19}\) grams.

0.00000000000000000047

Exercise \(\PageIndex{40}\)

A mitochondrion is the energy-producing element of a cell. A mitochondrion is about \(1.5 \times 10^{-6}\) meters in diameter.

Exercise \(\PageIndex{41}\)

There is a species of frogs in Cuba that attain a length of at most \(1.25 \times 10^{-2}\) meters.

Perform the following operations.

Exercise \(\PageIndex{42}\)

\((2 \times 10^4)(3 \times 10^5)\)

Exercise \(\PageIndex{43}\)

\((4 \times 10^2)(8 \times 10^6)\)

\(3.2 \times 10^9\)

Exercise \(\PageIndex{44}\)

\((6 \times 10^{14})(6 \times 10^{-10})\)

Exercise \(\PageIndex{45}\)

\((3 \times 10^{-5})(8 \times 10^7)\)

\(2.4 \times 10^3\)

Exercise \(\PageIndex{46}\)

\((2 \times 10^{-1})(3 \times 10^{-5})\)

Exercise \(\PageIndex{47}\)

\((9 \times 10^{-5})(1 \times 10^{-11})\)

\(9 \times 10^{-16}\)

Exercise \(\PageIndex{48}\)

\((3.1 \times 10^4)(3.1 \times 10^{-6})\)

Exercise \(\PageIndex{49}\)

\(4.2 \times 10^{-12})(3.6 \times 10^{-20})\)

\(1.512 \times 10^{-31}\)

Exercise \(\PageIndex{50}\)

\((1.1 \times 10^6)^2\)

Exercises for Review

Exercise \(\pageindex{51}\).

What integers can replace \(x\) so that the statement \(-6 < x < -2\) is true?

\(-5, -4, -3\)

Exercise \(\PageIndex{52}\)

Simplify \((5x^2y^4)(2xy^5)\)

Exercise \(\PageIndex{53}\)

Determine the value of \(-[-(-|-5|)]\).

Exercise \(\PageIndex{54}\)

Write \(\dfrac{x^3y^{-5}}{z^{-4}\) so that only positive exponents appear.

Study Guides > ALGEBRA / TRIG I

Problem solving with scientific notation, learning outcomes.

• Solve application problems involving scientific notation

Solve application problems

Think about it.

[latex]\begin{array}{c}\text{ density }=\frac{2\times10^{-11}\text{ grams }}{10^{-6}\text{ meters }^3}\\\text{ }\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=2\times10^{-11-\left(-6\right)}\frac{\text{ grams }}{\text{ meters }^3}\\\text{ }\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=2\times10^{-5}\frac{\text{ grams }}{\text{ meters }^3}\\\end{array}[/latex]

The average density of a human cell is [latex]2\times10^{-5}\frac{\text{ grams }}{\text{ meters }^3}[/latex]

[latex]\begin{array}{l}d=1.5\times10^{11}\\r=3\times10^{8}\frac{\text{ meters }}{\text{ second }}\\t=\text{ ? }\end{array}[/latex]

Write and Solve:  Substitute the values we are given into the [latex]d=r\cdot{t}[/latex] equation. We will work without units to make it easier. Often, scientists will work with units to make sure they have made correct calculations.

[latex]\begin{array}{c}d=r\cdot{t}\\1.5\times10^{11}=3\times10^{8}\cdot{t}\end{array}[/latex]

Divide both sides of the equation by [latex]3\times10^{8}[/latex] to isolate  t.

[latex]\begin{array}{c}1.5\times10^{11}=3\times10^{8}\cdot{t}\\\text{ }\\\frac{1.5\times10^{11}}{3\times10^{8}}=\frac{3\times10^{8}}{3\times10^{8}}\cdot{t}\end{array}[/latex]

On the left side, you will need to use the quotient rule of exponents to simplify, and on the right, you are left with  t. 

[latex]\begin{array}{c}\frac{1.5\times10^{11}}{3\times10^{8}}=\frac{3\times10^{8}}{3\times10^{8}}\cdot{t}\\\text{ }\\\left(\frac{1.5}{3}\right)\times\left(\frac{10^{11}}{10^{8}}\right)=t\\\text{ }\\\left(0.5\right)\times\left(10^{11-8}\right)=t\\0.5\times10^3=t\end{array}[/latex]

This answer is not in scientific notation, so we will move the decimal to the right, which means we need to subtract one factor of [latex]10[/latex].

[latex]0.5\times10^3=5.0\times10^2=t[/latex]

Contribute!

Licenses & attributions, cc licensed content, original.

• Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution .
• Application of Scientific Notation - Quotient 1 (Number of Times Around the Earth). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution .
• Application of Scientific Notation - Quotient 2 (Time for Computer Operations). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution .
• Screenshot: water molecule. Provided by: Lumen Learning License: CC BY: Attribution .
• Screenshot: red blood cells. Provided by: Lumen Learning License: CC BY: Attribution .
• Screenshot: light traveling from the sun to the earth. Provided by: Lumen Learning License: CC BY: Attribution .

CC licensed content, Shared previously

• Unit 11: Exponents and Polynomials, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology and Education Located at: https://www.nroc.org/. License: CC BY: Attribution .

Please add a message.

Message received. Thanks for the feedback.