case study questions on linear equations in two variables

Bihar Board

CFA Institute

Srm university.

Rajasthan 10th Result
Rajasthan Board Result
Shiv Khera Special
Education News
Web Stories
Current Affairs
School & Boards
College Admission
Govt Jobs Alert & Prep
GK & Aptitude
CBSE Class 10 Study Material

CBSE Class 10 Maths Case Study Questions for Chapter 3 - Pair of Linear Equations in Two Variables (Published by CBSE)

Cbse's question bank on case study for class 10 maths chapter 3 is available here. these questions will be very helpful to prepare for the cbse class 10 maths exam 2022..

Case study questions are going to be new for CBSE Class 10 students. These are the competency-based questions that are completely new to class 10 students. To help students understand the format of the questions, CBSE has released a question bank on case study for class 10 Maths. Students must practice with these questions to get familiarised with the concepts and logic used in the case study and understand how to answers them correctly. You may check below the case study questions for CBSE Class 10 Maths Chapter 3 - Pair of Linear Equations in Two Variables. You can also check the right answer at the end of each question.

Check Case Study Questions for Class 10 Maths Chapter 3 - Pair of Linear Equations in Two Variables

CASE STUDY-1:

1. If answer to all questions he attempted by guessing were wrong, then how many questions did he answer correctly?

2. How many questions did he guess?

3. If answer to all questions he attempted by guessing were wrong and answered 80 correctly, then how many marks he got?

4. If answer to all questions he attempted by guessing were wrong, then how many questions answered correctly to score 95 marks?

Let the no of questions whose answer is known to the student x and questions attempted by cheating be y

x – 1/4y =90

solving these two

x = 96 and y = 24

1. He answered 96 questions correctly.

2. He attempted 24 questions by guessing.

3. Marks = 80- ¼ 0f 40 =70

4. x – 1/4 of (120 – x) = 95

5x = 500, x = 100

CASE STUDY-2:

Amit is planning to buy a house and the layout is given below. The design and the measurement has been made such that areas of two bedrooms and kitchen together is 95 sq.m.

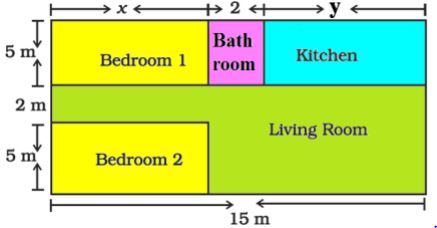
case study questions on linear equations in two variables

Based on the above information, answer the following questions:

1. Form the pair of linear equations in two variables from this situation.

2. Find the length of the outer boundary of the layout.

3. Find the area of each bedroom and kitchen in the layout.

4. Find the area of living room in the layout.

5. Find the cost of laying tiles in kitchen at the rate of Rs. 50 per sq.m.

1. Area of two bedrooms= 10x sq.m

Area of kitchen = 5y sq.m

10x + 5y = 95

Also, x + 2+ y = 15

2. Length of outer boundary = 12 + 15 + 12 + 15 = 54m

3. On solving two equation part(i)

x = 6m and y = 7m

area of bedroom = 5 x 6 = 30m

area of kitchen = 5 x 7 = 35m

4. Area of living room = (15 x 7) – 30 = 105 – 30 = 75 sq.m

5. Total cost of laying tiles in the kitchen = Rs50 x 35 = Rs1750

Case study-3 :

It is common that Governments revise travel fares from time to time based on various factors such as inflation ( a general increase in prices and fall in the purchasing value of money) on different types of vehicles like auto, Rickshaws, taxis, Radio cab etc. The auto charges in a city comprise of a fixed charge together with the charge for the distance covered. Study the following situations:

Situation 1: In city A, for a journey of 10 km, the charge paid is Rs 75 and for a journey of 15 km, the charge paid is Rs 110.

Situation 2: In a city B, for a journey of 8km, the charge paid is Rs91 and for a journey of 14km, the charge paid is Rs 145.

Refer situation 1

1. If the fixed charges of auto rickshaw be Rs x and the running charges be Rs y km/hr, the pair of linear equations representing the situation is

a) x + 10y =110, x + 15y = 75

b) x + 10y = 75, x + 15y = 110

c) 10x + y = 110, 15x + y = 75

d) 10x + y = 75, 15x + y = 110

Answer: b) x + 10y = 75, x + 15y = 110

2. A person travels a distance of 50km. The amount he has to pay is

Answer: c) Rs.355

Refer situation 2

3. What will a person have to pay for travelling a distance of 30km?

Answer: b) Rs.289

4. The graph of lines representing the conditions are: (situation 2)

Answer: (iii)

Also Check:

CBSE Case Study Questions for Class 10 Maths - All Chapters

Tips to Solve Case Study Based Questions Accurately

Get here latest School , CBSE and Govt Jobs notification in English and Hindi for Sarkari Naukari and Sarkari Result . Download the Jagran Josh Sarkari Naukri App . Check Board Result 2024 for Class 10 and Class 12 like CBSE Board Result , UP Board Result , Bihar Board Result , MP Board Result , Rajasthan Board Result and Other States Boards.

HPSC AEE Admit Card 2024
RBSE Result 2024
rajshaladarpan.nic.in 5th, 8th Result 2024
rajshaladarpan.nic.in Result 2024
Rajasthan Board Class 8th, 5th Result 2024 Roll Number
RBSE Class 5th Result 2024 Roll Number
Rajasthan 5th 8th Class Result 2024
8th, 5th Board Result 2024 Rajasthan
RBSE 10th Result 2024
UPSC CSE Admit Card 2024
CBSE Study Material
CBSE Class 10

Latest Education News

UK Board Class 12 Physics Syllabus 2024-25: Download Physics Syllabus PDF For Free

These forts of Asia have mesmerized the masses for years! Check the list

UP Board Class 9 Agriculture Syllabus 2024-25 OUT: Download Now!

GK Quiz on Exit Polls: The Ultimate Exit Polls Quiz to Test if Are You an Expert

World Environment Day 2024: Top 7 Drawing Ideas For School Students!

ICC T20 World Cup 2024 Points Table: पॉइंट्स टेबल में कौन-सी टीम किस स्थान पर देखें यहां

UPSC CSE Admit Card 2024 Live Updates: Civil Service, IFS Prelims Call Letter Soon on upsc.gov.in

Most Runs In T20 World Cup 2024

You have 20/20 vision if you can find the hidden cat in 8 seconds!

World Environment Day 2024: विश्व पर्यावरण दिवस पर निबंध, Essay on in Hindi

CUSAT Result 2024 OUT at cusat.ac.in, Direct Link to Download UG and PG Marksheet

CUSAT CAT Result 2024 OUT at cusat.ac.in, Direct Link to Download Ranklist PDF

IBPS RRB 2024 Recruitment Notification: Check Exam Dates, Eligibility and Latest Updates

Genius IQ Test: Find the value of the triangle in 11 seconds!

UK Board Class 12 Maths Syllabus 2024-25: Download Maths Syllabus PDF For Board Exam

AP LAWCET 2024 Hall Ticket Download Link Active at cets.apsche.ap.gov.in, Steps to Download Admit Card Here

UPSC NDA 2 Apply Online 2024 Last Date: Direct Link to Online Form for 404 Vacancies

UP Board Class 9 Hindi Syllabus 2025: Download UPMSP 9th Hindi Syllabus 2024-25 PDF Here

TS POLYCET Results 2024 Manabadi Declared: Direct Link to Check TS Polycet Result at polycet.sbtet.telangana.gov.in, Download Rank Card Here

Newton’s Laws Of Motion: Definition, Formula, Applications And Examples

Class 10 Maths Case Study Questions Chapter 3 Pair of Linear Equations in Two Variables

Post author: studyrate
Post published:
Post category: class 10th
Post comments: 0 Comments

Case study Questions in the Class 10 Mathematics Chapter 3 are very important to solve for your exam. Class 10 Maths Chapter 3 Case Study Questions have been prepared for the latest exam pattern. You can check your knowledge by solving case study-based questions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables

Join our Telegram Channel, there you will get various e-books for CBSE 2024 Boards exams for Class 9th, 10th, 11th, and 12th.

In CBSE Class 10 Maths Paper, Students will have to answer some questions based on Assertion and Reason. There will be a few questions based on case studies and passage-based as well. In that, a paragraph will be given, and then the MCQ questions based on it will be asked.

Pair of Linear Equations in Two Variables Case Study Questions With Answers

Here, we have provided case-based/passage-based questions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables

Case Study/Passage-Based Questions

(i) 1 st situation can be represented algebraically as

Answer: (d) 2x+3y=46

(ii) 2 nd situation can be represented algebraically as

Answer: (c) 3x + 5y = 74

(iii), Fare from Ben~aluru to Malleswaram is

Answer: (b) Rs 8

(iv) Fare from Bengaluru to Yeswanthpur is

Answer: (a) Rs 10

(v) The system oflinear equations represented by both situations has

Answer: (c) unique solution

Case Study 2: The scissors which are so common in our daily life use, its blades represent the graph of linear equations.

Let the blades of a scissor are represented by the system of linear equations:

x + 3y = 6 and 2x – 3y = 12

(i) The pivot point (point of intersection) of the blades represented by the linear equation x + 3y = 6 and 2x – 3y = 12 of the scissor is (a) (2, 3) (b) (6, 0) (c) (3, 2) (d) (2, 6)

Answer: (b) (6, 0)

(ii) The points at which linear equations x + 3y = 6 and 2x – 3y = 12 intersect y – axis respectively are (a) (0, 2) and (0, 6) (b) (0, 2) and (6, 0) (c) (0, 2) and (0, –4) (d) (2, 0) and (0, –4)

Answer: (c) (0, 2) and (0, –4)

(iii) The number of solution of the system of linear equations x + 2y – 8 = 0 and 2x + 4y = 16 is (a) 0 (b) 1 (c) 2 (d) infinitely many

Answer: (d) infinitely many

(iv) If (1, 2) is the solution of linear equations ax + y = 3 and 2x + by = 12, then values of a and b are respectively (a) 1, 5 (b) 2, 3 (c) –1, 5 (d) 3, 5

Answer: (a) 1, 5

(v) If a pair of linear equations in two variables is consistent, then the lines represented by two equations are (a) intersecting (b) parallel (c) always coincident (d) intersecting or coincident

Answer: (d) intersecting or coincident

Hope the information shed above regarding Case Study and Passage Based Questions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables with Answers Pdf free download has been useful to an extent. If you have any other queries about CBSE Class 10 Maths Pair of Linear Equations in Two Variables Case Study and Passage Based Questions with Answers, feel free to comment below so that we can revert back to us at the earliest possible By Team Study Rate

Mcq class 10 social science geography water resources quiz with answers, extra questions of class 10 social science economics chapter 8 novels, society and history pdf download, class 10 maths case study questions of chapter 1 real numbers, leave a reply cancel reply.

Save my name, email, and website in this browser for the next time I comment.

Gurukul of Excellence

Classes for Physics, Chemistry and Mathematics by IITians

Join our Telegram Channel for Free PDF Download

Case Study Questions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables

Last modified on: 10 months ago
Reading Time: 5 Minutes

Case Study Questions

Question 1:

The scissors which is so common in our daily life use, its blades represent the graph of linear equations.

Let the blades of a scissor are represented by the system of linear equations:

x + 3y = 6 and 2x – 3y = 12

(i) The pivot point (point of intersection) of the blades represented by the linear equation x + 3y = 6 and 2x – 3y = 12 of the scissor is (a) (2, 3) (b) (6, 0) (c) (3, 2) (d) (2, 6)

(iii) The number of solution of the system of linear equations x + 2y – 8 = 0 and 2x + 4y = 16 is (a) 0 (b) 1 (c) 2 (d) infinitely many

(iv) If (1, 2) is the solution of linear equations ax + y = 3 and 2x + by = 12, then values of a and b are respectively (a) 1, 5 (b) 2, 3 (c) –1, 5 (d) 3, 5

(v) If a pair of linear equations in two variables is consistent, then the lines represented by two equations are (a) intersecting (b) parallel (c) always coincident (d) intersecting or coincident

✨ Free Quizzes, Test Series and Learning Videos for CBSE Class 10 Maths

Download CBSE Books

Exam Special Series:

Sample Question Paper for CBSE Class 10 Science (for 2024)
Sample Question Paper for CBSE Class 10 Maths (for 2024)
CBSE Most Repeated Questions for Class 10 Science Board Exams
CBSE Important Diagram Based Questions Class 10 Physics Board Exams
CBSE Important Numericals Class 10 Physics Board Exams
CBSE Practical Based Questions for Class 10 Science Board Exams
CBSE Important “Differentiate Between” Based Questions Class 10 Social Science
Sample Question Papers for CBSE Class 12 Physics (for 2024)
Sample Question Papers for CBSE Class 12 Chemistry (for 2024)
Sample Question Papers for CBSE Class 12 Maths (for 2024)
Sample Question Papers for CBSE Class 12 Biology (for 2024)
CBSE Important Diagrams & Graphs Asked in Board Exams Class 12 Physics
Master Organic Conversions CBSE Class 12 Chemistry Board Exams
CBSE Important Numericals Class 12 Physics Board Exams
CBSE Important Definitions Class 12 Physics Board Exams
CBSE Important Laws & Principles Class 12 Physics Board Exams
10 Years CBSE Class 12 Chemistry Previous Year-Wise Solved Papers (2023-2024)
10 Years CBSE Class 12 Physics Previous Year-Wise Solved Papers (2023-2024)
10 Years CBSE Class 12 Maths Previous Year-Wise Solved Papers (2023-2024)
10 Years CBSE Class 12 Biology Previous Year-Wise Solved Papers (2023-2024)
ICSE Important Numericals Class 10 Physics BOARD Exams (215 Numericals)
ICSE Important Figure Based Questions Class 10 Physics BOARD Exams (230 Questions)
ICSE Mole Concept and Stoichiometry Numericals Class 10 Chemistry (65 Numericals)
ICSE Reasoning Based Questions Class 10 Chemistry BOARD Exams (150 Qs)
ICSE Important Functions and Locations Based Questions Class 10 Biology
ICSE Reasoning Based Questions Class 10 Biology BOARD Exams (100 Qs)

✨ Join our Online JEE Test Series for 499/- Only (Web + App) for 1 Year

✨ Join our Online NEET Test Series for 499/- Only for 1 Year

Discover more from Gurukul of Excellence

Subscribe now to keep reading and get access to the full archive.

Type your email…

Andhra Pradesh
Chhattisgarh
West Bengal
Madhya Pradesh
Maharashtra
Jammu & Kashmir
NCERT Books 2022-23
NCERT Solutions
NCERT Notes
NCERT Exemplar Books
NCERT Exemplar Solution
States UT Book
School Kits & Lab Manual
NCERT Books 2021-22
NCERT Books 2020-21
NCERT Book 2019-2020
NCERT Book 2015-2016
RD Sharma Solution
TS Grewal Solution
TR Jain Solution
Selina Solution
Frank Solution
Lakhmir Singh and Manjit Kaur Solution
I.E.Irodov solutions
ICSE - Goyal Brothers Park
ICSE - Dorothy M. Noronhe
Sandeep Garg Textbook Solution
Micheal Vaz Solution
S.S. Krotov Solution
Evergreen Science
KC Sinha Solution
ICSE - ISC Jayanti Sengupta, Oxford
ICSE Focus on History
ICSE GeoGraphy Voyage
ICSE Hindi Solution
ICSE Treasure Trove Solution
Thomas & Finney Solution
SL Loney Solution
SB Mathur Solution
P Bahadur Solution
Narendra Awasthi Solution
MS Chauhan Solution
LA Sena Solution
Integral Calculus Amit Agarwal Solution
IA Maron Solution
Hall & Knight Solution
Errorless Solution
Pradeep's KL Gogia Solution
OP Tandon Solutions
Sample Papers
Previous Year Question Paper
Value Based Questions
CBSE Syllabus
CBSE MCQs PDF
Assertion & Reason
New Revision Notes
Revision Notes
HOTS Question
Marks Wise Question
Toppers Answer Sheets
Exam Paper Aalysis
Concept Map
CBSE Text Book
Additional Practice Questions
Vocational Book
CBSE - Concept
KVS NCERT CBSE Worksheets
Formula Class Wise
Formula Chapter Wise
JEE Crash Course
JEE Previous Year Paper
Important Info
JEE Mock Test
JEE Sample Papers
SRM-JEEE Mock Test
VITEEE Mock Test
BITSAT Mock Test
Manipal Engineering Mock Test
AP EAMCET Previous Year Paper
COMEDK Previous Year Paper
GUJCET Previous Year Paper
KCET Previous Year Paper
KEAM Previous Year Paper
Manipal Previous Year Paper
MHT CET Previous Year Paper
WBJEE Previous Year Paper
AMU Previous Year Paper
TS EAMCET Previous Year Paper
SRM-JEEE Previous Year Paper
VITEEE Previous Year Paper
BITSAT Previous Year Paper
UPSEE Previous Year Paper
CGPET Previous Year Paper
CUSAT Previous Year Paper
AEEE Previous Year Paper
Crash Course
Previous Year Paper
NCERT Based Short Notes
NCERT Based Tests
NEET Sample Paper
Previous Year Papers
Quantitative Aptitude
Numerical Aptitude Data Interpretation
General Knowledge
Mathematics
Agriculture
Accountancy
Business Studies
Political science
Enviromental Studies
Mass Media Communication
Teaching Aptitude
NAVODAYA VIDYALAYA
SAINIK SCHOOL (AISSEE)
Mechanical Engineering
Electrical Engineering
Electronics & Communication Engineering
Civil Engineering
Computer Science Engineering
CBSE Board News
Scholarship Olympiad
School Admissions
Entrance Exams
All Board Updates
Miscellaneous
State Wise Books
Engineering Exam

Case Study on Pair of Equations in Two Variables Class 10 Maths PDF

The passage-based questions are commonly known as case study questions. Students looking for Case Study on Pair of Equations in Two Variables Class 10 Maths can use this page to download the PDF file.

The case study questions on Pair of Equations in Two Variables are based on the CBSE Class 10 Maths Syllabus, and therefore, referring to the Pair of Equations in Two Variables case study questions enable students to gain the appropriate knowledge and prepare better for the Class 10 Maths board examination. Continue reading to know how should students answer it and why it is essential to solve it, etc.

Case Study on Pair of Equations in Two Variables Class 10 Maths with Solutions in PDF

Our experts have also kept in mind the challenges students may face while solving the case study on Pair of Equations in Two Variables, therefore, they prepared a set of solutions along with the case study questions on Pair of Equations in Two Variables.

The case study on Pair of Equations in Two Variables Class 10 Maths with solutions in PDF helps students tackle questions that appear confusing or difficult to answer. The answers to the Pair of Equations in Two Variables case study questions are very easy to grasp from the PDF - download links are given on this page.

Why Solve Pair of Equations in Two Variables Case Study Questions on Class 10 Maths?

There are three major reasons why one should solve Pair of Equations in Two Variables case study questions on Class 10 Maths - all those major reasons are discussed below:

To Prepare for the Board Examination: For many years CBSE board is asking case-based questions to the Class 10 Maths students, therefore, it is important to solve Pair of Equations in Two Variables Case study questions as it will help better prepare for the Class 10 board exam preparation.
Develop Problem-Solving Skills: Class 10 Maths Pair of Equations in Two Variables case study questions require students to analyze a given situation, identify the key issues, and apply relevant concepts to find out a solution. This can help CBSE Class 10 students develop their problem-solving skills, which are essential for success in any profession rather than Class 10 board exam preparation.
Understand Real-Life Applications: Several Pair of Equations in Two Variables Class 10 Maths Case Study questions are linked with real-life applications, therefore, solving them enables students to gain the theoretical knowledge of Pair of Equations in Two Variables as well as real-life implications of those learnings too.

How to Answer Case Study Questions on Pair of Equations in Two Variables?

Students can choose their own way to answer Case Study on Pair of Equations in Two Variables Class 10 Maths, however, we believe following these three steps would help a lot in answering Class 10 Maths Pair of Equations in Two Variables Case Study questions.

Read Question Properly: Many make mistakes in the first step which is not reading the questions properly, therefore, it is important to read the question properly and answer questions accordingly.
Highlight Important Points Discussed in the Clause: While reading the paragraph, highlight the important points discussed as it will help you save your time and answer Pair of Equations in Two Variables questions quickly.
Go Through Each Question One-By-One: Ideally, going through each question gradually is advised so, that a sync between each question and the answer can be maintained. When you are solving Pair of Equations in Two Variables Class 10 Maths case study questions make sure you are approaching each question in a step-wise manner.

What to Know to Solve Case Study Questions on Class 10 Pair of Equations in Two Variables?

A few essential things to know to solve Case Study Questions on Class 10 Pair of Equations in Two Variables are -

Basic Formulas of Pair of Equations in Two Variables: One of the most important things to know to solve Case Study Questions on Class 10 Pair of Equations in Two Variables is to learn about the basic formulas or revise them before solving the case-based questions on Pair of Equations in Two Variables.
To Think Analytically: Analytical thinkers have the ability to detect patterns and that is why it is an essential skill to learn to solve the CBSE Class 10 Maths Pair of Equations in Two Variables case study questions.
Strong Command of Calculations: Another important thing to do is to build a strong command of calculations especially, mental Maths calculations.

Where to Find Case Study on Pair of Equations in Two Variables Class 10 Maths?

Use Selfstudys.com to find Case Study on Pair of Equations in Two Variables Class 10 Maths. For ease, here is a step-wise procedure to download the Pair of Equations in Two Variables Case Study for Class 10 Maths in PDF for free of cost.

Since you are already on this page, you can scroll to the top section of this page to get access to the Case Study on Pair of Equations in Two Variables. To help others reach this page let them know these steps:

Open Selfstudys.com on your computer/laptop or Smartphone
Once the website gets loaded, click on the navigation button

Case Study on Pair of Equations in Two Variables Class 10 Maths, Maths Case Study on Pair of Equations in Two Variables Class 10, Class 10 Maths Case Study on Pair of Equations in Two Variables, Pair of Equations in Two Variables Case Study for Class 10 Maths, Case Study on Pair of Equations in Two Variables Class 10 Maths with Solutions, Pair of Equations in Two Variables Case Study Questions, Case Study Questions on Pair of Equations in Two Variables, Case Study Questions on Class 10 Pair of Equations in Two Variables

Find CBSE from the given menu

Click on Case Study

Choose Class 10
Search Maths and then navigate to the Pair of Equations in Two Variables Class 10 Maths Case Study

NCERT Solutions for Class 12 Maths
NCERT Solutions for Class 10 Maths
CBSE Syllabus 2023-24
Social Media Channels
Login Customize Your Notification Preferences

One Last Step...

Second click on the toggle icon

Provide prime members with unlimited access to all study materials in PDF format.

Allow prime members to attempt MCQ tests multiple times to enhance their learning and understanding.

Provide prime users with access to exclusive PDF study materials that are not available to regular users.

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons

Margin Size

Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

5.10: Systems of Linear Equations in Two Variables

Last updated
Save as PDF
Page ID 129561

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$Baskets of vegetables are displayed at a farmers' market.$

Learning Objectives

After completing this section, you should be able to:

Determine and show whether an ordered pair is a solution to a system of equations.
Solve systems of linear equations using graphical methods.
Solve systems of linear equations using substitution.
Solve systems of linear equations using elimination.
Identify systems with no solution or infinitely many solutions.
Solve applications of systems of linear equations.

In this section, we will learn how to solve systems of linear equations in two variables. There are several real-world scenarios that can be represented by systems of linear equalities. Suppose two friends, Andrea and Bart, go shopping at a farmers market to buy some vegetables. Andrea buys 2 tomatoes and 4 cucumbers and spends $2.00. Bart buys 4 tomatoes and 5 cucumbers and spends $2.95. What is the price of each vegetable?

Determining If an Ordered Pair Is a Solution to a System of Equations

When we solved linear equations in Linear Equations in One Variable with Applications and Linear Inequalities in One Variable with Applications, we learned how to solve linear equations with one variable. Now we will work with two or more linear equations grouped together, which is known as a system of linear equations .

In this section, we will focus our work on systems of two linear equations in two unknowns (variables) and applications of systems of linear equations. An example of a system of two linear equations is shown below. We use a brace to show the two equations are grouped together to form a system of equations.

{ 2 x + y = 7 x − 2 y = 6 { 2 x + y = 7 x − 2 y = 6

A linear equation in two variables, such as 2 x + y = 7 2 x + y = 7 , has an infinite number of solutions. Its graph is a line. Remember, every point on the line is a solution to the equation and every solution to the equation is a point on the line. To solve a system of two linear equations, we want to find the values of the variables that are solutions to both equations. In other words, we are looking for the ordered pairs ( x x , y y ) that make both equations true. These are called the solutions of a system of equations .

To determine if an ordered pair is a solution to a system of two equations, we substitute the values of the variables into each equation. If the ordered pair makes both equations true, it is a solution to the system.

Example 5.81

Determining whether an ordered pair is a solution to the system.

Determine whether the ordered pair is a solution to the system.

{ x − y = − 1 2 x − y = − 5 { x − y = − 1 2 x − y = − 5

( − 2 , − 1 ) ( − 2 , − 1 )
( − 4 , − 3 ) ( − 4 , − 3 )

x − y = − 1 − 2 − ( − 1 ) = ? − 1 − 1 = − 1 ✓ 2 x − y = − 5 2 ( − 2 ) - ( − 1 ) = ? − 5 - 3 ≠ − 5 x − y = − 1 − 2 − ( − 1 ) = ? − 1 − 1 = − 1 ✓ 2 x − y = − 5 2 ( − 2 ) - ( − 1 ) = ? − 5 - 3 ≠ − 5

x − y = − 1 − 4 − ( − 3 ) = ? − 1 − 1 = − 1 ✓ 2 x − y = − 5 2 • ( − 4 ) − ( − 3 ) = ? − 5 − 5 = − 5 ✓ x − y = − 1 − 4 − ( − 3 ) = ? − 1 − 1 = − 1 ✓ 2 x − y = − 5 2 • ( − 4 ) − ( − 3 ) = ? − 5 − 5 = − 5 ✓

Your Turn 5.81

Example 5.82.

Determine whether the ordered pair is a solution to the system

{ y = 3 2 x + 1 2 x − 3 y = 7 { y = 3 2 x + 1 2 x − 3 y = 7

( − 4 , − 5 ) ( − 4 , − 5 )
( − 4 , 5 ) ( − 4 , 5 )

− 5 = ? 3 2 ( − 4 ) + 1 − 5 = ? 3 ( − 2 ) + 1 − 5 = ? − 6 + 1 − 5 = − 5 ✓ 2 ( − 4 ) − 3 ( − 5 ) = ? 7 ( − 8 ) − ( − 15 ) = ? 7 − 8 + 15 = ? 7 7 = 7 ✓ − 5 = ? 3 2 ( − 4 ) + 1 − 5 = ? 3 ( − 2 ) + 1 − 5 = ? − 6 + 1 − 5 = − 5 ✓ 2 ( − 4 ) − 3 ( − 5 ) = ? 7 ( − 8 ) − ( − 15 ) = ? 7 − 8 + 15 = ? 7 7 = 7 ✓

5 = ? 3 2 ( − 4 ) + 1 5 = ? 3 ( − 2 ) + 1 5 = ? − 6 + 1 5 ≠ − 5 2 ( − 4 ) − 3 ( 5 ) = ? 7 ( − 8 ) − ( 15 ) = ? 7 − 8 − 15 = ? 7 − 23 ≠ 7 5 = ? 3 2 ( − 4 ) + 1 5 = ? 3 ( − 2 ) + 1 5 = ? − 6 + 1 5 ≠ − 5 2 ( − 4 ) − 3 ( 5 ) = ? 7 ( − 8 ) − ( 15 ) = ? 7 − 8 − 15 = ? 7 − 23 ≠ 7

Your Turn 5.82

Solving systems of linear equations using graphical methods.

We will use three methods to solve a system of linear equations. The first method we will use is graphing. The graph of a linear equation is a line. Each point on the line is a solution to the equation. For a system of two equations, we will graph two lines. Then we can see all the points that are solutions to each equation. And, by finding what points the lines have in common, we will find the solution to the system.

Most linear equations in one variable have one solution; but for some equations called contradictions , there are no solutions, and for other equations called identities , all numbers are solutions. Similarly, when we solve a system of two linear equations represented by a graph of two lines in the same plane, there are three possible cases, as shown in Figure 5.93.

$Three coordinate planes. The first coordinate plane shows one line passing through the points, (0, 7) and (3.5, 0) and a second line passing through the points, (0, negative 3) and (6, 0). The two lines intersect at the point (4, negative 1). Text reads, The lines intersect. Intersecting line shave one point in common. There is one solution to this system. The second coordinate plane shows one line passing through the points, (negative 8, 0) and (0, 3) and a second line passing through the points, (0, negative 2) and (5, 0). The lines do not intersect. Text reads, The lines are parallel. Parallel lines have no points in common. There is no solution to this system. The third coordinate plane shows a line passing through the points, (0, negative 3) and (1.5, 0). Text reads, Both equations give the same line. Because we have just one line, there are infinitely many solutions.$

Each time we demonstrate a new method, we will use it on the same system of linear equations. At the end you will decide which method was the most convenient way to solve this system.

The steps to use to solve a system of linear equations by graphing are shown here.

Step 1: Graph the first equation.

Step 2: Graph the second equation on the same rectangular coordinate system.

Step 3: Determine whether the lines intersect, are parallel, or are the same line.

Step 4: Identify the solution to the system.

If the lines intersect, identify the point of intersection. This is the solution to the system.

If the lines are parallel, the system has no solution.

If the lines are the same, the system has an infinite number of solutions.

Step 5: Check the solution in both equations.

Example 5.83

Solving a system of linear equations by graphing.

Solve this system of linear equations by graphing.

To graph the second line, use intercepts.

x - 2 y = 6 ( 0 , - 3 ) ( 6 , 0 ) x - 2 y = 6 ( 0 , - 3 ) ( 6 , 0 )

$Two lines are plotted on an x y coordinate plane. The x and y axes range from negative 7 to 7, in increments of 1. The first line passes through the points, (0, 7), (3.5, 0), and (7, negative 7). The second line passes through the points, (negative 6, negative 6), (0, negative 3), and (6, 0). The two lines intersect at (4, negative 1).$

If the lines intersect, identify the point of intersection. Check to make sure it is a solution to both equations. This is the solution to the system.

Since the lines intersect, find the point of intersection.

Check the point in both equations.

The lines intersect at ( 4 , - 1 ) ( 4 , - 1 ) .

2 x + y = 7 2 ( 4 ) + ( - 1 ) = ? 7 8 - 1 = ? 7 7 = 7 ✓ x - 2 y = 6 4 - 2 ( - 1 ) = ? 6 6 = 6 ✓ 2 x + y = 7 2 ( 4 ) + ( - 1 ) = ? 7 8 - 1 = ? 7 7 = 7 ✓ x - 2 y = 6 4 - 2 ( - 1 ) = ? 6 6 = 6 ✓

The solution is ( 4 , - 1 ) ( 4 , - 1 ) .

Your Turn 5.83

Solving systems of linear equations using substitution.

We will now solve systems of linear equations by the substitution method. We will use the same system we used for graphing.

We will first solve one of the equations for either x x or y y . We can choose either equation and solve for either variable—but we’ll try to make a choice that will keep the work easy. Then, we substitute that expression into the other equation. The result is an equation with just one variable—and we know how to solve those!

After we find the value of one variable, we will substitute that value into one of the original equations and solve for the other variable. Finally, we check our solution and make sure it makes both equations true. This process is summarized here:

Step 1: Solve one of the equations for either variable.

Step 2: Substitute the expression from Step 1 into the other equation.

Step 3: Solve the resulting equation.

Step 4: Substitute the solution in Step 3 into either of the original equations to find the other variable.

Step 5: Write the solution as an ordered pair.

Step 6: Check that the ordered pair is a solution to both original equations.

Example 5.84

Solving a system of linear equations using substitution.

Solve this system of linear equations by substitution:

Your Turn 5.84

Solving systems of linear equations using elimination.

We have solved systems of linear equations by graphing and by substitution. Graphing works well when the variable coefficients are small, and the solution has integer values. Substitution works well when we can easily solve one equation for one of the variables and not have too many fractions in the resulting expression.

The third method of solving systems of linear equations is called the elimination method. When we solved a system by substitution, we started with two equations and two variables and reduced it to one equation with one variable. This is what we’ll do with the elimination method, too, but we’ll have a different way to get there.

The elimination method is based on the Addition Property of Equality. The Addition Property of Equality says that when you add the same quantity to both sides of an equation, you still have equality. We will extend the Addition Property of Equality to say that when you add equal quantities to both sides of an equation, the results are equal. For any expressions a a , b b , c c , and d d :

if a = b a = b

and c = d c = d

then a + c = b + d a + c = b + d .

To solve a system of equations by elimination, we start with both equations in standard form. Then we decide which variable will be easiest to eliminate. How do we decide? We want to have the coefficients of one variable be opposites, so that we can add the equations together and eliminate that variable. Notice how that works when we add these two equations together:

The y y ’s add to zero and we have one equation with one variable. Let us try another one:

{ x + 4 y = − 2 2 x + 5 y = − 2 { x + 4 y = − 2 2 x + 5 y = − 2

This time we do not see a variable that can be immediately eliminated if we add the equations. But if we multiply the first equation by − 2 − 2 , we will make the coefficients of x x opposites. We must multiply every term on both sides of the equation by − 2 − 2 .

{ − 2 ( x + 4 y ) = − 2 ( 2 ) 2 x + 5 y = − 2 { − 2 ( x + 4 y ) = − 2 ( 2 ) 2 x + 5 y = − 2

Then rewrite the system of equations.

{ − 2 x − 8 y = − 4 2 x + 5 y = − 2 { − 2 x − 8 y = − 4 2 x + 5 y = − 2

Now we see that the coefficients of the x x terms are opposites, so x x will be eliminated when we add these two equations.

{ − 2 x − 8 y = − 4 2 x + 5 y = − 2 _ − 3 y = − 6 { − 2 x − 8 y = − 4 2 x + 5 y = − 2 _ − 3 y = − 6

Once we get an equation with just one variable, we solve it. Then we substitute that value into one of the original equations to solve for the remaining variable. And, as always, we check our answer to make sure it is a solution to both of the original equations. Here’s a summary of using the elimination method:

Step 1: Write both equations in standard form. If any coefficients are fractions, clear them.

Step 2: Make the coefficients of one variable opposites.

Decide which variable you will eliminate.

Multiply one or both equations so that the coefficients of that variable are opposites.

Step 3: Add the equations resulting from Step 2 to eliminate one variable.

Step 4: Solve for the remaining variable.

Step 5: Substitute the solution from Step 4 into one of the original equations. Then solve for the other variable.

Step 6: Write the solution as an ordered pair.

Step 7: Check that the ordered pair is a solution to both original equations.

Example 5.85

Solving a system of linear equations using elimination.

Solve this system of linear equations by elimination:

Your Turn 5.85

Identifying systems with no solution or infinitely many solutions.

In all the systems of linear equations so far, the lines intersected, and the solution was one point. In Example 5.86 and Example 5.87, we will look at a system of equations that has no solution and at a system of equations that has an infinite number of solutions.

Example 5.86

Solving a system of linear equations with no solution.

Solve the system by a method of your choice:

Let us solve the system of linear equations by graphing.

To graph the first equation, we will use its slope and y y -intercept.

y = 1 2 x − 3 m = 1 2 b = − 3 y = 1 2 x − 3 m = 1 2 b = − 3

To graph the second equation, we will use the intercepts.

x − 2 y = 4 x − 2 y = 4

Graph the lines (Figure 5.94).

$Two lines are plotted on an x y coordinate plane. The x and y axes range from negative 7 to 7, in increments of 1. The first line passes through the points, (negative 6, negative 5), (0, negative 2), (4, 0), and (6, 1). The second line passes through the points, (negative 6, negative 6), (0, negative 3), and (6, 0). The two lines do not intersect.$

Determine the points of intersection. The lines are parallel. Since no point is on both lines, there is no ordered pair that makes both equations true. There is no solution to this system.

Your Turn 5.86

Example 5.87, solving a system of linear equations with infinite solutions.

{ y = 2 x − 3 − 6 x + 3 y = − 9 { y = 2 x − 3 − 6 x + 3 y = − 9

Find the slope and y y -intercept of the first equation.

y = 2 x − 3 m = 2 b = − 3 y = 2 x − 3 m = 2 b = − 3

Find the intercepts of the second equation.

− 6 x + 3 y = − 9 − 6 x + 3 y = − 9

Graph the lines (Figure 5.95).

$A line is plotted on an x y coordinate plane. The x and y axes range from negative 7 to 7, in increments of 1. The line passes through the points, (negative 2, negative 7), (0, negative 3), and (5, 7).$

The lines are the same! Since every point on the line makes both equations true, there are infinitely many ordered pairs that make both equations true.

There are infinitely many solutions to this system.

Your Turn 5.87

In the previous example, if you write the second equation in slope-intercept form, you may recognize that the equations have the same slope and same y y -intercept. Since every point on the line makes both equations true, there are infinitely many ordered pairs that make both equations true. There are infinitely many solutions to the system. We say the two lines are coincident. Coincident lines have the same slope and same y y -intercept. A system of equations that has at least one solution is called a consistent system . A system with parallel lines has no solution. We call a system of equations like this an inconsistent system . It has no solution.

We also categorize the equations in a system of equations by calling the equations independent or dependent. If two equations are independent, they each have their own set of solutions. Intersecting lines and parallel lines are independent. If two equations are dependent, all the solutions of one equation are also solutions of the other equation. When we graph two dependent equations, we get coincident lines. Let us sum this up by looking at the graphs of the three types of systems. See Figure 5.96 and the table that follows

$Three coordinate planes. The first coordinate plane is labeled, Intersecting. One line passes through the points, (0, 3.5) and (1.75, 0). A second line passes through the points, (0, negative 1.5) and (3, 0). The two lines intersect at the point (2, negative 0.5). The second coordinate plane is labeled, Parallel. One line passes through the points, (negative 0.5, 0) and (0, 1). A second line passes through the points, (0, negative 1.5) and (1, 0). The lines do not intersect. The third coordinate plane is labeled, Coincident. A line passes through the points, (0, negative 1.5) and (0.75, 0).$

WORK IT OUT

Using matrices and cramer’s rule to solve systems of linear equations.

An m m by n n matrix is an array with m m rows and n n columns, where each item in the matrix is a number. Matrices are used for many things, but one thing they can be used for is to represent systems of linear equations. For example, the system of linear equations

can be represented by the following matrix:

To use Cramer’s Rule, you need to be able to take the determinant of a matrix. The determinant of a 2 by 2 matrix A A , denoted | A | | A | , is

| A | = | a 11 a 12 a 21 a 22 | = ( a 11 × a 22 ) + ( a 21 × a 12 ) | A | = | a 11 a 12 a 21 a 22 | = ( a 11 × a 22 ) + ( a 21 × a 12 )

For example, the determinant of the matrix | 2 1 3 − 2 | = ( 2 × − 2 ) − ( 3 × 1 ) = − 4 − 3 = − 7. | 2 1 3 − 2 | = ( 2 × − 2 ) − ( 3 × 1 ) = − 4 − 3 = − 7.

Cramer’s Rule involves taking three determinants:

The determinant of the first two columns, denoted | D | | D | ;
The determinant of the first column and the third column, denoted | D y | | D y | ;
The determinant of the third column and the first column, denoted | D x | | D x | .

Going back to the original matrix [ 2 1 7 1 − 2 6 ] [ 2 1 7 1 − 2 6 ]

| D | = | 2 1 1 − 2 | = − 4 − 1 = − 5 | D | = | 2 1 1 − 2 | = − 4 − 1 = − 5

| D y | = | 2 7 1 6 | = 12 − 7 = 5 | D y | = | 2 7 1 6 | = 12 − 7 = 5

| D x | = | 7 1 6 − 2 | = − 14 − 6 = − 20 | D x | = | 7 1 6 − 2 | = − 14 − 6 = − 20

Now Cramer’s Rule for the solution of the system will be:

x = | D x | | D | , y = | D y | | D | x = | D x | | D | , y = | D y | | D |

Putting in the values for these determinants, we have x = − 20 − 5 = 4 ; y = 5 − 5 = − 1. x = − 20 − 5 = 4 ; y = 5 − 5 = − 1. The solution to the system is the ordered pair ( 4 , − 1 ) ( 4 , − 1 ) .

Solving Applications of Systems of Linear Equations

Systems of linear equations are very useful for solving applications. Some people find setting up word problems with two variables easier than setting them up with just one variable. To solve an application, we will first translate the words into a system of linear equations. Then we will decide the most convenient method to use, and then solve the system.

Step 1 : Read the problem. Make sure all the words and ideas are understood.

Step 2: Identify what we are looking for.

Step 3: Name what we are looking for. Choose variables to represent those quantities.

Step 4: Translate into a system of equations.

Step 5: Solve the system of equations using good algebra techniques.

Step 6: Check the answer in the problem and make sure it makes sense.

Step 7: Answer the question with a complete sentence.

Example 5.88

Applying system to a real-world application.

Heather has been offered two options for her salary as a trainer at the gym. Option A would pay her $25,000 a year plus $15 for each training session. Option B would pay her $10,000 a year plus $40 for each training session. How many training sessions would make the salary options equal?

Step 1: Read the problem.

We are looking for the number of training sessions that would make the pay equal.

Step 3: Name what we are looking for.

Let s = Heather’s salary s = Heather’s salary , and n = the number of training sessions n = the number of training sessions

Option A would pay her $25,000 plus $15 for each training session.

s = 25,000 + 15 n s = 25,000 + 15 n

Option B would pay her $10,000 + $40 for each training session.

s = 10,000 + 40 n s = 10,000 + 40 n

The system is shown.

{ s = 25,000 + 15 n s = 10,000 + 40 n { s = 25,000 + 15 n s = 10,000 + 40 n

Step 5: Solve the system of equations.

We will use substitution.

Substitute 25,000 + 15 n 25,000 + 15 n for s s in the second equation

s = 25,000 + 15 n s = 10,000 + 40 n s = 25,000 + 15 n s = 10,000 + 40 n

Solve for n n .

25,000 + 15 n = 10,000 + 40 n 25,000 = 10,000 + 25 n 15,000 = 25 n 600 = n 25,000 + 15 n = 10,000 + 40 n 25,000 = 10,000 + 25 n 15,000 = 25 n 600 = n

Step 6: Check the answer.

Are 600 training sessions a year reasonable?

Are the two options equal when n = 600 n = 600 ?

Substitute into each equation.

s = 25 , 000 + 15 ( 600 ) = 34 , 000 s = 10 , 000 + 40 ( 600 ) = 34 , 000 s = 25 , 000 + 15 ( 600 ) = 34 , 000 s = 10 , 000 + 40 ( 600 ) = 34 , 000

Step 7: Answer the question.

The salary options would be equal for 600 training sessions.

Your Turn 5.88

Practice with Solving Applications of Systems of Equations

Applications of Systems of Linear Equations

Check Your Understanding

Section 5.9 exercises.

4.1 Solve Systems of Linear Equations with Two Variables

Learning objectives.

By the end of this section, you will be able to:

Determine whether an ordered pair is a solution of a system of equations
Solve a system of linear equations by graphing
Solve a system of equations by substitution
Solve a system of equations by elimination
Choose the most convenient method to solve a system of linear equations

Be Prepared 4.1

Before you get started, take this readiness quiz.

For the equation y = 2 3 x − 4 , y = 2 3 x − 4 , ⓐ Is ( 6 , 0 ) ( 6 , 0 ) a solution? ⓑ Is ( −3 , −2 ) ( −3 , −2 ) a solution? If you missed this problem, review Example 3.2 .

Be Prepared 4.2

Find the slope and y -intercept of the line 3 x − y = 12 . 3 x − y = 12 . If you missed this problem, review Example 3.16 .

Be Prepared 4.3

Find the x- and y -intercepts of the line 2 x − 3 y = 12 . 2 x − 3 y = 12 . If you missed this problem, review Example 3.8 .

Determine Whether an Ordered Pair is a Solution of a System of Equations

In Solving Linear Equations , we learned how to solve linear equations with one variable. Now we will work with two or more linear equations grouped together, which is known as a system of linear equations .

System of Linear Equations

When two or more linear equations are grouped together, they form a system of linear equations .

In this section, we will focus our work on systems of two linear equations in two unknowns. We will solve larger systems of equations later in this chapter.

An example of a system of two linear equations is shown below. We use a brace to show the two equations are grouped together to form a system of equations.

A linear equation in two variables, such as 2 x + y = 7 , 2 x + y = 7 , has an infinite number of solutions. Its graph is a line. Remember, every point on the line is a solution to the equation and every solution to the equation is a point on the line.

To solve a system of two linear equations, we want to find the values of the variables that are solutions to both equations. In other words, we are looking for the ordered pairs ( x , y ) ( x , y ) that make both equations true. These are called the solutions of a system of equations .

Solutions of a System of Equations

The solutions of a system of equations are the values of the variables that make all the equations true. A solution of a system of two linear equations is represented by an ordered pair ( x , y ) . ( x , y ) .

Example 4.1

Determine whether the ordered pair is a solution to the system { x − y = −1 2 x − y = −5 . { x − y = −1 2 x − y = −5 .

ⓐ ( −2 , −1 ) ( −2 , −1 ) ⓑ ( −4 , −3 ) ( −4 , −3 )

Determine whether the ordered pair is a solution to the system { 3 x + y = 0 x + 2 y = −5 . { 3 x + y = 0 x + 2 y = −5 .

ⓐ ( 1 , −3 ) ( 1 , −3 ) ⓑ ( 0 , 0 ) ( 0 , 0 )

Determine whether the ordered pair is a solution to the system { x − 3 y = −8 − 3 x − y = 4 . { x − 3 y = −8 − 3 x − y = 4 .

ⓐ ( 2 , −2 ) ( 2 , −2 ) ⓑ ( −2 , 2 ) ( −2 , 2 )

Solve a System of Linear Equations by Graphing

In this section, we will use three methods to solve a system of linear equations. The first method we’ll use is graphing.

The graph of a linear equation is a line. Each point on the line is a solution to the equation. For a system of two equations, we will graph two lines. Then we can see all the points that are solutions to each equation. And, by finding what the lines have in common, we’ll find the solution to the system.

Most linear equations in one variable have one solution, but we saw that some equations, called contradictions, have no solutions and for other equations, called identities, all numbers are solutions.

Similarly, when we solve a system of two linear equations represented by a graph of two lines in the same plane, there are three possible cases, as shown.

Each time we demonstrate a new method, we will use it on the same system of linear equations. At the end of the section you’ll decide which method was the most convenient way to solve this system.

Example 4.2

How to solve a system of equations by graphing.

Solve the system by graphing { 2 x + y = 7 x − 2 y = 6 . { 2 x + y = 7 x − 2 y = 6 .

Solve the system by graphing: { x − 3 y = −3 x + y = 5 . { x − 3 y = −3 x + y = 5 .

Solve the system by graphing: { − x + y = 1 3 x + 2 y = 12 . { − x + y = 1 3 x + 2 y = 12 .

The steps to use to solve a system of linear equations by graphing are shown here.

Solve a system of linear equations by graphing.

Step 1. Graph the first equation.
Step 2. Graph the second equation on the same rectangular coordinate system.
Step 3. Determine whether the lines intersect, are parallel, or are the same line.
If the lines intersect, identify the point of intersection. This is the solution to the system.
If the lines are parallel, the system has no solution.
If the lines are the same, the system has an infinite number of solutions.
Step 5. Check the solution in both equations.

In the next example, we’ll first re-write the equations into slope–intercept form as this will make it easy for us to quickly graph the lines.

Example 4.3

Solve the system by graphing: { 3 x + y = − 1 2 x + y = 0 . { 3 x + y = − 1 2 x + y = 0 .

We’ll solve both of these equations for y y so that we can easily graph them using their slopes and y -intercepts.

Solve the system by graphing: { − x + y = 1 2 x + y = 10 . { − x + y = 1 2 x + y = 10 .

Solve the system by graphing: { 2 x + y = 6 x + y = 1 . { 2 x + y = 6 x + y = 1 .

In all the systems of linear equations so far, the lines intersected and the solution was one point. In the next two examples, we’ll look at a system of equations that has no solution and at a system of equations that has an infinite number of solutions.

Example 4.4

Solve the system by graphing: { y = 1 2 x − 3 x − 2 y = 4 . { y = 1 2 x − 3 x − 2 y = 4 .

Solve the system by graphing: { y = − 1 4 x + 2 x + 4 y = − 8 . { y = − 1 4 x + 2 x + 4 y = − 8 .

Solve the system by graphing: { y = 3 x − 1 6 x − 2 y = 6 . { y = 3 x − 1 6 x − 2 y = 6 .

Sometimes the equations in a system represent the same line. Since every point on the line makes both equations true, there are infinitely many ordered pairs that make both equations true. There are infinitely many solutions to the system.

Example 4.5

Solve the system by graphing: { y = 2 x − 3 − 6 x + 3 y = − 9 . { y = 2 x − 3 − 6 x + 3 y = − 9 .

If you write the second equation in slope-intercept form, you may recognize that the equations have the same slope and same y -intercept.

Solve the system by graphing: { y = − 3 x − 6 6 x + 2 y = − 12 . { y = − 3 x − 6 6 x + 2 y = − 12 .

Try It 4.10

Solve the system by graphing: { y = 1 2 x − 4 2 x − 4 y = 16 . { y = 1 2 x − 4 2 x − 4 y = 16 .

When we graphed the second line in the last example, we drew it right over the first line. We say the two lines are coincident . Coincident lines have the same slope and same y- intercept.

Coincident Lines

Coincident lines have the same slope and same y- intercept.

The systems of equations in Example 4.2 and Example 4.3 each had two intersecting lines. Each system had one solution.

In Example 4.5 , the equations gave coincident lines, and so the system had infinitely many solutions.

The systems in those three examples had at least one solution. A system of equations that has at least one solution is called a consistent system.

A system with parallel lines, like Example 4.4 , has no solution. We call a system of equations like this inconsistent. It has no solution.

Consistent and Inconsistent Systems

A consistent system of equations is a system of equations with at least one solution.

An inconsistent system of equations is a system of equations with no solution.

If two equations are dependent, all the solutions of one equation are also solutions of the other equation. When we graph two dependent equations, we get coincident lines.

Let’s sum this up by looking at the graphs of the three types of systems. See below and Table 4.1 .

Example 4.6

Without graphing, determine the number of solutions and then classify the system of equations.

ⓐ { y = 3 x − 1 6 x − 2 y = 12 { y = 3 x − 1 6 x − 2 y = 12 ⓑ { 2 x + y = − 3 x − 5 y = 5 { 2 x + y = − 3 x − 5 y = 5

ⓐ We will compare the slopes and intercepts of the two lines.

A system of equations whose graphs are parallel lines has no solution and is inconsistent and independent.

ⓑ We will compare the slope and intercepts of the two lines.

A system of equations whose graphs are intersect has 1 solution and is consistent and independent.

Try It 4.11

ⓐ { y = −2 x − 4 4 x + 2 y = 9 { y = −2 x − 4 4 x + 2 y = 9 ⓑ { 3 x + 2 y = 2 2 x + y = 1 { 3 x + 2 y = 2 2 x + y = 1

Try It 4.12

ⓐ { y = 1 3 x − 5 x − 3 y = 6 { y = 1 3 x − 5 x − 3 y = 6 ⓑ { x + 4 y = 12 − x + y = 3 { x + 4 y = 12 − x + y = 3

Solving systems of linear equations by graphing is a good way to visualize the types of solutions that may result. However, there are many cases where solving a system by graphing is inconvenient or imprecise. If the graphs extend beyond the small grid with x and y both between −10 −10 and 10, graphing the lines may be cumbersome. And if the solutions to the system are not integers, it can be hard to read their values precisely from a graph.

Solve a System of Equations by Substitution

We will now solve systems of linear equations by the substitution method.

We will use the same system we used first for graphing.

We will first solve one of the equations for either x or y . We can choose either equation and solve for either variable—but we’ll try to make a choice that will keep the work easy.

Then we substitute that expression into the other equation. The result is an equation with just one variable—and we know how to solve those!

Example 4.7

How to solve a system of equations by substitution.

Solve the system by substitution: { 2 x + y = 7 x − 2 y = 6 . { 2 x + y = 7 x − 2 y = 6 .

Try It 4.13

Solve the system by substitution: { − 2 x + y = −11 x + 3 y = 9 . { − 2 x + y = −11 x + 3 y = 9 .

Try It 4.14

Solve the system by substitution: { 2 x + y = −1 4 x + 3 y = 3 . { 2 x + y = −1 4 x + 3 y = 3 .

Solve a system of equations by substitution.

Step 1. Solve one of the equations for either variable.
Step 2. Substitute the expression from Step 1 into the other equation.
Step 3. Solve the resulting equation.
Step 4. Substitute the solution in Step 3 into either of the original equations to find the other variable.
Step 5. Write the solution as an ordered pair.
Step 6. Check that the ordered pair is a solution to both original equations.

Be very careful with the signs in the next example.

Example 4.8

Solve the system by substitution: { 4 x + 2 y = 4 6 x − y = 8 . { 4 x + 2 y = 4 6 x − y = 8 .

We need to solve one equation for one variable. We will solve the first equation for y .

Try It 4.15

Solve the system by substitution: { x − 4 y = −4 − 3 x + 4 y = 0 . { x − 4 y = −4 − 3 x + 4 y = 0 .

Try It 4.16

Solve the system by substitution: { 4 x − y = 0 2 x − 3 y = 5 . { 4 x − y = 0 2 x − 3 y = 5 .

Solve a System of Equations by Elimination

We have solved systems of linear equations by graphing and by substitution. Graphing works well when the variable coefficients are small and the solution has integer values. Substitution works well when we can easily solve one equation for one of the variables and not have too many fractions in the resulting expression.

The third method of solving systems of linear equations is called the Elimination Method. When we solved a system by substitution, we started with two equations and two variables and reduced it to one equation with one variable. This is what we’ll do with the elimination method, too, but we’ll have a different way to get there.

The Elimination Method is based on the Addition Property of Equality. The Addition Property of Equality says that when you add the same quantity to both sides of an equation, you still have equality. We will extend the Addition Property of Equality to say that when you add equal quantities to both sides of an equation, the results are equal.

For any expressions a, b, c, and d .

Notice how that works when we add these two equations together:

The y ’s add to zero and we have one equation with one variable.

Let’s try another one:

This time we don’t see a variable that can be immediately eliminated if we add the equations.

But if we multiply the first equation by −2 , −2 , we will make the coefficients of x opposites. We must multiply every term on both sides of the equation by −2 . −2 .

Then rewrite the system of equations.

Now we see that the coefficients of the x terms are opposites, so x will be eliminated when we add these two equations.

Now we’ll see how to use elimination to solve the same system of equations we solved by graphing and by substitution.

Example 4.9

How to solve a system of equations by elimination.

Solve the system by elimination: { 2 x + y = 7 x − 2 y = 6 . { 2 x + y = 7 x − 2 y = 6 .

Try It 4.17

Solve the system by elimination: { 3 x + y = 5 2 x − 3 y = 7 . { 3 x + y = 5 2 x − 3 y = 7 .

Try It 4.18

Solve the system by elimination: { 4 x + y = − 5 − 2 x − 2 y = − 2 . { 4 x + y = − 5 − 2 x − 2 y = − 2 .

The steps are listed here for easy reference.

Solve a system of equations by elimination.

Step 1. Write both equations in standard form. If any coefficients are fractions, clear them.
Decide which variable you will eliminate.
Multiply one or both equations so that the coefficients of that variable are opposites.
Step 3. Add the equations resulting from Step 2 to eliminate one variable.
Step 4. Solve for the remaining variable.
Step 5. Substitute the solution from Step 4 into one of the original equations. Then solve for the other variable.
Step 6. Write the solution as an ordered pair.
Step 7. Check that the ordered pair is a solution to both original equations.

Now we’ll do an example where we need to multiply both equations by constants in order to make the coefficients of one variable opposites.

Example 4.10

Solve the system by elimination: { 4 x − 3 y = 9 7 x + 2 y = −6 . { 4 x − 3 y = 9 7 x + 2 y = −6 .

In this example, we cannot multiply just one equation by any constant to get opposite coefficients. So we will strategically multiply both equations by different constants to get the opposites.

Try It 4.19

Solve the system by elimination: { 3 x − 4 y = − 9 5 x + 3 y = 14 . { 3 x − 4 y = − 9 5 x + 3 y = 14 .

Try It 4.20

Solve each system by elimination: { 7 x + 8 y = 4 3 x − 5 y = 27 . { 7 x + 8 y = 4 3 x − 5 y = 27 .

When the system of equations contains fractions, we will first clear the fractions by multiplying each equation by the LCD of all the fractions in the equation.

Example 4.11

Solve the system by elimination: { x + 1 2 y = 6 3 2 x + 2 3 y = 17 2 . { x + 1 2 y = 6 3 2 x + 2 3 y = 17 2 .

In this example, both equations have fractions. Our first step will be to multiply each equation by the LCD of all the fractions in the equation to clear the fractions.

Try It 4.21

Solve each system by elimination: { 1 3 x − 1 2 y = 1 3 4 x − y = 5 2 . { 1 3 x − 1 2 y = 1 3 4 x − y = 5 2 .

Try It 4.22

Solve each system by elimination: { x + 3 5 y = − 1 5 − 1 2 x − 2 3 y = 5 6 . { x + 3 5 y = − 1 5 − 1 2 x − 2 3 y = 5 6 .

When we solved the system by graphing, we saw that not all systems of linear equations have a single ordered pair as a solution. When the two equations were really the same line, there were infinitely many solutions. We called that a consistent system. When the two equations described parallel lines, there was no solution. We called that an inconsistent system.

The same is true using substitution or elimination. If the equation at the end of substitution or elimination is a true statement, we have a consistent but dependent system and the system of equations has infinitely many solutions. If the equation at the end of substitution or elimination is a false statement, we have an inconsistent system and the system of equations has no solution.

Example 4.12

Solve the system by elimination: { 3 x + 4 y = 12 y = 3 − 3 4 x . { 3 x + 4 y = 12 y = 3 − 3 4 x .

This is a true statement. The equations are consistent but dependent. Their graphs would be the same line. The system has infinitely many solutions.

After we cleared the fractions in the second equation, did you notice that the two equations were the same? That means we have coincident lines.

Try It 4.23

Solve the system by elimination: { 5 x − 3 y = 15 y = − 5 + 5 3 x . { 5 x − 3 y = 15 y = − 5 + 5 3 x .

Try It 4.24

Solve the system by elimination: { x + 2 y = 6 y = − 1 2 x + 3 . { x + 2 y = 6 y = − 1 2 x + 3 .

Choose the Most Convenient Method to Solve a System of Linear Equations

When you solve a system of linear equations in in an application, you will not be told which method to use. You will need to make that decision yourself. So you’ll want to choose the method that is easiest to do and minimizes your chance of making mistakes.

Example 4.13

For each system of linear equations, decide whether it would be more convenient to solve it by substitution or elimination. Explain your answer.

ⓐ { 3 x + 8 y = 40 7 x − 4 y = −32 { 3 x + 8 y = 40 7 x − 4 y = −32 ⓑ { 5 x + 6 y = 12 y = 2 3 x − 1 { 5 x + 6 y = 12 y = 2 3 x − 1

Since both equations are in standard form, using elimination will be most convenient.

Since one equation is already solved for y , using substitution will be most convenient.

Try It 4.25

For each system of linear equations decide whether it would be more convenient to solve it by substitution or elimination. Explain your answer.

ⓐ { 4 x − 5 y = −32 3 x + 2 y = −1 { 4 x − 5 y = −32 3 x + 2 y = −1 ⓑ { x = 2 y − 1 3 x − 5 y = −7 { x = 2 y − 1 3 x − 5 y = −7

Try It 4.26

ⓐ { y = 2 x − 1 3 x − 4 y = − 6 { y = 2 x − 1 3 x − 4 y = − 6 ⓑ { 6 x − 2 y = 12 3 x + 7 y = −13 { 6 x − 2 y = 12 3 x + 7 y = −13

Section 4.1 Exercises

Practice makes perfect.

In the following exercises, determine if the following points are solutions to the given system of equations.

{ 2 x − 6 y = 0 3 x − 4 y = 5 { 2 x − 6 y = 0 3 x − 4 y = 5

ⓐ ( 3 , 1 ) ( 3 , 1 ) ⓑ ( −3 , 4 ) ( −3 , 4 )

{ − 3 x + y = 8 − x + 2 y = −9 { − 3 x + y = 8 − x + 2 y = −9

ⓐ ( −5 , −7 ) ( −5 , −7 ) ⓑ ( −5 , 7 ) ( −5 , 7 )

{ x + y = 2 y = 3 4 x { x + y = 2 y = 3 4 x

ⓐ ( 8 7 , 6 7 ) ( 8 7 , 6 7 ) ⓑ ( 1 , 3 4 ) ( 1 , 3 4 )

{ 2 x + 3 y = 6 y = 2 3 x + 2 { 2 x + 3 y = 6 y = 2 3 x + 2 ⓐ ( −6 , 2 ) ( −6 , 2 ) ⓑ ( −3 , 4 ) ( −3 , 4 )

In the following exercises, solve the following systems of equations by graphing.

{ 3 x + y = −3 2 x + 3 y = 5 { 3 x + y = −3 2 x + 3 y = 5

{ − x + y = 2 2 x + y = −4 { − x + y = 2 2 x + y = −4

{ y = x + 2 y = −2 x + 2 { y = x + 2 y = −2 x + 2

{ y = x − 2 y = −3 x + 2 { y = x − 2 y = −3 x + 2

{ y = 3 2 x + 1 y = − 1 2 x + 5 { y = 3 2 x + 1 y = − 1 2 x + 5

{ y = 2 3 x − 2 y = − 1 3 x − 5 { y = 2 3 x − 2 y = − 1 3 x − 5

{ x + y = −4 − x + 2 y = −2 { x + y = −4 − x + 2 y = −2

{ − x + 3 y = 3 x + 3 y = 3 { − x + 3 y = 3 x + 3 y = 3

{ − 2 x + 3 y = 3 x + 3 y = 12 { − 2 x + 3 y = 3 x + 3 y = 12

{ 2 x − y = 4 2 x + 3 y = 12 { 2 x − y = 4 2 x + 3 y = 12

{ x + 3 y = −6 y = − 4 3 x + 4 { x + 3 y = −6 y = − 4 3 x + 4

{ − x + 2 y = −6 y = − 1 2 x − 1 { − x + 2 y = −6 y = − 1 2 x − 1

{ − 2 x + 4 y = 4 y = 1 2 x { − 2 x + 4 y = 4 y = 1 2 x

{ 3 x + 5 y = 10 y = − 3 5 x + 1 { 3 x + 5 y = 10 y = − 3 5 x + 1

{ 4 x − 3 y = 8 8 x − 6 y = 14 { 4 x − 3 y = 8 8 x − 6 y = 14

{ x + 3 y = 4 − 2 x − 6 y = 3 { x + 3 y = 4 − 2 x − 6 y = 3

{ x = −3 y + 4 2 x + 6 y = 8 { x = −3 y + 4 2 x + 6 y = 8

{ 4 x = 3 y + 7 8 x − 6 y = 14 { 4 x = 3 y + 7 8 x − 6 y = 14

{ 2 x + y = 6 − 8 x − 4 y = −24 { 2 x + y = 6 − 8 x − 4 y = −24

{ 5 x + 2 y = 7 − 10 x − 4 y = −14 { 5 x + 2 y = 7 − 10 x − 4 y = −14

{ y = 2 3 x + 1 − 2 x + 3 y = 5 { y = 2 3 x + 1 − 2 x + 3 y = 5

{ y = 3 2 x + 1 2 x − 3 y = 7 { y = 3 2 x + 1 2 x − 3 y = 7

{ 5 x + 3 y = 4 2 x − 3 y = 5 { 5 x + 3 y = 4 2 x − 3 y = 5

{ y = − 1 2 x + 5 x + 2 y = 10 { y = − 1 2 x + 5 x + 2 y = 10

{ 5 x − 2 y = 10 y = 5 2 x − 5 { 5 x − 2 y = 10 y = 5 2 x − 5

In the following exercises, solve the systems of equations by substitution.

{ 2 x + y = −4 3 x − 2 y = −6 { 2 x + y = −4 3 x − 2 y = −6

{ 2 x + y = −2 3 x − y = 7 { 2 x + y = −2 3 x − y = 7

{ x − 2 y = −5 2 x − 3 y = −4 { x − 2 y = −5 2 x − 3 y = −4

{ x − 3 y = −9 2 x + 5 y = 4 { x − 3 y = −9 2 x + 5 y = 4

{ 5 x − 2 y = −6 y = 3 x + 3 { 5 x − 2 y = −6 y = 3 x + 3

{ − 2 x + 2 y = 6 y = −3 x + 1 { − 2 x + 2 y = 6 y = −3 x + 1

{ 2 x + 5 y = 1 y = 1 3 x − 2 { 2 x + 5 y = 1 y = 1 3 x − 2

{ 3 x + 4 y = 1 y = − 2 5 x + 2 { 3 x + 4 y = 1 y = − 2 5 x + 2

{ 2 x + y = 5 x − 2 y = −15 { 2 x + y = 5 x − 2 y = −15

{ 4 x + y = 10 x − 2 y = −20 { 4 x + y = 10 x − 2 y = −20

{ y = −2 x − 1 y = − 1 3 x + 4 { y = −2 x − 1 y = − 1 3 x + 4

{ y = x − 6 y = − 3 2 x + 4 { y = x − 6 y = − 3 2 x + 4

{ x = 2 y 4 x − 8 y = 0 { x = 2 y 4 x − 8 y = 0

{ 2 x − 16 y = 8 − x − 8 y = −4 { 2 x − 16 y = 8 − x − 8 y = −4

{ y = 7 8 x + 4 − 7 x + 8 y = 6 { y = 7 8 x + 4 − 7 x + 8 y = 6

{ y = − 2 3 x + 5 2 x + 3 y = 11 { y = − 2 3 x + 5 2 x + 3 y = 11

In the following exercises, solve the systems of equations by elimination.

{ 5 x + 2 y = 2 − 3 x − y = 0 { 5 x + 2 y = 2 − 3 x − y = 0

{ 6 x − 5 y = −1 2 x + y = 13 { 6 x − 5 y = −1 2 x + y = 13

{ 2 x − 5 y = 7 3 x − y = 17 { 2 x − 5 y = 7 3 x − y = 17

{ 5 x − 3 y = −1 2 x − y = 2 { 5 x − 3 y = −1 2 x − y = 2

{ 3 x − 5 y = −9 5 x + 2 y = 16 { 3 x − 5 y = −9 5 x + 2 y = 16

{ 4 x − 3 y = 3 2 x + 5 y = −31 { 4 x − 3 y = 3 2 x + 5 y = −31

{ 3 x + 8 y = −3 2 x + 5 y = −3 { 3 x + 8 y = −3 2 x + 5 y = −3

{ 11 x + 9 y = −5 7 x + 5 y = −1 { 11 x + 9 y = −5 7 x + 5 y = −1

{ 3 x + 8 y = 67 5 x + 3 y = 60 { 3 x + 8 y = 67 5 x + 3 y = 60

{ 2 x + 9 y = −4 3 x + 13 y = −7 { 2 x + 9 y = −4 3 x + 13 y = −7

{ 1 3 x − y = −3 x + 5 2 y = 2 { 1 3 x − y = −3 x + 5 2 y = 2

{ x + 1 2 y = 3 2 1 5 x − 1 5 y = 3 { x + 1 2 y = 3 2 1 5 x − 1 5 y = 3

{ x + 1 3 y = −1 1 3 x + 1 2 y = 1 { x + 1 3 y = −1 1 3 x + 1 2 y = 1

{ 1 3 x − y = −3 2 3 x + 5 2 y = 3 { 1 3 x − y = −3 2 3 x + 5 2 y = 3

{ 2 x + y = 3 6 x + 3 y = 9 { 2 x + y = 3 6 x + 3 y = 9

{ x − 4 y = −1 − 3 x + 12 y = 3 { x − 4 y = −1 − 3 x + 12 y = 3

{ − 3 x − y = 8 6 x + 2 y = −16 { − 3 x − y = 8 6 x + 2 y = −16

{ 4 x + 3 y = 2 20 x + 15 y = 10 { 4 x + 3 y = 2 20 x + 15 y = 10

In the following exercises, decide whether it would be more convenient to solve the system of equations by substitution or elimination.

ⓐ { 8 x − 15 y = −32 6 x + 3 y = −5 { 8 x − 15 y = −32 6 x + 3 y = −5 ⓑ { x = 4 y − 3 4 x − 2 y = −6 { x = 4 y − 3 4 x − 2 y = −6

ⓐ { y = 7 x − 5 3 x − 2 y = 16 { y = 7 x − 5 3 x − 2 y = 16 ⓑ { 12 x − 5 y = −42 3 x + 7 y = −15 { 12 x − 5 y = −42 3 x + 7 y = −15

ⓐ { y = 4 x + 9 5 x − 2 y = −21 { y = 4 x + 9 5 x − 2 y = −21 ⓑ { 9 x − 4 y = 24 3 x + 5 y = −14 { 9 x − 4 y = 24 3 x + 5 y = −14

ⓐ { 14 x − 15 y = −30 7 x + 2 y = 10 { 14 x − 15 y = −30 7 x + 2 y = 10 ⓑ { x = 9 y − 11 2 x − 7 y = −27 { x = 9 y − 11 2 x − 7 y = −27

Writing Exercises

In a system of linear equations, the two equations have the same intercepts. Describe the possible solutions to the system.

Solve the system of equations by substitution and explain all your steps in words: { 3 x + y = 12 x = y − 8 . { 3 x + y = 12 x = y − 8 .

Solve the system of equations by elimination and explain all your steps in words: { 5 x + 4 y = 10 2 x = 3 y + 27 . { 5 x + 4 y = 10 2 x = 3 y + 27 .

Solve the system of equations { x + y = 10 x − y = 6 { x + y = 10 x − y = 6

ⓐ by graphing ⓑ by substitution ⓒ Which method do you prefer? Why?

After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

If most of your checks were:

…confidently. Congratulations! You have achieved the objectives in this section. Reflect on the study skills you used so that you can continue to use them. What did you do to become confident of your ability to do these things? Be specific.

…with some help. This must be addressed quickly because topics you do not master become potholes in your road to success. In math every topic builds upon previous work. It is important to make sure you have a strong foundation before you move on. Whom can you ask for help?Your fellow classmates and instructor are good resources. Is there a place on campus where math tutors are available? Can your study skills be improved?

…no - I don’t get it! This is a warning sign and you must not ignore it. You should get help right away or you will quickly be overwhelmed. See your instructor as soon as you can to discuss your situation. Together you can come up with a plan to get you the help you need.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction

Authors: Lynn Marecek, Andrea Honeycutt Mathis
Publisher/website: OpenStax
Book title: Intermediate Algebra 2e
Publication date: May 6, 2020
Location: Houston, Texas
Book URL: https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction
Section URL: https://openstax.org/books/intermediate-algebra-2e/pages/4-1-solve-systems-of-linear-equations-with-two-variables

© Jan 23, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

CBSE Expert

CBSE Class 10 Maths: Case Study Questions of Chapter 3 Pair of Linear Equations in Two Variables PDF Download

In CBSE Class 10 Maths Paper, Students will have to answer some questions based on Assertion and Reason . There will be a few questions based on case studies and passage-based as well. In that, a paragraph will be given, and then the MCQ questions based on it will be asked.

Pair of Linear Equations in Two Variables Case Study Questions With answers

Here, we have provided case-based/passage-based questions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables

Case Study/Passage-Based Questions

Question 1:

(i) 1 st situation can be represented algebraically as

Answer: (d) 2x+3y=46

(ii) 2 nd situation can be represented algebraically as

Answer: (c) 3x + 5y = 74

(iii), Fare from Ben~aluru to Malleswaram is

Answer: (b) Rs 8

(iv) Fare from Bengaluru to Yeswanthpur is

Answer: (a) Rs 10

(v) The system oflinear equations represented by both situations has

Answer: (c) unique solution

Question 2:

The scissors which is so common in our daily life use, its blades represent the graph of linear equations.

Let the blades of a scissor are represented by the system of linear equations:

x + 3y = 6 and 2x – 3y = 12

(i) The pivot point (point of intersection) of the blades represented by the linear equation x + 3y = 6 and 2x – 3y = 12 of the scissor is (a) (2, 3) (b) (6, 0) (c) (3, 2) (d) (2, 6)

Answer: (b) (6, 0)

Answer: (c) (0, 2) and (0, –4)

(iii) The number of solution of the system of linear equations x + 2y – 8 = 0 and 2x + 4y = 16 is (a) 0 (b) 1 (c) 2 (d) infinitely many

Answer: (d) infinitely many

(iv) If (1, 2) is the solution of linear equations ax + y = 3 and 2x + by = 12, then values of a and b are respectively (a) 1, 5 (b) 2, 3 (c) –1, 5 (d) 3, 5

Answer: (a) 1, 5

(v) If a pair of linear equations in two variables is consistent, then the lines represented by two equations are (a) intersecting (b) parallel (c) always coincident (d) intersecting or coincident

Answer: (d) intersecting or coincident

Download India's best Exam Preparation App Now.

Key Features

Revision Notes
Important Questions
Previous Years Questions
Case-Based Questions
Assertion and Reason Questions

No thanks, I’m not interested!

CBSE Maths Important Questions
Class 9 Maths
Chapter 4: Linear Equations Two Variables

Important Questions CBSE Class 9 Maths Chapter 4-Linear Equation in Two Variables

Important Questions of CBSE Class 9 Maths Chapter 4 -Linear equations in two variables with solutions are available for the students who are preparing 9th final exam. These problems are solved by our experts, as per NCERT book formulated by CBSE board. It covers all the questions according to the syllabus, which is important as per the exam point of view.

Students can reach us at BYJU’S to get important questions for all chapter CBSE class 9 Maths . Practising these extra questions will also help them to revise all the concepts and get good marks in the examination.

Also Check:

Important 2 Marks Questions for CBSE 9th Maths
Important 3 Marks Questions for CBSE 9th Maths
Important 4 Marks Questions for CBSE 9th Maths

Important Questions & Solutions For Class 9 Maths Chapter 4 (Linear Equation in Two Variables)

Q.1: Express the following linear equations in the form ax + by + c = 0 and indicate the values of a, b and c in each case:

(i) x – y/5 – 10 = 0

(ii) -2x+3y = 6

(iii) y – 2 = 0

(i) The equation x-y/5-10 = 0 can be written as:

(1)x + (-1/5) y + (-10) = 0

Now compare the above equation with ax + by + c = 0

Thus, we get;

(ii) –2x + 3y = 6

Re-arranging the given equation, we get,

–2x + 3y – 6 = 0

The equation –2x + 3y – 6 = 0 can be written as,

(–2)x + 3y +(– 6) = 0

Now comparing (–2)x + 3y +(– 6) = 0 with ax + by + c = 0

We get, a = –2

(iii) y – 2 = 0

The equation y – 2 = 0 can be written as,

0x + 1y + (–2) = 0

Now comparing 0x + 1y + (–2) = 0with ax + by + c = 0

We get, a = 0

Q.2. Write four solutions for each of the following equations:

(i) 2x + y = 7

To find the four solutions of 2x + y = 7 we substitute different values for x and y

(2×0)+y = 7

(2×1)+y = 7

The solutions are (0, 7), (1,5), (3,1), (2,3)

(ii) πx + y = 9

To find the four solutions of πx + y = 9 we substitute different values for x and y

(π × 0)+y = 9

(π×1)+y = 9

(π(-1))+y = 9

The solutions are (0,9), (1,9-π),(9/π,0),(-1,9+π)

Q.3: Find the value of k, if x = 2, y = 1 is a solution of the equation 2x + 3y = k.

The given equation is

2x + 3y = k

According to the question, x = 2 and y = 1.

Now, Substituting the values of x and y in the equation 2x + 3y = k,

⇒(2 x 2)+ (3 × 1) = k

The value of k, if x = 2, y = 1 is a solution of the equation 2x + 3y = k, is 7.

Q.4: Draw the graph of each of the following linear equations in two variables:

To draw a graph of linear equations in two variables, let us find out the points to plot.

To find out the points, we have to find the values for which x and y satisfies the given equation.

Substituting the values for x,

When x = 0,

When x = 1,

The points to be plotted are (0, 0) and (1, 3)

Class 9 maths Chapter 4 Important Question 4.i

(ii) 3 = 2x + y

⇒ 3 = 2(0) + y

⇒ 3 = 0 + y

⇒ 3 = 2(1) + y

⇒ 3 = 2 + y

⇒ y = 3 – 2

The points to be plotted are (0, 3) and (1, 1)

Class 9 Maths Chapter 4 Important Questions 4.ii

Q.5: If the point (3, 4) lies on the graph of the equation 3y = ax + 7, find the value of a.

3y = ax + 7

According to the question, x = 3 and y = 4

Now, Substituting the values of x and y in the equation 3y = ax + 7,

(3×4) = (ax3) + 7

⇒ 12 = 3a+7

⇒ 3a = 12–7

The value of a, if the point (3, 4) lies on the graph of the equation 3y = ax + 7 is 5/3.

Q.6: Show that the points A (1, 2), B ( – 1, – 16) and C (0, – 7) lie on the graph of the linear equation y = 9x – 7.

We have the equation,

For A (1, 2),

Substituting (x,y) = (1, 2),

2 = 9(1) – 7

For B (–1, –16),

Substituting (x,y) = (–1, –16),

–16 = 9(–1) – 7

-16 = – 9 – 7

For C (0, –7),

Substituting (x,y) = (0, –7),

– 7 = 9(0) – 7

Hence, the points A (1, 2), B (–1, –16) and C (0, –7) satisfy the line y = 9x – 7.

Thus, A (1, 2), B (–1, –16) and C (0, –7) are solutions of the linear equation y = 9x – 7

Therefore, the points A (1, 2), B (–1, –16), C (0, –7) lie on the graph of linear equation y = 9x – 7.

Q.7: Draw the graph of the linear equation 3x + 4y = 6. At what points, the graph cuts X and Y-axis?

Solution: Given equation,

3x + 4y = 6.

We need at least 2 points on the graph to draw the graph of this equation,

Thus, the points the graph cuts

Since the point is on the x-axis, we have y = 0.

Substituting y = 0 in the equation, 3x + 4y = 6,

3x + 4×0 = 6

Hence, the point at which the graph cuts x-axis = (2, 0).

(ii) y-axis

Since the point is on the y-axis, we have, x = 0.

Substituting x = 0 in the equation, 3x + 4y = 6,

3×0 + 4y = 6

Hence, the point at which the graph cuts y-axis = (0, 1.5).

Plotting the points (0, 1.5) and (2, 0) on the graph.

Class 9 maths chapter 4 important question 7

Extra Questions For Class 9 Maths Chapter 4

The taxi fare in a city is as follows: For the first kilometre, the fare is ₹ 8 and for the subsequent distance it is ₹5 per km. Taking the distance covered as x km and total fare as ₹ y, write a linear equation for this information, and draw its graph.
in one variable
in two variables
Write the linear equation such that each point on its graph has an ordinate 3 times its abscissa.

Register with BYJU'S & Download Free PDFs

New QB365-SLMS
NEET Materials
JEE Materials
Banking first yr Materials
TNPSC Materials
DIPLOMA COURSE Materials
5th Standard Materials
12th Standard Materials
11th Standard Materials
10th Standard Materials
9th Standard Materials
8th Standard Materials
7th Standard Materials
6th Standard Materials
12th Standard CBSE Materials
11th Standard CBSE Materials
10th Standard CBSE Materials
9th Standard CBSE Materials
8th Standard CBSE Materials
7th Standard CBSE Materials
6th Standard CBSE Materials
Tamilnadu Stateboard
Scholarship Exams
Scholarships

Class 9th Maths - Linear Equations in Two Variables Case Study Questions and Answers 2022 - 2023

By QB365 on 08 Sep, 2022

QB365 provides a detailed and simple solution for every Possible Case Study Questions in Class 9th Maths Subject - Linear Equations in Two Variables, CBSE. It will help Students to get more practice questions, Students can Practice these question papers in addition to score best marks.

QB365 - Question Bank Software

Linear equations in two variables case study questions with answer key.

9th Standard CBSE

Final Semester - June 2015

Mathematics

(ii) Find the length of the outer boundary of the layout.

(iii) The pair of linear equation in two variables formed from the statements are (a) x + y = 13, x + y = 9 (b) 2x + y = 13, x + y = 9 (c) x + y = 13, 2x + y = 9 (d) None of the above (iv) Which is the solution satisfying both the equations formed in (iii)?

(v) Find the area of each bedroom.

(iii) Find the cost of one pen?

(iv) Find the total cost if they will purchase the same type of 15 notebooks and 12 pens.

(v) Find whose estimation is correct in the given statement.

(b) How to represent the above situation in linear equations in two variables ?

(d) If both contributed equally, then how much is contributed by each?

(e) Which is the standard form of linear equations x = – 5 ?

(ii) Which is the solution of the equations formed in (i)?

(d) If the cost of one notebook is twice the cost of one pen, then find the cost of one pen?

(e) Which is the standard form of linear equations y = 4 ?

(b) If the number of children is 15, then find the number of adults?

(d) Find the value of b, if x = 5, y = 0 is a solution of the equation 3x + 5y = b.

(e) Which is the standard form of linear equations in two variables: y - x = 5?

(b) If the cost of chocolates A is 5, then find the cost of chocolates B?

(d) The point where the line x + y = 7 intersect y-axis is

(e) For what value of k, x = 2 and y = -1 is a soluation of x + 3y -k = 0.

*****************************************

Linear equations in two variables case study questions with answer key answer keys.

(i) (b) 10x, 5y Area of one bedroom = 5x sq.m Area of two bedrooms = 10x sq.m Area of kitchen = 5y sq. m (ii) (d) 54 m Length of outer boundary = 12 + 15 + 12 + 15 = 54 m (iii) (d) None of the above Area of two bedrooms = 10x sq.m Area of kitchen = 5y sq. m So, 10x + 5y = 95  2x + y = 19 Also, x + 2 + y = 15 x + y = 13 (iv) (c) x = 6, y = 7 x + y = 6 + 7 = 13 2x + y = 2(6) + 7 = 19 x = 6, y = 7 x + y = 6 + 7 = 13 2x + y = 2(6) + 7 = 19 x = 6, y = 7 (v) (a) 30 sq. m Area of living room = (15 x 7) – 30 = 105 – 30 =75 sq. m

(i) (a) 3x + 2y = 80 and 4x + 3y = 110 Here, the cost of one notebook be Rs. x and that of pen be Rs. y. According to the statement, we have 3x + 2y = 80 and 4x + 3y = 110 (ii) (b) x = 20, y = 10 3x + 2y = 3(20) + 2(10) = 60 + 20 = 80 4x + 3y = 4(20) + 3(10) = 80 + 30 = 110 (b) x = 20, y = 10 (iii) (b) Rs. 10 Cost of 1 pen = Rs. 10 (b) Rs. 10 (iv) (d) Rs. 420 Total cost = Rs. 15 x 20 + Rs. 12 x 10 = 300 + 120 = Rs. 420 (v) (a) Deepak Ram said that price of each notebook could be Rs. 25. Ajay felt that Rs. 2.50 for one pen was too little. It should be at least Rs. 16 Deepak guess the cost of one pen is Rs. 10 and Lohith guess the cost of one notebook is Rs. 30 Therefore, estimation of Deepak is correct

(a) (iii) x2 + x = 1 (b) (ii) x + y = 200 Here, x represents Sita's contribution and y represents Gita's contribution. (c) (iii) Rs. 124 If x = 76 then 76 + y = 200 y = 200 - 76 y = 124 (d) (ii) Rs. 100, Rs. 100 If x = y then x + x = 200 2x = 200 x = 200/2 = 100 (e) (iii) 1.x + 0.y + 5 = 0 Since, x = -5 ⇒ x + 5 = 0 Thus, standard form of x = -5 is 1.x + 0.y + 5 = 0.

(i) (d) 5x + 2y = 120 Here, the cost of one notebook be Rs. x and that of pen be Rs. y. According to the statement, we have 5x + 2y = 120 (ii) (b) x = 20, y = 10 5x + 2y = 5(10) + 2(20) = 50 + 40 = 90 ≠ 120 5x + 2y = 5(20) + 2(10) = 100 + 20 = 120 5x + 2y = 5(15) + 2(15) = 75 + 30 = 105 ≠ 120 (c) (ii) Rs. 95 5x + 2y = 5(15) + 2(10) = 75 + 20 = 95 (d) (b) Rs. 10 Here, x = 2y 5(2y) + 2y = 10y + 2y = 12y = 120 ⇒ y = 10 (e) (iv) 0.x + 1.y – 4 = 0 Since, y = 4 ⇒ y – 4 = 0 Thus, standard form of y = 4 is 0.x + 1.y – 4 = 0

(a) (iii) 2x + 3y = 60 Let the number of children be x and the number of adults be y then the linear equation in two variable for the given situation is 2x + 3y = 60. (b) (i) 10 2x + 3y =60 ⇒ 2(15) + 3y = 60 ⇒ 3y = 60 - 30 = 30 ⇒ y = 10 (c) (i) 12 2x + 3y = 60 ⇒ 2x + 3(12) = 60 ⇒ 2x 60 - 36 = 24 ⇒ x = 12 (d) (iii) 15 On putting x = 5 and y = 0 in the equation 3x + 5y = b, we have 3 x 5 + 5 x 0 = b ⇒ 15 + 0 = b ⇒ b = 15 (e) (ii) 1.x - 1.y + 5 = 0 y - x = 5 ⇒ y = x + 5 ⇒ x - y + 5 = 0 ⇒ 1.x - 1.y + 5 = 0

(a) (iii) x + y = 7 (b) (iv) 2 x + y = 7 ⇒ 5 + y = 7 ⇒ y = 7 - 5 = 2 (c) (i) (3, 4) (d) (iv) (0, 7) (e) (iii) -1 On putting x = 2 and y = -1 in the equation x + 3y - k = 0, we have 2 + 3(-1) - k = 0 ⇒ 2 - 3 = k ⇒ k = -1

Related 9th Standard CBSE Mathematics Materials

9th standard cbse syllabus & materials, class 10th social science - pastoralists case study questions and answers 2022 - 2023, class 9th social science - forest society and colonialism case study questions and answers 2022 - 2023, class 9th social science - nazism and the rise of hitler case study questions and answers 2022 - 2023, class 9th social science - socialism in europe and the russian revolution case study questions and answers 2022 - 2023, class 9th social science - the french revolution case study questions and answers 2022 - 2023, class 9th science - work and energy case study questions and answers 2022 - 2023, class 9th science - force and laws of motion case study questions and answers 2022 - 2023, class 9th science - motion case study questions and answers 2022 - 2023, class 9th science - the fundamental unit of life case study questions and answers 2022 - 2023, class 9th science - is matter around us pure case study questions and answers 2022 - 2023, class 9th science - matter in our surroundings case study questions and answers 2022 - 2023, xam idea 9th standard economics ncert solutions for food security in india, xam idea 9th standard economics ncert solutions for poverty as a challenge, xam idea 9th standard economics ncert solutions for people as resource, xam idea 9th standard economics ncert solutions for the story of village palampur.

Class VI to XII

Tn state board / cbse, 3000+ q&a's per subject, score high marks.

9th Standard CBSE Study Materials

9th Standard CBSE Subjects

The Site is down as we are performing important server maintenance, during which time the server will be unavailable for approximately 24 hours. Please hold off on any critical actions until we are finished. As always your feedback is appreciated.

Study Packages
NCERT Solutions
Sample Papers
Online Test

Questions Bank
Mathematics
Pair of Linear Equations in Two Variables
Test Series
Ncert Solutions
Solved Papers
Current Affairs
JEE Main & Advanced
Pre-Primary
MP State Exams
UP State Exams
Rajasthan State Exams
Jharkhand State Exams
Chhattisgarh State Exams
Bihar State Exams
Haryana State Exams
Gujarat State Exams
MH State Exams
Himachal State Exams
Delhi State Exams
Uttarakhand State Exams
Punjab State Exams
J&K State Exams

10th Class Mathematics Pair of Linear Equations in Two Variables Question Bank

Done case based (mcqs) - pair of linear equations in two variables total questions - 40.

A) \[2x+y=19,\,\,x+y=13\] done clear

B) \[x+2y=19,\,\,x+y=18\] done clear

C) \[x+y=19,\,\,x+2y=13\] done clear

D) \[x+3y=19,2\,x+y=15\] done clear

question_answer 2) Find the perimeter of the outer boundary of the Layout

A) \[45\,m\] done clear

B) \[54m\] done clear

C) \[44m\] done clear

D) \[55m\] done clear

question_answer 3) Find the area of each bedroom and kitchen in the Layout

A) Area of each bedroom\[=\text{35 sq}.\text{ m}\] Area of kitchen \[=\text{3}0\text{ sq}.\text{ m}\] done clear

B) Area of each bedroom \[=\text{53 sq}.\text{ m}\] Area of kitchen \[=\text{3}0\text{ sq}.\text{ m}\] done clear

C) Area of each bedroom \[=\text{3}0\text{ sq}.\text{ m}\] Area of kitchen \[=\text{35 sq}.\text{ m}\] done clear

D) None of the above done clear

question_answer 4) Find the area of living room in the layout

A) \[\text{75 sq}.\text{ m}\] done clear

B) \[\text{57 sq}.\text{ m}\] done clear

C) \[\text{55 sq}.\text{ m}\] done clear

D) \[\text{77 sq}.\text{ m}\] done clear

question_answer 5) Find the cost of laying tiles in kitchen at the rate of Rs.50 per sq. m.

A) Rs.1250 done clear

B) Rs.1575 done clear

C) Rs.1700 done clear

D) Rs.1750 done clear

A) \[\text{8 km}/\text{h}\] done clear

B) \[\text{1}0\text{ km}/\text{h}\] done clear

C) \[\text{12 km}/\text{h}\] done clear

D) \[\text{14 km}/\text{h}\] done clear

question_answer 7) The speed of stream is:

A) \[\text{3 km}/\text{h}\] done clear

B) \[\text{4 km}/\text{h}\] done clear

C) \[\text{5 km}/\text{h}\] done clear

D) \[\text{6 km}/\text{h}\] done clear

question_answer 8) Which mathematical concept is used in above problem?

A) Pair of linear equations done clear

B) Cross-multiplication method done clear

C) Factorisation method done clear

D) None of the above done clear

question_answer 9) The direction in which the speed is maximum, is:

A) upstream done clear

B) downstream done clear

C) both have equal speed done clear

D) None of these done clear

question_answer 10) The average speed of stream and boat in still water is:

A) \[\text{7 km}/\text{h}\] done clear

B) \[\text{10 km}/\text{h}\] done clear

D) \[\text{5 km}/\text{h}\] done clear

A) \[\text{x}-\text{2y}=0\]and \[\text{3x}+\text{4y}=\text{2}0\] done clear

B) \[\text{x}+\text{2y}=0\]and \[\text{3x}-\text{4y}=\text{2}0\] done clear

C) \[\text{x}-\text{2y}=0\]and \[\text{4x}+\text{3y}=\text{2}0\] done clear

D) \[None\,\, of\,\, the\,\,above\] done clear

question_answer 12) Graphically, if the pair of equations intersect at one point, then the pair of equation is:

A) Consistent done clear

B) inconsistent done clear

C) consistent or inconsistent done clear

D) None of these done clear

question_answer 13) The intersection point of two lines is:

A) \[(-4,-2)\] done clear

B) \[(4,3)\] done clear

C) \[(2,4)\] done clear

D) \[(4,2)\] done clear

question_answer 14) Intersection points of the line \[x-2y=0\]on x and y-axes are:

A) \[(2,0),\,\,(0,1)\] done clear

B) \[(1,0),\,\,(0,2)\] done clear

C) \[(0,0)\] done clear

D) \[None\,\, of\,\, these\] done clear

question_answer 15) Intersection points of the line \[\text{3x}+\text{4y}=\text{2}0\]on x and y-axes -are:

A) \[\left( \frac{20}{3},0 \right),\,(0,5)\] done clear

B) \[(2,0),\,\,(0,1)\] done clear

C) \[(5,0),\left( 0,\frac{20}{3} \right)\] done clear

A) Length = 6 m, breadth = 4 m done clear

B) length = 10 m, breadth = 6 m done clear

C) length =10 m, breadth =4 m done clear

D) length = 6 m, breadth = 2m done clear

question_answer 17) If the graphs of the equations in the given situation are plotted on the same graph paper, then:

A) The lines will be parallel done clear

B) The lines will coincide done clear

C) The lines will intersect done clear

D) Can't say done clear

question_answer 18) The coordinates of the points where the two Lines, when plotted on a graph paper, intersect the x-axis are:

A) \[(4,0)\] and \[(8,0)\] done clear

B) \[(-4,0)\] and \[(8,0)\] done clear

C) \[(4,0)\]and \[(-8,0)\] done clear

D) \[(-4,0)\] and \[(-8,0)\] done clear

question_answer 19) The value of k for which the system of equations \[\text{x+y}-\text{4=0}\]and \[\text{2x}+\text{ky}=\text{3}\] has no solution, is:

A) \[-2\] done clear

B) \[\ne 2\] done clear

C) 2 done clear

D) 3 done clear

question_answer 20) The equation of a line parallel to the line whose equation is given by \[\text{3x}-\text{2y}=\text{8}\] can be:

A) \[\text{3x}+\text{2y}=8\] done clear

B) \[3x-2y=8\] done clear

C) \[6x+4y=16\] done clear

D) \[15x-10y=45\] done clear

A) \[\frac{{{a}_{1}}}{{{a}_{2}}}\ne \frac{{{b}_{1}}}{{{b}_{2}}}=\frac{{{c}_{1}}}{{{c}_{2}}}\] done clear

B) \[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{{{b}_{1}}}{{{b}_{2}}}=\frac{{{c}_{1}}}{{{c}_{2}}}\] done clear

C) \[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{{{b}_{1}}}{{{b}_{2}}}\ne \frac{{{c}_{1}}}{{{c}_{2}}}\] done clear

question_answer 22) If pair of lines are parallel, then pair of linear equations is:

A) inconsistent done clear

B) consistent done clear

D) None of these done clear

question_answer 23) Check weather the two paths will cross each other or not.

A) yes done clear

B) no done clear

C) do not say done clear

question_answer 24) How many point(s) lie on the Line \[\text{x}-\text{3y}=\text{2}\]?

A) one done clear

B) two done clear

C) three done clear

D) infinitely done clear

question_answer 25) If the line \[\text{2x}+\text{6y}=\text{5}\] intersect the X-axis, then find its coordinate.

A) \[(-2.5,0)\] done clear

B) \[(2.5,0)\] done clear

C) \[(0,2.5)\] done clear

D) \[(0,-2.5)\] done clear

A) \[-\text{4x}-\text{3y}=-\text{4}\]and \[\text{4x}+\text{3y}=\text{2}0\] done clear

B) \[\text{4x}-\text{3y}=\text{4}\]and \[\text{4x}+\text{3y}=\text{2}0\] done clear

C) \[\text{4x}-\text{3y}=-\text{4}\]and \[\text{4x}+\text{3y}=\text{2}0\] done clear

D) \[-\text{4x}+\text{3y}=-\text{4}\]and \[\text{4x}+\text{3y}=\text{2}0\] done clear

question_answer 27) The cost of one ring game and one balloon game is:

A) Rs.2and Rs.4 done clear

B) Rs.4 and Rs.2 done clear

C) Rs.8 and Rs.2 done clear

D) Rs.6 and Rs.3 done clear

question_answer 28) The points where the line represented by the equation \[\text{4x}-\text{3y}=-\text{ 4}\] intersects the x-axis and y-axis, respectively are given by:

A) \[(1,0),\,\,\left( 0,\frac{4}{3} \right)\] done clear

B) \[(1,0),\,\,\left( 0,\frac{4}{3} \right)\] done clear

C) \[(-1,0),\,\,\left( 0,-\frac{4}{3} \right)\] done clear

D) \[(1,0),\,\,\left( 0,-\frac{4}{3} \right)\] done clear

question_answer 29) The area of the triangle formed by the two lines and the x-axis is:

A) 4 sq. units done clear

B) 6 sq. units done clear

C) 8 sq. units done clear

D) 12 sq. units done clear

question_answer 30) The value of k for which the pair of linear equations \[-x+y=-1,\] \[x+ky=5\] will be inconsistent, is:

A) \[k=1\] done clear

B) \[k=-1\] done clear

C) \[k\ne -1\] done clear

D) \[k\ne 1\] done clear

A) \[\text{x}+\text{ y}=\text{2}000\]and \[x+2y=2800\] done clear

B) \[\text{x}+\text{2y}=\text{2}000\]and \[\text{x}+\text{y}=\text{28}00\] done clear

C) \[\text{2x}+\text{y}=\text{2}000\]and \[\text{x}+\text{y}=\text{28}00\] done clear

D) \[\text{x}+y=\text{2}000\]and \[\text{2x}+\text{y}=\text{28}00\] done clear

question_answer 32) Find the number of children and adults who bought tickets on that particular day are:

A) 1100 and 900 done clear

B) 1200 and 800 done clear

C) 1300 and 700 done clear

D) 1500 and 300 done clear

question_answer 33) Find the value(s) of k for which the pair of linear equations given by \[\text{2x}+\text{5y}=\text{2};\] \[(k+2)x+(2k+1)y=2(k-1)\] will have infinitely many solutions.

A) \[6\] done clear

B) \[-4\] done clear

C) \[4\] done clear

D) \[-6\] done clear

question_answer 34) Find the points where the lines represented by the equations \[\text{2x}-\text{5y}+\text{4}=0\]and \[\text{x}+\text{2y}-\text{5}=0\]respectively intersect the x-axis.

A) \[(-3,0)\] and \[(4,0)\] done clear

B) \[(-2,0)\] and \[(5,0)\] done clear

C) \[(-1,0)\] and \[(6,0)\] done clear

D) \[(2,0)\] and \[(4,0)\] done clear

question_answer 35) Write the number of solutions of the system of linear equations \[\text{2x}-\text{3y}+\text{4}=0\] and \[\text{x}+\text{2y}-\text{5=0}\].

A) 1 done clear

B) 2 done clear

C) 0 done clear

D) infinite done clear

A) 24 done clear

B) 96 done clear

C) 70 done clear

D) 100 done clear

question_answer 37) How many questions did he guess?

B) 70 done clear

C) 100 done clear

D) 96 done clear

question_answer 38) If answer to all questions he attempted by guessing were wrong and answered 80 correctly, then how many marks he got?

A) 96 done clear

B) 24 done clear

D) 70 done clear

question_answer 39) If answer to all questions be attempted by guessing were wrong, then how many questions answered correctly to score 90 marks?

B) 70 done clear

C) 96 done clear

question_answer 40) If answer to all questions he attempter by guessing were wrong and answered \[\text{5}0%\]correctly, then how many marks he got?

A) 45 done clear

B) 55 done clear

C) 65 done clear

D) 40 done clear

Study Package

Case Based (MCQs) - Pair of Linear Equations in Two Variables

Reset Password.

OTP has been sent to your mobile number and is valid for one hour

Mobile Number Verified

Your mobile number is verified.

Talk to our experts

1800-120-456-456

Important Questions for CBSE Class 9 Maths Chapter 4 - Linear Equations in Two Variables

Class 9 Important Question
Chapter 4: Linear Equations In Two Variables

Download Important Questions for Class 9 Maths Chapter 4 - Linear Equations in Two Variables - Free PDF

Vedantu has important questions for CBSE Class 9 Mathematics Chapter 4 - Linear Equations in Two Variables. These questions are developed in accordance with the most recent NCERT Curriculum Syllabus and are commonly asked in many sorts of examinations. These questions and answers will help students discover distinct patterns of conceptual issues that may appear on the final exam.

Download these Important Questions for Class 9 Maths Chapter 4 with Solutions PDF for free and use them to practice. Prepare the chapter well by using the solution format designed by the experts. You can also download NCERT Solutions for Class 9 Maths to help you to revise the complete syllabus and score more marks in your examinations. Students can also avail of NCERT Solutions Class 9 Science from our website. Besides, find CBSE Solutions to get more understanding of various subjects.

Download CBSE Class 9 Maths Important Questions 2024-25 PDF

Also, check CBSE Class 9 Maths Important Questions for other chapters:

Topics Covered in CBSE Class 9 Maths Chapter 4 - Linear Equations in Two Variables are as follows:

Linear Equations

Solution of a Linear Equation

Graph of a Linear Equation In Two Variables

Equations of Lines Parallel to the x-axis and y-axis

Important Questions from Linear Equations in Two Variables (Short, Long & Practice)

Short answer type questions.

1. Linear equation x – 2 = 0 is parallel to which axis?

2. If (1, -2) is a solution of the equation 2x – y = p, then find the value of p.

3. Express x/4 – 3y = – 7 in the form of ax + by + c = 0.

Long Answer Type Questions

1. If (2,3) and (4, 0) lie on the graph of equation ax + by = 1. Find the value of a and b. Plot the graph of the equation obtained.

2. Draw the graphs of the following equations on the same graph sheet: x = 4,x = 2,y = l and y – 3 = 0

3. Represent 2x + 3y = 6 by a graph. Write the coordinates of the point where it meets: (a) x-axis (b) y-axis

Practice Questions

1. Find the two solutions of the linear equation 2x – 3y = 12.

2. Find the value of m if (5,8) is a solution of the equation 11 x-2y = 3m, then find one more solution of this equation.

3. On the graph paper draw the straight line 3x – 2y = 4 and x + y – 3 = 0. Also, find their point of intersection on the graph.

Class 9 Maths Chapter 4 Linear Equations in Two Variables Important Questions: Summary

As mentioned earlier, the 4 th chapter concentrates on the linear equations in two variables. The students will learn how an equation is formed using two variables and how they are solved. These new concepts will be used later in the advanced classes to understand the concepts of Cartesian coordinates and higher equations. To develop the concepts in this class even better, follow the Important Questions for Class 9 Maths Chapter 4 . The solutions are also provided for the questions.

These questions are prepared in accordance with the principles covered in the chapter. Students will learn how to employ these concepts in new and sophisticated ways by doing these questions. As a result, the primary goal of teachers is to demonstrate how formulae and concepts may be utilised to look forward and solve new issues. Teachers are aware of the kind of questions that will be asked on final examinations. Some will be simple, while others will be mentally hard. This is where solving Linear Equations in Two Variables Class 9 Crucial Questions will come in handy. Discover a few additional types of questions and how to answer them fast.

The 4 th chapter will teach how one variable is used to form an equation. It will also describe the different terms used in a linear equation. You will then proceed to learn how an equation is formed using two variables. Find out the difference between the linear equation of one variable and two variables. Check out Chapter 4 Maths Class 9 Important Questions to understand the new concepts even better.

How Can You Use Chapter 4 Maths Class 9 Important Questions?

Apart from studying the chapter and solving the exercise questions, adding these important questions for Class 9 Maths Chapter 4 to the study material is ideal. Let us check how you can use these questions for your betterment.

Solving Important Questions for Class 9 Maths Chapter 4 to Gain Another Perspective

The exercise-based questions are solved by all the students. What if you want to learn how different questions are formed for this chapter? This is where downloading these important questions can help you find out the different formats based on the same concepts taught in the chapter.

Answering these new questions will help you develop a new perspective to tackle the exam questions. You can use the solution provided to check how the teachers have formulated the approaches to solve these questions. Hence, your conceptual development will be a step ahead of the competition.

Easy Recapitulation of the Concepts

You can use the Class 9 Maths Chapter 4 Important Questions as a platform to recapitulate the new concepts you have learned in this chapter. Solving the same exercise questions might not give you the thrill. You will need the essence of these new questions to intellectually challenge your problem-solving skills. Find out your preparation level by answering these questions. You can also refer to the solution to learn how to solve these problems better.

Faster Completion of Preparation

How can you find out whether you are done with the preparation of a chapter? Use the Important Questions of Linear Equations in Two Variables Class 9 to find out whether you can solve them or not. If yes, then you are good to go. If not, then proceed to the solution section. Find out how the teachers have designed the solution and learn the chapter again efficiently.

Key Features of Important Questions CBSE Class 9 Maths Chapter 4 - Linear Equations in Two Variables

All the important questions are curated as per the exam point of view to help students score better.

Solutions are explained in a step-by-step manner for all questions.

All solutions are easy to understand and learn as they are clearly written by subject experts to match the curriculum.

These important questions help in developing a good conceptual foundation for students, which is important in the final stages of preparation for board and competitive exams.

These solutions are absolutely free and available in PDF format.

Key Concerns CBSE Class 9 Mathematics Chapter 4 Linear Equations in Two Variables is a valuable resource for students studying for the Class 9 Test. We have provided problems with solutions from highly significant areas covered by the NCERT Class 9 Linear Equations in Two Variables Syllabus. Students will also get an understanding of the kind of questions and methods used in the final test.

Important Related Links for CBSE Class 9

FAQs on Important Questions for CBSE Class 9 Maths Chapter 4 - Linear Equations in Two Variables

1. How can You Find More Questions Based on Linear Equations for Class 9?

The best way to find different kinds of questions is by downloading the Important Questions for Class 9 Maths Chapter 4 with Solutions. You will find a list of questions that can be used to prepare for new formats and challenges before an exam.

2. Why Should I Prefer Vedantu for Important Questions Related to Linear Equations of Class 9?

Vedantu is a one-stop online portal for Mathematics for Class 9 Students. They find quality NCERT solutions for Mathematics and sample papers to solve. They also find the Class 9 Maths Chapter 4 Important Questions to make their foundation of concepts better.

3. Are important questions of Chapter 4 of Class 9 Maths important from the exam point of view?

Yes, important questions of Chapter 4 of Class 9 Maths are important from an exam point of view as these questions will help you save your time and get accurate answers to all the questions. You can prepare from these questions a day before your exam and cross-check all the solutions so as not to write wrong answers in your exams. The solutions are accurate, and you can rely on them to even understand the right method to solve your problems. The important questions are available free of cost on the Vedantu website and the Vedantu app.

4. Give me a summary of exercises present in Chapter 4 of Class 9 Maths.

It has the following topics; Introduction, Linear Equation, Solution Of Linear Equations, Graphs In Two Variables, Equations To Lines Parallel To X And Y-axis. Visit the official Vedantu website for additional details. There are important questions in this chapter that will assist you to pass your tests. These answers will cover all of the major themes that have been compiled from the exam's perspective. These questions are available for download and storage on your computer.

5. Express the following linear equations in the form ax + by + c = 0 and indicate the values of a, b and c in each case:

x –(y/5)–10 = 0

This equation x –(y/5)-10 = 0 can also be written as

Comparing 1x+(-⅕)y +(-10)=0 with ax+by+c=0

a= 1, b = -(⅕), c= -10

6. In the NCERT Solutions for Class 9 Maths linear equations in two variables, how many questions are there?

There are 16 questions in four exercises in NCERT Class 9 Maths Chapter 4 Linear Equations in Two Variables. All of these problems are paced in a way that allows students to gain a thorough understanding of linear equations, their solutions, and graphing. To arrange a time-based practise and preparation, divide these 16 questions into three categories: long replies, short level, and easy. NCERT Math solutions for Class 9 exercises on writing linear equations, finding solutions to linear equations, graphing linear equations, and graphical depiction of equations of lines parallel to the x and y axes are included in Chapter 4 linear equations in two variables.

7. Why must students build a strong foundation of Chapter 4 of Class 9 Maths?

The application of many algebraic ideas studied in higher grades requires the use of linear equations in two variables. Many real-life calculations, such as calculating profits, estimating values, and so on, are also vital to comprehend. As a result, students must have a solid foundation in this subject. The NCERT Solutions for Chapter 4 “Linear Equations in Two Variables” of Class 9 Maths carefully explain all of the key concepts so that students can easily absorb the knowledge.

CBSE Class 9 Maths Important Questions

Cbse study materials.

Trending Now
Foundational Courses
Data Science
Practice Problem
Machine Learning
System Design
DevOps Tutorial

Understanding Two-Variable Equations

Two-variable equations involve relationships between two different variables, often represented as 𝑥 x and 𝑦 y . These equations are fundamental in understanding how variables interact and change in relation to one another. In middle school, students learn to solve, graph, and interpret these equations, which form the basis for more advanced algebraic concepts. Mastery of two-variable equations enhances problem-solving skills and prepares students for topics such as linear equations, systems of equations, and coordinate geometry.

Which of the following pairs (𝑥,𝑦) is a solution to the equation 𝑦=2𝑥+3?

What is the y-intercept of the equation 𝑦=−3𝑥+4?

Solve for 𝑦 in the equation 2𝑥+𝑦=7 when 𝑥=2.

What is the slope of the line represented by the equation 𝑦=1/2𝑥−1?

What is the solution to the system of equations 𝑦=𝑥+2 and 𝑦=2𝑥−1?

There are 5 questions to complete.

IMAGES

CBSE Class 10 Case Study Questions for Maths Chapter 3
Case Study Based Questions
linear equations word problems two variables
Pair of Linear Equations in Two Variables: Introduction, Videos, Examples
Case Study Questions CBSE Class 10 Maths
Pair of Linear Equations in Two Variables Class 10 Extra Questions

VIDEO

Linear Equations Word Problems Class -10th
Case based questions || Case Study Questions || Linear equations in one variable || Class- 8 || CBSE
Math 21
Tricks 1: Linear Equations two variables (BY: Mayank Sir). #gaganpratapmaths #physicswallah
NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex3.2 Q3.1
L3: Basics of Linear Algebra Part 1/7

COMMENTS

Linear Equations in two variables Case Study Questions With Answers
He paid 110 for 4 notebooks and 3 pens. Later, Deepak guesses the cost of one pen is Rs. 10 and Lohith guess the cost of one notebook is Rs. 30. (i) Form the pair of linear equations in two variables from this situation by taking the cost of one notebook as Rs. x and the cost of one pen as Rs. y. (a) 3x + 2y = 80 and 4x + 3y = 110.
CBSE Class 10 Case Study Questions for Maths Chapter 3
CBSE Class 10 Maths Case Study Questions for Chapter 3 - Pair of Linear Equations in Two Variables (Published by CBSE) CBSE's question bank on case study for Class 10 Maths Chapter 3 is available ...
Pair of Linear Equations in Two Variables Case Study Questions With Answers
Case Study 2: The scissors which are so common in our daily life use, its blades represent the graph of linear equations. Let the blades of a scissor are represented by the system of linear equations: x + 3y = 6 and 2x - 3y = 12. (i) The pivot point (point of intersection) of the blades represented by the linear equation x + 3y = 6 and 2x ...
Case Study Questions for Class 9 Maths Chapter 4 Linear Equations in
Case Study Questions for Class 9 Maths Chapter 4 Linear Equations in Two Variables Case Study Questions Question 1: Anil went to buy some vegetables, he bought 'x' kgs. of tomato and 'y' kgs. of potato. The total cost of vegetables comes out to be of Rs. 200. Now if the cost of 1 kg … Continue reading Case Study Questions for Class 9 Maths Chapter 4 Linear Equations in Two Variables
Case Study Questions for Class 10 Maths Chapter 3 Pair of Linear
Case Study Questions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables. Case Study Questions. Question 1: The scissors which is so common in our daily life use, its blades represent the graph of linear equations. Let the blades of a scissor are represented by the system of linear equations: x + 3y = 6 and 2x - 3y = 12
CBSE Case Study Questions For Class 10 Maths Linear Equations In Two
Mere Bacchon, you must practice the CBSE Case Study Questions Class 10 Maths Linear Equations in Two Variables in order to fully complete your preparation.They are very very important from exam point of view. These tricky Case Study Based Questions can act as a villain in your heroic exams!. I have made sure the questions (along with the solutions) prepare you fully for the upcoming exams.
Case Study on Pair of Equations in Two Variables Class 10 ...
Develop Problem-Solving Skills: Class 10 Maths Pair of Equations in Two Variables case study questions require students to analyze a given situation, identify the key issues, and apply relevant concepts to find out a solution. This can help CBSE Class 10 students develop their problem-solving skills, which are essential for success in any ...
5.10: Systems of Linear Equations in Two Variables
An example of a system of two linear equations is shown below. We use a brace to show the two equations are grouped together to form a system of equations. {2 x + y = 7 x − 2 y = 6 {2 x + y = 7 x − 2 y = 6. A linear equation in two variables, such as 2 x + y = 7 2 x + y = 7, has an infinite number of solutions. Its graph is a line.
4.1 Solve Systems of Linear Equations with Two Variables
A linear equation in two variables, such as 2 x + y = 7, 2 x + y = 7, has an infinite number of solutions. Its graph is a line. Remember, every point on the line is a solution to the equation and every solution to the equation is a point on the line. ... Reflect on the study skills you used so that you can continue to use them. What did you do ...
Linear Equations in Two Variables
The graphical representation of a linear equation in two variables is a straight line. Solution of Linear Equation in Two Variables: If x = 𝛼 and y = 𝛽 is the solution of the expression ax + by + c then a𝛼 + b𝛽 + c = 0. Simultaneous Equations: Pair of linear equations in two variables are said to be simultaneous equations if both ...
CBSE 10th Standard Maths Pair of Linear Equation in Two Variables Case
CBSE 10th Standard Maths Subject Pair of Linear Equation in Two Variables Case Study Questions With Solution 2021 Answer Keys. Case Study Questions. (i) (d): 1 st situation can be represented algebraically as 2x + 3y = 46. (ii) (c): 2 nd situation can be represented algebraically as 3x + 5y = 74.
Class 9th Maths
Class 9th Maths - Linear Equations in Two Variables Case Study Questions and Answers 2022 - 2023 - Complete list of 9th Standard CBSE question papers, syllabus, exam tips, study material, previous year exam question papers, centum tips, formula, answer keys, solutions etc..
Class 10 Maths
This video explains the detailed solution and explanation of Case Study Based Questions related to Chapter 3 Pair Of Linear Equations In Two Variables.This v...
CBSE Class 10 Maths: Case Study Questions of Chapter 3 Pair of Linear
Pair of Linear Equations in Two Variables Case Study Questions With answers. Here, we have provided case-based/passage-based questions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables. Case Study/Passage-Based Questions. Question 1: From Bengaluru bus stand, if Riddhima buys 2 tickets to Malleswaram and 3 tickets to ...
RD Sharma Solutions for Class 10 Maths Chapter 3 Pair of Linear
RD Sharma Solutions Class 10 Maths Chapter 3 - Free PDF Download. RD Sharma Solutions for Class 10 Maths Chapter 3 - Pair of Linear Equations In Two Variables are given here for students to study and prepare for their board exams. The subject of Mathematics is well understood with the right methods and tools for studying it.
Important Questions CBSE Class 9 Maths Chapter 4-Linear Equation in Two
Q.4: Draw the graph of each of the following linear equations in two variables: (i)y = 3x. Solution: To draw a graph of linear equations in two variables, let us find out the points to plot. To find out the points, we have to find the values for which x and y satisfies the given equation. Here, y=3x. Substituting the values for x, When x = 0, y ...
9th Maths Linear Equations in Two Variables Case Study Questions and
QB365 provides a detailed and simple solution for every Possible Case Study Questions in Class 9th Maths Subject - Linear Equations in Two Variables, CBSE. It will help Students to get more practice questions, Students can Practice these question papers in addition to score best marks.
10th Class Mathematics Pair of Linear Equations in Two Variables
Case Study : Q. 16 to 20 : The residents of a group housing society at Jaipur decided to build a rectangular garden to beautify the garden. One of the members of the society made some calculations and informed that if the length of the rectangular garden is increased by 2 m and the breadth reduced by 2 m, the area gets reduced by 12 sq. m.
Linear Equations in Two Variables
🔴👉 For Adbhut Batch Registration: https://www.magnetbrains.com/adbhut-batch-english-medium-live-classes🔴👉For Batch Enquiry Fill This Form:- https://www.m...
Case Study Based Questions
ABOUT THIS VIDEO : Case Study Based Questions | Pair of Linear Equations in two variables | Chapter - 3 | Class 10 | Math-----...
Two-variable linear equations intro (video)
Good question! In x and/or y, any linear equation is equivalent to one of two forms: x=a or y=mx+b where a, m, and b are constants. (Yes, this already includes the form where y is a constant, because this would be the result of taking m to be 0 in the equation y=mx+b).
CBSE Class 9 Maths Chapter 4
Long Answer Type Questions. 1. If (2,3) and (4, 0) lie on the graph of equation ax + by = 1. Find the value of a and b. Plot the graph of the equation obtained. 2. Draw the graphs of the following equations on the same graph sheet: x = 4,x = 2,y = l and y - 3 = 0. 3. Represent 2x + 3y = 6 by a graph.
Linear equations in two variables
Unit 11: Linear equations in two variables. 1,000 possible mastery points. Mastered. Proficient. Familiar. Attempted. Not started. Quiz. Unit test. ... Complete solutions to 2-variable equations Get 3 of 4 questions to level up! Algebraic methods. Learn. Systems of equations with substitution: -3x-4y=-2 & y=2x-5
Quiz about Understanding Two-Variable Equations
Understanding Two-Variable Equations. Two-variable equations involve relationships between two different variables, often represented as 𝑥x and 𝑦y. These equations are fundamental in understanding how variables interact and change in relation to one another. In middle school, students learn to solve, graph, and interpret these equations ...

CFA Institute

CBSE Class 10 Maths Case Study Questions for Chapter 3 - Pair of Linear Equations in Two Variables (Published by CBSE)

Latest Education News

Class 10 Maths Case Study Questions Chapter 3 Pair of Linear Equations in Two Variables

Pair of Linear Equations in Two Variables Case Study Questions With Answers

You Might Also Like

Case Study Questions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables

Download CBSE Books

Leave a Reply Cancel reply

Discover more from Gurukul of Excellence

Case Study on Pair of Equations in Two Variables Class 10 Maths PDF

Case Study on Pair of Equations in Two Variables Class 10 Maths with Solutions in PDF

Why Solve Pair of Equations in Two Variables Case Study Questions on Class 10 Maths?

How to Answer Case Study Questions on Pair of Equations in Two Variables?

What to Know to Solve Case Study Questions on Class 10 Pair of Equations in Two Variables?

Where to Find Case Study on Pair of Equations in Two Variables Class 10 Maths?

One Last Step...

Margin Size

5.10: Systems of Linear Equations in Two Variables

Learning Objectives

Determining If an Ordered Pair Is a Solution to a System of Equations

Example 5.81

Your Turn 5.81

Your Turn 5.82

Example 5.83

Your Turn 5.83

Example 5.84

Your Turn 5.84

Example 5.85

Your Turn 5.85

Example 5.86

Your Turn 5.86

Your Turn 5.87

WORK IT OUT

Solving Applications of Systems of Linear Equations

Example 5.88

Your Turn 5.88

Check Your Understanding

4.1 Solve Systems of Linear Equations with Two Variables

Be Prepared 4.1

Be Prepared 4.2

Be Prepared 4.3

System of Linear Equations

Solutions of a System of Equations

Example 4.1

Example 4.2

Solve a system of linear equations by graphing.

Example 4.3

Example 4.4

Example 4.5

Try It 4.10

Coincident Lines

Consistent and Inconsistent Systems

Example 4.6

Try It 4.11

Try It 4.12

Example 4.7

Try It 4.13

Try It 4.14

Solve a system of equations by substitution.

Example 4.8

Try It 4.15

Try It 4.16

Example 4.9

Try It 4.17

Try It 4.18

Solve a system of equations by elimination.

Example 4.10

Try It 4.19

Try It 4.20

Example 4.11

Try It 4.21

Try It 4.22

Example 4.12

Try It 4.23

Try It 4.24

Example 4.13

Try It 4.25

Try It 4.26

Section 4.1 Exercises

Extra Questions For Class 9 Maths Chapter 4