describe a research study that uses statistics

Statistics Made Easy

The Importance of Statistics in Research (With Examples)

The field of statistics is concerned with collecting, analyzing, interpreting, and presenting data.

In the field of research, statistics is important for the following reasons:

Reason 1 : Statistics allows researchers to design studies such that the findings from the studies can be extrapolated to a larger population.

Reason 2 : Statistics allows researchers to perform hypothesis tests to determine if some claim about a new drug, new procedure, new manufacturing method, etc. is true.

Reason 3 : Statistics allows researchers to create confidence intervals to capture uncertainty around population estimates.

In the rest of this article, we elaborate on each of these reasons.

Reason 1: Statistics Allows Researchers to Design Studies

Researchers are often interested in answering questions about populations like:

• What is the average weight of a certain species of bird?
• What is the average height of a certain species of plant?
• What percentage of citizens in a certain city support a certain law?

One way to answer these questions is to go around and collect data on every single individual in the population of interest.

However, this is typically too costly and time-consuming which is why researchers instead take a  sample  of the population and use the data from the sample to draw conclusions about the population as a whole.

There are many different methods researchers can potentially use to obtain individuals to be in a sample. These are known as  sampling methods .

There are two classes of sampling methods:

• Probability sampling methods : Every member in a population has an equal probability of being selected to be in the sample.
• Non-probability sampling methods : Not every member in a population has an equal probability of being selected to be in the sample.

By using probability sampling methods, researchers can maximize the chances that they obtain a sample that is representative of the overall population.

This allows researchers to extrapolate the findings from the sample to the overall population.

Read more about the two classes of sampling methods here .

Reason 2: Statistics Allows Researchers to Perform Hypothesis Tests

Another way that statistics is used in research is in the form of hypothesis tests .

These are tests that researchers can use to determine if there is a statistical significance between different medical procedures or treatments.

For example, suppose a scientist believes that a new drug is able to reduce blood pressure in obese patients. To test this, he measures the blood pressure of 30 patients before and after using the new drug for one month.

He then performs a paired samples t- test using the following hypotheses:

• H 0 : μ after = μ before (the mean blood pressure is the same before and after using the drug)
• H A : μ after < μ before (the mean blood pressure is less after using the drug)

If the p-value of the test is less than some significance level (e.g. α = .05), then he can reject the null hypothesis and conclude that the new drug leads to reduced blood pressure.

Note : This is just one example of a hypothesis test that is used in research. Other common tests include a one sample t-test , two sample t-test , one-way ANOVA , and two-way ANOVA .

Reason 3: Statistics Allows Researchers to Create Confidence Intervals

Another way that statistics is used in research is in the form of confidence intervals .

A confidence interval is a range of values that is likely to contain a population parameter with a certain level of confidence.

For example, suppose researchers are interested in estimating the mean weight of a certain species of turtle.

Instead of going around and weighing every single turtle in the population, researchers may instead take a simple random sample of turtles with the following information:

• Sample size  n = 25
• Sample mean weight  x  = 300
• Sample standard deviation  s = 18.5

Using the confidence interval for a mean formula , researchers may then construct the following 95% confidence interval:

95% Confidence Interval:  300 +/-  1.96*(18.5/√ 25 ) =  [292.75, 307.25]

The researchers would then claim that they’re 95% confident that the true mean weight for this population of turtles is between 292.75 pounds and 307.25 pounds.

Additional Resources

The following articles explain the importance of statistics in other fields:

The Importance of Statistics in Healthcare The Importance of Statistics in Nursing The Importance of Statistics in Business The Importance of Statistics in Economics The Importance of Statistics in Education

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Join the Statology Community

I have read and agree to the terms & conditions

Introduction: Statistics as a Research Tool

• First Online: 24 February 2021

Cite this chapter

• David Weisburd 5 , 6 ,
• Chester Britt 7 ,
• David B. Wilson 5 &
• Alese Wooditch 8  

2455 Accesses

Statistics seem intimidating because they are associated with complex mathematical formulas and computations. Although some knowledge of math is required, an understanding of the concepts is much more important than an in-depth understanding of the computations. The researcher’s aim in using statistics is to communicate findings in a clear and simple form. As a result, the researcher should always choose the simplest statistic appropriate for answering the research question. Statistics offer commonsense solutions to research problems. The following principles apply to all types of statistics: (1) in developing statistics, we seek to reduce the level of error as much as possible; (2) statistics based on more information are generally preferred over those based on less information; (3) outliers present a significant problem in choosing and interpreting statistics; and (4) the researcher must strive to systematize the procedures used in data collection and analysis. There are two principal uses of statistics discussed in this book. In descriptive statistics, the researcher summarizes large amounts of information in an efficient manner. Two types of descriptive statistics that go hand in hand are measures of central tendency, which describe the characteristics of the average case, and measures of dispersion, which tell us just how typical this average case is. We use inferential statistics to make statements about a population on the basis of a sample drawn from that population.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

• Available as EPUB and PDF
• Read on any device
• Instant download
• Own it forever
• Compact, lightweight edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info
• Durable hardcover edition

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Reiss, A. J., Jr. (1971). Systematic Observation of Natural Social Phenomena. Sociological Methodology, 3,  3–33. doi:10.2307/270816

Google Scholar  

National Institute of Justice (2016).  National Institute of Justice Annual Report: 2016.  Washington, DC: U.S. Department of Justice, Office of Justice Programs, National Institute of Justice.

Download references

Author information

Authors and affiliations.

Department of Criminology, Law and Society, George Mason University, Fairfax, VA, USA

David Weisburd & David B. Wilson

Institute of Criminology, Faculty of Law, Hebrew University of Jerusalem, Jerusalem, Israel

David Weisburd

Iowa State University, Ames, IA, USA

Chester Britt

Department of Criminal Justice, Temple University, Philadelphia, PA, USA

Alese Wooditch

You can also search for this author in PubMed   Google Scholar

Rights and permissions

Reprints and permissions

Copyright information

© 2020 Springer Nature Switzerland AG

About this chapter

Weisburd, D., Britt, C., Wilson, D.B., Wooditch, A. (2020). Introduction: Statistics as a Research Tool. In: Basic Statistics in Criminology and Criminal Justice. Springer, Cham. https://doi.org/10.1007/978-3-030-47967-1_1

Download citation

DOI : https://doi.org/10.1007/978-3-030-47967-1_1

Published : 24 February 2021

Publisher Name : Springer, Cham

Print ISBN : 978-3-030-47966-4

Online ISBN : 978-3-030-47967-1

eBook Packages : Law and Criminology Law and Criminology (R0)

Share this chapter

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

Effective Use of Statistics in Research – Methods and Tools for Data Analysis

Remember that impending feeling you get when you are asked to analyze your data! Now that you have all the required raw data, you need to statistically prove your hypothesis. Representing your numerical data as part of statistics in research will also help in breaking the stereotype of being a biology student who can’t do math.

Statistical methods are essential for scientific research. In fact, statistical methods dominate the scientific research as they include planning, designing, collecting data, analyzing, drawing meaningful interpretation and reporting of research findings. Furthermore, the results acquired from research project are meaningless raw data unless analyzed with statistical tools. Therefore, determining statistics in research is of utmost necessity to justify research findings. In this article, we will discuss how using statistical methods for biology could help draw meaningful conclusion to analyze biological studies.

Table of Contents

Role of Statistics in Biological Research

Statistics is a branch of science that deals with collection, organization and analysis of data from the sample to the whole population. Moreover, it aids in designing a study more meticulously and also give a logical reasoning in concluding the hypothesis. Furthermore, biology study focuses on study of living organisms and their complex living pathways, which are very dynamic and cannot be explained with logical reasoning. However, statistics is more complex a field of study that defines and explains study patterns based on the sample sizes used. To be precise, statistics provides a trend in the conducted study.

Biological researchers often disregard the use of statistics in their research planning, and mainly use statistical tools at the end of their experiment. Therefore, giving rise to a complicated set of results which are not easily analyzed from statistical tools in research. Statistics in research can help a researcher approach the study in a stepwise manner, wherein the statistical analysis in research follows –

1. Establishing a Sample Size

Usually, a biological experiment starts with choosing samples and selecting the right number of repetitive experiments. Statistics in research deals with basics in statistics that provides statistical randomness and law of using large samples. Statistics teaches how choosing a sample size from a random large pool of sample helps extrapolate statistical findings and reduce experimental bias and errors.

2. Testing of Hypothesis

When conducting a statistical study with large sample pool, biological researchers must make sure that a conclusion is statistically significant. To achieve this, a researcher must create a hypothesis before examining the distribution of data. Furthermore, statistics in research helps interpret the data clustered near the mean of distributed data or spread across the distribution. These trends help analyze the sample and signify the hypothesis.

3. Data Interpretation Through Analysis

When dealing with large data, statistics in research assist in data analysis. This helps researchers to draw an effective conclusion from their experiment and observations. Concluding the study manually or from visual observation may give erroneous results; therefore, thorough statistical analysis will take into consideration all the other statistical measures and variance in the sample to provide a detailed interpretation of the data. Therefore, researchers produce a detailed and important data to support the conclusion.

Types of Statistical Research Methods That Aid in Data Analysis

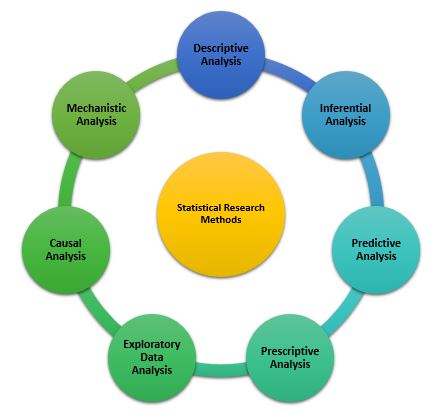
Statistical analysis is the process of analyzing samples of data into patterns or trends that help researchers anticipate situations and make appropriate research conclusions. Based on the type of data, statistical analyses are of the following type:

1. Descriptive Analysis

The descriptive statistical analysis allows organizing and summarizing the large data into graphs and tables . Descriptive analysis involves various processes such as tabulation, measure of central tendency, measure of dispersion or variance, skewness measurements etc.

2. Inferential Analysis

The inferential statistical analysis allows to extrapolate the data acquired from a small sample size to the complete population. This analysis helps draw conclusions and make decisions about the whole population on the basis of sample data. It is a highly recommended statistical method for research projects that work with smaller sample size and meaning to extrapolate conclusion for large population.

3. Predictive Analysis

Predictive analysis is used to make a prediction of future events. This analysis is approached by marketing companies, insurance organizations, online service providers, data-driven marketing, and financial corporations.

4. Prescriptive Analysis

Prescriptive analysis examines data to find out what can be done next. It is widely used in business analysis for finding out the best possible outcome for a situation. It is nearly related to descriptive and predictive analysis. However, prescriptive analysis deals with giving appropriate suggestions among the available preferences.

5. Exploratory Data Analysis

EDA is generally the first step of the data analysis process that is conducted before performing any other statistical analysis technique. It completely focuses on analyzing patterns in the data to recognize potential relationships. EDA is used to discover unknown associations within data, inspect missing data from collected data and obtain maximum insights.

6. Causal Analysis

Causal analysis assists in understanding and determining the reasons behind “why” things happen in a certain way, as they appear. This analysis helps identify root cause of failures or simply find the basic reason why something could happen. For example, causal analysis is used to understand what will happen to the provided variable if another variable changes.

7. Mechanistic Analysis

This is a least common type of statistical analysis. The mechanistic analysis is used in the process of big data analytics and biological science. It uses the concept of understanding individual changes in variables that cause changes in other variables correspondingly while excluding external influences.

Important Statistical Tools In Research

Researchers in the biological field find statistical analysis in research as the scariest aspect of completing research. However, statistical tools in research can help researchers understand what to do with data and how to interpret the results, making this process as easy as possible.

1. Statistical Package for Social Science (SPSS)

It is a widely used software package for human behavior research. SPSS can compile descriptive statistics, as well as graphical depictions of result. Moreover, it includes the option to create scripts that automate analysis or carry out more advanced statistical processing.

2. R Foundation for Statistical Computing

This software package is used among human behavior research and other fields. R is a powerful tool and has a steep learning curve. However, it requires a certain level of coding. Furthermore, it comes with an active community that is engaged in building and enhancing the software and the associated plugins.

3. MATLAB (The Mathworks)

It is an analytical platform and a programming language. Researchers and engineers use this software and create their own code and help answer their research question. While MatLab can be a difficult tool to use for novices, it offers flexibility in terms of what the researcher needs.

4. Microsoft Excel

Not the best solution for statistical analysis in research, but MS Excel offers wide variety of tools for data visualization and simple statistics. It is easy to generate summary and customizable graphs and figures. MS Excel is the most accessible option for those wanting to start with statistics.

5. Statistical Analysis Software (SAS)

It is a statistical platform used in business, healthcare, and human behavior research alike. It can carry out advanced analyzes and produce publication-worthy figures, tables and charts .

6. GraphPad Prism

It is a premium software that is primarily used among biology researchers. But, it offers a range of variety to be used in various other fields. Similar to SPSS, GraphPad gives scripting option to automate analyses to carry out complex statistical calculations.

This software offers basic as well as advanced statistical tools for data analysis. However, similar to GraphPad and SPSS, minitab needs command over coding and can offer automated analyses.

Use of Statistical Tools In Research and Data Analysis

Statistical tools manage the large data. Many biological studies use large data to analyze the trends and patterns in studies. Therefore, using statistical tools becomes essential, as they manage the large data sets, making data processing more convenient.

Following these steps will help biological researchers to showcase the statistics in research in detail, and develop accurate hypothesis and use correct tools for it.

There are a range of statistical tools in research which can help researchers manage their research data and improve the outcome of their research by better interpretation of data. You could use statistics in research by understanding the research question, knowledge of statistics and your personal experience in coding.

Have you faced challenges while using statistics in research? How did you manage it? Did you use any of the statistical tools to help you with your research data? Do write to us or comment below!

Frequently Asked Questions

Statistics in research can help a researcher approach the study in a stepwise manner: 1. Establishing a sample size 2. Testing of hypothesis 3. Data interpretation through analysis

Statistical methods are essential for scientific research. In fact, statistical methods dominate the scientific research as they include planning, designing, collecting data, analyzing, drawing meaningful interpretation and reporting of research findings. Furthermore, the results acquired from research project are meaningless raw data unless analyzed with statistical tools. Therefore, determining statistics in research is of utmost necessity to justify research findings.

Statistical tools in research can help researchers understand what to do with data and how to interpret the results, making this process as easy as possible. They can manage large data sets, making data processing more convenient. A great number of tools are available to carry out statistical analysis of data like SPSS, SAS (Statistical Analysis Software), and Minitab.

nice article to read

Holistic but delineating. A very good read.

Rate this article Cancel Reply

Your email address will not be published.

Enago Academy's Most Popular Articles

• Promoting Research
• Thought Leadership
• Trending Now

How Enago Academy Contributes to Sustainable Development Goals (SDGs) Through Empowering Researchers

The United Nations Sustainable Development Goals (SDGs) are a universal call to action to end…

• Reporting Research

Research Interviews: An effective and insightful way of data collection

Research interviews play a pivotal role in collecting data for various academic, scientific, and professional…

Planning Your Data Collection: Designing methods for effective research

Planning your research is very important to obtain desirable results. In research, the relevance of…

• Language & Grammar

Best Plagiarism Checker Tool for Researchers — Top 4 to choose from!

While common writing issues like language enhancement, punctuation errors, grammatical errors, etc. can be dealt…

• Industry News
• Publishing News

2022 in a Nutshell — Reminiscing the year when opportunities were seized and feats were achieved!

It’s beginning to look a lot like success! Some of the greatest opportunities to research…

2022 in a Nutshell — Reminiscing the year when opportunities were seized and feats…

Sign-up to read more

Subscribe for free to get unrestricted access to all our resources on research writing and academic publishing including:

• 2000+ blog articles
• 50+ Webinars
• 10+ Expert podcasts
• 50+ Infographics
• 10+ Checklists
• Research Guides

We hate spam too. We promise to protect your privacy and never spam you.

I am looking for Editing/ Proofreading services for my manuscript Tentative date of next journal submission:

As a researcher, what do you consider most when choosing an image manipulation detector?

Understanding and Using Statistical Methods

Statistics is a set of tools used to organize and analyze data. Data must either be numeric in origin or transformed by researchers into numbers. For instance, statistics could be used to analyze percentage scores English students receive on a grammar test: the percentage scores ranging from 0 to 100 are already in numeric form. Statistics could also be used to analyze grades on an essay by assigning numeric values to the letter grades, e.g., A=4, B=3, C=2, D=1, and F=0.

Employing statistics serves two purposes, (1) description and (2) prediction. Statistics are used to describe the characteristics of groups. These characteristics are referred to as variables . Data is gathered and recorded for each variable. Descriptive statistics can then be used to reveal the distribution of the data in each variable.

Statistics is also frequently used for purposes of prediction. Prediction is based on the concept of generalizability : if enough data is compiled about a particular context (e.g., students studying writing in a specific set of classrooms), the patterns revealed through analysis of the data collected about that context can be generalized (or predicted to occur in) similar contexts. The prediction of what will happen in a similar context is probabilistic . That is, the researcher is not certain that the same things will happen in other contexts; instead, the researcher can only reasonably expect that the same things will happen.

Prediction is a method employed by individuals throughout daily life. For instance, if writing students begin class every day for the first half of the semester with a five-minute freewriting exercise, then they will likely come to class the first day of the second half of the semester prepared to again freewrite for the first five minutes of class. The students will have made a prediction about the class content based on their previous experiences in the class: Because they began all previous class sessions with freewriting, it would be probable that their next class session will begin the same way. Statistics is used to perform the same function; the difference is that precise probabilities are determined in terms of the percentage chance that an outcome will occur, complete with a range of error. Prediction is a primary goal of inferential statistics.

Revealing Patterns Using Descriptive Statistics

Descriptive statistics, not surprisingly, "describe" data that have been collected. Commonly used descriptive statistics include frequency counts, ranges (high and low scores or values), means, modes, median scores, and standard deviations. Two concepts are essential to understanding descriptive statistics: variables and distributions .

Statistics are used to explore numerical data (Levin, 1991). Numerical data are observations which are recorded in the form of numbers (Runyon, 1976). Numbers are variable in nature, which means that quantities vary according to certain factors. For examples, when analyzing the grades on student essays, scores will vary for reasons such as the writing ability of the student, the students' knowledge of the subject, and so on. In statistics, these reasons are called variables. Variables are divided into three basic categories:

Nominal Variables

Nominal variables classify data into categories. This process involves labeling categories and then counting frequencies of occurrence (Runyon, 1991). A researcher might wish to compare essay grades between male and female students. Tabulations would be compiled using the categories "male" and "female." Sex would be a nominal variable. Note that the categories themselves are not quantified. Maleness or femaleness are not numerical in nature, rather the frequencies of each category results in data that is quantified -- 11 males and 9 females.

Ordinal Variables

Ordinal variables order (or rank) data in terms of degree. Ordinal variables do not establish the numeric difference between data points. They indicate only that one data point is ranked higher or lower than another (Runyon, 1991). For instance, a researcher might want to analyze the letter grades given on student essays. An A would be ranked higher than a B, and a B higher than a C. However, the difference between these data points, the precise distance between an A and a B, is not defined. Letter grades are an example of an ordinal variable.

Interval Variables

Interval variables score data. Thus the order of data is known as well as the precise numeric distance between data points (Runyon, 1991). A researcher might analyze the actual percentage scores of the essays, assuming that percentage scores are given by the instructor. A score of 98 (A) ranks higher than a score of 87 (B), which ranks higher than a score of 72 (C). Not only is the order of these three data points known, but so is the exact distance between them -- 11 percentage points between the first two, 15 percentage points between the second two and 26 percentage points between the first and last data points.

Distributions

A distribution is a graphic representation of data. The line formed by connecting data points is called a frequency distribution. This line may take many shapes. The single most important shape is that of the bell-shaped curve, which characterizes the distribution as "normal." A perfectly normal distribution is only a theoretical ideal. This ideal, however, is an essential ingredient in statistical decision-making (Levin, 1991). A perfectly normal distribution is a mathematical construct which carries with it certain mathematical properties helpful in describing the attributes of the distribution. Although frequency distribution based on actual data points seldom, if ever, completely matches a perfectly normal distribution, a frequency distribution often can approach such a normal curve.

The closer a frequency distribution resembles a normal curve, the more probable that the distribution maintains those same mathematical properties as the normal curve. This is an important factor in describing the characteristics of a frequency distribution. As a frequency distribution approaches a normal curve, generalizations about the data set from which the distribution was derived can be made with greater certainty. And it is this notion of generalizability upon which statistics is founded. It is important to remember that not all frequency distributions approach a normal curve. Some are skewed. When a frequency distribution is skewed, the characteristics inherent to a normal curve no longer apply.

Making Predictions Using Inferential Statistics

Inferential statistics are used to draw conclusions and make predictions based on the descriptions of data. In this section, we explore inferential statistics by using an extended example of experimental studies. Key concepts used in our discussion are probability, populations, and sampling.

Experiments

A typical experimental study involves collecting data on the behaviors, attitudes, or actions of two or more groups and attempting to answer a research question (often called a hypothesis). Based on the analysis of the data, a researcher might then attempt to develop a causal model that can be generalized to populations.

A question that might be addressed through experimental research might be "Does grammar-based writing instruction produce better writers than process-based writing instruction?" Because it would be impossible and impractical to observe, interview, survey, etc. all first-year writing students and instructors in classes using one or the other of these instructional approaches, a researcher would study a sample – or a subset – of a population. Sampling – or the creation of this subset of a population – is used by many researchers who desire to make sense of some phenomenon.

To analyze differences in the ability of student writers who are taught in each type of classroom, the researcher would compare the writing performance of the two groups of students.

Dependent Variables

In an experimental study, a variable whose score depends on (or is determined or caused by) another variable is called a dependent variable. For instance, an experiment might explore the extent to which the writing quality of final drafts of student papers is affected by the kind of instruction they received. In this case, the dependent variable would be writing quality of final drafts.

Independent Variables

In an experimental study, a variable that determines (or causes) the score of a dependent variable is called an independent variable. For instance, an experiment might explore the extent to which the writing quality of final drafts of student papers is affected by the kind of instruction they received. In this case, the independent variable would be the kind of instruction students received.

Probability

Beginning researchers most often use the word probability to express a subjective judgment about the likelihood, or degree of certainty, that a particular event will occur. People say such things as: "It will probably rain tomorrow." "It is unlikely that we will win the ball game." It is possible to assign a number to the event being predicted, a number between 0 and 1, which represents degree of confidence that the event will occur. For example, a student might say that the likelihood an instructor will give an exam next week is about 90 percent, or .9. Where 100 percent, or 1.00, represents certainty, .9 would mean the student is almost certain the instructor will give an exam. If the student assigned the number .6, the likelihood of an exam would be just slightly greater than the likelihood of no exam. A rating of 0 would indicate complete certainty that no exam would be given(Shoeninger, 1971).

The probability of a particular outcome or set of outcomes is called a p-value . In our discussion, a p-value will be symbolized by a p followed by parentheses enclosing a symbol of the outcome or set of outcomes. For example, p(X) should be read, "the probability of a given X score" (Shoeninger). Thus p(exam) should be read, "the probability an instructor will give an exam next week."

A population is a group which is studied. In educational research, the population is usually a group of people. Researchers seldom are able to study every member of a population. Usually, they instead study a representative sample – or subset – of a population. Researchers then generalize their findings about the sample to the population as a whole.

Sampling is performed so that a population under study can be reduced to a manageable size. This can be accomplished via random sampling, discussed below, or via matching.

Random sampling is a procedure used by researchers in which all samples of a particular size have an equal chance to be chosen for an observation, experiment, etc (Runyon and Haber, 1976). There is no predetermination as to which members are chosen for the sample. This type of sampling is done in order to minimize scientific biases and offers the greatest likelihood that a sample will indeed be representative of the larger population. The aim here is to make the sample as representative of the population as possible. Note that the closer a sample distribution approximates the population distribution, the more generalizable the results of the sample study are to the population. Notions of probability apply here. Random sampling provides the greatest probability that the distribution of scores in a sample will closely approximate the distribution of scores in the overall population.

Matching is a method used by researchers to gain accurate and precise results of a study so that they may be applicable to a larger population. After a population has been examined and a sample has been chosen, a researcher must then consider variables, or extrinsic factors, that might affect the study. Matching methods apply when researchers are aware of extrinsic variables before conducting a study. Two methods used to match groups are:

Precision Matching

In precision matching , there is an experimental group that is matched with a control group. Both groups, in essence, have the same characteristics. Thus, the proposed causal relationship/model being examined allows for the probabilistic assumption that the result is generalizable.

Frequency Distribution

Frequency distribution is more manageable and efficient than precision matching. Instead of one-to-one matching that must be administered in precision matching, frequency distribution allows the comparison of an experimental and control group through relevant variables. If three Communications majors and four English majors are chosen for the control group, then an equal proportion of three Communications major and four English majors should be allotted to the experiment group. Of course, beyond their majors, the characteristics of the matched sets of participants may in fact be vastly different.

Although, in theory, matching tends to produce valid conclusions, a rather obvious difficulty arises in finding subjects which are compatible. Researchers may even believe that experimental and control groups are identical when, in fact, a number of variables have been overlooked. For these reasons, researchers tend to reject matching methods in favor of random sampling.

Statistics can be used to analyze individual variables, relationships among variables, and differences between groups. In this section, we explore a range of statistical methods for conducting these analyses.

Statistics can be used to analyze individual variables, relationships among variables, and differences between groups.

Analyzing Individual Variables

The statistical procedures used to analyze a single variable describing a group (such as a population or representative sample) involve measures of central tendency and measures of variation . To explore these measures, a researcher first needs to consider the distribution , or range of values of a particular variable in a population or sample. Normal distribution occurs if the distribution of a population is completely normal. When graphed, this type of distribution will look like a bell curve; it is symmetrical and most of the scores cluster toward the middle. Skewed Distribution simply means the distribution of a population is not normal. The scores might cluster toward the right or the left side of the curve, for instance. Or there might be two or more clusters of scores, so that the distribution looks like a series of hills.

Once frequency distributions have been determined, researchers can calculate measures of central tendency and measures of variation. Measures of central tendency indicate averages of the distribution, and measures of variation indicate the spread, or range, of the distribution (Hinkle, Wiersma and Jurs 1988).

Measures of Central Tendency

Central tendency is measured in three ways: mean , median and mode . The mean is simply the average score of a distribution. The median is the center, or middle score within a distribution. The mode is the most frequent score within a distribution. In a normal distribution, the mean, median and mode are identical.

Measures of Variation

Measures of variation determine the range of the distribution, relative to the measures of central tendency. Where the measures of central tendency are specific data points, measures of variation are lengths between various points within the distribution. Variation is measured in terms of range, mean deviation, variance, and standard deviation (Hinkle, Wiersma and Jurs 1988).

The range is the distance between the lowest data point and the highest data point. Deviation scores are the distances between each data point and the mean.

Mean deviation is the average of the absolute values of the deviation scores; that is, mean deviation is the average distance between the mean and the data points. Closely related to the measure of mean deviation is the measure of variance .

Variance also indicates a relationship between the mean of a distribution and the data points; it is determined by averaging the sum of the squared deviations. Squaring the differences instead of taking the absolute values allows for greater flexibility in calculating further algebraic manipulations of the data. Another measure of variation is the standard deviation .

Standard deviation is the square root of the variance. This calculation is useful because it allows for the same flexibility as variance regarding further calculations and yet also expresses variation in the same units as the original measurements (Hinkle, Wiersma and Jurs 1988).

Analyzing Differences Between Groups

Statistical tests can be used to analyze differences in the scores of two or more groups. The following statistical tests are commonly used to analyze differences between groups:

A t-test is used to determine if the scores of two groups differ on a single variable. A t-test is designed to test for the differences in mean scores. For instance, you could use a t-test to determine whether writing ability differs among students in two classrooms.

Note: A t-test is appropriate only when looking at paired data. It is useful in analyzing scores of two groups of participants on a particular variable or in analyzing scores of a single group of participants on two variables.

Matched Pairs T-Test

This type of t-test could be used to determine if the scores of the same participants in a study differ under different conditions. For instance, this sort of t-test could be used to determine if people write better essays after taking a writing class than they did before taking the writing class.

Analysis of Variance (ANOVA)

The ANOVA (analysis of variance) is a statistical test which makes a single, overall decision as to whether a significant difference is present among three or more sample means (Levin 484). An ANOVA is similar to a t-test. However, the ANOVA can also test multiple groups to see if they differ on one or more variables. The ANOVA can be used to test between-groups and within-groups differences. There are two types of ANOVAs:

One-Way ANOVA: This tests a group or groups to determine if there are differences on a single set of scores. For instance, a one-way ANOVA could determine whether freshmen, sophomores, juniors, and seniors differed in their reading ability.

Multiple ANOVA (MANOVA): This tests a group or groups to determine if there are differences on two or more variables. For instance, a MANOVA could determine whether freshmen, sophomores, juniors, and seniors differed in reading ability and whether those differences were reflected by gender. In this case, a researcher could determine (1) whether reading ability differed across class levels, (2) whether reading ability differed across gender, and (3) whether there was an interaction between class level and gender.

Analyzing Relationships Among Variables

Statistical relationships between variables rely on notions of correlation and regression. These two concepts aim to describe the ways in which variables relate to one another:

Correlation

Correlation tests are used to determine how strongly the scores of two variables are associated or correlated with each other. A researcher might want to know, for instance, whether a correlation exists between students' writing placement examination scores and their scores on a standardized test such as the ACT or SAT. Correlation is measured using values between +1.0 and -1.0. Correlations close to 0 indicate little or no relationship between two variables, while correlations close to +1.0 (or -1.0) indicate strong positive (or negative) relationships (Hayes et al. 554).

Correlation denotes positive or negative association between variables in a study. Two variables are positively associated when larger values of one tend to be accompanied by larger values of the other. The variables are negatively associated when larger values of one tend to be accompanied by smaller values of the other (Moore 208).

An example of a strong positive correlation would be the correlation between age and job experience. Typically, the longer people are alive, the more job experience they might have.

An example of a strong negative relationship might occur between the strength of people's party affiliations and their willingness to vote for a candidate from different parties. In many elections, Democrats are unlikely to vote for Republicans, and vice versa.

Regression analysis attempts to determine the best "fit" between two or more variables. The independent variable in a regression analysis is a continuous variable, and thus allows you to determine how one or more independent variables predict the values of a dependent variable.

Simple Linear Regression is the simplest form of regression. Like a correlation, it determines the extent to which one independent variables predicts a dependent variable. You can think of a simple linear regression as a correlation line. Regression analysis provides you with more information than correlation does, however. It tells you how well the line "fits" the data. That is, it tells you how closely the line comes to all of your data points. The line in the figure indicates the regression line drawn to find the best fit among a set of data points. Each dot represents a person and the axes indicate the amount of job experience and the age of that person. The dotted lines indicate the distance from the regression line. A smaller total distance indicates a better fit. Some of the information provided in a regression analysis, as a result, indicates the slope of the regression line, the R value (or correlation), and the strength of the fit (an indication of the extent to which the line can account for variations among the data points).

Multiple Linear Regression allows one to determine how well multiple independent variables predict the value of a dependent variable. A researcher might examine, for instance, how well age and experience predict a person's salary. The interesting thing here is that one would no longer be dealing with a regression "line." Instead, since the study deals with three dimensions (age, experience, and salary), it would be dealing with a plane, that is, with a two-dimensional figure. If a fourth variable was added to the equations, one would be dealing with a three-dimensional figure, and so on.

Misuses of Statistics

Statistics consists of tests used to analyze data. These tests provide an analytic framework within which researchers can pursue their research questions. This framework provides one way of working with observable information. Like other analytic frameworks, statistical tests can be misused, resulting in potential misinterpretation and misrepresentation. Researchers decide which research questions to ask, which groups to study, how those groups should be divided, which variables to focus upon, and how best to categorize and measure such variables. The point is that researchers retain the ability to manipulate any study even as they decide what to study and how to study it.

Potential Misuses:

• Manipulating scale to change the appearance of the distribution of data
• Eliminating high/low scores for more coherent presentation
• Inappropriately focusing on certain variables to the exclusion of other variables
• Presenting correlation as causation

Measures Against Potential Misuses:

• Testing for reliability and validity
• Testing for statistical significance
• Critically reading statistics

Annotated Bibliography

Dear, K. (1997, August 28). SurfStat australia . Available: http://surfstat.newcastle.edu.au/surfstat/main/surfstat-main.html

A comprehensive site contain an online textbook, links together statistics sites, exercises, and a hotlist for Java applets.

de Leeuw, J. (1997, May 13 ). Statistics: The study of stability in variation . Available: http://www.stat.ucla.edu/textbook/ [1997, December 8].

An online textbook providing discussions specifically regarding variability.

Ewen, R.B. (1988). The workbook for introductory statistics for the behavioral sciences. Orlando, FL: Harcourt Brace Jovanovich.

A workbook providing sample problems typical of the statistical applications in social sciences.

Glass, G. (1996, August 26). COE 502: Introduction to quantitative methods . Available: http://seamonkey.ed.asu.edu/~gene/502/home.html

Outline of a basic statistics course in the college of education at Arizona State University, including a list of statistic resources on the Internet and access to online programs using forms and PERL to analyze data.

Hartwig, F., Dearing, B.E. (1979). Exploratory data analysis . Newberry Park, CA: Sage Publications, Inc.

Hayes, J. R., Young, R.E., Matchett, M.L., McCaffrey, M., Cochran, C., and Hajduk, T., eds. (1992). Reading empirical research studies: The rhetoric of research . Hillsdale, NJ: Lawrence Erlbaum Associates.

A text focusing on the language of research. Topics vary from "Communicating with Low-Literate Adults" to "Reporting on Journalists."

Hinkle, Dennis E., Wiersma, W. and Jurs, S.G. (1988). Applied statistics for the behavioral sciences . Boston: Houghton.

This is an introductory text book on statistics. Each of 22 chapters includes a summary, sample exercises and highlighted main points. The book also includes an index by subject.

Kleinbaum, David G., Kupper, L.L. and Muller K.E. Applied regression analysis and other multivariable methods 2nd ed . Boston: PWS-KENT Publishing Company.

An introductory text with emphasis on statistical analyses. Chapters contain exercises.

Kolstoe, R.H. (1969). Introduction to statistics for the behavioral sciences . Homewood, ILL: Dorsey.

Though more than 25-years-old, this textbook uses concise chapters to explain many essential statistical concepts. Information is organized in a simple and straightforward manner.

Levin, J., and James, A.F. (1991). Elementary statistics in social research, 5th ed . New York: HarperCollins.

This textbook presents statistics in three major sections: Description, From Description to Decision Making and Decision Making. The first chapter underlies reasons for using statistics in social research. Subsequent chapters detail the process of conducting and presenting statistics.

Liebetrau, A.M. (1983). Measures of association . Newberry Park, CA: Sage Publications, Inc.

Mendenhall, W.(1975). Introduction to probability and statistics, 4th ed. North Scltuate, MA: Duxbury Press.

An introductory textbook. A good overview of statistics. Includes clear definitions and exercises.

Moore, David S. (1979). Statistics: Concepts and controversies , 2nd ed . New York: W. H. Freeman and Company.

Introductory text. Basic overview of statistical concepts. Includes discussions of concrete applications such as opinion polls and Consumer Price Index.

Mosier, C.T. (1997). MG284 Statistics I - notes. Available: http://phoenix.som.clarkson.edu/~cmosier/statistics/main/outline/index.html

Explanations of fundamental statistical concepts.

Newton, H.J., Carrol, J.H., Wang, N., & Whiting, D.(1996, Fall). Statistics 30X class notes. Available: http://stat.tamu.edu/stat30x/trydouble2.html [1997, December 10].

This site contains a hyperlinked list of very comprehensive course notes from and introductory statistics class. A large variety of statistical concepts are covered.

Runyon, R.P., and Haber, A. (1976). Fundamentals of behavioral statistics , 3rd ed . Reading, MA: Addison-Wesley Publishing Company.

This is a textbook that divides statistics into categories of descriptive statistics and inferential statistics. It presents statistical procedures primarily through examples. This book includes sectional reviews, reviews of basic mathematics and also a glossary of symbols common to statistics.

Schoeninger, D.W. and Insko, C.A. (1971). Introductory statistics for the behavioral sciences . Boston: Allyn and Bacon, Inc.

An introductory text including discussions of correlation, probability, distribution, and variance. Includes statistical tables in the appendices.

Stevens, J. (1986). Applied multivariate statistics for the social sciences . Hillsdale, NJ: Lawrence Erlbaum Associates.

Stockberger, D. W. (1996). Introductory statistics: Concepts, models and applications . Available: http://www.psychstat.smsu.edu/ [1997, December 8].

Describes various statistical analyses. Includes statistical tables in the appendix.

Local Resources

If you are a member of the Colorado State University community and seek more in-depth help with analyzing data from your research (e.g., from an undergraduate or graduate research project), please contact CSU's Graybill Statistical Laboratory for statistical consulting assistance at http://www.stat.colostate.edu/statlab.html .

Jackson, Shawna, Karen Marcus, Cara McDonald, Timothy Wehner, & Mike Palmquist. (2005). Statistics: An Introduction. Writing@CSU . Colorado State University. https://writing.colostate.edu/guides/guide.cfm?guideid=67

Top 9 Statistical Tools Used in Research

Well-designed research requires a well-chosen study sample and a suitable statistical test selection . To plan an epidemiological study or a clinical trial, you’ll need a solid understanding of the data . Improper inferences from it could lead to false conclusions and  unethical behavior . And given the ocean of data available nowadays, it’s often a daunting task for researchers to gauge its credibility and do statistical analysis on it.

With that said, thanks to all the statistical tools available in the market that help researchers make such studies much more manageable.  Statistical tools are   extensively used in academic and research sectors  to study human, animal, and material behaviors and reactions.

Statistical tools  aid in the interpretation and use of data. They can be used to evaluate and comprehend any form of data. Some statistical tools can help you see trends, forecast future sales, and create links between causes and effects. When you’re unsure where to go with your study, other tools can assist you in navigating through enormous amounts of data.

In this article, we will  discuss some  of the best statistical tools and their key features . So, let’s start without any further ado.

What is Statistics? And its Importance in Research

Statistics is the study of collecting, arranging, and interpreting data from samples and inferring it to the total population.  Also  known  as the “Science of Data,” it allows us to derive conclusions from a data set. It may also assist people in all industries in answering research or business queries and forecast outcomes, such as what show you should watch next on your favorite video app.

Statistical Tools Used in Research

Researchers often cannot discern a simple truth from a set of data. They can only draw conclusions from data after statistical analysis. On the other hand, creating a statistical analysis is a difficult task. This is when statistical tools come into play. Researchers can use statistical tools to back up their claims, make sense of a vast set of data, graphically show complex data, or help clarify many things in a short period. 

Let’s go through  the top 9 best statistical tools used in research  below:

SPSS (Statistical Package for the Social Sciences)  is a collection of software tools compiled as a single package. This program’s primary function is to analyze scientific data in social science. This information can be utilized for market research, surveys, and data mining, among other things. It is mainly used in the following areas like marketing, healthcare, educational research, etc.

SPSS first stores and organizes the data, then compile the data set to generate appropriate output. SPSS is intended to work with a wide range of variable data formats.

Some of the  highlights of SPSS :

• It gives you greater tools for analyzing and comprehending your data. With SPSS’s excellent interface, you can easily handle complex commercial and research challenges.
•  It assists you in making accurate and high-quality decisions.
• It also comes with a variety of deployment options for managing your software.
• You may also use a point-and-click interface to produce unique visualizations and reports. To start using SPSS, you don’t need prior coding skills.
•  It provides the best views of missing data patterns and summarizes variable distributions.

R  is a statistical computing and graphics programming language that you may use to clean, analyze and graph your data. It is frequently used to estimate and display results by researchers from various fields and lecturers of statistics and research methodologies. It’s free, making it an appealing option, but it relies upon programming code rather than drop-down menus or buttons. 

Some of the  highlights of R :

• It offers efficient storage and data handling facility.
• R has the most robust set of operators. They are used for array calculations, namely matrices.
• It has the best data analysis tools.
• It’s a full-featured high-level programming language with conditional loops, decision statements, and various functions.

SAS  is a statistical analysis tool that allows users to build scripts for more advanced analyses or use the GUI. It’s a high-end solution frequently used in industries including business, healthcare, and human behavior research. Advanced analysis and publication-worthy figures and charts are conceivable, albeit coding can be a challenging transition for people who aren’t used to this approach.

Many big tech companies are using SAS due to its support and integration for vast teams. Setting up the tool might be a bit time-consuming initially, but once it’s up and running, it’ll surely streamline your statistical processes.

Some of the  highlights of SAS  are:

• , with a range of tutorials available.
• Its package includes a wide range of statistics tools.
• It has the best technical support available.
• It gives reports of excellent quality and aesthetic appeal
• It provides the best assistance for detecting spelling and grammar issues. As a result, the analysis is more precise.

MATLAB  is one of the most well-reputed statistical analysis tools and statistical programming languages. It has a toolbox with several features that make programming languages simple. With MATLAB, you may perform the most complex statistical analysis, such as  EEG data analysis . Add-ons for toolboxes can be used to increase the capability of MATLAB.

Moreover, MATLAB provides a multi-paradigm numerical computing environment, which means that the language may be used for both procedural and object-oriented programming. MATLAB is ideal for matrix manipulation, including data function plotting, algorithm implementation, and user interface design, among other things. Last but not least, MATLAB can also  run programs  written in other programming languages. 

Some of the  highlights of MATLAB :

• MATLAB toolboxes are meticulously developed and professionally executed. It is also put through its paces by the tester under various settings. Aside from that, MATLAB provides complete documents.
• MATLAB is a production-oriented programming language. As a result, the MATLAB code is ready for production. All that is required is the integration of data sources and business systems with corporate systems.
• It has the ability to convert MATLAB algorithms to C, C++, and CUDA cores.
• For users, MATLAB is the best simulation platform.
• It provides the optimum conditions for performing data analysis procedures.

Some of the  highlights of Tableau  are:

• It gives the most compelling end-to-end analytics.
• It provides us with a system of high-level security.
• It is compatible with practically all screen resolutions.

Minitab  is a data analysis program that includes basic and advanced statistical features. The GUI and written instructions can be used to execute commands, making it accessible to beginners and those wishing to perform more advanced analysis.

Some of the  highlights of Minitab  are:

• Minitab can be used to perform various sorts of analysis, such as measurement systems analysis, capability analysis, graphical analysis, hypothesis analysis, regression, non-regression, etcetera.
• , such as scatterplots, box plots, dot plots, histograms, time series plots, and so on.
• Minitab also allows you to run a variety of statistical tests, including one-sample Z-tests, one-sample, two-sample t-tests, paired t-tests, and so on.

7. MS EXCEL:

You can apply various formulas and functions to your data in Excel without prior knowledge of statistics. The learning curve is great, and even freshers can achieve great results quickly since everything is just a click away. This makes Excel a great choice not only for amateurs but beginners as well.

Some of the  highlights of MS Excel  are:

• It has the best GUI for data visualization solutions, allowing you to generate various graphs with it.
• MS Excel has practically every tool needed to undertake any type of data analysis.
• It enables you to do basic to complicated computations.
• Excel has a lot of built-in formulas that make it a good choice for performing extensive data jobs.

8. RAPIDMINER:

RapidMiner  is a valuable platform for data preparation, machine learning, and the deployment of predictive models. RapidMiner makes it simple to develop a data model from the beginning to the end. It comes with a complete data science suite. Machine learning, deep learning, text mining, and predictive analytics are all possible with it.

Some of the  highlights of RapidMiner  are:

• It has outstanding security features.
• It allows for seamless integration with a variety of third-party applications.
• RapidMiner’s primary functionality can be extended with the help of plugins.
• It provides an excellent platform for data processing and visualization of results.
• It has the ability to track and analyze data in real-time.

9. APACHE HADOOP:

Apache Hadoop  is an open-source software that is best known for its top-of-the-drawer scaling capabilities. It is capable of resolving the most challenging computational issues and excels at data-intensive activities as well, given its  distributed architecture . The primary reason why it outperforms its contenders in terms of computational power and speed is that it does not directly transfer files to the node. It divides enormous files into smaller bits and transmits them to separate nodes with specific instructions using  HDFS . More about it  here .

So, if you have massive data on your hands and want something that doesn’t slow you down and works in a distributed way, Hadoop is the way to go.

Some of the  highlights of Apache Hadoop  are:

• It is cost-effective.
• Apache Hadoop offers built-in tools that automatically schedule tasks and manage clusters.
• It can effortlessly integrate with third-party applications and apps.
• Apache Hadoop is also simple to use for beginners. It includes a framework for managing distributed computing with user intervention.

Learn more about Statistics and Key Tools

Elasticity of Demand Explained in Plain Terms

When you think of “elasticity,” you probably think of flexibility or the ability of an object to bounce back to its original conditions after some change. The type of elasticity

Learn More…

An Introduction to Statistical Power And A/B Testing

Statistical power is an integral part of A/B testing. And in this article, you will learn everything you need to know about it and how it is applied in A/B testing. A/B

What Data Analytics Tools Are And How To Use Them

When it comes to improving the quality of your products and services, data analytic tools are the antidotes. Regardless, people often have questions. What are data analytic tools? Why are

There are a variety of software tools available, each of which offers something slightly different to the user – which one you choose will be determined by several things, including your research question, statistical understanding, and coding experience. These factors may indicate that you are on the cutting edge of data analysis, but the quality of the data acquired depends on the study execution, as with any research.

It’s worth noting that even if you have the most powerful statistical software (and the knowledge to utilize it), the results would be meaningless if they weren’t collected properly. Some online statistics tools are an alternative to the above-mentioned statistical tools. However, each of these tools is the finest in its domain. Hence, you really don’t need a second opinion to use any of these tools. But it’s always recommended to get your hands dirty a little and see what works best for your specific use case before choosing it.

Emidio Amadebai

As an IT Engineer, who is passionate about learning and sharing. I have worked and learned quite a bit from Data Engineers, Data Analysts, Business Analysts, and Key Decision Makers almost for the past 5 years. Interested in learning more about Data Science and How to leverage it for better decision-making in my business and hopefully help you do the same in yours.

Recent Posts

Causal vs Evidential Decision-making (How to Make Businesses More Effective) 

In today’s fast-paced business landscape, it is crucial to make informed decisions to stay in the competition which makes it important to understand the concept of the different characteristics and...

Bootstrapping vs. Boosting

Over the past decade, the field of machine learning has witnessed remarkable advancements in predictive techniques and ensemble learning methods. Ensemble techniques are very popular in machine...

Child Care and Early Education Research Connections

Descriptive research studies.

Descriptive research is a type of research that is used to describe the characteristics of a population. It collects data that are used to answer a wide range of what, when, and how questions pertaining to a particular population or group. For example, descriptive studies might be used to answer questions such as: What percentage of Head Start teachers have a bachelor's degree or higher? What is the average reading ability of 5-year-olds when they first enter kindergarten? What kinds of math activities are used in early childhood programs? When do children first receive regular child care from someone other than their parents? When are children with developmental disabilities first diagnosed and when do they first receive services? What factors do programs consider when making decisions about the type of assessments that will be used to assess the skills of the children in their programs? How do the types of services children receive from their early childhood program change as children age?

Descriptive research does not answer questions about why a certain phenomenon occurs or what the causes are. Answers to such questions are best obtained from  randomized and quasi-experimental studies . However, data from descriptive studies can be used to examine the relationships (correlations) among variables. While the findings from correlational analyses are not evidence of causality, they can help to distinguish variables that may be important in explaining a phenomenon from those that are not. Thus, descriptive research is often used to generate hypotheses that should be tested using more rigorous designs.

A variety of data collection methods may be used alone or in combination to answer the types of questions guiding descriptive research. Some of the more common methods include surveys, interviews, observations, case studies, and portfolios. The data collected through these methods can be either quantitative or qualitative. Quantitative data are typically analyzed and presenting using  descriptive statistics . Using quantitative data, researchers may describe the characteristics of a sample or population in terms of percentages (e.g., percentage of population that belong to different racial/ethnic groups, percentage of low-income families that receive different government services) or averages (e.g., average household income, average scores of reading, mathematics and language assessments). Quantitative data, such as narrative data collected as part of a case study, may be used to organize, classify, and used to identify patterns of behaviors, attitudes, and other characteristics of groups.

Descriptive studies have an important role in early care and education research. Studies such as the  National Survey of Early Care and Education  and the  National Household Education Surveys Program  have greatly increased our knowledge of the supply of and demand for child care in the U.S. The  Head Start Family and Child Experiences Survey  and the  Early Childhood Longitudinal Study Program  have provided researchers, policy makers and practitioners with rich information about school readiness skills of children in the U.S.

Each of the methods used to collect descriptive data have their own strengths and limitations. The following are some of the strengths and limitations of descriptive research studies in general.

Study participants are questioned or observed in a natural setting (e.g., their homes, child care or educational settings).

Study data can be used to identify the prevalence of particular problems and the need for new or additional services to address these problems.

Descriptive research may identify areas in need of additional research and relationships between variables that require future study. Descriptive research is often referred to as "hypothesis generating research."

Depending on the data collection method used, descriptive studies can generate rich datasets on large and diverse samples.

Limitations:

Descriptive studies cannot be used to establish cause and effect relationships.

Respondents may not be truthful when answering survey questions or may give socially desirable responses.

The choice and wording of questions on a questionnaire may influence the descriptive findings.

Depending on the type and size of sample, the findings may not be generalizable or produce an accurate description of the population of interest.

Have a thesis expert improve your writing

Check your thesis for plagiarism in 10 minutes, generate your apa citations for free.

• Knowledge Base

The Beginner's Guide to Statistical Analysis | 5 Steps & Examples

Statistical analysis means investigating trends, patterns, and relationships using quantitative data . It is an important research tool used by scientists, governments, businesses, and other organisations.

To draw valid conclusions, statistical analysis requires careful planning from the very start of the research process . You need to specify your hypotheses and make decisions about your research design, sample size, and sampling procedure.

After collecting data from your sample, you can organise and summarise the data using descriptive statistics . Then, you can use inferential statistics to formally test hypotheses and make estimates about the population. Finally, you can interpret and generalise your findings.

This article is a practical introduction to statistical analysis for students and researchers. We’ll walk you through the steps using two research examples. The first investigates a potential cause-and-effect relationship, while the second investigates a potential correlation between variables.

Table of contents

Step 1: write your hypotheses and plan your research design, step 2: collect data from a sample, step 3: summarise your data with descriptive statistics, step 4: test hypotheses or make estimates with inferential statistics, step 5: interpret your results, frequently asked questions about statistics.

To collect valid data for statistical analysis, you first need to specify your hypotheses and plan out your research design.

Writing statistical hypotheses

The goal of research is often to investigate a relationship between variables within a population . You start with a prediction, and use statistical analysis to test that prediction.

A statistical hypothesis is a formal way of writing a prediction about a population. Every research prediction is rephrased into null and alternative hypotheses that can be tested using sample data.

While the null hypothesis always predicts no effect or no relationship between variables, the alternative hypothesis states your research prediction of an effect or relationship.

• Null hypothesis: A 5-minute meditation exercise will have no effect on math test scores in teenagers.
• Alternative hypothesis: A 5-minute meditation exercise will improve math test scores in teenagers.
• Null hypothesis: Parental income and GPA have no relationship with each other in college students.
• Alternative hypothesis: Parental income and GPA are positively correlated in college students.

Planning your research design

A research design is your overall strategy for data collection and analysis. It determines the statistical tests you can use to test your hypothesis later on.

First, decide whether your research will use a descriptive, correlational, or experimental design. Experiments directly influence variables, whereas descriptive and correlational studies only measure variables.

• In an experimental design , you can assess a cause-and-effect relationship (e.g., the effect of meditation on test scores) using statistical tests of comparison or regression.
• In a correlational design , you can explore relationships between variables (e.g., parental income and GPA) without any assumption of causality using correlation coefficients and significance tests.
• In a descriptive design , you can study the characteristics of a population or phenomenon (e.g., the prevalence of anxiety in U.S. college students) using statistical tests to draw inferences from sample data.

Your research design also concerns whether you’ll compare participants at the group level or individual level, or both.

• In a between-subjects design , you compare the group-level outcomes of participants who have been exposed to different treatments (e.g., those who performed a meditation exercise vs those who didn’t).
• In a within-subjects design , you compare repeated measures from participants who have participated in all treatments of a study (e.g., scores from before and after performing a meditation exercise).
• In a mixed (factorial) design , one variable is altered between subjects and another is altered within subjects (e.g., pretest and posttest scores from participants who either did or didn’t do a meditation exercise).
• Experimental
• Correlational

First, you’ll take baseline test scores from participants. Then, your participants will undergo a 5-minute meditation exercise. Finally, you’ll record participants’ scores from a second math test.

In this experiment, the independent variable is the 5-minute meditation exercise, and the dependent variable is the math test score from before and after the intervention. Example: Correlational research design In a correlational study, you test whether there is a relationship between parental income and GPA in graduating college students. To collect your data, you will ask participants to fill in a survey and self-report their parents’ incomes and their own GPA.

Measuring variables

When planning a research design, you should operationalise your variables and decide exactly how you will measure them.

For statistical analysis, it’s important to consider the level of measurement of your variables, which tells you what kind of data they contain:

• Categorical data represents groupings. These may be nominal (e.g., gender) or ordinal (e.g. level of language ability).
• Quantitative data represents amounts. These may be on an interval scale (e.g. test score) or a ratio scale (e.g. age).

Many variables can be measured at different levels of precision. For example, age data can be quantitative (8 years old) or categorical (young). If a variable is coded numerically (e.g., level of agreement from 1–5), it doesn’t automatically mean that it’s quantitative instead of categorical.

Identifying the measurement level is important for choosing appropriate statistics and hypothesis tests. For example, you can calculate a mean score with quantitative data, but not with categorical data.

In a research study, along with measures of your variables of interest, you’ll often collect data on relevant participant characteristics.

In most cases, it’s too difficult or expensive to collect data from every member of the population you’re interested in studying. Instead, you’ll collect data from a sample.

Statistical analysis allows you to apply your findings beyond your own sample as long as you use appropriate sampling procedures . You should aim for a sample that is representative of the population.

Sampling for statistical analysis

There are two main approaches to selecting a sample.

• Probability sampling: every member of the population has a chance of being selected for the study through random selection.
• Non-probability sampling: some members of the population are more likely than others to be selected for the study because of criteria such as convenience or voluntary self-selection.

In theory, for highly generalisable findings, you should use a probability sampling method. Random selection reduces sampling bias and ensures that data from your sample is actually typical of the population. Parametric tests can be used to make strong statistical inferences when data are collected using probability sampling.

But in practice, it’s rarely possible to gather the ideal sample. While non-probability samples are more likely to be biased, they are much easier to recruit and collect data from. Non-parametric tests are more appropriate for non-probability samples, but they result in weaker inferences about the population.

If you want to use parametric tests for non-probability samples, you have to make the case that:

• your sample is representative of the population you’re generalising your findings to.
• your sample lacks systematic bias.

Keep in mind that external validity means that you can only generalise your conclusions to others who share the characteristics of your sample. For instance, results from Western, Educated, Industrialised, Rich and Democratic samples (e.g., college students in the US) aren’t automatically applicable to all non-WEIRD populations.

If you apply parametric tests to data from non-probability samples, be sure to elaborate on the limitations of how far your results can be generalised in your discussion section .

Create an appropriate sampling procedure

Based on the resources available for your research, decide on how you’ll recruit participants.

• Will you have resources to advertise your study widely, including outside of your university setting?
• Will you have the means to recruit a diverse sample that represents a broad population?
• Do you have time to contact and follow up with members of hard-to-reach groups?

Your participants are self-selected by their schools. Although you’re using a non-probability sample, you aim for a diverse and representative sample. Example: Sampling (correlational study) Your main population of interest is male college students in the US. Using social media advertising, you recruit senior-year male college students from a smaller subpopulation: seven universities in the Boston area.

Calculate sufficient sample size

Before recruiting participants, decide on your sample size either by looking at other studies in your field or using statistics. A sample that’s too small may be unrepresentative of the sample, while a sample that’s too large will be more costly than necessary.

There are many sample size calculators online. Different formulas are used depending on whether you have subgroups or how rigorous your study should be (e.g., in clinical research). As a rule of thumb, a minimum of 30 units or more per subgroup is necessary.

To use these calculators, you have to understand and input these key components:

• Significance level (alpha): the risk of rejecting a true null hypothesis that you are willing to take, usually set at 5%.
• Statistical power : the probability of your study detecting an effect of a certain size if there is one, usually 80% or higher.
• Expected effect size : a standardised indication of how large the expected result of your study will be, usually based on other similar studies.
• Population standard deviation: an estimate of the population parameter based on a previous study or a pilot study of your own.

Once you’ve collected all of your data, you can inspect them and calculate descriptive statistics that summarise them.

Inspect your data

There are various ways to inspect your data, including the following:

• Organising data from each variable in frequency distribution tables .
• Displaying data from a key variable in a bar chart to view the distribution of responses.
• Visualising the relationship between two variables using a scatter plot .

By visualising your data in tables and graphs, you can assess whether your data follow a skewed or normal distribution and whether there are any outliers or missing data.

A normal distribution means that your data are symmetrically distributed around a center where most values lie, with the values tapering off at the tail ends.

In contrast, a skewed distribution is asymmetric and has more values on one end than the other. The shape of the distribution is important to keep in mind because only some descriptive statistics should be used with skewed distributions.

Extreme outliers can also produce misleading statistics, so you may need a systematic approach to dealing with these values.

Calculate measures of central tendency

Measures of central tendency describe where most of the values in a data set lie. Three main measures of central tendency are often reported:

• Mode : the most popular response or value in the data set.
• Median : the value in the exact middle of the data set when ordered from low to high.
• Mean : the sum of all values divided by the number of values.

However, depending on the shape of the distribution and level of measurement, only one or two of these measures may be appropriate. For example, many demographic characteristics can only be described using the mode or proportions, while a variable like reaction time may not have a mode at all.

Calculate measures of variability

Measures of variability tell you how spread out the values in a data set are. Four main measures of variability are often reported:

• Range : the highest value minus the lowest value of the data set.
• Interquartile range : the range of the middle half of the data set.
• Standard deviation : the average distance between each value in your data set and the mean.
• Variance : the square of the standard deviation.

Once again, the shape of the distribution and level of measurement should guide your choice of variability statistics. The interquartile range is the best measure for skewed distributions, while standard deviation and variance provide the best information for normal distributions.

Using your table, you should check whether the units of the descriptive statistics are comparable for pretest and posttest scores. For example, are the variance levels similar across the groups? Are there any extreme values? If there are, you may need to identify and remove extreme outliers in your data set or transform your data before performing a statistical test.

From this table, we can see that the mean score increased after the meditation exercise, and the variances of the two scores are comparable. Next, we can perform a statistical test to find out if this improvement in test scores is statistically significant in the population. Example: Descriptive statistics (correlational study) After collecting data from 653 students, you tabulate descriptive statistics for annual parental income and GPA.

It’s important to check whether you have a broad range of data points. If you don’t, your data may be skewed towards some groups more than others (e.g., high academic achievers), and only limited inferences can be made about a relationship.

A number that describes a sample is called a statistic , while a number describing a population is called a parameter . Using inferential statistics , you can make conclusions about population parameters based on sample statistics.

Researchers often use two main methods (simultaneously) to make inferences in statistics.

• Estimation: calculating population parameters based on sample statistics.
• Hypothesis testing: a formal process for testing research predictions about the population using samples.

You can make two types of estimates of population parameters from sample statistics:

• A point estimate : a value that represents your best guess of the exact parameter.
• An interval estimate : a range of values that represent your best guess of where the parameter lies.

If your aim is to infer and report population characteristics from sample data, it’s best to use both point and interval estimates in your paper.

You can consider a sample statistic a point estimate for the population parameter when you have a representative sample (e.g., in a wide public opinion poll, the proportion of a sample that supports the current government is taken as the population proportion of government supporters).

There’s always error involved in estimation, so you should also provide a confidence interval as an interval estimate to show the variability around a point estimate.

A confidence interval uses the standard error and the z score from the standard normal distribution to convey where you’d generally expect to find the population parameter most of the time.

Hypothesis testing

Using data from a sample, you can test hypotheses about relationships between variables in the population. Hypothesis testing starts with the assumption that the null hypothesis is true in the population, and you use statistical tests to assess whether the null hypothesis can be rejected or not.

Statistical tests determine where your sample data would lie on an expected distribution of sample data if the null hypothesis were true. These tests give two main outputs:

• A test statistic tells you how much your data differs from the null hypothesis of the test.
• A p value tells you the likelihood of obtaining your results if the null hypothesis is actually true in the population.

Statistical tests come in three main varieties:

• Comparison tests assess group differences in outcomes.
• Regression tests assess cause-and-effect relationships between variables.
• Correlation tests assess relationships between variables without assuming causation.

Your choice of statistical test depends on your research questions, research design, sampling method, and data characteristics.

Parametric tests

Parametric tests make powerful inferences about the population based on sample data. But to use them, some assumptions must be met, and only some types of variables can be used. If your data violate these assumptions, you can perform appropriate data transformations or use alternative non-parametric tests instead.

A regression models the extent to which changes in a predictor variable results in changes in outcome variable(s).

• A simple linear regression includes one predictor variable and one outcome variable.
• A multiple linear regression includes two or more predictor variables and one outcome variable.

Comparison tests usually compare the means of groups. These may be the means of different groups within a sample (e.g., a treatment and control group), the means of one sample group taken at different times (e.g., pretest and posttest scores), or a sample mean and a population mean.

• A t test is for exactly 1 or 2 groups when the sample is small (30 or less).
• A z test is for exactly 1 or 2 groups when the sample is large.
• An ANOVA is for 3 or more groups.

The z and t tests have subtypes based on the number and types of samples and the hypotheses:

• If you have only one sample that you want to compare to a population mean, use a one-sample test .
• If you have paired measurements (within-subjects design), use a dependent (paired) samples test .
• If you have completely separate measurements from two unmatched groups (between-subjects design), use an independent (unpaired) samples test .
• If you expect a difference between groups in a specific direction, use a one-tailed test .
• If you don’t have any expectations for the direction of a difference between groups, use a two-tailed test .

The only parametric correlation test is Pearson’s r . The correlation coefficient ( r ) tells you the strength of a linear relationship between two quantitative variables.

However, to test whether the correlation in the sample is strong enough to be important in the population, you also need to perform a significance test of the correlation coefficient, usually a t test, to obtain a p value. This test uses your sample size to calculate how much the correlation coefficient differs from zero in the population.

You use a dependent-samples, one-tailed t test to assess whether the meditation exercise significantly improved math test scores. The test gives you:

• a t value (test statistic) of 3.00
• a p value of 0.0028

Although Pearson’s r is a test statistic, it doesn’t tell you anything about how significant the correlation is in the population. You also need to test whether this sample correlation coefficient is large enough to demonstrate a correlation in the population.

A t test can also determine how significantly a correlation coefficient differs from zero based on sample size. Since you expect a positive correlation between parental income and GPA, you use a one-sample, one-tailed t test. The t test gives you:

• a t value of 3.08
• a p value of 0.001

The final step of statistical analysis is interpreting your results.

Statistical significance

In hypothesis testing, statistical significance is the main criterion for forming conclusions. You compare your p value to a set significance level (usually 0.05) to decide whether your results are statistically significant or non-significant.

Statistically significant results are considered unlikely to have arisen solely due to chance. There is only a very low chance of such a result occurring if the null hypothesis is true in the population.

This means that you believe the meditation intervention, rather than random factors, directly caused the increase in test scores. Example: Interpret your results (correlational study) You compare your p value of 0.001 to your significance threshold of 0.05. With a p value under this threshold, you can reject the null hypothesis. This indicates a statistically significant correlation between parental income and GPA in male college students.

Note that correlation doesn’t always mean causation, because there are often many underlying factors contributing to a complex variable like GPA. Even if one variable is related to another, this may be because of a third variable influencing both of them, or indirect links between the two variables.

Effect size

A statistically significant result doesn’t necessarily mean that there are important real life applications or clinical outcomes for a finding.

In contrast, the effect size indicates the practical significance of your results. It’s important to report effect sizes along with your inferential statistics for a complete picture of your results. You should also report interval estimates of effect sizes if you’re writing an APA style paper .

With a Cohen’s d of 0.72, there’s medium to high practical significance to your finding that the meditation exercise improved test scores. Example: Effect size (correlational study) To determine the effect size of the correlation coefficient, you compare your Pearson’s r value to Cohen’s effect size criteria.

Decision errors

Type I and Type II errors are mistakes made in research conclusions. A Type I error means rejecting the null hypothesis when it’s actually true, while a Type II error means failing to reject the null hypothesis when it’s false.

You can aim to minimise the risk of these errors by selecting an optimal significance level and ensuring high power . However, there’s a trade-off between the two errors, so a fine balance is necessary.

Frequentist versus Bayesian statistics

Traditionally, frequentist statistics emphasises null hypothesis significance testing and always starts with the assumption of a true null hypothesis.

However, Bayesian statistics has grown in popularity as an alternative approach in the last few decades. In this approach, you use previous research to continually update your hypotheses based on your expectations and observations.

Bayes factor compares the relative strength of evidence for the null versus the alternative hypothesis rather than making a conclusion about rejecting the null hypothesis or not.

Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.

The research methods you use depend on the type of data you need to answer your research question .

• If you want to measure something or test a hypothesis , use quantitative methods . If you want to explore ideas, thoughts, and meanings, use qualitative methods .
• If you want to analyse a large amount of readily available data, use secondary data. If you want data specific to your purposes with control over how they are generated, collect primary data.
• If you want to establish cause-and-effect relationships between variables , use experimental methods. If you want to understand the characteristics of a research subject, use descriptive methods.

Statistical analysis is the main method for analyzing quantitative research data . It uses probabilities and models to test predictions about a population from sample data.

Is this article helpful?

Other students also liked, a quick guide to experimental design | 5 steps & examples, controlled experiments | methods & examples of control, between-subjects design | examples, pros & cons, more interesting articles.

• Central Limit Theorem | Formula, Definition & Examples
• Central Tendency | Understanding the Mean, Median & Mode
• Correlation Coefficient | Types, Formulas & Examples
• Descriptive Statistics | Definitions, Types, Examples
• How to Calculate Standard Deviation (Guide) | Calculator & Examples
• How to Calculate Variance | Calculator, Analysis & Examples
• How to Find Degrees of Freedom | Definition & Formula
• How to Find Interquartile Range (IQR) | Calculator & Examples
• How to Find Outliers | Meaning, Formula & Examples
• How to Find the Geometric Mean | Calculator & Formula
• How to Find the Mean | Definition, Examples & Calculator
• How to Find the Median | Definition, Examples & Calculator
• How to Find the Range of a Data Set | Calculator & Formula
• Inferential Statistics | An Easy Introduction & Examples
• Levels of measurement: Nominal, ordinal, interval, ratio
• Missing Data | Types, Explanation, & Imputation
• Normal Distribution | Examples, Formulas, & Uses
• Null and Alternative Hypotheses | Definitions & Examples
• Poisson Distributions | Definition, Formula & Examples
• Skewness | Definition, Examples & Formula
• T-Distribution | What It Is and How To Use It (With Examples)
• The Standard Normal Distribution | Calculator, Examples & Uses
• Type I & Type II Errors | Differences, Examples, Visualizations
• Understanding Confidence Intervals | Easy Examples & Formulas
• Variability | Calculating Range, IQR, Variance, Standard Deviation
• What is Effect Size and Why Does It Matter? (Examples)
• What Is Interval Data? | Examples & Definition
• What Is Nominal Data? | Examples & Definition
• What Is Ordinal Data? | Examples & Definition
• What Is Ratio Data? | Examples & Definition
• What Is the Mode in Statistics? | Definition, Examples & Calculator

Microsoft and LinkedIn release the 2024 Work Trend Index on the state of AI at work

May 8, 2024 | Microsoft Source

• Share on Facebook (opens new window)
• Share on LinkedIn (opens new window)
• Share on Twitter (opens new window)

New data shows most employees are experimenting with AI and growing their skills — now, the job of every leader is to channel this experimentation into business impact

REDMOND, Wash. — May 8, 2024 — On Wednesday, Microsoft Corp. and LinkedIn released the 2024 Work Trend Index, a joint report on the state of AI at work titled, “ AI at work is here. Now comes the hard part .” The research — based on a survey of 31,000 people across 31 countries, labor and hiring trends on LinkedIn, trillions of Microsoft 365 productivity signals, and research with Fortune 500 customers — shows how, just one year in, AI is influencing the way people work, lead and hire around the world. Microsoft also announced new capabilities in Copilot for Microsoft 365, and LinkedIn made free more than 50 learning courses for LinkedIn Premium subscribers designed to empower professionals at all levels to advance their AI aptitude. [1]

The data is in: 2024 is the year AI at work gets real. Use of generative AI at work has nearly doubled in the past six months. LinkedIn is seeing a significant increase in professionals adding AI skills to their profiles, and most leaders say they wouldn’t hire someone without AI skills. But with many leaders worried their company lacks an AI vision, and employees bringing their own AI tools to work, leaders have reached the hard part of any tech disruption: moving from experimentation to tangible business impact.

“AI is democratizing expertise across the workforce,” said Satya Nadella, chairman and CEO, Microsoft. “Our latest research highlights the opportunity for every organization to apply this technology to drive better decision-making, collaboration — and ultimately business outcomes.”

The report highlights three insights every leader and professional needs to know about AI’s impact on work and the labor market in the year ahead:

• Employees want AI at work — and won’t wait for companies to catch up: Seventy-five percent of knowledge workers now use AI at work. Employees, many of them struggling to keep up with the pace and volume of work, say AI saves time, boosts creativity, and allows them to focus on their most important work. But although 79% of leaders agree AI adoption is critical to remain competitive, 59% worry about quantifying the productivity gains of AI and 60% say their company lacks a vision and plan to implement it. So, employees are taking things into their own hands. 78% of AI users are bringing their own tools to work — Bring Your Own AI (BYOAI) — missing out on the benefits that come from strategic AI use at scale and putting company data at risk. The opportunity for every leader is to channel this momentum into business impact at scale.
• For employees, AI raises the bar and breaks the career ceiling : Although AI and job loss are top of mind for many, the data offers a more nuanced view — one with a hidden talent shortage, employees eyeing a career change, and massive opportunity for those willing to skill up on AI. A majority of leaders (55%) are concerned about having enough talent to fill roles this year with leaders in cybersecurity, engineering and creative design feeling the pinch most. And professionals are looking. Forty-six percent across the globe are considering quitting in the year ahead — an all-time high since the Great Reshuffle of 2021. A separate LinkedIn study found U.S. numbers to be even higher with 85% eyeing career moves. Although two-thirds of leaders (66%) wouldn’t hire someone without AI skills, only 39% of users have received AI training from their company and only 25% of companies expect to offer it this year. So, professionals are skilling up on their own. As of late last year, we’ve seen a 142x increase in LinkedIn members adding AI skills like Copilot and ChatGPT to their profiles and a 160% increase in nontechnical professionals using LinkedIn Learning courses to build their AI aptitude. In a world where AI mentions in LinkedIn job posts drive a 17% bump in application growth, it’s a two-way street: Organizations that empower employees with AI tools and training will attract the best talent, and professionals who skill up will have the edge.
• The rise of the AI power user — and what they reveal about the future: Four types of AI users emerged in the research — from skeptics who rarely use AI to power users who use it extensively. Compared to skeptics, AI power users have reoriented their workdays in fundamental ways, reimagining business processes and saving over 30 minutes per day. Over 90% of power users say AI makes their overwhelming workload more manageable and their work more enjoyable, but they aren’t doing it on their own. These users are 61% more likely to have heard from their CEO on the importance of using generative AI at work, 53% more likely to receive encouragement from leadership to consider how AI can transform their function, and 35% more likely to receive tailored AI training for their specific role or function.

“AI is redefining work, and it’s clear we need new playbooks,” said Ryan Roslansky, CEO of LinkedIn. “It’s the leaders who build for agility instead of stability and invest in skill building internally that will give their organizations a competitive advantage and create more efficient, engaged and equitable teams.”

Microsoft is also announcing Copilot for Microsoft 365 innovations to help people get started with AI.

• A new auto-complete feature is coming to the prompt box. Copilot will now help people who have the start of a prompt by offering to complete it, suggesting a more detailed prompt based on what is being typed, to deliver a stronger result.
• When people know what they want, but don’t have the right words, the new rewrite feature in Copilot will turn a basic prompt into a rich one with the click of a button.
• Catch Up is a new chat interface that surfaces personal insights based on recent activity and provides responsive recommendations. For example, Copilot will flag an upcoming meeting and provide relevant information to help participants prepare.
• And new capabilities in Copilot Lab will enable people to create, publish and manage prompts tailored to them, and to their specific team, role and function.

These features will be available in the coming months.

LinkedIn is also providing AI tools to enable you to stay ahead in your career.

• For upskilling. LinkedIn Learning offers more than 22,000 courses, including more than 600 AI courses, to build aptitude in generative AI , empower your teams to make GAI-powered business investments , or simply to keep your skills sharp. This includes over 50 new AI learning courses to empower professionals at all skill levels. New courses are free and available for everyone to use through July 8. Additionally, our new AI-Powered Coaching in LinkedIn Learning helps learners find the content they need to grow their skills faster, with greater personalization and guided conversational learning.
• For career advancement. For LinkedIn Premium subscribers, AI-powered personalized takeaways on LinkedIn Feed on posts, articles or videos (from the article to the commentary) can also help you daily in your career with personalized, relevant insights and opportunities including ideas and actions you can take.
• For job seeking. And if you’re looking to change your job, we’re also making it easier and faster to find your ideal job. With new AI-powered tools, you can now assess your fit for a role in seconds based on your experience and skills, get advice on how to stand out, and subscribers will also see nudges, for example suggestions for skills to build, professionals in your network to reach out to, and more . So far, more than 90% of subscribers who have access shared it’s been helpful in job search.

To learn more, visit the Official Microsoft Blog , the 2024 Work Trend Index Report , and head to LinkedIn to hear more from the company’s Chief Economist, Karin Kimbrough.

About Microsoft

Microsoft (Nasdaq “MSFT” @microsoft) creates platforms and tools powered by AI to deliver innovative solutions that meet the evolving needs of our customers. The technology company is committed to making AI available broadly and doing so responsibly, with a mission to empower every person and every organization on the planet to achieve more.

About LinkedIn

LinkedIn connects the world’s professionals to make them more productive and successful and transforms the way companies hire, learn, market and sell. Our vision is to create economic opportunity for every member of the global workforce through the ongoing development of the world’s first Economic Graph. LinkedIn has more than 1 billion members and has offices around the globe.

For more information, press only:

Microsoft Media Relations, WE Communications, (425) 638-7777,  [email protected]

LinkedIn Press Line, [email protected]

Note to editors:  For more information, news and perspectives from Microsoft, please visit the Microsoft News Center at  http://news.microsoft.com . Web links, telephone numbers and titles were correct at time of publication but may have changed. For additional assistance, journalists and analysts may contact Microsoft’s Rapid Response Team or other appropriate contacts listed at  https://news.microsoft.com/microsoft-public-relations-contacts .

[1] Courses will be available for free until July 8, 2024.

Related Posts

ServiceNow and Microsoft expand strategic alliance, combining generative AI capabilities to enhance choice and flexibility

Microsoft announces $3.3 billion investment in Wisconsin to spur artificial intelligence innovation and economic growth

Axel Springer and Microsoft expand partnership across advertising, AI, content and Azure services 

The Estée Lauder Companies and Microsoft increase collaboration to power prestige beauty with generative AI

Microsoft earnings press release available on Investor Relations website

• Check us out on RSS

Share this page: