example of anova null hypothesis

Statistics Made Easy

Understanding the Null Hypothesis for ANOVA Models

A one-way ANOVA is used to determine if there is a statistically significant difference between the mean of three or more independent groups.

A one-way ANOVA uses the following null and alternative hypotheses:

H 0 : μ 1 = μ 2 = μ 3 = … = μ k (all of the group means are equal)
H A : At least one group mean is different from the rest

To decide if we should reject or fail to reject the null hypothesis, we must refer to the p-value in the output of the ANOVA table.

If the p-value is less than some significance level (e.g. 0.05) then we can reject the null hypothesis and conclude that not all group means are equal.

A two-way ANOVA is used to determine whether or not there is a statistically significant difference between the means of three or more independent groups that have been split on two variables (sometimes called “factors”).

A two-way ANOVA tests three null hypotheses at the same time:

All group means are equal at each level of the first variable
All group means are equal at each level of the second variable
There is no interaction effect between the two variables

To decide if we should reject or fail to reject each null hypothesis, we must refer to the p-values in the output of the two-way ANOVA table.

The following examples show how to decide to reject or fail to reject the null hypothesis in both a one-way ANOVA and two-way ANOVA.

Example 1: One-Way ANOVA

Suppose we want to know whether or not three different exam prep programs lead to different mean scores on a certain exam. To test this, we recruit 30 students to participate in a study and split them into three groups.

The students in each group are randomly assigned to use one of the three exam prep programs for the next three weeks to prepare for an exam. At the end of the three weeks, all of the students take the same exam.

The exam scores for each group are shown below:

When we enter these values into the One-Way ANOVA Calculator , we receive the following ANOVA table as the output:

Notice that the p-value is 0.11385 .

For this particular example, we would use the following null and alternative hypotheses:

H 0 : μ 1 = μ 2 = μ 3 (the mean exam score for each group is equal)

Since the p-value from the ANOVA table is not less than 0.05, we fail to reject the null hypothesis.

This means we don’t have sufficient evidence to say that there is a statistically significant difference between the mean exam scores of the three groups.

Example 2: Two-Way ANOVA

Suppose a botanist wants to know whether or not plant growth is influenced by sunlight exposure and watering frequency.

She plants 40 seeds and lets them grow for two months under different conditions for sunlight exposure and watering frequency. After two months, she records the height of each plant. The results are shown below:

In the table above, we see that there were five plants grown under each combination of conditions.

For example, there were five plants grown with daily watering and no sunlight and their heights after two months were 4.8 inches, 4.4 inches, 3.2 inches, 3.9 inches, and 4.4 inches:

She performs a two-way ANOVA in Excel and ends up with the following output:

We can see the following p-values in the output of the two-way ANOVA table:

The p-value for watering frequency is 0.975975 . This is not statistically significant at a significance level of 0.05.
The p-value for sunlight exposure is 3.9E-8 (0.000000039) . This is statistically significant at a significance level of 0.05.
The p-value for the interaction between watering frequency and sunlight exposure is 0.310898 . This is not statistically significant at a significance level of 0.05.

These results indicate that sunlight exposure is the only factor that has a statistically significant effect on plant height.

And because there is no interaction effect, the effect of sunlight exposure is consistent across each level of watering frequency.

That is, whether a plant is watered daily or weekly has no impact on how sunlight exposure affects a plant.

Additional Resources

The following tutorials provide additional information about ANOVA models:

How to Interpret the F-Value and P-Value in ANOVA How to Calculate Sum of Squares in ANOVA What Does a High F Value Mean in ANOVA?

Featured Posts

5 Regularization Techniques You Should Know

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike. My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Statistics and probability

Course: statistics and probability > unit 16.

ANOVA 1: Calculating SST (total sum of squares)
ANOVA 2: Calculating SSW and SSB (total sum of squares within and between)

ANOVA 3: Hypothesis test with F-statistic

Want to join the conversation.

Upvote Button navigates to signup page
Downvote Button navigates to signup page
Flag Button navigates to signup page

Video transcript

13.1 One-Way ANOVA

The purpose of a one-way ANOVA test is to determine the existence of a statistically significant difference among several group means. The test uses variances to help determine if the means are equal or not. To perform a one-way ANOVA test, there are five basic assumptions to be fulfilled:

Each population from which a sample is taken is assumed to be normal.
All samples are randomly selected and independent.
The populations are assumed to have equal standard deviations (or variances).
The factor is a categorical variable.
The response is a numerical variable.

The Null and Alternative Hypotheses

The null hypothesis is that all the group population means are the same. The alternative hypothesis is that at least one pair of means is different. For example, if there are k groups

H 0 : μ 1 = μ 2 = μ 3 = ... = μ k

H a : At least two of the group means μ 1 , μ 2 , μ 3 , ..., μ k are not equal. That is, μ i ≠ μ j for some i ≠ j .

The graphs, a set of box plots representing the distribution of values with the group means indicated by a horizontal line through the box, help in the understanding of the hypothesis test. In the first graph (red box plots), H 0 : μ 1 = μ 2 = μ 3 and the three populations have the same distribution if the null hypothesis is true. The variance of the combined data is approximately the same as the variance of each of the populations.

If the null hypothesis is false, then the variance of the combined data is larger, which is caused by the different means as shown in the second graph (green box plots).

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.

Access for free at https://openstax.org/books/statistics/pages/1-introduction

Authors: Barbara Illowsky, Susan Dean
Publisher/website: OpenStax
Book title: Statistics
Publication date: Mar 27, 2020
Location: Houston, Texas
Book URL: https://openstax.org/books/statistics/pages/1-introduction
Section URL: https://openstax.org/books/statistics/pages/13-1-one-way-anova

© Jan 23, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Hypothesis Testing - Analysis of Variance (ANOVA)

The ANOVA Approach

Test statistic for anova.

All Modules

Table of F-Statistic Values

Consider an example with four independent groups and a continuous outcome measure. The independent groups might be defined by a particular characteristic of the participants such as BMI (e.g., underweight, normal weight, overweight, obese) or by the investigator (e.g., randomizing participants to one of four competing treatments, call them A, B, C and D). Suppose that the outcome is systolic blood pressure, and we wish to test whether there is a statistically significant difference in mean systolic blood pressures among the four groups. The sample data are organized as follows:

The hypotheses of interest in an ANOVA are as follows:

H 0 : μ 1 = μ 2 = μ 3 ... = μ k
H 1 : Means are not all equal.

where k = the number of independent comparison groups.

In this example, the hypotheses are:

H 0 : μ 1 = μ 2 = μ 3 = μ 4
H 1 : The means are not all equal.

The null hypothesis in ANOVA is always that there is no difference in means. The research or alternative hypothesis is always that the means are not all equal and is usually written in words rather than in mathematical symbols. The research hypothesis captures any difference in means and includes, for example, the situation where all four means are unequal, where one is different from the other three, where two are different, and so on. The alternative hypothesis, as shown above, capture all possible situations other than equality of all means specified in the null hypothesis.

The test statistic for testing H 0 : μ 1 = μ 2 = ... = μ k is:

and the critical value is found in a table of probability values for the F distribution with (degrees of freedom) df 1 = k-1, df 2 =N-k. The table can be found in "Other Resources" on the left side of the pages.

NOTE: The test statistic F assumes equal variability in the k populations (i.e., the population variances are equal, or s 1 2 = s 2 2 = ... = s k 2 ). This means that the outcome is equally variable in each of the comparison populations. This assumption is the same as that assumed for appropriate use of the test statistic to test equality of two independent means. It is possible to assess the likelihood that the assumption of equal variances is true and the test can be conducted in most statistical computing packages. If the variability in the k comparison groups is not similar, then alternative techniques must be used.

The F statistic is computed by taking the ratio of what is called the "between treatment" variability to the "residual or error" variability. This is where the name of the procedure originates. In analysis of variance we are testing for a difference in means (H 0 : means are all equal versus H 1 : means are not all equal) by evaluating variability in the data. The numerator captures between treatment variability (i.e., differences among the sample means) and the denominator contains an estimate of the variability in the outcome. The test statistic is a measure that allows us to assess whether the differences among the sample means (numerator) are more than would be expected by chance if the null hypothesis is true. Recall in the two independent sample test, the test statistic was computed by taking the ratio of the difference in sample means (numerator) to the variability in the outcome (estimated by Sp).

The decision rule for the F test in ANOVA is set up in a similar way to decision rules we established for t tests. The decision rule again depends on the level of significance and the degrees of freedom. The F statistic has two degrees of freedom. These are denoted df 1 and df 2 , and called the numerator and denominator degrees of freedom, respectively. The degrees of freedom are defined as follows:

df 1 = k-1 and df 2 =N-k,

where k is the number of comparison groups and N is the total number of observations in the analysis. If the null hypothesis is true, the between treatment variation (numerator) will not exceed the residual or error variation (denominator) and the F statistic will small. If the null hypothesis is false, then the F statistic will be large. The rejection region for the F test is always in the upper (right-hand) tail of the distribution as shown below.

Rejection Region for F Test with a =0.05, df 1 =3 and df 2 =36 (k=4, N=40)

Graph of rejection region for the F statistic with alpha=0.05

For the scenario depicted here, the decision rule is: Reject H 0 if F > 2.87.

return to top | previous page | next page

Home » ANOVA (Analysis of variance) – Formulas, Types, and Examples

ANOVA (Analysis of variance) – Formulas, Types, and Examples

Table of Contents

Analysis of Variance (ANOVA)

Analysis of Variance (ANOVA) is a statistical method used to test differences between two or more means. It is similar to the t-test, but the t-test is generally used for comparing two means, while ANOVA is used when you have more than two means to compare.

ANOVA is based on comparing the variance (or variation) between the data samples to the variation within each particular sample. If the between-group variance is high and the within-group variance is low, this provides evidence that the means of the groups are significantly different.

ANOVA Terminology

When discussing ANOVA, there are several key terms to understand:

Factor : This is another term for the independent variable in your analysis. In a one-way ANOVA, there is one factor, while in a two-way ANOVA, there are two factors.
Levels : These are the different groups or categories within a factor. For example, if the factor is ‘diet’ the levels might be ‘low fat’, ‘medium fat’, and ‘high fat’.
Response Variable : This is the dependent variable or the outcome that you are measuring.
Within-group Variance : This is the variance or spread of scores within each level of your factor.
Between-group Variance : This is the variance or spread of scores between the different levels of your factor.
Grand Mean : This is the overall mean when you consider all the data together, regardless of the factor level.
Treatment Sums of Squares (SS) : This represents the between-group variability. It is the sum of the squared differences between the group means and the grand mean.
Error Sums of Squares (SS) : This represents the within-group variability. It’s the sum of the squared differences between each observation and its group mean.
Total Sums of Squares (SS) : This is the sum of the Treatment SS and the Error SS. It represents the total variability in the data.
Degrees of Freedom (df) : The degrees of freedom are the number of values that have the freedom to vary when computing a statistic. For example, if you have ‘n’ observations in one group, then the degrees of freedom for that group is ‘n-1’.
Mean Square (MS) : Mean Square is the average squared deviation and is calculated by dividing the sum of squares by the corresponding degrees of freedom.
F-Ratio : This is the test statistic for ANOVAs, and it’s the ratio of the between-group variance to the within-group variance. If the between-group variance is significantly larger than the within-group variance, the F-ratio will be large and likely significant.
Null Hypothesis (H0) : This is the hypothesis that there is no difference between the group means.
Alternative Hypothesis (H1) : This is the hypothesis that there is a difference between at least two of the group means.
p-value : This is the probability of obtaining a test statistic as extreme as the one that was actually observed, assuming that the null hypothesis is true. If the p-value is less than the significance level (usually 0.05), then the null hypothesis is rejected in favor of the alternative hypothesis.
Post-hoc tests : These are follow-up tests conducted after an ANOVA when the null hypothesis is rejected, to determine which specific groups’ means (levels) are different from each other. Examples include Tukey’s HSD, Scheffe, Bonferroni, among others.

Types of ANOVA

Types of ANOVA are as follows:

One-way (or one-factor) ANOVA

This is the simplest type of ANOVA, which involves one independent variable . For example, comparing the effect of different types of diet (vegetarian, pescatarian, omnivore) on cholesterol level.

Two-way (or two-factor) ANOVA

This involves two independent variables. This allows for testing the effect of each independent variable on the dependent variable , as well as testing if there’s an interaction effect between the independent variables on the dependent variable.

Repeated Measures ANOVA

This is used when the same subjects are measured multiple times under different conditions, or at different points in time. This type of ANOVA is often used in longitudinal studies.

Mixed Design ANOVA

This combines features of both between-subjects (independent groups) and within-subjects (repeated measures) designs. In this model, one factor is a between-subjects variable and the other is a within-subjects variable.

Multivariate Analysis of Variance (MANOVA)

This is used when there are two or more dependent variables. It tests whether changes in the independent variable(s) correspond to changes in the dependent variables.

Analysis of Covariance (ANCOVA)

This combines ANOVA and regression. ANCOVA tests whether certain factors have an effect on the outcome variable after removing the variance for which quantitative covariates (interval variables) account. This allows the comparison of one variable outcome between groups, while statistically controlling for the effect of other continuous variables that are not of primary interest.

Nested ANOVA

This model is used when the groups can be clustered into categories. For example, if you were comparing students’ performance from different classrooms and different schools, “classroom” could be nested within “school.”

ANOVA Formulas

ANOVA Formulas are as follows:

Sum of Squares Total (SST)

This represents the total variability in the data. It is the sum of the squared differences between each observation and the overall mean.

yi represents each individual data point
y_mean represents the grand mean (mean of all observations)

Sum of Squares Within (SSW)

This represents the variability within each group or factor level. It is the sum of the squared differences between each observation and its group mean.

yij represents each individual data point within a group
y_meani represents the mean of the ith group

Sum of Squares Between (SSB)

This represents the variability between the groups. It is the sum of the squared differences between the group means and the grand mean, multiplied by the number of observations in each group.

ni represents the number of observations in each group
y_mean represents the grand mean

Degrees of Freedom

The degrees of freedom are the number of values that have the freedom to vary when calculating a statistic.

For within groups (dfW):

For between groups (dfB):

For total (dfT):

N represents the total number of observations
k represents the number of groups

Mean Squares

Mean squares are the sum of squares divided by the respective degrees of freedom.

Mean Squares Between (MSB):

Mean Squares Within (MSW):

F-Statistic

The F-statistic is used to test whether the variability between the groups is significantly greater than the variability within the groups.

If the F-statistic is significantly higher than what would be expected by chance, we reject the null hypothesis that all group means are equal.

Examples of ANOVA

Examples 1:

Suppose a psychologist wants to test the effect of three different types of exercise (yoga, aerobic exercise, and weight training) on stress reduction. The dependent variable is the stress level, which can be measured using a stress rating scale.

Here are hypothetical stress ratings for a group of participants after they followed each of the exercise regimes for a period:

Yoga: [3, 2, 2, 1, 2, 2, 3, 2, 1, 2]
Aerobic Exercise: [2, 3, 3, 2, 3, 2, 3, 3, 2, 2]
Weight Training: [4, 4, 5, 5, 4, 5, 4, 5, 4, 5]

The psychologist wants to determine if there is a statistically significant difference in stress levels between these different types of exercise.

To conduct the ANOVA:

1. State the hypotheses:

Null Hypothesis (H0): There is no difference in mean stress levels between the three types of exercise.
Alternative Hypothesis (H1): There is a difference in mean stress levels between at least two of the types of exercise.

2. Calculate the ANOVA statistics:

Compute the Sum of Squares Between (SSB), Sum of Squares Within (SSW), and Sum of Squares Total (SST).
Calculate the Degrees of Freedom (dfB, dfW, dfT).
Calculate the Mean Squares Between (MSB) and Mean Squares Within (MSW).
Compute the F-statistic (F = MSB / MSW).

3. Check the p-value associated with the calculated F-statistic.

If the p-value is less than the chosen significance level (often 0.05), then we reject the null hypothesis in favor of the alternative hypothesis. This suggests there is a statistically significant difference in mean stress levels between the three exercise types.

4. Post-hoc tests

If we reject the null hypothesis, we conduct a post-hoc test to determine which specific groups’ means (exercise types) are different from each other.

Examples 2:

Suppose an agricultural scientist wants to compare the yield of three varieties of wheat. The scientist randomly selects four fields for each variety and plants them. After harvest, the yield from each field is measured in bushels. Here are the hypothetical yields:

The scientist wants to know if the differences in yields are due to the different varieties or just random variation.

Here’s how to apply the one-way ANOVA to this situation:

Null Hypothesis (H0): The means of the three populations are equal.
Alternative Hypothesis (H1): At least one population mean is different.
Calculate the Degrees of Freedom (dfB for between groups, dfW for within groups, dfT for total).
If the p-value is less than the chosen significance level (often 0.05), then we reject the null hypothesis in favor of the alternative hypothesis. This would suggest there is a statistically significant difference in mean yields among the three varieties.
If we reject the null hypothesis, we conduct a post-hoc test to determine which specific groups’ means (wheat varieties) are different from each other.

How to Conduct ANOVA

Conducting an Analysis of Variance (ANOVA) involves several steps. Here’s a general guideline on how to perform it:

Null Hypothesis (H0): The means of all groups are equal.
Alternative Hypothesis (H1): At least one group mean is different from the others.
The significance level (often denoted as α) is usually set at 0.05. This implies that you are willing to accept a 5% chance that you are wrong in rejecting the null hypothesis.
Data should be collected for each group under study. Make sure that the data meet the assumptions of an ANOVA: normality, independence, and homogeneity of variances.
Calculate the Degrees of Freedom (df) for each sum of squares (dfB, dfW, dfT).
Compute the Mean Squares Between (MSB) and Mean Squares Within (MSW) by dividing the sum of squares by the corresponding degrees of freedom.
Compute the F-statistic as the ratio of MSB to MSW.
Determine the critical F-value from the F-distribution table using dfB and dfW.
If the calculated F-statistic is greater than the critical F-value, reject the null hypothesis.
If the p-value associated with the calculated F-statistic is smaller than the significance level (0.05 typically), you reject the null hypothesis.
If you rejected the null hypothesis, you can conduct post-hoc tests (like Tukey’s HSD) to determine which specific groups’ means (if you have more than two groups) are different from each other.
Regardless of the result, report your findings in a clear, understandable manner. This typically includes reporting the test statistic, p-value, and whether the null hypothesis was rejected.

When to use ANOVA

ANOVA (Analysis of Variance) is used when you have three or more groups and you want to compare their means to see if they are significantly different from each other. It is a statistical method that is used in a variety of research scenarios. Here are some examples of when you might use ANOVA:

Comparing Groups : If you want to compare the performance of more than two groups, for example, testing the effectiveness of different teaching methods on student performance.
Evaluating Interactions : In a two-way or factorial ANOVA, you can test for an interaction effect. This means you are not only interested in the effect of each individual factor, but also whether the effect of one factor depends on the level of another factor.
Repeated Measures : If you have measured the same subjects under different conditions or at different time points, you can use repeated measures ANOVA to compare the means of these repeated measures while accounting for the correlation between measures from the same subject.
Experimental Designs : ANOVA is often used in experimental research designs when subjects are randomly assigned to different conditions and the goal is to compare the means of the conditions.

Here are the assumptions that must be met to use ANOVA:

Normality : The data should be approximately normally distributed.
Homogeneity of Variances : The variances of the groups you are comparing should be roughly equal. This assumption can be tested using Levene’s test or Bartlett’s test.
Independence : The observations should be independent of each other. This assumption is met if the data is collected appropriately with no related groups (e.g., twins, matched pairs, repeated measures).

Applications of ANOVA

The Analysis of Variance (ANOVA) is a powerful statistical technique that is used widely across various fields and industries. Here are some of its key applications:

Agriculture

ANOVA is commonly used in agricultural research to compare the effectiveness of different types of fertilizers, crop varieties, or farming methods. For example, an agricultural researcher could use ANOVA to determine if there are significant differences in the yields of several varieties of wheat under the same conditions.

Manufacturing and Quality Control

ANOVA is used to determine if different manufacturing processes or machines produce different levels of product quality. For instance, an engineer might use it to test whether there are differences in the strength of a product based on the machine that produced it.

Marketing Research

Marketers often use ANOVA to test the effectiveness of different advertising strategies. For example, a marketer could use ANOVA to determine whether different marketing messages have a significant impact on consumer purchase intentions.

Healthcare and Medicine

In medical research, ANOVA can be used to compare the effectiveness of different treatments or drugs. For example, a medical researcher could use ANOVA to test whether there are significant differences in recovery times for patients who receive different types of therapy.

ANOVA is used in educational research to compare the effectiveness of different teaching methods or educational interventions. For example, an educator could use it to test whether students perform significantly differently when taught with different teaching methods.

Psychology and Social Sciences

Psychologists and social scientists use ANOVA to compare group means on various psychological and social variables. For example, a psychologist could use it to determine if there are significant differences in stress levels among individuals in different occupations.

Biology and Environmental Sciences

Biologists and environmental scientists use ANOVA to compare different biological and environmental conditions. For example, an environmental scientist could use it to determine if there are significant differences in the levels of a pollutant in different bodies of water.

Advantages of ANOVA

Here are some advantages of using ANOVA:

Comparing Multiple Groups: One of the key advantages of ANOVA is the ability to compare the means of three or more groups. This makes it more powerful and flexible than the t-test, which is limited to comparing only two groups.

Control of Type I Error: When comparing multiple groups, the chances of making a Type I error (false positive) increases. One of the strengths of ANOVA is that it controls the Type I error rate across all comparisons. This is in contrast to performing multiple pairwise t-tests which can inflate the Type I error rate.

Testing Interactions: In factorial ANOVA, you can test not only the main effect of each factor, but also the interaction effect between factors. This can provide valuable insights into how different factors or variables interact with each other.

Handling Continuous and Categorical Variables: ANOVA can handle both continuous and categorical variables . The dependent variable is continuous and the independent variables are categorical.

Robustness: ANOVA is considered robust to violations of normality assumption when group sizes are equal. This means that even if your data do not perfectly meet the normality assumption, you might still get valid results.

Provides Detailed Analysis: ANOVA provides a detailed breakdown of variances and interactions between variables which can be useful in understanding the underlying factors affecting the outcome.

Capability to Handle Complex Experimental Designs: Advanced types of ANOVA (like repeated measures ANOVA, MANOVA, etc.) can handle more complex experimental designs, including those where measurements are taken on the same subjects over time, or when you want to analyze multiple dependent variables at once.

Disadvantages of ANOVA

Some limitations or disadvantages that are important to consider:

Assumptions: ANOVA relies on several assumptions including normality (the data follows a normal distribution), independence (the observations are independent of each other), and homogeneity of variances (the variances of the groups are roughly equal). If these assumptions are violated, the results of the ANOVA may not be valid.

Sensitivity to Outliers: ANOVA can be sensitive to outliers. A single extreme value in one group can affect the sum of squares and consequently influence the F-statistic and the overall result of the test.

Dichotomous Variables: ANOVA is not suitable for dichotomous variables (variables that can take only two values, like yes/no or male/female). It is used to compare the means of groups for a continuous dependent variable.

Lack of Specificity: Although ANOVA can tell you that there is a significant difference between groups, it doesn’t tell you which specific groups are significantly different from each other. You need to carry out further post-hoc tests (like Tukey’s HSD or Bonferroni) for these pairwise comparisons.

Complexity with Multiple Factors: When dealing with multiple factors and interactions in factorial ANOVA, interpretation can become complex. The presence of interaction effects can make main effects difficult to interpret.

Requires Larger Sample Sizes: To detect an effect of a certain size, ANOVA generally requires larger sample sizes than a t-test.

Equal Group Sizes: While not always a strict requirement, ANOVA is most powerful and its assumptions are most likely to be met when groups are of equal or similar sizes.

About the author

Muhammad Hassan

Researcher, Academic Writer, Web developer

Cluster Analysis – Types, Methods and Examples

Discriminant Analysis – Methods, Types and...

MANOVA (Multivariate Analysis of Variance) –...

Documentary Analysis – Methods, Applications and...

Graphical Methods – Types, Examples and Guide

Substantive Framework – Types, Methods and...

Understanding the Null Hypothesis for ANOVA Models

A one-way ANOVA is used to determine if there is a statistically significant difference between the mean of three or more independent groups.

A one-way ANOVA uses the following null and alternative hypotheses:

H 0 : μ 1 = μ 2 = μ 3 = … = μ k (all of the group means are equal)
H A : At least one group mean is different from the rest

To decide if we should reject or fail to reject the null hypothesis, we must refer to the p-value in the output of the ANOVA table.

If the p-value is less than some significance level (e.g. 0.05) then we can reject the null hypothesis and conclude that not all group means are equal.

A two-way ANOVA tests three null hypotheses at the same time:

All group means are equal at each level of the first variable
All group means are equal at each level of the second variable
There is no interaction effect between the two variables

To decide if we should reject or fail to reject each null hypothesis, we must refer to the p-values in the output of the two-way ANOVA table.

The following examples show how to decide to reject or fail to reject the null hypothesis in both a one-way ANOVA and two-way ANOVA.

Example 1: One-Way ANOVA

The exam scores for each group are shown below:

When we enter these values into the One-Way ANOVA Calculator , we receive the following ANOVA table as the output:

Notice that the p-value is 0.11385 .

For this particular example, we would use the following null and alternative hypotheses:

H 0 : μ 1 = μ 2 = μ 3 (the mean exam score for each group is equal)

Since the p-value from the ANOVA table is not less than 0.05, we fail to reject the null hypothesis.

This means we don’t have sufficient evidence to say that there is a statistically significant difference between the mean exam scores of the three groups.

Example 2: Two-Way ANOVA

Suppose a botanist wants to know whether or not plant growth is influenced by sunlight exposure and watering frequency.

In the table above, we see that there were five plants grown under each combination of conditions.

For example, there were five plants grown with daily watering and no sunlight and their heights after two months were 4.8 inches, 4.4 inches, 3.2 inches, 3.9 inches, and 4.4 inches:

She performs a two-way ANOVA in Excel and ends up with the following output:

We can see the following p-values in the output of the two-way ANOVA table:

The p-value for watering frequency is 0.975975 . This is not statistically significant at a significance level of 0.05.
The p-value for sunlight exposure is 3.9E-8 (0.000000039) . This is statistically significant at a significance level of 0.05.
The p-value for the interaction between watering frequency and sunlight exposure is 0.310898 . This is not statistically significant at a significance level of 0.05.

These results indicate that sunlight exposure is the only factor that has a statistically significant effect on plant height.

And because there is no interaction effect, the effect of sunlight exposure is consistent across each level of watering frequency.

That is, whether a plant is watered daily or weekly has no impact on how sunlight exposure affects a plant.

Additional Resources

The following tutorials provide additional information about ANOVA models:

How to Interpret the F-Value and P-Value in ANOVA How to Calculate Sum of Squares in ANOVA What Does a High F Value Mean in ANOVA?

How to Fix in R: incomplete final line found by readTableHeader

Pandas: how to add subtotals to pivot table, related posts, how to normalize data between -1 and 1, vba: how to check if string contains another..., how to interpret f-values in a two-way anova, how to create a vector of ones in..., how to determine if a probability distribution is..., what is a symmetric histogram (definition & examples), how to find the mode of a histogram..., how to find quartiles in even and odd..., how to calculate sxy in statistics (with example), how to calculate sxx in statistics (with example).

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

11.4 One-Way ANOVA and Hypothesis Tests for Three or More Population Means

Learning objectives.

Conduct and interpret hypothesis tests for three or more population means using one-way ANOVA.

The purpose of a one-way ANOVA (analysis of variance) test is to determine the existence of a statistically significant difference among the means of three or more populations. The test actually uses variances to help determine if the population means are equal or not.

Throughout this section, we will use subscripts to identify the values for the means, sample sizes, and standard deviations for the populations:

[latex]k[/latex] is the number of populations under study, [latex]n[/latex] is the total number of observations in all of the samples combined, and [latex]\overline{\overline{x}}[/latex] is the mean of the sample means.

[latex]\begin{eqnarray*} n & = & n_1+n_2+\cdots+n_k \\ \\ \overline{\overline{x}} & = & \frac{n_1 \times \overline{x}_1 +n_2 \times \overline{x}_2 +\cdots+n_k \times \overline{x}_k}{n} \end{eqnarray*}[/latex]

One-Way ANOVA

A predictor variable is called a factor or independent variable . For example age, temperature, and gender are factors. The groups or samples are often referred to as treatments . This terminology comes from the use of ANOVA procedures in medical and psychological research to determine if there is a difference in the effects of different treatments.

A local college wants to compare the mean GPA for players on four of its sports teams: basketball, baseball, hockey, and lacrosse. A random sample of players was taken from each team and their GPA recorded in the table below.

In this example, the factor is the sports team.

[latex]\begin{eqnarray*} k & = & 4 \\ \\ n & = & n_1+n_2+n_3+n_4 \\ & = & 5+5+5+5 \\ & = & 20 \\ \\ \overline{\overline{x}} & = & \frac{n_1 \times \overline{x}_1+n_2 \times \overline{x}_2+n_3 \times \overline{x}_3+n_4 \times \overline{x}_4}{n} \\ & = & \frac{5 \times 3.22+5 \times 3.02+5 \times 3+5 \times 2.94}{20} \\& = & 3.045 \end{eqnarray*}[/latex]

The following assumptions are required to use a one-way ANOVA test:

Each population from which a sample is taken is normally distributed.
All samples are randomly selected and independently taken from the populations.
The populations are assumed to have equal variances.
The population data is numerical (interval or ratio level).

The logic behind one-way ANOVA is to compare population means based on two independent estimates of the (assumed) equal variance [latex]\sigma^2[/latex] between the populations:

One estimate of the equal variance [latex]\sigma^2[/latex] is based on the variability among the sample means themselves (called the between-groups estimate of population variance).
One estimate of the equal variance [latex]\sigma^2[/latex] is based on the variability of the data within each sample (called the within-groups estimate of population variance).

The one-way ANOVA procedure compares these two estimates of the population variance [latex]\sigma^2[/latex] to determine if the population means are equal or if there is a difference in the population means. Because ANOVA involves the comparison of two estimates of variance, an [latex]F[/latex]-distribution is used to conduct the ANOVA test. The test statistic is an [latex]F[/latex]-score that is the ratio of the two estimates of population variance:

[latex]\displaystyle{F=\frac{\mbox{variance between groups}}{\mbox{variance within groups}}}[/latex]

The degrees of freedom for the [latex]F[/latex]-distribution are [latex]df_1=k-1[/latex] and [latex]df_2=n-k[/latex] where [latex]k[/latex] is the number of populations and [latex]n[/latex] is the total number of observations in all of the samples combined.

The variance between groups estimate of the population variance is called the mean square due to treatment , [latex]MST[/latex]. The [latex]MST[/latex] is the estimate of the population variance determined by the variance of the sample means from the overall sample mean [latex]\overline{\overline{x}}[/latex]. When the population means are equal, [latex]MST[/latex] provides an unbiased estimate of the population variance. When the population means are not equal, [latex]MST[/latex] provides an overestimate of the population variance.

[latex]\begin{eqnarray*} SST & = & n_1 \times (\overline{x}_1-\overline{\overline{x}})^2+n_2\times (\overline{x}_2-\overline{\overline{x}})^2+ \cdots +n_k \times (\overline{x}_k-\overline{\overline{x}})^2 \\ \\ MST & =& \frac{SST}{k-1} \end{eqnarray*}[/latex]

The variance within groups estimate of the population variance is called the mean square due to error , [latex]MSE[/latex]. The [latex]MSE[/latex] is the pooled estimate of the population variance using the sample variances as estimates for the population variance. The [latex]MSE[/latex] always provides an unbiased estimate of the population variance because it is not affected by whether or not the population means are equal.

[latex]\begin{eqnarray*} SSE & = & (n_1-1) \times s_1^2+ (n_2-1) \times s_2^2+ \cdots + (n_k-1) \times s_k^2\\ \\ MSE & =& \frac{SSE}{n -k} \end{eqnarray*}[/latex]

The one-way ANOVA test depends on the fact that the variance between groups [latex]MST[/latex] is influenced by differences between the population means, which results in [latex]MST[/latex] being either an unbiased or overestimate of the population variance. Because the variance within groups [latex]MSE[/latex] compares values of each group to its own group mean, [latex]MSE[/latex] is not affected by differences between the population means and is always an unbiased estimate of the population variance.

The null hypothesis in a one-way ANOVA test is that the population means are all equal and the alternative hypothesis is that there is a difference in the population means. The [latex]F[/latex]-score for the one-way ANOVA test is [latex]\displaystyle{F=\frac{MST}{MSE}}[/latex] with [latex]df_1=k-1[/latex] and [latex]df_2=n-k[/latex]. The p -value for the test is the area in the right tail of the [latex]F[/latex]-distribution, to the right of the [latex]F[/latex]-score.

When the variance between groups [latex]MST[/latex] and variance within groups [latex]MSE[/latex] are close in value, the [latex]F[/latex]-score is close to 1 and results in a large p -value. In this case, the conclusion is that the population means are equal.
When the variance between groups [latex]MST[/latex] is significantly larger than the variability within groups [latex]MSE[/latex], the [latex]F[/latex]-score is large and results in a small p -value. In this case, the conclusion is that there is a difference in the population means.

Steps to Conduct a Hypothesis Test for Three or More Population Means

Verify that the one-way ANOVA assumptions are met.

[latex]\begin{eqnarray*} \\ H_0: & & \mu_1=\mu_2=\cdots=\mu_k\end{eqnarray*}[/latex].

[latex]\begin{eqnarray*} \\ H_a: & & \mbox{at least one population mean is different from the others} \\ \\ \end{eqnarray*}[/latex]

Collect the sample information for the test and identify the significance level [latex]\alpha[/latex].

[latex]\begin{eqnarray*}F & = & \frac{MST}{MSE} \\ \\ df_1 & = & k-1 \\ \\ df_2 & = & n-k \\ \\ \end{eqnarray*}[/latex]

The results of the sample data are significant. There is sufficient evidence to conclude that the null hypothesis [latex]H_0[/latex] is an incorrect belief and that the alternative hypothesis [latex]H_a[/latex] is most likely correct.
The results of the sample data are not significant. There is not sufficient evidence to conclude that the alternative hypothesis [latex]H_a[/latex] may be correct.
Write down a concluding sentence specific to the context of the question.

Assume the populations are normally distributed and have equal variances. At the 5% significance level, is there a difference in the average GPA between the sports team.

Let basketball be population 1, let baseball be population 2, let hockey be population 3, and let lacrosse be population 4. From the question we have the following information:

Previously, we found [latex]k=4[/latex], [latex]n=20[/latex], and [latex]\overline{\overline{x}}=3.045[/latex].

Hypotheses:

[latex]\begin{eqnarray*} H_0: & & \mu_1=\mu_2=\mu_3=\mu_4 \\ H_a: & & \mbox{at least one population mean is different from the others} \end{eqnarray*}[/latex]

To calculate out the [latex]F[/latex]-score, we need to find [latex]MST[/latex] and [latex]MSE[/latex].

[latex]\begin{eqnarray*} SST & = & n_1 \times (\overline{x}_1-\overline{\overline{x}})^2+n_2\times (\overline{x}_2-\overline{\overline{x}})^2+n_3 \times (\overline{x}_3-\overline{\overline{x}})^2 +n_4 \times (\overline{x}_4-\overline{\overline{x}})^2\\ & = & 5 \times (3.22-3.045)^2+5 \times (3.02-3.045)^2+5 \times (3-3.045)^2 \\ & & +5 \times (2.94 -3.045)^2 \\ & = & 0.2215 \\ \\ MST & = & \frac{SST}{k-1} \\ & = & \frac{0.2215 }{4-1} \\ & = & 0.0738...\\ \\ SSE & = & (n_1-1) \times s_1^2+ (n_2-1) \times s_2^2+ (n_3-1) \times s_3^2+ (n_4-1) \times s_4^2\\ & = &( 5-1) \times 0.277+(5-1) \times 0.487+(5-1) \times 0.56 +(5-1)\times 0.623 \\ & = & 7.788 \\ \\ MSE & = & \frac{SSE}{n-k} \\ & = & \frac{7.788 }{20-4} \\ & = & 0.48675\end{eqnarray*}[/latex]

The p -value is the area in the right tail of the [latex]F[/latex]-distribution. To use the f.dist.rt function, we need to calculate out the [latex]F[/latex]-score and the degrees of freedom:

[latex]\begin{eqnarray*} F & = &\frac{MST}{MSE} \\ & = & \frac{0.0738...}{0.48675} \\ & = & 0.15168... \\ \\ df_1 & = & k-1 \\ & = & 4-1 \\ & = & 3 \\ \\df_2 & = & n-k \\ & = & 20-4 \\ & = & 16\end{eqnarray*}[/latex]

So the p -value[latex]=0.9271[/latex].

Conclusion:

Because p -value[latex]=0.9271 \gt 0.05=\alpha[/latex], we do not reject the null hypothesis. At the 5% significance level there is enough evidence to suggest that the mean GPA for the sports teams are the same.

The null hypothesis [latex]\mu_1=\mu_2=\mu_3=\mu_4[/latex] is the claim that the mean GPA for the sports teams are all equal.
The alternative hypothesis is the claim that at least one of the population means is not equal to the others. The alternative hypothesis does not say that all of the population means are not equal, only that at least one of them is not equal to the others.
The function is f.dist.rt because we are finding the area in the right tail of an [latex]F[/latex]-distribution.
Field 1 is the value of [latex]F[/latex].
Field 2 is the value of [latex]df_1[/latex].
Field 3 is the value of [latex]df_2[/latex].
The p -value of 0.9271 is a large probability compared to the significance level, and so is likely to happen assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis. In other words, the population means are all equal.

ANOVA Summary Tables

The calculation of the [latex]MST[/latex], [latex]MSE[/latex], and the [latex]F[/latex]-score for a one-way ANOVA test can be time consuming, even with the help of software like Excel. However, Excel has a built-in one-way ANOVA summary table that not only generates the averages, variances, [latex]MST[/latex] and [latex]MSE[/latex], but also calculates the required [latex]F[/latex]-score and p -value for the test.

USING EXCEL TO CREATE A ONE-WAY ANOVA SUMMARY TABLE

In order to create a one-way ANOVA summary table, we need to use the Analysis ToolPak. Follow these instructions to add the Analysis ToolPak.

Enter the data into an Excel worksheet.
Go to the Data tab and click on Data Analysis . If you do not see Data Analysis in the Data tab, you will need to install the Analysis ToolPak.
In the Data Analysis window, select Anova: Single Factor . Click OK .
In the Inpu t range, enter the cell range for the data.
In the Grouped By box, select rows if your data is entered as rows (the default is columns).
Click on Labels in first row if the you included the column headings in the input range.
In the Alpha box, enter the significance level for the test.
From the Output Options , select the location where you want the output to appear.

This website provides additional information on using Excel to create a one-way ANOVA summary table.

Because we are using the p -value approach to hypothesis testing, it is not crucial that we enter the actual significance level we are using for the test. The p -value (the area in the right tail of the [latex]F[/latex]-distribution) is not affected by significance level. For the critical-value approach to hypothesis testing, we must enter the correct significance level for the test because the critical value does depend on the significance level.

Let basketball be population 1, let baseball be population 2, let hockey be population 3, and let lacrosse be population 4.

The ANOVA summary table generated by Excel is shown below:

The p -value for the test is in the P -value column of the between groups row . So the p -value[latex]=0.9271[/latex].

In the top part of the ANOVA summary table (under the Summary heading), we have the averages and variances for each of the groups (basketball, baseball, hockey, and lacrosse).
The value of [latex]SST[/latex] (in the SS column of the between groups row).
The value of [latex]MST[/latex] (in the MS column of the between group s row).
The value of [latex]SSE[/latex] (in the SS column of the within groups row).
The value of [latex]MSE[/latex] (in the MS column of the within groups row).
The value of the [latex]F[/latex]-score (in the F column of the between groups row).
The p -value (in the p -value column of the between groups row).

A fourth grade class is studying the environment. One of the assignments is to grow bean plants in different soils. Tommy chose to grow his bean plants in soil found outside his classroom mixed with dryer lint. Tara chose to grow her bean plants in potting soil bought at the local nursery. Nick chose to grow his bean plants in soil from his mother’s garden. No chemicals were used on the plants, only water. They were grown inside the classroom next to a large window. Each child grew five plants. At the end of the growing period, each plant was measured, producing the data (in inches) in the table below.

Assume the heights of the plants are normally distribution and have equal variance. At the 5% significance level, does it appear that the three media in which the bean plants were grown produced the same mean height?

Let Tommy’s plants be population 1, let Tara’s plants be population 2, and let Nick’s plants be population 3.

[latex]\begin{eqnarray*} H_0: & & \mu_1=\mu_2=\mu_3 \\ H_a: & & \mbox{at least one population mean is different from the others} \end{eqnarray*}[/latex]

So the p -value[latex]=0.8760[/latex].

Because p -value[latex]=0.8760 \gt 0.05=\alpha[/latex], we do not reject the null hypothesis. At the 5% significance level there is enough evidence to suggest that the mean heights of the plants grown in three media are the same.

The null hypothesis [latex]\mu_1=\mu_2=\mu_3[/latex] is the claim that the mean heights of the plants grown in the three different media are all equal.
The p -value of 0.8760 is a large probability compared to the significance level, and so is likely to happen assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis. In other words, the population means are all equal.

A statistics professor wants to study the average GPA of students in four different programs: marketing, management, accounting, and human resources. The professor took a random sample of GPAs of students in those programs at the end of the past semester. The data is recorded in the table below.

Assume the GPAs of the students are normally distributed and have equal variance. At the 5% significance level, is there a difference in the average GPA of the students in the different programs?

Let marketing be population 1, let management be population 2, let accounting be population 3, and let human resources be population 4.

[latex]\begin{eqnarray*} H_0: & & \mu_1=\mu_2=\mu_3=\mu_4\\ H_a: & & \mbox{at least one population mean is different from the others} \end{eqnarray*}[/latex]

So the p -value[latex]=0.0462[/latex].

Because p -value[latex]=0.0462 \lt 0.05=\alpha[/latex], we reject the null hypothesis in favour of the alternative hypothesis. At the 5% significance level there is enough evidence to suggest that there is a difference in the average GPA of the students in the different programs.

A manufacturing company runs three different production lines to produce one of its products. The company wants to know if the average production rate is the same for the three lines. For each production line, a sample of eight hour shifts was taken and the number of items produced during each shift was recorded in the table below.

Assume the numbers of items produced on each line during an eight hour shift are normally distributed and have equal variance. At the 1% significance level, is there a difference in the average production rate for the three lines?

Let Line 1 be population 1, let Line 2 be population 2, and let Line 3 be population 3.

So the p -value[latex]=0.0073[/latex].

Because p -value[latex]=0.0073 \lt 0.01=\alpha[/latex], we reject the null hypothesis in favour of the alternative hypothesis. At the 1% significance level there is enough evidence to suggest that there is a difference in the average production rate of the three lines.

Concept Review

A one-way ANOVA hypothesis test determines if several population means are equal. In order to conduct a one-way ANOVA test, the following assumptions must be met:

Each population from which a sample is taken is assumed to be normal.
All samples are randomly selected and independent.

The analysis of variance procedure compares the variation between groups [latex]MST[/latex] to the variation within groups [latex]MSE[/latex]. The ratio of these two estimates of variance is the [latex]F[/latex]-score from an [latex]F[/latex]-distribution with [latex]df_1=k-1[/latex] and [latex]df_2=n-k[/latex]. The p -value for the test is the area in the right tail of the [latex]F[/latex]-distribution. The statistics used in an ANOVA test are summarized in the ANOVA summary table generated by Excel.

The one-way ANOVA hypothesis test for three or more population means is a well established process:

Write down the null and alternative hypotheses in terms of the population means. The null hypothesis is the claim that the population means are all equal and the alternative hypothesis is the claim that at least one of the population means is different from the others.
Collect the sample information for the test and identify the significance level.
The p -value is the area in the right tail of the [latex]F[/latex]-distribution. Use the ANOVA summary table generated by Excel to find the p -value.
Compare the p -value to the significance level and state the outcome of the test.

Attribution

“ 13.1 One-Way ANOVA “ and “ 13.2 The F Distribution and the F-Ratio “ in Introductory Statistics by OpenStax is licensed under a Creative Commons Attribution 4.0 International License .

Lean Six Sigma Training Certification

Facebook Instagram Twitter LinkedIn YouTube
(877) 497-4462

Mood’s Median Non-Parametric Hypothesis Test. A Complete Guide

May 17th, 2024

Often in stats research, teams encounter the imperative for comparing groups/samples’ central tendencies. While ANOVA frequently helps, it requires normalcy and homogeneity. When extremes or non-normality mar data, non-parametric exams better interpret. One such is Mood’s median test, which bears its discoverer’s name.

Designed by comparing medians of independent sets, it proves beneficial for exploratory or skewed information interpreters. Mood’s median examines central data proclivities without distorted normal prerequisites.

Particularly valued amid non-normalcy or outliers plaguing parametric test suppositions, it remains sturdy against aberrations.

By flagging central fixtures reliably notwithstanding abnormalities, Mood’s median grasps realities obscured to others. For teams grappling information information-defying widespread methods, it enlightens the next moves without parametric bonds.

Its sturdiness aids comprehension through hindrances to standard stats’ works, steering steady problem-solving as demands evolve. Joined insight lifts enterprises serving communities enduringly.

Key Highlights

Mood’s median test gauges medians between independent sets or samples non-parametrically. It proves an alternative when normalcy and homogeneity fail one-way ANOVA demands.
Stemming from chi-squared distributions, it examines normally distributed, equal medians hypotheses crosswise multitudes. Unperturbed by outliers or skews, suitability expands to non-regular figures.
Allowing bi-sample or multi-sample examination, suppositions include detachment, continued or ordered information alongside near underlying designing forms.
Furnishing test analytics and p-values, researchers determine if discernments distinguish significantly. Applicable where aberrations undermine orthodox techniques, it champions comprehension through unforeseen hurdles materializing.
By flagging median divergences reliably regardless of incongruences, Mood’s median guides choice-making, and optimization cooperatively sailed.

What is Mood’s Median Test?

Mood’s median test compares groups/samples’ midpoints non-parametrically unlike parametric exams demanding specific distributions.

Not requiring normalized information lets it interpret where those prerequisites limit. It expands bi-sample median investigations to abundance.

Null proposes population-wide medians align against another differing, tested against multi-treatment, independent demographic, or non-regular set median divergences.

Keys involve:

Examining multiple test subject brackets
Assessing treatment effects on non-standardized figures
Analyzing where regular assumptions constrain

While ANOVA outpaces spotting central tendency changes on normalized information, Mood’s median soundly detects divergences without such presumptions.

Proposed in ‘54 by Alexander Mood, it approximates chi-squared as repeats enlarge, providing valid conclusions minus distribution stipulations. For teams grappling with non-parametric realities, it highlights and provides choices.

Assumptions of Mood’s Median Test

Before running it, it’s important to check that the assumptions of the test are met. Violating these assumptions can lead to invalid results and conclusions. The key assumptions are:

Random Samples : The data must be collected using random sampling from the respective populations. This ensures the representativeness of the samples.
Independent Observations : The observations within each sample should be independent of each other. There should be no relationship between the observations that could influence the values.
Continuous or Ordinal Data : It requires the data to be continuous (measured on an interval or ratio scale) or ordinal (ranked data).
Similar Shape Distributions : While it does not require the distributions to be normal, the distributions should have similar shapes and spread. Dissimilar shapes can affect the validity of the results.
No Outliers : Extreme outliers in the data can significantly influence the median values and distort the test results. It’s recommended to check for and handle any outliers before conducting the test.
Tied Values : It can handle tied values (observations with the same value) within the samples. However, an excessive number of ties can reduce the test’s power and sensitivity.

Checking these assumptions is crucial as violations can increase the risk of Type I (false positive) or Type II (false negative) errors. Various graphical and statistical methods, such as histograms , boxplots , and normality tests , can be used to assess the assumptions.

If assumptions are violated, appropriate data transformations or non-parametric alternatives may be considered.

Hypothesis Testing in Mood’s Median Test

The Mood’s median test is a non-parametric hypothesis test that allows you to determine if the medians of two or more groups differ. It tests the null hypothesis that the medians of the groups are equal, against the alternative that at least one population median is different.

Null Hypothesis

The null hypothesis (H0) states that the medians of all groups are equal. Mathematically, this can be represented as:

H0: Median1 = Median2 = … = Mediank

Where k is the number of groups being compared.

Alternative Hypothesis

The alternative hypothesis (Ha) states that at least one median is different from the others. There are three possible alternative hypotheses:

1) Two-tailed test : At least one median differs

Ha : Not all medians are equal

2) Upper-tailed test : At least one median is larger

Ha : At least one median is larger than the others

3) Lower-tailed test : At least one median is smaller

Ha : At least one median is smaller than the others

The choice between one-tailed or two-tailed depends on the research question.

Test Statistic

Mood’s median test uses a chi-square test statistic to evaluate the null hypothesis. The test statistic follows a chi-square distribution with k-1 degrees of freedom when the null is true.

The test statistic is calculated from the number of observations above and below the grand median in each group. Larger deviations from the expected counts indicate greater evidence against the null hypothesis of equal medians.

The p-value is the probability of observing a test statistic as extreme as the one calculated, assuming the null hypothesis is true. A small p-value (typically <0.05) indicates strong evidence against the null, allowing you to reject it.

Interpretation

If the p-value is less than the chosen significance level (e.g. 0.05), you reject the null hypothesis. This means at least one group median is statistically different from the others. Effect sizes and confidence intervals help quantify the median differences.

The test makes no assumptions about the distribution shapes, making it a robust non-parametric alternative to the one-way ANOVA when data violates normality assumptions.

Performing Mood’s Median Test

To perform it, there are several steps to follow. First, you need to state the null and alternative hypotheses. The null hypothesis (H0) is that the medians of the groups are equal, while the alternative hypothesis (Ha) is that at least one median is different.

Next, you’ll need to combine all the data points across groups and find the overall median. This combined median serves as the test criterion.

For each group, count how many data points are greater than, less than, or equal to the combined median. These counts form the frequencies needed to calculate the test statistic.

It follows a chi-square distribution with k-1 degrees of freedom, where k is the number of groups. Calculate this test statistic based on the frequency counts and degrees of freedom.

Compare the test statistic to the critical value from the chi-square distribution for your chosen alpha level (e.g. 0.05). If the test statistic exceeds the critical value, you reject the null hypothesis. Otherwise, you fail to reject it.

Calculating the test statistic can be tedious by hand for larger sample sizes. Most statistical software like R, Python, Minitab , etc. have built-in functions to run Mood’s median test and provide the p-value directly. The p-value approach is equivalent – if p < alpha, reject H0.

It’s good practice to report the test statistic value, degrees of freedom, p-value, sample sizes, and your conclusion about the null hypothesis. Effect sizes can also provide more insight into the practical significance beyond statistical significance.

Mood’s Median Test in Statistical Software

It can be performed using various statistical software packages. While the test calculations can be done manually, using software is much more efficient, especially for larger datasets. Here are some examples of how to implement it in popular statistical programs:

Mood’s Median Test in R

In R, the mood.test() function from the RVAideMemoire package allows you to perform Mood’s median test. Here is an example:

install.packages(“RVAideMemoire”)

library(RVAideMemoire)

# Example data

x1 <- c(42, 37, 39, 44, 36, 38)

x2 <- c(40, 39, 38, 37, 31, 43)

# Perform Mood’s test

mood.test(x1, x2)

This will output the test statistic, p-value, and other relevant metrics for Mood’s median test on the two sample vectors x1 and x2.

Mood’s Median Test in Python

For Python, the scipy.stats module provides the median_test() function to conduct the test. Here’s an example:

“`python

from scipy import stats

# Example data

x1 = [42, 37, 39, 44, 36, 38]

x2 = [40, 39, 38, 37, 31, 43]

stats.median_test(x1, x2)

The median_test() function returns the chi-square statistic and p-value for the test.

Mood’s Median Test in Excel

Excel does not have a built-in function for this test. However, you can use add-ins or write custom VBA code to perform the test.

The Real Statistics Resource Pack provides a Mood’s Median Test data analysis tool for Excel.

Mood’s Median Test in SPSS, SAS, Minitab

Most major statistical software like SPSS , SAS, and Minitab provide the functionality to run this test, albeit through different function names and syntax. Refer to the respective documentation for implementation details.

No matter which software you use, be sure to verify the assumptions of this test before interpreting the results. Additionally, report the test statistic, p-value, sample sizes, and any other relevant metrics when presenting your findings.

Comparing Mood’s Median Test

When choosing a statistical test, it’s important to understand how Mood’s median test compares to other commonly used non-parametric tests like the Wilcoxon rank-sum test , the Kruskal-Wallis test , and the analysis of variance (ANOVA).

Mood’s Median Test vs Wilcoxon Rank-Sum Test

Both Mood’s median test and the Wilcoxon rank-sum test are non-parametric alternatives to the two-sample t-test . However, the Wilcoxon test assumes that the distributions have the same shape, while Mood’s test does not require this assumption.

Mood’s test is preferred when you cannot make the equal distribution shape assumption.

Mood’s Median Test vs Kruskal-Wallis Test

The Kruskal-Wallis test is a non-parametric alternative to one-way ANOVA for comparing more than two independent groups.

Like the Wilcoxon test, it assumes the distributions have the same shape. This test can be used when this assumption is violated, making it more robust for certain data sets.

Mood’s Median Test vs ANOVA

The key difference is that ANOVA is a parametric test that requires assumptions like normality and homogeneity of variances. The test is a non-parametric alternative when these assumptions are not met. It tests for differences in medians rather than means.

While sacrificing some statistical power compared to parametric tests when assumptions are met, this test is a robust option for non-normal data or heterogeneous variances across groups. The choice depends on whether the parametric assumptions can be reasonably satisfied.

Post-Hoc Analysis

If Mood’s median test detects a statistically significant difference among groups, post-hoc tests may be needed to determine which specific groups differ. Options include pairwise Mood’s median tests with a multiplicity adjustment.

Additional Considerations

While this is a useful non-parametric alternative to the one-way ANOVA, there are some additional points to keep in mind:

Power and Sample Size

Like other statistical tests, the power of Mood’s median test to detect an effect depends on the sample size.

With small samples, the test may not have enough power to find a significant difference even if one exists. Researchers should perform power analysis ahead of data collection to ensure adequate sample sizes.

Mood’s median test can handle tied observations within groups. However, it cannot deal with ties across different groups of medians. If there are ties across medians, the test may not be valid and an alternative like the Kruskal-Wallis test should be used instead.

If the overall test is significant, indicating differences between some of the medians, post-hoc tests are needed to determine which specific pairs of groups differ. Common post-hoc approaches include the Mann-Whitney U test or Dunn’s test .

Assumption Violations

While Mood’s test has fewer assumptions than the one-way ANOVA, the assumptions of random sampling and independence of observations still apply. Violations can increase the chance of false positives or false negatives.

Effect Size

Like other hypothesis tests, a significant p-value does not convey the degree of difference between groups. Effect sizes like the probability of superiority should be calculated and interpreted along with the p-value.

When reporting the results, good practice involves stating the test statistic value, degrees of freedom, p-value, sample sizes, medians, and effect size estimate. Graphical displays like boxplots can also aid interpretation.

Overall, Mood’s median test is a robust non-parametric tool. Still, careful checking of assumptions, appropriate sample sizing, post-hoc testing if needed, and comprehensive reporting of results is recommended for valid inference.

SixSigma.us offers both Live Virtual classes as well as Online Self-Paced training. Most option includes access to the same great Master Black Belt instructors that teach our World Class in-person sessions. Sign-up today!

Virtual Classroom Training Programs Self-Paced Online Training Programs

SixSigma.us Accreditation & Affiliations

Monthly Management Tips

Be the first one to receive the latest updates and information from 6Sigma
Get curated resources from industry-experts
Gain an edge with complete guides and other exclusive materials
Become a part of one of the largest Six Sigma community
Unlock your path to become a Six Sigma professional

" * " indicates required fields

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons

Margin Size

Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

4.3: Two-Way ANOVA models and hypothesis tests

Last updated
Save as PDF
Page ID 33241

Mark Greenwood
Montana State University

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

To assess interactions with two variables, we need to fully describe models for the additive and interaction scenarios and then develop a method for assessing evidence of the need for different aspects of the models. First, we need to define the notation for these models:

\(j = 1,\ldots,J\) \(J\) is the number of levels of A
\(k = 1,\ldots,K\) \(K\) is the number of levels of B
\(i = 1,\ldots,n_{jk}\) \(n_{jk}\) is the sample size for level \(j\) of factor A and level \(k\) of factor B
\(N = \Sigma_j\Sigma_k n_{jk}\) is the total sample size (sum of the number of observations across all \(JK\) groups)

We need to extend our previous discussion of reference-coded models to develop a Two-Way ANOVA model. We start with the Two-Way ANOVA interaction model :

\[y_{ijk} = \alpha + \tau_j + \gamma_k + \omega_{jk} + \varepsilon_{ijk},\]

where \(\alpha\) is the baseline group mean (for level 1 of A and level 1 of B), \(\tau_j\) is the deviation for the main effect of A from the baseline for levels \(2,\ldots,J\) , \(\gamma_k\) (gamma \(k\) ) is the deviation for the main effect of B from the baseline for levels \(2,\ldots,K\) , and \(\omega_{jk}\) (omega \(jk\) ) is the adjustment for the interaction effect for level \(j\) of factor A and level \(k\) of factor B for \(j = 1,\ldots,J\) and \(k = 1,\ldots,K\) . In this model, \(\tau_1\) , \(\gamma_1\) , and \(\omega_{11}\) are all fixed at 0 because \(\alpha\) is the mean for the combination of the baseline levels of both variables and so no adjustments are needed. Additionally, any \(\omega_{jk}\) ’s that contain the baseline category of either factor A or B are also set to 0 and the model for these levels just involves \(\tau_j\) or \(\gamma_k\) added to the intercept. Exploring the R output will help clarify which coefficients are present or set to 0 (so not displayed) in these models. As in Chapter 3, R will typically choose the baseline categories alphabetically but now it is choosing a baseline for both variables and so our detective work will be doubled to sort this out.

If the interaction term is not important, usually based on the interaction test presented below, the \(\omega_{jk}\text{'s}\) can be dropped from the model and we get a model that corresponds to Scenario 4 above. Scenario 4 is where there are two main effects in the model but no interaction between them. The additive Two-Way model is

\[y_{ijk} = \alpha + \tau_j + \gamma_k + \varepsilon_{ijk},\]

where each component is defined as in the interaction model. The difference between the interaction and additive models is setting all the \(\omega_{jk}\text{'s}\) to 0 that are present in the interaction model. When we set parameters to 0 in models it removes them from the model. Setting parameters to 0 is also how we will develop our hypotheses to test for an interaction, by assessing evidence against a null hypothesis that all \(\omega_{jk}\text{'s} = 0\) .

The interaction test hypotheses are

\(H_0\) : No interaction between A and B on response in population \(\Leftrightarrow\) All \(\omega_{jk}\text{'s} = 0\) .
\(H_A\) : Interaction between A and B on response in population \(\Leftrightarrow\) At least one \(\omega_{jk}\ne 0\) .

To perform this test, a new ANOVA \(F\) -test is required (presented below) but there are also hypotheses relating to the main effects of A ( \(\tau_j\text{'s}\) ) and B ( \(\gamma_k\text{'s}\) ). If you decide that there is sufficient evidence against the null hypothesis that no interaction is present to conclude that one is likely present, then it is dangerous to ignore the interaction and test for the main effects because important main effects can be masked by interactions (examples later). It is important to note that, by definition, both variables matter if an interaction is found to be important so the main effect tests may not be very interesting in an interaction model. If the interaction is found to be important based on the test and so is retained in the model, you should focus on the interaction model (also called the full model ) in order to understand and describe the form of the interaction among the variables.

If the interaction test does not return a small p-value and you decide that you do not have enough evidence against the null hypothesis to suggest that the interaction is needed, the interaction can be dropped from the model. In this situation, we would re-fit the model and focus on the results provided by the additive model – performing tests for the two additive main effects. For the first, but not last time, we encounter a model with more than one variable and more than one test of potential interest. In models with multiple variables at similar levels (here both are main effects), we are interested in the results for each variable given that the other variable is in the model. In many situations, including more than one variable in a model changes the results for the other variable even if those variables do not interact. The reason for this is more clear in Chapter 8 and really only matters here if we have unbalanced designs, but we need to start adding a short modifier to our discussions of main effects – they are the results conditional on or adjusting for or, simply, given , the other variable(s) in the model. Specifically, the hypotheses for the two main effects are:

\(\Leftrightarrow\) All \(\tau_j\text{'s} = 0\) in additive model.

\(\Leftrightarrow\) At least one \(\tau_j \ne 0\) , in additive model.

\(\Leftrightarrow\) All \(\gamma_k\text{'s} = 0\) in additive model.

\(\Leftrightarrow\) At least one \(\gamma_k \ne 0\) , in additive model.

In order to test these effects (interaction in the interaction model and main effects in the additive model), \(F\) -tests are developed using Sums of Squares, Mean Squares, and degrees of freedom similar to those in Chapter 3. We won’t worry about the details of the sums of squares formulas but you should remember the sums of squares decomposition, which still applies 84 . Table 4.1 summarizes the ANOVA results you will obtain for the interaction model and Table 4.2 provides the similar general results for the additive model. As we saw in Chapter 3, the degrees of freedom are the amount of information that is free to vary at a particular level and that rule generally holds here. For example, for factor A with \(J\) levels, there are \(J-1\) parameters that are free since the baseline is fixed. The residual degrees of freedom for both models are not as easily explained but have a simple formula. Note that the sum of the degrees of freedom from the main effects, (interaction if present), and error need to equal \(N-1\) , just like in the One-Way ANOVA table.

The mean squares are formed by taking the sums of squares (we’ll let R find those for us) and dividing by the \(df\) in the row. The \(F\) -ratios are found by taking the mean squares from the row and dividing by the mean squared error ( \(\text{MS}_E\) ). They follow \(F\) -distributions with numerator degrees of freedom from the row and denominator degrees of freedom from the Error row (in R output this the Residuals row). It is possible to develop permutation tests for these methods but some technical issues arise in doing permutation tests for interaction model components so we will not use them here. This means we will have to place even more emphasis on the data not presenting clear violations of assumptions since we only have the parametric method available.

With some basic expectations about the ANOVA tables and \(F\) -statistic construction in mind, we can get to actually estimating the models and exploring the results. The first example involves the fake paper towel data displayed in Figure 4.1 and 4.2. It appeared that Scenario 5 was the correct story since the lines appeared to be non-parallel, but we need to know whether there is sufficient evidence to suggest that the interaction is “real” and we get that through the interaction hypothesis test. To fit the interaction model using lm , the general formulation is lm(y ~ x1 * x2, data = ...) . The order of the variables doesn’t matter as the most important part of the model, to start with, relates to the interaction of the variables.

The ANOVA table output shows the results for the interaction model obtained by running the anova function on the model called m1 . Specifically, the test that \(H_0: \text{ All } \omega_{jk}\text{'s} = 0\) has a test statistic of \(F(2,24) = 1.92\) (in the output from the row with brands:drops) and a p-value of 0.17. So there is weak evidence against the null hypothesis of no interaction, with a 17% chance we would observe a difference in the \(\omega_{jk}\text{'s}\) like we did or more extreme if the \(\omega_{jk}\text{'s}\) really were all 0. So we would conclude that the interaction is probably not needed 85 . Note that for the interaction model components, R presents them with a colon, : , between the variable names.

It is useful to display the estimates from this model and we can utilize plot(allEffects(MODELNAME)) to visualize the results for the terms in our models. If we turn on the options for grid = T , multiline = T , and ci.style = "bars" we get a useful version of the basic “effect plot” for Two-Way ANOVA models with interaction. I also added lty = c(1:2) to change the line type for the two lines (replace 2 with the number of levels in the variable driving the different lines. The results of the estimated interaction model are displayed in Figure 4.7, which looks very similar to our previous interaction plot. The only difference is that this comes from model that assumes equal variance and these plots show 95% confidence intervals for the means instead of the \(\pm\) 1 SE used in the intplot where each SE is calculated using the variance of the observations at each combination of levels. Note that other than the lines connecting the means, this plot also is similar to the pirate-plot in Figure 4.1 that also displayed the original responses for each of the six combinations of the two explanatory variables. That plot then provides a place to assess assumptions of the equal variance and distributions for each group as well as explore differences in the group means.

Plot of estimated results of interaction model for the paper towel performance data.

In the absence of sufficient evidence to include the interaction, the model should be simplified to the additive model and the interpretation focused on each main effect, conditional on having the other variable in the model. To fit an additive model and not include an interaction, the model formula involves a “+” instead of a “ * ” between the explanatory variables.

The p-values for the main effects of brand and drops change slightly from the results in the interaction model due to changes in the \(\text{MS}_E\) from 0.4118 to 0.4409 (more variability is left over in the simpler model) and the \(\text{DF}_{\text{error}}\) that increases from 24 to 26. In both models, the \(\text{SS}_{\text{Total}}\) is the same (20.6544). In the interaction model,

\[\begin{array}{rl} \text{SS}_{\text{Total}} & = \text{SS}_{\text{brand}} + \text{SS}_{\text{drops}} + \text{SS}_{\text{brand:drops}} + \text{SS}_{\text{E}}\\ & = 4.3322 + 4.8581 + 1.5801 + 9.8840\\ & = 20.6544.\\ \end{array}\]

In the additive model, the variability that was attributed to the interaction term in the interaction model ( \(\text{SS}_{\text{brand:drops}} = 1.5801\) ) is pushed into the \(\text{SS}_{\text{E}}\) , which increases from 9.884 to 11.4641. The sums of squares decomposition in the additive model is

\[\begin{array}{rl} \text{SS}_{\text{Total}} & = \text{SS}_{\text{brand}} + \text{SS}_{\text{drops}} + \text{SS}_{\text{E}} \\ & = 4.3322 + 4.8581 + 11.4641 \\ & = 20.6544. \\ \end{array}\]

This shows that the sums of squares decomposition applies in these more complicated models as it did in the One-Way ANOVA. It also shows that if the interaction is removed from the model, that variability is lumped in with the other unexplained variability that goes in the \(\text{SS}_{\text{E}}\) in any model.

The fact that the sums of squares decomposition can be applied here is useful, except that there is a small issue with the main effect tests in the ANOVA table results that follow this decomposition when the design is not balanced. It ends up that the tests in a typical ANOVA table are only conditional on the tests higher up in the table. For example, in the additive model ANOVA table, the Brand test is not conditional on the Drops effect, but the Drops effect is conditional on the Brand effect. In balanced designs, conditioning on the other variable does not change the results but in unbalanced designs, the order does matter. To get both results to be similarly conditional on the other variable, we have to use another type of sums of squares, called Type II sums of squares . These sums of squares will no longer always follow the rules of the sums of squares decomposition but they will test the desired hypotheses. Specifically, they provide each test conditional on any other terms at the same level of the model and match the hypotheses written out earlier in this section. To get the “correct” ANOVA results, the car package ( Fox, Weisberg, and Price ( 2022a ) , Fox and Weisberg ( 2011 ) ) is required. We use the Anova function on our linear models from here forward to get the “right” tests in our ANOVA tables 86 . Note how the case-sensitive nature of R code shows up in the use of the capital “A” Anova function instead of the lower-case “a” anova function used previously. In this situation, because the design was balanced, the results are the same using either function. Observational studies rarely generate balanced designs (some designed studies can result in unbalanced designs too) so we will generally just use the Type II version of the sums of squares to give us the desired results across different data sets we might analyze. The Anova results using the Type II sums of squares are slightly more conservative than the results from anova , which are called Type I sums of squares. The sums of squares decomposition no longer applies, but it is a small sacrifice to get each test after adjusting for all other variables 87 .

The new output switches the columns around and doesn’t show you the mean squares, but gives the most critical parts of the output. Here, there is no change in results because it is a balanced design with equal counts of responses in each combination of the two explanatory variables.

The additive model, when appropriate, provides simpler interpretations for each explanatory variable compared to models with interactions because the effect of one variable is the same regardless of the levels of the other variable and vice versa. There are two tools to aid in understanding the impacts of the two variables in the additive model. First, the model summary provides estimated coefficients with interpretations like those seen in Chapter 3 (deviation of group \(j\) or \(k\) from the baseline group’s mean), except with the additional wording of “controlling for” the other variable added to any of the discussion. Second, the term-plots now show each main effect and how the groups differ with one panel for each of the two explanatory variables in the model. These term-plots are created by holding the other variable constant at one of its levels (the most frequently occurring or first if the there are multiple groups tied for being most frequent) and presenting the estimated means across the levels of the variable in the plot.

In the model summary, the baseline combination estimated in the (Intercept) row is for Brand B1 and Drops 10 and estimates the mean failure time as 1.85 seconds for this combination. As before, the group labels that do not show up are the baseline but there are two variables’ baselines to identify. Now the “simple” aspects of the additive model show up. The interpretation of the Brands B2 coefficient is as a deviation from the baseline but it applies regardless of the level of Drops . Any difference between B1 and B2 involves a shift up of 0.76 seconds in the estimated mean failure time. Similarly, going from 10 (baseline) to 20 drops results in a drop in the estimated failure mean of 0.47 seconds and going from 10 to 30 drops results in a drop of almost 1 second in the average time to failure, both estimated changes are the same regardless of the brand of paper towel being considered. Sometimes, especially in observational studies, we use the terminology “controlled for” to remind the reader that the other variable was present in the model 88 and also explained some of the variability in the responses. The term-plots for the additive model (Figure 4.8) help us visualize the impacts of changes brand and changing water levels, holding the other variable constant. The differences in heights in each panel correspond to the coefficients just discussed.

Term-plots of additive model for paper towel data. Left panel displays results for two brands and right panel for number of drops of water, each after controlling for the other.

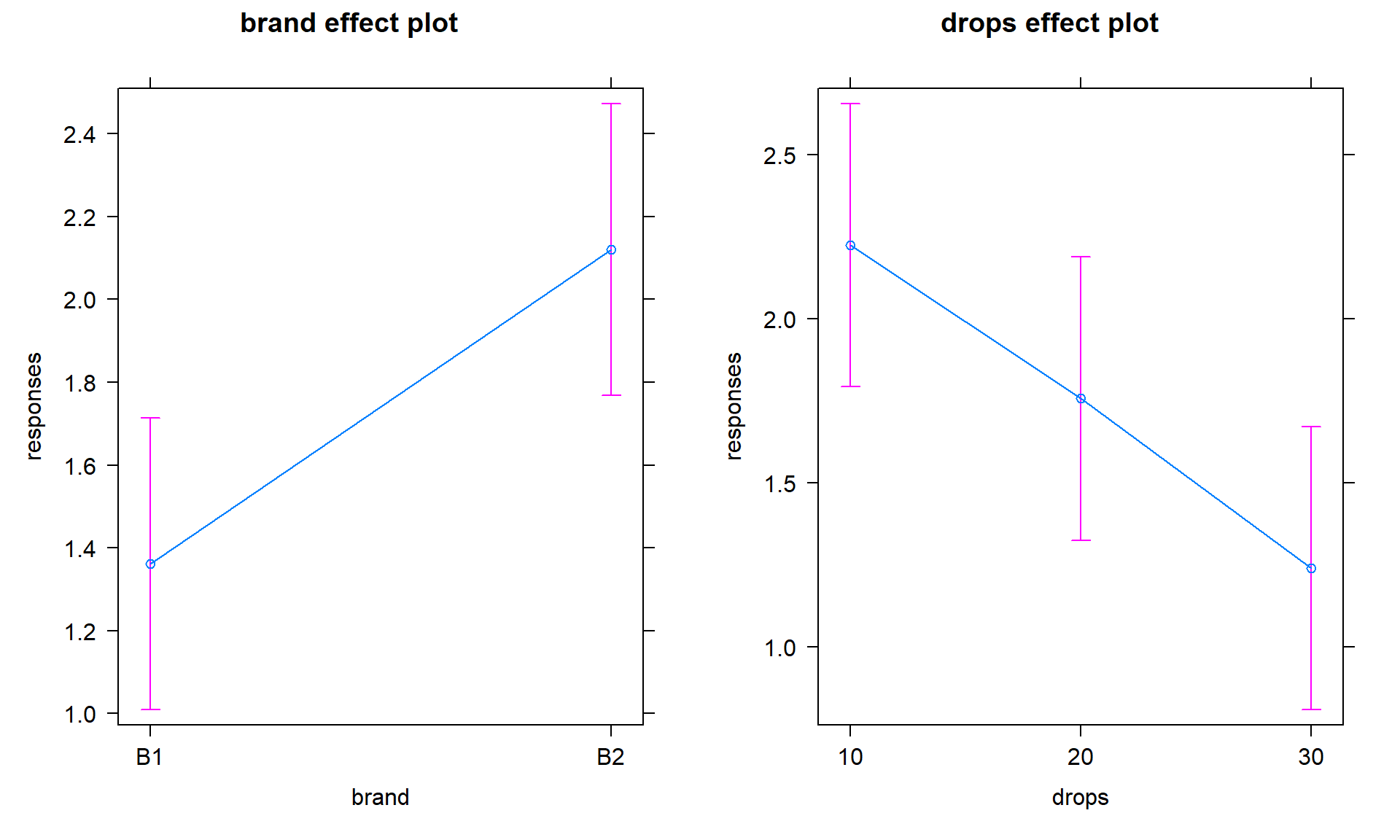
With the first additive model we have considered, it is now the first time where we are working with a model where we can’t display the observations together with the means that the model is producing because the results for each predictor are averaged across the levels of the other predictor. To visualize some aspects of the original observations with the estimates from each group, we can turn on an option in the term-plots ( residuals = T ) to obtain the partial residuals that show the residuals as a function of one variable after adjusting for the effects/impacts of other variables. We will avoid the specifics of the calculations for now, but you can use these to explore the residuals at different levels of each predictor. They will be most useful in the Chapters 7 and 8 but give us some insights in unexplained variation in each level of the predictors once we remove the impacts of other predictors in the model. Use plots like Figure 4.9 to look for different variability at different levels of the predictors and locations of possible outliers in these models. Note that the points (open circles) are jittered to aid in seeing all of them, the means of each group of residuals are indicated by a filled large circle, and the smaller circles in the center of the bars for the 95% confidence intervals are the means from the model. Term-plots with partial residuals accompany our regular diagnostic plots for assessing equal variance assumptions in these models – in some cases adding the residuals will clutter the term-plots so much that reporting them is not useful since one of the main purposes of the term-plots is to visualize the model estimates. So use the residuals = T option judiciously.

Term-plots of additive model for paper towel data with partial residuals added. Relatively similar variability seems to be present in each of the groups of residuals after adjusting for the other variable except for the residuals for the 10 drops where the variability is smaller, especially if one small outlier is ignored.

For the One-Way and Two-Way interaction models, the partial residuals are just the original observations so present similar information as the pirate-plots but do show the model estimated 95% confidence intervals. With interaction models, you can use the default settings in effects when adding in the partial residuals as seen below in Figure 4.12.

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
Duis aute irure dolor in reprehenderit in voluptate
Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

Minitab quick guide.

Minitab ®

Access Minitab Web , using Google Chrome .

Click on the section to view the Minitab procedures.

After saving the Minitab File to your computer or cloud location, you must first open Minitab .

To open a Minitab project (.mpx file): File > Open > Project
To open a data file (.mtw, .csv or .xlsx): File > Open > Worksheet

Descriptive, graphical

Bar Chart : Graph > Bar Chart > Counts of unique values > One Variable
Pie Chart : Graph > Pie Chart > Counts of unique values > Select Options > Under Label Slices With choose Percent

Descriptive, numerical

Frequency Tables : Stat > Tables > Tally Individual Variables

Inference (one proportion)

Hypothesis Test

With raw data : Stat > Basic Statistics > 1 Proportion > Select variable > Check Perform hypothesis test and enter null value > Select Options tab > Choose correct alternative > Under method , choose Normal approximation
With summarized data : Stat > Basic Statistics > 1 Proportion > Choose Summarized data from the dropdown menu > Enter data > Check Perform hypothesis test and enter null value > Select Options tab > Choose correct alternative > Under method, choose Normal approximation

Confidence Interval

With raw data : Stat > Basic Statistics > 1 Proportion > Select variable > Select Options tab > Enter correct confidence level, make sure the alternative is set as not-equal, and choose Normal approximation method
Histogram : Graph > Histogram > Simple
Dotplot : Graph > Dotplot > One Y, Simple
Boxplot : Graph > Boxplot > One Y, Simple
Mean, Std. Dev., 5-number Summary, etc .: Stat > Basic Statistics > Display Descriptive Statistics > Select Statistics tab to choose exactly what you want to display

Inference (one mean)

With raw data : Stat > Basic Statistics > 1-Sample t > Select variable > Check Perform hypothesis test and enter null value > Select Options tab > Choose the correct alternative
With summarized data : Stat > Basic Statistics > 1-Sample t > Select Summarized data from the dropdown menu > Enter data (n, x-bar, s) > Check Perform hypothesis test and enter null value > Select Options tab > Choose correct alternative
With raw data : Stat > Basic Statistics > 1-Sample t > Select variable > Select Options tab > Enter correct confidence level and make sure the alternative is set as not-equal
With summarized data : Stat > Basic Statistics > 1-Sample t > Select Summarized data from the dropdown menu > Enter data (n, x-bar, s) > Select Options tab > Enter correct confidence level and make sure the alternative is set as not-equal
Side-by-side Histograms : Graph > Histogram > Under One Y Variable , select Groups Displayed Separately > Enter the categorical variable under Group Variables > Choose In separate panels of one graph under Display Groups
Side-by-side Dotplots : Graph > Dotplot > One Y Variable , Groups Displayed on the Scale
Side-by-side Boxplots : Graph > Boxplot > One Y, With Categorical Variables
Mean, Std. Dev., 5-number Summary, etc .: Stat > Basic Statistics > Display Descriptive Statistics > Select variables (enter the categorical variable under By variables ) > Select Statistics tab to choose exactly what you want to display

Inference (independent samples)

With raw data : Stat > Basic Statistics > 2-Sample t > Select variables (response/quantitative as Samples and explanatory/categorical as Sample IDs ) > Select Options tab > Choose correct alternative
With summarized data : Stat > Basic Statistics > 2-Sample t > Select Summarized data from the dropdown menu > Enter data > Select Options tab > Choose correct alternative
Same as above, choose confidence level and make sure the alternative is set as not-equal

Inference (paired difference)

Stat > Basic Statistics > Paired t > Enter correct columns in Sample 1 and Sample 2 boxes > Select Options tab > Choose correct alternative
Scatterplot : Graph > Scatterplot > Simple > Enter the response variable under Y variables and the explanatory variable under X variables
Fitted Line Plot : Stat > Regression > Fitted Line Plot > Enter the response variable under Response (y) and the explanatory variable under Predictor (x)
Correlation : Stat > Basic Statistics > Correlation > Select Graphs tab > Click Statistics to display on plot and select Correlations
Correlation : Stat > Basic Statistics > Correlation > Select Graphs tab > Click Statistics to display on plot and select Correlations and p-values
Regression Line : Stat > Regression > Regression > Fit Regression Model > Enter the response variable under Responses and the explanatory variable under Continuous predictors > Select Results tab > Click Display of results and select Basic tables ( Note : if you want the confidence interval for the population slope, change “display of results” to “expanded table.” With the expanded table, you will get a lot of information on the output that you will not understand.)
Side-by-side Bar Charts with raw data : Graph > Bar Chart > Counts of unique values > Multiple Variables
Side-by-side Bar Charts with a two-way table : Graph > Bar Chart > Summarized Data in a Table > Under Two-Way Table choose Clustered or Stacked > Enter the columns that contain the data under Y-variables and enter the column that contains your row labels under Row labels
Two-way Table : Stat > Tables > Cross Tabulation and Chi-square

Inference (difference in proportions)

Using a dataset : Stat > Basic Statistics > 2 Proportions > Select variables (enter response variable as Samples and explanatory variable as Sample IDs ) > Select Options tab > Choose correct alternative
Using a summary table : Stat > Basic Statistics > 2 Proportions > Select Summarized data from the dropdown menu > Enter data > Select Options tab > Choose correct alternative
Same as above, choose confidence level and make sure the alternative is set as not equal

Inference (Chi-squared test of association)

Stat > Tables > Chi-Square Test for Association > Choose correct data option (raw or summarized) > Select variables > Select Statistics tab to choose the statistics you want to display
Fit multiple regression model : Stat > Regression > Regression > Fit Regression Model > Enter the response variable under Responses , the quantitative explanatory variables under Continuous predictors , and any categorical explanatory variables under Categorical predictors > Select Results tab > Click Display of results and select Basic tables ( Note : if you want the confidence intervals for the coefficients, change display of results to expanded table . You will get a lot of information on the output that you will not understand.)
Make a prediction or prediction interval using a fitted model : Stat > Regression > Regression > Predict > Enter values for each explanatory variable

IMAGES

Anova by Hazilah Mohd Amin
PPT
Analysis of Variance (ANOVA) Explained with Formula, and an Example
ANOVA: Definition, one-way, two-way, table, examples, uses
15 Null Hypothesis Examples (2024)
PPT

VIDEO

When the null hypothesis for an ANOVA analysis comparing four treatment means, is rejected
Statistics
Null and Alternative Hypothesis (with samples and activity to answer)
SPSS: Multivariate Analysis Of Variance or MANOVA; Two way, Part 3 of 3
Two way ANOVA Example
Understanding the Difference: Null Hypothesis vs. Alternative Hypothesis in Statistics |Math Dot Com

COMMENTS

Understanding the Null Hypothesis for ANOVA Models
Since the p-value from the ANOVA table is not less than 0.05, we fail to reject the null hypothesis. This means we don't have sufficient evidence to say that there is a statistically significant difference between the mean exam scores of the three groups. Example 2: Two-Way ANOVA
Hypothesis Testing
The null hypothesis in ANOVA is always that there is no difference in means. The research or alternative hypothesis is always that the means are not all equal and is usually written in words rather than in mathematical symbols. ... This is an example of a two-factor ANOVA where the factors are treatment (with 5 levels) and sex (with 2 levels ...
PDF Lecture 7: Hypothesis Testing and ANOVA
The intent of hypothesis testing is formally examine two opposing conjectures (hypotheses), H0 and HA. These two hypotheses are mutually exclusive and exhaustive so that one is true to the exclusion of the other. We accumulate evidence - collect and analyze sample information - for the purpose of determining which of the two hypotheses is true ...
ANOVA Test: Definition, Types, Examples, SPSS
The null hypothesis for the test is that the two means are equal. Therefore, a significant result means that the two means are unequal. Examples of when to use a one way ANOVA. Situation 1: You have a group of individuals randomly split into smaller groups and completing different tasks. For example, you might be studying the effects of tea on ...
One-way ANOVA
One-way ANOVA example As a crop researcher, you want to test the effect of three different fertilizer mixtures on crop yield. You can use a one-way ANOVA to find out if there is a difference in crop yields between the three groups. ... The null hypothesis (H 0) of ANOVA is that there is no difference among group means. The alternative ...
One Way ANOVA Overview & Example
Null hypothesis: All population group means are equal. Alternative hypothesis: Not all population group means are equal.; Reject the null when your p-value is less than your significance level (e.g., 0.05). The differences between the means are statistically significant. Your sample provides sufficiently strong evidence to conclude that the population means are not all equal.
ANOVA Explained by Example. Manually Calculating an ANOVA Table…
Compare the p-value and significance level to decide whether or not to reject the null hypothesis. 1. Formulate a Hypotheses. As with nearly all statistical significance tests, ANOVA starts with formulating a null and alternative hypothesis. For this example, the hypotheses are as follows:
ANOVA 3: Hypothesis test with F-statistic
ANOVA is inherently a 2-sided test. Say you have two groups, A and B, and you want to run a 2-sample t-test on them, with the alternative hypothesis being: Ha: µ.a ≠ µ.b. You will get some test statistic, call it t, and some p-value, call it p1. If you then run an ANOVA on these two groups, you will get an test statistic, f, and a p-value p2.
11.1: One-Way ANOVA
The F-test (for ANOVA) is a statistical test for testing the equality of \ (k\) population means. The one-way ANOVA F-test is a statistical test for testing the equality of \ (k\) population means from 3 or more groups within one variable or factor. There are many different types of ANOVA; for now, we are going to start with what is commonly ...
13.1 One-Way ANOVA
The test uses variances to help determine if the means are equal or not. To perform a one-way ANOVA test, there are five basic assumptions to be fulfilled: Each population from which a sample is taken is assumed to be normal. All samples are randomly selected and independent. The populations are assumed to have equal standard deviations (or ...
13.2: One-Way ANOVA
We test the null hypothesis of equal means of the response in every group versus the alternative hypothesis of one or more group means being different from the others. A one-way ANOVA hypothesis test determines if several population means are equal. The distribution for the test is the \(F\) distribution with two different degrees of freedom.
11.3: Hypotheses in ANOVA
Statistical sentence: F (df) = = F-calc, p<.05 (fill in the df and the calculated F) Statistical sentence: F (df) = = F-calc, p>.05 (fill in the df and the calculated F) This page titled 11.3: Hypotheses in ANOVA is shared under a license and was authored, remixed, and/or curated by . With three or more groups, research hypothesis get more ...
The ANOVA Approach
The sample data are organized as follows: The hypotheses of interest in an ANOVA are as follows: H 1: Means are not all equal. where k = the number of independent comparison groups. In this example, the hypotheses are: H 1: The means are not all equal. The null hypothesis in ANOVA is always that there is no difference in means.
ANOVA (Analysis of variance)
Null Hypothesis (H0): This is the hypothesis that there is no difference between the group means. ... Examples of ANOVA. Examples 1: Suppose a psychologist wants to test the effect of three different types of exercise (yoga, aerobic exercise, and weight training) on stress reduction. The dependent variable is the stress level, which can be ...
Understanding the Null Hypothesis for ANOVA Models
The following examples show how to decide to reject or fail to reject the null hypothesis in both a one-way ANOVA and two-way ANOVA. Example 1: One-Way ANOVA. Suppose we want to know whether or not three different exam prep programs lead to different mean scores on a certain exam. To test this, we recruit 30 students to participate in a study ...
Null Hypothesis: Definition, Rejecting & Examples
When your sample contains sufficient evidence, you can reject the null and conclude that the effect is statistically significant. Statisticians often denote the null hypothesis as H 0 or H A.. Null Hypothesis H 0: No effect exists in the population.; Alternative Hypothesis H A: The effect exists in the population.; In every study or experiment, researchers assess an effect or relationship.
ANOVA in R
The null hypothesis (H 0) of the ANOVA is no difference in means, and the alternative hypothesis (H a) is that the means are different from one another. In this guide, ... Two-way ANOVA example In the two-way ANOVA, we add an additional independent variable: planting density. We test the effects of 3 types of fertilizer and 2 different planting ...
11.4 One-Way ANOVA and Hypothesis Tests for Three or More Population
The alternative hypothesis does not say that all of the population means are not equal, only that at least one of them is not equal to the others. The p-value of 0.8760 is a large probability compared to the significance level, and so is likely to happen assuming the null hypothesis is true. This suggests that the assumption that the null ...
1.2: The 7-Step Process of Statistical Hypothesis Testing
The null hypothesis can be thought of as the opposite of the "guess" the researchers made: in this example, the biologist thinks the plant height will be different for the fertilizers. So the null would be that there will be no difference among the groups of plants. Specifically, in more statistical language the null for an ANOVA is that the ...
Two-Way ANOVA
When to use a two-way ANOVA. You can use a two-way ANOVA when you have collected data on a quantitative dependent variable at multiple levels of two categorical independent variables.. A quantitative variable represents amounts or counts of things. It can be divided to find a group mean. Bushels per acre is a quantitative variable because it represents the amount of crop produced.
Mood's Median Non-Parametric Hypothesis Test. A Complete Guide
Hypothesis Testing in Mood's Median Test. The Mood's median test is a non-parametric hypothesis test that allows you to determine if the medians of two or more groups differ. It tests the null hypothesis that the medians of the groups are equal, against the alternative that at least one population median is different.
Understanding Two-Way ANOVA: Practical Examples and
17 The ANOVA is already completed, with the assumption that the values within groups are same. Throughout this example, the null hypothesis is that the ranges are identical. Because of this, the p-value is lower than 0.0001. We deny the null hypothesis of equality of variation since it is extremely important. So, Welch's weighted variance ANOVA is chosen.
Null & Alternative Hypotheses
The null and alternative hypotheses offer competing answers to your research question. When the research question asks "Does the independent variable affect the dependent variable?": The null hypothesis ( H0) answers "No, there's no effect in the population.". The alternative hypothesis ( Ha) answers "Yes, there is an effect in the ...
4.3: Two-Way ANOVA models and hypothesis tests
We need to extend our previous discussion of reference-coded models to develop a Two-Way ANOVA model. We start with the Two-Way ANOVA interaction model: yijk = α + τj + γk + ωjk + εijk, where α is the baseline group mean (for level 1 of A and level 1 of B), τj is the deviation for the main effect of A from the baseline for levels 2 ...
Minitab Quick Guide
Hypothesis Test. With raw data: Stat > Basic Statistics > 1-Sample t > Select variable > Check Perform hypothesis test and enter null value > Select Options tab > Choose the correct alternative; With summarized data: Stat > Basic Statistics > 1-Sample t > Select Summarized data from the dropdown menu > Enter data (n, x-bar, s) > Check Perform hypothesis test and enter null value > Select ...

Understanding the Null Hypothesis for ANOVA Models

Example 1: One-Way ANOVA

Example 2: Two-Way ANOVA

Additional Resources

Featured Posts

Leave a Reply Cancel reply

Join the Statology Community

Statistics and probability

ANOVA 3: Hypothesis test with F-statistic

Video transcript

13.1 One-Way ANOVA

The Null and Alternative Hypotheses

Hypothesis Testing - Analysis of Variance (ANOVA)

The ANOVA Approach

ANOVA (Analysis of variance) – Formulas, Types, and Examples

Analysis of Variance (ANOVA)

ANOVA Terminology

Types of ANOVA

One-way (or one-factor) ANOVA

Two-way (or two-factor) ANOVA

Repeated Measures ANOVA

Mixed Design ANOVA

Multivariate Analysis of Variance (MANOVA)

Analysis of Covariance (ANCOVA)

Nested ANOVA

ANOVA Formulas

Examples of ANOVA

How to Conduct ANOVA

When to use ANOVA

Applications of ANOVA

Advantages of ANOVA

Disadvantages of ANOVA

About the author

Muhammad Hassan

You may also like

Cluster Analysis – Types, Methods and Examples

Discriminant Analysis – Methods, Types and...

MANOVA (Multivariate Analysis of Variance) –...

Documentary Analysis – Methods, Applications and...

Graphical Methods – Types, Examples and Guide

Substantive Framework – Types, Methods and...

Understanding the Null Hypothesis for ANOVA Models

Example 1: One-Way ANOVA

Example 2: Two-Way ANOVA

Additional Resources

How to Fix in R: incomplete final line found by readTableHeader

11.4 One-Way ANOVA and Hypothesis Tests for Three or More Population Means

One-Way ANOVA

Steps to Conduct a Hypothesis Test for Three or More Population Means

ANOVA Summary Tables

USING EXCEL TO CREATE A ONE-WAY ANOVA SUMMARY TABLE

Concept Review

Attribution

Mood’s Median Non-Parametric Hypothesis Test. A Complete Guide

Key Highlights

What is Mood’s Median Test?

Assumptions of Mood’s Median Test

Hypothesis Testing in Mood’s Median Test

Null Hypothesis

Alternative Hypothesis

Test Statistic

Interpretation

Performing Mood’s Median Test

Mood’s Median Test in Statistical Software

Mood’s Median Test in R

Mood’s Median Test in Python

Mood’s Median Test in Excel

Mood’s Median Test in SPSS, SAS, Minitab

Comparing Mood’s Median Test

Mood’s Median Test vs Wilcoxon Rank-Sum Test

Mood’s Median Test vs Kruskal-Wallis Test

Mood’s Median Test vs ANOVA

Post-Hoc Analysis

Additional Considerations

Power and Sample Size

Assumption Violations

Effect Size

SixSigma.us Accreditation & Affiliations

Monthly Management Tips

Margin Size