math problem solving questions geometry

Geometry Math Problems - Perimeters

In these lessons, we will learn to solve geometry math problems that involve perimeter.

Related Pages Geometry math problems involving area Area Formula Geometry math problems involving angles More Algebra Word Problems

Geometry word problems involves geometric figures and angles described in words. You would need to be familiar with the formulas in geometry.

Making a sketch of the geometric figure is often helpful.

Geometry Word Problems Involving Perimeter

Example: A triangle has a perimeter of 50. If 2 of its sides are equal and the third side is 5 more than the equal sides, what is the length of the third side?

Solution: Step 1: Assign variables:

Let x = length of the equal sides Sketch the figure

Step 2: Write out the formula for perimeter of triangle .

P = sum of the three sides

Step 3: Plug in the values from the question and from the sketch.

50 = x + x + x+ 5

Combine like terms 50 = 3x + 5

Isolate variable x 3x = 50 – 5 3x = 45 x = 15

Be careful! The question requires the length of the third side.

The length of third side = 15 + 5 = 20

Answer: The length of third side is 20.

Geometry Math Problem involving the perimeter of a rectangle

The following two videos give the perimeter of a rectangle, a relationship between the length and width of the rectangle, and use that information to find the exact value of the length and width.

Example: A rectangular garden is 2.5 times as long as it is wide. It has a perimeter of 168 ft. How long and wide is the garden?

Example: A rectangular landing strip for an airplane has perimeter 8000 ft. If the length is 10 ft longer than 35 times the width, what is the length and width?

Examples of perimeter geometry word problems This video shows how to write an equation and find the dimensions of a rectangle knowing the perimeter and some information about the about the length and width.

Example: The width of a rectangle is 3 ft less than its length. The perimeter of the rectangle is 110 ft. Find the dimensions.

Perimeter Word Problems

Example: The length of a rectangle is 7 cm more than 4 times its width. Its perimeter is 124 cm. Find its dimensions.

Geometry Math Problem involving the perimeter of a triangle

The following two videos give the perimeter of a triangle, a relationship between the sides of the triangle, and use that information to find the exact value or values of the required side or sides.

Example: Patrick’s bike ride follows a triangular path; two legs are equal, the third is 8 miles longer than the other legs. If Patrick rides 30 miles total, what is the length of the longest leg?

Example: The perimeter of a triangle is 56 cm. The first side is 6 cm shorter than the second side. The third side is 2 cm shorter than twice the length of the first side. What is the length of each side?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

• Skip to main content
• Skip to primary sidebar
• Skip to footer

Additional menu

Khan Academy Blog

Free Math Worksheets — Over 100k free practice problems on Khan Academy

Looking for free math worksheets.

You’ve found something even better!

That’s because Khan Academy has over 100,000 free practice questions. And they’re even better than traditional math worksheets – more instantaneous, more interactive, and more fun!

Just choose your grade level or topic to get access to 100% free practice questions:

Kindergarten, basic geometry, pre-algebra, algebra basics, high school geometry.

• Trigonometry

Statistics and probability

High school statistics, ap®︎/college statistics, precalculus, differential calculus, integral calculus, ap®︎/college calculus ab, ap®︎/college calculus bc, multivariable calculus, differential equations, linear algebra.

• Addition and subtraction
• Place value (tens and hundreds)
• Addition and subtraction within 20
• Addition and subtraction within 100
• Addition and subtraction within 1000
• Measurement and data
• Counting and place value
• Measurement and geometry
• Place value
• Measurement, data, and geometry
• Add and subtract within 20
• Add and subtract within 100
• Add and subtract within 1,000
• Money and time
• Measurement
• Intro to multiplication
• 1-digit multiplication
• Addition, subtraction, and estimation
• Intro to division
• Understand fractions
• Equivalent fractions and comparing fractions
• More with multiplication and division
• Arithmetic patterns and problem solving
• Quadrilaterals
• Represent and interpret data
• Multiply by 1-digit numbers
• Multiply by 2-digit numbers
• Factors, multiples and patterns
• Add and subtract fractions
• Multiply fractions
• Understand decimals
• Plane figures
• Measuring angles
• Area and perimeter
• Units of measurement
• Decimal place value
• Add decimals
• Subtract decimals
• Multi-digit multiplication and division
• Divide fractions
• Multiply decimals
• Divide decimals
• Powers of ten
• Coordinate plane
• Algebraic thinking
• Converting units of measure
• Properties of shapes
• Ratios, rates, & percentages
• Arithmetic operations
• Negative numbers
• Properties of numbers
• Variables & expressions
• Equations & inequalities introduction
• Data and statistics
• Negative numbers: addition and subtraction
• Negative numbers: multiplication and division
• Fractions, decimals, & percentages
• Rates & proportional relationships
• Expressions, equations, & inequalities
• Numbers and operations
• Solving equations with one unknown
• Linear equations and functions
• Systems of equations
• Geometric transformations
• Data and modeling
• Volume and surface area
• Pythagorean theorem
• Transformations, congruence, and similarity
• Arithmetic properties
• Factors and multiples
• Reading and interpreting data
• Negative numbers and coordinate plane
• Ratios, rates, proportions
• Equations, expressions, and inequalities
• Exponents, radicals, and scientific notation
• Foundations
• Algebraic expressions
• Linear equations and inequalities
• Graphing lines and slope
• Expressions with exponents
• Quadratics and polynomials
• Equations and geometry
• Algebra foundations
• Solving equations & inequalities
• Working with units
• Linear equations & graphs
• Forms of linear equations
• Inequalities (systems & graphs)
• Absolute value & piecewise functions
• Exponents & radicals
• Exponential growth & decay
• Quadratics: Multiplying & factoring
• Quadratic functions & equations
• Irrational numbers
• Performing transformations
• Transformation properties and proofs
• Right triangles & trigonometry
• Non-right triangles & trigonometry (Advanced)
• Analytic geometry
• Conic sections
• Solid geometry
• Polynomial arithmetic
• Complex numbers
• Polynomial factorization
• Polynomial division
• Polynomial graphs
• Rational exponents and radicals
• Exponential models
• Transformations of functions
• Rational functions
• Trigonometric functions
• Non-right triangles & trigonometry
• Trigonometric equations and identities
• Analyzing categorical data
• Displaying and comparing quantitative data
• Summarizing quantitative data
• Modeling data distributions
• Exploring bivariate numerical data
• Study design
• Probability
• Counting, permutations, and combinations
• Random variables
• Sampling distributions
• Confidence intervals
• Significance tests (hypothesis testing)
• Two-sample inference for the difference between groups
• Inference for categorical data (chi-square tests)
• Advanced regression (inference and transforming)
• Analysis of variance (ANOVA)
• Scatterplots
• Data distributions
• Two-way tables
• Binomial probability
• Normal distributions
• Displaying and describing quantitative data
• Inference comparing two groups or populations
• Chi-square tests for categorical data
• More on regression
• Prepare for the 2020 AP®︎ Statistics Exam
• AP®︎ Statistics Standards mappings
• Polynomials
• Composite functions
• Probability and combinatorics
• Limits and continuity
• Derivatives: definition and basic rules
• Derivatives: chain rule and other advanced topics
• Applications of derivatives
• Analyzing functions
• Parametric equations, polar coordinates, and vector-valued functions
• Applications of integrals
• Differentiation: definition and basic derivative rules
• Differentiation: composite, implicit, and inverse functions
• Contextual applications of differentiation
• Applying derivatives to analyze functions
• Integration and accumulation of change
• Applications of integration
• AP Calculus AB solved free response questions from past exams
• AP®︎ Calculus AB Standards mappings
• Infinite sequences and series
• AP Calculus BC solved exams
• AP®︎ Calculus BC Standards mappings
• Integrals review
• Integration techniques
• Thinking about multivariable functions
• Derivatives of multivariable functions
• Applications of multivariable derivatives
• Integrating multivariable functions
• Green’s, Stokes’, and the divergence theorems
• First order differential equations
• Second order linear equations
• Laplace transform
• Vectors and spaces
• Matrix transformations
• Alternate coordinate systems (bases)

Frequently Asked Questions about Khan Academy and Math Worksheets

Why is khan academy even better than traditional math worksheets.

Khan Academy’s 100,000+ free practice questions give instant feedback, don’t need to be graded, and don’t require a printer.

What do Khan Academy’s interactive math worksheets look like?

Here’s an example:

What are teachers saying about Khan Academy’s interactive math worksheets?

“My students love Khan Academy because they can immediately learn from their mistakes, unlike traditional worksheets.”

Is Khan Academy free?

Khan Academy’s practice questions are 100% free—with no ads or subscriptions.

What do Khan Academy’s interactive math worksheets cover?

Our 100,000+ practice questions cover every math topic from arithmetic to calculus, as well as ELA, Science, Social Studies, and more.

Is Khan Academy a company?

Khan Academy is a nonprofit with a mission to provide a free, world-class education to anyone, anywhere.

Want to get even more out of Khan Academy?

Then be sure to check out our teacher tools . They’ll help you assign the perfect practice for each student from our full math curriculum and track your students’ progress across the year. Plus, they’re also 100% free — with no subscriptions and no ads.

Get Khanmigo

The best way to learn and teach with AI is here. Ace the school year with our AI-powered guide, Khanmigo. 

For learners     For teachers     For parents

Geometry Questions

Geometry questions, with answers, are provided for students to help them understand the topic more easily. Geometry is a chapter that has been included in almost all classes. The questions will be provided in accordance with NCERT guidelines. The use of geometry can be seen in both mathematics and everyday life. Thus, the fundamentals of this topic must be understood. The questions here will cover both the fundamentals and more difficult problems for students of all levels. As a result, students will be skilled in using it to solve geometry problems. Click here to learn more about Geometry.

Here, we are going to discuss different geometry questions, based on different concepts with solutions.

Geometry Questions with Solutions

1. The lines that are equidistant from each other and never meet are called ____.

Parallel lines are the lines that are equidistant from each other and never meet. The parallel lines are represented with a pair of vertical lines and its symbol is “||”. If AB and CD are the two parallel lines, it is denoted as AB || CD.

2. If two or more points lie on the same line, they are called _____.

If two or more points lie on the same line, they are called collinear points. If points A, B and C lie on the same line “l”, then we can say that the points are collinear.

3. Find the number of angles in the following figure.

In the given figure, there are three individual angles, (i.e.) 30°, 20° and 40°.

Two angles in a pair of 2. (i.e.) 20° + 30° = 50° and 20 + 40 = 60°

One angle in a pair of 3 (i.e) 20° + 30° + 40° = 90°

Hence, the total number of possible angles in the given figure is 6 .

4. In the given figure, ∠BAC = 90°, and AD is perpendicular to BC. Find the number of right triangles in the given figure.

Given: ∠BAC = 90° and AD⊥BC.

Since AD⊥BC, the two possible right triangles obtained are ∠ADB and ∠ADC.

Hence, the number of right triangles in the given figure is 3.

I.e., ∠BAC = ∠ADB = ∠ADC = 90°.

5. The length of a rectangle is 3 more inches than its breadth. The area of the rectangle is 40 in 2 . What is the perimeter of the rectangle?

Given: Area = 40 in 2 .

Let “l” be the length and “b” be the breadth of the rectangle.

According to the given question,

b = b and l = 3+b

We know that the area of a rectangle is lb units.

So, 40 = (3+b)b

40 = 3b +b 2

This can be written as b 2 +3b-40 = 0

On factoring the above equation, we get b= 5 and b= -8.

Since the value of length cannot be negative, we have b = 5 inches.

Substitute b = 5 in l = 3 + b, we get

l = 3 + 5 = 8 inches.

As we know, the perimeter of a rectangle is 2(l+b) units

P = 2 ( 8 + 5)

P = 2 (13) = 26

Hence, the perimeter of a rectangle is 26 inches.

6. What is the area of a circle in terms of π, whose diameter is 16 cm?

Given: Diameter = 16 cm.

Hence, Radius, r = 8 cm

We know that the area of a circle = πr 2 square units.

Now, substitute r = 8 cm in the formula, we get

A = π(8) 2 cm 2

A = 64π cm 2

Hence, the area of a circle whose diameter is 16 cm = 64π cm 2 .

7. Find the missing angle in the given figure.

Given two angles are 35° and 95°.

Let the unknown angle be “x”.

We know that sum of angles of a triangle is 180°

Therefore, 35°+95°+x = 180°

130°+ x = 180°

x = 180° – 130°

Hence, the missing angle is 50°.

8. Find the curved surface area of a hemisphere whose radius is 14 cm.

Given: Radius = 14 cm.

As we know, the curved surface area of a hemisphere is 2πr 2 square units.

CSA of hemisphere = 2×(22/7)×14×14

CSA = 2×22×2×14

Hence, the curved surface area of a hemisphere is 1232 cm 2 .

9. Find the volume of a cone in terms π, whose radius is 3 cm and height is 4 cm.

Given: Radius = 3 cm

Height = 4 cm

We know that the formula to find the volume of a cone is V = (⅓)πr 2 h cubic units.

Now, substitute the values in the formula, we get

V = (⅓)π(3) 2 (4)

V = π(3)(4)

V = 12π cm 3

Hence, the volume of a cone in terms of π is 12π cm 3 .

10. The base area of a cylinder is 154 cm 2 and height is 5 cm. Find the volume of a cylinder.

Given: Base area of a cylinder = 154 cm 2 .

As the base area of a cylinder is a circle, we can write πr 2 = 154cm 2 .

We know that the volume of a cylinder is πr 2 h cubic units.

V = 154(5) cm 3

V = 770 cm 3

Hence, the volume of a cylinder is 770 cm 2 .

Practice Questions

• Find the area of a square whose side length is 6 cm.
• Find the number of obtuse angles in the given figure.

            3. Find the number of line segments in the given figure and name them.

Stay tuned to BYJU’S – The Learning App, and download the app to learn all Maths concepts by exploring more videos.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

15 Challenging Geometry Problems and Their Step-by-Step Solutions

• Author: Noreen Niazi
• Last Updated on: August 22, 2023

Introduction to Geometry Problems

The area of mathematics known as geometry is concerned with the study of the positions, dimensions, and shapes of objects.Geometry has applications in various fields, such as engineering, architecture, and physics. Geometry problems are among the most challenging and exciting problems in mathematics. Understanding and mastering geometry problems is essential for anyone who wants to pursue a career in any field requiring a good understanding of geometry.

Importance of Practicing Geometry Problems

Practicing geometry problems is essential for anyone who wants to master geometry. Geometry problems require a good understanding of the concepts, formulas, and theorems. By practicing geometry problems, you will develop a deep understanding of the concepts and the formulas.

You will also be able to identify the issues and the strategies to solve them. Practicing geometry problems will also help you to improve your problem-solving skills, which will be helpful in other areas of your life.

Types of Geometry Problems

There are several types of geometry problems. Some of the common types of geometry problems include:

• Congruence problems: These problems involve proving that two or more shapes are congruent.
• Similarity problems: These problems involve proving that two or more shapes are similar.
• Area and perimeter problems: These problems involve finding the area and perimeter of various shapes.
• Volume and surface area problems: These problems involve finding the volume and surface area of various shapes.
• Coordinate geometry problems: These problems involve finding the coordinates of various points on a graph.

Strategies for Solving Geometry Problems

To solve geometry problems, you must understand the concepts, formulas, and theorems well. You also need to have a systematic approach to solving problems. Some of the strategies for solving geometry problems include:

• Read the problem carefully: You must read the situation carefully and understand what is required.
• Draw a diagram: You need to draw a diagram representing the problem. This will help you to visualize the problem and identify the relationships between the shapes.
• Identify the type of problem: You need to identify the problem type and the applicable formulas and theorems.
• Solve the problem step by step: You need to solve the problem step by step, showing all your work.
• Check your answer: You must check it to ensure it is correct.

Common Geometry Formulas and Theorems

To solve geometry problems, you must understand the standard formulas and theorems well. Some of the common procedures and theorems include:

• Area of a square: side × side.
• Pythagoras theorem: a² + b² = c², where a and b are the lengths of the two sides of a right-angled triangle, and c is the hypotenuse length.
• Area of a rectangle: length × breadth.
• Circumference of a circle : 2 × π × radius.
• Area of a triangle : ½ × base × height.
• Congruent triangles theorem: Triangles are congruent if they have the same shape and size.
• Area of a circle: π × radius².
• Similar triangles theorem: Triangles are similar if they have the same shape but different sizes.

Problem 1: Lets the length of three sides of triangle be 3 cm, 4 cm, and 5 cm. Calculate the area of a right-angled triangle.

Using the Pythagoras theorem:

$$a² + b² = c²$$

where a = 3 cm, b = 4 cm, and c = 5 cm.

$$3² + 4² = 5²$$

$$9 + 16 = 25$$

Therefore, $$c² = 25$$, and $$c = √25 = 5 cm$$.

• The area of the triangle = $$½ × \text{base} × \text{height}$$ 

$$= ½ × 3 cm × 4 cm $$

$$= 6 cm².$$

Problem 2:If the length of each side of an equilateral triangle is 10 cm then calculate its perimeter.

As the perimeter of an equilateral triangle = $$3 × side length.$$

• Therefore, the perimeter of the triangle $$= 3 × 10 cm = 30 cm.$$

Problem 3: If cylinder has 4cm radius and 10 cm height then what is the volume of a cylinder.

The volume of a cylinder = $$π × radius² × height.$$

• Therefore, the volume of the cylinder $$= π × 4² × 10 cm = 160π cm³$$.

Problem 4: If radius of a circle is given by 5cm and central angle 60° then what is the area of sector of a circle.

The area of a sector of a circle $$= (central angle ÷ 360°) × π × radius².$$

• Therefore, the area of the sector $$= (60° ÷ 360°) × π × 5² c = 4.36 cm².$$

Problem 5: Find the hypotenuse of right-angled triangle, if its other two sides are of 8 cm and 15 cm.

Using the Pythagoras theorem :

Where a = 8 cm, b = 15 cm , and c is the hypotenuse length.

$$8² + 15² = c²$$

$$64 + 225 = c²$$

• Therefore, $$c² = 289,$$ and $$c = √289 = 17 cm.$$

Problem 6: If two parallel sides of trapezium are of length 5 cm and 10 cm and height 8 cm. Calculate the area of a trapezium.

The area of a trapezium = $$½ × (sum of parallel sides) × height.$$

• Therefore, the area of the trapezium $$= ½ × (5 cm + 10 cm) × 8 cm = 60 cm².$$

Problem 7: Radius and height of cone is given by 6cm and 12 cm respectively. Calculate its volume.

The volume of a cone $$= ⅓ × π × radius² × height.$$

• Therefore, the volume of the cone $$= ⅓ × π × 6² × 12 cm³ = 452.39 cm³.$$

Problem 8:What is the length of side of square if its area is 64 cm².

The area of a square $$= side × side.$$

• Therefore, $$side = √64 cm = 8 cm.$$

Problem 9: If length rectangle is 10cm and breadth is 6cm. Calculate its diagonal.

Where $$a = 10 cm$$, $$b = 6 cm$$, and c is the diagonal length.

$$10² + 6² = c²$$

$$100 + 36 = c²$$

• Therefore, $$c² = 136,$$ and $$c = √136 cm = 11.66 cm.$$

Problem 10: If one side of regular hexagon is of 8cm then what is the area of a regular hexagon.

The area of a regular hexagon $$= 6 × (side length)² × (√3 ÷ 4).$$

• Therefore, the area of the hexagon $$= 6 × 8² × (√3 ÷ 4) cm² = 96√3 cm².$$

Problem 11: If radius of sphere is 7 cm, then what is its volume.

The volume of a sphere = $$⅔ × π × radius³.$$

• Therefore, the volume of the sphere $$= ⅔ × π × 7³ cm³ = 1436.76 cm³.$$

Problem 12: Find the hypotenuse length of a right-angled triangle with sides of 6 cm and 8 cm.

Where a = 6 cm, b = 8 cm, and c is the hypotenuse length.

$$6² + 8² = c²$$

$$36 + 64 = c²$$

Therefore, $$c² = 100,$$ and $$c = √100 cm = 10 cm.$$

Problem 13: Find the area of a rhombus with 12 cm and 16 cm diagonals.

The area of a rhombus = (diagonal 1 × diagonal 2) ÷ 2.

• Therefore, the area of the rhombus = (12 cm × 16 cm) ÷ 2 = 96 cm².

Problem 14: If radius and central angle of circle is 4cm and 45° respectively then what is the length oof arc of circle.

The length of the arc of a circle = (central angle ÷ 360°) × 2 × π × radius.

• Therefore, the length of the arc = (45° ÷ 360°) × 2 × π × 4 cm

Problem 15: Find the length of the side of a regular octagon with the radius of the inscribed circle measuring 4 cm.

The length of the side of a regular octagon = (radius of the inscribed circle) × √2.

Therefore, the length of the side of the octagon = 4 cm × √2 

Online Resources for Geometry Practice Problems

There are several online resources that you can use to practice geometry problems. Some of the popular online resources include:

• Khan Academy : On the free online learning platform Khan Academy, you may find practise questions and video lectures on a variety of subjects, including geometry.
• Mathway : Mathway is an online tool that can solve various math problems, including geometry problems.
• IXL :IXL is a website that provides practise questions and tests on a variety of subjects, including geometry.

Q: What is geometry?

A: Geometry is the branch of mathematics that studies objects’ shapes, sizes, and positions.

Q: Why is practicing geometry problems significant?

A: Practicing geometry problems is essential for anyone who wants to master geometry. Geometry problems require a good understanding of the concepts, formulas, and theorems. By practicing geometry problems, you will develop a deep understanding of the concepts and the formulas.

Q: What are some standard geometry formulas and theorems?

A: Some of the standard geometry formulas and theorems include the Pythagoras theorem, area of a triangle, area of a square, area of a rectangle, area of a circle, circumference of a circle, congruent triangles theorem, and similar triangles theorem.

Geometry problems are among the most challenging and exciting problems in mathematics. Understanding and mastering geometry problems is essential for anyone who wants to pursue a career in any field requiring a good understanding of geometry. By practicing geometry problems and using the strategies and formulas discussed in this article, you can master geometry and improve your problem-solving skills.

• Math Tutorials
• Trigonometry
• Cookie Policy
• Privacy Policy and Terms of Use

Connect With Us

• LearnAboutMath Newsletter

The Best Math Website for Learning and Practice

By signing up you are agreeing to receive emails according to our privacy policy.

Stay tuned with our latest math posts

Missing Angles Practice Questions

Click here for questions, click here for answers.

angle, right, straight line, point, full turn, vertically, opposite, basic, facts, triangle, quadrilateral

GCSE Revision Cards

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2024

Math Solver

Geogebra math solver.

Get accurate solutions and step-by-step explanations for algebra and other math problems, while enhancing your problem-solving skills!

Kite Questions with Solutions

Kite formulas.

We define the length of segments \( AC \), \( BD \) and \( AO \) using small letters as follows: \( AC = e\), \( BD = f \) and \( AO = g \). We now present the formulas that may be used to find the sides, the area, perimeter and angles of the kite. Note that: \( OC = AC - AO = e - g\) and \( BO = OD = f/2 \) Area of triangle \( AOB = (1/2)(BO)(AO) = (1/4) f g \) Area of triangle \( BOC = (1/2)(BO)(CO) = (1/4) f (e-g) \) Area of triangle \( ABC = (1/4) f g + (1/4) f (e-g) = (1/4) f g \) Area \( A \) of Kite: \[ \displaystyle A = 2 \times \text{Area of tringle} ABC = \dfrac{f \cdot e}{2} \] Use the Pythagorean theorem in the right triangle \( BOC \) Sides \( a \) and \( b \): \[ \displaystyle a = b = \sqrt{ \left(\dfrac{f}{2}\right)^2 + (e-g)^2} \] Use the Pythagorean theorem in the right triangle \( AOB \) Sides \( c \) and \( d \): \[ \displaystyle d = c = \sqrt{ \left(\dfrac{f}{2}\right)^2 + g^2} \] Perimeter: \( \displaystyle p = 2 a + 2 d \) Use the right triangle \( AOB \) to write: \( \tan(\alpha / 2) = \dfrac{f/2}{g} \), which gives Angle \( \alpha \): \[ \displaystyle \alpha = 2 \arctan (\dfrac{f}{2g}) \] Use the right triangle \( BOC \) to write: \( \tan(\gamma / 2) = \dfrac{f/2}{e-g} \), which gives Angle\( \gamma \) : \[ \displaystyle \gamma = 2 \arctan \left(\dfrac{f}{2(e-g)}\right) \] The sum of all angles in triangle \( ABC \) is equal to \( 180^{\circ} \), hence Angle \( \beta \): \[ \displaystyle \beta = 180 - \dfrac{\gamma}{2} - \dfrac{\alpha}{2} \] A kite calculator is included and may be used to check answers to calculations.

Questions with Solutions

Question 1 Calculate the sides \( a \) and \( d \), the area, the perimeter and the angles \( \alpha, \beta \) and \( \gamma \) of a kite with the diagonal axis of \( 0.8 \) meters, the second diagonal \( 0.40 \) meters and distance \( AO \) of \( 0.2 \) meters. Solution Given: \( e = 0.8 \), \( f = 0.4\) and \( g = 0.2\) Area: \( \displaystyle A = \dfrac{f \cdot e}{2} = \dfrac{0.4 \cdot 0.8}{2} = 0.16 \) square meters Sides: \( \displaystyle a = b = \sqrt{ \left(\dfrac{f}{2}\right)^2 + (e-g)^2} = \sqrt{ \left(\dfrac{0.4}{2}\right)^2 + (0.8-0.2)^2} \approx 0.63 \) meters Sides: \( \displaystyle d = c = \sqrt{ \left(\dfrac{f}{2}\right)^2 + g^2} = \sqrt{ \left(\dfrac{0.4}{2}\right)^2 + 0.2^2} \approx 0.28 \) meters Perimeter: \( \displaystyle p = 2 a + 2 d = 2 \cdot 0.68 + 2 \cdot 0.28 \approx 1.92 \) meters Angle: \( \displaystyle \alpha = 2 \arctan (\dfrac{f}{2g}) = 2 \arctan (\dfrac{0.4}{2\cdot0.2}) = 90^{\circ}\) Angle: \( \displaystyle \gamma = 2 \arctan (\dfrac{f}{2(e-g)}) = 2 \arctan (\dfrac{0.4}{2(0.8-0.2)}) = 36.87^{\circ}\) Angle: \( \displaystyle \beta = 180 - \dfrac{\gamma}{2} - \dfrac{\alpha}{2} = 180 - \dfrac{36.87}{2} - \dfrac{90}{2} = 116.57^{\circ} \)

Question 2 Calculate the sides \( a \) and \( d \), the angles \( \beta \), \( \gamma \), the area, the perimeter of a kite with the diagonal axis of \( e = 1.5 \) meters, the second diagonal \( f = 0.50 \) meters and angle \( \alpha = 30^{\circ} \). Solution Use triangle \( AOB \) to write: \( \sin(\alpha/2) = \dfrac{f/2}{d} \) The above gives: \( d = \dfrac{f/2}{\sin(\alpha/2)} = \dfrac{0.5/2}{\sin(15^{\circ}} = 0.97 \) meters Use triangle \( AOB \) to write: \( \tan(\alpha/2) = \dfrac{f/2}{OA} \) The above gives: \( g = OA = \dfrac{f/2}{\tan(\alpha/2)} = \dfrac{0.5/2}{\tan(15^{\circ}} = 0.933 \) meters Use triangle \( BOC \) to write: \( \tan(\gamma/2) = \dfrac{f/2}{AC-AO} = \dfrac{0.5/2}{1.5 - 0.933} = 0.44091\) The above gives: \( \gamma = 2 \arctan(0.44091) = 47.59^{\circ} \) Side: \( a = \sqrt { (1.5 - 0.933)^2 + (0.5/2)^2} = 0.63 \) meters Angle: \( \displaystyle \beta = 180 - \dfrac{\gamma}{2} - \dfrac{\alpha}{2} = 180 - \dfrac{47.59}{2} - \dfrac{30}{2} = 141.21^{\circ} \) Perimeter: \( \displaystyle p = 2 a + 2 d = 2 \cdot 0.63 + 2 \cdot 0.97 \approx 3.2 \) meters Area: \( \displaystyle A = \dfrac{f \cdot e}{2} = \dfrac{0.5 \cdot 1.5}{2} = 0.375 \) square meters

Question 3 Given the second diagonal \( f = 0.60 \) meters and angles \( \alpha = 30^{\circ} \) and \( \beta = 120^{\circ} \), calculate the lengths of the diagonal axis \( AC = e\) the second diagonal \( BD = f \) and angle \( \gamma \) Solution Use triangle \( AOB \) to write: \( \tan(\alpha/2) = \dfrac{f/2}{OA} \) Which gives: \(OA = g = \dfrac{f/2}{\tan(\alpha/2)} = \dfrac{0.60/2}{\tan(15^{\circ})} = 1.12 \) meters Use triangle \( ABC \) to write: \( \alpha / 2 + \gamma /2 + \beta = 180^{\circ} \) Hence: \( \gamma = 2(180 - \alpha / 2 - \beta) = 2(180 - 15 - 120) = 90^{\circ} \) Use triangle \( BOC \) to write: \( \tan(\gamma / 2) = \dfrac{BO}{OC} \) Which gives: \( OC = e - g = \dfrac{BO}{\tan(\gamma / 2)} = \dfrac{0.6/2}{45^{\circ}} = 0.3 \) Hence: \( e = 0.38 + g = 0.3 + 1.12 = 1.42 \) meters.

More References and Links

Game Central

Get step-by-step explanations

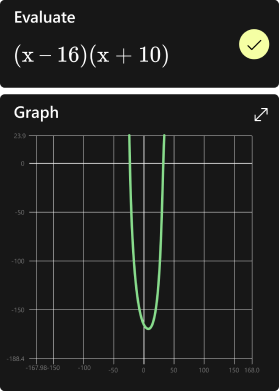
Graph your math problems

Practice, practice, practice

Upload a screenshot and solve any math, physics, or accounting problem instantly with MathGPT!

Drag & drop an image file here, or click to select an image.

Math with Bad Drawings

Lover of math. Bad at drawing.

Twenty Questions (Of Maddening, Delicious Geometry)

SURGEON GENERAL’S WARNING: BEWARE THESE PUZZLES. SIDE EFFECTS CAN INCLUDE LOST AFTERNOONS, HAIR PULLED OUT IN CLUMPS, AND EXCLAMATIONS OF “OHHHHHHH, THAT’S HOW YOU DO IT” SO LOUD THEY CAN DAMAGE WINDOWS.

I came across  Catriona Shearer ‘s math puzzles on Twitter a few months ago. I was immediately drawn in: they’re so tactile, so handcrafted, so ripe for solving. Each of her gorgeously tricksy problems can swallow an hour in a single bite.

She agreed to let me  brainfish you folks by sharing 20 of her favorites. She even indulged my curiosity and admiration with an interview (see the bottom of the post).

Enjoy. And don’t say the Surgeon General didn’t warn you.

1. The Garden of Clocks

“Unfortunately, my favourite one of the six is the only one I didn’t come up with myself,” says Catriona, “the dark blue one.”

2. The Toppled Square

(This one feels like an instant classic to me.)

3. It’s a Trap

“A ‘second attempt’ puzzle that was nicer than the first one I came up with.”

4. Three Square Meals

“I quite like this one – I drew lots of pretty patterns based on it.”

5. Shear Beauty

“Probably my all-time favourite. It just looks impossible! Apparently the solution method used here is called shearing (unfortunately, not in my honour).”

6. All Men are Created Equilateral

“Another corollary that I much prefer to the original.”

7. Semicircle Turducken

9. Tale of Two Circles

“This was a corollary to a different puzzle, but I like it more than the original!”

“I think this one’s quite neat, although it looks like a massive rip-off of Ed Southall’s puzzles.”

11. All in the Square

“I like the fact that although you can work out all the dimensions of the orange triangle from the information here (and I did when I solved it), you don’t actually need to – using the area and the hypotenuse is enough.”

12. Spike in the Hive

“This one’s quite neat – I like the fact that you don’t need to work out any of the actual side lengths, which are almost certainly horrible.”

13. Isosceles I Saw

“I think the wording of this one is my favourite. Lots of people missed the important information and concluded there were infintely many solutions!

14. Green vs. Blue

“Another one of my favourites.”

15. Jewel Cutters

“The best thing about this one: the really nice dissection solutions that were posted.”

16. Going, Going, ‘gon

“This one isn’t so neat, but the answer really surprised me. I think because it’s harder it didn’t get so much traction on twitter!

17. Just One Fact

“This is one of my favourites, as it just doesn’t look like there’s enough information.”

18. The Tumble Dryer

“I like the higgledy-piggledy squares here, like they’re rattling around in a tumble dryer. And the answer is surprisingly neat too.”

19. Fly the Flags

“This one’s quite simple, once you see it – but I didn’t straight away so the simplicity of the answer surprised me.”

20. The Tiger-gon

“This one I nearly didn’t post. But the picture reminded me of Tony the Tiger.”

BONUS: Sunset Over Square City

“I like this one because it reminds me of a sunrise over a city of squares.”

In case you’ve made it this far down the post – in which case, it’s probably 6 months after you started, and your desk is surrounded by crumpled papers and empty Chinese food containers – then here are some questions I had for Catriona.

How did you get into designing these puzzles?

I went on holiday to the Scottish Highlands, but forgot to take a coat with me, so I ended up spending more time inside than my friends did! I kept doodling along the lines of “I wonder if I could work out…”

I wasn’t expecting it to turn into a hobby, but it gets a bit addictive – especially when people reply with their solutions, which I love. There’s almost always a neat shortcut that I’ve missed.

What’s your creative process like?

It just starts with doodling. I’ll end up with a whole page of overlapping squares at different angles, or regular(ish) pentagons with different parts shaded in, and then see if there’s any nice Maths hiding there – relationships between lengths or areas or angles.

Lots of your images are marker on paper. Why the low-tech approach?

I did try using Desmos and Geogebra, but I’m not very good. I found it way quicker to draw an inscribed circle by getting my compass out and doing a bit of trial and error than by constructing it nicely in geometry software.

Also, with felt tips you can fudge things because the lines are so thick. It’s a nice compromise between it looking ‘right’ but also knowing you can’t just get your ruler out and measure it.

One of the nice things about geometry is it’s very forgiving – I can show you a hopeless picture of a square or a circle, but it’s enough to communicate the concept because they’re so well defined.

Several of your puzzles provide  just  enough information. How do you find that boundary, where a diagram is  just barely  determined?

Sometimes giving the bare minimum is actually a giveaway, because it only leaves one avenue. My preference is for giving slightly too much information, so there are a couple of decoy routes. This also means I get to see more variety when people reply with their solutions!

I’ve posted a couple of puzzles that were impossible – luckily someone usually points it out quite quickly!

I’ve also posted puzzles that I’ve massively over-specified, because I didn’t see a nice shortcut that would only use half the information.

Advice for would-be puzzle makers?

Ok, my imposter syndrome has fully kicked in here. I’m definitely still a novice – I’ve only been doing this since August! On the other hand, I’ve discovered I enjoy making puzzles and reading solutions even more than I like solving them myself.

A puzzle’s primary purpose should be amusement – that’s what marks it out from a standard Maths problem. So you need at least two of:

• A neat set up . Perhaps just enough information, so that the reader is wondering how on earth this is possible. Or several tantalising pieces of information that each feel like they offer a way in. Regular polygons and circles are a fantastic two-birds-one-stone here, because they disguise a wealth of information, without the specifically useful bits being marked on the diagram.
• A neat method . A trick, or a shortcut, or an insight that simplifies the whole thing. This might not be the most obvious method – I can think of lots of puzzles I’ve solved with lines of algebra, or surds, or horrible expressions with pi, only for it all to cancel out at the end and I realise there must have been an easier way.
• A neat answer . It’s a bit unsatisfying to work through a puzzle to get to a messy answer.

Basically, get drawing – find a puzzle you enjoyed solving and see what happens if you extend it, or change some elements of it. If you find a relationship that surprises you, chances are it will also surprise the rest of us, so put it out there. Twitter’s a great platform as people can post their own diagrams in reply.

Also, while you’re here: check out Math with Bad Drawings: The Book of All New and Wildly Enjoyable Stuff!

Leave a Reply Cancel reply

Discover more from math with bad drawings.

Subscribe now to keep reading and get access to the full archive.

Type your email…

Continue reading

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 2: Angles

About this unit.

In this topic, we will learn what an angle is and how to label, measure and construct them. We will also explore special types of angles.

Angle introduction

• Angles: introduction (Opens a modal)
• Naming angles (Opens a modal)
• Angle basics review (Opens a modal)
• Angle basics 4 questions Practice
• Name angles 4 questions Practice

Measuring angles

• Measuring angles in degrees (Opens a modal)
• Measuring angles using a protractor (Opens a modal)
• Measuring angles using a protractor 2 (Opens a modal)
• Measuring angles review (Opens a modal)
• Measure angles 4 questions Practice

Constructing angles

• Constructing angles (Opens a modal)
• Constructing angles review (Opens a modal)
• Draw angles 7 questions Practice

Angles in circles

• Angle measurement & circle arcs (Opens a modal)
• Angles in circles word problems (Opens a modal)
• Angles in circles 7 questions Practice

Angle types

• Recognizing angles (Opens a modal)
• Drawing acute, right and obtuse angles (Opens a modal)
• Identifying an angle (Opens a modal)
• Angle types review (Opens a modal)
• Angle types 4 questions Practice
• Recognize angles in figures 4 questions Practice
• Draw right, acute, and obtuse angles 7 questions Practice
• Benchmark angles 7 questions Practice

Vertical, complementary, and supplementary angles

• Complementary & supplementary angles (Opens a modal)
• Complementary and supplementary angles review (Opens a modal)
• Vertical angles review (Opens a modal)
• Angle relationships example (Opens a modal)
• Vertical angles are congruent proof (Opens a modal)
• Identifying supplementary, complementary, and vertical angles 7 questions Practice
• Complementary and supplementary angles (visual) 4 questions Practice
• Complementary and supplementary angles (no visual) 7 questions Practice
• Vertical angles 4 questions Practice

Angles between intersecting lines

• Angles, parallel lines, & transversals (Opens a modal)
• Parallel & perpendicular lines (Opens a modal)
• Missing angles with a transversal (Opens a modal)
• Parallel lines & corresponding angles proof (Opens a modal)
• Missing angles (CA geometry) (Opens a modal)
• Proving angles are congruent (Opens a modal)
• Proofs with transformations (Opens a modal)
• Angle relationships with parallel lines 7 questions Practice
• Line and angle proofs 4 questions Practice

Sal's old angle videos

• Intro to angles (old) (Opens a modal)
• Angles (part 2) (Opens a modal)
• Angles (part 3) (Opens a modal)
• Angles formed between transversals and parallel lines (Opens a modal)
• Angles of parallel lines 2 (Opens a modal)
• The angle game (Opens a modal)
• The angle game (part 2) (Opens a modal)
• Acute, right, & obtuse angles (Opens a modal)

• Solve equations and inequalities
• Simplify expressions
• Factor polynomials
• Graph equations and inequalities
• Advanced solvers
• All solvers
• Arithmetics
• Determinant
• Percentages
• Scientific Notation
• Inequalities

What can QuickMath do?

QuickMath will automatically answer the most common problems in algebra, equations and calculus faced by high-school and college students.

• The algebra section allows you to expand, factor or simplify virtually any expression you choose. It also has commands for splitting fractions into partial fractions, combining several fractions into one and cancelling common factors within a fraction.
• The equations section lets you solve an equation or system of equations. You can usually find the exact answer or, if necessary, a numerical answer to almost any accuracy you require.
• The inequalities section lets you solve an inequality or a system of inequalities for a single variable. You can also plot inequalities in two variables.
• The calculus section will carry out differentiation as well as definite and indefinite integration.
• The matrices section contains commands for the arithmetic manipulation of matrices.
• The graphs section contains commands for plotting equations and inequalities.
• The numbers section has a percentages command for explaining the most common types of percentage problems and a section for dealing with scientific notation.

Math Topics

More solvers.

• Add Fractions
• Simplify Fractions

Watch CBS News

How two high school students solved a 2,000-year-old math puzzle

By Bill Whitaker , Aliza Chasan , Sara Kuzmarov, Mariah Campbell

May 5, 2024 / 7:00 PM EDT / CBS News

A high school math teacher at St. Mary's Academy in New Orleans, Michelle Blouin Williams, was looking for ingenuity when she and her colleagues set a school-wide math contest with a challenging bonus question. That bonus question asked students to create a new proof for the Pythagorean Theorem, a fundamental principle of geometry, using trigonometry. The teachers weren't necessarily expecting anyone to solve it, as proofs of the Pythagorean Theorem using trigonometry were believed to be impossible for nearly 2,000 years.

But then, in December 2022, Calcea Johnson and Ne'Kiya Jackson, seniors at St. Mary's Academy, stepped up to the challenge. The $500 prize money was a motivating factor.

After months of work, they submitted their innovative proofs to their teachers. With the contest behind them, their teachers encouraged the students to present at a mathematics conference, and then to seek to publish their work. And even today, they're not done. Now in college, they've been working on further proofs of the Pythagorean Theorem and believe they have found five more proofs. Amazingly, despite their impressive achievements, they insist they're not math geniuses.

"I think that's a stretch," Calcea said.

The St. Mary's math contest

When the pair started working on the math contest they were familiar with the Pythagorean Theorem's equation: A² + B² = C², which explains that by knowing the length of two sides of a right triangle, it's possible to figure out the length of the third side.

When Calcea and Ne'Kiya set out to create a new Pythagorean Theorem proof, they didn't know that for thousands of years, one using trigonometry was thought to be impossible.  In 2009, mathematician Jason Zimba submitted one, and now Calcea and Ne'Kiya are adding to the canon.

Calcea and Ne'Kiya had studied geometry and some trigonometry when they started working on their proofs, but said they didn't feel math was easy. As the contest went on, they spent almost all their free time developing their ideas.

"The garbage can was full of papers, which she would, you know, work out the problems and if that didn't work, she would ball it up, throw it in the trash," Cal Johnson, Calcea's dad, said.

Neliska Jackson, Ne'Kiya's mother, says lightheartedly, that most of the time, her daughter's work was beyond her. 

To document Calcea and Ne'Kiya's work, math teachers at St. Mary's submitted their proofs to an American Mathematical Society conference in Atlanta in March 2023.

"Well, our teacher approached us and was like, 'Hey, you might be able to actually present this,'" Ne'Kiya said. "I was like, 'Are you joking?' But she wasn't. So we went. I got up there. We presented and it went well, and it blew up."

Why Calcea' and Ne'kiya's work "blew up"

The reaction was insane and unexpected, Calcea said. News of their accomplishment spread around the world. The pair got a write-up in South Korea and a shoutout from former first lady Michelle Obama. They got a commendation from the governor and keys to the city of New Orleans. 

Calcea and Ne'Kiya said they think there's several reasons why people found their work so impressive. 

"Probably because we're African American, one," Ne'Kiya said. "And we're also women. So I think-- oh, and our age. Of course our ages probably played a big part."

Ne'Kiya said she'd like their accomplishment to be celebrated for what it is: "a great mathematical achievement."

In spite of the community's celebration of the students' work, St. Mary's Academy president and interim principal Pamela Rogers said that with recognition came racist calls and comments. 

"[People said] 'they could not have done it. African Americans don't have the brains to do it.' Of course, we sheltered our girls from that," Rogers said. "But we absolutely did not expect it to come in the volume that it came."

Rogers said too often society has a vision of who can be successful.

"To some people, it is not always an African American female," Rogers said. "And to us, it's always an African American female."

Success at St. Marys 

St. Mary's, a private Catholic elementary and high school, was started for young Black women just after the Civil War. Ne'Kiya and Calcea follow a long line of barrier-breaking graduates. Leah Chase , the late queen of Creole cuisine, was an alum. So was Michelle Woodfork, the first African American female New Orleans police chief, and Dana Douglas, a judge for the Fifth Circuit Court of Appeals. 

Math teacher Michelle Blouin Williams, who initiated the math contest, said Calcea and Ne'Kiya are typical St. Mary's students. She said if they're "unicorns," then every student who's matriculated through the school is a "beautiful, Black unicorn."

Students hear that message from the moment they walk in the door, Rogers said. 

"We believe all students can succeed, all students can learn," the principal said. "It does not matter the environment that you live in."

About half the students at St. Mary's get scholarships, subsidized by fundraising to defray the $8,000 a year tuition. There's no test to get in, but expectations are high and rules are strict: cellphones are not allowed and modest skirts and hair in its natural color are required. 

Students said they appreciate the rules and rigor.

"Especially the standards that they set for us," junior Rayah Siddiq said. "They're very high. And I don't think that's ever going to change." 

What's next for Ne'Kiya and Calcea

Last year when Ne'Kiya and Calcea graduated, all their classmates were accepted into college and received scholarship offers. The school has had a 100% graduation rate and a 100% college acceptance rate for 17 years, according to Rogers.

Ne'Kiya got a full ride in the pharmacy department at Xavier University in New Orleans. Calcea, the class valedictorian, is studying environmental engineering at Louisiana State University. Neither one is pursuing a career in math, though Calcea said she may minor in math.

"People might expect too much out of me if I become a mathematician," Ne'Kiya said wryly. 

Bill Whitaker is an award-winning journalist and 60 Minutes correspondent who has covered major news stories, domestically and across the globe, for more than four decades with CBS News.

More from CBS News

Is a $10,000 deposit into a high-yield savings account worth it?

L. Franklin Devine retires from 60 Minutes

The young SS "helpers" at Auschwitz concentration camp

Pope Francis discusses same-sex couples, surrogacy during rare interview

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&