practice assignment understanding distributions through sampling

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons

Margin Size

Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

5.1: Introduction to Sampling Distributions

Last updated
Save as PDF
Page ID 28896

Rice University

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

Learning Objectives

Define inferential statistics
Graph a probability distribution for the mean of a discrete variable
Describe a sampling distribution in terms of "all possible outcomes"
Describe a sampling distribution in terms of repeated sampling
Describe the role of sampling distributions in inferential statistics
Define the standard error of the mean

Suppose you randomly sampled $10$ people from the population of women in Houston, Texas, between the ages of $21$ and $35$ years and computed the mean height of your sample. You would not expect your sample mean to be equal to the mean of all women in Houston. It might be somewhat lower or it might be somewhat higher, but it would not equal the population mean exactly. Similarly, if you took a second sample of $10$ people from the same population, you would not expect the mean of this second sample to equal the mean of the first sample.

Recall that inferential statistics concern generalizing from a sample to a population. A critical part of inferential statistics involves determining how far sample statistics are likely to vary from each other and from the population parameter. (In this example, the sample statistics are the sample means and the population parameter is the population mean.) As the later portions of this chapter show, these determinations are based on sampling distributions.

Discrete Distributions

We will illustrate the concept of sampling distributions with a simple example. Figure $\PageIndex{1}$ shows three pool balls, each with a number on it. Two of the balls are selected randomly (with replacement) and the average of their numbers is computed.

All possible outcomes are shown below in Table $\PageIndex{1}$.

Notice that all the means are either $1.0$, $1.5$, $2.0$, $2.5$, or $3.0$. The frequencies of these means are shown in Table $\PageIndex{2}$. The relative frequencies are equal to the frequencies divided by nine because there are nine possible outcomes.

Figure $\PageIndex{2}$ shows a relative frequency distribution of the means based on Table $\PageIndex{2}$. This distribution is also a probability distribution since the $Y$-axis is the probability of obtaining a given mean from a sample of two balls in addition to being the relative frequency.

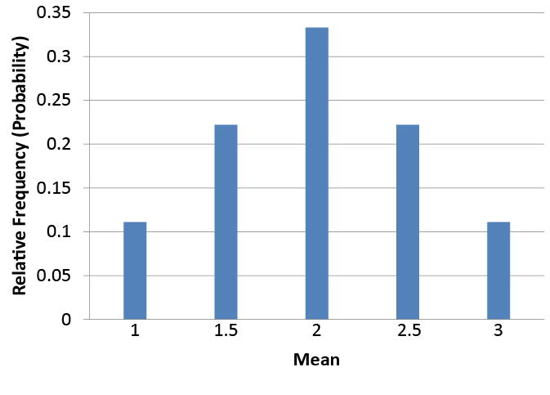
The distribution shown in Figure $\PageIndex{2}$ is called the sampling distribution of the mean. Specifically, it is the sampling distribution of the mean for a sample size of $2$ ($N = 2$). For this simple example, the distribution of pool balls and the sampling distribution are both discrete distributions. The pool balls have only the values $1$, $2$, and $3$, and a sample mean can have one of only five values shown in Table $\PageIndex{2}$.

There is an alternative way of conceptualizing a sampling distribution that will be useful for more complex distributions. Imagine that two balls are sampled (with replacement) and the mean of the two balls is computed and recorded. Then this process is repeated for a second sample, a third sample, and eventually thousands of samples. After thousands of samples are taken and the mean computed for each, a relative frequency distribution is drawn. The more samples, the closer the relative frequency distribution will come to the sampling distribution shown in Figure $\PageIndex{2}$. As the number of samples approaches infinity, the relative frequency distribution will approach the sampling distribution. This means that you can conceive of a sampling distribution as being a relative frequency distribution based on a very large number of samples. To be strictly correct, the relative frequency distribution approaches the sampling distribution as the number of samples approaches infinity.

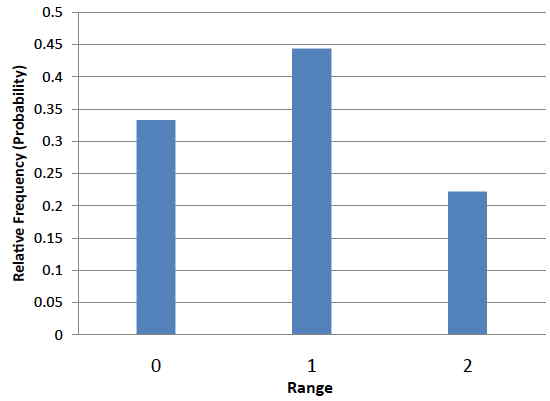
It is important to keep in mind that every statistic, not just the mean, has a sampling distribution. For example, Table $\PageIndex{3}$ shows all possible outcomes for the range of two numbers (larger number minus the smaller number). Table $\PageIndex{4}$ shows the frequencies for each of the possible ranges and Figure $\PageIndex{3}$ shows the sampling distribution of the range.

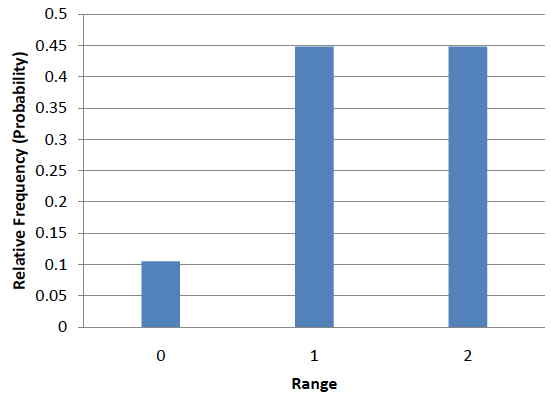
It is also important to keep in mind that there is a sampling distribution for various sample sizes. For simplicity, we have been using $N = 2$. The sampling distribution of the range for $N = 3$ is shown in Figure $\PageIndex{4}$.

Continuous Distributions

In the previous section, the population consisted of three pool balls. Now we will consider sampling distributions when the population distribution is continuous. What if we had a thousand pool balls with numbers ranging from $0.001$ to $1.000$ in equal steps? (Although this distribution is not really continuous, it is close enough to be considered continuous for practical purposes.) As before, we are interested in the distribution of means we would get if we sampled two balls and computed the mean of these two balls. In the previous example, we started by computing the mean for each of the nine possible outcomes. This would get a bit tedious for this example since there are $1,000,000$ possible outcomes ($1,000$ for the first ball x $1,000$ for the second). Therefore, it is more convenient to use our second conceptualization of sampling distributions which conceives of sampling distributions in terms of relative frequency distributions. Specifically, the relative frequency distribution that would occur if samples of two balls were repeatedly taken and the mean of each sample computed.

When we have a truly continuous distribution, it is not only impractical but actually impossible to enumerate all possible outcomes. Moreover, in continuous distributions, the probability of obtaining any single value is zero. Therefore, as discussed in the section "Introduction to Distributions," these values are called probability densities rather than probabilities.

Sampling Distributions and Inferential Statistics

As we stated in the beginning of this chapter, sampling distributions are important for inferential statistics. In the examples given so far, a population was specified and the sampling distribution of the mean and the range were determined. In practice, the process proceeds the other way: you collect sample data and from these data you estimate parameters of the sampling distribution. This knowledge of the sampling distribution can be very useful. For example, knowing the degree to which means from different samples would differ from each other and from the population mean would give you a sense of how close your particular sample mean is likely to be to the population mean. Fortunately, this information is directly available from a sampling distribution. The most common measure of how much sample means differ from each other is the standard deviation of the sampling distribution of the mean. This standard deviation is called the standard error of the mean. If all the sample means were very close to the population mean, then the standard error of the mean would be small. On the other hand, if the sample means varied considerably, then the standard error of the mean would be large.

To be specific, assume your sample mean were $125$ and you estimated that the standard error of the mean were $5$ (using a method shown in a later section). If you had a normal distribution, then it would be likely that your sample mean would be within $10$ units of the population mean since most of a normal distribution is within two standard deviations of the mean.

Keep in mind that all statistics have sampling distributions, not just the mean. In later sections we will be discussing the sampling distribution of the variance, the sampling distribution of the difference between means, and the sampling distribution of Pearson's correlation, among others.

If you could change one thing about college, what would it be?

Graduate faster

Better quality online classes

Flexible schedule

Access to top-rated instructors

Understanding Sampling Distributions: What Are They and How Do They Work?

10.06.2021 • 12 min read

Sarah Thomas

Subject Matter Expert

Sampling distribution is a key tool in the process of drawing inferences from statistical data sets. Here, we'll take you through how sampling distributions work and explore some common types.

Imagine trying to estimate the mean income of commuters who take the New Jersey Transit rail system into New York City. More than one hundred thousand commuters take these trains each day, so there’s no way you can survey every rider. Instead, you draw a random sample of 80 commuters from this population and ask each person in the sample what their household income is. You find that the mean household income for the sample is x ˉ 1 \bar{x}_{1} x ˉ 1 = $92,382. This figure is a sample statistic. It’s a number that summarizes your sample data, and you can use it to estimate the population parameter. In this case, the population parameter you are interested in is the mean income of all commuters who use the New Jersey Transit rail system to get to New York City.

Now that you’ve drawn one sample, say you draw 99 more. You now have 100 random samples of sample size n=80, and for each sample, you can calculate a sample mean. We’ll denote these means as x ˉ 1 \bar{x}_1 x ˉ 1 , x ˉ 2 \bar{x}_2 x ˉ 2 , … x ˉ 100 \bar{x}_{100} x ˉ 100 , where the subscript indicates the sample for which the mean was calculated. The value of these means will vary. For the first sample, we found a mean income of $92,382, but in another sample, the mean may be higher or lower depending on who gets sampled. In this way, the sample statistic x ˉ \bar{x} x ˉ becomes its own random variable with its own probability distribution. Tallying the values of the sample means and plotting them on a relative frequency histogram gives you the sampling distribution of x ˉ \bar{x} x ˉ (the sampling distribution of the sample mean).

Graph showing sampling distribution of sample medians

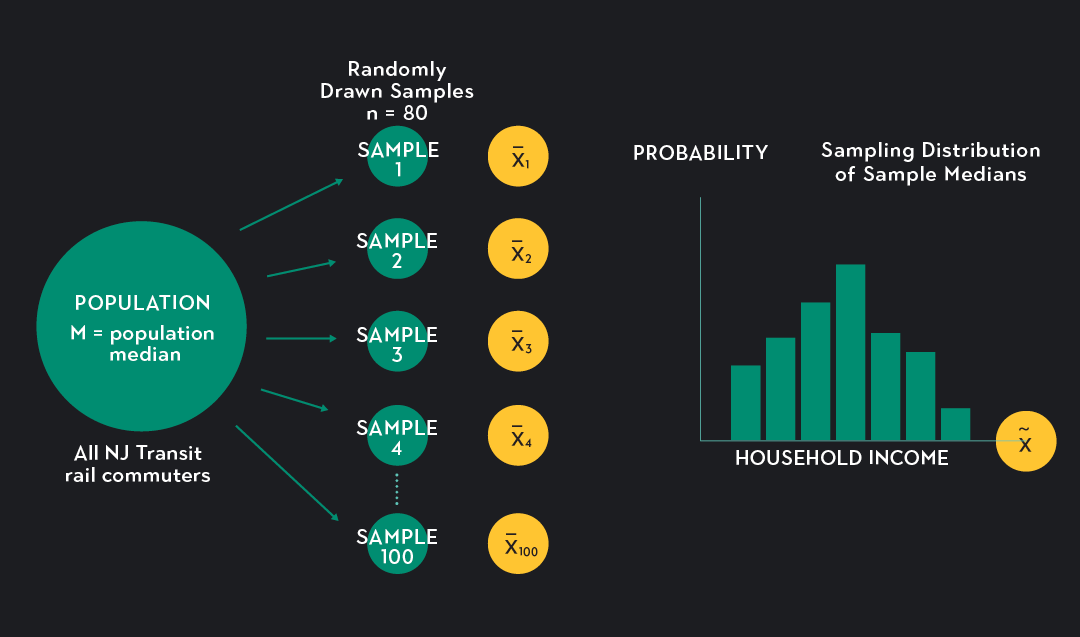
Don’t get confused! The sampling distribution is not the same thing as the probability distribution for the underlying population or the probability distribution of any one of your samples.

In our New Jersey Transit example:

The population distribution is the distribution of household income for all NJ Transit rail commuters.

The sample distribution is the distribution of income for a particular sample of eighty riders randomly drawn from the population.

The sampling distribution is the distribution of the sample statistic x ˉ \bar{x} x ˉ . This is the distribution of the 100 sample means you got from drawing 100 samples.

Sampling distributions are closely linked to one of the most important tools in statistics: the central limit theorem. There is plenty to say about the central limit theorem, but in short, and for the sake of this article, it tells us two crucial things about properly drawn samples and the shape of sampling distributions:

If you draw a large enough random sample from a population, the distribution of the sample should resemble the distribution of the population.

As the number of drawn samples gets larger and larger, and if certain conditions are met, the sampling distribution will approach a normal distribution.

What conditions need to be met for the central limit theorem to hold?

The central limit theorem applies in situations where the underlying data for the population is normally distributed or in cases where the size of the samples being drawn is greater than or equal to 30 (n≥30). In either case, samples need to be drawn randomly and with replacement.

Here is the magic behind sampling distributions and the central limit theorem. If we know that a sampling distribution is approximately normal, we can use the rules of probability (such as the empirical rule, z-transformations, and more) to make powerful statistical inferences. This is true even if the underlying distribution for the population is not normal or even if the shape of the underlying distribution is unknown. So long as the sample size is equal to or greater than 30, we can use the normal approximation of the sampling distribution to get a better estimate of what the underlying population is like.

A refresher on normal distributions and the empirical rule:

The normal distribution is a bell-shaped distribution that is symmetric around the mean and unimodal.

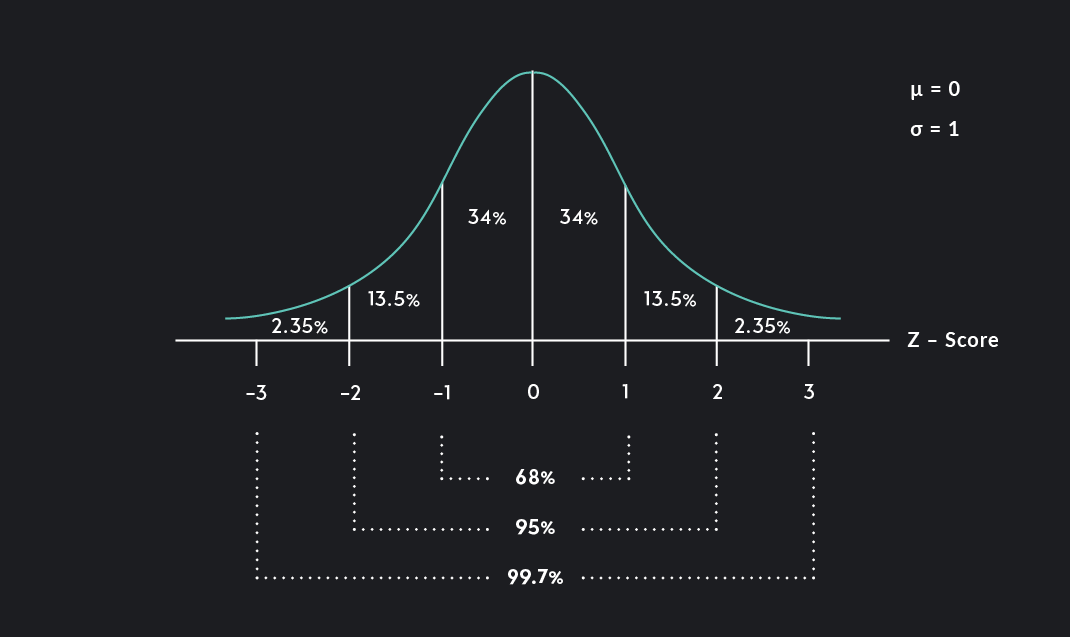
The empirical rule tells us that 68% of all observations in a normal distribution lie within one standard deviation of the mean, 95% of all observations lie within two standard deviations of the mean, and 99.7% of all observations lie within three standard deviations of the mean.

A refresher on standard normal distributions and z-transformations:

A standard normal distribution is a normal distribution with a mean equal to zero and a standard deviation equal to one.

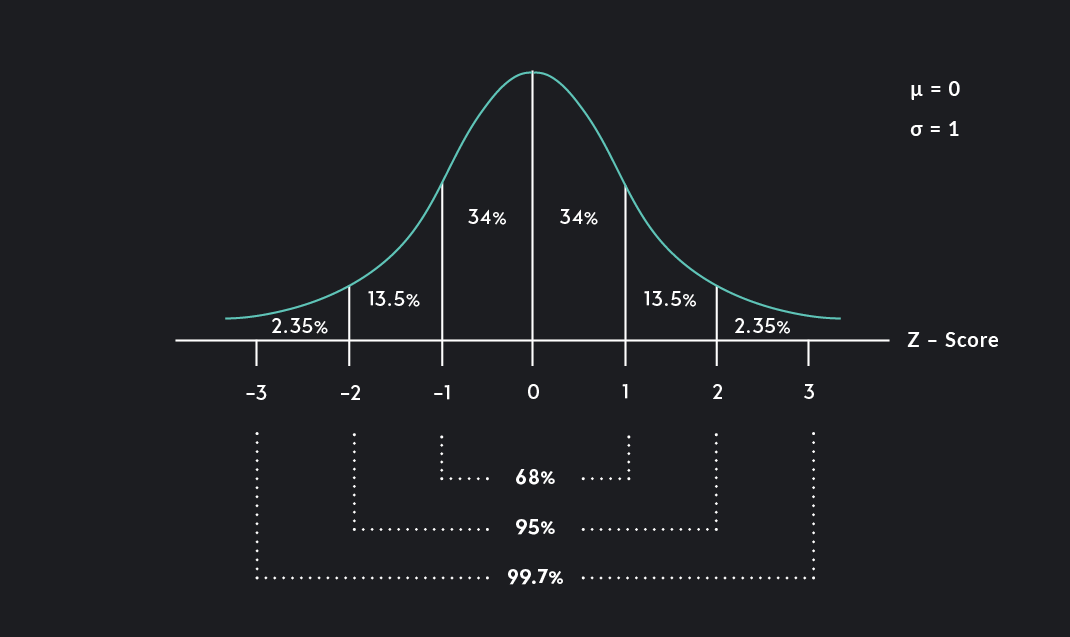
Any value from a normal distribution can be mapped to a value on the standard normal distribution using a z-transformation.

Z = ( x − μ ) σ Z =\frac{(x-\mu)}{\sigma} Z = σ ( x − μ )

Sampling distributions can be constructed for any random-sample-based statistic, so there are many types of sampling distributions. We’ll end this article by briefly exploring the characteristics of two of the most commonly used sampling distributions: the sampling distribution of sample means and the sampling distribution of sample sums. Both of these sampling distributions approach a normal distribution with a particular mean and standard deviation. The standard deviation of a sampling distribution is called the standard error .

If the central limit theorem holds, the sampling distribution of sample means will approach a normal distribution with a mean equal to the population mean, μ \mu μ , and a standard error equal to the population standard deviation divided by the square root of the sample size, σ n \frac{\sigma}{\sqrt{n}} n σ .

The fact that the distribution of sample means is centered around the population mean is an important one. This means that the expectation of a sample mean is the true population mean, μ \mu μ , and using the empirical rule, we can assert that if large enough samples of size n are drawn with replacement, 99.7% of the sample means will fall within 3 standard errors of the population mean. Lastly, sampling distribution of means allows you to use z-transformations to make probability statements about the likelihood that a sample mean, x ˉ \bar{x} x ˉ , calculated from a sample of size n, will be between, greater than, or equal to some value(s).

The sampling distribution of sample means:

The sampling distribution of the sample means, x ˉ \bar{x} x ˉ , approaches a normal distribution with mean, μ \mu μ , and a standard deviation, σ n \frac{\sigma}{\sqrt{n}} n σ ).

Sampling distribution showing probability and standard error

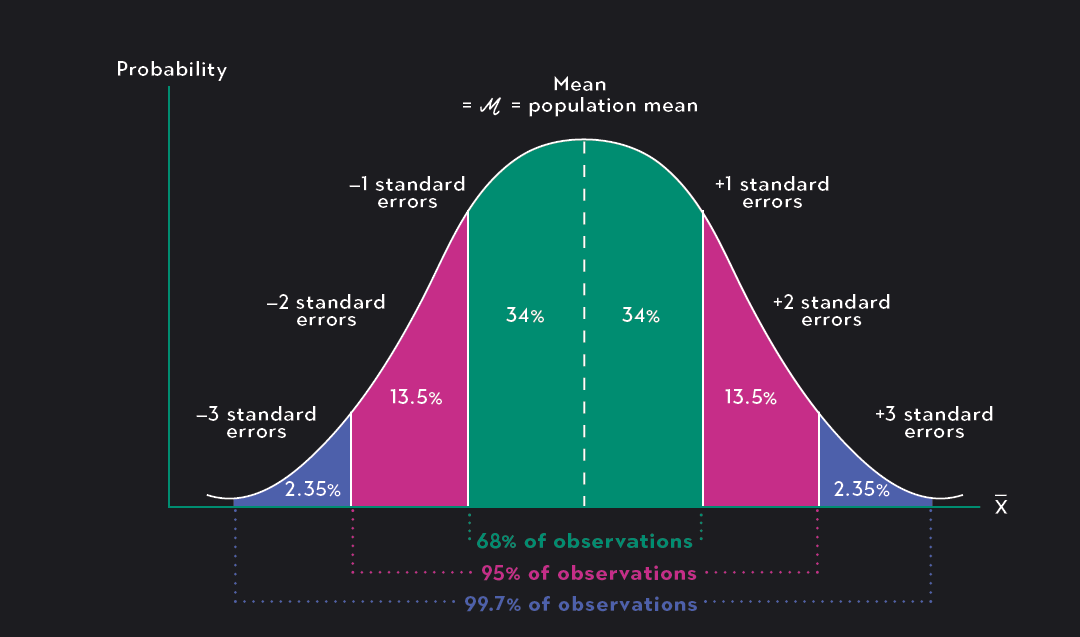
x ˉ \bar{x} x ˉ ~ N( μ \mu μ , σ n \frac{\sigma}{\sqrt{n}} n σ ) where μ \mu μ is the population mean, σ \sigma σ is the population standard deviation, and n is the sample size

Just as the sampling distribution of sample means approaches a normal distribution with a unique mean and standard, so does the sampling distribution of sample sums. A sample sum, Σ \Sigma Σ , is just the sum of all values in a sample.

The sampling distribution of sample sums is centered around a mean equal to the sample size multiplied by the population mean, n μ \mu μ , and the standard error of sums is equal to the square root of the sample size multiplied by the standard deviation of the population: ( n \sqrt{n} n )( σ \sigma σ ).

The sampling distribution of sample sums:

The sampling distribution of the sample sums, Σ \Sigma Σ , approaches a normal distribution with mean, n μ \mu μ , and a standard deviation, ( n \sqrt{n} n )( σ \sigma σ ).

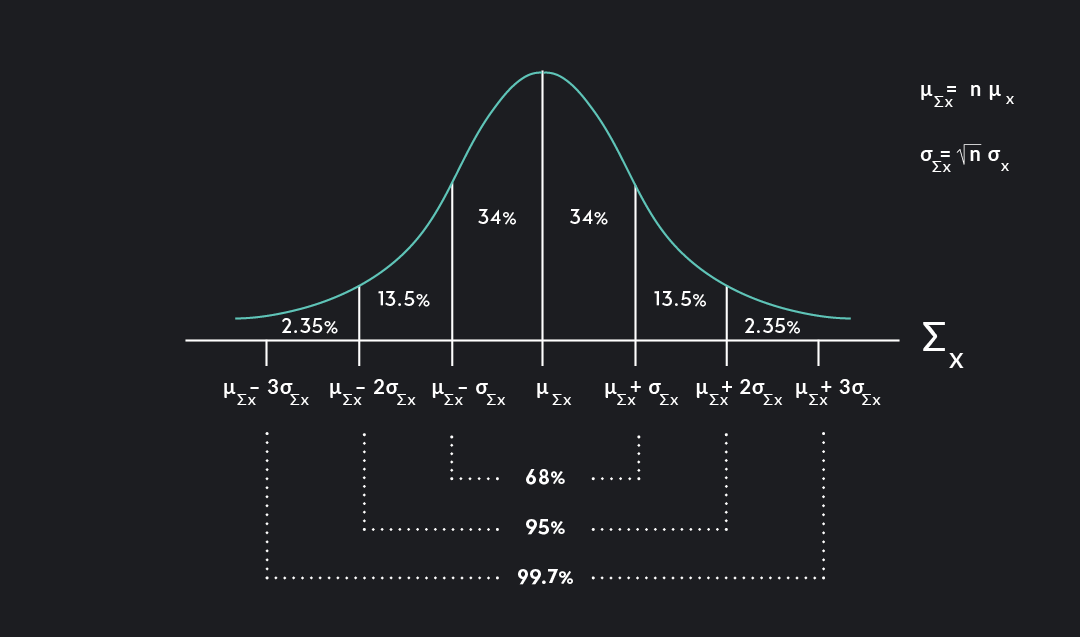
Σ x \Sigma_x Σ x ~ N(n μ x \mu_x μ x , ( n \sqrt{n} n )( σ x \sigma_x σ x ))

The mean of the sampling distribution of sums μ Σ x \mu_{\Sigma_{x}} μ Σ x = (n)( μ \mu μ )

The standard deviation of the sampling distribution of sums σ Σ x \sigma_{\Sigma_{x}} σ Σ x : ( n \sqrt{n} n )( σ \sigma σ )

One last reminder:

Remember, the standard error is just a name given to the standard deviation of a sampling distribution.

The standard error of means is the standard deviation for the sampling distribution of means. It equals σ n \frac{\sigma}{\sqrt{n}} n σ when the central limit theorem holds.

The standard error of sums is the standard deviation of the sampling distribution of sum. It equals ( n \sqrt{n} n )( σ \sigma σ ) when the central limit theorem holds.

Explore Outlier's Award-Winning For-Credit Courses

Outlier (from the co-founder of MasterClass) has brought together some of the world's best instructors, game designers, and filmmakers to create the future of online college.

Check out these related courses:

Intro to Statistics

How data describes our world.

Precalculus

Master the building blocks of Calculus.

The mathematics of change.

Intro to Microeconomics

Why small choices have big impact.

A Step-by-Step Guide on How to Calculate Standard Deviation

Standard deviation is one of the most crucial concepts in the field of Statistics. Here, we'll take you through its definition and uses, and then teach you step by step how to calculate it for any data set.

What Is the Power Rule?

The Power Rule is one of the fundamental derivative rules in the field of Calculus. In this article, we'll first discuss its definition and how to use it, and then take a deeper dive by looking at its application to a number of specific functions.

view up of a circling stairway representing a derivative in calculus

What Is a Derivative in Calculus?

In this article, we’ll discuss the meaning of slope, tangent, and the derivative. We’ll learn how to derive the limit definition of the derivative. Then, we’ll examine the most common derivative rules and practice with some examples.

Rachel McLean

Introduction to Statistics and Data Science

Chapter 9 Sampling Distributions

In Chapter 8 we introduced inferential statistics by discussing several ways to take a random sample from a population and that estimates calculated from random samples can be used to make inferences regarding parameter values in populations. In this chapter we focus on how these inferences can be made using the theory of repeated sampling .

Needed packages

Let's load all the packages needed for this chapter (this assumes you've already installed them). If needed, read Section 1.3 for information on how to install and load R packages.

9.1 Distributions

Recall from Section 2.5 that histograms allow us to visualize the distribution of a numerical variable: where the values center, how they vary, and the shape in terms of modality and symmetry/skew. Figure 9.1 shows examples of some common distribution shapes.

FIGURE 9.1: Common distribution shapes

When you visualize your population or sample data in a histogram, often times it will follow what is called a parametric distribution. Or simply put, a distribution with a fixed set of parameters. There are many known discrete and continuous distributions, however we will only focus on three common distributions:

Normal distribution
T-distribution
Chi-squared distribution.

9.1.1 Normal Distribution

The Normal Distribution is the most common and important of all distributions. It is characterized by two parameters: $\mu$ , which determines the center of the distribution, and $\sigma$ which determines the spread. In Figure 9.17 , the solid- and dashed-line curves have the same standard deviation (i.e. $\sigma = 1$ ), so they have identical spread, but they have different means, so the dashed curve is simply shifted to the right to be centered at $\mu = 2$ . On the other hand, the solid- and dotted-line curves are centered around the same value (i.e. $\mu = 0$ ), but the dotted curve has a larger standard deviation and is therefore more spread out. The solid line is a special case of the Normal distribution called the Standard Normal distribution , which has mean 0 and standard deviation 1. Importantly, for all possible values of $\mu$ and $\sigma$ , the Normal distribution is symmetric and unimodal .

FIGURE 9.2: Normal distribution

Normally distributed random variables arise naturally in many contexts. For examples, IQ, birth weight, height, shoe size, SAT scores, and the sum of two dice all tend to be Normally distributed. Let's consider the birth weight of babies from the babies data frame included in the UsingR package. We will use a histogram to visualize the distribution of weight for babies. Note that it is often difficult to obtain population data, for the sake of this example let's assume we have the entire population.

practice assignment understanding distributions through sampling

Visually we can see that the distribution is bell-shaped, that is, unimodal and approximately symmetric. It clearly resembles a Normal distribution from the shape aspect with a mean weight of 119.6 ounces and standard deviation of 18.2 ounces. However, not all bell shaped distributions are Normally distributed.

The Normal distribution has a very convenient property that says approximately 68%, 95%, and 99.7% of data fall within 1, 2, and 3 standard deviations of the mean, respectively. How can we confirm that the disbursement of birth weights adheres to this property? That would be difficult to visually check with a histogram. We could manually calculate the actual proportion of data that is within one, two, and three standard deviations of the mean, however that can be tedious. Luckily, a convenient tool exists for confirming that the disbursement of data is Normally distributed called a QQ plot, or quantile-quantile plot. A QQ plot is a scatterplot created by plotting two sets of quantiles (percentiles) against one another. That is, it plots the quantiles from our sample data against the theoretical quantiles of a Normal distribution. If the data really is Normally distributed, the sample (data) quantiles should match-up with the theoretical quantiles. The data should match up with theory! Graphically we should see the points fall along the line of identity, where data matches theory. Let's see if the QQ plot of birth weights suggest that the distribution is Normal.

The points in the QQ plot appear to fall along the line of identity, for the most part. Notice points at each end deviate slightly from the line at the. Meaning sample quartiles deviate more from theoretical quartiles at the tails. The QQ plot is suggesting that our sample data has more extreme data in the tails than an exact Normal distribution would suggest. Similar to a histogram this is a visual check and not an airtight proof. Given that our birth weight data is unimodal, symmetric, and the points of the QQ plot fall close enough to the line of identity, we can say the data is approximately Normally distributed. It is common to drop the approximately and say Normally distributed.

9.1.2 Empirical Rule

FIGURE 9.3: Empirical Rule: property of the Normal Distribution

The property that approximately 68%, 95%, and 99.7% of data falls within 1, 2, and 3 standard deviations of the mean, respectively is known as the Empirical Rule. Figure 9.3 displays this phenomenon. Note this is a property of the Normal distribution in general, for all values of $\mu$ and $\sigma$ .

If you were to plot the distribution of a Normally distributed random variable, this means you would expect:

Approximately 68% of values to fall between $\mu-\sigma$ and $\mu+\sigma$
Approximately 95% of values to fall between $\mu-2\sigma$ and $\mu+2\sigma$
Approximately 99.7% of values to fall between $\mu-3\sigma$ and $\mu+3\sigma$

Let's continue to consider our birth weight data from the babies data set. We calculated above a mean $\mu= 119.6$ ounces and standard deviation $\sigma=18.2$ ounces. Remember, we are assuming this is population data for this example. Using the empirical rule we expect 68% of data to fall between 101.4 and 137.8 ounces; 95% of data to fall between 83.2 and 155.6 ounces; and 99.7% of data to fall between 65 and 174.2 ounces. It is important to note that the total area under the distribution curve is 1 or 100%.

We can validate the empirical rule by comparing it to the actual values.

We can see that the actual proportion of data within 1 standard deviation is 69.6% compared to the expected 68%; within 2 standard deviations is 94.7% compared to the expected 95%; within 3 standard deviations is 99.4% compared to the expected 99.7%. Since all proportions are reasonably close, we find that the empirical rule is a very convenient approximation.

9.1.3 Standardization

A special case of the Normal distribution is called the Standard Normal distribution , which has mean 0 and standard deviation 1. Any Normally distributed random variable can be standardized , or in other words converted into a Standard Normal distribution using the formula:

\[STAT = \frac{x-\mu}{\sigma}.\]

Figure 9.4 demonstrates the relationship between a Normally distributed random variable, $X$ , and its standardized statistic.

FIGURE 9.4: Converting normally distributed data to standard normal.

In some literature, STAT is called a Z-score or test statistic. Standardization is a useful statistical tool as it allows us to put measures that are on different scales all onto the same scale. For example, if we have a STAT value of 2.5, we know it will fall fairly far out in the right tail of the distribution. Or if we have a STAT value of -0.5, we know it falls slightly to the left of center. This is displayed in Figure 9.5 .

FIGURE 9.5: N(0,1) example values: STAT = -0.5, STAT = 2.5

Continuing our example of babies birth weight, let's observe the relationship between weight and the standardized statistic, STAT.

FIGURE 9.6: Standardized birth weight distribution.

What if we wanted to know the percent of babies that weigh less than 95 ounces at birth? Start by converting the value 95 to STAT.

\[STAT = \frac{x-\mu}{\sigma} = \frac{95-119.6}{18.2}= -1.35\] Meaning that 95 ounces is 1.35 standard deviations below the mean. The standardized statistic already gives us an idea for a range of babies that weight less than 95 ounces because it falls somewhere between -2 and -1 standard deviations. Based on the empirical rule we know this probability should be between 2.5% and 16%, see Figure 9.7 for details.

FIGURE 9.7: Standardized birth weight distribution.

We can calculate the exact probability of a baby weighing less than 95 ounces using the pnorm() function.

There is an 8.8% chance a baby weights less than 95 ounces. Notice that you can use either the data value or standardized value, the two functions give you the same results and any difference is simply due to rounding. By default, pnorm() calculates the area less than or to the left of a specified value.

What if instead we want to calculate a value based on a percent. For example, 25% of babies weigh less than what weight? This is essentially the reverse of our previous question.

FIGURE 9.8: Standardized birth weight distribution.

We will use the function qnorm() .

This returns the weight of 107.3 or STAT of -0.67. Meaning 25% of babies weigh less than 107.3 ounces or in other words are 0.67 standard deviations below the mean. Notice by default in qnorm() you are specifying the area less than or to the left of the value. If you need to calculate the area greater than a value or use a probability that is greater than a value, you can specify the upper tail by adding on the statement lower.tail=FALSE .

9.1.4 T-Distribution

The t-distribution is a type of probability distribution that arises while sampling a normally distributed population when the sample size is small and the standard deviation of the population is unknown. The t-distribution (denoted $t(df)$ ) depends on one parameter, $df$ , and has a mean of 0 and a standard deviation of $\sqrt{\frac{df}{df-2}}$ . Degrees of freedom are dependent on the sample size and statistic (e.g. $df = n - 1$ ).

In general, the t-distribution has the same shape as the Standard Normal distribution (symmetric, unimodal), but it has heavier tails . As sample size increases (and therefore degrees of freedom increases), the t-distribution becomes a very close approximation to the Normal distribution.

FIGURE 9.9: t-distribution with example 95% cutoff values

Because the exact shape of the t-distribution depends on the sample size, we can't define one nice rule like the Empirical Rule to know which "cutoff" values correspond to 95% of the data, for example. If $df = 30$ , for example, it can be shown that 95% of the data will fall between -2.04 and 2.04, but if $df = 2$ , 95% of the data will fall between -4.3 and 4.3. This is what we mean by the t-distribution having "heavier tails"; more of the observations fall farther out in the tails of the distribution, compared to the Normal distribution.

Similar to the Normal distribution we can calculate probabilities and test statistics from a t-distribution using the pt() and qt() function, respectively. You must specify the df parameter which recall is a function of sample size, $n$ , and dependent on the statistic. We will learn more about the df of different statistics in Section 9.4 .

9.1.5 Normal vs T

The Normal distribution and t-distribution are very closely related, how do we know when to use which one? The t-distribution is used when the standard deviation of the population, $\sigma$ , is unknown. The normal distribution is used when the population standard deviation, $\sigma$ , is known. The fatter tail in the t-distribution allows us to take into account the uncertainty in not knowing the true population standard deviation.

9.1.6 Chi-squared Distribution

The Chi-squared distribution is unimodal but skewed right. The Chi-squared distribution depends on one parameter $df$ .

9.2 Repeated Sampling

A vast majority of the time we do not have data for the entire population of interest. Instead we take a sample from the population and use this sample to make generalizations and inferences about the population. How certain can we be that our sample estimate is close to the true population? In order to answer that question we must first delve into a theoretical framework, and use the theory of repeated sampling to develop the Cental Limit Theorem (CLT) and confidence intervals for our estimates.

9.2.1 Theory of Repeated Samples

Imagine that you want to know the average age of individuals at a football game, so you take a random sample of $n=100$ people. In this sample, you find the average age is $\bar{x} = 28.2$ . This average age is an estimate of the population average age $\mu$ . Does this mean that the population mean is $\mu = 28.2$ ? The sample was selected randomly, so inferences are straightforward, right?

It’s not this simple! Statisticians approach this problem by focusing not on the sample in hand, but instead on possible other samples . We will call this counter-factual thinking . This means that in order to understand the relationship between a sample estimate we are able to compute in our data and the population parameter, we have to understand how results might differ if instead of our sample, we had another possible (equally likely) sample . That is,

How would our estimate of the average age change if instead of these $n = 100$ individuals we had randomly selected a different $n = 100$ individuals?

While it is not possible to travel back in time for this particular question, we could instead generate a way to study this exact question by creating a simulation . We will discuss simulations further in Sections 9.2.2 and 9.2.3 and actually conduct one, but for now, let's just do a thought experiment. Imagine that we create a hypothetical situation in which we know the outcome (e.g., age) for every individual or observation in a population. As a result, we know what the population parameter value is (e.g., $\mu = 32.4$ ). Then we would randomly select a sample of $n = 100$ observations and calculate the sample mean (e.g. $\bar{x} = 28.2$ ). And then we could repeat this sampling process – each time selecting a different possible sample of $n = 100$ – many, many, many times (e.g., $10,000$ different samples of $n = 100$ ), each time calculating the sample mean. At the end of this process, we would then have many different estimates of the population mean, each equally likely.

We do this type of simulation in order to understand how close any one sample’s estimate is to the true population mean. For example, it may be that we are usually within $\pm 2$ years? Or maybe $\pm 5$ years? We can ask further questions, like: on average, is the sample mean the same as the population mean?

It is important to emphasize here that this process is theoretical . In real life, you do not know the values for all individuals or observations in a population. (If you did, why sample?) And in real life, you will not take repeated samples. Instead, you will have in front of you a single sample that you will need to use to make inferences to a population. What simulation exercises provide are properties that can help you understand how far off the sample estimate you have in hand might be for the population parameter you care about .

9.2.2 Sampling Activity

In the previous section, we provided an overview of repeated sampling and why the theoretical exercise is useful for understanding how to make inferences. This way of thinking, however, can be hard in the abstract.

**What proportion of this bowl's balls are red?**

In this section, we provide a concrete example, based upon a classroom activity completed in an introductory statistics class with 33 students. In the class, there is a large bowl of balls that contains red and white balls. Importantly, we know that 37.5% of the balls are red (someone counted this!).

FIGURE 9.10: A bowl with red and white balls.

The goal of the activity is to understand what would happen if we didn’t actually count all of the red balls (a census), but instead estimated the proportion that are red based upon a smaller random sample (e.g., n = 50).

**Taking one random sample**

We begin by taking a random sample of n = 50 balls. To do so, we insert a shovel into the bowl, as seen in Figure 9.11 .

FIGURE 9.11: Inserting a shovel into the bowl.

Using the shovel, we remove a number of balls as seen in Figure 9.12 .

FIGURE 9.12: Fifty balls from the bowl.

Observe that 17 of the balls are red. There are a total of 5 x 10 = 50 balls, and thus 0.34 = 34% of the shovel's balls are red. We can view the proportion of balls that are red in this shovel as a guess of the proportion of balls that are red in the entire bowl . While not as exact as doing an exhaustive count, our guess of 34% took much less time and energy to obtain.

**Everyone takes a random sample (i.e., repeating this 33 times)**

In our random sample, we estimated the proportion of red balls to be 34%. But what if we were to have gotten a different random sample? Would we remove exactly 17 red balls again? In other words, would our guess at the proportion of the bowl's balls that are red be exactly 34% again? Maybe? What if we repeated this exercise several times? Would we obtain exactly 17 red balls each time? In other words, would our guess at the proportion of the bowl's balls that are red be exactly 34% every time? Surely not.

To explore this, every student in the introductory statistics class repeated the same activity. Each person:

Used the shovel to remove 50 balls,
Counted the number of red balls,
Used this number to compute the proportion of the 50 balls they removed that are red,
Returned the balls into the bowl, and
Mixed the contents of the bowl a little to not let a previous group’s results influence the next group’s set of results.

FIGURE 9.13: Repeating sampling activity 33 times.

However, before returning the balls into the bowl, they are going to mark the proportion of the 50 balls they removed that are red in a histogram as seen in Figure 9.14 .

FIGURE 9.14: Constructing a histogram of proportions.

Recall from Section 2.5 that histograms allow us to visualize the distribution of a numerical variable: where the values center and in particular how they vary. The resulting hand-drawn histogram can be seen in Figure 9.15 .

FIGURE 9.15: Hand-drawn histogram of 33 proportions.

Observe the following about the histogram in Figure 9.15 :

At the low end, one group removed 50 balls from the bowl with proportion between 0.20 = 20% and 0.25 = 25%
At the high end, another group removed 50 balls from the bowl with proportion between 0.45 = 45% and 0.5 = 50% red.
However the most frequently occurring proportions were between 0.30 = 30% and 0.35 = 35% red, right in the middle of the distribution.
The shape of this distribution is somewhat bell-shaped.

Let's construct this same hand-drawn histogram in R using your data visualization skills that you honed in Chapter 2 . Each of the 33 student's proportion red is saved in a data frame tactile_prop_red which is included in the moderndive package you loaded earlier.

Let's display only the first 10 out of 33 rows of tactile_prop_red 's contents in Table 9.1 .

Observe for each student we have their names, the number of red_balls they obtained, and the corresponding proportion out of 50 balls that were red named prop_red . Observe, we also have a variable replicate enumerating each of the 33 students; we chose this name because each row can be viewed as one instance of a replicated activity: using the shovel to remove 50 balls and computing the proportion of those balls that are red.

We visualize the distribution of these 33 proportions using a geom_histogram() with binwidth = 0.05 in Figure 9.16 , which is appropriate since the variable prop_red is numerical. This computer-generated histogram matches our hand-drawn histogram from the earlier Figure 9.15 .

FIGURE 9.16: Distribution of 33 proportions based on 33 samples of size 50

**What are we doing here?**

We just worked through a thought experiment in which we imagined 33 different realities that could have occurred. In each, a different random sample of size 50 balls was selected and the proportion of balls that were red was calculated, providing an estimate of the true proportion of balls that are red in the entire bowl. We then compared these estimates to the true parameter value.

We found that there is variation in these estimates – what we call sampling variability – and that while the estimates are somewhat near to the population parameter, they are not typically equal to the population parameter value. That is, in some of these realities, the sample estimate was larger than the population value, while in others, the sample estimate was smaller.

But why did we do this? It may seem like a strange activity, since we already know the value of the population proportion. Why do we need to imagine these other realities? By understanding how close (or far) a sample estimate can be from a population parameter in a situation when we know the true value of the parameter , we are able to deduce properties of the estimator more generally, which we can use in real-life situations in which we do not know the value of the population parameter and have to estimate it.

Unfortunately, the thought exercise we just completed wasn’t very precise – certainly there are more than 33 possible alternative realities and samples that we could have drawn. Put another way, if we really want to understand properties of an estimator, we need to repeat this activity thousands of times. Doing this by hand – as illustrated in this section – would take forever. For this reason, in Section 9.2.3 we’ll extend the hands-on sampling activity we just performed by using a computer simulation .

Using a computer, not only will we be able to repeat the hands-on activity a very large number of times, but it will also allow us to use shovels with different numbers of slots than just 50. The purpose of these simulations is to develop an understanding of two key concepts relating to repeated sampling: understanding the concept of sampling variation and the role that sample size plays in this variation.

9.2.3 Computer simulation

In the previous Section 9.2.2 , we began imagining other realities and the other possible samples we could have gotten other than our own. To do so, we read about an activity in which a physical bowl of balls and a physical shovel were used by 33 members of a statistics class. We began with this approach so that we could develop a firm understanding of the root ideas behind the theory of repeated sampling.

In this section, we’ll extend this activity to include 10,000 other realities and possible samples using a computer. We focus on 10,000 hypothetical samples since it is enough to get a strong understanding of the properties of an estimator, while remaining computationally simple to implement.

**Using the virtual shovel once**

Let's start by performing the virtual analogue of the tactile sampling simulation we performed in 9.2.2 . We first need a virtual analogue of the bowl seen in Figure 9.10 . To this end, we included a data frame bowl in the moderndive package whose rows correspond exactly with the contents of the actual bowl.

Observe in the output that bowl has 2400 rows, telling us that the bowl contains 2400 equally-sized balls. The first variable ball_ID is used merely as an "identification variable" for this data frame; none of the balls in the actual bowl are marked with numbers. The second variable color indicates whether a particular virtual ball is red or white. View the contents of the bowl in RStudio's data viewer and scroll through the contents to convince yourselves that bowl is indeed a virtual version of the actual bowl in Figure 9.10 .

Now that we have a virtual analogue of our bowl, we now need a virtual analogue for the shovel seen in Figure 9.11 ; we'll use this virtual shovel to generate our virtual random samples of 50 balls. We're going to use the rep_sample_n() function included in the moderndive package. This function allows us to take rep eated, or rep licated, samples of size n . Run the following and explore virtual_shovel 's contents in the RStudio viewer.

Let's display only the first 10 out of 50 rows of virtual_shovel 's contents in Table 9.2 .

The ball_ID variable identifies which of the balls from bowl are included in our sample of 50 balls and color denotes its color. However what does the replicate variable indicate? In virtual_shovel 's case, replicate is equal to 1 for all 50 rows. This is telling us that these 50 rows correspond to a first repeated/replicated use of the shovel, in our case our first sample. We'll see below when we "virtually" take 10,000 samples, replicate will take values between 1 and 10,000. Before we do this, let's compute the proportion of balls in our virtual sample of size 50 that are red using the dplyr data wrangling verbs you learned in Chapter 3 . Let's breakdown the steps individually:

First, for each of our 50 sampled balls, identify if it is red using a test for equality using == . For every row where color == "red" , the Boolean TRUE is returned and for every row where color is not equal to "red" , the Boolean FALSE is returned. Let's create a new Boolean variable is_red using the mutate() function from Section 3.5 :

Second, we compute the number of balls out of 50 that are red using the summarize() function. Recall from Section 3.3 that summarize() takes a data frame with many rows and returns a data frame with a single row containing summary statistics that you specify, like mean() and median() . In this case we use the sum() :

Why does this work? Because R treats TRUE like the number 1 and FALSE like the number 0 . So summing the number of TRUE 's and FALSE 's is equivalent to summing 1 's and 0 's, which in the end counts the number of balls where color is red . In our case, 12 of the 50 balls were red.

Third and last, we compute the proportion of the 50 sampled balls that are red by dividing num_red by 50:

In other words, this "virtual" sample's balls were 24% red. Let's make the above code a little more compact and succinct by combining the first mutate() and the summarize() as follows:

Great! 24% of virtual_shovel 's 50 balls were red! So based on this particular sample, our guess at the proportion of the bowl 's balls that are red is 24%. But remember from our earlier tactile sampling activity that if we repeated this sampling, we would not necessarily obtain a sample of 50 balls with 24% of them being red again; there will likely be some variation. In fact in Table 9.1 we displayed 33 such proportions based on 33 tactile samples and then in Figure 9.15 we visualized the distribution of the 33 proportions in a histogram. Let's now perform the virtual analogue of having 10,000 students use the sampling shovel!

**Using the virtual shovel 10,000 times**

Recall that in our tactile sampling exercise in Section 9.2.2 we had 33 students each use the shovel, yielding 33 samples of size 50 balls, which we then used to compute 33 proportions. In other words we repeated/replicated using the shovel 33 times. We can perform this repeated/replicated sampling virtually by once again using our virtual shovel function rep_sample_n() , but by adding the reps = 10000 argument, indicating we want to repeat the sampling 10,000 times. Be sure to scroll through the contents of virtual_samples in RStudio's viewer.

Observe that while the first 50 rows of replicate are equal to 1 , the next 50 rows of replicate are equal to 2 . This is telling us that the first 50 rows correspond to the first sample of 50 balls while the next 50 correspond to the second sample of 50 balls. This pattern continues for all reps = 10000 replicates and thus virtual_samples has 10,000 $\times$ 50 = 500,000 rows.

Let's now take the data frame virtual_samples with 10,000 $\times$ 50 = 500,000 rows corresponding to 10,000 samples of size 50 balls and compute the resulting 10,000 proportions red. We'll use the same dplyr verbs as we did in the previous section, but this time with an additional group_by() of the replicate variable. Recall from Section 3.4 that by assigning the grouping variable "meta-data" before summarizing() , we'll obtain 10,000 different proportions red:

Let's display only the first 10 out of 10,000 rows of virtual_prop_red 's contents in Table 9.1 . As one would expect, there is variation in the resulting prop_red proportions red for the first 10 out 10,000 repeated/replicated samples.

Let's visualize the distribution of these 10,000 proportions red based on 10,000 virtual samples using a histogram with binwidth = 0.05 in Figure 9.17 .

FIGURE 9.17: Distribution of 10,000 proportions based on 10,000 samples of size 50

Observe that every now and then, we obtain proportions as low as between 20% and 25%, and others as high as between 55% and 60%. These are rare however. However, the most frequently occurring proportions red out of 50 balls were between 35% and 40%. Why do we have these differences in proportions red? Because of sampling variation .

As a wrap up to this section, let’s reflect now on what we learned. First, we began with a situation in which we know the right answer – that the true proportion of red balls in the bowl (population) is 0.375 – and then we simulated drawing a random sample of size n = 50 balls and estimating the proportion of balls that are red from this sample. We then repeated this simulation another 9,999 times, each time randomly selecting a different sample and estimating the population proportion from the sample data. At the end, we collected 10,000 estimates of the proportion of balls that are red in the bowl (population) and created a histogram showing the distribution of these estimates. Just as in the case with the 33 samples of balls selected randomly by students (in Section 9.2), the resulting distribution indicates that there is sampling variability – that is, that some of the estimates are bigger and others smaller than the true proportion. In the next section, we will continue this discussion, providing new language and concepts for summarizing this distribution.

9.3 Properties of Sampling Distributions

In the previous sections, you were introduced to sampling distributions via both an example of a hands-on activity and one using computer simulation. In both cases, you explored the idea that the sample you see in your data is one of many, many possible samples of data that you could observe. To do so, you conducted a thought experiment in which you began with a population parameter (the proportion of red balls) that you knew, and then simulated 10,000 different hypothetical random samples of the same size that you used to calculate 10,000 estimates of the population proportion. At the end, you produced a histogram of these estimated values.

The histogram you produced is formally called a sampling distribution . While this is a nice visualization, it is not particularly helpful to summarize this only with a figure. For this reason, statisticians summarize the sampling distribution by answering three questions:

How can you characterize its distribution? (Also: Is it a known distribution?)
What is the average value in this distribution? How does that compare to the population parameter?
What is the standard deviation of this distribution? What range of values are likely to occur in samples of size $n$ ?

Hopefully you were able to see that in Figure 9.17 that the sampling distribution of $\hat{\pi}$ follows a Normal distribution. As a result of the Central Limit Theorem (CLT), when sample sizes are large, most sampling distributions will be approximated well by a Normal Distribution. We will discuss the CLT further in Section 9.6 .

Throughout this section, it is imperative that you remember that this is a theoretical exercise. By beginning with a situation in which we know the right answer, we will be able to deduce properties of estimators that we can leverage in cases in which we do not know the right answer (i.e., when you are conducting actual data analyses!).

9.3.1 Mean of the sampling distribution

If we were to summarize a dataset beyond the distribution, the first statistic we would likely report is the mean of the distribution. This is true with sampling distributions as well. With sampling distributions, however, we do not simply want to know what the mean is – we want to know how similar or different this is from the population parameter value that the sample statistic is estimating. Any difference in these two values is called bias . That is:

\[Bias = Average \ \ value \ \ of \ \ sampling \ \ distribution - True \ \ population \ \ parameter \ \ value\]

A sample statistic is a biased estimator of a population parameter if its average value is more or less than the population parameter it is meant to estimate.
A sample statistic is an unbiased estimator of a population parameter if in the average sample it equals the population parameter value.

We can calculate the mean of our simulated sampling distribution of proportion of red balls $\hat{\pi}$ and compare it to the true population proportion $\pi$ .

Here we see that $\hat{\pi}=$ 0.375, which is a good approximation to the true proportion of red balls in the bowl ( $\pi =$ 0.375). This is because the sample proportion $\hat{\pi} = \frac{\# \ of \ successes}{\# \ of \ trials}$ is an unbiased estimator of the population proportion $\pi$ .

The difficulty with introducing this idea of bias in an introductory course is that most statistics used at this level (e.g., proportions, means, regression coefficients) are unbiased. Examples of biased statistics are more common in more complex models. One example, however, that illustrates this bias concept is that of sample variance estimator.

Recall that we have used standard deviation as a summary statistic for how spread out data is. Variance is simply standard deviation squared , and thus it is also a measure of spread. The sample standard deviation is usually denoted by the letter $s$ , and sample variance by $s^2$ . These are estimators for the population standard deviation (denoted $\sigma$ ) and the population variance (denoted $\sigma^2$ ). We estimate the sample variance using $s^2= \frac{\sum_{i = 1}^n(x_i - \bar{x})^2}{(n-1)}$ , where $n$ is the sample size (check out A if you are unfamiliar with the $\sum$ notation and using subscripts $i$ ). When we use the sd() function in R, it is using the square root of this function in the background: $s= \sqrt{s^2} = \sqrt{\frac{\sum_{i = 1}^n(x_i - \bar{x})^2}{(n-1)}}$ . Until now, we have simply used this estimator without reason. You might ask: why is this divided by $n – 1$ instead of simply by $n$ like the formula for the mean (i.e. $\frac{\sum x_i}{n}$ )? To see why, let's look at an example.

The gapminder dataset in the dslabs package has life expectancy data on 185 countries in 2016. We will consider these 185 countries to be our population. The true variance of life expectancy in this population is $\sigma^2 = 57.5$ .

Let's draw 10,000 repeated samples of n = 5 countries from this population. The data for the first 2 samples (replicates) is shown in 9.4 .

We can then calculate the variance for each sample (replicate) using two different formulas:

$s_n^2= \frac{\sum(x_i - \bar{x})^2}{n}$

$s^2= \frac{\sum(x_i - \bar{x})^2}{(n-1)}$

Table 9.5 shows the results for the first 10 samples. Let's look at the average of $s_n^2$ and $s^2$ across all 10,000 samples.

Remember that the true value of the variance in this population is $\sigma^2 = 57.5$ . We can see that $s_n^2$ is biased; on average it is equal to 45.913. By dividing by $n – 1$ instead of $n$ , however, the bias is removed; the average value of $s^2$ = 57.391. Therefore we use $s^2= \frac{\sum(x_i - \bar{x})^2}{(n-1)}$ as our usual estimator for $\sigma^2$ because it is unbiased.

In Figure 9.18 we visualize the sampling distribution of $s_n^2$ and $s^2$ . The black dotted line corresponds to the population variance ( $\sigma^2$ ), and we can see that the mean of the $s^2$ s line up with it very well (blue vertical line), but on average the $s_n^2$ s are an underestimate (red vertical line).

FIGURE 9.18: Sample variance estimates for 10,000 samples of size n = 5

Notice that the sampling distribution of the sample variance shown in Figure 9.18 is not Normal but rather is skewed right; in fact, it follows a chi-square distribution with $n-1$ degrees of freedom.

9.3.2 Standard deviation of the sampling distribution

In Section 9.3.1 we mentioned that one desirable characteristic of an estimator is that it be unbiased . Another desirable characteristic of an estimator is that it be precise . An estimator is precise when the estimate is close to the average of its sampling distribution in most samples. In other words, the estimates do not vary greatly from one (theoretical) sample to another.

If we were analyzing a dataset in general, we might characterize this precision by a measure of the distribution’s spread, such as the standard deviation. We can do this with sampling distributions, too. The standard error of an estimator is the standard deviation of its sampling distribution:

A large standard error means that an estimate (e.g., in the sample you have) may be far from the average of its sampling distribution. This means the estimate is imprecise .
A small standard error means an estimate (e.g., in the sample you have) is likely to be close to the average of its sampling distribution. This means the estimate is precise .

In statistics, we prefer estimators that are precise over those that are not. Again, this is tricky to understand at an introductory level, since nearly all sample statistics at this level can be proven to be the most precise estimators (out of all possible estimators) of the population parameters they are estimating. In more complex models, however, there are often competing estimators, and statisticians spend time studying the behavior of these estimators in comparison to one another.

Figure 9.19 illustrates the concepts of bias and precision. Note that an estimator can be precise but also biased. That is, all of the estimates tend to be close to one another (i.e. the sampling distribution has a small standard error), but they are centered around the wrong average value. Conversely, it's possible for an estimator to be unbiased (i.e. it's centered around the true population parameter value) but imprecise (i.e. large standard error, the estimates vary quite a bit from one (theoretical) sample to another). Most of the estimators you use in this class (e.g. $\bar{x}, s^2, \hat{\pi}$ ) are both precise and unbiased, which is clearly the preferred set of characteristics.

FIGURE 9.19: Bias vs. Precision

9.3.3 Confusing concepts

On one level, sampling distributions should seem straightforward and like simple extensions to methods you’ve learned already in this course. That is, just like sample data you have in front of you, we can summarize these sampling distributions in terms of their shape (distribution), mean (bias), and standard deviation (standard error). But this similarity to data analysis is exactly what makes this tricky.

It is imperative to remember that sampling distributions are inherently theoretical constructs :

Even if your estimator is unbiased, the number you see in your data (the value of the estimator) may not be the value of the parameter in the population.
The standard deviation is a measure of spread in your data. The standard error is a property of an estimator across repeated samples.
The distribution of a variable is something you can directly examine in your data. The sampling distribution is a property of an estimator across repeated samples.

Remember, a sample statistic is a tool we use to estimate a parameter value in a population. The sampling distribution tells us how good this tool is: Does it work on average (bias)? Does it work most of the time (standard error)? Does it tend to over- or under- estimate (distribution)?

9.4 Common statistics and their theoretical distributions

In the previous sections, we demonstrated that every statistic has a sampling distribution and that this distribution is used to make inferences between a statistic (estimate) calculated in a sample and its unknown (parameter) value in the population. For example, you now know that the sample mean’s sampling distribution is a normal distribution and that the sample variance’s sampling distribution is a chi-squared distribution.

9.4.1 Standard Errors based on Theory

In Section 9.3.2 we explained that the standard error gives you a sense of how far from the average value an estimate might be in an observed sample. In simulations, you could see that a wide distribution meant a large standard error, while a narrow distribution meant a small standard error. We could see this relationship by beginning with a case in which we knew the right answer (e.g., the population mean) and then simulating random samples of the same size, estimating this parameter in each possible sample.

But we can be more precise than this. Using mathematical properties of the normal distribution, a formula can be derived for this standard error. For example, for the sample mean, the standard error is, \[SE(\bar{x}) = \frac{\sigma}{\sqrt{n}} = \frac{s}{\sqrt{n}},\] where $s = \sqrt{\frac{\sum (x_i – \bar{x})^2}{n – 1}}$ is the sample standard deviation.

Note that this standard error is a function of both the spread of the underlying data (the $x_i$ ’s) and the sample size ( $n$ ). We will discuss more about the role of sample size in Section 9.5 .

In Table 9.6 we provide properties of some estimators, including their standard errors, for many common statistics. Note that this is not exhaustive – there are many more estimators in the world of statistics, but the ones listed here are common and provide a solid introduction.

Recall if the population standard deviation is unknown, we use $s$ and the sampling distribution is the t-distribution. If the population standard deviation is known we replace the $s$ 's in these formulas with $\sigma's$ and the sampling distribution is the Normal distribution.

The fact that there is a formula for this standard error means that we can know properties of the sampling distribution without having to do a simulation and can use this knowledge to make inferences. For example, let’s pretend we’re estimating a population mean, which we don’t know. To do so, we take a random sample of the population and estimate the mean ( $\bar{x} = 5.2$ ) and standard deviation ( $s = 2.1$ ) based upon $n = 10$ observations. Now, looking at Table 9.6 , we know that the sample mean:

Is an unbiased estimate of the population mean (so, on average, we get the right answer),
That the sampling distribution is a t-distribution, and that
The standard error (spread) of this distribution can be calculated as $SE(\bar{x}) = \frac{\sigma}{\sqrt{n}} = \frac{s}{\sqrt{n}} = \frac{2.1}{\sqrt{10}} = 0.664$ .

At this point, this is all you know, but in Chapters 10 – 12 , we will put these properties to good use.

9.5 Sample Size and Sampling Distributions

Let’s return to our football stadium thought experiment. Let’s say you could estimate the average age of fans by selecting a sample of $n = 10$ or by selecting a sample of $n = 100$ . Which would be better? Why? A larger sample will certainly cost more – is this worth it? What about a sample of $n = 500$ ? Is that worth it?

This question of appropriate sample size drives much of statistics. For example, you might be conducting an experiment in a psychology lab and ask: how many participants do I need to estimate this treatment effect precisely? Or you might be conducting a survey and need to know: how many respondents do I need in order to estimate the relationship between income and education well?

These questions are inherently about how sample size affects sampling distributions, in general, and in particular, how sample size affects standard errors (precision).

9.5.1 Sampling balls with different sized shovels

Returning to our ball example, now say instead of just one shovel, you had three choices of shovels to extract a sample of balls with.

If your goal was still to estimate the proportion of the bowl's balls that were red, which shovel would you choose? In our experience, most people would choose the shovel with 100 slots since it has the biggest sample size and hence would yield the "best" guess of the proportion of the bowl's 2400 balls that are red. Using our newly developed tools for virtual sampling simulations, let's unpack the effect of having different sample sizes! In other words, let's use rep_sample_n() with size = 25 , size = 50 , and size = 100 , while keeping the number of repeated/replicated samples at 10,000:

Virtually use the appropriate shovel to generate 10,000 samples with size balls.
Compute the resulting 10,000 replicates of the proportion of the shovel's balls that are red.
Visualize the distribution of these 10,000 proportion red using a histogram.

Run each of the following code segments individually and then compare the three resulting histograms.

For easy comparison, we present the three resulting histograms in a single row with matching x and y axes in Figure 9.20 . What do you observe?

FIGURE 9.20: Comparing the distributions of proportion red for different sample sizes

Observe that as the sample size increases, the spread of the 10,000 replicates of the proportion red decreases. In other words, as the sample size increases, there are less differences due to sampling variation and the distribution centers more tightly around the same value. Eyeballing Figure 9.20 , things appear to center tightly around roughly 40%.

We can be numerically explicit about the amount of spread in our 3 sets of 10,000 values of prop_red by computing the standard deviation for each of the three sampling distributions. For all three sample sizes, let's compute the standard deviation of the 10,000 proportions red by running the following data wrangling code that uses the sd() summary function.

Let's compare these 3 measures of spread of the distributions in Table 9.7 .

As we observed visually in Figure 9.20 , as the sample size increases our numerical measure of spread (i.e. our standard error) decreases; there is less variation in our proportions red. In other words, as the sample size increases, our guesses at the true proportion of the bowl's balls that are red get more consistent and precise. Remember that because we are computing the standard deviation of an estimator $\hat{\pi}$ 's sampling distribution, we call this the standard error of $\hat{\pi}$ .

Overall, this simulation shows that compared to a smaller sample size (e.g., $n = 10$ ), with a larger sample size (e.g., $n = 100$ ), the sampling distribution has less spread and a smaller standard error. This means that an estimate from a larger sample is likely closer to the population parameter value than one from a smaller sample.

Note that this is exactly what we would expect by looking at the standard error formulas in Table 9.6 . Sample size $n$ appears in some form on the denominator in each formula, and we know by simple arithmetic that dividing by a larger number causes the calculation to result in a smaller value. Therefore it is a general mathematical property that increasing sample size will decrease the standard error.

9.6 Central Limit Theorem (CLT)

There is a very useful result in statistics called the Central Limit Theorem which tells us that the sampling distribution of the sample mean is well approximated by the normal distribution. While not all variables follow a normal distribution, many estimators have sampling distributions that are normal. We have already seen this to be true with the sample proportion.

More formally, the CLT tells us that \[\bar{x} \sim N(mean = \mu, SE = \frac{\sigma}{\sqrt{n}}),\] where $\mu$ is the population mean of X, $\sigma$ is the population standard deviation of X, and $n$ is the sample size.

Note that we if we standardize the sample mean, it will follow the standard normal distribution. That is: \[STAT = \frac{\bar{x} - \mu}{\frac{\sigma}{\sqrt{n}}} \sim N(0,1)\] .

9.6.1 CLT conditions

Certain conditions must be met for the CLT to apply:

Independence : Sampled observations must be independent. This is difficult to verify, but is more likely if

random sampling / assignment is used, and
Sample size n < 10% of the population

Sample size / skew : Either the population distribution is normal, or if the population distribution is skewed, the sample size is large.

the more skewed the population distribution, the larger sample size we need for the CLT to apply
for moderately skewed distributions n > 30 is a widely used rule of thumb.

This is also difficult to verify for the population, but we can check it using the sample data, and assume that the sample mirrors the population.

9.6.2 CLT example

Let's return to the gapminder dataset, this time looking at the variable infant_mortality . We'll first subset our data to only include the year 2015, and we'll exclude the 7 countries that have missing data for infant_mortality . Figure 9.21 shows the distribution of infant_mortality , which is skewed right.

FIGURE 9.21: Infant mortality rates per 1,000 live births across 178 countries in 2015

Let's run 3 simulations where we take 10,000 samples of size $n = 5$ , $n = 30$ and $n = 100$ and plot the sampling distribution of the mean for each.

FIGURE 9.22: Sampling distributions of the mean infant mortality for various sample sizes

Figure 9.22 shows that for samples of size $n = 5$ , the sampling distribution is still skewed slightly right. However, with even a moderate sample size of $n = 30$ , the Central Limit Theorem kicks in, and we see that the sampling distribution of the mean ( $\bar{x}$ ) is normal, even though the underlying data was skewed. We again see that the standard error of the estimate decreases as the sample size increases.

Overall, this simulation shows that not only might the precision of an estimate differ as a result of a larger sample size, but also the sampling distribution might be different for a smaller sample size (e.g., $n = 5$ ) than for a larger sample size (e.g., $n=100$ ).

9.7 Conclusion

In this chapter, you’ve been introduced to the theory of repeated sampling that undergirds our ability to connect estimates from samples to parameters from populations that we wish to know about. In order to make these inferences, we need to understand how our results might change if – in a different reality – a different random sample was collected, or, more generally, how our results might differ across the many, many possible random samples we could have drawn. This led us to simulate the sampling distribution for our estimator of the population proportion.

You also learned that statisticians summarize this sampling distribution in three ways. We showed that for the population proportion:

The sampling distribution of the sample proportion is symmetric, unimodal, and follows a normal distribution (when n = 50),
The sample proportion is an unbiased estimate of the population proportion, and
The sample proportion does not always equal the population proportion, i.e., there is some sampling variability , making it not uncommon to see values of the sample proportion larger or smaller than the population proportion.

In the next section of the book, we will build upon this theoretical foundation, developing approaches – based upon these properties – that we can use to make inferences from the sample we have to the population we wish to know about.

Manage cookies

In this window you can switch the placement of cookies on and off. Only the Functional Cookies cannot be switched off. Your cookies preferences will be stored for 9 months, after which they will be set to default again. You can always manage your preferences and revoke your marketing consent via the Cookie Statement page in the lower left corner of the website.

Like you, we love to learn. That is why we and third parties we work with, use functional and analytical cookies (and comparable techniques) to improve your experience. By accepting all cookies you allow us to place cookies for marketing purposes too, in line with our Privacy Policy . These allow us to track your surfing behavior on and outside of Springest so we and third parties can adapt our website, advertisements and communication to you. Find more information and manage your preferences via the Cookie statement .

check Accept all Cookies

cancel Reject optional Cookies

settings Manage cookies

Applied Plotting, Charting & Data Representation in Python

Price completeness: This price is complete, there are no hidden additional costs.

Need more information? Get more details on the site of the provider.

Description

When you enroll for courses through Coursera you get to choose for a paid plan or for a free plan .

Free plan: No certicification and/or audit only. You will have access to all course materials except graded items.
Paid plan: Commit to earning a Certificate—it's a trusted, shareable way to showcase your new skills.

Read the complete description

Frequently asked questions

There are no frequently asked questions yet. If you have any more questions or need help, contact our customer service .

Didn't find what you were looking for? See also: Python , R Programming , Information Management , IT Management & Strategy , and IT Security .

About this course: This course will introduce the learner to information visualization basics, with a focus on reporting and charting using the matplotlib library. The course will start with a design and information literacy perspective, touching on what makes a good and bad visualization, and what statistical measures translate into in terms of visualizations. The second week will focus on the technology used to make visualizations in python, matplotlib, and introduce users to best practices when creating basic charts and how to realize design decisions in the framework. The third week will describe the gamut of functionality available in matplotlib, and demonstrate a variety of basic statistical charts helping learners to identify when a particular method is good for a particular problem. The course will end with a discussion of other forms of structuring and visualizing data. This course should be taken after Introduction to Data Science in Python and before the remainder of the Applied Data Science with Python courses: Applied Machine Learning in Python, Applied Text Mining in Python, and Applied Social Network Analysis in Python.

Who is this class for: This course is part of “Applied Data Science with Python“ and is intended for learners who have basic python or programming background, and want to apply statistics, machine learning, information visualization, social network analysis, and text analysis techniques to gain new insight into data. Only minimal statistics background is expected, and the first course contains a refresh of these basic concepts. There are no geographic restrictions. Learners with a formal training in Computer Science but without formal training in data science will still find the skills they acquire in these courses valuable in their studies and careers.

Taught by: Christopher Brooks

Each course is like an interactive textbook, featuring pre-recorded videos, quizzes and projects.

Connect with thousands of other learners and debate ideas, discuss course material, and get help mastering concepts.

Earn official recognition for your work, and share your success with friends, colleagues, and employers.

Video: Introduction
Reading: Syllabus
Reading: Help us learn more about you!
Video: About the Professor: Christopher Brooks
Video: Tools for Thinking about Design (Alberto Cairo)
LTI Item: Hands-on Visualization Wheel
Video: Graphical heuristics: Data-ink ratio (Edward Tufte)
Reading: Dark Horse Analytics (Optional)
Video: Graphical heuristics: Chart junk (Edward Tufte)
Reading: Useful Junk?: The Effects of Visual Embellishment on Comprehension and Memorability of Charts
Video: Graphical heuristics: Lie Factor and Spark Lines (Edward Tufte)
Video: The Truthful Art (Alberto Cairo)
Discussion Prompt: Must a visual be enlightening?
Reading: Graphics Lies, Misleading Visuals
Notebook: Module 2 Jupyter Notebook
Video: Matplotlib Architecture
Reading: Matplotlib
Reading: Ten Simple Rules for Better Figures
Video: Basic Plotting with Matplotlib
Video: Scatterplots
Video: Line Plots
Video: Bar Charts
Video: Dejunkifying a Plot
Notebook: Plotting Weather Patterns
Notebook: Module 3 Jupyter Notebook
Video: Subplots
Video: Histograms
Reading: Selecting the Number of Bins in a Histogram: A Decision Theoretic Approach (Optional)
Video: Box Plots
Video: Heatmaps
Video: Animation
Video: Interactivity
Notebook: Practice Assignment: Understanding Distributions Through Sampling
Peer Review: Practice Assignment: Understanding Distributions Through Sampling
Notebook: Building a Custom Visualization
Reading: Assignment Reading
Notebook: Module 4 Jupyter Notebook
Video: Plotting with Pandas
Video: Seaborn
Reading: Spurious Correlations
Video: Becoming an Independent Data Scientist
Notebook: Project Description
Reading: Post-course Survey
View related products with reviews: Python .

Share your review

Privacy Policy
Cookie statement
Your reference ID is: X8L9F
The Netherlands
United Kingdom

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

AP®︎/College Statistics

Course: ap®︎/college statistics > unit 6.

Techniques for generating a simple random sample
Simple random samples
Techniques for random sampling and avoiding bias
Systematic random sampling

Sampling methods

Sampling method considerations
(Choice A) Simple random sample A Simple random sample
(Choice B) Stratified random sample B Stratified random sample
(Choice C) Cluster random sample C Cluster random sample
(Choice D) Systematic random sample D Systematic random sample
(Choice E) None of the above E None of the above

Instantly share code, notes, and snippets.

Recently created
Least recently created
Recently updated
Least recently updated

Data Science
Data Analysis
Data Visualization
Machine Learning
Deep Learning
Computer Vision
Artificial Intelligence
AI ML DS Interview Series
AI ML DS Projects series
Data Engineering
Web Scrapping
Probability Distribution
Poisson Distribution In R
How to Calculate Sampling Distributions in R
Cluster Sampling in R
Plot t Distribution in R
Exploring Data Distribution | Set 1
Normal Distribution in R
Exploring Data Distribution | Set 2
Uniform Distribution Formula
Cluster Sampling
Triangular Distribution in Excel
Cluster Sampling in Pandas
Distribution of Population: Facts & Figures
Inverse t-distribution in R
Understanding the t-distribution in R
Binomial Distribution in R Programming
Sampling distribution Using Python
Frequency Distribution
Introduction to Resampling methods

Sampling Distributions in Data Science

Sampling distributions are like the building blocks of statistics. Exploring sampling distributions gives us valuable insights into the data’s meaning and the confidence level in our findings. In this, article we will explore more about sampling distributions.

Table of Content

What is Sampling distributions?

Importance sampling distribution in data science, types of sampling distributions.

1. Sampling Distribution of the Sample Mean (\bar{x})

2. Sampling Distribution of the Sample Proportion ($p$)

3. sampling distribution of the sample variance ($s^2$), central limit theorem in sampling distributions, how clt shapes sampling distributions, understanding the distribution of sample means, understanding the distribution of sample proportions, understanding the distribution of sample variances, significance of standard error in sampling, characteristics of sampling distributions, factors that influence sampling distributions.

A sampling distribution is a statistical idea that helps us understand data better. It shows the values of a statistic when we take lots of samples from a population. For example, if we want to know the average height of people in a city, we might take many random groups and find their average height. The sampling distribution helps us understand the potential variability in average heights. By analyzing this distribution, entities like governments and businesses can make more informed decisions based on their collected data.

Sampling distributions allow data scientists to:

Estimate Population Parameters : By analyzing the distribution of sample statistics, data scientists can make inferences about population parameters (e.g., population mean or proportion).
Quantify Uncertainty : Sampling distributions provide a measure of the variability of a statistic, which is crucial for constructing confidence intervals and hypothesis tests.
Model Performance Evaluation : They help in understanding the variability and performance of models, especially when dealing with small datasets or conducting resampling techniques like bootstrap.

1. Sampling Distribution of the Sample Mean ( [Tex]\bar{x}[/Tex] )

If the population is normally distributed or the sample size is sufficiently large (according to the Central Limit Theorem ), the sampling distribution of the sample mean is approximately normal with mean ( [Tex]\mu[/Tex] ) and standard error ( [Tex]\frac{\sigma}{\sqrt{n}} [/Tex] ).

If the conditions for using the normal approximation to the binomial distribution are met (e.g., large sample size, [Tex]np ≥ 10, n(1-p) ≥ 10), the sampling distribution of the sample proportion is approximately normal with mean (p) and standard error \sqrt{\frac{p(1-p)}{n}}[/Tex]

Population is normally distributed, the sampling distribution of the sample variance follows a chi-square distribution with $n-1$ degrees of freedom

The Central Limit Theorem (CLT) is a fundamental concept in statistics. It states that when we take many samples from any population and calculate their averages, the distribution of these sample averages will tend to follow a bell-shaped curve, or a normal distribution , regardless of the shape of the original population distribution.

This is important because it allows us to make predictions and draw conclusions about population parameters, like the population mean, even when we only have information about sample averages. So basically, the CLT helps us understand and predict the behavior of sample averages, making it a key tool in statistical analysis.

The Central Limit Theorem (CLT) shapes sampling distributions by providing insights into how the distribution of sample means behaves as the sample size increases.

Approach to Normality: Regardless of the shape of the population distribution, the sampling distribution of the sample mean tends to become more normally distributed as the sample size increases. This means that even if the population distribution is not normal, the distribution of sample means will approximate a normal distribution.
Stability of Parameters: The mean of the sampling distribution of the sample mean is equal to the population mean. This means that as you take larger and larger samples, the average of those samples will converge to the population mean.
Decrease in Variability: The variance of the sampling distribution of the sample mean decreases as the sample size increases. Specifically, the variance of the sample mean is equal to the population variance divided by the sample size. This means that larger sample sizes lead to less variability in the sample means.
Predictability: With larger sample sizes, the sampling distribution becomes more predictable and consistent. This is because the sample mean tends to be closer to the population mean, and the spread of the distribution becomes narrower.
Use of Normal Distribution: The CLT allows statisticians to use the properties of the normal distribution to make inferences about population parameters. For example, confidence intervals and hypothesis tests often rely on the assumption of normality, which is justified by the CLT when dealing with sample means.
The Distribution of Sample Means, also known as the sampling distribution of the sample mean, depicts the distribution of sample means obtained from multiple samples of the same size taken from a population.
Central Limit Theorem states that as the sample size increases, distribution of sample means approaches a normal distribution, regardless of the shape of the population distribution.
This distribution is crucial because it allows us to make inferences about population parameters based on sample statistics, such as estimating population means and constructing confidence intervals.

import numpy as np import matplotlib.pyplot as plt # Generate population data (normal distribution) population_mean = 50 population_std = 10 population_size = 1000 population_data = np . random . normal ( population_mean , population_std , population_size ) # Sample size and number of samples sample_size = 30 num_samples = 1000 # Calculate sample means sample_means = [ np . mean ( np . random . choice ( population_data , sample_size )) for _ in range ( num_samples )] # Plot histogram of sample means plt . hist ( sample_means , bins = 30 , edgecolor = 'black' ) plt . xlabel ( 'Sample Mean' ) plt . ylabel ( 'Frequency' ) plt . title ( 'Distribution of Sample Means' ) plt . show ()

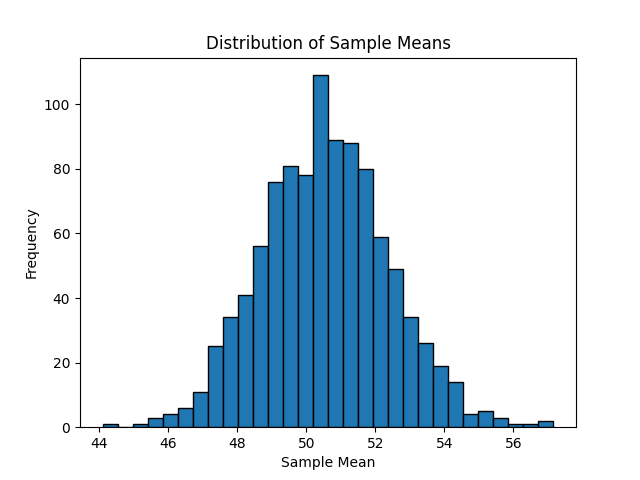
Distribution of Sample Means

The output graph is a histogram that peaks around the population of 50 showing that the average of the sample means is a good estimator of the population mean.

The Distribution of Sample Proportions describes the distribution of sample proportions (e.g., the proportion of successes) obtained from multiple samples of the same size taken from a population.
When the sample size is sufficiently large (usually greater than 30) and sampling method is random, the distribution of sample proportions can be approximated by a normal distribution.
The distribution is also fundamental in various applications, such as estimating population proportions, testing hypotheses about proportions, and constructing confidence intervals for proportions.

import numpy as np import matplotlib.pyplot as plt # Generate population data (binomial distribution) population_size = 1000 population_proportion = 0.6 population_data = np . random . binomial ( 1 , population_proportion , population_size ) # Sample size and number of samples sample_size = 50 num_samples = 1000 # Calculate sample proportions sample_proportions = [ np . mean ( np . random . choice ( population_data , sample_size , replace = True )) for _ in range ( num_samples )] # Plot histogram of sample proportions plt . hist ( sample_proportions , bins = 30 , edgecolor = 'black' ) plt . xlabel ( 'Sample Proportion' ) plt . ylabel ( 'Frequency' ) plt . title ( 'Distribution of Sample Proportions' ) plt . show ()

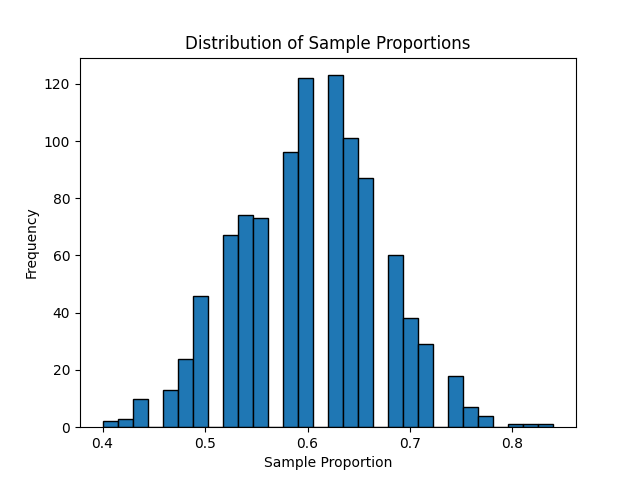
Distribution of Sample Proportions

The output graph displays the frequency distribution of the generate data, the peak of the histogram the is around population proportion (0.6), indicating that the average of the sample proportions is a good estimator of the population proportion.

The Distribution of Sample Variances showcases the distribution of sample variances obtained from multiple samples of the same size taken from a population.
Unlike the sample mean, distribution of sample variances does not necessarily follow a normal distribution, especially for small sample sizes or non-normally distributed populations.
Understanding this distribution is essential in statistical analysis, particularly in assessing the variability of data and making inferences about population variances.

import numpy as np import matplotlib.pyplot as plt # Generate population data (uniform distribution) population_data = np . random . uniform ( 0 , 100 , 1000 ) # Sample size and number of samples sample_size = 50 num_samples = 1000 # Calculate sample variances sample_variances = [ np . var ( np . random . choice ( population_data , sample_size )) for _ in range ( num_samples )] # Plot histogram of sample variances plt . hist ( sample_variances , bins = 30 , edgecolor = 'black' ) plt . xlabel ( 'Sample Variance' ) plt . ylabel ( 'Frequency' ) plt . title ( 'Distribution of Sample Variances' ) plt . show ()

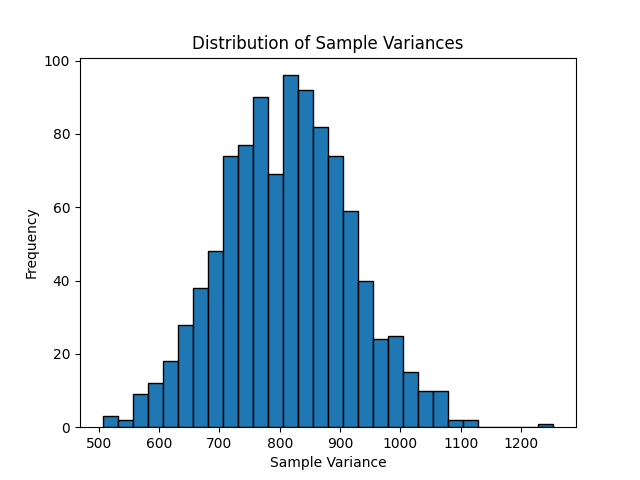
Distribution of Sample Variances

The peak of the histogram should be around the true population variance (833.33), but there will be variability due to the sampling process. The histogram will demonstrate the variability in the estimation of variance when drawing different samples from the same population.

Standard error (SE) is like a measure of how much we can trust our sample to represent the whole population. Let’s discuss it significance:

Reliability: The SE tells us how much the sample statistic (like the mean or proportion) might differ from the true population parameter. A smaller SE means we can trust our sample more because it’s closer to the population truth.
Precision: A smaller SE means our estimate is more precise. It gives us a better idea of how confident we can be in our sample data. For example, if the SE of a mean is low, we can be more confident that our sample mean is close to the true population mean.
Inference: We use SE to make inferences about the population based on our sample. For instance, in hypothesis testing, we compare the difference between sample means or proportions to the SE to see if it’s statistically significant or just due to chance.
Central Tendency: Sampling distributions have measures like mean, median, and mode, which represent the average or typical value.
Variability: They exhibit variability, quantified by measures like standard deviation or standard error, indicating how spread out the sample statistics are.
Shape: The shape depends on the population distribution and sample size. With larger samples, they tend to resemble a bell-shaped curve (normal distribution).
Bias: Sampling methods can introduce bias, leading to systematic underestimation or overestimation of population parameters.
Sampling Distribution of Sample Means: This distribution has a mean equal to the population mean and a standard deviation (or standard error) that decreases with larger sample sizes.
Sampling Distribution of Sample Proportions: Describes the variability in proportions across different samples, often used in studies involving categorical data.
Inference: Sampling distributions are foundational for statistical inference, enabling us to make probabilistic statements about population parameters based on sample statistics.
Sample Size: Larger samples lead to more representative distributions, with smaller variability.
Population Variability: More variability in the population means more variability in sample statistics.
Sampling Method: Random sampling tends to produce unbiased estimates, while non-random methods may introduce bias.
Population Distribution: Extreme skewness or outliers may affect the shape of the sampling distribution.
Parameter of Interest: Different parameters (mean, proportion, variance) may have distinct sampling distributions.
Measurement Error: Errors in data collection can increase variability in the sampling distribution.
Sampling Frame: The representativeness of the sample is influenced by the sampling frame, affecting the characteristics of the distribution.

Please Login to comment...

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

IMAGES

A Practical Introduction to Sampling Distributions
Sampling Distributions What is a sampling distribution? Section 7.1
Understanding Sampling Distributions: Calculating Test Average
Understanding Sampling Distributions: What Are They and How Do They
BSB123 THA 5 Sampling Distributions
Practice Questions on Sampling Distributions

VIDEO

MATH 1342
ASSIGNMENT INTRODUCTION CONTENT l 8 MUST HAVE POINTS l PART 1
Chapter 17: Sampling Distributions (AP Statistics)
Unlocking Investment Profits: Understanding Distributions
random sampling & assignment
Solved Example#14.7 to 14.9 ||Chapter#14 ||Survey Sampling & Sampling Distribution

COMMENTS

Practice Assignment: Understanding Distributions Through Sampling
Practice Assignment: Understanding Distributions Through Sampling. This assignment is optional, and I encourage you to share your solutions with me and your peers in the discussion forums! To complete this assignment, create a code cell that: Creates a number of subplots using the pyplot subplots or matplotlib gridspec functionality.
Applied Plotting, Charting & Data Representation in Python
Practice Assignment: Understanding Distributions Through Sampling: This assignment is optional, and I encourage you to share your solutions with me and your peers in the discussion forums! To complete this assignment, create a code cell that: Creates a number of subplots using the pyplot subplots or matplotlib gridspec functionality.
GitHub: Let's build from here · GitHub
* Creates an animation, pulling between 100 and 1000 samples from each of the random variables (`x1`, `x2`, `x3`, `x4`) for each plot and plotting this as we did in the lecture on animation.","# * **Bonus:** Go above and beyond and \"wow\" your classmates (and me!) by looking into matplotlib widgets and adding a widget which allows for ...
GitHub
Assignment 3 - practice. Understanding distributions through sampling Plot: different distributions - approximations by number of bins Assignment 3. Adding interactivity to the plot. Plot: clickable barplot that is redrawn depending on the mouseclick-indicated threshold, based on the level of confidence.
6.E: Sampling Distributions (Exercises)
In one study it was found that 86% of all homes have a functional smoke detector. Suppose this proportion is valid for all homes. Find the probability that in a random sample of 600 homes, between 80% and 90% will have a functional smoke detector. You may assume that the normal distribution applies.
Applied Plotting, Charting & Data Representation in Python
Practice Assignment: Understanding Distributions Through Sampling • 120 minutes; Building a Custom Visualization • 120 minutes; 3 ungraded labs • Total 180 minutes. Module 3 Jupyter Notebooks • 60 minutes; Practice Assignment: Understanding Distributions Through Sampling ...
Sampling distributions
Sampling distribution of a sample mean. If I take a sample, I don't always get the same results. However, sampling distributions—ways to show every possible result if you're taking a sample—help us to identify the different results we can get from repeated sampling, which helps us understand and use repeated samples.
GitHub
n\","," \" var button = $(' ');\\n\","," \" button.click(function (evt) { fig.handle_close(fig, {}); } );\\n\","," \" button.mouseover('Stop Interaction', toolbar ...
5.1: Introduction to Sampling Distributions
The distribution shown in Figure $\PageIndex{2}$ is called the sampling distribution of the mean. Specifically, it is the sampling distribution of the mean for a sample size of $2$ ($N = 2$). For this simple example, the distribution of pool balls and the sampling distribution are both discrete distributions.
Sampling distributions
Unit 9: Sampling distributions. A sampling distribution shows every possible result a statistic can take in every possible sample from a population and how often each result happens - and can help us use samples to make predictions about the chance tht something will occur. This unit covers how sample proportions and sample means behave in ...
Understanding Sampling Distributions: What Are They and How Do They
The sample distribution is the distribution of income for a particular sample of eighty riders randomly drawn from the population. The sampling distribution is the distribution of the sample statistic \bar {x} xˉ. This is the distribution of the 100 sample means you got from drawing 100 samples.
Practice Assignment for Week 3 of Applied Plotting, Charting and Data
Practice Assignment for Week 3 of Applied Plotting, Charting and Data Representation in Python Coursera course - UnderstandingDistributionsThroughSampling.ipynb
Chapter 9 Sampling Distributions
Chapter 9 Sampling Distributions. In Chapter 8 we introduced inferential statistics by discussing several ways to take a random sample from a population and that estimates calculated from random samples can be used to make inferences regarding parameter values in populations. In this chapter we focus on how these inferences can be made using the theory of repeated sampling.
Full article: Simulation Methods for Teaching Sampling Distributions
Indeed, an examination of the effect of hands-on activities using an assessment instrument that directly measures understanding of sampling distributions through more than a few items is needed. Though the study was designed to control for TA effects and other variables, the treatment is still associated with other factors.
Sampling Distributions
In this lesson, the students will use simulations to develop an intuitive understanding of sample distributions. The students will use the simulations to estimate population parameters and explore bias and unbias estimators.
Applied Plotting, Charting & Data Representation in Python
Notebook: Practice Assignment: Understanding Distributions Through Sampling; Peer Review: Practice Assignment: Understanding Distributions Through Sampling; Notebook: Building a Custom Visualization; Reading: Assignment Reading; Graded: Building a Custom Visualization WEEK 4 Module 4: Applied Visualizations In this module, then everything ...
GitHub
* Creates an animation, pulling between 100 and 1000 samples from each of the random variables (`x1`, `x2`, `x3`, `x4`) for each plot and plotting this as we did in the lecture on animation.","# * **Bonus:** Go above and beyond and \"wow\" your classmates (and me!) by looking into matplotlib widgets and adding a widget which allows for ...
PDF Compiling Toward an Understanding of Sampling Distributions
sampling. The assignment was designed for use within a business curriculum. Access to Excel and a basic understanding of Excel operations are sufficient for student success. Results suggest that this experience improved student understanding of the sampling distribution identity.
Sampling methods (practice)
None of the above. Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more. Khan Academy is a nonprofit with the mission of providing a free, world-class education for anyone, anywhere.
LalehT's gists · GitHub
Practice Assignment: Understanding Distributions Through Sampling: This assignment is optional, and I encourage you to share your solutions with me and your peers in the discussion forums! To complete this assignment, create a code cell that: Creates a number of subplots using the pyplot subplots or matplotlib gridspec functionality.
QiangUM/Understanding-Distributions-Through-Sampling
This is Cousera Applied plot practice assigment. Contribute to QiangUM/Understanding-Distributions-Through-Sampling development by creating an account on GitHub.
UnderstandingDistributionsThroughSampling.py
# coding: utf-8 # # Practice Assignment: Understanding Distributions Through Sampling # # ** *This assignment is optional, and I encourage you to share your solutions with me and your peers in the discussion forums!* ** # # # To complete this assignment, create a code cell that: # * Creates a number of subplots using the `pyplot subplots` or `matplotlib gridspec` functionality.
{"payload":{"allShortcutsEnabled":false,"fileTree":{"Pratice Assignment
{"payload":{"allShortcutsEnabled":false,"fileTree":{"Pratice Assignment":{"items":[{"name":"WHAT_TO_DO.txt","path":"Pratice Assignment/WHAT_TO_DO.txt","contentType ...
Sampling Distributions in Data Science
Central Limit Theorem in Sampling Distributions. The Central Limit Theorem (CLT) is a fundamental concept in statistics. It states that when we take many samples from any population and calculate their averages, the distribution of these sample averages will tend to follow a bell-shaped curve, or a normal distribution, regardless of the shape of the original population distribution.