problem solving net force

StickMan Physics

Animated Physics Lessons

F=ma Practice Problems

F=ma problem set.

Practice solving for net force, using Newtons second law (F=ma), and relating F=ma to the acceleration equations.

In these practice problems we will either use F=ma or our 1D motion acceleration equations to solve force problems.

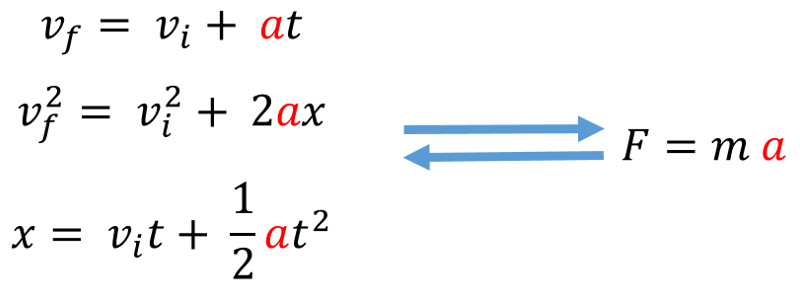
1. What is the acceleration of the 15 kg box that has 500 N of force applied to the right?

a = 33.33 m/s 2 Right

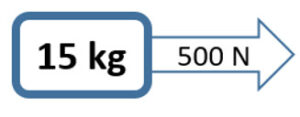
2. What is the acceleration of the 25 kg box that has 50 N of force applied to the right?

                a=2.0 m/s 2 Right

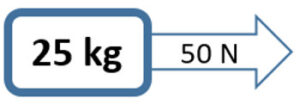
3. What is the acceleration of the 3 kg box that has 25 N of force applied to the right and 55 N left?

               a = 10.0 m/s 2 Left

4. What is the acceleration of the 5 kg box that has a 25 N force and 50 N force applied both right?

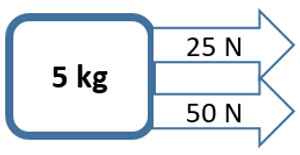
            a = 15.0 m/s 2 Right

5. What is the acceleration of the 25 kg box that has a 100 N force north and 50 N force east applied?

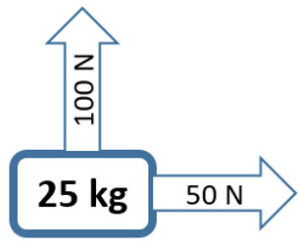
             a= 4.47 m/s 2

5b. What direction would this box accelerate?

            63.43° North of East

6. Does a 795 kg Lorinser speedy, 6300 kg elephant, or 8.6 kg wagon have more inertia and why?

            6300 kg Elephant

            The more mass the more inertia

7. How much force is required to accelerate a 795 kg Lorinser Speedy by 15 m/s 2 ?

            F = 11925 N

8. How much force is required to accelerate an 8.6 kg wagon by 15 m/s 2 ?

            F = 129 N

9. How much does a 6300 kg elephant accelerate when you apply 500 N of force?

            a = 0.0794 m/s 2

10. What is the mass of an object if it takes a net force of 40 N to accelerate at a rate of 0.88 m/s 2 ?

            m = 45.45 kg

11. How much force is required to accelerate a 0.142 kg baseball to 44.7 m/s during a pitchers 1.5 meter delivery?

            F = 94.58 N

12. A 0.050 kg golf ball leaves the tee at a speed of 75.0 m/s. The club is in contact with the ball for 0.020 s. What is the net force of the club on the ball?

                F = 187.5 N

13. A 90.0 kg astronaut receives a 30.0 N force from her jetpack. How much faster is she be moving after 2.00 seconds?

            0.667 m/s faster

14. A 795 kg car starts from rest and travels 41 m in 3.0 s. How much force did the car engine provide?

            F = 7242 N

15. Joe and his sailboat have a combined weight of 450 kg. How far has Joe sailed when he started at 5 m/s and a gust of wind provided 600 Newtons of force for 4 seconds?

            x = 30.64 m

16. Tom pulls a 45 kilogram wagon with a force of 200 Newtons at a 15° angle to the horizontal from rest. How much faster will the wagon be moving after 2 seconds?

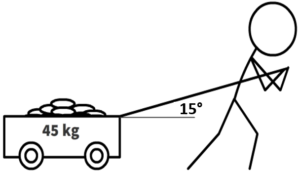
            v f = 8.58 m/s

• Back to the Newtons Second Law Lesson
• Continue to Mass and Weight
• Back to the Main Forces Page
• Back to the Stickman Physics Home Page
• Equation Sheet

Terms and Conditions - Privacy Policy

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

High school physics - NGSS

Course: high school physics - ngss   >   unit 1.

• Newton's first law of motion introduction
• Applying Newton's first law of motion
• Newton's second law of motion
• More on Newton's second law

Newton's second law review

• Understand: force, mass, and acceleration
• Apply: force, mass, and acceleration

Newton’s second law of motion

Solving problems using newton’s second law, what else should i know about newton’s second law of motion.

• Balanced forces can cause the net force of an object to be zero. Multiple forces can act on an object. If the forces are balanced, the net force is zero and the object’s acceleration is also zero.
• There are limitations to Newton’s laws. Newton’s laws are excellent for modeling our experience of the world. When we start investigating objects that are approaching the speed of light or are on the atomic scale, Newton’s laws are no longer accurate. Physicists have had to come up with additional models for these situations.]

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Physics Bootcamp

Samuel J. Ling

Section 6.4 Net Force

What happens when several forces act on a single body? For simplicity, here we consider a body of fixed mass \(m \text{.}\) Second law already tells us what to do - each force will cause acceleration. The acceleration we will observe is the net acceleration. For \(n \) forces, \(\vec F_1\text{,}\) \(\vec F_2\text{,}\) \(\cdots \text{,}\) \(\vec F_n\text{,}\) let the accelerations be \(\vec a_1\text{,}\) \(\vec a_2\text{,}\) \(\cdots \text{,}\) \(\vec a_n\text{,}\) respectively, the acceleration of the body will be

where each individual acceleration is given by the second law as

Adding them all, we get the observed acceleration, from the sum of all forces.

For instance, if you are pushed by two friends with equal-magnitude forces, one pointed East and the other pointed West. The net force on you will be zero and you will have no acceleration.

But, you know that if only one of your friends pushed on you, say the friend who was pushing in the East direction, you will have acceleration towards East. We say that, when both friends were pushing on you from opposite directions, each of your friend caused their own acceleration, but their vector sum cancelled out, resulting in no acceleration for you.

Now, if one friend pushed you towards East and the other towards North with an equal-magnitude force, your net acceleration will be in the North-East direction. The friend pushing East caused acceleration towards East, and the friend pushing North caused acceleration towards North.

The net result is the vector sum of the two, which is the observed acceleration. Therefore, rather than compute accelerations of each and then compute the vector sum of accelerations, we compute the vector sum of the forces, and then compute one acceleration from the net force.

We call the sum of all forces, the net force .

Often, we write \(\vec a_{\text{net}} \) simply as \(\vec a\text{,}\) and write the result in the following way.

We may also omit \(\text{net}\) from the force and indicate the net force as simply \(\vec F\text{.}\)

Subsection 6.4.1 Free-body Diagram

If out object of interest is a point particle, all forces on that particle will act at one point, i.e., the point where the object is currently located. But, when an object has a finite size, forces on the object can act any of the outer surface and at volume points occupied by the object. The forces acting throughout the volume include gravitational, eletric, and magnetic. The forces on the surface include friction, air drag, normal force, etc.

To find the net force on a finite object, we first identify all forces at the point they act and draw them out on the body accordingly. For gravity, we assume forces acting at all volume points add up and can be placed on a special point, called center of gravity of the body. This is the first step.

But, then, to add them vectorially, especially using the analytic method of vector addition, we draw another figure in which we replace the finite body by a single point and draw force arrows coming out of that point . This new diagram is is called free-body diagram (FBD) .

For instance, Figure 6.4.1 shows three forces on a block on an inclined surface - (1) weight (the name for the gravity force) \(\vec W\text{,}\) is placed acting on the center of gravity, (2) normal (the upward push by the incline surface) \(\vec F_N\text{,}\) and (3) friction (from the incline surface horizontal to the incline surface) \(\vec F_\text{fr}\text{.}\) Corresponding free-body diagram removes the block and replaces it wth a point.

Subsection 6.4.2 (Calculus) General Case

For the general case, we will need to work with the general equation, Eq. (6.2.6) , in which the force would now be the net force, Eq. (6.4.3) , and the momentum will the momentum of the body, \(\vec p = m \vec v\text{.}\)

We can derive this equation by setting up \(n \) equations, one for each force, causing its own rate of momentum change, and then summing them all will result in net rate at which the observed momentum changes.

Example 6.4.2 . Net Force on a Box Pulled by Two Forces in Perpendicular Directions.

A box is pulled by a force of \(40\text{ N}\) in the horizontal direction and a force of \(30\text{ N}\) also horizontally but at an angle of \(90^{\circ}\) to the direction of the other force. Find the magnitude and direction of the net force by these two forces in the horizontal plane.

Add the forces by vector rules.

\(50\ N,\ 37^{\circ}\) counterclockwise from the postitive \(x \) axis.

This problem can be done either graphically or analytically by setting up a coordinate system and using the components. We will do it analytically here. First, note that the forces of weight and normal force from the floor are not in the horizontal plane, therefore, we will ignore them since the question is only about forces that act in the horizontal plane.

First, we draw the forces in a figure so that the tails of the force vectors of interest are at the same point. This diagram of forces is called a free-body diagram . Then, we pick axes for a Cartesian coordinate system that would be very helpful in calculating the components as illustrated in the figure shown here.

Computational Steps. Using the chosen axes, we compute the Cartesian components of each force. Note that while the magnitude of a force is always positive, the components can be positive or negative. Finally, we add the \(x \) components of the forces separately from their \(y \) components to obtain the \(x \) and \(y \) components of the net force. The strength of the force is the magnitude. Therefore, we calculate the magnitude and direction of the net force from the \(x \) and \(y \) components as we would for any vector quantity.

The implementation in the present case. The table below summarizes the components found for each force.

For simplicity in writing, let us denote the net force by \(\vec F \) rather than \(\vec F_{\text{net}}\text{.}\) Therefore, the \(x \) and \(y \) components of the net force are

Therefore, the magnitude of the force is

and the angle from the positive \(x \) axis is

Since \((40,\ 30)\) is in the first quadrant, the direction is \(37^{\circ}\) counterclockwise from the postitive \(x \) axis.

Checkpoint 6.4.3 . Net Force of Two Forces Simple Case.

The figure shows all the forces acting on a body. What is the net force on the body?

You can use \(x \) and \(y\) axes.

\(361\text{ N}\) \(56.3^{\circ}\) counterclockwise from the positive \(x\) axis.

We choose the positive \(x \) axis to the right and the positive \(y \) axis pointed up. Let us denote the horizontal force by \(\vec F_1 \) and the vertical force by \(\vec F_2\text{.}\) Then, we have the components of the two forces as follows.

Let us denote the net force by \(\vec F\text{.}\) Therefore, the components of the net force are

From these we get the magnitude of the net force to be

We will get the direction from the angle \(\theta \text{,}\)

Since, the point \((F_x, F_y)=(200\text{ N}, 300\text{ N}) \) is in the first quadrant, this angle says that, the direction of the net force is \(56.3^{\circ}\) counterclockwise from the positive \(x\) axis.

Checkpoint 6.4.4 . Net Force of Two Forces General Case.

\(265\text{ N}\) \(49.1^{\circ}\) clockwise from the positive \(x\) axis.

We choose the positive \(x \) axis to the right and the positive \(y \) axis pointed up. Then, we have the components of the two forces as follows.

Since, the point \((F_x, F_y)=(173.2\text{ N}, -200\text{ N}) \) is in the first quadrant, this angle says that, the direction of the net force is \(49.1^{\circ}\) clockwise from the positive \(x\) axis.

Checkpoint 6.4.5 . Net Force of Three Forces Simple Case.

\(202\text{ N}\) \(82.4^{\circ}\) counterclockwise from the negative \(x\) axis.

We choose positive \(x \) axis to the right and the positive \(y \) axis pointed up. Then, we have the components of the three forces as follows.

Since, the point \((F_x, F_y)=(-26.8\text{ N}, -200\text{ N}) \) is in the third quadrant, this angle says that, the direction of the net force is \(82.4^{\circ}\) counterclockwise from the negative \(x\) axis.

Checkpoint 6.4.6 . Three Balanced Forces - Find Magnitude and Direction of One.

The figure shows all the forces acting on a body. The net acceleration of the body is zero. Find the magnitude and direction of the unknown force.

Set the net force to zero.

\(265\text{ N}\text{,}\) \(49.1^{\circ}\) clockwise from the negative \(x \) axis.

From the second law of motion, since net acceleration is zero, the net force is zero.

In a plane, this will lead to two equations along the two axes. To be concrete, we choose the positive \(x \) axis to the right and the positive \(y \) axis pointed up. Then, we have the components of the four forces as follows.

Setting the \(x \) and \(y\) components of the net force to zero separately, we get the two equations.

From these we get the components of \(\vec T \) to be

From these, we find the magnitude

The angle with \(x \) axis:

Since \((-173.2, 200)\) is in the second quadrant, the direction is \(49.1^{\circ}\) clockwise from the negative \(x \) axis.

Checkpoint 6.4.7 . Four Balanced Forces - Find Magnitudes of Two.

The figure shows all the forces acting on a body. The net acceleration of the body is zero. Find the magnitudes of the two forces whose symbols are \(F \) and \(T \text{.}\)

\(F = 230\text{ N}\text{,}\) \(T = 194\text{ N}\text{.}\)

From these we get the magnitudes to be

practice problem 1

For all solutions, let T 1 be the cable on the left and T 2 be the cable on the right. The sign always has weight ( W ), which points down. The sign isn't going anywhere (it's not accelerating), therefore the three forces are in equilibrium. Describe this state using the language of physics — equations; in particular, component analysis equations. As always, make a nice drawing to show what's going on. Use a ruler and a protractor if you wish.

The two upward components should equal one another. Together they should equal the weight, which means each one is carrying half the load.

Weight points down (270°) and T 1 points to the left (180°). These are both good vectors — good in the sense that they are easy to deal with. T 1 is the troublemaker. Break it up into components and state the conditions for equilibrium in the vertical and horizontal directions. I like to put negative vectors on the left side of the equals sign and positive vectors on the right side. I also suggest working through the vertical equation first.

Weight is the only force with a convenient direction. Resolve the tensions into their components. State the equilibrium condition along both axes. I suggest working with the horizontal equation first.

That's the end of the physics. The rest of the work is math. Solve the horizontal equation for T 1 .

Substitute the result into the vertical equation.

Solve that for T 2 , substitute values, and compute T 2 .

Substitute back into the horizontal equation and compute T 1 .

My, that last one wasn't very much fun. Let's see if there isn't a simpler solution. We used component analysis since it's the default approach. Whenever you're given a pile of vectors and you need to combine them, components is the way to go — especially if you have no expectation of any special relationships among the vectors. We use this brainless, brute force approach to problems all the time. Understand the rules, describe them using commands a computer understands, put numbers in, get answers out.

Sometimes, however, there are clever solutions available. They don't work all the time, but when they do we should use them. In this practice problem, the vectors are rigged so that the alternate solution is easier than the default solution. The graphical method for addition of vectors requires placing them head to tail. The sum would be the resultant vector connecting the tail of the first vector to the head of the last. When forces are in equilibrium, their sum is zero and their will be no resultant. This means, it should be possible to arrange the three vectors in this practice problem into a closed figure — a triangle. Let's try it.

This is what we call a degenerate triangle. Sure it has three sides, but it covers no area. The two short sides lie on top of the long side. Symmetry tells us the two short sides should have equal length. Thus each tension equals half the weight. We already said this, so there is no advantage to this method over the previous one.

The horizontal tension and the vertical weight are the legs of a 45–45–90 triangle whose hypotenuse is the diagonal tension. These forces should form the ratio 1:1:√2.

The two tensions are the legs of a 30–60–90 triangle and weight is the hypotenuse. This means the sides should form the ratio 1:√3:2. Just be sure to get the tensions to correspond to the correct parts of this ratio.

And there are probably other ways to solve this problem.

practice problem 2

• What is the net force?
• What fourth force will put the point in equilibrium?

Compute the x and y components of each vector. Arrange the results in a table like this one.

Add the components…

Use pythagorean theorem to get the magnitude of the resultant force…

Use tangent to get the direction…

Add these numbers to the table…

The fourth force that would put this arrangement in equilibrium (the equilibrant) is equal and opposite the resultant. The components work this way too. To get the opposite direction angle, add on 180°.

practice problem 3

• Draw a free body diagram of the crate.
• the component of the crate's weight that is perpendicular to the ramp
• the component of the crate's weight that is parallel to the ramp
• the normal force between the crate and the ramp
• the static friction force between the crate and the ramp
• At what angle will the crate just begin to slip?

This is an example of a classic physics problem that students have been solving since the 17th century. It starts as an equilibrium problem, since the crate isn't going anywhere.

The component of the crate's weight perpendicular to the ramp is found using the cosine function. An object's weight is entirely pushing into a surface when the surface is level (a 0° angle of inclination). None of that weight is pushing into the surface when the surface is vertical, like a wall (a 90° angle of inclination). Cosine is a maximum when the angle is zero and zero when the angle is 90°. This is how the perpendicular component works.

The component of the crate's weight parallel to the ramp is found using the sine function. An object's weight has no sideways component on a level floor (a floor with no inclination). An object's weight is entirely parallel to a wall (a floor with a 90° inclination, in a sense). Sine is zero when the angle is zero and a maximum when the angle is 90°. This is how the parallel component works.

Normal forces are normal — that is, perpendicular to a tangent drawn to a curve or surface. This crate isn't currently going anywhere, so all the forces perpendicular to the incline must cancel. For a static crate on an incline, the force normal to the incline equals the perpendicular component of its weight.

Friction is a sideways, lateral, or tangential force — that is, parallel to a tangent drawn to a curve or surface. I'll say it again, this crate isn't going anywhere, so all the forces parallel to the incline should cancel. For a static crate on an incline, the static friction force equals the parallel component of the crate's weight.

The component of the crate's weight parallel to the incline pulls the crate down the incline while the frictional force tries to keep it in place. Since nothing is going anywhere, these two forces must balance each other.

As the angle of inclination increases, so to does the static friction, but it can't keep doing this forever. At some angle, the parallel component of the weight will equal the maximum static friction. Friction won't be strong enough and the crate will slip.

Cancel the weight.

μ s  cos θ = sin θ

Do some trig.

tan θ = μ s

Enter numbers.

tan θ =  0.28

Compute. The angle at which the crate just begins to slip is…

θ =  16°

This number is known as the critical angle (because it marks a critical value separating two types of behavior — sticking vs. sliding), angle of friction (because you gotta call it something), angle of repose (because granular materials will settle, or repose, in conical piles with this angle), or critical angle of repose (because adding grains to a pile with this angle will make it slump ).

practice problem 4

• Physics Formulas

Net Force Formula

The net force is defined as is the sum of all the forces acting on an object. Net force can accelerate a mass. Some other force acts on a body either at rest or motion. The net force is a term used in a system when there is a significant number of forces.  

Formula of Net Force

If N is the number of forces acting on a body, the net force formula is given by,

F Net = F 1 + F 2 + F 3 ….+ F N

F 1 , F 2 , F 3 …F N is the force acting on a body.

When the body is at rest, the net force formula is given by,

F Net = F a + F g .

F a = applied force,

F g = gravitational force. Net force when a body is in motion:

When a force is applied to the body, not only is the applied force acting, there are many other forces like gravitational force  Fg, frictional force Ff and the normal force that balances the other force.

Therefore, the net force formula is given by,

F Ne t = F a + F g + F f + F N .

• F a  is applied force,
• F g  is the gravitational force,
• F f  is the frictional force,
• FN is a normal force.

Examples of Net Force

In a tug of war, a fat man pulls with a force of 100 N on a side, and a lean man pulls with 90 N on the other side. Determine the net force.

Force F 1 = 100 N

Force F 2 = -90 N

The net force formula is given by

F Net = F 1 + F 2

F Net   = 100 – 90

F Net   = 10 N

Therefore, the net force is 10 N.

A toy car is at rest, and a force of 70 N is applied to it. If the frictional force of 20 N, determine the net force.

Applied force F a = 70 N

Frictional force F f = -20 N

F Net = F a + F f

 F Net  = 70 – 20

F Net   = 50 N

Therefore, the net force is 50 N

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

HIGH SCHOOL

• ACT Tutoring
• SAT Tutoring
• PSAT Tutoring
• ASPIRE Tutoring
• SHSAT Tutoring
• STAAR Tutoring

GRADUATE SCHOOL

• MCAT Tutoring
• GRE Tutoring
• LSAT Tutoring
• GMAT Tutoring
• AIMS Tutoring
• HSPT Tutoring
• ISAT Tutoring
• SSAT Tutoring

Search 50+ Tests

Loading Page

math tutoring

• Elementary Math
• Pre-Calculus
• Trigonometry

science tutoring

Foreign languages.

• Mandarin Chinese

elementary tutoring

• Computer Science

Search 350+ Subjects

• Video Overview
• Tutor Selection Process
• Online Tutoring
• Mobile Tutoring
• Instant Tutoring
• How We Operate
• Our Guarantee
• Impact of Tutoring
• Reviews & Testimonials
• Media Coverage
• About Varsity Tutors

High School Physics : Calculating Force

Study concepts, example questions & explanations for high school physics, all high school physics resources, example questions, example question #1 : net force.

Plug these into the equation to solve for acceleration.

Example Question #2 : Calculating Force

Plug in the values given to us and solve for the force.

Example Question #1 : Calculating Force

Plug in the given values to solve for the mass.

(Assume the only two forces acting on the object are friction and Derek).

Plug in the information we've been given so far to find the force of friction.

Friction will be negative because it acts in the direction opposite to the force of Derek.

Newton's third law states that when one object exerts a force on a second object, the second object exerts a force equal in size, but opposite in direction to the first. That means that the force of the hammer on the nail and the nail on the hammer will be equal in size, but opposite in direction.

Example Question #6 : Calculating Force

We can find the net force by adding the individual force together.

If the object has a constant velocity, that means that the net acceleration must be zero.

In conjunction with Newton's second law, we can see that the net force is also zero. If there is no net acceleration, then there is no net force.

Since Franklin is lifting the weight vertically, that means there will be two force acting upon the weight: his lifting force and gravity. The net force will be equal to the sum of the forces acting on the weight.

We know the mass of the weight and we know the acceleration, so we can solve for the lifting force.

We are given the mass, but we will need to calculate the acceleration to use in the formula.

Plug in our given values and solve for acceleration.

Now we know both the acceleration and the mass, allowing us to solve for the force.

Example Question #9 : Calculating Force

We can calculate the gravitational force using the mass.

Example Question #10 : Calculating Force

Report an issue with this question

If you've found an issue with this question, please let us know. With the help of the community we can continue to improve our educational resources.

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC 101 S. Hanley Rd, Suite 300 St. Louis, MO 63105

Or fill out the form below:

Contact Information

Complaint details.

• Pre-algebra lessons
• Pre-algebra word problems
• Algebra lessons
• Algebra word problems
• Algebra proofs
• Advanced algebra
• Geometry lessons
• Geometry word problems
• Geometry proofs
• Trigonometry lessons
• Consumer math
• Baseball math
• Math for nurses
• Statistics made easy
• High school physics
• Basic mathematics store
• SAT Math Prep
• Math skills by grade level
• Ask an expert
• Other websites
• K-12 worksheets
• Worksheets generator
• Algebra worksheets
• Geometry worksheets
• Free math problem solver
• Pre-algebra calculators
• Algebra Calculators
• Geometry Calculators
• Math puzzles
• Math tricks
• Member login

Net force word problems 

Find here in this lesson some easy and challenging net force word problems.  

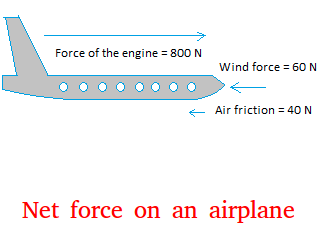
Problem #1:

What is the net force on the airplane in the figure below?

The airplane is moving with a force of 800 N. However, there are two forces moving in the opposite direction on the airplane.

Just add these two forces: 40 N + 60 N = 100 N

Subtract to get the net force: 800 N  - 100 N  = 700 N

The net force is 700 N.

The airplane will move with a force of 700 N as a result of air friction and wind. 

Problem #2 : You and your brother are pushing a car with a dead battery with forces of 20 N and 25 N in the same direction. What is the net force applied on the car?

Solution: 

Since you are pushing the car in the same direction, the forces will be added together.

Net force = 20 N + 25 N

Net force  = 45 N.

Problem #3 : A brother is pulling a toy from his sister with a force of 6  N. The sister is pulling back with a force of 8 N. 

Who gets the toy?

What is the net force? 

The sister gets the toy of course since she is pulling with a stronger force.

Net force = 8 N - 6 N

Net force  = 2 N.

More challenging net force word problems

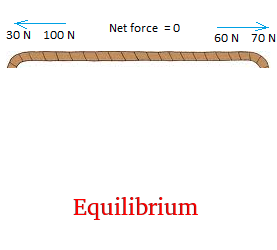
Problem #4 :

4 people are playing a tug of war. Two are pulling on the right side. Two are pulling on the left side.  On the right side, one is pulling with a force of 60 N and the other with a force of 70 N. On the left side, one is pulling with a force of 30 N. How much force should the second person on the left apply to keep the rope in equilibrium? 

The rope will be in equilibrium is the net force is 0.

The forces on the right is equal to 60 N + 70 N = 130 N

Let x be the force that must be applied by the second person on the left.

30 N + x = 130 N

Since 30 N + 100 N = 130 N,  x = 100 N

The other person should pull with a force of 100 N to keep the rope in equilibrium.

Problem #5 :

Your friend is pulling upward on an object with force of 3 N. You are pulling to the right with a force of 4 N.

Find the net force and the direction the object moves.

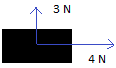
Just build the rectangle and find the resultant. The red arrow shows the direction the object will move. 

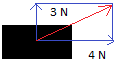
This net force word problem is a little challenging. To find the net force, we need use the Pythagorean Theorem .

What is a net force?

Recent Articles

How to divide any number by 5 in 2 seconds.

Feb 28, 24 11:07 AM

Math Trick to Square Numbers from 50 to 59

Feb 23, 24 04:46 AM

Sum of Consecutive Odd Numbers

Feb 22, 24 10:07 AM

100 Tough Algebra Word Problems. If you can solve these problems with no help, you must be a genius!

 Recommended

About me :: Privacy policy :: Disclaimer :: Donate   Careers in mathematics  

Copyright © 2008-2021. Basic-mathematics.com. All right reserved

6.1 Solving Problems with Newton’s Laws

Learning objectives.

By the end of this section, you will be able to:

• Apply problem-solving techniques to solve for quantities in more complex systems of forces
• Use concepts from kinematics to solve problems using Newton’s laws of motion
• Solve more complex equilibrium problems
• Solve more complex acceleration problems
• Apply calculus to more advanced dynamics problems

Success in problem solving is necessary to understand and apply physical principles. We developed a pattern of analyzing and setting up the solutions to problems involving Newton’s laws in Newton’s Laws of Motion ; in this chapter, we continue to discuss these strategies and apply a step-by-step process.

Problem-Solving Strategies

We follow here the basics of problem solving presented earlier in this text, but we emphasize specific strategies that are useful in applying Newton’s laws of motion . Once you identify the physical principles involved in the problem and determine that they include Newton’s laws of motion, you can apply these steps to find a solution. These techniques also reinforce concepts that are useful in many other areas of physics. Many problem-solving strategies are stated outright in the worked examples, so the following techniques should reinforce skills you have already begun to develop.

Problem-Solving Strategy

Applying newton’s laws of motion.

• Identify the physical principles involved by listing the givens and the quantities to be calculated.
• Sketch the situation, using arrows to represent all forces.
• Determine the system of interest. The result is a free-body diagram that is essential to solving the problem.
• Apply Newton’s second law to solve the problem. If necessary, apply appropriate kinematic equations from the chapter on motion along a straight line.
• Check the solution to see whether it is reasonable.

Let’s apply this problem-solving strategy to the challenge of lifting a grand piano into a second-story apartment. Once we have determined that Newton’s laws of motion are involved (if the problem involves forces), it is particularly important to draw a careful sketch of the situation. Such a sketch is shown in Figure 6.2 (a). Then, as in Figure 6.2 (b), we can represent all forces with arrows. Whenever sufficient information exists, it is best to label these arrows carefully and make the length and direction of each correspond to the represented force.

As with most problems, we next need to identify what needs to be determined and what is known or can be inferred from the problem as stated, that is, make a list of knowns and unknowns. It is particularly crucial to identify the system of interest, since Newton’s second law involves only external forces. We can then determine which forces are external and which are internal, a necessary step to employ Newton’s second law. (See Figure 6.2 (c).) Newton’s third law may be used to identify whether forces are exerted between components of a system (internal) or between the system and something outside (external). As illustrated in Newton’s Laws of Motion , the system of interest depends on the question we need to answer. Only forces are shown in free-body diagrams, not acceleration or velocity. We have drawn several free-body diagrams in previous worked examples. Figure 6.2 (c) shows a free-body diagram for the system of interest. Note that no internal forces are shown in a free-body diagram.

Once a free-body diagram is drawn, we apply Newton’s second law. This is done in Figure 6.2 (d) for a particular situation. In general, once external forces are clearly identified in free-body diagrams, it should be a straightforward task to put them into equation form and solve for the unknown, as done in all previous examples. If the problem is one-dimensional—that is, if all forces are parallel—then the forces can be handled algebraically. If the problem is two-dimensional, then it must be broken down into a pair of one-dimensional problems. We do this by projecting the force vectors onto a set of axes chosen for convenience. As seen in previous examples, the choice of axes can simplify the problem. For example, when an incline is involved, a set of axes with one axis parallel to the incline and one perpendicular to it is most convenient. It is almost always convenient to make one axis parallel to the direction of motion, if this is known. Generally, just write Newton’s second law in components along the different directions. Then, you have the following equations:

(If, for example, the system is accelerating horizontally, then you can then set a y = 0 . a y = 0 . ) We need this information to determine unknown forces acting on a system.

As always, we must check the solution. In some cases, it is easy to tell whether the solution is reasonable. For example, it is reasonable to find that friction causes an object to slide down an incline more slowly than when no friction exists. In practice, intuition develops gradually through problem solving; with experience, it becomes progressively easier to judge whether an answer is reasonable. Another way to check a solution is to check the units. If we are solving for force and end up with units of millimeters per second, then we have made a mistake.

There are many interesting applications of Newton’s laws of motion, a few more of which are presented in this section. These serve also to illustrate some further subtleties of physics and to help build problem-solving skills. We look first at problems involving particle equilibrium, which make use of Newton’s first law, and then consider particle acceleration, which involves Newton’s second law.

Particle Equilibrium

Recall that a particle in equilibrium is one for which the external forces are balanced. Static equilibrium involves objects at rest, and dynamic equilibrium involves objects in motion without acceleration, but it is important to remember that these conditions are relative. For example, an object may be at rest when viewed from our frame of reference, but the same object would appear to be in motion when viewed by someone moving at a constant velocity. We now make use of the knowledge attained in Newton’s Laws of Motion , regarding the different types of forces and the use of free-body diagrams, to solve additional problems in particle equilibrium .

Example 6.1

Different tensions at different angles.

Thus, as you might expect,

This gives us the following relationship:

Note that T 1 T 1 and T 2 T 2 are not equal in this case because the angles on either side are not equal. It is reasonable that T 2 T 2 ends up being greater than T 1 T 1 because it is exerted more vertically than T 1 . T 1 .

Now consider the force components along the vertical or y -axis:

This implies

Substituting the expressions for the vertical components gives

There are two unknowns in this equation, but substituting the expression for T 2 T 2 in terms of T 1 T 1 reduces this to one equation with one unknown:

which yields

Solving this last equation gives the magnitude of T 1 T 1 to be

Finally, we find the magnitude of T 2 T 2 by using the relationship between them, T 2 = 1.225 T 1 T 2 = 1.225 T 1 , found above. Thus we obtain

Significance

Particle acceleration.

We have given a variety of examples of particles in equilibrium. We now turn our attention to particle acceleration problems, which are the result of a nonzero net force. Refer again to the steps given at the beginning of this section, and notice how they are applied to the following examples.

Example 6.2

Drag force on a barge.

The drag of the water F → D F → D is in the direction opposite to the direction of motion of the boat; this force thus works against F → app , F → app , as shown in the free-body diagram in Figure 6.4 (b). The system of interest here is the barge, since the forces on it are given as well as its acceleration. Because the applied forces are perpendicular, the x - and y -axes are in the same direction as F → 1 F → 1 and F → 2 . F → 2 . The problem quickly becomes a one-dimensional problem along the direction of F → app F → app , since friction is in the direction opposite to F → app . F → app . Our strategy is to find the magnitude and direction of the net applied force F → app F → app and then apply Newton’s second law to solve for the drag force F → D . F → D .

The angle is given by

From Newton’s first law, we know this is the same direction as the acceleration. We also know that F → D F → D is in the opposite direction of F → app , F → app , since it acts to slow down the acceleration. Therefore, the net external force is in the same direction as F → app , F → app , but its magnitude is slightly less than F → app . F → app . The problem is now one-dimensional. From the free-body diagram, we can see that

However, Newton’s second law states that

This can be solved for the magnitude of the drag force of the water F D F D in terms of known quantities:

Substituting known values gives

The direction of F → D F → D has already been determined to be in the direction opposite to F → app , F → app , or at an angle of 53 ° 53 ° south of west.

In Newton’s Laws of Motion , we discussed the normal force , which is a contact force that acts normal to the surface so that an object does not have an acceleration perpendicular to the surface. The bathroom scale is an excellent example of a normal force acting on a body. It provides a quantitative reading of how much it must push upward to support the weight of an object. But can you predict what you would see on the dial of a bathroom scale if you stood on it during an elevator ride? Will you see a value greater than your weight when the elevator starts up? What about when the elevator moves upward at a constant speed? Take a guess before reading the next example.

Example 6.3

What does the bathroom scale read in an elevator.

From the free-body diagram, we see that F → net = F → s − w → , F → net = F → s − w → , so we have

Solving for F s F s gives us an equation with only one unknown:

or, because w = m g , w = m g , simply

No assumptions were made about the acceleration, so this solution should be valid for a variety of accelerations in addition to those in this situation. ( Note: We are considering the case when the elevator is accelerating upward. If the elevator is accelerating downward, Newton’s second law becomes F s − w = − m a . F s − w = − m a . )

• We have a = 1.20 m/s 2 , a = 1.20 m/s 2 , so that F s = ( 75.0 kg ) ( 9.80 m/s 2 ) + ( 75.0 kg ) ( 1.20 m/s 2 ) F s = ( 75.0 kg ) ( 9.80 m/s 2 ) + ( 75.0 kg ) ( 1.20 m/s 2 ) yielding F s = 825 N . F s = 825 N .
• Now, what happens when the elevator reaches a constant upward velocity? Will the scale still read more than his weight? For any constant velocity—up, down, or stationary—acceleration is zero because a = Δ v Δ t a = Δ v Δ t and Δ v = 0 . Δ v = 0 . Thus, F s = m a + m g = 0 + m g F s = m a + m g = 0 + m g or F s = ( 75.0 kg ) ( 9.80 m/s 2 ) , F s = ( 75.0 kg ) ( 9.80 m/s 2 ) , which gives F s = 735 N . F s = 735 N .

Thus, the scale reading in the elevator is greater than his 735-N (165-lb.) weight. This means that the scale is pushing up on the person with a force greater than his weight, as it must in order to accelerate him upward. Clearly, the greater the acceleration of the elevator, the greater the scale reading, consistent with what you feel in rapidly accelerating versus slowly accelerating elevators. In Figure 6.5 (b), the scale reading is 735 N, which equals the person’s weight. This is the case whenever the elevator has a constant velocity—moving up, moving down, or stationary.

Check Your Understanding 6.1

Now calculate the scale reading when the elevator accelerates downward at a rate of 1.20 m/s 2 . 1.20 m/s 2 .

The solution to the previous example also applies to an elevator accelerating downward, as mentioned. When an elevator accelerates downward, a is negative, and the scale reading is less than the weight of the person. If a constant downward velocity is reached, the scale reading again becomes equal to the person’s weight. If the elevator is in free fall and accelerating downward at g , then the scale reading is zero and the person appears to be weightless.

Example 6.4

Two attached blocks.

For block 1: T → + w → 1 + N → = m 1 a → 1 T → + w → 1 + N → = m 1 a → 1

For block 2: T → + w → 2 = m 2 a → 2 . T → + w → 2 = m 2 a → 2 .

Notice that T → T → is the same for both blocks. Since the string and the pulley have negligible mass, and since there is no friction in the pulley, the tension is the same throughout the string. We can now write component equations for each block. All forces are either horizontal or vertical, so we can use the same horizontal/vertical coordinate system for both objects

When block 1 moves to the right, block 2 travels an equal distance downward; thus, a 1 x = − a 2 y . a 1 x = − a 2 y . Writing the common acceleration of the blocks as a = a 1 x = − a 2 y , a = a 1 x = − a 2 y , we now have

From these two equations, we can express a and T in terms of the masses m 1 and m 2 , and g : m 1 and m 2 , and g :

Check Your Understanding 6.2

Calculate the acceleration of the system, and the tension in the string, when the masses are m 1 = 5.00 kg m 1 = 5.00 kg and m 2 = 3.00 kg . m 2 = 3.00 kg .

Example 6.5

Atwood machine.

• We have For m 1 , ∑ F y = T − m 1 g = m 1 a . For m 2 , ∑ F y = T − m 2 g = − m 2 a . For m 1 , ∑ F y = T − m 1 g = m 1 a . For m 2 , ∑ F y = T − m 2 g = − m 2 a . (The negative sign in front of m 2 a m 2 a indicates that m 2 m 2 accelerates downward; both blocks accelerate at the same rate, but in opposite directions.) Solve the two equations simultaneously (subtract them) and the result is ( m 2 − m 1 ) g = ( m 1 + m 2 ) a . ( m 2 − m 1 ) g = ( m 1 + m 2 ) a . Solving for a : a = m 2 − m 1 m 1 + m 2 g = 4 kg − 2 kg 4 kg + 2 kg ( 9.8 m/s 2 ) = 3.27 m/s 2 . a = m 2 − m 1 m 1 + m 2 g = 4 kg − 2 kg 4 kg + 2 kg ( 9.8 m/s 2 ) = 3.27 m/s 2 .
• Observing the first block, we see that T − m 1 g = m 1 a T = m 1 ( g + a ) = ( 2 kg ) ( 9.8 m/s 2 + 3.27 m/s 2 ) = 26.1 N . T − m 1 g = m 1 a T = m 1 ( g + a ) = ( 2 kg ) ( 9.8 m/s 2 + 3.27 m/s 2 ) = 26.1 N .

Check Your Understanding 6.3

Determine a general formula in terms of m 1 , m 2 m 1 , m 2 and g for calculating the tension in the string for the Atwood machine shown above.

Newton’s Laws of Motion and Kinematics

Physics is most interesting and most powerful when applied to general situations that involve more than a narrow set of physical principles. Newton’s laws of motion can also be integrated with other concepts that have been discussed previously in this text to solve problems of motion. For example, forces produce accelerations, a topic of kinematics , and hence the relevance of earlier chapters.

When approaching problems that involve various types of forces, acceleration, velocity, and/or position, listing the givens and the quantities to be calculated will allow you to identify the principles involved. Then, you can refer to the chapters that deal with a particular topic and solve the problem using strategies outlined in the text. The following worked example illustrates how the problem-solving strategy given earlier in this chapter, as well as strategies presented in other chapters, is applied to an integrated concept problem.

Example 6.6

What force must a soccer player exert to reach top speed.

• We are given the initial and final velocities (zero and 8.00 m/s forward); thus, the change in velocity is Δ v = 8.00 m/s Δ v = 8.00 m/s . We are given the elapsed time, so Δ t = 2.50 s . Δ t = 2.50 s . The unknown is acceleration, which can be found from its definition: a = Δ v Δ t . a = Δ v Δ t . Substituting the known values yields a = 8.00 m/s 2.50 s = 3.20 m/s 2 . a = 8.00 m/s 2.50 s = 3.20 m/s 2 .
• Here we are asked to find the average force the ground exerts on the runner to produce this acceleration. (Remember that we are dealing with the force or forces acting on the object of interest.) This is the reaction force to that exerted by the player backward against the ground, by Newton’s third law. Neglecting air resistance, this would be equal in magnitude to the net external force on the player, since this force causes her acceleration. Since we now know the player’s acceleration and are given her mass, we can use Newton’s second law to find the force exerted. That is, F net = m a . F net = m a . Substituting the known values of m and a gives F net = ( 70.0 kg ) ( 3.20 m/s 2 ) = 224 N . F net = ( 70.0 kg ) ( 3.20 m/s 2 ) = 224 N .

This is a reasonable result: The acceleration is attainable for an athlete in good condition. The force is about 50 pounds, a reasonable average force.

Check Your Understanding 6.4

The soccer player stops after completing the play described above, but now notices that the ball is in position to be stolen. If she now experiences a force of 126 N to attempt to steal the ball, which is 2.00 m away from her, how long will it take her to get to the ball?

Example 6.7

What force acts on a model helicopter.

The magnitude of the force is now easily found:

Check Your Understanding 6.5

Find the direction of the resultant for the 1.50-kg model helicopter.

Example 6.8

Baggage tractor.

• ∑ F x = m system a x ∑ F x = m system a x and ∑ F x = 820.0 t , ∑ F x = 820.0 t , so 820.0 t = ( 650.0 + 250.0 + 150.0 ) a a = 0.7809 t . 820.0 t = ( 650.0 + 250.0 + 150.0 ) a a = 0.7809 t . Since acceleration is a function of time, we can determine the velocity of the tractor by using a = d v d t a = d v d t with the initial condition that v 0 = 0 v 0 = 0 at t = 0 . t = 0 . We integrate from t = 0 t = 0 to t = 3 : t = 3 : d v = a d t , ∫ 0 3 d v = ∫ 0 3.00 a d t = ∫ 0 3.00 0.7809 t d t , v = 0.3905 t 2 ] 0 3.00 = 3.51 m/s . d v = a d t , ∫ 0 3 d v = ∫ 0 3.00 a d t = ∫ 0 3.00 0.7809 t d t , v = 0.3905 t 2 ] 0 3.00 = 3.51 m/s .
• Refer to the free-body diagram in Figure 6.8 (b). ∑ F x = m tractor a x 820.0 t − T = m tractor ( 0.7805 ) t ( 820.0 ) ( 3.00 ) − T = ( 650.0 ) ( 0.7805 ) ( 3.00 ) T = 938 N . ∑ F x = m tractor a x 820.0 t − T = m tractor ( 0.7805 ) t ( 820.0 ) ( 3.00 ) − T = ( 650.0 ) ( 0.7805 ) ( 3.00 ) T = 938 N .

Recall that v = d s d t v = d s d t and a = d v d t a = d v d t . If acceleration is a function of time, we can use the calculus forms developed in Motion Along a Straight Line , as shown in this example. However, sometimes acceleration is a function of displacement. In this case, we can derive an important result from these calculus relations. Solving for dt in each, we have d t = d s v d t = d s v and d t = d v a . d t = d v a . Now, equating these expressions, we have d s v = d v a . d s v = d v a . We can rearrange this to obtain a d s = v d v . a d s = v d v .

Example 6.9

Motion of a projectile fired vertically.

The acceleration depends on v and is therefore variable. Since a = f ( v ) , a = f ( v ) , we can relate a to v using the rearrangement described above,

We replace ds with dy because we are dealing with the vertical direction,

We now separate the variables ( v ’s and dv ’s on one side; dy on the other):

Thus, h = 114 m . h = 114 m .

Check Your Understanding 6.6

If atmospheric resistance is neglected, find the maximum height for the mortar shell. Is calculus required for this solution?

Interactive

Explore the forces at work in this simulation when you try to push a filing cabinet. Create an applied force and see the resulting frictional force and total force acting on the cabinet. Charts show the forces, position, velocity, and acceleration vs. time. View a free-body diagram of all the forces (including gravitational and normal forces).

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/university-physics-volume-1/pages/1-introduction

• Authors: William Moebs, Samuel J. Ling, Jeff Sanny
• Publisher/website: OpenStax
• Book title: University Physics Volume 1
• Publication date: Sep 19, 2016
• Location: Houston, Texas
• Book URL: https://openstax.org/books/university-physics-volume-1/pages/1-introduction
• Section URL: https://openstax.org/books/university-physics-volume-1/pages/6-1-solving-problems-with-newtons-laws

© Jan 19, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
• EDIT Edit this Article
• EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
• Browse Articles
• Learn Something New
• Quizzes Hot
• This Or That Game
• Train Your Brain
• Explore More
• Support wikiHow
• About wikiHow
• Log in / Sign up
• Education and Communications
• Classical Mechanics

How to Find Net Force

Last Updated: March 6, 2023 Fact Checked

This article was reviewed by Grace Imson, MA . Grace Imson is a math teacher with over 40 years of teaching experience. Grace is currently a math instructor at the City College of San Francisco and was previously in the Math Department at Saint Louis University. She has taught math at the elementary, middle, high school, and college levels. She has an MA in Education, specializing in Administration and Supervision from Saint Louis University. There are 8 references cited in this article, which can be found at the bottom of the page. This article has been fact-checked, ensuring the accuracy of any cited facts and confirming the authority of its sources. This article has been viewed 114,969 times.

Net force is the total amount of force acting on an object when you take into account both magnitude and direction. An object with a net force of zero is stationary. An unbalanced force, or net force of a magnitude greater than or less than zero, leads to acceleration of the object. [1] X Research source Once you have calculated or measured the magnitude of a force, combining them to find the net force is simple. Sketching a simple force diagram and making sure all of the forces are labelled and in the correct direction makes calculating net force a breeze.

Determining Net Force

• For example: Calculate the net force of an object weighing 20 N sitting on a table being pushed towards the right with 5 N of force, but staying still because of a friction force of 5 N.

• If you are working with multiple force diagrams, make sure you keep the directions consistent throughout.
• Label the magnitude of each force with a “+” or “-“ sign based on the direction of the arrow you’ve drawn on the force diagram.
• For example: The force of gravity is a downward force making it negative. The normal force is upward making it positive. The push force is to the right making it positive, while the friction force acts to oppose this force towards the left (negative).

• A standard way to label forces is with a capital F and a subscript of first letter of the force. For example, if there is a force due to friction, label it F f .
• Force due to gravity: F g = -20 N
• Normal force: F n = +20 N
• Friction force: F f = -5 N
• Push force: F p = +5 N

• For example: F net = F g + F n + F f + F p = -20 + 20 -5 + 5 = 0 N. Because the net force is 0 N, the object is stationary.

Calculating Diagonal Force

• Draw the force diagram including the angle of the diagonal force.
• Sketch each arrow in the proper direction the force is acting and label it with the proper magnitude.
• For example: Sketch the diagram for a 10 N object experiencing a 25 N force up and to the right at an angle of 45°. There is also a friction force to the left of 10 N.
• Forces include: F g = -10 N, F n = + 10 N, F p = 25 N, F f = -10 N.

• Remember, CAH: cosine(θ) = adjacent/hypotenuse. F x = cos θ * F = cos(45°) * 25 = 17.68 N.
• Remember, SOH: sine(θ) = opposite/hypotenuse. F y = sin θ * F = sin(45°) * 25 = 17.68 N.
• Note that there may be multiple diagonal forces acting on an object simultaneously, so you'll have to find F x and F y of each force in the problem. Then sum the F x values to obtain the total force in the horizontal direction and sum the F y values for the total force in the vertical direction.

• For example, instead of one diagonal force, the diagram will now have one vertical force pointing up with a magnitude of 17.68 N and one horizontal force pointing to the right with a magnitude of 17.68 N.

• For example: Horizontal vectors are all forces along the x axis: F netx = 17.68 – 10 = 7.68 N.
• Vertical vectors are all forces along the y axis: F nety = 17.68 + 10 - 10 = 17.68 N.

• For example: F netx = 7.68 N and F nety = 17.68 N
• Plug into equation: F net = √ (F netx 2 + F nety 2 ) = √ (7.68 2 + 17.68 2 )
• Solve: F net = √ (7.68 2 + 17.68 2 ) = √(58.98 + 35.36) = √94.34 = 9.71 N.
• The magnitude of force is 9.71 N in a diagonal up and to the right.

Community Q&A

You Might Also Like

• ↑ http://www.physicsclassroom.com/class/newtlaws/Lesson-2/Determining-the-Net-Force
• ↑ https://www.youtube.com/watch?v=qPaqDfRKBI4
• ↑ https://www.youtube.com/watch?v=JTfBvzscE8c
• ↑ https://www.youtube.com/watch?v=EQJe6x-83_w
• ↑ https://www.youtube.com/watch?v=yUZ6_cY37FY
• ↑ http://www.physicsclassroom.com/class/vectors/Lesson-3/Resolution-of-Forces
• ↑ https://www.mathsisfun.com/pythagoras.html

About This Article

To find net force, start by drawing a diagram of the object being acted upon, including arrows to represent all of the forces acting on it that are listed in the problem. Then, make all of the arrows pointing upward or to the right positive, and the arrows pointing downward or to the left negative. Next, label all of the forces in the problem, as well as the force of gravity, which is equal to -20 newtons, and the normal force, which is equal to 20 newtons. Finally, sum the magnitude of all the forces to find the net force. To learn how to calculate diagonal force, scroll down! Did this summary help you? Yes No

• Send fan mail to authors

Did this article help you?

Featured Articles

Trending Articles

Watch Articles

• Terms of Use
• Privacy Policy
• Do Not Sell or Share My Info
• Not Selling Info

wikiHow Tech Help Pro:

Develop the tech skills you need for work and life

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.6: Problem-Solving Strategies

• Last updated
• Save as PDF
• Page ID 1502

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

By the end of this section, you will be able to:

• Understand and apply a problem-solving procedure to solve problems using Newton’s laws of motion.

Success in problem solving is obviously necessary to understand and apply physical principles, not to mention the more immediate need of passing exams. The basics of problem solving, presented earlier in this text, are followed here, but specific strategies useful in applying Newton’s laws of motion are emphasized. These techniques also reinforce concepts that are useful in many other areas of physics. Many problem-solving strategies are stated outright in the worked examples, and so the following techniques should reinforce skills you have already begun to develop.

Problem-Solving Strategy for Newton’s Laws of Motion

Step 1. As usual, it is first necessary to identify the physical principles involved. Once it is determined that Newton’s laws of motion are involved (if the problem involves forces), it is particularly important to draw a careful sketch of the situation . Such a sketch is shown in Figure (a). Then, as in Figure (b), use arrows to represent all forces, label them carefully, and make their lengths and directions correspond to the forces they represent (whenever sufficient information exists).

Step 2. Identify what needs to be determined and what is known or can be inferred from the problem as stated. That is, make a list of knowns and unknowns. Then carefully determine the system of interest . This decision is a crucial step, since Newton’s second law involves only external forces. Once the system of interest has been identified, it becomes possible to determine which forces are external and which are internal, a necessary step to employ Newton’s second law. (See Figure (c).) Newton’s third law may be used to identify whether forces are exerted between components of a system (internal) or between the system and something outside (external). As illustrated earlier in this chapter, the system of interest depends on what question we need to answer. This choice becomes easier with practice, eventually developing into an almost unconscious process. Skill in clearly defining systems will be beneficial in later chapters as well.

A diagram showing the system of interest and all of the external forces is called a free-body diagram . Only forces are shown on free-body diagrams, not acceleration or velocity. We have drawn several of these in worked examples. Figure (c) shows a free-body diagram for the system of interest. Note that no internal forces are shown in a free-body diagram.

Step 3. Once a free-body diagram is drawn, Newton’s second law can be applied to solve the problem . This is done in Figure (d) for a particular situation. In general, once external forces are clearly identified in free-body diagrams, it should be a straightforward task to put them into equation form and solve for the unknown, as done in all previous examples. If the problem is one-dimensional—that is, if all forces are parallel—then they add like scalars. If the problem is two-dimensional, then it must be broken down into a pair of one-dimensional problems. This is done by projecting the force vectors onto a set of axes chosen for convenience. As seen in previous examples, the choice of axes can simplify the problem. For example, when an incline is involved, a set of axes with one axis parallel to the incline and one perpendicular to it is most convenient. It is almost always convenient to make one axis parallel to the direction of motion, if this is known.

APPLYING NEWTON'S SECOND LAW

Before you write net force equations, it is critical to determine whether the system is accelerating in a particular direction. If the acceleration is zero in a particular direction, then the net force is zero in that direction. Similarly, if the acceleration is nonzero in a particular direction, then the net force is described by the equation: \(F_{net} = ma\)

For example, if the system is accelerating in the horizontal direction, but it is not accelerating in the vertical direction, then you will have the following conclusions: \[ F_{net \, x} = ma \]

\[ F_{net \, y} = 0 \]

You will need this information in order to determine unknown forces acting in a system.

Step 4. As always, check the solution to see whether it is reasonable . In some cases, this is obvious. For example, it is reasonable to find that friction causes an object to slide down an incline more slowly than when no friction exists. In practice, intuition develops gradually through problem solving, and with experience it becomes progressively easier to judge whether an answer is reasonable. Another way to check your solution is to check the units. If you are solving for force and end up with units of m/s, then you have made a mistake.

• To solve problems involving Newton’s laws of motion, follow the procedure described:
• Draw a sketch of the problem.
• Identify known and unknown quantities, and identify the system of interest. Draw a free-body diagram, which is a sketch showing all of the forces acting on an object. The object is represented by a dot, and the forces are represented by vectors extending in different directions from the dot. If vectors act in directions that are not horizontal or vertical, resolve the vectors into horizontal and vertical components and draw them on the free-body diagram.
• Write Newton’s second law in the horizontal and vertical directions and add the forces acting on the object. If the object does not accelerate in a particular direction (for example, the \(x\)-direction) then \(F_{net \, x} = 0 \). If the object does accelerate in that direction, \(F_{net \, x} = ma \).
• Check your answer. Is the answer reasonable? Are the units correct?

The Cognition Sentinel

Guarding Knowledge, Inspiring Minds

Understanding Net Force: A Comprehensive Guide to Calculation and Application

Introduction

Net force is a fundamental concept in physics, essential for understanding the way objects move and interact with their environment. It is the sum of all the forces acting on an object, and it determines the object’s resulting motion. Whether you’re a student in physics class or simply interested in understanding the laws that govern our world, this guide will provide a comprehensive overview of net force and how to calculate it.

Understanding Net Force

At its core, net force is the result of all forces acting upon an object. Forces can be any push or pull, and each force has its own magnitude and direction. Net force is the sum total of all of these forces, so an object can either be accelerating, decelerating, or at a constant speed.

In addition to its magnitude and direction, a force also has an associated property called a vector, which describes how it acts on the object. The net force is thus a vector quantity that takes into account both the magnitude and direction of all the forces acting on an object.

The formula for calculating net force is relatively straightforward. Take all of the forces that are acting on the object, and add them all together. Then, determine the resulting vector that describes the net force.

One of the most common misconceptions about net force is the concept of “canceling out” forces. For example, if you have two forces of equal magnitude but opposite directions, you might assume that they simply “cancel out,” resulting in a net force of zero. In reality, every force acting on an object has an impact on its motion, and they do not cancel each other out. Rather, they work together to determine the net force.

Step-by-Step Guide to Calculate Net Force

Now that you understand the basics of net force, let’s dive into the details of how to calculate it. Here is a step-by-step guide for finding the net force:

Step 1: Identify All Forces Acting on the Object

The first step is to identify all of the forces that are acting on the object. Forces can come from a variety of sources, including gravity, friction, air resistance, and contact forces. Make sure to account for all of them in your calculations.

Step 2: Determine the Magnitude and Direction of Each Force

Once you have identified all of the forces acting on the object, you need to determine the magnitude and direction of each force. This information will be critical for adding them all together in the next step.

Step 3: Add All of the Forces Together

Next, add all of the forces together to find the total force acting on the object. Keep in mind that forces can act in different directions, so you may need to use negative values to reflect this.

Step 4: Determine the Resulting Vector of the Net Force

Finally, determine the resulting vector that represents the net force by combining all of the forces you have identified. This will provide you with a complete picture of how the object will move as a result of the forces acting on it.

Applying these steps to specific scenarios can help you better understand how to calculate net force in practice. Let’s take a look at some examples.

Visuals-Based Walkthrough

For many students, seeing is believing. That’s why visual aids can be so helpful when it comes to understanding net force. By using diagrams, images, and animations, you can better visualize the concept of net force, making it more concrete and easier to comprehend.

For example, you might use a diagram to illustrate the different forces acting on an object, and how they combine to result in the net force. Alternatively, you might use an animation to show how the forces interact over time, providing a more dynamic and engaging experience.

If you’re looking for visuals to help teach net force, there are plenty of resources available online. Many physics websites and educational platforms offer interactive tools and resources that can help students learn in a fun and engaging way.

Problem-Solving Examples

The best way to truly master net force is through practice. That’s why problem-solving examples are so valuable for students and professionals alike. By working through examples step by step, you can build your understanding of net force, and learn how to apply it in real-world scenarios.

Let’s take a look at some sample problem-solving scenarios, along with step-by-step walkthroughs for solving them.

Example 1: A box with a mass of 10 kg is being pulled to the right by a force of 30 N, while another force of 20 N pulls it to the left. What is the net force acting on the box?

The two forces acting on the box are the 30 N force to the right and the 20 N force to the left.

The 30 N force is in the positive direction, while the 20 N force is in the negative direction.

The total force acting on the box is 30 N – 20 N = 10 N.

The resulting vector of the net force is 10 N to the right.

Example 2: An object is thrown vertically upward, with a force of 100 N. As it rises, it experiences a force of 50 N due to air resistance. What is the net force acting on the object at its peak height?

The two forces acting on the object are the force of 100 N upward and the force of 50 N due to air resistance acting in the opposite direction, downward.

The 100 N force is in the positive direction, while the 50 N force is in the negative direction.

The total force acting on the object is 100 N – 50 N = 50 N.

The resulting vector of the net force is 50 N upward.

As you can see, these examples illustrate how net force can be calculated based on specific scenarios, and the resulting vector can help determine the direction and magnitude of the object’s motion.

Historical Perspective

Net force has a rich history, dating back to ancient Greek philosophers who pondered the nature of motion and force. Over time, scientists and mathematicians built upon these foundations, developing complex theories to describe the workings of the universe.

One of the most significant contributions to the understanding of net force came from Sir Isaac Newton in the seventeenth century. His laws of motion, particularly the second law, laid the groundwork for modern physics. Newton’s laws helped establish the relationship between force, mass, and acceleration, providing a framework for calculating and understanding net force.

Over the centuries, many other scientists and mathematicians have contributed to the understanding of net force, including Galileo Galilei, Albert Einstein, and Richard Feynman. Each new discovery and development has built upon the work of those who came before, adding new layers to our understanding of the laws of physics and the role of net force in the world around us.

Comparison to Other Concepts

Net force is just one of many concepts related to the study of physics and motion. Other concepts include friction, acceleration, and velocity, to name just a few. Understanding how these concepts relate to one another can provide a more holistic view of how objects move and interact.

Friction, for example, can resist motion and affect the net force acting upon an object. Acceleration reflects changes in the speed or direction of an object over time, while velocity describes the object’s speed and direction at a specific moment in time. By understanding the relationship between these different concepts, it becomes easier to calculate and predict how an object will behave in a given situation.

Real-world examples can help illustrate these concepts in action. For instance, a car’s acceleration may be influenced by the friction between its tires and the road. Understanding how these factors work together can help drivers make more informed decisions and stay safe on the road.

Relevant Everyday Scenarios

Net force is at play in countless real-world scenarios, from the motion of planets in our solar system to the way a paper airplane glides through the air. Here are a few examples of everyday scenarios that involve net force:

• A person lifting a box off the ground. The force applied to lift the box must overcome the force of gravity acting upon it, resulting in a net force that determines the box’s resulting motion.
• A baseball player swinging a bat. The force applied to the bat must be greater than the combined force of gravity and air resistance, resulting in a net force that sends the ball flying through the air.
• A train pulling a heavy load. The locomotive’s engine applies a force that overcomes the force of friction and hauls the cargo along the tracks, resulting in a net force that propels the train forward.

By considering the net force at play in these scenarios, we can gain a better understanding of the physical laws that govern them. This, in turn, can help us make more informed decisions and develop a deeper appreciation for the world around us.

Net force is a fundamental concept in physics, but it can also be applied to countless real-world scenarios. By understanding how to calculate net force, you can gain a deeper appreciation for the laws that govern the world around us. Beyond just calculations, this guide has explored the history and context of net force, as well as how it relates to other physics concepts and everyday scenarios. Applying these principles to practice can help improve your understanding and even your problem-solving skills.

We hope that this guide has helped demystify this complex concept and encouraged you to explore further on your own. Whether you’re a student studying physics, a professional working in engineering, or simply someone with a thirst for knowledge, understanding net force is an essential component of a well-rounded education in the physical sciences.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

Related News

How to Find Yourself: A Journey of Self-Discovery

How to Download Google Chrome: A Comprehensive Guide

You may have missed.

How to Add Photos to Hidden Folders: A Comprehensive Guide to Privacy and Security

How to Stop Feeling Lightheaded from Anxiety: Coping Techniques, Lifestyle Changes, and More

How to Bake Polymer Clay: A Step-by-Step Guide

How to Make Yourself Go to Sleep: Creating Healthy Bedtime Habits

Dynamics: Force and Newton’s Laws of Motion

Problem-solving strategies, learning objective.

By the end of this section, you will be able to:

• Understand and apply a problem-solving procedure to solve problems using Newton’s laws of motion.

Success in problem solving is obviously necessary to understand and apply physical principles, not to mention the more immediate need of passing exams. The basics of problem solving, presented earlier in this text, are followed here, but specific strategies useful in applying Newton’s laws of motion are emphasized. These techniques also reinforce concepts that are useful in many other areas of physics. Many problem-solving strategies are stated outright in the worked examples, and so the following techniques should reinforce skills you have already begun to develop.

Problem-Solving Strategy for Newton’s Laws of Motion

Step 1. As usual, it is first necessary to identify the physical principles involved. Once it is determined that Newton’s laws of motion are involved (if the problem involves forces), it is particularly important to draw a careful sketch of the situation . Such a sketch is shown in Figure 1(a). Then, as in Figure 1(b), use arrows to represent all forces, label them carefully, and make their lengths and directions correspond to the forces they represent (whenever sufficient information exists).

Figure 1. (a) A sketch of Tarzan hanging from a vine. (b) Arrows are used to represent all forces. T is the tension in the vine above Tarzan, F T is the force he exerts on the vine, and w is his weight. All other forces, such as the nudge of a breeze, are assumed negligible. (c) Suppose we are given the ape man’s mass and asked to find the tension in the vine. We then define the system of interest as shown and draw a free-body diagram. F T is no longer shown, because it is not a force acting on the system of interest; rather, F T  acts on the outside world. (d) Showing only the arrows, the head-to-tail method of addition is used. It is apparent that T = –w , if Tarzan is stationary.

Step 2. Identify what needs to be determined and what is known or can be inferred from the problem as stated. That is, make a list of knowns and unknowns. Then carefully determine the system of interest . This decision is a crucial step, since Newton’s second law involves only external forces. Once the system of interest has been identified, it becomes possible to determine which forces are external and which are internal, a necessary step to employ Newton’s second law. (See Figure 1(c).) Newton’s third law may be used to identify whether forces are exerted between components of a system (internal) or between the system and something outside (external). As illustrated earlier in this chapter, the system of interest depends on what question we need to answer. This choice becomes easier with practice, eventually developing into an almost unconscious process. Skill in clearly defining systems will be beneficial in later chapters as well.

A diagram showing the system of interest and all of the external forces is called a free-body diagram . Only forces are shown on free-body diagrams, not acceleration or velocity. We have drawn several of these in worked examples. Figure 1(c) shows a free-body diagram for the system of interest. Note that no internal forces are shown in a free-body diagram.

Step 3. Once a free-body diagram is drawn, Newton’s second law can be applied to solve the problem . This is done in Figure 1(d) for a particular situation. In general, once external forces are clearly identified in free-body diagrams, it should be a straightforward task to put them into equation form and solve for the unknown, as done in all previous examples. If the problem is one-dimensional—that is, if all forces are parallel—then they add like scalars. If the problem is two-dimensional, then it must be broken down into a pair of one-dimensional problems. This is done by projecting the force vectors onto a set of axes chosen for convenience. As seen in previous examples, the choice of axes can simplify the problem. For example, when an incline is involved, a set of axes with one axis parallel to the incline and one perpendicular to it is most convenient. It is almost always convenient to make one axis parallel to the direction of motion, if this is known.

Applying Newton’s Second Law

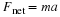
F net x  = ma ,

F net y = 0.

You will need this information in order to determine unknown forces acting in a system.

Step 4. As always, check the solution to see whether it is reasonable . In some cases, this is obvious. For example, it is reasonable to find that friction causes an object to slide down an incline more slowly than when no friction exists. In practice, intuition develops gradually through problem solving, and with experience it becomes progressively easier to judge whether an answer is reasonable. Another way to check your solution is to check the units. If you are solving for force and end up with units of m/s, then you have made a mistake.

Section Summary

To solve problems involving Newton’s laws of motion, follow the procedure described:

• Draw a sketch of the problem.
• Identify known and unknown quantities, and identify the system of interest. Draw a free-body diagram, which is a sketch showing all of the forces acting on an object. The object is represented by a dot, and the forces are represented by vectors extending in different directions from the dot. If vectors act in directions that are not horizontal or vertical, resolve the vectors into horizontal and vertical components and draw them on the free-body diagram.
• Write Newton’s second law in the horizontal and vertical directions and add the forces acting on the object. If the object does not accelerate in a particular direction (for example, the x-direction) then  F net x  = 0 . If the object does accelerate in that direction,  F net x  = ma .
• Check your answer. Is the answer reasonable? Are the units correct?

Problems & Exercises

1. A 5.00 × 10 5 -kg rocket is accelerating straight up. Its engines produce 1.250 × 10 7  of thrust, and air resistance is 4.50 × 10 6 N. What is the rocket’s acceleration? Explicitly show how you follow the steps in the Problem-Solving Strategy for Newton’s laws of motion.

2. The wheels of a midsize car exert a force of 2100 N backward on the road to accelerate the car in the forward direction. If the force of friction including air resistance is 250 N and the acceleration of the car is 1.80 m/s 2 , what is the mass of the car plus its occupants? Explicitly show how you follow the steps in the Problem-Solving Strategy for Newton’s laws of motion. For this situation, draw a free-body diagram and write the net force equation.

3. Calculate the force a 70.0-kg high jumper must exert on the ground to produce an upward acceleration 4.00 times the acceleration due to gravity. Explicitly show how you follow the steps in the Problem-Solving Strategy for Newton’s laws of motion.

4. When landing after a spectacular somersault, a 40.0-kg gymnast decelerates by pushing straight down on the mat. Calculate the force she must exert if her deceleration is 7.00 times the acceleration due to gravity. Explicitly show how you follow the steps in the Problem-Solving Strategy for Newton’s laws of motion.

5. A freight train consists of two 8.00 × 10 4   engines and 45 cars with average masses of 5.50 × 10 4 kg . (a) What force must each engine exert backward on the track to accelerate the train at a rate of 5.00 × 10 -2  if the force of friction is 7.50 × 10 5 , assuming the engines exert identical forces? This is not a large frictional force for such a massive system. Rolling friction for trains is small, and consequently trains are very energy-efficient transportation systems. (b) What is the force in the coupling between the 37th and 38th cars (this is the force each exerts on the other), assuming all cars have the same mass and that friction is evenly distributed among all of the cars and engines?

6. Commercial airplanes are sometimes pushed out of the passenger loading area by a tractor. (a) An 1800-kg tractor exerts a force of 1.75 × 10 5  backward on the pavement, and the system experiences forces resisting motion that total 2400 N. If the acceleration is 0.150 m/s 2 , what is the mass of the airplane? (b) Calculate the force exerted by the tractor on the airplane, assuming 2200 N of the friction is experienced by the airplane. (c) Draw two sketches showing the systems of interest used to solve each part, including the free-body diagrams for each.

7. A 1100-kg car pulls a boat on a trailer. (a) What total force resists the motion of the car, boat, and trailer, if the car exerts a 1900-N force on the road and produces an acceleration of 0.550 m/s 2 ? The mass of the boat plus trailer is 700 kg. (b) What is the force in the hitch between the car and the trailer if 80% of the resisting forces are experienced by the boat and trailer?

8. (a) Find the magnitudes of the forces F 1 and F 2  that add to give the total force F tot  shown in Figure 4. This may be done either graphically or by using trigonometry. (b) Show graphically that the same total force is obtained independent of the order of addition of   F 1 and F 2 . (c) Find the direction and magnitude of some other pair of vectors that add to give F tot . Draw these to scale on the same drawing used in part (b) or a similar picture.

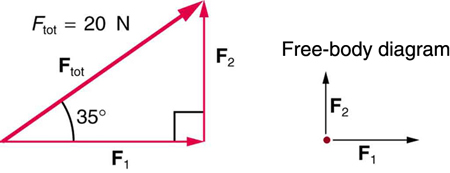
9. Two children pull a third child on a snow saucer sled exerting forces  F 1 and F 2 as shown from above in Figure 4 . Find the acceleration of the 49.00-kg sled and child system. Note that the direction of the frictional force is unspecified; it will be in the opposite direction of the sum of  F 1 and F 2 .

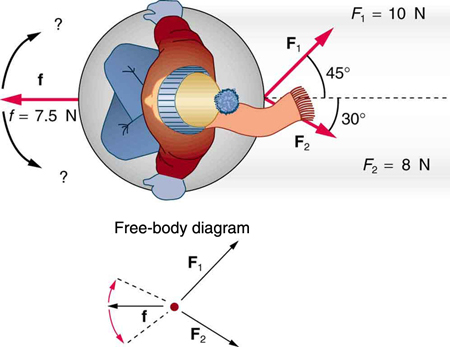
10. Suppose your car was mired deeply in the mud and you wanted to use the method illustrated in Figure 6 to pull it out. (a) What force would you have to exert perpendicular to the center of the rope to produce a force of 12,000 N on the car if the angle is 2.00°? In this part, explicitly show how you follow the steps in the Problem-Solving Strategy for Newton’s laws of motion. (b) Real ropes stretch under such forces. What force would be exerted on the car if the angle increases to 7.00° and you still apply the force found in part (a) to its center?

11. What force is exerted on the tooth in Figure 7 if the tension in the wire is 25.0 N? Note that the force applied to the tooth is smaller than the tension in the wire, but this is necessitated by practical considerations of how force can be applied in the mouth. Explicitly show how you follow steps in the Problem-Solving Strategy for Newton’s laws of motion.

Figure 7. Braces are used to apply forces to teeth to realign them. Shown in this figure are the tensions applied by the wire to the protruding tooth. The total force applied to the tooth by the wire, F app , points straight toward the back of the mouth.

12. Figure 9 shows Superhero and Trusty Sidekick hanging motionless from a rope. Superhero’s mass is 90.0 kg, while Trusty Sidekick’s is 55.0 kg, and the mass of the rope is negligible. (a) Draw a free-body diagram of the situation showing all forces acting on Superhero, Trusty Sidekick, and the rope. (b) Find the tension in the rope above Superhero. (c) Find the tension in the rope between Superhero and Trusty Sidekick. Indicate on your free-body diagram the system of interest used to solve each part.

Figure 9. Superhero and Trusty Sidekick hang motionless on a rope as they try to figure out what to do next. Will the tension be the same everywhere in the rope?

13. A nurse pushes a cart by exerting a force on the handle at a downward angle 35.0º below the horizontal. The loaded cart has a mass of 28.0 kg, and the force of friction is 60.0 N. (a) Draw a free-body diagram for the system of interest. (b) What force must the nurse exert to move at a constant velocity?

14. Construct Your Own Problem Consider the tension in an elevator cable during the time the elevator starts from rest and accelerates its load upward to some cruising velocity. Taking the elevator and its load to be the system of interest, draw a free-body diagram. Then calculate the tension in the cable. Among the things to consider are the mass of the elevator and its load, the final velocity, and the time taken to reach that velocity.

15. Construct Your Own Problem Consider two people pushing a toboggan with four children on it up a snow-covered slope. Construct a problem in which you calculate the acceleration of the toboggan and its load. Include a free-body diagram of the appropriate system of interest as the basis for your analysis. Show vector forces and their components and explain the choice of coordinates. Among the things to be considered are the forces exerted by those pushing, the angle of the slope, and the masses of the toboggan and children.

16. Unreasonable Results (a) Repeat Exercise 7, but assume an acceleration of 1.20 m/s 2  is produced. (b) What is unreasonable about the result? (c) Which premise is unreasonable, and why is it unreasonable?

17. Unreasonable Results (a) What is the initial acceleration of a rocket that has a mass of 1.50 × 10 6  at takeoff, the engines of which produce a thrust of 2.00 × 10 6 ? Do not neglect gravity. (b) What is unreasonable about the result? (This result has been unintentionally achieved by several real rockets.) (c) Which premise is unreasonable, or which premises are inconsistent? (You may find it useful to compare this problem to the rocket problem earlier in this section.)

Selected Solutions to Problems & Exercises

1. Using the free-body diagram:

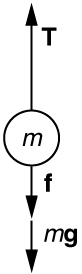
• [latex]{F}_{\text{net}}=T-f-mg=\text{ma}\\[/latex] ,

[latex]a=\frac{T-f-\text{mg}}{m}=\frac{1\text{.}\text{250}\times {\text{10}}^{7}\text{N}-4.50\times {\text{10}}^{\text{6}}N-\left(5.00\times {\text{10}}^{5}\text{kg}\right)\left(9.{\text{80 m/s}}^{2}\right)}{5.00\times {\text{10}}^{5}\text{kg}}=\text{6.20}{\text{m/s}}^{2}\\[/latex]

3. Use Newton’s laws of motion.

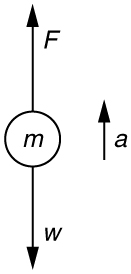
[latex]F=\left(\text{70.0 kg}\right)\left[\left(\text{39}\text{.}{\text{2 m/s}}^{2}\right)+\left(9\text{.}{\text{80 m/s}}^{2}\right)\right]\\[/latex] [latex]=3.\text{43}\times {\text{10}}^{3}\text{N}\\[/latex].  The force exerted by the high-jumper is actually down on the ground, but F is up from the ground and makes him jump.

• This result is reasonable, since it is quite possible for a person to exert a force of the magnitude of 10 3 N.

5. (a) 4.41 × 10 5 N (b) 1.50 × 10 5 N

7. (a) 910 N (b) 1.11 × 10 3

9. (a) a = 0.139 m/s, θ = 12.4º

11. Use Newton’s laws since we are looking for forces.

• Draw a free-body diagram:

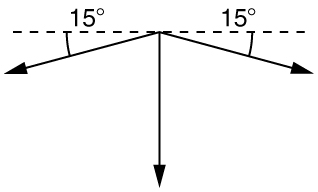
• The tension is given as T = 25.0 N. Find F app . Using Newton’s laws gives:[latex]\sigma{F}_{y}=0\\[/latex], so that applied force is due to the y -components of the two tensions: F app = 2 T  sin  θ  = 2(25.0 N) sin(15º) = 12.9 N The x -components of the tension cancel. [latex]\sum{F}_{x}=0\\[/latex].
• This seems reasonable, since the applied tensions should be greater than the force applied to the tooth.
• College Physics. Authored by : OpenStax College. Located at : http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a/College_Physics . License : CC BY: Attribution . License Terms : Located at License

• Net force formula

Update: This page’s content is moving to a new address in the upcoming months.

The information on this page is ✔ fact-checked.

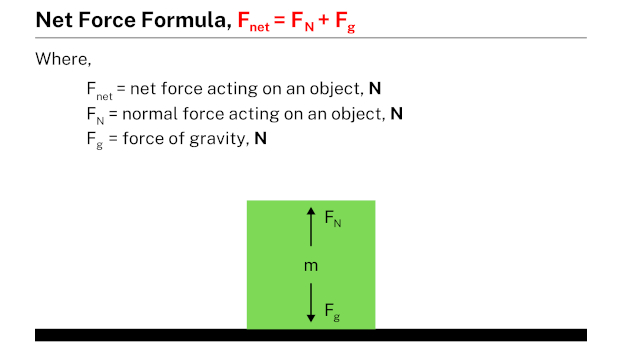
The net force formula is used to determine the total force acting on an object in different scenarios. When an object is at rest, the net force, represented as F net , is determined by adding the values of the normal force , denoted as F N , and the force of gravity , symbolized as F g . This relationship can be expressed using the equation F net = F N + F g .

In situations where the object is in motion, the net force formula becomes more comprehensive. It includes additional forces such as applied force (F a ) and frictional force (F f ), in addition to the normal force (F N ) and the force of gravity (F g ). The formula for calculating the net force in such cases is expressed as F net = F a + F f + F N + F g .

When an object is subjected to multiple forces (F 1 , F 2 , F 3 , …, F n ), the net force formula can be expanded accordingly. In this case, the net force (F net ) is determined by adding up all the individual forces acting on the object, leading to the formula F net = F 1 + F 2 + F 3 + … + F n .

Practice problems

A block is resting on the floor and is balanced by a normal force of 6 N and a gravitational force of 6 N. Determine the net force acting on the block.

Given data:

• Normal force acting on a block, F N = 6 N
• Force of gravity acting on a block, F g = -6 N (downward)
• Net force acting on a block, F net = ?

Applying the formula, when an object is at rest:

• F net = F N + F g
• F net = 6 – 6
• F net = 0 N

Therefore, the net force acting on a block is 0 N .

A book is lying on a desk. When a force of 15 N is applied to the book, a friction force of 5 N acts in the opposite direction. If the book is balanced by a normal force of 20 N and the force of gravity, calculate the net force acting on it.

• Applied force acting on a book, F a = 15 N
• Friction force acting on a book, F f = -5 N (left)
• Normal force acting on a book, F N = 20 N
• Force of gravity acting on a book, F g = -20 N (downward)
• Net force acting on a book, F net = ?

Applying the formula, when an object is in motion:

• F net = F a + F f + F N + F g
• F net = 15 – 5 + 20 – 20
• F net = 10 N

Therefore, the net force acting on a book is 10 N .

Two persons, Person 1 (standing on the right side) and Person 2 (standing on the left side), are pulling a rope in opposite directions. Person 1 applies a force of 40 N, and Person 2 applies a force of 15 N. Calculate the net force acting on the rope.

• Force acting on the rope, F 1 = 40 N
• Force acting on the rope, F 2 = -15 N (left)
• Net force acting on the rope, F net = ?

Applying the formula, when multiple forces are acting on an object:

• F net = F 1 + F 2
• F net = 40 – 15
• F net = 25 N

Therefore, the net force acting on the rope is 25 N .

A car gets stuck on the road, and six people are pushing it in the right direction. The six individuals apply the following forces: 3 N, 4 N, 5 N, 3 N, 7 N, and 2 N. Calculate the net force acting on the car.

• Force acting on the car, F 1 = 3 N
• Force acting on the car, F 2 = 4 N
• Force acting on the car, F 3 = 5 N
• Force acting on the car, F 4 = 3 N
• Force acting on the car, F 5 = 7 N
• Force acting on the car, F 6 = 2 N
• F net = F 1 + F 2 + F 3 + F 4 + F 5 + F 6
• F net = 3 + 4 + 5 + 3 + 7 + 2
• F net = 24 N

Therefore, the net force acting on the car is 24 N .

📝 Your feedback matters. Visit our contact page.

• Force equation
• Normal force equation
• Applied force formula
• Magnetic force equation
• Centripetal force equation
• Centrifugal force equation
• Spring force equation
• Tension force formula
• Electric force equation

External links

• Finding the Net Force: Equation & Examples – Study.com
• Determining the Net Force – The Physics Classroom
• How to Find Net Force: 9 Steps (with Pictures) – wikiHow
• Force Calculator | How to Find Force? – Omni Calculator
• Net Force: Definition, Equation, How to Calculate – Sciencing
• High School Physics : Net Force – Varsity Tutors
• Calculating Acceleration from Force and Mass – CK-12
• What is the formula for finding net force? – Brainly
• Net force – Wikipedia
• Lesson 19: Net Force – Studyphysics
• Force, Mass, Acceleration – Zona Land Education
• How do we calculate net force and acceleration? – Quora
• Force Calculator – How to Find Net Force with Formula – Calculator-online.net
• Calculating Net Force and Acceleration – Dummies
• Net Force Calculator – CalcTool

Learnool.com was founded by Deep Rana, who is a mechanical engineer by profession and a blogger by passion. He has a good conceptual knowledge on different educational topics and he provides the same on this website. He loves to learn something new everyday and believes that the best utilization of free time is developing a new skill.

Leave a Comment Cancel reply

Save my name, email, and website in this browser for the next time I comment.

Problem solving in the Middle East

23 May 2024

If there’s an issue on the airfield, Air Force Corporal John Chapman can get it done. 

The ground support equipment technician, deployed to Australia’s main operating base in the Middle East on Operation Accordion, has become the person coalition forces turn to in a bind. 

That’s what happened on April 1 when the mechanic from Muswellbrook, NSW, received a late-night call for help. 

A large Egyptian military cargo plane was stuck on the runway and needed an air start before it could take off. 

For more than two decades, international partner nations have been guests on the Emirati base. Corporal Chapman, the only Air Force technician deployed on Operation Accordion, was the only person on the base with the right tools and experience to get the job done. 

The right tools in this case was an air-start cart – a turbine compressor on wheels that pumps pressurised air into a jet engine to ‘jump start’ the turbines. 

It was well after midnight and the phone was ringing off the hook. 

“Our partners requested help, I was pretty sure I could make it happen but I wasn’t 100 per cent sure it was going to work,” Corporal Chapman said. 

Luckily, the Egyptian aeroplane was similar to the Australian C-130 Hercules and the equipment could be attached to the Antonov without issue. 

“[The Egyptians] were all smiles when we got the prop started and they got on their way,” he said. 

It wasn’t the first time the Australian has been called on to help partner militaries. 

Over his eight-month deployment to the Middle East, he has helped United States generals and become mates with the British. 

When a US general visited the base, they needed equipment to power their plane when it was on the runway. 

Then there was the time the British blew a tire and needed compressed nitrogen. 

Luckily, the Australian workshop was able to help. 

“That’s how it is between the international countries here,” Corporal Chapman said. 

“We just call each other up if we need a hand – there’s a lot of favours for favours.” 

With less than a month until he returns to Australia, Corporal Chapman will look back on his deployment as a career highlight. 

“I’m operating by myself and I’ve used every workshop and airside skill I’ve been taught,” he said. 

“I love getting asked, ‘how do I solve this?’ Mechanics love to solve problems.” 

Related services

Recommended stories.

Navy service spans three generations

When HMAS Brisbane II passed under Tower Bridge in London, Able Seaman Leslie Birch realised his dream to see the world.

Conquering the Marathon des Sables endurance race

This year, an Air Force sergeant was the first Australian to cross the finish line of the world's toughest race.

Stranded Aussies welcomed aboard C-130

An Air Force C-130J Hercules has assisted with the first ADF repatriation flight out of New Caledonia.

Rehoming wild horses won't solve the brumby problem, but it transforms lives for horses and owners

At 14, Ruby Wild would rather demonstrate her connection with horses than explain it.

Whether she's prompting the more than 500-kilogram animal to lie down or waiting for the mare to be still enough to stand on her back, the bond between the teenager and her horses is undeniable.

"If you don't have a strong connection, it's hard to do anything," Ruby said.

But her herd of four aren't regular domestic horses, they were once wild brumbies.

"We grew up together because she was only little. She was only two when we got her," she said.

Her mum Kylie Wild said, while Ruby was supervised, her young daughter had a natural intuition with horses.

"Ruby and Gidget built this connection together and it never really crossed my mind that she was a wild brumby," Ms Wild said.

Ruby's love of brumbies is one she shares with her cousin, 17-year-old Brooke Wild.

"Brumbies, they're definitely underestimated, that's for sure," Brooke said.

"Brumbies are just so, so versatile, anything you put them to: jumps, cattle, whatever. They'll just pick it up like that and they just learn so quickly."

Where did brumbies come from?

Horses came to Australia on the First Fleet in 1788. Escaped animals become the country's first brumbies.

Over time, other domestic breeds have gone feral and now descendants of thoroughbreds, stock, quarter and heavy horses can be found in the wild.

It is estimated there are more than 400,000 brumbies in Australia and when concentrated in high numbers, their hard hooves pose a risk to the environment and native species.

Horse trainer Anna Uhrig runs a brumby rehoming camp in south-east Queensland, using horses trapped in local forests and from central Queensland.

"We can't solve the brumby problem but we're doing what we can," Ms Uhrig said.

"It's a very small part of the puzzle: the amount of horses we rehome. It's not thousands but I think the work adds quality of life to those horses."

Ecologist Dave Berman has been managing brumby populations for 40 years across the country.

For most of the past decade, he has managed the brumby herds of Tuan and Toolara state forests, which consist of pine plantations and native species north of Noosa.

The growing population has brought wild horses close to roads, putting drivers at risk.

"We catch them and find homes for them to reduce the risk of collisions between horses and people," Dr Berman said.

"Usually it's the horses that get killed, but eventually, you know, there will be people killed.

"Originally in about 2009 there were about four horses killed per year, we removed all the horses regularly crossing the road and then there were no collisions, so we showed that worked."

What's a brumby rehoming camp?

Ms Uhrig's 10-day intensive camp attracts participants from all over the country to choose, train and adopt a brumby.

"Yarding, drafting and then coming to these yards is totally new for the brumbies so it can be quite scary for them," Ms Uhrig said.

In less than two weeks, some of the horses go from not letting a human within 100 metres to being ridden.

"I just love seeing the transformation and I love giving people the opportunity to learn those skills," Ms Uhrig said.

"I could break in a brumby continuously and I still wouldn't be able to rehome as many as we can through the camps."

Melissa Teunis's brumby Valour will join her herd of domestic horses used for equine therapy.

"I've loved horses forever and I just wanted the opportunity to start [training] my own [horse]," she said. 

"It's the perfect place to come. Anna is amazing and just knows the process and talks and walks you through every step."

But Ms Uhrig said rehoming brumbies wouldn't work everywhere.

"In terms of the whole management debate, it's not a closed book. We don't have the answers necessarily," Ms Uhrig said.

"There's been some research done in some targeted areas and we think we have the answers and we can apply those but generally it's a nationwide issue and the management implications are different in each area."

How are the horses trapped?

Dr Berman said   the trapping process was slow and targeted brumbies who grazed near or regularly crossed roads.

"We use electric fences and we build a really large electric fence area that can be up to 4 kilometres long," he said.

"We'll build that around the horses and gradually make it smaller and then get them into a laneway and then into hessian panels, and then into panel yards."

He said patience and a respect for the animals were required.

"If you put too much pressure on, they go. They'll go through the fence anyway," he said.

Giving the horses a second chance can take weeks and sometimes months.

It's an emotional process for Dr Berman who creates a strong connection with the brumbies during the process.

"They're wonderful animals," he said.

A national problem

Brumby management differs across the country.

Dr Berman said rehoming was becoming more common, but wasn't the solution alone.

"In a lot of other parts of Australia where populations are getting too much, horses can be shot from the air or the ground," he said.

In New South Wales's largest national park, Kosciuszko, the government is culling horses in the hundreds . 

In 2022, the NSW government estimated about 18,000 horses lived in the park, with a population range between 14,501 and 23,535 horses .

Under the state government management plan, more than 15,000 brumbies could be killed or rehomed to reduce the population to 3,000 by mid-2027, to the despair of some of the locals.

Meanwhile, a Kosciuszko brumby rehoming program has been suspended  after hundreds of horse carcasses were found on a property near Wagga Wagga .

Further north in NSW, the officers from the Local Land Services have a different approach, working with landholders and rescue groups to trap and rehome wild horses near Grafton.

"It's not just about safety for people. It's the safety of the horses as a number of them have been hit on the road," senior biosecurity officer Tiffany Felton said.

"But it's not just that, they're a hard-hoofed animals so they do, and especially in these dry times, start affecting the waterways and in environmentally sensitive areas."

In the past three years more than 130 have been captured and rehomed under the state government's Biosecurity Act.

"Previously, there have been probably far harsher approaches to wild horse management, and that's not what the community wanted," said Louise Orr of North Coast Local Land Services.

Untapped potential

After just seven days at brumby camp, some of the horses are almost unrecognisable for participants, including Melissa Teunis.

"It's amazing to think that when we got here last Friday, he'd never been touched," Ms Teunis said.

"It shows you how resilient they are and just how willing — oh this will make me cry — how willing they are to try for us and, and give us all that they have."

Lilly Anderson, 14, could put a saddle on her horse Rain by day four of the course and three days later, she was able to ride the animal.

"Like, for me, that's incredible. That's like just gone so quickly. But she's also so just amazing," Lilly said.

The camp is the first stage of the horses transitioning to domestic life with more time and effort required after they leave.

"Once you give them a chance, they'll do anything for you," Lilly said. 

"She's just so smart to catch on and she'll do anything for lucerne as well. Loves a bit of food."

Past participants of the camp said the biggest challenge with rehoming a brumby was fighting off the temptation to buy another.

"It's been hard but it gets better. The highs are really high," Ava Cloherty said.

Watch ABC TV's Landline at 12:30pm on Sunday or on  ABC iview .

• X (formerly Twitter)

Related Stories

Nsw suspends brumby rehoming after discovery of hundreds of dead horses.

Brumby re-homing program under investigation after mass horse carcass find on farm

'Versatile and amazing' brumbies show what they can do

• Equine Production
• Human Interest
• Maroochydore
• Perisher Valley

• TPC and eLearning
• What's NEW at TPC?
• Read Watch Interact
• Practice Review Test
• Teacher-Tools
• Subscription Selection
• Seat Calculator
• Ad Free Account
• Edit Profile Settings
• Classes (Version 2)
• Student Progress Edit
• Task Properties
• Export Student Progress
• Task, Activities, and Scores
• Metric Conversions Questions
• Metric System Questions
• Metric Estimation Questions
• Significant Digits Questions
• Proportional Reasoning
• Acceleration
• Distance-Displacement
• Dots and Graphs
• Graph That Motion
• Match That Graph
• Name That Motion
• Motion Diagrams
• Pos'n Time Graphs Numerical
• Pos'n Time Graphs Conceptual
• Up And Down - Questions
• Balanced vs. Unbalanced Forces
• Change of State
• Force and Motion
• Mass and Weight
• Match That Free-Body Diagram
• Net Force (and Acceleration) Ranking Tasks
• Newton's Second Law
• Normal Force Card Sort
• Recognizing Forces
• Air Resistance and Skydiving
• Solve It! with Newton's Second Law
• Which One Doesn't Belong?
• Component Addition Questions
• Head-to-Tail Vector Addition
• Projectile Mathematics
• Trajectory - Angle Launched Projectiles
• Trajectory - Horizontally Launched Projectiles
• Vector Addition
• Vector Direction
• Which One Doesn't Belong? Projectile Motion
• Forces in 2-Dimensions
• Being Impulsive About Momentum
• Explosions - Law Breakers
• Hit and Stick Collisions - Law Breakers
• Case Studies: Impulse and Force
• Impulse-Momentum Change Table
• Keeping Track of Momentum - Hit and Stick
• Keeping Track of Momentum - Hit and Bounce
• What's Up (and Down) with KE and PE?
• Energy Conservation Questions
• Energy Dissipation Questions
• Energy Ranking Tasks
• LOL Charts (a.k.a., Energy Bar Charts)
• Match That Bar Chart
• Words and Charts Questions
• Name That Energy
• Stepping Up with PE and KE Questions
• Case Studies - Circular Motion
• Circular Logic
• Forces and Free-Body Diagrams in Circular Motion
• Gravitational Field Strength
• Universal Gravitation
• Angular Position and Displacement
• Linear and Angular Velocity
• Angular Acceleration
• Rotational Inertia
• Balanced vs. Unbalanced Torques
• Getting a Handle on Torque
• Torque-ing About Rotation
• Properties of Matter
• Fluid Pressure
• Buoyant Force
• Sinking, Floating, and Hanging
• Pascal's Principle
• Flow Velocity
• Bernoulli's Principle
• Balloon Interactions
• Charge and Charging
• Charge Interactions
• Charging by Induction
• Conductors and Insulators
• Coulombs Law
• Electric Field
• Electric Field Intensity
• Polarization
• Case Studies: Electric Power
• Know Your Potential
• Light Bulb Anatomy
• I = ∆V/R Equations as a Guide to Thinking
• Parallel Circuits - ∆V = I•R Calculations
• Resistance Ranking Tasks
• Series Circuits - ∆V = I•R Calculations
• Series vs. Parallel Circuits
• Equivalent Resistance
• Period and Frequency of a Pendulum
• Pendulum Motion: Velocity and Force
• Energy of a Pendulum
• Period and Frequency of a Mass on a Spring
• Horizontal Springs: Velocity and Force
• Vertical Springs: Velocity and Force
• Energy of a Mass on a Spring
• Decibel Scale
• Frequency and Period
• Closed-End Air Columns
• Name That Harmonic: Strings
• Rocking the Boat
• Wave Basics
• Matching Pairs: Wave Characteristics
• Wave Interference
• Waves - Case Studies
• Color Addition and Subtraction
• Color Filters
• If This, Then That: Color Subtraction
• Light Intensity
• Color Pigments
• Converging Lenses
• Curved Mirror Images
• Law of Reflection
• Refraction and Lenses
• Total Internal Reflection
• Who Can See Who?
• Formulas and Atom Counting
• Atomic Models
• Bond Polarity
• Entropy Questions
• Cell Voltage Questions
• Heat of Formation Questions
• Reduction Potential Questions
• Oxidation States Questions
• Measuring the Quantity of Heat
• Hess's Law
• Oxidation-Reduction Questions
• Galvanic Cells Questions
• Thermal Stoichiometry
• Molecular Polarity
• Quantum Mechanics
• Balancing Chemical Equations
• Bronsted-Lowry Model of Acids and Bases
• Classification of Matter
• Collision Model of Reaction Rates
• Density Ranking Tasks
• Dissociation Reactions
• Complete Electron Configurations
• Elemental Measures
• Enthalpy Change Questions
• Equilibrium Concept
• Equilibrium Constant Expression
• Equilibrium Calculations - Questions
• Equilibrium ICE Table
• Intermolecular Forces Questions
• Ionic Bonding
• Lewis Electron Dot Structures
• Limiting Reactants
• Line Spectra Questions
• Mass Stoichiometry
• Measurement and Numbers
• Metals, Nonmetals, and Metalloids
• Metric Estimations
• Metric System
• Molarity Ranking Tasks
• Mole Conversions
• Name That Element
• Names to Formulas
• Names to Formulas 2
• Nuclear Decay
• Particles, Words, and Formulas
• Periodic Trends
• Precipitation Reactions and Net Ionic Equations
• Pressure Concepts
• Pressure-Temperature Gas Law
• Pressure-Volume Gas Law
• Chemical Reaction Types
• Significant Digits and Measurement
• States Of Matter Exercise
• Stoichiometry Law Breakers
• Stoichiometry - Math Relationships
• Subatomic Particles
• Spontaneity and Driving Forces
• Gibbs Free Energy
• Volume-Temperature Gas Law
• Acid-Base Properties
• Energy and Chemical Reactions
• Chemical and Physical Properties
• Valence Shell Electron Pair Repulsion Theory
• Writing Balanced Chemical Equations
• Mission CG1
• Mission CG10
• Mission CG2
• Mission CG3
• Mission CG4
• Mission CG5
• Mission CG6
• Mission CG7
• Mission CG8
• Mission CG9
• Mission EC1
• Mission EC10
• Mission EC11
• Mission EC12
• Mission EC2
• Mission EC3
• Mission EC4
• Mission EC5
• Mission EC6
• Mission EC7
• Mission EC8
• Mission EC9
• Mission RL1
• Mission RL2
• Mission RL3
• Mission RL4
• Mission RL5
• Mission RL6
• Mission KG7
• Mission RL8
• Mission KG9
• Mission RL10
• Mission RL11
• Mission RM1
• Mission RM2
• Mission RM3
• Mission RM4
• Mission RM5
• Mission RM6
• Mission RM8
• Mission RM10
• Mission LC1
• Mission RM11
• Mission LC2
• Mission LC3
• Mission LC4
• Mission LC5
• Mission LC6
• Mission LC8
• Mission SM1
• Mission SM2
• Mission SM3
• Mission SM4
• Mission SM5
• Mission SM6
• Mission SM8
• Mission SM10
• Mission KG10
• Mission SM11
• Mission KG2
• Mission KG3
• Mission KG4
• Mission KG5
• Mission KG6
• Mission KG8
• Mission KG11
• Mission F2D1
• Mission F2D2
• Mission F2D3
• Mission F2D4
• Mission F2D5
• Mission F2D6
• Mission KC1
• Mission KC2
• Mission KC3
• Mission KC4
• Mission KC5
• Mission KC6
• Mission KC7
• Mission KC8
• Mission AAA
• Mission SM9
• Mission LC7
• Mission LC9
• Mission NL1
• Mission NL2
• Mission NL3
• Mission NL4
• Mission NL5
• Mission NL6
• Mission NL7
• Mission NL8
• Mission NL9
• Mission NL10
• Mission NL11
• Mission NL12
• Mission MC1
• Mission MC10
• Mission MC2
• Mission MC3
• Mission MC4
• Mission MC5
• Mission MC6
• Mission MC7
• Mission MC8
• Mission MC9
• Mission RM7
• Mission RM9
• Mission RL7
• Mission RL9
• Mission SM7
• Mission SE1
• Mission SE10
• Mission SE11
• Mission SE12
• Mission SE2
• Mission SE3
• Mission SE4
• Mission SE5
• Mission SE6
• Mission SE7
• Mission SE8
• Mission SE9
• Mission VP1
• Mission VP10
• Mission VP2
• Mission VP3
• Mission VP4
• Mission VP5
• Mission VP6
• Mission VP7
• Mission VP8
• Mission VP9
• Mission WM1
• Mission WM2
• Mission WM3
• Mission WM4
• Mission WM5
• Mission WM6
• Mission WM7
• Mission WM8
• Mission WE1
• Mission WE10
• Mission WE2
• Mission WE3
• Mission WE4
• Mission WE5
• Mission WE6
• Mission WE7
• Mission WE8
• Mission WE9
• Vector Walk Interactive
• Name That Motion Interactive
• Kinematic Graphing 1 Concept Checker
• Kinematic Graphing 2 Concept Checker
• Graph That Motion Interactive
• Two Stage Rocket Interactive
• Rocket Sled Concept Checker
• Force Concept Checker
• Free-Body Diagrams Concept Checker
• Free-Body Diagrams The Sequel Concept Checker
• Skydiving Concept Checker
• Elevator Ride Concept Checker
• Vector Addition Concept Checker
• Vector Walk in Two Dimensions Interactive
• Name That Vector Interactive
• River Boat Simulator Concept Checker
• Projectile Simulator 2 Concept Checker
• Projectile Simulator 3 Concept Checker
• Hit the Target Interactive
• Turd the Target 1 Interactive
• Turd the Target 2 Interactive
• Balance It Interactive
• Go For The Gold Interactive
• Egg Drop Concept Checker
• Fish Catch Concept Checker
• Exploding Carts Concept Checker
• Collision Carts - Inelastic Collisions Concept Checker
• Its All Uphill Concept Checker
• Stopping Distance Concept Checker
• Chart That Motion Interactive
• Roller Coaster Model Concept Checker
• Uniform Circular Motion Concept Checker
• Horizontal Circle Simulation Concept Checker
• Vertical Circle Simulation Concept Checker
• Race Track Concept Checker
• Gravitational Fields Concept Checker
• Orbital Motion Concept Checker
• Angular Acceleration Concept Checker
• Balance Beam Concept Checker
• Torque Balancer Concept Checker
• Aluminum Can Polarization Concept Checker
• Charging Concept Checker
• Name That Charge Simulation
• Coulomb's Law Concept Checker
• Electric Field Lines Concept Checker
• Put the Charge in the Goal Concept Checker
• Circuit Builder Concept Checker (Series Circuits)
• Circuit Builder Concept Checker (Parallel Circuits)
• Circuit Builder Concept Checker (∆V-I-R)
• Circuit Builder Concept Checker (Voltage Drop)
• Equivalent Resistance Interactive
• Pendulum Motion Simulation Concept Checker
• Mass on a Spring Simulation Concept Checker
• Particle Wave Simulation Concept Checker
• Boundary Behavior Simulation Concept Checker
• Slinky Wave Simulator Concept Checker
• Simple Wave Simulator Concept Checker
• Wave Addition Simulation Concept Checker
• Standing Wave Maker Simulation Concept Checker
• Color Addition Concept Checker
• Painting With CMY Concept Checker
• Stage Lighting Concept Checker
• Filtering Away Concept Checker
• InterferencePatterns Concept Checker
• Young's Experiment Interactive
• Plane Mirror Images Interactive
• Who Can See Who Concept Checker
• Optics Bench (Mirrors) Concept Checker
• Name That Image (Mirrors) Interactive
• Refraction Concept Checker
• Total Internal Reflection Concept Checker
• Optics Bench (Lenses) Concept Checker
• Kinematics Preview
• Velocity Time Graphs Preview
• Moving Cart on an Inclined Plane Preview
• Stopping Distance Preview
• Cart, Bricks, and Bands Preview
• Fan Cart Study Preview
• Friction Preview
• Coffee Filter Lab Preview
• Friction, Speed, and Stopping Distance Preview
• Up and Down Preview
• Projectile Range Preview
• Ballistics Preview
• Juggling Preview
• Marshmallow Launcher Preview
• Air Bag Safety Preview
• Colliding Carts Preview
• Collisions Preview
• Engineering Safer Helmets Preview
• Push the Plow Preview
• Its All Uphill Preview
• Energy on an Incline Preview
• Modeling Roller Coasters Preview
• Hot Wheels Stopping Distance Preview
• Ball Bat Collision Preview
• Energy in Fields Preview
• Weightlessness Training Preview
• Roller Coaster Loops Preview
• Universal Gravitation Preview
• Keplers Laws Preview
• Kepler's Third Law Preview
• Charge Interactions Preview
• Sticky Tape Experiments Preview
• Wire Gauge Preview
• Voltage, Current, and Resistance Preview
• Light Bulb Resistance Preview
• Series and Parallel Circuits Preview
• Thermal Equilibrium Preview
• Linear Expansion Preview
• Heating Curves Preview
• Electricity and Magnetism - Part 1 Preview
• Electricity and Magnetism - Part 2 Preview
• Vibrating Mass on a Spring Preview
• Period of a Pendulum Preview
• Wave Speed Preview
• Slinky-Experiments Preview
• Standing Waves in a Rope Preview
• Sound as a Pressure Wave Preview
• DeciBel Scale Preview
• DeciBels, Phons, and Sones Preview
• Sound of Music Preview
• Shedding Light on Light Bulbs Preview
• Models of Light Preview
• Electromagnetic Radiation Preview
• Electromagnetic Spectrum Preview
• EM Wave Communication Preview
• Digitized Data Preview
• Light Intensity Preview
• Concave Mirrors Preview
• Object Image Relations Preview
• Snells Law Preview
• Reflection vs. Transmission Preview
• Magnification Lab Preview
• Reactivity Preview
• Ions and the Periodic Table Preview
• Periodic Trends Preview
• Intermolecular Forces Preview
• Melting Points and Boiling Points Preview
• Bond Energy and Reactions Preview
• Reaction Rates Preview
• Ammonia Factory Preview
• Stoichiometry Preview
• Nuclear Chemistry Preview
• Gaining Teacher Access
• Tasks and Classes
• Tasks - Classic
• Subscription
• Subscription Locator
• 1-D Kinematics
• Newton's Laws
• Vectors - Motion and Forces in Two Dimensions
• Momentum and Its Conservation
• Work and Energy
• Circular Motion and Satellite Motion
• Thermal Physics
• Static Electricity
• Electric Circuits
• Vibrations and Waves
• Sound Waves and Music
• Light and Color
• Reflection and Mirrors
• About the Physics Interactives
• Task Tracker
• Usage Policy
• Newtons Laws
• Vectors and Projectiles
• Forces in 2D
• Momentum and Collisions
• Circular and Satellite Motion
• Balance and Rotation
• Electromagnetism
• Waves and Sound
• Atomic Physics
• Forces in Two Dimensions
• Work, Energy, and Power
• Circular Motion and Gravitation
• Sound Waves
• 1-Dimensional Kinematics
• Circular, Satellite, and Rotational Motion
• Einstein's Theory of Special Relativity
• Waves, Sound and Light
• QuickTime Movies
• About the Concept Builders
• Pricing For Schools
• Directions for Version 2
• Measurement and Units
• Relationships and Graphs
• Rotation and Balance
• Vibrational Motion
• Reflection and Refraction
• Teacher Accounts
• Task Tracker Directions
• Kinematic Concepts
• Kinematic Graphing
• Wave Motion
• Sound and Music
• About CalcPad
• 1D Kinematics
• Vectors and Forces in 2D
• Simple Harmonic Motion
• Rotational Kinematics
• Rotation and Torque
• Rotational Dynamics
• Electric Fields, Potential, and Capacitance
• Transient RC Circuits
• Light Waves
• Units and Measurement
• Stoichiometry
• Molarity and Solutions
• Thermal Chemistry
• Acids and Bases
• Kinetics and Equilibrium
• Solution Equilibria
• Oxidation-Reduction
• Nuclear Chemistry
• Newton's Laws of Motion
• Work and Energy Packet
• Static Electricity Review
• NGSS Alignments
• 1D-Kinematics
• Projectiles
• Circular Motion
• Magnetism and Electromagnetism
• Graphing Practice
• About the ACT
• ACT Preparation
• For Teachers
• Other Resources
• Solutions Guide
• Solutions Guide Digital Download
• Motion in One Dimension
• Work, Energy and Power
• Algebra Based Physics
• Other Tools
• Frequently Asked Questions
• Purchasing the Download
• Purchasing the CD
• Purchasing the Digital Download
• About the NGSS Corner
• NGSS Search
• Force and Motion DCIs - High School
• Energy DCIs - High School
• Wave Applications DCIs - High School
• Force and Motion PEs - High School
• Energy PEs - High School
• Wave Applications PEs - High School
• Crosscutting Concepts
• The Practices
• Physics Topics
• NGSS Corner: Activity List
• NGSS Corner: Infographics
• About the Toolkits
• Position-Velocity-Acceleration
• Position-Time Graphs
• Velocity-Time Graphs
• Newton's First Law
• Newton's Second Law
• Newton's Third Law
• Terminal Velocity
• Projectile Motion
• Forces in 2 Dimensions
• Impulse and Momentum Change
• Momentum Conservation
• Work-Energy Fundamentals
• Work-Energy Relationship
• Roller Coaster Physics
• Satellite Motion
• Electric Fields
• Circuit Concepts
• Series Circuits
• Parallel Circuits
• Describing-Waves
• Wave Behavior Toolkit
• Standing Wave Patterns
• Resonating Air Columns
• Wave Model of Light
• Plane Mirrors
• Curved Mirrors
• Teacher Guide
• Using Lab Notebooks
• Current Electricity
• Light Waves and Color
• Reflection and Ray Model of Light
• Refraction and Ray Model of Light
• Classes (Legacy Version)
• Teacher Resources
• Subscriptions

• Newton's Laws
• Einstein's Theory of Special Relativity
• About Concept Checkers
• School Pricing
• Newton's Laws of Motion
• Newton's First Law
• Newton's Third Law

Mechanics: Vectors and Forces in Two-Dimensions

Calculator pad, version 2, vectors and forces in 2-d: problem set.

For each collection of listed forces, determine the vector sum or the net force.

• Audio Guided Solution
• Show Answer

Hector is walking his dog (Fido) around the neighborhood. Upon arriving at Fidella's house (a friend of Fido's), Fido turns part mule and refuses to continue on the walk. Hector yanks on the chain with a 67.0 N force at an angle of 30.0° above the horizontal. Determine the horizontal and vertical components of the tension force.

Helen is parasailing. She sits in a seat harness which is attached by a tow rope to a speedboat. The rope makes an angle of 51° with the horizontal and has a tension of 350 N. Determine the horizontal and vertical components of the tension force.

At one moment during a walk around the block, there are four forces exerted upon Fido - a 10.0 kg dog. The forces are:

F app = 67.0 N at 30.0° above the horizontal (rightward and upward) F norm = 64.5 N, up F frict = 27.6 N, left F grav = 98 N, down

Resolve the applied force (F app ) into horizontal and vertical components, then add the forces up as vectors to determine the net force.

Jerome and Michael, linebackers for South’s varsity football team, delivered a big hit to the halfback in last weekend’s game. Striking the halfback simultaneously from different directions with the following forces:

F Jerome = 1230 N at 53° F Michael = 1450 at 107°

Determine the resultant force applied by Jerome and Michael to the halfback. (The directions of the two forces are stated as counter-clockwise angles of rotation with East.)

A pack of three Artic wolves are fighting over the carcass of a dead polar bear. A top view of the magnitude and direction of the three forces is shown in the diagram to the right.

a. Determine the resultant or net force acting upon the carcass. b. Determine the acceleration of the 750-kg polar bear carcass.

Lee Mealone is sledding with his friends. Disgruntled by a coarse comment, he decides to separate from the group. He momentarily exerts a 31 N force on the rope which is attached to his 2.5-kg sled. The rope makes an angle of 22° with the nearly frictionless surface. Use the structure provided below to determine the net force on and acceleration of the sled.

Renee is on Spring Break and pulling her 21-kg suitcase through the airport at a constant speed of 0.47 m/s. She pulls on the strap with 120 N of force at an angle of 38° above the horizontal. Determine the normal force and the total resistance force (friction and air resistance) experienced by the suitcase.

Ben Laborin works for the South bookstore during the summer months to help prepare for Fall sales. Books from one supplier are shipped to the school in large crates equipped with rope handles on all sides. On one occasion, Ben momentarily pulled with a force of 692 N at an angle of 36.0° above the horizontal to accelerate a 112-kg crate of books. The coefficient of friction between the crates and the vinyl floor is 0.548. Determine the acceleration experienced by the crate. (Suggestion: Begin with a free body diagram.)

Problem 10:

A fire breaks out on a high rise building and a rescue helicopter is called to the scene. The helicopter is equipped with a rescue basket attached by a strong cable to a winch on the helicopter. The rescue basket is lowered to the roof and some occupants of the top floor escape to the roof and enter the basket. As the helicopter takes off, the cable momentarily makes a 78.2° angle to the horizontal, imparting a slight horizontal acceleration to the 621-kg basket and occupants across the roof top. The coefficient of friction between the basket and the roof top is 0.568 and the tension in the cable is 4980 N. Determine the acceleration of the basket and occupants. (Suggestion: Begin with a free body diagram.)

Problem 11:

The custodians clean the field house gym floor between games at the annual Holiday Basketball Classic. Chuck exerts a force on a 1.1-kg push broom as he walks across the floor at a constant speed. The coefficient of friction between the floor and the broom is 0.45 and the broom handle makes an angle of 41° with the horizontal. Determine the amount of force with which Chuck pushes downward (along the handle of the broom) in order to achieve this constant speed motion. (Suggestion: Begin with a free body diagram.)

Problem 12:

Lon Mauer is cleaning up the driveway after mowing the grass. He exerts a sudden downward force of 56.8 N at a constant angle of 54.7° below the horizontal in order to accelerate his 1.05-kg broom from rest. The coefficient of friction between the broom bristles and the driveway is 0.567. Determine the rate of acceleration of the broom. (Suggestion: Begin with a free body diagram.)

Problem 13:

South still displays with great pride the large sign boasting of their 1996 State Championship Girl’s Basketball Team. The 43.1-kg sign hangs from two cables which make an angle of 34.5° with the horizontal. Determine the tension in each of the cables.

Problem 14:

A massive light hangs over the table in Jeremy's dining room. The light is supported by four strong chains which make an angle of 75.0° with the horizontal. The force in each chain is 35.8 N.

a. Determine the force with which a single chain pulls horizontally and vertically upon the light. b. Determine the mass of the light.

Problem 15:

Troy Ginometri, owner of the local floral shop, displays the sale of the month in the front window of his shop. The 5.6-kg flower pot is suspended by three chains from the ceiling. The chains make an angle of 25° with the vertical. Determine the tension in one of the chains.

Problem 16:

The historic Stanley Center for the Arts in Utica, New York is the proud owner of the world’s largest LED chandelier. The chandelier is 35 feet wide, 17 feet tall and has a mass of 2900 kg. It is directly supported by four cables which make an angle of 63° with the horizontal. Determine the tension in the cables.

Problem 17:

Xavier went rock climbing this past weekend. During one climb through a narrow vertical chimney, he supported his weight by leaning with his back against one wall of the chimney and pushing off the opposite wall with his legs. His left leg made a 26° angle with the horizontal. The coefficient of frcition between his back and the chimney wall is 0.508. Determine the minimum amount of tension which would be required to support the weight of his 86-kg body.

a. Determine the tension in his left leg. b. Determine the normal force of the chimney wall pushing upon his back.

Problem 18:

Charles Blondin is famous for having crossed the Niagra Falls on an 1100-foot long tight-rope at a height of 160 feet above the gorge. He accomplished the feet several times in a variety of ways – blindfolded, in a sack, carrying his manager on his shoulders, pushing a wheelbarrow and walking on stilts. Suppose the 65-kg Blondin is at the midpoint of the tight-rope and has stopped to cook and eat an omelet. If the tightrope makes an angle of 5° with the horizontal, determine the tension in the rope.

Problem 19:

Mom and Dad have tied a rope to Matthew’s sled and are momentarily pulling him through the snow. Dad is pulling with force A and Mom with force B.

A: 54 N at 65° north of east B: 130 N at 22° south of east

a. Determine the resultant force of A and B. b. Determine the acceleration that these momentary forces would create for a 39-kg sled and child (assuming negligible friction).

Problem 20:

A local automobile dealership has chosen to hang a car outside the entry to their showroom. The car has been modified so that its mass is 645 kg. The car's weight will be supported by a heavy-duty chain which pulls upwards and leftwards. A beam will push outward to balance the wallward pull of the chain. The manufacturer of the chain claims it has a breaking strength of 17400 Newtons. Village code requires that there be a safety factor of 2.20. That is, the actual tension in the chain must be no more than 1/2.20 of the breaking strength. What is the minimum angle (between the chain and the horizontal ) at which the dealership can hang the car?

Problem 21:

Lab partners Anna Litical and Noah Formula placed a 0.500-kg glider on their air track and inclined the track at 15.0° above the horizontal. Determine the net force and acceleration of the glider along the frictionless track. Use the structure provided with the free body diagram shown below.

Problem 22:

Anna Litical and Noah Formula now place a 1.38-kg brick on a wooden board and incline the board at 24.0° above the horizontal. The coefficient of friction between the brick and the board is 0. 328. Determine the net force and the acceleration of the brick. Use the structure provided with the free body diagram shown below.

Problem 23:

Ben Laborin exerts a force on an 86-kg crate of books to push it up the ramp of the loading dock at a constant speed of 24 cm/s. The ramp makes an angle of 12° with the horizontal. The coefficient of friction between the crate and the ramp is 0.74. Assuming that Ben is pushing parallel to the inclined plane, determine the force with which he is pushing. (Suggestion: Begin with a free body diagram.)

Problem 24:

The infamous Lombard Street in San Francisco has an abnormally steep block which consists of several tight hairpin turns. On average, the roadway on this block of the street is inclined at 16°. Determine the force which would be required to pull a 23-kg wagon and child up the hill at constant speed. Assume the force is exerted parallel to the road and that friction is negligible.

Problem 25:

In an effort to determine the coefficient of friction between a wood block and a metal track, Anna Litical and Noah Formula place the block on the track and slowly elevate one of its ends until the block finally budges from rest and slides down the incline. Anna and Noah repeat several trials and determine that the block accelerates from its rest position when the track makes an angle of 38° above the horizontal. Use this angle value to determine the coefficient of friction. (Suggestion: Begin with a free body diagram.)

Problem 26:

The Splash Mountain flume ride at Walt Disney World's Magic Kingdom in Orlando, Florida boasts one of the steepest flume rides in the world. The boats plunge 52 feet down a 43-degree incline near the final stage of the ride. Assuming a coefficient of friction of 0.12, determine the acceleration of the boat and riders. (Suggestion: Begin with a free body diagram.)

Problem 27:

Ethan recently found out that the sledding hill on the west side of Lake Bluebird is more of a shredding hill than a sledding hill. He boarded his 60-inch sled and descended the steepest section near the tall trees. Before his ride ended at the location of a tree stump buried a few inches below the snow, he was accelerating at 2.5 m/s/s down the 19° incline. Determine the coefficient of friction between the sled and the snow. (Suggestion: Begin with a free body diagram.)

Return to Overview

View Audio Guided Solution for Problem:

Millennials have a fresh take on the FIRE movement, and it's less about taking it easy in retirement

At age 36, Jace Mattinson is already over retirement . Four years ago, he sold his lumber company for seven figures, and he had enough saved that he never needed to work again.

He said that was an enticing idea after five "extremely tough" years of owning a business. During that time, he was away from his home in Austin a few nights a week and hustling to run the 135-year-old company he'd acquired. After selling the company, he needed a long break from anything laborious.

"I was golfing three, four times a week. I was going to the lake. I was doing all my hobbies that I really cared about and enjoyed, ones that for the greater part of a decade I didn't have as much time to do," Mattinson told Business Insider.

But after eight months, he decided retirement was not nearly as fulfilling as he'd imagined. He returned to a job in lumber distribution and revived his financial podcast. He said he wanted to continue to model a good work ethic for his kids.

Mattinson has all the trappings of someone in the FIRE movement . The acronym, which stands for financial independence, retire early, was coined in the 1990s in the book "Your Money or Your Life" and popularized on blogs like Mr. Money Mustache and the investment site Motley Fool. The idea was to work hard, ideally with multiple income streams, live a life of austerity, invest prudently, and build a big enough nest egg to walk away from work well before the average retirement age of 64.

But millennials, including Mattinson, who finds himself happiest when he has a balance of work and leisure, said they're not as interested in early retirement — and are creating their own versions of life after work.

Millennials often want the FI without the RE

Devotees of the FIRE movement often save or invest the majority of their income . Some take on extra jobs or delay major life milestones like marriage or having kids.

It's an exclusive club, and many hungry millennials are eager to join it. ChooseFI's Facebook group has over 108,000 members, while the r/financialindependence subreddit has 2.2 million members. But for some FIRE wannabes, the "FI" part of the equation is the biggest focus, and the "RE" half seems to be less of a foregone conclusion.

A popular rule of thumb among this group is the "4% rule," which says you should aim to save 25 times your annual expenses so you can withdraw 4% of your funds each year after you quit working. Some FIRE participants told BI that their target savings goal is between $1.5 million and $2.5 million, though many are working toward more for even greater security.

To be sure, early retirees are a small slice of the population. According to Business Insider's analysis of American retirees, just 2.2% are 50 or younger. Less than 1% are below age 35. Just 0.75% of all Americans over 18 and under 50 are retired. Still, many BI spoke with retire unofficially or partially retire, taking on less responsibility at a company or moving to a lower-stakes position.

BI spoke to a dozen millennials who have achieved or are on track to achieve financial independence. While some have retired and told BI they're enjoying it, most feel retirement is pointless and still want to build their careers or give back to their communities.

"The thing I have noticed shift most is the emphasis on FI and less on RE," Scott Rieckens, the executive producer of the film " Playing With FIRE ," said. "I think it's awesome to see, as it signals that financial independence is the key motive, which it is, and that work and purpose are actually really important. Retiring early to nothing is a bad idea."

Brad Barrett, the host of the "ChooseFI" podcast, said "vanishingly few" people with the wherewithal to reach financial independence are retiring early. To him, reaching financial independence allows someone to live the life they want, but retiring early signifies turning away from everything you've worked toward.

For many, financial freedom goes beyond quitting a job you don't like. Some said it's the ability to spend on travel or leisure without much stress — which has become even more important after the pandemic's peak. Others said it helps them lead a life of purpose, whether that means educating people on a podcast or leading charity efforts.

The problem with retirement seems to be that people want to add value to their communities and within their own lives — and they believe work is the way to do that. As Bill Schaninger, a speaker, author, and thought leader on the future of work, found in research he conducted with Naina Dhingra for McKinsey , 70% of people who were surveyed said they define their purpose through work.

"Many people figured out one of the things that I get a lot of validation from is being clever, solving problems, participating, and working on something bigger than me," Schaninger told BI.

COVID-19 may have amplified this, he added. "The fragility of our condition, I think, was brought home in a way that maybe many of us had taken for granted," he said. "And so now it's like, 'Well, if I'm going to do this, it has to matter.'"

The millennial version of early retirement

Mitch, 37, said he is about to quit his high-stress job and take a mini-retirement — he has a 22-stop national parks trip planned this summer.

The Minnesota resident and vice president of a building-maintenance company, who asked that only his first name be used because of an ongoing job transition, has a net worth of about $2 million but said he's only planning to take a few months off before returning to the workforce in a lower-stress position. All the sources BI spoke with provided documentation of their net worth.

Mitch said he stumbled into the online personal-finance community in his early 30s, which inspired him and his wife to increase their savings to at least 75% of their income by avoiding spending on luxury items. He said even his high savings won't affect his decision to quit working.

"I think a lot of traditional retirees lack purpose — they take a year or two of retirement and hate it because they do whatever and lose purpose," Mitch said. "The ones that volunteer, continue to coach and consult, or do whatever it is to sharpen their brain and really have a purpose tend to be some of the happiest retirees."

Brian Luebben, a financially independent millennial , described having a panic attack shortly after he hit FI and quit his sales job.

"If you have anxiety, financial freedom is not going to solve it," he said. "If you have depression, financial freedom is not going to solve it. Be careful of the mountaintop moments. When you become a millionaire, when you become financially free, when you do all this stuff, no mariachi band follows you around and performs."

He argued that achieving financial independence and hitting a specific number is "the simplest part." After all, there's a playbook for wealth-building strategies like investing in real estate or building an e-commerce business.

"The most difficult part is figuring out what you do when you have nothing to do all day," he said. "What do you choose to work on?"

Luebben, who hosts a podcast and runs the entrepreneur resource The Action Academy to help other people achieve financial freedom, said people should think through four core questions before they're even close to achieving financial independence: "What does the perfect day look like? What does the perfect week look like? Who was with you? And where?"

Going through that exercise can help ensure that your identity doesn't become wrapped up in achieving FIRE, which is something that Grant Sabatier, who took a year and a half off from work after achieving financial independence, struggled with.

"I defined myself by the pursuit of financial independence," Sabatier, the author of " Financial Freedom ," said. "Then, once I reached it, it was like, now I no longer had to do that thing, so what am I going to do? I encourage people on the path to do that inner work. Don't delay figuring out what you really want, why you're pursuing financial independence, and what you want to do after."

Balancing work and fun

Instead of a traditional retirement, many financially independent millennials are finding a balance between work and leisure that works for them.

For Sabina Horrocks, 41, becoming a millionaire was "quite boring." She and her husband worked in six-figure managerial positions, recently achieving a net worth of about $2 million, then had a daughter in 2021. They "plowed money into investments early on," kept daily expenditures low, and purchased rental properties they eventually sold.

She quit her sales operations job but has no intention of stopping work. She's a stay-at-home mom and plans to continue her blog The Moneyaires ; she'd also like to become a financial coach or planner.

Blogging and coaching were common post-FI pursuits among the would-be early retirees BI spoke to. Michelle Schroeder-Gardner, 34, runs the blog Making Sense of Cents , and over the past decade, she and her husband have lived mostly in an RV or a sailboat.

By 2017, their blog, advertising sales, and a course they created called Making Sense of Affiliate Marketing had generated nearly $1.2 million in revenue. By 2018, they had achieved financial independence. After years of 100-hour workweeks, she now spends 10 hours a week on her business, which generates $600,000 a year.

"I'm able to travel whenever I want. I can work whenever I want. Nothing's really dependent on my work hours," she said. "My plan is pretty much to continue doing this while I like it and continue to make a little bit more money and save as much as I can."

Lauren and Steven Keys, who quit their full-time jobs in their 20s , have a similar outlook.

Steven does freelance work for his former employer but spends much of his time on an online-tutoring service called CramBetter that he cofounded in 2023. Lauren has one social-media client she works with a couple of hours a month. They also run a financial-independence blog, Trip of a Lifestyle , and earn rental income from a fully paid-off investment property.

"There's this misconception about early retirement that you'll never make another penny ever again and just sit on the beach all day for the rest of your life," Steven said. "We're never going to stop making any money whatsoever."

Are you part of the FIRE movement or living by some of its principles? Reach out these reporters at [email protected] or [email protected] .

Related stories

More from Economy

Most popular

• Main content

• Share full article

For more audio journalism and storytelling, download New York Times Audio , a new iOS app available for news subscribers.

• May 23, 2024   •   34:24 I.C.C. Prosecutor Requests Warrants for Israeli and Hamas Leaders
• May 22, 2024   •   23:20 Biden’s Open War on Hidden Fees
• May 21, 2024   •   24:14 The Crypto Comeback
• May 20, 2024   •   31:51 Was the 401(k) a Mistake?
• May 19, 2024   •   33:23 The Sunday Read: ‘Why Did This Guy Put a Song About Me on Spotify?’
• May 17, 2024   •   51:10 The Campus Protesters Explain Themselves
• May 16, 2024   •   30:47 The Make-or-Break Testimony of Michael Cohen
• May 15, 2024   •   27:03 The Possible Collapse of the U.S. Home Insurance System
• May 14, 2024   •   35:20 Voters Want Change. In Our Poll, They See It in Trump.
• May 13, 2024   •   27:46 How Biden Adopted Trump’s Trade War With China
• May 10, 2024   •   27:42 Stormy Daniels Takes the Stand
• May 9, 2024   •   34:42 One Strongman, One Billion Voters, and the Future of India

The Sunday Read: ‘Why Did This Guy Put a Song About Me on Spotify?’

The answer involves a remarkable — and lucrative, and ridiculous — scheme to game the way we find music today..

By Brett Martin

Read by Eric Jason Martin

Produced by Adrienne Hurst and Aaron Esposito

Narration produced by Tanya Pérez and Krish Seenivasan

Edited by John Woo

Original music by Aaron Esposito

Engineered by Sophia Lanman and Devin Murphy

Listen and follow The Daily Apple Podcasts | Spotify

Have you heard the song “Brett Martin, You a Nice Man, Yes”?

Probably not. On Spotify, “Brett Martin, You a Nice Man, Yes” has not yet accumulated enough streams to even register a tally. Even Brett Martin, a contributing writer for The New York Times Magazine and the titular Nice Man, didn’t hear the 1 minute 14 second song until last summer, a full 11 years after it was uploaded by an artist credited as Papa Razzi and the Photogs.

When Martin stumbled on “Brett Martin, You a Nice Man, Yes,” he naturally assumed it was about a different, more famous Brett Martin: perhaps Brett Martin, the left-handed reliever who until recently played for the Texas Rangers; or Brett Martin, the legendary Australian squash player; or even Clara Brett Martin, the Canadian who in 1897 became the British Empire’s first female lawyer. Only when the singer began referencing details of stories that he made for public radio’s “This American Life” almost 20 years ago did he realize the song was actually about him. The song ended, “I really like you/Will you be my friend?/Will you call me on the phone?” Then it gave a phone number, with a New Hampshire area code.

So, he called.

There are a lot of ways to listen to ‘The Daily.’ Here’s how.

We want to hear from you. Tune in, and tell us what you think. Email us at [email protected] . Follow Michael Barbaro on X: @mikiebarb . And if you’re interested in advertising with The Daily, write to us at [email protected] .

Additional production for The Sunday Read was contributed by Isabella Anderson, Anna Diamond, Sarah Diamond, Elena Hecht, Emma Kehlbeck, Tanya Pérez, Frannie Carr Toth and Krish Seenivasan.

Advertisement

Opinion | Letters: Country’s problems can’t be solved…

Share this:.

• Click to share on Facebook (Opens in new window)
• Click to share on X (Opens in new window)

Daily e-Edition

Evening e-Edition

• Readers React

Breaking News

Opinion | lehigh county man fatally shot wife, then himself, coroner says, opinion | letters: country’s problems can’t be solved through the use of force.

Criminal history wasn’t needed in report on couple’s death

An elderly couple were fatally hit by a car Friday night and their names were not released until Tuesday’s edition of local news. Was it really necessary to say that the victim was found guilty of a crime in 2008 and prior to that in 1990?  What does that have to do with the accident? How about if they have any family and this is what is mentioned about the accident?

Denise Williams

Lower Macungie Township

Sheer force not the answer to solving country’s problems

A recent letter to the editor recounted a list of problems the nation faces and suggested they’re all the result of weak leadership. But the alternative, Donald Trump, though he has a forceful personality, knows very little about how anything in government works. If you need confirmation of the last part of that sentence, read the commentaries of some of his top advisers when he was president — Rex Tillerson, John Kelly, John Bolton, William Barr, etc. — and about the difficulty they had getting him to understand any kind of complexity, or even some fairly basic principles. A plumber or electrician, faced with a complex problem, wouldn’t get very far trying to solve it with strength alone; he would need to understand what’s going on. The problems facing the nation today won’t be helped by a sledgehammer. I’ll take Biden any day of the week over the alternative. I haven’t been happy with every one of his moves — there’s never been a politician about whom I could say that — but he has several landmark achievements in his presidency already, and he’s worked credibly, if incrementally, on most of the issues before us now.

Quality is important emphasis in Rick Anderson interview

Some thoughts on Rick Anderson’s two-hour interview, “St. Luke’s CEO talks local health care” (April 21). Anderson is to be congratulated on his nearly 39-year run as St. Luke’s CEO. He successfully navigated many turbulent waters, and is in good company: Warren Buffett chaired Berkshire-Hathaway for over 50 years and Thomas Watson chaired IBM for 42 years.

I like Anderson’s recurring emphasis on quality — highly important in health care — although the article said nothing about the metrics St. Luke’s uses to measure quality. Nor was the managerial role of physicians at St. Luke’s addressed (it is physicians who swear to uphold the Hippocratic oath).

Physicians’ private entrepreneurial practices are gradually being absorbed by hospital networks and doctors become employees. To what extent are professional managers and bean counters supplanting physicians’ expertise in health care decisions?

The planned merger/acquisition of Jefferson Health in Philadelphia and Lehigh Valley Health Network reminds me of the Philadelphia Electric Co. (PECO) proposal to take over our local PPL electric utility some 20 years ago. Public concern in the Lehigh Valley eventually put the kibosh on that proposal.

I wish Mr. Anderson well and hope that his “quality” theme continues to improve health care outcomes and strengthens physicians’ role in St. Luke’s health care decisions.

James Largay

Upper Saucon Township

Help pay decent wage for child care workers

Quality child care teachers are a primary component of the quality of a child care program. My children love their teacher and that relationship is central to fostering their love for learning. I’m one of the fortunate families who are able to have their children in high quality child care. Unfortunately, in Pennsylvania less than half of children in child care are enrolled in a high quality program.

Thousands of families are struggling to find child care because of the staffing crisis. Many classrooms are closed and waitlists are the norm. In fact, Sonya Sue’s Daycare, where my children go, has multiple children on the waiting list. Child care programs are simply unable to compete with rising wages and benefits now being offered by companies requiring less specialized skill.

To ensure my children and children across Pennsylvania are able to find the high-quality care and education they deserve, our lawmakers must prioritize funding to help programs pay teachers a livable wage.

Samantha Shive

Stuttering Foundation has resources available

May 12-18 is National Stuttering Awareness Week. One in every 100 people stutter. That’s 80 million people worldwide. Yet stuttering is often misunderstood and even laughed at.

To address the many myths surrounding this complex disorder, the Stuttering Foundation has compiled a list of “75 Must-Use Resources for the Stuttering Community” — available for free on at StutteringHelp.org.

The foundation’s most popular content represents a mix of time-tested favorites and newer innovations:

* Drawings and letters from kids featuring submissions from children around the world and published in our magazine

* “Answers for Employers” brochure answering frequent questions from employers received by the foundation each year

* “Self-Therapy for the Stutterer” e-book written by founder Malcolm Fraser in 1978

* List of famous people who stutter continuously updated with many celebrities, sports heroes, writers and world leaders.

* A podcast, now in its sixth season with more than 100,000 listeners.

* “Advice to Those Who Stutter” audio book, drafted in 1972 and updated by 28 therapists who stutter themselves.

* I Stutter ID card, helping people identify themselves in a nonverbal way.

All resources are available at StutteringHelp.org.

Jane Fraser

The writer is the president of The Stuttering Foundation.

Mackenzie’s help earned him a vote for Congress

On Nov. 5, Ryan Mackenzie will have my vote for U.S. Congress. Like most people, I didn’t used to think a lot about identity theft. It was something I’d heard about, but I never thought it would happen to me. Then, like millions of Americans, I discovered that I had become a victim. This was a scary time for me. When I got a bill for an account that was opened fraudulently, it couldn’t be canceled. I wasn’t sure where to turn, so I tried the offices of Susan Wild and some of my other representatives. Unfortunately, no one seemed to know how to help me, and I felt alone and frustrated. That’s when I ran into state Rep. Ryan Mackenzie at a local event. He wasn’t even my state representative, but when I mentioned my problem, he promised to take care of it. About a week later, everything was taken care of, and I am thankful to him and his office for helping me. I’ll always be grateful to Ryan Mackenzie for stepping up to help when no one else would. That’s why he will have my vote for U.S. Congress.

Mona Chibber

Whitehall Township

The Morning Call encourages community dialogue on important issues. Submit a letter to the editor at  [email protected] .

More in Opinion

SUBSCRIBER ONLY

Opinion | browse political cartoons for the week of may 20.

Opinion | Your View: Fixing the way Washington regulates manufacturers would benefit them and the Lehigh Valley

Opinion | Letters to the Editor: Alley houses plan for Bethlehem will create more problems than it will solve

Opinion | Your View: Honor the efforts of women, Black Americans during World War II