problem solving nzmaths

The home of mathematics education in New Zealand.

• Forgot password ?
• Teaching material
• Problem solving activities

Problem Solving

The Ministry is migrating nzmaths content to Tāhurangi.             Relevant and up-to-date teaching resources are being moved to Tāhūrangi (tahurangi.education.govt.nz).  When all identified resources have been successfully moved, this website will close. We expect this to be in June 2024.  e-ako maths, e-ako Pāngarau, and e-ako PLD 360 will continue to be available. 

For more information visit https://tahurangi.education.govt.nz/updates-to-nzmaths

This section of the nzmaths website has problem-solving lessons that you can use in your maths programme. The lessons provide coverage of Levels 1 to 6 of The New Zealand Curriculum. The lessons are organised by level and curriculum strand.  Accompanying each lesson is a copymaster of the problem in English and in Māori. 

Choose a problem that involves your students in applying current learning. Remember that the context of most problems can be adapted to suit your students and your current class inquiry. Customise the problems for your class.

• Level 1 Problems
• Level 2 Problems
• Level 3 Problems
• Level 4 Problems
• Level 5 Problems
• Level 6 Problems

The site also includes Problem Solving Information . This provides you with practical information about how to implement problem solving in your maths programme as well as some of the philosophical ideas behind problem solving. We also have a collection of problems and solutions for students to use independently.

Or search by topic

Number and algebra

• The Number System and Place Value
• Calculations and Numerical Methods
• Fractions, Decimals, Percentages, Ratio and Proportion
• Properties of Numbers
• Patterns, Sequences and Structure
• Algebraic expressions, equations and formulae
• Coordinates, Functions and Graphs

Geometry and measure

• Angles, Polygons, and Geometrical Proof
• 3D Geometry, Shape and Space
• Measuring and calculating with units
• Transformations and constructions
• Pythagoras and Trigonometry
• Vectors and Matrices

Probability and statistics

• Handling, Processing and Representing Data
• Probability

Working mathematically

• Thinking mathematically
• Mathematical mindsets
• Cross-curricular contexts
• Physical and digital manipulatives

For younger learners

• Early Years Foundation Stage

Advanced mathematics

• Decision Mathematics and Combinatorics
• Advanced Probability and Statistics

Problem Solving

Problem Solving and the New Curriculum   Age 5 to 11

Developing a Classroom Culture That Supports a Problem-solving Approach to Mathematics   Age 5 to 11

Developing Excellence in Problem Solving with Young Learners   Age 5 to 11

Using NRICH Tasks to Develop Key Problem-solving Skills   Age 5 to 11

Trial and Improvement at KS1   Age 5 to 7

Trial and Improvement at KS2   Age 7 to 11

Working Systematically - Primary Teachers   Age 5 to 11

Number Patterns   Age 5 to 11

Working Backwards at KS1   Age 5 to 7

Working Backwards at KS2   Age 7 to 11

Reasoning   Age 5 to 11

Visualising at KS1 - Primary Teachers   Age 5 to 7

Visualising at KS2 - Primary Teachers   Age 7 to 11

Conjecturing and Generalising at KS1 - Primary Teachers   Age 5 to 7

Conjecturing and Generalising at KS2 - Primary Teachers   Age 7 to 11

• Mathematical Problem Solving in the Early Years
• Low Threshold High Ceiling - an Introduction
• What's All the Talking About?
• Group-worthy Tasks and Their Potential to Support Children to Develop Independent Problem-solving Skills
• Developing the Classroom Culture: Using the Dotty Six Activity as a Springboard for Investigation

Maths Links

A directory of useful objects found on the web for teaching Maths.

NZMaths Problem Solving

http://nzmaths.co.nz/problem-solving

Lesson, Resources

Problem-solving lessons that can be integrated in normal teaching programs. The problems cover a variety of levels and curriculum strands.

27 May 2015 Edit: 27 May 2015

User submitted, thanks to Belinda Keir

Submit a correction to this link | Help align this link to NSW Mathematics Syllabuses align this link to The Australian Curriculum

Enter this in the address bar:

gomaths.net/4109

Teachers, use the Short Address .

Short Address

This short address will bring you back to this page. It is shorter to write in documents to reference this link.

Add to List

Register or login.

To use the lists feature, first Sign up for free

or if already registered, Sign in

How have you used this link in your classroom? Share your teaching ideas or leave a review about this link.

Sign in to leave a comment.

There are no comments for this link.

Get updates…

• Patterns and Algebra
• Measurement
• Space and Geometry
• more …
• Australian Curriculum
• NSW Syllabus

Figure it Out Books all online

Jun 16, 2020 | AMA News

This week nzmaths finished uploading PDF’s of all the english medium Figure it Out activities to their website.

Figure It Out is a series of mathematics curriculum support books designed to supplement existing classroom programmes. Along with the student activities you will find a teachers book with suggested approaches, links to achievement objectives, ideas for extension and the answers

You can find activities by:

• searching the activity’s name if you know it
• using the carousel interface: https://nzmaths.co.nz/figure-it-out-carousel-interface . Scroll through the books by title then dive inside

A number of the books contain activities focussed around theme  including

• Sport [l3-4]
• At Camp [L3]
• Technology in practice [3+-4+]
• Using resources [3+-4+]
• Forces [2+-3+]

Have a browse

• Skills by Standard
• Skills by Grade
• Skills by Category

Go to profile

• Assignments
• Assessments
• Report Cards
• Our Teachers

New Zealand Mathematics Curriculum

Students are entering a new section of math that consists of algebra, geometry, decimals, and more complicated division problems. When there is not a parent or teacher around, students have access to on-demand videos for their sixth-grade mathematical lessons. Our video tutorials are taught by math teachers who go through the problem solving process.

• The key to learning math is repetition, and our math teachers go through multiple examples. 
• Math teachers show students step-by-step directions on how to solve these more complex problems.
• Students learn money, ratios, decimals, graphing, and other concepts from the 6th grade curriculum.

Not a Member?

Read more about the Member Benefits of MAV and find out how to join MAV or renew your membership.

• Authentic tasks
• F - 10 Resources

Authentic tasks are designed to help students see mathematics as worthwhile and important. When students understand the purpose of a given problem in mathematics, they are more likely to persist when challenged. Authentic tasks generally have an ‘open middle’ which means that students can use different representations and solutions to communicate their knowledge and reasoning.

These curated links provide MAV members with access to nine authentic tasks from some of our primary consultants’ favourite resources. The 11 criteria provide MAV members with a research-informed context to consider each task’s potential impact on student thinking, ways of working, attitudes towards mathematics, their knowledge and understanding.

The following criteria was used to select the tasks based on their potential:

Used with permission © Martin Holt Educational Consultant 2017

If you would like to learn more about this approach to assessing or using tasks contact [email protected]

Statistics and probability

Measurement and geometry, number and algebra.

These support pages were produced using Strategic Partnership Program funding from the Department of Education and Training.

• Document Listing
• Undergrad and first year teachers
• Picture books
• Mathspiration
• News and research
• Curriculum and resources
• VCE Resources
• Investigations - Vinculum
• Learning Activities Years F to 9
• Town Squared-game
• Mathematics in Careers

The Common Denominator 2/24

DOWNLOAD NOW

• Join or Renew Membership
• Register for Professional Learning
• Maths Talent Quest
• Girls in STEM
• VCE Revision Lectures
• Resources in the MAV Shop

Log in / Sign up

About NZCER Contact Us Our Team Latest News NZCER Blog Careers NZCER Assist Login Newsletter signup 

Search form

You are here, problem solving in mathematics.

Not all teachers are comfortable with using the technique of problem solving, which is an attempt to find the answer to a problem when the method of solution is not known. This research shows how problem solving can be used in secondary school mathematics classes.

PROBLEM SOLVING In Mathematics

Derek Holton Department of Mathematics and Statistics, University of Otago

Jim Neyland Mathematics and Science Education Centre, Victoria University of Wellington

Julie Anderson Department of Mathematics and Statistics, University of Otago

WHERE ARE WE?

In 1993, a new national mathematics curriculum which emphasised the importance of problem solving was introduced in New Zealand. Three years later there was evidence that a significant proportion of teachers believe problem solving to be important and many are making some effort to incorporate problem solving into their teaching. However, despite this evident commitment, problem solving does not seem to occupy a regular place in most classrooms.

By problem solving we mean the attempt to find the answer to a problem when the method of solution is not known. In problem-solving situations the solver has to use strategic skills to find appropriate mathematical techniques which will settle the question. Neyland (1995) discusses the similarities and differences between the problem-solving approach and seven other approaches to teaching mathematics.

It is worth noting that what is a problem to one person may not be a problem to another. For a five-year-old determining the number of legs three sheep have will almost certainly be a problem. However, it should not be a problem for most 15-year-olds. The five-year-old may need to draw, use equipment, or employ some other method to solve the problem. The 15-year-old will just say “3 times 4 equals 12”.

Word problems do not necessarily involve problem solving. If a word problem is introduced to practise a technique which has just been acquired, it should be reasonably obvious what technique has to be used. On the other hand, problem-solving situations may be presented as wordy problems, though this is not always the case.

According to the National Council of Teachers of Mathematics:

Problem Solving should be the central focus of the mathematics curriculum. As such it is a primary goal of all mathematics instruction and an integral part of all mathematical activity. Problem Solving is not a distinct topic but a process that should permeate the entire program and provide the context in which concepts and skills can be learned.

We would like to underline the last sentence of the above quote as we find it difficult to differentiate between problem solving on the one hand and mathematics, or its essential nature, on the other.

In Australia, these views are reflected in A National Statement on Mathematics for Australian Schools (1990), where problem solving is one of four sub-headings in the Mathematical Inquiry strand:

The mathematical processes described within this strand cannot be developed in isolation from the work of other strands. They should pervade the whole curriculum.

In New Zealand, the importance of problem solving has been underscored by the Ministry of Education publication Implementing Mathematical Processes in Mathematics in the New Zealand Curriculum (1995):

Problem solving is the first heading in the Mathematical Processes strand; unless the ability to solve problems is developed, there is little point in studying mathematics.

The Mathematical Processes strand in the Mathematics in the New Zealand Curriculum document provides the umbrella for learning in the other five strands of Number, Measurement, Geometry, Algebra, and Statistics. It incorporates three areas: problem solving, developing logic and reasoning, and communicating mathematical ideas. We have decided to focus our attention on problem solving because it can provide the medium for both developing mathematical processes and interlacing the learning of specific knowledge and skills. However, is problem solving valued in our classrooms?

THE STUDIES

The work in this paper is based upon two pieces of research. The first was a questionnaire that was given to 11 secondary school mathematics departments in a provincial city of New Zealand. Some 53 teachers responded to the questionnaire (representing a 100 percent response rate from the schools) and the issues raised were discussed with seven experienced mathematics teachers.

The second study involved observations of problem-solving sessions in five secondary classrooms at the form 3 and 4 level [year 9 and 10 in New Zealand; year 8 and 9 in Australia].

The main questions in the questionnaire were:

How is problem solving being used and how often?

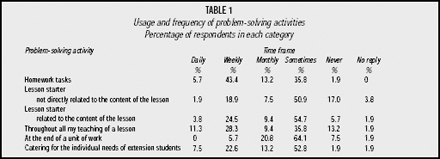
There are a variety of approaches to problem solving in the classroom. The questionnaire avoided questions about specific types of activities (open-ended tasks, investigations, short challenging tasks, projects, or mathematical modelling) and concentrated on broader areas of usage that had been observed in classrooms. The six categories considered were homework tasks, lesson starters not directly related to the content of the lesson, lesson starters related to the content of the lesson, throughout lesson, at the end of a unit of work, and catering for the needs of more able students. See table 1 for results.

Homework tasks

From table 1, we see that problem-solving activities are being used as homework tasks more regularly than any of the other five categories surveyed. However, of those teachers using homework tasks at least weekly, under half (48 percent) used problem solving through all of a lesson at least weekly. This suggests that homework tasks are often independent activities which are not supported by problem solving in the classroom.

Lesson starters

One of the teaching approaches identified by Sigurdson et al. (1994) is the problem-process approach , which involves using simple problems related to the mathematical content of the lesson, solving these problems through student-teacher interaction in a whole class setting and focusing on the processes being used. While using problems as lesson starters seems a good starting-off point for the implementation of a problemsolving approach, over half of the teachers surveyed never used problemsolving starters or used them only sometimes. Less than four percent use lesson starters related to content daily. But, more surprisingly, stand-alone problems are used as lesson starters at least once a week by only 21 percent of respondents. This suggests that teachers should be encouraged to use short challenging tasks to initiate problem solving in their classroom. This might be a useful point to begin teacher professional development in this area.

Throughout lesson

Over one-third of teachers (40 percent) stated that they were using a problem-solving approach throughout all of their teaching of a lesson, at least weekly. This suggests that a regular integrated approach to problem solving is occurring in a number of classrooms. However, evidence from later written responses suggested there may have been an overstatement of the actual situation.

The reason for the relatively small percentage of teachers using a problem-solving approach regularly through all lessons may be found in Burkhardt (1988). He believes that standard teaching methods are largely single track and depend on the method being explained by the teacher. On the other hand, problem solving is multi-track and is led by the methods proposed by individual students. Burkhardt feels that problem solving is difficult for the teacher. He identifies three areas giving rise to this difficulty— mathematical, pedagogical, and personal .

Mathematically the teacher must scan the different approaches that students are using and assess how useful each of these may be. The teacher then has to decide how best to complete the mathematical task from each of these starting points.

Pedagogically the teacher must decide when to help and when not to help, and what support and questioning to provide for each student or each group of students.

Personally there is the problem of teacher confidence. Because teachers may be confronted with approaches that they have not considered before, they need to believe that they can determine, possibly with student help, which approaches lead to solutions and which don’t. This is a potentially non-trivial barrier to tackling problem solving in class.

End of unit

In the past it has been the practice to include word problems at the end of a section in order for students to practise newly learned skills in potentially novel situations. Some 27 percent of the respondents are using problem solving in this way at least monthly. It is worth noting though that all but one of the teachers who used problem solving at the end of a unit of work was also using problem-solving lesson starters or was also using problem solving throughout all of their teaching weekly. Applying skills to problems at the end of a unit of work seems to be only one component of a teacher’s problem-solving repertoire.

Extension students

Many schools encourage their capable students to experience independent problem solving in a variety of ways. These include mathematics or computer clubs, small groups working apart from the normal class, through mathematics competitions, or via individual extension material. In a survey of talented mathematics students, Curran, Holton, Daniel, and Pek (1992) found that such students enjoyed the challenge and the open approach of problemsolving tasks. Burkhardt (1988) highlights a common belief in the need for problem solving for the gifted child but is reserved about how best to balance this need in the gifted students’ mathematical diet.

The survey shows that, at least monthly, individual students are being given specific extension opportunities in the area of problem solving by 43 percent of teachers. Other able students will benefit from being exposed to regular classroom problem-solving activities. However, of the 57 percent of classrooms which are not providing specific problem-solving experiences regularly for their capable students, some 41 percent do not provide opportunities for problem solving in the regular classroom at least monthly. Hence, in over 23 percent of classrooms, bright students are only occasionally being exposed to any form of problem solving.

What strategies are being promoted?

Pólya (1973) stresses the importance of strategies for solving problems. Strategies are just means to discover a solution. They are almost always not the method of solution nor a justification of the answer. They are, however, a mechanism by which the answer may be found and then justified, if necessary, by some other means.

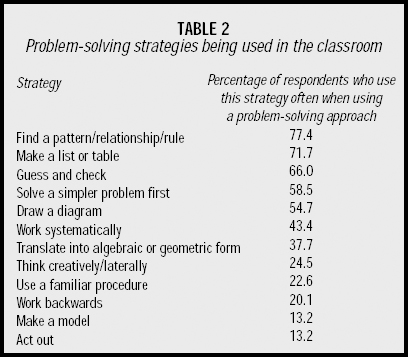
The suggested learning experiences in the problem-solving section of Mathematics in the New Zealand Curriculum include the “devising, using, and modifying of problem solving strategies”. The questionnaire in our study referred to 12 strategies from Mathematics in the New Zealand Curriculum . These were the strategies that we thought would be commonly used by teachers. The results are summarised in table 2.

The predominance of Find a pattern, etc is perhaps to be expected. It is one of the easiest techniques to promote because of the natural occurrence of patterning in students’ environments. In addition, children come to secondary school with a history of patterning experience from primary school for teachers to draw on. Further, the emphasis on patterning is encouraged by Mathematics in the New Zealand Curriculum . Exploring patterns and relationships is an achievement objective for all levels.

We believe that Make a list and Guess and check are also popular because they are easy to teach and can be applied to a range of problems. Equally it may be that these strategies are well suited to the types of problems that are frequently used in the early years of high school.

Surprisingly though, Draw a diagram was only rated as a commonly-used strategy by just over half of the teachers. It is not clear whether this is because teachers feel that this is not “proper” mathematics at the secondary level or whether its value as a tool is not appreciated. In the research project we have seen diagrams being of great value, especially to weaker students. It provides a closer representation of the problem than, for instance, algebra does, and hence may make some problems more accessible to students.

A similar accessibility can be provided through the strategies Make a model or Act out . These heuristics (or the means by which a solution is sought) give more control of the problem to the students and can provide motivation. Lovitt and Clarke (1988) advocate these approaches, referring to them as “kinesthetic”. It is now acknowledged that children learn in different ways and the tactile, physical, pictorial thinkers could well benefit if these strategies and Draw a diagram were used more often. It may be that some teachers avoid these strategies because they view them as being more appropriate for primary schools. They may also find the strategies too difficult to implement because of the resources needed and the time constraints on their lessons. Only a quarter of respondents regularly discuss Thinking creatively . It is difficult for a teacher to model with students that “flash of brilliance” which seems to come from nowhere. However, the fostering of such insights by discussion and brain storming is vital if we are to extend the horizons of students’ thinking and to enable them to strike out in new directions.

Strategies need to be taught

Our research supports the conclusion that strategies need to be taught. They also need to be practised otherwise they become forgotten. This seems to be especially true for young students and students who are weak mathematically.

Generally a number of strategies can be used in one problem. For example:

Greedygrimes Charlie ate a total of 100 jellybeans in 5 days, each day eating 6 more than the previous day. How many jellybeans did he eat on the third day?

This problem was solved by students in form 4 [year 10 in New Zealand, year 9 in Australia] using:

The Australian National Statement on Mathematics says that the methods of good problem solvers are likely to be “idiosyncratic” and that students need to discuss a variety of strategies to increase their “awareness of the range of techniques available”. This is supported by Beagle (1979), Pólya (1973), and Schoenfeld (1992). The first of these authors states:

… problem solving strategies are both problem and student specific often enough to suggest that finding one (or few) strategies which should be taught to all, or most students, is far too simplistic.

It is not clear, though, how heuristics should be taught. Holton (1994) and Neyland (1994) share a concern that teaching should not lead to strategies being employed like another set of algorithms or rules. They also say that students should be encouraged to see how to translate strategies to other problems and situations. Strategy usage and teaching is not straightforward and much more research is required in these areas.

How would you like to use problem solving in the future?

Just under 60 percent of the teachers surveyed want to use problem solving more often, suggesting that a receptive environment for future development does exist. They do identify a number of common difficulties though. Among these are:

Our experience is that problem solving does take more time, especially in the early stages. However, time can be saved later. One of the teachers in the research project commented that using a group investigative approach to construction tasks and locus problems enabled her students to develop a number of concepts in one lesson which usually took her two or three lessons of more structured teaching. This approach also freed her to help individuals who were struggling, resulting in all students achieving more than usual in the time.

There is a real concern for the needs of less-able students. This relates in particular to their reading ability. One of the classes in our research project is a low-ability class. They work effectively at problem solving. This may be because all the students are of comparable ability, because the teacher uses problems that can be completed in ten to fifteen minutes, because the reading level required by the problems is not too high, or because the teacher chooses problems in a single lesson that require the same strategies.

What help do you need with problem solving?

The teachers in the survey overwhelmingly requested pre-prepared resources and problems that would fit in with content strands. Some 74 percent of the respondents asked for resources of this kind. Some typical comments regarding teacher needs were:

As Neyland (1994) and Lovitt (1995) say, problem-solving activities by themselves are not enough to guarantee good problem solving. However, a start in this direction cannot be made without these activities. There is an urgent need to produce them in a form which makes them easily used.

Other comments by teachers included the provision of appropriate physical environments for problem solving. This meant appropriate equipment as well as space. Teachers also felt they needed help and training in scaffolding, heuristics, and metacognition (thinking about thinking—an important aspect of problem solving). Some assistance in extension work for bright students would also be appreciated.

Two valuable suggestions were made which could usefully be explored. These are:

With the change of the political environment, teachers may find the Ministry of Education in New Zealand will no longer provide the continuing services it has done in the past. Resources for teachers are less likely to be seen as a central responsibility and if not contracted out may be left to private enterprise to produce. Until these appear on the scene the next phase of teacher development will be largely left in the hands of the teachers themselves.

A TEACHING PERSPECTIVE

In the short period since the implementation of the new curriculum, it appears that most teachers are making at least some effort to incorporate problem-solving approaches into their mathematics classrooms. At present, problem solving is not a regular feature of most classrooms but it is clear that teachers are prepared to increase their use of problem solving. This increased use can be facilitated by the production of appropriate content-related problems. Indeed the teachers surveyed see this as the first priority to the further implementation of a problem-solving approach to mathematics.

ADVANTAGES OF PROBLEM SOLVING

The advantages proposed for problem solving in school are that it:

Unfortunately simply giving teachers good reasons for teaching problem solving, and giving them good problems to pass on to their students, does not produce good problem solving. As Lovitt (1995) says:

All the early problem-solving efforts were mostly devoted to the creation of suitable problems in the belief that teachers could present these in classrooms and generate effective learning with the same maths they used for expository teaching. It has taken some time to recognise that this is not the case …

Neyland (1994) expresses the same view:

Some well designed [problem-solving activities] do not result in the active learning event intended. There appear to be two main reasons for this. Firstly, the way the activity was originally presented to the class diminished its potential. And secondly, the interactive component of the teaching–learning process was not adequately prepared and unanticipated problems arose. [emphasis in original]

Before starting to teach problem solving, teachers should be clear why, apart from the fact that it is in the curriculum, they intend teaching it. It is important too, to note that the problem-solving approach to teaching mathematics is different from what has become the traditional approach. However, much of the problem-solving approach is not new. Scaffolding, which is not limited to problem solving, has its origins in the Socratic method. Heuristics too have a long pedigree. So how is problem solving different from what has become the standard “chalk and talk” method for teaching mathematics?

The main difference is one of attitude or philosophy on the part of the teacher. The shift is from the so-called “sage on the stage” to the “guide by the side”. Philosophically, the teacher needs to change from a giving role to an encouraging role, from “here is how to solve a linear equation” to “how might we solve this linear equation? ”

Naturally the students will not be able to invent all the mathematics they need for themselves. There will still be things that they need to be told. They will still need to practise both skills and problemsolving processes. However, more time needs to be spent by the students exploring mathematics with the teacher as a guide. During this exploration, seeds will be planted and students will develop connections between various parts of their learning which will increase learning, understanding and retention later ( see Hiebert and Carpenter, 1992).

So, instead of teachers taking students down well-trodden paths in a sequential unfolding of mathematical structures, there should be more emphasis on the students themselves structuring mathematical knowledge for specific problem contexts. Certainly the structures that are formed this way have to be justified but not necessarily in the one way shown in the textbook. Where possible, students should be given the opportunity to provide their own justifications. Many of these will be correct and may well be different from the text-book proof.

This is not to say that the development of mathematics during the year is anarchic. Teachers should know from the start what material is to be covered. However, there should be some flexibility in the manner and order in which the content arises. Of course, in highstakes years, when there are external examinations, the course may have to be slightly more structured. Nevertheless, it is important even on these occasions for teachers’ questioning to be open rather than closed in order to stimulate students’ thinking.

In the problem-solving approach then, there is less emphasis on students applying rules to problems which have been carefully chosen to fit those rules. There is greater emphasis on the creative construction of mathematical structures and solutions in non-routine situations and over a range of contexts.

Incorporating process and model

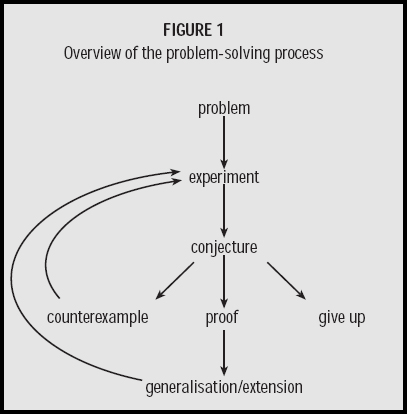
In order to give the following five-part overview of the problem-solving process we combine the model of problem solving given in Holton and Neyland (1996) with the heuristics and metacognition discussed in that paper ( see figure 1).

We recall that heuristics are means by which a solution is sought. Most of the heuristics of Begg (1994) are covered in this overview of the problem-solving process. We also show that certain heuristics tend naturally to appear at certain stages. In what follows, heuristics are emphasised in italics.

I Getting started

This is the first part of problem solving and includes “problem” and “experiment” from figure 1. It also covers the first two phases of Póya’s four-phase model.

1. Understand the problem

The problem will either be posed by the students themselves, presented in writing, or given verbally. If the problem is not one posed by the students, a first and crucial step is for them to make the problem their own; to become familiar with its conditions, characteristics, and variables. If it is in writing the solver has to read the problem and read it carefully. Many a solver has begun by solving a problem they thought was there but was actually not.

As the solvers read the problem they should be asking the various questions posed by Pólya. They should also be looking for key words . These are words which, if changed, will lead to a quite different problem. They are words or phrases which are essential in the solution of the problem. For novice problem solvers, underlining key words is a useful strategy. It is also a good idea for the problem solver to restate the problem for themselves . This helps to emphasise the key aspects of the problem. Other strategies such as experimenting with special cases also help the student to understand the problem.

Consider the problem below.

Peter is 18 years older than his daughter Sue who is 7 years old. How old will Peter be when he is twice as old as Sue?

In this problem, “18”, “7”, and “twice as old” all appear to be key words or phrases. The question, and more importantly the answer, is altered if key words are changed. (In actual fact, “7” is an extraneous piece of information here.) On the other hand, “Peter” could be “Peta” and “Sue”, “Sam” without changing the answer or the method of solution.

In this particular problem it is obvious that both Peter and Sue age at the same rate, one year at a time. This is nowhere explicitly stated but it is an hidden assumption . Many problems have implicit conditions that turn out to be important in finding a solution. So it is vital to make sure that hidden assumptions have been noted.

One of the metacognitive aspects of problem solving is to know when to come back to the original problem and read it again. This may be necessary to see if you are on the right track of a solution or if you have inadvertently started to solve another problem. It may also help you to try another approach if you have made no progress with a particular method of attack or change the point of view . Once an answer has been obtained it is important to reread the question to ensure that the solution you have obtained does indeed solve the original problem.

Apart from the metacognition (or “thinking about thinking”) at the start of a problem—which largely relates to monitoring and controlling the problem-solving processes—it is necessary for solvers to go through a mental list of heuristics in an effort to find a few which will get them started.

It is worth asking the following Pólya questions:

In addition it is worth considering:

3. Experiment

This is often an early stage in the problem-solving process. It has two main functions. The first is to get a feel for the problem. The second is to start to produce some evidence for a conjecture. The experiments may be calculations or measurements or a variety of things depending on the problem in hand.

The experiments should be systematic . The aim is to get central, useful information that can be collated in some way, rather than an unconnected jumble of, say, numbers. And the results of experiments should be recorded in some logical fashion— in a list, table , or diagram . When appropriate, consider the case n = 1, then n = 2 and so on. It is worth keeping these experiments until the problem has been completely solved. They may well be useful to provide or inspire a counterexample later.

Another problem that is useful to illustrate some ideas here is the frog problem.

Four spotted frogs (S) and four green frogs (G) are sitting on lilypads as in figure 2. Frogs can move to the next lilypad if it is free or they can jump over another frog if there is an empty lilypad on the other side. What is the smallest number of moves which can interchange the green and the spotted frogs?

There is a certain amount of symmetry in this problem. Whatever happens next, certainly it doesn’t matter whether a spotted or a green frog starts first.

This is a good problem too, to illustrate solving a simpler problem first . It’s easier to do the problem above once you’ve tried moving one frog of each type, two frogs of each type, and so on.

This is a common feeling at the start of a new problem. Success and experience will give the solver confidence to continue. However, even expert problem solvers face panic on occasions. Be prepared to think “there is no way I will ever do this problem” and then get on and realise you can.

II Conjecturing

The next process in problem solving involves conjecture.

This can be the most enjoyable and interesting part of the problemsolving process. In more difficult problems it is necessary to find a pattern, rule , or relation in order to produce a conjecture.

Some problems give up the correct conjecture immediately, other problems take more time. In harder problems it may be necessary to discard a number of conjectures before obtaining the right one. Some people find some problems easier to make conjectures about than others. And conjectures require practice. So it is necessary to start with simple problems and work up.

Does the conjecture make sense? Is it consistent with previous knowledge and the data that has been assembled in the experimental phase? Does the conjecture imply anything that feels wrong? Intuition and common sense can and should be used here. A conjecture which implies that the height of a mountain is five centimetres must surely be wrong. Any conjecture should be justifiable . Even though it cannot be proved at this stage, there should be good reasons for choosing one conjecture over another.

III Proof/Counter example

The more difficult problems will require the solver to trade off conjecture against proofs against counterexamples. The process is a dynamic one which is only completed when the final step in the solution is written down. Frequently, trying to prove a conjecture gives an idea for a counterexample and looking for a counterexample can give an idea for a proof. Whether starting down the proof or counterexample trail the solver may see that the conjecture needs adjusting and the process starts again.

It is difficult to see whether to first try to justify a conjecture or show it is wrong. The decision as to which to try first depends on the solver and the problem. If testing a few cases will cover all possible counterexamples, then the solver should go that route. This will either produce a counterexample or strongly confirm the conjecture. In the latter case, of course, a proof will still be required.

Some problems look like others and this may suggest a way to proceed to a proof. A slight change of a known proof might work. Or the problem may be one which suggests a well-known proof technique such as proof by contradiction or mathematical induction .

1. Extreme cases

In trying to find counterexamples it is often valuable to try extreme examples or extreme cases . These examples are somehow at the edge of the spectrum of values that are being used. For instance, what happens if a number is very small or what happens as “n” approaches infinity? What happens if the triangle is isosceles? Extreme cases are usually easier to handle than more general situations so it is worth testing a few before trying a proof. Even if they do not provide a counterexample they may well give the solver some useful information which can be used later. Here is a problem which can be quickly solved by looking at an extreme case: Do all one-litre milk containers have the same surface area? The answer, no, can be easily obtained by imagining a one-litre box-shaped milk container with a base the size of a tennis court and a height a fraction of a millimetre. Clearly this one-litre container has a surface area much larger than the one in the fridge.

2. Special cases

A conjecture can also be tested against special cases rather than extreme cases. Special cases are typical cases such as the ones during the experimental phase. Where possible, cases would be tested because they are straight forward or easy to test. But sometimes more complicated cases are forced on the solver.

3. Simpler problems

Sometimes problems are far too difficult to solve the first time. They may involve far too many variables to be able to understand easily. In that case reduce the problem to a simpler problem in some way. For instance, in the frog problem using fewer frogs is a good way to start. Similarly a gambling problem involving five dice might be reduced at first to one involving only two. Insight gained from the two dice case may well lead to the solution of the original problem. Here the aim is to keep as many of the essentials of the problem as possible while reducing the problem to a manageable size. Using simpler problems is also something that is useful at the experimental stage, as we saw earlier. Sometimes problems can be simplified in more than one way and students should learn to choose the best from the range of available simplified situations.

4. Exhaust all possibilities

One of the very simple methods of proof is to exhaust all possibilities . If there are sufficiently few cases to handle (under 50, say), then by looking at each one in turn, the solver can learn about the entire problem. This way any conjecture about the situation is immediately verified or disproved. Simple combinatorial problems such as the behaviour of two dice are often open to this approach. For instance, how many different ways are there for two dice to give a sum of four?

When a solution has been obtained by older children by the exhaustive approach, it is worth asking the Pólya phase four question “Can you derive the result differently?” They should be looking for more sophisticated approaches. There are times, however, when no other method is available. Certainly this will be the case with younger children. And finding a justification, any justification, is better than no justification at all.

5. Guess and check

One of the simplest ways of tackling a problem is guess and check . This is sometimes also called trial and error . In the problem of Peter and Sue, an answer can be found by guessing and checking. It is therefore a good strategy for simple problems. There are drawbacks, however. First, if the problem involved has a large number of cases, for instance the five dice gambling game we alluded to earlier, then it may not be easy to guess the correct answer in a reasonable time. Second, guessing and checking will give an answer. However, the method cannot tell you whether the answer is unique. It may well be that the problem has a number of answers. Only an exhaustive search will be able to determine all answers in such a problem. Finally, the guess and check method in complicated situations may only reveal the conjecture required; it may not justify that conjecture.

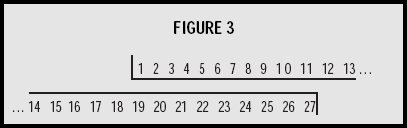
The efficiency of guess and check can be increased with metacognition by using guess and improve . Here subsequent guesses are improved using the data of past guesses. Again in simple problems where a unique answer is almost certain, this is a useful strategy. In Peter and Sue’s problem, we could first guess that Peter was 30, in which case Sue would be 12. The check 2 × 12≤ 30, shows that we have guessed incorrectly. We could then guess, say 40. Now 2 × 22 = 44 which is more than 30. The next guess should then be directed between 30 and 40. Guessing and thinking allows us to hone in on the correct answer.

To make sure that we don’t keep making the same guesses, the results could be recorded in a table such as that in figure 3. Another advantage of the table is that it enables us to move our guesses in the right direction; it enables us to see how best to use guess and improve.

We actually came across a nice solution of this problem where the student had made a model . On the edges of two pieces of paper he wrote the numbers 1 to 30. He then put the edges of the paper side by side and moved one of them until corresponding numbers were 18 higher on one edge ( see figure 3). He then looked along the edges to try to find where one number was twice the other. (Actually he didn’t put down enough numbers, but what he had was enough to enable him to see the right answer.)

6. Work backwards

Work backwards is often useful in problems which involve a sequence of moves, events, or operations leading to a known end point. By reversing the process the starting configuration can be obtained; this is a bit like running a video in reverse. It is useful for investigating two-person games. Start from the last move and work back to the starting position. Work backwards is the basis of many commonly used methods for solving equations. This strategy is also useful when dealing with proofs of trigonometric identities.

6. All information

If the solver is unable to make any headway it is often worth re-reading the question in an attempt to ensure that all of the information given in the problem has been used. Sometimes there is an implicit detail that is not mentioned specifically but which is vital to the solution. Knowing general facts such as the sum of the dots on opposite sides of a dice is seven may well be required to solve a problem. (See hidden information in the experimental stage.)

Having obtained a complete solution the solver should go through the justification and check every step. Even if the proof passes the check test, sometimes the solver still has a nagging doubt. In all cases it is a good idea for the solver to get someone else to check their solutions. At this stage too, sometimes a solver may see a quicker, more efficient, way to solve the problem. The new method needs to be written down and checked too.

IV GENERALISATION/EXTENSION

1. generalisation.

A generalisation is a problem which contains the original problem as a subset or special case. Generalisations can often be found by increasing the number of digits (in some number problems), stepping up the dimension (in a geometry problem), or by increasing the number of variables in some way. For instance, you may want to do the frog problem with an arbitrary number of frogs (n, say) on either side. This is a generalisation of the four frog case.

The reason for considering generalisations is that they give a result which is true for a much wider class of objects. One difficulty with generalisations is that they may require a quite different justification from the justification used in the original problem.

2. Extension

An extension of a problem is one which is related to the original problem but not by way of a generalisation. These can be found by changing one of the conditions of the original problem in some way. It may be that a problem can be extended by changing addition to multiplication. As with generalisations, the proof of an extension may not be linked in any way to the proof of the original problem.

The final part of the problem-solving process may in fact be to give it up!

Some problems are too difficult to be solved right now. So, at times, students will have to abandon some problems. If they are forced to abandon all problems they tackle then the problems are too difficult.

This will depend on the teacher and the student. It becomes a matter of priorities. However, any reasonable problem will take more than 10 minutes and less than two hours (unless it is an extended investigation). In general, we suspect that students can go further than we usually expect. This is especially true of the better students. And it should be remembered that expert problem solvers like to sleep on a problem if no solution is at first forthcoming.

In cases where the problem is too hard for both the teacher and the student, outside help should be summoned. This may be from another teacher, a book, or a local university.

Implementing problem solving

If you are a teacher who has been convinced philosophically of the importance of problem solving in mathematics, or if you see it in the curriculum and feel a responsibility to teach problem solving, the next question to be resolved is how ? The first thing to point out is that there is no unique way to teach problem solving. Teachers and schools will need to develop their own styles. Each teacher will need to develop an individual style which will no doubt develop and be a function of the school, the students, and many other things. An easy way to start is by using a series of one-off problems that may not necessarily be related to the content of the remainder of the lesson. This allows the teacher to gain confidence and gather together a string of useful problems. However, the danger is that students will not realise the relevance and importance of problem solving that stands alone, not integrated with the rest of the curriculum.

Our research suggests that problem-solving lessons work well around a three-stage format. The first stage is a whole-class format, where the problem is discussed by teachers and students, and students may suggest possible heuristics.

In the second stage, students work in small groups. The aim of this stage is to enable students to become involved with the problem and attempt to solve it for themselves. During this period, the teacher is able to go from group to group to provide scaffolding. However, our research suggests that most scaffolding during group work is undertaken by the students themselves as they give peer tuition to their group members.

The third stage is a reporting back stage which gives the students an opportunity to say what they have done and how they did it. Here the spotlight is again on the students who are reporting on their work. Different methods of solution are to be encouraged during this stage. It is important that student thinking and learning takes place in this final stage. One reason for the reporting is to improve students’ ability to communicate but even more important is the chance for students to see alternative approaches to a problem. These alternative approaches should be useful on future occasions. In this stage too, there is an opportunity for students to see links between different parts of mathematics which is again another aid towards understanding.

We have observed these three stages in a variety of problem-solving classes. They seem to work equally well with weak and strong students and with young and old students. A general rule of thumb is that the three-stage cycle should be repeated with young students and weak students. For these children the three stages should take no more than 15 minutes. Very good students may only go around the cycle once in a one-hour lesson.

Problem solving is not easy for many teachers as it involves a rethinking of their whole approach to teaching mathematics. The difficulties arise for many reasons. Some relate to potential loss of control in going from a closed to an open environment where it is never clear in which direction the students will head next. Some relate to the wider range of teaching skills required to handle the situation. Other difficulties are due to social phenomena, including student expectation. But it is our experience that most of these difficulties are surmountable by many teachers, even though at times they may be close to giving up. In our current research, one teacher was in despair after what she thought was a bad lesson. The next problem-solving lesson she taught was extremely successful, with the students seeing links that she herself had not previously seen. From that moment she has been sold on problem solving.

Another teacher had worked solidly doing a competent job for over two terms with a weak-streamed class. In a regular third-term exam (not based on problem solving) her students were 10 percent above similar students in another class. Her students had gained considerably on word problems. The practice they had had in problem-solving situations had given them confidence to successfully tackle the word problems in the exam.

DEREK HOLTON is Professor in the Department of Mathematics and Statistics, University of Otago. E-mail: [email protected]

JIM NEYLAND is Lecturer of Mathematics Education in the Mathematics and Science Education Centre, Victoria University of Wellington. E-mail: [email protected]

JULIE ANDERSON is in the Department of Mathematics and Statistics, University of Otago, and St Hilda’s College, Dunedin.

We would like to thank the Ministry of Education, Research Section, for the financial support which allowed us to engage in the research on which this paper is based. Our thanks also go to the many teachers and students who allowed us into their classrooms.

For more details of this research, see:

Holton D., Spicer, T., & Thomas, G. (1995). Is problem solving too hard? Proceedings of Mathematics Education Research Group of Australasia , 345–351.

Holton D., Spicer T., Thomas G., & Young, S. (1996). The benefits of problem solving in the learning of mathematics (Report to the Ministry of Education). Dunedin: Otago University, Department of Mathematics and Statistics.

The New Zealand curriculum documents are:

Ministry of Education. (1992). Mathematics in the New Zealand curriculum . Wellington: Learning Media Ltd.

Ministry of Education. (1995). Implementing mathematical processes in the New Zealand curriculum . Wellington: Learning Media Ltd.

The Australian curriculum documents are:

Australian Education Council. (1990). A national statement on mathematics for Australian schools . Carlton, Vic: Curriculum Corporation.

That problem solving should be the central focus of the mathematics curriculum is from page 23 of:

National Council of Teachers of Mathematics. (1989). Curriculum and evaluation standards for school mathematic . Reston, VA: Author.

The problem-process approach is described by:

Sigurdson, S. E., Olson, A. T., & Mason, R. (1994). Problem solving and mathematics learning. Journal of Mathematical Behaviour 13, 361–388.

That talented mathematics students enjoyed the challenge and the open approach of problem-solving tasks is noted by:

Curran, J., Holton, D., Daniel, C., & Pek, W. H. (1992). A survey of talented secondary mathematics students . Dunedin: Department of Mathematics and Statistics, University of Otago.

A common belief in the need for problem solving for the gifted child is highlighted in:

Burkhardt, H. (1988). Teaching problem solving. In H. Burkhardt, S. Groves, A. Schoenfeld & K. Stacey (Eds.), Problem solving: A world view (pp. 17–42). Nottingham, UK: Shell Centre.

The importance of strategies for solving problems is noted in:

Pólya, G. (1973). How to solve it (3rd ed.). Princeton, NJ: Princeton University Press.

The kinesthetic approaches are advocated by:

Lovitt, C., & Clarke, D. J. (1988). Mathematics curriculum and teaching program, activity bank (Vols. 1 and 2). Canberra, ACT: Curriculum Development Centre.

That the methods of good problem solvers are likely to be “idiosyncratic” is supported by:

Beagle (1979) pp. 145–146, see above.

Pólya (1973), see above.

Schoenfeld, A. H. (1992). Learning to think mathematically: Problem solving, meta-cognition and sense making in mathematics. In Douglas A. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 334–370). New York: Macmillan.

That students should be encouraged to see how to translate strategies to other problems and situations is stated by:

Holton, D. (1994). Problem solving. In J. Neyland (Ed.), Mathematics education: A handbook for teachers (Vol. 1, pp. 18–30). Wellington: Wellington College of Education.

Neyland, J. (1994). Designing rich mathematical activities. In J. Neyland (Ed.), Mathematics education: A handbook for teachers (Vol. 1, pp.106–122). Wellington: Wellington College of Education.

That problem-solving activities by themselves are not enough to guarantee good problem solving is stated by:

Lovitt, C. (1995). Personal communication.

That time needs to be spent by the students exploring mathematics with the teacher as a guide is noted by:

Hiebert, J. & Carpenter, J. P. (1996). The benefits of problem solving to the learning of mathematics (Report to the Ministry of Education, Wellington). Dunedin: University of Otago, Department of Mathematics and Statistics.

For more details of the heuristics used in the problemsolving process see:

Begg, A. (1994). Mathematics: Content and process. In J. Neyland (Ed.), Mathematics education: A handbook for teacher (Vol. 1, pp. 183–192). Wellington: Wellington College of Education.

Ministry of Education. (1995). Implementing mathematical process in mathematics in the New Zealand curriculum . Wellington: Learning Media, Ltd.

National Council of Teachers of Mathematics. (1980). An agenda for action . Reston, VA: Author.

National Council of Teachers of Mathematics. (1989). Curriculum and evaluation standards for school mathematics . Reston, VA: Author.

Neyland, J. (1995). Eight approaches to teaching mathematics. In J. Neyland (Ed.), Mathematical education: A handbook for teachers (Vol. 2, pp. 34–48). Wellington: Wellington College of Education.

For a good example of problem-solving teachers include:

Stacey, K. & Groves, S. (1985). Strategies for problem solving . Camberwell, Vic: Lattude Publications.

Problem Solving

You are using an outdated browser. Please upgrade your browser to improve your experience.

Issues We Care About

• Digital Divide
• Affordability
• College Readiness
• Environmental Barriers

Measuring Impact

• WGU's Success Metrics
• Policy Priorities
• Annual Report
• WGU's Story
• Careers at WGU
• Impact Blog

4 Jobs for People Who Like Problem-Solving

• Information Technology
• Career Development
• See More Tags

Picture these scenarios: An attorney strives to represent their client in court but must prepare a thorough and persuasive brief to do so. A data analyst seeks to improve a business’s customer base but first needs to use data collection software to measure audience engagement. A middle school principal sets goals to improve next year’s standardized test scores but has to assess teacher performance and curriculums beforehand.

What do these jobs have in common? Even though the settings and duties differ for each, all three roles involve critical thinking and problem-solving abilities to achieve a positive outcome.

If you consider yourself a goal-oriented, problem-solving enthusiast, you might feel overwhelmed at the sheer number of careers that provide opportunities for overcoming complex challenges. This blog discusses four jobs that are ideal for people who like problem-solving and seeking concrete results. Read on to learn about these jobs and how you can find a career that rewards your problem-solving skills.

Top Problem-Solving Jobs in Today’s Market

While many—if not all—careers demand some form of problem-solving, some industries may call for more extensive and straightforward attention to detail than others. The jobs listed below belong to the fields of business, information technology (IT), and healthcare. Each job includes a description of day-to-day responsibilities and common examples of problem-solving abilities where critical thinking and analytical skills are key to success.

Software Engineer

Software engineers —sometimes called software developers—have become invaluable as digital technology has advanced over the last several decades. These professionals create and optimize software programs, applications, and operating systems for consumers, businesses, and other organizations.

Software engineers usually concept and ideate on a vision before collaborating with other developers and programmers to build it out for a specific purpose. For example, a software engineer may design an account management program for an insurance company or develop a word processing program for individual use. Common tasks for software engineers include the following:

• Assessing software needs for users
• Creating and maintaining software and underlying operating systems
• Writing, testing, and debugging program code
• Communicating with IT teams, organization leaders, and stakeholders
• Implementing security features into software

Questions such as “What do users need in a program?” and “How can I make software accessible for users?” are important for software engineers to ponder. Since so many people rely on computers for business, communication, banking, and more, software engineers need to be agile, logical, and collaborative, keeping speed and scalability in mind as they develop software solutions tailored to user needs.

Financial Planner

Managing finances includes more than just being thrifty or saving money. Entire careers—like those of financial advisors and financial planners—are dedicated to helping individuals and organizations achieve their financial goals. Financial planners provide expert advice on various financial matters like spending, saving, investing, paying taxes, and more.

Daily job duties of financial planners include:

• Consulting with clients to establish expectations and answer questions
• Discussing financial goals with clients
• Forecasting financial trends for clients
• Reviewing and optimizing client budgets
• Making recommendations based on client income and spending habits

If clients have questions about retirement funds, mortgages, insurance premiums, or any number of similar financial subjects, a financial planner can clarify and help them navigate their concerns. This means that financial planners need to communicate effectively and actively listen. They consider all available solutions, then choose the one that best meets a client’s needs based on their unique circumstances.

Data Analyst

According to the data aggregator site Statista.com, the total amount of data created and consumed in the world reached about 64.2 zettabytes in 2020. That figure is forecasted to increase to 180 zettabytes by 2025. For reference, one zettabyte is equal to one trillion gigabytes.

How is it Possible to Manage This Much Data and Harness it For Use?

Data analysts are trained to collect, analyze, and parse all kinds of data to glean actionable information. These specialists use computer programs and machine learning technologies to spot patterns in raw data that could—after proper interpretation—benefit individual or organizational decision-making. Data analysis requires logical reasoning, critical thinking, and inference skills—all of which are common traits of problem-solvers.

Many data analysts work to research market trends, enhance business goals, assess demographic behaviors, and more. Others work as actuaries with an emphasis on risk analysis. The empirical evidence produced through iterative data analysis can then be used to support myriad organizational initiatives, programs, or campaigns.

Registered Nurse

Registered nurses compose the backbone of functional healthcare systems. A registered nurse (RN) is a licensed healthcare professional that cares for and educates patients of all ages. Whether it involves measuring patient vitals, administering treatment, or consulting with physicians and therapists, nurses help patients on their path to healthy, happy lifestyles.

Regarding their day-to-day job responsibilities, nurses maintain a balanced skill set in interpersonal communication, medical knowledge, and technical problem-solving. Common tasks include the following:

• Working in tandem with doctors to treat patients
• Collecting and recording patient medical histories
• Conducting diagnostic tests on patients
• Using and maintaining medical equipment
• Establishing treatment plans based on patient diagnoses

It’s important for nurses to practice empathy toward their patients, including helping them understand the nature of their illness or injury. Many patients may not know how to manage their condition upon being diagnosed. To overcome this challenge, RNs should answer a patient’s questions as accurately as possible and provide encouragement as needed.

Building a Career in Critical Thinking and Problem-Solving

To determine whether you’d thrive in a role oriented to problem-solving, consider reflecting on your professional skills and workplace attitude. Do you enjoy the challenges inherent in business , IT , healthcare, or other dynamic, growing fields? Do you like being the go-to person that people come to when they have an issue? Could you see yourself finding fulfillment in solving work-related problems five or 10 years from now? Are you willing to gain the education or credentials you need for the job?

Answering questions like these can help you feel more confident as you search for jobs that align with your interests.

As you prepare for the problem-solving career of your dreams, look to WGU. We offer more than 75 online, accredited bachelor’s and master’s programs in IT, business, education, and healthcare. Each program is designed with input from industry experts, granting you the skills that employers love to see. Additionally, WGU’s competency-based education model means that you advance through coursework as quickly as you show mastery of the material, so you can potentially graduate faster and save money. Get started today.

Ready to Start Your Journey?

HEALTH & NURSING

Recommended Articles

Take a look at other articles from WGU. Our articles feature information on a wide variety of subjects, written with the help of subject matter experts and researchers who are well-versed in their industries. This allows us to provide articles with interesting, relevant, and accurate information. 

Types of Supply Chain Management Software: An In-Depth Guide

Top Qualities And Skills Of A Good Teacher

IgnitED: Rethinking Financial Aid Amid a Changing Higher Ed Landscape

IgnitED: The Quest to Serve Rising Talent

8 HR Careers for a Human Resources Degree

The university.

• Accessibility
• Accreditation

For Students

• Student Portal
• Alumni Services

Most Visited Links

• Business Programs
• Bachelor's Degrees
• Student Experience
• Online Degrees
• Scholarships
• Financial Aid
• Diversity, Equity, and Inclusion
• Testimonials
• Student Communities

Watch CBS News

Teens come up with trigonometry proof for Pythagorean Theorem, a problem that stumped math world for centuries

By Bill Whitaker

May 5, 2024 / 7:00 PM EDT / CBS News

As the school year ends, many students will be only too happy to see math classes in their rearview mirrors. It may seem to some of us non-mathematicians that geometry and trigonometry were created by the Greeks as a form of torture, so imagine our amazement when we heard two high school seniors had proved a mathematical puzzle that was thought to be impossible for 2,000 years. 

We met Calcea Johnson and Ne'Kiya Jackson at their all-girls Catholic high school in New Orleans. We expected to find two mathematical prodigies.

Instead, we found at St. Mary's Academy , all students are told their possibilities are boundless.

Come Mardi Gras season, New Orleans is alive with colorful parades, replete with floats, and beads, and high school marching bands.

In a city where uniqueness is celebrated, St. Mary's stands out – with young African American women playing trombones and tubas, twirling batons and dancing - doing it all, which defines St. Mary's, students told us.

Junior Christina Blazio says the school instills in them they have the ability to accomplish anything. 

Christina Blazio: That is kinda a standard here. So we aim very high - like, our aim is excellence for all students. 

The private Catholic elementary and high school sits behind the Sisters of the Holy Family Convent in New Orleans East. The academy was started by an African American nun for young Black women just after the Civil War. The church still supports the school with the help of alumni.

In December 2022, seniors Ne'Kiya Jackson and Calcea Johnson were working on a school-wide math contest that came with a cash prize.

Ne'Kiya Jackson: I was motivated because there was a monetary incentive.

Calcea Johnson: 'Cause I was like, "$500 is a lot of money. So I-- I would like to at least try."

Both were staring down the thorny bonus question.

Bill Whitaker: So tell me, what was this bonus question?

Calcea Johnson: It was to create a new proof of the Pythagorean Theorem. And it kind of gave you a few guidelines on how would you start a proof.

The seniors were familiar with the Pythagorean Theorem, a fundamental principle of geometry. You may remember it from high school: a² + b² = c². In plain English, when you know the length of two sides of a right triangle, you can figure out the length of the third.

Both had studied geometry and some trigonometry, and both told us math was not easy. What no one told  them  was there had been more than 300 documented proofs of the Pythagorean Theorem using algebra and geometry, but for 2,000 years a proof using trigonometry was thought to be impossible, … and that was the bonus question facing them.

Bill Whitaker: When you looked at the question did you think, "Boy, this is hard"?

Ne'Kiya Jackson: Yeah. 

Bill Whitaker: What motivated you to say, "Well, I'm going to try this"?

Calcea Johnson: I think I was like, "I started something. I need to finish it." 

Bill Whitaker: So you just kept on going.

Calcea Johnson: Yeah.

For two months that winter, they spent almost all their free time working on the proof.

CeCe Johnson: She was like, "Mom, this is a little bit too much."

CeCe and Cal Johnson are Calcea's parents.

CeCe Johnson:   So then I started looking at what she really was doing. And it was pages and pages and pages of, like, over 20 or 30 pages for this one problem.

Cal Johnson: Yeah, the garbage can was full of papers, which she would, you know, work out the problems and-- if that didn't work she would ball it up, throw it in the trash. 

Bill Whitaker: Did you look at the problem? 

Neliska Jackson is Ne'Kiya's mother.

Neliska Jackson: Personally I did not. 'Cause most of the time I don't understand what she's doing (laughter).

Michelle Blouin Williams: What if we did this, what if I write this? Does this help? ax² plus ….

Their math teacher, Michelle Blouin Williams, initiated the math contest.

Bill Whitaker: And did you think anyone would solve it?

Michelle Blouin Williams: Well, I wasn't necessarily looking for a solve. So, no, I didn't—

Bill Whitaker: What were you looking for?

Michelle Blouin Williams: I was just looking for some ingenuity, you know—

Calcea and Ne'Kiya delivered on that! They tried to explain their groundbreaking work to 60 Minutes. Calcea's proof is appropriately titled the Waffle Cone.

Calcea Johnson: So to start the proof, we start with just a regular right triangle where the angle in the corner is 90°. And the two angles are alpha and beta.

Bill Whitaker: Uh-huh

Calcea Johnson: So then what we do next is we draw a second congruent, which means they're equal in size. But then we start creating similar but smaller right triangles going in a pattern like this. And then it continues for infinity. And eventually it creates this larger waffle cone shape.

Calcea Johnson: Am I going a little too—

Bill Whitaker: You've been beyond me since the beginning. (laughter) 

Bill Whitaker: So how did you figure out the proof?

Ne'Kiya Jackson: Okay. So you have a right triangle, 90° angle, alpha and beta.

Bill Whitaker: Then what did you do?

Ne'Kiya Jackson: Okay, I have a right triangle inside of the circle. And I have a perpendicular bisector at OP to divide the triangle to make that small right triangle. And that's basically what I used for the proof. That's the proof.

Bill Whitaker: That's what I call amazing.

Ne'Kiya Jackson: Well, thank you.

There had been one other documented proof of the theorem using trigonometry by mathematician Jason Zimba in 2009 – one in 2,000 years. Now it seems Ne'Kiya and Calcea have joined perhaps the most exclusive club in mathematics. 

Bill Whitaker: So you both independently came up with proof that only used trigonometry.

Ne'Kiya Jackson: Yes.

Bill Whitaker: So are you math geniuses?

Calcea Johnson: I think that's a stretch. 

Bill Whitaker: If not genius, you're really smart at math.

Ne'Kiya Jackson: Not at all. (laugh) 

To document Calcea and Ne'Kiya's work, math teachers at St. Mary's submitted their proofs to an American Mathematical Society conference in Atlanta in March 2023.

Ne'Kiya Jackson: Well, our teacher approached us and was like, "Hey, you might be able to actually present this," I was like, "Are you joking?" But she wasn't. So we went. I got up there. We presented and it went well, and it blew up.

Bill Whitaker: It blew up.

Calcea Johnson: Yeah. 

Ne'Kiya Jackson: It blew up.

Bill Whitaker: Yeah. What was the blowup like?

Calcea Johnson: Insane, unexpected, crazy, honestly.

It took millenia to prove, but just a minute for word of their accomplishment to go around the world. They got a write-up in South Korea and a shout-out from former first lady Michelle Obama, a commendation from the governor and keys to the city of New Orleans. 

Bill Whitaker: Why do you think so many people found what you did to be so impressive?

Ne'Kiya Jackson: Probably because we're African American, one. And we're also women. So I think-- oh, and our age. Of course our ages probably played a big part.

Bill Whitaker: So you think people were surprised that young African American women, could do such a thing?

Calcea Johnson: Yeah, definitely.

Ne'Kiya Jackson: I'd like to actually be celebrated for what it is. Like, it's a great mathematical achievement.

Achievement, that's a word you hear often around St. Mary's academy. Calcea and Ne'Kiya follow a long line of barrier-breaking graduates. 

The late queen of Creole cooking, Leah Chase , was an alum. so was the first African-American female New Orleans police chief, Michelle Woodfork …

And judge for the Fifth Circuit Court of Appeals, Dana Douglas. Math teacher Michelle Blouin Williams told us Calcea and Ne'Kiya are typical St. Mary's students.  

Bill Whitaker: They're not unicorns.

Michelle Blouin Williams: Oh, no no. If they are unicorns, then every single lady that has matriculated through this school is a beautiful, Black unicorn.

Pamela Rogers: You're good?

Pamela Rogers, St. Mary's president and interim principal, told us the students hear that message from the moment they walk in the door.

Pamela Rogers: We believe all students can succeed, all students can learn. It does not matter the environment that you live in. 

Bill Whitaker: So when word went out that two of your students had solved this almost impossible math problem, were they universally applauded?

Pamela Rogers: In this community, they were greatly applauded. Across the country, there were many naysayers.

Bill Whitaker: What were they saying?

Pamela Rogers: They were saying, "Oh, they could not have done it. African Americans don't have the brains to do it." Of course, we sheltered our girls from that. But we absolutely did not expect it to come in the volume that it came.  

Bill Whitaker: And after such a wonderful achievement.

Pamela Rogers: People-- have a vision of who can be successful. And-- to some people, it is not always an African American female. And to us, it's always an African American female.

Gloria Ladson-Billings: What we know is when teachers lay out some expectations that say, "You can do this," kids will work as hard as they can to do it.

Gloria Ladson-Billings, professor emeritus at the University of Wisconsin, has studied how best to teach African American students. She told us an encouraging teacher can change a life.

Bill Whitaker: And what's the difference, say, between having a teacher like that and a whole school dedicated to the excellence of these students?

Gloria Ladson-Billings: So a whole school is almost like being in Heaven. 

Bill Whitaker: What do you mean by that?

Gloria Ladson-Billings: Many of our young people have their ceilings lowered, that somewhere around fourth or fifth grade, their thoughts are, "I'm not going to be anything special." What I think is probably happening at St. Mary's is young women come in as, perhaps, ninth graders and are told, "Here's what we expect to happen. And here's how we're going to help you get there."

At St. Mary's, half the students get scholarships, subsidized by fundraising to defray the $8,000 a year tuition. Here, there's no test to get in, but expectations are high and rules are strict: no cellphones, modest skirts, hair must be its natural color.

Students Rayah Siddiq, Summer Forde, Carissa Washington, Tatum Williams and Christina Blazio told us they appreciate the rules and rigor.

Rayah Siddiq: Especially the standards that they set for us. They're very high. And I don't think that's ever going to change.

Bill Whitaker: So is there a heart, a philosophy, an essence to St. Mary's?

Summer Forde: The sisterhood—

Carissa Washington: Sisterhood.

Tatum Williams: Sisterhood.

Bill Whitaker: The sisterhood?

Voices: Yes.

Bill Whitaker: And you don't mean the nuns. You mean-- (laughter)

Christina Blazio: I mean, yeah. The community—

Bill Whitaker: So when you're here, there's just no question that you're going to go on to college.

Rayah Siddiq: College is all they talk about. (laughter) 

Pamela Rogers: … and Arizona State University (Cheering)

Principal Rogers announces to her 615 students the colleges where every senior has been accepted.

Bill Whitaker: So for 17 years, you've had a 100% graduation rate—

Pamela Rogers: Yes.

Bill Whitaker: --and a 100% college acceptance rate?

Pamela Rogers: That's correct.

Last year when Ne'Kiya and Calcea graduated, all their classmates went to college and got scholarships. Ne'Kiya got a full ride to the pharmacy school at Xavier University in New Orleans. Calcea, the class valedictorian, is studying environmental engineering at Louisiana State University.

Bill Whitaker: So wait a minute. Neither one of you is going to pursue a career in math?

Both: No. (laugh)

Calcea Johnson: I may take up a minor in math. But I don't want that to be my job job.

Ne'Kiya Jackson: Yeah. People might expect too much out of me if (laugh) I become a mathematician. (laugh)

But math is not completely in their rear-view mirrors. This spring they submitted their high school proofs for final peer review and publication … and are still working on further proofs of the Pythagorean Theorem. Since their first two …

Calcea Johnson: We found five. And then we found a general format that could potentially produce at least five additional proofs.

Bill Whitaker: And you're not math geniuses?

Bill Whitaker: I'm not buying it. (laughs)

Produced by Sara Kuzmarov. Associate producer, Mariah B. Campbell. Edited by Daniel J. Glucksman.

Bill Whitaker is an award-winning journalist and 60 Minutes correspondent who has covered major news stories, domestically and across the globe, for more than four decades with CBS News.

More from CBS News

Heineken vows nearly $50 million to transform "tired pubs" in U.K.

Should you use a reverse mortgage to cover long-term care costs?

Afghan diplomat accused of smuggling gold into India resigns

How technology helped a nonspeaking autistic woman find her voice

• Student Resources
• Alumni Resources

Master of Product Design and Development Management (mpd²) at the Segal Design Institute, McCormick School of Engineering

• Inside Our Program

Solving Problems and Nurturing Future Problem Solvers

Courtney welton helps guide curriculum alignment for the mpd2 program in addition to her work promoting compliance,ethics, and transformation at allstate..

There is no such thing as an average day for Courtney Welton, and that's exactly how she likes it.  

Welton is senior vice president and general counsel for business law and compliance at Allstate. She also serves as the insurance company’s chief ethics and privacy officer.

Since 2022, Welton has been sharing her knowledge and expertise with Northwestern Engineering's Master of Product Design and Development Management (MPD2) program as a member of the Industry Advisory Board (IAB). The IAB is charged with ensuring course offerings remain aligned with industry needs.

“So many customer problems remain unsolved,” she said. “I love the idea of helping foster the next generation of product professionals who will solve important problems."

Welton has been addressing customer problems at Allstate for more than five years. She provides legal advice and promotes compliance and ethical activity for more than 20 business units and subsidiaries. She created Allstate’s first innovation legal team, focused on cybersecurity, privacy, data, intellectual property, and international law.

Welton joined Allstate after nearly a decade working in technology, including as global general counsel for Motorola Mobility. There, she crossed paths with current MPD2 director Jim Wicks, who served as senior vice president of design for Motorola from 2007 to 2016.

Welton eagerly accepted Wicks’ offer to join the IAB.

“I knew what an inspiring leader and creative product designer Jim was then and still is,” she said. “I was thrilled to hear about his work in academia and with students. I instantly wanted to be a part of it.”

Welton's work is vital to Allstate's transformation into a data and technology company. She’s also working on the ongoing transformation of its compliance function to make it more agile and adaptable to emerging technologies like generative artificial intelligence.

“To me, innovation is finding new ways of thinking, working, and problem solving,” she said. “I love to see the intersection of diversity sparking innovation because it opens up possibilities for new and different ways to solve problems for our customers and employees.”

Her passion is a more diverse and inclusive society. She’s a board member of Legal Prep Charter Academy in Chicago, helping diverse young adults succeed in Chicago's only legal-themed high school. She’s also on the board of REDF, a nonprofit that invests in and supports businesses that help people break through barriers to employment.

It’s all part of her focus on brighter futures. Which is why she’s excited about her work with MPD2, helping guide a product design curriculum that’s both inspiring and pragmatic. She’s eager to see the impact MPD2 students have.

“I appreciate the opportunity to work with the talented students of MPD2,” she said. “I look forward to seeing them make a difference for customers as they take their learnings into action after graduation.”

REQUEST INFO

Request your program and application guide.