case study class 9 maths chapter 7

CBSE Expert

CBSE Case Study Questions Class 9 Maths Chapter 7 Triangles PDF Download

Case Study Questions Class 9 Maths Chapter 7   are very important to solve for your exam. Class 9 Maths Chapter 7 Case Study Questions have been prepared for the latest exam pattern. You can check your knowledge by solving  case study-based   questions for Class 9 Maths Chapter 7 Triangles

Case Study Questions Class 9 Maths Chapter 7 Triangles

Case Study 1. A group of students is studying the properties of triangles. They came across the following scenario:

Three friends, Ankit, Bhavna, and Chetan, were discussing their recent hiking trip. During their hike, they noticed a triangular-shaped lake. They observed the following:

• The lake has three sides of different lengths.
• The sum of the lengths of any two sides of the lake is greater than the length of the third side.
• The largest angle of the lake is less than 90 degrees.
• The smallest angle of the lake is greater than 30 degrees.

Based on this information, the students were asked to analyze the properties of the triangle formed by the lake. Let’s see if you can answer the questions correctly:

MCQ Questions:

Q1. The type of triangle formed by the lake is: (a) Equilateral (b) Isosceles (c) Scalene (d) Right-angled

Answer: (c) Scalene

Q2. The sum of the measures of the three angles of the lake’s triangle is: (a) 180 degrees (b) 90 degrees (c) 360 degrees (d) It cannot be determined

Answer: (a) 180 degrees

Q3. The lake’s triangle is an example of a triangle that satisfies the: (a) Angle-side-angle (ASA) condition (b) Side-angle-side (SAS) condition (c) Side-side-side (SSS) condition (d) None of the above

Answer: (c) Side-side-side (SSS) condition

Q4. The measure of the largest angle of the lake’s triangle is: (a) 30 degrees (b) 60 degrees (c) 90 degrees (d) More than 90 degrees

Answer: (c) 90 degrees

Q5. The measure of the smallest angle of the lake’s triangle is: (a) 30 degrees (b) 60 degrees (c) 90 degrees (d) Less than 30 degrees

Answer: (d) Less than 30 degrees

Case Study 2. A group of students is studying the properties of triangles. They encountered the following scenario:

Three friends, Rahul, Sana, and Tina, participated in a kite-flying competition. They noticed that their kites formed a triangular shape in the sky. They made the following observations:

• The lengths of two sides of the kite triangle are equal.
• The measure of the largest angle of the kite triangle is 90 degrees.
• The sum of the measures of the three angles of the kite triangle is 180 degrees.
• The lengths of the three sides of the kite triangle are in the ratio 3:4:5.

Based on this information, the students were asked to analyze the properties of the triangle formed by their kites. Let’s see if you can answer the questions correctly:

Q1. The type of triangle formed by their kites is: (a) Equilateral (b) Isosceles (c) Scalene (d) Right-angled

Answer: (b) Isosceles

Q2. The length of the third side of the kite triangle is: (a) 3 units (b) 4 units (c) 5 units (d) It cannot be determined

Answer: (c) 5 units

Q3. The kite triangle is an example of a triangle that satisfies the: (a) Angle-side-angle (ASA) condition (b) Side-angle-side (SAS) condition (c) Side-side-side (SSS) condition (d) None of the above

Answer: (b) Side-angle-side (SAS) condition

Q4. The measure of the smallest angle of the kite triangle is: (a) 30 degrees (b) 45 degrees (c) 60 degrees (d) 90 degrees

Answer: (a) 30 degrees

Q5. The lengths of the two equal sides of the kite triangle are: (a) 3 units each (b) 4 units each (c) 5 units each (d) It cannot be determined

Answer: (c) 5 units each

Hope the information shed above regarding Case Study and Passage Based Questions for Case Study Questions Class 9 Maths Chapter 7 Triangles with Answers Pdf free download has been useful to an extent. If you have any other queries about Case Study Questions Class 9 Maths Chapter 7 Triangles and Passage-Based Questions with Answers, feel free to comment below so that we can revert back to us at the earliest possible.

Leave a Comment Cancel reply

Save my name, email, and website in this browser for the next time I comment.

Download India's best Exam Preparation App Now.

Key Features

• Revision Notes
• Important Questions
• Previous Years Questions
• Case-Based Questions
• Assertion and Reason Questions

No thanks, I’m not interested!

(Education-Your Door To The Future)

CBSE Class 9 Maths Most Important Case Study Based Questions With Solution

Cbse class 9 mathematics case study questions.

In this post I have provided CBSE Class 9 Maths Case Study Based Questions With Solution. These questions are very important for those students who are preparing for their final class 9 maths exam.

All these questions provided in this article are with solution which will help students for solving the problems. Dear students need to practice all these questions carefully with the help of given solutions.

As you know CBSE Class 9 Maths exam will have a set of cased study based questions in the form of MCQs. CBSE Class 9 Maths Question Bank given in this article can be very helpful in understanding the new format of questions for new session.

All Of You Can Also Read

Case studies in class 9 mathematics.

The Central Board of Secondary Education (CBSE) has included case study based questions in the Class 9 Mathematics paper in current session. According to new pattern CBSE Class 9 Mathematics students will have to solve case based questions. This is a departure from the usual theoretical conceptual questions that are asked in Class 9 Maths exam in this year.

Each question provided in this post has five sub-questions, each followed by four options and one correct answer. All CBSE Class 9th Maths Students can easily download these questions in PDF form with the help of given download Links and refer for exam preparation.

There is many more free study materials are available at Maths And Physics With Pandey Sir website. For many more books and free study material all of you can visit at this website.

Given Below Are CBSE Class 9th Maths Case Based Questions With Their Respective Download Links.

myCBSEguide

• Mathematics
• CBSE Class 9 Mathematics...

CBSE Class 9 Mathematics Case Study Questions

Table of Contents

myCBSEguide App

Download the app to get CBSE Sample Papers 2023-24, NCERT Solutions (Revised), Most Important Questions, Previous Year Question Bank, Mock Tests, and Detailed Notes.

If you’re looking for a comprehensive and reliable study resource and case study questions for class 9 CBSE, myCBSEguide is the perfect door to enter. With over 10,000 study notes, solved sample papers and practice questions, it’s got everything you need to ace your exams. Plus, it’s updated regularly to keep you aligned with the latest CBSE syllabus . So why wait? Start your journey to success with myCBSEguide today!

Significance of Mathematics in Class 9

Mathematics is an important subject for students of all ages. It helps students to develop problem-solving and critical-thinking skills, and to think logically and creatively. In addition, mathematics is essential for understanding and using many other subjects, such as science, engineering, and finance.

CBSE Class 9 is an important year for students, as it is the foundation year for the Class 10 board exams. In Class 9, students learn many important concepts in mathematics that will help them to succeed in their board exams and in their future studies. Therefore, it is essential for students to understand and master the concepts taught in Class 9 Mathematics .

Case studies in Class 9 Mathematics

A case study in mathematics is a detailed analysis of a particular mathematical problem or situation. Case studies are often used to examine the relationship between theory and practice, and to explore the connections between different areas of mathematics. Often, a case study will focus on a single problem or situation and will use a variety of methods to examine it. These methods may include algebraic, geometric, and/or statistical analysis.

Example of Case study questions in Class 9 Mathematics

The Central Board of Secondary Education (CBSE) has included case study questions in the Class 9 Mathematics paper. This means that Class 9 Mathematics students will have to solve questions based on real-life scenarios. This is a departure from the usual theoretical questions that are asked in Class 9 Mathematics exams.

The following are some examples of case study questions from Class 9 Mathematics:

Class 9 Mathematics Case study question 1

There is a square park ABCD in the middle of Saket colony in Delhi. Four children Deepak, Ashok, Arjun and Deepa went to play with their balls. The colour of the ball of Ashok, Deepak,  Arjun and Deepa are red, blue, yellow and green respectively. All four children roll their ball from centre point O in the direction of   XOY, X’OY, X’OY’ and XOY’ . Their balls stopped as shown in the above image.

Answer the following questions:

Answer Key:

Class 9 Mathematics Case study question 2

• Now he told Raju to draw another line CD as in the figure
• The teacher told Ajay to mark  ∠ AOD  as 2z
• Suraj was told to mark  ∠ AOC as 4y
• Clive Made and angle  ∠ COE = 60°
• Peter marked  ∠ BOE and  ∠ BOD as y and x respectively

Now answer the following questions:

• 2y + z = 90°
• 2y + z = 180°
• 4y + 2z = 120°
• (a) 2y + z = 90°

Class 9 Mathematics Case study question 3

• (a) 31.6 m²
• (c) 513.3 m³
• (b) 422.4 m²

Class 9 Mathematics Case study question 4

How to Answer Class 9 Mathematics Case study questions

To crack case study questions, Class 9 Mathematics students need to apply their mathematical knowledge to real-life situations. They should first read the question carefully and identify the key information. They should then identify the relevant mathematical concepts that can be applied to solve the question. Once they have done this, they can start solving the Class 9 Mathematics case study question.

Students need to be careful while solving the Class 9 Mathematics case study questions. They should not make any assumptions and should always check their answers. If they are stuck on a question, they should take a break and come back to it later. With some practice, the Class 9 Mathematics students will be able to crack case study questions with ease.

Class 9 Mathematics Curriculum at Glance

At the secondary level, the curriculum focuses on improving students’ ability to use Mathematics to solve real-world problems and to study the subject as a separate discipline. Students are expected to learn how to solve issues using algebraic approaches and how to apply their understanding of simple trigonometry to height and distance problems. Experimenting with numbers and geometric forms, making hypotheses, and validating them with more observations are all part of Math learning at this level.

The suggested curriculum covers number systems, algebra, geometry, trigonometry, mensuration, statistics, graphing, and coordinate geometry, among other topics. Math should be taught through activities that include the use of concrete materials, models, patterns, charts, photographs, posters, and other visual aids.

CBSE Class 9 Mathematics (Code No. 041)

Class 9 Mathematics question paper design

The CBSE Class 9 mathematics question paper design is intended to measure students’ grasp of the subject’s fundamental ideas. The paper will put their problem-solving and analytical skills to the test. Class 9 mathematics students are advised to go through the question paper pattern thoroughly before they start preparing for their examinations. This will help them understand the paper better and enable them to score maximum marks. Refer to the given Class 9 Mathematics question paper design.

QUESTION PAPER DESIGN (CLASS 9 MATHEMATICS)

Mycbseguide: blessing in disguise.

Class 9 is an important milestone in a student’s life. It is the last year of high school and the last chance to score well in the CBSE board exams. myCBSEguide is the perfect platform for students to get started on their preparations for Class 9 Mathematics. myCBSEguide provides comprehensive study material for all subjects, including practice questions, sample papers, case study questions and mock tests. It also offers tips and tricks on how to score well in exams. myCBSEguide is the perfect door to enter for class 9 CBSE preparations.

Test Generator

Create question paper PDF and online tests with your own name & logo in minutes.

Question Bank, Mock Tests, Exam Papers, NCERT Solutions, Sample Papers, Notes

Related Posts

• Competency Based Learning in CBSE Schools
• Class 11 Physical Education Case Study Questions
• Class 11 Sociology Case Study Questions
• Class 12 Applied Mathematics Case Study Questions
• Class 11 Applied Mathematics Case Study Questions
• Class 11 Mathematics Case Study Questions
• Class 11 Biology Case Study Questions
• Class 12 Physical Education Case Study Questions

14 thoughts on “CBSE Class 9 Mathematics Case Study Questions”

This method is not easy for me

aarti and rashika are two classmates. due to exams approaching in some days both decided to study together. during revision hour both find difficulties and they solved each other’s problems. aarti explains simplification of 2+ ?2 by rationalising the denominator and rashika explains 4+ ?2 simplification of (v10-?5)(v10+ ?5) by using the identity (a – b)(a+b). based on above information, answer the following questions: 1) what is the rationalising factor of the denominator of 2+ ?2 a) 2-?2 b) 2?2 c) 2+ ?2 by rationalising the denominator of aarti got the answer d) a) 4+3?2 b) 3+?2 c) 3-?2 4+ ?2 2+ ?2 d) 2-?3 the identity applied to solve (?10-?5) (v10+ ?5) is a) (a+b)(a – b) = (a – b)² c) (a – b)(a+b) = a² – b² d) (a-b)(a+b)=2(a² + b²) ii) b) (a+b)(a – b) = (a + b

MATHS PAAGAL HAI

All questions was easy but search ? hard questions. These questions was not comparable with cbse. It was totally wastage of time.

Where is search ? bar

maths is love

Can I have more questions without downloading the app.

I love math

Hello l am Devanshu chahal and l am an entorpinior. I am started my card bord business and remanded all the existing things this all possible by math now my business is 120 crore and my business profit is 25 crore in a month. l find the worker team because my business is going well Thanks

Leave a Comment

Save my name, email, and website in this browser for the next time I comment.

• Andhra Pradesh
• Chhattisgarh
• West Bengal
• Madhya Pradesh
• Maharashtra
• Jammu & Kashmir
• NCERT Books 2022-23
• NCERT Solutions
• NCERT Notes
• NCERT Exemplar Books
• NCERT Exemplar Solution
• States UT Book
• School Kits & Lab Manual
• NCERT Books 2021-22
• NCERT Books 2020-21
• NCERT Book 2019-2020
• NCERT Book 2015-2016
• RD Sharma Solution
• TS Grewal Solution
• TR Jain Solution
• Selina Solution
• Frank Solution
• Lakhmir Singh and Manjit Kaur Solution
• I.E.Irodov solutions
• ICSE - Goyal Brothers Park
• ICSE - Dorothy M. Noronhe
• Sandeep Garg Textbook Solution
• Micheal Vaz Solution
• S.S. Krotov Solution
• Evergreen Science
• KC Sinha Solution
• ICSE - ISC Jayanti Sengupta, Oxford
• ICSE Focus on History
• ICSE GeoGraphy Voyage
• ICSE Hindi Solution
• ICSE Treasure Trove Solution
• Thomas & Finney Solution
• SL Loney Solution
• SB Mathur Solution
• P Bahadur Solution
• Narendra Awasthi Solution
• MS Chauhan Solution
• LA Sena Solution
• Integral Calculus Amit Agarwal Solution
• IA Maron Solution
• Hall & Knight Solution
• Errorless Solution
• Pradeep's KL Gogia Solution
• OP Tandon Solutions
• Sample Papers
• Previous Year Question Paper
• Value Based Questions
• CBSE Syllabus
• CBSE MCQs PDF
• Assertion & Reason
• New Revision Notes
• Revision Notes
• HOTS Question
• Marks Wise Question
• Toppers Answer Sheets
• Exam Paper Aalysis
• Concept Map
• CBSE Text Book
• Additional Practice Questions
• Vocational Book
• CBSE - Concept
• KVS NCERT CBSE Worksheets
• Formula Class Wise
• Formula Chapter Wise
• JEE Crash Course
• JEE Previous Year Paper
• Important Info
• JEE Mock Test
• JEE Sample Papers
• SRM-JEEE Mock Test
• VITEEE Mock Test
• BITSAT Mock Test
• Manipal Engineering Mock Test
• AP EAMCET Previous Year Paper
• COMEDK Previous Year Paper
• GUJCET Previous Year Paper
• KCET Previous Year Paper
• KEAM Previous Year Paper
• Manipal Previous Year Paper
• MHT CET Previous Year Paper
• WBJEE Previous Year Paper
• AMU Previous Year Paper
• TS EAMCET Previous Year Paper
• SRM-JEEE Previous Year Paper
• VITEEE Previous Year Paper
• BITSAT Previous Year Paper
• UPSEE Previous Year Paper
• CGPET Previous Year Paper
• CUSAT Previous Year Paper
• AEEE Previous Year Paper
• Crash Course
• Previous Year Paper
• NCERT Based Short Notes
• NCERT Based Tests
• NEET Sample Paper
• Previous Year Papers
• Quantitative Aptitude
• Numerical Aptitude Data Interpretation
• General Knowledge
• Mathematics
• Agriculture
• Accountancy
• Business Studies
• Political science
• Enviromental Studies
• Mass Media Communication
• Teaching Aptitude
• NAVODAYA VIDYALAYA
• SAINIK SCHOOL (AISSEE)
• Mechanical Engineering
• Electrical Engineering
• Electronics & Communication Engineering
• Civil Engineering
• Computer Science Engineering
• CBSE Board News
• Scholarship Olympiad
• School Admissions
• Entrance Exams
• All Board Updates
• Miscellaneous
• State Wise Books
• Engineering Exam

CBSE Class 9th Maths 2023 : 30 Most Important Case Study Questions with Answers; Download PDF

SHARING IS CARING If our Website helped you a little, then kindly spread our voice using Social Networks. Spread our word to your readers, friends, teachers, students & all those close ones who deserve to know what you know now.

CBSE Class 9 Maths exam 2022-23 will have a set of questions based on case studies in the form of MCQs. CBSE Class 9 Maths Question Bank on Case Studies given in this article can be very helpful in understanding the new format of questions.

Each question has five sub-questions, each followed by four options and one correct answer. Students can easily download these questions in PDF format and refer to them for exam preparation.

CBSE Class 9 All Students can also Download here Class 9 Other Study Materials in PDF Format.

• NCERT Solutions for Class 12 Maths
• NCERT Solutions for Class 10 Maths
• CBSE Syllabus 2023-24
• Social Media Channels
• Login Customize Your Notification Preferences
• CBSE Class 9th 2023-24 : Science Practical Syllabus; Download PDF 19 April, 2023, 4:52 pm
• CBSE Class 9 Maths Practice Book 2023 (Released By CBSE) 23 March, 2023, 6:16 pm
• CBSE Class 9 Science Practice Book 2023 (Released By CBSE) 23 March, 2023, 5:56 pm
• CBSE Class 9th Maths 2023 : 30 Most Important Case Study Questions with Answers; Download PDF 10 February, 2023, 6:20 pm
• CBSE Class 9th Maths 2023 : Important Assertion Reason Question with Solution Download Pdf 9 February, 2023, 12:16 pm
• CBSE Class 9th Exam 2023 : Social Science Most Important Short Notes; Download PDF 16 January, 2023, 4:29 pm
• CBSE Class 9th Mathematics 2023 : Most Important Short Notes with Solutions 27 December, 2022, 6:05 pm
• CBSE Class 9th English 2023 : Chapter-wise Competency-Based Test Items with Answer; Download PDF 21 December, 2022, 5:16 pm
• CBSE Class 9th Science 2023 : Chapter-wise Competency-Based Test Items with Answers; Download PDF 20 December, 2022, 5:37 pm

• Second click on the toggle icon

Provide prime members with unlimited access to all study materials in PDF format.

Allow prime members to attempt MCQ tests multiple times to enhance their learning and understanding.

Provide prime users with access to exclusive PDF study materials that are not available to regular users.

• NCERT Solutions
• NCERT Class 9
• NCERT 9 Maths
• Chapter 7: Geometry Of Triangles

NCERT Solutions for Class 9 Maths Chapter 7 - Triangles

Ncert solutions for class 9 maths chapter 7 – cbse free pdf download.

NCERT Solutions for Class 9 Maths Chapter 7 Triangles provides the answers and questions related to the chapter as included in the CBSE Syllabus for 2023-24. The word triangle itself describes its meaning. “Tri” means “three”,; so a closed figure formed by three intersecting lines is known as a Triangle. Students must have already studied the angle sum property of a triangle in Chapter 6 of NCERT Class 9 Maths. Now, in continuation to it, Chapter 7 of NCERT Solutions for Class 9 Maths will brief students about the congruence of triangles and the rules of congruence. Also, they will learn a few more properties of triangles and inequalities in a triangle.

Download Exclusively Curated Chapter Notes for Class 9 Maths Chapter – 7 Goemetry of Triangles

Download most important questions for class 9 maths chapter – 7 goemetry of triangles.

Here we have provided the complete Class 9 Maths NCERT Solutions Chapter 7  Triangles in PDF format solved by experienced teachers. Students can download the free PDF of these NCERT Solutions for Class 9 by clicking on the link below to keep it handy for future reference.

• Chapter 1 Number System
• Chapter 2 Polynomials
• Chapter 3 Coordinate Geometry
• Chapter 4 Linear Equations in Two Variables
• Chapter 5 Introduction to Euclids Geometry
• Chapter 6 Lines and Angles
• Chapter 7 Triangles
• Chapter 8 Quadrilaterals
• Chapter 9 Areas of Parallelograms and Triangles
• Chapter 10 Circles
• Chapter 11 Constructions
• Chapter 12 Heron’s Formula
• Chapter 13 Surface Areas and Volumes
• Chapter 14 Statistics
• Chapter 15 Inroduction to Probability

NCERT Solutions for Class 9 Maths Chapter 7 – Triangles

carouselExampleControls112

Previous Next

List of Exercises in NCERT Class 9 Maths Chapter 7

Exercise 7.1 Solution 8 Questions (6 Short Answer Questions, 2 Long Answer Question) Exercise 7.2 Solution  8 Questions (6 Short Answer Questions, 2 Long Answer Question) Exercise 7.3 Solution  5 Questions (3 Short Answer Questions, 2 Long Answer Question) Exercise 7.4 Solution 6 Questions (5 Short Answer Questions, 1 Long Answer Question) Exercise 7.5 (Optional) Solution 4 Questions

Access Answers of Maths NCERT Class 9 Chapter 7 – Triangles

Exercise: 7.1 (Page No: 118)

1. In quadrilateral ACBD, AC = AD and AB bisect ∠A (see Fig. 7.16). Show that ΔABC≅ ΔABD. What can you say about BC and BD?

It is given that AC and AD are equal i.e. AC = AD and the line segment AB bisects ∠A.

We will have to now prove that the two triangles ABC and ABD are similar i.e. ΔABC ≅ ΔABD

Consider the triangles ΔABC and ΔABD,

(i) AC = AD (It is given in the question)

(ii) AB = AB (Common)

(iii) ∠CAB = ∠DAB (Since AB is the bisector of angle A)

So, by SAS congruency criterion , ΔABC ≅  ΔABD.

For the 2 nd part of the question, BC and BD are of equal lengths by the rule of C.P.C.T.

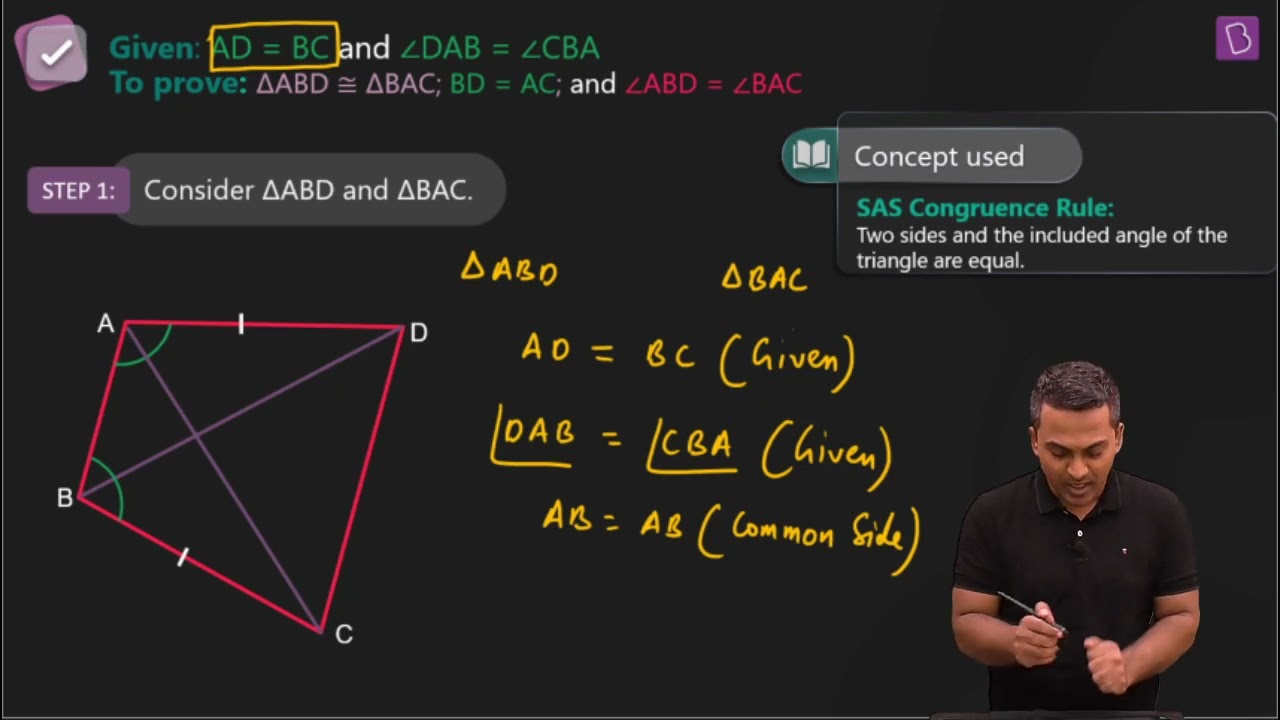
2. ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA (see Fig. 7.17). Prove that

(i) ΔABD ≅  ΔBAC

(ii) BD = AC

(iii) ∠ ABD = ∠ BAC.

The given parameters from the questions are ∠ DAB = ∠ CBA and AD = BC.

(i) ΔABD and ΔBAC are similar by SAS congruency as

AB = BA (It is the common arm)

∠ DAB = ∠ CBA and AD = BC (These are given in the question)

So, triangles ABD and BAC are similar i.e. ΔABD ≅  ΔBAC. (Hence proved).

(ii) It is now known that ΔABD ≅  ΔBAC so,

BD = AC (by the rule of CPCT).

(iii) Since ΔABD ≅  ΔBAC so,

Angles ∠ ABD = ∠ BAC (by the rule of CPCT).

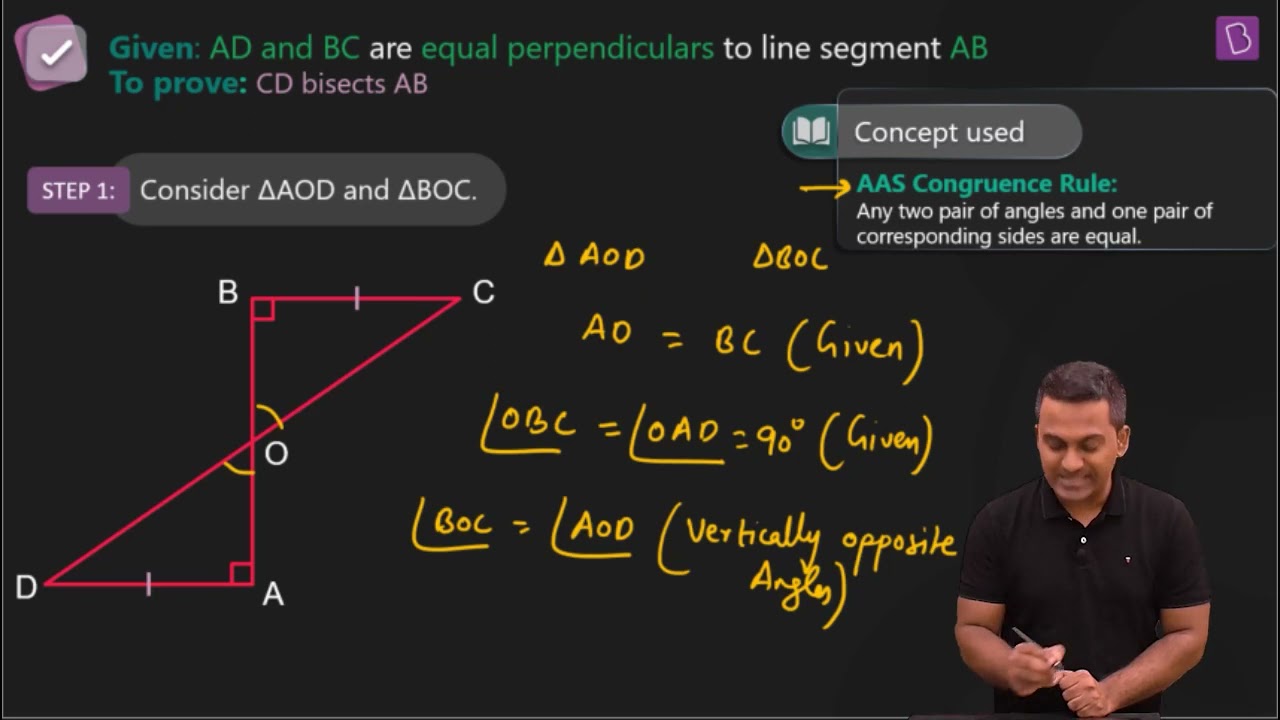
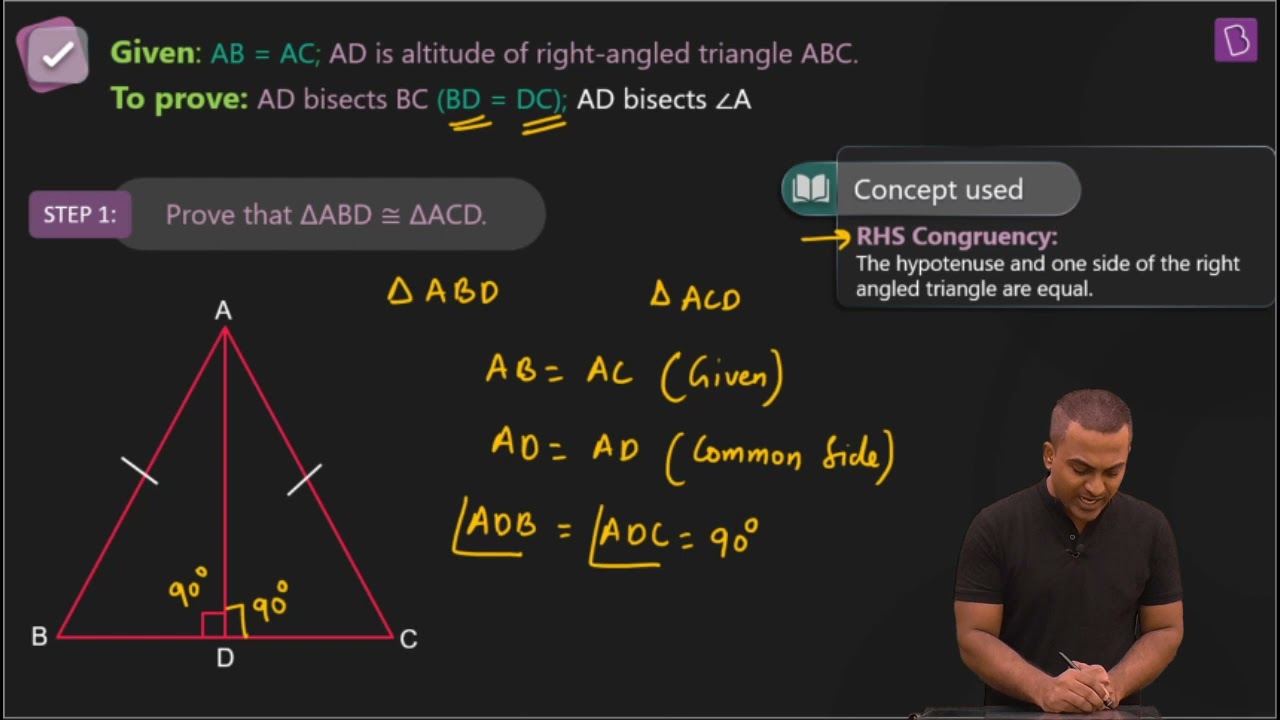
3. AD and BC are equal perpendiculars to a line segment AB (see Fig. 7.18). Show that CD bisects AB.

It is given that AD and BC are two equal perpendiculars to AB.

We will have to prove that CD is the bisector of AB

Triangles ΔAOD and ΔBOC are similar by AAS congruency since:

(i) ∠A = ∠B (They are perpendiculars)

(ii) AD = BC (As given in the question)

(iii) ∠AOD = ∠BOC (They are vertically opposite angles)

∴ ΔAOD ≅ ΔBOC.

So, AO = OB (by the rule of CPCT).

Thus, CD bisects AB (Hence proved).

4. l and m are two parallel lines intersected by another pair of parallel lines p and q (see Fig. 7.19). Show that ΔABC ≅ ΔCDA.

It is given that p || q and l || m

Triangles ABC and CDA are similar i.e. ΔABC ≅ ΔCDA

Consider the ΔABC and ΔCDA,

(i) ∠BCA = ∠DAC and ∠BAC = ∠DCA Since they are alternate interior angles

(ii) AC = CA as it is the common arm

So, by ASA congruency criterion, ΔABC ≅ ΔCDA.

5. Line l is the bisector of an angle ∠A and B is any point on l . BP and BQ are perpendiculars from B to the arms of ∠A (see Fig. 7.20). Show that:

(i) ΔAPB ≅ ΔAQB

(ii) BP = BQ or B is equidistant from the arms of ∠A.

It is given that the line “ l ” is the bisector of angle ∠A and the line segments BP and BQ are perpendiculars drawn from l .

(i) ΔAPB and ΔAQB are similar by AAS congruency because:

∠P = ∠Q (They are the two right angles)

AB = AB (It is the common arm)

∠BAP = ∠BAQ (As line l is the bisector of angle A)

So, ΔAPB ≅ ΔAQB.

(ii) By the rule of CPCT, BP = BQ. So, it can be said the point B is equidistant from the arms of ∠A.

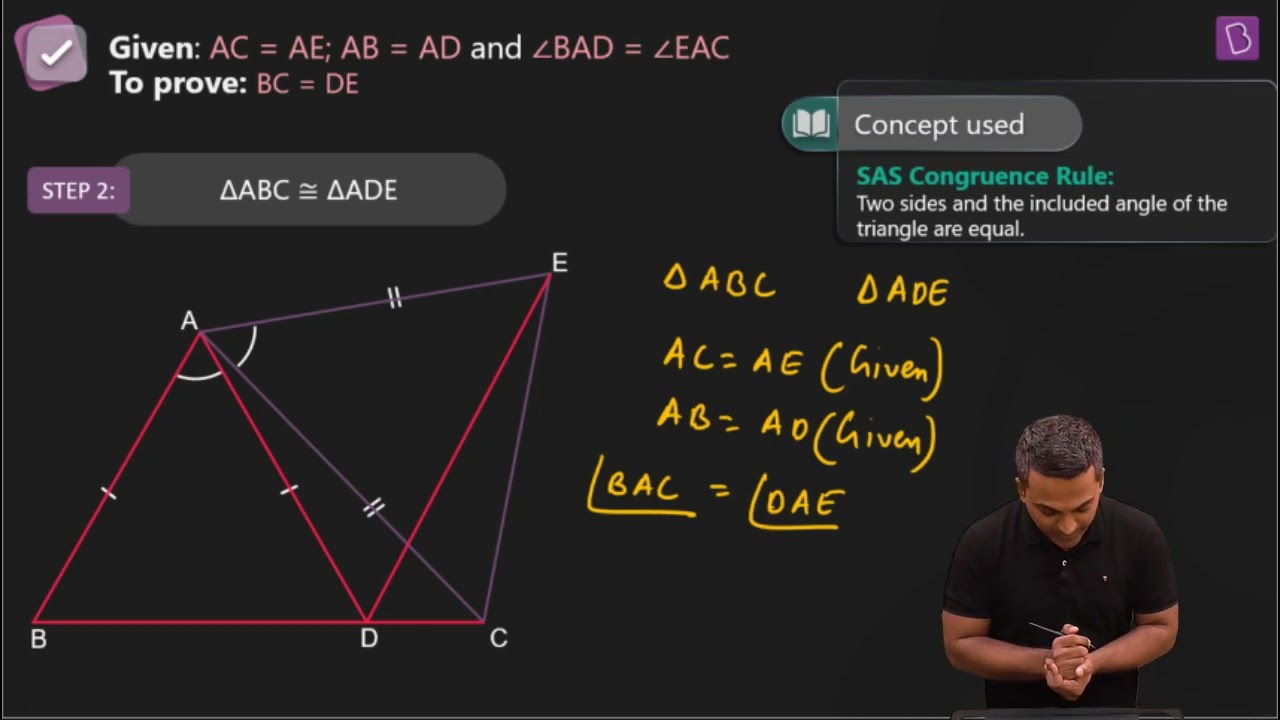
6. In Fig. 7.21, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

It is given in the question that AB = AD, AC = AE, and ∠BAD = ∠EAC

The line segment BC and DE are similar i.e. BC = DE

We know that ∠BAD = ∠EAC

Now, by adding ∠DAC on both sides we get,

∠BAD + ∠DAC = ∠EAC +∠DAC

This implies, ∠BAC = ∠EAD

Now, ΔABC and ΔADE are similar by SAS congruency since:

(i) AC = AE (As given in the question)

(ii) ∠BAC = ∠EAD

(iii) AB = AD (It is also given in the question)

∴ Triangles ABC and ADE are similar i.e. ΔABC ≅ ΔADE.

So, by the rule of CPCT, it can be said that BC = DE.

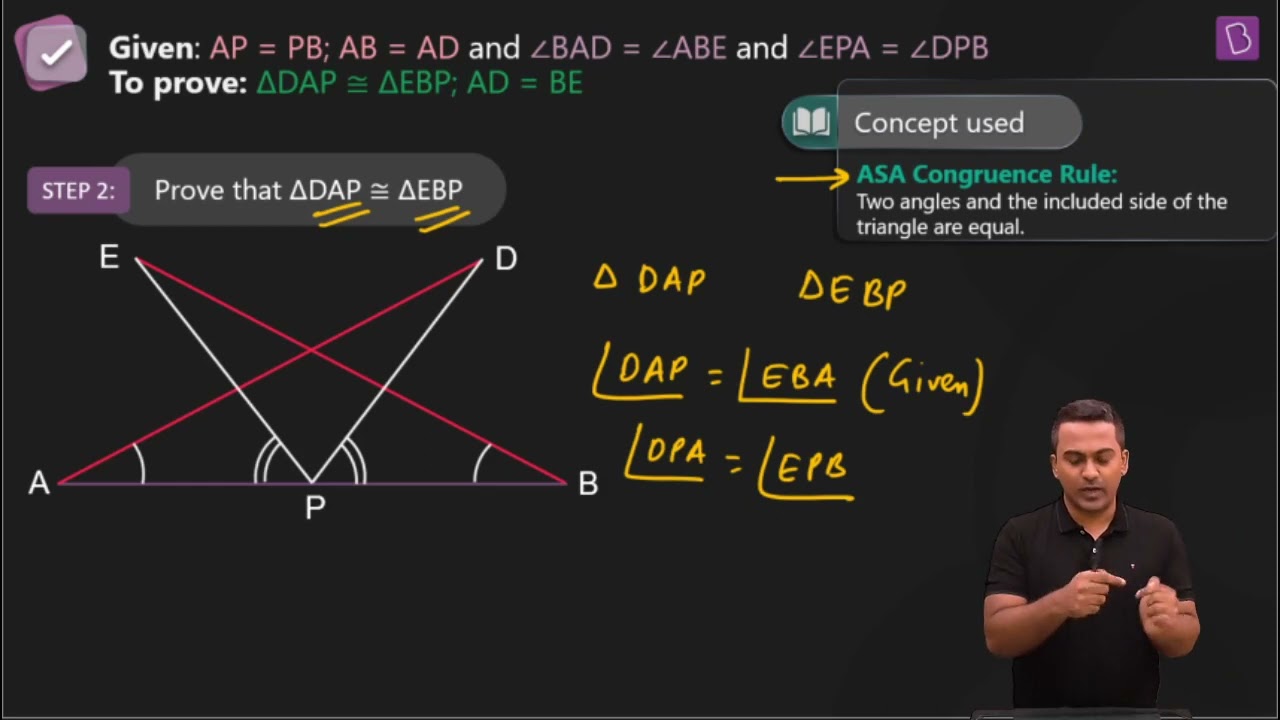
7. AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (see Fig. 7.22). Show that

(i) ΔDAP ≅ ΔEBP

(ii) AD = BE

In the question, it is given that P is the mid-point of line segment AB. Also, ∠BAD = ∠ABE and ∠EPA = ∠DPB

(i) It is given that ∠EPA = ∠DPB

Now, add ∠DPE on both sides,

∠EPA +∠DPE = ∠DPB+∠DPE

This implies that angles DPA and EPB are equal i.e. ∠DPA = ∠EPB

Now, consider the triangles DAP and EBP.

∠DPA = ∠EPB

AP = BP (Since P is the mid-point of the line segment AB)

∠BAD = ∠ABE (As given in the question)

So, by ASA congruency , ΔDAP ≅ ΔEBP.

(ii) By the rule of CPCT, AD = BE.

8. In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see Fig. 7.23). Show that:

(i) ΔAMC ≅ ΔBMD

(ii) ∠DBC is a right angle.

(iii) ΔDBC ≅ ΔACB

(iv) CM = ½ AB

It is given that M is the mid-point of the line segment AB, ∠C = 90°, and DM = CM

(i) Consider the triangles ΔAMC and ΔBMD:

AM = BM (Since M is the mid-point)

CM = DM (Given in the question)

∠CMA = ∠DMB (They are vertically opposite angles)

So, by SAS congruency criterion , ΔAMC ≅ ΔBMD.

(ii) ∠ACM = ∠BDM (by CPCT)

∴ AC || BD as alternate interior angles are equal.

Now, ∠ACB +∠DBC = 180° (Since they are co-interiors angles)

⇒ 90° +∠B = 180°

∴ ∠DBC = 90°

(iii) In ΔDBC and ΔACB,

BC = CB (Common side)

∠ACB = ∠DBC (They are right angles)

DB = AC (by CPCT)

So, ΔDBC ≅ ΔACB by SAS congruency .

(iv) DC = AB (Since ΔDBC ≅ ΔACB)

⇒ DM = CM = AM = BM (Since M the is mid-point)

So, DM + CM = BM+AM

Hence, CM + CM = AB

⇒ CM = (½) AB

Exercise: 7.2 (Page No: 123)

1. In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that:

(i) OB = OC (ii) AO bisects ∠A

AB = AC and

the bisectors of ∠B and ∠C intersect each other at O

(i) Since ABC is an isosceles with AB = AC,

½ ∠B = ½ ∠C

⇒ ∠OBC = ∠OCB (Angle bisectors)

∴ OB = OC (Side opposite to the equal angles are equal.)

(ii) In ΔAOB and ΔAOC,

AB = AC (Given in the question)

AO = AO (Common arm)

OB = OC (As Proved Already)

So, ΔAOB ≅ ΔAOC by SSS congruence condition.

BAO = CAO (by CPCT)

Thus, AO bisects ∠A.

2. In ΔABC, AD is the perpendicular bisector of BC (see Fig. 7.30). Show that ΔABC is an isosceles triangle in which AB = AC.

It is given that AD is the perpendicular bisector of BC

In ΔADB and ΔADC,

AD = AD (It is the Common arm)

∠ADB = ∠ADC

BD = CD (Since AD is the perpendicular bisector)

So, ΔADB ≅ ΔADC by SAS congruency criterion .

AB = AC (by CPCT)

3. ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see Fig. 7.31). Show that these altitudes are equal.

(i) BE and CF are altitudes.

(ii) AC = AB

Triangles ΔAEB and ΔAFC are similar by AAS congruency since

∠A = ∠A (It is the common arm)

∠AEB = ∠AFC (They are right angles)

∴ ΔAEB ≅ ΔAFC and so, BE = CF (by CPCT).

4. ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig. 7.32). Show that

(i) ΔABE ≅ ΔACF

(ii) AB = AC, i.e., ABC is an isosceles triangle.

It is given that BE = CF

(i) In ΔABE and ΔACF,

∠A = ∠A (It is the common angle)

BE = CF (Given in the question)

∴ ΔABE ≅ ΔACF by AAS congruency condition .

(ii) AB = AC by CPCT and so, ABC is an isosceles triangle.

5. ABC and DBC are two isosceles triangles on the same base BC (see Fig. 7.33). Show that ∠ABD = ∠ACD.

In the question, it is given that ABC and DBC are two isosceles triangles.

We will have to show that ∠ABD = ∠ACD

Triangles ΔABD and ΔACD are similar by SSS congruency since

AD = AD (It is the common arm)

AB = AC (Since ABC is an isosceles triangle)

BD = CD (Since BCD is an isosceles triangle)

So, ΔABD ≅ ΔACD.

∴ ∠ABD = ∠ACD by CPCT.

6. ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see Fig. 7.34). Show that ∠BCD is a right angle.

It is given that AB = AC and AD = AB

We will have to now prove ∠BCD is a right angle.

Consider ΔABC,

AB = AC (It is given in the question)

Also, ∠ACB = ∠ABC (They are angles opposite to the equal sides and so, they are equal)

Now, consider ΔACD,

Also, ∠ADC = ∠ACD (They are angles opposite to the equal sides and so, they are equal)

∠CAB + ∠ACB + ∠ABC = 180°

So, ∠CAB + 2∠ACB = 180°

⇒ ∠CAB = 180° – 2∠ACB — (i)

Similarly, in ΔADC,

∠CAD = 180° – 2∠ACD — (ii)

∠CAB + ∠CAD = 180° (BD is a straight line.)

Adding (i) and (ii) we get,

∠CAB + ∠CAD = 180° – 2∠ACB+180° – 2∠ACD

⇒ 180° = 360° – 2∠ACB-2∠ACD

⇒ 2(∠ACB+∠ACD) = 180°

⇒ ∠BCD = 90°

7. ABC is a right-angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.

In the question, it is given that

∠A = 90° and AB = AC

⇒ ∠B = ∠C (They are angles opposite to the equal sides and so, they are equal)

∠A+∠B+∠C = 180° (Since the sum of the interior angles of the triangle)

∴ 90° + 2∠B = 180°

⇒ 2∠B = 90°

So, ∠B = ∠C = 45°

8. Show that the angles of an equilateral triangle are 60° each.

Let ABC be an equilateral triangle as shown below:

Here, BC = AC = AB (Since the length of all sides is same)

⇒ ∠A = ∠B =∠C (Sides opposite to the equal angles are equal.)

Also, we know that

∠A+∠B+∠C = 180°

⇒ 3∠A = 180°

∴ ∠A = ∠B = ∠C = 60°

So, the angles of an equilateral triangle are always 60° each.

Exercise: 7.3 (Page No: 128)

1. ΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that

(i) ΔABD ≅ ΔACD

(ii) ΔABP ≅ ΔACP

(iii) AP bisects ∠A as well as ∠D.

(iv) AP is the perpendicular bisector of BC.

In the above question, it is given that ΔABC and ΔDBC are two isosceles triangles.

(i) ΔABD and ΔACD are similar by SSS congruency because:

AB = AC (Since ΔABC is isosceles)

BD = CD (Since ΔDBC is isosceles)

∴ ΔABD ≅ ΔACD.

(ii) ΔABP and ΔACP are similar as:

AP = AP (It is the common side)

∠PAB = ∠PAC (by CPCT since ΔABD ≅ ΔACD)

So, ΔABP ≅ ΔACP by SAS congruency condition.

(iii) ∠PAB = ∠PAC by CPCT as ΔABD ≅ ΔACD.

AP bisects ∠A. — (i)

Also, ΔBPD and ΔCPD are similar by SSS congruency as

PD = PD (It is the common side)

BD = CD (Since ΔDBC is isosceles.)

BP = CP (by CPCT as ΔABP ≅ ΔACP)

So, ΔBPD ≅ ΔCPD.

Thus, ∠BDP = ∠CDP by CPCT. — (ii)

Now by comparing (i) and (ii) it can be said that AP bisects ∠A as well as ∠D.

(iv) ∠BPD = ∠CPD (by CPCT as ΔBPD ΔCPD)

and BP = CP — (i)

∠BPD +∠CPD = 180° (Since BC is a straight line.)

⇒ 2∠BPD = 180°

⇒ ∠BPD = 90° —(ii)

Now, from equations (i) and (ii), it can be said that

AP is the perpendicular bisector of BC.

2. AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that

(i) AD bisects BC (ii) AD bisects ∠A.

It is given that AD is an altitude and AB = AC. The diagram is as follows:

(i) In ΔABD and ΔACD,

∠ADB = ∠ADC = 90°

AD = AD (Common arm)

∴ ΔABD ≅ ΔACD by RHS congruence condition.

Now, by the rule of CPCT,

So, AD bisects BC

(ii) Again, by the rule of CPCT, ∠BAD = ∠CAD

Hence, AD bisects ∠A.

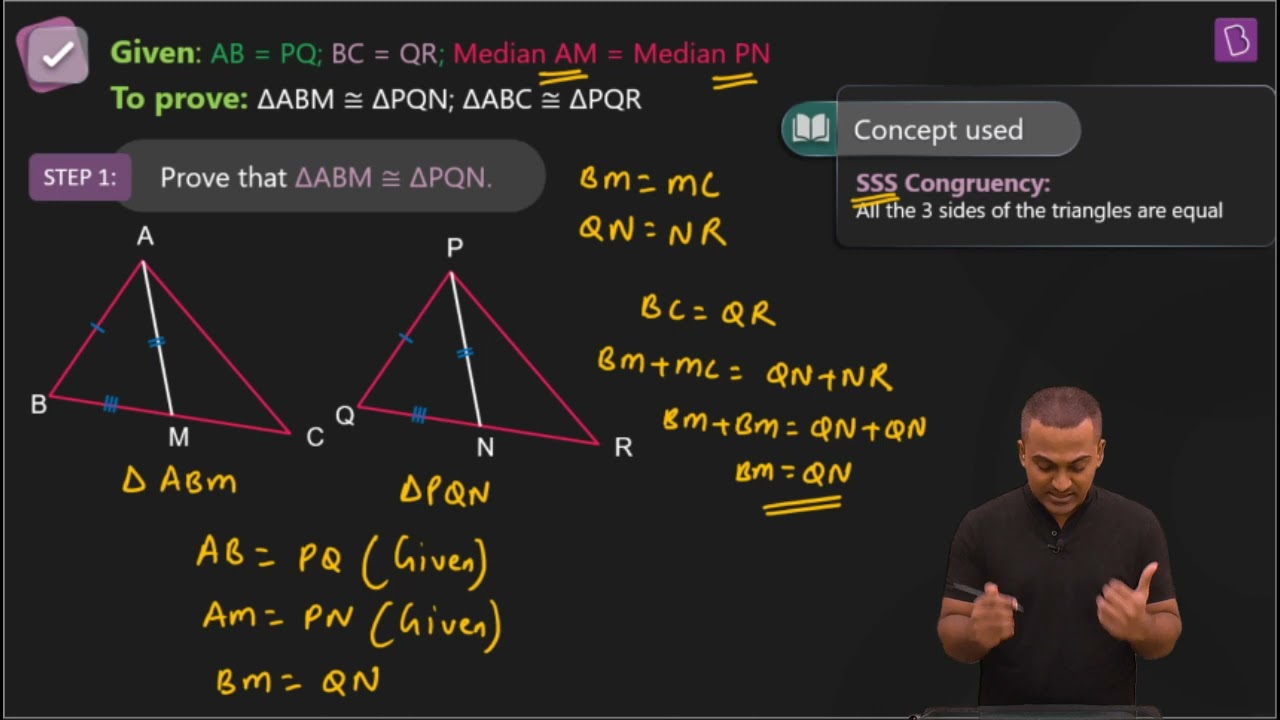
3. Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ΔPQR (see Fig. 7.40). Show that:

(i) ΔABM ≅ ΔPQN

(ii) ΔABC ≅ ΔPQR

Given parameters are:

BC = QR and

(i) ½ BC = BM and ½ QR = QN (Since AM and PN are medians)

Also, BC = QR

So, ½ BC = ½ QR

In ΔABM and ΔPQN,

AM = PN and AB = PQ (As given in the question)

BM = QN (Already proved)

∴ ΔABM ≅ ΔPQN by SSS congruency.

(ii) In ΔABC and ΔPQR,

AB = PQ and BC = QR (As given in the question)

∠ABC = ∠PQR (by CPCT)

So, ΔABC ≅ ΔPQR by SAS congruency.

4. BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.

It is known that BE and CF are two equal altitudes.

Now, in ΔBEC and ΔCFB,

∠BEC = ∠CFB = 90° (Same Altitudes)

BE = CF (Common side)

So, ΔBEC ≅ ΔCFB by RHS congruence criterion.

Also, ∠C = ∠B (by CPCT)

Therefore, AB = AC as sides opposite to the equal angles is always equal.

5. ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC to show that ∠B = ∠C.

In the question, it is given that AB = AC

Now, ΔABP and ΔACP are similar by RHS congruency as

∠APB = ∠APC = 90° (AP is altitude)

AP = AP (Common side)

So, ΔABP ≅ ΔACP.

∴ ∠B = ∠C (by CPCT)

Exercise: 7.4 (Page No: 132)

1. Show that in a right-angled triangle, the hypotenuse is the longest side.

It is known that ABC is a triangle right angled at B.

We know that,

∠A +∠B+∠C = 180°

Now, if ∠B+∠C = 90° then ∠A has to be 90°.

Since A is the largest angle of the triangle, the side opposite to it must be the largest.

So, AB is the hypotenuse which will be the largest side of the above right-angled triangle i.e. ΔABC.

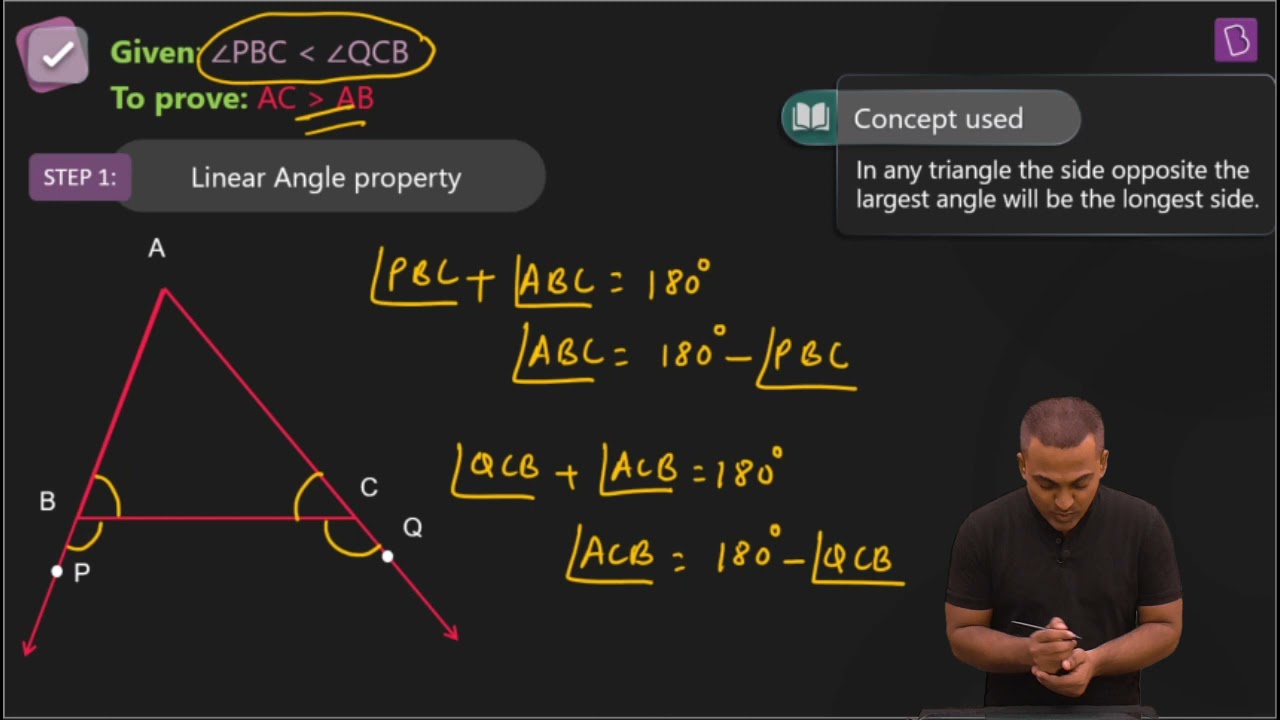
2. In Fig. 7.48, sides AB and AC of ΔABC are extended to points P and Q respectively. Also, ∠PBC < ∠QCB. Show that AC > AB.

It is given that ∠PBC < ∠QCB

We know that ∠ABC + ∠PBC = 180°

So, ∠ABC = 180°-∠PBC

∠ACB +∠QCB = 180°

Therefore ∠ACB = 180° -∠QCB

Now, since ∠PBC < ∠QCB,

∴ ∠ABC > ∠ACB

Hence, AC > AB as sides opposite to the larger angle is always larger.

3. In Fig. 7.49, ∠B < ∠A and ∠C < ∠D. Show that AD < BC.

In the question, it is mentioned that angles B and angle C is smaller than angles A and D respectively i.e. ∠B < ∠A and ∠C < ∠D.

Since the side opposite to the smaller angle is always smaller

AO < BO — (i)

And OD < OC —(ii)

By adding equation (i) and equation (ii) we get

AO+OD < BO + OC

So, AD < BC

4. AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see Fig. 7.50).

Show that ∠A > ∠C and ∠B > ∠D.

In ΔABD, we see that

AB < AD < BD

So, ∠ADB < ∠ABD — (i) (Since angle opposite to longer side is always larger)

Now, in ΔBCD,

BC < DC < BD

Hence, it can be concluded that

∠BDC < ∠CBD — (ii)

Now, by adding equation (i) and equation (ii) we get,

∠ADB + ∠BDC < ∠ABD + ∠CBD

∠ADC < ∠ABC

Similarly, In triangle ABC,

∠ACB < ∠BAC — (iii) (Since the angle opposite to the longer side is always larger)

Now, In ΔADC,

∠DCA < ∠DAC — (iv)

By adding equation (iii) and equation (iv) we get,

∠ACB + ∠DCA < ∠BAC+∠DAC

⇒ ∠BCD < ∠BAD

∴ ∠A > ∠C

5. In Fig 7.51, PR > PQ and PS bisect ∠QPR. Prove that ∠PSR > ∠PSQ.

It is given that PR > PQ and PS bisects ∠QPR

Now we will have to prove that angle PSR is smaller than PSQ i.e. ∠PSR > ∠PSQ

∠QPS = ∠RPS — (ii) (As PS bisects ∠QPR)

∠PQR > ∠PRQ — (i) (Since PR > PQ as angle opposite to the larger side is always larger)

∠PSR = ∠PQR + ∠QPS — (iii) (Since the exterior angle of a triangle equals to the sum of opposite interior angles)

∠PSQ = ∠PRQ + ∠RPS — (iv) (As the exterior angle of a triangle equals to the sum of opposite interior angles)

By adding (i) and (ii)

∠PQR +∠QPS > ∠PRQ +∠RPS

Thus, from (i), (ii), (iii) and (iv), we get

∠PSR > ∠PSQ

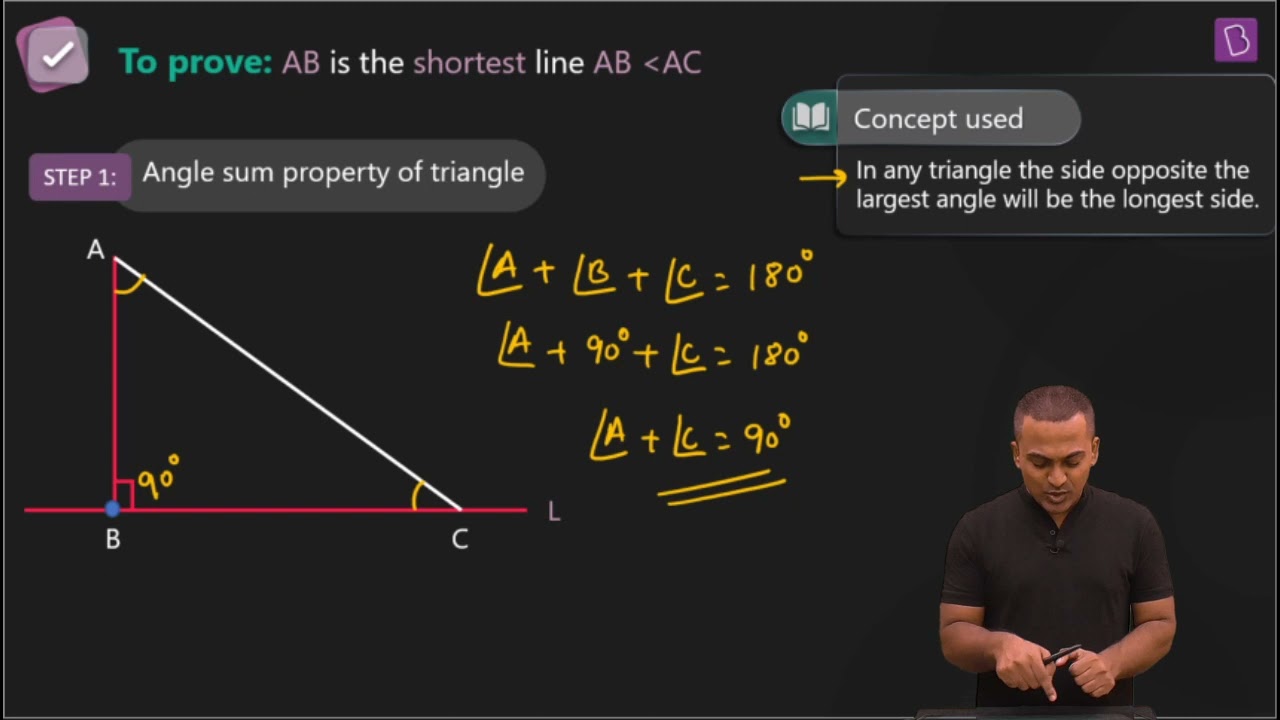
6. Show that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.

First, let “ l ” be a line segment and “B” be a point lying on it. A line AB perpendicular to l is now drawn. Also, let C be any other point on l . The diagram will be as follows:

In ΔABC, ∠B = 90°

Now, we know that

∴ ∠A +∠C = 90°

Hence, ∠C must be an acute angle which implies ∠C < ∠B

So, AB < AC (As the side opposite to the larger angle is always larger)

Summary of NCERT Solutions for Class 9 Maths Chapter 7 Triangles

Triangle is a part of Geometry. However, the complete Geometry of Class 9 constitutes a weightage of 22 marks out of 80 marks. Have a look at the types of questions that are expected from Geometry in the annual exam of class 9 Maths paper.

Students should practise all the questions from the exercise to score high marks in the Class 9 Maths paper. The step-by-step solution to all the exercises of NCERT Class 9 Maths Chapter 7 is provided below:

In previous classes, students must have used the properties of triangles for solving the questions, but now in the  NCERT Textbook of Class 9 Maths Chapter 7, students will learn how to prove these properties. For solving the questions related to this topic, it is very necessary that students should know the congruence rule. First, go through the theory and then look at the solved examples that are already there in the book. After that, start solving the exercise problems.

Students can also have a look at the NCERT Solutions of Class 9 for Science subject to know the answers of all the chapters with a detailed explanation.

Important Concepts Learned in NCERT Class 9 Maths Chapter 7 – Triangles

The aim of including this Triangle Chapter in the Class 9 Maths NCERT textbook is to make students know the following concepts:

• Congruence of triangles.
• Criteria for congruence of triangles (SAS congruence rule, ASA congruence rule, SSS congruence rule, RHS congruence rule).
• Properties of triangles.
• Inequalities of triangles.

We hope this information on “ NCERT Solution Class 9 Maths Chapter 7 ” is useful for students. Click on NCERT Solutions to get the solved answers from the NCERT book for all the classes. Stay tuned for further updates on CBSE and other competitive exams. To access interactive Maths and Science Videos, download BYJU’S App and subscribe to our YouTube Channel.

Triangles is a very important chapter as the fundamental concepts introduced here are carried forward to higher levels of education. For this purpose, after completing the questions from the NCERT Textbook, students are recommended to solve the other textbooks which are prescribed by the CBSE Board.

• RD Sharma Solutions for Class 9 Maths Chapter 9 Triangle and its Angles

Disclaimer:

Dropped Topics –  7.6 Inequalities in triangles.

Frequently Asked Questions on NCERT Solutions for Class 9 Maths Chapter 7

List out the important topics covered in ncert solutions for class 9 maths chapter 7., what is the meaning of congruence of triangles in ncert solutions for class 9 maths chapter 7, how is ncert solutions for class 9 maths chapter 7 helpful for cbse exam preparation, leave a comment cancel reply.

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

• New QB365-SLMS
• NEET Materials
• JEE Materials
• Banking first yr Materials
• TNPSC Materials
• DIPLOMA COURSE Materials
• 5th Standard Materials
• 12th Standard Materials
• 11th Standard Materials
• 10th Standard Materials
• 9th Standard Materials
• 8th Standard Materials
• 7th Standard Materials
• 6th Standard Materials
• 12th Standard CBSE Materials
• 11th Standard CBSE Materials
• 10th Standard CBSE Materials
• 9th Standard CBSE Materials
• 8th Standard CBSE Materials
• 7th Standard CBSE Materials
• 6th Standard CBSE Materials
• Tamilnadu Stateboard
• Scholarship Exams
• Scholarships

Class 9th Maths - Coordinate Geometry Case Study Questions and Answers 2022 - 2023

By QB365 on 08 Sep, 2022

QB365 provides a detailed and simple solution for every Possible Case Study Questions in Class 9th Maths Subject - Coordinate Geometry, CBSE. It will help Students to get more practice questions, Students can Practice these question papers in addition to score best marks.

QB365 - Question Bank Software

Coordinate geometry case study questions with answer key.

9th Standard CBSE

Final Semester - June 2015

Mathematics

(b) What are the coordinates of C and D respectively?

(c) What is the distance between B and D?

(d) What is the distance between A and C?

(e) What are the coordinates of the point of intersection of AC and BD?

(ii) What are the coordinates of Police Station?

(iii) Distance between school and police station:

(iv) What are the coordinates of Library?

(v) In which quadrant the point (-1, 4) lies?  

(b) What are the coordinates of A and B respectively?

(c) The coordinates of point O in the sketch -2 is

(d) The point on the y-axis ( in sketch 2) which is equidistant from the points B and C is 

(e) The point on the x-axis ( in sketch 2) which is equidistant from the points C and D is

(b) What are the coordinates of R, taking A as origin?

(c) Side of lawn is :

(d) Shape of lawn is :

(e) Area of lawn is :

(ii) What are the coordinates of position 'D'?

(iii) What are the coordinates of position 'H'?

(iv) In which quadrant, the point 'C' lie?

(v) Find the perpendicular distance of the point E from the y-axis.

*****************************************

Coordinate geometry case study questions with answer key answer keys.

(a) (iii) A(3, 5); B(7, 9) (b) (i) C(11, 5); D(7, 1) (c) (iii) 8 units (d) (iii) 8 units (e) (i) (7, 5)

(i) (b) (2, 3) (ii) (a) (2, -1) (iii) (a) 4 (iv) (d) (6, 2) (v) (b) II

(a) (ii) A(13, 10); B(19, 10) (b) (iv) A(19, 6); B(13, 6) (c) (ii) (16, 8) (d) (i) (0, 8) (e)  (ii) (16, 0)

(a) (iv) C(10, 6) (b) (iii) R(5, 6) (c) (ii)   \(\sqrt{34}\)  units PS 2 = AS 2 + AP 2 = 5 2 + 3 2 = 25 + 9 = 34 ⇒ PS =  \(\sqrt{34}\) (d) (iv) Rhombus (e) (i) 30 sq. units Area of rhombus =  \(1 / 2\)  x product of diagonals =  \(1 / 2\)  x 6 x 10  = 30 sq. units

(i) (d) (-4, 3)  (ii) (b) (-3, -2) (iii) (b) (8, 4.5) (iv) (d) IV (v) (b) 10 units

Related 9th Standard CBSE Mathematics Materials

9th standard cbse syllabus & materials, class 10th social science - pastoralists case study questions and answers 2022 - 2023, class 9th social science - forest society and colonialism case study questions and answers 2022 - 2023, class 9th social science - nazism and the rise of hitler case study questions and answers 2022 - 2023, class 9th social science - socialism in europe and the russian revolution case study questions and answers 2022 - 2023, class 9th social science - the french revolution case study questions and answers 2022 - 2023, class 9th science - work and energy case study questions and answers 2022 - 2023, class 9th science - force and laws of motion case study questions and answers 2022 - 2023, class 9th science - motion case study questions and answers 2022 - 2023, class 9th science - the fundamental unit of life case study questions and answers 2022 - 2023, class 9th science - is matter around us pure case study questions and answers 2022 - 2023, class 9th science - matter in our surroundings case study questions and answers 2022 - 2023, xam idea 9th standard economics ncert solutions for food security in india, xam idea 9th standard economics ncert solutions for poverty as a challenge, xam idea 9th standard economics ncert solutions for people as resource, xam idea 9th standard economics ncert solutions for the story of village palampur.

Class VI to XII

Tn state board / cbse, 3000+ q&a's per subject, score high marks.

9th Standard CBSE Study Materials

9th Standard CBSE Subjects

NCERT Solutions for Class 9 Maths Chapter 7 Triangles

NCERT Solutions for Class 9 Maths Chapter 7 Triangles are provided here. Our NCERT Maths solutions contain all the questions of the NCERT textbook that are solved and explained beautifully. Here you will get complete NCERT Solutions for Class 9 Maths Chapter 7 all exercises Exercise in one place. These solutions are prepared by the subject experts and as per the latest NCERT syllabus and guidelines. CBSE Class 9 Students who wish to score good marks in the maths exam must practice these questions regularly.

Class 9 Maths Chapter 7 Triangles NCERT Solutions

Below we have provided the solutions of each exercise of the chapter. Go through the links to access the solutions of exercises you want. You should also check out our NCERT Class 9 Solutions for other subjects to score good marks in the exams.

NCERT Solutions for Class 9 Maths Chapter 7 Exercise 7.1

NCERT Solutions for Class 9 Maths Chapter 7 Exercise 7.2

NCERT Solutions for Class 9 Maths Chapter 7 Exercise 7.3

NCERT Solutions for Class 9 Maths Chapter 7 Exercise 7.4

NCERT Solutions for Class 9 Maths Chapter 7 Exercise 7.5

NCERT Solutions for Class 9 Maths Chapter 7 – Topic Discussion

Below we have listed the topics that have been discussed in this chapter.

• Congruence of triangles.
• Criteria for congruence of triangles (SAS congruence rule, ASA congruence rule, SSS congruence rule, RHS congruence rule).
• Properties of triangles.
• Inequalities of triangle.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

CBSE Case Study Questions for Class 9 Maths - Pdf PDF Download

Cbse case study questions for class  9 maths.

CBSE Case Study Questions for Class 9 Maths are a type of assessment where students are given a real-world scenario or situation and they need to apply mathematical concepts to solve the problem. These types of questions help students to develop their problem-solving skills and apply their knowledge of mathematics to real-life situations.

Chapter Wise Case Based Questions for Class 9 Maths

The CBSE Class 9 Case Based Questions can be accessed from Chapetrwise Links provided below:

Chapter-wise case-based questions for Class 9 Maths are a set of questions based on specific chapters or topics covered in the maths textbook. These questions are designed to help students apply their understanding of mathematical concepts to real-world situations and events.

Chapter 1: Number System

• Case Based Questions: Number System

Chapter 2: Polynomial

• Case Based Questions: Polynomial

Chapter 3: Coordinate Geometry

• Case Based Questions: Coordinate Geometry

Chapter 4: Linear Equations

• Case Based Questions: Linear Equations - 1
• Case Based Questions: Linear Equations -2

Chapter 5: Introduction to Euclid’s Geometry

• Case Based Questions: Lines and Angles

Chapter 7: Triangles

• Case Based Questions: Triangles

Chapter 8: Quadrilaterals

• Case Based Questions: Quadrilaterals - 1
• Case Based Questions: Quadrilaterals - 2

Chapter 9: Areas of Parallelograms

• Case Based Questions: Circles

Chapter 11: Constructions

• Case Based Questions: Constructions

Chapter 12: Heron’s Formula

• Case Based Questions: Heron’s Formula

Chapter 13: Surface Areas and Volumes

• Case Based Questions: Surface Areas and Volumes

Chapter 14: Statistics

• Case Based Questions: Statistics

Chapter 15: Probability

• Case Based Questions: Probability

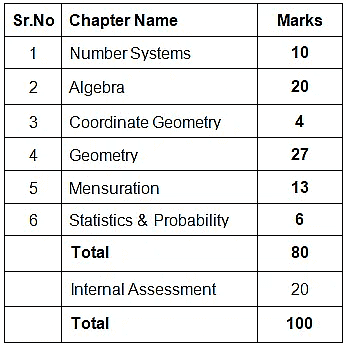
Weightage of Case Based Questions in Class 9 Maths

Why are Case Study Questions important in Maths Class  9?

• Enhance critical thinking:  Case study questions require students to analyze a real-life scenario and think critically to identify the problem and come up with possible solutions. This enhances their critical thinking and problem-solving skills.
• Apply theoretical concepts:  Case study questions allow students to apply theoretical concepts that they have learned in the classroom to real-life situations. This helps them to understand the practical application of the concepts and reinforces their learning.
• Develop decision-making skills:  Case study questions challenge students to make decisions based on the information provided in the scenario. This helps them to develop their decision-making skills and learn how to make informed decisions.
• Improve communication skills:  Case study questions often require students to present their findings and recommendations in written or oral form. This helps them to improve their communication skills and learn how to present their ideas effectively.
• Enhance teamwork skills:  Case study questions can also be done in groups, which helps students to develop teamwork skills and learn how to work collaboratively to solve problems.

In summary, case study questions are important in Class 9 because they enhance critical thinking, apply theoretical concepts, develop decision-making skills, improve communication skills, and enhance teamwork skills. They provide a practical and engaging way for students to learn and apply their knowledge and skills to real-life situations.

Class 9 Maths Curriculum at Glance

The Class 9 Maths curriculum in India covers a wide range of topics and concepts. Here is a brief overview of the Maths curriculum at a glance:

• Number Systems:  Students learn about the real number system, irrational numbers, rational numbers, decimal representation of rational numbers, and their properties.
• Algebra:  The Algebra section includes topics such as polynomials, linear equations in two variables, quadratic equations, and their solutions.
• Coordinate Geometry:  Students learn about the coordinate plane, distance formula, section formula, and slope of a line.
• Geometry:  This section includes topics such as Euclid’s geometry, lines and angles, triangles, and circles.
• Trigonometry: Students learn about trigonometric ratios, trigonometric identities, and their applications.
• Mensuration: This section includes topics such as area, volume, surface area, and their applications.
• Statistics and Probability:  Students learn about measures of central tendency, graphical representation of data, and probability.

The Class 9 Maths curriculum is designed to provide a strong foundation in mathematics and prepare students for higher education in the field. The curriculum is structured to develop critical thinking, problem-solving, and analytical skills, and to promote the application of mathematical concepts in real-life situations. The curriculum is also designed to help students prepare for competitive exams and develop a strong mathematical base for future academic and professional pursuits.

Students can also access Case Based Questions of all subjects of CBSE Class 9

• Case Based Questions for Class 9 Science
• Case Based Questions for Class 9 Social Science
• Case Based Questions for Class 9 English
• Case Based Questions for Class 9 Hindi
• Case Based Questions for Class 9 Sanskrit

Frequently Asked Questions (FAQs) on Case Based Questions for Class 9 Maths

What is case-based questions.

Case-Based Questions (CBQs) are open-ended problem solving tasks that require students to draw upon their knowledge of Maths concepts and processes to solve a novel problem. CBQs are often used as formative or summative assessments, as they can provide insights into how students reason through and apply mathematical principles in real-world problems.

What are case-based questions in Maths?

Case-based questions in Maths are problem-solving tasks that require students to apply their mathematical knowledge and skills to real-world situations or scenarios.

What are some common types of case-based questions in class 9 Maths?

Common types of case-based questions in class 9 Maths include word problems, real-world scenarios, and mathematical modeling tasks.

Top Courses for Class 9

Faqs on cbse case study questions for class 9 maths - pdf, study material, cbse case study questions for class 9 maths - pdf, video lectures, extra questions, viva questions, semester notes, objective type questions, important questions, mock tests for examination, sample paper, practice quizzes, previous year questions with solutions, shortcuts and tricks, past year papers.

CBSE Case Study Questions for Class 9 Maths - Pdf Free PDF Download

Importance of cbse case study questions for class 9 maths - pdf, cbse case study questions for class 9 maths - pdf notes, cbse case study questions for class 9 maths - pdf class 9, study cbse case study questions for class 9 maths - pdf on the app, welcome back, create your account for free.

Forgot Password

Unattempted tests, change country, practice & revise.

NCERT Solutions for Class 9 Maths Chapter 7 Triangles

Ncert solutions for class 9 maths chapter 7 triangles| pdf download.

Page No: 118

• Exercise 7.1 Chapter 7 Class 9 Maths NCERT Solutions
• Exercise 7.2 Chapter 7 Class 9 Maths NCERT Solutions
• Exercise 7.3 Chapter 7 Class 9 Maths NCERT Solutions
• Exercise 7.4 Chapter 7 Class 9 Maths NCERT Solutions
• Exercise 7.5 Chapter 7 Class 9 Maths NCERT Solutions

NCERT Solutions for Class 9 Maths Chapters:

How many exercises in chapter 7 triangles, each of the equal angles of an isosceles triangle is 38°, what is the measure of the third angle, find the measure of each of acute angle in a right angle isosceles triangle., if two angles are (30 ∠ a)º and (125 + 2a)º and they are supplement of each other. find the value of ‘a’., contact form.

Gurukul of Excellence

Classes for Physics, Chemistry and Mathematics by IITians

Category: Case Study Questions for Class 9 Maths

Join our Telegram Channel for Free PDF Download

Case Study Questions for Class 9 Maths Chapter 12 Herons Formula

Case study questions for class 9 maths chapter 9 areas of parallelograms and triangles, case study questions for class 9 maths chapter 6 lines and angles, case study questions for class 9 maths chapter 7 triangles, case study questions for class 9 maths chapter 5 introduction to euclid’s geometry, case study and passage based questions for class 9 maths chapter 14 statistics, case study questions for class 9 maths chapter 1 real numbers, case study questions for class 9 maths chapter 4 linear equations in two variables, case study questions for class 9 maths chapter 3 coordinate geometry, case study questions for class 9 maths chapter 15 probability, case study questions for class 9 maths chapter 13 surface area and volume, case study questions for class 9 maths chapter 10 circles, case study questions for class 9 maths chapter 9 quadrilaterals, case study questions for class 9 maths chapter 2 polynomials.

Join our Online Test Series for CBSE, ICSE, JEE, NEET and Other Exams

Editable Study Materials for Your Institute - CBSE, ICSE, State Boards (Maharashtra & Karnataka), JEE, NEET, FOUNDATION, OLYMPIADS, PPTs

CBSE Case Study Questions for Class 9 Maths Circles Free PDF

Mere Bacchon, you must practice the CBSE Case Study Questions Class 9 Maths Circles  in order to fully complete your preparation . They are very very important from exam point of view. These tricky Case Study Based Questions can act as a villain in your heroic exams!

I have made sure the questions (along with the solutions) prepare you fully for the upcoming exams. To download the latest CBSE Case Study Questions , just click ‘ Download PDF ’.

CBSE Case Study Questions for Class 9 Maths Circles PDF

Checkout our case study questions for other chapters.

• Chapter 8 Quadrilaterals Case Study Questions
• Chapter 9 Areas of Parallelograms and Triangles Case Study Questions
• Chapter 11 Constructions Case Study Questions
• Chapter 12 Heron’s Formula Case Study Questions

How should I study for my upcoming exams?

First, learn to sit for at least 2 hours at a stretch

Solve every question of NCERT by hand, without looking at the solution.

Solve NCERT Exemplar (if available)

Sit through chapter wise FULLY INVIGILATED TESTS

Practice MCQ Questions (Very Important)

Practice Assertion Reason & Case Study Based Questions

Sit through FULLY INVIGILATED TESTS involving MCQs. Assertion reason & Case Study Based Questions

After Completing everything mentioned above, Sit for atleast 6 full syllabus TESTS.

Contact Form

Privacy Policy

Class 9 Maths Case Study Questions Chapter 4 Linear Equations in two variables

• Post author: studyrate
• Post published:
• Post category: class 9th
• Post comments: 0 Comments

Case study Questions in Class 9 Mathematics Chapter 4  are very important to solve for your exam. Class 9 Maths Chapter 4 Case Study Questions have been prepared for the latest exam pattern. You can check your knowledge by solving  Class 9 Maths Case Study Questions Chapter 4 Linear Equations in two variables

Join our Telegram Channel, there you will get various e-books for CBSE 2024 Boards exams for Class 9th, 10th, 11th, and 12th.

In CBSE Class 9 Maths Paper, Students will have to answer some questions based on Assertion and Reason. There will be a few questions based on case studies and passage-based as well. In that, a paragraph will be given, and then the MCQ questions based on it will be asked.

Linear Equations in two variables Case Study Questions With Answers

Here, we have provided case-based/passage-based questions for Class 9 Maths Chapter 4 Linear Equations in two variables

Case Study/Passage-Based Questions

Case Study 1: Deepak bought 3 notebooks and 2 pens for Rs. 80. His friend Ram said that the price of each notebook could be Rs. 25. Then three notebooks would cost Rs.75, the two pens would cost Rs.5 and each pen could be Rs. 2.50. Another friend Ajay felt that Rs. 2.50 for one pen was too little. It should be at least Rs. 16. Then the price of each notebook would also be Rs.16

Lohith also bought the same types of notebooks and pens as Aditya. He paid 110 for 4 notebooks and 3 pens. Later, Deepak guesses the cost of one pen is Rs. 10 and Lohith guess the cost of one notebook is Rs. 30.

(i) Form the pair of linear equations in two variables from this situation by taking the cost of one notebook as Rs. x and the cost of one pen as Rs. y. (a) 3x + 2y = 80 and 4x + 3y = 110 (b) 2x + 3y = 80 and 3x + 4y = 110 (c) x + y = 80 and x + y = 110 (d) 3x + 2y = 110 and 4x + 3y = 80

Answer: (a) 3x + 2y = 80 and 4x + 3y = 110

(ii) Which is the solution satisfying both the equations formed in (i)? (a) x = 10, y = 20 (b) x = 20, y = 10 (c) x = 15, y = 15 (d) none of these

Answer: (b) x = 20, y = 10

(iii) Find the cost of one pen? (a) Rs. 20 (b) Rs. 10 (c) Rs. 5 (d) Rs. 15

Answer: (b) Rs. 10

(iv) Find the total cost if they will purchase the same type of 15 notebooks and 12 pens. (a) Rs. 400 (b) Rs. 350 (c) Rs. 450 (d) Rs. 420

Answer: (d) Rs. 420

(v) Find whose estimation is correct in the given statement. (a) Deepak (b) Lohith (c) Ram (d) Ajay

Answer: (a) Deepak

Case Study 2: In the below given layout, the design and measurements have been made such that area of two bedrooms and Kitchen together is 95 sq. m.

(i) The area of two bedrooms and kitchen are respectively equal to (a) 5x, 5y (b) 10x, 5y (c) 5x, 10y (c) x, y

(ii) Find the length of the outer boundary of the layout. (a) 27 m (b) 15 m (c) 50 m (d) 54 m

(iii) The pair of linear equations in two variables formed from the statements are (a) x + y = 13, x + y = 9 (b) 2x + y = 13, x + y = 9 (c) x + y = 13, 2x + y = 9 (d) None of the above

(iv) Which is the solution satisfying both the equations formed in (iii)? (a) x = 7, y = 6 (b) x = 8, y = 5 (c) x = 6, y = 7 (d) x = 5, y = 8

(v) Find the area of each bedroom. (a) 30 sq. m (b) 35 sq. m (c) 65 sq. m (d) 42 sq. m

Hope the information shed above regarding Case Study and Passage Based Questions for Class 9 Mathematics Chapter 4 Linear Equations in two variables with Answers Pdf free download has been useful to an extent. If you have any other queries about CBSE Class 9 Maths Linear Equations in two variables Case Study and Passage Based Questions with Answers, feel free to comment below so that we can revert back to us at the earliest possible By Team Study Rate

You Might Also Like

Mcq questions of class 9 maths chapter 11 constructions with answers, class 9 science case study questions chapter 12 sound, class 9 history case study questions chapter 2 socialism in europe and the russian revolution, leave a reply cancel reply.

Save my name, email, and website in this browser for the next time I comment.