case study questions class 11 physics chapter 6

Class 11 Physics Case Study Questions Chapter 6 Work, Energy, and Power

Post author: studyrate
Post published:
Post category: Class 11
Post comments: 0 Comments

In Class 11 Final Exams there will be Case studies and Passage Based Questions will be asked, So practice these types of questions. Study Rate is always there to help you. Free PDF Downloads of CBSE Class 11 Physics Chapter 6 Case Study and Passage-Based Question s with Answers were Prepared Based on the Latest Exam Pattern. Students can solve Class 11 Physics Case Study Questions Work, Energy, and Power to know their preparation level.

Join our Telegram Channel, there you will get various e-books for CBSE 2024 Boards exams for Class 9th, 10th, 11th, and 12th.

In CBSE Class 11 Physics Paper, There will be a few questions based on case studies and passage-based as well. In that, a paragraph will be given, and then the MCQ questions based on it will be asked.

Work, Energy, and Power Case Study Questions With Answers

Here, we have provided case-based/passage-based questions for Class 11 Physics Chapter 6 Work, Energy, and Power

Case Study/Passage-Based Questions

Case Study 1: The kinetic energy possessed by an object of mass, m, and moving with a uniform velocity, v is

case study questions class 11 physics chapter 6

Kinetic energy is a scalar quantity. The kinetic energy of an object is a measure of the work and The energy possessed by an object is thus measured in terms of its capacity of doing work. The unit of energy is, therefore, the same as that of work, that is, joule (J).

Work energy theorem: The change in kinetic energy of a particle is equal to the work done on it by the net force. Mathematically

K f – K i = W

Where K i and K f are respectively the initial and final kinetic energies of the object. Work refers to the force and the displacement over which it acts. Work is done by a force on the body over a certain displacement.

1) Kinetic energy is

a) Scalar quantity
b) Vector quantity
c) None of these

Answer: a) Scalar quantity

2) Which of the following has the same unit?

a) Potential energy and work
b) Kinetic energy and work
c) Force and weight
d) All of the above

Answer: d) All of the above

3) A car with an initial kinetic energy of 400 J is brought to a stop by applying brakes. How much work is done by the brakes? a) -400 J b) 0 J c) 400 J d) 800 J

Answer: a) -400 J

4) What happens to the kinetic energy of an object if its velocity is doubled? a) It remains the same. b) It becomes four times. c) It becomes half. d) It becomes twice.

Answer: b) It becomes four times.

5) According to the work-energy theorem, if a body’s kinetic energy decreases, the work done by the net force must be: a) Positive b) Negative c) Zero d) Infinite

Answer: b) Negative

What is the kinetic energy of an object with a mass of 10 kg and a velocity of 5 m/s? a) 125 J b) 250 J c) 500 J d) 50 J

Answer: a) 125 J

Case Study 2: The work-energy theorem states that – the change in the kinetic energy of a body is equal to the work done by the net force. In deriving the theorem, it is assumed that force is effective only in changing the KE. When the force and displacement are in the same direction, KE increases and work done is positive. When the force and displacement are in opposite directions, KE decreases and work done is negative. When the body is in uniform motion, KE does not change and work done by centripetal force is zero.

(i) A body of mass 10 kg initially at rest, acquires a velocity of 10 m/s. The work done is: (a) -500J (b) 500J (c) 50J (d) – 50J

Answer: (a) -500J

(ii) How much work must be done by a force on a 50 kg body in order to accelerate from rest to 20 m/s in 10 sec? (a) 10 3 J (b) 10 4 J (c) 2 X 10 3 J (d) 4 X 10 4 J

Answer: (b) 104 J

(iii) A gun of mass M fires a bullet of mass m with maximum speed v. The KE of gun will be? (a) ½ mv2 (b) 1/2 Mv2 (c) more than ½ mv2 (d) less than½ mv2

Answer: (d) less than½ mv2

(iv) An unloaded car moving with velocity v on a frictionless road can be stopped in a distance s. If the passengers add 40% to its weight and the breaking force remains the same then the stopping distance will be: (a) 1.4 s (b) 1.5 s (c) 1.6 s (d) 1.8 s

Answer: (a) 1.4 s

(v) A block of mass 10 kg is moving in the x direction with a constant speed of 10 m/s. It is subjected to a retarding force F = – 0.1 xj/m during its travel from x=20m to x=30m. Final KE will be (a) 250J (b) 275J (c) 450J (d) 475J

Answer: (d) 475J

Hope the information shed above regarding Case Study and Passage Based Questions for Class 11 Physics Chapter 6 Work, Energy, and Power with Answers Pdf free download has been useful to an extent. If you have any other queries about CBSE Class 11 Physics Work, Energy, and Power Case Study and Passage Based Questions with Answers, feel free to comment below so that we can revert back to us at the earliest possible. By Team Study Rate

Mcq questions class 11 business studies chapter 4 business services with answers, mcq questions class 11 english snapshots chapter 4 albert einstein at school with answers, mcq questions class 11 business studies chapter 9 small business with answers, leave a reply cancel reply.

Save my name, email, and website in this browser for the next time I comment.

This site uses Akismet to reduce spam. Learn how your comment data is processed .

The Topper Combo Flashcards

Contains the Latest NCERT in just 350 flashcards.
Colourful and Interactive
Summarised Important reactions according to the latest PYQs of NEET(UG) and JEE

No thanks, I’m not interested!

CBSE Expert

CBSE Case Study Questions Class 11 Physics PDF Download

Are you a Class 11 Physics student looking to enhance your understanding and prepare effectively for your exams? Look no further! In this comprehensive guide, we present a curated collection of CBSE Case Study Questions Class 11 Physics that will help you grasp the core concepts of Physics while reinforcing your problem-solving skills.

CBSE 11th Standard CBSE Physics question papers, important notes, study materials, Previous Year Questions, Syllabus, and exam patterns. Free 11th Standard CBSE Physics books and syllabus online. Important keywords, Case Study Questions, and Solutions.

Class 11 Physics Case Study Questions

CBSE Class 11 Physics question paper will have case study questions too. These case-based questions will be objective type in nature. So, Class 11 Physics students must prepare themselves for such questions. First of all, you should study NCERT Textbooks line by line, and then you should practice as many questions as possible.

Chapter-wise Solved Case Study Questions for Class 11 Physics

Chapter 1: Physical World
Chapter 2: Units and Measurements
Chapter 3: Motion in a Straight Line
Chapter 4: Motion in a Plane
Chapter 5: Laws of Motion
Chapter 6: Work, Energy, and Power
Chapter 7: System of Particles and Rotational Motion
Chapter 8: Gravitation
Chapter 9: Mechanical Properties of Solids
Chapter 10: Mechanical Properties of Fluids
Chapter 11: Thermal Properties of Matter
Chapter 12: Thermodynamics
Chapter 13: Kinetic Theory
Chapter 14: Oscillations
Chapter 15: Waves

Class 11 students should go through important Case Study problems for Physics before the exams. This will help them to understand the type of Case Study questions that can be asked in Grade 11 Physics examinations. Our expert faculty for standard 11 Physics have designed these questions based on the trend of questions that have been asked in last year’s exams. The solutions have been designed in a manner to help the grade 11 students understand the concepts and also easy-to-learn solutions.

Class 11 Books for Boards

Why Case Study Questions Matter

Case study questions are an invaluable resource for Class 11 Physics students. Unlike traditional textbook exercises, these questions simulate real-life scenarios, challenging students to apply theoretical knowledge to practical situations. This approach fosters critical thinking and helps students build a deep understanding of the subject matter.

Let’s delve into the different topics covered in this collection of case study questions:

1. Motion and Gravitation

In this section, we explore questions related to motion, velocity, acceleration, and the force of gravity. These questions are designed to test your grasp of the fundamental principles governing motion and gravitation.

2. Work, Energy, and Power

This set of questions delves into the concepts of work, energy, and power. You will encounter scenarios that require you to calculate work done, potential and kinetic energy, and power in various contexts.

3. Mechanical Properties of Solids and Fluids

This section presents case study questions about the mechanical properties of solids and fluids. From stress and strain calculations to understanding the behavior of fluids in different situations, these questions cover a wide range of applications.

4. Thermodynamics

Thermodynamics can be a challenging topic, but fear not! This part of the guide offers case study questions that will clarify the laws of thermodynamics, heat transfer, and thermal expansion, among other concepts.

5. Oscillations and Waves

Get ready to explore questions related to oscillations, simple harmonic motion, and wave characteristics. These questions will deepen your understanding of wave propagation and the behavior of oscillatory systems.

6. Kinetic Theory and Laws of Motion

Kinetic theory and the laws of motion can be complex, but with our case study questions, you’ll find yourself mastering these topics effortlessly.

Discover a wide array of questions dealing with light, lenses, and mirrors. This section will improve your problem-solving skills in optics and enhance your ability to analyze optical phenomena.

8. Electrical Effects of Current

Electricity and circuits are fundamental to physics. The case study questions in this section will challenge you to apply Ohm’s law, Kirchhoff’s laws, and other principles in various electrical circuits.

9. Magnetic Effects of Current

Delve into the fascinating world of magnets and magnetic fields. This set of questions will strengthen your understanding of magnetic effects and their applications.

10. Electromagnetic Induction

The final section covers electromagnetic induction, Faraday’s law, and Lenz’s law. You’ll be presented with scenarios that test your ability to predict induced electromotive forces and analyze electromagnetic phenomena.

In conclusion, mastering Class 11 Physics requires a thorough understanding of fundamental concepts and their practical applications. The case study questions provided in this guide will undoubtedly assist you in achieving a deeper comprehension of the subject.

Remember, practice is key! Regularly attempt these case study questions to strengthen your problem-solving abilities and boost your confidence for the exams. Happy studying, and may you excel in your Physics journey!

Download India's best Exam Preparation App Now.

Key Features

Revision Notes
Important Questions
Previous Years Questions
Case-Based Questions
Assertion and Reason Questions

No thanks, I’m not interested!

myCBSEguide

Class 11 Physics Case...

Class 11 Physics Case Study Questions

Table of Contents

myCBSEguide App

Download the app to get CBSE Sample Papers 2023-24, NCERT Solutions (Revised), Most Important Questions, Previous Year Question Bank, Mock Tests, and Detailed Notes.

Looking for complete and comprehensive case study questions for class 11 Physics? myCBSEguide is just a click away! With extensive study materials, sample papers, case study questions and mock tests, myCBSEguide is your one-stop solution for class 11 Physics exam preparation needs. So, what are you waiting for? Log on to myCBSEguide and get started today!

What is the purpose of physics?

Physics is the study of the fundamental principles governing the natural world. It is a vital part of the scientific enterprise, providing the foundation on which other sciences are built. Physics is essential for understanding how the world works, from the smallest particles to the largest structures in the Universe. In class 11 Physics, students are introduced to the basic concepts of physics and learn about the fundamental principles governing the natural world. Class 11 Physics concepts are essential for understanding the world around us and for further study in physics and other sciences.

What are case study questions in physics?

In physics, case study questions are intended to evaluate a student’s ability to apply theoretical principles to real-life situations. These questions usually ask the student to assess data from a specific experiment or setting in order to discover what physical principles are at play. Problem-solving and critical-thinking skills are developed through case study questions, which are an important aspect of physics education.

CBSE Case Study Questions in Class 11 Physics

CBSE Class 11 Physics question paper pattern includes case study questions. Class 11 Physics case study questions assess a student’s ability to apply physics principles to real-world environments. The questions are usually focused on a situation provided in the Class 11 Physics question paper, and they demand the student to answer the problem using their physics knowledge. Class 11 Physics case study questions are an important aspect of the CBSE physics curriculum. Class 11 Physics case study questions are a useful way to assess a student’s expertise in the subject.

Sample Class 11 Physics Case Study Questions

Expert educators at myCBSEguide have created a collection of Class 11 physics case study questions. The samples of Class 11 physics case study questions are given below. Class 11 physics case study questions are designed to test your understanding of the concepts and principles of physics. They are not meant to be easy, but they should be done if you have a good grasp of the subject. So, take a look at the questions and see how you fare. Good luck!

Class 11 Physics Case Study Question 1

Read the case study given below and answer any four subparts: Potential energy is the energy stored within an object, due to the object’s position, arrangement or state. Potential energy is one of the two main forms of energy, along with kinetic energy. Potential energy depends on the force acting on the two objects.

kinetic energy
potential energy
mechanical energy
none of these
potential energy decreases
potential energy increases
kinetic energy decreases
kinetic energy increases
only when spring is stretched
only when spring is compressed
both a and b
5 × 10 4 J
5 × 10 5 J

Answer Key:

Class 11 Physics Case Study Question 2

distance between body
source of heat
all of the above
convection and radiation
(b) convection
(d) all of the above
(a) convection
(a) increase
(c) radiation

Class 11 Physics Case Study Question 3

internal energy.
1 +(T 2 /T 1 )
(T 1 /T 2 )+1
(T 1 /T 2 )- 1
1 – (T 2 / T 1 )
increase or decrease depending upon temperature ratio
first increase and then decrease
(d) 1- (T 2 / T 1 )
(b) increase
(c) constant

Class 11 Physics Case Study Question 4

It is far away from the surface of the earth
Its surface temperature is 10°C
The r.m.s. velocity of all the gas molecules is more than the escape velocity of the moon’s surface
The escape velocity of the moon’s surface is more than the r.m.s velocity of all molecules
T(H 2 ) = T(N 2 )
T(H 2 ) < T(N 2 )
T(H 2 ) > T(N 2 )

The given samples of Class 11 Physics case study questions will help Class 11 Physics students to get an idea on how to solve it. These Class 11 Physics case study questions are based on the topics covered in the Class 11 Physics syllabus and are designed to test the student’s conceptual understanding. The questions are of varying difficulty levels and cover a wide range of topics. By solving these Class 11 Physics case study questions, students will be able to develop their problem-solving skills and improve their understanding of the concepts.

Examining Class 11 Physics syllabus

Senior Secondary school education is a transitional step from general education to a discipline-based curriculum concentration. The current curriculum of Class 11 Physics takes into account the rigour and complexity of the disciplinary approach, as well as the learners’ comprehension level. Class 11 Physics syllabus has also been carefully crafted to be similar to international norms.

The following are some of the Class 11 Physics syllabus’s most notable features:

Emphasis is placed on gaining a fundamental conceptual knowledge of the material.
Use of SI units, symbols, naming of physical quantities, and formulations in accordance with international standards are emphasised.
For enhanced learning, provide logical sequencing of subject matter units and suitable placement of concepts with their links.
Eliminating overlapping concepts/content within the field and between disciplines to reduce the curricular load.
Process skills, problem-solving ability, and the application of Physics principles are all encouraged.

CBSE Class 11 Physics (Code No. 042)

myCBSEguide: A true saviour for many students

myCBSEguide has been a true saviour for many students who struggle to find resources elsewhere. It is a reliable source of information and provides students with everything they need to excel in their academics. myCBSEguide has helped many students score high marks in their exams and has been a valuable resource for their studies. Teachers recommend myCBSEguide to all CBSE students. And best of all, it’s available 24/7, so you can study at your own pace, anytime, anywhere. So why wait? Get started today and see the difference myCBSEguide can make to your studies.

Test Generator

Create question paper PDF and online tests with your own name & logo in minutes.

Question Bank, Mock Tests, Exam Papers, NCERT Solutions, Sample Papers, Notes

Competency Based Learning in CBSE Schools
Class 11 Physical Education Case Study Questions
Class 11 Sociology Case Study Questions
Class 12 Applied Mathematics Case Study Questions
Class 11 Applied Mathematics Case Study Questions
Class 11 Mathematics Case Study Questions
Class 11 Biology Case Study Questions
Class 12 Physical Education Case Study Questions

Save my name, email, and website in this browser for the next time I comment.

CBSE Class 10th

CBSE Class 12th

UP Board 10th
UP Board 12th
Bihar Board 10th
Bihar Board 12th
Top Schools in India
Top Schools in Delhi
Top Schools in Mumbai
Top Schools in Chennai
Top Schools in Hyderabad
Top Schools in Kolkata
Top Schools in Pune
Top Schools in Bangalore

Products & Resources

JEE Main Knockout April
Free Sample Papers
Free Ebooks
NCERT Notes

NCERT Syllabus

NCERT Books
RD Sharma Solutions
Navodaya Vidyalaya Admission 2024-25

NCERT Solutions

NCERT Solutions for Class 12
NCERT Solutions for Class 11
NCERT solutions for Class 10
NCERT solutions for Class 9
NCERT solutions for Class 8
NCERT Solutions for Class 7
JEE Main 2024
MHT CET 2024
JEE Advanced 2024
BITSAT 2024
View All Engineering Exams
Colleges Accepting B.Tech Applications
Top Engineering Colleges in India
Engineering Colleges in India
Engineering Colleges in Tamil Nadu
Engineering Colleges Accepting JEE Main
Top IITs in India
Top NITs in India
Top IIITs in India
JEE Main College Predictor
JEE Main Rank Predictor
MHT CET College Predictor
AP EAMCET College Predictor
GATE College Predictor
KCET College Predictor
JEE Advanced College Predictor
View All College Predictors
JEE Main Question Paper
JEE Main Cutoff
JEE Main Advanced Admit Card
JEE Advanced Admit Card 2024
Download E-Books and Sample Papers
Compare Colleges
B.Tech College Applications
KCET Result
MAH MBA CET Exam
View All Management Exams

Colleges & Courses

MBA College Admissions
MBA Colleges in India
Top IIMs Colleges in India
Top Online MBA Colleges in India
MBA Colleges Accepting XAT Score
BBA Colleges in India
XAT College Predictor 2024
SNAP College Predictor
NMAT College Predictor
MAT College Predictor 2024
CMAT College Predictor 2024
CAT Percentile Predictor 2023
CAT 2023 College Predictor
CMAT 2024 Admit Card
TS ICET 2024 Hall Ticket
CMAT Result 2024
MAH MBA CET Cutoff 2024
Download Helpful Ebooks
List of Popular Branches
QnA - Get answers to your doubts
IIM Fees Structure
AIIMS Nursing
Top Medical Colleges in India
Top Medical Colleges in India accepting NEET Score
Medical Colleges accepting NEET
List of Medical Colleges in India
List of AIIMS Colleges In India
Medical Colleges in Maharashtra
Medical Colleges in India Accepting NEET PG
NEET College Predictor
NEET PG College Predictor
NEET MDS College Predictor
NEET Rank Predictor
DNB PDCET College Predictor
NEET Admit Card 2024
NEET PG Application Form 2024
NEET Cut off
NEET Online Preparation
Download Helpful E-books
Colleges Accepting Admissions
Top Law Colleges in India
Law College Accepting CLAT Score
List of Law Colleges in India
Top Law Colleges in Delhi
Top NLUs Colleges in India
Top Law Colleges in Chandigarh
Top Law Collages in Lucknow

Predictors & E-Books

CLAT College Predictor
MHCET Law ( 5 Year L.L.B) College Predictor
AILET College Predictor
Sample Papers
Compare Law Collages
Careers360 Youtube Channel
CLAT Syllabus 2025
CLAT Previous Year Question Paper
NID DAT Exam
Pearl Academy Exam

Predictors & Articles

NIFT College Predictor
UCEED College Predictor
NID DAT College Predictor
NID DAT Syllabus 2025
NID DAT 2025
Design Colleges in India
Top NIFT Colleges in India
Fashion Design Colleges in India
Top Interior Design Colleges in India
Top Graphic Designing Colleges in India
Fashion Design Colleges in Delhi
Fashion Design Colleges in Mumbai
Top Interior Design Colleges in Bangalore
NIFT Result 2024
NIFT Fees Structure
NIFT Syllabus 2025
Free Design E-books
List of Branches
Careers360 Youtube channel
IPU CET BJMC
JMI Mass Communication Entrance Exam
IIMC Entrance Exam
Media & Journalism colleges in Delhi
Media & Journalism colleges in Bangalore
Media & Journalism colleges in Mumbai
List of Media & Journalism Colleges in India
CA Intermediate
CA Foundation
CS Executive
CS Professional
Difference between CA and CS
Difference between CA and CMA
CA Full form
CMA Full form
CS Full form
CA Salary In India

Top Courses & Careers

Bachelor of Commerce (B.Com)
Master of Commerce (M.Com)
Company Secretary
Cost Accountant
Charted Accountant
Credit Manager
Financial Advisor
Top Commerce Colleges in India
Top Government Commerce Colleges in India
Top Private Commerce Colleges in India
Top M.Com Colleges in Mumbai
Top B.Com Colleges in India
IT Colleges in Tamil Nadu
IT Colleges in Uttar Pradesh
MCA Colleges in India
BCA Colleges in India

Diploma Colleges

Top Diploma Colleges in Maharashtra
UPSC IAS 2024
SSC CGL 2024
IBPS RRB 2024
Previous Year Sample Papers
Free Competition E-books
Sarkari Result
QnA- Get your doubts answered
UPSC Previous Year Sample Papers
CTET Previous Year Sample Papers
SBI Clerk Previous Year Sample Papers
NDA Previous Year Sample Papers

Upcoming Events

NDA Application Form 2024
UPSC IAS Application Form 2024
CDS Application Form 2024
CTET Admit card 2024
HP TET Result 2023
SSC GD Constable Admit Card 2024
UPTET Notification 2024
SBI Clerk Result 2024

Other Exams

SSC CHSL 2024
UP PCS 2024
UGC NET 2024
RRB NTPC 2024
IBPS PO 2024
IBPS Clerk 2024
IBPS SO 2024
Top University in USA
Top University in Canada
Top University in Ireland
Top Universities in UK
Top Universities in Australia
Best MBA Colleges in Abroad
Business Management Studies Colleges

Top Countries

Study in USA
Study in UK
Study in Canada
Study in Australia
Study in Ireland
Study in Germany
Study in China
Study in Europe

Student Visas

Student Visa Canada
Student Visa UK
Student Visa USA
Student Visa Australia
Student Visa Germany
Student Visa New Zealand
Student Visa Ireland
CUET PG 2024
IGNOU B.Ed Admission 2024
DU Admission 2024
UP B.Ed JEE 2024
LPU NEST 2024
IIT JAM 2024
IGNOU Online Admission 2024
Universities in India
Top Universities in India 2024
Top Colleges in India
Top Universities in Uttar Pradesh 2024
Top Universities in Bihar
Top Universities in Madhya Pradesh 2024
Top Universities in Tamil Nadu 2024
Central Universities in India
CUET Exam City Intimation Slip 2024
IGNOU Date Sheet
CUET Mock Test 2024
CUET Admit card 2024
CUET PG Syllabus 2024
CUET Participating Universities 2024
CUET Previous Year Question Paper
CUET Syllabus 2024 for Science Students
E-Books and Sample Papers
CUET Exam Pattern 2024
CUET Exam Date 2024
CUET Cut Off 2024
CUET Exam Analysis 2024
IGNOU Exam Form 2024
CUET 2024 Exam Live
CUET Answer Key 2024

Engineering Preparation

Knockout JEE Main 2024
Test Series JEE Main 2024
JEE Main 2024 Rank Booster

Medical Preparation

Knockout NEET 2024
Test Series NEET 2024
Rank Booster NEET 2024

Online Courses

JEE Main One Month Course
NEET One Month Course
IBSAT Free Mock Tests
IIT JEE Foundation Course
Knockout BITSAT 2024
Career Guidance Tool

Top Streams

IT & Software Certification Courses
Engineering and Architecture Certification Courses
Programming And Development Certification Courses
Business and Management Certification Courses
Marketing Certification Courses
Health and Fitness Certification Courses
Design Certification Courses

Specializations

Digital Marketing Certification Courses
Cyber Security Certification Courses
Artificial Intelligence Certification Courses
Business Analytics Certification Courses
Data Science Certification Courses
Cloud Computing Certification Courses
Machine Learning Certification Courses
View All Certification Courses
UG Degree Courses
PG Degree Courses
Short Term Courses
Free Courses
Online Degrees and Diplomas
Compare Courses

Top Providers

Coursera Courses
Udemy Courses
Edx Courses
Swayam Courses
upGrad Courses
Simplilearn Courses
Great Learning Courses

NCERT Solutions for Class 11 Physics Chapter 6 Work Energy and Power

NCERT Solutions for Class 11 Physics Chapter 6 – Download Free PDF

NCERT Solutions for Class 11 Physics Chapter 6 Work Energy and Power play a crucial role in the mechanics section of the 11th grade. Moreover, this chapter of NCERT Solution serves as the cornerstone for several subsequent chapters. To achieve high scores in your Class 11 exams or competitive tests like JEE and NEET, it's essential to grasp work energy and power Class 11 numericals with solutions thoroughly and efficiently tackle its questions.

JEE Main Scholarship Test Kit (Class 11): Narayana | Physics Wallah | Aakash | Unacademy

NEET Scholarship Test Kit (Class 11): Narayana | Physics Wallah | Aakash | ALLEN

Suggested: JEE Main: high scoring chapters | Past 10 year's papers

New: Aakash iACST Scholarship Test. Up to 90% Scholarship. Register Now

NCERT Solutions for Class 11 Physics Chapter 6 Work, Energy and Power

Ncert solutions for class 11 physics chapter 6 work energy and power - exercise questions, ncert solutions for class 11 physics chapter 6 work energy and power additional exercise, ncert solutions for class 11 physics chapter wise, tips to score good marks in class 11 physics chapter 6 ncert solutions, some of the main points on work energy and power class 11 topic-collisions, importance of ncert solutions for class 11 physics chapter 6 work energy and power, subject wise ncert exemplar solutions, subject wise ncert solutions.

On this page of Careers360, you will find comprehensive class 11 physics chapter 6 exercise solutions from Question 6.1 to 6.30. along with, additional exercise questions designed by subject experts. These solutions are presented in a clear, step-by-step manner that is easy to understand.

Consider that you are carrying a 10 Kg stationary in your hand and you are not moving. In this situation, you are doing work physically according to you. But according to physics, you are doing zero work. Can you find out why work is zero here? Work Energy and Power ch 6 Physics class 11 has questions based on the concepts of work and types of work, the relation between work and energy and the concept of power. In the CBSE NCERT solutions for Class 11 Physics Chapter 6 Work Energy and Power , you will study problems on the law of conservation of energy (energy can be neither created nor destroyed).

NCERT solutions for Class 11 Physics Chapter 6 Work Energy and Power also give answers to the questions based on the concepts of collision, which are important for the exam. Solutions of NCERT are helpful in scoring well in class and board exams. Solutions for both exercise and additional exercise in the NCERT are given. Students can also download Work Energy and Power Class 11 NCERT solutions pdf by clicking on the link download PDF for free.

NCERT Class 11 Physics Chapter 6 Exercise Solutions pdf download for free.

** According to the CBSE Syllabus for the academic year 2023-24, the chapter you previously referred to as Chapter 6, "Work, Energy and Power" has been renumbered as Chapter 5.

Download PDF

Q1(a) The sign of work done by a force on a body is important to understand. State carefully if the following quantities are positive or negative:

work done by a man in lifting a bucket out of a well by means of a rope tied to the bucket.

In this case, the direction of force and displacement are the same, this work done is positive .

Q1(b) The sign of work done by a force on a body is important to understand. State carefully if the following quantities are positive or negative: (b) work done by gravitational force in the above case

In this case, the direction of displacement is upward and the direction of force is downward. Thus work done is negative in nature.

Q1 (c) The sign of work done by a force on a body is important to understand. State carefully if the following quantities are positive or negative: work done by friction on a body sliding down an inclined plane,

We know that friction acts in the direction opposite to the direction of motion. Hence work done by the frictional force is negative .

Q 1 (d) The sign of work done by a force on a body is important to understand. State carefully if the following quantities are positive or negative: work done by an applied force on a body moving on a rough horizontal plane with uniform velocity

In this case, the applied force supports the motion of the object (balances frictional force). Thus work done by the force is positive .

Q1 (e) The sign of work done by a force on a body is important to understand. State carefully if the following quantities are positive or negative: work done by the resistive force of air on a vibrating pendulum in bringing it to rest.

Work done in this case is negative as the direction of force and motion are not identical.

Q2 (a) A body of mass 2 kg initially at rest moves under the action of an applied horizontal force of 7 N on a table with coefficient of kinetic friction = 0.1. Compute the work done by the applied force in 10 s,

Using Newton's law we can write :

$a\ =\ \frac{F}{m}$

The frictional force is given by :

$f\ =\ \mu mg$

Its direction will be opposite of the direction of the motion. Thus acceleration produced will be negative.

$a\ =\ \frac{-1.96}{2}\ =\ -0.98\ m/s^2$

Thus the net acceleration is = 3.5 - 0.98 = 2.52 m/s 2 .

The total distance travelled is given by :

$s\ =\ ut\ +\ \frac{1}{2}at^2$

Hence the work done by applied force is given by :

$W\ =\ F.s\ =\ 7\times 126\ =\ 882\ J$

Q2 (b) A body of mass 2 kg initially at rest moves under the action of an applied horizontal force of 7 N on a table with coefficient of kinetic friction = 0.1. Compute the work done by friction in 10 s,

The work done by frictional force will be negative as the force opposes the motion.

$W\ =\ f.s\ =\ -1.96\times 126\ =\ -247\ J$

Q2 (c) A body of mass 2 kg initially at rest moves under the action of an applied horizontal force of 7 N on a table with coefficient of kinetic friction = 0.1. Compute the work done by the net force on the body in 10 s,

The net work done will be the sum of work done by applied force and work done by frictional force.

$W\ =\ 882\ -\ 247\ =\ 635\ J$

Q2 (d) A body of mass 2 kg initially at rest moves under the action of an applied horizontal force of 7 N on a table with coefficient of kinetic friction = 0.1. Compute the change in kinetic energy of the body in 10 s

It is given that initial velocity is zero. The final velocity can be calculated by the equation of motion :

$v\ =\ u\ +\ at$

Thus change is kinetic energy is :

$\Delta K\ =\ \frac{1}{2}mv^2\ -\ \frac{1}{2}mu^2$

Total energy = kinetic energy (KE) + potential energy(PE)

KE > 0 since m and v 2 is positive. If KE <0 particles cannot be find. If PE>TE, then KE<0 (now in all graph check for this condition)

In case 1 kinetic energy is negative for x<a. So at x<a particle cannot be found.

In case 2 for x<a and for x> b kinetic energy is negative. So the particle cannot be found in these regions.

$a<x<b$

The kinetic energy in this case is given by :

$K.E.\ =\ E\ -\ (-V_1)\ =\ E\ +\ V_1$

And the minimum energy of particle is - V 1 .

In the fourth case , the particle will not exist in the states which will have potential energy greater than the total energy.

$\frac{-b}{2}<x<\frac{b}{2}$

The minimum energy of particle will be - V 1 as it is the minimum potential energy.

$V ( x ) = k x^2 /2$

The total energy of the particle is given by :

$E\ =\ K.E\ +\ P.E$

At the extreme position, the velocity of the object is zero thus its kinetic energy at that point is zero.

$E\ =\ \frac{1}{2} kx^2$

Q5 (a) Answer the following : The casing of a rocket in flight burns up due to friction. At whose expense is the heat energy required for burning obtained? The rocket or the atmosphere?

The total energy is given by :

$=\ \frac{1}{2}mv^2\ +\ mgh$

The burning of casing results in a reduction in the mass of the rocket. This leads to a lowering in the total energy.

Thus heat required for burning is obtained from the expenses of the rocket .

Q5 (b) Comets move around the sun in highly elliptical orbits. The gravitational force on the comet due to the sun is not normal to the comet’s velocity in general. Yet the work done by the gravitational force over every complete orbit of the comet is zero. Why?

This is because the gravitational force is a conservative force. And we know that the work done by a conservative force in a closed path is always zero. That's why the work done by the gravitational force is zero in a complete orbit revolution.

Q5 (c) An artificial satellite orbiting the earth in very thin atmosphere loses its energy gradually due to dissipation against atmospheric resistance, however small. Why then does its speed increase progressively as it comes closer and closer to the earth?

The total energy of artificial satellite remains constant. Thus when it approaches towards the earth the distance between them decreases. This results in a decrease in the potential energy of the satellite. By energy conservation, the kinetic energy of satellite increases and so does the velocity.

Q5 (d) In Fig. 6.13(i) the man walks 2 m carrying a mass of 15 kg on his hands. In Fig. 6.13(ii), he walks the same distance pulling the rope behind him. The rope goes over a pulley, and a mass of 15 kg hangs at its other end. In which case is the work done greater?

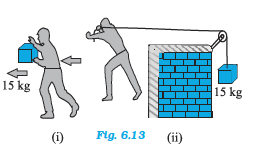
In the first case,

Work done is :

$W\ =\ F.s\ =\ Fs \cos \Theta$

In the second case :

$W\ =\ Fs \cos \Theta$

Thus work done in the second case is greater than the first case.

Q6 (a) When a conservative force does positive work on a body, the potential energy of the body increases/decreases/remains unaltered.

It is given that work done by the conservative force is positive, thus the force acts in the direction of the motion. This results in a decrease in distance between the bodies. Thus it's potential energy decreases .

Q6 (b) Work done by a body against friction always results in a loss of its kinetic/potential energy.

Work done by the body against friction results in a decrease in the velocity of the body. Thus the kinetic energy of the body decreases.

Q6 (c) The rate of change of total momentum of a many-particle system is proportional to the external force/sum of the internal forces on the system.

The internal force cannot produce a change in the total momentum as no external force is acting. Thus the change in total momentum is proportional to the external forces acting on the body.

Q6(d) In an inelastic collision of two bodies, the quantities which do not change after the collision are the total kinetic energy/total linear momentum/total energy of the system of two bodies.

The conservation of total linear momentum doesn't depend upon the fact whether it is an elastic collision or an inelastic collision.

Q7(a) State if each of the following statements is true or false. Give reasons for your answer.

In an elastic collision of two bodies, the momentum and energy of each body is conserved.

False: - The linear momentum and energy will be conserved if both are considered in a system. But for individual bodies, this conservation of momentum and energy doesn't hold. This is because the impact during the collision may transfer energy/momentum of one ball to the other ball.

Q7 (b) State if each of the following statements is true or false. Give reasons for your answer. (b) Total energy of a system is always conserved, no matter what internal and external forces on the body are present.

False: - Internal forces will not change the energy of the system but external forces can change the total energy by changing their magnitude or direction.

Q7 (c) State if each of the following statements is true or false. Give reasons for your answer. Work done in the motion of a body over a closed loop is zero for every force in nature.

False:- This is true only for conservative forces e.g. gravitational force. For e.g in case of frictional force (non-conservative force), the work done in a closed-loop cannot be zero as energy is wasted throughout.

Q7 (d) State if each of the following statements is true or false. Give reasons for your answer. In an inelastic collision, the final kinetic energy is always less than the initial kinetic energy of the system.

True but not always:- In the case of inelastic collisions, few amounts of energy is converted into other forms of energy such as sound or in deformation. Thus final kinetic energy is always less as compared to initial kinetic energy. But in case of the explosion of a bomb final kinetic energy is greater than the initial kinetic energy

Q8 (a) Answer carefully, with reasons: In an elastic collision of two billiard balls, is the total kinetic energy conserved during the short time of collision of the balls (i.e. when they are in contact)?

No, because at the time of the collision, the kinetic energy is converted to the potential energy. Thus total kinetic energy is not constant at the collision.

Q8 (b) Is the total linear momentum conserved during the short time of an elastic collision of two balls?

Yes, in case of elastic collision the total linear momentum of the system remains conserved as no external force is acting on the system of balls.

Q8 (c) What are the answers to (a) and (b) for an inelastic collision?

The total kinetic energy of the system cannot be conserved in case of inelastic collision as there is loss of energy in the form of deformation. But the total linear momentum of the system remains constant even in the case of inelastic collision as no external force is acting.

Q8 (d) If the potential energy of two billiard balls depends only on the separation distance between their centres, is the collision elastic or inelastic? (Note, we are talking here of potential energy corresponding to the force during collision, not gravitational potential energy).

Since the potential energy of the system depends upon the separation between the bodies thus the forces acting on the body are conservative in nature. We know that conservative forces produce elastic collisions.

$(i) t^{1/2}\: \: (ii) t \: \: (iii) t^{3/2}\: \: (iv) t^2$

It is given that acceleration is constant thus force will also be constant (by Newton's law of motion F = ma).

$a\ =\ \frac{dv}{dt}\ =\ constant$

Now, the work done by the force is given by :

$P\ =\ F.v$

Hence power is directly proportional to the time.

Q10 A body is moving unidirectionally under the influence of a source of constant power. Its displacement in time t is proportional to

We know that the power is given by :

$=\ ma.v$

It is given that power is constant, thus :

$mv\frac{dv}{dt}\ =\ constant$

By integrating both sides, we get

$v\ =\ \left ( \sqrt{\frac{2Ct}{m}} \right )$

Also, we can write :

$v\ =\ \frac{dx}{dt}$

By integrating we get the relation :

$x\ \propto \ \ t^\frac{3}{2}$

Force is given to be :

And the displacement is :

$s\ =\ 4 \hat k\ m$

Thus the work done is given by :

$W\ =\ F.s$

The kinetic energy of the electron is given by :

$K_e\ =\ \frac{1}{2}mv_e^2$

Thus velocity is obtained as :

$v_e\ =\ \sqrt{\frac{2\times 1.6\times 10^{-15}}{9.11\times 10^{-31}}}$

Similarly, we can find the velocity of the proton :

$K_p\ =\ \frac{1}{2}mv_p^2$

Thus the ratio of their velocities is :

$\frac{v_e}{v_p}\ =\ \frac{5.93\times 10^{7}}{4.38\times 10^6}\ =\ 13.54$

The volume of the drop is :

$V\ =\ \frac{4}{3}\pi r^3\ =\ \frac{4}{3}\times 3.14\times (2\times 10^{-3})^3$

Thus the mass of raindrop is :

$m\ =\ \rho v$

Now the total energy at the peak point is :

$E_p\ =\ mgh\ +\ 0\ =\ mgh$

And the energy at the ground is :

$E_b\ =\ 0\ +\ \frac{1}{2}mv^2\ =\ \frac{1}{2}mv^2$

Thus work done by the resistive force is :

$=\ 1.67\times 10^{-3} \ J\ -\ 0.164\ J\ =\ -\ 0.162\ J$

The momentum is conserved in the collision as no external force is acting on the system. In the given case the rebound velocity is the same as the initial velocity thus the kinetic energy of the molecule initially and finally are same. Hence this is an elastic collision.

Q15 A pump on the ground floor of a building can pump up water to fill a tank of volume 30 m 3 in 15 min. If the tank is 40 m above the ground, and the efficiency of the pump is 30%, how much electric power is consumed by the pump?

Mass of the water is :

$=\ 30\times10^3 \ Kg$

Thus the output power is given by :

$Power\ =\ \frac{Work\ done}{Time}$

Also, we are given that efficiency is 30 per cent.

Thus the input power is :

$P_i\ =\ \frac{13.067}{\frac{30}{100}}\times 10^3$

Q16 Two identical ball bearings in contact with each other and resting on a frictionless table are hit head-on by another ball bearing of the same mass moving initially with a speed V. If the collision is elastic, which of the following (Fig. 6.14) is a possible result after collision?

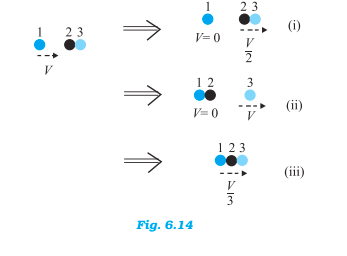
The initial kinetic energy of the system is given by :

$=\ \frac{1}{2}mv^2\ -\ \frac{1}{2}2m(0)$

Case (i):- The final kinetic energy is :

$=\ \frac{1}{2}m.0\ -\ \frac{1}{2}2m(\frac{v}{2})^2\ =\ \frac{1}{4}mv^2$

Thus the kinetic energy is not conserved in this case.

Case (ii):- The final kinetic energy is :

$=\ \frac{1}{2}2m.0\ -\ \frac{1}{2}mv^2\ =\ \frac{1}{2}mv^2$

Thus kinetic energy is conserved in this case.

Case (iii):- The final kinetic energy is:-

$=\ \frac{1}{2}\times 3m\times \left ( \frac{v}{3} \right )^2$

Q17 The bob A of a pendulum released from 30o to the vertical hits another bob B of the same mass at rest on a table as shown in Fig. 6.15. How high does the bob A rise after the collision? Neglect the size of the bobs and assume the collision to be elastic.

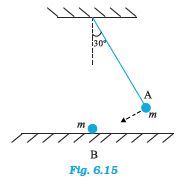
This is an elastic collision thus the transfer of momentum will take place. It is given that bob B is at rest and bob A has some velocity. So in momentum transfer, bob B will gain the velocity in the left direction whereas bob A will come to rest (complete momentum transfer takes place).

Hence bob A will not rise.

Q18 The bob of a pendulum is released from a horizontal position. If the length of the pendulum is 1.5 m, what is the speed with which the bob arrives at the lowermost point, given that it dissipated 5% of its initial energy against air resistance?

Consider the extreme position (horizintal) :-

The kinetic energy at this position is zero as velocity is zero.

$=\ mgl\ +\ 0 \ =\ mgl$

Now consider the mean position (lowermost point) :

Here the potential energy of bob is zero.

Whereas kinetic energy is :

Further, it is given that 5 per cent of energy is dissipated due to air resistance while coming down.

Thus energy equation becomes (conservation of energy):-

$\frac{1}{2}mv^2\ =\ \frac{95}{100}\times mgl$

Since the sand is falling in the trolley thus the force generated on the system (trolley and sandbag) is an internal force. There is no external force thus momentum of the system doesn't change. Hence speed remains the same i.e., 27 Km/hr.

$v = ax ^{3/2}$

The relation between work done and the kinetic energy is given by :

$Work\ =\ \frac{1}{2}mv^2\ -\ \frac{1}{2}mu^2$

Initial velocity = 0 (at x = 0 )

$10\sqrt{2}\ m/s$

Thus work done is :

$Work\ =\ \frac{1}{2}m(v^2\ -\ u^2)$

Q21 (a) The blades of a windmill sweep out a circle of area A. If the wind flows at a velocity v perpendicular to the circle, what is the mass of the air passing through it in time t?

$Av$

Q21 (b) The blades of a windmill sweep out a circle of area A. What is the kinetic energy of the air?

The kinetic energy is given by :

$=\ \frac{1}{2}\ \rho Avt\ v^2$

It is given that 25 per cent of wind energy is converted into electrical energy.

Thus electric energy produced is :

$=\ \frac{25}{100} \times \frac{1}{2}\ \rho At v^3$

Now the electric power is given by :

$Power\ =\ \frac{Energy}{Time}$

Q22 (a) A person trying to lose weight (dieter) lifts a 10 kg mass, one thousand times, to a height of 0.5 m each time. Assume that the potential energy lost each time she lowers the mass is dissipated. How much work does she do against the gravitational force?

The work done against the gravitational force is given by :

$\times$

Efficiency is given to be 20 per cent.

Thus energy supplied by the person :

$=\ \frac{20}{100}\times 3.8\times 10^7$

Thus the amount of fat lost is :

$=\ \frac{49\times 10^3}{\frac{20}{100}\times 3.8\times 10^7}$

Q23 (a) A family uses 8 kW of power. Direct solar energy is incident on the horizontal surface at an average rate of 200 W per square meter. If 20% of this energy can be converted to useful electrical energy, how large an area is needed to supply 8 kW?

It is given that the efficiency of energy conversion is 20 per cent.

According to question, we can write (equating power used by family) :

$8\times 10^3\ =\ \frac{20}{100}\times A\times 200$

Thus required area is 200 m 2 .

Q23 (b) A family uses 8 kW of power. Compare this area to that of the roof of a typical house.

$14 \times 14\ m^2$

This is nearly equal to the area required for the production of the given amount of electricity.

$70 ms^{-1}$

We are given :

Mass of the bullet m: 0.012 Kg

Mass of the block M: 0.4 Kg

The initial velocity of the bullet u: 70 m/s

The initial velocity of the block : 0

The final velocity of the system (bullet + block): v

For finding the final speed of system we will apply the law of conservation of momentum :

$mu_b\ +\ M(0)\ =\ (m\ +\ M)v$

Now for the system, we will apply the law of conservation of energy :

The potential energy at the highest point = Kinetic energy at the lowest point

$(m+M)gh\ =\ \frac{1}{2}(m+M)v^2$

Hence heat produced is :

$=\ \frac{1}{2}mu^2\ -\ \frac{1}{2}(m\ +\ M)v^2$

The FBD of the track is shown in the figure below :

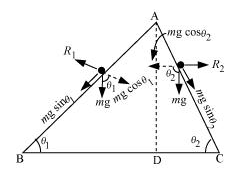
Using the law of conservation of energy we have :

$\frac{1}{2}mv_1^2\ =\ \frac{1}{2}mv_2^2$

Hence both stones will reach the bottom with the same speed.

For stone 1 we can write :

$F\ =\ mg\sin \Theta_1$

For stone 2 we have :

$a_2\ =\ g\sin \Theta_2$

Also, using the equation of motion,

$t\ =\ \frac{v}{a}$

Hence, the stone travelling on the steep plane will reach before.

For finding speed and time we can use conservation of energy.

$mgh\ =\ \frac{1}{2}mv^2$

And the time is given by :

$t_1\ =\ \frac{v}{a_1}\ =\ \frac{14}{9.8\times \sin 30^{\circ}}\ =\ 2.86\ s$

Displacement (x) of the block is given as : = 0.1 m.

Using equilibrium conditions we can write :

$R\ =\ mg \cos 37^{\circ}$

We can write work done in terms of potential energy as :

$mg\ \left ( \sin 37^{\circ}\ -\ \mu \cos 37^{\circ} \right )x\ =\ \frac{1}{2}kx^2$

Thus the coefficient of friction is 0.125.

$7 m s ^{-1}$

In this case, the heat produced is the loss in the potential energy.

heat produced = mg h

$=\ 0.3\times 9.8\times 3$

The heat produced (when the lift is stationary) will remain the same as the relative velocity of the bolt with respect lift still remains zero.

$4 ms ^{-1}$

The initial momentum of the system (boy + trolley) is given as :

$=\ (m\ +\ M)V$

Now assume v ' is the final velocity of the trolley with respect to the ground.

Then the final momentum will be :

$=\ Mv'\ +\ m(v'\ -\ 4)\ =\ 220v'\ -\ 80$

Conserving momentum :

$220v'\ -\ 80\ =\ 2200$

The time taken by the boy is :

$=\ \frac{10}{4}\ =\ 2.5\ s$

Hence the distance moved by the trolley is :

$=\ 10.36\times 2.5 \ =\ 25.9\ m$

Q29 Which of the following potential energy curves in Fig. 6.18 cannot possibly describe the elastic collision of two billiard balls? Here r is the distance between centres of the balls.

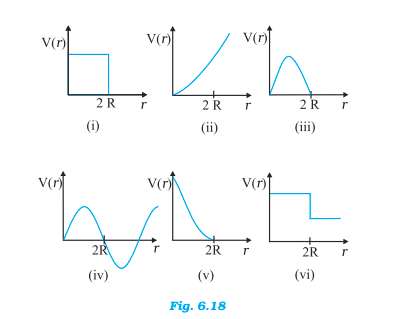
The potential energy of the system depends inversely on the separation between the balls. Thus the potential energy will decrease as the balls will come closer and will become zero as they touch each other.

Thus elastic collision is best described only by the graph (v).

Q30 Consider the decay of a free neutron at rest: Show that the two-body decay of this type must necessarily give an electron of fixed energy and, therefore, cannot account for the observed continuous energy distribution in the of a neutron or a nucleus (Fig. 6.19).

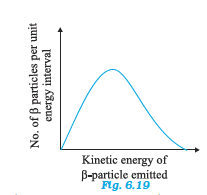
By Einstein’s mass-energy relation we can write :

$Energy\ =\ \Delta mc^2$

class 11 physics chapter 6 ncert solutions consist of a total of thirty questions. These questions cover topics such as basic work energy and Power, Enistein's mass-energy relation, friction in an inclined plane, total energy and more. Step-by-step solutions made by subject matter experts of Careers360 can provide students with a comprehensive understanding of these concepts and help them prepare for exams. By studying NCERT Solutions for Class 11 Physics Chapter 6 PDF, students can improve their problem-solving skills and gain confidence in their ability to tackle physics problems.

Class 11 Physics chapter 6 exercise solutions: Important Formulas and Diagrams + eBook link

Knowing how important formulas and diagrams are in Class 11th Physics, Chapter 6 NCERT Solutions is key. These tools really help understand concepts and solve problems well. To help you learn better, here are the important formulas and diagrams for this chapter:

$W= Fcos\theta \times \bigtriangleup s=\vec{F}.\Delta s=\int \vec{F} \cdot \mathrm{d} \vec{S}$

[SI unit = joule (J) and dimension = ML 2 T 2 ]

Kinetic energy

(KE) = 1/2mv 2 =P 2 /2m

Potential Energy

U SPRING = 1/2kx 2

Work-Energy Theorem

W = Change in K. E. of a body =Δ KE

To score good marks in Physics Class 11 Chapter 6, you can follow these steps using NCERT Solutions:

Understand the Concepts: Read the chapter work power energy class 11 thoroughly to understand the concepts and principles involved in it. Try to understand the definitions, laws, and equations used in the chapter.

NCERT solution: Use chapter 6 physics class 11 ncert solutions provided on our careers360 website. These solutions provide detailed explanations and solutions to all the problems given in the textbook.

Practice Problems: Practice the problems provided in the NCERT Solutions chapter-wise and try to solve them on your own. This will help you understand the concepts better and improve your problem-solving skills.

Revise Regularly: Revise the concepts regularly to ensure that you have a strong foundation in the subject.

Solve Sample Papers and Previous Years' Question Papers: Practice sample papers and previous years' question and NCERT Exemplar Class 11 Physics Solutions .

By following these steps, you can use the class 11th physics chapter 6 ncert solutions to score good marks in your exams.

For an elastic collision, Law of conservation of momentum and that of Kinetic Energy holds good
For inelastic collision Law of conservation of momentum hold good but kinetic energy is not conserved
Coefficient of restitution is the ratio of relative velocity after the collision to relative velocity before the collision
For a perfectly elastic collision coefficient of restitution is one
For inelastic collision coefficient of restitution is less than one
For a perfectly inelastic collision coefficient of restitution is zero

Key Features of NCERT Class 11 physics chapter 6 exercise solutions

Expert-Crafted Solutions: The work energy and power class 11 numericals with solutions have been meticulously prepared by subject matter experts, ensuring a comprehensive understanding of each question. The use of simple language makes it easier for students to follow along.

Thorough Explanation: All thirty questions in the exercise are explained in detail, breaking down each step to clarify the reasoning behind the solution approach. This helps students grasp not only the answer but also the underlying concepts.

Additional Exercise Questions: In addition to the main exercise questions, there are extra practice questions included. These extra questions are designed to enhance problem-solving skills and reinforce the chapter's concepts.

Comprehensive Coverage: The class 11th physics chapter 6 ncert solutions cover all aspects of the chapter, including key concepts, formulas, and diagrams. This ensures a well-rounded understanding of the topics discussed in Chapter 6.

Easy Accessibility: Students can access these solutions conveniently, enabling them to study and revise the chapter effectively, ultimately leading to a stronger grasp of the subject matter.

Many questions were answered in the solutions of NCERT Class 11 Physics chapter 6 Work Energy and Power based on the concept of the work-energy theorem which is important throughout the physics course. The concept will be used in class 12 also.
NCERT solutions for class 11 will help to score well in-class exams and also competitive exams like NEET.
Learning NCERT solutions will help to solve problems from other reference books also.

NCERT Physics Exemplar Solutions Class 11 For All The Chapters:

NCERT Exemplar Class 11th Solutions
NCERT Exemplar Class 11th Maths
NCERT Exemplar Class 11th Physics
NCERT Exemplar Class 11th Chemistry
NCERT Exemplar Class 11th Biology

Also Check NCERT Books and NCERT Syllabus here

NCERT Books Class 11 Physics
NCERT Syllabus Class 11 Physics
NCERT Books Class 11
NCERT Syllabus Class 11
NCERT solutions for class 11 Mathematics
NCERT solutions for class 11 Chemistry
NCERT solutions for class 11 Physics
NCERT solutions for class 11 Biology

Frequently Asked Question (FAQs)

On an average 4% questions are asked for NEET from Work Energy and Power. To prepare for NEET exam NCERT book is the one of the preffered materials. Along with NCERT exercise questions students can also practice NCERT exemplar and NEET previous year papers.

One or two question can be expected from the chapter Work Energy and Power for JEE Main based on the previous year paper analysis. But the concepts studied in Work Energy and Power Class 11 chapter will be used in other chapters of Class 11 and Class 12 Physics.

In Class 11 more analysis is done using Mathematics (vector and calculus) and some more concepts are added. The concepts of collision is not explained in the Class 9 NCERT Science book.

To download the PDF version of work energy and power class 11 solutions click on NCERT Solutions for Class 11 Physics and select the chapter according to your comfort and click on the download PDF.

A collision is an event that happens when two objects come into direct contact with each other and exert forces on each other for a relatively short period of time. This can involve two or more bodies interacting with one another, resulting in changes in their motion and momentum.

Latest Articles
Popular Articles

Upcoming School Exams

National institute of open schooling 12th examination.

Admit Card Date : 28 March,2024 - 22 May,2024

National Institute of Open Schooling 10th examination

Uttar pradesh board 12th examination.

Application Date : 07 May,2024 - 31 May,2024

Uttar Pradesh Board 10th examination

Exam Date : 07 May,2024 - 31 May,2024

Goa Board Higher Secondary School Certificate Examination

Admit Card Date : 13 May,2024 - 07 June,2024

Colleges After 12th

Popular course after 12th.

DUET (DU JAT)
BHU UET,BUMAT,
MAH CET Law
JEE Advanced
COMEDK UGET
JEE Main Paper 2
AAT (JEE Advanced)
ISI Admission Test

Applications for Admissions are open.

Aakash iACST Scholarship Test 2024

Get up to 90% scholarship on NEET, JEE & Foundation courses

ALLEN Digital Scholarship Admission Test (ADSAT)

JEE Main Important Physics formulas

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

PW JEE Coaching

Enrol in PW Vidyapeeth center for JEE coaching

PW NEET Coaching

Enrol in PW Vidyapeeth center for NEET coaching

JEE Main Important Chemistry formulas

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

Explore on Careers360

Board Exams
Top Schools
Navodaya Vidyalaya
NCERT Solutions for Class 10
NCERT Solutions for Class 9
NCERT Solutions for Class 8
NCERT Solutions for Class 6

NCERT Exemplars

NCERT Exemplar
NCERT Exemplar Class 9 solutions
NCERT Exemplar Class 10 solutions
NCERT Exemplar Class 11 Solutions
NCERT Exemplar Class 12 Solutions
NCERT Books for class 6
NCERT Books for class 7
NCERT Books for class 8
NCERT Books for class 9
NCERT Books for Class 10
NCERT Books for Class 11
NCERT Books for Class 12
NCERT Notes for Class 9
NCERT Notes for Class 10
NCERT Notes for Class 11
NCERT Notes for Class 12
NCERT Syllabus for Class 6
NCERT Syllabus for Class 7
NCERT Syllabus for class 8
NCERT Syllabus for class 9
NCERT Syllabus for Class 10
NCERT Syllabus for Class 11
NCERT Syllabus for Class 12
CBSE Date Sheet
CBSE Syllabus
CBSE Admit Card
CBSE Result
CBSE Result Name and State Wise
CBSE Passing Marks

CBSE Class 10

CBSE Board Class 10th
CBSE Class 10 Date Sheet
CBSE Class 10 Syllabus
CBSE 10th Exam Pattern
CBSE Class 10 Answer Key
CBSE 10th Admit Card
CBSE 10th Result
CBSE 10th Toppers
CBSE Board Class 12th
CBSE Class 12 Date Sheet
CBSE Class 12 Admit Card
CBSE Class 12 Syllabus
CBSE Class 12 Exam Pattern
CBSE Class 12 Answer Key
CBSE 12th Result
CBSE Class 12 Toppers

CISCE Board 10th

ICSE 10th time table
ICSE 10th Syllabus
ICSE 10th exam pattern
ICSE 10th Question Papers
ICSE 10th Result
ICSE 10th Toppers
ISC 12th Board
ISC 12th Time Table
ISC Syllabus
ISC 12th Question Papers
ISC 12th Result
IMO Syllabus
IMO Sample Papers
IMO Answer Key
IEO Syllabus
IEO Answer Key
NSO Syllabus
NSO Sample Papers
NSO Answer Key
NMMS Application form
NMMS Scholarship
NMMS Eligibility
NMMS Exam Pattern
NMMS Admit Card
NMMS Question Paper
NMMS Answer Key
NMMS Syllabus
NMMS Result
NTSE Application Form
NTSE Eligibility Criteria
NTSE Exam Pattern
NTSE Admit Card
NTSE Syllabus
NTSE Question Papers
NTSE Answer Key
NTSE Cutoff
NTSE Result

Schools By Medium

Malayalam Medium Schools in India
Urdu Medium Schools in India
Telugu Medium Schools in India
Karnataka Board PUE Schools in India
Bengali Medium Schools in India
Marathi Medium Schools in India

By Ownership

Central Government Schools in India
Private Schools in India
Schools in Delhi
Schools in Lucknow
Schools in Kolkata
Schools in Pune
Schools in Bangalore
Schools in Chennai
Schools in Mumbai
Schools in Hyderabad
Schools in Gurgaon
Schools in Ahmedabad
Schools in Uttar Pradesh
Schools in Maharashtra
Schools in Karnataka
Schools in Haryana
Schools in Punjab
Schools in Andhra Pradesh
Schools in Madhya Pradesh
Schools in Rajasthan
Schools in Tamil Nadu
NVS Admit Card
Navodaya Result
Navodaya Exam Date
Navodaya Vidyalaya Admission Class 6
JNVST admit card for class 6
JNVST class 6 answer key
JNVST class 6 Result
JNVST Class 6 Exam Pattern
Navodaya Vidyalaya Admission
JNVST class 9 exam pattern
JNVST class 9 answer key
JNVST class 9 Result

Download Careers360 App's

Regular exam updates, QnA, Predictors, College Applications & E-books now on your Mobile

Certifications

We Appeared in

School Solutions
Star Program
NCERT Solutions Class 12 Maths
NCERT Solutions Class 12 Physics
NCERT Solutions Class 12 Chemistry
NCERT Solutions Class 12 Biology
NCERT Solutions Class 12 Commerce
NCERT Solutions Class 12 Economics
NCERT Solutions Class 12 Accountancy
NCERT Solutions Class 12 English
NCERT Solutions Class 12 Hindi
NCERT Solutions Class 11 Maths
NCERT Solutions Class 11 Physics
NCERT Solutions Class 11 Chemistry
NCERT Solutions Class 11 Biology
NCERT Solutions Class 11 Commerce
NCERT Solutions Class 11 Accountancy
NCERT Solutions Class 11 English
NCERT Solutions Class 11 Hindi
NCERT Solutions Class 11 Statistics
NCERT Solutions Class 10 Maths
NCERT Solutions Class 10 Science
NCERT Solutions Class 10 English
NCERT Solutions Class 10 Hindi
NCERT Solutions Class 10 Social Science
NCERT Solutions Class 9 Maths
NCERT Solutions Class 9 Science
NCERT Solutions Class 9 English
NCERT Solutions Class 9 Hindi
NCERT Solutions Class 9 Social Science
NCERT Solutions Class 8 Maths
NCERT Solutions Class 8 Science
NCERT Solutions Class 8 English
NCERT Solutions Class 8 Hindi
NCERT Solutions Class 8 Social Science
NCERT Solutions Class 7 Maths
NCERT Solutions Class 7 Science
NCERT Solutions Class 7 English
NCERT Solutions Class 7 Hindi
NCERT Solutions Class 7 Social Science
NCERT Solutions Class 6 Maths
NCERT Solutions Class 6 Science
NCERT Solutions Class 6 English
NCERT Solutions Class 6 Hindi
NCERT Solutions Class 6 Social Science
NCERT Solutions Class 5 Maths
NCERT Solutions Class 5 English
NCERT Solutions Class 5 EVS
NCERT Solutions Class 4 Maths
NCERT Solutions Class 4 English
NCERT Solutions Class 4 EVS
NCERT Solutions Class 4 Hindi
NCERT Solutions Class 3 Maths
NCERT Solutions Class 3 English
NCERT Solutions Class 3 EVS
NCERT Solutions Class 3 Hindi
NCERT Solutions Class 2 Maths
NCERT Solutions Class 2 English
NCERT Solutions Class 2 Hindi
NCERT Solutions Class 1 Maths
NCERT Solutions Class 1 English
NCERT Solutions Class 1 Hindi
NCERT Books Class 12
NCERT Books Class 11
NCERT Books Class 10
NCERT Books Class 9
NCERT Books Class 8
NCERT Books Class 7
NCERT Books Class 6
NCERT Books Class 5
NCERT Books Class 4
NCERT Books Class 3
NCERT Books Class 2
NCERT Books Class 1
Important Questions Class 12
Important Questions Class 11
Important Questions Class 10
Important Questions Class 9
Important Questions Class 8
Important Questions Class 7
important questions class 6
CBSE Class 12 Revision Notes
CBSE Class 11 Revision Notes
CBSE Class 10 Revision Notes
CBSE Class 9 Revision Notes
CBSE Class 8 Revision Notes
CBSE Class 7 Revision Notes
CBSE Class 6 Revision Notes
CBSE Class 12 Syllabus
CBSE Class 11 Syllabus
CBSE Class 10 Syllabus
CBSE Class 9 Syllabus
CBSE Class 8 Syllabus
CBSE Class 7 Syllabus
CBSE Class 6 Syllabus
CBSE Class 5 Syllabus
CBSE Class 4 Syllabus
CBSE Class 3 Syllabus
CBSE Class 2 Syllabus
CBSE Class 1 Syllabus
CBSE Sample Question Papers For Class 12
CBSE Sample Question Papers For Class 11
CBSE Sample Question Papers For Class 10
CBSE Sample Question Papers For Class 9
CBSE Sample Question Papers For Class 8
CBSE Sample Question Papers For Class 7
CBSE Sample Question Papers For Class 6
CBSE Sample Question Papers For Class 5
CBSE Sample Question Papers For Class 4
CBSE Sample Question Papers For Class 3
CBSE Sample Question Papers For Class 2
CBSE Sample Question Papers For Class 1
CBSE Previous Year Question Papers Class 12
CBSE Previous Year Question Papers Class 10
Extra Questions For Class 8 Maths
Extra Questions For Class 8 Science
Extra Questions For Class 9 Maths
Extra Questions For Class 9 Science
Extra Questions For Class 10 Maths
Extra Questions For Class 10 Science
NEET 2021 Question Paper
NEET 2020 Question Paper
NEET 2019 Question Paper
NEET 2018 Question Paper
NEET 2017 Question Paper
NEET 2016 Question Paper
NEET 2015 Question Paper
NEET Physics Questions
NEET Chemistry Questions
NEET Biology Questions
NEET Sample Papers
NEET Physics Syllabus
NEET Chemistry Syllabus
NEET Biology Syllabus
NEET Mock Test
NEET Eligibility Criteria
JEE Main 2021 Question Paper
JEE Main 2020 Question Paper
JEE Main 2019 Question Paper
JEE Main 2018 Question Paper
JEE Main 2017 Question Paper
JEE Main 2016 Question Paper
JEE Main 2015 Question Paper
JEE Main Sample Papers
JEE Main Physics Syllabus
JEE Main Chemistry Syllabus
JEE Main Maths Syllabus
JEE Main Physics Questions
JEE Main Chemistry Questions
JEE Main Maths Questions
JEE main revision notes
JEE Main Mock Test
JEE Advanced Physics Questions
JEE Advanced Chemistry Questions
JEE Advanced Maths Questions
JEE Advanced 2021 Question Paper
JEE Advanced 2020 Question Paper
JEE Advanced 2019 Question Paper
JEE Advanced 2018 Question Paper
JEE Advanced 2017 Question Paper
JEE Advanced 2016 Question Paper
JEE Advanced 2015 Question Paper
JEE Advanced Physics Syllabus
JEE Advanced Chemistry Syllabus
JEE Advanced Maths Syllabus
JEE Advanced Mock Test
ISC Class 12 Syllabus
ISC Class 11 Syllabus
ICSE Class 10 Syllabus
ICSE Class 9 Syllabus
ICSE Class 8 Syllabus
ICSE Class 7 Syllabus
ICSE Class 6 Syllabus
ISC Sample Question Papers for Class 12
ISC Sample Question Papers for Class 11
ICSE Sample Question Papers for Class 10
ICSE Sample Question Papers for Class 9
ICSE Sample Question Papers for Class 8
ICSE Sample Question Papers for Class 7
ICSE Sample Question Papers for Class 6
ICSE Class 10 Revision Notes
ICSE Class 9 Revision Notes
ISC Important Questions for Class 12
ISC Important Questions for Class 11
ICSE Important Questions for Class 10
ICSE Important Questions for Class 9
ICSE Important Questions for Class 8
ICSE Important Questions for Class 7
ICSE Important Questions for Class 6
ISC Class 12 Question Paper
ICSE Class 10 Question Paper
Maharashtra Board Syllabus
Maharashtra Board Sample Question Paper
Maharashtra Board Previous Year Question Paper
AP Board Syllabus
AP Board Sample Question Paper
AP Board Previous Year Question Paper
Tamilnadu Board Syllabus
Tamilnadu Board Sample Question Paper
Tamilnadu Board Previous Year Question Paper
Telangana Board Syllabus
Telangana Board Sample Question Paper
Telangana Board Previous Year Question Paper
Karnataka Board Syllabus
Karnataka Board Sample Question Paper
Karnataka Board Previous Year Question Paper
Examination Full Forms
Physics Full Forms
Chemistry Full Forms
Biology Full Forms
Educational Full Form
CUET Eligibility Criteria
CUET Exam Pattern
CUET Cutoff
CUET Syllabus
CUET Admit Card
CUET Counselling
CUET Previous Year Question Papers
CUET Application Form
CUET Sample Papers
CUET Exam Centers
CUET Exam Dates
CUET Results
Physics Formulas
Chemistry Formulas
Math Formulas
Algebra Formulas
Geometry Formulas
Trigonometry Formulas
Subscription

Important Questions Class 11 Physics Chapter 6

Home » CBSE » Important Questions Class 11 Physics Chapter 6

CBSE Important Questions
Important Questions Class 6
CBSE Previous Year Question Papers
CBSE Revision Notes
CBSE Syllabus
CBSE Extra Questions
CBSE Sample Papers
ISC & ICSE Syllabus
ICSE Syllabus Class 9
ICSE Syllabus Class 8
ICSE Syllabus Class 7
ICSE Syllabus Class 6
ICSE Syllabus Class 10
ICSE Question Paper
ICSE Sample Question Papers
ISC Sample Question Papers For Class 12
ISC Sample Question Papers For Class 11
ICSE Sample Question Papers For Class 10
ICSE Sample Question Papers For Class 9
ICSE Sample Question Papers For Class 8
ICSE Sample Question Papers For Class 7
ICSE Sample Question Papers For Class 6
ICSE Revision Notes
ICSE Important Questions
ISC Important Questions For Class 12
ISC Important Questions For Class 11
ICSE Important Questions For Class 10
ICSE Important Questions For Class 9
ICSE Important Questions For Class 8
ICSE Important Questions For Class 7
ICSE Important Questions For Class 6
Maharashtra board
Rajasthan-Board
Andhrapradesh Board
AP Board syllabus
Telangana Board
Tamilnadu Board
Tamilnadu Sample Question Paper
Tamilnadu Syllabus
Tamilnadu Previous Year Question Paper
NCERT Solutions Class 12
NCERT Solutions Class 10
NCERT Solutions Class 11
NCERT Solutions Class 9
NCERT Solutions Class 8
NCERT Solutions Class 7
NCERT Solutions Class 6
NCERT Solutions Class 5
NCERT Solutions Class 4
NCERT Solutions Class 3
NCERT Solutions Class 2
NCERT Solutions Class 1
JEE Main Question Papers
JEE Main Syllabus
JEE Main Questions
JEE Main Revision Notes
JEE Advanced Question Papers
JEE Advanced Syllabus
JEE Advanced Questions
JEE Advanced Sample Papers
NEET Question Papers
Neet 2021 Question Paper
Neet 2020 Question Paper
Neet 2019 Question Paper
Neet 2018 Question Paper
Neet 2017 Question Paper
Neet 2016 Question Paper
Neet 2015 Question Paper
NEET Syllabus

Important Questions for CBSE Class 11 Physics Chapter 6 – Work, Energy and Power

The words “work,” “energy,” and “power” are frequently heard. But in physics, work has a specific and definite meaning. In Chapter 6 of Class 11 Physics, a variety of important concepts are discussed. Students can refer to the set of Class 11 Physics Chapter 6 Important Questions to score high marks on final exams. These solutions can help them learn the most important concepts.

Quick Links

The topics that are covered in this chapter are as follows.

The work-energy theorem
Kinetic energy
Work done by a variable force
The work-energy theorem for a variable force
The concept of potential energy
The conservation of mechanical energy
The potential energy of a spring
Law of conservation of energy

CBSE Class 11 Physics Chapter 6 Important Questions – Free Download

Study Important Questions for Class 11 Physics Chapter 6 – Work, Energy and Power

Here, students will find some of the Important Questions for Class 11 Physics Chapter 6. They can additionally access the link provided to review the complete set.

Very Short Answers and Questions- 1 Mark

Q1. Will two bodies which stick together after a collision be elastic or inelastic?

A1. An inelastic collision occurs when two bodies stick together after a collision.

Q2. What happens to an air bubble’s potential energy when it rises in water?

A2. When an air bubble rises in water, its potential energy decreases because work is done by upthrusting on the bubble.

Short Answers and Questions- 2 Marks

Q1. A ball is dropped from height h1 and bounces back to height h2. Determine the value of the restitution coefficient.

A1. As the ball falls from height h1,

The approach velocity will be v1 = √2gh1.

The ball then rebounds to height h2.

As a result, the velocity of separation is v2 = √2gh2.

The restitution coefficient is given by

e = v2v1 = 2gh2√2gh1√

⇒e = h2h1−−√

Q2. When two bodies of different temperatures, T1 and T2 come into thermal contact, they do not always settle to their mean temperature. Why?

A2. Two bodies of different temperatures, T1 and T2, come into thermal contact. Because the thermal capacities of two bodies are not always equal, they do not always settle at their mean temperature.

Q3. List the benefits and drawbacks of a Platinum Resistance thermometer.

A3. The following are the benefits of using a platinum resistance thermometer.

High measurement precision
Temperature measurements can be taken over a wide temperature range, from 2600C to 12000C.

The following are the disadvantages of the Platinum Resistance thermometer.

Additional equipment is required, such as a bridge circuit and a power supply.

Long Answers and Questions- 3 Marks

Q1. It is critical to comprehend the sign of work done by a force on a body. Determine whether the following quantities are positive or negative.

(i) A man’s work in lifting a bucket out of a well using a rope tied to the bucket:

Ans: A positive sign of completed work. Force and displacement are both in the same direction in the given case. As a result, the sign of completed work is positive. The work is done on the bucket in this case.

(ii) In the preceding example, work is done by gravitational force:

Ans: The sign of completed work is negative. The directions of force (vertically downward) and displacement (vertically upward) are opposite in the given case. As a result, the sign of completed work is negative.

(iii) Frictional work done on a body sliding down an inclined plane:

Ans: The sign of completed work is negative. Because the frictional force acts in the opposite direction of motion, the work done by the frictional force is negative in this case.

(iv) Work done by an applied force on a body moving with uniform velocity in a rough horizontal plane:

Ans: A positive sign of completed work. The body is moving on a rough horizontal plane in this case. The frictional force is the force that opposes the motion of the body. As a result, a uniform force must be applied to the body in order to maintain a uniform velocity. Because the applied force acts in the direction of the body’s motion, the work done is positive.

(v) The work done by air’s resistive force on a vibrating pendulum to bring it to rest:

Ans: The sign of completed work is negative. The air’s resistive force acts in the opposite direction of the pendulum’s motion. As a result, the work done in this case is negative.

Q2. A 0.5 kg body travels in a straight line with velocity v = ax32, where a = 5m/s2. What is the net force work done during its displacement from x = 0 to x = 2 m?

A2. Ans: In the above question it is given that,

Mass of the body, m= 0.5 kg

Velocity of the body is governed by the equation,

v = ax32 where a = 5m/s2.

Initial velocity, u (at x = 0) = 0

Final velocity v (at x = 2 m) = 102–√m/s

Work done, W = Change in kinetic energy

= 12m(v2−u2)

= 12×0.5×((102–√)2−0)

Long Answers and Questions- 4 Marks

Q1. On a frictionless track, a trolley weighing 200 kg moves at a constant speed of 36 km/h. A child of 20 kg runs on the trolley from one end to the other (10 m away) at a speed of 4 relative to the trolley in the opposite direction of its motion and jumps out. What is the trolley’s top speed? How far has the trolley moved since the child began to run?

A1. In the above question, it is given that,

Mass of the trolley, M = 200 kg

Speed of the trolley, v = 36 km/h = 10 m/s

Mass of the boy, m = 20 kg

The initial momentum of the system of the boy and the trolley

= (200+20)×10

= 2200 kg m/s

Let ‘v’ be the final velocity of the trolley with respect to the ground.

The final velocity of the boy with respect to the ground = v′−4

Final momentum = Mv′+m(v′−4)

= 200v′+20v′−80

As per the law of conservation of momentum,

Initial momentum = Final momentum

2200 = 220v′−80

⇒v′ = 2280220 = 10.36m/s

Length of the trolley, l = 10 m

Speed of the boy, v′′ = 4 m/s

Time taken by the boy to run, t = 104 = 2.5s.

Thus, the distance moved by the trolley = v′′×t = 10.36×2.5 = 25.9m.

Long Answer Questions- 5 Marks

Q1. (a) Define the term potential energy. Give some examples.

Ans. (a) Potential energy is defined as the energy possessed by a body as a result of its position in a field or a change in its configuration, such as a gas compressed in a cylinder, the water wound spring, water raised to an overhead tank in a house, and so on.

(b) Create a graph that depicts the variation of potential energy, kinetic energy, and total energy of a body falling freely on earth from h?

Ans. (b) The graph below depicts the variation of potential energy, kinetic energy, and total energy of a body falling freely on earth from a height h.

(i) The gravitational potential energy decreases as the body falls down until it reaches zero at the earth’s surface.

(ii) Kinetic energy increases as the body fall downward and reaches its peak when the body hits the ground.

(iii) The total mechanical (KE + PE) energy remains constant according to the law of conservation of energy.

Download Important Questions For Class 11 Physics Chapter 6

Chapter 6 of Class 11 Physics Work, Power and Energy is an important topic for students to cover and achieve high marks in both exams and competitive exams. Students can learn Chapter 6 Work, Power and Energy by practising more and more questions with the help of Important Questions for Class 11 Physics Chapter 6 which is available on the Extramarks platform.

Work Energy And Power Class 11 Important Questions With Answers

The chapter contains interesting topics such as the work-energy theorem, kinetic energy, potential energy, energy conservation, power, collisions, and so on.

Students preparing for exams must be well-versed in the chapter. By practising questions from related topics, students can adapt and approach any type of question they face in the exam. Before beginning to practise Class 11 Physics Work, Energy and Power Important Questions, students should review the chapter.

Physics Chapter 6 – Work, Energy and Power

Work, energy, and power are crucial chapters in the CBSE Syllabus for Physics in terms of examinations. Students are familiar with the terms “work,” “energy,” and “power” from elementary school. Regular studies and practice are required to master any subject. Work, Energy, and Power is a chapter that can be learned through practice exams. Work, Energy, and Power Class 11 Important Questions covers all of the questions with appropriate examples that students can quickly understand.

Students should understand the entire chapter and remember a few topics in order to answer important questions from Work, Energy, and Power Class 11.

Work is simply the transfer of energy through force.

Work Done: When an external force acts on a body in steady motion, it will experience some displacement; this action is referred to as work done.

Energy is defined as the ability to do work. There are various types of energy, such as electrical energy, solar energy, mechanical energy, and so on. This chapter will primarily cover mechanical energy and its various forms. Mechanical energy is classified into two types:

Kinetic Energy: The energy gained by an object as a result of its motion is referred to as the object’s kinetic energy.
Potential Energy: The energy gained by an object as a result of its position is referred to as the object’s potential energy.

Power is the rate at which work is completed.

Work Energy Theorem: The Work-Energy theorem states that the work done on an object by external forces is equal to the change in its kinetic energy.

Law of conservation of energy states that energy can neither be created nor destroyed.

Why Go For Extramarks?

Extramarks provides a comprehensive set of Important Questions for all subjects and chapters. Our subject matter experts choose questions based on the exam pattern and past years’ questions. These questions provide a thorough understanding of Class 11 Physics Chapter 6 Work, Energy and Power with step-by-step solutions.

Important Questions for Class 11 Physics Work, Energy and Power are essential for students preparing for exams. Students will gain an understanding of the types of questions in the final examination from the discussion above. These Important Questions have been curated in a concise manner by subject-matter experts.

Click to share on Facebook (Opens in new window)
Click to share on Twitter (Opens in new window)
Click to share on LinkedIn (Opens in new window)
Click to share on WhatsApp (Opens in new window)

Read the assertion and reason carefully to mark the correct option out of the options given below.

Assertion: The v-t graph of the particle is shown in the figure. The work is done in the interval AB is positive while in CD is negative.

Reason: Work done on the system is equal to the change in kinetic energy.

Assertion is true but reason is false.

Assertion and reason both are false.

Both assertion and reason are true and the reason is the correct explanation of the assertion.

Both assertion and reason are true but reason is not the correct explanation of the assertion.

The expression of ?work-energy?theorem is, W?=???K.E. W?= 1 2 m V f 2 ?V i 2 ? Here,? V f ? is the final velocity and V i is the inital velocity. In segment AB, V f ? is equal to v and V i is equal to u. So, work done in time interval 0 to t is, W 0?t ?= 1 2 m v 2 ? 0 2 = 1 2 mv 2 ???(+ve?value)? In segment CD, V f ? is equal to 0 and V i is equal to v. So, work done in time interval 3t to 4t, W 3t?4t = 1 2 m 0 2 ? v 2 =? 1 2 mv 2 ????(?ve value)?

If the mass and velocity of a body is doubled, then its new kinetic energy is

eight times the original kinetic energy.

four times the original kinetic energy.

twice the original kinetic energy.

half the original kinetic energy.

The mass of a pendulum bob is 100 g and the length of its string is 1 m. The bob is held such that the string is horizontal and is then allowed to fall. The kinetic energy when the string makes an angle of 30° with the vertical, is

Q.4 What happens to the potential energy of a body when conservative force does positive work?

When conservative forces do positive work, potential energy of a body decreases.

Q.5 Two bodies of masses 5kg and 3kg moving in the same direction along the same straight line with velocities 5m/s and 3m/s respectively suffers one dimensional elastic collision. Find the velocities of two bodies after the collision.

Please register to view this section

Faqs (frequently asked questions), 1. what is the triple point of water.

A1. A substance’s triple point is the combination of temperature and pressure at which it can exist in all three states—solid, liquid, and gas. The triple point of water is 273.16 K and the vapour pressure is 611.66 Pascal. Water can now exist in all three states—vapour, liquid, and ice by varying the pressure and temperature.

2. What do you mean by Internal Forces? Give examples.

A2. Internal forces are the types of forces that exist within the body and act on it. Internal forces include gravity, magnetic force, electrical force, and spring force. The gravitational force is invisible to us, but it affects every object that remains on Earth. The concept is the same in all of the preceding examples.

3. What is the Law of Conservation of Energy in reference to Class 11 Chapter 6?

A3. The law of energy conservation states two things. First, energy is neither created nor destroyed. Second, energy can be converted between forms. As a result, the total energy of any object is never lost, and thus this law is known as the Law of Conservation of Energy. As a result, when a system is isolated, it has a fixed amount of energy because no energy is added from an external source.

Fill this form to view question paper

Otp verification.

Talk to our experts

1800-120-456-456

Important Questions for CBSE Class 11 Physics Chapter 6 - Work, Energy and Power

CBSE Class 11 Physics Chapter-6 Important Questions - Free PDF Download

Important Questions for Class 11 Physics Chapter 6 - Work, Energy and Power are available in Vedantu. All Questions are designed as per the latest Syllabus of NCERT with reference to frequent questions in exams. We hear the words 'work,' 'energy,' & 'power' all the time. A person carrying materials, a farmer cultivating, a student studying for exams are all said to be performing their work. Work has a specific and definite meaning in physics. In this article we will Solve lot of important questions that will definitely help students to score good marks in final exams. Students can use these solutions for learning the most important concepts and prepare for their board exams.

Download CBSE Class 11 Physics Important Questions 2024-25 PDF

Also, check CBSE Class 11 Physics Important Questions for other chapters:

Topics Covered in Class 11 Physics Chapter 6 - Work, Energy and Power are as follows:

The work-energy theorem

Kinetic energy

Work done by a variable force

The work-energy theorem for a variable force

The concept of potential energy

The conservation of mechanical energy

The potential energy of a spring

Law of conservation of energy

Study Important Questions for Class 11 Physics Chapter 6 - Work, Energy and Power

Very Short Answer Questions 1 Mark

1. If two bodies stick together after collision, will the collision be elastic or inelastic?

Ans : If two bodies stick together after the collision the collision will be an inelastic collision.

2. When an air bubble rises in water, what happens to its potential energy?

Ans: When an air bubble rises in water, the potential energy of the air bubble decreases because work is done by upthrust on the bubble.

3. A spring is kept compressed by pressing its ends together lightly. It is then placed in a strong acid, and released. What happens to its stored potential energy?

Ans: When spring is kept compressed by pressing its ends together lightly and further placed in strong acid and released, t he loss in potential energy appears as kinetic energy of the molecules of the acid.

4. Define the triple point of water.

Ans: Triple point of water indicates the values of pressure and temperature at which water co-exists in equilibrium in all the three states of matter.

5. State Dulong and Petit law.

Ans: According to Dulong and Petit law, the specific heat of all the solids is constant at room temperature and is equal to \[3R\].

6. Why are the clock pendulums made of invar, a material of low value of coefficient of linear expansion?

Ans: The clock pendulums are made of Inver as it has a low value of α (coefficient of linear expansion) i.e., for a small change in temperature, there won’t be much change in the length of the pendulum.

7. Why is mercury used in making thermometers?

Ans: Mercury is used in making thermometers as it has a wide and useful temperature range and has a uniform rate of expansion.

8. How would a thermometer be different if glass expanded more with increasing temperature than mercury?

Ans: If glass expanded more with increasing temperature than mercury, the scale of the thermometer would be upside down.

9. Show the variation of specific heat at constant pressure with temperature.

Ans: Here is the required variation:

10. Two thermometers are constructed in the same way except that one has a spherical bulb and the other an elongated cylindrical bulb. Which one will respond quickly to temperature change?

Ans: The thermometer with a cylindrical bulb will respond quickly to temperature changes as the surface area of the cylindrical bulb is greater than that of a spherical bulb.

11. A body constrained to move along the z-axis of a coordinate system is subject to a constant force F given by \[F=-\overset{\wedge }{\mathop{i}}\,+2\overset{\wedge }{\mathop{j}}\,+3\overset{\wedge }{\mathop{k}}\,N\]. Where \[\overset{\wedge }{\mathop{i}}\,,\overset{\wedge }{\mathop{j}}\,,\overset{\wedge }{\mathop{k}}\,\] are unit vectors along the x, y and z axis of the system respectively. What is the work done by this force in moving the body a distance of 4 m along the z axis?

Ans: Force exerted on the body is \[F=-\overset{\wedge }{\mathop{i}}\,+2\overset{\wedge }{\mathop{j}}\,+3\overset{\wedge }{\mathop{k}}\,N\].

Displacement, \[s\text{ }=4\overset{\wedge }{\mathop{k}}\,\text{ }m\]

Work done, \[W\text{ }=F.s\]

\[=\left( -\overset{\wedge }{\mathop{i}}\,+2\overset{\wedge }{\mathop{j}}\,+3\overset{\wedge }{\mathop{k}}\, \right).\left( 4\overset{\wedge }{\mathop{k}}\, \right)\]

$=12\text{ }J$

Thus, \[12\text{ }J\] of work is done by the force on the body.

12. A molecule in a gas container hits a horizontal wall with speed and angle 30° with the normal, and rebounds with the same speed. Is momentum conserved in the collision? Is the collision elastic or inelastic?

Ans: Yes; the collision is elastic. The momentum of the gas molecule remains conserved whether the collision is elastic or inelastic. The gas molecule moves with a velocity of \[200\text{ }m/s\] and strikes the stationary wall of the container and rebounds with the same speed. This shows that the rebound velocity of the wall remains zero. Thus, the total kinetic energy of the molecule remains conserved during the collision. The given collision is an example of an elastic collision.

13. The bob A of a pendulum released from 30° to the vertical hits another bob B of the same mass at rest on a table as shown in Fig. 6.15. How high does the bob A rise after the collision? Neglect the size of the bobs and assume the collision to be elastic.

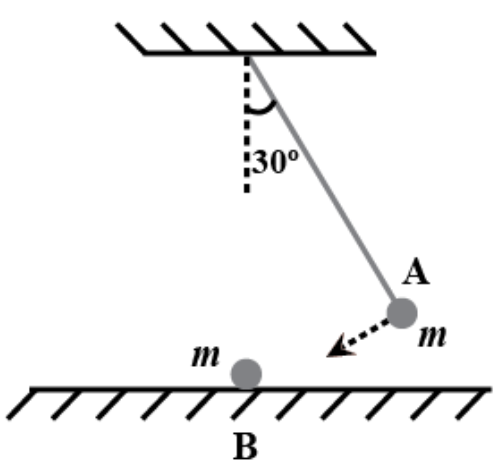
Ans: Bob A won’t rise at all. For an elastic collision between two equal masses in which one is stationary, while the other is moving with some velocity, the stationary mass acquires the same velocity, while the moving mass immediately comes to rest after collision. Here a complete transfer of momentum takes place from the moving mass to the stationary mass. Thus, bob A of mass m, will come to rest after colliding with bob B of equal mass, while bob B will move with the velocity of bob A at the instant of collision.

14. A trolley of mass 300 kg carrying a sandbag of 25 kg is moving uniformly with a speed of 27 km/h on a frictionless track. After a while, sand starts leaking out of a hole on the floor of the trolley at the rate of 0.05 kg/s. What is the speed of the trolley after the entire sand bag is empty?

Ans: The sand bag is placed on a trolley that is moving with a uniform speed of \[27\text{ }km/h\]. The external forces acting on the system of the sandbag and the trolley is zero. As the leaking action does not produce any external force on the system, the sand starts leaking from the bag with no change in the velocity of the trolley. This is in accordance with Newton's first law of motion. Thus, the speed of the trolley will remain \[27\text{ }km/h\].

15. Which of the following potential energy curves in Fig. 6.18 cannot possibly describe the elastic collision of two billiard balls? Here r is the distance between centres of the balls.

Potential Energy Curves with Respect to Distance between Centers of the Balls.

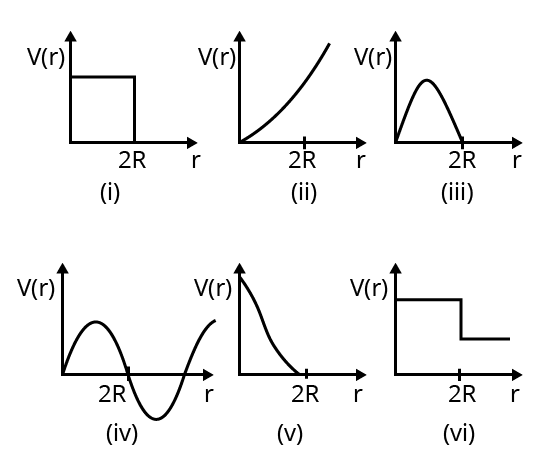
Ans: From the figure given in the question, (i), (ii), (iii), (iv), and (vi) cannot possibly describe the elastic collision of two billiard balls. We know that the potential energy of a system of two masses is inversely proportional to the separation between them. Here the potential energy of the system of the two balls will decrease as they come closer to each other. It will become zero (i.e., \[V\left( r \right)\text{ }=\text{ }0\]) when the two balls touch each other, i.e., at \[r\text{ }=\text{ }2R\], where R is the radius of each billiard ball. The potential energy curves given in figures (i), (ii), (iii), (iv), and (vi) do not satisfy these two conditions. Thus, they do not describe the elastic collisions between them.

Short Answer Questions 2 Marks

1. A body is moving along Z – axis of a co – ordinate system is subjected to a constant force F is given by $\overset{\to }{\mathop{F}}\,=-\overset{\wedge }{\mathop{i}}\,+2\overset{\wedge }{\mathop{j}}\,+3\overset{\wedge }{\mathop{k}}\,N$. Where \[\overset{\wedge }{\mathop{i}}\,,\overset{\wedge }{\mathop{j}}\,,\overset{\wedge }{\mathop{k}}\,\] are unit vector along the x, y and z – axis of the system respectively. What is the work done by this force in moving the body a distance of 4m along the Z – axis?

Ans: Force exerted on the body is,

\[F=-\overset{\wedge }{\mathop{i}}\,+2\overset{\wedge }{\mathop{j}}\,+3\overset{\wedge }{\mathop{k}}\,N\].

2. A ball is dropped from the height \[{{h}_{1}}\] and if re-bounces to a height \[{{h}_{2}}\]. Find the value of coefficient of restitution.

Ans: As the ball drops from height \[{{h}_{1}}\] ,

Velocity of approach will be ${{v}_{1}}=\sqrt{2g{{h}_{1}}}$

And the ball rebounds to height \[{{h}_{2}}\] .

Therefore, velocity of separation is ${{v}_{2}}=\sqrt{2g{{h}_{2}}}$

Coefficient of restitution is given by:

$e=\frac{{{v}_{2}}}{{{v}_{1}}}=\frac{\sqrt{2g{{h}_{2}}}}{\sqrt{2g{{h}_{1}}}}$

$\Rightarrow e=\sqrt{\frac{{{h}_{2}}}{{{h}_{1}}}}$

3. State and prove work energy theorem analytically.

Ans: The work-energy theorem states that work done by force acting on a body is equal to the change produced in its kinetic energy.

If $\vec{F}$ force is applied to move an object through a distance $d\vec{s}$.

Then $dw=\vec{F}.d\vec{s}$

$F=m\vec{a}$

$dw=m\vec{a}.d\vec{s}$

$dw=m\frac{d\vec{v}}{dt}.d\vec{s}$

\[dw=m\frac{d\vec{s}}{dt}.d\vec{v}\]

\[\Rightarrow dw=mv.d\vec{v}\]

On integrating,

\[\sum{dw}=W=\int\limits_{u}^{v}{mv.d\vec{v}}\]

\[W=m\left| \frac{v}{2} \right|_{u}^{v}\]

\[\Rightarrow W=\frac{m{{v}^{2}}}{2}-\frac{m{{u}^{2}}}{2}\]

Hence \[W\text{ }=\text{ }{{K}_{f}}\text{ }\text{ }{{K}_{i}}\] Where \[{{K}_{f}}\] and \[{{K}_{i}}\] are final and initial kinetic energy.

4. An object of mass 0.4kg moving with a velocity of 4m/s collides with another object of mass 0.6kg moving in the same direction with a velocity of 2m/s. If the collision is perfectly inelastic, what is the loss of K.E. due to impact?

Ans: In the above question it is given that:

\[{{m}_{1\text{ }}}=\text{ }0.4kg\],

\[{{u}_{1}}\text{ }=\text{ }4m/s\],

\[{{m}_{2\text{ }}}=\text{ }0.6kg\] And

\[{{u}_{2\text{ }}}=\text{ }2m/s\].

Total K.E. before collision is given by:

${{K}_{i}}=\frac{1}{2}{{m}_{1}}{{u}_{1}}^{2}+\frac{1}{2}{{m}_{2}}{{u}_{2}}^{2}$

\[\Rightarrow {{K}_{i}}=\frac{1}{2}\left( 0.4 \right){{\left( 4 \right)}^{2}}+\frac{1}{2}\left( 0.6 \right){{\left( 2 \right)}^{2}}\]

\[\Rightarrow {{K}_{i}}=4.4J\]

Since collision is perfectly inelastic,

$v=\frac{{{m}_{1}}{{u}_{1}}+{{m}_{2}}{{u}_{2}}}{{{m}_{1}}+{{m}_{2}}}=2.8m/s$

Total K.E. after collision is given by:

${{K}_{f}}=\frac{1}{2}\left( {{m}_{1}}+{{m}_{2}} \right){{v}^{2}}$

$\Rightarrow {{K}_{f}}=\frac{1}{2}\left( 0.4+0.6 \right){{2.8}^{2}}$

$\Rightarrow {{K}_{f}}=3.92J$

Thus, loss in K.E. will be:

$\Delta K={{K}_{i}}-{{K}_{f}}$

$\Rightarrow \Delta K=4.4-3.92=0.48J$

5. Why does the density of solid/liquid decreases with rise in temperature?

Ans: Consider P to be Density of solid/liquid at temperature T.

\[{{P}_{1}}\text{ }=\text{ }Density\text{ }of\text{ }solid/liquid\text{ }at\text{ }Temperature\text{ }T+\Delta T\].

As, \[Density=\frac{Mass}{Volume}\]

\[P=\frac{M}{V}\] …… (1)

\[{{P}_{1}}=\frac{M}{{{V}_{1}}}\] …… (2)

\[{{V}_{1}}=\text{ }Volume\text{ }of\text{ }solid\text{ }at\text{ }temperature\text{ }T\text{ }+\text{ }\Delta T\]

\[V\text{ }=\text{ }Volume\text{ }of\text{ }solid\text{ }at\text{ }temperature\text{ }T\]

As on increasing the temperature, solids/liquids expand, that is their volume increases, so by equation 1) & 2) Density is inversely proportional to volumes. Therefore, if the volume increases on increasing the temperature, Density will decrease.

6. Two bodies at different temperatures \[{{\mathbf{T}}_{\mathbf{1}}}\], and \[{{\mathbf{T}}_{\mathbf{2}}}\] are brought in thermal contact do not necessarily settle down to the mean temperature of \[{{\mathbf{T}}_{\mathbf{1}}}\] and \[{{\mathbf{T}}_{\mathbf{2}}}\] . Why?

Ans: When two bodies at different temperatures \[{{\mathbf{T}}_{\mathbf{1}}}\] and \[{{\mathbf{T}}_{\mathbf{2}}}\] are in thermal contact. They do not always settle at their mean temperature because the thermal capacities of two bodies may not always be equal.

7. The resistance of certain platinum resistance thermometer is found to be \[2.56\text{ }\Omega \] at ${{0}^{\circ }}C$ and \[3.56\text{ }\Omega \] at \[{{1000}^{\circ }}C\]. When the thermometer is immersed in a given liquid, its resistance is observed to \[5.06\text{ }\Omega \]. Determine the temperature of liquid?

\[{{R}_{o}}\text{ }=\text{ }Resistance\]at ${{0}^{\circ }}C=2.56\Omega $

\[{{R}_{t}}\text{ }=\text{ }Resistance\text{ }at\text{ }temperature\text{ }T\text{ }=\text{ }{{1000}^{\circ }}\text{C is 3}.56\text{ }\Omega \]

\[{{R}_{t}}\text{ }=\text{ }Resistance\text{ }at\text{ }unknown\text{ }temperature\text{ }t\];

\[{{R}_{t\text{ }}}=\text{ }5.06\Omega \]

As $t=\frac{{{R}_{t}}-{{R}_{0}}}{{{R}_{100}}-{{R}_{0}}}\times 100$

$\Rightarrow t=\frac{5.06-2.56}{3.56-2.56}\times 100={{250}^{\circ }}C$

8. A ball is dropped on a floor from a height of 2cm. After the collision, it rises up to a height of 1.5m. Assuming that 40% of mechanical energy lost goes to thermal energy into the ball. Calculate the rise in temperature of the ball in the collision. Specific heat capacity of the ball is 800J/k. Take \[g\text{ }=\text{ }10m/{{s}^{2}}\].

\[Initial\text{ }height\text{ }=\text{ }{{h}_{1}}=2m\]

\[Final\text{ }height\text{ }=\text{ }{{h}_{2}}=1.5m\]

\[Since\text{ }potential\text{ }energy\text{ }=\text{ }mechanical\text{ }energy\text{ }for\text{ }a\text{ }body\text{ }at\text{ }rest\text{ }as\text{ }K.E\text{ }=0\]

\[Mechanical\text{ }energy\text{ }lost\text{ }=\left| mg\left( {{h}_{1}}-{{h}_{2}} \right) \right|\]

$=\left| 1\times 10\left( 105-2 \right) \right|=5J$

Now \[\left( mechanical\text{ }energy\text{ }lost \right)\text{ }\times \text{ }40%\text{ }=\text{ }heat\text{ }gained\text{ }by\text{ }ball\]

$\frac{40}{100}\times 5=Cm\Delta T$

$\Rightarrow \frac{40}{100}\times 5=800\times 1\times \Delta T$

Therefore,

\[\Delta T=\frac{100\times 800}{40\times 5}=2.5\times {{10}^{-3}}{{\text{ }}^{o}}C\], which is the required rise in temperature.

9. A thermometer has wrong calibration. It reads the melting point of ice as \[\text{ }\mathbf{1}{{\mathbf{0}}^{\mathbf{0}}}\mathbf{C}\]. It reads \[\mathbf{6}{{\mathbf{0}}^{\mathbf{0}}}\mathbf{C}\] in place of \[\mathbf{5}{{\mathbf{0}}^{\mathbf{0}}}\mathbf{C}\]. What is the temperature of boiling point of water on the scale?

Lower fixed point on the wrong scale is \[\text{ }\mathbf{1}{{\mathbf{0}}^{\mathbf{0}}}\mathbf{C}\].

Let \[n\text{ }=\text{ }no.\text{ }divisions\text{ }between\text{ }upper\text{ }and\text{ }lower\text{ }fixed\text{ }points\text{ }on\text{ }this\text{ }scale\].

If \[Q\text{ }=\text{ }reading\text{ }on\text{ }this\text{ }scale\], then

$\frac{C-0}{100}=\frac{Q-\left( -10 \right)}{n}$

Now, \[C\text{ }=\text{ }Incorrect\text{ }Reading\text{ }=\text{ }{{60}^{0}}C\]

\[Q\text{ }=\text{ }Correct\text{ }Reading\text{ }=\text{ }{{50}^{0}}C\]

$\frac{50-0}{100}=\frac{60-\left( -10 \right)}{n}$

$\frac{50}{100}=\frac{70}{n}$

\[n\text{ }=\text{ }140\]

On the Celsius scale, Boiling point of water is \[{{100}^{0}}C\]

$\frac{100-0}{100}=\frac{Q+10}{140}$

\[Q\text{ }=\text{ }{{130}^{0}}C\], which is the temperature of boiling point of water on this scale.

10. Write the advantages and disadvantages of platinum resistance thermometer.

Ans: Advantages of Platinum Resistance thermometer are as follows:

High accuracy of measurement

Measurements of temperature can be made over a wide range of temperature i.e., from \[{{260}^{0}}C\text{ }to\text{ }{{1200}^{0}}C\].

Disadvantages of Platinum Resistance thermometer are as follows:

Requires additional equipment such as bridge circuit, Power supply etc.

11. If the volume of block of metal changes by 0.12% when it is heated through 200C. What is the co-efficient of linear expansion of the metal?

Ans: The co-efficient of cubical expansion y of the metal is given by:

$Y=\frac{1}{V}\times \frac{\Delta V}{\Delta T}$

$\Rightarrow Y=\frac{\Delta V}{V}\times \frac{1}{\Delta T}$

Here, $\frac{\Delta V}{V}=\frac{0.12}{100}$

$\Delta T={{20}^{0}}C$

$Y=\frac{0.12}{100}\times \frac{1}{20}$

$\Rightarrow Y=6\times {{10}^{-5}}{{/}^{0}}C$

$\therefore$ Co-efficient of linear expansion of the metal is:

$\alpha =\frac{Y}{3}=\frac{6\times {{10}^{-5}}}{3}=2\times {{10}^{-5}}{{/}^{0}}C$

12. The density of a solid at00C and 5000C is in the ratio 1.027: 1. Find the co-efficient of linear expansion of the solid?

\[Density\text{ }at\text{ }{{0}^{0}}C\text{ }=\text{ }{{S}_{O}}\]

\[Density\text{ }at\text{ }{{500}^{0}}C\text{ }=\text{ }{{S}_{500}}\]

Now, \[{{S}_{O}}\text{ }=\text{ }{{S}_{500}}\left( 1+Y\Delta T \right)\]

Where, \[Y\text{ }=\text{ }Co-efficient\text{ }of\text{ }volume\text{ }expansion\]

\[\Delta T\text{ }=\text{ }Change\text{ }in\text{ }temperature\]

$\frac{{{S}_{O}}}{{{S}_{500}}}=\frac{1.027}{1}$

\[\Delta T\text{ }=\text{ }Final\text{ }Temperature\text{ }\text{ }Initial\text{ }temperature\]

\[\Delta T\text{ }=\text{ }500\text{ }-\text{ }{{0}^{0}}C\]

\[\Delta T\text{ }=\text{ }{{500}^{0}}C\]

Or $1.027=1\times \left( 1+Y\Delta T \right)$

$1.027=1+Y\Delta T$

$\Rightarrow 1.027-1=Y\Delta T$

$\Rightarrow 0.027=Y\Delta T$

$\Rightarrow \frac{0.027}{500}=Y$

$\Rightarrow Y=54\times {{10}^{-5}}{{/}^{0}}C$

Now, the co-efficient of linear expansion \[\left( \alpha \right)\] is related to co-efficient of volume expansion (Y) as:

\[\alpha =\frac{Y}{3}=\frac{54\times {{10}^{-5}}}{3}=18\times {{10}^{-5}}{{/}^{0}}C\]

13. If one Mole of a monatomic gas is mixed with 3 moles of a diatomic gas. What is the molecular specific heat of the mixture at constant volume?

Ans: We know that:

For, a monatomic gas, \[Specific\text{ }heat\text{ }at\text{ }consent\text{ }volume\text{ }=\text{ }{{C}_{V1}}\text{ }=\frac{3}{2}R\] ;

\[R\text{ }=\text{ }Universal\text{ }Gas\text{ }Constant\]

\[No.\text{ }of\text{ }moles\text{ }of\text{ }monatomic\text{ }gas\text{ }=\text{ }{{n}_{1}}\text{ }=\text{ }1\text{ }mole\]

\[No.\text{ }of\text{ }moles\text{ }of\text{ }diatomic\text{ }gas\text{ }=\text{ }{{n}_{2}}\text{ }=\text{ }3\text{ }moles\].

For, diatomic gas, specific heat at constant volume, \[{{C}_{V2}}\text{ }=\frac{5}{2}R\]

Applying, conservation of energy.

Let \[{{C}_{V}}\text{ }=\text{ }Specific\text{ }heat\text{ }of\text{ }the\text{ }mixture\];

${{C}_{V}}=\frac{{{n}_{1}}{{C}_{{{v}_{1}}}}+{{n}_{2}}{{C}_{{{n}_{2}}}}}{{{n}_{1}}+{{n}_{2}}}$

$\Rightarrow {{C}_{V}}=\frac{1\times \frac{3}{2}R+3\times \frac{5}{2}R}{1+3}$

$\Rightarrow {{C}_{V}}=\frac{\frac{3}{2}R+\frac{15}{2}R}{4}$

R = Universal Gas constant

$\Rightarrow {{C}_{V}}=\frac{9R}{4}=\frac{9\times 8.31}{4}=18.7J/mol/K$

14. Calculate the difference between two principal specific heats of 1g of helium gas at N. T. P. Given Molecular weight of Helium = 4 and J = 4.186 J/cal and Universal Gas constant, R = 8.314J / mole / K?

\[Molecular\text{ }weight\text{ }of\text{ }Helium\text{ }=\text{ }M\text{ }=\text{ }4\]

\[Universal\text{ }Gas\text{ }Constant,\text{ }R\text{ }=\text{ }8.31J/mole/K\]

\[{{C}_{P}}\text{ }=\text{ }specific\text{ }heat\text{ }at\text{ }constant\text{ }Pressure\]

\[{{C}_{V}}\text{ }=\text{ }specific\text{ }heat\text{ }at\text{ }constant\text{ }Volume\]

Now, ${{C}_{P}}-{{C}_{V}}=\frac{r}{J}$ for 1 mole of gas.

${{C}_{P}}-{{C}_{V}}=\frac{R}{MJ}$

Where, \[R\text{ }=\text{ }Universal\text{ }Gas\text{ }Constant\text{ }=\text{ }8.31J/mole/K\]

\[J\text{ }=\text{ }4.186\text{ }J/cal\]

\[M\text{ }=\text{ }Molecular\text{ }weight\text{ }of\text{ }Helium\text{ }=\text{ }4\]

$\Rightarrow {{C}_{P}}-{{C}_{V}}=\frac{8.31}{4\times 4.186}$

$\Rightarrow {{C}_{P}}-{{C}_{V}}=0.496cal/g/K$, which is the required difference.

15. Why does heat flow from a body at higher temperature to a body at lower temperature?

Ans: If a body at a higher temperature is in contact with a body at a lower temperature, molecules with a more kinetic energy that are in contact with less energetic molecules give some of their kinetic energy to the less energetic ones.

16. A one litre flask contains some mercury. IT is found that at different temperatures, then volume of air inside the flask remains the same. What is the volume of mercury in the flask? Given the co-efficient of linear expansion of glass \[=\text{ }9\text{ }\times \text{ }{{10}^{-6}}\text{ }/{{\text{ }}^{0}}C\] and co- efficient of volume expansion of mercury \[=\text{ }1.8\text{ }\times \text{ }{{10}^{-4}}\text{ }/{{\text{ }}^{0}}C\].

Ans: It is given that the volume of air in the flask remains the same at different temperatures. This is possible only when the expansion of glass is exactly equal to the expansion of mercury, Co-efficient of cubical expansion of glass is:-

${{\gamma }_{g}}=3{{\alpha }_{g}}=3\times 9\times {{10}^{-5}}=27\times {{10}^{-5}}{{/}^{0}}C$

The co-efficient of cubical expansion of mercury is:

${{\gamma }_{m}}=1.8\times {{10}^{-4}}{{/}^{0}}C$

Volume of flask, \[V\text{ }=\text{ }1\text{ }liter\text{ }=\text{ }1000\text{ }c{{m}^{3}}\].

Let \[{{V}_{m}}\text{ c}{{m}^{3}}\] be the volume of mercury in the flask.

\[Expansion\text{ }of\text{ }flask\text{ }=\text{ }Expansion\text{ }of\text{ }Mercury\]

$C\times {{\gamma }_{g}}\times t={{V}_{m}}\times {{\gamma }_{m}}\times t$

∴ Volume of Mercury, ${{V}_{m}}=\frac{V\times {{\gamma }_{g}}}{{{\gamma }_{m}}}$

$\Rightarrow {{V}_{m}}=\frac{1000\times 27\times {{10}^{-5}}}{1.8\times {{10}^{-4}}}=150c{{m}^{3}}$

17. The potential energy function for a particle executing linear simple harmonic motion is given by \[\mathbf{V}\left( \mathbf{x} \right)\text{ }=k{{x}^{2}}/\mathbf{2}\] , where k is the force constant of the oscillator. For k = 0.5 N/m, the graph of V(x) versus x is shown in Fig. 6.12. Show that a particle of total energy 1 J moving under this potential must 'turn back' when it reaches x = ± 2 m.

Potential Energy Curve for a Particle Executing Linear SHM

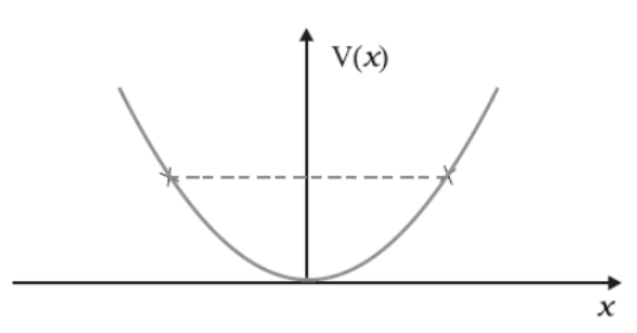
Total energy of the particle, \[E=\text{ }1J\].

Force constant, \[k=\text{ }0.5\text{ }N/m\].

Kinetic energy of the particle, \[K\text{ }=\frac{1}{2}m{{v}^{2}}\]

According to the conservation law:

\[E=\text{ }V\text{ }+\text{ }K\]

\[1=\text{ }\frac{1}{2}k{{x}^{2}}\text{ }+\text{ }\frac{1}{2}m{{v}^{2}}\]

At the moment of ‘turn back', velocity (and hence K) becomes zero.

$\therefore 1=\frac{1}{2}k{{x}^{2}}$

$\frac{1}{2}\times 0.5{{x}^{2}}=1$

${{x}^{2}}=4$

Thus, the particle turns back when it reaches $x=\pm 2$m.

18. State if each of the following statements is true or false. Give reasons for your Answer.

In an elastic collision of two bodies, the momentum and energy of each body is conserved.

Ans: The above statement is false. This is because in an elastic collision, the total energy and momentum of both the bodies, and not of each individual body, is conserved.

Total energy of a system is always conserved, no matter what internal and external forces on the body are present.

Ans: The above statement is false. This is because although internal forces are balanced, they cause no work to be done on a body. It is the external forces that have the ability to do work. Hence, external forces are able to change the energy of a system.

Work done in the motion of a body over a closed loop is zero for every force in nature.

Ans: The above statement is false. This is because the work done in the motion of a body over a closed loop is zero for a conservation force only.

In an inelastic collision, the final kinetic energy is always less than the initial kinetic energy of the system.

Ans: The above statement is true. This is because in an inelastic collision, the final kinetic energy is always less than the initial kinetic energy of the system. This is because in such collisions, there is always a loss of energy in the form of heat, sound, etc.

19. A body is initially at rest. It undergoes one-dimensional motion with constant acceleration. The power delivered to it at time t is proportional to

(i) ${{t}^{\frac{1}{2}}}$

(ii) t

(iii) \[{{t}^{\frac{3}{2}}}\]

(iv) ${{t}^{2}}$

Ans: The power delivered to it at time t is proportional to t i.e., option (ii) t is the correct choice.

\[Mass\text{ }of\text{ }the\text{ }body\text{ }=\text{ }m\]

\[Acceleration\text{ }of\text{ }the\text{ }body\text{ }=\text{ }a\]

Using Newton's second law of motion, the force experienced by the body is given by: \[F\text{ }=\text{ }ma\].

Both m and a are constants. Hence, force F will also be a constant.

\[F\text{ }=\text{ }ma\text{ }=\text{ }Constant\] ..... (i)

For velocity v, acceleration is given as,

$a=\frac{dv}{dt}=c\text{onstant}$

$dv=c\text{onstant}\times \text{dt}$

$v=\alpha t$ …… (ii)

Where, $\alpha $ is another constant.

$v\propto t$ …… (iii)

Power is given by the relation:

\[P\text{ }=\text{ }F.v\]

Using equations (i) and (iii), we have:

$P\propto t$

Hence, power is directly proportional to time.

20. A body is moving unidirectionally under the influence of a source of constant power. Its displacement in time t is proportional to

Ans: Its displacement in time t is proportional to \[{{t}^{\frac{3}{2}}}\], $\therefore$ option (iii) is the right answer.

$=mav=mv\frac{dv}{dt}=\text{constant=k}$

$\Rightarrow vdv=\frac{k}{m}dt$

Integrating both sides:

$\frac{{{v}^{2}}}{2}=\frac{k}{m}t$

$v=\sqrt{\frac{2kt}{m}}$

For displacement of the body, we have:

$v=\frac{dx}{dt}=\sqrt{\frac{2k}{m}}{{t}^{\frac{1}{2}}}$

$dx=k'{{t}^{\frac{1}{2}}}dt$

Where $k'=\sqrt{\frac{2k}{3}}=$ New constant

On integrating both sides, we get:

$x=\frac{2}{3}k'{{t}^{\frac{3}{2}}}$

$\Rightarrow x\propto {{t}^{\frac{3}{2}}}$, which is the required proportionality.

21. A pump on the ground floor of a building can pump up water to fill a tank of volume $30{{m}^{3}}$ in 15 min. If the tank is 40 m above the ground, and the efficiency of the pump is 30%, how much electric power is consumed by the pump?

Volume of the tank, $V=30{{m}^{3}}$ .

Time of operation, \[t=\text{ }15\text{ }min\text{ }=\text{ }15\text{ }\times 60\text{ }=\text{ }900\text{ }s\].

Height of the tank, \[h=\text{ }40\text{ }m\].

Efficiency of the pump, \[\eta =\text{ }30%\]

Density of water, $\rho ={{10}^{3}}kg/{{m}^{3}}$

Mass of water, \[m=\rho V=30\times {{10}^{3}}kg\]

Output power can be obtained as:

${{P}_{0}}=\frac{Wo\text{rk d}one}{Time}=\frac{mgh}{t}$

$\frac{30\times {{10}^{3}}\times 9.8\times 40}{900}=13.067\times {{10}^{3}}W$

For input power, efficiency is given by the relation:

$\eta =\frac{{{P}_{0}}}{{{P}_{1}}}=30%$

$\Rightarrow {{P}_{1}}=\frac{13.067}{30}\times 100\times {{10}^{3}}$

$\Rightarrow {{P}_{1}}=43.6kW$, which is the required power consumption.

22. A body of mass 0.5 kg travels in a straight line with velocity $v=a{{x}^{\frac{3}{2}}}$ where $a=5m/{{s}^{2}}$. What is the work done by the net force during its displacement from x = 0 to x = 2 m?

Mass of the body, \[m=\text{ }0.5\text{ }kg\].

Velocity of the body is governed by the equation,

$v=a{{x}^{\frac{3}{2}}}$ where $a=5m/{{s}^{2}}$.

Initial velocity, \[u\text{ }\left( at\text{ }x\text{ }=\text{ }0 \right)\text{ }=\text{ }0\]

Final velocity \[v\text{ }\left( at\text{ }x\text{ }=\text{ }2\text{ }m \right)=10\sqrt{2}m/s\]

Work done, \[W\text{ }=\text{ }Change\text{ }in\text{ }kinetic\text{ }energy\]

$=\frac{1}{2}m\left( {{v}^{2}}-{{u}^{2}} \right)$

$=\frac{1}{2}\times 0.5\times \left( {{\left( 10\sqrt{2} \right)}^{2}}-0 \right)$

23. A family uses 8 kW of power.

Direct solar energy is incident on the horizontal surface at an average rate of 200 W per square meter. If 20% of this energy can be converted to useful electrical energy, how large an area is needed to supply 8 kW?

Power used by the family, \[P\text{ }=\text{ }8\text{ }kW\text{ }=\text{ 8}\times {{10}^{3}}W\]

Solar energy received per square metre \[=\text{ }200\text{ }W\]

Efficiency of conversion from solar to electricity energy \[=\text{ }20\text{ }%\]

Area required to generate the desired electricity \[=\text{ }A\]

As per the information given in the question,

\[\text{8}\times {{10}^{3}}=20%\times \left( A\times 200 \right)\]$=\frac{20}{100}\times A\times 200$

$\Rightarrow A=200{{m}^{2}}$

Compare this area to that of the roof of a typical house.

Ans: The area of a solar plate required to generate \[8\text{ }kW\] of electricity is almost equivalent to the area of the roof of a building having dimensions \[14\text{ }m\times 14\text{ }m\].

24. A bolt of mass 0.3 kg falls from the ceiling of an elevator moving down with a uniform speed of 7m/s. It hits the floor of the elevator (length of the elevator = 3 m) and does not rebound. What is the heat produced by the impact? Would your answer be different if the elevator were stationary?

Mass of the bolt, \[m=\text{ }0.3\text{ }kg\].

\[Speed\text{ }of\text{ }the\text{ }elevator\text{ }=\text{ }7\text{ }m/s\].

Height, \[h\text{ }=\text{ }3\text{ }m\].

As the relative velocity of the bolt with respect to the lift is zero, at the time of impact, potential energy gets converted into heat energy.

\[Heat\text{ }produced\text{ }=\text{ }Loss\text{ }of\text{ }potential\text{ }energy\text{ }=\text{ }mgh\text{ }=\text{ }=\text{ }8.82\text{ }J\]

The heat produced will remain the same even if the lift is stationary. This is due to the fact that the relative velocity of the bolt with respect to the lift will remain zero.

25. Consider the decay of a free neutron at rest: \[n\text{ }\to \text{ }p+\text{ }e-\]. Show that the two-body decay of this type must necessarily give an electron of fixed energy and, therefore, cannot account for the observed continuous energy distribution in the $\beta $ decay of a neutron or a nucleus (Fig. 6.19).

Graph Between Number of Beta Particles Per Unit Energy Interval Vs Kinetic Energy of the Emitted Beta Particle

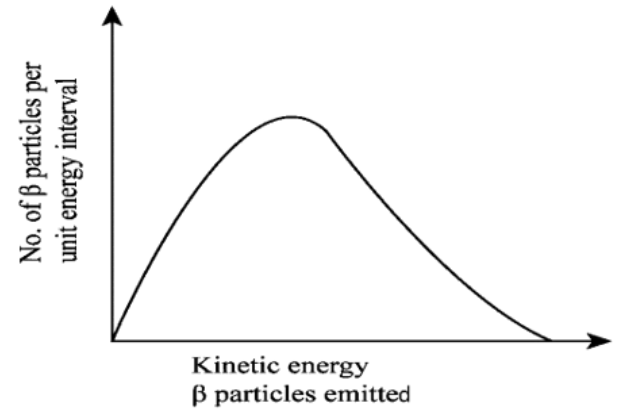
(Note: The simple result of this exercise was one among the several arguments advanced by W. Pauli to predict the existence of a third particle in the decay products of $\beta $ decay. This particle is known as neutrino. We now know that it is a particle of intrinsic spin 1/2 (like e-, p or n), but is neutral, and either massless or having an extremely small mass (compared to the mass of electron) and which interacts very weakly with matter. The correct decay process of neutron is: \[n\text{ }\to \text{ }p+\text{ }e-\])

Ans: The decay process of free neutron at rest is \[n\text{ }\to \text{ }p+\text{ }e-\].

Using Einstein's mass-energy relation, we have the energy of electron as $\Delta m{{c}^{2}}$.

\[\Delta m=\text{ }Mass\text{ }defect\text{ }=\text{ }Mass\text{ }of\text{ }neutron-\left( Mass\text{ }of\text{ }proton\text{ }+\text{ }Mass\text{ }of\text{ }electron \right)\]

\[c\text{ }=\text{ }Speed\text{ }of\text{ }light\]

\[\Delta m\] and c are constants. Thus, the given two-body decay is unable to explain the continuous energy distribution in the $\beta $ decay of a neutron or a nucleus. The presence of neutrino on the LHS of the decay correctly interprets the continuous energy distribution.

Long Answer Questions 3 Marks

1. Prove that in an elastic collision in one dimension the relative velocity of approach before impact is equal to the relative velocity of separation after impact.

Ans: Consider the figure given below:

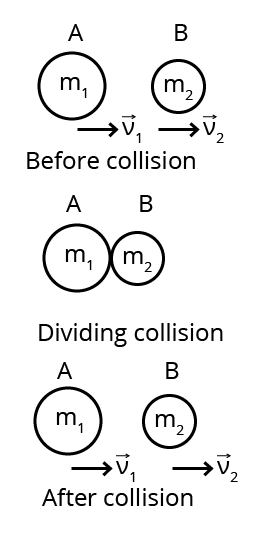
According to law of conservation of linear momentum

${{m}_{1}}{{u}_{1}}+{{m}_{2}}{{u}_{2}}={{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}}$

\[{{m}_{1}}\left( {{u}_{1}}-{{v}_{1}} \right)={{m}_{2}}\left( {{v}_{2}}-{{u}_{2}} \right)\] …… (1)

K.E. also remains conserved.

$\frac{1}{2}{{m}_{1}}{{u}_{1}}^{2}+\frac{1}{2}{{m}_{2}}{{u}_{2}}^{2}=\frac{1}{2}{{m}_{1}}{{v}_{1}}^{2}+\frac{1}{2}{{m}_{2}}{{v}_{2}}^{2}$

${{m}_{1}}\left( {{u}_{1}}^{2}-{{v}_{1}}^{2} \right)={{m}_{2}}\left( {{v}_{2}}^{2}-{{u}_{2}}^{2} \right)$ …… (2)

Dividing (2) by (1)

${{u}_{1}}-{{v}_{1}}={{v}_{2}}+{{u}_{2}}$

${{u}_{1}}-{{u}_{2}}={{v}_{2}}-{{v}_{1}}$

i.e., \[Relative\text{ }velocity\text{ }of\text{ }approach\text{ }=\text{ }Relative\text{ }velocity\text{ }of\text{ }separation\].

2. Calculate \[{{C}_{p}}\] for air, given that \[{{C}_{v}}\text{ }=0.162\text{ }cal\text{ }{{g}^{-1}}\text{ }{{k}^{-1}}\] and density air at N.T. P is \[0.001293\text{ }g/c{{m}^{3}}\].

\[Specific\text{ }heat\text{ }at\text{ }constant\text{ }volume\text{ }=\text{ }{{C}_{v\text{ }}}=\text{ }0.162\text{ }Cal\text{ }{{g}^{-1\text{ }}}{{k}^{-1}}\]

Specific heat at constant pressure = \[{{C}_{p}}=\text{ }?\]

Now, \[{{C}_{p}}\text{ }\text{ }{{C}_{v\text{ }}}=\frac{r}{J}=\frac{PV}{TJ}\left( \because PV=nRT \right)\]

\[{{C}_{p}}\text{ }\text{ }{{C}_{v\text{ }}}=\frac{P\times 1}{s\times TJ}\left( s=Density \right)\]

\[\Rightarrow {{C}_{p}}\text{ }\text{ }{{C}_{v\text{ }}}=\frac{1.01\times {{10}^{5}}}{273\times 4.2\times {{10}^{7}}\times 1.293\times {{10}^{-3}}}\]

\[\Rightarrow {{C}_{p}}\text{ }\text{ }{{C}_{v\text{ }}}=\frac{1.01\times {{10}^{6+3-7}}}{273\times 4.2\times {{10}^{7}}\times 1.293}\]

\[\Rightarrow {{C}_{p}}\text{ }\text{ }{{C}_{v\text{ }}}=\frac{1.01\times {{10}^{2}}}{1482.5}=6.8\times {{10}^{-2}}\]

\[\Rightarrow {{C}_{p}}\text{ }\text{ }{{C}_{v\text{ }}}=0.068\]

\[\Rightarrow {{C}_{p}}\text{ }=\text{ }0.162+0.068\]

\[\Rightarrow {{C}_{p}}\text{ }=\text{ }0.23\text{ c}al\text{ }{{g}^{-1}}\text{ }{{k}^{-1}}\], which is the required value asked to determine.

3. Develop a relation between the co-efficient of linear expansion, co-efficient superficial expansion and coefficient of cubical expansion of a solid.

Ans: As the \[co-efficient\text{ }of\text{ }linear\text{ }expansion\text{ }=\text{ }\alpha \text{ }=\frac{\Delta L}{L\Delta T}\]

\[\Delta L\text{ }=\text{ }change\text{ }in\text{ }length\]

\[L\text{ }=\text{ }length\]

\[\Delta T\text{ }=\text{ }change\text{ }in\text{ }temperature\].

In the same way,

\[Co-efficient\text{ }of\text{ }superficial\text{ }expansion\text{ }=\text{ }\beta \text{ }=\frac{\Delta S}{S\Delta T}\]

\[\Delta S\text{ }=\text{ }change\text{ }in\text{ }area\]

\[S\text{ }=\text{ }original\text{ }area\]

\[\Delta T\text{ }=\text{ }change\text{ }in\text{ }temperature\]

Co-efficient of cubical expansion, \[Y\text{ }=\frac{\Delta V}{V\Delta T}\]

\[\Delta V\text{ }=\text{ }change\text{ }in\text{ }volume\]

\[V\text{ }=\text{ }original\text{ }volume\]

\[\Delta L=\alpha L\text{ }\Delta T\]

\[\Rightarrow L\text{ }+\text{ }\Delta L\text{ }=\text{ }L\text{ }+\text{ }\alpha L\text{ }\Delta T\]

\[\Rightarrow L\text{ }+\text{ }\Delta L\text{ }=\text{ }L\text{ }\left( 1+\alpha \Delta T \right)\] …… (1)

\[V+\text{ }\Delta V\text{ }=\text{ }V\text{ }\left( 1+Y\Delta T \right)\] ……. (2)

\[S+\Delta S=S\text{ }\left( 1+\beta \Delta T \right)\] …… (3)

Also,

\[\left( V+\Delta V \right)\text{ }=\text{ }{{\left( L+\Delta L \right)}^{3}}\]

\[\Rightarrow V+\Delta V={{L}^{3}}\left( 1+3\alpha \Delta T+3{{\alpha }^{2}}\Delta {{T}^{2}}+{{\alpha }^{3}}{{T}^{3}} \right)\]

Since \[{{\alpha }^{2}},\text{ }{{\alpha }^{3}}\] are negligible, so,

\[V+\gamma \text{ }V\Delta T=\text{ }V\left( 1+3\alpha \Delta T \right)\] \[\left[ as\text{ }{{L}^{3\text{ }}}=\text{ }V \right]\]

\[V+\gamma V\Delta T\text{ }=\text{ }V+V3\alpha \Delta T\]

\[\Rightarrow \gamma V\Delta T\text{ }=\text{ }3\alpha \Delta T\]

\[\Rightarrow \gamma \text{ }=\text{ }3\alpha \]

Similarly, \[\beta \text{ }=\text{ }2\alpha \] (using \[{{L}^{2}}\text{ }=\text{ }S\text{ }\left( Area \right)\])

\[\alpha =\frac{\beta }{2}=\frac{\gamma }{3}\], which is the required relation.

4. Calculate the amount of heat required to convert 1.00kg of ice at \[\text{ }\mathbf{1}{{\mathbf{0}}^{\mathbf{0}}}C\] into steam at \[\mathbf{10}{{\mathbf{0}}^{\mathbf{0}}}C\] at normal pressure. Specific heat of ice = 2100J/kg/k. Latent heat of fusion of ice = 3.36x105 J/kg, specific heat of water = 4200J/kg/k. Latent heat of vaporization of water \[=\text{ }2.25\times {{10}^{6}}J/kg\].

Heat is required to raise the temperature of ice from \[\text{ }{{10}^{0}}C\text{ }to\text{ }{{0}^{0}}C.\]

Thus, change in temperature \[=\text{ }\Delta T\text{ }=\text{ }T2-T1\text{ }=\text{ }0-\left( -10 \right)\text{ }=\text{ }{{10}^{0}}C\].

So, \[\Delta Q1=cm\Delta T\]

\[C\text{ }=\text{ }specific\text{ }heat\text{ }of\text{ }ice\]

\[M\text{ }=\text{ }Mass\text{ }of\text{ }ice\]

\[\Delta T\text{ }=\text{ }{{10}^{0}}C\]

\[\Delta {{Q}_{1}}\text{ }=\text{ }2100\times 1\times 10=21000J\]

(2) Heat required to melt the ice to \[{{0}^{0}}C\] water:

\[\Delta {{Q}_{2}}=\text{ }mL\]

\[L\text{ }=\text{ }Latent\text{ }heat\text{ }of\text{ }fusion\text{ }of\text{ }ice\text{ }=\text{ }3.36\times 105\text{ }J/kg\]

\[m\text{ }=\text{ }Mass\text{ }of\text{ }ice\]

\[\Rightarrow \Delta {{Q}_{2}}=1\times 3.36\times 105\text{ }J/kg\]

\[\Rightarrow \Delta {{Q}_{2}}=3.36\times 105\text{ }J\]

\[\Rightarrow \Delta {{Q}_{2}}=336000J\]

(3) Heat required to raise the temperature of water from \[{{0}^{0}}C\] to \[{{100}^{0}}C\]:-

\[\Delta T\text{ }=\text{ }T2-T1\text{ }=\text{ }100-0={{100}^{0}}C\]

\[\Delta {{Q}_{3}}=\text{ }cm\Delta Tc\text{ }=\text{ }specific\text{ }heat\text{ }of\text{ }water\]

\[\Rightarrow \Delta {{Q}_{3}}=4200\times 1\times 100\]

\[\Rightarrow \Delta {{Q}_{3}}=420,000J\]

(4) Heat required to convert 1000C water to steam at 1000C

\[\Delta {{Q}_{4}}=\text{ }mL\]

Where, \[L\text{ }=\text{ }Latent\text{ }heat\text{ }of\text{ }vapourisation\text{ }=\text{ }2.25\times {{10}^{6}}J/kg\]

\[\Rightarrow \Delta {{Q}_{4}}=\text{ }1\times 2.25\times 106J/kg\]

\[\Rightarrow \Delta {{Q}_{4}}=2250000J\]

\[Total\text{ }Heat\text{ }required\text{ }=\Delta {{Q}_{1}}+\Delta {{Q}_{2}}+\Delta {{Q}_{3}}+\Delta {{Q}_{4}}\]

\[\Rightarrow \Delta {{Q}_{total}}=\text{ }21000+336000+420000+2250000\]

\[\Rightarrow \Delta {{Q}_{total}}=\text{ }3027000J\]

\[\Rightarrow \Delta {{Q}_{total}}=\text{ }3.027\times {{10}^{6}}J\]

5. The sign of work done by a force on a body is important to understand. State carefully if the following quantities are positive or negative:

Work done by a man in lifting a bucket out of a well by means of a rope tied to the bucket.

Ans: The sign of work done is positive. In the given case, force and displacement are in the same direction. Hence, the sign of work done is positive. In this case, the work is done on the bucket.

Work done by gravitational force in the above case,

Ans: The sign of work done is negative. In the given case, the direction of force (vertically downward) and displacement (vertically upward) are opposite to each other. Hence, the sign of work done is negative.

Work done by friction on a body sliding down an inclined plane,

Ans: The sign of work done is negative. Since the direction of frictional force is opposite to the direction of motion, the work done by the frictional force is negative in this case.

Work done by an applied force on a body moving on a rough horizontal plane with uniform velocity,

Ans: The sign of work done is positive. Here the body is moving on a rough horizontal plane. Frictional force opposes the motion of the body. Therefore, in order to maintain a uniform velocity, a uniform force must be applied to the body. Since the applied force acts in the direction of motion of the body, the work done is positive.

Work done by the resistive force of air on a vibrating pendulum in bringing it to rest.

Ans: The sign of work done is negative. The resistive force of air acts in the direction opposite to the direction of motion of the pendulum. Hence, the work done is negative in this case.

6. Choose the correct alternative:

When a conservative force does positive work on a body, the potential energy of the body increases/decreases/remains unaltered.

Ans: Decreases, this is because:

A conservative force does a positive work on a body when it displaces the body in the direction of force. As a result, the body advances toward the centre of force. It decreases the separation between the two, thereby decreasing the potential energy of the body.

Work done by a body against friction always results in a loss of its kinetic/potential energy.

Ans: Kinetic energy, this is because:

The work done against the direction of friction reduces the velocity of a body. Hence, there is a loss of kinetic energy of the body.

The rate of change of total momentum of a many-particle system is proportional to the external force/sum of the internal forces on the system.

Ans: External force, this is because:

Internal forces, irrespective of their direction, cannot produce any change in the total momentum of a body. Hence, the total momentum of a many- particle system is proportional to the external forces acting on the system.

In an inelastic collision of two bodies, the quantities which do not change after the collision are the total kinetic energy/total linear momentum/total energy of the system of two bodies.

Ans: Total linear momentum, this is because:

The total linear momentum always remains conserved whether it is an elastic collision or an inelastic collision.

7. Answer carefully, with reasons:

In an elastic collision of two billiard balls, is the total kinetic energy conserved during the short time of collision of the balls (i.e., when they are in contact)

Ans: No. This is because in an elastic collision, the total initial kinetic energy of the balls will be equal to the total final kinetic energy of the balls. This kinetic energy is not conserved at the instant the two balls are in contact with each other. In fact, at the time of collision, the kinetic energy of the balls will get converted into potential energy.

Is the total linear momentum conserved during the short time of an elastic collision of two balls?

Ans: Yes. This is because in an elastic collision, the total linear momentum of the system always remains conserved.

What are the answers to (a) and (b) for an inelastic collision?

Ans: No; Yes. This is because in an inelastic collision, there is always a loss of kinetic energy, i.e., the total kinetic energy of the billiard balls before collision will always be greater than that after collision. The total linear momentum of the system of billiards balls will remain conserved even in the case of an inelastic collision.

If the potential energy of two billiard balls depends only on the separation distance between their centres, is the collision elastic or inelastic? (Note, we are talking here of potential energy corresponding to the force during collision, not gravitational potential energy).

Ans: Elastic. This is because in the given case, the forces involved are conservation. This is because they depend on the separation between the centres of the billiard balls. Hence, the collision is elastic.

8. A person trying to lose weight (dieter) lifts a 10 kg mass, one thousand times, to a height of 0.5 m each time. Assume that the potential energy lost each time she lowers the mass is dissipated.

How much work does she do against the gravitational force?

Mass of the weight, \[m\text{ }=\text{ }10\text{ }kg\].

Height to which the person lifts the weight, \[h\text{ }=\text{ }0.5\text{ }m\].

Number of times the weight is lifted, \[n\text{ }=\text{ }1000\]

$\therefore$ Work done against gravitational force is:

$=1000\times 10\times 9.8\times 0.5$

Fat supplies J of energy per kilogram which is converted to mechanical energy with a 20% efficiency rate. How much fat will the dieter use up?

\[Energy\text{ }equivalent\text{ }of\text{ }1\text{ }kg\text{ }of\text{ }fat\text{ }=\text{ 3}\text{.8}\times \text{1}{{\text{0}}^{7}}J\]

\[Efficiency\text{ }rate\text{ }=\text{ }20%\]

Mechanical energy supplied by the person's body will be:

$=\frac{20}{100}\times 3.8\times {{10}^{7}}$

$=\frac{1}{5}\times 3.8\times {{10}^{7}}$

Equivalent mass of fat lost by the dieter will be:

$=\frac{1}{\frac{1}{5}\times 3.8\times {{10}^{7}}}\times 49\times {{10}^{3}}$

$=6.45\times {{10}^{-3}}kg$

Long Answer Questions 4 Marks

1. A body of mass 2 kg initially at rest moves under the action of an applied horizontal force of 7 N on a table with coefficient of kinetic friction = 0.1.

Compute the following:

(a) Work done by the applied force in 10 s,

(b) Work done by friction in 10 s,

(d) Change in kinetic energy of the body in 10 s, and interpret your results.

Mass of the body, \[m=\text{ }2\text{ }kg\].

Applied force, \[F\text{ }=\text{ }7\text{ }N\].

Coefficient of kinetic friction, \[\mu =\text{ }0.1\]

Initial velocity, \[u=\text{ }0\]

Time, \[t\text{ }=\text{ }10\text{ }s\].

The acceleration produced in the body by the applied force is given by Newton's second law of motion as:

$a'=\frac{F}{m}=\frac{7}{2}=3.5m/{{s}^{2}}$

Frictional force is given as:

$f=\mu mg=0.1\times 2\times 9.8=-1.96N$

The acceleration produced by the frictional force:

$a''=-\frac{1.96}{2}=0.98m/{{s}^{2}}$

Total acceleration of the body:

$a=a'+a''=3.5-0.98=2.52m/{{s}^{2}}$

The distance travelled by the body is given by the equation of motion:

$s=ut+\frac{1}{2}a{{t}^{2}}$$=0+\frac{1}{2}\times 2.52\times {{10}^{2}}=126m$

Work done by the applied force, ${{W}_{s}}=F\times s=7\times 126=882J$

Work done by the frictional force, ${{W}_{f}}=F\times s=-1.96\times 126=-247J$

Net force \[~=7-1.96=\text{ }5.04\text{ }N\]

Work done by the net force, \[{{W}_{net}}=\text{ }5.04\text{ }\times 126\text{ }=\text{ }635\text{ }J\].

From the first equation of motion, final velocity can be calculated as:

$v=u+at$$=0+2.52\times 10=25.2m/s$

Change in kinetic energy

$=\frac{1}{2}m{{v}^{2}}-\frac{1}{2}m{{u}^{2}}$

$=\frac{1}{2} 2\left ( v^{2}-u^{2} \right)=\left ( -25.2 \right )^{2}-0^{2}=635 J$

2. A trolley of mass 200 kg moves with a uniform speed of 36 km/h on a frictionless track. A child of mass 20 kg runs on the trolley from one end to the other (10 m away) with a speed of 4 relative to the trolley in a direction opposite to its motion, and jumps out of the trolley. What is the final speed of the trolley? How much has the trolley moved from the time the child begins to run?

Mass of the trolley, \[M=\text{ }200\text{ }kg\].

Speed of the trolley, \[v=\text{ }36\text{ }km/h\text{ }=\text{ }10\text{ }m/s\].

Mass of the boy, \[m=\text{ }20\text{ }kg\].

Initial momentum of the system of the boy and the trolley

\[=\text{ }\left( M+\text{ }m \right)v\]

$=\left( 200+20 \right)\times 10$

\[=\text{ }2200\text{ }kg\text{ }m/s\]

Let v' be the final velocity of the trolley with respect to the ground.

Final velocity of the boy with respect to the ground $=v'-4$

Final momentum $=Mv'+m\left( v'-4 \right)$

$=200v'+20v'-80$

$=220v'-80$

As per the law of conservation of momentum:

\[Initial\text{ }momentum\text{ }=\text{ }Final\text{ }momentum\]

\[2200\text{ }=220v'-80\]

$\Rightarrow v'=\frac{2280}{220}=10.36m/s$

Length of the trolley, \[l=\text{ }10\text{ }m\].

Speed of the boy, \[v''\text{ }=\text{ }4\text{ }m/s\].

Time taken by the boy to run, $t=\frac{10}{4}=2.5s$.

Thus, the distance moved by the trolley $=v''\times t=10.36\times 2.5=25.9m$.

3. A 1 kg block situated on a rough incline is connected to a spring of spring constant 100 N/m as shown in Fig. 6.17. The block is released from rest with the spring in the unstretched position. The block moves 10 cm down the incline before coming to rest. Find the coefficient of friction between the block and the incline. Assume that the spring has a negligible mass and the pulley is frictionless.

Spring and block system on a rough inclined plane

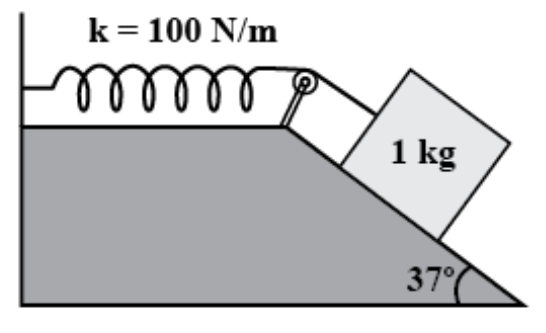
Mass of the block, \[m=\text{ }1\text{ }kg\]

Spring constant, \[k=100N/m\]

Displacement in the block, \[x=\text{ }10\text{ }cm\text{ }=\text{ }0.1\text{ }m\]

The given situation can be shown as in the following figure.

Free body diagram of a Spring and block system on a rough inclined plane.

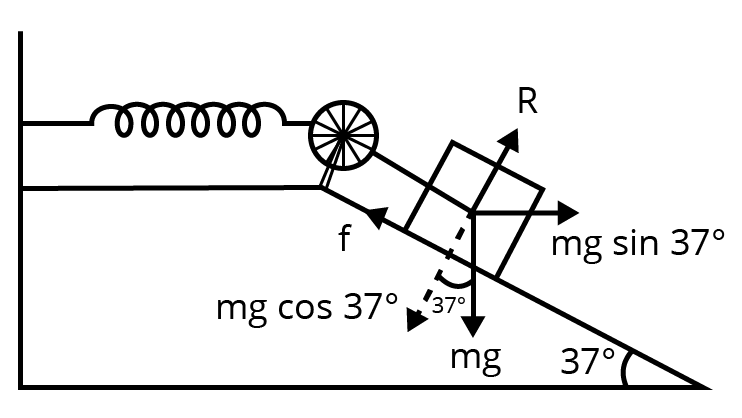
At equilibrium:

Normal reaction, \[R=\text{ }mg\text{ }cos\text{ }37{}^\circ \]

Frictional force, \[f\text{ = }\mu R\text{ }=\text{ }mg\text{ }sin\text{ }37{}^\circ \]

Where, \[\mu \] is the coefficient of friction.

Net force acting on the block \[=mg\sin {{37}^{0}}-f\]

\[=mg\sin {{37}^{0}}-\mu mgco\operatorname{s}{{37}^{0}}\]

\[=mg\left( \sin {{37}^{0}}-\mu co\operatorname{s}{{37}^{0}} \right)\]

At equilibrium, the work done by the block is equal to the potential energy of the spring, i.e.,

\[mg\left( \sin {{37}^{0}}-\mu mgco\operatorname{s}{{37}^{0}} \right)x=\frac{1}{2}k{{x}^{2}}\]

\[\Rightarrow 1\times 9.8\left( \sin {{37}^{0}}-\mu mgco\operatorname{s}{{37}^{0}} \right)x=\frac{1}{2}100\times {{0.1}^{2}}\]

$\Rightarrow 0.602-\mu \times 0.799=0.510$

$\Rightarrow \mu =\frac{0.092}{0.799}=0.115$, which is the required coefficient of friction.

4. Given in Fig. 6.11 are examples of some potential energy functions in one dimension. The total energy of the particle is indicated by a cross on the ordinate axis. In each case, specify the regions, if any, in which the particle cannot be found for the given energy. Also, indicate the minimum total energy the particle must have in each case. Think of simple physical contexts for which these potential energy shapes are relevant.

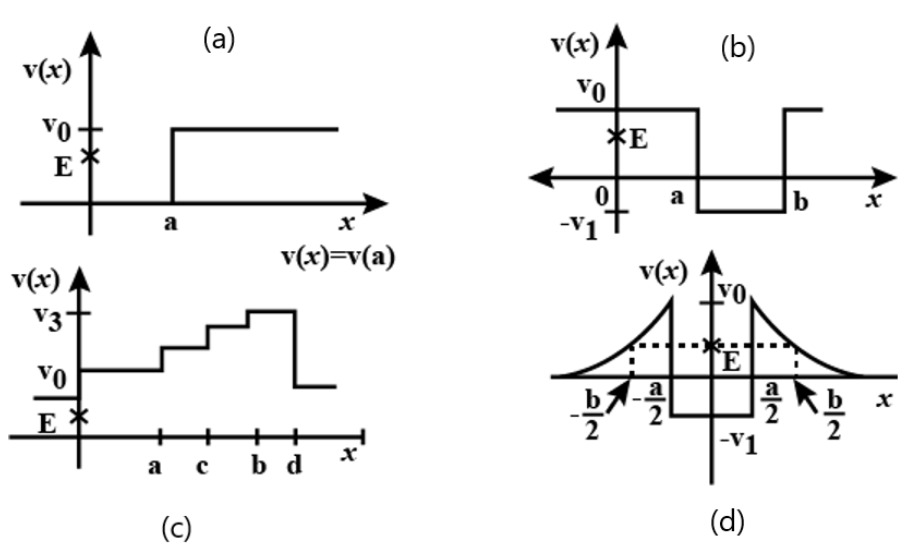
From the given figure: \[x\text{ }>\text{ }a;\text{ 0}\]

Total energy of a system is:\[E\text{ }=\text{ }P.E.\text{ }+\text{ }K.\text{ }E.\]

The kinetic energy of a body is a positive quantity. It cannot be negative. Therefore, the particle will not exist in a region where K.E. becomes negative. In this case, the potential energy $\left( {{V}_{0}} \right)$ of the particle becomes greater than total energy (E) for \[x\text{ }>\text{ }a\]. Hence, kinetic energy becomes negative in this region. Therefore, the particle will not exist in this region. The minimum total energy of the particle is zero.

From the given figure, all the regions the particle cannot be found for the given energy. In the given case, the potential energy (PE) is greater than total energy (E) in all regions. Hence, the particle will not exist in this region.

From the given figure: $x>a$ and \[x\text{ }<\text{ }b;-{{V}_{1}}\]

In the given case, the condition regarding the positivity of K.E. is satisfied only in the region between $x>a$ and \[x\text{ }<\text{ }b\].The minimum potential energy in this case is \[{{V}_{1}}\]. Therefore,

\[KE=\text{ }E-\left( -{{V}_{1}} \right)=E+{{V}_{1}}\].

Therefore, for the positivity of the kinetic energy, the total energy of the particle must be greater than \[{{V}_{1}}\]. So, the minimum total energy the particle must have is \[{{V}_{1}}\].

From the given figure: $-\frac{b}{2}<x<\frac{a}{2};-\frac{a}{2}<x<\frac{a}{2};-{{V}_{1}}$

In the given case, the potential energy \[\left( \text{ }{{\text{V}}_{0}} \right)\] of the particle becomes greater than the total energy (E) for $-\frac{b}{2}<x<\frac{a}{2}$ and $-\frac{a}{2}<x<\frac{a}{2}$. Therefore, the particle will not exist in these regions.

The minimum potential energy in this case is $-{{V}_{1}}$. Therefore,\[KE=\text{ }E-\left( -{{V}_{1}} \right)=E+{{V}_{1}}\].

Therefore, for the positivity of the kinetic energy, the total energy of the particle must be greater than $-{{V}_{1}}$. So, the minimum total energy the particle must have is $-{{V}_{1}}$.

5. An electron and a proton are detected in a cosmic ray experiment, the first with kinetic energy 10 keV, and the second with 100 keV. Which is faster, the electron or the proton? Obtain the ratio of their speeds.

(electron mass \[=9.11\times {{10}^{-31}}\text{ }kg\], proton mass \[=1.67\times {{10}^{-27}}\text{ }kg\], \[1\text{ }eV\text{ }=\text{ 1}\text{.60}\times \text{1}{{\text{0}}^{-19}}J\]).

Mass of the electron \[=9.11\times {{10}^{-31}}\text{ }kg\]

Mass of the proton \[=1.67\times {{10}^{-27}}\text{ }kg\]

Kinetic energy of the electron, \[{{E}_{Ke}}=\text{ }10\text{ }keV\text{ }=\text{ 1}{{\text{0}}^{4}}eV\]

\[=\text{1}{{\text{0}}^{4}}\times \text{1}\text{.60}\times \text{1}{{\text{0}}^{-19}}\text{=1}\text{.60}\times \text{1}{{\text{0}}^{-15}}J\]

Kinetic energy of the proton, ${{E}_{Kp}}=100keV={{10}^{5}}eV=1.60\times {{10}^{-14}}J$.

For the velocity of an electron ${{v}_{e}}$, its kinetic energy is given by the relation:

${{E}_{Ke}}=\frac{1}{2}m{{v}_{e}}^{2}$

$\Rightarrow {{v}_{e}}=\sqrt{\frac{2\times {{E}_{Ke}}}{m}}$$=\sqrt{\frac{2\times 1.60\times {{10}^{-15}}}{9.11\times {{10}^{-31}}}}=5.93\times {{10}^{7}}m/s$

For the velocity of a proton ${{v}_{p}}$, its kinetic energy is given by the relation:

${{E}_{Kp}}=\frac{1}{2}m{{v}_{p}}^{2}$

$\Rightarrow {{v}_{p}}=\sqrt{\frac{2\times {{E}_{Kp}}}{m}}$$=\sqrt{\frac{2\times 1.60\times {{10}^{-15}}}{1.67\times {{10}^{-27}}}}=4.38\times {{10}^{6}}m/s$

Hence, the electron is moving faster than the proton.

The ratio of their speeds:

$\frac{{{v}_{e}}}{{{v}_{p}}}=\frac{5.93\times {{10}^{7}}}{4.38\times {{10}^{6}}}=13.54:1$

It is clear that electrons are faster; Ratio of speeds is \[13.54:\text{ }1\].

6. The bob of a pendulum is released from a horizontal position. If the length of the pendulum is 1.5 m, what is the speed with which the bob arrives at the lowermost point, given that it dissipated 5% of its initial energy against air resistance?

Length of the pendulum, \[l\text{ }=\text{ }1.5\text{ }m\]

Mass of the bob \[=\text{ }m\]

Energy dissipated \[=\text{ }5%\]

Using the law of conservation of energy, the total energy of the system remains constant.

At the horizontal position:

Potential energy of the bob, \[EP\text{ }=\text{ }mgl\]

Kinetic energy of the bob, \[EK\text{ }=\text{ }0\]

\[Total\text{ }energy\text{ }=\text{ }mgl\] ... (i)

At the lowermost point (mean position):

Potential energy of the bob, \[EP\text{ }=\text{ }0\]

Kinetic energy of the bob, ${{E}_{k}}=\frac{1}{2}m{{v}^{2}}$.

Total energy, ${{E}_{k}}=\frac{1}{2}m{{v}^{2}}$... (ii)

As the bob moves from the horizontal position to the lowermost point, 5% of its energy gets dissipated. The total energy at the lowermost point is equal to 95% of the total energy at the horizontal point, i.e.,

$\frac{1}{2}m{{v}^{2}}=\frac{95}{100}\times mgl$

$\Rightarrow v=\sqrt{\frac{2\times 95\times 1.5\times 9.8}{100}}=528m/s$, which is the required speed.

7. The blades of a windmill sweep out a circle of area A. (a) If the wind flows at a velocity v perpendicular to the circle, what is the mass of the air passing through it in time t? (b) What is the kinetic energy of the air? (c) Assume that the windmill converts 25% of the wind's energy into electrical energy, and that A = $30{{m}^{2}}$ , v = 36 km/h and the density of air is \[\mathbf{1}.\mathbf{2}\text{ }\mathbf{kg}/{{m}^{3}}\]. What is the electrical power produced?

\[Area\text{ }of\text{ }the\text{ }circle\text{ }swept\text{ }by\text{ }the\text{ }windmill\text{ }=\text{ }A\]

\[Velocity\text{ }of\text{ }the\text{ }wind\text{ }=\text{ }v\]

\[Density\text{ }of\text{ }air\text{ }=\rho \]

Volume of the wind flowing through the windmill per sec \[=\text{ }Av\]

Mass of the wind flowing through the windmill per sec \[=\text{ }\rho Av\]. Mass m, of the wind flowing through the windmill in time \[t=\rho Avt\]

Kinetic energy of air $=\frac{1}{2}m{{v}^{2}}=\frac{1}{2}\left( \rho Avt \right){{v}^{2}}=\frac{1}{2}\rho A{{v}^{3}}t$

Area of the circle swept by the windmill \[=\text{ }A\text{ }=\text{ }30\text{ }{{m}^{2}}\]

Velocity of the wind \[=\text{ }v=\text{ }36\text{ }km/h\]

Density of air, $\rho =1.2kg/{{m}^{3}}$

\[Electric\text{ }energy\text{ }produced\text{ }=\text{ }25%\text{ }of\text{ }the\text{ }wind\text{ }energy\]

$=\frac{25}{100}\times Kinet\text{ic energy of a}ir$

$=\frac{1}{8}\rho A{{v}^{3}}t$

\[Electrical\text{ }power=\frac{Electrica\text{l e}nergy}{Time}\]

$=\frac{1}{8}\frac{\rho A{{v}^{3}}t}{t}=\frac{1}{8}\rho A{{v}^{3}}$

$=\frac{1}{8}\times 1.2\times 30\times {{10}^{3}}=4.5kW$

5 Marks Questions

Define potential energy. Give examples.

Ans: Potential energy is defined as the energy possessed by a body by virtue of its position in a field or due to change in its configuration example – A gas compressed in a cylinder, A wound spring of a water, water raised to the overhead tank in a house etc.

Draw a graph showing the variation of potential energy, kinetic energy and the total energy of a body freely falling on earth from a height h?

Ans: The graph below shows the variation of potential energy, kinetic energy and the total energy of a body freely falling on earth from a height h:

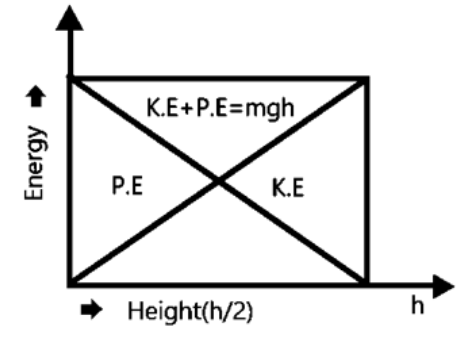
(i) Gravitational potential energy decreases as the body falls downwards and is zero at the earth

(ii) Kinetic energy increases as the body falls downwards and is maximum when the body just strikes the ground.

(iii) According to the law of conservation of energy, total mechanical (KE + PE) energy remains constant.

2. Answer the following:

The casing of a rocket in flight burns up due to friction. At whose expense is the heat energy required for burning obtained? The rocket or the atmosphere?

Ans: At rocket’s expense the heat energy required for burning is obtained. The burning of the casing of a rocket in flight (due to friction) results in the reduction of the mass of the rocket. According to the conservation of energy:

\[Total\text{ }Energy\left( T.E. \right)=\text{ }Potential\text{ }enegry\left( P.E. \right)+Kinetic\text{ }energy\left( K.E. \right)\]

$mgh+\frac{1}{2}m{{v}^{2}}$

The reduction in the rocket's mass causes a drop in the total energy. Therefore, the heat energy required for the burning is obtained from the rocket.

Comets move around the sun in highly elliptical orbits. The gravitational force on the comet due to the sun is not normal to the comet's velocity in general. Yet the work done by the gravitational force over every complete orbit of the comet is zero. Why?

Ans: Gravitational force is a conservative force. As the work done by a conservative force over a closed path is zero, the work done by the gravitational force over every complete orbit of a comet is zero.

An artificial satellite orbiting the earth in a very thin atmosphere loses its energy gradually due to dissipation against atmospheric resistance, however small. Why then does its speed increase progressively as it comes closer and closer to the earth?

Ans: When an artificial satellite, orbiting around earth, moves closer to earth, its potential energy decreases due to the reduction in the height. As the total energy of the system remains constant, the reduction in P.E. results in an increase in K.E. Hence, the velocity of the satellite increases. However, due to atmospheric friction, the total energy of the satellite decreases by a small amount.

In Fig. 6.13(i) the man walks 2 m carrying a mass of 15 kg on his hands. In Fig. 6.13(ii), he walks the same distance pulling the rope behind him. The rope goes over a pulley, and a mass of 15 kg hangs at its other end. In which case is the work done greater?

(i) Shows a man walking carrying a mass of 15 kg on his hands, (ii) Man walks the same distance pulling the rope behind him.

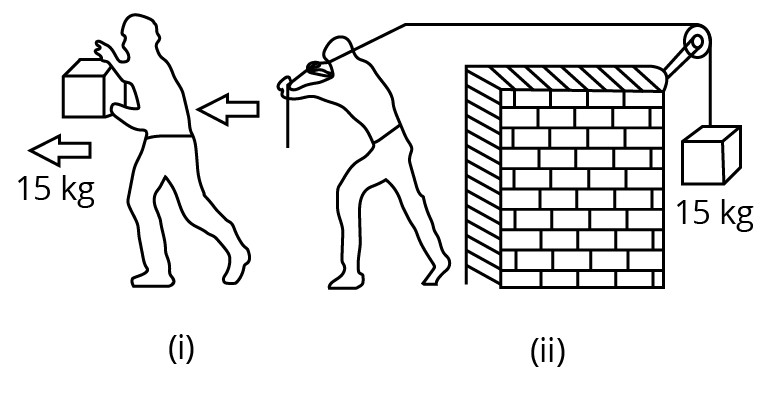
Ans: In the second case, the work done is greater.

Mass, \[m\text{ }=\text{ }15\text{ }kg\]

Displacement, \[s\text{ }=\text{ }2\text{ }m\]

Work done, \[W=Fs\cos \theta \]

Where, \[\theta =Angle\text{ }between\text{ }force\text{ }and\text{ }displacement\]

\[W=mgs\cos \theta =15\times 2\times 9.8\cos {{90}^{0}}=0\]

Here, the direction of the force applied on the rope and the direction of the displacement of the rope are the same.

Therefore, the angle between them, $\theta ={{0}^{0}}$

As, $\cos {{0}^{0}}=1$

Work done, \[W={{F}_{s}}\cos \theta =mgs\]$=15\times 9.8\times 2=294J$

Thus, work done in the second case is greater.

3. A rain drop of radius 2 mm falls from a height of 500 m above the ground. It falls with decreasing acceleration (due to viscous resistance of the air) until at half its original height, it attains its maximum (terminal) speed, and moves with uniform speed thereafter. What is the work done by the gravitational force on the drop in the first and second half of its journey? What is the work done by the resistive force in the entire journey if its speed on reaching the ground is $10m/s$?

Radius of the rain drop, \[r=\text{ }2\text{ }mm\text{ }=\text{ 2}\times {{10}^{-3}}m\].

Volume of the rain drop, \[V=\frac{4}{3}\pi {{r}^{3}}\]

\[=\frac{4}{3}\times 3.14\times {{\left( \text{2}\times {{10}^{-3}} \right)}^{3}}\times {{10}^{3}}kg\]

Mass of the rain drop, \[m=\rho V\]

Gravitational force, \[F\text{ }=\text{ }mg\]

\[=\frac{4}{3}\times 3.14\times {{\left( \text{2}\times {{10}^{-3}} \right)}^{3}}\times {{10}^{3}}\times 9.8N\]

The work done by the gravitational force on the drop in the first half of its journey:

${{W}_{1}}=Fs$

\[=\frac{4}{3}\times 3.14\times {{\left( \text{2}\times {{10}^{-3}} \right)}^{3}}\times {{10}^{3}}\times 9.8\times 250\]

\[=\text{ }0.082\text{ }J\]

This amount of work is equal to the work done by the gravitational force on the drop in the second half of its journey, i.e., \[{{W}_{II}}=\text{ }0.082\text{ }J\]As per the law of conservation of energy, if no resistive force is present, then the total energy of the rain drop will remain the same.

Total energy at the top will be:

${{E}_{T}}=mgh+0$

\[=\frac{4}{3}\times 3.14\times {{\left( \text{2}\times {{10}^{-3}} \right)}^{3}}\times {{10}^{3}}\times 9.8\times 500\times {{10}^{-5}}\]

Due to the presence of a resistive force, the drop hits the ground with a velocity of 10 m/s.

Total energy at the ground will be:

${{E}_{G}}=\frac{1}{2}m=\frac{4}{3}\times 3.14\times {{\left( \text{2}\times {{10}^{-3}} \right)}^{3}}\times {{10}^{3}}\times 9.8\times {{10}^{2}}$

$=1.675\times {{10}^{-3}}J$

\[Work\text{ }done\text{ }by\text{ }resistive\text{ }force\text{ }={{E}_{G}}-{{E}_{T}}=-0.162J\]

4. Two identical ball bearings in contact with each other and resting on a frictionless table are hit head-on by another ball bearing of the same mass moving initially with a speed V. If the collision is elastic, which of the following figures is a possible result after collision?

Collision between two identical balls in contact with another identical ball.

Ans:

Case (i) result is possible after a collision

It is observed that the total momentum before and after collision in each case is constant. For an elastic collision, the total kinetic energy of a system remains conserved before and after the collision. For the mass of each ball bearing m,

The total kinetic energy of the system before collision:

$=\frac{1}{2}m{{v}^{2}}-\frac{1}{2}\left( 2m \right)0$

$=\frac{1}{2}m{{v}^{2}}$

Case (ii): Total kinetic energy of the system after collision:

$=\frac{1}{2}\left( m \right)0+\frac{1}{2}\left( 2m \right){{\left( \frac{v}{2} \right)}^{2}}$

$=\frac{1}{4}m{{v}^{2}}$

Hence, the kinetic energy of the system is not conserved in case (i).

Case (iii): Total kinetic energy of the system after collision:

$=\frac{1}{2}\left( 2m \right)0+\frac{1}{2}m{{v}^{2}}$

Thus, the kinetic energy of the system is conserved in case (ii).

Case (vi): Total kinetic energy of the system after collision:

$=\frac{1}{2}\left( 3m \right){{\left( \frac{v}{3} \right)}^{2}}$

$=\frac{1}{6}m{{v}^{2}}$

Thus, the kinetic energy of the system is not conserved in case (iii).

5. A bullet of mass 0.012 kg and horizontal speed of $70m/s$ strikes a block of wood of mass 0.4 kg and instantly comes to rest with respect to the block. The block is suspended from the ceiling by means of thin wires. Calculate the height to which the block rises. Also, estimate the amount of heat produced in the block.

Mass of the bullet, \[m=\text{ }0.012\text{ }kg\]

Initial speed of the bullet, \[{{u}_{b}}=\text{ }70\text{ }m/s\].

Mass of the wooden block, \[M=\text{ }0.4\text{ }kg\]

Initial speed of the wooden block, \[{{u}_{g}}=\text{ }0\]

Final speed of the system of the bullet and the block \[=\text{ }v\]

Applying the law of conservation of momentum:

$m{{u}_{b}}+M{{u}_{g}}=\left( m+M \right)v$

$0.012\times 70+0.4\times 0=\left( 0.012+0.4 \right)v$

$\Rightarrow v=\frac{0.84}{0.412}=2.041m/s$

For the system of the bullet and the wooden block:

Mass of the system, \[m'\text{ }=\text{ }0.412\text{ }kg\]

Velocity of the system \[=\text{ }2.04\text{ }m/s\]

Height up to which the system rises \[=\text{ }h\]

Applying the law of conservation of energy to this system:

\[Potential\text{ }energy\text{ }at\text{ }the\text{ }highest\text{ }point\text{ }=\text{ }Kinetic\text{ }energy\text{ }at\text{ }the\text{ }lowest\text{ }point\]

$m'gh=\frac{1}{2}m'{{v}^{2}}$

$\Rightarrow h=\frac{1}{2}\left( \frac{{{v}^{2}}}{g} \right)$$=\frac{1}{2}\times \frac{{{\left( 2.04 \right)}^{2}}}{9.8}$$=0.2123m$

The wooden block will rise to a height of \[0.2123\text{ }m\].

\[Heat\text{ }produced\text{ }=\text{ }Kinetic\text{ }energy\text{ }of\text{ }the\text{ }bullet\text{ }-\text{ }Kinetic\text{ }energy\text{ }of\text{ }the\text{ }system\]

$\Rightarrow \frac{1}{2}m{{u}^{2}}-\frac{1}{2}m'{{v}^{2}}$\[=\frac{1}{2}\times 0.012\times {{70}^{2}}-\frac{1}{2}\times 0.412\times {{2.04}^{2}}=28.54J\]

6. Two inclined frictionless tracks, one gradual and the other steep, meet at A from where two stones are allowed to slide down from rest, one on each track (Fig. 6.16). Will the stones reach the bottom at the same time? Will they reach there with the same speed? Explain. Given \[{{\theta }_{1}}=\text{ }30{}^\circ ,\text{ }{{\theta }_{2}}=\text{ }60{}^\circ ,\]and h = 10 m, what are the speeds and times taken by the two stones?

Ans: No, they won’t reach there with the same speed.

The stone moving down the steep plane will reach the bottom first.

Yes; the stones will reach the bottom with the same speed

\[{{v}_{b}}={{v}_{c}}=\text{ }14\text{ }m/s\]

\[{{t}_{1}}=\text{ }2.86\text{ }s;\text{ }{{\text{t}}_{2}}=\text{ }1.65\text{ }s\]

The given situation can be shown as in the following figure:

${{v}_{b}}={{v}_{c}}=\text{ }14\text{ }m/s\] \[{{t}_{1}}=\text{ }2.86\text{ }s;\text{ }{{\text{t}}_{2}}=\text{ }1.65\text{ }s$

Here, the initial height (AD) for both stones is the same (h). Hence, both will have the same potential energy at point A.

As per the law of conservation of energy, the kinetic energy of the stones at points B and C will also be the same, i.e.,

$\frac{1}{2}m{{v}_{1}}^{2}=\frac{1}{2}m{{v}_{2}}^{2}$

Consider, ${{v}_{1}}={{v}_{2}}=v$

\[m\text{ }=\text{ }Mass\text{ }of\text{ }each\text{ }stone\]

\[v=\text{ }Speed\text{ }of\text{ }each\text{ }stone\text{ }at\text{ }points\text{ }B\text{ }and\text{ }C\]

Hence, both stones will reach the bottom with the same speed, v.

For stone I:

Net force acting on this stone is given by:

${{F}_{net}}=m{{a}_{1}}=mg\sin {{\theta }_{1}}$

$\Rightarrow {{a}_{1}}=g\sin {{\theta }_{1}}$

For stone II:

${{a}_{2}}=g\sin {{\theta }_{2}}$

$\Rightarrow {{\theta }_{2}}>{{\theta }_{1}}$

$\Rightarrow {{a}_{2}}>{{a}_{1}}$

Using the first equation of motion, the time of slide can be obtained as:

$\Rightarrow t=\frac{v}{a}\left( \because u=0 \right)$

${{t}_{1}}=\frac{v}{{{a}_{1}}}$

${{t}_{2}}=\frac{v}{{{a}_{2}}}$

$\Rightarrow {{t}_{2}}<{{t}_{1}}$

Thus, the stone moving down the steep plane will reach the bottom first.

The speed (v) of each stone at points B and C is given by the relation obtained from the law of conservation of energy.

$mgh=\frac{1}{2}m{{v}^{2}}$

$\Rightarrow v=\sqrt{2gh}=\sqrt{2\times 9.8\times 10}=14m/s$

${{t}_{1}}=\frac{v}{{{a}_{1}}}=\frac{v}{g\sin {{\theta }_{1}}}=\frac{14}{9.8\times \sin {{30}^{0}}}=2.86s$

${{t}_{2}}=\frac{v}{{{a}_{2}}}=\frac{v}{g\sin {{\theta }_{2}}}=\frac{14}{9.8\times \sin {{60}^{0}}}=1.65s$, which are the corresponding times taken by both the stones.

Important Questions from Work, Energy and Power (Short, Long & Practice)

Short answer type questions.

1. A spring is stretched. Is the work done by the stretching force positive or negative?

2. What is the work done by the centripetal force? Why?

3. What is the work done by the tension in the string of a simple pendulum?

Long Answer Type Questions

1. Prove that instantaneous power is given, by the dot product of force and velocity i.e. P = F.v.

2. State and prove work-energy theorem or principle.

3. State and prove the law of conservation of energy.

4. A 10 kg block slides without acceleration down a rough inclined plane making an angle of 20° with the horizontal. Calculate the work done over a distance of 1.2 m when the inclination of the plane is increased to 30°.

Practice Questions

1. A bullet of mass 20 g moving with a velocity of 500 ms -1 strikes a tree and goes out from the other end. with a velocity of 400 ms -1 . Calculate the work done in passing through the tree.

2. A stone of mass 5 kg falls from the top of a cliff 30 m high and buries itself one metre deep into the sand. Find the average resistance offered and time taken to penetrate into the sand.

3. A wooden ball is dropped from a height of 2 m. What is the height up to which the ball will rebound if the coefficient of restitution is 0.5?

Download Important Questions For Class 11 Physics Chapter 6

Chapter 6 of Class 11 Physics Work, Power, and Energy is an important topic to be covered by the students for securing good scores in the Board exams as well as in the competitive exams. Students find Chapter 6 Work, Power, and Energy as one of the difficult topics to be covered in Physics, but students will be able to tackle this by practising more and more questions with the help of work energy and power Class 11 important questions with answers Pdf available on the Vedantu platform. Class 11 Physics Chapter 6 Important Questions Pdf is prepared for students in such a way that they will be able to solve the questions effortlessly.

Work Energy And Power Class 11 Important Questions With Answers

Students must be familiar with Chapter 6 Work, Power, and Energy for attempting Class 11 Physics Chapter 6 Important Questions . The chapter includes interesting topics like a work-energy theorem, kinetic energy, potential energy, conservation of energy, power, collisions, etc…

Students must be well versed with Chapter 6 for appearing in the CBSE board exams. The most common difficulty encountered by the students is how to approach the question. The approach of the question is understood by practising questions from related topics. Before starting with the practice of Class 11 Physics work energy and power important questions students should have a brief revision of the chapter which is available on the Vedantu website.

Physics Chapter 6 - Work, Energy, and Power

In NCERT Physics syllabus Work, Energy, and Power chapter is of high importance from an examination point of view. Students must be familiar with the terms of work, energy, and power from their elementary classes. In our everyday life, we use these terms so casually but the Physics behind them is interesting. In order to have a hold on any subject, it is only possible with regular studies and practice. Work, Energy, and Power is a chapter that can be understood with real-life exams. Work energy and power Class 11 important questions with answers covered all the questions with suitable examples students can relate it to quickly.

Students should start studying by questioning, for example, now we are on Chapter 6 Work, Energy, and Power. The very first question that arises in a student's mind is what is work. Work and energy are two terms that we come across most often, work and energy are interrelated concepts. For solving important questions from work energy and power Class 11 , students should understand the complete chapter and remember a few topics such as :

Work: Work is just energy transferred by force.

Work Done: Work done is defined as when an external force acts upon a body in steady motion; it will experience some displacement; this action is termed as the work is done.

Energy: The ability to do work is known as energy. There are several types of energy like electrical energy, solar energy, mechanical energy, etc. In this chapter, we will focus mainly on mechanical energy and its types. There are basically two types of mechanical energy:

Kinetic Energy: The energy gained by an object due to its motion is known as the kinetic energy of that object.

Potential Energy: The energy gained by an object due to its position is known as the potential energy of that object.

Power: The rate of doing work is known as power.

Work Energy Theorem: Work energy theorem states that work done by the external forces on an object is equal to the change in its kinetic energy.

Conservation of Energy: Conservation of energy can be stated as- energy is a conserved quantity it can neither be created nor be destroyed.

Like these, there are many more interesting concepts included in Chapter 6 of Class 11 Physics. Not only these we will also come across topics like momentum, conservation of momentum, collisions, type of collision, etc… There are high chances of getting numerical type problems in competitive exams from this chapter. Not only numerical type questions we also get to see questions that demand for graphical methods, derivations, and multiple choices type questions.

The work, energy, and power chapter compiled of many more important topics that can be mastered by practicing Class 11 Physics Chapter 6 Important Questions . The work, Energy and Power chapter mainly focus on bringing the idea of how work is defined, the difference between work and work done, Mechanical energy and its types, etc… Refer to the material available on the Vedantu for a detailed explanation.

Chapter 6 of Class 11 Physics syllabus as prescribed by CBSE, NCERT board have numerous topics, derivations, diagrams, graphs. Students must focus on derivation parts carefully with clear understanding. Numerical problems, MCQs, Revision notes of Chapter 6 are available on the Vedantu website and they are prepared by experts after deep research and analysis of CBSE, NEET , JEE exam papers and students find them reliable. Before starting with the preparation of the exams, students should go through the chapters thoroughly without skipping any topic as in Physics every topic will be related to another topic.

Key Features of Important Questions for Class 11 Physics Chapter 6 - Work, Energy and Power

Important Questions are curated in the right manner to help students in quickly finding solutions.

Step-by-step explanations for all questions from previous years are included.

All solutions are easy to understand as they are solved by subject experts to match the syllabus.

These Important Questions on Work, Energy and Power help students in developing strong conceptual foundations for students, which is important in the final stages of preparation for board and competitive exams.

These Important Questions are available in PDF format and can be downloaded for free.

Important Questions on Class 11 Physics Work, Energy and Power are a very important material for students preparing for Class XI Examination as well as competitive exams. From the discussion above, students will get an idea about the type of questions in the final examination. Students can rely on these Important Questions as they are curated by experts.

Important Related Links for CBSE Class 11

FAQs on Important Questions for CBSE Class 11 Physics Chapter 6 - Work, Energy and Power

1. Is Chapter 6-Work, Power, and Energy of Class 11 Physics difficult?

Chapter 6-Work, Power, and Energy of Class 11 Physics is an important chapter from the exam's point of view. Students find this chapter difficult because there are many different concepts given in the chapter. Students have to learn the formulae, solve the numerical, and understand the definitions given in this chapter for scoring high marks in CBSE exams. Students can score high marks by practising important questions available on Vedantu app and website. Students can visit Vedantu to download PDFs of important questions free of cost.

2. Do I have to learn the definitions given in Chapter 6 of Class 11 Physics?

Yes, students have to learn important definitions in Class 11 Physics Chapter 6 and can understand all the basic concepts easily. They can download the important definitions and important questions from Vedantu and can prepare for their exams effortlessly by preparing short notes. Important questions for Class 11 Physics Chapter 6 are prepared by expert and qualified teachers to help students understand the concepts easily.

3. What are the important topics given in Chapter 6-Work, Power, and Energy of Class 11 Physics?

Important topics covered in Chapter 6 of Class 11 Physics include an introduction, the theorem related to work, energy, and power, different types of energies such as kinetic energy, potential energy, and mechanical energy. Students will also learn the concept of conservation of energy and laws related to the conservation of energy. Students can understand all important topics given in Class 11 Physics Chapter 6 by practicing important questions given on Vedantu.

4. How important is Class 11 Physics Chapter 6 for JEE and NEET Exams?

Class 11 Physics Chapter 6 is very important for JEE and NEET exams. Students should understand the basic concepts of this chapter to score high marks in the board exams and entrance exams. They should practice formulas and numerical for solving numerical problems. Students can get high marks in the board exams and entrance exams.

5. Where can I find Important Questions for Class 11 Physics Chapter 6 Work, Energy and Power?

Vedantu offers a well-prepared set of Important Questions for all subjects. Our experts select questions based on the exam pattern and questions from the previous papers. These questions are solved by subject matter experts to provide a thorough understanding of the Class 11 Physics Chapter 6 Work, Energy and Power with step by step solutions.

CBSE Class 11 Physics Important Questions

Cbse study materials.

Andhra Pradesh
Chhattisgarh
West Bengal
Madhya Pradesh
Maharashtra
Jammu & Kashmir
NCERT Books 2022-23
NCERT Solutions
NCERT Notes
NCERT Exemplar Books
NCERT Exemplar Solution
States UT Book
School Kits & Lab Manual
NCERT Books 2021-22
NCERT Books 2020-21
NCERT Book 2019-2020
NCERT Book 2015-2016
RD Sharma Solution
TS Grewal Solution
TR Jain Solution
Selina Solution
Frank Solution
ML Aggarwal Solution
Lakhmir Singh and Manjit Kaur Solution
I.E.Irodov solutions
ICSE - Goyal Brothers Park
ICSE - Dorothy M. Noronhe
Sandeep Garg Textbook Solution
Micheal Vaz Solution
S.S. Krotov Solution
Evergreen Science
KC Sinha Solution
ICSE - ISC Jayanti Sengupta, Oxford
ICSE Focus on History
ICSE GeoGraphy Voyage
ICSE Hindi Solution
ICSE Treasure Trove Solution
Thomas & Finney Solution
SL Loney Solution
SB Mathur Solution
P Bahadur Solution
Narendra Awasthi Solution
MS Chauhan Solution
LA Sena Solution
Integral Calculus Amit Agarwal Solution
IA Maron Solution
Hall & Knight Solution
Errorless Solution
Pradeep's KL Gogia Solution
OP Tandon Solutions
Sample Papers
Previous Year Question Paper
Value Based Questions
CBSE Syllabus
CBSE MCQs PDF
Assertion & Reason
New Revision Notes
Revision Notes
HOTS Question
Marks Wise Question
Toppers Answer Sheets
Exam Paper Aalysis
Concept Map
CBSE Text Book
Additional Practice Questions
Vocational Book
CBSE - Concept
KVS NCERT CBSE Worksheets
Formula Class Wise
Formula Chapter Wise
JEE Crash Course
JEE Previous Year Paper
Important Info
JEE Mock Test
JEE Sample Papers
SRM-JEEE Mock Test
VITEEE Mock Test
BITSAT Mock Test
Manipal Engineering Mock Test
AP EAMCET Previous Year Paper
COMEDK Previous Year Paper
GUJCET Previous Year Paper
KCET Previous Year Paper
KEAM Previous Year Paper
Manipal Previous Year Paper
MHT CET Previous Year Paper
WBJEE Previous Year Paper
AMU Previous Year Paper
TS EAMCET Previous Year Paper
SRM-JEEE Previous Year Paper
VITEEE Previous Year Paper
BITSAT Previous Year Paper
UPSEE Previous Year Paper
CGPET Previous Year Paper
CUSAT Previous Year Paper
AEEE Previous Year Paper
Crash Course
Previous Year Paper
NCERT Based Short Notes
NCERT Based Tests
NEET Sample Paper
Previous Year Papers
Quantitative Aptitude
Numerical Aptitude Data Interpretation
General Knowledge
Mathematics
Agriculture
Accountancy
Business Studies
Political science
Enviromental Studies
Mass Media Communication
Teaching Aptitude
NAVODAYA VIDYALAYA
SAINIK SCHOOL (AISSEE)
Mechanical Engineering
Electrical Engineering
Electronics & Communication Engineering
Civil Engineering
Computer Science Engineering
CBSE Board News
Scholarship Olympiad
School Admissions
Entrance Exams
All Board Updates
Miscellaneous
State Wise Books
Engineering Exam

CBSE Class 11th Physics Value Based Questions Chapter 6 Work Energy and Power PDF Download

CBSE Class 11th Physics Value Based Questions Chapter 6 Work Energy and Power are the easiest questions which you see in your question paper and the scoring one all student who attempt it surely get they are just little bit difficult and examine your basic knowledge regarding the particular chapter. Physics Value Based Questions for Class 11th are available here at Free of cost. These questions are expected to be asked in the Class 11th board examination. These Physics Value Based Questions are from complete CBSE Syllabus.

CBSE Class 11th Physics Value Based Questions Chapter 6 Work Energy and Power

Most of these Physics Value Based Questions are quite easy and students need only a basic knowledge of the chapter to answer these questions. Download CBSE Physics Value Based Questions for board examinations. These Physics Value Based Questions are prepared by Directorate of Education, Delhi.

CBSE Physics Value Based Questions Class 11th Chapter 6 Work Energy and Power PDF

The purpose of the Physics Value Based Questions is to make students aware of how basic values are needed in the analysis of different situations and how students require to recognize those values in their daily lives. Some questions are subject related. But even if they are not, that one-minute awareness of what we write about value without any specific preparation is a good step indeed.

CBSE Physics Value Based Questions for Class 11th Chapter 6 Work Energy and Power download here in PDF format. The most CBSE Physics Value Based Questions for annual examination are given here for free of cost. The additional questions for practice the Class 11th exam are collected from various sources. It covers questions asked in previous year examinations.

CBSE Physics Value Based Questions for Class 11th Chapter 6 Work Energy and Power Free PDF

Class 11th books have many questions. These questions are regularly asked in exams in one or other way. Practising such most CBSE Physics Value Based Questions Chapter 6 Work Energy and Power certainly help students to obtain good marks in the examinations.

Manipal MET 2024 Application (Released) (All Pages)

NCERT Solutions for Class 12 Maths
NCERT Solutions for Class 10 Maths
CBSE Syllabus 2023-24
Social Media Channels
Login Customize Your Notification Preferences

One Last Step...

Second click on the toggle icon

Provide prime members with unlimited access to all study materials in PDF format.

Allow prime members to attempt MCQ tests multiple times to enhance their learning and understanding.

Provide prime users with access to exclusive PDF study materials that are not available to regular users.

Physics Important Questions
Class 11 Physics

CBSE Important Questions for Class 11 Physics

CBSE Important Questions for Class 11 Physics provide you with excellent strategies to prepare for the Physics examination. Questions can be framed from any corner of the book or outside the textbook for the final exams. Thus, you need advanced knowledge rather than practising only through textbooks. This page provides you with CBSE Important Questions Class 11 with medium to advance level Physics questions, helping you to become well-prepared for the competitive examinations.

CBSE Class 11 Physics Important Questions

Important questions for Class 11 Physics are framed according to the NCERT syllabus. Students can click the link below to access the chapter-wise important questions of CBSE Class 11 Physics.

The repeatedly asked questions and the questions of high priority according to the syllabus are provided with answers, at BYJU’S for free. Thus, CBSE Important Questions are essential in building clear concepts and excelling in the Class 11 examination. It plays a major role in helping students face exams confidently and achieve good grades.

Register with BYJU'S & Download Free PDFs

Gurukul of Excellence

Classes for Physics, Chemistry and Mathematics by IITians

Category: Case Study Questions for Class 11 Physics

Join our Telegram Channel for Free PDF Download

Case Study Questions for Class 11 Physics Chapter 15 Waves

Case study questions for class 11 physics chapter 14 oscillations, case study questions for class 11 physics chapter 11 thermal properties of matter, case study questions for class 11 physics chapter 10 mechanical properties of fluids, case study questions for class 11 physics chapter 9 mechanical properties of solids, case study questions for class 11 physics chapter 8 gravitation, case study questions for class 11 physics chapter 7 system of particles and rotational motion, case study questions for class 11 physics chapter 6 work energy and power, case study questions for class 11 physics chapter 5 laws of motion, case study questions for class 11 physics chapter 4 motion in a plane, case study questions for class 11 physics chapter 3 motion in a straight line, case study questions for class 11 physics chapter 2 units and measurements.

Join our Online Test Series for CBSE, ICSE, JEE, NEET and Other Exams

Editable Study Materials for Your Institute - CBSE, ICSE, State Boards (Maharashtra & Karnataka), JEE, NEET, FOUNDATION, OLYMPIADS, PPTs

Question and Answer forum for K12 Students

MCQ Questions for Class 11 Physics Chapter 6 Work, Energy and Power with Answers

We have compiled the NCERT MCQ Questions for Class 11 Physics Chapter 6 Work, Energy and Power with Answers Pdf free download covering the entire syllabus. Practice MCQ Questions for Class 11 Physics with Answers on a daily basis and score well in exams. Refer to the Work, Energy and Power Class 11 MCQs Questions with Answers here along with a detailed explanation.

Work, Energy and Power Class 11 MCQs Questions with Answers

Multiple Choice Type Questions

Question 1. A bullet is fired horizontally and gets embedded in a block kept on a table. If the table is frictionless, then (a) only momentum is conserved. (b) only potential energy is conserved. (c) only K.E. is conserved. (d) both (a) and (b).

Answer: (d) both (a) and (b).

Work, Energy and Power with Questions and Answers

Question 2. A shell is fired from a canon with a velocity v ms -1 at an angle 6 with the horizontal direction. At the highest point in its path, it explodes into two pieces of equal mass. One of the pieces retraces its path to the canon and the speed of the other piece (in ms -1 ) just after the explosion is (a) v cos θ (b) 3v cos θ (c) 2v cos θ (d) $\frac {v}{2}$ cos θ

Answer: (b) 3v cos θ

Question 3. The work performed on an object does not depend upon (a) the displacement. (b) the force applied. (c) the angle at which the force is applied to the displacement (d) initial velocity of the object.

Answer: (d) initial velocity of the object.

Question 4. A ball is dropped from a height of 15 m. It gets embedded in sand by 10 mm and then stops. Which of the following is conserved? (a) Temperature (b) Momentum (c) Kinetic energy (d) Both (a) and (c)

Answer: (b) Momentum

Question 5. A chain of length L and mass M is held on a smooth table with its $\frac {1}{n}$ th part hanging over the edge. The work done in pulling the chain is directly proportional to (a) n -3 (b) √n (c) n (d) n -2

Answer: (d) n -2

Question 6. A pump delivers water at the rate of V cubic meter per second. By what factor its power should be raised so that it delivers water at the rate of nV cubic metre per second. (a) n³ (b) √n (c) n (d) n²

Answer: (a) n³

Question 7. Liquid of density ρ flows along a horizontal pipe of uniform area of cross-section ‘a’ with a velocity v through a right angled bend. What force should be applied to the bend to hold it in equilibrium? (a) $\frac {av^2ρ}{2}$ (b) $\frac {av^2ρ}{√2}$ (c) 2av²ρ (d) √2 av²ρ

Answer: (c) 2av²ρ

Question 8. A body of mass M accelerates uniformly from rest to a velocity v in time t. What is the instantaneous power delivered to the body at time T. (a) $\frac {mv}{t}$T (b) $\frac {mv^2}{t}$T (c) $\frac {m^2v^2}{t^2}$T (d) $\frac {mv^2}{t^2}$T

Answer: (d) $\frac {mv^2}{t^2}$T

Question 9. A man weighing 50 kgf carries a load of 10 kgf to the top of the building in 5 minutes. The work done by him is 10 5 J. If he carries the same load in 10 minutes, the work done by him will be: (a) 10 5 J (b) 5 × 10 5 J (c) 12 × 10 5 J (d) 2.5 × 10 5 J

Answer: (a) 10 5 J

Question 10. If v be the instantaneous velocity of a body dropped from the top of a tower, when it is located at a height h, then which of the following remains constant? (a) gh + $\frac {1}{2}$ v² (b) gh – $\frac {1}{2}$ v² (c) gh + v² (d) gh – v²

Answer: (a) gh + $\frac {1}{2}$ v²

Question 11. A ball B 1 of mass m is moving with a velocity v along north. It collides with another ball B 2 of same mass moving with a velocity v along east. After the collision, both the balls stick together and move along north east. The velocity of the combination is (a) $\frac {v}{√2}$ (b) √2v (c) 2v (d) v

Answer: (a) $\frac {v}{√2}$

Question 12. A ball B 1 of mass m moving with velocity u, collides head on with another ball B 2 of the same mass at rest. Given that the coefficient of restitution is e. Then the ratio of velocities of two balls after collision will be (a) $\frac {1+e}{1-e}$ (b) e (c) $\frac {1+e}{2}$ (d) $\frac {1-e}{2}$

Answer: (a) $\frac {1+e}{1-e}$

Question 13. A vehicle of mass m is moving on a rough horizontal road with a momentum p. If the coefficient of friction between the tyres and the road be µ, then the stopping distance is given by (a) $\frac {p}{2µm^2g}$ (b) $\frac {p}{2µmg}$ (c) $\frac {p^2}{2µmg}$ (d) $\frac {p^2}{2µm^2g}$

Answer: (d) $\frac {p^2}{2µm^2g}$

Question 14. A uniform chain of length l and mass m is lying on a smooth table and one-third of its length is hanging vertically down over the edge of the table. If g be the acceleration due to gravity, then the work required to pull the hanging part on the table is : (a) $\frac {mg l}{3}$ (b) $\frac {mgl}{9}$ (c) $\frac {mgl}{18}$ (d) mg l

Answer: (c) $\frac {mgl}{18}$

MCQ Questions for Class 11 Physics Chapter 6 Work, Energy and Power with Answers 1

Answer: (d) $\frac {2mg(h+x)}{x^2}$

Question 16. The slope of the potential energy versus position vector gives (a) momentum (b) force (c) work done (d) power

Answer: (b) force

Question 17. The slope of the kinetic energy versus position vector gives the time rate of change of: (a) momentum (b) force (c) work done (d) power

Answer: (a) momentum

Question 18. A bus weighing 100 quintals moves on a rough road with a constant speed of 72 kmh -1 . The friction of the road is 9% of its weight and that of air is 1 % of its weight. What is the power of the engine? Take g = 10 ms -2 . (a) 100 kW (b) 150 kW (c) 200 kW (d) 50 kW

Answer: (c) 200 kW

Question 19. A metre rod is pivoted at its end and stands vertically. If it is displaced through 60° with the vertical, what will be the ratio of its potential energy in this position to its maximum potential energy? (a) 0.25 (b) 0.75 (c) 0.80 (d) 0.50

Answer: (d) 0.50

Question 20. A bullet is fired into a block of sand and its velocity decreases by 50% when it penetrates through 9 cm. What will be the total distance penetrated by the bullet? (a) 9 cm (b) 10 cm (c) 12 cm (d) 18 cm

Answer: (c) 12 cm

Fill in the blanks

Question 1. When a body is dropped from a certain height on the ground, the work is done on the body ……………. and is ……………….

Answer: by the force of gravity, positive

Question 2. When it is lifted from the ground to a certain height, the work is done on the body ……………. and is ……………

Answer: against the force of gravity, negative

Question 3. The statement that inertial mass of a body is equal to the gravitational mass is called ……………

Answer: principle of equivalence

Question 4. When a vertical force equal to the weight of a body is applied to it, then its acceleration is ……………..

Answer: zero.

Question 5. When work done is zero, then the speed of a body is ……………..

Answer: uniform

Question 6. Coefficient of restitution is one for ……………… collision.

Answer: perfectly elastic collision

Question 7. The coefficient of restitution is zero (e = 0) for ……………… collision which means that ……………….. of the colliding body is lost and is changed to other forms like ………………. or …………………..

Answer: perfectly inelastic, kinetic energy, sound energy, or heat energy

Question 8. The mass of a body increases with the increase in the velocity of the particle according to the relation ………………..

Answer: m = $\frac {m_0}{\sqrt{1-\frac{v^2}{c^2}}}$

Question 9. Mass of the particle becomes infinite if it moves with the ……………….. and the acceleration produced in the body by a given force F becomes ………………

Answer: velocity of light c = 3 × 10 8 ms -1 , zero (∵ a = $\frac {F}{m}$ = $\frac {F}{∞}$ = 0)

Question 10. E = mc² shows that mass and energy are …………….

Answer: inter convertible

Energy is transferred from one form to another. Name the transformations of energy in the following in the form ……………….. to ……………….. Question 11. lifting of a book by a boy ………………..

Answer: Lifting of a book by a boy transforms energy from chemical to gravitational.

Question 12. burning of candle ………………..

Answer: Burning of candle transforms energy from chemical to light and heat.

Question 13. a moving truck on a road ………………..

Answer: A moving truck on a road transforms energy from chemical to kinetic energy of motion.

Question 14. emission of light by Sun ………………..

Answer: Emission of light by Sun transforms energy from nuclear to electromagnetic energy.

Question 15. The work done against friction is ……………….. proportional to the force with which the surfaces are pressed together.

Answer: directly

Question 16. If the momentum of a body is doubled then its K.E. becomes ………………..

Answer: four times

Question 17. The sum of K.E. and P.E. for an isolated system is always ………………..

Answer: constant

Question 18. If the range of a projectile be R, then its K.E. is minimum when horizontal distance covered by it is ………………..

Answer: $\frac {R}{2}$

Question 19. ………………. is not conserved during an inelastic collision.

Answer: K.E.

Question 20. When a bullet striking a block gets embedded in it, then the nature of collision is ……………….

Answer: perfectly inelastic

Question 21. ………………. is a non-conservative force.

Answer: friction

Question 22. For a perfectly inelastic collision, the coefficient of restitution is ……………….

Answer: zero

Question 23. The work done …………….. updn the time taken in doing it.

Answer: does not depend

Question 24. The work done by the conservative force 1s always ……………..

Answer: positive

Question 25. The P.E. gained by the body raised from the surface of Earth by a height equal to radius of Earth is ……………..

Answer: mg $\frac {R}{2}$

Question 26. K.E. of a projectile is …………….. at the highest point of its trajectory.

Answer: minimum

Question 27. The work done on a body by a resultant external force is always ………………. to the change in its K.E.

Answer: equal

Question 28. A body is suspended by vertical string. The work done on the body by the tension in the string is …………….

Question 29. Power is ………………. of force and velocity.

Answer: scalar product

Question 30. Work is ………………. of force and displacement.

Question 31. 1 kwh is the energy consumed by an appliance of power I kw in ………….

Answer: 1 hour

Question 32. The work done by a conservative force moving an object on a closed path is …………….

Question 33. In a perfectly inelastic collision, the two bodies ………………… after collision.

Answer: stick together

Question 34. For an inelastic collision, the coefficient of restitution lies between ………………

Question 35. Kinetic energy increases during a ……………….

Answer: super elastic collision

Question 36. ………………. energy results from the chemical bounding between the atoms.

Answer: Chemical

Question 37. ………………. energy results due to the separation between two objects in the gravitational field.

Answer: Gravitational

Question 38. ………………… energy between two nucleons is due to nuclear force.

Answer: Nuclear

Question 39. Chemical, gravitational and nuclear energies are the ……………….. for different types of forces in nature.

Answer: Potential energies

True/False Type Questions

1. Which of the following statement is True/False? (a) Work done can be positive, negative and zero. (b) A teacher sitting in a chair is dong work. (c) Work is the cross product of force and displacement. (d) Work done by a coolie in carrying a bag on his head is zero.

Answer: (a) True (b) False (c) False (d) True

2. Which of the following statement is True/False? (a) The principle of conservation of linear momentum can be strictly applied during a collision between two particles provided the time of impact is extremely small. (b) In an inelastic collision, the linear momentum is conserved but not the kinetic energy. (c) The collision is said to be elastic if two bodies stick together after collision. (d) The unit of energy is increased by 16 times if the unit of force and length be each increased by 4 times.

Answer: (a) True (b) True (c) False (d) True

3. Tell which of the following statement is True/False? (a) Momentum is conserved in elastic collision but not in inelastic collision. (b) Total kinetic energy is conserved in elastic collision but momentum is not conserved in elastic collision. (c) Both K.E. and momentum are conserved in all types of collision. (d) Total energy, K.E. and the momentum is conserved in elastic collision.

Answer: (a) False (b) False (c) False (d) True

4. Which of the following statement is True/False? (a) Both momentum and energy are conserved in an inelastic collision. (b) Neither momentum nor energy is conserved in an inelastic collision. (c) Momentum is conserved but not the K.E. in an inelastic collision. (d) Momentum is not conserved but the K.E. is conserved in an inelastic collision.

Answer: (a) False (b) False (c) True (d) False

5. Which of the following statement is True/False? There will be an increase in potential energy of the system if work is done upon the system by (a) a conservative force. (b) a non-conservative force. (c) any conservative or non-conservative force.

Answer: (a) True (b) False (c) False

6. Which of the following statement is True/False? (a) The gain in the P.E. of an object of mass m raised from the surface of earth to a height equal to the radius R is $\frac {mgR}{2}$. (b) 1 eV = 1.6 × 10 -19 J (c) Power is the cross-product of force and velocity. (d) Work is the dot product of force and displacement.

7. Which of the following statement is True/False? (a) A teacher rubbing the blockboard by a duster is doing no work. (b) A light and a heavy body have equal K.E. of translation. The heavier body has larger momentum. (c) A bullet is fired from a rifle. If the rifle recoils freely, then the K.E. of the rifle is greater than that of the bullet. (d) The energy produced when 10 gram of coal is burnt is 9 × 10 4 J.

8. Tell which one of the following statement is True/False? (a) A truck and car having same K.E. cover equal distances before stopping after applying equal retarding force through brakes. (b) 1 kg m = 9.8 J (c) 1 J = 10 7 erg (d) For an elastic collision, the velocity of separation after collision is always equal to the velocity of approach before collision.

Answer: (a) True (b) True (c) True (d) True

9. Tell which of the following statement is True/False? (a) Friction is non-conservative force. (b) Gravity is a conservative force. (c) No work is done against gravity while moving an object along horizontal. (d) Kilowatt-hour is the unit of energy.

10. Tell which of the following statements are True/False? (a) The forces involved during the elastic collision are conservative in nature. (b) K.E. lost in an inelastic collision appears in some other form of energy such as heat, sound etc. (c) Mechanical energy is not converted into any other form of energy in an elastic collision. (d) Coefficient of restitution is zero (e = 0) for a perfectly inelastic collosion.

Match Type Questions

Hope the information shed above regarding NCERT MCQ Questions for Class 11 Physics Chapter 6 Work, Energy and Power with Answers Pdf free download has been useful to an extent. If you have any other queries of CBSE Class 11 Physics Work, Energy and Power MCQs Multiple Choice Questions with Answers, feel free to reach us so that we can revert back to us at the earliest possible.

Book Solutions
State Boards

Case Study Questions Class 11 Physics Oscillations

Case study questions class 11 physics chapter 14 oscillations.

CBSE Class 11 Case Study Questions Physics Oscillations. Important Case Study Questions for Class 11 Board Exam Students. Here we have arranged some Important Case Base Questions for students who are searching for Paragraph Based Questions Oscillations.

At Case Study Questions there will given a Paragraph. In where some Important Questions will made on that respective Case Based Study. There will various types of marks will given 1 marks, 2 marks, 3 marks, 4 marks.

CBSE Case Study Questions Class 11 Physics Oscillations

Case study – 1.

A motion that repeats itself at regular intervals of time is called periodic motion. Very often, the body undergoing periodic motion has an equilibrium position somewhere inside its path. When the body is at this position no net external force acts on it. Therefore, if it is left there at rest, it remains there forever. If the body is given a small displacement from the position, a force comes into play which tries to bring the body back to the equilibrium point, giving rise to oscillations or vibrations . Every oscillatory motion is periodic, but every periodic motion need not be oscillatory. Circular motion is a periodic motion, but it is not oscillatory. The smallest interval of time after which the motion is repeated is called its period. Let us denote the period by the symbol T. Its SI unit is second. The reciprocal of T gives the number of repetitions that occur per unit time. This quantity is called the frequency of the periodic motion. It is represented by the symbol n. The relation between n and T is n = 1/T. The unit of n is thus s -1 . After the discoverer of radio waves, Heinrich Rudolph Hertz (1857–1894), a special name has been given to the unit of frequency. It is called hertz (abbreviated as Hz). Answer the following.

1) Every oscillatory motion is periodic motion true or false?

2) Circular motion is

a) Oscillatory motion

b) Periodic motion

c) Rotational motion

d) None of these

3) Define period. Give its SI unit and dimensions

4) Define frequency of periodic motion. How it is related to time period

5) What is oscillatory motion

Answer key – 1

3) The smallest interval of time after which the motion is repeated is called its period. Its SI unit is second and dimensions are [T 1 ].

4) Reciprocal of Time period (T) gives the number of repetitions that occur per unit time. This quantity is called the frequency of the periodic motion. It is represented by the symbol n. The relation between n and T is n = 1/T i.e. they are inversely proportional to each other. The unit of n is thus s -1 or hertz.

5) Oscillatory motion is type of periodic motion in which body performs periodic to and fro motion about some mean position. Every oscillatory motion is periodic, but every periodic motion need not be oscillatory.

Case Study – 2

There are no physical examples of absolutely pure simple harmonic motion. In practice we come across systems that execute simple harmonic motion approximately under certain conditions.

Oscillations due to a spring:

The simplest observable example of simple harmonic motion is the small oscillations of a block of mass m fixed to a spring, which in turn is fixed to a rigid wall. The block is placed on a frictionless horizontal surface. If the block is pulled on one side and is released, it then executes a to and fro motion about the mean position. Let x = 0, indicate the position of the centre of the block when the spring is in equilibrium. The positions marked as –A and +A indicate the maximum displacements to the left and the right of the mean position. We have already learnt that springs have special properties, which were first discovered by the English physicist Robert Hooke. He had shown that such a system when deformed is subject to a restoring force, the magnitude of which is proportional to the deformation or the displacement and acts in opposite direction. This is known as Hooke’s law. It holds good for displacements small in comparison to the length of the spring. At any time t, if the displacement of the block from its mean position is x, the restoring force F acting on the block is,

F (x) = –k x

The constant of proportionality, k, is called the spring constant, its value is governed by the elastic properties of the spring. A stiff spring has large k and a soft spring has small k. Equation is same as the force law for SHM and therefore the system executes a simple harmonic motion.

Damped oscillations

We know that the motion of a simple pendulum, swinging in air, dies out eventually. Why does it happen? This is because the air drag and the friction at the support oppose the motion of the pendulum and dissipate its energy gradually. The pendulum is said to execute damped oscillations. In damped oscillations, the energy of the system is dissipated continuously; but, for small damping, the oscillations remain approximately periodic. The dissipating forces are generally the frictional forces.

The damping force is generally proportional to velocity of the bob and acts opposite to the direction of velocity. If the damping force is denoted by F d , we have

where the positive constant b depends on characteristics of the medium (viscosity, for example) and the size and shape of the block, is usually valid only for small velocity.

1) Damping force is directly proportional to

a) Velocity

c) Acceleration

2) Oscillations due to spring performs SHM for

a) Only small oscillations of spring

b) Only for large oscillations of spring

c) Both large as well as small oscillations of spring

3) Give expression for restoring force in spring while performing small SHM oscillations.

4) Explain damped oscillations

5) Explain oscillations due to spring

Answer key-2

3) At any time t, if the displacement of the block from its mean position is x, the restoring force F acting on the block is,

The constant of proportionality, k, is called the spring constant, its value is governed by the elastic properties of the spring

4) In the motion of a simple pendulum, swinging in air amplitude became zero after some time. This is because the air drag and the friction oppose the motion of the pendulum and dissipate its energy gradually. The pendulum is said to execute damped oscillations. In damped oscillations, the energy of the system is dissipated continuously. The damping force is generally proportional to velocity of the bob and acts opposite to the direction of velocity. If the damping force is denoted by F d , we have F d = –b v. Where the positive constant b depends on characteristics of the medium and the size and shape of the block.

5) the small oscillations of a block of mass m fixed to a spring, which in turn is fixed to a rigid wall. The block is placed on a frictionless horizontal surface. If the block is pulled on one side and is released, it then executes to and fro motion about the mean position. Let x = 0, indicate the position of the centre of the block when the spring is in equilibrium. We know that springs have special property that when deformed is subject to a restoring force, the magnitude of which is proportional to the deformation or the displacement and acts in opposite direction. It holds good for displacements small in comparison to the length of the spring. At any time t, if the displacement of the block from its mean position is x, the restoring force F acting on the block is,

Case Study – 3

When a system (such as a simple pendulum or a block attached to a spring) is displaced from its equilibrium position and released, it oscillates with its natural frequency ω, and the oscillations are called free oscillations. All free oscillations eventually die out because of the ever present damping forces. However, an external agency can maintain these oscillations. These are called forced or driven oscillations. We consider the case when the external force is itself periodic, with a frequency w d called the driven frequency. The most important fact of forced periodic oscillations is that the system oscillates not with its natural frequency ω, but at the frequency ω d of the external agency; the free oscillations die out due to damping. The most familiar example of forced oscillation is when a child in a garden swing periodically presses his feet against the ground (or someone else periodically gives the child a push) to maintain the oscillations. The maximum possible amplitude for a given driving frequency is governed by the driving frequency and the damping, and is never infinity. The phenomenon of increase in amplitude when the driving force is close to the natural frequency of the oscillator is called resonance . In our daily life, we encounter phenomena which involve resonance. Your experience with swings is a good example of resonance. You might have realized that the skill in swinging to greater heights lies in the synchronization of the rhythm of pushing against the ground with the natural frequency of the swing.

1) When a system oscillates with its natural frequency ω, and the oscillations are called

a) Free oscillations

b) Forced oscillations

2) All free oscillations eventually die out because of

a) Damping force

b) electromagnetic force

c) None of these

3) What is free oscillation?

4) What is forced oscillations?

5) What is resonance?

Answer key – 3

3) When a system (such as a simple pendulum or a block attached to a spring) is displaced from its equilibrium position and released, it oscillates with its natural frequency ω, and the oscillations are called free oscillations.

4) Forced oscillations are oscillations where external force drives the oscillations with frequency given by external force.

5) The phenomenon of increase in amplitude when the driving force is close to the natural frequency of the oscillator is called resonance. In our daily life, we encounter phenomena which involve resonance. Your experience with swings is a good example of resonance. You might have realized that the skill in swinging to greater heights lies in the synchronization of the rhythm of pushing against the ground with the natural frequency of the swing.

We have a strong team of experienced Teachers who are here to solve all your exam preparation doubts

West bengal board class 9 english solution chapter 11 a shipwrecked sailor, 2025 solved specimen paper icse class 10 biology, 2025 solved icse specimen paper class 10 english paper 1, west bengal board class 9 english solution chapter 10 the price of bananas.

Username or Email Address

Remember Me

IMAGES

Case Study Questions for Class 11 Physics Chapter 6 Work Energy and
chapter 6 numerical questions class 11 physics
NCERT Solutions for Class 11 Physics Chapter 6
Ncert Solution for Class 11 Physics Chapter 6
NCERT Solutions for Class 11 Physics Chapter 6 Work Energy and power
NCERT Solutions for Class 11 Physics Chapter 6 Work, Energy and Power

VIDEO

Work Energy and Power Class 11 Questions
CLASS_11(Chapter-6)(EXERCISE-6.22)
Class 11 Physics NCERT Example Solutions
Numericals chapter 6 class 11 physics
Class 11th Physics 2019 Question paper jac board||Annual Examination 2019 physics jac board||
Physics Most Important MCQs Class 11th Physics Revision Part 2

COMMENTS

Class 11 Physics Case Study Questions Chapter 6 Work ...
Here, we have provided case-based/passage-based questions for Class 11 Physics Chapter 6 Work, Energy, and Power. Case Study/Passage-Based Questions. Case Study 1: The kinetic energy possessed by an object of mass, m, and moving with a uniform velocity, v is. Kinetic energy is a scalar quantity.
Case Study Questions for Class 11 Physics Chapter 6 Work Energy and
Case Study Questions for Class 11 Physics Chapter 6 Work Energy and Power Here we are providing case study questions for class 11 physics chapter 6 Work, Energy and Power. Students can practice these questions for better understanding of case study type questions. Case Study Questions: Question 1: Potential Energy of SpringThere are many types … Continue reading Case Study Questions for ...
CBSE Case Study Questions Class 11 Physics PDF Download
Chapter-wise Solved Case Study Questions for Class 11 Physics. Chapter 1: Physical World. Chapter 2: Units and Measurements. Chapter 3: Motion in a Straight Line. Chapter 4: Motion in a Plane. Chapter 5: Laws of Motion. Chapter 6: Work, Energy, and Power. Chapter 7: System of Particles and Rotational Motion.
Class 11 Physics Case Study Questions
Class 11 Physics Case Study Question 1. Read the case study given below and answer any four subparts: Potential energy is the energy stored within an object, due to the object's position, arrangement or state. Potential energy is one of the two main forms of energy, along with kinetic energy. Potential energy depends on the force acting on ...
Case Study Questions Class 11 Physics Work, Energy And Power
CBSE Case Study Questions Class 11 Physics Work, Energy And Power. Case Study - 1. 1) The scalar product or dot product of any two vectors A and B, denoted as A.B (read A dot B) is defined as. A.B = A B cos θ. Where q is the angle between the two vectors.
Class 11 Physics Case Study Question Chapter 1 to 15
Case Study Question Class 11 Physics (CBSE / NCERT Board) CBSE Class 11 Physics Case Study Question. There are total 15 chapter Physical World, Units and Measurement, Motion in a Straight Line, Motion in a Plane, Laws of Motion, Work, Energy and Power, Systems of Particles and Rotational Motion, Gravitation, Mechanical Properties of Solids ...
NCERT Solutions for Class 11 Physics Chapter 6 Work, Energy and Power
NCERT Solutions for Class 11 Physics Chapter 6 - Free PDF Download *According to the CBSE Syllabus 2023-24, this chapter has been renumbered as Chapter 5. NCERT Solutions Class 11 Physics Chapter 6 Work, Energy and Power are provided in PDF format for easy access and download. Students can get answers to the textbook questions, extra questions, exemplary problems and worksheets, which will ...
NCERT Exemplar for Class 11 Physics Chapter 6
The sixth chapter of NCERT class 11 Physics book tells us about the dissipation or transformation of different forms of energy that we use to get work done. The scalar or dot product of two or more vectors is the foundation of this chapter as described in the introductory section 6.1.
NCERT Solutions for Class 11 Physics Chapter 6 Work Energy ...
Solutions for both exercise and additional exercise in the NCERT are given. Students can also download Work Energy and Power Class 11 NCERT solutions pdf by clicking on the link download PDF for free. NCERT Class 11 Physics Chapter 6 Exercise Solutions pdf download for free. ** According to the CBSE Syllabus for the academic year 2023-24, the ...
NCERT Solutions for Class 11 Physics Chapter 6 Work Energy and Power
Therefore,θ= 0°. W = F s cosθ = mg x s cos0°. W = 15 x 9.8 x 2 x 1 = 294 joule. ∴ Work done is greater in 2 nd case. Question 6. Underline the correct alternative: (a) When a conservative force does positive work on a body, the potential energy of the body increases/decreases/remains unaltered.
NCERT Solutions for Class 11 Physics Chapter 6
NCERT Solution of Work, Energy, and Power Class 11 also comes in handy for students who are preparing for competitive exams like JEE. These solutions efficiently cover all the essential concepts within the chapter. Students often find Physics Ch 6 Class 11 Work, Energy, and Power to be extremely difficult. But you'll be able to effortlessly ...
NCERT Solutions for Class 11 Physics Chapter 6 Work Energy and Power
7. State if each of the following statements is true or false. Give reasons for your answer. (a) In an elastic collision of two bodies, the momentum and energy of each body is conserved. (b) Total energy of a system is always conserved, no matter what internal and external forces on the body are present. (c) Work done in the motion of a body ...
Important Questions Class 11 Physics Chapter 6
Important Questions for CBSE Class 11 Physics Chapter 6 - Work, Energy and Power The words "work," "energy," and "power" are frequently heard. But in physics, work has a specific and definite meaning. In Chapter 6 of Class 11 Physics, a variety of important concepts are discussed. Students can refer to the set of Class […]
Important Questions for CBSE Class 11 Physics Chapter 6
Important Questions for Class 11 Physics Chapter 6 - Work, Energy and Power are available in Vedantu. All Questions are designed as per the latest Syllabus of NCERT with reference to frequent questions in exams. We hear the words 'work,' 'energy,' & 'power' all the time. A person carrying materials, a farmer cultivating, a student studying for exams are all said to be performing their work.
CBSE Class 11th Physics Value Based Questions Chapter 6 ...
CBSE Physics Value Based Questions for Class 11th Chapter 6 Work Energy and Power download here in PDF format. The most CBSE Physics Value Based Questions for annual examination are given here for free of cost. The additional questions for practice the Class 11th exam are collected from various sources. It covers questions asked in previous ...
Assertion and Reason Questions for Class 11 Physics Chapter 6 Work
Directions: Each of these questions contain two statements, Assertion and Reason. Each of these questions also has four alternative choices, only one of which is the correct answer. You have to select one of the codes (a), (b), (c) and (d) given below.(a) Assertion is correct, reason is correct; reason is a correct explanation for assertion.(b) … Continue reading Assertion and Reason ...
Important questions for class 11 Physics Chapter 6 System of Particles
Chapter 6 - System of Particles and Rotational Motion. CBSE Class 11 Physics Important Questions Chapter 6 System of Particles and Rotational Motion are available here for students. Solving these questions will boost their exam preparation and help them scoring more marks in the exam. By practising these questions, students will also get ...
Work, Energy and Power Class 11 Important Extra Questions Physics Chapter 6
Question 1. An engine draws a train up an incline of 1 in 100 at the rate of 36 km h -1. If the resistance due to friction is 5 kg wt per ton, calculate the power of the engine. Mass of train and engine is 100. Answer: Here, m = 100 metric ton = 100 × 1000 kg. Total force of friction, f1 = 100 × 5 = 500 kg wt.
CBSE Important Questions for Class 11 Physics
Students can click the link below to access the chapter-wise important questions of CBSE Class 11 Physics. Important Questions Chapter 1 - Units and Measurements. Important Questions Chapter 2 - Motion in a Straight Line. Important Questions Chapter 3 - Motion in a Plane. Important Questions Chapter 4 - Laws of Motion.
Category: Case Study Questions for Class 11 Physics
January 9, 2023 July 29, 2023 Physics Gurukul Leave a Comment on Case Study Questions for Class 11 Physics Chapter 10 Mechanical Properties of Fluids. ... September 25, 2022 July 29, 2023 Physics Gurukul Leave a Comment on Case Study Questions for Class 11 Physics Chapter 7 System of Particles and Rotational Motion.
MCQ Questions for Class 11 Physics Chapter 6 Work, Energy and Power
Answer. Question 11. A ball B 1 of mass m is moving with a velocity v along north. It collides with another ball B 2 of same mass moving with a velocity v along east. After the collision, both the balls stick together and move along north east. The velocity of the combination is. (a) v √2. (b) √2v. (c) 2v.
Case Study Questions Class 11 Physics
At Case Study Questions there will given a Paragraph. In where some Important Questions will made on that respective Case Based Study. There will various types of marks will given 1 marks, 2 marks, 3 marks, 4 marks. CBSE Case Study Questions Class 11 Physics Oscillations Case Study - 1

Class 11 Physics Case Study Questions Chapter 6 Work, Energy, and Power

Work, Energy, and Power Case Study Questions With Answers

You Might Also Like

The Topper Combo Flashcards

CBSE Case Study Questions Class 11 Physics PDF Download

Class 11 Physics Case Study Questions

Chapter-wise Solved Case Study Questions for Class 11 Physics

Class 11 Books for Boards

Leave a Comment Cancel reply

Download India's best Exam Preparation App Now.

Class 11 Physics Case Study Questions

myCBSEguide App

What is the purpose of physics?

What are case study questions in physics?

CBSE Case Study Questions in Class 11 Physics

Sample Class 11 Physics Case Study Questions

Class 11 Physics Case Study Question 1

Class 11 Physics Case Study Question 2

Class 11 Physics Case Study Question 3

Class 11 Physics Case Study Question 4

Examining Class 11 Physics syllabus

myCBSEguide: A true saviour for many students

Related Posts

Leave a Comment

CBSE Class 12th

Products & Resources

NCERT Syllabus

NCERT Solutions

Colleges & Courses

Predictors & E-Books

Predictors & Articles

Top Courses & Careers

Quick Links

Diploma Colleges

Upcoming Events

Other Exams

Top Countries

Student Visas

Engineering Preparation

Medical Preparation

Online Courses

Top Streams

Specializations

Top Providers

NCERT Solutions for Class 11 Physics Chapter 6 Work Energy and Power

NCERT Solutions for Class 11 Physics Chapter 6 Work, Energy and Power

Class 11 Physics chapter 6 exercise solutions: Important Formulas and Diagrams + eBook link

Kinetic energy

Potential Energy

Work-Energy Theorem

Key Features of NCERT Class 11 physics chapter 6 exercise solutions

Also Check NCERT Books and NCERT Syllabus here

Frequently Asked Question (FAQs)

Upcoming School Exams

National Institute of Open Schooling 10th examination

Uttar Pradesh Board 10th examination

Goa Board Higher Secondary School Certificate Examination

Popular Questions

Colleges After 12th

Applications for Admissions are open.

Aakash iACST Scholarship Test 2024

ALLEN Digital Scholarship Admission Test (ADSAT)

JEE Main Important Physics formulas

PW JEE Coaching

PW NEET Coaching

JEE Main Important Chemistry formulas

Explore on Careers360

NCERT Exemplars

CBSE Class 10

CISCE Board 10th

Schools By Medium

By Ownership

Download Careers360 App's

We Appeared in

Important Questions Class 11 Physics Chapter 6

Important Questions for CBSE Class 11 Physics Chapter 6 – Work, Energy and Power

CBSE Class 11 Physics Chapter 6 Important Questions – Free Download

Download Important Questions For Class 11 Physics Chapter 6

Physics Chapter 6 – Work, Energy and Power

Why Go For Extramarks?