how flowchart helps in problem solving

We use essential cookies to make Venngage work. By clicking “Accept All Cookies”, you agree to the storing of cookies on your device to enhance site navigation, analyze site usage, and assist in our marketing efforts.

Manage Cookies

Cookies and similar technologies collect certain information about how you’re using our website. Some of them are essential, and without them you wouldn’t be able to use Venngage. But others are optional, and you get to choose whether we use them or not.

Strictly Necessary Cookies

These cookies are always on, as they’re essential for making Venngage work, and making it safe. Without these cookies, services you’ve asked for can’t be provided.

Show cookie providers

• Google Login

Functionality Cookies

These cookies help us provide enhanced functionality and personalisation, and remember your settings. They may be set by us or by third party providers.

Performance Cookies

These cookies help us analyze how many people are using Venngage, where they come from and how they're using it. If you opt out of these cookies, we can’t get feedback to make Venngage better for you and all our users.

• Google Analytics

Targeting Cookies

These cookies are set by our advertising partners to track your activity and show you relevant Venngage ads on other sites as you browse the internet.

• Google Tag Manager
• Infographics
• Daily Infographics
• Popular Templates
• Accessibility
• Graphic Design
• Graphs and Charts
• Data Visualization
• Human Resources
• Beginner Guides

Blog Business What is a Problem-Solving Flowchart & How to Make One

What is a Problem-Solving Flowchart & How to Make One

Written by: Danesh Ramuthi Aug 10, 2023

Problem-Solving Flowcharts, contrary to what many believe aren’t just aesthetic wonders — they’re almost like magical blueprints for troubleshooting those pesky problems that many of us face.

Flowcharts take business challenges and turn them into a navigable pathway. In this post, I will guide you on key aspects of problem-solving flowcharts such as what it is, the advantages of problem-solving flowcharts, how to create one and more.

Besides, you’ll also discover how to create problem-solving flowcharts with the help of Venngage’s Flowchart Maker.

And for those of you thinking, “I’m no designer, how can I create one?” worry not! I’ve got you covered. Just hop on Venggage’s Flowchart Templates and you’ll be charting your way to problem-solving glory in no time.

Click to jump ahead:

What are problem-solving flowcharts?

When to use problem-solving flowcharts, what are the advantages of flowcharts in problem-solving, what are the 7 steps of problem-solving flowcharts.

• 5 different types of problem-solving flowcharts

Best practices for designing effective problem-solving flowcharts

How to make a flowchart using venngage , problem-solving flowcharts faqs.

• Final Thoughts

Problem-Solving Flowcharts is a graphical representation used to break down problem or process into smaller, manageable parts, identify the root causes and outline a step-by-step solution. 

It helps in visually organizing information and showing the relationships between various parts of the problem.

This type of flowcharts consists of different symbols and arrows, each representing different components or steps in the problem-solving process. 

By following the flow of the chart, individuals or teams can methodically approach problem, analyze different aspects of it and come to a well-informed solution.

Problem-Solving Flowcharts is a versatile tool that can be used in various scenarios. Here’s when to consider utilizing one:

• Complex Problems: When faced with a multifaceted issue that involves multiple steps or variables, flowcharts can help break down the complexity into digestible parts.
• Team Collaboration: If you’re working with a team and need a common understanding of problem and its potential solutions then a flowchart provides a visual that everyone can refer to.
• Analyzing Processes: In a situation where you need to understand a particular process, whether it’s within a project or a part of regular operations then mapping it out in a flowchart can offer clarity.
• Decision Making: When various paths or decisions might be taken, a flowchart can outline the potential outcomes of each aiding in making an informed choice.
• Training and Onboarding: Flowcharts can be used in training materials to help new employees understand complex processes or procedures which makes the learning curve smoother.
• Identifying Root Causes: If you’re looking to identify the underlying causes of problem then a flowchart can facilitate a systematic approach to reaching the root of the issue.

Related: How to Use Fishbone Diagrams to Solve Complex Problems

Problem-solving flowcharts can offer several benefits to the users who are looking to solve a particular problem. Few advantages of flowcharts in problem solving are: 

Visual Clarity

When you’re dealing with multifaceted problems or processes, words alone can make the situation seem even more tangled. Flowcharts distill these complexities into easily understandable visual elements. 

By mapping out each phase or component of problem, flowcharts offer a bird’s eye view enabling individuals to grasp the bigger picture and the finer details simultaneously.

Sequential Representation

Flowcharts excel in laying out the sequence of events or actions. By indicating a clear starting point and illustrating each subsequent step, they guide users through a process or solution path methodically. 

This linear representation ensures that no step is overlooked and each is executed in the right order.  

Collaboration

Problem-solving often requires team effort and flowcharts are instrumental in fostering collaborative environments. 

When a team is discussing potential solutions or trying to understand problem’s intricacies, a flowchart serves as a collective reference point. 

It aids in synchronizing everyone’s understanding, minimizing miscommunications and promoting constructive discussions. 

Read more about: Flowcharts Symbols and Meaning

1. Define the Problem  

Before anything else, it’s essential to articulate the problem or task you want to solve clearly and accurately. By understanding exactly what needs to be addressed you can ensure that subsequent steps align with the core issue.

2. Identify the Inputs and Outputs  

Determine what inputs (such as data, information or resources) will be required to solve the problem and what the desired outputs or outcomes are. Identifying these factors will guide you in structuring the steps needed to reach the end goal and ensure that all necessary resources are at hand.

3. Identify the Main Steps  

Break down the problem-solving process into its main steps or subtasks. This involves pinpointing the essential actions or stages necessary to reach the solution. Create a roadmap that helps in understanding how to approach the problem methodically.

4. Use Decision Symbols  

In problem-solving, decisions often lead to different paths or outcomes. Using standard symbols to represent these decision points in the flowcharts allows for a clear understanding of these critical junctures. It helps visually present various scenarios and their consequences.

5. Add Descriptions and Details  

A well-designed flowcharts is concise but clear in its labeling. Using arrows and short, descriptive phrases to explain what happens at each step or decision point ensures that the flowcharts communicates the process without unnecessary complexity. 

6. Revise and Refine  

Creating a flowcharts is not always a one-and-done process. It may require revisions to improve its clarity, accuracy or comprehensiveness. Necessary refinement ensures that the flowcharts precisely reflects the problem-solving process and is free from errors or ambiguities.

7. Use Flowchart Tool  

While it’s possible to draw a flowcharts manually, using a flowcharts tool like Venngage’s Flowchart Maker and Venngage’s Flowchart Templates can make the process more efficient and flexible. These tools come with pre-designed templates and intuitive interfaces that make it easy to create, modify and share flowcharts. 

5 different types of problem-solving flowcharts 

Let’s have a look at 5 most common types of flowcharts that individuals and organizations often use. 

1. Process Flowchart s

A process flowcharts is a visual representation of the sequence of steps and decisions involved in executing a particular process or procedure. 

It serves as a blueprint that showcases how different stages or functions are interconnected in a systematic flow and it highlights the direction of the process from its beginning to its end.

Process flowcharts are instrumental in training and onboarding, sales process , process optimization, documentation, recruitment and in any scenario where clear communication of a process is crucial.

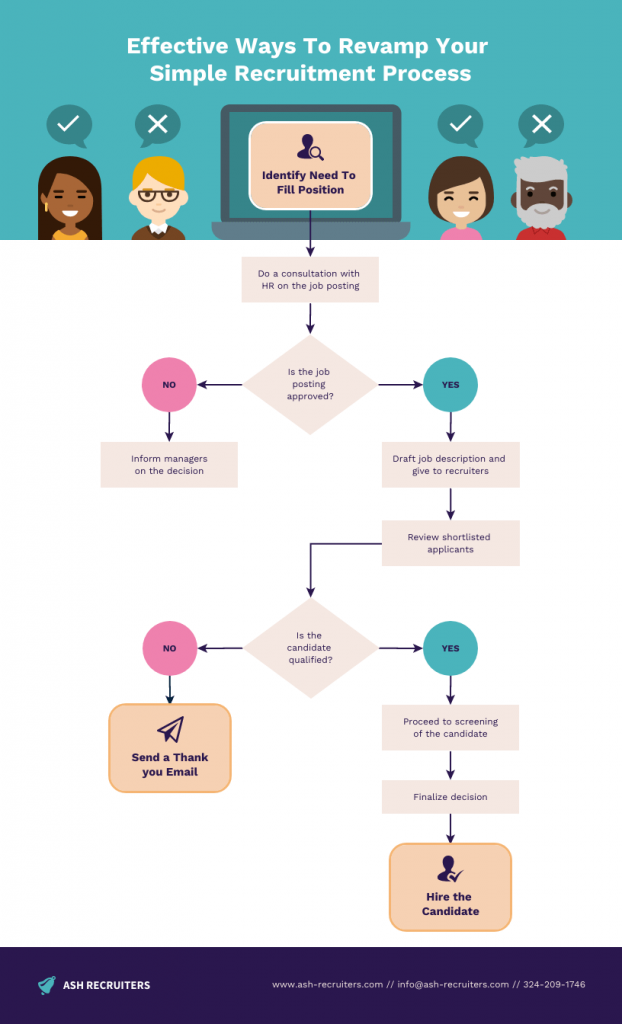
2. Flowcharts Infographic 

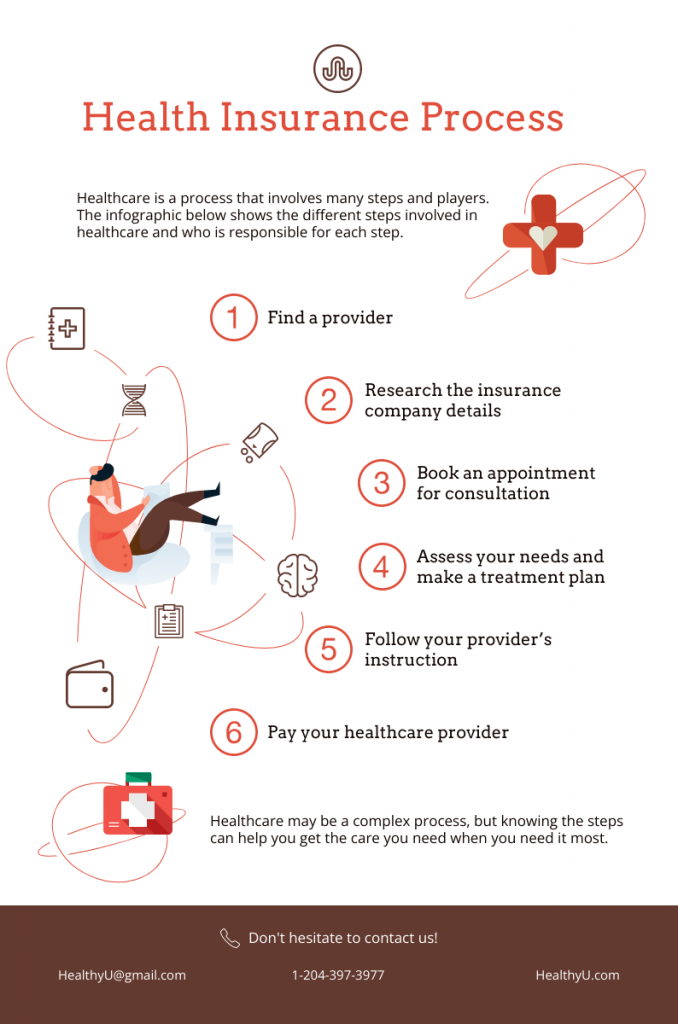
A flowcharts infographic is a great way to showcase the process or a series of steps using a combination of graphics, icons, symbols and concise text. It aims to communicate complex information in a clear and easy-to-understand manner, making it a popular tool for conveying information, data and instructions in a visually engaging way.

For example, you can use this flowchart to illustrate a health insurance process that visually explains the steps involved from finding a provider to paying for your healthcare provider. 

3. Circular Flowcharts

A circular flowcharts is used to illustrate the flow of information, goods, services or money within a closed system or process. It gets its name from its circular shape, which emphasizes the continuous and cyclical nature of the flow. 

Circular flowcharts are widely used in various fields such as economics, business, engineering and process management to help visualize and understand complex systems.

In a circular flowcharts , elements are represented using various shapes and connected with arrows to indicate the direction of flow. The circular arrangement indicates that the process is ongoing and repeats itself over time.

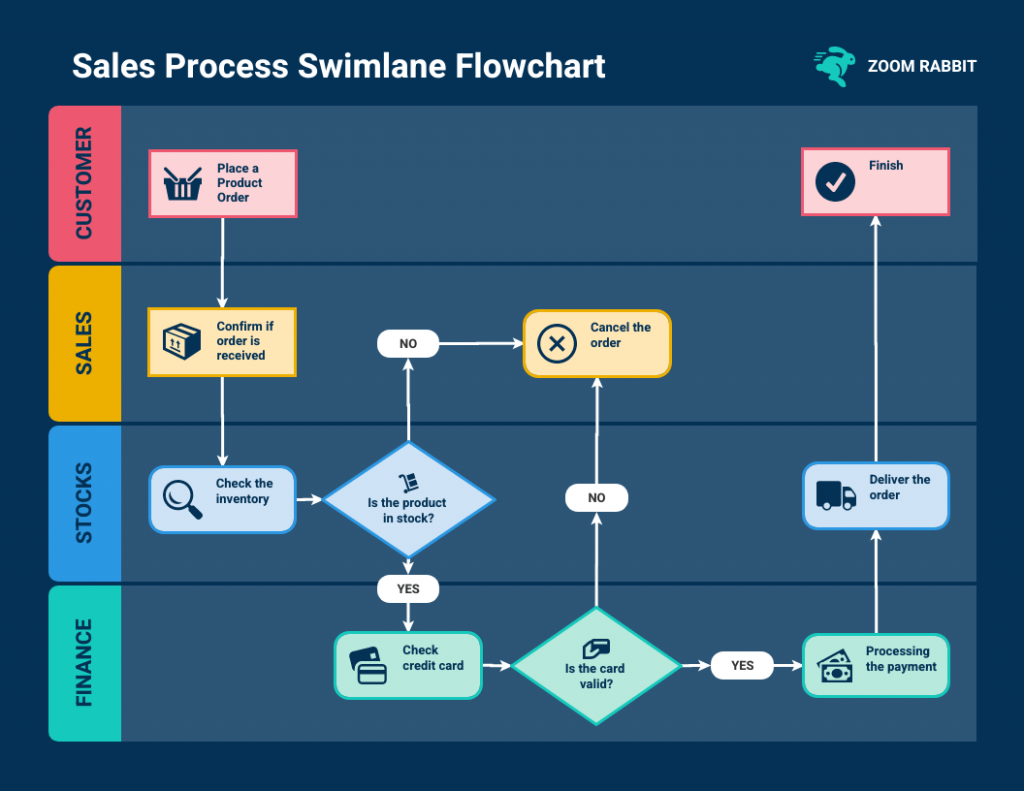
4. Swimlane flowcharts

Swimlane flowcharts , also known as cross-functional flowcharts are a specific type of flowchart that organizes the process flow into lanes or “swimlanes.” 

Each lane represents a different participant or functional area involved in the process and the flowchart shows how activities or information move between these participants. 

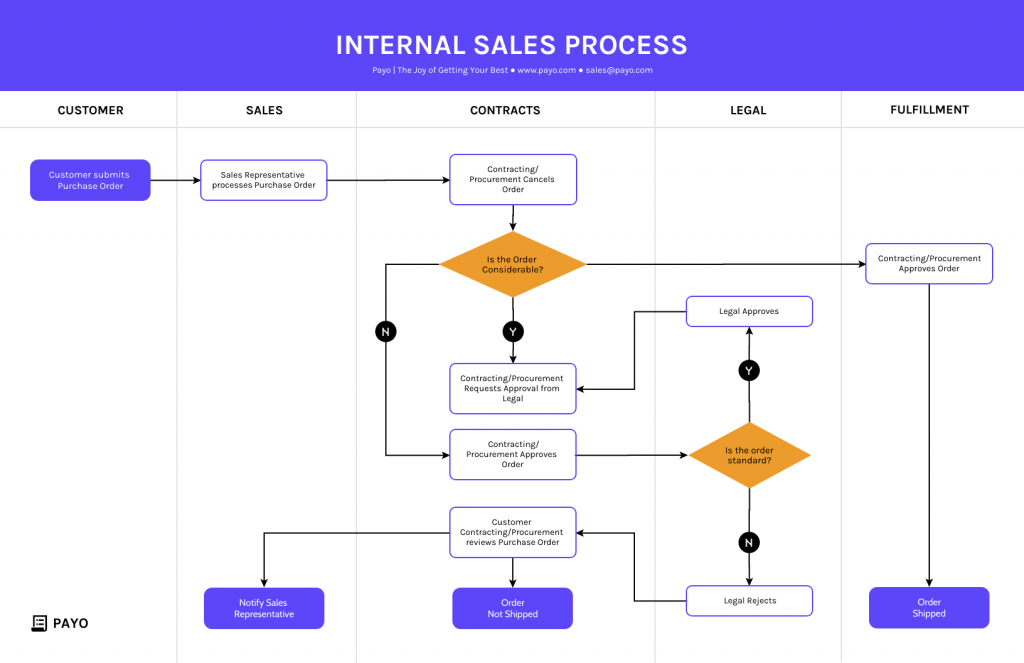
Swimlane flowcharts are particularly useful for illustrating complex processes that involve multiple stakeholders or departments.

In a swimlane flowcharts, the process is divided horizontally into lanes and each lane is labeled with the name of the department, person or role responsible for that part of the process. Vertically, the flowchart displays the sequence of steps or actions taken in the process.

5. Decision Flowchart s

Decision flowcharts, also known as decision trees or flow diagrams are graphical representations that illustrate the process of making decisions or solving problems. 

They are widely used in various fields such as computer science, business mapping , engineering and problem-solving scenarios. 

Decision flowcharts help break down complex decision-making processes into simple, sequential steps, making it easier to understand and follow.

A decision tree is a specialized flowchart used to visually represent the process of decision-making. 

Businesses and other individuals can employ a decision tree analysis as a tool to aid in evaluating different options and the possible consequences associated with each choice.

Decision trees Infographics can be used to create a more nuanced type of flowchart that is more informative and visually appealing by combining a decision flowchart and the flowchart infographic. 

Decision flowcharts are valuable tools for visualizing decision-making processes, analyzing complex problems and communicating them effectively to others.

Designing effective problem-solving flowcharts involves careful consideration of various factors to ensure clarity, accuracy and usability. Here are some best practices to create efficient and useful problem-solving flowcharts:

• Understand the problem first & clearly define it
• Keep it simple
• Use standard & recognizable symbols
• Ensure that the flowchart follows a logical and sequential order
• Clearly label each decision point, action and outcome
• Verify the flowchart’s accuracy by testing it
• Clearly state the decision criteria that lead to different branches
• Provide context when the flowchart is part of a larger process or system
• Review and revise the flowchart

Creating problem-solving flowchart on Venngage is incredibly simple. All you have to do is:

• Start by Signing Up and Creating an Account with Venngage
• Choose a flowchart template that best suits your needs from our library.
• Start editing your flowchart by choosing the desired shapes, labels and colors.
• You can also enhance your flowchart by incorporating icons, illustrations or backgrounds all of which are readily available in our library.
• Once done, you will have 2 options to choose from, either sharing it online for free or downloading your flowchart to your desktop by subscribing to the Premium or Business Plan. 

Is flowchart the representation of problem solutions?

Flowcharts are not the representation of problem solutions per se; rather, they are a visual representation of processes, decision-making steps and actions taken to arrive at a solution to problem.

What are the 3 basic structures of flowcharts?

3 Basic Structures of Flowcharts are:

• Sequence: Simplify Complexity
• Selection (Decision): Embrace Choices
• Repetition (Loop): Emphasize Iteration

What are the elements of a good flowchart?

A good flowchart should exhibit clarity and simplicity, using consistent symbols and labels to depict a logical sequence of steps. It should be readable, with appropriate white space to avoid clutter while eliminating ambiguity through well-defined decision criteria and paths.

Can flowcharts be used for both simple and complex problem-solving?

Yes, flowcharts can be used for both simple and complex problem-solving scenarios. Flowcharts are versatile visual tools that can effectively represent various processes, decision-making steps and problem-solving approaches regardless of their complexity.

In both cases, flowcharts offer a systematic and visual means of organizing information, identifying potential problems and facilitating collaboration among team members.

Can problem-solving flowcharts be used in any industry or domain?

Problem-solving flowcharts can be used in virtually any industry or domain. The versatility and effectiveness of flowcharts make them applicable to a wide range of fields such as Business and Management, Software Development and IT, Healthcare, Education, Finance, Marketing & Sales and a lot more other industries. 

Final thoughts

Problem-solving flowcharts are a valuable and versatile tool that empowers individuals and teams to tackle complex problems with clarity and efficiency.

By visually representing the step-by-step process of identifying, analyzing and resolving issues, flowcharts serve as navigational guides simplifying intricate challenges into digestible parts.

With the aid of modern tools like Venngage’s Flowchart Maker and Venngage’s Flowchart Templates , designing impactful flowcharts becomes accessible to all while revolutionizing the way problems are approached and solved.

Discover popular designs

Infographic maker

Brochure maker

White paper online

Newsletter creator

Flyer maker

Timeline maker

Letterhead maker

Mind map maker

Ebook maker

How to create a problem-solving flow chart

Problem-solving is one of those topics that we’ve often discussed on this site (check out our Problem Solving guide ). We think it’s one of  THE  vital skills of business. Why? Because you’ll come across problems every day, and you need to arm yourself with the right tools to solve them.

A problem-solving flowchart is one of those tools. It’ll help you take a problem statement, break the problem down into likely causes helping you get to the bottom of what’s gone wrong.

In this post, we’ll cover

• What is a Problem Solving Flow Chart
• How to create a Problem Solving flow chart
• Example 1 of Problem Solving flow chart
• Example 2 of Problem Solving Flow chart
• What flow chart shapes to use
• When should you use a flow chart
• 7 tips on creating your Problem Solving chart

Key Benefits & Likely issues with the tool

Let’s get started!

What is a Problem Solving Flowchart

A Problem Solving flow chart is a diagram that uses shapes, arrows, and text to show a moving sequence of actions and/or activities that help solve a problem.  

How to create a Problem Solving flowchart

• Describe your problem.
• Pose Yes/No Questions that can help identify the cause of the problem
• Question each stage of the process until it is fully examined
• Repeat steps 2 & 3 until you have identified a solution
• Try the solution; if it is successful in addressing the root cause, then you’ve fixed your problem. If not, repeat the process until you have a solution that works.

A problem-solving flowchart attempts to identify a root cause/solution to the trigger that is causing the problem allowing you to change the process and prevent the problem from occurring. 

Let’s now demonstrate the effectiveness of a problem solving flowchart by showing some examples.

Example 1 Problem solving flow chart

In our first example, we’re going to start with something simple to show you the principle of the tool.

We have been given a cup of tea and we don’t like it!  

Let’s use a problem-solving flow chart to find out what’s gone wrong.

We’ve used Excel to capture this flow chart using flowchart shapes (insert –> shapes), you can, of course, use other applications to do this, you don’t’ have to have specialized flow chart software to do this. ( there’s a great flowchart in Excel video here ). Or you can simply use a pen and paper.

Use a rectangle and add your problem statement.

Remember to keep your problem statement unambiguous and straightforward. Here we’ve used “I don’t like my cup of tea.”

Now that we’ve got our problem statement, we’re going to start asking questions.

We’re going to examine the variables that go into a cup of tea in an attempt to find out what’s gone wrong.

** TIP** – Work through your process – rather than start from scratch, if you have a documented process, work through that examining each step to ascertain if there are issues. If not, you might find it useful to research and sketch out the process before starting with your flowchart.

We have a process for the cup of tea, which is:

1/ Boil Water

2/ Place Breakfast Tea teabag in the cup

3/ Add Water

4/ Leave to sit for 2 mins

4/ Remove teabag

5/ Add milk

6/ Add sugar

So our problem solving flow chart needs to examine each of those steps to determine where the failure has occurred. 

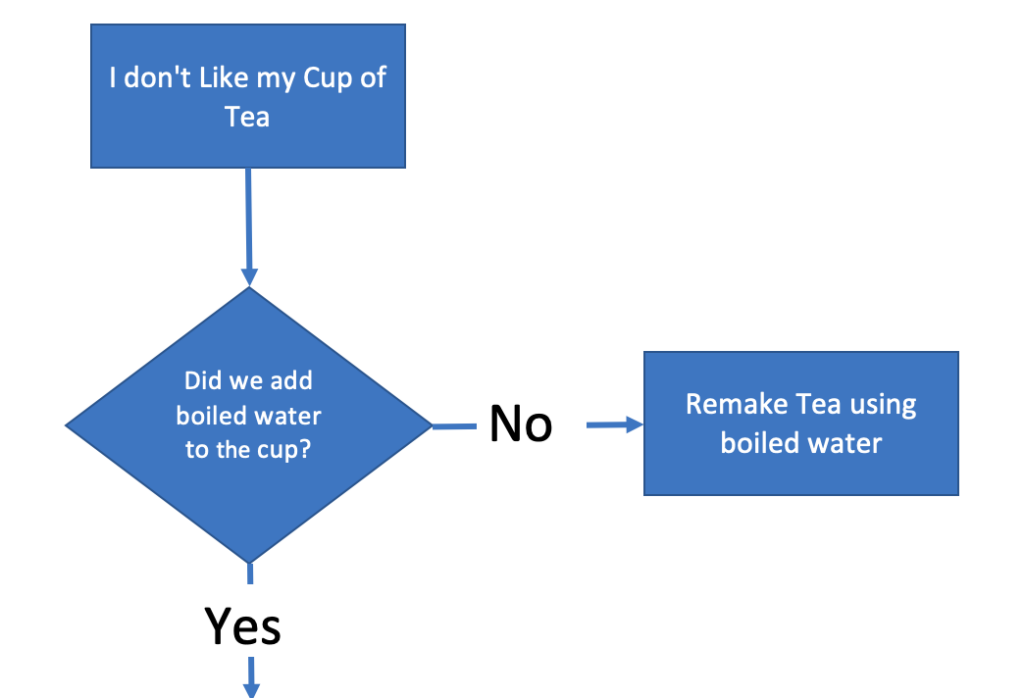
We’ll add a question shape (diamond), connect out problem statement to it using an arrow to check if we boiled the kettle. Our Diagram will now look like:

As a question, we want two possible routes – Yes and No.

Our process asks us to boil the kettle if we did, and the answer is Yes, then we can go to the next process step.

If the answer is No, then we have a problem. Our tea will be cold. 

Here we can do one of two things. We can terminate the flow chart, or we can add an activity to rectify the problem (this might be to remake the drink or to perhaps heat the drink up in the microwave).

Our flow chart now looks like this:

Step 2 in our Tea making process was to add a Breakfast-tea tea bag.

So, once again, we’ll ask a question about that step.

“Did we add an English Breakfast teabag.”

As before, we’ll use a question shape, using Yes or No answers. If we performed the process step correctly, we’d move on. If we didn’t, we’ll either end the problem solving (we’ve found the root cause), or we’ll add a corrective action.

Now we’ll repeat this process until we’ve reviewed the whole process.

Our finished flowchart looks like this.

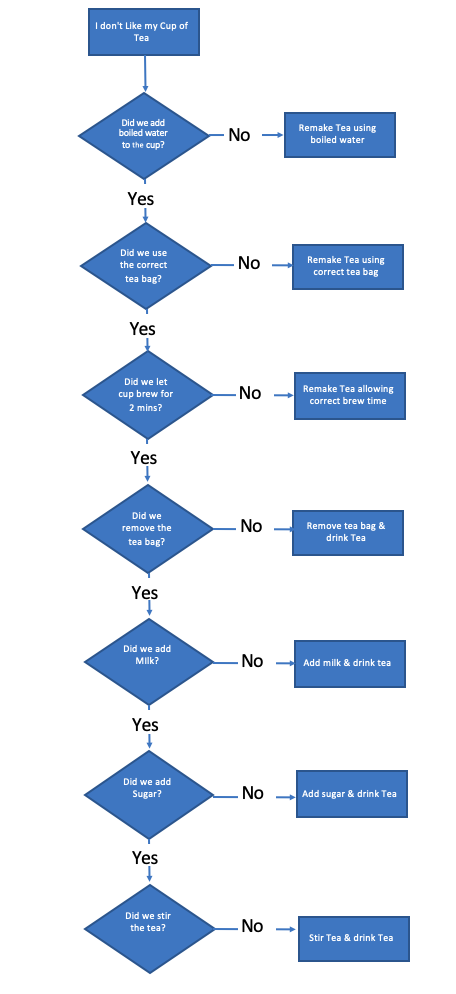
However, we’re not finished.

What happens if we follow the flow chart, and we find we didn’t use boiled water. We remake the tea using boiled water, and we still don’t like it?  

We need to ask some further questions.

We need to update our flow chart to validate that we solved the problem and what to do if we didn’t.

So for each step of the process, our problem solving flowchart now looks like this.

Here’s our completed flow chart.

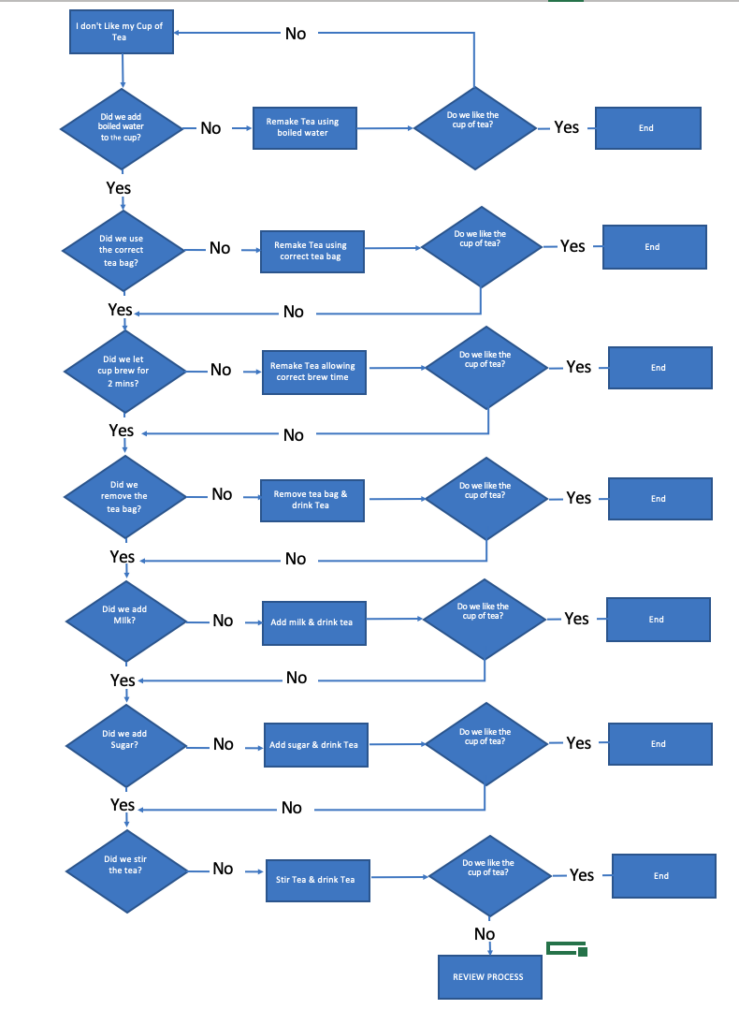
As you can see, we’ve identified the problem, and we’ve described a corrective action.

But there’s a problem here. With this flowchart, you can still follow it, validating the process, and still end up with a cup of tea that’s unsatisfactory. 

Why is that?

Well, it’s perfectly possible that we started out with a process that’s incorrect. What happens if the process called for using an incorrect tea bag from the start?

So we’ll simplify things by adding a block at the end that if you’re still not happy at the end of reviewing the steps, a full review of the process will be undertaken. This is a simple answer to this problem, and I would expect that you would expand this section in more detail if you were creating a flowchart yourself.

So what does a more complex process look like, how about we look at a business problem?

Example 2 Problem Solving flow chart

OK, so example 1 may have been a bit simple, and you are maybe looking for something in a business context.

So in Example 2, let’s look at a scenario that’s a little more complex.

Let’s assume that your organization has received a non-conforming part. You have been assigned to work with the Vendor to:

• Find out what went wrong
• Prevent recurrence

We’re going to use a problem solving flow chart to help us do that.

As with the first example, we’re going to state the problem.

“The part is non conforming.”

Using the production process from the Vendor, we’ll work through the stages to see if we can spot what’s gone wrong.

The diagram below shows an analysis of the first two steps of the production process using a problem-solving flow chart.

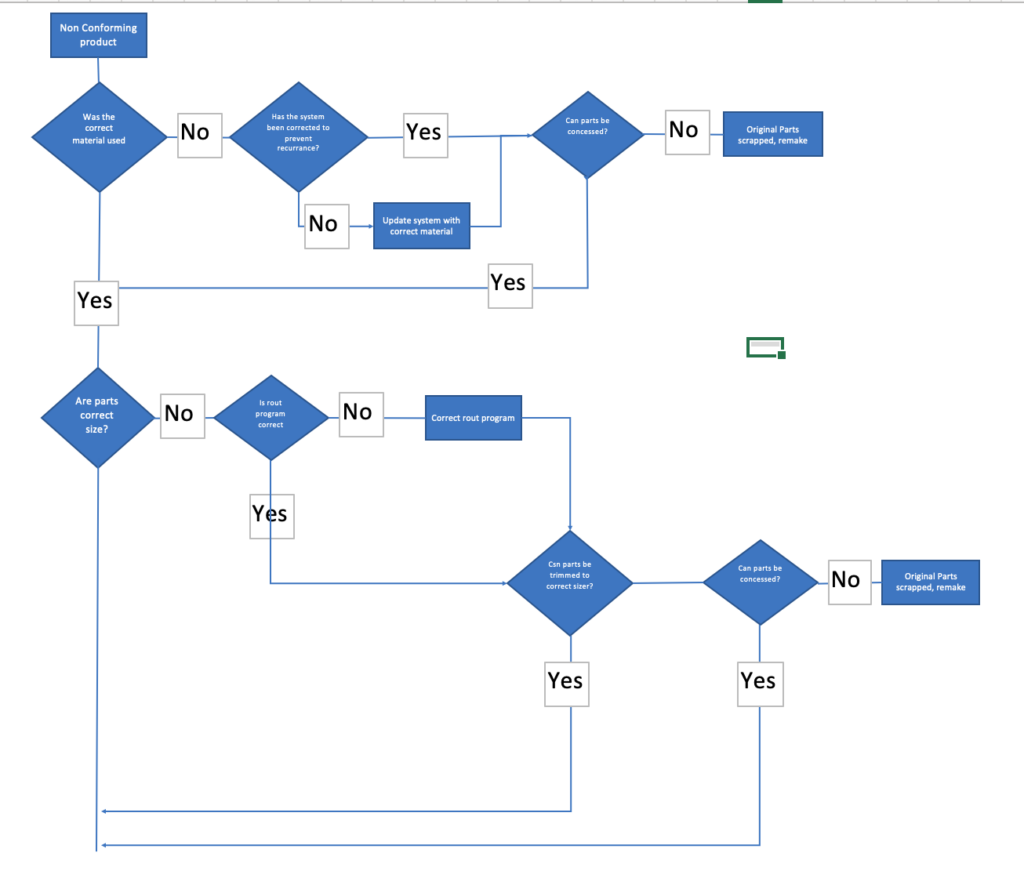
The first thing you’ll notice is that on one process step, there may be many questions to ascertain the potential issue.  

Some of these may be complex and require careful thought.

There may be multiple variables (systems, processes, tools, inputs, etc.) that may require attention.

You will need to analyze each process step, in full, to be sure you have caught all the possible causes of the fault.

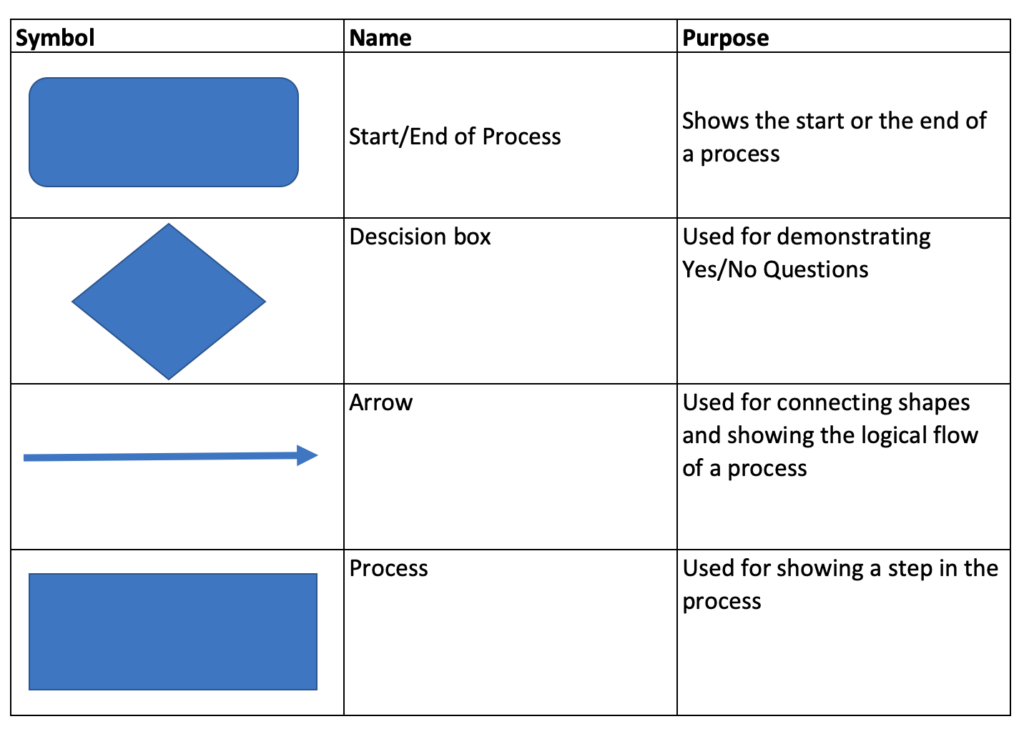
Which Flow chart shapes should you use.

A problem solving flow chart usually utilizes only a small number of shapes. We show these in the table below.

When should you use a Problem Solving flow chart

There are many many problem tools available.

A flow chart lends itself to be used when:

• You are looking for a tool that is simple to use
• You are looking to use a tool that does not require complex software
• You want to validate a  process.
• You want something that facilitates collaboration
• You want something that you can use to communicate with others

7 Tips on creating great problem solving flow charts

1/ Use standard shapes!

2/ Make it easy to follow!

3/ Keep things on one page

4/ Don’t overload your boxes with text

5/ Go into enough detail. Don’t try and simplify activities as it might hide problems from being seen.

6/ Collaborate. Where you can utilize a team to help document the problem and the activities do so. The more knowledge of the process, the better chance you’ll have of locating the issue.

7/ Use a consistent direction to flow your process, moving things around the page can confuse people who might look at it.

A flow chart can provide you with a great advantage when looking to solve problems. Some of the key benefits include

• A visual aide that’s easy to understand
• Simple to use, does not require hours and hours of training
• A tool that facilitates collaboration
• Effective for aiding communication
• Provides an effective method of analysing a process

However, as with everything, there are some issues to look out for

• Flowchart fails to capture all process steps and therefore root cause analysis is hit and miss
• Lack of knowledge of the process by the individual compiling the flowchart results in inaccurate problem solving
• Inconsistent flow of process makes maps confusing
• Complex processes may be better suited to other tools (fishbone etc)
• Inconsistent formatting and/or use of shapes result in flowchart that is difficult to utilise.

There are a great many tools out there for problem-solving, and flow charts can be used either as a stand-alone tool or conjunction with one of these other tools.

Flowcharts can make for a great problem-solving tool.  

They’re simple to use, effective, and facilitate collaboration.

We hope you’ve found our article useful, in particular the example walkthroughs.

If you’re looking to use the tool, we’d love some feedback from you and hearing how you’ve got on. Why not fire us a message on twitter or use the comments section below.

This article is part of our Problem Solving Guide.   

Our Content

• Calculators
• Career Skills
• Communications
• Human Resources
• Strategy and Leadership
• Supply Chain Management

How it works

For Business

Join Mind Tools

Article • 9 min read

Flow Charts

Identify and communicate your optimal process.

By the Mind Tools Content Team

How often have you thought about streamlining a process in your organization but not been sure where to start? Or perhaps you've struggled to understand a process when it's described to you in detail.

Flow charts are a useful tool in these situations, as they make a process easy to understand at a glance. Using just a few words and some simple symbols, they show clearly what happens at each stage and how this affects other decisions and actions.

In this article and video, we look at how to create and use flow charts, and explore how they can help you to solve problems in your processes.

What Is a Flow Chart?

Flow charts are easy-to-understand diagrams that show how the steps of a process fit together. American engineer Frank Gilbreth is widely believed to be the first person to document a process flow, having introduced the concept of a "Process Chart" to the American Society of Mechanical Engineers in 1921.

Flow charts tend to consist of four main symbols, linked with arrows that show the direction of flow:

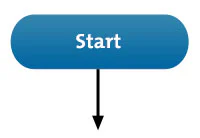
1. Elongated circles, which signify the start or end of a process.

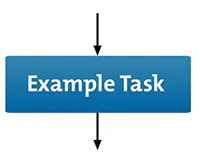
2. Rectangles, which show instructions or actions.

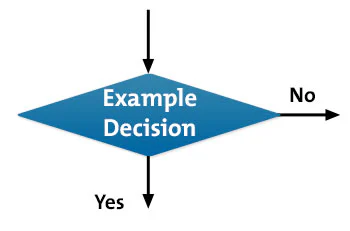
3. Diamonds, which highlight where you must make a decision.

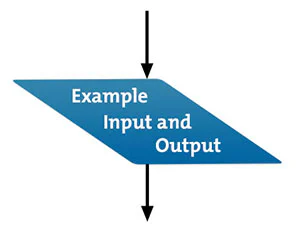
4. Parallelograms, which show input and output. This can include materials, services or people.

You can use many other symbols in a flow chart but remember that these diagrams are used for communication . If you use symbols that only a few people understand, you may fail to get your message across. So, be sure to keep things simple !

When to Use a Flow Chart

All manner of organizations use flow charts to:

• Define a process.
• Standardize a process.
• Communicate a process.
• Identify bottlenecks or waste in a process.
• Solve a problem .
• Improve a process.

For example, software developers can use them to work out how the automated and manual parts of a process join up. Inexperienced team members might follow a flow chart to help them to complete activities in the right order. A manufacturer could ensure that it keeps to its values by applying a quality-control flow chart that presents questions and decision points. And an HR department might combine a flow chart with an organogram to show people who to contact about issues and when.

Why Use Flow Charts?

This tool's simplicity makes communicating and documenting a process quick and clear, so that the process will more likely be understood and applied correctly and consistently. It can also help you to estimate the timescale of the process, as you're better able to gauge the time needed for each task along the way. And you'll more likely identify who you should involve and at what stage, such as senior management or a compliance authority.

But you can also benefit from the process of creating a flow chart itself, as you build it step by step. You'll be able to focus on the detail of each individual stage, without feeling overwhelmed by the rest of the process, and then "zoom out" again to see the wider picture.

If your process or project involves several people or teams, you might find it more useful to use a Swim Lane Diagram rather than a flow chart – this helps you to show process flows between people and teams.

How to Create a Flow Chart

Follow these four steps:

Step 1: Identify Tasks

Begin by listing all of the tasks in a process in chronological order. Ask questions such as, "What happens next in the process?" or, "Do you need to make a decision before the next step?" or, "What approvals are required before you move on to the next task?"

Put yourself in the shoes of the person using the process, possibly for the first time. Talk to team members who work with the process directly, and get their opinions on where improvements could be made. Better yet, take a hands-on approach and go through the procedure yourself, and think about the practicalities of each stage. Use Customer Experience Mapping if your flow chart focuses on customer service, so that you can gain a better understanding of the process.

Step 2: Organize and Document Tasks

Next, start your flow chart by drawing the elongated circle shape and labeling it "Start."

Then, work through your whole process, and show the actions and decisions in the order that they happen. Link them with arrows to illustrate the flow of the process.

Where you need to make a decision, draw arrows from the decision diamond to each possible solution, and then label each arrow with the decision made. Remember to show the end of the process by using an elongated circle labeled "Finish."

Step 3: Double-Check the Process

When you've completed your flow chart, go back to the start and try it out to make sure that you haven't overlooked anything. Work through each step, and ask yourself whether you've represented the sequence of actions and the decisions involved correctly. Are there more decisions to be made at certain stages?

Then show your flow chart to other people, especially those who work directly with the process. Ask them to test that it works and to tell you if there are any problems or omissions.

Step 4: Challenge the Flow Chart

Finally, you might want to improve the process rather than just record it. So, see whether any of the steps that you've described are unnecessary or overly complicated. Identify any major bottlenecks , and deal with them to improve performance.

Are there any missing steps, no matter how small or seemingly insignificant, that you should add? And have you assigned tasks and decisions to the right people or automated them where it's most appropriate? Make any changes and then challenge the chart again.

As you challenge your flow chart, you might also be challenging your team members' tried and tested ways of working. So, take time to win support for your ideas, and don't expect to change people's habits overnight.

You may find that SIPOC diagrams will give you the detailed information that you need to introduce change in a controlled and effective way.

Flow Chart Software

You'll likely start with drawing flow charts by hand, but it's often more convenient to use a diagramming app to save, amend and share your charts.

Such apps vary from the simple and free, such as draw.io , creately and Pencil Project , to the more complex and paid-for, such as gliffy™ , Lucidchart , SmartDraw™ , and Visio® .

Flow charts can quickly become long and complicated, so that you can't represent them on a single piece of paper. This is where you can use "connectors" (shown as numbered circles) to link the flow when moving from one page to another. The user can follow the matching numbers to trace the flow of the process.

The image below shows part of a flow chart for how the receptionists in an example company should route incoming phone calls to the correct department:

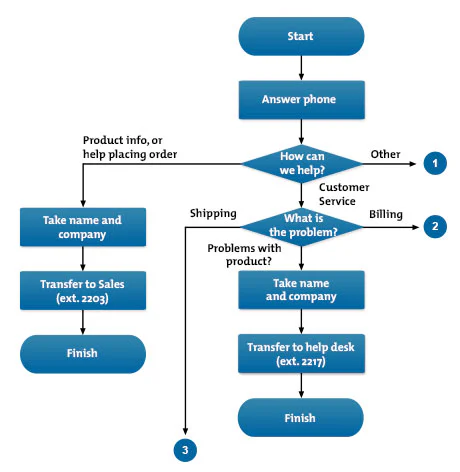
Flow charts are simple diagrams that map out a process, so that you can easily communicate it to other people. You can also use them to define and analyze a process, build a step-by-step picture of it, and then standardize or improve it.

To draw a flow chart, identify the tasks and decisions that you make during a process, and write them down in order.

Then, arrange these steps in the flow chart format, using the appropriate symbols.

Finally, check and challenge your flow chart to make sure that it accurately represents the process, and that it shows the most efficient way of doing the job.

You've accessed 1 of your 2 free resources.

Get unlimited access

Discover more content

How to spot fake news.

Separating Fact From Fiction

How to Spot Real and Fake News

Critically Appraising Information

Add comment

Comments (0)

Be the first to comment!

Get 30% off your first year of Mind Tools

Great teams begin with empowered leaders. Our tools and resources offer the support to let you flourish into leadership. Join today!

Sign-up to our newsletter

Subscribing to the Mind Tools newsletter will keep you up-to-date with our latest updates and newest resources.

Subscribe now

Business Skills

Personal Development

Leadership and Management

Member Extras

Most Popular

Latest Updates

Top Tips for Distributed Leadership

Mind Tools Store

About Mind Tools Content

Discover something new today

Leadership in hard times.

Leading – and Succeeding – in a Downturn

Pain Points Podcast - Building Trust

Developing and Strengthening Trust at Work

How Emotionally Intelligent Are You?

Boosting Your People Skills

Self-Assessment

What's Your Leadership Style?

Learn About the Strengths and Weaknesses of the Way You Like to Lead

Recommended for you

Deep work: rules for focused success in a distracted world.

Cal Newport

Book Insights

Business Operations and Process Management

Strategy Tools

Customer Service

Business Ethics and Values

Handling Information and Data

Project Management

Knowledge Management

Self-Development and Goal Setting

Time Management

Presentation Skills

Learning Skills

Career Skills

Communication Skills

Negotiation, Persuasion and Influence

Working With Others

Difficult Conversations

Creativity Tools

Self-Management

Work-Life Balance

Stress Management and Wellbeing

Coaching and Mentoring

Change Management

Team Management

Managing Conflict

Delegation and Empowerment

Performance Management

Leadership Skills

Developing Your Team

Talent Management

Problem Solving

Decision Making

Member Podcast

• Demo Videos
• Interactive Product Tours
• Request Demo

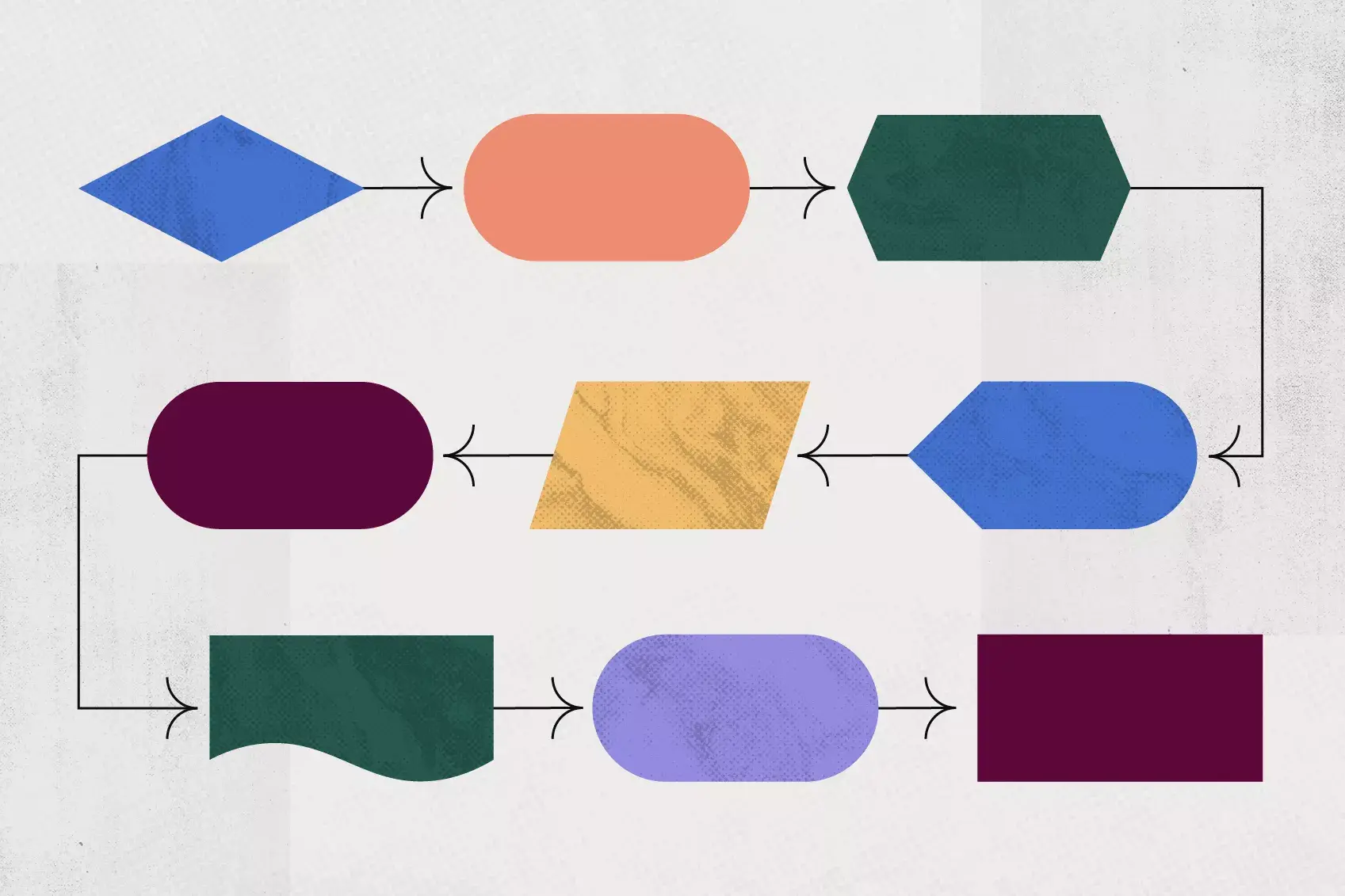
Flowchart Tutorial (with Symbols, Guide and Examples)

A flowchart is simply a graphical representation of steps. It shows steps in sequential order and is widely used in presenting the flow of algorithms, workflow or processes. Typically, a flowchart shows the steps as boxes of various kinds, and their order by connecting them with arrows.

What is a Flowchart?

A flowchart is a graphical representations of steps. It was originated from computer science as a tool for representing algorithms and programming logic but had extended to use in all other kinds of processes. Nowadays, flowcharts play an extremely important role in displaying information and assisting reasoning. They help us visualize complex processes, or make explicit the structure of problems and tasks. A flowchart can also be used to define a process or project to be implemented.

Flowchart Symbols

Different flowchart shapes have different conventional meanings. The meanings of some of the more common shapes are as follows:

The terminator symbol represents the starting or ending point of the system.

A box indicates some particular operation.

This represents a printout, such as a document or a report.

A diamond represents a decision or branching point. Lines coming out from the diamond indicates different possible situations, leading to different sub-processes.

It represents information entering or leaving the system. An input might be an order from a customer. Output can be a product to be delivered.

On-Page Reference

This symbol would contain a letter inside. It indicates that the flow continues on a matching symbol containing the same letter somewhere else on the same page.

Off-Page Reference

This symbol would contain a letter inside. It indicates that the flow continues on a matching symbol containing the same letter somewhere else on a different page.

Delay or Bottleneck

Identifies a delay or a bottleneck.

Lines represent the flow of the sequence and direction of a process.

When to Draw Flowchart?

Using a flowchart has a variety of benefits:

• It helps to clarify complex processes.
• It identifies steps that do not add value to the internal or external customer, including delays; needless storage and transportation; unnecessary work, duplication, and added expense; breakdowns in communication.
• It helps team members gain a shared understanding of the process and use this knowledge to collect data, identify problems, focus discussions, and identify resources.
• It serves as a basis for designing new processes.

Flowchart examples

Here are several flowchart examples. See how you can apply a flowchart practically.

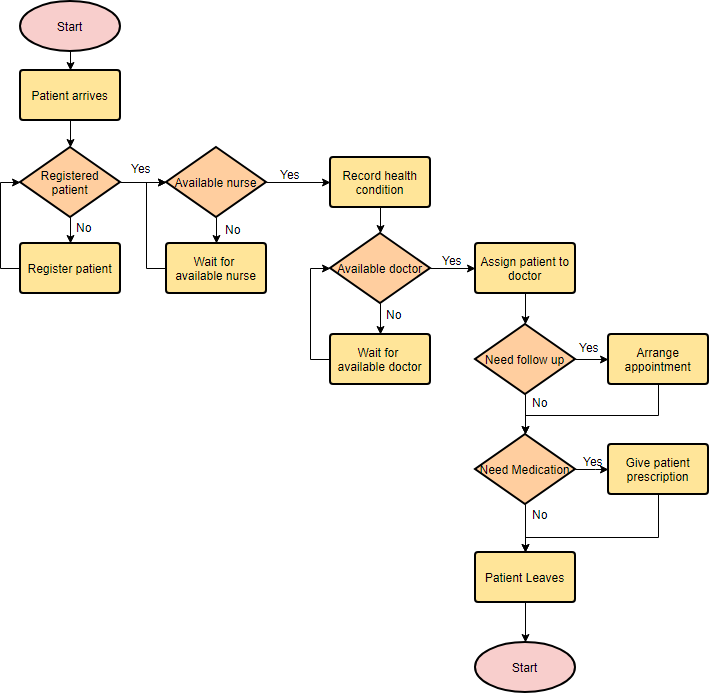
Flowchart Example – Medical Service

This is a hospital flowchart example that shows how clinical cases shall be processed. This flowchart uses decision shapes intensively in representing alternative flows.

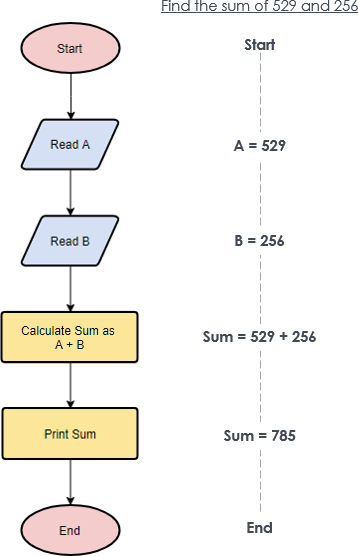
Flowchart Example – Simple Algorithms

A flowchart can also be used in visualizing algorithms, regardless of its complexity. Here is an example that shows how flowchart can be used in showing a simple summation process.

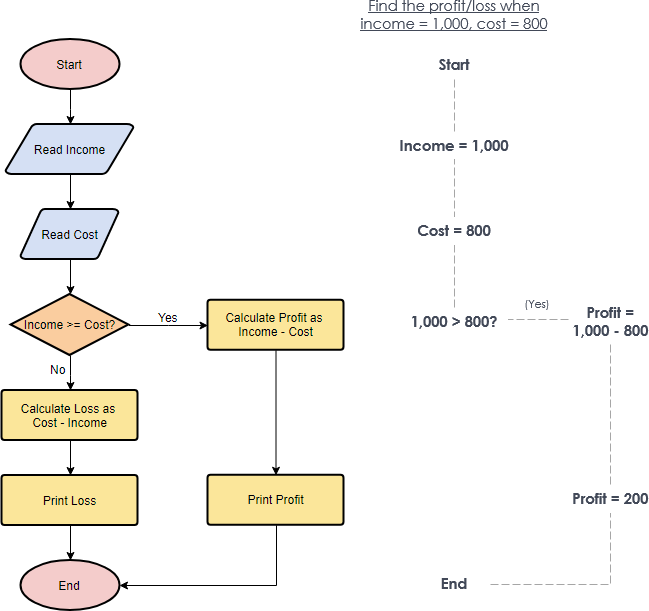
Flowchart Example – Calculate Profit and Loss

The flowchart example below shows how profit and loss can be calculated.

Creating a Flowchart in Visual Paradigm

Let’s see how to draw a flowchart in Visual Paradigm. We will use a very simple flowchart example here. You may expand the example when finished this tutorial.

• Select Diagram > New from the main menu.

• Enter the name of the flowchart and click OK .

• Enter Add items to Cart as the name of the process.

Turn every software project into a successful one.

We use cookies to offer you a better experience. By visiting our website, you agree to the use of cookies as described in our Cookie Policy .

© 2024 by Visual Paradigm. All rights reserved.

• Privacy statement

Visual Problem Solving with Mind Maps and Flowcharts

Updated on: 25 July 2023

Everyone has problems, and we spend most of our working lives solving them. For those who find this quite negative, problems can be also termed as Issues, Challenges or Opportunities.

Some people are especially gifted at problem-solving while others struggle. Some are only good at solving some types of problems, while some other are simply great at finding viable solutions for any problem. Society generally calls the latter, smart.

What if I was to tell you that there’s a simple way to solve any problem you may encounter. In fact, it can be regarded as the smart way to solve problems.

Before we get into it, let’s see how people really fail at solving problems.

Problem-Solving   Fails

You Solve the Wrong Problem

Well, if you don’t know what the problem area is and don’t understand it very well, you’ll probably solve a problem that actually doesn’t exist while the actual problem remains as it is.

You Solve It Half Way

Again, this happens if you don’t know what the full problem is. Identifying and understanding the problem is so important before you start.

You Solve it but New Problems Show Up

This is typical when you don’t know much about the background about the problem area. If you know nothing about computers and you try to fix a broken computer, you probably won’t get very far and will likely make it worse.

You Don’t Know How

Well, obviously if you are trying to solve a problem that you have no clue about, this is going to be hard. When that’s the case, get the help of an expert in the domain the problem you are trying to solve belong to.

How to Solve Any Problem

As it’s quite clear the first step to solving any problem is understanding it thoroughly. Apart from getting a domain expert involved, the best trick I can bring you in is to draw it out. If you are a visual person this is the first thing you should do.

Different kinds of problems require different diagrams, but mind maps and flowcharts are common solutions to most problems.

Thinking Around the Problem

To get a background idea on what the problem and problem area is, mind maps can help greatly. Start with the core idea and branch out as you think about various aspects of the problem.

A mind map is a good place to start visual problem solving ( click on image to create your own mind map )

After thinking about wide aspects of the problem, it’s best to document what the immediate context of the issue is.

To do this, a concept map helps. A concept map is a diagram where you use various shapes to show areas of the problem and how they are connected.

Breaking It Down

Any big problem can be broken into a series of smaller problems. These are usually connected so a flowchart helps . Break the problem into smaller steps with a flowchart.

If you are analyzing an existing solution and trying to optimize it, a flowchart makes perfect sense as it also does the ‘defining’ part of the problem as well.

Analyze your problem further with a flowchart

Once you have broken down the problem into smaller easily solvable problems in a flow chart, you can start creating another chart for the solution as well.

Getting Help

You should always get help if it’s available when you are solving any problem. A second opinion or a second pair of eyes can help a lot in getting the optimal solution.

Tools to Aid Visual Problem Solving

While there is a myriad of tools to help you draw things, Creately is definitely one of the easiest ways to visualize your problem.

We support mind maps, flowcharts, concept maps and 50+ other diagram types which you can use for visual problem-solving.

Our professionally designed templates and productivity features  help you just focus on the drawing as it’s really easy to draw a beautiful diagram in it.

It also comes with built-in real-time collaboration so it helps when you want to get someone else to collaborate on your problem.

Other choices for drawing diagrams to solve problems include Dia, Google Draw or even Microsoft office packages.

Join over thousands of organizations that use Creately to brainstorm, plan, analyze, and execute their projects successfully.

More Related Articles

Leave a comment Cancel reply

Please enter an answer in digits: 17 + 2 =

Download our all-new eBook for tips on 50 powerful Business Diagrams for Strategic Planning.

What is a Flowchart

What do you want to do with flowcharts, i want to create my own flowchart on lucidchart., i want to create a flowchart from a ready-made template..

This comprehensive guide offers everything you need to know about flowcharts, including definitions, history, use cases, symbols, tips, and how to use our flowchart maker to get you started.

9 minute read

Want to create a flowchart of your own? Try Lucidchart. It's fast, easy, and totally free.

More flowchart tips

• Keep your audience in mind and gear the detail in your chart to them. Clear communication is a key goal of flowcharts.
• If the process you are charting involves different teams or departments, consider using a Swimlane Diagram to clearly delineate responsibilities and handoffs.
• Use on-page or off-page connectors to “edit” your chart and make it flow logically. This can allow you to break up a chart into separate pages and still flow well.

What is a flowchart?

Flowcharts to document business processes came into use in the 1920s and ‘30s. In 1921, industrial engineers Frank and Lillian Gilbreth introduced the “Flow Process Chart” to the American Society of Mechanical Engineers (ASME).  In the early 1930s, industrial engineer Allan H. Morgensen used Gilbreth’s tools to present conferences on making work more efficient to business people at his company.  In the 1940s, two Morgensen students, Art Spinanger and Ben S. Graham, spread the methods more widely. Spinanger introduced the work simplification methods to Procter and Gamble. Graham, a director at Standard Register Industrial, adapted flow process charts to information processing. In 1947, ASME adopted a symbol system for Flow Process Charts, derived from the Gilbreths’ original work.

Also in the late ‘40s, Herman Goldstine and John Van Neumann used flowcharts to develop computer programs, and diagramming soon became increasingly popular for computer programs and algorithms of all kinds. Flowcharts are still used for programming today, although pseudocode, a combination of words and coding language meant for human reading, is often used to depict deeper levels of detail and get closer to a final product.

In Japan, Kaoru Ishikawa (1915-1989), a key figure in quality initiatives in manufacturing, named flowcharts as one of the key tools of quality control, along with complementary tools such as the Histogram, Check Sheet and Cause-and-Effect Diagram, now often called the Ishikawa Diagram.

Flowchart symbols

Here are some of the common flowchart symbols. For a more comprehensive list, see our full flowchart symbols page .

Flowcharts for computer programming/algorithms

As a visual representation of data flow, flowcharts are useful in writing a program or algorithm and explaining it to others or collaborating with them on it. You can use an algorithm flowchart to spell out the logic behind a program before ever starting to code the automated process. It can help to organize big-picture thinking and provide a guide when it comes time to code. More specifically, flowcharts can:

• Demonstrate the way code is organized.
• Visualize the execution of code within a program.
• Show the structure of a website or application.
• Understand how users navigate a website or program.

Often, programmers may write pseudocode, a combination of natural language and computer language able to be read by people. This may allow greater detail than the flowchart and serve either as a replacement for the flowchart or as a next step to actual code.

Related diagrams used in computer software include:

• Unified Modeling Language (UML): This is a general-purpose language used in software engineering for modeling.
• Nassi-Shneiderman Diagrams: Used for structured computer programming. Named after Isaac Nassi and Ben Shneiderman, who developed it in 1972 at SUNY-Stony Brook. Also called Structograms.
• DRAKON charts: DRAKON is an algorithmic visual programming language used to produce flowcharts.

How flowcharts are used in numerous other fields

Beyond computer programming, flowcharts have many uses in many diverse fields.

In any field:

• Document and analyze a process.
• Standardize a process for efficiency and quality.
• Communicate a process for training or understanding by other parts of the organization.
• Identify bottlenecks, redundancies and unnecessary steps in a process and improve it.
• Plan coursework and academic requirements.
• Create a lesson plan or oral presentation.
• Organize a group or individual project.
• Show a legal or civil process, like voter registration.
• Plan and structure creative writing, like lyrics or poetry.
• Demonstrate character development for literature and film.
• Represent the flow of algorithms or logic puzzles.
• Understand a scientific process, like the Krebs cycle.
• Chart an anatomical process, such as digestion.
• Map out symptoms and treatment for diseases/disorders.
• Communicate hypotheses and theories, like Maslow’s hierarchy of needs.

Sales and marketing:

• Plot out the flow of a survey.
• Chart a sales process.
• Plan research strategies.
• Show registration flows.
• Disseminate communication policies, like an emergency PR plan.
• Understand order and procurement processes.
• Represent an employee’s tasks or daily routine.
• Understand the paths that users take on a website or in a store.
• Develop a business plan or product realization plan.
• Document a process in preparation for an audit, including for regulatory compliance, such as under the Sarbanes-Oxley Act.
• Document a process in preparation for a sale or consolidation.

Manufacturing:

• Denote the physical or chemical makeup of a product.
• Illustrate the manufacturing process from beginning to end.
• Discover and solve inefficiencies in a manufacturing or procurement process.

Engineering:

• Represent process flows or system flows.
• Design and update chemical and plant processes.
• Assess the life cycle of a structure.
• Chart a reverse-engineering flow.
• Demonstrate the design and prototype phase of a new structure or product.

Types of flowcharts

Different authors describe various types of flowcharts in different terms. These people include published experts such as Alan B. Sterneckert, Andrew Veronis, Marilyn Bohl and Mark A. Fryman.

Sterneckert, in his 2003 book Critical Incident Management , listed four popular flowchart types, framed around the concept of flow controls rather than the flow itself:

Document Flowcharts:

Data flowcharts:, system flowcharts:, program flowcharts:.

Veronis , in his 1978 book Microprocessors: Design and Applications , outlined three flowchart types based on scope and level of detail:

System Flowchart:

General flowchart:, detailed flowchart:.

Bohl, in her 1978 book A Guide for Programmers, listed only two:

System Flowchart.

Program flowchart..

But Fryman, in his 2001 book Quality and Process Improvement , differentiated the types in multiple ways from more of a business perspective than a computer perspective:

Decision Flowchart.

Logic flowchart., systems flowchart., product flowchart., process flowchart..

Additional flowchart types defined by others include:

Swimlane Diagram, a.k.a Swimlane Flowchart:

Workflow flowchart:, event-driven process chain (epc) flowchart:, specification and description language (sdl) flowchart:.

These related diagrams are also sometimes thought of as types of flowcharts:

Data Flow Diagram (DFD):

Process flow diagram (pfd), a.k.a. process flowchart:, business process model and notation (bpmn 2.0):, how to plan and draw a basic flowchart, define your purpose and scope., identify the tasks in chronological order., organize them by type and corresponding shape,, draw your chart,, confirm your flowchart,, helpful resources.

• How to Make a Flowchart in Excel
• What is a flowchart and how to create one
• Flowchart Symbols and Notation
• How to Make a Flowchart
• How to Make a Flowchart in PowerPoint
• How to Make a Flowchart in Word

Creating flowcharts in Lucidchart is simple and intuitive. Simply drag shapes onto the canvas and draw lines to connect them. If you're not sure where to begin, check out our tutorial for tips on how to draw a flowchart .

Please log in to save materials. Log in

• Problem Solving / Decision Making

Problem Solving Diagrams - Flowcharts

A flow chart can be a useful tool in problem solving. You can see at a glance how your decisions and actions affect the outcome of your problem solving process. This lesson will help you learn the symbols and steps for writing a flowchart. 

Video - Introduction to Creating Flowcharts

Video - lucidchart introduction, "what is my grade" flowchart.

Computer programmers use flowcharts and other types of diagrams to help visualize the steps and  flow  of the program. This can help to see any errors in the logic before they begin to program. Flowcharts can be used no matter what computer language the program will be written in.

If you wanted to write a computer program that inputs a quiz score and then outputs the letter grade that corresponds to that quiz score, you may want to think about the steps that you would use to create this program.

Task Instructions:

1. View the tutorial above for information on how to use Lucidchart to create a flowchart.

2. This is the algorithm that your flowchart should follow:

Input test score

Decision: Is score greater than 89?

Decision: Is score between 80 and 89?

Decision: Is score between 70 and 79?

Decision: Is score between 60 and 69?

Decision: Is score less than 60?

2. You will use the following symbols for this flowchart: Start/End symbols (this symbol is called Terminator in Lucidchart), Decision symbols, Input/Output (Data) symbols 

3.  Click here for the What is my Grade Flowchart Template .  Click on  File , then  Make Copy

4.   Create your flowchart according to the instructions on the template.

"Time For Lunch" Flowchart

Summarize the lesson by discussing with the students the reasons a computer programmer might use a flowchart.

You want to order lunch at a fast food restaurant. You know you want a hamburger, but aren't sure if you'd like fries and a drink. To practice creating a flowchart, think about the steps that you take to solve this problem. Instructions:

Click HERE to go to Lucidchart.com . 

Click HERE to open the TIME FOR LUNCH Flowchart

Click on  File  and choose to  Make a Copy

• Follow the instructions on the  TIME FOR LUNCH Flowchart  to fill in the correct text in the flowchart symbols.   Click HERE to view a tutorial on how to properly fill out this chart .

Version History

• Product overview
• All features
• App integrations

CAPABILITIES

• project icon Project management
• Project views
• Custom fields
• Status updates
• goal icon Goals and reporting
• Reporting dashboards
• workflow icon Workflows and automation
• portfolio icon Resource management
• Time tracking
• my-task icon Admin and security
• Admin console
• asana-intelligence icon Asana Intelligence
• list icon Personal
• premium icon Starter
• briefcase icon Advanced
• Goal management
• Organizational planning
• Campaign management
• Creative production
• Content calendars
• Marketing strategic planning
• Resource planning
• Project intake
• Product launches
• Employee onboarding
• View all uses arrow-right icon
• Project plans
• Team goals & objectives
• Team continuity
• Meeting agenda
• View all templates arrow-right icon
• Work management resources Discover best practices, watch webinars, get insights
• What's new Learn about the latest and greatest from Asana
• Customer stories See how the world's best organizations drive work innovation with Asana
• Help Center Get lots of tips, tricks, and advice to get the most from Asana
• Asana Academy Sign up for interactive courses and webinars to learn Asana
• Developers Learn more about building apps on the Asana platform
• Community programs Connect with and learn from Asana customers around the world
• Events Find out about upcoming events near you
• Partners Learn more about our partner programs
• Support Need help? Contact the Asana support team
• Asana for nonprofits Get more information on our nonprofit discount program, and apply.

Featured Reads

• Project management |
• Flowchart 101: Symbols, types, and how ...

Flowchart 101: Symbols, types, and how to create them

A flowchart is the perfect way to visualize a complex process for your team. There are over 30 standardized symbols you can use to create a flowchart. These symbols can indicate anything from a process to a document or decisions that need to be made. In this article, you’ll learn what the different shapes mean, when a flowchart can be useful, and what types of flowcharts you can implement at work.

Whether you're a business owner looking to streamline operations, a project manager aiming to keep your team on track, or a software developer designing a new application, flowcharts can be an invaluable tool. By breaking down complex processes into clear, logical steps, flowcharts help you identify potential bottlenecks, optimize workflows, and communicate ideas effectively. In this comprehensive guide, we'll explore the fundamentals of flowcharts, including their symbols, types, and practical applications.

What is a flowchart?

Industrial engineers Frank and Lillian Gilbreth introduced the flowchart concept for the first time in 1921 when they presented it to the American Society of Mechanical Engineers (ASME). Since then, flowcharts have been refined and standardized to optimize processes across various industries.

If you want to learn more about the variety of different types of flowcharts and flowchart symbols, you’ve come to the right place. We’re also going to cover how you can create flowchart diagrams and provide a few examples for inspiration.

When to use flowcharts

Flowcharts can be helpful in a variety of scenarios, including when you need to:

1. Documenting and standardizing processes

A flowchart is a wonderful way to map out and document a collaborative project or process. Once your flowchart is done, you can reuse it for similar projects and processes. This can save you and your team time—and stress—in the long run.

2. Visualizing complex ideas and systems

Not everyone on your team will have the time (or resources) to read through a complicated and lengthy process document. A flowchart allows everyone to follow the workflow, understand the tasks, and analyze the individual steps quickly and easily.

3. Organizing teams and assigning tasks

Visually representing a process can make it easier for you to assign tasks to team members and organize your team’s work so it all flows better.

4. Making data-driven decisions

Decisions often look way less intimidating and complicated when they’re mapped out in a flowchart. A flowchart can also help you see the consequences of your decisions, which makes it easier to anticipate and justify next steps.

5. Identifying and preventing bottlenecks

Flowcharts help you uncover bottlenecks or problems before they become issues. By mapping out the entire process with this visual guide, you can follow each step and ensure that you allocate enough time and resources to every task.

6. Planning and tracking project progress

Since it’s so easy to follow the steps in your flowchart, you can always pinpoint where your team is currently at in the project or process. This makes tracking progress very easy and also gives you a great overview of the tasks that still need to be completed.

Flowchart symbols and definitions

Flowcharts vary from quickly hand-drawn visualizations to help document or plan a process to comprehensive workflow diagrams created with a designated software. To make it easier for you to understand flowcharts across teams, departments, and even industries, the American National Standards Institute (ANSI) set official standards in the 1960s, which were adopted by the International Organization for Standardization (ISO) in 1970 and are continuously updated and improved. The latest version of this standard was confirmed in 2019 .

When reading a flowchart, follow the Western standard, meaning you’ll read it from the top to the bottom and from the left to the right. Let’s take a look at some of the most commonly used flowchart shapes, symbols, names, and meanings.

Flowline: The flowline shows the process’s direction by connecting two blocks with one another.

Termina or Terminator: The terminal or terminator represents the start or end points of a flowchart process.

Process: The process symbol is the most common component of a flowchart and indicates a step in the process.

Comment or Annotation: You can indicate additional information about a step with a comment or annotation.

Decision: This symbol represents a decision you or your team need to make to get to the next step of the process. Typically, it’s a true or false decision or a yes or no question that you need to answer.

Stored data: This symbolizes a data file or database.

“Or” symbol: This indicates that the process flow continues in three or more branches.

Input/Output: The input/output symbol represents the process of inputting or outputting external data.

Display: This indicates a step that displays relevant information.

Document: This symbol represents a single document.

Delay: This symbol allows you to plan and represent any delay periods that will be part of the process.

Manual input: This symbol represents data or information that needs to be manually entered into a system.

Manual operation: This symbolizes a manual operation or adjustment to the process.

Off-page connector: This symbol is used to connect two symbols that are on different pages.

On-page connector: This dot can connect two symbols and replace long lines, which allows for a cleaner flowchart.

Summoning junction symbol: This symbol is used to converge multiple branches back into a single process.

Alternate process: The lines to this symbol are usually dotted. The symbol itself stands for an alternative to the normal process step, in case one is needed.

Predefined process: This symbol indicates a process that is already defined elsewhere.

Multiple documents: This symbolizes multiple documents.

Preparation or initialization: This symbol indicates a preparation or initialization step in the process.

Once you’ve learned what the symbols represent, you can read—or create—pretty much any type of flowchart and gain a better understanding of the visualized process. When you create a flowchart that needs different shapes or symbols, include a legend so it’s still accessible to your teammates.

Common types of flowcharts

Flowcharts come in various types, each serving a specific purpose in visualizing and analyzing different aspects of a process or system. Understanding the common types of flowcharts can help you choose the right one for your needs, whether you're documenting a workflow, designing an algorithm, or managing a complex project. Here are some of the most widely used types of flowcharts:

Decision flowchart

A decision flowchart focuses on the decision-making process, outlining the different paths and outcomes based on specific conditions or criteria. It helps teams evaluate and improve their decision-making strategies.

Process flowchart

Also known as a process flow diagram or process map, a process flowchart provides a step-by-step representation of a process, showcasing the sequence of tasks, decision points, and endpoints. It is useful for documenting, analyzing, and optimizing business processes.

Workflow diagram

A workflow diagram illustrates the flow of work and information between people, departments, or systems. It helps streamline processes, identify bottlenecks, and ensure efficient collaboration among team members.

Swimlane flowchart

Also called a cross-functional flowchart or swimlane diagram, this type of flowchart separates the process steps into lanes representing different actors, such as departments or roles. It is ideal for visualizing complex processes that involve multiple stakeholders.

Data flow diagram (DFD)

A data flow diagram (DFD) maps out the flow of data within a system, showcasing how data is processed, stored, and transmitted. DFDs are commonly used in computer programming and systems analysis to design and document information systems.

Program flowchart

A program flowchart represents the sequence of steps and decisions in a computer program or algorithm. It helps programmers design, document, and debug software applications using standard flowchart symbols and shapes.

System flowchart

A system flowchart represents the architecture and components of a system, including hardware, software, and their interactions. It is useful for designing, documenting, and troubleshooting complex systems.

Process flow diagram (PFD)

Similar to a process flowchart, a process flow diagram (PFD) provides a high-level overview of a process, focusing on the major equipment, material flows, and control loops. This type of diagram is commonly used in chemical engineering and industrial processes.

Event-Driven Process Chain (EPC) flowchart

An event-driven process chain (EPC) flowchart is a specialized type of flowchart used to model business processes in terms of events, functions, and logical connectors. EPCs are often used in conjunction with other process modeling methodologies, such as BPMN (Business Process Model and Notation).

Specification and Description Language (SDL) flowchart

SDL flowcharts are used in the design and documentation of real-time systems, particularly in the telecommunications industry. They provide a graphical representation of a system's behavior, including states, transitions, and actions.

By understanding these common types of flowcharts and their applications, you can select the most appropriate one for your project, whether you're using a flowchart template, a flowchart maker, or creating one from scratch.

Tip: You can find a process document flowchart in our article on process documentation and check out PERT charts for another common flowchart example.

How to create a flowchart: Step-by-step guide

Creating a flowchart may seem daunting at first, but by following these simple steps, you can easily visualize your processes, workflows, or algorithms using a flowchart maker or software. Whether you're creating process charts, a decision flowchart, or a swimlane diagram, this guide will help you get started.

1. Define your purpose and scope.

Before you begin creating your flowchart, clearly define its purpose and scope. Are you documenting a business process, designing an algorithm, or visualizing a complex workflow? Understanding your goal will help you choose the right type of flowchart and determine the level of detail required.

2. Identify and organize tasks

Gather information about the process, workflow, or system you want to visualize. Brainstorm with team members and stakeholders to identify the key steps, decision points, inputs, and outputs. Use a whiteboard or sticky notes to organize your ideas and create a rough draft of your flowchart, outlining the main steps and structure.

3. Select the right flowchart symbols

Familiarize yourself with the standard flowchart symbols and shapes, including connectors, decision points, and end points. Choose the most appropriate symbols based on the type of flowchart you're creating, such as a process flowchart, data flow diagram (DFD), or swimlane diagram. Consistency in symbol usage ensures clarity and readability.

4. Draw and refine your flowchart

Use a flowchart maker or software like Microsoft Visio or Lucidchart to create a polished, digital version of your flowchart. These tools offer a wide range of templates, shapes, and connectors, making it easy to create professional-looking flowcharts for various use cases. Arrange the steps and decision points in a logical order, and use connectors to show the flow between them. Add annotations and labels to provide additional context and clarity.

5. Implement and optimize

Share your completed flowchart with your team members and stakeholders, and encourage feedback. Collaborate to ensure that everyone understands the process or workflow represented in the flowchart. Implement the flowchart in your organization and monitor its effectiveness. Continuously review and optimize your flowchart based on real-world experience and feedback, making adjustments as needed to improve efficiency and productivity.

By following these steps and leveraging the power of flowchart software and templates, you can create clear, effective flowcharts that help streamline your processes, workflows, and decision-making.

Use flowchart templates to maximize your productivity

A flowchart is supposed to make your life easier, so utilize computer programs or app integrations like Lucidchart to create them. The Lucidchart + Asana integration seamlessly embeds diagrams, flowcharts, and process maps into your Asana project. Choose from thousands of templates to create all the flowcharts you need.

FAQ: Flowchart

What is the difference between a flowchart and a process map?

Flowcharts focus on the sequence of steps and decisions in a process, using simple shapes and symbols. Process maps provide a more detailed view, including inputs, outputs, relationships between steps, and additional information like time and resources required.

How do I choose the right type of flowchart for my project?

Choose a flowchart type based on the purpose and complexity of your project. Basic flowcharts work for simple, linear processes. Swimlane diagrams or cross-functional flowcharts are better for processes with multiple stakeholders or parallel steps. Program flowcharts or data flow diagrams (DFDs), suit technical projects.

Can flowcharts be used for non-technical processes?

Yes, flowcharts can visualize and optimize processes in any industry or domain, such as customer service, marketing, or creative projects. By breaking down complex processes into clear steps, flowcharts help identify bottlenecks and improve efficiency in any field.

Related resources

What are story points? Six easy steps to estimate work in Agile

How to choose project management software for your team

7 steps to complete a social media audit (with template)

3 visual project management layouts (and how to use them)

• Skip to main content
• Skip to primary sidebar
• Skip to footer

Additional menu

Nine essential problem solving tools: The ultimate guide to finding a solution

October 26, 2023 by MindManager Blog

Problem solving may unfold differently depending on the industry, or even the department you work in. However, most agree that before you can fix any issue, you need to be clear on what it is, why it’s happening, and what your ideal long-term solution will achieve.

Understanding both the nature and the cause of a problem is the only way to figure out which actions will help you resolve it.

Given that most problem-solving processes are part inspiration and part perspiration, you’ll be more successful if you can reach for a problem solving tool that facilitates collaboration, encourages creative thinking, and makes it easier to implement the fix you devise.

The problem solving tools include three unique categories: problem solving diagrams, problem solving mind maps, and problem solving software solutions.

They include:

• Fishbone diagrams
• Strategy maps
• Mental maps
• Concept maps
• Layered process audit software
• Charting software
• MindManager

In this article, we’ve put together a roundup of versatile problem solving tools and software to help you and your team map out and repair workplace issues as efficiently as possible.

Let’s get started!

Problem solving diagrams

Mapping your way out of a problem is the simplest way to see where you are, and where you need to end up.

Not only do visual problem maps let you plot the most efficient route from Point A (dysfunctional situation) to Point B (flawless process), problem mapping diagrams make it easier to see:

• The root cause of a dilemma.
• The steps, resources, and personnel associated with each possible solution.
• The least time-consuming, most cost-effective options.

A visual problem solving process help to solidify understanding. Furthermore, it’s a great way for you and your team to transform abstract ideas into a practical, reconstructive plan.

Here are three examples of common problem mapping diagrams you can try with your team:

1. Fishbone diagrams

Fishbone diagrams are a common problem solving tool so-named because, once complete, they resemble the skeleton of a fish.

With the possible root causes of an issue (the ribs) branching off from either side of a spine line attached to the head (the problem), dynamic fishbone diagrams let you:

• Lay out a related set of possible reasons for an existing problem
• Investigate each possibility by breaking it out into sub-causes
• See how contributing factors relate to one another

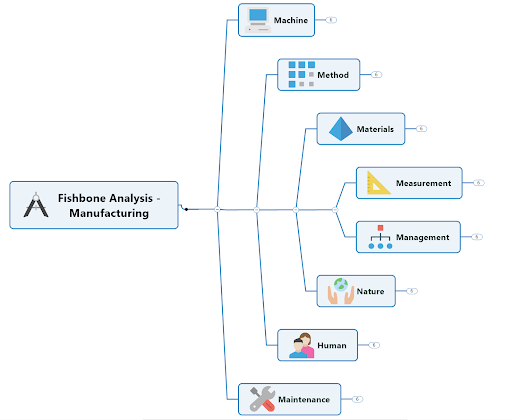
Fishbone diagrams are also known as cause and effect or Ishikawa diagrams.

2. Flowcharts

A flowchart is an easy-to-understand diagram with a variety of applications. But you can use it to outline and examine how the steps of a flawed process connect.

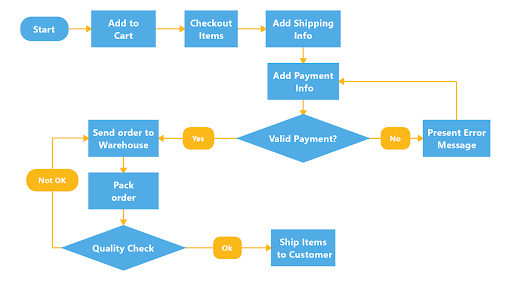
Made up of a few simple symbols linked with arrows indicating workflow direction, flowcharts clearly illustrate what happens at each stage of a process – and how each event impacts other events and decisions.

3. Strategy maps

Frequently used as a strategic planning tool, strategy maps also work well as problem mapping diagrams. Based on a hierarchal system, thoughts and ideas can be arranged on a single page to flesh out a potential resolution.

Once you’ve got a few tactics you feel are worth exploring as possible ways to overcome a challenge, a strategy map will help you establish the best route to your problem-solving goal.

Problem solving mind maps

Problem solving mind maps are especially valuable in visualization. Because they facilitate the brainstorming process that plays a key role in both root cause analysis and the identification of potential solutions, they help make problems more solvable.

Mind maps are diagrams that represent your thinking. Since many people struggle taking or working with hand-written or typed notes, mind maps were designed to let you lay out and structure your thoughts visually so you can play with ideas, concepts, and solutions the same way your brain does.

By starting with a single notion that branches out into greater detail, problem solving mind maps make it easy to:

• Explain unfamiliar problems or processes in less time
• Share and elaborate on novel ideas
• Achieve better group comprehension that can lead to more effective solutions

Mind maps are a valuable problem solving tool because they’re geared toward bringing out the flexible thinking that creative solutions require. Here are three types of problem solving mind maps you can use to facilitate the brainstorming process.

4. Mental maps

A mental map helps you get your thoughts about what might be causing a workplace issue out of your head and onto a shared digital space.

Because mental maps mirror the way our brains take in and analyze new information, using them to describe your theories visually will help you and your team work through and test those thought models.

5. Idea maps

Idea maps let you take advantage of a wide assortment of colors and images to lay down and organize your scattered thought process. Idea maps are ideal brainstorming tools because they allow you to present and explore ideas about the best way to solve a problem collaboratively, and with a shared sense of enthusiasm for outside-the-box thinking.

6. Concept maps

Concept maps are one of the best ways to shape your thoughts around a potential solution because they let you create interlinked, visual representations of intricate concepts.

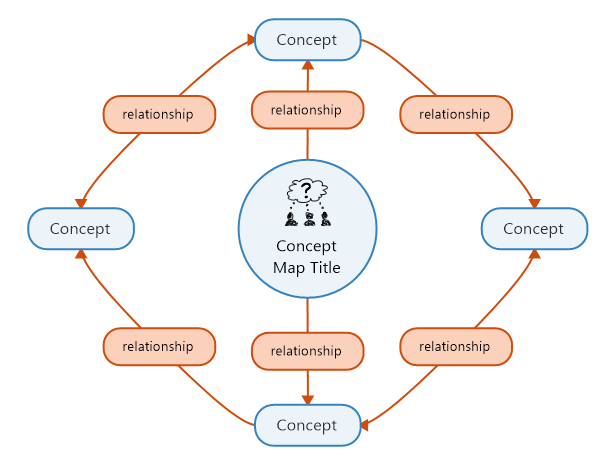
By laying out your suggested problem-solving process digitally – and using lines to form and define relationship connections – your group will be able to see how each piece of the solution puzzle connects with another.

Problem solving software solutions

Problem solving software is the best way to take advantage of multiple problem solving tools in one platform. While some software programs are geared toward specific industries or processes – like manufacturing or customer relationship management, for example – others, like MindManager , are purpose-built to work across multiple trades, departments, and teams.

Here are three problem-solving software examples.

7. Layered process audit software

Layered process audits (LPAs) help companies oversee production processes and keep an eye on the cost and quality of the goods they create. Dedicated LPA software makes problem solving easier for manufacturers because it helps them see where costly leaks are occurring and allows all levels of management to get involved in repairing those leaks.

8. Charting software

Charting software comes in all shapes and sizes to fit a variety of business sectors. Pareto charts, for example, combine bar charts with line graphs so companies can compare different problems or contributing factors to determine their frequency, cost, and significance. Charting software is often used in marketing, where a variety of bar charts and X-Y axis diagrams make it possible to display and examine competitor profiles, customer segmentation, and sales trends.

9. MindManager

No matter where you work, or what your problem-solving role looks like, MindManager is a problem solving software that will make your team more productive in figuring out why a process, plan, or project isn’t working the way it should.

Once you know why an obstruction, shortfall, or difficulty exists, you can use MindManager’s wide range of brainstorming and problem mapping diagrams to:

• Find the most promising way to correct the situation
• Activate your chosen solution, and
• Conduct regular checks to make sure your repair work is sustainable

MindManager is the ultimate problem solving software.

Not only is it versatile enough to use as your go-to system for puzzling out all types of workplace problems, MindManager’s built-in forecasting tools, timeline charts, and warning indicators let you plan, implement, and monitor your solutions.

By allowing your group to work together more effectively to break down problems, uncover solutions, and rebuild processes and workflows, MindManager’s versatile collection of problem solving tools will help make everyone on your team a more efficient problem solver.

Download a free trial today to get started!

Ready to take the next step?

MindManager helps boost collaboration and productivity among remote and hybrid teams to achieve better results, faster.

Why choose MindManager?

MindManager® helps individuals, teams, and enterprises bring greater clarity and structure to plans, projects, and processes. It provides visual productivity tools and mind mapping software to help take you and your organization to where you want to be.

Explore MindManager

Culture Online

What is the significance of a flowchart?

This is a great question, there are many ways we can use diagrams and maps to make information easier to process visually.

2 June 2021

A flowchart is a diagram depicting a process, a system or a computer algorithm. It is a diagrammatic representation of the solution to a given problem but, more importantly, it provides a breakdown of the essential steps to solving the problem.

When designing and planning a process, flowcharts can help you identify its essential steps and simultaneously offer the bigger picture of the process. It organises the tasks in chronological order and identify them by type, e.g. process, decision, data, etc.

Each step is independent of implementation as the flowchart only describes what should happen at that step, what input is needed and what the output of the step is but it says nothing about how to implement the step.

Once a flowchart is in place, it can help find less obvious features of the process that can then be refined to improve its efficiency, i.e. bottlenecks, flaws, unnecessary steps. It should be seen as an evolving diagram.

Flowcharts are limited in what they can represent and are usually employed alongside other types of diagrams. They do have historical importance. They were first introduced in 1921 as flow process chart to members of the American Society of Mechanical Engineers and were popular in early computing in the 50s. Visual Programming Languages used in computing are sophisticated flowcharts.

There is a brilliant commentary on flowcharts by xkcd :

Follow question:

“What is the most important part of a flow chart?"

Readability is probably the most important aspect of a flowchart. As the diagrammatic representation of a process, the flowchart aims to offer a visual description of a process to help us understand what is going on. However flowcharts can get a bit out of control and you can end up with something so complicated that it defeats the purpose of having one.

Answered by:

Luciano Rila

Information security, Maths Careers, and Image Processing

View more questions

Meet our experts

Ask a question

If you'd like to provide feedback on the website itself,  tell us what you think here . 

• Introduction to Algorithms and Flowcharts

Problem Solving

Today, we use computers in every field for various purposes. But, we know that they cannot solve the problems all by themselves. Furthermore, we have to give step by step instructions to the computer for solving the problem. We can define problem-solving as a process of understanding the problem, finding solutions for the problem, and finally implementing the solution to it. We can design the solution before coding in the form of algorithms and flowcharts. Moreover, the identification of arithmetic and logical operations is very important in developing the program.

Therefore, we can say that a successful problem-solving process depends on the following factors:

• understanding the problem and defining it precisely.
• designing proper algorithms and flowcharts of the solution.
• implementing the algorithm successfully.

When the problems are easy we can easily search out a solution. Whereas, complex problems require step by step process to solve. Hence, this means that we have to apply problem-solving techniques to solve the problem. Furthermore, this starts with finding a precise definition of the problem and ends with a successful solution. Moreover, the identification of arithmetic and logical operations plays a vital role while designing the algorithm. Here, we will study the algorithms and flowcharts.

Designing the solution

After understanding the relationship between input and output and the functionalities required we have to design an algorithm or flowchart. Furthermore, the algorithm should contain all the necessary functions to solve the problem. Moreover, it should produce a proper output for every input.

Hence, we can say that before writing the exact code for the problem it is necessary to define a solution. We can do this by starting with an initial plan and improvising it till it gives perfect results. Moreover, there can be more than one possible solution for a problem. Therefore, it is the responsibility of the programmer to choose the best solution.

While designing a problem we can represent it in algorithms and flowcharts. Hence, before writing the program code we can design the solution either in the form of an algorithm or a flowchart.

Browse more Topics Under Problem Solving Methodologies

• Understanding of the Problem
• Solution for the Problem
• Breaking Down Solution into Simple Steps
• Identification of Arithmetic and Logical Operations
• Control Structure

Introduction to Algorithms

An algorithm is basically a procedure of steps that we exactly follow to solve a particular task or problem. We can say that it is a set of rules that we need to follow while developing a program code during problem-solving. Furthermore, if we write an algorithm before actually writing a code, it becomes easy to perform the coding part. Moreover, the algorithm is in simple English language hence, others can also easily understand it and develop the code.

Features of an algorithm

The features of an algorithm are as follows:

The algorithm should be very clear and unambiguous in its meaning. It should be simple so that one can understand it easily.

• Well-defined inputs

A program may require to take input from the user. Therefore, the algorithm should clearly define the inputs.

• Well-defined outputs

The algorithm should clearly specify the output that the program will produce.

The algorithm should have a termination point. This means that the algorithm should not be such that it runs infinite times or end up in loops.

• Feasibility

The algorithm should be such that we can implement it easily. Hence, it should be simple and practical to implement.

• Language independent

It should be in simple English language. Since the code implementation should result in the same output no matter which programming language we use while writing the code.

Introduction to Flowcharts

It is basically a diagrammatic representation of an algorithm. Furthermore, it uses various symbols and arrows to describe the beginning, ending, and flow of the program. Moreover, the programmers use it to depicting the flow of data and instructions while problem-solving. F lowcharting is the process of drawing a flowchart for an algorithm.

Symbols in a flowchart

The flowchart uses various symbols in the representation. These basic symbols are as follows:

It represents the start, stop, or halt in a program’s flow. The flowchart always starts and ends with this symbol. Besides, we represent it using an oval shape.

Input/Output

We represent it using a parallelogram . It indicates any input from the user or output of the program.

We represent it using a rectangle . It indicates any arithmetic operation’s processing such as addition, subtraction, multiplication, division, etc.

We represent it using the diamond symbol. It represents any type of decision in a program that results in true or false. For example. if-conditions.

We represent it using a circle . Whenever a flowchart is too large we can use connectors to avoid confusion.

These are basically arrows that represent the flow of the program.

Frequently Asked Questions (FAQs)

Q1. What are the main steps in problem-solving?

A1. A successful problem-solving process depends on the following factors:

• understanding the problem.
• designing proper algorithms and flowcharts.
• implementing the algorithm.

Q2. What is problem-solving?

A2. We can define problem-solving as a process of understanding the problem, finding solution for the problem, and finally implementing the solution to it.

Q3. What is an algorithm?

A3. An algorithm is basically a procedure of steps that we exactly follow to solve a particular task or problem.

Q4. What is a flowchart?

A4. It is basically a diagrammatic representation of an algorithm. Furthermore, it uses various symbols and arrows to describe the beginning, ending, and flow of the program.

Q5. Name the features of an algorithm.

A5. The features of an algorithm are as follows:

Customize your course in 30 seconds

Which class are you in.

Problem Solving Methodologies

• Control Structures
• Identification of Arithmetic and Logical Operations Required for Solution
• Understanding the Problem

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Download the App

How to Make a Flowchart?

Contents page

The Power of Flowcharts

Why use flowcharts, understanding flowcharts: definition and purpose, types of flow charts and workflow diagrams, how does a flowchart look like, how to make a flowchart: step-by-step guide, tips for creating effective flowcharts, harnessing the power of flowcharts.

Try timeCamp Planner App and streamline your team collaboration

Flowcharts are powerful visual tools that help organizations map out processes, identify inefficiencies, and streamline workflows. They are used across industries to enhance communication, facilitate problem-solving, and simplify complex information.

In this comprehensive guide, we will explore the definition of a flowchart, its types, and how to make a flowchart that will transform your business processes.

Flowcharts are powerful tools for visualizing and organizing complex processes or decision-making workflows. They offer several advantages that make them valuable in various fields, including software development, project management, system analysis, and problem-solving.

Here are some key benefits of using flowcharts. If you're facing project management and organizational problems and you'd like to introduce a flowchart to your team, take a look at these advantages.

Clarity and Communication

Flowcharts provide a clear and concise representation of a process or system . By using standardized symbols and arrows to depict the flow of information or actions, flowcharts make it easier for people to understand complex concepts, even without prior knowledge of the subject matter.

They are especially useful for explaining procedures to stakeholders, clients, or team members who may have different levels of expertise.

Process Analysis and Optimization

Flowcharts allow for a detailed analysis of each step within a process . By breaking down complex procedures into individual components, basic shapes, and split paths, it becomes easier to identify bottlenecks, redundancies, or areas for improvement.

Analyzing a flowchart can help identify inefficiencies or areas of potential optimization, leading to streamlined workflows and increased productivity.

Decision-making and Problem-solving

Flowcharts can be used to map out decision trees or problem-solving methodologies . By representing different options and outcomes, all the shapes on flowcharts provide a systematic approach to decision-making.

They enable users to visualize the consequences of various choices, facilitating more informed and efficient decision-making processes.

Standardization and Documentation

Flowcharts serve as a standardized method for documenting processes and procedures . They capture the logical flow, inputs, outputs, and decision points within a system, making it easier for others to understand and replicate the process.

Flowcharts also facilitate process improvement by providing a clear reference point for identifying areas of potential change or enhancement.

Collaboration and Teamwork

Flowcharts promote collaboration and teamwork by providing a common visual representation that can be easily shared among team members. They facilitate discussions, brainstorming sessions, and problem-solving exercises by allowing participants to contribute ideas, identify dependencies, and suggest modifications.

Flowcharts encourage a shared understanding of processes, fostering effective communication and collaboration within a team.

Error Identification and Debugging

Flowcharts are useful for identifying errors, bugs, or flaws within a process . By visually tracing the flow of actions or information, it becomes easier to pinpoint potential issues or areas of concern.

Flowcharts enable users to systematically analyze each step, making it easier to locate and rectify errors.

Training and Onboarding

Flowcharts are valuable tools for training new employees or guiding individuals through complex processes. By providing a visual representation of the steps and decisions involved, flowcharts facilitate a step-by-step understanding of the workflow.

They can be used as reference materials for new hires, reducing the learning curve and ensuring consistency in operations.

A flowchart (a.k.a. process flow diagram or process flowchart) is a diagram that represents a process, workflow, or system through the use of symbols, arrows, and text.

It illustrates the steps, decisions, and relationships between various elements, making it easier to understand and communicate complex information.

Here are the four main reasons why you should use flowcharts:

Identify inefficiencies and bottlenecks in a process.

Visualize and analyze workflows.

Simplify complex information for better understanding.

Facilitate communication and collaboration.

In summary, flowcharts are powerful because their versatility and ease of use make them an indispensable tool in a wide range of industries and applications.

There are several types of flowcharts and workflow diagrams, each suited for different purposes and industries.

Here are the most common types of a flowchart:

Process flowchart : represents the steps in a process, showing the sequence of actions and decisions.

Swimlane flowchart : organizes the steps of a process into distinct "lanes" or categories, often representing different departments or roles.

Data Flow Diagram : focuses on the flow of data between various system components.

Work Breakdown Structure (WBS) : displays the tasks and subtasks involved in a project, organized hierarchically.

Workflow Diagram : represents the flow of tasks, activities, or actions within a specific workflow or business process. It focuses on the sequence of tasks and the relationships between them, providing an overview of how work progresses from start to finish.

Data Flow Diagram (DFD) : DFDs focus on the movement of data within a system or process. They illustrate how data is input, processed, stored, and output, showing the interactions between various components and data entities.

Decision Tree : symbolizes decision-making process or algorithms. It uses nodes to represent decisions, branches to represent different options, and leaves to represent outcomes or actions. Decision trees are useful for modeling complex decision paths and understanding the consequences of different choices.

Value Stream Map (VSM) : VSM is a flowchart used primarily in lean manufacturing and process improvement methodologies such as Lean Six Sigma. It represents the flow of materials, information, and activities across the entire value stream, from the supplier to the customer. VSM helps identify areas of waste, bottlenecks, and opportunities for improvement.

Gantt Chart : While not a traditional flowchart, a Gantt chart is a popular visual tool used in project management. It represents project schedules and timelines, showing the start and end dates of tasks, dependencies, and milestones. Gantt charts provide a clear overview of the project's progress and help with scheduling and resource allocation.

It's most useful to choose a flowchart that is best for your planning process. Also, you can mix, combine, and customize the entire flowchart for a better planning process.

First of all, to create a flowchart, you'll need to use the right tool. For example, one of the most popular is Microsoft Word.

You can create a basic flowchart by starting with the right page layout and shape outline with common shapes. You can use one shape for all your tasks, two shapes, or add as many other shapes as you want for a more complex structure.

Additional elements you can find on a flowchart are more shapes (each depicts different parts of the process), text pane, and design tab. You can also adjust font size, font style, add text fill, and more to better document workflow.

All the shapes represent each single process step, sub-process, and other elements such as related resources, activities, sequences, etc.

You can create a flowchart by using a flowchart template or with the SmartArt graphic in Microsoft Word. And the options to create a flowchart are limitless—data flowcharts, basic structure flowchart, swimlane diagram, and many more.

Once you know how to make a flowchart with flowchart symbols, it's easier to identify everything you need to consider in your project planning.

Here's a short guide on how to make a flowchart faster.

1. Define the Purpose

Before creating a flowchart, determine the objective and scope of the diagram. What process, workflow, or system do you want to represent? Who is the intended audience?

To define the purpose of a flowchart in a concise manner, you can:

Identify the specific process or workflow that the flowchart will represent.

Determine the goals and objectives of creating the flowchart, such as improving understanding or streamlining operations.

Consider the audience and their needs to tailor the flowchart accordingly.

Refine and articulate the purpose in a clear statement, aligning it with the desired outcomes of the flowchart.

2. Gather Information

Research and gather all necessary information about the process, including input from relevant stakeholders.

To gather all the information, you need to identify steps and actions, collect relevant data and information associated with each step or action in the process (inputs, outputs, decision criteria, and dependencies).

Don't forget to document symbols and connections on a blank canvas or using flowchart software. Connect the symbols with arrows to indicate the flow between steps.

3. Choose the Flowchart Type

Select the most appropriate type of flowchart based on your objective and the information you have gathered.

Use flowchart symbols to represent different elements of the process. Common symbols include rectangles for process steps, diamonds for decision points, and arrows for the flow of information or actions. Consult flowchart symbol references or libraries to ensure accurate representation.

Additionally, many tools comes with flowchart templates. A good flowchart template can improve the planning process.

4. Use a Flowchart Tool or Software

Leverage a flowchart tool or software to create a professional-looking diagram. Many tools offer customizable templates and shapes to streamline the process.

Just a few clicks are all it takes to create most flowcharts. With various software and online tools available, designing a flowchart has become a straightforward process.

These tools provide a user-friendly interface with a drag-and-drop feature, and a wide range of pre-designed shapes and templates, making it easy to create flowcharts that suit your specific needs.

5. Start with a Clear Starting Point

Begin your flow chart with a clear starting point, typically represented by a rectangle or oval shape.

When creating a flowchart, you can start with the basic steps of the process and gradually add more details.

The design concepts behind flowcharts are simple yet effective, allowing you to visually represent the flow of information and actions in a logical manner.

6. Add Process Steps and Decision Points

Use appropriate symbols and flowchart shapes to represent the steps and decisions in your process. Connect the elements using arrows to indicate the flow of information or actions.

Your flowchart doesn't have to be perfect at the beginning. Add shapes in the process so you keep it all clear and avoid confusion.

7. Review and Refine

Review your flow chart for accuracy, clarity, and completeness. Make any necessary adjustments and solicit feedback from stakeholders to ensure the diagram accurately represents the process.

A good flowchart should reflect your customer's needs, so make sure all the components demonstrate the purpose, and don't be afraid to make changes.

Regular feedback and reviews can help improve your flowchart and planning process.

If you're new to flowchart planning or want to improve your project management, there are certain things that will make it easier.

Take a look at what you can do to better plan your work with flowcharts:

Keep it simple : use clear and concise language, and avoid cluttering the diagram with too much information. Avoid adding shapes that aren't necessary.

Follow a logical flow : ensure that the flow chart follows a logical sequence, with arrows indicating the direction of the process.

Use standard symbols : stick to common flowchart symbols and shapes to maintain consistency and ease of understanding.

Opt for color-coding : color-code elements or lanes to enhance visual clarity and make the diagram more engaging.

Use the right tool : you can opt for a dedicated software or combine it with, for example, a good flowchart template.

Creating an effective flowchart requires a clear understanding of the process, a suitable flow chart type, and a logical, visually appealing design.

By mastering the art of flow chart creation, you can streamline your organization's procedures, enhance communication, and make data-driven decisions that drive success. Remember, practice makes perfect— so start creating flow charts today and unleash the potential of your business processes.

Computersciencementor | Hardware, Software, Networking and programming

Algorithm and flowchart explained with examples, what is algorithm and flowchart.

Algorithm and flowchart are programming tools. A Programmer uses various programming languages to create programs. But before actually writing a program in a programming language, a programmer first needs to find a procedure for solving the problem which is known as planning the program. The program written without proper pre-planning have higher chances of errors. The tools that are used to plan or design the problem are known as programming tools. Algorithm and flowchart are widely used programming tools.

The word “algorithm” relates to the name of the mathematician Al- khowarizmi , which means a procedure or a technique. Programmer commonly uses an algorithm for planning and solving the problems.

An algorithm is a specific set of meaningful instructions written in a specific order for carrying out or solving a specific problem.

Types of Algorithm:

The algorithm and flowchart are classified into three types of control structures.

• Branching(Selection)
• Loop(Repetition)

According to the condition and requirement, these three control structures can be used.

In the  sequence structure, statements are placed one after the other and the execution takes place starting from up to down.

Whereas in branch control, there is a condition and according to a condition, a decision of either TRUE or FALSE is achieved. In the case of TRUE, one of the two branches is explored; but in the case of FALSE condition, the other alternative is taken. Generally, the ‘IF-THEN’ is used to represent branch control.

Write an algorithm to find the smallest number between two numbers

Write an algorithm to check odd or even number.

The Loop or Repetition allows a statements or block of statements to be executed repeatedly based on certain loop condition. ‘While’ and ‘for’ construct are used to represent the loop structure in most programming languages. Loops are of two types: Bounded and Unbounded loop. In bounded loop, the number of iterations is fixed while in unbounded loops the condition has to satisfy to end the loop.

An algorithm to calculate even numbers between 20 and 40

Write an algorithm to input a natural number, n, and calculate the odd numbers equal or less than n.

Characteristics of a good algorithm.

• The Finite number of steps:

After starting an algorithm for any problem, it has to terminate at some point.

• Easy Modification.

There can be numbers of steps in an algorithm depending on the type of problem. It supports easy modification of Steps.

• Easy and simple to understand

A Simple English language is used while writing an algorithm. It is not dependent on any particular programming language. People without the knowledge of programming can read and understand the steps in the algorithm.

An algorithm is just a design of a program. Every program needs to display certain output after processing the input data. So one always expects the result as an output from an algorithm. It can give output at different stages. The result obtained at the end of an algorithm is known as an end result and if the result is obtained at an intermediate stage of process or operation then the result is known as an intermediate result. Also, the output has to be as expected having some relation to the inputs.

The first design of flowchart goes back to 1945 which was designed by John Von Neumann . Unlike an algorithm, Flowchart uses different symbols to design a solution to a problem. It is another commonly used programming tool.

In general, a flowchart is a diagram that uses different symbols to visually present the flow of data. By looking at a flow chart one can understand the operations and sequence of operations performed in a system. This is why flowchart is often considered as a blueprint of a design used for solving a specific problem.

A flowchart is defined as a symbolic or a graphical representation of an algorithm that uses different standard symbols.

Flowchart Symbols:

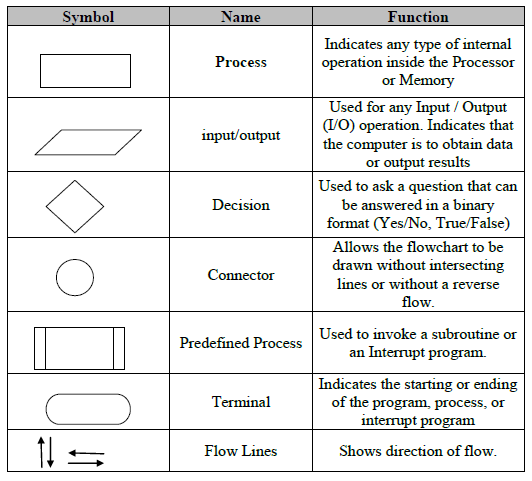
Guidelines for drawing a flowchart.

• The Title for every flowchart is compulsory.
• There must be START and END point for every flowchart.
• The symbols used in flowchart should have only one entry point on the top. The exit point for symbols (except for decision/diamond symbol) is on the button.
• There should be two exit points for decision symbol; exit points can be on the bottom and one side or on the sides.
• The flow of flowchart is generally from top to bottom. But in some cases, it can also flow to upward direction
• The direction of the flow of control should be indicated by arrowheads.
• The operations for every step should be written inside the symbol.
• The language used in flowchart should be simple so that it can be easily understood.
• The flowlines that show the direction of flow of flowchart must not cross each other.
• While connecting different pages of the same flowchart, Connectors must be used.

Some examples of algorithm and flowchart.

Example1: To calculate the area of a circle

Step1: Start

Step2: Input radius of the circle say r

Step3: Use the formula πr 2 and store result in a variable AREA

Step4: Print AREA

Step5: Stop Flowchart:

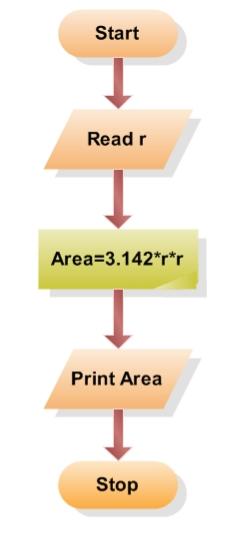
Related Posts

Sampurna shrestha

Save my name, email, and website in this browser for the next time I comment.

How can procedural flowcharts support the development of mathematics problem-solving skills?

• Original Article
• Open access
• Published: 22 February 2024

Cite this article

You have full access to this open access article

• Musarurwa David Chinofunga   ORCID: orcid.org/0000-0002-0262-3039 1 ,
• Philemon Chigeza   ORCID: orcid.org/0000-0001-9964-0988 1 &
• Subhashni Taylor   ORCID: orcid.org/0000-0002-1624-0901 1  

1014 Accesses

1 Altmetric

Explore all metrics

Supporting students’ problem-solving skills, solution planning and sequencing of different stages that are involved in successfully developing a meaningful solution to a problem has been a challenge for teachers. This case study was informed by reflective investigation methodology which explored how procedural flowcharts can support student mathematics problem solving in a senior Mathematical Methods subject in Queensland. The paper used thematic analysis to analyse and report on teachers’ perceptions of the utility of procedural flowcharts during problem solving as well as content analysis on how student-developed flowcharts can support their problem-solving skills. Results show that development of procedural flowcharts can support problem solving as it helps with integration of problem-solving stages.

Similar content being viewed by others

Identifying Students’ Misconceptions on Basic Algorithmic Concepts Through Flowchart Analysis

Students’ individual schematization pathways - empirical reconstructions for the case of part-of-part determination for fractions.

Identifying Metacognitive Behavior in Problem-Posing Processes

Avoid common mistakes on your manuscript.

Introduction

Problem solving is central to teaching and learning of mathematics (see Cai, 2010 ; Lester, 2013 ; Schoenfeld et al., 2014 ). For decades, research in mathematics problem solving, including special issues from leading mathematics education journals (see, Educational Studies in Mathematics, (Vol. 83, no. 2013); The Mathematics Enthusiast, (Vol. 10, nos. 1–2); ZDM , (Vol. 39, nos. 5–6)), have offered significant insights but struggled to produce well-articulated guidelines for educational practice (English & Gainsburg, 2016 ). This could possibly be the reason why mathematics teachers’ efforts to improve students’ problem-solving skills have not produced the desired results (Anderson, 2014 ; English & Gainsburg, 2016 ). Despite Polya’s ( 1945 ) heuristics being so valuable in problem solving, there appears to be limited success when translated into the classroom environment (English & Gainsburg, 2016 ). English and Gainsburg went further to posit that one of the issues to be addressed is how to support problem-solving competency in students during the process of problem solving. Thus, teachers’ perceptions in this study are a valuable part in evaluating how procedural flowcharts can support problem solving.

The problem-solving process is a dialogue between the prior knowledge the problem solver possesses, the tentative plan of solving the problem and other relevant thoughts and facts (Schoenfeld, 1983 ). However, research is still needed on tools that teachers can use to support students during problem solving (Lester & Cai, 2016 ). Although research in mathematics problem solving has been progressing, it has remained largely theoretical (Lester, 2013 ). Schoenfeld ( 2013 ) suggests that research focus should now advance from the framework for examining problem solving to explore how ideas grow and are presented and shared during the problem-solving process. Recently, Kaitera and Harmoinen ( 2022 ) emphasised the need to support teachers through resources that can help students develop problem solving skills. They went on to posit that resources that can assist students in presenting different approaches to a solution and displaying their understanding are critical to build their problem-solving skills.

The study by Kaitera and Harmoinen ( 2022 ) introduced mathematics students to ‘problem-solving keys’ which are heuristics for problem solving that students are to follow as they engage with tasks. Their conclusion was also noted by Vale and Barbosa ( 2018 ) who observed that a key area that would benefit from further research is the identification of strategies or plan that support students’ ability to construct and present their mathematical knowledge effectively during problem solving, particularly if complex processes such as integration and modification of several procedures are involved. Similarly, students face challenges in connecting or bringing all the ideas together and showing how they relate as they work towards the solution (Reinholz, 2020 ). Problem solving in mathematics is challenging for students (Ahmad et al., 2010 ), and therefore, supporting students’ problem-solving skills needs urgent attention (Schoenfeld, 2016 ). Furthermore, Mason ( 2016 ) posits that the crucial yet not significantly understood issue for adopting a problem-solving approach to teaching is the issue of “when to introduce explanatory tasks, when to intervene and in what way” (p. 263). Therefore, teachers also need resources to support the teaching of problem-solving skills, often because they were not taught these approaches when they were school students (Kaitera & Harmoinen, 2022 ; Sakshaug & Wohlhuter, 2010 ).

Flowcharts have been widely used in problem solving across different fields. In a technology-rich learning environment such as Lego Robotics, creating flowcharts to explain processes was observed to facilitate understanding, thinking, making sense of how procedures relate, investigating and communicating the solution (Norton et al., 2007 ). They are effective in guiding students during problem solving (Gencer, 2023 ), enhancing achievement and improving problem-solving skills in game-based intelligent tutoring (Hooshyar et al., 2016 ). Flowcharts have been identified as an effective problem-solving tool in health administration (McGowan & Boscia, 2016 ). In mathematics education, heuristic trees and flowcharts were observed to supplement each other in influencing students’ problem solving behaviour (Bos & van den Bogaart, 2022 ). Importantly, McGowan and Boscia emphasised that “one of the greatest advantages of a flowchart is its ability to provide for the visualisation of complex processes, aiding in the understanding of the flow of work, identifying nonvalue-adding activities and areas of concern, and leading to improved problem-solving and decision-making” (p. 213). Identifying the most appropriate strategy and making the correct decision at the right stage are keys to problem solving. Teaching students to use visual representations like flowcharts as part of problem solving supports the ability to easily identify new relationships among different procedures and assess the solution being communicated faster as visual representations are more understandable (Vale et al., 2018 ).

The purpose of this case study was to explore, through an in-depth teacher’s interview, and student-developed artefacts, the utility of procedural flowcharts in supporting the development of students’ problem-solving skills in mathematics. The study will focus on problem solving in Mathematical Methods which is one of the calculus-based mathematics subjects at senior school in Queensland. The aim was to investigate if the development of procedural flowcharts supported students in planning, logically connecting and integrating mathematical procedures (knowledge) and to communicate the solution effectively during problem solving. The use of flowcharts in this study was underpinned by the understanding that visual aids that support cognitive processes and interlinking of ideas and procedures influence decision-making, which is vital in problem-based learning (McGowan & Boscia, 2016 ). Moreover, flowcharts are effective tools for communicating the processes that need to be followed in problem solving (Krohn, 1983 ).

Problem-solving learning in mathematics education

The drive to embrace a problem-solving approach to develop and deepen students’ mathematics knowledge has been a priority in mathematics education (Koellner et al., 2011 ; Sztajn et al., 2017 ). In the problem-solving approach, the teacher provides the problem to be investigated by students who then design ways to solve it (Colburn, 2000 ). To engage in problem solving, students are expected to use concepts and procedures that they have learnt (prior knowledge) and apply them in unfamiliar situations (Matty, 2016 ). Teachers are encouraged to promote problem-solving activities as they involve students engaging with a mathematics task where the procedure or method to the solution is not known in advance (National Council of Teachers of Mathematics [NCTM], 2000 ), thus providing opportunities for deep understanding as well as providing students with the opportunity to develop a unique solution (Queensland Curriculum and Assessment Authority [QCAA], 2018 ). Using this approach, students are given a more active role through applying and adapting procedures to solve a non-routine problem and then communicating the method (Karp & Wasserman, 2015 ). The central role problem solving plays in developing students’ mathematical understanding has resulted in the development of different problem-solving models over the years.

The process of problem solving in mathematics requires knowledge to be organised as the solution is developed and then communicated. Polya is among the first to systematise problem solving in mathematics (Voskoglou, 2021 ). Students need to understand the problem, plan the solution, execute the plan and reflect on the solution and process (Polya, 1971 ). Voskoglou’s ( 2021 ) problem-solving model emphasised that the process of modelling involves analysis of problem, mathematisation, solution development, validation and implementation. Similarly, problem solving is guided by four phases: discover, devise, develop and defend (Makar, 2012 ). During problem solving, students engage with an unfamiliar real-world problem, develop plans in response, justify mathematically through representation, then evaluate and communicate the solution (Artigue & Blomhøj, 2013 ). Furthermore, Schoenfeld ( 1980 ) posited that problem solving involves problem analysis, exploration, design, implementation and verification of the solution. When using a problem-solving approach, students can pose questions, develop way(s) to answer problems (which might include drawing diagrams, carrying out calculations, defining relationships and making conclusions), interpreting, evaluating and communicating the solution (Artigue et al., 2020 ; Dorier & Maass, 2020 ). Problem solving involves understanding the problem, devising and executing the plan and evaluating (Nieuwoudt, 2015 ). Likewise, Blum and Leiß ( 2007 ) developed a modelling approach that was informed by these stages, understanding, simplifying, mathematising, working mathematically, interpreting and validating.

Similarly, mathematical modelling involves problem identification from a contextualised real-world problem, linking the solution to mathematics concepts, carrying out mathematic manipulations, justifying and evaluating the solution in relation to the problem and communicating findings (Geiger et al., 2021 ). Likewise, in modelling, Galbraith and Stillman ( 2006 ) suggested that further research is needed in fostering students’ ability to transition effectively from one phase to the next. “Mathematical modelling is a special kind of problem solving which formulates and solves mathematically real-world problems connected to science and everyday life situations” (Voskoglou, 2021 p. 85). As part of problem solving, mathematical modelling requires students to interpret information from a variety of narrative, expository and graphic texts that reflect authentic real-life situations (Doyle, 2005 ).

There are different approaches to problem solving and modelling, but all of them focus on the solving of real-world problems using mathematical procedures and strategies (Hankeln, 2020 ). A literature synthesis is critical where several models exist as it can be used to develop an overarching conceptual model (Snyder, 2019 ). Torraco ( 2005 ) noted that literature synthesis can be used to integrate different models that address the same phenomenon. For example, in this study, it was used to integrate problem solving models cited in the literature. Moreover, the review was necessitated by the need to reconceptualise the problem-solving model by Polya ( 1971 ) to include the understanding that the definition of problem solving has now broadened to include modelling. Torraco went further to suggest that as literature grows, and knowledge expands on a topic which might accommodate new insights, there is a need for literature synthesis with the aim to reflect the changes. Thus, the model in Fig.  1 took into consideration the key stages broadly identified by the researchers and the understanding that modelling is part of problem solving. Problem solving and modelling is generally a linear process that can include loops depending on how the problem identification, mathematisation and implementation effectively address the problem (Blum & Leiß, 2007 ; Polya, 1957 ).

Stages of mathematics problem solving

Figure  1 identifies the main stages that inform mathematics problem solving from the literature.

Problem identification and the design to solve the problem might be revisited if the procedures that were identified and their mathematical justification do not address the problem. Likewise, justification and evaluation after implementation might prompt the problem solver to realise that the problem was incorrectly identified. The loop is identified by the backward arrow, and the main problem-solving stages are identified by the linear arrows. The Australian Curriculum, Assessment and Reporting Authority notes that during problem solving:

Students solve problems when they use mathematics to represent unfamiliar situations, when they design investigations and plan their approaches, when they apply their existing knowledge to seek solutions, and when they verify that their answers are reasonable. Students develop the ability to make choices, interpret, formulate, model and investigate problem situations, and communicate solutions effectively. (Australia Curriculum and Reporting Authority, 2014 , p. 5)

Therefore, during problem solving, students have to plan the solution to the problem and be able to communicate all the key processes involved. However, although problem solving is highly recommended in mathematics education, it presents several challenges for teachers in terms of how they can best support students to connect the processes and mathematics concepts into something coherent that can lead to a meaningful solution (Hacker, 1998 ). Therefore, relevant tools that support problem solving and decision-making can make a difference for both mathematics teachers and students (McGowan & Boscia, 2016 ).

Students can solve problems better if they can think critically (Kules, 2016 ). Problem solving requires their active engagement in analysing, conceptualising, applying concepts, evaluating, comparing, sequencing, synthesising, reasoning, reflecting and communicating, which are skills that are said to promote critical thinking (Kim et al., 2012 ; King, 1995 ; Moon, 2008 ; QCAA, 2018 ). Similarly, the ability to undertake problem solving is supported when students are provided with the opportunity to sequence ideas logically and evaluate the optimal strategy to solve the problem (Parvaneh & Duncan, 2021 ). However, finding tools that can support problem solving has been a focus for researchers for a long time but with very limited breakthroughs (McCormick et al., 2015 ). This study explored how procedural flowcharts as visual representations can support students in organising ideas, execute procedures, justify solutions and communicate their solution.

Importance of visual representations in mathematics problem-solving

Research on how visual representations support mathematics discovery and structural thinking in problem solving has come a long way (see Hadamard, 1945 ; Krutetskii, 1976 ; Polya, 1957 ). Visual representations are classified as graphs, tables, maps, diagrams, networks and icons and are widely used to convey information in a recognisable form that can be easily interpreted without resorting to tedious computations (Lohse et al., 1994 ). Visual representations can be used as a tool to capture mathematics relations and processes (van Garderen et al., 2021 ) and used in many cognitive tasks such as problem solving, reasoning and decision making (Zhang, 1997 ). Indeed, representations can be modes of communicating during concepts exploration and problem solving (Roth & McGinn, 1998 ). Likewise, visual representations can be a powerful way of presenting the solution to a problem, including self-monitoring on how the problem is being solved (Kingsdorf & Krawec, 2014 ; Krawec, 2014 ). Using visualisations created by teachers or students in mathematics can support students’ problem-solving abilities (Csíkos et al., 2012 ).

Visual representations show thoughts in non-linguistic format, which is effective for communication and reflection. “Visual representations serve as tools for thinking about and solving problems. They also help students communicate their thinking to others” (NCTM, 2000 , p. 206). In mathematics, visual representation plays a significant role in showing the cognitive constructs of the solution (Owens & Clements, 1998 ), a view echoed by Arcavi ( 2003 ), who said that visual representations can be appreciated as a central part of reasoning and as a resource to use in problem solving. More importantly, they can be used to represent the logical progression of ideas and reasoning during problem solving (Roam, 2009 ). However, there is need to explore how visual representations can be used to support and illustrate the problem-solving process and to create connections among concepts (Stylianou, 2010 ). Importantly, developing diagrams is often a recommended strategy for solving mathematics problems (Pape & Tchoshanov, 2001 ; Jitendra et al., 2013 ; Zahner & Corter, 2010 ). Therefore, this study will explore the utility of procedural flowcharts as a visual representation and resource in supporting problem analysis, problem understanding, solution development and evaluation, while communicating the whole problem-solving process effectively. It will go further to explore how development of procedural flowcharts can support educational practice in Mathematical Methods subject.

Procedural flowcharts are a visual representation of procedures, corresponding steps and stages of evaluation of a solution to a problem (Chinofunga et al., 2022 ). These authors noted that procedural flowcharts developed by the teacher can guide students during the inquiry process and highlight key procedures and stages for decision-making during the process of problem solving. This is because “a procedural flowchart graphically displays the information–decision–action sequences in the proposed order” (Krohn, 1983 , p. 573). Similarly, Chinofunga and colleagues ( 2022 ) emphasised that procedural flowcharts can be used to visually represent procedural flexibility as more than one procedure can be accommodated, making it easier to compare the effectiveness of different procedures as they are being applied. They further posited that student-developed procedural flowcharts provide students with the opportunity to comprehensively engage with the problem and brainstorm different ways of solving it, thus deepening their mathematics knowledge. Moreover, a procedural flowchart can be a visual presentation of an individual or group solution during problem solving.

Research has identified extended benefits of problem solving in small groups (Laughlin et al., 2006 ). Giving groups an opportunity to present a solution visually can be a quicker way to evaluate a group solution because visual representations can represent large amounts of information (even from different sources) in a simple way (Raiyn, 2016 ). Equally, Vale and colleagues encouraged visual representation of solutions with multisolutions as a tool to teach students problem solving ( 2018 ). Therefore, students can be asked to develop procedural flowcharts individually then come together to synthesise different procedural flowcharts.

Similarly, flowcharts are a visual aid used to represent how procedures interrelate and function together. “They are tools to visually break down complex information into individual building blocks and how the blocks are connected” (Grosskinsky et al., 2019 , p. 24). They outlay steps in a procedure and show how they can be applied, thus helping to visualise the process (Ledin & Machin, 2020 ; Reingewertz, 2013 ). Flowcharts can also be used when a logical and sequenced approach is needed to address a problem (Cantatore & Stevens, 2016 ). Importantly, in schools, Norton and colleagues ( 2007 ) noted that “planning facilitated through the use of flow charts should be actively encouraged and scaffolded so that students can appreciate the potential of flow charts to facilitate problem-solving capabilities” (p. 15). This was because the use of flowcharts in problem solving provided a mental representation of a proposed approach to solve a task (Jonassen, 2012 ). The success of flowcharts in problem solving in different fields can be attributed to their ability to facilitate deep engagement in planning the solution to the problem.

Flowcharts use has distinct advantages that can benefit problem solving. Norton and colleagues ( 2007 ) posited that using a well-planned and well-constructed flowchart in problem solving results in a good-quality solution. Furthermore, flowcharts can also be a two-way communication resource between a teacher and students or among students (Grosskinsky et al., 2019 ). These authors further noted that flowcharts can help in checking students’ progress, tracking their progress and guide them. They can also be used to highlight important procedures that students can follow during the process of problem solving.

Similarly, flowcharts can be used to provide a bigger picture of the solution to a problem (Davidowitz & Rollnick, 2001 ). Flowcharts help students gain an overall and coherent understanding of the procedures involved in solving the problem as they promote conceptual chunking (Norton et al., 2007 ). Importantly, “they may function to amplify the zone of proximal development for students by simplifying tasks in the zone” (Davidowitz & Rollnick, 2001 , p. 22). Use of flowcharts by students reduces the cognitive load which then may help them focus on more complex tasks (Berger, 1998 ; Sweller et al., 2019 ). Indeed, development of problem-solving skills can be supported when teachers introduce learning tools such as flowcharts, because they can help structure how the solution is organised (Santoso & Syarifuddin, 2020 ). Therefore, the use of procedural flowcharts in mathematics problem solving has the potential to transform the process.

The research question in this study was informed by the understanding that limited resources are available to teachers to support students’ problem-solving abilities. In addition, the literature indicates that visual representation such as procedural flowcharts can support students’ potential in problem solving. Therefore, the research described in this study addressed the following research question: What are teachers’ perceptions of how procedural flowcharts can support the development of students’ problem-solving skills in the Mathematical Methods subject?

Methodology

The case study draws from the reflective investigation methodology (Trouche et al., 2018 ,  2020 ). The methodology explores how teaching and learning was supported by facilitating a teacher’s reflection on the unexpected use of a resource, in this case procedural flowcharts. The reflective methodology emphasises a teacher’s active participation through soliciting views on the current practice and recollection on previous work (Trouche et al., 2020 ). Using the methodology, a teacher is asked to reflect on and describe the resource used, the structure (related to the activity), the implementation and the outcomes (Huang et al., 2023 ).

This case study focuses on phases three and four of a broad PhD study that involved four phases. The broad study was informed by constructivism. Firstly, phase one investigated Queensland senior students’ mathematics enrolment in different mathematics curricula options from 2010 to 2020. Secondly, phase two developed and introduced pedagogical resources that could support planning, teaching and learning of calculus-based mathematics with a special focus on functions in mathematical methods. The pedagogical resources included a framework on mathematics content sequencing which was developed through literature synthesis to guide teachers on how to sequence mathematics content during planning. Furthermore, the phase also introduced concept maps as a resource for linking prior knowledge to new knowledge in a constructivist setting. Procedural flowcharts were also introduced to teachers in this phase as a resource to support development of procedural fluency in mathematics. Importantly, a conference workshop organised by the Queensland Association of Mathematics Teachers (Cairns Region) provided an opportunity for teachers to contribute their observations on ways that concept maps and procedural flowcharts can be used to support teaching. Thirdly, phase three was a mixed-method study that focused on evaluating the pedagogical resources that were developed or introduced in phase two with 16 purposively sampled senior mathematics teachers in Queensland who had been given a full school term to use the resources in their practice. Some qualitative data collected through semistructured interviews from phase three were included in the results of the study reported here. During the analysis of the qualitative data, a new theme emerged which pointed to the unexpected use of procedural flowcharts during teaching and learning beyond developing procedural fluency. As a result, the researchers decided to explore how development of procedural flowcharts supported teaching and learning of mathematics as an additional phase. Phase four involved an in-depth interview with Ms. Simon (pseudonym) a teacher who had unexpectedly applied procedural flowcharts in a problem-solving task, which warranted further investigation. Ms. Simon’s use of procedural flowcharts was unexpected as she had used them outside the context and original focus of the broader study. Importantly, in phase four, artefacts created by the teacher and her four students in the problem-solving task were also collected.

Ms. Simon (pseudonym) had explored the use of procedural flowcharts in a problem-solving and modelling task (PSMT) in her year 11 Mathematical Methods class. This included an introduction to procedural flowcharts, followed by setting the students a task whereby they were asked to develop a procedural flowchart as an overview on how they would approach a problem-solving task. The students were expected to first develop the procedural flowcharts independently then to work collaboratively to develop and structure an alternative solution to the same task. The student-developed procedural flowcharts (artefacts) and the in-depth interview with Ms. Simon were included in the analysis. As this was an additional study, an ethics amendment was applied for and granted by the James Cook University Ethics committee, approval Number H8201, as the collection of students’ artefacts was not covered by the main study ethics approval for teachers.

Research context of phase four of the study

In the state of Queensland, senior mathematics students engage with three formal assessments (set by schools but endorsed by QCAA) in year 12 before the end of year external examination. The formal internal assessments consist of two written examinations and a problem-solving and modelling task (PSMT). The PSMT is expected to cover content from Unit 3 (Further Calculus). The summative external examination contributes 50% and the PSMT 20% of the overall final mark, demonstrating that the PSMT carries the highest weight among the three formal internal assessments.

The PSMT is the first assessment in the first term of year 12 and is set to be completed in 4 weeks. Students are given 3 h of class time to work on the task within the 4 weeks and write a report of up to 10 pages or 2000 words. The 4 weeks are divided into four check points, one per week with the fourth being the submission date. On the other three checkpoints, students are expected to email their progress to the teacher. At checkpoint one, the student will formulate a general plan on how to solve the problem which is detailed enough for the teacher to provide meaningful feedback. Checkpoint one is where this study expects teachers to provide students with the opportunity to develop a procedural flowchart of the plan to reach the solution. Importantly at checkpoint one, teachers are interested in understanding which mathematics concepts students will select and apply to try and solve the problem and how the concepts integrate or complement each other to develop a mathematically coherent, valid and appropriate solution. Moreover, teachers are expected to have provided students with opportunities to develop skills in undertaking problem-solving and modelling task before they engage with this formal internal assessment. The QCAA has provided a flowchart to guide teachers and students on how to approach a PSMT ( Appendix 1 )

Participants in phase four of the study

Ms. Simon and a group of four students were the participants in this study. Ms. Simon had studied mathematics as part of her undergraduate education degree, which set her as a highly qualified mathematics teacher. At the time of this study, she was the Head of Science and Mathematics and a senior mathematics teacher at one of the state high schools in Queensland. She had 35 years’ experience in teaching mathematics across Australia in both private and state schools, 15 of which were as a curriculum leader. She was also part of the science, technology, engineering and mathematics (STEM) state-wide professional working group. Since the inception of the external examination in Queensland in 2020, she had been an external examination marker and an assessment endorser for Mathematical Methods with QCAA. The students who were part of this study were aged between 17 and 18 years and were from Ms. Simon’s Mathematical Methods senior class. Two artefacts were from individual students, and the third was a collaborative work from the two students.

Phase four data collection

First, data were collected through an in-depth interview between the researcher and Ms. Simon. The researcher used pre-prepared questions and incidental questions arising from the interview. The questions focused on exploring how she had used procedural flowcharts in a PSMT with her students. The interview also focused on her experiences, observations, opinions, perceptions and results, comparing the new experience with how she had previously engaged her students in such tasks. The interview lasted 40 min, was transcribed and coded so as to provide evidence of the processes involved in the problem solving. Some of the pre-prepared questions were as follows:

What made you consider procedural flowcharts as a resource that can be used in a PSMT?

How have you used procedural flowcharts in PSMT?

How has the use of procedural flowcharts transformed students’ problem-solving skills?

How have you integrated procedural flowcharts to complement the QCAA flowchart on PSMT in mathematics?

What was your experience of using procedural flowcharts in a collaborative setting?

How can procedural flowcharts aid scaffolding of problem-solving tasks?

Second, Ms. Simon shared her formative practice PSMT task (described in detail below), and three of her students’ artefacts. The artefacts that she shared (with the students’ permission) were a critical source of data as they were a demonstration of how procedural flowcharts produced by students can support the development of problem solving and provided an insight into the use of procedural flowcharts in a PSMT.

Problem-solving and assessment task

The formative practice PSMT that Ms. Simon shared is summarised below under the subheadings: Scenario, Task, Checkpoints and Scaffolding.

You are part of a team that is working on opening a new upmarket Coffee Café. Your team has decided to cater for mainly three different types of customers. Those who:

Consume their coffee fast.

Have a fairly good amount of time to finish their coffee.

Want to drink their coffee very slowly as they may be reading a book or chatting.

The team has tasked you to come up with a mode or models that can be used to understand the cooling of coffee in relation to the material the cup is made from and the temperature of the surroundings.

Write a mathematical report of at most 2000 words or up to 10 pages that explains how you developed the cooling model/s and took into consideration the open cup, the material the cup was made from, the cooling time, the initial temperature of the coffee and the temperature of the surroundings.

Design an experiment that investigates the differences in the time of cooling of a liquid in open cups made from different materials. Record your data in a table.

Develop a procedural flowchart that shows the steps that you used to arrive at a solution for the problem.

Justify your procedures and decisions by explaining mathematical reasoning.

Provide a mathematical analysis of formulating and evaluating models using both mathematical manipulation and technology.

Provide a mathematical analysis that involves differentiation (rate of change) and/or anti-differentiation (area under a curve) to satisfy the needs of each category of customers.

Evaluate the reasonableness of solutions.

You must consider Newton’s Law of Cooling which states that the rate of change of the temperature of an object is proportional to the difference between its own temperature and the temperature of its surroundings. For a body that has a higher temperature than its surroundings, Newton’s Law of Cooling can model the rate at which the object is cooling in its surroundings through an exponential equation. This equation can be used to model any object cooling in its surroundings: 

y is the difference between the temperature of the body and its surroundings after t minutes,

A 0 is the difference between the initial temperature of the body and its surroundings,

k is the cooling constant.

Checkpoints

Week 1: Students provide individual data from the experiment and create a procedural flowchart showing the proposed solution to the problem. Teacher provides individual feedback. Week 2: Students provide a consolidated group procedural flowchart. Teacher provides group feedback Week 3: Students email a copy of their individually developed draft report for feedback. Week 4: Students submit individual final response in digital (PDF format) by emailing a copy to their teacher, providing a printed copy to their teacher and saving a copy in their Maths folder.

Additional requirements/instructions

The response must be presented using an appropriate mathematical genre (i.e., a mathematical report).

The approach to problem-solving and mathematical modelling must be used.

All sources must be referenced.

Data analysis

The analysis of data includes some observations and perceptions of mathematics teachers which were collected through surveys and interviews from phase three of the broader PhD study. The survey and interviews data in the broader study including phase four in-depth interview with Ms. Simon were transcribed and coded using thematic analysis (TA). TA is widely used in qualitative research to identify and describe patterns of meaning within data (Braun & Clarke, 2006 ; Ozuem et al., 2022 ). The thematic validity was ensured using theory triangulation. It involves sharing qualitative responses among colleagues at different status positions in the field and then comparing findings and conclusions (Guion et al., 2011 ). The study adopted the inductive approach which produces codes that are solely reflective of the contents of the data (Byrne, 2022 ).

Coding was done with no pre-set codes, and line-by-line coding was used as this was mainly an inductive analysis. The research team comprising of the researcher and two advisors/supervisors met to set the initial coding mechanism and code part of the data for consistency before independent coding of all the data. This is supported by King ( 2004 ) who suggested that when searching for themes, it is best to start with a few codes to help guide analysis. The data covered a wide variety of concepts, so initially the different concepts that grouped the research questions as ‘conceptual themes’ were utilised to organise the data. The research team examined the codes, checking their meaning and relationships between them to determine which ones were underpinned by a central concept. In Excel, codes that shared a core idea from the initial phase that used data from the open-ended responses and interview transcripts were colour coded. After the independent thematic analysis, the filter function in Excel was used to sort the codes using cell colour. Moreover, Excel provided the opportunity to identify duplicates as codes were collated from the three researchers. Same coloured codes were synthesised to develop a general pattern of meaning, which we referred to as candidate themes. The sorting and collation approach would bring together all codes under each theme which then would facilitate further analysis and review (Bree et al., 2014 ).

The research team went on to review the relationship of the data and the codes that informed the themes. This is supported by Braun and Clarke ( 2012 , 2021 ) who posited that researchers should conduct a recursive review of the candidate themes in relation to the coded data items and the entire dataset. During the review, whenever themes were integrated or codes were moved to another theme, a new spreadsheet was created so that if further review was necessary, the old data and layout would still be available. Importantly, if the codes form a coherent and meaningful pattern, the theme makes a logical argument and may be representative of the data (Nowell et al., 2017 ). Furthermore, the team also reviewed the themes in relation to the data. This is because Nowell and others posited that themes should provide the most accurate interpretation of the data. The research team also discussed and wrote detailed analysis for each candidate theme identifying the main story behind each theme and how each one fit into the overall story about the data through the lens of the research questions. Finally, the researchers also linked quotes to final themes reached during the analysis. Illustrating findings with direct quotations from the participants strengthen the face validity and credibility of the research (Bryne, 2022 ; Patton, 2002 ; Nowell et al., 2017 ).

Student artefacts

The students’ artefacts (procedural flowcharts) in Figs.  5 , 6 and 7 were analysed using content analysis. Content analysis can be used to analyse written, verbal or visual representations (Cole, 1988 ; Elo & Kyngäs, 2008 ). Content analysis is ideal when there is a greater need to identify critical processes (Lederman, 1991 ). Unlike interviews, documents that are ideal for qualitative analysis should be developed independently without the researcher’s involvement (Merriam & Tisdell, 2015 ). In fact, the documents should not have been prepared for the purpose of research (Hughes & Goodwin, 2014 ), hence they are a stable and discrete data source (De Massis & Kotlar, 2014 ; Merriam & Tisdell, 2015 ). The students’ artefacts used in this study were not prepared for the purpose of the study but as a mathematics task. Deductive content analysis is used when the structure of analysis is implemented on the basis of previous knowledge and the purpose of the study is model testing or confirmation (Burns & Grove, 2009 ). Similarly, it is an analytical method that aims to test existing concepts, models or hypotheses in a new context (Kyngäs et al., 2020 ). They went further to note that researchers can use deductive analysis to determine how a model fit a new context.

Deductive content analysis follows three main stages: preparation, organising and reporting (Elo et al., 2014 ; Elo & Kyngäs, 2008 ). Firstly, preparation involves identifying the unit of analysis (Guthrie et al., 2004 ). In this study, the unit of analysis are the artefacts developed by the students. Furthermore, the phase requires the researcher to be immersed in the data reading and digesting to make sense of the whole set of data through reflexivity, open-mindedness and following the rationale of what guided participants’ narratives or in developing the artefact (Azungah, 2018 ). Secondly, a categorisation matrix based on existing knowledge should be developed or identified to facilitate the coding of the data according to categories (Hsieh & Shannon, 2005 ) (Table  1 ). Importantly, when using deductive content analysis, researchers require a theoretical structure or model from which they can build an analysis matrix (Kyngäs et al., 2020 ). Finally, the analysis results should be reported in ways that promote interpretation of the data and the results, for example, in tabular form (Elo & Kyngäs, 2008 ) (Fig.  2 ).

Stages followed during analysis of procedural flowcharts

The students’ procedural flowcharts were coded and interpreted on how they respond to different stages of problem solving. The researcher’s codes, interpretations and findings should be clearly derived and justified using the available data and then inform conclusions and interpretations for confirmability (Tobin & Begley, 2004 ). The artefacts were shared between the researcher and his supervisors; the analysis was done independently then reviewed by the researcher and his supervisors. Schreier ( 2012 ) recommended that analysis should be done by more than one person to promote thoroughness and broaden the interpretation of the data. Schreier went further to note that if the categorisation matrix is clear and of high quality, the coding should produce very little discrepancies. Very little discrepancies were observed except that some stages on the students’ procedural flowcharts overlapped between skills.

This section presents results from the analysis of the interviews data and student artefacts.

Semi-structured interviews

The thematic analysis of interviews resulted in two themes:

The utility of procedural flowcharts in supporting mathematics problem solving.

The utility of procedural flowcharts in supporting the integration of the four stages of mathematics problem solving.

In phase three, which prompted the targeted phase four study described in this study, teachers were asked the question, “How have you used procedural flowcharts to enhance teaching and learning of mathematics?” The question was not specific to problem solving but the teachers’ observations and perceptions strongly related to problem-solving and student-centred learning.

Theme 1 The utility of procedural flowcharts generally supports mathematics problem solving

The visual nature of procedural flowcharts was seen as an advantage to both teachers and students. For students, drawing a flowchart was easier than writing paragraphs to explain how they had arrived at the intended solution. For teachers, the flowchart was easier to process for timely feedback to students. Developing a procedural flowchart at the first checkpoint in the PSMT allows teachers to provide valuable feedback as the procedural flowchart can be used to represent several processes compared to written because of its visual nature. Engagement can be promoted because students can use the targeted feedback to improve their solutions as they will have provided a detailed overview of how they propose to solve the problem.

They present steps in diagrammatic form which is easy to process and easy to understand and process… students prefer them more as its in diagrammatic form and I have witnessed more students engaging. (Participant 8, phase three study) I find it (visual) a really efficient way for me to look at the proposed individual students processes and provide relevant feedback to the student or for the student to consider. And, you know, once the students are comfortable with using these procedural flowcharts you know, I find it much easier for me to give them relevant feedback, and I actually find that feedback more worthwhile than feedback we used to give them, you know, that was just based on what they wrote in paragraphs,…students get to practice in creating their own visual display, which communicates their intended strategies to solve the problem, then they have opportunities to use it, and fine tune it as they work out the problem … student developed procedural flow charts, they represent a student’s maths knowledge in a visual way. (Ms. Simon).

Identifying students’ competencies early was seen as central to successful problem solving as it provided opportunities for early intervention. Results showed that teachers viewed procedural flowcharts as a resource that could be used to identify gaps in skills, level of understanding and misconceptions that could affect successful and meaningful execution of a problem-solving task. Going through a student-developed flowchart during problem solving provided the teachers with insight into the student’s level of understanding of the problem and how the effectiveness of the procedures proposed to address the problem. This is critical for tasks that require students to develop a report detailing the solution at the end of developing the solution. Teachers can get the opportunity to gain an insight of the proposed solution before the student commit to write the report. The procedural flowchart provides the bigger picture of the solution plan which might expose gaps in knowledge.

I found it quite useful because I can identify what kids or which kids are competent in what, which sort of problem-solving skills. And I can identify misconceptions that students have or gaps in students understanding. (Participant 1, phase three study) It also to me highlights gaps in students’ knowledge in unique ways that students intend to reach a solution because the use of the procedural flow chart encourages students to explain the steps or procedures behind any mathematical manipulation that you know they're intending to use. And it's something that was much more difficult to determine prior to using procedural flow charts… I've also used you know, student developed procedural flow charts to ascertain how narrow or wide the students’ knowledge is and that's also something that wasn't obvious to make a judgement about prior to using procedural flow charts. (Ms. Simon)

Problem solving was seen as student-centred. If procedural flowcharts could be used to support problem solving, then they could facilitate an environment where students were the ones to do most of the work. The students could develop procedural flowcharts showing how they will solve a PSMT task using concepts and procedures they have learnt. The open-ended nature of the problem in a PSMT provides opportunities for diverse solutions that are validated through mathematical justifications. The visual nature of procedural flowcharts makes them more efficient to navigate compared to text.

Mathematics goes from being very dry and dusty to being something which is actually creative and interesting and evolving, starting to get kids actually engaging and having to back themselves. (Participant 7, phase three study) As a teacher, I find that procedural flowcharts are a really efficient way to ascertain the ways that students have considered and how they are going to solve a problem … It engages the students from start to finish, you know in different ways this method demands students to compare, interpret, analyse, reason, evaluate, and to an extent justify as they develop this solution. (Ms. Simon)

Similarly, results showed that procedural flowcharts could be used as a resource to promote collaborative learning and scaffolding. Students could be asked to collaboratively develop a procedural flowchart or could be provided with one to follow as they worked towards solving the problem. Collaborative development of procedural flowcharts can support problem solving as students can bring their different mathematical understanding to develop a solution from different perspectives.

Sometimes, you know, I get students to work on it in groups as they share ideas and get that mathematisation happening. So, it's really helpful there … I looked at the PSMT and its Marking Guide, and develop a more detailed procedural flowchart for students to use as a scaffold to guide them through the process. So, procedural flowcharts provide a structure in a more visual way for students to know what to do next. (Ms. Simon)

Ms. Simon shared her detailed procedural flowchart in Fig.  3 that she used to guide students in PSMTs.

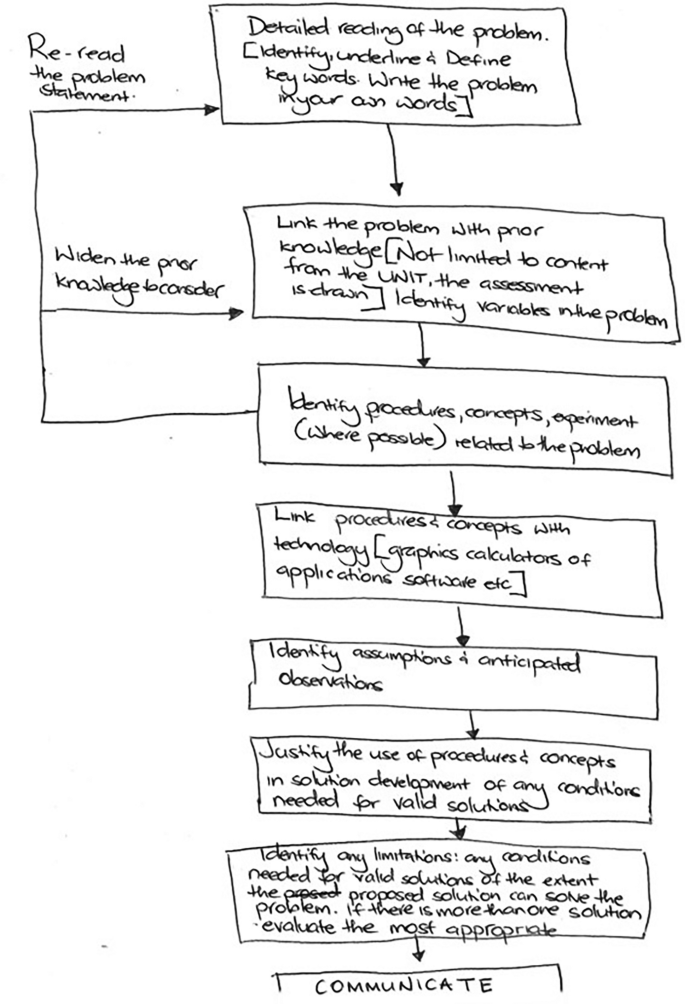
Ms. Simon’s procedural flowchart on problem solving

The participants also observed that procedural flowcharts could be used to promote opportunities for solution evaluation which played an important role in problem solving. Loops can be introduced in procedural flowcharts to provide opportunities for reflection and reasoning as alternative paths provide flexibility while the solution is being developed. Following Fig.  4 are participants’ comments referring to the figure which was among procedural flowcharts shared with participants as examples of how they can be used to teach syllabus identified Mathematical Methods concepts. The Mathematical Methods syllabus expects students to “recognise the distinction between functions and relations and use the vertical line test to determine whether a relation is a function” (QCAA, 2018 p. 20).

The cycle approach, the feeding back in the feeding back out that type of stuff, you know, that is when we starting to teach students how to think . (Participant 7, phase three study) Complex procedural flowcharts like the one you provided guide students in making key decisions as they work through solutions which is key to critical thinking and judgement and these two are very important in maths. (Participant 8, phase three study) I also sincerely believe that procedural flowcharts are a way to get students to develop and demonstrate the critical thinking skills, which PSMTs are designed to assess. Students inadvertently have to use their critical thinking skills to analyse and reason as they search for different ways to obtain a solution to the problem presented in the PSMT … the use of procedural flowcharts naturally permits students to develop their critical thinking skills as it gets their brain into a problem-solving mode as they go through higher order thinking skills such as analysis, reasoning and synthesis and the like … this visual way of presenting solution provides students with opportunities to think differently, which they're not used to do, and it leads them to reflect and compare. (Ms. Simon)

Procedural flowchart on distinguishing functions and relations

Problem solving of non-routine problems uses a structure that should be followed. Resources that are intended to support problem solving in students can be used to support the integration of the stages involved in problem solving.

Theme 2 The utility of procedural flowcharts in supporting the integration of the four stages of mathematics problem solving.

Procedural flowcharts can support the flow of ideas and processes in the four stages during problem-solving and modelling task in Mathematical Methods subject. Literature synthesis in this study identified the four stages as:

Identification of problem and mathematics strategies than can solve the problem.

Implementation.

Evaluation and justification.

Communicating the solution.

Similarly, QCAA flowchart on PSMT identifies the four stages as formulate, solve, evaluate and verify, and communicate.

The logical sequencing of the stages of mathematics problem solving is crucial to solving and communicating the solution to the problem. Development of procedural flowcharts can play an important role in problem solving through fostering the logical sequencing of processes to reach a solution. Participants noted that the development of procedural flowcharts provides opportunities for showing the flow of ideas and processes which lay out an overview of how different stages connect into a bigger framework of the solution. Furthermore, it can help show how different pieces of a puzzle interconnect, in this case how all the components of the solution interconnect and develop to address the problem. In fact, procedural flowcharts can be used to show how the different mathematics concepts students have learnt can be brought together in a logical way to respond to a problem.

Procedural flowcharts help students sum up and connect the pieces together… connect the bits of knowledge together. (Participant 4, phase three study) Really good how it organises the steps and explains where you need to go if you're at a certain part in a procedure. (Participant 2, phase three study) Potentially, it's also an excellent visual presentation, which shows a student's draft of their logical sequence of processes that they're intending to develop to solve the problem … So, the steps students need to follow actually flows logically. So really given a real-life scenario they need to solve in a PSMT students need to mathematise it and turn it into a math plan, where they execute their process, evaluate and verify it and then conclude … so we use procedural flowcharts to reinforce the structure of how to approach problem-solving … kids, you know, they really struggling, you know, presenting things in a logical way, because they presume that we know what they're thinking . (Ms. Simon)

Developing procedural flowcharts provided students with opportunities to plan the solution informed by the stages of problem solving. Teachers could reinforce the structure of problem solving by telling students what they could expect to be included on the procedural flowchart. Procedural flowcharts can be used as a visual tool to highlight all the critical stages that are included during the planning of the solution.

I tell the students, “I need to see how you have interpreted the problem that you need to solve. I need to see how you formulated your model that involves the process of mathematisation, where you move from the real world into the maths world, and I need to see all the different skills you're intending to use to arrive at your solution.” (Ms. Simon)

Similarly, procedural flowcharts could visually represent more than one strategy in the “identify and execute mathematics procedures that can solve the problem” stage, thereby providing a critical resource to demonstrate flexibility. When there are multiple ways of addressing a problem, developing a procedural flowchart can provide an opportunity of showing all possible paths or relationships between different paths to the solution, thus promoting flexibility. Procedural flowcharts provide an opportunity to show how different procedures can be used or integrated to solve a problem.

Students are expected to show evidence that they have the knowledge of solving the problem using several ways to get to the same solution. So, it goes beyond the students’ preferred way of answering a question and actually highlights the importance of flexibility when it comes to processes and strategies of solving a problem … By using procedural flowcharts, I'm saying to the students, “Apart from your preferred way of solving the problem, give me a map of other routes, you can also use to get to your destination.” (Ms. Simon)

The results also indicated that procedural flowcharts could be used to identify strengths and limitations of procedures in the “evaluate solution” stage and thus demonstrate the reasonableness of the answer. Having more than one way of solving a problem on a procedural flowchart helps in comparing and evaluating the most ideal way to address the problem.

And I'm finding that, you know, as students go through, and they compare the different processes, you know, the strengths and limitations, literally stare them in the face. So, they don't have to. They're not ... they don't struggle as much as they used to in coming up with those sorts of answers … it's also a really easy way that once the students reach the next phase, which is the evaluating verified stage, they can go back to their procedural flow chart and identify and explain strengths and limitations of their model … It's a convenient way for students to show their reasonableness of their solution by comparing strengths and weaknesses of all the strategies presented on the procedural flowchart, something that they've struggled with in the past. (Ms. Simon)

The results from the interview show that the procedural flowcharts supported efficient communication of the steps to be followed in developing the solution to the problem. Student-developed procedural flowcharts allowed the teacher to have an insight and overview of the solution to the problem earlier in the assessment task. In addition, they provided an alternative way of presenting their solution to the teacher.

I expect students to use the procedural flowchart as a way to communicate to me how they're planning to solve the scenario in the PSMT…It's also one of the parts that students are expected to hand in to me on one of the check points, and I find it a really efficient way for me to look at, you know, a proposed individual students processes, and provide relevant feedback to the student to consider in a really efficient way…I just found that it helps students communicate their solution to a problem in lots of different ways that challenges students to logically present a solution. (Ms. Simon)

She went on to say,

Students also found it challenging to communicate their ideas in one or two paragraphs, when more than one process or step was required to solve the problem. So, I found that, you know, procedural flowcharts, have filled this gap really nicely, as that provides students with a simple tool that they can use to present a visual overview of the processes they've chosen to use to solve the problem. And so, for me, as a teacher, procedural flowcharts are an efficient way for me to scan the intended processes that an individual student is proposing to use to solve the problem in their authentic way and provide them with valuable feedback.

In summary, the teacher’s experiences, views and perceptions showed that procedural flowcharts can be a valuable resource in supporting students in all four stages of problem solving.

Students’ artefacts

The student-generated flowcharts in this part of the research gave an insight into students’ understanding as they planned how to solve the problem presented to them. Students were expected to use the problem-solving stages to successfully develop solutions to problems. Their de-identified procedural flowcharts are shown in Figs.  5 , 6 and 7 .

Procedural flowchart developed by student 1

Procedural flowchart developed by student 2

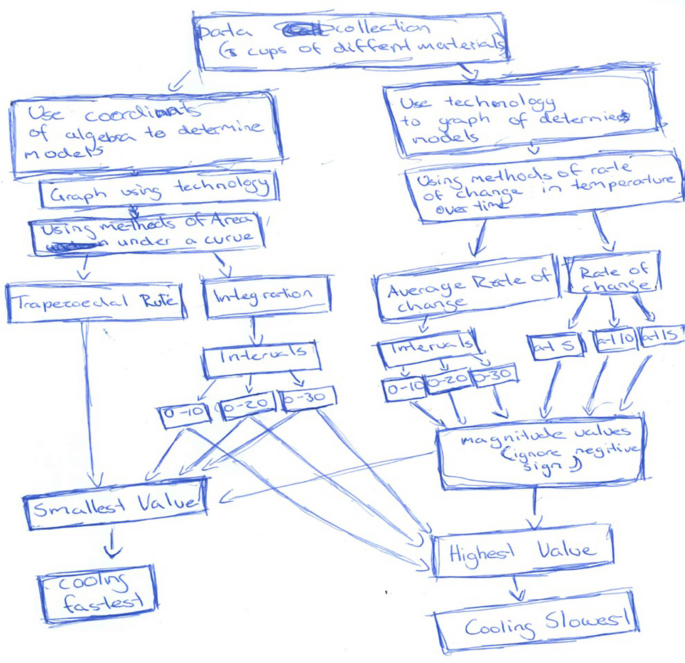
Collaboratively developed procedural flowchart

Students 1 and 2 also collaboratively developed a procedural flowchart, shown as Fig.  7 .

This discussion is presented as two sections: (1) how developing procedural flowcharts can support mathematics problem solving and (2) how developing procedural flowcharts support the integration of the different stages of mathematics problem solving. This study although limited by sample size highlighted how developing procedural flowcharts can support mathematics problem solving, can reinforce the structure of the solution to a problem and can help develop metacognitive skills among students. The different stages involved in problem solving inform the process of developing the solution to the problem. The focus on problem-based learning has signified the need to introduce resources that can support students and teachers in developing and structuring solutions to problems. Results from this study have also provided discussion points on how procedural flowcharts can have a positive impact in mathematics problem solving.

Procedural flowcharts can support mathematics problem solving

Procedural flowcharts help in visualising the process of problem solving. The results described in this study show that student-generated flowcharts can provide an overview of the proposed solution to the problem. The study noted that students preferred developing procedural flowcharts rather than writing how they planned to find a solution to the problem. The teachers also preferred visual aids because they were easier and quicker to process and facilitated understanding of the steps taken to reach the solution. These results are consistent with the findings of other researchers (McGowan & Boscia, 2016 ; Raiyn, 2016 ). The results are also consistent with Grosskinsky and colleagues’ ( 2019 ) findings that flowcharts break complex information into different tasks and show how they are connected, thereby enhancing understanding of the process. Consequently, they allow teachers to provide timely feedback at a checkpoint compared to the time a teacher would take to go through a written draft. Procedural flowcharts connect procedures and processes in a solution to the problem (Chinofunga et al., 2022 ). Thus, the feedback provided by the teacher can be more targeted to a particular stage identified on the procedural flowchart, making the feedback more effective and worthwhile. The development of a procedural flowchart during problem solving can be viewed as a visual representation of students’ plan and understanding of how they plan to solve the problem as demonstrated in Figs.  5 , 6 and 7 .

In this study, Ms. Simon noted that procedural flowcharts can represented students’ knowledge or thinking in a visual form, which is consistent with Owens and Clements’ ( 1998 ) findings that visual representations are cognitive constructs. Consequently, they can facilitate evaluation of such knowledge. This study noted that developing procedural flowcharts can provide opportunities to identify gaps in students’ understanding and problem-solving skills. It also noted that providing students with opportunities to develop procedural flowcharts may expose students’ misconceptions, the depth and breadth of their understanding of the problem and how they plan to solve the problem. This is supported by significant research (Grosskinsky et al., 2019 ; Norton et al., 2007 ; Vale & Barbosa, 2018 ), which identified flowcharts as a resource in helping visualise and recognise students’ understanding of a problem and communication of the solution. Thus, providing teachers with opportunities to have an insight into students’ thinking can facilitate intervention early in the process. The results in this study showed that when students develop their own plan on how to respond to a problem, they are at the centre of their learning. However, scaffolding and collaborative learning can also support problem solving.

Vygotsky ( 1978 ) posited that in the Zone of Proximal Development, collaborative learning and scaffolding can facilitate understanding. In this study, the results indicated that a teacher-developed procedural flowchart can be used to guide students in developing a solution to a problem. These results are consistent with Davidowitz and Rollnick’s study that concluded that flowcharts provide a bigger picture of how to solve the problem. In Queensland, the QCAA has developed a flowchart (see Appendix 1 ) to guide schools on problem-solving and modelling tasks. It highlights the significant stages to be considered during the process and how they relate to each other. Teachers are encouraged to contextualise official documents to suit their school and classes. In such cases, a procedural flowchart acts as a scaffolding resource in directing students on how to develop the solution to the problem. The findings are consistent with previous literature that flowcharts can give an overall direction of the process, help explain what is involved, may help reduce cognitive load and allow students to focus on complex tasks (Davidowitz & Rollnick, 2001 ; Norton et al., 2007 ; Sweller et al., 2019 ).

In addition to being a scaffolding resource, results showed that procedural flowcharts can be developed collaboratively providing students with an opportunity to share their solution to the problem. Being a scaffolding resource or a resource to use in a community of learning highlights the importance of procedural flowcharts in promoting learning within a zone of proximal development, as posited by Davidowitz and Rollnick ( 2001 ). Scaffolding students to problem solve and develop procedural flowcharts collaboratively provides students with the opportunity to be at the centre of problem solving.

Research has identified problem solving as student-centred learning (Ahmad et al., 2010 ; Karp & Wasserman, 2015 ; Reinholz, 2020 ; Vale & Barbosa, 2018 ). The process of developing the procedural flowcharts as students plan for the solution provides students with opportunities to engage more with the problem. Results showed that when students developed procedural flowcharts themselves, mathematics learning transformed from students just being told what to do or follow procedures into something creative and interesting. As students develop procedural flowcharts, they use concepts they have learnt to develop a solution to an unfamiliar problem (Matty, 2016 ), thus engaging with learning from the beginning of the process until they finalise the solution. The results indicated that developing procedural flowcharts promoted students’ ability to not only integrate different procedures to solve the problem but also determine how and when the conditions were ideal to address the problem, providing opportunities to justify and evaluate the procedures that were used.

Deeper understanding of mathematics and relationships between concepts plays an important role in problem solving, and the results from this study showed that different procedures can be integrated to develop a solution to a problem. The participants observed that developing procedural flowcharts could support the brainstorming ideas as they developed the flowchart, as ideas may interlink in a non-linear way. Moreover, students are expected at different stages to make key decisions about the direction they will need to take to reach the solution to the problem, as more than one strategy may be available. For example, student 1 planned on using only technology to develop the models while student 2 considered both technology and algebra. This showed that student 2 applied flexibility in using alternative methods, thus demonstrating a deeper understanding of the problem. Equally important, Ms. Simon observed that as students developed their procedural flowcharts while planning the steps to reach a solution, they were required to analyse, conceptualise, reason, analyse, synthesise and evaluate, which are important attributes of deeper understanding. Fostering deeper understanding of mathematics is the key goal of using problem solving (Kim et al., 2012 ; King, 1995 ; Moon, 2008 ; QCAA, 2018 ). The results are additionally consistent with findings from Owens and Clements ( 1998 ) and Roam ( 2009 ), who posited that visual aids foster reasoning and show cognitive constructs. Similarly, logical sequencing of procedures and ways to execute a strategy expected when developing procedural flowchart can support deeper understanding, as posited by Parvaneh and Duncan ( 2021 ). When developing procedural flowchart, students are required to link ideas that are related or feed into another, creating a web of knowledge. Students are also required to identify the ways in which a concept is applied as they develop a solution, and this requires deeper understanding of mathematics. Working collaboratively can also support deeper and broader understanding of mathematics.

The procedural flowchart that was developed collaboratively by the two students demonstrated some of the skills that they did not demonstrate in their individual procedural flowcharts. Like student 2, the collaboratively developed flowchart included use of technology and algebra to determine the models for the three different cups. The students considered both rate of change and area under a curve in the task analysis. Apart from planning to use rate at a point, average rate and definite integration, they added the trapezoidal rule. Both average rate and definite integration were to be applied within the same intervals, building the scope for comparison. The trapezoidal rule would also compare with integration. The complexity of the collaboratively developed procedural flowchart concurred with Rogoff and others ( 1984 ) and Stone ( 1998 ), who suggested that a community of learning can expand current skills to higher levels than individuals could achieve on their own. It seems the students used the feedback provided by the teacher on their individually developed procedural flowcharts as scaffolding to develop a much more complex procedural flowchart with competing procedures to address the problem. Their individually developed flowcharts might have acted as reference points, as their initial plans were still included in the collaboratively developed plan but with better clarity. This observation is consistent with Guk and Kellogg ( 2007 ), Kirova and Jamison ( 2018 ) and Ouyang and colleagues ( 2022 ), who noted that scaffolding involving peers, teacher and other resources enhances complex problem-solving tasks and transfer of skills.

Supporting the integration of the different stages of mathematics problem solving

When students develop procedural flowcharts, it supports the logical sequencing of ideas from different stages into a process that ends with a solution. Problem solving follows a proposed order and procedural flowcharts visually display decision and/or action sequences in a logical order (Krohn, 1983 ). They are used when a sequenced order of ideas is emphasised, such as in problem solving (Cantatore & Stevens, 2016 ). This study concurs with Krohn, Cantatore and Stevens, as the results showed that procedural flowcharts could be used to organise steps and ideas logically as students worked towards developing a solution. Students’ procedural flowcharts are expected to be developed through the following stages: problem identification, problem mathematisation, planning and execution and finally evaluation. Such a structure can be reinforced by teachers by sharing a generic problem-solving flowchart outlining the stages so that students can then develop a problem-specific version. Importantly, students’ artefacts in Figs.  5 , 6 and 7 provided evidence of how procedural flowcharts support the different stages of problem-solving stages to create a logical and sequential flow of the solution (see Appendix 1 ). Similarly, Ms. Simon noted that while her students had previously had problems in presenting the steps to their solution in a logical way, she witnessed a significant improvement after she asked them to develop procedural flowcharts first. Further, the results are consistent with Chinofunga et al.’s ( 2022 ) work that procedural flowcharts can support procedural flexibility, as they can accommodate more than one procedure in the “identify and execute mathematics procedures that can solve the problem” stage. Thus, stages that require one procedure or more than one procedure can all be accommodated in a single procedural flowchart. Evaluating the different procedures is also a key stage in problem solving.

As students develop the solution to the problem and identify ways to address the problem, they also have to evaluate the procedures, reflecting on the limitations and strengths of the solutions they offer. Ms. Simon observed that her students had previously struggled with identifying strengths and weaknesses of different procedures. However, she noted that procedural flowcharts gave students the opportunity to reflect and compare as they planned the solution. For example, students could have the opportunity to reflect and compare rate at a point, average rate and integration so they can evaluate which strategy can best address he problem. The artefacts identified the different procedures the students used in planning the solution, enabling them to evaluate the effectiveness of each strategy. Thus, enhancing students’ capacity to make decisions and identify the optimal strategy to solve a problem aligns with the work of McGowan and Boscia ( 2016 ). Similarly, Chinofunga and colleagues’ findings noted that developing procedural flowcharts can be effective in evaluating different procedures as they can accommodate several procedures. The different stages that need to be followed during problem solving and the way the solution to the problem is logically presented are central to how the final product is communicated.

In this study, procedural flowcharts were used to communicate the plan to reach the solution to a problem. The length of time given to students to work on their problem-solving tasks in Queensland is fairly long (4 weeks) and students may struggle to remember some key processes along the way. Developing procedural flowcharts to gain an overview of the solution to the problem and share it with the teacher at an early checkpoint is of significant importance. In this study, Ms. Simon expected her students to share their procedural flowcharts early in the process for her to give feedback, thus making the flowcharts a communication tool. The procedural flowcharts developed by the students in Figs.  5 , 6 and 7 show how students proposed solving the problem. This result lends further support to the NCTM ( 2000 ) findings that visual representations can help students communicate their thinking before applying those thoughts to solving a problem. Ms. Simon also noted that before introducing students to procedural flowcharts, they did not have an overall coherent structure to follow, which presented challenges when they wanted to communicate a plan that involved more than one strategy. However, the students’ artefacts were meaningful, clearly articulating how the solution to the problem was being developed, thus demonstrating that procedural flowcharts can provide the structure that supports the coherent and logical communication of the solution to the problem by both teachers and students (Norton et al., 2007 ). The visual nature of the students’ responses in the form of procedural flowcharts is key to communicating the proposed solution to the problem.

Visual representations are a favourable alternative to narrative communication. Procedural flowcharts can help teachers to check students’ work faster and provide critical feedback in a timely manner. Ms. Simon noted that the use of procedural flowcharts provided her with the opportunity to provide feedback faster and more effectively earlier in the task because the charts provided her with an overview of the whole proposed solution. Considering that students are expected to write a report of 2000 words or 10 pages on the task, the procedural flowchart provides the opportunity to present large amounts of information in just one visual representation. Raiyn ( 2016 ) noted that visual representations can be a quicker way to evaluate a solution and represent large amounts of information.

The procedural flowcharts that were created by students in this study demonstrate that they can be effective in supporting the development of problem-solving skills. This study suggests that including procedural flowcharts in problem solving may support teachers and students in communicating efficiently about how to solve the problem. For students, it is a resource that provides the solution overview, while teachers can consider it as a mental representation of students’ thinking as they plan the steps to reach a solution. Student-developed procedural flowcharts may represent how a student visualises a solution to a problem after brainstorming different pathways and different decision-making stages.

Moreover, as highlighted in this study, the visual nature of procedural flowcharts may offer a diverse range of support for problem solving. Procedural flowcharts make it easy to process and provide timely feedback that in turn might help students engage with the problem meaningfully. Furthermore, they may also provide a structure of the problem-solving process and guide students through the problem-solving process. Navigating through stages of problem solving might be supported by having students design procedural flowcharts first and then execute the plan. Indeed, this study showed that the ability of procedural flowcharts to represent multiple procedures, evaluation stages or loops and alternative paths helps students reflect and think about how to present a logically cohesive solution. Importantly, procedural flowcharts have also been identified as a resource that can help students communicate the solution to the problem. Procedural flowcharts have been noted to support deeper understanding as it may facilitate analysis, logical sequencing, reflection, reasoning, evaluation and communication. Although the in-depth study involved one teacher and three artefacts from her students, which is a very small sample to be conclusive, it identified the numerous advantages that procedural flowcharts bring to mathematics learning and teaching, particularly in terms of supporting the development of problem-solving skills. The study calls for further investigation on how procedural flowcharts can support students’ problem solving.

Ahmad, A., Tarmizi, R. A., & Nawawi, M. (2010). Visual representations in mathematical word problem-solving among form four students in malacca. Procedia - Social and Behavioral Sciences, 8 , 356–361. https://doi.org/10.1016/j.sbspro.2010.12.050

Article   Google Scholar  

Anderson, J. (2014). Forging new opportunities for problem solving in Australian mathematics classrooms through the first national mathematics curriculum. In Y. Li & G. Lappan (Eds.), Mathematics curriculum in school education (pp. 209–230). Springer.

Chapter   Google Scholar  

Arcavi, A. (2003). The role of visual representations in the learning of mathematics. Educational Studies in Mathematics, 52 (3), 215–241. https://doi.org/10.1023/A:1024312321077

Artigue, M., & Blomhøj, M. (2013). Conceptualizing Inquiry-Based Education in Mathematics. ZDM, 45 (6), 797–810. https://doi.org/10.1007/s11858-013-0506-6

Artigue, M., Bosch, M., Doorman, M., Juhász, P., Kvasz, L., & Maass, K. (2020). Inquiry based mathematics education and the development of learning trajectories. Teaching Mathematics and Computer Science, 18 (3), 63–89. https://doi.org/10.5485/TMCS.2020.0505

Australia Curriculum and Reporting Authority. (2014). Mathematics proficiencies (Version 8.4) . https://www.australiancurriculum.edu.au/resources/mathematics-proficiencies/portfolios/problem-solving/

Azungah, T. (2018). Qualitative research: deductive and inductive approaches to data analysis. Qualitative Research Journal, 18 (4), 383–400. https://doi.org/10.1108/QRJ-D-18-00035

Berger, M. (1998). Graphic calculators: An Interpretative framework. For the Learning of Mathematics, 18 (2), 13–20.

Google Scholar  

Blum, W., & Leiß, D. (2007). Deal with modelling problems. Mathematical Modelling: Education, Engineering and Economics, 12 , 222. https://doi.org/10.1533/9780857099419.5.221

Bos, R., & van den Bogaart, T. (2022). Heuristic trees as a digital tool to foster compression and decompression in problem-solving. Digital Experiences in Mathematics Education, 8 (2), 157–182. https://doi.org/10.1007/s40751-022-00101-6

Braun, V., & Clarke, V. (2006). Using thematic analysis in psychology. Qualitative Research in Psychology, 3 (2), 77–101. https://doi.org/10.1191/1478088706qp063oa

Braun, V., & Clarke, V. (2012). Thematic analysis. In H. Cooper, P. M. Camic, D. L. Long, A. T. Panter, D. Rindskopf, & K. J. Sher (Eds.), APA Handbook of Research Methods in Psychology, Research Designs (Vol. 2, pp. 57–71). American Psychological Association.

Braun, V., & Clarke, V. (2021). One size fits all? What counts as quality practice in (reflexive) thematic analysis? Qualitative Research in Psychology, 18 (3), 328–352. https://doi.org/10.1080/14780887.2020.1769238

Bree, R. T., Dunne, K., Brereton, B., Gallagher, G., & Dallat, J. (2014). Engaging learning and addressing over-assessment in the Science laboratory: Solving a pervasive problem. The All-Ireland Journal of Teaching and Learning in Higher Education, 6 (3), 206.1–206.36. http://ojs.aishe.org/index.php/aishe-j/article/viewFile/206/290

Burns, N., & Grove, S. (2009). The practice of nursing research: Appraisal, synthesis and generation of evidence (6th ed.). St. Louis: Saunders Elsevier. https://doi.org/10.7748/ns2013.04.27.31.30.b1488

Book   Google Scholar  

Byrne, D. (2022). A worked example of Braun and Clarke’s approach to reflexive thematic analysis. Quality & Quantity, 56 (3), 1391–1412. https://doi.org/10.1007/s11135-021-01182-y

Cai, J. (2010). Helping elementary school students become successful mathematical problem solvers. In D. Lambdin (Ed.), Teaching and learning mathematics: Translating research to the elementary classroom (pp. 9–14). Reston, VA: National Council of Teachers of Mathematics.

Cantatore, F., & Stevens, I. (2016). Making connections : Incorporating visual learning in law subjects through mind mapping and flowcharts. Canterbury Law Review, 22 (1), 153–170. https://doi.org/10.3316/agis_archive.20173661

Chinofunga, M. D., Chigeza, P., & Taylor, S. (2022). Procedural flowcharts can enhance senior secondary mathematics. In N. Fitzallen, C. Murphy, & V. Hatisaru (Eds.), Mathematical confluences and journeys (Proceedings of the 44th Annual Conference of the Mathematics Education Research Group of Australasia, July 3-7) (pp. 130–137). Launceston: MERGA. https://files.eric.ed.gov/fulltext/ED623874.pdf

Colburn, A. (2000). An inquiry primer. Science Scope, 23 (6), 42–44. http://www.cyberbee.com/inquiryprimer.pdf

Cole, F. L. (1988). Content analysis: Process and application. Clinical Nurse Specialist, 2 (1), 53–57. https://doi.org/10.1097/00002800-198800210-00025

Article   CAS   PubMed   Google Scholar  

Csíkos, C., Szitányi, J., & Kelemen, R. (2012). The effects of using drawings in developing young children’s mathematical word problem solving: A design experiment with third-grade Hungarian students. Educational Studies in Mathematics, 81 , 47–65. https://doi.org/10.1007/s10649-011-9360-z

Davidowitz, B., & Rollnick, M. (2001). Effectiveness of flow diagrams as a strategy for learning in laboratories. Australian Journal of Education in Chemistry, (57), 18–24. https://search.informit.org/doi/10.3316/aeipt.129151

De Massis, A., & Kotlar, J. (2014). The case study method in family business research: Guidelines for qualitative scholarship. Journal of Family Business Strategy, 5 (1), 15–29. https://doi.org/10.1016/j.jfbs.2014.01.007

Dorier, J.-L., & Maass, K. (2020). Inquiry-based mathematics education. In S. Lerman (Ed.), Encyclopedia of mathematics education (pp. 384–388). Springer. https://doi.org/10.1007/978-3-030-15789-0_176

Doyle, K. M. (2005). Mathematical problem solving: A need for literacy. In F. Bryer, B. Bartlett, & D. Roebuck (Eds.), Proceedings Stimulating the “Action” as participants in participatory research 2 (pp. 39–45). Australia: Surfers Paradise.

Elo, S., & Kyngäs, H. (2008). The qualitative content analysis process. Journal of Advanced Nursing, 62 (1), 107–115. https://doi.org/10.1111/j.1365-2648.2007.04569.x

Article   PubMed   Google Scholar  

Elo, S., Kääriäinen, M., Kanste, O., Pölkki, T., Utriainen, K., & Kyngäs, H. (2014). Qualitative content analysis: A focus on trustworthiness. SAGE Open, 4 (1), 215824401452263. https://doi.org/10.1177/2158244014522633

English, L., & Gainsburg, J. (2016). Problem solving in a 21st-century mathematics curriculum. In L. English & D. Kirshner (Eds.), Handbook of international research in mathematics education (3rd ed., pp. 313–335). New York, NY: Routledge.

Galbraith, P., & Stillman, G. (2006). A framework for identifying student blockages during transitions in the modelling process. ZDM – Mathematics Education, 38 (2), 143–162. https://doi.org/10.1007/BF02655886

Geiger, V., Galbraith, P., Niss, M., & Delzoppo, C. (2021). Developing a task design and implementation framework for fostering mathematical modelling competencies. Educational Studies in Mathematics, 109 (2), 313–336. https://doi.org/10.1007/s10649-021-10039-y

Gencer, S. (2023). Development and use of flowchart for preservice chemistry teachers’ problem solving on the first law of thermodynamics. Journal of Chemical Education, 100 (9), 3393–3401. https://doi.org/10.1021/acs.jchemed.3c00224

Article   CAS   ADS   Google Scholar  

Grosskinsky, D. K., Jørgensen, K., & Hammer úr Skúoy, K. (2019). A flowchart as a tool to support student learning in a laboratory exercise. Dansk Universitetspædagogisk Tidsskrift, 14 (26), 23–35. https://doi.org/10.7146/dut.v14i26.104402

Guion, L. A., Diehl, D. C., & McDonald, D. (2011). Triangulation: Establishing the validity of qualitative studies. EDIS, (8), 3–3. https://doi.org/10.32473/edis-fy394-2011

Guk, I., & Kellogg, D. (2007). The ZPD and whole class teaching: Teacher-led and student-led interactional mediation of tasks. Language Teaching Research, 11 (3), 281–299. https://doi.org/10.1177/1362168807077561

Guthrie, J., Petty, R., Yongvanich, K., & Ricceri, F. (2004). Using content analysis as a research method to inquire into intellectual capital reporting. Journal of Intellectual Capital, 5 (2), 282–293. https://doi.org/10.1108/14691930410533704

Hacker, D. J., Dunlosky, J., & Graesser, A. C. (Eds.). (1998). Metacognition in educational theory and practice (1st ed.). Routledge. https://doi.org/10.4324/9781410602350

Hadamard, J. (1945). The psychology of invention in the mathematical field . Princeton, NJ: Princeton University Press.

Hankeln, C. (2020). Mathematical modeling in Germany and France: A comparison of students’ modeling processes. Educational Studies in Mathematics, 103 (2), 209–229. https://doi.org/10.1007/s10649-019-09931-5

Hooshyar, D., Ahmad, R. B., Yousefi, M., Fathi, M., Horng, S.-J., & Lim, H. (2016). Applying an online game-based formative assessment in a flowchart-based intelligent tutoring system for improving problem-solving skills. Computers and Education, 94 , 18–36. https://doi.org/10.1016/j.compedu.2015.10.013

Hsieh, H.-F., & Shannon, S. E. (2005). Three approaches to qualitative content analysis. Qualitative Health Research, 15 (9), 1277–1288. https://doi.org/10.1177/1049732305276687

Huang, X., Huang, R., & Trouche, L. (2023). Teachers’ learning from addressing the challenges of online teaching in a time of pandemic: A case in Shanghai. Educational Studies in Mathematics, 112 (1), 103–121. https://doi.org/10.1007/s10649-022-10172-2

Hughes, J. R. A., & Goodwin, J. (2014). Editors’ introduction: Human documents and archival research . University of Leicester. Chapter. https://hdl.handle.net/2381/31547

Jitendra, A. K., Dupuis, D. N., Rodriguez, M. C., Zaslofsky, A. F., Slater, S., Cozine-Corroy, K., & Church, C. (2013). A randomized controlled trial of the impact of schema-based instruction on mathematical outcomes for third-grade students with mathematics difficulties. The Elementary School Journal, 114 (2), 252–276. https://doi.org/10.1086/673199

Jonassen, D. H. (2012). Designing for decision making. Educational Technology Research and Development, 60 (2), 341–359. https://doi.org/10.1007/s11423-011-9230-5

Kaitera, S., & Harmoinen, S. (2022). Developing mathematical problem-solving skills in primary school by using visual representations on heuristics. LUMAT: International Journal on Math, Science and Technology Education, 10 (2), 111–146. https://doi.org/10.31129/LUMAT.10.2.1696

Karp, A., & Wasserman, N. (2015). Mathematics in middle and secondary school: A problem-solving approach . Charlotte, North Carolina: Information Age Publishing Inc.

Kim, K., Sharma, P., Land, S. M., & Furlong, K. P. (2012). Effects of active learning on enhancing student critical thinking in an undergraduate general science course. Innovative Higher Education, 38 (3), 223–235. https://doi.org/10.1007/s10755-012-9236-x

King, A. (1995). Designing the instructional process to enhance critical thinking across the curriculum: Inquiring minds really do want to know: Using questioning to teach critical thinking. Teaching of Psychology, 22 (1), 13–17. https://doi.org/10.1207/s15328023top2201_5

Article   MathSciNet   Google Scholar  

King, N. (2004). Using templates in the thematic analysis of text. In C. Cassell & G. Symon (Eds.), Essential guide to qualitative methods in organizational research (pp. 257–270). London, UK: Sage. https://doi.org/10.4135/9781446280119

Kingsdorf, S., & Krawec, J. (2014). Error analysis of mathematical word problem solving across students with and without learning disabilities. Learning Disabilities Research & Practice, 29 (2), 66–74. https://doi.org/10.1111/ldrp.12029

Kirova, A., & Jamison, N. M. (2018). Peer scaffolding techniques and approaches in preschool children’s multiliteracy practices with iPads. Journal of Early Childhood Research, 16 (3), 245–257. https://doi.org/10.1177/1476718X18775762

Koellner, K., Jacobs, J., & Borko, H. (2011). Mathematics professional development: Critical features for developing leadership skills and building teachers’ capacity. Mathematics Teacher Education & Development, 13 (1), 115–136. Retrieved from https://files.eric.ed.gov/fulltext/EJ960952.pdf

Krawec, J. L. (2014). Problem representation and mathematical problem solving of students of varying math ability. Journal of Learning Disabilities, 47 , 103–115. https://doi.org/10.1177/0022219412436976

Krohn, G. S. (1983). Flowcharts used for procedural instructions. Human Factors, 25 (5), 573–581. https://doi.org/10.1177/001872088302500511

Krutetskii, V. A. (1976). The psychology of mathematical abilities in schoolchildren . Chicago: University of Chicago Press.

Kules, B. (2016). Computational thinking is critical thinking: Connecting to university discourse, goals, and learning outcomes. Proceedings of the Association for Information Science and Technology, 53 (1), 1–6. https://doi.org/10.1002/pra2.2016.14505301092

Kyngäs, H., Mikkonen, K., & Kääriäinen, M. (2020). The application of content analysis in nursing science research . Cham: Springer. https://doi.org/10.1007/978-3-030-30199-6

Laughlin, P. R., Hatch, E. C., Silver, J. S., & Boh, L. (2006). Groups perform better than the best individuals on letters-to-numbers problems: Effects of group size. Journal of Personality and Social Psychology, 90 (4), 644–651. https://doi.org/10.1037/0022-3514.90.4.644

Lederman, R. P. (1991). Content analysis: Steps to a more precise coding procedure. MCN, The American Journal of Maternal Child Nursing, 16 (5), 275–275. https://doi.org/10.1097/00005721-199109000-00012

Ledin, P., & Machin, D. (2020). The misleading nature of flow charts and diagrams in organizational communication: The case of performance management of preschools in Sweden. Semiotica, 2020 (236), 405–425. https://doi.org/10.1515/sem-2020-0032

Lester, F. (2013). Thoughts about research on mathematical problem-solving instruction. The Mathematics Enthusiast, 10 (1–2), 245–278.

Lester, F. K., & Cai, J. (2016). Can mathematical problem solving be taught? Preliminary answers from 30 years of research. In P. Felmer, E. Pehkonen, & J. Kilpatrick (Eds.), Posing and solving mathematical problems: Advances and new perspectives (pp. 117–135). Springer International Publishing. https://doi.org/10.1007/978-3-319-28023-3_8

Lohse, G., Biolsi, K., Walker, N., & Rueter, H. (1994). A classification of visual representations. Communications of the ACM, 37 (12), 36–49. https://doi.org/10.1145/198366.198376

Makar, K. (2012). The pedagogy of mathematical inquiry. In R. Gillies (Ed.), Pedagogy: New developments in the learning sciences (pp. 371–397). Hauppauge, N.Y.: Nova Science Publishers.

Mason, J. (2016). When is a problem…? “When” is actually the problem! In P. Felmer, E. Pehkonen, & J. Kilpatrick (Eds.), Posing and solving mathematical problems. Advances and new perspectives (pp. 263–287). Switzerland: Springer. https://doi.org/10.1007/978-3-319-28023-3_16

Matty, A. N. (2016). A study on how inquiry based instruction impacts student achievement in mathematics at the high school level . ProQuest Dissertations Publishing. https://www.proquest.com/openview/da895b80797c90f9382f0c9a948f7f68/1?pq-origsite=gscholar&cbl=18750

McCormick, N. J., Clark, L. M., & Raines, J. M. (2015). Engaging students in critical thinking and problem-solving: A brief review of the literature. Journal of Studies in Education, 5 (4), 100–113. https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.960.810&rep=rep1&type=pdf

McGowan, M. M., & Boscia, M. W. (2016). Opening more than just a bag: Unlocking the flowchart as an effective problem-solving tool. The Journal of Health Administration Education, 33 (1), 211–219.

Merriam, S. B., & Tisdell, E. J. (2015). Qualitative research: A guide to design and implementation (4th ed.). Newark: Wiley.

Moon, J. (2008). Critical thinking: An exploration of theory and practice . Routledge. https://doi.org/10.4324/9780203944882

National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics . Reston, VA: National Council of Teachers of Mathematics.

Nieuwoudt, S. (2015). Developing a model for problem-solving in a Grade 4 mathematics classroom. Pythagoras, 36 (2), 1–7. https://doi.org/10.4102/pythagoras.v36i2.275

Norton, S. J., McRobbie, C. J., & Ginns, I. S. (2007). Problem-solving in a middle school robotics design classroom. Research in Science Education, 37 (3), 261–277. https://doi.org/10.1007/s11165-006-9025-6

Article   ADS   Google Scholar  

Nowell, L. S., Norris, J. M., White, D. E., & Moules, N. J. (2017). Thematic analysis: Striving to meet the trustworthiness criteria. International Journal of Qualitative Methods, 16 (1), 1609406917733847. https://doi.org/10.1177/1609406917733847

Ouyang, F., Chen, S., Yang, Y., & Chen, Y. (2022). Examining the effects of three group-level metacognitive scaffoldings on in-service teachers’ knowledge building. Journal of Educational Computing Research, 60 (2), 352–379. https://doi.org/10.1177/07356331211030847

Owens, K. D., & Clements, M. A. (1998). Representations in spatial problem-solving in the classroom. The Journal of Mathematical Behavior, 17 (2), 197–218. https://doi.org/10.1016/S0364-0213(99)80059-7

Ozuem, W., Willis, M., & Howell, K. (2022). Thematic analysis without paradox: Sensemaking and context. Qualitative Market Research, 25 (1), 143–157. https://doi.org/10.1108/QMR-07-2021-0092

Pape, S. J., & Tchoshanov, M. A. (2001). The role of representation(s) in developing mathematical understanding. Theory into Practice, 40 (2), 118–127. https://doi.org/10.1207/s15430421tip4002_6

Parvaneh, H., & Duncan, G. J. (2021). The role of robotics in the development of creativity, critical thinking and algorithmic thinking. Australian Primary Mathematics Classroom, 26 (3), 9–13. https://doi.org/10.3316/informit.448545849534966

Patton, M. Q. (2002). Qualitative research and evaluation methods (3rd ed.). Sage Publications.

Polya, G. (1945). How to solve it: A new aspect of mathematical method . Princeton, NJ: Princeton University Press.

Polya, G. (1957). How to solve it: A new aspect of mathematical method . Princeton: Princeton University Press.

Polya, G. (1971). How to solve it: A new aspect of mathematical method (2nd ed.). Princeton University Press.

Queensland Curriculum and Assessment Authority (QCAA). (2018). Mathematical methods. general senior syllabus . Brisbane: Queensland Curriculum and Assessment Authority. https://www.qcaa.qld.edu.au/downloads/senior-qce/syllabuses/snr_maths_methods_19_syll.pdf

Raiyn, J. (2016). The role of visual learning in improving students’ high-order thinking skills. Journal of Education and Practice, 7 , 115–121. https://www.learntechlib.org/p/195092/

Reingewertz, Y. (2013). Teaching macroeconomics through flowcharts. International Review of Economics Education, 14 , 86–93. https://doi.org/10.1016/j.iree.2013.10.004

Reinholz, D. L. (2020). Five practices for supporting inquiry in analysis. Problems Resources and Issues in Mathematics Undergraduate Studies, 30 (1), 19–35. https://doi.org/10.1080/10511970.2018.1500955

Roam, D. (2009). The back of the napkin: Solving problems and selling ideas with pictures (1st ed.). Singapore: Marshall Cavendish International (Asia) Private Limited.

Rogoff, B., Malkin, C., & Gilbride, K. (1984). Interaction with babies as guidance in development. New Directions for Child and Adolescent Development, 1984 (23), 31–44. https://doi.org/10.1002/cd.23219842305

Roth, W. M., & McGinn, M. (1998). Inscriptions: Toward a theory of representing as social practice. Review of Educational Research, 68 (1), 35–59.

Sakshaug, L. E., & Wohlhuter, K. A. (2010). Journey toward teaching mathematics through problem-solving. School Science and Mathematics, 110 (8), 397–409. https://doi.org/10.1111/j.1949-8594.2010.00051.x

Santoso, B., & Syarifuddin, H. (2020). Validity of mathematic learning teaching administration on realistic mathematics education based approach to improve problem-solving. Journal of Physics. Conference Series, 1554 (1), 12001. https://doi.org/10.1088/1742-6596/1554/1/012001

Schoenfeld, A. H. (1980). Teaching problem-solving skills. The American Mathematical Monthly, 87 (10), 794. https://doi.org/10.2307/2320787

Schoenfeld, A. H. (1983). Problem solving in the mathematics curriculum . The Mathematical Association of America.

Schoenfeld, A. H. (2013). Reflections on problem-solving theory and practice. The Mathematics Enthusiast, 10 (1/2), 9.

Schoenfeld, A. H. (2016). Learning to think mathematically: Problem-solving, metacognition, and sense making in mathematics (Reprint). Journal of Education, 196 (2), 1–38. https://doi.org/10.1177/002205741619600202

Schoenfeld, A. H., Floden, R. E., & The algebra teaching study and mathematics assessment project. (2014). An introduction to the TRU Math document suite . Berkeley, CA & E. Lansing, MI: Graduate School of Education, University of California, Berkeley & College of Education, Michigan State University. Retrieved from: http://ats.berkeley.edu/tools.html

Schreier, M. (2012). Qualitative content analysis in practice . London: SAGE.

Snyder, H. (2019). Literature review as a research methodology: An overview and guidelines. Journal of Business Research, 104 , 333–339. https://doi.org/10.1016/j.jbusres.2019.07.039

Stone, C. A. (1998). Should we salvage the scaffolding metaphor? Journal of Learning Disabilities, 31 (4), 409–413. https://doi.org/10.1177/002221949803100411

Stylianou, D. A. (2010). Teachers’ conceptions of representation in middle school mathematics. Journal of Mathematics Teacher Education, 13 (4), 325–343. https://doi.org/10.1007/s10857-010-9143-y

Sweller, J., Van Merrienboer, J. J. G., & Paas, F. (2019). Cognitive architecture and instructional design: 20 years later. Educational Psychology Review, 31 (2), 261–292. https://doi.org/10.1007/s10648-019-09465-5

Sztajn, P., Borko, H., & Smith, T. (2017). Research on mathematics professional development. In J. Cai (Ed.), Compendium for research in mathematics education (Chapter 29, pp. 213–243). Reston, VA: National Council of Teachers of Mathematics.

Tobin, G. A., & Begley, C. M. (2004). Methodological rigor within a qualitative framework. Journal of Advanced Nursing, 48 , 388–396. https://doi.org/10.1111/j.1365-2648.2004.03207.x

Torraco, R. J. (2005). Writing integrative literature reviews: Guidelines and examples. Human Resource Development Review, 4 (3), 356–367. https://doi.org/10.1177/1534484305278283

Trouche, L., Gueudet, G., & Pepin, B. (2018). Documentational approach to didactics. In S. Lerman (Ed.), Encyclopedia of mathematics education. Cham: Springer. https://doi.org/10.1007/978-3-319-77487-9_100011-1

Trouche, L., Rocha, K., Gueudet, G., & Pepin, B. (2020). Transition to digital resources as a critical process in teachers’ trajectories: The case of Anna’s documentation work. ZDM Mathematics Education, 52 (7), 1243–1257. https://doi.org/10.1007/s11858-020-01164-8

Vale, I., & Barbosa, A. (2018). Mathematical problems: The advantages of visual strategies. Journal of the European Teacher Education Network, 13 , 23–33.

Vale, I., Pimentel, T., & Barbosa, A. (2018). The power of seeing in problem solving and creativity: An issue under discussion. In S. Carreira, N. Amado, & K. Jones (Eds.), Broadening the scope of research on mathematical problem-solving: A focus on technology, creativity and affect (pp. 243–272). Switzerland: Springer.

van Garderen, D., Scheuermann, A., Sadler, K., Hopkins, S., & Hirt, S. M. (2021). Preparing pre-service teachers to use visual representations as strategy to solve mathematics problems: What did they learn? Teacher Education and Special Education, 44 (4), 319–339. https://doi.org/10.1177/0888406421996070

Voskoglou, M. (2021). Problem solving and mathematical modelling. American Journal of Educational Research, 9 (2), 85–90. https://doi.org/10.12691/education-9-2-6

Vygotsky, L. S. (1978). Mind in society . Cambridge, MA: Harvard University Press.

Zahner, D., & Corter, J. E. (2010). The process of probability problem solving: Use of external visual representations. Mathematical Thinking and Learning, 12 (2), 177–204. https://doi.org/10.1080/10986061003654240

Zhang, J. (1997). The nature of external representations in problem solving. Cognitive Science, 21 (2), 179–217. https://doi.org/10.1207/s15516709cog2102_3

Download references

Acknowledgements

We would like to acknowledge and thank the teachers and students involved in the research.

Open Access funding enabled and organized by CAUL and its Member Institutions The study was financially supported by James Cook University Higher degree by research grant.

Author information

Authors and affiliations.

College of Arts, Society and Education, James Cook University, Cairns, Australia

Musarurwa David Chinofunga, Philemon Chigeza & Subhashni Taylor

You can also search for this author in PubMed   Google Scholar

Contributions

David: developed original idea, completed literature review, data analysis and authored the first draft of the article (80%). Philemon and Subhashni contributed to the data analysis, coherence of ideas and editing of the article (10% each).

Corresponding author

Correspondence to Musarurwa David Chinofunga .

Ethics declarations

Ethics approval.

This research was approved by the Human Research Ethics Committee, James Cook University (Approval Number H8201).

Informed consent

Informed consent was sought from all participants in accordance with the above ethics approval conditions. Before seeking consent from participants, permission was first obtained from the Queensland Department of Education and school principals of participating schools. The information sheets and consent forms were sent to participating mathematics teachers. An information sheet and consent form for students to share their artifacts was send through their teacher and consent was obtained directly from them as young adults (17–18 years). Consent forms and the data collected has been deidentified to protect participants and stored in the university repository.

Conflict of interest

The authors declare no competing interests.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

A research report which is part of a PhD study by the first author who is an experienced high school mathematics teacher in Queensland, Australia. The second and third authors are primary and secondary advisors respectively. Correspondence concerning this article should be addressed to David Chinofunga, College of Arts, Society and Education, Nguma-bada Campus, Smithfield, Building A4, Cairns, PO Box 6811 Cairns QLD 4870, Australia.

Appendix 1 An approach to problem solving and mathematical modelling

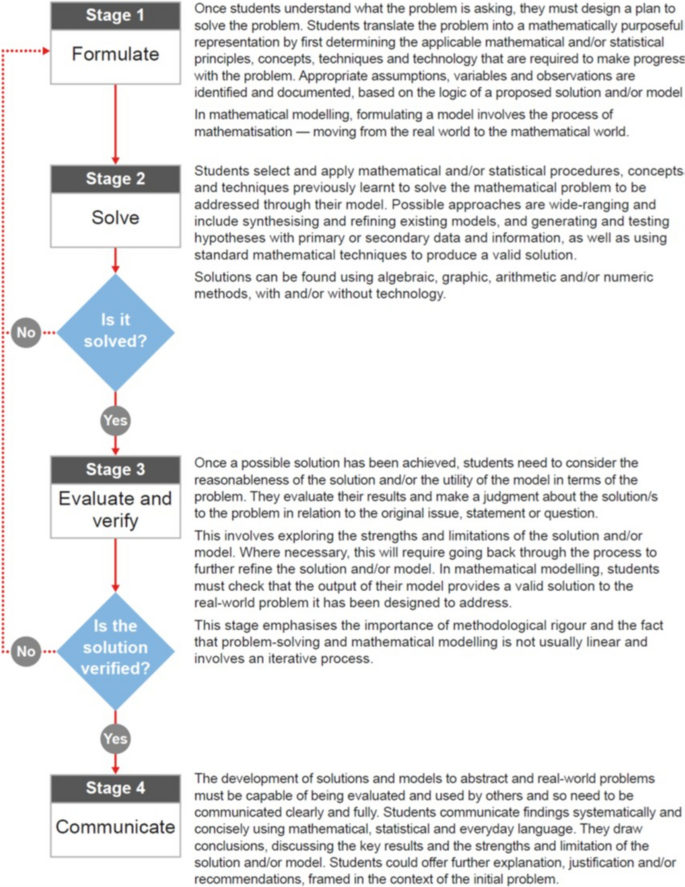
Appendix 2 Phases three and four thematic analysis themes

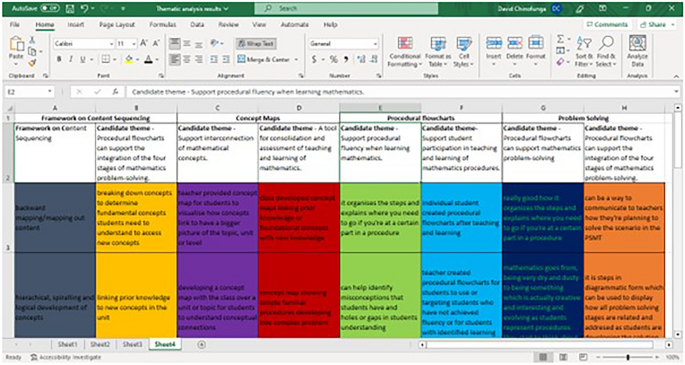
Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Chinofunga, M.D., Chigeza, P. & Taylor, S. How can procedural flowcharts support the development of mathematics problem-solving skills?. Math Ed Res J (2024). https://doi.org/10.1007/s13394-024-00483-3

Download citation

Received : 09 February 2023

Revised : 28 November 2023

Accepted : 06 January 2024

Published : 22 February 2024

DOI : https://doi.org/10.1007/s13394-024-00483-3

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Problem solving
• Procedural flowcharts
• Problem-solving stages
• Solution planning
• Visual representation
• Find a journal
• Publish with us
• Track your research

• System Design Tutorial
• What is System Design
• System Design Life Cycle
• High Level Design HLD
• Low Level Design LLD
• Design Patterns
• UML Diagrams
• System Design Interview Guide
• Crack System Design Round
• System Design Bootcamp
• System Design Interview Questions
• Microservices
• Scalability

An introduction to Flowcharts

• What is a Flowchart and its Types?
• Creating Interactive Plots with R and Highcharts
• Interactive Bubble Chart in R
• Charts.js Introduction
• RAPTOR Tool - A Flowchart Interpreter
• Introduction to Graphs | Class 8 Maths
• Python | Bar Charts in Vincent
• Pygal Introduction
• Introduction of Algorithmic State Machines (ASMs)
• Introduction to Matplotlib
• Flowchart for basic Machine Learning models
• Charts.js Installation Guide
• Dual Combination Chart in Tableau
• Data Visualization with Highcharter in R
• Short Note on Gantt Chart
• Gantt Chart in Tableau
• How to build Animated Charts like Hans Rosling
• How to Make a Gantt Chart in Excel
• Power BI - Cluster Bar and Column Charts

What is a Flowchart?   Flowchart is a graphical representation of an algorithm. Programmers often use it as a program-planning tool to solve a problem. It makes use of symbols which are connected among them to indicate the flow of information and processing.  The process of drawing a flowchart for an algorithm is known as “flowcharting”. 

Basic Symbols used in Flowchart Designs

• Terminal: The oval symbol indicates Start, Stop and Halt in a program’s logic flow. A pause/halt is generally used in a program logic under some error conditions. Terminal is the first and last symbols in the flowchart.   

• Input/Output: A parallelogram denotes any function of input/output type. Program instructions that take input from input devices and display output on output devices are indicated with parallelogram in a flowchart.   

• Processing: A box represents arithmetic instructions. All arithmetic processes such as adding, subtracting, multiplication and division are indicated by action or process symbol.   

• Decision Diamond symbol represents a decision point. Decision based operations such as yes/no question or true/false are indicated by diamond in flowchart.   

• Connectors: Whenever flowchart becomes complex or it spreads over more than one page, it is useful to use connectors to avoid any confusions. It is represented by a circle.   

• Flow lines: Flow lines indicate the exact sequence in which instructions are executed. Arrows represent the direction of flow of control and relationship among different symbols of flowchart. 

Rules For Creating Flowchart :

A flowchart is a graphical representation of an algorithm.it should follow some rules while creating a flowchart Rule 1: Flowchart opening statement must be ‘start’ keyword. Rule 2:  Flowchart ending statement must be ‘end’ keyword. Rule 3: All symbols in the flowchart must be connected with an arrow line. Rule 4: The decision symbol in the flowchart is associated with the arrow line.  

Advantages of Flowchart:

• Flowcharts are a better way of communicating the logic of the system.
• Flowcharts act as a guide for blueprint during program designed.
• Flowcharts help in debugging process.
• With the help of flowcharts programs can be easily analyzed.
• It provides better documentation.
• Flowcharts serve as a good proper documentation.
• Easy to trace errors in the software.
• Easy to understand.
• The flowchart can be reused for inconvenience in the future.
• It helps to provide correct logic.  

Disadvantages of Flowchart:

• It is difficult to draw flowcharts for large and complex programs.
• There is no standard to determine the amount of detail.
• Difficult to reproduce the flowcharts.
• It is very difficult to modify the Flowchart.
• Making a flowchart is costly.
• Some developer thinks that it is waste of time.
• It makes software processes low.
• If changes are done in software, then the flowchart must be redrawn  

Example : Draw a flowchart to input two numbers from the user and display the largest of two numbers    

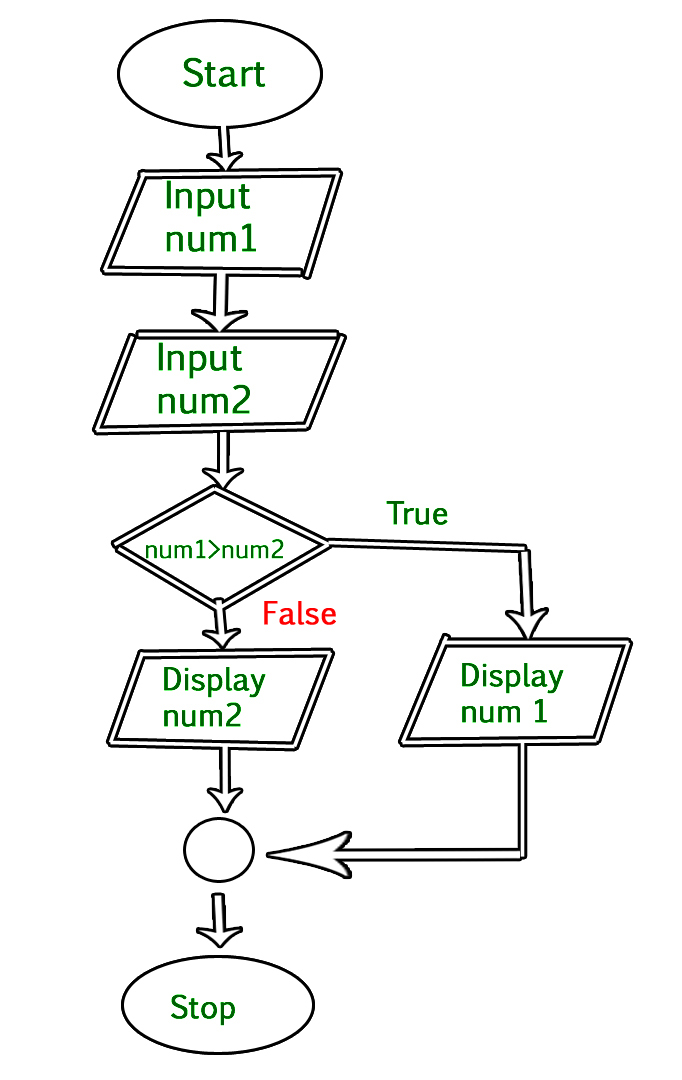
References:   Computer Fundamentals by Pradeep K. Sinha and Priti Sinha  

Please Login to comment...

Similar reads.

• CBSE - Class 11
• school-programming
• Design Pattern
• School Programming
• System Design
• Technical Scripter

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Problem-solving – Flowchart example

The flowchart starts with identifying a problem. After the problem is identified, data is gathered and analyzed. Then, the solution is developed and the best solution is identified. If it isn’t successful, the solution development process starts again. If successful, the plan is implemented and is improved continuously.

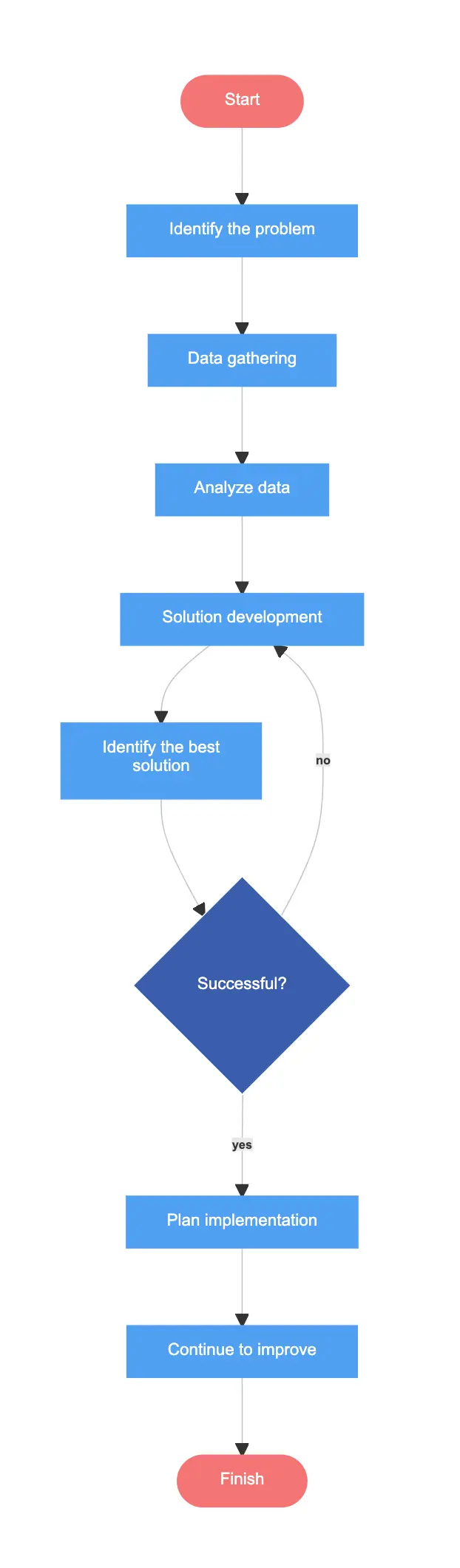
Edit this diagram in Gleek

Problem-Solving diagram code in Gleek

Start:queue Identify the problem Data gathering Analyze data Solution development Identify the best solution Successful?:diamond Plan implementation Continue to improve Finish:queue Start–>Identify the problem Identify the problem–>Data gathering Data gathering–>Analyze data Analyze data–>Solution development Solution development–>Identify the best solution Identify the best solution–>Successful? Successful?-no->Solution development Successful?-yes->Plan implementation Plan implementation–>Continue to improve Continue to improve–>Finish

About Flowcharts

A flowchart, or flow chart, is a type of diagram that shows a step-by-step view of a process. Flowcharts document the tasks and decisions needed to achieve a specific goal. A basic flowchart is easy to make and understand. Businesses, engineers and software designers often use flowcharts to diagram their ideas.

Similar flowchart examples

Product development flowchart

A/B testing flowchart

Patient transfer in hospital flowchart

Credit card payment process flowchart

Alarm clock flowchart

Mike Taylor

Ask. Learn. Share.

The L&D Detective: Solving Performance Mysteries with Mager’s Flowchart

As an L&D professional, you may feel overwhelmed by the challenges of diagnosing and solving performance problems in your organization. Fortunately, there’s a powerful tool that can guide you through this process: Mager’s Performance Consulting Flowchart. In this blog post, we’ll break down Mager’s flowchart, explain why it’s so helpful, and highlight the benefits of using it in your L&D practice.

This flow chart comes from Mager & Pipe’s book “ Analyzing Performance Problems: Or, You Really Oughta Wanna–How to Figure out Why People Aren’t Doing What They Should Be, and What to do About It “. One of the most important things this flow chart does is to emphasize the importance of identifying non-training solutions before considering training as a solution.

What is Mager’s Performance Consulting Flowchart?

This Performance Consulting Flowchart, developed by Robert F. Mager and Peter Pipe, is a widely used step-by-step guide that helps L&D professionals diagnose performance issues and determine the most effective solutions. This structured approach allows you to systematically analyze performance gaps, identify the root causes of performance problems, and decide whether training or other interventions are needed to improve performance.

The Steps in Mager’s Flowchart

• Determine if there is a gap between expected performance and actual performance. This involves observing employees, collecting performance data, and comparing it to the desired standards.
• Assess the impact of the performance problem. If the gap significantly affects the organization’s goals or operations, it’s worth addressing. If not, it might be better to focus on more critical issues.
• Look for quick and simple solutions that can immediately improve performance. These “fast fixes” can provide temporary relief while you work on more comprehensive solutions.
• Identify any barriers preventing optimal performance. These could be environmental factors, lack of resources, or systemic issues within the organization.
• Determine if the performance problem is due to a lack of skills or knowledge. If employees don’t have the necessary competencies, training or development programs may be needed.
• Examine whether there are appropriate incentives and consequences linked to performance. This includes rewards for good performance and penalties for poor performance.
• Ensure that employees receive regular and constructive feedback on their performance. Feedback helps employees understand how they are doing and where they can improve.
• Verify that performance expectations are clearly communicated. Employees need to know what is expected of them and what standards they should meet.

Why Use Mager’s Flowchart?

Mager’s flowchart is a game-changer for L&D professionals because it provides a systematic, data-driven approach to problem-solving. By following the flowchart, you can:

• Identify the root causes of performance issues
• Determine whether training or other interventions are needed
• Make informed decisions backed by evidence
• Communicate clearly with stakeholders
• Enhance your credibility as a strategic problem-solver

A crucial point to remember is that not all performance gaps can be addressed by training. It’s essential to recognize when training is not the appropriate solution and avoid sending training to do a job it’s not capable of.

Mager’s flowchart helps you make this distinction, ensuring that you choose the most effective intervention for each situation.

For example, let’s say a sales team is struggling to meet its quarterly targets. By using Mager’s flowchart, an L&D professional might discover that the issue isn’t a lack of skills, but rather a lack of clear performance expectations and feedback. By addressing these root causes, the team’s performance could significantly improve without the need for additional training.

Using Mager’s flowchart consistently can lead to:

• Improved employee performance
• Cost-effective solutions that save time and resources
• Increased accountability and motivation among employees
• Greater trust and collaboration with stakeholders

Mager’s Performance Consulting Flowchart is an invaluable tool for L&D professionals, especially those new to the field. By providing a structured, logical approach to diagnosing and solving performance problems, it ensures that you can deliver effective, targeted interventions that drive real improvements in your organization.

Remember, not all performance issues require training. By using Mager’s flowchart, you’ll be able to identify when training is the right solution and when other interventions are more appropriate. This will help you avoid the costly mistake of sending training to do a job it’s not suited for, and instead focus on implementing solutions that directly address the root causes of performance gaps.

Embrace Mager’s flowchart, and you’ll be well on your way to becoming a trusted, partner your organization.

Share this:

• Click to share on LinkedIn (Opens in new window)
• Click to share on Twitter (Opens in new window)
• Click to share on Pinterest (Opens in new window)
• Click to share on Pocket (Opens in new window)
• Click to share on Facebook (Opens in new window)
• Click to email a link to a friend (Opens in new window)
• Click to print (Opens in new window)

Published by Mike Taylor

Born with a life-long passion for learning, I have the great fortune to work at the intersection of learning, design, technology & collaboration. View more posts

Leave a comment Cancel reply

This site uses Akismet to reduce spam. Learn how your comment data is processed .

• Already have a WordPress.com account? Log in now.
• Subscribe Subscribed
• Copy shortlink
• Report this content
• View post in Reader
• Manage subscriptions
• Collapse this bar