relationship between thinking and problem solving

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

7 Thinking, Language, and Problem Solving

What is the best way to solve a problem? How does a person who has never seen or touched snow in real life develop an understanding of the concept of snow? How do young children acquire the ability to learn language with no formal instruction? Psychologists who study thinking explore questions like these and are called cognitive psychologists.

In other chapters, we discussed the cognitive processes of perception, learning, and memory. In this chapter, we will focus on high-level cognitive processes. As a part of this discussion, we will consider thinking and briefly explore the development and use of language. We will also discuss problem solving and creativity. After finishing this chapter, you will have a greater appreciation of the higher-level cognitive processes that contribute to our distinctiveness as a species.

Table of Contents

7.1 What is Cognition? 7.2 Language 7.3 Problem Solving

7.1 What is Cognition?

Learning Objectives

By the end of this section, you will be able to:

• Describe cognition
• Distinguish concepts and prototypes
• Explain the difference between natural and artificial concepts
• Describe how schemata are organized and constructed

Imagine all of your thoughts as if they were physical entities, swirling rapidly inside your mind. How is it possible that the brain is able to move from one thought to the next in an organized, orderly fashion? The brain is endlessly perceiving, processing, planning, organizing, and remembering—it is always active. Yet, you don’t notice most of your brain’s activity as you move throughout your daily routine. This is only one facet of the complex processes involved in cognition . Simply put,  cognition  is thinking, and it encompasses the processes associated with perception, knowledge, problem solving, judgment, language, and memory. Scientists who study cognition are searching for ways to understand how we integrate, organize, and utilize our conscious cognitive experiences without being aware of all of the unconscious work that our brains are doing (for example, Kahneman, 2011).

Upon waking each morning, you begin thinking—contemplating the tasks that you must complete that day. In what order should you run your errands? Should you go to the bank, the cleaners, or the grocery store first? Can you get these things done before you head to class or will they need to wait until school is done? These thoughts are one example of cognition at work. Exceptionally complex, cognition is an essential feature of human consciousness, yet not all aspects of cognition are consciously experienced.

Cognitive psychology  is the field of psychology dedicated to examining how people think. It attempts to explain how and why we think the way we do by studying the interactions among human thinking, emotion, creativity, language, and problem solving, in addition to other cognitive processes. Cognitive psychologists strive to determine and measure different types of intelligence, why some people are better at problem solving than others, and how emotional intelligence affects success in the workplace, among countless other topics. They also sometimes focus on how we organize thoughts and information gathered from our environments into meaningful categories of thought, which will be discussed later.

Concepts and Prototypes

The human nervous system is capable of handling endless streams of information. The senses serve as the interface between the mind and the external environment, receiving stimuli and translating it into nervous impulses that are transmitted to the brain. The brain then processes this information and uses the relevant pieces to create thoughts, which can then be expressed through language or stored in memory for future use. To make this process more complex, the brain does not gather information from external environments only. When thoughts are formed, the mind synthesizes information from emotions and memories ( Figure 7.2 ). Emotion and memory are powerful influences on both our thoughts and behaviors.

Concepts are informed by our semantic memory (you will learn more about semantic memory in a later chapter) and are present in every aspect of our lives; however, one of the easiest places to notice concepts is inside a classroom, where they are discussed explicitly. When you study United States history, for example, you learn about more than just individual events that have happened in America’s past. You absorb a large quantity of information by listening to and participating in discussions, examining maps, and reading first-hand accounts of people’s lives. Your brain analyzes these details and develops an overall understanding of American history. In the process, your brain gathers details that inform and refine your understanding of related concepts like democracy, power, and freedom.

Concepts can be complex and abstract, like justice, or more concrete, like types of birds. Some concepts, like tolerance, are agreed upon by many people, because they have been used in various ways over many years. Other concepts, like the characteristics of your ideal friend or your family’s birthday traditions, are personal and individualized. In this way, concepts touch every aspect of our lives, from our many daily routines to the guiding principles behind the way governments function.

Another technique used by your brain to organize information is the identification of prototypes for the concepts you have developed. A  prototype  is the best example or representation of a concept. For example, what comes to your mind when you think of a dog? Most likely your early experiences with dogs will shape what you imagine. If your first pet was a Golden Retriever, there is a good chance that this would be your prototype for the category of dogs.

Natural and Artificial Concepts

In psychology, concepts can be divided into two categories, natural and artificial. Natural concepts  are created “naturally” through your experiences and can be developed from either direct or indirect experiences. For example, if you live in Essex Junction, Vermont, you have probably had a lot of direct experience with snow. You’ve watched it fall from the sky, you’ve seen lightly falling snow that barely covers the windshield of your car, and you’ve shoveled out 18 inches of fluffy white snow as you’ve thought, “This is perfect for skiing.” You’ve thrown snowballs at your best friend and gone sledding down the steepest hill in town. In short, you know snow. You know what it looks like, smells like, tastes like, and feels like. If, however, you’ve lived your whole life on the island of Saint Vincent in the Caribbean, you may never have actually seen snow, much less tasted, smelled, or touched it. You know snow from the indirect experience of seeing pictures of falling snow—or from watching films that feature snow as part of the setting. Either way, snow is a natural concept because you can construct an understanding of it through direct observations, experiences with snow, or indirect knowledge (such as from films or books) ( Figure 7.3 ).

An  artificial concept , on the other hand, is a concept that is defined by a specific set of characteristics. Various properties of geometric shapes, like squares and triangles, serve as useful examples of artificial concepts. A triangle always has three angles and three sides. A square always has four equal sides and four right angles. Mathematical formulas, like the equation for area (length × width) are artificial concepts defined by specific sets of characteristics that are always the same. Artificial concepts can enhance the understanding of a topic by building on one another. For example, before learning the concept of “area of a square” (and the formula to find it), you must understand what a square is. Once the concept of “area of a square” is understood, an understanding of area for other geometric shapes can be built upon the original understanding of area. The use of artificial concepts to define an idea is crucial to communicating with others and engaging in complex thought. According to Goldstone and Kersten (2003), concepts act as building blocks and can be connected in countless combinations to create complex thoughts.

A  schema (plural: schemata)  is a mental construct consisting of a cluster or collection of related concepts (Bartlett, 1932). There are many different types of schemata, and they all have one thing in common: schemata are a method of organizing information that allows the brain to work more efficiently. When a schema is activated, the brain makes immediate assumptions about the person or object being observed.

There are several types of schemata. A  role schema  makes assumptions about how individuals in certain roles will behave (Callero, 1994). For example, imagine you meet someone who introduces himself as a firefighter. When this happens, your brain automatically activates the “firefighter schema” and begins making assumptions that this person is brave, selfless, and community-oriented. Despite not knowing this person, already you have unknowingly made judgments about him. Schemata also help you fill in gaps in the information you receive from the world around you. While schemata allow for more efficient information processing, there can be problems with schemata, regardless of whether they are accurate: Perhaps this particular firefighter is not brave, he just works as a firefighter to pay the bills while studying to become a children’s librarian.

An  event schema , also known as a  cognitive script , is a set of behaviors that can feel like a routine. Think about what you do when you walk into an elevator ( Figure 7.4 ). First, the doors open and you wait to let exiting passengers leave the elevator car. Then, you step into the elevator and turn around to face the doors, looking for the correct button to push. You never face the back of the elevator, do you? And when you’re riding in a crowded elevator and you can’t face the front, it feels uncomfortable, doesn’t it? Interestingly, event schemata can vary widely among different cultures and countries. For example, while it is quite common for people to greet one another with a handshake in the United States, in Tibet, you greet someone by sticking your tongue out at them, and in Belize, you bump fists (Cairns Regional Council, n.d.)

Because event schemata are automatic, they can be difficult to change. Imagine that you are driving home from work or school. This event schema involves getting in the car, shutting the door, and buckling your seatbelt before putting the key in the ignition. You might perform this script two or three times each day. As you drive home, you hear your phone’s ring tone. Typically, the event schema that occurs when you hear your phone ringing involves locating the phone and answering it or responding to your latest text message. So without thinking, you reach for your phone, which could be in your pocket, in your bag, or on the passenger seat of the car. This powerful event schema is informed by your pattern of behavior and the pleasurable stimulation that a phone call or text message gives your brain. Because it is a schema, it is extremely challenging for us to stop reaching for the phone, even though we know that we endanger our own lives and the lives of others while we do it (Neyfakh, 2013) ( Figure 7.5 ).

Remember the elevator? It feels almost impossible to walk in and  not  face the door. Our powerful event schema dictates our behavior in the elevator, and it is no different with our phones. Current research suggests that it is the habit, or event schema, of checking our phones in many different situations that makes refraining from checking them while driving especially difficult (Bayer & Campbell, 2012). Because texting and driving has become a dangerous epidemic in recent years, psychologists are looking at ways to help people interrupt the “phone schema” while driving. Event schemata like these are the reason why many habits are difficult to break once they have been acquired. As we continue to examine thinking, keep in mind how powerful the forces of concepts and schemata are to our understanding of the world.

7.2 LAnguage

• Define language and demonstrate familiarity with the components of language
• Understand the development of language
• Explain the relationship between language and thinking

Language  is a communication system that involves using words and systematic rules to organize those words to transmit information from one individual to another. While language is a form of communication, not all communication is language. Many species communicate with one another through their postures, movements, odors, or vocalizations. This communication is crucial for species that need to interact and develop social relationships with their conspecifics. However, many people have asserted that it is language that makes humans unique among all of the animal species (Corballis & Suddendorf, 2007; Tomasello & Rakoczy, 2003). This section will focus on what distinguishes language as a special form of communication, how the use of language develops, and how language affects the way we think.

Components of Language

Language, be it spoken, signed, or written, has specific components: a lexicon and lexicon grammar .  Lexicon  refers to the words of a given language. Thus, lexicon is a language’s vocabulary.  Grammar  refers to the set of rules that are used to convey meaning through the use of the lexicon (Fernández & Cairns, 2011). For instance, English grammar dictates that most verbs receive an “-ed” at the end to indicate past tense.

Words are formed by combining the various phonemes that make up the language. A  phoneme  (e.g., the sounds “ah” vs. “eh”) is a basic sound unit of a given language, and different languages have different sets of phonemes. For example, the phoneme English speakers associate with the letter ‘L’ is not used in the Japanese language. Similarly, many Southern African languages use phonemes, sometimes referred to as ‘click consonants’ that are not used in English.

Phonemes are combined to form  morphemes , which are the smallest units of language that convey some type of meaning. Some words are morphemes, but not all morphemes are words.  For example, “-ed” is a morpheme used to convey the past-tense in English, but it is not a word. The word “review” contains two morphemes: re- (meaning to do something again) and view (to see). Finally, some words like “I” and “a” are both a phonemes and morphemes.

We use semantics and syntax to construct language. Semantics and syntax are part of a language’s grammar.  Semantics  refers to the process by which we derive meaning from morphemes and words by connecting those morphemes and words to stored concepts.  Syntax  refers to the way words are organized into sentences (Chomsky, 1965; Fernández & Cairns, 2011). For example, you would never say “the dog walked I today” to let someone know you took your dog for a walk–that sentence does not obey English syntax and is therefore difficult to make sense of.

We apply the rules of grammar to organize the lexicon in novel and creative ways, which allow us to communicate information about both concrete and abstract concepts. We can talk about our immediate and observable surroundings as well as the surface of unseen planets. We can share our innermost thoughts, our plans for the future, and debate the value of a college education. We can provide detailed instructions for cooking a meal, fixing a car, or building a fire. Through our use of words and language, we are able to form, organize, and express ideas, schema, and artificial concepts.

Language Development

Given the remarkable complexity of a language, one might expect that mastering a language would be an especially arduous task; indeed, for those of us trying to learn a second language as adults, this might seem to be true. However, young children master language very quickly with relative ease. B. F.  Skinner  (1957) proposed that language is learned through reinforcement. Noam  Chomsky  (1965) criticized this behaviorist approach, asserting instead that the mechanisms underlying language acquisition are biologically determined. The use of language develops in the absence of formal instruction and appears to follow a very similar pattern in children from vastly different cultures and backgrounds. It would seem, therefore, that we are born with a biological predisposition to acquire a language (Chomsky, 1965; Fernández & Cairns, 2011). Moreover, it appears that there is a critical period for language acquisition, such that this proficiency at acquiring language is maximal early in life; generally, as people age, the ease with which they acquire and master new languages diminishes (Johnson & Newport, 1989; Lenneberg, 1967; Singleton, 1995).

Children begin to learn about language from a very early age ( Table 7.1 ). In fact, it appears that this is occurring even before we are born. Newborns show preference for their mother’s voice and appear to be able to discriminate between the language spoken by their mother and other languages. Babies are also attuned to the languages being used around them and show preferences for videos of faces that are moving in synchrony with the audio of spoken language versus videos that do not synchronize with the audio (Blossom & Morgan, 2006; Pickens, 1994; Spelke & Cortelyou, 1981).

DIG DEEPER: The Case of Genie

In the fall of 1970, a social worker in the Los Angeles area found a 13-year-old girl who was being raised in extremely neglectful and abusive conditions. The girl, who came to be known as Genie, had lived most of her life tied to a potty chair or confined to a crib in a small room that was kept closed with the curtains drawn. For a little over a decade, Genie had virtually no social interaction and no access to the outside world. As a result of these conditions, Genie was unable to stand up, chew solid food, or speak (Fromkin, Krashen, Curtiss, Rigler, & Rigler, 1974; Rymer, 1993). The police took Genie into protective custody.

Genie’s abilities improved dramatically following her removal from her abusive environment, and early on, it appeared she was acquiring language—much later than would be predicted by critical period hypotheses that had been posited at the time (Fromkin et al., 1974). Genie managed to amass an impressive vocabulary in a relatively short amount of time. However, she never developed a mastery of the grammatical aspects of language (Curtiss, 1981). Perhaps being deprived of the opportunity to learn language during a critical period impeded Genie’s ability to fully acquire and use language.

You may recall that each language has its own set of phonemes that are used to generate morphemes, words, and so on. Babies can discriminate among the sounds that make up a language (for example, they can tell the difference between the “s” in vision and the “ss” in fission); early on, they can differentiate between the sounds of all human languages, even those that do not occur in the languages that are used in their environments. However, by the time that they are about 1 year old, they can only discriminate among those phonemes that are used in the language or languages in their environments (Jensen, 2011; Werker & Lalonde, 1988; Werker & Tees, 1984).

After the first few months of life, babies enter what is known as the babbling stage, during which time they tend to produce single syllables that are repeated over and over. As time passes, more variations appear in the syllables that they produce. During this time, it is unlikely that the babies are trying to communicate; they are just as likely to babble when they are alone as when they are with their caregivers (Fernández & Cairns, 2011). Interestingly, babies who are raised in environments in which sign language is used will also begin to show babbling in the gestures of their hands during this stage (Petitto, Holowka, Sergio, Levy, & Ostry, 2004).

Generally, a child’s first word is uttered sometime between the ages of 1 year to 18 months, and for the next few months, the child will remain in the “one word” stage of language development. During this time, children know a number of words, but they only produce one-word utterances. The child’s early vocabulary is limited to familiar objects or events, often nouns. Although children in this stage only make one-word utterances, these words often carry larger meaning (Fernández & Cairns, 2011). So, for example, a child saying “cookie” could be identifying a cookie or asking for a cookie.

As a child’s lexicon grows, she begins to utter simple sentences and to acquire new vocabulary at a very rapid pace. In addition, children begin to demonstrate a clear understanding of the specific rules that apply to their language(s). Even the mistakes that children sometimes make provide evidence of just how much they understand about those rules. This is sometimes seen in the form of  overgeneralization . In this context, overgeneralization refers to an extension of a language rule to an exception to the rule. For example, in English, it is usually the case that an “s” is added to the end of a word to indicate plurality. For example, we speak of one dog versus two dogs. Young children will overgeneralize this rule to cases that are exceptions to the “add an s to the end of the word” rule and say things like “those two gooses” or “three mouses.” Clearly, the rules of the language are understood, even if the exceptions to the rules are still being learned (Moskowitz, 1978).

Language and Thought

When we speak one language, we agree that words are representations of ideas, people, places, and events. The given language that children learn is connected to their culture and surroundings. But can words themselves shape the way we think about things? Psychologists have long investigated the question of whether language shapes thoughts and actions, or whether our thoughts and beliefs shape our language. Two researchers, Edward Sapir and Benjamin Lee Whorf, began this investigation in the 1940s. They wanted to understand how the language habits of a community encourage members of that community to interpret language in a particular manner (Sapir, 1941/1964). Sapir and Whorf proposed that language determines thought. For example, in some languages there are many different words for love. However, in English we use the word love for all types of love. Does this affect how we think about love depending on the language that we speak (Whorf, 1956)? Researchers have since identified this view as too absolute, pointing out a lack of empiricism behind what Sapir and Whorf proposed (Abler, 2013; Boroditsky, 2011; van Troyer, 1994). Today, psychologists continue to study and debate the relationship between language and thought.

WHAT DO YOU THINK? The Meaning of Language

Think about what you know of other languages; perhaps you even speak multiple languages. Imagine for a moment that your closest friend fluently speaks more than one language. Do you think that friend thinks differently, depending on which language is being spoken? You may know a few words that are not translatable from their original language into English. For example, the Portuguese word  saudade  originated during the 15th century, when Portuguese sailors left home to explore the seas and travel to Africa or Asia. Those left behind described the emptiness and fondness they felt as  saudade  ( Figure 7.6 ) .  The word came to express many meanings, including loss, nostalgia, yearning, warm memories, and hope. There is no single word in English that includes all of those emotions in a single description. Do words such as  saudade  indicate that different languages produce different patterns of thought in people? What do you think??

One group of researchers who wanted to investigate how language influences thought compared how English speakers and the Dani people of Papua New Guinea think and speak about color. The Dani have two words for color: one word for  light  and one word for  dark . In contrast, the English language has 11 color words. Researchers hypothesized that the number of color terms could limit the ways that the Dani people conceptualized color. However, the Dani were able to distinguish colors with the same ability as English speakers, despite having fewer words at their disposal (Berlin & Kay, 1969). A recent review of research aimed at determining how language might affect something like color perception suggests that language can influence perceptual phenomena, especially in the left hemisphere of the brain. You may recall from earlier chapters that the left hemisphere is associated with language for most people. However, the right (less linguistic hemisphere) of the brain is less affected by linguistic influences on perception (Regier & Kay, 2009)

7.3 Problem Solving

• Describe problem solving strategies
• Define algorithm and heuristic
• Explain some common roadblocks to effective problem solving and decision making

People face problems every day—usually, multiple problems throughout the day. Sometimes these problems are straightforward: To double a recipe for pizza dough, for example, all that is required is that each ingredient in the recipe be doubled. Sometimes, however, the problems we encounter are more complex. For example, say you have a work deadline, and you must mail a printed copy of a report to your supervisor by the end of the business day. The report is time-sensitive and must be sent overnight. You finished the report last night, but your printer will not work today. What should you do? First, you need to identify the problem and then apply a strategy for solving the problem.

Problem-Solving Strategies

When you are presented with a problem—whether it is a complex mathematical problem or a broken printer, how do you solve it? Before finding a solution to the problem, the problem must first be clearly identified. After that, one of many problem solving strategies can be applied, hopefully resulting in a solution.

A  problem-solving strategy  is a plan of action used to find a solution. Different strategies have different action plans associated with them ( Table 7.2 ). For example, a well-known strategy is  trial and error . The old adage, “If at first you don’t succeed, try, try again” describes trial and error. In terms of your broken printer, you could try checking the ink levels, and if that doesn’t work, you could check to make sure the paper tray isn’t jammed. Or maybe the printer isn’t actually connected to your laptop. When using trial and error, you would continue to try different solutions until you solved your problem. Although trial and error is not typically one of the most time-efficient strategies, it is a commonly used one.

Another type of strategy is an algorithm. An  algorithm  is a problem-solving formula that provides you with step-by-step instructions used to achieve a desired outcome (Kahneman, 2011). You can think of an algorithm as a recipe with highly detailed instructions that produce the same result every time they are performed. Algorithms are used frequently in our everyday lives, especially in computer science. When you run a search on the Internet, search engines like Google use algorithms to decide which entries will appear first in your list of results. Facebook also uses algorithms to decide which posts to display on your newsfeed. Can you identify other situations in which algorithms are used?

A heuristic is another type of problem solving strategy. While an algorithm must be followed exactly to produce a correct result, a  heuristic  is a general problem-solving framework (Tversky & Kahneman, 1974). You can think of these as mental shortcuts that are used to solve problems. A “rule of thumb” is an example of a heuristic. Such a rule saves the person time and energy when making a decision, but despite its time-saving characteristics, it is not always the best method for making a rational decision. Different types of heuristics are used in different types of situations, but the impulse to use a heuristic occurs when one of five conditions is met (Pratkanis, 1989):

• When one is faced with too much information
• When the time to make a decision is limited
• When the decision to be made is unimportant
• When there is access to very little information to use in making the decision
• When an appropriate heuristic happens to come to mind in the same moment

Working backwards  is a useful heuristic in which you begin solving the problem by focusing on the end result. Consider this example: You live in Washington, D.C. and have been invited to a wedding at 4 PM on Saturday in Philadelphia. Knowing that Interstate 95 tends to back up any day of the week, you need to plan your route and time your departure accordingly. If you want to be at the wedding service by 3:30 PM, and it takes 2.5 hours to get to Philadelphia without traffic, what time should you leave your house? You use the working backwards heuristic to plan the events of your day on a regular basis, probably without even thinking about it.

Another useful heuristic is the practice of accomplishing a large goal or task by breaking it into a series of smaller steps. Students often use this common method to complete a large research project or long essay for school. For example, students typically brainstorm, develop a thesis or main topic, research the chosen topic, organize their information into an outline, write a rough draft, revise and edit the rough draft, develop a final draft, organize the references list, and proofread their work before turning in the project. The large task becomes less overwhelming when it is broken down into a series of small steps.

EVERYDAY CONNECTION: Solving Puzzles

Problem-solving abilities can improve with practice. Many people challenge themselves every day with puzzles and other mental exercises to sharpen their problem-solving skills. Sudoku puzzles appear daily in most newspapers. Typically, a sudoku puzzle is a 9×9 grid. The simple sudoku below ( Figure 7.7 ) is a 4×4 grid. To solve the puzzle, fill in the empty boxes with a single digit: 1, 2, 3, or 4. Here are the rules: The numbers must total 10 in each bolded box, each row, and each column; however, each digit can only appear once in a bolded box, row, and column. Time yourself as you solve this puzzle and compare your time with a classmate.

Here is another popular type of puzzle ( Figure 7.8 ) that challenges your spatial reasoning skills. Connect all nine dots with four connecting straight lines without lifting your pencil from the paper:

Not all problems are successfully solved, however. What challenges stop us from successfully solving a problem? Albert Einstein once said, “Insanity is doing the same thing over and over again and expecting a different result.” Imagine a person in a room that has four doorways. One doorway that has always been open in the past is now locked. The person, accustomed to exiting the room by that particular doorway, keeps trying to get out through the same doorway even though the other three doorways are open. The person is stuck—but she just needs to go to another doorway, instead of trying to get out through the locked doorway. A  mental set  is where you persist in approaching a problem in a way that has worked in the past but is clearly not working now.

Functional fixedness  is a type of mental set where you cannot perceive an object being used for something other than what it was designed for. Duncker (1945) conducted foundational research on functional fixedness. He created an experiment in which participants were given a candle, a book of matches, and a box of thumbtacks. They were instructed to use those items to attach the candle to the wall so that it did not drip wax onto the table below. Participants had to use functional fixedness to solve the problem ( Figure 7.10 ). During the  Apollo 13  mission to the moon, NASA engineers at Mission Control had to overcome functional fixedness to save the lives of the astronauts aboard the spacecraft. An explosion in a module of the spacecraft damaged multiple systems. The astronauts were in danger of being poisoned by rising levels of carbon dioxide because of problems with the carbon dioxide filters. The engineers found a way for the astronauts to use spare plastic bags, tape, and air hoses to create a makeshift air filter, which saved the lives of the astronauts.

Researchers have investigated whether functional fixedness is affected by culture. In one experiment, individuals from the Shuar group in Ecuador were asked to use an object for a purpose other than that for which the object was originally intended. For example, the participants were told a story about a bear and a rabbit that were separated by a river and asked to select among various objects, including a spoon, a cup, erasers, and so on, to help the animals. The spoon was the only object long enough to span the imaginary river, but if the spoon was presented in a way that reflected its normal usage, it took participants longer to choose the spoon to solve the problem. (German & Barrett, 2005). The researchers wanted to know if exposure to highly specialized tools, as occurs with individuals in industrialized nations, affects their ability to transcend functional fixedness. It was determined that functional fixedness is experienced in both industrialized and nonindustrialized cultures (German & Barrett, 2005).

In order to make good decisions, we use our knowledge and our reasoning. Often, this knowledge and reasoning is sound and solid. Sometimes, however, we are swayed by biases or by others manipulating a situation. For example, let’s say you and three friends wanted to rent a house and had a combined target budget of $1,600. The realtor shows you only very run-down houses for $1,600 and then shows you a very nice house for $2,000. Might you ask each person to pay more in rent to get the $2,000 home? Why would the realtor show you the run-down houses and the nice house? The realtor may be challenging your anchoring bias. An  anchoring bias  occurs when you focus on one piece of information when making a decision or solving a problem. In this case, you’re so focused on the amount of money you are willing to spend that you may not recognize what kinds of houses are available at that price point.

The  confirmation bias  is the tendency to focus on information that confirms your existing beliefs. For example, if you think that your professor is not very nice, you notice all of the instances of rude behavior exhibited by the professor while ignoring the countless pleasant interactions he is involved in on a daily basis.  Hindsight bias  leads you to believe that the event you just experienced was predictable, even though it really wasn’t. In other words, you knew all along that things would turn out the way they did.  Representative bias  describes a faulty way of thinking, in which you unintentionally stereotype someone or something; for example, you may assume that your professors spend their free time reading books and engaging in intellectual conversation, because the idea of them spending their time playing volleyball or visiting an amusement park does not fit in with your stereotypes of professors.

Finally, the  availability heuristic  is a heuristic in which you make a decision based on an example, information, or recent experience that is that readily available to you, even though it may not be the best example to inform your decision .  Biases tend to “preserve that which is already established—to maintain our preexisting knowledge, beliefs, attitudes, and hypotheses” (Aronson, 1995; Kahneman, 2011). These biases are summarized in  Table 7.3 .

Were you able to determine how many marbles are needed to balance the scales in  Figure 7.9 ? You need nine. Were you able to solve the problems in  Figure 7.7  and  Figure 7.8 ? Here are the answers ( Figure 7.11 ).

Chapter Summary

7.1 what is cognition.

In this section, you were introduced to cognitive psychology, which is the study of cognition, or the brain’s ability to think, perceive, plan, analyze, and remember. Concepts and their corresponding prototypes help us quickly organize our thinking by creating categories into which we can sort new information. We also develop schemata, which are clusters of related concepts. Some schemata involve routines of thought and behavior, and these help us function properly in various situations without having to “think twice” about them. Schemata show up in social situations and routines of daily behavior.

7.2 Language

Language is a communication system that has both a lexicon and a system of grammar. Language acquisition occurs naturally and effortlessly during the early stages of life, and this acquisition occurs in a predictable sequence for individuals around the world. Language has a strong influence on thought, and the concept of how language may influence cognition remains an area of study and debate in psychology.

Many different strategies exist for solving problems. Typical strategies include trial and error, applying algorithms, and using heuristics. To solve a large, complicated problem, it often helps to break the problem into smaller steps that can be accomplished individually, leading to an overall solution. Roadblocks to problem solving include a mental set, functional fixedness, and various biases that can cloud decision making skills.

thinking; or, all of the processes associated with perception, knowledge, problem solving, judgement, language, and memory.

A modern school of psychological thought that empirically examines mental processes such as perception, memory, language, and judgement.

a category or grouping of linguistic information, images, ideas or memories, such as life experiences.

knowledge about words, concepts, and language-based knowledge and facts

the best example or representation of a concept, specific to an individual

concepts developed through direct or indirect experiences with the world

a concept defined by a specific set of characteristics.

a mental construct consisting of a cluster of related concepts

a set of ideas relating to how individuals in certain roles will behave.

also known as a cognitive script; a set of behaviors associated with a particular place or event

also known as an event schema; a set of behaviors associated with a particular place or event

a communication system that involves using words and systematic rules to organize those words to transmit information from one individual to another.

the words of a language

the rules of a language used to convey meaning through the use of the lexicon

the basic sounds that make up a language

the smallest unit of language that conveys meaning

the process by which we derive meaning from morphemes and words

the rules guiding the organization of morphemes into words and words into sentences.

Psychology 2e Copyright © 2020 by Openstax is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

7 Module 7: Thinking, Reasoning, and Problem-Solving

This module is about how a solid working knowledge of psychological principles can help you to think more effectively, so you can succeed in school and life. You might be inclined to believe that—because you have been thinking for as long as you can remember, because you are able to figure out the solution to many problems, because you feel capable of using logic to argue a point, because you can evaluate whether the things you read and hear make sense—you do not need any special training in thinking. But this, of course, is one of the key barriers to helping people think better. If you do not believe that there is anything wrong, why try to fix it?

The human brain is indeed a remarkable thinking machine, capable of amazing, complex, creative, logical thoughts. Why, then, are we telling you that you need to learn how to think? Mainly because one major lesson from cognitive psychology is that these capabilities of the human brain are relatively infrequently realized. Many psychologists believe that people are essentially “cognitive misers.” It is not that we are lazy, but that we have a tendency to expend the least amount of mental effort necessary. Although you may not realize it, it actually takes a great deal of energy to think. Careful, deliberative reasoning and critical thinking are very difficult. Because we seem to be successful without going to the trouble of using these skills well, it feels unnecessary to develop them. As you shall see, however, there are many pitfalls in the cognitive processes described in this module. When people do not devote extra effort to learning and improving reasoning, problem solving, and critical thinking skills, they make many errors.

As is true for memory, if you develop the cognitive skills presented in this module, you will be more successful in school. It is important that you realize, however, that these skills will help you far beyond school, even more so than a good memory will. Although it is somewhat useful to have a good memory, ten years from now no potential employer will care how many questions you got right on multiple choice exams during college. All of them will, however, recognize whether you are a logical, analytical, critical thinker. With these thinking skills, you will be an effective, persuasive communicator and an excellent problem solver.

The module begins by describing different kinds of thought and knowledge, especially conceptual knowledge and critical thinking. An understanding of these differences will be valuable as you progress through school and encounter different assignments that require you to tap into different kinds of knowledge. The second section covers deductive and inductive reasoning, which are processes we use to construct and evaluate strong arguments. They are essential skills to have whenever you are trying to persuade someone (including yourself) of some point, or to respond to someone’s efforts to persuade you. The module ends with a section about problem solving. A solid understanding of the key processes involved in problem solving will help you to handle many daily challenges.

7.1. Different kinds of thought

7.2. Reasoning and Judgment

7.3. Problem Solving

READING WITH PURPOSE

Remember and understand.

By reading and studying Module 7, you should be able to remember and describe:

• Concepts and inferences (7.1)
• Procedural knowledge (7.1)
• Metacognition (7.1)
• Characteristics of critical thinking:  skepticism; identify biases, distortions, omissions, and assumptions; reasoning and problem solving skills  (7.1)
• Reasoning:  deductive reasoning, deductively valid argument, inductive reasoning, inductively strong argument, availability heuristic, representativeness heuristic  (7.2)
• Fixation:  functional fixedness, mental set  (7.3)
• Algorithms, heuristics, and the role of confirmation bias (7.3)
• Effective problem solving sequence (7.3)

By reading and thinking about how the concepts in Module 6 apply to real life, you should be able to:

• Identify which type of knowledge a piece of information is (7.1)
• Recognize examples of deductive and inductive reasoning (7.2)
• Recognize judgments that have probably been influenced by the availability heuristic (7.2)
• Recognize examples of problem solving heuristics and algorithms (7.3)

Analyze, Evaluate, and Create

By reading and thinking about Module 6, participating in classroom activities, and completing out-of-class assignments, you should be able to:

• Use the principles of critical thinking to evaluate information (7.1)
• Explain whether examples of reasoning arguments are deductively valid or inductively strong (7.2)
• Outline how you could try to solve a problem from your life using the effective problem solving sequence (7.3)

7.1. Different kinds of thought and knowledge

• Take a few minutes to write down everything that you know about dogs.
• Do you believe that:
• Psychic ability exists?
• Hypnosis is an altered state of consciousness?
• Magnet therapy is effective for relieving pain?
• Aerobic exercise is an effective treatment for depression?
• UFO’s from outer space have visited earth?

On what do you base your belief or disbelief for the questions above?

Of course, we all know what is meant by the words  think  and  knowledge . You probably also realize that they are not unitary concepts; there are different kinds of thought and knowledge. In this section, let us look at some of these differences. If you are familiar with these different kinds of thought and pay attention to them in your classes, it will help you to focus on the right goals, learn more effectively, and succeed in school. Different assignments and requirements in school call on you to use different kinds of knowledge or thought, so it will be very helpful for you to learn to recognize them (Anderson, et al. 2001).

Factual and conceptual knowledge

Module 5 introduced the idea of declarative memory, which is composed of facts and episodes. If you have ever played a trivia game or watched Jeopardy on TV, you realize that the human brain is able to hold an extraordinary number of facts. Likewise, you realize that each of us has an enormous store of episodes, essentially facts about events that happened in our own lives. It may be difficult to keep that in mind when we are struggling to retrieve one of those facts while taking an exam, however. Part of the problem is that, in contradiction to the advice from Module 5, many students continue to try to memorize course material as a series of unrelated facts (picture a history student simply trying to memorize history as a set of unrelated dates without any coherent story tying them together). Facts in the real world are not random and unorganized, however. It is the way that they are organized that constitutes a second key kind of knowledge, conceptual.

Concepts are nothing more than our mental representations of categories of things in the world. For example, think about dogs. When you do this, you might remember specific facts about dogs, such as they have fur and they bark. You may also recall dogs that you have encountered and picture them in your mind. All of this information (and more) makes up your concept of dog. You can have concepts of simple categories (e.g., triangle), complex categories (e.g., small dogs that sleep all day, eat out of the garbage, and bark at leaves), kinds of people (e.g., psychology professors), events (e.g., birthday parties), and abstract ideas (e.g., justice). Gregory Murphy (2002) refers to concepts as the “glue that holds our mental life together” (p. 1). Very simply, summarizing the world by using concepts is one of the most important cognitive tasks that we do. Our conceptual knowledge  is  our knowledge about the world. Individual concepts are related to each other to form a rich interconnected network of knowledge. For example, think about how the following concepts might be related to each other: dog, pet, play, Frisbee, chew toy, shoe. Or, of more obvious use to you now, how these concepts are related: working memory, long-term memory, declarative memory, procedural memory, and rehearsal? Because our minds have a natural tendency to organize information conceptually, when students try to remember course material as isolated facts, they are working against their strengths.

One last important point about concepts is that they allow you to instantly know a great deal of information about something. For example, if someone hands you a small red object and says, “here is an apple,” they do not have to tell you, “it is something you can eat.” You already know that you can eat it because it is true by virtue of the fact that the object is an apple; this is called drawing an  inference , assuming that something is true on the basis of your previous knowledge (for example, of category membership or of how the world works) or logical reasoning.

Procedural knowledge

Physical skills, such as tying your shoes, doing a cartwheel, and driving a car (or doing all three at the same time, but don’t try this at home) are certainly a kind of knowledge. They are procedural knowledge, the same idea as procedural memory that you saw in Module 5. Mental skills, such as reading, debating, and planning a psychology experiment, are procedural knowledge, as well. In short, procedural knowledge is the knowledge how to do something (Cohen & Eichenbaum, 1993).

Metacognitive knowledge

Floyd used to think that he had a great memory. Now, he has a better memory. Why? Because he finally realized that his memory was not as great as he once thought it was. Because Floyd eventually learned that he often forgets where he put things, he finally developed the habit of putting things in the same place. (Unfortunately, he did not learn this lesson before losing at least 5 watches and a wedding ring.) Because he finally realized that he often forgets to do things, he finally started using the To Do list app on his phone. And so on. Floyd’s insights about the real limitations of his memory have allowed him to remember things that he used to forget.

All of us have knowledge about the way our own minds work. You may know that you have a good memory for people’s names and a poor memory for math formulas. Someone else might realize that they have difficulty remembering to do things, like stopping at the store on the way home. Others still know that they tend to overlook details. This knowledge about our own thinking is actually quite important; it is called metacognitive knowledge, or  metacognition . Like other kinds of thinking skills, it is subject to error. For example, in unpublished research, one of the authors surveyed about 120 General Psychology students on the first day of the term. Among other questions, the students were asked them to predict their grade in the class and report their current Grade Point Average. Two-thirds of the students predicted that their grade in the course would be higher than their GPA. (The reality is that at our college, students tend to earn lower grades in psychology than their overall GPA.) Another example: Students routinely report that they thought they had done well on an exam, only to discover, to their dismay, that they were wrong (more on that important problem in a moment). Both errors reveal a breakdown in metacognition.

The Dunning-Kruger Effect

In general, most college students probably do not study enough. For example, using data from the National Survey of Student Engagement, Fosnacht, McCormack, and Lerma (2018) reported that first-year students at 4-year colleges in the U.S. averaged less than 14 hours per week preparing for classes. The typical suggestion is that you should spend two hours outside of class for every hour in class, or 24 – 30 hours per week for a full-time student. Clearly, students in general are nowhere near that recommended mark. Many observers, including some faculty, believe that this shortfall is a result of students being too busy or lazy. Now, it may be true that many students are too busy, with work and family obligations, for example. Others, are not particularly motivated in school, and therefore might correctly be labeled lazy. A third possible explanation, however, is that some students might not think they need to spend this much time. And this is a matter of metacognition. Consider the scenario that we mentioned above, students thinking they had done well on an exam only to discover that they did not. Justin Kruger and David Dunning examined scenarios very much like this in 1999. Kruger and Dunning gave research participants tests measuring humor, logic, and grammar. Then, they asked the participants to assess their own abilities and test performance in these areas. They found that participants in general tended to overestimate their abilities, already a problem with metacognition. Importantly, the participants who scored the lowest overestimated their abilities the most. Specifically, students who scored in the bottom quarter (averaging in the 12th percentile) thought they had scored in the 62nd percentile. This has become known as the  Dunning-Kruger effect . Many individual faculty members have replicated these results with their own student on their course exams, including the authors of this book. Think about it. Some students who just took an exam and performed poorly believe that they did well before seeing their score. It seems very likely that these are the very same students who stopped studying the night before because they thought they were “done.” Quite simply, it is not just that they did not know the material. They did not know that they did not know the material. That is poor metacognition.

In order to develop good metacognitive skills, you should continually monitor your thinking and seek frequent feedback on the accuracy of your thinking (Medina, Castleberry, & Persky 2017). For example, in classes get in the habit of predicting your exam grades. As soon as possible after taking an exam, try to find out which questions you missed and try to figure out why. If you do this soon enough, you may be able to recall the way it felt when you originally answered the question. Did you feel confident that you had answered the question correctly? Then you have just discovered an opportunity to improve your metacognition. Be on the lookout for that feeling and respond with caution.

concept :  a mental representation of a category of things in the world

Dunning-Kruger effect : individuals who are less competent tend to overestimate their abilities more than individuals who are more competent do

inference : an assumption about the truth of something that is not stated. Inferences come from our prior knowledge and experience, and from logical reasoning

metacognition :  knowledge about one’s own cognitive processes; thinking about your thinking

Critical thinking

One particular kind of knowledge or thinking skill that is related to metacognition is  critical thinking (Chew, 2020). You may have noticed that critical thinking is an objective in many college courses, and thus it could be a legitimate topic to cover in nearly any college course. It is particularly appropriate in psychology, however. As the science of (behavior and) mental processes, psychology is obviously well suited to be the discipline through which you should be introduced to this important way of thinking.

More importantly, there is a particular need to use critical thinking in psychology. We are all, in a way, experts in human behavior and mental processes, having engaged in them literally since birth. Thus, perhaps more than in any other class, students typically approach psychology with very clear ideas and opinions about its subject matter. That is, students already “know” a lot about psychology. The problem is, “it ain’t so much the things we don’t know that get us into trouble. It’s the things we know that just ain’t so” (Ward, quoted in Gilovich 1991). Indeed, many of students’ preconceptions about psychology are just plain wrong. Randolph Smith (2002) wrote a book about critical thinking in psychology called  Challenging Your Preconceptions,  highlighting this fact. On the other hand, many of students’ preconceptions about psychology are just plain right! But wait, how do you know which of your preconceptions are right and which are wrong? And when you come across a research finding or theory in this class that contradicts your preconceptions, what will you do? Will you stick to your original idea, discounting the information from the class? Will you immediately change your mind? Critical thinking can help us sort through this confusing mess.

But what is critical thinking? The goal of critical thinking is simple to state (but extraordinarily difficult to achieve): it is to be right, to draw the correct conclusions, to believe in things that are true and to disbelieve things that are false. We will provide two definitions of critical thinking (or, if you like, one large definition with two distinct parts). First, a more conceptual one: Critical thinking is thinking like a scientist in your everyday life (Schmaltz, Jansen, & Wenckowski, 2017).  Our second definition is more operational; it is simply a list of skills that are essential to be a critical thinker. Critical thinking entails solid reasoning and problem solving skills; skepticism; and an ability to identify biases, distortions, omissions, and assumptions. Excellent deductive and inductive reasoning, and problem solving skills contribute to critical thinking. So, you can consider the subject matter of sections 7.2 and 7.3 to be part of critical thinking. Because we will be devoting considerable time to these concepts in the rest of the module, let us begin with a discussion about the other aspects of critical thinking.

Let’s address that first part of the definition. Scientists form hypotheses, or predictions about some possible future observations. Then, they collect data, or information (think of this as making those future observations). They do their best to make unbiased observations using reliable techniques that have been verified by others. Then, and only then, they draw a conclusion about what those observations mean. Oh, and do not forget the most important part. “Conclusion” is probably not the most appropriate word because this conclusion is only tentative. A scientist is always prepared that someone else might come along and produce new observations that would require a new conclusion be drawn. Wow! If you like to be right, you could do a lot worse than using a process like this.

A Critical Thinker’s Toolkit 

Now for the second part of the definition. Good critical thinkers (and scientists) rely on a variety of tools to evaluate information. Perhaps the most recognizable tool for critical thinking is  skepticism (and this term provides the clearest link to the thinking like a scientist definition, as you are about to see). Some people intend it as an insult when they call someone a skeptic. But if someone calls you a skeptic, if they are using the term correctly, you should consider it a great compliment. Simply put, skepticism is a way of thinking in which you refrain from drawing a conclusion or changing your mind until good evidence has been provided. People from Missouri should recognize this principle, as Missouri is known as the Show-Me State. As a skeptic, you are not inclined to believe something just because someone said so, because someone else believes it, or because it sounds reasonable. You must be persuaded by high quality evidence.

Of course, if that evidence is produced, you have a responsibility as a skeptic to change your belief. Failure to change a belief in the face of good evidence is not skepticism; skepticism has open mindedness at its core. M. Neil Browne and Stuart Keeley (2018) use the term weak sense critical thinking to describe critical thinking behaviors that are used only to strengthen a prior belief. Strong sense critical thinking, on the other hand, has as its goal reaching the best conclusion. Sometimes that means strengthening your prior belief, but sometimes it means changing your belief to accommodate the better evidence.

Many times, a failure to think critically or weak sense critical thinking is related to a  bias , an inclination, tendency, leaning, or prejudice. Everybody has biases, but many people are unaware of them. Awareness of your own biases gives you the opportunity to control or counteract them. Unfortunately, however, many people are happy to let their biases creep into their attempts to persuade others; indeed, it is a key part of their persuasive strategy. To see how these biases influence messages, just look at the different descriptions and explanations of the same events given by people of different ages or income brackets, or conservative versus liberal commentators, or by commentators from different parts of the world. Of course, to be successful, these people who are consciously using their biases must disguise them. Even undisguised biases can be difficult to identify, so disguised ones can be nearly impossible.

Here are some common sources of biases:

• Personal values and beliefs.  Some people believe that human beings are basically driven to seek power and that they are typically in competition with one another over scarce resources. These beliefs are similar to the world-view that political scientists call “realism.” Other people believe that human beings prefer to cooperate and that, given the chance, they will do so. These beliefs are similar to the world-view known as “idealism.” For many people, these deeply held beliefs can influence, or bias, their interpretations of such wide ranging situations as the behavior of nations and their leaders or the behavior of the driver in the car ahead of you. For example, if your worldview is that people are typically in competition and someone cuts you off on the highway, you may assume that the driver did it purposely to get ahead of you. Other types of beliefs about the way the world is or the way the world should be, for example, political beliefs, can similarly become a significant source of bias.
• Racism, sexism, ageism and other forms of prejudice and bigotry.  These are, sadly, a common source of bias in many people. They are essentially a special kind of “belief about the way the world is.” These beliefs—for example, that women do not make effective leaders—lead people to ignore contradictory evidence (examples of effective women leaders, or research that disputes the belief) and to interpret ambiguous evidence in a way consistent with the belief.
• Self-interest.  When particular people benefit from things turning out a certain way, they can sometimes be very susceptible to letting that interest bias them. For example, a company that will earn a profit if they sell their product may have a bias in the way that they give information about their product. A union that will benefit if its members get a generous contract might have a bias in the way it presents information about salaries at competing organizations. (Note that our inclusion of examples describing both companies and unions is an explicit attempt to control for our own personal biases). Home buyers are often dismayed to discover that they purchased their dream house from someone whose self-interest led them to lie about flooding problems in the basement or back yard. This principle, the biasing power of self-interest, is likely what led to the famous phrase  Caveat Emptor  (let the buyer beware) .  

Knowing that these types of biases exist will help you evaluate evidence more critically. Do not forget, though, that people are not always keen to let you discover the sources of biases in their arguments. For example, companies or political organizations can sometimes disguise their support of a research study by contracting with a university professor, who comes complete with a seemingly unbiased institutional affiliation, to conduct the study.

People’s biases, conscious or unconscious, can lead them to make omissions, distortions, and assumptions that undermine our ability to correctly evaluate evidence. It is essential that you look for these elements. Always ask, what is missing, what is not as it appears, and what is being assumed here? For example, consider this (fictional) chart from an ad reporting customer satisfaction at 4 local health clubs.

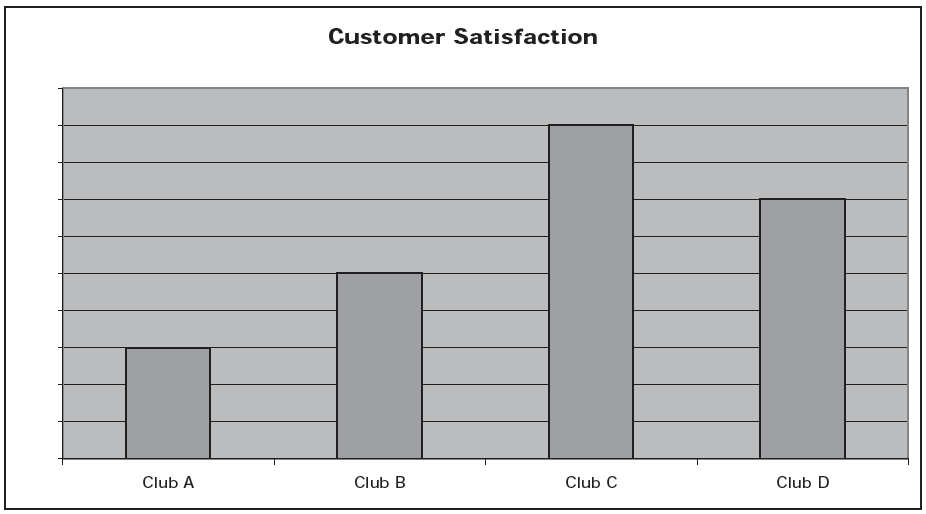
Clearly, from the results of the chart, one would be tempted to give Club C a try, as customer satisfaction is much higher than for the other 3 clubs.

There are so many distortions and omissions in this chart, however, that it is actually quite meaningless. First, how was satisfaction measured? Do the bars represent responses to a survey? If so, how were the questions asked? Most importantly, where is the missing scale for the chart? Although the differences look quite large, are they really?

Well, here is the same chart, with a different scale, this time labeled:

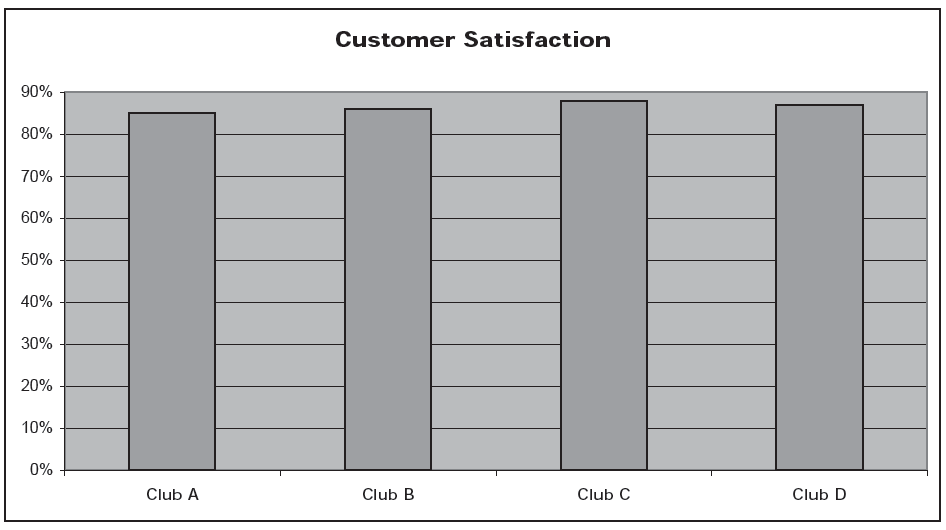
Club C is not so impressive any more, is it? In fact, all of the health clubs have customer satisfaction ratings (whatever that means) between 85% and 88%. In the first chart, the entire scale of the graph included only the percentages between 83 and 89. This “judicious” choice of scale—some would call it a distortion—and omission of that scale from the chart make the tiny differences among the clubs seem important, however.

Also, in order to be a critical thinker, you need to learn to pay attention to the assumptions that underlie a message. Let us briefly illustrate the role of assumptions by touching on some people’s beliefs about the criminal justice system in the US. Some believe that a major problem with our judicial system is that many criminals go free because of legal technicalities. Others believe that a major problem is that many innocent people are convicted of crimes. The simple fact is, both types of errors occur. A person’s conclusion about which flaw in our judicial system is the greater tragedy is based on an assumption about which of these is the more serious error (letting the guilty go free or convicting the innocent). This type of assumption is called a value assumption (Browne and Keeley, 2018). It reflects the differences in values that people develop, differences that may lead us to disregard valid evidence that does not fit in with our particular values.

Oh, by the way, some students probably noticed this, but the seven tips for evaluating information that we shared in Module 1 are related to this. Actually, they are part of this section. The tips are, to a very large degree, set of ideas you can use to help you identify biases, distortions, omissions, and assumptions. If you do not remember this section, we strongly recommend you take a few minutes to review it.

skepticism :  a way of thinking in which you refrain from drawing a conclusion or changing your mind until good evidence has been provided

bias : an inclination, tendency, leaning, or prejudice

• Which of your beliefs (or disbeliefs) from the Activate exercise for this section were derived from a process of critical thinking? If some of your beliefs were not based on critical thinking, are you willing to reassess these beliefs? If the answer is no, why do you think that is? If the answer is yes, what concrete steps will you take?

7.2 Reasoning and Judgment

• What percentage of kidnappings are committed by strangers?
• Which area of the house is riskiest: kitchen, bathroom, or stairs?
• What is the most common cancer in the US?
• What percentage of workplace homicides are committed by co-workers?

An essential set of procedural thinking skills is  reasoning , the ability to generate and evaluate solid conclusions from a set of statements or evidence. You should note that these conclusions (when they are generated instead of being evaluated) are one key type of inference that we described in Section 7.1. There are two main types of reasoning, deductive and inductive.

Deductive reasoning

Suppose your teacher tells you that if you get an A on the final exam in a course, you will get an A for the whole course. Then, you get an A on the final exam. What will your final course grade be? Most people can see instantly that you can conclude with certainty that you will get an A for the course. This is a type of reasoning called  deductive reasoning , which is defined as reasoning in which a conclusion is guaranteed to be true as long as the statements leading to it are true. The three statements can be listed as an  argument , with two beginning statements and a conclusion:

Statement 1: If you get an A on the final exam, you will get an A for the course

Statement 2: You get an A on the final exam

Conclusion: You will get an A for the course

This particular arrangement, in which true beginning statements lead to a guaranteed true conclusion, is known as a  deductively valid argument . Although deductive reasoning is often the subject of abstract, brain-teasing, puzzle-like word problems, it is actually an extremely important type of everyday reasoning. It is just hard to recognize sometimes. For example, imagine that you are looking for your car keys and you realize that they are either in the kitchen drawer or in your book bag. After looking in the kitchen drawer, you instantly know that they must be in your book bag. That conclusion results from a simple deductive reasoning argument. In addition, solid deductive reasoning skills are necessary for you to succeed in the sciences, philosophy, math, computer programming, and any endeavor involving the use of logic to persuade others to your point of view or to evaluate others’ arguments.

Cognitive psychologists, and before them philosophers, have been quite interested in deductive reasoning, not so much for its practical applications, but for the insights it can offer them about the ways that human beings think. One of the early ideas to emerge from the examination of deductive reasoning is that people learn (or develop) mental versions of rules that allow them to solve these types of reasoning problems (Braine, 1978; Braine, Reiser, & Rumain, 1984). The best way to see this point of view is to realize that there are different possible rules, and some of them are very simple. For example, consider this rule of logic:

therefore q

Logical rules are often presented abstractly, as letters, in order to imply that they can be used in very many specific situations. Here is a concrete version of the of the same rule:

I’ll either have pizza or a hamburger for dinner tonight (p or q)

I won’t have pizza (not p)

Therefore, I’ll have a hamburger (therefore q)

This kind of reasoning seems so natural, so easy, that it is quite plausible that we would use a version of this rule in our daily lives. At least, it seems more plausible than some of the alternative possibilities—for example, that we need to have experience with the specific situation (pizza or hamburger, in this case) in order to solve this type of problem easily. So perhaps there is a form of natural logic (Rips, 1990) that contains very simple versions of logical rules. When we are faced with a reasoning problem that maps onto one of these rules, we use the rule.

But be very careful; things are not always as easy as they seem. Even these simple rules are not so simple. For example, consider the following rule. Many people fail to realize that this rule is just as valid as the pizza or hamburger rule above.

if p, then q

therefore, not p

Concrete version:

If I eat dinner, then I will have dessert

I did not have dessert

Therefore, I did not eat dinner

The simple fact is, it can be very difficult for people to apply rules of deductive logic correctly; as a result, they make many errors when trying to do so. Is this a deductively valid argument or not?

Students who like school study a lot

Students who study a lot get good grades

Jane does not like school

Therefore, Jane does not get good grades

Many people are surprised to discover that this is not a logically valid argument; the conclusion is not guaranteed to be true from the beginning statements. Although the first statement says that students who like school study a lot, it does NOT say that students who do not like school do not study a lot. In other words, it may very well be possible to study a lot without liking school. Even people who sometimes get problems like this right might not be using the rules of deductive reasoning. Instead, they might just be making judgments for examples they know, in this case, remembering instances of people who get good grades despite not liking school.

Making deductive reasoning even more difficult is the fact that there are two important properties that an argument may have. One, it can be valid or invalid (meaning that the conclusion does or does not follow logically from the statements leading up to it). Two, an argument (or more correctly, its conclusion) can be true or false. Here is an example of an argument that is logically valid, but has a false conclusion (at least we think it is false).

Either you are eleven feet tall or the Grand Canyon was created by a spaceship crashing into the earth.

You are not eleven feet tall

Therefore the Grand Canyon was created by a spaceship crashing into the earth

This argument has the exact same form as the pizza or hamburger argument above, making it is deductively valid. The conclusion is so false, however, that it is absurd (of course, the reason the conclusion is false is that the first statement is false). When people are judging arguments, they tend to not observe the difference between deductive validity and the empirical truth of statements or conclusions. If the elements of an argument happen to be true, people are likely to judge the argument logically valid; if the elements are false, they will very likely judge it invalid (Markovits & Bouffard-Bouchard, 1992; Moshman & Franks, 1986). Thus, it seems a stretch to say that people are using these logical rules to judge the validity of arguments. Many psychologists believe that most people actually have very limited deductive reasoning skills (Johnson-Laird, 1999). They argue that when faced with a problem for which deductive logic is required, people resort to some simpler technique, such as matching terms that appear in the statements and the conclusion (Evans, 1982). This might not seem like a problem, but what if reasoners believe that the elements are true and they happen to be wrong; they will would believe that they are using a form of reasoning that guarantees they are correct and yet be wrong.

deductive reasoning :  a type of reasoning in which the conclusion is guaranteed to be true any time the statements leading up to it are true

argument :  a set of statements in which the beginning statements lead to a conclusion

deductively valid argument :  an argument for which true beginning statements guarantee that the conclusion is true

Inductive reasoning and judgment

Every day, you make many judgments about the likelihood of one thing or another. Whether you realize it or not, you are practicing  inductive reasoning   on a daily basis. In inductive reasoning arguments, a conclusion is likely whenever the statements preceding it are true. The first thing to notice about inductive reasoning is that, by definition, you can never be sure about your conclusion; you can only estimate how likely the conclusion is. Inductive reasoning may lead you to focus on Memory Encoding and Recoding when you study for the exam, but it is possible the instructor will ask more questions about Memory Retrieval instead. Unlike deductive reasoning, the conclusions you reach through inductive reasoning are only probable, not certain. That is why scientists consider inductive reasoning weaker than deductive reasoning. But imagine how hard it would be for us to function if we could not act unless we were certain about the outcome.

Inductive reasoning can be represented as logical arguments consisting of statements and a conclusion, just as deductive reasoning can be. In an inductive argument, you are given some statements and a conclusion (or you are given some statements and must draw a conclusion). An argument is  inductively strong   if the conclusion would be very probable whenever the statements are true. So, for example, here is an inductively strong argument:

• Statement #1: The forecaster on Channel 2 said it is going to rain today.
• Statement #2: The forecaster on Channel 5 said it is going to rain today.
• Statement #3: It is very cloudy and humid.
• Statement #4: You just heard thunder.
• Conclusion (or judgment): It is going to rain today.

Think of the statements as evidence, on the basis of which you will draw a conclusion. So, based on the evidence presented in the four statements, it is very likely that it will rain today. Will it definitely rain today? Certainly not. We can all think of times that the weather forecaster was wrong.

A true story: Some years ago psychology student was watching a baseball playoff game between the St. Louis Cardinals and the Los Angeles Dodgers. A graphic on the screen had just informed the audience that the Cardinal at bat, (Hall of Fame shortstop) Ozzie Smith, a switch hitter batting left-handed for this plate appearance, had never, in nearly 3000 career at-bats, hit a home run left-handed. The student, who had just learned about inductive reasoning in his psychology class, turned to his companion (a Cardinals fan) and smugly said, “It is an inductively strong argument that Ozzie Smith will not hit a home run.” He turned back to face the television just in time to watch the ball sail over the right field fence for a home run. Although the student felt foolish at the time, he was not wrong. It was an inductively strong argument; 3000 at-bats is an awful lot of evidence suggesting that the Wizard of Ozz (as he was known) would not be hitting one out of the park (think of each at-bat without a home run as a statement in an inductive argument). Sadly (for the die-hard Cubs fan and Cardinals-hating student), despite the strength of the argument, the conclusion was wrong.

Given the possibility that we might draw an incorrect conclusion even with an inductively strong argument, we really want to be sure that we do, in fact, make inductively strong arguments. If we judge something probable, it had better be probable. If we judge something nearly impossible, it had better not happen. Think of inductive reasoning, then, as making reasonably accurate judgments of the probability of some conclusion given a set of evidence.

We base many decisions in our lives on inductive reasoning. For example:

Statement #1: Psychology is not my best subject

Statement #2: My psychology instructor has a reputation for giving difficult exams

Statement #3: My first psychology exam was much harder than I expected

Judgment: The next exam will probably be very difficult.

Decision: I will study tonight instead of watching Netflix.

Some other examples of judgments that people commonly make in a school context include judgments of the likelihood that:

• A particular class will be interesting/useful/difficult
• You will be able to finish writing a paper by next week if you go out tonight
• Your laptop’s battery will last through the next trip to the library
• You will not miss anything important if you skip class tomorrow
• Your instructor will not notice if you skip class tomorrow
• You will be able to find a book that you will need for a paper
• There will be an essay question about Memory Encoding on the next exam

Tversky and Kahneman (1983) recognized that there are two general ways that we might make these judgments; they termed them extensional (i.e., following the laws of probability) and intuitive (i.e., using shortcuts or heuristics, see below). We will use a similar distinction between Type 1 and Type 2 thinking, as described by Keith Stanovich and his colleagues (Evans and Stanovich, 2013; Stanovich and West, 2000). Type 1 thinking is fast, automatic, effortful, and emotional. In fact, it is hardly fair to call it reasoning at all, as judgments just seem to pop into one’s head. Type 2 thinking , on the other hand, is slow, effortful, and logical. So obviously, it is more likely to lead to a correct judgment, or an optimal decision. The problem is, we tend to over-rely on Type 1. Now, we are not saying that Type 2 is the right way to go for every decision or judgment we make. It seems a bit much, for example, to engage in a step-by-step logical reasoning procedure to decide whether we will have chicken or fish for dinner tonight.

Many bad decisions in some very important contexts, however, can be traced back to poor judgments of the likelihood of certain risks or outcomes that result from the use of Type 1 when a more logical reasoning process would have been more appropriate. For example:

Statement #1: It is late at night.

Statement #2: Albert has been drinking beer for the past five hours at a party.

Statement #3: Albert is not exactly sure where he is or how far away home is.

Judgment: Albert will have no difficulty walking home.

Decision: He walks home alone.

As you can see in this example, the three statements backing up the judgment do not really support it. In other words, this argument is not inductively strong because it is based on judgments that ignore the laws of probability. What are the chances that someone facing these conditions will be able to walk home alone easily? And one need not be drunk to make poor decisions based on judgments that just pop into our heads.

The truth is that many of our probability judgments do not come very close to what the laws of probability say they should be. Think about it. In order for us to reason in accordance with these laws, we would need to know the laws of probability, which would allow us to calculate the relationship between particular pieces of evidence and the probability of some outcome (i.e., how much likelihood should change given a piece of evidence), and we would have to do these heavy math calculations in our heads. After all, that is what Type 2 requires. Needless to say, even if we were motivated, we often do not even know how to apply Type 2 reasoning in many cases.

So what do we do when we don’t have the knowledge, skills, or time required to make the correct mathematical judgment? Do we hold off and wait until we can get better evidence? Do we read up on probability and fire up our calculator app so we can compute the correct probability? Of course not. We rely on Type 1 thinking. We “wing it.” That is, we come up with a likelihood estimate using some means at our disposal. Psychologists use the term heuristic to describe the type of “winging it” we are talking about. A  heuristic   is a shortcut strategy that we use to make some judgment or solve some problem (see Section 7.3). Heuristics are easy and quick, think of them as the basic procedures that are characteristic of Type 1.  They can absolutely lead to reasonably good judgments and decisions in some situations (like choosing between chicken and fish for dinner). They are, however, far from foolproof. There are, in fact, quite a lot of situations in which heuristics can lead us to make incorrect judgments, and in many cases the decisions based on those judgments can have serious consequences.

Let us return to the activity that begins this section. You were asked to judge the likelihood (or frequency) of certain events and risks. You were free to come up with your own evidence (or statements) to make these judgments. This is where a heuristic crops up. As a judgment shortcut, we tend to generate specific examples of those very events to help us decide their likelihood or frequency. For example, if we are asked to judge how common, frequent, or likely a particular type of cancer is, many of our statements would be examples of specific cancer cases:

Statement #1: Andy Kaufman (comedian) had lung cancer.

Statement #2: Colin Powell (US Secretary of State) had prostate cancer.

Statement #3: Bob Marley (musician) had skin and brain cancer

Statement #4: Sandra Day O’Connor (Supreme Court Justice) had breast cancer.

Statement #5: Fred Rogers (children’s entertainer) had stomach cancer.

Statement #6: Robin Roberts (news anchor) had breast cancer.

Statement #7: Bette Davis (actress) had breast cancer.

Judgment: Breast cancer is the most common type.

Your own experience or memory may also tell you that breast cancer is the most common type. But it is not (although it is common). Actually, skin cancer is the most common type in the US. We make the same types of misjudgments all the time because we do not generate the examples or evidence according to their actual frequencies or probabilities. Instead, we have a tendency (or bias) to search for the examples in memory; if they are easy to retrieve, we assume that they are common. To rephrase this in the language of the heuristic, events seem more likely to the extent that they are available to memory. This bias has been termed the  availability heuristic   (Kahneman and Tversky, 1974).

The fact that we use the availability heuristic does not automatically mean that our judgment is wrong. The reason we use heuristics in the first place is that they work fairly well in many cases (and, of course that they are easy to use). So, the easiest examples to think of sometimes are the most common ones. Is it more likely that a member of the U.S. Senate is a man or a woman? Most people have a much easier time generating examples of male senators. And as it turns out, the U.S. Senate has many more men than women (74 to 26 in 2020). In this case, then, the availability heuristic would lead you to make the correct judgment; it is far more likely that a senator would be a man.

In many other cases, however, the availability heuristic will lead us astray. This is because events can be memorable for many reasons other than their frequency. Section 5.2, Encoding Meaning, suggested that one good way to encode the meaning of some information is to form a mental image of it. Thus, information that has been pictured mentally will be more available to memory. Indeed, an event that is vivid and easily pictured will trick many people into supposing that type of event is more common than it actually is. Repetition of information will also make it more memorable. So, if the same event is described to you in a magazine, on the evening news, on a podcast that you listen to, and in your Facebook feed; it will be very available to memory. Again, the availability heuristic will cause you to misperceive the frequency of these types of events.

Most interestingly, information that is unusual is more memorable. Suppose we give you the following list of words to remember: box, flower, letter, platypus, oven, boat, newspaper, purse, drum, car. Very likely, the easiest word to remember would be platypus, the unusual one. The same thing occurs with memories of events. An event may be available to memory because it is unusual, yet the availability heuristic leads us to judge that the event is common. Did you catch that? In these cases, the availability heuristic makes us think the exact opposite of the true frequency. We end up thinking something is common because it is unusual (and therefore memorable). Yikes.

The misapplication of the availability heuristic sometimes has unfortunate results. For example, if you went to K-12 school in the US over the past 10 years, it is extremely likely that you have participated in lockdown and active shooter drills. Of course, everyone is trying to prevent the tragedy of another school shooting. And believe us, we are not trying to minimize how terrible the tragedy is. But the truth of the matter is, school shootings are extremely rare. Because the federal government does not keep a database of school shootings, the Washington Post has maintained their own running tally. Between 1999 and January 2020 (the date of the most recent school shooting with a death in the US at of the time this paragraph was written), the Post reported a total of 254 people died in school shootings in the US. Not 254 per year, 254 total. That is an average of 12 per year. Of course, that is 254 people who should not have died (particularly because many were children), but in a country with approximately 60,000,000 students and teachers, this is a very small risk.

But many students and teachers are terrified that they will be victims of school shootings because of the availability heuristic. It is so easy to think of examples (they are very available to memory) that people believe the event is very common. It is not. And there is a downside to this. We happen to believe that there is an enormous gun violence problem in the United States. According the the Centers for Disease Control and Prevention, there were 39,773 firearm deaths in the US in 2017. Fifteen of those deaths were in school shootings, according to the Post. 60% of those deaths were suicides. When people pay attention to the school shooting risk (low), they often fail to notice the much larger risk.

And examples like this are by no means unique. The authors of this book have been teaching psychology since the 1990’s. We have been able to make the exact same arguments about the misapplication of the availability heuristics and keep them current by simply swapping out for the “fear of the day.” In the 1990’s it was children being kidnapped by strangers (it was known as “stranger danger”) despite the facts that kidnappings accounted for only 2% of the violent crimes committed against children, and only 24% of kidnappings are committed by strangers (US Department of Justice, 2007). This fear overlapped with the fear of terrorism that gripped the country after the 2001 terrorist attacks on the World Trade Center and US Pentagon and still plagues the population of the US somewhat in 2020. After a well-publicized, sensational act of violence, people are extremely likely to increase their estimates of the chances that they, too, will be victims of terror. Think about the reality, however. In October of 2001, a terrorist mailed anthrax spores to members of the US government and a number of media companies. A total of five people died as a result of this attack. The nation was nearly paralyzed by the fear of dying from the attack; in reality the probability of an individual person dying was 0.00000002.

The availability heuristic can lead you to make incorrect judgments in a school setting as well. For example, suppose you are trying to decide if you should take a class from a particular math professor. You might try to make a judgment of how good a teacher she is by recalling instances of friends and acquaintances making comments about her teaching skill. You may have some examples that suggest that she is a poor teacher very available to memory, so on the basis of the availability heuristic you judge her a poor teacher and decide to take the class from someone else. What if, however, the instances you recalled were all from the same person, and this person happens to be a very colorful storyteller? The subsequent ease of remembering the instances might not indicate that the professor is a poor teacher after all.

Although the availability heuristic is obviously important, it is not the only judgment heuristic we use. Amos Tversky and Daniel Kahneman examined the role of heuristics in inductive reasoning in a long series of studies. Kahneman received a Nobel Prize in Economics for this research in 2002, and Tversky would have certainly received one as well if he had not died of melanoma at age 59 in 1996 (Nobel Prizes are not awarded posthumously). Kahneman and Tversky demonstrated repeatedly that people do not reason in ways that are consistent with the laws of probability. They identified several heuristic strategies that people use instead to make judgments about likelihood. The importance of this work for economics (and the reason that Kahneman was awarded the Nobel Prize) is that earlier economic theories had assumed that people do make judgments rationally, that is, in agreement with the laws of probability.

Another common heuristic that people use for making judgments is the  representativeness heuristic (Kahneman & Tversky 1973). Suppose we describe a person to you. He is quiet and shy, has an unassuming personality, and likes to work with numbers. Is this person more likely to be an accountant or an attorney? If you said accountant, you were probably using the representativeness heuristic. Our imaginary person is judged likely to be an accountant because he resembles, or is representative of the concept of, an accountant. When research participants are asked to make judgments such as these, the only thing that seems to matter is the representativeness of the description. For example, if told that the person described is in a room that contains 70 attorneys and 30 accountants, participants will still assume that he is an accountant.

inductive reasoning :  a type of reasoning in which we make judgments about likelihood from sets of evidence

inductively strong argument :  an inductive argument in which the beginning statements lead to a conclusion that is probably true

heuristic :  a shortcut strategy that we use to make judgments and solve problems. Although they are easy to use, they do not guarantee correct judgments and solutions

availability heuristic :  judging the frequency or likelihood of some event type according to how easily examples of the event can be called to mind (i.e., how available they are to memory)

representativeness heuristic:   judging the likelihood that something is a member of a category on the basis of how much it resembles a typical category member (i.e., how representative it is of the category)

Type 1 thinking : fast, automatic, and emotional thinking.

Type 2 thinking : slow, effortful, and logical thinking.

• What percentage of workplace homicides are co-worker violence?

Many people get these questions wrong. The answers are 10%; stairs; skin; 6%. How close were your answers? Explain how the availability heuristic might have led you to make the incorrect judgments.

• Can you think of some other judgments that you have made (or beliefs that you have) that might have been influenced by the availability heuristic?

7.3 Problem Solving

• Please take a few minutes to list a number of problems that you are facing right now.
• Now write about a problem that you recently solved.
• What is your definition of a problem?

Mary has a problem. Her daughter, ordinarily quite eager to please, appears to delight in being the last person to do anything. Whether getting ready for school, going to piano lessons or karate class, or even going out with her friends, she seems unwilling or unable to get ready on time. Other people have different kinds of problems. For example, many students work at jobs, have numerous family commitments, and are facing a course schedule full of difficult exams, assignments, papers, and speeches. How can they find enough time to devote to their studies and still fulfill their other obligations? Speaking of students and their problems: Show that a ball thrown vertically upward with initial velocity v0 takes twice as much time to return as to reach the highest point (from Spiegel, 1981).

These are three very different situations, but we have called them all problems. What makes them all the same, despite the differences? A psychologist might define a  problem   as a situation with an initial state, a goal state, and a set of possible intermediate states. Somewhat more meaningfully, we might consider a problem a situation in which you are in here one state (e.g., daughter is always late), you want to be there in another state (e.g., daughter is not always late), and with no obvious way to get from here to there. Defined this way, each of the three situations we outlined can now be seen as an example of the same general concept, a problem. At this point, you might begin to wonder what is not a problem, given such a general definition. It seems that nearly every non-routine task we engage in could qualify as a problem. As long as you realize that problems are not necessarily bad (it can be quite fun and satisfying to rise to the challenge and solve a problem), this may be a useful way to think about it.

Can we identify a set of problem-solving skills that would apply to these very different kinds of situations? That task, in a nutshell, is a major goal of this section. Let us try to begin to make sense of the wide variety of ways that problems can be solved with an important observation: the process of solving problems can be divided into two key parts. First, people have to notice, comprehend, and represent the problem properly in their minds (called  problem representation ). Second, they have to apply some kind of solution strategy to the problem. Psychologists have studied both of these key parts of the process in detail.

When you first think about the problem-solving process, you might guess that most of our difficulties would occur because we are failing in the second step, the application of strategies. Although this can be a significant difficulty much of the time, the more important source of difficulty is probably problem representation. In short, we often fail to solve a problem because we are looking at it, or thinking about it, the wrong way.

problem :  a situation in which we are in an initial state, have a desired goal state, and there is a number of possible intermediate states (i.e., there is no obvious way to get from the initial to the goal state)

problem representation :  noticing, comprehending and forming a mental conception of a problem

Defining and Mentally Representing Problems in Order to Solve Them

So, the main obstacle to solving a problem is that we do not clearly understand exactly what the problem is. Recall the problem with Mary’s daughter always being late. One way to represent, or to think about, this problem is that she is being defiant. She refuses to get ready in time. This type of representation or definition suggests a particular type of solution. Another way to think about the problem, however, is to consider the possibility that she is simply being sidetracked by interesting diversions. This different conception of what the problem is (i.e., different representation) suggests a very different solution strategy. For example, if Mary defines the problem as defiance, she may be tempted to solve the problem using some kind of coercive tactics, that is, to assert her authority as her mother and force her to listen. On the other hand, if Mary defines the problem as distraction, she may try to solve it by simply removing the distracting objects.

As you might guess, when a problem is represented one way, the solution may seem very difficult, or even impossible. Seen another way, the solution might be very easy. For example, consider the following problem (from Nasar, 1998):

Two bicyclists start 20 miles apart and head toward each other, each going at a steady rate of 10 miles per hour. At the same time, a fly that travels at a steady 15 miles per hour starts from the front wheel of the southbound bicycle and flies to the front wheel of the northbound one, then turns around and flies to the front wheel of the southbound one again, and continues in this manner until he is crushed between the two front wheels. Question: what total distance did the fly cover?

Please take a few minutes to try to solve this problem.

Most people represent this problem as a question about a fly because, well, that is how the question is asked. The solution, using this representation, is to figure out how far the fly travels on the first leg of its journey, then add this total to how far it travels on the second leg of its journey (when it turns around and returns to the first bicycle), then continue to add the smaller distance from each leg of the journey until you converge on the correct answer. You would have to be quite skilled at math to solve this problem, and you would probably need some time and pencil and paper to do it.

If you consider a different representation, however, you can solve this problem in your head. Instead of thinking about it as a question about a fly, think about it as a question about the bicycles. They are 20 miles apart, and each is traveling 10 miles per hour. How long will it take for the bicycles to reach each other? Right, one hour. The fly is traveling 15 miles per hour; therefore, it will travel a total of 15 miles back and forth in the hour before the bicycles meet. Represented one way (as a problem about a fly), the problem is quite difficult. Represented another way (as a problem about two bicycles), it is easy. Changing your representation of a problem is sometimes the best—sometimes the only—way to solve it.

Unfortunately, however, changing a problem’s representation is not the easiest thing in the world to do. Often, problem solvers get stuck looking at a problem one way. This is called  fixation . Most people who represent the preceding problem as a problem about a fly probably do not pause to reconsider, and consequently change, their representation. A parent who thinks her daughter is being defiant is unlikely to consider the possibility that her behavior is far less purposeful.

Problem-solving fixation was examined by a group of German psychologists called Gestalt psychologists during the 1930’s and 1940’s. Karl Dunker, for example, discovered an important type of failure to take a different perspective called  functional fixedness . Imagine being a participant in one of his experiments. You are asked to figure out how to mount two candles on a door and are given an assortment of odds and ends, including a small empty cardboard box and some thumbtacks. Perhaps you have already figured out a solution: tack the box to the door so it forms a platform, then put the candles on top of the box. Most people are able to arrive at this solution. Imagine a slight variation of the procedure, however. What if, instead of being empty, the box had matches in it? Most people given this version of the problem do not arrive at the solution given above. Why? Because it seems to people that when the box contains matches, it already has a function; it is a matchbox. People are unlikely to consider a new function for an object that already has a function. This is functional fixedness.

Mental set is a type of fixation in which the problem solver gets stuck using the same solution strategy that has been successful in the past, even though the solution may no longer be useful. It is commonly seen when students do math problems for homework. Often, several problems in a row require the reapplication of the same solution strategy. Then, without warning, the next problem in the set requires a new strategy. Many students attempt to apply the formerly successful strategy on the new problem and therefore cannot come up with a correct answer.

The thing to remember is that you cannot solve a problem unless you correctly identify what it is to begin with (initial state) and what you want the end result to be (goal state). That may mean looking at the problem from a different angle and representing it in a new way. The correct representation does not guarantee a successful solution, but it certainly puts you on the right track.

A bit more optimistically, the Gestalt psychologists discovered what may be considered the opposite of fixation, namely  insight . Sometimes the solution to a problem just seems to pop into your head. Wolfgang Kohler examined insight by posing many different problems to chimpanzees, principally problems pertaining to their acquisition of out-of-reach food. In one version, a banana was placed outside of a chimpanzee’s cage and a short stick inside the cage. The stick was too short to retrieve the banana, but was long enough to retrieve a longer stick also located outside of the cage. This second stick was long enough to retrieve the banana. After trying, and failing, to reach the banana with the shorter stick, the chimpanzee would try a couple of random-seeming attempts, react with some apparent frustration or anger, then suddenly rush to the longer stick, the correct solution fully realized at this point. This sudden appearance of the solution, observed many times with many different problems, was termed insight by Kohler.

Lest you think it pertains to chimpanzees only, Karl Dunker demonstrated that children also solve problems through insight in the 1930s. More importantly, you have probably experienced insight yourself. Think back to a time when you were trying to solve a difficult problem. After struggling for a while, you gave up. Hours later, the solution just popped into your head, perhaps when you were taking a walk, eating dinner, or lying in bed.

fixation :  when a problem solver gets stuck looking at a problem a particular way and cannot change his or her representation of it (or his or her intended solution strategy)

functional fixedness :  a specific type of fixation in which a problem solver cannot think of a new use for an object that already has a function

mental set :  a specific type of fixation in which a problem solver gets stuck using the same solution strategy that has been successful in the past

insight :  a sudden realization of a solution to a problem

Solving Problems by Trial and Error

Correctly identifying the problem and your goal for a solution is a good start, but recall the psychologist’s definition of a problem: it includes a set of possible intermediate states. Viewed this way, a problem can be solved satisfactorily only if one can find a path through some of these intermediate states to the goal. Imagine a fairly routine problem, finding a new route to school when your ordinary route is blocked (by road construction, for example). At each intersection, you may turn left, turn right, or go straight. A satisfactory solution to the problem (of getting to school) is a sequence of selections at each intersection that allows you to wind up at school.

If you had all the time in the world to get to school, you might try choosing intermediate states randomly. At one corner you turn left, the next you go straight, then you go left again, then right, then right, then straight. Unfortunately, trial and error will not necessarily get you where you want to go, and even if it does, it is not the fastest way to get there. For example, when a friend of ours was in college, he got lost on the way to a concert and attempted to find the venue by choosing streets to turn onto randomly (this was long before the use of GPS). Amazingly enough, the strategy worked, although he did end up missing two out of the three bands who played that night.

Trial and error is not all bad, however. B.F. Skinner, a prominent behaviorist psychologist, suggested that people often behave randomly in order to see what effect the behavior has on the environment and what subsequent effect this environmental change has on them. This seems particularly true for the very young person. Picture a child filling a household’s fish tank with toilet paper, for example. To a child trying to develop a repertoire of creative problem-solving strategies, an odd and random behavior might be just the ticket. Eventually, the exasperated parent hopes, the child will discover that many of these random behaviors do not successfully solve problems; in fact, in many cases they create problems. Thus, one would expect a decrease in this random behavior as a child matures. You should realize, however, that the opposite extreme is equally counterproductive. If the children become too rigid, never trying something unexpected and new, their problem solving skills can become too limited.

Effective problem solving seems to call for a happy medium that strikes a balance between using well-founded old strategies and trying new ground and territory. The individual who recognizes a situation in which an old problem-solving strategy would work best, and who can also recognize a situation in which a new untested strategy is necessary is halfway to success.

Solving Problems with Algorithms and Heuristics

For many problems there is a possible strategy available that will guarantee a correct solution. For example, think about math problems. Math lessons often consist of step-by-step procedures that can be used to solve the problems. If you apply the strategy without error, you are guaranteed to arrive at the correct solution to the problem. This approach is called using an  algorithm , a term that denotes the step-by-step procedure that guarantees a correct solution. Because algorithms are sometimes available and come with a guarantee, you might think that most people use them frequently. Unfortunately, however, they do not. As the experience of many students who have struggled through math classes can attest, algorithms can be extremely difficult to use, even when the problem solver knows which algorithm is supposed to work in solving the problem. In problems outside of math class, we often do not even know if an algorithm is available. It is probably fair to say, then, that algorithms are rarely used when people try to solve problems.

Because algorithms are so difficult to use, people often pass up the opportunity to guarantee a correct solution in favor of a strategy that is much easier to use and yields a reasonable chance of coming up with a correct solution. These strategies are called  problem solving heuristics . Similar to what you saw in section 6.2 with reasoning heuristics, a problem solving heuristic is a shortcut strategy that people use when trying to solve problems. It usually works pretty well, but does not guarantee a correct solution to the problem. For example, one problem solving heuristic might be “always move toward the goal” (so when trying to get to school when your regular route is blocked, you would always turn in the direction you think the school is). A heuristic that people might use when doing math homework is “use the same solution strategy that you just used for the previous problem.”

By the way, we hope these last two paragraphs feel familiar to you. They seem to parallel a distinction that you recently learned. Indeed, algorithms and problem-solving heuristics are another example of the distinction between Type 1 thinking and Type 2 thinking.

Although it is probably not worth describing a large number of specific heuristics, two observations about heuristics are worth mentioning. First, heuristics can be very general or they can be very specific, pertaining to a particular type of problem only. For example, “always move toward the goal” is a general strategy that you can apply to countless problem situations. On the other hand, “when you are lost without a functioning gps, pick the most expensive car you can see and follow it” is specific to the problem of being lost. Second, all heuristics are not equally useful. One heuristic that many students know is “when in doubt, choose c for a question on a multiple-choice exam.” This is a dreadful strategy because many instructors intentionally randomize the order of answer choices. Another test-taking heuristic, somewhat more useful, is “look for the answer to one question somewhere else on the exam.”

You really should pay attention to the application of heuristics to test taking. Imagine that while reviewing your answers for a multiple-choice exam before turning it in, you come across a question for which you originally thought the answer was c. Upon reflection, you now think that the answer might be b. Should you change the answer to b, or should you stick with your first impression? Most people will apply the heuristic strategy to “stick with your first impression.” What they do not realize, of course, is that this is a very poor strategy (Lilienfeld et al, 2009). Most of the errors on exams come on questions that were answered wrong originally and were not changed (so they remain wrong). There are many fewer errors where we change a correct answer to an incorrect answer. And, of course, sometimes we change an incorrect answer to a correct answer. In fact, research has shown that it is more common to change a wrong answer to a right answer than vice versa (Bruno, 2001).

The belief in this poor test-taking strategy (stick with your first impression) is based on the  confirmation bias   (Nickerson, 1998; Wason, 1960). You first saw the confirmation bias in Module 1, but because it is so important, we will repeat the information here. People have a bias, or tendency, to notice information that confirms what they already believe. Somebody at one time told you to stick with your first impression, so when you look at the results of an exam you have taken, you will tend to notice the cases that are consistent with that belief. That is, you will notice the cases in which you originally had an answer correct and changed it to the wrong answer. You tend not to notice the other two important (and more common) cases, changing an answer from wrong to right, and leaving a wrong answer unchanged.

Because heuristics by definition do not guarantee a correct solution to a problem, mistakes are bound to occur when we employ them. A poor choice of a specific heuristic will lead to an even higher likelihood of making an error.

algorithm :  a step-by-step procedure that guarantees a correct solution to a problem

problem solving heuristic :  a shortcut strategy that we use to solve problems. Although they are easy to use, they do not guarantee correct judgments and solutions

confirmation bias :  people’s tendency to notice information that confirms what they already believe

An Effective Problem-Solving Sequence

You may be left with a big question: If algorithms are hard to use and heuristics often don’t work, how am I supposed to solve problems? Robert Sternberg (1996), as part of his theory of what makes people successfully intelligent (Module 8) described a problem-solving sequence that has been shown to work rather well:

• Identify the existence of a problem.  In school, problem identification is often easy; problems that you encounter in math classes, for example, are conveniently labeled as problems for you. Outside of school, however, realizing that you have a problem is a key difficulty that you must get past in order to begin solving it. You must be very sensitive to the symptoms that indicate a problem.
• Define the problem.  Suppose you realize that you have been having many headaches recently. Very likely, you would identify this as a problem. If you define the problem as “headaches,” the solution would probably be to take aspirin or ibuprofen or some other anti-inflammatory medication. If the headaches keep returning, however, you have not really solved the problem—likely because you have mistaken a symptom for the problem itself. Instead, you must find the root cause of the headaches. Stress might be the real problem. For you to successfully solve many problems it may be necessary for you to overcome your fixations and represent the problems differently. One specific strategy that you might find useful is to try to define the problem from someone else’s perspective. How would your parents, spouse, significant other, doctor, etc. define the problem? Somewhere in these different perspectives may lurk the key definition that will allow you to find an easier and permanent solution.
• Formulate strategy.  Now it is time to begin planning exactly how the problem will be solved. Is there an algorithm or heuristic available for you to use? Remember, heuristics by their very nature guarantee that occasionally you will not be able to solve the problem. One point to keep in mind is that you should look for long-range solutions, which are more likely to address the root cause of a problem than short-range solutions.
• Represent and organize information.  Similar to the way that the problem itself can be defined, or represented in multiple ways, information within the problem is open to different interpretations. Suppose you are studying for a big exam. You have chapters from a textbook and from a supplemental reader, along with lecture notes that all need to be studied. How should you (represent and) organize these materials? Should you separate them by type of material (text versus reader versus lecture notes), or should you separate them by topic? To solve problems effectively, you must learn to find the most useful representation and organization of information.
• Allocate resources.  This is perhaps the simplest principle of the problem solving sequence, but it is extremely difficult for many people. First, you must decide whether time, money, skills, effort, goodwill, or some other resource would help to solve the problem Then, you must make the hard choice of deciding which resources to use, realizing that you cannot devote maximum resources to every problem. Very often, the solution to problem is simply to change how resources are allocated (for example, spending more time studying in order to improve grades).
• Monitor and evaluate solutions.  Pay attention to the solution strategy while you are applying it. If it is not working, you may be able to select another strategy. Another fact you should realize about problem solving is that it never does end. Solving one problem frequently brings up new ones. Good monitoring and evaluation of your problem solutions can help you to anticipate and get a jump on solving the inevitable new problems that will arise.

Please note that this as  an  effective problem-solving sequence, not  the  effective problem solving sequence. Just as you can become fixated and end up representing the problem incorrectly or trying an inefficient solution, you can become stuck applying the problem-solving sequence in an inflexible way. Clearly there are problem situations that can be solved without using these skills in this order.

Additionally, many real-world problems may require that you go back and redefine a problem several times as the situation changes (Sternberg et al. 2000). For example, consider the problem with Mary’s daughter one last time. At first, Mary did represent the problem as one of defiance. When her early strategy of pleading and threatening punishment was unsuccessful, Mary began to observe her daughter more carefully. She noticed that, indeed, her daughter’s attention would be drawn by an irresistible distraction or book. Fresh with a re-representation of the problem, she began a new solution strategy. She began to remind her daughter every few minutes to stay on task and remind her that if she is ready before it is time to leave, she may return to the book or other distracting object at that time. Fortunately, this strategy was successful, so Mary did not have to go back and redefine the problem again.

Pick one or two of the problems that you listed when you first started studying this section and try to work out the steps of Sternberg’s problem solving sequence for each one.

a mental representation of a category of things in the world

an assumption about the truth of something that is not stated. Inferences come from our prior knowledge and experience, and from logical reasoning

knowledge about one’s own cognitive processes; thinking about your thinking

individuals who are less competent tend to overestimate their abilities more than individuals who are more competent do

Thinking like a scientist in your everyday life for the purpose of drawing correct conclusions. It entails skepticism; an ability to identify biases, distortions, omissions, and assumptions; and excellent deductive and inductive reasoning, and problem solving skills.

a way of thinking in which you refrain from drawing a conclusion or changing your mind until good evidence has been provided

an inclination, tendency, leaning, or prejudice

a type of reasoning in which the conclusion is guaranteed to be true any time the statements leading up to it are true

a set of statements in which the beginning statements lead to a conclusion

an argument for which true beginning statements guarantee that the conclusion is true

a type of reasoning in which we make judgments about likelihood from sets of evidence

an inductive argument in which the beginning statements lead to a conclusion that is probably true

fast, automatic, and emotional thinking

slow, effortful, and logical thinking

a shortcut strategy that we use to make judgments and solve problems. Although they are easy to use, they do not guarantee correct judgments and solutions

udging the frequency or likelihood of some event type according to how easily examples of the event can be called to mind (i.e., how available they are to memory)

judging the likelihood that something is a member of a category on the basis of how much it resembles a typical category member (i.e., how representative it is of the category)

a situation in which we are in an initial state, have a desired goal state, and there is a number of possible intermediate states (i.e., there is no obvious way to get from the initial to the goal state)

noticing, comprehending and forming a mental conception of a problem

when a problem solver gets stuck looking at a problem a particular way and cannot change his or her representation of it (or his or her intended solution strategy)

a specific type of fixation in which a problem solver cannot think of a new use for an object that already has a function

a specific type of fixation in which a problem solver gets stuck using the same solution strategy that has been successful in the past

a sudden realization of a solution to a problem

a step-by-step procedure that guarantees a correct solution to a problem

The tendency to notice and pay attention to information that confirms your prior beliefs and to ignore information that disconfirms them.

a shortcut strategy that we use to solve problems. Although they are easy to use, they do not guarantee correct judgments and solutions

Introduction to Psychology Copyright © 2020 by Ken Gray; Elizabeth Arnott-Hill; and Or'Shaundra Benson is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

What is the relationship between thinking and problem solving?

Thinking and problem solving are two fundamental cognitive processes that are closely intertwined. Thinking involves the mental processes of perception, reasoning, and judgment, while problem solving is the ability to find solutions to complex or challenging situations. The relationship between thinking and problem solving is crucial, as effective problem solving requires the use of critical thinking skills. In this essay, we will explore the intricacies of this relationship and how thinking plays a crucial role in the problem-solving process. We will also discuss how different thinking styles can impact problem-solving abilities and the importance of incorporating critical thinking skills in problem-solving strategies.

Thinking or Thought Process refers to ideas or arrangements of ideas that are the result of the process of thinking. Though thinking is an activity considered essential to humanity, there is no consensus as to how we define or understand it.

Because thought underlies many human actions and interactions, understanding its physical and metaphysical origins, processes, and effects has been a longstanding goal of many academic disciplines including linguistics, psychology, neuroscience, philosophy, artificial intelligence, biology, sociology and cognitive science.

Thinking allows humans to make sense of, interpret, represent or model the world they experience, and to make predictions about that world. It is therefore helpful to an organism with needs, objectives, and desires as it makes plans or otherwise attempts to accomplish those goals.

The word thought comes from Old English þoht, or geþoht, from stem of þencan “to conceive of in the mind, consider”.

The word “thought” may mean:

• a single product of thinking or a single idea (“My first thought was ‘no.’”)
• the product of mental activity (“Mathematics is a large body of thought.”)
• the act or system of thinking (“I was frazzled from too much thought.”)
• the capacity to think, reason, imagine, and so on (“All her thought was applied to her work.”)
• the consideration of or reflection on an idea (“The thought of death terrifies me.”)
• recollection or contemplation (“I thought about my childhood.”)
• half-formed or imperfect intention (“I had some thought of going.”)
• anticipation or expectation (“She had no thought of seeing him again.”)
• consideration, attention, care, or regard (“He took no thought of his appearance” and “I did it without thinking.”)
• judgment, opinion, or belief (“According to his thought, honesty is the best policy.”)
• the ideas characteristic of a particular place, class, or time (“Greek thought”)
• the state of being conscious of something (“It made me think of my grandmother.”)
• tending to believe in something, especially with less than full confidence (“I think that it will rain, but I am not sure.”)

Definitions may or may not require that thought:

• take place within a human brain (see anthropomorphism),
• take place as part of a living biological system (see Alan Turing and Computing Machinery and Intelligence),
• take place only at a conscious level of awareness (see Unconscious Thought Theory),
• require language,
• is principally or even only conceptual, abstract (“formal”),
• involve other concepts such as drawing analogies, interpreting, evaluating, imagining, planning, and remembering.

Definitions of thought may also be derived directly or indirectly from theories of thought.

• “Outline of a theory of thought-processes and thinking machines” (Caianiello) – thought processes and mental phenomena modeled by sets of mathematical equations
• Surfaces and Essences: Analogy as the Fuel and Fire of Thinking (Hofstadter and Sander) – a theory built on analogies
• The Neural Theory of Language and Thought (Feldman and Lakoff) – neural modeling of language and spatial relations
• ThoughtForms – The Structure, Power, and Limitations of Thought (Baum) – a theory built on mental models
• Unconscious Thought Theory – thought that is not conscious
• Linguistics theories – The Stuff of Thought (Steven Pinker, Noam Chomsky) – The linguistic and cognitive theory that thought is based on syntactic and linguistic recursion processes

What is most thought-provoking in these thought-provoking times, is that we are still not thinking.

— Martin Heidegger

The phenomenology movement in philosophy saw a radical change in the way in which we understand thought. Martin Heidegger’s phenomenological analyses of the existential structure of man in Being and Time cast new light on the issue of thinking, unsettling traditional cognitive or rational interpretations of man which affect the way we understand thought. The notion of the fundamental role of non-cognitive understanding in rendering possible thematic consciousness informed the discussion surrounding Artificial Intelligence during the 1970s and 1980s.

Phenomenology, however, is not the only approach to thinking in modern Western philosophy. Philosophy of mind is a branch of philosophy that studies the nature of the mind, mental events, mental functions, mental properties, consciousness and their relationship to the physical body, particularly the brain. The mind-body problem, i.e. the relationship of the mind to the body, is commonly seen as the central issue in philosophy of mind, although there are other issues concerning the nature of the mind that do not involve its relation to the physical body.

The mind-body problem

The mind-body problem concerns the explanation of the relationship that exists between minds, or mental processes, and bodily states or processes. The main aim of philosophers working in this area is to determine the nature of the mind and mental states/processes, and how—or even if—minds are affected by and can affect the body.

Human perceptual experiences depend on stimuli which arrive at one’s various sensory organs from the external world and these stimuli cause changes in one’s mental state, ultimately causing one to feel a sensation, which may be pleasant or unpleasant. Someone’s desire for a slice of pizza, for example, will tend to cause that person to move his or her body in a specific manner and in a specific direction to obtain what he or she wants. The question, then, is how it can be possible for conscious experiences to arise out of a lump of gray matter endowed with nothing but electrochemical properties. A related problem is to explain how someone’s propositional attitudes (e.g. beliefs and desires) can cause that individual’s neurons to fire and his muscles to contract in exactly the correct manner. These comprise some of the puzzles that have confronted epistemologists and philosophers of mind from at least the time of René Descartes.

Functionalism vs. embodiment

The above reflects a classical, functional description of how we work as cognitive, thinking systems. However the apparently irresolvable mind-body problem is said to be overcome, and bypassed, by the embodied cognition approach, with its roots in the work of Heidegger, Piaget, Vygotsky, Merleau-Ponty and the pragmatist John Dewey.

This approach states that the classical approach of separating the mind and analysing its processes is misguided: instead, we should see that the mind, actions of an embodied agent, and the environment it perceives and envisions, are all parts of a whole which determine each other. Therefore, functional analysis of the mind alone will always leave us with the mind-body problem which cannot be solved.

A neuron (also known as a neurone or nerve cell) is an excitable cell in the nervous system that processes and transmits information by electrochemical signaling. Neurons are the core components of the brain, the vertebrate spinal cord, the invertebrate ventral nerve cord, and the peripheral nerves. A number of specialized types of neurons exist: sensory neurons respond to touch, sound, light and numerous other stimuli affecting cells of the sensory organs that then send signals to the spinal cord and brain. Motor neurons receive signals from the brain and spinal cord and cause muscle contractions and affect glands. Interneurons connect neurons to other neurons within the brain and spinal cord. Neurons respond to stimuli, and communicate the presence of stimuli to the central nervous system, which processes that information and sends responses to other parts of the body for action. Neurons do not go through mitosis, and usually cannot be replaced after being destroyed,[dubious – discuss] although astrocytes have been observed to turn into neurons as they are sometimes pluripotent.

Psychologists have concentrated on thinking as an intellectual exertion aimed at finding an answer to a question or the solution of a practical problem. Cognitive psychology is a branch of psychology that investigates internal mental processes such as problem solving, memory, and language. The school of thought arising from this approach is known as cognitivism which is interested in how people mentally represent information processing. It had its foundations in the Gestalt psychology of Max Wertheimer, Wolfgang Köhler, and Kurt Koffka, and in the work of Jean Piaget, who provided a theory of stages/phases that describe children’s cognitive development.

Cognitive psychologists use psychophysical and experimental approaches to understand, diagnose, and solve problems, concerning themselves with the mental processes which mediate between stimulus and response. They study various aspects of thinking, including the psychology of reasoning, and how people make decisions and choices, solve problems, as well as engage in creative discovery and imaginative thought. Cognitive theory contends that solutions to problems take the form of algorithms—rules that are not necessarily understood but promise a solution, or heuristics—rules that are understood but that do not always guarantee solutions. Cognitive science differs from cognitive psychology in that algorithms that are intended to simulate human behavior are implemented or implementable on a computer. In other instances, solutions may be found through insight, a sudden awareness of relationships.

In developmental psychology, Jean Piaget was a pioneer in the study of the development of thought from birth to maturity. In his theory of cognitive development, thought is based on actions on the environment. That is, Piaget suggests that the environment is understood through assimilations of objects in the available schemes of action and these accommodate to the objects to the extent that the available schemes fall short of the demands. As a result of this interplay between assimilation and accommodation, thought develops through a sequence of stages that differ qualitatively from each other in mode of representation and complexity of inference and understanding. That is, thought evolves from being based on perceptions and actions at the sensorimotor stage in the first two years of life to internal representations in early childhood. Subsequently, representations are gradually organized into logical structures which first operate on the concrete properties of the reality, in the stage of concrete operations, and then operate on abstract principles that organize concrete properties, in the stage of formal operations. In recent years, the Piagetian conception of thought was integrated with information processing conceptions. Thus, thought is considered as the result of mechanisms that are responsible for the representation and processing of information. In this conception, speed of processing, cognitive control, and working memory are the main functions underlying thought. In the neo-Piagetian theories of cognitive development, the development of thought is considered to come from increasing speed of processing, enhanced cognitive control, and increasing working memory.

Positive psychology emphasizes the positive aspects of human psychology as equally important as the focus on mood disorders and other negative symptoms. In Character Strengths and Virtues, Peterson and Seligman list a series of positive characteristics. One person is not expected to have every strength, nor are they meant to fully capsulate that characteristic entirely. The list encourages positive thought that builds on a person’s strengths, rather than how to “fix” their “symptoms”.

Psychoanalysis

“Id”, “ego”, and “super-ego” are the three parts of the “psychic apparatus” defined in Sigmund Freud’s structural model of the psyche; they are the three theoretical constructs in terms of whose activity and interaction mental life is described. According to this model, the uncoordinated instinctual trends are the “id”; the organized realistic part of the psyche is the “ego,” and the critical and moralizing function the “super-ego.”

The unconscious was considered by Freud throughout the evolution of his psychoanalytic theory a sentient force of will influenced by human desire and yet operating well below the perceptual conscious mind. For Freud, the unconscious is the storehouse of instinctual desires, needs, and psychic drives. While past thoughts and reminiscences may be concealed from immediate consciousness, they direct the thoughts and feelings of the individual from the realm of the unconscious.

For psychoanalysis, the unconscious does not include all that is not conscious, rather only what is actively repressed from conscious thought or what the person is averse to knowing consciously. In a sense this view places the self in relationship to their unconscious as an adversary, warring with itself to keep what is unconscious hidden. If a person feels pain, all he can think of is alleviating the pain. Any of his desires, to get rid of pain or enjoy something, command the mind what to do. For Freud, the unconscious was a repository for socially unacceptable ideas, wishes or desires, traumatic memories, and painful emotions put out of mind by the mechanism of psychological repression. However, the contents did not necessarily have to be solely negative. In the psychoanalytic view, the unconscious is a force that can only be recognized by its effects—it expresses itself in the symptom.

Social psychology is the study of how people and groups interact. Scholars in this interdisciplinary area are typically either psychologists or sociologists, though all social psychologists employ both the individual and the group as their units of analysis.

Despite their similarity, psychological and sociological researchers tend to differ in their goals, approaches, methods, and terminology. They also favor separate academic journals and professional societies. The greatest period of collaboration between sociologists and psychologists was during the years immediately following World War II. Although there has been increasing isolation and specialization in recent years, some degree of overlap and influence remains between the two disciplines.

The collective unconscious, sometimes known as collective subconscious, is a term of analytical psychology, coined by Carl Jung. It is a part of the unconscious mind, shared by a society, a people, or all humanity, in an interconnected system that is the product of all common experiences and contains such concepts as science, religion, and morality. While Freud did not distinguish between an “individual psychology” and a “collective psychology,” Jung distinguished the collective unconscious from the personal subconscious particular to each human being. The collective unconscious is also known as “a reservoir of the experiences of our species.”

In the “Definitions” chapter of Jung’s seminal work Psychological Types, under the definition of “collective” Jung references representations collectives, a term coined by Lucien Lévy-Bruhl in his 1910 book How Natives Think. Jung says this is what he describes as the collective unconscious. Freud, on the other hand, did not accept the idea of a collective unconscious.

Problem Solving

Problem solving consists of using generic or ad hoc methods, in an orderly manner, for finding solutions to problems. Some of the problem-solving techniques developed and used in artificial intelligence, computer science, engineering, mathematics, or medicine are related to mental problem-solving techniques studied in psychology.

The term problem solving is used in many disciplines, sometimes with different perspectives, and often with different terminologies. For instance, it is a mental process in psychology and a computerized process in computer science. Problems can also be classified into two different types (ill-defined and well-defined) from which appropriate solutions are to be made. Ill-defined problems are those that do not have clear goals, solution paths, or expected solution. Well-defined problems have specific goals, clearly defined solution paths, and clear expected solutions. These problems also allow for more initial planning than ill-defined problems. Being able to solve problems sometimes involves dealing with pragmatics (logic) and semantics (interpretation of the problem). The ability to understand what the goal of the problem is and what rules could be applied represent the key to solving the problem. Sometimes the problem requires some abstract thinking and coming up with a creative solution.

Thomas J. D’Zurilla in 1988 defined problem solving as a “cognitive–affective–behavioral process through which an individual (or group) attempts to identify, discover, or invent effective means of coping with problems encountered in every day living”. It is an evolutionary drive for living organisms and an important coping skill for dealing with a variety of concerns. Problem solving specifically in psychology refers to a state of desire for reaching a definite ‘goal’ from a present condition that either is not directly moving toward the goal, is far from it, or needs more complex logic for finding a missing description of conditions or steps toward the goal. In each case “where you want to be” is an imagined (or written) state in which you would like to be and the solutions are situation- or context-specific. This process includes problem finding or ‘problem analysis’, problem shaping, generating alternative strategies, implementation and verification of the selected solution. Distinguished feature of a problem is that there is a goal to be reached and how you get there depends upon problem orientation (problem-solving coping style and skills) and systematic analysis. The nature of human problem solving processes and methods is a field of study and work for mental health professionals. Methods of studying problem solving include introspection, behaviorism, simulation, computer modeling, and experiment. Social psychologists look into the person-environment relationship aspect of the problem and independent and interdependent problem-solving methods. Problem solving has been defined as a higher-order cognitive process and intellectual function that requires the modulation and control of more routine or fundamental skills.

Problem solving has two major domains: mathematical problem solving and personal problem solving both are seen in terms of some difficulty or barrier is encountered. Empirical researches show that self-interest and interpersonal skills; collaborative and instrumental problem approach (it helps in reflective and expansive understanding of the problem situation and its preferable outcome); strategy fluency (the number and diversity of strategies) and conceptual clarity that can lead to an action-identification (Vallacher & Wegner, 1987); temporal lifespan perspective that lead to selectivity in strategy (problem focused and emotion focused strategies); self-efficacy and problem familiarity; formation of ‘carry over’ relationships (egalitarian friendship, romantic ties, cliques, hygge’s, etc.) that helps individuals mutually move through life and provide a sense of identity (Antonucci, Birditt, & Ajrouch, 2011); negotiation; type of relationships (obligatory vs. voluntary); gender typing; problem focused and emotion focused strategies as some strategies and factors that influence everyday problem solving. Neuropsychologists have studied that individuals with frontal lobe injuries with deficits in emotional control and reasoning can be remediated with effective rehabilitation and could improve the capacity of injured persons to resolve everyday problems (Rath, Simon, Langenbahn, Sherr, & Diller, 2003).

Interpersonal everyday problem solving is dependent upon the individual personal motivational and contextual components. One such component is the emotional valence of “real-world” problems and it can either impede or aid problem-solving performance. Researchers have focused on the role of emotions in problem solving (D’Zurilla & Goldfried, 1971; D’Zurilla & Nezu, 1982), demonstrating that poor emotional control can disrupt focus on the target task and impede problem resolution and likely lead to negative outcomes such as fatigue, depression, and inertia (Rath, Langenbahn, Simon, Sherr, & Diller, 2004). In conceptualization, human problem solving consists of two related processes: problem orientation, the motivational/attitudinal/affective approach to problematic situations and problem-solving skills. Studies conclude people’s strategies cohere with their goals (Hoppmann & Blanchard-Fields, 2010, Berg et al., 1998) and they are stemmed from the natural process of comparing oneself with others (Sonstegard and Bitter, 1998).

Cognitive sciences

The early experimental work of the Gestaltists in Germany placed the beginning of problem solving study (e.g., Karl Duncker in 1935 with his book The psychology of productive thinking). Later this experimental work continued through the 1960s and early 1970s with research conducted on relatively simple (but novel for participants) laboratory tasks of problem solving. Choosing simple novel tasks was based on the clearly defined optimal solutions and their short time for solving, which made it possible for the researchers to trace participants’ steps in problem-solving process. Researchers’ underlying assumption was that simple tasks such as the Tower of Hanoi correspond to the main properties of “real world” problems and thus the characteristic cognitive processes within participants’ attempts to solve simple problems are the same for “real world” problems too; simple problems were used for reasons of convenience and with the expectation that thought generalizations to more complex problems would become possible. Perhaps the best-known and most impressive example of this line of research is the work by Allen Newell and Herbert A. Simon. Other experts have shown that the principle of decomposition improves the ability of the problem solver to make good judgment.

Computer science and algorithmics

In computer science and in the part of artificial intelligence that deals with algorithms (“algorithmics”), problem solving encompasses a number of techniques known as algorithms, heuristics, root cause analysis, etc. In these disciplines, problem solving is part of a larger process that encompasses problem determination, de-duplication, analysis, diagnosis, repair, etc.

Engineering

Problem solving is used in when products or processes fail, so corrective action can be taken to prevent further failures. It can also be applied to a product or process prior to an actual fail event, i.e., when a potential problem can be predicted and analyzed, and mitigation applied so the problem never actually occurs. Techniques such as Failure Mode Effects Analysis can be used to proactively reduce the likelihood of problems occurring.

Military science

In military science, problem solving is linked to the concept of “end-states”, the desired condition or situation that strategists wish to generate.:xiii, E-2 The ability to solve problems is important at any military rank, but is highly critical at the command and control level, where it is strictly correlated to the deep understanding of qualitative and quantitative scenarios. Effectiveness of problem solving is “a criterion used to assess changes in system behavior, capability, or operational environment that is tied to measuring the attainment of an end state, achievement of an objective, or creation of an effect”. Planning for problem-solving is a “process that determines and describes how to employ ‘means’ in specific ‘ways’ to achieve ‘ends’ (the problem’s solution).”

• Forensic engineering is an important technique of failure analysis that involves tracing product defects and flaws. Corrective action can then be taken to prevent further failures.
• Reverse engineering attempts to discover the original problem-solving logic used in developing a product by taking it apart.
• Other problem solving tools are linear and nonlinear programming, queuing systems, and simulation.

Problem-solving strategies

Problem-solving strategies are the steps that one would use to find the problem(s) that are in the way to getting to one’s own goal. Firend’s problem solving model (PSM) is practical in application and incorporates the conventional 5WH approach, with a systematic process of investigation, implementation and assessment cycle.[non-primary source needed] Some would refer to this as the “problem-solving cycle” (Bransford & Stein, 1993). In this cycle one will recognize the problem, define the problem, develop a strategy to fix the problem, organize the knowledge of the problem cycle, figure out the resources at the user’s disposal, monitor one’s progress, and evaluate the solution for accuracy. The reason it is called a cycle is that once one is completed with a problem another usually will pop up.

Blanchard-Fields (2007) looks at problem solving from one of two facets. The first looking at those problems that only have one solution (like mathematical problems, or fact-based questions) which are grounded in psychometric intelligence. The other that is socioemotional in nature and are unpredictable with answers that are constantly changing (like what’s your favorite color or what you should get someone for Christmas).

The following techniques are usually called problem-solving strategies’

• Abstraction: solving the problem in a model of the system before applying it to the real system
• Analogy: using a solution that solves an analogous problem
• Brainstorming: (especially among groups of people) suggesting a large number of solutions or ideas and combining and developing them until an optimum solution is found
• Divide and conquer: breaking down a large, complex problem into smaller, solvable problems
• Hypothesis testing: assuming a possible explanation to the problem and trying to prove (or, in some contexts, disprove) the assumption
• Lateral thinking: approaching solutions indirectly and creatively
• Means-ends analysis: choosing an action at each step to move closer to the goal
• Method of focal objects: synthesizing seemingly non-matching characteristics of different objects into something new
• Morphological analysis: assessing the output and interactions of an entire system
• Proof: try to prove that the problem cannot be solved. The point where the proof fails will be the starting point for solving it
• Reduction: transforming the problem into another problem for which solutions exist
• Research: employing existing ideas or adapting existing solutions to similar problems
• Root cause analysis: identifying the cause of a problem
• Trial-and-error: testing possible solutions until the right one is found

Problem-solving methods

• Eight Disciplines Problem Solving
• How to Solve It
• OODA loop (observe, orient, decide, and act)
• PDCA (plan–do–check–act)
• Root cause analysis
• RPR problem diagnosis (rapid problem resolution)
• TRIZ (in Russian: Teoriya Resheniya Izobretatelskikh Zadach, “theory of solving inventor’s problems”)
• A3 problem solving
• System dynamics

Common barriers to problem solving

Common barriers to problem solving are mental constructs that impede our ability to correctly solve problems. These barriers prevent people from solving problems in the most efficient manner possible. Five of the most common processes and factors that researchers have identified as barriers to problem solving are confirmation bias, mental set, functional fixedness, unnecessary constraints, and irrelevant information.

Confirmation bias

Within the field of science there exists a set of fundamental standards, the scientific method, which outlines the process of discovering facts or truths about the world through unbiased consideration of all pertinent information and through impartial observation of and/or experimentation with that information. According to this method, one is able to most accurately find a solution to a perceived problem by performing the aforementioned steps. The scientific method does not prescribe a process that is limited to scientists, but rather one that all people can practice in their respective fields of work as well as in their personal lives. Confirmation bias can be described as one’s unconscious or unintentional corruption of the scientific method. Thus when one demonstrates confirmation bias, one is formally or informally collecting data and then subsequently observing and experimenting with that data in such a way that favors a preconceived notion that may or may not have motivation. Research has found that professionals within scientific fields of study also experience confirmation bias. Andreas Hergovich, Reinhard Schott, and Christoph Burger’s experiment conducted online, for instance, suggested that professionals within the field of psychological research are likely to view scientific studies that are congruent with their preconceived understandings more favorably than studies that are incongruent with their established beliefs.

Motivation refers to one’s desire to defend or find substantiation for beliefs (e.g., religious beliefs) that are important to one. According to Raymond Nickerson, one can see the consequences of confirmation bias in real-life situations, which range in severity from inefficient government policies to genocide. With respect to the latter and most severe ramification of this cognitive barrier, Nickerson argued that those involved in committing genocide of persons accused of witchcraft, an atrocity that occurred from the 15th to 17th centuries, demonstrated confirmation bias with motivation. Researcher Michael Allen found evidence for confirmation bias with motivation in school children who worked to manipulate their science experiments in such a way that would produce their hoped for results. However, confirmation bias does not necessarily require motivation. In 1960, Peter Cathcart Wason conducted an experiment in which participants first viewed three numbers and then created a hypothesis that proposed a rule that could have been used to create that triplet of numbers. When testing their hypotheses, participants tended to only create additional triplets of numbers that would confirm their hypotheses, and tended not to create triplets that would negate or disprove their hypotheses. Thus research also shows that people can and do work to confirm theories or ideas that do not support or engage personally significant beliefs.

Mental set was first articulated by Abraham Luchins in the 1940s and demonstrated in his well-known water jug experiments. In these experiments, participants were asked to fill one jug with a specific amount of water using only other jugs (typically three) with different maximum capacities as tools. After Luchins gave his participants a set of water jug problems that could all be solved by employing a single technique, he would then give them a problem that could either be solved using that same technique or a novel and simpler method. Luchins discovered that his participants tended to use the same technique that they had become accustomed to despite the possibility of using a simpler alternative. Thus mental set describes one’s inclination to attempt to solve problems in such a way that has proved successful in previous experiences. However, as Luchins’ work revealed, such methods for finding a solution that have worked in the past may not be adequate or optimal for certain new but similar problems. Therefore, it is often necessary for people to move beyond their mental sets in order to find solutions. This was again demonstrated in Norman Maier’s 1931 experiment, which challenged participants to solve a problem by using a household object (pliers) in an unconventional manner. Maier observed that participants were often unable to view the object in a way that strayed from its typical use, a phenomenon regarded as a particular form of mental set (more specifically known as functional fixedness, which is the topic of the following section). When people cling rigidly to their mental sets, they are said to be experiencing fixation, a seeming obsession or preoccupation with attempted strategies that are repeatedly unsuccessful. In the late 1990s, researcher Jennifer Wiley worked to reveal that expertise can work to create a mental set in persons considered to be experts in certain fields, and she furthermore gained evidence that the mental set created by expertise could lead to the development of fixation.

Functional fixedness

Functional fixedness is a specific form of mental set and fixation, which was alluded to earlier in the Maier experiment, and furthermore it is another way in which cognitive bias can be seen throughout daily life. Tim German and Clark Barrett describe this barrier as the fixed design of an object hindering the individual’s ability to see it serving other functions. In more technical terms, these researchers explained that “[s]ubjects become “fixed” on the design function of the objects, and problem solving suffers relative to control conditions in which the object’s function is not demonstrated.” Functional fixedness is defined as only having that primary function of the object itself hinder the ability of it serving another purpose other than its original function. In research that highlighted the primary reasons that young children are immune to functional fixedness, it was stated that “functional fixedness…[is when]subjects are hindered in reaching the solution to a problem by their knowledge of an object’s conventional function.” Furthermore, it is important to note that functional fixedness can be easily expressed in commonplace situations. For instance, imagine the following situation: a man sees a bug on the floor that he wants to kill, but the only thing in his hand at the moment is a can of air freshener. If the man starts looking around for something in the house to kill the bug with instead of realizing that the can of air freshener could in fact be used not only as having its main function as to freshen the air, he is said to be experiencing functional fixedness. The man’s knowledge of the can being served as purely an air freshener hindered his ability to realize that it too could have been used to serve another purpose, which in this instance was as an instrument to kill the bug. Functional fixedness can happen on multiple occasions and can cause us to have certain cognitive biases. If we only see an object as serving one primary focus than we fail to realize that the object can be used in various ways other than its intended purpose. This can in turn cause many issues with regards to problem solving. Common sense seems to be a plausible answer to functional fixedness. One could make this argument because it seems rather simple to consider possible alternative uses for an object. Perhaps using common sense to solve this issue could be the most accurate answer within this context. With the previous stated example, it seems as if it would make perfect sense to use the can of air freshener to kill the bug rather than to search for something else to serve that function but, as research shows, this is often not the case.

Functional fixedness limits the ability for people to solve problems accurately by causing one to have a very narrow way of thinking. Functional fixedness can be seen in other types of learning behaviors as well. For instance, research has discovered the presence of functional fixedness in many educational instances. Researchers Furio, Calatayud, Baracenas, and Padilla stated that “… functional fixedness may be found in learning concepts as well as in solving chemistry problems.” There was more emphasis on this function being seen in this type of subject and others.

There are several hypotheses in regards to how functional fixedness relates to problem solving. There are also many ways in which a person can run into problems while thinking of a particular object with having this function. If there is one way in which a person usually thinks of something rather than multiple ways then this can lead to a constraint in how the person thinks of that particular object. This can be seen as narrow minded thinking, which is defined as a way in which one is not able to see or accept certain ideas in a particular context. Functional fixedness is very closely related to this as previously mentioned. This can be done intentionally and or unintentionally, but for the most part it seems as if this process to problem solving is done in an unintentional way.

Functional fixedness can affect problem solvers in at least two particular ways. The first is with regards to time, as functional fixedness causes people to use more time than necessary to solve any given problem. Secondly, functional fixedness often causes solvers to make more attempts to solve a problem than they would have made if they were not experiencing this cognitive barrier. In the worst case, functional fixedness can completely prevent a person from realizing a solution to a problem. Functional fixedness is a commonplace occurrence, which affects the lives of many people.

Unnecessary constraints

Unnecessary constraints are another very common barrier that people face while attempting to problem-solve. This particular phenomenon occurs when the subject, trying to solve the problem subconsciously, places boundaries on the task at hand, which in turn forces him or her to strain to be more innovative in their thinking. The solver hits a barrier when they become fixated on only one way to solve their problem, and it becomes increasingly difficult to see anything but the method they have chosen. Typically, the solver experiences this when attempting to use a method they have already experienced success from, and they can not help but try to make it work in the present circumstances as well, even if they see that it is counterproductive.

Groupthink, or taking on the mindset of the rest of the group members, can also act as an unnecessary constraint while trying to solve problems. This is due to the fact that with everybody thinking the same thing, stopping on the same conclusions, and inhibiting themselves to think beyond this. This is very common, but the most well-known example of this barrier making itself present is in the famous example of the dot problem. In this example, there are nine dots lying in a square- three dots across, and three dots running up and down. The solver is then asked to draw no more than four lines, without lifting their pen or pencil from the paper. This series of lines should connect all of the dots on the paper. Then, what typically happens is the subject creates an assumption in their mind that they must connect the dots without letting his or her pen or pencil go outside of the square of dots. Standardized procedures like this can often bring mentally invented constraints of this kind, and researchers have found a 0% correct solution rate in the time allotted for the task to be completed. The imposed constraint inhibits the solver to think beyond the bounds of the dots. It is from this phenomenon that the expression “think outside the box” is derived.

This problem can be quickly solved with a dawning of realization, or insight. A few minutes of struggling over a problem can bring these sudden insights, where the solver quickly sees the solution clearly. Problems such as this are most typically solved via insight and can be very difficult for the subject depending on either how they have structured the problem in their minds, how they draw on their past experiences, and how much they juggle this information in their working memories In the case of the nine-dot example, the solver has already been structured incorrectly in their minds because of the constraint that they have placed upon the solution. In addition to this, people experience struggles when they try to compare the problem to their prior knowledge, and they think they must keep their lines within the dots and not go beyond. They do this because trying to envision the dots connected outside of the basic square puts a strain on their working memory.

Luckily, the solution to the problem becomes obvious as insight occurs following incremental movements made toward the solution. These tiny movements happen without the solver knowing. Then when the insight is realized fully, the “aha” moment happens for the subject. These moments of insight can take a long while to manifest or not so long at other times, but the way that the solution is arrived at after toiling over these barriers stays the same.

Irrelevant information

Irrelevant information is information presented within a problem that is unrelated or unimportant to the specific problem. Within the specific context of the problem, irrelevant information would serve no purpose in helping solve that particular problem. Often irrelevant information is detrimental to the problem solving process. It is a common barrier that many people have trouble getting through, especially if they are not aware of it. Irrelevant information makes solving otherwise relatively simple problems much harder.

For example: “Fifteen percent of the people in Topeka have unlisted telephone numbers. You select 200 names at random from the Topeka phone book. How many of these people have unlisted phone numbers?”

The people that are not listed in the phone book would not be among the 200 names you selected. The individuals looking at this task would have naturally wanted to use the 15% given to them in the problem. They see that there is information present and they immediately think that it needs to be used. This of course is not true. These kinds of questions are often used to test students taking aptitude tests or cognitive evaluations. They aren’t meant to be difficult but they are meant to require thinking that is not necessarily common. Irrelevant Information is commonly represented in math problems, word problems specifically, where numerical information is put for the purpose of challenging the individual.

One reason irrelevant information is so effective at keeping a person off topic and away from the relevant information, is in how it is represented. The way information is represented can make a vast difference in how difficult the problem is to be overcome. Whether a problem is represented visually, verbally, spatially, or mathematically, irrelevant information can have a profound effect on how long a problem takes to be solved; or if it’s even possible. The Buddhist monk problem is a classic example of irrelevant information and how it can be represented in different ways:

A Buddhist monk begins at dawn one day walking up a mountain, reaches the top at sunset, meditates at the top for several days until one dawn when he begins to walk back to the foot of the mountain, which he reaches at sunset. Making no assumptions about his starting or stopping or about his pace during the trips, prove that there is a place on the path which he occupies at the same hour of the day on the two separate journeys.

This problem is near impossible to solve because of how the information is represented. Because it is written out in a way that represents the information verbally, it causes us to try and create a mental image of the paragraph. This is often very difficult to do especially with all the irrelevant information involved in the question. This example is made much easier to understand when the paragraph is represented visually. Now if the same problem was asked, but it was also accompanied by a corresponding graph, it would be far easier to answer this question; irrelevant information no longer serves as a road block. By representing the problem visually, there are no difficult words to understand or scenarios to imagine. The visual representation of this problem has removed the difficulty of solving it.

These types of representations are often used to make difficult problems easier. They can be used on tests as a strategy to remove Irrelevant Information, which is one of the most common forms of barriers when discussing the issues of problem solving. Identifying crucial information presented in a problem and then being able to correctly identify its usefulness is essential. Being aware of irrelevant information is the first step in overcoming this common barrier.

Cognitive sciences: two schools

In cognitive sciences, researchers’ realization that problem-solving processes differ across knowledge domains and across levels of expertise (e.g. Sternberg, 1995) and that, consequently, findings obtained in the laboratory cannot necessarily generalize to problem-solving situations outside the laboratory, has led to an emphasis on real-world problem solving since the 1990s. This emphasis has been expressed quite differently in North America and Europe, however. Whereas North American research has typically concentrated on studying problem solving in separate, natural knowledge domains, much of the European research has focused on novel, complex problems, and has been performed with computerized scenarios (see Funke, 1991, for an overview).

In Europe, two main approaches have surfaced, one initiated by Donald Broadbent (1977; see Berry & Broadbent, 1995) in the United Kingdom and the other one by Dietrich Dörner (1975, 1985; see Dörner & Wearing, 1995) in Germany. The two approaches share an emphasis on relatively complex, semantically rich, computerized laboratory tasks, constructed to resemble real-life problems. The approaches differ somewhat in their theoretical goals and methodology, however. The tradition initiated by Broadbent emphasizes the distinction between cognitive problem-solving processes that operate under awareness versus outside of awareness, and typically employs mathematically well-defined computerized systems. The tradition initiated by Dörner, on the other hand, has an interest in the interplay of the cognitive, motivational, and social components of problem solving, and utilizes very complex computerized scenarios that contain up to 2,000 highly interconnected variables (e.g., Dörner, Kreuzig, Reither & Stäudel’s 1983 LOHHAUSEN project; Ringelband, Misiak & Kluwe, 1990). Buchner (1995) describes the two traditions in detail.

North America

In North America, initiated by the work of Herbert A. Simon on “learning by doing” in semantically rich domains (e.g. Anzai & Simon, 1979; Bhaskar & Simon, 1977), researchers began to investigate problem solving separately in different natural knowledge domains – such as physics, writing, or chess playing – thus relinquishing their attempts to extract a global theory of problem solving (e.g. Sternberg & Frensch, 1991). Instead, these researchers have frequently focused on the development of problem solving within a certain domain, that is on the development of expertise (e.g. Anderson, Boyle & Reiser, 1985; Chase & Simon, 1973; Chi, Feltovich & Glaser, 1981).

Areas that have attracted rather intensive attention in North America include:

• Reading (Stanovich & Cunningham, 1991)
• Writing (Bryson, Bereiter, Scardamalia & Joram, 1991)
• Calculation (Sokol & McCloskey, 1991)
• Political decision making (Voss, Wolfe, Lawrence & Engle, 1991)
• Managerial problem solving (Wagner, 1991)
• Lawyers’ reasoning (Amsel, Langer & Loutzenhiser, 1991)
• Mechanical problem solving (Hegarty, 1991)
• Problem solving in electronics (Lesgold & Lajoie, 1991)
• Computer skills (Kay, 1991)
• Game playing (Frensch & Sternberg, 1991)
• Personal problem solving (Heppner & Krauskopf, 1987)
• Mathematical problem solving (Pólya, 1945; Schoenfeld, 1985)
• Social problem solving (D’Zurilla & Goldfreid, 1971; D’Zurilla & Nezu, 1982)
• Problem solving for innovations and inventions: TRIZ (Altshuller, 1994)

Characteristics of complex problems

As elucidated by Dietrich Dörner and later expanded upon by Joachim Funke, complex problems have some typical characteristics that can be summarized as follows:

• Complexity (large numbers of items, interrelations and decisions)
• enumerability
• heterogeneity
• connectivity (hierarchy relation, communication relation, allocation relation)
• Dynamics (time considerations)
• temporal constraints
• temporal sensitivity
• phase effects
• dynamic unpredictability
• Intransparency (lack of clarity of the situation)
• commencement opacity
• continuation opacity
• Polytely (multiple goals)
• inexpressiveness

Collective problem solving

Problem solving is applied on many different levels − from the individual to the civilizational. Collective problem solving refers to problem solving performed collectively.

Social issues and global issues can typically only be solved collectively.

It has been noted that the complexity of contemporary problems has exceeded the cognitive capacity of any individual and requires different but complementary expertise and collective problem solving ability.

Collective intelligence is shared or group intelligence that emerges from the collaboration, collective efforts, and competition of many individuals.

In a 1962 research report, Douglas Engelbart linked collective intelligence to organizational effectiveness, and predicted that pro-actively ‘augmenting human intellect’ would yield a multiplier effect in group problem solving: “Three people working together in this augmented mode [would] seem to be more than three times as effective in solving a complex problem as is one augmented person working alone”.

Henry Jenkins, a key theorist of new media and media convergence draws on the theory that collective intelligence can be attributed to media convergence and participatory culture. He criticizes contemporary education for failing to incorporate online trends of collective problem solving into the classroom, stating “whereas a collective intelligence community encourages ownership of work as a group, schools grade individuals”. Jenkins argues that interaction within a knowledge community builds vital skills for young people, and teamwork through collective intelligence communities contribute to the development of such skills.

Collective impact is the commitment of a group of actors from different sectors to a common agenda for solving a specific social problem, using a structured form of collaboration.

After World War II the UN, the Bretton Woods organization and the WTO were created and collective problem solving on the international level crystallized since the 1980s around these 3 types of organizations. As these global institutions remain state-like or state-centric it has been called unsurprising that these continue state-like or state-centric approaches to collective problem-solving rather than alternative ones.

It has been observed that models of liberal democracy provide neither adequate designs for collective problem solving nor handling the substantive challenges in society such as crime, war, economic decline, illness and environmental degradation to produce satisfying outcomes.

Crowdsourcing is a process of accumulating the ideas, thoughts or information from many independent participants, with aim to find the best solution for a given challenge. Modern information technologies allow for massive number of subjects to be involved as well as systems of managing these suggestions that provide good results. With the Internet a new capacity for collective, including planetary-scale, problem solving was created.

Click on the topics below to explore further:

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

5.3: Using Critical Thinking Skills- Decision Making and Problem Solving

• Last updated
• Save as PDF
• Page ID 24260

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Introduction

In previous lessons, you learned about characteristics of critical thinkers and information literacy. In this module, you will learn how to put those skills into action through the important processes of decision making and problem solving.

As with the process of developing information literacy, asking questions is an important part of decision making and problem solving. Thinking is born of questions. Questions wake us up. Questions alert us to hidden assumptions. Questions promote curiosity and create new distinctions. Questions open up options that otherwise go unexplored. Besides, teachers love questions.

We make decisions all the time, whether we realize it or not. Even avoiding decisions is a form of decision making. The student who puts off studying for a test until the last minute, for example, might really be saying, “I’ve decided this course is not important” or “I’ve decided not to give this course much time.”

Decisions are specific and lead to focused action. When we decide, we narrow down. We give up actions that are inconsistent with our decision.

In addition to decision making, critical thinking skills are important to solving problems. We encounter problems every single day, and having a solid process in place is important to solving them.

At the end of the lesson, you will learn how to put your critical thinking skills to use by reviewing an example of how critical thinking skills can help with making those everyday decisions.

Using Critical Thinking Skills: Asking Questions

Questions have practical power. Asking for directions can shave hours off a trip. Asking a librarian for help can save hours of research time. Asking how to address an instructor—by first name or formal title—can change your relationship with that person. Asking your academic advisor a question can alter your entire education. Asking people about their career plans can alter your career plans.

You can use the following strategies to develop questions for problem solving and decision making:

Ask questions that create possibilities. At any moment, you can ask a question that opens up a new possibility for someone.

• Suppose a friend walks up to you and says, “People just never listen to me.” You listen carefully. Then you say, “Let me make sure I understand. Who, specifically, doesn’t listen to you? And how do you know they’re not listening?”
• Another friend tells you, “I just lost my job to someone who has less experience. That should never happen.” You respond, “Wow, that’s hard. I’m sorry you lost your job. Who can help you find another job?”
• A relative seeks your advice. “My mother-in-law makes me mad,” she says. “You’re having a hard time with this person,” you say. “What does she say and do when you feel mad at her? And are there times when you don’t get mad at her?”

These kinds of questions—asked with compassion and a sense of timing—can help people move from complaining about problems to solving them.

Discover new questions. Students sometimes say, “I don’t know what questions to ask.” Consider the following ways to create questions about any subject you want to study or about any

area of your life that you want to change:

• Let your pen start moving. Sometimes you can access a deeper level of knowledge by taking out your pen, putting it on a piece of paper, and writing down questions—even before you know what to write. Don’t think. Just watch the pen move across the paper. Notice what appears. The results might be surprising.
• Ask about what’s missing . Another way to invent useful questions is to notice what’s missing from your life and then ask how to supply it. For example, if you want to take better notes, you can write, “What’s missing is skill in note taking. How can I gain more skill in taking notes?” If you always feel rushed, you can write, “What’s missing is time. How do I create enough time in my day to actually do the things that I say I want to do?”
• Pretend to be someone else. Another way to invent questions is first to think of someone you greatly respect. Then pretend you’re that person. Ask the questions you think she would ask.
• What can I do when ... an instructor calls on me in class and I have no idea what to say? When a teacher doesn’t show up for class on time? When I feel overwhelmed with assignments?
• How can I ... take the kind of courses that I want? Expand my career options? Become much more effective as a student, starting today?
• When do I ... decide on a major? Transfer to another school? Meet with an instructor to discuss an upcoming term paper?
• What else do I want to know about ... my academic plan? My career plan? My options for job hunting? My friends? My relatives? My spouse?
• Who can I ask about ... my career options? My major? My love life? My values and purpose in life?

Many times you can quickly generate questions by simply asking yourself, “What else do I want to know?” Ask this question immediately after you read a paragraph in a book or listen to someone speak.

Start from the assumption that you are brilliant. Then ask questions to unlock your brilliance.

Using Critical Thinking Skills in Decision Making

As you develop your critical thinking skills, you can apply them as you make decisions. The following suggestions can help in your decision-making process:

Recognize decisions. Decisions are more than wishes or desires. There’s a world of difference between “I wish I could be a better student” and “I will take more powerful notes, read with greater retention, and review my class notes daily.” Deciding to eat fruit for dessert instead of ice cream rules out the next trip to the ice cream store.

Establish priorities. Some decisions are trivial. No matter what the outcome, your life is not affected much. Other decisions can shape your circumstances for years. Devote more time and energy to the decisions with big outcomes.

Base decisions on a life plan. The benefit of having long-term goals for our lives is that they provide a basis for many of our daily decisions. Being certain about what we want to accomplish this year and this month makes today’s choices more clear.

Balance learning styles in decision making. To make decisions more effectively, use all four modes of learning explained in a previous lesson. The key is to balance reflection with action, and thinking with experience. First, take the time to think creatively, and generate many options. Then think critically about the possible consequences of each option before choosing one. Remember, however, that thinking is no substitute for experience. Act on your chosen option, and notice what happens. If you’re not getting the results you want, then quickly return to creative thinking to invent new options.

Choose an overall strategy. Every time you make a decision, you choose a strategy—even when you’re not aware of it. Effective decision makers can articulate and choose from among several strategies. For example:

• Find all of the available options, and choose one deliberately. Save this strategy for times when you have a relatively small number of options, each of which leads to noticeably different results.
• Find all of the available options, and choose one randomly. This strategy can be risky. Save it for times when your options are basically similar and fairness is the main issue.
• Limit the options, and then choose. When deciding which search engine to use, visit many search sites and then narrow the list down to two or three from which to choose.

Use time as an ally. Sometimes we face dilemmas—situations in which any course of action leads to undesirable consequences. In such cases, consider putting a decision on hold. Wait it out. Do nothing until the circumstances change, making one alternative clearly preferable to another.

Use intuition. Some decisions seem to make themselves. A solution pops into your mind, and you gain newfound clarity. Using intuition is not the same as forgetting about the decision or refusing to make it. Intuitive decisions usually arrive after we’ve gathered the relevant facts and faced a problem for some time.

Evaluate your decision. Hindsight is a source of insight. After you act on a decision, observe the consequences over time. Reflect on how well your decision worked and what you might have done differently.

Think of choices. This final suggestion involves some creative thinking. Consider that the word decide derives from the same roots as suicide and homicide . In the spirit of those words, a decision forever “kills” all other options. That’s kind of heavy. Instead, use the word choice , and see whether it frees up your thinking. When you choose , you express a preference for one option over others. However, those options remain live possibilities for the future. Choose for today, knowing that as you gain more wisdom and experience, you can choose again.

Using Critical Thinking Skills in Problem Solving

Think of problem solving as a process with four Ps : Define the problem , generate possibilities ,

create a plan , and perform your plan.

Step 1: Define the problem. To define a problem effectively, understand what a problem is—a mismatch between what you want and what you have. Problem solving is all about reducing the gap between these two factors.

Tell the truth about what’s present in your life right now, without shame or blame. For example: “I often get sleepy while reading my physics assignments, and after closing the book I cannot remember what I just read.”

Next, describe in detail what you want. Go for specifics: “I want to remain alert as I read about physics. I also want to accurately summarize each chapter I read.”

Remember that when we define a problem in limiting ways, our solutions merely generate new problems. As Albert Einstein said, “The world we have made is a result of the level of thinking we have done thus far. We cannot solve problems at the same level at which we created them” (Calaprice 2000).

This idea has many applications for success in school. An example is the student who struggles with note taking. The problem, she thinks, is that her notes are too sketchy. The logical solution, she decides, is to take more notes; her new goal is to write down almost everything her instructors say. No matter how fast and furiously she writes, she cannot capture all of the instructors’ comments.

Consider what happens when this student defines the problem in a new way. After more thought, she decides that her dilemma is not the quantity of her notes but their quality . She adopts a new format for taking notes, dividing her notepaper into two columns. In the right-hand column, she writes down only the main points of each lecture. In the left-hand column, she notes two or three supporting details for each point.

Over time, this student makes the joyous discovery that there are usually just three or four core ideas to remember from each lecture. She originally thought the solution was to take more notes. What really worked was taking notes in a new way.

Step 2: Generate possibilities. Now put on your creative thinking hat. Open up. Brainstorm as many possible solutions to the problem as you can. At this stage, quantity counts. As you generate possibilities, gather relevant facts. For example, when you’re faced with a dilemma about what courses to take next semester, get information on class times, locations, and instructors. If you haven’t decided which summer job offer to accept, gather information on salary, benefits, and working conditions.

Step 3: Create a plan. After rereading your problem definition and list of possible solutions, choose the solution that seems most workable. Think about specific actions that will reduce the gap between what you have and what you want. Visualize the steps you will take to make this solution a reality, and arrange them in chronological order. To make your plan even more powerful, put it in writing.

Step 4: Perform your plan. This step gets you off your chair and out into the world. Now you actually do what you have planned.

Ultimately, your skill in solving problems lies in how well you perform your plan. Through the quality of your actions, you become the architect of your own success.

When facing problems, experiment with these four Ps, and remember that the order of steps is not absolute. Also remember that any solution has the potential to create new problems. If that happens, cycle through the four Ps of problem solving again.

Critical Thinking Skills in Action: Thinking About Your Major, Part 1

One decision that troubles many students in higher education is the choice of a major. Weighing the benefits, costs, and outcomes of a possible major is an intellectual challenge. This choice is an opportunity to apply your critical thinking, decision-making, and problem-solving skills. The following suggestions will guide you through this seemingly overwhelming process.

The first step is to discover options. You can use the following suggestions to discover options for choosing your major:

Follow the fun. Perhaps you look forward to attending one of your classes and even like completing the assignments. This is a clue to your choice of major.

See whether you can find lasting patterns in the subjects and extracurricular activities that you’ve enjoyed over the years. Look for a major that allows you to continue and expand on these experiences.

Also, sit down with a stack of 3 × 5 cards and brainstorm answers to the following questions:

• What do you enjoy doing most with your unscheduled time?
• Imagine that you’re at a party and having a fascinating conversation. What is this conversation about?
• What kind of problems do you enjoy solving—those that involve people? Products? Ideas?
• What interests are revealed by your choices of reading material, television shows, and other entertainment?
• What would an ideal day look like for you? Describe where you would live, who would be with you, and what you would do throughout the day. Do any of these visions suggest a possible major?

Questions like these can uncover a “fun factor” that energizes you to finish the work of completing a major.

Consider your abilities. In choosing a major, ability counts as much as interest. In addition to considering what you enjoy, think about times and places when you excelled. List the courses that you aced, the work assignments that you mastered, and the hobbies that led to rewards or recognition. Let your choice of a major reflect a discovery of your passions and potentials.

Use formal techniques for self-discovery. Explore questionnaires and inventories that are designed to correlate your interests with specific majors. Examples include the Strong Interest Inventory and the Self-Directed Search. Your academic advisor or someone in your school’s career planning office can give you more details about these and related assessments. For some fun, take several of them and meet with an advisor to interpret the results. Remember inventories can help you gain self-knowledge, and other people can offer valuable perspectives. However, what you do with all this input is entirely up to you.

Critical Thinking Skills in Action: Thinking About Your Major, Part 2

As you review the following additional suggestions of discovering options, think about what strategies you already use in your own decision-making process. Also think about what new strategies you might try in the future.

Link to long-term goals. Your choice of a major can fall into place once you determine what you want in life. Before you choose a major, back up to a bigger picture. List your core values, such as contributing to society, achieving financial security and professional recognition, enjoying good health, or making time for fun. Also write down specific goals that you want to accomplish 5 years, 10 years, or even 50 years from today.

Many students find that the prospect of getting what they want in life justifies all of the time, money, and day-to-day effort invested in going to school. Having a major gives you a powerful incentive for attending classes, taking part in discussions, reading textbooks, writing papers, and completing other assignments. When you see a clear connection between finishing school and creating the life of your dreams, the daily tasks of higher education become charged with meaning.

Ask other people. Key people in your life might have valuable suggestions about your choice of major. Ask for their ideas, and listen with an open mind. At the same time, distance yourself from any pressure to choose a major or career that fails to interest you. If you make a choice solely on the basis of the expectations of other people, you could end up with a major or even a career you don’t enjoy.

Gather information. Check your school’s catalog or website for a list of available majors. Here is a gold mine of information. Take a quick glance, and highlight all the majors that interest you. Then talk to students who have declared these majors. Also read the descriptions of courses required for these majors. Do you get excited about the chance to enroll in them? Pay attention to your gut feelings.

Also chat with instructors who teach courses in a specific major. Ask for copies of their class syllabi. Go to the bookstore and browse the required texts. Based on all of this information, write a list of prospective majors. Discuss them with an academic advisor and someone at your school’s career-planning center.

Invent a major. When choosing a major, you might not need to limit yourself to those listed in your school catalog. Many schools now have flexible programs that allow for independent study. Through such programs, you might be able to combine two existing majors or invent an entirely new one of your own.

Consider a complementary minor. You can add flexibility to your academic program by choosing a minor to complement or contrast with your major. The student who wants to be a minister could opt for a minor in English; all of those courses in composition can help in writing sermons. Or the student with a major in psychology might choose a minor in business administration, with the idea of managing a counseling service some day. An effective choice of a minor can expand your skills and career options.

Think critically about the link between your major and your career. Your career goals might have a significant impact on your choice of major.

You could pursue a rewarding career by choosing among several different majors. Even students planning to apply for law school or medical school have flexibility in their choice of majors. In addition, after graduation, many people tend to be employed in jobs that have little relationship to their major. And you might choose a career in the future that is unrelated to any currently available major.

Critical Thinking Skills in Action: Thinking About Your Major, Part 3

Once you have discovered all of your options, you can move on to the next step in the process— making a trial choice.

Make a Trial Choice

Pretend that you have to choose a major today. Based on the options for a major that you’ve already discovered, write down the first three ideas that come to mind. Review the list for a few minutes, and then choose one.

Evaluate Your Trial Choice

When you’ve made a trial choice of major, take on the role of a scientist. Treat your choice as a hypothesis, and then design a series of experiments to evaluate and test it. For example:

• Schedule office meetings with instructors who teach courses in the major. Ask about required course work and career options in the field.
• Discuss your trial choice with an academic advisor or career counselor.
• Enroll in a course related to your possible major. Remember that introductory courses might not give you a realistic picture of the workload involved in advanced courses. Also, you might not be able to register for certain courses until you’ve actually declared a related major.
• Find a volunteer experience, internship, part-time job, or service-learning experience related to the major.
• Interview students who have declared the same major. Ask them in detail about their experiences and suggestions for success.
• Interview people who work in a field related to the major and “shadow” them—that is, spend time with those people during their workday.
• Think about whether you can complete your major given the amount of time and money that you plan to invest in higher education.
• Consider whether declaring this major would require a transfer to another program or even another school.

If your “experiments” confirm your choice of major, celebrate that fact. If they result in choosing a new major, celebrate that outcome as well.

Also remember that higher education represents a safe place to test your choice of major—and to change your mind. As you sort through your options, help is always available from administrators, instructors, advisors, and peers.

Choose Again

Keep your choice of a major in perspective. There is probably no single “correct” choice. Your unique collection of skills is likely to provide the basis for majoring in several fields.

Odds are that you’ll change your major at least once—and that you’ll change careers several times during your life. One benefit of higher education is mobility. You gain the general skills and knowledge that can help you move into a new major or career field at any time.

Viewing a major as a one-time choice that determines your entire future can raise your stress levels. Instead, look at choosing a major as the start of a continuing path that involves discovery, choice, and passionate action.

As you review this example of how you can use critical thinking to make a decision about choosing your major, think about how you will use your critical thinking to make decisions and solve problems in the future.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Ch 8: Thinking and Language

Thinking and language.

Why is it so difficult to break habits—like reaching for your ringing phone even when you shouldn’t, such as when you’re driving? Why is it hard to pay attention to a conversation when typing out a text message? How does a person who has never seen or touched snow in real life develop an understanding of the concept of snow? How do young children acquire the ability to learn language with no formal instruction? Psychologists who study thinking explore questions like these.

As a part of this discussion, we will consider thinking, and briefly explore the development and use of language. We will also discuss problem solving and creativity. After finishing this chapter, you will have a greater appreciation of the higher-level cognitive processes that contribute to our distinctiveness as a species.

Learning Objectives

• Understand why selective attention is important and how it can be studied.
• Learn about different models of when and how selection can occur.
• Understand how divided attention or multitasking is studied, and implications of multitasking in situations such as distracted driving.

Thinking and Problem-Solving

Imagine all of your thoughts as if they were physical entities, swirling rapidly inside your mind. How is it possible that the brain is able to move from one thought to the next in an organized, orderly fashion? The brain is endlessly perceiving, processing, planning, organizing, and remembering—it is always active. Yet, you don’t notice most of your brain’s activity as you move throughout your daily routine. This is only one facet of the complex processes involved in cognition. Simply put, cognition is thinking, and it encompasses the processes associated with perception, knowledge, problem solving, judgment, language, and memory. Scientists who study cognition are searching for ways to understand how we integrate, organize, and utilize our conscious cognitive experiences without being aware of all of the unconscious work that our brains are doing (for example, Kahneman, 2011).

• Distinguish between concepts and prototypes
• Explain the difference between natural and artificial concepts
• Describe problem solving strategies, including algorithms and heuristics
• Explain some common roadblocks to effective problem solving

What is Cognition?

Categories and concepts, concepts and prototypes.

The human nervous system is capable of handling endless streams of information. The senses serve as the interface between the mind and the external environment, receiving stimuli and translating it into nerve impulses that are transmitted to the brain. The brain then processes this information and uses the relevant pieces to create thoughts, which can then be expressed through language or stored in memory for future use. To make this process more complex, the brain does not gather information from external environments only. When thoughts are formed, the brain also pulls information from emotions and memories (Figure 9). Emotion and memory are powerful influences on both our thoughts and behaviors.

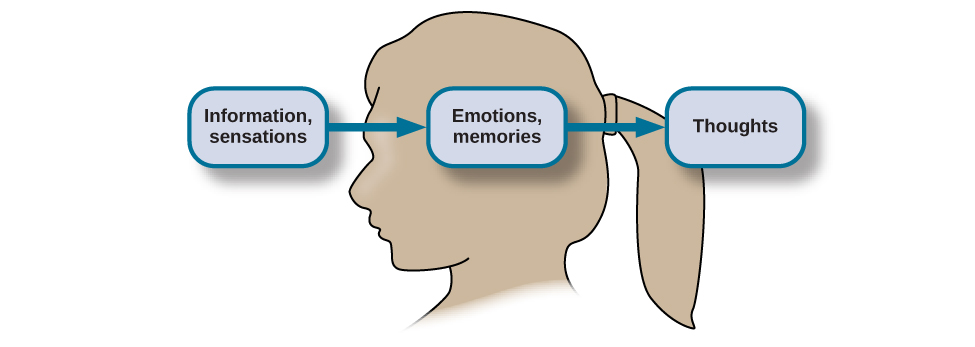
In order to organize this staggering amount of information, the brain has developed a file cabinet of sorts in the mind. The different files stored in the file cabinet are called concepts. Concepts  are categories or groupings of linguistic information, images, ideas, or memories, such as life experiences. Concepts are, in many ways, big ideas that are generated by observing details, and categorizing and combining these details into cognitive structures. You use concepts to see the relationships among the different elements of your experiences and to keep the information in your mind organized and accessible.

Concepts are informed by our semantic memory (you will learn more about this concept when you study memory) and are present in every aspect of our lives; however, one of the easiest places to notice concepts is inside a classroom, where they are discussed explicitly. When you study United States history, for example, you learn about more than just individual events that have happened in America’s past. You absorb a large quantity of information by listening to and participating in discussions, examining maps, and reading first-hand accounts of people’s lives. Your brain analyzes these details and develops an overall understanding of American history. In the process, your brain gathers details that inform and refine your understanding of related concepts like democracy, power, and freedom.

Concepts can be complex and abstract, like justice, or more concrete, like types of birds. In psychology, for example, Piaget’s stages of development are abstract concepts. Some concepts, like tolerance, are agreed upon by many people because they have been used in various ways over many years. Other concepts, like the characteristics of your ideal friend or your family’s birthday traditions, are personal and individualized. In this way, concepts touch every aspect of our lives, from our many daily routines to the guiding principles behind the way governments function.

Concepts are at the core of intelligent behavior. We expect people to be able to know what to do in new situations and when confronting new objects. If you go into a new classroom and see chairs, a blackboard, a projector, and a screen, you know what these things are and how they will be used. You’ll sit on one of the chairs and expect the instructor to write on the blackboard or project something onto the screen. You do this even if you have never seen any of these particular objects before , because you have concepts of classrooms, chairs, projectors, and so forth, that tell you what they are and what you’re supposed to do with them. Furthermore, if someone tells you a new fact about the projector—for example, that it has a halogen bulb—you are likely to extend this fact to other projectors you encounter. In short, concepts allow you to extend what you have learned about a limited number of objects to a potentially infinite set of entities.

Another technique used by your brain to organize information is the identification of prototypes for the concepts you have developed. A prototype  is the best example or representation of a concept. For example, for the category of civil disobedience, your prototype could be Rosa Parks. Her peaceful resistance to segregation on a city bus in Montgomery, Alabama, is a recognizable example of civil disobedience. Or your prototype could be Mohandas Gandhi, sometimes called Mahatma Gandhi (“Mahatma” is an honorific title) (Figure 10).

Mohandas Gandhi served as a nonviolent force for independence for India while simultaneously demanding that Buddhist, Hindu, Muslim, and Christian leaders—both Indian and British—collaborate peacefully. Although he was not always successful in preventing violence around him, his life provides a steadfast example of the civil disobedience prototype (Constitutional Rights Foundation, 2013). Just as concepts can be abstract or concrete, we can make a distinction between concepts that are functions of our direct experience with the world and those that are more artificial in nature.

Link to Learning

Natural and artificial concepts.

In psychology, concepts can be divided into two categories, natural and artificial. Natural concepts  are created “naturally” through your experiences and can be developed from either direct or indirect experiences. For example, if you live in Essex Junction, Vermont, you have probably had a lot of direct experience with snow. You’ve watched it fall from the sky, you’ve seen lightly falling snow that barely covers the windshield of your car, and you’ve shoveled out 18 inches of fluffy white snow as you’ve thought, “This is perfect for skiing.” You’ve thrown snowballs at your best friend and gone sledding down the steepest hill in town. In short, you know snow. You know what it looks like, smells like, tastes like, and feels like. If, however, you’ve lived your whole life on the island of Saint Vincent in the Caribbean, you may never have actually seen snow, much less tasted, smelled, or touched it. You know snow from the indirect experience of seeing pictures of falling snow—or from watching films that feature snow as part of the setting. Either way, snow is a natural concept because you can construct an understanding of it through direct observations or experiences of snow (Figure 11).

An artificial concept  on the other hand, is a concept that is defined by a specific set of characteristics. Various properties of geometric shapes, like squares and triangles, serve as useful examples of artificial concepts. A triangle always has three angles and three sides. A square always has four equal sides and four right angles. Mathematical formulas, like the equation for area (length × width) are artificial concepts defined by specific sets of characteristics that are always the same. Artificial concepts can enhance the understanding of a topic by building on one another. For example, before learning the concept of “area of a square” (and the formula to find it), you must understand what a square is. Once the concept of “area of a square” is understood, an understanding of area for other geometric shapes can be built upon the original understanding of area. The use of artificial concepts to define an idea is crucial to communicating with others and engaging in complex thought. According to Goldstone and Kersten (2003), concepts act as building blocks and can be connected in countless combinations to create complex thoughts.

A schema is a mental construct consisting of a cluster or collection of related concepts (Bartlett, 1932). There are many different types of schemata, and they all have one thing in common: schemata are a method of organizing information that allows the brain to work more efficiently. When a schema is activated, the brain makes immediate assumptions about the person or object being observed.

There are several types of schemata. A role schema makes assumptions about how individuals in certain roles will behave (Callero, 1994). For example, imagine you meet someone who introduces himself as a firefighter. When this happens, your brain automatically activates the “firefighter schema” and begins making assumptions that this person is brave, selfless, and community-oriented. Despite not knowing this person, already you have unknowingly made judgments about him. Schemata also help you fill in gaps in the information you receive from the world around you. While schemata allow for more efficient information processing, there can be problems with schemata, regardless of whether they are accurate: Perhaps this particular firefighter is not brave, he just works as a firefighter to pay the bills while studying to become a children’s librarian.

An event schema , also known as a cognitive script , is a set of behaviors that can feel like a routine. Think about what you do when you walk into an elevator (Figure 12). First, the doors open and you wait to let exiting passengers leave the elevator car. Then, you step into the elevator and turn around to face the doors, looking for the correct button to push. You never face the back of the elevator, do you? And when you’re riding in a crowded elevator and you can’t face the front, it feels uncomfortable, doesn’t it? Interestingly, event schemata can vary widely among different cultures and countries. For example, while it is quite common for people to greet one another with a handshake in the United States, in Tibet, you greet someone by sticking your tongue out at them, and in Belize, you bump fists (Cairns Regional Council, n.d.)

Because event schemata are automatic, they can be difficult to change. Imagine that you are driving home from work or school. This event schema involves getting in the car, shutting the door, and buckling your seatbelt before putting the key in the ignition. You might perform this script two or three times each day. As you drive home, you hear your phone’s ring tone. Typically, the event schema that occurs when you hear your phone ringing involves locating the phone and answering it or responding to your latest text message. So without thinking, you reach for your phone, which could be in your pocket, in your bag, or on the passenger seat of the car. This powerful event schema is informed by your pattern of behavior and the pleasurable stimulation that a phone call or text message gives your brain. Because it is a schema, it is extremely challenging for us to stop reaching for the phone, even though we know that we endanger our own lives and the lives of others while we do it (Neyfakh, 2013) (Figure 13).

Remember the elevator? It feels almost impossible to walk in and not face the door. Our powerful event schema dictates our behavior in the elevator, and it is no different with our phones. Current research suggests that it is the habit, or event schema, of checking our phones in many different situations that makes refraining from checking them while driving especially difficult (Bayer & Campbell, 2012). Because texting and driving has become a dangerous epidemic in recent years, psychologists are looking at ways to help people interrupt the “phone schema” while driving. Event schemata like these are the reason why many habits are difficult to break once they have been acquired. As we continue to examine thinking, keep in mind how powerful the forces of concepts and schemata are to our understanding of the world.

Watch this CrashCourse video to see more examples of concepts and prototypes. You’ll also get a preview on other key topics in cognition, including problem-solving strategies like algorithms and heuristics.

You can view the transcript for “Cognition – How Your Mind Can Amaze and Betray You: Crash Course Psychology #15” here (opens in new window) .

Think It Over

People face problems every day—usually, multiple problems throughout the day. Sometimes these problems are straightforward: To double a recipe for pizza dough, for example, all that is required is that each ingredient in the recipe be doubled. Sometimes, however, the problems we encounter are more complex. For example, say you have a work deadline, and you must mail a printed copy of a report to your supervisor by the end of the business day. The report is time-sensitive and must be sent overnight. You finished the report last night, but your printer will not work today. What should you do? First, you need to identify the problem and then apply a strategy for solving the problem.

Problem-Solving Strategies

When you are presented with a problem—whether it is a complex mathematical problem or a broken printer, how do you solve it? Before finding a solution to the problem, the problem must first be clearly identified. After that, one of many problem solving strategies can be applied, hopefully resulting in a solution.

A problem-solving strategy is a plan of action used to find a solution. Different strategies have different action plans associated with them. For example, a well-known strategy is trial and error . The old adage, “If at first you don’t succeed, try, try again” describes trial and error. In terms of your broken printer, you could try checking the ink levels, and if that doesn’t work, you could check to make sure the paper tray isn’t jammed. Or maybe the printer isn’t actually connected to your laptop. When using trial and error, you would continue to try different solutions until you solved your problem. Although trial and error is not typically one of the most time-efficient strategies, it is a commonly used one.

Another type of strategy is an algorithm. An algorithm  is a problem-solving formula that provides you with step-by-step instructions used to achieve a desired outcome (Kahneman, 2011). You can think of an algorithm as a recipe with highly detailed instructions that produce the same result every time they are performed. Algorithms are used frequently in our everyday lives, especially in computer science. When you run a search on the Internet, search engines like Google use algorithms to decide which entries will appear first in your list of results. Facebook also uses algorithms to decide which posts to display on your newsfeed. Can you identify other situations in which algorithms are used?

A heuristic  is another type of problem solving strategy. While an algorithm must be followed exactly to produce a correct result, a heuristic is a general problem-solving framework (Tversky & Kahneman, 1974). You can think of these as mental shortcuts that are used to solve problems. A “rule of thumb” is an example of a heuristic. Such a rule saves the person time and energy when making a decision, but despite its time-saving characteristics, it is not always the best method for making a rational decision. Different types of heuristics are used in different types of situations, but the impulse to use a heuristic occurs when one of five conditions is met (Pratkanis, 1989):

• When one is faced with too much information
• When the time to make a decision is limited
• When the decision to be made is unimportant
• When there is access to very little information to use in making the decision
• When an appropriate heuristic happens to come to mind in the same moment

Working backwards  is a useful heuristic in which you begin solving the problem by focusing on the end result. Consider this example: You live in Washington, D.C. and have been invited to a wedding at 4 PM on Saturday in Philadelphia. Knowing that Interstate 95 tends to back up any day of the week, you need to plan your route and time your departure accordingly. If you want to be at the wedding service by 3:30 PM, and it takes 2.5 hours to get to Philadelphia without traffic, what time should you leave your house? You use the working backwards heuristic to plan the events of your day on a regular basis, probably without even thinking about it.

What problem-solving method could you use to solve Einstein’s famous riddle?

You can view the transcript for “Can you solve “Einstein’s Riddle”? – Dan Van der Vieren” here (opens in new window) .

Another useful heuristic is the practice of accomplishing a large goal or task by breaking it into a series of smaller steps. Students often use this common method to complete a large research project or long essay for school. For example, students typically brainstorm, develop a thesis or main topic, research the chosen topic, organize their information into an outline, write a rough draft, revise and edit the rough draft, develop a final draft, organize the references list, and proofread their work before turning in the project. The large task becomes less overwhelming when it is broken down into a series of small steps.

Everyday Connections: Solving Puzzles

Problem-solving abilities can improve with practice. Many people challenge themselves every day with puzzles and other mental exercises to sharpen their problem-solving skills. Sudoku puzzles appear daily in most newspapers. Typically, a sudoku puzzle is a 9×9 grid. The simple sudoku below (Figure 14) is a 4×4 grid. To solve the puzzle, fill in the empty boxes with a single digit: 1, 2, 3, or 4. Here are the rules: The numbers must total 10 in each bolded box, each row, and each column; however, each digit can only appear once in a bolded box, row, and column. Time yourself as you solve this puzzle and compare your time with a classmate.

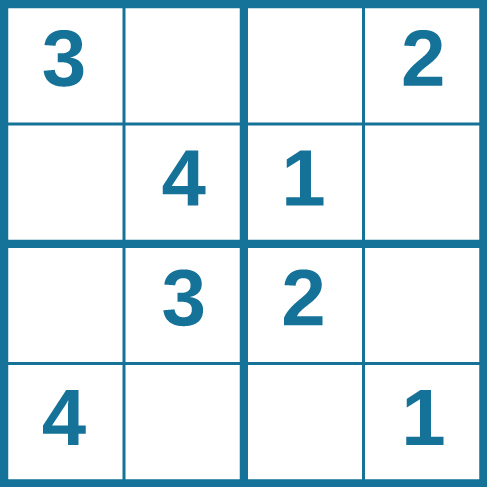
Here is another popular type of puzzle that challenges your spatial reasoning skills. Connect all nine dots with four connecting straight lines without lifting your pencil from the paper:

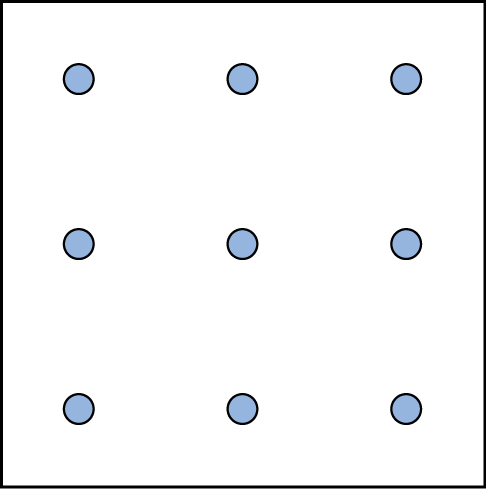
Take a look at the “Puzzling Scales” logic puzzle below (Figure 16). Sam Loyd, a well-known puzzle master, created and refined countless puzzles throughout his lifetime (Cyclopedia of Puzzles, n.d.).

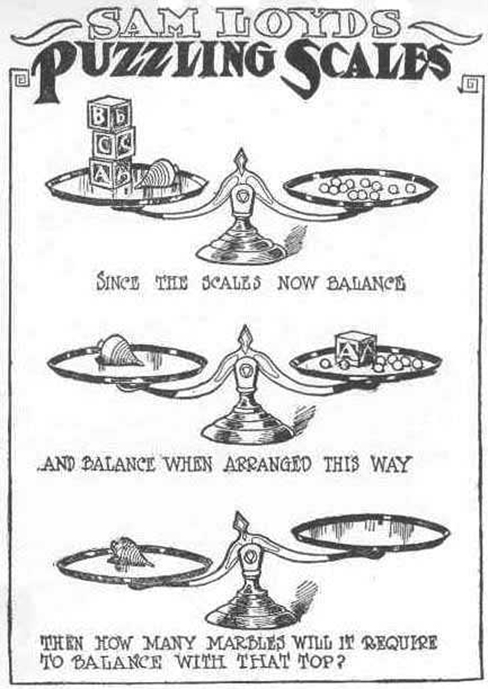
Were you able to determine how many marbles are needed to balance the scales in the Puzzling Scales? You need nine. Were you able to solve the other problems above? Here are the answers:

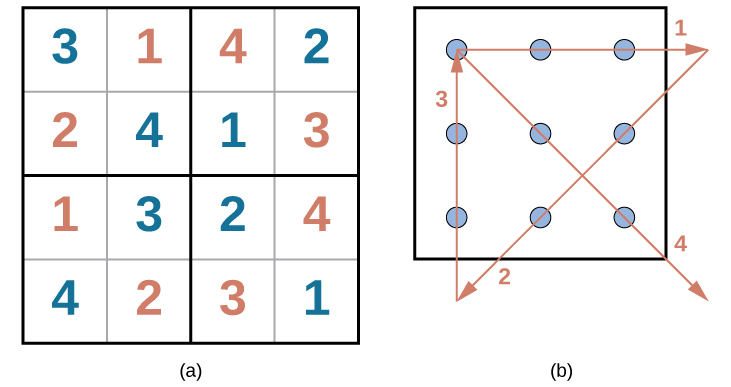
Pitfalls to Problem Solving

Not all problems are successfully solved, however. What challenges stop us from successfully solving a problem? Albert Einstein once said, “Insanity is doing the same thing over and over again and expecting a different result.” Imagine a person in a room that has four doorways. One doorway that has always been open in the past is now locked. The person, accustomed to exiting the room by that particular doorway, keeps trying to get out through the same doorway even though the other three doorways are open. The person is stuck—but she just needs to go to another doorway, instead of trying to get out through the locked doorway. A mental set  is where you persist in approaching a problem in a way that has worked in the past but is clearly not working now. Functional fixedness   is a type of mental set where you cannot perceive an object being used for something other than what it was designed for. During the Apollo 13 mission to the moon, NASA engineers at Mission Control had to overcome functional fixedness to save the lives of the astronauts aboard the spacecraft. An explosion in a module of the spacecraft damaged multiple systems. The astronauts were in danger of being poisoned by rising levels of carbon dioxide because of problems with the carbon dioxide filters. The engineers found a way for the astronauts to use spare plastic bags, tape, and air hoses to create a makeshift air filter, which saved the lives of the astronauts.

In order to make good decisions, we use our knowledge and our reasoning. Often, this knowledge and reasoning is sound and solid. Sometimes, however, we are swayed by biases or by others manipulating a situation. For example, let’s say you and three friends wanted to rent a house and had a combined target budget of $1,600. The realtor shows you only very run-down houses for $1,600 and then shows you a very nice house for $2,000. Might you ask each person to pay more in rent to get the $2,000 home? Why would the realtor show you the run-down houses and the nice house? The realtor may be challenging your anchoring bias. An anchoring bias  occurs when you focus on one piece of information when making a decision or solving a problem. In this case, you’re so focused on the amount of money you are willing to spend that you may not recognize what kinds of houses are available at that price point.

The confirmation bias is the tendency to focus on information that confirms your existing beliefs. For example, if you think that your professor is not very nice, you notice all of the instances of rude behavior exhibited by the professor while ignoring the countless pleasant interactions he is involved in on a daily basis. This bias proves that first impressions do matter and that we tend to look for information to confirm our initial judgments of others.

Watch this video from the Big Think to learn more about the confirmation bias.

You can view the transcript for “Confirmation Bias: Your Brain is So Judgmental” here (opens in new window) .

Hindsight bias leads you to believe that the event you just experienced was predictable, even though it really wasn’t. In other words, you knew all along that things would turn out the way they did. Representative bias  describes a faulty way of thinking, in which you unintentionally stereotype someone or something; for example, you may assume that your professors spend their free time reading books and engaging in intellectual conversation, because the idea of them spending their time playing volleyball or visiting an amusement park does not fit in with your stereotypes of professors.

Finally, the availability heuristic is a heuristic in which you make a decision based on an example, information, or recent experience that is that readily available to you, even though it may not be the best example to inform your decision . To use a common example, would you guess there are more murders or more suicides in America each year? When asked, most people would guess there are more murders. In truth, there are twice as many suicides as there are murders each year. However, murders seem more common because we hear a lot more about murders on an average day. Unless someone we know or someone famous takes their own life, it does not make the news. Murders, on the other hand, we see in the news every day. This leads to the erroneous assumption that the easier it is to think of instances of something, the more often that thing occurs.

Watch the following video for an example of the availability heuristic.

You can view the transcript for “Availability Heuristic: Are Planes More Dangerous Than Cars?” here (opens in new window) .

Biases tend to “preserve that which is already established—to maintain our preexisting knowledge, beliefs, attitudes, and hypotheses” (Aronson, 1995; Kahneman, 2011). These biases are summarized in Table 2 below.

Learn more about heuristics and common biases through the article, “ 8 Common Thinking Mistakes Our Brains Make Every Day and How to Prevent Them ” by Belle Beth Cooper.

You can also watch this clever music video explaining these and other cognitive biases.

Which type of bias do you recognize in your own decision making processes? How has this bias affected how you’ve made decisions in the past and how can you use your awareness of it to improve your decisions making skills in the future?

• Understand how the use of language develops
• Explain the relationship between language and thinking

Language Development

Language is a communication system that involves using words and systematic rules to organize those words to transmit information from one individual to another. While language is a form of communication, not all communication is language. Many species communicate with one another through their postures, movements, odors, or vocalizations. This communication is crucial for species that need to interact and develop social relationships with their conspecifics. However, many people have asserted that it is language that makes humans unique among all of the animal species (Corballis & Suddendorf, 2007; Tomasello & Rakoczy, 2003). This section will focus on what distinguishes language as a special form of communication, how the use of language develops, and how language affects the way we think.

Components of Language

Language , be it spoken, signed, or written, has specific components: a lexicon and grammar. Lexicon refers to the words of a given language. Thus, lexicon is a language’s vocabulary. Grammar  refers to the set of rules that are used to convey meaning through the use of the lexicon (Fernández & Cairns, 2011). For instance, English grammar dictates that most verbs receive an “-ed” at the end to indicate past tense.

Words are formed by combining the various phonemes that make up the language. A phoneme  (e.g., the sounds “ah” vs. “eh”) is a basic sound unit of a given language, and different languages have different sets of phonemes. Phonemes are combined to form morphemes , which are the smallest units of language that convey some type of meaning (e.g., “I” is both a phoneme and a morpheme).  Further, a morpheme is not the same as a word. The main difference is that a morpheme sometimes does not stand alone, but a word, by definition, always stands alone.

We use semantics and syntax to construct language. Semantics and syntax are part of a language’s grammar. Semantics refers to the process by which we derive meaning from morphemes and words. Syntax  refers to the way words are organized into sentences (Chomsky, 1965; Fernández & Cairns, 2011).

We apply the rules of grammar to organize the lexicon in novel and creative ways, which allow us to communicate information about both concrete and abstract concepts. We can talk about our immediate and observable surroundings as well as the surface of unseen planets. We can share our innermost thoughts, our plans for the future, and debate the value of a college education. We can provide detailed instructions for cooking a meal, fixing a car, or building a fire. The flexibility that language provides to relay vastly different types of information is a property that makes language so distinct as a mode of communication among humans.

Given the remarkable complexity of a language, one might expect that mastering a language would be an especially arduous task; indeed, for those of us trying to learn a second language as adults, this might seem to be true. However, young children master language very quickly with relative ease. B. F. Skinner (1957) proposed that language is learned through reinforcement. Noam Chomsky (1965) criticized this behaviorist approach, asserting instead that the mechanisms underlying language acquisition are biologically determined. The use of language develops in the absence of formal instruction and appears to follow a very similar pattern in children from vastly different cultures and backgrounds. It would seem, therefore, that we are born with a biological predisposition to acquire a language (Chomsky, 1965; Fernández & Cairns, 2011). Moreover, it appears that there is a critical period for language acquisition, such that this proficiency at acquiring language is maximal early in life; generally, as people age, the ease with which they acquire and master new languages diminishes (Johnson & Newport, 1989; Lenneberg, 1967; Singleton, 1995).

Children begin to learn about language from a very early age (Table 1). In fact, it appears that this is occurring even before we are born. Newborns show preference for their mother’s voice and appear to be able to discriminate between the language spoken by their mother and other languages. Babies are also attuned to the languages being used around them and show preferences for videos of faces that are moving in synchrony with the audio of spoken language versus videos that do not synchronize with the audio (Blossom & Morgan, 2006; Pickens, 1994; Spelke & Cortelyou, 1981).

Dig Deeper: The Case of Genie

In the fall of 1970, a social worker in the Los Angeles area found a 13-year-old girl who was being raised in extremely neglectful and abusive conditions. The girl, who came to be known as Genie, had lived most of her life tied to a potty chair or confined to a crib in a small room that was kept closed with the curtains drawn. For a little over a decade, Genie had virtually no social interaction and no access to the outside world. As a result of these conditions, Genie was unable to stand up, chew solid food, or speak (Fromkin, Krashen, Curtiss, Rigler, & Rigler, 1974; Rymer, 1993). The police took Genie into protective custody.

Genie’s abilities improved dramatically following her removal from her abusive environment, and early on, it appeared she was acquiring language—much later than would be predicted by critical period hypotheses that had been posited at the time (Fromkin et al., 1974). Genie managed to amass an impressive vocabulary in a relatively short amount of time. However, she never developed a mastery of the grammatical aspects of language (Curtiss, 1981). Perhaps being deprived of the opportunity to learn language during a critical period impeded Genie’s ability to fully acquire and use language.

You may recall that each language has its own set of phonemes that are used to generate morphemes, words, and so on. Babies can discriminate among the sounds that make up a language (for example, they can tell the difference between the “s” in vision and the “ss” in fission); early on, they can differentiate between the sounds of all human languages, even those that do not occur in the languages that are used in their environments. However, by the time that they are about 1 year old, they can only discriminate among those phonemes that are used in the language or languages in their environments (Jensen, 2011; Werker & Lalonde, 1988; Werker & Tees, 1984).

After the first few months of life, babies enter what is known as the babbling stage, during which time they tend to produce single syllables that are repeated over and over. As time passes, more variations appear in the syllables that they produce. During this time, it is unlikely that the babies are trying to communicate; they are just as likely to babble when they are alone as when they are with their caregivers (Fernández & Cairns, 2011). Interestingly, babies who are raised in environments in which sign language is used will also begin to show babbling in the gestures of their hands during this stage (Petitto, Holowka, Sergio, Levy, & Ostry, 2004).

Generally, a child’s first word is uttered sometime between the ages of 1 year to 18 months, and for the next few months, the child will remain in the “one word” stage of language development. During this time, children know a number of words, but they only produce one-word utterances. The child’s early vocabulary is limited to familiar objects or events, often nouns. Although children in this stage only make one-word utterances, these words often carry larger meaning (Fernández & Cairns, 2011). So, for example, a child saying “cookie” could be identifying a cookie or asking for a cookie.

As a child’s lexicon grows, she begins to utter simple sentences and to acquire new vocabulary at a very rapid pace. In addition, children begin to demonstrate a clear understanding of the specific rules that apply to their language(s). Even the mistakes that children sometimes make provide evidence of just how much they understand about those rules. This is sometimes seen in the form of overgeneralization . In this context, overgeneralization refers to an extension of a language rule to an exception to the rule. For example, in English, it is usually the case that an “s” is added to the end of a word to indicate plurality. For example, we speak of one dog versus two dogs. Young children will overgeneralize this rule to cases that are exceptions to the “add an s to the end of the word” rule and say things like “those two gooses” or “three mouses.” Clearly, the rules of the language are understood, even if the exceptions to the rules are still being learned (Moskowitz, 1978).

Language and Thinking

Think about it:  the meaning of language.

Think about what you know of other languages; perhaps you even speak multiple languages. Imagine for a moment that your closest friend fluently speaks more than one language. Do you think that friend thinks differently, depending on which language is being spoken? You may know a few words that are not translatable from their original language into English. For example, the Portuguese word saudade originated during the 15th century, when Portuguese sailors left home to explore the seas and travel to Africa or Asia. Those left behind described the emptiness and fondness they felt as saudade (Figure 20) . The word came to express many meanings, including loss, nostalgia, yearning, warm memories, and hope. There is no single word in English that includes all of those emotions in a single description. Do words such as saudade indicate that different languages produce different patterns of thought in people? What do you think??

Language may indeed influence the way that we think, an idea known as linguistic determinism. One recent demonstration of this phenomenon involved differences in the way that English and Mandarin Chinese speakers talk and think about time. English speakers tend to talk about time using terms that describe changes along a horizontal dimension, for example, saying something like “I’m running behind schedule” or “Don’t get ahead of yourself.” While Mandarin Chinese speakers also describe time in horizontal terms, it is not uncommon to also use terms associated with a vertical arrangement. For example, the past might be described as being “up” and the future as being “down.” It turns out that these differences in language translate into differences in performance on cognitive tests designed to measure how quickly an individual can recognize temporal relationships. Specifically, when given a series of tasks with vertical priming, Mandarin Chinese speakers were faster at recognizing temporal relationships between months. Indeed, Boroditsky (2001) sees these results as suggesting that “habits in language encourage habits in thought” (p. 12).

Language does not completely determine our thoughts—our thoughts are far too flexible for that—but habitual uses of language can influence our habit of thought and action. For instance, some linguistic practice seems to be associated even with cultural values and social institution. Pronoun drop is the case in point. Pronouns such as “I” and “you” are used to represent the speaker and listener of a speech in English. In an English sentence, these pronouns cannot be dropped if they are used as the subject of a sentence. So, for instance, “I went to the movie last night” is fine, but “Went to the movie last night” is not in standard English. However, in other languages such as Japanese, pronouns can be, and in fact often are, dropped from sentences. It turned out that people living in those countries where pronoun drop languages are spoken tend to have more collectivistic values (e.g., employees having greater loyalty toward their employers) than those who use non–pronoun drop languages such as English (Kashima & Kashima, 1998). It was argued that the explicit reference to “you” and “I” may remind speakers the distinction between the self and other, and the differentiation between individuals. Such a linguistic practice may act as a constant reminder of the cultural value, which, in turn, may encourage people to perform the linguistic practice.

One group of researchers who wanted to investigate how language influences thought compared how English speakers and the Dani people of Papua New Guinea think and speak about color. The Dani have two words for color: one word for light and one word for dark . In contrast, the English language has 11 color words. Researchers hypothesized that the number of color terms could limit the ways that the Dani people conceptualized color. However, the Dani were able to distinguish colors with the same ability as English speakers, despite having fewer words at their disposal (Berlin & Kay, 1969). A recent review of research aimed at determining how language might affect something like color perception suggests that language can influence perceptual phenomena, especially in the left hemisphere of the brain. You may recall from earlier chapters that the left hemisphere is associated with language for most people. However, the right (less linguistic hemisphere) of the brain is less affected by linguistic influences on perception (Regier & Kay, 2009)

Learn more about language, language acquisition, and especially the connection between language and thought in the following CrashCourse video:

You can view the transcript for “Language: Crash Course Psychology #16” here (opens in new window) .

In this chapter, you learned to

• describe attention
• describe cognition and problem-solving strategies
• describe language acquisition and the role language plays in communication and thought

You learned about non-memory cognitive processes in this chapter. Because each of you reading this is using language in some shape or form, we will end with a quick summary and a video on this topic. Language is a communication system that has both a lexicon and a system of grammar. Language acquisition occurs naturally and effortlessly during the early stages of life, and this acquisition occurs in a predictable sequence for individuals around the world. Language has a strong influence on thought, and the concept of how language may influence cognition remains an area of study and debate in psychology.

In this TED talk, Lera Boroditsky summarizes unique ways that language and culture intersect with some basic cognitive processes. How was your language shaped your thinking?

Abler, W. (2013). Sapir, Harris, and Chomsky in the twentieth century. Cognitive Critique, 7, 29–48.

Aronson, E. (Ed.). (1995). Social cognition. In The social animal (p. 151). New York: W.H. Freeman and Company.

Bartlett, F. C. (1932). Remembering: A study in experimental and social psychology. Cambridge, England: Cambridge University Press.

Bayer, J. B., & Campbell, S. W. (2012). Texting while driving on automatic: Considering the frequency-independent side of habit. Computers in Human Behavior, 28, 2083–2090.

Beilock, S. L., & Carr, T. H. (2001). On the fragility of skilled performance: What governs choking under pressure?  Journal of Experimental Psychology: General, 130 , 701–725.

Berlin, B., & Kay, P. (1969). Basic color terms: Their universality and evolution. Berkley: University of California Press.

Blossom, M., & Morgan, J. L. (2006). Does the face say what the mouth says? A study of infants’ sensitivity to visual prosody. In the 30th annual Boston University Conference on Language Development, Somerville, MA.

Boroditsky, L. (2001). Does language shape thought? Mandarin and English speakers’ conceptions of time. Cognitive Psychology, 43, 1–22.

Boroditsky, L. (2011, February). How language shapes thought. Scientific American, 63–65.Chomsky, N. (1965). Aspects of the theory of syntax. Cambridge, MA: MIT Press

Broadbent, D. A. (1958).  Perception and communication . London, England: Pergamon Press.

Cairns Regional Council. (n.d.). Cultural greetings. Retrieved from http://www.cairns.qld.gov.au/__data/assets/pdf_file/0007/8953/CulturalGreetingExercise.pdf

Callero, P. L. (1994). From role-playing to role-using: Understanding role as resource. Social Psychology Quarterly, 57, 228–243.

Cherry, E. C. (1953). Experiments on the recognition of speech with one and two ears.  Journal of the Acoustical Society of America, 25 , 975–979.

Chomsky, N.(1965). Aspects of the theory of syntax. Cambridge, MA: MIT Press

Corballis, M. C., & Suddendorf, T. (2007). Memory, time, and language. In C. Pasternak (Ed.), What makes us human (pp. 17–36). Oxford, UK: Oneworld Publications.

Curtiss, S. (1981). Dissociations between language and cognition: Cases and implications. Journal of Autism and Developmental Disorders, 11(1), 15–30.

Cyclopedia of Puzzles. (n.d.) Retrieved from http://www.mathpuzzle.com/loyd/

Deutsch, J. A., & Deutsch, D. (1963). Attention: some theoretical considerations.  Psychological Review, 70 , 80–90.

Fernández, E. M., & Cairns, H. S. (2011). Fundamentals of psycholinguistics. West Sussex, UK: Wiley-Blackwell.

Fromkin, V., Krashen, S., Curtiss, S., Rigler, D., & Rigler, M. (1974). The development of language in Genie: A case of language acquisition beyond the critical period. Brain and Language, 1, 81–107.

German, T. P., & Barrett, H. C. (2005). Functional fixedness in a technologically sparse culture. Psychological Science, 16, 1–5.

Goldstone, R. L., & Kersten, A. (2003). Concepts and categorization. In A. F. Healy, R. W. Proctor, & I.B. Weiner (Eds.), Handbook of psychology (Volume IV, pp. 599–622). Hoboken, New Jersey: John Wiley & Sons, Inc.

Hirst, W. C., Neisser, U., & Spelke, E. S. (1978). Divided attention.  Human Nature, 1 , 54–61.

James, W. (1983).  The principles of psychology . Cambridge, MA: Harvard University Press. (Original work published 1890)

Jensen, J. (2011). Phoneme acquisition: Infants and second language learners. The Language Teacher, 35(6), 24–28.

Johnson, J. S., & Newport, E. L. (1989). Critical period effects in second language learning: The influence of maturational state on the acquisition of English as a second language. Cognitive Psychology, 21, 60–99.

Johnston, W. A., & Heinz, S. P. (1978). Flexibility and capacity demands of attention.  Journal of Experimental Psychology: General, 107 , 420–435.

Kahneman, D. (2011). Thinking, fast and slow. New York: Farrar, Straus, and Giroux.

Lenneberg, E. (1967). Biological foundations of language. New York: Wiley.

Monsell, S. (2003). Task switching.  Trends in Cognitive Science, 7 (3), 134–140.

Moray, N. (1959). Attention in dichotic listening: Affective cues and the influence of instructions.  Quarterly Journal of Experimental Psychology, 11 , 56–60.

Moskowitz, B. A. (1978). The acquisition of language. Scientific American, 239, 92–108. Petitto, L. A., Holowka, S., Sergio, L. E., Levy, B., & Ostry, D. J. (2004). Baby hands that move to the rhythm of language: Hearing babies acquiring sign languages babble silently on the hands. Cognition, 93, 43–73.

Neyfakh, L. (2013, October 7). “Why you can’t stop checking your phone.” Retrieved from http://www.bostonglobe.com/ideas/2013/10/06/why-you-can-stop-checking-your-phone/rrBJzyBGDAr1YlEH5JQDcM/story.html

Petitto, L. A., Holowka, S., Sergio, L. E., Levy, B., & Ostry, D. J. (2004). Baby hands that move to the rhythm of language: Hearing babies acquiring sign languages babble silently on the hands. Cognition, 93, 43–73.

Pickens, J. (1994). Full-term and preterm infants’ perception of face-voice synchrony. Infant Behavior and Development, 17, 447–455.

Pratkanis, A. (1989). The cognitive representation of attitudes. In A. R. Pratkanis, S. J. Breckler, & A. G. Greenwald (Eds.), Attitude structure and function (pp. 71–98). Hillsdale, NJ: Erlbaum.

Regier, T., & Kay, P. (2009). Language, thought, and color: Whorf was half right. Trends in Cognitive Sciences, 13(10), 439–446.

Rymer, R. (1993). Genie: A Scientific Tragedy. New York: Harper Collins.

Sapir, E. (1964). Culture, language, and personality. Berkley: University of California Press. (Original work published 1941)

Simons, D. J., & Chabris, C. F. (1999). Gorillas in our midst: Sustained inattentional blindness for dynamic events.  Perception, 28 , 1059–1074.

Skinner, B. F. (1957). Verbal behavior. Acton, MA: Copley Publishing Group.

Spelke, E. S., & Cortelyou, A. (1981). Perceptual aspects of social knowing: Looking and listening in infancy. In M.E. Lamb & L.R. Sherrod (Eds.), Infant social cognition: Empirical and theoretical considerations (pp. 61–83). Hillsdale, NJ: Erlbaum.

Spelke, E. S., Hirst, W. C., & Neisser, U. (1976). Skills of divided attention.  Cognition, 4 , 215–250.

Strayer, D. L., & Drews, F. A. (2007). Cell-phone induced inattention blindness.  Current Directions in Psychological Science, 16 , 128–131.

Strayer, D. L., & Johnston, W. A. (2001). Driven to distraction: Dual-task studies of simulated driving and conversing on a cellular telephone.  Psychological Science, 12 , 462–466.

Strayer, D. L., Watson, J. M., & Drews, F. A. (2011) Cognitive distraction while multitasking in the automobile. In Brian Ross (Ed.),  The Psychology of Learning and Motivation  (Vol. 54, pp. 29–58). Burlington, VT: Academic Press.

Tomasello, M., & Rakoczy, H. (2003). What makes human cognition unique? From individual to shared to collective intentionality. Mind & Language, 18(2), 121–147.

Treisman, A. (1960). Contextual cues in selective listening.  Quarterly Journal of Experimental Psychology, 12 , 242–248.

Tversky, A., & Kahneman, D. (1974). Judgment under uncertainty: Heuristics and biases. Science, 185(4157), 1124–1131.

van Troyer, G. (1994). Linguistic determinism and mutability: The Sapir-Whorf “hypothesis” and intercultural communication. JALT Journal, 2, 163–178.

Watson, J. M., & Strayer, D. L. (2010). Supertaskers: Profiles in extraordinary multitasking ability.  Psychonomic Bulletin & Review, 17 , 479–485.

Werker, J. F., & Lalonde, C. E. (1988). Cross-language speech perception: Initial capabilities and developmental change. Developmental Psychology, 24, 672–683.

Werker, J. F., & Tees, R. C. (1984). Cross-language speech perception: Evidence for perceptual reorganization during the first year of life. Infant Behavior and Development, 7, 49–63.

Whorf, B. L. (1956). Language, thought and relativity. Cambridge, MA: MIT Press.

CC original content.

Attention, Thinking and Language.  Authored by:  Karenna Malavanti Provided by: PressBooks. License: CC BY-SA: Attribution-ShareAlike

CC licensed content, Shared previously

• Why It Matters: Thinking and Intelligence.  Authored by : Lumen Learning License :  CC BY: Attribution   Located at :  https://pressbooks.online.ucf.edu/lumenpsychology/chapter/introduction-10/
• Attention. Authored by: Frances Friedrich. Located at NOBA Psychology. License: CC-BY-NC-SA. Retrieved from: Retrieved from  http://noba.to/uv9x8df5
• Introduction to Thinking and Intelligence. Authored by : OpenStax College. License : CC BY: Attribution . License Terms : Download for free at https://openstax.org/books/psychology-2e/pages/1-introduction   Located at : https://openstax.org/books/psychology-2e/pages/7-introduction .
• What Is Cognition?. Authored by : OpenStax College. License : CC BY: Attribution . License Terms : Download for free at https://openstax.org/books/psychology-2e/pages/1-introduction   Located at : https://openstax.org/books/psychology-2e/pages/7-1-what-is-cognition .
• A Thinking Man Image. Authored by : Wesley Nitsckie. License : CC BY-SA: Attribution-ShareAlike   Located at : https://www.flickr.com/photos/nitsckie/5507777269 .
• What Is Cognition?.  Authored by : Lumen Learning License :  CC BY: Attribution   Located at :  https://pressbooks.online.ucf.edu/lumenpsychology/chapter/what-is-cognition/
• Categories and Concepts. Authored by : Gregory Murphy. Provided by : New York University. Project : The Noba Project. License : CC BY-NC-SA: Attribution-NonCommercial-ShareAlike   Located at : http://nobaproject.com/textbooks/wendy-king-introduction-to-psychology-the-full-noba-collection/modules/categories-and-concepts .
• Solving Problems.  Authored by : Lumen Learning License :  CC BY: Attribution   Located at : https://pressbooks.online.ucf.edu/lumenpsychology/chapter/problem-solving/
• Problem-Solving. Authored by : OpenStax College. License : CC BY: Attribution . License Terms : Download for free at https://openstax.org/books/psychology-2e/pages/1-introduction . Located at : https://openstax.org/books/psychology-2e/pages/7-3-problem-solving .
• Pitfalls to Problem Solving.  Authored by : Lumen Learning License :  CC BY: Attribution   Located at :  https://pressbooks.online.ucf.edu/lumenpsychology/chapter/reading-pitfalls-to-problem/
• Introduction to Language.  Authored by : Lumen Learning License :  CC BY: Attribution   Located at :  https://pressbooks.online.ucf.edu/lumenpsychology/chapter/outcome-language/
• Language. Authored by : OpenStax College.  License : CC BY: Attribution . License Terms : Download for free at https://openstax.org/books/psychology-2e/pages/1-introduction   Located at : https://openstax.org/books/psychology-2e/pages/7-2-language .
• Language. Authored by : geralt. Provided by : Pixabay. License : CC0: No Rights Reserved   Located at : https://pixabay.com/en/school-board-languages-blackboard-1063556/ .
• Language and Language Use.  Authored by : Lumen Learning License :  CC BY: Attribution   Located at :  https://pressbooks.online.ucf.edu/lumenpsychology/chapter/language-and-language-use/
• Language and Language Use. Authored by : Yoshihisa Kashima. Project : The Noba Project. License : CC BY-NC-SA: Attribution-NonCommercial-ShareAlike   Located at : http://nobaproject.com/textbooks/introduction-to-psychology-the-full-noba-collection/modules/language-and-language-use .
• Language Development.  Authored by : Lumen Learning License :  CC BY: Attribution   Located at :  https://pressbooks.online.ucf.edu/lumenpsychology/chapter/language/
• Morpheme. Provided by : Wikipedia. License : CC BY-SA: Attribution-ShareAlike   Located at : https://en.wikipedia.org/wiki/Morpheme .
• Language and Thinking.  Authored by : Lumen Learning License :  CC BY: Attribution   Located at :  https://pressbooks.online.ucf.edu/lumenpsychology/chapter/reading-language-and-thought/
• Summary. Authored by : OpenStax College. License : CC BY: Attribution . License Terms : Download for free at https://openstax.org/books/psychology-2e/pages/1-introduction . Located at : https://openstax.org/books/psychology-2e/pages/7-summary .

All rights reserved content

• Cognition: How Your Mind Can Amaze and Betray You – Crash Course Psychology #15. Provided by : CrashCourse. License : All Rights Reserved . License Terms : Standard YouTube License   Located at : https://www.youtube.com/watch?v=R-sVnmmw6WY&feature=youtu.be&list=PL8dPuuaLjXtOPRKzVLY0jJY-uHOH9KVU6 .
• Can you solve Einsteinu2019s Riddle? . Authored by : Dan Van der Vieren. Provided by : Ted-Ed. License : Other . License Terms : Standard YouTube License .  Located at : https://www.youtube.com/watch?v=1rDVz_Fb6HQ&index=3&list=PLUmyCeox8XCwB8FrEfDQtQZmCc2qYMS5a .
• Language: Crash Course Psychology #16. Authored by : CrashCourse. License : Other . License Terms : Standard YouTube License .  Located at : https://www.youtube.com/watch?v=s9shPouRWCs&feature=youtu.be&list=PL8dPuuaLjXtOPRKzVLY0jJY-uHOH9KVU6 .
• How language shapes the way we think Authored by: Lera Boroditsky.  Provided by :  TED.  License : Other . License Terms : Standard YouTube License .  Located at :  https://youtu.be/RKK7wGAYP6k

thinking, including perception, learning, problem solving, judgment, and memory

field of psychology dedicated to studying every aspect of how people think

a set of objects that can be treated as equivalent in some way

category or grouping of linguistic information, objects, ideas, or life experiences

best representation of a concept

mental groupings that are created “naturally” through your experiences

concept that is defined by a very specific set of characteristics

(plural = schemata) mental construct consisting of a cluster or collection of related concepts

set of expectations that define the behaviors of a person occupying a particular role

set of behaviors that are performed the same way each time; also referred to as a cognitive script

set of behaviors that are performed the same way each time; also referred to as an event schema

method for solving problems

problem-solving strategy in which multiple solutions are attempted until the correct one is found

problem-solving strategy characterized by a specific set of instructions

mental shortcut that saves time when solving a problem

heuristic in which you begin to solve a problem by focusing on the end result

continually using an old solution to a problem without results

inability to see an object as useful for any other use other than the one for which it was intended

faulty heuristic in which you fixate on a single aspect of a problem to find a solution

belief that the event just experienced was predictable, even though it really wasn’t

subset of the population that accurately represents the general population

faulty heuristic in which you make a decision based on information readily available to you

communication system that involves using words to transmit information from one individual to another

Words and expressions.

set of rules that are used to convey meaning through the use of a lexicon

basic sound unit of a given language

smallest unit of language that conveys some type of meaning

process by which we derive meaning from morphemes and words

manner by which words are organized into sentences

extension of a rule that exists in a given language to an exception to the rule

Psychological Science: Understanding Human Behavior Copyright © by Karenna Malavanti is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

• Get started with computers
• Learn Microsoft Office
• Apply for a job
• Improve my work skills
• Design nice-looking docs
• Getting Started
• Smartphones & Tablets
• Typing Tutorial
• Online Learning
• Basic Internet Skills
• Online Safety
• Social Media
• Zoom Basics
• Google Docs
• Google Sheets
• Career Planning
• Resume Writing
• Cover Letters
• Job Search and Networking
• Business Communication
• Entrepreneurship 101
• Careers without College
• Job Hunt for Today
• 3D Printing
• Freelancing 101
• Personal Finance
• Sharing Economy
• Decision-Making
• Graphic Design
• Photography
• Image Editing
• Learning WordPress
• Language Learning
• Critical Thinking
• For Educators
• Translations
• Staff Picks
• English expand_more expand_less

Critical Thinking and Decision-Making  - What is Critical Thinking?

Critical thinking and decision-making  -, what is critical thinking, critical thinking and decision-making what is critical thinking.

Critical Thinking and Decision-Making: What is Critical Thinking?

Lesson 1: what is critical thinking, what is critical thinking.

Critical thinking is a term that gets thrown around a lot. You've probably heard it used often throughout the years whether it was in school, at work, or in everyday conversation. But when you stop to think about it, what exactly is critical thinking and how do you do it ?

Watch the video below to learn more about critical thinking.

Simply put, critical thinking is the act of deliberately analyzing information so that you can make better judgements and decisions . It involves using things like logic, reasoning, and creativity, to draw conclusions and generally understand things better.

This may sound like a pretty broad definition, and that's because critical thinking is a broad skill that can be applied to so many different situations. You can use it to prepare for a job interview, manage your time better, make decisions about purchasing things, and so much more.

The process

As humans, we are constantly thinking . It's something we can't turn off. But not all of it is critical thinking. No one thinks critically 100% of the time... that would be pretty exhausting! Instead, it's an intentional process , something that we consciously use when we're presented with difficult problems or important decisions.

Improving your critical thinking

In order to become a better critical thinker, it's important to ask questions when you're presented with a problem or decision, before jumping to any conclusions. You can start with simple ones like What do I currently know? and How do I know this? These can help to give you a better idea of what you're working with and, in some cases, simplify more complex issues.  

Real-world applications

Let's take a look at how we can use critical thinking to evaluate online information . Say a friend of yours posts a news article on social media and you're drawn to its headline. If you were to use your everyday automatic thinking, you might accept it as fact and move on. But if you were thinking critically, you would first analyze the available information and ask some questions :

• What's the source of this article?
• Is the headline potentially misleading?
• What are my friend's general beliefs?
• Do their beliefs inform why they might have shared this?

After analyzing all of this information, you can draw a conclusion about whether or not you think the article is trustworthy.

Critical thinking has a wide range of real-world applications . It can help you to make better decisions, become more hireable, and generally better understand the world around you.

/en/problem-solving-and-decision-making/why-is-it-so-hard-to-make-decisions/content/

• Business Essentials
• Leadership & Management
• Credential of Leadership, Impact, and Management in Business (CLIMB)
• Entrepreneurship & Innovation
• Digital Transformation
• Finance & Accounting
• Business in Society
• For Organizations
• Support Portal
• Media Coverage
• Founding Donors
• Leadership Team

• Harvard Business School →
• HBS Online →
• Business Insights →

Business Insights

Harvard Business School Online's Business Insights Blog provides the career insights you need to achieve your goals and gain confidence in your business skills.

• Career Development
• Communication
• Decision-Making
• Earning Your MBA
• Negotiation
• News & Events
• Productivity
• Staff Spotlight
• Student Profiles
• Work-Life Balance
• AI Essentials for Business
• Alternative Investments
• Business Analytics
• Business Strategy
• Business and Climate Change
• Design Thinking and Innovation
• Digital Marketing Strategy
• Disruptive Strategy
• Economics for Managers
• Entrepreneurship Essentials
• Financial Accounting
• Global Business
• Launching Tech Ventures
• Leadership Principles
• Leadership, Ethics, and Corporate Accountability
• Leading Change and Organizational Renewal
• Leading with Finance
• Management Essentials
• Negotiation Mastery
• Organizational Leadership
• Power and Influence for Positive Impact
• Strategy Execution
• Sustainable Business Strategy
• Sustainable Investing
• Winning with Digital Platforms

What Is Creative Problem-Solving & Why Is It Important?

• 01 Feb 2022

One of the biggest hindrances to innovation is complacency—it can be more comfortable to do what you know than venture into the unknown. Business leaders can overcome this barrier by mobilizing creative team members and providing space to innovate.

There are several tools you can use to encourage creativity in the workplace. Creative problem-solving is one of them, which facilitates the development of innovative solutions to difficult problems.

Here’s an overview of creative problem-solving and why it’s important in business.

Access your free e-book today.

What Is Creative Problem-Solving?

Research is necessary when solving a problem. But there are situations where a problem’s specific cause is difficult to pinpoint. This can occur when there’s not enough time to narrow down the problem’s source or there are differing opinions about its root cause.

In such cases, you can use creative problem-solving , which allows you to explore potential solutions regardless of whether a problem has been defined.

Creative problem-solving is less structured than other innovation processes and encourages exploring open-ended solutions. It also focuses on developing new perspectives and fostering creativity in the workplace . Its benefits include:

• Finding creative solutions to complex problems : User research can insufficiently illustrate a situation’s complexity. While other innovation processes rely on this information, creative problem-solving can yield solutions without it.
• Adapting to change : Business is constantly changing, and business leaders need to adapt. Creative problem-solving helps overcome unforeseen challenges and find solutions to unconventional problems.
• Fueling innovation and growth : In addition to solutions, creative problem-solving can spark innovative ideas that drive company growth. These ideas can lead to new product lines, services, or a modified operations structure that improves efficiency.

Creative problem-solving is traditionally based on the following key principles :

1. Balance Divergent and Convergent Thinking

Creative problem-solving uses two primary tools to find solutions: divergence and convergence. Divergence generates ideas in response to a problem, while convergence narrows them down to a shortlist. It balances these two practices and turns ideas into concrete solutions.

2. Reframe Problems as Questions

By framing problems as questions, you shift from focusing on obstacles to solutions. This provides the freedom to brainstorm potential ideas.

3. Defer Judgment of Ideas

When brainstorming, it can be natural to reject or accept ideas right away. Yet, immediate judgments interfere with the idea generation process. Even ideas that seem implausible can turn into outstanding innovations upon further exploration and development.

4. Focus on "Yes, And" Instead of "No, But"

Using negative words like "no" discourages creative thinking. Instead, use positive language to build and maintain an environment that fosters the development of creative and innovative ideas.

Creative Problem-Solving and Design Thinking

Whereas creative problem-solving facilitates developing innovative ideas through a less structured workflow, design thinking takes a far more organized approach.

Design thinking is a human-centered, solutions-based process that fosters the ideation and development of solutions. In the online course Design Thinking and Innovation , Harvard Business School Dean Srikant Datar leverages a four-phase framework to explain design thinking.

The four stages are:

• Clarify: The clarification stage allows you to empathize with the user and identify problems. Observations and insights are informed by thorough research. Findings are then reframed as problem statements or questions.
• Ideate: Ideation is the process of coming up with innovative ideas. The divergence of ideas involved with creative problem-solving is a major focus.
• Develop: In the development stage, ideas evolve into experiments and tests. Ideas converge and are explored through prototyping and open critique.
• Implement: Implementation involves continuing to test and experiment to refine the solution and encourage its adoption.

Creative problem-solving primarily operates in the ideate phase of design thinking but can be applied to others. This is because design thinking is an iterative process that moves between the stages as ideas are generated and pursued. This is normal and encouraged, as innovation requires exploring multiple ideas.

Creative Problem-Solving Tools

While there are many useful tools in the creative problem-solving process, here are three you should know:

Creating a Problem Story

One way to innovate is by creating a story about a problem to understand how it affects users and what solutions best fit their needs. Here are the steps you need to take to use this tool properly.

1. Identify a UDP

Create a problem story to identify the undesired phenomena (UDP). For example, consider a company that produces printers that overheat. In this case, the UDP is "our printers overheat."

2. Move Forward in Time

To move forward in time, ask: “Why is this a problem?” For example, minor damage could be one result of the machines overheating. In more extreme cases, printers may catch fire. Don't be afraid to create multiple problem stories if you think of more than one UDP.

3. Move Backward in Time

To move backward in time, ask: “What caused this UDP?” If you can't identify the root problem, think about what typically causes the UDP to occur. For the overheating printers, overuse could be a cause.

Following the three-step framework above helps illustrate a clear problem story:

• The printer is overused.
• The printer overheats.
• The printer breaks down.

You can extend the problem story in either direction if you think of additional cause-and-effect relationships.

4. Break the Chains

By this point, you’ll have multiple UDP storylines. Take two that are similar and focus on breaking the chains connecting them. This can be accomplished through inversion or neutralization.

• Inversion: Inversion changes the relationship between two UDPs so the cause is the same but the effect is the opposite. For example, if the UDP is "the more X happens, the more likely Y is to happen," inversion changes the equation to "the more X happens, the less likely Y is to happen." Using the printer example, inversion would consider: "What if the more a printer is used, the less likely it’s going to overheat?" Innovation requires an open mind. Just because a solution initially seems unlikely doesn't mean it can't be pursued further or spark additional ideas.
• Neutralization: Neutralization completely eliminates the cause-and-effect relationship between X and Y. This changes the above equation to "the more or less X happens has no effect on Y." In the case of the printers, neutralization would rephrase the relationship to "the more or less a printer is used has no effect on whether it overheats."

Even if creating a problem story doesn't provide a solution, it can offer useful context to users’ problems and additional ideas to be explored. Given that divergence is one of the fundamental practices of creative problem-solving, it’s a good idea to incorporate it into each tool you use.

Brainstorming

Brainstorming is a tool that can be highly effective when guided by the iterative qualities of the design thinking process. It involves openly discussing and debating ideas and topics in a group setting. This facilitates idea generation and exploration as different team members consider the same concept from multiple perspectives.

Hosting brainstorming sessions can result in problems, such as groupthink or social loafing. To combat this, leverage a three-step brainstorming method involving divergence and convergence :

• Have each group member come up with as many ideas as possible and write them down to ensure the brainstorming session is productive.
• Continue the divergence of ideas by collectively sharing and exploring each idea as a group. The goal is to create a setting where new ideas are inspired by open discussion.
• Begin the convergence of ideas by narrowing them down to a few explorable options. There’s no "right number of ideas." Don't be afraid to consider exploring all of them, as long as you have the resources to do so.

Alternate Worlds

The alternate worlds tool is an empathetic approach to creative problem-solving. It encourages you to consider how someone in another world would approach your situation.

For example, if you’re concerned that the printers you produce overheat and catch fire, consider how a different industry would approach the problem. How would an automotive expert solve it? How would a firefighter?

Be creative as you consider and research alternate worlds. The purpose is not to nail down a solution right away but to continue the ideation process through diverging and exploring ideas.

Continue Developing Your Skills

Whether you’re an entrepreneur, marketer, or business leader, learning the ropes of design thinking can be an effective way to build your skills and foster creativity and innovation in any setting.

If you're ready to develop your design thinking and creative problem-solving skills, explore Design Thinking and Innovation , one of our online entrepreneurship and innovation courses. If you aren't sure which course is the right fit, download our free course flowchart to determine which best aligns with your goals.

About the Author

Mediating effects of self-directed learning on the relationship between critical thinking and problem-solving in student nurses attending online classes: A cross-sectional descriptive study

Affiliations.

• 1 Kyungpook National University, College of Nursing, Research Institute of Nursing Science, Daegu, South Korea. Electronic address: [email protected].
• 2 Kyungpook National University, College of Nursing, Research Institute of Nursing Science, Daegu, South Korea. Electronic address: [email protected].
• 3 Kyungpook National University, College of Nursing, Research Institute of Nursing Science, Daegu, South Korea.
• PMID: 34972030
• DOI: 10.1016/j.nedt.2021.105227

Background: With the increased prevalence of online education due to the coronavirus 2019 pandemic and advancements in information technology, essential competencies, such as critical thinking, self-directed learning, and problem-solving ability, should be examined among student nurses taking online classes.

Objectives: Based on the findings of several studies suggesting that critical thinking does not affect problem-solving, this study aimed to examine the relationship among critical thinking, self-directed learning, and problem-solving in student nurses attending online classes, and to determine whether self-directed learning could mediate the relationship between critical thinking and problem-solving.

Design: Cross-sectional, descriptive design.

Setting: K University in South Korea.

Participants: In total, 138 junior and senior nursing students were enrolled.

Methods: The critical thinking disposition scale for nursing students, self-directed learning scale, and problem-solving scale for college students were used to quantify participants' responses.

Results: Our results revealed significant positive correlations among critical thinking, self-directed learning, and problem-solving. Furthermore, self-directed learning (β = 0.78, p < 0.001) had a significant mediating effect on the relationship between critical thinking and problem-solving ability (Z = 5.10, p < 0.001).

Conclusion: Developing and implementing appropriate self-directed learning programs are critical for improving problem-solving ability affected by critical thinking among student nurses engaged in online education.

Keywords: Critical thinking; Online education; Problem-solving; Self-directed learning; Student nurses.

Copyright © 2021 Elsevier Ltd. All rights reserved.

• Cross-Sectional Studies
• Problem Solving
• Students, Nursing*

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• Front Psychol

Intelligence and Creativity in Problem Solving: The Importance of Test Features in Cognition Research

Associated data.

This paper discusses the importance of three features of psychometric tests for cognition research: construct definition, problem space, and knowledge domain. Definition of constructs, e.g., intelligence or creativity, forms the theoretical basis for test construction. Problem space, being well or ill-defined, is determined by the cognitive abilities considered to belong to the constructs, e.g., convergent thinking to intelligence, divergent thinking to creativity. Knowledge domain and the possibilities it offers cognition are reflected in test results. We argue that (a) comparing results of tests with different problem spaces is more informative when cognition operates in both tests on an identical knowledge domain, and (b) intertwining of abilities related to both constructs can only be expected in tests developed to instigate such a process. Test features should guarantee that abilities can contribute to self-generated and goal-directed processes bringing forth solutions that are both new and applicable. We propose and discuss a test example that was developed to address these issues.

The definition of the construct a test is to measure is most important in test construction and application, because cognitive processes reflect the possibilities a task offers. For instance, a test constructed to assess intelligence will operationalize the definition of this construct, being, in short, finding the correct answer. Also, the definition of a construct becomes important when selecting tests for the confirmation of a specific hypothesis. One can only find confirmation for a hypothesis if the chosen task instigates the necessary cognitive operations. For instance, in trying to confirm the assumed intertwining of certain cognitive abilities (e.g., convergent thinking and divergent thinking), tasks should be applied that have shown to yield the necessary cognitive process.

The second test feature, problem space , determines the degrees of freedom cognition has to its disposal in solving a problem. For instance, cognition will go through a wider search path when problem constraints are less well defined and, consequently, data will differ accordingly.

The third test feature, knowledge domain , is important when comparing results from two different tests. When tests differ in problem space, it is not advisable they should differ in knowledge domain. For instance, when studying the differences in cognitive abilities between tests constructed to asses convergent thinking (mostly defined problem space) and divergent thinking (mostly ill-defined problem space), in general test practice, both tests also differ in knowledge domain. Hence, data will reflect cognition operating not only in different problem spaces, but also operating on different knowledge domains, which makes the interpretation of results ambiguous.

The proposed approach for test development and test application holds the promise of, firstly, studying cognitive abilities in different problem spaces while operating on an identical knowledge domain. Although cognitions’ operations have been studied extensively and superbly in both contexts separately, they have rarely been studied in test situations where one or the other test feature is controlled for. The proposed approach also presents a unique method for studying thinking processes in which cognitive abilities intertwine. On the basis of defined abilities, tasks can be developed that have a higher probability of yielding the hypothesized results.

The construct of intelligence is defined as the ability to produce the single best (or correct) answer to a clearly defined question, such as a proof to a theorem ( Simon, 1973 ). It may also be seen as a domain-general ability ( g -factor; Spearman, 1904 ; Cattell, 1967 ) that has much in common with meta cognitive functions, such as metacognitive knowledge, metacognitive monitoring, and metacognitive control ( Saraç et al., 2014 ).

The construct of creativity, in contrast, is defined as the ability to innovate and move beyond what is already known ( Wertheimer , 1945/1968 ; Ghiselin , 1952/1985 ; Vernon, 1970 ). In other words, it emphasizes the aspect of innovation. This involves the ability to consider things from an uncommon perspective, transcend the old order ( Ghiselin , 1952/1985 ; Chi, 1997 ; Ward, 2007 ), and explore loosely associated ideas ( Guilford, 1950 ; Mednick, 1962 ; Koestler, 1964 ; Gentner, 1983 ; Boden, 1990 ; Christensen, 2007 ). Creativity could also be defined as the ability to generate a solution to problems with ill-defined problem spaces ( Wertheimer , 1945/1968 ; Getzels and Csikszentmihalyi, 1976 ). In this sense it involves the ability to identify problematic aspects of a given situation ( Ghiselin , 1952/1985 ) and, in a wider sense, the ability to define completely new problems ( Getzels, 1975 , 1987 ).

Guilford (1956) introduced the constructs of convergent thinking and divergent thinking abilities. Both thinking abilities are important because they allow us insights in human problem solving. On the basis of their definitions convergent and divergent thinking help us to structurally study human cognitive operations in different situations and over different developmental stages. Convergent thinking is defined as the ability to apply conventional and logical search, recognition, and decision-making strategies to stored information in order to produce an already known answer ( Cropley, 2006 ). Divergent thinking, by contrast, is defined as the ability to produce new approaches and original ideas by forming unexpected combinations from available information and by applying such abilities as semantic flexibility, and fluency of association, ideation, and transformation ( Guilford, 1959 , as cited in Cropley, 2006 , p. 1). Divergent thinking brings forth answers that may never have existed before and are often novel, unusual, or surprising ( Cropley, 2006 ).

Guilford (1967) introduced convergent and divergent thinking as part of a set of five operations that apply in his Structure of Intellect model (SOI model) on six products and four kinds of content, to produce 120 different factors of cognitive abilities. With the SOI model Guilford wanted to give the construct of intelligence a comprehensive model. He wanted the model to include all aspects of intelligence, many of which had been seriously neglected in traditional intelligence testing because of a persistent adherence to the belief in Spearman’s g ( Guilford, 1967 , p. vii). Hence, Guilford envisaged cognition to embrace, among other abilities, both convergent and divergent thinking abilities. After these new constructs were introduced and defined, tests for convergent and divergent thinking emerged. Despite the fact that Guilford reported significant loadings of tests for divergent production on tests constructed to measure convergent production ( Guilford, 1967 , p. 155), over the years, both modes of thinking were considered as separate identities where convergent thinking tests associated with intelligence and divergent thinking tests with creativity ( Cropley, 2006 ; Shye and Yuhas, 2004 ). Even intelligence tests that assess aspects of intelligence that supposedly reflect creative abilities do not actually measure creativity ( Kaufman, 2015 ).

The idea that both convergent and divergent thinking are important for solving problems, and that intelligence helps in the creative process, is not really new. In literature we find models of the creative process that define certain stages to convergent and divergent thinking; the stages of purposeful preparation at the start and those of critical verification at the end of the process, respectively ( Wallas, 1926 ; Webb Young , 1939/2003 ). In this view, divergent thinking enables the generation of new ideas whereas the exploratory activities of convergent thinking enable the conversion of ideas into something new and appropriate ( Cropley and Cropley, 2008 ).

We argue that studying the abilities of divergent and convergent thinking in isolation does not suffice to give us complete insight of all possible aspects of human problem solving, its constituent abilities and the structure of its processes. Processes that in a sequence of thoughts and actions lead to novel and adaptive productions ( Lubart, 2001 ) are more demanding of cognition for understanding the situation at hand and planning a path to a possible solution, than abilities involved in less complex situations ( Jaušovec, 1999 ). Processes that yield self-generated and goal-directed thought are the most complex cognitive processes that can be studied ( Beaty et al., 2016 ). Creative cognition literature is moving toward the view that especially in those processes that yield original and appropriate solutions within a specific context, convergent and divergent abilities intertwine ( Cropley, 2006 ; Ward, 2007 ; Gabora, 2010 ).

The approach of intertwining cognitive abilities is also developed within cognitive neuroscience by focusing on the intertwining of brain networks ( Beaty et al., 2016 ). In this approach divergent thinking relates to the default brain network. This network operates in defocused or associative mode of thought yielding spontaneous and self-generated cognition ( Beaty et al., 2015 ). Convergent thinking relates to the executive control network operating in focused or analytic modes of thought, yielding updating, shifting, and inhibition ( Benedek et al., 2014 ). Defocused attention theory ( Mendelssohn, 1976 ) states that less creative individuals operate with a more focused attention than do creative individuals. This theory argues that e.g., attending to two things at the same time, might result in one analogy, while attending to four things might yield six analogies ( Martindale, 1999 ).

In the process of shifting back and forth along the spectrum between associative and analytic modes of thinking, the fruits of associative thought become ingredients for analytic thought processes, and vice versa ( Gabora, 2010 ). In this process, mental imagery is involved as one sensory aspect of the human ability to gather and process information ( Jung and Haier, 2013 ). Mental imagery is fed by scenes in the environment that provide crucial visual clues for creative problem solving and actuates the need for sketching ( Verstijnen et al., 2001 ).

Creative problem solving processes often involve an interactive relationship between imagining, sketching, and evaluating the result of the sketch ( van Leeuwen et al., 1999 ). This interactive process evolves within a type of imagery called “visual reasoning” where forms and shapes are manipulated in order to specify the configurations and properties of the design entities ( Goldschmidt, 2013 ). The originality of inventions is predicted by the application of visualization, whereas their practicality is predicted by the vividness of imagery ( Palmiero et al., 2015 ). Imaginative thought processes emerge from our conceptual knowledge of the world that is represented in our semantic memory system. In constrained divergent thinking, the neural correlates of this semantic memory system partially overlap with those of the creative cognition system ( Abraham and Bubic, 2015 ).

Studies of convergent and divergent thinking abilities have yielded innumerable valuable insights on the cognitive and neurological aspects involved, e.g., reaction times, strategies, brain areas involved, mental representations, and short and long time memory components. Studies on the relationship between both constructs suggest that it is unlikely that individuals employ similar cognitive strategies when solving more convergent than more divergent thinking tasks ( Jaušovec, 2000 ). However, to arrive at a quality formulation the creative process cannot do without the application of both, convergent and divergent thinking abilities (e.g., Kaufmann, 2003 ; Runco, 2003 ; Sternberg, 2005 ; Dietrich, 2007 ; Cropley and Cropley, 2008 ; Silvia et al., 2013 ; Jung, 2014 ).

When it is our aim to study the networks addressed by the intertwining of convergent and divergent thinking processes that are considered to operate when new, original, and yet appropriate solutions are generated, then traditional thinking tests like intelligence tests and creativity tests are not appropriate; they yield processes related to the definition of one or the other type of construct.

Creative Reasoning Task

According to the new insights gained in cognition research, we need tasks that are developed with the aim to instigate precisely the kind of thinking processes we are looking for. Tasks should also provide a method of scoring independently the contribution of convergent and divergent thinking. As one possible solution for such tasks we present the Creative Reasoning Task (CRT; Jaarsveld, 2007 ; Jaarsveld et al., 2010 , 2012 , 2013 ).

The CRT presents participants with an empty 3 × 3 matrix and asks them to fill it out, as original and complex as possible, by creating components and the relationships that connect them. The created matrix can, in principle, be solved by another person. The creation of components is entirely free, as is the generation of the relationships that connects them into a completed pattern. Created matrices are scored with two sub scores; Relations , which scores the logical complexity of a matrix and is, therefore, considered a measure for convergent thinking, and Components and Specifications , which scores the originality, fluency, and flexibility and, therefore, is considered an indication for divergent thinking (for a more detailed description of the score method, see Appendix 1 in Supplementary Material).

Psychometric studies with the CRT showed, firstly, that convergent and divergent thinking abilities apply within this task and can be assessed independently. The CRT sub score Relations correlated with the Standard Progressive Matrices test (SPM) and the CRT sub score Components and Specifications correlated with a standard creativity test (TCT–DP, Test of Creative Thinking–Drawing Production; Urban and Jellen, 1995 ; Jaarsveld et al., 2010 , 2012 , 2013 ). Studies further showed that, although a correlation was observed for the intelligence and creativity test scores, no correlation was observed between the CRT sub scores relating to intelligent and creative performances ( Jaarsveld et al., 2012 , 2013 ; for further details about the CRT’s objectivity, validity, and reliability, see Appendix 2 in Supplementary Material).

Reasoning in creative thinking can be defined as the involvement of executive/convergent abilities in the inhibition of ideas and the updating of information ( Benedek et al., 2014 ). Jung (2014) describes a dichotomy for cognitive abilities with at one end the dedicated system that relies on explicit and conscious knowledge and at the other end the improvisational system that relies more upon implicit or unconscious knowledge systems. The link between explicit and implicit systems can actually be traced back to Kris’ psychoanalytic approach to creativity dating from the 1950s. The implicit system refers to Kris’ primary process of adaptive regression, where unmodulated thoughts intrude into consciousness; the explicit system refers to the secondary process, where the reworking and transformation of primary process material takes place through reality-oriented and ego-controlled thinking ( Sternberg and Lubart, 1999 ). The interaction between explicit and implicit systems can be seen to form the basis of creative reasoning, i.e., the cognitive ability to solve problems in an effective and adaptive way. This interaction evolved as a cognitive mechanism when human survival depended on finding effective solutions to both common and novel problem situations ( Gabora and Kaufman, 2010 ). Creative reasoning solves that minority of problems that are unforeseen and yet of high adaptability ( Jung, 2014 ).

Hence, common tests are insufficient when it comes to solving problems that are unforeseen and yet of high adaptability, because they present problems that are either unforeseen and measure certain abilities contained in the construct of creativity or they address adaptability and measure certain abilities contained in the construct of intelligence. The CRT presents participants with a problem that they could not have foreseen; the form is blank and offers no stimuli. All tests, even creativity tests, present participants with some kind of stimuli. The CRT addresses adaptability; to invent from scratch a coherent structure that can be solved by another person, like creating a crossword puzzle. Problems, that are unforeseen and of high adaptability, are solved by the application of abilities from both constructs.

Neuroscience of Creative Cognition

Studies in neuroscience showed that cognition operating in ill-defined problem space not only applies divergent thinking but also benefits from additional convergent operations ( Gabora, 2010 ; Jung, 2014 ). Understanding creative cognition may be advanced when we study the flow of information among brain areas ( Jung et al., 2010 ).

In a cognitive neuroscience study with the CRT we focused on the cognitive process evolving within this task. Participants performed the CRT while EEG alpha activity was registered. EEG alpha synchronization in frontal areas is understood as an indication of top-down control ( Cooper et al., 2003 ). When observed in frontal areas, for divergent and convergent thinking tasks, it may not reflect a brain state that is specific for creative cognition but could be attributed to the high processing demands typically involved in creative thinking ( Benedek et al., 2011 ). Top-down control, relates to volitionally focusing attention to task demands ( Buschman and Miller, 2007 ). That this control plays a role in tasks with an ill-defined problem space showed when electroencephalography (EEG) alpha synchronization was stronger for individuals engaged in creative ideation tasks compared to an intelligence related tasks ( Fink et al., 2007 , 2009 ; Fink and Benedek, 2014 ). This activation was also found for the CRT; task related alpha synchronization showed that convergent thinking was integrated in the divergent thinking processes. Analyzes of the stages in the CRT process showed that this alpha synchronization was especially visible at the start of the creative process at prefrontal and frontal sites when information processing was most demanding, i.e., due to multiplicity of ideas, and it was visible at the end of the process, due to narrowing down of alternatives ( Jaarsveld et al., 2015 ).

A functional magnetic resonance imaging (fMRI) study ( Beaty et al., 2015 ) with a creativity task in which cognition had to meet specific constraints, showed the networks involved. The default mode network which drives toward abstraction and metaphorical thinking and the executive control network driving toward certainty ( Jung, 2014 ). Control involves not only maintenance of patterns of activity that represent goals and the means to achieve those ( Miller and Cohen, 2001 ), but also their voluntary suppression when no longer needed, as well as the flexible shift between different goals and mental sets ( Abraham and Windmann, 2007 ). Attention can be focused volitionally by top-down signals derived from task demands and automatically by bottom-up signals from salient stimuli ( Buschman and Miller, 2007 ). Intertwining between top-down and bottom-up attention processes in creative cognition ensures a broadening of attention in free associative thinking ( Abraham and Windmann, 2007 ).

These studies support and enhance the findings of creative cognition research in showing that the generation of original and applicable ideas involves an intertwining between different abilities, networks, and attention processes.

Problem Space

A problem space is an abstract representation, in the mind of the problem solver, of the encountered problem and of the asked for solution ( Simon and Newell, 1971 ; Simon, 1973 ; Hayes and Flowers, 1986 ; Kulkarni and Simon, 1988 ; Runco, 2007 ). The space that comes with a certain problem can, according to the constraints that are formulated for the solution, be labeled well-defined or ill-defined ( Simon and Newell, 1971 ). Consequently, the original problems are labeled closed and open problems, respectively ( Jaušovec, 2000 ).

A problem space contains all possible states that are accessible to the problem solver from the initial state , through iterative application of transformation rules , to the goal state ( Newell and Simon, 1972 ; Anderson, 1983 ). The initial state presents the problem solver with a task description that defines which requirements a solution has to answer. The goal state represents the solution. The proposed solution is a product of the application of transformation rules (algorithms and heuristics) on a series of successive intermediate solutions. The proposed solution is also a product of the iterative evaluations of preceding solutions and decisions based upon these evaluations ( Boden, 1990 ; Gabora, 2002 ; Jaarsveld and van Leeuwen, 2005 ; Goldschmidt, 2014 ). Whether all possible states need to be passed through depends on the problem space being well or ill-defined and this, in turn, depends on the character of the task descriptions.

When task descriptions clearly state which requirements a solution has to answer then the inferences made will show little idiosyncratic aspects and will adhere to the task constraints. As a result, fewer options for alternative paths are open to the problem solver and search for a solution evolves in a well-defined space. Vice versa, when task or problem descriptions are fuzzy and under specified, the problem solver’s inferences are more idiosyncratic; the resulting process will evolve within an ill-defined space and will contain more generative-evaluative cycles in which new goals are set, and the cycle is repeated ( Dennett, 1978 , as cited in Gabora, 2002 , p. 126).

Tasks that evolve in defined problem space are, e.g., traditional intelligence tests (e.g., Wechsler Adult Intelligence Scale, WAIS; and SPM, Raven , 1938/1998 ). The above tests consist of different types of questions, each testing a different component of intelligence. They are used in test practice to assess reasoning abilities in diverse domains, such as, abstract, logical, spatial, verbal, numerical, and mathematical domains. These tests have clearly stated task descriptions and each item has one and only one correct solution that has to be generated from memory or chosen from a set of alternatives, like in multiple choice formats. Tests can be constructed to assess crystallized or fluid intelligence. Crystallized intelligence represents abilities acquired through learning, practice, and exposure to education, while fluid intelligence represents a more basic capacity that is valuable to reasoning and problem solving in contexts not necessarily related to school education ( Carroll, 1982 ).

Tasks that evolve in ill-defined problem space are, e.g., standard creativity tests. These types of test ask for a multitude of ideas to be generated in association with a given item or situation (e.g., “think of as many titles for this story”). Therefore, they are also labeled as divergent thinking test. Although they assess originality, fluency, flexibility of responses, and elaboration, they are not constructed, however, to score appropriateness or applicability. Divergent thinking tests assess one limited aspect of what makes an individual creative. Creativity depends also on variables like affect and intuition; therefore, divergent thinking can only be considered an indication of an individual’s creative potential ( Runco, 2008 ). More precisely, divergent thinking explains just under half of the variance in adult creative potential, which is more than three times that of the contribution of intelligence ( Plucker, 1999 , p. 103). Creative achievement , by contrast, is commonly assessed by means of self-reports such as biographical questionnaires in which participants indicate their achievement across various domains (e.g., literature, music, or theater).

Studies with the CRT showed that problem space differently affects processing of and comprehension of relationships between components. Problem space did not affect the ability to process complex information. This ability showed equal performance in well and ill-defined problem spaces ( Jaarsveld et al., 2012 , 2013 ). However, problem space did affect the comprehension of relationships, which showed in the different frequencies of relationships solved and created ( Jaarsveld et al., 2010 , 2012 ). Problem space also affected the neurological activity as displayed when individuals solve open or closed problems ( Jaušovec, 2000 ).

Problem space further affected trends over grade levels of primary school children for relationships solved in well-defined and applied in ill-defined problem space. Only one of the 12 relationships defined in the CRT, namely Combination, showed an increase with grade for both types of problem spaces ( Jaarsveld et al., 2013 ). In the same study, cognitive development in the CRT showed in the shifts of preference for a certain relationship. These shifts seem to correspond to Piaget’s developmental stages ( Piaget et al., 1977 ; Siegler, 1998 ) which are in evidence in the CRT, but not in the SPM ( Jaarsveld et al., 2013 ).

Design Problems

A sub category of problems with an ill-defined problem space are represented by design problems. In contrast to divergent thinking tasks that ask for the generation of a multitude of ideas, in design tasks interim ideas are nurtured and incrementally developed until they are appropriate for the task. Ideas are rarely discarded and replaced with new ideas ( Goel and Pirolli, 1992 ). The CRT could be considered a design problem because it yields (a) one possible solution and (b) an iterative thinking process that involves the realization of a vague initial idea. In the CRT a created matrix, which is a closed problem, is created within an ill-defined problem space. Design problems can be found, e.g., in engineering, industrial design, advertising, software design, and architecture ( Sakar and Chakrabarti, 2013 ), however, they can also be found in the arts, e.g., poetry, sculpting, and dance geography.

These complex problems are partly determined by unalterable needs, requirements and intentions but the major part of the design problem is undetermined ( Dorst, 2004 ). This author points out that besides containing an original and a functional value, these types of problems contain an aesthetic value. He further states that the interpretation of the design problem and the creation and selection of possible suitable solutions can only be decided during the design process on the basis of proposals made by the designer.

In design problems the generation stage may be considered a divergent thinking process. However, not in the sense that it moves in multiple directions or generates multiple possibilities as in a divergent thinking tests, but in the sense that it unrolls by considering an initially vague idea from different perspectives until it comes into focus and requires further processing to become viable. These processes can be characterized by a set of invariant features ( Goel and Pirolli, 1992 ), e.g., structuring. iteration , and coherence .

Structuring of the initial situation is required in design processes before solving can commence. The problem contains little structured and clear information about its initial state and about the requirements of its solution. Therefore, design problems allow or even require re-interpretation of transformation rules; for instance, rearranging the location of furniture in a room according to a set of desirable outcomes. Here one uncovers implicit requirements that introduce a set of new transformations and/or eliminate existing ones ( Barsalou, 1992 ; Goel and Pirolli, 1992 ) or, when conflicting requirements arise, one creates alternatives and/or introduces new trade-offs between the conflicting constraints ( Yamamoto et al., 2000 ; Dorst, 2011 ).

A second aspect of design processes is their iterative character. After structuring and planning a vague idea emerges, which is the result of the merging of memory items. A vague idea is a cognitive structure that, halfway the creative process is still ill defined and, therefore, can be said to exist in a state of potentiality ( Gabora and Saab, 2011 ). Design processes unroll in an iterative way by the inspection and adjustment of the generated ideas ( Goldschmidt, 2014 ). New meanings are created and realized while the creative mind imposes its own order and meaning on the sensory data and through creative production furthers its own understanding of the world ( Arnheim , 1962/1974 , as cited in Grube and Davis, 1988 , pp. 263–264).

A third aspect of design processes is coherence. Coherence theories characterize coherence in, for instance, philosophical problems and psychological processes, in terms of maximal satisfaction of multiple constraints and compute coherence by using, a.o., connectionist algorithms ( Thagard and Verbeurgt, 1998 ). Another measure of coherence is characterized as continuity in design processes. This measure was developed for a design task ( Jaarsveld and van Leeuwen, 2005 ) and calculated by the occurrence of a given pair of objects in a sketch, expressed as a percentage of all the sketches of a series. In a series of sketches participants designed a logo for a new soft drink. Design series strong in coherence also received a high score for their final design, as assessed by professionals in various domains. Indicating that participants with a high score for the creative quality of their final sketch seemed better in assessing their design activity in relation to the continuity in the process and, thereby, seemed better in navigating the ill-defined space of a design problem ( Jaarsveld and van Leeuwen, 2005 ). In design problems the quality of cognitive production depends, in part, on the abilities to reflect on one’s own creative behavior ( Boden, 1996 ) and to monitor how far along in the process one is in solving it ( Gabora, 2002 ). Hence, design problems are especially suited to study more complex problem solving processes.

Knowledge Domain

Knowledge domain represents disciplines or fields of study organized by general principles, e.g., domains of various arts and sciences. It contains accumulated knowledge that can be divided in diverse content domains, and the relevant algorithms and heuristics. We also speak of knowledge domains when referring to, e.g., visuo-spatial and verbal domains. This latter differentiation may refer to the method by which performance in a certain knowledge domain is assessed, e.g., a visuo-spatial physics task that assesses the content domain of the workings of mass and weights of objects.

In comparing tests results, we should keep in mind that apart from reflecting cognitive processes evolving in different problem spaces, the results also arise from cognition operating on different knowledge domains. We argue that, the still contradictory and inconclusive discussion about the relationship between intelligence and creativity ( Silvia, 2008 ), should involve the issue of knowledge domain.

Intelligence tests contain items that pertain to, e.g., verbal, abstract, mechanical and spatial reasoning abilities, while their content mostly operates on knowledge domains that are related to contents contained in school curricula. Items of creativity tests, by contrast, pertain to more idiosyncratic knowledge domains, their contents relating to associations between stored personal experiences ( Karmiloff-Smith, 1992 ). The influence of knowledge domain on the relationships between different test scores was already mentioned by Guilford (1956 , p. 169). This author expected a higher correlation between scores from a typical intelligence test and a divergent thinking test than between scores from two divergent thinking tests because the former pair operated on identical information and the latter pair on different information.

Studies with the CRT showed that when knowledge domain is controlled for, the development of intelligence operating in ill-defined problem space does not compare to that of traditional intelligence but develops more similarly to the development of creativity ( Welter et al., in press ).

Relationship Intelligence and Creativity

The Threshold theory ( Guilford, 1967 ) predicts a relationship between intelligence and creativity up to approximately an intelligence quotient (IQ) level of 120 but not beyond ( Lubart, 2003 ; Runco, 2007 ). Threshold theory was corroborated when creative potential was found to be related to intelligence up to certain IQ levels; however, the theory was refuted, when focusing on achievement in creative domains; it showed that creative achievement benefited from higher intelligence even at fairly high levels of intellectual ability ( Jauk et al., 2013 ).

Distinguishing between subtypes of general intelligence known as fluent and crystallized intelligence ( Cattell, 1967 ), Sligh et al. (2005) observed an inverse threshold effect with fluid IQ: a correlation with creativity test scores in the high IQ group but not in the average IQ group. Also creative achievement showed to be affected by fluid intelligence ( Beaty et al., 2014 ). Intelligence, defined as fluid IQ, verbal fluency, and strategic abilities, showed a higher correlation with creativity scores ( Silvia, 2008 ) than when defined as crystallized intelligence. Creativity tests, which involved convergent thinking (e.g., Remote Association Test; Mednick, 1962 ) showed higher correlations with intelligence than ones that involved only divergent thinking (e.g., the Alternate Uses Test; Guilford et al., 1978 ).

That the Remote Association test also involves convergent thinking follows from the instructions; one is asked, when presented with a stimulus word (e.g., table) to produce the first word one thinks of (e.g., chair). The word pair table–chair is a common association, more remote is the pair table–plate, and quite remote is table–shark. According to Mednick’s theory (a) all cognitive work is done essentially by combining or associating ideas and (b) individuals with more commonplace associations have an advantage in well-defined problem spaces, because the class of relevant associations is already implicit in the statement of the problem ( Eysenck, 2003 ).

To circumvent the problem of tests differing in knowledge domain, one can develop out of one task a more divergent and a more convergent thinking task by asking, on the one hand, for the generation of original responses, and by asking, on the other hand, for more common responses ( Jauk et al., 2012 ). By changing the instruction of a task, from convergent to divergent, one changes the constraints the solution has to answer and, thereby, one changes for cognition its freedom of operation ( Razumnikova et al., 2009 ; Limb, 2010 ; Jauk et al., 2012 ). However, asking for more common responses is still a divergent thinking task because it instigates a generative and ideational process.

Indeed, studying the relationship between intelligence and creativity with knowledge domain controlled for yielded different results as defined in the Threshold theory. A study in which knowledge domain was controlled for showed, firstly, that intelligence is no predictor for the development of creativity ( Welter et al., 2016 ). Secondly, that the relationship between scores of intelligence and creativity tests as defined under the Threshold theory was only observed in a small subset of primary school children, namely, female children in Grade 4 ( Welter et al., 2016 ). We state that relating results of operations yielded by cognitive abilities performing in defined and in ill-defined problem spaces can only be informative when it is ensured that cognitive processes also operate on an identical knowledge domain.

Intertwining of Cognitive Abilities

Eysenck (2003) observed that there is little justification for considering the constructs of divergent and convergent thinking in categorical terms in which one construct excludes the other. In processes that yield original and appropriate solutions convergent and divergent thinking both operate on the same large knowledge base and the underlying cognitive processes are not entirely dissimilar ( Eysenck, 2003 , p. 110–111).

Divergent thinking is especially effective when it is coupled with convergent thinking ( Runco, 2003 ; Gabora and Ranjan, 2013 ). A design problem study ( Jaarsveld and van Leeuwen, 2005 ) showed that divergent production was active throughout the design, as new meanings are continuously added to the evolving structure ( Akin, 1986 ), and that convergent production was increasingly important toward the end of the process, as earlier productions are wrapped up and integrated in the final design. These findings are in line with the assumptions of Wertheimer (1945/1968) who stated that thinking within ill-defined problem space is characterized by two points of focus; one is to work on the parts, the other to make the central idea clearer.

Parallel to the discussion about the intertwining of convergent and divergent thinking abilities in processes that evolve in ill-defined problem space we find the discussion about how intelligence may facilitate creative thought. This showed when top-down cognitive control advanced divergent processing in the generation of original ideas and a certain measure of cognitive inhibition advanced the fluency of idea generation ( Nusbaum and Silvia, 2011 ). Fluid intelligence and broad retrieval considered as intelligence factors in a structural equation study contributed both to the production of creative ideas in a metaphor generation task ( Beaty and Silvia, 2013 ). The notion that creative thought involves top-down, executive processes showed in a latent variable analysis where inhibition primarily promoted the fluency of ideas, and intelligence promoted their originality ( Benedek et al., 2012 ).

Definitions of the Constructs Intelligence and Creativity

The various definitions of the constructs of intelligence and creativity show a problematic overlap. This overlap stems from the enormous endeavor to unanimously agree on valid descriptions for each construct. Spearman (1927) , after having attended many symposia that aimed at defining intelligence, stated that “in truth, ‘intelligence’ has become a mere vocal sound, a word with so many meanings that finally it has none” (p. 14).

Intelligence is expressed in terms of adaptive, goal-directed behavior; and the subset of such behavior that is labeled “intelligent” seems to be determined in large part by cultural or societal norms ( Sternberg and Salter, 1982 ). The development of the IQ measure is discussed by Carroll (1982) : “Binet (around 1905) realized that intelligent behavior or mental ability can be ranged along a scale. Not much later, Stern (around 1912) noticed that, as chronological age increased, variation in mental age changes proportionally. He developed the IQ ratio, whose standard deviation would be approximately constant over chronological age if mental age was divided by chronological age. With the development of multiple-factor-analyses (Thurstone, around 1935) it could be shown that intelligence is not a simple unitary trait because at least seven somewhat independent factors of mental ability were identified.”

Creativity is defined as a combined manifestation of novelty and usefulness ( Jung et al., 2010 ). Although it is identified with divergent thinking, and performance on divergent thinking tasks predicts, e.g., quantity of creative achievements ( Torrance, 1988 , as cited in Beaty et al., 2014 ) and quality of creative performance ( Beaty et al., 2013 ), it cannot be identified uniquely with divergent thinking.

Divergent thinking often leads to highly original ideas that are honed to appropriate ideas by evaluative processes of critical thinking, and valuative and appreciative considerations ( Runco, 2008 ). Divergent thinking tests should be more considered as estimates of creative problem solving potential rather than of actual creativity ( Runco, 1991 ). Divergent thinking is not specific enough to help us understand what, exactly, are the mental processes—or the cognitive abilities—that yield creative thoughts ( Dietrich, 2007 ).

Although current definitions of intelligence and creativity try to determine for each separate construct a unique set of cognitive abilities, analyses show that definitions vary in the degree to which each includes abilities that are generally considered to belong to the other construct ( Runco, 2003 ; Jaarsveld et al., 2012 ). Abilities considered belonging to the construct of intelligence such as hypothesis testing, inhibition of alternative responses, and creating mental images of new actions or plans are also considered to be involved in creative thinking ( Fuster, 1997 , as cited in Colom et al., 2009 , p. 215). The ability, for instance, to evaluate , which is considered to belong to the construct of intelligence and assesses the match between a proposed solution and task constraints, has long been considered to play a role in creative processes that goes beyond the mere generation of a series of ideas as in creativity tasks ( Wallas, 1926 , as cited in Gabora, 2002 , p. 1; Boden, 1990 ).

The Geneplore model ( Finke et al., 1992 ) explicitly models this idea; after stages in which objects are merely generated, follow phases in which an object’s utility is explored and estimated. The generation phase brings forth pre inventive objects, imaginary objects that are generated without any constraints in mind. In exploration, these objects are evaluated for their possible functionalities. In anticipating the functional characteristics of generated ideas, convergent thinking is needed to apprehend the situation, make evaluations ( Kozbelt, 2008 ), and consider the consequences of a chosen solution ( Goel and Pirolli, 1992 ). Convergent reasoning in creativity tasks invokes criteria of functionality and appropriateness ( Halpern, 2003 ; Kaufmann, 2003 ), goal directedness and adaptive behavior ( Sternberg, 1982 ), as well as the abilities of planning and attention. Convergent thinking stages may even require divergent thinking sub processes to identify restrictions on proposed new ideas and suggest requisite revision strategies ( Mumford et al., 2007 ). Hence, evaluation, which is considered to belong to the construct of intelligence, is also functional in creative processes.

In contrast, the ability of flexibility , which is considered to belong to the construct of creativity and denotes an openness of mind that ensures the generation of ideas from different domains, showed, as a factor component for latent divergent thinking, a relationship with intelligence ( Silvia, 2008 ). Flexibility was also found to play an important role in intelligent behavior where it enables us to do novel things smartly in new situations ( Colunga and Smith, 2008 ). These authors studied children’s generalizations of novel nouns and concluded that if we are to understand human intelligence, we must understand the processes that make inventiveness. They propose to include the construct of flexibility within that of intelligence. Therefore, definitions of the constructs we are to measure affect test construction and the resulting data. However, an overlap between definitions, as discussed, yields a test diversity that makes it impossible to interpret the different findings across studies with any confidence ( Arden et al., 2010 ). Also Kim (2005) concluded that because of differences in tests and administration methods, the observed correlation between intelligence and creativity was negligible. As the various definitions of the constructs of intelligence and creativity show problematic overlap, we propose to circumvent the discussion about which cognitive abilities are assessed by which construct, and to consider both constructs as being involved in one design process. This approach allows us to study the contribution to this process of the various defined abilities, without one construct excluding the other.

Reasoning Abilities

The CRT is a psychometrical tool constructed on the basis of an alternative construct of human cognitive functioning that considers creative reasoning as a thinking process understood as the cooperation between cognitive abilities related to intelligent and creative thinking.

In generating relationships for a matrix, reasoning and more specifically the ability of rule invention is applied. The ability of rule invention could be considered as an extension of the sequence of abilities of rule learning, rule inference, and rule application, implying that creativity is an extension of intelligence ( Shye and Goldzweig, 1999 ). According to this model, we could expect different results between a task assessing abilities of rule learning and rule inference, and a task assessing abilities of rule application. In two studies rule learning and rule inference was assessed with the RPM and rule application was assessed with the CRT. Results showed that from Grades 1 to 4, the frequencies of relationships applied did not correlate with those solved ( Jaarsveld et al., 2010 , 2012 ). Results showed that performance in the CRT allows an insight of cognitive abilities operating on relationships among components that differs from the insight based on performance within the same knowledge domain in a matrix solving task. Hence, reasoning abilities lead to different performances when applied in solving closed as to open problems.

We assume that reasoning abilities are more clearly reflected when one formulates a matrix from scratch; in the process of thinking and drawing one has, so to speak, to solve one’s own matrix. In doing so one explains to oneself the relationship(s) realized so far and what one would like to attain. Drawing is thinking aloud a problem and aids the designer’s thinking processes in providing some “talk-back” ( Cross and Clayburn Cross, 1996 ). Explanatory activity enhances learning through increased depth of processing ( Siegler, 2005 ). Analyzing explanations of examples given with physics problems showed that they clarify and specify the conditions and consequences of actions, and that they explicate tacit knowledge; thereby enhancing and completing an individual’s understanding of principles relevant to the task ( Chi and VanLehn, 1991 ). Constraint of the CRT is that the matrix, in principle, can be solved by another person. Therefore, in a kind of inner explanatory discussion, the designer makes observations of progress, and uses evaluations and decisions to answer this constraint. Because of this, open problems where certain constraints have to be met, constitute a powerful mechanism for promoting understanding and conceptual advancement ( Chi and VanLehn, 1991 ; Mestre, 2002 ; Siegler, 2005 ).

Convergent and divergent thinking processes have been studied with a variety of intelligence and creativity tests, respectively. Relationships between performances on these tests have been demonstrated and a large number of research questions have been addressed. However, the fact that intelligence and creativity tests vary in the definition of their construct, in their problem space, and in their knowledge domain, poses methodological problems regarding the validity of comparisons of test results. When we want to focus on one cognitive process, e.g., intelligent thinking, and on its different performances in well or ill-defined problem situations, we need pairs of tasks that are constructed along identical definitions of the construct to be assessed, that differ, however, in the description of their constraints but are identical regarding their knowledge domain.

One such possible pair, the Progressive Matrices Test and the CRT was suggested here. The CRT was developed on the basis of creative reasoning , a construct that assumes the intertwining of intelligent and creativity related abilities when looking for original and applicable solutions. Matched with the Matrices test, results indicated that, besides similarities, intelligent thinking also yielded considerable differences for both problem spaces. Hence, with knowledge domain controlled, and only differences in problem space remaining, comparison of data yielded new results on intelligence’s operations. Data gathered from intelligence and creativity tests, whether they are performance scores or physiological measurements on the basis of, e.g., EEG, and fMRI methods, are reflections of cognitive processes performing on a certain test that was constructed on the basis of a certain definition of the construct it was meant to measure. Data are also reflections of the processes evolving within a certain problem space and of cognitive abilities operating on a certain knowledge domain.

Data can unhide brain networks that are involved in the performance of certain tasks, e.g., traditional intelligence and creativity tests, but data will always be related to the characteristics of the task. The characteristics of the task, such as problem space and knowledge domain originated at the construction of the task, and the construction, on its turn, is affected by the definition of the construct the task is meant to measure.

Here we present the CRT as one possible solution for the described problems in cognition research. However, for research on relationships among test scores other pairs of tests are imaginable, e.g., pairs of tasks operating on the same domain where one task has a defined problem space and the other one an ill-defined space. It is conceivable that pairs of test could operate, besides on the domain of mathematics, on content of e.g., visuo-spatial, verbal, and musical domains. Pairs of test have been constructed by changing the instruction of a task; instructions instigated a more convergent or a more a divergent mode of response ( Razumnikova et al., 2009 ; Limb, 2010 ; Jauk et al., 2012 ; Beaty et al., 2013 ).

The CRT involves the creation of components and their relationships for a 3 × 3 matrix. Hence, matrices created in the CRT are original in the sense that they all bear individual markers and they are applicable in the sense, that they can, in principle, be solved by another person. We showed that the CRT instigates a real design process; creators’ cognitive abilities are wrapped up in a process that should produce a closed problem within an ill-defined problem space.

For research on the relationship among convergent and divergent thinking, we need pairs of test that differ in the problem spaces related to each test but are identical in the knowledge domain on which cognition operates. The test pair of RPM and CRT provides such a pair. For research on the intertwining of convergent and divergent thinking, we need tasks that measure more than tests assessing each construct alone. We need tasks that are developed on the definition of intertwining cognitive abilities; the CRT is one such test.

Hence, we hope to have sufficiently discussed and demonstrated the importance of the three test features, construct definition, problem space, and knowledge domain, for research questions in creative cognition research.

Author Contributions

All authors listed, have made substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: http://journal.frontiersin.org/article/10.3389/fpsyg.2017.00134/full#supplementary-material

• Abraham A., Bubic A. (2015). Semantic memory as the root of imagination. Front. Psychol. 6 : 325 10.3389/fpsyg.2015.00325 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Abraham A., Windmann S. (2007). Creative cognition: the diverse operations and the prospect of applying a cognitive neuroscience perspective. Methods 42 38–48. 10.1016/j.ymeth.2006.12.007 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Akin O. (1986). Psychology of Architectural Design London: Pion. [ Google Scholar ]
• Anderson J. R. (1983). The Architecture of Cognition Cambridge, MA: Harvard University Press. [ Google Scholar ]
• Arden R., Chavez R. S., Grazioplene R., Jung R. E. (2010). Neuroimaging creativity: a psychometric view. Behav. Brain Res. 214 143–156. 10.1016/j.bbr.2010.05.015 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Arnheim R. (1962/1974). Picasso’s Guernica Berkeley: University of California Press. [ Google Scholar ]
• Barsalou L. W. (1992). Cognitive Psychology: An Overview for Cognitive Scientists Hillsdale, NJ: LEA. [ Google Scholar ]
• Beaty R. E., Benedek M., Silvia P. J., Schacter D. L. (2016). Creative cognition and brain network dynamics. Trends Cogn. Sci. 20 87–95. 10.1016/j.tics.2015.10.004 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Beaty R. E., Kaufman S. B., Benedek M., Jung R. E., Kenett Y. N., Jauk E., et al. (2015). Personality and complex brain networks: the role of openness to experience in default network efficiency. Hum. Brain Mapp. 37 773–777. 10.1002/hbm.23065 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Beaty R. E., Nusbaum E. C., Silvia P. J. (2014). Does insight problem solving predict real-world creativity? Psychol. Aesthet. Creat. Arts 8 287–292. 10.1037/a0035727 [ CrossRef ] [ Google Scholar ]
• Beaty R. E., Silvia R. E. (2013). Metaphorically speaking: cognitive abilities and the production of figurative language. Mem. Cognit. 41 255–267. 10.3758/s13421-012-0258-5 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Beaty R. E., Smeekens B. A., Silvia P. J., Hodges D. A., Kane M. J. (2013). A first look at the role of domain-general cognitive and creative abilities in jazz improvisation. Psychomusicology 23 262–268. 10.1037/a0034968 [ CrossRef ] [ Google Scholar ]
• Benedek M., Bergner S., Konen T., Fink A., Neubauer A. C. (2011). EEG alpha synchronization is related to top-down processing in convergent and divergent thinking. Neuropsychologia 49 3505–3511. 10.1016/j.neuropsychologia.2011.09.004 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Benedek M., Franz F., Heene M., Neubauer A. C. (2012). Differential effects of cognitive inhibition and intelligence on creativity. Pers. Individ. Dif. 53 480–485. 10.1016/j.paid.2012.04.014 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Benedek M., Jauk E., Sommer M., Arendasy M., Neubauer A. C. (2014). Intelligence, creativity, and cognitive control: the common and differential involvement of executive functions in intelligence and creativity. Intelligence 46 73–83. 10.1016/j.intell.2014.05.007 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Boden M. A. (1990). The Creative Mind: Myths and Mechanisms London: Abacus. [ Google Scholar ]
• Boden M. A. (1996). Artificial Intelligence New York, NY: Academic. [ Google Scholar ]
• Buschman T. J., Miller E. K. (2007). Top-down versus bottom-up control of attention in the prefrontal and posterior parietal cortices. Science 315 1860–1862. 10.1126/science.1138071 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Carroll J. B. (1982). “The measurement of Intelligence,” in Handbook of Human Intelligence , ed. Sternberg R. J. (New York, NY: Cambridge University Press; ), 29–120. [ Google Scholar ]
• Cattell R. B. (1967). The theory of fluid and crystallized general intelligence checked at the 5-6 year-old level. Br. J. Educ. Psychol. 37 209–224. 10.1111/j.2044-8279.1967.tb01930.x [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Chi M. T. H. (1997). “ Creativity: Shifting across ontological categories flexibly ,” in Creative Thought: An Investigation of Conceptual Structures and Processes , eds Ward T., Smith S., Vaid J. (Washington, DC: American Psychological Association; ), 209–234. [ Google Scholar ]
• Chi M. T. H., VanLehn K. A. (1991). The content of physics self-explanations. J. Learn. Sci. 1 69–105. 10.1207/s15327809jls0101_4 [ CrossRef ] [ Google Scholar ]
• Christensen B. T. (2007). The relationship of analogical distance to analogical function and preinventive structure: the case of engineering design. Mem. Cogn. 35 29–38. 10.3758/BF03195939 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Colom R., Haier R. J., Head K., Álvarez-Linera J., Quiroga M. A., Shih P. C., et al. (2009). Gray matter correlates of fluid, crystallized, and spatial intelligence: testing the P-FIT model. Intelligence 37 124–135. 10.1016/j.intell.2008.07.007 [ CrossRef ] [ Google Scholar ]
• Colunga E., Smith L. B. (2008). Flexibility and variability: essential to human cognition and the study of human cognition. New Ideas Psychol. 26 158–192. 10.1016/j.newideapsych.2007.07.012 [ CrossRef ] [ Google Scholar ]
• Cooper N. R., Croft R. J., Dominey S. J. J., Burgess A. P., Gruzelier J. H. (2003). Paradox lost? Exploring the role of alpha oscillations during externally vs. internally directed attention and the implications for idling and inhibition hypotheses. Int. J. Psychophysiol. 47 65–74. 10.1016/S0167-8760(02)00107-1 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Cropley A. (2006). In praise of convergent thinking. Creat. Res. J. 18 391–404. 10.1207/s15326934crj1803_13 [ CrossRef ] [ Google Scholar ]
• Cropley A., Cropley D. (2008). Resolving the paradoxes of creativity: an extended phase model. Camb. J. Educ. 38 355–373. 10.1080/03057640802286871 [ CrossRef ] [ Google Scholar ]
• Cross N., Clayburn Cross A. (1996). Winning by design: the methods of Gordon Murray, racing car designer. Des. Stud. 17 91–107. 10.1016/0142-694X(95)00027-O [ CrossRef ] [ Google Scholar ]
• Dennett D. (1978). Brainstorms: Philosophical Essays on Mind and Psychology Montgomery, VT: Bradford Books. [ Google Scholar ]
• Dietrich A. (2007). Who’s afraid of a cognitive neuroscience of creativity? Methods 42 22–27. 10.1016/j.ymeth.2006.12.009 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Dorst K. (2004). The problem of design problems: Problem solving and design expertise. J. Design Res. 4 10.1504/JDR.2004.009841 [ CrossRef ] [ Google Scholar ]
• Dorst K. (2011). The core of ‘design thinking’ and its application. Des. Stud. 32 521–532. 10.1016/j.destud.2011.07.006 [ CrossRef ] [ Google Scholar ]
• Eysenck H. J. (2003). “Creativity, personality and the convergent-divergent continuum,” in Critical Creative Processes , ed. Runco M. A. (Cresskill, NJ: Hampton Press; ), 95–114. [ Google Scholar ]
• Fink A., Benedek M. (2014). EEG alpha power and creative ideation. Neurosci. Biobehav. Rev. 44 111–123. 10.1016/j.neubiorev.2012.12.002 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Fink A., Benedek M., Grabner R. H., Staudt B., Neubauer A. C. (2007). Creativity meets neuroscience: experimental tasks for the neuroscientific study of creative thinking. Methods 42 68–76. 10.1016/j.ymeth.2006.12.001 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Fink A., Grabner R. H., Benedek M., Reishofer G., Hauswirth V., Fally M., et al. (2009). The creative brain: investigation of brain activity during creative problem solving by means of EEG and FMRI. Hum. Brain Mapp. 30 734–748. 10.1002/hbm.20538 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Finke R. A., Ward T. B., Smith S. M. (1992). Creative Cognition: Theory, Research, and Applications Cambridge, MA: MIT Press. [ Google Scholar ]
• Fuster J. M. (1997). Network memory. Trends Neurosci. 20 451–459. 10.1016/S0166-2236(97)01128-4 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Gabora L. (2002). “Cognitive mechanisms underlying the creative process,” in Proceedings of the Fourth International Conference on Creativity and Cognition , eds Hewett T., Kavanagh T. (Loughborough: Loughborough University; ), 126–133. [ Google Scholar ]
• Gabora L. (2010). Revenge of the ‘neurds’: Characterizing creative thought in terms of the structure and dynamics of human memory. Creat. Res. J. 22 1–13. 10.1080/10400410903579494 [ CrossRef ] [ Google Scholar ]
• Gabora L., Kaufman S. B. (2010). “Evolutionary approaches to creativity,” in The Cambridge Handbook of Creativity , eds Kaufman J. S., Sternberg R. J. (Cambridge: Cambridge University Press; ), 279–300. [ Google Scholar ]
• Gabora L., Ranjan A. (2013). “How insight emerges in a distributed, content-addressable memory,” in The Neuroscience of Creativity , eds Bristol A., Vartanian O., Kaufman J. (Cambridge: MIT Press; ), 19–43. [ Google Scholar ]
• Gabora L., Saab A. (2011). “Creative inference and states of potentiality in analogy problem solving,” in Proceedings of the Annual Meeting of the Cognitive Science Society , Boston, MA, 3506–3511. [ Google Scholar ]
• Gentner D. (1983). Structure mapping: a theoretical framework for analogy. Cogn. Sci. 7 155–170. 10.1207/s15516709cog0702_3 [ CrossRef ] [ Google Scholar ]
• Getzels J. W. (1975). Problem finding and the inventiveness of solutions. J. Creat. Behav. 9 12–18. 10.1002/j.2162-6057.1975.tb00552.x [ CrossRef ] [ Google Scholar ]
• Getzels J. W. (1987). “Creativity, intelligence, and problem finding: retrospect and prospect,” in Frontiers of Creativity Research: Beyond the Basics , ed. Isaksen S. G. (Buffalo, NY: Bearly Limited; ), 88–102. [ Google Scholar ]
• Getzels J. W., Csikszentmihalyi M. (1976). The Creative Vision: A Longitudinal Study of Problem Finding in Art New York, NY: Wiley. [ Google Scholar ]
• Ghiselin B. (ed.) (1952/1985). The Creative Process Los Angeles: University of California. [ Google Scholar ]
• Goel V., Pirolli P. (1992). The structure of design problem spaces. Cogn. Sci. 16 395–429. 10.1207/s15516709cog1603_3 [ CrossRef ] [ Google Scholar ]
• Goldschmidt G. (2013). “A micro view of design reasoning: two-way shifts between embodiment and rationale,” in Creativity and Rationale: Enhancing Human Experience by Design, Human-Computer Interaction Series , ed. Carroll J. M. (London: Springer Verlag; ). 10.1007/978-1-4471-2_3 [ CrossRef ] [ Google Scholar ]
• Goldschmidt G. (2014). Linkography: Unfolding the Design Process Cambridge, MA: MIT Press. [ Google Scholar ]
• Grube H. E., Davis S. N. (1988). “Inching our way up mount Olympus: The evolving-systems approach to creative thinking,” in The Nature of Creativity , ed. Sternberg R. J. (New York, NY: Cambridge University Press; ), 243–270. [ Google Scholar ]
• Guilford J. P. (1950). Creativity. Am. Psychol. 5 444–454. 10.1037/h0063487 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Guilford J. P. (1956). The structure of intellect model. Psychol. Bull. 53 267–293. 10.1037/h0040755 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Guilford J. P. (1959). “Traits of creativity,” in Creativity and its Cultivation , ed. Anderson H. H. (New York: Harper; ), 142–161. [ Google Scholar ]
• Guilford J. P. (1967). The Nature of Human Intelligence New York, NY: McGraw-Hill, Inc. [ Google Scholar ]
• Guilford J. P., Christensen P. R., Merrifield P. R., Wilson R. C. (1978). Alternate Uses: Manual of Instructions and Interpretation Orange, CA: Sheridan Psychological Services. [ Google Scholar ]
• Halpern D. F. (2003). “Thinking critically about creative thinking,” in Critical Creative Processes , ed. Runco M. A. (Cresskill, NJ: Hampton Press; ), 189–208. [ Google Scholar ]
• Hayes J. R., Flowers L. S. (1986). Writing research and the writer. Am. Psychol. 41 1106–1113. 10.1037/0003-066X.41.10.1106 [ CrossRef ] [ Google Scholar ]
• Jaarsveld S. (2007). Creative Cognition: New Perspectives on Creative Thinking Kaiserslautern: University of Kaiserslautern Press. [ Google Scholar ]
• Jaarsveld S., Fink A., Rinner M., Schwab D., Benedek M., Lachmann T. (2015). Intelligence in creative processes; an EEG study. Intelligence 49 171–178. 10.1016/j.ijpsycho.2012.02.012 [ CrossRef ] [ Google Scholar ]
• Jaarsveld S., Lachmann T., Hamel R., van Leeuwen C. (2010). Solving and creating Raven Progressive Matrices: reasoning in well and ill defined problem spaces. Creat. Res. J. 22 304–319. 10.1080/10400419.2010.503541 [ CrossRef ] [ Google Scholar ]
• Jaarsveld S., Lachmann T., van Leeuwen C. (2012). Creative reasoning across developmental levels: convergence and divergence in problem creation. Intelligence 40 172–188. 10.1016/j.intell.2012.01.002 [ CrossRef ] [ Google Scholar ]
• Jaarsveld S., Lachmann T., van Leeuwen C. (2013). “The impact of problem space on reasoning: Solving versus creating matrices,” in Proceedings of the 35th Annual Conference of the Cognitive Science Society , eds Knauff M., Pauen M., Sebanz N., Wachsmuth I. (Austin, TX: Cognitive Science Society; ), 2632–2638. [ Google Scholar ]
• Jaarsveld S., van Leeuwen C. (2005). Sketches from a design process: creative cognition inferred from intermediate products. Cogn. Sci. 29 79–101. 10.1207/s15516709cog2901_4 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Jauk E., Benedek M., Dunst B., Neubauer A. C. (2013). The relationship between intelligence and creativity: new support for the threshold hypothesis by means of empirical breakpoint detection. Intelligence 41 212–221. 10.1016/j.intell.2013.03.003 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Jauk E., Benedek M., Neubauer A. C. (2012). Tackling creativity at its roots: evidence for different patterns of EEG alpha activity related to convergent and divergent modes of task processing. Int. J. Psychophysiol. 84 219–225. 10.1016/j.ijpsycho.2012.02.012 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Jaušovec N. (1999). “Brain biology and brain functioning,” in Encyclopedia of Creativity , eds Runco M. A., Pritzker S. R. (San Diego, CA: Academic Press; ), 203–212. [ Google Scholar ]
• Jaušovec N. (2000). Differences in cognitive processes between gifted, intelligent, creative, and average individuals while solving complex problems: an EEG Study. Intelligence 28 213–237. 10.1016/S0160-2896(00)00037-4 [ CrossRef ] [ Google Scholar ]
• Jung R. E. (2014). Evolution, creativity, intelligence, and madness: “here be dragons”. Front. Psychol 5 : 784 10.3389/fpsyg.2014.00784 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Jung R. E., Haier R. J. (2013). “Creativity and intelligence,” in Neuroscience of Creativity , eds Vartanian O., Bristol A. S., Kaufman J. C. (Cambridge, MA: MIT Press; ), 233–254. [ Google Scholar ]
• Jung R. E., Segall J. M., Bockholt H. J., Flores R. A., Smith S. M., Chavez R. S., et al. (2010). Neuroanatomy of creativity. Hum. Brain Mapp. 31 398–409. 10.1002/hbm.20874 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Karmiloff-Smith A. (1992). Beyond Modularity: A Developmental Perspective on Cognitive Science Cambridge, MA: MIT Press. [ Google Scholar ]
• Kaufman J. C. (2015). Why creativity isn’t in IQ tests, why it matters, and why it won’t change anytime soon probably. Intelligence 3 59–72. 10.3390/jintelligence303005 [ CrossRef ] [ Google Scholar ]
• Kaufmann G. (2003). What to measure? A new look at the concept of creativity. Scand. J. Educ. Res. 47 235–251. 10.1080/00313830308604 [ CrossRef ] [ Google Scholar ]
• Kim K. H. (2005). Can only intelligent people be creative? J. Second. Gift. Educ. 16 57–66. [ Google Scholar ]
• Koestler A. (1964). The Act of Creation London: Penguin. [ Google Scholar ]
• Kozbelt A. (2008). Hierarchical linear modeling of creative artists’ problem solving behaviors. J. Creat. Behav. 42 181–200. 10.1002/j.2162-6057.2008.tb01294.x [ CrossRef ] [ Google Scholar ]
• Kulkarni D., Simon H. A. (1988). The processes of scientific discovery: the strategy of experimentation. Cogn. Sci. 12 139–175. 10.1016/j.coph.2009.08.004 [ CrossRef ] [ Google Scholar ]
• Limb C. J. (2010). Your Brain on Improve Available at: http://www.ted.com/talks/charles_limb_your_brain_on_improv [ Google Scholar ]
• Lubart T. I. (2001). Models of the creative process: past, present and future. Creat. Res. J. 13 295–308. 10.1207/S15326934CRJ1334_07 [ CrossRef ] [ Google Scholar ]
• Lubart T. I. (2003). Psychologie de la Créativité. Cursus. Psychologie Paris: Armand Colin. [ Google Scholar ]
• Martindale C. (1999). “Biological basis of creativity,” in Handbook of Creativity , ed. Sternberg R. J. (New York, NY: Cambridge University Press; ), 137–152. [ Google Scholar ]
• Mednick S. A. (1962). The associative basis of the creative process. Psychol. Rev. 69 220–232. 10.1037/h0048850 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Mendelssohn G. A. (1976). Associational and attentional processes in creative performance. J. Pers. 44 341–369. 10.1111/j.1467-6494.1976.tb00127.x [ CrossRef ] [ Google Scholar ]
• Mestre J. P. (2002). Probing adults’ conceptual understanding and transfer of learning via problem posing. Appl. Dev. Psychol. 23 9–50. 10.1016/S0193-3973(01)00101-0 [ CrossRef ] [ Google Scholar ]
• Miller E. K., Cohen J. D. (2001). An integrative theory of prefrontal cortex function. Annu. Rev. Neurosci. 24 167–202. 10.1146/annurev.neuro.24.1.167 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Mumford M. D., Hunter S. T., Eubanks D. L., Bedell K. E., Murphy S. T. (2007). Developing leaders for creative efforts: a domain-based approach to leadership development. Hum. Res. Manag. Rev. 17 402–417. 10.1016/j.hrmr.2007.08.002 [ CrossRef ] [ Google Scholar ]
• Newell A., Simon H. A. (1972). “The theory of human problem solving,” in Human Problem Solving , eds Newell A., Simon H. (Englewood Cliffs, NJ: Prentice Hall; ), 787–868. [ Google Scholar ]
• Nusbaum E. C., Silvia P. J. (2011). Are intelligence and creativity really so different? Intelligence 39 36–40. 10.1016/j.intell.2010.11.002 [ CrossRef ] [ Google Scholar ]
• Palmiero M., Nori R., Aloisi V., Ferrara M., Piccardi L. (2015). Domain-specificity of creativity: a study on the relationship between visual creativity and visual mental imagery. Front. Psychol. 6 : 1870 10.3389/fpsyg.2015.01870 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Piaget J., Montangero J., Billeter J. (1977). “La formation des correlats,” in Recherches sur L’abstraction Reflechissante I , ed. Piaget J. (Paris: Presse Universitaires de France; ), 115–129. [ Google Scholar ]
• Plucker J. (1999). Is the proof in the pudding? Reanalyses of torrance’s (1958 to present) longitudinal study data. Creat. Res. J. 12 103–114. 10.1207/s15326934crj1202_3 [ CrossRef ] [ Google Scholar ]
• Raven J. C. (1938/1998). Standard Progressive Matrices, Sets A, B, C, D & E Oxford: Oxford Psychologists Press. [ Google Scholar ]
• Razumnikova O. M., Volf N. V., Tarasova I. V. (2009). Strategy and results: sex differences in electrographic correlates of verbal and figural creativity. Hum. Physiol. 35 285–294. 10.1134/S0362119709030049 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Runco M. A. (1991). The evaluative, valuative, and divergent thinking of children. J. Creat. Behav. 25 311–319. 10.1177/1073858414568317 [ CrossRef ] [ Google Scholar ]
• Runco M. A. (2003). “Idea evaluation, divergent thinking, and creativity,” in Critical Creative Processes , ed. Runco M. A. (Cresskill, NJ: Hampton Press; ), 69–94. [ Google Scholar ]
• Runco M. A. (2007). Creativity, Theories and Themes: Research, Development, and Practice New York, NY: Elsevier. [ Google Scholar ]
• Runco M. A. (2008). Commentary: divergent thinking is not synonymous with creativity. Psychol. Aesthet. Creat. Arts 2 93–96. 10.1037/1931-3896.2.2.93 [ CrossRef ] [ Google Scholar ]
• Sakar P., Chakrabarti A. (2013). Support for protocol analyses in design research. Des. Issues 29 70–81. 10.1162/DESI_a_00231 [ CrossRef ] [ Google Scholar ]
• Saraç S., Önder A., Karakelle S. (2014). The relations among general intelligence, metacognition and text learning performance. Educ. Sci. 39 40–53. [ Google Scholar ]
• Shye S., Goldzweig G. (1999). Creativity as an extension of intelligence: Faceted definition and structural hypotheses. Megamot 40 31–53. [ Google Scholar ]
• Shye S., Yuhas I. (2004). Creativity in problem solving. Tech. Rep. 10.13140/2.1.1940.0643 [ CrossRef ] [ Google Scholar ]
• Siegler R. S. (1998). Children’s Thinking , 3rd Edn Upper Saddle River, NJ: Prentice Hall, 28–50. [ Google Scholar ]
• Siegler R. S. (2005). Children’s learning. Am. Psychol. 60 769–778. 10.1037/0003-066X.60.8.769 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Silvia P. J. (2008). Creativity and intelligence revisited: a reanalysis of Wallach and Kogan (1965). Creat. Res. J. 20 34–39. 10.1080/10400410701841807 [ CrossRef ] [ Google Scholar ]
• Silvia P. J., Beaty R. E., Nussbaum E. C. (2013). Verbal fluency and creativity: general and specific contributions of broad retrieval ability (Gr) factors to divergent thinking. Intelligence 41 328–340. 10.1016/j.intell.2013.05.004 [ CrossRef ] [ Google Scholar ]
• Simon H. A. (1973). The structure of ill structured problems. Artif. Intell. 4 1012–1021. 10.1016/0004-3702(73)90011-8 [ CrossRef ] [ Google Scholar ]
• Simon H. A., Newell A. (1971). Human problem solving: state of theory in 1970. Am. Psychol. 26 145–159. 10.1037/h0030806 [ CrossRef ] [ Google Scholar ]
• Sligh A. C., Conners F. A., Roskos-Ewoldsen B. (2005). Relation of creativity to fluid and crystallized intelligence. J. Creat. Behav. 39 123–136. 10.1002/j.2162-6057.2005.tb01254.x [ CrossRef ] [ Google Scholar ]
• Spearman C. (1904). ‘General intelligence,’ objectively determined and measured. Am. J. Psychol. 15 201–293. 10.2307/1412107 [ CrossRef ] [ Google Scholar ]
• Spearman C. (1927). The Abilities of Man London: Macmillan. [ Google Scholar ]
• Sternberg R. J. (1982). “Conceptions of intelligence,” in Handbook of Human Intelligence , ed. Sternberg R. J. (New York, NY: Cambridge University Press; ), 3–28. [ Google Scholar ]
• Sternberg R. J. (2005). “The WICS model of giftedness,” in Conceptions of Giftedness , 2nd Edn, eds Sternberg R. J., Davidson J. E. (New York, NY: Cambridge University Press; ), 237–243. [ Google Scholar ]
• Sternberg R. J., Lubart T. I. (1999). “The concept of creativity: Prospects and paradigms,” in Handbook of Creativity , ed. Sternberg R. J. (New York, NY: Cambridge University Press; ), 3–15. [ Google Scholar ]
• Sternberg R. J., Salter W. (1982). “The nature of intelligence and its measurements,” in Handbook of Human Intelligence , ed. Sternberg R. J. (New York, NY: Cambridge University Press; ), 3–24. [ Google Scholar ]
• Thagard P., Verbeurgt K. (1998). Coherence as constraint satisfaction. Cogn. Sci. 22 l–24. 10.1207/s15516709cog2201_1 [ CrossRef ] [ Google Scholar ]
• Torrance E. P. (1988). “The nature of creativity as manifest in its testing,” in The Nature of Creativity: Contemporary Psychological Perspectives , ed. Sternberg R. J. (New York, NY: Cambridge University Press; ), 43–75. [ Google Scholar ]
• Urban K. K., Jellen H. G. (1995). Test of Creative Thinking – Drawing Production Frankfurt: Swets Test Services. [ Google Scholar ]
• van Leeuwen C., Verstijnen I. M., Hekkert P. (1999). “Common unconscious dynamics underlie uncommon conscious effect: a case study in the iterative nature of perception and creation,” in Modeling Consciousness Across the Disciplines , ed. Jordan J. S. (Lanham, MD: University Press of America; ), 179–218. [ Google Scholar ]
• Vernon P. E. (ed.) (1970). Creativity London: Penguin. [ Google Scholar ]
• Verstijnen I. M., Heylighen A., Wagemans J., Neuckermans H. (2001). “Sketching, analogies, and creativity,” in Visual and Spatial Reasoning in Design, II. Key Centre of Design Computing and Cognition , eds Gero J. S., Tversky B., Purcell T. (Sydney, NSW: University of Sydney; ). [ Google Scholar ]
• Wallas G. (1926). The Art of Thought New York, NY: Harcourt, Brace & World. [ Google Scholar ]
• Ward T. B. (2007). Creative cognition as a window on creativity. Methods 42 28–37. 10.1016/j.ymeth.2006.12.002 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Webb Young J. (1939/2003). A Technique for Producing Ideas New York, NY: McGraw-Hill. [ Google Scholar ]
• Welter M. M., Jaarsveld S., Lachmann T. Problem space matters: development of creativity and intelligence in primary school children. Creat. Res. J. (in press) [ Google Scholar ]
• Welter M. M., Jaarsveld S., van Leeuwen C., Lachmann T. (2016). Intelligence and creativity; over the threshold together? Creat. Res. J. 28 212–218. 10.1080/10400419.2016.1162564 [ CrossRef ] [ Google Scholar ]
• Wertheimer M. (1945/1968). Productive Thinking (Enlarged Edition) London: Tavistock. [ Google Scholar ]
• Yamamoto Y., Nakakoji K., Takada S. (2000). Hand on representations in two dimensional spaces for early stages of design. Knowl. Based Syst. 13 357–384. 10.1016/S0950-7051(00)00078-2 [ CrossRef ] [ Google Scholar ]

More From Forbes

Success in sustainability: two cognitive strategies for effective problem-solving.

• Share to Facebook
• Share to Twitter
• Share to Linkedin

Thomas Lim is the Vice-Dean of Centre for Systems Leadership at SIM Academy. He is an AI+Web3 practitioner & author of Think.Coach.Thrive!

Systems thinking and critical thinking are distinct yet complementary cognitive tools essential for effective problem-solving. Systems thinking allows businesses to understand and address the broad impacts of their actions on an interconnected system, while critical thinking sharpens decision-making, ensuring that outcomes are viable, ethical and based on solid reasoning.

Systems thinking provides a holistic perspective, focusing on how various components of a system interact and affect each other within a broader context. It emphasizes understanding the interconnections, dynamics, long-term impacts and patterns within systems to predict future behaviors and develop sustainable solutions.

This approach is particularly valuable in complex environments like organizational change, environmental management, and technological systems, where understanding the big picture is crucial.

On the other hand, critical thinking adopts a more analytical approach, concentrating on evaluating information and arguments, identifying logical inconsistencies, and making reasoned judgments. It involves dissecting complex problems into manageable parts, emphasizing evidence-based decision-making and rigorous evaluation of ideas and assumptions.

Critical thinking is key in activities that require clear, structured thinking, such as logical reasoning, decision-making, and solution evaluation, often focusing on scrutinizing existing solutions and preventing errors.

Best Buy Memorial Day Sale: 70 Deals On TVs, Tablets And Appliances

Nyt strands 84 hints spangram and answers for sunday may 26th, saw the eclipse and aurora now comes a third once in a lifetime event.

Together, these methodologies enhance decision-making and problem-solving by providing both macro and micro analytical perspectives to the challenge at hand.

Integrating both of these ways of thinking into sustainability initiatives offers organizations a robust framework for tackling complex challenges through a structured yet flexible approach. It helps organizations transform their approach to sustainability from fragmented efforts into a coherent, strategic agenda that drives real change.

Here's how organizations can implement these two ways of thinking effectively:

Step 1: Articulating Vision And Current Reality

Begin by defining a clear sustainability vision and objectively assess the current state to identify gaps. What is the desired future and the existing barriers or deficiencies preventing its realization? Engaging in this step ensures that all stakeholders have a unified understanding of the objectives and challenges.

For instance, a government agency might aim for sustainable urban development while recognizing current inefficiencies in urban infrastructure. The systemic structure would take into consideration manpower availability, lifetime cost of building projects and green funding availability.

Step 2: Structuring Decisions Based On Evidence

Detail decisions across all levels from strategic to tactical, ensuring that each decision aligns with the overarching sustainability goals.

This step often involves using decision hierarchies to maintain clarity and relevance at every level, thus preventing duplications and identifying gaps in strategies.

For example, a multinational corporation might structure decisions around reducing its carbon footprint through supplier engagement programs. Using critical thinking methodologies, they could create an analytical and evidence-based workflow and test assumptions on handoffs to ensure compliance.

Step 3: Prioritizing Challenges At Different Levels Of Perspectives

Identify the most impactful sustainability challenge and focus resources and efforts on areas where they can make the most significant difference to help maximize impact.

For example, a healthcare provider may prioritize waste reduction in its facilities by improving waste segregation and processing and develop the necessary systems and processes in keeping with the new disposal methods. They may modify or eliminate altogether outdated policies, leading to new behaviors of pattern over time in personnel involved.

Step 4: Developing Nested Solutions

Use both systems and critical thinking to create comprehensive, innovative and interconnected solutions. This might involve using systems diagrams to visualize problems and how they relate and employing logical reasoning to evaluate potential solutions for effectiveness and feasibility.

Remember the government agency aiming for sustainable urban development? In this scenario, they may create a stakeholder map aligning and enabling various parties to translate purpose into strategy. This would allow them to co-create multifaceted urban plans that integrate green spaces and renewable energy solutions. As a result, corresponding tactics and activities happen in an integrated, not haphazard, way.

Step 5: Crafting A Theory of Success

Develop a clear and actionable theory of success that outlines the key actions and leverage points. This theory should detail how the proposed solutions will address the identified challenges and lead to the desired change, identifying where small interventions could lead to significant systemic improvements.

In the case of the multinational corporation, their leverage was in incentivizing suppliers to adopt low-carbon technologies. Their theory of success was not in "shifting the burden" but in creating a positive reinforcement loop where they focused on the quality of relationships for long-term commitment.

Step 6: Implementing And Adjusting The Strategy

Put the strategies into action while establishing mechanisms for ongoing monitoring and adaptation. This includes setting up feedback loops to continuously gather data on the effectiveness of the interventions and making necessary adjustments based on empirical evidence and changing conditions.

For the healthcare provider addressing waste management challenges, this might involve adjusting waste management procedures based on ongoing feedback and outcomes. They might realize they are oftentimes reactive in their problem solving and therefore intend to conduct an intentional analysis and internalize and operationalize key insights.

As businesses become more complex and interconnected, the ability to think both systemically and critically isn’t just an advantage; it’s essential to survival and success in an interconnected world.

Forbes Coaches Council is an invitation-only community for leading business and career coaches. Do I qualify?

• Editorial Standards
• Reprints & Permissions

Along with Stanford news and stories, show me:

• Student information
• Faculty/Staff information

We want to provide announcements, events, leadership messages and resources that are relevant to you. Your selection is stored in a browser cookie which you can remove at any time using “Clear all personalization” below.

For everyone whose relationship with mathematics is distant or broken, Jo Boaler , a professor at Stanford Graduate School of Education (GSE), has ideas for repairing it. She particularly wants young people to feel comfortable with numbers from the start – to approach the subject with playfulness and curiosity, not anxiety or dread.

“Most people have only ever experienced what I call narrow mathematics – a set of procedures they need to follow, at speed,” Boaler says. “Mathematics should be flexible, conceptual, a place where we play with ideas and make connections. If we open it up and invite more creativity, more diverse thinking, we can completely transform the experience.”

Boaler, the Nomellini and Olivier Professor of Education at the GSE, is the co-founder and faculty director of Youcubed , a Stanford research center that provides resources for math learning that has reached more than 230 million students in over 140 countries. In 2013 Boaler, a former high school math teacher, produced How to Learn Math , the first massive open online course (MOOC) on mathematics education. She leads workshops and leadership summits for teachers and administrators, and her online courses have been taken by over a million users.

In her new book, Math-ish: Finding Creativity, Diversity, and Meaning in Mathematics , Boaler argues for a broad, inclusive approach to math education, offering strategies and activities for learners at any age. We spoke with her about why creativity is an important part of mathematics, the impact of representing numbers visually and physically, and how what she calls “ishing” a math problem can help students make better sense of the answer.

What do you mean by “math-ish” thinking?

It’s a way of thinking about numbers in the real world, which are usually imprecise estimates. If someone asks how old you are, how warm it is outside, how long it takes to drive to the airport – these are generally answered with what I call “ish” numbers, and that’s very different from the way we use and learn numbers in school.

In the book I share an example of a multiple-choice question from a nationwide exam where students are asked to estimate the sum of two fractions: 12/13 + 7/8. They’re given four choices for the closest answer: 1, 2, 19, or 21. Each of the fractions in the question is very close to 1, so the answer would be 2 – but the most common answer 13-year-olds gave was 19. The second most common was 21.

I’m not surprised, because when students learn fractions, they often don’t learn to think conceptually or to consider the relationship between the numerator or denominator. They learn rules about creating common denominators and adding or subtracting the numerators, without making sense of the fraction as a whole. But stepping back and judging whether a calculation is reasonable might be the most valuable mathematical skill a person can develop.

But don’t you also risk sending the message that mathematical precision isn’t important?

I’m not saying precision isn’t important. What I’m suggesting is that we ask students to estimate before they calculate, so when they come up with a precise answer, they’ll have a real sense for whether it makes sense. This also helps students learn how to move between big-picture and focused thinking, which are two different but equally important modes of reasoning.

Some people ask me, “Isn’t ‘ishing’ just estimating?” It is, but when we ask students to estimate, they often groan, thinking it’s yet another mathematical method. But when we ask them to “ish” a number, they're more willing to offer their thinking.

Ishing helps students develop a sense for numbers and shapes. It can help soften the sharp edges in mathematics, making it easier for kids to jump in and engage. It can buffer students against the dangers of perfectionism, which we know can be a damaging mindset. I think we all need a little more ish in our lives.

You also argue that mathematics should be taught in more visual ways. What do you mean by that?

For most people, mathematics is an almost entirely symbolic, numerical experience. Any visuals are usually sterile images in a textbook, showing bisecting angles, or circles divided into slices. But the way we function in life is by developing models of things in our minds. Take a stapler: Knowing what it looks like, what it feels and sounds like, how to interact with it, how it changes things – all of that contributes to our understanding of how it works.

There’s an activity we do with middle-school students where we show them an image of a 4 x 4 x 4 cm cube made up of smaller 1 cm cubes, like a Rubik’s Cube. The larger cube is dipped into a can of blue paint, and we ask the students, if they could take apart the little cubes, how many sides would be painted blue? Sometimes we give the students sugar cubes and have them physically build a larger 4 x 4 x 4 cube. This is an activity that leads into algebraic thinking.

Some years back we were interviewing students a year after they’d done that activity in our summer camp and asked what had stayed with them. One student said, “I’m in geometry class now, and I still remember that sugar cube, what it looked like and felt like.” His class had been asked to estimate the volume of their shoes, and he said he’d imagined his shoes filled with 1 cm sugar cubes in order to solve that question. He had built a mental model of a cube.

When we learn about cubes, most of us don’t get to see and manipulate them. When we learn about square roots, we don’t take squares and look at their diagonals. We just manipulate numbers.

I wonder if people consider the physical representations more appropriate for younger kids.

That’s the thing – elementary school teachers are amazing at giving kids those experiences, but it dies out in middle school, and by high school it’s all symbolic. There’s a myth that there’s a hierarchy of sophistication where you start out with visual and physical representations and then build up to the symbolic. But so much of high-level mathematical work now is visual. Here in Silicon Valley, if you look at Tesla engineers, they're drawing, they're sketching, they're building models, and nobody says that's elementary mathematics.

There’s an example in the book where you’ve asked students how they would calculate 38 x 5 in their heads, and they come up with several different ways of arriving at the same answer. The creativity is fascinating, but wouldn’t it be easier to teach students one standard method?

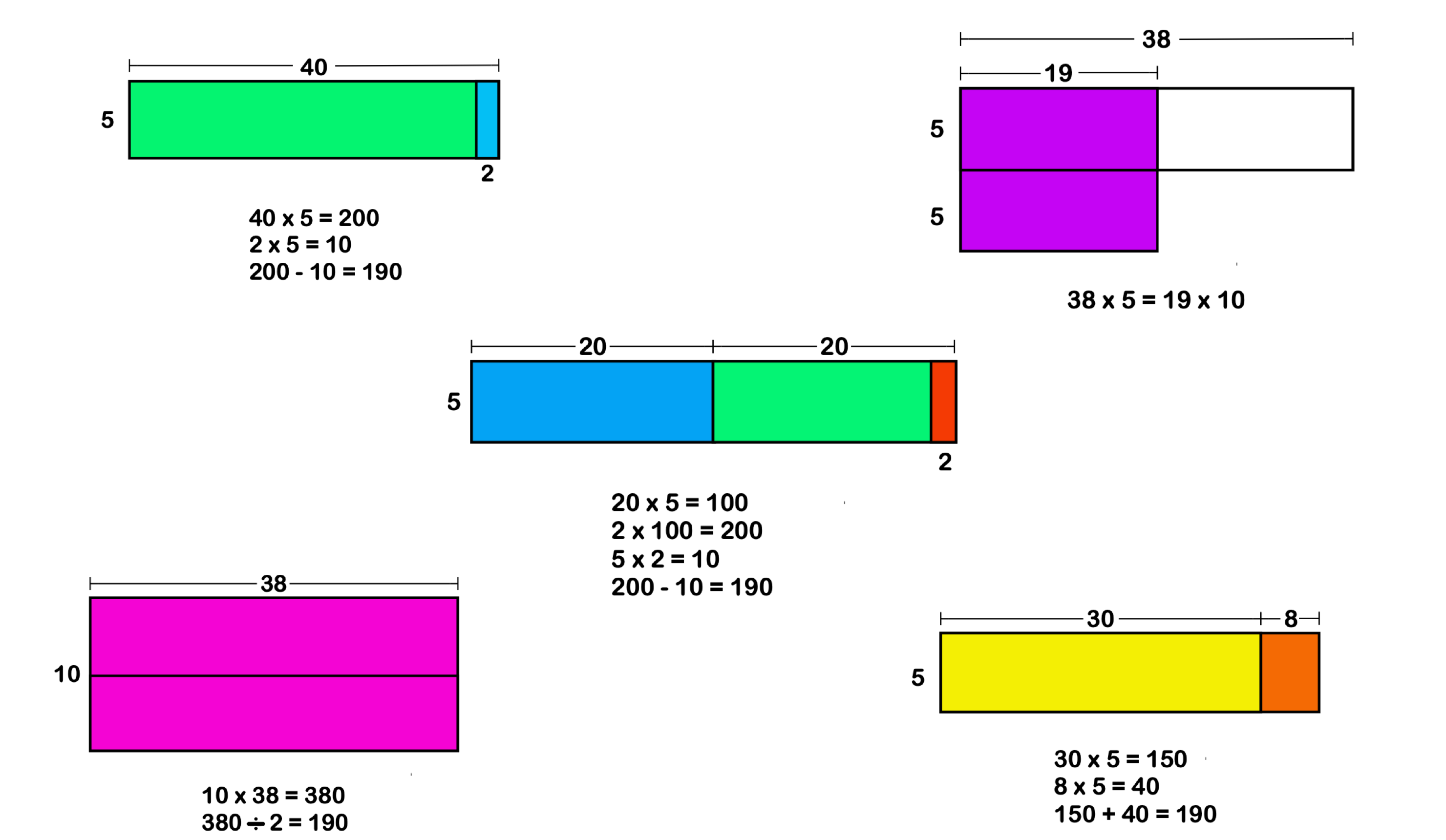
A depiction of various ways to calculate 38 x 5, numerically and visually. | Courtesy Jo Boaler

That narrow, rigid version of mathematics where there’s only one right approach is what most students experience, and it’s a big part of why people have such math trauma. It keeps them from realizing the full range and power of mathematics. When you only have students blindly memorizing math facts, they’re not developing number sense. They don’t learn how to use numbers flexibly in different situations. It also makes students who think differently believe there’s something wrong with them.

When we open mathematics to acknowledge the different ways a concept or problem can be viewed, we also open the subject to many more students. Mathematical diversity, to me, is a concept that includes both the value of diversity in people and the diverse ways we can see and learn mathematics. When we bring those forms of diversity together, it’s powerful. If we want to value different ways of thinking and problem-solving in the world, we need to embrace mathematical diversity.

• SUGGESTED TOPICS
• The Magazine
• Newsletters
• Managing Yourself
• Managing Teams
• Work-life Balance
• The Big Idea
• Data & Visuals
• Reading Lists
• Case Selections
• HBR Learning
• Topic Feeds
• Account Settings
• Email Preferences

Share Podcast

A Better Framework for Solving Tough Problems

Start with trust and end with speed.

• Apple Podcasts

When it comes to solving complicated problems, the default for many organizational leaders is to take their time to work through the issues at hand. Unfortunately, that often leads to patchwork solutions or problems not truly getting resolved.

But Anne Morriss offers a different framework. In this episode, she outlines a five-step process for solving any problem and explains why starting with trust and ending with speed is so important for effective change leadership. As she says, “Let’s get into dialogue with the people who are also impacted by the problem before we start running down the path of solving it.”

Morriss is an entrepreneur and leadership coach. She’s also the coauthor of the book, Move Fast and Fix Things: The Trusted Leader’s Guide to Solving Hard Problems .

Key episode topics include: strategy, decision making and problem solving, strategy execution, managing people, collaboration and teams, trustworthiness, organizational culture, change leadership, problem solving, leadership.

HBR On Strategy curates the best case studies and conversations with the world’s top business and management experts, to help you unlock new ways of doing business. New episodes every week.

• Listen to the full HBR IdeaCast episode: How to Solve Tough Problems Better and Faster (2023)
• Find more episodes of HBR IdeaCast
• Discover 100 years of Harvard Business Review articles, case studies, podcasts, and more at HBR.org .

HANNAH BATES: Welcome to HBR On Strategy , case studies and conversations with the world’s top business and management experts, hand-selected to help you unlock new ways of doing business.

When it comes to solving complicated problems, many leaders only focus on the most apparent issues. Unfortunately that often leads to patchwork or partial solutions. But Anne Morriss offers a different framework that aims to truly tackle big problems by first leaning into trust and then focusing on speed.

Morriss is an entrepreneur and leadership coach. She’s also the co-author of the book, Move Fast and Fix Things: The Trusted Leader’s Guide to Solving Hard Problems . In this episode, she outlines a five-step process for solving any problem. Some, she says, can be solved in a week, while others take much longer. She also explains why starting with trust and ending with speed is so important for effective change leadership.

This episode originally aired on HBR IdeaCast in October 2023. Here it is.

CURT NICKISCH: Welcome to the HBR IdeaCast from Harvard Business Review. I’m Curt Nickisch.

Problems can be intimidating. Sure, some problems are fun to dig into. You roll up your sleeves, you just take care of them; but others, well, they’re complicated. Sometimes it’s hard to wrap your brain around a problem, much less fix it.

And that’s especially true for leaders in organizations where problems are often layered and complex. They sometimes demand technical, financial, or interpersonal knowledge to fix. And whether it’s avoidance on the leaders’ part or just the perception that a problem is systemic or even intractable, problems find a way to endure, to keep going, to keep being a problem that everyone tries to work around or just puts up with.

But today’s guest says that just compounds it and makes the problem harder to fix. Instead, she says, speed and momentum are key to overcoming a problem.

Anne Morriss is an entrepreneur, leadership coach and founder of the Leadership Consortium and with Harvard Business School Professor Francis Frei, she wrote the new book, Move Fast and Fix Things: The Trusted Leaders Guide to Solving Hard Problems . Anne, welcome back to the show.

ANNE MORRISS: Curt, thank you so much for having me.

CURT NICKISCH: So, to generate momentum at an organization, you say that you really need speed and trust. We’ll get into those essential ingredients some more, but why are those two essential?

ANNE MORRISS: Yeah. Well, the essential pattern that we observed was that the most effective change leaders out there were building trust and speed, and it didn’t seem to be a well-known observation. We all know the phrase, “Move fast and break things,” but the people who were really getting it right were moving fast and fixing things, and that was really our jumping off point. So when we dug into the pattern, what we observed was they were building trust first and then speed. This foundation of trust was what allowed them to fix more things and break fewer.

CURT NICKISCH: Trust sounds like a slow thing, right? If you talk about building trust, that is something that takes interactions, it takes communication, it takes experiences. Does that run counter to the speed idea?

ANNE MORRISS: Yeah. Well, this issue of trust is something we’ve been looking at for over a decade. One of the headlines in our research is it’s actually something we’re building and rebuilding and breaking all the time. And so instead of being this precious, almost farbege egg, it’s this thing that is constantly in motion and this thing that we can really impact when we’re deliberate about our choices and have some self-awareness around where it’s breaking down and how it’s breaking down.

CURT NICKISCH: You said break trust in there, which is intriguing, right? That you may have to break trust to build trust. Can you explain that a little?

ANNE MORRISS:  Yeah, well, I’ll clarify. It’s not that you have to break it in order to build it. It’s just that we all do it some of the time. Most of us are trusted most of the time. Most of your listeners I imagine are trusted most of the time, but all of us have a pattern where we break trust or where we don’t build as much as could be possible.

CURT NICKISCH: I want to talk about speed, this other essential ingredient that’s so intriguing, right? Because you think about solving hard problems as something that just takes a lot of time and thinking and coordination and planning and designing. Explain what you mean by it? And also, just  how we maybe approach problems wrong by taking them on too slowly?

ANNE MORRISS: Well, Curt, no one has ever said to us, “I wish I had taken longer and done less.” We hear the opposite all the time, by the way. So what we really set out to do was to create a playbook that anyone can use to take less time to do more of the things that are going to make your teams and organizations stronger.

And the way we set up the book is okay, it’s really a five step process. Speed is the last step. It’s the payoff for the hard work you’re going to do to figure out your problem, build or rebuild trust, expand the team in thoughtful and strategic ways, and then tell a real and compelling story about the change you’re leading.

Only then do you get to go fast, but that’s an essential part of the process, and we find that either people under emphasize it or speed has gotten a bad name in this world of moving fast and breaking things. And part of our mission for sure was to rehabilitate speed’s reputation because it is an essential part of the change leader’s equation. It can be the difference between good intentions and getting anything done at all.

CURT NICKISCH: You know, the fact that nobody ever tells you, “I wish we had done less and taken more time.” I think we all feel that, right? Sometimes we do something and then realize, “Oh, that wasn’t that hard and why did it take me so long to do it? And I wish I’d done this a long time ago.” Is it ever possible to solve a problem too quickly?

ANNE MORRISS: Absolutely. And we see that all the time too. What we push people to do in those scenarios is really take a look at the underlying issue because in most cases, the solution is not to take your foot off the accelerator per se and slow down. The solution is to get into the underlying problem. So if it’s burnout or a strategic disconnect between what you’re building and the marketplace you’re serving, what we find is the anxiety that people attach to speed or the frustration people attach to speed is often misplaced.

CURT NICKISCH: What is a good timeline to think about solving a problem then? Because if we by default take too long or else jump ahead and we don’t fix it right, what’s a good target time to have in your mind for how long solving a problem should take?

ANNE MORRISS: Yeah. Well, we’re playful in the book and talking about the idea that many problems can be solved in a week. We set the book up five chapters. They’re titled Monday, Tuesday, Wednesday, Thursday, Friday, and we’re definitely having fun with that. And yet, if you count the hours in a week, there are a lot of them. Many of our problems, if you were to spend a focused 40 hours of effort on a problem, you’re going to get pretty far.

But our main message is, listen, of course it’s going to depend on the nature of the problem, and you’re going to take weeks and maybe even some cases months to get to the other side. What we don’t want you to do is take years, which tends to be our default timeline for solving hard problems.

CURT NICKISCH: So you say to start with identifying the problem that’s holding you back, seems kind of obvious. But where do companies go right and wrong with this first step of just identifying the problem that’s holding you back?

ANNE MORRISS: And our goal is that all of these are going to feel obvious in retrospect. The problem is we skip over a lot of these steps and this is why we wanted to underline them. So this one is really rooted in our observation and I think the pattern of our species that we tend to be overconfident in the quality of our thoughts, particularly when it comes to diagnosing problems.

And so we want to invite you to start in a very humble and curious place, which tends not to be our default mode when we’re showing up for work. We convince ourselves that we’re being paid for our judgment. That’s exactly what gets reinforced everywhere. And so we tend to counterintuitively, given what we just talked about, we tend to move too quickly through the diagnostic phase.

CURT NICKISCH: “I know what to do, that’s why you hired me.”

ANNE MORRISS: Exactly. “I know what to do. That’s why you hired me. I’ve seen this before. I have a plan. Follow me.” We get rewarded for the expression of confidence and clarity. And so what we’re inviting people to do here is actually pause and really lean into what are the root causes of the problem you’re seeing? What are some alternative explanations? Let’s get into dialogue with the people who are also impacted by the problem before we start running down the path of solving it.

CURT NICKISCH: So what do you recommend for this step, for getting to the root of the problem? What are questions you should ask? What’s the right thought process? What do you do on Monday of the week?

ANNE MORRISS: In our experience of doing this work, people tend to undervalue the power of conversation, particularly with other people in the organization. So we will often advocate putting together a team of problem solvers, make it a temporary team, really pull in people who have a particular perspective on the problem and create the space, make it as psychologically safe as you can for people to really, as Chris Argyris so beautifully articulated, discuss the undiscussable.

And so the conditions for that are going to look different in every organization depending on the problem, but if you can get a space where smart people who have direct experience of a problem are in a room and talking honestly with each other, you can make an extraordinary amount of progress, certainly in a day.

CURT NICKISCH: Yeah, that gets back to the trust piece.

ANNE MORRISS: Definitely.

CURT NICKISCH: How do you like to start that meeting, or how do you like to talk about it? I’m just curious what somebody on that team might hear in that meeting, just to get the sense that it’s psychologically safe, you can discuss the undiscussable and you’re also focusing on the identification part. What’s key to communicate there?

ANNE MORRISS: Yeah. Well, we sometimes encourage people to do a little bit of data gathering before those conversations. So the power of a quick anonymous survey around whatever problem you’re solving, but also be really thoughtful about the questions you’re going to ask in the moment. So a little bit of preparation can go a long way and a little bit of thoughtfulness about the power dynamic. So who’s going to walk in there with license to speak and who’s going to hold back? So being thoughtful about the agenda, about the questions you’re asking about the room, about the facilitation, and then courage is a very infectious emotion.

So if you can early on create the conditions for people to show up bravely in that conversation, then the chance that you’re going to get good information and that you’re going to walk out of that room with new insight in the problem that you didn’t have when you walked in is extraordinarily high.

CURT NICKISCH: Now, in those discussions, you may have people who have different perspectives on what the problem really is. They also bear different costs of addressing the problem or solving it. You talked about the power dynamic, but there’s also an unfairness dynamic of who’s going to actually have to do the work to take care of it, and I wonder how you create a culture in that meeting where it’s the most productive?

ANNE MORRISS: For sure, the burden of work is not going to be equitably distributed around the room. But I would say, Curt, the dynamic that we see most often is that people are deeply relieved that hard problems are being addressed. So it really can create, and more often than not in our experience, it does create this beautiful flywheel of action, creativity, optimism. Often when problems haven’t been addressed, there is a fair amount of anxiety in the organization, frustration, stagnation. And so credible movement towards action and progress is often the best antidote. So even if the plan isn’t super clear yet, if it’s credible, given who’s in the room and their decision rights and mandate, if there’s real momentum coming out of that to make progress, then that tends to be deeply energizing to people.

CURT NICKISCH: I wonder if there’s an organization that you’ve worked with that you could talk about how this rolled out and how this took shape?

ANNE MORRISS: When we started working with Uber, that was wrestling with some very public issues of culture and trust with a range of stakeholders internally, the organization, also external, that work really started with a campaign of listening and really trying to understand where trust was breaking down from the perspective of these stakeholders?

So whether it was female employees or regulators or riders who had safety concerns getting into the car with a stranger. This work, it starts with an honest internal dialogue, but often the problem has threads that go external. And so bringing that same commitment to curiosity and humility and dialogue to anyone who’s impacted by the problem is the fastest way to surface what’s really going on.

CURT NICKISCH: There’s a step in this process that you lay out and that’s communicating powerfully as a leader. So we’ve heard about listening and trust building, but now you’re talking about powerful communication. How do you do this and why is it maybe this step in the process rather than the first thing you do or the last thing you do?

ANNE MORRISS: So in our process, again, it’s the days of the week. On Monday you figured out the problem. Tuesday you really got into the sandbox in figuring out what a good enough plan is for building trust. Wednesday, step three, you made it better. You created an even better plan, bringing in new perspectives. Thursday, this fourth step is the day we’re saying you got to go get buy-in. You got to bring other people along. And again, this is a step where we see people often underinvest in the power and payoff of really executing it well.

CURT NICKISCH: How does that go wrong?

ANNE MORRISS: Yeah, people don’t know the why. Human behavior and the change in human behavior really depends on a strong why. It’s not just a selfish, “What’s in it for me?” Although that’s helpful, but where are we going? I may be invested in a status quo and I need to understand, okay, if you’re going to ask me to change, if you’re going to invite me into this uncomfortable place of doing things differently, why am I here? Help me understand it and articulate the way forward and language that not only I can understand, but also that’s going to be motivating to me.

CURT NICKISCH: And who on my team was part of this process and all that kind of stuff?

ANNE MORRISS: Oh, yeah. I may have some really important questions that may be in the way of my buy-in and commitment to this plan. So certainly creating a space where those questions can be addressed is essential. But what we found is that there is an architecture of a great change story, and it starts with honoring the past, honoring the starting place. Sometimes we’re so excited about the change and animated about the change that what has happened before or what is even happening in the present tense is low on our list of priorities.

Or we want to label it bad, because that’s the way we’ve thought about the change, but really pausing and honoring what came before you and all the reasonable decisions that led up to it, I think can be really helpful to getting people emotionally where you want them to be willing to be guided by you. Going back to Uber, when Dara Khosrowshahi came in.

CURT NICKISCH: This is the new CEO.

ANNE MORRISS: The new CEO.

CURT NICKISCH: Replaced Travis Kalanick, the founder and first CEO, yeah.

ANNE MORRISS: Yeah, and had his first all-hands meeting. One of his key messages, and this is a quote, was that he was going to retain the edge that had made Uber, “A force of nature.” And in that meeting, the crowd went wild because this is also a company that had been beaten up publicly for months and months and months, and it was a really powerful choice. And his predecessor, Travis was in the room, and he also honored Travis’ incredible work and investment in bringing the company to the place where it was.

And I would use words like grace to also describe those choices, but there’s also an incredible strategic value to naming the starting place for everybody in the room because in most cases, most people in that room played a role in getting to that starting place, and you’re acknowledging that.

CURT NICKISCH: You can call it grace. Somebody else might call it diplomatic or strategic. But yeah, I guess like it or not, it’s helpful to call out and honor the complexity of the way things have been done and also the change that’s happening.

ANNE MORRISS: Yeah, and the value. Sometimes honoring the past is also owning what didn’t work or what wasn’t working for stakeholders or segments of the employee team, and we see that around culture change. Sometimes you’ve got to acknowledge that it was not an equitable environment, but whatever the worker, everyone in that room is bringing that pass with them. So again, making it discussable and using it as the jumping off place is where we advise people to start.

Then you’ve earned the right to talk about the change mandate, which we suggest using clear and compelling language about the why. “This is what happened, this is where we are, this is the good and the bad of it, and here’s the case for change.”

And then the last part, which is to describe a rigorous and optimistic way forward. It’s a simple past, present, future arc, which will be familiar to human beings. We love stories as human beings. It’s among the most powerful currency we have to make sense of the world.

CURT NICKISCH: Yeah. Chronological is a pretty powerful order.

ANNE MORRISS: Right. But again, the change leaders we see really get it right, are investing an incredible amount of time into the storytelling part of their job. Ursula Burns, the Head of Xerox is famous for the months and years she spent on the road just telling the story of Xerox’s change, its pivot into services to everyone who would listen, and that was a huge part of her success.

CURT NICKISCH: So Friday or your fifth step, you end with empowering teams and removing roadblocks. That seems obvious, but it’s critical. Can you dig into that a little bit?

ANNE MORRISS: Yeah. Friday is the fun day. Friday’s the release of energy into the system. Again, you’ve now earned the right to go fast. You have a plan, you’re pretty confident it’s going to work. You’ve told the story of change the organization, and now you get to sprint. So this is about really executing with urgency, and it’s about a lot of the tactics of speed is where we focus in the book. So the tactics of empowerment, making tough strategic trade-offs so that your priorities are clear and clearly communicated, creating mechanisms to fast-track progress. At Etsy, CEO Josh Silverman, he labeled these projects ambulances. It’s an unfortunate metaphor, but it’s super memorable. These are the products that get to speed out in front of the other ones because the stakes are high and the clock is sticking.

CURT NICKISCH: You pull over and let it go by.

ANNE MORRISS: Yeah, exactly. And so we have to agree as an organization on how to do something like that. And so we see lots of great examples both in young organizations and big complex biotech companies with lots of regulatory guardrails have still found ways to do this gracefully.

And I think we end with this idea of conflict debt, which is a term we really love. Leanne Davey, who’s a team scholar and researcher, and anyone in a tech company will recognize the idea of tech debt, which is this weight the organization drags around until they resolve it. Conflict debt is a beautiful metaphor because it is this weight that we drag around and slows us down until we decide to clean it up and fix it. The organizations that are really getting speed right have figured out either formally or informally, how to create an environment where conflict and disagreements can be gracefully resolved.

CURT NICKISCH: Well, let’s talk about this speed more, right? Because I think this is one of those places that maybe people go wrong or take too long, and then you lose the awareness of the problem, you lose that urgency. And then that also just makes it less effective, right? It’s not just about getting the problem solved as quickly as possible. It’s also just speed in some ways helps solve the problem.

ANNE MORRISS: Oh, yeah. It really is the difference between imagining the change you want to lead and really being able to bring it to life. Speed is the thing that unlocks your ability to lead change. It needs a foundation, and that’s what Monday through Thursday is all about, steps one through four, but the finish line is executing with urgency, and it’s that urgency that releases the system’s energy, that communicates your priorities, that creates the conditions for your team to make progress.

CURT NICKISCH: Moving fast is something that entrepreneurs and tech companies certainly understand, but there’s also this awareness that with big companies, the bigger the organization, the harder it is to turn the aircraft carrier around, right? Is speed relative when you get at those levels, or do you think this is something that any company should be able to apply equally?

ANNE MORRISS: We think this applies to any company. The culture really lives at the level of team. So we believe you can make a tremendous amount of progress even within your circle of control as a team leader. I want to bring some humility to this and careful of words like universal, but we do think there’s some universal truths here around the value of speed, and then some of the byproducts like keeping fantastic people. Your best people want to solve problems, they want to execute, they want to make progress and speed, and the ability to do that is going to be a variable in their own equation of whether they stay or they go somewhere else where they can have an impact.

CURT NICKISCH: Right. They want to accomplish something before they go or before they retire or finish something out. And if you’re able to just bring more things on the horizon and have it not feel like it’s going to be another two years to do something meaningful.

ANNE MORRISS: People – I mean, they want to make stuff happen and they want to be around the energy and the vitality of making things happen, which again, is also a super infectious phenomenon. One of the most important jobs of a leader, we believe, is to set the metabolic pace of their teams and organizations. And so what we really dig into on Friday is, well, what does that look like to speed something up? What are the tactics of that?

CURT NICKISCH: I wonder if that universal truth, that a body in motion stays in motion applies to organizations, right? If an organization in motion stays in motion, there is something to that.

ANNE MORRISS: Absolutely.

CURT NICKISCH: Do you have a favorite client story to share, just where you saw speed just become a bit of a flywheel or just a positive reinforcement loop for more positive change at the organization?

ANNE MORRISS: Yeah. We work with a fair number of organizations that are on fire. We do a fair amount of firefighting, but we also less dramatically do a lot of fire prevention. So we’re brought into organizations that are working well and want to get better, looking out on the horizon. That work is super gratifying, and there is always a component of, well, how do we speed this up?

What I love about that work is there’s often already a high foundation of trust, and so it’s, well, how do we maintain that foundation but move this flywheel, as you said, even faster? And it’s really energizing because often there’s a lot of pent-up energy that… There’s a lot of loyalty to the organization, but often it’s also frustration and pent-up energy. And so when that gets released, when good people get the opportunity to sprint for the first time in a little while, it’s incredibly energizing, not just for us, but for the whole organization.

CURT NICKISCH: Anne, this is great. I think finding a way to solve problems better but also faster is going to be really helpful. So thanks for coming on the show to talk about it.

ANNE MORRISS:  Oh, Curt, it was such a pleasure. This is my favorite conversation. I’m delighted to have it anytime.

HANNAH BATES: That was entrepreneur, leadership coach, and author Anne Morriss – in conversation with Curt Nickisch on HBR IdeaCast.

We’ll be back next Wednesday with another hand-picked conversation about business strategy from Harvard Business Review. If you found this episode helpful, share it with your friends and colleagues, and follow our show on Apple Podcasts, Spotify, or wherever you get your podcasts. While you’re there, be sure to leave us a review.

When you’re ready for more podcasts, articles, case studies, books, and videos with the world’s top business and management experts, you’ll find it all at HBR.org.

This episode was produced by Mary Dooe, Anne Saini, and me, Hannah Bates. Ian Fox is our editor. Special thanks to Rob Eckhardt, Maureen Hoch, Erica Truxler, Ramsey Khabbaz, Nicole Smith, Anne Bartholomew, and you – our listener. See you next week.

• Subscribe On:

Latest in this series

This article is about strategy.

• Decision making and problem solving
• Strategy execution
• Leadership and managing people
• Collaboration and teams
• Trustworthiness
• Organizational culture

Partner Center

The relationship between problem-solving skills and environmental literacy of class X students

[email protected]

[email protected]

[email protected]

[email protected]

[email protected]

• Split-Screen
• Article contents
• Figures & tables
• Supplementary Data
• Peer Review
• Open the PDF for in another window
• Reprints and Permissions
• Cite Icon Cite
• Search Site

Mimien Henie Irawati AL Muhdhar , Ardelia Delinda , Racy Rizky Abdillah , Nurhikma Ramadhana , Lely Mardiyanti , Wiedia Carullina Purwanti; The relationship between problem-solving skills and environmental literacy of class X students. AIP Conf. Proc. 24 May 2024; 3106 (1): 030044. https://doi.org/10.1063/5.0215783

Download citation file:

• Ris (Zotero)
• Reference Manager

Environmental literacy is an individual’s ability to build an understanding of the main concepts based on phenomena and apply knowledge to improve environmental problems. Environmental literacy focuses on real behaviour, not just knowledge about the environment. Problem-solving skills are one of the skills in the world of education that include the process of identifying problems, considering options, and making informed choices. This study aims to determine the relationship between problem-solving skills and environmental literacy of class X students at SMAN 8 Malang. The population in this study includes all students of class X at SMAN 8 Malang. The research sample was taken randomly from as many as 112 students of class X majoring in Mathematics and Natural Sciences at SMAN 8 Malang. The instrument used is a test of problem-solving skills based on Greenstein and an environmental literacy test based on the Middle School Environmental Literacy Survey. The results showed that the average problem-solving skills score of students was 1.9 in the medium category, and the average environmental literacy score was 279.3 in the medium category. Data analysis using Pearson Correlation obtained a significance value of 0.112 > 0.05. The correlation test shows that there is no relationship between the problem-solving skills and environmental literacy of class X students at SMAN 8 Malang. The results of the correlation test, which are not significant, indicate that further research is needed to determine the relationship between problem-solving skills indicators and environmental literacy indicators.

Citing articles via

Publish with us - request a quote.

Sign up for alerts

• Online ISSN 1551-7616
• Print ISSN 0094-243X
• For Researchers
• For Librarians
• For Advertisers
• Our Publishing Partners  
• Physics Today
• Conference Proceedings
• Special Topics

pubs.aip.org

• Privacy Policy
• Terms of Use

Connect with AIP Publishing

This feature is available to subscribers only.

Sign In or Create an Account

Relationships between computational thinking and the quality of computer programs

• Open access
• Published: 03 March 2022
• Volume 27 , pages 8289–8310, ( 2022 )

Cite this article

You have full access to this open access article

• Kay-Dennis Boom 1 ,
• Matt Bower   ORCID: orcid.org/0000-0002-4161-5816 2 ,
• Jens Siemon 1 &
• Amaël Arguel 3  

16 Citations

5 Altmetric

Explore all metrics

Computational thinking – the ability to reformulate and solve problems in ways that can be undertaken by computers – has been heralded as a foundational capability for the 21st Century. However, there are potentially different ways to conceptualise and measure computational thinking, for instance, as generalized problem solving capabilities or as applied practice during computer programming tasks, and there is little evidence to substantiate whether higher computational thinking capabilities using either of these measures result in better quality computer programs. This study examines the relationship between different forms of computational thinking and two different measures of programming quality for a group of 37 pairs of pre-service teachers. General computational thinking capabilities were measured using Bebras tests, while applied computational thinking processes were measured using a Computational Thinking Behavioural Scheme. The quality of computer programs was measured using a qualitative rubric, and programs were also assessed using the Dr Scratch auto-grading platform. The Test of Nonverbal Intelligence (3rd edition, TONI-3) was used to test for confounding effects. While significant correlations between both measures of computational thinking and program quality were detected, regression analysis revealed that only applied computational thinking processes significantly predicted program quality (general computational thinking capability and non-verbal intelligence were not significant predictors). The results highlight the importance of students developing applied computational thinking procedural capabilities more than generalized computational thinking capabilities in order to improve the quality of their computer programs.

Similar content being viewed by others

Developing Computational Thinking Practices in Primary Education. Outcomes from a School-Year Instructional Intervention

A valid and reliable tool for examining computational thinking skills

Assessing Computational Thinking: The Relation of Different Assessment Instruments and Learning Tools

Avoid common mistakes on your manuscript.

1 Introduction

1.1 context of the problem.

Since its first major appearance in 2006 by Wing, computational thinking has been intensively discussed in the field of computer science education (Tang, Chou, & Tsai, 2020 ). CT can be regarded as the ability to reformulate problems in ways that computers can then be used to help solve those problems (International Society for Technology in Education [ISTE] & the Computer Science Teachers Association [CSTA], 2011 ). The value proposition of computational thinking capabilities in a digital age is that they can help people solve a range of problems that lead to personal satisfaction and success, not only in the technology area but also life more broadly. However, the conjecture that possessing computational thinking knowledge, or applying computational thinking skills while solving problems, leads to higher quality solutions, has rarely been empirically validated.

One aspect of computational thinking that is often emphasized by advocates is that it is not simply computer programming capability. Research about the effects of computational thinking knowledge and/or skill can be divided into the area of effects regarding computational problem solving (e.g. computer programming) and effects regarding diverse non-programming problems or tasks. For example, a wide range of problems, from finding the shortest route between map locations to designing an online shopping platforms, rely on people applying computational thinking processes while they are writing computer programs to solve those problems. However, computational thinking skills (such as problem decomposition, pattern recognition, algorithmic thinking and abstraction) can also be used to solve a range problems that do not involve computer programming, such as finding a way through a maze or specifying the steps in a dance sequence. While learning computer programming relies on people utilizing and applying computational thinking as part of the process they undertake, instructional settings will often use computational thinking foundations to teach subjects and ideas that do not involve computer programming (e.g. Bull, Garofalo, & Hguyen, 2020 ). In fact, a literature review conducted by Tang et al. ( 2020 ) concluded that there were far more computational thinking effects analyzed in subject areas not related to computer science ( n = 240) than for effects related to computer science ( n = 78). However, we note that while computational thinking can be applied in a range of disciplines, it is considered absolutely essential and fundamental to successful computer programming (Angeli & Giannakos, 2020 ; Lye & Koh, 2014 ). Yet, we could not find any studies amongst the literature that examined whether or not computational thinking capabilities did in fact relate to higher quality computer programs.

The purpose of this study is to evaluate the extent to which general computational thinking knowledge, as well as computational thinking processes applied during problem solving tasks, influence the quality of computer-programming solutions. This was achieved by comparing university students’ computational knowledge (as measured by Bebras tests) and the computational thinking processes observed while they wrote computer programs with the quality of the final computing products that they produced. The findings of this study have implications for how computational thinking is framed, conceptualized and emphasized within education and society.

2 Literature review

2.1 defining computational thinking and its subcomponents.

Computational thinking is generally seen as an attitude and skill for solving problems, designing complex systems, and understanding human thoughts and behaviors, based on concepts fundamental to computer science (Lye & Koh, 2014 ). Recent reviews of computational thinking definitions and components by Shute, Sun and Asbell-Clarke ( 2017 ) and Ezeamuzie and Leung ( 2021 ) point out the lack of consistent definition regarding what is meant by computational thinking, though with some terms being more popular (such as abstraction, algorithm design, decomposition, and pattern recognition as generalisation), particularly when academics devise explicit definitions with relation to their research. Some inconsistency between definitions of components can occur, at times not because there is disagreement about what computational thinking involves, but because other frequently used terms such as ‘sequencing’, ‘conditional logic’ and ‘loops’ can conceptually fall within overarching categories (in this case, ‘algorithm design’).

In this study, we will draw upon generally accepted core components of computational thinking as being comprised of problem decomposition, pattern recognition (generalisation) algorithmic thinking and abstraction, which accords with other definitional work from the research field (Angeli & Giannakos, 2020 ; Cansu & Cansu, 2019 ; Tsai, Liang, Lee, & Hsu, 2021 ). We acknowledge that there are other aspects of computational thinking that are identified in some studies, such as ‘parallelism’, ‘data collection’, and ‘modelling’, as outlined by Shute et al. ( 2017 ), however, as Ezeamuzie and Leung ( 2021 ) points out, these sorts of other terms are relatively uncommon, and they are not processes utilised for all computational thinking problems. Selecting problem decomposition, pattern recognition (as generalisation), algorithmic thinking and abstraction as the components of computational thinking in this study also corresponds with approaches adopted in industry (for example, Csizmadia, Curzon, Dorling, Humphreys, Ng, Selby, & Woollard, 2015 ; McNicholl, 2019 ).

One crucial part of any computational thinking task is problem decomposition , the division of a problem into smaller chunks. Problem decomposition has been identified as a general problem solving strategy well before the advent of computational thinking (Anderson, 2015 ). In computational problems, decomposition is particularly important because of its relationship to modularity, where the complexity of a task can be simplified by identifying smaller parts that can each be addressed separately (Atmatzidou & Demetriadis, 2016 ). For example, when programming a multimedia story, one might first identify the different scenes that occur, and then break each scene into a series of actions by the characters.

Another component of computational thinking is abstraction , in terms of ignoring unimportant details and instead focusing on relevant information. From a psychological perspective, abstraction is a thought process that is used to achieve organised thinking (Shivhare & Kumar, 2016 ). In computational problems, abstraction enables people to concentrate on the essential, relevant, and important parts of the context and solution (Thalheim, 2009 ). For instance, when writing a multimedia story to have characters dance about a screen, a person may recognise that their program only needs to attend to the coordinates of the characters and their size, and the routines that they write can be applied to numerous characters irrespective of their colours or costumes.

A further critical thought process when engaging in computational thinking is pattern recognition . Pattern recognition involves being able to infer rules based on observations and apply these rules to instances that have never been encountered (visa vi Posner & Keele, 1968 ). Pattern recognition is crucial when solving computational problems, because rules inferred based on observations can then be translated into instructions that can be used to solve problems. For instance, when a person realises that a square can be drawn by drawing a straight line and then turning 90 degrees four times, then they can easily and efficiently specify a set of instructions for a computer (or human) to execute the process. It is important to note that pattern recognition is closely related to abstraction as a form of ignoring irrelevant details, but is generally regarded as distinct by virtue of distilling those aspects of a situation that repeat or reoccur in certain ways.

The fourth computational thinking category in this study is algorithmic thinking . An algorithm is a well-defined procedure or ‘recipe’ that defines how inputs can be used to achieve a specific objective (Cormen et al, 2014 ; Sipser, 2013 ). Algorithmic thinking has roots in cognitive psychology in the form of scripts, that help people to know how to behave in social or behavioural contexts (for instance, going to a restaurant or playing a game, see Schank & Abelson, 1977 ). When solving computational problems, algorithmic thinking enables people to translate their abstract ideas and the patterns that they recognise into a set of procedures, for instance having a robot trace out a square and then dance on the spot. For the purposes of this study, algorithmic thinking also includes the thinking required to resolve errors that occur in early versions of algorithm designs (the process known in computing as ‘debugging’), thus overcoming issues associated with delineating these two intrinsically interrelated processes.

2.2 Ways of measuring computational thinking

When defining a skill, the question arises whether it is possible to measure and differentiate it from other, possibly overlapping or more general skills. For computational thinking, the existing measurement methods that can be broadly divided into assessment of computational thinking as knowledge that is applied or tested (input), the assessment of computational thinking as a skill observed during a problem solving activity (process) and (theoretically also) the assessment of computations thinking by analyzing the result of a task (output). All measures are subsequently used as indicators for the existence and the grade/level of the respective type of the computational thinking competence.

The most internationally well-known instruments for measuring general computational thinking knowledge are the Bebras Challenges. The main idea behind Bebras Challenges has been to create abstract, non-computing problems that require specific cognitive abilities rather than technical knowledge or coding experience (Dagienė & Sentance, 2016 ). Examples of Bebras tasks can be found at https://www.bebras.org/examples.html . Different studies have shown that abilities such as breaking down problems into parts, interpreting patterns and models, and designing and implementing algorithms are needed to solve Bebras problems (Lockwood & Mooney, 2018 ; Araujo, Andrade, Guerrero, & Melo, 2019 ). There are also other approaches to measuring general computational thinking knowledge, both within computer programming contexts and also other disciplinary contexts, many of which have been applied in the training of teachers. For instance, Zha, Jin, Moore, and Gaston ( 2020 ) used multiple choice knowledge quizzes about computational thinking and Hopscotch coding to measure the impact of a team-based and flipped learning introduction to the Hopscotch block coding platform. In a study exploring the effects of a 13 week algorithm education course on 24 preservice teachers, Türker & Pala ( 2020 ) used the “Computational Thinking Skills Scale” (CTSS, from Korucu, Gencturk & Gundogdu, 2017 ) comprising the computational thinking facets creativity, algorithmic thinking, collaboration, critical thinking and problem solving. Suters and Suters ( 2020 ) report on a paper-and-pencil based computational thinking knowledge assessment to measure the effects of an extend summer institute for middle school mathematics teachers ( n = 22) undertaking training in computer programming with Bootstrap Algebra and Lego® Mindstorms® robotics. The content assessment consisted of items that integrated mathematics common core content with facets of computational thinking, in line with research endeavors recognizing the need to contextualize computational thinking within specific disciplines (Gadanidis, 2017 ; Grover & Pea, 2013 ; Weintrop et al., 2016 ). All of these approaches to computational thinking knowledge assessment share an emphasis on short, often multiple choice, closed questioning to measure computational thinking, rather than examining the computational thinking that arises as part of authentic and more extended problem solving contexts.

In a second variant of possible computational thinking measurement, the process of solving a context-dependent task – mostly typically a programming task – is observed and analyzed with regard to the abilities which are considered to be part of computational thinking skill. Skill analysis based on observations is a comparatively underdeveloped field. Brennan & Resnick ( 2012 ) seminally investigated the computational thinking processes and practices that children undertook while designing their programs using the visual programming platform Scratch, noting that “framing computational thinking solely around concepts insufficiently represented other elements of students learning” (p. 6). Their qualitative observations and interviews identified computational thinking practices such as being incremental and iterative, testing and debugging, reusing and remixing, and abstracting and modularizing. However, their results were not reported based on any sort of observational coding of participants, so that there is no indication of time spent on each of these processes while solving computing problems.

While analysis of learner pre- and/or post- interview narratives has been previously conducted to determine evidence of computational thinking (Grover, 2011 ; Portelance & Bers, 2015 ), we were not able to find any computational thinking analyses involving systematic examination of narratives emerging from participants while they were solving authentic programming problems. However, there are examples of observing and thematically categorizing computer programming processes and narratives (Bower & Hedberg, 2010 ; Knobelsdorf & Frede, 2016 ). These approaches provide a basis for in-situ observation and subsequent qualitative analysis of programming activity for computational thinking constructs such as problem deconstruction, abstraction, pattern recognition and algorithmic thinking, and our study is based on these more systematic observational approaches.

2.3 Measuring the quality of computer programs

There are a range of qualities that can be used to evaluate the quality of computer programs, such as the extent to which the code functionally achieves its intentions, avoids unnecessary repetition, is well organized, and so on (Martin, 2009 ). Much of the research relating to evaluating the quality of computer programs examines how to ways of auto-assessing student work (for instance, Ihantola, Ahoniemi, Karavirta, & Seppälä, 2010 ; Pieterse, 2013 ). However, automated tools struggle to accurately assess computational thinking (Poulakis & Politis, 2021 ), and recent work points out the need to look beyond raw functionality and ‘black-box’ testing of outputs, to examine the inner working of code and algorithms (Jin & Charpentia, 2020 ). Some research also examines the extent to which computational thinking is evident with the final programming product itself, by virtue of the code fragments that are used and their sophistication. Brennan and Resnick ( 2012 ) examined whether aspects of computational thinking were present in students’ block-based Scratch programs. Grover et al. have manually evaluated computational thinking evident in students’ Scratch programs, though without providing detail of the process and rubrics (Grover, 2017 ; Grover, Pea, & Cooper, 2015 ). An increasingly renown innovation, Dr Scratch, combines automated assessment, examination of the inner workings of programs, and analysis of computational thinking to provide a measure of program quality for Scratch programs (Moreno-León & Robles, 2015 ). One study has established a strong correlation ( r = 0.682) between the Dr Scratch automated assessment of computational thinking evident within students’ Scratch programs and manual evaluation of computational thinking within Scratch programs by human experts (Moreno-León et al., 2017 ). However, the computational thinking within a computer program is not necessarily a proxy for overall program quality, and the extent to which program quality relates to the computational thinking knowledge and computational thinking processes of program authors is an open question.

2.4 Research question

Thus, having established the lack of empirical evidence to suggest that general computational thinking knowledge or in-situ computational thinking processes is related to computing performance, and armed with potential ways to operationalize and measure computational thinking knowledge, computational thinking processes, and quality of computer programs, this study examines the following research questions:

Is the quality of computer programming solutions that people produce related to their general computational thinking knowledge?

Is the quality of computer programming solutions that people produce related to the applied computational thinking processes that they undertake?

3.1 Participants

The sample for this study was drawn from 74 pre-service teachers completing a digital creativity and learning course at an Australian university. Among them 68% were female, 30% male and 2% preferred not to say. On average, participants were 23.9 years old ( SD = 5.2). In terms of language proficiency, 97% indicated that they spoke English fluently or were native speakers. In terms of prior knowledge, 97% had no or only little prior programming experience and none of the participants were familiar with the Scratch programming environment that was used for the study.

3.2 Instruments

3.2.1 measuring computational thinking knowledge.

To measure computational thinking knowledge as it arises in general problem solving contexts, participants solved an online version of adapted Bebras tasks. All tasks were chosen from the Australian versions of the Bebras contests from 2014 (Schulz & Hobson, 2015 ) and 2015 (Schulz, Hobson, & Zagami, 2016 ). Only tasks from the oldest available age group were selected (i.e., for adolescents 16 to 18 years of age and school levels 11 and 12, respectively). The tasks were slightly revised and presented without any iconic beavers or other comical pictures in order to be more appropriate for the university participants in this study. Although there is still a considerably age gap between the targeted age group of the tasks and the actual age of participants, it was not expected that this difference would cause any problems (e.g., ceiling effects) because pre-service teachers on the whole were not expected to be familiar with or particularly adept at computational thinking tasks. The scoring of participant performance was based on the recommended scoring system of the founder of the Australian version of the Bebras tasks (Schulz et al., 2016 ). There were eight tasks considered as easy level (worth two points), seven medium (three points), and five hard tasks (four points) resulting in 20 tasks in total with a maximum achievable score of 57.

3.2.2 Observing computational thinking processes

To enable participants to demonstrate how much time they spent on computational thinking-relevant processes while programming, participants were set a Scratch programming task. Scratch itself was developed in 2003 at MIT Media Laboratory and publicly launched in 2007 (Resnick et al., 2009 ). It is one the first and one of the most popular open-source visual programming environments. In visual programming environments, users connects code blocks with each other instead of actual writing a code as common in real programming languages.

To prepare students for the task, they were given 45 min to review the Scratch tutorials available from within the Scratch platform. They were also allowed to access these tutorials during the programming task. The task itself was defined as follows: “ Program a story or a game where a hero has to overcome a challenge in order to defeat the villain(s) .”

This task was chosen because it is somewhat open-ended and can be solved in the chosen Scratch development framework without prior programming knowledge. Furthermore, computational thinking subskills (problem decomposition, pattern recognition, abstraction, algorithm design) would most likely have to be used to solve the task. The way in which the Scratch programming environment, task, and participants may influence the generalizability of results is considered in the Discussion section of this paper.

To reliably assess the amount of time they spent on computational thinking processes during their Scratch programming session, a computational thinking behavior scheme (CTBS) was developed. The CTBS was based on event sampling, involving analysis of how often and for how long specific behavioral cues occur. Based on the literature review, four components were identified as main features of computational thinking and which are the latent constructs in the CTBS: decomposition, abstraction (as in ignoring unimportant details), pattern recognition, and designing and applying algorithms (see operationalization of these constructs in Table  1 below). Two researchers coded five entire videos independently to assess inter-rater reliability. As a result, at least two third of the events were identified by both raters. The range of the frequency of agreement for the five videos laid between 66.67% and 72.50% and the κ coefficients ranged from 0.58 to 0.67. Overall, the reliability can be interpreted as moderate (Landis & Koch, 1977 ). Note that the CTBS measured the time spent on computational thinking components, not the correctness of the computational thinking processes. It is to be expected that during the process of solving computational problems that people may not always immediately have correct thoughts about the right course of action, and this study sought to examine relationship between the time spent on computational thinking processes and the quality of programming products.

3.2.3 Measuring program quality

To measure participants’ program quality, two measures were used. For one, a rubric scheme loosely based on “Clean code” of Martin ( 2009 ) was developed specially for this study. The program quality criteria were based on five categories: richness of project , variety of code usage , organization and tidiness , functionality of code and coding efficiency . Richness of project described how much was happening in the Scratch project. Lower scores were given when only one element was programmed to perform only one behaviour, while Scratch projects consisting of several programmed elements that were related to each other received higher scores. The variety of code usage depended on the kinds of code blocks were used. Scratch projects were rated lower when they mainly consisted of simple code chunks such as motion or looks and high when more advanced chunks like control or sensing were used. The category organization and tidiness took into account the extent to which the control section in Scratch was organized, with more organized Scratch projects receiving higher scores. Functionality was assessed based on whether the intention of the Scratch project was clear and whether it worked as intended. Projects received higher scores when they ran smoothly and the intention was easy to understand. The category efficiency described the usage of code controlling the flow of execution, and the number unnecessary duplications. Lower scores were given to projects having many such duplicates, while more generalized and more abstract code scripts received higher scores. An example of a program with unnecessary duplication is shown in Fig.  1 (left), compared to a more efficiently represented code block in Fig.  1 (right).

Two examples of the same function but coded differently. An example with unnecessary duplicates is shown on the left and a more efficient version is seen on the right

The five code quality categories were all rated on a scale including 0 ( not evident ), 1 ( poor ), 2 ( satisfactory ), 3 ( good ), up to 4 ( excellent ). A weighted mean over all categories was calculated to provide a general assessment. The weight for each category was based on their importance for program quality, resulting in extent and richness, variety, and functionality being weighted 20% each, efficiency 30%, and organization and tidiness 10% to the weighted mean. Quality criteria and the (weighted) scoring system of the scheme were discussed with two computer science education professionals to uphold the content validity of the measure. In addition, one of the CS education professionals rated the Scratch projects to obtain reliability assessment. Inter-rater reliability was high with ICC(3,1), 95% CI [0.87, 0.96].

The second measure for program quality was based on Dr Scratch (Moreno-León & Robles, 2015 ). Dr Scratch provides a measure of program quality based on seven dimensions relevant to CS: abstraction and problem decomposition, parallelism, logical thinking, synchronization, algorithmic notions of flow control, user interactivity and data representation. Dimensions are judged as 0 ( not evident ), 1 ( Basic ), 2 ( Developing ), and 3 ( Proficient ). Scores are aggregated over all dimensions resulting in a total evaluation score (mastery score) from 0 to 21. Mastery scores between 8 and 14 are regarded as general developing ; lower than 8 is regarded as generally basic , and more than 14 as general proficient . High correlations between Dr Scratch mastery scores and experts judgments of program quality can be used as an indicator of satisfactory criterion validity (Moreno-León, Román-González, Harteveld, & Robles, 2017 ). While Dr Scratch focuses primarily on computational thinking elements as opposed to other aspects of computer programming (e.g. organization of code, efficiency), it is based on the final computer programming solution that is produced, and thus provides an interesting alternative measure of program quality for this computational thinking study.

3.2.4 Test of nonverbal intelligence

To take account for potential confounding effect, participants’ nonverbal intelligence was also measured. For this the Test of Nonverbal Intelligence (3rd edition; TONI-3, Brown, Sherbeernou, & Johnson, 1997 ) was used. The TONI-3 is a classic culture fair test (i.e., minimally linguistically demanding) and as in many of them participants need to recognize a correct figure in a set of abstract and geometrical pictures. The test consists of 45 items and has an average testing time of 15 min and has a satisfactory level of psychometrical properties (Banks & Franzen, 2010 ).

3.3 Procedure

Initially, participants completed the Bebras Computational Thinking Knowledge test and the test of nonverbal intelligence (TONI-3 online). One week later, the second phase took place at university’s classrooms and participants attempted the task in Scratch. To collect rich video material with many verbal and nonverbal indicators for the research team to analyze, participants were organized in pairs. It was hoped that working in pairs would encourage participants to talk and engage more with each other. The pairs were formed based on similar Bebras scores to minimize any effects due to large differences in competences. In total, 37 pairs were formed and filmed while working on the task, forming the corpus for the analysis.

3.4 Analysis

All statistical analysis was conducted using the R statistics programming environment. In order to acquire a sense of the data, basic descriptive statistics including means and standard deviations were calculated for all five measures (Bebras scores, time spent on different computational thinking processes, program quality rubric score, Dr Scratch score, TONI-3 non-verbal intelligence score). Because participants worked on the programming task in pairs, all programming assessments based on the rubric scheme, the additional Scratch evaluation assessment based on Dr Scratch, and the assessment of how much time participants spent on computational thinking behavior based on CTBS, were paired values. Scores on the Bebras tasks and TONI-3 test were averaged for each pair. Of the 37 pairs of participants who agreed to complete the Bebras test and have their final programs used in the study, 27 agreed to be video recorded for the purposes of the CTBS analysis, and 32 pairs agreed to complete the TONI-3 test.

Spearman’s ρ were computed between all five measures using all available data, to determine whether the underlying variables were directly correlated. Finally, in order to account for the possibility of moderating variables, two regression models were estimated with the two program quality measures as outcomes (program quality rubric score and Dr Scratch score). These two regression models used the Bebras task scores, the CTBS, and the TONI-3 IQ scores as predictors, so that it was possible to detect if any of these were moderating variables.

4.1 Descriptive statistics and measurement outcomes

The average score for the measure of general computational thinking capability (Bebras task) was 57.03% ( SD = 18.6%). The range was from 21% to one participant who achieved 100%. Results indicated a medium level of test difficulty, with no serious problems due to ceiling or floor effects. In TONI-3-IQ, participants achieved an average intelligence score of 113.12 ( SD = 14.17). The mean of this sample was slightly higher than the expected value of the population (µ = 100, see, for example, Sternberg, 2017 ), which can be explained by the fact the sample was drawn from university students. The time participants needed to complete the Bebras tasks ( Md = 55 min) and the TONI-3-IQ ( Md = 22 min) roughly aligned with the expected time of 60 min (Dagienė & Futschek, 2008 ) and 15 min (Brown et al., 1997 ), respectively.

Table  2 shows that while writing their programs, coded participants spent nearly half of their time on computational thinking behaviors, with algorithmic design having the largest contribution and little time spent on decomposition and pattern recognition. Pattern recognition was observed in less than half of all pairs. No sign of abstraction in the sense of neglecting information was observed for any pair.

Table 3 contains an overview of scores achieved by the pairs of participants in the rubric scheme for program quality. The full range of the rating scales (0 to 4) was used. The distributions of all five dimensions had their center at around 2 (i.e., satisfactory level).

In comparison, participants’ Scratch projects typically only achieved a basic rating according to Dr Scratch, with only two dimensions rated as developing (See Table  4 ).

4.2 Correlations between variables

As a first step towards analyzing which of the two computational thinking measures (general computational thinking knowledge as measured by Bebras versus computational thinking processes as observed in practice) have a greater relationship to program quality, Spearman’s ρ were computed (see Table  4 ). Correlation between the two measures of program quality (weighted means based on the developed rubric scheme and Dr Scratch mastery scores) revealed a significant relationship, ρ = 0.61, p < .001. Based on common interpretation of effect sizes (Cohen, 1988 ), this correlation can be interpreted as large. The large correlation between the two measures of program quality reveals a degree of consistency in their assessment of student programs.

Significant positive correlations were found between general computational thinking knowledge (Bebras scores) and both measures of program quality, with a borderline small to medium effect sizes (see Table  5 ). Significant positive correlations between time spent on computational thinking processes while programming and both measures of program quality, with quite large effects.

Because of some potential (partial) conceptual overlaps between nonverbal intelligence and computational thinking, the correlations between the TONI-3 IQ and computational thinking measures were calculated as well. On one hand, the correlation between the TONI-3 IQ and the Bebras scores was significant and positive with a medium to large effect size, ρ = 0.49, p = 0.002. On the other hand, correlation between TONI-3-IQ and time spent on computational thinking processes while programming was not statistically significant, ρ = 0.09, p = 0.346

4.3 Regression analysis

As explained in the Methodology section, two regression models were estimated with both program quality measures as outcomes and the both computational thinking measures and the TONI-3 IQ scores as predictors. Standardized parameter estimations and tests of significance of the regression model are shown in Table  6 . The regression models only partly supported the findings from the correlations. The positive correlation between the Bebras score and both measures of program quality vanished when taking into account the effect of TONI-3 IQ. The only significant predictor for both measures of programming quality was the computational thinking process scores.

Post hoc analyses for both regression models were performed for power estimation. Based on the given parameters ( N = 24, number of predictors = 3, effect size = R 2 pro.qual = 0.50, R 2 DrScratch = 0.44, and α = 0.05), a power of > 0.99 for both models was achieved. Because of the small sample size, assumptions about linear multiple regressions such as homoscedasticity, multicollinearity, and residuals were rigorously checked. No serious violations of any assumption could be found, though it should be noted that the residuals when the outcome was programming quality were not normally distributed, based on Shapiro-Francias test, with W’ = 0.88, p = 0.011. In conclusion, the power of both regression models were sufficiently high enough and the regression coefficients can be interpreted as “best linear regression estimations”.

5 Discussion

The general computational thinking knowledge scores (Bebras) and the computational thinking procedural performance (as indicated by the CTBS), were both positively correlated with both program quality measures (the rubric scheme and Dr Scratch mastery score). Therefore, a general interpretation could be that the higher the level of both general computational thinking knowledge and applied computational thinking in practice, the better the program quality. However, this interpretation would be premature because regression analyses revealed that only one — the applied computational thinking in practice — was a significant predictor of program quality when controlling for other variables such as the level of nonverbal intelligence and general computational thinking knowledge. The reason why the two different computational thinking measures predict programming differently might lie in different perspectives underlying the two different measures of computational thinking, and how these might mediate the relationship with program quality.

The Bebras tasks focus on general and conceptual aspects of computational thinking. Correlations between the Bebras score and the TONI-3-IQ were between moderate and strong. As for the most instruments for nonverbal intelligence, TONI-3 is based on pictures in which participants need to identify similar instances and recognize patterns. Many of the Bebras tasks are designed in a similar fashion. The original idea behind the Bebras tasks was to create a test about CS concepts “independent from specific systems” to avoid contestants being dependent on prior knowledge of any specific IT system (Dagienė & Futschek, 2008 , p. 22). This may have led to some items being similar to those of nonverbal intelligence tests.

As found in some prior studies, this also caused confusion for some Bebras contestants. Vaníček ( 2014 ) asked participants for their opinions about the Bebras tasks. Some questioned the purpose and validity of the test, stating “I wonder what the contest questions have to do with informatics. Maybe nothing at all?”. If (at least some) Bebras tasks are similar to those of nonverbal intelligence tests and there is a high and significant positive correlation between both measures, it is possible that both tests measure similar constructs. This would explain why the relationship between the Bebras scores and program quality vanished when controlled for TONI-3-IQ. The Bebras tasks are validated by several studies (Dagienė & Stupuriene, 2016 ; Dolgopolovas, Jevsikova, Savulionienė, & Dagienė, 2015 ; Lockwood & Mooney, 2018 ) but none of these studies controlled for any potential confounding effects on similar psychological constructs such as nonverbal intelligence. We could only find one study in which the potential relationship between the Bebras tasks and nonverbal intelligence has been discussed, with similar findings to our study (Román-González, Pérez-González, & Jiménez-Fernández, 2017 ). Thus, it is possible that the Bebras tasks indeed measure computational thinking but mainly the facet of abstract thinking and pattern recognition.

It is possible that these abstract parts of computational thinking alone are not a good predictor of programming quality because extensive cognitive effort is required to transfer the skills for application in different situations and settings. Even though some similar skills are required to solve both kinds of tasks (the Bebras tasks as well as the programming task in this study), it would require a high level of transferability from these abstract logical quizzes to real applied programming situations. Moreover, according to the authors of the Bebras tasks, participants need to apply the same cognitive abilities as needed for programming tasks such as problem deconstruction, thinking abstractly, recognizing patterns, and being able to understand, design, and evaluate algorithms (Dagienė & Sentance, 2016 ). However, the content of the Bebras tasks (as for many ‘unplugged’ methods) is very different from real programming tasks. This may lead to general computational thinking as measured by Bebras tasks not providing a good predictor of program quality above and beyond that which is captured and controlled for by general measures of intelligence (such as the TONI-3-IQ).

In our opinion, the results can be well explained in terms of the thesis of disproportion between application extensity and intensity of use (Weinert, 1994 ). This theory asserts that, the more general a rule or strategy is, the more minor its contribution to solving challenging, content-specific problems. This could also apply to the computational thinking skills of the Bebras tasks. The measured skills are very general and partly overlap with general facets of intelligence. Their contribution to solving a challenging, content-specific problem might therefore be rather small and statistically hard to detect. At least, this would be one possible interpretation of the rather weak correlation and the lost connection in the regression analysis with regard to general computational thinking knowledge and program quality.

In contrast to the Bebras tasks, the focus of the CTBS lies on participants’ applied computational thinking processes in practice. Correlations indicated that the more participants spent on applied computational thinking processes, the better the programming quality of their Scratch project. It must be pointed that this was mostly due to algorithmic design, with algorithmic design being the most frequently applied computational thinking activity measured. As stated before, participants were working on their code from the start of the session and so there is a logical interpretation that the longer and the more participants spent on algorithmic design, the better the quality of their programs. Even after controlling for other measures, this relationship was still significant and persisted in both regression models with the programming quality rubric and Dr Scratch project evaluation as outcome, respectively. What is even more remarkable is that computational thinking processes were significantly correlated with program quality even though the correctness of the computational thinking processes was not assessed in this study. That is to say, that the more time spent thinking about computational thinking components while solving the computing problem led to better quality programming solutions, even when at times that computational thinking may not have necessarily been ‘right’. This is in line with the learning concept of ‘productive failure’, where thinking deeply about problems and exploring incorrect solutions can ultimately lead to greater learning overall (Kafai, De Liema, Fields, Lewandowski & Lewis, 2019 ).

These results indicate that the computational thinking process capabilities observed by the CTBS are more strongly related to program quality than computational thinking knowledge as measured by Bebras. While the Bebras Challenge is undoubtedly a valuable competition for students worldwide, the results from this study indicate the ability to solve Bebras problems may not be a good indicator of the ability to solve authentic informatics problems that involve computer programming. In fact, the result challenges the premise that generalised computational thinking knowledge underpins the ability to solve authentic programming problems to any substantial extent. The capacity to apply computational thinking processes in-situ has been shown in this study to be far more relevant and influential in terms of being able to derive high quality programming solutions than solving general computational thinking knowledge problems. To this extent, from a pedagogical perspective, educators who wish to use computational thinking as a basis for improving the ability of their students to solve programming problems should focus on developing students’ abilities to apply computational thinking processes in practice (algorithm design, problem decomposition, pattern recognition, abstraction) rather than their computational thinking knowledge in a more detached and decontextualized sense.

5.1 Limitations of the Study

In this study, students worked together in pairs as a naturalistic way to provoke social interaction and make otherwise unobservable thoughts accessible. This contributed to the authenticity of the study, with pair programming often occurring in industry and education. Moreover, pair-programming settings have been used in prior studies in terms of measuring computational thinking and programming knowledge for novices (Denner, Werner, Campe, & Ortiz, 2014 ; Wu, Hu, Ruis, & Wang, 2019 ). However, this approach involved some inherent challenges. It was not possible to perfectly group pairs according to identical levels of computational thinking, intelligence, or programming quality. Some might argue that the results and overall conclusion might have been different if all measures were obtained and analyzed solely on an individual basis. However, gauging individual measures of computational thinking programming skills from a behavioral perspective also involves challenges, as it is difficult to encourage individual participants to verbalize their thinking for the entire duration of the programming process. We believe that the benefits of analyzing computational thinking arising from a more naturalistic setting outweigh those from measuring the computational thinking of individuals, in terms of the validity of results.

It is also worth mentioning that the CTBS and the programming quality instrument were designed specifically for the purpose of this study. That means these instruments have not been tested in other studies yet. Interrater reliability assessments indicated a satisfactory level of agreement, but the results based on CTBS and programming quality rubric scheme deserve to be interpreted with caution. Some indicators of the computational thinking behavior are dependent on the environment used. For instance, the computational thinking component algorithmic design category of the scheme and encompasses all utterance and actions with the purpose of designing an algorithmic solution to a problem. The programming task in this study was designed in Scratch, for which the only way to create algorithmic solutions was to drag and drop code chunks together. If another programming environment were used, or indeed different programming problems, or even other cohorts of participants, other indicators may be identified. This potentially limits the generalization of the results of the study.

6 Conclusion and future work

Computational thinking is promoted as the literacy of the 21st century and is already implemented in various curricula all over the world. Some refer to computational thinking even as the foundation of programming and CS (Lu & Fletcher, 2009 ). Thus, the goal of this study was to analyses the role of computational thinking in promoting high quality programming products. Results showed that the answer to the question of how computational thinking is related to program quality depends on whether computational thinking is seen as a set of general conceptual understandings or a set of procedural skills in use. The results of our study found that computational thinking as general conceptual knowledge (such as that used to solve Bebras challenges) was not significantly related to program quality. On the other hand, we found that computational thinking as a set of procedural skills applied in practice was significantly related to programming quality, even when controlling for general intelligence. Thus, when discussing the role of computational thinking in developing computer programming capacity, we suggest that educators and policy makers focus on the importance of cultivating computational thinking procedural capabilities rather than in more abstract, knowledge-based and context free forms.

There are several potential avenues for research to build upon the results of this study. Visual programming environments such as Scratch are usually used to introduce computational thinking or programming concepts to people who have no knowledge about programming, as was the case in this study. In future, researchers could analyse how computational thinking is applied when experienced programmers solve a programming task in a programming language such as Java or C++. The way programmers approach problems develops over time as they gain more knowledge (Teague & Lister, 2014 ). It is possible that the level of computational thinking for experienced programmers differs from the level of novices, which might mediate the relationship between both concepts. A range of different tasks could be examined, for instance, to gauge differences in computational thinking prevalence and relationships to program quality for tasks with more closed solutions as opposed to being more open-ended in nature. Future research could attempt to analyze all concepts individually rather than in pairs as an alternative way to examine the relationship between the constructs in question. In any case, it is intended that the frameworks and methods presented in this paper provide a strong foundation for these future analyses.

Anderson, J. R. (2015). Cognitive psychology and its implications (8th.). New York, NY: Worth Publishers

Google Scholar  

Angeli, & Giannakos, M. (2020). Computational thinking education: Issues and challenges. Computers in Human Behavior , 105, 106185. https://doi.org/10.1016/j.chb.2019.106185

Article   Google Scholar  

Araujo, A. L. S. O., Andrade, W. L., Guerrero, D. D. S., & Melo, M. R. A. (2019). How many abilities can we measure in computational thinking? A study on Bebras challenge. Proceedings of the 50th ACM Technical Symposium on Computer Science Education (pp. 545–551). https://doi.org/10.1145/3287324#issue-downloads

Atmatzidou, & Demetriadis, S. (2016). Advancing students’ computational thinking skills through educational robotics: A study on age and gender relevant differences. Robotics and Autonomous Systems , 75, 661–670. https://doi.org/10.1016/j.robot.2015.10.008

Banks, S. H., & Franzen, M. D. (2010). Concurrent validity of the TONI-3. Journal of Psychoeducational Assessment , 28(1), 70–79. https://doi.org/10.1177/0734282909336935

Brennan, K., & Resnick, M. (2012). New frameworks for studying and assessing the development of computational thinking. In Proceedings of the 2012 annual meeting of the American Educational Research Association, Vancouver, Canada

Bower, M., & Hedberg, J. G. (2010). A quantitative multimodal discourse analysis of teaching and learning in a web-conferencing environment–the efficacy of student-centred learning designs. Computers & Education , 54(2), 462–478

Brown, L., Sherbeernou, R. J., & Johnson, S. K. (1997). Test of nonverbal intelligence-3 . Austin, TX: PRO-ED

Bull, G., Garofalo, J., & Hguyen, N. R. (2020). Thinking about computational thinking. Journal of Digital Learning in Teacher Education , 36(1), 6–18. https://doi.org/10.1080/21532974.2019.1694381

Cansu, F. K., & Cansu, S. K. (2019). An overview of computational thinking. International Journal of Computer Science Education in Schools , 3(1), 17–30. https://doi.org/10.21585/ijcses.v3i1.53

Article   MATH   Google Scholar  

Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2nd ed.). Hillsdale, N.J.: L. Erlbaum Associates

MATH   Google Scholar  

Cormen, T. H., Leiserson, C. E., Rivest, R. L., & Stein, C. (2014). Introduction to algorithms (3rd ed.). Cambridge, MA, London: MIT Press

Csizmadia, A., Curzon, P., Dorling, M., Humphreys, S., Ng, T., Selby, C., & Woollard, J. (2015). Computational thinking - A guide for teachers . Swindon: Computing at School. http://eprints.soton.ac.uk/id/eprint/424545

Dagienė, V., & Futschek, G. (2008). Bebras international contest on informatics and computer literacy: Criteria for good tasks. In R. T. Mittermeir & M. M. Sysło (Eds.), Informatics Education - Supporting Computational Thinking: Third International Conference on Informatics in Secondary Schools - Evolution and Perspectives, ISSEP 2008 Torun Poland, July 1-4, 2008 Proceedings (pp. 19–30). Berlin, Heidelberg: Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-540-69924-8_2

Dagienė, V., & Sentance, S. (2016). It’s computational thinking! Bebras tasks in the curriculum. In A. Brodnik & F. Tort (Eds.), Lecture Notes in Computer Science. Informatics in Schools: 9th International Conference on Informatics in Schools: Situation, Evolution, and Perspectives, Proceedings (Vol. 9973, pp. 28–39). Cham: Springer Verlag. https://doi.org/10.1007/978-3-319-46747-4_3

Dagienė, V., & Stupuriene, G. (2016). Bebras - A sustainable community building model for the concept based learning of informatics and computational thinking. Informatics in Education , 15(1), 25–44. https://doi.org/10.15388/infedu.2016.02

Denner, J., Werner, L., Campe, S., & Ortiz, E. (2014). Pair programming: Under what conditions is it advantageous for middle school students? Journal of Research on Technology in Education , 46(3), 277–296. https://doi.org/10.1080/15391523.2014.888272

Dolgopolovas, V., Jevsikova, T., Savulionienė, L., & Dagienė, V. (2015). On evaluation of computational thinking of software engineering novice students. In A. Brodnik & C. Lewin (Eds.), IFIP TC3 Working Conference “A New Culture of Learning: Computing and next Generations” . Vilnius, Lithuania: Vilnius University

Ezeamuzie, & Leung, J. S. C. (2021). Computational thinking through an empirical lens: A systematic review of literature. Journal of Educational Computing Research , Vol. 59, https://doi.org/10.1177/07356331211033158

Gadanidis, G. (2017). Five affordances of computational thinking to support elementary mathematics education. Journal of Computers in Mathematics and Science Teaching , 36(2), 143–151

Grover, S. (2011). Robotics and engineering for middle and high school students to develop computational thinking. In Annual Meeting of the American Educational Research Association, New Orleans, LA

Grover, S. (2017). Assessing algorithmic and computational thinking in K-12: Lessons from a Middle School Classroom. In P. J. Rich, & C. B. Hodges (Eds.), Emerging Research, Practice, and Policy on Computational Thinking (31 vol., pp. 269–288). Cham: Springer International Publishing. https://doi.org/10.1007/978-3-319-52691-1_17

Chapter   Google Scholar  

Grover, S., & Pea, R. (2013). Computational thinking in K–12: A review of the state of the field. Educational Researcher , 42(1), 38–43

Grover, S., Pea, R., & Cooper, S. (2015). Designing for deeper learning in a blended computer science course for middle school students. Computer Science Education , 25(2), 199–237. https://doi.org/10.1080/08993408.2015.1033142

Ihantola, P., Ahoniemi, T., Karavirta, V., & Seppälä, O. (2010). Review of recent systems for automatic assessment of programming assignments. Proceedings of the 10th Koli Calling International Conference on Computing Education Research , 86–93. https://doi.org/10.1145/1930464.1930480

International Society for Technology in Education [ISTE] & the Computer Science Teachers Association [CSTA] (2011). Operational definition of computational thinking for K–12 education. Retrieved from https://csta.acm.org/Curriculum/sub/CurrFiles/CompThinkingFlyer.pdf

Jin, K. H., & Charpentier, M. (2020). Automatic programming assignment assessment beyond black-box testing. Journal of Computing Sciences in Colleges , 35(8), 116–125

Kafai, Y. B., De Liema, D., Fields, D. A., Lewandowski, G., & Lewis, C. (2019). Rethinking debugging as productive failure for CS Education. In S. Heckman & J. Zhang (Eds.), Proceedings of the 50th ACM technical symposium on Computer Science Education . New York, NY: ACM

Knobelsdorf, M., & Frede, C. (2016, August). Analyzing student practices in theory of computation in light of distributed cognition theory. In Proceedings of the 2016 ACM Conference on International Computing Education Research (pp. 73–81).

Korucu, A. T., Gencturk, A. T., & Gundogdu, M. M. (2017). Examination of the computational thinking skills of students. Journal of Learning and Teaching in Digital Age , 2 (1), 11–19. Retrieved from https://eric.ed.gov/?id=ED572684

Landis, R., & Koch, G. G. (1977). The measurement of observer agreement for categorial data. Biometrics , 33, 159–174

Lockwood, J., & Mooney, A. (2018). Computational thinking in secondary education: Where does it fit? A systematic literary review. International Journal of Computer Science Education in Schools , 2(1), pp. 1–20. https://doi.org/10.21585/ijcses.v2i1.26

Lu, J. J., & Fletcher, G. H. L. (2009). Thinking about computational thinking. In S. Fitzgerald (Ed.), Proceedings of the 40th ACM technical symposium on Computer science education . New York, NY: ACM

Lye, S. Y., & Koh, J. H. L. (2014). Review on teaching and learning of computational thinking through programming: What is next for K-12? Computers in Human Behavior , 41, 51–61. https://doi.org/10.1016/j.chb.2014.09.012

Martin, R. C. (2009). Clean code: A handbook of agile software craftsmanship . Pearson Prentice Hall

McNicholl, R. (2019). Computational thinking using Code.org. Hello World , 4, 36–37. https://issuu.com/raspberry314/docs/helloworld04

Moreno-León, J., & Robles, G. (2015). Dr. Scratch: a web tool to automatically evaluate scratch projects. In J. Gal-Ezer, S. Sentance, & J. Vahrenhold (Eds.), Proceedings of the Workshop in Primary and Secondary Computing Education, London, United Kingdom, November 09 - 11, 2015 (pp. 132–133). New York: ACM. https://doi.org/10.1145/2818314.2818338

Moreno-León, J., Román-González, M., Harteveld, C., & Robles, G. (2017). On the automatic assessment of computational thinking skills. In G. Mark, S. Fussell, C. Lampe, m. schraefel, J. P. Hourcade, C. Appert, & D. Wigdor (Eds.), CHI’17: Extended abstracts: proceedings of the 2017 ACM SIGCHI Conference on Human Factors in Computing Systems : May 6-11, 2017, Denver, CO, USA (pp. 2788–2795). New York, New York: The Association for Computing Machinery. https://doi.org/10.1145/3027063.3053216

Pieterse, V. (2013). Automated assessment of programming assignments. Proceedings of the 3rd Computer Science Education Research Conference , 13 , 4–5. https://doi.org/10.5555/2541917.2541921

Portelance, D. J., & Bers, M. U. (2015). Code and tell: Assessing young Children’s learning of computational thinking using peer video interviews with ScratchJr. In M. U. Bers & G. L. Revelle (Eds.), IDC ‘15: Proceedings of the 14th international conference on interaction design and children (pp. 271–274). New York: ACM

Posner, M. I., & Keele, S. W. (1968). On the genesis of abstract ideas. Journal of Experimental Psychology , 77, 353–363. https://doi.org/10.1037/h0025953

Poulakis, E., & Politis, P. (2021). Computational Thinking Assessment: Literature Review. Research on E-Learning and ICT in Education: Technological, Pedagogical and Instructional Perspectives , 111–128

Resnick, M., Silverman, B., Kafai, Y., Maloney, J., Monroy-Hernández, A., Rusk, N., & Silver, J. (2009). Scratch: Programming for all. Communications of the ACM , 52(11), 60. https://doi.org/10.1145/1592761.1592779

Román-González, M., Pérez-González, J. C., & Jiménez-Fernández, C. (2017). Which cognitive abilities underlie computational thinking?: Criterion validity of the Computational Thinking Test. Computers in Human Behavior , 72, 678–691. https://doi.org/10.1016/j.chb.2016.08.047

Schank, R. C., & Abelson, R. P. (1977). Scripts, plans, goals and understanding: An inquiry into human knowledge structures . Hillsdale, NJ: L. Erlbaum Associates. Artificial intelligence series

Schulz, K., & Hobson, S. (2015). Bebras Australia computational thinking challenge tasks and solutions 2014 . Brisbane, Australia: Digital Careers

Schulz, K., Hobson, S., & Zagami, J. (2016). Bebras Austrlia computational thinking challenge - tasks and solution 2016 . Brisbane, Australia: Digital Careers

Shivhare, & Kumar, C. A. (2016). On the Cognitive process of abstraction. Procedia Computer Science , 89, 243–252. https://doi.org/10.1016/j.procs.2016.06.051

Shute, V. J., Sun, C., & Asbell-Clarke, J. (2017). Demystifying computational thinking. Educational Research Review , 22, 142–158. https://doi.org/10.1016/j.edurev.2017.09.003

Sipser, M. (2013). Introduction to the theory of computation (3rd ed.). Boston: Cengage Learning

Sternberg, R. J. (2017). Human intelligence. Encyclopaedia Britannica . Retrieved from https://www.britannica.com/topic/human-intelligence-psychology/Development-of-intelligence#ref13354

Suters, L., & Suters, H. (2020). Coding for the core: Computational thinking and middle grades mathematics. Contemporary Issues in Technology and Teacher Education (CITE Journal) , 20 (3). Retrieved from https://citejournal.org/volume-20/issue-3-20/mathematics/coding-for-the-core-computational-thinking-and-middle-grades-mathematics/

Tang, K. Y., Chou, T. L., & Tsai, C. C. (2020). A content analysis of computational thinking research: An international publication trends and research typology. Asia-Pacific Education Researcher , 29(1), 9–19. https://doi.org/10.1007/s40299-019-00442-8

Teague, D., & Lister, R. (2014). Longitudinal think aloud study of a novice programmer. In J. Whalley (Ed.), Proceedings of the Sixteenth Australasian Computing Education Conference - Volume 148 . Darlinghurst, Australia: Australian Computer Society, Inc

Thalheim, B. (2009). Abstraction. In L. Liu, & M. T. Özsu (Eds.), Springer reference. Encyclopedia of database systems , 1–3. New York, NY: Springer

Tsai, Liang, J. C., Lee, S. W. Y., & Hsu, C. Y. (2021). Structural validation for the developmental model of computational thinking. Journal of Educational Computing Research , Vol. 59, https://doi.org/10.1177/07356331211017794

Türker, P. M., & Pala, F. K. (2020). A Study on students’ computational thinking skills and self-efficacy of block-based programming. Journal on School Educational Technology , 15 (3), 18–31 (14 Seiten). Retrieved from https://imanagerpublications.com/article/16669/

Vaníček, J. (2014). Bebras informatics contest: Criteria for good tasks revised. In Y. Gülbahar & E. Karataş (Eds.), Informatics in Schools. Teaching and Learning Perspectives: 7th International Conference on Informatics in Schools: Situation, Evolution, and Perspectives, ISSEP 2014, Istanbul, Turkey, September 22-25, 2014. Proceedings (pp. 17–28). Cham: Springer International Publishing. https://doi.org/10.1007/978-3-319-09958-3_3

Weintrop, D., Beheshti, E., Horn, M., Orton, K., Jona, K., Trouille, L., & Wilensky, U. (2016). Defining computational thinking for mathematics and science classrooms. Journal of Science Education and Technology , 25(1), 127–147

Weinert, F. E. (1994). Lernen lernen und das eigene Lernen verstehen. [Learning how to learn and understanding the own learning]. In K. Reusser, & M. Reusser-Weyeneth (Eds.), Verstehen. Psychologischer Prozess und didaktische Aufgabe [Understanding. Psychological processes and didactical tasks.] (pp. 183–205). Bern: Huber

Wing, J. M. (2006). Computational thinking. Communications of the ACM , 49(3), 33–35. https://doi.org/10.1145/1118178.1118215

Wu, B., Hu, Y., Ruis, A. R., & Wang, M. (2019). Analysing computational thinking in collaborative programming: A quantitative ethnography approach. Journal of Computer Assisted Learning , 35(3), 421–434. https://doi.org/10.1111/jcal.12348

Zha, S., Jin, Y., Moore, P., & Gaston, J. (2020). Hopscotch into Coding: introducing pre-service teachers computational thinking. TechTrends , 64(1), 17–28. https://doi.org/10.1007/s11528-019-00423-0

Download references

Acknowledgements

Open Access funding enabled and organized by CAUL and its Member Institutions

Author information

Authors and affiliations.

Department of Vocational and Business Education, University of Hamburg, Hamburg, Germany

Kay-Dennis Boom & Jens Siemon

School of Education, Macquarie University, Building 29WW Room 238, Balaclava Rd North Ryde, 2109, NSW, Sydney, Australia

CLLE, University of Toulouse, CNRS, Toulouse, France

Amaël Arguel

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Matt Bower .

Ethics declarations

Conflict of interest, additional information, publisher’s note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Boom, KD., Bower, M., Siemon, J. et al. Relationships between computational thinking and the quality of computer programs. Educ Inf Technol 27 , 8289–8310 (2022). https://doi.org/10.1007/s10639-022-10921-z

Download citation

Received : 05 September 2021

Accepted : 27 January 2022

Published : 03 March 2022

Issue Date : July 2022

DOI : https://doi.org/10.1007/s10639-022-10921-z

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Computational thinking
• Visual programming
• Program quality
• Find a journal
• Publish with us
• Track your research

share this!

May 21, 2024

This article has been reviewed according to Science X's editorial process and policies . Editors have highlighted the following attributes while ensuring the content's credibility:

fact-checked

trusted source

The case for 'math-ish' thinking

by Stanford University

For everyone whose relationship with mathematics is distant or broken, Jo Boaler, a professor at Stanford Graduate School of Education (GSE), has ideas for repairing it. She particularly wants young people to feel comfortable with numbers from the start—to approach the subject with playfulness and curiosity, not anxiety or dread.

"Most people have only ever experienced what I call narrow mathematics—a set of procedures they need to follow, at speed," Boaler says. "Mathematics should be flexible, conceptual, a place where we play with ideas and make connections. If we open it up and invite more creativity, more diverse thinking, we can completely transform the experience."

Boaler, the Nomellini and Olivier Professor of Education at the GSE, is the co-founder and faculty director of Youcubed, a Stanford research center that provides resources for math learning that has reached more than 230 million students in over 140 countries. In 2013 Boaler, a former high school math teacher, produced How to Learn Math, the first massive open online course (MOOC) on mathematics education . She leads workshops and leadership summits for teachers and administrators, and her online courses have been taken by over a million users.

In her new book, " Math-ish: Finding Creativity, Diversity, and Meaning in Mathematics ," Boaler argues for a broad, inclusive approach to math education, offering strategies and activities for learners at any age. We spoke with her about why creativity is an important part of mathematics, the impact of representing numbers visually and physically, and how what she calls "ishing" a math problem can help students make better sense of the answer.

What do you mean by 'math-ish' thinking?

It's a way of thinking about numbers in the real world, which are usually imprecise estimates. If someone asks how old you are, how warm it is outside, how long it takes to drive to the airport—these are generally answered with what I call "ish" numbers, and that's very different from the way we use and learn numbers in school.

In the book I share an example of a multiple-choice question from a nationwide exam where students are asked to estimate the sum of two fractions: 12/13 + 7/8. They're given four choices for the closest answer: 1, 2, 19, or 21. Each of the fractions in the question is very close to 1, so the answer would be 2—but the most common answer 13-year-olds gave was 19. The second most common was 21.

I'm not surprised, because when students learn fractions, they often don't learn to think conceptually or to consider the relationship between the numerator or denominator. They learn rules about creating common denominators and adding or subtracting the numerators, without making sense of the fraction as a whole. But stepping back and judging whether a calculation is reasonable might be the most valuable mathematical skill a person can develop.

But don't you also risk sending the message that mathematical precision isn't important?

I'm not saying precision isn't important. What I'm suggesting is that we ask students to estimate before they calculate, so when they come up with a precise answer, they'll have a real sense for whether it makes sense. This also helps students learn how to move between big-picture and focused thinking, which are two different but equally important modes of reasoning.

Some people ask me, "Isn't 'ishing' just estimating?" It is, but when we ask students to estimate, they often groan, thinking it's yet another mathematical method. But when we ask them to "ish" a number, they're more willing to offer their thinking.

Ishing helps students develop a sense for numbers and shapes. It can help soften the sharp edges in mathematics, making it easier for kids to jump in and engage. It can buffer students against the dangers of perfectionism, which we know can be a damaging mindset. I think we all need a little more ish in our lives.

You also argue that mathematics should be taught in more visual ways. What do you mean by that?

For most people, mathematics is an almost entirely symbolic, numerical experience. Any visuals are usually sterile images in a textbook, showing bisecting angles, or circles divided into slices. But the way we function in life is by developing models of things in our minds. Take a stapler: Knowing what it looks like, what it feels and sounds like, how to interact with it, how it changes things—all of that contributes to our understanding of how it works.

There's an activity we do with middle-school students where we show them an image of a 4 x 4 x 4 cm cube made up of smaller 1 cm cubes, like a Rubik's Cube. The larger cube is dipped into a can of blue paint, and we ask the students, if they could take apart the little cubes, how many sides would be painted blue? Sometimes we give the students sugar cubes and have them physically build a larger 4 x 4 x 4 cube. This is an activity that leads into algebraic thinking.

Some years back we were interviewing students a year after they'd done that activity in our summer camp and asked what had stayed with them. One student said, "I'm in geometry class now, and I still remember that sugar cube, what it looked like and felt like." His class had been asked to estimate the volume of their shoes, and he said he'd imagined his shoes filled with 1 cm sugar cubes in order to solve that question. He had built a mental model of a cube.

When we learn about cubes, most of us don't get to see and manipulate them. When we learn about square roots, we don't take squares and look at their diagonals. We just manipulate numbers.

I wonder if people consider the physical representations more appropriate for younger kids.

That's the thing—elementary school teachers are amazing at giving kids those experiences, but it dies out in middle school, and by high school it's all symbolic. There's a myth that there's a hierarchy of sophistication where you start out with visual and physical representations and then build up to the symbolic. But so much of high-level mathematical work now is visual. Here in Silicon Valley, if you look at Tesla engineers, they're drawing, they're sketching, they're building models, and nobody says that's elementary mathematics.

There's an example in the book where you've asked students how they would calculate 38 x 5 in their heads, and they come up with several different ways of arriving at the same answer. The creativity is fascinating, but wouldn't it be easier to teach students one standard method?

That narrow, rigid version of mathematics where there's only one right approach is what most students experience, and it's a big part of why people have such math trauma. It keeps them from realizing the full range and power of mathematics. When you only have students blindly memorizing math facts, they're not developing number sense.

They don't learn how to use numbers flexibly in different situations. It also makes students who think differently believe there's something wrong with them.

When we open mathematics to acknowledge the different ways a concept or problem can be viewed, we also open the subject to many more students. Mathematical diversity, to me, is a concept that includes both the value of diversity in people and the diverse ways we can see and learn mathematics.

When we bring those forms of diversity together, it's powerful. If we want to value different ways of thinking and problem-solving in the world, we need to embrace mathematical diversity.

Provided by Stanford University

Explore further

Feedback to editors

Improved refrigeration could save nearly half of the 1.3 billion tons of food wasted each year globally

1 minute ago

Researchers develop reusable 'sponge' for soaking up marine oil spills—even in chilly northern waters

10 minutes ago

Novel carbon nanotube yarns can generate electricity from waste heat

35 minutes ago

The death of Vulcan: Study reveals planet is actually an astronomical illusion caused by stellar activity

40 minutes ago

Economists report on a modest intervention that helps low-income families beat the poverty trap

New approach uses 'cloaked' proteins to deliver cancer-killing therapeutics into cells

3 hours ago

Speeding up calculations that reveal how electrons interact in materials

Small birds boast range of flight styles thanks to evolutionary edge

Florida fossil porcupine solves a prickly dilemma 10 million years in the making

4 hours ago

GPT's inaccuracies in agriculture could lead to crop losses and food crises

Relevant physicsforums posts, question about branch of logarithm, memorizing trigonometric identities.

May 26, 2024

Graphing trip efficiency - distance over time

May 20, 2024

Help with Recurrence Equation

May 18, 2024

Numerically how to approximate exponential decay in a discrete signal

May 16, 2024

Flat surface to curved surface

May 13, 2024

More from General Math

Related Stories

Changing students' attitudes to mathematics improves test scores

May 10, 2018

Math degrees are becoming less accessible—and this is a problem for business, government and innovation

May 5, 2024

Former math teacher explains why some students are 'good' at math and others lag behind

Nov 3, 2022

Studies recommend increased research into achievement, engagement to raise student math scores

Feb 15, 2024

5 tips to get your children excited about math

Jan 17, 2020

Future teachers often think memorization is the best way to teach math and science – until they learn a different way

Sep 17, 2020

Recommended for you

Math discovery provides new method to study cell activity, aging

First-generation medical students face unique challenges and need more targeted support, say researchers

Mechanistic model shows how much gossip is needed to foster social cooperation

May 15, 2024

Random processes shape science and math: Researchers propose a unified, probabilistic framework

May 9, 2024

Study of new method used to preserve privacy with US census data suggests accuracy has suffered

May 6, 2024

New study is first to use statistical physics to corroborate 1940s social balance theory

May 3, 2024

Let us know if there is a problem with our content

Use this form if you have come across a typo, inaccuracy or would like to send an edit request for the content on this page. For general inquiries, please use our contact form . For general feedback, use the public comments section below (please adhere to guidelines ).

Please select the most appropriate category to facilitate processing of your request

Thank you for taking time to provide your feedback to the editors.

Your feedback is important to us. However, we do not guarantee individual replies due to the high volume of messages.

E-mail the story

Your email address is used only to let the recipient know who sent the email. Neither your address nor the recipient's address will be used for any other purpose. The information you enter will appear in your e-mail message and is not retained by Phys.org in any form.

Newsletter sign up

Get weekly and/or daily updates delivered to your inbox. You can unsubscribe at any time and we'll never share your details to third parties.

More information Privacy policy

Donate and enjoy an ad-free experience

We keep our content available to everyone. Consider supporting Science X's mission by getting a premium account.

E-mail newsletter