what is insight problem solving psychology

Insight Learning Theory: Definition, Stages, and Examples

Categories Learning

Insight learning theory is all about those “lightbulb moments” we experience when we suddenly understand something. Instead of slowly figuring things out through trial and error, insight theory says we can suddenly see the solution to a problem in our minds. 

This theory is super important because it helps us understand how our brains work when we learn and solve problems. It can help teachers find better ways to teach and improve our problem-solving skills and creativity. It’s not just useful in school—insight theory also greatly impacts science, technology, and business.

Table of Contents

What Is Insight Learning?

Insight learning is like having a lightbulb moment in your brain. It’s when you suddenly understand something without needing to go through a step-by-step process. Instead of slowly figuring things out by trial and error, insight learning happens in a flash. One moment, you’re stuck, and the next, you have the solution. 

This type of learning is all about those “aha” experiences that feel like magic. The key principles of insight learning involve recognizing patterns, making connections, and restructuring our thoughts. It’s as if our brains suddenly rearrange the pieces of a puzzle, revealing the big picture. So, next time you have a brilliant idea pop into your head out of nowhere, you might just be experiencing insight learning in action!

Three Components of Insight Learning Theory

Insight learning, a concept rooted in psychology, comprises three distinct properties that characterize its unique nature:

1. Sudden Realization

Unlike gradual problem-solving methods, insight learning involves sudden and profound understanding. Individuals may be stuck on a problem for a while, but then, seemingly out of nowhere, the solution becomes clear. This sudden “aha” moment marks the culmination of mental processes that have been working behind the scenes to reorganize information and generate a new perspective .

2. Restructuring of Problem-Solving Strategies

Insight learning often involves a restructuring of mental representations or problem-solving strategies . Instead of simply trying different approaches until stumbling upon the correct one, individuals experience a shift in how they perceive and approach the problem. This restructuring allows for a more efficient and direct path to the solution once insight occurs.

3. Aha Moments

A hallmark of insight learning is the experience of “aha” moments. These moments are characterized by a sudden sense of clarity and understanding, often accompanied by a feeling of satisfaction or excitement. It’s as if a mental lightbulb turns on, illuminating the solution to a previously perplexing problem. 

These moments of insight can be deeply rewarding and serve as powerful motivators for further learning and problem-solving endeavors.

Four Stages of Insight Learning Theory

Insight learning unfolds in a series of distinct stages, each contributing to the journey from problem recognition to the sudden realization of a solution. These stages are as follows:

1. Problem Recognition

The first stage of insight learning involves recognizing and defining the problem at hand. This may entail identifying obstacles, discrepancies, or gaps in understanding that need to be addressed. Problem recognition sets the stage for the subsequent stages of insight learning by framing the problem and guiding the individual’s cognitive processes toward finding a solution.

2. Incubation

After recognizing the problem, individuals often enter a period of incubation where the mind continues to work on the problem unconsciously. During this stage, the brain engages in background processing, making connections, and reorganizing information without the individual’s conscious awareness. 

While it may seem like a period of inactivity on the surface, incubation is a crucial phase where ideas gestate, and creative solutions take shape beneath the surface of conscious thought.

3. Illumination

The illumination stage marks the sudden emergence of insight or understanding. It is characterized by a moment of clarity and realization, where the solution to the problem becomes apparent in a flash of insight. 

This “aha” moment often feels spontaneous and surprising, as if the solution has been waiting just below the surface of conscious awareness to be revealed. Illumination is the culmination of the cognitive processes initiated during problem recognition and incubation, resulting in a breakthrough in understanding.

4. Verification

Following the illumination stage, individuals verify the validity and feasibility of their insights by testing the proposed solution. This may involve applying the solution in practice, checking it against existing knowledge or expertise, or seeking feedback from others. 

Verification serves to confirm the efficacy of the newfound understanding and ensure its practical applicability in solving the problem at hand. It also provides an opportunity to refine and iterate on the solution based on real-world feedback and experience.

Famous Examples of Insight Learning

Examples of insight learning can be observed in various contexts, ranging from everyday problem-solving to scientific discoveries and creative breakthroughs. Some well-known examples of how insight learning theory works include the following:

Archimedes’ Principle

According to legend, the ancient Greek mathematician Archimedes experienced a moment of insight while taking a bath. He noticed that the water level rose as he immersed his body, leading him to realize that the volume of water displaced was equal to the volume of the submerged object. This insight led to the formulation of Archimedes’ principle, a fundamental concept in fluid mechanics.

Köhler’s Chimpanzee Experiments

In Wolfgang Köhler’s experiments with chimpanzees on Tenerife in the 1920s, the primates demonstrated insight learning in solving novel problems. One famous example involved a chimpanzee named Sultan, who used sticks to reach bananas placed outside his cage. After unsuccessful attempts at using a single stick, Sultan suddenly combined two sticks to create a longer tool, demonstrating insight into the problem and the ability to use tools creatively.

Eureka Moments in Science

Many scientific discoveries are the result of insight learning. For instance, the famed naturalist Charles Darwin had many eureka moments where he gained sudden insights that led to the formation of his influential theories.

Everyday Examples of Insight Learning Theory

You can probably think of some good examples of the role that insight learning theory plays in your everyday life. A few common real-life examples include:

• Finding a lost item : You might spend a lot of time searching for a lost item, like your keys or phone, but suddenly remember exactly where you left them when you’re doing something completely unrelated. This sudden recollection is an example of insight learning.
• Untangling knots : When trying to untangle a particularly tricky knot, you might struggle with it for a while without making progress. Then, suddenly, you realize a new approach or see a pattern that helps you quickly unravel the knot.
• Cooking improvisation : If you’re cooking and run out of a particular ingredient, you might suddenly come up with a creative substitution or alteration to the recipe that works surprisingly well. This moment of improvisation demonstrates insight learning in action.
• Solving riddles or brain teasers : You might initially be stumped when trying to solve a riddle or a brain teaser. However, after some time pondering the problem, you suddenly grasp the solution in a moment of insight.
• Learning a new skill : Learning to ride a bike or play a musical instrument often involves moments of insight. You might struggle with a certain technique or concept but then suddenly “get it” and experience a significant improvement in your performance.
• Navigating a maze : While navigating through a maze, you might encounter dead ends and wrong turns. However, after some exploration, you suddenly realize the correct path to take and reach the exit efficiently.
• Remembering information : When studying for a test, you might find yourself unable to recall a particular piece of information. Then, when you least expect it, the answer suddenly comes to you in a moment of insight.

These everyday examples illustrate how insight learning is a common and natural part of problem-solving and learning in our daily lives.

Exploring the Uses of Insight Learning

Insight learning isn’t an interesting explanation for how we suddenly come up with a solution to a problem—it also has many practical applications. Here are just a few ways that people can use insight learning in real life:

Problem-Solving

Insight learning helps us solve all sorts of problems, from finding lost items to untangling knots. When we’re stuck, our brains might suddenly come up with a genius idea or a new approach that saves the day. It’s like having a mental superhero swoop in to rescue us when we least expect it!

Ever had a brilliant idea pop into your head out of nowhere? That’s insight learning at work! Whether you’re writing a story, composing music, or designing something new, insight can spark creativity and help you come up with fresh, innovative ideas.

Learning New Skills

Learning isn’t always about memorizing facts or following step-by-step instructions. Sometimes, it’s about having those “aha” moments that make everything click into place. Insight learning can help us grasp tricky concepts, master difficult skills, and become better learners overall.

Insight learning isn’t just for individuals—it’s also crucial for innovation and progress in society. Scientists, inventors, and entrepreneurs rely on insight to make groundbreaking discoveries and develop new technologies that improve our lives. Who knows? The next big invention could start with someone having a brilliant idea in the shower!

Overcoming Challenges

Life is full of challenges, but insight learning can help us tackle them with confidence. Whether it’s navigating a maze, solving a puzzle, or facing a tough decision, insight can provide the clarity and creativity we need to overcome obstacles and achieve our goals.

The next time you’re feeling stuck or uninspired, remember: the solution might be just one “aha” moment away!

Alternatives to Insight Learning Theory

While insight learning theory emphasizes sudden understanding and restructuring of problem-solving strategies, several alternative theories offer different perspectives on how learning and problem-solving occur. Here are some of the key alternative theories:

Behaviorism

Behaviorism is a theory that focuses on observable, overt behaviors and the external factors that influence them. According to behaviorists like B.F. Skinner, learning is a result of conditioning, where behaviors are reinforced or punished based on their consequences. 

In contrast to insight learning theory, behaviorism suggests that learning occurs gradually through repeated associations between stimuli and responses rather than sudden insights or realizations.

Cognitive Learning Theory

Cognitive learning theory, influenced by psychologists such as Jean Piaget and Lev Vygotsky , emphasizes the role of mental processes in learning. This theory suggests that individuals actively construct knowledge and understanding through processes like perception, memory, and problem-solving. 

Cognitive learning theory acknowledges the importance of insight and problem-solving strategies but places greater emphasis on cognitive structures and processes underlying learning.

Gestalt Psychology

Gestalt psychology, which influenced insight learning theory, proposes that learning and problem-solving involve the organization of perceptions into meaningful wholes or “gestalts.” 

Gestalt psychologists like Max Wertheimer emphasized the role of insight and restructuring in problem-solving, but their theories also consider other factors, such as perceptual organization, pattern recognition, and the influence of context.

Information Processing Theory

Information processing theory views the mind as a computer-like system that processes information through various stages, including input, processing, storage, and output. This theory emphasizes the role of attention, memory, and problem-solving strategies in learning and problem-solving. 

While insight learning theory focuses on sudden insights and restructuring, information processing theory considers how individuals encode, manipulate, and retrieve information to solve problems.

Related reading:

• What Is Kolb’s Learning Cycle?
• What Is Latent Learning?
• What Is Scaffolding in Psychology?
• What Is Observational Learning?

Kizilirmak, J. M., Fischer, L., Krause, J., Soch, J., Richter, A., & Schott, B. H. (2021). Learning by insight-like sudden comprehension as a potential strategy to improve memory encoding in older adults .  Frontiers in Aging Neuroscience ,  13 , 661346. https://doi.org/10.3389/fnagi.2021.661346

Lind, J., Enquist, M. (2012). Insight learning and shaping . In: Seel, N.M. (eds) Encyclopedia of the Sciences of Learning . Springer, Boston, MA. https://doi.org/10.1007/978-1-4419-1428-6_851

Osuna-Mascaró, A. J., & Auersperg, A. M. I. (2021). Current understanding of the “insight” phenomenon across disciplines . Frontiers in Psychology , 12, 791398. https://doi.org/10.3389/fpsyg.2021.791398

Salmon-Mordekovich, N., & Leikin, M. (2023). Insight problem solving is not that special, but business is not quite ‘as usual’: typical versus exceptional problem-solving strategies .  Psychological Research ,  87 (6), 1995–2009. https://doi.org/10.1007/s00426-022-01786-5

Insight Learning (Definition+ 4 Stages + Examples)

Have you ever been so focused on a problem that it took stepping away for you to figure it out? You can’t find the solution when you’re looking at all of the moving parts, but once you get distracted with something else - “A-ha!” you have it. 

When a problem cannot be solved by applying an obvious step-by-step solving sequence,   Insight learning occurs when the mind rearranges the elements of the problem and finds connections that were not obvious in the initial presentation of the problem. People experience this as a sudden A-ha moment.

Humans aren’t the only species that have these “A-ha” moments. Work with other species helped psychologists understand the definition and stages of Insight Learning. This video is going to break down those stages and how you can help to move these “a-ha” moments along. 

What Is Insight Learning? 

Insight learning is a process that leads to a sudden realization regarding a problem. Often, the learner has tried to understand the problem, but steps away before the change in perception occurs. Insight learning is often compared to trial-and-error learning, but it’s slightly different.

Rather than just trying different random solutions, insight learning requires more comprehension. Learners aim to understand the relationships between the pieces of the puzzle. They use patterns, organization, and past knowledge to solve the problem at hand. 

Is Insight Learning Only Observed In Humans? 

Humans aren’t the only species that learn with insight. Not all species use this process - just the ones that are closest to us intellectually. Insight learning was first discovered not by observing humans, but by observing chimps. 

In the early 1900s, Wolfgang Köhler observed chimpanzees as they solved problems. Köhler’s most famous subject was a chimp named Sultan. The psychologist gave Sultan two sticks of different sizes and placed a banana outside of Sultan’s cage. He watched as Sultan looked at the sticks and tried to reach for the banana with no success. Eventually, Sultan gave up and got distracted. But it was during this time that Köhler noticed Sultan having an “epiphany.” The chimp went back to the sticks, placed one inside of the other, and used this to bring the banana to him. 

Since Köhler’s original observations took place, psychologists looked deeper into the insight process and when you are more likely to experience that “a-ha” moment. There isn’t an exact science to insight learning, but certain theories suggest that some places are better for epiphanies than others. 

Four Stages of Insight Learning 

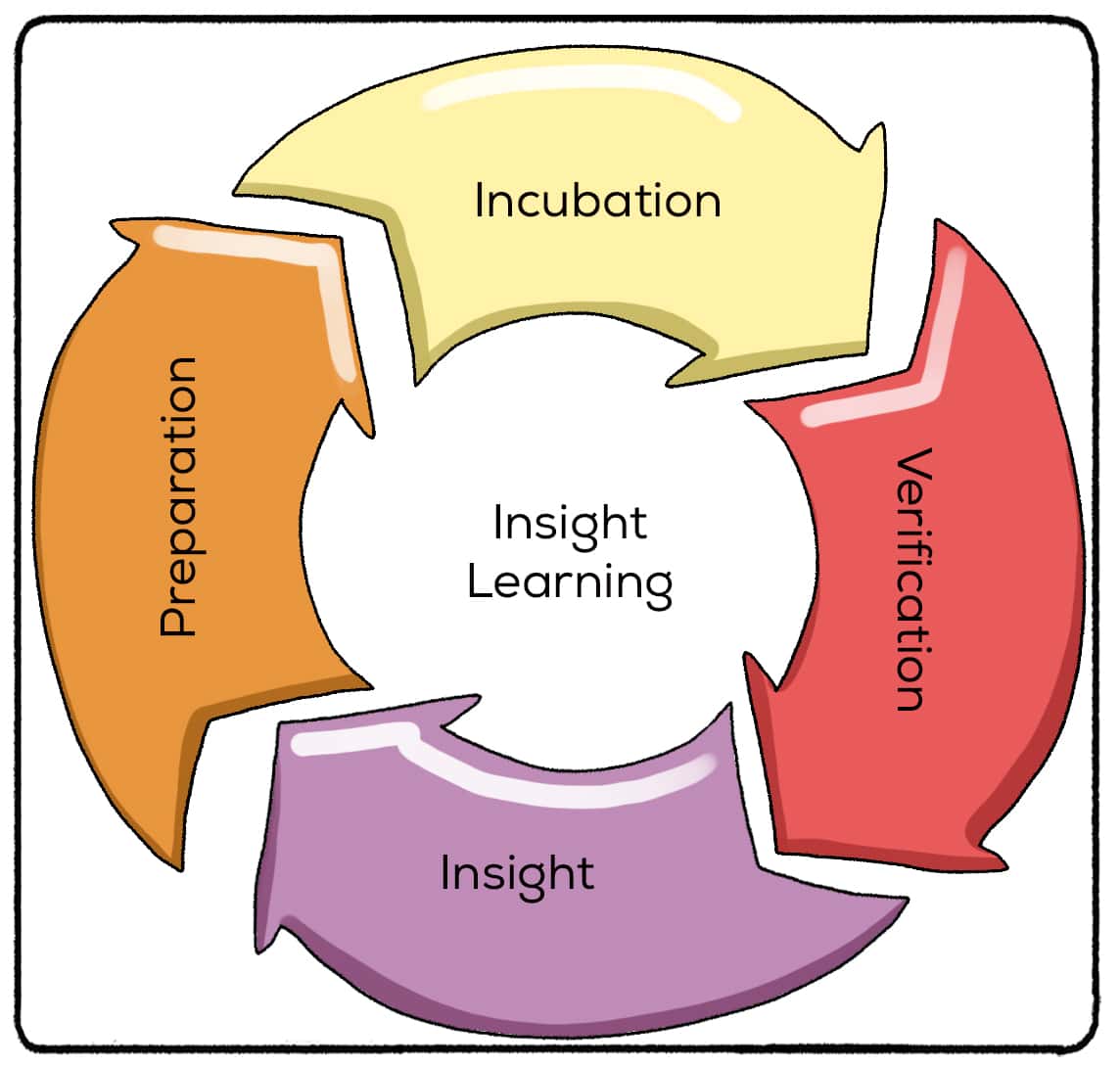
But how does insight learning happen? Multiple models have been developed, but the four-stage model is the most popular. The four stages of insight learning are preparation, incubation, insight, and verification. 

Preparation

The process begins as you try to solve the problem. You have the materials and information in front of you and begin to make connections. Although you see the relationships between the materials, things just haven’t “clicked” yet. This is the stage where you start to get frustrated. 

During the incubation period, you “give up” for a short period of time. Although you’ve abandoned the project, your brain is still making connections on an unconscious level. 

When the right connections have been made in your mind, the “a-ha” moment occurs. Eureka! You have an epiphany! 

Verification

Now, you just have to make sure that your epiphany is right. You test out your solution and hopefully, it works! This is a great moment in your learning journey. The connections you make solving this problem are likely to help you in the future. 

Examples of Insight Learning

Insight learning refers to the sudden realization or understanding of a solution to a problem without the need for trial-and-error attempts. It's like a "light bulb" moment when things suddenly make sense. Here are some examples of insight learning:

• The Matchstick Problem : Realizing you can light a match and use it to illuminate a dark room instead of fumbling around in the dark.
• Sudoku Puzzles : Suddenly seeing a pattern or number placement that you hadn't noticed before, allowing you to complete the puzzle.
• The Two Rope Problem : In an experiment, a person is given two ropes hanging from the ceiling and is asked to tie them together. The solution involves swinging one rope like a pendulum and grabbing it with the other.
• Opening Jars : After struggling to open a jar, you remember you can tap its lid lightly or use a rubber grip to make it easier.
• Tangram Puzzles : Suddenly realizing how to arrange the geometric pieces to complete the picture without any gaps.
• Escape Rooms : Having an "aha" moment about a clue that helps you solve a puzzle and move to the next challenge.
• The Nine Dot Problem : Connecting all nine dots using only four straight lines without lifting the pen.
• Cooking : Realizing you can soften butter quickly by grating it or placing it between two sheets of parchment paper and rolling it.
• Math Problems : Suddenly understanding a complex math concept or solution method after pondering it for a while.
• Guitar Tuning : Realizing you can use the fifth fret of one string to tune the next string.
• Traffic Routes : Discovering a faster or more efficient route to your destination without using a GPS.
• Packing Suitcases : Figuring out how to fit everything by rolling clothes or rearranging items in a specific order.
• The Crow and the Pitcher : A famous Aesop's fable where a thirsty crow drops pebbles into a pitcher to raise the water level and drink.
• Computer Shortcuts : Discovering a keyboard shortcut that makes a task you frequently do much quicker.
• Gardening : Realizing you can use eggshells or coffee grounds as a natural fertilizer.
• Physics Problems : After struggling with a concept, suddenly understanding the relationship between two variables in an equation.
• Art : Discovering a new technique or perspective that transforms your artwork.
• Sports : Realizing a different way to grip a tennis racket or baseball bat that improves your game.
• Language Learning : Suddenly understanding the grammar or pronunciation rule that was previously confusing.
• DIY Projects : Figuring out a way to repurpose old items in your home, like using an old ladder as a bookshelf.

Where Is the Best Place to Have an Epiphany? 

But what if you want to have an epiphany? You’re stuck on a problem and you can’t take it anymore. You want to abandon it, but you’re not sure what you should do for this epiphany to take place. Although an “a-ha” moment isn’t guaranteed, studies suggest that the following activities or places can help you solve a tough problem. 

The Three B’s of Creativity 

Creativity and divergent thinking are key to solving problems. And some places encourage creativity more than others. Researchers believe that you can kickstart divergent thinking with the three B’s: bed, bath, and the bus. 

Sleep 

“Bed” might be your best bet out of the three. Studies show that if you get a full night’s sleep, you will be twice as likely to solve a problem than if you stay up all night. This could be due to the REM sleep that you get throughout the night. During REM sleep , your brain is hard at work processing the day’s information and securing connections. Who knows - maybe you’ll dream up the answer to your problems tonight!

Meditation 

The word for “insight” in the Pali language is vipassana. If you have ever been interested in meditation , you might have seen this word before. You can do a vipassana meditation at home, or you can go to a 10-day retreat. These retreats are often silent and are set up to cultivate mind-body awareness. 

You certainly don’t have to sign up for a 10-day silent retreat to solve a problem that is bugging you. (Although, you may have a series of breakthroughs!) Try meditating for 20 minutes at a time. Studies show that this can increase the likelihood of solving a problem. 

Laugh! 

How do you feel when you have an epiphany? Good, right? The next time you’re trying to solve a problem, check in with your emotions. You are more likely to experience insight when you’re in a positive mood. Positivity opens your mind and gives your mind more freedom to explore. That exploration may just lead you to your solution. 

Be patient when you’re trying to solve problems. Take breaks when you need to and make sure that you are taking care of yourself. This approach will help you solve problems faster and more efficiently!

Insight Vs. Other Types Of Learning.

Learning by insight is  not  learning by trial and  error, nor by observation  and imitation. Learning by insight is a learning theory accepted by the Gestalt  school of psychology, which disagrees with the behaviorist  school, which claims that all learning occurs through conditioning from the  external environment.

Gestalt is a German word that approximately translates as ‘an organized whole  that has properties  and elements in addition to the sum of its parts .’ By viewing a problem as a ‘gestalt’ , the learner does not simply react to whatever she observes at the moment. She also imagines elements that could be present but are not and uses her imagination to combine parts of the problem that are presently not so combined in fact.  

Insight Vs. Trial And Error Learning

Imagine yourself in a maze-running competition. You and your rivals each have 10 goes. The first one to run the maze successfully wins $500. You may adopt a trial-and-error strategy, making random turning decisions and remembering whether those particular turns were successful or not for your next try. If you have a good memory and with a bit of luck, you will get to the exit and win the prize.

Completing the maze through trial and error requires no insight. If you had to run a different maze, you would have no advantage over running previous mazes with different designs. You have now learned to run this particular maze as predicted by behaviorist psychologists. External factors condition your maze running behavior. The cash prize motivates  you to run the maze in the first place. All maze dead ends act as punishments , which you remember not to repeat. All correct turns act as rewards , which you remember to repeat.

If you viewed the maze running competition as a gestalt, you might notice that it doesn't explicitly state in the competition rules that you must run along the designated paths to reach the exit.

Suppose you further noticed that the maze walls were made from cardboard. In that case, you may combine those 2 observations in your imagination and realize that you could just punch big holes in the walls or tear them down completely, to see around corners and directly run to the now visible exit.

Insight Vs. Learning Through Observation, Imitation, And Repetition

Observation, imitation, and repetition are at the heart of training. The violin teacher shows you how to hold your bow correctly; you practice your scales countless times before learning to play a sonata from Beethoven flawlessly. Mastering a sport or a musical instrument rarely comes from a flash of insight but a lot of repetition and error correction from your teacher.

Herbert Lawford, the Scottish tennis player, and 1887 Wimbledon champion, is credited for being the first player to play a topspin. Who could have taught it to him? Who could he have imitated? One can only speculate since no player at that time was being coached on how to hit topspin.

He could have only learned to play a topspin by having a novel insight. One possibility is that he played one by accident during training, by mistakenly hitting the ball at a flatter angle than normal. He could then have observed that his opponent was disorientated by the flatter and quicker bounce of the ball and realized the benefit of his ‘mistake’ .

Behaviorist theories of learning can probably explain how most successful and good tennis players are produced, but you need a Gestalt insight learning theory to explain Herbert Lawford.

Another interesting famous anecdote illustrating insight learning concerned Carl Friedrich Gauss when he was a 7-year-old pupil at school. His mathematics teacher seems to have adopted strict behaviorism in his teaching since the original story implies that he beat students with a switch.

One day the teacher set classwork requiring the students to add up all the numbers from 1 to 100. He expected his pupils to perform this calculation in how they were trained. He expected it to be a laborious and time-consuming task, giving him a long break. In just a few moments, young Gauss handed in the correct answer after having to make at most 2 calculations, which are easy to do in your head. How did he do it? Gauss saw the arithmetic sequence as a gestalt instead of adding all the numbers one at a time: 1+2+3+4…. +99+100 as he expected.

He realized that by breaking this sequence in half at 50, then snaking the last number (100) under the first number (1), and then adding the 2 halves of the arithmetic sequence like so:  

    1         +        2       +        3      +       4      +       5         +    ………….      +        48        +        49             +       50

100        +       99       +      98      +     97      +      96       +    …………...    +        53        +         52           +       51

101        +      101      +    101     +    101      +     101     +   …………….     +     101        +       101           +     101    

Arranged in this way, each number column adds up to 101, so all Gauss needed to do was calculate 50 x 101 = 5050.

Can Major Scientific Breakthroughs be made through observation and experiment alone?

Science is unapologetically an evidence-based inquiry. Observations, repeatable experiments, and hard, measurable data must support theories and explanations.

Since countless things can be observed and comparisons made, they cannot be done randomly for observations and experiments to advance knowledge. They must be guided by a good question and a  testable hypothesis. Before performing actual experiments and observations, scientists often first perform thought experiments . They think of ideal situations by imagining ways things could be or imaging away things that are.

Atoms were talked about long before electron microscopes could observe them. How could atoms be seriously discussed in ancient Greece long before the discoveries of modern chemistry? Pre-Socratic philosophers were puzzled by a purely philosophical problem, which they termed the problem of the one and many .  

People long observed that the world was made of many different things that didn't remain static but continuously changed into other various things. For example, a seed different from a tree changed into a tree over time. Small infants change into adults yet remain the same person. Boiling water became steam, and frozen water became ice.

Observing all of this in the world, philosophers didn’t simply take it for granted and aimed to profit from it practically through stimulus-response and trial and error learning. They were puzzled by how the world fit together as a whole.

To make sense of all this observable changing multiplicity, one needed to imagine an unobservable sameness behind it all. Yet, there is no obvious or immediate punishment or reward. Therefore, there seems to be no satisfying behaviorist reason behind philosophical speculations.

Thinkers such as Empedocles and Aristotle made associations between general properties in the world wetness, dryness, temperature, and phases of matter as follows:

• Earth :  dry, cold     
• Fire:  dry, hot
• Water:  wet, cold
• Air: hot or wet, depending on whether moisture or heat prevails in the atmosphere.

These 4 primitive elements transformed and combined give rise to the diversity we see in the world. However, this view was still too sensually based  to provide the world with sought-for coherence and unity. How could a multiplicity of truly basic stuff interact? Doesn't such an interaction presuppose something more fundamental in common?

The ratio of these 4 elements was thought to affect the properties of things. Stone contained more earth, while a rabbit had more water and fire, thus making it soft and giving it life. Although this theory correctly predicted that seemingly basic things like stones were complex compounds, it had some serious flaws.

For example, if you break a stone in half many times, the pieces never resemble fire, air, water, or earth.   

To account for how different things could be the same on one level and different on another level, Leucippus and his student Democritus reasoned that all things are the same in that they were made from some common primitive indivisible stuff but different due to the different ways or patterns in which this indivisible stuff or atoms could be arranged.

For atoms to be able to rearrange and recombine into different patterns led thinkers to the insight that if the atom idea was true, then logically, there had to be free spaces between the atoms for them to shift into. They had to imagine a vacuum, another phenomenon not directly observable since every nook and cranny in the world seems to be filled with some liquid, solid, or gas.  

This ancient notion of vacuum proved to be more than just a made-up story since it led to modern practical applications in the form of vacuum cleaners and food vacuum packing.

This insight that atoms and void exist makes no sense from a behaviorist learning standpoint. It cannot be explained in terms of stimulus-response or environmental conditioning and made no practical difference in the lives of ancient Greeks.  

For philosophers to feel compelled to hold onto notions, which at the time weren’t directly useful, it suggests that they must have felt some need to understand the universe as an intelligible ‘gestalt’ One may even argue that the word Cosmos, from the Greek word Kosmos, which roughly translates to ‘harmonious arrangement’ is at least a partial synonym.  

The Historical Development Of The Theory of Insight Learning

Wolfgang Kohler , the German gestalt psychologist, is credited for formulating the theory of insight learning, one of the first cognitive learning theories. He came up with the theory while first conducting experiments  in 1913 on 7 chimpanzees  on the island of Tenerife to observe how they learned to solve problems.

In one experiment, he dangled a banana from the top of a high cage. Boxes and poles were left in the cage with the chimpanzees. At first, the chimps used trial and error to get at the banana. They tried to jump up to the banana without success. After many failed attempts, Kohler noticed that they paused to think  for a while.  

After some time, they behaved more methodically by stacking the boxes on top of each other, making a raised platform from which they could swipe at the banana using the available poles. Kohler believed that chimps, like humans, were capable of experiencing flashes of insight, just like humans.

In another experiment, he placed a peanut down a long narrow tube attached to the cage's outer side. The chimpanzee tried scooping the peanut out with his hand and fingers, but to no avail, since the tube was too long and narrow. After sitting down to think, the chimp filled its mouth with water from a nearby water container in the cage and spat it into the tube.

The peanut floated up the tube within the chimp's reach. What is essential is that the chimp realized it could use water as a tool in a flash of insight, something it had never done before or never shown how  to do .  Kohler's conclusions contrasted with those of American psychologist Edward Thorndike , who, years back, conducted learning experiments on cats, dogs, and monkeys.

Through his experiments and research, Thorndike concluded that although there was a vast difference in learning speed and potential between monkey dogs and cats, he concluded that all animals, unlike humans, are not capable of genuine reasoned thought. According to him, Animals can only learn through stimulus-response conditioning, trial and error, and solve problems accidentally.

Kohler’s 4 Stage Model Of Insight Learning

From his observations of how chimpanzees solve complex problems, he concluded that the learning process went through the following 4 stages:

• Preparation:  Learners encounter the problem and begin to survey all relevant information and materials. They process stimuli and begin to make connections.
• Incubation: Learners get frustrated and may even seem to observers as giving up. However, their brains carry on processing information unconsciously.
• Insight: The learner finally achieves a breakthrough, otherwise called an epiphany or ‘Aha’ moment. This insight comes in a flash and is often a radical reorganization of the problem. It is a discontinuous leap in understanding rather than continuous with reasoning undertaken in the preparation phase.
• Verification: The learner now formally tests the new insight and sees if it works in multiple different situations. Mathematical insights are formally proved.

The 2 nd  and 3 rd  stages of insight learning are well described in anecdotes of famous scientific breakthroughs. In 1861, August Kekulé was contemplating the structure of the Benzene molecule. He knew it was a chain of 6 carbon atoms attached to 6 hydrogen atoms. Still, He got stuck   (incubation phase)  on working out how they could fit together to remain chemically stable.

He turned away from his desk and, facing the fireplace, fell asleep. He dreamt of a snake eating its tail and then spinning around. He woke up and realized (insight phase)  that these carbon-hydrogen chains can close onto themselves to form hexagonal rings. He then worked out the consequences of his new insight on Benzene rings. (Verification phase)

Suitably prepared minds can experience insights while observing ordinary day-to-day events. Many people must have seen apples fall from trees and thought nothing of it. When Newton saw an apple fall, he connected its fall to the action of the moon. If an unseen force pulls the apple from the tree top, couldn't the same force extends to the moon? This same force must be keeping the moon tethered in orbit around the earth, keeping it from whizzing off into space. Of course, this seems counterintuitive because if the moon is like the apple, should it not be crashing down to earth?

Newton's prepared mind understood the moon to be continuously falling to earth around the horizon's curve. Earth's gravitational pull on the moon balanced its horizontal velocity tangential to its orbit. If the apple were shot fast enough over the horizon from a cannon, it too, like the moon, would stay in orbit.

So, although before Newton, everyone was aware of gravity in a stimulus-response kind of way and even made practical use of it to weigh things, no one understood its universal implications.

Applying Insight Learning To The Classroom

The preparation-incubation-insight- verification cycle could be implemented by teachers in the classroom. Gestalt theory predicts that students learn best when they engage with the material; they are mentally prepared  for age, and maturity, having had experiences enabling them to relate to the material and having background knowledge that allows them to contextualize the material. When first presenting content they want to teach the students, teachers must make sure students are suitably prepared to receive the material, to successfully go through the preparation stage of learning.

Teachers should present the material holistically and contextually. For example, when teaching about the human heart, they should also teach where it is in the human body and its functional importance and relationship to other organs and parts of the body. Teachers could also connect other fields, such as comparing hearts to mechanical pumps.

Once the teacher has imparted sufficient background information to students, they should set a problem for their students to solve independently or in groups. The problem should require the students to apply what they have learned in a new way and make novel connections not explicitly made by the teacher during the lesson.

However, they must already know and be familiar with all the material they need to solve the problem. Students must be allowed to fumble their way to a solution  and make many mistakes , as this is vital for the incubation phase. The teacher should resist the temptation to spoon-feed them. Instead, teachers should use the Socratic method to coax the students into arriving at solutions and answers themselves.

Allowing the students to go through a sufficiently challenging incubation phase engages all their higher cognitive functions, such as logical and abstract reasoning, visualization, and imagination. It also habituates them to a bit of frustration to build the mental toughness to stay focused.

It also forces their brains to work hard in processing combining information to sufficiently own the insights they achieve, making it more likely that they will retain  the knowledge they gained and be able to apply it across different contexts.

Once students have written down their insights and solutions, the teacher should guide them through the verification phase. The teacher and students need to check and test the validity of the answers. Solutions should be checked for errors and inconsistencies and checked against the norms and standards of the field.

However, one should remember that mass education is aimed at students of average capacity and that not all students are always equally capable of learning through insight. Also, students need to be prepared to gain the ability and potential to have fruitful insights.  

Learning purely from stimulus-response conditioning is insufficient for progress and major breakthroughs to be made in the sciences. For breakthroughs to be made, humans need to be increasingly capable of higher and higher levels of abstract thinking.

However, we are not all equally capable of having epiphanies on the cutting edge of scientific research. Most education aims to elevate average reasoning, knowledge, and skill acquisition. For insight, learning must build on rather than replace behaviorist teaching practices.

Related posts:

• The Psychology of Long Distance Relationships
• Beck’s Depression Inventory (BDI Test)
• Operant Conditioning (Examples + Research)
• Variable Interval Reinforcement Schedule (Examples)
• Concrete Operational Stage (3rd Cognitive Development)

Reference this article:

About The Author

Operant Conditioning

Classical Conditioning

Observational Learning

Latent Learning

Experiential Learning

The Little Albert Study

Bobo Doll Experiment

Spacing Effect

Von Restorff Effect

PracticalPie.com is a participant in the Amazon Associates Program. As an Amazon Associate we earn from qualifying purchases.

Follow Us On:

Youtube Facebook Instagram X/Twitter

Psychology Resources

Developmental

Personality

Relationships

Psychologists

Serial Killers

Psychology Tests

Personality Quiz

Memory Test

Depression test

Type A/B Personality Test

© PracticalPsychology. All rights reserved

Privacy Policy | Terms of Use

What Is Insight? Definition, Psychology, And Practical Examples

The Merriam-Webster dictionary defines insight as “the act or result of apprehending the inner nature of things or of seeing intuitively.” Psychology sees insight not as a means of acquiring insightful knowledge but rather as the act of becoming aware of insightful solutions. It can be helpful to understand both definitions of insight to know how to use it to improve your mental health. 

What’s the difference between insight and knowledge? 

Some subjects may be taught directly, while you can learn others from observation and repetition. You might notice that some knowledge seems to appear out of thin air. Before understanding insight psychology, taking a detour to understanding knowledge can be beneficial. 

What is knowledge? 

Knowledge is an awareness or familiarity with objects, events, ideas, or actions learned from experience, being taught, or instinct from birth. Articulation of this concept can be found in the movie  Memento  (2000) when the main character, who experiences short-term memory loss, explains that, despite not being able to remember what he had completed a few moments ago, he could understand inherent knowledge. For example, he knew the sound of knocking on wood and the feeling of lifting a glass of water. He says this type of knowledge is different because it is a form of memory.

How does insight relate to knowledge? 

Wolfgang Kohler and his work with the  Gestalt theory led him to some interesting findings in the early 1900s. He experimented with his chimp Sultan. In his experiment, Sultan was hungry. A banana was held out of reach. The only tools Sultan could use to reach the banana were two bamboo sticks of differing lengths, neither long enough to reach the banana.

Eventually, Sultan figured out that he could fit them together by playing with the sticks to form one long rod that would reach the banana. Unlike trial and error, Sultan used reason for this solution. He had given up actively trying different ways to get the banana when he discovered the sticks could be combined. The answer came to him in what is commonly referred to as an “Aha!” moment.

The key to this insight psychology is idleness or a reduced ability to see the finish line. Like Sultan, the subject or client may give up on finding a solution. As desperation approaches, they may use creativity and insight by combining their current knowledge of events with new knowledge. 

How psychologists interpret insight

Among psychologists, there are varying interpretations of how knowledge and reasoning combine to present the consciousness with a viable solution to a given task. Below are a few theories. 

The nothing special view 

In the “nothing special” theory, insight occurs as a natural process of the brain continually taking in information and working to make the best use of it. A solution may arrive when presented with a task or issue due to how a person processes information. In this theory, no special or esoteric significance is given to intuition. 

The neo-Gestaltist view

As with Kohler and Sultan, the Gestaltist view states that insight solution problem solving is not simple. Instead, they believe it has a special quality, placing it cognitively higher than routine problem-solving.

The three process view 

The three-process view posits that there are three individual types of insight, including the following: 

• Selective-Encoding Insight: Distinguishing relevant from irrelevant information
• Selective-Comparison Insight: Renewed perception of the relationship between old information and new information
• Selective-Combination Insight: Using encoded information and applying it in a novel way.

The four stages of behavioral processes

Insight is marked by four stages of behavioral processes, including impasse, fixation, incubation, and the eureka moment.

• Impasse: An impasse occurs when one gives up or reaches an area they struggle to solve. 
• Fixation: Fixation may be a particular solution attempted that is ineffective but attempted more than once, often with an obsessive focus. 
• Incubation: Incubation is a gap in solution attempts allowing the mind to clear itself of irrelevant information pertaining to the solution. 
• Eureka: Eureka involves the appearance of a solution in the individual’s mind that suddenly becomes clear. 

What does psychological research say about insight? 

Insight may affect how you live your life, tackle obstacles, and practice mental health and well-being. Below are a few studies on insight. 

Graham Wallas and the nine dot puzzle

When dealing with abstract concepts, reframing them into concrete examples may be helpful. For example, Graham Wallas used the nine-dot puzzle in 1926 to show how individuals can arrive at solutions by insight. The goal was to connect all nine dots with a pencil without lifting the pencil off the paper and using the fewest possible lines. At first glance, it may seem impossible to complete the task due to a narrow perception.

Because the dots appear to be in a rectangle shape, your brain may assume the solution must be derived by drawing a rectangle. Once the insight that the rectangle does not exist or limit the puzzle, the solution to “go outside the lines” may be more prominent. You may be able to solve the puzzle using triangles or a zig-zag pattern. 

Responses to the nine dot puzzle and banana problem

When you apply the insight psychology definition to mental health, it is not a banana or a puzzle on a piece of paper but rather an insight into the psyche. Many symptoms of mental health conditions are challenging to treat because of a lack of insight.

Not being aware that a symptom is a symptom of a mental health condition can be detrimental to finding the correct treatment. For example, those who experience substance use disorders may struggle to see that their substance use is a problem, rationalizing it by saying they can stop when they want to. Believing they do not have a problem can be a lack of insight. In these cases, having a guiding voice like a therapist can be beneficial. 

If you are struggling with substance use, contact the SAMHSA National Helpline at (800) 662-4357 to receive support and resources. Support is available 24/7.

What are a few examples of insight? 

Anyone can use insight, which doesn’t necessarily relate to psychology or treating mental illness. Problem-solving comes in all different shapes and sizes. In relationships, conflict can be an area where individuals use insight. Whether in familial or romantic relationships, you may find yourself at an impasse stage, feeling you’ve exhausted all options. Conflict at an impasse can be stressful for all parties and make the relationship seem hopeless. Below are a couple of examples that showcase insight. 

Relationship example 

If two spouses experience a pattern of constantly arguing, with communication breaking down, there can be a tendency to want to give up on the marriage. Taking time to step back from the situation, let emotions settle, and allow reason to prevail can provide insight.  Introspection psychology , an act of examining or observing thoughts, emotions, and perceptions, allows individuals to gain insight. Knowledge of oneself and time to breathe can offer a different perspective for the “Aha!” moment to occur. A relationship is often complex and unique. Applying these concepts when appropriate may help you avoid conflict and stress. 

Therapy example 

Insight can also be helpful in a therapeutic session. For example, clients with social anxiety can shift their paradigm from fear of social situations to learning to manage their symptoms from within. Someone who pushes people away but craves intimacy can benefit from the insight that their actions may stem from a fear of abandonment. Many people may experience “Aha!” moments of eureka in therapy. 

What to expect from insight psychology therapy

While it can be empowering to become aware of the above processes and apply them in your personal life, it can be overwhelming to wade through the ideas in your mind alone. In therapy, you can discuss these concerns with your therapist while maintaining an open, trusting relationship. If this is not your experience or you find in-person therapy inaccessible due to finances, location, or accessibility, you might try online therapy through a platform like BetterHelp. 

Some methods of therapy have been aligned to elicit insight. For example, researchers have developed metacognitive insight and reflection therapy (MERIT) to help individuals recover from psychosis. Following a three-month trial,  a 2020 study found significantly improved metacognition and other benefits from administering MERIT. 

These insights were particularly pronounced among those who did not understand or believe that they had a problem, a common effect of psychosis. MERIT is increasingly available to psychologists around the US, as well as those who practice online.  A recent survey revealed  that nearly a third of respondents would not seek in-person counseling but would do so if online therapy were available. Online therapy continues to gain popularity, with four out of ten Americans using it since 2021. 

Therapy is insight: Learn more about insight and insight therapy

Please find us inside these links:

If you need a crisis hotline or want more insight into therapy, please see below:

• RAINN  (Rape, Abuse, and Incest National Network) -  1-800-656-4673
• The National Suicide Prevention Lifeline -  1-800-273-8255
• National Domestic Violence Hotline  -  1-800-799-7233
• NAMI Helpline (National Alliance on Mental Illness) -  1-800-950-6264

For more insight on mental health, please see:

• SAMHSA (Substance Abuse and Mental Health Services Administration)  SAMHSA Facebook ,  SAMHSA Twitter ,  SAMHSA LinkedIn
• Mental Health America,  MHA Twitter ,  MHA Facebook ,  MHA Instagram ,  MHA Pinterest ,  MHA LinkedIn
• WebMD,  WebMD Facebook ,  WebMD Twitter ,  WebMD Pinterest ,  WebMD LinkedIn
• NIMH (National Institute of Mental Health),  NIMH Facebook ,  NIMH Twitter, NIMH YouTube ,  NIMH LinkedIn
• APA  (American Psychiatric Association),  APA Twitter ,  APA Facebook ,  APA LinkedIn ,  APA Instagram

Get help and insight now:

• Emergency: 911
• National Domestic Violence Hotline: 1-  800-799-7233
• National Suicide Prevention Lifeline: 1-800-273-TALK (8255)
• National Hopeline Network: 1-800-SUICIDE (784-2433)
• Crisis Text Line: Text “DESERVE” TO 741-741
• Lifeline Crisis Chat (Online live messaging): https://suicidepreventionlifeline.org/chat/
• What Is Theory Of Mind? Psychology And Knowledge Of Self And Others Medically reviewed by April Justice , LICSW
• Memory Consolidation: Definition And Examples In Psychology Medically reviewed by Laura Angers Maddox , NCC, LPC
• Psychologists
• Relationships and Relations

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Review Article
• Published: 14 December 2023

Restructuring processes and Aha! experiences in insight problem solving

• Jennifer Wiley   ORCID: orcid.org/0000-0002-2590-7392 1 &
• Amory H. Danek   ORCID: orcid.org/0000-0002-2849-8774 2  

Nature Reviews Psychology volume  3 ,  pages 42–55 ( 2024 ) Cite this article

496 Accesses

2 Citations

6 Altmetric

Metrics details

• Human behaviour

Insightful solution processes represent cases of problem solving in which the emergence of a new interpretation allows for an abrupt shift from bewilderment to clarity. One approach to researching insight problem solving emphasizes cognitive restructuring of the problem representation as a defining feature of the insightful solution process. By contrast, another approach emphasizes phenomenological Aha! experiences. In this Review, we summarize both approaches, considering the restructuring processes involved in finding a solution and the Aha! experiences that might accompany solutions. We then consider the extent to which Aha! experiences co-occur with restructuring, and the critical observation that sometimes they do not. We conclude by proposing avenues for future research that combine the methodologies used to study restructuring and Aha! experiences to better understand the cognitive and phenomenological underpinnings of insight problem solving and the connections between them.

This is a preview of subscription content, access via your institution

Access options

Subscribe to this journal

Receive 12 digital issues and online access to articles

55,14 € per year

only 4,60 € per issue

Buy this article

• Purchase on Springer Link
• Instant access to full article PDF

Prices may be subject to local taxes which are calculated during checkout

Similar content being viewed by others

Testing theory of mind in large language models and humans

Microdosing with psilocybin mushrooms: a double-blind placebo-controlled study

Simple Behavioral Analysis (SimBA) as a platform for explainable machine learning in behavioral neuroscience

Duncker, K. On problem-solving. Psychol. Monogr. 58 , 270 (1945).

Article   Google Scholar  

Ellen, P. Direction, past experience, and hints in creative problem solving: reply to Weisberg and Alba. J. Exp. Psychol. 111 , 316–325 (1982).

Katona, G. Organizing and Memorizing: Studies in the Psychology of Learning and Teaching (Columbia Univ. Press, 1940).

Köhler, W. An aspect of Gestalt psychology. Ped. Sem. J. Genet. Psychol. 32 , 691–723 (1925).

Google Scholar  

Luchins, A. S. Mechanization in problem solving: the effect of Einstellung . Psychol. Monogr. 54 , i–95 (1945).

Maier, N. R. F. Reasoning in humans. I. On direction. J. Comp. Psychol. 10 , 115–143 (1930).

Maier, N. R. F. Reasoning in humans. II. The solution of a problem and its appearance in consciousness. J. Comp. Psychol. 12 , 181–194 (1931).

Wertheimer, M. Productive Thinking Enlarged edn (Harper and Brothers, 1945/1959).

Ash, I. K., Cushen, P. J., & Wiley, J. Obstacles in investigating the role of restructuring in insightful problem solving. J. Probl. Solving https://doi.org/10.7771/1932-6246.1056 (2009).

Ohlsson, S. in Advances in the Psychology of Thinking (eds Keane, M. T. & Gilhooly, K. J.) 1–44 (Harvester Wheatsheaf, 1992).

Ohlsson, S. Deep Learning: How the Mind Overrides Experience (Cambridge Univ. Press, 2011).

Bühler, K. Tatsachen und Probleme zu einer Psychologie der Denkvorgänge. II. Über Gedankenzusammenhänge. Arch. Gesamte Psychol. 12 , 1–23 (1908).

Bowden, E. M. The effect of reportable and unreportable hints on anagram solution and the Aha! Experience. Conscious. Cogn. 6 , 545–573 (1997).

Article   PubMed   Google Scholar  

Bowden, E. M., Jung-Beeman, M., Fleck, J. I. & Kounios, J. New approaches to demystifying insight. Trends Cogn. Sci. 9 , 322–328 (2005).

Danek, A. H. in Routledge International Handbook of Creative Cognition (eds Ball, L. J. & Vallée-Tourangeau, F.) (Routledge, 2023).

Kaplan, C. A. & Simon, H. A. In search of insight. Cogn. Psychol. 22 , 374–419 (1990).

Kounios, J. & Beeman, M. The cognitive neuroscience of insight. Annu. Rev. Psychol. 65 , 71–93 (2014).

Smith, R. W. & Kounios, J. Sudden insight: all-or-none processing revealed by speed–accuracy decomposition. J. Exp. Psychol. Learn. Mem. Cogn. 22 , 1443–1462 (1996).

Gilhooly, K. J. Incubation and intuition in creative problem solving. Front. Psychol. 7 , 1076 (2016).

Article   PubMed   PubMed Central   Google Scholar  

Metcalfe, J. Premonitions of insight predict impending error. J. Exp. Psychol. Learn. Mem. Cogn. 12 , 623–634 (1986).

Metcalfe, J. & Wiebe, D. Intuition in insight and noninsight problem solving. Mem. Cogn. 15 , 238–246 (1987).

Newell, A., & Simon, H. A. Human Problem Solving (Prentice-Hall, 1972).

Davidson, J. E. in The Nature of Insight (eds Sternberg, R. J. & Davidson, J. E.) 125–155 (MIT Press, 1995).

MacGregor, J. N., Ormerod, T. C. & Chronicle, E. P. Information processing and insight: a process model of performance on the nine-dot and related problems. J. Exp. Psychol. Learn. Mem. Cogn. 27 , 176–201 (2001).

Weisberg, R. W. in The Nature of Insight (Sternberg, R. J. & Davidson, J. E.) 157–196 (MIT Press, 1995).

Ash, I. K. & Wiley, J. The nature of restructuring in insight: an individual-differences approach. Psychon. Bull. Rev. 13 , 66–73 (2006).

Cushen, P. J. & Wiley, J. Cues to solution, restructuring patterns, and reports of insight in creative problem solving. Consc. Cogn. 21 , 1166–1175 (2012).

Fedor, A., Szathmáry, E. & Öllinger, M. Problem solving stages in the five square problem. Front. Psychol. 6 , 1050 (2015).

Knoblich, G., Ohlsson, S., Haider, H. & Rhenius, D. Constraint relaxation and chunk decomposition in insight problem solving. J. Exp. Psychol. Learn. Mem. Cogn. 25 , 1534–1555 (1999).

Ormerod, T. C., MacGregor, J. N. & Chronicle, E. P. Dynamics and constraints in insight problem solving. J. Exp. Psychol. Learn. Mem. Cogn. 28 , 791–799 (2002).

Danek, A. H., Fraps, T., von Müller, A., Grothe, B. & Öllinger, M. Working wonders? Investigating insight with magic tricks. Cognition 130 , 174–185 (2014).

Hedne, M. R., Norman, E. & Metcalfe, J. Intuitive feelings of warmth and confidence in insight and noninsight problem solving of magic tricks. Front. Psychol. 7 , 1314 (2016).

Thomas, C., Didierjean, A. & Kuhn, G. It is magic! How impossible solutions prevent the discovery of obvious ones. Q. J. Exp. Psychol. 71 , 2481–2487 (2018).

Danek, A. H., Wiley, J. & Öllinger, M. Solving classical insight problems without Aha! experience: 9 dot, 8 coin, and matchstick arithmetic problems. J. Probl. Solving https://doi.org/10.7771/1932-6246.1183 (2016).

Gilhooly, K. J. & Murphy, P. Differentiating insight from non-insight problems. Think. Reason. 11 , 279–302 (2005).

Öllinger, M., Jones, G. & Knoblich, G. The dynamics of search, impasse, and representational change provide a coherent explanation of difficulty in the nine-dot problem. Psychol. Res. 78 , 266–275 (2014).

Webb, M. E., Little, D. R. & Cropper, S. J. Insight is not in the problem: investigating insight in problem solving across task types. Front. Psychol. 7 , 1424 (2016).

Dygert, S. K. & Jarosz, A. F. Individual differences in creative cognition. J. Exp. Psychol. Gen. 149 , 1249–1274 (2020).

MacGregor, J. N. & Cunningham, J. B. Rebus puzzles as insight problems. Behav. Res. Meth. 40 , 263–268 (2008).

Salvi, C., Costantini, G., Bricolo, E., Perugini, M. & Beeman, M. Validation of Italian rebus puzzles and compound remote associate problems. Behav. Res. Meth. 48 , 664–685 (2016).

Smith, S. M. & Blankenship, S. E. Incubation effects. Bull. Psychon. Soc. 27 , 311–314 (1989).

Threadgold, E., Marsh, J. E. & Ball, L. J. Normative data for 84 UK English rebus puzzles. Front. Psychol. 9 , 2513 (2018).

Mednick, S. The associative basis of the creative process. Psychol. Rev. 69 , 220–232 (1962).

Bowden, E. M. & Beeman, M. J. Getting the right idea: semantic activation in the right hemisphere may help solve insight problems. Psychol. Sci. 9 , 435–440 (1998).

Bowers, K. S., Regehr, G., Balthazard, C. & Parker, K. Intuition in the context of discovery. Cogn. Psychol. 22 , 72–110 (1990).

Schooler, J. W. & Melcher, J. in The Creative Cognition Approach (Smith, S. M., Ward, T. B. & Finke, R. A.) 97–143 (MIT Press, 1995).

Smith, S. M. & Blankenship, S. E. Incubation and the persistence of fixation in problem solving. Am. J. Psychol. 104 , 61–87 (1991).

Wiley, J. Expertise as mental set: the effects of domain knowledge in creative problem solving. Mem. Cogn 26 , 716–730 (1998).

Beeftink, F., Van Eerde, W. & Rutte, C. G. The effect of interruptions and breaks on insight and impasses: do you need a break right now? Creativ. Res. J. 20 , 358–364 (2008).

Friedlander, K. J. & Fine, P. A. “The penny drops”: investigating insight through the medium of cryptic crosswords. Front. Psychol. 9 , 904 (2018).

Bowden, E. M. & Jung-Beeman, M. Normative data for 144 compound remote associate problems. Behav. Res. Meth. Instrum. Comput. 35 , 634–639 (2003).

Cranford, E. A. & Moss, J. Is insight always the same? A protocol analysis of insight in compound remote associate problems. J. Probl. Solving 4 , https://doi.org/10.7771/1932-6246.1129 (2012).

Öllinger, M. & von Müller, A. Search and coherence-building in intuition and insight problem solving. Front. Psychol. 8 , 827 (2017).

Zander, T., Öllinger, M. & Volz, K. G. Intuition and insight: two processes that build on each other or fundamentally differ? Front. Psychol. 7 , 1395 (2016).

Ellis, J. J., Glaholt, M. G. & Reingold, E. M. Eye movements reveal solution knowledge prior to insight. Consc. Cogn. 20 , 768–776 (2011).

Novick, L. R. & Sherman, S. J. On the nature of insight solutions: evidence from skill differences in anagram solution. Q. J. Exp. Psychol. A 56 , 351–382 (2003).

Rees, H. J. & Israel, H. E. An investigation of the establishment and operation of mental sets. Psychol. Monogr. 46 , 1–26 (1935).

Tempel, T. & Frings, C. Directed forgetting in problem solving. Acta Psychol. 201 , 102955 (2019).

Jacoby, L. L. On interpreting the effects of repetition: solving a problem versus remembering a solution. J. Verb. Learn. Verb. Behav. 17 , 649–667 (1978).

Koppel, R. H. & Storm, B. C. Unblocking memory through directed forgetting. J. Cogn. Psychol. 24 , 901–907 (2012).

Smith, S. M. & Beda, Z. Old problems in new contexts: the context-dependent fixation hypothesis. J. Exp. Psychol. Gen. 149 , 192–197 (2020).

Auble, P. M., Franks, J. J. & Soraci, S. A. Effort toward comprehension: elaboration or “Aha”? Mem. Cogn. 7 , 426–434 (1979).

Bar-Hillel, M. Stumpers: an annotated compendium. Think. Reason. 27 , 536–566 (2021).

Bowden, E. M. Accessing relevant information during problem solving: time constraints on search in the problem space. Mem. Cogn. 13 , 280–286 (1985).

Dow, G. T. & Mayer, R. E. Teaching students to solve insight problems: evidence for domain specificity in creativity training. Creativ. Res. J. 16 , 389–398 (2004).

Durso, F. T., Rea, C. B. & Dayton, T. Graph-theoretic confirmation of restructuring during insight. Psychol. Sci. 5 , 94–98 (1994).

Lockhart, R. S., Lamon, M. & Gick, M. L. Conceptual transfer in simple insight problems. Mem. Cogn. 16 , 36–44 (1988).

Patrick, J. & Ahmed, A. Facilitating representation change in insight problems through training. J. Exp. Psychol. Learn. Mem. Cogn. 40 , 532–543 (2014).

Bar-Hillel, M., Noah, T. & Frederick, S. Solving stumpers, CRT and CRAT: are the abilities related? Judgm. Decis. Mak. 14 , 620–623 (2019).

Webb, M. E., Little, D. R. & Cropper, S. J. Once more with feeling: normative data for the Aha experience in insight and noninsight problems. Behav. Res. Meth. 50 , 2035–2056 (2018).

Beilock, S. L. & DeCaro, M. S. From poor performance to success under stress: working memory, strategy selection, and mathematical problem solving under pressure. J. Exp. Psychol. Learn. Mem. Cogn. 33 , 983–998 (2007).

DeCaro, M. S., Van Stockum, C. A. & Wieth, M. B. When higher working memory capacity hinders insight. J. Exp. Psychol. Learn. Mem. Cogn. 42 , 39–49 (2016).

Van Stockum Jr, C. A. & DeCaro, M. S. When working memory mechanisms compete: predicting cognitive flexibility versus mental set. Cognition 201 , 104313 (2020).

Koppel, R., George, T. & Wiley, J. in The Emergence of Insight (Cambridge Press, 2024).

Bilalić, M., McLeod, P. & Gobet, F. The mechanism of the Einstellung (set) effect: a pervasive source of cognitive bias. Curr. Dir. Psychol. Sci. 19 , 111–115 (2010).

Sheridan, H. & Reingold, E. M. The mechanisms and boundary conditions of the Einstellung effect in chess: evidence from eye movements. PLoS One 8 , e75796 (2013).

Ellis, J. J. & Reingold, E. M. The Einstellung effect in anagram problem solving: evidence from eye movements. Front. Psychol. 5 , 679 (2014).

Beda, Z. & Smith, S. M. Chasing red herrings: memory of distractors causes fixation in creative problem solving. Mem. Cogn. 46 , 671–684 (2018).

Howe, M. L. & Garner, S. R. Can false memories prime alternative solutions to ambiguous problems? Memory 26 , 96–105 (2018).

Smith, S. M. in The Nature of Insight (Sternberg, R. J. & Davidson, J. E.) 229–251 (MIT Press, 1995).

Kohn, N. & Smith, S. M. Partly versus completely out of your mind: effects of incubation and distraction on resolving fixation. J. Creativ. Behav. 43 , 102–118 (2009).

Koppel, R. H. & Storm, B. C. Escaping mental fixation: incubation and inhibition in creative problem solving. Memory 22 , 340–348 (2014).

May, C. P. Synchrony effects in cognition: the costs and a benefit. Psychon. Bull. Rev. 6 , 142–147 (1999).

Penaloza, A. A. & Calvillo, D. P. Incubation provides relief from artificial fixation in problem solving. Creativ. Res. J. 24 , 338–344 (2012).

Storm, B. C. & Angello, G. Overcoming fixation: creative problem solving and retrieval-induced forgetting. Psychol. Sci. 21 , 1263–1265 (2010).

Storm, B. C. & Hickman, M. L. Mental fixation and metacognitive predictions of insight in creative problem solving. Q. J. Exp. Psychol. 68 , 802–813 (2015).

Vul, E. & Pashler, H. Incubation benefits only after people have been misdirected. Mem. Cogn. 35 , 701–710 (2007).

Ricks, T. R., Turley-Ames, K. J. & Wiley, J. Effects of working memory capacity on mental set due to domain knowledge. Mem. Cogn. 35 , 1456–1462 (2007).

Dodds, R. A., Ward, T. B. & Smith, S. M. in Creativity Research Handbook (ed. Runco, M. A.) 291–322 (Hampton Press, 2012).

Sio, U. N. & Ormerod, T. C. Does incubation enhance problem solving? A meta-analytic review. Psychol. Bull. 135 , 94–120 (2009).

Caravona, L. & Macchi, L. Different incubation tasks in insight problem solving: evidence for unconscious analytic thought. Think. Reason. 29 , 559–593 (2023).

Sanders, K. E. & Beeman, M. Sleep and incubation: using problem reactivation during sleep to study forgetting fixation and unconscious processing during sleep incubation. J. Cogn. Psychol. 33 , 738–756 (2021).

Cai, D. J., Mednick, S. A., Harrison, E. M., Kanady, J. C. & Mednick, S. C. REM, not incubation, improves creativity by priming associative networks. Proc. Natl Acad. Sci. USA 106 , 10130–10134 (2009).

Stickgold, R. & Walker, M. P. Sleep-dependent memory triage: evolving generalization through selective processing. Nat. Neurosci. 16 , 139–145 (2013).

Segal, E. Incubation in insight problem solving. Creativ. Res. J. 16 , 141–148 (2004).

George, T. & Wiley, J. Fixation, flexibility, and forgetting during alternate uses tasks. Psychol. Aesth. Creativ. Arts 13 , 305–313 (2019).

Lu, J. G., Akinola, M. & Mason, M. F. “Switching on” creativity: task switching can increase creativity by reducing cognitive fixation. Organ. Behav. Hum. Decis. Process. 139 , 63–75 (2017).

Smith, S. M., Gerkens, D. R. & Angello, G. Alternating incubation effects in the generation of category exemplars. J. Creativ. Behav. 51 , 95–106 (2017).

Ansburg, P. I. & Hill, K. Creative and analytic thinkers differ in their use of attentional resources. Pers. Individ. Differ. 34 , 1141–1152 (2003).

Kim, S., Hasher, L. & Zacks, R. T. Aging and a benefit of distractibility. Psychon. Bull. Rev. 14 , 301–305 (2007).

Reverberi, C., Toraldo, A., D’Agostini, S. & Skrap, M. Better without (lateral) frontal cortex? Insight problems solved by frontal patients. Brain 128 , 2882–2890 (2005).

Wiley, J. & Jarosz, A. How working memory capacity affects problem solving. Psychol. Learn. Motiv. 56 , 185–227 (2012).

Zmigrod, S., Zmigrod, L. & Hommel, B. The relevance of the irrelevant: attentional distractor-response binding predicts performance in the remote associates task. Psychol. Aesth. Creativ. Arts 13 , 15–23 (2019).

Ninomiya, Y. et al. Effect of cognitive load and working memory capacity on the efficiency of discovering better alternatives: a survival analysis. Mem. Cogn . https://doi.org/10.3758/s13421-023-01448-w (2023).

Tan, T., Zou, H., Chen, C. & Luo, J. Mind wandering and the incubation effect in insight problem solving. Creativ. Res. J. 27 , 375–382 (2015).

Yang, T. & Wu, G. Spontaneous or deliberate: the dual influence of mind wandering on creative incubation. J. Creativ. Behav. 56 , 584–600 (2022).

Zedelius, C. M. & Schooler, J. W. Mind wandering “Ahas” versus mindful reasoning: alternative routes to creative solutions. Front. Psychol. 6 , 834 (2015).

Benedek, M., Panzierer, L., Jauk, E. & Neubauer, A. C. Creativity on tap? Effects of alcohol intoxication on creative cognition. Consc. Cogn. 56 , 128–134 (2017).

Jarosz, A. F., Colflesh, G. J. & Wiley, J. Uncorking the muse: alcohol intoxication facilitates creative problem solving. Consc. Cogn. 21 , 487–493 (2012).

Wieth, M. B. & Zacks, R. T. Time of day effects on problem solving: when the non-optimal is optimal. Think. Reason. 17 , 387–401 (2011).

Bolte, A., Goschke, T. & Kuhl, J. Emotion and intuition: effects of positive and negative mood on implicit judgments of semantic coherence. Psychol. Sci. 14 , 416–421 (2003).

Rowe, G., Hirsh, J. B. & Anderson, A. K. Positive affect increases the breadth of attentional selection. Proc. Natl Acad. Sci. USA 104 , 383–388 (2007).

Aiello, D. A., Jarosz, A. F., Cushen, P. J. & Wiley, J. Firing the executive: when an analytic approach to problem solving helps and hurts. J. Probl. Solving https://doi.org/10.7771/1932-6246.1128 (2012).

Ellis, D. M., Robison, M. K. & Brewer, G. A. The cognitive underpinnings of multiply-constrained problem solving. J. Intell. 9 , 7 (2021).

Chein, J. M., Weisberg, R. W., Streeter, N. L. & Kwok, S. Working memory and insight in the nine-dot problem. Mem. Cogn. 38 , 883–892 (2010).

Kershaw, T. C. & Ohlsson, S. Multiple causes of difficulty in insight: the case of the nine-dot problem. J. Exp. Psychol. Learn. Mem. Cogn. 30 , 3–13 (2004).

Lung, C. T. & Dominowski, R. L. Effects of strategy instructions and practice on nine-dot problem solving. J. Exp. Psychol. Learn. Mem. Cogn. 11 , 804–811 (1985).

Öllinger, M., Jones, G., Faber, A. H. & Knoblich, G. Cognitive mechanisms of insight: the role of heuristics and representational change in solving the eight-coin problem. J. Exp. Psychol. Learn. Mem. Cogn. 39 , 931–939 (2013).

Thomas, L. E. & Lleras, A. Swinging into thought: directed movement guides insight in problem solving. Psychon Bull. Rev. 16 , 719–723 (2009).

Hattori, M., Sloman, S. A. & Orita, R. Effects of subliminal hints on insight problem solving. Psychon. Bull. Rev. 20 , 790–797 (2013).

Moss, J., Kotovsky, K. & Cagan, J. The influence of open goals on the acquisition of problem-relevant information. J. Exp. Psychol. Learn. Mem. Cogn. 33 , 876–891 (2007).

Moss, J., Kotovsky, K. & Cagan, J. The effect of incidental hints when problems are suspended before, during, or after an impasse. J. Exp. Psychol. Learn. Mem. Cogn. 37 , 140–148 (2011).

Pétervári, J. & Danek, A. H. Problem solving of magic tricks: guiding to and through an impasse with solution cues. Think. Reason. 26 , 502–533 (2020).

Seifert, C. M., Meyer, D. E., Davidson, N., Patalano, A. L., & Yaniv, I. in The Nature of Insight (Sternberg, R. J. & Davidson, J. E.) 65–124 (MIT Press, 1995).

Gick, M. L. & McGarry, S. J. Learning from mistakes: inducing analogous solution failures to a source problem produces later successes in analogical transfer. J. Exp. Psychol. Learn. Mem. Cogn. 18 , 623–639 (1992).

Ash, I. K., Jee, B. D. & Wiley, J. Investigating insight as sudden learning. J. Probl. Solving https://doi.org/10.7771/1932-6246.1123 (2012).

Ansburg, P. I. & Dominowski, R. I. Promoting insightful problem solving. J. Creat. Behav. 34 , 30–60 (2000).

Bianchi, I., Branchini, E., Burro, R., Capitani, E. & Savardi, U. Overtly prompting people to “think in opposites” supports insight problem solving. Think. Reason. 26 , 31–67 (2020).

Chrysikou, E. G. When shoes become hammers: goal-derived categorization training enhances problem-solving performance. J. Exp. Psychol. Learn. Mem. Cogn. 32 , 935–942 (2006).

Blech, C., Gaschler, R. & Bilalić, M. Why do people fail to see simple solutions? Using think-aloud protocols to uncover the mechanism behind the Einstellung (mental set) effect. Think. Reason. 26 , 552–580 (2020).

Fleck, J. I. & Weisberg, R. W. The use of verbal protocols as data: an analysis of insight in the candle problem. Mem. Cogn. 32 , 990–1006 (2004).

Fleck, J. I. & Weisberg, R. W. Insight versus analysis: evidence for diverse methods in problem solving. J. Cogn. Psychol. 25 , 436–463 (2013).

Tidikis, V. & Ash, I. K. Working in dyads and alone: examining process variables in solving insight problems. Creativ. Res. J. 25 , 189–198 (2013).

Gupta, N., Jang, Y., Mednick, S. C. & Huber, D. E. The road not taken: creative solutions require avoidance of high-frequency responses. Psychol. Sci. 23 , 288–294 (2012).

Bilalić, M., Graf, M., Vaci, N. & Danek, A. H. The temporal dynamics of insight problem solving—restructuring might not always be sudden. Think. Reason. 27 , 1–37 (2021).

Knoblich, G., Ohlsson, S. & Raney, G. E. An eye movement study of insight problem solving. Mem. Cogn. 29 , 1000–1009 (2001).

Nathan, M. J., Schenck, K. E., Vinsonhaler, R., Michaelis, J. E., Swart, M. I. & Walkington, C. Embodied geometric reasoning: dynamic gestures during intuition, insight, and proof. J. Educ. Psychol. 113 , 929–948 (2020).

Vallée-Tourangeau, F., Ross, W., Ruffatto Rech, R. & Vallée-Tourangeau, G. Insight as discovery. J. Cogn. Psychol. 33 , 718–737 (2021).

Loesche, F., Goslin, J. & Bugmann, G. Paving the way to Eureka—introducing “Dira” as an experimental paradigm to observe the process of creative problem solving. Front. Psychol. 9 , 1773 (2018).

Ash, I. K. & Wiley, J. Hindsight bias in insight and mathematical problem solving: evidence of different reconstruction mechanisms for metacognitive versus situational judgments. Mem. Cogn. 36 , 822–837 (2008).

Danek, A. H. & Wiley, J. What causes the insight memory advantage? Cognition 205 , 104411 (2020).

Danek, A. H., Williams, J. & Wiley, J. Closing the gap: connecting sudden representational change to the subjective Aha! experience in insightful problem solving. Psychol. Res. 84 , 111–119 (2020).

Bowden, E. M. & Grunewald, K. in Insight: On the Origins of New Ideas F. (ed. Vallée-Tourangeau, F.) 28–50 (Routledge, 2018).

Gick, M. L., & Lockhart, R. S. in The Nature of Insight (Sternberg, R. J. & Davidson, J. E.) 197–228 (MIT Press, 1995).

Bilalić, M., Graf, M., Vaci, N., & Danek, A. H. When the solution is on the doorstep: better solving performance, but diminished Aha! experience for chess experts on the mutilated checkerboard problem. Cogn. Sci. 43 , e12771 (2019).

Laukkonen, R. E., Ingledew, D. J., Grimmer, H. J., Schooler, J. W. & Tangen, J. M. Getting a grip on insight: real-time and embodied Aha experiences predict correct solutions. Cogn. Emot. 35 , 918–935 (2021).

Ross, W. & Vallée-Tourangeau, F. Insight with stumpers: normative solution data for 25 stumpers and a fresh perspective on the accuracy effect. Think. Skills Creat. 46 , 101114 (2022).

Köhler, W. The Task of Gestalt Psychology (Princeton Univ. Press, 1969).

Ovington, L. A., Saliba, A. J., Moran, C. C., Goldring, J. & MacDonald, J. B. Do people really have insights in the shower? The when, where and who of the Aha! moment. J. Creativ. Behav. 52 , 21–34 (2018).

Gable, S. L., Hopper, E. A. & Schooler, J. W. When the muses strike: creative ideas of physicists and writers routinely occur during mind wandering. Psychol. Sci. 30 , 396–404 (2019).

Jung-Beeman, M. et al. Neural activity when people solve verbal problems with insight. PLoS Biol. 2 , 500–510 (2004).

Danek, A. H. & Wiley, J. What about false insights? Deconstructing the Aha! experience along its multiple dimensions for correct and incorrect solutions separately. Front. Psychol. 7 , 2077 (2017).

Danek, A. H., Fraps, T., von Müller, A., Grothe, B., & Öllinger, M. It’s a kind of magic — what self-reports can reveal about the phenomenology of insight problem solving. Front. Psychol.   5 , 1408 (2014).

Thagard, P. & Stewart, T. C. The Aha! experience: creativity through emergent binding in neural networks. Cogn. Sci. 35 , 1–33 (2011).

Gruber, H. E. in The Nature of Insight (Sternberg, R. J. & Davidson, J. E.) 397–431 (MIT Press, 1995).

Skaar, Ø. O. & Reber, R. Motivation through insight: the phenomenological correlates of insight and spatial ability tasks. J. Cogn. Psychol. 33 , 631–643 (2021).

Spiridonov, V., Loginov, N. & Ardislamov, V. Dissociation between the subjective experience of insight and performance in the CRA paradigm. J. Cogn. Psychol. 33 , 685–699 (2021).

Stuyck, H., Aben, B., Cleeremans, A. & Van den Bussche, E. The Aha! moment: is insight a different form of problem solving? Consc. Cogn. 90 , 103055 (2021).

Webb, M. E., Cropper, S. J. & Little, D. R. Unusual uses and experiences are good for feeling insightful, but not for problem solving: contributions of schizotypy, divergent thinking, and fluid reasoning, to insight moments. J. Cogn. Psychol. 33 , 770–792 (2021).

Kizilirmak, J. M., Serger, V., Kehl, J., Öllinger, M., Folta-Schoofs, K. & Richardson-Klavehn, A. Feelings-of-warmth increase more abruptly for verbal riddles solved with in contrast to without Aha! experience. Front. Psychol. 9 , 1404 (2018).

Becker, M., Kühn, S. & Sommer, T. Verbal insight revisited—dissociable neurocognitive processes underlying solutions accompanied by an Aha! experience with and without prior restructuring. J. Cogn. Psychol. 33 , 659–684 (2021).

Topolinski, S. & Reber, R. Gaining insight into the “Aha” experience. Curr. Dir. Psychol. Sci. 19 , 402–405 (2010).

Salvi, C., Simoncini, C., Grafman, J. & Beeman, M. Oculometric signature of switch into awareness? Pupil size predicts sudden insight whereas microsaccades predict problem-solving via analysis. NeuroImage 217 , 116933 (2020).

Danek, A. H. & Salvi, C. Moment of truth: why Aha! experiences are correct. J. Creativ. Behav. 54 , 484–486 (2020).

Dietrich, A. & Haider, H. Human creativity, evolutionary algorithms, and predictive representations: the mechanics of thought trials. Psychon. Bull. Rev. 22 , 897–915 (2015).

Salvi, C., Bricolo, E., Kounios, J., Bowden, E. M. & Beeman, M. Insight solutions are correct more often than analytic solutions. Think. Reason. 22 , 1–18 (2016).

Webb, M. E., Laukkonen, R. E., Cropper, S. J. & Little, D. R. Commentary: moment of (perceived) truth: exploring accuracy of Aha! experiences. J. Creativ. Behav. 55 , 289–293 (2021).

Shen, W., Tong, Y., Yuan, Y., Zhan, H., Liu, C., Luo, J. & Cai, H. Feeling the insight: uncovering somatic markers of the “Aha” experience. Appl. Psychophysiol. Biofeedback 43 , 13–21 (2018).

Stuyck, H., Cleeremans, A. & Van den Bussche, E. Aha! under pressure: the Aha! experience is not constrained by cognitive load. Cognition 219 , 104946 (2022).

Strickland, T., Wiley, J. & Ohlsson, S. Hints and the Aha-accuracy effect in insight problem solving. Proc. Annu. Meet. Cogn. Sci. Soc. 44 , 3209–3215 (2022).

Kizilirmak, J. M., Gallisch, N., Schott, B. H. & Folta-Schoofs, K. Insight is not always the same: differences between true, false, and induced insights in the matchstick arithmetic task. J. Cogn. Psychol. 33 , 700–717 (2021).

Webb, M. E., Cropper, S. J. & Little, D. R. “Aha!” is stronger when preceded by a “huh?”: presentation of a solution affects ratings of Aha experience conditional on accuracy. Think. Reason. 25 , 324–364 (2019).

Kizilirmak, J. M., Galvao Gomes da Silva, J., Imamoglu, F. & Richardson-Klavehn, A. Generation and the subjective feeling of “Aha!” are independently related to learning from insight. Psychol. Res. 80 , 1059–1074 (2016).

Kounios, J., Fleck, J. I., Green, D. L., Payne, L., Stevenson, J. L., Bowden, E. M. & Jung-Beeman, M. The origins of insight in resting-state brain activity. Neuropsychologia 46 , 281–291 (2008).

Sadler-Smith, E. Wallas’ four-stage model of the creative process: more than meets the eye? Creativ. Res. J. 27 , 342–352 (2015).

Wallas, G. The Art of Thought (Harcourt and Brace, 1926).

Chronicle, E. P., MacGregor, J. N. & Ormerod, T. C. What makes an insight problem? The roles of heuristics, goal conception, and solution recoding in knowledge-lean problems. J. Exp. Psychol. Learn. Mem. Cogn. 30 , 14–27 (2004).

Grimmer, H., Laukkonen, R., Tangen, J. & von Hippel, W. Eliciting false insights with semantic priming. Psychon. Bull. Rev. 29 , 954–970 (2022).

Laukkonen, R. E., Kaveladze, B. T., Tangen, J. M. & Schooler, J. W. The dark side of Eureka: artificially induced Aha moments make facts feel true. Cognition 196 , 104122 (2020).

Laukkonen, R. E., Kaveladze, B. T., Protzko, J., Tangen, J. M., von Hippel, W. & Schooler, J. W. Irrelevant insights make worldviews ring true. Sci. Rep. 12 , 2075 (2022).

Metcalfe, J., Schwartz, B. L., & Bloom, P. A. The tip-of-the-tongue state and curiosity. Cogn. Res. Princ. Implic.   2 , 31 (2017).  

Bianchi, I., Branchini, E., Canestrari, C. & Burro, R. On pleasures of the mind related to humour and insight problem solving: an investigation of people’s awareness of what they like and why. J. Cogn. Psychol. 34 , 778–795 (2022).

Kozbelt, A. & Nishioka, K. Humor comprehension, humor production, and insight: an exploratory study. Int. J. Humor Res. 23 , 375–401 (2010).

Chesebrough, C., Chrysikou, E. G., Holyoak, K. J., Zhang, F. & Kounios, J. Conceptual change induced by analogical reasoning sparks aha moments. Creativ. Res. J. 35 , 1–23 (2010).

George T., & Wiley, J. in Insight: On the Origin of New Ideas (ed. Vallée-Tourangeau, F.) 143–168 (Routledge, 2018).

Lv, K. The involvement of working memory and inhibition functions in the different phases of insight problem solving. Mem. Cogn. 43 , 709–722 (2015).

Weisberg, R. W. Toward an integrated theory of insight in problem solving. Think. Reason. 21 , 5–39 (2015).

Slamecka, N. J. & Graf, P. The generation effect: delineation of a phenomenon. J. Exp. Psychol. Hum. Learn. Mem. 4 , 592–604 (1978).

Buyer, L. S. & Dominowski, R. L. Retention of solutions: it is better to give than to receive. Am. J. Psychol. 102 , 353–363 (1989).

Kizilirmak, J. M., Wiegmann, B. & Richardson-Klavehn, A. Problem solving as an encoding task: a special case of the generation effect. J. Probl. Solving 9 , 59–76 (2016).

Patalano, A. L. & Seifert, C. M. Memory for impasses during problem solving. Mem. Cogn. 22 , 234–242 (1994).

Dominowski, R. L. & Buyer, L. S. Retention of problem solutions: the re-solution effect. Am. J. Psychol. 113 , 249–274 (2000).

Schwartz, D. & Martin, T. Inventing to prepare for future learning: the hidden efficiency of encouraging original student production in statistics instruction. Cogn. Instr. 22 , 129–184 (2004).

Jarosz, A. F., Goldenberg, O. & Wiley, J. Learning by invention: small group discussion activities that support learning in statistics. Discourse Process. 54 , 285–302 (2017).

Sinha, T. & Kapur, M. When problem solving followed by instruction works: evidence for productive failure. Rev. Educ. Res. 91 , 761–798 (2021).

Danek, A. H., Fraps, T., von Müller, A., Grothe, B. & Öllinger, M. Aha! experiences leave a mark: facilitated recall of insight solutions. Psychol. Res. 77 , 659–669 (2013).

Liljedahl, P. G. Mathematical discovery and affect: the effect of Aha! experiences on undergraduate mathematics students. Int. J. Math. Educ. Sci. Technol. 36 , 219–234 (2005).

Metcalfe, J., Schwartz, B. L. & Eich, T. S. Epistemic curiosity and the region of proximal learning. Curr. Opin. Behav. Sci. 35 , 40–47 (2020).

Van de Cruys, S., Damiano, C., Boddez, Y., Król, M., Goetschalckx, L. & Wagemans, J. Visual affects: linking curiosity, Aha-Erlebnis, and memory through information gain. Cognition 212 , 104698 (2021).

Kizilirmak, J. M., Thuerich, H., Folta-Schoofs, K., Schott, B. H. & Richardson-Klavehn, A. Neural correlates of learning from induced insight: a case for reward-based episodic encoding. Front. Psychol. 7 , 1693 (2016). (2016).

Oh, Y., Chesebrough, C., Erickson, B., Zhang, F. & Kounios, J. An insight-related neural reward signal. NeuroImage 214 , 116757 (2020).

Salvi, C., Leiker, E. K., Baricca, B., Molinari, M. A., Eleopra, R., Nichelli, P. F., Grafman, J. & Dunsmoor, J. E. The effect of dopaminergic replacement therapy on creative thinking and insight problem-solving in Parkinson’s disease patients. Front. Psychol. 12 , 646448 (2021).

Tik, M., Sladky, R., Luft, C. D. B., Willinger, D., Hoffmann, A., Banissy, M. J. & Windischberger, C. Ultra‐high‐field fMRI insights on insight: neural correlates of the Aha!‐moment. Hum. Brain Mapp. 39 , 3241–3252 (2018).

Download references

Acknowledgements

The authors thank I. K. Ash, P. J. Cushen, T. George, A. F. Jarosz, T. S. Miller and S. Ohlsson for discussion on these topics.

Author information

Authors and affiliations.

Department of Psychology, University of Illinois at Chicago, Chicago, IL, USA

Jennifer Wiley

Department of Psychology, Heidelberg University, Heidelberg, Germany

Amory H. Danek

You can also search for this author in PubMed   Google Scholar

Contributions

The authors contributed equally to all aspects of the article.

Corresponding author

Correspondence to Jennifer Wiley .

Ethics declarations

Competing interests.

The authors declare no competing interests.

Peer review

Peer review information.

Nature Reviews Psychology thanks Rolf Reber and the other anonymous, reviewers for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Cite this article.

Wiley, J., Danek, A.H. Restructuring processes and Aha! experiences in insight problem solving. Nat Rev Psychol 3 , 42–55 (2024). https://doi.org/10.1038/s44159-023-00257-x

Download citation

Accepted : 30 October 2023

Published : 14 December 2023

Issue Date : January 2024

DOI : https://doi.org/10.1038/s44159-023-00257-x

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

HYPOTHESIS AND THEORY article

Intuition and insight: two processes that build on each other or fundamentally differ.

• 1 Department of Psychology, University of Basel, Basel, Switzerland
• 2 Parmenides Foundation, Munich, Germany
• 3 Department Psychology, Ludwig-Maximilians-Universität München, Munich, Germany
• 4 Werner Reichardt Centre for Integrative Neuroscience, University of Tübingen, Tübingen, Germany

Intuition and insight are intriguing phenomena of non-analytical mental functioning: whereas intuition denotes ideas that have been reached by sensing the solution without any explicit representation of it, insight has been understood as the sudden and unexpected apprehension of the solution by recombining the single elements of a problem. By face validity, the two processes appear similar; according to a lay perspective, it is assumed that intuition precedes insight. Yet, predominant scientific conceptualizations of intuition and insight consider the two processes to differ with regard to their (dis-)continuous unfolding. That is, intuition has been understood as an experience-based and gradual process, whereas insight is regarded as a genuinely discontinuous phenomenon. Unfortunately, both processes have been investigated differently and without much reference to each other. In this contribution, we therefore set out to fill this lacuna by examining the conceptualizations of the assumed underlying cognitive processes of both phenomena, and by also referring to the research traditions and paradigms of the respective field. Based on early work put forward by Bowers et al. (1990 , 1995 ), we referred to semantic coherence tasks consisting of convergent word triads (i.e., the solution has the same meaning to all three clue words) and/or divergent word triads (i.e., the solution means something different with respect to each clue word) as an excellent kind of paradigm that may be used in the future to disentangle intuition and insight experimentally. By scrutinizing the underlying mechanisms of intuition and insight, with this theoretical contribution, we hope to launch lacking but needed experimental studies and to initiate scientific cooperation between the research fields of intuition and insight that are currently still separated from each other.

Introduction

There are situations, in which decision makers arrive at an idea or a decision not by analytically inferring the solution but by either sensing the correct solution without being able to give reasons for it, or by realizing the solution all of a sudden without being able to report on the solution process. Roughly, the former phenomenon has been called intuition, the latter insight. Both have fascinated the public as well as the scientific audience.

Here are two historical cases that illustrate the two phenomena ( Gladwell, 2005 ; Mclean, as cited in Klein and Jarosz, 2011 ): The first is known as the Getty kouros and happened to the J. Paul Getty Museum in Los Angeles at the end of the 20th century. The museum was offered to add an over-life-sized statue in form of a kouros – allegedly from Ancient Greece, and thus several millions worth – to its art collection. Before the contract could be concluded, several experts set out to assure the authenticity of the statue and its origin thereby using a substantial number of high-tech methods for their analyses. After a year of thorough inspection, the experts reached the conclusion that the statue was authentic. At the same time, the former curator of the Metropolitan Museum of Art in New York, by chance, cast a glance at the artwork and spontaneously raised doubts regarding its authenticity. Thereupon, other men of renown who were asked for their spontaneous assessment of the kouros, also reported that they felt that something was wrong with it – without being able to tell the reason for this impression (cf. Gladwell, 2005 ). Interestingly, up to now, it could not be entirely cleared whether the statue stems from Ancient Greece or whether it is a modern forgery. Yet, the curator – instantaneously “feeling” that something was wrong and acting upon this impression although not being able to name a specific reason – is a paramount example of what it means to have an intuition being strong enough to act accordingly.

For an example of a sudden insight into the solution of a complex problem, consider Wagner Dodge, a smokejumper who survived the Mann Gulch Fire in August 1949 (Mclean, as cited in Klein and Jarosz, 2011 ). On a very hot day, a fire broke out in Mann Gulch, a canyon near Helena in Montana. Sixteen smokejumpers were flown close to the fire in order to extinguish it. After they had parachuted out of the aircraft, they realized that the fire was much worse than expected: They faced an uncontrollable blaze. The biggest problem was that they were in the danger of being entrapped by the fire. They could not escape and thus their lives were immediately threatened. For a moment they were desperately helpless and bustled around without a plan. They faced an impasse : well-known routines would not bring them forward and they might be caught in a mental set , that is, the tendency to try to solve a problem based on previous successful solution attempts to similar kinds of problems that are inefficient or cannot be transferred to the problem at hand (see Luchins and Luchins, 1959 , as well as Öllinger et al., 2008 ). After a while, all at once, Wagner Dodge had the sudden idea to ignite an “escape fire” ahead of the group (i.e., he had a sudden aha-experience ). Although he had never heard of such a possibility, he abruptly realized that when he could quickly stub an area of vegetation, the blaze would have no basis to continue when arriving at the cinder. He put his idea into action, ignited an additional fire and stepped into the middle of the newly burnt area. This way, he could save his life; the other smokejumpers who did not trust him lost their lives in the fire. Today, escape fires belong to the standard practice of fire services in the wild (Mclean, as cited in Klein and Jarosz, 2011 ).

Based on these examples, both phenomena – intuition and insight – may be conceived of as non-analytical thought processes that result in certain behavior that is not based on an exclusively deliberate and stepwise search for a solution. Non-analytical thought means a thought process in which no deliberate deduction takes place: individuals are not engaged in the consecutive testing of the obvious and/or typical routes to solution that define deliberate analysis. Instead, intuitions are characterized by the decision maker feeling out the solution without an available, tangible explanation for it; insights are characterized by the fact that the solution suddenly and unexpectedly pops into the mind of the decision maker or problem solver being instantaneously self-evident. Despite these apparent similarities of the two phenomena, intuition and insight have been conceptualized rather differently in the scientific literature up to now with regard to the underlying cognitive mechanisms as well as to the experimental designs routinely being used to gain empirical evidence. The aim of our contribution is therefore to scrutinize the similarities and differences of the cognitive mechanisms underlying intuition and insight by drawing on and extending early ideas by Bowers et al. (1990 , 1995 ). The gripping question is whether intuition and insight are two qualitatively distinct phenomena, appearing similar only by face validity, or whether they are indeed similar/related and may only unfold on different levels of processing. To address this question, we draw on the latest contributions in the field and include recent research findings that have not been available in Bowers et al. (1990 , 1995 ) time.

First, we will give an overview of predominant definitions of intuition and insight from a cognitive-psychological perspective. Second, we will elaborate on the underlying cognitive processes of both phenomena, thereby aiming to pin down similarities and differences. Both, similarities and differences will be addressed against the background of the research history of intuition and insight as well as in light of predominant, experimental paradigms that have been used to investigate the two phenomena. The paper ends by outlining open questions and highlighting future directions in scientific research that may progress our understanding of the underlying cognitive processes of intuition and insight (as well as on their relatedness).

Defining Intuition and Insight

Theoretical characterization of intuition.

Although most people “intuitively” know what an intuition is, the scientific community is split over its definition as well as its conceptualization. Despite disagreement about any definition, common ground is that intuition is an experienced-based process resulting in a spontaneous tendency toward a hunch or a hypothesis ( Bowers et al., 1990 ; Volz and Zander, 2014 ). Taking all major definitions into consideration, it is possible to distil certain characteristics that prominent definitions of intuition have in common ( Glöckner and Witteman, 2010 ; Volz and Zander, 2014 ).

Firstly, there is the aspect of non-conscious processing , which means that intuition occurs with very little awareness about the underlying cognitive processes so that people are mostly not able to report on these. Yet, intuitive processes can partly or completely be made conscious at some point in the entire judgmental process (e.g., Gigerenzer, 2008 ). In this regard, intuitive processing is not directly conscious or non-conscious, but can be viewed as reflecting cognitive processing on the fringe of human consciousness ( Mangan, 1993 , 2001 , 2015 ; Norman, 2002 , 2016 ; Price, 2002 ; Norman et al., 2006 , 2010 ). Secondly, there is the aspect of automaticity or uncontrollability . Intuitive processing appears in the form of spontaneous and instantaneous ideas or hunches that cannot be intentionally controlled in the way that they cannot be neither intentionally evoked nor ignored (e.g., Topolinski and Strack, 2008 ). The unintentional nature of intuition implies that intuition comes along without attentional effort and thus intuitive processing has been described as fast and effortless (e.g., Hogarth, 2001 ). Thirdly, there is the aspect of experientiality . Intuitive processing is based on tacit knowledge that has been acquired without attention during a person’s life and is thus fueled by it (e.g., Bowers et al., 1990 ). In combination these aspects result in the subjective experience of “knowing without knowing why” as Claxton (1998 , p. 217) put it. Lastly, there is the aspect of the initiation of action . The non-conscious, experience-based, and unintentional process finally results in a strong tendency toward a hunch, which serves as a go-signal that is strong enough to initiate action. As a result, people act in accordance with their intuitive impression or feeling (e.g., Gigerenzer, 2008 ). For a more detailed overview of the different aspects, consult Glöckner and Witteman (2010) or Volz and Zander (2014) .

In line with these aspects, Gigerenzer (2008) has focused, inter alia, on the experiential basis of intuition and states that intuition may hardly be possible without pre-existing knowledge and experiences. To revert to the example of the Getty kouros, the interplay of the given (visible) information was dissonant for someone who had seen lots of antique statues before; a beginner to the field may have arrived at a completely different judgment. By intuitively apprehending the situation, the curator relied on specific long-term-memory content that had been primarily acquired by studying, analyzing, and reflecting about a great number of statues resulting in associative and unattended learning. Volz and Zander (2014) refer to this kind of memory content as tacitly (in)formed cue-criterion relationships . On this view, different environmental cues can have different predictive power with respect to the criterion at hand; the situational validity of the cues will moderate whether the cue is used outright. In the above example, the curator judged the grade of authenticity of the kouros (criterion) from the subjective impression that the statue’s outer appearance had on him (cue). By doing this, the curator could not only rely on the given information (i.e., the visible kouros), but had to non-consciously activate further relevant knowledge from memory, that is to activate associatively learned cue-criterion relationships. Thus, the mental representation constructed during intuitive processing goes beyond the existing, perceivable information. Consequently, the curator’s feeling of unease when having a look at the statue resulted from an incomplete cue-criterion relationship that was taken as diagnostic for the assessment of the statue’s authenticity.

In addition to the aspect of experientiality and the unconscious read-out of implicitly learned cue-criterion relationships, Gigerenzer (2008) describes intuition as felt knowledge that aids decision making not only in cases, in which the decision maker already has a huge amount of prior experiences with a particular situation, but also when time and cognitive capacity is limited. According to the author, shadowy situations – either caused by a blurry sensory input that is only hardly detectable, or by the temporary non-availability of necessary information about the individual decisional components, which does not allow for foreseeing all consequences of a decision – foster intuitive processing. Intuition then manifests itself in the use of certain heuristics that may form highly successful, cognitive shortcuts ( Gigerenzer, 2008 ; Gigerenzer and Gaissmaier, 2011 ).

Insight and Aha-Experience

In contrast to the above elaborations on intuition, the term insight has been used to refer to the sudden and unexpected understanding of a previously incomprehensible problem or concept. In this sense, Jung-Beeman et al. (2004 , p. 506) explicate the nature of insight as “the recognition of new connections across existing knowledge.” Sometimes the solution to a difficult problem may suddenly pop out in the mind and the decision maker or problem solver may immediately recognize the complex nexuses, as formerly illustrated in the episode of the smokejumper Wagner Dodge. Problems seem to be processed and solved by re-grouping or re-combining (i.e., re-structuring) existing information in a new way so that self-imposed constraints can elegantly be relaxed ( Duncker, 1935 ; Wertheimer, 1959 ; Ohlsson, 1992 ). Wagner Dodge had prior knowledge: For instance, he knew how fires most commonly can be extinguished and that fires need vegetation or some other foundation to burn on. Furthermore, he knew about terrestrial conditions, and most important, he knew that smoke and fire could kill him. The solution to the problem occurred when he non-consciously combined all pieces of knowledge with each other in a new way so as to circumvent the fire death.

Such insightful solutions are associated with a privileged storage in long-term memory. Likewise as single trial learning. Recent studies observed a memory advantage for items that were solved by insight compared with non-insight solutions ( Danek et al., 2013 ) as well as compared with items that were not self-generated ( Kizilirmak et al., 2015 ). So, it is very likely, that Wagner Dodge never forgot how to ignite escape fires in the wild.

Yet, it has to be emphasized that an exact definition of the term insight has proven to be difficult, not least because the term insight has been used in many different ways in problem-solving research. Another hindrance is that it is very difficult to empirically operationalize the psychological construct of insight ( Knoblich and Öllinger, 2006 ), which is a similar problem as in research on intuition. Hitherto, researchers disagree whether there are certain necessary and/or sufficient conditions to determine whether an insight has occurred. For example, due to the absence of objective physiological markers indicating the occurrence of an insight, mainly reports in form of the subjective aha-experience have been used ex post to determine whether an insight has occurred during the solution process of a certain problem (e.g., Gick and Lockhardt, 1995 ; Bowden et al., 2005 ; Danek et al., 2013 ). Danek et al. (2013 , p. 2) state that the aha-experience is “the clearest defining characteristic of insight problem solving.” Topolinski and Reber (2010) define the aha-experience as the sudden and unexpected understanding of the solution, which comes with ease and is accompanied by positive affect as well as confidence in the truth of the solution. Given scientific endeavors to (objectively) pin down whether an insight had occurred, it can be summarized that insight and aha-experience have been equated. However, to date, there is disagreement whether (a) every insight is accompanied by an aha-experience, and (b) aha-experiences can only accompany insights and do never occur for presented solutions (i.e., solutions that are not generated by the individual herself; cf. Klein and Jarosz, 2011 ; Kizilirmak et al., 2015 ).

In order to help clarifying the conceptual muddle on insight, Knoblich and Öllinger (2006) proposed a classification of insight on three dimensions: first, on a phenomenological dimension, insight is opposed to a systematic and stepwise solution approach. Instead, it can be described as the sudden, unintended, and unexpected appearance of a solution idea, which is accompanied by a strong emotional component – the subjective and involuntary aha-experience. Second, on a task dimension, the literature on insight distinguishes between predefined insight problems and non-insight problems, with insight problems requiring sudden solution ideas and non-insight problems requiring a rather incremental solution approach. In case such an insight problem is solved, it is inferred that it is very likely that an insight has taken place. For example, the nine-dot problem ( Maier, 1930 ), the eight-coin problem ( Ormerod et al., 2002 ), and the candle problem ( Duncker, 1935 ) belong to such classical insight problems. However, a disadvantage of this distinction is that there are no unique criteria for an insight problem, and most of these problem could be solved with or without having an insight ( Öllinger et al., 2014 ); the most proposed criteria refer back to the subjective experience of aha, which has led to a circular definition of insight and insight problems. To circumvent this disadvantage, Bowden et al. (2005) have suggested using a class of problems that can be solved either with insight or without insight. Last, on a process dimension, recent research is concerned with the underlying cognitive mechanisms of insight and how these are different from non-insight problem solving. The predominant assumption here is that the non-conscious cognitive process of a mental set shift enables a changed representation of the problem’s elements ( Ohlsson, 1992 , 2011 ), which in turn leads to a sudden insight into the solution. For instance, in the nine-dot problem, the sudden realization that moves beyond the virtual nine-dot square are possible may lead to the relaxation of the perceptually driven boundary constraints and thus to a representational change of the problem space, which in the following enable insightful solutions (for a detailed explanation of the three dimensions consult Knoblich and Öllinger, 2006 ) 1 .

Different Research Traditions of Intuition and Insight

After having defined both cognitive phenomena, intuition and insight, it becomes obvious that both share a similarity in terms of persisting conceptual difficulties. Moreover, with regard to the subjective phenomenology they reveal a distinct picture: While intuition means to non-consciously understand environmental patterns and to act according with this first impression without being able to justify it ( Bowers et al., 1990 ), insight problem solving deals with situations in which a solution pops into a person’s mind out of the blue ( Durso et al., 1994 ). Yet, both processes can be viewed as non-analytical solution or thought processes, where no incremental search takes place. In the following, we will critically elaborate on the cognitive processes assumed to underlie intuition and insight. Starting point will be a few words on the research history of both, which allow to understand why both fields of research have developed independently over time.

The Single- vs. Dual-System View on Intuition

Intuition research has been deeply integrated in research on judgment and decision making that investigates how humans decide between alternatives and judge situations ( Plessner et al., 2008 ). Yet this took some time, in which intuition had been neglected due to its elusiveness ( Betsch, 2008 ). Now researchers agree that “intuition need not to be “magical” – it can be defined and explained scientifically” ( Sadler-Smith, 2008 , p. 1). It has to be emphasized, though, that, historically, the concept of intuition has fallen between (at least) two stools: The fast-and-frugal-heuristic approach – which sees the concept in a positive light as it serves as the basis for heuristics and thus is a valid strategy successfully be used when time and cognitive capacity is limited in a fuzzy real world ( Gigerenzer et al., 1999 ) –, and the heuristics-and-biases approach – which conceives of heuristics based on intuition as a source of erroneous and biased thinking that demonstrates human cognitive fallibility ( Kahneman and Tversky, 1974 ). Both approaches have localized the concept of intuition completely differently within human thought processes and assign qualitatively different functions to it. Today, due to their continuing, fundamentally contradictory assumptions concerning human cognition, the fast-and-frugal-heuristic approach and the heuristics-and-biases approach pit themselves against each other. Conceptually, the key difference may be that Kahneman and Tversky (1974) and Kahneman (2011) advocate a dual-system view on human thinking (intuition vs. deliberation), whereas Kruglanski and Gigerenzer (2011) and Mega et al. (2015) favor a single system view of unified processes in thinking and reasoning. Additionally, it has to be emphasized that, since interest in intuition has mainly originated from the area of judgment and decision making, implications for intuition with respect to problem solving processes (and insight) are rather hard to derive from this kind of research. This may have complicated experimentally clarifying the relationship between intuition and insight.

Intuition As Experienced-Based Perception of Coherence and As an Antecedent of Insight

To anticipate elaboration taking place later in this contribution, we mention a third approach in intuition research, which has developed independently from any dual- or single perspective and has its roots in the creativity and problem-solving literature ( Mednick, 1962 ; Bowers et al., 1995 ; Dorfman et al., 1996 ). Intuition is here conceived as the experience-based perception or recognition of environmental meaning/coherence in terms of a sensitization toward the detection of hidden patterns whose structure cannot be immediately verbalized. For example, in the different versions of the semantic coherence task originally developed by Bowers et al. (1990) , participants are asked to judge the semantic coherence of word triads and to name a forth word that may be the semantic link between the words, if it exists. Research found out that in these tasks participants are able to correctly categorize word triads as semantic coherent or incoherent – intriguingly even when they are not able to name the forth word, which is a paramount example of intuitive processing (e.g., Bowers et al., 1990 ; Bolte and Goschke, 2005 ). They rather feel the semantic link between the three words, but are not (yet) able to report on the reasons in terms of a solution concept that describes the semantic associations between the triad’s constituents. The concept of fringe consciousness ( Mangan, 1993 , 2001 , 2015 ) may be helpful to further understand intuition as the preliminary perception of environmental coherence. Price and Norman (2008) , referring to the concept of fringe consciousness, have explained that the stream of consciousness does not only include a nucleus of consciously available information , but also a non-conscious fringe that contains cognitive signals of temporarily unavailable, non-conscious information processing that is constantly going on in the background (as it accompanies cognition). These signals are continuously going on as cognitive byproducts of cognitive processes . Yet, they are only consciously experienced when attention is drawn to them ( Reber et al., 2004 ). Regarding the semantic coherence task, the product of this non-conscious processing on the fringe (i.e., the subjectively experienced intuition) is consciously perceivable, but its antecedents, direct content, and underlying processing mechanisms are outside of awareness (see also Topolinski and Strack, 2009a ).

On this view, intuitive responses have been understood as “intuitive antecedents of insight” ( Bowers et al., 1995 , p. 27). As far as we know, this has been the first (and only) conception that up to now has addressed a potential link between intuition and insight. Their early work allows deriving assumptions concerning the interaction of intuition and insight in more detail. Moreover, this conceptualization produced valuable empirical paradigms (e.g., semantic and visual coherence judgment tasks) that are particularly suited to investigate insight and its intuitive precursors. Therefore, we will elaborate on this conception later in this contribution when aiming to clarify the conceptual relationship between intuition and insight 2 .

The Special-Process vs. Nothing-Special View on Insight

In contrast, research on insightful thinking has its roots in Gestalt psychology, which investigated the integration and ordering mechanisms of human perception and problem solving (e.g., Köhler, 1921 ; Duncker, 1945 ; Metzger, 1953 ). Similar to intuition research, the research on insight problem solving is also located between two different views: The special-process view – which posits that insight problem solving involves a unique cognitive process that is qualitatively different from the processes non-insight problem solving utilizes – and the business-as-usual or nothing-special view – which assumes that mainly the same cognitive processes are involved in insight and non-insight problem solving ( Seifert et al., 1995 ). Despite these two views, scientists have been highly fascinated by the topic since its early description by the Gestalt psychologists. This great interest culminated in the seminal book “The nature of insight,” which mainly deals with the Gestalt psychologist’s view on insight problem solving ( Sternberg and Davidson, 1995 ).

Interim Summary I

In sum, both concepts, due to their elusiveness, had to fight for recognition as an established field of research. Nevertheless, regrettably, research on intuition and research on insight has developed mostly independently from each other. However, this is in sharp contrast to a lay perspective on the two phenomena, which would rather endorse the perspective that intuition and insight are inherently intertwined with intuition being an antecedent of insight (in terms of a slight previous impression on the fringe of consciousness). Yet, the two branches of research evolved from different research traditions using different scientific paradigms and, unfortunately, have referred to one another only marginally (i.e., for instance by Bowers et al., 1990 ). Therefore, we think it is now time to scrutinize the relationship between the two phenomena in greater depth. Based on Bowers et al. (1990 , 1995 ) work, we will do this by elaborating on the cognitive similarities and differences of the two phenomena and by offering preliminary process ideas on their relationship.

Differences in the Cognitive Processes Assumed to Underlie Intuition and Insight

The continuity model of intuition: intuition as a gradual process.

In the majority of conceptualizations, intuitive processing has been described within a continuity model locating intuition on one end of the continuum and insight on the other. A prominent example is the two-stage model put forward by Bowers et al. (1990) . The authors determine intuition as the preliminary perception of coherence in the environment triggered by tacit knowledge that has been acquired unintentionally during a person’s life (i.e., the cue-criterion relationships that we addressed earlier in this contribution, see also Volz and Zander, 2014 ). While tacit, or implicit, knowledge is seen as the foundation on which intuitions are based (e.g., Lieberman, 2000 ), in our view, intuition must not be regarded solely as a phenomenon of or even be equated with implicit memory processing. As Volz and Zander (2014) clarify, there are several important differences between intuition and implicit memory concerning both the format in which information is stored in memory and the kind of signal that accompanies the respective cognitive process. The fact that implicit knowledge is seen only as one component of processing is similar to the field of implicit cognition in general. Here, implicit knowledge is assumed to be supplemented and/or completed by antecedent hunches of correct solution, the subjectively experienced nearness to the solution ( Reber et al., 2007 ).

Based on Polanyi’s (1966) concept of tacit knowledge, Bowers (1984 , p. 256) defined intuition as “sensitivity and responsiveness to information that is not consciously represented, but which nevertheless guides inquiry toward productive and sometimes profound insights.” According to the author, the cognitive processing from an intuitive hunch toward an explicit insight is gradual and proceeds in two stages. In the first stage, the guiding or intuitive stage , environmental cues trigger the activation of tacit knowledge associatively connected in semantic memory, which results in an implicit perception of coherence that (yet) cannot be explained verbally. This process is characterized by the automatic spread of activation proposed by Collins and Loftus (1975) . In the second stage of intuition, the integrative or insight stage , information becomes consciously available, which is enabled via a gradual accumulation of the previously activated concepts. The previous, implicit activation becomes now explicitly represented, which may thus be also interpreted as a form of insight processing. Hence, in Bowers et al. (1990 , 1995 ) conception, intuition precedes insight in the way that explicit representations are anticipated by the sensitization of environmental pattern or structure. Yet, besides the idea of a gradual, successive accumulation of activated concepts in associative memory, unfortunately, it has remained unclear which cognitive and/or physiological conditions foster the transition from sensed intuition to justified insight.

Bowers et al. (1990) approach is not only theoretically important it also carries paradigmatic weight. In order to empirically test their model’s assumptions, the authors developed several novel paradigms (verbal as well as perceptual ones), which today, after slight revisions, belong to the standard paradigms of intuition research (e.g., Bolte and Goschke, 2005 ; Volz and von Cramon, 2006 ; Topolinski and Strack, 2009b ; Hicks et al., 2010 ; Remmers et al., 2014 ; Zander et al., 2015 ). One of them is the semantic coherence task mentioned above, consisting of word triads that can be either semantically coherent (e.g., SALT, DEEP, and FOAM) or incoherent (DREAM; BALL; BOOK). Semantic coherence is determined via a fourth word each word of the word triad’s constituents associatively hints at (e.g., SEA for the coherent triad). Participants are instructed to perform a semantic coherence judgment , that is, to indicate via button press whether a given triad is coherent or incoherent. Researchers found that people showed an above-chance discrimination between coherent and incoherent triads even when they are not able to name the forth word (e.g., Bowers et al., 1990 ; Bolte and Goschke, 2005 ). In other words, people were intuitively sensitized to the detection of coherence prior to its explicit recognition (i.e., before having an explicit insight into the underlying semantic structure). Using a similar task, which consists of up to 15 semantically target-related clue words (i.e., the Accumulated Clues Task), it could be observed that participants continuously approached the explicit representation of environmental patterns/meaning ( Bowers et al., 1990 ; Reber et al., 2007 ), which could be recently also demonstrated on a neuronal level when using the semantic coherence task ( Zander et al., 2015 ). These results are perfectly in line with Bowers et al. (1990) definition of intuition and the corresponding gradual two-stage model. As another important aspect concerning the link between intuition and insight, Bowers et al. (1990) suggested the concept of semantic convergence to differentiate between triads that are rather easily solved by non-consciously reading out the common association (i.e., convergent triads) and triads that require a reorganization of semantic associations (i.e., divergent triads; see also the section Bridging the gap between the underlying processes of insight and intuition , second part).

To put it in a nutshell, according to the continuity model, – as Bowers et al. (1990) defined and tested it by means of verbal and visual coherence tasks – intuition and insight (in terms of an explicit representation that can be verbalized) are inherently intertwined: intuition and insight build upon each other and the one can hardly occur without the other. That is, intuitive processing is the non-conscious precursor of insight and thus, intuition and insight build on each other evolving on different processing stages. Accordingly, intuition and insight are not considered qualitatively distinct or mutually exclusive. Instead a crosstalk between the two is possible and even required to some extent. Importantly, Bowers et al. (1995) noted, that a thought process that appears to be sudden on a phenomenological level (like an aha-experience) nevertheless could have continuous underlying processes that have led to the particular subjective experience. Thus, they do not exclude the existence of subjective aha-experiences accompanying the successful solution generation in their verbal tasks.

Along these lines, when investigating insights from a naturalistic perspective (i.e., in a field setting and not in controlled laboratory settings), Klein and Jarosz (2011) found out that a substantial number of insights occurred gradually and in an (non-conscious) evidence-accumulating fashion. Following the naturalistic-decision-making approach ( Zsambok and Klein, 1997 ), the authors aimed at investigating the natural occurrence of insights by analyzing a collection of reported insight incidents (comprising a radical shift in understanding) having occurred in the different domains of everyday life of different occupation (e.g., invention, firefighting, management, and the like). The authors found out that (a) impasses did not occur in each insight case, (b) not every incident of an insight was accompanied by an aha-experience, and (c) an intuitive feeling of how near the solution might be occurred in many cases before the actual solution was reached. These results indicate that insights in a naturalistic setting may differ from insights synthetically induced by the class of pre-defined insight problems (e.g., eight-coin-problem, Ormerod et al., 2002 ) according to the degree with which the solution is derived gradually. Thus, in the naturalistic setting, a continuous solution approach (as advocated in intuition research) may be adoptable.

The Discontinuity Model of Insight: Insight As the Result of a Mental Restructuring Process

Contrary to the idea of a gradual solution approach, there is the discontinuity model of problem solving: insight is strongly linked to cognitive processes that restructure mental problem representations in order to allow the generation of a solution to a complex problem. A prominent example of a discontinuity model is the representational change theory put forward by Ohlsson (1992 , 2011 ) that combines the Gestalt psychological approach (characterized by a person being unable to report conscious solution strategies, cf. Duncker, 1945 ) and the information-processing view on problem solving (characterized by a conscious search through alternatives in a problem space, which is a controllable and reportable process, cf. Newell and Simon, 1972 ). According to the representational change theory, and in sharp contrast to the two-stage model developed by Bowers et al. (1990) , prior knowledge and experiences are postulated to hamper (instead of promote) the generation of solutions since they easily turn into constraints ( Knoblich et al., 1999 ). Based on this, Ohlsson (1992) introduced the idea that an impasse, that is a “blind lane” where one is caught in wrong solution attempts finding no expedient or problem solving attempts ceases, is the precondition for a representational change that results in an insight. According to the author, a restructuring process is required, during which self-imposed constraints of the problem representation change and the problem solver obtains a “fresh look” at the problem. Problem solvers may then be able to rearrange either the individual components or the general assumptions how to solve the problem. A putative mechanism assumed to drive such restructuring processes is the relaxation of self-imposed constraints . The representational change theory became very influential; there are several studies that have tested and could corroborate its assumptions (e.g., Knoblich et al., 2001 ; Kershaw and Ohlsson, 2004 ; Öllinger et al., 2006 , 2013 ).

In an eye movement study, for example, participants were asked to transform an incorrect arithmetic statement, which is made up of Roman numbers made of matchsticks, into a correct one moving only one single matchstick. Interestingly, it could be observed that before the correct solution of difficult problems was generated, suddenly, solvers attended such problem elements of the equation (e.g., the operators) longer that they had hardly noticed before. This was taken as evidence that successful solvers overcame self-imposed constraints ( Knoblich et al., 2001 ). Research on the underlying cognition of the representational change theory could also help in understanding the subjective aha-experience as a subjective marker of insight: a recent study conducted by Danek et al. (2016) provides first evidence that the self-reported rates of aha-experiences depend on the degree of constraint relaxation that is necessary to solve the given problem. The authors found that the more constraints had to be relaxed, the less aha-experiences were reported, which was interpreted such that the execution of several necessary solution steps (that are needed to gain a representational change) minimizes or even eliminates the experience of suddenness as a key attribute of subjective aha-experiences.

Interim Summary II

To summarize, according to a discontinuity model, the cognitive processes of intuition and insight seem to be qualitatively distinct. No crosstalk between them is possible. Moreover, the first (intuitive) look on a problem resulting in a mental impasse biases the subsequent solution. To be more precise, the intuitive apprehension of a problem necessarily leads to an impasse and restructuring processes are needed so as to overcome the bias and to solve the problem. This can be demonstrated, for example, via the utilization of magic tricks in order to probe insight problem solving. To explicate, Danek et al. (2013) recently introduced a novel paradigm consisting of magic tricks to investigate the cognitive underpinnings of insight problem solving. When viewing these magic tricks, the intuitive viewing pattern, which the magician intentionally utilizes, will very likely prohibit the understanding of the trick, that is, to first impede the solution to the problem. The solution is only within reach when the intuitive apprehension of the magic-trick situation, that is the first and rapidly formed impression, can be overcome. Classical insight problems as for example the famous candle problem ( Duncker, 1935 ) utilize the same rationale.

Bridging the Gap between the Underlying Processes of Insight and Intuition

Dual-system models of thinking and reasoning.

This discontinuity approach resembles the experimental procedure in typical judgment and decision-making studies conducted within the heuristics-and-biases framework ( Kahneman, 2011 ). This framework draws on a class of psychological models that are very well known in social and cognitive psychology and are called dual-system or dual-process models (e.g., Evans and Frankish, 2009 ; Kahneman, 2011 ). These models assume two different modes of thinking, which Stanovich and West (2000) called System 1 (described as e.g., non-conscious, fast, associative, holistic, automatic, and emotional) and System 2 (described as e.g., conscious, slow, analytic, serial, controlled, and affect-free). In other words, according to dual-system models, judgments may be formed via two qualitatively distinct processes or systems – an intuitive one (System 1) or a deliberate one (System 2). The intuitive strategy, thereby, is thought to require some sort of a feeling that “tells” a person which option is the optimal one. Thus, affective feelings are here seen as a crucial component that is inherent to the entire decision process. In contrast, when thoroughly deliberating on the pros and cons of multiple options, the solution to the decision process is considered to come to mind by way of logic and exhaustively sensible considerations of probable consequences. Thus, System 2 processing is here thought to not need or even to not involve any affective contribution.

Despite the large number of contributions that support the dual-systems view both theoretically and empirically, such theories have nevertheless recently come under strong fire ( Keren and Schul, 2009 ; Kruglanski and Gigerenzer, 2011 ). The main point of criticism put forward by Keren and Schul (2009 , p. 534) is that “the different dual-system theories lack conceptual clarity, that they are based upon methodological methods that are questionable, and that they rely on insufficient (and often inadequate) empirical evidence.” Kruglanski and Gigerenzer (2011) provide a unified approach and explain that both, intuition and deliberation, rely on the same functional principles (i.e., they are based on if – then rules), which is dependent on environmental conditions. As a reply to such criticism, Evans and Stanovich (2013) recently riposted that it is overstated since such criticism refers to dual-system models as a class of purely the same theoretical assumptions. They clarify that there are indeed different assumptions and terminologies subsumed under the dual-system framework, which needs to be considered. Nevertheless, there is also neuronal evidence against the assumptions of the dual-system approach ( Mega et al., 2015 ). The authors did a functional-magnetic-resonance-imaging study and asked participants to judge either intuitively or deliberately the authenticity of emotional facial expressions. Interestingly, the authors found that intuition and deliberation recruit the same neuronal networks – a finding well in line with Kruglanski and Gigerenzer’s (2011) proposal. It can be summarized that the dual-system framework is being much debated at the moment (see also volume 8 of Perspectives on Psychological Science , 2013) and therefore, it is very likely that there will be a revised conception in the foreseeable future.

Dual-System Models and the Discontinuity Model of Insight: Intuition As the First and Biased Problem Representation

After having shortly named the key assumptions of the dual-system framework as well as potential critical points, we will continue by elaborating on why we think the experimental approach of the insight problem solving literature (e.g., Danek et al., 2013 ) is similar to the one pursued by the heuristics-and-biases framework ( Kahneman, 2011 ). A typical task used by researchers of the heuristics-and-biases approach is the bat and the ball problem . Participants are told that a bat and ball together cost $ 1.10 in total and that the bat costs $ 1 more than the ball. Then they are asked to state how much the ball costs. A vast number of experiments showed that the first “intuitive answer,” following Kahneman’s terminology, is 10 cent, but after a while of conscious deliberation (i.e., analytical thought) participants find out that the correct answer is 5 cent ( Kahneman, 2011 ). Here is employed the same principle as in the magic-trick paradigm: the first and rapidly formed judgment, which is intentionally induced by the task material, is incorrect and hampers the generation of the correct solution (here 5 cent). In terms of the representational change theory an over-constraint problem representation is activated, where a simple goal representation is set up: total sum minus bat results immediately in the cost of the ball. Overcoming these assumptions seems difficult and requires a more sophisticated goal representation that combines two sets of information: (1) bat - ball = 1 AND (2) bat + ball = 1.10 => 1 in (2) ball + ball + 1 = 1.10 => ball = 0.05).

Together, experiments from both scientific fields show that by exploiting peoples’ intuitive apprehension of a problem, the solution is precluded from the beginning. To overcome the impasse or bias, it is suggested that the problem solver may engage in restructuring the problem space or in analytic strategies so as to eventually being able to solve the problem and to arrive at the objectively correct answer. Thus, there might be a reasonable mapping of the discontinuity model to the common dual-system model: first, the intuitive system starts (whether by default first or in parallel to System 2), and will lead to an over-constrained or biased problem representation that subsequently may lead to an impasse or conflict. Essential for reaching a solution is, (i) that the problem solver or decision maker realizes that the fast initial apprehension of the problem precludes its solution and (ii) engages in a representational change to overcome the initial problem representation ( Öllinger et al., 2014 ). Since, by definition, System 2 processing is slower than System 1 processing it can smooth out the first and hasty attempts made by System 1. In the diction of dual system theorists, the analytic mind is called up when encountering an impasse or conflict and will attempt to deliberately solve the problem by applying certain rational strategies. Importantly, Systems 1 and 2, or intuition and insight, are here considered to be qualitatively different – “hare and tortoise.”

Equally important, System 1 is considered subordinate to System 2 and its hasty responses needs to be tamed (cf. Kahneman, 2011 , p. 185). Kahneman (2011 , p. 44) states: “One of the main functions of System 2 is to monitor and control thought and actions “suggested” by System 1, allowing some to be expressed directly in behavior and suppressing or modifying others.” Given such an understanding of intuition and insight, the discontinuity model may suffer from the very same conceptual problem as a dual-system account of reasoning: that is, how and by which factors is a conflict or impasse detected? “Who” eventually launches restructuring processes that are needed to overcome the error? How does restructuring of the first problem representation take place? This may be viewed as a variation of the “homunculus problem.”

Hence, within the discontinuity conception of insight, intuition is not regarded as helpful or diagnostic for the generation of a pending insight. In line with this idea, Metcalfe and Wiebe (1987) investigated feeling of warmth accompanying insight and incremental problem solving using classical insight problems and algebraic problems. They used feeling-of-warmth ratings as the assessment of how close participants intuitively felt to the solution, which was taken to indicate the subjective nearness to the solution . Interestingly, they found out that these subjective feelings of warmth differed for insight and non-insight solutions insofar that they could predict performance only on incremental algebra problems. For insight problems such intuitive feelings were lacking. Given this result, one may conclude that intuition differs from insight concerning the (introspective) access to non-conscious processing: whereas decision makers intuit the solution to a problem, people solving the problem by insight show to lack such hunches. Thus, additionally to the continuity/discontinuity distinction, insightful solutions as in contrast to intuitive ones seem to be discrete phenomena in terms of availability to awareness. However, it could be also possible that the conscious assessment of how close/far the solution is, just easier for non-insight tasks. Since non-insight tasks are well-defined insofar that there are clear starts, solution paths, and goals, which enables exact planning of the necessary steps and its order (as for example in algebraic problems). Conversely, classical insight problems may be technically well-defined (in that there is also a clear start and goal, see e.g., the famous nine-dot problem), but since the problem’s different components are unhelpfully represented in the problem solvers mental set, it is difficult or rather impossible to estimate how far/close the solution is.

Interim Summary III

As an interim summary, it may be concluded that intuition research advocates a continuity model, in which intuition and insight build upon each other in a gradual and cumulative fashion: people are non-consciously sensitized toward pattern or meaning in the environment and act accordingly (e.g., Bowers et al., 1990 ). In contrast, insight research focuses on a discontinuity model, in which the initial representation of the problem (i.e., early intuition) biases later solution attempts and has to be overcome in order to reach a solution. Here, no intuitive precursors of insight in terms of a subjectively felt nearness toward the solution are assumed. This latter model resembles famous, yet recently heavily criticized, dual-system models in judgment and decision-making research insofar as in both approaches the participants first intuitive apprehension of a problem biases its later solution.

Semantic Coherence Tasks Used in Intuition and Insight Research: Word Triads and Remote Associates

Interestingly, in the semantic domain, intuition research following Bowers et al. (1990) approach and contemporary insight research do have used similar stimuli yet with different task rationales, which could be used as an excellent starting point for necessary, and up to now lacking, common investigations. As described earlier in this contribution, in the tradition of Bowers et al. (1990 , 1995 ), typical coherence judgment tasks include semantically coherent and incoherent word triads – a task that dates back to the work of Mednick (1962) . Here, response patterns of both triad types (i.e., coherent vs. incoherent) are compared to each other. In recent research on insight problem solving, Bowden et al. (2005) presented a novel framework and a new class of problems in order to probe insight problem solving. The authors equate subjectively reported aha-experiences with insight. The authors have used word triads based on Mednick’s (1962) task to investigate the neuronal underpinnings of insight. They presented a large number of problems that can be solved either by insight or by non-insight (i.e., Aha! vs. Non-Aha!) and do not require a lot of time to be solved ( Kounios and Beeman, 2014 ). As a result they found that Aha! solutions revealed distinguish neural patterns than Non-Aha!-solutions. Unlike intuition research, they (1) only applied word triads that are principally solvable (i.e., no incoherent triads), and (2) word triads that consist of compound remote associate.

Bowers et al. (1990) , distinguished two types of triads and termed them convergent and divergent triads , respectively. For convergent triads the common associate means the same with respect to each clue word, whereas for divergent triads the common associate is more remote and changes its meaning with respect to each clue word. An example for a coherent convergent triad is SALT DEEP FOAM– SEA; and an example for a divergent triad is AGE MILE SAND– STONE. Unlike convergent triads, divergent triads are built in a way one need to detect the multiple meanings of the solution word to associate it with the meanings of the three clue words. As divergent triads may require a restructuring of the different meanings of the clues with respect to the solution, these kinds of triads could be nicely seen as an insight condition.

According to Bowden and Jung-Beeman (2007) , divergent triads are not as complex as classical insight problems, but they can nevertheless be used as a kind of insight problems. Like typical insight tasks (1) they misdirect retrieval processes (i.e., the first word of a divergent triad biases later thought toward a specific, yet wrong direction), (2) the strategy that has led to the correct solution cannot be reported by the problem solver, and (3) aha-experiences can occur.

For such divergent triads, Cranford and Moss (2012) , using a verbal protocol method, found out that there are two different types of insight problems, for which only one type shows the typical traditional characteristics of an insight. It has to be emphasized that, unlike Bowden et al. (2005) , the authors consider all three components, subjective aha-experience, impasse, and restructuring, as necessary for an insight to occur. They could show that some problems, consisting of divergent triads, could be solved via immediate insight , whereas others were solved by non-immediate or delayed insight . Interestingly, only the latter type of insights showed the supposed phases of insight. Fedor et al. (2015) detailed on this question and found that the classical insight sequence (i.e., constrained search, impasse, insight, extended search, and solution) is a rather rare event. They found that participants showed much more often fairly different insight sequences (i.e., a flexible order of the different problem-solving stages), which has to be further specified in the future. We consider this line of research ( Cranford and Moss, 2012 ; Kounios and Beeman, 2014 ; Fedor et al., 2015 ) as promising and important for future endeavors, which may initiate the common investigations of intuition and insight.

Conclusion, Open Research Questions, and Future Directions

To conclude, we set out to disentangle the underlying mechanisms of intuition and insight so as to clarify their relationship. At first sight, intuition and insight seem to be very differently conceptualized: while the intuition literature favors a continuity model, insight has been described within in a discontinuity model. In a continuity model, early (semantic) readout processes are taken as diagnostic for the non-conscious detection of environmental patterns and/or meaning (in terms of an antecedent of later explicit mental representation or insight). Intuition is described as aiding decision making and problem solving when time and cognitive capacity is limited and necessary information is temporarily unavailable. Contrary to this, in a discontinuity model early intuitive responses misdirect the generation of a correct solution or are experimentally utilized to bias solution attempts. In this case, intuitions lead people astray. Instead of employing intuition, mental restructuring processes (i.e., qualitative changes in the non-conscious search processes) are needed to overcome biased intuitive impressions or apprehensions so as to eventually solve the problem. In that respect, a discontinuity model resembles dual-process accounts in judgment and decision making.

Except early work by Bowers et al. (1990 , 1995 ) and Dorfman et al. (1996) , there have not been much empirical investigations so far aiming at exploring similarities and differences in the underlying neurocognitive mechanisms of intuition and insight. A major drawback here may be that there are no tasks that easily enable a direct empirical comparison between the two concepts. Nevertheless, we consider it very important to test intuitive and insight solution processes by means of exactly the same task and within the same participants. Such a task needs to be created. With this theoretical contribution, we therefore aim to initiate common investigations of both fields of research to detect neurocognitive similarities and differences between intuitive processing and insight problem solving. A good starting point for common empirical investigations may be the use of different types of triads [as for example divergent and convergent triads, as formerly suggested by Bowers et al. (1990) ] in order to induce gradual and discontinuous solution attempts. We also consider it important to investigate not only the cognitive processes that may underlie intuition and insight, but also the neuronal processes involved. Future studies may shed light on the specific (and maybe distinct) neuronal correlates, which will then also allow drawing conclusions about the theoretical conceptualization of the two phenomena. Interesting research questions would be (as non-exhaustive list): (1) Are the neuronal correlates different for the two types of triads (convergent versus divergent triads)? (2) Do aha-experiences also occur for convergent triads? (3) Do feelings-of-warmth ratings occur for both types of triads or only for convergent triads? (4) Do verbal protocols differ for the two types of triads? (5) How can the assumed recursive coherence building process be neuronally mapped? The further investigation of the underlying cognitive and neuronal processes of restructuring may also deeply progress our understanding of the topic. Here, Öllinger et al. (2006 , 2013 ) reached influential results that may be carried forward in future research. Equally important, following Kounios and Beeman (2014) in using current neuroimaging techniques may promote the detection of objective physiological markers of insight (in form of a specific neuronal or electrophysiological activation pattern accompanying the experience of impasses and aha’s as well as correlating mental restructuring processes). Kounios and Beeman (2014) as well as Sandkühler and Bhattacharya (2008) already gained promising results in this respect, thus their research may be a good starting point for the future. To sum up, intuition and insight are intriguing (non-analytical) mental phenomena that need to be further investigated in the future.

Author Contributions

TZ developed the theoretical conception; wrote the article. MÖ developed the theoretical conception; revised the manuscript. KV developed the theoretical conception; revised the manuscript.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work was funded by the Werner Reichardt Centre for Integrative Neuroscience (CIN) at the University of Tübingen (an Excellence Cluster within the framework of the Excellence Initiative (EXG 307) funded by the Deutsche Forschungsgemeinschaft (DFG).

• ^ There is the idea that a period, in which a person after encountering an impasse is not being consciously engaged in finding the solution anymore and puts the problem aside (i.e., the incubation period ) fosters sudden insights of the solution (e.g., Gilhooly et al., 2012 ). Ritter and Dijksterhuis (2014) explain that unconscious thought processes continue to find the problem’s solution by re-organizing memory content eventually resulting in gist-based representations. This occurs in the absence of a person’s conscious attempts. It has to be emphasized, however, that empirical studies revealed different results as to whether incubation periods are beneficial for problem solving. The specific conditions under which positive incubation effects take place have to be further investigated ( Sio and Ormerod, 2009 ).
• ^ For the sake of completeness, it has to be emphasized that metacognitive processes may play a role as well in intuitive processing. To strengthen the scope of our argumentation, we decided not to detail on this notion. Please see Mealor and Dienes (2013) ; Storm and Hickman (2015) , or Thompson et al. (2011) . A particular emphasize may be laid on the concept of experience-based metacognitive feelings (e.g., Koriat and Levy-Sadot, 1999 ).

Betsch, T. (2008). “The nature of intuition and its neglect in research on judgment and decision making,” in Intuition in Judgment and Decision Making , eds H. Plessner, C. Betsch, and T. Betsch (New York, NY: Lawrence Erlbaum Associates), 3–22.

Google Scholar

Bolte, A., and Goschke, T. (2005). On the speed of intuition: intuitive judgments of semantic coherence under different response deadlines. Mem. Cognit. 33, 1248–1255. doi: 10.3758/BF03193226

CrossRef Full Text | Google Scholar

Bowden, E. M., and Jung-Beeman, M. (2007). Methods for investigating the neural components of insight. Methods 42, 87–99. doi: 10.1016/j.ymeth.2006.11.007

Bowden, E. M., Jung-Beeman, M., Fleck, J., and Kounios, J. (2005). New approaches to demystifying insight. Trends Cogn. Sci. 9, 322–328. doi: 10.1016/j.tics.2005.05.012

Bowers, K. S. (1984). “On being unconsciously influenced and informed,” in The Unconscious Reconsidered , eds K. S. Bowers and D. Meichenbaum (New York, NY: John Wiley & Sons), 227–272.

Bowers, K. S., Farvolden, P., and Mermigis, L. (1995). “Intuitive antecedents of insight,” in The Creative Cognition Approach , eds S. M. Smith, T. B. Ward, and R. A. Finke (Cambridge, MA: The MIT Press), 27–51.

Bowers, K. S., Regehr, G., Balthazard, C., and Parker, K. (1990). Intuition in the context of discovery. Cognit. Psychol. 22, 72–110. doi: 10.1016/0010-0285(90)90004-N

Claxton, G. (1998). Investigating human intuition: knowing without knowing why. Psychologist 11, 217–220. doi: 10.3758/s13415-014-0286-7

Collins, A. M., and Loftus, E. F. (1975). A spreading-activation theory of semantic processing. Psychol. Rev. 82, 407–428. doi: 10.1037/0033-295X.82.6.407

Cranford, E. A., and Moss, J. (2012). Is insight always the same? A verbal protocol analysis of insight in compound remote associate problems. J. Probl. Solving 4, 128–153.

Danek, A. H., Fraps, T., von Müller, A., Grothe, B., and Öllinger, M. (2013). Aha! experiences leave a mark: facilitated recall of insight solutions. Psychol. Res. 77, 659–669. doi: 10.1007/s00426-012-0454-8

Danek, A. H., Wiley, J., and Öllinger, M. (2016). Solving classical insight problems without Aha! experience: 9 dot, 8 coin, and matchstick arithmetic problems. J. Probl. Solving 9, 47–57. doi: 10.7771/1932-6246.1183

Dorfman, J., Shames, V. A., and Kihlstrom, J. F. (1996). “Intuition, incubation and insight: implicit cognition in problem solving,” in Implicit Cognition , ed. G. Underwood (Oxford: Oxford University Press), 257–296.

Duncker, K. (1935). Zur Psychologie des Produktiven Denkens [On the psychology of productive Thinking]. Berlin: Springer.

Duncker, K. (1945). On problem solving. Psychol. Monogr. 58:270. doi: 10.1037/h0093599

Durso, F. T. F., Rea, C. C. B., and Dayton, T. (1994). Graph-theoretic confirmation of restructuring during insight. Psychol. Sci. 5, 94–97. doi: 10.1111/j.1467-9280.1994.tb00637.x

Evans, J., and Frankish, K. (eds) (2009). In Two Minds: Dual Processes and Beyond . Oxford: Oxford University Press.

Evans, J., and Stanovich, K. S. (2013). Dual-process theories of higher cognition: advancing the debate. Perspect. Psychol. Sci. 8, 223–241. doi: 10.1177/1745691612460685

Fedor, A., Szatmary, E., and Öllinger, M. (2015). Problem solving stages in the five square problem. Front. Psychol. 6:1050. doi: 10.3389/fpsyg.2015.01050

Gick, M. L., and Lockhardt, R. S. (1995). “Cognitive and affective components of insight,” in The Nature of Insight , eds R. J. Sternberg and J. E. Davidson (Cambridge, MA: The MIT Press), 197–228.

Gigerenzer, G. (2008). Gut Feelings: The Intelligence of the Unconscious . New York, NY: Viking.

Gigerenzer, G., and Gaissmaier, W. (2011). Heuristic decision making. Annu. Rev. Psychol. 62, 451–482. doi: 10.1146/annurev-psych-120709-145346

Gigerenzer, G., Todd, P. M., and The Abc Research Group. (eds) (1999). Simple Heuristics that Make us Smart. New York, NY: Oxford University Press.

Gilhooly, K. J., Georgiou, G. J., Garrison, J., Reston, J. D., and Sirota, M. (2012). Don’t wait to incubate: immediate versus delayed incubation in divergent thinking. Mem. Cognit. 40, 966–975. doi: 10.3758/s13421-012-0199-z

Gladwell, M. (2005). Blink. The Power of Thinking Without Thinking. London: Penguin Books.

Glöckner, A., and Witteman, C. (2010). “Foundations for tracing intuition: models, findings, categorizations,” in Foundations for Tracing Intuition: Challenges and Methods , eds A. Glöckner, and C. Witteman (East Sussex: Psychology Press), 1–23.

Hicks, J. A., Burton, C. M., Cicero, D. C., Trent, J., and King, L. A. (2010). Positive affect, intuition, and feelings of meaning. J. Pers. Soc. Psychol. 89, 967–979. doi: 10.1037/a0019377

Hogarth, R. M. (2001). Educating Intuition. Chicago, IL: University of Chicago Press.

Jung-Beeman, M., Bowden, E. M., Haberman, J., Frymiare, J. L., Arambel-Liu, S., Greenblatt, R., et al. (2004). Neural activity when people solve verbal problems with insight. PLoS Biol. 2:E97. doi: 10.1371/journal.pbio.0020097

Kahneman, D. (2011). Thinking, Fast and Slow . London: Penguin Books.

Kahneman, D., and Tversky, A. (1974). Judgment under uncertainty: heuristics and biases. Science 185, 1124–1131. doi: 10.1126/science.185.4157.1124

Keren, G., and Schul, Y. (2009). Two is not always better than one: a critical evaluation of two-system theories. Perspect. Psychol. Sci. 4, 533–550. doi: 10.1111/j.1745-6924.2009.01164.x

Kershaw, T. C., and Ohlsson, S. (2004). Multiple causes of difficulty in insight: the case of thenine-dot problem. J. Exp. Psychol. Learn. Mem. Cogn. 30, 3–13. doi: 10.1037/0278-7393.30.1.3

Kizilirmak, J., Galvao Gomes da Silva, J., Imamoglu, F., and Richardsohn-Klavehn, R. (2015). Generation and the subjective feeling of “aha!” are independently related to learning from insight. Psychol. Res. doi: 10.1007/s00426-015-0697-2 [Epub ahead of print].

Klein, G., and Jarosz, A. (2011). A naturalistic study of insight. J. Cogn. Eng. Decis. Mak. 5, 335–351. doi: 10.1177/1555343411427013

Knoblich, G., Ohlsson, S., Haider, H., and Rhenius, D. (1999). Constraint relaxation and chunk decomposition in insight problem solving. J. Exp. Psychol. Learn. Mem. Cogn. 25, 1534–1555. doi: 10.1037/0278-7393.25.6.1534

Knoblich, G., Ohlsson, S., and Raney, G. E. (2001). An eye movement study of insight problem solving. Mem. Cognit. 29, 1000–1009. doi: 10.3758/BF03195762

Knoblich, G., and Öllinger, M. (2006). “Einsicht und umstrukturierung beim problemlösen [insight and restructering in problem solving],” in Denken und Problemlösen. Enzyklopädie der Psychologie [Thinking and Problem Solving. Encyclopedia of Psychology] , ed. J. Funke (Göttingen: Hogrefe), 3–86.

Köhler, W. (1921). Intelligenzprüfungen am Menschenaffen [Investigating intelligence in great apes] . Berlin: Springer.

Koriat, A., and Levy-Sadot, R. (1999). “Processes underlying metacognitive judgments: information-based and experience-based monitoring of one’s own knowledge,” in Dual-Process Theories in Social Psychology , eds S. Chaiken and Y. Trope (New York, NY: Guilford Press), 483–502.

Kounios, J., and Beeman, M. (2014). The cognitive neuroscience of insight. Annu. Rev. Psychol. 65, 71–93. doi: 10.1146/annurev-psych-010213-115154

Kruglanski, A. W., and Gigerenzer, G. (2011). Intuitive and deliberate judgments are based on common principles. Psychol. Rev. 118, 97–109. doi: 10.1037/a0020762

Lieberman, M. D. (2000). Intuition: a social cognitive neuroscience approach. Psychol. Bull. 126, 109–137. doi: 10.1037/0033-2909.126.1.109

Luchins, A. S., and Luchins, E. H. (1959). Rigidity of Behavior: A Variational Approach to the Effect of Einstellung . Eugene, OR: University of Oregon Books.

Maier, N. R. F. (1930). Reasoning in humans. I. On direction. J. Comp. Psychol. 10, 115–143. doi: 10.1037/h0073232

Mangan, B. (1993). Taking phenomenology seriously: the “fringe” and its implications for cognitive research. Consci. Cogn. 2, 89–108. doi: 10.1006/ccog.1993.1008

Mangan, B. (2001). Sensation’s ghost. The non-sensory “fringe” of consciousness. Psyche 7.

Mangan, B. (2015). The uncanny valley as fringe experience. Interact. Stud. 16, 193–199. doi: 10.1075/is.16.2.05man

Mealor, A. D., and Dienes, Z. (2013). The speed of metacognition: taking time to get to know one’s structural knowledge. Conscious. Cogn. 22, 123–136. doi: 10.1016/j.concog.2012.11.009

Mednick, S. A. (1962). The associative basis of the creative process. Psychol. Rev. 69, 220–232. doi: 10.1037/h0048850

Mega, L. F., Gigerenzer, G., and Volz, K. G. (2015). Do intuitive and deliberate judgments rely on two distinct neural systems? A case study in face processing. Front. Hum. Neurosci. 9:456. doi: 10.3389/fnhum.2015.00465

Metcalfe, J., and Wiebe, D. (1987). Intuition in insight and noninsight problem solving. Mem. Cognit. 15, 238–246. doi: 10.3758/BF03197722

Metzger, W. (1953). Gesetze des Sehens [Rules of vision]. Frankfurt: Kramer.

Newell, A., and Simon, H. A. (1972). Human Problem Solving. Englewood Cliffs, NJ: Prentice Hall.

Norman, E. (2002). Subcategories of “fringe consciousness” and their related nonconscious contexts. Psyche 8, 1–15.

Norman, E. (2016). Metacognition and minfulness: the role of fringe consciousness. Mindfulness doi: 10.1007/s12671-016-0494-z

Norman, E., Price, M. C., and Duff, S. C. (2006). Fringe consciousness in sequence learning: the influence of individual differences. Consci. Cogn. 15, 723–760. doi: 10.1016/j.concog.2005.06.003

Norman, E., Price, M. C., and Duff, S. C. (2010). “Fringe consciousness: a useful framework for clarifying the nature of experience-based feelings,” in Trends and Prospects in Metacognition Research , eds A. Efklides and P. Misailidi (New York, NY: Springer), 63–89.

Ohlsson, S. (1992). “Information-processing explanations of insight and related phenomena,” in Advances in the Psychology of Thinking , eds M. Keane and K. Gilhooly (London: Harvester-Wheatsheaf), 1–44.

Ohlsson, S. (2011). Deep Learning. How the Mind Overrides Experience. New York, NY: Cambridge University Press.

Öllinger, M., Jones, G., Faber, A. H., and Knoblich, G. (2013). Cognitive mechanisms of insight: the role of heuristics and the representational change in solving the eight-coin problem. J. Exp. Psychol. Learn. Mem. Cogn. 39, 931–939. doi: 10.1037/a0029194

Öllinger, M., Jones, G., and Knoblich, G. (2006). Heuristics and representational change in two-move matchstick arithmetic task. Adv. Cogn. Psychol. 2, 239–253. doi: 10.2478/v10053-008-0059-3

CrossRef Full Text

Öllinger, M., Jones, G., and Knoblich, G. (2008). Investigating the effect of mental set on insight problem solving. Exp. Psychol. 55, 270–282.

Öllinger, M., Jones, G., and Knoblich, G. (2014). The dynamics of search, impasse, and representational change provide a coherent explanation of difficulty in the nine-dot problem. Psychol. Res. 78, 266–275. doi: 10.1007/s00426-013-0494-8

Ormerod, T. C., MacGregor, J. N., and Chronicle, E. P. (2002). Dynamics and constraints in insight problem solving. J. Exp. Psychol. Learn. Mem. Cogn. 28, 791–799. doi: 10.1037/0278-7393.28.4.791

Plessner, H., Betsch, C., and Betsch, T. (eds). (2008). Intuition in Judgment and Decision Making. New York, NY: Lawrence Erlbaum Associates.

Polanyi, M. (1966). Implizites Wissen [The tacit dimension]. Frankfurt: Suhrkamp.

Price, M. C. (2002). Measuring the fringe of experience. Psyche 8, 1–24.

Price, M. C., and Norman, E. (2008). Intuitive feelings on the fringe of consciousness: are they conscious and does it matter? Judgm. Decis. Mak. 3, 28–41.

Reber, R., Ruch-Monachon, M.-A., and Perrig, W. J. (2007). Decomposing intuitive components in a conceptual problem solving task. Conscious. Cogn. 16, 294–309. doi: 10.1016/j.concog.2006.05.004

Reber, R., Schwarz, N., and Winkielmann, P. (2004). Processing fluency and aesthetic pleasure: is beauty in the perceiver’s processing experience? Pers. Soc. Psychol. Rev. 8, 364–382. doi: 10.1207/s15327957pspr0804_3

Remmers, C., Topolinski, T., Dietrich, D. E., and Michalak, J. (2014). Impaired intuition in pateints with major depressive disorder. Br. J. Clin. Psychol. 54, 200–213. doi: 10.1111/bjc.12069

Ritter, S., and Dijksterhuis, A. (2014). Creativity – the unconscious foundations of the incubation period. Front. Hum. Neurosci. 8:215. doi: 10.3389/fnhum.2014.00215

Sadler-Smith, E. (2008). Inside Intuition. Abingdon: Routledge.

Sandkühler, S., and Bhattacharya, J. (2008). Deconstructing insight: EEG correlates of insightful problem solving. PLoS ONE 3:1459. doi: 10.1371/journal.pone.0001459

Seifert, C. M., Meyer, D. E., Davidson, N., Patalano, A. L., and Yaniv, I. (1995). “Demystification of cognitive insight: opportunistic assimilation and the prepared-mind perspective,” in The Nature of Insight , eds R. J. Sternberg and J. E. Davidson (Cambridge, MA: The MIT Press), 65–124.

Sio, U. N., and Ormerod, T. C. (2009). Does incubation enhance problem solving? A meta- analytic review. Psychol. Bull. 135, 94–120. doi: 10.1037/a0014212

Stanovich, K. E., and West, R. F. (2000). Individual differences in reasoning: implications for the rationality debate. Behav. Brain Sci. 23, 645–665. doi: 10.1017/S0140525X00003435

Sternberg, R. J., and Davidson, J. E. (eds). (1995). The Nature of Insight. Cambridge, MA: The MIT Press.

Storm, B. C., and Hickman, M. L. (2015). Mental fixation and metacognitive predictions of insight in creative problem solving. Q. J. Exp. Psychol. 68, 802–813. doi: 10.1080/17470218.2014.966730

Thompson, V. A., Prowse Turner, J. A., and Pennycook, G. (2011). Intuition, reason, and metacognition. Cognit. Psychol. 63, 107–140. doi: 10.1016/j.cogpsych.2011.06.001

Topolinski, S., and Reber, R. (2010). Gaining insight into the “aha” experience. Curr. Dir. Psychol. Sci. 19, 402–405. doi: 10.3389/fpsyg.2014.01408

Topolinski, S., and Strack, F. (2008). Where there’s a will – there’s no intuition. The unintentional basis of semantic coherence judgments. J. Mem. Lang. 58, 1032–1048. doi: 10.1016/j.jml.2008.01.002

Topolinski, S., and Strack, F. (2009a). Scanning the “fringe” of consciousness: what is felt and what is not felt in intuitions about semantic coherence. Consci. Cogn. 18, 608–618. doi: 10.1016/j.concog.2008.06.002

Topolinski, S., and Strack, F. (2009b). The analysis of intuition: processing fluency and affect in judgments of semantic coherence. Cogn. Emot. 23, 1465–1503. doi: 10.1080/02699930802420745

Volz, K. G., and von Cramon, D. Y. (2006). What neuroscience can tell about intuitive processes in the context of perceptual discovery. J. Cogn. Neurosci. 18, 1–11. doi: 10.1162/jocn.2006.18.12.2077

Volz, K. G., and Zander, T. (2014). Primed for intuition? Neurosci. Decis. Mak. 1, 26–34. doi: 10.2478/ndm-2014-0001

Wertheimer, M. (1959). Productive Thinking. New York, NY: Harper.

Zander, T., Horr, N. K., Bolte, A., and Volz, K. G. (2015). Intuition as a gradual process: investigating intuition-based and priming-based decisions with fMRI. Brain Behav. 6:e00420. doi: 10.1002/brb3.420

Zsambok, C. E., and Klein, G. (eds). (1997). Naturalistic Decision Making. New York, NY: Routlege.

Keywords : intuitive decision making, insight problem solving, continuity, discontinuity, non-analytical solution processes

Citation: Zander T, Öllinger M and Volz KG (2016) Intuition and Insight: Two Processes That Build on Each Other or Fundamentally Differ? Front. Psychol. 7:1395. doi: 10.3389/fpsyg.2016.01395

Received: 02 May 2016; Accepted: 31 August 2016; Published: 13 September 2016.

Reviewed by:

Copyright © 2016 Zander, Öllinger and Volz. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY) . The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.

*Correspondence: Thea Zander, [email protected]

Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.

Incubation and interactivity in insight problem solving

• Original Article
• Open access
• Published: 26 February 2018
• Volume 84 , pages 128–139, ( 2020 )

Cite this article

You have full access to this open access article

• Niyat Henok 1 ,
• Frédéric Vallée-Tourangeau   ORCID: orcid.org/0000-0002-9554-5294 2 &
• Gaëlle Vallée-Tourangeau 1  

5826 Accesses

12 Citations

10 Altmetric

Explore all metrics

Insight is commonly viewed as originating from the restructuring of a mental representation. Distributed cognition frameworks such as the Systemic Thinking Model (SysTM, Vallée-Tourangeau and Vallée-Tourangeau, Cognition beyond the brain: interactivity and human thinking, pp 133–154, 2017 ), however, assumes that information processing can be transformed when it is distributed across mental and material resources. The experiments reported here investigated whether interactivity enhanced incubation effects with the cheap necklace problem. Participants attempted to solve the problem in a low-interactivity condition with pen and paper or in a high-interactivity condition with a set of metal chains. Performance was substantially better in a task environment that fostered a higher degree of interactivity at Time 1. There was evidence of an incubation effect as participants significantly improved in performance after a 2-week gap, particularly in the high-interactivity condition. Experiment 2 showed that the context within which people can enact their thinking following incubation is key to improve problem-solving performance. When the problem presentation changed after a 2-week gap (low interactivity to high interactivity or high interactivity to low interactivity), performance only improved for those who worked on a highly interactive task at Time 2. Taken together, these findings underscore the importance of adopting a systemic perspective when investigating incubation effects in problem solving.

Similar content being viewed by others

Cognition Beyond the Classical Information Processing Model: Cognitive Interactivity and the Systemic Thinking Model (SysTM)

Insight Problem Solving and Unconscious Analytic Thought. New Lines of Research

The end of science? On human cognitive limitations and how to overcome them

Avoid common mistakes on your manuscript.

In general day-to-day activities, problems range in nature and complexity. Different strategies are used to solve these problems based on previous experience, seeking help from others, utilising information and tools immediately available, and so on. Traditionally, psychologists classify problems into two broad categories: transformation and insight. Transformation problems are well defined with a clear specified goal, such as the Tower of Hanoi. The problem space identifies the sequence of steps that transforms the problem from the initial state to the goal state. By contrast, insight problems are less well defined, and are formulated in a manner that derails participants’ ability to anticipate a path to solution.

The cheap necklace problem (CNP) is one such insight problem. Introduced by Silveira ( 1971 ), the CNP is a difficult problem with a solution rate often less than 10% (Fioratou & Cowley, 2009 ; Fioratou, Flin, & Glavin, 2010 ; Silveira, 1971 ). In its standard form, participants are presented with a diagram of four chains each consisting of three links, alongside a diagram of a complete 12-link necklace. Figure  1 presents a slightly modified version wherein actual chains are shown in a photograph rather than illustrated with a schematic diagram. Participants are asked to reconstruct the necklace by connecting the four separate chains at a cost: namely, 2¢ to open a link, 3¢ to close a link, with a maximum spending of 15¢. It is not possible to solve this task by simply connecting the ends of each chain, as this will exceed the 15¢ allowed. Joining the ends of each chain suggests optimal progress towards the solution as the initial move of joining two chains together only cost 5¢, yet makes half of the necklace. This path, however, leads to a dead end as it will eventually cost 20¢. Although joining the ends of the chains does not work, participants have been observed to persevere with this strategy (Chu, Dewald & Chronicle, 2007 ). The solution requires all the links in one chain to be opened at a cost of 6¢, then connecting the remaining three chains together using those open links, at a cost of 9¢. The solution to break up the chain with the aim of making a complete necklace is counterintuitive.

Given and goal states in the cheap necklace problem

When struggling to solve a problem, it may pay off to leave it aside for some time before attempting to discover a solution. In problem-solving research, the initial period of unsuccessful labour is sometimes referred as a ‘preparation’ phase and the interpolated break period the ‘incubation’ phase (Wallas, 1926 ). There is evidence that taking a break from the CNP after struggling to solve it results in higher solution rates later. Silveira ( 1971 , Experiment 2) sought to establish whether the difficult CNP would be made easier when delays were placed between an initial intense period of working on the problem and a subsequent attempt at completing it. In her study, participants were shown the CNP on a sheet of paper. They were told they were free to make notes on the paper while they thought about the problem. They were also made aware that they would be interrupted, but were not told when. Thirteen minutes after reaching an impasse (for example, closing a circle of chains and realising they would go over budget), participants were interrupted to complete a short questionnaire about their performance. A control group could resume work on the problem as soon as the questionnaire was completed. The experimental group was given a 4-h break before resuming work on the CNP. After this incubation period, they were given the same sheet they had previously been working with and continued searching for a solution. Participants across all conditions performed well in the task, with successful performance at 38 and 81%, respectively. Overall successful performance was very high in this study in comparison to subsequent studies on the CNP, which may be explained by the extended period of time people were allowed to work on the problem (González-Vallejo, Lassiter, Bellezza, & Lindberg, 2008 ).

Sio and Ormerod’s ( 2009 ) meta-analysis examined incubation effects for three types of problems, creative (e.g. unusual uses test), visual insight problems (of which the CNP is an example, see Sio & Ormerod, p. 113), and linguistic insight problems (e.g. remote associate problems). Their meta-analysis reported significant incubation effects for all three types of problems. The main moderator of incubation effects for visual insight problems was the length of the preparation phase. Thus, a stronger incubation effect is observed the longer a participant struggles to solve the problem before the interpolated break period.

Incubation in tasks such as the CNP may help problem solving through restructuring following impasse (MacGregor, Ormerod, & Chronicle, 2001 ). Restructuring is conceived as the reorganisation of a reasoner’s mental representation in a more productive form, enabling a more adequate use of the problem information to reach a solution (Sio & Ormerod, 2009 ). Restructuring can proceed through switching search strategies for possible moves (e.g. MacGregor et al., 2001 ), relaxing constraints on possible moves as well as decomposing familiar patterns of features or “chunks” (e.g. Knoblich, Ohlsson Haider & Rhenius, 1999 ); some of these mental processes may be unconscious rather than reflecting a conscious deliberate analysis of the problem elements. In addition, withdrawing attention from a problem that resists a solution (and its concomitant incorrect representation) can enhance solution rates once the problem is revisited (Segal, 2004 , Sio & Ormerod, 2009 ). One never steps into the same idea twice (to adapt Ingold, 2014 ) and returning to the problem after a delay may help defuse incorrect assumptions and encourage a different perspective on the problem.

Breaking one of the four chains into three separate links is the breakthrough required to solve the CNP problem. The difficulty in solving this problem is often attributed to the (mental) representation of the small chains as tight perceptual chunks. From the perspective of Ohlsson’s ( 1992 ) Representational Change Theory, for instance, a solution is more likely achieved if the representation is restructured such that individuated links are segmented and hence can be decomposed. Alternatively, the Criterion for Satisfactory Progress theory (Chu et al., 2007 ) proposes that hints aimed at defusing the first obvious move—namely to connect two chains to form half the necklace—may help reasoners solve the problem. In a series of experiments, Chu et al. established that a mix of hints to prevent selecting the obvious first move as well as presenting one of the four chains as made up of three links each of a separate colour was most efficient in improving solution rates. These findings suggest that both perceptual chunking and criterion for satisfactory progress contribute to the impasse.

Cognitive interactivity and the systemic thinking model (SysTM)

Despite being worded as an active task where links are opened and closed, the CNP problem is traditionally offered as a pen and paper exercise. Yet, outside the psychologist’s laboratory, situations that require problem solving are rarely encountered in this manner. Anthropologists, cognitive archaeologists, human factors engineers, and designers are keenly aware of the role of artefacts in supporting and transforming thinking (e.g. Baber, Chemero, & Hall, 2017 ; Hutchins, 1995 ; Kirsh, 2013 ; Malafouris, 2014 ; Norman, 1993 ; Toon, 2011 ). Recently, the systemic thinking model (SysTM, Vallée-Tourangeau, Abadie, & Vallée-Tourangeau, 2015 ; Vallée-Tourangeau & Vallée-Tourangeau, 2017 ) was developed to account for interactivity, defined as the processes involved when thinking and problem solving take place in environments where people and things exert a reciprocal influence upon one another. (see Fig.  2 ).

(SysTM, adapted from Vallée-Tourangeau & Vallée-Tourangeau, 2017 )

Systemic thinking model

SysTM highlights that when participants can act directly upon the material presentation of the information, thinking no longer results exclusively from the deductive processing of a mental representation (Rumelhart, Smolensky, McClelland, & Hinton, 1986 ). Rather, solutions to problems emerge from a situated agent–environment ecosystem: that is, from an agent situated in, interacting with, and being influenced by her physical environment. Extending our conception of cognitive activity beyond the remits of deductive mental processing allows introducing a different type of information processing, namely inductive processing, which may also transform, and possibly augment, thinking performance (Kirsh, 2017 ). Specifically, SysTM proposes that enabling the physical manipulation of one’s immediate environment supports the perception of “micro-affordances” (Ellis & Tucker, 2000 ), or possible actions within one’s environment that are perceived without being mediated by mental representations. As individuals act upon these perceived micro-affordances (e.g. by grasping a chain), they transform the perceptual input. This affordance-driven physical rearrangement allows cognition to proceed through an inductive processing loop where the physical manipulation of the material layout without a clear mental plan multiplies the opportunities to achieve different and potentially fruitful perceptual perspectives.

It follows that agent–environment ecosystems can be characterised by the level of interactivity they afford, that is, the extent to which the cognitive agent has the opportunity to transform the material instantiation of a cognitive task and, conversely, to be influenced by the task’s changing perceptual layout. One of the key predictions of SysTM is, therefore, that increasing the opportunities to physically manipulate information through highly interactive environments will increase the likelihood of successful problem solving.

Consistent with this view, increasing opportunities to interact with the problem material has been shown to increase performance with matchstick algebra problems (Weller, Villejoubert, & Vallée-Tourangeau, 2011 ) as well as the CNP (Fioratou & Cowley, 2009 ). To measure the impact of increasing interactivity in the CNP, Fioratou and Cowley ( 2009 ) compared two problem versions: an “abstract” paper-and-pencil version where participants were given a pen and could draw possible solutions and a “concrete (physical)” version where participants were presented with opening and closing metal chains to work on the problem. In line with the SysTM terminology, we will thereafter distinguish these versions by the level of interactivity they afford, and refer to them as “low-interactivity” and “high-interactivity” versions, respectively. With 10 min to reach a solution, fewer than 3% of the participants solved the problem with the low-interactivity version. This performance rate rose to 30% when participants were given the opportunity to interact with a physical model of the problem in the high-interactivity version. To summarise, when thinking can be reflected and prompted by changes in the world, the resulting perceptual change may highlight cues to new strategies, thus enabling better planning and efficiency in progressing towards a solution (Vallée-Tourangeau & Vallée-Tourangeau, 2017 ; Vallée-Tourangeau, 2014 ; Vallée-Tourangeau, Abadie, & Vallée-Tourangeau, 2015 ).

Interactivity and incubation

Sio and Ormerod ( 2009 ) identify six possible moderators of incubation effects in problem solving, including length of the preparation phase and nature of the interpolated task (see pp. 95–97); however, they do not consider the interactive nature of the task environment. Rather, their perspective on problem solving is couched in cognitive terms aimed at eventually developing a ‘computational model of insight problem solving’ (p. 110), moderated by psychometric variables such as executive function and working memory capacity. Yet, as we mentioned above, another way to increase performance is to increase the interactivity afforded by the task presentation by giving participants the opportunity to manipulate actual chains. Participants in Silveira’s ( 1971 ) experiment did not have access to a material presentation of the cheap necklace. Thus, whether and how incubation effects may interact with higher degrees of task interactivity remains to be established.

Following the SysTM perspective, we can assume that working on a problem that offers limited opportunities for manipulating the task materials—as in the low-interactivity “pen-and-paper” version of the task—cognition will be constrained to follow deductive processing loops where actions (e.g. symbolic marks on the paper) proceed from a mentally represented plan. An unproductive task representation may lead to an impasse and restructuring may be hindered by the relative invariance of the informational input. Consider, by contrast, an information input which affords manipulation—as in the high-interactivity version mentioned above. Each manipulation of the metal chains has the potential to reconfigure the perceptual input. Akin to reasoners working on the low-interactivity version of the CNP, those engaged in interactive manipulation of metal chains in the high-interactivity version may restructure an unproductive task representation through planned hypothetico-deductive processing. The increased level of interactivity, however, also enables unplanned inductive processing. This does not only create more opportunities to identify a productive path to solution while they are working on the task, but it also fosters a richer, experiential and multisensory representation of the task information. This more dynamic and distributed representation may facilitate the discovery of new strategies and facilitate the relaxation of unproductive interpretations and constraints. Increased interactivity, we thus hypothesise, may favour productive restructuring when participants who failed to solve the problem at their first attempt may now be more likely to solve it on a second attempt after taking a break from working on the problem. In other words, an incubation effect may be more strongly manifested in a context that offers opportunities for action.

The SysTM perspective does not directly address whether incubation might be the product of largely deliberate conscious processing or unconscious processing—such as spread of activation or selective forgetting during the interpolated break. This is largely because the debate in its current form (e.g. Sio & Ormerod, 2009 , pp. 94–95) is couched in computationalist terms: in those accounts, the issue is not whether insight is mediated by physical processing in one’s immediate environment, but rather whether it occurs through mental unconscious processes or mental conscious processes. In other words, the current debate is formulated in a manner that validates rather than challenges commitments to the traditional mentalist framework. This being noted, the SysTM perspective offers the opportunity to broaden the debate by exploring how inductive processing and unplanned physical actions contribute to insight. Thus, in addition to exploring the impact of interactivity on solving the CNP, the experiments reported here tested the prediction that participants who failed to solve the problem at Time 1 would be more likely to solve it after a delay when they worked on the problem in a high-interactivity condition compared to those who returned to work on the problem in a low-interactivity task environment.

Operationalising incubation under laboratory conditions often proceeds with an intervening task that encourages reasoners to abandon working on the primary solving task for a short period of time, usually a few minutes (e.g. Patrick, 1986 ; Segal, 2004 ; Silveira, 1971 ), although it is sometimes difficult to determine the exact length of the incubation period (Sio & Ormerod, 2009 ). Anecdotal examples of incubation in science and the arts, however, span much longer periods of time, weeks or months (Weisberg, 2014 ). We were thus interested in exploring the impact of an incubation period that spanned weeks rather than minutes. Although it may be more difficult to control the nature of the activities that participants engage in during that period, it offers a test that is much closer to incubation as it manifests outside the psychologist’s laboratory.

Experiment 1

The aim of Experiment 1 was to examine whether interactivity would moderate incubation in the CNP task. Participants worked on the CNP either in a low- or high-interactivity condition. Based on previous findings, we expected performance to be influenced by the degree of interactivity afforded by the task environment: manipulating the physical elements of the problem should yield a higher solution rate than simulating moves mentally. Our main objective, however, was to test whether a higher degree of interactivity would promote a more pronounced incubation effect when participants returned to the problem after a substantial delay.

In addition to measuring solution rates, we also explored how solution latencies may be affected by increasing interactivity, as well as whether participants’ memory abilities may moderate the impact of increasing interactivity. There is increasing evidence to suggest that working memory is implicated in insight problem solving (e.g. Chudersky, 2014 ). However, tests and measures of working memory and problem-solving performance that inform correlational analyses usually proceed in task environments that afford little or no interactivity. Interacting with a physical model of the problem has been shown to functionally enhance a participant’s working memory resources when working on a mental arithmetic task, since the physical model stores information and cues actions that may be more difficult to rehearse and simulate mentally (Vallée-Tourangeau, Sirota, & Vallée-Tourangeau, 2016a ). We were interested in determining the extent to which working memory was also implicated in performance on the CNP task, and whether its implication depended on the level of interactivity afforded by the task.

We also developed a long-term memory task based on the material reported in Roediger and Karpicke ( 2006 ); participants were presented with a short description of the Sun––qua celestial body––and were tested for their memory of that material at Time 1 and again at Time 2, computing a difference score to determine the rate of memory decline. This measure was designed to explore whether a long-term memory index discriminated between solvers and non-solvers at Time 2. This was exploratory because we were not in a position to make a specific prediction: On the one hand, better long-term memory skills may make it easier for participants to remember strategies employed at Time 1, but not whether these were successful or not. On the other hand, better memory skills may help participants remember more quickly what strategies were unsuccessful and hence support their dismissal.

Experiment 1: method

Participants.

Sixty-three undergraduate and postgraduate psychology students (53 females) volunteered to participate in exchange for course credits ( M age  = 22.05, SD  = 4.05). All participants were naïve to the CNP prior to participation.

A six-page problem pack was given to participants at both Times 1 and 2. The packs included an informed consent form, a short informative article about the Sun (only given at Time 1), the CNP with instructions and a set of four metal chains consisting of three links, which could be opened and closed by screwing the top of each link for participants in the high-interactivity condition. Low-interactivity participants were presented the task on a sheet of paper, including a picture of the chains, with the problem written at the top and lined space to work on a solution below.

Design and procedure

This experiment employed a 2 × 2 mixed design, where the between-subjects factor was the level of interactivity (low interactivity vs. high interactivity) and time was a repeated measures factor (Time 1 vs. Time 2). At Time 1 participants initially attempted to solve the CNP in either a low interactivity or high interactivity, which they again attempted in the same interactivity condition at Time 2, 2 weeks later.

All testing was conducted individually in a quiet room. At Time 1, participants were given 5 min to read a short summary about the Sun that contained 30 separate ideas written in 256 words (taken from Roediger & Karpicke, 2006 ). They were then presented with the CNP and the instructions were read aloud by the researcher. The picture of the CNP (as illustrated in Fig.  1 ) was shown to participants in both conditions. In both interactivity conditions, participants had up to 30 min to complete the task, with the option to stop whenever they chose. Once they were ready to announce their answer to the problem, participants in both interactivity conditions were asked to write it down and the time taken to completion was noted. Participants were then given a recall sheet, and were given 5 min to recall in either full sentences or bullet points any information they could remember from the short article they read before attempting the CNP. Participants were then debriefed, but no feedback on performance was given. At this time, they were asked to return to the laboratory 2 weeks later and not to discuss or work on the CNP during that period.

Two weeks later, participants were given 5 min at the start of the session to note anything they could remember from the short description of the Sun presented at Time 1. Long-term memory performance was indexed by taking the difference in the number of distinct ideas recalled at Time 1 and Time 2: The greater the difference in recall, the sharper was the decline in memory performance at Time 2. They were then presented with the CNP and given 30 min to solve the problem. Once they noted their solution, the time taken to complete the task was noted. A computation span (C-Span) working memory task was then presented to the participants (adapted from Ashcraft & Kirk, 2001 ). In the C-Span, participants solved a series of simple arithmetic expressions. The series were composed of two to six expressions. At the end of each series, participants were asked to remember the second number for each expression presented in their order of presentation.

Experiment 1: results

Cnp performance, solution rates.

Successful performance was classified using Silveira’s ( 1971 ) solution of deconstructing one chain into three links at a cost of 6¢, and using those three separate links to combine the remaining three chains into a single circle at a cost of 9¢. Solution rates are reported in Table  1 : Twelve (or 43%) of the participants solved the problem in the high-interactivity condition at Time 1, while two (or 6%) solved the problem in the low-interactivity condition; the difference in solution rates was significant, χ 2 (1, N  = 63) = 12.42, p  < .001. At Time 2, all the participants who solved the problem at Time 1, in both interactivity conditions, offered a correct solution. Of the 16 participants who had not solved the problem in the high-interactivity condition at Time 1, 7 (or 44%) solved it at Time 2; of the 33 participants who were unable to solve the problem in the low-interactivity condition at Time 1, 5 (or 15%) solved it at Time 2; the difference was significant, χ 2 (1, N  = 49) = 4.77, p  = .029. Because one of the four cells of the contingency table had expected frequencies lower than five, we also conducted a Fisher exact test, which was significant, p  = .040, and supported the initial chi square test.

Solution latencies

Latency to solution were considerably lower at Time 2 compared to Time 1 for those participants who had solved the problem at Time 1 (see Table  1 ). In a 2 × 2 mixed ANOVA, the main effect of time was significant, F (1, 12) = 26.8, p  < .001, but the main effect of level of interactivity, F  < 1, and the interaction between time and interactivity, F  < 1, were not. If the latencies for the participants who only solved the problem at Time 2 are compared with the latencies for those who solved the problem at Time 1, the main effect of time was significant, F (1, 21) = 11.1, p  = .003, but the main effect of interactivity, F  < 1, and the interaction between time and levels of interactivity, were not significant, F (1, 21) = 2.28, p  = .146.

Of the unsuccessful participants in the low-interactivity condition, seven participants persevered for 30 min. In the high-interactivity condition, among the 16 unsuccessful participants, 3 worked on the problem for 30 min. However, a better measure of diligence might be offered by the time spent on the problem by those who gave up before the allocated 30 min. Participants who gave up working on the problem did so quicker in the low-interactivity ( M  = 521 s, SD  = 472) than in the high-interactivity ( M  = 764 s, SD  = 447) condition, a marginally significant difference, t (37) = − 1.99, p  = .054. In light of the fact that the length of the preparation phase was identified as a significant moderator of incubation effects in Sio and Ormerod’s ( 2009 ) meta-analysis, time working on the problem for the unsuccessful participants at Time 1 might predict success at Time 2, independent of the level of interactivity. While participants who first solved the problem at Time 2 spent on average of four additional minutes working on the problem during Time 1 ( M  = 1029.0, SD  = 632.8) compared to those who did not solve the problem at Time 2 ( M  = 787.5, SD  = 571.1), this difference was not significant, t (47) = 1.24, p  = .221.

Long-term and working memory performance

Participants’ long-term memory was indexed on the basis of difference in their ability to recall separate ideas expressed in the Sun vignette at Times 1 and 2; the mean decline in performance is reported for participants who solved and did not solve the problem at Time 2 in both interactivity conditions in Table  1 . Memory decline was constant across participants in both conditions and as a function of having solved the problem. A 2(solved, did not solve) × 2(low, high interactivity) between subjects’ ANOVA confirmed those impressions: the main effects of having solved the problem, F  < 1, and interactivity, F  < 1, were not significant, nor was the interaction, F (1, 59) = 1.54, p  = .220.

Participants’ working memory capacity as gauged by their performance on a computation span test is reported in Table  1 . Participants who solved the problem generally had higher C-Span scores than those who did not solve the problem, and this pattern was observed in both interactivity conditions. In a 2 × 2 between-subjects ANOVA, those who solved the problem ( M  = 21.3, SD  = 9.0) scored significantly higher on the C-Span than those who did not ( M  = 14.1, SD  = 8.0), F (1, 59) = 6.84, p  = .011, but working memory capacity did not differ between participants in the high-interactivity condition ( M  = 20.7, SD  = 10.3) and low-interactivity condition ( M  = 13.3, SD  = 8.9), F (1, 59) = 1.64, p  = .206; the interaction was not significant, F  < 1.

Experiment 1: discussion

Experiment 1 sought to explore the impact of interactivity on the ability to solve the CNP as well as the degree of incubation manifested in performance at Time 2 as a function of the level of interactivity. The CNP is a difficult problem, and the solution rates observed here are similar to those reported previously (e.g. Fioratou & Cowley, 2009 ; Fioratou, Flin, & Glavin, 2010 ; Silveira, 1971 ). Upon first encounter in the low-interactivity condition, only two participants could find the solution. This low solution rate is in part explained by how quickly participants gave up on the task: Generally, participants were less diligent in the low-interactivity condition.

Performance on the CNP was significantly better when participants could use and manipulate tangible chains in the high-interactivity condition than when restricted to just a pen and paper to find the solution. Higher working memory capacity, however, was associated with higher solution rates in both conditions, a finding that lends support to the role of working memory in insight problem solving.

More participants completed the CNP at Time 2, and those participants who completed the task successfully on both attempts were quicker to find the solution during their second attempt. As we had anticipated, the incubation effect was distinctly stronger in the high-interactivity condition: participants who did not solve the problem at Time 1 in the high-interactivity condition were more likely to solve the problem at Time 2 than the unsuccessful participants in the low-interactivity condition at Time 1. Thus, incubation effects were more clearly manifested in a high-interactivity context. In addition, performance at Time 2 could not be explained in terms of better long-term memory; memory decline was similar in both conditions.

We assumed higher levels of interactivity in the initial context would provide multiple opportunities for unplanned interactions, thus resulting in a richer, more dynamic initial representation of the task in terms of possible moves and possible paths to solution. However, it remains to be established whether the greater increase in solution rates at Time 2 with the high-interactivity version of the CNP is driven by restructuration through incubation on a richer, more dynamic representation of the task fostered at Time 1 (an incubation-driven performance improvement) or by restructuration through enactment on the high-interactivity version of the CNP at Time 2 (an enactment-driven performance improvement). If the richness of the initial representation is indeed key to the incubation effect, performance after incubation should therefore remain high when people work on the high-interactivity version at Time 1, and are presented with the paper-and-pencil version at Time 2. Conversely, when presented with the paper-and-pencil at Time 1, the resulting initial representation should be less amenable to restructuration and thus offer limited advantage to improve performance at Time 2. There is an alternative possibility, however: it may be that incubation effects are realised in situ. If this is the case, we should expect that working within a context with limited action possibilities at Time 2 (i.e. using the paper-and-pencil CNP version) would impede performance improvement even if reasoners were able to interact with a high-interactivity version at Time 1. Conversely, a context replete with action possibilities (i.e. using the high-interactivity CNP version) at Time 2 should allow performance to leap up. These conflicting predictions are summarised in Table  2 and were tested in Experiment 2.

Experiment 2: method

Sixty-one undergraduate and postgraduate psychology students (56 females) were recruited to participate in exchange for course credits ( M age  = 21.43, SD  = 4.21). All participants were naïve to the CNP prior to participation.

The same materials from Experiment 1 were used.

Experiment 2 employed a 2 × 2 mixed design, with time as a repeated measures factor and interactivity level switch as a between subjects factor (low interactivity at Time 1 switched to high interactivity at Time 2 vs. high interactivity at Time 1 switched to low interactivity at Time 2). A similar procedure as that of Experiment 1 was employed aside from one key change: the interactivity level switch for participants at Time 2.

Experiment 2: results

As in Experiment 1, successful performance was classified using Silveira’s ( 1971 ) solution criterion. Solution rates are reported in Table  3 : Fourteen (or 41%) of the participants solved the problem in the high-interactivity condition at Time 1, while four (or 15%) solved the problem in the low-interactivity condition; the difference in solution rates was significant, χ 2 (1, N  = 55) = 5.03, p  = .025; this pattern of solution rates replicates the pattern observed at Time 1 in Experiment 1. At Time 2, all 14 participants who solved the problem in the high interactivity at Time 1 solved the problem in the low-interactivity condition. Among the remaining 20 participants who had not solved it at Time 1 in the high-interactivity condition, only 1 (or 5%) solved the problem in the low-interactivity condition at Time 2 All four participants who solved the problem in the low interactivity at Time 1 solved it in the high-interactivity condition at Time 2; of the remaining 23 who did not solve the problem in the low-interactivity condition at Time 1, 14 (or 61%) now solved the problem when they switched to the high-interactivity condition at Time 2.

The switch in the level of interactivity substantially affected performance. This is particularly clearly revealed on the basis of cross experiment comparisons. Thus, of the participants who did not solve the CNP in a low-interactivity condition in Experiment 1 at Time 1, 5 (or 15%) solved the same version of the problem at Time 2. In Experiment 2, of the participants who did not solve the low-interactivity version of the problem at Time 1, 14 (or 61%) subsequently solved the problem in the high-interactivity condition at Time 2. Thus, incubation following the paper-and-pencil task (low interactivity) led to significantly higher rate of solution in a highly interactive realisation context, χ 2 (1, N  = 56) = 12.64, p  < .001. Conversely, the switch to a low-interactivity condition for participants who started in a high-interactivity condition depressed performance considerably. Of the 20 participants who failed to solve the problem at Time 1 in Experiment 2 in the high-interactivity condition, only 1 (or 5%) solved it at Time 2 in the low-interactivity condition. In Experiment 1, of the 16 participants who had not solved the problem at Time 1 in the high-interactivity condition, 7 (or 44%) solved it at Time 2. In other words, incubation following the high-interactivity task version resulted in a significantly lower rate of solution in the “paper-and-pencil” low-interactivity realisation context, χ 2 (1, N  = 36) = 7.22, p  = .007. Because two of the four cells of the contingency table had expected frequencies lower than 5, we also conducted a Fisher exact test, which was significant, p  = .012, and supported the initial chi square test. Taken together, these results support the enactment-driven performance hypothesis (see Table  2 ), since, as Table  4 illustrates, switching from a high to a low level of interactivity resulted in a much smaller increase in performance than switching from a low-interactivity to a high-interactivity level.

Latency to solution were lower at Time 2 compared to Time 1 for those participants who had solved the problem at Time 1 (see Table  3 ). In a 2 × 2 mixed ANOVA, the main effect of time was significant, F (1, 16) = 38.7, p  < .001, but neither the main effect of order (high to low or low to high), F  < 1, nor the interaction, F (1, 16) = 3.78, p  = .07, was significant. Looking at how quickly participants solved the problem at Time 2, for those who had not solved the problem at Time 1, the analysis could only be conducted for participants in the low- to high-interactivity condition, since only one participant in the high to low condition solved the problem at Time 2. In the low to high condition, Time 2 successful participants were not faster than those who had solved the problem at Time 1, t (16) = − 0.299, p  = .769. There was no difference in the level of perseverance among participants who did not solve the problem at Time 1 in the high-interactivity condition ( M  = 693 s, SD  = 464) and in the low-interactivity ( M  = 716 s, SD  = 386) condition, t (33) = 0.16, p  = .875.

Participants’ long-term memory was indexed on the basis of the difference in their ability to recall separate ideas expressed in the Sun vignette at Times 1 and 2. The mean decline in performance for participants who solved, and did not solve, the problem at Time 2 in both interactivity conditions is reported in Table  3 . Pooling the data across interactivity conditions, memory decline was a little less steep among participants who solved the problem ( M  = − 3.45, SD  = 1.76) than among those who did not solve the problem ( M  = − 4.85, SD  = 2.85). In a 2(solved, did not solve) × 2(low to high, high to low) between subjects ANOVA, the main effect of having solved the problem, F (1, 56) = 4.22, p  = .045, was significant; however, memory scores did not differ between experimental conditions, F  < 1; the interaction between success and experimental condition was not significant, F  < 1.

Participants’ working memory capacity as gauged by their performance on a computation span test is reported in Table  3 . Pooling the data across conditions, participants who solved the problem generally had higher C-Span scores ( M  = 22.52, SD  = 9.21) than those who did not solve the problem ( M  = 18.85, SD  = 24.94). However, in a 2(solved, did not solve it) × 2(low to high, high to low) between subjects ANOVA, the main effect of solving the problem was not significant, F  < 1, nor was the main effect of the experimental condition, F (1, 56) = 1.63, p  = .206; the interaction was also not significant, F  < 1.

Experiment 2: discussion

In Experiment 2 participants switched from a low- to a high-interactivity context or vice versa when they encountered the problem a second time 2 weeks later. At Time 1, participants were much more likely to solve the problem in the high- than the low-interactivity condition, replicating the pattern observed in Experiment 1. The effect of incubation was strongest when it was realised in a high-interactivity context. That is, the solution rate among participants who first encountered the CNP in a low-interactivity condition to then tackle the problem in the high-interactivity condition was significantly higher than when participants tackled the problem in a low-interactivity condition after initially working on the problem in a high-interactivity condition. This suggests that performance at Time 2 is primarily driven by the context of enactment rather than by the nature of the problem representation achieved prior to incubation. In addition, diligence among unsuccessful participants at Time 1 in Experiment 2 did not differ significantly between the low- and high-interactivity condition. Pooling the data across the interactivity conditions, participants who scored better on the long-term memory task were more likely to solve the problem at Time 2, suggesting that long-term memory might be implicated in moderating the learning effect across exposure to the problem; however, working memory capacity as measured with a computation span test did not differ between participants who solved and did not solve the problem at Time 2.

General discussion

The present experiments investigated incubation and interactivity in problem solving using the CNP. In Experiment 1, participants reattempted the task with the same level of interactivity as with their initial encounter. In Experiment 2, participants reattempted the task with a different scope of action possibilities; they switched from low interactivity to high interactivity or high interactivity to low interactivity. As expected, in both Experiment 1 and Experiment 2, participants in the high-interactivity conditions solved the problem more frequently than those in the low interactivity at Time 1. Informed by the Systemic Thinking Model (Vallée-Tourangeau & Vallée-Tourangeau, 2017 ), we predicted that incubation would differ markedly as a function of the level of interactivity. This is indeed what was observed in Experiment 1. Experiment 2 enabled us to refine this finding by demonstrating that higher levels of interactivity also play a critical role in facilitating solution following incubation, in the realisation context. All participants who interacted with the high-interactivity version of the CNP were able to transfer their solution to the low-interactivity version. Meanwhile, participants who did not solve the problem in the initial context using a paper-and-pencil version were able to overcome their impasse when they could manipulate chains following a 2-week break. However, for those who did not overcome their impasse at Time 1 while working on a high-interactivity version of the CNP, incubation on a presumably richer representation of the problem elements did not facilitate insight when their thinking was later constrained in a deductive processing loop while working on a paper-and-pencil version at Time 2 This finding suggests that task realism or “concreteness” cannot account for the effect of interactivity, since having encountered the more concrete high-interactivity version of the CNP at Time 1 was not sufficient to promote success regardless of the interactivity level of the task at Time 2. This is an important finding which suggests that restructuring following impasse is not a purely representational process; the unique SysTM perspective paves the way for moving beyond comparing and contrasting predictions from purely internalist accounts, such as those from representational change theory or the criterion of satisfactory progress hypothesis, to consider how increasing interactivity and, by way of consequence, increasing reasoners’ opportunities to process perceptual inputs through physical manipulation of the problem elements plays a critical role in the enactment of insight.

Future research may further distil this finding by examining more closely the nature of the representations created by the low-interactivity and high-interactivity versions of the CNP and their actual role in overcoming the impasse. The SysTM assumes that inductive processing results from unplanned actions driven by the perception of affordances. Therefore, we purposely did not use verbal protocols to avoid artificially forcing participants to engage in a deductive processing loop where they would actively plan each of their moves instead of being guided by the action possibilities they perceived. In other words, SysTM would predict that instructing participants to narrate their concurrent thought processes might reduce performance under high levels of interactivity as this would encourage more deductive processing, and limit or constraint opportunistic insights emerging from unplanned actions triggered by the perception of affordances.

Likewise, SysTM would predict that a passive observation of physical movements (e.g. where a participant is observing another participant who attempts to solve the task in a high-interactivity context) would not be as successful, since this would presumably increase the load of deliberative thinking as the observer attemps to uncover the intentions of the actor’s moves.

Admittedly higher degrees of interactivity engage a number of different physical and cognitive processes. The relatively blunt measure of problem-solving success reported in these experiments does not in itself identify their relative contributions. Future research may also explore whether, and by which processes, higher interactivity fosters unplanned actions and richer task representations through a more refined analysis of action possibilities and their impact on cognitive processes (see, e.g. Steffensen et al., 2016 for a probatonic analysis of another insight task, the 17 animals problem).

The results in the present study were in line with other results showing that interaction with artefacts enhances problem-solving success (Fioratou & Cowley, 2009 ; Vallée-Tourangeau, et al., 2015 ; Vallée-Tourangeau et al., 2016b ). The performance in the present experiments were considerably higher than those reported by Fioratou and Cowley ( 2009 ). This difference may be explained by the length of time permitted for participants to complete the task. Fioratou and Cowley allowed a maximum of 10 min, while participants in the experiments reported here could work on the problem for 30 min during each of the two testing sessions. Nonetheless, both the results of the present experiments and Fioratou and Cowley underscore the importance of working with a highly interactive version of the problem.

If an incubation effect is in part driven by participants adopting a fresh perspective on the problem, we would expect long-term memory scores to be higher for those who did not solve the problems at Time 2; however, if anything long-term memory scores were slightly higher among those who solved the problem at Time 2. In turn, while working memory capacity has been implicated in solving insight problems (e.g. Chuderski, 2014 ), the evidence is mixed (e.g. DeCaro, Van Stockum, & Wieth, 2016 ), and more important, previous work that explored problem solving in a high-interactivity task environment found no association between working memory scores and solution rates with a so-called insight problem (e.g. Vallée-Tourangeau et al., 2016b ).

The CNP remains a difficult problem to solve due to the non-obvious solution required, namely breaking one of the chains into its separate components to use as bridging links to create the full necklace. Working with a highy interactive version of the problem facilitates discovering the solution. Walking away from the problem is also a good thing. We observed here that participants who did not solve the problem at Time 1 were more likely to solve it at Time 2. The novel and original findings reported here indicate that an effect of incubation was most clearly present when participants worked on the problem in a high-interactivity condition at Time 2. These findings highlight the importance of examining problem solving in different task environments as well as gauging incubation as a function of the scope of action possibilities afforded by the level of interactivity. Interactivity matters and helps participants recognise more quickly a path to solution when they previously failed to solve the problem.

Aschraft, M. H., & Kirk, E. P. (2001). The relationships among working memory, math anxiety, and performance. Journal of Experimental Psychology: General, 130 , 224. https://doi.org/10.1037/0096-3445.130.2.224 .

Article   Google Scholar  

Baber, C., Chemero, T., & Hall, J. (2017). What the jeweller’s hand tells the jeweller’s brain: Tool use, creativity and embodied cognition. Philosophy & Technology . https://doi.org/10.1007/s13347-017-0292-0 .

Chu, Y., Dewald, A. D., & Chronicle, E. P. (2007). Theory-driven hints in the Cheap Necklace Problem: A preliminary investigation. Journal of Problem Solving, 1 , 18–32. https://doi.org/10.7771/1932-6246.1010 .

Chuderski, A. (2014). How well can storage capacity, executive control, and fluid reasoning explain insight problem solving. Intelligence, 46 , 258–270. https://doi.org/10.1016/j.intell.2014.07.010 .

DeCaro, M. S., Van Stockum, C. A. Jr., & Wieth, M. (2016). When higher working memory capacity hinders insight. Journal of Experimental Psychology: Learning, Memory, and Cognition, 42 , 39–49. https://doi.org/10.1037/xlm0000152 .

Article   PubMed   Google Scholar  

Ellis, R., & Tucker, M. (2000). Micro-affordance: The potentiation of components of action by seen objects. British Journal of Psychology, 91 , 451–471. https://doi.org/10.1348/000712600161934 .

Fioratou, E., & Cowley, S. J. (2009). Insightful thinking: cognitive dynamics and material artifacts. Pragmatics & Cognition, 17 , 549–572. https://doi.org/10.1075/pc.17.3.04fio .

Fioratou, E., Flin, R., & Glavin, R. (2010). No simple fix for fixation errors: Cognitive processes and their clinical applications. Anaesthesia, 65 , 61–69. https://doi.org/10.1111/j.1365-2044.2009.05994.x .

Gilhooly, K. J., & Fioratou, E. (2009). Executive functions in insight versus non-insight problem solving: An individual differences approach. Thinking & Reasoning, 15 , 355–376. https://doi.org/10.1080/13546780903178615 .

González-Vallejo, C., Lassiter, G. D., Bellezza, F. S., & Lindberg, M. J. (2008). Save angels perhaps”: A critical examination of unconscious thought theory and the deliberation-without-attention effect. Review of General Psychology, 12 , 282–296. https://doi.org/10.1037/a0013134 .

Hutchins, E. (1995). How a cockpit remembers its speeds. Cognitive Sciencs, 19 , 265–288. https://doi.org/10.1207/s15516709cog1903_1 .

Ingold, T. (2014). The creativity of undergoing. Pragmatics & Cognition, 22 , 124–139. https://doi.org/10.1075/pc.22.1.07ing .

Kirsh, D. (2013). Embodied cognition and the magical future of interaction design. ACM Transactions on Computer–Human Interaction, 20 (1–3), 30. https://doi.org/10.1145/2442106.2442109 .

Kirsh, D. (2017). Thinking with external representations. In S. Cowley & F. Vallée-Tourangeau (Eds.), Cognition beyond the brain: Interactivity and human thinking (2nd edn., pp. 61–84). London: Springer.

Chapter   Google Scholar  

Knoblich, G., Ohlsson, S., Haider, H., & Rhenius, D. (1999). Constraint relaxation and chunk decomposition in insight problem solving. Journal of Experimental Psychology-Learning Memory and Cognition, 25 , 1534–1555. https://doi.org/10.1037/0278-7393.25.6.1534 .

MacGregor, J. N., Ormerod, T. C., & Chronicle, E. P. (2001). Information processing and insight. Journal of Experimental Psychology: Learning, Memory, and Cognition, 27 , 176–120. https://doi.org/10.1037/0278-7393.27.1.176 .

Malafouris, L. (2014). Creative thinging: The feeling of and for clay. Pragmatics & Cognition, 22 , 140–158. https://doi.org/10.1075/pc.22.1.08mal .

Norman, D. A. (1993). Cognition in the head and in the world: An introduction to the special issue on situated action. Cognitive Science, 17 , 1–6. https://doi.org/10.1207/s15516709cog1701_1 .

Ohlsson, S. (1992). Information-processing explanations of insight and related phenomena. In M. Keane & K. J. Gilhooly (Eds.), Advances in the psychology of thinking . London: Harvester-Wheatsheaf.

Google Scholar  

Ormerod, T. C., Fioratou, E., Chronicle, E. P., & MacGregor, J. N. (2006). The remnants of insight. In R. Sun & N. Miyake. Proceedings of the 28th Annual Conference of Cognitive Science Society (pp. 1893–1898). Austin, TX: Cognitive Science Society.

Patrick, A. S. (1986). The role of ability in creative ‘incubation’. Personality and Individual Differences, 7 , 169–174. https://doi.org/10.1016/0191-8869(86)90052-8 .

Roediger, H. L., III, & Karpicke, J. D. (2006). Test enhanced learning: Taking memory tests improves long-term retention. Psychological Science, 17 , 249–255. https://doi.org/10.1111/j.1467-9280.2006.01693.x .

Rumelhart, D. E., Smolensky, P., McClelland, J. L., & Hinton, G. E. (1986). Schemata and sequential thought processes in PDP models. In J. L. McClelland & D. E. Rumelhart, & the PDP Research Group (Eds.), Parallel distributed processing: Explorations in the microstructure of cognition (Vol. 2, pp. 7–57). Cambridge MA: MIT Press.

Segal, E. (2004). Incubation in insight problem solving. Creativity Research Journal, 16 , 141–148. https://doi.org/10.1207/s15326934crj1601_13 .

Silveira, J. M. (1971). Incubation: The effect of timing and lenght on problem solution and quality of problem processing . Unpublished thesis, University of Oregon.

Sio, U. N., & Ormerod, T. C. (2009). Does incubation enhance problem solving? A meta-analytic review. Psychological Bulletin, 135 , 94–120. https://doi.org/10.1037/a0014212 .

Steffensen, S. V., Vallée-Tourangeau, F., & Vallée-Tourangeau, G. (2016). Cognitive events in a problem-solving task: Qualitative methods for investigating interactivity in the 17 animals problem. Journal of Cognitive Psychology, 28 , 79–105. https://doi.org/10.1080/20445911.2015.1095193 .

Toon, A. (2011). Playing with molecules. Studies in History and Philosophy of Science Part A, 42 , 580–589. https://doi.org/10.1016/j.shpsa.2011.08.002 .

Vallée-Tourangeau, F. (2014). Insight, interactivity and materiality. Pragmatics & Cognition, 22 , 27–44. https://doi.org/10.1075/pc.22.1.02val .

Vallée-Tourangeau, F., Sirota, M., & Vallée-Tourangeau, G. (2016a). Interactivity mitigates the impact of working memory depletion on mental arithmetic performance. Cognitive Research: Principles and Implications, 1 , 26. https://doi.org/10.1186/s41235-016-0027-2 .

Vallée-Tourangeau, F., Steffensen, S. V., Vallée-Tourangeau, G., & Sirota, M. (2016b). Insight with hands and things. Acta Psychologica, 170 , 195–205. https://doi.org/10.1016/j.actpsy.2016.08.006 .

Vallée-Tourangeau, G., Abadie, M., & Vallée-Tourangeau, F. (2015). Interactivity fosters Bayesian reasoning without instruction. Journal of Experimental Psychology: General, 144 , 581–603. https://doi.org/10.1037/a0039161 .

Vallée-Tourangeau, G., & Vallée-Tourangeau, F. (2017). Cognition beyond the classical information processing model: Cognitive interactivity and the systemic thinking model (SysTM). In S. Cowley & F. Vallée-Tourangeau (Eds.), Cognition beyond the brain: Interactivity and human thinking (2nd edn., pp. 133–154). London: Springer.

Wallas, G. (1926). The art of thought . London: Cape.

Weisberg, R. W. (2014). Toward an integrated theory of insight in problem solving. Thinking & Reasoning, 21 , 5–39. https://doi.org/10.1080/13546783.2014.886625 .

Weller, A., Villejoubert, G., & Vallée-Tourangeau, F. (2011). Interactive insight problem solving. Thinking & Reasoning, 17 , 424–439. https://doi.org/10.1080/13546783.2011.629081 .

Download references

This study was not funded by an external grant agency, charity, private or public corporation.

Author information

Authors and affiliations.

Department of Management, Kingston University Business School, Kingston-upon-Thames, KT2 7LB, UK

Niyat Henok & Gaëlle Vallée-Tourangeau

Department of Psychology, Kingston University, Kingston-upon-Thames, KT1 2EE, UK

Frédéric Vallée-Tourangeau

You can also search for this author in PubMed   Google Scholar

Corresponding authors

Correspondence to Niyat Henok , Frédéric Vallée-Tourangeau or Gaëlle Vallée-Tourangeau .

Ethics declarations

Conflict of interest.

Niyat Henok declares that she has no conflict of interest. Frédéric Vallée-Tourangeau declares that he has no conflict of interest. Gaëlle Vallée-Tourangeau declares that she has no conflict of interest.

Ethical approval

All procedures performed in the experiments reported here involving human participants were conferred a favourable opinion from Kingston University’s Faculty of Arts and Social Sciences Research Ethics Committee and were in accordance with the British Psychological Society Code of Ethics and Conduct and with the 1964 Helsinki Declaration and its later amendments.

Informed consent

Informed consent was obtained from all individual participants included in the two experiments reported here.

Rights and permissions

Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License ( http://creativecommons.org/licenses/by/4.0/ ), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Reprints and permissions

About this article

Henok, N., Vallée-Tourangeau, F. & Vallée-Tourangeau, G. Incubation and interactivity in insight problem solving. Psychological Research 84 , 128–139 (2020). https://doi.org/10.1007/s00426-018-0992-9

Download citation

Received : 18 July 2017

Accepted : 12 February 2018

Published : 26 February 2018

Issue Date : February 2020

DOI : https://doi.org/10.1007/s00426-018-0992-9

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Find a journal
• Publish with us
• Track your research

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• PMC10219327

Tracing Cognitive Processes in Insight Problem Solving: Using GAMs and Change Point Analysis to Uncover Restructuring

1 Institute of Psychology, University of Klagenfurt, 9020 Klagenfurt, Austria

Amory H. Danek

2 Department of Psychology, Heidelberg University, 69117 Heidelberg, Germany

Nemanja Vaci

3 Department of Psychology, Sheffield University, Sheffield S10 2BP, UK

Merim Bilalić

4 Department of Psychology, University of Northumbria at Newcastle, Newcastle upon Tyne NE1 8ST, UK

Associated Data

Technical details, such as data and code for the analysis, is available at https://osf.io/pwuhs/?view_only=7c52bda4e6fa481e826e5d7570b6ef34 (accessed on 25 April 2023).

Insight problems are likely to trigger an initial, incorrect mental representation, which needs to be restructured in order to find the solution. Despite the widespread theoretical assumption that this restructuring process happens suddenly, leading to the typical “Aha!” experience, the evidence is inconclusive. Among the reasons for this lack of clarity is that many measures of insight rely solely on the solvers’ subjective experience of the solution process. In our previous paper, we used matchstick arithmetic problems to demonstrate that it is possible to objectively trace problem-solving processes by combining eye movements with new analytical and statistical approaches. Specifically, we divided the problem-solving process into ten (relative) temporal phases to better capture possible small changes in problem representation. Here, we go a step further to demonstrate that classical statistical procedures, such as ANOVA, cannot capture sudden representational change processes, which are typical for insight problems. Only nonlinear statistical models, such as generalized additive (mixed) models (GAMs) and change points analysis, correctly identified the abrupt representational change. Additionally, we demonstrate that explicit hints reorient participants’ focus in a qualitatively different manner, changing the dynamics of restructuring in insight problem solving. While insight problems may indeed require a sudden restructuring of the initial mental representation, more sophisticated analytical and statistical approaches are necessary to uncover their true nature.

1. Introduction

In cognitive science, the temporal dynamics of problem-solving processes have always been an important topic of investigation. Most problems are assumed to be solved gradually, by piecing together information in order to arrive at a solution ( Newell and Simon 1972 ). To investigate these problems, several tools have been developed, which allow for the observation of each step of the problem-solving process (e.g., Tower of Hanoi, Hobbits and Orcs problem). In the case of “insight problems”, the solution often comes seemingly out of nowhere ( Duncker 1945 ), despite the problem appearing unsolvable just a moment earlier. To be solved, insight problems are thought to require a fundamental, sudden change in the way the problem is perceived, a process referred to as restructuring or representational change ( Ohlsson 1992 ; Wertheimer 1925 ). The restructuring from the initial, incorrect mental representation to the correct one is the key component in modern theories such as representational change theory (RCT) ( Knoblich et al. 1999 ; Ohlsson 1984 , 1992 , 2011 ).

Although the sudden nature of the underlying restructuring process is a main theoretical assumption about insight, the evidence for this claim is inconclusive. Ohlsson ( 1992 ) even hypothesized that “the sudden appearance of the complete solution in consciousness is an illusion caused by our lack of introspective access to our cognitive processes (...)” (p. 17). To truly understand the temporal nature of insight, the cognitive component of insight (restructuring) must be examined with appropriate tools. Observing changes in solvers’ mental problem representation is a methodological and statistical challenge, which is addressed in the present work. Among the reasons for this lack of clarity is that many measures of insight rely solely on the solvers’ subjective experience of the solution process. Using matchstick arithmetic problems, we demonstrate that it is possible to objectively trace problem-solving processes.

We first review the research on representational change, focusing on the experimental designs. After that, we describe a novel analytical approach that improves upon previous attempts. Finally, and arguably most importantly, we show that this analytical approach needs to be combined with appropriate statistical tools in order to work properly. We demonstrate the feasibility of this approach by re-analyzing eye-tracking data from an already published study ( Bilalić et al. 2019 ). The paper is accompanied by an online supplement , with technical details, such as data and code for the analysis, which is freely available at https://osf.io/pwuhs/?view_only=7c52bda4e6fa481e826e5d7570b6ef3 (accessed on 25 April 2023).

1.1. Temporal Dynamics of the Restructuring Process

In 1994, Durso and colleagues conducted an early study on the temporal dynamics of insight problem solving. They asked participants to rate the relatedness of word pairs in a word puzzle and found that, on average, solution-relevant pairs were rated as increasingly similar as participants approached a solution. The authors concluded that “[l]ike dynamite, the insightful solution explodes on the solver’s cognitive landscape with breathtaking suddenness, but if one looks closely, a long fuse warns of the impending reorganization” ( Durso et al. 1994, p. 98 ). Novick and Sherman ( 2003 ; Experiment 2) provided similar evidence. They asked participants to indicate within a short time window (250 ms after stimulus offset) whether presented anagrams were solvable. They found that, although participants could not find the solution within the allotted time, they were increasingly better at differentiating between solvable and unsolvable anagrams as the presentation time of the anagrams increased. The authors concluded that solvers gradually accumulate information relevant for solving the anagrams.

Several studies have focused on the concept of restructuring in insight problem solving, but have typically not measured the dynamics of the solving process (e.g., Ash et al. 2012 ; Ash and Wiley 2006 , 2008 ; Fleck and Weisberg 2013 ; MacGregor and Cunningham 2009 ). However, a number of studies have attempted to measure the temporal dynamics of restructuring, using different methods to acquire trace data. Some used repeated ratings of problem elements, either regarding their similarity ( Durso et al. 1994 ) or with regard to their relevance for the solution ( Cushen and Wiley 2012 ; Danek et al. 2020 ). Others recorded eye movements ( Ellis et al. 2011 ; Knoblich et al. 2001 ; Bilalić et al. 2019 ; Tseng et al. 2014 ) or employed solvability judgments ( Novick and Sherman 2003 ). In some of these studies, both incremental and sudden solution patterns were found ( Cushen and Wiley 2012 ; Danek et al. 2020 ; Novick and Sherman 2003 ), whereas other studies found only incremental patterns ( Durso et al. 1994 ).

1.2. Eye Movements and Matchstick Arithmetic Problems

Here, we will take a closer look at using eye movement recordings to measure the temporal dynamics of restructuring in insight problems (for a comprehensive overview on eye movements, please see Holmqvist et al. 2011 ). In general, eye movements provide an objective measure of cognitive processes, as they are closely linked to attention (e.g., Just and Carpenter 1976 ; Rayner 1995 ; Reingold et al. 2001 ). Specifically, eye fixations reveal when people pay attention to certain features of a problem and for how long. More importantly, eye tracking is particularly useful when participants might not remember or even concurrently report that they are paying attention to these elements ( Bilalić and McLeod 2014 ; Bilalić et al. 2008 , 2010 ; Kuhn and Land 2006 ; Kuhn et al. 2009 ). This is particularly relevant in the case of insight problems, where it is possible that people are not aware of the dynamics of their solution process.

We use the matchstick arithmetic problems introduced by Knoblich et al. ( 1999 ). Matchstick arithmetic problems are suitable for investigation with eye tracking, as was powerfully demonstrated by the seminal study of Knoblich et al. ( 2001 ). A matchstick arithmetic problem consists of a false arithmetic statement written using Roman numerals, arithmetic operators, and equal signs, all formed using matchsticks ( Knoblich et al. 1999 , 2001 ; see also Figure 1 below). The task is to transform the false arithmetic statement into a true statement by moving only a single stick. Four types of matchstick arithmetic problems have been defined with varying levels of difficulty, depending on the constraints that need to be relaxed and the tightness of the chunks that need to be decomposed. These problem types were theoretically derived from the representational change theory ( Ohlsson 1992 ) and have been empirically confirmed ( Knoblich et al. 1999 ; Öllinger et al. 2006 , 2008 ). The use of matchstick arithmetic problems enables us to build on a well-researched task domain. It is known which problem type should elicit the restructuring process ( Knoblich et al. 1999 ; Öllinger et al. 2006 , 2008 ), and it is possible to contrast it with a type which requires no restructuring. Additionally, based on Knoblich’s study (2001), predictions about eye movement patterns can be made. Furthermore, the matchstick arithmetic domain is well suited for eye tracking because each problem consists of individual matchsticks that do not overlap, allowing for precise differentiation of fixations. In other words, we can determine at any point in time which aspect of the problem is attended to.

Matchstick arithmetic problem. Participants are required to transform the false arithmetic statement to a true statement by moving a single matchstick. This problem requires restructuring, because the initial assumption that only the matchsticks from values can be manipulated needs to be changed. In this case, the operator “+” can be decomposed and its vertical matchstick moved to make another “=” sign (VI = VI = VI). The “+” sign is the critical element that needs to be changed for solution.

Knoblich et al. ( 2001 ) investigated constraint relaxation type problems, which are considered to require restructuring; see Figure 1 for an example. They found that for this problem (constraint relaxation type), both solvers and non-solvers examined the values in the beginning and spent most of their time doing so. This can be seen as an indication that participants were using an initial incorrect problem representation, triggered by previous knowledge, where only values can be changed. Only in the final third of the problem- solving period did later solvers change their mental representation, as demonstrated by their eye movements. Solvers started to pay attention more to the operators and less to the values. In contrast, non-solvers remained stuck in their initial representation, as they continued to attend to values rather than to operators. Similar results for the same problem were found by another eye-tracking study ( Tseng et al. 2014 ).

The Knoblich et al. ( 2001 ) study provides strong evidence for the claim that in problems that require constraint relaxation, a restructuring of the problem representation took place. However, it did not answer the question of whether this change was a sudden or a gradual one. In the final third of the allotted time, solvers paid attention to the important but previously ignored features, which could be interpreted as a result of sudden restructuring. It is nevertheless not that clear, since the final period may have lasted minutes, given that they took around five minutes to solve the problem. Thus, the restructuring might have been a continuous process over time. On the other hand, an eye-tracking study on anagrams by Ellis et al. ( 2011 ; see also Ellis and Reingold 2014 ) found that participants started disregarding the irrelevant problem elements several seconds before they came up with the solution. The viewing times on that problem elements were decreasing gradually. Most intriguingly, both participant groups, those who experienced pop-out insight-like solutions and those who did not, displayed the same gradual accumulation of solution knowledge.

1.3. Metacognitive Processes and Insight Problems

There is evidence that the problem-solving process benefits from hints (e.g., Bowden 1997 ; Bilalić et al. 2019 ; Ammalainen and Moroshkina 2021 ; Becker et al. 2021 ; Korovkin and Savinova 2021 ; Spiridonov et al. 2021 ). This is the case even when hints were unreportable; that is, hints even work when presented briefly below the threshold of consciousness. Ammalainen and Moroshkina ( 2021 ) found evidence that hints can influence the problem-solving ability, which can be both, positive and negative. In a positive way, hints which are helpful to find the solution increase solution rates. On the other hand, misleading hints can negatively affect solution rates by distracting problem solvers and leading to a decrease in their success rate. In our paper ( Bilalić et al. 2019 ), we also provided hints when participants were unable to find the correct solution after a certain time.

These hints serve two purposes: a practical and a theoretical one. On a practical level, they provide an additional check on the main assumption behind the restructuring process. On a theoretical level, they serve as explicit clues that tap into metacognitive processes ( Takeuchi et al. 2019 ; Metcalfe and Shimamura 1994 ). Hints make participants aware of important aspects in the problem, drawing their attention towards elements that may have been neglected. They also change participants’ knowledge about the problem, potentially affecting the way they solve insight problems ( Bowden 1997 ; Bilalić et al. 2019 ; Korovkin and Savinova 2021 ).

The present work is a re-analysis of our paper ( Bilalić et al. 2019 ). In our paper, we also combined solving of insight and non-insight problems with eye tracking. We presented first a non-insight matchstick problem and then the matchstick insight problem depicted here (see Figure 1 ) to 61 participants (5 male; M age = 22.8; SD age = 6.5). The study was designed to take into account the methodological issue discussed in the previous section. It built upon previous attempts that utilized more time periods and sometimes presented the last 5 or 10 s separately (see also Bilalić et al. 2008 , 2010 , 2014 ). In the 2019 study, we provided a more fine-grained temporal analysis of the solution process by using ten time periods of equal length for our eye movement analysis 1 (for more information, please refer to Bilalić et al. 2019 ). We demonstrated that the restructuring is a gradual process on the insight problem as the solvers started paying attention to the important aspects of the problem long before they found the solution. Here, we provide another set of data where the jump is sudden; that is, the solvers started paying attention to the important aspects immediately before they found the solution (as reported by Knoblich et al. 2001 ). This is done to illustrate (1) how classical ways of analyzing data, such as ANOVA, are inappropriate for discovering the sudden changes, and (2) how other non-linear approaches are required.

We expected that all participants would initially focus on the values. Solvers would shift their attention towards the critical element (the “+” operator), while non-solvers would remain fixated on the values. The first question of interest is whether the representational shift in eventual solvers will be sudden or rather incremental. The second question of interest is whether the explicit cue, that is, the hint, will produce a sudden rearrangement of attention towards the critical elements (here “+”, but also “=” because “=” is also an operator). In our design, we included hints for participants who had not solved the problem within five minutes. The hint provided at this point was ‘You can change the operators, too.’ We were interested in whether the hints change the dynamics of problem solving, specifically whether the solution process remains sudden even after receiving an explicit cue.

The problem proved difficult as only 34% found the solution. After the hint was provided, an additional 11% of participants were able to find the solution. We present the eye data analysis below, with a particular focus on the critical element of the problem, the plus sign (+). Additionally, when analyzing the impact of hints, we also focused on the equal sign (=) as the hints should also affect the attention drawn to this operator through metacognitive control. For analysis of other problem elements, please refer to the supplementary materials .

3.1. Is Insight Sudden or Incremental? (Solvers vs. Non-Solvers: First 5 Min Analysis)

In Figure 2 , raw data and means for each bin of the critical element for the first five minutes are presented. 2 The solving pattern follows the typical sudden pattern, where there is not much difference between eventual solvers and non-solvers with regard to the time spent on the critical element (+) until the end of the first five minutes. Solvers suddenly increase their dwell time just before announcing the solution, while non-solvers continue to observe the critical element sporadically until the end of the solving period.

Raw data and means for each bin of the critical element (+). The raw data represents every data point of each participant over the entire problem-solving period. The problem-solving period was divided in 10 proportional bins, each representing 10% of the total problem-solving time. The error bars represent the 68% confidence interval. This figure illustrates a nonlinear increase in the amount of time that solvers spend on the critical element. In the case of solvers, the 100% bin means the participant provided a solution.

The crucial question is how to analyze the temporal changes presented in Figure 2 . The traditional method, which we had chosen in our previous paper ( Bilalić et al. 2019 ), is to use an analysis of variance (ANOVA) where the bins and groups are factors that predict the amount of time spent on the critical element. However, ANOVA not only requires a completely balanced dataset, but it also ignores the clustered nature of data ( van Rij et al. 2020 ). Furthermore, it is based on linear regression, which is not suitable for capturing sudden attentional shifts, which are nonlinear in nature. In order to capture the sudden shift as depicted in Figure 2 (the 100% bin for the solvers), ANOVA would need to adjust the linear trend throughout the whole problem-solving period. In other words, a sudden trend may appear as an incremental one as ANOVA adjusts by increasing previous periods (see Figure 3 , left panel).

Estimated model means based on ( a ) ANOVA with linear term; ( b ) ANOVA with both linear and quadratic terms. Y-Axis: Time on the problem element (%). Please refer to supplementary material for the detailed analysis.

ANOVA can be expressed as linear regression, where an additional quadratic polynomial term is included next to the linear one, in an attempt to capture the shift. However, even in this case, the predicted shift by the ANOVA model would begin earlier, namely at the 80% bin, than it does in the raw data (see Figure 3 , right panel). The general limitation of linear regression, with or without polynomial terms, is that it heavily relies on previous trends. If the change is sudden, the previous time periods will also be adjusted accordingly.

One way around this problem is generalized additive (mixed) modeling (GAM). These models are specifically designed to handle nonlinear relationships, as they are data-driven and use non-linear mixed-effects regression ( van Rij et al. 2020 ). A key benefit of GAMs is that they do not require the user to specify the shape of the nonlinear regression line, as the model determines this based on the data. However, while GAMs have a high level of flexibility in modeling nonlinear changes in time series data, they only allow for the exploration of changes in the function and do not provide parametric estimates such as standard error of estimate or its impact on predictive accuracy of the model. More specifically, GAMs do not provide parametric estimates, which means that they do not give us a set of parameters that describe the shape of the nonlinear function. However, the present work intends to demonstrate the advantages and downsides of the available analysis tools in question, which is why GAMs are included here.

Arguably the most reliable way of checking the assumption of suddenness is the use of change point analysis, which looks for significant deviance from previous trends ( Raftery and Akman 1986 ). Unlike the standard regression analysis (ANOVA) and nonlinear GAMs, change point regression estimates the moment of the function inflection. In other words, it includes the possibility to estimate additional parameters, such as intercept and slope of regression, time point when the function changes, and how the intercept and/or slope of regression changes (see the figures of the MCP analysis for illustrations). This makes the technique particularly valuable in detecting increasing patterns as one would expect several points of change in the attentional pattern on the way towards the solution. In this instance, we use the one implemented in the Multiple Change Points package (MCP; Lindeløv 2020 ).

Below, we address the three main questions using both GAM and MCP analysis. In the supplemental material , we provide the model-estimated values for each case, which include the results and, in the case of the MCPs, how well the model fits the data and which model was used. We begin with the GAM analysis of solvers and non-solvers for the first five minutes to determine whether the insight is sudden or incremental. Figure 4 provides the estimated trend lines for both solvers and non-solvers, as well as the time periods (shaded in orange) where the difference between the two is statistically significant. The model estimates closely follow the raw data (see Figure 2 ), and the difference between solvers and non-solvers is indeed significant at the beginning of the solving phase, as well as at the 90% bin and the 100% bin.

GAM: the difference between two estimated trend lines for solvers and non-solvers of the critical element (+). This figure illustrates that the GAM also found a nonlinear increase in the amount of time that non-solvers spend on the critical element. The orange area determines where the differences between solvers and non-solvers were significant.

Figure 5 shows the results of the MCP analysis for the same data as the GAM above. Similarly to the GAM, the MCP analysis identified a change point around the 90% bin for the solvers, which captures an attentional shift they made. While some non-solvers also shifted their attention towards the “+” sign at the end, it was not as clear as in the case of the solvers.

MCP analysis of the critical element (+) for non-solvers and solvers. This figure illustrates every data point of each participant over the problem-solving period. Lines at the bottom of the figure illustrate the posterior density (estimated likelihood) of the change point for each MCMC chain. There is a nonlinear increase in the amount of time that solvers spend on the critical element.

3.2. Do Explicit Cues Rearrange Attentional Distribution? (An Immediate Change after the Hint)

Figure 6 illustrates the impact of providing an explicit hint to the non-solvers from the first five minutes (presented here as a single group; solvers from the first five minutes are not included in this graph). The attentional shift from values towards operators, “+” and “=”, is substantial immediately after the hint. The operator “=” is attended to twice as much immediately after the hint than before. The change for “+” is slightly less dramatic at first (only 4%), but by the 20% bin, the dwell time has doubled in comparison to before the hint was provided. Note that only non-solvers are shown here, since solvers did not receive any hints.

Raw data and means for each bin of the operators (“+” upper panel; “=” lower panel) in the period before and after the hint. The raw data represents every data point of each participant (non-solvers only) over the problem-solving periods. Each of both problem-solving periods (before and after the hint was provided) were divided in 10 proportional bins, each representing 10% of the total problem-solving time. It is necessary to view the problem-solving periods as distinct periods; therefore, each period is labeled from beginning to end (10% to 100%) to differentiate them. The error bars represent the 68% confidence interval. This figure illustrates the attentional shifts from values (mostly attended to before the hint) towards operators (attended to after the hint was given).

The GAM analysis effectively captures the attentional shift, as depicted in Figure 7 . However, it predicts that the change occurs prior to the hint being provided, starting already at the 90% bin, which is not a correct reflection of the actual data. While GAM is considerably more flexible than regressions with polynomial terms, the same problem of interdependence of neighboring phases remains. The shift caused by the explicit cue is so drastic that the GAM needs to adjust the increase to begin earlier in order to account for it.

GAM: estimated trend line for non-solvers of the critical element (+; upper panel) and the other operator (=; lower panel). This figure illustrates that the GAM also found a nonlinear increase in the amount of time that non-solvers spend on the critical element after receiving a hint. The orange area indicates where there is a significant shift in attention.

In contrast, the switch points of the MCP analysis correctly capture where the change in attention allocation happens (see Figure 8 ).

MCP analysis of the critical element (+; upper panel) and the other operator (=; lower panel). This figure illustrates that the switch points of the MCP analysis correctly captures where the shift in attention happens.

3.3. Does Metacognition Influence Insight Problem Solving? (Solvers vs. Non-Solvers after the Hint)

The final question we aimed to address was whether the explicit cue, and the additional knowledge about the problem associated with it, would alter the way the problem was solved. Figure 9 indicates that both solvers and non-solvers maintain the level of attention on the critical aspects throughout the problem-solving period, which is a direct consequence of the explicit cue. However, this was not sufficient for finding the solution. The eventual solvers initially shifted their attention to “=” around the 30% bin, but starting from the 50% bin, they increasingly focused on “+”. This means that at this point in time, the solvers may have realized that the “+” symbol was the critical element they needed to solve the problem. Consequently, they gathered more information about the symbol by attending to it more closely.

Raw data and means for each bin of the critical element (+; upper panel) and the other operator (=; lower panel) after the hint was provided. The raw data represent every data point of each participant over the remaining problem-solving period after the hint was given. The error bars represent the 68% confidence interval. This figure illustrates a nonlinear increase or decrease in the time solvers spend on the critical element.

This incremental pattern of solving is well captured by GAMs, as Figure 10 illustrates. While the non-solvers attended to the critical “+” operator consistently over the entire problem-solving period, but on a rather low level of 25% of their time, solvers gradually increased their attention towards it. Significant differences were found in the middle and the end of the problem-solving period. This was also the case for the other operator (=). Non-solvers attended to “=” in a consistent manner throughout the problem-solving period, while the solvers attended to “=” more in the middle of the problem-solving period and less at the very end of it, probably because they were then already focusing more on the “+” sign which needs to be changed for a solution.

GAM: the difference between two estimated trend lines for solvers and non-solvers of the critical element (+; upper panel) and the other operator (=; lower panel). This figure illustrates that the GAM also found a nonlinear increase in the time solvers spend on that particular element. The orange area in the figure indicates regions where there are statistically significant differences between the attention patterns of solvers and non-solvers.

Figure 11 illustrates that the attentional shifts after receiving a hint are effectively captured by the MCP analysis. Again, non-solvers attended to the “+” operator on a consistently low level throughout the entire problem-solving process, while solvers attended to the “+” operator more and more. The same trend is observed for the “=” operator. Non-solvers attended to it less, while solvers shifted their attention to it in the middle of the problem-solving process. Towards the end of the problem-solving process, the data suggest that solvers became aware that the “=” operator was not as important for solving the problem and began to focus more on the “+” operator.

MCP analysis of the critical element after the hint (+; upper panel) and the other operator (=; lower panel) for non-solvers and solvers. This figure demonstrates that the switch points of the MCP analysis correctly captures the incremental pattern of solving for the critical element (+). It also demonstrates that after the hint, the non-solvers attended to the noncritical element (=) more in the beginning but not the critical element (+). As the GAMs showed already, the non-solvers attended to the critical element (+) in the same way throughout the whole problem-solving period.

4. Discussion

We have demonstrated that recording eye movements is a valuable method for gaining insight into complex cognitive processes, including mental restructuring in insight problems. It is also an adequate tool for investigating attentional shifts after receiving hints. However, it is important to use eye movement recording with appropriate analytical approaches. Our results show that it is necessary to conduct a more fine-grained analysis of the eye movement data to capture the temporal dynamics of the problem-solving process. This is particularly relevant for insight problems such as the one used here, which are believed to feature a sudden change in eye movement patterns reflecting a change in mental representation.

We were able to identify the point at which solvers and non-solvers start to differ in their attentional patterns by dividing the problem-solving period into ten equal bins. The temporal resolution of the problem-solving period is one aspect, but it is also important to choose an appropriate statistical procedure. We have demonstrated that nonlinear statistical models, such as GAM and MCP, can effectively capture the sudden change that is a hallmark of insight problem solving. The GAM analysis can effectively capture the attentional shift; however, it predicts that the change occurs prior to the correct reflection of the actual data. While GAM is considerably more flexible than regressions with polynomial terms, the same problem of interdependence of neighboring phases remains. The shift caused by the explicit cue is so drastic that the GAM needs to adjust the increase to begin earlier to account for it. In contrast, the change points of the MCP analysis correctly capture where the change in attention allocation happens. A change point is a time point where the statistical properties of a time series change abruptly. However, in contrast to GAMs, one needs a priori knowledge about the number of change points and the form of the segments in between ( Lindeløv 2020 ). Therefore, one might decide from case to case which statistical procedure is appropriate.

Our example illustrates the importance of considering theoretical assumptions when choosing analytical and statistical procedures. The restructuring of mental representations is a key concept in theories of insight ( Knoblich et al. 1999 ; Ohlsson 1984 , 1992 , 2011 ). It is a nonlinear process in essence, which can be operationalized as a sudden burst of attention to the relevant aspects of a problem ( Bilalić et al. 2019 ). The shift inevitably deviates significantly from participants’ previous problem solving. Seen as a part of the overall problem-solving continuum, the sudden shift is difficult to capture with linear statistical procedures. Only truly nonlinear statistical procedures can appropriately capture the sudden nature of representational change.

Providing explicit hints typically alters the dynamics of problem solving. It is obvious that the given hints were effective, as participants’ patterns of attention show a drastic change, which is very well captured by both GAM and MCP. However, it is important to note that the eventual solvers, after receiving the hint, exhibit a gradual, incremental shift, with increasing attention to the main elements during the problem-solving period. In contrast, non-solvers display an immediate burst of refocusing following the hint, but subsequently, their attention to the important aspects diminishes.

Both the analytical procedure for capturing the temporal resolution and the nonlinear statistical procedures can be easily extended beyond eye movements to other tracing methods. For example, “importance-to-solution” ratings of individual problem elements that are made repeatedly during the solving process ( Durso et al. 1994 ; Cushen and Wiley 2012 ; Danek et al. 2020 ; Danek and Wiley 2020 ) often reveal patterns of sudden change which could be effectively captured by GAMs and MCPs. Similarly, “Feelings-of-Warmth” that are used to assess metacognitive knowledge about solution progress ( Kizilirmak et al. 2018 ; Hedne et al. 2016 ; Pétervári and Danek 2020 ) are another suitable candidate for nonlinear modeling with GAMs. Other tracing methods, such as mouse-tracing data ( Loesche et al. 2018 ; van Rij et al. 2020 ), think-aloud protocols ( Gilhooly et al. 2010 ; Schooler et al. 1993 ; Blech et al. 2020 ), or even self-reports ( Fedor et al. 2015 ), are also better modeled with GAMs than with commonly applied linear methods, even if they are more appropriate than the classical ANOVA.

5. Conclusions

Our results indicate that for insight problems, the restructuring process leaves a discernible trace of suddenness. Eye movements suggest that just prior to solving the problems, participants shift their focus from elements that constituted the initial problem representation to those crucial for the solution. Our results also demonstrate that receiving hints leads to attentional shifts towards critical aspects, which in turn facilitates the generation of a correct solution. However, in order to accurately capture the sudden shift in attention, a combination of the appropriate methodological approach and statistical procedure is necessary. These nonlinear processes are best captured by nonlinear statistical procedures, such as GAMs and MCPs.

Acknowledgments

The help and cooperation from participants is greatly appreciated, as is Matthew Bladen’s contribution in preparing the text.

Supplementary Materials

The following supporting information can be downloaded at: https://osf.io/pwuhs/?view_only=7c52bda4e6fa481e826e5d7570b6ef34 .

Funding Statement

This research was funded by Talent Austria der OeAD-GmbH, finanziert aus Mitteln des österreichischen Bundesministeriums für Wissenschaft, Forschung und Wirtschaft (BMWFW), grant number ICM-2017-07423 given to the first author.

Author Contributions

Conceptualization, M.B. and M.G.; methodology, M.B. and M.G.; software, M.G.; validation, M.B., N.V., A.H.D., and M.G.; formal analysis, M.G. and N.V.; investigation, M.G.; data curation, M.G.; writing—original draft preparation, M.G.; writing—review and editing, M.B., A.H.D., N.V., and M.G.; visualization, M.G., N.V., and M.B.; project administration, M.G. and M.B.; funding acquisition, M.G. All authors have read and agreed to the published version of the manuscript.

Institutional Review Board Statement

Since this is a re-analysis of our paper ( Bilalić et al. 2019 ), please refer to the original paper for the Institutional Review Board Statement.

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

Conflicts of interest.

The authors declare no conflict of interest.

1 The length of time taken to solve (or not solve) a problem is different from person to person, meaning that one cannot compare the eye tracking data directly between people. For example, some may need only 45 s to solve the problem, whereas others need four minutes to find a solution. In consequence, the data must be transformed in order to be able to compare the data between people properly. While the problem-solving period can be extended by adding more time phases, it is important to note that the duration should not be prolonged beyond a certain point. Utilizing too many time frames may leave too little data (e.g., a 10-second trial should not be divided into 100 bins, as each bin will have the duration of only 100 ms). This can lead to distorted eye movement patterns, masking the underlying effects present before the data were binned. On the other hand, choosing too few bins may not capture the full temporal dynamics of the problem-solving process. In either case, ANOVA is not suitable for analyzing a large number of problem-solving periods, unlike GAM and multiple change point analysis, which can easily accommodate a large number of time frames. MCP analysis is another adequate tool for this type of analysis as it can capture the shift of attention. However, in contrast to GAMs, one needs a priori knowledge about the number of change points and the form of the segments in between ( Lindeløv 2020 ).

2 Please note that the data presented here are simulated to represent a sudden shift, which is difficult to capture by classical analyses. The original data in Bilalić et al. ( 2019 ) indicate a gradual shift.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

• Ammalainen Artur, Moroshkina Nadezhda. The effect of true and false unreportable hints on anagram problem solving, restructuring, and the Aha!-experience. Journal of Cognitive Psychology. 2021; 33 :644–58. doi: 10.1080/20445911.2020.1844722. [ CrossRef ] [ Google Scholar ]
• Ash Ivan K., Wiley Jennifer. The nature of restructuring in insight: An individual-differences approach. Psychonomic Bulletin & Review. 2006; 13 :66–73. [ PubMed ] [ Google Scholar ]
• Ash Ivan K., Wiley Jennifer. Hindsight bias in insight and mathematical problem solving: Evidence of different reconstruction mechanisms for metacognitive versus situational judgments. Memory & Cognition. 2008; 36 :822–37. doi: 10.3758/MC.36.4.822. [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Ash Ivan K., Jee Benjamin, Wiley Jennifer. Investigating insight as sudden learning. The Journal of Problem Solving. 2012; 4 :150–76. doi: 10.7771/1932-6246.1123. [ CrossRef ] [ Google Scholar ]
• Becker Maxi, Kühn Simone, Sommer Tobias. Verbal insight revisited—Dissociable neurocognitive processes underlying solutions accompanied by an AHA! experience with and without prior restructuring. Journal of Cognitive Psychology. 2021; 33 :659–84. doi: 10.1080/20445911.2020.1819297. [ CrossRef ] [ Google Scholar ]
• Bilalić Merim, McLeod Peter. Why good thoughts block better ones. Scientific American. 2014; 310 :74–79. doi: 10.1038/scientificamerican0314-74. [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Bilalić Merim, McLeod Peter, Gobet Fernand. Why good thoughts block better ones: The mechanism of the pernicious Einstellung (set) effect. Cognition. 2008; 108 :652–61. doi: 10.1016/j.cognition.2008.05.005. [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Bilalić Merim, McLeod Peter, Gobet Fernand. The Mechanism of the Einstellung (Set) Effect: A Pervasive Source of Cognitive Bias. Current Directions in Psychological Science. 2010; 19 :111–15. doi: 10.1177/0963721410363571. [ CrossRef ] [ Google Scholar ]
• Bilalić Merim, Graf Mario, Vaci Nemanja, Danek Amory H. The temporal dynamics of insight problem solving–restructuring might not always be sudden. Thinking & Reasoning. 2019; 27 :1–37. [ Google Scholar ]
• Blech Christine, Gaschler Robert, Bilalić Merim. Why do people fail to see simple solutions? Using think-aloud protocols to uncover the mechanism behind the Einstellung (mental set) effect. Thinking & Reasoning. 2020; 26 :552–80. [ Google Scholar ]
• Bowden Edward M. The effect of reportable and unreportable hints on anagram solution and the Aha! Experience. Consciousness and Cognition. 1997; 6 :545–73. doi: 10.1006/ccog.1997.0325. [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Cushen Patrick J., Wiley Jennifer. Cues to solution, restructuring patterns, and reports of insight in creative problem solving. Consciousness and Cognition. 2012; 21 :1166–75. doi: 10.1016/j.concog.2012.03.013. [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Danek Amory H., Wiley Joshua. What causes the insight memory advantage? Cognition. 2020; 205 :104411. doi: 10.1016/j.cognition.2020.104411. [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Danek Amory H., Williams Joshua, Wiley Jennifer. Closing the gap: Connecting sudden representational change to the subjective Aha! experience in insightful problem solving. Psychological Research. 2020; 84 :111–19. doi: 10.1007/s00426-018-0977-8. [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Duncker Karl. On problem-solving. Psychological Monographs. 1945; 58 :270. doi: 10.1037/h0093599. [ CrossRef ] [ Google Scholar ]
• Durso Francis T., Rea Cornelia B., Dayton Tom. Graph-theoretic confirmation of restructuring during insight. Psychological Science. 1994; 5 :94–97. doi: 10.1111/j.1467-9280.1994.tb00637.x. [ CrossRef ] [ Google Scholar ]
• Ellis Jessica J., Reingold Eyal M. The Einstellung effect in anagram problem solving: Evidence from eye movements. Frontiers in Psychology. 2014; 5 :679. doi: 10.3389/fpsyg.2014.00679. [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Ellis Jessica J., Glaholt Mackenzie G., Reingold Eyal M. Eye movements reveal solution knowledge prior to insight. Consciousness and Cognition. 2011; 20 :768–76. doi: 10.1016/j.concog.2010.12.007. [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Fedor Anna, Szathmáry Eörs, Öllinger Michael. Problem solving stages in the five square problem. Frontiers in Psychology. 2015; 6 :1050. doi: 10.3389/fpsyg.2015.01050. [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Fleck Jessica I., Weisberg Robert W. Insight versus analysis: Evidence for diverse methods in problem solving. Journal of Cognitive Psychology. 2013; 25 :436–63. doi: 10.1080/20445911.2013.779248. [ CrossRef ] [ Google Scholar ]
• Gilhooly Ken J., Fioratou Evie, Henretty N. Verbalization and problem solving: Insight and spatial factors. British Journal of Psychology. 2010; 101 :81–93. doi: 10.1348/000712609X422656. [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Hedne Mikael R., Norman Elisabeth, Metcalfe Janet. Intuitive feelings of warmth and confidence in insight and noninsight problem solving of magic tricks. Frontiers in Psychology. 2016; 7 :1314. doi: 10.3389/fpsyg.2016.01314. [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Holmqvist Kenneth, Nyström Marcus, Andersson Richard, Dewhurst Richard, Halszka Jarodzka, Van de Weijer Joost. Eye Tracking: A Comprehensive Guide to Methods and Measures. OUP Oxford; Oxford: 2011. [ Google Scholar ]
• Just Marcel A., Carpenter Patricia A. Eye fixations and cognitive processes. Cognitive Psychology. 1976; 8 :441–80. doi: 10.1016/0010-0285(76)90015-3. [ CrossRef ] [ Google Scholar ]
• Kizilirmak Jasmin M., Serger Violetta, Kehl Judith, Öllinger Michael, Folta-Schoofs Kristian, Richardson-Klavehn Alan. Feelings-of-warmth increase more abruptly for verbal riddles solved with in contrast to without Aha! Experience. Frontiers in Psychology. 2018; 9 :1404. doi: 10.3389/fpsyg.2018.01404. [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Knoblich Günther, Ohlsson Stellan, Haider Hilde, Rhenius Detlef. Constraint relaxation and chunk decomposition in insight problem solving. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1999; 25 :1534–55. doi: 10.1037/0278-7393.25.6.1534. [ CrossRef ] [ Google Scholar ]
• Knoblich Günther, Ohlsson Stellan, Raney Gary E. An eye movement study of insight problem solving. Memory & Cognition. 2001; 29 :1000–9. doi: 10.3758/BF03195762. [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Korovkin Sergey, Savinova Anna. The Effectiveness of Metacognitive Hints in Insight Problem Solving. In: Velichkovsky Boris M., Balaban Pavel M., Ushakov Vadim L., editors. Advances in Cognitive Research, Artificial Intelligence and Neuroinformatics. Vol. 1358. Springer; Cham: 2021. Intercognsci 2020. Advances in Intelligent Systems and Computing. [ CrossRef ] [ Google Scholar ]
• Kuhn Gustav, Land Michael F. There’s more to magic than meets the eye. Current Biology. 2006; 16 :R950–R51. doi: 10.1016/j.cub.2006.10.012. [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Kuhn Gustav, Tatler Benjamin W., Cole Geoff. G. You look where I look! Effect of gaze cues on overt and covert attention in misdirection. Visual Cognition. 2009; 17 :925–44. doi: 10.1080/13506280902826775. [ CrossRef ] [ Google Scholar ]
• Lindeløv Jonas K. mcp: An R Package for Regression with Multiple Change Points. OSF Preprints. 2020 doi: 10.31219/osf.io/fzqxv. [ CrossRef ] [ Google Scholar ]
• Loesche Frank, Goslin Jeremy, Bugmann Guido. Paving the way to eureka—Introducing “dira” as an experimental paradigm to observe the process of creative problem solving. Frontiers in Psychology. 2018; 9 :1773. doi: 10.3389/fpsyg.2018.01773. [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• MacGregor James N., Cunningham J. Barton. The effects of number and level of restructuring in insight problem solving. The Journal of Problem Solving. 2009; 2 :7. doi: 10.7771/1932-6246.1062. [ CrossRef ] [ Google Scholar ]
• Metcalfe Janet, Shimamura Arthur P., editors. Metacognition: Knowing about Knowing. MIT Press; Cambridge: 1994. [ Google Scholar ]
• Newell Allen, Simon Herbert A. Human Problem Solving. Prentice Hall; Englewood Cliffs: 1972. [ Google Scholar ]
• Novick Laura R., Sherman Steven J. On the nature of insight solutions: Evidence from skill differences in anagram solution. The Quarterly Journal of Experimental Psychology Section A. 2003; 56 :351–82. doi: 10.1080/02724980244000288. [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Ohlsson Stellan. Restructuring revisited: II. An information processing theory of restructuring and insight. Scandinavian Journal of Psychology. 1984; 25 :117–29. doi: 10.1111/j.1467-9450.1984.tb01005.x. [ CrossRef ] [ Google Scholar ]
• Ohlsson Stellan. Information-processing explanations of insight and related phenomena. In: Keane M., Gilhooly K. J., editors. Advances in the Psychology of Thinking. Harvester-Wheatsheaf; London: 1992. pp. 1–44. [ Google Scholar ]
• Ohlsson Stellan. Deep Learning: How the Mind Overrides Experience. Cambridge University Press; New York: 2011. [ Google Scholar ]
• Öllinger Michael, Jones Gary, Knoblich Günther. Heuristics and representational change in two-move matchstick arithmetic tasks. Advances in Cognitive Psychology. 2006; 2 :239–53. doi: 10.2478/v10053-008-0059-3. [ CrossRef ] [ Google Scholar ]
• Öllinger Michael, Jones Gary, Knoblich Günther. Investigating the effect of mental set on insight problem solving. Experimental Psychology. 2008; 55 :270–82. doi: 10.1027/1618-3169.55.4.269. [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Pétervári Judit, Danek Amory H. Problem solving of magic tricks: Guiding to and through an impasse with solution cues. Thinking & Reasoning. 2020; 26 :502–33. doi: 10.1080/13546783.2019.1668479. [ CrossRef ] [ Google Scholar ]
• Raftery Adrian E., Akman V. E. Bayesian analysis of a Poisson process with a change-point. Biometrika. 1986; 73 :85–89. doi: 10.1093/biomet/73.1.85. [ CrossRef ] [ Google Scholar ]
• Rayner Keith. Studies in Visual Information Processing. Vol. 6. Elsevier; Amsterdam: 1995. Eye movements and cognitive processes in reading, visual search, and scene perception; pp. 3–22. [ Google Scholar ]
• Reingold Eyal M., Charness Neil, Schultetus Richard S., Stampe Dave M. Perceptual automaticity in expert chess players: Parallel encoding of chess relations. Psychonomic Bulletin & Review. 2001; 8 :504–10. [ PubMed ] [ Google Scholar ]
• Schooler Jonathan W., Ohlsson Stellan, Brooks Kevin. Thoughts beyond words: When language overshadows insight. Journal of Experimental Psychology: General. 1993; 122 :166. doi: 10.1037/0096-3445.122.2.166. [ CrossRef ] [ Google Scholar ]
• Spiridonov Vladimir, Loginov Nikita, Ardislamov Vladlen. Dissociation between the subjective experience of insight and performance in the CRA paradigm. Journal of Cognitive Psychology. 2021; 33 :685–99. doi: 10.1080/20445911.2021.1900198. [ CrossRef ] [ Google Scholar ]
• Takeuchi Naoyuki, Mori Takayuki, Suzukamo Yoshimi, Izumi Shin I. Activity of prefrontal cortex in teachers and students during teaching of an insight problem. Mind, Brain, and Education. 2019; 13 :167–75. doi: 10.1111/mbe.12207. [ CrossRef ] [ Google Scholar ]
• Tseng Chien-Chih, Chen Ching-Hui, Chen Hsueh-Chih, Sung Yao-Ting, Chang Kuo-En. Verification of Dual Factors theory with eye movements during a matchstick arithmetic insight problem. Thinking Skills and Creativity. 2014; 13 :129–40. doi: 10.1016/j.tsc.2014.04.004. [ CrossRef ] [ Google Scholar ]
• van Rij Jacolien, Vaci Nemanja, Wurm Lee, Feldman Laurie. Alternative quantitative methods in psycholingistics: Implications for theory and design. In: Pirrelli Vito, Plag Ingo, Dressler Wolfgang., editors. Word Knowledge and Word Usage: A Cross-Disciplinary Guide to the Mental Lexicon. De Gruyter Mouton; Berlin and Boston: 2020. pp. 83–126. [ CrossRef ] [ Google Scholar ]
• Wertheimer Max. Über Schlussprozesse im produktiven Denken. In: Wertheimer Max., editor. Drei Abhandlungen zur Gestalttheorie. Verlag der Philosophischen Akademie; Erlangen: 1925. pp. 164–84. [ Google Scholar ]

• Testimonials

Insight: Creative Problem Solving

In the business world, there is more and more pressure for creative problem solving for developing new products, streamlining delivery systems, optimizing managerial structure, and dealing with personnel and clients. Constant innovation is the game. But what do we do when we’re faced with a problem that we don’t know how to solve? In fact, what we know may actually get in the way of a new solution: Our brain’s electrical activity may inhibit other circuits, and other ideas. We tend to think of creativity in terms of art and music. We recognize that artists and musicians are creative people, but what about the rest of us? Does that mean we’re not at all creative or that creativity is not useful in our lives?

Key Takeaway

Insight is the sudden solution to a long-vexing problem, a sudden recognition of a new idea, or a sudden understanding of a complex situation, an Aha! moment. Solutions found through insight are often more accurate than those found through step-by-step analysis. In the several seconds before people have an insight, or an Aha! moment, brain activity slows down, attention becomes more diffuse and less focused on the problem. To encourage insight, this means that we need to step back and let our minds wander or sleep on the problem. Insight cannot happen when our minds are constantly engaged.

One form of creativity is insight. It’s the sudden solution to a long-vexing problem, a sudden recognition of a new idea, or a sudden understanding of a complex situation, an Aha! moment. Einstein once described how he achieved his insights by making “a great speculative leap” to a conclusion and then tracing back the connections to verify the idea.

Insight may also be an important agent of change for helping people change their habits and way of thinking because of the enhanced and perhaps distinctive way in which people remember ideas achieved through insight. And we can all get closer to that magical spark of insight thanks to what we’ve learned from the neuroscience of insight.

Some people are "insight machines"

Enter John Kounios and Mark Beeman, two researchers who have studied the neuroscience of insight extensively. They have found that, in the several seconds before people have an insight, or an Aha! moment, their brain activity slows down ! Their attention becomes more diffuse, less focused on the problem. At the moment of insight, their brain activity spikes. Mark Beeman has seen this so often, that he can tell by people’s brain activity who will solve the problem analytically, in a step by step fashion, and who will solve the problem using insight: He calls such people “insight machines”.

Solutions found through insight are often more accurate than solutions using analytical thinking. But, not all solutions reached through insight are accurate. So after you have a moment of insight, it's important to evaluate your solution.

Solutions found through insight are often more accurate than solutions using analytical thinking. That’s because insight is an all-or-nothing phenomenon while analytic solving is incremental. Incremental, step-by-step analytic solving produces partial information on which you can base a guess, and guessing increases the likelihood of being wrong. Insightful, all-or-none solving does not yield intermediate results and people will not offer a solution unless they “know” it is right. Nevertheless, not all solutions reached through insight are accurate. So after you have a moment of insight, it’s important to evaluate your solution.

Insight can't be forced. To increase your insight potential, cultivate a quiet mind, daydream, or sleep on the problem. Insight cannot happen with a cluttered mind.

What can you do to increase your insight potential? Insight can’t be forced, but there are things you can do to foster it. Engage in activities that encourage an open mind. Gather a wide base of knowledge, ask how you could do this differently, engage in a new hobby that uses completely different skills, or just generally relax and let your mind wander. Sleeping on the problem, meditating, or stepping away from it and concentrating on something else may help your unconscious mind to cultivate a creative solution. Insight cannot happen with a cluttered mind. This is why insight, or Aha! moments, can happen in the shower or when you’re daydreaming, when your mind isn’t focused on anything in particular.

Thank you Irena,

I am not sure why I am responding and hoping I will understand by the time I finish.

I think it may be that I have discovered who I am rather that what I do, as I identify with this model closely. In some ways I have felt pressure from the world to get on this sequential train with a definite end position. Rather than an Insightful approach which I feel is more of a parrallel thought mechanism, that can take you anywhere and everywhere.

I am often criticised because I think slow and talk slow, but I am frustrated because people don’t see far and don’t look at possibilities. I now know I am not slow, just thinking about a whole lot more.

I feel that this insightful way of looking at things (parallel thinking) is my right-hand and the analytical process (sequential thinking) is my left-hand. I am a capable analytical thinker but but clumsy and very deliberate.

When I gain insight and analyse the solution, I tend to make it complex and the task of moving ahead becomes huge. I am beginning to learn to start the solution phase and work out the details as I go, so long as others are not involved.

However, when I look at the world I see people who I call solution fitters, these are people, who have gained insight and are trying to fit the problem to the insight.

I think it is like many things, there is a process that must followed, insight is good, but we need to go back to first principal thinking, what is it that we want to create, a solution or art and what is true.

Art in my view is simply an open communication that inspires others to think about something from a fresh point of view or through a new medium. (Purist may well put me straight on this point). So there is giving insight and receiving insight and the pleasure is always in the giving.

Solving a problem with insight and creativity is self satisfy and may benefit us in many ways, but I think the real satisfaction comes from being useful to others, even if we are paid for it.

So why did I respond to this article; – Above all we should value peoples strengths and not be afraid of the opposites (Analytical thinkers and insightful thinkers) and know they have a place in The Process. – This article and my responce has provided clarity for myself and I feel happy with who I am. – I question if we can be good at both ways of thinking, it is a bit like being lefthanded and righthanded, it is possible to be good with both but it is rare. – I am greatful that you took the time to write this article, it has given me insight how I think and may move forward in the future. – Many other thoughts beyond this article have sprung up from writing this response, so I shall finish and hope that my input may trigger others and provide them with similar insight and clarity about themselves.

Good Luck and happy thinking David

Thank you David for you thoughtful comment. I agree that we all prefer one way of thinking over the other. But, both kinds of thinking are valuable. That doesn’t mean that we shouldn’t explore ways of thinking that don’t come easily to us. Insightful thinkers must analyze their insights because they’re not always the best solution. And analytical thinkers would benefit from expanding their world. Like you, I’m an analytical thinker and quite slow too, and it’s because we analyze everything. Insight happens in an instant, which is one reason why insightful thinkers tend to be faster.

Even if our preferred way of thinking is analytical, we can still benefit from insight. Haven’t you slept on a problem overnight and woken up to a solution? That’s insight! This happens to me all the time as I’m writing or preparing a Masterclass: When I get stuck, I know to let it go and when I come back to it later in the day or the next morning, I have a way to move forward! We just need to let our minds wander.

Happy thinking to you too David.

Great insight… Excuse the pun! Thanks Irena

You’re welcome, Alan.

Get ten neuroscience strategies to work with your clients' brains

Session expired

Please log in again. The login page will open in a new tab. After logging in you can close it and return to this page.

Powered by WishList Member - Membership Software

What is insight learning? (Definition and theory)

Insight learning is a type of learning that happens suddenly, in the flash of a moment. It’s those “a-ha” moments, the light bulbs that people typically get long after they’ve abandoned a problem.

It’s believed that insight learning has been behind many creative inventions, discoveries, and solutions throughout history.

In this article, we’ll explore what’s behind those “a-ha” moments. We’ll look at how we learn , how we solve problems, and how insight fits into the picture of problem-solving.

Associative learning vs Insight learning

Behavioural psychologists in the mid-twentieth century had come up with good theories of how we learn by association. Their work was largely based on Thorndike’s experiments, where he put animals in a puzzle box with many levers on the inside.

To get out of the box, the animals had to hit the right lever. The animals randomly moved levers before they figured out which one opened the door. This is associative learning. The animal associated the movement of the right lever with the opening of the door.

As Thorndike repeated the experiments, the animals got better and better at figuring out the right lever. In other words, the number of trials required by the animals to solve the problem decreased over time.

Behavioral psychologists are infamous for not paying any attention to cognitive processes. In Thorndike’s, Pavlov’s, Watson’s, and Skinner’s experiments, the subjects learn things purely from their environments. There’s no mental work involved except association.

Gestalt psychologists, on the other hand, were fascinated by how the brain could perceive the same thing in different ways. They were inspired by optical illusions such as the reversible cube shown below, which can be perceived in two ways.

Instead of focusing on the parts, they were interested in the sum of the parts, the whole. Given their interest in perception (a cognitive process), Gestalt psychologists were interested in the role cognition could play in learning.

Along came Kohler, who observed that apes, after they couldn’t solve a problem for a while, had sudden insights and seemed to figure out the solution.

For example, to reach bananas that were out of their reach, the apes joined two sticks together in a moment of insight. To reach a bunch of bananas hanging high from the ceiling, they placed crates that were lying around on top of each other.

Clearly, in these experiments, the animals didn’t solve their problems with associative learning. Some other cognitive process was going on. Gestalt psychologists called it insight learning.

The apes didn’t learn to solve the problems purely by association or feedback from the environment. They used reasoning or cognitive trial-and-error (as opposed to behaviorism’s behavioral trial-and-error) to arrive at the solution. 1

How does insight learning occur?

To understand how we experience insight, it’s helpful to look at how we solve problems . When we encounter a problem, one of the following situations may arise:

1. The problem is easy

When we encounter a problem, our mind searches our memory for similar problems we’ve faced in the past. Then it applies solutions that have worked in our past to the current problem.

The easiest problem to solve is the one you’ve encountered before. It might take you only a few trials or just one trial to solve it. You don’t experience any insight. You solve the problem by reasoning or analytic thinking.

2. The problem is harder

The second possibility is that the problem is a bit harder. You probably have faced similar, but not too similar, problems in the past. So you apply solutions that have worked for you in the past to the current problem.

However, in this case, you need to think harder. You need to re-arrange elements of the problem or restructure the problem or your approach to solving it.

Eventually, you solve it, but in more trials than were required in the previous case. You’re more likely to experience insight in this case than in the previous one.

3. The problem is complex

This is where people mostly experience insight. When you encounter an ill-defined or a complex problem, you exhaust all the solutions you can derive from memory. You hit a wall and you don’t know what to do.

You abandon the problem. Later, when you’re doing something unrelated to the problem, a flash of insight appears in your mind that helps you solve the problem.

We usually solve such problems after a maximum number of trials. The more trials a problem takes to solve, the more you have to re-arrange the elements of a problem or restructure it.

Now that we have contextualized the insight experience, let’s look at the stages involved in insight learning.

Stages of insight learning

The stage decomposition theory of Wallas 2 states that the insight experience involves the following stages:

1. Preparation

This is the analytic thinking stage in which the problem-solver tries all kinds of approaches to solving a problem using logic and reasoning. If the solution is found, the next stages don’t occur.

If the problem is complex, the problem-solver exhausts their options and cannot find a solution. They feel frustrated and abandon the problem.

2. Incubation

If you’ve ever abandoned a difficult problem, you must have noticed that it lingers in the back of your mind. So does some frustration and a slight bad mood . During the incubation period, you don’t pay much attention to your problem and engage in other routine activities.

This period can last from a few minutes to many years. Studies have shown that this period increases the probability of finding the solution. 3

3. Insight (Illumination)

Insight occurs when the solution manifests spontaneously in conscious thought. This suddenness is important. It seems like a leap to the solution, not a slow, step-wise arrival to it as in analytic thinking.

4. Verification

The solution reached via insight may or may not be correct and so needs to be tested. Verifying the solution, again, is a deliberative process like analytic thinking. If the solution found via insight turns out to be false, then the Preparation stage is repeated.

I know what you’re thinking:

“It’s all fine and dandy- the stages and everything. But how exactly do we get insights?”

Let’s talk about that for a moment.

The Explicit-Implicit Interaction (EII) theory

An interesting theory put forward to explain how we get insights is the Explicit-Implicit Interaction (EII) theory. 4

The theory states that there’s a constant interaction that happens between our conscious and unconscious processes. We’re rarely fully conscious or unconscious when interacting with the world.

Conscious (or explicit) processing largely involves rule-based processing that activates a specific set of concepts during problem-solving .

When you’re solving a problem analytically, you do it with a limited approach based on your experience. The brain’s left hemisphere handles this type of processing.

Unconscious (or implicit) processing or intuition involves the right hemisphere. It activates a broad range of concepts when you’re trying to solve a problem. It helps you look at the big picture.

When you learn to ride a bicycle for the first time, for example, you’re given a set of rules to follow. Do this and don’t do that. Your conscious mind is active. After you’ve learned the skill, it becomes part of your unconscious or implicit memory. This is called implicitation.

When the same thing happens in reverse, we have explicitation or insight. That is, we get insight when unconscious processing transfers information to the conscious mind.

In support of this theory, studies have shown that just before having an insight, the right hemisphere sends a signal to the left hemisphere. 5

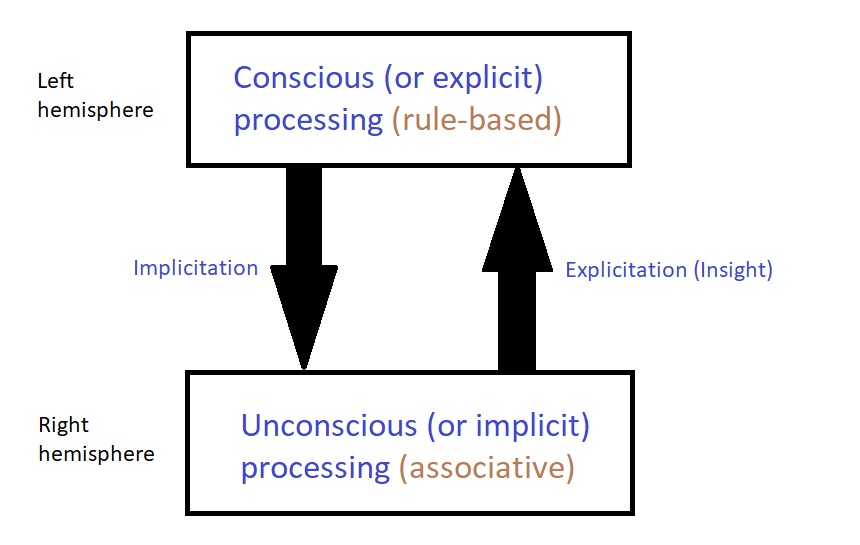
The above figure tells us that when a person abandons a problem (i.e. inhibits conscious processing), their unconscious still tries to make associative connections to reach the solution.

When it finds the right connection- voila! The insight appears in the conscious mind.

Note that this connection may arise spontaneously in the mind or some external stimulus (an image, sound or a word) might trigger it.

I’m sure you’ve experienced or observed one of those moments where you’re talking to a problem-solver and something you said triggered their insight. They look pleasantly surprised , ditch the conversation, and rush to solve their problem.

Further insights into the nature of insight

There’s more to insight than what we’ve discussed. Turns out, this dichotomy between analytic problem-solving and insight problem solving doesn’t always hold up.

Sometimes insight can be reached via analytic thinking. Other times, you don’t need to have abandoned a problem to experience insight. 6

Therefore, we need a novel way to look at insight that can account for these facts.

For that, I want you to think of problem-solving as going from point A (first encountering the problem) to point B (solving the problem).

Imagine that between points A and B, you have puzzle pieces scattered all around. Arranging these pieces in the right manner would be akin to solving the problem. You’ll have created a path from A to B.

If you encounter an easy problem, you’ve probably solved a similar problem in the past. You only need to arrange a few pieces in the right order to solve the problem. The pattern in which the pieces will fit together is easy to figure out.

This re-arranging of the pieces is analytic thinking.

Almost always, insight is experienced when you’re facing a complex problem. When the problem is complex, you’ll have to spend a long time re-arranging the pieces. You’ll have to take many trials. You’re playing with more pieces.

If you’re unable to solve the problem while you’re shuffling too many pieces, it leads to frustration. If you keep going and don’t abandon the problem, you might experience an insight. You finally found a pattern for the puzzle pieces that can lead you from A to B.

This feeling of having found a solution pattern to a complex problem produces insight, irrespective of whether you abandon the problem.

Think about how insight feels. It is pleasant, exciting, and brings relief. It is essentially a relief from overt or covert frustration. You’re relieved because you feel you’ve found a solution pattern for a complex problem- a needle in a haystack.

What happens when you abandon the problem?

As EII theory explains, it’s likely that you hand over sifting through the puzzle pieces to your unconscious mind in the process of implicitation. Just as you hand over cycling to your unconscious after you’ve done it for a while.

This is what’s likely to be responsible for that feeling of the problem lingering in the back of your mind.

While you’re engaged in other activities, the subconscious keeps re-arranging the puzzle pieces. It uses more pieces than you could’ve used consciously (activation of a wide range of concepts by the right hemisphere).

When your subconscious is done doing the re-arranging and believes it has reached a solution- a way to move from A to B- you get the “a-ha” moment. This solution pattern detection marks the end of a long period of frustration.

If you find that the solution pattern doesn’t actually solve the problem, you go back to re-arranging the puzzle pieces.

Re-structuring the approach, not the problem

Gestalt psychologists proposed that the incubation period helps the problem-solver to re-structure the problem i.e. see the problem itself differently.

In our puzzle pieces analogy, the pieces refer to elements of the problem, the problem itself, as well as the approach to solving the problem. So, when you’re re-arranging the puzzle pieces, you may do one or more of these things.

To highlight the difference between restructuring the problem itself and changing just the approach, I want to narrate an example from personal experience.

The 9-dot problem is a famous insight problem that requires you to think outside the box. When my father first showed this problem to me, I was clueless. I just couldn’t solve it. Then he finally showed me the solution, and I had an “a-ha” moment.

Since then, every time I’ve come across the problem, I’ve been able to solve it in just a few trials. The first time it took me many trials, and I failed.

Note that what I had learned from my “a-ha” moment was how to approach the problem differently. I didn’t re-structure the problem itself, only my approach to it. I didn’t memorize the solution. I just knew the right way to go about it.

When I knew the right way to approach it, I solved in a few trials every single time, despite not knowing what the solution looked like exactly.

This is true for so many complex problems in life. If some problem is taking you too many trials, perhaps you should reconsider how you’re approaching it before you start playing with other puzzle pieces.

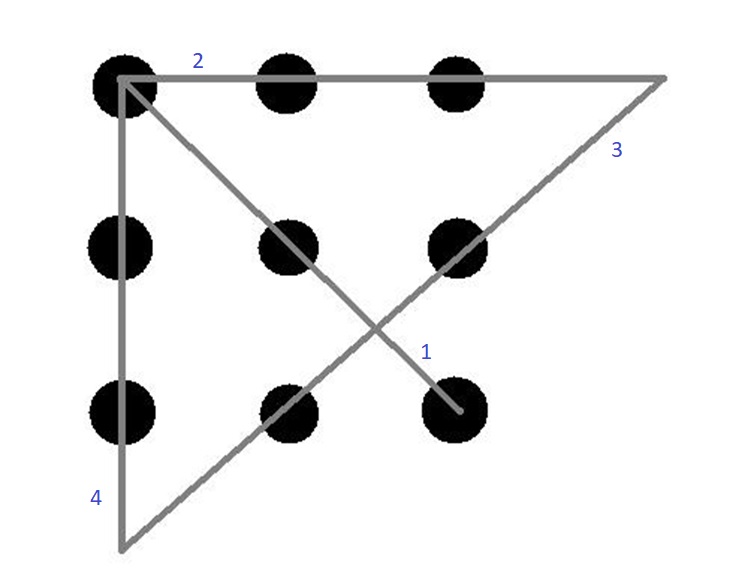
• Ash, I. K., Jee, B. D., & Wiley, J. (2012). Investigating insight as sudden learning.  The Journal of Problem Solving ,  4 (2).
• Wallas, G. (1926). The art of thought. J. Cape: London.
• Dodds, R. A., Smith, S. M., & Ward, T. B. (2002). The use of environmental clues during incubation.  Creativity Research Journal ,  14 (3-4), 287-304.
• Hélie, S., & Sun, R. (2010). Incubation, insight, and creative problem solving: a unified theory and a connectionist model.  Psychological review ,  117 (3), 994.
• Bowden, E. M., Jung-Beeman, M., Fleck, J., & Kounios, J. (2005). New approaches to demystifying insight.  Trends in cognitive sciences ,  9 (7), 322-328.
• Weisberg, R. W. (2015). Toward an integrated theory of insight in problem solving.  Thinking & Reasoning ,  21 (1), 5-39.

Hi, I’m Hanan Parvez (MA Psychology). I’ve published over 500 articles and authored one book. My work has been featured in Forbes , Business Insider , Reader’s Digest , and Entrepreneur .

The Roots of Intuition and Emotional Intelligence

Decoding the neuroscience of gut feelings and sudden insights..

Posted May 28, 2024 | Reviewed by Gary Drevitch

What is it to be intuitive? Have you ever experienced a gut feeling, or sensed an instinctive urge to make a decision based on a subtle emotion ? Intuition is often described as a mysterious force influencing our emotions and choices, and it plays a significant role in our lives. While traditionally seen as something unexplainable, neuroscience is now shedding light on the true nature of intuition. It turns out that it is not a product of magic but instad may be deeply rooted in the emotional surges in our brains.

The gut-brain axis

The gut-brain axis is a superhighway of communication between your gut and your brain that is crucial for intuition. The activity of neurotransmitters like serotonin influence everything from your immune system to your mood. According to Mayer and his colleagues (2014), the bacteria living in your gut, or gut microbiota, can actually mess with neurotransmitter production. That can have a significant impact on your cognitive processes and emotions, and even affect intuition: The bacteria living in the gut may actually make us intuitive.

Emotional Intelligence vs. Logical Analysis

Our emotions and rationality are in perpetual tension. While rational analysis prioritizes logical reasoning, emotional intelligence leverages intuition and emotional cues. So being emotionally intelligent goes beyond conscious awareness, drawing from past experiences and intuitive insights, in contrast to the linear approach of rational analysis. LeDoux (1996) delves into the mysterious underpinnings of emotional life, shedding light on these intricate workings. By exploring the neural mechanisms behind emotions, we can find valuable insights into how intuition arises from the depths of our emotional brain.

The Emotional Brain and Intuitive Insights

Intuition is intimately linked to our emotions, arising from complex neural circuits dedicated to the information processing of our feelings. Key brain regions like the amygdala, insula, and ventromedial prefrontal cortex play crucial roles. The amygdala processes emotional stimuli, shaping instinctual reactions even before we become consciously aware. The insula integrates bodily sensations with environmental cues, further contributing to intuitive insights. The ventromedial prefrontal cortex evaluates the significance and aids in understanding our feelings and how we might respond. Together, these brain regions form a dynamic network that orchestrates an intricate dance between emotions and intuition. By integrating emotional cues from our surroundings with internal bodily sensations, this neural circuitry generates intuitive responses that shape our thoughts, actions, and decisions even before we are consciously aware.

Cultivating Intuition through Experience

The power of intuition lies in its reliance on unconscious emotional processing. Our brains can rapidly evaluate emotional cues and generate intuitive insights without conscious effort. This unconscious emotional processing allows us to make split-second decisions based on deeply ingrained emotional knowledge. As we navigate the complexities of life, we accumulate a wealth of emotional experiences that shape our intuitive responses, and ou emotional experience serves as the crucible through which intuition is forged.

Let’s consider a few examples:

• The Therapist's Empathic Insight: Dr. Alex, a seasoned therapist, relies on her emotional intuition to guide her therapeutic interventions. Through listening and empathic attunement, she uncovers hidden emotional truths with her clients which can foster profound healing.
• The Negotiator's Intuitive Rapport: Sarah, a skilled negotiator, leverages her intuition to build rapport and trust with her counterparts. By reading the room and tuning into subtle emotional cues, she navigates negotiations to achieve mutually beneficial outcomes.
• The Leader's Intuitive Leadership : Mark harnesses his intuition to inspire and motivate his team. Through empathetic understanding and emotional resonance, he fosters a culture of collaboration and innovation , driving team success. One notable instance of his intuitive leadership occurred during a crucial team meeting: Sensing subtle cues in his team's body language and vocal tone, he intuited tension and unease among his colleagues. Drawing on his basic knowledge of social neuroscience (he had read Social by M. Lieberman, 2014), he understood the importance for productivity of fostering open communication. Leveraging his intuition, Mark skillfully addressed members' underlying concerns, creating a safe space for them to express themselves. This proactive approach improved the team's emotional state and enhanced their engagement and cohesion, as per research by Edmondson, A. (1999) on psychological safety.
• Tom, a diligent executive in a fast-paced construction company, found himself constantly facing challenging time-sensitive decisions. However, he noticed that some of his most successful choices weren't solely based on rational analysis but also on a gut feeling; his deep-seated intuition guided him toward the right choice or path. Harnessing intuition became a pivotal aspect of Tom's expertise as he learned to recognize subtle cues from his emotions and trust his instincts. He became more confident and effective in decision-making both personally and professionally.

The enigmatic phenomenon of intuition finds its roots not solely in the brain but also in the intricate interplay between various physiological systems. It manifests in bodily sensations, subtle cues, and flashes of insight that bypass conscious thought. Tuning into these signals allows us to grasp emotional nuances, understand relationships, and deepen self-awareness. By embracing intuition, we can enhance decision-making, empathy, and connection. Understanding its neuroscience provides insight into intuitive processes. How might you harness your intuition to enrich your life choices? Maybe you need a sign, like a butterfly in your belly, or a shiver down your spine.

Barrett, L. F., & Satpute, A. B. (2013). Large-scale brain networks in affective and social neuroscience: Towards an integrative functional architecture of the brain. Current Opinion in Neurobiology, 23(3), 361–372. DOI: 10.1016/j.conb.2013.02.004

Edmondson, A. (1999). Psychological safety and learning behavior in work teams. Administrative Science Quarterly, 44(2), 350–383. DOI: 10.2307/2666999

Kahneman, D. (2011). Thinking, fast and slow. Farrar, Straus and Giroux.

Kandel ER, Koester JD, Mack SH 2021, Siegelbaum SA. Principles of Neural Science, 6th ed. McGraw-Hill, New York. ISBN 978-1-25-964224-1

LeDoux, J. E. (1996). The emotional brain: The mysterious underpinnings of emotional life. (apa.org) . https://psycnet.apa.org/record/1996-98824-000

Lieberman, M. Social: Why Our Brains Are Wired to Connect - amazon.com, 2014.

Justin James Kennedy, Ph.D., is a professor of applied neuroscience and organisational behaviour at UGSM-Monarch Business School in Switzerland and the author of Brain Re-Boot.

• Find a Therapist
• Find a Treatment Center
• Find a Psychiatrist
• Find a Support Group
• Find Online Therapy
• International
• New Zealand
• South Africa
• Switzerland
• Asperger's
• Bipolar Disorder
• Chronic Pain
• Eating Disorders
• Passive Aggression
• Personality
• Goal Setting
• Positive Psychology
• Stopping Smoking
• Low Sexual Desire
• Relationships
• Child Development
• Self Tests NEW
• Therapy Center
• Diagnosis Dictionary
• Types of Therapy

At any moment, someone’s aggravating behavior or our own bad luck can set us off on an emotional spiral that threatens to derail our entire day. Here’s how we can face our triggers with less reactivity so that we can get on with our lives.

• Emotional Intelligence
• Gaslighting
• Affective Forecasting
• Neuroscience