2 steps problem solving

Two-Step Equations

Two step equations are equations that can be solved within exactly two steps. Two step equations are extremely easy to solve. As the name suggests, two step equations take only two steps to solve. These equations are just a little complicated than the one step equations. While solving a two step equation, we need to perform the operation on both sides of the equals to sign.

In this article, we will understand the meaning of two step equations with integers, decimals, and fractions, how to solve them, the golden rule to solve two step equations along with some examples for a better understanding.

What are Two Step Equations?

Two step equations are algebraic problems that take just two steps to solve. The two step equation is a linear equation in one variable . While performing an operation for solving a two step equation, we need to perform the same operation on both sides of the equation. We isolate the variable on one side of the equation to determine its value.

Two Step Equations Definition

Two step equations are algebraic equations and are the equations that can be solved in exactly two steps and gives the final value of the variable in two steps. Generally, two step equations are of the form ax + b = c, where a, b, c are real numbers. A few examples of two step equations are:

• 0.3y + 5 = 1
• (2/3)z - 12 = 10

Solving Two Step Equations

Two step equations are very easy to solve. It includes just one extra step as compared to one-step equations to solve. We can solve a two-step equation by isolating the variable (usually represented by an alphabet or letter) on one side of the equation and all other values on the other side. The general two steps to solve the two-step equations are:

• Step 1: Addition and subtraction to isolate the variable.
• Step 2: Multiplication  or division  to determine the value of the variable.

Let us consider a few examples and solve two-step equations to understand the concept of solving two-step equations.

Example 1: Solve the equation 2x + 6 = 12.

To solve the two step equation 2x + 6 = 12, we need to determine the value of x. Let us solve it step-wise.

Step 1: Subtract -6 from both sides of the equation to isolate the variable x.

2x + 6 - 6 = 12 - 6

Step 2: Divide both sides of the equation by 2 to solve for x.

Hence, we have solved the equation 2x + 3 = 12 in just two steps.

Thus the two-step equation can be easily solved in a sequence of steps, as presented above.

Two-Step Equations with Decimals and Fractions

Two step equations that have decimals and fractions as the coefficient of the variable and constant term are said to be two step equations with decimals and fractions. A few examples of two step equations with fractions and decimals are:

• 0.3 x + 2/3 = 1
• 3x - 0.5 = 1.2
• (1/3) x + 4/5 = 3/4

These equations are solved in the same manner as the general two steps equations and the same steps are followed to determine the value of the variable.

Golden Rule to Solve Two Step Equations

The golden rule to solve two step equations is to perform all operations simultaneously on both sides of the equation. To isolate the variable on one side of the equation and to determine its value, we first add or subtract on both sides of the equation and then multiply or divide on both sides to get the final solution of the two step equation.

Important Notes on Two Step Equations

• Remove the parentheses and combine like terms to simplify each side of the two-step equation.
• Always remove the constant first by adding or subtracting the appropriate number.
• Always verify the solution in the end.

Topics Related to Two Step Equations

• Equations in Math
• Simple equations
• Algebraic formulas

Two Step Equations Examples

Example 1: Solve the two step equation (x/6) - 7 = 11

Solution: To solve the given two step equation, we will follow the steps discussed above in the article.

Step 1: Add 7 to both sides of the given two step equation

(x/6) - 7 + 7 = 11 + 7

⇒ (x/6) = 18

Step 2: Multiply both sides of the equation by 6.

6 × x/6 = 6 × 18

Answer: Hence the solution to the given two step equation (x/6) - 7 = 11 is x = 108.

Example 2: Determine the solution of the two step equation (2/3) z + 0.8 = 1.5

Step 1: Subtract 0.8 from both sides of the given two step equation

(2/3) z + 0.8 - 0.8 = 1.5 - 0.8

⇒ (2/3) z = 0.7

Step 2: Multiply both sides of the equation by (3/2).

(3/2) × (2/3) z = (3/2) × 0.7

Answer: Hence the solution to the given two step equation (2/3) z + 0.8 = 1.5 is x = 1.05

go to slide go to slide

Book a Free Trial Class

Practice Questions on Two Step Equations

Faqs on two step equations, what are two step equations in algebra.

Two step equations are algebraic equations that take just two steps to solve.First, the variable is isolated by adding or subtracting a numeric value on both sides of the equation. Secondly, the value of the variable is computed by multiplying or dividing the variable by an appropriate number.

What are the Steps to Solve Two Step Equations?

The general two steps to solve two step equations are:

• Step 1: Simplify the given equation by removing all brackets and parenthesis:
• Step 2: Add or subtract to isolate the variable.
• Step 2: Multiply or divide to determine the value of the variable.
• Step: Verify the answer by substituting it in the given equation .

How to Solve Two Step Equations?

Two step equations can be solved by following two quick steps:

• Step 1: Add or subtract numbers on either sides, to isolate the variable.

IS Two Step Equation the Same as A Multi-Step Equation?

Two-step equation can also be called a multi-step equation since it involves more than one step. And a multi-step equation can have two or more steps, in the process of solving the equation.

What is the Difference Between One Step and Two Step Equations?

One step equations take just one step to solve whereas two steps equations take two steps to get to the solution. Two-step equations include just one extra step as compared to one step equations to solve.

What is the Goal of Solving Two Step Equations?

The goal of solving two step equations is to isolate the variable and determine the value of the variable. And in the end, the variable should satisfy the given two step equation.

JavaScript is not active on your browser. This webite requires JavaScript in order to function.

Two-step word problems.

Two-step word problems have three numbers which must be operated on separately, and in the right order. They take much more understanding of the problem than simple word problems because they provide the information in a less structured form.

• Addition, then Subtraction
• Addition, then Multiplication
• Addition, then Division
• Subtraction, then Addition
• Subtraction, then Multiplication
• Subtraction, then Division
• Multiplication, then Addition
• Multiplication, then Division

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• x^{2}-x-6=0
• -x+3\gt 2x+1
• line\:(1,\:2),\:(3,\:1)
• prove\:\tan^2(x)-\sin^2(x)=\tan^2(x)\sin^2(x)
• \frac{d}{dx}(\frac{3x+9}{2-x})
• (\sin^2(\theta))'
• \lim _{x\to 0}(x\ln (x))
• \int e^x\cos (x)dx
• \int_{0}^{\pi}\sin(x)dx
• \sum_{n=0}^{\infty}\frac{3}{2^n}
• Is there a step by step calculator for math?
• Symbolab is the best step by step calculator for a wide range of math problems, from basic arithmetic to advanced calculus and linear algebra. It shows you the solution, graph, detailed steps and explanations for each problem.
• Is there a step by step calculator for physics?
• Symbolab is the best step by step calculator for a wide range of physics problems, including mechanics, electricity and magnetism, and thermodynamics. It shows you the steps and explanations for each problem, so you can learn as you go.
• How to solve math problems step-by-step?
• To solve math problems step-by-step start by reading the problem carefully and understand what you are being asked to find. Next, identify the relevant information, define the variables, and plan a strategy for solving the problem.
• My Notebook, the Symbolab way Math notebooks have been around for hundreds of years. You write down problems, solutions and notes to go back...

Please add a message.

Message received. Thanks for the feedback.

• Bipolar Disorder
• Therapy Center
• When To See a Therapist
• Types of Therapy
• Best Online Therapy
• Best Couples Therapy
• Best Family Therapy
• Managing Stress
• Sleep and Dreaming
• Understanding Emotions
• Self-Improvement
• Healthy Relationships
• Student Resources
• Personality Types
• Guided Meditations
• Verywell Mind Insights
• 2024 Verywell Mind 25
• Mental Health in the Classroom
• Editorial Process
• Meet Our Review Board
• Crisis Support

Overview of the Problem-Solving Mental Process

Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

Rachel Goldman, PhD FTOS, is a licensed psychologist, clinical assistant professor, speaker, wellness expert specializing in eating behaviors, stress management, and health behavior change.

• Identify the Problem
• Define the Problem
• Form a Strategy
• Organize Information
• Allocate Resources
• Monitor Progress
• Evaluate the Results

Frequently Asked Questions

Problem-solving is a mental process that involves discovering, analyzing, and solving problems. The ultimate goal of problem-solving is to overcome obstacles and find a solution that best resolves the issue.

The best strategy for solving a problem depends largely on the unique situation. In some cases, people are better off learning everything they can about the issue and then using factual knowledge to come up with a solution. In other instances, creativity and insight are the best options.

It is not necessary to follow problem-solving steps sequentially, It is common to skip steps or even go back through steps multiple times until the desired solution is reached.

In order to correctly solve a problem, it is often important to follow a series of steps. Researchers sometimes refer to this as the problem-solving cycle. While this cycle is portrayed sequentially, people rarely follow a rigid series of steps to find a solution.

The following steps include developing strategies and organizing knowledge.

1. Identifying the Problem

While it may seem like an obvious step, identifying the problem is not always as simple as it sounds. In some cases, people might mistakenly identify the wrong source of a problem, which will make attempts to solve it inefficient or even useless.

Some strategies that you might use to figure out the source of a problem include :

• Asking questions about the problem
• Breaking the problem down into smaller pieces
• Looking at the problem from different perspectives
• Conducting research to figure out what relationships exist between different variables

2. Defining the Problem

After the problem has been identified, it is important to fully define the problem so that it can be solved. You can define a problem by operationally defining each aspect of the problem and setting goals for what aspects of the problem you will address

At this point, you should focus on figuring out which aspects of the problems are facts and which are opinions. State the problem clearly and identify the scope of the solution.

3. Forming a Strategy

After the problem has been identified, it is time to start brainstorming potential solutions. This step usually involves generating as many ideas as possible without judging their quality. Once several possibilities have been generated, they can be evaluated and narrowed down.

The next step is to develop a strategy to solve the problem. The approach used will vary depending upon the situation and the individual's unique preferences. Common problem-solving strategies include heuristics and algorithms.

• Heuristics are mental shortcuts that are often based on solutions that have worked in the past. They can work well if the problem is similar to something you have encountered before and are often the best choice if you need a fast solution.
• Algorithms are step-by-step strategies that are guaranteed to produce a correct result. While this approach is great for accuracy, it can also consume time and resources.

Heuristics are often best used when time is of the essence, while algorithms are a better choice when a decision needs to be as accurate as possible.

4. Organizing Information

Before coming up with a solution, you need to first organize the available information. What do you know about the problem? What do you not know? The more information that is available the better prepared you will be to come up with an accurate solution.

When approaching a problem, it is important to make sure that you have all the data you need. Making a decision without adequate information can lead to biased or inaccurate results.

5. Allocating Resources

Of course, we don't always have unlimited money, time, and other resources to solve a problem. Before you begin to solve a problem, you need to determine how high priority it is.

If it is an important problem, it is probably worth allocating more resources to solving it. If, however, it is a fairly unimportant problem, then you do not want to spend too much of your available resources on coming up with a solution.

At this stage, it is important to consider all of the factors that might affect the problem at hand. This includes looking at the available resources, deadlines that need to be met, and any possible risks involved in each solution. After careful evaluation, a decision can be made about which solution to pursue.

6. Monitoring Progress

After selecting a problem-solving strategy, it is time to put the plan into action and see if it works. This step might involve trying out different solutions to see which one is the most effective.

It is also important to monitor the situation after implementing a solution to ensure that the problem has been solved and that no new problems have arisen as a result of the proposed solution.

Effective problem-solvers tend to monitor their progress as they work towards a solution. If they are not making good progress toward reaching their goal, they will reevaluate their approach or look for new strategies .

7. Evaluating the Results

After a solution has been reached, it is important to evaluate the results to determine if it is the best possible solution to the problem. This evaluation might be immediate, such as checking the results of a math problem to ensure the answer is correct, or it can be delayed, such as evaluating the success of a therapy program after several months of treatment.

Once a problem has been solved, it is important to take some time to reflect on the process that was used and evaluate the results. This will help you to improve your problem-solving skills and become more efficient at solving future problems.

A Word From Verywell​

It is important to remember that there are many different problem-solving processes with different steps, and this is just one example. Problem-solving in real-world situations requires a great deal of resourcefulness, flexibility, resilience, and continuous interaction with the environment.

Get Advice From The Verywell Mind Podcast

Hosted by therapist Amy Morin, LCSW, this episode of The Verywell Mind Podcast shares how you can stop dwelling in a negative mindset.

Follow Now : Apple Podcasts / Spotify / Google Podcasts

You can become a better problem solving by:

• Practicing brainstorming and coming up with multiple potential solutions to problems
• Being open-minded and considering all possible options before making a decision
• Breaking down problems into smaller, more manageable pieces
• Asking for help when needed
• Researching different problem-solving techniques and trying out new ones
• Learning from mistakes and using them as opportunities to grow

It's important to communicate openly and honestly with your partner about what's going on. Try to see things from their perspective as well as your own. Work together to find a resolution that works for both of you. Be willing to compromise and accept that there may not be a perfect solution.

Take breaks if things are getting too heated, and come back to the problem when you feel calm and collected. Don't try to fix every problem on your own—consider asking a therapist or counselor for help and insight.

If you've tried everything and there doesn't seem to be a way to fix the problem, you may have to learn to accept it. This can be difficult, but try to focus on the positive aspects of your life and remember that every situation is temporary. Don't dwell on what's going wrong—instead, think about what's going right. Find support by talking to friends or family. Seek professional help if you're having trouble coping.

Davidson JE, Sternberg RJ, editors.  The Psychology of Problem Solving .  Cambridge University Press; 2003. doi:10.1017/CBO9780511615771

Sarathy V. Real world problem-solving .  Front Hum Neurosci . 2018;12:261. Published 2018 Jun 26. doi:10.3389/fnhum.2018.00261

By Kendra Cherry, MSEd Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

• Solve equations and inequalities
• Simplify expressions
• Factor polynomials
• Graph equations and inequalities
• Advanced solvers
• All solvers
• Arithmetics
• Determinant
• Percentages
• Scientific Notation
• Inequalities

What can QuickMath do?

QuickMath will automatically answer the most common problems in algebra, equations and calculus faced by high-school and college students.

• The algebra section allows you to expand, factor or simplify virtually any expression you choose. It also has commands for splitting fractions into partial fractions, combining several fractions into one and cancelling common factors within a fraction.
• The equations section lets you solve an equation or system of equations. You can usually find the exact answer or, if necessary, a numerical answer to almost any accuracy you require.
• The inequalities section lets you solve an inequality or a system of inequalities for a single variable. You can also plot inequalities in two variables.
• The calculus section will carry out differentiation as well as definite and indefinite integration.
• The matrices section contains commands for the arithmetic manipulation of matrices.
• The graphs section contains commands for plotting equations and inequalities.
• The numbers section has a percentages command for explaining the most common types of percentage problems and a section for dealing with scientific notation.

Math Topics

More solvers.

• Add Fractions
• Simplify Fractions

• The Art of Effective Problem Solving: A Step-by-Step Guide

Daniel Croft

Daniel Croft is an experienced continuous improvement manager with a Lean Six Sigma Black Belt and a Bachelor's degree in Business Management. With more than ten years of experience applying his skills across various industries, Daniel specializes in optimizing processes and improving efficiency. His approach combines practical experience with a deep understanding of business fundamentals to drive meaningful change.

• Last Updated: February 6, 2023
• Learn Lean Sigma
• Problem Solving

Whether we realise it or not, problem solving skills are an important part of our daily lives. From resolving a minor annoyance at home to tackling complex business challenges at work, our ability to solve problems has a significant impact on our success and happiness. However, not everyone is naturally gifted at problem-solving, and even those who are can always improve their skills. In this blog post, we will go over the art of effective problem-solving step by step.

You will learn how to define a problem, gather information, assess alternatives, and implement a solution, all while honing your critical thinking and creative problem-solving skills. Whether you’re a seasoned problem solver or just getting started, this guide will arm you with the knowledge and tools you need to face any challenge with confidence. So let’s get started!

Problem Solving Methodologies

Individuals and organisations can use a variety of problem-solving methodologies to address complex challenges. 8D and A3 problem solving techniques are two popular methodologies in the Lean Six Sigma framework.

Methodology of 8D (Eight Discipline) Problem Solving:

The 8D problem solving methodology is a systematic, team-based approach to problem solving. It is a method that guides a team through eight distinct steps to solve a problem in a systematic and comprehensive manner.

The 8D process consists of the following steps:

• Form a team: Assemble a group of people who have the necessary expertise to work on the problem.
• Define the issue: Clearly identify and define the problem, including the root cause and the customer impact.
• Create a temporary containment plan: Put in place a plan to lessen the impact of the problem until a permanent solution can be found.
• Identify the root cause: To identify the underlying causes of the problem, use root cause analysis techniques such as Fishbone diagrams and Pareto charts.
• Create and test long-term corrective actions: Create and test a long-term solution to eliminate the root cause of the problem.
• Implement and validate the permanent solution: Implement and validate the permanent solution’s effectiveness.
• Prevent recurrence: Put in place measures to keep the problem from recurring.
• Recognize and reward the team: Recognize and reward the team for its efforts.

Download the 8D Problem Solving Template

A3 Problem Solving Method:

The A3 problem solving technique is a visual, team-based problem-solving approach that is frequently used in Lean Six Sigma projects. The A3 report is a one-page document that clearly and concisely outlines the problem, root cause analysis, and proposed solution.

The A3 problem-solving procedure consists of the following steps:

• Determine the issue: Define the issue clearly, including its impact on the customer.
• Perform root cause analysis: Identify the underlying causes of the problem using root cause analysis techniques.
• Create and implement a solution: Create and implement a solution that addresses the problem’s root cause.
• Monitor and improve the solution: Keep an eye on the solution’s effectiveness and make any necessary changes.

Subsequently, in the Lean Six Sigma framework, the 8D and A3 problem solving methodologies are two popular approaches to problem solving. Both methodologies provide a structured, team-based problem-solving approach that guides individuals through a comprehensive and systematic process of identifying, analysing, and resolving problems in an effective and efficient manner.

Step 1 – Define the Problem

The definition of the problem is the first step in effective problem solving. This may appear to be a simple task, but it is actually quite difficult. This is because problems are frequently complex and multi-layered, making it easy to confuse symptoms with the underlying cause. To avoid this pitfall, it is critical to thoroughly understand the problem.

To begin, ask yourself some clarifying questions:

• What exactly is the issue?
• What are the problem’s symptoms or consequences?
• Who or what is impacted by the issue?
• When and where does the issue arise?

Answering these questions will assist you in determining the scope of the problem. However, simply describing the problem is not always sufficient; you must also identify the root cause. The root cause is the underlying cause of the problem and is usually the key to resolving it permanently.

Try asking “why” questions to find the root cause:

• What causes the problem?
• Why does it continue?
• Why does it have the effects that it does?

By repeatedly asking “ why ,” you’ll eventually get to the bottom of the problem. This is an important step in the problem-solving process because it ensures that you’re dealing with the root cause rather than just the symptoms.

Once you have a firm grasp on the issue, it is time to divide it into smaller, more manageable chunks. This makes tackling the problem easier and reduces the risk of becoming overwhelmed. For example, if you’re attempting to solve a complex business problem, you might divide it into smaller components like market research, product development, and sales strategies.

To summarise step 1, defining the problem is an important first step in effective problem-solving. You will be able to identify the root cause and break it down into manageable parts if you take the time to thoroughly understand the problem. This will prepare you for the next step in the problem-solving process, which is gathering information and brainstorming ideas.

Step 2 – Gather Information and Brainstorm Ideas

Gathering information and brainstorming ideas is the next step in effective problem solving. This entails researching the problem and relevant information, collaborating with others, and coming up with a variety of potential solutions. This increases your chances of finding the best solution to the problem.

Begin by researching the problem and relevant information. This could include reading articles, conducting surveys, or consulting with experts. The goal is to collect as much information as possible in order to better understand the problem and possible solutions.

Next, work with others to gather a variety of perspectives. Brainstorming with others can be an excellent way to come up with new and creative ideas. Encourage everyone to share their thoughts and ideas when working in a group, and make an effort to actively listen to what others have to say. Be open to new and unconventional ideas and resist the urge to dismiss them too quickly.

Finally, use brainstorming to generate a wide range of potential solutions. This is the place where you can let your imagination run wild. At this stage, don’t worry about the feasibility or practicality of the solutions; instead, focus on generating as many ideas as possible. Write down everything that comes to mind, no matter how ridiculous or unusual it may appear. This can be done individually or in groups.

Once you’ve compiled a list of potential solutions, it’s time to assess them and select the best one. This is the next step in the problem-solving process, which we’ll go over in greater detail in the following section.

Step 3 – Evaluate Options and Choose the Best Solution

Once you’ve compiled a list of potential solutions, it’s time to assess them and select the best one. This is the third step in effective problem solving, and it entails weighing the advantages and disadvantages of each solution, considering their feasibility and practicability, and selecting the solution that is most likely to solve the problem effectively.

To begin, weigh the advantages and disadvantages of each solution. This will assist you in determining the potential outcomes of each solution and deciding which is the best option. For example, a quick and easy solution may not be the most effective in the long run, whereas a more complex and time-consuming solution may be more effective in solving the problem in the long run.

Consider each solution’s feasibility and practicability. Consider the following:

• Can the solution be implemented within the available resources, time, and budget?
• What are the possible barriers to implementing the solution?
• Is the solution feasible in today’s political, economic, and social environment?

You’ll be able to tell which solutions are likely to succeed and which aren’t by assessing their feasibility and practicability.

Finally, choose the solution that is most likely to effectively solve the problem. This solution should be based on the criteria you’ve established, such as the advantages and disadvantages of each solution, their feasibility and practicability, and your overall goals.

It is critical to remember that there is no one-size-fits-all solution to problems. What is effective for one person or situation may not be effective for another. This is why it is critical to consider a wide range of solutions and evaluate each one based on its ability to effectively solve the problem.

Step 4 – Implement and Monitor the Solution

When you’ve decided on the best solution, it’s time to put it into action. The fourth and final step in effective problem solving is to put the solution into action, monitor its progress, and make any necessary adjustments.

To begin, implement the solution. This may entail delegating tasks, developing a strategy, and allocating resources. Ascertain that everyone involved understands their role and responsibilities in the solution’s implementation.

Next, keep an eye on the solution’s progress. This may entail scheduling regular check-ins, tracking metrics, and soliciting feedback from others. You will be able to identify any potential roadblocks and make any necessary adjustments in a timely manner if you monitor the progress of the solution.

Finally, make any necessary modifications to the solution. This could entail changing the solution, altering the plan of action, or delegating different tasks. Be willing to make changes if they will improve the solution or help it solve the problem more effectively.

It’s important to remember that problem solving is an iterative process, and there may be times when you need to start from scratch. This is especially true if the initial solution does not effectively solve the problem. In these situations, it’s critical to be adaptable and flexible and to keep trying new solutions until you find the one that works best.

To summarise, effective problem solving is a critical skill that can assist individuals and organisations in overcoming challenges and achieving their objectives. Effective problem solving consists of four key steps: defining the problem, generating potential solutions, evaluating alternatives and selecting the best solution, and implementing the solution.

You can increase your chances of success in problem solving by following these steps and considering factors such as the pros and cons of each solution, their feasibility and practicability, and making any necessary adjustments. Furthermore, keep in mind that problem solving is an iterative process, and there may be times when you need to go back to the beginning and restart. Maintain your adaptability and try new solutions until you find the one that works best for you.

• Novick, L.R. and Bassok, M., 2005.  Problem Solving . Cambridge University Press.

Was this helpful?

Daniel Croft is a seasoned continuous improvement manager with a Black Belt in Lean Six Sigma. With over 10 years of real-world application experience across diverse sectors, Daniel has a passion for optimizing processes and fostering a culture of efficiency. He's not just a practitioner but also an avid learner, constantly seeking to expand his knowledge. Outside of his professional life, Daniel has a keen Investing, statistics and knowledge-sharing, which led him to create the website learnleansigma.com, a platform dedicated to Lean Six Sigma and process improvement insights.

Understanding the Cost of Good Quality: Investing in Quality Pays Off

From Good to Great: Transformation with Continuous Improvement

Free lean six sigma templates.

Improve your Lean Six Sigma projects with our free templates. They're designed to make implementation and management easier, helping you achieve better results.

5S Floor Marking Best Practices

In lean manufacturing, the 5S System is a foundational tool, involving the steps: Sort, Set…

How to Measure the ROI of Continuous Improvement Initiatives

When it comes to business, knowing the value you’re getting for your money is crucial,…

8D Problem-Solving: Common Mistakes to Avoid

In today’s competitive business landscape, effective problem-solving is the cornerstone of organizational success. The 8D…

The Evolution of 8D Problem-Solving: From Basics to Excellence

In a world where efficiency and effectiveness are more than just buzzwords, the need for…

8D: Tools and Techniques

Are you grappling with recurring problems in your organization and searching for a structured way…

How to Select the Right Lean Six Sigma Projects: A Comprehensive Guide

Going on a Lean Six Sigma journey is an invigorating experience filled with opportunities for…

How it works

Transform your enterprise with the scalable mindsets, skills, & behavior change that drive performance.

Explore how BetterUp connects to your core business systems.

We pair AI with the latest in human-centered coaching to drive powerful, lasting learning and behavior change.

Build leaders that accelerate team performance and engagement.

Unlock performance potential at scale with AI-powered curated growth journeys.

Build resilience, well-being and agility to drive performance across your entire enterprise.

Transform your business, starting with your sales leaders.

Unlock business impact from the top with executive coaching.

Foster a culture of inclusion and belonging.

Accelerate the performance and potential of your agencies and employees.

See how innovative organizations use BetterUp to build a thriving workforce.

Discover how BetterUp measurably impacts key business outcomes for organizations like yours.

A demo is the first step to transforming your business. Meet with us to develop a plan for attaining your goals.

• What is coaching?

Learn how 1:1 coaching works, who its for, and if it's right for you.

Accelerate your personal and professional growth with the expert guidance of a BetterUp Coach.

Types of Coaching

Navigate career transitions, accelerate your professional growth, and achieve your career goals with expert coaching.

Enhance your communication skills for better personal and professional relationships, with tailored coaching that focuses on your needs.

Find balance, resilience, and well-being in all areas of your life with holistic coaching designed to empower you.

Discover your perfect match : Take our 5-minute assessment and let us pair you with one of our top Coaches tailored just for you.

Research, expert insights, and resources to develop courageous leaders within your organization.

Best practices, research, and tools to fuel individual and business growth.

View on-demand BetterUp events and learn about upcoming live discussions.

The latest insights and ideas for building a high-performing workplace.

• BetterUp Briefing

The online magazine that helps you understand tomorrow's workforce trends, today.

Innovative research featured in peer-reviewed journals, press, and more.

Founded in 2022 to deepen the understanding of the intersection of well-being, purpose, and performance

We're on a mission to help everyone live with clarity, purpose, and passion.

Join us and create impactful change.

Read the buzz about BetterUp.

Meet the leadership that's passionate about empowering your workforce.

For Business

For Individuals

10 Problem-solving strategies to turn challenges on their head

Jump to section

What is an example of problem-solving?

What are the 5 steps to problem-solving, 10 effective problem-solving strategies, what skills do efficient problem solvers have, how to improve your problem-solving skills.

Problems come in all shapes and sizes — from workplace conflict to budget cuts.

Creative problem-solving is one of the most in-demand skills in all roles and industries. It can boost an organization’s human capital and give it a competitive edge. 

Problem-solving strategies are ways of approaching problems that can help you look beyond the obvious answers and find the best solution to your problem . 

Let’s take a look at a five-step problem-solving process and how to combine it with proven problem-solving strategies. This will give you the tools and skills to solve even your most complex problems.

Good problem-solving is an essential part of the decision-making process . To see what a problem-solving process might look like in real life, let’s take a common problem for SaaS brands — decreasing customer churn rates.

To solve this problem, the company must first identify it. In this case, the problem is that the churn rate is too high. 

Next, they need to identify the root causes of the problem. This could be anything from their customer service experience to their email marketing campaigns. If there are several problems, they will need a separate problem-solving process for each one. 

Let’s say the problem is with email marketing — they’re not nurturing existing customers. Now that they’ve identified the problem, they can start using problem-solving strategies to look for solutions. 

This might look like coming up with special offers, discounts, or bonuses for existing customers. They need to find ways to remind them to use their products and services while providing added value. This will encourage customers to keep paying their monthly subscriptions.

They might also want to add incentives, such as access to a premium service at no extra cost after 12 months of membership. They could publish blog posts that help their customers solve common problems and share them as an email newsletter.

The company should set targets and a time frame in which to achieve them. This will allow leaders to measure progress and identify which actions yield the best results.

Perhaps you’ve got a problem you need to tackle. Or maybe you want to be prepared the next time one arises. Either way, it’s a good idea to get familiar with the five steps of problem-solving. 

Use this step-by-step problem-solving method with the strategies in the following section to find possible solutions to your problem.

1. Identify the problem

The first step is to know which problem you need to solve. Then, you need to find the root cause of the problem. 

The best course of action is to gather as much data as possible, speak to the people involved, and separate facts from opinions. 

Once this is done, formulate a statement that describes the problem. Use rational persuasion to make sure your team agrees .

2. Break the problem down 

Identifying the problem allows you to see which steps need to be taken to solve it. 

First, break the problem down into achievable blocks. Then, use strategic planning to set a time frame in which to solve the problem and establish a timeline for the completion of each stage.

3. Generate potential solutions

At this stage, the aim isn’t to evaluate possible solutions but to generate as many ideas as possible. 

Encourage your team to use creative thinking and be patient — the best solution may not be the first or most obvious one.

Use one or more of the different strategies in the following section to help come up with solutions — the more creative, the better.

4. Evaluate the possible solutions

Once you’ve generated potential solutions, narrow them down to a shortlist. Then, evaluate the options on your shortlist. 

There are usually many factors to consider. So when evaluating a solution, ask yourself the following questions:

• Will my team be on board with the proposition?
• Does the solution align with organizational goals ?
• Is the solution likely to achieve the desired outcomes?
• Is the solution realistic and possible with current resources and constraints?
• Will the solution solve the problem without causing additional unintended problems?

5. Implement and monitor the solutions

Once you’ve identified your solution and got buy-in from your team, it’s time to implement it. 

But the work doesn’t stop there. You need to monitor your solution to see whether it actually solves your problem. 

Request regular feedback from the team members involved and have a monitoring and evaluation plan in place to measure progress.

If the solution doesn’t achieve your desired results, start this step-by-step process again.

There are many different ways to approach problem-solving. Each is suitable for different types of problems. 

The most appropriate problem-solving techniques will depend on your specific problem. You may need to experiment with several strategies before you find a workable solution.

Here are 10 effective problem-solving strategies for you to try:

• Use a solution that worked before
• Brainstorming
• Work backward
• Use the Kipling method
• Draw the problem
• Use trial and error
• Sleep on it
• Get advice from your peers
• Use the Pareto principle
• Add successful solutions to your toolkit

Let’s break each of these down.

1. Use a solution that worked before

It might seem obvious, but if you’ve faced similar problems in the past, look back to what worked then. See if any of the solutions could apply to your current situation and, if so, replicate them.

2. Brainstorming

The more people you enlist to help solve the problem, the more potential solutions you can come up with.

Use different brainstorming techniques to workshop potential solutions with your team. They’ll likely bring something you haven’t thought of to the table.

3. Work backward

Working backward is a way to reverse engineer your problem. Imagine your problem has been solved, and make that the starting point.

Then, retrace your steps back to where you are now. This can help you see which course of action may be most effective.

4. Use the Kipling method

This is a method that poses six questions based on Rudyard Kipling’s poem, “ I Keep Six Honest Serving Men .” 

• What is the problem?
• Why is the problem important?
• When did the problem arise, and when does it need to be solved?
• How did the problem happen?
• Where is the problem occurring?
• Who does the problem affect?

Answering these questions can help you identify possible solutions.

5. Draw the problem

Sometimes it can be difficult to visualize all the components and moving parts of a problem and its solution. Drawing a diagram can help.

This technique is particularly helpful for solving process-related problems. For example, a product development team might want to decrease the time they take to fix bugs and create new iterations. Drawing the processes involved can help you see where improvements can be made.

6. Use trial-and-error

A trial-and-error approach can be useful when you have several possible solutions and want to test them to see which one works best.

7. Sleep on it

Finding the best solution to a problem is a process. Remember to take breaks and get enough rest . Sometimes, a walk around the block can bring inspiration, but you should sleep on it if possible.

A good night’s sleep helps us find creative solutions to problems. This is because when you sleep, your brain sorts through the day’s events and stores them as memories. This enables you to process your ideas at a subconscious level. 

If possible, give yourself a few days to develop and analyze possible solutions. You may find you have greater clarity after sleeping on it. Your mind will also be fresh, so you’ll be able to make better decisions.

8. Get advice from your peers

Getting input from a group of people can help you find solutions you may not have thought of on your own. 

For solo entrepreneurs or freelancers, this might look like hiring a coach or mentor or joining a mastermind group. 

For leaders , it might be consulting other members of the leadership team or working with a business coach .

It’s important to recognize you might not have all the skills, experience, or knowledge necessary to find a solution alone. 

9. Use the Pareto principle

The Pareto principle — also known as the 80/20 rule — can help you identify possible root causes and potential solutions for your problems.

Although it’s not a mathematical law, it’s a principle found throughout many aspects of business and life. For example, 20% of the sales reps in a company might close 80% of the sales. 

You may be able to narrow down the causes of your problem by applying the Pareto principle. This can also help you identify the most appropriate solutions.

10. Add successful solutions to your toolkit

Every situation is different, and the same solutions might not always work. But by keeping a record of successful problem-solving strategies, you can build up a solutions toolkit. 

These solutions may be applicable to future problems. Even if not, they may save you some of the time and work needed to come up with a new solution.

Improving problem-solving skills is essential for professional development — both yours and your team’s. Here are some of the key skills of effective problem solvers:

• Critical thinking and analytical skills
• Communication skills , including active listening
• Decision-making
• Planning and prioritization
• Emotional intelligence , including empathy and emotional regulation
• Time management
• Data analysis
• Research skills
• Project management

And they see problems as opportunities. Everyone is born with problem-solving skills. But accessing these abilities depends on how we view problems. Effective problem-solvers see problems as opportunities to learn and improve.

Ready to work on your problem-solving abilities? Get started with these seven tips.

1. Build your problem-solving skills

One of the best ways to improve your problem-solving skills is to learn from experts. Consider enrolling in organizational training , shadowing a mentor , or working with a coach .

2. Practice

Practice using your new problem-solving skills by applying them to smaller problems you might encounter in your daily life. 

Alternatively, imagine problematic scenarios that might arise at work and use problem-solving strategies to find hypothetical solutions.

3. Don’t try to find a solution right away

Often, the first solution you think of to solve a problem isn’t the most appropriate or effective.

Instead of thinking on the spot, give yourself time and use one or more of the problem-solving strategies above to activate your creative thinking. 

4. Ask for feedback

Receiving feedback is always important for learning and growth. Your perception of your problem-solving skills may be different from that of your colleagues. They can provide insights that help you improve. 

5. Learn new approaches and methodologies

There are entire books written about problem-solving methodologies if you want to take a deep dive into the subject. 

We recommend starting with “ Fixed — How to Perfect the Fine Art of Problem Solving ” by Amy E. Herman. 

6. Experiment

Tried-and-tested problem-solving techniques can be useful. However, they don’t teach you how to innovate and develop your own problem-solving approaches. 

Sometimes, an unconventional approach can lead to the development of a brilliant new idea or strategy. So don’t be afraid to suggest your most “out there” ideas.

7. Analyze the success of your competitors

Do you have competitors who have already solved the problem you’re facing? Look at what they did, and work backward to solve your own problem. 

For example, Netflix started in the 1990s as a DVD mail-rental company. Its main competitor at the time was Blockbuster. 

But when streaming became the norm in the early 2000s, both companies faced a crisis. Netflix innovated, unveiling its streaming service in 2007. 

If Blockbuster had followed Netflix’s example, it might have survived. Instead, it declared bankruptcy in 2010.

Use problem-solving strategies to uplevel your business

When facing a problem, it’s worth taking the time to find the right solution. 

Otherwise, we risk either running away from our problems or headlong into solutions. When we do this, we might miss out on other, better options.

Use the problem-solving strategies outlined above to find innovative solutions to your business’ most perplexing problems.

If you’re ready to take problem-solving to the next level, request a demo with BetterUp . Our expert coaches specialize in helping teams develop and implement strategies that work.

Boost your productivity

Maximize your time and productivity with strategies from our expert coaches.

Elizabeth Perry, ACC

Elizabeth Perry is a Coach Community Manager at BetterUp. She uses strategic engagement strategies to cultivate a learning community across a global network of Coaches through in-person and virtual experiences, technology-enabled platforms, and strategic coaching industry partnerships. With over 3 years of coaching experience and a certification in transformative leadership and life coaching from Sofia University, Elizabeth leverages transpersonal psychology expertise to help coaches and clients gain awareness of their behavioral and thought patterns, discover their purpose and passions, and elevate their potential. She is a lifelong student of psychology, personal growth, and human potential as well as an ICF-certified ACC transpersonal life and leadership Coach.

8 creative solutions to your most challenging problems

5 problem-solving questions to prepare you for your next interview, what are metacognitive skills examples in everyday life, what is lateral thinking 7 techniques to encourage creative ideas, 31 examples of problem solving performance review phrases, learn what process mapping is and how to create one (+ examples), leadership activities that encourage employee engagement, can dreams help you solve problems 6 ways to try, how much do distractions cost 8 effects of lack of focus, similar articles, the pareto principle: how the 80/20 rule can help you do more with less, thinking outside the box: 8 ways to become a creative problem solver, 3 problem statement examples and steps to write your own, contingency planning: 4 steps to prepare for the unexpected, adaptability in the workplace: defining and improving this key skill, stay connected with betterup, get our newsletter, event invites, plus product insights and research..

3100 E 5th Street, Suite 350 Austin, TX 78702

• Platform Overview
• Integrations
• Powered by AI
• BetterUp Lead™
• BetterUp Manage™
• BetterUp Care®
• Sales Performance
• Diversity & Inclusion
• Case Studies
• Why BetterUp?
• About Coaching
• Find your Coach
• Career Coaching
• Communication Coaching
• Life Coaching
• News and Press
• Leadership Team
• Become a BetterUp Coach
• BetterUp Labs
• Center for Purpose & Performance
• Leadership Training
• Business Coaching
• Contact Support
• Contact Sales
• Privacy Policy
• Acceptable Use Policy
• Trust & Security
• Cookie Preferences

What is Problem Solving? (Steps, Techniques, Examples)

By Status.net Editorial Team on May 7, 2023 — 5 minutes to read

What Is Problem Solving?

Definition and importance.

Problem solving is the process of finding solutions to obstacles or challenges you encounter in your life or work. It is a crucial skill that allows you to tackle complex situations, adapt to changes, and overcome difficulties with ease. Mastering this ability will contribute to both your personal and professional growth, leading to more successful outcomes and better decision-making.

Problem-Solving Steps

The problem-solving process typically includes the following steps:

• Identify the issue : Recognize the problem that needs to be solved.
• Analyze the situation : Examine the issue in depth, gather all relevant information, and consider any limitations or constraints that may be present.
• Generate potential solutions : Brainstorm a list of possible solutions to the issue, without immediately judging or evaluating them.
• Evaluate options : Weigh the pros and cons of each potential solution, considering factors such as feasibility, effectiveness, and potential risks.
• Select the best solution : Choose the option that best addresses the problem and aligns with your objectives.
• Implement the solution : Put the selected solution into action and monitor the results to ensure it resolves the issue.
• Review and learn : Reflect on the problem-solving process, identify any improvements or adjustments that can be made, and apply these learnings to future situations.

Defining the Problem

To start tackling a problem, first, identify and understand it. Analyzing the issue thoroughly helps to clarify its scope and nature. Ask questions to gather information and consider the problem from various angles. Some strategies to define the problem include:

• Brainstorming with others
• Asking the 5 Ws and 1 H (Who, What, When, Where, Why, and How)
• Analyzing cause and effect
• Creating a problem statement

Generating Solutions

Once the problem is clearly understood, brainstorm possible solutions. Think creatively and keep an open mind, as well as considering lessons from past experiences. Consider:

• Creating a list of potential ideas to solve the problem
• Grouping and categorizing similar solutions
• Prioritizing potential solutions based on feasibility, cost, and resources required
• Involving others to share diverse opinions and inputs

Evaluating and Selecting Solutions

Evaluate each potential solution, weighing its pros and cons. To facilitate decision-making, use techniques such as:

• SWOT analysis (Strengths, Weaknesses, Opportunities, Threats)
• Decision-making matrices
• Pros and cons lists
• Risk assessments

After evaluating, choose the most suitable solution based on effectiveness, cost, and time constraints.

Implementing and Monitoring the Solution

Implement the chosen solution and monitor its progress. Key actions include:

• Communicating the solution to relevant parties
• Setting timelines and milestones
• Assigning tasks and responsibilities
• Monitoring the solution and making adjustments as necessary
• Evaluating the effectiveness of the solution after implementation

Utilize feedback from stakeholders and consider potential improvements. Remember that problem-solving is an ongoing process that can always be refined and enhanced.

Problem-Solving Techniques

During each step, you may find it helpful to utilize various problem-solving techniques, such as:

• Brainstorming : A free-flowing, open-minded session where ideas are generated and listed without judgment, to encourage creativity and innovative thinking.
• Root cause analysis : A method that explores the underlying causes of a problem to find the most effective solution rather than addressing superficial symptoms.
• SWOT analysis : A tool used to evaluate the strengths, weaknesses, opportunities, and threats related to a problem or decision, providing a comprehensive view of the situation.
• Mind mapping : A visual technique that uses diagrams to organize and connect ideas, helping to identify patterns, relationships, and possible solutions.

Brainstorming

When facing a problem, start by conducting a brainstorming session. Gather your team and encourage an open discussion where everyone contributes ideas, no matter how outlandish they may seem. This helps you:

• Generate a diverse range of solutions
• Encourage all team members to participate
• Foster creative thinking

When brainstorming, remember to:

• Reserve judgment until the session is over
• Encourage wild ideas
• Combine and improve upon ideas

Root Cause Analysis

For effective problem-solving, identifying the root cause of the issue at hand is crucial. Try these methods:

• 5 Whys : Ask “why” five times to get to the underlying cause.
• Fishbone Diagram : Create a diagram representing the problem and break it down into categories of potential causes.
• Pareto Analysis : Determine the few most significant causes underlying the majority of problems.

SWOT Analysis

SWOT analysis helps you examine the Strengths, Weaknesses, Opportunities, and Threats related to your problem. To perform a SWOT analysis:

• List your problem’s strengths, such as relevant resources or strong partnerships.
• Identify its weaknesses, such as knowledge gaps or limited resources.
• Explore opportunities, like trends or new technologies, that could help solve the problem.
• Recognize potential threats, like competition or regulatory barriers.

SWOT analysis aids in understanding the internal and external factors affecting the problem, which can help guide your solution.

Mind Mapping

A mind map is a visual representation of your problem and potential solutions. It enables you to organize information in a structured and intuitive manner. To create a mind map:

• Write the problem in the center of a blank page.
• Draw branches from the central problem to related sub-problems or contributing factors.
• Add more branches to represent potential solutions or further ideas.

Mind mapping allows you to visually see connections between ideas and promotes creativity in problem-solving.

Examples of Problem Solving in Various Contexts

In the business world, you might encounter problems related to finances, operations, or communication. Applying problem-solving skills in these situations could look like:

• Identifying areas of improvement in your company’s financial performance and implementing cost-saving measures
• Resolving internal conflicts among team members by listening and understanding different perspectives, then proposing and negotiating solutions
• Streamlining a process for better productivity by removing redundancies, automating tasks, or re-allocating resources

In educational contexts, problem-solving can be seen in various aspects, such as:

• Addressing a gap in students’ understanding by employing diverse teaching methods to cater to different learning styles
• Developing a strategy for successful time management to balance academic responsibilities and extracurricular activities
• Seeking resources and support to provide equal opportunities for learners with special needs or disabilities

Everyday life is full of challenges that require problem-solving skills. Some examples include:

• Overcoming a personal obstacle, such as improving your fitness level, by establishing achievable goals, measuring progress, and adjusting your approach accordingly
• Navigating a new environment or city by researching your surroundings, asking for directions, or using technology like GPS to guide you
• Dealing with a sudden change, like a change in your work schedule, by assessing the situation, identifying potential impacts, and adapting your plans to accommodate the change.
• How to Resolve Employee Conflict at Work [Steps, Tips, Examples]
• How to Write Inspiring Core Values? 5 Steps with Examples
• 30 Employee Feedback Examples (Positive & Negative)

How it works

For Business

Join Mind Tools

Article • 4 min read

The Problem-Solving Process

Looking at the basic problem-solving process to help keep you on the right track.

By the Mind Tools Content Team

Problem-solving is an important part of planning and decision-making. The process has much in common with the decision-making process, and in the case of complex decisions, can form part of the process itself.

We face and solve problems every day, in a variety of guises and of differing complexity. Some, such as the resolution of a serious complaint, require a significant amount of time, thought and investigation. Others, such as a printer running out of paper, are so quickly resolved they barely register as a problem at all.

Despite the everyday occurrence of problems, many people lack confidence when it comes to solving them, and as a result may chose to stay with the status quo rather than tackle the issue. Broken down into steps, however, the problem-solving process is very simple. While there are many tools and techniques available to help us solve problems, the outline process remains the same.

The main stages of problem-solving are outlined below, though not all are required for every problem that needs to be solved.

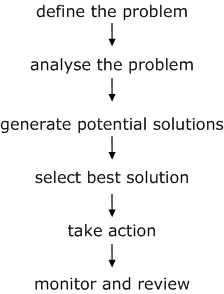
1. Define the Problem

Clarify the problem before trying to solve it. A common mistake with problem-solving is to react to what the problem appears to be, rather than what it actually is. Write down a simple statement of the problem, and then underline the key words. Be certain there are no hidden assumptions in the key words you have underlined. One way of doing this is to use a synonym to replace the key words. For example, ‘We need to encourage higher productivity ’ might become ‘We need to promote superior output ’ which has a different meaning.

2. Analyze the Problem

Ask yourself, and others, the following questions.

• Where is the problem occurring?
• When is it occurring?
• Why is it happening?

Be careful not to jump to ‘who is causing the problem?’. When stressed and faced with a problem it is all too easy to assign blame. This, however, can cause negative feeling and does not help to solve the problem. As an example, if an employee is underperforming, the root of the problem might lie in a number of areas, such as lack of training, workplace bullying or management style. To assign immediate blame to the employee would not therefore resolve the underlying issue.

Once the answers to the where, when and why have been determined, the following questions should also be asked:

• Where can further information be found?
• Is this information correct, up-to-date and unbiased?
• What does this information mean in terms of the available options?

3. Generate Potential Solutions

When generating potential solutions it can be a good idea to have a mixture of ‘right brain’ and ‘left brain’ thinkers. In other words, some people who think laterally and some who think logically. This provides a balance in terms of generating the widest possible variety of solutions while also being realistic about what can be achieved. There are many tools and techniques which can help produce solutions, including thinking about the problem from a number of different perspectives, and brainstorming, where a team or individual write as many possibilities as they can think of to encourage lateral thinking and generate a broad range of potential solutions.

4. Select Best Solution

When selecting the best solution, consider:

• Is this a long-term solution, or a ‘quick fix’?
• Is the solution achievable in terms of available resources and time?
• Are there any risks associated with the chosen solution?
• Could the solution, in itself, lead to other problems?

This stage in particular demonstrates why problem-solving and decision-making are so closely related.

5. Take Action

In order to implement the chosen solution effectively, consider the following:

• What will the situation look like when the problem is resolved?
• What needs to be done to implement the solution? Are there systems or processes that need to be adjusted?
• What will be the success indicators?
• What are the timescales for the implementation? Does the scale of the problem/implementation require a project plan?
• Who is responsible?

Once the answers to all the above questions are written down, they can form the basis of an action plan.

6. Monitor and Review

One of the most important factors in successful problem-solving is continual observation and feedback. Use the success indicators in the action plan to monitor progress on a regular basis. Is everything as expected? Is everything on schedule? Keep an eye on priorities and timelines to prevent them from slipping.

If the indicators are not being met, or if timescales are slipping, consider what can be done. Was the plan realistic? If so, are sufficient resources being made available? Are these resources targeting the correct part of the plan? Or does the plan need to be amended? Regular review and discussion of the action plan is important so small adjustments can be made on a regular basis to help keep everything on track.

Once all the indicators have been met and the problem has been resolved, consider what steps can now be taken to prevent this type of problem recurring? It may be that the chosen solution already prevents a recurrence, however if an interim or partial solution has been chosen it is important not to lose momentum.

Problems, by their very nature, will not always fit neatly into a structured problem-solving process. This process, therefore, is designed as a framework which can be adapted to individual needs and nature.

Join Mind Tools and get access to exclusive content.

This resource is only available to Mind Tools members.

Already a member? Please Login here

Sign-up to our newsletter

Subscribing to the Mind Tools newsletter will keep you up-to-date with our latest updates and newest resources.

Subscribe now

Business Skills

Personal Development

Leadership and Management

Member Extras

Most Popular

Latest Updates

Pain Points Podcast - Presentations Pt 2

NEW! Pain Points - How Do I Decide?

Mind Tools Store

About Mind Tools Content

Discover something new today

Finding the Best Mix in Training Methods

Using Mediation To Resolve Conflict

Resolving conflicts peacefully with mediation

How Emotionally Intelligent Are You?

Boosting Your People Skills

Self-Assessment

What's Your Leadership Style?

Learn About the Strengths and Weaknesses of the Way You Like to Lead

Recommended for you

Talent management overview.

This Document Provides an Overview of Talent Management

Business Operations and Process Management

Strategy Tools

Customer Service

Business Ethics and Values

Handling Information and Data

Project Management

Knowledge Management

Self-Development and Goal Setting

Time Management

Presentation Skills

Learning Skills

Career Skills

Communication Skills

Negotiation, Persuasion and Influence

Working With Others

Difficult Conversations

Creativity Tools

Self-Management

Work-Life Balance

Stress Management and Wellbeing

Coaching and Mentoring

Change Management

Team Management

Managing Conflict

Delegation and Empowerment

Performance Management

Leadership Skills

Developing Your Team

Talent Management

Problem Solving

Decision Making

Member Podcast

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

• Math for Kids
• Parenting Resources
• ELA for Kids
• Teaching Resources

How to Teach Long Division to Kids in 6 Easy Steps

15 Famous Mathematicians in History That Kids Should Know

11 Best Multiplication Apps for Kids

How to Teach Number Formation in 5 Easy Steps

13 Best Resources for Math Videos for Kids: Math Made Fun

6 Best Alternatives to Public Schooling: A Guide for Parents

How to Cope With Test Anxiety in 12 Easy Ways

Developmental Milestones for 4 Year Olds: The Ultimate Guide

Simple & Stress-Free After School Schedule for Kids of All Ages

When Do Kids Start Preschool: Age & Readiness Skills

How to Teach Letter Recognition in 6 Easy Steps

20 Fun Limericks for Kids

How to Improve Reading Comprehension: Strategies & Tips

40 Best Summer Writing Prompts for Kids of All Ages

12 Best Ways to Teach Rhyming Words to Kids

12 Best Tips for Substitute Teachers

30 Best Classroom Reward Ideas for Elementary Students

12 Best Websites for English Teachers

10 Best Game-Based Learning Platforms for Kids

60 Fun Animal Facts for Kids

Step 1: Start with Division Vocabulary

Step 2: introduce long division layout, step 3: demonstrate with an examples, step 4: practice without bringing down zeros, step 5: teach bringing down zeros, step 6: explain problems with remainders.

Long division can be challenging for kids because it involves many steps and new vocabulary, making it easy to lose track of the process. This complexity often confuses students, especially when bringing down digits or handling remainders. Teaching long division step by step helps kids understand it better. This guide on “ how to teach long division to kids ” will provide clear steps to simplify learning for kids, making it less overwhelming.

Math & ELA | PreK To Grade 5

Kids see fun ., you see real learning outcomes ..

Watch your kids fall in love with math & reading through our scientifically designed curriculum.

What Should My Child Know Before Learning Long Division?

Before diving into teaching long division, children must have a solid foundation in several key areas. These pre-requisites ensure that they are prepared for the complexities of long division:

• Understanding Multiplication: Kids should be comfortable with multiplication facts up to 12. This knowledge is fundamental because long division requires frequent multiplication to check and subtract products during the division steps.

Here are some fun activities to brush up your child’s understanding of multiplication facts:

• Basic Division Concepts: Ensure children understand the concept of division as sharing or grouping equally. They should be able to perform simple division tasks without remainders, using numbers that are easy to handle.

Here are some fun activities to brush up your child’s understanding of division facts:

• Familiarity with Subtraction: Subtraction is a significant part of the long division process, used to find the difference after multiplying the divisor. Children should be confident in subtracting large numbers, as they will need to do this repeatedly in each step of long division.

Assess how well your kids are versed with subtraction with these fun subtraction games :

• Number Sense: Good number sense , or an understanding of how numbers work and relate to each other, helps children anticipate the results of multiplication and division, making the process of long division smoother and more intuitive.

Ensuring kids are proficient in these areas makes teaching long division more effective, setting them up for success.

How to Teach Long Division in 6 Steps

Before learning the steps of long division, kids need to understand the key terms used throughout the process. Knowing these will help them follow long division strategies more easily.

• Dividend: This is the number being divided in the problem. In the long division layout, the dividend is written inside the long division bracket (often called the “house”).
• Divisor: The number dividing the dividend is called the divisor . The divisor is placed outside the long division bracket.
• Quotient: The quotient is the answer or the result of the division problem. This is written above the bracket, aligned with the digits of the dividend being divided.
• Remainder: If the division isn’t exact, there’s an amount left over called the remainder . The remainder is written as “R” followed by the remaining value after the division process.

Setting up a long division problem correctly is an essential skill for kids to learn. Here’s how to structure it visually:

• Write the Dividend Inside: Start by placing the dividend (the number being divided) inside the long division bracket, often called the “house.” This makes it clear that this number is the one being split into smaller groups.
• Place the Divisor Outside: Write the divisor (the number doing the dividing) outside, to the left of the bracket. This shows which number will be used repeatedly to divide the dividend into smaller groups.
• Draw Lines for the Quotient: The space above the bracket is where the quotient (the result of the division) will be written. Each digit of the quotient will align above the digit or digits of the dividend that are being divided.

1: Set Up the Problem

Write 1564 under the division bar and 27 outside the division bar.

• Look at the first two digits of the dividend (15). Since 15 is less than 27, we need to include the next digit, making it 156.
• Now, determine how many times 27 can fit into 156. 27 goes into 156 a total of 5 times because 27 multiplied by 6 (the next higher number) would exceed 156.

3. Multiply

• Multiply the quotient digit found (5) by the divisor (27), which equals 135.
• Write 135 under 156.

4. Subtract

• Subtract 135 from 156, which equals 21.
• Write 21 below 135.

5. Bring Down

Bring down the next digit of the dividend (the 4 in 1564), making the new number 214.

6. Repeat the Process

• Determine how many times 27 can fit into 214. It fits 7 times (since 27 multiplied by 8 exceeds 214).
• Multiply 27 by 7 (the next quotient digit) to get 189.
• Write 189 under 214, and subtract to find the difference: 214 – 189 = 25.

7. Remainder

• Since there are no more digits to bring down, 25 is the remainder.
• The complete quotient is 57 with a remainder of 25.

After understanding the layout, kids can apply what they’ve learned by playing these games in, each focusing on different levels of difficulty: 

• Dividing 2-Digit Numbers by 1-Digit

• Dividing 3-Digit Numbers by 1-Digit

• Dividing 4-Digit Numbers by 1-Digit

• Divide 4-Digit By 2-Digit Numbers

To build a strong foundation in long division, it’s crucial for children to practice problems where they bring down each digit consecutively without the complication of zeros . This helps them focus on mastering the basic steps of division:

Sequential Bringing Down: Start with simpler numbers where each digit in the dividend needs to be brought down one at a time. This practice solidifies their understanding of the division process step by step.

Example Problems:

• 21 ÷ 3: Begin by dividing the first digit. Since 2 divided by 3 doesn’t work, we use 21. 21 divided by 3 equals 7, so 7 is written above the division bar.
• 154 ÷ 7: Start with the first digit. 1 divided by 7 is not possible, so consider the first two digits, 15. 15 divided by 7 equals 2. Write 2 above the division bar, multiply 2 by 7 (which is 14), subtract 14 from 15 to get 1, then bring down the next digit to make it 14. Continue this way.

Handling zeros can be tricky, but it’s one of the key ways to teach long division. Here’s how to approach problems involving zeros:

Example: 120 ÷ 4

• Divide: Start by dividing the first non-zero digit. Since 1 is smaller than 4, look at the first two digits, 12. Divide 12 by 4 to get 3.
• Write the Quotient: Write 3 above the long division bracket.
• Multiply and Subtract: Multiply 3 by 4 (giving 12) and subtract this from 12, leaving 0.
• Bring Down Zeros: Bring down the next digit, which is 0, making it 0. Divide this 0 by 4 to get 0. Write 0 next to the 3 in the quotient.
• Multiply and Subtract: Multiply 0 by 4 to get 0 and subtract, leaving no remainder.

In some cases, division doesn’t result in an even quotient. This means there’s an amount leftover, called a remainder. Here’s how to handle it:

Example: 29 ÷ 4

• Divide: Start by dividing the first digit, 2, by 4. Since 2 is smaller than 4, consider the first two digits, 29.
• Find the Quotient: Divide 29 by 4 to get 7. Write 7 above the long division bracket.
• Multiply and Subtract: Multiply 7 by 4, which gives 28. Subtract 28 from 29, leaving 1.
• Write the Remainder: Since there’s nothing left to bring down, write “R1” (remainder of 1) next to the 7.

Knowing how to recognize and handle remainders is one of the essential long division tricks that help kids understand why not all division problems divide evenly. 

5 Fun Ways to Teach Long Division

Practicing long division is crucial for reinforcing the steps and strategies. Here are five effective ways to help kids master this skill:

• Online Long Division Games 

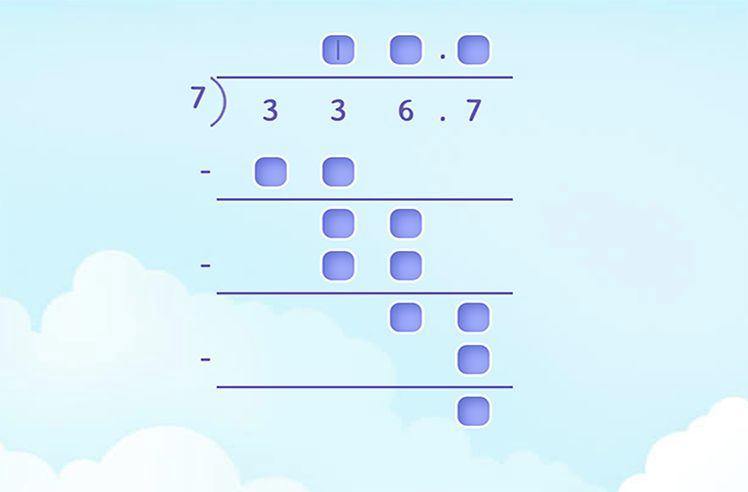
Use interactive online games that challenge students to solve division problems step-by-step. These games make learning fun while providing instant feedback to help them understand mistakes.

• Long Division Worksheets

Provide worksheets that start with simpler problems and progressively increase in complexity. Use colorful designs and real-world scenarios to keep kids engaged.

Create or find flashcards that present division problems on one side and answers on the other. This simple tool is a quick way to reinforce division facts and promote speedy calculations.

• Real-Life Problems

Apply division concepts to real-world situations, like dividing treats among friends or organizing items into equal groups. This practical approach makes long division relatable.

• Group Activities

Collaborative exercises where kids work together to solve division problems encourage discussion and peer learning. This can help clarify challenging steps and foster teamwork.

Learning long division can be challenging, but kids can grasp the concept effectively with clear steps, consistent practice, and engaging resources like games and worksheets. With these strategies on how to teach long division, children will build confidence and become proficient problem-solvers at their own pace.

Frequently Asked Questions (FAQs)

What is an easy way to learn division.

An easy way to learn division is by starting with simple problems and using visual aids like counters or drawings to illustrate the process. Gradually move to more complex problems as confidence builds.

What are some tips for teaching long division to struggling students?

Break down the steps into smaller, manageable parts, and offer lots of practice with engaging resources like games and worksheets. Provide positive reinforcement to encourage their progress and address specific challenges with patience.

• Pre-Kindergarten
• Kindergarten

Most Popular

15 Best Report Card Comments Samples

117 Best Riddles for Kids (With Answers)

40 Best Good Vibes Quotes to Brighten Your Day

Recent posts.

15 Best Fourth of July Crafts for Preschoolers

Math & ELA | PreK To Grade 5

Kids see fun., you see real learning outcomes..

Watch your kids fall in love with math & reading through our scientifically designed curriculum.

Parents, try for free Teachers, use for free

• Games for Kids
• Worksheets for Kids
• Math Worksheets
• ELA Worksheets
• Math Vocabulary
• Number Games
• Addition Games
• Subtraction Games
• Multiplication Games
• Division Games
• Addition Worksheets
• Subtraction Worksheets
• Multiplication Worksheets
• Division Worksheets
• Times Tables Worksheets
• Reading Games
• Writing Games
• Phonics Games
• Sight Words Games
• Letter Tracing Games
• Reading Worksheets
• Writing Worksheets
• Phonics Worksheets
• Sight Words Worksheets
• Letter Tracing Worksheets
• Prime Number
• Order of Operations
• Long multiplication
• Place value
• Parallelogram
• SplashLearn Success Stories
• SplashLearn Apps
• [email protected]

© Copyright - SplashLearn

Make study-time fun with 14,000+ games & activities, 450+ lesson plans, and more—free forever.

Parents, Try for Free Teachers, Use for Free

Product Overview

• Donor Database Use a CRM built for nonprofits.
• Fundraising Tools Drive impact with modern giving solutions.
• Volunteer Management Volunteer experiences that inspire.
• Membership Management Unify your donor and member data.
• Marketing & Engagement Reach out and grow your donor network.
• Reporting & Analytics Easily generate accurate reports.
• Data Management Gather and update donor insights.
• Mobile App Fundraise from anywhere.
• Integrations
• Professional Services & Support
• API Documentation

Learn & Connect

• Articles Read the latest from our community of fundraising professionals.
• Guides & Templates Download free guides and templates.
• Webinars & Events Watch informational webinars and attend industry events.
• DEI Resources Get DEI resources from respected and experienced leaders.
• Ask An Expert Real fundraising questions, answered.
• Bloomerang Academy Learn from our team of fundraising and technology experts.
• Consultant Directory
• Comms Audit Tool
• Donor Retention Calculator
• Compare Bloomerang
• Volunteer Management

Why Our Definition Of Nonprofits Restricts Problem Solving

• Fundraising

Easily Manage Your Donor & Fundraising Needs in Bloomerang!

I’ve often wondered why we’re the only sector that defines ourselves by what we’re NOT.

Non profit.

Why not what we ARE? Social benefit. Or, as Dan Palotta once suggested, “ humanity sector .”

Rather than focusing so much on how to scrimp and save and be as cost- efficient as possible, shouldn’t we be focusing on how to spend and grow and be as big and effective as possible?

Nonprofits are stuck in a vicious cycle, jeopardizing their ability to generate the resources they need to succeed. 

Let’s take a look at six underlying reasons for the sector’s inability to build sustainable capacity to solve the world’s pressing problems.

1. Where are our cultures of philanthropy?

To be loving, one must begin with a loving stance..

Over a decade ago,  CompassPoint  and the  Evelyn and Walter Haas, Jr. Fund published a three-part series of reports exploring culture of philanthropy. Or what I like to call a love-train culture . The first, UnderDeveloped: A National Study of Challenges Facing Nonprofit Fundraising , concluded:

“Organizations need to make fundamental changes in the way they lead and resource fund development in order to build the capacity, the systems, and the culture to support fundraising success. Among the signs that an organization is up to the task: It invests in its fundraising capacity and in the technologies and other fund development systems it needs ; The staff, the executive director, and the board are deeply engaged in fundraising as ambassadors and in many cases as solicitors; Fund development and philanthropy are understood and valued across the organization.”

Alas, a culture of philanthropy essential to long-term success in the sector is still largely absent from our institutions. 

Huge instability in the development director role is just one symptom of a larger problem: lack of basic fundraising systems and inadequate attention to fund development across the board.

2. Why aren’t we investing in greater impact?

To drive impact, one must truly value that impact..

Also, a decade ago, Dan Pallotta gave what’s become a famous TED talk, “ The way we think about charity is dead wrong .” He talks about how the ways we’ve been taught to think about social innovation, and the role charity plays, are undermining the causes we love and our profound yearning to change the world.

“ It’s time to change how society thinks about charity and social reform. The donating public is obsessed with restrictions—nonprofits shouldn’t pay executives too much, or spend a lot on overhead or take risks with donated dollars. It should be asking whether these organizations have what they need to actually solve problems. The conventional wisdom is that low costs serve the higher good. But this view is killing the ability of nonprofits to make progress against our most pressing problems. Long-term solutions require investment in things that don’t show results in the short term.”

In his book, Charity Case: How the Nonprofit Community Can Stand Up For Itself and Really Change the World , Pallota writes:

“The nonprofit sector is critical to our dream of changing the world. Yet there is no greater injustice than the double standard that exists between the for-profit and nonprofit sectors . One gets to feast on marketing, risk-taking, capital and financial incentive, the other is sentenced to begging.”

A culture of investment, where overhead is not seen as the enemy, is hugely lacking within the social benefit (aka nonprofit) sector and among the public at large. 

There is a separate rule book for charities that has a chilling effect on risk-taking, social innovation, and entrepreneurship .

3. Why aren’t we attracting social capital?

To be of social benefit, one must sell impact..

More than a decade ago, Jason Saul published  The End of Fundraising: Raise More Money by Selling Your Impact . He argued we need to look more to the vast ‘social capital market’ – which is approximately 20 times the size of the philanthropic market. The fact that we aren’t set up to engage people who attach real economic value to social outcomes (rather than simply the psychological “feel good” individual donors get as a result of giving) is vastly limiting our ability to attract the social capital we need to survive and thrive.

Social benefit organizations must stop begging for charity and start selling impact. 

It’s a subtle shift in approach that can pack a big punch. Saul details four steps for nonprofits to follow:

• Get a deep understanding of the impact you have and express it in clear terms.
• Identify those who want and can pay for impact (e.g., corporate partners, social and impact investors, and service providers).
• Understand your impact on buyers’ specific needs.
• Ensure your value proposition is clearly defined.

4. Why are we fighting amongst ourselves?

To solve pressing problems, people must come together..

Over the past several years, a whole new movement has entered into the fray –  community-centric fundraising – as a counter balance to what is deemed the nonprofit industrial complex . The distinguishing argument veers from simply “not enriching shareholders” (evil for-profits) to “not reinforcing capitalism, patriarchy, white supremacy and more” (evil nonprofits).

We’re faced with an evolving definition of the sector that shifts from the concept of “social good” to one positing most nonprofits, by definition , reinforce “social ills” by upholding oppressive ways society is organized.

Perhaps. But by creating division and erecting barriers to giving, and fundraising, “philanthropy” (aka “ love of humanity ”) suffers. While some within this movement would say this is a good thing, arguing the sector (by any name) should not exist, and society should simply be restructured to embrace a diverse, equitable, and inclusive model, I’m not convinced.

I can’t argue with this utopian vision, yet I’m not ready to throw the baby (the “sector”) out with the bathwater (fundraising). Too many problems need solving, and Eden is not just around the corner. Which is why I advocate a practice of “philanthropy, not fundraising .” Love, not money.

5. Why are we fighting with donors?

To empower people to be the change they want to see, one must facilitate philanthropy..

This means making giving easy, not hard . Because so many problems need solving, it’s just not fruitful to get into a determination of which donors should be entitled to give, which should not, and how they should be rewarded. It’s important for fundraisers to fully embrace philanthropy as a positive, not a negative .

I always say “ if you want gifts you must give them ,” and in four decades of fundraising I’ve found one constant in donors who remain loyal and passionate — they repeatedly tell me:

“I get so much more out of this than I give.”

That’s how you  want  donors to feel. Because it’s what keeps them coming back. The more you can help people – donors included – secure what they most yearn for, the more successful you’ll be in driving purpose-filled actions, creating a community that cares for its members. All of them.

The “us” vs. “them” attitudes, roughly lumped under the mantle of “community-centric fundraising,” are unfortunate. 

Because they do the opposite of making people feel connected to your community, enveloped in your  loving   (the “ philos ” of philanthropy) embrace.

6. Why do we persist in thinking small?

To do the greatest good, one must think expansively..

I am constantly counseling social benefit organizations to think and dream bigger. Ask yourself:

• What’s our real vision?
• How much more could we accomplish with more resources?
• Why are we limiting ourselves?
• What else could we innovate?

Everything I’ve written thus far points to the fact it’s really all about how you invest in philanthropic work — both in terms of the money you spend and the human capital you involve.

Big problems will never be solved by small solutions.

When you silo the resource development function to one person, one department or one board committee, you think too small to scale your solutions to match the worthy needs you seek to address via your mission.  Thinking small this way, you’ll never attain your vision .

Concluding thoughts

It’s going to take a culture shift to move the needle..

I fear we’re racing to the bottom with our emphasis on lean and mean. As the inimitable Seth Godin notes in Cheaper than that , “ Once we’ve cut every corner, all that’s left is the brutality of less … The problem with the race to the bottom is that you might win.”

Studies like “ Underdeveloped ,” books like Jason Saul’s, TED talks like Dan Pallota’s, and movements like community-centric fundraising that seek a transformational approach to the task of repairing the world can help. But only if nonprofit leaders take them to heart, thoughtfully consider their implications and implementation, and actively commit to essential change and innovation. We need to:

• Stop demanding charities cut, cut, cut expenses rather than encouraging them to invest, invest, invest in ways to grow impact.
• Talk more about vision and what it will take to get there.
• Insist on finding ways to actually solve some of our intractable problems.
• Clearly articulate our impact and results in order to attract social investing.
• Spread the love around, centering our light on staff, board members, donors, volunteers, beneficiaries, and the entire community that stands to benefit when we all fight the good fight together .
• Figure out a way to prioritize community without cutting donors out of the picture – empowering both donors and beneficiaries alike.

Are you up for the challenge?

How to Write a Fundraising Plan in 2 Steps!

Exclusive Resources

Related Articles

An efficient ODE-solving method based on heuristic and statistical computations: αII-(2 + 3)P method

• Published: 31 May 2024

Cite this article

• Mehdi Babaei 1  

The main goal of this paper is to develop a new class of sixth- and fourth-order implicit Runge–Kutta methods to treat linear and nonlinear initial value ordinary differential equations (ODEs) in applied science and engineering. In this regard, a completely unconventional approach is taken to derive the new formulations. They are derived through a computational approach without involving in the rigorous theory of order conditions. The new formulation has two distinctive parts, namely integration and interpolation. In the first part, we introduce a form of multi-stage single-step numerical integrator with unknown weights. These weights are determined by four simple interconnectivity rules that relate them to minimize the error of the integrator. Some of these rules are based on our expertise gathered from the available prominent quadratures. However, the most important one, the so-called fundamental weighting rule (FWR), is obtained from evolutionary and statistical computations. The second part of this research focuses on developing efficient tools for evaluating the internal stages of the integrator. Accordingly, a series of strong Hermite interpolators has been extended to approximate the solution values at the internal stages. They effectively collaborate with the integrator in several numerical algorithms, the so-called \(\alpha II-(q+r)P\) algorithms, to solve applied ODEs. Development of the integrator, its weighting rules, and the interpolators constitutes the central contribution of this research. Numerical studies demonstrate that the presented algorithms exhibit a high level of accuracy when approximating high-frequency problems as well as long-term solutions of linear and nonlinear ODEs.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Availability of data and material

Not applicable.

Abelman S, Patidar KC (2008) Comparison of some recent numerical methods for initial-value problems for stiff ordinary differential equations. Comput Math Appl 55(4):733–744

Article   MathSciNet   Google Scholar  

Anastassi ZA, Simos TE (2005) An optimized Runge-Kutta method for the solution of orbital problems. J Comput Appl Math 175(1):1–9

Soroushian A (2008) A technique for time integration analysis with steps larger than the excitation steps. Commun Numer Methods Eng 24(12):2087–2111

Soroushian A, Farjoodi J (2003) More reliable responses for time integration analyses. Struct Eng Mech Int J 16(2):219–240

Article   Google Scholar  

Babaei M (2013) A general approach to approximate solutions of nonlinear differential equations using particle swarm optimization. Appl Soft Comput 13(7):3354–3365

Babaei M (2024) A Swarm-Intelligence Based Formulation for Solving Nonlinear ODEs: γβII-(2+ 3) P method. Appl Soft Comput, 111424. https://doi.org/10.1016/j.asoc.2024.111424

Babaei M (2022) Numerical solution of beam equation using neural networks and evolutionary optimization tools. Adv Comput Des 7(1):1–17. https://doi.org/10.12989/acd.2022.7.1.001

MathSciNet   Google Scholar  

Babaei M, Jalilkhani M, Ghasemi SH, Mollaei S (2022) New methods for dynamic analysis of structural systems under earthquake loads. J Rehabilit Civil Eng 10(3):81–99. https://doi.org/10.22075/JRCE.2021.23323.1506

Google Scholar  

Babaei M, Farzi J (2023) Derivation of weighting rules for developing a class of A-stable numerical integration scheme: αI-(2+3)P method. J Difference Equat Appl, pp 1–30. https://doi.org/10.1080/10236198.2023.2219785

Babaei M (2024) Optimized Gauss–Legendre–Hermite 2-point (O-GLH-2P) method for nonlinear time-history analysis of structures. Mechanica, pp 1–28, https://doi.org/10.1007/s11012-023-01752-4

Babaei M, Hanafi MR (2024) A novel method for nonlinear time-history analysis of structural systems: improved Newton–Cotes-Hermite-5P Method. (in press). https://doi.org/10.1007/s40996-024-01345-5

Boyce WE, DiPrima RC, Meade DB (2021) Elementary differential equations and boundary value problems. Wiley, New York

Burden Richard L (2011) Numerical analysis. Brooks/Cole Cengage Learning.

Burrage K, Butcher JC (1979) Stability criteria for implicit Runge-Kutta methods. SIAM J Numer Anal 16(1):46–57

Butcher JC (1964) Implicit Runge-Kutta processes. Math Comp 18(85):50–64

Butcher JC (1996) A history of Runge-Kutta methods. Appl Numer Math 20(3):247–260

Butcher JC, Wanner G (1996) Runge-Kutta methods: some historical notes. Appl Numer Math 22(1–3):113–151

Butcher JC (2000) Numerical methods for ordinary differential equations in the 20th century. J Comput Appl Math 125(1–2):1–29

Butcher JC (2016) Numerical methods for ordinary differential equations. John Wiley & Sons, Wiley

Book   Google Scholar  

Carpenter MH, Gottlieb D, Abarbanel S, Don WS (1993) The theoretical accuracy of Runge-Kutta time discretizations for the initial boundary value problem: a careful study of the boundary error (No. NAS 1.26: 191561). NASA.

Cash JR, Considine S (1992) An MEBDF code for stiff initial value problems. ACM Trans Math Softw (TOMS) 18(2):142–155

Chan RP, Tsai AY (2010) On explicit two-derivative Runge-Kutta methods. Numer Algorithms 53:171–194

Chicone C (2006) Ordinary differential equations with applications (Vol. 34). Springer, Cham.

Chopra AK (2012) Dynamics of structures: theory and applications to earthquake engineering, 4th edn. Prentice Hall, Upper Saddle River, NJ

Clough RW, Penzien J (2003) Dynamics of structures. Computers and Structures, Berkeley, CA

Coddington EA (2012) An introduction to ordinary differential equations. Courier Corporation.

Cooper G (1987) Stability of Runge-Kutta methods for trajectory problems. IMA J Numer Anal 7(1):1–13

Cooper GJ, Vignesvaran R (1993) Some schemes for the implementation of implicit Runge-Kutta methods. J Comput Appl Math 45(1–2):213–225

Craig Jr RR, Kurdila AJ (2006) Fundamentals of structural dynamics. Wiley, New York

D'Alembert JBLR (1767) Mélanges de littérature, d'histoire, et de philosophie: Part 5 (Vol. 5). Z. Chatelain & fils.

Davis PJ (1975) Interpolation and approximation. Courier Corporation.

Dowdy S, Wearden S, Chilko D (2011) Statistics for research. Wiley, New York

Epperson JF (2021) An introduction to numerical methods and analysis. Wiley, New York

Euler L (1824) Institutionum calculi integralis (Vol. 1). Impensis Academiae imperialis scientiarum.

Fathoni MF, Wuryandari AI (2015) Comparison between Euler, Heun, Runge-Kutta and Adams-Bashforth-Moulton integration methods in the particle dynamic simulation. In: 2015 4th International Conference on Interactive Digital Media (ICIDM) (pp. 1–7). IEEE, New York.

Gadisa G, Garoma H (2017) Comparison of higher order Taylor’s method and Runge-Kutta methods for solving first order ordinary differential equations. J Comp Math Sci 8(1):12–23

Gatti PL (2014) Applied structural and mechanical vibrations: theory and methods. CRC Press, Boca Raton.

Gautschi W (2011) Numerical analysis. Springer, Cham

Gear CW (1971) Numerical initial value problems in ordinary differential equations. Prentice-Hall series in automatic computation, New Jersey.

Greenberg MD (2012) Ordinary differential equations. Wiley, New York

Griffiths DF, Higham DJ (2010) Numerical methods for ordinary differential equations: initial value problems, vol 5. Springer, London

Gupta SC, Kapoor VK (2020) Fundamentals of mathematical statistics. Sultan Chand & Sons, Delhi

Hairer E, Wanner G, Nørsett SP (2008) Solving ordinary differential equations I: Nonstiff problems. Springer, Berlin Heidelberg, Germany

Hairer E, Wanner G (1973) Multistep-multistage-multiderivative methods for ordinary differential equations. Computing 11(3):287–303

Hairer E, Wanner G (2015) Runge–Kutta methods, explicit, implicit. Encyclopedia of Applied and Computational Mathematics, pp 1282–1285.

Hermann M, Saravi M (2016) Nonlinear ordinary differential equations. Springer, Berlin

Islam MA (2015) A comparative study on numerical solutions of initial value problems (IVP) for ordinary differential equations (ODE) with Euler and Runge Kutta Methods. Am J Comput Math 5(03):393

Islam MA (2015) Accurate solutions of initial value problems for ordinary differential equations with the fourth order Runge Kutta method. J Math Res 7(3):41

Islam MA (2015) Accuracy Analysis of Numerical solutions of initial value problems (IVP) for ordinary differential equations (ODE). IOSR J Math 11(3):18–23

Jator SN (2010) Solving second order initial value problems by a hybrid multistep method without predictors. Appl Math Comput 217(8):4036–4046

Jeon Y, Bak S, Bu S (2019) Reinterpretation of multi-Stage methods for stiff systems: a comprehensive review on current perspectives and recommendations. Mathematics 7(12):1158

Kalogiratou Z, Monovasilis T, Simos TE (2010) New modified Runge–Kutta–Nyström methods for the numerical integration of the Schrödinger equation. Comput Math Appl 60(6):1639–1647

Katsikadelis JT (2013) A new direct time integration scheme for the nonlinear equations of motion in structural dynamics. In: 10 the HSTAM international congress on mechanics, May, pp. 25–27.

Katsikadelis JT (2021) A new method for numerical integration of higher-order ordinary differential equations without losing the periodic responses. Front Built Environ 7:40

Katsikadelis JT (2020) Dynamic analysis of structures, 1st edn. Elsevier Amsterdam.

Kutta M (1901) Beitrag zur näherungsweisen Integration totaler Differentialgleichungen. Zeitschrift für Mathematik und Physik 46:435–453

Lambert JD (1973) Computational methods in ordinary differential equations. (No Title).

Lapidus L, Seinfeld JH (1971) Numerical solution of ordinary differential equations. Academic Press, New York.

Larsen RJ, Marx ML (2005) An introduction to mathematical statistics. Prentice Hall, Hoboken, NJ

Lian J, Hui G (2024) Human evolutionary optimization algorithm. Expert Syst Appl 241:122638

Lotkin M (1951) On the accuracy of Runge-Kutta’s method. Math Tables Other Aids Comput 5(35):128–133

Mechee M, Senu N, Ismail F, Nikouravan B, Siri Z (2013) A three-stage fifth-order Runge-Kutta method for directly solving special third-order differential equation with application to thin film flow problem. Math Problems Eng. 2013, ID 795397: 1-7

Meriam JL, Kraige LG, Bolton JN (2020) Engineering mechanics: dynamics. Wiley, New York

Mohammed AA, Hamza A, Mohammed U (2013) A self-starting hybrid linear multistep method for a direct solution of the general second-order initial value problem, IOSR Journal of Mathematics (IOSR-JM) 4(6): 7-13

Montiel O, Castillo O, Melin P, Díaz AR, Sepúlveda R (2007) Human evolutionary model: a new approach to optimization. Inf Sci 177(10):2075–2098

Murphy GM (2011) Ordinary differential equations and their solutions. Courier Corporation.

Ogunrinde RB, Fadugba SE, Okunlola JT (2012) On some numerical methods for solving initial value problems in ordinary differential equations. IOSR Journal of Mathematics (IOSRJM) 1(3): 25-31

Omar Z, Adeyeye O (2016) Numerical solution of first order initial value problems using a self-starting implicit two-step Obrechkoff-type block method. J Math Stat 12(2):127–134

Paz M, Leigh W (2004) Structural dynamics: theory and computation, 5th edn. Springer, New York

Rabiei F, Ismail F, Suleiman M (2013) Improved Runge-Kutta methods for solving ordinary differential equations. Sains Malaysiana 42(11):1679–1687

Runge C (1895) Über die numerische Auflösung von Differentialgleichungen. Math Ann 46(2):167–178

Sakhnovich LA (2012) Interpolation theory and its applications, Vol. 428. Springer, Cham.

Saremi S, Mirjalili S, Lewis A (2017) Grasshopper optimisation algorithm: theory and application. Adv Eng Softw 105:30–47

Sasser JE (1992) History of ordinary differential equations: the first hundred years. In: Proceedings of the Midwest Mathematics History Society, p 1.

Simmons GF (2016) Differential equations with applications and historical notes. CRC Press, Boca Raton

Stoer J, Bulirsch R, Bartels R, Gautschi W, Witzgall C (1980) Introduction to numerical analysis, vol 1993. Springer, New York

Sunday J, Odekunle MR (2012) A New Numerical integrator for the solution of initial value problems in ordinary differential equations. Pacific J Sci Technol 13(1):221–227

Tedesco J, McDougal WG, Ross CA (2000) Structural dynamics. Pearson Education, London, UK.

Tsitouras C, Famelis IT, Simos TE (2011) On modified Runge-Kutta trees and methods. Comput Math Appl 62(4):2101–2111

Thomson W(2018) Theory of vibration with applications. CRC Press, Boca Raton.

Walter W (2013) Ordinary differential equations, Vol. 182. Springer, Cham.

Wang ZQ, Guo BY (2012) Legendre-Gauss-Radau collocation method for solving initial value problems of first order ordinary differential equations. J Sci Comput 52(1):226–255

Wanner G, Hairer E (1996) Solving ordinary differential equations II (Vol. 375). Computing 52(1):226–255.

Witte RS, Witte JS (2017) Statistics. Wiley, New York

Wright K (1964) Chebyshev collocation methods for ordinary differential equations. Comput J 6(4):358–365

Zervoudakis K, Tsafarakis S (2022) A global optimizer inspired from the survival strategies of flying foxes. Eng Comp, pp 1–34.

Download references

Acknowledgements

I would like to express my sincere thanks to the reviewers of this paper for their valuable feedback and constructive comments. Their insightful suggestions greatly improved the scientific quality of this work. I am truly appreciative of their time and expertise in reviewing this manuscript.

No funding was received for conducting this study.

Author information

Authors and affiliations.

Department of Civil Engineering, University of Bonab, P.O. Box 55513-95133, Bonab, Iran

Mehdi Babaei

You can also search for this author in PubMed   Google Scholar

Contributions

The whole paper is worked by M. Babaei, the single author of the paper.

Corresponding author

Correspondence to Mehdi Babaei .

Ethics declarations

Conflict of interests.

There is no conflict of interest.

Ethics approval and consent to participate

Consent for publication, additional information, publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Babaei, M. An efficient ODE-solving method based on heuristic and statistical computations: αII-(2 + 3)P method. J Supercomput (2024). https://doi.org/10.1007/s11227-024-06137-2

Download citation

Accepted : 09 April 2024

Published : 31 May 2024

DOI : https://doi.org/10.1007/s11227-024-06137-2

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

•  Initial value problem (IVP)
•  Ordinary differential equation (ODE)
• Runge–Kutta method
• Numerical Integration
• Hermite Interpolation
• Long-term solution
• Optimization
• Find a journal
• Publish with us
• Track your research