math reasoning or problem solving lesson plan

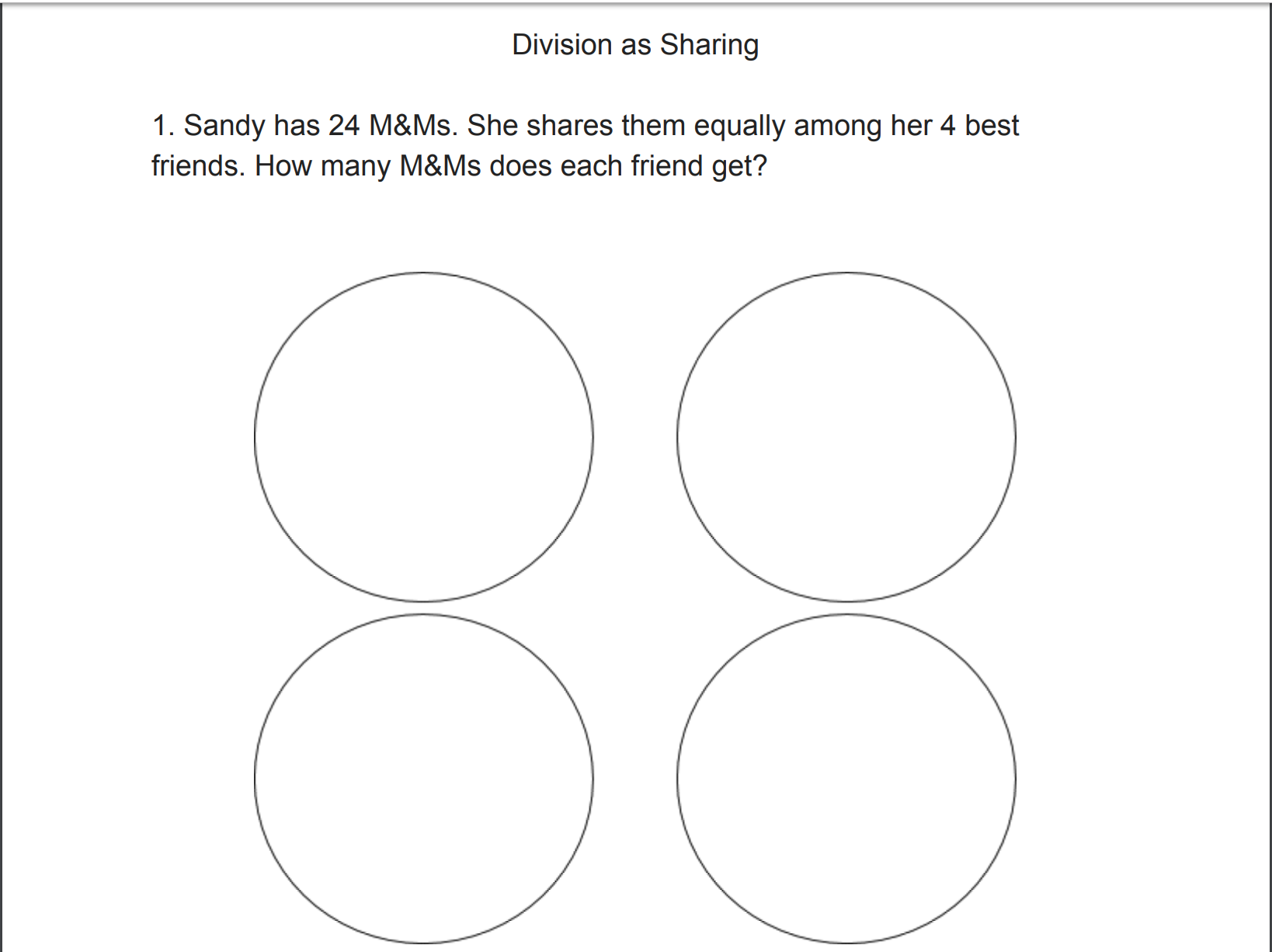
High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Free ready-to-use math resources

Hundreds of free math resources created by experienced math teachers to save time, build engagement and accelerate growth

20 Effective Math Strategies To Approach Problem-Solving 

Katie Keeton

Math strategies for problem-solving help students use a range of approaches to solve many different types of problems. It involves identifying the problem and carrying out a plan of action to find the answer to mathematical problems.  

Problem-solving skills are essential to math in the general classroom and real-life. They require logical reasoning and critical thinking skills. Students must be equipped with strategies to help them find solutions to problems.

This article explores mathematical problem solving strategies, logical reasoning and critical thinking skills to help learners with solving math word problems independently in real-life situations. 

What are problem-solving strategies?

Problem-solving strategies in math are methods students can use to figure out solutions to math problems. Some problem-solving strategies: 

• Draw a model
• Use different approaches
• Check the inverse to make sure the answer is correct

Students need to have a toolkit of math problem-solving strategies at their disposal to provide different ways to approach math problems. This makes it easier to find solutions and understand math better. 

Strategies can help guide students to the solution when it is difficult ot know when to start.

The ultimate guide to problem solving techniques

Download these ready-to-go problem solving techniques that every student should know. Includes printable tasks for students including challenges, short explanations for teachers with questioning prompts.

20 Math Strategies For Problem-Solving

Different problem-solving math strategies are required for different parts of the problem. It is unlikely that students will use the same strategy to understand and solve the problem. 

Here are 20 strategies to help students develop their problem-solving skills. 

Strategies to understand the problem

Strategies that help students understand the problem before solving it helps ensure they understand: 

• The context
• What the key information is
• How to form a plan to solve it

Following these steps leads students to the correct solution and makes the math word problem easier .

Here are five strategies to help students understand the content of the problem and identify key information. 

1. Read the problem aloud

Read a word problem aloud to help understand it. Hearing the words engages auditory processing. This can make it easier to process and comprehend the context of the situation.

2. Highlight keywords 

When keywords are highlighted in a word problem, it helps the student focus on the essential information needed to solve it. Some important keywords help determine which operation is needed.  For example, if the word problem asks how many are left, the problem likely requires subtraction.  Ensure students highlight the keywords carefully and do not highlight every number or keyword. There is likely irrelevant information in the word problem.

3. Summarize the information

Read the problem aloud, highlight the key information and then summarize the information. Students can do this in their heads or write down a quick summary.  Summaries should include only the important information and be in simple terms that help contextualize the problem.

4. Determine the unknown

A common problem that students have when solving a word problem is misunderstanding what they are solving. Determine what the unknown information is before finding the answer.  Often, a word problem contains a question where you can find the unknown information you need to solve. For example, in the question ‘How many apples are left?’ students need to find the number of apples left over.

5. Make a plan

Once students understand the context of the word problem, have dentified the important information and determined the unknown, they can make a plan to solve it.  The plan will depend on the type of problem. Some problems involve more than one step to solve them as some require more than one answer.  Encourage students to make a list of each step they need to take to solve the problem before getting started.

Strategies for solving the problem 

1. draw a model or diagram.

Students may find it useful to draw a model, picture, diagram, or other visual aid to help with the problem solving process.  It can help to visualize the problem to understand the relationships between the numbers in the problem. In turn, this helps students see the solution.

Similarly, you could draw a model to represent the objects in the problem:

2. Act it out

This particular strategy is applicable at any grade level but is especially helpful in math investigation in elementary school . It involves a physical demonstration or students acting out the problem using movements, concrete resources and math manipulatives .  When students act out a problem, they can visualize and contectualize the word problem in another way and secure an understanding of the math concepts.  The examples below show how 1st-grade students could “act out” an addition and subtraction problem:

3. Work backwards

Working backwards is a popular problem-solving strategy. It involves starting with a possible solution and deciding what steps to take to arrive at that solution.  This strategy can be particularly helpful when students solve math word problems involving multiple steps. They can start at the end and think carefully about each step taken as opposed to jumping to the end of the problem and missing steps in between.

For example,

To solve this problem working backwards, start with the final condition, which is Sam’s grandmother’s age (71) and work backwards to find Sam’s age. Subtract 20 from the grandmother’s age, which is 71.  Then, divide the result by 3 to get Sam’s age. 71 – 20 = 51 51 ÷ 3 = 17 Sam is 17 years old.

4. Write a number sentence

When faced with a word problem, encourage students to write a number sentence based on the information. This helps translate the information in the word problem into a math equation or expression, which is more easily solved.  It is important to fully understand the context of the word problem and what students need to solve before writing an equation to represent it.

5. Use a formula

Specific formulas help solve many math problems. For example, if a problem asks students to find the area of a rug, they would use the area formula (area = length × width) to solve.   Make sure students know the important mathematical formulas they will need in tests and real-life. It can help to display these around the classroom or, for those who need more support, on students’ desks.

Strategies for checking the solution 

Once the problem is solved using an appropriate strategy, it is equally important to check the solution to ensure it is correct and makes sense. 

There are many strategies to check the solution. The strategy for a specific problem is dependent on the problem type and math content involved.

Here are five strategies to help students check their solutions. 

1. Use the Inverse Operation

For simpler problems, a quick and easy problem solving strategy is to use the inverse operation. For example, if the operation to solve a word problem is 56 ÷ 8 = 7 students can check the answer is correct by multiplying 8 × 7. As good practice, encourage students to use the inverse operation routinely to check their work. 

2. Estimate to check for reasonableness

Once students reach an answer, they can use estimation or rounding to see if the answer is reasonable.  Round each number in the equation to a number that’s close and easy to work with, usually a multiple of ten.  For example, if the question was 216 ÷ 18 and the quotient was 12, students might round 216 to 200 and round 18 to 20. Then use mental math to solve 200 ÷ 20, which is 10.  When the estimate is clear the two numbers are close. This means your answer is reasonable. 

3. Plug-In Method

This method is particularly useful for algebraic equations. Specifically when working with variables.  To use the plug-in method, students solve the problem as asked and arrive at an answer. They can then plug the answer into the original equation to see if it works. If it does, the answer is correct.

If students use the equation 20m+80=300 to solve this problem and find that m = 11, they can plug that value back into the equation to see if it is correct. 20m + 80 = 300 20 (11) + 80 = 300 220 + 80 = 300 300 = 300 ✓

4. Peer Review

Peer review is a great tool to use at any grade level as it promotes critical thinking and collaboration between students. The reviewers can look at the problem from a different view as they check to see if the problem was solved correctly.   Problem solvers receive immediate feedback and the opportunity to discuss their thinking with their peers. This strategy is effective with mixed-ability partners or similar-ability partners. In mixed-ability groups, the partner with stronger skills provides guidance and support to the partner with weaker skills, while reinforcing their own understanding of the content and communication skills.  If partners have comparable ability levels and problem-solving skills, they may find that they approach problems differently or have unique insights to offer each other about the problem-solving process.

5. Use a Calculator

A calculator can be introduced at any grade level but may be best for older students who already have a foundational understanding of basic math operations. Provide students with a calculator to allow them to check their solutions independently, accurately, and quickly. Since calculators are so readily available on smartphones and tablets, they allow students to develop practical skills that apply to real-world situations.  

Step-by-step problem-solving processes for your classroom

In his book, How to Solve It , published in 1945, mathematician George Polya introduced a 4-step process to solve problems. 

Polya’s 4 steps include:

• Understand the problem
• Devise a plan
• Carry out the plan

Today, in the style of George Polya, many problem-solving strategies use various acronyms and steps to help students recall. 

Many teachers create posters and anchor charts of their chosen process to display in their classrooms. They can be implemented in any elementary, middle school or high school classroom. 

Here are 5 problem-solving strategies to introduce to students and use in the classroom.

How Third Space Learning improves problem-solving 

Resources .

Third Space Learning offers a free resource library is filled with hundreds of high-quality resources. A team of experienced math experts carefully created each resource to develop students mental arithmetic, problem solving and critical thinking. 

Explore the range of problem solving resources for 2nd to 8th grade students. 

One-on-one tutoring 

Third Space Learning offers one-on-one math tutoring to help students improve their math skills. Highly qualified tutors deliver high-quality lessons aligned to state standards. 

Former teachers and math experts write all of Third Space Learning’s tutoring lessons. Expertly designed lessons follow a “my turn, follow me, your turn” pedagogy to help students move from guided instruction and problem-solving to independent practice. 

Throughout each lesson, tutors ask higher-level thinking questions to promote critical thinking and ensure students are developing a deep understanding of the content and problem-solving skills.

Problem-solving

Educators can use many different strategies to teach problem-solving and help students develop and carry out a plan when solving math problems. Incorporate these math strategies into any math program and use them with a variety of math concepts, from whole numbers and fractions to algebra. 

Teaching students how to choose and implement problem-solving strategies helps them develop mathematical reasoning skills and critical thinking they can apply to real-life problem-solving.

READ MORE : 8 Common Core math examples

There are many different strategies for problem-solving; Here are 5 problem-solving strategies: • draw a model  • act it out  • work backwards  • write a number sentence • use a formula

Here are 10 strategies of problem-solving: • Read the problem aloud • Highlight keywords • Summarize the information • Determine the unknown • Make a plan • Draw a model  • Act it out  • Work backwards  • Write a number sentence • Use a formula

1. Understand the problem 2. Devise a plan 3. Carry out the plan 4. Look back

Some strategies you can use to solve challenging math problems are: breaking the problem into smaller parts, using diagrams or models, applying logical reasoning, and trying different approaches.

Related articles

Why Student Centered Learning Is Important: A Guide For Educators

13 Effective Learning Strategies: A Guide to Using them in your Math Classroom

Differentiated Instruction: 9 Differentiated Curriculum And Instruction Strategies For Teachers 

5 Math Mastery Strategies To Incorporate Into Your 4th and 5th Grade Classrooms

Ultimate Guide to Metacognition [FREE]

Looking for a summary on metacognition in relation to math teaching and learning?

Check out this guide featuring practical examples, tips and strategies to successfully embed metacognition across your school to accelerate math growth.

Privacy Overview

Teaching Problem Solving in Math

• Freebies , Math , Planning

Every year my students can be fantastic at math…until they start to see math with words. For some reason, once math gets translated into reading, even my best readers start to panic. There is just something about word problems, or problem-solving, that causes children to think they don’t know how to complete them.

Every year in math, I start off by teaching my students problem-solving skills and strategies. Every year they moan and groan that they know them. Every year – paragraph one above. It was a vicious cycle. I needed something new.

I put together a problem-solving unit that would focus a bit more on strategies and steps in hopes that that would create problem-solving stars.

The Problem Solving Strategies

First, I wanted to make sure my students all learned the different strategies to solve problems, such as guess-and-check, using visuals (draw a picture, act it out, and modeling it), working backward, and organizational methods (tables, charts, and lists). In the past, I had used worksheet pages that would introduce one and provide the students with plenty of problems practicing that one strategy. I did like that because students could focus more on practicing the strategy itself, but I also wanted students to know when to use it, too, so I made sure they had both to practice.

I provided students with plenty of practice of the strategies, such as in this guess-and-check game.

There’s also this visuals strategy wheel practice.

I also provided them with paper dolls and a variety of clothing to create an organized list to determine just how many outfits their “friend” would have.

Then, as I said above, we practiced in a variety of ways to make sure we knew exactly when to use them. I really wanted to make sure they had this down!

Anyway, after I knew they had down the various strategies and when to use them, then we went into the actual problem-solving steps.

The Problem Solving Steps

I wanted students to understand that when they see a story problem, it isn’t scary. Really, it’s just the equation written out in words in a real-life situation. Then, I provided them with the “keys to success.”

S tep 1 – Understand the Problem.   To help students understand the problem, I provided them with sample problems, and together we did five important things:

• read the problem carefully
• restated the problem in our own words
• crossed out unimportant information
• circled any important information
• stated the goal or question to be solved

We did this over and over with example problems.

Once I felt the students had it down, we practiced it in a game of problem-solving relay. Students raced one another to see how quickly they could get down to the nitty-gritty of the word problems. We weren’t solving the problems – yet.

Then, we were on to Step 2 – Make a Plan . We talked about how this was where we were going to choose which strategy we were going to use. We also discussed how this was where we were going to figure out what operation to use. I taught the students Sheila Melton’s operation concept map.

We talked about how if you know the total and know if it is equal or not, that will determine what operation you are doing. So, we took an example problem, such as:

Sheldon wants to make a cupcake for each of his 28 classmates. He can make 7 cupcakes with one box of cupcake mix. How many boxes will he need to buy?

We started off by asking ourselves, “Do we know the total?” We know there are a total of 28 classmates. So, yes, we are separating. Then, we ask, “Is it equal?” Yes, he wants to make a cupcake for EACH of his classmates. So, we are dividing: 28 divided by 7 = 4. He will need to buy 4 boxes. (I actually went ahead and solved it here – which is the next step, too.)

Step 3 – Solving the problem . We talked about how solving the problem involves the following:

• taking our time
• working the problem out
• showing all our work
• estimating the answer
• using thinking strategies

We talked specifically about thinking strategies. Just like in reading, there are thinking strategies in math. I wanted students to be aware that sometimes when we are working on a problem, a particular strategy may not be working, and we may need to switch strategies. We also discussed that sometimes we may need to rethink the problem, to think of related content, or to even start over. We discussed these thinking strategies:

• switch strategies or try a different one
• rethink the problem
• think of related content
• decide if you need to make changes
• check your work
• but most important…don’t give up!

To make sure they were getting in practice utilizing these thinking strategies, I gave each group chart paper with a letter from a fellow “student” (not a real student), and they had to give advice on how to help them solve their problem using the thinking strategies above.

Finally, Step 4 – Check It.   This is the step that students often miss. I wanted to emphasize just how important it is! I went over it with them, discussing that when they check their problems, they should always look for these things:

• compare your answer to your estimate
• check for reasonableness
• check your calculations
• add the units
• restate the question in the answer
• explain how you solved the problem

Then, I gave students practice cards. I provided them with example cards of “students” who had completed their assignments already, and I wanted them to be the teacher. They needed to check the work and make sure it was completed correctly. If it wasn’t, then they needed to tell what they missed and correct it.

To demonstrate their understanding of the entire unit, we completed an adorable lap book (my first time ever putting together one or even creating one – I was surprised how well it turned out, actually). It was a great way to put everything we discussed in there.

Once we were all done, students were officially Problem Solving S.T.A.R.S. I just reminded students frequently of this acronym.

Stop – Don’t rush with any solution; just take your time and look everything over.

Think – Take your time to think about the problem and solution.

Act  – Act on a strategy and try it out.

Review – Look it over and see if you got all the parts.

Wow, you are a true trooper sticking it out in this lengthy post! To sum up the majority of what I have written here, I have some problem-solving bookmarks FREE to help you remember and to help your students!

You can grab these problem-solving bookmarks for FREE by clicking here .

You can do any of these ideas without having to purchase anything. However, if you are looking to save some time and energy, then they are all found in my Math Workshop Problem Solving Unit . The unit is for grade three, but it  may work for other grade levels. The practice problems are all for the early third-grade level.

• freebie , Math Workshop , Problem Solving

FIND IT NOW!

Check me out on tpt.

CHECK THESE OUT

Three Types of Rocks and Minerals with Rock Cycle Circle Book

Partitioning Shapes Equal Share Fractions Halves, Thirds, Fourths Math Puzzles

Want to save time?

COPYRIGHT © 2016-2024. The Owl Teacher | Privacy page | Disclosure Page | Shipping | Returns/Refunds

BOGO on EVERYTHING!

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

5 Teaching Mathematics Through Problem Solving

Janet Stramel

In his book “How to Solve It,” George Pólya (1945) said, “One of the most important tasks of the teacher is to help his students. This task is not quite easy; it demands time, practice, devotion, and sound principles. The student should acquire as much experience of independent work as possible. But if he is left alone with his problem without any help, he may make no progress at all. If the teacher helps too much, nothing is left to the student. The teacher should help, but not too much and not too little, so that the student shall have a reasonable share of the work.” (page 1)

What is a problem  in mathematics? A problem is “any task or activity for which the students have no prescribed or memorized rules or methods, nor is there a perception by students that there is a specific ‘correct’ solution method” (Hiebert, et. al., 1997). Problem solving in mathematics is one of the most important topics to teach; learning to problem solve helps students develop a sense of solving real-life problems and apply mathematics to real world situations. It is also used for a deeper understanding of mathematical concepts. Learning “math facts” is not enough; students must also learn how to use these facts to develop their thinking skills.

According to NCTM (2010), the term “problem solving” refers to mathematical tasks that have the potential to provide intellectual challenges for enhancing students’ mathematical understanding and development. When you first hear “problem solving,” what do you think about? Story problems or word problems? Story problems may be limited to and not “problematic” enough. For example, you may ask students to find the area of a rectangle, given the length and width. This type of problem is an exercise in computation and can be completed mindlessly without understanding the concept of area. Worthwhile problems  includes problems that are truly problematic and have the potential to provide contexts for students’ mathematical development.

There are three ways to solve problems: teaching for problem solving, teaching about problem solving, and teaching through problem solving.

Teaching for problem solving begins with learning a skill. For example, students are learning how to multiply a two-digit number by a one-digit number, and the story problems you select are multiplication problems. Be sure when you are teaching for problem solving, you select or develop tasks that can promote the development of mathematical understanding.

Teaching about problem solving begins with suggested strategies to solve a problem. For example, “draw a picture,” “make a table,” etc. You may see posters in teachers’ classrooms of the “Problem Solving Method” such as: 1) Read the problem, 2) Devise a plan, 3) Solve the problem, and 4) Check your work. There is little or no evidence that students’ problem-solving abilities are improved when teaching about problem solving. Students will see a word problem as a separate endeavor and focus on the steps to follow rather than the mathematics. In addition, students will tend to use trial and error instead of focusing on sense making.

Teaching through problem solving  focuses students’ attention on ideas and sense making and develops mathematical practices. Teaching through problem solving also develops a student’s confidence and builds on their strengths. It allows for collaboration among students and engages students in their own learning.

Consider the following worthwhile-problem criteria developed by Lappan and Phillips (1998):

• The problem has important, useful mathematics embedded in it.
• The problem requires high-level thinking and problem solving.
• The problem contributes to the conceptual development of students.
• The problem creates an opportunity for the teacher to assess what his or her students are learning and where they are experiencing difficulty.
• The problem can be approached by students in multiple ways using different solution strategies.
• The problem has various solutions or allows different decisions or positions to be taken and defended.
• The problem encourages student engagement and discourse.
• The problem connects to other important mathematical ideas.
• The problem promotes the skillful use of mathematics.
• The problem provides an opportunity to practice important skills.

Of course, not every problem will include all of the above. Sometimes, you will choose a problem because your students need an opportunity to practice a certain skill.

Key features of a good mathematics problem includes:

• It must begin where the students are mathematically.
• The feature of the problem must be the mathematics that students are to learn.
• It must require justifications and explanations for both answers and methods of solving.

Problem solving is not a  neat and orderly process. Think about needlework. On the front side, it is neat and perfect and pretty.

But look at the b ack.

It is messy and full of knots and loops. Problem solving in mathematics is also like this and we need to help our students be “messy” with problem solving; they need to go through those knots and loops and learn how to solve problems with the teacher’s guidance.

When you teach through problem solving , your students are focused on ideas and sense-making and they develop confidence in mathematics!

Mathematics Tasks and Activities that Promote Teaching through Problem Solving

Choosing the Right Task

Selecting activities and/or tasks is the most significant decision teachers make that will affect students’ learning. Consider the following questions:

• Teachers must do the activity first. What is problematic about the activity? What will you need to do BEFORE the activity and AFTER the activity? Additionally, think how your students would do the activity.
• What mathematical ideas will the activity develop? Are there connections to other related mathematics topics, or other content areas?
• Can the activity accomplish your learning objective/goals?

Low Floor High Ceiling Tasks

By definition, a “ low floor/high ceiling task ” is a mathematical activity where everyone in the group can begin and then work on at their own level of engagement. Low Floor High Ceiling Tasks are activities that everyone can begin and work on based on their own level, and have many possibilities for students to do more challenging mathematics. One gauge of knowing whether an activity is a Low Floor High Ceiling Task is when the work on the problems becomes more important than the answer itself, and leads to rich mathematical discourse [Hover: ways of representing, thinking, talking, agreeing, and disagreeing; the way ideas are exchanged and what the ideas entail; and as being shaped by the tasks in which students engage as well as by the nature of the learning environment].

The strengths of using Low Floor High Ceiling Tasks:

• Allows students to show what they can do, not what they can’t.
• Provides differentiation to all students.
• Promotes a positive classroom environment.
• Advances a growth mindset in students
• Aligns with the Standards for Mathematical Practice

Examples of some Low Floor High Ceiling Tasks can be found at the following sites:

• YouCubed – under grades choose Low Floor High Ceiling
• NRICH Creating a Low Threshold High Ceiling Classroom
• Inside Mathematics Problems of the Month

Math in 3-Acts

Math in 3-Acts was developed by Dan Meyer to spark an interest in and engage students in thought-provoking mathematical inquiry. Math in 3-Acts is a whole-group mathematics task consisting of three distinct parts:

Act One is about noticing and wondering. The teacher shares with students an image, video, or other situation that is engaging and perplexing. Students then generate questions about the situation.

In Act Two , the teacher offers some information for the students to use as they find the solutions to the problem.

Act Three is the “reveal.” Students share their thinking as well as their solutions.

“Math in 3 Acts” is a fun way to engage your students, there is a low entry point that gives students confidence, there are multiple paths to a solution, and it encourages students to work in groups to solve the problem. Some examples of Math in 3-Acts can be found at the following websites:

• Dan Meyer’s Three-Act Math Tasks
• Graham Fletcher3-Act Tasks ]
• Math in 3-Acts: Real World Math Problems to Make Math Contextual, Visual and Concrete

Number Talks

Number talks are brief, 5-15 minute discussions that focus on student solutions for a mental math computation problem. Students share their different mental math processes aloud while the teacher records their thinking visually on a chart or board. In addition, students learn from each other’s strategies as they question, critique, or build on the strategies that are shared.. To use a “number talk,” you would include the following steps:

• The teacher presents a problem for students to solve mentally.
• Provide adequate “ wait time .”
• The teacher calls on a students and asks, “What were you thinking?” and “Explain your thinking.”
• For each student who volunteers to share their strategy, write their thinking on the board. Make sure to accurately record their thinking; do not correct their responses.
• Invite students to question each other about their strategies, compare and contrast the strategies, and ask for clarification about strategies that are confusing.

“Number Talks” can be used as an introduction, a warm up to a lesson, or an extension. Some examples of Number Talks can be found at the following websites:

• Inside Mathematics Number Talks
• Number Talks Build Numerical Reasoning

Saying “This is Easy”

“This is easy.” Three little words that can have a big impact on students. What may be “easy” for one person, may be more “difficult” for someone else. And saying “this is easy” defeats the purpose of a growth mindset classroom, where students are comfortable making mistakes.

When the teacher says, “this is easy,” students may think,

• “Everyone else understands and I don’t. I can’t do this!”
• Students may just give up and surrender the mathematics to their classmates.
• Students may shut down.

Instead, you and your students could say the following:

• “I think I can do this.”
• “I have an idea I want to try.”
• “I’ve seen this kind of problem before.”

Tracy Zager wrote a short article, “This is easy”: The Little Phrase That Causes Big Problems” that can give you more information. Read Tracy Zager’s article here.

Using “Worksheets”

Do you want your students to memorize concepts, or do you want them to understand and apply the mathematics for different situations?

What is a “worksheet” in mathematics? It is a paper and pencil assignment when no other materials are used. A worksheet does not allow your students to use hands-on materials/manipulatives [Hover: physical objects that are used as teaching tools to engage students in the hands-on learning of mathematics]; and worksheets are many times “naked number” with no context. And a worksheet should not be used to enhance a hands-on activity.

Students need time to explore and manipulate materials in order to learn the mathematics concept. Worksheets are just a test of rote memory. Students need to develop those higher-order thinking skills, and worksheets will not allow them to do that.

One productive belief from the NCTM publication, Principles to Action (2014), states, “Students at all grade levels can benefit from the use of physical and virtual manipulative materials to provide visual models of a range of mathematical ideas.”

You may need an “activity sheet,” a “graphic organizer,” etc. as you plan your mathematics activities/lessons, but be sure to include hands-on manipulatives. Using manipulatives can

• Provide your students a bridge between the concrete and abstract
• Serve as models that support students’ thinking
• Provide another representation
• Support student engagement
• Give students ownership of their own learning.

Adapted from “ The Top 5 Reasons for Using Manipulatives in the Classroom ”.

any task or activity for which the students have no prescribed or memorized rules or methods, nor is there a perception by students that there is a specific ‘correct’ solution method

should be intriguing and contain a level of challenge that invites speculation and hard work, and directs students to investigate important mathematical ideas and ways of thinking toward the learning

involves teaching a skill so that a student can later solve a story problem

when we teach students how to problem solve

teaching mathematics content through real contexts, problems, situations, and models

a mathematical activity where everyone in the group can begin and then work on at their own level of engagement

20 seconds to 2 minutes for students to make sense of questions

Mathematics Methods for Early Childhood Copyright © 2021 by Janet Stramel is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

Module 1: Problem Solving Strategies

• Last updated
• Save as PDF
• Page ID 10352

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Unlike exercises, there is never a simple recipe for solving a problem. You can get better and better at solving problems, both by building up your background knowledge and by simply practicing. As you solve more problems (and learn how other people solved them), you learn strategies and techniques that can be useful. But no single strategy works every time.

Pólya’s How to Solve It

George Pólya was a great champion in the field of teaching effective problem solving skills. He was born in Hungary in 1887, received his Ph.D. at the University of Budapest, and was a professor at Stanford University (among other universities). He wrote many mathematical papers along with three books, most famously, “How to Solve it.” Pólya died at the age 98 in 1985.1

1. Image of Pólya by Thane Plambeck from Palo Alto, California (Flickr) [CC BY

In 1945, Pólya published the short book How to Solve It , which gave a four-step method for solving mathematical problems:

First, you have to understand the problem.

After understanding, then make a plan.

Carry out the plan.

Look back on your work. How could it be better?

This is all well and good, but how do you actually do these steps?!?! Steps 1. and 2. are particularly mysterious! How do you “make a plan?” That is where you need some tools in your toolbox, and some experience to draw upon.

Much has been written since 1945 to explain these steps in more detail, but the truth is that they are more art than science. This is where math becomes a creative endeavor (and where it becomes so much fun). We will articulate some useful problem solving strategies, but no such list will ever be complete. This is really just a start to help you on your way. The best way to become a skilled problem solver is to learn the background material well, and then to solve a lot of problems!

Problem Solving Strategy 1 (Guess and Test)

Make a guess and test to see if it satisfies the demands of the problem. If it doesn't, alter the guess appropriately and check again. Keep doing this until you find a solution.

Mr. Jones has a total of 25 chickens and cows on his farm. How many of each does he have if all together there are 76 feet?

Step 1: Understanding the problem

We are given in the problem that there are 25 chickens and cows.

All together there are 76 feet.

Chickens have 2 feet and cows have 4 feet.

We are trying to determine how many cows and how many chickens Mr. Jones has on his farm.

Step 2: Devise a plan

Going to use Guess and test along with making a tab

Many times the strategy below is used with guess and test.

Make a table and look for a pattern:

Procedure: Make a table reflecting the data in the problem. If done in an orderly way, such a table will often reveal patterns and relationships that suggest how the problem can be solved.

Step 3: Carry out the plan:

Notice we are going in the wrong direction! The total number of feet is decreasing!

Better! The total number of feet are increasing!

Step 4: Looking back:

Check: 12 + 13 = 25 heads

24 + 52 = 76 feet.

We have found the solution to this problem. I could use this strategy when there are a limited number of possible answers and when two items are the same but they have one characteristic that is different.

Videos to watch:

1. Click on this link to see an example of “Guess and Test”

http://www.mathstories.com/strategies.htm

2. Click on this link to see another example of Guess and Test.

http://www.mathinaction.org/problem-solving-strategies.html

Check in question 1:

Place the digits 8, 10, 11, 12, and 13 in the circles to make the sums across and vertically equal 31. (5 points)

Check in question 2:

Old McDonald has 250 chickens and goats in the barnyard. Altogether there are 760 feet . How many of each animal does he have? Make sure you use Polya’s 4 problem solving steps. (12 points)

Problem Solving Strategy 2 (Draw a Picture). Some problems are obviously about a geometric situation, and it is clear you want to draw a picture and mark down all of the given information before you try to solve it. But even for a problem that is not geometric thinking visually can help!

Videos to watch demonstrating how to use "Draw a Picture".

1. Click on this link to see an example of “Draw a Picture”

2. Click on this link to see another example of Draw a Picture.

Problem Solving Strategy 3 ( Using a variable to find the sum of a sequence.)

Gauss's strategy for sequences.

last term = fixed number ( n -1) + first term

The fix number is the the amount each term is increasing or decreasing by. "n" is the number of terms you have. You can use this formula to find the last term in the sequence or the number of terms you have in a sequence.

Ex: 2, 5, 8, ... Find the 200th term.

Last term = 3(200-1) +2

Last term is 599.

To find the sum of a sequence: sum = [(first term + last term) (number of terms)]/ 2

Sum = (2 + 599) (200) then divide by 2

Sum = 60,100

Check in question 3: (10 points)

Find the 320 th term of 7, 10, 13, 16 …

Then find the sum of the first 320 terms.

Problem Solving Strategy 4 (Working Backwards)

This is considered a strategy in many schools. If you are given an answer, and the steps that were taken to arrive at that answer, you should be able to determine the starting point.

Videos to watch demonstrating of “Working Backwards”

https://www.youtube.com/watch?v=5FFWTsMEeJw

Karen is thinking of a number. If you double it, and subtract 7, you obtain 11. What is Karen’s number?

1. We start with 11 and work backwards.

2. The opposite of subtraction is addition. We will add 7 to 11. We are now at 18.

3. The opposite of doubling something is dividing by 2. 18/2 = 9

4. This should be our answer. Looking back:

9 x 2 = 18 -7 = 11

5. We have the right answer.

Check in question 4:

Christina is thinking of a number.

If you multiply her number by 93, add 6, and divide by 3, you obtain 436. What is her number? Solve this problem by working backwards. (5 points)

Problem Solving Strategy 5 (Looking for a Pattern)

Definition: A sequence is a pattern involving an ordered arrangement of numbers.

We first need to find a pattern.

Ask yourself as you search for a pattern – are the numbers growing steadily larger? Steadily smaller? How is each number related?

Example 1: 1, 4, 7, 10, 13…

Find the next 2 numbers. The pattern is each number is increasing by 3. The next two numbers would be 16 and 19.

Example 2: 1, 4, 9, 16 … find the next 2 numbers. It looks like each successive number is increase by the next odd number. 1 + 3 = 4.

So the next number would be

25 + 11 = 36

Example 3: 10, 7, 4, 1, -2… find the next 2 numbers.

In this sequence, the numbers are decreasing by 3. So the next 2 numbers would be -2 -3 = -5

-5 – 3 = -8

Example 4: 1, 2, 4, 8 … find the next two numbers.

This example is a little bit harder. The numbers are increasing but not by a constant. Maybe a factor?

So each number is being multiplied by 2.

16 x 2 = 32

1. Click on this link to see an example of “Looking for a Pattern”

2. Click on this link to see another example of Looking for a Pattern.

Problem Solving Strategy 6 (Make a List)

Example 1 : Can perfect squares end in a 2 or a 3?

List all the squares of the numbers 1 to 20.

1 4 9 16 25 36 49 64 81 100 121 144 169 196 225 256 289 324 361 400.

Now look at the number in the ones digits. Notice they are 0, 1, 4, 5, 6, or 9. Notice none of the perfect squares end in 2, 3, 7, or 8. This list suggests that perfect squares cannot end in a 2, 3, 7 or 8.

How many different amounts of money can you have in your pocket if you have only three coins including only dimes and quarters?

Quarter’s dimes

0 3 30 cents

1 2 45 cents

2 1 60 cents

3 0 75 cents

Videos demonstrating "Make a List"

Check in question 5:

How many ways can you make change for 23 cents using only pennies, nickels, and dimes? (10 points)

Problem Solving Strategy 7 (Solve a Simpler Problem)

Geometric Sequences:

How would we find the nth term?

Solve a simpler problem:

1, 3, 9, 27.

1. To get from 1 to 3 what did we do?

2. To get from 3 to 9 what did we do?

Let’s set up a table:

Term Number what did we do

Looking back: How would you find the nth term?

Find the 10 th term of the above sequence.

Let L = the tenth term

Problem Solving Strategy 8 (Process of Elimination)

This strategy can be used when there is only one possible solution.

I’m thinking of a number.

The number is odd.

It is more than 1 but less than 100.

It is greater than 20.

It is less than 5 times 7.

The sum of the digits is 7.

It is evenly divisible by 5.

a. We know it is an odd number between 1 and 100.

b. It is greater than 20 but less than 35

21, 23, 25, 27, 29, 31, 33, 35. These are the possibilities.

c. The sum of the digits is 7

21 (2+1=3) No 23 (2+3 = 5) No 25 (2 + 5= 7) Yes Using the same process we see there are no other numbers that meet this criteria. Also we notice 25 is divisible by 5. By using the strategy elimination, we have found our answer.

Check in question 6: (8 points)

Jose is thinking of a number.

The number is not odd.

The sum of the digits is divisible by 2.

The number is a multiple of 11.

It is greater than 5 times 4.

It is a multiple of 6

It is less than 7 times 8 +23

What is the number?

Click on this link for a quick review of the problem solving strategies.

https://garyhall.org.uk/maths-problem-solving-strategies.html

• Visit Two Rivers Public Charter School to see the school that inspired the Two Rivers Learning Institute.
• Course Login

Problem-Based Tasks in Math

Want to learn more about our work?

Dive deeper into our Instructional Practices and methodology by taking one of our online courses.

Providing students with opportunities to grapple with math has led to amazing things happening in my class. Students are totally excited and are driven to figure out not just how to solve a problem but why it works.

– Jessica Proffitt, Fifth-Grade Teacher at Two Rivers

Watch two rivers’s teachers and students at work on problem-based tasks in math.

Problem-Based Tasks Require Students to Apply Their Knowledge in New Contexts

Problem-based tasks are math lessons built around a single, compelling problem. The problems are truly “problematic” for students — that is, they do not offer an immediate solution.

The problems provide an opportunity for students to build conceptual understanding. Problem-based tasks require students to apply their current understanding and skills to new contexts that highlight core math concepts. For example, when students solve a problem that could be solved with multiplication before they have formally been taught what multiplication is and how it works, they build an understanding that multiplication is repeated addition.

Well-designed problem-based tasks provide multiple entry points for students to engage in problem solving, ensuring that all students have access to the same concepts. When students solve the problems in different ways—including drawing pictures, acting out the problem, writing algorithms, and using manipulatives—they make connections between the variety of models that all accurately illustrate the underlying mathematics.

Problem-Based Tasks in Math Resources

Or search by topic

Number and algebra

• The Number System and Place Value
• Calculations and Numerical Methods
• Fractions, Decimals, Percentages, Ratio and Proportion
• Properties of Numbers
• Patterns, Sequences and Structure
• Algebraic expressions, equations and formulae
• Coordinates, Functions and Graphs

Geometry and measure

• Angles, Polygons, and Geometrical Proof
• 3D Geometry, Shape and Space
• Measuring and calculating with units
• Transformations and constructions
• Pythagoras and Trigonometry
• Vectors and Matrices

Probability and statistics

• Handling, Processing and Representing Data
• Probability

Working mathematically

• Thinking mathematically
• Mathematical mindsets
• Cross-curricular contexts
• Physical and digital manipulatives

For younger learners

• Early Years Foundation Stage

Advanced mathematics

• Decision Mathematics and Combinatorics
• Advanced Probability and Statistics

Problem Solving

Problem Solving and the New Curriculum   Age 5 to 11

Developing a Classroom Culture That Supports a Problem-solving Approach to Mathematics   Age 5 to 11

Developing Excellence in Problem Solving with Young Learners   Age 5 to 11

Using NRICH Tasks to Develop Key Problem-solving Skills   Age 5 to 11

Trial and Improvement at KS1   Age 5 to 7

Trial and Improvement at KS2   Age 7 to 11

Working Systematically - Primary Teachers   Age 5 to 11

Number Patterns   Age 5 to 11

Working Backwards at KS1   Age 5 to 7

Working Backwards at KS2   Age 7 to 11

Reasoning   Age 5 to 11

Visualising at KS1 - Primary Teachers   Age 5 to 7

Visualising at KS2 - Primary Teachers   Age 7 to 11

Conjecturing and Generalising at KS1 - Primary Teachers   Age 5 to 7

Conjecturing and Generalising at KS2 - Primary Teachers   Age 7 to 11

• Mathematical Problem Solving in the Early Years
• Low Threshold High Ceiling - an Introduction
• What's All the Talking About?
• Group-worthy Tasks and Their Potential to Support Children to Develop Independent Problem-solving Skills
• Developing the Classroom Culture: Using the Dotty Six Activity as a Springboard for Investigation

Math Interventions

Introduction.

• Subitizing Interventions
• Counting Interventions: Whole Numbers Less Than 30
• Counting Interventions: Whole Numbers Greater Than 30 (Place Value)
• Counting Interventions: Fractions
• Counting Interventions: Decimals
• Composing and Decomposing Numbers Interventions
• Rounding Interventions
• Number Sense Lesson Plans
• Addition and Subtraction Facts
• Multiplication and Division Facts
• Computational Fluency Lesson Plans
• Understanding the Problem Interventions
• Planning and Executing a Solution Interventions
• Monitoring Progress & Reflecting on a Solution Interventions
• Problem-Solving Process Interventions
• Problem-Solving Lesson Plans
• Identifying Essential Variables Interventions
• Direct Models Interventions
• Counting On/Back Interventions
• Deriving Interventions
• Interpreting the Results Interventions
• Mathematical Modeling Lesson Plans
• Math Rules and Concepts Interventions
• Math Rules and Concepts Lesson Plans

You can use either  Explicit Instruction  or Self-Regulated Strategy Development when you intervene to support your student's problem solving skills. The following lesson plan targets a specific problem-solving skill using explicit instruction. As you read this plan, consider: 

How does this plan support objective mastery?

Problem Solving Intervention Plan

Art, E. (2017). Problem solving intervention packet. New York, NY: Relay Graduate School of Education.

This lesson plan supports objective mastery because the teacher employs Principles of Specialized instruction to help the student visualize Part/Part/Whole (Part Unknown) problems to identify what she is supposed to figure out. In this lesson plan, she isolates the skill (identifying what the problem is), and uses explicit instruction to teach the student how to identify two what is happening in the story and what she is trying to figure out. After she explains the process she'll take, she uses metacognition and shows the student how she asks these two questions as she is reading. Finally, she builds in multiple at-bats so that the student has the opportunity to practice this strategy over and over so that she can reach her objective.

• << Previous: Problem-Solving Process Interventions
• Next: Identifying Essential Variables Interventions >>
• Last Updated: Feb 14, 2024 6:46 PM
• URL: https://relay.libguides.com/math-interventions

• Try for free

Math Lesson Plans for Teachers

• Most Popular
• Most Recent

• Teaching Students Mathematical Reasoning Skills

Students can build upon their basic math skills and become higher order thinkers when we encourage the following principles.

By Jacqueline Dwyer

Mathematical reasoning is essential to bridging the gap between basic skills and higher-order thinking. In fact, research has shown that students who are taught reasoning skills early on ultimately become more confident, independent learners; they have a deeper understanding of how a concept can be applied in a variety of situations and are willing to take risks to see what works and what doesn’t. What follows are some ways you can actively engage your students in the reasoning process.

Multiple Ways to Solve a Problem

Since every student learns in a different way, they generally problem solve in unique ways as well. That is why it’s important to create and encourage multiple ways for students to approach topics. Here is a sample problem: Robin has $5. How many more dollars does she need to buy a journal that costs $12? The teacher can lay out plastic cubes and play money , and encourage students to count on their fingers, write down their calculations, or use mental math to figure out the answer. Students can then take turns explaining their reasoning and justifying their explanations. By using this approach, students will then be able to compare the different strategies they used for solving the same problem. A problem like this also allows students to solve problems according to their developmental level. I’ve found that by allowing students to develop their own strategies for solving addition problems, they intuitively start to use the commutative and associative properties.

Thinking It Through

Students who are successful problem solvers take a learned skill and apply it in different ways to a variety of situations. For this reason, you should reassure children that it’s ok to make mistakes, as what you’re really interested in is how they think through a problem, not whether they get the answer right. Here's another reasoning problem you can use to help students build on their subtraction skills.

• Pose the following question: How can you weigh a suitcase that is too large to fit on a bathroom scale?
• Be sure to listen carefully to the students’ answers, try out some of their suggestions, if possible, and praise them for thinking through the problem.
• If they don’t come up with a solution, tell them that one way to find the weight of the suitcase is for one person to stand on the scales while holding it. Ask another student to write the total weight.
• Then put the suitcase aside and let the child weigh himself again, while another child notes his weight. If the student subtracts his weight from the total weight, the number remaining is the weight of the suitcase.

Hands-On Problem Solving

There are many ways to provide older students with hands-on, manipulative-based reasoning activities. Here is one example in which students explore the relationships between different sized balls. Begin by showing the class a set of up to ten sports balls and invite them to talk about what they notice. They are likely to suggest all sorts of things, perhaps related to the sport that each is used for, or the material each is made of, in addition to their spherical shape.

• Draw a line on the ground and ask students the following questions: If the balls are put on the line, with each ball touching the one in front and the one behind, which arrangement makes the shortest line of balls?
• Which arrangement makes the longest line of balls?
• Let students try many different arrangements of balls, then ask them to share their results with the class.
• Hopefully they’ll discover that to get a shorter line you have to put the smaller balls between the big balls because the bigger balls tower over the smaller balls with their curve allowing the smaller to fit in under resulting in a smaller distance used.
• By changing the order of the balls, students will naturally come to a better understanding of the properties of circles.
• You can extend the activity for older students by printing out copies of the balls to scale, then asking them to place the equipment in lines that make up an equilateral triangle or a square.

Here are some more mathematical reasoning lessons and activities you can use to challenge your students.

Math Reasoning Lesson Plans

Math Sleuths Students use their problem-solving skills to complete an online Math Hunt. Their share their answers and justify their thought processes with the class. Math in Everyday Life Students work with a partner to come up a with word problems, involving time, money, and simple fractions. They then share their word problems with other students. Lift the Math Curse Students read the book Math Curse by Jon Scieszka. Then they write story about a day in their life that includes up to fifteen math problems with an answer key. Students share their books with the class. Patterns, Functions, and Algebraic Reasoning Younger students use a calculator to explore, generate, and predict patterns in math.

Start Your 10-Day Free Trial

• Search 350,000+ online teacher resources.
• Find lesson plans, worksheets, videos, and more.
• Inspire your students with great lessons.

Lesson Search Terms

• "Mathematical Reasoning"
• Mathematical Reasoning 12
• Mathematical Reasoning Grid
• Mathematical Reasoning Shapes
• Mathematical Reasoning 1.2

Recent Math Articles

• Making Math Merry
• Math and Your Local Restaurant
• Why Mastery of Math Facts is Important
• Four Fundamentals of Addition First Graders Should Know By June

5. Teaching Mathematical Reasoning: Critical Math Thinking Through Problem-Solving and Modeling

• Mathematical problem-solving : This approach makes students think conceptually about problems before applying tools they’ve learned.
• Mathematical modeling : Modeling projects give students experience in weighing several factors against one another and using mathematical knowledge to make decisions.

I. Mathematical Problem-Solving

An emphasis on open-ended mathematical problem-solving can help develop mathematical reasoning skills and address a problem teachers have long been concerned about: too much “rote” learning in math. 

Too often students spend time in math class memorizing procedures and applying them mindlessly to problems. This leads to errors when students are confronted with unfamiliar problems. It also contributes to a widespread misperception of math as boring and lacking relevance to everyday life. 

On the other hand, attempting to remedy this problem by giving students open-ended problems has its own drawbacks. Without the conceptual and methodological tools to solve these problems students become frustrated and disengaged. It can end up being an inefficient way to spend class time.  

Although learning fundamental math skills like algorithms for adding, subtracting, multiplying, and dividing is absolutely critical for students in the early grades, the deeper mathematical problem-solving skills are the ones we really want students to graduate with. How can we ensure they do?

The deeper mathematical problem-solving skills are the ones we really want students to graduate with.

Evidence suggests that skills in mathematical problem-solving lead to more general improvements in outcomes related to math. They help students acquire a deeper understanding of mathematical reasoning and concepts. 

For instance, the commutative property, which most students learn applies to addition and multiplication problems (changing the order of the operations doesn’t affect the outcome), also applies to other logical and practical situations. A familiarity with some of these situations fosters deeper conceptual understanding, and deeper conceptual understanding leads to better critical thinking.

And learning these skills helps students improve outcomes related to critical thinking more generally. For example, students who become skilled in mathematical problem-solving tend to also:

• Create beneficial habits of mind — persistence, thoroughness, creativity in solution-finding, and improved self-monitoring.
• Break down hard problems into easier parts or reframing problems so that they can think about them more clearly. 
• Some problem solving tactics are applicable to situations well beyond math: making a visualization of a situation to understand it more clearly; creating a simplified version of the problem to more easily address the essence of the problem; creating branches of possibilities to solve the problem; creating “what if” example cases to test key assumptions, etc.
• Elevate the value of discussion and argumentation over simple appeals to authority.

Small-group mathematical problem solving targets skills that traditional mathematics instruction doesn’t. Instead of just finding a match between an algorithm and a question, students must: adapt or create an algorithm; evaluate and debate the merits of different solution paths; and verify their solution through additional evidence.

Small-group mathematical problem solving targets skills that traditional mathematics instruction doesn’t.

This process continues until the class has thoroughly explored the problem space, revealing multiple solution paths and exploring variations on the problem or contrasting problem-types.

Of course, the usefulness of a question like this depends on what students already know. If students don’t already know that chickens have two legs and pigs have four, they’re just going to be confused by the problem (and the explanation of the solution). It also requires some other basic skills—for instance, that if one chicken has two legs, four chickens would have eight.

As a way of evaluating student growth, teachers could also include some of these open-ended problems in homework assignments or as extra credit assignments.

Lesson Plan Outline

An example that might be appropriate for fifth grade is something like the following: A farmer has some pigs and some chickens. He finds that together they have 70 heads and 200 legs. How many pigs and how many chickens does he have? Divide the class into student groups of three to four. Have students spend a few minutes reading over the problem individually. Then let student groups discuss possible solution paths. The teacher walks around the classroom, monitoring the groups. Then the teacher leads a whole-class discussion about the problem.

• So how did you go about thinking about the problem?
• Show us how you got your answer and why you think it’s right. This might mean that a student goes up to the board to illustrate something if a verbal explanation is inadequate.
• And what was the answer you got?
• Does anyone else have a different way of thinking about the problem? If there are other ways of solving the problem that students didn’t come up with, teachers can introduce these other ways themselves.

Developing Math Problem-Solving Skills

Teachers should keep in mind the following as they bring mathematical problem-solving activities into their classrooms:

• Problem selection . Teachers have to select grade-appropriate problems. A question like “John is taller than Mary. Mary is taller than Peter. Who is the shortest of the three children?” may be considered an exercise to older students — that is, a question where the solutions steps are already known — but a genuine problem to younger students. It’s also helpful when problems can be extended in various ways. Adding variation and complexity to a problem lets students explore a class of related problems in greater depth.
• Managing student expectations . Introducing open-ended math problems to students who haven’t experienced them before can also be confusing for the students. Students who are used to applying algorithms to problems can be confused about what teachers expect them to do with open-ended problems, because no algorithm is available.
• Asking why . Asking students to explain the rationale behind their answer is critical to improving their thinking. Teachers need to make clear that these rationales or justifications are even more important than the answer itself. These justifications give us confidence that an answer is right. That is, if the student can’t justify her answer, it almost doesn’t matter if it’s correct, because there’s no way of verifying it.

II. Mathematical Modeling

Another approach is mathematical modeling. Usually used for students in middle or high school, mathematical modeling brings math tools to bear on real-world problems, keeping students engaged and helping them to develop deeper mathematical reasoning and critical thinking skills.

Math modeling is an extremely common practice in the professional world. Investors model returns and the effects of various events on the market; business owners model revenue and expenses, buying behavior, and more; ecologists model population growth, rainfall, water levels, and soil composition, among many other things. 

But, despite these many applications and the contributions it can make to general mathematical reasoning and critical thinking skills, mathematical modeling is rarely a main component of the math curriculum. Although textbook examples occasionally refer to real-world phenomena, the modeling process is not commonly practiced in the classroom.

Modeling involves engaging students in a big, messy real-world problem. The goals are for students to:

• refine their understanding of the situation by asking questions and making assumptions,
• leverage mathematical tools to solve the problem,
• make their own decisions about how to go about solving the problem,
• explain whether and how their methods and solutions make sense,
• and test or revise their solutions if necessary.

Mathematical modeling typically takes place over the course of several class sessions and involves working collaboratively with other students in small groups.

Modeling is not just about getting to a “right” answer — it’s about considering factors beyond mathematics as well.

Modeling also offers the opportunity to integrate other material across the curriculum and to “think mathematically” in several different contexts. Modeling is not just about getting to a “right” answer — it’s about considering factors beyond mathematics as well. For example, students deal with questions like:

• What is a “fair” split? 
• What level of risk should someone tolerate?
• What tradeoffs should a society make?

In others words, students come to see mathematics as the socially indispensable tool that it is, rather than an abstract (and sometimes frustrating) school subject.

Mathematical Modeling and Critical Thinking

Research suggests that the ability to solve abstractly framed academic math problems is not necessarily related to mathematical reasoning more broadly: that is, the ability to use math well in everyday life or to integrate mathematical thinking into one’s decision-making. Students may be able to follow procedures when given certain cues, but unable to reason about underlying concepts. 

It’s also very common to hear complaints from students about math — that either they aren’t “ math people ,” that math is irrelevant, or that math is simply boring.

Mathematical modeling is one approach to resolving both these problems. It asks students to move between the concreteness of real — or at least relatively realistic — situations and the abstraction of mathematical models. Well-chosen problems can engage student interest. And the practice emphasizes revision, step-by-step improvement, and tradeoffs over single solution paths and single right-or-wrong answers.

Mathematical modeling often begins with a general question, one that may initially seem only loosely related to mathematics:

• how to design an efficient elevator system, given certain constraints;
• what the best gas station is to visit in our local area;
• how to distinguish between two kinds of flies, given some data about their physical attributes.

Then, over the course of the modeling process, students develop more specific questions or cases, adding constraints or assumptions to simplify the problem. Along the way, students identify the important variables — what’s changing, and what’s not changing? Which variables are playing the biggest role in the desired outcomes?

Students with little experience in modeling can leap too quickly into looking for a generalized solution, before they have developed a feel for the problem. They may also need assistance in developing those specific cases. During this part of the process, it can be easiest to use well-defined values for some variables. These values may then become variables later on.

After students explore some simplifying cases, then they work on extensions of these cases to reach ever more general solutions.

A key part of this activity is letting students be creative — students will often come up with unusual or especially innovative solutions.

Throughout the modeling process, the teacher may need to point out missing assumptions or constraints, or offer other ways of reframing the problem. For any given modeling problem, some solutions are usually more obvious than others, which leads to common stages students may reach as they solve the problem. But a key part of this activity is letting students be creative — students will often come up with unusual or especially innovative solutions.

A sample problem, from the Guidelines for Assessment and Instruction in Mathematical Modeling Education is below:

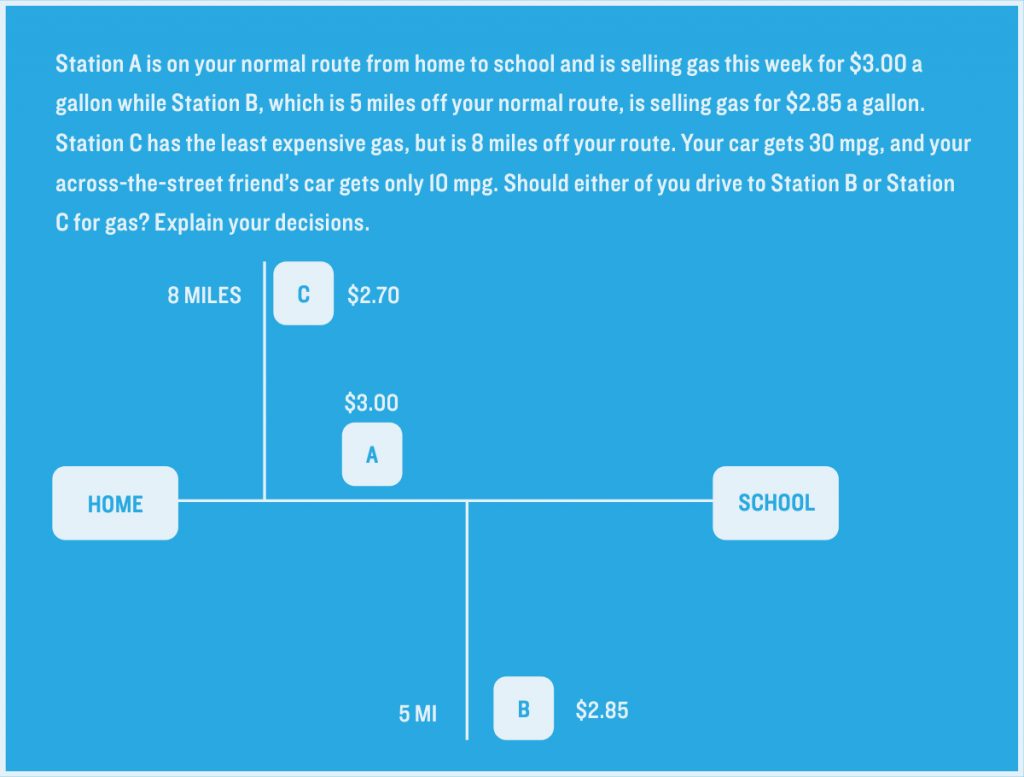
This problem involves variables that aren’t necessarily immediately apparent to students. For instance, the size of the gas tank, and how much gas you fill up on per trip. As students manage this specific case, they can take other hypothetical scenarios to generalize their solution: if it’s 10 miles away, how cheap would the gas have to be to make it worth it? What about the time spent in the car — is there a value to put on that?

Many modeling problems can be arbitrarily extended in various directions. Instead of just considering the best gas station to go to for a single car, for instance, students can explore the behavior of a fleet of trucks on set routes or seasonal changes to gas prices.

It’s also possible to include shorter modeling activities, where students work together in pairs or small groups to extend a problem or interpret the meaning of a solution.

These kinds of modeling activities are not reserved solely for older students. One example of a modeling problem for students in elementary school might be something like: what should go in a lunchbox? Students can talk about what kinds of things are important to them for lunch, “mathematize” the problem by counting student preferences or coming up with an equation (e.g., lunch = sandwich + vegetable + dessert + drink); and even explore geometrically how to fit such items into a lunchbox of a certain size.

Teaching Mathematical Modeling: Further Key Factors

Mathematical modeling activities can be challenging for both teachers and students. 

Often, mathematical modeling activities stretch over several class periods. Fitting modeling activities in, especially if standardized tests are focused on mathematical content, can be challenging. One approach is to design modeling activities that support the overall content goals.

The teacher’s role during mathematical modeling is more like a facilitator than a lecturer. Mathematical modeling activities are considerably more open-ended than typical math activities, and require active organization, monitoring, and regrouping by the teacher. Deciding when to let students persevere on a problem for a bit longer and when to stop the class to provide additional guidance is a key skill that only comes with practice.

The teacher’s role during math modeling is more like a facilitator than a lecturer.

Students — especially students who have traditionally been successful in previous math classes — may also experience frustration when encountering modeling activities for the first time. Traditional math problems involve applying the right procedure to a well-defined problem. But expertise at this kind of mathematical reasoning differs markedly from tackling yet-to-be-defined problems with many possible solutions, each of which has tradeoffs and assumptions. Students might feel unprepared or even that they’re being treated unfairly.

Students also have to have some knowledge about the situation to reason mathematically about it. If the question is about elevators, for example, they need to know that elevators in tall buildings might go to different sets of floors; that elevators have a maximum capacity; that elevators occasionally break and need to be repaired. 

Finally, the mathematical question needs to be tailored to students’ experience and interests. Asking a group of students who don’t drive about how to efficiently purchase gas won’t garner student interest. Teachers should use their familiarity with their students to find and design compelling modeling projects. This is chance for both students and teachers to be creative. 

To download the PDF of the Teachers’ Guide

(please click here)

Sources and Resources

O’Connell, S. (2000). Introduction to Problem Solving: Strategies for The Elementary Classroom . Heinemann. A recent handbook for teachers with tips on how to implement small-group problem solving.

Youcubed.org , managed by Jo Boaler.  A community with lots of resources for small-group problem solving instruction.

Yackel, E., Cobb, P., & Wood, T. (1991). Small group interactions as a source of learning opportunities in second-grade mathematics . Journal for research in mathematics education , 390-408. Education research that illustrates how small-group problem solving leads to different kinds of learning opportunities than traditional instruction.

Guidelines for Assessment and Instruction in Mathematical Modeling Education , 2nd ed. (2019). Consortium for Mathematics and its Applications & Society for Industrial and Applied Mathematics.  An extensive guide for teaching mathematical modeling at all grade levels.

Hernández, M. L., Levy, R., Felton-Koestler, M. D., & Zbiek, R. M. (March/April 2017). Mathematical modeling in the high school curriculum . The variable , 2(2). A discussion of the advantages of mathematical modeling at the high school level.

Privacy Overview

Mastering Division Facts and Word Problems - Lesson Plan

Join us on a mathematical journey as we explore division facts and problem-solving strategies. this lesson is designed to help students strengthen their understanding of division, practice division facts, and apply their knowledge to solve word problems. through engaging activities and real-world scenarios, students will develop confidence in their division skills and enhance their problem-solving abilities. get ready to dive into the world of division.

Know more about Mastering Division Facts and Word Problems - Lesson Plan

The main objectives of this lesson plan are to reinforce division facts, develop problem-solving skills, and apply division to real-world situations.

This lesson plan helps students improve their math skills by providing opportunities to practice division facts, develop problem-solving strategies, and apply their knowledge to solve word problems.

Students can expect to learn how to recall division facts, use related multiplication facts, divide multiples of 10, write division equations for real-world situations, and think multiplication when solving division problems.

Your one stop solution for all grade learning needs.

• International
• Schools directory
• Resources Jobs Schools directory News Search

Maths Problem Solving Lesson Plan Year 5 and 6

Subject: Mathematics

Age range: 7-11

Resource type: Lesson (complete)

Last updated

30 September 2014

• Share through email
• Share through twitter
• Share through linkedin
• Share through facebook
• Share through pinterest

Tes classic free licence

Your rating is required to reflect your happiness.

It's good to leave some feedback.

Something went wrong, please try again later.

Surely you should not be sharing planning that contains children's names....

Empty reply does not make any sense for the end user

shaymaismail321

Thank you. The slides are helpful.<br />

I hate to say this: I used the lesson plan and resources today, Sept. 30th 2014. I felt the lesson went really well, the children were v enthusiastic, and worked with real concentration. Unfortunately, the lesson was being observed by the Head and Deputy. The preliminary feedback (more tomorrow) is that the lesson isnt &quot;age appropriate&quot; for Years 5 and 6. Will keep updated on further feedback.........

missRhughes

Thanks for the resources brillaint lesson! Some help needed though- I am definately over thinking this but what is the final formula for the Nth term? Thanks

Report this resource to let us know if it violates our terms and conditions. Our customer service team will review your report and will be in touch.

Not quite what you were looking for? Search by keyword to find the right resource:

Got any suggestions?

We want to hear from you! Send us a message and help improve Slidesgo

Top searches

Trending searches

memorial day

12 templates

66 templates

american history

75 templates

music video

21 templates

150 templates

Problem Solving and Mathematical Reasoning

It seems that you like this template, problem solving and mathematical reasoning presentation, free google slides theme, powerpoint template, and canva presentation template.

Let's make math learning more fun, especially at early levels of education. This new template has some cute illustrations and lots of elements related to math, including backgrounds that look like blackboards. This is a great choice for teachers who want to turn their classes into a more entertaining experience for their students. Customize the slides to add your own activities or explanations!

Features of this template

• 100% editable and easy to modify
• 36 different slides to impress your audience
• Contains easy-to-edit graphics such as graphs, maps, tables, timelines and mockups
• Includes 500+ icons and Flaticon’s extension for customizing your slides
• Designed to be used in Google Slides, Canva, and Microsoft PowerPoint
• 16:9 widescreen format suitable for all types of screens
• Includes information about fonts, colors, and credits of the free resources used

How can I use the template?

Am I free to use the templates?

How to attribute?

Combines with:

This template can be combined with this other one to create the perfect presentation:

Attribution required If you are a free user, you must attribute Slidesgo by keeping the slide where the credits appear. How to attribute?

Related posts on our blog.

How to Add, Duplicate, Move, Delete or Hide Slides in Google Slides

How to Change Layouts in PowerPoint

How to Change the Slide Size in Google Slides

Related presentations.

Premium template

Unlock this template and gain unlimited access

Along with Stanford news and stories, show me:

• Student information
• Faculty/Staff information

We want to provide announcements, events, leadership messages and resources that are relevant to you. Your selection is stored in a browser cookie which you can remove at any time using “Clear all personalization” below.

For everyone whose relationship with mathematics is distant or broken, Jo Boaler , a professor at Stanford Graduate School of Education (GSE), has ideas for repairing it. She particularly wants young people to feel comfortable with numbers from the start – to approach the subject with playfulness and curiosity, not anxiety or dread.

“Most people have only ever experienced what I call narrow mathematics – a set of procedures they need to follow, at speed,” Boaler says. “Mathematics should be flexible, conceptual, a place where we play with ideas and make connections. If we open it up and invite more creativity, more diverse thinking, we can completely transform the experience.”

Boaler, the Nomellini and Olivier Professor of Education at the GSE, is the co-founder and faculty director of Youcubed , a Stanford research center that provides resources for math learning that has reached more than 230 million students in over 140 countries. In 2013 Boaler, a former high school math teacher, produced How to Learn Math , the first massive open online course (MOOC) on mathematics education. She leads workshops and leadership summits for teachers and administrators, and her online courses have been taken by over a million users.

In her new book, Math-ish: Finding Creativity, Diversity, and Meaning in Mathematics , Boaler argues for a broad, inclusive approach to math education, offering strategies and activities for learners at any age. We spoke with her about why creativity is an important part of mathematics, the impact of representing numbers visually and physically, and how what she calls “ishing” a math problem can help students make better sense of the answer.

What do you mean by “math-ish” thinking?

It’s a way of thinking about numbers in the real world, which are usually imprecise estimates. If someone asks how old you are, how warm it is outside, how long it takes to drive to the airport – these are generally answered with what I call “ish” numbers, and that’s very different from the way we use and learn numbers in school.

In the book I share an example of a multiple-choice question from a nationwide exam where students are asked to estimate the sum of two fractions: 12/13 + 7/8. They’re given four choices for the closest answer: 1, 2, 19, or 21. Each of the fractions in the question is very close to 1, so the answer would be 2 – but the most common answer 13-year-olds gave was 19. The second most common was 21.

I’m not surprised, because when students learn fractions, they often don’t learn to think conceptually or to consider the relationship between the numerator or denominator. They learn rules about creating common denominators and adding or subtracting the numerators, without making sense of the fraction as a whole. But stepping back and judging whether a calculation is reasonable might be the most valuable mathematical skill a person can develop.

But don’t you also risk sending the message that mathematical precision isn’t important?

I’m not saying precision isn’t important. What I’m suggesting is that we ask students to estimate before they calculate, so when they come up with a precise answer, they’ll have a real sense for whether it makes sense. This also helps students learn how to move between big-picture and focused thinking, which are two different but equally important modes of reasoning.

Some people ask me, “Isn’t ‘ishing’ just estimating?” It is, but when we ask students to estimate, they often groan, thinking it’s yet another mathematical method. But when we ask them to “ish” a number, they're more willing to offer their thinking.

Ishing helps students develop a sense for numbers and shapes. It can help soften the sharp edges in mathematics, making it easier for kids to jump in and engage. It can buffer students against the dangers of perfectionism, which we know can be a damaging mindset. I think we all need a little more ish in our lives.

You also argue that mathematics should be taught in more visual ways. What do you mean by that?

For most people, mathematics is an almost entirely symbolic, numerical experience. Any visuals are usually sterile images in a textbook, showing bisecting angles, or circles divided into slices. But the way we function in life is by developing models of things in our minds. Take a stapler: Knowing what it looks like, what it feels and sounds like, how to interact with it, how it changes things – all of that contributes to our understanding of how it works.

There’s an activity we do with middle-school students where we show them an image of a 4 x 4 x 4 cm cube made up of smaller 1 cm cubes, like a Rubik’s Cube. The larger cube is dipped into a can of blue paint, and we ask the students, if they could take apart the little cubes, how many sides would be painted blue? Sometimes we give the students sugar cubes and have them physically build a larger 4 x 4 x 4 cube. This is an activity that leads into algebraic thinking.

Some years back we were interviewing students a year after they’d done that activity in our summer camp and asked what had stayed with them. One student said, “I’m in geometry class now, and I still remember that sugar cube, what it looked like and felt like.” His class had been asked to estimate the volume of their shoes, and he said he’d imagined his shoes filled with 1 cm sugar cubes in order to solve that question. He had built a mental model of a cube.

When we learn about cubes, most of us don’t get to see and manipulate them. When we learn about square roots, we don’t take squares and look at their diagonals. We just manipulate numbers.

I wonder if people consider the physical representations more appropriate for younger kids.

That’s the thing – elementary school teachers are amazing at giving kids those experiences, but it dies out in middle school, and by high school it’s all symbolic. There’s a myth that there’s a hierarchy of sophistication where you start out with visual and physical representations and then build up to the symbolic. But so much of high-level mathematical work now is visual. Here in Silicon Valley, if you look at Tesla engineers, they're drawing, they're sketching, they're building models, and nobody says that's elementary mathematics.

There’s an example in the book where you’ve asked students how they would calculate 38 x 5 in their heads, and they come up with several different ways of arriving at the same answer. The creativity is fascinating, but wouldn’t it be easier to teach students one standard method?

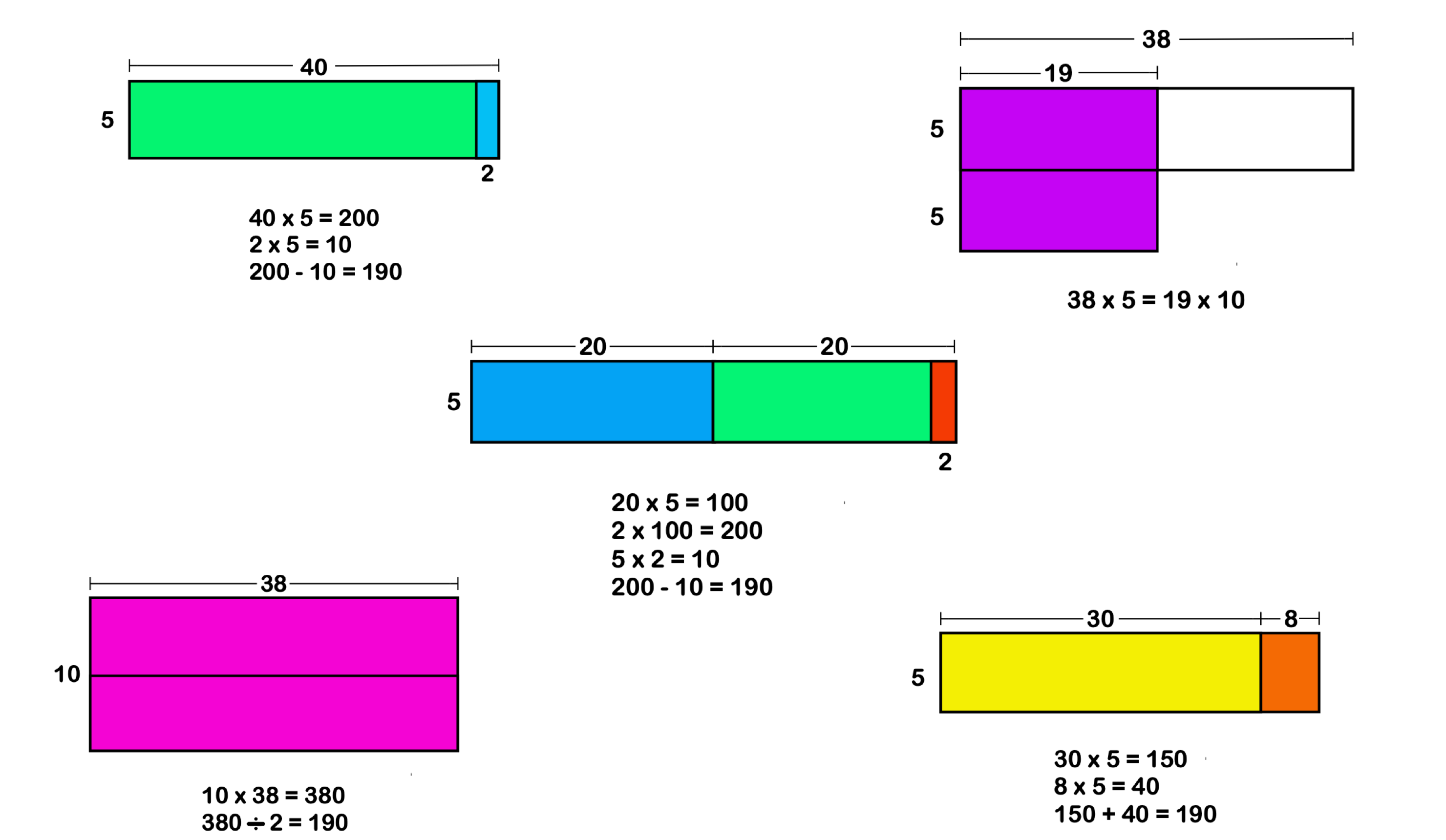
A depiction of various ways to calculate 38 x 5, numerically and visually. | Courtesy Jo Boaler

That narrow, rigid version of mathematics where there’s only one right approach is what most students experience, and it’s a big part of why people have such math trauma. It keeps them from realizing the full range and power of mathematics. When you only have students blindly memorizing math facts, they’re not developing number sense. They don’t learn how to use numbers flexibly in different situations. It also makes students who think differently believe there’s something wrong with them.

When we open mathematics to acknowledge the different ways a concept or problem can be viewed, we also open the subject to many more students. Mathematical diversity, to me, is a concept that includes both the value of diversity in people and the diverse ways we can see and learn mathematics. When we bring those forms of diversity together, it’s powerful. If we want to value different ways of thinking and problem-solving in the world, we need to embrace mathematical diversity.

Promoting biology students’ scientific reasoning in plant physiology lessons using problem-based learning (PBL)

[email protected]

[email protected]

[email protected]

[email protected]

[email protected]

• Split-Screen
• Article contents
• Figures & tables
• Supplementary Data
• Peer Review
• Open the PDF for in another window
• Reprints and Permissions
• Cite Icon Cite
• Search Site

Maisuna Kundariati , Rahel Natalia Saragih Munthe , Maria Rosalia Ijung Anggur , Herawati Susilo , Balqis Balqis , Frida Kunti Setiowati; Promoting biology students’ scientific reasoning in plant physiology lessons using problem-based learning (PBL). AIP Conf. Proc. 24 May 2024; 3106 (1): 030031. https://doi.org/10.1063/5.0214972

Download citation file:

• Ris (Zotero)
• Reference Manager

Scientific reasoning skills now days become discussed among scholars because its importance in every daily life. As a part of 21 st -century skills, it is necessary to promote it in science courses, especially in biology lessons. The purpose of this research is to enhance students’ scientific reasoning skills. Students who participate in this research were enrolled for the plant physiology course. The research was conducted during September-December 2022 at Universitas Negeri Malang. The learning process was carried out through Problem-based Learning. Classroom learning is done by implementing lesson study to improve each learning process. The research instruments were chapter design. Lesson design, lesson plan, and essay test of scientific reasoning skills refer to the rubric of scientific reasoning by the AACU (2010). The scientific reasoning achievement of students in the Plant Physiology course has increased from the initial, middle, and final tests. The average achievement of scientific reasoning on the initial, middle, and final tests, respectively, is 54.17, 63.13, and 72.56. The n-gain score of the scientific reasoning skills of students is 0.65 in the medium category. Meanwhile, the achievement of students’ scientific reasoning on the Topic or Argument Selection indicator is 0.58 in the medium category; Existing Knowledge, Research, and/or Views of 0.75 in the high category; Analysis of 0.64 in the medium category; and Conclusions, Limitations, and Implications of 0.57 in the medium category.

Citing articles via

Publish with us - request a quote.

Sign up for alerts

• Online ISSN 1551-7616
• Print ISSN 0094-243X
• For Researchers
• For Librarians
• For Advertisers
• Our Publishing Partners  
• Physics Today
• Conference Proceedings
• Special Topics

pubs.aip.org

• Privacy Policy
• Terms of Use

Connect with AIP Publishing

This feature is available to subscribers only.

Sign In or Create an Account

• Skip to content
• Skip to search
• Student portal
• Staff portal (Inside the department)
• Edit this site
• Edit this page

Plumpton High School

Make a payment

• School planning and reporting
• Location and transport
• Financial contributions and assistance
• Rules and policies
• Going green
• Useful links
• General information
• Payment - School Bytes
• School counselling service
• Student Health
• Volunteering at school
• Parent-teacher interviews
• International Students
• Caring for our students
• Special needs support
• Positive Behaviour for Learning
• Student Leadership at PHS
• Inclusive learning support
• Learning from home
• Creative arts
• Human society and its environment
• Mathematics
• Personal development, health and physical education
• Technology and applied studies
• Religion and ethics
• Assessment Schedules
• Scholarships and awards
• Duke of Edinburgh
• Learning support
• Academic Opportunities
• Student leadership
• Remote Learning at Plumpton
• Our successes
• Plans, dreams and ambitions
• New possibilities
• Help your child learn
• Immunisation information
• Subject selection for year 11
• Make a payment |
• Enrolment |
• Newsletter |

Achieving Excellence in Teaching and Learning

T: Telephone 02 9625 7020

E: Email [email protected]

High Potential & Gifted Education Mathematics Day – Plumpton Regional Champions

10 May 2024

Outstanding High Potential and Gifted Education (HPGE) Mathematics Day organised by 'Inquisitive Minds’ at Plumpton High School proved to be a highly effective way for representing schools to provide high quality and fun maths activities for their students.

Plumpton High School's outstanding performance was notable, as they secured first place in the competition. Plumpton High School was also declared the 'Inquisitive Minds Talented Maths Champions' of the Greater Western Sydney Region, solidifying their ability in mathematical problem-solving and teamwork.

Students from Plumpton High School achieved individual success, with Year 9 students Year 9 students Ysabela Marasigan and Lanvy Nguyen earning 1st place and Jericho Villareal and Jordan Villareal placing third. Year 8 students Taha Ali and Zakariya Al-Shible also achieved winning scores while collaborating with students from another school. In the Engineering Competition, Plumpton High School secured second place, with the group led by Dev Patel constructing a bridge with a remarkable span of 57.5m.

The event exposed HPGE maths students from Year 8 and Year 9 to four hours of problem-solving activities, including an interactive lesson and engineering competition. It enabled advanced problem-solving strategies and critical thinking skills to be developed and practiced. With participation from four schools (Riverstone High School, St Johns Park High, Jamieson High School and Plumpton High School), the day facilitated collaborative learning and practical application of mathematical concepts, demonstrating the value of hands-on, interactive experiences in promoting mathematical proficiency.

A huge thank you to Ms Prasad, Ms Zhang and Ms Deni-Savio for organising the successful event and other schools for their participation in healthy competition that has built complex mathematical reasoning and problem solving.

Tim Lloyd, Principal

For more photos of the event, please visit our image gallery .

General enquiries

address 141 Hyatts Road Plumpton NSW, 2761

telephone 02 9625 7020

email [email protected]

Get directions

We would like to pay our respects and acknowledge the traditional custodians of the land and also pay respect to Elders both past and present.

Copyright for this website is owned by the State of New South Wales through the Department of Education. For more information go to http://www.dec.nsw.gov.au/footer/copyright.