math word problem solving techniques

MAKE WAVES WITH THIS FREE WEEKLONG VOCABULARY UNIT!

Strategies for Solving Word Problems – Math

It’s one thing to solve a math equation when all of the numbers are given to you but with word problems, when you start adding reading to the mix, that’s when it gets especially tricky.

The simple addition of those words ramps up the difficulty (and sometimes the math anxiety) by about 100!

How can you help your students become confident word problem solvers? By teaching your students to solve word problems in a step by step, organized way, you will give them the tools they need to solve word problems in a much more effective way.

Here are the seven strategies I use to help students solve word problems.

1. read the entire word problem.

Before students look for keywords and try to figure out what to do, they need to slow down a bit and read the whole word problem once (and even better, twice). This helps kids get the bigger picture to be able to understand it a little better too.

2. Think About the Word Problem

Students need to ask themselves three questions every time they are faced with a word problem. These questions will help them to set up a plan for solving the problem.

Here are the questions:

A. what exactly is the question.

What is the problem asking? Often times, curriculum writers include extra information in the problem for seemingly no good reason, except maybe to train kids to ignore that extraneous information (grrrr!). Students need to be able to stay focused, ignore those extra details, and find out what the real question is in a particular problem.

B. What do I need in order to find the answer?

Students need to narrow it down, even more, to figure out what is needed to solve the problem, whether it’s adding, subtracting, multiplying, dividing, or some combination of those. They’ll need a general idea of which information will be used (or not used) and what they’ll be doing.

This is where key words become very helpful. When students learn to recognize that certain words mean to add (like in all, altogether, combined ), while others mean to subtract, multiply, or to divide, it helps them decide how to proceed a little better

Here’s a Key Words Chart I like to use for teaching word problems. The handout could be copied at a smaller size and glued into interactive math notebooks. It could be placed in math folders or in binders under the math section if your students use binders.

One year I made huge math signs (addition, subtraction, multiplication, and divide symbols) and wrote the keywords around the symbols. These served as a permanent reminder of keywords for word problems in the classroom.

If you’d like to download this FREE Key Words handout, click here:

C. What information do I already have?

This is where students will focus in on the numbers which will be used to solve the problem.

3. Write on the Word Problem

This step reinforces the thinking which took place in step number two. Students use a pencil or colored pencils to notate information on worksheets (not books of course, unless they’re consumable). There are lots of ways to do this, but here’s what I like to do:

• Circle any numbers you’ll use.
• Lightly cross out any information you don’t need.
• Underline the phrase or sentence which tells exactly what you’ll need to find.

4. Draw a Simple Picture and Label It

Drawing pictures using simple shapes like squares, circles, and rectangles help students visualize problems. Adding numbers or names as labels help too.

For example, if the word problem says that there were five boxes and each box had 4 apples in it, kids can draw five squares with the number four in each square. Instantly, kids can see the answer so much more easily!

5. Estimate the Answer Before Solving

Having a general idea of a ballpark answer for the problem lets students know if their actual answer is reasonable or not. This quick, rough estimate is a good math habit to get into. It helps students really think about their answer’s accuracy when the problem is finally solved.

6. Check Your Work When Done

This strategy goes along with the fifth strategy. One of the phrases I constantly use during math time is, Is your answer reasonable ? I want students to do more than to be number crunchers but to really think about what those numbers mean.

Also, when students get into the habit of checking work, they are more apt to catch careless mistakes, which are often the root of incorrect answers.

7. Practice Word Problems Often

Just like it takes practice to learn to play the clarinet, to dribble a ball in soccer, and to draw realistically, it takes practice to become a master word problem solver.

When students practice word problems, often several things happen. Word problems become less scary (no, really).

They start to notice similarities in types of problems and are able to more quickly understand how to solve them. They will gain confidence even when dealing with new types of word problems, knowing that they have successfully solved many word problems in the past.

If you’re looking for some word problem task cards, I have quite a few of them for 3rd – 5th graders.

This 3rd grade math task cards bundle has word problems in almost every one of its 30 task card sets..

There are also specific sets that are dedicated to word problems and two-step word problems too. I love these because there’s a task card set for every standard.

CLICK HERE to take a look at 3rd grade:

This 4th Grade Math Task Cards Bundle also has lots of word problems in almost every single of its 30 task card sets. These cards are perfect for centers, whole class, and for one on one.

CLICK HERE to see 4th grade:

This 5th Grade Math Task Cards Bundle is also loaded with word problems to give your students focused practice.

CLICK HERE to take a look at 5th grade:

Want to try a FREE set of math task cards to see what you think?

3rd Grade: Rounding Whole Numbers Task Cards

4th Grade: Convert Fractions and Decimals Task Cards

5th Grade: Read, Write, and Compare Decimals Task Cards

Thanks so much for stopping by!

• Read more about: Math

You might also like...

Fraction Activities Students Love – Math

Fractions can be tough! While it takes time and repeated exposure with fractions for students to have a real understanding of them, there are lots

Math Games Using Dice

Games are an important part of math class, in my opinion. Not only are kids able to practice the skills that we have been focusing

Math Games Using Dominoes

Math games have always been part of our math time. I love the fact that any time I introduce a math game, I know I’ll

Hi, I’m Jenn, CEO and owner of The Teacher Next Door!

I know that you strive to be an effective upper elementary teacher while maintaining a healthy work-life balance.

In order to do that, you need resources that are impactful, yet simple .

The problem is that most resources and curriculums out there are far from simple. The pages upon pages of daily lesson plans are just plain overwhelming .

At TTND, we believe teachers should be living their lives outside of the classroom, and not spend hours lesson planning and searching for resources.

We understand that now, more than ever, teachers need space to be themselves which is why we create and support teachers with timesaving tips and standards-aligned resources.

Want access to TTND's Free Resource Library? Sign up for our newsletter and we'll email you the exclusive password!

Trending posts.

SEARCH BY TOPIC

• Classroom Ideas
• Holidays and Seasonal
• Mentor Texts
• Reading Block
• Uncategorized
• Writing & Grammar

POPULAR RESOURCES

Facebook Group

Teachers Pay Teachers

Free Resource Library

💌 Contact Us

Disclosures

Privacy Policy

Refund Policy

Purchase Orders

Your Downloads

Reward Points

©  The Teacher Next Door, LLC. All rights reserved.

* Please note: If your school has strong email filters, you may wish to use your personal email to ensure access.

• Grades 6-12
• School Leaders

Don't Miss the Grand Prize: A $2,500 Office Depot/OfficeMax Card!

14 Effective Ways to Help Your Students Conquer Math Word Problems

If a train leaving Minneapolis is traveling at 87 miles an hour…

Word problems can be tricky for a lot of students, but they’re incredibly important to master. After all, in the real world, most math is in the form of word problems. “If one gallon of paint covers 400 square feet, and my wall measures 34 feet by 8 feet, how many gallons do I need?” “This sweater costs $135, but it’s on sale for 35% off. So how much is that?” Here are the best teacher-tested ideas for helping kids get a handle on these problems.

1. Solve word problems regularly

This might be the most important tip of all. Word problems should be part of everyday math practice, especially for older kids. Whenever possible, use word problems every time you teach a new math skill. Even better: give students a daily word problem to solve so they’ll get comfortable with the process.

Learn more: Teaching With Jennifer Findlay

2. Teach problem-solving routines

There are a LOT of strategies out there for teaching kids how to solve word problems (keep reading to see some terrific examples). The important thing to remember is that what works for one student may not work for another. So introduce a basic routine like Plan-Solve-Check that every kid can use every time. You can expand on the Plan and Solve steps in a variety of ways, but this basic 3-step process ensures kids slow down and take their time.

Learn more: Word Problems Made Easy

[contextly_auto_sidebar]

3. Visualize or model the problem

Encourage students to think of word problems as an actual story or scenario. Try acting the problem out if possible, and draw pictures, diagrams, or models. Learn more about this method and get free printable templates at the link.

Learn more: Math Geek Mama

4. Make sure they identify the actual question

Educator Robert Kaplinsky asked 32 eighth grade students to answer this nonsensical word problem. Only 25% of them realized they didn’t have the right information to answer the actual question; the other 75% gave a variety of numerical answers that involved adding, subtracting, or dividing the two numbers. That tells us kids really need to be trained to identify the actual question being asked before they proceed. 

Learn more: Robert Kaplinsky

5. Remove the numbers

It seems counterintuitive … math without numbers? But this word problem strategy really forces kids to slow down and examine the problem itself, without focusing on numbers at first. If the numbers were removed from the sheep/shepherd problem above, students would have no choice but to slow down and read more carefully, rather than plowing ahead without thinking. 

Learn more: Where the Magic Happens Teaching

6. Try the CUBES method

This is a tried-and-true method for teaching word problems, and it’s really effective for kids who are prone to working too fast and missing details. By taking the time to circle, box, and underline important information, students are more likely to find the correct answer to the question actually being asked.

Learn more: Teaching With a Mountain View

7. Show word problems the LOVE

Here’s another fun acronym for tackling word problems: LOVE. Using this method, kids Label numbers and other key info, then explain Our thinking by writing the equation as a sentence. They use Visuals or models to help plan and list any and all Equations they’ll use. 

8. Consider teaching word problem key words

This is one of those methods that some teachers love and others hate. Those who like it feel it offers kids a simple tool for making sense of words and how they relate to math. Others feel it’s outdated, and prefer to teach word problems using context and situations instead (see below). You might just consider this one more trick to keep in your toolbox for students who need it.

Learn more: Book Units Teacher

9. Determine the operation for the situation

Instead of (or in addition to) key words, have kids really analyze the situation presented to determine the right operation(s) to use. Some key words, like “total,” can be pretty vague. It’s worth taking the time to dig deeper into what the problem is really asking. Get a free printable chart and learn how to use this method at the link.

Learn more: Solving Word Problems With Jennifer Findlay

10. Differentiate word problems to build skills

Sometimes students get so distracted by numbers that look big or scary that they give up right off the bat. For those cases, try working your way up to the skill at hand. For instance, instead of jumping right to subtracting 4 digit numbers, make the numbers smaller to start. Each successive problem can be a little more difficult, but kids will see they can use the same method regardless of the numbers themselves.

Learn more: Differentiating Math 

11. Ensure they can justify their answers

One of the quickest ways to find mistakes is to look closely at your answer and ensure it makes sense. If students can explain how they came to their conclusion, they’re much more likely to get the answer right. That’s why teachers have been asking students to “show their work” for decades now.

Learn more: Madly Learning

12. Write the answer in a sentence

When you think about it, this one makes so much sense. Word problems are presented in complete sentences, so the answers should be too. This helps students make certain they’re actually answering the question being asked… part of justifying their answer.

Learn more: Multi-Step Word Problems

13. Add rigor to your word problems

A smart way to help kids conquer word problems is to, well… give them better problems to conquer. A rich math word problem is accessible and feels real to students, like something that matters. It should allow for different ways to solve it and be open for discussion. A series of problems should be varied, using different operations and situations when possible, and even include multiple steps. Visit both of the links below for excellent tips on adding rigor to your math word problems.

Learn more: The Routty Math Teacher and Alyssa Teaches

14. Use a problem-solving rounds activity.

Put all those word problem strategies and skills together with this whole-class activity. Start by reading the problem as a group and sharing important information. Then, have students work with a partner to plan how they’ll solve it. In round three, kids use those plans to solve the problem individually. Finally, they share their answer and methods with their partner and the class. Be sure to recognize and respect all problem-solving strategies that lead to the correct answer.

Learn more: Teacher Trap

Like these word problem tips and tricks? Learn more about Why It’s Important to Honor All Math Strategies .

Plus, 60+ Awesome Websites For Teaching and Learning Math .

You Might Also Like

Check Out These 50 First-Grade Math Word Problems of the Day

Desmond saw 5 bunnies. Continue Reading

Copyright © 2024. All rights reserved. 5335 Gate Parkway, Jacksonville, FL 32256

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Free ready-to-use math resources

Hundreds of free math resources created by experienced math teachers to save time, build engagement and accelerate growth

20 Effective Math Strategies To Approach Problem-Solving 

Katie Keeton

Math strategies for problem-solving help students use a range of approaches to solve many different types of problems. It involves identifying the problem and carrying out a plan of action to find the answer to mathematical problems.  

Problem-solving skills are essential to math in the general classroom and real-life. They require logical reasoning and critical thinking skills. Students must be equipped with strategies to help them find solutions to problems.

This article explores mathematical problem solving strategies, logical reasoning and critical thinking skills to help learners with solving math word problems independently in real-life situations. 

What are problem-solving strategies?

Problem-solving strategies in math are methods students can use to figure out solutions to math problems. Some problem-solving strategies: 

• Draw a model
• Use different approaches
• Check the inverse to make sure the answer is correct

Students need to have a toolkit of math problem-solving strategies at their disposal to provide different ways to approach math problems. This makes it easier to find solutions and understand math better. 

Strategies can help guide students to the solution when it is difficult ot know when to start.

The ultimate guide to problem solving techniques

Download these ready-to-go problem solving techniques that every student should know. Includes printable tasks for students including challenges, short explanations for teachers with questioning prompts.

20 Math Strategies For Problem-Solving

Different problem-solving math strategies are required for different parts of the problem. It is unlikely that students will use the same strategy to understand and solve the problem. 

Here are 20 strategies to help students develop their problem-solving skills. 

Strategies to understand the problem

Strategies that help students understand the problem before solving it helps ensure they understand: 

• The context
• What the key information is
• How to form a plan to solve it

Following these steps leads students to the correct solution and makes the math word problem easier .

Here are five strategies to help students understand the content of the problem and identify key information. 

1. Read the problem aloud

Read a word problem aloud to help understand it. Hearing the words engages auditory processing. This can make it easier to process and comprehend the context of the situation.

2. Highlight keywords 

When keywords are highlighted in a word problem, it helps the student focus on the essential information needed to solve it. Some important keywords help determine which operation is needed.  For example, if the word problem asks how many are left, the problem likely requires subtraction.  Ensure students highlight the keywords carefully and do not highlight every number or keyword. There is likely irrelevant information in the word problem.

3. Summarize the information

Read the problem aloud, highlight the key information and then summarize the information. Students can do this in their heads or write down a quick summary.  Summaries should include only the important information and be in simple terms that help contextualize the problem.

4. Determine the unknown

A common problem that students have when solving a word problem is misunderstanding what they are solving. Determine what the unknown information is before finding the answer.  Often, a word problem contains a question where you can find the unknown information you need to solve. For example, in the question ‘How many apples are left?’ students need to find the number of apples left over.

5. Make a plan

Once students understand the context of the word problem, have dentified the important information and determined the unknown, they can make a plan to solve it.  The plan will depend on the type of problem. Some problems involve more than one step to solve them as some require more than one answer.  Encourage students to make a list of each step they need to take to solve the problem before getting started.

Strategies for solving the problem 

1. draw a model or diagram.

Students may find it useful to draw a model, picture, diagram, or other visual aid to help with the problem solving process.  It can help to visualize the problem to understand the relationships between the numbers in the problem. In turn, this helps students see the solution.

Similarly, you could draw a model to represent the objects in the problem:

2. Act it out

This particular strategy is applicable at any grade level but is especially helpful in math investigation in elementary school . It involves a physical demonstration or students acting out the problem using movements, concrete resources and math manipulatives .  When students act out a problem, they can visualize and contectualize the word problem in another way and secure an understanding of the math concepts.  The examples below show how 1st-grade students could “act out” an addition and subtraction problem:

3. Work backwards

Working backwards is a popular problem-solving strategy. It involves starting with a possible solution and deciding what steps to take to arrive at that solution.  This strategy can be particularly helpful when students solve math word problems involving multiple steps. They can start at the end and think carefully about each step taken as opposed to jumping to the end of the problem and missing steps in between.

For example,

To solve this problem working backwards, start with the final condition, which is Sam’s grandmother’s age (71) and work backwards to find Sam’s age. Subtract 20 from the grandmother’s age, which is 71.  Then, divide the result by 3 to get Sam’s age. 71 – 20 = 51 51 ÷ 3 = 17 Sam is 17 years old.

4. Write a number sentence

When faced with a word problem, encourage students to write a number sentence based on the information. This helps translate the information in the word problem into a math equation or expression, which is more easily solved.  It is important to fully understand the context of the word problem and what students need to solve before writing an equation to represent it.

5. Use a formula

Specific formulas help solve many math problems. For example, if a problem asks students to find the area of a rug, they would use the area formula (area = length × width) to solve.   Make sure students know the important mathematical formulas they will need in tests and real-life. It can help to display these around the classroom or, for those who need more support, on students’ desks.

Strategies for checking the solution 

Once the problem is solved using an appropriate strategy, it is equally important to check the solution to ensure it is correct and makes sense. 

There are many strategies to check the solution. The strategy for a specific problem is dependent on the problem type and math content involved.

Here are five strategies to help students check their solutions. 

1. Use the Inverse Operation

For simpler problems, a quick and easy problem solving strategy is to use the inverse operation. For example, if the operation to solve a word problem is 56 ÷ 8 = 7 students can check the answer is correct by multiplying 8 × 7. As good practice, encourage students to use the inverse operation routinely to check their work. 

2. Estimate to check for reasonableness

Once students reach an answer, they can use estimation or rounding to see if the answer is reasonable.  Round each number in the equation to a number that’s close and easy to work with, usually a multiple of ten.  For example, if the question was 216 ÷ 18 and the quotient was 12, students might round 216 to 200 and round 18 to 20. Then use mental math to solve 200 ÷ 20, which is 10.  When the estimate is clear the two numbers are close. This means your answer is reasonable. 

3. Plug-In Method

This method is particularly useful for algebraic equations. Specifically when working with variables.  To use the plug-in method, students solve the problem as asked and arrive at an answer. They can then plug the answer into the original equation to see if it works. If it does, the answer is correct.

If students use the equation 20m+80=300 to solve this problem and find that m = 11, they can plug that value back into the equation to see if it is correct. 20m + 80 = 300 20 (11) + 80 = 300 220 + 80 = 300 300 = 300 ✓

4. Peer Review

Peer review is a great tool to use at any grade level as it promotes critical thinking and collaboration between students. The reviewers can look at the problem from a different view as they check to see if the problem was solved correctly.   Problem solvers receive immediate feedback and the opportunity to discuss their thinking with their peers. This strategy is effective with mixed-ability partners or similar-ability partners. In mixed-ability groups, the partner with stronger skills provides guidance and support to the partner with weaker skills, while reinforcing their own understanding of the content and communication skills.  If partners have comparable ability levels and problem-solving skills, they may find that they approach problems differently or have unique insights to offer each other about the problem-solving process.

5. Use a Calculator

A calculator can be introduced at any grade level but may be best for older students who already have a foundational understanding of basic math operations. Provide students with a calculator to allow them to check their solutions independently, accurately, and quickly. Since calculators are so readily available on smartphones and tablets, they allow students to develop practical skills that apply to real-world situations.  

Step-by-step problem-solving processes for your classroom

In his book, How to Solve It , published in 1945, mathematician George Polya introduced a 4-step process to solve problems. 

Polya’s 4 steps include:

• Understand the problem
• Devise a plan
• Carry out the plan

Today, in the style of George Polya, many problem-solving strategies use various acronyms and steps to help students recall. 

Many teachers create posters and anchor charts of their chosen process to display in their classrooms. They can be implemented in any elementary, middle school or high school classroom. 

Here are 5 problem-solving strategies to introduce to students and use in the classroom.

How Third Space Learning improves problem-solving 

Resources .

Third Space Learning offers a free resource library is filled with hundreds of high-quality resources. A team of experienced math experts carefully created each resource to develop students mental arithmetic, problem solving and critical thinking. 

Explore the range of problem solving resources for 2nd to 8th grade students. 

One-on-one tutoring 

Third Space Learning offers one-on-one math tutoring to help students improve their math skills. Highly qualified tutors deliver high-quality lessons aligned to state standards. 

Former teachers and math experts write all of Third Space Learning’s tutoring lessons. Expertly designed lessons follow a “my turn, follow me, your turn” pedagogy to help students move from guided instruction and problem-solving to independent practice. 

Throughout each lesson, tutors ask higher-level thinking questions to promote critical thinking and ensure students are developing a deep understanding of the content and problem-solving skills.

Problem-solving

Educators can use many different strategies to teach problem-solving and help students develop and carry out a plan when solving math problems. Incorporate these math strategies into any math program and use them with a variety of math concepts, from whole numbers and fractions to algebra. 

Teaching students how to choose and implement problem-solving strategies helps them develop mathematical reasoning skills and critical thinking they can apply to real-life problem-solving.

READ MORE : 8 Common Core math examples

There are many different strategies for problem-solving; Here are 5 problem-solving strategies: • draw a model  • act it out  • work backwards  • write a number sentence • use a formula

Here are 10 strategies of problem-solving: • Read the problem aloud • Highlight keywords • Summarize the information • Determine the unknown • Make a plan • Draw a model  • Act it out  • Work backwards  • Write a number sentence • Use a formula

1. Understand the problem 2. Devise a plan 3. Carry out the plan 4. Look back

Some strategies you can use to solve challenging math problems are: breaking the problem into smaller parts, using diagrams or models, applying logical reasoning, and trying different approaches.

Related articles

Why Student Centered Learning Is Important: A Guide For Educators

13 Effective Learning Strategies: A Guide to Using them in your Math Classroom

Differentiated Instruction: 9 Differentiated Curriculum And Instruction Strategies For Teachers 

5 Math Mastery Strategies To Incorporate Into Your 4th and 5th Grade Classrooms

Ultimate Guide to Metacognition [FREE]

Looking for a summary on metacognition in relation to math teaching and learning?

Check out this guide featuring practical examples, tips and strategies to successfully embed metacognition across your school to accelerate math growth.

Privacy Overview

Resources and

Guiding Curiosity, Igniting Imagination!

4 Math Word Problem Solving Strategies

5 Strategies to Learn to Solve Math Word Problems

A critical step in math fluency is the ability to solve math word problems. The funny thing about solving math word problems is that it isn’t just about math. Students need to have strong reading skills as well as the growth mindset needed for problem-solving. Strong problem solving skills need to be taught as well. In this article, let’s go over some strategies to help students improve their math problem solving skills when it comes to math word problems. These skills are great for students of all levels but especially important for students that struggle with math anxiety or students with animosity toward math.

Signs of Students Struggling with Math Word Problems

It is important to look at the root cause of what is causing the student to struggle with math problems. If you are in a tutoring situation, you can check your students reading level to see if that is contributing to the issue. You can also support the student in understanding math keywords and key phrases that they might need unpacked. Next, students might need to slow their thinking down and be taught to tackle the word problem bit by bit.

How to Help Students Solve Math Word Problems

Focus on math keywords and mathematical key phrases.

The first step in helping students with math word problems is focusing on keywords and phrases. For example, the words combined or increased by can mean addition. If you teach keywords and phrases they should watch out for students will gain the cues needed to go about solving a word problem. It might be a good idea to have them underline or highlight these words.

Cross out Extra Information

Along with highlighting important keywords students should also try to decipher the important from unimportant information. To help emphasize what is important in the problem, ask your students to cross out the unimportant distracting information.  This way, it will allow them to focus on what they can use to solve the problem.

Encourage Asking Questions

As you give them time to read, allow them to have time to ask questions on what they just read. Asking questions will help them understand what to focus on and what to ignore. Once they get through that, they can figure out the right math questions and add another item under their problem-solving strategies.

Draw the Problem

A fun way to help your students understand the problem is through letting them draw it on graph paper. For example, if a math problem asks a student to count the number of fruits that Farmer John has, ask them to draw each fruit while counting them. This is a great strategy for visual learners.

Check Back Once They Answer

Once they figured out the answer to the math problem, ask them to recheck their answer. Checking their answer is a good habit for learning and one that should be encouraged but students need to be taught how to check their answer. So the first step would be to review the word problem to make sure that they are solving the correct problem. Then to make sure that they set it up right. This is important because sometimes students will check their equation but will not reread the word problem and make sure that the equation is set up right. So always have them do this first! Once students believe that they have read and set up the correct equation, they should be taught to check their work and redo the problem, I also like to teach them to use the opposite to double check, for example if their equation is 2+3=5, I will show them how to take 5 which is the whole and check their work backwards 5-3 and that should equal 2. This is an important step and solidifies mathematical thinking in children.

Mnemonic Devices

Mnemonic devices are a great way to remember all of the types of math strategy in this post. The following are ones that I have heard of and wanted to share:

CUBES Word Problem Strategy

Cubes is a mnemonic to remember the following steps in solving math word problems:

C: Circle the numbers

U: Underline the question

B: Box in the key words

E: Eliminate the information

S: Solve the problem & show your work

RISE Word Problem Strategy

Rise is another way to explain the steps needed to solve problems:

R: Read and reread

I: Illustrate what is being asked

S: Solve by writing your equation or number sentences

E: Explain your thinking

COINS Word Problem Strategy

C: Comprehend the questions

O: Observe the data

I: Illustrate the problem

N: Write the number sentence (equation)

Understand -Plan – Solve – Check Word Problem Strategy

This is a simple step solution to show students the big picture. I think this along with one of the mnemonic devices helps students with better understanding of the approach.

Understand: What is the question asking? Do you understand all the words?

Plan: What would be a reasonable answer? In this stage students are formulating their approach to the word problem. 

Solve: What strategies will I use to solve this problem? Am I showing my thinking? Here students use the strategies outlined in this post to attack the problem.

Check: Students will ask themselves if they answered the question and if their answer makes sense. 

If you need word problems to use with your classroom, you can check out my word problems resource below.

Teaching students how to approach and solve math word problems is an important skill. Solving word problems is the closest math skill that resembles math in the real world. Encouraging students to slow their thinking, examine and analyze the word problem and encourage the habit of answer checking will give your students the learning skills that can be applied not only to math but to all learning. I also wrote a blog post on a specific type of math word problem called cognitively guided instruction you can read information on that too. It is just a different way that math problems are written and worth understanding to teach problem solving, click here to read .

Share This Story, Choose Your Platform!

Related posts.

How to play the card game Garbage

Teaching Number Tracing and Formation to Students

fun games with math

Leave a comment cancel reply.

 subscribe to our newsletter

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

Module 1: Problem Solving Strategies

• Last updated
• Save as PDF
• Page ID 10352

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Unlike exercises, there is never a simple recipe for solving a problem. You can get better and better at solving problems, both by building up your background knowledge and by simply practicing. As you solve more problems (and learn how other people solved them), you learn strategies and techniques that can be useful. But no single strategy works every time.

Pólya’s How to Solve It

George Pólya was a great champion in the field of teaching effective problem solving skills. He was born in Hungary in 1887, received his Ph.D. at the University of Budapest, and was a professor at Stanford University (among other universities). He wrote many mathematical papers along with three books, most famously, “How to Solve it.” Pólya died at the age 98 in 1985.1

1. Image of Pólya by Thane Plambeck from Palo Alto, California (Flickr) [CC BY

In 1945, Pólya published the short book How to Solve It , which gave a four-step method for solving mathematical problems:

First, you have to understand the problem.

After understanding, then make a plan.

Carry out the plan.

Look back on your work. How could it be better?

This is all well and good, but how do you actually do these steps?!?! Steps 1. and 2. are particularly mysterious! How do you “make a plan?” That is where you need some tools in your toolbox, and some experience to draw upon.

Much has been written since 1945 to explain these steps in more detail, but the truth is that they are more art than science. This is where math becomes a creative endeavor (and where it becomes so much fun). We will articulate some useful problem solving strategies, but no such list will ever be complete. This is really just a start to help you on your way. The best way to become a skilled problem solver is to learn the background material well, and then to solve a lot of problems!

Problem Solving Strategy 1 (Guess and Test)

Make a guess and test to see if it satisfies the demands of the problem. If it doesn't, alter the guess appropriately and check again. Keep doing this until you find a solution.

Mr. Jones has a total of 25 chickens and cows on his farm. How many of each does he have if all together there are 76 feet?

Step 1: Understanding the problem

We are given in the problem that there are 25 chickens and cows.

All together there are 76 feet.

Chickens have 2 feet and cows have 4 feet.

We are trying to determine how many cows and how many chickens Mr. Jones has on his farm.

Step 2: Devise a plan

Going to use Guess and test along with making a tab

Many times the strategy below is used with guess and test.

Make a table and look for a pattern:

Procedure: Make a table reflecting the data in the problem. If done in an orderly way, such a table will often reveal patterns and relationships that suggest how the problem can be solved.

Step 3: Carry out the plan:

Notice we are going in the wrong direction! The total number of feet is decreasing!

Better! The total number of feet are increasing!

Step 4: Looking back:

Check: 12 + 13 = 25 heads

24 + 52 = 76 feet.

We have found the solution to this problem. I could use this strategy when there are a limited number of possible answers and when two items are the same but they have one characteristic that is different.

Videos to watch:

1. Click on this link to see an example of “Guess and Test”

http://www.mathstories.com/strategies.htm

2. Click on this link to see another example of Guess and Test.

http://www.mathinaction.org/problem-solving-strategies.html

Check in question 1:

Place the digits 8, 10, 11, 12, and 13 in the circles to make the sums across and vertically equal 31. (5 points)

Check in question 2:

Old McDonald has 250 chickens and goats in the barnyard. Altogether there are 760 feet . How many of each animal does he have? Make sure you use Polya’s 4 problem solving steps. (12 points)

Problem Solving Strategy 2 (Draw a Picture). Some problems are obviously about a geometric situation, and it is clear you want to draw a picture and mark down all of the given information before you try to solve it. But even for a problem that is not geometric thinking visually can help!

Videos to watch demonstrating how to use "Draw a Picture".

1. Click on this link to see an example of “Draw a Picture”

2. Click on this link to see another example of Draw a Picture.

Problem Solving Strategy 3 ( Using a variable to find the sum of a sequence.)

Gauss's strategy for sequences.

last term = fixed number ( n -1) + first term

The fix number is the the amount each term is increasing or decreasing by. "n" is the number of terms you have. You can use this formula to find the last term in the sequence or the number of terms you have in a sequence.

Ex: 2, 5, 8, ... Find the 200th term.

Last term = 3(200-1) +2

Last term is 599.

To find the sum of a sequence: sum = [(first term + last term) (number of terms)]/ 2

Sum = (2 + 599) (200) then divide by 2

Sum = 60,100

Check in question 3: (10 points)

Find the 320 th term of 7, 10, 13, 16 …

Then find the sum of the first 320 terms.

Problem Solving Strategy 4 (Working Backwards)

This is considered a strategy in many schools. If you are given an answer, and the steps that were taken to arrive at that answer, you should be able to determine the starting point.

Videos to watch demonstrating of “Working Backwards”

https://www.youtube.com/watch?v=5FFWTsMEeJw

Karen is thinking of a number. If you double it, and subtract 7, you obtain 11. What is Karen’s number?

1. We start with 11 and work backwards.

2. The opposite of subtraction is addition. We will add 7 to 11. We are now at 18.

3. The opposite of doubling something is dividing by 2. 18/2 = 9

4. This should be our answer. Looking back:

9 x 2 = 18 -7 = 11

5. We have the right answer.

Check in question 4:

Christina is thinking of a number.

If you multiply her number by 93, add 6, and divide by 3, you obtain 436. What is her number? Solve this problem by working backwards. (5 points)

Problem Solving Strategy 5 (Looking for a Pattern)

Definition: A sequence is a pattern involving an ordered arrangement of numbers.

We first need to find a pattern.

Ask yourself as you search for a pattern – are the numbers growing steadily larger? Steadily smaller? How is each number related?

Example 1: 1, 4, 7, 10, 13…

Find the next 2 numbers. The pattern is each number is increasing by 3. The next two numbers would be 16 and 19.

Example 2: 1, 4, 9, 16 … find the next 2 numbers. It looks like each successive number is increase by the next odd number. 1 + 3 = 4.

So the next number would be

25 + 11 = 36

Example 3: 10, 7, 4, 1, -2… find the next 2 numbers.

In this sequence, the numbers are decreasing by 3. So the next 2 numbers would be -2 -3 = -5

-5 – 3 = -8

Example 4: 1, 2, 4, 8 … find the next two numbers.

This example is a little bit harder. The numbers are increasing but not by a constant. Maybe a factor?

So each number is being multiplied by 2.

16 x 2 = 32

1. Click on this link to see an example of “Looking for a Pattern”

2. Click on this link to see another example of Looking for a Pattern.

Problem Solving Strategy 6 (Make a List)

Example 1 : Can perfect squares end in a 2 or a 3?

List all the squares of the numbers 1 to 20.

1 4 9 16 25 36 49 64 81 100 121 144 169 196 225 256 289 324 361 400.

Now look at the number in the ones digits. Notice they are 0, 1, 4, 5, 6, or 9. Notice none of the perfect squares end in 2, 3, 7, or 8. This list suggests that perfect squares cannot end in a 2, 3, 7 or 8.

How many different amounts of money can you have in your pocket if you have only three coins including only dimes and quarters?

Quarter’s dimes

0 3 30 cents

1 2 45 cents

2 1 60 cents

3 0 75 cents

Videos demonstrating "Make a List"

Check in question 5:

How many ways can you make change for 23 cents using only pennies, nickels, and dimes? (10 points)

Problem Solving Strategy 7 (Solve a Simpler Problem)

Geometric Sequences:

How would we find the nth term?

Solve a simpler problem:

1, 3, 9, 27.

1. To get from 1 to 3 what did we do?

2. To get from 3 to 9 what did we do?

Let’s set up a table:

Term Number what did we do

Looking back: How would you find the nth term?

Find the 10 th term of the above sequence.

Let L = the tenth term

Problem Solving Strategy 8 (Process of Elimination)

This strategy can be used when there is only one possible solution.

I’m thinking of a number.

The number is odd.

It is more than 1 but less than 100.

It is greater than 20.

It is less than 5 times 7.

The sum of the digits is 7.

It is evenly divisible by 5.

a. We know it is an odd number between 1 and 100.

b. It is greater than 20 but less than 35

21, 23, 25, 27, 29, 31, 33, 35. These are the possibilities.

c. The sum of the digits is 7

21 (2+1=3) No 23 (2+3 = 5) No 25 (2 + 5= 7) Yes Using the same process we see there are no other numbers that meet this criteria. Also we notice 25 is divisible by 5. By using the strategy elimination, we have found our answer.

Check in question 6: (8 points)

Jose is thinking of a number.

The number is not odd.

The sum of the digits is divisible by 2.

The number is a multiple of 11.

It is greater than 5 times 4.

It is a multiple of 6

It is less than 7 times 8 +23

What is the number?

Click on this link for a quick review of the problem solving strategies.

https://garyhall.org.uk/maths-problem-solving-strategies.html

3 Strategies to Conquer Math Word Problems

Here’s a word problem for you:

Miss Friday’s class does a daily word problem. Ten of her students are great at word problems involving addition, and only 7 seem to understand subtraction word problems. Five of her students are bored with the easy problems. Thirteen students are still struggling with basic math facts and 3 have trouble reading the word problems at all. How many of her students are engaged and learning?

Here’s a better question: “How do you grow confident and effective problem solvers?”

Why Students Struggle with Math Word Problems

Students struggle with math word problems for many reasons, but three of the biggest I’ve encountered include:

Issue #1: Student Confidence For many students, just looking at a word problem leads to anxiety. No one can think clearly with a sense of dread or fear of failure looming!

Issue #2: Flexible Thinking Many kids are taught to solve word problems methodically, with a prescriptive step-by-step plan using key words that don’t always work. Plans are great, but not when students use them as a crutch rather than a tool. Today’s standardized tests and real-world applications require creative thinking and flexibility with strategies.

Issue #3: Differentiation Teachers want students to excel quickly and often push too fast, too soon. In the case of word problems, you have to go slow to go fast. Just like in Guided Reading, you’ll want to give lots of practice with “just-right” problems and provide guided practice with problems just-above the students’ level.

3 Problem Solving Strategies

The solution is to conquer math word problems with engaging classroom strategies that counteract the above issues!

1. Teach a Problem-Solving Routine 

Kids (and adults) are notoriously impulsive problem solvers. Many students see a word problem and want to immediately snatch out those numbers and “do something” with them. When I was in elementary school, this was actually a pretty reliable strategy! But today, kids are asked to solve much more complex problems, often with tricky wording or intentional distractors.

Grow flexible thinkers and build confidence by teaching a routine. A problem solving routine simply encourages students to slow down and think before and after solving. I’ve seen lots of effective routines but my favorites always include a “before, during, and after” mindset.

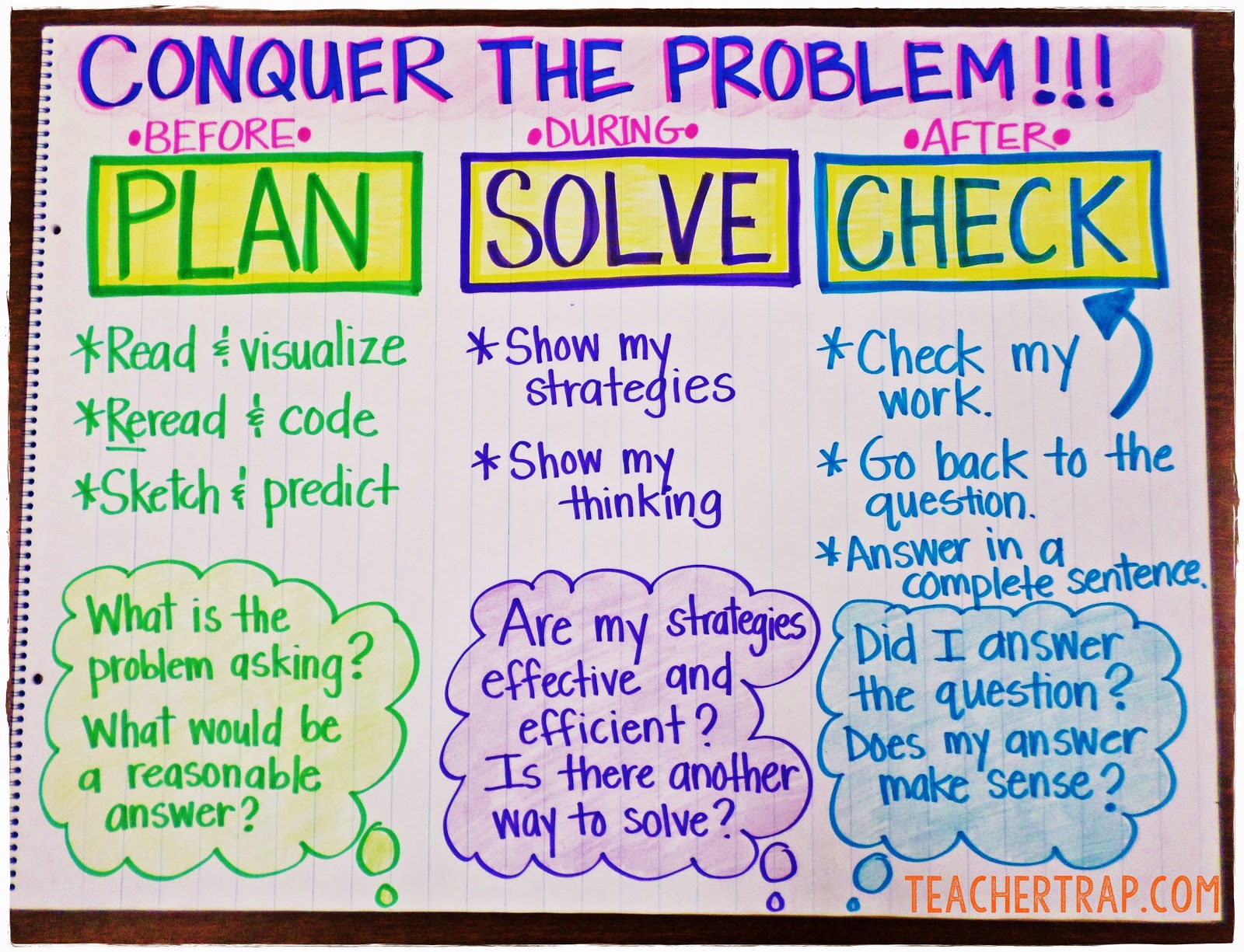
To make the problem solving routine meaningful and effective:

• Use it often (daily if possible)
• Incorporate “Turn & Teach” (Students orally explain their thinking and process to a partner.)
• Allow for “Strategy Share” after solving (Selected students explain their method and thinking.)

2. Differentiate Word Problems 

No, this doesn’t mean to write a different word problem for every student! This can be as simple as adjusting the numbers in a problem or removing distractors for struggling students. Scaffolding word problems will grow confidence and improve problem solving skills by gradually increasing the level difficulty as the child is ready. This is especially effective when you are trying to teach students different structures of word problems to go with a certain operation.

For example, comparison subtraction problems are very challenging for some students. By starting with a simple version, you allow students to focus on the problem itself, rather than becoming intimidated or frustrated.

I’ve had great success in using scaffolded problems with my guided math groups. After solving the easier problem, students realize that it’s not that tricky and are ready to take on the tougher ones!

3. Compare Problems Side-by-Side 

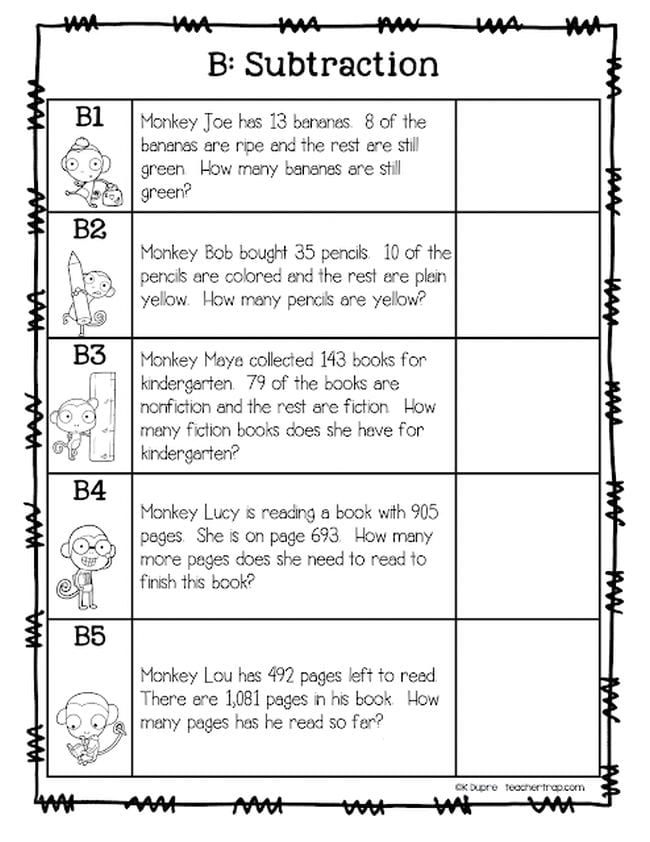
To develop flexible thinking, nothing is more powerful than analyzing and comparing word problems. Start by using problems that have similar stories and numbers, but different problem structures. Encourage conversation, use visual representations, and have students explain the difference in structure and operation. Here’s an example showing student work on two similar problems about monkeys. Click here to download a blank copy of these problems. My freebie includes several variations to help you differentiate.

Use these three strategies to get kids thinking and talking about their problem solving strategies while building that “oh-so-important” confidence, and you CAN conquer math word problems!

Kady Dupre has worked as a classroom teacher, instructional coach, and intervention teacher in elementary grades. She loves creating learning resources for students and teachers. She authors Teacher Trap , a blog aimed at sharing her challenges, successes, and insights as a teacher.

Candler's Classroom Connections

• Growth Mindset
• Literature Circles
• Cooperative Learning

Strategies for Solving Math Word Problems

Math word problems can be tricky and often challenging to solve. Employing the SQRQCQ method can make solving math word problems easier and less intimidating.

The SQRQCQ method is particularly useful for children with learning disabilities and can be used effectively in special education programs. SQRQCQ is an abbreviation for Survey, Question, Read, Question, Compute, and Question.

Step 1 – SURVEY the Math Problem

The first step to solving a math word problem is to read the problem in its entirety to understand what you are being asked to solve. After you read it, you can decide the most relevant aspects of the problem that need to be solved and what aspects are not relevant to solving the problem. The idea here is to get a general understanding.

Step 2 – QUESTION

Once you have an idea of what you’re attempting to solve, you need to determine what formulas, steps, or equations should be utilized in order to find the correct answer. It is impossible to find an answer if you can’t determine what needs to be solved. Basically, what are the questions being asked by the problem?

Step 3 – REREAD

Now that you’ve determined what needs to be solved, reread the problem and pay close attention to specific details. Determine which aspects of the problem are interrelated. Identify all relevant facts and information needed to solve the problem. As you do, write them down.

Step 4 – QUESTION

Now that you’re familiar with specific details and how different facts and information within the problem are interrelated, determine what formulas or equations must be used to set up and solve the problem. Be sure to write down what steps or operations you will use for easy reference.

Step 5 – COMPUTE

Use the formulas and/or equations identified in the previous step to complete the calculations. Be sure to follow the steps you outlined while setting up an equation or using a formula. As you complete each step, check it off your list.

Step 6 – QUESTION

Once you’ve completed the calculations, review the final answer and make sure it is correct and accurate. If it does not appear logical, review the steps you took to find the answer and look for calculation or set-up errors. Recalculate the numbers or make other changes until you get an answer that makes sense.

How does SQRQCQ help students with learning disabilities?

Math word problems tend to be especially challenging for Learning Disabled (LD) students. LD students often lack “Concept Imagery”, or the ability to visualize the whole problem by creating a complete mental image. They often jump right into calculations and computations without understanding what the problem is asking or what they’re looking for.

LD students may also struggle to understand the words or wording within math word problems correctly. The inability to correctly interpret and understand wording greatly impacts their math reasoning skills and often leads them to making the wrong calculations and arriving incorrect conclusions.

Remembering and manipulating information and details in their working memory is another challenge some LD students face as they try to see the whole picture. Slow processing of information, followed by frustration and anxiety, will often lead LD students to try and get through math word problems as quickly as possible – which is why they often jump straight into computations in their attempt to make it to the finish line as quickly as possible.

SQRQCQ is a metacognitive guide that provides LD students with a logical order for solving math word problems. It provides just enough direction to guide them through the reasoning process without overwhelming them. SQRQCQ is also a mnemonic that is easy for students to remember and which they can fall back on when completing homework or taking tests.

Read also: – A Guide for St u dying Math

Similar Posts:

• Discover Your Learning Style – Comprehensive Guide on Different Learning Styles
• 15 Learning Theories in Education (A Complete Summary)
• 35 of the BEST Educational Apps for Teachers (Updated 2024)

Leave a Comment Cancel reply

Save my name and email in this browser for the next time I comment.

• Get started with computers
• Learn Microsoft Office
• Apply for a job
• Improve my work skills
• Design nice-looking docs
• Getting Started
• Smartphones & Tablets
• Typing Tutorial
• Online Learning
• Basic Internet Skills
• Online Safety
• Social Media
• Zoom Basics
• Google Docs
• Google Sheets
• Career Planning
• Resume Writing
• Cover Letters
• Job Search and Networking
• Business Communication
• Entrepreneurship 101
• Careers without College
• Job Hunt for Today
• 3D Printing
• Freelancing 101
• Personal Finance
• Sharing Economy
• Decision-Making
• Graphic Design
• Photography
• Image Editing
• Learning WordPress
• Language Learning
• Critical Thinking
• For Educators
• Translations
• Staff Picks
• English expand_more expand_less

Algebra Topics  - Introduction to Word Problems

Algebra topics  -, introduction to word problems, algebra topics introduction to word problems.

Algebra Topics: Introduction to Word Problems

Lesson 9: introduction to word problems.

/en/algebra-topics/solving-equations/content/

What are word problems?

A word problem is a math problem written out as a short story or scenario. Basically, it describes a realistic problem and asks you to imagine how you would solve it using math. If you've ever taken a math class, you've probably solved a word problem. For instance, does this sound familiar?

Johnny has 12 apples. If he gives four to Susie, how many will he have left?

You could solve this problem by looking at the numbers and figuring out what the problem is asking you to do. In this case, you're supposed to find out how many apples Johnny has left at the end of the problem. By reading the problem, you know Johnny starts out with 12 apples. By the end, he has 4 less because he gave them away. You could write this as:

12 - 4 = 8 , so you know Johnny has 8 apples left.

Word problems in algebra

If you were able to solve this problem, you should also be able to solve algebra word problems. Yes, they involve more complicated math, but they use the same basic problem-solving skills as simpler word problems.

You can tackle any word problem by following these five steps:

• Read through the problem carefully, and figure out what it's about.
• Represent unknown numbers with variables.
• Translate the rest of the problem into a mathematical expression.
• Solve the problem.
• Check your work.

We'll work through an algebra word problem using these steps. Here's a typical problem:

The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took two days, and the van cost $360. How many miles did she drive?

It might seem complicated at first glance, but we already have all of the information we need to solve it. Let's go through it step by step.

Step 1: Read through the problem carefully.

With any problem, start by reading through the problem. As you're reading, consider:

• What question is the problem asking?
• What information do you already have?

Let's take a look at our problem again. What question is the problem asking? In other words, what are you trying to find out?

The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took 2 days, and the van cost $360. How many miles did she drive?

There's only one question here. We're trying to find out how many miles Jada drove . Now we need to locate any information that will help us answer this question.

There are a few important things we know that will help us figure out the total mileage Jada drove:

• The van cost $30 per day.
• In addition to paying a daily charge, Jada paid $0.50 per mile.
• Jada had the van for 2 days.
• The total cost was $360 .

Step 2: Represent unknown numbers with variables.

In algebra, you represent unknown numbers with letters called variables . (To learn more about variables, see our lesson on reading algebraic expressions .) You can use a variable in the place of any amount you don't know. Looking at our problem, do you see a quantity we should represent with a variable? It's often the number we're trying to find out.

Since we're trying to find the total number of miles Jada drove, we'll represent that amount with a variable—at least until we know it. We'll use the variable m for miles . Of course, we could use any variable, but m should be easy to remember.

Step 3: Translate the rest of the problem.

Let's take another look at the problem, with the facts we'll use to solve it highlighted.

The rate to rent a small moving van is $30 per day , plus $0.50 per mile . Jada rented a van to drive to her new home. It took 2 days , and the van cost $360 . How many miles did she drive?

We know the total cost of the van, and we know that it includes a fee for the number of days, plus another fee for the number of miles. It's $30 per day, and $0.50 per mile. A simpler way to say this would be:

$30 per day plus $0.50 per mile is $360.

If you look at this sentence and the original problem, you can see that they basically say the same thing: It cost Jada $30 per day and $0.50 per mile, and her total cost was $360 . The shorter version will be easier to translate into a mathematical expression.

Let's start by translating $30 per day . To calculate the cost of something that costs a certain amount per day, you'd multiply the per-day cost by the number of days—in other words, 30 per day could be written as 30 ⋅ days, or 30 times the number of days . (Not sure why you'd translate it this way? Check out our lesson on writing algebraic expressions .)

$30 per day and $.50 per mile is $360

$30 ⋅ day + $.50 ⋅ mile = $360

As you can see, there were a few other words we could translate into operators, so and $.50 became + $.50 , $.50 per mile became $.50 ⋅ mile , and is became = .

Next, we'll add in the numbers and variables we already know. We already know the number of days Jada drove, 2 , so we can replace that. We've also already said we'll use m to represent the number of miles, so we can replace that too. We should also take the dollar signs off of the money amounts to make them consistent with the other numbers.

30 ⋅ 2 + .5 ⋅ m = 360

Now we have our expression. All that's left to do is solve it.

Step 4: Solve the problem.

This problem will take a few steps to solve. (If you're not sure how to do the math in this section, you might want to review our lesson on simplifying expressions .) First, let's simplify the expression as much as possible. We can multiply 30 and 2, so let's go ahead and do that. We can also write .5 ⋅ m as 0.5 m .

60 + .5m = 360

Next, we need to do what we can to get the m alone on the left side of the equals sign. Once we do that, we'll know what m is equal to—in other words, it will let us know the number of miles in our word problem.

We can start by getting rid of the 60 on the left side by subtracting it from both sides .

The only thing left to get rid of is .5 . Since it's being multiplied with m , we'll do the reverse and divide both sides of the equation with it.

.5 m / .5 is m and 300 / 0.50 is 600 , so m = 600 . In other words, the answer to our problem is 600 —we now know Jada drove 600 miles.

Step 5: Check the problem.

To make sure we solved the problem correctly, we should check our work. To do this, we can use the answer we just got— 600 —and calculate backward to find another of the quantities in our problem. In other words, if our answer for Jada's distance is correct, we should be able to use it to work backward and find another value, like the total cost. Let's take another look at the problem.

According to the problem, the van costs $30 per day and $0.50 per mile. If Jada really did drive 600 miles in 2 days, she could calculate the cost like this:

$30 per day and $0.50 per mile

30 ⋅ day + .5 ⋅ mile

30 ⋅ 2 + .5 ⋅ 600

According to our math, the van would cost $360, which is exactly what the problem says. This means our solution was correct. We're done!

While some word problems will be more complicated than others, you can use these basic steps to approach any word problem. On the next page, you can try it for yourself.

Let's practice with a couple more problems. You can solve these problems the same way we solved the first one—just follow the problem-solving steps we covered earlier. For your reference, these steps are:

If you get stuck, you might want to review the problem on page 1. You can also take a look at our lesson on writing algebraic expressions for some tips on translating written words into math.

Try completing this problem on your own. When you're done, move on to the next page to check your answer and see an explanation of the steps.

A single ticket to the fair costs $8. A family pass costs $25 more than half of that. How much does a family pass cost?

Here's another problem to do on your own. As with the last problem, you can find the answer and explanation to this one on the next page.

Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?

Problem 1 Answer

Here's Problem 1:

A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?

Answer: $29

Let's solve this problem step by step. We'll solve it the same way we solved the problem on page 1.

Step 1: Read through the problem carefully

The first in solving any word problem is to find out what question the problem is asking you to solve and identify the information that will help you solve it . Let's look at the problem again. The question is right there in plain sight:

So is the information we'll need to answer the question:

• A single ticket costs $8 .
• The family pass costs $25 more than half the price of the single ticket.

Step 2: Represent the unknown numbers with variables

The unknown number in this problem is the cost of the family pass . We'll represent it with the variable f .

Step 3: Translate the rest of the problem

Let's look at the problem again. This time, the important facts are highlighted.

A single ticket to the fair costs $8 . A family pass costs $25 more than half that . How much does a family pass cost?

In other words, we could say that the cost of a family pass equals half of $8, plus $25 . To turn this into a problem we can solve, we'll have to translate it into math. Here's how:

• First, replace the cost of a family pass with our variable f .

f equals half of $8 plus $25

• Next, take out the dollar signs and replace words like plus and equals with operators.

f = half of 8 + 25

• Finally, translate the rest of the problem. Half of can be written as 1/2 times , or 1/2 ⋅ :

f = 1/2 ⋅ 8 + 25

Step 4: Solve the problem

Now all we have to do is solve our problem. Like with any problem, we can solve this one by following the order of operations.

• f is already alone on the left side of the equation, so all we have to do is calculate the right side.
• First, multiply 1/2 by 8 . 1/2 ⋅ 8 is 4 .
• Next, add 4 and 25. 4 + 25 equals 29 .

That's it! f is equal to 29. In other words, the cost of a family pass is $29 .

Step 5: Check your work

Finally, let's check our work by working backward from our answer. In this case, we should be able to correctly calculate the cost of a single ticket by using the cost we calculated for the family pass. Let's look at the original problem again.

We calculated that a family pass costs $29. Our problem says the pass costs $25 more than half the cost of a single ticket. In other words, half the cost of a single ticket will be $25 less than $29.

• We could translate this into this equation, with s standing for the cost of a single ticket.

1/2s = 29 - 25

• Let's work on the right side first. 29 - 25 is 4 .
• To find the value of s , we have to get it alone on the left side of the equation. This means getting rid of 1/2 . To do this, we'll multiply each side by the inverse of 1/2: 2 .

According to our math, s = 8 . In other words, if the family pass costs $29, the single ticket will cost $8. Looking at our original problem, that's correct!

So now we're sure about the answer to our problem: The cost of a family pass is $29 .

Problem 2 Answer

Here's Problem 2:

Answer: $70

Let's go through this problem one step at a time.

Start by asking what question the problem is asking you to solve and identifying the information that will help you solve it . What's the question here?

To solve the problem, you'll have to find out how much money Mo gave to charity. All the important information you need is in the problem:

• The amount Flor donated is three times as much the amount Mo donated
• Flor and Mo's donations add up to $280 total

The unknown number we're trying to identify in this problem is Mo's donation . We'll represent it with the variable m .

Here's the problem again. This time, the important facts are highlighted.

Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo . Between the two of them, they donated $280 . How much money did Mo give?

The important facts of the problem could also be expressed this way:

Mo's donation plus Flor's donation equals $280

Because we know that Flor's donation is three times as much as Mo's donation, we could go even further and say:

Mo's donation plus three times Mo's donation equals $280

We can translate this into a math problem in only a few steps. Here's how:

• Because we've already said we'll represent the amount of Mo's donation with the variable m , let's start by replacing Mo's donation with m .

m plus three times m equals $280

• Next, we can put in mathematical operators in place of certain words. We'll also take out the dollar sign.

m + three times m = 280

• Finally, let's write three times mathematically. Three times m can also be written as 3 ⋅ m , or just 3 m .

m + 3m = 280

It will only take a few steps to solve this problem.

• To get the correct answer, we'll have to get m alone on one side of the equation.
• To start, let's add m and 3 m . That's 4 m .
• We can get rid of the 4 next to the m by dividing both sides by 4. 4 m / 4 is m , and 280 / 4 is 70 .

We've got our answer: m = 70 . In other words, Mo donated $70 .

The answer to our problem is $70 , but we should check just to be sure. Let's look at our problem again.

If our answer is correct, $70 and three times $70 should add up to $280 .

• We can write our new equation like this:

70 + 3 ⋅ 70 = 280

• The order of operations calls for us to multiply first. 3 ⋅ 70 is 210.

70 + 210 = 280

• The last step is to add 70 and 210. 70 plus 210 equals 280 .

280 is the combined cost of the tickets in our original problem. Our answer is correct : Mo gave $70 to charity.

/en/algebra-topics/distance-word-problems/content/

• Prodigy Math
• Prodigy English
• Is a Premium Membership Worth It?
• Promote a Growth Mindset
• Help Your Child Who's Struggling with Math
• Parent's Guide to Prodigy
• Assessments
• Math Curriculum Coverage
• English Curriculum Coverage
• Game Portal

How to Solve Math Problems Faster: 15 Techniques to Show Students

Written by Marcus Guido

• Teaching Strategies

“Test time. No calculators.”

You’ll intimidate many students by saying this, but teaching techniques to solve math problems with ease and speed can make it less daunting.

This can also  make math more rewarding . Instead of relying on calculators, students learn strategies that can improve their concentration and estimation skills while building number sense. And, while there are educators who  oppose math “tricks”  for valid reasons, proponents point to benefits such as increased confidence to handle difficult problems.

Here are 15 techniques to show students,  helping them solve math problems faster:

Addition and Subtraction

1. two-step addition.

Many students struggle when learning to add integers of three digits or higher together, but changing the process’s steps can make it easier.

The first step is to  add what’s easy.  The second step is to  add the rest.

Let’s say students must find the sum of 393 and 89. They should quickly see that adding 7 onto 393 will equal 400 — an easier number to work with. To balance the equation, they can then subtract 7 from 89.

Broken down, the process is:

• (393 + 7) + (89 – 7)

With this fast technique, big numbers won’t look as scary now.

2. Two-Step Subtraction

There’s a similar method for subtraction.

Remove what’s easy. Then remove what’s left.

Suppose students must find the difference of 567 and 153. Most will feel that 500 is a simpler number than 567. So, they just have to take away 67 from the minuend — 567 — and the subtrahend — 153 — before solving the equation.

Here’s the process:

• (567 – 67) – (153 – 67)

Instead of two complex numbers, students will only have to tackle one.

3. Subtracting from 1,000

You can  give students confidence  to handle four-digit integers with this fast technique.

To subtract a number from 1,000, subtract that number’s first two digits from 9. Then, subtract the final digit from 10.

Let’s say students must solve 1,000 – 438.  Here are the steps:

This also applies to 10,000, 100,000 and other integers that follow this pattern.

Multiplication and Division

4. doubling and halving.

When students have to multiply two integers, they can speed up the process when one is an even number. They just need to  halve the even number and double the other number.

Students can stop the process when they can no longer halve the even integer, or when the equation becomes manageable.

Using 33 x 48 as an example,  here’s the process:

The only prerequisite is understanding the 2 times table.

5. Multiplying by Powers of 2

This tactic is a speedy variation of doubling and halving.

It simplifies multiplication if a number in the equation is a power of 2, meaning it works for 2, 4, 8, 16 and so on.

Here’s what to do:  For each power of 2 that makes up that number, double the other number.

For example, 9 x 16 is the same thing as 9 x (2 x 2 x 2 x 2) or 9 x 24. Students can therefore double 9 four times to reach the answer:

Unlike doubling and halving, this technique demands an understanding of exponents along with a strong command of the 2 times table.

6. Multiplying by 9

For most students, multiplying by 9 — or 99, 999 and any number that follows this pattern — is difficult compared with multiplying by a power of 10.

But there’s an easy tactic to solve this issue, and  it has two parts.

First, students round up the 9  to 10. Second, after solving the new equation, they subtract the number they just multiplied by 10 from the answer.

For example, 67 x 9 will lead to the same answer as 67 x 10 – 67. Following the order of operations will give a result of 603. Similarly, 67 x 99 is the same as 67 x 100 – 67.

Despite more steps, altering the equation this way is usually faster.

7. Multiplying by 11

There’s an easier way for multiplying two-digit integers by 11.

Let’s say students must find the product of 11 x 34.

The idea is to put a space between the digits, making it 3_4. Then, add the two digits together and put the sum in the space.

The answer is 374.

What happens if the sum is two digits? Students would put the second digit in the space and add 1 to the digit to the left of the space.  For example:

It’s multiplication without having to multiply.

8. Multiplying Even Numbers by 5

This technique only requires basic division skills.

There are two steps,  and 5 x 6 serves as an example. First, divide the number being multiplied by 5 — which is 6 — in half. Second, add 0 to the right of number.

The result is 30, which is the correct answer.

It’s an ideal, easy technique for students mastering the 5 times table.

9. Multiplying Odd Numbers by 5

This is another time-saving tactic that works well when teaching students the 5 times table.

This one has three steps,  which 5 x 7 exemplifies.

First, subtract 1 from the number being multiplied by 5, making it an even number. Second, cut that number in half — from 6 to 3 in this instance. Third, add 5 to the right of the number.

The answer is 35.

Who needs a calculator?

10. Squaring a Two-Digit Number that Ends with 1

Squaring a high two-digit number can be tedious, but there’s a shortcut if 1 is the second digit.

There are four steps to this shortcut,  which 812 exemplifies:

• Subtract 1 from the integer: 81 – 1 = 80
• Square the integer, which is now an easier number: 80 x 80 = 6,400
• Add the integer with the resulting square twice: 6,400 + 80 + 80 = 6,560
• Add 1: 6,560 + 1 = 6,561

This work-around eliminates the difficulty surrounding the second digit, allowing students to work with multiples of 10.

11. Squaring a Two-Digit Numbers that Ends with 5

Squaring numbers ending in 5 is easier, as there are  only two parts of the process.

First, students will always make 25 the product’s last digits.

Second, to determine the product’s first digits, students must multiply the number’s first digit — 9, for example — by the integer that’s one higher — 10, in this case.

So, students would solve 952 by designating 25 as the last two digits. They would then multiply 9 x 10 to receive 90. Putting these numbers together, the  result is 9,025.

Just like that, a hard problem becomes easy multiplication for many students.

12. Calculating Percentages

Cross-multiplication is an  important skill  to develop, but there’s an easier way to calculate percentages.

For example, if students want to know what 65% of 175 is, they can multiply the numbers together and move the decimal place two digits to the left.

The result is 113.75, which is indeed the correct answer.

This shortcut is a useful timesaver on tests and quizzes.

13. Balancing Averages

To determine the average among a set of numbers, students can balance them instead of using a complex formula.

Suppose a student wants to volunteer for an average of 10 hours a week over a period of four weeks. In the first three weeks, the student worked for 10, 12 and 14 hours.

To determine the number of hours required in the fourth week, the student must  add how much he or she surpassed or missed the target average  in the other weeks:

• 14 hours – 10 hours = 4 hours
• 12 – 10 = 2
• 10 – 10 = 0
• 4 hours + 2 hours + 0 hours = 6 hours

To learn the number of hours for the final week, the student must  subtract the sum from the target average:

• 10 hours – 6 hours = 4 hours

With practice, this method may not even require pencil and paper. That’s how easy it is. 

Word Problems

14. identifying buzzwords.

Students who struggle to translate  word problems  into equations will benefit from learning how to spot buzzwords — phrases that indicate specific actions.

This isn’t a trick. It’s a tactic.

Teach students to look for these buzzwords,  and what skill they align with in most contexts:

Be sure to include buzzwords that typically appear in their textbooks (or other classroom  math books ), as well as ones you use on tests and assignments.

As a result, they should have an  easier time processing word problems .

15. Creating Sub-Questions

For complex word problems, show students how to dissect the question by answering three specific sub-questions.

Each student should ask him or herself:

• What am I looking for?  — Students should read the question over and over, looking for buzzwords and identifying important details.
• What information do I need?  — Students should determine which facts, figures and variables they need to solve the question. For example, if they determine the question is rooted in subtraction, they need the minuend and subtrahend.
• What information do I have?  — Students should be able to create the core equation using the information in the word problem, after determining which details are important.

These sub-questions help students avoid overload.

Instead of writing and analyzing each detail of the question, they’ll be able to identify key information. If you identify students who are struggling with these, you can use  peer learning  as needed.  

For more fresh approaches to teaching math in your classroom, consider treating your students to a range of  fun math activities .

Final Thoughts About these Ways to Solve Math Problems Faster

Showing these 15 techniques to students can give them the  confidence to tackle tough questions .

They’re also  mental math  exercises, helping them build skills related to focus, logic and critical thinking.

A rewarding class equals an  engaging class . That’s an easy equation to remember.

> Create or log into your teacher account on Prodigy  — a free, adaptive math game that adjusts content to accommodate player trouble spots and learning speeds. Aligned to US and Canadian curricula, it’s loved by more than 500,000 teachers and 15 million students.

• ELEMENTARY TEACHING , MATH

How to Teach Word Problems: Strategies for Elementary Teachers

If you are looking for tips and ideas for how to teach word problems to your elementary students, then you’ve found the right place! We know that teaching elementary students how to solve word problems is important for math concept and skill application, but it sure can feel like a daunting charge without knowing about the different types, the best practices for teaching them, and common misconceptions to plan in advance for, as well as having the resources you need. All this information will make you feel confident about how to teach addition, subtraction, multiplication, and division word problems! Teaching students how to solve word problems will be so much easier!

This blog post will address the following questions:

• What is a word problem?
• What is a multi-step word problem?
• Why are elementary math word problems important?
• Why are math word problems so hard for elementary students?
• What are the types of word problems?
• How do I teach math word problems in a systematic way?
• What are the best elementary math word problem strategies I can teach my students and what are some tips for how to teach math word problems strategies?
• Do you have any helpful tips for how to teach word problems?
• What are the common mistakes I should look for that my students may make?
• How do I address my students’ common misconceptions surrounding elementary math word problems?

What is a Word Problem?

A word problem is a math situation that calls for an equation to be solved.  Students must apply their critical thinking skills to determine how to solve the problem.  Word problems give students the opportunity to practice turning situations into numbers.  This is critical as students progress in their education, as well as in their day-to-day life.  By teaching students how to solve word problems in a strategic way, you are setting them up for future success!

What is a Multi-Step Word Problem?

A multi-step word problem , also known as a two-step word problem or two-step equation word problem, is a math situation that involves more than one equation having to be answered in order to solve the ultimate question.  This requires students to apply their problem solving skills to determine which operation or operations to use to tackle the problem and find the necessary information.  In some cases, the situation may call for mixed operations, and in others the operations will be the same.  Multi-step word problems offer students the opportunity to practice the skill of applying different math concepts with a given problem.

Why are Word Problems Important in Math?

Word problems are essential in math because they give students the opportunity to apply what they have learned to a real life situation.  In addition, it facilitates students in developing their higher order thinking and critical thinking skills, creativity, positive mindset toward persevering while problem solving, and confidence in their math abilities.  Word problems are an effective tool for teachers to determine whether or not students understand and can apply the concepts and skills they learned to a real life situation.

Why do Students Struggle with Math Word Problems?

Knowing why students have trouble with word problems will help you better understand how to teach them. The reason why math word problems are difficult for your students is because of a few different reasons. First, students need to be able to fluently read and comprehend the text. Second, they need to be able to identify which operations and steps are needed to find the answer. Finally, they need to be able to accurately calculate the answer. If you have students who struggle with reading or English is their second language (ESL), they may not be able to accurately show what they know and can do because of language and literacy barriers. In these cases, it is appropriate to read the text aloud to them or have it translated into their native language for assignments and assessments.

Types of Word Problems

Knowing the different types of word problems will help you better understand how to teach math word problems. Read below to learn about the four types of basic one-step addition and subtraction word problems, the subcategories within each of them, and specific examples for all of them. Two-step equation word problems can encompass two of the same type or two separate types (also known as mixed operation word problems).

This type of word problem involves an action that increases the original amount. There are three kinds: Result unknown, change unknown, and initial quantity unknown.

Result Unknown

Example : There were 7 kids swimming in the pool. 3 more kids jumped in. How many kids are in the pool now? (7 + 3 = ?)

Change Unknown

Example : There were 8 kids swimming in the pool. More kids jumped in. Now there are 15 kids in the pool. How many kids jumped in? (8 + ? = 15)

Initial Quantity Unknown

Example : There were kids swimming in the pool. 2 kids jumped in. Now there are 6 kids in the pool. How many kids were swimming in the pool at first? (? + 2 = 6)

2. Separate

This type of word problem involves an action that decreases the original amount. There are three kinds: Result unknown, change unknown, and initial quantity unknown.

Example: There were 12 kids swimming in the pool. 6 of the kids got out of the pool. How many kids are in the pool now? (12 – 6 = ?)

Example: There were 9 kids swimming in the pool. Some of the kids got out of the pool. Now there are 4 kids in the pool. How many kids got out of the pool? (9 – ? = 4)

Example: There were kids swimming in the pool. 3 of the kids got out of the pool. Now there are 2 kids in the pool. How many kids were in the pool at first? (? – 3 = 2)

3. Part-Part-Whole

This type of word problem does not involve an action like the join and separate types. Instead, it is about defining relationships among a whole and two parts. There are two kinds: result unknown and part unknown.

Example: There are 5 boys and 9 girls swimming in the pool. How many kids are in the pool? (5 + 9 = ?)

Part Unknown

Example: There are 12 kids swimming in the pool. 8 of them are girls and the rest of them are boys. How many boys are swimming in the pool? (8 + ? = 12)

This type of word problem does not involve an action or relationship like the three other types. Instead, it is about comparing two different unrelated items. There are two kinds: Difference unknown and quantity unknown.

Difference Unknown

Example: There are 2 kids in the pool. There are 7 kids in the yard. How many more kids are in the yard than in the pool? (2 + ? = 7 or 7 – 2 = ?)

Quantity Unknown

Example 1: There are 5 kids in the pool. There are 3 fewer kids playing in the yard. How many kids are playing in the yard? (5 – 3 = ?)

Example 2: There are 2 kids in the pool. There are 10 more kids playing in the yard than in the pool. How many kids are playing in the yard? (2 + 10 = ?)

How to Solve Word Problems in 5 Easy Steps

Here are 5 steps that will help you teach word problems to your 1st, 2nd, 3rd, 4th or 5th grade students:

• Read the problem.
• Read the problem a second time and make meaning of it by visualizing, drawing pictures, and highlighting important information (numbers, phrases, and questions).
• Plan how you will solve the problem by organizing information in a graphic organizer and writing down equations and formulas that you will need to solve.
• Implement the plan and determine answer.
• Reflect on your answer and determine if it is reasonable.  If not, check your work and start back at step one if needed.  If the answer is reasonable, check your answer and be prepared to explain how you solved it and why you chose the strategies you did.

5 Math Word Problem Strategies

Here are 5 strategies for how to teach elementary word problems:

Understand the math situation and what the question is asking by picturing what you read in your head while you are reading.

Draw Pictures

Make meaning of what the word problem is asking by drawing a picture of the math situation.

Make Models

Use math tools like base-ten blocks to model what is happening in the math situation.

Highlight Important Information

Underline or highlight important numbers, phrases, and questions.

Engage in Word Study

Look for key words and phrases like “less” or “in all.” Check out this blog post if you are interested in learning more about math word problem keywords and their limitations.

10 Tips for Teaching Students How to Solve Math Word Problems

Here are 10 tips for how to teach math word problems:

• Model a positive attitude toward word problems and math.
• Embody a growth mindset.
• Model! Provide plenty of direct instruction.
• Give lots of opportunities to practice.
• Explicitly teach strategies and post anchor charts so students can access them and remember prior learning.
• Celebrate the strategies and process rather than the correct answer.
• Encourage students to continue persevering when they get stuck.
• Invite students to act as peer tutors.
• Provide opportunities for students to write their own word problems.
• Engage in whole-group discussions when solving word problems as a class.

Common Misconceptions and Errors When Students Learn How to Solve Math Word Problems

Here are 5 common misconceptions or errors elementary students have or make surrounding math word problems:

1. Use the Incorrect Operation

Elementary students often apply the incorrect operations because they pull the numbers from a word problem and add them without considering what the question is asking them or they misunderstand what the problem is asking.  Early in their experience with word problems, this strategy may work most of the time; however, its effectiveness will cease as the math gets more complex.  It is important to instruct students to develop and apply problem-solving strategies.

Although helpful in determining the meaning, elementary students rely solely on key words and phrases in a word problem to determine what operation is being called for. Again, this may be an effective strategy early on in their math career, but it should not be the only strategy students use to determine what their plan of attack is.

2. Get Stuck in a Fixed Mindset

Some elementary students give up before starting a word problem because they think all word problems are too hard.  It is essential to instill a positive mindset towards math in students. The best way to do that is through modeling. If you portray an excitement for math, many of your students will share that same feeling.

3. Struggle with Reading Skills Component

For first and second graders (as well as struggling readers and ESL students), it is common for students to decode the text incorrectly. Along the same lines, some elementary students think they can’t solve word problems because they do not know how to read yet.  The purpose of word problems is not to assess whether a child can read or not.  Instead, the purpose is to assess their critical thinking and problem-solving skills.  As a result, it is appropriate to read word problems to elementary students.

4. Calculate Incorrectly

You’ll find instances where students will understand what the question is asking, but they will calculate the addends or the subtrahend from the minuend incorrectly. This type of error is important to note when analyzing student responses because it gives you valuable information for when you plan your instruction.

5. Encode Response Incorrectly

Another error that is important to note when analyzing student responses is when you find that they encode their solution in writing incorrectly. This means they understand what the problem is asking, they solve the operations correctly, document their work meticulously, but then write the incorrect answer on the line.

How to Address Common Misconceptions Surrounding Math Word Problems

You might be wondering, “What can I do in response to some of these misconceptions and errors?” After collecting and analyzing the data, forming groups based on the results, and planning differentiated instruction, you may want to consider trying out these prompts:

• Can you reread the question aloud to me?
• What is the question asking us to do?
• How can we represent the information and question?
• Can we represent the information and question with an equation?
• What is our first step?
• What is our next step?
• Can you think of any strategies we use to help us solve?
• How did you find your answer?
• Can you walk me through how you found your answer step by step?
• What do we need to remember when recording our answer?

Now that you have all these tips and ideas for how to teach word problems, we would love for you to try these word problem resources with your students. They offer students opportunities to practice solving word problems after having learned how to solve word problems. You can download word problem worksheets specific to your grade level (along with lots of other math freebies) in our free printable math resources bundle using this link: free printable math activities for elementary teachers .

Check out my monthly word problem resources !

• 1st Grade Word Problems
• 2nd Grade Word Problems
• 3rd Grade Word Problems
• 4th Grade Word Problems
• 5th Grade Word Problems

You might also like...

Increasing Parent Participation in Elementary Math (Grades 1-5)

100+ Math Accommodations for Elementary Teachers

Vertical Alignment Curriculum in Math Education (Grades 1-5)

Join the newsletter.

• CLUTTER-FREE TEACHER CLUB
• FACEBOOK GROUPS
• EMAIL COMMUNITY
• OUR TEACHER STORE
• ALL-ACCESS MEMBERSHIPS
• OUR TPT SHOP
• JODI & COMPANY
• TERMS OF USE
• Privacy Policy

Get a collection of FREE MATH RESOURCES for your grade level!

• --> --> --> --> -->