powerpoint presentation on adding and subtracting fractions

Got any suggestions?

We want to hear from you! Send us a message and help improve Slidesgo

Top searches

Trending searches

11 templates

teacher appreciation

mother teresa

18 templates

memorial day

12 templates

summer vacation

25 templates

Math Subject for Elementary - 5th Grade: Fractions I

Math subject for elementary - 5th grade: fractions i presentation, free google slides theme, powerpoint template, and canva presentation template.

Who says Maths have to be boring? Introduce elementary school students to the wonders of fractions with this cool template. Its fun and approachable design is filled with colors and makes each slide look like a page ripped out from a spiral notebook. Also, its many color illustrations add a touch of whimsy to the subject that goes a long way towards making it palatable and interesting to young pupils!

Features of this template

• 100% editable and easy to modify
• 36 different slides to impress your audience
• Available in different colors
• Contains easy-to-edit graphics such as graphs, maps, tables, timelines and mockups
• Includes 500+ icons and Flaticon’s extension for customizing your slides
• Designed to be used in Google Slides, Canva, and Microsoft PowerPoint
• 16:9 widescreen format suitable for all types of screens
• Includes information about fonts, colors, and credits of the resources used

How can I use the template?

Am I free to use the templates?

How to attribute?

Combines with:

This template can be combined with this other one to create the perfect presentation:

Attribution required If you are a free user, you must attribute Slidesgo by keeping the slide where the credits appear. How to attribute?

Available colors.

Original Color

Related posts on our blog

How to Add, Duplicate, Move, Delete or Hide Slides in Google Slides

How to Change Layouts in PowerPoint

How to Change the Slide Size in Google Slides

Related presentations.

Premium template

Unlock this template and gain unlimited access

Adding and Subtracting Fractions - PowerPoint

In this educational resource designed for Year 3 students, the focus is on understanding and practising the addition and subtraction of fractions with the same denominator. The lesson begins by defining fractions as equal parts of a whole, which can represent parts of an object, quantity, or number. Students recap the structure of fractions, identifying the numerator and denominator in a fraction written as a numeral. The numerator indicates the number of equal parts being considered, while the denominator shows into how many parts the whole is divided.

The lesson then moves on to explain the straightforward process of adding fractions with the same denominator, where only the numerators are added while the denominator remains unchanged. This concept is visualised through diagrams that help students see the fractions being combined. Similarly, subtracting fractions is taught by subtracting the numerators and keeping the denominator constant. Students are encouraged to practise these operations through various exercises and word problems provided in worksheets. These activities aim to reinforce their understanding and application of adding and subtracting fractions in different contexts.

• International
• Schools directory
• Resources Jobs Schools directory News Search

Adding and Subtracting Fractions.

Subject: Mathematics

Age range: 14-16

Resource type: Worksheet/Activity

Last updated

• Share through email
• Share through twitter
• Share through linkedin
• Share through facebook
• Share through pinterest

We have two differentiated worksheets to help you learn adding fractions. First, you’ll work with fractions that have the same bottom number (same denominator). Then, we’ll move on to fractions where one denominator is a factor of the other. Next, you’ll practice adding fractions with different denominators. After that, we’ll move to adding mixed numbers. Finally, we’ll tackle some word problems that involve fractions.“ We provide detailed step-by-step solutions for all the questions on the worksheets. This means you’ll get clear explanations for each problem, helping you understand how to add fractions better

Tes paid licence How can I reuse this?

Your rating is required to reflect your happiness.

It's good to leave some feedback.

Something went wrong, please try again later.

This resource hasn't been reviewed yet

To ensure quality for our reviews, only customers who have purchased this resource can review it

Report this resource to let us know if it violates our terms and conditions. Our customer service team will review your report and will be in touch.

Not quite what you were looking for? Search by keyword to find the right resource:

Adding And Subtracting Algebraic Fractions

Jan 04, 2020

260 likes | 371 Views

Adding And Subtracting Algebraic Fractions.

Share Presentation

• common denominator
• basic factors

Presentation Transcript

When adding and subtracting fractions, it is necessary to find a common denominator – preferably the lowest common denominator (LCD). This is what makes addition and subtraction of fractions more tedious than multiplication and division. A common denominator is NOT required for multiplication or division. The process of determining the LCD is critical when adding or subtracting fractions but before dealing with examples where the denominators are different, it might be useful to work with some where the denominators are the same. In these cases, it will not be necessary to determine the LCD because the denominators will start out that way.

When the denominators of the fractions being added or subtracted start out the same, it is necessary to combine the numerators over that same denominator. It may be possible to factor the denominator and the newly combined numerator in a later step.

2x2 + 15x – 8 2x2 – 1x + 16x – 8 x(2x – 1) + 8(2x – 1) (2x – 1)(x + 8) 2 × - 8 = -16 -1 16 -2 8 -4 4 3 × - 8 = -24 3x2 - 10x – 8 3x2 + 2x - 12x – 8 x(3x + 2) - 4(3x + 2) (3x + 2)(x - 4) 1 -24 2 -12 3 -8 4 -6

When adding and subtracting fractions where the denominators are different, it is necessary to find the LCD. This is what makes addition and subtraction of fractions more tedious than multiplication and division. A common denominator is NOT required for multiplication or division. The LCD is basically the simplest expression that all of the starting denominators can divide into. If the denominators are just numerical, then the LCD is actually the lowest common multiple of each of the original denominators. Multiples of 5 = 5, 10, 15, 20, 25, 30, 35, 45, 50 ,55, … Multiples of 18 = 18, 36, 54, 72, 90, 108, … Multiples of 9 = 9, 18, 27, 36, 45, 54 ,63, … Multiples of 12 = 12, 24, 36, 48, 60, 72, 84, …  LCM = 45  LCM = 36

The steps involved in the addition of algebraic fractions can be appreciated by analyzing the steps of adding of a simpler pair of numeric fractions. To add these 2 fractions, we must find the lowest multiple of denominators 6 and 8 – in other words ‘the lowest common denominator’. LCD = 24 The LCD for these 2 fractions is 24 because 24 is the lowest number that both 6 and 8 can divide into evenly. 24  8 = 3 and 24  6 = 4 After choosing the LCD, it is now necessary to rewrite each of the fractions with the LCD instead of the original denominators. NOTE: If the denominator is changed then the numerator must be changed by the same factor to preserve the value of the original fractions. 9 20

Once the fractions have been written with a common denominator, the operation can be completed in the numerator. This whole process basically has 3 critical steps: • Choosing the LCD. • - Technically any common denominator will yield the correct answer (not just the lowest), however if a greater denominator is used it causes all the numbers thereafter to be bigger and therefore more difficult to work with. When working with algebraic fractions a common denominator that is NOT as small as possible will often be crippling and make the expressions too complicated to work with. • Adjusting the numerator of each fraction. • - When the denominator of a fraction is changed to the LCD, the numerator must be changed by the same factor. • Performing operations in numerator. • - Only the numerators are added/subtracted. The denominator remains whatever the LCD is.

When adding or subtracting fractions with different denominators, we will deal with them first by working with fractions that have monomial (one-term) denominators. LCD = 6 15x 14x 7x LCD = 12 8x

To determine the LCD for monomial expressions involving variables, it is helpful to visualize the basic or prime factors of each of the denominators of the fractions being added or subtracted. 6x2y3z = 2  3  x  x  y  y  y  z  8 basic factors 9xy3z2 = 3  3  x  y  y  y  z  z  8 basic factors The LCD must contain all of those basic factors. If a factor exists in one of the original denominators more than once, then it must also be in the LCD more than once. However, if a factor is in both denominators only once, then it only needs to be in the LCD once.

6x2y3z = 2  3  x  x  y  y  y  z  8 basic factors 9xy3z2 = 3  3  x  y  y  y  z  z  8 basic factors Referring to the example, the LCD must contain a factor of 2 and 3 because these are factors of 6x2y3z. LCD = 2  3  3  x  x  y  y  y  z  z = 18x2y3z2 It must contain a second factor of 3 because there are two factors of 3 in 9xy3z2. It must contain two factors of x because there are two factors of x in 6x2y3z. 9xy3z2 has only 1 factor of x and it is already there once. It must contain a three factors of y because there are 3 factors of y in 6x2y3z. 9xy3z2 also has 3 factors of y but it is already part of the LCD 3 times. It must contain a factor of z because there is a factor of z in 6x2y3z. 9xy3z2 has 2 factors of z. The LCD already has been given one but it must be given a second. The LCD has 10 basic factors.

Another way to determine the LCD is to determine the numeric part of the LCD by choosing the lowest common multiple and then determine the variable part by choosing the greatest exponent from each of the variables of the original denominators. Multiples of 6 = 6, 12, 18, 24, 30, 36, 42, … LCM = 18 Multiples of 9 = 9, 18, 27, 36, 45, 54, … 6x2y3z 9xy3z2 The LCD for the x variable will be x2 because 2 is the greatest exponent for the x variable. The LCD for the y variable will be y3 because 3 is the greatest exponent for the y variable. The LCD for the z variable will be z2 because 2 is the greatest exponent for the z variable. LCM = 18x2y3z2

LCD = xy 5y 7x LCD = x2 5x 3

25x LCD = 30x3y3 9y2 a3bd LCD = ab2c2d2 c3

To determine the LCD for denominators having expressions involving 2 or more terms, it is again helpful to visualize the basic or prime factors of each of the denominators of the fractions being added or subtracted. For this reason, it is necessary to factor the denominators to their most basic factors at the very beginning. There are 2 factors in each denominator. The LCD must contain those factors. The first denominator has the factors (x + 2) and (x + 4) so they must be a part of the LCD. The second denominator has the factors (x + 2) and (x - 2) so they must be a part of the LCD. Since (x + 2) already is there, it doesn’t need to be placed there a second time. LCD = (x + 2)(x + 4) (x – 2)

There are 6 factors in the first denominator and 5 factors in the second. The LCD must contain those factors. The first denominator has the factors 2, 3, x, x a second time, (x + 2) and (x + 4) so they must be a part of the LCD. The second denominator has the factors 3, 3 a second time, x, (x + 2) and (x + 2) a second time so they must be a part of the LCD. Since 3, x, and (x + 2) are already there one time, they don’t need to be placed there again. However because 3 and (x + 2) are in the second denominator twice, they must be a part of the LCD twice. LCD = 23xx(x + 2)(x + 4) 3(x + 2) = 233xx (x + 2)(x + 2)(x + 4) = 18x2(x + 2)2(x + 4)

LCD = 18x2(x + 2)2(x + 4) 21(x + 2) 28x(x + 4)

Be careful with subtraction of fractions. LCD = 18x2(x + 2)2(x + 4) 21(x + 2) 28x(x + 4)

LCD = (x + 3)(x + 4)(x – 2) 1(x – 2) 5(x + 4)

• More by User

Adding and Subtracting Fractions

Adding and Subtracting Fractions. By: Maren Miller. Review. What is a numerator? What is a denominator? What does a normal fraction look like? What does a improper fraction look like? What does a mixed number look like?. Like Fractions.

499 views • 16 slides

Adding and Subtracting Fractions. Let’s look at a model of adding fractions. Example: . First we need a fraction bar representation of each addend. We will stack these so that the shading of the second starts where the shading of the first ends .

353 views • 11 slides

Adding and Subtracting Fractions. Chapter X, Lesson Y.Z. Mr. Borowski January 29, 2012. At the end of this lesson we will be able to answer the following questions:. How do we add or subtract fractions? How do we add or subtract different fractions with different denominators?

451 views • 11 slides

Adding and subtracting fractions

Adding and subtracting fractions. Fractions with the same denominator. Check the answers to these questions on your calculator: a. b. c. d. . Fractions with the same denominator. Check the answers to these questions on your calculator:

420 views • 18 slides

Adding and Subtracting Fractions. Unit 7. Question #1. 1 + 2 5 3. Question #1. 1 + 2 = 13 5 3 15. Question #2. Answer #2. Answer is 2. Question #3. Answer #3. Answer is = 2 = 3 = 15 = 33. Question #4. Answer #4. Answer is = 6 .

526 views • 41 slides

Adding and Subtracting Fractions. Warm up. Find a the missing numbers . What is the lowest common multiple of:. 2. 6. =. 3 and 4. 12. 15. 5. 5 and 6. 30. 3. 15. =. 8. 4 and 6. 12. 40. 3 and 8. 24. 25. 5. =. 6. 5 and 10. 10. 30. Adding and Subtracting Fractions.

310 views • 10 slides

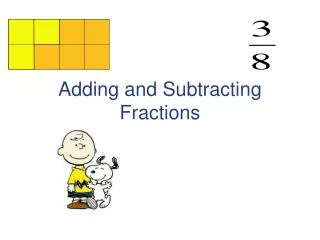
Adding and Subtracting Fractions. Adding Fractions with common denominators. Adding Fractions with different denominators. Problem: You can ’ t add fractions with different denominators without getting them ready first. They will be ready to add when they have common denominators.

1.44k views • 10 slides

Adding and Subtracting Fractions. 5.3. Common Denominators. Add or subtract the numerators Keep the denominator reduce. Examples. Unlike Denominators. Find the LCM of the denominators (LCD) Rename the fractions Add or subtract the numerators Keep the denominators reduce. Examples.

224 views • 8 slides

Adding and Subtracting Fractions. Example #1. When adding and subtracting fractions, we need a common denominator. Once the fractions have a common denominator, you will add or subtract the numerators and keep the denominators the same. Example #2. Find common denominators.

251 views • 8 slides

Adding and Subtracting Fractions. DON’T COPY. 3 Apples + 5 Apples = 7 Oranges + 4 Oranges = 5 Apples – 2 Apples = 2 Quarters + 5 Quarters = 4 Fifths + 3 Fifths = 7 Halves + 2 Halves = 4 Apples + 6 Oranges = 4 Halves + 6 Fifths = You cannot add things that are not the same type. .

421 views • 12 slides

Adding and Subtracting Fractions. 6.1. Common Denominators. Add or subtract the numerators Keep the denominator reduce. Examples. Unlike Denominators. Find the LCM of the denominators (LCD) Rename the fractions Add or subtract the numerators Keep the denominators reduce. Examples.

362 views • 11 slides

Adding and Subtracting Fractions. Number Sense 1.2. In order to add/subtract fractions, the denominator must be the same. Example: ¼ + 2/4 = ¾

146 views • 6 slides

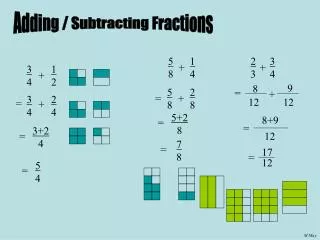
Adding / Subtracting Fractions

5 8. 1 4. 2 3. 3 4. +. +. 3 4. 1 2. +. +. 12. 12. 12. 12. Adding / Subtracting Fractions. 9. 8. 5 8. 2 8. =. =. +. 3 4. 2 4. =. +. 5+2 8. 8+9. =. =. 3+2 4. =. 7 8. =. 17. =. 5 4. =. 4 5. 6 7. x. 120. x. 91. 15÷3=5. =. =. =. =. =. =.

120 views • 2 slides

Chapter 3. Adding and Subtracting Fractions. Least Common Multiple. 3.2. Finding the Least Common Multiple Using Multiples. Method 1: Find the LCM of a List of Numbers Using Multiples of the Largest Number

294 views • 10 slides

ADDING AND SUBTRACTING FRACTIONS

ADDING AND SUBTRACTING FRACTIONS. Objective:- to learn to add and subtract fractions. Num/Den. Numerator. REMEMBER:. Denominator. Addition/Subtraction of Fractions. Same Den. Adding and subtracting simple fractions. 7 – 3. 4. –. 8. 8. 3. 1. 7. 2. 8. 8. 1. =. =. =. 2.

561 views • 16 slides

ADDING AND SUBTRACTING FRACTIONS. Parts of a Fraction Changing Improper Fractions into Mixed Numbers and Vice-Versa How to Add Fractions How to Add Mixed Numbers How to Subtract Fractions How to Subtract Mixed Numbers How to Borrow When Subtracting Fractions. 6 th Grade HomePage.

280 views • 14 slides

Adding and Subtracting Fractions. By Graeme Henchel. http://hench-maths.wikispaces.com. Adding Fractions with common denominators. Adding Fractions with different denominators. Problem:

265 views • 10 slides

Adding and Subtracting FRACTIONS

Adding and Subtracting FRACTIONS. By Lawrence Maxwell Hartman. FIRST,.

106 views • 3 slides

Adding and Subtracting Fractions. NS 2.1 Solve problems involving addition, subtraction , multiplication, and division of positive fractions and explain why a particular operation was used for a given situation.

256 views • 13 slides

306 views • 18 slides

Chapter 3. Adding and Subtracting Fractions. Adding and Subtracting Like Fractions. 3.1. Adding Like Fractions. Fractions with the same denominator are called like fractions . Fractions that have different denominators are called unlike fractions. Adding Like Fractions.

925 views • 13 slides

Adding and Subtracting Fractions. Add and Subtract Fractions Key fact You can only do this when the denominator is the SAME. Same Denominator. ⅜ + ⅛. ⅗ + ⅘. Improper/Mixed Number Fractions. Different Denominator. Mixed number fractions.

77 views • 6 slides