unit 5 trigonometric functions homework 8 law of cosines answers

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

3.2: The Law of Cosines

• Last updated
• Save as PDF
• Page ID 112421

• Katherine Yoshiwara
• Los Angeles Pierce College

If we know two angles and one side of a triangle, we can use the Law of Sines to solve the triangle. We can also use the Law of Sines when we know two sides and the angle opposite one of them. But the Law of Sines is not helpful for the problem that opened this chapter, finding the distance from Avery to Clio. In this case we know two sides of the triangle, \(a\) and \(c\), and the included angle, \(B\).

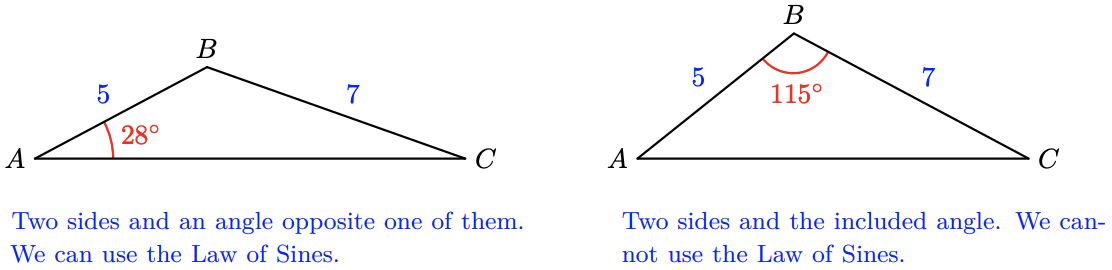
To solve a triangle when we know two sides and the included angle, we will need a generalization of the Pythagorean theorem known as the Law of Cosines.

In a right triangle, with \(C = 90^{\circ}\), the Pythagorean theorem tells us that

\(c^2 = a^2 + b^2\)

If we allow angle \(C\) to vary, but keep \(a\) and \(b\) the same length, the side \(c\) will grow or shrink, depending on whether we increase or decrease the angle \(C\), as shown below.

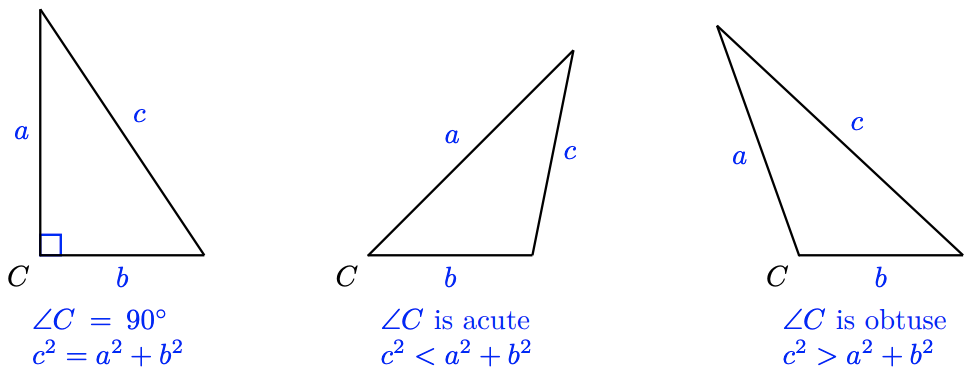
The Pythagorean theorem is actually a special case of a more general law that applies to all triangles, no matter what the size of angle \(C\). The equation relating the three sides of a triangle is

\(c^2=a^2+b^2-2 a b \cos C\)

You can see that when \(C\) is a right angle, \(\cos 90^{\circ}=0\), so the equation reduces to the Pythagorean theorem.

We can write similar equations involving the angles or \(A\) or \(B\). The three equations are all versions of the Law of Cosines.

Law of Cosines.

If the angles of a triangle are \(A, B\), and \(C\), and the opposite sides are respectively \(a, b\), and \(c\), then

\begin{aligned} &a^2=b^2+c^2-2 b c \cos A \\ &b^2=a^2+c^2-2 a c \cos B \\ &c^2=a^2+b^2-2 a b \cos C \end{aligned}

Note 3.38 For a proof of the Law of Cosines, see Homework Problems 57 and 58.

Finding a Side

Now we can solve the problem of the distance from Avery to Clio. Here is the figure from Section 3.1 showing the location of the three towns.

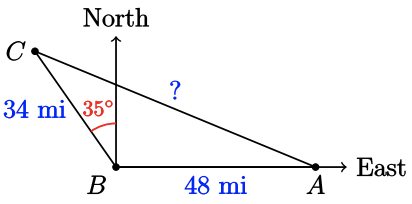
Example 3.39

How far is it from Avery to Clio?

The angle \(\angle A B C=35^{\circ}+90^{\circ}=125^{\circ}\). Thus, in \(\triangle A B C\) we have \(a=34, c=48\) and \(B=125^{\circ}\). The distance from Avery to Clio is represented by \(b\) in the figure.

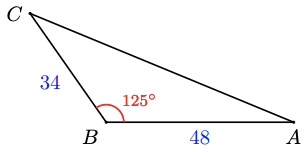
We know two sides and the included angle, and we choose the version of the Law of Cosines that uses our known angle, \(B\).

\begin{aligned} b^2 &= a^2 + c^2 - 2ac \cos B \quad \quad &&\text{Substitute the known values.} \\ b^2 &= 34^2 + 48^2 - 2(34)(48)\cos 125^{\circ} &&\text{Simplify the right side.} \\ b^2 &= 3460 - 3264\cos 125^{\circ} = 5332.153 &&\text{Take square roots.} \\ b &= 73.02 \end{aligned}

Avery is about 73 miles from Clio.

Caution 3.40

When simplifying the Law of Cosines, be careful to follow the order of operations. In the previous example, the right side of the equation

\(b^2=34^2+48^2-2(34)(48) \cos 125^{\circ}\)

has three terms, and simplifies to

\begin{aligned} &b^2=1156+2304-3264 \cos 125^{\circ} \\ &b^2=3460-3264(-0.573567364 \ldots) \end{aligned}

Note that 3264 is the coefficient of \(\cos 125^{\circ}\), so it would be incorrect to subtract 3264 from 3460. If you are using a graphing calculator, you can enter the right side of the equation exactly as it is written.

Checkpoint 3.41

In \(\triangle A B C, a=11, c=23\), and \(B=87^{\circ}\). Find \(b\), and round your answer to two decimal places.

Finding an Angle

We can also use the Law of Cosines to find an angle when we know all three sides of a triangle. Pay close attention to the algebraic steps used to solve the equation in the next example.

Example 3.42

In the triangle at right, \(a = 6, b = 7\), and \(c = 11\). Find angle \(C\).

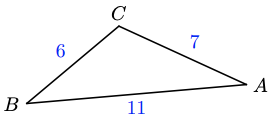
We choose the version of the Law of Cosines that uses angle \(C\).

\begin{aligned} c^2 &= a^2 + b^2 - 2ab\cos C \quad \quad &&\text{Substitute the known values.} \\ 11^2 &= 6^2 + 7^2 - 2(6)(7)\cos C &&\text{Simplify each side.} \\ 121 &= 36 + 49 - 84\cos C &&\text{Isolate the cosine term.} \\ 36 &= -84\cos C &&\text{Solve for }\cos C. \\ \dfrac{-3}{7} &= \cos C &&\text{Solve for }C. \\ C &= \cos^{-1}\left(\dfrac{-3}{7}\right) = 115.4^{\circ} \end{aligned}

Angle \(C\) is about \(115.4^{\circ}\).

Checkpoint 3.43

In \(\triangle A B C, a=5.3, b=4.7\), and \(c=6.1\). Find angle \(B\), and round your answer to two decimal places.

\(48.07^{\circ}\)

Once we have calculated one of the angles in a triangle, we can use either the Law of Sines or the Law of Cosines to find a second angle. Here is how we would use the Law of Sines to find angle \(A\) in the previous example.

\begin{aligned} \dfrac{\sin A}{a} &=\dfrac{\sin C}{c} \quad \quad &&\text{Substitute the known values}.\\ \dfrac{\sin A}{6} &=\dfrac{\sin 115.4^{\circ}}{11} &&\text{Solve for }\sin A.\\ \sin A &=6 \cdot \dfrac{\sin 115.4^{\circ}}{11} \approx 0.4928 \end{aligned}

Thus, \(A=\sin ^{-1}(0.4928)=29.5^{\circ}\). (We know that \(A\) is an acute angle because it is opposite the shortest side of the triangle.) Finally,

\(B=180^{\circ}-(A+C) \approx 35.1^{\circ}\)

Alternatively, we can use the Law of Cosines to find angle \(A\).

\begin{aligned} a^2 &=b^2+c^2-2 b c \cos A & & \text { Substitute the known values. } \\ 6^2 &=7^2+11^2-2(7)(11) \cos A & & \text { Simplify each side. } \\ 36 &=49+121-154 \cos A & & \text { Isolate the cosine term. } \\ -134 &=-154 \cos A & & \text { Solve for } \cos \boldsymbol{A} . \\ \dfrac{67}{77} &=\cos A & & \text { Solve for A. } \\ A &=\cos ^{-1}\left(\dfrac{67}{77}\right)=29.5^{\circ} & & \end{aligned}

Note 3.44 Using the Law of Sines requires fewer calculations than the Law of Cosines, but the Law of Cosines uses only the original values, instead of the results of our previous calculations and approximations.

Whenever we round off a number, we introduce inaccuracy into the calculations, and these inaccuracies grow with each additional calculation. Thus, for the sake of accuracy, it is best to use given values in preference to calculated values whenever possible.

Using the Law of Cosines for the Ambiguous Case

In Section 3.2 we encountered the ambiguous case:

If we know two sides \(a\) and \(b\) of a triangle and the acute angle \(\alpha\) opposite one of them, there may be one solution, two solutions, or no solution, depending on the size of \(a\) in relation to \(b\) and \(\alpha\), as shown below.

The Ambiguous Case.

1 No solution: \(a < b \sin \alpha\)

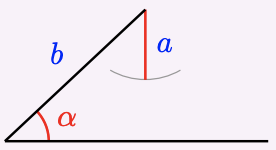
\(\alpha\) is too short to make a triangle.

2 One solution: \(a = b \sin \alpha\)

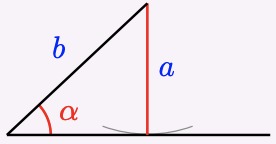
\(\alpha\) is exactly the right length to make a right triangle.

3 Two solutions: \(b \sin \alpha < a < b\)

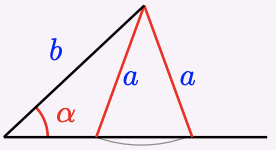
4 One solution: \(a > b\)

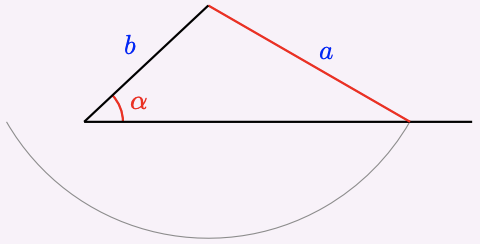
If \(\alpha\) is an obtuse angle, things are simpler: there is one solution if \(a>b\), and no solution if \(a \leq b\). Because there are always two angles with a given sine, if we use the Law of Sines for the ambiguous case, we must check whether both possible angles result in a triangle. But here is another approach: We can apply the Law of Cosines to find the third side first. With that method, we'll need the quadratic formula.

Quadratic Formula.

The solutions of the quadratic equation \(a x^2+b x+c=0, \quad a \neq 0\), are given by

\(x=\dfrac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)

A quadratic equation can have one solution, two solutions, or no solution, depending on the value of the discriminant , \(b^2-4 a c\). If we use the Law of Cosines to find a side in the ambiguous case, the quadratic formula will tell us how many triangles have the given properties.

• If the quadratic equation has one positive solutions, there is one triangle.
• If the quadratic equation has two positive solutions, there are two triangles.
• If the quadratic equation has no positive solutions, there is no triangle with the given properties.

Example 3.45

In \(\triangle A B C, B=14.4^{\circ}, a=8\), and \(b=3\). Solve the triangle.

We begin by finding the third side of the triangle. Using the Law of Cosines, we have

\begin{aligned} b^2 &= a^2 + c^2 - 2ac \cos B \quad \quad &&\text{Substitute the known values.} \\ 3^2 &= 8^2 + c^2 - 2(8)c\cos 14.4^{\circ} &&\text{Simplify.} \\ 9 &= 64 + c^2 - 16c(0.9686) &&\text{Write the quadratic equation in standard from.} \\ 0 &= c^2 - 15.497c + 55 &&\text{Apply the quadratic formula.} \end{aligned}

\begin{aligned} c &= \dfrac{15.497 \pm \sqrt{(-15.497)^2 - 4(1)(55)}}{2(1)} \quad \quad &&\text{Simplify.} \\ &= \dfrac{15.497 \pm 4.490}{2} = 5.503 \text{ or } 9.994 \end{aligned}

Because there are two positive solutions for side \(c\), either \(c=5.503\) or \(c=9.994\), there are two triangles with the given properties. We apply the Law of Cosines again to find angle \(C\) in each triangle.

For the triangle with \(c=5.503\), we have

\begin{aligned} c^2 &= a^2 + b^2 - 2ab\cos C \quad \quad &&\text{Substitute the known values.} \\ 5.503^2 &= 8^2 +3^2 - 2(8)(3)\cos C &&\text{Solve for }\cos C. \\ \cos C &= \dfrac{5.503^2 - 64 - 9}{-48} = 0.889876 \\ C &= \cos^{-1} 0.889876) = 27.1^{\circ} \end{aligned}

and \(A = 180^{\circ} − (14.4^{\circ} + 27.1^{\circ} ) = 138.5^{\circ}\).

For the triangle with \(c = 9.994\), we have

\begin{aligned} c^2 &= a^2 + b^2 - 2ab\cos C \quad \quad &&\text{Substitute the known values.} \\ 9.994^2 &= 8^2 + 3^2 - 2(8)(3)\cos C &&\text{Solve for }\cos C. \\ \cos C &= \dfrac{9.994^2 - 64 - 9}{-48} = -0.560027 \\ C &= \cos^{-1}(-0.560027) = 124.1^{\circ} \end{aligned}

and \(A = 180^{\circ} - (14.4^{\circ} + 124.1^{\circ}) = 41.5^{\circ}\). Both triangles are shown below.

Note 3.46 In the previous example, notice that we used the Law of Cosines instead of the Law of Sines to find a second angle in the triangle, because there is only one angle between \(0^{\circ}\) and \(180^{\circ}\) with a given cosine. We don't have to check the results, as we would if we used the Law of Sines.

Checkpoint 3.47

Use the Law of Cosines to find all triangles \(A B C\) with \(A=48^{\circ}, a=10\), and \(b=15\).

No Solution.

Even with the aid of GPS (Global Positioning System) instruments, aircraft pilots and ship captains need to understand navigation based on trigonometry.

Example 3.48

The sailing club leaves the marina on a heading \(15^{\circ}\) east of north and sails for 18 miles. They then change course, and after traveling for 12 miles on a heading \(35^{\circ}\) east of north, they experience engine trouble and radio for help. The marina sends a speed boat to rescue them. How far should the speed boat go, and on what heading?

We'd like to find the distance \(x\) and the angle \(\theta\) shown in the figure. In \(\triangle A B C\), we can calculate the angle at point \(B\) where the sailing club changed course:

\(B = 180^{\circ} - 35^{\circ} + 15^{\circ} = 160^{\circ}\)

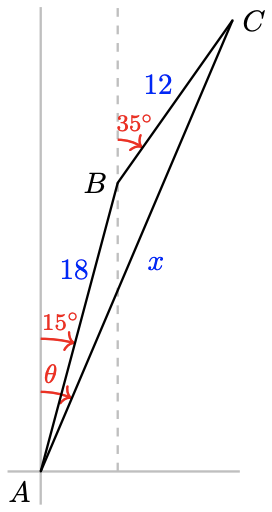
We know \(a = 12\) and \(c = 18\). We use the Law of Cosines to find \(b\) and \(\angle A\).

\begin{aligned} b^2 &= a^2 + c^2 - 2ac\cos B \quad \quad &&\text{Substitute the known values.} \\ &= 12^2 + 18^2 - 2(12)18\cos 160^{\circ} &&\text{Evaluate.} \\ &= 873.95 &&\text{Take positive square root.} \\ b&= 29.56 \end{aligned}

Next, we apply the Law of Cosines again to find \(\angle A\).

\begin{aligned} a^2 &=b^2+c^2-2 b c \cos A & & \text { Substitute the known values. } \\ 12^2 &=29.56^2+18^2-2(29.56)(18) \cos A & & \text { Solve for } \cos \boldsymbol{A} \\ \cos A &=\dfrac{12^2-29.56^2-18^2}{-2(29.56)(18)}=0.9903 & \\ C &=\cos ^{-1}(0.9903)=8^{\circ} & \end{aligned}

Thus, \(x=29.56\) and \(\theta=8^{\circ}+15^{\circ}=23^{\circ}\). The speed boat should travel \(29.56\) miles on a heading \(23^{\circ}\) east of north.

Checkpoint 3.49

Howard wants to fly from Anchorage to Nome, Alaska, a distance of 540 miles on a heading \(57^{\circ}\) west of north. After flying for some time, he discovers that his heading is in error, and he is actually flying \(47^{\circ}\) west of north. Howard corrects his flight plan and changes course when he is exactly 200 miles from Anchorage. What is his new heading, and how far is he from Nome?

\(62.8^{\circ}\) west of north, \(344.8\) miles

Which Law to Use

How can we decide which law, the Law of Sines or the Law of Cosines, is appropriate for a given problem?

• If we are solving a right triangle, we don’t need the Laws of Sines and Cosines; all we need are the definitions of the trigonometric ratios.
• But for oblique triangles, we can identify the following cases:

How to Solve an Oblique Triangle.

Note 3.50 In the ambiguous case, SSA, the Law of Sines is easier to apply, but there will be two possible angles, and we must check each angle to see if it produces a solution. Using the Law of Cosines involves solving a quadratic equation, but each positive solution of the equation yields a solution of the triangle.

Example 3.51

In the triangle at right, which law should you use to find \(\angle B\)? Which law should you use to find \(c\)?

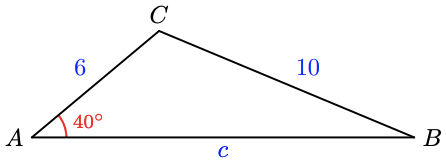
We know two sides of the triangle and the angle opposite one of them. We can use the Law of Sines to find \(\angle B\).

\begin{aligned} \dfrac{\sin B}{6} &=\dfrac{\sin 40^{\circ}}{10} \\ \sin B &=0.3857 \end{aligned}

This is the ambiguous case; there are two angles between \(0^{\circ}\) and \(180^{\circ}\) with sine \(0.3857\), and we must check each angle to see if it produces a solution.

If instead we start by finding side \(c\), we use the Law of Cosines.

\begin{aligned} 10^2 &=6^2+c^2-2(6) c \cos 40^{\circ} \\ c^2-\left(12 \cos 40^{\circ}\right) c-64 &=0 \\ c &=\dfrac{12 \cos 40^{\circ} \pm \sqrt{\left(-12 \cos 40^{\circ}\right)^2-4(1)(-64)}}{2(1)} \end{aligned}

You can check that the quadratic equation has only one positive solution for \(c\) (or notice that because \(a>b\), angle \(B\) must be acute).

Checkpoint 3.52

In the triangle at right, which part of the triangle can you find, and which law should you use?

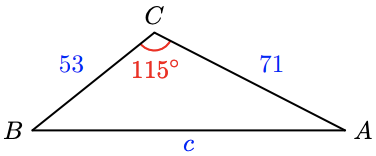
We first find side \(c\) using the Law of Cosines

Review the following skills you will need for this section.

Algebra Refresher 3.4

Solve each quadratic equation.

1 \(2.5x^2 + 6.2 = 816.2\)

2 \(0.8x^2 - 124 = 376\)

3 \(2x(2x-3) = 208\)

4 \(3x(x+5) = 900\)

5 \(2x^2 - 6x = 233.12\)

6 \(0.5x^2 + 1.5x = 464\)

1 \(\pm 8\)

2 \(\pm 25\)

3 \(8, -6.5\)

4 \(15, -20\)

5 \(12.4, -9.4\)

6 \(29, -32\)

Section 3.3 Summary

• Quadratic equation

• Quadratic formula

• Discriminant

1 The Law of Sines is not helpful when we know two sides of the triangle and the included angle. In this case we need the Law of Cosines.

2 If the angles of a triangle are \(A, B\), and \(C\), and the opposite sides are respectively \(a, b\), and \(c\), then

3 We can also use the Law of Cosines to find an angle when we know all three sides of a triangle.

4 We can use the Law of Cosines to solve the ambiguous case.

Study Questions

1 The Law of Cosines is really a generalization of what familiar theorem?

2 If you know all three sides of a triangle and one angle, what might be the advantage in using the Law of Cosines o find another angle, instead of the Law of Sines?

3 State the quadratic formula from memory. Try to sing the quadratic formula to the tune of ”Pop Goes the Weasel.”

4 Francine is solving a triangle in which \(a = 20, b = 16\), and \(A = 26^{\circ}\). She finds that \(\sin B = 0.3507\). How does she know that \(B = 20.5^{\circ}\), and not \(159.5^{\circ}\)?

1 Use the Law of Cosines to find the side opposite an angle #7-12

2 Use the Law of Cosines to find an angle #13-20

3 Use the Law of Cosines to find a side adjacent to an angle #21-26

4 Decide which law to use #27-34

5 Solve a triangle #35-42

6 Solve problems using the Law of Cosines #43-56

Homework 3.3

a Simplify \(5^2+7^2-2(5)(7) \cos \theta\) b Evaluate the expression in part (a) for \(\theta=29^{\circ}\) c Evaluate the expression in part (a) for \(\theta=151^{\circ}\)

a Simplify \(26.1^2+32.5^2-2(26.1)(32.5) \cos \phi\) b Evaluate the expression in part (a) for \(\phi=64^{\circ}\) c Evaluate the expression in part (a) for \(\phi=116^{\circ}\)

a Solve \(b^2=a^2+c^2-2 a c \cos \beta\) for \(\cos \beta\) b For the equation in part (a), find \(\cos \beta\) if \(a=5, b=11\), and \(c=8\).

a Solve \(a^2=b^2+c^2-2 b c \cos \alpha\) for \(\cos \alpha\) b For the equation in part (a), find \(\cos \alpha\) if \(a=4.6, b=7.2\), and \(c=9.4\).

a The equation \(9^2=b^2+4^2-2 b(4) \cos \alpha\) is quadratic in \(b\). Write the equation in standard form. b Solve the equation in part (a) for \(b\) if \(\alpha=48^{\circ}\).

a The equation \(5^2=6^2+c^2-2(5) c \cos \beta\) is quadratic in \(c\)

b Solve the equation in part (a) for \(c\) if \(\beta = 126^{\circ}.

For Problems 7–12, use the Law of Cosines to find the indicated side. Round to two decimal places.

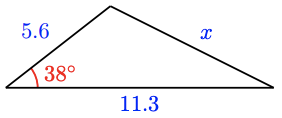
For Problems 13–16,use the Law of Cosines to find the indicated angle. Round to two decimal places.

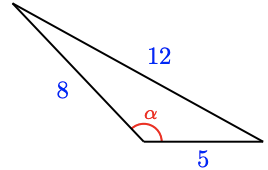
For Problems 17–20, find the angles of the triangle. Round answers to two decimal places.

17. \(a = 23, b = 14, c = 18\)

18. \(a = 18, b = 25, c = 19\)

19. \(a = 16.3, b = 28.1, c = 19.4\)

20. \(a = 82.3, b = 22.5, c = 66.8\)

For Problems 21–26, use the Law of Cosines to find the unknown side. Round your answers to two decimal places.

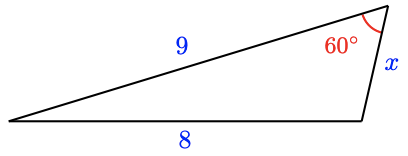
For Problems 27–34, which law should you use to find the labeled unknown value, the Law of Sines or the Law of Cosines? Write an equation you can solve to find the unknown value. For Problems 31-34, you may need two steps to find the unknown value.

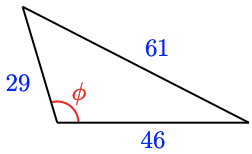
For Problems 35–42,

a Sketch and label the triangle.

b Solve the triangle. Round answers to two decimal places.

35. \(B = 47^{\circ} , a = 23, c = 17\)

36. \(C = 32^{\circ} , a = 14, b = 18\)

37. \(a = 8, b = 7, c = 9\)

38. \(a = 23, b = 34, c = 45\)

39. \(b = 72, c = 98, B = 38^{\circ}\)

40. \(a = 28, c = 41, A = 27^{\circ}\)

41. \(c = 5.7, A = 59^{\circ} , B = 82^{\circ}\)

42. \(b = 82, A = 11^{\circ}, C = 42^{\circ}\)

a Sketch and label a triangle to illustrate the problem.

b Solve the problem. Round answers to one decimal place.

43. A surveyor would like to know the distance \(P Q\) across a small lake, as shown in the figure. She stands at point \(O\) and measures the angle between the lines of sight to points \(P\) and \(Q\) at \(76^{\circ}\). She also finds \(OP = 1400\) meters and \(OQ = 600\) meters. Calculate the distance \(P Q\).

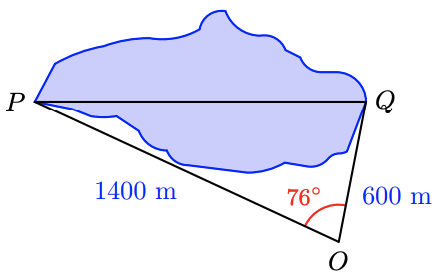
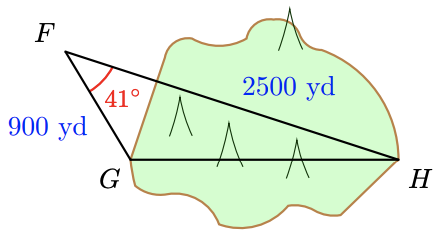
44. Highway engineers plan to drill a tunnel through Boney Mountain from \(G\) to \(H\), as shown in the figure. The angle at point \(F\) is \(41^{\circ}\), and the distances to \(G\) and \(H\) are \(900\) yards and \(2500\) yards, respectively. How long will the tunnel be?

45. Two pilots leave an airport at the same time. One pilot flies \(3^{\circ}\) east of north at a speed of \(320\) miles per hour, the other flies \(157^{\circ}\) east of north at a speed of \(406\) miles per hour. How far apart are the two pilots after \(3\) hours? What is the heading from the first plane to the second plane at that time?

46. Two boats leave port at the same time. One boat sails due west at a speed of \(17\) miles per hour, the other powers \(42^{\circ}\) east of north at a speed of \(23\) miles per hour. How far apart are the two boats after \(2\) hours? What is the heading from the first boat to the second boat at that time?

46. Two boats leave port at the same time. One boat sails due west at a speed of 17 miles per hour, the other powers \(42^{\circ}\) east of north at a speed of 23 miles per hour. How far apart are the two boats after 2 hours? What is the heading from the first boat to the second boat at that time?

47. Caroline wants to fly directly south from Indianapolis to Cancun, Mexico, a distance of 1290 miles. However, to avoid bad weather, she flies for 400 miles on a heading \(18^{\circ}\) east of south. What is the heading to Cancun from that location, and how far is it?

48. Alex sails 8 miles from Key West, Florida on a heading \(40^{\circ}\) east of south. He then changes course and sails for 10 miles due east. What is the heading back to Key West from that point, and how far is it?

49. The phone company wants to erect a cell tower on a steep hill inclined \(26^{\circ}\) to the horizontal. The installation crew plans to run a guy wire from a point on the ground 20 feet uphill from the base of the tower and attach it to the tower at a height of 100 feet. How long should the guy wire be?

50. Sandstone Peak rises 3500 above the desert. The Park Service plans to run an aerial tramway up the north face, which is inclined at an angle of \(68^{\circ}\) to the horizontal. The base station will be located 500 feet from the foot of Sandstone Peak. Ignoring any slack in the cable, how long should it be?

51. The sides of a triangle are 27 cm, 15 cm, and 20 cm. Find the area of the triangle. (Hint: Find one of the angles first.)

52. The sides of a parallelogram are 10 inches and 8 inches, and form an angle of \(130^{\circ}\). Find the lengths of the diagonals of the parallelogram.

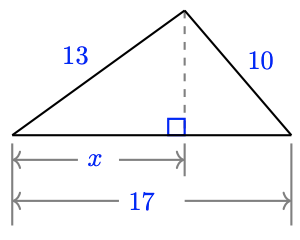
For Problems 53–56, find x, the distance from one vertex to the foot of the altitude.

Problems 57 and 58 prove the Law of Cosines.

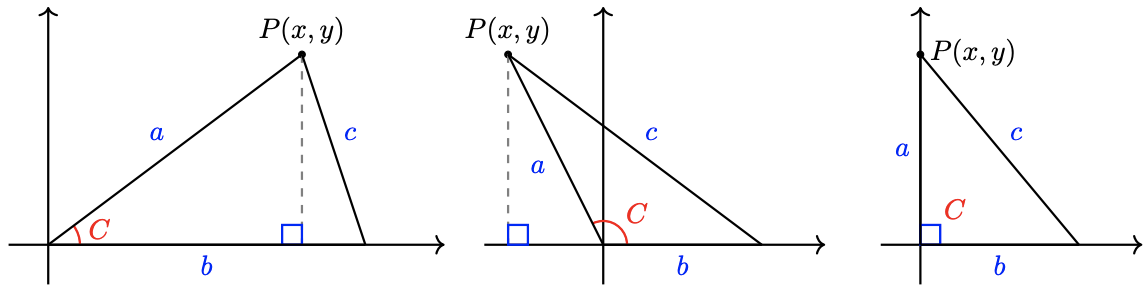
a Copy the three figures above showing the three possibilities for an angle \(C\) in a triangle: \(C\) is acute, obtuse, or a right angle. For each figure, explain why it is true that \(c^2=(b-x)^2+y^2\), then rewrite the right side to get \(c^2=\left(x^2+y^2\right)+b^2-2 b x\).

b For each figure, explain why it is true that \(x^2+y^2=a^2\).

c For all three figures, \(a\) is the distance from the origin to the point \((x, y)\). Use the definition of cosine to write \(\cos C\) in terms of \(a\) and \(x\), then solve your equation for \(x\).

d Start with the last equation from (a), and substitute expressions from (b) and (c) to conclude one case of the Law of Cosines.

58. Demonstrate the other two cases of the Law of Cosines:

• \(a^2=b^2+c^2-2 b c \cos A\)
• \(b^2=a^2+c^2-2 a c \cos B\)

(Hint: See Problem 57 and switch the roles of \(a\) and \(c\), etc.)

59. Use the Law of Cosines to prove the projection laws:

\begin{aligned} a &=b \cos C+c \cos B \\ b &=c \cos A+a \cos C \\ c &=a \cos B+b \cos A \end{aligned}

Illustrate with a sketch. (Hint: Add together two of the versions of the Law of Cosines.)

60. If \(\triangle A B C\) is isosceles with \(a=b\), show that \(c^2=2 a^2(1-\cos C)\).

61. Use the Law of Cosines to prove:

\begin{aligned} 1+\cos A &=\dfrac{(a+b+c)(-a+b+C)}{2 b c} \\ 1-\cos A &=\dfrac{(a-b+c)(-a+b+C)}{2 b c} \end{aligned}

62. Prove that

\(\dfrac{\cos A}{a}+\dfrac{\cos B}{b}+\dfrac{\cos C}{c}=\dfrac{a^2+b^2+c^2}{2 a b c}\)

8.1 Graphs of the Sine and Cosine Functions

1 2 1 2 compressed

π 2 ; π 2 ; right

midline: y = 0 ; y = 0 ; amplitude: | A | = 1 2 ; | A | = 1 2 ; period: P = 2 π | B | = 6 π ; P = 2 π | B | = 6 π ; phase shift: C B = π C B = π

f ( x ) = sin ( x ) + 2 f ( x ) = sin ( x ) + 2

two possibilities: y = 4 sin ( π 5 x − π 5 ) + 4 y = 4 sin ( π 5 x − π 5 ) + 4 or y = − 4 sin ( π 5 x + 4 π 5 ) + 4 y = − 4 sin ( π 5 x + 4 π 5 ) + 4

midline: y = 0 ; y = 0 ; amplitude: | A | = 0.8 ; | A | = 0.8 ; period: P = 2 π | B | = π ; P = 2 π | B | = π ; phase shift: C B = 0 C B = 0 or none

midline: y = 0 ; y = 0 ; amplitude: | A | = 2 ; | A | = 2 ; period: P = 2 π | B | = 6 ; P = 2 π | B | = 6 ; phase shift: C B = − 1 2 C B = − 1 2

y = 3 cos ( x ) − 4 y = 3 cos ( x ) − 4

8.2 Graphs of the Other Trigonometric Functions

It would be reflected across the line y = − 1 , y = − 1 , becoming an increasing function.

g ( x ) = 4 tan ( 2 x ) g ( x ) = 4 tan ( 2 x )

This is a vertical reflection of the preceding graph because A A is negative.

8.3 Inverse Trigonometric Functions

arccos ( 0.8776 ) ≈ 0.5 arccos ( 0.8776 ) ≈ 0.5

• ⓐ − π 2 ; − π 2 ;
• ⓑ − π 4 ; − π 4 ;

1.9823 or 113.578°

sin −1 ( 0.6 ) = 36.87° = 0.6435 sin −1 ( 0.6 ) = 36.87° = 0.6435 radians

π 8 ; 2 π 9 π 8 ; 2 π 9

3 π 4 3 π 4

12 13 12 13

4 2 9 4 2 9

4 x 16 x 2 + 1 4 x 16 x 2 + 1

8.1 Section Exercises

The sine and cosine functions have the property that f ( x + P ) = f ( x ) f ( x + P ) = f ( x ) for a certain P . P . This means that the function values repeat for every P P units on the x -axis.

The absolute value of the constant A A (amplitude) increases the total range and the constant D D (vertical shift) shifts the graph vertically.

At the point where the terminal side of t t intersects the unit circle, you can determine that the sin t sin t equals the y -coordinate of the point.

amplitude: 2 3 ; 2 3 ; period: 2 π ; 2 π ; midline: y = 0 ; y = 0 ; maximum: y = 2 3 y = 2 3 occurs at x = 0 ; x = 0 ; minimum: y = − 2 3 y = − 2 3 occurs at x = π ; x = π ; for one period, the graph starts at 0 and ends at 2 π 2 π

amplitude: 4; period: 2 π ; 2 π ; midline: y = 0 ; y = 0 ; maximum y = 4 y = 4 occurs at x = π 2 ; x = π 2 ; minimum: y = − 4 y = − 4 occurs at x = 3 π 2 ; x = 3 π 2 ; one full period occurs from x = 0 x = 0 to x = 2 π x = 2 π

amplitude: 1; period: π ; π ; midline: y = 0 ; y = 0 ; maximum: y = 1 y = 1 occurs at x = π ; x = π ; minimum: y = − 1 y = − 1 occurs at x = π 2 ; x = π 2 ; one full period is graphed from x = 0 x = 0 to x = π x = π

amplitude: 4; period: 2; midline: y = 0 ; y = 0 ; maximum: y = 4 y = 4 occurs at x = 0 ; x = 0 ; minimum: y = − 4 y = − 4 occurs at x = 1 x = 1

amplitude: 3; period: π 4 ; π 4 ; midline: y = 5 ; y = 5 ; maximum: y = 8 y = 8 occurs at x = 0.12 ; x = 0.12 ; minimum: y = 2 y = 2 occurs at x = 0.516 ; x = 0.516 ; horizontal shift: − 4 ; − 4 ; vertical translation 5; one period occurs from x = 0 x = 0 to x = π 4 x = π 4

amplitude: 5; period: 2 π 5 ; 2 π 5 ; midline: y = −2 ; y = −2 ; maximum: y = 3 y = 3 occurs at x = 0.08 ; x = 0.08 ; minimum: y = −7 y = −7 occurs at x = 0.71; x = 0.71; phase shift: −4 ; −4 ; vertical translation: −2; −2; one full period can be graphed on x = 0 x = 0 to x = 2 π 5 x = 2 π 5

amplitude: 1 ; period: 2 π ; 2 π ; midline: y = 1 ; y = 1 ; maximum: y = 2 y = 2 occurs at x = 2.09 ; x = 2.09 ; maximum: y = 2 y = 2 occurs at t = 2.09 ; t = 2.09 ; minimum: y = 0 y = 0 occurs at t = 5.24 ; t = 5.24 ; phase shift: − π 3 ; − π 3 ; vertical translation: 1; one full period is from t = 0 t = 0 to t = 2 π t = 2 π

amplitude: 1; period: 4 π ; 4 π ; midline: y = 0 ; y = 0 ; maximum: y = 1 y = 1 occurs at t = 11.52 ; t = 11.52 ; minimum: y = − 1 y = − 1 occurs at t = 5.24 ; t = 5.24 ; phase shift: − 10 π 3 ; − 10 π 3 ; vertical shift: 0

amplitude: 2; midline: y = − 3 ; y = − 3 ; period: 4; equation: f ( x ) = 2 sin ( π 2 x ) − 3 f ( x ) = 2 sin ( π 2 x ) − 3

amplitude: 2; period: 5; midline: y = 3 ; y = 3 ; equation: f ( x ) = − 2 cos ( 2 π 5 x ) + 3 f ( x ) = − 2 cos ( 2 π 5 x ) + 3

amplitude: 4; period: 2; midline: y = 0 ; y = 0 ; equation: f ( x ) = − 4 cos ( π ( x − π 2 ) ) f ( x ) = − 4 cos ( π ( x − π 2 ) )

amplitude: 2; period: 2; midline y = 1 ; y = 1 ; equation: f ( x ) = 2 cos ( π x ) + 1 f ( x ) = 2 cos ( π x ) + 1

0 , π 0 , π

sin ( π 2 ) = 1 sin ( π 2 ) = 1

f ( x ) = sin x f ( x ) = sin x is symmetric

π 3 , 5 π 3 π 3 , 5 π 3

Maximum: 1 1 at x = 0 x = 0 ; minimum: -1 -1 at x = π x = π

A linear function is added to a periodic sine function. The graph does not have an amplitude because as the linear function increases without bound the combined function h ( x ) = x + sin x h ( x ) = x + sin x will increase without bound as well. The graph is bounded between the graphs of y = x + 1 y = x + 1 and y = x - 1 y = x - 1 because sine oscillates between −1 and 1.

There is no amplitude because the function is not bounded.

The graph is symmetric with respect to the y-axis and there is no amplitude because the function’s bounds decrease as | x | | x | grows. There appears to be a horizontal asymptote at y = 0 y = 0 .

8.2 Section Exercises

Since y = csc x y = csc x is the reciprocal function of y = sin x , y = sin x , you can plot the reciprocal of the coordinates on the graph of y = sin x y = sin x to obtain the y -coordinates of y = csc x . y = csc x . The x -intercepts of the graph y = sin x y = sin x are the vertical asymptotes for the graph of y = csc x . y = csc x .

Answers will vary. Using the unit circle, one can show that tan ( x + π ) = tan x . tan ( x + π ) = tan x .

The period is the same: 2 π . 2 π .

period: 8; horizontal shift: 1 unit to left

− cot x cos x − sin x − cot x cos x − sin x

stretching factor: 2; period: π 4 ; π 4 ; asymptotes: x = 1 4 ( π 2 + π k ) + 8 ,  where  k  is an integer x = 1 4 ( π 2 + π k ) + 8 ,  where  k  is an integer

stretching factor: 6; period: 6; asymptotes: x = 3 k ,  where  k  is an integer x = 3 k ,  where  k  is an integer

stretching factor: 1; period: π ; π ; asymptotes: x = π k ,  where  k  is an integer x = π k ,  where  k  is an integer

Stretching factor: 1; period: π ; π ; asymptotes: x = π 4 + π k ,  where  k  is an integer x = π 4 + π k ,  where  k  is an integer

stretching factor: 2; period: 2 π ; 2 π ; asymptotes: x = π k ,  where  k  is an integer x = π k ,  where  k  is an integer

stretching factor: 4; period: 2 π 3 ; 2 π 3 ; asymptotes: x = π 6 k ,  where  k  is an odd integer x = π 6 k ,  where  k  is an odd integer

stretching factor: 7; period: 2 π 5 ; 2 π 5 ; asymptotes: x = π 10 k ,  where  k  is an odd integer x = π 10 k ,  where  k  is an odd integer

stretching factor: 2; period: 2 π ; 2 π ; asymptotes: x = − π 4 + π k ,  where  k  is an integer x = − π 4 + π k ,  where  k  is an integer

stretching factor: 7 5 ; 7 5 ; period: 2 π ; 2 π ; asymptotes: x = π 4 + π k ,  where  k  is an integer x = π 4 + π k ,  where  k  is an integer

y = tan ( 3 ( x − π 4 ) ) + 2 y = tan ( 3 ( x − π 4 ) ) + 2

f ( x ) = csc ( 2 x ) f ( x ) = csc ( 2 x )

f ( x ) = csc ( 4 x ) f ( x ) = csc ( 4 x )

f ( x ) = 2 csc x f ( x ) = 2 csc x

f ( x ) = 1 2 tan ( 100 π x ) f ( x ) = 1 2 tan ( 100 π x )

• ⓐ ( − π 2 , π 2 ) ; ( − π 2 , π 2 ) ;
• ⓒ x = − π 2 x = − π 2 and x = π 2 ; x = π 2 ; the distance grows without bound as | x | | x | approaches π 2 π 2 —i.e., at right angles to the line representing due north, the boat would be so far away, the fisherman could not see it;
• ⓓ 3; when x = − π 3 , x = − π 3 , the boat is 3 km away;
• ⓔ 1.73; when x = π 6 , x = π 6 , the boat is about 1.73 km away;
• ⓕ 1.5 km; when x = 0 x = 0
• ⓐ h ( x ) = 2 tan ( π 120 x ) ; h ( x ) = 2 tan ( π 120 x ) ;
• ⓒ h ( 0 ) = 0 : h ( 0 ) = 0 : after 0 seconds, the rocket is 0 mi above the ground; h ( 30 ) = 2 : h ( 30 ) = 2 : after 30 seconds, the rockets is 2 mi high;
• ⓓ As x x approaches 60 seconds, the values of h ( x ) h ( x ) grow increasingly large. The distance to the rocket is growing so large that the camera can no longer track it.

8.3 Section Exercises

The function y = sin x y = sin x is one-to-one on [ − π 2 , π 2 ] ; [ − π 2 , π 2 ] ; thus, this interval is the range of the inverse function of y = sin x , y = sin x , f ( x ) = sin − 1 x . f ( x ) = sin − 1 x . The function y = cos x y = cos x is one-to-one on [ 0 , π ] ; [ 0 , π ] ; thus, this interval is the range of the inverse function of y = cos x , f ( x ) = cos − 1 x . y = cos x , f ( x ) = cos − 1 x .

π 6 π 6 is the radian measure of an angle between − π 2 − π 2 and π 2 π 2 whose sine is 0.5.

In order for any function to have an inverse, the function must be one-to-one and must pass the horizontal line test. The regular sine function is not one-to-one unless its domain is restricted in some way. Mathematicians have agreed to restrict the sine function to the interval [ − π 2 , π 2 ] [ − π 2 , π 2 ] so that it is one-to-one and possesses an inverse.

True . The angle, θ 1 θ 1 that equals arccos ( − x ) arccos ( − x ) , x > 0 x > 0 , will be a second quadrant angle with reference angle, θ 2 θ 2 , where θ 2 θ 2 equals arccos x arccos x , x > 0 x > 0 . Since θ 2 θ 2 is the reference angle for θ 1 θ 1 , θ 2 = π − θ 1 θ 2 = π − θ 1 and arccos ( − x ) arccos ( − x ) = π − arccos x π − arccos x -

− π 6 − π 6

− π 3 − π 3

0.56 radians

− π 4 − π 4

x − 1 − x 2 + 2 x x − 1 − x 2 + 2 x

x 2 − 1 x x 2 − 1 x

x + 0.5 − x 2 − x + 3 4 x + 0.5 − x 2 − x + 3 4

2 x + 1 x + 1 2 x + 1 x + 1

2 x + 1 x 2 x + 1 x

domain [ − 1 , 1 ] ; [ − 1 , 1 ] ; range [ 0 , π ] [ 0 , π ]

approximately x = 0.00 x = 0.00

0.395 radians

1.11 radians

1.25 radians

0.405 radians

No. The angle the ladder makes with the horizontal is 60 degrees.

Review Exercises

amplitude: 3; period: 2 π ; 2 π ; midline: y = 3 ; y = 3 ; no asymptotes

amplitude: 3; period: 2 π ; 2 π ; midline: y = 0 ; y = 0 ; no asymptotes

amplitude: 3; period: 2 π ; 2 π ; midline: y = − 4 ; y = − 4 ; no asymptotes

amplitude: 6; period: 2 π 3 ; 2 π 3 ; midline: y = − 1 ; y = − 1 ; no asymptotes

stretching factor: none; period: π ; π ; midline: y = − 4 ; y = − 4 ; asymptotes: x = π 2 + π k , x = π 2 + π k , where k k is an integer

stretching factor: 3; period: π 4 ; π 4 ; midline: y = − 2 ; y = − 2 ; asymptotes: x = π 8 + π 4 k , x = π 8 + π 4 k , where k k is an integer

amplitude: none; period: 2 π ; 2 π ; no phase shift; asymptotes: x = π 2 k , x = π 2 k , where k k is an odd integer

amplitude: none; period: 2 π 5 ; 2 π 5 ; no phase shift; asymptotes: x = π 5 k , x = π 5 k , where k k is an integer

amplitude: none; period: 4 π ; 4 π ; no phase shift; asymptotes: x = 2 π k , x = 2 π k , where k k is an integer

largest: 20,000; smallest: 4,000

amplitude: 8,000; period: 10; phase shift: 0

In 2007, the predicted population is 4,413. In 2010, the population will be 11,924.

No solution

The graphs are not symmetrical with respect to the line y = x . y = x . They are symmetrical with respect to the y y -axis.

The graphs appear to be identical.

Practice Test

amplitude: 0.5; period: 2 π ; 2 π ; midline y = 0 y = 0

amplitude: 5; period: 2 π ; 2 π ; midline: y = 0 y = 0

amplitude: 1; period: 2 π ; 2 π ; midline: y = 1 y = 1

amplitude: 3; period: 6 π ; 6 π ; midline: y = 0 y = 0

amplitude: none; period: π ; π ; midline: y = 0 , y = 0 , asymptotes: x = 2 π 3 + π k , x = 2 π 3 + π k , where k k is an integer

amplitude: none; period: 2 π 3 ; 2 π 3 ; midline: y = 0 , y = 0 , asymptotes: x = π 3 k , x = π 3 k , where k k is an integer

amplitude: none; period: 2 π ; 2 π ; midline: y = − 3 y = − 3

amplitude: 2; period: 2; midline: y = 0 ; y = 0 ; f ( x ) = 2 sin ( π ( x − 1 ) ) f ( x ) = 2 sin ( π ( x − 1 ) )

amplitude: 1; period: 12; phase shift: −6 ; −6 ; midline y = −3 y = −3

D ( t ) = 68 − 12 sin ( π 12 x ) D ( t ) = 68 − 12 sin ( π 12 x )

period: π 6 ; π 6 ; horizontal shift: −7 −7

f ( x ) = sec ( π x ) ; f ( x ) = sec ( π x ) ; period: 2; phase shift: 0

The views are different because the period of the wave is 1 25 . 1 25 . Over a bigger domain, there will be more cycles of the graph.

On the approximate intervals ( 0.5 , 1 ) , ( 1.6 , 2.1 ) , ( 2.6 , 3.1 ) , ( 3.7 , 4.2 ) , ( 4.7 , 5.2 ) , ( 5.6 , 6.28 ) ( 0.5 , 1 ) , ( 1.6 , 2.1 ) , ( 2.6 , 3.1 ) , ( 3.7 , 4.2 ) , ( 4.7 , 5.2 ) , ( 5.6 , 6.28 )

f ( x ) = 2 cos ( 12 ( x + π 4 ) ) + 3 f ( x ) = 2 cos ( 12 ( x + π 4 ) ) + 3

This graph is periodic with a period of 2 π . 2 π .

1 − ( 1 − 2 x ) 2 1 − ( 1 − 2 x ) 2

1 1 + x 4 1 1 + x 4

x + 1 x x + 1 x

approximately 0.07 radians

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/algebra-and-trigonometry/pages/1-introduction-to-prerequisites

• Authors: Jay Abramson
• Publisher/website: OpenStax
• Book title: Algebra and Trigonometry
• Publication date: Feb 13, 2015
• Location: Houston, Texas
• Book URL: https://openstax.org/books/algebra-and-trigonometry/pages/1-introduction-to-prerequisites
• Section URL: https://openstax.org/books/algebra-and-trigonometry/pages/chapter-8

© Dec 8, 2021 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• Skip to main content

PAYMENT PLANS ARE NOW AVAILABLE • VISIT THE SHOP TO LEARN MORE!

All Things Algebra®

Pre-Calculus Unit 5: Trigonometric Functions

This unit includes 93 pages of guided notes, homework assignments, four quizzes, a study guide, and a unit test that cover the topics listed in the description below.

• Description
• Additional Information
• What Educators Are Saying

This unit contains the following topics:

• Angles in Standard Position • Degrees and Radians • Coterminal Angles • Degree-Minute-Second (DMS) Form • Arc Lengths • Area of Sectors • Circular Motion: Linear Speed and Angular Speed • Six Trigonometric Functions (Sine, Cosine, Tangent, Cosecant, Secant, Cotangent) • Trigonometric Functions Values in Special Right Triangles • Finding Sides and Angles in Right Triangles • Solving Right Triangles • Right Triangle Applications (Angle of Elevation and Angle of Depression) • Trigonometric Functions of Angle Angle • Reference Angles • The Unit Circle • Law of Sines • Law of Cosines • Applications of Law of Sines and Law of Cosines • Area of Triangles and Heron’s Formula • Graphing Sine, Cosine, and Tangent Functions • Translating Trigonometric Functions (Vertical and Horizontal Phase Shifts) • Graphing Reciprocal Functions (with and without translations) • Evaluating Inverse Trigonometric Functions • Graphing Inverse Trigonometric Functions • Compositions of Trigonometric Functions

This unit does not contain activities.

This is the guided notes, homework assignments, quizzes, study guide, and unit test only.  For suggested activities to go with this unit, check out the ATA Activity Alignment Guides .

This resource is included in the following bundle(s):

Pre-Calculus Curriculum

License Terms:

This purchase includes a single non-transferable license, meaning it is for one teacher only for personal use in their classroom and can not be passed from one teacher to another.  No part of this resource is to be shared with colleagues or used by an entire grade level, school, or district without purchasing the proper number of licenses.  A t ransferable license is not available for this resource.

Copyright Terms:

No part of this resource may be uploaded to the internet in any form, including classroom/personal websites or network drives, unless the site is password protected and can only be accessed by students.

What standards is this curriculum aligned to?

What format are the files in, will i have access to materials if they are updated, are answer keys included, are videos included.

Excellent Resource as always! Students understand the material, are engaged, and retain the information for a long time. Logically presented and easy to follow!

Excellent resource! Very helpful in filling in the gaps - a lifesaver for me, saving me hours of writing my own!!

I love using Gina Wilson's materials. They are easy for my students to follow, and I like that they are designed with the Cornell Notetaking method in mind. It allows for the teacher to decide if more practice is needed after teaching the concepts.

Law of Sines Worksheet

Students will practice applying the law of sines to calculate side lengths and angle measurements. This worksheet includes word problems as well as challenging bonus problems.

Example Questions

Visual Aids

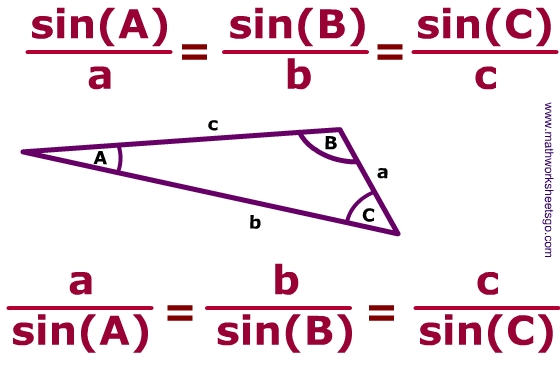
Other Details

This is a 5 part worksheet:

• Part I Model Problems
• Part II Practice Problems (1-6)
• Part III Practice (harder) & Word Problems (7 - 18)
• Part IV Challenge Problems
• Part V Answer Key
• Pictures of Law of Sines (triangles, formula and more..)
• Law of Sines and Cosines Worksheets

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!

Popular pages @ mathwarehouse.com.