what is hypothesis population mean

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

10.26: Hypothesis Test for a Population Mean (5 of 5)

• Last updated
• Save as PDF
• Page ID 14164

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Interpret the P-value as a conditional probability.

We finish our discussion of the hypothesis test for a population mean with a review of the meaning of the P-value, along with a review of type I and type II errors.

Review of the Meaning of the P-value

At this point, we assume you know how to use a P-value to make a decision in a hypothesis test. The logic is always the same. If we pick a level of significance (α), then we compare the P-value to α.

• If the P-value ≤ α, reject the null hypothesis. The data supports the alternative hypothesis.
• If the P-value > α, do not reject the null hypothesis. The data is not strong enough to support the alternative hypothesis.

In fact, we find that we treat these as “rules” and apply them without thinking about what the P-value means. So let’s pause here and review the meaning of the P-value, since it is the connection between probability and decision-making in inference.

Birth Weights in a Town

Let’s return to the familiar context of birth weights for babies in a town. Suppose that babies in the town had a mean birth weight of 3,500 grams in 2010. This year, a random sample of 50 babies has a mean weight of about 3,400 grams with a standard deviation of about 500 grams. Here is the distribution of birth weights in the sample.

Obviously, this sample weighs less on average than the population of babies in the town in 2010. A decrease in the town’s mean birth weight could indicate a decline in overall health of the town. But does this sample give strong evidence that the town’s mean birth weight is less than 3,500 grams this year?

We now know how to answer this question with a hypothesis test. Let’s use a significance level of 5%.

Let μ = mean birth weight in the town this year. The null hypothesis says there is “no change from 2010.”

• H 0 : μ < 3,500
• H a : μ = 3,500

Since the sample is large, we can conduct the T-test (without worrying about the shape of the distribution of birth weights for individual babies.)

Statistical software tells us the P-value is 0.082 = 8.2%. Since the P-value is greater than 0.05, we fail to reject the null hypothesis.

Our conclusion: This sample does not suggest that the mean birth weight this year is less than 3,500 grams ( P -value = 0.082). The sample from this year has a mean of 3,400 grams, which is 100 grams lower than the mean in 2010. But this difference is not statistically significant. It can be explained by the chance fluctuation we expect to see in random sampling.

What Does the P-Value of 0.082 Tell Us?

A simulation can help us understand the P-value. In a simulation, we assume that the population mean is 3,500 grams. This is the null hypothesis. We assume the null hypothesis is true and select 1,000 random samples from a population with a mean of 3,500 grams. The mean of the sampling distribution is at 3,500 (as predicted by the null hypothesis.) We see this in the simulated sampling distribution.

In the simulation, we can see that about 8.6% of the samples have a mean less than 3,400. Since probability is the relative frequency of an event in the long run, we say there is an 8.6% chance that a random sample of 500 babies has a mean less than 3,400 if the population mean is 3,500. We can see that the corresponding area to the left of T = −1.41 in the T-model (with df = 49) also gives us a good estimate of the probability. This area is the P-value, about 8.2%.

If we generalize this statement, we say the P-value is the probability that random samples have results more extreme than the data if the null hypothesis is true. (By more extreme, we mean further from value of the parameter, in the direction of the alternative hypothesis.) We can also describe the P-value in terms of T-scores. The P-value is the probability that the test statistic from a random sample has a value more extreme than that associated with the data if the null hypothesis is true.

What Does a P-Value Mean?

Do women who smoke run the risk of shorter pregnancy and premature birth? The mean pregnancy length is 266 days. We test the following hypotheses.

• H 0 : μ = 266
• H a : μ < 266

Suppose a random sample of 40 women who smoke during their pregnancy have a mean pregnancy length of 260 days with a standard deviation of 21 days. The P-value is 0.04.

What probability does the P-value of 0.04 describe? Label each of the following interpretations as valid or invalid.

https://assessments.lumenlearning.co...sessments/3654

https://assessments.lumenlearning.co...sessments/3655

https://assessments.lumenlearning.co...sessments/3656

Review of Type I and Type II Errors

We know that statistical inference is based on probability, so there is always some chance of making a wrong decision. Recall that there are two types of wrong decisions that can be made in hypothesis testing. When we reject a null hypothesis that is true, we commit a type I error. When we fail to reject a null hypothesis that is false, we commit a type II error.

The following table summarizes the logic behind type I and type II errors.

It is possible to have some influence over the likelihoods of committing these errors. But decreasing the chance of a type I error increases the chance of a type II error. We have to decide which error is more serious for a given situation. Sometimes a type I error is more serious. Other times a type II error is more serious. Sometimes neither is serious.

Recall that if the null hypothesis is true, the probability of committing a type I error is α. Why is this? Well, when we choose a level of significance (α), we are choosing a benchmark for rejecting the null hypothesis. If the null hypothesis is true, then the probability that we will reject a true null hypothesis is α. So the smaller α is, the smaller the probability of a type I error.

It is more complicated to calculate the probability of a type II error. The best way to reduce the probability of a type II error is to increase the sample size. But once the sample size is set, larger values of α will decrease the probability of a type II error (while increasing the probability of a type I error).

General Guidelines for Choosing a Level of Significance

• If the consequences of a type I error are more serious, choose a small level of significance (α).
• If the consequences of a type II error are more serious, choose a larger level of significance (α). But remember that the level of significance is the probability of committing a type I error.
• In general, we pick the largest level of significance that we can tolerate as the chance of a type I error.

Let’s return to the investigation of the impact of smoking on pregnancy length.

Recap of the hypothesis test: The mean human pregnancy length is 266 days. We test the following hypotheses.

https://assessments.lumenlearning.co...sessments/3778

https://assessments.lumenlearning.co...sessments/3779

https://assessments.lumenlearning.co...sessments/3780

Let’s Summarize

In this “Hypothesis Test for a Population Mean,” we looked at the four steps of a hypothesis test as they relate to a claim about a population mean.

Step 1: Determine the hypotheses.

• The hypotheses are claims about the population mean, µ.
• The null hypothesis is a hypothesis that the mean equals a specific value, µ 0 .

Step 2: Collect the data.

Since the hypothesis test is based on probability, random selection or assignment is essential in data production. Additionally, we need to check whether the t-model is a good fit for the sampling distribution of sample means. To use the t-model, the variable must be normally distributed in the population or the sample size must be more than 30. In practice, it is often impossible to verify that the variable is normally distributed in the population. If this is the case and the sample size is not more than 30, researchers often use the t-model if the sample is not strongly skewed and does not have outliers.

Step 3: Assess the evidence.

• If a t-model is appropriate, determine the t-test statistic for the data’s sample mean.
• Use the test statistic, together with the alternative hypothesis, to determine the P-value.
• The P-value is the probability of finding a random sample with a mean at least as extreme as our sample mean, assuming that the null hypothesis is true.
• As in all hypothesis tests, if the alternative hypothesis is greater than, the P-value is the area to the right of the test statistic. If the alternative hypothesis is less than, the P-value is the area to the left of the test statistic. If the alternative hypothesis is not equal to, the P-value is equal to double the tail area beyond the test statistic.

Step 4: Give the conclusion.

The logic of the hypothesis test is always the same. To state a conclusion about H 0 , we compare the P-value to the significance level, α.

• If P ≤ α, we reject H 0 . We conclude there is significant evidence in favor of H a .
• If P > α, we fail to reject H 0 . We conclude the sample does not provide significant evidence in favor of H a .
• We write the conclusion in the context of the research question. Our conclusion is usually a statement about the alternative hypothesis (we accept H a or fail to acceptH a ) and should include the P-value.

Other Hypothesis Testing Notes

• Remember that the P-value is the probability of seeing a sample mean at least as extreme as the one from the data if the null hypothesis is true. The probability is about the random sample; it is not a “chance” statement about the null or alternative hypothesis.
• If our test results in rejecting a null hypothesis that is actually true, then it is called a type I error.
• If our test results in failing to reject a null hypothesis that is actually false, then it is called a type II error.
• If rejecting a null hypothesis would be very expensive, controversial, or dangerous, then we really want to avoid a type I error. In this case, we would set a strict significance level (a small value of α, such as 0.01).
• Finally, remember the phrase “garbage in, garbage out.” If the data collection methods are poor, then the results of a hypothesis test are meaningless.

Contributors and Attributions

• Concepts in Statistics. Provided by : Open Learning Initiative. Located at : http://oli.cmu.edu . License : CC BY: Attribution

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

8.7 Hypothesis Tests for a Population Mean with Unknown Population Standard Deviation

Learning objectives.

• Conduct and interpret hypothesis tests for a population mean with unknown population standard deviation.

Some notes about conducting a hypothesis test:

• The null hypothesis [latex]H_0[/latex] is always an “equal to.”  The null hypothesis is the original claim about the population parameter.
• The alternative hypothesis [latex]H_a[/latex] is a “less than,” “greater than,” or “not equal to.”  The form of the alternative hypothesis depends on the context of the question.
• If the alternative hypothesis is a “less than”,  then the test is left-tail.  The p -value is the area in the left-tail of the distribution.
• If the alternative hypothesis is a “greater than”, then the test is right-tail.  The p -value is the area in the right-tail of the distribution.
• If the alternative hypothesis is a “not equal to”, then the test is two-tail.  The p -value is the sum of the area in the two-tails of the distribution.  Each tail represents exactly half of the p -value.
• Think about the meaning of the p -value.  A data analyst (and anyone else) should have more confidence that they made the correct decision to reject the null hypothesis with a smaller p -value (for example, 0.001 as opposed to 0.04) even if using a significance level of  0.05.  Similarly, for a large p -value such as 0.4, as opposed to a p -value of 0.056 (a significance level of 0.05 is less than either number), a data analyst should have more confidence that they made the correct decision in not rejecting the null hypothesis.  This makes the data analyst use judgment rather than mindlessly applying rules.
• The significance level must be identified before collecting the sample data and conducting the test.  Generally, the significance level will be included in the question.  If no significance level is given, a common standard is to use a significance level of 5%.
• An alternative approach for hypothesis testing is to use what is called the critical value approach .  In this book, we will only use the p -value approach.  Some of the videos below may mention the critical value approach, but this approach will not be used in this book.

Steps to Conduct a Hypothesis Test for a Population Mean with Unknown Population Standard Deviation

• Write down the null and alternative hypotheses in terms of the population mean [latex]\mu[/latex].  Include appropriate units with the values of the mean.
• Use the form of the alternative hypothesis to determine if the test is left-tailed, right-tailed, or two-tailed.
• Collect the sample information for the test and identify the significance level [latex]\alpha[/latex].

[latex]\begin{eqnarray*} t & = & \frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}} \\ \\ df & = & n-1 \\ \\ \end{eqnarray*}[/latex]

• The results of the sample data are significant. There is sufficient evidence to conclude that the null hypothesis [latex]H_0[/latex] is an incorrect belief and that the alternative hypothesis [latex]H_a[/latex] is most likely correct.
• The results of the sample data are not significant. There is not sufficient evidence to conclude that the alternative hypothesis [latex]H_a[/latex] may be correct.
• Write down a concluding sentence specific to the context of the question.

USING EXCEL TO CALCULE THE P -VALUE FOR A HYPOTHESIS TEST ON A POPULATION MEAN WITH UNKNOWN POPULATION STANDARD DEVIATION

The p -value for a hypothesis test on a population mean is the area in the tail(s) of the distribution of the sample mean.  When the population standard deviation is unknown, use the [latex]t[/latex]-distribution to find the p -value.

If the p -value is the area in the left-tail:

• For t-score , enter the value of [latex]t[/latex] calculated from [latex]\displaystyle{t=\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}}[/latex].
• For degrees of freedom , enter the degrees of freedom for the [latex]t[/latex]-distribution [latex]n-1[/latex].
• For the logic operator , enter true .  Note:  Because we are calculating the area under the curve, we always enter true for the logic operator.
• The output from the t.dist function is the area under the [latex]t[/latex]-distribution to the left of the entered [latex]t[/latex]-score.
• Visit the Microsoft page for more information about the t.dist function.

If the p -value is the area in the right-tail:

• The output from the t.dist.rt function is the area under the [latex]t[/latex]-distribution to the right of the entered [latex]t[/latex]-score.
• Visit the Microsoft page for more information about the t.dist.rt function.

If the p -value is the sum of area in the tails:

• For t-score , enter the absolute value of [latex]t[/latex] calculated from [latex]\displaystyle{t=\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}}[/latex].  Note:  In the t.dist.2t function, the value of the [latex]t[/latex]-score must be a positive number.  If the [latex]t[/latex]-score is negative, enter the absolute value of the [latex]t[/latex]-score into the t.dist.2t function.
• The output from the t.dist.2t function is the sum of areas in the tails under the [latex]t[/latex]-distribution.
• Visit the Microsoft page for more information about the t.dist.2t function.

Statistics students believe that the mean score on the first statistics test is 65.  A statistics instructor thinks the mean score is higher than 65.  He samples ten statistics students and obtains the following scores:

The instructor performs a hypothesis test using a 1% level of significance. The test scores are assumed to be from a normal distribution.

Hypotheses:

[latex]\begin{eqnarray*} H_0: & & \mu=65  \\ H_a: & & \mu \gt 65  \end{eqnarray*}[/latex]

From the question, we have [latex]n=10[/latex], [latex]\overline{x}=67[/latex], [latex]s=3.1972...[/latex] and [latex]\alpha=0.01[/latex].

This is a test on a population mean where the population standard deviation is unknown (we only know the sample standard deviation [latex]s=3.1972...[/latex]).  So we use a [latex]t[/latex]-distribution to calculate the p -value.  Because the alternative hypothesis is a [latex]\gt[/latex], the p -value is the area in the right-tail of the distribution.

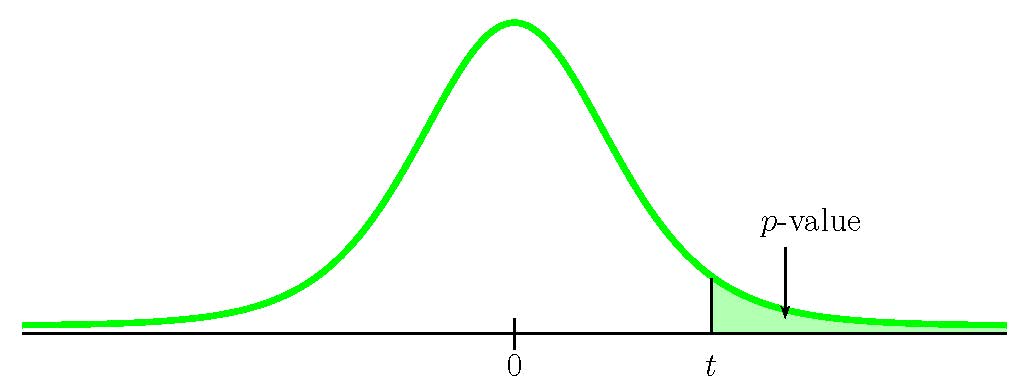
To use the t.dist.rt function, we need to calculate out the [latex]t[/latex]-score:

[latex]\begin{eqnarray*} t & = & \frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}} \\ & = & \frac{67-65}{\frac{3.1972...}{\sqrt{10}}} \\ & = & 1.9781... \end{eqnarray*}[/latex]

The degrees of freedom for the [latex]t[/latex]-distribution is [latex]n-1=10-1=9[/latex].

So the p -value[latex]=0.0396[/latex].

Conclusion:

Because p -value[latex]=0.0396 \gt 0.01=\alpha[/latex], we do not reject the null hypothesis.  At the 1% significance level there is not enough evidence to suggest that mean score on the test is greater than 65.

• The null hypothesis [latex]\mu=65[/latex] is the claim that the mean test score is 65.
• The alternative hypothesis [latex]\mu \gt 65[/latex] is the claim that the mean test score is greater than 65.
• Keep all of the decimals throughout the calculation (i.e. in the sample standard deviation, the [latex]t[/latex]-score, etc.) to avoid any round-off error in the calculation of the p -value.  This ensures that we get the most accurate value for the p -value.
• The p -value is the area in the right-tail of the [latex]t[/latex]-distribution, to the right of [latex]t=1.9781...[/latex].
• The p -value of 0.0396 tells us that under the assumption that the mean test score is 65 (the null hypothesis), there is a 3.96% chance that the mean test score is 65 or more.  Compared to the 1% significance level, this is a large probability, and so is likely to happen assuming the null hypothesis is true.  This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis.

A company claims that the average change in the value of their stock is $3.50 per week.  An investor believes this average is too high. The investor records the changes in the company’s stock price over 30 weeks and finds the average change in the stock price is $2.60 with a standard deviation of $1.80.  At the 5% significance level, is the average change in the company’s stock price lower than the company claims?

[latex]\begin{eqnarray*} H_0: & & \mu=$3.50  \\ H_a: & & \mu \lt $3.50  \end{eqnarray*}[/latex]

From the question, we have [latex]n=30[/latex], [latex]\overline{x}=2.6[/latex], [latex]s=1.8[/latex] and [latex]\alpha=0.05[/latex].

This is a test on a population mean where the population standard deviation is unknown (we only know the sample standard deviation [latex]s=1.8.[/latex]).  So we use a [latex]t[/latex]-distribution to calculate the p -value.  Because the alternative hypothesis is a [latex]\lt[/latex], the p -value is the area in the left-tail of the distribution.

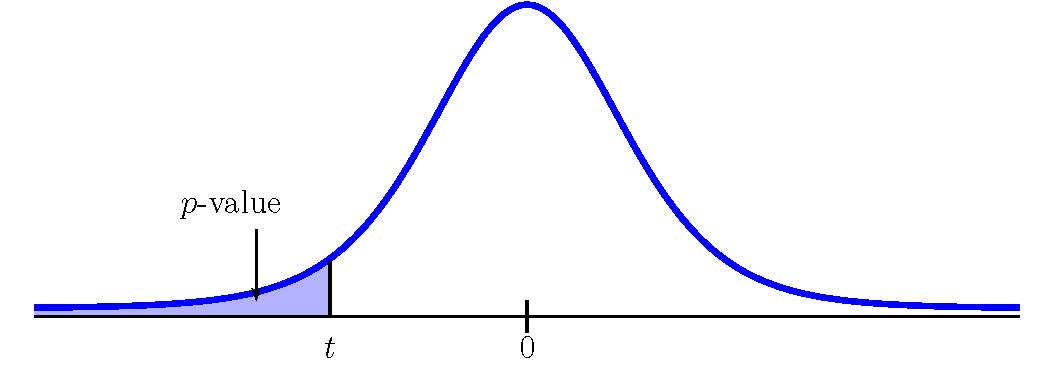
To use the t.dist function, we need to calculate out the [latex]t[/latex]-score:

[latex]\begin{eqnarray*} t & = & \frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}} \\ & = & \frac{2.6-3.5}{\frac{1.8}{\sqrt{30}}} \\ & = & -1.5699... \end{eqnarray*}[/latex]

The degrees of freedom for the [latex]t[/latex]-distribution is [latex]n-1=30-1=29[/latex].

So the p -value[latex]=0.0636[/latex].

Because p -value[latex]=0.0636 \gt 0.05=\alpha[/latex], we do not reject the null hypothesis.  At the 5% significance level there is not enough evidence to suggest that average change in the stock price is lower than $3.50.

• The null hypothesis [latex]\mu=$3.50[/latex] is the claim that the average change in the company’s stock is $3.50 per week.
• The alternative hypothesis [latex]\mu \lt $3.50[/latex] is the claim that the average change in the company’s stock is less than $3.50 per week.
• The p -value is the area in the left-tail of the [latex]t[/latex]-distribution, to the left of [latex]t=-1.5699...[/latex].
• The p -value of 0.0636 tells us that under the assumption that the average change in the stock is $3.50 (the null hypothesis), there is a 6.36% chance that the average change is $3.50 or less.  Compared to the 5% significance level, this is a large probability, and so is likely to happen assuming the null hypothesis is true.  This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis.  In other words, the company’s claim that the average change in their stock price is $3.50 per week is most likely correct.

A paint manufacturer has their production line set-up so that the average volume of paint in a can is 3.78 liters.  The quality control manager at the plant believes that something has happened with the production and the average volume of paint in the cans has changed.  The quality control department takes a sample of 100 cans and finds the average volume is 3.62 liters with a standard deviation of 0.7 liters.  At the 5% significance level, has the volume of paint in a can changed?

[latex]\begin{eqnarray*} H_0: & & \mu=3.78 \mbox{ liters}  \\ H_a: & & \mu \neq 3.78 \mbox{ liters}  \end{eqnarray*}[/latex]

From the question, we have [latex]n=100[/latex], [latex]\overline{x}=3.62[/latex], [latex]s=0.7[/latex] and [latex]\alpha=0.05[/latex].

This is a test on a population mean where the population standard deviation is unknown (we only know the sample standard deviation [latex]s=0.7[/latex]).  So we use a [latex]t[/latex]-distribution to calculate the p -value.  Because the alternative hypothesis is a [latex]\neq[/latex], the p -value is the sum of area in the tails of the distribution.

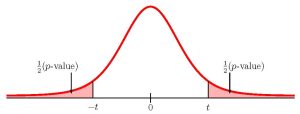
To use the t.dist.2t function, we need to calculate out the [latex]t[/latex]-score:

[latex]\begin{eqnarray*} t & = & \frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}} \\ & = & \frac{3.62-3.78}{\frac{0.07}{\sqrt{100}}} \\ & = & -2.2857... \end{eqnarray*}[/latex]

The degrees of freedom for the [latex]t[/latex]-distribution is [latex]n-1=100-1=99[/latex].

So the p -value[latex]=0.0244[/latex].

Because p -value[latex]=0.0244 \lt 0.05=\alpha[/latex], we reject the null hypothesis in favour of the alternative hypothesis.  At the 5% significance level there is enough evidence to suggest that average volume of paint in the cans has changed.

• The null hypothesis [latex]\mu=3.78[/latex] is the claim that the average volume of paint in the cans is 3.78.
• The alternative hypothesis [latex]\mu \neq 3.78[/latex] is the claim that the average volume of paint in the cans is not 3.78.
• Keep all of the decimals throughout the calculation (i.e. in the [latex]t[/latex]-score) to avoid any round-off error in the calculation of the p -value.  This ensures that we get the most accurate value for the p -value.
• The p -value is the sum of the area in the two tails.  The output from the t.dist.2t function is exactly the sum of the area in the two tails, and so is the p -value required for the test.  No additional calculations are required.
• The t.dist.2t function requires that the value entered for the [latex]t[/latex]-score is positive .  A negative [latex]t[/latex]-score entered into the t.dist.2t function generates an error in Excel.  In this case, the value of the [latex]t[/latex]-score is negative, so we must enter the absolute value of this [latex]t[/latex]-score into field 1.
• The p -value of 0.0244 is a small probability compared to the significance level, and so is unlikely to happen assuming the null hypothesis is true.  This suggests that the assumption that the null hypothesis is true is most likely incorrect, and so the conclusion of the test is to reject the null hypothesis in favour of the alternative hypothesis.  In other words, the average volume of paint in the cans has most likely changed from 3.78 liters.

Watch this video: Hypothesis Testing: t -test, right tail by ExcelIsFun [11:02]

Watch this video: Hypothesis Testing: t -test, left tail by ExcelIsFun [7:48]

Watch this video: Hypothesis Testing: t -test, two tail by ExcelIsFun [8:54]

Concept Review

The hypothesis test for a population mean is a well established process:

• Collect the sample information for the test and identify the significance level.
• When the population standard deviation is unknown, find the p -value (the area in the corresponding tail) for the test using the [latex]t[/latex]-distribution with [latex]\displaystyle{t=\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}}[/latex] and [latex]df=n-1[/latex].
• Compare the p -value to the significance level and state the outcome of the test.

Attribution

“ 9.6   Hypothesis Testing of a Single Mean and Single Proportion “ in Introductory Statistics by OpenStax  is licensed under a  Creative Commons Attribution 4.0 International License.

Introduction to Statistics Copyright © 2022 by Valerie Watts is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Teach yourself statistics

Hypothesis Test for a Mean

This lesson explains how to conduct a hypothesis test of a mean, when the following conditions are met:

• The sampling method is simple random sampling .
• The sampling distribution is normal or nearly normal.

Generally, the sampling distribution will be approximately normally distributed if any of the following conditions apply.

• The population distribution is normal.
• The population distribution is symmetric , unimodal , without outliers , and the sample size is 15 or less.
• The population distribution is moderately skewed , unimodal, without outliers, and the sample size is between 16 and 40.
• The sample size is greater than 40, without outliers.

This approach consists of four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results.

State the Hypotheses

Every hypothesis test requires the analyst to state a null hypothesis and an alternative hypothesis . The hypotheses are stated in such a way that they are mutually exclusive. That is, if one is true, the other must be false; and vice versa.

The table below shows three sets of hypotheses. Each makes a statement about how the population mean μ is related to a specified value M . (In the table, the symbol ≠ means " not equal to ".)

The first set of hypotheses (Set 1) is an example of a two-tailed test , since an extreme value on either side of the sampling distribution would cause a researcher to reject the null hypothesis. The other two sets of hypotheses (Sets 2 and 3) are one-tailed tests , since an extreme value on only one side of the sampling distribution would cause a researcher to reject the null hypothesis.

Formulate an Analysis Plan

The analysis plan describes how to use sample data to accept or reject the null hypothesis. It should specify the following elements.

• Significance level. Often, researchers choose significance levels equal to 0.01, 0.05, or 0.10; but any value between 0 and 1 can be used.
• Test method. Use the one-sample t-test to determine whether the hypothesized mean differs significantly from the observed sample mean.

Analyze Sample Data

Using sample data, conduct a one-sample t-test. This involves finding the standard error, degrees of freedom, test statistic, and the P-value associated with the test statistic.

SE = s * sqrt{ ( 1/n ) * [ ( N - n ) / ( N - 1 ) ] }

SE = s / sqrt( n )

• Degrees of freedom. The degrees of freedom (DF) is equal to the sample size (n) minus one. Thus, DF = n - 1.

t = ( x - μ) / SE

• P-value. The P-value is the probability of observing a sample statistic as extreme as the test statistic. Since the test statistic is a t statistic, use the t Distribution Calculator to assess the probability associated with the t statistic, given the degrees of freedom computed above. (See sample problems at the end of this lesson for examples of how this is done.)

Sample Size Calculator

As you probably noticed, the process of hypothesis testing can be complex. When you need to test a hypothesis about a mean score, consider using the Sample Size Calculator. The calculator is fairly easy to use, and it is free. You can find the Sample Size Calculator in Stat Trek's main menu under the Stat Tools tab. Or you can tap the button below.

Interpret Results

If the sample findings are unlikely, given the null hypothesis, the researcher rejects the null hypothesis. Typically, this involves comparing the P-value to the significance level , and rejecting the null hypothesis when the P-value is less than the significance level.

Test Your Understanding

In this section, two sample problems illustrate how to conduct a hypothesis test of a mean score. The first problem involves a two-tailed test; the second problem, a one-tailed test.

Problem 1: Two-Tailed Test

An inventor has developed a new, energy-efficient lawn mower engine. He claims that the engine will run continuously for 5 hours (300 minutes) on a single gallon of regular gasoline. From his stock of 2000 engines, the inventor selects a simple random sample of 50 engines for testing. The engines run for an average of 295 minutes, with a standard deviation of 20 minutes. Test the null hypothesis that the mean run time is 300 minutes against the alternative hypothesis that the mean run time is not 300 minutes. Use a 0.05 level of significance. (Assume that run times for the population of engines are normally distributed.)

Solution: The solution to this problem takes four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results. We work through those steps below:

Null hypothesis: μ = 300

Alternative hypothesis: μ ≠ 300

• Formulate an analysis plan . For this analysis, the significance level is 0.05. The test method is a one-sample t-test .

SE = s / sqrt(n) = 20 / sqrt(50) = 20/7.07 = 2.83

DF = n - 1 = 50 - 1 = 49

t = ( x - μ) / SE = (295 - 300)/2.83 = -1.77

where s is the standard deviation of the sample, x is the sample mean, μ is the hypothesized population mean, and n is the sample size.

Since we have a two-tailed test , the P-value is the probability that the t statistic having 49 degrees of freedom is less than -1.77 or greater than 1.77. We use the t Distribution Calculator to find P(t < -1.77) is about 0.04.

• If you enter 1.77 as the sample mean in the t Distribution Calculator, you will find the that the P(t < 1.77) is about 0.04. Therefore, P(t >  1.77) is 1 minus 0.96 or 0.04. Thus, the P-value = 0.04 + 0.04 = 0.08.
• Interpret results . Since the P-value (0.08) is greater than the significance level (0.05), we cannot reject the null hypothesis.

Note: If you use this approach on an exam, you may also want to mention why this approach is appropriate. Specifically, the approach is appropriate because the sampling method was simple random sampling, the population was normally distributed, and the sample size was small relative to the population size (less than 5%).

Problem 2: One-Tailed Test

Bon Air Elementary School has 1000 students. The principal of the school thinks that the average IQ of students at Bon Air is at least 110. To prove her point, she administers an IQ test to 20 randomly selected students. Among the sampled students, the average IQ is 108 with a standard deviation of 10. Based on these results, should the principal accept or reject her original hypothesis? Assume a significance level of 0.01. (Assume that test scores in the population of engines are normally distributed.)

Null hypothesis: μ >= 110

Alternative hypothesis: μ < 110

• Formulate an analysis plan . For this analysis, the significance level is 0.01. The test method is a one-sample t-test .

SE = s / sqrt(n) = 10 / sqrt(20) = 10/4.472 = 2.236

DF = n - 1 = 20 - 1 = 19

t = ( x - μ) / SE = (108 - 110)/2.236 = -0.894

Here is the logic of the analysis: Given the alternative hypothesis (μ < 110), we want to know whether the observed sample mean is small enough to cause us to reject the null hypothesis.

The observed sample mean produced a t statistic test statistic of -0.894. We use the t Distribution Calculator to find P(t < -0.894) is about 0.19.

• This means we would expect to find a sample mean of 108 or smaller in 19 percent of our samples, if the true population IQ were 110. Thus the P-value in this analysis is 0.19.
• Interpret results . Since the P-value (0.19) is greater than the significance level (0.01), we cannot reject the null hypothesis.

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

5.2 - writing hypotheses.

The first step in conducting a hypothesis test is to write the hypothesis statements that are going to be tested. For each test you will have a null hypothesis (\(H_0\)) and an alternative hypothesis (\(H_a\)).

When writing hypotheses there are three things that we need to know: (1) the parameter that we are testing (2) the direction of the test (non-directional, right-tailed or left-tailed), and (3) the value of the hypothesized parameter.

• At this point we can write hypotheses for a single mean (\(\mu\)), paired means(\(\mu_d\)), a single proportion (\(p\)), the difference between two independent means (\(\mu_1-\mu_2\)), the difference between two proportions (\(p_1-p_2\)), a simple linear regression slope (\(\beta\)), and a correlation (\(\rho\)). 
• The research question will give us the information necessary to determine if the test is two-tailed (e.g., "different from," "not equal to"), right-tailed (e.g., "greater than," "more than"), or left-tailed (e.g., "less than," "fewer than").
• The research question will also give us the hypothesized parameter value. This is the number that goes in the hypothesis statements (i.e., \(\mu_0\) and \(p_0\)). For the difference between two groups, regression, and correlation, this value is typically 0.

Hypotheses are always written in terms of population parameters (e.g., \(p\) and \(\mu\)).  The tables below display all of the possible hypotheses for the parameters that we have learned thus far. Note that the null hypothesis always includes the equality (i.e., =).

9.1 Null and Alternative Hypotheses

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 , the — null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.

H a —, the alternative hypothesis: a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are reject H 0 if the sample information favors the alternative hypothesis or do not reject H 0 or decline to reject H 0 if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

Example 9.1

H 0 : No more than 30 percent of the registered voters in Santa Clara County voted in the primary election. p ≤ 30 H a : More than 30 percent of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25 percent. State the null and alternative hypotheses.

Example 9.2

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are the following: H 0 : μ = 2.0 H a : μ ≠ 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ __ 66
• H a : μ __ 66

Example 9.3

We want to test if college students take fewer than five years to graduate from college, on the average. The null and alternative hypotheses are the following: H 0 : μ ≥ 5 H a : μ < 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ __ 45
• H a : μ __ 45

Example 9.4

An article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third of the students pass. The same article stated that 6.6 percent of U.S. students take advanced placement exams and 4.4 percent pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6 percent. State the null and alternative hypotheses. H 0 : p ≤ 0.066 H a : p > 0.066

On a state driver’s test, about 40 percent pass the test on the first try. We want to test if more than 40 percent pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : p __ 0.40
• H a : p __ 0.40

Collaborative Exercise

Bring to class a newspaper, some news magazines, and some internet articles. In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.

Access for free at https://openstax.org/books/statistics/pages/1-introduction

• Authors: Barbara Illowsky, Susan Dean
• Publisher/website: OpenStax
• Book title: Statistics
• Publication date: Mar 27, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/statistics/pages/1-introduction
• Section URL: https://openstax.org/books/statistics/pages/9-1-null-and-alternative-hypotheses

© Jan 23, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Module: Inference for Means

Hypothesis test for a population mean (3 of 5), learning objectives.

• Under appropriate conditions, conduct a hypothesis test about a mean for a matched pairs design. State a conclusion in context.

Another common use of the t-test for a population mean is in “before and after” situations. In this situation, we have two quantitative measurements from a single sample of individuals. This is an example of a matched-pairs design.

Drinking and Driving

The Centers for Disease Control and Prevention (CDC) website cites studies from the National Highway Traffic Safety Administration to support this statement: “Alcohol use slows reaction time and impairs judgment and coordination, which are all skills needed to drive a car safely. The more alcohol consumed, the greater the impairment.” All states in the United States have adopted a blood alcohol concentration of 0.08% (80 mg/dL) as the legal limit for operating a motor vehicle. The CDC website continues, “Note: Legal limits do not define a level below which it is safe to operate a vehicle or engage in some other activity. Impairment due to alcohol use begins to occur at levels well below the legal limit.”

It is this last statement that may be surprising to drivers. Interviews with drunk drivers who were involved in accidents reveal that drunk drivers do not realize how drunk they are. “I only had one or two drinks – I am okay to drive” is a common sentiment. Suppose a college conducts a study to call attention to this issue. Researchers use a random sample of 20 college students to examine the effect of drinking two beers on reaction times. They use a driving simulator to measure each student’s reaction time before and after drinking two beers. The reaction time is the time it takes the student to hit the brakes in the simulator when an obstacle appears in the road.

Click here to see the data.

In this situation, we have two quantitative measurements for each student. To measure the effect of the two beers, we subtract the two reaction times to create one measurement of “change” or “effect.” This controls the effects of individual characteristics that could influence reaction time, such as driving experience or natural quickness.

Here is a partial list of the data. We define the difference as “before minus after.” If the “after” reaction time is longer, then the difference is negative. A negative value means the reaction time is slower after drinking.

Note: It is common to define the difference in measurements as “before minus after.” But we could also define the difference the other way around as “after minus before.” In this definition, if the “after” reaction time is longer, then the difference is positive, so a slower reaction time after drinking corresponds to a positive value. This makes less intuitive sense to us. We want “negative” to mean “drinking has a negative effect,” so we used the other definition, “before minus after.”

Step 1: Determine the hypotheses.

The null hypothesis is a claim of “no change” or “no effect.” The alternative hypothesis reflects the claim.

• H 0 : Drinking two beers has no effect on reaction time.
• H a : Drinking two beers slows reaction time.

If drinking two beers has no effect on reaction time, then the mean of the differences in reaction times (before minus after) will be zero. If drinking two beers slows reaction time, then the mean of the differences in reaction times (before minus after) will be negative. So we can rewrite our hypotheses as follows.

• H 0 : μ = 0
• H a : μ < 0

where µ is the mean of the difference in reaction time (before minus after) for all students at this college after drinking two beers.

Suppose researchers set a significance level of 5%.

Note: if we defined the difference in reverse order as “after minus before,” then a positive difference corresponds to a slower reaction time. This changes the alternative hypothesis to H a : µ > 0. This will not effect the P-value or our conclusion. You just have to make sure the alternative hypothesis says what you want it to say given the way you define the difference.

Note: In some textbooks and other statistical materials, you will see the “mean of the difference” written as μ d .

Step 2: Collect the data.

Here is the (made-up) data from this sample of 20 college students. The mean of the differences (before minus after) is approximately −0.46 seconds, and the standard deviation is approximately 0.87 seconds.

Step 3: Assess the evidence.

Check the Criteria for Use of a T-Model

The sample size is only 20, and we do not know if these differences would be normally distributed in general when comparing these two treatments in the population of all college students. We therefore do not meet the conditions for use of a t-model. Some researchers would stop here and not complete the hypothesis test. Others would check the shape of the distribution of differences in the sample. If the sample is approximately normal (or at least not heavily skewed), then they view this as a hopeful indication that the distribution in the population will also be approximately normal, and they continue with the hypothesis test, adding a disclaimer to the conclusion.

Here is a histogram of the differences in the sample.

The data is not heavily skewed, so we are willing to proceed with the t-test.

Compute the Test Statistic

[latex]\text{estimated}\text{}\text{standard}\text{}\text{error}\text{}=\text{}\frac{s}{\sqrt{n}}\text{}=\text{}\frac{0.87}{\sqrt{20}}\text{}\approx \text{}0.195[/latex]

[latex]\text{T}\text{}=\text{}\frac{\text{statistic}-\text{parameter}}{\text{estimated standard error}}\text{}=\text{}\frac{-0.46-0}{0.195}\text{}\approx \text{}-2.36[/latex]

Find the P-value.

We use the simulation with the t-model for 19 degrees of freedom ( df = n − 1 = 20 − 1 = 19). The P-value is approximately 0.015.

Step 4: State a conclusion.

The P-value (0.015) is less than the significance level (0.05), so we reject the null and accept the alternative hypothesis that µ < 0.

This study suggests that reactions times when driving are significantly slower after drinking two beers for students at this college. ( P = 0.015).

It is good practice to include a disclaimer with this conclusion because the sample is small. We might add the following to our conclusion if we were publicly presenting these results: “The sample was too small to formally met the requirements for a t-test. On the basis of the data, we are assuming that the difference in reaction times would be normally distributed in general when comparing these two treatments in the population of all college students. The conclusion from this test is valid only if this assumption is true.”

From this study, can we generalize to a larger population of “all college students” or “all drivers”? Technically, such a generalization requires that the sample be randomly selected from the more general population. Is this type of random sampling done in practice? Not always. The matched pairs design controls for individual differences that would otherwise confound such a generalization. This is one of the reasons that researchers run hypothesis tests with data gathered by groups like the National Highway Traffic Safety Administration, even when participants are not randomly selected. But ideally we should select samples randomly from the population of interest.

Can we make a cause-and-effect conclusion from this study?

We should be cautious about a cause-and-effect conclusion here because there is no random assignment. We take measurements from every student in both the treatment and the control setting without randomizing the treatment order. Every participant did the driving test sober, then drank two beers and did the driving test again. Technically, we need a more sophisticated study design that uses random assignment in order to make cause-and-effect conclusions. For example, we could randomly assign the treatment order for each student by flipping a coin, assigning some students do the first driving test while sober and others do the first driving test after drinking two beers. Then everyone comes back on another day to complete the part of the experiment that he or she had not done.

The following activities give you an opportunity to practice parts of the hypothesis testing process. In each of these activities, the study is a matched-pairs design, so the population mean represents a mean of differences in paired measurements. Later you will have the opportunity to practice the hypothesis test from start to finish.

Learn By Doing

• Concepts in Statistics. Provided by : Open Learning Initiative. Located at : http://oli.cmu.edu . License : CC BY: Attribution

Privacy Policy

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Statistics and probability

Course: statistics and probability   >   unit 13.

• Comparing population proportions 1
• Comparing population proportions 2

Hypothesis test comparing population proportions

Want to join the conversation.

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

• School Guide
• Mathematics
• Number System and Arithmetic
• Trigonometry
• Probability
• Mensuration
• Maths Formulas
• Class 8 Maths Notes
• Class 9 Maths Notes
• Class 10 Maths Notes
• Class 11 Maths Notes
• Class 12 Maths Notes
• Data Analysis with Python

Introduction to Data Analysis

• What is Data Analysis?
• Data Analytics and its type
• How to Install Numpy on Windows?
• How to Install Pandas in Python?
• How to Install Matplotlib on python?
• How to Install Python Tensorflow in Windows?

Data Analysis Libraries

• Pandas Tutorial
• NumPy Tutorial - Python Library
• Data Analysis with SciPy
• Introduction to TensorFlow

Data Visulization Libraries

• Matplotlib Tutorial
• Python Seaborn Tutorial
• Plotly tutorial
• Introduction to Bokeh in Python

Exploratory Data Analysis (EDA)

• Univariate, Bivariate and Multivariate data and its analysis
• Measures of Central Tendency in Statistics
• Measures of spread - Range, Variance, and Standard Deviation
• Interquartile Range and Quartile Deviation using NumPy and SciPy
• Anova Formula
• Skewness of Statistical Data
• How to Calculate Skewness and Kurtosis in Python?
• Difference Between Skewness and Kurtosis
• Histogram | Meaning, Example, Types and Steps to Draw
• Interpretations of Histogram
• Quantile Quantile plots
• What is Univariate, Bivariate & Multivariate Analysis in Data Visualisation?
• Using pandas crosstab to create a bar plot
• Exploring Correlation in Python
• Mathematics | Covariance and Correlation
• Factor Analysis | Data Analysis
• Data Mining - Cluster Analysis
• MANOVA Test in R Programming
• Python - Central Limit Theorem
• Probability Distribution Function
• Probability Density Estimation & Maximum Likelihood Estimation
• Exponential Distribution in R Programming - dexp(), pexp(), qexp(), and rexp() Functions
• Mathematics | Probability Distributions Set 4 (Binomial Distribution)
• Poisson Distribution - Definition, Formula, Table and Examples
• P-Value: Comprehensive Guide to Understand, Apply, and Interpret
• Z-Score in Statistics
• How to Calculate Point Estimates in R?
• Confidence Interval
• Chi-square test in Machine Learning

Understanding Hypothesis Testing

Data preprocessing.

• ML | Data Preprocessing in Python
• ML | Overview of Data Cleaning
• ML | Handling Missing Values
• Detect and Remove the Outliers using Python

Data Transformation

• Data Normalization Machine Learning
• Sampling distribution Using Python

Time Series Data Analysis

• Data Mining - Time-Series, Symbolic and Biological Sequences Data
• Basic DateTime Operations in Python
• Time Series Analysis & Visualization in Python
• How to deal with missing values in a Timeseries in Python?
• How to calculate MOVING AVERAGE in a Pandas DataFrame?
• What is a trend in time series?
• How to Perform an Augmented Dickey-Fuller Test in R
• AutoCorrelation

Case Studies and Projects

• Top 8 Free Dataset Sources to Use for Data Science Projects
• Step by Step Predictive Analysis - Machine Learning
• 6 Tips for Creating Effective Data Visualizations

Hypothesis testing involves formulating assumptions about population parameters based on sample statistics and rigorously evaluating these assumptions against empirical evidence. This article sheds light on the significance of hypothesis testing and the critical steps involved in the process.

What is Hypothesis Testing?

Hypothesis testing is a statistical method that is used to make a statistical decision using experimental data. Hypothesis testing is basically an assumption that we make about a population parameter. It evaluates two mutually exclusive statements about a population to determine which statement is best supported by the sample data. 

Example: You say an average height in the class is 30 or a boy is taller than a girl. All of these is an assumption that we are assuming, and we need some statistical way to prove these. We need some mathematical conclusion whatever we are assuming is true.

Defining Hypotheses

Key Terms of Hypothesis Testing

• P-value: The P value , or calculated probability, is the probability of finding the observed/extreme results when the null hypothesis(H0) of a study-given problem is true. If your P-value is less than the chosen significance level then you reject the null hypothesis i.e. accept that your sample claims to support the alternative hypothesis.
• Test Statistic: The test statistic is a numerical value calculated from sample data during a hypothesis test, used to determine whether to reject the null hypothesis. It is compared to a critical value or p-value to make decisions about the statistical significance of the observed results.
• Critical value : The critical value in statistics is a threshold or cutoff point used to determine whether to reject the null hypothesis in a hypothesis test.
• Degrees of freedom: Degrees of freedom are associated with the variability or freedom one has in estimating a parameter. The degrees of freedom are related to the sample size and determine the shape.

Why do we use Hypothesis Testing?

Hypothesis testing is an important procedure in statistics. Hypothesis testing evaluates two mutually exclusive population statements to determine which statement is most supported by sample data. When we say that the findings are statistically significant, thanks to hypothesis testing. 

One-Tailed and Two-Tailed Test

One tailed test focuses on one direction, either greater than or less than a specified value. We use a one-tailed test when there is a clear directional expectation based on prior knowledge or theory. The critical region is located on only one side of the distribution curve. If the sample falls into this critical region, the null hypothesis is rejected in favor of the alternative hypothesis.

One-Tailed Test

There are two types of one-tailed test:

Two-Tailed Test

A two-tailed test considers both directions, greater than and less than a specified value.We use a two-tailed test when there is no specific directional expectation, and want to detect any significant difference.

What are Type 1 and Type 2 errors in Hypothesis Testing?

In hypothesis testing, Type I and Type II errors are two possible errors that researchers can make when drawing conclusions about a population based on a sample of data. These errors are associated with the decisions made regarding the null hypothesis and the alternative hypothesis.

How does Hypothesis Testing work?

Step 1: define null and alternative hypothesis.

We first identify the problem about which we want to make an assumption keeping in mind that our assumption should be contradictory to one another, assuming Normally distributed data.

Step 2 – Choose significance level

Step 3 – Collect and Analyze data.

Gather relevant data through observation or experimentation. Analyze the data using appropriate statistical methods to obtain a test statistic.

Step 4-Calculate Test Statistic

The data for the tests are evaluated in this step we look for various scores based on the characteristics of data. The choice of the test statistic depends on the type of hypothesis test being conducted.

There are various hypothesis tests, each appropriate for various goal to calculate our test. This could be a Z-test , Chi-square , T-test , and so on.

• Z-test : If population means and standard deviations are known. Z-statistic is commonly used.
• t-test : If population standard deviations are unknown. and sample size is small than t-test statistic is more appropriate.
• Chi-square test : Chi-square test is used for categorical data or for testing independence in contingency tables
• F-test : F-test is often used in analysis of variance (ANOVA) to compare variances or test the equality of means across multiple groups.

We have a smaller dataset, So, T-test is more appropriate to test our hypothesis.

T-statistic is a measure of the difference between the means of two groups relative to the variability within each group. It is calculated as the difference between the sample means divided by the standard error of the difference. It is also known as the t-value or t-score.

Step 5 – Comparing Test Statistic:

In this stage, we decide where we should accept the null hypothesis or reject the null hypothesis. There are two ways to decide where we should accept or reject the null hypothesis.

Method A: Using Crtical values

Comparing the test statistic and tabulated critical value we have,

• If Test Statistic>Critical Value: Reject the null hypothesis.
• If Test Statistic≤Critical Value: Fail to reject the null hypothesis.

Note: Critical values are predetermined threshold values that are used to make a decision in hypothesis testing. To determine critical values for hypothesis testing, we typically refer to a statistical distribution table , such as the normal distribution or t-distribution tables based on.

Method B: Using P-values

We can also come to an conclusion using the p-value,

Note : The p-value is the probability of obtaining a test statistic as extreme as, or more extreme than, the one observed in the sample, assuming the null hypothesis is true. To determine p-value for hypothesis testing, we typically refer to a statistical distribution table , such as the normal distribution or t-distribution tables based on.

Step 7- Interpret the Results

At last, we can conclude our experiment using method A or B.

Calculating test statistic

To validate our hypothesis about a population parameter we use statistical functions . We use the z-score, p-value, and level of significance(alpha) to make evidence for our hypothesis for normally distributed data .

1. Z-statistics:

When population means and standard deviations are known.

• μ represents the population mean, 
• σ is the standard deviation
• and n is the size of the sample.

2. T-Statistics

T test is used when n<30,

t-statistic calculation is given by:

• t = t-score,
• x̄ = sample mean
• μ = population mean,
• s = standard deviation of the sample,
• n = sample size

3. Chi-Square Test

Chi-Square Test for Independence categorical Data (Non-normally distributed) using:

• i,j are the rows and columns index respectively.

Real life Hypothesis Testing example

Let’s examine hypothesis testing using two real life situations,

Case A: D oes a New Drug Affect Blood Pressure?

Imagine a pharmaceutical company has developed a new drug that they believe can effectively lower blood pressure in patients with hypertension. Before bringing the drug to market, they need to conduct a study to assess its impact on blood pressure.

• Before Treatment: 120, 122, 118, 130, 125, 128, 115, 121, 123, 119
• After Treatment: 115, 120, 112, 128, 122, 125, 110, 117, 119, 114

Step 1 : Define the Hypothesis

• Null Hypothesis : (H 0 )The new drug has no effect on blood pressure.
• Alternate Hypothesis : (H 1 )The new drug has an effect on blood pressure.

Step 2: Define the Significance level

Let’s consider the Significance level at 0.05, indicating rejection of the null hypothesis.

If the evidence suggests less than a 5% chance of observing the results due to random variation.

Step 3 : Compute the test statistic

Using paired T-test analyze the data to obtain a test statistic and a p-value.

The test statistic (e.g., T-statistic) is calculated based on the differences between blood pressure measurements before and after treatment.

t = m/(s/√n)

• m  = mean of the difference i.e X after, X before
• s  = standard deviation of the difference (d) i.e d i ​= X after, i ​− X before,
• n  = sample size,

then, m= -3.9, s= 1.8 and n= 10

we, calculate the , T-statistic = -9 based on the formula for paired t test

Step 4: Find the p-value

The calculated t-statistic is -9 and degrees of freedom df = 9, you can find the p-value using statistical software or a t-distribution table.

thus, p-value = 8.538051223166285e-06

Step 5: Result

• If the p-value is less than or equal to 0.05, the researchers reject the null hypothesis.
• If the p-value is greater than 0.05, they fail to reject the null hypothesis.

Conclusion: Since the p-value (8.538051223166285e-06) is less than the significance level (0.05), the researchers reject the null hypothesis. There is statistically significant evidence that the average blood pressure before and after treatment with the new drug is different.

Python Implementation of Hypothesis Testing

Let’s create hypothesis testing with python, where we are testing whether a new drug affects blood pressure. For this example, we will use a paired T-test. We’ll use the scipy.stats library for the T-test.

Scipy is a mathematical library in Python that is mostly used for mathematical equations and computations.

We will implement our first real life problem via python,

In the above example, given the T-statistic of approximately -9 and an extremely small p-value, the results indicate a strong case to reject the null hypothesis at a significance level of 0.05. 

• The results suggest that the new drug, treatment, or intervention has a significant effect on lowering blood pressure.
• The negative T-statistic indicates that the mean blood pressure after treatment is significantly lower than the assumed population mean before treatment.

Case B : Cholesterol level in a population

Data: A sample of 25 individuals is taken, and their cholesterol levels are measured.

Cholesterol Levels (mg/dL): 205, 198, 210, 190, 215, 205, 200, 192, 198, 205, 198, 202, 208, 200, 205, 198, 205, 210, 192, 205, 198, 205, 210, 192, 205.

Populations Mean = 200

Population Standard Deviation (σ): 5 mg/dL(given for this problem)

Step 1: Define the Hypothesis

• Null Hypothesis (H 0 ): The average cholesterol level in a population is 200 mg/dL.
• Alternate Hypothesis (H 1 ): The average cholesterol level in a population is different from 200 mg/dL.

As the direction of deviation is not given , we assume a two-tailed test, and based on a normal distribution table, the critical values for a significance level of 0.05 (two-tailed) can be calculated through the z-table and are approximately -1.96 and 1.96.

Step 4: Result

Since the absolute value of the test statistic (2.04) is greater than the critical value (1.96), we reject the null hypothesis. And conclude that, there is statistically significant evidence that the average cholesterol level in the population is different from 200 mg/dL

Limitations of Hypothesis Testing

• Although a useful technique, hypothesis testing does not offer a comprehensive grasp of the topic being studied. Without fully reflecting the intricacy or whole context of the phenomena, it concentrates on certain hypotheses and statistical significance.
• The accuracy of hypothesis testing results is contingent on the quality of available data and the appropriateness of statistical methods used. Inaccurate data or poorly formulated hypotheses can lead to incorrect conclusions.
• Relying solely on hypothesis testing may cause analysts to overlook significant patterns or relationships in the data that are not captured by the specific hypotheses being tested. This limitation underscores the importance of complimenting hypothesis testing with other analytical approaches.

Hypothesis testing stands as a cornerstone in statistical analysis, enabling data scientists to navigate uncertainties and draw credible inferences from sample data. By systematically defining null and alternative hypotheses, choosing significance levels, and leveraging statistical tests, researchers can assess the validity of their assumptions. The article also elucidates the critical distinction between Type I and Type II errors, providing a comprehensive understanding of the nuanced decision-making process inherent in hypothesis testing. The real-life example of testing a new drug’s effect on blood pressure using a paired T-test showcases the practical application of these principles, underscoring the importance of statistical rigor in data-driven decision-making.

Frequently Asked Questions (FAQs)

1. what are the 3 types of hypothesis test.

There are three types of hypothesis tests: right-tailed, left-tailed, and two-tailed. Right-tailed tests assess if a parameter is greater, left-tailed if lesser. Two-tailed tests check for non-directional differences, greater or lesser.

2.What are the 4 components of hypothesis testing?

Null Hypothesis ( ): No effect or difference exists. Alternative Hypothesis ( ): An effect or difference exists. Significance Level ( ): Risk of rejecting null hypothesis when it’s true (Type I error). Test Statistic: Numerical value representing observed evidence against null hypothesis.

3.What is hypothesis testing in ML?

Statistical method to evaluate the performance and validity of machine learning models. Tests specific hypotheses about model behavior, like whether features influence predictions or if a model generalizes well to unseen data.

4.What is the difference between Pytest and hypothesis in Python?

Pytest purposes general testing framework for Python code while Hypothesis is a Property-based testing framework for Python, focusing on generating test cases based on specified properties of the code.

Please Login to comment...

Similar reads.

• data-science
• Data Science
• Machine Learning

Improve your Coding Skills with Practice

What kind of Experience do you want to share?