how to apply hypothesis testing in r

Statistics Made Easy

The Complete Guide: Hypothesis Testing in R

A hypothesis test is a formal statistical test we use to reject or fail to reject some statistical hypothesis.

This tutorial explains how to perform the following hypothesis tests in R:

One sample t-test
Two sample t-test
Paired samples t-test

We can use the t.test() function in R to perform each type of test:

x, y: The two samples of data.
alternative: The alternative hypothesis of the test.
mu: The true value of the mean.
paired: Whether to perform a paired t-test or not.
var.equal: Whether to assume the variances are equal between the samples.
conf.level: The confidence level to use.

The following examples show how to use this function in practice.

Example 1: One Sample t-test in R

A one sample t-test is used to test whether or not the mean of a population is equal to some value.

For example, suppose we want to know whether or not the mean weight of a certain species of some turtle is equal to 310 pounds. We go out and collect a simple random sample of turtles with the following weights:

Weights : 300, 315, 320, 311, 314, 309, 300, 308, 305, 303, 305, 301, 303

The following code shows how to perform this one sample t-test in R:

From the output we can see:

t-test statistic: -1.5848
degrees of freedom: 12
p-value: 0.139
95% confidence interval for true mean: [303.4236, 311.0379]
mean of turtle weights: 307.230

Since the p-value of the test (0.139) is not less than .05, we fail to reject the null hypothesis.

This means we do not have sufficient evidence to say that the mean weight of this species of turtle is different from 310 pounds.

Example 2: Two Sample t-test in R

A two sample t-test is used to test whether or not the means of two populations are equal.

For example, suppose we want to know whether or not the mean weight between two different species of turtles is equal. To test this, we collect a simple random sample of turtles from each species with the following weights:

Sample 1 : 300, 315, 320, 311, 314, 309, 300, 308, 305, 303, 305, 301, 303

Sample 2 : 335, 329, 322, 321, 324, 319, 304, 308, 305, 311, 307, 300, 305

The following code shows how to perform this two sample t-test in R:

t-test statistic: -2.1009
degrees of freedom: 19.112
p-value: 0.04914
95% confidence interval for true mean difference: [-14.74, -0.03]
mean of sample 1 weights: 307.2308
mean of sample 2 weights: 314.6154

Since the p-value of the test (0.04914) is less than .05, we reject the null hypothesis.

This means we have sufficient evidence to say that the mean weight between the two species is not equal.

Example 3: Paired Samples t-test in R

A paired samples t-test is used to compare the means of two samples when each observation in one sample can be paired with an observation in the other sample.

For example, suppose we want to know whether or not a certain training program is able to increase the max vertical jump (in inches) of basketball players.

To test this, we may recruit a simple random sample of 12 college basketball players and measure each of their max vertical jumps. Then, we may have each player use the training program for one month and then measure their max vertical jump again at the end of the month.

The following data shows the max jump height (in inches) before and after using the training program for each player:

Before : 22, 24, 20, 19, 19, 20, 22, 25, 24, 23, 22, 21

After : 23, 25, 20, 24, 18, 22, 23, 28, 24, 25, 24, 20

The following code shows how to perform this paired samples t-test in R:

t-test statistic: -2.5289
degrees of freedom: 11
p-value: 0.02803
95% confidence interval for true mean difference: [-2.34, -0.16]
mean difference between before and after: -1.25

Since the p-value of the test (0.02803) is less than .05, we reject the null hypothesis.

This means we have sufficient evidence to say that the mean jump height before and after using the training program is not equal.

Additional Resources

Use the following online calculators to automatically perform various t-tests:

One Sample t-test Calculator Two Sample t-test Calculator Paired Samples t-test Calculator

Featured Posts

5 Regularization Techniques You Should Know

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike. My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

The Complete Guide: Hypothesis Testing in R

A hypothesis test is a formal statistical test we use to reject or fail to reject some statistical hypothesis.

This tutorial explains how to perform the following hypothesis tests in R:

One sample t-test
Two sample t-test
Paired samples t-test

We can use the t.test() function in R to perform each type of test:

x, y: The two samples of data.
alternative: The alternative hypothesis of the test.
mu: The true value of the mean.
paired: Whether to perform a paired t-test or not.
var.equal: Whether to assume the variances are equal between the samples.
conf.level: The confidence level to use.

The following examples show how to use this function in practice.

Example 1: One Sample t-test in R

A one sample t-test is used to test whether or not the mean of a population is equal to some value.

Weights : 300, 315, 320, 311, 314, 309, 300, 308, 305, 303, 305, 301, 303

The following code shows how to perform this one sample t-test in R:

From the output we can see:

t-test statistic: -1.5848
degrees of freedom: 12
p-value: 0.139
95% confidence interval for true mean: [303.4236, 311.0379]
mean of turtle weights: 307.230

Since the p-value of the test (0.139) is not less than .05, we fail to reject the null hypothesis.

This means we do not have sufficient evidence to say that the mean weight of this species of turtle is different from 310 pounds.

Example 2: Two Sample t-test in R

A two sample t-test is used to test whether or not the means of two populations are equal.

Sample 1 : 300, 315, 320, 311, 314, 309, 300, 308, 305, 303, 305, 301, 303

Sample 2 : 335, 329, 322, 321, 324, 319, 304, 308, 305, 311, 307, 300, 305

The following code shows how to perform this two sample t-test in R:

t-test statistic: -2.1009
degrees of freedom: 19.112
p-value: 0.04914
95% confidence interval for true mean difference: [-14.74, -0.03]
mean of sample 1 weights: 307.2308
mean of sample 2 weights: 314.6154

Since the p-value of the test (0.04914) is less than .05, we reject the null hypothesis.

This means we have sufficient evidence to say that the mean weight between the two species is not equal.

Example 3: Paired Samples t-test in R

A paired samples t-test is used to compare the means of two samples when each observation in one sample can be paired with an observation in the other sample.

For example, suppose we want to know whether or not a certain training program is able to increase the max vertical jump (in inches) of basketball players.

The following data shows the max jump height (in inches) before and after using the training program for each player:

Before : 22, 24, 20, 19, 19, 20, 22, 25, 24, 23, 22, 21

After : 23, 25, 20, 24, 18, 22, 23, 28, 24, 25, 24, 20

The following code shows how to perform this paired samples t-test in R:

t-test statistic: -2.5289
degrees of freedom: 11
p-value: 0.02803
95% confidence interval for true mean difference: [-2.34, -0.16]
mean difference between before and after: -1.25

Since the p-value of the test (0.02803) is less than .05, we reject the null hypothesis.

This means we have sufficient evidence to say that the mean jump height before and after using the training program is not equal.

Additional Resources

Use the following online calculators to automatically perform various t-tests:

One Sample t-test Calculator Two Sample t-test Calculator Paired Samples t-test Calculator

How to Calculate Mode from Frequency Table (With Examples)

How to use write.table in r (with examples), related posts, how to create a stem-and-leaf plot in spss, how to create a correlation matrix in spss, excel: how to use if function with text..., excel: how to use greater than or equal..., excel: how to use if function with multiple..., how to convert date of birth to age..., excel: how to highlight entire row based on..., how to add target line to graph in..., excel: how to use if function with negative..., how to extract number from string in pandas.

Hypothesis Tests in R

This tutorial covers basic hypothesis testing in R.

Normality tests
Shapiro-Wilk normality test
Kolmogorov-Smirnov test
Comparing central tendencies: Tests with continuous / discrete data
One-sample t-test : Normally-distributed sample vs. expected mean
Two-sample t-test : Two normally-distributed samples
Wilcoxen rank sum : Two non-normally-distributed samples
Weighted two-sample t-test : Two continuous samples with weights
Comparing proportions: Tests with categorical data
Chi-squared goodness of fit test : Sampled frequencies of categorical values vs. expected frequencies
Chi-squared independence test : Two sampled frequencies of categorical values
Weighted chi-squared independence test : Two weighted sampled frequencies of categorical values
Comparing multiple groups: Tests with categorical and continuous / discrete data
Analysis of Variation (ANOVA) : Normally-distributed samples in groups defined by categorical variable(s)
Kruskal-Wallace One-Way Analysis of Variance : Nonparametric test of the significance of differences between two or more groups

Hypothesis Testing

Science is "knowledge or a system of knowledge covering general truths or the operation of general laws especially as obtained and tested through scientific method" (Merriam-Webster 2022) .

The idealized world of the scientific method is question-driven , with the collection and analysis of data determined by the formulation of research questions and the testing of hypotheses. Hypotheses are tentative assumptions about what the answers to your research questions may be.

Formulate questions: How can I understand some phenomenon?
Literature review: What does existing research say about my questions?
Formulate hypotheses: What do I think the answers to my questions will be?
Collect data: What data can I gather to test my hypothesis?
Test hypotheses: Does the data support my hypothesis?
Communicate results: Who else needs to know about this?
Formulate questions: Frame missing knowledge about a phenomenon as research question(s).
Literature review: A literature review is an investigation of what existing research says about the phenomenon you are studying. A thorough literature review is essential to identify gaps in existing knowledge you can fill, and to avoid unnecessarily duplicating existing research.
Formulate hypotheses: Develop possible answers to your research questions.
Collect data: Acquire data that supports or refutes the hypothesis.
Test hypotheses: Run tools to determine if the data corroborates the hypothesis.
Communicate results: Share your findings with the broader community that might find them useful.

While the process of knowledge production is, in practice, often more iterative than this waterfall model, the testing of hypotheses is usually a fundamental element of scientific endeavors involving quantitative data.

The Problem of Induction

The scientific method looks to the past or present to build a model that can be used to infer what will happen in the future. General knowledge asserts that given a particular set of conditions, a particular outcome will or is likely to occur.

The problem of induction is that we cannot be 100% certain that what we are assuming is a general principle is not, in fact, specific to the particular set of conditions when we made our empirical observations. We cannot prove that that such principles will hold true under future conditions or different locations that we have not yet experienced (Vickers 2014) .

The problem of induction is often associated with the 18th-century British philosopher David Hume . This problem is especially vexing in the study of human beings, where behaviors are a function of complex social interactions that vary over both space and time.

Falsification

One way of addressing the problem of induction was proposed by the 20th-century Viennese philosopher Karl Popper .

Rather than try to prove a hypothesis is true, which we cannot do because we cannot know all possible situations that will arise in the future, we should instead concentrate on falsification , where we try to find situations where a hypothesis is false. While you cannot prove your hypothesis will always be true, you only need to find one situation where the hypothesis is false to demonstrate that the hypothesis can be false (Popper 1962) .

If a hypothesis is not demonstrated to be false by a particular test, we have corroborated that hypothesis. While corroboration does not "prove" anything with 100% certainty, by subjecting a hypothesis to multiple tests that fail to demonstrate that it is false, we can have increasing confidence that our hypothesis reflects reality.

Null and Alternative Hypotheses

In scientific inquiry, we are often concerned with whether a factor we are considering (such as taking a specific drug) results in a specific effect (such as reduced recovery time).

To evaluate whether a factor results in an effect, we will perform an experiment and / or gather data. For example, in a clinical drug trial, half of the test subjects will be given the drug, and half will be given a placebo (something that appears to be the drug but is actually a neutral substance).

Because the data we gather will usually only be a portion (sample) of total possible people or places that could be affected (population), there is a possibility that the sample is unrepresentative of the population. We use a statistical test that considers that uncertainty when assessing whether an effect is associated with a factor.

Statistical testing begins with an alternative hypothesis (H 1 ) that states that the factor we are considering results in a particular effect. The alternative hypothesis is based on the research question and the type of statistical test being used.
Because of the problem of induction , we cannot prove our alternative hypothesis. However, under the concept of falsification , we can evaluate the data to see if there is a significant probability that our data falsifies our alternative hypothesis (Wilkinson 2012) .
The null hypothesis (H 0 ) states that the factor has no effect. The null hypothesis is the opposite of the alternative hypothesis. The null hypothesis is what we are testing when we perform a hypothesis test.

The output of a statistical test like the t-test is a p -value. A p -value is the probability that any effects we see in the sampled data are the result of random sampling error (chance).

If a p -value is greater than the significance level (0.05 for 5% significance) we fail to reject the null hypothesis since there is a significant possibility that our results falsify our alternative hypothesis.
If a p -value is lower than the significance level (0.05 for 5% significance) we reject the null hypothesis and have corroborated (provided evidence for) our alternative hypothesis.

The calculation and interpretation of the p -value goes back to the central limit theorem , which states that random sampling error has a normal distribution.

Using our example of a clinical drug trial, if the mean recovery times for the two groups are close enough together that there is a significant possibility ( p > 0.05) that the recovery times are the same (falsification), we fail to reject the null hypothesis.

However, if the mean recovery times for the two groups are far enough apart that the probability they are the same is under the level of significance ( p < 0.05), we reject the null hypothesis and have corroborated our alternative hypothesis.

Significance means that an effect is "probably caused by something other than mere chance" (Merriam-Webster 2022) .

The significance level (α) is the threshold for significance and, by convention, is usually 5%, 10%, or 1%, which corresponds to 95% confidence, 90% confidence, or 99% confidence, respectively.
A factor is considered statistically significant if the probability that the effect we see in the data is a result of random sampling error (the p -value) is below the chosen significance level.
A statistical test is used to evaluate whether a factor being considered is statistically significant (Gallo 2016) .

Type I vs. Type II Errors

Although we are making a binary choice between rejecting and failing to reject the null hypothesis, because we are using sampled data, there is always the possibility that the choice we have made is an error.

There are two types of errors that can occur in hypothesis testing.

Type I error (false positive) occurs when a low p -value causes us to reject the null hypothesis, but the factor does not actually result in the effect.
Type II error (false negative) occurs when a high p -value causes us to fail to reject the null hypothesis, but the factor does actually result in the effect.

The numbering of the errors reflects the predisposition of the scientific method to be fundamentally skeptical . Accepting a fact about the world as true when it is not true is considered worse than rejecting a fact about the world that actually is true.

Statistical Significance vs. Importance

When we fail to reject the null hypothesis, we have found information that is commonly called statistically significant . But there are multiple challenges with this terminology.

First, statistical significance is distinct from importance (NIST 2012) . For example, if sampled data reveals a statistically significant difference in cancer rates, that does not mean that the increased risk is important enough to justify expensive mitigation measures. All statistical results require critical interpretation within the context of the phenomenon being observed. People with different values and incentives can have different interpretations of whether statistically significant results are important.

Second, the use of 95% probability for defining confidence intervals is an arbitrary convention. This creates a good vs. bad binary that suggests a "finality and certitude that are rarely justified." Alternative approaches like Beyesian statistics that express results as probabilities can offer more nuanced ways of dealing with complexity and uncertainty (Clayton 2022) .

Science vs. Non-science

Not all ideas can be falsified, and Popper uses the distinction between falsifiable and non-falsifiable ideas to make a distinction between science and non-science. In order for an idea to be science it must be an idea that can be demonstrated to be false.

While Popper asserts there is still value in ideas that are not falsifiable, such ideas are not science in his conception of what science is. Such non-science ideas often involve questions of subjective values or unseen forces that are complex, amorphous, or difficult to objectively observe.

Example Data

As example data, this tutorial will use a table of anonymized individual responses from the CDC's Behavioral Risk Factor Surveillance System . The BRFSS is a "system of health-related telephone surveys that collect state data about U.S. residents regarding their health-related risk behaviors, chronic health conditions, and use of preventive services" (CDC 2019) .

A CSV file with the selected variables used in this tutorial is available here and can be imported into R with read.csv() .

Guidance on how to download and process this data directly from the CDC website is available here...

Variable Types

The publicly-available BRFSS data contains a wide variety of discrete, ordinal, and categorical variables. Variables often contain special codes for non-responsiveness or missing (NA) values. Examples of how to clean these variables are given here...

The BRFSS has a codebook that gives the survey questions associated with each variable, and the way that responses are encoded in the variable values.

Normality Tests

Tests are commonly divided into two groups depending on whether they are built on the assumption that the continuous variable has a normal distribution.

Parametric tests presume a normal distribution.
Non-parametric tests can work with normal and non-normal distributions.

The distinction between parametric and non-parametric techniques is especially important when working with small numbers of samples (less than 40 or so) from a larger population.

The normality tests given below do not work with large numbers of values, but with many statistical techniques, violations of normality assumptions do not cause major problems when large sample sizes are used. (Ghasemi and Sahediasi 2012) .

The Shapiro-Wilk Normality Test

Data: A continuous or discrete sampled variable
R Function: shapiro.test()
Null hypothesis (H 0 ): The population distribution from which the sample is drawn is not normal
History: Samuel Sanford Shapiro and Martin Wilk (1965)

This is an example with random values from a normal distribution.

This is an example with random values from a uniform (non-normal) distribution.

The Kolmogorov-Smirnov Test

The Kolmogorov-Smirnov is a more-generalized test than the Shapiro-Wilks test that can be used to test whether a sample is drawn from any type of distribution.

Data: A continuous or discrete sampled variable and a reference probability distribution
R Function: ks.test()
Null hypothesis (H 0 ): The population distribution from which the sample is drawn does not match the reference distribution
History: Andrey Kolmogorov (1933) and Nikolai Smirnov (1948)
pearson.test() The Pearson Chi-square Normality Test from the nortest library. Lower p-values (closer to 0) means to reject the reject the null hypothesis that the distribution IS normal.

Modality Tests of Samples

Comparing two central tendencies: tests with continuous / discrete data, one sample t-test (two-sided).

The one-sample t-test tests the significance of the difference between the mean of a sample and an expected mean.

Data: A continuous or discrete sampled variable and a single expected mean (μ)
Parametric (normal distributions)
R Function: t.test()
Null hypothesis (H 0 ): The means of the sampled distribution matches the expected mean.
History: William Sealy Gosset (1908)

t = ( Χ - μ) / (σ̂ / √ n )

t : The value of t used to find the p-value
Χ : The sample mean
μ: The population mean
σ̂: The estimate of the standard deviation of the population (usually the stdev of the sample
n : The sample size

T-tests should only be used when the population is at least 20 times larger than its respective sample. If the sample size is too large, the low p-value makes the insignificant look significant. .

For example, we test a hypothesis that the mean weight in IL in 2020 is different than the 2005 continental mean weight.

Walpole et al. (2012) estimated that the average adult weight in North America in 2005 was 178 pounds. We could presume that Illinois is a comparatively normal North American state that would follow the trend of both increased age and increased weight (CDC 2021) .

The low p-value leads us to reject the null hypothesis and corroborate our alternative hypothesis that mean weight changed between 2005 and 2020 in Illinois.

One Sample T-Test (One-Sided)

Because we were expecting an increase, we can modify our hypothesis that the mean weight in 2020 is higher than the continental weight in 2005. We can perform a one-sided t-test using the alternative="greater" parameter.

The low p-value leads us to again reject the null hypothesis and corroborate our alternative hypothesis that mean weight in 2020 is higher than the continental weight in 2005.

Note that this does not clearly evaluate whether weight increased specifically in Illinois, or, if it did, whether that was caused by an aging population or decreasingly healthy diets. Hypotheses based on such questions would require more detailed analysis of individual data.

Although we can see that the mean cancer incidence rate is higher for counties near nuclear plants, there is the possiblity that the difference in means happened by accident and the nuclear plants have nothing to do with those higher rates.

The t-test allows us to test a hypothesis. Note that a t-test does not "prove" or "disprove" anything. It only gives the probability that the differences we see between two areas happened by chance. It also does not evaluate whether there are other problems with the data, such as a third variable, or inaccurate cancer incidence rate estimates.

Note that this does not prove that nuclear power plants present a higher cancer risk to their neighbors. It simply says that the slightly higher risk is probably not due to chance alone. But there are a wide variety of other other related or unrelated social, environmental, or economic factors that could contribute to this difference.

Box-and-Whisker Chart

One visualization commonly used when comparing distributions (collections of numbers) is a box-and-whisker chart. The boxes show the range of values in the middle 25% to 50% to 75% of the distribution and the whiskers show the extreme high and low values.

Although Google Sheets does not provide the capability to create box-and-whisker charts, Google Sheets does have candlestick charts , which are similar to box-and-whisker charts, and which are normally used to display the range of stock price changes over a period of time.

This video shows how to create a candlestick chart comparing the distributions of cancer incidence rates. The QUARTILE() function gets the values that divide the distribution into four equally-sized parts. This shows that while the range of incidence rates in the non-nuclear counties are wider, the bulk of the rates are below the rates in nuclear counties, giving a visual demonstration of the numeric output of our t-test.

While categorical data can often be reduced to dichotomous data and used with proportions tests or t-tests, there are situations where you are sampling data that falls into more than two categories and you would like to make hypothesis tests about those categories. This tutorial describes a group of tests that can be used with that type of data.

Two-Sample T-Test

When comparing means of values from two different groups in your sample, a two-sample t-test is in order.

The two-sample t-test tests the significance of the difference between the means of two different samples.

Two normally-distributed, continuous or discrete sampled variables, OR
A normally-distributed continuous or sampled variable and a parallel dichotomous variable indicating what group each of the values in the first variable belong to
Null hypothesis (H 0 ): The means of the two sampled distributions are equal.

For example, given the low incomes and delicious foods prevalent in Mississippi, we might presume that average weight in Mississippi would be higher than in Illinois.

We test a hypothesis that the mean weight in IL in 2020 is less than the 2020 mean weight in Mississippi.

The low p-value leads us to reject the null hypothesis and corroborate our alternative hypothesis that mean weight in Illinois is less than in Mississippi.

While the difference in means is statistically significant, it is small (182 vs. 187), which should lead to caution in interpretation that you avoid using your analysis simply to reinforce unhelpful stigmatization.

Wilcoxen Rank Sum Test (Mann-Whitney U-Test)

The Wilcoxen rank sum test tests the significance of the difference between the means of two different samples. This is a non-parametric alternative to the t-test.

Data: Two continuous sampled variables
Non-parametric (normal or non-normal distributions)
R Function: wilcox.test()
Null hypothesis (H 0 ): For randomly selected values X and Y from two populations, the probability of X being greater than Y is equal to the probability of Y being greater than X.
History: Frank Wilcoxon (1945) and Henry Mann and Donald Whitney (1947)

The test is is implemented with the wilcox.test() function.

When the test is performed on one sample in comparison to an expected value around which the distribution is symmetrical (μ), the test is known as a Mann-Whitney U test .
When the test is performed to compare two samples, the test is known as a Wilcoxon rank sum test .

For this example, we will use AVEDRNK3: During the past 30 days, on the days when you drank, about how many drinks did you drink on the average?

1 - 76: Number of drinks
77: Don’t know/Not sure
99: Refused
NA: Not asked or Missing

The histogram clearly shows this to be a non-normal distribution.

Continuing the comparison of Illinois and Mississippi from above, we might presume that with all that warm weather and excellent food in Mississippi, they might be inclined to drink more. The means of average number of drinks per month seem to suggest that Mississippians do drink more than Illinoians.

We can test use wilcox.test() to test a hypothesis that the average amount of drinking in Illinois is different than in Mississippi. Like the t-test, the alternative can be specified as two-sided or one-sided, and for this example we will test whether the sampled Illinois value is indeed less than the Mississippi value.

The low p-value leads us to reject the null hypothesis and corroborates our hypothesis that average drinking is lower in Illinois than in Mississippi. As before, this tells us nothing about why this is the case.

Weighted Two-Sample T-Test

The downloadable BRFSS data is raw, anonymized survey data that is biased by uneven geographic coverage of survey administration (noncoverage) and lack of responsiveness from some segments of the population (nonresponse). The X_LLCPWT field (landline, cellphone weighting) is a weighting factor added by the CDC that can be assigned to each response to compensate for these biases.

The wtd.t.test() function from the weights library has a weights parameter that can be used to include a weighting factor as part of the t-test.

Comparing Proportions: Tests with Categorical Data

Chi-squared goodness of fit.

Tests the significance of the difference between sampled frequencies of different values and expected frequencies of those values
Data: A categorical sampled variable and a table of expected frequencies for each of the categories
R Function: chisq.test()
Null hypothesis (H 0 ): The relative proportions of categories in one variable are different from the expected proportions
History: Karl Pearson (1900)
Example Question: Are the voting preferences of voters in my district significantly different from the current national polls?

For example, we test a hypothesis that smoking rates changed between 2000 and 2020.

In 2000, the estimated rate of adult smoking in Illinois was 22.3% (Illinois Department of Public Health 2004) .

The variable we will use is SMOKDAY2: Do you now smoke cigarettes every day, some days, or not at all?

1: Current smoker - now smokes every day
2: Current smoker - now smokes some days
3: Not at all
7: Don't know
NA: Not asked or missing - NA is used for people who have never smoked

We subset only yes/no responses in Illinois and convert into a dummy variable (yes = 1, no = 0).

The listing of the table as percentages indicates that smoking rates were halved between 2000 and 2020, but since this is sampled data, we need to run a chi-squared test to make sure the difference can't be explained by the randomness of sampling.

In this case, the very low p-value leads us to reject the null hypothesis and corroborates the alternative hypothesis that smoking rates changed between 2000 and 2020.

Chi-Squared Contingency Analysis / Test of Independence

Tests the significance of the difference between frequencies between two different groups
Data: Two categorical sampled variables
Null hypothesis (H 0 ): The relative proportions of one variable are independent of the second variable.

We can also compare categorical proportions between two sets of sampled categorical variables.

The chi-squared test can is used to determine if two categorical variables are independent. What is passed as the parameter is a contingency table created with the table() function that cross-classifies the number of rows that are in the categories specified by the two categorical variables.

The null hypothesis with this test is that the two categories are independent. The alternative hypothesis is that there is some dependency between the two categories.

For this example, we can compare the three categories of smokers (daily = 1, occasionally = 2, never = 3) across the two categories of states (Illinois and Mississippi).

The low p-value leads us to reject the null hypotheses that the categories are independent and corroborates our hypotheses that smoking behaviors in the two states are indeed different.

p-value = 1.516e-09

Weighted Chi-Squared Contingency Analysis

As with the weighted t-test above, the weights library contains the wtd.chi.sq() function for incorporating weighting into chi-squared contingency analysis.

As above, the even lower p-value leads us to again reject the null hypothesis that smoking behaviors are independent in the two states.

Suppose that the Macrander campaign would like to know how partisan this election is. If people are largely choosing to vote along party lines, the campaign will seek to get their base voters out to the polls. If people are splitting their ticket, the campaign may focus their efforts more broadly.

In the example below, the Macrander campaign took a small poll of 30 people asking who they wished to vote for AND what party they most strongly affiliate with.

The output of table() shows fairly strong relationship between party affiliation and candidates. Democrats tend to vote for Macrander, while Republicans tend to vote for Stewart, while independents all vote for Miller.

This is reflected in the very low p-value from the chi-squared test. This indicates that there is a very low probability that the two categories are independent. Therefore we reject the null hypothesis.

In contrast, suppose that the poll results had showed there were a number of people crossing party lines to vote for candidates outside their party. The simulated data below uses the runif() function to randomly choose 50 party names.

The contingency table() shows no clear relationship between party affiliation and candidate. This is validated quantitatively by the chi-squared test. The fairly high p-value of 0.4018 indicates a 40% chance that the two categories are independent. Therefore, we fail to reject the null hypothesis and the campaign should focus their efforts on the broader electorate.

The warning message given by the chisq.test() function indicates that the sample size is too small to make an accurate analysis. The simulate.p.value = T parameter adds Monte Carlo simulation to the test to improve the estimation and get rid of the warning message. However, the best way to get rid of this message is to get a larger sample.

Comparing Categorical and Continuous Variables

Analysis of variation (anova).

Analysis of Variance (ANOVA) is a test that you can use when you have a categorical variable and a continuous variable. It is a test that considers variability between means for different categories as well as the variability of observations within groups.

There are a wide variety of different extensions of ANOVA that deal with covariance (ANCOVA), multiple variables (MANOVA), and both of those together (MANCOVA). These techniques can become quite complicated and also assume that the values in the continuous variables have a normal distribution.

Data: One or more categorical (independent) variables and one continuous (dependent) sampled variable
R Function: aov()
Null hypothesis (H 0 ): There is no difference in means of the groups defined by each level of the categorical (independent) variable
History: Ronald Fisher (1921)
Example Question: Do low-, middle- and high-income people vary in the amount of time they spend watching TV?

As an example, we look at the continuous weight variable (WEIGHT2) split into groups by the eight income categories in INCOME2: Is your annual household income from all sources?

1: Less than $10,000
2: $10,000 to less than $15,000
3: $15,000 to less than $20,000
4: $20,000 to less than $25,000
5: $25,000 to less than $35,000
6: $35,000 to less than $50,000
7: $50,000 to less than $75,000)
8: $75,000 or more

The barplot() of means does show variation among groups, although there is no clear linear relationship between income and weight.

To test whether this variation could be explained by randomness in the sample, we run the ANOVA test.

The low p-value leads us to reject the null hypothesis that there is no difference in the means of the different groups, and corroborates the alternative hypothesis that mean weights differ based on income group.

However, it gives us no clear model for describing that relationship and offers no insights into why income would affect weight, especially in such a nonlinear manner.

Suppose you are performing research into obesity in your city. You take a sample of 30 people in three different neighborhoods (90 people total), collecting information on health and lifestyle. Two variables you collect are height and weight so you can calculate body mass index . Although this index can be misleading for some populations (notably very athletic people), ordinary sedentary people can be classified according to BMI:

Average BMI in the US from 2007-2010 was around 28.6 and rising, standard deviation of around 5 .

You would like to know if there is a difference in BMI between different neighborhoods so you can know whether to target specific neighborhoods or make broader city-wide efforts. Since you have more than two groups, you cannot use a t-test().

Kruskal-Wallace One-Way Analysis of Variance

A somewhat simpler test is the Kruskal-Wallace test which is a nonparametric analogue to ANOVA for testing the significance of differences between two or more groups.

R Function: kruskal.test()
Null hypothesis (H 0 ): The samples come from the same distribution.
History: William Kruskal and W. Allen Wallis (1952)

For this example, we will investigate whether mean weight varies between the three major US urban states: New York, Illinois, and California.

To test whether this variation could be explained by randomness in the sample, we run the Kruskal-Wallace test.

The low p-value leads us to reject the null hypothesis that the samples come from the same distribution. This corroborates the alternative hypothesis that mean weights differ based on state.

A convienent way of visualizing a comparison between continuous and categorical data is with a box plot , which shows the distribution of a continuous variable across different groups:

A percentile is the level at which a given percentage of the values in the distribution are below: the 5th percentile means that five percent of the numbers are below that value.

The quartiles divide the distribution into four parts. 25% of the numbers are below the first quartile. 75% are below the third quartile. 50% are below the second quartile, making it the median.

Box plots can be used with both sampled data and population data.

The first parameter to the box plot is a formula: the continuous variable as a function of (the tilde) the second variable. A data= parameter can be added if you are using variables in a data frame.

The chi-squared test can be used to determine if two categorical variables are independent of each other.

Introduction to Statistics with R

6.2 hypothesis tests, 6.2.1 illustrating a hypothesis test.

Let’s say we have a batch of chocolate bars, and we’re not sure if they are from Theo’s. What can the weight of these bars tell us about the probability that these are Theo’s chocolate?

Now, let’s perform a hypothesis test on this chocolate of an unknown origin.

What is the sampling distribution of the bar weight under the null hypothesis that the bars from Theo’s weigh 40 grams on average? We’ll need to specify the standard deviation to obtain the sampling distribution, and here we’ll use $\sigma_X = 2$ (since that’s the value we used for the distribution we sampled from).

The null hypothesis is \[H_0: \mu = 40\] since we know the mean weight of Theo’s chocolate bars is 40 grams.

The sample distribution of the sample mean is: \[ \overline{X} \sim {\cal N}\left(\mu, \frac{\sigma}{\sqrt{n}}\right) = {\cal N}\left(40, \frac{2}{\sqrt{20}}\right). \] We can visualize the situation by plotting the p.d.f. of the sampling distribution under $H_0$ along with the location of our observed sample mean.

6.2.2 Hypothesis Tests for Means

6.2.2.1 known standard deviation.

It is simple to calculate a hypothesis test in R (in fact, we already implicitly did this in the previous section). When we know the population standard deviation, we use a hypothesis test based on the standard normal, known as a $z$ -test. Here, let’s assume $\sigma_X = 2$ (because that is the standard deviation of the distribution we simulated from above) and specify the alternative hypothesis to be \[ H_A: \mu \neq 40. \] We will the z.test() function from the BSDA package, specifying the confidence level via conf.level , which is $1 - \alpha = 1 - 0.05 = 0.95$ , for our test:

6.2.2.2 Unknown Standard Deviation

If we do not know the population standard deviation, we typically use the t.test() function included in base R. We know that: \[\frac{\overline{X} - \mu}{\frac{s_x}{\sqrt{n}}} \sim t_{n-1},\] where $t_{n-1}$ denotes Student’s $t$ distribution with $n - 1$ degrees of freedom. We only need to supply the confidence level here:

We note that the $p$ -value here (rounded to 4 decimal places) is 0.0031, so again, we can detect it’s not likely that these bars are from Theo’s. Even with a very small sample, the difference is large enough (and the standard deviation small enough) that the $t$ -test can detect it.

6.2.3 Two-sample Tests

6.2.3.1 unpooled two-sample t-test.

Now suppose we have two batches of chocolate bars, one of size 40 and one of size 45. We want to test whether they come from the same factory. However we have no information about the distributions of the chocolate bars. Therefore, we cannot conduct a one sample t-test like above as that would require some knowledge about $\mu_0$ , the population mean of chocolate bars.

We will generate the samples from normal distribution with mean 45 and 47 respectively. However, let’s assume we do not know this information. The population standard deviation of the distributions we are sampling from are both 2, but we will assume we do not know that either. Let us denote the unknown true population means by $\mu_1$ and $\mu_2$ .

Consider the test $H_0:\mu_1=\mu_2$ versus $H_1:\mu_1\neq\mu_2$ . We can use R function t.test again, since this function can perform one- and two-sided tests. In fact, t.test assumes a two-sided test by default, so we do not have to specify that here.

The p-value is much less than .05, so we can quite confidently reject the null hypothesis. Indeed, we know from simulating the data that $\mu_1\neq\mu_2$ , so our test led us to the correct conclusion!

Consider instead testing $H_0:\mu_1=\mu_2$ versus $H_1:\mu_1\leq\mu_2$ .

As we would expect, this test also rejects the null hypothesis. One-sided tests are more common in practice as they provide a more principled description of the relationship between the datasets. For example, if you are comparing your new drug’s performance to a “gold standard”, you really only care if your drug’s performance is “better” (a one-sided alternative), and not that your drug’s performance is merely “different” (a two-sided alternative).

6.2.3.2 Pooled Two-sample t-test

Suppose you knew that the samples are coming from distributions with same standard deviations. Then it makes sense to carry out a pooled 2 sample t-test. You specify this in the t.test function as follows.

6.2.3.3 Paired t-test

Suppose we take a batch of chocolate bars and stamp the Theo’s logo on them. We want to know if the stamping process significantly changes the weight of the chocolate bars. Let’s suppose that the true change in weight is distributed as a ${\cal N}(-0.3, 0.2^2)$ random variable:

Let $\mu_1$ and $\mu_2$ be the true means of the distributions of chocolate weights before and after the stamping process. Suppose we want to test $H_0:\mu_1=\mu_2$ versus $\mu_1\neq\mu_2$ . We can use the R function t.test() for this by choosing paired = TRUE , which indicates that we are looking at pairs of observations corresponding to the same experimental subject and testing whether or not the difference in distribution means is zero.

We can also perform the same test as a one sample t-test using choc.after - choc.batch .

Notice that we get the exact same $p$ -value for these two tests.

Since the p-value is less than .05, we reject the null hypothesis at level .05. Hence, we have enough evidence in the data to claim that stamping a chocolate bar significantly reduces its weight.

6.2.4 Tests for Proportions

Let’s look at the proportion of Theo’s chocolate bars with a weight exceeding 38g:

Going back to that first batch of 20 chocolate bars of unknown origin, let’s see if we can test whether they’re from Theo’s based on the proportion weighing > 38g.

Recall from our test on the means that we rejected the null hypothesis that the means from the two batches were equal. In this case, a one-sided test is appropiate, and our hypothesis is:

Null hypothesis: $H_0: p = 0.85$ . Alternative: $H_A: p > 0.85$ .

We want to test this hypothesis at a level $\alpha = 0.05$ .

In R, there is a function called prop.test() that you can use to perform tests for proportions. Note that prop.test() only gives you an approximate result.

Similarly, you can use the binom.test() function for an exact result.

The $p$ -value for both tests is around 0.18, which is much greater than 0.05. So, we cannot reject the hypothesis that the unknown bars come from Theo’s. This is not because the tests are less accurate than the ones we ran before, but because we are testing a less sensitive measure: the proportion weighing > 38 grams, rather than the mean weights. Also, note that this doesn’t mean that we can conclude that these bars do come from Theo’s – why not?

The prop.test() function is the more versatile function in that it can deal with contingency tables, larger number of groups, etc. The binom.test() function gives you exact results, but you can only apply it to one-sample questions.

6.2.5 Power

Let’s think about when we reject the null hypothesis. We would reject the null hypothesis if we observe data with too small of a $p$ -value. We can calculate the critical value where we would reject the null if we were to observe data that would lead to a more extreme value.

Suppose we take a sample of chocolate bars of size n = 20 , and our null hypothesis is that the bars come from Theo’s ( $H_0$ : mean = 40, sd = 2 ). Then for a one-sided test (versus larger alternatives), we can calculate the critical value by using the quantile function in R, specifiying the mean and sd of the sampling distribution of $\overline X$ under $H_0$ :

Now suppose we want to calculate the power of our hypothesis test: the probability of rejecting the null hypothesis when the null hypothesis is false. In order to do so, we need to compare the null to a specific alternative, so we choose $H_A$ : mean = 42, sd = 2 . Then the probability that we reject the null under this specific alternative is

We can use R to perform the same calculations using the power.z.test from the asbio package:

Introduction

R installation
Working directory
Getting help
Install packages

Data structures

Data Wrangling

Sort and order
Merge data frames

Programming

Creating functions
If else statement
apply function
sapply function
tapply function

Import & export

Read TXT files
Import CSV files
Read Excel files
Read SQL databases
Export data
plot function
Scatter plot
Density plot
Tutorials Introduction Data wrangling Graphics Statistics See all

HYPOTHESIS TESTING IN R

Hypothesis testing is a statistical procedure used to make decisions or draw conclusions about the characteristics of a population based on information provided by a sample

NORMALITY TESTS

Normality tests are used to evaluate whether a data sample follows a normal distribution. These tests allow to verify if the data have a behavior similar to that of a Gaussian distribution, being useful to determine if the assumptions of certain parametric statistical analyses that require normality in the data are met

Shapiro Wilk normality test

shapiro.test()

Lilliefors normality test

lillie.test()

GOODNESS OF FIT TESTS

These tests are used to verify whether a proposed theoretical distribution adequately matches the observed data. They are useful to assess whether a specific distribution fits the data well, allowing to determine whether a theoretical model accurately represents the observed data distribution

Pearson's Chi-squared test with chisq.test()

chisq.test()

Kolmogorov-Smirnov test in R with ks.test()

Kolmogorov-Smirnov test with ks.test()

Median tests.

Median tests are used to test whether the medians of two or more groups are statistically different, thus identifying whether there are significant differences in medians between populations or treatments

Wilcoxon signed rank test

wilcox.test()

Wilcoxon rank sum test (Mann-Whitney U test)

Kruskal Wallis rank sum test (H test)

kruskal.test()

OTHER TYPES OF TESTS

There are other types of tests, such as tests for comparing means, for equality of variances or for equality of proportions

T-test to compare means

F test with var.test() to compare two variances

Test for proportions with prop.test()

prop.test()

Try adjusting your search query

👉 If you haven’t found what you’re looking for, consider clicking the checkbox to activate the extended search on R CHARTS for additional graphs tutorials, try searching a synonym of your query if possible (e.g., ‘bar plot’ -> ‘bar chart’), search for a more generic query or if you are searching for a specific function activate the functions search or use the functions search bar .

An R Introduction to Statistics

Hypothesis Testing

$fractal-10h$

In the following tutorials, we demonstrate the procedure of hypothesis testing in R first with the intuitive critical value approach. Then we discuss the popular p-value approach as alternative.

Lower Tail Test of Population Mean with Known Variance
Upper Tail Test of Population Mean with Known Variance
Two-Tailed Test of Population Mean with Known Variance
Lower Tail Test of Population Mean with Unknown Variance
Upper Tail Test of Population Mean with Unknown Variance
Two-Tailed Test of Population Mean with Unknown Variance
Lower Tail Test of Population Proportion
Upper Tail Test of Population Proportion
Two-Tailed Test of Population Proportion
Elementary Statistics with R
hypothesis testing
significance level
type I error

R Tutorial eBook

R Tutorials

Combining Vectors
Vector Arithmetics
Vector Index
Numeric Index Vector
Logical Index Vector
Named Vector Members
Matrix Construction
Named List Members
Data Frame Column Vector
Data Frame Column Slice
Data Frame Row Slice
Data Import
Frequency Distribution of Qualitative Data
Relative Frequency Distribution of Qualitative Data
Category Statistics
Frequency Distribution of Quantitative Data
Relative Frequency Distribution of Quantitative Data
Cumulative Frequency Distribution
Cumulative Frequency Graph
Cumulative Relative Frequency Distribution
Cumulative Relative Frequency Graph
Stem-and-Leaf Plot
Scatter Plot
Interquartile Range
Standard Deviation
Correlation Coefficient
Central Moment
Binomial Distribution
Poisson Distribution
Continuous Uniform Distribution
Exponential Distribution
Normal Distribution
Chi-squared Distribution
Student t Distribution
F Distribution
Point Estimate of Population Mean
Interval Estimate of Population Mean with Known Variance
Interval Estimate of Population Mean with Unknown Variance
Sampling Size of Population Mean
Point Estimate of Population Proportion
Interval Estimate of Population Proportion
Sampling Size of Population Proportion
Type II Error in Lower Tail Test of Population Mean with Known Variance
Type II Error in Upper Tail Test of Population Mean with Known Variance
Type II Error in Two-Tailed Test of Population Mean with Known Variance
Type II Error in Lower Tail Test of Population Mean with Unknown Variance
Type II Error in Upper Tail Test of Population Mean with Unknown Variance
Type II Error in Two-Tailed Test of Population Mean with Unknown Variance
Population Mean Between Two Matched Samples
Population Mean Between Two Independent Samples
Comparison of Two Population Proportions
Multinomial Goodness of Fit
Chi-squared Test of Independence
Completely Randomized Design
Randomized Block Design
Factorial Design
Wilcoxon Signed-Rank Test
Mann-Whitney-Wilcoxon Test
Kruskal-Wallis Test
Estimated Simple Regression Equation
Coefficient of Determination
Significance Test for Linear Regression
Confidence Interval for Linear Regression
Prediction Interval for Linear Regression
Residual Plot
Standardized Residual
Normal Probability Plot of Residuals
Estimated Multiple Regression Equation
Multiple Coefficient of Determination
Adjusted Coefficient of Determination
Significance Test for MLR
Confidence Interval for MLR
Prediction Interval for MLR
Estimated Logistic Regression Equation
Significance Test for Logistic Regression
Distance Matrix by GPU
Hierarchical Cluster Analysis
Kendall Rank Coefficient
Significance Test for Kendall's Tau-b
Support Vector Machine with GPU
Support Vector Machine with GPU, Part II
Bayesian Classification with Gaussian Process
Hierarchical Linear Model
Installing GPU Packages

Statistics with R
R Objects, Numbers, Attributes, Vectors, Coercion
Matrices, Lists, Factors
Data Frames in R
Control Structures in R
Functions in R
Data Basics: Compute Summary Statistics in R
Central Tendency and Spread in R Programming
Data Basics: Plotting – Charts and Graphs
Normal Distribution in R
Skewness of statistical data
Bernoulli Distribution in R
Binomial Distribution in R Programming
Compute Randomly Drawn Negative Binomial Density in R Programming
Poisson Functions in R Programming
How to Use the Multinomial Distribution in R
Beta Distribution in R
Chi-Square Distribution in R
Exponential Distribution in R Programming
Log Normal Distribution in R
Continuous Uniform Distribution in R
Understanding the t-distribution in R
Gamma Distribution in R Programming
How to Calculate Conditional Probability in R?

How to Plot a Weibull Distribution in R

Hypothesis testing in r programming.

One Sample T-test in R
Two sample T-test in R
Paired Sample T-test in R
Type I Error in R
Type II Error in R
Confidence Intervals in R
Covariance and Correlation in R
Covariance Matrix in R
Pearson Correlation in R
Normal Probability Plot in R

Hypothesis testing is a statistical method used to determine whether there is enough evidence to reject a null hypothesis in favor of an alternative hypothesis. In R programming, you can perform various types of hypothesis tests, such as t-tests, chi-squared tests, and ANOVA tests, among others.

In R programming, you can perform hypothesis testing using various built-in functions. Here’s an overview of some commonly used hypothesis testing methods in R:

T-test (one-sample, paired, and independent two-sample)
Chi-square test
ANOVA (Analysis of Variance)
Wilcoxon signed-rank test
Mann-Whitney U test

1. One-sample t-test:

The one-sample t-test is used to compare the mean of a sample to a known value (usually a population mean) to see if there is a significant difference.

2. Two-sample t-test:

The two-sample t-test is used to compare the means of two independent samples to see if there is a significant difference.

3. Paired t-test:

The paired t-test is used to compare the means of two dependent samples, usually to test the effect of a treatment or intervention.

4. Chi-squared test:

The chi-squared test is used to test the association between two categorical variables.

5. One-way ANOVA

For a one-way ANOVA, use the aov() and summary() functions:

6. Wilcoxon signed-rank test

7. mann-whitney u test.

For a Mann-Whitney U test, use the wilcox.test() function with the paired argument set to FALSE :

Steps for conducting a Hypothesis Testing

Hypothesis testing is a statistical method used to make inferences about population parameters based on sample data. In R programming, you can perform various types of hypothesis tests, such as t-tests, chi-squared tests, and ANOVA, depending on the nature of your data and research question.

Here, I’ll walk you through the steps for conducting a t-test (one of the most common hypothesis tests) in R. A t-test is used to compare the means of two groups, often in order to determine whether there’s a significant difference between them.

1. Prepare your data:

First, you’ll need to have your data in R. You can either read data from a file (e.g., using read.csv() ), or you can create vectors directly in R. For this example, I’ll create two sample vectors for Group 1 and Group 2:

2. State your null and alternative hypotheses:

In hypothesis testing, we start with a null hypothesis (H0) and an alternative hypothesis (H1). For a t-test, the null hypothesis is typically that there’s no difference between the means of the two groups, while the alternative hypothesis is that there is a difference. In this example:

H0: μ1 = μ2 (the means of Group 1 and Group 2 are equal)
H1: μ1 ≠ μ2 (the means of Group 1 and Group 2 are not equal)

3. Perform the t-test:

Use the t.test() function to perform the t-test on your data. You can specify the type of t-test (independent samples, paired, or one-sample) with the appropriate arguments. In this case, we’ll perform an independent samples t-test:

4. Interpret the results:

The t-test result will include the t-value, degrees of freedom, and the p-value, among other information. The p-value is particularly important, as it helps you determine whether to accept or reject the null hypothesis. A common significance level (alpha) is 0.05. If the p-value is less than alpha, you can reject the null hypothesis, otherwise you fail to reject it.

5. Make a decision:

Based on the p-value and your chosen significance level, make a decision about whether to reject or fail to reject the null hypothesis. If the p-value is less than 0.05, you would reject the null hypothesis and conclude that there is a significant difference between the means of the two groups.

Keep in mind that this example demonstrates the basic process of hypothesis testing using a t-test in R. Different tests and data may require additional steps, arguments, or functions. Be sure to consult R documentation and resources to ensure you’re using the appropriate test and interpreting the results correctly.

Few more examples of hypothesis tests using R

1. one-sample t-test: compares the mean of a sample to a known value., 2. two-sample t-test: compares the means of two independent samples., 3. paired t-test: compares the means of two paired samples., 4. chi-squared test: tests the independence between two categorical variables., 5. anova: compares the means of three or more independent samples..

Remember to interpret the results (p-value) according to the significance level (commonly 0.05). If the p-value is less than the significance level, you can reject the null hypothesis in favor of the alternative hypothesis.

T-Test in R Programming

Quantitative Methods Using R

10 hypothesis testing.

Hypothesis testing is a method used to make decisions about population parameters based on sample data.

10.1 Hypothesis

A hypothesis is an educated guess or statement about the relationship between variables or the characteristics of a population. In hypothesis testing, there are two main hypotheses:

10.1.1 Null hypothesis (H0):

This hypothesis states that there is no effect or no relationship between variables. It is typically the hypothesis that the researcher wants to disprove.

10.1.2 Alternative hypothesis (H1):

This hypothesis states that there is an effect or a relationship between variables. It is the hypothesis that the researcher wants to prove or provide evidence for.

10.2 Decision Type Error

When performing hypothesis testing, there are two types of decision errors:

Type I Error (α): This error occurs when the null hypothesis is rejected when it is actually true. In other words, it’s a false positive. The probability of committing a Type I error is denoted by the significance level (α), which is typically set at 0.05 or 0.01. Type II Error (β): This error occurs when the null hypothesis is not rejected when it is actually false. In other words, it’s a false negative. The probability of committing a Type II error is denoted by β. The power of a test (1 - β) measures the ability of the test to detect an effect when it truly exists. Here is a graphical representation of the types of decision errors:

Hypothesis Testing Errors

This table represents the different outcomes when making decisions based on hypothesis testing. The columns represent the reality (i.e., whether the null hypothesis is true or false), and the rows represent the decision made based on the hypothesis test (i.e., whether to reject or not reject the null hypothesis). The cells show the types of decision errors (Type I and Type II errors) and the correct decisions.

10.3 Level of Signficance

The level of significance is a critical component in hypothesis testing because it sets a threshold for determining whether an observed effect is statistically significant or not.

The level of significance is denoted by the Greek letter α (alpha) and represents the probability of making a Type I error. A Type I error occurs when we reject the null hypothesis (H0) when it is actually true. By choosing a level of significance, researchers define the risk they are willing to take when rejecting a true null hypothesis. Common levels of significance are 0.05 (5%) and 0.01 (1%).

To better understand the role of the level of significance in hypothesis testing, let’s consider the following steps:

Formulate the null hypothesis (H0) and the alternative hypothesis (H1): The null hypothesis typically states that there is no effect or relationship between variables, while the alternative hypothesis states that there is an effect or relationship.

Choose a level of significance (α): Determine the threshold for the probability of making a Type I error. For example, if α is set to 0.05, there is a 5% chance of rejecting a true null hypothesis.

Perform the statistical test and calculate the test statistic: The test statistic is calculated using the sample data, and it helps determine how far the observed sample mean is from the hypothesized population mean. In the case of a single mean, a one-sample t-test is commonly used, and the test statistic is the t-value.

Determine the critical value or p-value: Compare the calculated test statistic with the critical value or the p-value (probability value) to make a decision about the null hypothesis. The critical value is a threshold value that depends on the chosen level of significance and the distribution of the test statistic. The p-value represents the probability of obtaining a test statistic as extreme or more extreme than the observed test statistic under the assumption that the null hypothesis is true.

Make a decision: If the test statistic is more extreme than the critical value, or if the p-value is less than the level of significance (α), reject the null hypothesis. Otherwise, fail to reject the null hypothesis.

10.4 T-statistic

The t-statistic is a standardized measure used in hypothesis testing to compare the observed sample mean with the hypothesized population mean. It takes into account the sample mean, the hypothesized population mean, and the standard error of the mean. Mathematically, the t-statistic can be calculated using the following formula:

t = (X̄ - μ) / (s / √n)

t is the t-statistic X̄ is the sample mean μ is the hypothesized population mean s is the sample standard deviation n is the sample size

10.4.1 T-distribution

The t-distribution, also known as the Student’s t-distribution, is a probability distribution that is used when the population standard deviation is unknown and the sample size is small. It is similar to the normal distribution but has thicker tails, which accounts for the increased variability due to using the sample standard deviation as an estimate of the population standard deviation. The shape of the t-distribution depends on the degrees of freedom (df), which is related to the sample size (df = n - 1). As the sample size increases, the t-distribution approaches the normal distribution.

To calculate the t-statistic in R, you can use the following code:

To perform a one-sample t-test in R, which calculates the t-statistic and p-value automatically, you can use the t.test() function:

10.4.2 Intepreting Normality Evidence

When using a t-test, the assumption of normality is important. The data should follow a normal distribution to ensure the validity of the test results. To assess the normality of the data, we can use visual methods (histograms, Q-Q plots) and statistical tests (e.g., Shapiro-Wilk test).

This is important because the t-test assumes that the data follow a normal distribution, and verifying this assumption helps ensure the validity of the test results.

To generate normality evidence after performing a t-test, you can use the following methods:

Visual methods: Histograms and Q-Q plots can provide a visual assessment of the normality of the data.

Statistical tests: Shapiro-Wilk test and Kolmogorov-Smirnov test are commonly used to test for normality. These tests generate p-values, which can be compared with a chosen significance level (e.g., 0.05) to determine if the data deviate significantly from normality.

In R, you can create a histogram and Q-Q plot using the following code:

Create a histogram and Q-Q plot:

Perform the Shapiro-Wilk test:

To interpret the normality evidence, follow these guidelines:

Visual methods: Inspect the histogram and Q-Q plot. If the histogram is roughly bell-shaped and the points on the Q-Q plot fall approximately on the reference line, the data can be considered approximately normally distributed.

Statistical tests: Check the p-values of the normality tests. If the p-value is greater than the chosen significance level (e.g., 0.05), the null hypothesis (i.e., the data follow a normal distribution) cannot be rejected. This suggests that the data do not deviate significantly from normality.

Keep in mind that no single method is foolproof, and it’s often a good idea to use a combination of visual and statistical methods to assess normality. If the data appear to be non-normal, you might consider using non-parametric alternatives to the t-test or transforming the data to achieve normality.

10.5 Statistical Power

Statistical power is the probability of correctly rejecting the null hypothesis when it is false, which means not committing a Type II error. Power is influenced by factors such as sample size, effect size, and the chosen significance level (α). Power analysis helps researchers determine the appropriate sample size needed to achieve a desired level of power, typically 0.8 or higher.

To perform power analysis in R, you can use the pwr package, which provides a set of functions for power calculations in various statistical tests, including the t-test.

Here’s a step-by-step procedure for generating and testing power using R:

Install and load the pwr package:
Define the parameters for power analysis. You will need to specify the effect size (Cohen’s d), sample size, and significance level (α):
Use the pwr.t.test() function to calculate the power for a one-sample t-test:

The output will show the calculated power, sample size, effect size, and significance level. If the power is below the desired level (e.g., 0.8), you can adjust the sample size or effect size and recalculate the power to determine the necessary changes for achieving the desired power level.

It’s essential to consider the practical implications of the effect size and sample size when planning a study. A large effect size may be easier to detect but might not occur frequently in real-world situations. Conversely, a small effect size might be more difficult to detect and may require a larger sample size to achieve adequate power.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

11 Hypothesis testing

The process of induction is the process of assuming the simplest law that can be made to harmonize with our experience. This process, however, has no logical foundation but only a psychological one. It is clear that there are no grounds for believing that the simplest course of events will really happen. It is an hypothesis that the sun will rise tomorrow: and this means that we do not know whether it will rise. – Ludwig Wittgenstein 157

In the last chapter, I discussed the ideas behind estimation, which is one of the two “big ideas” in inferential statistics. It’s now time to turn out attention to the other big idea, which is hypothesis testing . In its most abstract form, hypothesis testing really a very simple idea: the researcher has some theory about the world, and wants to determine whether or not the data actually support that theory. However, the details are messy, and most people find the theory of hypothesis testing to be the most frustrating part of statistics. The structure of the chapter is as follows. Firstly, I’ll describe how hypothesis testing works, in a fair amount of detail, using a simple running example to show you how a hypothesis test is “built”. I’ll try to avoid being too dogmatic while doing so, and focus instead on the underlying logic of the testing procedure. 158 Afterwards, I’ll spend a bit of time talking about the various dogmas, rules and heresies that surround the theory of hypothesis testing.

11.1 A menagerie of hypotheses

Eventually we all succumb to madness. For me, that day will arrive once I’m finally promoted to full professor. Safely ensconced in my ivory tower, happily protected by tenure, I will finally be able to take leave of my senses (so to speak), and indulge in that most thoroughly unproductive line of psychological research: the search for extrasensory perception (ESP). 159

Let’s suppose that this glorious day has come. My first study is a simple one, in which I seek to test whether clairvoyance exists. Each participant sits down at a table, and is shown a card by an experimenter. The card is black on one side and white on the other. The experimenter takes the card away, and places it on a table in an adjacent room. The card is placed black side up or white side up completely at random, with the randomisation occurring only after the experimenter has left the room with the participant. A second experimenter comes in and asks the participant which side of the card is now facing upwards. It’s purely a one-shot experiment. Each person sees only one card, and gives only one answer; and at no stage is the participant actually in contact with someone who knows the right answer. My data set, therefore, is very simple. I have asked the question of $N$ people, and some number $X$ of these people have given the correct response. To make things concrete, let’s suppose that I have tested $N = 100$ people, and $X = 62$ of these got the answer right… a surprisingly large number, sure, but is it large enough for me to feel safe in claiming I’ve found evidence for ESP? This is the situation where hypothesis testing comes in useful. However, before we talk about how to test hypotheses, we need to be clear about what we mean by hypotheses.

11.1.1 Research hypotheses versus statistical hypotheses

The first distinction that you need to keep clear in your mind is between research hypotheses and statistical hypotheses. In my ESP study, my overall scientific goal is to demonstrate that clairvoyance exists. In this situation, I have a clear research goal: I am hoping to discover evidence for ESP. In other situations I might actually be a lot more neutral than that, so I might say that my research goal is to determine whether or not clairvoyance exists. Regardless of how I want to portray myself, the basic point that I’m trying to convey here is that a research hypothesis involves making a substantive, testable scientific claim… if you are a psychologist, then your research hypotheses are fundamentally about psychological constructs. Any of the following would count as research hypotheses :

Listening to music reduces your ability to pay attention to other things. This is a claim about the causal relationship between two psychologically meaningful concepts (listening to music and paying attention to things), so it’s a perfectly reasonable research hypothesis.
Intelligence is related to personality . Like the last one, this is a relational claim about two psychological constructs (intelligence and personality), but the claim is weaker: correlational not causal.
Intelligence is* speed of information processing . This hypothesis has a quite different character: it’s not actually a relational claim at all. It’s an ontological claim about the fundamental character of intelligence (and I’m pretty sure it’s wrong). It’s worth expanding on this one actually: It’s usually easier to think about how to construct experiments to test research hypotheses of the form “does X affect Y?” than it is to address claims like “what is X?” And in practice, what usually happens is that you find ways of testing relational claims that follow from your ontological ones. For instance, if I believe that intelligence is* speed of information processing in the brain, my experiments will often involve looking for relationships between measures of intelligence and measures of speed. As a consequence, most everyday research questions do tend to be relational in nature, but they’re almost always motivated by deeper ontological questions about the state of nature.

Notice that in practice, my research hypotheses could overlap a lot. My ultimate goal in the ESP experiment might be to test an ontological claim like “ESP exists”, but I might operationally restrict myself to a narrower hypothesis like “Some people can `see’ objects in a clairvoyant fashion”. That said, there are some things that really don’t count as proper research hypotheses in any meaningful sense:

Love is a battlefield . This is too vague to be testable. While it’s okay for a research hypothesis to have a degree of vagueness to it, it has to be possible to operationalise your theoretical ideas. Maybe I’m just not creative enough to see it, but I can’t see how this can be converted into any concrete research design. If that’s true, then this isn’t a scientific research hypothesis, it’s a pop song. That doesn’t mean it’s not interesting – a lot of deep questions that humans have fall into this category. Maybe one day science will be able to construct testable theories of love, or to test to see if God exists, and so on; but right now we can’t, and I wouldn’t bet on ever seeing a satisfying scientific approach to either.
The first rule of tautology club is the first rule of tautology club . This is not a substantive claim of any kind. It’s true by definition. No conceivable state of nature could possibly be inconsistent with this claim. As such, we say that this is an unfalsifiable hypothesis, and as such it is outside the domain of science. Whatever else you do in science, your claims must have the possibility of being wrong.
More people in my experiment will say “yes” than “no” . This one fails as a research hypothesis because it’s a claim about the data set, not about the psychology (unless of course your actual research question is whether people have some kind of “yes” bias!). As we’ll see shortly, this hypothesis is starting to sound more like a statistical hypothesis than a research hypothesis.

As you can see, research hypotheses can be somewhat messy at times; and ultimately they are scientific claims. Statistical hypotheses are neither of these two things. Statistical hypotheses must be mathematically precise, and they must correspond to specific claims about the characteristics of the data generating mechanism (i.e., the “population”). Even so, the intent is that statistical hypotheses bear a clear relationship to the substantive research hypotheses that you care about! For instance, in my ESP study my research hypothesis is that some people are able to see through walls or whatever. What I want to do is to “map” this onto a statement about how the data were generated. So let’s think about what that statement would be. The quantity that I’m interested in within the experiment is $P(\mbox{“correct”})$ , the true-but-unknown probability with which the participants in my experiment answer the question correctly. Let’s use the Greek letter $\theta$ (theta) to refer to this probability. Here are four different statistical hypotheses:

If ESP doesn’t exist and if my experiment is well designed, then my participants are just guessing. So I should expect them to get it right half of the time and so my statistical hypothesis is that the true probability of choosing correctly is $\theta = 0.5$ .
Alternatively, suppose ESP does exist and participants can see the card. If that’s true, people will perform better than chance. The statistical hypotheis would be that $\theta > 0.5$ .
A third possibility is that ESP does exist, but the colours are all reversed and people don’t realise it (okay, that’s wacky, but you never know…). If that’s how it works then you’d expect people’s performance to be below chance. This would correspond to a statistical hypothesis that $\theta < 0.5$ .
Finally, suppose ESP exists, but I have no idea whether people are seeing the right colour or the wrong one. In that case, the only claim I could make about the data would be that the probability of making the correct answer is not equal to 50. This corresponds to the statistical hypothesis that $\theta \neq 0.5$ .

All of these are legitimate examples of a statistical hypothesis because they are statements about a population parameter and are meaningfully related to my experiment.

What this discussion makes clear, I hope, is that when attempting to construct a statistical hypothesis test the researcher actually has two quite distinct hypotheses to consider. First, he or she has a research hypothesis (a claim about psychology), and this corresponds to a statistical hypothesis (a claim about the data generating population). In my ESP example, these might be

And the key thing to recognise is this: a statistical hypothesis test is a test of the statistical hypothesis, not the research hypothesis . If your study is badly designed, then the link between your research hypothesis and your statistical hypothesis is broken. To give a silly example, suppose that my ESP study was conducted in a situation where the participant can actually see the card reflected in a window; if that happens, I would be able to find very strong evidence that $\theta \neq 0.5$ , but this would tell us nothing about whether “ESP exists”.

11.1.2 Null hypotheses and alternative hypotheses

So far, so good. I have a research hypothesis that corresponds to what I want to believe about the world, and I can map it onto a statistical hypothesis that corresponds to what I want to believe about how the data were generated. It’s at this point that things get somewhat counterintuitive for a lot of people. Because what I’m about to do is invent a new statistical hypothesis (the “null” hypothesis, $H_0$ ) that corresponds to the exact opposite of what I want to believe, and then focus exclusively on that, almost to the neglect of the thing I’m actually interested in (which is now called the “alternative” hypothesis, $H_1$ ). In our ESP example, the null hypothesis is that $\theta = 0.5$ , since that’s what we’d expect if ESP didn’t exist. My hope, of course, is that ESP is totally real, and so the alternative to this null hypothesis is $\theta \neq 0.5$ . In essence, what we’re doing here is dividing up the possible values of $\theta$ into two groups: those values that I really hope aren’t true (the null), and those values that I’d be happy with if they turn out to be right (the alternative). Having done so, the important thing to recognise is that the goal of a hypothesis test is not to show that the alternative hypothesis is (probably) true; the goal is to show that the null hypothesis is (probably) false. Most people find this pretty weird.

The best way to think about it, in my experience, is to imagine that a hypothesis test is a criminal trial 160 … the trial of the null hypothesis . The null hypothesis is the defendant, the researcher is the prosecutor, and the statistical test itself is the judge. Just like a criminal trial, there is a presumption of innocence: the null hypothesis is deemed to be true unless you, the researcher, can prove beyond a reasonable doubt that it is false. You are free to design your experiment however you like (within reason, obviously!), and your goal when doing so is to maximise the chance that the data will yield a conviction… for the crime of being false. The catch is that the statistical test sets the rules of the trial, and those rules are designed to protect the null hypothesis – specifically to ensure that if the null hypothesis is actually true, the chances of a false conviction are guaranteed to be low. This is pretty important: after all, the null hypothesis doesn’t get a lawyer. And given that the researcher is trying desperately to prove it to be false, someone has to protect it.

11.2 Two types of errors

Before going into details about how a statistical test is constructed, it’s useful to understand the philosophy behind it. I hinted at it when pointing out the similarity between a null hypothesis test and a criminal trial, but I should now be explicit. Ideally, we would like to construct our test so that we never make any errors. Unfortunately, since the world is messy, this is never possible. Sometimes you’re just really unlucky: for instance, suppose you flip a coin 10 times in a row and it comes up heads all 10 times. That feels like very strong evidence that the coin is biased (and it is!), but of course there’s a 1 in 1024 chance that this would happen even if the coin was totally fair. In other words, in real life we always have to accept that there’s a chance that we did the wrong thing. As a consequence, the goal behind statistical hypothesis testing is not to eliminate errors, but to minimise them.

At this point, we need to be a bit more precise about what we mean by “errors”. Firstly, let’s state the obvious: it is either the case that the null hypothesis is true, or it is false; and our test will either reject the null hypothesis or retain it. 161 So, as the table below illustrates, after we run the test and make our choice, one of four things might have happened:

As a consequence there are actually two different types of error here. If we reject a null hypothesis that is actually true, then we have made a type I error . On the other hand, if we retain the null hypothesis when it is in fact false, then we have made a type II error .

Remember how I said that statistical testing was kind of like a criminal trial? Well, I meant it. A criminal trial requires that you establish “beyond a reasonable doubt” that the defendant did it. All of the evidentiary rules are (in theory, at least) designed to ensure that there’s (almost) no chance of wrongfully convicting an innocent defendant. The trial is designed to protect the rights of a defendant: as the English jurist William Blackstone famously said, it is “better that ten guilty persons escape than that one innocent suffer.” In other words, a criminal trial doesn’t treat the two types of error in the same way~… punishing the innocent is deemed to be much worse than letting the guilty go free. A statistical test is pretty much the same: the single most important design principle of the test is to control the probability of a type I error, to keep it below some fixed probability. This probability, which is denoted $\alpha$ , is called the significance level of the test (or sometimes, the size of the test). And I’ll say it again, because it is so central to the whole set-up~… a hypothesis test is said to have significance level $\alpha$ if the type I error rate is no larger than $\alpha$ .

So, what about the type II error rate? Well, we’d also like to keep those under control too, and we denote this probability by $\beta$ . However, it’s much more common to refer to the power of the test, which is the probability with which we reject a null hypothesis when it really is false, which is $1-\beta$ . To help keep this straight, here’s the same table again, but with the relevant numbers added:

A “powerful” hypothesis test is one that has a small value of $\beta$ , while still keeping $\alpha$ fixed at some (small) desired level. By convention, scientists make use of three different $\alpha$ levels: $.05$ , $.01$ and $.001$ . Notice the asymmetry here~… the tests are designed to ensure that the $\alpha$ level is kept small, but there’s no corresponding guarantee regarding $\beta$ . We’d certainly like the type II error rate to be small, and we try to design tests that keep it small, but this is very much secondary to the overwhelming need to control the type I error rate. As Blackstone might have said if he were a statistician, it is “better to retain 10 false null hypotheses than to reject a single true one”. To be honest, I don’t know that I agree with this philosophy – there are situations where I think it makes sense, and situations where I think it doesn’t – but that’s neither here nor there. It’s how the tests are built.

11.3 Test statistics and sampling distributions

At this point we need to start talking specifics about how a hypothesis test is constructed. To that end, let’s return to the ESP example. Let’s ignore the actual data that we obtained, for the moment, and think about the structure of the experiment. Regardless of what the actual numbers are, the form of the data is that $X$ out of $N$ people correctly identified the colour of the hidden card. Moreover, let’s suppose for the moment that the null hypothesis really is true: ESP doesn’t exist, and the true probability that anyone picks the correct colour is exactly $\theta = 0.5$ . What would we expect the data to look like? Well, obviously, we’d expect the proportion of people who make the correct response to be pretty close to 50%. Or, to phrase this in more mathematical terms, we’d say that $X/N$ is approximately $0.5$ . Of course, we wouldn’t expect this fraction to be exactly 0.5: if, for example we tested $N=100$ people, and $X = 53$ of them got the question right, we’d probably be forced to concede that the data are quite consistent with the null hypothesis. On the other hand, if $X = 99$ of our participants got the question right, then we’d feel pretty confident that the null hypothesis is wrong. Similarly, if only $X=3$ people got the answer right, we’d be similarly confident that the null was wrong. Let’s be a little more technical about this: we have a quantity $X$ that we can calculate by looking at our data; after looking at the value of $X$ , we make a decision about whether to believe that the null hypothesis is correct, or to reject the null hypothesis in favour of the alternative. The name for this thing that we calculate to guide our choices is a test statistic .

Having chosen a test statistic, the next step is to state precisely which values of the test statistic would cause is to reject the null hypothesis, and which values would cause us to keep it. In order to do so, we need to determine what the sampling distribution of the test statistic would be if the null hypothesis were actually true (we talked about sampling distributions earlier in Section 10.3.1 ). Why do we need this? Because this distribution tells us exactly what values of $X$ our null hypothesis would lead us to expect. And therefore, we can use this distribution as a tool for assessing how closely the null hypothesis agrees with our data.

$The sampling distribution for our test statistic $X$ when the null hypothesis is true. For our ESP scenario, this is a binomial distribution. Not surprisingly, since the null hypothesis says that the probability of a correct response is $\theta = .5$, the sampling distribution says that the most likely value is 50 (our of 100) correct responses. Most of the probability mass lies between 40 and 60.$

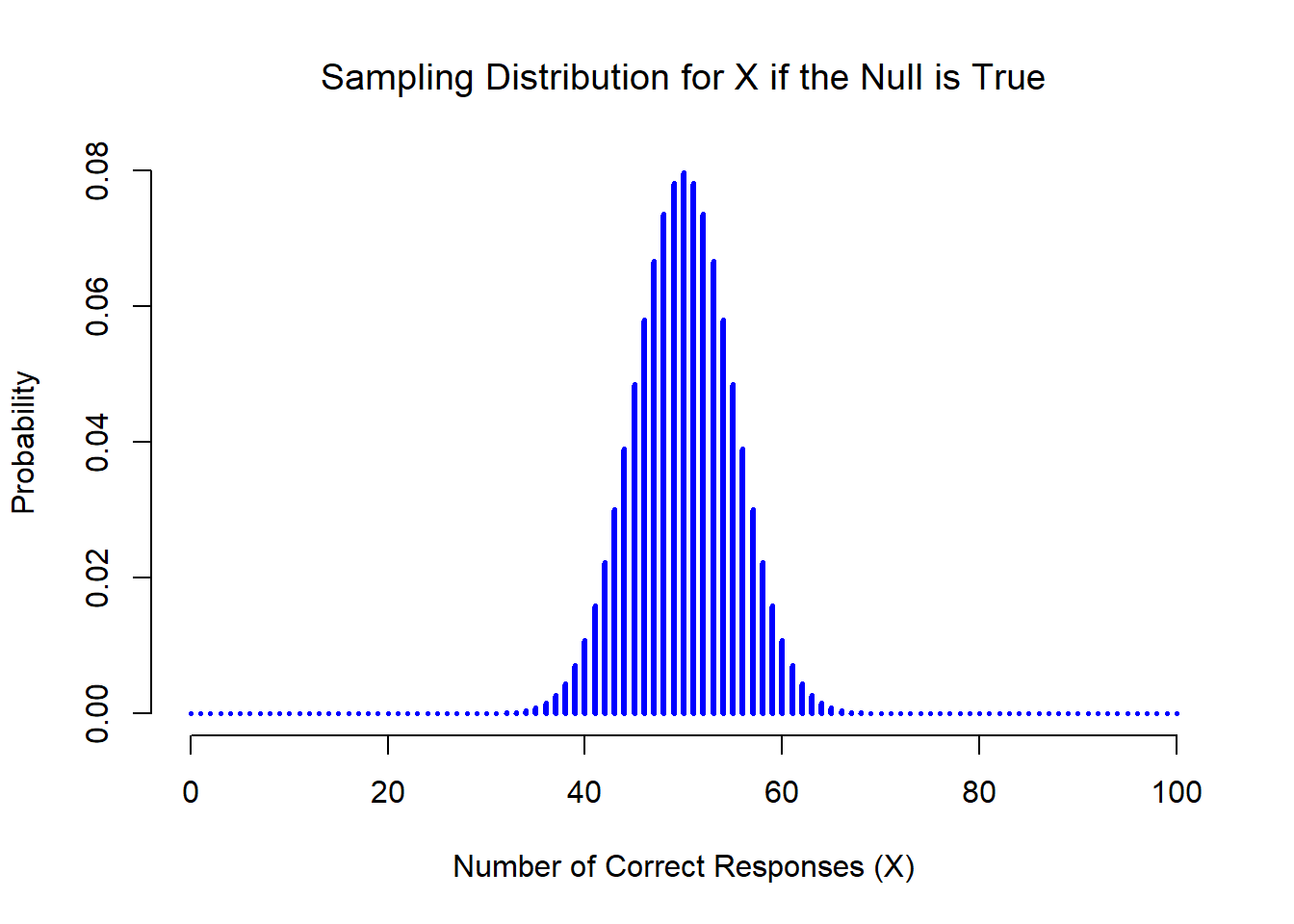
Figure 11.1: The sampling distribution for our test statistic $X$ when the null hypothesis is true. For our ESP scenario, this is a binomial distribution. Not surprisingly, since the null hypothesis says that the probability of a correct response is $\theta = .5$ , the sampling distribution says that the most likely value is 50 (our of 100) correct responses. Most of the probability mass lies between 40 and 60.

How do we actually determine the sampling distribution of the test statistic? For a lot of hypothesis tests this step is actually quite complicated, and later on in the book you’ll see me being slightly evasive about it for some of the tests (some of them I don’t even understand myself). However, sometimes it’s very easy. And, fortunately for us, our ESP example provides us with one of the easiest cases. Our population parameter $\theta$ is just the overall probability that people respond correctly when asked the question, and our test statistic $X$ is the count of the number of people who did so, out of a sample size of $N$ . We’ve seen a distribution like this before, in Section 9.4 : that’s exactly what the binomial distribution describes! So, to use the notation and terminology that I introduced in that section, we would say that the null hypothesis predicts that $X$ is binomially distributed, which is written \[ X \sim \mbox{Binomial}(\theta,N) \] Since the null hypothesis states that $\theta = 0.5$ and our experiment has $N=100$ people, we have the sampling distribution we need. This sampling distribution is plotted in Figure 11.1 . No surprises really: the null hypothesis says that $X=50$ is the most likely outcome, and it says that we’re almost certain to see somewhere between 40 and 60 correct responses.

11.4 Making decisions

Okay, we’re very close to being finished. We’ve constructed a test statistic ( $X$ ), and we chose this test statistic in such a way that we’re pretty confident that if $X$ is close to $N/2$ then we should retain the null, and if not we should reject it. The question that remains is this: exactly which values of the test statistic should we associate with the null hypothesis, and which exactly values go with the alternative hypothesis? In my ESP study, for example, I’ve observed a value of $X=62$ . What decision should I make? Should I choose to believe the null hypothesis, or the alternative hypothesis?

11.4.1 Critical regions and critical values

To answer this question, we need to introduce the concept of a critical region for the test statistic $X$ . The critical region of the test corresponds to those values of $X$ that would lead us to reject null hypothesis (which is why the critical region is also sometimes called the rejection region). How do we find this critical region? Well, let’s consider what we know:

$X$ should be very big or very small in order to reject the null hypothesis.
If the null hypothesis is true, the sampling distribution of $X$ is Binomial $(0.5, N)$ .
If $\alpha =.05$ , the critical region must cover 5% of this sampling distribution.

It’s important to make sure you understand this last point: the critical region corresponds to those values of $X$ for which we would reject the null hypothesis, and the sampling distribution in question describes the probability that we would obtain a particular value of $X$ if the null hypothesis were actually true. Now, let’s suppose that we chose a critical region that covers 20% of the sampling distribution, and suppose that the null hypothesis is actually true. What would be the probability of incorrectly rejecting the null? The answer is of course 20%. And therefore, we would have built a test that had an $\alpha$ level of $0.2$ . If we want $\alpha = .05$ , the critical region is only allowed to cover 5% of the sampling distribution of our test statistic.

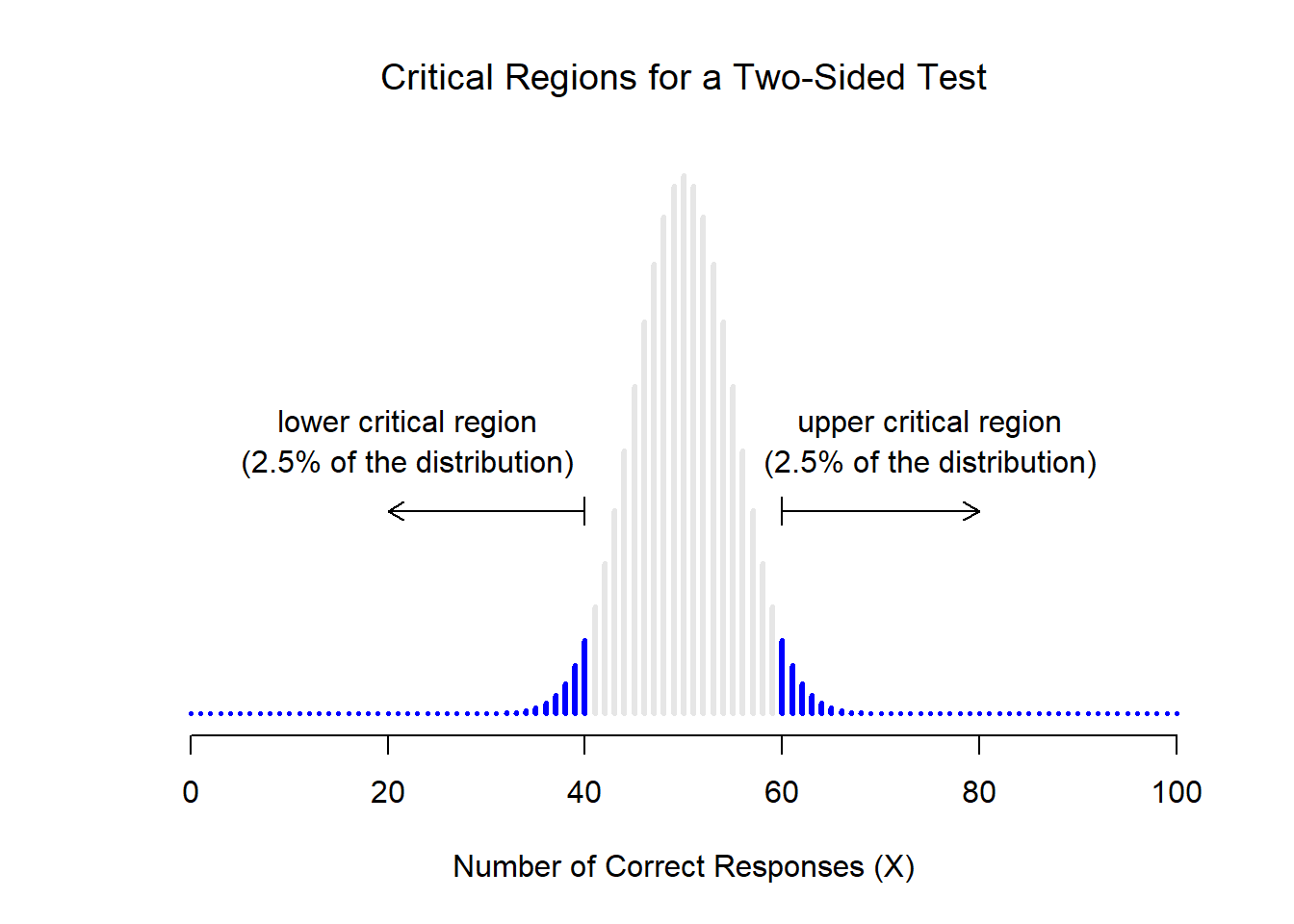
Figure 11.2: The critical region associated with the hypothesis test for the ESP study, for a hypothesis test with a significance level of $\alpha = .05$ . The plot itself shows the sampling distribution of $X$ under the null hypothesis: the grey bars correspond to those values of $X$ for which we would retain the null hypothesis. The black bars show the critical region: those values of $X$ for which we would reject the null. Because the alternative hypothesis is two sided (i.e., allows both $\theta <.5$ and $\theta >.5$ ), the critical region covers both tails of the distribution. To ensure an $\alpha$ level of $.05$ , we need to ensure that each of the two regions encompasses 2.5% of the sampling distribution.

As it turns out, those three things uniquely solve the problem: our critical region consists of the most extreme values , known as the tails of the distribution. This is illustrated in Figure 11.2 . As it turns out, if we want $\alpha = .05$ , then our critical regions correspond to $X \leq 40$ and $X \geq 60$ . 162 That is, if the number of people saying “true” is between 41 and 59, then we should retain the null hypothesis. If the number is between 0 to 40 or between 60 to 100, then we should reject the null hypothesis. The numbers 40 and 60 are often referred to as the critical values , since they define the edges of the critical region.

At this point, our hypothesis test is essentially complete: (1) we choose an $\alpha$ level (e.g., $\alpha = .05$ , (2) come up with some test statistic (e.g., $X$ ) that does a good job (in some meaningful sense) of comparing $H_0$ to $H_1$ , (3) figure out the sampling distribution of the test statistic on the assumption that the null hypothesis is true (in this case, binomial) and then (4) calculate the critical region that produces an appropriate $\alpha$ level (0-40 and 60-100). All that we have to do now is calculate the value of the test statistic for the real data (e.g., $X = 62$ ) and then compare it to the critical values to make our decision. Since 62 is greater than the critical value of 60, we would reject the null hypothesis. Or, to phrase it slightly differently, we say that the test has produced a significant result.

11.4.2 A note on statistical “significance”

Like other occult techniques of divination, the statistical method has a private jargon deliberately contrived to obscure its methods from non-practitioners. – Attributed to G. O. Ashley 163

A very brief digression is in order at this point, regarding the word “significant”. The concept of statistical significance is actually a very simple one, but has a very unfortunate name. If the data allow us to reject the null hypothesis, we say that “the result is statistically significant ”, which is often shortened to “the result is significant”. This terminology is rather old, and dates back to a time when “significant” just meant something like “indicated”, rather than its modern meaning, which is much closer to “important”. As a result, a lot of modern readers get very confused when they start learning statistics, because they think that a “significant result” must be an important one. It doesn’t mean that at all. All that “statistically significant” means is that the data allowed us to reject a null hypothesis. Whether or not the result is actually important in the real world is a very different question, and depends on all sorts of other things.

11.4.3 The difference between one sided and two sided tests

There’s one more thing I want to point out about the hypothesis test that I’ve just constructed. If we take a moment to think about the statistical hypotheses I’ve been using, \[ \begin{array}{cc} H_0 : & \theta = .5 \\ H_1 : & \theta \neq .5 \end{array} \] we notice that the alternative hypothesis covers both the possibility that $\theta < .5$ and the possibility that $\theta > .5$ . This makes sense if I really think that ESP could produce better-than-chance performance or worse-than-chance performance (and there are some people who think that). In statistical language, this is an example of a two-sided test . It’s called this because the alternative hypothesis covers the area on both “sides” of the null hypothesis, and as a consequence the critical region of the test covers both tails of the sampling distribution (2.5% on either side if $\alpha =.05$ ), as illustrated earlier in Figure 11.2 .

However, that’s not the only possibility. It might be the case, for example, that I’m only willing to believe in ESP if it produces better than chance performance. If so, then my alternative hypothesis would only covers the possibility that $\theta > .5$ , and as a consequence the null hypothesis now becomes $\theta \leq .5$ : \[ \begin{array}{cc} H_0 : & \theta \leq .5 \\ H_1 : & \theta > .5 \end{array} \] When this happens, we have what’s called a one-sided test , and when this happens the critical region only covers one tail of the sampling distribution. This is illustrated in Figure 11.3 .

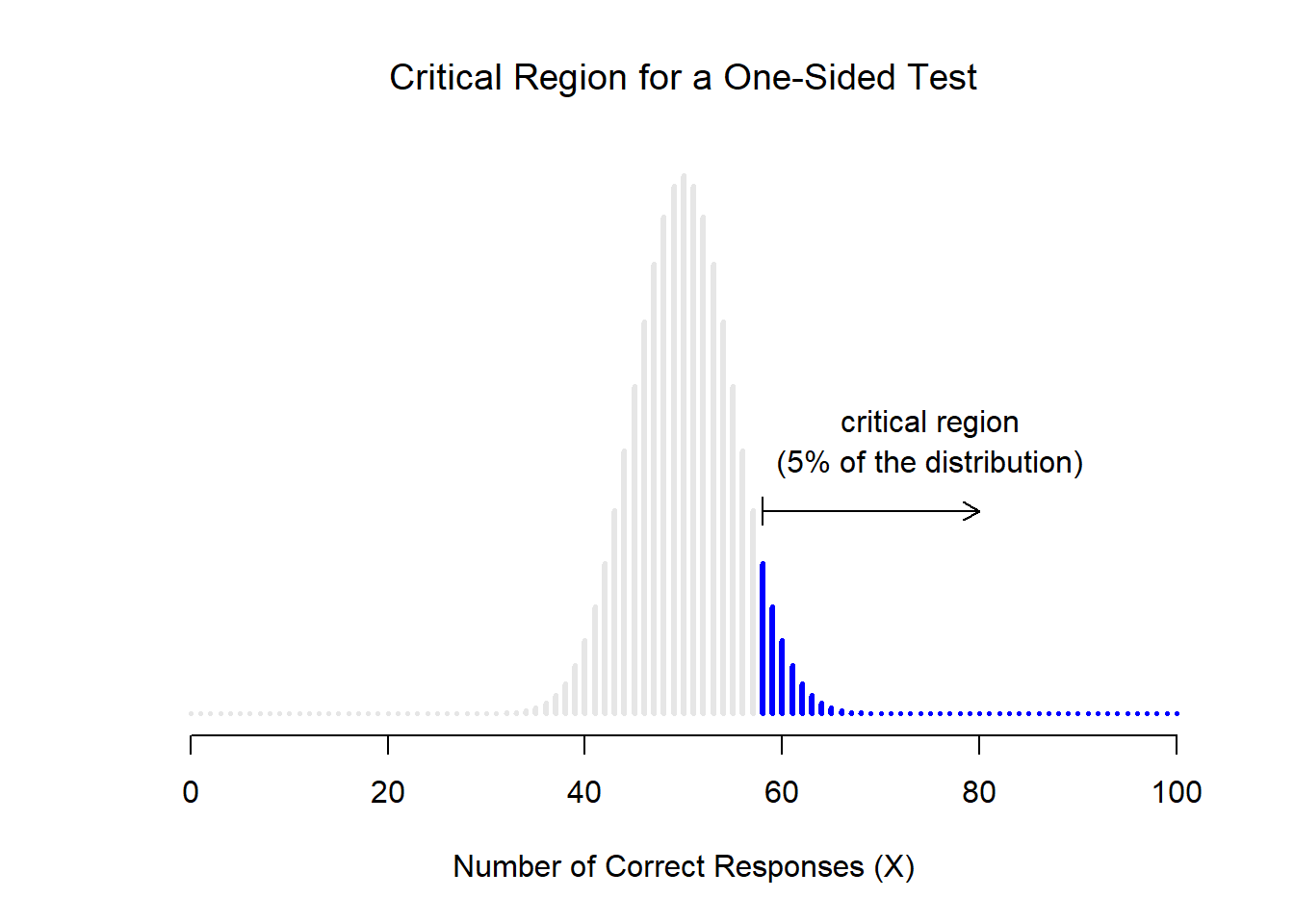
Figure 11.3: The critical region for a one sided test. In this case, the alternative hypothesis is that $\theta > .05$ , so we would only reject the null hypothesis for large values of $X$ . As a consequence, the critical region only covers the upper tail of the sampling distribution; specifically the upper 5% of the distribution. Contrast this to the two-sided version earlier)

11.5 The $p$ value of a test

In one sense, our hypothesis test is complete; we’ve constructed a test statistic, figured out its sampling distribution if the null hypothesis is true, and then constructed the critical region for the test. Nevertheless, I’ve actually omitted the most important number of all: the $p$ value . It is to this topic that we now turn. There are two somewhat different ways of interpreting a $p$ value, one proposed by Sir Ronald Fisher and the other by Jerzy Neyman. Both versions are legitimate, though they reflect very different ways of thinking about hypothesis tests. Most introductory textbooks tend to give Fisher’s version only, but I think that’s a bit of a shame. To my mind, Neyman’s version is cleaner, and actually better reflects the logic of the null hypothesis test. You might disagree though, so I’ve included both. I’ll start with Neyman’s version…

11.5.1 A softer view of decision making

One problem with the hypothesis testing procedure that I’ve described is that it makes no distinction at all between a result this “barely significant” and those that are “highly significant”. For instance, in my ESP study the data I obtained only just fell inside the critical region – so I did get a significant effect, but was a pretty near thing. In contrast, suppose that I’d run a study in which $X=97$ out of my $N=100$ participants got the answer right. This would obviously be significant too, but my a much larger margin; there’s really no ambiguity about this at all. The procedure that I described makes no distinction between the two. If I adopt the standard convention of allowing $\alpha = .05$ as my acceptable Type I error rate, then both of these are significant results.

This is where the $p$ value comes in handy. To understand how it works, let’s suppose that we ran lots of hypothesis tests on the same data set: but with a different value of $\alpha$ in each case. When we do that for my original ESP data, what we’d get is something like this

When we test ESP data ( $X=62$ successes out of $N=100$ observations) using $\alpha$ levels of .03 and above, we’d always find ourselves rejecting the null hypothesis. For $\alpha$ levels of .02 and below, we always end up retaining the null hypothesis. Therefore, somewhere between .02 and .03 there must be a smallest value of $\alpha$ that would allow us to reject the null hypothesis for this data. This is the $p$ value; as it turns out the ESP data has $p = .021$ . In short:

$p$ is defined to be the smallest Type I error rate ( $\alpha$ ) that you have to be willing to tolerate if you want to reject the null hypothesis.

If it turns out that $p$ describes an error rate that you find intolerable, then you must retain the null. If you’re comfortable with an error rate equal to $p$ , then it’s okay to reject the null hypothesis in favour of your preferred alternative.

In effect, $p$ is a summary of all the possible hypothesis tests that you could have run, taken across all possible $\alpha$ values. And as a consequence it has the effect of “softening” our decision process. For those tests in which $p \leq \alpha$ you would have rejected the null hypothesis, whereas for those tests in which $p > \alpha$ you would have retained the null. In my ESP study I obtained $X=62$ , and as a consequence I’ve ended up with $p = .021$ . So the error rate I have to tolerate is 2.1%. In contrast, suppose my experiment had yielded $X=97$ . What happens to my $p$ value now? This time it’s shrunk to $p = 1.36 \times 10^{-25}$ , which is a tiny, tiny 164 Type I error rate. For this second case I would be able to reject the null hypothesis with a lot more confidence, because I only have to be “willing” to tolerate a type I error rate of about 1 in 10 trillion trillion in order to justify my decision to reject.

11.5.2 The probability of extreme data

The second definition of the $p$ -value comes from Sir Ronald Fisher, and it’s actually this one that you tend to see in most introductory statistics textbooks. Notice how, when I constructed the critical region, it corresponded to the tails (i.e., extreme values) of the sampling distribution? That’s not a coincidence: almost all “good” tests have this characteristic (good in the sense of minimising our type II error rate, $\beta$ ). The reason for that is that a good critical region almost always corresponds to those values of the test statistic that are least likely to be observed if the null hypothesis is true. If this rule is true, then we can define the $p$ -value as the probability that we would have observed a test statistic that is at least as extreme as the one we actually did get. In other words, if the data are extremely implausible according to the null hypothesis, then the null hypothesis is probably wrong.

11.5.3 A common mistake

Okay, so you can see that there are two rather different but legitimate ways to interpret the $p$ value, one based on Neyman’s approach to hypothesis testing and the other based on Fisher’s. Unfortunately, there is a third explanation that people sometimes give, especially when they’re first learning statistics, and it is absolutely and completely wrong . This mistaken approach is to refer to the $p$ value as “the probability that the null hypothesis is true”. It’s an intuitively appealing way to think, but it’s wrong in two key respects: (1) null hypothesis testing is a frequentist tool, and the frequentist approach to probability does not allow you to assign probabilities to the null hypothesis… according to this view of probability, the null hypothesis is either true or it is not; it cannot have a “5% chance” of being true. (2) even within the Bayesian approach, which does let you assign probabilities to hypotheses, the $p$ value would not correspond to the probability that the null is true; this interpretation is entirely inconsistent with the mathematics of how the $p$ value is calculated. Put bluntly, despite the intuitive appeal of thinking this way, there is no justification for interpreting a $p$ value this way. Never do it.

11.6 Reporting the results of a hypothesis test

When writing up the results of a hypothesis test, there’s usually several pieces of information that you need to report, but it varies a fair bit from test to test. Throughout the rest of the book I’ll spend a little time talking about how to report the results of different tests (see Section 12.1.9 for a particularly detailed example), so that you can get a feel for how it’s usually done. However, regardless of what test you’re doing, the one thing that you always have to do is say something about the $p$ value, and whether or not the outcome was significant.

The fact that you have to do this is unsurprising; it’s the whole point of doing the test. What might be surprising is the fact that there is some contention over exactly how you’re supposed to do it. Leaving aside those people who completely disagree with the entire framework underpinning null hypothesis testing, there’s a certain amount of tension that exists regarding whether or not to report the exact $p$ value that you obtained, or if you should state only that $p < \alpha$ for a significance level that you chose in advance (e.g., $p<.05$ ).

11.6.1 The issue

To see why this is an issue, the key thing to recognise is that $p$ values are terribly convenient. In practice, the fact that we can compute a $p$ value means that we don’t actually have to specify any $\alpha$ level at all in order to run the test. Instead, what you can do is calculate your $p$ value and interpret it directly: if you get $p = .062$ , then it means that you’d have to be willing to tolerate a Type I error rate of 6.2% to justify rejecting the null. If you personally find 6.2% intolerable, then you retain the null. Therefore, the argument goes, why don’t we just report the actual $p$ value and let the reader make up their own minds about what an acceptable Type I error rate is? This approach has the big advantage of “softening” the decision making process – in fact, if you accept the Neyman definition of the $p$ value, that’s the whole point of the $p$ value. We no longer have a fixed significance level of $\alpha = .05$ as a bright line separating “accept” from “reject” decisions; and this removes the rather pathological problem of being forced to treat $p = .051$ in a fundamentally different way to $p = .049$ .

This flexibility is both the advantage and the disadvantage to the $p$ value. The reason why a lot of people don’t like the idea of reporting an exact $p$ value is that it gives the researcher a bit too much freedom. In particular, it lets you change your mind about what error tolerance you’re willing to put up with after you look at the data. For instance, consider my ESP experiment. Suppose I ran my test, and ended up with a $p$ value of .09. Should I accept or reject? Now, to be honest, I haven’t yet bothered to think about what level of Type I error I’m “really” willing to accept. I don’t have an opinion on that topic. But I do have an opinion about whether or not ESP exists, and I definitely have an opinion about whether my research should be published in a reputable scientific journal. And amazingly, now that I’ve looked at the data I’m starting to think that a 9% error rate isn’t so bad, especially when compared to how annoying it would be to have to admit to the world that my experiment has failed. So, to avoid looking like I just made it up after the fact, I now say that my $\alpha$ is .1: a 10% type I error rate isn’t too bad, and at that level my test is significant! I win.

In other words, the worry here is that I might have the best of intentions, and be the most honest of people, but the temptation to just “shade” things a little bit here and there is really, really strong. As anyone who has ever run an experiment can attest, it’s a long and difficult process, and you often get very attached to your hypotheses. It’s hard to let go and admit the experiment didn’t find what you wanted it to find. And that’s the danger here. If we use the “raw” $p$ -value, people will start interpreting the data in terms of what they want to believe, not what the data are actually saying… and if we allow that, well, why are we bothering to do science at all? Why not let everyone believe whatever they like about anything, regardless of what the facts are? Okay, that’s a bit extreme, but that’s where the worry comes from. According to this view, you really must specify your $\alpha$ value in advance, and then only report whether the test was significant or not. It’s the only way to keep ourselves honest.

11.6.2 Two proposed solutions

In practice, it’s pretty rare for a researcher to specify a single $\alpha$ level ahead of time. Instead, the convention is that scientists rely on three standard significance levels: .05, .01 and .001. When reporting your results, you indicate which (if any) of these significance levels allow you to reject the null hypothesis. This is summarised in Table 11.1 . This allows us to soften the decision rule a little bit, since $p<.01$ implies that the data meet a stronger evidentiary standard than $p<.05$ would. Nevertheless, since these levels are fixed in advance by convention, it does prevent people choosing their $\alpha$ level after looking at the data.

Nevertheless, quite a lot of people still prefer to report exact $p$ values. To many people, the advantage of allowing the reader to make up their own mind about how to interpret $p = .06$ outweighs any disadvantages. In practice, however, even among those researchers who prefer exact $p$ values it is quite common to just write $p<.001$ instead of reporting an exact value for small $p$ . This is in part because a lot of software doesn’t actually print out the $p$ value when it’s that small (e.g., SPSS just writes $p = .000$ whenever $p<.001$ ), and in part because a very small $p$ value can be kind of misleading. The human mind sees a number like .0000000001 and it’s hard to suppress the gut feeling that the evidence in favour of the alternative hypothesis is a near certainty. In practice however, this is usually wrong. Life is a big, messy, complicated thing: and every statistical test ever invented relies on simplifications, approximations and assumptions. As a consequence, it’s probably not reasonable to walk away from any statistical analysis with a feeling of confidence stronger than $p<.001$ implies. In other words, $p<.001$ is really code for “as far as this test is concerned, the evidence is overwhelming.”

In light of all this, you might be wondering exactly what you should do. There’s a fair bit of contradictory advice on the topic, with some people arguing that you should report the exact $p$ value, and other people arguing that you should use the tiered approach illustrated in Table 11.1 . As a result, the best advice I can give is to suggest that you look at papers/reports written in your field and see what the convention seems to be. If there doesn’t seem to be any consistent pattern, then use whichever method you prefer.

11.7 Running the hypothesis test in practice

At this point some of you might be wondering if this is a “real” hypothesis test, or just a toy example that I made up. It’s real. In the previous discussion I built the test from first principles, thinking that it was the simplest possible problem that you might ever encounter in real life. However, this test already exists: it’s called the binomial test , and it’s implemented by an R function called binom.test() . To test the null hypothesis that the response probability is one-half p = .5 , 165 using data in which x = 62 of n = 100 people made the correct response, here’s how to do it in R:

Right now, this output looks pretty unfamiliar to you, but you can see that it’s telling you more or less the right things. Specifically, the $p$ -value of 0.02 is less than the usual choice of $\alpha = .05$ , so you can reject the null. We’ll talk a lot more about how to read this sort of output as we go along; and after a while you’ll hopefully find it quite easy to read and understand. For now, however, I just wanted to make the point that R contains a whole lot of functions corresponding to different kinds of hypothesis test. And while I’ll usually spend quite a lot of time explaining the logic behind how the tests are built, every time I discuss a hypothesis test the discussion will end with me showing you a fairly simple R command that you can use to run the test in practice.

11.8 Effect size, sample size and power

In previous sections I’ve emphasised the fact that the major design principle behind statistical hypothesis testing is that we try to control our Type I error rate. When we fix $\alpha = .05$ we are attempting to ensure that only 5% of true null hypotheses are incorrectly rejected. However, this doesn’t mean that we don’t care about Type II errors. In fact, from the researcher’s perspective, the error of failing to reject the null when it is actually false is an extremely annoying one. With that in mind, a secondary goal of hypothesis testing is to try to minimise $\beta$ , the Type II error rate, although we don’t usually talk in terms of minimising Type II errors. Instead, we talk about maximising the power of the test. Since power is defined as $1-\beta$ , this is the same thing.

11.8.1 The power function

$Sampling distribution under the *alternative* hypothesis, for a population parameter value of $\theta = 0.55$. A reasonable proportion of the distribution lies in the rejection region.$

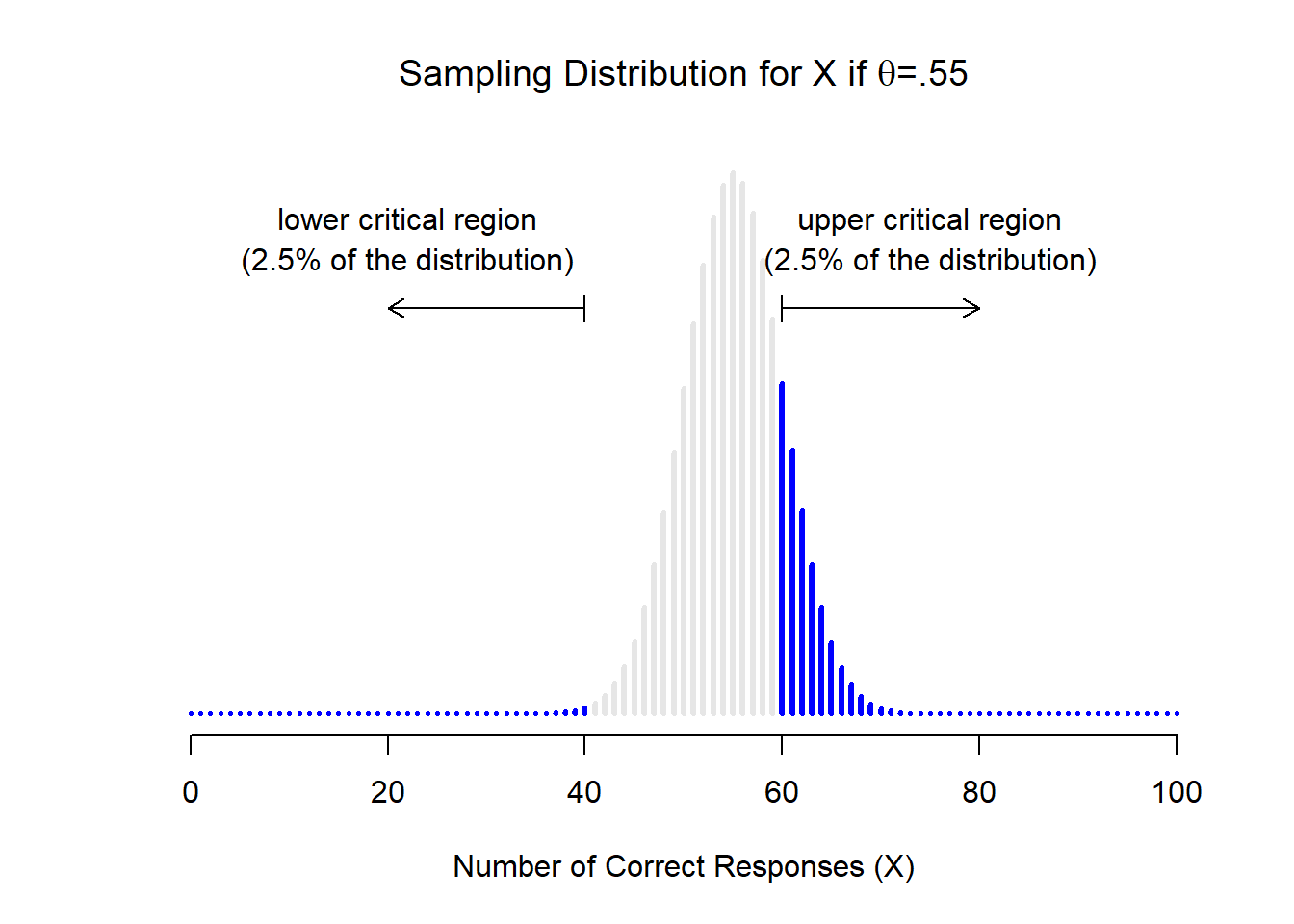
Figure 11.4: Sampling distribution under the alternative hypothesis, for a population parameter value of $\theta = 0.55$ . A reasonable proportion of the distribution lies in the rejection region.

Let’s take a moment to think about what a Type II error actually is. A Type II error occurs when the alternative hypothesis is true, but we are nevertheless unable to reject the null hypothesis. Ideally, we’d be able to calculate a single number $\beta$ that tells us the Type II error rate, in the same way that we can set $\alpha = .05$ for the Type I error rate. Unfortunately, this is a lot trickier to do. To see this, notice that in my ESP study the alternative hypothesis actually corresponds to lots of possible values of $\theta$ . In fact, the alternative hypothesis corresponds to every value of $\theta$ except 0.5. Let’s suppose that the true probability of someone choosing the correct response is 55% (i.e., $\theta = .55$ ). If so, then the true sampling distribution for $X$ is not the same one that the null hypothesis predicts: the most likely value for $X$ is now 55 out of 100. Not only that, the whole sampling distribution has now shifted, as shown in Figure 11.4 . The critical regions, of course, do not change: by definition, the critical regions are based on what the null hypothesis predicts. What we’re seeing in this figure is the fact that when the null hypothesis is wrong, a much larger proportion of the sampling distribution distribution falls in the critical region. And of course that’s what should happen: the probability of rejecting the null hypothesis is larger when the null hypothesis is actually false! However $\theta = .55$ is not the only possibility consistent with the alternative hypothesis. Let’s instead suppose that the true value of $\theta$ is actually 0.7. What happens to the sampling distribution when this occurs? The answer, shown in Figure 11.5 , is that almost the entirety of the sampling distribution has now moved into the critical region. Therefore, if $\theta = 0.7$ the probability of us correctly rejecting the null hypothesis (i.e., the power of the test) is much larger than if $\theta = 0.55$ . In short, while $\theta = .55$ and $\theta = .70$ are both part of the alternative hypothesis, the Type II error rate is different.

$Sampling distribution under the *alternative* hypothesis, for a population parameter value of $\theta = 0.70$. Almost all of the distribution lies in the rejection region.$

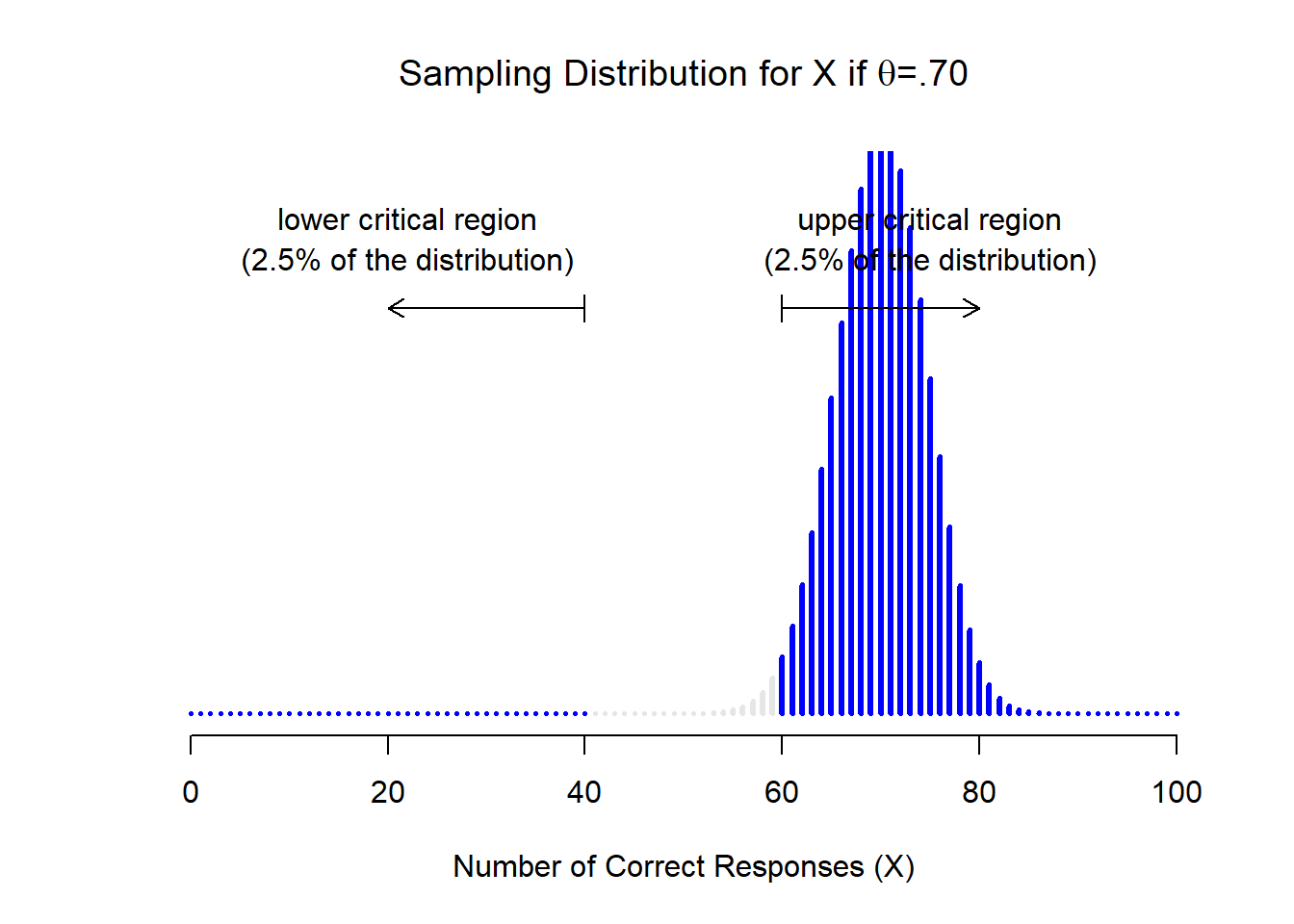
Figure 11.5: Sampling distribution under the alternative hypothesis, for a population parameter value of $\theta = 0.70$ . Almost all of the distribution lies in the rejection region.

$The probability that we will reject the null hypothesis, plotted as a function of the true value of $\theta$. Obviously, the test is more powerful (greater chance of correct rejection) if the true value of $\theta$ is very different from the value that the null hypothesis specifies (i.e., $\theta=.5$). Notice that when $\theta$ actually is equal to .5 (plotted as a black dot), the null hypothesis is in fact true: rejecting the null hypothesis in this instance would be a Type I error.$

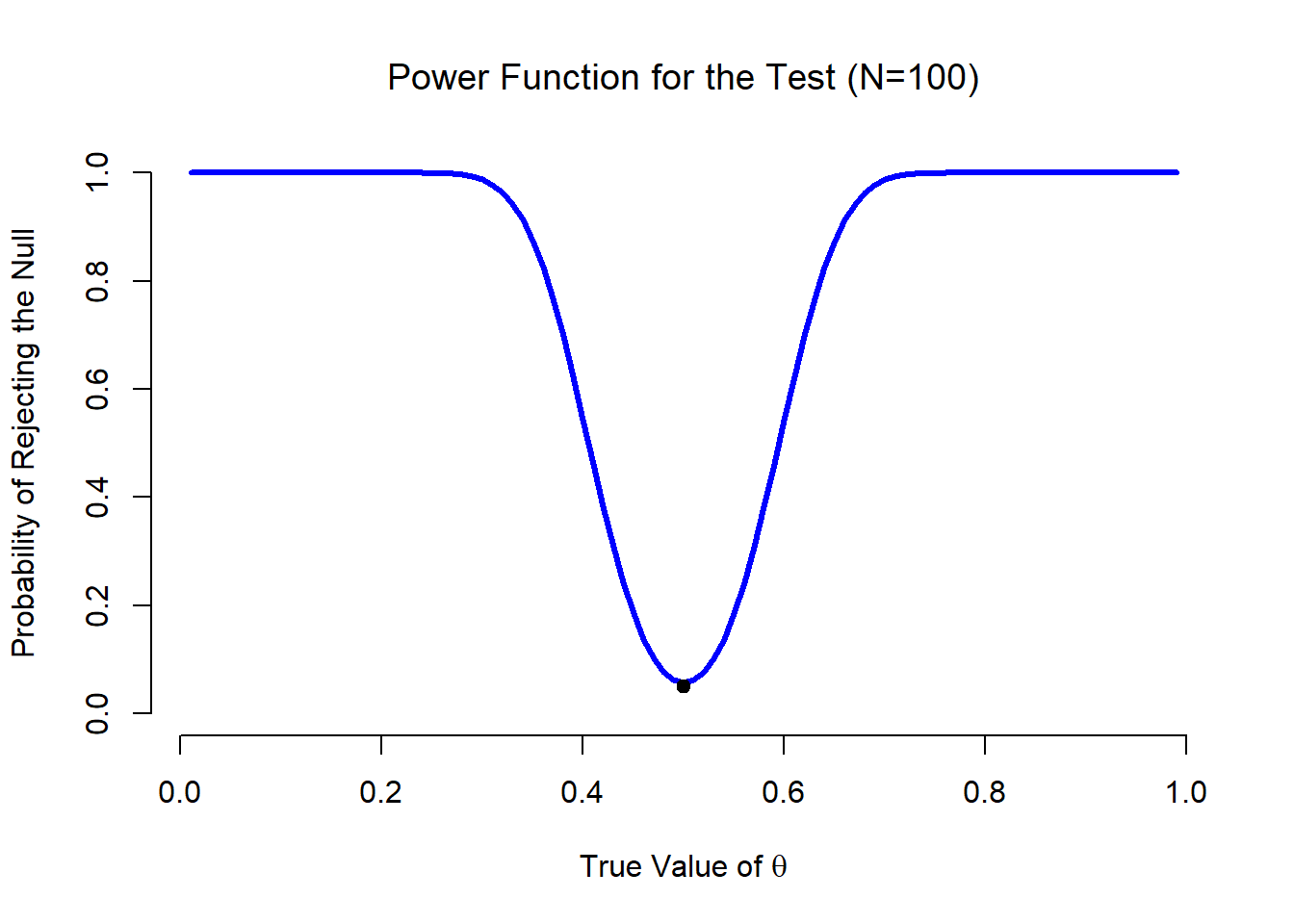
Figure 11.6: The probability that we will reject the null hypothesis, plotted as a function of the true value of $\theta$ . Obviously, the test is more powerful (greater chance of correct rejection) if the true value of $\theta$ is very different from the value that the null hypothesis specifies (i.e., $\theta=.5$ ). Notice that when $\theta$ actually is equal to .5 (plotted as a black dot), the null hypothesis is in fact true: rejecting the null hypothesis in this instance would be a Type I error.

What all this means is that the power of a test (i.e., $1-\beta$ ) depends on the true value of $\theta$ . To illustrate this, I’ve calculated the expected probability of rejecting the null hypothesis for all values of $\theta$ , and plotted it in Figure 11.6 . This plot describes what is usually called the power function of the test. It’s a nice summary of how good the test is, because it actually tells you the power ( $1-\beta$ ) for all possible values of $\theta$ . As you can see, when the true value of $\theta$ is very close to 0.5, the power of the test drops very sharply, but when it is further away, the power is large.

11.8.2 Effect size

Since all models are wrong the scientist must be alert to what is importantly wrong. It is inappropriate to be concerned with mice when there are tigers abroad – George Box 1976

The plot shown in Figure 11.6 captures a fairly basic point about hypothesis testing. If the true state of the world is very different from what the null hypothesis predicts, then your power will be very high; but if the true state of the world is similar to the null (but not identical) then the power of the test is going to be very low. Therefore, it’s useful to be able to have some way of quantifying how “similar” the true state of the world is to the null hypothesis. A statistic that does this is called a measure of effect size (e.g. Cohen 1988 ; Ellis 2010 ) . Effect size is defined slightly differently in different contexts, 166 (and so this section just talks in general terms) but the qualitative idea that it tries to capture is always the same: how big is the difference between the true population parameters, and the parameter values that are assumed by the null hypothesis? In our ESP example, if we let $\theta_0 = 0.5$ denote the value assumed by the null hypothesis, and let $\theta$ denote the true value, then a simple measure of effect size could be something like the difference between the true value and null (i.e., $\theta – \theta_0$ ), or possibly just the magnitude of this difference, $\mbox{abs}(\theta – \theta_0)$ .

Why calculate effect size? Let’s assume that you’ve run your experiment, collected the data, and gotten a significant effect when you ran your hypothesis test. Isn’t it enough just to say that you’ve gotten a significant effect? Surely that’s the point of hypothesis testing? Well, sort of. Yes, the point of doing a hypothesis test is to try to demonstrate that the null hypothesis is wrong, but that’s hardly the only thing we’re interested in. If the null hypothesis claimed that $\theta = .5$ , and we show that it’s wrong, we’ve only really told half of the story. Rejecting the null hypothesis implies that we believe that $\theta \neq .5$ , but there’s a big difference between $\theta = .51$ and $\theta = .8$ . If we find that $\theta = .8$ , then not only have we found that the null hypothesis is wrong, it appears to be very wrong. On the other hand, suppose we’ve successfully rejected the null hypothesis, but it looks like the true value of $\theta$ is only .51 (this would only be possible with a large study). Sure, the null hypothesis is wrong, but it’s not at all clear that we actually care , because the effect size is so small. In the context of my ESP study we might still care, since any demonstration of real psychic powers would actually be pretty cool 167 , but in other contexts a 1% difference isn’t very interesting, even if it is a real difference. For instance, suppose we’re looking at differences in high school exam scores between males and females, and it turns out that the female scores are 1% higher on average than the males. If I’ve got data from thousands of students, then this difference will almost certainly be statistically significant , but regardless of how small the $p$ value is it’s just not very interesting. You’d hardly want to go around proclaiming a crisis in boys education on the basis of such a tiny difference would you? It’s for this reason that it is becoming more standard (slowly, but surely) to report some kind of standard measure of effect size along with the the results of the hypothesis test. The hypothesis test itself tells you whether you should believe that the effect you have observed is real (i.e., not just due to chance); the effect size tells you whether or not you should care.

11.8.3 Increasing the power of your study

Not surprisingly, scientists are fairly obsessed with maximising the power of their experiments. We want our experiments to work, and so we want to maximise the chance of rejecting the null hypothesis if it is false (and of course we usually want to believe that it is false!) As we’ve seen, one factor that influences power is the effect size. So the first thing you can do to increase your power is to increase the effect size. In practice, what this means is that you want to design your study in such a way that the effect size gets magnified. For instance, in my ESP study I might believe that psychic powers work best in a quiet, darkened room; with fewer distractions to cloud the mind. Therefore I would try to conduct my experiments in just such an environment: if I can strengthen people’s ESP abilities somehow, then the true value of $\theta$ will go up 168 and therefore my effect size will be larger. In short, clever experimental design is one way to boost power; because it can alter the effect size.

Unfortunately, it’s often the case that even with the best of experimental designs you may have only a small effect. Perhaps, for example, ESP really does exist, but even under the best of conditions it’s very very weak. Under those circumstances, your best bet for increasing power is to increase the sample size. In general, the more observations that you have available, the more likely it is that you can discriminate between two hypotheses. If I ran my ESP experiment with 10 participants, and 7 of them correctly guessed the colour of the hidden card, you wouldn’t be terribly impressed. But if I ran it with 10,000 participants and 7,000 of them got the answer right, you would be much more likely to think I had discovered something. In other words, power increases with the sample size. This is illustrated in Figure 11.7 , which shows the power of the test for a true parameter of $\theta = 0.7$ , for all sample sizes $N$ from 1 to 100, where I’m assuming that the null hypothesis predicts that $\theta_0 = 0.5$ .

$The power of our test, plotted as a function of the sample size $N$. In this case, the true value of $\theta$ is 0.7, but the null hypothesis is that $\theta = 0.5$. Overall, larger $N$ means greater power. (The small zig-zags in this function occur because of some odd interactions between $\theta$, $\alpha$ and the fact that the binomial distribution is discrete; it doesn't matter for any serious purpose)$

Figure 11.7: The power of our test, plotted as a function of the sample size $N$ . In this case, the true value of $\theta$ is 0.7, but the null hypothesis is that $\theta = 0.5$ . Overall, larger $N$ means greater power. (The small zig-zags in this function occur because of some odd interactions between $\theta$ , $\alpha$ and the fact that the binomial distribution is discrete; it doesn’t matter for any serious purpose)

Because power is important, whenever you’re contemplating running an experiment it would be pretty useful to know how much power you’re likely to have. It’s never possible to know for sure, since you can’t possibly know what your effect size is. However, it’s often (well, sometimes) possible to guess how big it should be. If so, you can guess what sample size you need! This idea is called power analysis , and if it’s feasible to do it, then it’s very helpful, since it can tell you something about whether you have enough time or money to be able to run the experiment successfully. It’s increasingly common to see people arguing that power analysis should be a required part of experimental design, so it’s worth knowing about. I don’t discuss power analysis in this book, however. This is partly for a boring reason and partly for a substantive one. The boring reason is that I haven’t had time to write about power analysis yet. The substantive one is that I’m still a little suspicious of power analysis. Speaking as a researcher, I have very rarely found myself in a position to be able to do one – it’s either the case that (a) my experiment is a bit non-standard and I don’t know how to define effect size properly, (b) I literally have so little idea about what the effect size will be that I wouldn’t know how to interpret the answers. Not only that, after extensive conversations with someone who does stats consulting for a living (my wife, as it happens), I can’t help but notice that in practice the only time anyone ever asks her for a power analysis is when she’s helping someone write a grant application. In other words, the only time any scientist ever seems to want a power analysis in real life is when they’re being forced to do it by bureaucratic process. It’s not part of anyone’s day to day work. In short, I’ve always been of the view that while power is an important concept, power analysis is not as useful as people make it sound, except in the rare cases where (a) someone has figured out how to calculate power for your actual experimental design and (b) you have a pretty good idea what the effect size is likely to be. Maybe other people have had better experiences than me, but I’ve personally never been in a situation where both (a) and (b) were true. Maybe I’ll be convinced otherwise in the future, and probably a future version of this book would include a more detailed discussion of power analysis, but for now this is about as much as I’m comfortable saying about the topic.

11.9 Some issues to consider

What I’ve described to you in this chapter is the orthodox framework for null hypothesis significance testing (NHST). Understanding how NHST works is an absolute necessity, since it has been the dominant approach to inferential statistics ever since it came to prominence in the early 20th century. It’s what the vast majority of working scientists rely on for their data analysis, so even if you hate it you need to know it. However, the approach is not without problems. There are a number of quirks in the framework, historical oddities in how it came to be, theoretical disputes over whether or not the framework is right, and a lot of practical traps for the unwary. I’m not going to go into a lot of detail on this topic, but I think it’s worth briefly discussing a few of these issues.

11.9.1 Neyman versus Fisher

The first thing you should be aware of is that orthodox NHST is actually a mash-up of two rather different approaches to hypothesis testing, one proposed by Sir Ronald Fisher and the other proposed by Jerzy Neyman (for a historical summary see Lehmann 2011 ) . The history is messy because Fisher and Neyman were real people whose opinions changed over time, and at no point did either of them offer “the definitive statement” of how we should interpret their work many decades later. That said, here’s a quick summary of what I take these two approaches to be.

First, let’s talk about Fisher’s approach. As far as I can tell, Fisher assumed that you only had the one hypothesis (the null), and what you want to do is find out if the null hypothesis is inconsistent with the data. From his perspective, what you should do is check to see if the data are “sufficiently unlikely” according to the null. In fact, if you remember back to our earlier discussion, that’s how Fisher defines the $p$ -value. According to Fisher, if the null hypothesis provided a very poor account of the data, you could safely reject it. But, since you don’t have any other hypotheses to compare it to, there’s no way of “accepting the alternative” because you don’t necessarily have an explicitly stated alternative. That’s more or less all that there was to it.

In contrast, Neyman thought that the point of hypothesis testing was as a guide to action, and his approach was somewhat more formal than Fisher’s. His view was that there are multiple things that you could do (accept the null or accept the alternative) and the point of the test was to tell you which one the data support. From this perspective, it is critical to specify your alternative hypothesis properly. If you don’t know what the alternative hypothesis is, then you don’t know how powerful the test is, or even which action makes sense. His framework genuinely requires a competition between different hypotheses. For Neyman, the $p$ value didn’t directly measure the probability of the data (or data more extreme) under the null, it was more of an abstract description about which “possible tests” were telling you to accept the null, and which “possible tests” were telling you to accept the alternative.

As you can see, what we have today is an odd mishmash of the two. We talk about having both a null hypothesis and an alternative (Neyman), but usually 169 define the $p$ value in terms of exreme data (Fisher), but we still have $\alpha$ values (Neyman). Some of the statistical tests have explicitly specified alternatives (Neyman) but others are quite vague about it (Fisher). And, according to some people at least, we’re not allowed to talk about accepting the alternative (Fisher). It’s a mess: but I hope this at least explains why it’s a mess.

11.9.2 Bayesians versus frequentists

Earlier on in this chapter I was quite emphatic about the fact that you cannot interpret the $p$ value as the probability that the null hypothesis is true. NHST is fundamentally a frequentist tool (see Chapter 9 ) and as such it does not allow you to assign probabilities to hypotheses: the null hypothesis is either true or it is not. The Bayesian approach to statistics interprets probability as a degree of belief, so it’s totally okay to say that there is a 10% chance that the null hypothesis is true: that’s just a reflection of the degree of confidence that you have in this hypothesis. You aren’t allowed to do this within the frequentist approach. Remember, if you’re a frequentist, a probability can only be defined in terms of what happens after a large number of independent replications (i.e., a long run frequency). If this is your interpretation of probability, talking about the “probability” that the null hypothesis is true is complete gibberish: a null hypothesis is either true or it is false. There’s no way you can talk about a long run frequency for this statement. To talk about “the probability of the null hypothesis” is as meaningless as “the colour of freedom”. It doesn’t have one!

Most importantly, this isn’t a purely ideological matter. If you decide that you are a Bayesian and that you’re okay with making probability statements about hypotheses, you have to follow the Bayesian rules for calculating those probabilities. I’ll talk more about this in Chapter 17 , but for now what I want to point out to you is the $p$ value is a terrible approximation to the probability that $H_0$ is true. If what you want to know is the probability of the null, then the $p$ value is not what you’re looking for!

11.9.3 Traps

As you can see, the theory behind hypothesis testing is a mess, and even now there are arguments in statistics about how it “should” work. However, disagreements among statisticians are not our real concern here. Our real concern is practical data analysis. And while the “orthodox” approach to null hypothesis significance testing has many drawbacks, even an unrepentant Bayesian like myself would agree that they can be useful if used responsibly. Most of the time they give sensible answers, and you can use them to learn interesting things. Setting aside the various ideologies and historical confusions that we’ve discussed, the fact remains that the biggest danger in all of statistics is thoughtlessness . I don’t mean stupidity, here: I literally mean thoughtlessness. The rush to interpret a result without spending time thinking through what each test actually says about the data, and checking whether that’s consistent with how you’ve interpreted it. That’s where the biggest trap lies.

To give an example of this, consider the following example (see Gelman and Stern 2006 ) . Suppose I’m running my ESP study, and I’ve decided to analyse the data separately for the male participants and the female participants. Of the male participants, 33 out of 50 guessed the colour of the card correctly. This is a significant effect ( $p = .03$ ). Of the female participants, 29 out of 50 guessed correctly. This is not a significant effect ( $p = .32$ ). Upon observing this, it is extremely tempting for people to start wondering why there is a difference between males and females in terms of their psychic abilities. However, this is wrong. If you think about it, we haven’t actually run a test that explicitly compares males to females. All we have done is compare males to chance (binomial test was significant) and compared females to chance (binomial test was non significant). If we want to argue that there is a real difference between the males and the females, we should probably run a test of the null hypothesis that there is no difference! We can do that using a different hypothesis test, 170 but when we do that it turns out that we have no evidence that males and females are significantly different ( $p = .54$ ). Now do you think that there’s anything fundamentally different between the two groups? Of course not. What’s happened here is that the data from both groups (male and female) are pretty borderline: by pure chance, one of them happened to end up on the magic side of the $p = .05$ line, and the other one didn’t. That doesn’t actually imply that males and females are different. This mistake is so common that you should always be wary of it: the difference between significant and not-significant is not evidence of a real difference – if you want to say that there’s a difference between two groups, then you have to test for that difference!

The example above is just that: an example. I’ve singled it out because it’s such a common one, but the bigger picture is that data analysis can be tricky to get right. Think about what it is you want to test, why you want to test it, and whether or not the answers that your test gives could possibly make any sense in the real world.

11.10 Summary

Null hypothesis testing is one of the most ubiquitous elements to statistical theory. The vast majority of scientific papers report the results of some hypothesis test or another. As a consequence it is almost impossible to get by in science without having at least a cursory understanding of what a $p$ -value means, making this one of the most important chapters in the book. As usual, I’ll end the chapter with a quick recap of the key ideas that we’ve talked about:

Research hypotheses and statistical hypotheses. Null and alternative hypotheses. (Section 11.1 ).
Type 1 and Type 2 errors (Section 11.2 )
Test statistics and sampling distributions (Section 11.3 )
Hypothesis testing as a decision making process (Section 11.4 )
$p$ -values as “soft” decisions (Section 11.5 )
Writing up the results of a hypothesis test (Section 11.6 )
Effect size and power (Section 11.8 )
A few issues to consider regarding hypothesis testing (Section 11.9 )

Later in the book, in Chapter 17 , I’ll revisit the theory of null hypothesis tests from a Bayesian perspective, and introduce a number of new tools that you can use if you aren’t particularly fond of the orthodox approach. But for now, though, we’re done with the abstract statistical theory, and we can start discussing specific data analysis tools.

Cohen, J. 1988. Statistical Power Analysis for the Behavioral Sciences . 2nd ed. Lawrence Erlbaum.

Ellis, P. D. 2010. The Essential Guide to Effect Sizes: Statistical Power, Meta-Analysis, and the Interpretation of Research Results . Cambridge, UK: Cambridge University Press.

Lehmann, Erich L. 2011. Fisher, Neyman, and the Creation of Classical Statistics . Springer.

Gelman, A., and H. Stern. 2006. “The Difference Between ‘Significant’ and ‘Not Significant’ Is Not Itself Statistically Significant.” The American Statistician 60: 328–31.

The quote comes from Wittgenstein’s (1922) text, Tractatus Logico-Philosphicus . ↩
A technical note. The description below differs subtly from the standard description given in a lot of introductory texts. The orthodox theory of null hypothesis testing emerged from the work of Sir Ronald Fisher and Jerzy Neyman in the early 20th century; but Fisher and Neyman actually had very different views about how it should work. The standard treatment of hypothesis testing that most texts use is a hybrid of the two approaches. The treatment here is a little more Neyman-style than the orthodox view, especially as regards the meaning of the $p$ value. ↩
My apologies to anyone who actually believes in this stuff, but on my reading of the literature on ESP, it’s just not reasonable to think this is real. To be fair, though, some of the studies are rigorously designed; so it’s actually an interesting area for thinking about psychological research design. And of course it’s a free country, so you can spend your own time and effort proving me wrong if you like, but I wouldn’t think that’s a terribly practical use of your intellect. ↩
This analogy only works if you’re from an adversarial legal system like UK/US/Australia. As I understand these things, the French inquisitorial system is quite different. ↩
An aside regarding the language you use to talk about hypothesis testing. Firstly, one thing you really want to avoid is the word “prove”: a statistical test really doesn’t prove that a hypothesis is true or false. Proof implies certainty, and as the saying goes, statistics means never having to say you’re certain. On that point almost everyone would agree. However, beyond that there’s a fair amount of confusion. Some people argue that you’re only allowed to make statements like “rejected the null”, “failed to reject the null”, or possibly “retained the null”. According to this line of thinking, you can’t say things like “accept the alternative” or “accept the null”. Personally I think this is too strong: in my opinion, this conflates null hypothesis testing with Karl Popper’s falsificationist view of the scientific process. While there are similarities between falsificationism and null hypothesis testing, they aren’t equivalent. However, while I personally think it’s fine to talk about accepting a hypothesis (on the proviso that “acceptance” doesn’t actually mean that it’s necessarily true, especially in the case of the null hypothesis), many people will disagree. And more to the point, you should be aware that this particular weirdness exists, so that you’re not caught unawares by it when writing up your own results. ↩
Strictly speaking, the test I just constructed has $\alpha = .057$ , which is a bit too generous. However, if I’d chosen 39 and 61 to be the boundaries for the critical region, then the critical region only covers 3.5% of the distribution. I figured that it makes more sense to use 40 and 60 as my critical values, and be willing to tolerate a 5.7% type I error rate, since that’s as close as I can get to a value of $\alpha = .05$ . ↩
The internet seems fairly convinced that Ashley said this, though I can’t for the life of me find anyone willing to give a source for the claim. ↩
That’s $p = .000000000000000000000000136$ for folks that don’t like scientific notation! ↩
Note that the p here has nothing to do with a $p$ value. The p argument in the binom.test() function corresponds to the probability of making a correct response, according to the null hypothesis. In other words, it’s the $\theta$ value. ↩
There’s an R package called compute.es that can be used for calculating a very broad range of effect size measures; but for the purposes of the current book we won’t need it: all of the effect size measures that I’ll talk about here have functions in the lsr package ↩
Although in practice a very small effect size is worrying, because even very minor methodological flaws might be responsible for the effect; and in practice no experiment is perfect, so there are always methodological issues to worry about. ↩
Notice that the true population parameter $\theta$ doesn’t necessarily correspond to an immutable fact of nature. In this context $\theta$ is just the true probability that people would correctly guess the colour of the card in the other room. As such the population parameter can be influenced by all sorts of things. Of course, this is all on the assumption that ESP actually exists! ↩
Although this book describes both Neyman’s and Fisher’s definition of the $p$ value, most don’t. Most introductory textbooks will only give you the Fisher version. ↩
In this case, the Pearson chi-square test of independence (Chapter 12 ; chisq.test() in R) is what we use; see also the prop.test() function. ↩

Share This Book

R news and tutorials contributed by hundreds of R bloggers

Hypothesis testing in r.

Posted on December 3, 2022 by Jim in R bloggers | 0 Comments

The post Hypothesis Testing in R appeared first on Data Science Tutorials

What do you have to lose?. Check out Data Science tutorials here Data Science Tutorials .

Hypothesis Testing in R, A formal statistical test called a hypothesis test is used to confirm or disprove a statistical hypothesis.

The following R hypothesis tests are demonstrated in this course.

T-test with one sample
T-Test of two samples
T-test for paired samples

Each type of test can be run using the R function t.test().

How to Create an Interaction Plot in R? – Data Science Tutorials

one sample t-test

x, y: The two samples of data.

alternative: The alternative hypothesis of the test.

mu: The true value of the mean.

paired: whether or not to run a paired t-test.

var.equal: Whether to assume that the variances between the samples are equal.

conf.level: The confidence level to use.

The following examples show how to use this function in practice.

Example 1: One-Sample t-test in R

A one-sample t-test is used to determine whether the population’s mean is equal to a given value.

Consider the situation where we wish to determine whether the mean weight of a particular species of turtle is 310 pounds or not. We go out and gather a straightforward random sample of turtles with the weights listed below.

How to Find Unmatched Records in R – Data Science Tutorials

Weights: 301, 305, 312, 315, 318, 319, 310, 318, 305, 313, 305, 305, 305

The following code shows how to perform this one sample t-test in R:

specify a turtle weights vector

Now we can perform a one-sample t-test

From the output we can see:

t-test statistic: 045145

degrees of freedom: 12

p-value: 0. 9647

95% confidence interval for true mean: [306.3644, 313.7895]

mean of turtle weights: 310.0769We are unable to reject the null hypothesis since the test’s p-value of 0. 9647 is greater than or equal to.05.

This means that we lack adequate evidence to conclude that this species of turtle’s mean weight is different from 310 pounds.

Example 2: Two Sample t-test in R

To determine whether the means of two populations are equal, a two-sample t-test is employed.

Consider the situation where we want to determine whether the mean weight of two different species of turtles is equal. We gather a straightforward random sample of turtles from each species with the following weights to test this.

ggpairs in R – Data Science Tutorials

Sample 1: 310, 311, 310, 315, 311, 319, 310, 318, 315, 313, 315, 311, 313

Sample 2: 335, 339, 332, 331, 334, 339, 334, 318, 315, 331, 317, 330, 325

The following code shows how to perform this two-sample t-test in R:

Now we can create a vector of turtle weights for each sample

Let’s perform two sample t-tests

We reject the null hypothesis because the test’s p-value (6.029e-06) is smaller than.05.

Accordingly, we have enough data to conclude that the mean weight of the two species is not identical.

Example 3: Paired Samples t-test in R

When each observation in one sample can be paired with an observation in the other sample, a paired samples t-test is used to compare the means of the two samples.

For instance, let’s say we want to determine if a particular training program may help basketball players raise their maximum vertical jump (in inches).

How to create Anatogram plot in R – Data Science Tutorials

We may gather a small, random sample of 12 college basketball players to test this by measuring each player’s maximum vertical jump. Then, after each athlete has used the training regimen for a month, we might take another look at their max vertical leap.

The following information illustrates the maximum jump height (in inches) for each athlete before and after using the training program.

Before: 122, 124, 120, 119, 119, 120, 122, 125, 124, 123, 122, 121

After: 123, 125, 120, 124, 118, 122, 123, 128, 124, 125, 124, 120

The following code shows how to perform this paired samples t-test in R:

Let’s define before and after max jump heights

We can perform paired samples t-test

We reject the null hypothesis since the test’s p-value (0. 02803) is smaller than.05.

Autocorrelation and Partial Autocorrelation in Time Series (datasciencetut.com)

The mean jump height before and after implementing the training program is not equal, thus we have enough data to conclude so.

Check your inbox or spam folder to confirm your subscription.

Learn how to expert in the Data Science field with Data Science Tutorials .

Never miss an update! Subscribe to R-bloggers to receive e-mails with the latest R posts. (You will not see this message again.)

COMMENTS

The Complete Guide: Hypothesis Testing in R
A hypothesis test is a formal statistical test we use to reject or fail to reject some statistical hypothesis. This tutorial explains how to perform the following hypothesis tests in R: One sample t-test. Two sample t-test. Paired samples t-test. We can use the t.test () function in R to perform each type of test:
The Complete Guide: Hypothesis Testing in R
A hypothesis test is a formal statistical test we use to reject or fail to reject some statistical hypothesis. This tutorial explains how to perform the following hypothesis tests in R: One sample t-test. Two sample t-test. Paired samples t-test. We can use the t.test () function in R to perform each type of test:
Hypothesis Tests in R
R Function: t.test() Null hypothesis (H 0): The means of the sampled distribution matches the expected mean. History: William Sealy Gosset ; T-tests should only be used when the population is at least 20 times larger than its respective sample. If the sample size is too large, the low p-value makes the insignificant look significant..
6.2 Hypothesis Tests
6.2.2.1 Known Standard Deviation. It is simple to calculate a hypothesis test in R (in fact, we already implicitly did this in the previous section). When we know the population standard deviation, we use a hypothesis test based on the standard normal, known as a \ (z\) -test. Here, let's assume \ (\sigma_X = 2\) (because that is the standard ...
Introduction to Hypothesis Testing in R
With this R hypothesis testing tutorial, learn about the decision errors, two-sample T-test with unequal variance, one-sample T-testing, formula syntax and subsetting samples in T-test and μ test in R. ... You can apply a significance test to your correlations by using the cor.test() command. In this case, you can compare only two vectors at a ...
Hypothesis testing in R
👉 If you haven't found what you're looking for, consider clicking the checkbox to activate the extended search on R CHARTS for additional graphs tutorials, try searching a synonym of your query if possible (e.g., 'bar plot' -> 'bar chart'), search for a more generic query or if you are searching for a specific function activate the functions search or use the functions search bar.
Hypothesis Testing
In the following tutorials, we demonstrate the procedure of hypothesis testing in R first with the intuitive critical value approach. Then we discuss the popular p-value approach as alternative. Lower Tail Test of Population Mean with Known Variance
Hypothesis Testing in R Programming
Hypothesis Testing in R Programming. Hypothesis testing is a statistical method used to determine whether there is enough evidence to reject a null hypothesis in favor of an alternative hypothesis. In R programming, you can perform various types of hypothesis tests, such as t-tests, chi-squared tests, and ANOVA tests, among others.
Chapter 10 Hypothesis Testing
Here's a step-by-step procedure for generating and testing power using R: Install and load the pwr package: # Load the pwr package library ( pwr) #> Warning: package 'pwr' was built under R version 4.2.3. Define the parameters for power analysis.
Hypothesis testing
11. Hypothesis testing. The process of induction is the process of assuming the simplest law that can be made to harmonize with our experience. This process, however, has no logical foundation but only a psychological one. It is clear that there are no grounds for believing that the simplest course of events will really happen.
Hypothesis Testing in R: Elevating Your Data Analysis Skills
Practice Regularly: The more you apply hypothesis testing in different scenarios, the more skilled you'll become. Experiment with various datasets to enhance your understanding. Hypothesis testing in R is an invaluable skill for any data analyst or researcher. By understanding your data, choosing the appropriate test, interpreting results ...
Hypothesis Testing in R Programming
Four Step Process of Hypothesis Testing. There are 4 major steps in hypothesis testing: State the hypothesis- This step is started by stating null and alternative hypothesis which is presumed as true. Formulate an analysis plan and set the criteria for decision- In this step, a significance level of test is set.
15.5: Hypothesis Tests for Regression Models
Formally, our "null model" corresponds to the fairly trivial "regression" model in which we include 0 predictors, and only include the intercept term b 0. H 0 :Y i =b 0 +ϵ i. If our regression model has K predictors, the "alternative model" is described using the usual formula for a multiple regression model: H1: Yi = (∑K k=1 ...
Hypothesis Testing in R: Elevating Your Data Analysis Skills
With R, we can apply these concepts more easily, allowing us to draw meaningful conclusions from our data. ... Hypothesis testing in R is not just about performing calculations; it's about ...
R Tutorial : Hypothesis Testing
Want to learn more? Take the full course at https://learn.datacamp.com/courses/experimental-design-in-r at your own pace. More than a video, you'll learn han...
Hypothesis Testing in R Course
Discover Hypothesis Testing in R. Hypothesis testing lets you ask questions about your datasets and answer them in a statistically rigorous way. In this course, you'll learn how and when to use common tests like t-tests, proportion tests, and chi-square tests. You'll gain a deep understanding of how they work and the assumptions that underlie them.
Multiple Hypothesis Testing in R · R Views
In the first article of this series, we looked at understanding type I and type II errors in the context of an A/B test, and highlighted the issue of "peeking". In the second, we illustrated a way to calculate always-valid p-values that were immune to peeking. We will now explore multiple hypothesis testing, or what happens when multiple tests are conducted on the same family of data. We ...
Hypothesis Testing
Table of contents. Step 1: State your null and alternate hypothesis. Step 2: Collect data. Step 3: Perform a statistical test. Step 4: Decide whether to reject or fail to reject your null hypothesis. Step 5: Present your findings. Other interesting articles. Frequently asked questions about hypothesis testing.
Hypothesis test by hand
Step #1: Stating the null and alternative hypothesis. Step #2: Computing the test statistic. Step #3: Computing the p -value. Step #4: Concluding and interpreting the results. Method C: Comparing the target parameter with the confidence interval. Step #1: Stating the null and alternative hypothesis.
Hypothesis Testing in R
Now we can perform a one-sample t-test. t.test (x = weights, mu = 310) One Sample t-test data: weights t = 0.045145, df = 12, p-value = 0.9647 alternative hypothesis: true mean is not equal to 310 95 percent confidence interval: 306.3644 313.7895 sample estimates: mean of x 310.0769. From the output we can see:
Hypothesis Testing in R
Welcome to this project-based course Hypothesis Testing in R. In this project, you will learn how to perform extensive hypothesis tests for one and two samples in R. By the end of this 2-hour long project, you will understand the rationale behind performing hypothesis testing. Also, you will learn how to perform hypothesis tests for proportions ...
17: Hypothesis Testing in R
This page titled 17: Hypothesis Testing in R is shared under a CC BY-NC 2.0 license and was authored, remixed, and/or curated by Russell A. Poldrack via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.
ANOVA in R
Table of contents. Getting started in R. Step 1: Load the data into R. Step 2: Perform the ANOVA test. Step 3: Find the best-fit model. Step 4: Check for homoscedasticity. Step 5: Do a post-hoc test. Step 6: Plot the results in a graph. Step 7: Report the results.

The Complete Guide: Hypothesis Testing in R

Example 1: One Sample t-test in R

Example 2: Two Sample t-test in R

Example 3: Paired Samples t-test in R

Additional Resources

Featured Posts

Leave a Reply Cancel reply

Join the Statology Community

The Complete Guide: Hypothesis Testing in R

Example 1: One Sample t-test in R

Example 2: Two Sample t-test in R

Example 3: Paired Samples t-test in R

Additional Resources

How to Calculate Mode from Frequency Table (With Examples)

Hypothesis Tests in R

Hypothesis Testing

The Problem of Induction

Falsification

Null and Alternative Hypotheses

Type I vs. Type II Errors

Statistical Significance vs. Importance

Science vs. Non-science

Example Data

Variable Types

Normality Tests

The Shapiro-Wilk Normality Test

The Kolmogorov-Smirnov Test

Modality Tests of Samples

One Sample T-Test (One-Sided)

Box-and-Whisker Chart

Two-Sample T-Test

Wilcoxen Rank Sum Test (Mann-Whitney U-Test)

Weighted Two-Sample T-Test

Comparing Proportions: Tests with Categorical Data

Chi-Squared Contingency Analysis / Test of Independence

Weighted Chi-Squared Contingency Analysis

Comparing Categorical and Continuous Variables

Kruskal-Wallace One-Way Analysis of Variance

Introduction to Statistics with R

6.2.2 Hypothesis Tests for Means

6.2.2.2 Unknown Standard Deviation

6.2.3 Two-sample Tests

6.2.3.2 Pooled Two-sample t-test

6.2.3.3 Paired t-test

6.2.4 Tests for Proportions

6.2.5 Power

HYPOTHESIS TESTING IN R

NORMALITY TESTS

Shapiro Wilk normality test

Lilliefors normality test

GOODNESS OF FIT TESTS

Pearson's Chi-squared test with chisq.test()

Kolmogorov-Smirnov test with ks.test()

Wilcoxon signed rank test

Wilcoxon rank sum test (Mann-Whitney U test)

Kruskal Wallis rank sum test (H test)

OTHER TYPES OF TESTS

T-test to compare means

F test with var.test() to compare two variances

Test for proportions with prop.test()

An R Introduction to Statistics

Hypothesis Testing

R Tutorial eBook

R Tutorials

How to Plot a Weibull Distribution in R

1. One-sample t-test:

2. Two-sample t-test:

3. Paired t-test:

4. Chi-squared test:

5. One-way ANOVA

6. Wilcoxon signed-rank test

Steps for conducting a Hypothesis Testing

1. Prepare your data:

2. State your null and alternative hypotheses:

3. Perform the t-test:

4. Interpret the results:

5. Make a decision:

Few more examples of hypothesis tests using R

T-Test in R Programming

Quantitative Methods Using R