classical approach hypothesis testing calculator

Statistical Inference: A Short Course by Michael J. Panik

Get full access to Statistical Inference: A Short Course and 60K+ other titles, with a free 10-day trial of O'Reilly.

There are also live events, courses curated by job role, and more.

10.5 The Classical Approach to Hypothesis Testing

Armed with the concepts, we can now specify what is called the classical approach to hypothesis testing :

The classical approach to hypothesis testing is executed by the following stepwise procedure for hypothesis testing :

Get Statistical Inference: A Short Course now with the O’Reilly learning platform.

O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

Don’t leave empty-handed

Get Mark Richards’s Software Architecture Patterns ebook to better understand how to design components—and how they should interact.

It’s yours, free.

Check it out now on O’Reilly

Dive in for free with a 10-day trial of the O’Reilly learning platform—then explore all the other resources our members count on to build skills and solve problems every day.

• Media Upload

• Learning and Tutoring Center
• Supplemental Instruction

Hypothesis Testing - Classical Approach (Traditional Approach)

Critical Value Calculator

How to use critical value calculator, what is a critical value, critical value definition, how to calculate critical values, z critical values, t critical values, chi-square critical values (χ²), f critical values, behind the scenes of the critical value calculator.

Welcome to the critical value calculator! Here you can quickly determine the critical value(s) for two-tailed tests, as well as for one-tailed tests. It works for most common distributions in statistical testing: the standard normal distribution N(0,1) (that is when you have a Z-score), t-Student, chi-square, and F-distribution .

What is a critical value? And what is the critical value formula? Scroll down – we provide you with the critical value definition and explain how to calculate critical values in order to use them to construct rejection regions (also known as critical regions).

The critical value calculator is your go-to tool for swiftly determining critical values in statistical tests, be it one-tailed or two-tailed. To effectively use the calculator, follow these steps:

In the first field, input the distribution of your test statistic under the null hypothesis: is it a standard normal N (0,1), t-Student, chi-squared, or Snedecor's F? If you are not sure, check the sections below devoted to those distributions, and try to localize the test you need to perform.

In the field What type of test? choose the alternative hypothesis : two-tailed, right-tailed, or left-tailed.

If needed, specify the degrees of freedom of the test statistic's distribution. If you need more clarification, check the description of the test you are performing. You can learn more about the meaning of this quantity in statistics from the degrees of freedom calculator .

Set the significance level, α \alpha α . By default, we pre-set it to the most common value, 0.05, but you can adjust it to your needs.

The critical value calculator will display your critical value(s) and the rejection region(s).

Click the advanced mode if you need to increase the precision with which the critical values are computed.

For example, let's envision a scenario where you are conducting a one-tailed hypothesis test using a t-Student distribution with 15 degrees of freedom. You have opted for a right-tailed test and set a significance level (α) of 0.05. The results indicate that the critical value is 1.7531, and the critical region is (1.7531, ∞). This implies that if your test statistic exceeds 1.7531, you will reject the null hypothesis at the 0.05 significance level.

👩‍🏫 Want to learn more about critical values? Keep reading!

In hypothesis testing, critical values are one of the two approaches which allow you to decide whether to retain or reject the null hypothesis. The other approach is to calculate the p-value (for example, using the p-value calculator ).

The critical value approach consists of checking if the value of the test statistic generated by your sample belongs to the so-called rejection region , or critical region , which is the region where the test statistic is highly improbable to lie . A critical value is a cut-off value (or two cut-off values in the case of a two-tailed test) that constitutes the boundary of the rejection region(s). In other words, critical values divide the scale of your test statistic into the rejection region and the non-rejection region.

Once you have found the rejection region, check if the value of the test statistic generated by your sample belongs to it :

• If so, it means that you can reject the null hypothesis and accept the alternative hypothesis; and
• If not, then there is not enough evidence to reject H 0 .

But how to calculate critical values? First of all, you need to set a significance level , α \alpha α , which quantifies the probability of rejecting the null hypothesis when it is actually correct. The choice of α is arbitrary; in practice, we most often use a value of 0.05 or 0.01. Critical values also depend on the alternative hypothesis you choose for your test , elucidated in the next section .

To determine critical values, you need to know the distribution of your test statistic under the assumption that the null hypothesis holds. Critical values are then points with the property that the probability of your test statistic assuming values at least as extreme at those critical values is equal to the significance level α . Wow, quite a definition, isn't it? Don't worry, we'll explain what it all means.

First, let us point out it is the alternative hypothesis that determines what "extreme" means. In particular, if the test is one-sided, then there will be just one critical value; if it is two-sided, then there will be two of them: one to the left and the other to the right of the median value of the distribution.

Critical values can be conveniently depicted as the points with the property that the area under the density curve of the test statistic from those points to the tails is equal to α \alpha α :

Left-tailed test: the area under the density curve from the critical value to the left is equal to α \alpha α ;

Right-tailed test: the area under the density curve from the critical value to the right is equal to α \alpha α ; and

Two-tailed test: the area under the density curve from the left critical value to the left is equal to α / 2 \alpha/2 α /2 , and the area under the curve from the right critical value to the right is equal to α / 2 \alpha/2 α /2 as well; thus, total area equals α \alpha α .

As you can see, finding the critical values for a two-tailed test with significance α \alpha α boils down to finding both one-tailed critical values with a significance level of α / 2 \alpha/2 α /2 .

The formulae for the critical values involve the quantile function , Q Q Q , which is the inverse of the cumulative distribution function ( c d f \mathrm{cdf} cdf ) for the test statistic distribution (calculated under the assumption that H 0 holds!): Q = c d f − 1 Q = \mathrm{cdf}^{-1} Q = cdf − 1 .

Once we have agreed upon the value of α \alpha α , the critical value formulae are the following:

• Left-tailed test :
• Right-tailed test :
• Two-tailed test :

In the case of a distribution symmetric about 0 , the critical values for the two-tailed test are symmetric as well:

Unfortunately, the probability distributions that are the most widespread in hypothesis testing have somewhat complicated c d f \mathrm{cdf} cdf formulae. To find critical values by hand, you would need to use specialized software or statistical tables. In these cases, the best option is, of course, our critical value calculator! 😁

Use the Z (standard normal) option if your test statistic follows (at least approximately) the standard normal distribution N(0,1) .

In the formulae below, u u u denotes the quantile function of the standard normal distribution N(0,1):

Left-tailed Z critical value: u ( α ) u(\alpha) u ( α )

Right-tailed Z critical value: u ( 1 − α ) u(1-\alpha) u ( 1 − α )

Two-tailed Z critical value: ± u ( 1 − α / 2 ) \pm u(1- \alpha/2) ± u ( 1 − α /2 )

Check out Z-test calculator to learn more about the most common Z-test used on the population mean. There are also Z-tests for the difference between two population means, in particular, one between two proportions.

Use the t-Student option if your test statistic follows the t-Student distribution . This distribution is similar to N(0,1) , but its tails are fatter – the exact shape depends on the number of degrees of freedom . If this number is large (>30), which generically happens for large samples, then the t-Student distribution is practically indistinguishable from N(0,1). Check our t-statistic calculator to compute the related test statistic.

In the formulae below, Q t , d Q_{\text{t}, d} Q t , d ​ is the quantile function of the t-Student distribution with d d d degrees of freedom:

Left-tailed t critical value: Q t , d ( α ) Q_{\text{t}, d}(\alpha) Q t , d ​ ( α )

Right-tailed t critical value: Q t , d ( 1 − α ) Q_{\text{t}, d}(1 - \alpha) Q t , d ​ ( 1 − α )

Two-tailed t critical values: ± Q t , d ( 1 − α / 2 ) \pm Q_{\text{t}, d}(1 - \alpha/2) ± Q t , d ​ ( 1 − α /2 )

Visit the t-test calculator to learn more about various t-tests: the one for a population mean with an unknown population standard deviation , those for the difference between the means of two populations (with either equal or unequal population standard deviations), as well as about the t-test for paired samples .

Use the χ² (chi-square) option when performing a test in which the test statistic follows the χ²-distribution .

You need to determine the number of degrees of freedom of the χ²-distribution of your test statistic – below, we list them for the most commonly used χ²-tests.

Here we give the formulae for chi square critical values; Q χ 2 , d Q_{\chi^2, d} Q χ 2 , d ​ is the quantile function of the χ²-distribution with d d d degrees of freedom:

Left-tailed χ² critical value: Q χ 2 , d ( α ) Q_{\chi^2, d}(\alpha) Q χ 2 , d ​ ( α )

Right-tailed χ² critical value: Q χ 2 , d ( 1 − α ) Q_{\chi^2, d}(1 - \alpha) Q χ 2 , d ​ ( 1 − α )

Two-tailed χ² critical values: Q χ 2 , d ( α / 2 ) Q_{\chi^2, d}(\alpha/2) Q χ 2 , d ​ ( α /2 ) and Q χ 2 , d ( 1 − α / 2 ) Q_{\chi^2, d}(1 - \alpha/2) Q χ 2 , d ​ ( 1 − α /2 )

Several different tests lead to a χ²-score:

Goodness-of-fit test : does the empirical distribution agree with the expected distribution?

This test is right-tailed . Its test statistic follows the χ²-distribution with k − 1 k - 1 k − 1 degrees of freedom, where k k k is the number of classes into which the sample is divided.

Independence test : is there a statistically significant relationship between two variables?

This test is also right-tailed , and its test statistic is computed from the contingency table. There are ( r − 1 ) ( c − 1 ) (r - 1)(c - 1) ( r − 1 ) ( c − 1 ) degrees of freedom, where r r r is the number of rows, and c c c is the number of columns in the contingency table.

Test for the variance of normally distributed data : does this variance have some pre-determined value?

This test can be one- or two-tailed! Its test statistic has the χ²-distribution with n − 1 n - 1 n − 1 degrees of freedom, where n n n is the sample size.

Finally, choose F (Fisher-Snedecor) if your test statistic follows the F-distribution . This distribution has a pair of degrees of freedom .

Let us see how those degrees of freedom arise. Assume that you have two independent random variables, X X X and Y Y Y , that follow χ²-distributions with d 1 d_1 d 1 ​ and d 2 d_2 d 2 ​ degrees of freedom, respectively. If you now consider the ratio ( X d 1 ) : ( Y d 2 ) (\frac{X}{d_1}):(\frac{Y}{d_2}) ( d 1 ​ X ​ ) : ( d 2 ​ Y ​ ) , it turns out it follows the F-distribution with ( d 1 , d 2 ) (d_1, d_2) ( d 1 ​ , d 2 ​ ) degrees of freedom. That's the reason why we call d 1 d_1 d 1 ​ and d 2 d_2 d 2 ​ the numerator and denominator degrees of freedom , respectively.

In the formulae below, Q F , d 1 , d 2 Q_{\text{F}, d_1, d_2} Q F , d 1 ​ , d 2 ​ ​ stands for the quantile function of the F-distribution with ( d 1 , d 2 ) (d_1, d_2) ( d 1 ​ , d 2 ​ ) degrees of freedom:

Left-tailed F critical value: Q F , d 1 , d 2 ( α ) Q_{\text{F}, d_1, d_2}(\alpha) Q F , d 1 ​ , d 2 ​ ​ ( α )

Right-tailed F critical value: Q F , d 1 , d 2 ( 1 − α ) Q_{\text{F}, d_1, d_2}(1 - \alpha) Q F , d 1 ​ , d 2 ​ ​ ( 1 − α )

Two-tailed F critical values: Q F , d 1 , d 2 ( α / 2 ) Q_{\text{F}, d_1, d_2}(\alpha/2) Q F , d 1 ​ , d 2 ​ ​ ( α /2 ) and Q F , d 1 , d 2 ( 1 − α / 2 ) Q_{\text{F}, d_1, d_2}(1 -\alpha/2) Q F , d 1 ​ , d 2 ​ ​ ( 1 − α /2 )

Here we list the most important tests that produce F-scores: each of them is right-tailed .

ANOVA : tests the equality of means in three or more groups that come from normally distributed populations with equal variances. There are ( k − 1 , n − k ) (k - 1, n - k) ( k − 1 , n − k ) degrees of freedom, where k k k is the number of groups, and n n n is the total sample size (across every group).

Overall significance in regression analysis . The test statistic has ( k − 1 , n − k ) (k - 1, n - k) ( k − 1 , n − k ) degrees of freedom, where n n n is the sample size, and k k k is the number of variables (including the intercept).

Compare two nested regression models . The test statistic follows the F-distribution with ( k 2 − k 1 , n − k 2 ) (k_2 - k_1, n - k_2) ( k 2 ​ − k 1 ​ , n − k 2 ​ ) degrees of freedom, where k 1 k_1 k 1 ​ and k 2 k_2 k 2 ​ are the number of variables in the smaller and bigger models, respectively, and n n n is the sample size.

The equality of variances in two normally distributed populations . There are ( n − 1 , m − 1 ) (n - 1, m - 1) ( n − 1 , m − 1 ) degrees of freedom, where n n n and m m m are the respective sample sizes.

I'm Anna, the mastermind behind the critical value calculator and a PhD in mathematics from Jagiellonian University .

The idea for creating the tool originated from my experiences in teaching and research. Recognizing the need for a tool that simplifies the critical value determination process across various statistical distributions, I built a user-friendly calculator accessible to both students and professionals. After publishing the tool, I soon found myself using the calculator in my research and as a teaching aid.

Trust in this calculator is paramount to me. Each tool undergoes a rigorous review process , with peer-reviewed insights from experts and meticulous proofreading by native speakers. This commitment to accuracy and reliability ensures that users can be confident in the content. Please check the Editorial Policies page for more details on our standards.

What is a Z critical value?

A Z critical value is the value that defines the critical region in hypothesis testing when the test statistic follows the standard normal distribution . If the value of the test statistic falls into the critical region, you should reject the null hypothesis and accept the alternative hypothesis.

How do I calculate Z critical value?

To find a Z critical value for a given confidence level α :

Check if you perform a one- or two-tailed test .

For a one-tailed test:

Left -tailed: critical value is the α -th quantile of the standard normal distribution N(0,1).

Right -tailed: critical value is the (1-α) -th quantile.

Two-tailed test: critical value equals ±(1-α/2) -th quantile of N(0,1).

No quantile tables ? Use CDF tables! (The quantile function is the inverse of the CDF.)

Verify your answer with an online critical value calculator.

Is a t critical value the same as Z critical value?

In theory, no . In practice, very often, yes . The t-Student distribution is similar to the standard normal distribution, but it is not the same . However, if the number of degrees of freedom (which is, roughly speaking, the size of your sample) is large enough (>30), then the two distributions are practically indistinguishable , and so the t critical value has practically the same value as the Z critical value.

What is the Z critical value for 95% confidence?

The Z critical value for a 95% confidence interval is:

• 1.96 for a two-tailed test;
• 1.64 for a right-tailed test; and
• -1.64 for a left-tailed test.

Decimal random number generator

Permutation without repetition.

• Biology (100)
• Chemistry (100)
• Construction (144)
• Conversion (295)
• Ecology (30)
• Everyday life (262)
• Finance (570)
• Health (440)
• Physics (510)
• Sports (105)
• Statistics (184)
• Other (183)
• Discover Omni (40)

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants

Scientific Calculator

• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

29: Hypothesis Test for a Population Proportion Calculator

• Last updated
• Save as PDF
• Page ID 8351

• Larry Green
• Lake Tahoe Community College

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

hypothesis test for a population Proportion calculator

Fill in the sample size, n, the number of successes, x, the hypothesized population proportion \(p_0\), and indicate if the test is left tailed, <, right tailed, >, or two tailed, \(\neq\).  Then hit "Calculate" and the test statistic and p-Value will be calculated for you.

If there is one prayer that you should pray/sing every day and every hour, it is the LORD's prayer (Our FATHER in Heaven prayer) It is the most powerful prayer . A pure heart , a clean mind , and a clear conscience is necessary for it. - Samuel Dominic Chukwuemeka

For in GOD we live, and move, and have our being. - Acts 17:28

The Joy of a Teacher is the Success of his Students. - Samuel Chukwuemeka

Hypothesis Testing Calculators

Samuel Dominic Chukwuemeka (Samdom For Peace) B.Eng., A.A.T, M.Ed., M.S

One Sample Proportion: Left-Tailed

Given : CL To Find : α, -z α/2

The confidence level is in Percent Decimal

Given : α To Find : CL, -z α/2

The level of significance is in Percent Decimal

Given : p, p̂, α Test hypothesis using Classical Approach and P-value Approach

The population proportion is in Percent Decimal

The sample proportion is in Percent Decimal

The sample size is

Given : p, n, x, α Test hypothesis using Classical Approach and P-value Approach

The number of individuals is

Given : p, n, x of a Binomial Distribution; α Test hypothesis using P-value Approach

One Sample Proportion: Right-Tailed

Given : CL To Find : α, z α

Given : α To Find : CL, z α

One Sample Proportion: Two-Tailed

Given : σ, x, n, p Test hypothesis using the Classical Approach and the P-value Approach

The significance level is in Percent Decimal

Given :p, p̂, α Test hypothesis using Classical Approach and P-value Approach

Given : CL, x, n, p Test hypothesis using the Confidence Interval Method

Two Samples Proportion: Left-Tailed

Given : x 1 , n 1 , x 2 , n 2 , α Test hypothesis using Classical Approach and P-value Approach

The number of individuals from Population 1 is

The sample size from Population 1 is

The number of individuals from Population 2 is

The sample size from Population 2 is

Two Samples Proportion: Right-Tailed

Two samples proportion: two-tailed.

Given : σ, x, n, p Test hypothesis using Classical Approach and P-value Approach

Two Samples Proportion: Confidence Interval Estimate

Given : x 1 , n 1 , x 2 , n 2 , α To : Construct a confidence interval for p 1 - p 2

One Sample Mean: Left-Tailed

Given : CL, df To Find : α, critical t

The degrees of freedom is

Given : α df To Find : CL, critical t

Given : CL, n To Find : α, critical t

Given : α, n To Find : CL, critical t

Given : Raw dataset $X$ (from Sample) To calculate: sample size, mean, standard deviation

Please separate each value with a comma. Do not put a comma or a period at the end.

Given : sample size, test statistic To Calculate : degrees of freedom, P-value

The test statistic is

Given : μ x̄ , x̄, s, n, α Test hypothesis using Classical Approach and P-value Approach

The population mean is

The sample mean is

The sample standard deviation is

Given : μ x̄ , x̄, σ, n, α Test hypothesis using Classical Approach and P-value Approach

The population standard deviation is

One Sample Mean: Right-Tailed

One sample mean: two-tailed.

Given : μ x̄ , x̄, s, n, CL Test Hypothesis using the Confidence Interval Method

Two Samples Mean: Left-Tailed

Given : Raw datasets $X_1$ and $X_2$ (Samples) To Calculate : sample sizes, sample means, sample standard deviations, degrees of freedom (several ones: use whatever is applicable) Use for Independent Samples

Please separate each value with a comma. Do not put a comma or a period at the end. First Dataset

Please separate each value with a comma. Do not put a comma or a period at the end. Second Dataset

Given : Raw datasets $X_1$ and $X_2$ (Samples) To Calculate : differences between values; sample size, sample mean, and sample standard deviation of the difference, degrees of freedom Use for Dependent Samples

Two Independent Samples

Given: x̄ 1 , x̄ 2 , s 1 , s 2 , n 1 , n 2 , α Where: σ 1 and σ 2 are unknown, and are assumed to be equal Pooled Sample Variance is used Test hypothesis using Classical Approach and P-value Approach

The mean of the first sample is

The mean of the second sample is

The standard deviation of the first sample is

The standard deviation of the second sample is

The size of the first sample is

The size of the second sample is

Two Independent Samples: Confidence Interval Method

Given: x̄ 1 , x̄ 2 , s 1 , s 2 , n 1 , n 2 , CL Where: σ 1 and σ 2 are unknown, and are not assumed to be equal Pooled Sample Variance is used Construct a confidence interval for μ 1 - μ 2

The level of confidence is in Percent Decimal

Two Samples Mean: Right-Tailed

Two samples mean: two-tailed.

Given : Raw datasets $X_1$ and $X_2$ (Samples) To Calculate : sample sizes, sample means, sample standard deviations, degrees of freedom (several ones: use whatever is applicable)

First Dataset

Second Dataset

Given : x̄ 1 , x̄ 2 , s 1 , s 2 , n 1 , n 2 , α Where: σ 1 and σ 2 are unknown, and are assumed to be equal Pooled Sample Variance is used Test hypothesis using Classical Approach and P-value Approach

Two Independent Samples - Confidence Interval Method

Given: x̄ 1 , x̄ 2 , s 1 , s 2 , n 1 , n 2 , α Where: σ 1 and σ 2 are unknown, and are not assumed to be equal Test hypothesis using Classical Approach and P-value Approach

One Sample Standard Deviation: Left-Tailed

Given : n, s, σ, α Test hypothesis using Classical Approach and P-value Approach

Given: Raw dataset $X$ (from Sample) To Calculate: sample size, sample standard deviation

One Sample Standard Deviation: Right-Tailed

One sample standard deviation: two-tailed.

Given : n, s, σ, CL Test Hypothesis using the Confidence Interval Method

Goodness-of-Fit Test: Sample Data: Right-Tailed

Given : CL, df To Find : α, critical Chi-Square

Given : α, df To Find : CL, critical Chi-Square

Given: OV, EV To Calculate: df, Χ 2 (Show all steps), P-value

Please separate each value with a comma. Do not put a comma or a period at the end. $OV$ =

Please separate each value with a comma. Do not put a comma or a period at the end. $EV$ =

$OV - EV$ =

$(OV - EV)^2$ =

$\dfrac{(OV - EV)^2}{E}$ =

$\Sigma \dfrac{(OV - EV)^2}{E}$ =

Given: $OV$, Probabilities, Total Number of Trials OR Given: Benford's Law To Calculate $EV$, $df$, $\chi^2$ (Show all steps), P-value

Please separate each value with a comma. Do not put a comma or a period at the end. Probabilities (in decimals only) =

The total number of trials =

Given : $OV$, $EV$, α (Use 5% if not specified) Test Hypothesis Using Classical Approach and P-value Approach

Please separate each value with a comma. Do not put a comma or a period at the end. OV =

Please separate each value with a comma. Do not put a comma or a period at the end. EV =

Given: $OV$, Probabilities, Total Number of Trials, α (Use 5% if not specified) OR Given: Benford's Law, α (Use 5% if not specified) Test Hypothesis Using Classical Approach and P-value Approach

Contingency Table Test of Independence: Sample Data: Right-Tailed

Given : Contingency Table Test for Independence using the Critical Value Method and the P-value Method

How many rows (actual numeric rows) does your table have?

How many columns (actual numeric columns) does your table have?

Please fill in the actual data values. Leave extra boxes blank, or put zeros.

Σ R 1 = Σ R 2 = Σ R 3 = Σ R 4 = Σ R 5 = Σ R 6 = Σ R 7 =

Σ C 1 = Σ C 2 = Σ C 3 = Σ C 4 = Σ C 5 = Σ C 6 = Σ C 7 =

Σ R = Σ C = N =

The expected frequencies for each data value is listed below. Please ignore the zeros.

One-Way ANOVA: Three Samples of Equal Sizes

Given : Datasets 1, 2, and 3 Calculate the F test statistic (Show all work)

Dataset 1, $X_1$ =

Dataset 2, $X_2$ =

Dataset 3, $X_3$ =

Overall $n$ =

x̄ 1 =

x̄ 2 =

x̄ 3 =

Overall x̄ =

DF for Numerator =

X 1 - x̄ 1 =

(X 1 - x̄ 1 ) 2 =

Σ(X 1 - x̄ 1 ) 2 =

X 2 - x̄ 2 =

(X 2 - x̄ 2 ) 2 =

Σ(X 2 - x̄ 2 ) 2 =

X 3 - x̄ 3 =

(X 3 - x̄ 3 ) 2 =

Σ(X 3 - x̄ 3 ) 2 =

DF for Denominator =

Given: Datasets 1, 2, and 3 Test Hypothesis Using Classical Approach and P-value Approach

Please separate each value with a comma. Do not put a comma or a period at the end. Dataset 1, X 1 =

Please separate each value with a comma. Do not put a comma or a period at the end. Dataset 2, X 2 =

Please separate each value with a comma. Do not put a comma or a period at the end. Dataset 3, X 3 =

Two Samples Correlation: Left-Tailed

Given : datasets X and Y Test hypothesis using the Critical Value Method and the P-value Method

Please type each $x-value$ on a new line. No commas. No spaces. No period. No extra lines. X =

Please type each $y-value$ on a new line. No commas. No spaces. No period. No extra lines. Y =

Two Samples Correlation: Right-Tailed

Two samples correlation: two-tailed.

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

S.3.1 hypothesis testing (critical value approach).

The critical value approach involves determining "likely" or "unlikely" by determining whether or not the observed test statistic is more extreme than would be expected if the null hypothesis were true. That is, it entails comparing the observed test statistic to some cutoff value, called the " critical value ." If the test statistic is more extreme than the critical value, then the null hypothesis is rejected in favor of the alternative hypothesis. If the test statistic is not as extreme as the critical value, then the null hypothesis is not rejected.

Specifically, the four steps involved in using the critical value approach to conducting any hypothesis test are:

• Specify the null and alternative hypotheses.
• Using the sample data and assuming the null hypothesis is true, calculate the value of the test statistic. To conduct the hypothesis test for the population mean μ , we use the t -statistic \(t^*=\frac{\bar{x}-\mu}{s/\sqrt{n}}\) which follows a t -distribution with n - 1 degrees of freedom.
• Determine the critical value by finding the value of the known distribution of the test statistic such that the probability of making a Type I error — which is denoted \(\alpha\) (greek letter "alpha") and is called the " significance level of the test " — is small (typically 0.01, 0.05, or 0.10).
• Compare the test statistic to the critical value. If the test statistic is more extreme in the direction of the alternative than the critical value, reject the null hypothesis in favor of the alternative hypothesis. If the test statistic is less extreme than the critical value, do not reject the null hypothesis.

Example S.3.1.1

Mean gpa section  .

In our example concerning the mean grade point average, suppose we take a random sample of n = 15 students majoring in mathematics. Since n = 15, our test statistic t * has n - 1 = 14 degrees of freedom. Also, suppose we set our significance level α at 0.05 so that we have only a 5% chance of making a Type I error.

Right-Tailed

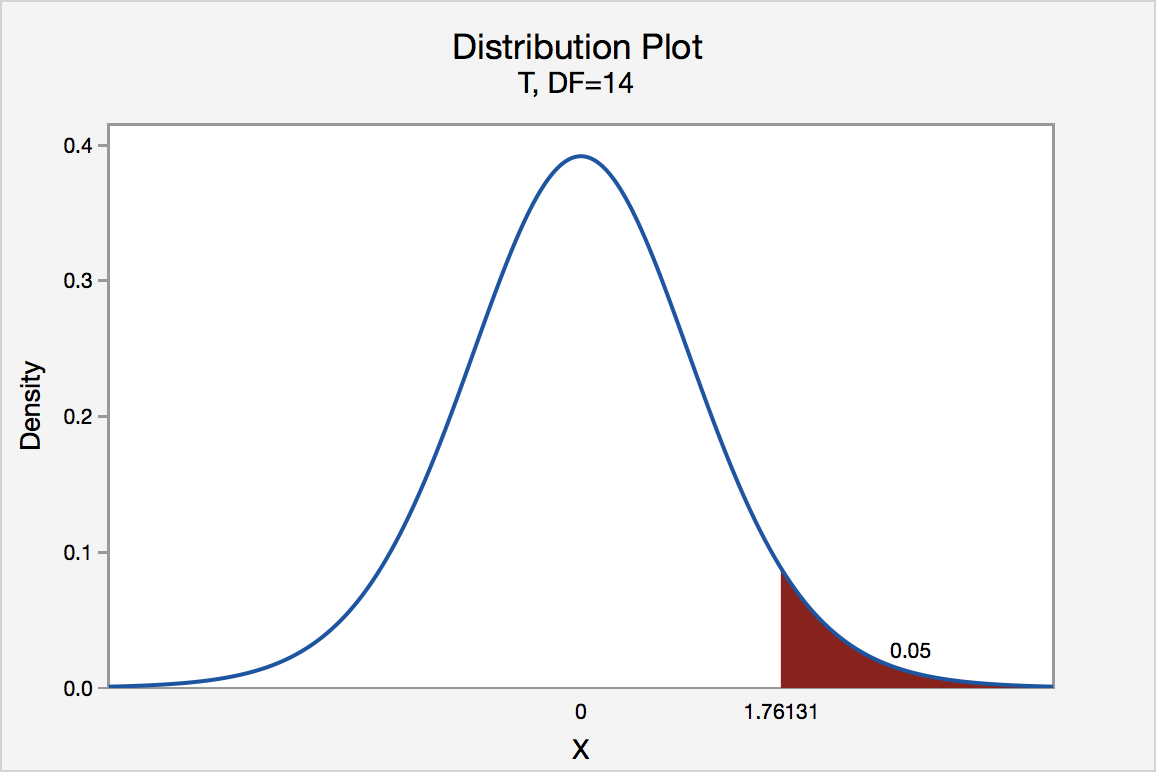
The critical value for conducting the right-tailed test H 0 : μ = 3 versus H A : μ > 3 is the t -value, denoted t \(\alpha\) , n - 1 , such that the probability to the right of it is \(\alpha\). It can be shown using either statistical software or a t -table that the critical value t 0.05,14 is 1.7613. That is, we would reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ > 3 if the test statistic t * is greater than 1.7613. Visually, the rejection region is shaded red in the graph.

Left-Tailed

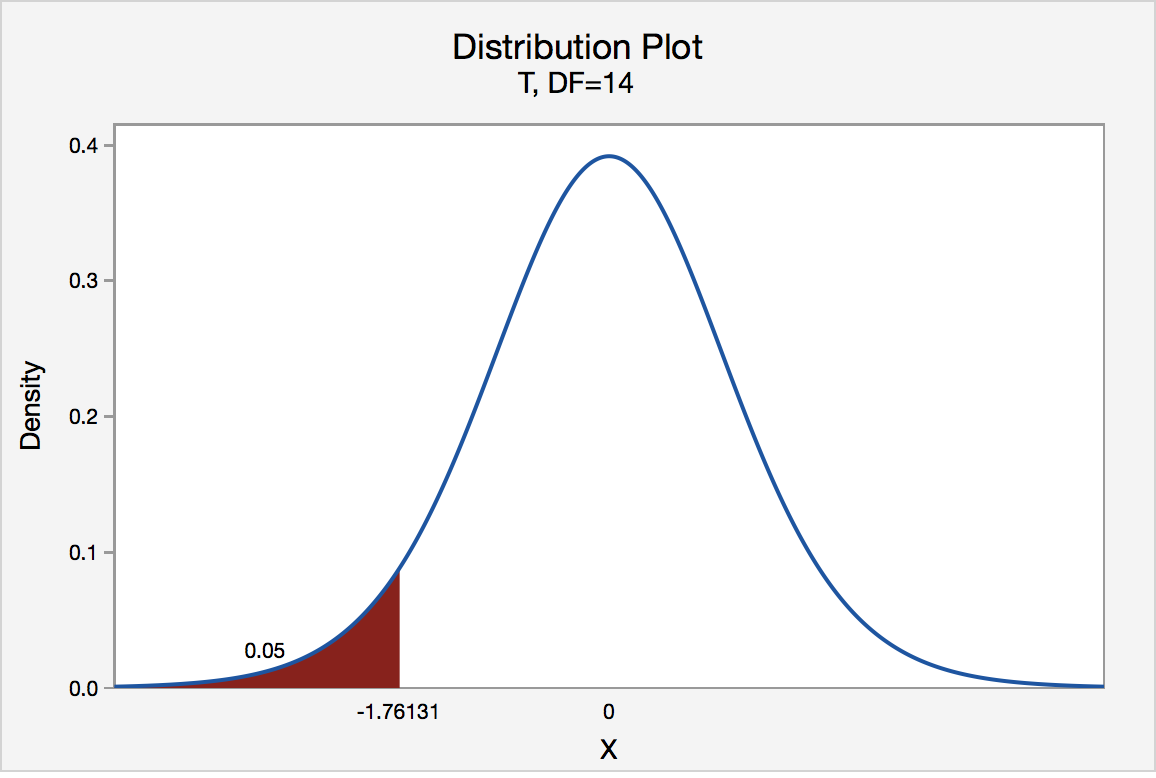
The critical value for conducting the left-tailed test H 0 : μ = 3 versus H A : μ < 3 is the t -value, denoted -t ( \(\alpha\) , n - 1) , such that the probability to the left of it is \(\alpha\). It can be shown using either statistical software or a t -table that the critical value -t 0.05,14 is -1.7613. That is, we would reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ < 3 if the test statistic t * is less than -1.7613. Visually, the rejection region is shaded red in the graph.

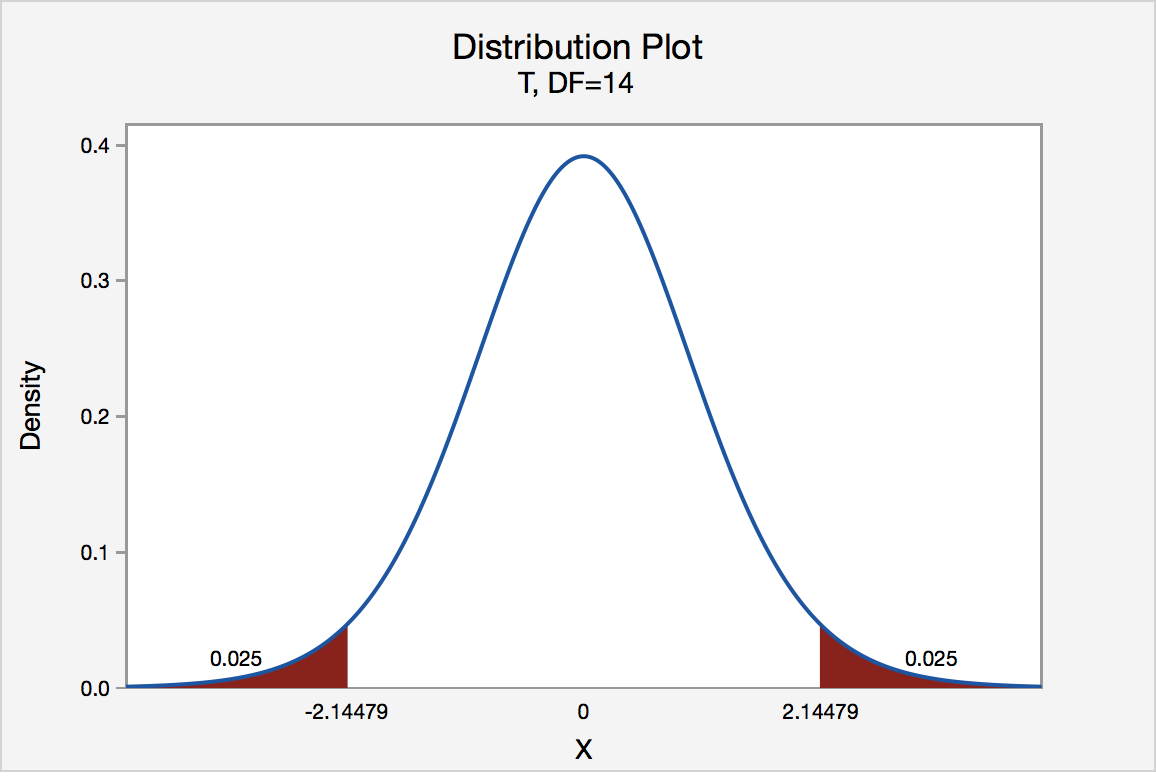
There are two critical values for the two-tailed test H 0 : μ = 3 versus H A : μ ≠ 3 — one for the left-tail denoted -t ( \(\alpha\) / 2, n - 1) and one for the right-tail denoted t ( \(\alpha\) / 2, n - 1) . The value - t ( \(\alpha\) /2, n - 1) is the t -value such that the probability to the left of it is \(\alpha\)/2, and the value t ( \(\alpha\) /2, n - 1) is the t -value such that the probability to the right of it is \(\alpha\)/2. It can be shown using either statistical software or a t -table that the critical value -t 0.025,14 is -2.1448 and the critical value t 0.025,14 is 2.1448. That is, we would reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ ≠ 3 if the test statistic t * is less than -2.1448 or greater than 2.1448. Visually, the rejection region is shaded red in the graph.

Statistics (iii): Classical Hypothesis Testing Theory

Cite this chapter.

Part of the book series: Statistics for Biology and Health ((SBH))

6242 Accesses

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Compact, lightweight edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info
• Durable hardcover edition

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Unable to display preview.  Download preview PDF.

Rights and permissions

Reprints and permissions

Copyright information

© 2005 Springer Science+Business Media, Inc.

About this chapter

(2005). Statistics (iii): Classical Hypothesis Testing Theory. In: Statistical Methods in Bioinformatics. Statistics for Biology and Health. Springer, New York, NY. https://doi.org/10.1007/0-387-26648-8_9

Download citation

DOI : https://doi.org/10.1007/0-387-26648-8_9

Publisher Name : Springer, New York, NY

Print ISBN : 978-0-387-40082-2

Online ISBN : 978-0-387-26648-0

eBook Packages : Mathematics and Statistics Mathematics and Statistics (R0)

Share this chapter

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research