maths assignment class 9 chapter 1

Search This Blog

Cbse mathematics.

Basic concepts, definitions and formulas of mathematics, mathematics assignments for 9th standard to 10+2 standard, maths study material for 8th, 9th, 10th, 11th, 12th classes, Mathematics lesson plan for classes 8th,10th and 12th standard, Interesting maths riddles and maths magic, Class-wise mathematics study material for students from 8th to 12. A complete resource centre of mathematics for students and teachers

Featured Posts

Mathematics class 10 lab manual | 21 lab activities, math assignment class ix ch -1| number system, maths assignment   class 9th chapter 1.

MATHEMATICS ASSIGNMENT CLASS IX  NUMBER SYSTEM

 (a) 1⁸ × 3⁰ × 5³ × 2²           Ans; 500,                

(b)  4 -3 × 4⁸ ÷ 4²                Ans; 64

(d) 3 -4 × 3 -5 ÷ 3¹⁰             Ans; 3 -19

Download complete pdf file 

Plese send us solution today is our test

Need solutions toooo

Post a Comment

Breaking news, popular post on this blog, lesson plan maths class 10 | for mathematics teacher.

Lesson Plan Maths Class XII | For Maths Teacher

Lesson Plan Maths Class X (Ch-5) | Arithmetic Progression

• Assignment 10 15
• Assignment 11 12
• Assignment 12 14
• Assignment 8 8
• Assignment 9 5
• Lesson plan 10 15
• Lesson Plan 12 14
• Lesson Plan 8 10
• Maths 10 20
• Maths 11 21
• Maths 12 17

SUBSCRIBE FOR NEW POSTS

Get new posts by email:.

NCERT Solutions for Class 9 Maths Chapter 1 Number Systems

NCERT Solutions for Class 9 Maths Chapter 1 Number Systems are provided here. Our NCERT Maths solutions contain all the questions of the NCERT textbook that are solved and explained beautifully. Here you will get complete NCERT Solutions for Class 9 Maths Chapter 1 all exercises Exercise in one place. These solutions are prepared by the subject experts and as per the latest NCERT syllabus and guidelines. CBSE Class 9 Students who wish to score good marks in the maths exam must practice these questions regularly.

Class 9 Maths Chapter 1 Number Systems NCERT Solutions

Below we have provided the solutions of each exercise of the chapter. Go through the links to access the solutions of exercises you want. You should also check out our NCERT Class 9 Solutions for other subjects to score good marks in the exams.

NCERT Solutions for Class 9 Maths Chapter 1 Exercise 1.1

NCERT Solutions for Class 9 Maths Chapter 1 Exercise 1.2

NCERT Solutions for Class 9 Maths Chapter 1 Exercise 1.3

NCERT Solutions for Class 9 Maths Chapter 1 Exercise 1.4

NCERT Solutions for Class 9 Maths Chapter 1 Exercise 1.5

NCERT Solutions for Class 9 Maths Chapter 1 Exercise 1.6

NCERT Solutions for Class 9 Maths Chapter 1 – Topic Discussion

Below we have listed the topics that have been discussed in this chapter. As Number System is one of the important topics in Maths, it has a weightage of 6 marks in class 9 Maths exams. 

• Introduction of Number Systems
• Irrational Numbers
• Real Numbers and Their Decimal Expansions
• Representing Real Numbers on the Number Line.
• Operations on Real Numbers
• Laws of Exponents for Real Numbers

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

NCERT Solutions for Class 9 Maths Chapter 1 Number Systems

Class 9 Maths Chapter 1 Solution for CBSE Board Class 9 Maths Exercise 1.1 in English Class 9 Maths Exercise 1.2 in English Class 9 Maths Exercise 1.3 in English Class 9 Maths Exercise 1.4 in English Class 9 Maths Exercise 1.5 in English

Class 9 Maths Chapter 1 Solution for State Boards Class 9 Maths Chapter 1 Exercise 1.1 Class 9 Maths Chapter 1 Exercise 1.2 Class 9 Maths Chapter 1 Exercise 1.3 Class 9 Maths Chapter 1 Exercise 1.4 Class 9 Maths Chapter 1 Exercise 1.5 Class 9 Maths Chapter 1 Exercise 1.6

Class 9 Maths Chapter 1 Solution in Hindi Class 9 Maths Exercise 1.1 in Hindi Class 9 Maths Exercise 1.2 in Hindi Class 9 Maths Exercise 1.3 in Hindi Class 9 Maths Exercise 1.4 in Hindi Class 9 Maths Exercise 1.5 in Hindi

NCERT Solutions for Class 9 Maths Chapter 1 Number Systems in Hindi Medium and English medium has been updated for academic session 2024-25. Tiwari Academy is a popular online platform that provides educational resources and solutions for students. As we continue to offer Class 9 Maths NCERT Solutions, here are some potential benefits of using Tiwari Academy for learning Class 9 Maths. Question-answers and solutions are modified as per revised NCERT book published for 2024-25 syllabus. We typically provides simple yet complete solutions to NCERT textbooks, including step-by-step explanations for each problem. This can be especially helpful for students who may find difficulty in understanding certain concepts.

All the Solutions for Class 9th Maths Chapter 1 have been updated according to latest CBSE Curriculum and NCERT Books for 2024-25. Since UP Board Students are using same NCERT Textbooks , they can also download UP Board Solutions for Class 9 Maths Chapter 1 in Hindi Medium or English Medium. Class 9 Maths NCERT Solutions have been provided by explaining the formulae and giving step by step explanation.

The content is according to the latest CBSE syllabus 2024-25 for the students of CBSE Board as well as UP Board and MP Board following the updated NCERT (https://ncert.nic.in/) Books for their final exams. Solutions for chapter 1 9th Maths are available in PDF format on our website Tiwari Academy and also through videos on Apps and website.

Study Materials on 9th Maths Chapter 1

• Study Material 9th Maths Chapter 1 for 2024-25 – English Medium
• Study Material 9th Maths Chapter 1 for 2024-25 – Hindi Medium
• Class 9 Mathematics Solutions Main Page

The topic Number Systems is the basis of Arithmetic. It is like learning the alphabets of any mathematics. We can say that 9th Maths chapter 1 is the foundation of Maths for secondary classes. CBSE NCERT Solutions for Class 9 mathematics Chapter 1 Number Systems in PDF format. These solutions are available for free download for session 2024-25. These are updated as per latest curriculum. Kindly visit the Discussion Forum and become a partner in knowledge sharing in mathematics. NCERT Solutions Offline Apps 2024-25, work without internet connection. Everything on Tiwari Academy website and Apps are available free of cost. No login or registration is required.

Important Questions on 9th Maths Chapter 1

Is zero a rational number can you write it in the form p/q, where p and q are integers and q≠0.

Yes, zero is a rational number. It can be written in the form of p/q. For example: 0/1, 0/2, 0/5 are rational numbers, where p and q are integers and q≠0.

Simplify each of the following expression: (3 + √3)(2 + √2)

(3 + √3)(2 + √2) = 6 + 3√2 + 2√3 + √6

Find six rational numbers between 3 and 4.

Six rational numbers between 3 and 4 are 3.1, 3.2, 3.3, 3.4, 3.5 and 3.6.

Express 0.99999… in the form of p/q . Are you surprised by your answer?

0.99999… Let x = 0.99999… … (i) Multiplying equation (i) by 10 both sides 10x = 9.99999… ⇒ 10x = 9 + 0.99999…… ⇒ 10x = 9 + x [From equation (i)] ⇒ 10x – x = 9 ⇒ 9x = 9 ⇒ x = 9/9 = 1 The answer makes sense as 0.99999… is very close to 1, that is why we can say that 0.99999=1.

Write three numbers whose decimal expansions are non-terminating non-recurring.

Three non-terminating non-recurring decimals: 0.414114111411114… 2.01001000100001… π=3.1416…

1. Natural numbers are those numbers which are used for counting. 2. Whole numbers are the collection of all natural numbers together with zero. 3. Integers are the collection of all whole numbers and negative of natural numbers. 4. Rational numbers are those numbers which can be expressed in the form of p/q, where p, q are integers and q is not equal to 0. 5. Irrational numbers are those numbers which cannot be expressed in the form of p/q, where p, q are integers and q is not = 0. 6. Real numbers are the collection of all rational and irrational numbers.

Two numbers are said to be equivalent, if numerators and denominators of both are in proportion or they are reducible to be equal. The decimal expansion of real numbers can be terminating or non-terminating repeating or non-terminating non-repeating. The decimal expansion of rational numbers can either be terminating or non-terminating and vice-versa. The decimal expansion of irrational numbers can either be non-recurring and vice-versa.

If a is a rational and b is an irrational, then a + b and a – b are irrational, and ab and a/b are irrational numbers, where b is not equal to 0. If a and b both are irrational, then a+b, a-b, ab and a/b may be rational or irrational. If a be any real number and n be any positive integer such that a^1/n = n√a is a real number, then ‘n’ is called exponent, a is called radical and √ is called radical sign.

How many questions in each exercise are given in chapter 1 of class 9 Maths?

There are 6 exercises in chapter 1 (Number systems) of class 9 Maths. In the first exercise (Ex 1.1), there are four questions. In the second exercise (Ex 1.2), there are four questions. In the third exercise (Ex 1.3), there are nine questions. In the fifth exercise (Ex 1.4), there are five questions. In the sixth exercise (Ex 1.5), there are three questions. So, there are in all 25 questions in chapter 1 (Number systems) of class 9 Maths. There are in all 20 examples in chapter 1 (Number systems) of class 9 Maths.

What are the core topics to study in chapter 1 Number systems of class 9 Mathematics?

In chapter 1, Number systems of class 9 Maths, students will study: 1. Natural Numbers, Whole Numbers, Integers, Rational Numbers. 2. Irrational Numbers. 3. Real Numbers and their Decimal Expansions. 4. Representing Real Numbers on the Number Line. 5. Operations on Real Numbers. 6. Laws of Exponents for Real Numbers.

Is chapter 1 of class 9th Maths difficult to solve?

Chapter 1 of class 9th Maths is not easy and not difficult. It lies in the middle of easy and difficult because some examples and questions of this chapter are easy, and some are difficult. However, the difficulty level of anything varies from student to student. So, Chapter 1 of class 9th Maths is easy or not depends on students also. Some students find it difficult, some find it easy, and some find it in the middle of easy and difficult.

How long it takes to study chapter 1 of class 9th Maths?

Students need a maximum of eight days to do chapter 1 of class 9th Maths if they give at least 2 hours per day to this chapter. This time also depends on student’s speed, efficiency, capability, and many other factors.

Chapter 2. Polynomials »

Mayank Tiwari

I have completed my B. Tech. in Computer Science and Engineering. Since, then I am working for Tiwari Academy as quality manager in content formation. I am currently Pursuing M. Tech. in Computer Science and Engineering with Specialization in Artificial Intelligence in Delhi.

Copyright 2024 by Tiwari Academy | A step towards Free Education

• Class 6 Maths
• Class 6 Science
• Class 6 Social Science
• Class 6 English
• Class 7 Maths
• Class 7 Science
• Class 7 Social Science
• Class 7 English
• Class 8 Maths
• Class 8 Science
• Class 8 Social Science
• Class 8 English
• Class 9 Maths
• Class 9 Science
• Class 9 Social Science
• Class 9 English
• Class 10 Maths
• Class 10 Science
• Class 10 Social Science
• Class 10 English
• Class 11 Maths
• Class 11 Computer Science (Python)
• Class 11 English
• Class 12 Maths
• Class 12 English
• Class 12 Economics
• Class 12 Accountancy
• Class 12 Physics
• Class 12 Chemistry
• Class 12 Biology
• Class 12 Computer Science (Python)
• Class 12 Physical Education
• GST and Accounting Course
• Excel Course
• Tally Course
• Finance and CMA Data Course
• Payroll Course

Interesting

• Learn English
• Learn Excel
• Learn Tally
• Learn GST (Goods and Services Tax)
• Learn Accounting and Finance
• GST Tax Invoice Format
• Accounts Tax Practical
• Tally Ledger List
• GSTR 2A - JSON to Excel

Are you in school ? Do you love Teachoo?

We would love to talk to you! Please fill this form so that we can contact you

You are learning...

Chapter 1 Class 9 Number Systems

Click on any of the links below to start learning from Teachoo ...

Get solutions of all NCERT Questions of Chapter 1 Class 9 Number System free at teachoo. Answers to all NCERT Exercises and Examples are solved for your reference. Theory of concepts is also made for your easy understanding

In this chapter, we will learn

• Different Types of numbers like Natural Numbers, Whole numbers, Integers, Rational numbers
• How to find rational numbers between two rational numbers
• What is an irrational number
• Checking if number is irrational or not
• And how to draw an irrational number on the number line
• Then, we will study What a real number is
• And find Decimal expansions - Terminating, Non terminating - repeating, Non terminating Non repeating
• Converting non-terminating repeating numbers into p/q form
• Finding irrational numbers between two numbers
• Representing real numbers on the number line (we use magnification)
• We will learn how to add , subtract and multiply numbers with square root (like 5√2 + 3√3 - 8√2)
• We will learn some identities of numbers with square root (like (√a + √b) 2 )
• How to rationalize numbers
• We will also do questions on Law of Exponents (here, the exponents can also be in fractions)

Click on an NCERT Exercise below to get started. 

Or you can also check the concepts from the Concept wise. Check it out now

Serial order wise

Concept wise.

What's in it?

Hi, it looks like you're using AdBlock :(

Please login to view more pages. it's free :), solve all your doubts with teachoo black.

CBSE NCERT Solutions

NCERT and CBSE Solutions for free

Class 9 Mathematics Assignments

We have provided below free printable Class 9 Mathematics Assignments for Download in PDF. The Assignments have been designed based on the latest NCERT Book for Class 9 Mathematics . These Assignments for Grade 9 Mathematics cover all important topics which can come in your standard 9 tests and examinations. Free printable Assignments for CBSE Class 9 Mathematics , school and class assignments, and practice test papers have been designed by our highly experienced class 9 faculty. You can free download CBSE NCERT printable Assignments for Mathematics Class 9 with solutions and answers. All Assignments and test sheets have been prepared by expert teachers as per the latest Syllabus in Mathematics Class 9. Students can click on the links below and download all Pdf Assignments for Mathematics class 9 for free. All latest Kendriya Vidyalaya Class 9 Mathematics Assignments with Answers and test papers are given below.

Mathematics Class 9 Assignments Pdf Download

We have provided below the biggest collection of free CBSE NCERT KVS Assignments for Class 9 Mathematics . Students and teachers can download and save all free Mathematics assignments in Pdf for grade 9th. Our expert faculty have covered Class 9 important questions and answers for Mathematics as per the latest syllabus for the current academic year. All test papers and question banks for Class 9 Mathematics and CBSE Assignments for Mathematics Class 9 will be really helpful for standard 9th students to prepare for the class tests and school examinations. Class 9th students can easily free download in Pdf all printable practice worksheets given below.

Topicwise Assignments for Class 9 Mathematics Download in Pdf

More assignments for class 9 mathematics.

Advantages of Class 9 Mathematics Assignments

• As we have the best and largest collection of Mathematics assignments for Grade 9, you will be able to easily get full list of solved important questions which can come in your examinations.
• Students will be able to go through all important and critical topics given in your CBSE Mathematics textbooks for Class 9 .
• All Mathematics assignments for Class 9 have been designed with answers. Students should solve them yourself and then compare with the solutions provided by us.
• Class 9 Students studying in per CBSE, NCERT and KVS schools will be able to free download all Mathematics chapter wise worksheets and assignments for free in Pdf
• Class 9 Mathematics question bank will help to improve subject understanding which will help to get better rank in exams

Frequently Asked Questions by Class 9 Mathematics students

At https://www.cbsencertsolutions.com, we have provided the biggest database of free assignments for Mathematics Class 9 which you can download in Pdf

We provide here Standard 9 Mathematics chapter-wise assignments which can be easily downloaded in Pdf format for free.

You can click on the links above and get assignments for Mathematics in Grade 9, all topic-wise question banks with solutions have been provided here. You can click on the links to download in Pdf.

We have provided here topic-wise Mathematics Grade 9 question banks, revision notes and questions for all difficult topics, and other study material.

We have provided the best collection of question bank and practice tests for Class 9 for all subjects. You can download them all and use them offline without the internet.

Related Posts

Class 9 English Assignments

Class 9 Assignments Download Pdf

Class 9 Mathematics Triangles Assignments

NCERT Solutions Class 9 Maths Chapter 1 Exercise 1.1 Number Systems

NCERT solutions class 9 maths chapter 1 exercise 1.1 number systems help the students understand the difference between natural, integer, and whole numbers , writing the correct format of real numbers , and also introduce the students to the concept of calculation of the rational numbers between any two numbers. NCERT solutions class 9 maths chapter 1 exercise 1.1 consists of 6 questions of which 5 are short and 1 long answer and are easy to solve.

The problems provided also help the students understand the notation of different numbers, like N for natural numbers , Z for integers. class 9 maths NCERT solutions chapter 1 exercise 1.1 number systems also come in a pdf format as below.

☛ Download NCERT Solutions Class 9 Maths Chapter 1 Exercise 1.1

Exercise 1.1 Class 9 Chapter 1   Download PDF

More Exercises in Class 9 Maths Chapter 1

• NCERT Solutions Class 9 Maths Chapter 1 Ex 1.2
• NCERT Solutions Class 9 Maths Chapter 1 Ex 1.3
• NCERT Solutions Class 9 Maths Chapter 1 Ex 1.4
• NCERT Solutions Class 9 Maths Chapter 1 Ex 1.5
• NCERT Solutions Class 9 Maths Chapter 1 Ex 1.6

NCERT Solutions Class 9 Maths Chapter 1 Exercise 1.1 Tips

NCERT solutions class 9 maths chapter 1 exercise 1.1 number systems are a good way to explore the number systems . Students are advised to go through each and every line of the chapter while also focusing on the examples which give easy explanations to solve the problems in a logical manner.

NCERT solutions class 9 maths chapter 1 exercise 1.1 will not only help the students get ready for their board exams but will also help in further competitive exams as well.

Download Cuemath NCERT Solutions PDF for free and start learning!

Class 9 Maths NCERT Solutions Video Chapter 1 Exercise 1.1

Talk to our experts

1800-120-456-456

CBSE Class 9 Maths Important Questions for Chapter 1 - Number System

• Class 9 Important Question
• Chapter 1: Number Systems

CBSE Class 9 Maths Important Questions Chapter 1 - Number System Free PDF Download

Chapter 1 of Mathematics Class 9 deals with an introduction to various other topics. Those who are planning to pursue a career in mathematics should prepare well for this chapter. Mathematics is the subject to deal with practical life calculations and Class 9 Maths Chapter 1 Important Questions will help set a good base for the students.

Based on these crucial questions, students can prepare for mathematics finals without any hassle. Class 9 is the base to prepare well for 10th boards. Hence students need to master their concepts and utilise their time efficiently. According to CBSE’s basic guidelines, these Important Questions for Class 9 Maths Chapter 1 Number System are prepared.

As a result, students do not need to be concerned or go elsewhere for answers to such inquiries. The first chapter of Mathematics 9th standard is Number System, which deals with whole numbers, rational and irrational numbers, and integers. Read about the topics included in the Crucial Questions for Class 9 Mathematics number system and comprehensive curriculum created by specialists in detail. Vedantu offers students a free PDF download option for all updated CBSE textbook solutions. Topics such as Science, Math, and English will become easier to study if you have access to NCERT Class 9 Science, Math, and other answers that are only accessible on Vedantu.

Download CBSE Class 9 Maths Important Questions 2024-25 PDF

Also, check CBSE Class 9 Maths Important Questions for other chapters:

Important Topics Covered in Class 9 Maths Chapter 1

Introduction to number system

Irrational Number

Real Number and Their Decimal Expansion

Representation of Real Number on Number Line

Operations on Real Number

Laws of Exponents for Real Number

Study Important Questions for Class 9 Maths Chapter 1 – Number Systems

1 Marks Questions

1. Are the square roots of all positive integers irrational? If not, give an example of the square root of a number that is irrational number.

Ans: We know that the square root of every positive integer will not yield an integer.

We know that \[\sqrt{4}\] is $2$, which is an integer. But, $\sqrt{7}$ or $\sqrt{10}$ will give an irrational number.

Therefore, we conclude that the square root of every positive integer is not an irrational number.

2. Write three numbers whose decimal expansions are non-terminating non-recurring.

Ans: The three numbers that have their expansions as non-terminating on recurring decimals are given below.

0.04004000400004.... 

0.07007000700007....

0.13001300013000013.... 

3. Find three different irrational numbers between the rational numbers $\frac{\text{5}}{\text{11}}$ and $\frac{\text{9}}{\text{11}}$ .

Ans: Let us convert $\frac{5}{11}$ and $\frac{9}{11}$ into decimal form, to get

$\frac{5}{7}=0.714285....and\frac{9}{11}=0.818181....$

Three irrational numbers that lie between $0.714285....$ and $0.818181....$ are:

0.73073007300073...

0.74074007400074.... 

0.76076007600076.... 

4. Which of the following rational numbers have terminating decimal representation?

 $(i)\frac{3}{5}$             

$(ii)\frac{2}{13} $

$(iii)\frac{40}{27}   $    

$(iv)\frac{23}{7}$

Ans: $(i)\frac{3}{5}$

5. How many rational numbers can be found between two distinct rational numbers?

(iv) Infinite

Ans: (iv) Infinite

6. The value of $\left( \text{2+}\sqrt{\text{3}} \right)\left( \text{2-}\sqrt{\text{3}} \right)$ in

(i) $\text{1}$

(ii) $\text{-1}$

(iii) $\text{2}$

(iv) none of these

Ans: (i) $1$

7. ${{\left( \text{27} \right)}^{\text{-2/3}}}$ is equal to

(i) $\text{9}$

(ii) $\text{1/9}$

(iii) $\text{3}$

Ans: (ii) $1/9$

8. Every natural number is

(i) not an integer

(ii) always a whole number

(iii) an irrational number

(iv) not a fraction

Ans: (ii) always a whole number

9. Select the correct statement from the following

(i) $\frac{\text{7}}{\text{9}}\text{}\frac{\text{4}}{\text{5}}$

(ii) $\frac{\text{2}}{\text{6}}\text{}\frac{\text{3}}{\text{9}}$

(iii) $\frac{\text{-2}}{\text{3}}\text{}\frac{\text{-4}}{\text{5}}$

(iv)$\frac{\text{-5}}{\text{7}}\text{}\frac{\text{-3}}{\text{4}}$

Ans: (iii) $\frac{-2}{3}>\frac{-4}{5}$

10. $\text{7}\text{.}\overline{\text{2}}$ is equal to

(i) $\frac{\text{68}}{\text{9}}$

(ii) $\frac{\text{64}}{\text{9}}$

(iii) $\frac{\text{65}}{\text{9}}$

(iv) $\frac{\text{63}}{\text{9}}$

Ans: (iii) $\frac{65}{9}$

11. $\text{0}\text{.83458456}......$ is

(i) an irrational number

(ii) rational number

(iii) a natural number

(iv) a whole number

Ans: (i) an irrational number

12. A terminating decimal is

(i) a natural number

(ii) a rational number

(iii) a whole number

(iv) an integer.

Ans: (ii) a rational number

13. The $\frac{\text{p}}{\text{q}}$ form of the number $\text{0}\text{.8}$ is

(i) $\frac{\text{8}}{\text{10}}$

(ii) $\frac{\text{8}}{\text{100}}$

(iii) $\frac{\text{1}}{\text{8}}$

(iv) $\text{1}$

Ans: (i) $\frac{8}{10}$

14. The value of $\sqrt[\text{3}]{\text{1000}}$ is

Ans: (ii) $10$

15. The sum of rational and an irrational number

(i) may be natural

(ii) may be irrational

(iii) is always irrational

(iv) is always rational

Ans: (iii) is always rational

16. The rational number not lying between $\frac{\text{3}}{\text{5}}$ and $\frac{\text{2}}{\text{3}}$ is

(i) $\frac{\text{49}}{\text{75}}$

(ii) $\frac{\text{50}}{\text{75}}$

(iii) \[\frac{\text{47}}{\text{75}}\]

(iv) $\frac{\text{46}}{\text{75}}$

Ans: (B) $\frac{50}{75}$

17. $\text{0}\text{.12}\overline{\text{3}}$ is equal to

(i) $\frac{\text{122}}{\text{90}}$

(ii) $\frac{\text{122}}{\text{100}}$

(iii) $\frac{\text{122}}{\text{99}}$

(iv) None of these

Ans: (a) $\frac{122}{990}$

18. The number ${{\left( \text{1+}\sqrt{\text{3}} \right)}^{\text{2}}}$ is

(a) natural number

(b) irrational number

(c) rational number

(d) integer

Ans: (b) irrational number

19. The simplest form of $\sqrt{\text{600}}$ is

(i) $\text{10}\sqrt{\text{60}}$

(ii) $\text{100}\sqrt{\text{6}}$

(iii) $\text{20}\sqrt{\text{3}}$

(iv) $\text{10}\sqrt{\text{6}}$

Ans: (D) $10\sqrt{6}$

20. The value of $\text{0}\text{.}\overline{\text{23}}\text{+0}\text{.}\overline{\text{22}}$ is

(i) $\text{0}\text{.4}\overline{\text{5}}$

(ii) $\text{0}\text{.4}\overline{\text{4}}$

(iii) $\text{0}\text{.}\overline{\text{45}}$

(iv) $\text{0}\text{.}\overline{\text{44}}$

Ans: (A) $0.\overline{23}=0.232323....$

$0.\overline{22}=0.222222....$

$0.\overline{23}+0.\overline{22}=0.454545....$

$=0.\overline{45}$

21. The value of ${{\text{2}}^{\frac{\text{1}}{\text{3}}}}\text{ }\!\!\times\!\!\text{ }{{\text{2}}^{\text{-}\frac{\text{4}}{\text{3}}}}$ is

(i) $\text{2}$

(ii) $\frac{\text{1}}{\text{2}}$

Ans: (B) ${{2}^{\frac{1}{3}}}\times {{2}^{-\frac{4}{3}}}={{2}^{\frac{1}{3}-\frac{4}{3}}}={{2}^{\frac{1-4}{3}}}={{2}^{-\frac{3}{3}}}$

22. \[\text{16}\sqrt{\text{13}}\text{ }\!\!\div\!\!\text{ 9}\sqrt{\text{52}}\] is equal to

(i) $\frac{\text{3}}{\text{9}}$

(ii) $\frac{\text{9}}{\text{8}}$

(iii) \[\frac{\text{8}}{\text{9}}\]

Ans: $16\sqrt{13}\div 9\sqrt{52}$

$\frac{16\sqrt{13}}{9\sqrt{52}}=\frac{16}{9}\sqrt{\frac{13}{52}}=\frac{8}{9}$

23. $\sqrt{\text{8}}$ is an

(i) natural number

(iii) integer

(iv) irrational number

Ans: (D) $\sqrt{8}$ is an irrational number

$\therefore \sqrt{4\times 2}=2\sqrt{2}$

2 Marks Questions

1. Is zero a rational number? Can you write it in the form $\frac{p}{q}$, where $p$ and $q$ are integers and $q\ne 0$?

Ans: Consider the definition of a rational number. A rational number is the one that can be written in the form $\frac{p}{q}$, where $p$ and $q$ are integers and $q\ne 0$.

Zero can be written as $\frac{0}{1},\frac{0}{2},\frac{0}{3},\frac{0}{4},\frac{0}{5}......$

So, we arrive at the conclusion that $0$ can be written in the form $\frac{p}{q}$, where $q$is any integer.

Therefore, zero is a rational number.

2. Find six rational numbers between $3$ and $4$.

Ans: We know that there are infinite rational numbers between any two numbers.

A rational number is the one that can be written in the form of $\frac{p}{q}$, where $p$ and $q$ are integers and $q\ne 0$.

We know that the numbers $3.1,3.2,3.3,3.4,3.5$ and $3.6$ all lie between $3$ and $4$.

We need to rewrite the numbers $3.1,3.2,3.3,3.4,3.5$ and $3.6$ in $\frac{p}{q}$ form to get the rational numbers between $3$ and $4$.

So, after converting we get $\frac{32}{10},\frac{32}{10},\frac{33}{10},\frac{34}{10},\frac{35}{10},$ and $\frac{36}{10},$ into lowest fractions.

On converting the fractions into lowest fractions, we get $\frac{16}{5},\frac{17}{5},\frac{7}{2}$ and $\frac{18}{5}$.

Therefore, six rational numbers between $3$ and $4$are \[\frac{31}{10},\frac{16}{5},\frac{33}{10},\frac{17}{5},\frac{7}{2}\] and $\frac{18}{5}$.

3. Find five rational numbers between $\frac{3}{5}$ and $\frac{4}{5}$.

We know that the numbers $\frac{3}{5}$ and $\frac{4}{5}$ can also be written as $0.6\text{ and }0.8$.

We can conclude that the numbers$0.61,0.62,0.63,0.64$ and $0.65$ in \[\frac{p}{q}\] form to get the rational numbers between $3\text{ and }4$.

So, after converting, we get $\frac{61}{100},\frac{62}{100},\frac{63}{100},\frac{64}{100}\text{ and }\frac{65}{100}$.

We can further convert the rational numbers $\frac{62}{100},\frac{64}{100}\text{ and }\frac{65}{100}$ into lowest fractions.

On converting the fractions, we get $\frac{31}{50},\frac{16}{25}\text{ and }\frac{13}{20}$.

Therefore, six rational numbers between $3\text{ and }4$ are $\frac{61}{100},\frac{31}{50},\frac{63}{100},\frac{16}{50}\text{ and }\frac{13}{50}$.

4. Show how $\sqrt{5}$ can be represented on the number line.

Ans: According to Pythagoras theorem, we can conclude that

${{\left( \sqrt{5} \right)}^{2}}={{\left( 2 \right)}^{2}}+{{\left( 1 \right)}^{2}}$.

We need to draw a line segment $AB\text{ of }1$unit on the number line. Then draw a straight line segment $BC\text{ of }2$ units. Then join the points $C$ and $A$, to form a line segment $BC$.

Then draw the arc $ACD$, to get the number $\sqrt{5}$ on the number line.

5. You know that $\frac{1}{7}=0.142857....$. Can you predict what the decimal expansion of $\frac{2}{7},\frac{3}{7},\frac{4}{7},\frac{5}{7},\frac{6}{7}$ are, without actually doing the long division? If so, how?

(Hint: Study the remainder while finding the value of $\frac{1}{7}$ carefully.)

Ans: We are given that $\frac{1}{7}=0.\overline{142857}$ or $\frac{1}{7}=0.142857....$

We need to find the value of \[\frac{2}{7},\frac{3}{7},\frac{4}{7},\frac{5}{7}\text{ and }\frac{6}{7}\], without performing long division.

We know that \[\frac{2}{7},\frac{3}{7},\frac{4}{7},\frac{5}{7}\text{ and }\frac{6}{7}\] can be rewritten as

$2\times \frac{1}{7},3\times \frac{1}{7},4\times \frac{1}{7},5\times \frac{1}{7}\text{ and }6\times \frac{1}{7}$.

On substituting value of $\frac{1}{7}$ as $0.142857....$, we get 

$2\times \frac{1}{7}=2\times 0.142857....=0.285714.... $

$3\times \frac{1}{7}=3\times 0.142857....=0.428571.... $ 

$4\times \frac{1}{7}=4\times 0.142857....=0.571428....$ 

$5\times \frac{1}{7}=5\times 0.142857....=0.714285.... $ 

 $6\times \frac{1}{7}=6\times 0.142857....=0.857142.... $ 

Therefore, we conclude that, we can predict the values of \[\frac{2}{7},\frac{3}{7},\frac{4}{7},\frac{5}{7}\text{ and }\frac{6}{7}\], without performing long division, to get 

\[\frac{2}{7}=0.\overline{285714},\frac{3}{7}=0.\overline{428571},\frac{4}{7}=0.\overline{571428},\frac{5}{7}=0.\overline{714285},\frac{6}{7}=0.\overline{857142}\]

6. Express $0.99999....$in the form $\frac{p}{q}$. Are you surprised by your answer? Discuss why the answer makes sense with your teacher and classmates.

Ans: Let $x=0.99999....\text{ }......(a)$

We need to multiply both sides by $10$ to get 

$10x=9.9999....\text{ }......(b)$

We need to subtract $(a)\text{ from }(b)$, to get

10x=9.99999.... 

x=0.99999.... 

_____________

We can also write $9x=9\text{ as }x=\frac{9}{9}\text{ or }x=1$.

Therefore, on converting $0.99999....$ in the $\frac{p}{q}$ form, we get the answer as $1$.

Yes, at a glance we are surprised at our answer. But the answer makes sense when we observe that $0.99999....$ goes on forever. So there is no gap between $1$  and $0.9999....$ and hence they are equal.

7. Visualize $3.765$ on the number line using successive magnification.

Ans: We know that the number $3.765$ will lie between $3.764\text{ and }3.766$.

We know that the number $3.764$and $3.766$ will lie between $3.76\text{ and }3.77$.

We know that the number $3.76\text{ and }3.77$. will lie between $3.7\text{ and }3.8$.

We know that the number  $3.7\text{ and }3.8$ will lie between $3\text{ and }~4$.

Therefore, we can conclude that we need to use the successive magnification, after locating numbers $3\text{ and }~4$ on the number line

(Image will be uploaded soon)

8. Visualize $4.\overline{26}$ on the number line, upto $4$decimal places.

Ans: We know that the number $4.\overline{26}$ can also be written as$4.262....$ .

We know that the number $4.262....$ will lie between $4.261\text{ and }4.263$.

We know that the number  $4.261\text{ and }4.263$ will lie between $4.26\text{ and }4.27$.

We know that the number $4.26\text{ and }4.27$ will lie between $4.2\text{ and }4.3$.

We know that the number $4.2\text{ and }4.3$ will lie between $4\text{ and }5$.

Therefore, we can conclude that we need to use the successive magnification, after locating numbers $4\text{ and }5$ on the number line.

9. Recall, $\pi $is defined as the ratio of the circumference (say $c$) of a circle of its diameter (say $d$). That is, $\pi =\frac{c}{d}$. This seems to contradict the fact that $\pi $ is irrational. How you resolve this contradiction?

Ans: We know that when we measure the length of the line or a figure by using a scaleneory device, we do not get an exact measurement. In fact, we get an approximate rational value. So, we are not able to realize that either the circumference ($c$) or diameter ($d$) of a circle is irrational.

Therefore, we can conclude that as such there is not any contradiction regarding the value of $\pi $ and we realize that the value of $\pi $ is irrational.

10. Represent $9.3$ on the number line.

Ans: Mark the distance $9.3$ units from a fixed point $A$ on a given line to obtain a point $B$ such that $AB=9.3$ units. From $B$ mark a distance of $1$ unit and call the new point as $C$. Find themid-point of $AC$ and call that point as $O$. Draw a semi-circle with centre $O$ and radius $OC=5.15$units. Draw a line perpendicular to $AC$ passing through $B$ cutting the semi-circle at $D$.

Then $BD=\sqrt{9.3}$.

11. Find (i) ${{64}^{\frac{1}{5}}}$ (ii) ${{32}^{\frac{1}{5}}}$ (iii) ${{125}^{\frac{1}{3}}}$

(i) ${{64}^{\frac{1}{2~}}}$

We know that${{a}^{\frac{1}{n}}}=\sqrt[n]{a},\text{ where }a>0$

We conclude that  ${{64}^{\frac{1}{2~}}}$can also be written as $\sqrt[2]{64}=\sqrt[2]{8\times 8}$

$\sqrt[2]{64}=\sqrt[2]{8\times 8}$$=8$

Therefore, the value of  ${{64}^{\frac{1}{2~}}}$will be $8$.

(ii) ${{32}^{\frac{1}{5}}}$

We conclude that  ${{32}^{\frac{1}{5}}}$can also be written as $\sqrt[5]{32}=\sqrt[5]{2\times 2\times 2\times 2\times 2}$

$\sqrt[5]{32}=\sqrt[5]{2\times 2\times 2\times 2\times 2}=2$

Therefore, the value of  ${{32}^{\frac{1}{5}}}$will be $2$.

(iii) ${{125}^{\frac{1}{3}}}$

We conclude that ${{125}^{\frac{1}{3}}}$can also be written as $\sqrt[3]{125}=\sqrt[3]{5\times 5\times 5}$

$\sqrt[3]{125}=\sqrt[3]{5\times 5\times 5}=5$

Therefore, the value of ${{125}^{\frac{1}{3}}}$will be $5$.

12. Simplify $\sqrt[3]{2}\times \sqrt[4]{3}$

Ans: $\sqrt[3]{2}\times \sqrt[4]{3}$

${{2}^{\frac{1}{3}}}\times {{3}^{\frac{1}{4}}}$

The LCM of $3\text{ and }4\text{ is }12$

$\therefore {{2}^{\frac{1}{3}}}={{2}^{\frac{4}{12}}}={{\left( {{2}^{4}} \right)}^{\frac{1}{12}}}={{16}^{\frac{1}{12}}} $

${{3}^{\frac{1}{4}}}={{3}^{\frac{3}{12}}}={{\left( {{3}^{3}} \right)}^{\frac{1}{12}}}={{27}^{\frac{1}{12}}} $

${{2}^{\frac{1}{3}}}\times {{3}^{\frac{1}{4}}}={{16}^{\frac{1}{12}}}\times {{27}^{\frac{1}{12}}}={{\left( 16\times 27 \right)}^{\frac{1}{12}}} $

$={{\left( 432 \right)}^{\frac{1}{12}}} $

13. Find the two rational numbers between$\frac{1}{2}$ and $\frac{1}{3}$.

Ans: First rational number between $\frac{1}{2}$ and $\frac{1}{3}$

$=\frac{1}{2}\left[ \frac{1}{2}+\frac{1}{3} \right]\Rightarrow \frac{1}{2}\left[ \frac{3+2}{6} \right]\Rightarrow \frac{5}{12} $

$ =\frac{1}{2},\frac{5}{12}\text{ and }\frac{1}{3} $

Second rational number between $\frac{1}{2}$ and $\frac{1}{3}$

$=\frac{1}{2}\left[ \frac{1}{2}+\frac{5}{12} \right]\Rightarrow \frac{1}{2}\left[ \frac{6+5}{12} \right]\Rightarrow \frac{11}{24}$

$=\frac{5}{12}\text{ and }\frac{11}{24}$ are two rational numbers between $\frac{1}{2}$ and $\frac{1}{3}$.

14. Find two rational numbers between $2$ and $3$.

Ans: Irrational numbers between $2$ and $3$ is $\sqrt{2\times 3}=\sqrt{6}$

Irrational number between $2$ and $3$ is $\sqrt{6}$.

$\sqrt{2\times \sqrt{6}}={{2}^{\frac{1}{2}}}\times {{6}^{\frac{1}{4}}}={{2}^{2\times \frac{1}{4}}}\times {{6}^{\frac{1}{4}}} $

$ ={{\left( {{2}^{2}} \right)}^{\frac{1}{4}}}\times {{6}^{\frac{1}{4}}}={{4}^{\frac{1}{4}}}\times {{6}^{\frac{1}{4}}}={{\left( 24 \right)}^{\frac{1}{4}}}=\sqrt[4]{24} $

$\sqrt{6}\text{ and }\sqrt{24}$ are two rational numbers between $2$ and $3$.

15. Multiply $\left( 3-\sqrt{5} \right)$ by $\left( 6+\sqrt{2} \right)$.

Ans: $\left( 3-\sqrt{5} \right)$$\left( 6+\sqrt{2} \right)$

$  =3\left( 6-\sqrt{2} \right)-\sqrt{5}\left( 6+\sqrt{2} \right) $

$=18+3\sqrt{2}-6\sqrt{5}-\sqrt{5}\times \sqrt{2} $

$  =18+3\sqrt{2}-6\sqrt{5}-\sqrt{10} $

16. Evaluate (i) $\sqrt[3]{125}$ (ii) $\sqrt[4]{1250}$

(i) $\sqrt[3]{125}$$={{\left( 5\times 5\times 5 \right)}^{\frac{1}{3}}}={{\left( {{5}^{3}} \right)}^{\frac{1}{3}}}=5$

(ii) $\sqrt[4]{1250}$$\begin{align}

$={{\left( 2\times 5\times 5\times 5\times 5 \right)}^{\frac{1}{4}}}={{\left( 2\times {{5}^{4}} \right)}^{\frac{1}{4}}} $ 

$={{2}^{\frac{1}{4}}}\times {{\left( {{5}^{4}} \right)}^{\frac{1}{4}}}=5\times \sqrt[4]{2} $

17. Find rationalizing factor of $\sqrt{300}$.

Ans: $\sqrt{300}=\sqrt{2\times 2\times 3\times 5\times 5}$

$  =\sqrt{{{2}^{2}}\times 3\times {{5}^{2}}} $

$ =2\times 5\sqrt{3}=10\sqrt{3} $

Rationalizing factor is $\sqrt{3}$

18. Rationalizing the denominator $\frac{1}{\sqrt{5}+\sqrt{2}}$ and subtract it from $\sqrt{5}-\sqrt{2}$.

Ans: $\frac{1}{\sqrt{5}+\sqrt{2}}\times \frac{\sqrt{5}-\sqrt{2}}{\sqrt{5}-\sqrt{2}}$

$=\frac{\sqrt{5}-\sqrt{2}}{{{\left( \sqrt{5} \right)}^{2}}-{{\left( \sqrt{2} \right)}^{2}}}=\frac{\sqrt{5}-\sqrt{2}}{5-2}=\frac{\sqrt{5}-\sqrt{2}}{3}$

Difference between $\left( \sqrt{5}-\sqrt{2} \right)\text{ and }\left( \sqrt{5}-\frac{\sqrt{2}}{3} \right)$

$=\sqrt{5}-\sqrt{2}-\left( \frac{\sqrt{5}-\sqrt{2}}{3} \right) $

$ =\sqrt{5}-\sqrt{2}-\frac{\sqrt{5}}{3}+\frac{\sqrt{2}}{3} $

$=\left( \sqrt{5}-\frac{\sqrt{5}}{3} \right)-\left( \sqrt{2}-\frac{\sqrt{2}}{3} \right) $

$=\frac{2\sqrt{5}}{3}-\frac{2\sqrt{2}}{3}=\frac{2}{3}\left( \sqrt{5}-\sqrt{2} \right) $

19. Show that $\sqrt{7}-3$ is irrational.

Ans: Suppose $\sqrt{7}-3$ is rational

Let $\sqrt{7}-3=x$ ($x$ is a rational number)

$\sqrt{7}=x+3$

$x$ is a rational number $3$ is also a rational number

$\therefore x+3$ is a rational number

But is $\sqrt{7}$ irrational number which is contradiction

$\therefore \sqrt{7}-3$ is an irrational number.

20. Find two rational numbers between $7$ and $5$.

Ans: First rational number $=\frac{1}{2}\left[ 7+5 \right]=\frac{12}{2}=6$

Second rational number $=\frac{1}{2}\left[ 7+6 \right]=\frac{1}{2}\times 13=\frac{13}{2}$

Two rational numbers between $7\text{ and }5\text{ are }6\text{ and }\frac{13}{2}$.

21. Show that $5+\sqrt{2}$ is not a rational number.

Ans: Let $5+\sqrt{2}$ is a rational number.

Say $5+\sqrt{2=x}$ i.e., $\sqrt{2}=x-5$

$x$ is a rational number $5$ is also rational number

$\therefore x-5$ is also a rational number.

But $\sqrt{2}$ is irrational number which is a contradiction

$\therefore 5+\sqrt{2}$ is an irrational number.

22. Simplify ${{\left( \sqrt{5}+\sqrt{2} \right)}^{2}}$.

Ans: ${{\left( \sqrt{5}+\sqrt{2} \right)}^{2}}={{\left( \sqrt{5} \right)}^{2}}+{{\left( \sqrt{2} \right)}^{2}}+2\sqrt{5}\times \sqrt{2}=5+2+2\sqrt{10}=7+2\sqrt{2}$

23. Evaluate $\frac{{{11}^{\frac{5}{2}}}}{{{11}^{\frac{3}{2}}}}$.

Ans: $\frac{{{11}^{\frac{5}{2}}}}{{{11}^{\frac{3}{2}}}}={{11}^{\frac{5}{2}-\frac{3}{2}}}\left[ \because \frac{{{a}^{m}}}{{{a}^{n}}}={{a}^{m-n}} \right]$

$ ={{11}^{\frac{5-3}{2}}}={{11}^{\frac{2}{2}}} $

$=11 $ 

24. Find four rational numbers between $\frac{3}{7}$ and $\frac{4}{7}$.

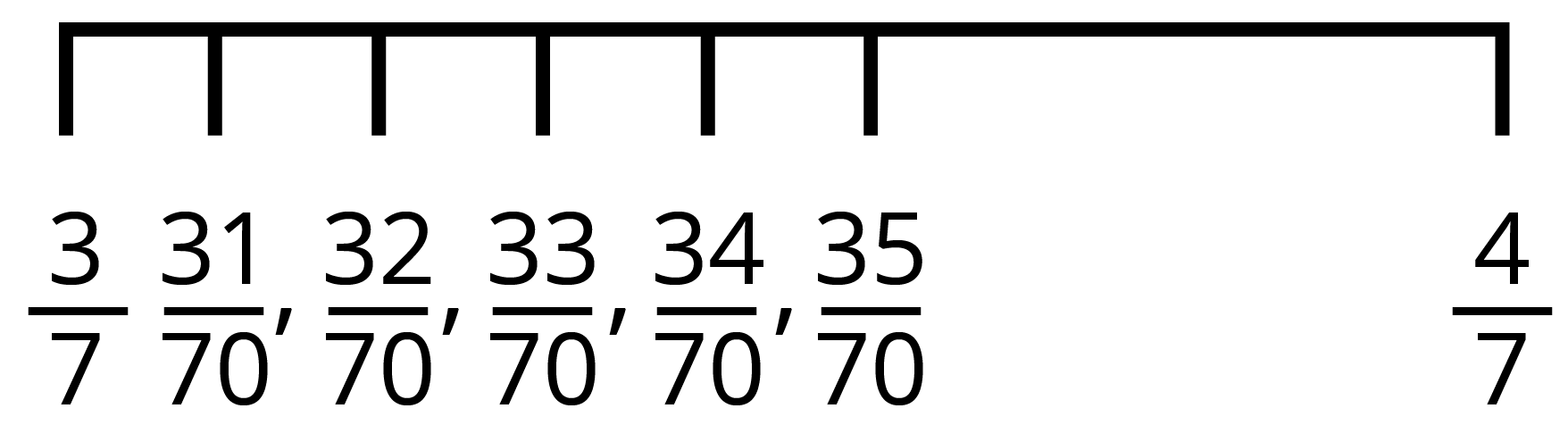
$\frac{3}{7}\times \frac{10}{10}=\frac{30}{70}\text{ and }\frac{4}{7}\times \frac{10}{10}=\frac{40}{70}$

Take any four rational numbers between $\frac{30}{70}\text{ and }\frac{40}{70}$ i.e., rational numbers between  $\frac{3}{7}$ and $\frac{4}{7}$ are $\frac{31}{70},\frac{32}{70},\frac{33}{70},\frac{34}{70},\frac{35}{70}$

25. Write the following in decimal form (i) $\frac{36}{100}$ (ii) $\frac{2}{11}$

(i) $\frac{36}{100}=0.36$

(ii) $\frac{2}{11}=0.\overline{18}$

26. Express $2.417\overline{8}$ in the form $\frac{a}{b}$

Ans: $x=2.4\overline{178}$

$10x=24.\overline{178}$$......(1)$$[\text{Multiplying both sides by }10]$

$10x=24.178178178.... $

$1000\times 10x=1000\times 24.178178178....$Multiplying both sides by 1000

$10,000x=24178.178178.... $

$ 10000x=24178.\overline{178}\text{ }......(2) $

Subtracting $(1)\text{ from }(2)$

$10,000x-x=24178.\overline{178}-24.\overline{178} $

$9990x=24154 $

$x=\frac{24154}{9990} $

$ 2.4\overline{178}=\frac{24154}{9990}+\frac{12077}{4995} $

27. Multiply $\sqrt{3}$ by $\sqrt[3]{5}$.

Ans: $\sqrt{3}\text{ and }\sqrt[3]{5}$

Or ${{3}^{\frac{1}{2}}}\text{ and }{{5}^{\frac{1}{3}}}$

$LCM\text{ of }2\text{ and }3\text{ is }6 $

${{3}^{\frac{1}{2}}}={{3}^{\frac{1}{2}\times \frac{3}{3}}}={{\left( {{3}^{3}} \right)}^{\frac{1}{6}}}={{\left( 27 \right)}^{\frac{1}{6}}} $

 ${{5}^{\frac{1}{3}}}={{5}^{\frac{1}{3}\times \frac{2}{2}}}={{\left( {{5}^{2}} \right)}^{\frac{1}{6}}}={{\left( 25 \right)}^{\frac{1}{6}}} $

 $\sqrt{3}\times \sqrt[3]{5}={{\left( 27 \right)}^{\frac{1}{6}}}\times {{\left( 25 \right)}^{\frac{1}{6}}}={{\left( 27\times 25 \right)}^{\frac{1}{6}}} $

$ ={{675}^{\frac{1}{6}}}=\sqrt[6]{675} $

28. Find the value of $\frac{\sqrt{2}+\sqrt{5}}{\sqrt{5}}$ if $\sqrt{5}=2.236$ and $\sqrt{10}=3.162$.

Ans: $\frac{\sqrt{2}+\sqrt{5}}{\sqrt{5}}\times \frac{\sqrt{5}}{\sqrt{5}}=\frac{\sqrt{10}+5}{5}=\frac{8.162}{5}=1.6324$

29. Convert $0.\overline{25}$ into rational number.

Ans: Let \[x=0.\overline{25}\]                            ......(i)

$x=0.252525....$

Multiply both sides by 100

$100x=25.252525....$

$100x=25.\overline{25}$                                                  ......(ii)

Subtract (i) from (ii)

$100x-x=25.\overline{25}-0.\overline{25} $

 $x=\frac{25}{99} $

30. Simplify $\left( 3\sqrt{3}+2\sqrt{2} \right)\left( 2\sqrt{3}+3\sqrt{2} \right)$.

Ans: By multiplying each terms in the given product we have,

 $ \left( 3\sqrt{3}+2\sqrt{2} \right)\left( 2\sqrt{3}+3\sqrt{2} \right) $

 $=3\sqrt{3}\left( 2\sqrt{3}+3\sqrt{2} \right)+2\sqrt{2}\left( 2\sqrt{3}+3\sqrt{2} \right) $

 $=18+9\sqrt{6}+4\sqrt{6}+12 $

 $ =30+\left( 9+4 \right)\sqrt{6} $

 $=30+13\sqrt{6} $

31. Simplify $\frac{{{9}^{\frac{3}{2}}}\times {{9}^{-\frac{4}{2}}}}{{{9}^{\frac{1}{2}}}}$.

Ans: By using the formulas of exponents with same base we get,

$\frac{{{9}^{\frac{3}{2}}}\times {{9}^{-\frac{4}{2}}}}{{{9}^{\frac{1}{2}}}}=\frac{{{9}^{\frac{3}{2}-\frac{4}{2}}}}{{{9}^{\frac{1}{2}}}}\left[ {{a}^{m}}.{{a}^{n}}={{a}^{m-n}} \right]$

$\frac{{{9}^{-\frac{1}{2}}}}{{{9}^{\frac{1}{2}}}}=\frac{1}{{{9}^{\frac{1}{2}+\frac{1}{2}}}}\left[ {{a}^{-m}}=\frac{1}{{{a}^{m}}} \right] $

$ =\frac{1}{{{9}^{\frac{2}{2}}}}=\frac{1}{9} $

3 Marks Questions

1. State whether the following statements are true or false. Give

reasons for your answers.

i. Every natural number is a whole number.

Separately, consider whole numbers and natural numbers.

We know that the whole number series is 0,1,2,3,4,5....

We know that the natural number series is 0,1,2,3,4,5....

As a result, every number in the natural number series may be found in the whole number series.

Therefore, we can safely conclude that any natural number is a whole number.

ii. Every integer is a whole number.

Ans: Separately, consider whole numbers and integers.

We know that integers are those numbers that can be written in the form of $\frac{p}{q}$ where q=1.

In the case of an integer series, we now have.... 4,3,2,1,0,1,2,3,4....

We can conclude that all whole number series numbers belong to the integer series.

However, the whole number series does not contain every number of integer series.

As a result, we can conclude that no integer is a whole number.

iii. Every rational number is a whole number.

Ans: Separately, consider whole numbers and rational numbers.

We know that integers are those numbers that can be written in the form of $\frac{p}{q}$ where $q\ne 0$.

We know that every number of whole number series can be written in the form of $\frac{p}{q}$ as $\frac{0}{1},\frac{1}{1},\frac{2}{1},\frac{3}{1},\frac{4}{1},\frac{5}{1}...$

We conclude that every number of the whole number series is a rational number. 

But, every rational number does not appear in the whole number series.

2. State whether the following statements are true or false. Justify your answers.

i. Every irrational number is a real number.

Ans: Separately, consider irrational numbers and real numbers.

We know that irrational numbers are the numbers that cannot be converted in the form $\frac{p}{q}$, where p and q are integers and $q\ne 0$.

A real number is made up of both rational and irrational numbers, as we all know.

As a result, we might conclude that any irrational number is, in fact, a real number.

ii. Every point on the number line is of the form $\sqrt{m}$, where m is a natural number.

Ans: Consider a number line. We know that we can express both negative and positive numbers on a number line.

We know that when we take the square root of any number, we cannot receive a negative value.

Therefore, we conclude that not every number point on the number line is of the form $\sqrt{m}$, where m is a natural number.

iii. Every real number is an irrational number.

As a result, we can deduce that any irrational number is actually a real number. However, not every real number is irrational.

Therefore, we conclude that every real number is not a rational number.

3. Express the following in the form $\frac{p}{q}$ where $p$ and $q$ are integers and $q\ne 0$.

i. $0.\overline{6}$

Let $x=0.\overline{6}$

$\Rightarrow x=0.6666$            ......(a)

Multiplying both sides by 10 we get

$10x=6.6666$             ......(b)

We need to subtract (a) from (b), to get

We can also write $9x=6$ as $x=\frac{6}{9}$ or $x=\frac{2}{3}$.

Therefore, on converting $0.\overline{6}$ in the $\frac{p}{q}$ form, we get the answer as $\frac{2}{3}$.

ii. $0.4\overline{7}$

Ans: Let $x=0.4\overline{7}\Rightarrow x=0.47777$                     ......(a)

Multiplying both sides by 10 we get 

$10x=4.7777$                                            ......(b)

We can also write $9x=4.3$ as $x=\frac{4.3}{9}$ or $x=\frac{43}{90}$

Therefore, on converting $0.4\overline{7}$ in the $\frac{p}{q}$ form, we get the answer as $\frac{43}{90}$.

iii. $0.\overline{001}$

Ans: Let $x=0.\overline{001}\Rightarrow x=0.001001$                     ......(a)

Multiplying both sides by 1000 we get 

$1000x=1.001001$                                         ......(b)

We can also write $999x=1$ as $x=\frac{1}{999}$

Therefore, on converting $0.\overline{001}$ in the $\frac{p}{q}$ form, we get the answer as $\frac{1}{999}$.

4. What can the maximum number of digits be in the recurring block of digits in the decimal expansion of $\frac{1}{17}$ ? Perform the division to check your answer.

Ans: The number of digits in the recurring block of $\frac{1}{17}$ must be determined.

To acquire the repeating block of $\frac{1}{17}$ we'll use long division.

We need to divide 1 by 17, to get 0.0588235294117647.... and we got the remainder as 1, which will continue to be 1 after carrying out 16 continuous divisions.

Therefore, we conclude that

\[\frac{1}{17}=0.0588235294117647\] or \[\frac{1}{17}=0.\overline{0588235294117647}\] which is a non-terminating decimal and recurring decimal.

5. Look at several examples of rational numbers in the form $\frac{p}{q}\left( q\ne 0 \right)$ where $p$ and $q$ are integers with no common factors other than 1 and having terminating decimal representations (expansions). Can you guess what property $q$ must satisfy?

Ans: Let us consider the examples of the form $\frac{p}{q}$ that are terminating decimals .

$ \frac{5}{2}=2.5 $ 

$ \frac{5}{4}=1.25 $ 

$ \frac{2}{5}=0.4 $

$  \frac{5}{16}=0.3125 $ 

It can be observed that the denominators of the above rational numbers have powers of 2,5 or both.

Therefore, we can conclude that property, which $q$ must satisfy in $\frac{p}{q}$ , so that the rational number $\frac{p}{q}$ is a terminating decimal is that q must have powers of 2,5 or both.

6. Classify the following numbers as rational or irrational:

i. $2-\sqrt{5}$

Ans: $2-\sqrt{5}$

We know that $\sqrt{5}=2.236....$, which is an irrational number.

$2-\sqrt{5}=2-2.236....$

$=-0.236...$, which is also an irrational number.

As a result, we can deduce that $2-\sqrt{5}$ is an irrational number.

ii. $\left( 3+\sqrt{23} \right)-\sqrt{23}$

Ans: $\left( 3+\sqrt{23} \right)-\sqrt{23}$

$\left( 3+\sqrt{23} \right)-\sqrt{23}=3+\sqrt{23}-\sqrt{23}=3$

As a result, we can deduce that $\left( 3+\sqrt{23} \right)-\sqrt{23}$ is a rational number.

iii. $\frac{2\sqrt{7}}{7\sqrt{7}}$

Ans: $\frac{2\sqrt{7}}{7\sqrt{7}}$

We can cancel $\sqrt{7}$ in the numerator and denominator to get $\frac{2\sqrt{7}}{7\sqrt{7}}=\frac{2}{7}$, because $\sqrt{7}$ is a common number in both the numerator and denominator.

iv. $\frac{1}{\sqrt{2}}$

Ans: $\frac{1}{\sqrt{2}}$

We know that $\sqrt{2}=1.4142...$, which is an irrational number.

$\frac{1}{\sqrt{2}}\times \frac{\sqrt{2}}{\sqrt{2}}=\frac{\sqrt{2}}{2}$

$=\frac{1.4142...}{2}=0.707...$ which is also an irrational number.

As a result, we can deduce that $\frac{1}{\sqrt{2}}$ is an irrational number.

Ans: $2\pi $

We know that $\pi =3.1415....,$ which is an irrational number.

We can conclude that $2\pi $ will also be an irrational number.

As a result, we can deduce that $2\pi $ is an irrational number.

7. Simplify each of the following expression:

i. $\left( 3+3\sqrt{3} \right)\left( 2+\sqrt{2} \right)$

$(3+3\sqrt{3})(2+\sqrt{2})$

Applying distributive law,

\[(3+3\sqrt{3})(2+\sqrt{2})=3(2+\sqrt{2})\sqrt{3}(2+\sqrt{2})\]

\[=6+3\sqrt{2}+2\sqrt{3}+\sqrt{6}\]

ii. \[\left( 3+3\sqrt{3} \right)3-\sqrt{3}\]

Ans: $(3+3\sqrt{3})(3-\sqrt{3})$

$  (3+3\sqrt{3})(3-\sqrt{3})=(3-\sqrt{3})+\sqrt{3}(3-\sqrt{3}) $ 

$ =9-3\sqrt{3}+3\sqrt{3}-3 $

iii. ${{\left( \sqrt{5}+\sqrt{2} \right)}^{2}}$

Ans: ${{\left( \sqrt{5}+\sqrt{2} \right)}^{2}}$

Applying the formula ${{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}$

${{\left( \sqrt{5}+\sqrt{2} \right)}^{2}}={{\left( \sqrt{5} \right)}^{2}}+2\times \sqrt{5}\times \sqrt{2}+{{\left( \sqrt{2} \right)}^{2}} $

$ =5+2\sqrt{10}+2 $

$=7+2\sqrt{10}$

iv. $\left( 5+\sqrt{2} \right)\left( 5+\sqrt{2} \right)$

Ans: $\left( 5+\sqrt{2} \right)\left( 5+\sqrt{2} \right)$

Applying the formula $\left( a-b \right)\left( a+b \right)={{a}^{2}}-{{b}^{2}}$

$ \left( 5+\sqrt{2} \right)\left( 5+\sqrt{2} \right)={{\left( \sqrt{5} \right)}^{2}}-{{\left( \sqrt{2} \right)}^{2}} $

8. Find 

i. ${{9}^{\frac{3}{2}}}$

Ans: We know that ${{a}^{\frac{1}{n}}}=\sqrt[n]{a},a>0$

As a result, we can deduce that ${{9}^{\frac{3}{2}}}$ can also be written as

$\sqrt[2]{{{\left( 9 \right)}^{3}}}=\sqrt[2]{9\times 9\times 9}=\sqrt[2]{3\times 3\times 3\times 3\times 3\times 3}$

$=3\times 3\times 3 $

Therefore, the value of ${{9}^{\frac{3}{2}}}$ will be $27$ .

ii. ${{32}^{\frac{2}{5}}}$

As a result, we can deduce that ${{32}^{\frac{2}{5}}}$ can also be written as

$ \sqrt[5]{{{\left( 32 \right)}^{2}}}=\sqrt[5]{\left( 2\times 2\times 2\times 2\times 2 \right)\left( 2\times 2\times 2\times 2\times 2 \right)} $

$=2\times 2 $ 

Therefore, the value of ${{32}^{\frac{2}{5}}}$ will be $4$.

iii. ${{16}^{\frac{3}{4}}}$

As a result, we can deduce that ${{16}^{\frac{3}{4}}}$ can also be written as 

$\sqrt[4]{{{\left( 16 \right)}^{3}}}=\sqrt[4]{\left( 2\times 2\times 2\times 2 \right)\left( 2\times 2\times 2\times 2 \right)\left( 2\times 2\times 2\times 2 \right)} $

$ =2\times 2\times 2 $

 & =8 $

Therefore, the value of ${{16}^{\frac{3}{4}}}$ will be $8$ .

iv. ${{125}^{-\frac{1}{3}}}$

Ans: We know that ${{a}^{-n}}=\frac{1}{{{a}^{n}}}$

As a result, we can deduce that ${{125}^{-\frac{1}{3}}}$ can also be written as $\frac{1}{{{125}^{\frac{1}{3}}}},or{{\left( \frac{1}{125} \right)}^{\frac{1}{3}}}$

We know that ${{a}^{\frac{1}{n}}}=\sqrt[n]{a},a>0$

$ \sqrt[3]{\frac{1}{125}}=\sqrt[3]{\left( \frac{1}{5}\times \frac{1}{5}\times \frac{1}{5} \right)} $

$=\frac{1}{5} $

Therefore, the value of ${{125}^{-\frac{1}{3}}}$ will be $\frac{1}{5}$.

9. Simplify

i. ${{2}^{\frac{2}{3}}}{{.2}^{\frac{1}{5}}}$

Ans: We know that ${{a}^{m}}.{{a}^{n}}={{a}^{\left( m+n \right)}}$

As a result, we can deduce that ${{2}^{\frac{2}{3}}}{{.2}^{\frac{1}{5}}}={{\left( 2 \right)}^{\frac{2}{3}+\frac{1}{5}}}$

${{2}^{\frac{2}{3}}}{{.2}^{\frac{1}{5}}}=\left( 2 \right)\frac{10+3}{15}={{\left( 2 \right)}^{\frac{13}{15}}}$

Therefore, the value of ${{2}^{\frac{2}{3}}}{{.2}^{\frac{1}{5}}}$ will be ${{\left( 2 \right)}^{\frac{13}{15}}}$.

ii. ${{\left( {{3}^{\frac{1}{3}}} \right)}^{7}}$

As a result, we can deduce that ${{\left( {{3}^{\frac{1}{3}}} \right)}^{7}}$ can also be written as ${{3}^{\frac{7}{3}}}$

iii. $\frac{{{11}^{\frac{1}{2}}}}{{{11}^{\frac{1}{4}}}}$

Ans: We know that $\frac{{{a}^{m}}}{{{a}^{n}}}={{a}^{\left( m-n \right)}}$

As a result, we can deduce that  $\begin{align}

$ \frac{{{11}^{\frac{1}{2}}}}{{{11}^{\frac{1}{4}}}}={{11}^{\frac{1}{2}}}-{{11}^{\frac{1}{4}}} $

$={{11}^{\frac{2-1}{4}}}={{11}^{\frac{1}{4}}} $

Therefore, the value of  $\frac{{{11}^{\frac{1}{2}}}}{{{11}^{\frac{1}{4}}}}$ will be ${{11}^{\frac{1}{4}}}$.

iv. ${{7}^{\frac{1}{2}}}{{.8}^{\frac{1}{2}}}$

Ans: We know that ${{a}^{m}}.{{b}^{m}}={{\left( a\times b \right)}^{m}}$

As a result, we can deduce that ${{7}^{\frac{1}{2}}}{{.8}^{\frac{1}{2}}}={{\left( 7\times 8 \right)}^{\frac{1}{2}}}.$

${{7}^{\frac{1}{2}}}{{.8}^{\frac{1}{2}}}={{\left( 7\times 8 \right)}^{\frac{1}{2}}}={{\left( 56 \right)}^{\frac{1}{2}}}.$

Therefore, the value of ${{7}^{\frac{1}{2}}}{{.8}^{\frac{1}{2}}}$ will be ${{\left( 56 \right)}^{\frac{1}{2}}}$.

10. Express $0.8888....$ in the form $\frac{p}{q}$.

Ans: Let us assume that the given decimal as,

$x=0.\overline{8}......\left( 1 \right)$

$10x=10\times 0.8888$ (Multiply both sides by 10)

$ 10x=8.8888 $

$10x=8.\overline{8}.....\left( 2 \right) $

$10x-x=8.\overline{8}-0.\overline{8}$ (Subtracting (1) from (2))

$x=\frac{8}{9} $

11.  Simplify by rationalizing denominator $\frac{7+3\sqrt{5}}{7-3\sqrt{5}}$.

Ans: We are given the fraction to rationalize. By rationalizing the denominator we get,

$\frac{7+3\sqrt{5}}{7-3\sqrt{5}}=\frac{7+3\sqrt{5}}{7-3\sqrt{5}}\times \frac{7+3\sqrt{5}}{7+3\sqrt{5}}$ 

$=\frac{{{\left( 7+3\sqrt{5} \right)}^{2}}}{{{7}^{2}}-{{\left( 3\sqrt{5} \right)}^{2}}} $

$ =\frac{{{7}^{2}}+{{\left( 3\sqrt{5} \right)}^{2}}+2\times 7\times 3\sqrt{5}}{49-{{3}^{2}}\times 5} $

$=\frac{49+9\times 5+42\sqrt{5}}{49-45} $

$=\frac{49+45+42\sqrt{5}}{4} $

$ =\frac{94+42\sqrt{5}}{4} $ 

$ =\frac{94}{4}+\frac{42}{4}\sqrt{5} $

$ =\frac{47}{2}+\frac{21}{2}\sqrt{5} $

12 . Simplify ${{\left\{ {{\left[ {{625}^{-}}^{\frac{1}{2}} \right]}^{-\frac{1}{4}}} \right\}}^{2}}$.

Ans:  Let us take the given expression to simplify and using the exponents formulas we get,

  \[{{\left\{ {{\left[ {{625}^{-}}^{\frac{1}{2}} \right]}^{-\frac{1}{4}}} \right\}}^{2}}\]

$ ={{\left\{ {{\left( \frac{1}{{{625}^{\frac{1}{2}}}} \right)}^{-\frac{1}{4}}} \right\}}^{2}} $

$={{\left\{ {{\left( \frac{1}{{{\left( {{25}^{2}} \right)}^{\frac{1}{2}}}} \right)}^{-\frac{1}{4}}} \right\}}^{2}}\left( {{a}^{-m}}=\frac{1}{{{a}^{m}}} \right) $

 $ =\left\{ {{\left( \frac{1}{25} \right)}^{-\frac{1}{4}\times 2}} \right\} $

$=\left( \frac{1}{{{25}^{-\frac{1}{2}}}} \right)=\frac{1}{{{\left( {{5}^{2}} \right)}^{-\frac{1}{2}}}}=\frac{1}{{{5}^{-1}}}=5 $

13. Visualize 3.76 on the number line using successive magnification.

14. Prove that $\frac{1}{1+{{x}^{b-a}}+{{x}^{c-a}}}+\frac{1}{1+{{x}^{a-b}}+{{x}^{c-b}}}+\frac{1}{1+{{x}^{a-c}}+{{x}^{b-c}}}=1$

Ans: We are asked to prove the expression,

$\frac{1}{1+{{x}^{b-a}}+{{x}^{c-a}}}+\frac{1}{1+{{x}^{a-b}}+{{x}^{c-b}}}+\frac{1}{1+{{x}^{a-c}}+{{x}^{b-c}}}=1$

Let us take the LHS of the given expression that is,

$LHS=\frac{1}{1+{{x}^{b}}.{{x}^{-a}}+{{x}^{c}}.{{x}^{-a}}}+\frac{1}{1+{{x}^{a}}.{{x}^{-b}}+{{x}^{c}}.{{x}^{-b}}}+\frac{1}{1+{{x}^{a}}.{{x}^{-c}}+{{x}^{b}}.{{x}^{-c}}} $

$=\frac{1}{{{x}^{-a}}.{{x}^{a}}+{{x}^{b}}.{{x}^{-a}}+{{x}^{c}}.{{x}^{-a}}}+\frac{1}{{{x}^{b}}.{{x}^{-b}}+{{x}^{a}}.{{x}^{-b}}+{{x}^{c}}.{{x}^{-b}}}+\frac{1}{{{x}^{c}}.{{x}^{-c}}+{{x}^{a}}.{{x}^{-c}}+{{x}^{b}}.{{x}^{-c}}} $

$ =\frac{1}{{{x}^{-a}}\left( {{x}^{a}}+{{x}^{b}}+{{x}^{c}} \right)}+\frac{1}{{{x}^{-b}}\left( {{x}^{a}}+{{x}^{b}}+{{x}^{c}} \right)}+\frac{1}{{{x}^{-c}}\left( {{x}^{a}}+{{x}^{b}}+{{x}^{c}} \right)} $

$=\frac{{{x}^{a}}}{\left( {{x}^{a}}+{{x}^{b}}+{{x}^{c}} \right)}+\frac{{{x}^{b}}}{\left( {{x}^{a}}+{{x}^{b}}+{{x}^{c}} \right)}+\frac{{{x}^{c}}}{\left( {{x}^{a}}+{{x}^{b}}+{{x}^{c}} \right)} $ $ =\frac{\left( {{x}^{a}}+{{x}^{b}}+{{x}^{c}} \right)}{\left( {{x}^{a}}+{{x}^{b}}+{{x}^{c}} \right)}=1 $

15. Represent $\sqrt{3}$ on number line.

Ans: Consider a number line $\text{OD}$ such that the construction to form two triangles is done as shown below.

Take $OA=AB=1$ unit.

And $\angle A=90{}^\circ $

In $\Delta OAB$, by using the Pythagorean theorem we get,

$O{{B}^{2}}={{1}^{2}}+{{1}^{2}}$

$O{{B}^{2}}=2 $

$ OB=\sqrt{2}$ 

Now from triangle $\text{ }\!\!\Delta\!\!\text{ OBD}$, using the Pythagorean theorem we get,

$O{{D}^{2}}=O{{B}^{2}}+B{{D}^{2}} $

$ O{{D}^{2}}={{\left( \sqrt{2} \right)}^{2}}+{{\left( 1 \right)}^{1}} $

$O{{D}^{2}}=2+1=3 $

$OD=\sqrt{3} $

Now, if the point $\text{O}$ is $0$ units then the point $\text{D}$ represents $\sqrt{3}$units.

16. Simplify ${{\left( 3\sqrt{2}+2\sqrt{3} \right)}^{2}}{{\left( 3\sqrt{2}-2\sqrt{3} \right)}^{2}}$.

Ans: We are given the expression as,

${{\left( 3\sqrt{2}+2\sqrt{3} \right)}^{2}}{{\left( 3\sqrt{2}-2\sqrt{3} \right)}^{2}}$

Now, by regrouping the terms in the above expression we have,

$ =\left( 3\sqrt{2}+2\sqrt{3} \right)\left( 3\sqrt{2}+2\sqrt{3} \right)\left( 3\sqrt{2}-2\sqrt{3} \right)\left( 3\sqrt{2}-2\sqrt{3} \right) $

$ =\left( 3\sqrt{2}+2\sqrt{3} \right)\left( 3\sqrt{2}-2\sqrt{3} \right)\left( 3\sqrt{2}+2\sqrt{3} \right)\left( 3\sqrt{2}-2\sqrt{3} \right) $

$=\left[ {{\left( 3\sqrt{2} \right)}^{2}}-{{\left( 2\sqrt{3} \right)}^{2}} \right]\left[ {{\left( 3\sqrt{2} \right)}^{2}}-{{\left( 2\sqrt{3} \right)}^{2}} \right] $

$ =\left[ 9\times 2-4\times 3 \right]\left[ 9\times 2-4\times 3 \right] $

$ =\left[ 18-12 \right]\left[ 18-12 \right] $ 

$=6\times 6=36 $

17. Express $2.\overline{4178}$ in the form $\frac{p}{q}$.

Ans: Let $\frac{p}{q}=2.\overline{4178}$

$\frac{p}{q}=2.4178178178$

Multiply by 10

$10\frac{p}{q}=24.178178$

Multiply by 1000

$10000\frac{p}{q}=1000\times 24.178178 $ 

$1000\frac{p}{q}-\frac{p}{q}=24178.178178-14.178178 $

$9999\frac{p}{q}=24154 $

$\frac{p}{q}=\frac{24154}{9999} $

18. Simplify ${{\left( 27 \right)}^{-\frac{2}{3}}}\div {{9}^{\frac{1}{2}}}{{.3}^{-\frac{3}{2}}}$.

Ans: ${{\left( 27 \right)}^{-\frac{2}{3}}}\div {{9}^{\frac{1}{2}}}{{.3}^{-\frac{3}{2}}}$

$ =\frac{{{\left( 3\times 3\times 3 \right)}^{-\frac{2}{3}}}\times {{3}^{\frac{3}{2}}}}{{{\left( 3\times 3 \right)}^{\frac{1}{2}}}}\left[ {{a}^{-m}}=\frac{1}{{{a}^{m}}} \right] $

$ =\frac{{{\left( {{3}^{3}} \right)}^{-\frac{2}{3}}}\times {{3}^{\frac{3}{2}}}}{{{\left( {{3}^{2}} \right)}^{\frac{1}{2}}}} $

$=\frac{{{3}^{\frac{3}{2}-2}}}{3}=\frac{{{3}^{-\frac{1}{3}}}}{3} $

$=\frac{1}{{{3}^{\frac{4}{3}}}}=\frac{1}{\sqrt[3]{81}} $

19. Find three rational numbers between $2.\overline{2}$ and $2.\overline{3}.$

Ans: The irrational numbers are the numbers that do not end after the decimal point nor repeat its numbers in a sequence. 

Representing the given numbers in decimal form we have,

$ 2.\overline{2}=2.222222222...... $

$ 2.\overline{3}=2.333333333....... $ 

So any numbers between these two numbers that do not end nor repeat in any sequence gives the required irrational numbers.

Three rational numbers between $2.\overline{2}$ and $2.\overline{3}$ are $2.222341365....$, $2.28945187364....$ and $2.2321453269....$

20. Give an example of two irrational numbers whose

i. Sum is a rational number

Ans: The required two irrational numbers are $2+\sqrt{2}$ and $2-\sqrt{2}$

Sum $2+\sqrt{2}+2-\sqrt{2}=4$ which is a rational number.

ii. Product is a rational number

Ans: The required two irrational numbers are $3\sqrt{2}$ and $6\sqrt{2}$

Product $3\sqrt{2}\times 6\sqrt{2}=18\times 2=36$ which is rational.

iii. Quotient is a rational number

Ans: The required two irrational numbers are $2\sqrt{125}$ and $3\sqrt{5}$

Quotient $\frac{2\sqrt{125}}{3\sqrt{5}}=\frac{2}{3}\sqrt{\frac{125}{5}}=\frac{2}{3}\times 5=\frac{10}{3}$

21 . If $\sqrt{2}=1.414$ and $\sqrt{3}=1.732$, find the value of $\frac{5}{\sqrt{2}+\sqrt{3}}$.

Ans: First let us take the given expression and by rationalizing the denominator we get,

$\frac{5}{\sqrt{2}+\sqrt{3}}\times \frac{\sqrt{2}-\sqrt{3}}{\sqrt{2}-\sqrt{3}}$ 

$\frac{5\left( \sqrt{2}-\sqrt{3} \right)}{{{\left( \sqrt{2} \right)}^{2}}-{{\left( \sqrt{3} \right)}^{2}}} $

$=\frac{5\left( \sqrt{2}-\sqrt{3} \right)}{2-3} $

Now, substituting the required values of irrational numbers we get,

$=-5\left[ 1.414-1.732 \right] $

$  =-5\times -0.318 $

$  =1.59 $ 

22. Visualize 2.4646 on the number line using successive magnification.

23. Rationalizing the denominator of $\frac{1}{4+2\sqrt{3}}$.

Ans: First let us take the given expression and rationalizing the denominator by multiplying the numerator and denominator with its conjugate we get,

$\frac{1}{4+2\sqrt{3}}=\frac{1}{4+2\sqrt{3}}\times \frac{4-2\sqrt{3}}{4+2\sqrt{3}} $

$ =\frac{4-2\sqrt{3}}{{{\left( 4 \right)}^{2}}-{{\left( 2\sqrt{3} \right)}^{2}}} $

$=\frac{4-2\sqrt{3}}{16-{{\left( 2\sqrt{3} \right)}^{2}}} $ 

$=\frac{4-2\sqrt{3}}{16-12} $ 

$  =\frac{4-2\sqrt{3}}{4} $

$ =\frac{2\left( 2-\sqrt{3} \right)}{4} $

$ =\frac{2-\sqrt{3}}{2} $

24. Visualize the representation of $5.3\overline{7}$ on the number line up to 3 decimal places.

Ans: The representation of $5.3\overline{7}$ on the number line is given below:

25. Show that \[5\sqrt{2}\] is not a rational number.

Ans: Let us assume that \[5\sqrt{2}\] is a rational number.

Take \[x=5\sqrt{2}\] , with \[x\]being rational as well.

\[x=5\sqrt{2}\]

\[\Rightarrow \frac{x}{5}=\sqrt{2}\]

Let us compare the terms in LHS and RHS.

In LHS, we have\[\frac{x}{5}\] , with \[x\] and $5$ being rational numbers (Here \[x\] is rational, based on our assumption). So \[\frac{x}{5}\] is a rational number.

In RHS, we have$\sqrt{2}$, which is not a rational number, but an irrational number.

This is a contradiction, i.e. $LHS\ne RHS$.

So, we can conclude that  \[5\sqrt{2}\] is not a rational number.

26. Simplify \[3\sqrt[3]{250}+7\sqrt[3]{16}-4\sqrt[3]{54}\].

Ans: Let us first find the cube roots of given numbers to their simplest forms by using the prime factorization then we get,

\[3\sqrt[3]{250}+7\sqrt[3]{16}-4\sqrt[3]{54}=3\sqrt[3]{5\times 5\times 5\times 2}+7\sqrt[3]{2\times 2\times 2\times 2}-4\sqrt[3]{3\times 3\times 3\times 2}\]

\[=\left( 3\times 5\sqrt[3]{2} \right)+\left( 7\times 2\sqrt[3]{2} \right)-\left( 4\times 3\sqrt[3]{2} \right)\]

\[=\left( 15\sqrt[3]{2} \right)+\left( 14\sqrt[3]{2} \right)-\left( 12\sqrt[3]{2} \right)\]

\[=\left( 15+14-12 \right)\sqrt[3]{2}\]

\[=17\sqrt[3]{2}\]

Thus, we get \[3\sqrt[3]{250}+7\sqrt[3]{16}-4\sqrt[3]{54}=17\sqrt[3]{2}\]

27. Simplify \[3\sqrt{48}-\frac{5}{2}\sqrt{\frac{1}{3}}+4\sqrt{3}\].

Ans: Let us first find the square roots of given numbers to their simplest forms by using the prime factorization then we get,

\[3\sqrt{48}-\frac{5}{2}\sqrt{\frac{1}{3}}+4\sqrt{3}=\left( 3\sqrt{2\times 2\times 2\times 2\times 3} \right)-\left[ \frac{5}{2}\left( \sqrt{\frac{1}{3}}\times \frac{\sqrt{3}}{\sqrt{3}} \right) \right]+\left( 4\sqrt{3} \right)\]

\[=\left( 3\times 2\times 2\sqrt{3} \right)-\left[ \frac{5}{2}\left( \frac{\sqrt{3}}{3} \right) \right]+\left( 4\sqrt{3} \right)\]

\[=\left( 12\sqrt{3} \right)-\left( \frac{5\sqrt{3}}{6} \right)+\left( 4\sqrt{3} \right)\]

\[=\left( 12-\frac{5}{6}+4 \right)\sqrt{3}\]

\[=\left( \frac{72-5+24}{6} \right)\sqrt{3}\]

\[=\frac{91}{6}\sqrt{3}\]

Thus, we get \[3\sqrt{48}-\frac{5}{2}\sqrt{\frac{1}{3}}+4\sqrt{3}=\frac{91}{6}\sqrt{3}\]

28. If $\frac{1}{7}=0.\overline{142857}$. Find the value of $\frac{2}{7},\frac{3}{7},\frac{4}{7}$

Ans: It is given that – $\frac{1}{7}=0.\overline{142857}$

(i) $\frac{2}{7}=2\times \frac{1}{7}$

$=2\times 0.\overline{142857}$

$=0.\overline{285714}$

$\Rightarrow \frac{2}{7}=0.\overline{285714}$

(ii) $\frac{3}{7}=3\times \frac{1}{7}$

$=3\times 0.\overline{142857}$

$=0.\overline{428571}$

$\Rightarrow \frac{3}{7}=0.\overline{428571}$

(iii) $\frac{4}{7}=4\times \frac{1}{7}$

$=4\times 0.\overline{142857}$

$=0.\overline{571428}$

$\Rightarrow \frac{4}{7}=0.\overline{571428}$

29. Find $6$ rational numbers between $\frac{6}{5}$ and $\frac{7}{5}$

Ans: It is possible to divide the interval between $\frac{6}{5}$ and $\frac{7}{5}$ into $10$ equal parts.

Then we will have – $\frac{6}{5},\frac{6.1}{5},\frac{6.2}{5},\frac{6.3}{5},\frac{6.4}{5},\frac{6.5}{5},\frac{6.6}{5},\frac{6.7}{5},\frac{6.8}{5},\frac{6.9}{5},\frac{7}{5}$

i.e. $\frac{60}{50},\frac{61}{50},\frac{62}{50},\frac{63}{50},\frac{64}{50},\frac{65}{50},\frac{66}{50},\frac{67}{50},\frac{68}{50},\frac{69}{50},\frac{70}{50}$

From these fractions, it is possible to choose $6$ rational numbers between $\frac{6}{5}$ and $\frac{7}{5}$

Thus , $6$ rational numbers between $\frac{6}{5}$ and $\frac{7}{5}$ are $\frac{61}{50},\frac{62}{50},\frac{63}{50},\frac{64}{50},\frac{65}{50},\frac{66}{50}$

30. Show how $\sqrt{4}$ can be represented on the number line.

Ans: Take $AB=OA=1\text{ }unit$ on a number line.

Also, $\angle A={{90}^{\circ }}$

In $\vartriangle OAB$, apply Pythagoras Theorem,

$\therefore O{{A}^{2}}+A{{B}^{2}}=O{{B}^{2}}$

$\Rightarrow O{{B}^{2}}={{1}^{2}}+{{1}^{2}}$

$\Rightarrow O{{B}^{2}}=1+1$

$\Rightarrow O{{B}^{2}}=2$

$\Rightarrow OB=\sqrt{2}$

Now, draw $OB=O{{A}_{1}}=\sqrt{2}$

And, ${{A}_{1}}{{B}_{1}}=1\text{ unit}$ with$\angle {{A}_{1}}={{90}^{\circ }}$

In \[\vartriangle O{{A}_{1}}{{B}_{1}}\], apply Pythagoras Theorem,

$\therefore O{{A}_{1}}^{2}+{{A}_{1}}{{B}_{1}}^{2}=O{{B}_{1}}^{2}$

$\Rightarrow O{{B}_{1}}^{2}={{\left( \sqrt{2} \right)}^{2}}+{{1}^{2}}$

$\Rightarrow O{{B}_{1}}^{2}=2+1$

$\Rightarrow O{{B}_{1}}^{2}=3$

$\Rightarrow O{{B}_{1}}=\sqrt{3}$

Now, draw $O{{B}_{1}}=O{{A}_{2}}=\sqrt{3}$

And, \[{{A}_{2}}{{B}_{2}}=1\text{ unit}\] with$\angle {{A}_{2}}={{90}^{\circ }}$

In \[\vartriangle O{{A}_{2}}{{B}_{2}}\], apply Pythagoras Theorem,

$\therefore O{{A}_{2}}^{2}+{{A}_{2}}{{B}_{2}}^{2}=O{{B}_{2}}^{2}$

$\Rightarrow O{{B}_{2}}^{2}={{\left( \sqrt{3} \right)}^{2}}+{{1}^{2}}$

$\Rightarrow O{{B}_{2}}^{2}=3+1$

$\Rightarrow O{{B}_{2}}^{2}=4$

$\Rightarrow O{{B}_{2}}=\sqrt{4}$

Now, draw $O{{B}_{2}}=O{{A}_{3}}=\sqrt{4}$

Thus line segment $O{{A}_{3}}=\sqrt{4}$

Short Answer Questions (4 Marks)

1. Write the following in decimal form and say what kind of decimal expansion each has:

i. $\frac{36}{100}$

Ans: Performing long division of $36$ by $100$

$\begin{matrix} &{0.36}\\ 100&{\overline{)\;36\quad}}\\ &\underline{-0\quad}\\ &360\\ &\underline{-300\quad}\\ &\;\;600\\ &\underline{-600}\\ &\underline{\quad 0 \;\;} \end{matrix}$

Thus, $\frac{36}{100}=0.36$ - this is a terminating decimal.

ii. $\frac{1}{11}$

Ans: Performing long division of $1$ by $11$

$\begin{matrix} {} & 0.0909.. \\ 11 & \overline{)\text{ }1\text{ }} \\ {} & \underline{-0} \\ {} & 10 \\ {} & \underline{-0} \\ {} & 100 \\ {} & \underline{-99} \\ {} & 10 \\ {} & \underline{-0} \\ {} & 100 \\ {} & \underline{-99} \\ {} & 1 \\ \end{matrix}$

It can be seen that performing further division will produce a reminder of $1$ continuously.

Thus, $\frac{1}{11}=0.09090...$ i.e. $\frac{1}{11}=0.\overline{09}$, this is a non-terminating, but recurring decimal.

iii. $4\frac{1}{8}$

Ans: First convert the mixed fraction into an improper fraction –

$4\frac{1}{8}=\frac{(4\times 8)+1}{8}=\frac{33}{8}$

Performing long division of $33$ by $8$

$\begin{matrix} {} & 4.125 \\ 8 & \overline{\left){\text{ }33\text{ }}\right.} \\ {} & \underline{-32} \\ {} & 10 \\ {} & \underline{-8} \\ {} & 20 \\ {} & \underline{-16} \\ {} & 40 \\ {} & \underline{-40} \\ {} & 0 \\ \end{matrix}$

Thus, $4\frac{1}{8}=4.125$ - this is a terminating decimal.

iv. $\frac{3}{13}$

Ans: Performing long division of $3$ by $13$

$\begin{matrix} {} & 0.230769.. \\ 13 & \overline{\left){\text{ }3\text{ }}\right.} \\ {} & \underline{-0} \\ {} & 30 \\ {} & \underline{-26} \\ {} & 40 \\ {} & \underline{-39} \\ {} & 10 \\ {} & \underline{-0} \\ {} & 100 \\ {} & \underline{-91} \\ {} & 90 \\ {} & \underline{-78} \\ {} & 120 \\ {} & \underline{-117} \\ {} & 3 \\ \end{matrix}$

It can be seen that performing further division will produce a reminder of $3$ periodically, after every six divisions.

Thus, $\frac{3}{13}=0.230769...$ i.e. \[\frac{3}{13}=0.\overline{230769}\], this is a non-terminating, but recurring decimal.

v. $\frac{2}{11}$

Ans: Performing long division of $2$ by $11$

$\begin{matrix} {} & 0.1818.. \\ 11 & \overline{)\text{ 2 }} \\ {} & \underline{-0} \\ {} & 20 \\ {} & \underline{-11} \\ {} & 90 \\ {} & \underline{-88} \\ {} & 20 \\ {} & \underline{-11} \\ {} & 90 \\ {} & \underline{-88} \\ {} & 2 \\ \end{matrix}$

It can be seen that performing further division will produce a reminder of $2$followed by $9$ alternatively.

Thus, $\frac{2}{11}=0.181818...$ i.e. $\frac{2}{11}=0.\overline{18}$this is a non-terminating, but recurring decimal.

vi. $\frac{329}{400}$

Ans: Performing long division of $33$ by $8$

$\begin{matrix} {} & 0.8225 \\ 400 & \overline{)\text{ 329 }} \\ {} & \underline{-0} \\ {} & 3290 \\ {} & \underline{-3200} \\ {} & 900 \\ {} & \underline{-800} \\ {} & 1000 \\ {} & \underline{-800} \\ {} & 2000 \\ {} & \underline{-2000} \\ {} & 0 \\ \end{matrix}$

Thus, $\frac{329}{400}=0.8225$ - this is a terminating decimal.

2. Classify the following as rational or irrational:

i. $\sqrt{23}$

Ans: It is known that the root of $23$ will produce a non-terminating and non-recurring decimal number (it is not a perfect square value), also it cannot be represented as a fraction. Thus we can say that $\sqrt{23}$ is an irrational number.

ii. $\sqrt{225}$

Ans: It is known that $\sqrt{225}=15$, which is an integer.

Thus $\sqrt{225}$ is a rational number.

iii. $0.3796$

Ans: Here, $0.3796$ is a terminating decimal number, and also it can be expressed as a fraction.

i.e. $0.3796=\frac{3796}{10000}=\frac{949}{2500}$

Thus $0.3796$ is a rational number.

iv. $7.478478...$

Ans: Here, $7.478478...$ is a non-terminating, but recurring decimal number, and also it can be expressed as a fraction.

i.e. $7.478478...=7.\overline{487}$

Converting it into fraction 

If $x=7.478478...\text{          (1)}$

Then $1000x=7478.478478...\text{          (2)}$

Subtract equations $(2)-(1)$

$ 1000x=7478.478478... $

$  \underline{-\text{      }x=\text{      }7.478478...} $

$ \text{  }999x=7471 $

Now, $999x=7471$

$\Rightarrow x=\frac{7471}{999}$

i.e. $7.\overline{478}=\frac{7471}{999}$

Thus $7.478478...$ is a rational number.

v. $1.101001000100001...$

Ans: Here,  $1.101001000100001...$ is a non-terminating and non-recurring decimal number and also it cannot be represented as a fraction. Thus we can say that $1.101001000100001...$ is an irrational number.

3. Rationalize the denominator of the following:

(i) $\frac{1}{\sqrt{7}}$

Ans: In order to rationalize the denominator, we multiply and divide $\frac{1}{\sqrt{7}}$ by $\sqrt{7}$

$\frac{1}{\sqrt{7}}\times \frac{\sqrt{7}}{\sqrt{7}}=\frac{\sqrt{7}}{7}$

Rationalizing the denominator of  $\frac{1}{\sqrt{7}}$ produces $\frac{\sqrt{7}}{7}$.

ii. $\frac{1}{\sqrt{7}-\sqrt{6}}$

Ans: In order to rationalize the denominator, we multiply and divide $\frac{1}{\sqrt{7}-\sqrt{6}}$ by $\sqrt{7}+\sqrt{6}$

$\frac{1}{\sqrt{7}-\sqrt{6}}\times \frac{\sqrt{7}+\sqrt{6}}{\sqrt{7}+\sqrt{6}}=\frac{\sqrt{7}+\sqrt{6}}{\left( \sqrt{7}-\sqrt{6} \right)\left( \sqrt{7}+\sqrt{6} \right)}$

Using the identity - \[(a+b)(a-b)={{a}^{2}}-{{b}^{2}}\]

$=\frac{\sqrt{7}+\sqrt{6}}{{{\left( \sqrt{7} \right)}^{2}}-{{\left( \sqrt{6} \right)}^{2}}}$

$=\frac{\sqrt{7}+\sqrt{6}}{7-6}$

$=\frac{\sqrt{7}+\sqrt{6}}{1}$

$\Rightarrow \frac{1}{\sqrt{7}-\sqrt{6}}=\sqrt{7}+\sqrt{6}$

Rationalizing the denominator of  $\frac{1}{\sqrt{7}-\sqrt{6}}$ produces $\sqrt{7}+\sqrt{6}$.

iii. $\frac{1}{\sqrt{5}+\sqrt{2}}$

Ans: In order to rationalize the denominator, we multiply and divide $\frac{1}{\sqrt{5}+\sqrt{2}}$ by $\sqrt{5}-\sqrt{2}$

$\frac{1}{\sqrt{5}+\sqrt{2}}\times \frac{\sqrt{5}-\sqrt{2}}{\sqrt{5}-\sqrt{2}}=\frac{\sqrt{5}-\sqrt{2}}{\left( \sqrt{5}+\sqrt{2} \right)\left( \sqrt{5}-\sqrt{2} \right)}$

$=\frac{\sqrt{5}-\sqrt{2}}{{{\left( \sqrt{5} \right)}^{2}}-{{\left( \sqrt{2} \right)}^{2}}}$

$=\frac{\sqrt{5}-\sqrt{2}}{5-2}$

$=\frac{\sqrt{5}-\sqrt{2}}{3}$

$\Rightarrow \frac{1}{\sqrt{5}+\sqrt{2}}=\frac{\sqrt{5}-\sqrt{2}}{3}$

Rationalizing the denominator of  $\frac{1}{\sqrt{5}+\sqrt{2}}$ produces $\frac{\sqrt{5}-\sqrt{2}}{3}$.

iv. $\frac{1}{\sqrt{7}-2}$

Ans: In order to rationalize the denominator, we multiply and divide $\frac{1}{\sqrt{7}-2}$ by $\sqrt{7}+2$

$\frac{1}{\sqrt{7}-2}\times \frac{\sqrt{7}+2}{\sqrt{7}+2}=\frac{\sqrt{7}+2}{\left( \sqrt{7}-2 \right)\left( \sqrt{7}+2 \right)}$

$=\frac{\sqrt{7}+2}{{{\left( \sqrt{7} \right)}^{2}}-{{\left( 2 \right)}^{2}}}$

$=\frac{\sqrt{7}+2}{7-4}$

$=\frac{\sqrt{7}+2}{3}$

$\Rightarrow \frac{1}{\sqrt{7}+2}=\frac{\sqrt{7}+2}{3}$

Rationalizing the denominator of  $\frac{1}{\sqrt{7}-2}$ produces $\frac{\sqrt{7}+2}{3}$.

Long Answer Questions (5 Marks)

It can be seen that performing further divisions will produce a reminder of $3$ periodically, after every six divisions.

Thus, $\frac{329}{400}=s0.8225$ - this is a terminating decimal.

4. If $\sqrt{5}=2.236$ and $\sqrt{3}=1.732$. Find the value of $\frac{2}{\sqrt{5}+\sqrt{3}}+\frac{7}{\sqrt{5}-\sqrt{3}}$.

Ans: It is given that – 

$\sqrt{5}=2.236$

$\sqrt{3}=1.732$

Now, $\frac{2}{\sqrt{5}+\sqrt{3}}+\frac{7}{\sqrt{5}-\sqrt{3}}$

$\frac{2}{\sqrt{5}+\sqrt{3}}+\frac{7}{\sqrt{5}-\sqrt{3}}=\left[ \frac{2}{\left( \sqrt{5}+\sqrt{3} \right)}\times \frac{\left( \sqrt{5}-\sqrt{3} \right)}{\left( \sqrt{5}-\sqrt{3} \right)} \right]+\left[ \frac{7}{\left( \sqrt{5}-\sqrt{3} \right)}\times \frac{\left( \sqrt{5}+\sqrt{3} \right)}{\left( \sqrt{5}+\sqrt{3} \right)} \right]$

$=\left[ \frac{2\left( \sqrt{5}-\sqrt{3} \right)}{\left( \sqrt{5}+\sqrt{3} \right)\left( \sqrt{5}-\sqrt{3} \right)} \right]+\left[ \frac{7\left( \sqrt{5}+\sqrt{3} \right)}{\left( \sqrt{5}-\sqrt{3} \right)\left( \sqrt{5}+\sqrt{3} \right)} \right]$

$=\left[ \frac{\left( 2\sqrt{5}-2\sqrt{3} \right)+\left( 7\sqrt{5}+7\sqrt{3} \right)}{\left( \sqrt{5}+\sqrt{3} \right)\left( \sqrt{5}-\sqrt{3} \right)} \right]$

$=\left[ \frac{2\sqrt{5}-2\sqrt{3}+7\sqrt{5}+7\sqrt{3}}{{{\left( \sqrt{5} \right)}^{2}}-{{\left( \sqrt{3} \right)}^{2}}} \right]$

$=\left[ \frac{(2+7)\sqrt{5}+(7-2)\sqrt{3}}{5-3} \right]$

$=\left[ \frac{9\sqrt{5}+5\sqrt{3}}{2} \right]$

Since, $\sqrt{5}=2.236$ and $\sqrt{3}=1.732$

$=\left[ \frac{(9\times 2.236)+(5\times 1.732)}{2} \right]$

$=\left[ \frac{20.124+8.66}{2} \right]$

$=\left[ \frac{28.784}{2} \right]$

Thus, $\frac{2}{\sqrt{5}+\sqrt{3}}+\frac{7}{\sqrt{5}-\sqrt{3}}=14.392$

5. Find the value of $\frac{3}{\sqrt{5}+\sqrt{2}}+\frac{7}{\sqrt{5}-\sqrt{2}}$, if $\sqrt{5}=2.236$ and $\sqrt{2}=1.414$.

$\sqrt{2}=1.414$

Now, $\frac{3}{\sqrt{5}+\sqrt{2}}+\frac{7}{\sqrt{5}-\sqrt{2}}$

$\frac{3}{\sqrt{5}+\sqrt{2}}+\frac{7}{\sqrt{5}-\sqrt{2}}=\left[ \frac{3}{\left( \sqrt{5}+\sqrt{2} \right)}\times \frac{\left( \sqrt{5}-\sqrt{2} \right)}{\left( \sqrt{5}-\sqrt{2} \right)} \right]+\left[ \frac{7}{\left( \sqrt{5}-\sqrt{2} \right)}\times \frac{\left( \sqrt{5}+\sqrt{2} \right)}{\left( \sqrt{5}+\sqrt{2} \right)} \right]$

$=\left[ \frac{3\left( \sqrt{5}-\sqrt{2} \right)}{\left( \sqrt{5}+\sqrt{2} \right)\left( \sqrt{5}-\sqrt{2} \right)} \right]+\left[ \frac{7\left( \sqrt{5}+\sqrt{2} \right)}{\left( \sqrt{5}-\sqrt{2} \right)\left( \sqrt{5}+\sqrt{2} \right)} \right]$

$=\left[ \frac{\left( 3\sqrt{5}-3\sqrt{2} \right)+\left( 7\sqrt{5}+7\sqrt{2} \right)}{\left( \sqrt{5}+\sqrt{2} \right)\left( \sqrt{5}-\sqrt{2} \right)} \right]$

$=\left[ \frac{3\sqrt{5}-3\sqrt{2}+7\sqrt{5}+7\sqrt{2}}{{{\left( \sqrt{5} \right)}^{2}}-{{\left( \sqrt{2} \right)}^{2}}} \right]$

$=\left[ \frac{(3+7)\sqrt{5}+(7-3)\sqrt{2}}{5-2} \right]$

$=\left[ \frac{10\sqrt{5}+4\sqrt{2}}{3} \right]$

Since, $\sqrt{5}=2.236$ and $\sqrt{2}=1.414$

$=\left[ \frac{(10\times 2.236)+(4\times 1.414)}{3} \right]$

$=\left[ \frac{22.36+5.656}{3} \right]$

$=\left[ \frac{28.016}{3} \right]$

Thus, $\frac{3}{\sqrt{5}+\sqrt{2}}+\frac{7}{\sqrt{5}-\sqrt{2}}=\frac{28.016}{3}$

6. Simplify $\frac{2+\sqrt{5}}{2-\sqrt{5}}+\frac{2-\sqrt{5}}{2+\sqrt{5}}$

Ans: $\frac{2+\sqrt{5}}{2-\sqrt{5}}+\frac{2-\sqrt{5}}{2+\sqrt{5}}$

\[\frac{2+\sqrt{5}}{2-\sqrt{5}}+\frac{2-\sqrt{5}}{2+\sqrt{5}}=\left[ \frac{2+\sqrt{5}}{2-\sqrt{5}}\times \frac{\left( 2+\sqrt{5} \right)}{\left( 2+\sqrt{5} \right)} \right]+\left[ \frac{2-\sqrt{5}}{2+\sqrt{5}}\times \frac{\left( 2-\sqrt{5} \right)}{\left( 2-\sqrt{5} \right)} \right]\]

\[=\left[ \frac{\left( 2+\sqrt{5} \right)\left( 2+\sqrt{5} \right)}{\left( 2-\sqrt{5} \right)\left( 2+\sqrt{5} \right)} \right]+\left[ \frac{\left( 2-\sqrt{5} \right)\left( 2-\sqrt{5} \right)}{\left( 2+\sqrt{5} \right)\left( 2-\sqrt{5} \right)} \right]\]

\[=\left[ \frac{{{\left( 2+\sqrt{5} \right)}^{2}}+{{\left( 2-\sqrt{5} \right)}^{2}}}{\left( 2-\sqrt{5} \right)\left( 2+\sqrt{5} \right)} \right]\]

Using the identities –

\[(a+b)(a-b)={{a}^{2}}-{{b}^{2}}\]

\[{{(a+b)}^{2}}={{a}^{2}}+{{b}^{2}}+2ab\]

\[{{(a-b)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab\]

\[=\left[ \frac{\left( {{\left( 2 \right)}^{2}}+{{\left( \sqrt{5} \right)}^{2}}+\left( 2\times 2\times \sqrt{5} \right) \right)+\left( {{\left( 2 \right)}^{2}}+{{\left( \sqrt{5} \right)}^{2}}-\left( 2\times 2\times \sqrt{5} \right) \right)}{{{\left( 2 \right)}^{2}}-{{\left( \sqrt{5} \right)}^{2}}} \right]\]

\[=\left[ \frac{\left( 4+5+\left( 4\sqrt{5} \right) \right)+\left( 4+5-\left( 4\sqrt{5} \right) \right)}{4-5} \right]\]

$=\left[ \frac{9+9}{-1} \right]$

$=\left[ \frac{18}{-1} \right]$

Thus, $\frac{2+\sqrt{5}}{2-\sqrt{5}}+\frac{2-\sqrt{5}}{2+\sqrt{5}}=\left( -18 \right)$

7. Find a and b, if $\frac{3-\sqrt{6}}{3+2\sqrt{6}}=a\sqrt{6}-b$

Ans: $\frac{3-\sqrt{6}}{3+2\sqrt{6}}=a\sqrt{6}-b$

Here, 

$LHS=\frac{3-\sqrt{6}}{3+2\sqrt{6}}$

$RHS=a\sqrt{6}-b$

Start by rationalizing the denominator in LHS

In order to rationalize the denominator, we multiply and divide $\frac{3-\sqrt{6}}{3+2\sqrt{6}}$ by $3+2\sqrt{6}$

$\frac{3-\sqrt{6}}{3+2\sqrt{6}}\times \frac{3-2\sqrt{6}}{3-2\sqrt{6}}=\frac{\left( 3-\sqrt{6} \right)\left( 3-2\sqrt{6} \right)}{\left( 3+2\sqrt{6} \right)\left( 3-2\sqrt{6} \right)}$

$=\frac{\left( 3\times 3 \right)-\left( 3\times 2\sqrt{6} \right)-\left( \sqrt{6}\times 3 \right)+\left( \sqrt{6}\times 2\sqrt{6} \right)}{{{\left( 3 \right)}^{2}}-{{\left( 2\sqrt{6} \right)}^{2}}}$

$=\frac{\left( 9 \right)-\left( 6\sqrt{6} \right)-\left( 3\sqrt{6} \right)+\left( 12 \right)}{9-24}$

$=\frac{\left( 21 \right)-\left( 9\sqrt{6} \right)}{-15}$

$=\frac{\left( 21 \right)}{-15}-\frac{\left( 9\sqrt{6} \right)}{-15}$

They are all divisible by $3$

$=-\frac{7}{5}+\frac{\left( 3\sqrt{6} \right)}{5}$

Thus, $LHS=\frac{3}{5}\sqrt{6}-\frac{7}{5}$

Comparing with RHS, we get – 

Thus, 

$a=\frac{3}{5}$

$b=\frac{7}{5}$

Important Questions for Class 9 Maths Chapter 1 - Free PDF Download

Class 9 is like beginning to your academics career, which is right before board 10th. Thus students need to be very serious regarding their studies during preparation. No matter what we learn in class 9, it is important to clarify your concepts better. Hence, clearing Number System concepts will help students further apply in electronics physics and higher maths. Thus it is better to build a good base in mathematics with these Important Questions Maths Class 9 Chapter 1.

Vedantu provides a free PDF to download for Class 9 Chapter 1 Important Questions such that students can prepare well according to the CBSE syllabus. CBSE is strict to its pattern and follows the same throughout the question paper set. Students need to understand these guidelines and find solutions with a proper explanation. This free PDF online will surely help students master their concepts and build a Number System base. This PDF covers all the important concepts in the form of question example to learn how to implement them during exams. Thus PDF proves to be magical for those who are weak in mathematics as they also get solutions to the concepts covered in the back exercise.

Number System Class 9 Important Questions

Before you begin practising Class 9 Chapter 1 Maths Important Questions, you need to know the different topics and subtopics to cover in the chapter. Chapter 1 of Mathematics Class 9 covers a total of 6 exercises with a small introduction of the number system, number lines, defining real numbers, natural numbers, whole numbers, rational, and irrational numbers. Also, students become familiar with the concepts of addition, subtraction, division, and multiplication of the real numbers. The last topic in the chapter will be covering the law of exponents in the real numbers.

Below are the mentioned section-wise topics and concepts that a student to prepare through important questions.

Exercise 1.1

Under exercise 1.1, students will become familiar with the basic understanding of rational and irrational numbers. There is also a revision on whole numbers, real number, integers, and natural numbers and definition. They will even know how to represent a number in the form of p/q, where q is not equal to 0.

Exercise 1.2

Further moving to in-depth study about rational and irrational numbers, there are questions on justification with true and false. Also, students become familiar with the concept of representing rational and irrational numbers on the number line. A new concept of constructing a square root spiral comes in exercise 1.2.

Exercise 1.3

Here the student will know how to represent fractions into decimal form and find if it is terminating or non-terminating. Thus the concepts of terminating and non-terminating fractions will further help to identify it is a rational or irrational number.

Exercise 1.4

A new concept of representing decimal expansion on the number line is introduced through exercise 1.4 mathematics class 9. Here students will learn about magnifying the number to the maximum requirement and representing it on the number line. These decimal places can be either terminating or non-terminating. Hence there are two different concepts in number line representation of decimal expansions.

Exercise 1.5

Now comes the basic calculations of different rational and irrational numbers. It includes addition, multiplication, subtraction, and division of the rational and irrational numbers. Questions will be based on such concepts, and thus you have to simplify the statement accordingly. Also, students become familiar with the concept of rationalising.

Exercise 1.6

Here students will learn to solve questions based with a number having power in fractional form. Also, it might cover the basic addition and subtraction of powers for in-depth conceptual and extra knowledge.

These are the six exercises which will be covered under Chapter 1 Maths Class 9 Important Questions. Hence students can prepare questions according to the concepts discussed above.

Chapter 1 Maths Class 9 Important Questions

According to the syllabus mentioned above exercise-wise, below are some important questions covered to let students prepare well for important questions for class 9 maths number system. These exercise-wise solutions will let students master each concept in detail. Below are some of the questions that are usually picked to set question paper as prepared by CBSE.

State if zero is a rational number. Justify your statement by representing it in p/q where q is not equal to 0 and p and q are both integers.

Find 5 different rational numbers between 5 and 6. Mention each step in detail.

Find out 5 different rational numbers between 12/11 and 10/11.

Justify your statement for the following terms stating true or false.

Rational numbers are real.

A number line having representation in the form of √m has m as a natural number.

A real number is always an irrational number.

Check if true or false. Square roots of all positive numbers will be irrational. Explain your answer statement with the help of an example.

Try to represent √5 on the number line.

Represent the following in the form of decimal expansion:

(i) 36/100  (ii) 1/11  (iii) 4⅛  (iv) 3/13  (v) 2/11  (vi) 329/400

Turn 2/7, 13/7, 4/7, 5/7, 6/7

into decimal expansions without actually doing any long division calculations. Here 1/7= 0.142857.

Express the following as fractional form p/q where q is not 0.

(i) \[0.\overline{6}\]

(ii) \[0.4 \overline{7}\]

(iii) \[0. \overline{001}\]

Represent 2.675 on the number line with number line magnification.

How will you visualise 6.2626…... on the number line up to 4 decimal places?

State if the numbers are rational or irrational.

(i) \[2 - \sqrt{5}\]  (ii)  \[(3 + \sqrt{23}) - \sqrt{23}\]  (iii) \[\frac{2\sqrt{7}}{7\sqrt{7}}\]  (iv) \[\frac{1}{\sqrt{2}}\]  (v) \[2 \pi\]

Simplify the following terms:

(i) \[(3 + \sqrt{3}) ( 2 + \sqrt{2})\] (ii) \[(3 + \sqrt{3}) (3 + \sqrt{3})\]

(iii) \[(\sqrt{5} + \sqrt{2})^{2}\] (iv)\[(\sqrt{5} - \sqrt{2})(\sqrt{5} + \sqrt{2})\]

Rationalise the following terms with their denominators:

(i) \[\frac{1}{7}\] (ii) \[\frac{1}{\sqrt{7} - \sqrt{6}}\] (iii) \[\frac{1}{\sqrt{5} + \sqrt{2}}\] (iv) \[\frac{1}{\sqrt{7} - 2}\]

(i) \[64^{1}{2}\] (ii) \[32^{1}{5}\] (iii) \[125^{1}{3}\]

Class 9 Maths Chapter 1 Extra Questions

Find three rational numbers between $\frac{1}{3}$ and $\frac{1}{2}$. 

Express 0.4323232 in the form of  $\frac{a}{b}$ where a and b are integers and b 0.

Simplify and find the value of $(729)^{1/6}$ .

Rationalise the denominator 1 9 + 5 + 6 .

Find 6 rational numbers between 4 and 6.

Simplify $\sqrt[3]{2}$+$\sqrt[4]{3}$ and $\sqrt{5}+\sqrt{2}$ .

Locate $\sqrt{5}$ on the number line.

Visualise the representation of 4.26 on the number line upto 3 decimal places.

Is 2 - 5   a rational number or irrational number?

Convert 0.45 into rational numbers.

Benefits of Important Questions for Class 9 Maths Number System

Number System Class 9 Important Questions PDF is prepared by Vedantu experts and is free of cost. Students can also schedule additional problems to prepare in-depth to clarify their concepts. These questions turn to be magical for those weak in mathematics or do not show interest in it. The questions are prepared precisely accordingly to CBSE guidelines for their question paper pattern such that students need not search them anywhere else.

Below are the mentioned reasons why students should refer to the Important Question of Maths Class 9 Chapter 1:

Students are free to access these important questions PDF. They need not pay for any study material on Vedantu website.

These Number System Class 9 Important Questions are helpful during exams and help students clarify their concepts of homework questions.

These crucial questions are available in PDF format, which can be easily downloaded through the website. Thus students need not unnecessarily waste their precious time in finding solutions to problems.

Students can print these PDF questions and solutions, which reduces the stress of preparing through soft copies.

All the questions and solutions to the questions are prepared according to CBSE guidelines. Thus it will help students to know question paper pattern.

There is a total of 100 marks for the Class 9 Mathematics paper where 20 marks are for internal assessment, and rest 80 is for the written exam. The marks weightage for Chapter 1 Maths Class 9 is 8 out of 80. Rest 72 marks are for rest of the syllabus of Class 9 Mathematics.

There are a total of 26 sums to be solved according to NCERT book for Chapter 1 Of Class 9 Maths in its six exercises. However, there are other Class 9 Maths Chapter 1 Important Questions prepared by the experts and solutions to each of them provided. Thus, students can build a good base in mathematics through this PDF of important questions available with Vedantu for free. According to exercise-wise, some questions describe different questions and situations that students generally encounter while sitting in the exam. Thus students need to struggle to find essential concepts in the chapter and solutions to each of them.

Important Related Links for CBSE Class 9 

FAQs on CBSE Class 9 Maths Important Questions for Chapter 1 - Number System

1. What number of questions are there in each exercise of Chapter 1 of Class 9 Maths?

Real numbers are used in the first chapter of Class 9 Mathematics. There are a total of six workouts. In Chapter 1, students will learn about several real number concepts. There are four questions in Exercise 1.1, four questions in Exercise 1.2, nine questions in Exercise 1.3, two questions in Exercise 1.4, five questions in Exercise 1.5, and three questions in Exercise 1.6. Students must rehearse all NCERT problems offered by Vedantu in order to understand Chapter 1 of Class 9 maths.

2. Is Chapter 1 of Class 9 Maths difficult to solve?

Students of Class 9 should understand the concepts of real numbers given in Chapter 1 of Class 9 Maths. It is not difficult to solve if students understand the basic concepts of real numbers. Students can take help from the NCERT solutions Class 9 Maths Chapter 1 given at Vedantu app and website. All concepts related to the real numbers are explained in a simple way for quick understanding of the students. 

3. Why are Class 9 Maths NCERT Solutions of Chapter 1 important?

Students should rehearse Class 9 Mathematics NCERT Answers for Chapter 1 to comprehend and practise real-world questions. The NCERT Answers are essential since students may face similar questions in their examinations. With the aid of these questions, students may simply tackle the actual numbers problems in the exam. Students may access complete NCERT Answers for Class 9 Mathematics Chapter 1 for free on the Vedantu platform.

4. What are five rational numbers between ⅖ and ⅗?

Students can find five or more rational numbers between the two given rational numbers easily. They can follow the given steps to find five rational numbers between ⅖ and ⅗. We have to multiply the numerator and denominator of the given rational numbers with the same number.

⅖ x 6/6 = 12/30

⅗ x 6/6= 18/30

Now, we can write five rational numbers between 12/30 and 18/30. Thus, the five rational numbers are 13/30, 14/30, 15/30, 16/30, 17/30.

5. What are the main topics covered in Chapter 1 of Class 9 Maths?

In Chapter 1 of Class 9 Mathematics, students will study about rational and irrational numbers. Students will learn about irrational numbers, how to represent real numbers on a number line, how to express real numbers in decimal form, different operations on real numbers, and real-world exponent rules. To comprehend the various principles of rational numbers in Class 9 Chapter 1, students should practise all NCERT problems offered in the textbook.

CBSE Class 9 Maths Important Questions

Cbse study materials.

NCERT Solutions for Class 9 Maths Chapter 1 Number Systems

Ncert solutions for class 9 maths chapter 1 number systems| pdf download.

• Exercise 1.1 Chapter 1 Class 9 Maths NCERT Solutions
• Exercise 1.2 Chapter 1 Class 9 Maths NCERT Solutions
• Exercise 1.3 Chapter 1 Class 9 Maths NCERT Solutions
• Exercise 1.4 Chapter 1 Class 9 Maths NCERT Solutions
• Exercise 1.5 Chapter 1 Class 9 Maths NCERT Solutions
• Exercise 1.6 Chapter 1 Class 9 Maths NCERT Solutions

NCERT Solutions for Class 9 Maths Chapters:

Why we should solve ncert solutions for chapter 1 number systems class 9, which three integers are equal to their own cube roots, find the sum of  (3√3 +7√2) and (√3 - 5√2)., how can i download pdf of chapter 1 number systems class 9 ncert solutions, contact form.

• NCERT Solutions
• NCERT Class 9
• NCERT 9 Maths
• Chapter 1: Number Systems
• Exercise 1.1

NCERT Solutions for class 9 Maths Chapter 1 - Number Systems Exercise 1.1

NCERT Solutions Class 9 Maths Chapter 1 Number Systems Exercise 1.1 are provided here. Our subject experts have prepared the NCERT Maths solutions for Class 9 chapter-wise so that it helps students to solve problems easily while using it as a reference. They also focus on creating solutions for these exercises in such a way that it is easy to understand for the students.

The first exercise in Number Systems Exercise 1.1 is the introduction. They provide a detailed and stepwise explanation of each answer to the questions given in the exercises in the NCERT textbook for Class 9. The NCERT Solutions are always prepared by following NCERT guidelines so that it covers the whole syllabus accordingly. These are very helpful in scoring well in CBSE examinations.

NCERT Solutions for Class 9 Maths Chapter 1- Number Systems Exercise 1.1

carouselExampleControls111

Previous Next

Exercise 1.2 Solutions 4 Questions (3 long and 1 short)

Exercise 1.3 Solutions 9 Questions (9 long)

Exercise 1.4 Solutions 2 Questions (2 long)

Exercise 1.5 Solutions 5 Questions (4 long and 1 short)

Exercise 1.6 Solutions 3 Questions (3 long)

Access Answers to Maths NCERT Class 9 Chapter 1 – Number Systems Exercise 1.1

1. Is zero a rational number? Can you write it in the form p/q where p and q are integers and q ≠ 0?

We know that a number is said to be rational if it can be written in the form p/q , where p and q are integers and q ≠ 0.

Taking the case of ‘0’,

Zero can be written in the form 0/1, 0/2, 0/3 … as well as , 0/1, 0/2, 0/3 ..

Since it satisfies the necessary condition, we can conclude that 0 can be written in the p/q form, where q can either be positive or negative number.

Hence, 0 is a rational number.

2. Find six rational numbers between 3 and 4.

There are infinite rational numbers between 3 and 4.

As we have to find 6 rational numbers between 3 and 4, we will multiply both the numbers, 3 and 4, with 6+1 = 7 (or any number greater than 6)

i.e., 3 × (7/7) = 21/7

and, 4 × (7/7) = 28/7. The numbers between 21/7 and 28/7 will be rational and will fall between 3 and 4.

Hence, 22/7, 23/7, 24/7, 25/7, 26/7, 27/7 are the 6 rational numbers between 3 and 4.

3. Find five rational numbers between 3/5 and 4/5.

There are infinite rational numbers between 3/5 and 4/5.

To find out 5 rational numbers between 3/5 and 4/5, we will multiply both the numbers 3/5 and 4/5

with 5+1=6 (or any number greater than 5)

i.e., (3/5) × (6/6) = 18/30

and, (4/5) × (6/6) = 24/30

The numbers between18/30 and 24/30 will be rational and will fall between 3/5 and 4/5.

Hence, 19/30, 20/30, 21/30, 22/30, 23/30 are the 5 rational numbers between 3/5 and 4/5

4. State whether the following statements are true or false. Give reasons for your answers.

(i) Every natural number is a whole number.

Natural numbers- Numbers starting from 1 to infinity (without fractions or decimals)

i.e., Natural numbers= 1,2,3,4…

Whole numbers- Numbers starting from 0 to infinity (without fractions or decimals)

i.e., Whole numbers= 0,1,2,3…

Or, we can say that whole numbers have all the elements of natural numbers and zero.

Every natural number is a whole number; however, every whole number is not a natural number.

(ii) Every integer is a whole number.

Integers- Integers are set of numbers that contain positive, negative and 0; excluding fractional and decimal numbers.

i.e., integers= {…-4,-3,-2,-1,0,1,2,3,4…}

i.e., Whole numbers= 0,1,2,3….

Hence, we can say that integers include whole numbers as well as negative numbers.

Every whole number is an integer; however, every integer is not a whole number.

(iii) Every rational number is a whole number.

Rational numbers- All numbers in the form p/q, where p and q are integers and q≠0.

i.e., Rational numbers = 0, 19/30 , 2, 9/-3, -12/7…

All whole numbers are rational; however, all rational numbers are not whole numbers.

NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Exercise 1.1 is the first exercise of Chapter 1 of Class 9 Maths. This exercise explains how to find rational numbers between two given numbers.

Key Features of NCERT Solutions for Class 9 Maths Chapter 1 – Number Systems Exercise 1.1

• These NCERT Solutions help you solve and revise all questions of Exercise 1.1.
• After going through the stepwise solutions given by our subject expert teachers, you will be able to score more marks.
• It follows NCERT guidelines which help in preparing the students accordingly.
• It contains all the important questions from the examination point of view.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.