progression in maths problem solving

Arithmetic Progression

An arithmetic progression (AP) is a sequence where the differences between every two consecutive terms are the same. For example, the sequence 2, 6, 10, 14, … is an arithmetic progression (AP) because it follows a pattern where each number is obtained by adding 4 to the previous term. A real-life example of an AP is the sequence formed by the annual income of an employee whose income increases by a fixed amount of $5000 every year.

In this article, we will explore the concept of arithmetic progression, the AP formulas to find its n th term, common difference, and the sum of n terms of an AP. We will solve various examples based on the arithmetic progression formula for a better understanding of the concept.

What is Arithmetic Progression?

An arithmetic progression (AP) is a sequence of numbers where the differences between every two consecutive terms are the same. In this progression, each term, except the first term, is obtained by adding a fixed number to its previous term. This fixed number is known as the common difference and is denoted by 'd'. The first term of an arithmetic progression is usually denoted by 'a' or 'a 1 '.

For example, 1, 5, 9, 13, 17, 21, 25, 29, 33, ... is an arithmetic progression as the differences between every two consecutive terms are the same (as 4). i.e., 5 - 1 = 9 - 5 = 13 - 9 = 17 - 13 = 21 - 17 = 25 - 21 = 29 - 25 = 33 - 29 = ... = 4. We can also notice that every term (except the first term) of this AP is obtained by adding 4 to its previous term. In this arithmetic progression:

• a = 1 (the first term)
• d = 4 (the "common difference" between terms)

Thus, an arithmetic progression, in general, can be written as: {a, a + d, a + 2d, a + 3d, ... }.

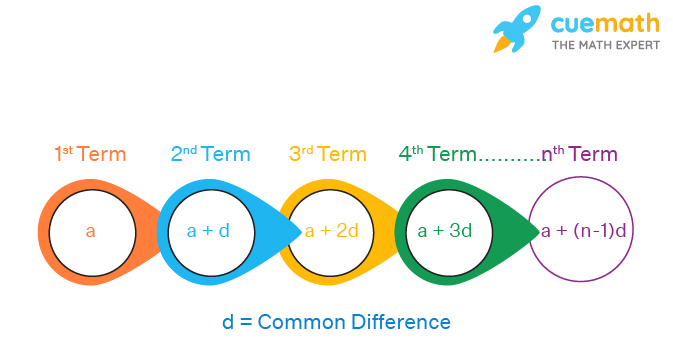
In the above example we have: {a, a + d, a + 2d, a + 3d, ... } = {1, 1 + 4, 1 + 2 × 4, 1 + 3 × 4, ... } = {1, 5, 9, 13, ... }

Arithmetic Progression Formula (AP Formulas)

For the first term 'a' of an AP and common difference 'd', given below is a list of arithmetic progression formulas that are commonly used to solve various problems related to AP:

• Common difference of an AP: d = a 2 - a 1 = a 3 - a 2 = a 4 - a 3 = ... = a n - a n-1
• n th term of an AP: a n = a + (n - 1)d
• Sum of n terms of an AP: S n = n/2 (2a + (n - 1) d) = n/2 (a + l), where l is the last term of the arithmetic progression.

The following image comprehends all AP formulas.

Common Terms Used in Arithmetic Progression

From now on, we will abbreviate arithmetic progression as AP. An AP generally is shown as follows: a 1 , a 2 , a 3 , . . . It involves the following terminology.

First Term of Arithmetic Progression:

As the name suggests, the first term of an AP is the first number of the progression. It is usually represented by a 1 (or) a. For example, in the sequence 6, 13, 20, 27, 34, . . . . the first term is 6. i.e., a 1 = 6 (or) a = 6.

Common Difference of Arithmetic Progression:

We know that an AP is a sequence where each term, except the first term, is obtained by adding a fixed number to its previous term. Here, the “fixed number” is called the “ common difference ” and is denoted by 'd' i.e., if the first term is a 1 , then: the second term is a 1 + d, the third term is a 1 + d + d = a 1 + 2d, and the fourth term is a 1 + 2d + d= a 1 + 3d and so on. For example, in the sequence 6, 13, 20, 27, 34,. . . , each term, except the first term, is obtained by the addition of 7 to its previous term. Thus, the common difference is, d=7. In general, the common difference is the difference between every two successive terms of an AP. Thus, the formula for calculating the common difference of an AP is: d = a n - a n-1 .

Here are some AP examples with their first term and common difference.

• 6, 13, 20, 27, 34, . . . . is an AP with the first term 6 and common difference 7.
• 91, 81, 71, 61, 51, . . . . is an AP with the first term 91 and common difference -10.
• π, 2π, 3π, 4π, 5π,… is an AP with the first term π and common difference π.
• -√3, −2√3, −3√3, −4√3, −5√3,… is an AP with the first term -√3 and common difference -√3.

Nth Term of Arithmetic Progression

The general term (or) n th term of an AP whose first term is 'a' and the common difference is 'd' is given by the formula a n = a + (n - 1) d. For example, to find the general term (or) n th term of the progression 6, 13, 20, 27, 34,. . . ., we substitute the first term, a 1 = 6, and the common difference, d = 7 in the formula for the n th term formula. Then we get, a n = a + (n - 1) d = 6 + (n - 1) 7 = 6 + 7n - 7 = 7n -1. Thus, the general term (or) n th term of this AP is: a n = 7n - 1. But what is the use of finding the general term of an AP? Let us see.

Use of AP Formula for General Term

We know that to find a term, we can add 'd' to its previous term. For example, if we have to find the 6 th term of 6, 13, 20, 27, 34, . . ., we can just add d = 7 to the 5 th term which is 34. Then 6 th term = 5 th term + 7 = 34 + 7 = 41. But what if we have to find the 102 nd term? Isn’t it difficult to calculate it manually? In this case, we can just substitute n = 102 (and also a = 6 and d = 7 in the formula of the n th term of an AP). Then we get:

a n = a + (n - 1) d

a 102 = 6 + (102 - 1) 7 = 6 + (101) 7 = 713

Therefore, the 102 nd term of the given AP 6, 13, 20, 27, 34, .... is 713. Thus, the general term (or) n th term of an AP is referred to as the arithmetic sequence explicit formula and can be used to find any term of the AP without finding its previous term.

The following table shows some AP examples and the first term, the common difference, and the general term in each case.

Sum of Arithmetic Progression

Consider an arithmetic progression (AP) whose first term is a 1 (or) a and the common difference is d.

• The sum of first n terms of an arithmetic progression when the n th term is NOT known is S n = (n/2) [2a + (n - 1) d]
• The sum of first n terms of an arithmetic progression when the n th term(a n ) is known is S n = n/2[a 1 + a n ]

Example: Mr. Kevin earns $400,000 per annum and his salary increases by $50,000 per annum. Then how much does he earn at the end of the first 3 years?

Solution: The amount earned by Mr. Kevin for the first year is, a = 4,00,000. The increment per annum is, d = 50,000. We have to calculate his earnings in the 3 years. So n = 3.

Substituting these values in the AP sum formula,

S n = n/2 [2a + (n - 1) d]

S n = 3/2(2(400000) + (3 - 1)(50000))

= 3/2 (800000 + 100000)

= 3/2 (900000)

He earned $1,350,000 in 3 years.

We can get the same answer by general thinking also as follows: The amount earned in 3 years = 400000 + 450000 + 500000 = 1350000. This could be calculated manually as n is a smaller value. But the above formulas are useful when n is a larger value.

Derivation of AP Sum Formula

Let us consider the first n terms of an arithmetic progression a 1 , a 1 + d, a 1 + 2d, ...., a 1 + (n - 1) d. Assume that the sum of these n terms is S n . Then

S n = a 1 + (a 1 + d) + (a 1 + 2d) + … + [a 1 + (n–1)d].

We can also start with the n th term and successively subtract the common difference, so,

S n = a n + (a n – d) + (a n – 2d) + … + [a n – (n–1)d].

Thus the sum of the arithmetic progression could be found in either of the ways. However, on adding those two equations together, we get

S n = a 1 + (a 1 + d) + (a 1 + 2d) + … + [a 1 + (n–1)d]

S n = a n + (a n – d) + (a n – 2d) + … + [a n – (n–1)d]

_________________________________________

2S n = (a 1 + a n ) + (a 1 + a n ) + (a 1 + a n ) + … + (a 1 + a n ).

____________________________________________

Notice all the d terms are cancelled out. So,

2S n = n (a 1 + a n )

⇒ S n = [n(a 1 + a n )]/2 --- (1)

By substituting a n = a 1 + (n – 1)d into the last formula, we have

S n = n/2 [a 1 + a 1 + (n – 1)d] ...Simplifying

S n = n/2 [2a 1 + (n – 1)d] --- (2)

These two formulas (1) and (2) help us to find the sum of an arithmetic series quickly.

Differences Between Arithmetic Progression and Geometric Progression

The following table explains the differences between arithmetic and geometric progression :

Important Notes on Arithmetic Progression:

• An AP is a list of numbers in which each term is obtained by adding a fixed number to the preceding number.
• a is represented as the first term, d is a common difference, a n as the n th term, and n as the number of terms.
• In general, AP can be represented as a, a + d, a + 2d, a + 3d, ...
• The n th term of an AP can be obtained by a n = a + (n − 1)d
• The sum of an AP can be obtained by s n = n/2 [2a + (n − 1) d]
• The graph of an AP is a straight line with the slope as the common difference.
• The common difference doesn't need to be positive always. For example, in the progression, 16, 8, 0, −8, −16, ... the common difference is negative (d = 8 - 16 = 0 - 8 = -8 - 0 = -16 - (-8) =... = -8).

☛ Related Articles:

• Arithmetic Sequence Calculator
• Sum of Arithmetic Sequence Calculator
• Sequence Calculator

Cuemath is one of the world's leading math learning platforms that offers LIVE 1-to-1 online math classes for grades K-12 . Our mission is to transform the way children learn math, to help them excel in school and competitive exams. Our expert tutors conduct 2 or more live classes per week, at a pace that matches the child's learning needs.

Arithmetic Progression Examples

Example 1: Find the general term of the arithmetic progression -3, -(1/2), 2…

The given progression is -3, -(1/2),2…

Here, the first term is a = -3, and the common difference is, d = -(1/2) - (-3) = -(1/2) + 3 = 5/2

By AP formulas , the general term of an AP is calculated by the formula:

a n = -3 + (n - 1) 5/2

= -3 + (5/2)n - 5/2

= 5n/2 - 11/2

Therefore, the general term of the given AP is:

Answer: a n = 5n/2 - 11/2

Example 2: Which term of the AP 3, 8, 13, 18,... is 78?

The given progression is 3,8,13,18,...

Here the first term is a = 3, and the common difference is, d = 8 - 3= 13 - 8 = ... = 5

Let us assume that the n th term is,

Substitute all these values in the general term of an arithmetic progression:

a n = a+(n - 1)d

78 = 3 +(n - 1)5

78 = 3 + 5n - 5

78 = 5n - 2

Answer: ∴ 78 is the 16 th term.

Example 3: Find the sum of the first 5 terms of the arithmetic progression whose first term is 3 and 5 th term is 11.

Solution: We have a 1 = a = 3 and a 5 = 11 and n = 5.

Using the AP formula for the sum of n terms, we have

S n = (n/2) (a + a n )

⇒ S 5 = (5/2) (3 + 11)

= (5/2) × 14

Answer: The required sum of the first 5 terms is 35.

go to slide go to slide go to slide

Book a Free Trial Class

Practice Questions on Arithmetic Progression

go to slide go to slide

FAQs on Arithmetic Progression

What is the meaning of arithmetic progression in maths.

A sequence of numbers where each term (other than the first term) is obtained by adding a fixed number to its previous term is called an arithmetic progression (A.P.). For example, is 3, 6, 9, 12, 15, 18, 21, … is an A.P. In simple words, we can say that an arithmetic progression is a sequence of numbers where the difference between each consecutive term is the same.

What is AP formula?

Here are the AP formulas corresponding to the AP a, a + d, a + 2d, a + 3d, . . . a + (n - 1)d:

• The formula to find the n th term is: a n = a + (n – 1) × d
• The formula to find the sum of n terms is S n = n/2 [2a + (n − 1) × d]

What are the Explicit Formula and Recursive Formula of AP?

For an AP a, a + d, a + 2d, ...

• the explicit formula to find the n th term is, a n = a + (n - 1) d
• the recursive formula to find the n th term is, a n = a n - 1 + d

How to Find the Sum of Arithmetic Progression?

To find the sum of arithmetic progression , we have to know the first term (a), the number of terms(n), and the common difference (d) between consecutive terms. Then substitute the values in the formula S n = n/2[2a + (n − 1) × d].

How to Find Number of Terms in Arithmetic Progression?

The number of terms in an arithmetic progression can be simply found by the division of the difference between the last and first terms by the common difference, and then adding 1.

What is the Sum of N Terms of the Arithmetic Progression Formula?

The sum of first n terms of an arithmetic progression can be calculated using one of the following two formulas:

• S n = n/2 [2a + (n - 1)d]
• S n = n/2 [a 1 + a n ].

How to Find Common Difference in Arithmetic Progression?

The common difference is the difference between every two consecutive terms in an arithmetic progression. Therefore, you can say that the formula to find the common difference of an arithmetic sequence is: d = a n - a n - 1 , where a n is the n th term in the progression, and a n - 1 is the previous term.

How to Find First Term in Arithmetic Progression?

If we know ‘d'(common difference) and any term (n th term) in the progression then we can find ‘a' (first term). If 5 th term is 10 and d = 2, then a 5 = a + 4d; 10 = a + 4(2); 10 = a + 8; a = 2.

What is the Difference Between Arithmetic Series and Arithmetic Progression?

Arithmetic progression is a progression in which the difference between every two consecutive terms is a constant whereas an arithmetic series is the sum of the elements of Arithmetic Progression.

What are the Types of Progressions in Maths?

There are three types of progressions in Maths. They are:

• Arithmetic Progression (AP)
• Geometric Progression (GP)
• Harmonic Progression (HP)

How do you Solve Arithmetic Progression Problems?

The following formulas help to solve arithmetic progression problems:

• Common difference of an AP: d = a n - a n-1 .
• Sum of n terms of an AP: S n = n/2 (2a + (n - 1)d)

Where is Arithmetic Progression Used?

A real-life application of arithmetic progression is seen when you take a taxi. Once you ride a taxi you will be charged an initial rate and then a per-mile or per-kilometre charge. This shows an arithmetic progression that for every kilometre you will be charged a certain fixed (constant) rate plus the initial rate.

What is Infinite Arithmetic Progression?

When the number of terms in an AP is infinite, we call it an infinite arithmetic progression. For example, 2, 4, 6, 8, 10, ... is an infinite AP; etc. The sum of an infinite arithmetic progression doesn't exist.

What is Nth Term in Arithmetic Progression?

The 'n th ' term in an AP is a formula with 'n' in it which enables you to find any term of a progression without having to go up from one term to the next. 'n' stands for the term number so to find the 50 th term we would just substitute 50 in the formula a n = a+ (n - 1)d in place of 'n'.

How to Find d in Arithmetic Progression?

To find d in an arithmetic progression, we take the difference between any two consecutive terms of the AP. It is always a term minus its previous term. An alternative way to find the common difference is just to see how much each term is getting added to get the next term.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Class 10 (Old)

Course: class 10 (old)   >   unit 5.

• Arithmetic progression applied to divisibility
• Sequences word problem: growth pattern
• nth term word problems

Word problems: Sum to n terms of an arithmetic progression

• Your answer should be
• an integer, like 6 ‍  
• a simplified proper fraction, like 3 / 5 ‍  
• a simplified improper fraction, like 7 / 4 ‍  
• a mixed number, like 1   3 / 4 ‍  
• an exact decimal, like 0.75 ‍  
• a multiple of pi, like 12   pi ‍   or 2 / 3   pi ‍  

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.1: Introduction to Problem Solving

• Last updated
• Save as PDF
• Page ID 9821

• Michelle Manes
• University of Hawaii

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

The Common Core State Standards for Mathematics ( http://www.corestandards.org/Math/Practice ) identify eight “Mathematical Practices” — the kinds of expertise that all teachers should try to foster in their students, but they go far beyond any particular piece of mathematics content. They describe what mathematics is really about, and why it is so valuable for students to master. The very first Mathematical Practice is:

Make sense of problems and persevere in solving them.

Mathematically proficient students start by explaining to themselves the meaning of a problem and looking for entry points to its solution. They analyze givens, constraints, relationships, and goals. They make conjectures about the form and meaning of the solution and plan a solution pathway rather than simply jumping into a solution attempt. They consider analogous problems, and try special cases and simpler forms of the original problem in order to gain insight into its solution. They monitor and evaluate their progress and change course if necessary.

This chapter will help you develop these very important mathematical skills, so that you will be better prepared to help your future students develop them. Let’s start with solving a problem!

Draw curves connecting A to A, B to B, and C to C. Your curves cannot cross or even touch each other,they cannot cross through any of the lettered boxes, and they cannot go outside the large box or even touch it’s sides.

Think / Pair / Share

After you have worked on the problem on your own for a while, talk through your ideas with a partner (even if you have not solved it).

• What did you try?
• What makes this problem difficult?
• Can you change the problem slightly so that it would be easier to solve?

Problem Solving Strategy 1 (Wishful Thinking).

Do you wish something in the problem was different? Would it then be easier to solve the problem?

For example, what if ABC problem had a picture like this:

Can you solve this case and use it to help you solve the original case? Think about moving the boxes around once the lines are already drawn.

Here is one possible solution.

• Math Article

Arithmetic Progression

Arithmetic Progression (AP) is a sequence of numbers in order, in which the difference between any two consecutive numbers is a constant value. It is also called Arithmetic Sequence. For example, the series of natural numbers : 1, 2, 3, 4, 5, 6,… is an Arithmetic Progression, which has a common difference between two successive terms (say 1 and 2) equal to 1 (2 -1). Even in the case of odd numbers and even numbers, we can see the common difference between two successive terms will be equal to 2.

Check: Mathematics for Grade 11

If we observe in our regular lives, we come across Arithmetic progression quite often. For example, Roll numbers of students in a class, days in a week or months in a year. This pattern of series and sequences has been generalized in Maths as progressions.

What is Arithmetic Progression?

In mathematics, there are three different types of progressions. They are:

• Arithmetic Progression (AP)
• Geometric Progression (GP)
• Harmonic Progression (HP)

A progression is a special type of sequence for which it is possible to obtain a formula for the nth term.  The Arithmetic Progression is the most commonly used sequence in maths with easy to understand formulas. 

Definition 1: A mathematical sequence in which the difference between two consecutive terms is always a constant and it is abbreviated as AP.

Definition 2: An arithmetic sequence or progression is defined as a sequence of numbers in which for every pair of consecutive terms, the second number is obtained by adding a fixed number to the first one.

The fixed number that must be added to any term of an AP to get the next term is known as the common difference of the AP.  Now, let us consider the sequence, 1, 4, 7, 10, 13, 16,…

It is considered as an arithmetic sequence (progression) with a common difference 3. 

Notation in Arithmetic Progression

In AP, we will come across some main terms, which are denoted as:

• First term (a)
• Common difference (d)
• nth Term (a n )
• Sum of the first n terms (S n )

All three terms represent the property of Arithmetic Progression. We will learn more about these three properties in the next section.

First Term of AP

The AP can also be written in terms of common differences, as follows;

where  “a” is the first term of the progression. 

Common Difference in Arithmetic Progression

In this progression, for a given series, the terms used are the first term, the common difference and nth term. Suppose,  a 1 , a 2 , a 3 , ……………., a n is an AP, then;   the common difference “ d ” can be obtained as;

Where “d” is a common difference. It can be positive, negative or zero.

Also, check:

General Form of an AP

Consider an AP to be:  a 1 , a 2 , a 3 , ……………., a n

Arithmetic Progression Formulas

• The nth term of AP
• Sum of the first n terms

nth Term of an AP

The formula for finding the n-th term of an AP is:

a = First term

d = Common difference

n = number of terms

a n  = nth term

Example: Find the nth term of AP: 1, 2, 3, 4, 5….,  a n , if the number of terms are 15.

Solution: Given, AP: 1, 2, 3, 4, 5….,  a n

By the formula we know, a n = a+(n-1)d

First-term, a =1

Common difference, d=2-1 =1

Therefore, a n  = a 15 = 1+(15-1)1 = 1+14 = 15

Note:  The behaviour of the sequence depends on the value of a common difference.

• If the value of “d” is positive, then the member terms will grow towards positive infinity
• If the value of “d” is negative, then the member terms grow towards negative infinity

Types of AP

Finite AP: An AP containing a finite number of terms is called finite AP . A finite AP has a last term.

For example: 3,5,7,9,11,13,15,17,19,21

Infinite AP: An AP which does not have a finite number of terms is called infinite AP. Such APs do not have a last term.

For example: 5,10,15,20,25,30, 35,40,45………………  

Sum of N Terms of AP

For an AP, the sum of the first n terms can be calculated if the first term, common difference and the total terms are known. The formula for the arithmetic progression sum is explained below:

Consider an AP consisting “n” terms.

This is the AP sum formula to find the sum of n terms in series.

Proof:  Consider an AP consisting “n” terms having the sequence a, a + d, a + 2d, …………., a + (n – 1) × d

Sum of first n terms = a + (a + d) + (a + 2d) + ………. + [a + (n – 1) × d] ——————-(i)

Writing the terms in reverse order, we have:

S n = [a + (n – 1) × d] + [a + (n – 2) × d] + [a + (n – 3) × d] + ……. (a) ———–(ii)

Adding both the equations term wise, we have:

2S n = [2a + (n – 1) × d] + [2a + (n – 1) × d] + [2a + (n – 1) × d] + …………. + [2a + (n – 1) ×d] (n-terms)

2S n = n × [2a + (n – 1) × d]

S n = n/2[2a + (n − 1) × d]

Example: Let us take the example of adding natural numbers up to 15 numbers.

AP = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15

Given, a = 1, d = 2-1 = 1 and a n = 15

Now, by the formula we know;

Hence, the sum of the first 15 natural numbers is 120.

Sum of AP when the Last Term is Given

Formula to find the sum of AP when first and last terms are given as follows:

List of Arithmetic Progression Formulas

The list of formulas is given in a tabular form used in AP. These formulas are useful to solve problems based on the series and sequence concept.

Arithmetic Progressions Solved Examples

Below are the problems to find the nth term and the sum of the sequence, which are solved using AP sum formulas in detail. Go through them once and solve the practice problems to excel in your skills.

Example 1: Find the value of n, if a = 10, d = 5, a n  = 95.

Solution:  Given, a = 10, d = 5, a n = 95

From the formula of general term, we have:

a n = a + (n − 1) × d

95 = 10 + (n − 1) × 5

(n − 1) × 5 =  95 – 10 = 85

(n − 1) =  85/ 5

(n − 1) = 17

Example 2: Find the 20 th term for the given AP: 3, 5, 7, 9, ……

Solution:  Given, 

3, 5, 7, 9, ……

a = 3, d = 5 – 3 = 2, n = 20

a 20 = 3 + (20 − 1) × 2

a 20 = 3 + 38

Example 3: Find the sum of the first 30 multiples of 4.

The first 30 multiples of 4 are: 4, 8, 12, ….., 120

Here,  a = 4, n = 30, d = 4

S 30 = n/2 [2a + (n − 1) × d]

S 30 = 30/2[2 (4) + (30 − 1) × 4]

S 30 = 15[8 + 116]

S 30 = 1860

Practice Problems on AP

Find the below questions based on Arithmetic sequence formulas and solve them for good practice.

Question 1: Find the a n and 10th term of the progression: 3, 1, 17, 24, ……

Question 2: If a = 2, d = 3 and n = 90. Find a n    and S n .

Question 3: The 7th term and 10th terms of an AP are 12 and 25. Find the 12th term.

Frequently Asked Questions on Arithmetic Progression

What is the general form of arithmetic progression, what is arithmetic progression give an example., how to find the sum of arithmetic progression, what are the types of progressions in maths, what is the use of arithmetic progression.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Maths related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

Awsome information 👍👍👍👍

This app is just a awesome app and I am using this byjus tablet for about 3 years. Every information given by them is very important and easy to understand.

Can anyone help me please.

it’s very informative. Thanks byjus 😍

Very well compiled!!

Awesome information 👍

very very useful. Thanks

This infromation is very usefull to children.

The n the term of an an arithmetic progression is an=4n+5 then the 3rd term is

The n the term of an arithmetic progression is an=4n+5. For the 3rd term, n = 3. Therefore, a3 = 4(3) + 5= 12+5 = 17

Very good explanation with various series option.

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Mastery-Aligned Maths Tutoring

“The best thing has been the increase in confidence and tutors being there to deal with any misunderstandings straight away."

FREE daily maths challenges

A new KS2 maths challenge every day. Perfect as lesson starters - no prep required!

Fluency, Reasoning and Problem Solving: What This Looks Like In Every Maths Lesson

Neil Almond

Fluency reasoning and problem solving have been central to the new maths national curriculum for primary schools introduced in 2014. Here we look at how these three approaches or elements of maths can be interwoven in a child’s maths education through KS1 and KS2. We look at what fluency, reasoning and problem solving are, how to teach them, and how to know how a child is progressing in each – as well as what to do when they’re not, and what to avoid.

The hope is that this blog will help primary school teachers think carefully about their practice and the pedagogical choices they make around the teaching of reasoning and problem solving in particular.

Before we can think about what this would look like in practice however, we need to understand the background tothese terms.

What is fluency in maths?

Fluency in maths is a fairly broad concept. The basics of mathematical fluency – as defined by the KS1 / KS2 National Curriculum for maths – involve knowing key mathematical facts and being able to recall them quickly and accurately.

But true fluency in maths (at least up to Key Stage 2) means being able to apply the same skill to multiple contexts, and being able to choose the most appropriate method for a particular task.

Fluency in maths lessons means we teach the content using a range of representations, to ensure that all pupils understand and have sufficient time to practise what is taught.

Read more: How the best schools develop maths fluency at KS2 .

What is reasoning in maths?

Reasoning in maths is the process of applying logical thinking to a situation to derive the correct problem solving strategy for a given question, and using this method to develop and describe a solution.

Put more simply, mathematical reasoning is the bridge between fluency and problem solving. It allows pupils to use the former to accurately carry out the latter.

Read more: Developing maths reasoning at KS2: the mathematical skills required and how to teach them .

What is problem solving in maths?

It’s sometimes easier to start off with what problem solving is not. Problem solving is not necessarily just about answering word problems in maths. If a child already has a readily available method to solve this sort of problem, problem solving has not occurred. Problem solving in maths is finding a way to apply knowledge and skills you have to answer unfamiliar types of problems.

Read more: Maths problem solving: strategies and resources for primary school teachers .

We are all problem solvers

First off, problem solving should not be seen as something that some pupils can do and some cannot. Every single person is born with an innate level of problem-solving ability.

Early on as a species on this planet, we solved problems like recognising faces we know, protecting ourselves against other species, and as babies the problem of getting food (by crying relentlessly until we were fed).

All these scenarios are a form of what the evolutionary psychologist David Geary (1995) calls biologically primary knowledge. We have been solving these problems for millennia and they are so ingrained in our DNA that we learn them without any specific instruction.

Why then, if we have this innate ability, does actually teaching problem solving seem so hard?

Mathematical problem solving is a  learned skill

As you might have guessed, the domain of mathematics is far from innate. Maths doesn’t just happen to us; we need to learn it. It needs to be passed down from experts that have the knowledge to novices who do not.

This is what Geary calls biologically secondary knowledge. Solving problems (within the domain of maths) is a mixture of both primary and secondary knowledge.

The issue is that problem solving in domains that are classified as biologically secondary knowledge (like maths) can only be improved by practising elements of that domain.

So there is no generic problem-solving skill that can be taught in isolation and transferred to other areas.

This will have important ramifications for pedagogical choices, which I will go into more detail about later on in this blog.

The educationalist Dylan Wiliam had this to say on the matter: ‘for…problem solving, the idea that pupils can learn these skills in one context and apply them in another is essentially wrong.’ (Wiliam, 2018)So what is the best method of teaching problem solving to primary maths pupils?

The answer is that we teach them plenty of domain specific biological secondary knowledge – in this case maths. Our ability to successfully problem solve requires us to have a deep understanding of content and fluency of facts and mathematical procedures.

Here is what cognitive psychologist Daniel Willingham (2010) has to say:

‘Data from the last thirty years lead to a conclusion that is not scientifically challengeable: thinking well requires knowing facts, and that’s true not simply because you need something to think about.

The very processes that teachers care about most—critical thinking processes such as reasoning and problem solving—are intimately intertwined with factual knowledge that is stored in long-term memory (not just found in the environment).’

Colin Foster (2019), a reader in Mathematics Education in the Mathematics Education Centre at Loughborough University, says, ‘I think of fluency and mathematical reasoning, not as ends in themselves, but as means to support pupils in the most important goal of all: solving problems.’

In that paper he produces this pyramid:

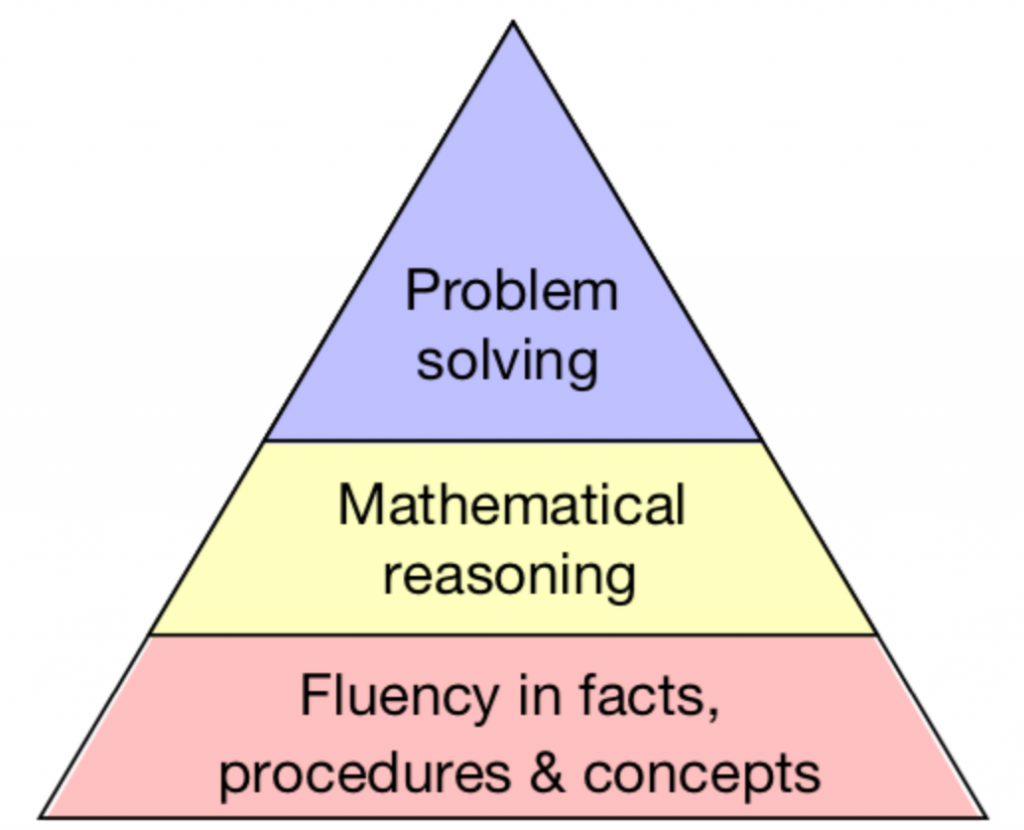
This is important for two reasons:

1)    It splits up reasoning skills and problem solving into two different entities

2)    It demonstrates that fluency is not something to be rushed through to get to the ‘problem solving’ stage but is rather the foundation of problem solving.

In my own work I adapt this model and turn it into a cone shape, as education seems to have a problem with pyramids and gross misinterpretation of them (think Bloom’s taxonomy).

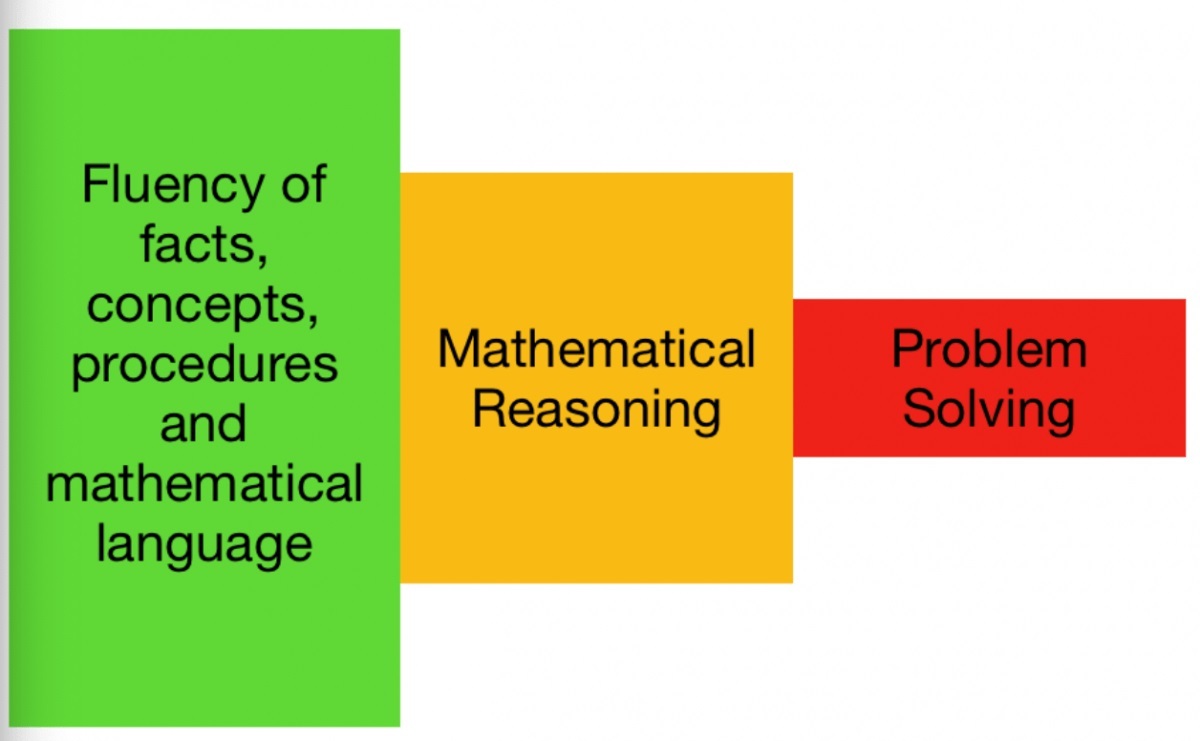
Notice how we need plenty of fluency of facts, concepts, procedures and mathematical language.

Having this fluency will help with improving logical reasoning skills, which will then lend themselves to solving mathematical problems – but only if it is truly learnt and there is systematic retrieval of this information carefully planned across the curriculum.

Performance vs learning: what to avoid when teaching fluency, reasoning, and problem solving

I mean to make no sweeping generalisation here; this was my experience both at university when training and from working in schools.

At some point schools become obsessed with the ridiculous notion of ‘accelerated progress’. I have heard it used in all manner of educational contexts while training and being a teacher. ‘You will need to show ‘ accelerated progress in maths ’ in this lesson,’ ‘Ofsted will be looking for ‘accelerated progress’ etc.

I have no doubt that all of this came from a good place and from those wanting the best possible outcomes – but it is misguided.

I remember being told that we needed to get pupils onto the problem solving questions as soon as possible to demonstrate this mystical ‘accelerated progress’.

This makes sense; you have a group of pupils and you have taken them from not knowing something to working out pretty sophisticated 2-step or multi-step word problems within an hour. How is that not ‘accelerated progress?’

This was a frequent feature of my lessons up until last academic year: teach a mathematical procedure; get the pupils to do about 10 of them in their books; mark these and if the majority were correct, model some reasoning/problem solving questions from the same content as the fluency content; set the pupils some reasoning and word problem questions and that was it.

I wondered if I was the only one who had been taught this while at university so I did a quick poll on Twitter and found that was not the case.

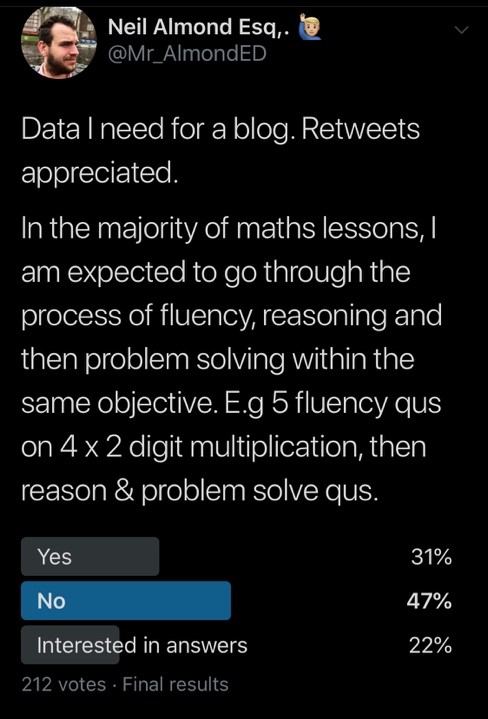
I know these numbers won’t be big enough for a representative sample but it still shows that others are familiar with this approach.

The issue with the lesson framework I mentioned above is that it does not take into account ‘performance vs learning.’

What IS performance vs learning’?

The premise is that performance in a lesson is not a good proxy for learning.

Yes, those pupils were performing well after I had modeled a mathematical procedure for them, and managed to get questions correct.

But if problem solving depends on a deep knowledge of mathematics, this approach to lesson structure is going to be very ineffective.

As mentioned earlier, the reasoning and problem solving questions were based on the same maths content as the fluency exercises, making it more likely that pupils would solve problems correctly whether they fully understood them or not.

Chances are that all they’d need to do is find the numbers in the questions and use the same method they used in the fluency section to get their answers – not exactly high level problem solving skills.

Teaching to “cover the curriculum” hinders development of strong problem solving skills.

This is one of my worries with ‘maths mastery schemes’ that block content so that, in some circumstances, it is not looked at again until the following year (and with new objectives).

The pressure for teachers to ‘get through the curriculum’ results in many opportunities to revisit content just not happening in the classroom.

Pupils are unintentionally forced to skip ahead in the fluency, reasoning, problem solving chain without proper consolidation of the earlier processes.

As David Didau (2019) puts it, ‘When novices face a problem for which they do not have a conveniently stored solution, they have to rely on the costlier means-end analysis.

This is likely to lead to cognitive overload because it involves trying to work through and hold in mind multiple possible solutions.

It’s a bit like trying to juggle five objects at once without previous practice. Solving problems is an inefficient way to get better at problem solving.’

Third Space's Ultimate Guide to Problem Solving Techniques

Download our free guide to problem solving techniques and get a head start on ensuring learning over performance!

Fluency and reasoning – Best practice in a lesson, a unit, and a term

By now I hope you have realised that when it comes to problem solving, fluency is king. As such we should look to mastery maths based teaching to ensure that the fluency that pupils need is there.

The answer to what fluency looks like will obviously depend on many factors, including the content being taught and the year group you find yourself teaching.

But we should not consider rushing them on to problem solving or logical reasoning in the early stages of this new content as it has not been learnt, only performed.

I would say that in the early stages of learning, content that requires the end goal of being fluent should take up the majority of lesson time – approximately 60%. The rest of the time should be spent rehearsing and retrieving other knowledge that is at risk of being forgotten about.

This blog on mental maths strategies pupils should learn in each year group is a good place to start when thinking about the core aspects of fluency that pupils should achieve.

Little and often is a good mantra when we think about fluency, particularly when revisiting the key mathematical skills of number bond fluency or multiplication fluency. So when it comes to what fluency could look like throughout the day, consider all the opportunities to get pupils practicing.

They could chant multiplications when transitioning. If a lesson in another subject has finished earlier than expected, use that time to quiz pupils on number bonds. Have fluency exercises as part of the morning work.

Read more: How to teach times tables KS1 and KS2 for total recall .

What about best practice over a longer period?

Thinking about what fluency could look like across a unit of work would again depend on the unit itself.

Look at this unit below from a popular scheme of work.

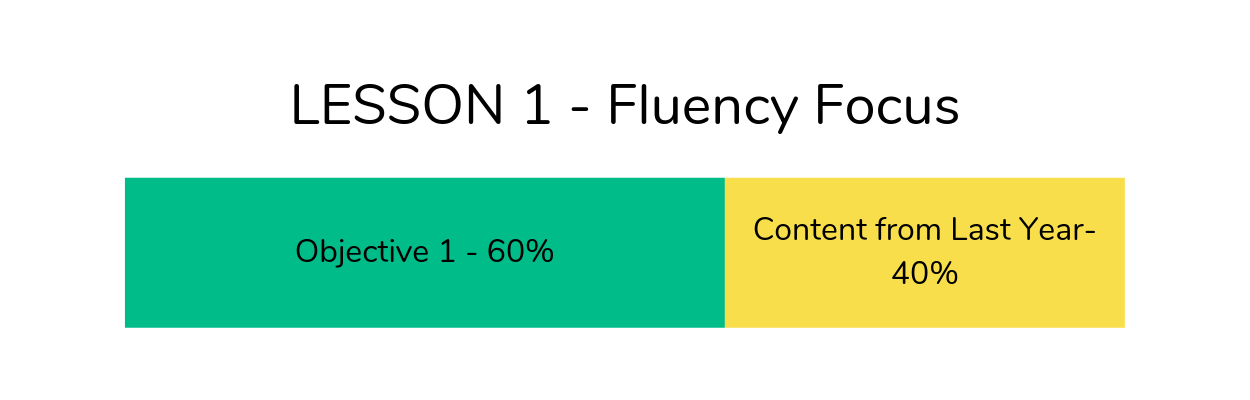
They recommend 20 days to cover 9 objectives. One of these specifically mentions problem solving so I will forget about that one at the moment – so that gives 8 objectives.

I would recommend that the fluency of this unit look something like this:

LY = Last Year

This type of structure is heavily borrowed from Mark McCourt’s phased learning idea from his book ‘Teaching for Mastery.’

This should not be seen as something set in stone; it would greatly depend on the needs of the class in front of you. But it gives an idea of what fluency could look like across a unit of lessons – though not necessarily all maths lessons.

When we think about a term, we can draw on similar ideas to the one above except that your lessons could also pull on content from previous units from that term.

So lesson one may focus 60% on the new unit and 40% on what was learnt in the previous unit.

The structure could then follow a similar pattern to the one above.

Best practice for problem solving in a lesson, a unit, and a term 

When an adult first learns something new, we cannot solve a problem with it straight away. We need to become familiar with the idea and practise before we can make connections, reason and problem solve with it.

The same is true for pupils. Indeed, it could take up to two years ‘between the mathematics a student can use in imitative exercises and that they have sufficiently absorbed and connected to use autonomously in non-routine problem solving.’ (Burkhardt, 2017).

Practise with facts that are secure

So when we plan for reasoning and problem solving, we need to be looking at content from 2 years ago to base these questions on.

Now given that much of the content of the KS2 SATs will come from years 5 and 6 it can be hard to stick to this two-year idea as pupils will need to solve problems with content that can be only weeks old to them.

But certainly in other year groups, the argument could be made that content should come from previous years.

You could get pupils in Year 4 to solve complicated place value problems with the numbers they should know from Year 2 or 3. This would lessen the cognitive load, freeing up valuable working memory so they can actually focus on solving the problems using content they are familiar with.

Read more: Cognitive load theory in the classroom

Increase complexity gradually.

Once they practise solving these types of problems, they can draw on this knowledge later when solving problems with more difficult numbers.

This is what Mark McCourt calls the ‘Behave’ phase. In his book he writes:

‘Many teachers find it an uncomfortable – perhaps even illogical – process to plan the ‘Behave’ phase as one that relates to much earlier learning rather than the new idea, but it is crucial to do so if we want to bring about optimal gains in learning, understanding and long term recall.’  (Mark McCourt, 2019)

This just shows the fallacy of ‘accelerated progress’; in the space of 20 minutes some teachers are taught to move pupils from fluency through to non-routine problem solving, or we are somehow not catering to the needs of the child.

When considering what problem solving lessons could look like, here’s an example structure based on the objectives above.

Fluency, Reasoning and Problem Solving should NOT be taught by rote 

It is important to reiterate that this is not something that should be set in stone. Key to getting the most out of this teaching for mastery approach is ensuring your pupils (across abilities) are interested and engaged in their work.

Depending on the previous attainment and abilities of the children in your class, you may find that a few have come across some of the mathematical ideas you have been teaching, and so they are able to problem solve effectively with these ideas.

Equally likely is encountering pupils on the opposite side of the spectrum, who may not have fully grasped the concept of place value and will need to go further back than 2 years and solve even simpler problems.

In order to have the greatest impact on class performance, you will have to account for these varying experiences in your lessons.

Read more: 

• Maths Mastery Toolkit : A Practical Guide To Mastery Teaching And Learning
• Year 6 Maths Reasoning Questions and Answers
• Get to Grips with Maths Problem Solving KS2
• Mixed Ability Teaching for Mastery: Classroom How To
• 21 Maths Challenges To Really Stretch Your More Able Pupils
• Maths Reasoning and Problem Solving CPD Powerpoint
• Why You Should Be Incorporating Stem Sentences Into Your Primary Maths Teaching

DO YOU HAVE STUDENTS WHO NEED MORE SUPPORT IN MATHS?

Every week Third Space Learning’s specialist online maths tutors support thousands of students across hundreds of schools with weekly online 1 to 1 maths lessons designed to plug gaps and boost progress.

Since 2013 these personalised one to 1 lessons have helped over 150,000 primary and secondary students become more confident, able mathematicians.

Learn how the programmes are aligned to maths mastery teaching or request a personalised quote for your school to speak to us about your school’s needs and how we can help.

Related articles

Maths Problem Solving: Engaging Your Students And Strengthening Their Mathematical Skills

Free Year 7 Maths Test With Answers And Mark Scheme: Mixed Topic Questions

What Is A Number Square? Explained For Primary School Teachers, Parents & Pupils

What Is Numicon? Explained For Primary School Teachers, Parents And Pupils

FREE Guide to Maths Mastery

All you need to know to successfully implement a mastery approach to mathematics in your primary school, at whatever stage of your journey.

Ideal for running staff meetings on mastery or sense checking your own approach to mastery.

Privacy Overview

• National Curriculum Resource Tool

Progression Maps for Key Stages 1 and 2

Progression maps.

The progression maps are structured using the topic headings as they appear in the National Curriculum

Each of the below categories has been divided into sub categories to illustrate progression in key areas.

All programmes of study statements are included and some appear twice. This is indicated in the text. This occurs where:

• The statement has central relevance to more than one sub category within a topic;
• The statement has central relevance to more than one mathematics topic. This is done to reflect the aims of the curriculum that pupils should make rich connections across mathematical ideas to develop fluency, mathematical reasoning and competence in solving increasingly sophisticated problems (Mathematics programmes of study: key stages 1 and 2 page 3). However the connections made are not intended to be exhaustive and teachers should seek to support pupils in making other connections.

Number and Place Value

Addition and subtraction, multiplication and division, fractions (including decimals and percentages), ratio and proportion, measurement, geometry - properties of shapes, geometry - position and direction, guidance notes.

The definitions in the glossary refer to the words and terms as they are used in the programmes of study. This document is based on an earlier publication Mathematics glossary for teachers in key stages 1 to 4 published by the Qualifications and Curriculum Authority in 2003. It is intended to be used alongside the 2014 National Curriculum for teachers to check the meaning of the terms.

Related Pages

Is there anything wrong with this page?

Subscribe to our newsletter

The NCETM is led and delivered by Tribal Education Services, with MEI as a key partner. Learn more about Tribal Education Services and what they do via the link to their website in 'About the NCETM'.

About this website

Stay connected.

Or search by topic

Number and algebra

• The Number System and Place Value
• Calculations and Numerical Methods
• Fractions, Decimals, Percentages, Ratio and Proportion
• Properties of Numbers
• Patterns, Sequences and Structure
• Algebraic expressions, equations and formulae
• Coordinates, Functions and Graphs

Geometry and measure

• Angles, Polygons, and Geometrical Proof
• 3D Geometry, Shape and Space
• Measuring and calculating with units
• Transformations and constructions
• Pythagoras and Trigonometry
• Vectors and Matrices

Probability and statistics

• Handling, Processing and Representing Data
• Probability

Working mathematically

• Thinking mathematically
• Mathematical mindsets
• Cross-curricular contexts
• Physical and digital manipulatives

For younger learners

• Early Years Foundation Stage

Advanced mathematics

• Decision Mathematics and Combinatorics
• Advanced Probability and Statistics

Fractions Unpacked - Progression in Fractions Through Problem Solving

These pictures show squares split into halves. Can you find other ways?

A Bowl of Fruit

Can you work out how many apples there are in this fruit bowl if you know what fraction there are?

Round the Dice Decimals 1

Use two dice to generate two numbers with one decimal place. What happens when you round these numbers to the nearest whole number?

Round the Dice Decimals 2

What happens when you round these numbers to the nearest whole number?

Andy's Marbles

Andy had a big bag of marbles but unfortunately the bottom of it split and all the marbles spilled out. Use the information to find out how many there were in the bag originally.

Spiralling Decimals

Take turns to place a decimal number on the spiral. Can you get three consecutive numbers?

Linked Chains

Can you find ways to make twenty-link chains from these smaller chains? This gives opportunities for different approaches.

Fraction Lengths

Can you find combinations of strips of paper which equal the length of the black strip? If the length of the black is 1, how could you write the sum of the strips?

Reset password New user? Sign up

Existing user? Log in

Geometric Progressions

Already have an account? Log in here.

Recommended Course

Algebra through puzzles.

Supercharge your algebraic intuition and problem solving skills!

• Shivam Jadhav
• Mahindra Jain
• Mohnish Chakravarti
• Kumar Saurav
• A Former Brilliant Member
• Rishik Jain
• David Kochergin
• pickle lamborghini
• Skanda Prasad
• Pranshu Gaba
• Marco Luca Sbodio
• Felipe Perestrelo
• Suyeon Khim
• Sam Solomon

A geometric progression (GP), also called a geometric sequence, is a sequence of numbers which differ from each other by a common ratio . For example, the sequence \(2, 4, 8, 16, \dots\) is a geometric sequence with common ratio \(2\).

We can find the common ratio of a GP by finding the ratio between any two adjacent terms.

The following sequence is a geometric progression with initial term \(10\) and common ratio \(3\):

\[\LARGE \color{blue}{10} \underbrace{\quad \quad }_{\times 3} \color{red}{30} \underbrace{\quad \quad }_{\times 3} \color{green}{90} \underbrace{\quad \quad }_{\times 3} \color{cyan}{270} \underbrace{\quad \quad }_{\times 3} \color{orangered}{810} \underbrace{\quad \quad }_{\times 3} \color{grey}{2430} \]

Describing Geometric Progressions

Sums of geometric progressions, sums of infinite geometric progressions, problem solving.

Important terminology

• Initial term: In a geometric progression, the first number is called the "initial term."
• Common ratio: The ratio between a term in the sequence and the term before it is called the "common ratio."

Recursive Formula

We can describe a geometric sequence with a recursive formula, which specifies how each term relates to the one before. Since in a geometric progression, each term is given by the product of the previous term and the common ratio, we can write a recursive description as follows:

\[ \text{Term} = \text{Previous term} \times \text{Common ratio}. \]

More concisely, with the common ratio \(r\), we have

\[a_n=a_{n-1} \times r.\]

Explicit Formula

While the recursive formula above allows us to describe the relationship between terms of the sequence, it is often helpful to be able to write an explicit description of the terms in the sequence, which would allow us to find any term.

If we know the initial term, the following terms are related to it by repeated multiplication of the common ratio. Thus, the explicit formula is

\[ \text{Term} = \text{Initial term} \times \underbrace{\text{Common ratio} \times \dots \times \text{Common ratio}}_{\text{Number of steps from the initial term}}. \]

Using exponents, we can write this with common ratio \(r\), as

\[a_n = a_1 \times r^{n-1}.\]

Note: It is sometimes easier to compute values in a geometric progression based on a term in the middle rather than the initial term. When we begin our calculations from the \(k^{\text{th}}\) term, the \(n^{\text{th}}\) term in the geometric progression is given by \[ a_n = a_k \times r ^ {n-k}.\]

Now let's work out some basic examples that can familiarize you with the above definitions.

What is the explicit formula for the geometric sequence \(4, 12, 36, 108, \dots?\) Reveal Answer The initial term is \(4\). Since each subsequent term is the product of the previous term and \(3\), the common ratio is \(3\). Thus the formula describing this sequence is \[ a_n = 4 \times 3^{n-1}.\ _\square\]

If the fourth term of a geometric progression with common ratio equal to half the initial term is \(32,\) what is the \(15^{\text{th}}\) term? Reveal Answer Let the initial term be \(a,\) and the common ratio \(r\). As stated in the problem, the \(4^{\text{th}} \) term is \(ar^{3} = 32\) and the initial term is \(a=2r\). Solving these two simultaneous equations gives \[2r^{4}=32 \implies r=2 \implies a=4.\] Hence, the \(15^{\text{th}}\) term is \[a_{15}=a \times r^{14}=4 \times 2^{14}=2^{16} . \ _\square\]

Which of the following is the explicit formula for the geometric progression

\[ 5, 10, 20, 40, \dots? \]

We sometimes want to find the sum of some terms of a geometric progression. When the number of terms we want to add is large, it can be difficult to add them all one at a time. The problem below illustrates a method that can be developed into a general technique:

Find the sum of the first \(10\) terms of the following geometric progression: \[3,\ 15,\ 75,\ 375,\ 1875,\, \ldots.\] Let the sum of the first \(10\) terms of the given series be \(A,\) then \[A=3+3 \cdot 5 +3 \cdot 5^2+ \cdots +3 \cdot 5^9. \qquad (1)\] Multiplying \(A\) by \(5,\) we get \[5A= 3 \cdot 5 +3 \cdot 5^2+3 \cdot 5^3+\cdots+3 \cdot 5^{10}. \qquad (2)\] Taking \((1)-(2)\) gives \[ \begin{array} { rllll} A&= 3+3 \cdot 5+3 \cdot 5^2&+\cdots+3 \cdot 5^{9} \\ 5A&= 0 +3\cdot 5+3 \cdot 5^2&+\cdots+3 \cdot 5^{9}&+3 \cdot 5^{10} \\ \hline A(1-5)& =3+0~\quad +0&+\cdots+0 &-3 \cdot 5^{10} \\ -4A&=3-3 \cdot 5^{10}\\\\ A&=\dfrac{3 \cdot 5^{10}-3}{4}. \ _\square \end{array}\]

In the example above, we multiplied the sum of the geometric progression by its common ratio and then subtracted the result from the original sum, finding that all the terms cancel out except the first and last ones. Now we can use the same approach to find the general formula for the sum.

For a geometric progression with initial term \( a\) and common ratio \(r,\) the sum of the first \(n\) terms is \[S_n = \begin{cases}\begin{array}{ll} a \cdot \left( \frac{ r^n -1 } { r - 1 } \right) && \text{for }r \neq 1 \\ a \cdot n && \text{for }r = 1.\end{array} \end{cases} \]

Suppose we wanted to add the first \(n\) terms of a geometric progression. If \( r = 1 \), then we have a constant sequence, and hence the sum is just \( n a \). Now, let's suppose that \( r \neq 1, \) then we would obtain \[ S_n = a + a \cdot r + a \cdot r^2 + \cdots + a \cdot r^{n-2} + a \cdot r ^ {n-1}. \qquad (1)\] Multiplying both sides by \(r\) gives \[ r S_n = a \cdot r + a \cdot r^2 + \cdots + a \cdot r^{n-1} + a \cdot r ^ {n}. \qquad (2)\] Taking \((1)-(2),\) we get \[ \begin{array} { rlllllllll} S_n&= a + a \cdot r& + a \cdot r^2& + \cdots + a \cdot r^{n-2}& + a \cdot r ^ {n-1} \\ r S_n& =0+a \cdot r & + a \cdot r^2 & + \cdots + a \cdot r^{n-2}& + a \cdot r ^ {n-1}& + a \cdot r^n \\ \hline S_n(1-r)& =a+0&+0&+\cdots+0& +0& - a \cdot r^{n} \\ (1-r) S_n &= a-a r^n. \end{array}\] Therefore, \[ S_n = a \times \left( \frac{ r^n - 1 } { r - 1 } \right) ~\text{for } r \neq 1 . \ _\square\]

What is the sum of the first \(10\) terms of a geometric progression with initial term \(2\) and common ratio \(3?\) Reveal Answer Applying the above formula for the sum of geometric progression terms, we have \[ 2 \times \frac{ 3^{10 } - 1 } { 3 - 1 } = 3^{10} - 1 = 59048. \ _\square\]

A girl puts \(1\) grain of rice in the first square of an 8 by 8 chess board. In the subsequent square, she puts twice that of the previous square, and she continues until she fills all the squares.

How many total grains does she need?

Find the sum of the geometric progression \(\frac{2}{3}, -1,\frac{3}{2},...\) up to \(7\) terms.

Now that we know how to find the sum of finitely many terms, let's move on to find the sum of infinitely many terms of a geometric progression. This is done in a similar way, and we do an example first.

Calculate the following geometric series: \[5+ \dfrac 53 +\dfrac 59 +\dfrac{5}{27}+\cdots.\] Let the given sum be \(S,\) then \[S=5+ \dfrac 53 +\dfrac 59 +\dfrac{5}{27}+\cdots. \qquad (1)\] Multiplying \(S\) by \(\frac 13\), we get \[\dfrac 13 S= \dfrac 53 +\dfrac 59 +\dfrac{5}{27}+\dfrac{5}{81}+\cdots. \qquad (2)\] Taking \((1)-(2)\) gives \[ \begin{array} {rlllllllll} S&=5+ \dfrac 53& +\dfrac 59& +\dfrac{5}{27}&+\cdots \\ \dfrac 13 S&=0+ \dfrac 53& +\dfrac 59& +\dfrac{5}{27}&+\dfrac{5}{81}&+\cdots \\ \hline S\left(1-\dfrac 13 \right)& =5+0&+0&+0&+0&+ \cdots \\ S \cdot \dfrac 23&=5\\ S&={\dfrac{15}{2}}. \ _\square \end{array}\]

Note that we're using the same trick of multiplying by the common ratio and subtracting! In fact, this trick can be used to find a general formula for the sum of the infinite terms of a geometric progression. Here we go:

For a geometric progression with initial term \( a \) and common ratio \(r\) satisfying \( |r| < 1 ,\) the sum of the infinite terms of the geometric progression is \[ S_{\infty} = \frac{ a } { 1-r }. \]

When \(-1 < r < 1\), as \(n\) becomes arbitrarily large, \(r^n\) tends to zero. Hence, taking the limit of the sequence , we get \[ S_\infty = \lim_{n \rightarrow \infty } S_n = \lim_{n \rightarrow \infty} \frac{ a ( 1 - r^n ) } { 1-r } = \frac{ a} { 1-r }. \ _\square \] Geometrical Proof : We can also think of this formula visually. If \(S\) is the sum of the series and the initial term is \(a\), we can construct a square and a triangle as follows: We can see that the large triangle and the inverted triangle on the left side of the square are similar. Therefore by similarity, \[\frac{S}{a} = \frac{a}{a-ar}.\] Solving for \(S\), we get \[S = \frac{a}{1-r}. \ _\square \]

After striking the floor, your tennis ball bounces to two-thirds of the height from which it has fallen. What is the total vertical distance it travels before coming to rest when it is dropped from a height of \(100 \text{ m}?\) Reveal Answer Let \(h\) be the height (in meters) from which the ball is dropped, and \(e\) a number such that \(0<e<1.\) Also, let \(S\) be the total vertical distance covered before the ball comes to rest. Then \[\begin{align} S&=h+2(eh)+2\big(e^2h\big)+2\big(e^3h\big)+2\big(e^4h\big)+\cdots \\ &=h +2eh\big(1+e+e^2+e^3+\cdots\big) \\ &=h+2eh \times \dfrac{1}{1-e} \qquad \qquad \qquad \qquad (\text{since } e<1) \\ &=\left( \dfrac{1+e}{1-e} \right) h. \end{align}\] Since we are given \(h=100\) and \(e=\frac23,\) \[S=\left( \dfrac{1+\frac 23}{1-\frac 23} \right) 100=500 \text{ (m)}. \ _\square\]

Find the sum of the geometric series \[5 - \frac{10}{3} + \frac{20}{9} - \frac{40}{27} +\cdots .\] Reveal Answer Observe that the given series is a geometric progression with initial term \(a= 5\) and common ratio \(r=\frac{-2}{3}.\) Then since \(-1<r<0,\) the series is convergent and we will use the formula for infinite sum \(S = \frac{a}{1-r}\) to evaluate the value of the given series. Hence \[S=\dfrac{5}{1-\left( \frac{-2}{3} \right) } = 3. \ _\square\]

As we are now familiar with the above concepts, let's try our hand at solving some problems below:

\[ \large \frac { 1 }{ { 2 }^{ 3 } } +\frac { 1 }{ { 2 }^{ 6 } } +\frac { 1 }{ { 2 }^{ 9 } } + \cdots = \, ? \]

If the first three terms of a geometric progression are given to be \( \sqrt2+1,1,\sqrt2-1, \) find the sum to infinity of all of its terms.

If the answer is in the form of \( \frac{a+b\sqrt c}d \) for positive integers \(a,b,c,\) and \(d\) with \(c\) square-free, find the minimum value of \(a+b+c+d\).

If each term of an infinite geometric progression is thrice the sum of the terms following it, then what is the common ratio of the geometric progression?

Cody has started running in a well-organized manner. He runs \(100 \text{ m}\) east, then turns left and runs another \(10 \text{ m}\) north, turns left and runs \(1 \text{ m},\) again turns left and runs \(0.1 \text{ m},\) and on the next turn \(0.01 \text{ m},\) and so on.

Assuming that Cody can run in this pattern infinitely, the displacement from his initial position can be written as \(\frac{a}{\sqrt{b}}\) with \(a\) and \(b\) being positive integers and \(b\) square-free.

What is the value of \( a \times b?\)

If an infinite GP of real numbers has second term \(x\) and sum \(4,\) where does \(x\) belong?

• Arithmetic Progressions
• Arithmetic and Geometric Progressions Problem Solving

Master concepts like these

Learn more in our Algebra through Puzzles course, built by experts for you.

Problem Loading...

Note Loading...

Set Loading...

Watch CBS News

Teens surprise math world with Pythagorean Theorem trigonometry proof | 60 Minutes

• Artificial Intelligence /

Google’s Circle to Search will help you with your math homework

Circle to search on android can now help students learn to solve mathematical word problems thanks to google’s new learnlm model..

By Umar Shakir , a news writer fond of the electric vehicle lifestyle and things that plug in via USB-C. He spent over 15 years in IT support before joining The Verge.

Share this story

Google is enhancing Android’s Circle to Search — the feature that lets you literally circle something on your Android phone’s screen to search it on Google — with a new ability to generate instructions on how to solve school math and physics problems .

Using an Android phone or tablet, students can now use Circle to Search to get AI assistance on mathematical word problems from their homework. The feature will help unpack the problem and list what the student needs to do to get the correct answer. According to Google, it won’t actually do the homework for you — only help you approach the problem.

Over the past year, the use of AI tools like ChatGPT has become a hot topic in the field of education, with plenty of concern over how students can and will use it to get work done quickly. Google, however, is explicitly positioning this as a feature to support education, potentially walking around some of the concerns about AI doing all of the work for students.

Later this year, Circle to Search will also gain the ability to solve complex math equations that involve formulas, diagrams, graphs, and more. Google is using LearnLM, its new AI model that’s fine-tuned for learning, to make the new Circle to Search abilities work.

Circle to Search first launched on  Samsung’s Galaxy S24 series in January and then on the Pixel 8 and 8 Pro later the same month. It’s one of the star new features of Android, and although iOS users can’t yet circle their math homework for help, anything is possible .

Lego Barad-dûr revealed: Sauron’s dark tower from The Lord of the Rings is $460

Google i/o 2024: everything announced, openai releases gpt-4o, a faster model that’s free for all chatgpt users, amazon web services ceo to step down, google i/o 2024: all the news from the developer conference regarding ai and more.

More from this stream Google I/O 2024: all the news from the developer conference regarding AI and more

Android apps will soon let you use your face to control your cursor, how to care for your ai., here’s sergey brin holding court with reporters at google i/o., google’s new learnlm ai model focuses on education.