problem solving measure and compare lesson 9.5

• Texas Go Math
• Big Ideas Math
• enVision Math
• EngageNY Math
• McGraw Hill My Math
• 180 Days of Math
• Math in Focus Answer Key
• Math Expressions Answer Key
• Privacy Policy

Go Math Grade 1 Chapter 9 Answer Key Pdf Measurement

Go Math Grade 1 Chapter 9 Answer Key Pdf: Primary School Go Math Grade 1 Chapter 9 Answer Key Measurement is designed by subject experts. Avail the handy preparation resources available here and get a good grip on the concepts. Download the First Grade HMH Go Math Answer Key Ch 9 Measurement for free and prepare from anywhere and anytime. Whether you are getting started or want to learn more Go Math Grade 1 Answer Key Chapter 9 Measurement is a great way to explore the curriculum.

Measurement Go Math Grade 1 Chapter 9 Answer Key Pdf

Refer to the HMH Go Math First Grade Ch 9 Measurement Solutions available to clear your queries. Practicing from the Go Math Grade 1 Chapter 9 Measurement you can understand the concepts clearly. In fact, you can learn the Problem Solving Approaches used here so that you can apply them to similar problems. Track your progress on the Topics of Go Math First Grade Measurement and Identify the Areas of Need.

Measurement

• Measurement Show What You Know – Page 510
• Measurement Vocabulary Builder – Page 511
• Measurement Game Measure UP! – Page 512
• Measurement Vocabulary Game – Page(512A-512D)

Lesson: 1 Order Length

• Lesson 9.1 Order Length – Page(513-518)
• Order Length Homework & Practice 9.1 – Page(517-518)

Lesson: 2 Indirect Measurement

• Lesson 9.2 Indirect Measurement – Page(519-524)
• Indirect Measurement Homework & Practice 9.2 – Page(523-524)

Lesson: 3 Use Nonstandard Units to Measure Length

• Lesson 9.3 Use Nonstandard Units to Measure Length – Page(525-530)
• Use Nonstandard Units to Measure Length Homework & Practice 9.3 – Page(529-530)

Lesson: 4 Make a Nonstandard Measuring Tool

• Lesson 9.4 Make a Nonstandard Measuring Tool – Page(531-536)
• Make a Nonstandard Measuring Tool Homework & Practice 9.4 – Page(535-536)

Lesson: 5 Problem Solving • Measure and Compare

• Lesson 9.5 Problem Solving • Measure and Compare – Page(537-542)
• Problem Solving • Measure and Compare Homework & Practice 9.5 – Page(541-542)

Mid-Chapter Checkpoint

• Measurement Mid-Chapter Checkpoint – Page 540

Lesson: 6 Time to the Hour

• Lesson 9.6 Time to the Hour – Page(543-548)
• Time to the Hour Homework & Practice 9.6 – Page(547-548)

Lesson: 7 Time to the Half Hour

• Lesson 9.7 Time to the Half Hour – Page(549-554)
• Time to the Half Hour Homework & Practice 9.7 – Page(553-554)

Lesson: 8 Tell Time to the Hour and Half Hour

• Lesson 9.8 Tell Time to the Hour and Half Hour – Page(555-560)
• Tell Time to the Hour and Half Hour Homework & Practice 9.8 – Page(559-560)

Lesson: 9 Practice Time to the Hour and Half Hour

• Lesson 9.9 Practice Time to the Hour and Half Hour – Page(561-566)
• Practice Time to the Hour and Half Hour Homework & Practice 9.9 – Page(565-566)
• Measurement Review/Test – Page(567-570)

Measurement Show What You Know

Measurement Vocabulary Builder

Understand Vocabulary Complete the sentences with the correct word. Question 1. A crayon is ______ than a marker. Answer: A crayon is shorter than a marker. Explanation: The length of the crayon is shorter when compared to marker based the lengths they are compared as longer or shorter.

Question 2. A toothbrush is _____ than a paper clip. Answer: A toothbrush is longer than a paper clip. Explanation : A toothbrush is longer when compared to a paper clip based the lengths they are compared as longer or shorter.

Measurement Game Measure UP!

• Your partner spins, moves, and takes that object.
• Compare the lengths of the two objects.

Measurement Vocabulary Game

• Follow these directions for the space where you land. White Space Read the math word or symbol. Tell its meaning. If you are correct, jump ahead to the next space with the same term. Green Space Follow the directions. If there are no directions, stay where you are.
• The first player to reach FINISH wins.
• If you land on one of these spaces: Blue Space Explain the math word or use it in a sentence. If your answer is correct, jump ahead to the next space with that word. Green Space Follow the directions in the space. If there are no directions, don’t move.

The Write Way Reflect Choose one idea. Draw and write about it.

• Julia has to measure an object. She does not have a ruler. Tell what Julia could do to solve her problem.
• Explain why it is important to learn how to tell time.

Lesson 9.1 Order Length

Essential Question How do you order objects by length?

Listen and Draw

MATHEMATICAL PRACTICES Compare the straw and the key. Which is longer? Which is shorter? Answer:

Model and Draw

Share and Show

On Your Own

MATHEMATICAL PRACTICE

Explanation : The Seventh line is shortest line and the Ninth line is longest line. So, the Eighth line should not be shortest nor longest so draw a line which is longer that shortest line and shorter than the longest line .

Problem Solving • Applications

TAKE HOME ACTIVITY • Show your child three different lengths of objects, such as three pencils or spoons. Ask him or her to order the objects from shortest to longest.

Order Length Homework & Practice 9.1

Lesson 9.2 Indirect Measurement

Essential Question How can you compare lengths of three objects to put them in order?

TAKE HOME ACTIVITY • Show your child the length of one object. Then show your child an object that is longer and an object that is shorter than the first object.

Indirect Measurement Homework & Practice 9.2

Spiral Review Question 2. What is the sum? Write the number. 42 + 20 = _____ Answer: 42 + 20 = 62 Explanation : When addend 20 is added to addend 42 we get the sum of 62 .

Lesson 9.3 Use Nonstandard Units to Measure Length

Essential Question How do you measure length using nonstandard units?

MATHEMATICAL PRACTICES Reasoning How do you draw the boat to be the right length? Answer:

Explanation : To Measure scissor we require 2 square object .

TAKE HOME ACTIVITY • Give your child paper clips or other small objects that are the same length. Have him or her estimate the lengths of objects around the house and then measure to check.

Use Nonstandard Units to Measure Length Homework & Practice 9.3

Question 3. Circle the number that is less. 51 50

Did tens or ones help you decide? tens ones

Lesson 9.4 Make a Nonstandard Measuring Tool

Essential Question How do you use a nonstandard measuring tool to measure length? Answer : Standard units are common units of measurement such as centimetres, grams and litres. Non-standard measurement units might include cups, cubes or sweets. For example: a child might be asked to measure the length of their table using their hand span. They would then record how many hand spans the table was and record this. They might then be asked to measure the length of a book.

TAKE HOME ACTIVITY • Have your child measure different objects around the house using a paper clip measuring tool.

Make a Nonstandard Measuring Tool Homework & Practice 9.4

Question 3. There are 12 books. 4 books are large. The rest are small. Write a number sentence that shows how to find the number of small books. ______ – ______ = ______ Answer: Number of books = 12 Number of large books = 4 Number of small books = 12 – 4 = 8 books

Lesson 9.5 Problem Solving • Measure and Compare

Essential Question How can acting it out help you solve measurement problems?

HOME CONNECTION • Have your child act out a measurement problem by finding the lengths of 3 objects and ordering them from shortest to longest.

TAKE HOME ACTIVITY • Have your child explain how he or she solved Exercise 4.

Problem Solving • Measure and Compare Homework & Practice 9.5

Spiral Review Question 2. What is the unknown number? Write the number. 4 + _____ = 13 Answer: 4 + ______ = 13 _______ = 13 – 4 = 9 So, the Unknown Number is 9

Go Math Grade 1 Chapter 9 Review Test Answer Key Question 3. Count by tens. What numbers are missing? Write the numbers. 17, 27, ____, ____, 57, 67 Answer: Count by tens : 17 , 27 , 37 , 47 , 57 , 67 Explanation : Count by tens means the every ten’s digit is increased by 1 from the previous ten’s value of the Number .

Measurement Mid-Chapter Checkpoint

Concepts and Skills

Lesson 9.6 Time to the Hour

Essential Question How do you tell time to the hour on a clock that has only an hour hand?

TAKE HOME ACTIVITY • Have your child describe what he or she did in this lesson.

Time to the Hour Homework & Practice 9.6

Spiral Review Question 3. What is the sum? Write the number. 40 + 30 = _____ Answer: 40 + 30 = 70

Question 4. What is the sum? Write the number 53 + 30 = ______ Answer: 53 + 30 = 83

Lesson 9.7 Time to the Half Hour

Essential Question How do you tell time to the half hour on a clock that has only an hour hand? Answer : To tell time to the half hour on a clock that an hour hand exactly halfway between the two numbers Example: To represent five and half an hour would be exactly here halfway between five and six .

MATHEMATICAL PRACTICES Reasoning Use before and after to describe the time shown on the middle clock. Answer:

TAKE HOME ACTIVITY • Say a time, such as half past 10:00. Ask your child to describe where the hour hand points at this time. Answer : half past 10 o’ clock Time is 10:30 Explanation: Half-past 10 is a short way of saying it’s half an hour (30 minutes) after 10:00. Here the short hand or hour hand points in between 11 and 10. so the Time is 10:30.

Time to the Half Hour Homework & Practice 9.7

Lesson 9.8 Tell Time to the Hour and Half Hour

Essential Question How are the minute hand and hour hand different for time to the hour and time to the half hour? Answer : Telling half hours Yes, at 1:30 the hour hand points exactly halfway between 1 and 2! The hour hand tells us a lot about the time! … The minute hand spins all the way around the clock every hour. It makes it easier to see if it’s 1:10, or 1:15, or even 1:12

MATHEMATICAL PRACTICES Use Tools Look at the top clock. Explain how you know which is the minute hand. Answer: The large hand on a clock that points to the minutes. It goes once around the clock every 60 minutes (one hour). Example: in the clock on the left, the minute hand is just past the “4”, and if you count the little marks from “12” it shows that it is 22 minutes past the hour.

Explanation: It is half past 3:00. The hour hand points between the 3 and the 4 . The minute hand points to the 6 .

Explanation: It is half past 7:00. The hour hand points between the 7 and the 8 . The minute hand points to the 6 .

TAKE HOME ACTIVITY • At times on the half hour, have your child show you the minute hand and the hour hand on a clock and tell what time it is.

Tell Time to the Hour and Half Hour Homework & Practice 9.8

Question 8. WRITE Draw a clock to show the time 1:30. Answer: Explanation: It is half past 1:00. The hour hand points between the 1 and the 2 . The minute hand points to the 6 . Explanation: It is half past 7:00. The hour hand points between the 7 and the 8 . The minute hand points to the 6 .

Spiral Review Question 3. What is the sum? Write the number. 48 + 20 = _____ Answer: 48 + 20 = 68 Explanation : Adding addend 48 and addend 20 we get sum 68 .

Lesson 9.9 Practice Time to the Hour and Half Hour

Essential Question How do you know whether to draw and write time to the hour or half hour? Answer : The short hand tells us the hour. The long hand tells us the minutes. When the long hand is pointing at the 6, it is half of the hour. Write in the time below each clock.

MATHEMATICAL PRACTICES Generalize Describe how you know which clock shows 1:30. Answer: The fifth clock Explanation : It is half past 1:00. The hour hand points between the 1 and the 2 . The minute hand points to the 6 .

TAKE HOME ACTIVITY • Show your child the time on a clock. Ask him or her what time it will be in 30 minutes

Practice Time to the Hour and Half Hour Homework & Practice 9.9

Problem Solving Solve. Question 4. Billy played outside for a half hour. Write how many minutes Billy played outside. _______ minutes Answer: Billy played outside for a half hour. half an hour = 30 minutes .

Spiral Review Question 2. What is the difference? Write the number. 80 – 30 = _____ Answer: 80 – 30 = 50

Measurement Review/Test

Final Words: We hope the given information is helpful for all the students of Grade 1. Get the step by step solutions of all the questions from HMH Go Math Grade 1 Answer Key Chapter 9 Measurement pdf.

Share this:

Leave a comment cancel reply.

You must be logged in to post a comment.

Chapter 9: Measurement

Chapter 9 Essential Question:

Chapter 9 objectives:.

• Order objects by length.
• Measure length using nonstandard units.
• Make a nonstandard measuring tool to measure length.
• Solve measurement problems using the strategy act it out.
• Write times to the hour and half hour shown on analog clocks.
• Tell times to the hour and half hour using analog and digital clocks.
• Use the hour hand to draw and write times on analog and digital clocks.

GO Math! is Online

iTools Primary

Interactive Student Edition-This is a great way to preview or review the math skills for the chapter!

• Lesson 9.1- Hands On: Order Length
• Lesson 9.2- Indirect Measurement
• Lesson 9.3- Hands On: Use Nonstandard Units to Measure Length
• Lesson 9.4- Hands On: Make and Nonstandard Measuring Tool
• Lesson 9.5- Problem Solving: Measure and Compare
• Lesson 9.6- Time to the Hour
• Lesson 9.7- Time to the Half Hour
• Lesson 9.8- Tell Time to the Hour and Half Hour
• Lesson 9.9- Practice Time to the Hour and Half Hour

Math On the Spot Videos-Cute videos that model problems within each lesson.

Animated Math Models-Practice some of your math skills with Curious George!

• Lesson 9.1 (Skill 39)- Compare Length
• Lesson 9.3 (Skill 40)-Use Nonstandard Units
• Lesson 9.6 (Skill 41)- Time to the Hour
• Lesson 9.7 (Skill 42)- Time to the Half Hour

Mega Math Games-Fun games that reinforce concepts taught within the chapter.

• Lesson 9.1- Shapes Ahoy, Made to Measure- Level C
• Lesson 9.2- Shapes Ahoy, Made to Measure- Level E
• Lesson 9.3, 9.4- Shapes Ahoy, Made to Measure- Level D
• Lesson 9.6, 9.8- Country Countdown, Clock a Doodle Doo- Level G
• Lesson 9.7, 9.8- Country Countdown, Clock a Doodle Doo- Level H

First Grade Team

Location: East Heritage Elementary School, East Constitution Way, Fontana, CA, United States Phone: 909-823-5696

• Texas Go Math
• Big Ideas Math
• Engageny Math
• McGraw Hill My Math
• enVision Math
• 180 Days of Math
• Math in Focus Answer Key
• Math Expressions Answer Key
• Privacy Policy

Go Math Grade 2 Answer Key Chapter 9 Length in Metric Units

Hey guys!!! Are you searching for the grade 2 answer key on various websites? If yes then you can stop your search now. Here you can get detailed explanations for all the questions on this page. As per your convenience, we have provided the Go Math Grade 2 Answer Key Chapter 9 Length in Metric Units in pdf format. Hence Download HMH Go Math Grade 2 Chapter 9 Solution Key Length in Metric Units Concepts for free of cost.

Go Math Grade 2 Chapter 9 Answer Key Length in Metric Units Concepts

Check out the topics before starting your preparation for the exams. We have provided solutions for all the questions as per the textbook. Test yourself by solving the problems given in the mid-chapter checkpoint and review the test. By solving the review test problems you can know how much you have learned from this chapter. Click on the below-given links and kickstart your preparation.

Chapter: 9 – Length in Metric Units

Length in Metric Units Show What You Know

Length in metric units vocabulary builder, length in metric units game estimating length, length in metric units vocabulary game.

Lesson: 1 Measure with a Centimeter Model

Lesson 9.1 Measure with a Centimeter Model

Measure with a centimeter model homework & practice 9.1.

Lesson: 2 Estimate Lengths in Centimeters

Lesson 9.2 Estimate Lengths in Centimeters

Estimate lengths in centimeters homework & practice 9.2.

Lesson: 3 Measure with a Centimeter Ruler

Lesson 9.3 Measure with a Centimeter Ruler

Measure with a centimeter ruler homework & practice 9.3.

Lesson: 4 Problem Solving • Add and Subtract Lengths

Lesson 9.4 Problem Solving • Add and Subtract Lengths

Problem solving • add and subtract lengths homework & practice 9.4.

Mid-Chapter Checkpoint

Length in Metric Units Mid-Chapter Checkpoint

Lesson: 5 Centimeters and Meters

Lesson 9.5 Centimeters and Meters

Centimeters and meters homework & practice 9.5.

Lesson: 6 Estimate Lengths in Meters

Lesson 9.6 Estimate Lengths in Meters

Estimate lengths in meters homework & practice 9.6.

Lesson: 7 Measure and Compare Lengths

Lesson 9.7 Measure and Compare Lengths

Measure and compare lengths homework & practice 9.7.

Review/Test

Length in Metric Units Review/Test

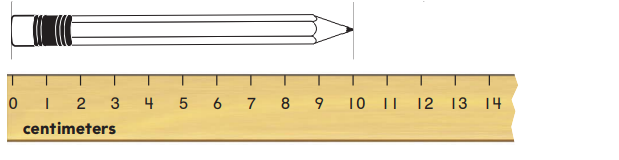
Explanation: Use the cube to measure the length of the pencil. The estimated measure of a pencil is 7

Question 3.

Explanation: Use the cube to measure the length of the pen. The estimated measure of a pen is 7.

• Take turns choosing a picture. Find the real object.
• Each player estimates the length of the object in cubes and then makes a cube train for his or her estimate.
• Compare the cube trains to the length of the object. The player with the closer estimate puts a counter on the picture. If there is a tie, both players put a counter on the picture.

For 3 players Materials

• 4 sets of word cards

How to Play

• Every player is dealt 5 cards. Put the rest face-down in a draw pile.
• If the player has the word card, he or she gives it to you. Put both cards in front of you. Take another turn.
• If the player does not have the word, he or she answers, “Go fish.” Take a card from the pile. If the word you get matches one you are holding, put both cards in front of you. Take another turn. If it does not match, your turn is over.

The Write Way Reflect Choose one idea. Write about it in the space below.

• Compare a centimeter to a meter. Explain how they are alike and how they are different.

Essential Question How do you use a centimeter model to measure the lengths of objects?

Listen and Draw

HOME CONNECTION • Your child used unit cubes as an introduction to measurement of length before using metric measurement tools.

MATHEMATICAL PRACTICES Use Tools Describe how to use unit cubes to measure an object’s length. Answer: We can measure the length of the object by locating the unit cubes in a sequence.

Share and Show

On Your Own

Problem Solving • Applications

TAKE HOME ACTIVITY • Have your child compare the lengths of other objects to those in this lesson.

Question 5. WRITE Write about using a unit cube to measure lengths in this lesson. ______________ _____________ Answer: Let us say your cube has the dimensions of 3 × 4 × 5 to find the area of the cube in the cubic measure you would multiply the three dimensions together and divide by the area of the cubes.

Question 4. Dan has a paper strip that is 28 inches long. He tears 6 inches off the strip. How long is the paper strip now? _________ inches Answer:  22 inches.

Explanation: Given Dan has a paper strip that is 28 inches long He tears 6 inches off the strip so 28 inches – 6 inches = 22 inches 22 inches long is the paper strip.

Question 5. Rita has 1 quarter, 1 dime, and 2 pennies. What is the total value of Rita’s coins? $ ______ or ______ cents Answer: Quarter = 25 cents dime = 10 cents 2 pennies = 2 cents 25 + 10 + 2 = 37 cents Thus the total value of Rita’s coins 37 cents.

Essential Question How do you use known lengths to estimate unknown lengths?

Find three classroom objects that are shorter than your 10-centimeter strip. Draw the objects. Write estimates for their lengths. about ________ centimeters

about ________ centimeters

HOME CONNECTION • Your child used a 10-centimeter strip of paper to practice estimating the lengths of some classroom objects.

Question 8. MATHEMATICAL PRACTICE Analyze Mr. Lott has 250 more centimeters of tape than Mrs. Sanchez. Mr. Lott has 775 centimeters of tape. How many centimeters of tape does Mrs. Sanchez have? ________ centimeters Answer: 525 centimeters

Explanation: Given, Mr. Lott has 250 more centimeters of tape than Mrs. Sanchez. Mr. Lott has 775 centimeters of tape. To find the length of tape we have to subtract 250 from 775 775 – 250 = 525 centimeters

TAKE HOME ACTIVITY • Give your child an object that is about 5 centimeters long. Have him or her use it to estimate the lengths of some other objects.

Question 4. WRITE Choose one exercise above. Describe how you decided which estimate was the best choice. Answer: Lesson 9.2 Estimate Lengths in Centimeters in this exercise we estimate the length of an object by comparing with the other object. So, this was the best choice.

Question 3. What is the sum? 14 + 65 = ______ Answer: 79

Question 4. Adrian has a cube train that is 13 inches long. He adds 6 inches of cubes to the train. How long is the cube train now? _______ inches Answer: 19 inches

Explanation: Given, Adrian has a cube train that is 13 inches long. He adds 6 inches of cubes to the train. 13 + 6 = 19 inches

Essential Question How do you use a centimeter ruler to measure lengths?

HOME CONNECTION • Your child used unit cubes to measure the lengths of some classroom objects as an introduction to measuring lengths in centimeters.

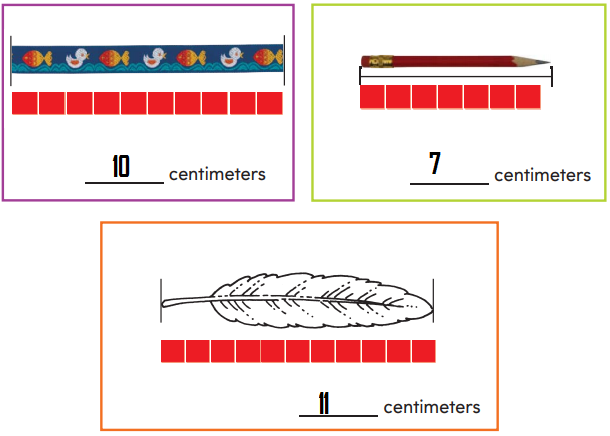
Question 8. GO DEEPER A marker is almost 13 centimeters long. This length ends between which two centimeter-marks on a ruler? ____________________ _____________________ Answer: It ends between 13 cm and 14 cm mark.

Explanation: Since this marker in the above question is almost 13 centimeters long and definitely ends between two centimeter marks, the two centimeters that the length of this marker ends between on a ruler should be 13cm and 14 cm marks on the ruler.

Explanation: Shown in the given figure that length of the crayon is between 3 to 11 cms hence 11-3 we get 8 centimeters

TAKE HOME ACTIVITY • Have your child measure the lengths of some objects using a centimeter ruler.

Question 4. WRITE Measure the length of the top of your desk in centimeters. Describe how you found the length. ___________________ ___________________ Answer: 12 centimeters by using rulers found the length of the desk

Essential Question How can drawing a diagram help when solving problems about lengths?

Nate had 23 centimeters of string. He gave 9 centimeters of string to Myra. How much string does Nate have now?

Unlock the Problem What information do I need to use? Nate had _________ centimeters of string. He gave _______ centimeters of string to Myra.

Answer: Nate has 14 centimeters of string now.

HOME CONNECTION • Your child drew a diagram to represent a problem about lengths. The diagram can be used to choose the operation for solving the problem.

Try Another Problem

MATHEMATICAL PRACTICES Explain how your diagram shows what happened in the first problem. Answer:

TAKE HOME ACTIVITY • Have your child explain how he or she used a diagram to solve one problem in this lesson.

Question 3. What is another way to write the time half past 7? _____ : ______ Answer: 07 : 30

Concepts and Skills

Essential Question How is measuring in meters different from measuring in centimeters?

MATHEMATICAL PRACTICES Describe how the lengths of the yarn and the sheet of paper are different. Answer:

TAKE HOME ACTIVITY • Have your child describe how centimeters and meters are different.

Problem Solving Question 3. Sally will measure the length of a wall in both centimeters and meters. Will there be fewer centimeters or fewer meters? Explain. _________________ _________________ Answer: There would be a fewer meter. Since 1 m=100 cm. Fewer centimeters because there will be fewer centimeters

Question 4. WRITE Would you measure the length of a bench in centimeters or in meters? Explain your choice. Answer: Meters

Step-by-step explanation: Reason: Usually, the bench length is bigger than the length of the chair and the table. So it will be measured using meters. If we use a meter it will easy to measure and accurate because it somewhat bigger in length than a chair and table. 1 meter = 100 centimeters. The standard length of a bench will 1.5 meters to 2 meters. Usually, 3 to 4 people will sit on the bench.

Question 3. Janet has a poster that is about 3 feet long. Fill in the blanks with the word inches or feet to make the statement true. 3 ______ is longer than 12 ________. Answer: The measurement of feets is longer than inches. 1 feet = 12 inches So, 3 feet is longer than 12 inches.

Question 5. List a group of coins with a value of $1.00? ______________ _____________ Answer: 100 pennies, 20 nickels, 10 dimes, or 4 quarters

Essential Question How do you estimate the lengths of objects in meters?

Is there a classroom object that is about 50 centimeters long? Draw and label it. Answer: No

MATHEMATICAL PRACTICES Describe how the lengths of the two real objects compare. Answer: Measure the length of an object twice, using length units of different lengths for the two measurements

Model and Draw

TAKE HOME ACTIVITY • With your child, estimate the lengths of some objects in meters.

Problem Solving Question 3. Barbara and Luke each placed 2 meter sticks end-to-end along the length of a large table. About how long is the table? about ________ meters Answer: 4 meters

Question 4. WRITE Choose one object from above. Describe how you estimated its length. __________________ __________________ Answer: Table By comparing with the real world we can estimate the length of the table.

Spiral Review Question 3. Sara has two $1 bills, 3 quarters, and 1 dime. How much money does she have? $ ____ . _____ Answer: $1 + $0.25 + $0.10 = $1.35

Essential Question How do you find the difference between the lengths of two objects?

HOME CONNECTION • Your child measured these lengths as an introduction to measuring and then comparing lengths.

MATHEMATICAL PRACTICES Name a classroom object that is longer than the paintbrush. Explain how you know. Answer: Chalk board as it is 2 meters long which is more than a paint brush

Analyze Relationships Question 6. Mark has a rope that is 23 centimeters long. He cuts 15 centimeters off. What is the length of the rope now? _________ centimeters Answer: 8 centimeters

Question 7. The yellow ribbon is 15 centimeters longer than the green ribbon. The green ribbon is 29 centimeters long. What is the length of the yellow ribbon? _________ centimeters Answer: 44 centimeters

TAKE HOME ACTIVITY • Have your child tell you how he or she solved one of the problems in this lesson.

Explanation: The length of the craft stick is 8 centimeters The length of chalk is 6 centimeters 11 – 8 = 3 Thus the craft stick is 3 centimeters longer than the chalk.

Problem Solving

Solve. Write or draw to explain. Question 2. A string is 11 centimeters long, a ribbon is 24 centimeters long, and a large paper clip is 5 centimeters long. How much longer is the ribbon than the string? ________ centimeters longer Answer: 19 centimeters longer

Question 3. WRITE Suppose the lengths of two strings are 10 centimeters and 17 centimeters. Describe how the lengths of these two strings compare. _____________________ ______________________ Answer: The length of the second string is 7 centimeters longer than the first string.

Question 3. What is a reasonable estimate for the length of a real chalkboard? _______ feet Answer: 5 feet

Question 4. Cindy leaves at half past 2. At what time does Cindy leave? ___ : ___ Answer: 02:30

Conclusion:

All the solutions that prevailed in the Go Math Grade 2 Answer Key Chapter 9 Length in Metric Units are prepared by the subject experts. Feel free to post your doubts in the below-mentioned comment box. Our team will try to clarify your doubts as early as possible. Keep in touch with our page to get Go Math Grade Answer Key for all the chapters.

Leave a Comment Cancel Reply

You must be logged in to post a comment.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

5.3: Numerical Measures of Center and Variation

• Last updated
• Save as PDF
• Page ID 50948

It is often desirable to use a few numbers to summarize a distribution. One important aspect of a distribution is where its center is located. Measures of central tendency are discussed first. A second aspect of a distribution is how spread out it is. In other words, how much the data in the distribution vary from one another. The second part of this section describes measures of variation.

Measures of Central Tendency

Let's begin by trying to find the most "typical" value of a data set.

Note that we just used the word "typical" although in many cases you might think of using the word "average." We need to be careful with the word "average" as it means different things to different people in different contexts. One of the most common uses of the word "average" is what mathematicians and statisticians call the “arithmetic mean”, or just plain old “mean” for short. "Arithmetic mean" sounds rather fancy, but you have likely calculated a mean many times without realizing it; the mean is what most people think of when they use the word "average.”

The mean of a set of data is the sum of the data values divided by the number of values.

Example \(\PageIndex{1}\)

Marci’s exam scores for her last math class were 79, 86, 82, 94. Find the mean.

The mean of these values would be:

79+86+82+944=85.25

Example \(\PageIndex{2}\)

The number of touchdown (TD) passes thrown by each of the 31 teams in the National Football League in the 2000 season are shown below.

37, 33, 33, 32, 29, 28, 28, 23, 22, 22, 22, 21, 21, 21, 20

20, 19, 19, 18, 18, 18, 18, 16, 15, 14, 14, 14, 12, 12, 9, 6

What is the mean number of touchdown passes thrown in the NFL in the 2000 season?

Adding these values, we get 634 total TDs. Dividing by 31, the number of data values, we get 634/31 = 20.4516. It would be appropriate to round this to 20.5.

It would be correct for us to report that “The mean number of touchdown passes thrown in the NFL in the 2000 season was 20.5 passes,” but it is not uncommon to see the more casual word “average” used in place of “mean.”

Try it Now 4

The prices of a jar of peanut butter at 5 stores were $3.29, $3.59, $3.79, $3.75, and $3.99. Find the mean price.

Example \(\PageIndex{3}\)

One hundred families in a particular neighborhood are asked their annual household income, to the nearest $5 thousand dollars. The results are summarized in a frequency table below.

Calculate the mean.

Calculating the mean by hand could get tricky if we try to type in all 100 values:

\[\dfrac{\overset{6 \text { terms }}{\overbrace{15+\cdots 15}}\; + \overset{8 \text { terms }}{\overbrace{20+\cdots 20}} + \overset{11 \text { terms }}{\overbrace{25+\cdots 25}} + \cdots}{100} \nonumber \]

We could calculate this more easily by noticing that adding 15 to itself six times is the same as 90. Using this simplification, we get:

\[\dfrac{15 \cdot 6+20 \cdot 8+25 \cdot 11+30 \cdot 17+35 \cdot 19+40 \cdot 20+45 \cdot 12+50 \cdot 7}{100}=\dfrac{3390}{100}=33.9 \nonumber \]

The mean household income of our sample is 33.9 thousand dollars ($33,900).

Example \(\PageIndex{4}\)

Extending off the last example, suppose a new family moves into the neighborhood example that has a household income of $5 million ($5000 thousand).

Adding this to our sample, our mean is now:

\[\dfrac{15 \cdot 6+20 \cdot 8+25 \cdot 11+30 \cdot 17+35 \cdot 19+40 \cdot 20+45 \cdot 12+50 \cdot 7+5000 \cdot 1}{101}=\frac{8390}{101}=83.069 \nonumber \]

While 83.1 thousand dollars ($83,069) is the correct mean household income, it no longer represents a “typical” value.

An extreme value, much bigger or much smaller than most other values in a given dataset, is called an “outlier”. An outlier can affect the mean.

Imagine the data values on a see-saw or balance scale. The mean is the value that keeps the data in balance, like in the picture below.

If we graph our household data, the $5 million data value is so far out to the right that the mean has to adjust up to keep things in balance.

In situations like this, where one value is much bigger or smaller than most other value in the data, there is a better measure of center than the mean.

The median of a set of data is the value in the middle when the data is in order.

To find the median, begin by listing the data in order from smallest to largest, or largest to smallest.

If the number of data values, \(N\), is odd, then the median is the middle data value. This can be found by rounding \(N/2\) up to the next whole number.

If the number of data values is even, there is no one middle value, so we find the mean of the two middle values (values \(N/2\) and \(N/2 + 1\) ).

Example \(\PageIndex{5}\)

Returning to the football touchdown data, we would start by listing the data in order. Luckily, it was already in decreasing order, so we can work with it without needing to reorder it first.

Find the median touchdown pass.

Since there are 31 data values, an odd number, the median will be the middle number, the 16th data value (31/2 = 15.5, round up to 16, leaving 15 values below and 15 above). The 16th data value is 20, so the median number of touchdown passes in the 2000 season was 20 passes. Notice that for this data, the median is fairly close to the mean we calculated earlier, 20.5.

Example \(\PageIndex{6}\)

Find the median of these quiz scores: 5, 10, 8, 6, 4, 8, 2, 5, 7, 7

We start by listing the data in order: 2, 4, 5, 5, 6, 7, 7, 8, 8, 10

Since there are 10 data values, an even number, there is no one middle number. So we find the mean of the two middle numbers, 6 and 7, and get (6+7)/2 = 6.5.

The median quiz score was 6.5.

Try it Now 5

The prices of a jar of peanut butter at 5 stores were $3.29, $3.59, $3.79, $3.75, and $3.99. Find the median price.

Example \(\PageIndex{7}\)

Let us return now to our original household income data.

Find the mean and median income.

Here we have 100 data values. If we didn’t already know that, we could find it by adding the frequencies. Since 100 is an even number, we need to find the mean of the middle two data values - the 50th and 51st data values. To find these, we start counting up from the bottom:

There are 6 data values of $15, so Values 1 to 6 are $15 thousand

The next 8 data values are $20, so Values 7 to (6+8)=14 are $20 thousand

The next 11 data values are $25, so Values 15 to (14+11)=25 are $25 thousand

The next 17 data values are $30, so Values 26 to (25+17)=42 are $30 thousand

The next 19 data values are $35, so Values 43 to (42+19)=61 are $35 thousand

From this we can tell that values 50 and 51 will be $35 thousand, and the mean of these two values is $35 thousand. The median income in this neighborhood is $35 thousand.

Example \(\PageIndex{8}\)

If we add in the new neighbor with a $5 million household income, how does the median change?

If we add in the new neighbor with a $5 million household income, then there will be 101 data values, and the 51st value will be the median. As we discovered in the last example, the 51st value is $35 thousand. Notice that the new neighbor did not affect the median in this case. The median is not swayed as much by outliers as the mean is.

This is the main reason the median, not the mean, is used to represent certain data, such as the average household income or home price.

In addition to the mean and the median, there is one other common measurement of the "typical" value of a data set: the mode.

The mode is the element of the data set that occurs most frequently.

The mode is fairly useless with data like weights or heights where there are a large number of possible values. The mode is most commonly used for categorical data, for which median and mean cannot be computed.

Example \(\PageIndex{9}\)

In our vehicle color survey, we collected the data

What is the mode?

For this data, Green is the mode, since it is the data value that occurred the most frequently.

It is possible for a data set to have more than one mode (if several categories have the same frequency), or no modes (if every category occurs only once.)

Try it Now 6

Reviewers were asked to rate a product on a scale of 1 to 5. Find

• The mean rating
• The median rating
• The mode rating

Measures of Variation

Consider these three sets of quiz scores:

Section A: 5, 5, 5, 5, 5, 5, 5, 5, 5, 5

Section B: 0, 0, 0, 0, 0, 10, 10, 10, 10, 10

Section C: 4, 4, 4, 5, 5, 5, 5, 6, 6, 6

All three of these sets of data have a mean of 5 and median of 5, yet the sets of scores are clearly quite different. In section A, everyone had the same score; in section B half the class got no points and the other half got a perfect score, assuming this was a 10-point quiz. Section C was not as consistent as section A, but not as widely varied as section B.

In addition to the mean and median, which are measures of the "typical" or "middle" value, we also need a measure of how "spread out" or varied each data set is.

There are several ways to measure this "spread" of the data. The first is the simplest and is called the range.

The range is the difference between the maximum value and the minimum value of the data.

Example \(\PageIndex{10}\)

Using the quiz scores from above, find the range for each section.

For section A, the range is 0 since both maximum and minimum are 5 and 5 – 5 = 0.

For section B, the range is 10 since 10 – 0 = 10.

For section C, the range is 2 since 6 – 4 = 2.

In the last example, the range seems to be revealing how spread out the data is.

However, suppose we add a fourth section, Section D, with scores 0, 5, 5, 5, 5, 5, 5, 5, 5, 10.

This section also has a mean and median of 5. The range is 10, yet this data set is quite different from Section B. To better illuminate the differences, we’ll have to turn to more sophisticated measures of variation.

Standard Deviation

The standard deviation is a measure of variation based on measuring how far each data value deviates, or is different, from the mean. A few important characteristics:

• Standard deviation is always positive. Standard deviation will be zero only if all the data values are equal and will get larger as the data spreads out.
• Standard deviation has the same unit as the original data.
• Standard deviation, like the mean, can be highly influenced by outliers.

Standard deviation is rather complicated. Let me explain below, step by step.

Using the data from section D (Example \(\PageIndex{10}\)), we could compute for each data value the difference between the data value and the mean:

We would like to get an idea of the "average" deviation from the mean, but if we find the average of the values in the second column, the negative and positive values cancel each other out, resulting in the average deviation of 0 (this will always happen). To prevent this we square every value in the second column:

We then add the squared deviations up to get 25 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 25 = 50. Ordinarily we would then divide by the number of scores, n (in this case, 10), to find the mean of the squares of the deviations. But we only do this if the data set represents a population; if the data set represents a sample (as it almost always does), we instead divide by \(n - 1\) (in this case, 10-1=9).

The quotient (by \(n\) or by \(n - 1\)) is called the “variance” of the data set.

So in our example, we would have 50/10 = 5 if section D represents a population and 50/9 = about 5.56 if section D represents a sample. These values (5 and 5.56) are called, respectively, the population variance and the sample variance for section D.

We are almost there—one more step, and we will find the standard deviation.

Variance can be a useful statistical concept, but note that the unit of variance in this instance would be points-squared since we squared all of the deviations. What are points-squared? Good question. We would rather deal with the units we started with (points in this case), so to convert back we take the square root and get:

Population standard deviation=\(\sqrt{\dfrac{50}{10}}=\sqrt{5} \approx 2.2\)

sample standard deviation=\(\sqrt{\dfrac{50}{9}} \approx 2.4\)

If we are unsure whether the data set is a sample or a population, we will usually assume it is a sample, and we will round answers to one more decimal place than the original data as we have done above.

As you can see, it takes multiple steps to calculate the standard deviation of a dataset. For most real-life applications, the calculations are performed using technology. Here is a brief summary.

To compute Standard Deviation

• Find the deviation of each data value from the mean. In other words, subtract the mean from the data value.
• Square each deviation.
• Add the squared deviations.
• Divide by \(n\), the number of data values, if the data represents a whole population; divide by \(n - 1\) if the data is from a sample.
• Compute the square root of the result.

Example \(\PageIndex{11}\)

Compute the standard deviation for Section B above

Computing the standard deviation for Section B above, we first calculate that the mean is 5. Using a table can help keep track of your computations for the standard deviation:

Assuming this data represents a population, we will add the squared deviations, divide by 10, the number of data values, and compute the square root:

\[\sqrt{\dfrac{25+25+25+25+25+25+25+25+25+25}{10}}=\sqrt{\dfrac{250}{10}}=5 \nonumber \]

Notice that the standard deviation of this data set is much larger than that of section D since the data in this set is more spread out.

For comparison, the standard deviations of all four sections are as follows:

Try it Now 7

The prices of a jar of peanut butter at 5 stores were: $3.29, $3.59, $3.79, $3.75, and $3.99. Find the standard deviation of the prices.

Where standard deviation is a measure of variation based on the mean, quartiles are based on the median.

Quartiles are values that divide the data in quarters.

The first quartile (Q1) is the value so that 25% of the data values are below it; the third quartile (Q3) is the value so that 75% of the data values are below it. You may have guessed that the second quartile is the same as the median, since the median is the value so that 50% of the data values are below it.

This divides the data into quarters; 25% of the data is between the minimum and Q1, 25% is between Q1 and the median, 25% is between the median and Q3, and 25% is between Q3 and the maximum value

While quartiles are not a 1-number summary of variation like standard deviation, the quartiles are used with the median, minimum, and maximum values to form a 5-number summary of the data.

Five-number Summary

The five-number summary takes this form:

Minimum, Q1, Median, Q3, Maximum.

To find the first quartile, we need to find the data value so that 25% of the data is below it.

But note that this is the same as the “median” of the first (lower) half of the dataset. So an easy way to find the first quartile is to split the original data set in half and find the median of the lower half. The third quartile is similar; find the median of the second (higher) half of the data set.

Warning: The precise definitions and method of finding quartiles vary slightly from book to book. You may see slightly different explanations in other resources.

Example \(\PageIndex{12}\)

Suppose we have measured 9 females and their heights (in inches), sorted from smallest to largest are:

59, 60, 62, 64, 66, 67, 69, 70, 72

Find Quartiles.

Note the median is 66.

The lower half, {59, 60, 62, 64}, has the median of 61, and the higher half, {67, 69, 70, 72}, has the median of 69.5.

So Q1 is 61, Q2 is 66, and Q3 is 69.5.

Example \(\PageIndex{13}\)

Suppose we had measured 8 females and their heights (in inches), sorted from smallest to largest are:

59, 60, 62, 64, 66, 67, 69, 70

Note the median in this case is 65, the mean of 64 and 66.

Then the lower half is the same as in Example 25 (its median is 61). The higher half now has the median 68.

So, Q1 is 61, Q2 is 65, and Q3 is 68.

The 5-number summary combines the first and third quartile with the minimum, median, and maximum values.

Example \(\PageIndex{14}\)

For the 9 female sample, the median is 66, the minimum is 59, and the maximum is 72. The 5- number summary is: 59, 61, 66, 69.5, 72.

For the 8 female sample, the median is 65, the minimum is 59, and the maximum is 70, so the 5- number summary would be: 59, 61, 65, 68, 70.

Example \(\PageIndex{15}\)

Returning to our quiz score data. In each case, there are 10 values, so the median is the mean of the 5th and 6th values. The first quartile will be the 3rd data value, and the third quartile will be the 8th data value. Creating the five-number summaries:

Of course, with a relatively small data set, finding a five-number summary is a bit silly since the summary contains almost as many values as the original data.

Try it Now 8

The total cost of textbooks for the term was collected from 36 students. Find the 5-number summary of this data.

$140 $160 $160 $165 $180 $220 $235 $240 $250 $260 $280 $285

$285 $285 $290 $300 $300 $305 $310 $310 $315 $315 $320 $320

$330 $340 $345 $350 $355 $360 $360 $380 $395 $420 $460 $460

Example \(\PageIndex{16}\)

Returning to the household income data from earlier, create the 5-number summary.

By adding the frequencies, we can see there are 100 data values represented in the table. In Example 20, we found the median was $35 thousand. We can see in the table that the minimum income is $15 thousand, and the maximum is $50 thousand.

Counting up in the data as we did before,

The lower half has 50 values, so Q1 is the mean of the 25th and the 26th values.

The 25th data value is $25 thousand, and the 26th data value is $30 thousand, so Q1 will be the mean of these: (25 + 30)/2 = $27.5 thousand.

Similarly, Q3 will be the mean of the 75th and 76th data values. Continuing our counting from earlier,

The next 20 data values are $40, so Values 61 to (61+20)=81 are $40 thousand

Both the 75th and 76th data values lie in this group, so Q3 will be $40 thousand.

Putting these values together into a five-number summary, we get: 15, 27.5, 35, 40, 50.

Note that the 5-number summary divides the data into four intervals, each of which will contain about 25% of the data. In the previous example, that means about 25% of households have income between $40 thousand and $50 thousand.

For visualizing data, there is a graphical representation of a 5-number summary called a box plot, or box and whisker graph.

A box plot is a graphical representation of a 5-number summary.

To create a box plot, a number line is first drawn. A box is drawn from the first quartile to the third quartile, and a line is drawn through the box at the median. “Whiskers” are extended out to the minimum and maximum values.

Example \(\PageIndex{17}\)

Draw a box plot below based on the 5-number summary:

59, 62, 66, 69, 72.

Example \(\PageIndex{18}\)

Draw a box plot below based on the household income data with 5 number summary:

15, 27.5, 35, 40, 50

Try it Now 9

Create a boxplot based on the textbook price data from the last Try it Now.

Box plots are particularly useful for comparing data from two populations.

Example \(\PageIndex{19}\)

The box plot of service times for two fast-food restaurants is shown below.

While store 2 had a slightly shorter median service time (2.1 minutes vs. 2.3 minutes), store 2 is less consistent, with a wider spread of the data.

At store 1, 75% of customers were served within 2.9 minutes, while at store 2, 75% of customers were served within 5.7 minutes.

Which store should you go to in a hurry?

That depends upon your opinions about luck – 25% of customers at store 2 had to wait between 5.7 and 9.6 minutes.

Example \(\PageIndex{20}\)

The boxplot below is based on the birth weights of infants with severe idiopathic respiratory distress syndrome (SIRDS). The boxplot is separated to show the birth weights of infants who survived and those that did not.

Compare the two groups to determine if birth weight is quite likely linked to survival of infants with SIRDS.

Comparing the two groups, the boxplot reveals that the birth weights of the infants that died appear to be, overall, smaller than the weights of infants that survived. In fact, we can see that the median birth weight of infants that survived is the same as the third quartile of the infants that died.

Similarly, we can see that the first quartile of the survivors is larger than the median weight of those that died, meaning that over 75% of the survivors had a birth weight larger than the median birth weight of those that died.

Looking at the maximum value for those that died and the third quartile of the survivors, we can see that over 25% of the survivors had birth weights higher than the heaviest infant that died.

The box plot gives us a quick, albeit informal, way to determine that birth weight is quite likely linked to survival of infants with SIRDS.

Contributors and Attributions

Saburo Matsumoto CC-BY-4.0

• AP Calculus
• AP Statistics
• Independent Study

Online Math Class

Mr. Math Blog

Thanks for your donation!  Every little bit helps me help you!  :-)

Problem Solving - Organize Data - Lesson 2.1

Use Picture Graphs - Lesson 2.2

Make Picture Graphs - Lesson 2.3

Use Bar Graphs - Lesson 2.4

Make a Bar Graph - Lesson 2.5

Solve Problems Using Data - Lesson 2.6

Use and Make Line Plots - Lesson 2.7

Number Patterns - Lesson 1.1

Round to Nearest Ten or Hundred - Lesson 1.2

Estimate Sums - Lesson 1.3

Mental Math Strategies for Addition - Lesson 1.4

Use Properties to Add - Lesson 1.5

Use the Break Apart Strategy to Add - Lesson 1.6

Use Place Value to Add - Lesson 1.7

Estimate Differences - Lesson 1.8

Mental Math Strategies for Subtraction - Lesson 1.9

Use Place Value to Subtract - Lesson 1.10

Combine Place Values to Subtract - Lesson 1.11

Describe Plane Shapes - Lesson 12.1

Describe Angles in Plane Shapes - Lesson 12.2

Identify Polygons - Lesson 12.3 ​

Describe Sides of Polygons - Lesson 12.4

​ Classify Quadrilaterals - Lesson 12.5

​Draw Quadrilaterals - Lesson 12.6

Describe Triangles - Lesson 12.7

Chapter 12 Performance Task Review For Test

Problem Solving - Compare Fractions - Lesson 9.1

Compare Fractions with the Same Denominator - Lesson 9.2

Compare Fractions with the Same Numerator - Lesson 9.3

Compare Fractions - Lesson 9.4

Compare and Order Fractions - Lesson 9.5

Model Equivalent Fractions - Lesson 9.6

Equivalent Fractions - Lesson 9.7

Divide by 2 - Lesson 7.1

Divide by 10 - Lesson 7.2

Divide by 5 - Lesson 7.3

Divide by 3 - Lesson 7.4

Divide by 4 - Lesson 7.5

Divide by 5 - Lesson 7.6

Mid-Chapter 7 Checkpoint on Division Facts and Strategies

Divide by 7 - Lesson 7.7

Divide by 8 - Lesson 7.8

Divide by 9 - Lesson 7.9

Problem Solving - Two-Step Problems - Lesson 7.10

Order of Operations - Lesson 7.11

Problem Solving - Model Division - Lesson 6.1

Size of Equal Groups - Lesson 6.2

Number of Equal Groups - Lesson 6.3

Model (Division) with Bar Model - Lesson 6.4

Relate Subtraction and Division - Lesson 6.5

Mid-Chapter 6 Checkpoint

Model (division) with Arrays - Lesson 6.6

Relate Multiplication and Division - Lesson 6.7

Write Related Facts - Lesson 6.8

Division Rules for 1 and 0 - Lesson 6.9

Chapter 6 Review for Test - Understanding Division

Multiply with 2 and 4 - Lesson 4.1

Multiply with 5 and 10 - Lesson 4.2

Multiply with 3 and 6 - Lesson 4.3

Distributive Property - Lesson 4.4

Multiply with 7 - Lesson 4.5

Associative Property of Multiplication - Lesson 4.6

Patterns on the Multiplication Table - Lesson 4.7

Multiply with 8 - Lesson 4.8

Multiply with 9 - Lesson 4.9

Review For Test on Chapter 4

Describe Patterns - Lesson 5.1

Find Unknown Factors - Lesson 5.2

Problem Solving: Using the Distributive Property - Lesson 5.3

Multiplication Strategies with Multiples of 10 - Lesson 5.4

Multiply Multiples of 10 by 1-Digit Numbers - Lesson 5.5

Chapter 5 Review on Multiplication Facts

Third Grade

      Math

• Second Grade Math
• Third Grade Math
• Fourth Grade Math
• Fifth Grade Math
• Sixth Grade Math
• Sixth Grade Math (CA)
• Seventh Grade Math (CA)
• Eighth Grade Math (CA)
• Integrated Math 1
• Integrated Math 2
• Integrated Math 3
• PreCalculus
• AP Statistics Exam Prep
• Elementary Statistics
• ELM Practice
• Percents and Decimals
• Sixth Grade Math (Big Ideas)

Model Perimeter - Lesson 11.1

Find Perimeter - Lesson 11.2

Find Unknown Side Lengths - Lesson 11.3

Understanding Area - Lesson 11.4

Measure Area - Lesson 11.5

Use Area Models - Lesson 11.6

Problem Solving - Area of Rectangles - Lesson 11.7

Area of Combined Rectangles - Lesson 11.8

Same Perimeter - Different Area - Lesson 11.9

Same Area - Different Perimeter - Lesson 11.10

Chapter 11 Review for Test on Perimeter and Area

Please Donate, if you're a regular!

The donate link is below. Thanks so much!!

Count Equal Groups - Lesson 3.1

Relate Addition and Multiplication - Lesson 3.2

Skip Count on a Number Line - Lesson 3.3

Problem Solving - Model Multiplication - Lesson 3.4

Model with Arrays - Lesson 3.5

Commutative Property of Multiplication - Lesson 3.6

Multiply with 1 and 0 - Lesson 3.7

Time to the Minute - Lesson 10.1

A.M. and P.M. - Lesson 10.2

Measure Time Intervals - Lesson 10.3

Use Time Intervals - Lesson 10.4

Problem Solving - Time Intervals - Lesson 10.5

Measure Length - Lesson 10.6

Estimate and Measure Liquid Volume - Lesson 10.7

Estimate and Measure Mass - Lesson 10.8

Equal Parts of a Whole - Lesson 8.1

Equal Shares - Lesson 8.2

Unit Fractions of a Whole - Lesson 8.3

Fractions of a Whole - Lesson 8.4

Fractions on a Number Line - Lesson 8.5

Relate Fractions and Whole Numbers - Lesson 8.6

Fractions of a Group - Lesson 8.7

Find Part of Group Using Unit Fractions - Lesson 8.8

Problem Solving: Find the Whole Using Unit Fractions - Lesson 8.9

Copyright 2013. All rights reserved.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: 5th grade   >   Unit 1

Comparing decimals: 9.97 and 9.798.

• Comparing decimals: 156.378 and 156.348
• Compare decimals through thousandths
• Ordering decimals
• Ordering decimals through thousandths
• Order decimals
• Comparing decimals in different representations
• Comparing decimals word problems
• Compare decimals word problems

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript