pythagorean theorem assignment calculate the measure of x in each

Pythagorean Theorem Calculator

How to use the pythagorean theorem calculator, what is the pythagorean theorem, how do i use pythagorean theorem, what is the hypotenuse formula, other considerations when dealing with triangles, the pythagorean theorem calculator in the making.

This Pythagorean theorem calculator will calculate the length of any of the missing sides of a right triangle, provided you know the lengths of its other two sides. This includes calculating the hypotenuse. The hypotenuse of the right triangle is the side opposite the right angle, and is the longest side. This side can be found using the hypotenuse formula, another term for the Pythagorean theorem when it's solving for the hypotenuse.

Recall that a right triangle is a triangle with an angle measuring 90 degrees. The other two angles must also total 90 degrees, as the sum of the measures of the angles of any triangle is 180. Read on to answer "what is the Pythagorean theorem and how is it used?"

The Pythagorean theorem calculator is one of the most accessible tools you will come across, despite the name being scary. All you need is any two of the three sides of a right triangle, and you are all set.

Let's take a look at the steps to use our Pythagorean theorem calculator.

Input leg a of the right triangle.

Next, input leg b of the right triangle.

And that is it. The tool will display the following results:

a. The hypotenuse (c) of the right triangle.

b. The area of the triangle.

c. And the perimeter of the triangle.

You don't necessarily have to input legs a and b. If you know the hypotenuse value and need to know any other legs, input the information accordingly.

The default unit is centimeter (cm) for length and cm² for area. You can change these to one of the listed of options according to your requirements. Remember to change the unit before you input the values.

How about we try to understand an example ? For instance, you are climbing a ladder to your roof, and you get curious about the length of the ladder . You notice that the distance from the roof to the ground is leg a , and the distance from the wall to the ladder's base is leg b . And the ladder itself is the hypotenuse. You input the measurements in the tool as leg a and b, 4 m and 3 m , respectively. (Remember to change the units from centimeters to meters first). The calculator instantly determines the hypotenuse as 5 m , the area as 6 m² , and the perimeter as 12 m .

Next time you get curious about any setup that looks like a right triangle, you can use our Pythagorean theorem calculator to determine the lengths of the legs.

The Pythagorean theorem describes how the three sides of a right triangle are related in Euclidean geometry. It states that the sum of the squares of the legs of a right triangle equals the square of the hypotenuse . You can also think of this theorem as the hypotenuse formula. If the legs of a right triangle are a and b and the hypotenuse is c , the formula is:

a² + b² = c²

The theorem was credited to the ancient Greek philosopher and mathematician Pythagoras, who lived in the sixth century BC. Although it was previously used by the Indians and Babylonians, Pythagoras (or his students) were credited with being the first to prove the theorem. It should be noted that there is no concrete evidence that Pythagoras himself worked on or proved this theorem.

Here's how to use Pythagorean theorem:

• Input the two lengths that you have into the formula. For example, suppose you know one leg a = 4 and the hypotenuse c = 8.94 . We want to find the length of the other leg b .
• After the values are put into the formula, we have 4² + b² = 8.94² .
• Square each term to get 16 + b² = 80 .
• Combine like terms to get b² = 64 .
• Take the square root of both sides of the equation to get b = 8 . Go ahead and check it with an online Pythagorean theorem calculator!

Note that if you are solving for a or b , rearrange the equation to isolate the desired variable before combining like terms and taking the square root

The Pythagorean theorem calculator will solve for the sides in the same manner that we displayed above. We have included the method to show you how you can solve your problem if you prefer to do it by hand.

The hypotenuse formula simply takes the Pythagorean theorem and solves for the hypotenuse, c . To solve for the hypotenuse, we simply take the square root of both sides of the equation a² + b² = c² and solve for c . When doing so, we get c = √(a² + b²) . This is just a reformulation of the Pythagorean theorem and is often associated with the name hypotenuse formula .

Notice the sides of a triangle have a certain degree of gradient or slope. We can use the slope calculator to determine the slope of each side. In a right triangle, the sides that form the right angle will have slopes whose product is -1. The formula for slope, if you wish to calculate by hand, is:

(y₂ − y₁)/(x₂ − x₁)

You can also figure out the missing side lengths and angles of a right triangle using the right triangle calculator . If the angles given in the problem are in degrees and you want to convert to radians or radians to degrees, check out our angle converter . There is an easy way to convert degrees to radians and radians to degrees.

If the angle is in radians:

• Multiply by 180/π .

If the angle is in degrees:

• Multiply by π/180 .

Sometimes you may encounter a problem where two lengths are missing. In such cases, the Pythagorean theorem calculator won't help – you will use trigonometric functions to solve for these missing pieces. Don't worry! We have an excellent trigonometric functions calculator available for you.

Indeed, all maths enthusiasts would be happy to have access to a Pythagorean theorem calculator. Even the students who have to complete their assignments would be thrilled. Now imagine how happy Mateusz and Piotr were when they decided to make a tool for one of the most sought-after mathematics concepts and successfully did so.

Mateusz Mucha is the brain behind Omni Calculator. His deep love for numbers with strategic vision and operational expertise is a testament to his career. He believes in a hands-on approach in all aspects of life, whether it is leadership, building some innovative calculator or digital product, or participating in a cycling marathon. He is a well-balanced blend of exemplary leadership and vision, with strategic thinking, innovation, and attention to detail being a few of the skills in his arsenal.

Piotr Małek is creative, athletic, and curious by nature, which makes him a person of remarkable discipline, high credibility, and determination. As a content writer, his ability to explain complex topics with a fairytale-like ease is genuinely fascinating. The diverse experiences he has gained over the years, his intellectual curiosity, and his lifestyle of continuous learning make him a credible voice in any field he is interested in exploring.

We ensure our tools are based on authentic information and proper research. After an expert makes the calculator, another expert in the field reviews it thoroughly. Then, a native language speaker proofreads the content, ensuring further refinement; only then is the tool released for our users. To learn more about our commitment to quality, please refer to our Editorial Policies page .

What is the hypotenuse given legs 7 and 9?

The hypotenuse is 11.40 .

You need to apply the Pythagorean theorem:

• Recall the formula a² + b² = c² , where a , and b are the legs and c is the hypotenuse.
• Put the length of the legs into the formula: 7² + 9² = c² .
• Squaring gives 49 + 81 = c² . That is, c² = 150 .
• Taking the square root, we obtain c = 11.40 . You can verify the result with an online Pythagorean theorem calculator.

What is the leg in an isosceles triangle with hypotenuse 10?

Each leg has length 10/√2 ≈ 7.07 . To arrive at this answer, we apply the Pythagorean theorem:

• In our case, a = b , so the formula reads 2a² = c² .
• Solving for a , we get a = c/√2 .
• Plugging in c = 10 , we get the final answer: a = 10/√2 ≈ 7.07 .

30 60 90 triangle

Black hole collision, center of mass, ideal egg boiling.

• Biology (100)
• Chemistry (100)
• Construction (144)
• Conversion (294)
• Ecology (30)
• Everyday life (262)
• Finance (569)
• Health (440)
• Physics (509)
• Sports (104)
• Statistics (182)
• Other (181)
• Discover Omni (40)

Pythagorean Theorem

How to Use The Pythagorean Theorem

The Formula

The picture below shows the formula for the Pythagorean theorem. For the purposes of the formula, side $$ \overline{c}$$ is always the hypotenuse . Remember that this formula only applies to right triangles .

Examples of the Pythagorean Theorem

When you use the Pythagorean theorem, just remember that the hypotenuse is always 'C' in the formula above. Look at the following examples to see pictures of the formula.

Conceptual Animation of Pythagorean Theorem

Demonstration #1.

More on the Pythagorean theorem

Demonstration #2

Video tutorial on how to use the pythagorean theorem.

Step By Step Examples of Using the Pythagorean Theorem

Example 1 (solving for the hypotenuse).

Use the Pythagorean theorem to determine the length of X.

Identify the legs and the hypotenuse of the right triangle .

The legs have length 6 and 8 . $$X $$ is the hypotenuse because it is opposite the right angle.

Substitute values into the formula (remember 'C' is the hypotenuse).

$ A^2+ B^2= \red C^2 \\ 6^2+ 8^2= \red X^2 $

$A^2+ B^2= \red X^2 \\ 100= \red X^2 \\ \sqrt {100} = \red X \\ 10= \red X $

Example 2 (solving for a Leg)

The legs have length 24 and $$X$$ are the legs. The hypotenuse is 26.

$ \red A^2+ B^2= C^2 \\ \red x^2 + 24^2= {26}^2 $

$ \red x^2 + 24^2= 26^2 \\ \red x^2 + 576= 676 \\ \red x^2 = 676 - 576 \\ \red x^2 = 100 \\ \red x = \sqrt { 100} \\ \red x = 10 $

Practice Problems

Find the length of X.

Remember our steps for how to use this theorem. This problems is like example 1 because we are solving for the hypotenuse .

The legs have length 14 and 48 . The hypotenuse is X.

$ A^2 + B^2 = C^2 \\ 14^2 + 48^2 = x^2 $

Solve for the unknown.

$ 14^2 + 48^2 = x^2 \\ 196 + 2304 = x^2 \\ \sqrt{2500} = x \\ \boxed{ 50 = x} $

Use the Pythagorean theorem to calculate the value of X. Round your answer to the nearest tenth.

Remember our steps for how to use this theorem. This problems is like example 2 because we are solving for one of the legs .

The legs have length 9 and X . The hypotenuse is 10.

$ A^2 + B^2 = C^2 \\ 9^2 + x^2 = 10^2 $

$ 9^2 + x^2 = 10^2 \\ 81 + x^2 = 100 \\ x^2 = 100 - 81 \\ x^2 = 19 \\ x = \sqrt{19} \approx 4.4 $

Use the Pythagorean theorem to calculate the value of X. Round your answer to the nearest hundredth.

The legs have length '10' and 'X'. The hypotenuse is 20.

$ A^2 + B^2 = C^2 \\ 10^2 + \red x^2 = 20^2 $

$ 10^2 + \red x^2 = 20^2 \\ 100 + \red x^2 = 400 \\ \red x^2 = 400 -100 \\ \red x^2 = 300 \\ \red x = \sqrt{300} \approx 17.32 $

• Pythagorean Theorem Shell Problem Cool challenging problem from involving pythagoren theorem, isosceles triangles and pattern recognition
• Free Triangle Worksheets
• Pythagorean Theorem Calculator

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!

Popular pages @ mathwarehouse.com.

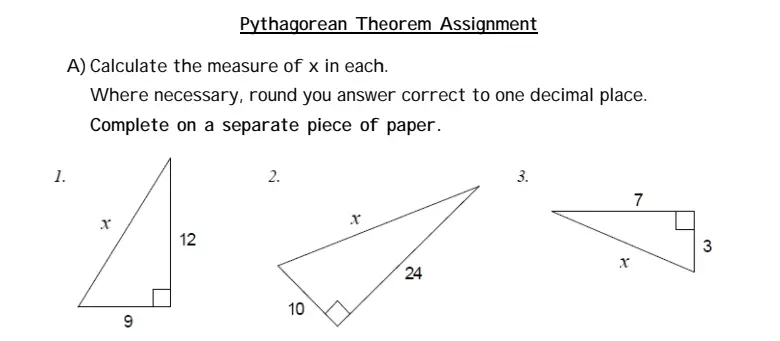
Pythagorean Theorem Assignment A) Calculate the measure of x in each. Where necessary, round you answer correct to one decimal place Complete on a separate piece of paper. 1. 2. 3.

Expert verified solution.

Answer by Ruby · Jun 17, 2021

Chapter 6: Introduction to Geometry

Using the pythagorean theorem to solve problems, learning outcomes.

• Use the pythagorean theorem to find the unknown length of a right triangle given the two other lengths

The Pythagorean Theorem is a special property of right triangles that has been used since ancient times. It is named after the Greek philosopher and mathematician Pythagoras who lived around [latex]500[/latex] BCE.

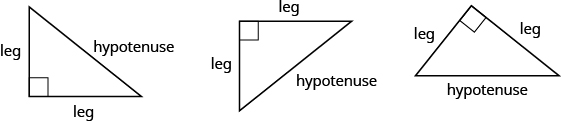
Remember that a right triangle has a [latex]90^\circ [/latex] angle, which we usually mark with a small square in the corner. The side of the triangle opposite the [latex]90^\circ [/latex] angle is called the hypotenuse, and the other two sides are called the legs. See the triangles below.

In a right triangle, the side opposite the [latex]90^\circ [/latex] angle is called the hypotenuse and each of the other sides is called a leg.

The Pythagorean Theorem

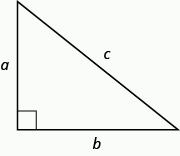
In any right triangle [latex]\Delta ABC[/latex],

[latex]{a}^{2}+{b}^{2}={c}^{2}[/latex]

where [latex]c[/latex] is the length of the hypotenuse [latex]a[/latex] and [latex]b[/latex] are the lengths of the legs.

To solve problems that use the Pythagorean Theorem, we will need to find square roots. In Simplify and Use Square Roots we introduced the notation [latex]\sqrt{m}[/latex] and defined it in this way:

[latex]\text{If }m={n}^{2},\text{ then }\sqrt{m}=n\text{ for }n\ge 0[/latex]

For example, we found that [latex]\sqrt{25}[/latex] is [latex]5[/latex] because [latex]{5}^{2}=25[/latex].

We will use this definition of square roots to solve for the length of a side in a right triangle.

Use the Pythagorean Theorem to find the length of the hypotenuse.

Use the Pythagorean Theorem to find the length of the longer leg.

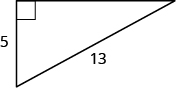
Kelvin is building a gazebo and wants to brace each corner by placing a [latex]\text{10-inch}[/latex] wooden bracket diagonally as shown. How far below the corner should he fasten the bracket if he wants the distances from the corner to each end of the bracket to be equal? Approximate to the nearest tenth of an inch.

In the following video we show two more examples of how to use the Pythagorean Theorem to solve application problems.

• Question ID 146918, 146916, 146914, 146913. Authored by : Lumen Learning. License : CC BY: Attribution
• Solve Applications Using the Pythagorean Theorem (c only). Authored by : James Sousa (mathispower4u.com). Located at : https://youtu.be/2P0dJxpwFMY . License : CC BY: Attribution
• Prealgebra. Provided by : OpenStax. License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]

Pythagorean Theorem Calculator

Enter the values of any two angles and any one side of a triangle below for which you want to find the length of the remaining two sides.

The Pythagorean theorem calculator finds the length of the remaining two sides of a given triangle using sine law or definitions of trigonometric functions.

If a given triangle is a right angle triangle, then the length of the remaining two sides of the triangle can be calculated using the definition of sine and cosine functions given by the formula-

sin θ = Opposite Side Hypotenuse

cos θ = Adjacent Side Hypotenuse

If a given triangle is not a right angle triangle, then the length of the remaining two sides of the triangle can be calculated using the sine law given by the formula-

Where A , B and C are angles of the triangle.

Click the blue arrow to submit. Choose "Find the Length of the Third Side" from the topic selector and click to see the result in our Trigonometry Calculator!

Find the Length of the Third Side

Popular Problems:

Find the Length of the Third Side Side Angle b = A = 90 c = B = 3 a = 4 C = Find the Length of the Third Side Side Angle b = A = 90 c = B = 1 a = 2 C = Find the Length of the Third Side Side Angle b = A = 90 c = B = 2 a = 2 C = Find the Length of the Third Side Side Angle b = A = 90 c = B = a = 4 C = 40 Find the Length of the Third Side Side Angle b = 4 A = 75 c = B = 20 a = C =

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

Pythagorean Theorem Calculator

Please provide any 2 values below to solve the Pythagorean equation: a 2 + b 2 = c 2 .

Related Triangle Calculator | Right Triangle Calculator

Pythagorean Theorem

The Pythagorean Theorem, also known as Pythagoras' theorem, is a fundamental relation between the three sides of a right triangle. Given a right triangle, which is a triangle in which one of the angles is 90°, the Pythagorean theorem states that the area of the square formed by the longest side of the right triangle (the hypotenuse) is equal to the sum of the area of the squares formed by the other two sides of the right triangle:

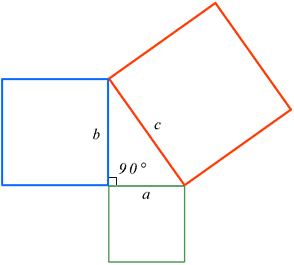
In other words, given that the longest side c = the hypotenuse, and a and b = the other sides of the triangle:

a 2 + b 2 = c 2

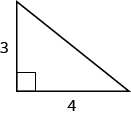
This is known as the Pythagorean equation, named after the ancient Greek thinker Pythagoras. This relationship is useful because if two sides of a right triangle are known, the Pythagorean theorem can be used to determine the length of the third side. Referencing the above diagram, if

a = 3 and b = 4

the length of c can be determined as:

c = √ a 2 + b 2 = √ 3 2 +4 2 = √ 25 = 5

It follows that the length of a and b can also be determined if the lengths of the other two sides are known using the following relationships:

a = √ c 2 - b 2

b = √ c 2 - a 2

The law of cosines is a generalization of the Pythagorean theorem that can be used to determine the length of any side of a triangle if the lengths and angles of the other two sides of the triangle are known. If the angle between the other sides is a right angle, the law of cosines reduces to the Pythagorean equation.

There are a multitude of proofs for the Pythagorean theorem, possibly even the greatest number of any mathematical theorem.

Algebraic proof:

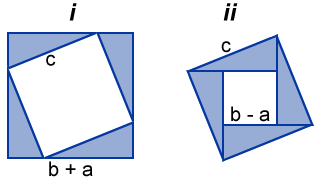
In the figure above, there are two orientations of copies of right triangles used to form a smaller and larger square, labeled i and ii, that depict two algebraic proofs of the Pythagorean theorem.

In the first one, i, the four copies of the same triangle are arranged around a square with sides c. This results in the formation of a larger square with sides of length b + a, and area of (b + a) 2 . The sum of the area of these four triangles and the smaller square must equal the area of the larger square such that:

which yields:

which is the Pythagorean equation.

Since the larger square has sides c and area c 2 , the above can be rewritten as:

c 2 = a 2 + b 2

which is again, the Pythagorean equation.

There are numerous other proofs ranging from algebraic and geometric proofs to proofs using differentials, but the above are two of the simplest versions.

• Math Article

Pythagoras Theorem

Pythagoras Theorem (also called Pythagorean Theorem) is an important topic in Mathematics, which explains the relation between the sides of a right-angled triangle . The sides of the right triangle are also called Pythagorean triples. The formula and proof of this theorem are explained here with examples.

Pythagoras theorem is basically used to find the length of an unknown side and the angle of a triangle. By this theorem, we can derive the base, perpendicular and hypotenuse formulas. Let us learn the mathematics of the Pythagorean theorem in detail here.

Pythagoras Theorem Statement

Pythagoras theorem states that “ In a right-angled triangle,  the square of the hypotenuse side is equal to the sum of squares of the other two sides “. The sides of this triangle have been named Perpendicular, Base and Hypotenuse. Here, the hypotenuse is the longest side, as it is opposite to the angle 90°. The sides of a right triangle (say a, b and c) which have positive integer values, when squared, are put into an equation, also called a Pythagorean triple.

The theorem is named after a Greek Mathematician called Pythagoras.

Pythagoras Theorem Formula

Consider the triangle given above:

Where “a” is the perpendicular,

“b” is the base,

“c” is the hypotenuse.

According to the definition, the Pythagoras Theorem formula is given as:

The side opposite to the right angle (90°)  is the longest side (known as Hypotenuse) because the side opposite to the greatest angle is the longest.

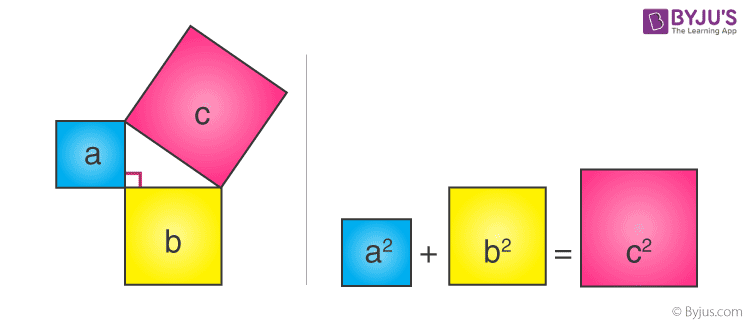
Consider three squares of sides a, b, c mounted on the three sides of a triangle having the same sides as shown.

By Pythagoras Theorem –

Area of square “a” + Area of square “b” = Area of square “c”

The examples of theorem and based on the statement given for right triangles is given below:

Consider a right triangle, given below:

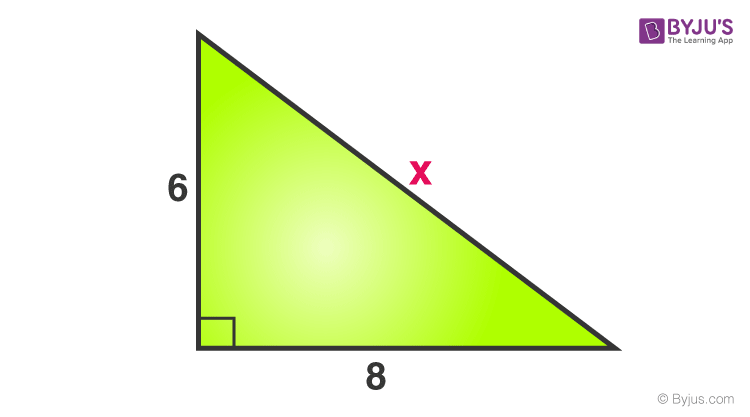
Find the value of x.

X is the side opposite to the right angle, hence it is a hypotenuse.

Now, by the theorem we know;

Hypotenuse 2  = Base 2 + Perpendicular 2

x 2 = 8 2 + 6 2

x 2 = 64+36 = 100

x = √100 = 10

Therefore, the value of x is 10.

Pythagoras Theorem Proof

Given: A right-angled triangle ABC, right-angled at B.

To Prove- AC 2 = AB 2 + BC 2

Construction: Draw a perpendicular BD meeting AC at D.

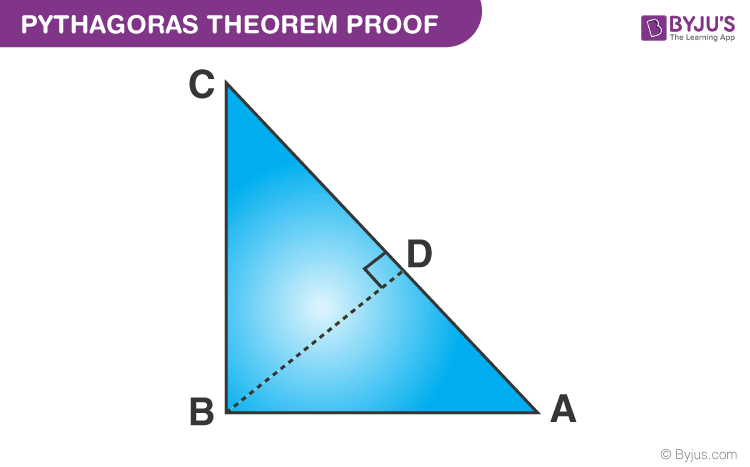
We know, △ ADB ~ △ABC

Therefore, \(\begin{array}{l}\frac{AD}{AB}=\frac{AB}{AC}\end{array} \) (corresponding sides of similar triangles)

Or, AB 2  = AD × AC …………………………….. ……..(1)

Also, △ BDC ~△ABC

Therefore, \(\begin{array}{l}\frac{CD}{BC}=\frac{BC}{AC}\end{array} \) (corresponding sides of similar triangles)

Or, BC 2 = CD × AC ……………………………… ……..(2)

Adding the equations (1) and (2) we get,

AB 2  + BC 2  = AD × AC + CD × AC

AB 2  + BC 2  = AC (AD + CD)

Since, AD + CD = AC

Therefore, AC 2 = AB 2 + BC 2

Hence, the Pythagorean theorem is proved.

Note:   Pythagorean theorem is only applicable to Right-Angled triangle.

Video Lesson on Pythagoras Theorem

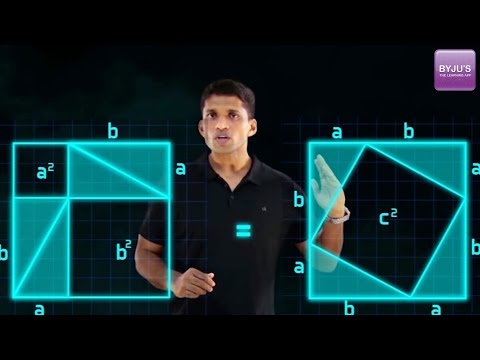
Applications of Pythagoras Theorem

• To know if the triangle is a right-angled triangle or not.
• In a right-angled triangle, we can calculate the length of any side if the other two sides are given.
• To find the diagonal of a square.

Pythagoras theorem is useful to find the sides of a right-angled triangle. If we know the two sides of a right triangle, then we can find the third side.

How to use Pythagoras Theorem?

To use Pythagoras theorem, remember the formula given below:

c 2 = a 2  + b 2

Where a, b and c are the sides of the right triangle.

For example, if the sides of a triangles are a, b and c, such that a = 3 cm, b = 4 cm and c is the hypotenuse. Find the value of c.

c 2 = 3 2 +4 2

c 2  = 9+16

Hence, the length of hypotenuse is 5 cm.

How to find whether a triangle is a right-angled triangle?

If we are provided with the length of three sides of a triangle, then to find whether the triangle is a right-angled triangle or not, we need to use the Pythagorean theorem.

Let us understand this statement with the help of an example.

Suppose a triangle with sides 10cm, 24cm, and 26cm are given. 

Clearly, 26 is the longest side.

It also satisfies the condition, 10 + 24 > 26

c 2  = a 2  + b 2     ………(1)

So, let a = 10, b = 24 and c = 26

First we will solve R.H.S. of equation 1.

a 2   + b 2 = 10 2  + 24 2  = 100 + 576 = 676

Now, taking L.H.S, we get;

c 2 = 26 2  = 676

We can see, 

Therefore, the given triangle is a right triangle, as it satisfies the Pythagoras theorem.

Related Articles

Pythagorean theorem solved examples.

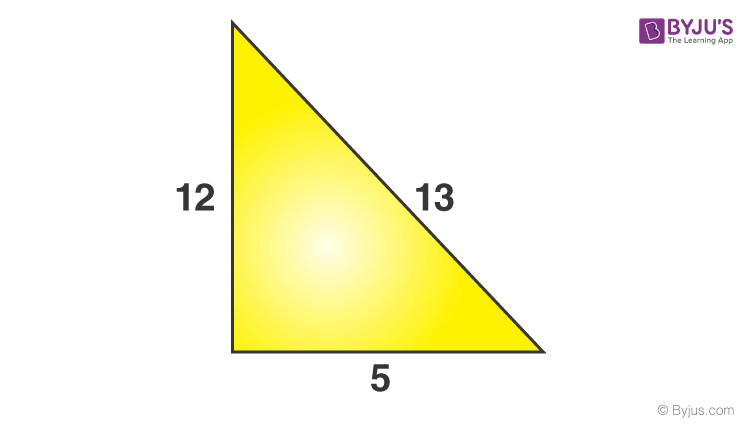
Problem 1:  The sides of a triangle are 5, 12 & 13 units. Check if it has a right angle or not.

Solution: From Pythagoras Theorem, we have;

Perpendicular 2 + Base 2 = Hypotenuse 2

P 2 + B 2 = H 2

Perpendicular (P) = 12 units

Base (B)= 5 units

Hypotenuse (H) = 13 units {since it is the longest side measure}

LHS = P 2 + B 2

⇒ 12 2 + 5 2

⇒ 169 = 169 

L.H.S. = R.H.S.

Therefore, the angle opposite to the 13 units side will be a right angle.

Problem 2:  The two sides of a right-angled triangle are given as shown in the figure. Find the third side.

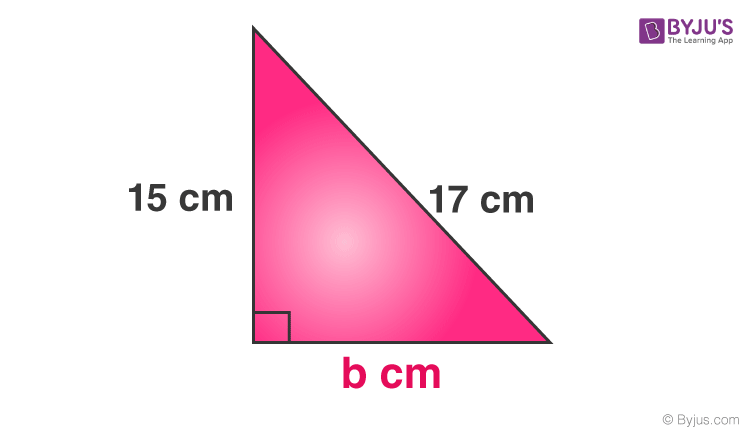
Perpendicular = 15 cm

Base = b cm

Hypotenuse = 17 cm

As per the Pythagorean Theorem, we have;

⇒15 2 + b 2 = 17 2

⇒225 + b 2 = 289

⇒b 2 = 289 – 225

Therefore,  b = 8 cm

Problem 3:  Given the side of a square to be 4 cm. Find the length of the diagonal .

Solution-  Given;

Sides of a square = 4 cm

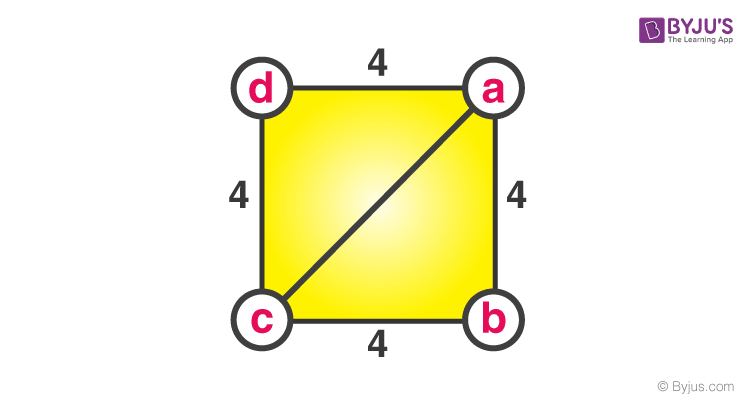
To Find- The length of diagonal ac.

Consider triangle abc (or can also be acd)

(ab) 2 +(bc) 2  = (ac) 2

(4) 2 +(4) 2 = (ac) 2

16 + 16 = (ac) 2

32 = (ac) 2

(ac) 2 = 32

Thus, the length of the diagonal is  4√2 cm.

Practice Problems on Pythagoras Theorem

• In a right triangle ABC, right-angled at B, the lengths of AB and BC are 7 units and 24 units, respectively. Find AC.
• If the length of the diagonal of a square is 10 cm, then find the length of the side of the square.
• A triangle is given whose sides are of length 11 cm, 60 cm, and 61 cm. Check whether these are the sides of a right-angled triangle.

Stay tuned with BYJU’S – The Learning App to learn all the important mathematical concepts and also watch interactive videos to learn with ease.

Frequently Asked Questions on Pythagoras Theorem

What is the formula for pythagorean theorem.

The formula for Pythagoras, for a right-angled triangle, is given by; P 2 + B 2 = H 2

What does Pythagoras theorem state?

Pythagoras theorem states that, in a right triangle, the square of the hypotenuse is equal to the sum of the square of the other two sides.

What is the formula for hypotenuse?

The hypotenuse is the longest side of the right-angled triangle, opposite to right angle, which is adjacent to base and perpendicular. Let base, perpendicular and hypotenuse be a, b and c respectively. Then the hypotenuse formula, from the Pythagoras statement will be; c  = √(a 2  + b 2 )

Can we apply the Pythagoras Theorem for any triangle?

No, this theorem is applicable only for the right-angled triangle.

What is the use of Pythagoras theorem?

Can the diagonals of a square be found using pythagoras theorem.

Yes, the diagonals of a square can be found using the Pythagoras theorem, as the diagonal divides the square into right triangles.

Explain the steps involved in finding the sides of a right triangle using Pythagoras theorem.

Step 1: To find the unknown sides of a right triangle, plug the known values in the Pythagoras theorem formula. Step 2: Simplify the equation to find the unknown side. Step 3: Solve the equation for the unknown side.

What are the different ways to prove Pythagoras theorem?

There are various approaches to prove the Pythagoras theorem. A few of them are listed below: Proof using similar triangles Proof using differentials Euclid’s proof Algebraic proof, and so on.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Maths related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

I want all before year question papers of 10th cbse please send me as soon as possible my exams are going to be start

I could understand this concept very well even though I’m in sixth grade. I learnt this for my math project. It was very helpful. thanks to Byju’ s.

Please explain about pythogorean theorem for side in detail for the project

I think that we children can use this website very well and it is also very helpful for us and I have used this website for the first time By the way I liked everything.

Yes I am satisfied this link 😊.

yes l am satisfied this link

Thanks to this website I will be the best student in my class thanks BYJUS I really appreciate it

Thank you very much byju’s for this. It really helped me in my math project.

Useful page and helped me understanding the concepts formulas I hope for much betterment

Hi , it is very useful page and thank you to byjus the are best learning app.

PLEASE DOWNLOAD THIS APP IT IS EXCELLENT APP

Very useful page for every students’. Thank you byjus!!

This link was very use ful for me 😊😊

I am very well satisfied with the explanation , helped me understand and grasp the concept well . This hep my math project also .Thank you 🙂

Thank you byju. It has helped me

Hi guys, Platform is awesome

According to this theorem, if a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side. Check the proof of Basic Proportionality Theorem converse theorem here.

Very interesting, good job, and thanks for sharing such a good blog.

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.37: Distance Formula and the Pythagorean Theorem

• Last updated
• Save as PDF
• Page ID 4972

Discover lengths of triangle sides using the Pythagorean Theorem. Identify distance as the hypotenuse of a right triangle. Determine distance between ordered pairs.

While walking to school one day, you decide to use your knowledge of the Pythagorean Theorem to determine how far it is between your home and school. You know that you walk 3 blocks east, and then turn and walk 7 blocks north to get to school. Is it possible to use the Pythagorean Theorem to help you determine the "straight line" distance between your home and school?

Determining the Distance Using the Pythagorean Theorem

You can use the Pythagorean Theorem is to find the distance between two points.

Consider the points \((-1, 6)\) and \((5, -3)\). If we plot these points on a grid and connect them, they make a diagonal line. Draw a vertical line down from \((-1, 6)\) and a horizontal line to the left of \((5, -3)\) to make a right triangle.

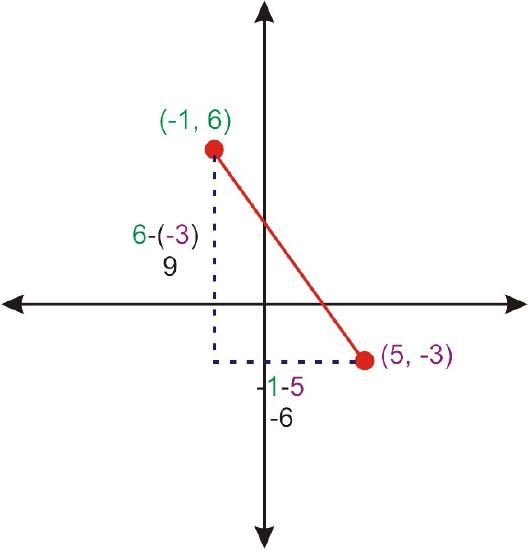
Now we can find the distance between these two points by using the vertical and horizontal distances that we determined from the graph.

\(\begin{align*} 9^2+(−6)^2&=d^2 \\ 81+36&=d^2 \\ 117&=d^2 \\ \sqrt{117}&=d \\ 3\sqrt{13}&=d\end{align*}\)

Notice, that the x−values were subtracted from each other to find the horizontal distance and the y−values were subtracted from each other to find the vertical distance. If this process is generalized for two points \((x_1, y_1) and \((x_2, y_2), the Distance Formula is derived.

\((x_1−x_2)^2+(y_1−y_2)^2=d^2\)

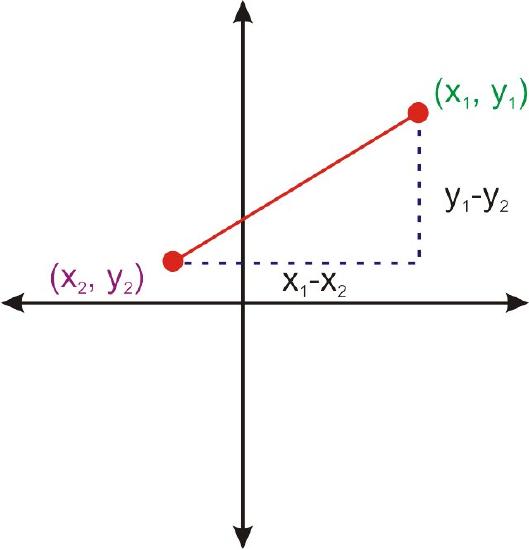
This is the Pythagorean Theorem with the vertical and horizontal differences between \((x_1, y_1)\) and \((x_2, y_2)\). Taking the square root of both sides will solve the right hand side for d, the distance.

\(\sqrt{(x_1−x_2)^2+(y_1−y_2)^2}=d\)

This is the Distance Formula. The following problems show how to apply the distance formula.

Applying the Distance Formula

1. Find the distance between the two points.

\((4, 2)\) and \((-9, 5)\)

Plug each pair of points into the distance formula.

\(\begin{align*}d & =\sqrt{(4−(−9))^2+(2−5)^2} \\ &=\sqrt{13^2+(−3)^2} \\ &=\sqrt{169+9} \\ &=\sqrt{178}\end{align*}\)

2. Find the distance between the two points.

\((-10, 3)\) and \((0, -15)\)

\(\begin{align*}d & =\sqrt{(−10−0)^2+(3−(−15))^2} \\ &=\sqrt{(−10)^2+(18)^2} \\ &=\sqrt{100+324} \\ &=\sqrt{424}=2\sqrt{106}\end{align*}\)

3. Find the distance between the two points.

\((3, 1)\) and \((2, -7)\)

\(\begin{align*}d&=\sqrt{(3−2)^2+(1−(−7))^2} \\ &=\sqrt{(1)^2+(8)^2} \\ &=\sqrt{1+64} \\ &=\sqrt{65}\end{align*}\)

Example \(\PageIndex{1}\)

Earlier, you were asked to use your knowledge of the Pythagorean Theorem to determine how far it is between your home and school.

Since you know that the trip to school involves walking 3 blocks east followed by 7 blocks north, you can construct a triangle on a coordinate system out of these lengths, like this:

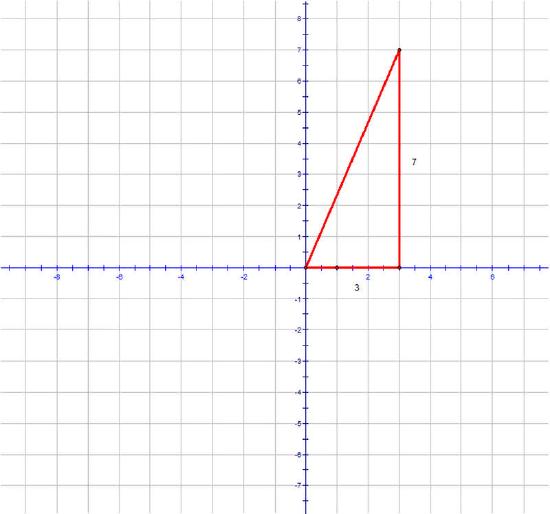
Since you went three blocks to the east, the school has an "\(x\)" coordinate of 3. Likewise, since you went 7 blocks north, the school has a "\(y\)" coordinate of 7. To find the straight-line distance to school, you can use the Distance Formula:

\(\begin{align*}d&=\sqrt{(3−0)^2+(7−0)^2} \\ &=\sqrt{(3)^2+(7)^2} \\ &=\sqrt{58}\end{align*}\)

This is a straight line distance of approximately 7.6 blocks.

Example \(\PageIndex{2}\)

Find the distance between the two points.

\((3, 1) and \((2, -7)

\(\begin{align*}d&=\sqrt{(3−2)^2+(1−(−7))^2 \\ &=\sqrt{(1)^2+(8)^2} \\ &=\sqrt{1+64} \\ &=\sqrt{65}\end{align*}\)

Example \(\PageIndex{3}\)

\((5, -8) and \((0, 3)

\(\begin{align*}d&=\sqrt{(5−0)^2+(−8−(3))^2} \\ &=\sqrt{(5)^2+(−11)^2} \\ &=\sqrt{25+121} \\ =\sqrt{146}\end{align*}\)

Example \(\PageIndex{4}\)

\((2, 6) \)and \((2, 9)\)

\(\begin{align*}d &=\sqrt{(2−2)^2+(6−9)^2} \\ &=\sqrt{(0)^2+(−3)^2 \\ &=\sqrt{9} \\ =3\end{align*}\)

Find the distance between each pair of points. Round each answer to the nearest tenth.

• \((2, 4)\) and \((5, 10)\)
• \((1, 5)\) and \((8, 9)\)
• \((-2, 3)\) and \((6, 4)\)
• \((5, 7)\) and \((5, 10)\)
• \((8, 12)\) and \((15, 12)\)
• \((1, -4)\) and \((25, -2)\)
• \((5, -6)\) and \((3, 7)\)
• \((12, -9)\) and \((-1, 5)\)
• \((-3, 14)\) and \((8, 10)\)
• \((-11, 3)\) and \((-5, 1)\)
• \((5, 2)\) and \((11, 13)\)
• \((8, 10)\) and \((9, -6)\)

Find the perimeter of each triangle. Round each answer to the nearest tenth.

• \(A(3,−5),\:B(−5,−8),\:C(−2,7)\)
• \(A(5,3),\:B(2,−7),\:C(−1,5)\)
• \(A(1,2),\:B(1,5),\:C(4,5)\)

Review (Answers)

To see the Review answers, open this PDF file and look for section 1.4.

Additional Resources

Interactive Element

Video: The Distance Formula

Practice: Distance Formula and the Pythagorean Theorem

Real World: It All Depends on Distance

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

9.4: Use Properties of Angles, Triangles, and the Pythagorean Theorem (Part 1)

• Last updated
• Save as PDF
• Page ID 5007

Learning Objectives

• Use the properties of angles
• Use the properties of triangles
• Use the Pythagorean Theorem

be prepared!

Before you get started, take this readiness quiz.

• Solve: x + 3 + 6 = 11. If you missed this problem, review Example 8.1.6 .
• Solve: \(\dfrac{a}{45} = \dfrac{4}{3}\). If you missed this problem, review Example 6.5.3 .
• Simplify: \(\sqrt{36 + 64}\). If you missed this problem, review Example 5.12.4 .

So far in this chapter, we have focused on solving word problems, which are similar to many real-world applications of algebra. In the next few sections, we will apply our problem-solving strategies to some common geometry problems.

Use the Properties of Angles

Are you familiar with the phrase ‘do a 180’? It means to turn so that you face the opposite direction. It comes from the fact that the measure of an angle that makes a straight line is 180 degrees. See Figure \(\PageIndex{1}\).

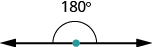
Figure \(\PageIndex{1}\)

An angle is formed by two rays that share a common endpoint. Each ray is called a side of the angle and the common endpoint is called the vertex . An angle is named by its vertex. In Figure \(\PageIndex{2}\), ∠A is the angle with vertex at point A. The measure of ∠A is written m ∠ A.

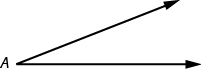
Figure \(\PageIndex{2}\) - ∠ A is the angle with vertex at point A.

We measure angles in degrees, and use the symbol ° to represent degrees. We use the abbreviation m for the measure of an angle. So if ∠A is 27°, we would write m ∠ A = 27.

If the sum of the measures of two angles is 180°, then they are called supplementary angles . In Figure \(\PageIndex{3}\), each pair of angles is supplementary because their measures add to 180°. Each angle is the supplement of the other.

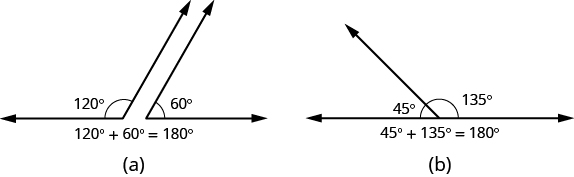
Figure \(\PageIndex{3}\) - The sum of the measures of supplementary angles is 180°.

If the sum of the measures of two angles is 90°, then the angles are complementary angles . In Figure \(\PageIndex{4}\), each pair of angles is complementary, because their measures add to 90°. Each angle is the complement of the other.

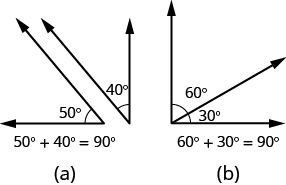
Figure \(\PageIndex{4}\) - The sum of the measures of complementary angles is 90°.

Definition: Supplementary and Complementary Angles

If the sum of the measures of two angles is 180°, then the angles are supplementary.

If ∠A and ∠B are supplementary, then m∠A + m∠B = 180°.

If the sum of the measures of two angles is 90°, then the angles are complementary.

If ∠A and ∠B are complementary, then m∠A + m∠B = 90°.

In this section and the next, you will be introduced to some common geometry formulas. We will adapt our Problem Solving Strategy for Geometry Applications. The geometry formula will name the variables and give us the equation to solve.

In addition, since these applications will all involve geometric shapes, it will be helpful to draw a figure and then label it with the information from the problem. We will include this step in the Problem Solving Strategy for Geometry Applications.

HOW TO: USE A PROBLEM SOLVING STRATEGY FOR GEOMETRY APPLICATIONS

Step 1. Read the problem and make sure you understand all the words and ideas. Draw a figure and label it with the given information.

Step 2. Identify what you are looking for

Step 3. Name what you are looking for and choose a variable to represent it.

Step 4. Translate into an equation by writing the appropriate formula or model for the situation. Substitute in the given information.

Step 5. Solve the equation using good algebra techniques.

Step 6. Check the answer in the problem and make sure it makes sense.

Step 7. Answer the question with a complete sentence.

The next example will show how you can use the Problem Solving Strategy for Geometry Applications to answer questions about supplementary and complementary angles.

Example \(\PageIndex{1}\):

An angle measures 40°. Find (a) its supplement, and (b) its complement.

Exercise \(\PageIndex{1}\):

An angle measures 25°. Find (a) its supplement, and (b) its complement.

Exercise \(\PageIndex{2}\):

An angle measures 77°. Find (a) its supplement, and (b) its complement.

Did you notice that the words complementary and supplementary are in alphabetical order just like 90 and 180 are in numerical order?

Example \(\PageIndex{2}\):

Two angles are supplementary. The larger angle is 30° more than the smaller angle. Find the measure of both angles.

Exercise \(\PageIndex{3}\):

Two angles are supplementary. The larger angle is 100° more than the smaller angle. Find the measures of both angles.

40°, 140°

Exercise \(\PageIndex{4}\):

Two angles are complementary. The larger angle is 40° more than the smaller angle. Find the measures of both angles.

25°, 65°

Use the Properties of Triangles

What do you already know about triangles? Triangle have three sides and three angles. Triangles are named by their vertices. The triangle in Figure \(\PageIndex{5}\) is called ΔABC, read ‘triangle ABC’. We label each side with a lower case letter to match the upper case letter of the opposite vertex.

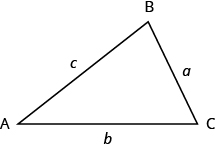
Figure \(\PageIndex{5}\) - ΔABC has vertices A, B, and C and sides a, b, and c.

The three angles of a triangle are related in a special way. The sum of their measures is 180°.

\[m \angle A + m \angle B + m \angle C = 180°\]

Definition: Sum of the Measures of the Angles of a Triangle

For any ΔABC, the sum of the measures of the angles is 180°.

Example \(\PageIndex{3}\):

The measures of two angles of a triangle are 55° and 82°. Find the measure of the third angle.

Exercise \(\PageIndex{5}\):

The measures of two angles of a triangle are 31° and 128°. Find the measure of the third angle.

Exercise \(\PageIndex{6}\):

A triangle has angles of 49° and 75°. Find the measure of the third angle.

Right Triangles

Some triangles have special names. We will look first at the right triangle . A right triangle has one 90° angle, which is often marked with the symbol shown in Figure \(\PageIndex{6}\).

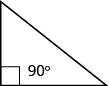
Figure \(\PageIndex{6}\)

If we know that a triangle is a right triangle, we know that one angle measures 90° so we only need the measure of one of the other angles in order to determine the measure of the third angle.

Example \(\PageIndex{4}\):

One angle of a right triangle measures 28°. What is the measure of the third angle?

Exercise \(\PageIndex{7}\):

One angle of a right triangle measures 56°. What is the measure of the other angle?

Exercise \(\PageIndex{8}\):

One angle of a right triangle measures 45°. What is the measure of the other angle?

In the examples so far, we could draw a figure and label it directly after reading the problem. In the next example, we will have to define one angle in terms of another. So we will wait to draw the figure until we write expressions for all the angles we are looking for.

Example \(\PageIndex{5}\):

The measure of one angle of a right triangle is 20° more than the measure of the smallest angle. Find the measures of all three angles.

Exercise \(\PageIndex{9}\):

The measure of one angle of a right triangle is 50° more than the measure of the smallest angle. Find the measures of all three angles.

20°, 70°, 90°

Exercise \(\PageIndex{10}\):

The measure of one angle of a right triangle is 30° more than the measure of the smallest angle. Find the measures of all three angles.

30°, 60°, 90°

Similar Triangles

When we use a map to plan a trip, a sketch to build a bookcase, or a pattern to sew a dress, we are working with similar figures. In geometry, if two figures have exactly the same shape but different sizes, we say they are similar figures . One is a scale model of the other. The corresponding sides of the two figures have the same ratio, and all their corresponding angles are have the same measures.

The two triangles in Figure \(\PageIndex{7}\) are similar. Each side of ΔABC is four times the length of the corresponding side of ΔXYZ and their corresponding angles have equal measures.

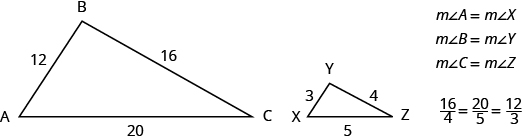
Figure \(\PageIndex{7}\) - ΔABC and ΔXYZ are similar triangles. Their corresponding sides have the same ratio and the corresponding angles have the same measure.

Definition: Properties of Similar Triangles

If two triangles are similar, then their corresponding angle measures are equal and their corresponding side lengths are in the same ratio.

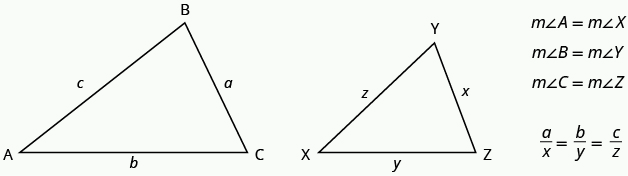
The length of a side of a triangle may be referred to by its endpoints, two vertices of the triangle. For example, in ΔABC:

the length a can also be written BC

the length b can also be written AC

the length c can also be written AB

We will often use this notation when we solve similar triangles because it will help us match up the corresponding side lengths.

Example \(\PageIndex{6}\):

ΔABC and ΔXYZ are similar triangles. The lengths of two sides of each triangle are shown. Find the lengths of the third side of each triangle.

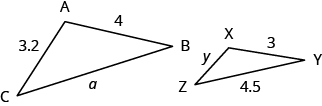
Exercise \(\PageIndex{11}\):

ΔABC is similar to ΔXYZ. Find a.

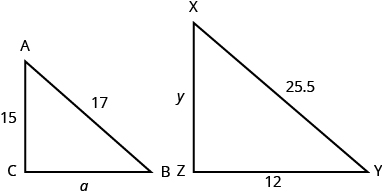
Exercise \(\PageIndex{12}\):

ΔABC is similar to ΔXYZ. Find y.

Contributors and Attributions

Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/[email protected] ."

Calculate a Side Measurement Using Pythagorean Theorem (A)

Welcome to The Calculate a Side Measurement Using Pythagorean Theorem (A) Math Worksheet from the Geometry Worksheets Page at Math-Drills.com. This math worksheet was created or last revised on 2017-05-23 and has been viewed 25 times this week and 415 times this month. It may be printed, downloaded or saved and used in your classroom, home school, or other educational environment to help someone learn math.

Teacher s can use math worksheets as test s, practice assignment s or teaching tool s (for example in group work , for scaffolding or in a learning center ). Parent s can work with their children to give them extra practice , to help them learn a new math skill or to keep their skills fresh over school breaks . Student s can use math worksheets to master a math skill through practice, in a study group or for peer tutoring .

Use the buttons below to print, open, or download the PDF version of the Calculate a Side Measurement Using Pythagorean Theorem (A) math worksheet . The size of the PDF file is 40552 bytes . Preview images of the first and second (if there is one) pages are shown. If there are more versions of this worksheet, the other versions will be available below the preview images. For more like this, use the search bar to look for some or all of these keywords: math, geometry, Pythagoras, Pythagorean, theorem, hypotenuse, cathetus, catheti, side, measurement .

Print Full Version

Open Full Version

Download Full Version

Print Student Version

Open Student Version

Download Student Version

The Print button initiates your browser's print dialog. The Open button opens the complete PDF file in a new browser tab. The Download button initiates a download of the PDF math worksheet. Teacher versions include both the question page and the answer key. Student versions, if present, include only the question page.

Other Versions:

More Geometry Worksheets

Copyright © 2005-2024 Math-Drills.com You may use the math worksheets on this website according to our Terms of Use to help students learn math.