13 4 problem solving with trigonometry answers

Want Better Math Grades?

✅ Unlimited Solutions

✅ Step-by-Step Answers

✅ Available 24/7

➕ Free Bonuses ($1085 value!)

On this page

• Search IntMath
• Math interactives
• About (site info)
• Uses of Trignometry
• ASCIIMath input, KaTeX output
• ASCIIMath input, LaTeX and KaTeX output
• Send Math in emails
• Syntax for ASCIIMathML
• Math Display Experiments
• Scientific Notebook
• Math Problem Solver

Related Sections

Math Tutoring

Need help? Chat with a tutor anytime, 24/7.

Trigonometry Problem Solver

This tool combines the power of mathematical computation engine that excels at solving mathematical formulas with the power of artificial intelligence large language models to parse and generate natural language answers. This creates a math problem solver that's more accurate than ChatGPT, more flexible than a math calculator, and provides answers faster than a human tutor.

Sign up for free here .

Problem Solver Subjects

Our math problem solver that lets you input a wide variety of trigonometry math problems and it will provide a step by step answer. This math solver excels at math word problems as well as a wide range of math subjects.

• Math Word Problems
• Pre-Algebra
• Geometry Graphing
• Trigonometry
• Precalculus
• Finite Math
• Linear Algebra

Here are example math problems within each subject that can be input into the calculator and solved. This list is constanstly growing as functionality is added to the calculator.

Basic Math Solutions

Below are examples of basic math problems that can be solved.

• Long Arithmetic
• Rational Numbers
• Operations with Fractions
• Ratios, Proportions, Percents
• Measurement, Area, and Volume
• Factors, Fractions, and Exponents
• Unit Conversions
• Data Measurement and Statistics
• Points and Line Segments

Math Word Problem Solutions

Math word problems require interpreting what is being asked and simplifying that into a basic math equation. Once you have the equation you can then enter that into the problem solver as a basic math or algebra question to be correctly solved. Below are math word problem examples and their simplified forms.

Word Problem: Rachel has 17 apples. She gives some to Sarah. Sarah now has 8 apples. How many apples did Rachel give her?

Simplified Equation: 17 - x = 8

Word Problem: Rhonda has 12 marbles more than Douglas. Douglas has 6 marbles more than Bertha. Rhonda has twice as many marbles as Bertha has. How many marbles does Douglas have?

Variables: Rhonda's marbles is represented by (r), Douglas' marbles is represented by (d) and Bertha's marbles is represented by (b)

Simplified Equation: {r = d + 12, d = b + 6, r = 2 �� b}

Word Problem: if there are 40 cookies all together and Angela takes 10 and Brett takes 5 how many are left?

Simplified: 40 - 10 - 5

Pre-Algebra Solutions

Below are examples of Pre-Algebra math problems that can be solved.

• Variables, Expressions, and Integers
• Simplifying and Evaluating Expressions
• Solving Equations
• Multi-Step Equations and Inequalities
• Ratios, Proportions, and Percents
• Linear Equations and Inequalities

Algebra Solutions

Below are examples of Algebra math problems that can be solved.

• Algebra Concepts and Expressions
• Points, Lines, and Line Segments
• Simplifying Polynomials
• Factoring Polynomials
• Linear Equations
• Absolute Value Expressions and Equations
• Radical Expressions and Equations
• Systems of Equations
• Quadratic Equations
• Inequalities
• Complex Numbers and Vector Analysis
• Logarithmic Expressions and Equations
• Exponential Expressions and Equations
• Conic Sections
• Vector Spaces
• 3d Coordinate System
• Eigenvalues and Eigenvectors
• Linear Transformations
• Number Sets
• Analytic Geometry

Trigonometry Solutions

Below are examples of Trigonometry math problems that can be solved.

• Algebra Concepts and Expressions Review
• Right Triangle Trigonometry
• Radian Measure and Circular Functions
• Graphing Trigonometric Functions
• Simplifying Trigonometric Expressions
• Verifying Trigonometric Identities
• Solving Trigonometric Equations
• Complex Numbers
• Analytic Geometry in Polar Coordinates
• Exponential and Logarithmic Functions
• Vector Arithmetic

Precalculus Solutions

Below are examples of Precalculus math problems that can be solved.

• Operations on Functions
• Rational Expressions and Equations
• Polynomial and Rational Functions
• Analytic Trigonometry
• Sequences and Series
• Analytic Geometry in Rectangular Coordinates
• Limits and an Introduction to Calculus

Calculus Solutions

Below are examples of Calculus math problems that can be solved.

• Evaluating Limits
• Derivatives
• Applications of Differentiation
• Applications of Integration
• Techniques of Integration
• Parametric Equations and Polar Coordinates
• Differential Equations

Statistics Solutions

Below are examples of Statistics problems that can be solved.

• Algebra Review
• Average Descriptive Statistics
• Dispersion Statistics
• Probability
• Probability Distributions
• Frequency Distribution
• Normal Distributions
• t-Distributions
• Hypothesis Testing
• Estimation and Sample Size
• Correlation and Regression

Finite Math Solutions

Below are examples of Finite Math problems that can be solved.

• Polynomials and Expressions
• Equations and Inequalities
• Linear Functions and Points
• Systems of Linear Equations
• Mathematics of Finance
• Statistical Distributions

Linear Algebra Solutions

Below are examples of Linear Algebra math problems that can be solved.

• Introduction to Matrices
• Linear Independence and Combinations

Chemistry Solutions

Below are examples of Chemistry problems that can be solved.

• Unit Conversion
• Atomic Structure
• Molecules and Compounds
• Chemical Equations and Reactions
• Behavior of Gases
• Solutions and Concentrations

Physics Solutions

Below are examples of Physics math problems that can be solved.

• Static Equilibrium
• Dynamic Equilibrium
• Kinematics Equations
• Electricity
• Thermodymanics

Geometry Graphing Solutions

Below are examples of Geometry and graphing math problems that can be solved.

• Step By Step Graphing
• Linear Equations and Functions
• Polar Equations

Looking for the old Mathway Calculator? We've moved it to here .

Tips, tricks, lessons, and tutoring to help reduce test anxiety and move to the top of the class.

Email Address Sign Up

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

13.4: Right Triangle Trigonometry

• Last updated
• Save as PDF
• Page ID 40841

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Use right triangles to evaluate trigonometric functions.
• Find function values for 30°(\(\dfrac{\pi}{6}\)),45°(\(\dfrac{\pi}{4}\)),and 60°(\(\dfrac{\pi}{3}\)).
• Use equal cofunctions of complementary angles.
• Use the definitions of trigonometric functions of any angle.
• Use right-triangle trigonometry to solve applied problems.

Mt. Everest, which straddles the border between China and Nepal, is the tallest mountain in the world. Measuring its height is no easy task and, in fact, the actual measurement has been a source of controversy for hundreds of years. The measurement process involves the use of triangles and a branch of mathematics known as trigonometry. In this section, we will define a new group of functions known as trigonometric functions, and find out how they can be used to measure heights, such as those of the tallest mountains.

We have previously defined the sine and cosine of an angle in terms of the coordinates of a point on the unit circle intersected by the terminal side of the angle:

\[ \begin{align*} \cos t &= x \\ \sin t &=y \end{align*} \]

In this section, we will see another way to define trigonometric functions using properties of right triangles .

Using Right Triangles to Evaluate Trigonometric Functions

In earlier sections, we used a unit circle to define the trigonometric functions . In this section, we will extend those definitions so that we can apply them to right triangles. The value of the sine or cosine function of \(t\) is its value at \(t\) radians. First, we need to create our right triangle. Figure \(\PageIndex{1}\) shows a point on a unit circle of radius 1. If we drop a vertical line segment from the point \((x,y)\) to the x -axis, we have a right triangle whose vertical side has length \(y\) and whose horizontal side has length \(x\). We can use this right triangle to redefine sine, cosine, and the other trigonometric functions as ratios of the sides of a right triangle.

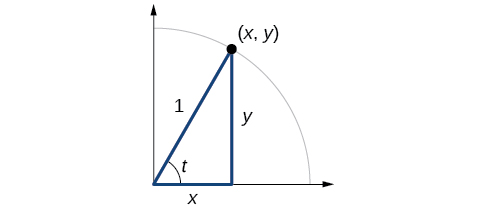
\[ \cos t= \frac{x}{1}=x \]

Likewise, we know

\[ \sin t= \frac{y}{1}=y \]

These ratios still apply to the sides of a right triangle when no unit circle is involved and when the triangle is not in standard position and is not being graphed using \((x,y)\) coordinates. To be able to use these ratios freely, we will give the sides more general names: Instead of \(x\),we will call the side between the given angle and the right angle the adjacent side to angle \(t\). (Adjacent means “next to.”) Instead of \(y\),we will call the side most distant from the given angle the opposite side from angle \(t\). And instead of \(1\),we will call the side of a right triangle opposite the right angle the hypotenuse . These sides are labeled in Figure \(\PageIndex{2}\).

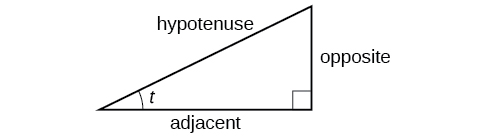
Understanding Right Triangle Relationships

Given a right triangle with an acute angle of \(t\),

\[\begin{align} \sin (t) &= \dfrac{\text{opposite}}{\text{hypotenuse}} \label{sindef}\\ \cos (t) &= \dfrac{\text{adjacent}}{\text{hypotenuse}} \label{cosdef}\\ \tan (t) &= \dfrac{\text{opposite}}{\text{adjacent}} \label{tandef}\end{align}\]

A common mnemonic for remembering these relationships is SohCahToa, formed from the first letters of “ S ine is o pposite over h ypotenuse, C osine is a djacent over h ypotenuse, T angent is o pposite over a djacent.”

how to: Given the side lengths of a right triangle and one of the acute angles, find the sine, cosine, and tangent of that angle

• Find the sine as the ratio of the opposite side to the hypotenuse.
• Find the cosine as the ratio of the adjacent side to the hypotenuse.
• Find the tangent is the ratio of the opposite side to the adjacent side.

Example \(\PageIndex{1}\): Evaluating a Trigonometric Function of a Right Triangle

Given the triangle shown in Figure \(\PageIndex{3}\), find the value of \(\cos α\).

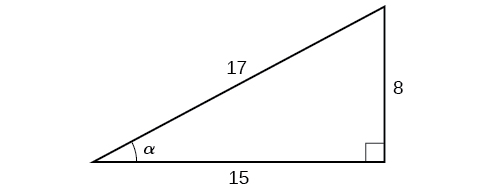
The side adjacent to the angle is 15, and the hypotenuse of the triangle is 17, so via Equation \ref{cosdef}:

\[\begin{align*} \cos (α) &= \dfrac{\text{adjacent}}{\text{hypotenuse}} \\[4pt] &= \dfrac{15}{17} \end{align*}\]

Exercise \(\PageIndex{1}\)

Given the triangle shown in Figure \(\PageIndex{4}\), find the value of \(\sin t\).

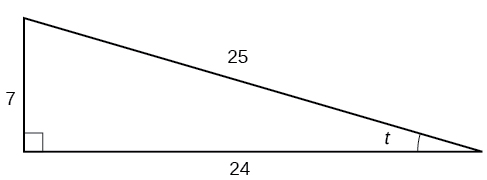
\(\frac{7}{25}\)

Relating Angles and Their Functions

When working with right triangles, the same rules apply regardless of the orientation of the triangle. In fact, we can evaluate the six trigonometric functions of either of the two acute angles in the triangle in Figure \(\PageIndex{5}\). The side opposite one acute angle is the side adjacent to the other acute angle, and vice versa.

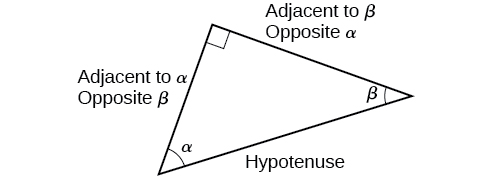
We will be asked to find all six trigonometric functions for a given angle in a triangle. Our strategy is to find the sine, cosine, and tangent of the angles first. Then, we can find the other trigonometric functions easily because we know that the reciprocal of sine is cosecant, the reciprocal of cosine is secant, and the reciprocal of tangent is cotangent.

how to: Given the side lengths of a right triangle, evaluate the six trigonometric functions of one of the acute angles

• If needed, draw the right triangle and label the angle provided.
• Identify the angle, the adjacent side, the side opposite the angle, and the hypotenuse of the right triangle.
• sine as the ratio of the opposite side to the hypotenuse
• cosine as the ratio of the adjacent side to the hypotenuse
• tangent as the ratio of the opposite side to the adjacent side
• secant as the ratio of the hypotenuse to the adjacent side
• cosecant as the ratio of the hypotenuse to the opposite side
• cotangent as the ratio of the adjacent side to the opposite side

Example \(\PageIndex{2}\): Evaluating Trigonometric Functions of Angles Not in Standard Position

Using the triangle shown in Figure \(\PageIndex{6}\), evaluate \( \sin α, \cos α, \tan α, \sec α, \csc α,\) and \( \cot α\).

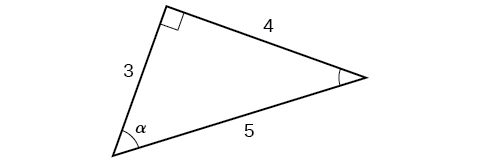
\[ \begin{align*} \sin α &= \dfrac{\text{opposite } α}{\text{hypotenuse}} = \dfrac{4}{5} \\ \cos α &= \dfrac{\text{adjacent to }α}{\text{hypotenuse}}=\dfrac{3}{5} \\ \tan α &= \dfrac{\text{opposite }α}{\text{adjacent to }α}=\dfrac{4}{3} \\ \sec α &= \dfrac{\text{hypotenuse}}{\text{adjacent to }α}= \dfrac{5}{3} \\ \csc α &= \dfrac{\text{hypotenuse}}{\text{opposite }α}=\dfrac{5}{4} \\ \cot α &= \dfrac{\text{adjacent to }α}{\text{opposite }α}=\dfrac{3}{4} \end{align*}\]

Exercise \(\PageIndex{2}\)

Using the triangle shown in Figure \(\PageIndex{7}\), evaluate \( \sin t, \cos t,\tan t, \sec t, \csc t,\) and \(\cot t\).

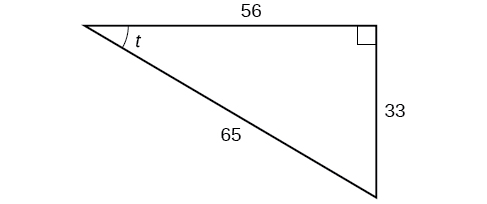
\[\begin{align*} \sin t &= \frac{33}{65}, \cos t= \frac{56}{65},\tan t= \frac{33}{56}, \\ \\ \sec t &= \frac{65}{56},\csc t= \frac{65}{33},\cot t= \frac{56}{33} \end{align*}\]

Finding Trigonometric Functions of Special Angles Using Side Lengths

We have already discussed the trigonometric functions as they relate to the special angles on the unit circle. Now, we can use those relationships to evaluate triangles that contain those special angles. We do this because when we evaluate the special angles in trigonometric functions, they have relatively friendly values, values that contain either no or just one square root in the ratio. Therefore, these are the angles often used in math and science problems. We will use multiples of \(30°, 60°,\) and \(45°\), however, remember that when dealing with right triangles, we are limited to angles between \(0° \text{ and } 90°\).

Suppose we have a \(30°,60°,90°\) triangle, which can also be described as a \(\frac{π}{6}, \frac{π}{3},\frac{π}{2}\) triangle. The sides have lengths in the relation \(s,\sqrt{3}s,2s.\) The sides of a \(45°,45°,90° \)triangle, which can also be described as a \(\frac{π}{4},\frac{π}{4},\frac{π}{2}\) triangle, have lengths in the relation \(s,s,\sqrt{2}s.\) These relations are shown in Figure \(\PageIndex{8}\).

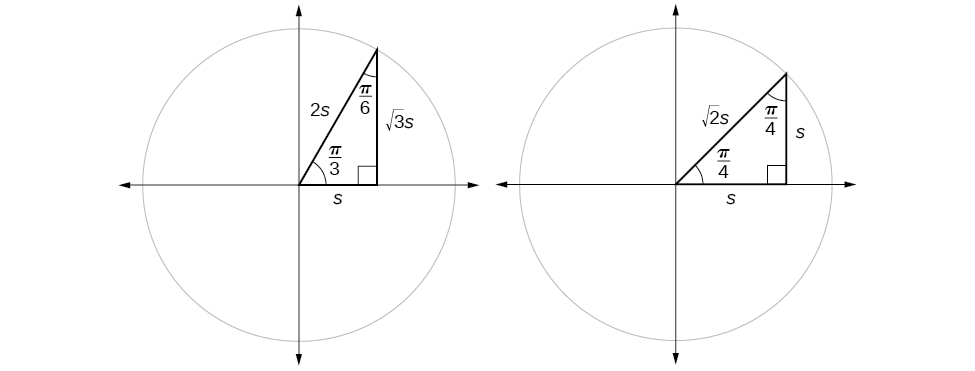
We can then use the ratios of the side lengths to evaluate trigonometric functions of special angles.

Given trigonometric functions of a special angle, evaluate using side lengths.

• Use the side lengths shown in Figure \(\PageIndex{8}\) for the special angle you wish to evaluate.
• Use the ratio of side lengths appropriate to the function you wish to evaluate.

Example \(\PageIndex{3}\): Evaluating Trigonometric Functions of Special Angles Using Side Lengths

Find the exact value of the trigonometric functions of \(\frac{π}{3}\), using side lengths.

\[\begin{align*} \sin (\dfrac{π}{3}) &= \dfrac{\text{opp}}{\text{hyp}}=\dfrac{\sqrt{3}s}{2s}=\dfrac{\sqrt{3}}{2} \\ \cos (\dfrac{π}{3}) &= \dfrac{\text{adj}}{\text{hyp}}=\dfrac{s}{2s}=\dfrac{1}{2} \\ \tan (\dfrac{π}{3}) &= \dfrac{\text{opp}}{\text{adj}} =\dfrac{\sqrt{3}s}{s}=\sqrt{3} \\ \sec (\dfrac{π}{3}) &= \dfrac{\text{hyp}}{\text{adj}} = \dfrac{2s}{s}=2 \\ \csc (\dfrac{π}{3}) &= \dfrac{\text{hyp}}{\text{opp}} =\dfrac{2s}{\sqrt{3}s}=\dfrac{2}{\sqrt{3}}=\dfrac{2\sqrt{3}}{3} \\ \cot (\dfrac{π}{3}) &= \dfrac{\text{adj}}{\text{opp}}=\dfrac{s}{\sqrt{3}s}=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3} \end{align*}\]

Exercise \(\PageIndex{3}\)

Find the exact value of the trigonometric functions of \(\frac{π}{4}\) using side lengths.

\( \sin (\frac{π}{4})=\frac{\sqrt{2}}{2}, \cos (\frac{π}{4})=\frac{\sqrt{2}}{2}, \tan (\frac{π}{4})=1,\)

\( \sec (\frac{π}{4})=\sqrt{2}, \csc (\frac{π}{4})=\sqrt{2}, \cot (\frac{π}{4}) =1 \)

Using Equal Cofunction of Complements

If we look more closely at the relationship between the sine and cosine of the special angles relative to the unit circle, we will notice a pattern. In a right triangle with angles of \(\frac{π}{6}\) and \(\frac{π}{3}\), we see that the sine of \(\frac{π}{3}\), namely \(\frac{\sqrt{3}}{2}\), is also the cosine of \(\frac{π}{6}\), while the sine of \(\frac{π}{6}\), namely \(\frac{1}{2},\) is also the cosine of \(\frac{π}{3}\) (Figure \(\PageIndex{9}\)).

\[\begin{align*} \sin \frac{π}{3} &= \cos \frac{π}{6}=\frac{\sqrt{3}s}{2s}=\frac{\sqrt{3}}{2} \\ \sin \frac{π}{6} &= \cos \frac{π}{3}=\frac{s}{2s}=\frac{1}{2} \end{align*}\]

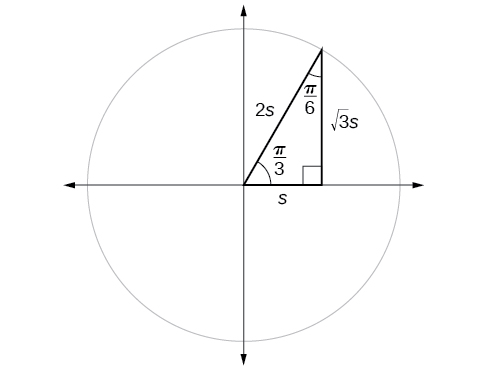
This result should not be surprising because, as we see from Figure \(\PageIndex{9}\), the side opposite the angle of \(\frac{π}{3}\) is also the side adjacent to \(\frac{π}{6}\), so \(\sin (\frac{π}{3})\) and \(\cos (\frac{π}{6})\) are exactly the same ratio of the same two sides, \(\sqrt{3} s\) and \(2s.\) Similarly, \( \cos (\frac{π}{3})\) and \( \sin (\frac{π}{6})\) are also the same ratio using the same two sides, \(s\) and \(2s\).

The interrelationship between the sines and cosines of \(\frac{π}{6}\) and \(\frac{π}{3}\) also holds for the two acute angles in any right triangle, since in every case, the ratio of the same two sides would constitute the sine of one angle and the cosine of the other. Since the three angles of a triangle add to π, π,and the right angle is \(\frac{π}{2}\), the remaining two angles must also add up to \(\frac{π}{2}\). That means that a right triangle can be formed with any two angles that add to \(\frac{π}{2}\)—in other words, any two complementary angles. So we may state a cofunction identity : If any two angles are complementary, the sine of one is the cosine of the other, and vice versa. This identity is illustrated in Figure \(\PageIndex{10}\).

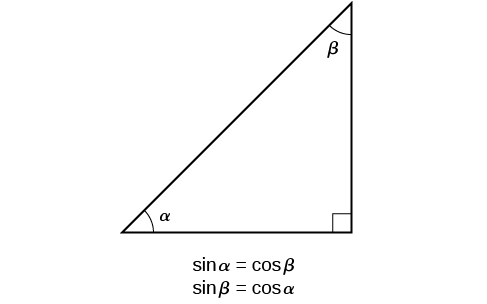
Using this identity, we can state without calculating, for instance, that the sine of \(\frac{π}{12}\) equals the cosine of \(\frac{5π}{12}\), and that the sine of \(\frac{5π}{12}\) equals the cosine of \(\frac{π}{12}\). We can also state that if, for a certain angle \(t, \cos t= \frac{5}{13},\) then \( \sin (\frac{π}{2}−t)=\frac{5}{13}\) as well.

COFUNCTION IDENTITIES

The cofunction identities in radians are listed in Table \(\PageIndex{1}\).

how to: Given the sine and cosine of an angle, find the sine or cosine of its complement.

• To find the sine of the complementary angle, find the cosine of the original angle.
• To find the cosine of the complementary angle, find the sine of the original angle.

Example \(\PageIndex{4}\): Using Cofunction Identities

If \( \sin t = \frac{5}{12},\) find \(( \cos \frac{π}{2}−t)\).

According to the cofunction identities for sine and cosine,

\[ \sin t= \cos (\dfrac{π}{2}−t). \nonumber\]

\[ \cos (\dfrac{π}{2}−t)= \dfrac{5}{12}. \nonumber\]

Exercise \(\PageIndex{4}\)

If \(\csc (\frac{π}{6})=2,\) find \( \sec (\frac{π}{3}).\)

Using Trigonometric Functions

In previous examples, we evaluated the sine and cosine in triangles where we knew all three sides. But the real power of right-triangle trigonometry emerges when we look at triangles in which we know an angle but do not know all the sides.

how to: Given a right triangle, the length of one side, and the measure of one acute angle, find the remaining sides

• For each side, select the trigonometric function that has the unknown side as either the numerator or the denominator. The known side will in turn be the denominator or the numerator.
• Write an equation setting the function value of the known angle equal to the ratio of the corresponding sides.
• Using the value of the trigonometric function and the known side length, solve for the missing side length.

Example \(\PageIndex{5}\): Finding Missing Side Lengths Using Trigonometric Ratios

Find the unknown sides of the triangle in Figure \(\PageIndex{11}\).

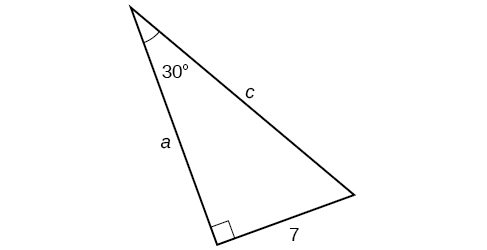
We know the angle and the opposite side, so we can use the tangent to find the adjacent side.

\[ \tan (30°)= \dfrac{7}{a} \nonumber\]

We rearrange to solve for \(a\).

\[\begin{align} a &=\dfrac{7}{ \tan (30°)} \\ & =12.1 \end{align} \nonumber\]

We can use the sine to find the hypotenuse.

\[ \sin (30°)= \dfrac{7}{c} \nonumber\]

Again, we rearrange to solve for \(c\).

\[\begin{align*} c &= \dfrac{7}{\sin (30°)} =14 \end{align*}\]

Exercise \(\PageIndex{5}\):

A right triangle has one angle of \(\frac{π}{3}\) and a hypotenuse of 20. Find the unknown sides and angle of the triangle.

\(\mathrm{adjacent=10; opposite=10 \sqrt{3}; }\) missing angle is \(\frac{π}{6}\)

Using Right Triangle Trigonometry to Solve Applied Problems

Right-triangle trigonometry has many practical applications. For example, the ability to compute the lengths of sides of a triangle makes it possible to find the height of a tall object without climbing to the top or having to extend a tape measure along its height. We do so by measuring a distance from the base of the object to a point on the ground some distance away, where we can look up to the top of the tall object at an angle. The angle of elevation of an object above an observer relative to the observer is the angle between the horizontal and the line from the object to the observer's eye. The right triangle this position creates has sides that represent the unknown height, the measured distance from the base, and the angled line of sight from the ground to the top of the object. Knowing the measured distance to the base of the object and the angle of the line of sight, we can use trigonometric functions to calculate the unknown height. Similarly, we can form a triangle from the top of a tall object by looking downward. The angle of depression of an object below an observer relative to the observer is the angle between the horizontal and the line from the object to the observer's eye. See Figure \(\PageIndex{12}\).

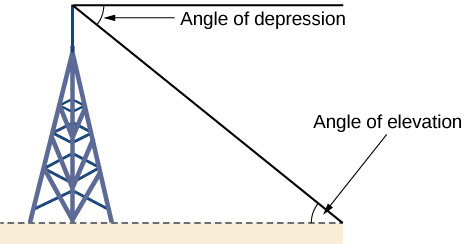
how to: Given a tall object, measure its height indirectly

• Make a sketch of the problem situation to keep track of known and unknown information.
• Lay out a measured distance from the base of the object to a point where the top of the object is clearly visible.
• At the other end of the measured distance, look up to the top of the object. Measure the angle the line of sight makes with the horizontal.
• Write an equation relating the unknown height, the measured distance, and the tangent of the angle of the line of sight.
• Solve the equation for the unknown height.

Example \(\PageIndex{6}\): Measuring a Distance Indirectly

To find the height of a tree, a person walks to a point 30 feet from the base of the tree. She measures an angle of 57° 57° between a line of sight to the top of the tree and the ground, as shown in Figure \(\PageIndex{13}\). Find the height of the tree.

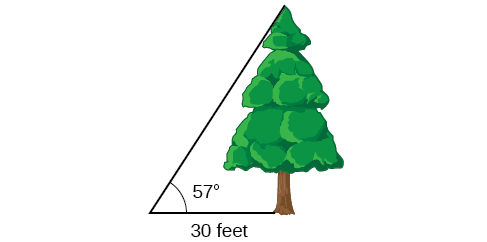
We know that the angle of elevation is \(57°\) and the adjacent side is 30 ft long. The opposite side is the unknown height.

The trigonometric function relating the side opposite to an angle and the side adjacent to the angle is the tangent. So we will state our information in terms of the tangent of \(57°\), letting \(h\) be the unknown height.

\[\begin{array}{cl} \tan θ = \dfrac{\text{opposite}}{\text{adjacent}} & \text{} \\ \tan (57°) = \dfrac{h}{30} & \text{Solve for }h. \\ h=30 \tan (57°) & \text{Multiply.} \\ h≈46.2 & \text{Use a calculator.} \end{array} \]

The tree is approximately 46 feet tall.

Exercise \(\PageIndex{6}\):

How long a ladder is needed to reach a windowsill 50 feet above the ground if the ladder rests against the building making an angle of \(\frac{5π}{12}\) with the ground? Round to the nearest foot.

About 52 ft

Access these online resources for additional instruction and practice with right triangle trigonometry.

• Finding Trig Functions on Calculator
• Finding Trig Functions Using a Right Triangle
• Relate Trig Functions to Sides of a Right Triangle
• Determine Six Trig Functions from a Triangle
• Determine Length of Right Triangle Side

Visit this website for additional practice questions from Learningpod.

Key Equations

Cofunction Identities

Key Concepts

• We can define trigonometric functions as ratios of the side lengths of a right triangle. See Example .
• The same side lengths can be used to evaluate the trigonometric functions of either acute angle in a right triangle. See Example .
• We can evaluate the trigonometric functions of special angles, knowing the side lengths of the triangles in which they occur. See Example .
• Any two complementary angles could be the two acute angles of a right triangle.
• If two angles are complementary, the cofunction identities state that the sine of one equals the cosine of the other and vice versa. See Example .
• We can use trigonometric functions of an angle to find unknown side lengths.
• Select the trigonometric function representing the ratio of the unknown side to the known side. See Example .
• Right-triangle trigonometry permits the measurement of inaccessible heights and distances.
• The unknown height or distance can be found by creating a right triangle in which the unknown height or distance is one of the sides, and another side and angle are known. See Example .

Game Central

Get step-by-step explanations

Graph your math problems

Practice, practice, practice

Get math help in your language

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Trigonometry

Unit 1: right triangles & trigonometry, unit 2: trigonometric functions, unit 3: non-right triangles & trigonometry, unit 4: trigonometric equations and identities, review articles.

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

Trigonometry Worksheets

Free worksheets with answer keys.

Enjoy these free sheets. Each one has model problems worked out step by step, practice problems, as well as challenge questions at the sheets end. Plus each one comes with an answer key.

(This sheet is a summative worksheet that focuses on deciding when to use the law of sines or cosines as well as on using both formulas to solve for a single triangle's side or angle)

• Law of Sines
• Ambiguous Case of the Law of Sines
• Law Of Cosines
• Sine, Cosine, Tangent, to Find Side Length
• Sine, Cosine, Tangent Chart
• Inverse Trig Functions
• Real World Applications of SOHCATOA
• Mixed Review
• Vector Worksheet
• Unit Circle Worksheet
• Graphing Sine and Cosine Worksheet

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!

Popular pages @ mathwarehouse.com.

Trigonometry Worksheets

Related Pages Math Worksheets Free Printable Worksheets

There are six sets of Trigonometry worksheets:

• Trig Ratios: Sin, Cos, Tan
• Sin & Cos of Complementary Angles
• Find Missing Sides
• Find Missing Angles
• Area of Triangle using Sine
• Law of Sines and Cosines

Sine, Cosine, & Tangent Worksheets

In these free math worksheets, students learn how to find the trig ratios: sine, cosine, and tangent.

There are five sets of Sine, Cosine, & Tangent worksheets: Trigonometry Worksheet (Learn Adjacent, Opposite, & Hypotenuse) Trigonometric Ratios Worksheets (Sine Ratio, Cosine Ratio, Tangent Ratio)

How to find Sine, Cosine, & Tangent worksheets? In the context of trigonometry, the sides of a right triangle are often described in relation to an angle within the triangle. The common terms used are:

Hypotenuse: The side opposite the right angle. It is the longest side of the right triangle.

Opposite: The side opposite a specified angle. In other words, if you’re looking at one of the non-right angles, the side opposite that angle is called the “opposite” side.

Adjacent: The side adjacent to a specified angle. It is the side that is next to the angle but is not the hypotenuse.

Sine (sin), cosine (cos), and tangent (tan) are three fundamental trigonometric functions that describe the relationships between the sides and angles of a right triangle. These functions are widely used in mathematics and various scientific fields.

Sine (sin): In a right triangle, the sine of an angle (θ) is the ratio of the length of the side opposite the angle to the length of the hypotenuse. sin(θ)= Opposite/Hypotenuse

Cosine (cos): The cosine of an angle (θ) in a right triangle is the ratio of the length of the side adjacent to the angle to the length of the hypotenuse. cos(θ)= Adjacent/Hypotenuse

Tangent (tan): The tangent of an angle (θ) in a right triangle is the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle. tan(θ)= Opposite/Adjacent

These functions are defined not only in the context of right triangles but also more broadly using the unit circle and as periodic functions. They have various applications in physics, engineering, computer science, and other fields where understanding the relationships between angles and sides is crucial.

Click on the following worksheet to get a printable pdf document. Scroll down the page for more Sine, Cosine, & Tangent Worksheets .

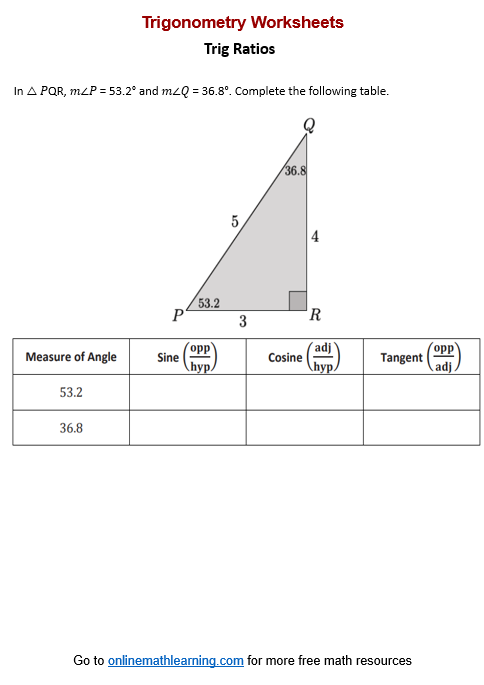
More Sine, Cosine, & Tangent Worksheets

Printable (Answers on the second page.) Trigonometry Worksheet #1 (Adjacent, Opposite, & Hypotenuse) Trig Ratios Worksheet #2 (Sin, Cos, Tan Ratios) Trig Ratios Worksheet #3 (Sin, Cos, Tan Ratios) Trig Ratios Worksheet #4 (Sin, Cos, Tan Ratios) Trig Ratios Worksheet #5 (Sin, Cos, Tan Ratios)

Online Trigonometry (sine, cosine, tangent) Trigonometry (sine, cosine, tangent) Trigonometry (using a calculator) Inverse Trigonometry (using a calculator) Trigonometry (find an unknown side) Trigonometry (find an unknown angle) Using Sine Using Cosine Using Tangent Using Sine, Cosine or Tangent Trigonometry Applications Problems Law of Sines or Sine Rule Law of Sines Law of Cosines or Cosine Rule Law of Cosines

Related Lessons & Worksheets

Trigonometry Lessons

More Printable Worksheets

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Trigonometry Questions

Trigonometry questions given here involve finding the missing sides of a triangle with the help of trigonometric ratios and proving trigonometry identities. We know that trigonometry is one of the most important chapters of Class 10 Maths. Hence, solving these questions will help you to improve your problem-solving skills.

What is Trigonometry?

The word ‘trigonometry’ is derived from the Greek words ‘tri’ (meaning three), ‘gon’ (meaning sides) and ‘metron’ (meaning measure). Trigonometry is the study of relationships between the sides and angles of a triangle.

The basic trigonometric ratios are defined as follows.

sine of ∠A = sin A = Side opposite to ∠A/ Hypotenuse

cosine of ∠A = cos A = Side adjacent to ∠A/ Hypotenuse

tangent of ∠A = tan A = (Side opposite to ∠A)/ (Side adjacent to ∠A)

cosecant of ∠A = cosec A = 1/sin A = Hypotenuse/ Side opposite to ∠A

secant of ∠A = sec A = 1/cos A = Hypotenuse/ Side adjacent to ∠A

cotangent of ∠A = cot A = 1/tan A = (Side adjacent to ∠A)/ (Side opposite to ∠A)

Also, tan A = sin A/cos A

cot A = cos A/sin A

Also, read: Trigonometry

Trigonometry Questions and Answers

1. From the given figure, find tan P – cot R.

From the given,

In the right triangle PQR, Q is right angle.

By Pythagoras theorem,

PR 2 = PQ 2 + QR 2

QR 2 = (13) 2 – (12) 2

= 169 – 144

tan P = QR/PQ = 5/12

cot R = QR/PQ = 5/12

So, tan P – cot R = (5/12) – (5/12) = 0

2. Prove that (sin 4 θ – cos 4 θ +1) cosec 2 θ = 2

L.H.S. = (sin 4 θ – cos 4 θ +1) cosec 2 θ

= [(sin 2 θ – cos 2 θ) (sin 2 θ + cos 2 θ) + 1] cosec 2 θ

Using the identity sin 2 A + cos 2 A = 1,

= (sin 2 θ – cos 2 θ + 1) cosec 2 θ

= [sin 2 θ – (1 – sin 2 θ) + 1] cosec 2 θ

= 2 sin 2 θ cosec 2 θ

= 2 sin 2 θ (1/sin 2 θ)

3. Prove that (√3 + 1) (3 – cot 30°) = tan 3 60° – 2 sin 60°.

LHS = (√3 + 1)(3 – cot 30°)

= (√3 + 1)(3 – √3)

= 3√3 – √3.√3 + 3 – √3

= 2√3 – 3 + 3

RHS = tan 3 60° – 2 sin 60°

= (√3) 3 – 2(√3/2)

= 3√3 – √3

Therefore, (√3 + 1) (3 – cot 30°) = tan 3 60° – 2 sin 60°.

Hence proved.

4. If tan(A + B) = √3 and tan(A – B) = 1/√3 ; 0° < A + B ≤ 90°; A > B, find A and B.

tan(A + B) = √3

tan(A + B) = tan 60°

A + B = 60°….(i)

tan(A – B) = 1/√3

tan(A – B) = tan 30°

A – B = 30°….(ii)

Adding (i) and (ii),

A + B + A – B = 60° + 30°

Substituting A = 45° in (i),

45° + B = 60°

B = 60° – 45° = 15°

Therefore, A = 45° and B = 15°.

5. If sin 3A = cos (A – 26°), where 3A is an acute angle, find the value of A.

sin 3A = cos(A – 26°); 3A is an acute angle

cos(90° – 3A) = cos(A – 26°) {since cos(90° – A) = sin A}

⇒ 90° – 3A = A – 26

⇒ 3A + A = 90° + 26°

⇒ 4A = 116°

⇒ A = 116°/4

6. If A, B and C are interior angles of a triangle ABC, show that sin (B + C/2) = cos A/2.

We know that, for a given triangle, the sum of all the interior angles of a triangle is equal to 180°

A + B + C = 180° ….(1)

B + C = 180° – A

Dividing both sides of this equation by 2, we get;

⇒ (B + C)/2 = (180° – A)/2

⇒ (B + C)/2 = 90° – A/2

Take sin on both sides,

sin (B + C)/2 = sin (90° – A/2)

⇒ sin (B + C)/2 = cos A/2 {since sin(90° – x) = cos x}

7. If tan θ + sec θ = l, prove that sec θ = (l 2 + 1)/2l.

tan θ + sec θ = l….(i)

We know that,

sec 2 θ – tan 2 θ = 1

(sec θ – tan θ)(sec θ + tan θ) = 1

(sec θ – tan θ) l = 1 {from (i)}

sec θ – tan θ = 1/l….(ii)

tan θ + sec θ + sec θ – tan θ = l + (1/l)

2 sec θ = (l 2 + 1)l

sec θ = (l 2 + 1)/2l

8. Prove that (cos A – sin A + 1)/ (cos A + sin A – 1) = cosec A + cot A, using the identity cosec 2 A = 1 + cot 2 A.

LHS = (cos A – sin A + 1)/ (cos A + sin A – 1)

Dividing the numerator and denominator by sin A, we get;

= (cot A – 1 + cosec A)/(cot A + 1 – cosec A)

Using the identity cosec 2 A = 1 + cot 2 A ⇒ cosec 2 A – cot 2 A = 1,

= [cot A – (cosec 2 A – cot 2 A) + cosec A]/ (cot A + 1 – cosec A)

= [(cosec A + cot A) – (cosec A – cot A)(cosec A + cot A)] / (cot A + 1 – cosec A)

= cosec A + cot A

9. Prove that: (cosec A – sin A)(sec A – cos A) = 1/(tan A + cot A)

[Hint: Simplify LHS and RHS separately]

LHS = (cosec A – sin A)(sec A – cos A)

= (cos 2 A/sin A) (sin 2 A/cos A)

= cos A sin A….(i)

RHS = 1/(tan A + cot A)

= (sin A cos A)/ (sin 2 A + cos 2 A)

= (sin A cos A)/1

= sin A cos A….(ii)

From (i) and (ii),

i.e. (cosec A – sin A)(sec A – cos A) = 1/(tan A + cot A)

10. If a sin θ + b cos θ = c, prove that a cosθ – b sinθ = √(a 2 + b 2 – c 2 ).

a sin θ + b cos θ = c

Squaring on both sides,

(a sin θ + b cos θ) 2 = c 2

a 2 sin 2 θ + b 2 cos 2 θ + 2ab sin θ cos θ = c 2

a 2 (1 – cos 2 θ) + b 2 (1 – sin 2 θ) + 2ab sin θ cos θ = c 2

a 2 – a 2 cos 2 θ + b 2 – b 2 sin 2 θ + 2ab sin θ cos θ = c 2

a 2 + b 2 – c 2 = a 2 cos 2 θ + b 2 sin 2 θ – 2ab sin θ cos θ

a 2 + b 2 – c 2 = (a cos θ – b sin θ ) 2

⇒ a cos θ – b sin θ = √(a 2 + b 2 – c 2 )

Video Lesson on Trigonometry

Practice Questions on Trigonometry

Solve the following trigonometry problems.

• Prove that (sin α + cos α) (tan α + cot α) = sec α + cosec α.
• If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.
• If sin θ + cos θ = √3, prove that tan θ + cot θ = 1.
• Evaluate: 2 tan 2 45° + cos 2 30° – sin 2 60°
• Express cot 85° + cos 75° in terms of trigonometric ratios of angles between 0° and 45°.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

HIGH SCHOOL

• ACT Tutoring
• SAT Tutoring
• PSAT Tutoring
• ASPIRE Tutoring
• SHSAT Tutoring
• STAAR Tutoring

GRADUATE SCHOOL

• MCAT Tutoring
• GRE Tutoring
• LSAT Tutoring
• GMAT Tutoring
• AIMS Tutoring
• HSPT Tutoring
• ISAT Tutoring
• SSAT Tutoring

Search 50+ Tests

Loading Page

math tutoring

• Elementary Math
• Pre-Calculus
• Trigonometry

science tutoring

Foreign languages.

• Mandarin Chinese

elementary tutoring

• Computer Science

Search 350+ Subjects

• Video Overview
• Tutor Selection Process
• Online Tutoring
• Mobile Tutoring
• Instant Tutoring
• How We Operate
• Our Guarantee
• Impact of Tutoring
• Reviews & Testimonials
• Media Coverage
• About Varsity Tutors

Trigonometry : Solving Word Problems with Trigonometry

Study concepts, example questions & explanations for trigonometry, all trigonometry resources, example questions, example question #1 : solving word problems with trigonometry.

You can draw the following right triangle using the information given by the question:

Since you want to find the height of the platform, you will need to use tangent.

You can draw the following right triangle from the information given by the question.

In order to find the height of the flagpole, you will need to use tangent.

You can draw the following right triangle from the information given in the question:

In order to find out how far up the ladder goes, you will need to use sine.

In right triangle ABC, where angle A measures 90 degrees, side AB measures 15 and side AC measures 36, what is the length of side BC?

This triangle cannot exist.

Example Question #5 : Solving Word Problems With Trigonometry

A support wire is anchored 10 meters up from the base of a flagpole, and the wire makes a 25 o angle with the ground. How long is the wire, w? Round your answer to two decimal places.

23.81 meters

28.31 meters

21.83 meters

To make sense of the problem, start by drawing a diagram. Label the angle of elevation as 25 o , the height between the ground and where the wire hits the flagpole as 10 meters, and our unknown, the length of the wire, as w. 

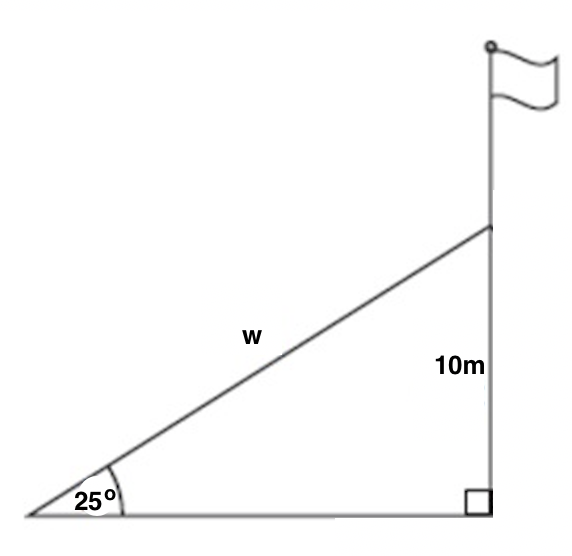
Now, we just need to solve for w using the information given in the diagram. We need to ask ourselves which parts of a triangle 10 and w are relative to our known angle of 25 o . 10 is opposite this angle, and w is the hypotenuse. Now, ask yourself which trig function(s) relate opposite and hypotenuse. There are two correct options: sine and cosecant. Using sine is probably the most common, but both options are detailed below.

We know that sine of a given angle is equal to the opposite divided by the hypotenuse, and cosecant of an angle is equal to the hypotenuse divided by the opposite (just the reciprocal of the sine function). Therefore:

To solve this problem instead using the cosecant function, we would get:

The reason that we got 23.7 here and 23.81 above is due to differences in rounding in the middle of the problem. 

Example Question #6 : Solving Word Problems With Trigonometry

When the sun is 22 o above the horizon, how long is the shadow cast by a building that is 60 meters high?

To solve this problem, first set up a diagram that shows all of the info given in the problem. 

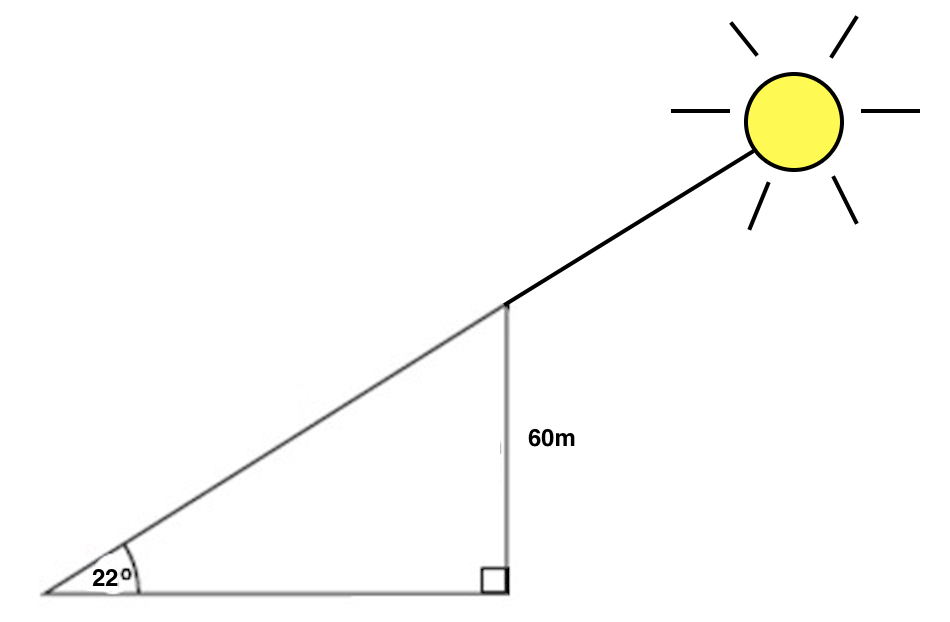
Next, we need to interpret which side length corresponds to the shadow of the building, which is what the problem is asking us to find. Is it the hypotenuse, or the base of the triangle? Think about when you look at a shadow. When you see a shadow, you are seeing it on something else, like the ground, the sidewalk, or another object. We see the shadow on the ground, which corresponds to the base of our triangle, so that is what we'll be solving for. We'll call this base b.

Therefore the shadow cast by the building is 150 meters long.

If you got one of the incorrect answers, you may have used sine or cosine instead of tangent, or you may have used the tangent function but inverted the fraction (adjacent over opposite instead of opposite over adjacent.)

Example Question #7 : Solving Word Problems With Trigonometry

From the top of a lighthouse that sits 105 meters above the sea, the angle of depression of a boat is 19 o . How far from the boat is the top of the lighthouse?

423.18 meters

318.18 meters

36.15 meters

110.53 meters

To solve this problem, we need to create a diagram, but in order to create that diagram, we need to understand the vocabulary that is being used in this question. The following diagram clarifies the difference between an angle of depression (an angle that looks downward; relevant to our problem) and the angle of elevation (an angle that looks upward; relevant to other problems, but not this specific one.) Imagine that the top of the blue altitude line is the top of the lighthouse, the green line labelled GroundHorizon is sea level, and point B is where the boat is.

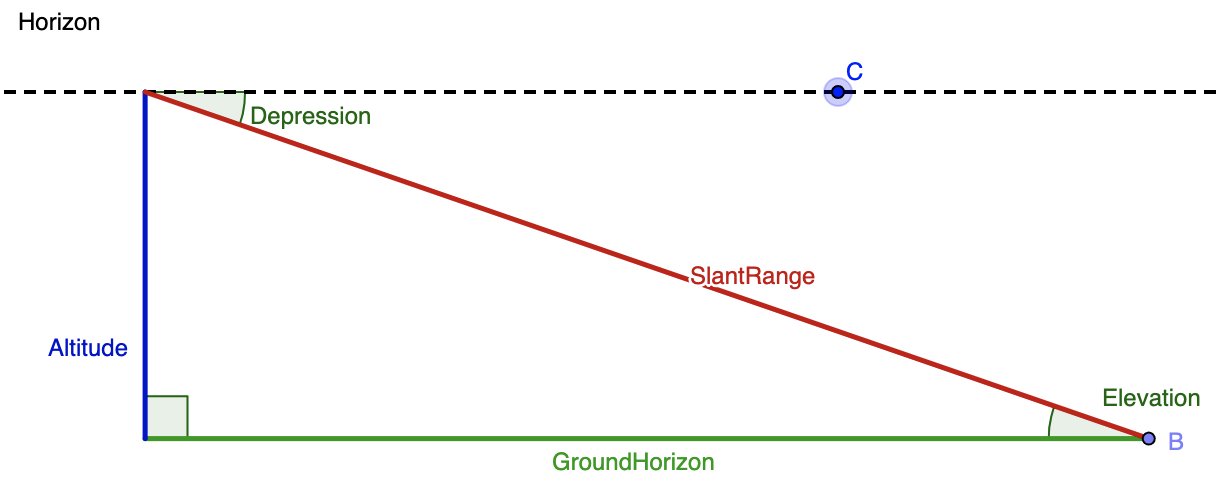
Merging together the given info and this diagram, we know that the angle of depression is 19 o  and and the altitude (blue line) is 105 meters. While the blue line is drawn on the left hand side in the diagram, we can assume is it is the same as the right hand side. Next, we need to think of the trig function that relates the given angle, the given side, and the side we want to solve for. The altitude or blue line is opposite the known angle, and we want to find the distance between the boat (point B) and the top of the lighthouse. That means that we want to determine the length of the hypotenuse, or red line labelled SlantRange. The sine function relates opposite and hypotenuse, so we'll use that here. We get:

Example Question #8 : Solving Word Problems With Trigonometry

Angelina just got a new car, and she wants to ride it to the top of a mountain and visit a lookout point. If she drives 4000 meters along a road that is inclined 22 o to the horizontal, how high above her starting point is she when she arrives at the lookout?

9.37 meters

1480 meters

3708.74 meters

10677.87 meters

1616.1 meters

As with other trig problems, begin with a sketch of a diagram of the given and sought after information.

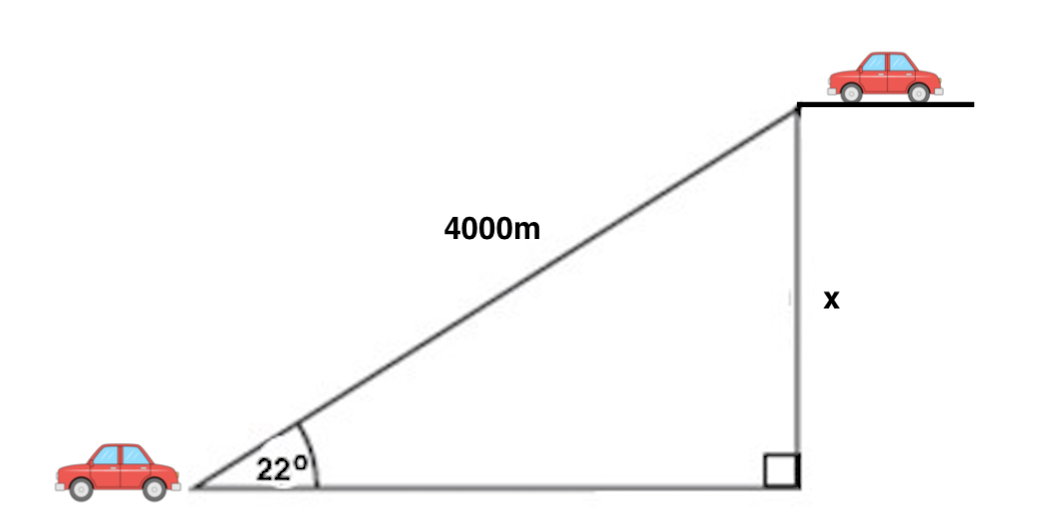
Angelina and her car start at the bottom left of the diagram. The road she is driving on is the hypotenuse of our triangle, and the angle of the road relative to flat ground is 22 o . Because we want to find the change in height (also called elevation), we want to determine the difference between her ending and starting heights, which is labelled x in the diagram. Next, consider which trig function relates together an angle and the sides opposite and hypotenuse relative to it; the correct one is sine. Then, set up:

Therefore the change in height between Angelina's starting and ending points is 1480 meters. 

Example Question #9 : Solving Word Problems With Trigonometry

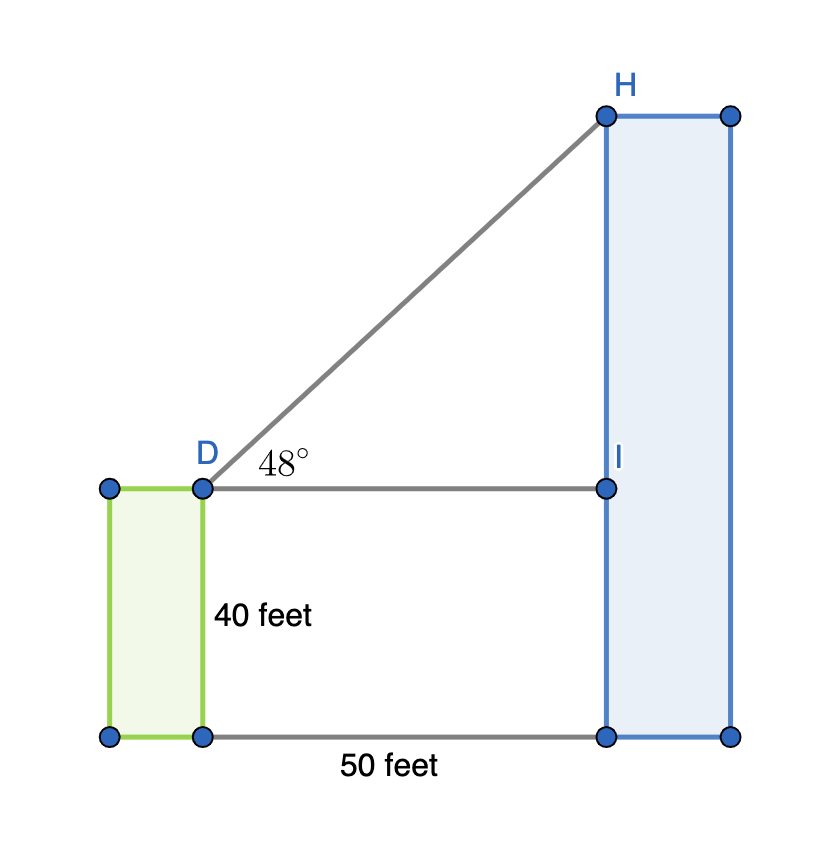
Two buildings with flat roofs are 50 feet apart. The shorter building is 40 feet tall. From the roof of the shorter building, the angle of elevation to the edge of the taller building is 48 o . How high is the taller building?

To solve this problem, let's start by drawing a diagram of the two buildings, the distance in between them, and the angle between the tops of the two buildings. Then, label in the given lengths and angle. 

Example Question #10 : Solving Word Problems With Trigonometry

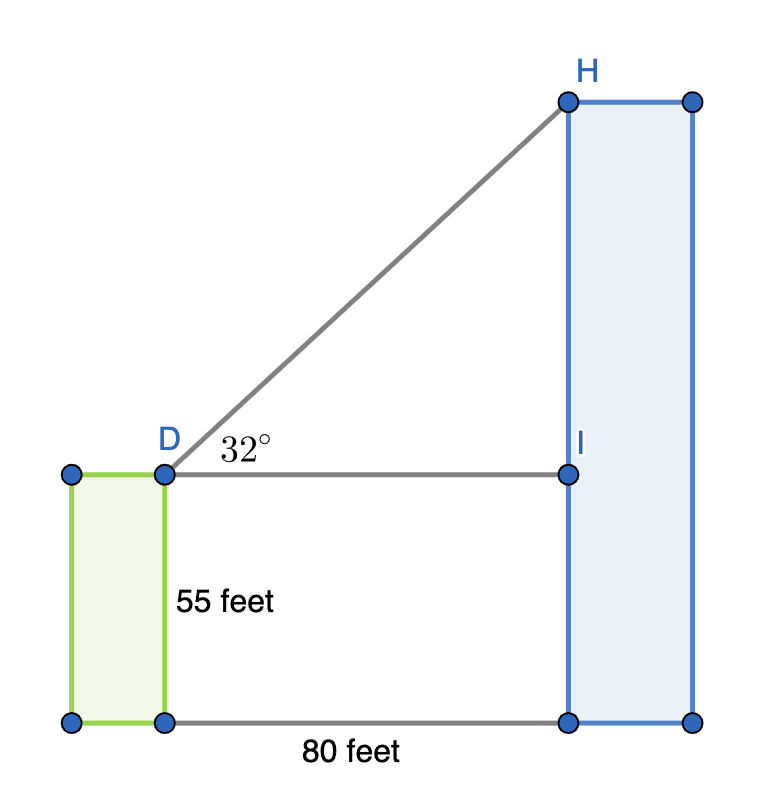
Two buildings with flat roofs are 80 feet apart. The shorter building is 55 feet tall. From the roof of the shorter building, the angle of elevation to the edge of the taller building is 32 o . How high is the taller building?

Report an issue with this question

If you've found an issue with this question, please let us know. With the help of the community we can continue to improve our educational resources.

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC 101 S. Hanley Rd, Suite 300 St. Louis, MO 63105

Or fill out the form below:

Contact Information

Complaint details.

Free Mathematics Tutorials

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• x^{2}-x-6=0
• -x+3\gt 2x+1
• line\:(1,\:2),\:(3,\:1)
• prove\:\tan^2(x)-\sin^2(x)=\tan^2(x)\sin^2(x)
• \frac{d}{dx}(\frac{3x+9}{2-x})
• (\sin^2(\theta))'
• \lim _{x\to 0}(x\ln (x))
• \int e^x\cos (x)dx
• \int_{0}^{\pi}\sin(x)dx
• \sum_{n=0}^{\infty}\frac{3}{2^n}
• Is there a step by step calculator for math?
• Symbolab is the best step by step calculator for a wide range of math problems, from basic arithmetic to advanced calculus and linear algebra. It shows you the solution, graph, detailed steps and explanations for each problem.
• Is there a step by step calculator for physics?
• Symbolab is the best step by step calculator for a wide range of physics problems, including mechanics, electricity and magnetism, and thermodynamics. It shows you the steps and explanations for each problem, so you can learn as you go.
• How to solve math problems step-by-step?
• To solve math problems step-by-step start by reading the problem carefully and understand what you are being asked to find. Next, identify the relevant information, define the variables, and plan a strategy for solving the problem.
• My Notebook, the Symbolab way Math notebooks have been around for hundreds of years. You write down problems, solutions and notes to go back...

Please add a message.

Message received. Thanks for the feedback.