literature review of data envelopment analysis

An official website of the United States government

Official websites use .gov A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS A lock ( Lock Locked padlock icon ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

• Publications
• Account settings
• Advanced Search
• Journal List

A data-envelopment analysis-based systematic review of the literature on innovation performance

Elangovan narayanan, wan rosmanira binti ismail, zainol bin mustafa.

• Author information
• Article notes
• Copyright and License information

Corresponding author. [email protected]

Received 2022 Mar 27; Revised 2022 Jul 11; Accepted 2022 Nov 18; Collection date 2022 Dec.

This is an open access article under the CC BY-NC-ND license (http://creativecommons.org/licenses/by-nc-nd/4.0/).

Innovation imbued in every sector in every part of the world is essential to growth and development. The National Innovation Systems (NIS) use their resources to support economies in different countries foster a novel environment. Therefore, this study is an attempt to examine the efficiency of NIS as measured by scholars in the past using Data Envelopment Analysis (DEA). Through a systematic literature review, this study aims to show the current dearth of studies on the efficiency of NIS. The literature is categorized accordingly and provides a framework with recommendations for future research. With the advent of technical tools, DEA programming methods other than traditional DEA such as network, relational network, dynamic network, slack based model, and super efficiency DEA have emerged. This enables the calculation of innovation efficiency to be efficient and reliable. As a result, DEA is regarded as a powerful tool for assessing the relative efficiency of NIS, which employs multiple inputs to generate multiple outputs. The results also suggest that future research is needed on the efficiency of innovation by paying more attention to cross-countries studies based on regions, geographical areas, participation in free trade blocs, and a group of tie-up countries involved, especially with comparative analyses regardless of the country classification. Another important observation is that there are few studies that focus on the efficiency of middle- and low-income countries. The comparative analysis of innovation efficiency across income groups enables NIS to benchmark itself against best-in-class innovators and improve their innovation performance and ranking. These findings provide an opportunity to further investigate how NIS add value and sustainability to countries by improving resource management capabilities to improve innovation efficiency.

Keywords: Data envelopment analysis, DEA, Efficiency, National innovation system, NIS, Technical efficiency

Data envelopment analysis; DEA; Efficiency; National innovation system; NIS; Technical efficiency

1. Introduction

The rapidly growing trend of globalization requires that each country creates unique competitive advantages to remain internationally competitive. Accordingly, countries around the world continue to plan and implement a variety of innovative measures to either maintain or create competitive advantages. Innovation is one of the key elements to improve competitiveness in the market ( Dereli, 2015 ; Ivanova and Cepel, 2018 ; Rajapathirana and Hui, 2018 ). The introduction of innovation by an organization encourages among others to find new methods to carve out a unique niche. However, the innovation process requires the support of various aspects. For example, technology is currently one of the most important features for advancing the frontiers of innovations ( Dodgson et al., 2006 ; Koellinger, 2008 ). Similarly, the need for appropriate conditions to facilitate these developments is paramount; including having suitable market-friendly business models and processes ( Bouwman et al., 2019 ).

We start with ideas presented in the very first papers that used the innovation system concept, namely Freeman (1982) and Lundvall (1985) . Freeman's analysis focuses on macro phenomena, while Lundvall (1985) focuses on micro phenomena. The theory of National Innovation Systems or NIS has been widely accepted since the mid-1980s, as the most competitive countries in the world have extensive and highly developed national innovation systems ( Freeman, 1987 ; Lundvall, 2007 ). The concept of NIS was developed solely as a networking medium between both the private and public sectors to help initiate, modify, import, and even disseminate the new technology-based innovations brought to the market ( Freeman, 1987 ). NIS has been defined as a set of linkages facilitated by the actors involved in innovation, creating an interactive network between them ( Gokhberg and Roud, 2016 ; Lala and Sinha, 2019 ). The network was built to provide an efficient background for innovation development while addressing regulatory requirements.

The main motive for establishing an agency similar to NIS is to develop and promote innovation practices, focus on research and development, and enable economic development by deploying these cutting-edge innovations through entrepreneurial ventures. Dahlman (1994) mentions in the definition of NIS, that it is a network of policies and an institution that enable the introduction of new technologies in the market. As innovation plays an important role in shaping global economic development in creating and maintaining competitiveness, researchers are increasingly interested in examining the concept of innovation from a global perspective. Since the mid-1980s, the NIS has been used as the primary analytical target in the study of innovation processes ( Diez and Kiese, 2009 ). Since the late 1990s, researchers have used the NIS concept in their study ( Edler and Fagerberg, 2017 ; Guan and Chen, 2012 ; Kuhlmann and Ordóñez-Matamoros, 2017 ; Liu et al., 2015 ; Watkins et al., 2015 ) and this concept can be helpful as a generalized conceptual framework for examining differences in efficiency across countries ( Teixeira, 2014 ).

The importance of NIS is quite high nowadays, especially given the increasing number of innovations proposed by various market players ( Golichenko, 2016 ; Lundvall, 2016 ). Recent changes in the global economy over time have led to new perspectives in measuring innovation performance. Communication and collaboration among stakeholders have driven the development of innovations and explained the growth patterns of nonlinear innovations ( Todttling and Trippl, 2005 ). This development has led to a shift in perspective in measuring innovation performance from a single input dimension to multiple input dimensions ( Pan et al., 2010 ). Since the innovation process is quite complex, its performance should be measured taking into account multiple dimensions rather than based on a single unit of input and output ( Tidd and Bessant, 2020 ).

The application and diffusion of NIS among the concerned actors in an economy are done through various non-parametric methods. This method essentially aims to measure the relative efficiency of a group of decision-making units (DMUs). Data Envelopment Analysis or DEA is one such technical product based on linear programming that can convert the inputs and outputs used into a single measure of performance ( Kong et al., 2021 ; Xiong et al., 2020 ). This technique based on frontier transformation has the potential to measure efficiency of different countries. It is a non-parametric method that does not require the inclusion of predetermined work processes to arrive at a decision state ( Afzal, 2014 ; Cooper et al., 2006 ). The DEA method has been used extensively in various cross-border studies to measure the efficiency of NIS ( Nasierowski and Arcelus, 2003 ). This approach was developed by Farrell (1957) and Charnes et al. (1978) . DEA is a mathematical programming method for determining efficiency levels using data to measure efficiency values when forming efficiency frontier patterns ( Kotsemir, 2013 ). Jaloudi (2019) , and Nasierowski and Arcelus (2012) state that DEA is used to convert the minimum number of input units to the maximum number of outputs when measuring the efficiency of the required sample.

Technical efficiency (TE) is a measure of how well a DMU succeeds in obtaining the maximum output from a given input. TE measures output relative to the output of an efficient isoquant curve. Efficient firms produce at the production frontier or in efficiently equal quantities. TE can be calculated from the ratio of the sum of weighted outputs to the sum of weighted inputs ( Cooper et al., 2006 ), as follows:

where ‘ x ’ and ‘ y ’ are inputs and outputs, ‘ v ’ and ‘ u ’ are input and output weights, respectively, ‘ q ’ is the number of inputs ( q = 1 , 2 , . . . , Q ); ‘ p ’ is the number of outputs ( p = 1 , 2 , . . , P ); and ‘ j ’ represents j th DMU.

The use of DEA in the NIS is the most common in the literature to date, given its flexibility compared to parametric approaches, both in practice and in theory ( Kou et al., 2016 )Several empirical studies have used the DEA approach to assess the efficiency of NIS ( Cai, 2011 ; Carayannis et al., 2016 , Carayannis et al., 2015 ; Liu et al., 2017 ; Xu and Cheng, 2013 ) of NIS ( Alnafrah, 2021 ; Bresciani et al., 2021 ; Kotsemir, 2013 ; Shin et al., 2018 ; Zeng et al., 2021 ; Zhang, 2013 ). Since both the DEA and NIS concepts are proving to be highly relevant and effective in today's world, this study attempts to merge the two concepts to determine the technical efficiency of NIS through the application of DEA. The main objective of this systematic review is to address the lack of literature regarding the efficiency of NIS based on the application of DEA. The research questions of the study are as follows:

How many previous studies have examined innovation systems at the national and regional levels?

What methods do researchers commonly use to assess the efficiency of innovation systems?

What country taxonomy is the focus of studies on innovation systems efficiency?

What DEA model have researchers used to assess innovation systems efficiency?

What types of measurements have the researchers used?

What income groups do the researchers consider when assessing innovation systems efficiency?

The study would be essentially entail the following steps ( Salim et al., 2019 ):

In the first phase, the research articles that contain the application of NIS, DEA and other relevant information sought in the objectives of the study would be shortlisted.

In the second phase, the short-listed articles would be classified and coded according to their specific characteristics and reviewed.

In the third phase, summary presentation the afore-mentioned review.

Finally, propose a framework for address gap of literature.

2. Research methodology

The study attempts to use a systematic literature review approach as this is an effective method ( Levy and Ellis, 2006 ; Snyder, 2019 ) to capture the results of a large amount of stored information ( Popay et al., 2006 ). Several researchers in the past have used the systematic review approach as a transparent filtering method for the literature reviewed in an unbiased approach ( Centobelli et al., 2017 ; Tranfield et al., 2003 ). It allows researchers to delve deeper into a topic and gain better insights. One of the advantages of a systematic literature review is that it allows researchers to publish the content of the literature review in question in relation to specific emerging issues while ensuring a smooth flow of information. According to Godinho and Veloso (2013) , the process of classifying the literature requires the following six steps:

1: Research of the relevant literature on the current state of knowledge;

2: A classification process using a structured code that includes logical reasoning;

3: Classification of the reviewed papers based on the classification process;

4: The results of the study are presented;

5: A detailed analysis of the existing gaps; and

6: Suggestions for future research.

Most of the articles used in this literature review were obtained from Google Scholar, Web of Science, and Scopus databases given the large database, high quality and authenticity of sources. The database was searched using keywords such as National Innovation Systems, Data Envelopment Analysis, NIS, DEA, efficiency and innovation systems, and for the period between 2010 and 2021. The total number of articles found was 387. With the gradual exclusion of studies based on applied criteria ( Liberati et al., 2009 ), only the articles dealing with NIS and the DEA approach were selected. The incomplete articles on this topic were excluded, leading to only 74 short-listed articles for review and data synthesis. Fig. 1 above illustrates the process of selecting articles for the review.

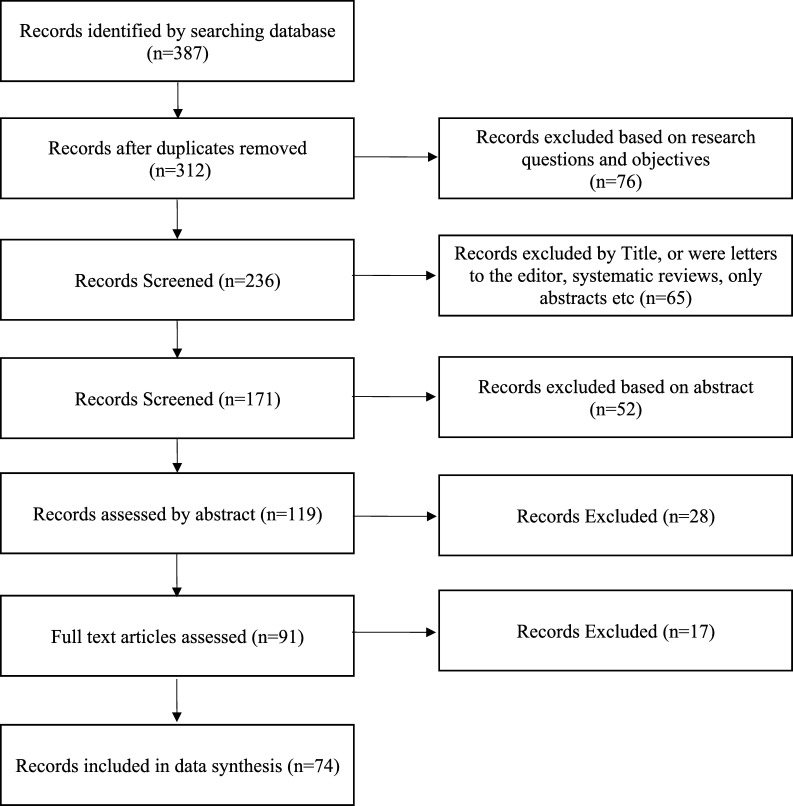
Records selection process.

2.1. Classification and coding

As mentioned earlier, the coding procedure used in this systematic literature review to classify articles and assign specific codes is detailed in Table 1 .

Classification and coding.

3. Results of the literature review

Table 2 provides information on the authors, the journals in which the articles were published, and the authors' origin.

Listed of selected articles.

Table 3 shows the code classification of the articles based on the six parameters identified for review.

Detailed review.

4. Descriptive analysis

The analysis of NIS can be divided into two approaches ( Belitz et al., 2011 ): a descriptive approach based on case studies ( Nelson, 1993 ) and a theoretical approach based on secondary research and quantitative indicators ( Lundvall, 2010 ). Fig. 2 shows the number of articles published per year. It was found that 13 articles were published in 2020, followed by 10 articles in 2019 and 2021 respectively, eight articles in 2016, and seven articles in 2014. Subsequently, five articles were published in 2018, follow by four articles in 2011, 2013, and 2017, and the fewest, three articles were published in 2010 and 2015. In comparison to the global development of innovation, the number of articles published on innovation performance is comparatively modest.

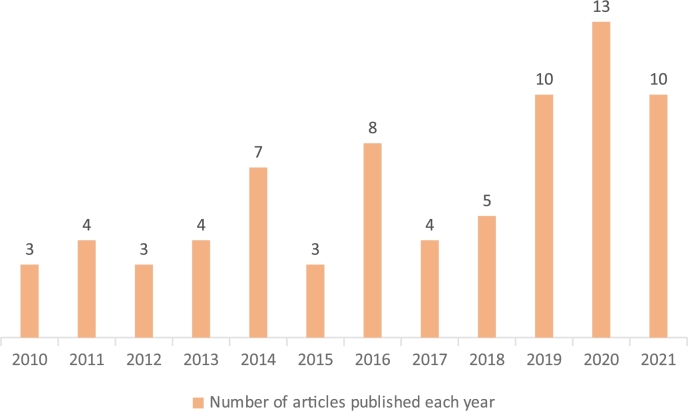
Number of articles published each year.

4.1. Context of determinants

An innovation system is a multi-level concept ( Carayannis et al., 2016 ) in which national, regional, and sectoral innovation systems ( Schrempf et al., 2013 ; Edquist, 2009 ; Archibugi, 1996 ) can coexist and develop together in the same country. Fig. 3 shows the overall distribution of articles in the national and regional context. As can be seen, the highest number of articles in the overview is actually the national context, up to 57%. The remaining 43% of the articles deal with a specific geographic region, which has been linked to the regional context in the studies. Nevertheless, more attention is paid to the national context ( Kou et al., 2016 ) than to the regional context. Therefore, strengthening regional innovation efficiency is necessary to bridge the innovation-based economic gap between heterogeneous regions and improve their innovation efficiency at the national level ( OECD, 2008 ).

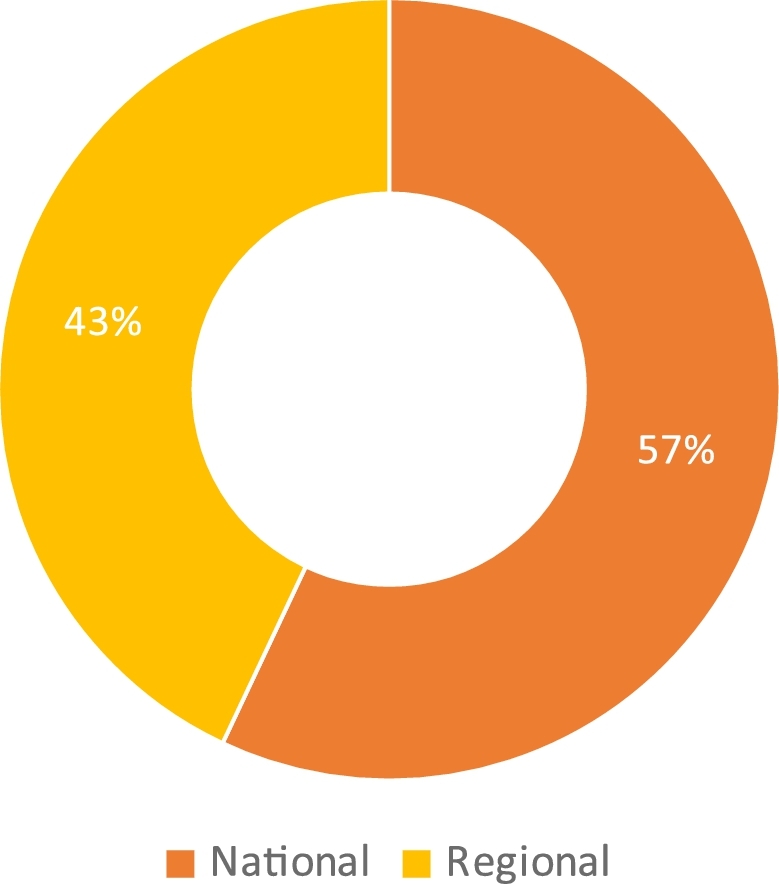
Distribution of determinants contexts.

4.2. Methodological context

According to Jabbour (2013) and Amui et al. (2017) , the methodological approach of each work is analyzed according to the following classifications: qualitative, quantitative, conceptual and/or, empirical, case studies and/or interviews and surveys. Fig. 4 shows the frequency of the methodological contexts used in this study. It is undeniable that all of the articles reviewed use a quantitative approach to measure the efficiency of innovation. Data sources could include either primary or secondary data with the methods used to collect them, including empirical data collected through survey or case study methods.

Distribution of research approaches.

4.3. National contexts

The categorization of the world's various economies into developed, developing and least developed countries (LDCs) has allowed researchers to specify the evidence required for each type of these countries. With the development of the innovation system concept, tools for evaluating and measuring such systems were developed in different countries ( Lacka and Brzezicki, 2021 ; Varblane et al., 2007 ). Fig. 5 shows the frequency of this study carried out according to the state of the national context. Studies on the innovation efficiency of developing countries are comparatively higher, reaching up to 89%, than those on developed countries (64%). It also demonstrates that studies on innovation efficiency involving the least developed countries are limited, signaling the need for more in-depth analyses of innovation efficiency in the LDCs to facilitate these countries develop good innovation policies.

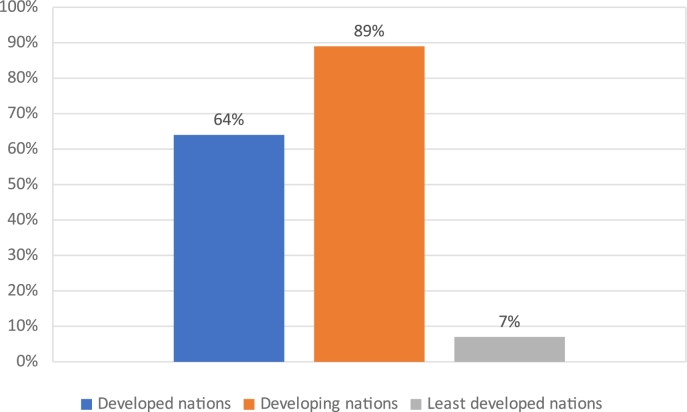
Distribution of national contexts.

4.4. DEA models

Most efficiency studies are motivated by the desire to estimate economic performance based on parametric or non-parametric methods ( Ajibefun, 2008 ; Asmare and Begashaw, 2018 ; Murillo-Zamorano and Vega-Cervera, 2001 ). The majority of the scholars evaluate innovation efficiency using DEA as a non-parametric approach. Fig. 6 shows the distribution of the DEA models. The traditional DEA model (39 studies) is used the most in measuring the efficiency of innovation, followed by the N-DEA model (16 studies). The B-DEA and RN-DEA models were used six times each, while the SMB-DEA and SE-DEA models were used in four different studies to assess innovation efficiency. Meanwhile, the DN-DEA model (2 studies) is the least used model in measuring innovation efficiency. As a result, in addition to T-DEA, evolved DEA models should be used to quantify innovation efficiency because they can provide reliable and scientifically established measurement values.

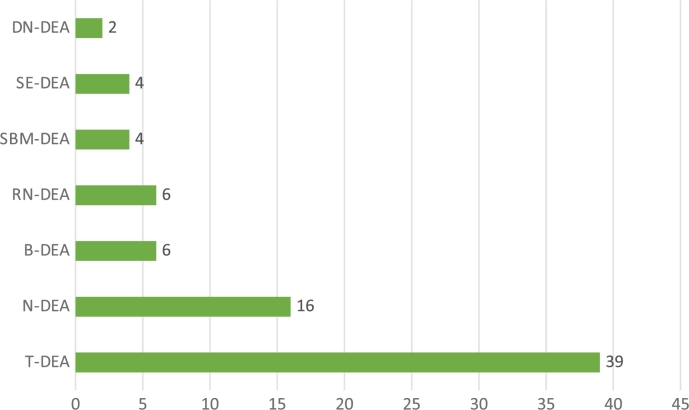
Distribution of DEA models.

4.5. Result areas

The NIS input and output variables can be quantified to assess a country's innovation efficiency and productivity ( Banker et al., 2013 ; Lacka and Brzezicki, 2021 ; Grilo and Santos, 2015 ). Fig. 7 shows the distribution of the result areas. Around 80% of articles used DEA to measure efficiency, while 11% of articles used Malmquist approach to measure productivity. In the meantime, only 9% of articles study both the efficiency and productivity of innovation. Also observed, regional innovation which assesses the efficiency and productivity of innovation is considerably low compared to national innovation. As a result, adequate attention should be paid to measuring efficiency and productivity at the regional level in order to improve regional innovation performance, which in turn will help to improve national innovation performance and ranking.

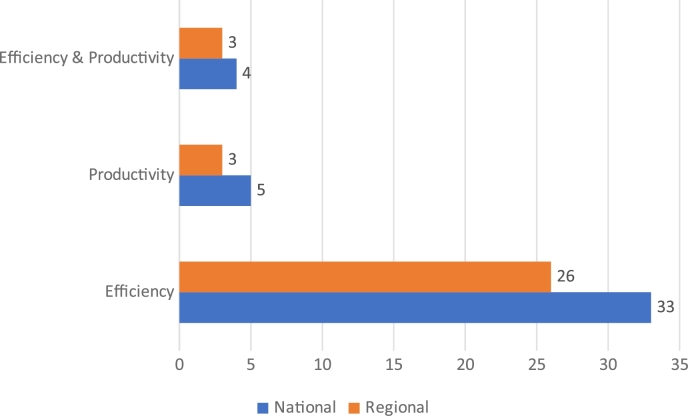
Distribution of result areas.

4.6. Income groups

The World Bank has divided countries around the world into high, upper-middle, lower-middle, and low-income countries based on their gross domestic product values. Choi and Zo (2019) and Leontitsis et al. (2018) assess the efficiency of NIS by classifying them by income group. Fig. 8 shows the distribution of the countries examined by income group. According to the review, 48% of the studies involved upper-middle income countries, while 33% involved high-income countries. However, the observation revealed that only 15% of low-middle income countries and 4% of low-income countries were sampled in the previous study, which is extremely concerning and indicates a lag in the field of innovation that requires appropriate intervention. Interestingly, three of the studies were conducted regardless of income group classification. According to the findings, low middle-income and low-income countries require more attention, particularly in determining the factors that stifle their innovation growth.

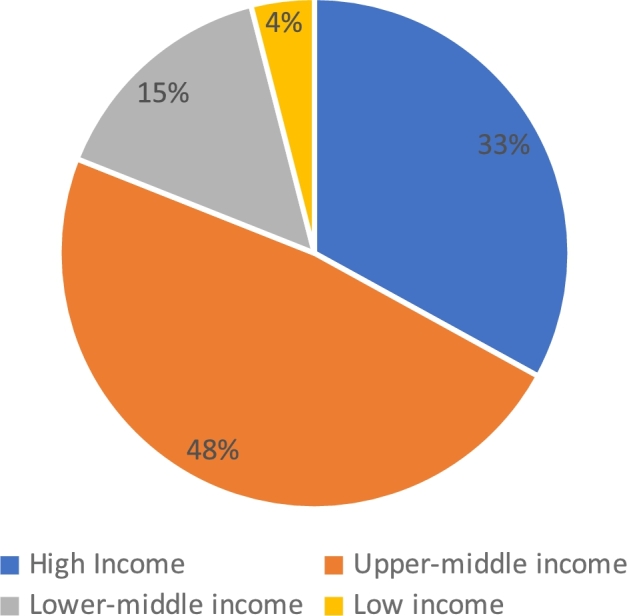
Distribution of countries by income groups.

5. Interpreting the research objectives

This article thoroughly examines the DEA used to assess innovation efficiency. Although the concept of NIS has been around since the late 1980s, the emphasis on using NIS to measure innovation is relatively new ( Balzat and Hanusch, 2004 ; Teixeira, 2014 ; Watkins et al., 2015 ). As a result, the DEA has employed a large number of researchers to examine the performance of NIS. The majority of the articles in the review can be found in a national context ( Carayannis et al., 2016 ; Guan and Chen, 2012 ; Kontolaimou et al., 2016 ; Kou et al., 2016 ; Liu et al., 2015 ; Lu et al., 2014 ; Nasierowski and Arcelus, 2003 ; Pan et al., 2010 ), and this context is an important factor for the analysis ( Jabbour, 2013 ; Mariano et al., 2015 ). While the term “Regional Innovation System” (RIS) is derived from the term “National Innovation System,” it focuses on a specific geographical area ( Iammarino, 2005 ). Empirical research has confirmed that spatial features have a significant impact on firms' innovative performance since 2000; however, the geographical dimension has characterized economic development and is assumed to be an exogenous explanatory variable ( Iammarino, 2005 ). Geographic, regional and local conditions, as well as the general macroeconomic situation of the NIS in which the regions are embedded, play a significant role in RIS performance ( Ho, 2009 ; Muscio, 2006 ) and long-term economic growth.

In addition, certain geographic regions such as the European Union – EU ( Carayannis et al., 2016 ; Dobrzanski, 2018 ; Hudec and Prochadzkova, 2013 ; Jurickova et al., 2017 ; Matei and Aldea, 2012 ; Pinto and Pereira, 2013 ; Samara et al., 2012 ), Central and Eastern Europe – CEEC ( Bielicki and Lesniak, 2016 ; Dobrzanski, 2018 ), Eastern Europe and Central Asian – EECA ( Yesilay and Halac, 2020 ) and Association of Southeast Asia Nations – ASEAN ( Afzal et al., 2019 ) were used to measure the efficiency of NIS. Meanwhile, Guan and Chen (2012) , Kotsemir (2013) , and Kou et al. (2016) have measured the OECD countries' innovation efficiency. On the other hand, Klevenhusen et al. (2020) considered the free trade bloc to which each country belongs as a context variable, such as the North American Free Trade Agreement (NAFTA), Asia-Pacific Economic Cooperation (APEC), EU, and ASEAN. This context variable arouses the interest of other countries participating in the free trade bloc to simulate the performance of innovations. In addition, there are several studies based on a group of tie-up countries such as BRICS (Brazil, Russia, India, People's Republic of China (China), and South Africa), OECD, CEEC, EECA and ASEAN, as well as a large number of studies focusing on the different regions in the EU. Future studies involving geographic regions, free trade bloc participants, and tie-up countries are required to provide input in formulating and developing innovation policies. Table 4 shows the examined countries by geographic region, and group of tie-up countries.

The examined countries by geographic region, and tie-up countries.

These studies are expected to be conducted in developed, developing, and least developed countries, which is consistent with previous research by Lacka and Brzezicki (2021) , Sharma and Thomas (2008) , and Yesilay and Halac (2020) . Most of these studies focus on developed countries ( Choi and Zo, 2019 ; Hudec and Prochadzkova, 2013 ; Kou et al., 2016 ; Matei and Aldea, 2012 ; Rousseau and Rousseau, 1997 ; Tarnawska and Mavroeidis, 2015 ) when looking at the individual numbers because innovation is an important driver of economic growth in developed countries ( Parkey, 2012 ; Kurniawati, 2020 ). Despite the fact that the percentage of examined developing nations is higher than the percentage of developed nations, but the frequency of countries sampled in developing nations is very limited, focusing only on Bulgaria, China, Romania, Russia, and Turkey. The studies recognize the difficulties that developing countries in particular face in embarking on innovations, as resources are limited, knowledge-based is relatively weak, economic conditions in developing countries are very heterogeneous ( Choi and Zo, 2019 ) and people are not as aware and skilled ( UNCTAD, 2021 ). The NIS concept has been used in developed and, more recently, developing countries, but it is more limited in LDCs ( Metcalfe and Ramlogan, 2008 ). Overall, the literature on innovation performance has not paid attention to less developed countries. Researchers focused on allowing these countries to mark themselves in the Global Innovation Index (GII), so studies focusing on developing and least developed countries can help them improve their innovation policies.

In terms of methodological analysis, it is clear that all articles used quantitative methods to assess the efficiency of innovation. This finding demonstrated that the quantitative approach is the most commonly used methodological approach by most researchers ( Bakhtiar et al., 2021 ; Cai, 2011 ; Carayannis et al., 2016 ; Firsova and Chernyshova, 2020 ; Kryzhko et al., 2020 ; Valdez and Balderrama, 2015 ; Zhang, 2013 ). These mainly involve the calculation of country key performance indicators by using previous data available for the NIS details. The studies often look at a specific year, period of time and collect the available data against the required factors and then analyze them using the various mathematical methods with statistical tools. Researchers prefer to collect data stored in various regional or global indices related to countries' performance in terms of stimulating innovation. This data can be used by researchers to implement DEA techniques and determine required country performance metrics once the study period has been determined. For example, Jankowska et al. (2017) , Jurickova et al. (2017) , Namazi and Mohammadi (2018) used secondary data from the GII provided by the World Intellectual Property Organization (WIPO) to measure innovation efficiency at the national level. In addition, Kudryavtseva et al. (2016) and Mahroum and Al-Saleh (2013) used the scoreboard's innovation information to assess a comparative assessment of innovation levels between the European Union and Russia.

The studies examined mainly focus on the use of non-parametric methods, especially DEA, as models to measure the innovation efficiency of the considered countries. Several researchers have emphasized that DEA is one of the most effective methods to measure the efficiency of countries on NIS ( Alnafrah, 2021 ; Bielicki and Lesniak, 2016 ; Botha et al., 2016 ; Carayannis et al., 2016 ; Fotia and Teclean, 2019 ; Krstic and Mimovic, 2018 ; Namazi and Mohammadi, 2018 ; Nasierowski and Arcelus, 2003 ; San, 2011 ; Yesilay and Halac, 2020 ). The traditional model of this DEA was developed to measure the efficiency of the DMU as a whole ( Kao, 2014 ) without considering the performance of other sub-processes within the unit ( Alnafrah, 2021 ). However, while conducting the study, some evolved DEA methods were encountered, including N-DEA, SBM-DEA, DN-DEA, RN-DEA, B-DEA, and SE-DEA. The evolution of the DEA method over time allows for the inclusion of intermediate results, making it easier to measure the contribution of these units to the units' overall performance ( Shewell and Migiro, 2016 ). Table 5 lists the benefits of evolved DEA models, and future studies should incorporate such DEA models to produce more reliable results.

The advantages of various DEA models.

The overall performance levels of innovation are evaluated, and the most important components used here are the effectiveness generated in the respected country with the implementation of NIS, and the total efficiency is measured using the DEA modeling. The input and output variables in the NIS can be quantified to measure a country's overall performance, and it includes the two major components of efficiency and productivity. The discovery reveals that DEA is widely used to measure efficiency ( Alnafrah, 2021 ; Guede-Cid et al., 2021 ; Kotsemir, 2013 ) rather than productivity. Although the rate of productivity measurement is still far below efficiency, measuring both productivity and the efficiency of innovation plays an important role in providing insight and input to policymakers.

Eventually, the study reveals that only a few previous studies have taken income grouping into account. Table 6 classifies the sampled countries based on their income levels. There have been very few studies that combine different income groups. Furthermore, few such middle- and low-income countries have been studied previously, so more samples from this income group are required to understand their innovation performance. At the same time, understanding the efficiency of innovation from a global perspective necessitates a non-income group study. Choi and Zo (2019) classified each cluster's member countries by income, allowing them to find closer targets related to economic resources in benchmarks. Meanwhile, Cai (2011) reinforces that the BRICS should improve NIS efficiency and boost innovation capacity in order to sustain rapid growth and escape the middle-income trap. Furthermore, Leontitsis et al. (2018) examined the results of multidimensional efficiency analysis scores by income group. Such cross-countries comparative studies are critical for providing insight into making innovation an explicit part of future strategic plans, as well as for solidifying the importance of and accountability for innovation.

The sampled countries based on their income levels.

Another significant finding revealed that previous studies sampled approximately 56% of 217 countries, as shown in Fig. 9 . Obviously, 44% of countries have yet to be sampled in studies on innovation efficiency. Previous studies also only looked at 44% of low-income countries, 55% of high-income countries, and 60% of middle-income countries. According to these studies, the frequency of high-income countries examined is higher than the middle- and low-income groups. However, 45% of high-income countries have yet to be sampled in previous studies. So, future studies should focus on comparative analysis regardless of income group taxonomy, including countries that have never been studied previously. Subsequently, the findings can help countries, that are lagging in the field of innovation to formulate and develop appropriate innovation policies.

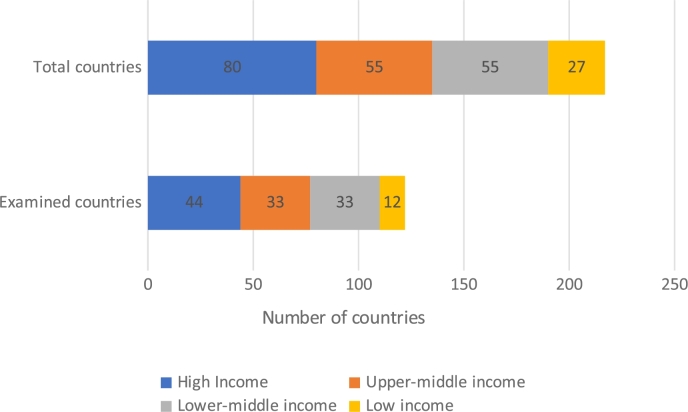
The distribution of nations evaluated in comparison to the total number of countries.

6. Discussion and research agenda

Based on the findings of the literature reviews, the final framework for future research is depicted in Fig. 10 . The research showed certain gaps existing in the present literature, including the measurement of innovation efficiencies using DEA. Although there have been many studies on the measurement of innovation efficiency at the national level, there is still a need to continue and increase the number of studies in cross countries. It is also important to note that the context, structure, and institutions that support innovation change over time ( Zabala-Iturriagagoitia et al., 2020 ) and volatile. So, further research to bridge the gap between global and national contexts is possible and necessary. If both the regional and sectoral innovation systems are strengthened, the innovation efficiency of the NIS can be increased. Innovation efficiency measurement based on certain geographic region, participation in free trade bloc and group of tie-up countries also would provide useful data and information to improve nation's efficiency. This is necessary in order to assess the impact of membership on each bloc's efficiency level. Comparative analysis allows countries or regions to benchmark against the ‘best in class’ innovator and improve their performance ( Shewell and Migiro, 2016 ).

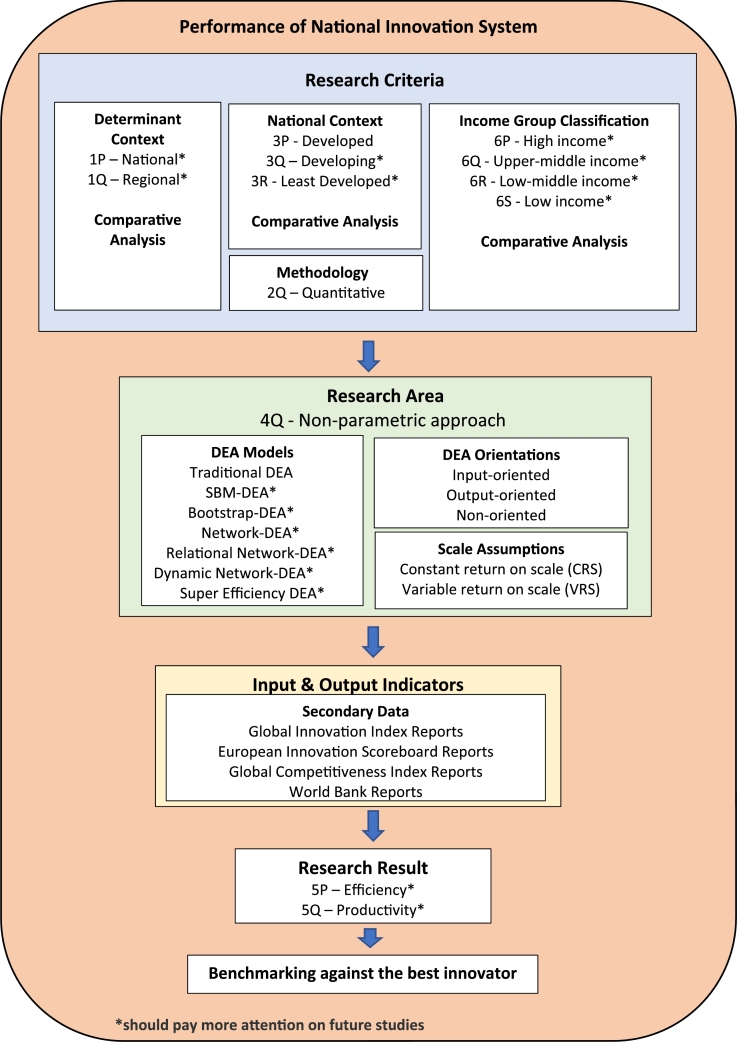
Framework for future research.

The reviewed articles undoubtedly included developed countries, primarily Europe countries (in terms of number of countries). This is because Europe has easy access to comparable and reliable data on NIS development ( Kotsemir, 2013 ). The studies on developed nations highlight the measures taken by them and how they have helped them to achieve a certain position in terms of innovation (refer Fig. 11 ). Moreover, it is reassuring to see that researchers in efficiencies measures on developing economies. Many developing countries are among the most prominent prime mover in innovation, and optimal innovation implementation can ensure further growth and development. Meanwhile, as most LDCs face significant structural obstacles to long-term development, future research should concentrate on developing nations and LDCs in order to help those countries understand inherent constraints and advantages and develop effective innovation strategies to improve their future innovation performance.

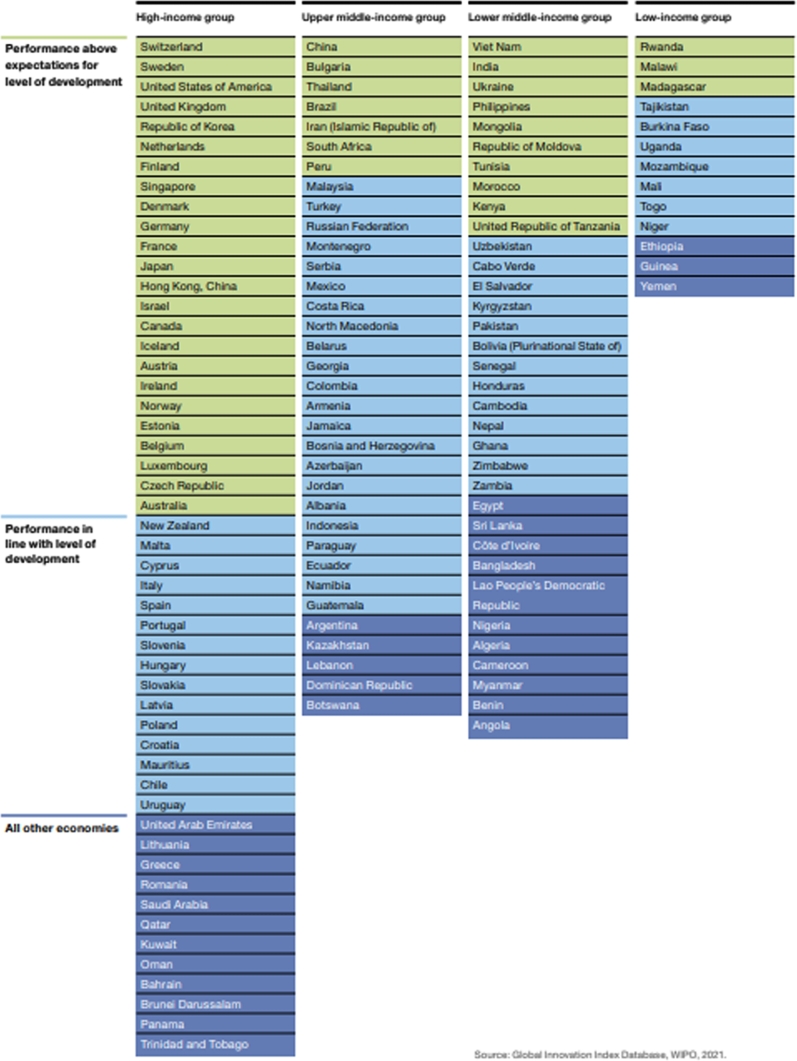
Innovation performance at different income levels, 2021 ( WIPO, 2021 ).

Given that the methodology applied is largely quantitative, an attempt using the other methods can be undertaken to determine the efficiency of NIS to locate other minute factors missed under the quantitative mode of study. The availability of secondary data, such as GII, Global Competitiveness Index, World Bank and European Innovation Scorecard reports, should optimally use to measure the efficiency of innovations. These reports provide a wealth of innovation-related data and information useful for future studies. Quantitative method research on innovation performance can help a country or region analyze its position and take appropriate actions/measures to enhance its innovation policies.

Another important observation made is that the studies focusing on efficiencies of low-income countries are scarce, although several low-income countries, such as Malawi, Rwanda, and Madagascar, have been innovating since 2012 ( WIPO, 2021 ). In addition, low-income sub-Saharan African economies are also effectively converting their limited innovation inputs and resources into innovative outputs ( WIPO, 2021 ). The frequency of middle-income countries examined in previous studies, on the other hand, is limited to a few countries, including Bulgaria, China, Romania, Russia, and Turkey. However, several lower-middle income countries, including India, Vietnam, and the Philippines, are experiencing a changing innovation landscape that has the potential to change the global innovation landscape ( WIPO, 2021 ). Fig. 11 depicts the level of innovation at various income levels. Therefore, upper middle-income economies will almost certainly continue to improve their performance and innovation systems in order to compete with higher-income countries. As a result, regardless of income group classification, a comparative analysis of the existing conditions on national and regional innovation can contribute to the current body of knowledge. These studies should provide a profile of member countries' national innovation policies as well as a comparative analysis of the most significant strengths and areas for improvement.

In a future study, comparative analysis among cross-countries, particular regions, country taxonomy and income groups on national efficiency through DEA will provide insights for countries to develop and implement effective innovation strategies for maximizing innovation outcomes. Comparative analysis helps peers benchmark with the best innovators to improve the efficiency of innovation and maintain international competitiveness and sustainability. Measuring innovation capacity and output provides clarity to decision-makers in government, business, and elsewhere, as they eagerly look forward to creating policies that empower their citizens to invent and create more efficiently. Ultimately, exploring future innovation performance will help countries develop and implement their innovation strategies towards integration to stimulate economic growth. A thorough examination of the efficiency of the national innovation system from a global perspective will be beneficial in developing an innovation research agenda and strategies for innovation sustainability.

7. Conclusion

The systematic review undertaken has been initiated to provide insights into the exponentially growing innovative measures across the world. The requirement for any country to innovate becomes utmost necessary at the present time. Hence, to facilitate innovative practices, the NIS was initiated to provide support to countries that want to innovate. While researchers in the past have provided several important insights into the matter, this study attempted to bring together similar contributions to present an overview for future researchers. Therefore, this study was conducted by using a classification and coding system as the main approach. This study fills the gap as previous researchers did not pay attention to the comparative analysis and cross-countries efficiency evaluation of NIS in their review articles. A comparative analysis of cross-countries innovation efficiency would give NIS insight on how to strengthen their ability and capacity to improve innovation performance. Subsequently, the framework also put forward an agenda for future research.

7.1. Implication for theory and practice

Innovation is inevitable. Innovation can have a significant impact on a country's performance and survival. In theory, the resulting framework conforms to the evolved DEA models, and comparative analysis regardless of income group taxonomy can provide a clear picture of the global efficiency of innovation. Countries must keep up with the ever-changing environment in this modern age of technological advancement and competitiveness. To adapt to the rapid environmental changes, it is critical to close the gaps identified in this study in order to assist countries in strengthening their innovation policies and strategies. Without appropriate enhancement, innovation capacities and capabilities will deteriorate over time. So, innovation resources should be used optimally to produce the highest level of innovation output. Furthermore, this study includes a systematic literature review process, with the results potentially presenting a more comprehensive framework for future research. The inclusion of a sectoral innovation system in a different context as a comparison for future research agendas can encourage a broader study.

7.2. Limitations

This study has some limitations. The types of input and output variables used in the studies were not considered in this review. To assess the efficiency of innovation, various inputs and outputs are used. Summarizing the factors identified during the study, the most important factors influencing NIS efficiency include the input factors corresponding to financial grants, the associated staff, and the number of units involved. The revenue from these innovative practices is the most important output factor, followed by the number of patents filed. These indicators affect the efficiency of the NIS, so it is best to examine the inputs and outputs when measuring innovation efficiency.

Declarations

Author contribution statement.

All authors listed have significantly contributed to the development and the writing of this article.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Data availability statement

Data included in article/supp. material/referenced in article.

Declaration of interests statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.

• Abbasi F., Hajihoseini H., Haukka S. Use of virtual index for measuring efficiency of innovation systems: a cross-country study. Int. J. Technol. Manag. Sustain. Dev. 2011;9(3):195–212. [ Google Scholar ]
• Afzal M.N.I. An empirical investigation of the National Innovation System (NIS) using Data Envelopment Analysis (DEA) and the TOBIT model. Int. Rev. Appl. Econ. 2014;28(4):507–523. [ Google Scholar ]
• Afzal M.N.I., Lawrey R., Gope J. Understanding national innovation system (NIS) using Porter's diamond model (PDM) of competitiveness in ASEAN-05. Compet. Rev. 2019;29(4):336–355. [ Google Scholar ]
• Ajibefun I.A. An evaluation of parametric and non-parametric methods of technical efficiency measurement: application to small scale food crop production in Nigeria. J. Agric. Soc. Sci. 2008;4(3):95–100. [ Google Scholar ]
• Alnafrah I. Efficiency evaluation of BRICS's national innovation systems based on bias-corrected network data envelopment analysis. J. Innov. Entrepreneurship. 2021;10(1):1–28. [ Google Scholar ]
• Amui L.B.L., Jabbour C.J.C., de Sousa Jabbour A.B.L., Kannan D. Sustainability as a dynamic organizational capability: a systematic review and a future agenda toward a sustainable transition. J. Clean. Prod. 2017;142:308–322. [ Google Scholar ]
• Andersen P., Petersen N.C. A procedure for ranking efficient units in data envelopment analysis. Manag. Sci. 1993;39(10):1261–1264. [ Google Scholar ]
• Anderson H.J., Stejskal J. Diffusion efficiency of innovation among EU member states: a data envelopment analysis. Economies. 2019;7(2):34. [ Google Scholar ]
• Aparicio J., Ortiz L., Pastor J.T., Mikel Zabala-Iturriagagoitia J. Introducing crossproductivity: a new approach for ranking productive units over time in data envelopment analysis. Comput. Ind. Eng. 2020;144 [ Google Scholar ]
• Archibugi D. National innovation systems. A comparative analysis: Richard R. Nelson (Editor), (Oxford University Press, New York and London, 1993) xii + 541 pp. Res. Policy. 1996;25(5):838–842. [ Google Scholar ]
• Asmare E., Begashaw A. Review on parametric and nonparametric methods of efficiency analysis. Open Access Bioinform. 2018;2(2):1–7. [ Google Scholar ]
• Aviles-Sacoto S.V., Cook W.D., Güemes-Castorena D., Zhu J. Modelling efficiency in regional innovation systems: a two-stage data envelopment analysis problem with shared outputs within groups of decision-making units. Eur. J. Oper. Res. 2020;287(2):572–582. [ Google Scholar ]
• Bakhtiar A., Ghazinoory S.S., Aslani A., Mafi V. Efficiency-effectiveness assessment of national innovation systems: comparative analysis. J. Sci. Technol. Policy Manag. 2021 [ Google Scholar ]
• Balzat M., Hanusch H. Recent trends in the research on national innovation systems. J. Evol. Econ. 2004;14(2):197–210. [ Google Scholar ]
• Banker R., Emrouznejad A., Bal H., Alp I., Cengiz M. Data envelopment analysis and performance measurement. Proceedings of the 11th International Conference of DEA; Samsun, Turkey, June 2013; 2013. [ Google Scholar ]
• Belitz H., Clemens M., von Hirschhausen C., SchmidtEhmcke J., Werwatz A., Zloczysti P. An indicator for national systems of innovation – methodology and application to industrialized countries. 2011. Discussion Paper.
• Bielicki M., Lesniak M. Proceedings of the 11th European Conference on Innovation and Entrepreneurship. 2016. CEE cross-country comparison of national innovation systems efficiency: DEA approach. [ Google Scholar ]
• Botha L., Grobbelaar S., Bam W. Towards a framework to guide the evaluation of innovation systems. S. Afr. J. Ind. Eng. 2016;27(3):64–78. [ Google Scholar ]
• Bouwman H., Nikou S., de Reuver M. Digitalization, business models, and SMEs: how do business model innovation practices improve performance of digitalizing SMEs? Telecommun. Policy. 2019;43(9) [ Google Scholar ]
• Bresciani S., Puertas R., Ferraris A., Santoro G. Innovation, environmental sustainability and economic development: DEA-Bootstrap and multilevel analysis to compare two regions. Technol. Forecast. Soc. Change. 2021;172(C) [ Google Scholar ]
• Broekel T., Rogge N., Brenner T. The innovation efficiency of German regions – a shared-input DEA approach. Rev. Reg. Res. 2017;38(1):77–109. [ Google Scholar ]
• Cai Y. Factors affecting the efficiency of the BRICSs' national innovation systems: a comparative study based on DEA and panel data analysis. 2011. Economics Discussion Papers, Kiel Institute for the World Economy (IfW)
• Carayannis E.G., Goletsis Y., Grigoroudis E. Multi-level multi-stage efficiency measurement: the case of innovation systems. Oper. Res. 2015;15(2):253–274. [ Google Scholar ]
• Carayannis E.G., Grigoroudis E., Goletsis Y. A multilevel and multistage efficiency evaluation of innovation systems: a multiobjective DEA approach. Expert Syst. Appl. 2016;62(C):63–80. [ Google Scholar ]
• Centobelli P., Cerchione R., Esposito E. Environmental sustainability in the service industry of transportation and logistics service providers: systematic literature review and research directions. Transp. Res., Part D, Transp. Environ. 2017;53:454–470. [ Google Scholar ]
• Chang C-C. Influences of knowledge spillover and utilization on the NIS performance: a multi-stage efficiency perspective. Qual. Quant. 2014;49(5):1945–1967. [ Google Scholar ]
• Charnes A., Cooper W.W., Rhodes E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978;2(6):429–444. [ Google Scholar ]
• Chen C.P., Hu J.L., Yang C.H. An international comparison of R&D efficiency of multiple innovative outputs: the role of the national innovation system. Innovation. 2011;13(3):341–360. [ Google Scholar ]
• Chen K., Guan J. Measuring the efficiency of China's regional innovation systems: application of network data envelopment analysis (DEA) Reg. Stud. 2012;46(3):355–377. [ Google Scholar ]
• Chen P-C., Hung S-W. An actor-network perspective on evaluating the R&D linking efficiency of innovation ecosystems. Technol. Forecast. Soc. Change. 2016;112:303–312. [ Google Scholar ]
• Choi H., Zo H. Assessing the efficiency of national innovation systems in developing countries. Sci. Public Policy. 2019;46(4):530–540. [ Google Scholar ]
• Cooper W.W., Seiford L.M., Tone K. Springer; New York, NY, USA: 2006. Introduction to Data Envelopment Analysis and Its Uses with DEA-Solver and References. [ Google Scholar ]
• Cooper W.W., Seiford L.M., Tone K. second edition. Springer-Verlag; US: 2007. Data Envelopment Analysis. [ Google Scholar ]
• Dahlman C.J. Technology strategy in East Asian developing countries. J. Asian Econ. 1994;5(4):541–572. [ Google Scholar ]
• Deng J., Zhang N., Ahmad F., Draz M.U. Local government competition, environmental regulation intensity and regional innovation performance: an empirical investigation of Chinese Provinces. Int. J. Environ. Res. Public Health. 2019;16(12):2130. doi: 10.3390/ijerph16122130. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Dereli D.D. Innovation management in global competition and competitive advantage. Proc., Soc. Behav. Sci. 2015;195:1365–1370. [ Google Scholar ]
• Didenko A., Loseva O., Abdikeev N. Measuring efficiency of regional innovation system with DEA and PCA. 2017 IEEE 11th International Conference on Application of Information and Communication Technologies; AICT; 2017. [ Google Scholar ]
• Diez J.R., Kiese M. In: International Encyclopedia of Human Geography. Kitchin R., Thrift N., editors. Elsevier; Oxford: 2009. Regional innovation systems; pp. 246–251. [ Google Scholar ]
• Dobrzanski P. Innovation expenditures efficiency in Central and Eastern European countries. Zb. Rad. Ekon. Fak. Rij. 2018;36(2):827–859. [ Google Scholar ]
• Dobrzanski P., Bobowski S., Chrysostome E., Velinov E., Strouhal J. Toward innovation-driven competitiveness across African countries: an analysis of efficiency of R&D expenditures. J. Compet. 2021;13(1):5–22. [ Google Scholar ]
• Dodgson M., Gann D., Salter A. The role of technology in the shift towards open innovation: the case of Procter & Gamble. R & D Manag. 2006;36(3):333–346. [ Google Scholar ]
• Edquist C. The Oxford Handbook of Innovation. 2009. Systems of innovation: perspectives and challenges. [ Google Scholar ]
• Edquist C., Zabala-Iturriagagoitia J.M. Assessing the performance of national innovation systems in Europe. 21st International Conference on Science and Technology Indicators; Spain; 2016. [ Google Scholar ]
• Edquist C., Zabala-Iturriagagoitia J.M., Barbero J., Zofío J.L. On the meaning of innovation performance: is the synthetic indicator of the Innovation Union Scoreboard flawed? Res. Eval. 2018:1–16. [ Google Scholar ]
• Edler J., Fagerberg J. Innovation policy: what, why, and how. Oxf. Rev. Econ. Policy. 2017;33(1):2–23. [ Google Scholar ]
• Fang J.-W., Chiu Y. Research on innovation efficiency and technology gap in China economic development. Asia-Pac. J. Oper. Res. 2017;34(2) (1-22) [ Google Scholar ]
• Fare R., Whittaker G. An intermediate input model of dairy production using complex survey data. J. Agric. Econ. 1995;46(2):201–213. [ Google Scholar ]
• Fare R., Grosskopf S. Network DEA. Socio-Econ. Plan. Sci. 2000;34(1):35–49. [ Google Scholar ]
• Farrell M.J. The measurement of productive efficiency. J. R. Stat. Soc. 1957;120(3):253–290. [ Google Scholar ]
• Firsova A., Chernyshova G. Efficiency analysis of regional innovation development based on DEA Malmquist Index. Information. 2020;11(6):294. [ Google Scholar ]
• Freeman, C., 1982. Technological infrastructure and international competitiveness. Draft paper submitted to the OECD Ad hoc group on Science, Technology and Competitiveness, August 1982. Mimeo. ; Freeman C. Technological infrastructure and international competitiveness. Ind. Corp. Change. 2004;13:541–569. Later published as. [ Google Scholar ]
• Freeman C. Pinter Publishers; London/New York: 1987. Technology and Economic Performance: Lessons from Japan. [ Google Scholar ]
• Foddi M., Usai S. Regional knowledge performance in Europe. Growth Change. 2013;44(2):258–286. [ Google Scholar ]
• Fotia A., Teclean C. The innovation efficiency in Central and Eastern Europe – an input-output comparative analysis between Czech Republic, Hungary, Poland and Romania. EURINT, Cent. Eur. Stud., Alexandru Ioan Cuza Univ. 2019;6(1):269–287. [ Google Scholar ]
• Godinho F.M., Veloso S.E. From time-based competition (TBC) to quick response manufacturing (QRM): the evolution of research aimed at lead time reduction. Int. J. Adv. Manuf. Technol. 2013;64:5–8. [ Google Scholar ]
• Gokhberg L., Roud V. Structural changes in the national innovation system: longitudinal study of innovation modes in the Russian industry. Econ. Change Restruct. 2016;49:269–288. [ Google Scholar ]
• Golichenko O.G. The national innovation system. Probl. Econ. Transit. 2016;58(5):463–481. [ Google Scholar ]
• Grilo A., Santos J. Measuring efficiency and productivity growth of new technology-based firms in business incubators: the Portuguese case study of Madan Parque. Sci. World J. 2015;2015 doi: 10.1155/2015/936252. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Guan J., Chen K. Modeling macro-R&D production frontier performance: an application to Chinese province-level R&D. Scientometrics. 2010;82(1):165–173. [ Google Scholar ]
• Guan J., Chen K. Modeling the relative efficiency of national innovation systems. Res. Policy. 2012;41(1):102–115. [ Google Scholar ]
• Guan J., Zuo K. A cross-country comparison of innovation efficiency. Scientometrics. 2014;100(2):541–575. [ Google Scholar ]
• Guede-Cid R., Rodas-Alfaya L., Leguey-Galán S., Cid-Cid A.I. Innovation efficiency in the Spanish service sectors, and open innovation. J. Open Innov. Technol. Market Complex. 2021;7(1):62. [ Google Scholar ]
• Gunay E.N., Kazazoglu G.R. Palgrave Macmillan Books, Palgrave Macmillan; 2016. National Innovation Efficiency During the Global Crisis. [ Google Scholar ]
• Halaskova M., Gavurova B., Kocisova K. Research and development efficiency in public and private sectors: an empirical analysis of EU countries by using DEA methodology. Sustainability. 2020;12(17):7050. [ Google Scholar ]
• Ho M.H-C. How regional innovation systems play a relative competitive role within knowledge networks. Eur. Plan. Stud. 2009;17(12):1881–1905. [ Google Scholar ]
• Hudec O., Prochadzkova M. The relative efficiency of knowledge innovation processes in EU countries. Stud. Reg. Sci. 2013;43(1):145–162. [ Google Scholar ]
• Hsu Y. Cross national comparison of innovation efficiency and policy application. Afr. J. Bus. Manag. 2011;5(4):1378–1387. [ Google Scholar ]
• Iammarino S. An evolutionary integrated view of regional systems of innovation: concepts, measures and historical perspectives. Eur. Plan. Stud. 2005;13(4):497–519. [ Google Scholar ]
• Ivanova E., Cepel M. The impact of innovation performance on the competitiveness of the Visegrad 4 countries. J. Compet. 2018;10(1):54–72. [ Google Scholar ]
• Jabbour C.J.C. Environmental training in organisations: from a literature review to a framework for future research. Resour. Conserv. Recycl. 2013;74:144–155. [ Google Scholar ]
• Jaloudi M.M. The efficiency of Jordan insurance companies and its determinants using DEA, slacks, and logit models. J. Asian Bus. Econ. Stud. 2019;26(1):153–166. [ Google Scholar ]
• Jankowska B., Matysek-Jędrych A., Mroczek-Dąbrowska K. Efficiency of national innovation systems: Poland and Bulgaria in the context of the global innovation index. Comp. Econ. Res. 2017;20(3):77–94. [ Google Scholar ]
• Jurickova E., Bobak R., Pilik M., Hrusecka D. Efficiency of innovation system in the Czech Republic: comparison with other European countries. New Trends Issues Proc. Humanit. Soc. Sci. 2017;4(10):90–96. [ Google Scholar ]
• Kaihua C., Mingting K. Staged efficiency and its determinants of regional innovation systems: a two-step analytical procedure. Ann. Reg. Sci. 2014;52(2):627–657. [ Google Scholar ]
• Kao C., Hwang S.N. Efficiency decomposition in two-stage data envelopment analysis: an application to non-life insurance companies in Taiwan. Eur. J. Oper. Res. 2008;185(1):418–429. [ Google Scholar ]
• Kao C. Network data envelopment analysis: a review. Eur. J. Oper. Res. 2014;239(1):1–16. [ Google Scholar ]
• Klevenhusen A., Coelho J., Warszawski L. Innovation efficiency in OECD countries: a non-parametric approach. J. Knowl. Econ. 2020;12(3):1064–1078. [ Google Scholar ]
• Koellinger P. The relationship between technology, innovation, and firm performance—empirical evidence from e-business in Europe. Res. Policy. 2008;37(8):1317–1328. [ Google Scholar ]
• Kong M., Wang X., Wu Q. The development efficiency of China's innovative industrial clusters-based on the DEA-Malmquist model. Arab. J. Geosci. 2021;14(7):1–15. [ Google Scholar ]
• Kontolaimou A., Giotopoulos I., Tsakanikas A. A typology of European countries based on innovation efficiency and technology gaps: the role of early-stage entrepreneurship. Econ. Model. 2016;52(PB):477–484. [ Google Scholar ]
• Kotsemir M.N. Higher School of Economics Research Papers, Paper no. WP BRP 16/STI/2013. National Research University Higher School of Economics; 2013. Measuring national innovation systems efficiency: a review of DEA approach. [ Google Scholar ]
• Kou M., Chen K., Wang S., Shao Y. Measuring efficiencies of multi-period and multi-division systems associated with DEA: an application to OECD countries' national innovation systems. Expert Syst. Appl. 2016;46(C):494–510. [ Google Scholar ]
• Kurniawati M.A. The role of ICT infrastructure, innovation and globalization on economic growth in OECD countries, 1996–2017. J. Sci. Technol. Policy Manag. 2020;11(2):193–215. [ Google Scholar ]
• Krstic A., Mimovic P. Measuring efficiency of the Serbian national innovation model: DEA approach. Contemporary Issues in Economics, Business and Management; EBM; 2018. [ Google Scholar ]
• Kryzhko D., Rudskaya I., Skhvediani A., Alamshoev A. Evaluation of technical efficiency of regional innovation system on the basis of DEA modeling. Proceedings of the 2nd International Scientific Conference on Innovations in Digital Economy; SPBPU IDE-2020; New York, NY, USA: Association for Computing Machinery; 2020. [ Google Scholar ]
• Kudryavtseva S.S., Shinkevich A.I., Ostanina S.S., Vodolazhskaya E.L., Chikisheva N.M., Lushchik I.V., Shirokova L.V., Khairullina E.R. The methods of national innovation systems assessing. Int. Rev. Manag. Mark. 2016;6(2S):225–230. [ Google Scholar ]
• Kuhlmann S., Ordóñez-Matamoros G., editors. Research Handbook on Innovation Governance for Emerging Economies. Towards Better Models. Edward Elgar Publishing; Cheltenham, UK: 2017. [ Google Scholar ]
• Lacka I., Brzezicki L. The efficiency and productivity evaluation of national innovation systems in Europe. Eur. Res. Stud. J. 2021;XXIV(3):471–496. [ Google Scholar ]
• Lafuente E., Szerb L., Zoltan J. Country level efficiency and national systems of entrepreneurship: a data envelopment analysis approach. J. Technol. Transf. 2016;41(6):1260–1283. [ Google Scholar ]
• Lala K., Sinha K. Role of technology incubation in India's innovation system: a case of the Indian Institute of Technology Kanpur Incubation Centre. Millenn. Asia. 2019;10(1):91–110. [ Google Scholar ]
• Leontitsis A., Philippas D., Sickles R., Tziogkidis P. Rice University, Department of Economics; 2018. Evaluating countries' innovation potential: an international perspective. Working Papers 18-011. [ Google Scholar ]
• Levy Y., Ellis T.J. A systems approach to conduct an effective literature review in support of information systems research. Informing Sci. J. 2006;9:182–212. [ Google Scholar ]
• Li R., Li Y., Cui Z. Application of data envelopment analysis to efficiency evaluation on R&D input and output. Open Autom. Control Syst. J. 2014;6:194–199. [ Google Scholar ]
• Liberati A., Altman D.G., Tetzlaff J., Mulrow C., Gøtzsche P.C., Ioannidis J.P.A., Clarke M., Devereaux P.J., Kleijnen J., Moher D. The PRISMA statement for reporting systematic reviews and meta-analyses of studies that evaluate health care interventions: explanation and elaboration. PLoS Med. 2009;6(7) doi: 10.1371/journal.pmed.1000100. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Lin T.-Y., Chiu S.-H., Yang H.-L. Performance evaluation for regional innovation systems development in China based on the two-stage SBM-DNDEA model. Socio-Econ. Plan. Sci. 2021 [ Google Scholar ]
• Liu M.C., Wang J.C., Wu M.T. Typology and knowledge productivity of regional innovation system: evidence from China. J. Bus. Econ. 2014;5(1):49–60. [ Google Scholar ]
• Liu J.S., Lu W.-M., Ho M.H.-C. National characteristics: innovation systems from the process efficiency perspective. R & D Manag. 2015;45(4):317–338. [ Google Scholar ]
• Liu Z., Chen X., Chu J., Zhu Q. Industrial development environment and innovation efficiency of high-tech industry: analysis based on the framework of innovation systems. Technol. Anal. Strateg. Manag. 2017;30(4):434–446. [ Google Scholar ]
• Lu W.M., Kweh Q.L., Huang C.L. Intellectual capital and national innovation systems performance. Knowl.-Based Syst. 2014;71(1):201–210. [ Google Scholar ]
• Lundvall B.-Å. Aalborg University Press; Aalborg: 1985. Product Innovation and User-Producer Interaction. [ Google Scholar ]
• Lundvall B.-A. National innovation systems-analytical concept and development tool. Ind. Innov. 2007;14(1):95–119. [ Google Scholar ]
• Lundvall B-A. vol. 2. Anthem Press; 2010. National Systems of Innovation: Toward a Theory of Innovation and Interactive Learning. (Anthem Other Canon Economics Series). [ Google Scholar ]
• Lundvall B.-A. The Learning Economy and the Economics of Hope. Anthem Press; 2016. National innovations systems and globalisation; pp. 351–374. Chapter 13. [ Google Scholar ]
• Mahroum S., Al-Saleh Y. Towards a functional framework for measuring national innovation efficacy. Technovation. 2013;33(10–11):320–332. [ Google Scholar ]
• Mariano E.B., Sobreiro V.A., do Nascimento Rebelatto D.A. Human development and data envelopment analysis: a structured literature review. Omega. 2015;54(C):33–49. [ Google Scholar ]
• Matei M.M., Aldea A. Ranking national innovation systems according to their technical efficiency. Proc., Soc. Behav. Sci. 2012;62:968–974. [ Google Scholar ]
• Metcalfe S., Ramlogan R. Innovation systems and the competitive process in developing economies. Q. Rev. Econ. Finance. 2008;48(2):433–446. [ Google Scholar ]
• Min S., Kim J., Sawng Y.W. The effect of innovation network size and public R&D investment on regional innovation efficiency. Technol. Forecast. Soc. Change. 2020;155 [ Google Scholar ]
• Murillo-Zamorano L.R., Vega-Cervera J.A. The use of parametric and non-parametric frontier methods to measure the productive efficiency in the industrial sector: a comparative study. Int. J. Prod. Econ. 2001;69(3):265–275. [ Google Scholar ]
• Muscio A. From regional innovation systems to local innovation systems: evidence from Italian industrial districts. Eur. Plan. Stud. 2006;6:773–789. [ Google Scholar ]
• Namazi M., Mohammadi E. Natural resource dependence and economic growth: a TOPSIS/DEA analysis of innovation efficiency. Resour. Policy. 2018;59(C):544–552. [ Google Scholar ]
• Nasierowski W. Technical efficiency of innovations in Poland from EU perspective. Pol. J. Econ. 2019;300(4):79–104. [ Google Scholar ]
• Nasierowski W., Arcelus F.J. On the efficiency of national innovation systems. Socio-Econ. Plan. Sci. 2003;37(3):215–234. [ Google Scholar ]
• Nasierowski W., Arcelus F.J. About efficiency of innovations: what can be learned from the Innovation Union Scoreboard Index. Proc., Soc. Behav. Sci. 2012;58:792–801. [ Google Scholar ]
• Nelson R.R., editor. National Innovation Systems. A Comparative Analysis. Oxford University Press; New York/Oxford: 1993. [ Google Scholar ]
• OECD . OECD; Paris: 2008. OECD Reviews of Regional Innovation: North of England, UK. [ Google Scholar ]
• Ozkan E.N.G., Kazazoglu G.N. Performance of national innovation systems during the global crisis: a cross-country analysis. PressAcademia Procedia. 2016;2(1):37–48. [ Google Scholar ]
• Pan T.-W., Hung S.-W., Lu W.-M. DEA performance measurement of the national innovation system in Asia and Europe. Asia-Pac. J. Oper. Res. 2010;27(03):369–392. [ Google Scholar ]
• Park K. Evaluating innovation capacities of Chinese provincial governments. The public sphere. J. Public Policy. 2021;9(1):53–81. [ Google Scholar ]
• Parkey M. Clemson University. TigerPrints; 2012. Assessing the national innovation system in a developing country context: a framework and evidence from Thailand. [ Google Scholar ]
• Pinto H., Pereira S.T. Efficiency of innovation systems in Europe: an institutional approach to the diversity of national profiles. Eur. Plan. Stud. 2013;21(6):755–779. [ Google Scholar ]
• Popay J., Roberts H., Sowden A., Petticrew M., Arai L., Rodgers M. 2006. Guidance on the Conduct of Narrative Synthesis in Systematic Reviews. A Product from the ESRC Methods Programme. Version 1. ESRC. [ Google Scholar ]
• Prokop V., Hajek P., Stejskal J. Configuration paths to efficient national innovation ecosystems. Technol. Forecast. Soc. Change. 2021;168(C) [ Google Scholar ]
• Rajapathirana R.P.J., Hui Y. Relationship between innovation capability, innovation type, and firm performance. J. Innov. Knowl. 2018;3(1):44–55. [ Google Scholar ]
• Ribeiro V.M., Varum C., Daniel A.D. Introducing microeconomic foundation in data envelopment analysis: effects of the ex ante regulation principle on regional performance. J. Knowl. Econ. 2020;12:1215–1244. [ Google Scholar ]
• Roman M. 2010. Regional efficiency of knowledge economy in the new EU countries: the Romanian and Bulgarian case. Munich Persona RePEc Archive, Romania. [ Google Scholar ]
• Rousseau S., Rousseau R. Data envelopment analysis as a tool for constructing scientometric indicators. Scientometrics. 1997;40(1):45–56. [ Google Scholar ]
• Salim N., Ab Rahman M.N., Abd Wahab D. A systematic literature review of internal capabilities for enhancing eco-innovation performance of manufacturing firms. J. Clean. Prod. 2019;209:1445–1460. [ Google Scholar ]
• Samara E., Georgiadis P., Bakouros I. The impact of innovation policies on the performance of national innovation systems: a system dynamics analysis. Technovation. 2012;32(11):624–638. [ Google Scholar ]
• San R.J.C. A multi criteria data envelopment analysis model to evaluate the efficiency of the renewable energy technologies. Renew. Energy. 2011;36(10):2742–2746. [ Google Scholar ]
• Schrempf B., Kaplan D., Schroeder D. National, regional, and sectoral systems of innovation – an overview. 2013. progressproject.eu Report for FP7 Project “Progress”.
• Sharma S., Thomas V.J. Inter-country R&D efficiency analysis: an application of data envelopment analysis. Scientometrics. 2008;76(3):483–501. [ Google Scholar ]
• Shewell P., Migiro S. Data envelopment analysis in performance measurement: a critical analysis of the literature. Probl. Perspect. Manag. 2016;14(3–3):705–713. [ Google Scholar ]
• Shin J., Kim C., Yang H. The effect of sustainability as innovation objectives on innovation efficiency. Sustainability. 2018;10(6) [ Google Scholar ]
• Silva W., Kimura H., Sobreiro V.A. An analysis of the literature on systemic financial risk: a survey. J. Financ. Stab. 2017;28(C):91–114. [ Google Scholar ]
• Simar L.O.L., Wilson P.W. Sensitivity analysis of efficiency scores: how to bootstrap in nonparametric frontier models? Manag. Sci. 1998;44(1):49–61. [ Google Scholar ]
• Simar L., Wilson P.W. A general methodology for bootstrapping in non-parametric frontier models. J. Appl. Stat. 2000;27(6):779–802. [ Google Scholar ]
• Snyder H. Literature review as a research methodology: an overview and guidelines. J. Bus. Res. 2019;104(C):333–339. [ Google Scholar ]
• Tasnim N., Afzal M.N.I. An empirical investigation of country level efficiency and national systems of entrepreneurship using Data Envelopment Analysis (DEA) and the TOBIT model. J. Glob. Entrep. Res. 2018 [ Google Scholar ]
• Tarnawska K., Mavroeidis V. Efficiency of the knowledge triangle policy in the EU member states: DEA approach. Triple Helix. 2015;2(1):1–22. [ Google Scholar ]
• Teixeira A. Evolution, roots and influence of the literature on national systems of innovation: a bibliometric account. Camb. J. Econ. 2014;38(1):181–214. [ Google Scholar ]
• Tidd J., Bessant J. 7th edition. John Wiley & Sons; Chichester: 2020. Managing Innovation: Integrating Technological, Market, and Organizational Change. [ Google Scholar ]
• Todttling F., Trippl M. One size fits all? Towards a differentiated regional innovation policy approach. Res. Policy. 2005;34(8):1203–1219. [ Google Scholar ]
• Tone K. A slacks-based measure of efficiency in data envelopment analysis. Eur. J. Oper. Res. 2001;130(3):498–509. [ Google Scholar ]
• Tone K. In: Handbook on Data Envelopment Analysis. Cooper W.W., Seiford L.M., Zhu J., editors. Springer; New York: 2011. Slacks-based measure of efficiency. [ Google Scholar ]
• Tone K., Tsutsui M. Dynamic DEA with network structure: a slacks-based measure approach. Omega. 2014;42(1):124–131. [ Google Scholar ]
• Tranfield D., Denyer D., Smart P. Towards a methodology for developing evidence-informed management knowledge by means of systematic review. Br. J. Manag. 2003;14(3):207–222. [ Google Scholar ]
• United Nations World economic situation and prospects. 2019. https://www.un.org/development/desa/dpad/wpcontent/uploads/sites/45/WESP2019_BOOK-ANNEX-en.pdf United Nations.
• UNCTAD . United Nations Conference on Trade and Development. 2021. Catching technological waves innovation with equity. Technology and Innovation Report 2021. [ Google Scholar ]
• Valdez L.C., Balderrama J.I.L. Efficiency of Mexico's regional innovation systems: an evaluation applying data envelopment analysis (DEA) Afr. J. Sci. Technol. Innov. Develop. 2015;7(1):36–44. [ Google Scholar ]
• Varblane U., Dyker D., Tamm D., von Tunzelmann N. Can the national innovation systems of the new EU member states be improved? Post-Communist Econ. 2007;19(4):399–416. [ Google Scholar ]
• Villaverde D., Paredes A., de los Angeles J. Assessment of innovation factors that impact competitiveness in the Mexican state entities through DEA analysis. Strategy Technol. Soc. 2020;10:11–35. [ Google Scholar ]
• Wang P., Lin X., Li S. Evaluation of government-supported provincial innovation competitiveness—evidence from China. Growth Change. 2019;50(2):587–608. [ Google Scholar ]
• Wang D., Zhao L., Yang F., Chen K. Performance evaluation of the Chinese high-tech industry: a two-stage DEA approach with feedback and shared resource. J. Ind. Manag. Optim. 2021 [ Google Scholar ]
• Wang Q., Tang J., Choi G. A two-stage eco-efficiency evaluation of China's industrial sectors: a dynamic network data envelopment analysis (DNDEA) approach. Process Saf. Environ. Prot. 2021;148:879–892. [ Google Scholar ]
• Watkins A., Papaioannou T., Mugwagwa J., Kale D. National innovation systems and the intermediary role of industry associations in building institutional capacities for innovation in developing countries: a critical review of the literature. Res. Policy. 2015;44(8):1407–1418. [ Google Scholar ]
• WIPO . World Intellectual Property Organization; Geneva: 2021. Global Innovation Index 2021: Tracking Innovation Through the COVID-19 Crisis. [ Google Scholar ]
• World Bank New World Bank country classifications by income level: 2021–2022. 2019. https://blogs.worldbank.org/opendata/new-world-bank-country-classifications-income-level-2021-2022
• Xiong X., Yang G., Guan Z. A parallel DEA-based method for evaluating parallel independent subunits with heterogeneous outputs. J. Informetr. 2020;14(3) [ Google Scholar ]
• Xu L., Cheng M. A study on Chinese regional scientific innovation efficiency with a perspective of synergy degree. Technol. Invest. 2013;4(4):229–235. [ Google Scholar ]
• Yesilay R.B., Halac U. Contemporary Studies in Economic and Financial Analysis. Emerald; Bingley, UK: 2020. An assessment of innovation efficiency in EECA countries using the DEA method; pp. 203–215. [ Google Scholar ]
• Yun Z., Yuan Z., Shichan F., Luyi C. The evolution and influencing factors of national innovation efficiency from the perspective of open economy. J. Ind. Technol. Econ. 2019 [ Google Scholar ]
• Zabala-Iturriagagoitia J.M., Aparicio J., Ortiz L., Carayannis E.G., Grigoroudis E. The productivity of national innovation systems in Europe: catching up or falling behind? Technovation. 2020;102(C) [ Google Scholar ]
• Zemtsov S., Kotsemir M. An assessment of regional innovation system efficiency in Russia: the application of the DEA approach. Scientometrics. 2019;120(2):375–404. [ Google Scholar ]
• Zeng J., Ribeiro-Soriano D., Ren J. Innovation efficiency: a bibliometric review and future research agenda. Asia Pac. Bus. Rev. 2021;27(2):1–20. [ Google Scholar ]
• Zhang J. International comparison of national innovation system efficiency. 2013. www.techmonitor.net/tm/images/d/da/13apr_jun_sf2.pdf Tech Monitor. April–June: 23–29.
• Zhang Y., Cui M. Determining the innovation efficiency of resource-based cities using a relational network DEA model: evidence from China. Extr. Ind. Soc. 2020;7(4):1557–1566. [ Google Scholar ]
• Zhang C., Wang X. The influence of ICT-driven innovation: a comparative study on national innovation efficiency between developed and emerging countries. Behav. Inf. Technol. 2019 [ Google Scholar ]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Data Availability Statement

• View on publisher site
• PDF (1.8 MB)
• Collections

Similar articles

Cited by other articles, links to ncbi databases.

• Download .nbib .nbib
• Format: AMA APA MLA NLM

Add to Collections

Applications of data envelopment analysis in acute care hospitals: a systematic literature review, 1984-2022

Affiliations.

• 1 School of Business Administration, Penn State Harrisburg, 777 West Harrisburg Pike, Middletown, PA, 17057, USA.
• 2 College of Business, Eastern Connecticut State University, 83 Windham St, Willimantic, CT, 06226, USA. [email protected].
• 3 Rochester Institute of Technology, Kate Gleason College of Engineering, Rochester, NY, 14623, USA.
• PMID: 38438649
• DOI: 10.1007/s10729-024-09669-4

This study reviews scholarly publications on data envelopment analysis (DEA) studies on acute care hospital (ACH) efficiency published between 1984 and 2022 in scholarly peer-reviewed journals. We employ systematic literature review (SLR) method to identify and analyze pertinent past research using predetermined steps. The SLR offers a comprehensive resource that meticulously analyzes DEA methodology for practitioners and researchers focusing on ACH efficiency measurement. The articles reviewed in the SLR are analyzed and synthesized based on the nature of the DEA modelling process and the key findings from the DEA models. The key findings from the DEA models are presented under the following sections: effects of different ownership structures; impacts of specific healthcare reforms or other policy interventions; international and multi-state comparisons; effects of changes in competitive environment; impacts of new technology implementations; effects of hospital location; impacts of quality management interventions; impact of COVID-19 on hospital performance; impact of teaching status, and impact of merger. Furthermore, the nature of DEA modelling process focuses on use of sensitivity analysis; choice of inputs and outputs; comparison with Stochastic Frontier Analysis; use of congestion analysis; use of bootstrapping; imposition of weight restrictions; use of DEA window analysis; and exogenous factors. The findings demonstrate that, despite several innovative DEA extensions and hospital applications, over half of the research used the conventional DEA models. The findings also show that the most often used inputs in the DEA models were labor-oriented inputs and hospital beds, whereas the most frequently used outputs were outpatient visits, followed by surgeries, admissions, and inpatient days. Further research on the impact of healthcare reforms and health information technology (HIT) on hospital performance is required, given the number of reforms being implemented in many countries and the role HIT plays in enhancing care quality and lowering costs. We conclude by offering several new research directions for future studies.

Keywords: Acute care hospitals; DEA; Systematic literature review.

© 2024. The Author(s), under exclusive licence to Springer Science+Business Media, LLC, part of Springer Nature.

Publication types

• Systematic Review
• COVID-19* / epidemiology
• Efficiency, Organizational*
• Hospital Administration / methods

A Review on the 40 Years of Existence of Data Envelopment Analysis Models: Historic Development and Current Trends

• Review article
• Published: 10 June 2022
• Volume 29 , pages 5397–5426, ( 2022 )

Cite this article

• Ankita Panwar 1 ,
• Maryam Olfati 2 ,
• Millie Pant 1 , 3 &
• Vaclav Snasel 2  

10k Accesses

39 Citations

Explore all metrics

DEA, incepted in 80s, has emerged as a popular decision-making technique, for determining the efficiency of similar units. Due to its simplicity and applicability, DEA has gained the attention of scientists and researchers working in diverse areas, which has contributed towards a rich literature both in terms of theoretical development as well as different applications. This paper tries to bring together the near 40 years of existence of DEA in a concise format by discussing the popular DEA models, their advantages and shortcomings, and different applications of DEA. It also provides a brief bibliometric analysis to highlight the development of DEA over the years in terms of publication trends, highly cited papers, journal citation, etc.

Similar content being viewed by others

Research Fronts and Prevailing Applications in Data Envelopment Analysis

Data Envelopment Analysis and Big Data: A Systematic Literature Review with Bibliometric Analysis

A sequence of targets toward a common best practice frontier in DEA

Avoid common mistakes on your manuscript.

1 Introduction

1.1 data envelopment analysis (dea).

The success of an organization or unit, whether government or private, depends on its efficiency. Measurement of efficiency of units of similar type, not only help in identifying the shortcomings of the unit, but also it helps in the development of the unit by eradicating or minimizing those shortcomings, thereby developing the country as a whole.

The first and the foremost principle of efficiency is to attain the best outcome through the minimum utilization of resources. Efficiency measurement and efficiency enhancement is a crucial and essential part of every organization for its future development [ 1 ]. However, measuring the efficiency, though extremely important, is not an easy task. For simple cases, when units have a single output and single input, efficiency could be measured as the ratio of the two. But, things become challenging when efficiency is to be calculated depending on multiple-input and output. This has attracted the scientists and researches working in the area of decision-making and operations research since many years.

Fifty years ago, in 1957, Farrel introduced the assessment of productivity efficiency in his classical paper [ 2 ]. Around twenty years later, in 1978, Charnes et al. [ 3 ] introduced a methodology named Data Envelopment Analysis (DEA) to calculate the relative efficiency of units based on multiple outputs and multiple inputs. He defined efficiency as the ratio of the weighted sum of the outputs to the weighted sum of inputs, and gave the mathematical representation described in detail are below. Some notable advantages of DEA are [ 4 ]:

It may maintain multiple outputs and multiple input variables, which may have different units.

It is able of engaging with qualitative as well as quantitative data.

It acts an effective decision-making tool in directing the attention of management to the area that can be improved.

Literature reveals that from 1978 to 1995, there has been a constant growth in the publications of DEA, but 1995 onwards there has been an exponential rise in the publications of DEA, both in terms of theoretical development and in terms of diverse applications such as banking [ 5 ], transportation [ 6 ], health sector [ 7 ], education [ 8 ], tourism [ 9 ], finance [ 10 ], sports [ 11 ], and many more. This trend is clearly reflected in Fig.  1 .

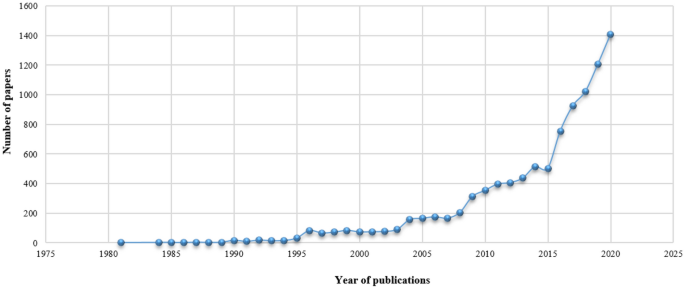
DEA publications since 1980

1.2 Basic DEA Model

We now come to the basic DEA model, which laid the foundation for several modified DEA variants. The idea was conceptualized by Charnes et al., in their highly cited paper published in 1978 [ 3 ]. DEA is a two-step process wherein the initial step the problem is formulated in the fractional form, which is simplified to the linear form in the second step [ 12 ].

Efficiency, by definition, is the ratio of the output upon the input as given in Eq. (1).

However, things become tricky in case of multiple input and multiple output, which is usually the case with real-life scenarios.

This is where, the notion of DEA comes to the rescue, according to which efficiency can be calculated as the weighted sum of output to the weighted sum of input, mathematically represented as Eq. (2).

To explain (2) in a better manner, let us assume that there are \(y_t\) and \(x_s\) output and input criteria respectively, where the output \(y_t\) is to be maximized, and input \(x_s\) is to be minimized. Here, we have considered M DMUs. Now, if we have to maximize the efficiency of the \(z^{th}\) DMU, then its mathematical representation can be the following equations:

If the efficiency score of a DMU is one, then it is known to be a relative efficient DMU otherwise it is said as a relative inefficient DMU [ 13 ]. Once the problem has been formulated considering the input and the output criteria, it is simplified into a linear programming (LP) model as followed.

where, \(E_{z}\) is the efficiency of the z th DMU, \(y_{tz}\) shows \(t^{th}\) output of the z th DMU, \(c_{tz}\) denotes the weight of the t th output, \(x_{sz}\) is the s th input of the z th DMU, and \(d_{sz}\) shows the weight of the s th input.

1.3 Significance of the Present Study

Many authors surveyed DEA literature in the past era on different aspects. Cooper et al. [ 14 ] in their review, discussed the theory of DEA models. Adler et al. [ 15 ] provided a review of different ranking methods of DEA. Kuah et al. [ 16 ] focused on the methodological development of DEA. Liu et al. [ 17 ] reviewed the citation-based survey from 1978-2010. An application of DEA-based literature was reviewed by Liu et al. [ 17 ]. Seiford [ 18 ] and Emrouznejad et al. [ 19 ] provided a bibliometric survey of taking into account 30 years of its development. Mardani et al. [ 20 ] and Xu et al. [ 21 ] provided a review on the energy efficiency evaluation based on DEA. The study aims to find a set of papers that cover the development in the DEA area in the last 40 years. The study adopts to review various DEA models, major application areas of DEA, details of the software, and bibliometric analysis. The present study is based on the following research questions (RQ):

RQ1: What are the different variants of DEA that have emerged during the 40 years of its existence?

RQ2: What are the advantages and disadvantages of different DEA models?

RQ3: what are the different application areas where DEA has been applied?

RQ4: what are major trends of DEA in terms of publications?

The paper is categorized into nine sections, including Sect. 1, a deep explanation of introduction of DEA. Section 2, examines the collecting of the information. Section 3 reviews selected DEA models, and Sect. 4 discusses the advantages and disadvantages of DEA models. Section 5 reviews the applications of the DEA and its variants. Section 6 discusses the software and conferences related to the DEA. A bibliometric analysis is propounded in Sect. 7, and conclusion and future measures are described in Sect. 8, and Sect. 9.

2 Collecting the Information

The purpose of this study is to abreast the reader with the historical and recent developments of DEA for which a large number of papers were surveyed through the standard ISI Web of Science (WOS) database.

According to the citation database, WOS is the world’s leading disciplinary coverage of high-impact journals in sciences, social sciences, as well as international progression. The selection of the publications is based on SCIE and SSCI index, Conference proceedings citation index-Science (CPCI-S), Art and humanities citation index (A& HCI), Conference proceeding citation index -social science & humanities (CPCI-SSH). More details are mentioned in Table  1 . We have tried to bring together the different models of DEA, discussed in detail in Sect. 3.

The search for research articles to be comprised of this paper is based on Journal Citation Report (JCR), and their impact factor (shown in Fig 12 ).

Choice of Keywords : We started the search by considering the following keywords:

‘Data Envelopment Analysis’, ‘Additive DEA approach’, ‘Slacks-Based DEA technique’, ‘Russel Measure DEA approach’, ‘Cross efficiency approach’, ‘Super efficiency DEA technique’, ‘Network DEA Models’, ‘Hierarchical DEA Models’, ‘Supply Chain DEA procedures’, ‘Stochastic DEA models’, ‘Fuzzy DEA model’, ‘Banking and DEA’, ‘Sports and DEA’, ‘Agriculture & farm and DEA’, ‘Transportation and DEA’, ‘Education and DEA’, ‘Communication and DEA’, ‘Fishery and DEA’, ‘Tourism and DEA’, ‘Health care and DEA’, ‘Automobile and DEA’, ‘Forestry and DEA’, ‘Water and DEA’, ‘Real estate and DEA’, ‘E-business and DEA’.

The number of articles that appeared using the above keywords are listed in Table  1 for the time window 1981 – 2021. Searching the database on the basis of applications of DEA, the data obtained is illustrated in Fig.  2 . In the subsequent sections we will discuss modified DEA models, their applications and so on Fig.  3 .

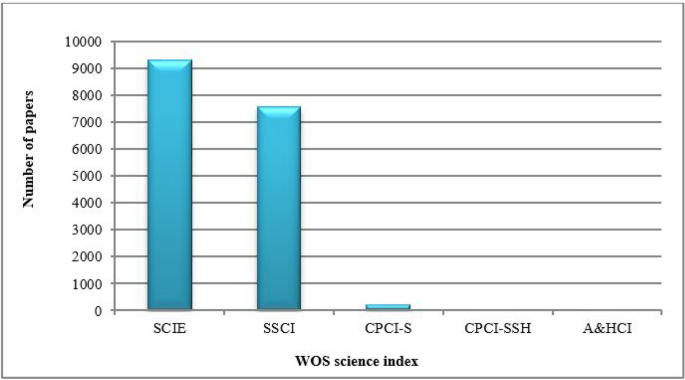
Science index of the DEA

Steps of the workflow for reviewing the literature of DEA

3 DEA Models

Nothing in the world is flawless, not even DEA, and though it gave an initial concept of efficiency measurement for units having multiple input and output, researchers realized that despite being an advantageous technique, there are certain drawbacks, listed below, associated with DEA.

It is a non-parametric approach, so statistical hypothesis testing is difficult.

Lack of discriminating power between the DMUs.

It cannot predict the performance of other DMUs.

Since the initial conceptualization of DEA, several models have been proposed to improve its performance. DEA models can also be segregated as per different terminologies one of which can be Radial and non-radial [ 4 ]. While radial models directly assume proportion change of output/input variable, and generally, resting slacks are indirectly accounted for inefficiency, the non-radial models deal with slacks of all output/input variable separately and combine them into an efficiency measure. In the present study we have segregated the models on the basis of their development as follows:

Classical DEA methods

Extended DEA methods

Multistage and multi-level DEA models

Stochastic and Fuzzy DEA techniques.

Hybrid DEA models

AI/ML assisted DEA models

3.1 Classical Models of DEA

The three models, viz. CCR, BCC and SE are placed under the classical model’s category. These models helped in designing DEA in the initial stage and also laid the foundation for other variants of DEA. In the following sub sections, we will describe the models one by one.

3.1.1 CCR (CRS) Model

CCR is the first DEA approach, and investigated by Charnes et al. in 1978 [ 3 ]; it is named as CCR model after the first letter of their names. The mathematical structure is the CCR model is shown in Eq. 4. Since the DMUs are M , the approach is run M times to recognize the relative efficiency value of all DMUs. Each DMU choose a collection of output weights \((c_{tz})\) and input weights \((d_{tz})\) which maximize the efficiency value. This model presumes constant returns to scale (CRS) supposition. The efficiency is also denominated as the overall technical efficiency (OTE) score.

3.1.2 BCC Model

It was observed that the CCR approach is focused on the proper DMU when it can consider all DMUs on an optimal scale. Some application areas like incomplete completion and restrictions on finance etc., may give rise to DMUs to operate away from the optimal scale. The extension technique of CCR technique was given via Banker, Charnes and Cooper in 1984 [ 13 ] and is also known as the VRS method. The efficient frontier of VRS is constituted by the convex hull of the DMUs which are available [ 16 ]. The efficiency measures obtained from the BCC technique, denominated pure technical efficiency (PTE) value. Mathematical form of the model is given below:

Main variation between the CCR and BCC techniques is convexity constraint. In the BCC technique, the sum of the \(\sum w_{q z}=1\) . If the value is \(\sum w_{q z}\le 1\) , instead of the \(\sum w_{q z}=1\) then the technique is Non-Increasing Returns to scale (NIRS) form. If the value is \(\sum w_{q z}\ge 1\) , instead the \(\sum w_{q z}=1\) thus, the approach is called Non-Decreasing Returns to scale (NDRS). CCR efficiency score is always less and equal to the BCC efficiency score.

Here, it is seen that the form of the BCC is different from the CCR model. This model has an extra convexity constraint, \(\sum w_{q z}=1\) . The difference between both models is explained by Fig.  4 .

Efficient frontier of CCR and BCC model

Here, it can be observed the straight-line “opqr”, which shows the CRS surface and the line “lsqwz” which shows the VRS.Under the CCR model, DMU q is efficient, and the remaining are inefficient DMUs. Under the VRS model, the efficient DMUs are s ,  q ,  w ,  and z . These efficient units are called BCC-efficient. The line segments s and q is IRS, and point q shows the CRS while the other point on right side of the q is experiencing decreasing returns to scale (DRS).

3.1.3 Scale Efficiency (SE) Model

The ratio of the CCR score into the BCC score shows the value of the scale efficiency [ 22 ]. It measures the influence on scale value on the efficiency of a DMU.

where, \(E_{CCR} = CCR\) score of the DMU, and \(E_{BCC}= BCC\) score of the DMU

3.2 Extended Versions of DEA Model

The traditional DEA approaches determine the relative efficiency of the DMUs, but they are not able to attain ranking for the efficient units. Lack of discriminating power is the major drawback of the model. If the number of input and output variables are greater than the number of decision units, it may reduce the discriminating tendency of the technique.

To deal with this drawback, researchers extended the basic model and proposed modifications in DEA to enhance its discriminatory power. Some extended models of the DEA are discussed in this section.

3.2.1 Additive DEA Model

The additive DEA model is non-radial and It proceeds the inefficient DMU to the efficient frontier by reducing the input and increasing output simultaneously. Also, This technique is called the Pareto Koopmans model and was presented by Charnes, Cooper, Golany, Seiford and Stutz in 1985 [ 23 ]. BCC and CCR models can be explained in the form of the additive model. The mathematical form is shown in Eq. (7).

\(s_{z}^{-}\) and \(s_{t}^{+}\) are show slacks, when \(s_{z}^{-}\) is input excesses and \(s_{t}^{+}\) is output shortfalls.

If the values of all slacks are zero, then DMU is called additive efficient at its optimum solution.

3.2.2 Slacks-Based Model (SBM)

SBM technique is used to surmount the drawback of the additive approach. This technique is a variation of the additive model and was recommended by Tone [ 24 ]. Efficiency measurement of the SBM model is shown in Eq. (8).

This fractional form can be transformed into the linear form, as shown in [ 25 ]. When all slacks are equal to 0, then the optimum solution of the SBM model is 1. SBM model is an example of the non-radial model.

3.2.3 Russel Measure Model (RM)

One of the other important DEA models is RM, introduced by Fare and Lovell [ 25 ] in 1978. Computationally, RM model is very complicated because it was formulated as a non-linear programming model (NLP)[ 26 ].

They revisited the RM model in 1999, called the Enhanced Russell Graph Measure model (EGRM). EGRM is an improved model of the RM model [ 26 ], and is calculated as the ratio among the average efficiency of the inputs to the average efficiency of outputs. EGRM is best model because it is capable of overcoming the computational complexity in the RM model. Pastor et al. published the development of RM. Without depending on EGRM, the second-order cone programming (SOCP) model is used directly to solve RM. The exact RM score can provide through the SOCP model.

3.2.4 Free Disposal Hull Model (FDH)

FDH [ 27 ] is an easy-to-use model and could be generated from the VRS or CRS model, with the extra restriction \(\delta _{u} \in \{0,1\}\) . In 1999, Thrall [ 28 ] challenge this idea, from the economic theory perspective which can be rebutted strongly by Cherchye et al. [ 29 ] and FDH remains a noteworthy technique for measuring efficiency. Figure  5 shows the “hull” of the boundary of sets and its connection concept of the FDH model [ 16 ].

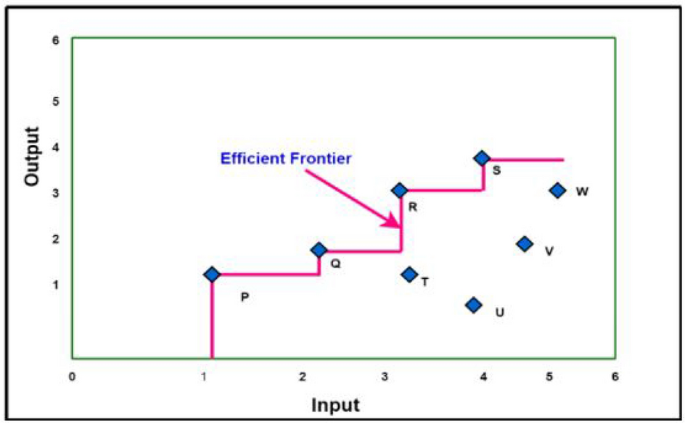
Efficient frontier of FDH model

3.2.5 Cross Efficiency DEA Model

This model was introduced by Sexton, Silkman, and Hogan in 1986 [ 30 ]. It evaluates the weights of outputs and inputs of each DMU with the help of the DEA. In the next step, weights of each DMU, using m sets of weights, and getting m efficiency value of each DMU. Finally, the cross-efficiency value of a DMU is the intermediate score of its efficiency score. According to cross efficiency value to give the rank of DMU. More discussion of the cross-efficiency model is mentioned in [ 31 ]. Some improved models along with applications are discussed in the references [ 32 , 33 ].

3.2.6 Super Efficiency Model (SE-DEA)

The SE-DEA model was introduced by Andersen and Petersen [ 34 ]. This model performs very well, however, the DMU is omitted from the peer set under the evaluation. The super-efficiency model has been extensively used in various application areas, as an example, measuring the efficiency regions [ 35 ], ranking of the efficient DMUs [ 34 ], and detecting the extreme efficient DMUs [ 36 ]. The mathematical form of the super efficiency model defined under DEA-CCR is expressed as [ 37 ]:

\(y_{ti}\) and \(x_{si}\) are the \(t\) th output and \(s\) th input respectively of the \(i\) th DMU, where \(i = 1, 2,\ldots ,I,\) and \(s=1,2,\ldots ,S, t=1,2,\ldots ,T\) .

Linear programming technique is used to solve each decision-making units above mathematical formulation [ 38 ]. The difference between the classical DEA (DEA-CCR) and the super-efficiency technique is exclusion of unit z as the constraint set in Eq. 10. When included unit z in Eq. 10, the maximum score of efficiency score is 1. Outputs are maximized when no longer in the second constraint ( i ) under the evaluation unit.

3.3 Multistage and Multilevel Models

Till now, the discussion was on the single-level DEA models. The concept of single level models extended further to multistage and multilevel DEA models. These models could be distinguished into three cliques: Network DEA approaches, Hierarchical DEA approaches and Supply Chain DEA models. These are explained briefly below:

3.3.1 Network DEA Models

Network model implements DEA for estimating the relative efficiency of the DMUs, taking its internal structure, which is not considered by the classical DEA models. Grosskopf and Fare [ 39 ] and Flare and Whittaker [ 40 ] proposed similar network models. Those models define the peer group for the DMU, as is the common practice in DEA that set of all convex linear compositions of DMUs. Some researchers also called the “black box” of DEA because in this model DMU is a black box. Fare et al. introduced the three general network DEA model as ( i ) static network model ( ii ) dynamic network model and ( iii ) technology adoption network model.

Lewis and Sexton [ 41 ] used the DEA technique in their paper to show the advantage of the network DEA model over the classical DEA technique. They took the Major League Baseball example. Network DEA Model could figure out inefficiencies that the efficient DEA Model displaces. Some examples of the network DEA model are; slack based DEA model [ 42 ], measuring the customer satisfaction and productivity of pharmacies [ 43 ]. The number of studies is increasing on the network DEA; thus, this is the future direction.

3.3.2 Hierarchical DEA Models

Few conditions of multistage efficiency assessment might include hierarchy structure. The concept of the model was established to determine the DMUs that fall naturally into a hierarchy. In this technique, measurement through pairwise comparisons by organizing the homogenous clusters of factors. Determining priority scales depend on the judgment of the experts. One of the applications of the hierarchical model is to find the power plant efficiency with several operating units [ 44 ].

The researchers determined the relative efficiency of each power unit and power plant, and hierarchical structure was observed as a multistage procedure. Green and Cook [ 45 ] modified the model, such that modified hierarchical efficiency assessment could be viewed at all levels concurrently.

3.3.3 Supply Chain DEA Model

One of the great competitive strategies is the supply chain, which modern enterprises can use because this strategy can influence the production of a variety of products at low expenses, high quality, and short lead times. Newly, DEA has been developed to specify the performance of supply chain operations and the recently proposed ‘supply chain model,’ is applied in the multistage DEA model. Optimization criteria in supply chains models have mentioned cost, inventory levels, profit, fill rates, stock out probability, product demand variance and system capacity. Present DEA-based supply chain models describe and calculate the efficiency of the supply chain. Authors showed that the DEA-based supply chain technique measures the efficiency of its member [ 46 ]. Another example is Wong and Wong [ 47 ] who studied efficiency of supply chain with the help of the DEA model.

3.4 Stochastic and Fuzzy DEA Model

One of the weaknesses of traditional DEA models is the fixed nature of input and output variables ignoring the stochastic fluctuations in output-input data, such as data entry and computational mistakes [ 36 ]. There are two DEA models viz. Stochastic DEA models and Fuzzy DEA models that can deal with the uncertainties associated with the data. These models are described below: If the final solutions are not accepted, then it gathers new data and proceeds next iterations of multi-criteria models,. There are two DEA methods, viz. Stochastic DEA approaches and Fuzzy DEA methods that can deal with the uncertainties associated with the data. These models are described below:

3.4.1 Stochastic DEA Model

Stochastic DEA model uses non-parametric convex hull reference techniques depend upon axioms via a statistical infrastructure in basis of axioms from statistics assumption that allow for an estimation reference technology [ 48 ]. Some researchers have included stochastic output and input variables into the DEA methodology.

Stochastic models allow the only inefficiency, but also statistical noise. They identify most quantile rile on assumptions of the composed error terms. These models allow for the probability of two-sided random disturbance, such as determine and specification error in output and input data.

These techniques attain the existence of data error in data and give probabilistic-based outcomes. Some applications are as follows: technical efficiency evaluated through the stochastic DEA, and other is Chance-Constrained Programming (CCP) approach [ 49 ]. Khodabakhshi and Asgharian [ 50 ] used the stochastic DEA model on input relaxation to measures of efficiency. CCP approaches used by Cooper et al. [ 49 ] used stochastic DEA to handle congestion issues.

3.4.2 Fuzzy DEA Models

To deal with the impreciseness of data in real life scenarios, concepts of fuzzy mathematical programming is integrated with DEA to provide a more realistic solution. For example, in [ 51 ] the authors incorporated fuzzy mathematical programming into the DEA model, and showed the performance of the DMU as a fuzzy efficiency.

Actually, DEA efficiency scores vary in (0, 1] and DEA methodologies assess the performance of different DMUs. Qin and Liu [ 52 ] used fuzzy inputs and outputs in the DEA methodology. Azadeh et al. [ 53 ] used integrated approaches like; computer simulation, fuzzy C-means, and fuzzy DEA to optimize operator allocation.

Fuzzy DEA models introduced by Peijun [ 54 ] extended the CCR technique to more general forms where crisp, fuzzy and hybrid data could be applied comfortably. Due to uncertainty existing in human contemplation and judgement, fuzzy DEA techniques could play a significant role in conceptual assessment problems comprehensively existing in the real-life.

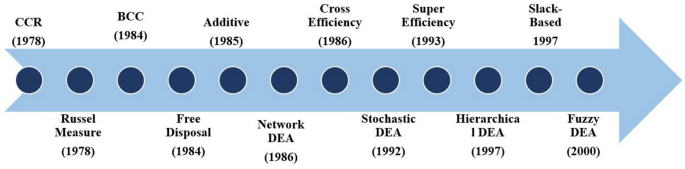
Timeline of DEA Models

3.5 Hybrid DEA Models

In this paper, we are referring to hybrid DEA models as the ones in which DEA is integrated with other techniques like soft-computing, machine learning, dimensionality reduction methods and other MCDM techniques.

3.5.1 DEA + Soft-Computing Techniques

Soft-Computing (SC), a vital area of study in computer science since the early 90s, originally referred to the umbrella term for Fuzzy Logic, Genetic Algorithms and Artificial Neural networks. However, with the passage of time, other nature inspired algorithms like Particle Swarm Optimization (PSO), Differential Evolution (DE) etc. are also considered to be a part of SC methods. For the more details of the SC techniques, the interested readers may refer to [ 55 , 56 , 57 ].

Here we are not discussing fuzzy logic embedded DEA because a portion of it has been discussed in component B of Section 3.4. In this article, the following papers have been reviewed covering the years between 2016 to 2021. Mogha and Yadav [ 58 ] proposed a simple DE (SDE) to solve the DEA-based models. Pelesaraei et al. [ 59 ] hybridized DEA with Multi-objective Genetic Algorithm (MOGA) to approximate the energy efficiency and GHG emissions of wheat production. Misiunas et al. [ 60 ] recommended DEANN, a hybrid of DEA and ANN called DEANN and applied it to predict the functional status of the patients. This technique expressed that DEA will assess efficiencies on an expanded set of DMUs by preparing data for the ANN (training set), a supernumerary ANN interpolated DMU for each of the principal DMU, and It uses it to figure the efficiency frontier by comprising all DMUs.

Jahuar et al. [ 61 ] combined DEA with Differential Evolution (DE) and multi-objective differential evolution (MODE) and showed that the integration enhances the discriminatory powers of DEA.

Pendharkar[ 62 ] introduced a hybrid GA and DEA framework to solve the constant cost allocation (FCA) problem. This framework allowed to compound various FCA sub-objectives for efficient and inefficient DMUs and solved the FCA problem, and the entire entropy of resource designation is maximized for efficient DMUs. Jauhar et al. [ 8 ] applied DE integrated DEA for calculating the performance of a remarkable educational supply chain.

Shabanpour et al. [ 63 ] proposed a hybrid of dynamic DEA and ANN, to forecast the future efficiency of the DMUs. Modhej et al. [ 64 ] integrated inverse DEA with neural network for preserving the relative efficiency value. Vlontzos and Pardalos [ 65 ] consider a combination of DEA with ANN to measure and prognosticate green house gas emissions of EU countries. Mozaffari et al. [ 66 ] presented a hybrid GA and ratio-DEA (R-DEA) technique to determine the efficiency of the sustainable supply chain.

Tsolas et al. [ 67 ] used a two-phase hybrid DEA and ANN technique (DEA-ANN), which is used as a preprocessor, to use the large size branch data of Greek commercial banks. Pendharkar [ 68 ] expressed that an ANN trained by sustainable power on the “efficient” training data subset is powerful than the predictive performance of an ANN trained on the “inefficient” training data subset. Bose et al. [ 69 ] have smoothened the efficiency frontier of DEA via training an artificial neural network from input/output prediction multiple of DMUs. Out of the various soft computing techniques, ANN is the one that is integrated the most with DEA.

3.5.2 DEA + Machine Learning Techniques

Potential of ML techniques have been leveraged by several researchers in diverse areas and the domain of DEA is no exception. In this section, we go through selected papers where the researchers have implemented the concepts of ML to enhance the performance of DEA.

Dariush et al. [ 70 ] proposed a new framework to reduce calculation time of efficiency when the number of DMU’s are more. Zhu et al. [ 71 ] recommended the algorithm to precipitate the computational procedure in the big data environment. The authors proposed DEA as a tool for data-oriented analysis to execute evaluation and benchmark testing. Although the calculation of algorithms has been introduced under the basis of traditional DEA to produce large scale of data (decisions making, units, input, and outputs), the precious knowledge is displayed by the network structure that should be hidden in big data and extracted by DEA [ 71 ]. The selected papers are from the years 2020 and 2021 only. More information of the Machine learning techniques can be found in [ 72 , 73 ].

Tayal et al. [ 74 ] measured the efficiency analysis for the stochastic dynamic facility layout problems by meta-heuristics, DEA, and machine learning techniques.They proposed three-stage techniques, where DEA was amplified with supervised and unsupervised ML technique to obtain the unique ranks and predicting the efficiency values of the layouts. Qu et al. [ 75 ] investigated the redevelopment of the urban centre blocks, and introduced a DEA, deep learning model. They introduced the DEA, and utilized a deep learning model to predict output-oriented indicators of non-intensive blocks.

Mirmozaffari et al. [ 76 ] integrated DEA with clustering algorithms to improve the accurecy of results. Aydin and Yurdakul [ 77 ] analyzed the performance of the 142 countries against the COVID-19 through a new three-staged framework by combining DEA approach with four ML algorithms viz. k-means, hierarchic clustering, decision tree, and random forest algorithms. Rebai et al. [ 78 ] predicted the performance of the secondary schools in Tunisia by the machine learning techniques. They used a two-level analysis part.

In the first stage, the directional distance function (DDF), estimated through the DEA, was used to deal with the desirable outputs while in the second stage, decision tree, and random forest algorithms were used to identify and visualize the variables of high-school performance. Salehi et al. [ 79 ] analyzed and improved the level of adaptive capacity of a the petrochemical plant. They used the DEA method for computing and analyzing the resilience engineering indicators, redundancy, and teamwork. They implemented multilayer perceptron (MLP) to estimate the level of adaptive capacity on the basis of the data.

Nandy and Singh [ 80 ] examined farm efficiency by machine learning and DEA techniques to predict the impact of the environmental factor on the farms’ performance. Jomthanachai et al. [ 81 ] introduced a cross-efficiency DEA model to find a set of risk factors obtained from failure mode and effect analysis (FMEA) and used ML techniques to predict the degree of remaining risk depending on simulated data corresponding to the risk treatment scenario. Thaker et al. [ 82 ] integrated random forest regression with DEA under a two-phase model and measured the corporate governance and bank efficiency.

Zhu et al. [ 83 ] combined the machine learning and DEA technique and used BPNN-DEA, GANN-DEA, ISVM-DEA, SVM-DEA techniques. They measured and predicted the efficiency of manufacturing companies of China. Jomthanachai et al. [ 84 ] used the DEA models with ML techniques to examine risk management. They used cross-efficiency DEA with ANN and predicted the level of risk. Zhong et al. [ 85 ] used an integrated DEA with machine learning technique, Super SBM-DEA-BPNN.

The aim of the authors is to improve the fusion efficiency. Taherinezhad and Alinezhad [ 86 ] used integrating DEAML techniques to predict the efficiency score of nations in the COVID-19 data. They used GANN, BPNN, SVM, and ISVM techniques and predicted the regression target (efficiency values). Nandy and Singh [ 80 ] determined the farm efficiency by the hybrid machine learning and data envelopment analysis. They used a two-stage DEA model with random forest and logistic regression techniques.

3.5.3 DEA + MCDM Techniques

Despite availability of various Multi criteria decision-making techniques[ 87 ], the application of DEA as a discrete alternative MCDM method is also an accepted way to attain reasonable decisions. The foundation of the MCDM techniques was laid in the 1950s and 1960s [ 88 ].

For more brief on MCDM techniques, the interested reader may refer to [ 89 , 90 ]. This section brings forward a succinct review of the recent work on the integration of the DEA with MCDM techniques. The selected papers are taken from the years 2020 and 2021 only.

Kaewfak et al. [ 91 ] fuzzy-AHP (FAHP) and DEA model to identify and measure quantitative risk. Bajec et al. [ 92 ] developed a distance-based AHP-DEA super efficiency technique to attain the demands of premeditated groups by applying the slack variables.

The purpose of the distance-based AHP model was to attain a hierarchy structure and weights for the criteria.

The aim of the DEA approach was the efficiency evaluation of the 21 fictional providers of the electric bike-sharing system. RezaHoseini et al. [ 93 ] used a Z-AHP and Z-DEA, and a Z-AHP-DEA model in their study. The Z-AHP model aimed to identify the conventional sustainability criteria and calculate importance weights. Z- DEA and Z-AHP-DEA models were introduced to measure project efficiency and concluded that Z-AHP-DEA model gave the more effective solution.

Banihashemi and Khalilzadeh [ 94 ] used the network DEA model to choose the best mode to mitigate the environmental impacts. Rank measurement of the different execution modes of each activity waas done through the TOPSIS. Wang et al. [ 95 ] presented a hybrid approach, DEA window analysis, and FTOPSIS and determined the abilities of 42 countries in terms of renewable energy capacity. Karasakal et al. [ 96 ] proposed two novels PROMETHEE based ranking approach to determine the weights and threshold values obtained by the DEA method.

Hoseini et al. [ 97 ] measured the performance of the research and development (R& D) organizations by hybridizing DEA and ANP. Lee et al. [ 98 ] utilized various DEA models and VIKOR to determine the 12 manufacturing industries in Taiwan. They compared different models of the DEA (CCR, super efficiency, cross efficiency, Doyal-Green efficiency) with MCDM approach VIKOR technique. Karami et al. [ 99 ] proposed a three-step integrated procedure, DEA-PCA-VIKOR to evaluate garment industry. PCA reduced the criteria, and the additive DEA model measured the efficiency of the suppliers or efficient suppliers.

Finally, VIKOR was activated to determine the ranking of the efficient suppliers. Mei and Chen [ 100 ] used the rough-fuzzy best-worst method and rough-fuzzy DEA to determine and select sustainable hydrogen production technologies. Here, the rough-fuzzy BWM was procedure is introduced for measuring the relative weights of the sustainability criteria, and rough-fuzzy DEA was introduced to prioritize the alternative HPTs. Tanasulis et al. [ 87 ] introduced a comprehensive technique of higher education teaching evaluation connecting AHP and DEA(fuzzy AHP is included).

AHP permits the regard of the different values of each teaching performance criteria, although DEA can create a comparison to the teaching perceived by the tutor and the student to understand the range of development for each tutor. Lee et al. [ 101 ] developed the integrated two-phase MCDM technique to recognize the relative weights of criteria and examine energy technologies’ relative efficiency against high oil prices. In the first phase, the fuzzy–AHP allocates the relative weights to criteria. In the second phase, the DEA technique determined the relative efficiency of energy technologies versus high oil prices from an economic standpoint.

3.5.4 Miscellaneous

In this section we have incorporated that the techniques that could not fit under the previous sections but play an important role in improving the performances of DEA. Here we have considered only the papers 2018 onwards. Zelenyuk [ 102 ] explored price-based aggregation to solve the large dimension. Lee and Cai [ 103 ] recommended the Least Absolute Shrinkage and Selection Operator (LASSO) variable selection technique, in data science to extract significant factors. They combined the LASSO and sign-constrained convex non-parametric the least squares (SCNLS), which could be represented as DEA estimators.

The proposed LASSO-SCNLS methods and their variants gave beneficial guidelines for DEA with small datasets. Chen et al. [ 104 ] used the latest version of LASSO, known as elastic net (EN), adapted it to DEA, and proposed the EN-DEA and used it for reducing the large dimensions into sparser. Limleamthong and Gosalbez [ 105 ] used the mixed-integer programming (MIP) technique for dimensionality reduction of the input and output variables. Main purpose of the authors has to elevate the prejudiced ability of classical DEA technique. Davoudabadi et al. [ 106 ] and Deng et al. [ 107 ] also used PCA technique to decrease the dimensions of the data.

Smirlis et al. [ 108 ], Azizi [ 109 ] solved the missing value problem in the crisp dataset by an interval DEA approach. Kuosmanen [ 110 ] used an alternative method, constructing the best-practice frontier technique to take missing values. Tao et al. [ 111 ] approach contributes to relaxing convexity assumption on production possibility set (PPS) in benchmarking using DEA and provides a powerful managerial instrument to improve the performance. Ren et al. [ 112 ] used DEA to identify the congestion in projects of universities.

4 Advantages and Disadvantages of the Models

Up till now we have seen that there exists a fair number of DEA models. Each model has advantages as well as disadvantages. These are summarized in Tables  2 and 3 [ 16 , 113 , 114 , 115 , 116 ], so that the user can identify the most appropriate model to be used for a particular problem.

5 Applications of the DEA and Its Variants

This section is segregated into two parts. In the first part we provide the implementation of different DEA models on different application problems, while in the second section we provide an overview of the different real life problems that have been solved through DEA or its variants.

DEA models described above have been implemented for solving a wide range of real life problems described in Tables  4 and Table  5 . While Table  4 lists the application of traditional DEA models, Table  5 provides the application of hybrid DEA models. It was observed that out of the papers reviewed for this study, Hierarchical DEA models and Stochastic DEA models have been used more for real life problem-solving in comparison to other methods. Hybrid DEA models, particularly DEA hybridized with soft-computing methods and DEA hybridized with each-other, appear to be more popular in comparison to the traditional DEA models. These Tables are prepared on the basis of the most cited papers.

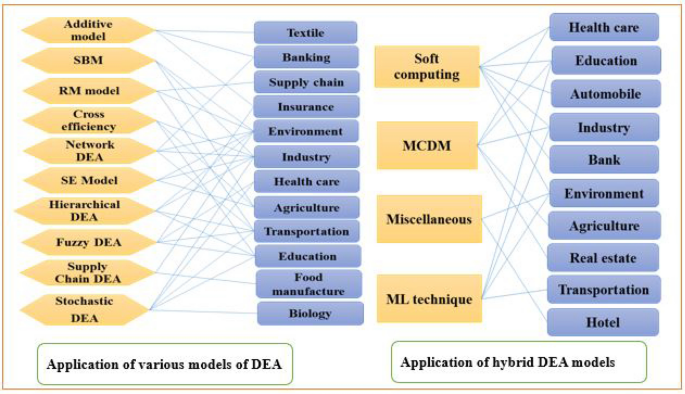
Application of various DEA models

5.1 Applications of DEA

In this subsection, the review has been done from the point of view of the application and which models have been applied for solving the applications.

5.1.1 Banking

One of the earliest applications DEA is found to be in the banking sector in the year 1984. David Sherman and Franklin Gold [ 162 ] determined the efficiency of 14 branch offices of a bank. They used the CCR model and compared operating efficiency between the branches. In 1987, Celik Parken [ 163 ] examined the performance of the thirty-five branches of the Canadian bank and measured the efficiency.

Rangan et al. [ 164 ] recommended the production frontier technique to determine the technical efficiency of the 215 US banks. Pastor et al. [ 165 ] introduced the DEA with Malmquist index techniques to study bank efficiency and productivity growth rate. Thompson et al. [ 166 ] integrated the sense of the confidence region with the DEA model (DEA/AR). They measured the 100 largest banks of the US. Soteriou and Zenios [ 167 ] used benchmarking technique of DEA to approximation the efficiency and credible charge of bank products at the branch level. Dekker and Post [ 168 ] used the Free Disposal Hull (FDH) model to find the efficiency of Dutch banks. Sueyoshi [ 169 ] used an extended DEA model, DEA-Discriminant Analysis (DEA-DA) to evaluate the performance of the Japanese bank.

Chen [ 170 ] examined the technical efficiency of 39 banks of Taiwan. He used chance-constrained data envelopment analysis (CC-DEA) and stochastic frontier analysis (SFA). Emrouznejad and Anouze [ 171 ] calculated the efficiency of the banking branches in the Gulf Cooperation Council countries. They proposed a DEA framework with a classification & regression model. Azad et al. [ 172 ] examined the efficiency of Islamic, the conventional banks in Malaysia. They used the customary efficiency sense, a black box with three-stage NDEA model. Thaker et al. [ 82 ] investigated the efficiency of Indian banks. They used a machine learning technique and random forest regression with DEA under a two-phase model and measured the efficiency of Indian bank.

5.1.2 Sports

Sueyoshi et al. [ 173 ] examined the efficiency of baseball players.They used a slack-adjusted (SA-DEA) model to determine their ranking scores. Lozano et al. [ 174 ] determined the efficiency of the nations at the recent five summers Olympic Games. Garcia-Sanchez [ 175 ] applied a three-phase DEA technique to specify the efficiency of the Spanish football teams. Gutierrez and Ruiz [ 176 ] introduced the DEA and cross-efficiency appraisement to measure the individual game performance of Spanish Premier League handball players. Dhordjevic et al. [ 177 ] evaluated the technical efficiency of the national football team for the 2010 FIFA World Cup.

They used the multi-stage DEA model. Villa and Lozano [ 178 ] determined the efficiency of the basketball performance on the basis of assessment of the players and the performance of the teams. The authors used the dynamic network DEA model. Adhikari et al. [ 179 ] used a modified DEA technique, namely supper efficiency DEA, to select the cricket players.

5.1.3 Agriculture & Farm

The first paper observed to be in the field of agriculture is by Fare et al. [ 180 ]. Who determined the technical efficiency (TE) of agriculture in Philippine. Cloutier and Rowley [ 181 ] measured the productive efficiency of the Quebec dairy farms at Quebec. Zaibet and P.S. Dharmapala used stochastic production frontier (SPF) and DEA methods to determine the percentage of the farmers. Majiwa et al. [ 182 ] have explained the network DEA technique to determine the PH efficiency of milling using the data of the rice procuring industry. Stefanos et al. [ 183 ] applied fuzzy DEA technique in the agriculture sector to determine the efficiency of the organic farms. Sefeedpari et al. [ 184 ] examined the efficiency assessment of dairy farming in Iran by implementing window data envelopment analysis (W-DEA) model with energy use as inputs and milk production as output for 25 provinces in Iran. Candemir [ 185 ] determined the efficiency of the cotton enterprises Kahramanmaras in Turkey. He obtained technical efficiency, pure technical efficiency (TE), scale efficiency (SE), allocative efficiency (AE), and economic efficiency (EE). Cecchini et al. [ 186 ] used the two-stage DEA model to measure the efficiency and super efficiency of the 76 meat-producing sheep farms. Their second objective was to examine the effect of animal welfare and management indicators on TE values.

5.1.4 Transportation

Michael Schefczyk [ 187 ] introduced the DEA methodology to examine the efficiency of 15 airlines. Their study analyzed the factor of the high profitability and performance of the airline. Oum and Yu [ 188 ] used a two-step procedure in their study. First, they examined the gross efficiency index from the panel data of 19 railways through DEA, and then they implied Tobit regression to identify the public subsidies. Cowie and Riddington [ 189 ] measured the efficiency of European railways. Nicole AdlerBoaz Golany [ 190 ] determined the deregulated railway networks used by combining DEA and principal component analysis (PCA). They studied the West European air transportation industry. Laya Olfat and Mahsa Pishdar [ 191 ] proposed fuzzy dynamic NDEA model based on the double production frontier for evaluating the sustainability of the Iranian airports. Sarmento et al. [ 192 ] in their paper measured the efficiency of the seven highway projects in Portugal by exploiting DEA and the Malmquist index techniques. Song et al. [ 193 ] introduced a three-stage DEA technique and measured the operational efficiency of the air transport industry in China. Chen et al. [ 194 ] utilized inverse DEA technique for analyzing the road safety issues in China.

5.1.5 Education

Charnes et al. [ 195 ] used the DEA model for measuring the efficiency of public schools’ education. One of the other studies in the school areas was Bessent and Bessent [ 196 ]. Sarrico and Dyson [ 197 ] introduced the DEA model to evaluate the performance of UK universities.Casu and Thanassoulis [ 198 ] measured the cost-efficiency in central administrative services in UK Universities. Kongar et al. [ 199 ] used a two-step DEA approach to determine the relative efficiency of the applicants to for graduate programs in engineering. Miranda et al. [ 200 ] introduced DEA and stochastic frontier analysis (SFA) models to examine the technical performance of the higher education institutions in the field of business administration courses. Thanassoulis et al. [ 87 ] evaluated higher education in Greece. They combined analytic hierarchy process along with DEA. Si and Qiao [ 201 ] determined the performance of the financial expenditure in science and maths education in China. Iulian [ 202 ] used the CRS DEA and Malmquist indicators models and measured the performance of the Romanian higher public education institutions. Foladi et al. [ 203 ] introduced the inverse dynamic DEA (IDDEA) approach for evaluating the faculties of the different departments of Urmia University. Chen and Chang [ 204 ] measured the efficiency of the National Chung Cheng University departments in Taiwan.

5.1.6 Communication

The DEA utilization, in communication, has attained great attention in the current years. The studies are mostly in the areas of computer network, telecom industry, Information and communication technology (ICT) etc.

Giokas and Pentzaropoulos [ 205 ] evaluated the operational efficiency of large-scale computer networks. Uri [ 206 ] calculated the technical and allocative efficiency of the local substitution carriers. Fernandez-Menendez et al. [ 207 ] showed in their paper the level of information and communication technology (ICT) within the organization. They measured the technical efficiency of the Spanish firms through the DEA. Goto [ 208 ] studied the fiscal effort of the world telecommunications industry via DEA–Discriminant Analysis (DEA-DA). Liao and Lien [ 209 ] measured the technology gaps related to the efficiency of Asia Pacific Economic Cooperation (APEC) integrated telecommunications operators using the DEA meta frontier technique. Lu et al. [ 210 ] investigated the influence of the information and communication technology (ICT) progress on construction labour productivity (CLP).

5.1.7 Fishery

Vestergaard et al. [ 211 ] measured the capacity and capacity utilization (CU) in the fishery through the DEA. Maravelias and Tsitsika [ 212 ] applied a simple DEA technique and found Mediterranean fisheries’ fleet capacity and economic efficiency. Rowe et al. [ 213 ] recommended a combination of life cycle assessment (LCA) and DEA technique life cycle assessment (LCA) and DEA to link socioeconomic and environmental evaluations of fisheries. Kim et al. [ 214 ] measured the productive efficiency of the sandfish coastal gillnet fishery through the stochastic frontier analysis (SFA). Espino et al. [ 215 ] examined the fishing valence and structure excess of fishing valence over the endurable level of the fleet. Wang et al. [ 216 ] evaluated the performance of fisheries enterprises using the Malmquist model.

5.1.8 Tourism

Onut and Soner [ 217 ] evaluated the energy efficiency of 32 five-star hotels in the Antalya regions. Sun and Lu [ 218 ] evaluated the Taiwan hotel industry by the weight slack–based technique. Chou et al. [ 219 ] measured human resource management in the tourism industry or agency through the Malmquist productivity index analysis technique. Taheri and Ansari et al. [ 220 ] determined the technical performance of the cultural-historical museums in Tehran, through DEA. Chiu and Wu [ 221 ] analyzed the efficiency of 49 international tourist hotels (ITHs). Shieh [ 222 ] investigated the connection between the green and cost efficiency in the international tourist hotels in Taiwan. Huang et al. [ 223 ] improved the two-stage DEA model and to investigate the effect on the productive efficiency, occupancy, and catering service of Taiwan’s hotels. Cuccia et al. [ 224 ] explored the influences of cultural heritage in fostering tourism through their paper. Their study checked the influences of UNESCO world heritage list inscription on tourism destination efficiency in Italy. In their empirical study, Yang et al. [ 225 ] took eight ethnic regions of China and evaluated the tourism investment and poverty alleviation.

5.1.9 Health care

The first paper in the area of healthcare was observed to be of Nunamaker [ 226 ], where the author provided an application of DEA to calculate the efficiency of the routine nursing service at the Wisconsin hospital. Jimtnez and Smith [ 227 ] judged the performance of primary health care through DEA. Johnston and Gerard [ 228 ] measured the relative efficiency of the breast screening units of UK. Kontodimopoulos and Niakas [ 229 ] measured the efficiency of the hemodialysis units in Greece. Rouse and Swales [ 230 ] identified the efficient expenditure level of public health care service through DEA. Ballestero and Maldonado [ 231 ] employed DEA to measure the rank of the hospital activities. Nayar and Ozcan [ 232 ] determined the technical efficiency of the hospital and measured the quality performance. Jat and Sebastian [ 233 ] determined the technical efficiency of the district hospitals in Madhya Pradesh, India. Arteaga et al. [ 234 ] evaluated the efficiency of kidney transplantation using DEA. Cinaroglu [ 235 ] examined the effect of hospital size on converts in the efficiencies of public hospitals.More recently, Hamzah [ 236 ] measured the efficiency of the healthcare system for COVID-19 restraint through the network DEA model.

5.1.10 Automobile

Brey et al. [ 237 ] applied a non-parametric technique to conduct the development of technologies in the automobile sector. Parameshwaran et al. [ 238 ] measured the performance of the automobile repair shops through integrating fuzzy AHP and DEA techniques. Hwang et al. [ 239 ] investigated the communication between the dynamic of price discounts at the dealership level and production efficiency in the auto market in Spanish. Wang et al. [ 240 ] analysed the performance of the world’s top 20 automakers by Malmquist productivity index [MPI], a DEA model. In the automobile area, the reviewed papers show that the CCR model, integrating fuzzy AHP and DEA, Malmquist productivity index [MPI], VRS multiplier DEA, techniques used.

5.1.11 Forestry

Vitala and Hanninen [ 241 ] measured the efficiency of the regional Forestry organization through the DEA. Bogetoft et al. [ 242 ] evaluated the different offices of the Danish Forestry extension service and Safak et al. [ 243 ] specified the efficiency of the forest sub-district in the Denizli Forestry Regional Directorate by fuzzy-DEA model. Limaei [ 244 ] examined the efficiency of the Iranian forest industry. Li et al. [ 245 ] determined performance of the China’s forestry resources and sustainable development of forestry. Lu et al. [ 246 ]studied the non-dynamic Slack-based DEA model and evaluated the energy efficiency of forestry areas.

5.1.12 Water

Lambert et al. [ 247 ] investigate the relative efficiencies of the publicly and privately owned water utilities. Thanassoulis [ 248 ] estimated the cost-saving for water companies in England. Daz et al. [ 249 ] studied of the irrigation districts in Andalusia, Southern Spain. Lilienfeld and Asmild [ 250 ] examined the influence of irrigation system type. Alsharif et al. [ 251 ] determined the efficiency of the water supply system for West Bank and Gaza. Frija et al. [ 252 ] investigate the technical efficiency of unheated greenhouse farms and measured the water efficiency used for irrigation. Rosas et al. [ 253 ] estimated the operational productivity of the Mexican water utilities and identified the context variables that influence their efficiency. Soltani et al. [ 254 ] developed a new water quality index (WQI) of the 47 Algerian dams.

5.1.13 Real estate

Lins et al. [ 255 ] measured the value range for real estate units. Wang examined the performance of the government real estate investment. Xue et al. [ 256 ] applied DEA base MPI technique to assess the performance of the construction industry in China. Chancellor and Lu [ 257 ] analyzed the regional productivity of Chinese construction industry. Li et al. [ 258 ] determined the performance of the contractors in China and Hong-Kong. Li et al. [ 259 ] studied the real estate market of China and determined the supply side efficiency of 29 provinces. Liu et al. [ 260 ] utilized the two-stage MPI in their paper and calculated the productivity efficiency of the real estate industry in China. Liu et al. [ 261 ] studied the same problem, but they used the meta-frontier SBM technique. Malmquist productivity index (MPI), Slack-based DEA, double perspective-DEA (DP-DEA), Färe-Primont DEA, techniques were used in the real estate application.

5.1.14 E-business

Cinca et al. [ 262 ] determined the efficiency in dot com firms. The objective of the firms is to obtain revenues from their activities and make an impact on the internet. Menendez et al. [ 207 ] examined the technical efficiency of Spanish firms by the information and communication technology (ICT). An et al. [ 263 ] measured the performance of the Chinese high-tech industries through the dynamic network DEA technique. Table 6 shows the various models used in the different application area (Table 6 ).

We were able to identify 18 software that can be utilized for application of DEA. Description of the software is provided in Table 7 [ 264 , 265 ].

7 Bibliometric Analysis

Bibliometric analysis is an excellent way of identifying the trends in a research area. Therefore, the remaining sections of this article are devoted to it. The bibliometric analysis is based on the database” web of science” for the years 1981 through 2021. The statistics is based on: year of publications, application area, journal quartile and its publication, area of research, and country-wise distribution and researcher statistics (Figs. 6 , 7 , 8 , 9 ).

7.1 Year-Wise Statistics

Since 1981 to 2021, the total number of papers listed in web of science database is 10,691. The first paper, published in 1981 [178], has more than 733 citations. In 1984 two papers were published on the basic concept of the efficiency measurement of the DMUs. 1994 onward, the number of papers on DEA started increasing. This trend is shown in Table  8 and a pictorial representation is given in Fig. 9  (Table 8 ). Table 9 shows the published number of articles in the year 1981 to 2021 and graphically representation shows in the Fig. 10 .

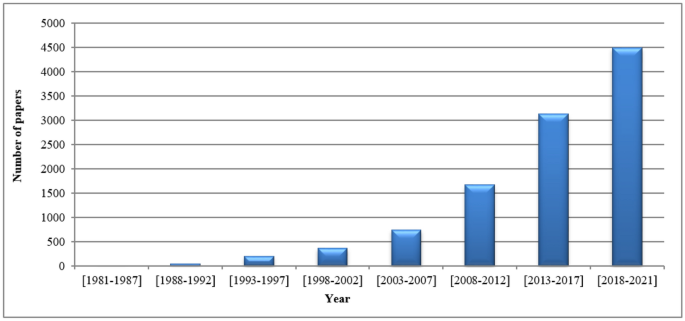
Year-wise publication of DEA papers

Quantitative analysis of the articles on the basis of article type

7.2 Statistical Analysis Based on the Quartile

Tables  10 , and 11 show the list of journals, along with their quartile, where DEA articles have been published (Fig. 10 ). A graphical representation of the impact factor of different journals is shown in Fig. 11 .

IF of different journals based on quartiles

7.3 Researchers Statistics

In this section, information about the most cited authors is listed in Table  12 . We have listed only the papers for which the citation is above ten thousand.

7.4 Recent Trends

In this section, we review the current trends of research in DEA, which includes articles from the years 2020 and 2021. The search results are taken from the WoS database (Table 13 ).

Number of publications of area of research

8 Conclusion

The main objective of this paper is to revel the 40 years of existence of DEA and to generate an interest among the new researchers towards DEA by bringing forward its variants, its applications and above all its potential. This article presents an overview of DEA (1981–2021). From the collected data and statistical analysis, the following conclusions may be drawn:

Since 1981, the graph of DEA is constantly rising with number of papers being more than 4000 between the period 2018 – 2021 in comparison to only 9 publications during the period 1981–1987. W.W. Cooper is to be the most cited author with around 40000 (forty thousand) citations till date.

Due to the applicability of DEA to diverse domains, one can find articles related to DEA in several journals. It was observed that there are around 169 journals that have published papers related to DEA, out of which 81 belongs to the first quartile or are Q1 journals, at the time of writing this report.

DEA has been hybridized with other methods so as to improve its efficiency and to increase its discriminatory power, a major shortcoming of DEA. Mostly DEA is used in conjugation with other MCDM method like AHP, TOPSIS etc. but it has also been combined with ANN.

From the application point of view, the two areas where DEA has been applied most frequently are education and banking. One of the reasons for this could be the availability of data that may be shared. In the last two years, business economics and operations research and some new emerging areas where DEA is being applied are remote sensing and polymer science.

In the last two years, the highest number of publications in the area of business economics (388), operational research (279), engineering (266), and science technology (229). These areas have seen the application of DEA earlier as well but it was interesting to see newer areas like geology, chemistry, physics, polymer science and remote sensing where application of DEA has started.

Out of the various DEA models proposed so far, Network DEA, hierarchical DEA, and stochastic DEA models are apparently, the most frequently used models in different application areas. All these models are the extension of classical DEA models. However, DEA has also been hybridized with other decision making techniques like AHP, TOPSIS etc.

Integration of DEA with Machine Learning models is one of the emerging areas of DEA which may have a lot of potential in the coming years due to the increase in volume of data, availability of good computing facilities and increase in the complexities of real world problems.

9 Future Directions

DEA is a versatile technique having immense scope from the development as well as from the application point of view. In the present review article, we saw areas like polymer science and remote sensing where DEA is applied likewise there can be new avenues where potential of DEA can be explored.

Integration of DEA with ML algorithms is another interesting area which seems to have a lot of potential. Both are decision making techniques but are conceptually different. DEA is mainly employed for determining the efficiency of the DMUs but after integrating it with ML techniques, one can also forecast the future efficiency of DMUs. Also for handling big data, ML and DEA can be combined for more efficient decision making.

Fuzzy DEA is an important concept which tries to incorporate the uncertainties of the real world scenarios. In this article we have devoted a small section to Fuzzy DEA, which probably is not justified considering the significance of the method. A separate detailed study can be prepared for Fuzzy DEA in the form of a review article.

Some of the important areas not included in this study are ranking methods and time series methods of DEA. A detailed analysis of these techniques will form an interesting piece of article. Further, a study on identifying and handling of undesirable input and output variables will also provide useful information to the researchers working in this area.

Kao C (2014) Network data envelopment analysis: a review. Eur J Oper Res 239(1):1–16

Article   MathSciNet   MATH   Google Scholar  

Farrell M (1957) The measurement of productive efficiency. J Royal Statist Soc 120(3):253–290

Article   Google Scholar  

Charnes A, Cooper WW, Rhodes E (1978) Measuring the efficiency of decision making units. Eur J Oper Res 2(6):429–444

Xie HSCQ, Zhu Y, Li Y (2021) Variations on the theme of slacks-based measure of efficiency: convex hull-based algorithms. Comput Ind Eng 159:8–14

Goyal RSJ, Singh M, Aggarwal A (2019) Efficiency and technology gaps in Indian banking sector: application of meta-frontier directional distance function dea approach, The Journal of Finance and Data. Science 5:156–172

Google Scholar  

Mahmoudi R, Emrouznejad A, Shetab-Boushehri S-N, Hejazi SR (2020) The origins, development and future directions of data envelopment analysis approach in transportation systems. Socioecon Plann Sci 69:100672

Yeşilyurt ME, Şahin E, Elbi MD, Kızılkaya A, Koyuncuoğlu MU, Akbaş-Yeşilyurt F (2021) A novel method for computing single output for dea with application in hospital efficiency. Socioecon Plann Sci 76:100995

Jauhar SK, Pant M, Nagar AK (2017) Sustainable educational supply chain performance measurement through dea and differential evolution: a case on indian hei. J Computat Sci 19:138–152

Paço CL, Pérez JMC The use of dea (data envelopment analysis) methodology to evaluate the impact of ict on productivity in the hotel sector, International Interdisciplinary Review of Tourism

Moon H, Min D (2020) A dea approach for evaluating the relationship between energy efficiency and financial performance for energy-intensive firms in korea. J Clean Prod 255:120283

Cooper WW, Ruiz JL, Sirvent I (2009) Selecting non-zero weights to evaluate effectiveness of basketball players with dea. Eur J Oper Res 195(2):563–574

Article   MATH   Google Scholar  

Panwar A, Tin M, Pant M (2021) Assessment of the basic education system of myanmar through the data envelopment analysis, In: Proceedings of International Conference on Scientific and Natural Computing, Springer, pp 221–232

Cook WD, Seiford LM (2009) Data envelopment analysis (dea)-thirty years on. Eur J Oper Res 192(1):1–17

Cooper W, Seiford L, Tone K, Zhu J (2007) Some models and measures for evaluating performances with dea: past accomplishments and future prospects. J Prod Anal 28(3):151–163

Adler LFN, Sinuany-Stern Z (2002) Review of ranking methods in the data envelopment analysis context. Eur J Oper Res 140(2):249–265

Kuah CT, Wong KY, Behrouzi F (2010) A review on data envelopment analysis (dea). In: 2010 fourth Asia international conference on mathematical/analytical modelling and computer simulation, IEEE, pp 168–173

Liu JS, Lu LY, Lu W-M, Lin BJ (2013) Data envelopment analysis 1978–2010: a citation-based literature survey. Omega 41(1):3–15

Seiford LM (1997) A bibliography for data envelopment analysis (1978–1996). Ann Oper Res 73:393–438

Emrouznejad A, Parker BR, Tavares G (2008) Evaluation of research in efficiency and productivity: a survey and analysis of the first 30 years of scholarly literature in dea. Socioecon Plann Sci 42(3):151–157

Mardani A, Zavadskas EK, Streimikiene D, Jusoh A, Khoshnoudi M (2017) A comprehensive review of data envelopment analysis (dea) approach in energy efficiency. Renew Sustain Energy Rev 70:1298–1322

Xu T, You J, Li H, Shao L (2020) Energy efficiency evaluation based on data envelopment analysis: a literature review. Energies 13(14):3548

Shahwan TM, Hassan YM. Efficiency analysis of uae banks using data envelopment analysis. J Econom Adm Sci

Charnes A, Cooper WW, Golany B, Seiford L, Stutz J (1985) Foundations of data envelopment analysis for pareto-koopmans efficient empirical production functions. J Econometr 30(1–2):91–107

Tone K (2011) Slacks-based measure of efficiency. In: Handbook on data envelopment analysis. Springer, pp 195–209

Färe R, Lovell CK (1978) Measuring the technical efficiency of production. J Econom Theory 19(1):150–162

Sirvent PJRJ (1999) I an enhanced dea russell graph efficiency measure. Eur J Opl Res 115:596–607

Zhu J (2006) Measuring labor efficiency in post offices (2006)

Thrall RM (1999) What is the economic meaning of fdh? J Prod Anal 11(3):243–250

Cherchye L, Kuosmanen T, Post T (2000) What is the economic meaning of fdh? a reply to thrall, J Product Analy 263–267

Sexton TR, Silkman RH, Hogan AJ (1986) Data envelopment analysis: critique and extensions. New Direct Program Evaluat 1986(32):73–105

Doyle J, Green R (1994) Efficiency and cross-efficiency in dea: derivations, meanings and uses. J Operat Res Soc 45(5):567–578

Green RH, Doyle JR, Cook WD (1996) Preference voting and project ranking using dea and cross-evaluation. Eur J Oper Res 90(3):461–472

Anderson TR (2002) A cross-evaluation model 249–255

Per Andersen NCP (1993) A procedure for ranking efficient units in data envelopment analysis. Manage Sci 39(10):1261–1264

Wilson PW (1993) Deterministic with nonparametric outputs multiple. J Bus Econ Stat 11(3):319–323

Thrall RM (1996) Duality, classification and slacks in dea. Ann Oper Res 66(2):109–138

Lee H-S, Chu C-W, Zhu J (2011) Super-efficiency dea in the presence of infeasibility. Eur J Oper Res 212(1):141–147

Liu W-B, Wongcha A, Peng K-C (2012) Adopting super-efficiency and tobit model on analyzing the efficiency of teacher’s colleges in thailand. Int J New Trends Educ Implicat 3(3):176–188

Färe R, Grosskopf S (1997) Intertemporal production frontiers: with dynamic dea. J Operat Res Soc 48(6):656–656

Färe R, Whittaker G (1995) An intermediate input model of dairy production using complex survey data. J Agric Econ 46(2):201–213

Lewis HF, Sexton TR (2004) Network dea: efficiency analysis of organizations with complex internal structure. Comput Operat Res 31(9):1365–1410

Tone K, Tsutsui M (2009) Network dea: a slacks-based measure approach. Eur J Oper Res 197(1):243–252

Löthgren M, Tambour M (1999) Productivity and customer satisfaction in swedish pharmacies: a dea network model. Eur J Oper Res 115(3):449–458

Cook WD, Chai D, Doyle J, Green R (1998) Hierarchies and groups in dea. J Prod Anal 10(2):177–198

Cook WD, Green RH (2005) Evaluating power plant efficiency: a hierarchical model. Comput Operat Res 32(4):813–823

Zhu J (2014) Quantitative models for performance evaluation and benchmarking: data envelopment analysis with spreadsheets, Vol. 213, Springer

Wong WP, Wong KY. Supply chain performance measurement system using dea modeling. Indus Manag Data Syst

Olesen OB, Petersen NC (2016) Stochastic data envelopment analysis-a review. Eur J Oper Res 251(1):2–21

Cooper WW, Deng H, Huang Z, Li SX (2004) Chance constrained programming approaches to congestion in stochastic data envelopment analysis. Eur J Oper Res 155(2):487–501

Khodabakhshi M, Asgharian M (2009) An input relaxation measure of efficiency in stochastic data envelopment analysis. Appl Math Model 33(4):2010–2023

León T, Liern V, Ruiz J, Sirvent I (2003) A fuzzy mathematical programming approach to the assessment of efficiency with dea models. Fuzzy Sets Syst 139(2):407–419

Qin R, Liu Y-K (2010) A new data envelopment analysis model with fuzzy random inputs and outputs. J Appl Math Comput 33(1):327–356

Azadeh A, Anvari M, Ziaei B, Sadeghi K (2010) An integrated fuzzy dea-fuzzy c-means-simulation for optimization of operator allocation in cellular manufacturing systems. Int J Adv Manuf Technol 46(1–4):361–375

Peijun G, Hideo T (2001) Fuzzy dea: a perceptual evaluation method. Fuzzy Sets Syst 119(1):149–160

Article   MathSciNet   Google Scholar  

Yan Y, Wang L, Wang T, Wang X, Hu Y, Duan Q (2018) Application of soft computing techniques to multiphase flow measurement: a review. Flow Meas Instrum 60:30–43

Chandrasekaran M, Muralidhar M, Krishna CM, Dixit U (2010) Application of soft computing techniques in machining performance prediction and optimization: a literature review. Int J Adv Manuf Technol 46(5):445–464

Saridakis KM, Dentsoras AJ (2008) Soft computing in engineering design-a review. Adv Eng Inform 22(2):202–221

Mogha SK, Yadav SP et al (2016) Application of differential evolution for data envelopment analysis. Int J Data Sci 1(3):247–258

Nabavi-Pelesaraei A, Hosseinzadeh-Bandbafha H, Qasemi-Kordkheili P, Kouchaki-Penchah H, Riahi-Dorcheh F (2016) Applying optimization techniques to improve of energy efficiency and ghg (greenhouse gas) emissions of wheat production. Energy 103:672–678

Misiunas N, Oztekin A, Chen Y, Chandra K (2016) Deann: A healthcare analytic methodology of data envelopment analysis and artificial neural networks for the prediction of organ recipient functional status. Omega 58:46–54

Jauhar SK, Pant M (2017) Integrating dea with de and mode for sustainable supplier selection. J Comput Sci 21:299–306

Pendharkar PC (2018) A hybrid genetic algorithm and dea approach for multi-criteria fixed cost allocation. Soft Comput 22(22):7315–7324

Shabanpour H, Yousefi S, Farzipoor Saen R (2017) forecasting efficiency of green suppliers by dynamic data envelopment analysis and artificial neural networks. J Clean Product 142

Modhej SMSNHFD (2017) Integrating inverse data envelopment analysis and neural network to preserve relative efficiency values. J Intell Fuzzy Syst 32(6):4047–4058

Vlontzos G, Pardalos P (2017) Assess and prognosticate green house gas emissions from agricultural production of eu countries, by implementing, dea window analysis and artificial neural networks. Renew Sustain Energy Rev 76:155–162

Mozaffari MR, Ostovan S, Fernandes Wanke P (2020) A hybrid genetic algorithm-ratio dea approach for assessing sustainable efficiency in two-echelon supply chains. Sustainability 12(19):8075

Tsolas IE, Charles V, Gherman T (2020) Supporting better practice benchmarking: a dea-ann approach to bank branch performance assessment. Expert Syst Appl 160:113599

Pendharkar RJAPC (2003) Technical efficiency-based selection of learning cases to improve forecasting accuracy of neural networks under monotonicity assumption. Decis Support Syst 117–136 (2003)

Bose A, Patel G (2015) “neuraldea”-a framework using neural network to re-evaluate dea benchmarks. OPSearch 52(1):18–41

Khezrimotlagh D, Zhu J, Cook WD, Toloo M (2019) Data envelopment analysis and big data. Eur J Oper Res 274(3):1047–1054

Zhu J (2020) Dea under big data: Data enabled analytics and network data envelopment analysis. Ann Operat Res 1–23 (2020)

Mishra S, Mishra D, Santra GH (2016) Applications of machine learning techniques in agricultural crop production: a review paper. Indian J Sci Technol 9(38):1–14

Tsai C.-F., Hsu Y.-F., Lin C.-Y., Lin W.-Y (2009) Intrusion detection by machine learning: a review. Exp Syst Appl 36(10):11994–12000

Tayal A, Kose U, Solanki A, Nayyar A, Saucedo JAM (2020) Efficiency analysis for stochastic dynamic facility layout problem using meta-heuristic, data envelopment analysis and machine learning. Comput Intell 36(1):172–202

Qu JLB, Ma J. Investigating the intensive redevelopment of urban central blocks using data envelopment analysis and deep learning: a case study of Nanjing, China. IEEE Access

Mirmozaffari M, Yazdani M, Boskabadi A, Ahady Dolatsara H, Kabirifar K, Amiri Golilarz N (2020) A novel machine learning approach combined with optimization models for eco-efficiency evaluation. Appl Sci 10(15):5210

Aydin N, Yurdakul G (2020) Assessing countries’ performances against covid-19 via wsidea and machine learning algorithms. Appl Soft Comput 97:106792

Rebai FBYS, Essid H graphically based machine learning approach to predict secondary schools performance in Tunisia. Socioecon Plann Sci 70

Salehi V, Veitch B, Musharraf M (2020) Measuring and improving adaptive capacity in resilient systems by means of an integrated dea-machine learning approach. Appl Ergon 82:102975

Nandy A, Singh PK (2020) Farm efficiency estimation using a hybrid approach of machine-learning and data envelopment analysis: evidence from rural eastern india. J Clean Prod 267:122106

Jomthanachai S, Wong W-P, Lim C-P An application of data envelopment analysis and machine learning approach to risk management. IEEE Access

Thaker K, Charles V, Pant A, Gherman T (2021) A dea and random forest regression approach to studying bank efficiency and corporate governance. J Operat Res Soc 1–28

Nan Zhu A. E, Zhu Chuanjin (2021) The dimensionality of counterproductivity: are all counterproductive behaviors created equal? J Manag Sci Eng 6(4):435–448

Jomthanachai S, Wong W-P, Lim C-P (2021) An application of data envelopment analysis and machine learning approach to risk management. IEEE Access 9:85978–85994

Zhong K, Wang Y, Pei J, Tang S, Han Z (2021) Super efficiency sbm-dea and neural network for performance evaluation. Inform Process Manag 58(6):102728

Taherinezhad A, Alinezhad A (2022) Nations performance evaluation during sars-cov-2 outbreak handling via data envelopment analysis and machine learning methods. Int J Syst Sci 1–18

Thanassoulis E, Dey PK, Petridis K, Goniadis I, Georgiou AC (2017) Evaluating higher education teaching performance using combined analytic hierarchy process and data envelopment analysis. J Operat Res Soc 68(4):431–445

Mardani A, Jusoh A, Nor K, Khalifah Z, Zakwan N, Valipour A (2015) Multiple criteria decision-making techniques and their applications-a review of the literature from 2000 to 2014. Econ Res-Ekonomska istraživanja 28(1):516–571

Stojčić M, Zavadskas EK, Pamučar D, Stević Ž, Mardani A (2019) Application of mcdm methods in sustainability engineering: a literature review 2008–2018. Symmetry 11(3):350

Kaya İ, Çolak M, Terzi F (2018) Use of mcdm techniques for energy policy and decision-making problems: a review. Int J Energy Res 42(7):2344–2372

Kaewfak K, Huynh V-N, Ammarapala V, Ratisoontorn N (2020) A risk analysis based on a two-stage model of fuzzy ahp-dea for multimodal freight transportation systems. IEEE Access 8:153756–153773

Bajec P, Tuljak-Suban D, Zalokar E (2021) A distance-based ahp-dea super-efficiency approach for selecting an electric bike sharing system provider: one step closer to sustainability and a win-win effect for all target groups. Sustainability 13(2):549

RezaHoseini A, Rahmani Z, BagherPour M (2021) Performance evaluation of sustainable projects: a possibilistic integrated novel analytic hierarchy process-data envelopment analysis approach using z-number information. Environ Devel Sustain 1–60 (2021)

Banihashemi SA, Khalilzadeh M (2021) Evaluating efficiency in construction projects with the topsis model and ndea method considering environmental effects and undesirable data, Iran. J Sci Technol - Trans Civ Eng

Wang C-N, Dang T-T, Tibo H, Duong D-H (2021) Assessing renewable energy production capabilities using dea window and fuzzy topsis model. Symmetry 13(2):334

Karasakal E, Eryılmaz U, Karasakal O (2021) Ranking using promethee when weights and thresholds are imprecise: a data envelopment analysis approach. J Operat Res Soc 1–18

Hoseini SA, Fallahpour A, Wong KY, Antuchevičienė J (2021) Developing an integrated model for evaluating r &d organizations’ performance: combination of dea-anp. Technol Econ Dev Econ 27(4):970–991

Lee Z-Y, Chu M-T, Wang Y-T, Chen K-J (2020) Industry performance appraisal using improved mcdm for next generation of Taiwan. Sustainability 12(13):5290

Karami S, Ghasemy Yaghin R, Mousazadegan F (2021) Supplier selection and evaluation in the garment supply chain: an integrated dea-pca-vikor approach. J Textile Instit 112(4):578–595

Mei M, Chen Z (2021) Evaluation and selection of sustainable hydrogen production technology with hybrid uncertain sustainability indicators based on rough-fuzzy bwm-dea. Renew Energy 165:716–730

Lee SK, Mogi G, Hui K (2013) A fuzzy analytic hierarchy process (ahp)/data envelopment analysis (dea) hybrid model for efficiently allocating energy r &d resources: In the case of energy technologies against high oil prices. Renew Sustain Energy Rev 21:347–355

Zelenyuk V (2020) Aggregation of inputs and outputs prior to data envelopment analysis under big data. Eur J Oper Res 282(1):172–187

Lee C-Y, Cai J-Y (2020) Lasso variable selection in data envelopment analysis with small datasets. Omega 91:102019

Chen Y, Tsionas MG, Zelenyuk V (2021) Lasso plus dea for small and big wide data. Omega-Int J Manag Sci 102

Limleamthong P, Guillen-Gosalbez G (2018) Mixed-integer programming approach for dimensionality reduction in data envelopment analysis: application to the sustainability assessment of technologies and solvents. Indus Eng Chem Res 57(30):9866–9878

Davoudabadi R, Mousavi SM, Sharifi E (2020) An integrated weighting and ranking model based on entropy, dea and pca considering two aggregation approaches for resilient supplier selection problem. J Comput Sci 40:101074

Deng F, Xu L, Fang Y, Gong Q, Li Z (2020) Pca-dea-tobit regression assessment with carbon emission constraints of china’s logistics industry. J Clean Prod 271:122548

Smirlis YG, Maragos EK, Despotis DK (2006) Data envelopment analysis with missing values: an interval dea approach. Appl Math Comput 177(1):1–10

MathSciNet   MATH   Google Scholar  

Azizi H (2013) A note on data envelopment analysis with missing values: an interval dea approach. Int J Adv Manuf Technol 66(9):1817–1823

Kuosmanen T (2009) Data envelopment analysis with missing data. J Operat Res Soc 60(12):1767–1774

Tao X, An Q, Xiong B, Chen Y, Goh M (2022) Benchmarking with nonconvex production possibility set through data envelopment analysis: an application to china’s transportation system. Expert Syst Appl 198:116872

Ren X-T, Fukuyama H, Yang G-L (2022) Eliminating congestion by increasing inputs in r &d activities of Chinese universities. Omega 110:102618

Shen W, Yang G, Zhou Z, Liu W (2019) Dea models with russell measures. Ann Oper Res 278(1):337–359

Aldamak A, Zolfaghari S (2017) Review of efficiency ranking methods in data envelopment analysis. Measurement 106:161–172

Wanke P, Barros CP, Emrouznejad A (2018) A comparison between stochastic dea and fuzzy dea approaches: revisiting efficiency in angolan banks. RAIRO-Operat Res 52(1):285–303

Ahmed NNSAM, Talib MA, Jani R (2022) A fuzzy data envelopment analysis model for measuring efficiency of malaysian public research universities, Palestine. J Mathem 11:109–124

Chen Y, Cook WD, Li N, Zhu J (2009) Additive efficiency decomposition in two-stage dea. Eur J Oper Res 196(3):1170–1176

Cook WD, Hababou M (2001) Sales performance measurement in bank branches. Omega 29(4):299–307

Wang K, Huang W, Wu J, Liu Y-N (2014) Efficiency measures of the chinese commercial banking system using an additive two-stage dea. Omega 44:5–20

Seiford LM, Zhu J (1998) Sensitivity analysis of dea models for simultaneous changes in all the data. J Operat Res Soc 49(10):1060–1071

Zhou P, Ang B, Poh K (2006) Slacks-based efficiency measures for modeling environmental performance. Ecol Econ 60(1):111–118

Choi Y, Zhang N, Zhou P (2012) Efficiency and abatement costs of energy-related co2 emissions in china: a slacks-based efficiency measure. Appl Energy 98:198–208

Tone K, Tsutsui M (2014) Dynamic dea with network structure: a slacks-based measure approach. Omega 42

Azadi M, Jafarian M, Saen RF, Mirhedayatian SM (2015) A new fuzzy dea model for evaluation of efficiency and effectiveness of suppliers in sustainable supply chain management context. Comput Operat Res 54:274–285

Lozano S, Gutiérrez E (2011) Efficiency analysis and target setting of spanish airports. Netw Spat Econ 11(1):139–157

Souto JE, Rodriguez A (2015) The problems of environmentally involved firms: innovation obstacles and essential issues in the achievement of environmental innovation. J Clean Prod 101:49–58

Lee K-H, Saen RF (2012) Measuring corporate sustainability management: a data envelopment analysis approach. Int J Prod Econ 140(1):219–226

Liang L, Wu J, Cook WD, Zhu J (2008) The dea game cross-efficiency model and its nash equilibrium. Oper Res 56(5):1278–1288

Chauhan NS, Mohapatra PK, Pandey KP (2006) Improving energy productivity in paddy production through benchmarking-an application of data envelopment analysis. Energy Convers Manage 47(9–10):1063–1085

Wang Y-M, Chin K-S (2010) A neutral dea model for cross-efficiency evaluation and its extension. Expert Syst Appl 37(5):3666–3675

Falagario M, Sciancalepore F, Costantino N, Pietroforte R (2012) Using a dea-cross efficiency approach in public procurement tenders. Eur J Oper Res 218(2):523–529

Vázquez-Rowe I, Villanueva-Rey P, Iribarren D, Moreira MT, Feijoo G (2012) Joint life cycle assessment and data envelopment analysis of grape production for vinification in the rías baixas appellation (nw spain). J Clean Prod 27:92–102

Li H, Shi J-F (2014) Energy efficiency analysis on chinese industrial sectors: an improved super-sbm model with undesirable outputs. J Clean Prod 65:97–107

Yang L, Ouyang H, Fang K, Ye L, Zhang J (2015) Evaluation of regional environmental efficiencies in china based on super-efficiency-dea. Ecol Ind 51:13–19

Mirhedayatian SM, Azadi M, Saen RF (2014) A novel network data envelopment analysis model for evaluating green supply chain management. Int J Prod Econ 147:544–554

Lozano S, Gutiérrez E, Moreno P (2013) Network dea approach to airports performance assessment considering undesirable outputs. Appl Math Model 37(4):1665–1676

Dotoli M, Falagario M (2012) A hierarchical model for optimal supplier selection in multiple sourcing contexts. Int J Prod Res 50(11):2953–2967

Eilat H, Golany B, Shtub A (2008) R &d project evaluation: An integrated dea and balanced scorecard approach. Omega 36(5):895–912

Liu W, Meng W, Zhang D (2008) Two-level dea approaches in research institute evaluation. Omega 36(6):950–957

Azadeh A, Ghaderi S, Maghsoudi A (2008) Location optimization of solar plants by an integrated hierarchical dea pca approach. Energy Policy 36(10):3993–4004

Azadeh A, Ghaderi S, Nasrollahi M (2011) Location optimization of wind plants in iran by an integrated hierarchical data envelopment analysis. Renew Energy 36(5):1621–1631

Azadeh A, Rahimi-Golkhandan A, Moghaddam M (2014) Location optimization of wind power generation-transmission systems under uncertainty using hierarchical fuzzy dea: A case study. Renew Sustain Energy Rev 30:877–885

Shen Y, Hermans E, Ruan D, Wets G, Brijs T, Vanhoof K (2011) A generalized multiple layer data envelopment analysis model for hierarchical structure assessment: a case study in road safety performance evaluation. Expert Syst Appl 38(12):15262–15272

Kumar A, Jain V, Kumar S (2014) A comprehensive environment friendly approach for supplier selection. Omega 42(1):109–123

Kuo RJ, Wang YC, Tien FC (2010) Integration of artificial neural network and mada methods for green supplier selection. J Clean Prod 18(12):1161–1170

Egilmez G, Kucukvar M, Tatari O, Bhutta MKS (2014) Supply chain sustainability assessment of the us food manufacturing sectors: a life cycle-based frontier approach. Resour Conserv Recycl 82:8–20

Pels E, Nijkamp P, Rietveld P (2003) Inefficiencies and scale economies of european airport operations. Transp Res Part E: Logist Transp Rev 39(5):341–361

Cullinane DWSK, Wang TF, Ji P (2006) The technical efficiency of container ports: comparing data envelopment analysis and stochastic frontier analysis. Transp. Res. Part A Policy Pract 40(4):354–374

Li M-J, Tao W-Q (2017) Review of methodologies and polices for evaluation of energy efficiency in high energy-consuming industry. Appl Energy 187:203–215

Sadjadi SJ, Omrani H (2008) Data envelopment analysis with uncertain data: an application for iranian electricity distribution companies. Energy Policy 36(11):4247–4254

De Witte K, López-Torres L (2017) Efficiency in education: a review of literature and a way forward. J Operat Res Soc 68(4):339–363

Linna M (1998) Measuring hospital cost efficiency with panel data models. Health Econ 7(5):415–427

Han Y, Geng Z, Zhu Q, Qu Y (2015) Energy efficiency analysis method based on fuzzy dea cross-model for ethylene production systems in chemical industry. Energy 83:685–695

Liu S-T (2014) Restricting weight flexibility in fuzzy two-stage dea. Comput Indus Eng 74:149–160

Gomez-Gallego JC, Gomez-Gallego M, Garcia-Garcia JF, Faura-Martinez U (2021) Evaluation of the efficiency of european health systems using fuzzy data envelopment analysis. In: Healthcare, Vol. 9, Multidisciplinary Digital Publishing Institute, p 1270

Jahani Sayyad Noveiri M, Kordrostami S (2021) Sustainability assessment using a fuzzy dea aggregation approach: a healthcare application. Soft Comput 25(16):10829–10849

Izadikhah M, Azadi M, Toloo M, Hussain FK (2021) Sustainably resilient supply chains evaluation in public transport: a fuzzy chance-constrained two-stage dea approach. Appl Soft Comput 113:107879

Pendharkar RJAPC (2003) Technical efficiency-based selection of learning cases to improve forecasting accuracy of neural networks under monotonicity assumption, Decision. Support Syst 36:117–136

Eftekhari SRN, Yazdani A, Shamohammadi A (2020) Data envelopment analysis based procedure for selection and ranking of ground motion prediction equations. Soil Dynam Earthquake Eng 137(4)

Bae J, Chung Y, Ko H (2021) Analysis of efficiency in public research activities in terms of knowledge spillover: focusing on earthquake r &d accomplishments. Nat Hazards 1–16

Zhang C (2021) Factors influencing the allocation of regional sci-tech financial resources based on the multiple regression model. Mathem Probl Eng

Sherman G, Gold FF (1985) Bank branch operating efficiency: evaluation with data envelopment analysis. J Bank Finance 9(2):297–315

Parkan C (1987) Measuring the efficiency of service operations: an application to bank branches. Eng Costs Product Econ 12(1–4):237–242

Rangan N, Grabowski R, Aly HY, Pasurka C (1988) The technical efficiency of us banks. Econ Lett 28(2):169–175

Pastor J, Perez F, Quesada J (1997) Efficiency analysis in banking firms: an international comparison. Eur J Oper Res 98(2):395–407

Thompson RG, Brinkmann EJ, Dharmapala P, Gonzalez-Lima M, Thrall RM (1997) Dea/ar profit ratios and sensitivity of 100 large us banks. Eur J Oper Res 98(2):213–229

Soteriou AC, Zenios SA (1999) Using data envelopment analysis for costing bank products. Eur J Oper Res 114(2):234–248

Dekker D, Post T (2001) A quasi-concave dea model with an application for bank branch performance evaluation. Eur J Oper Res 132(2):296–311

Sueyoshi T (2001) Extended dea-discriminant analysis. Eur J Oper Res 131(2):324–351

Chen T-Y (2002) A comparison of chance-constrained dea and stochastic frontier analysis: bank efficiency in taiwan. J Operat Res Soc 53(5):492–500

Emrouznejad A, Anouze AL (2010) Data envelopment analysis with classification and regression tree-a case of banking efficiency. Expert Syst 27(4):231–246

Azad AK, Kian-Teng K, Talib MA (2017) Unveiling black-box of bank efficiency: An adaptive network data envelopment analysis approach. Int J Islamic Middle Eastern Finance Manag

Sueyoshi T, Ohnishi K, Kinase Y (1999) A benchmark approach for baseball evaluation. Eur J Oper Res 115(3):429–448

Lozano S, Villa G, Guerrero F, Cortés P (2002) Measuring the performance of nations at the summer olympics using data envelopment analysis. J Operat Res Soc 53(5):501–511

García-Sánchez IM (2007) Efficiency and effectiveness of spanish football teams: a three-stage-dea approach. CEJOR 15(1):21–45

Gutiérrez Ruiz JL (2013) Data envelopment analysis and cross-efficiency evaluation in the management of sports teams: the assessment of game performance of players in the spanish handball league. J Sport Manag 27(3):217–229

Dijana Petrović Djordjević MM, Vujošević M (2015) Measuring efficiency of football teams by multi-stage dea model. https://doi.org/10.17559/TV-20140306134047

Villa G, Lozano S (2018) Dynamic network dea approach to basketball games efficiency. J Operat Res Soc 69(11):1738–1750

Adhikari A, Majumdar A, Gupta G, Bisi A (2020) An innovative super-efficiency data envelopment analysis, semi-variance, and shannon-entropy-based methodology for player selection: evidence from cricket. Ann Oper Res 284(1):1–32

Fare RGR, Grosskopf S (1985) Technical efficiency of philippine agriculture. Appl Econ 17(2):205–214

Cloutier LM, Rowley R (1993) Relative technical efficiency: data envelopment analysis and quebec’s dairy farms. Can J Agric Economics/Revue canadienne d’agroeconomie 41(2):169–176

Majiwa CWHFE, Lee BL, Managi S (2018) A network data envelopment analysis (ndea) model of post-harvest handling: the case of kenya’s rice processing industry. Food Sec 10(3):631–648

Nastis SA, Bournaris T, Karpouzos D (2019) Fuzzy data envelopment analysis of organic farms. Oper Res Int J 19(2):571–584

Sefeedpari P, Shokoohi Z, Pishgar-Komleh SH (2020) Dynamic energy efficiency assessment of dairy farming system in iran: application of window data envelopment analysis. J Clean Prod 275:124178

Candemir S (2021) Efficiency and functional analysis of cotton production in turkey: case of kahramanmaraş province. Custos e Agronegocio Line 17(2):100–122

Cecchini L, Vieceli L, D’Urso A, Magistrali CF, Forte C, Mignacca SA, Trabalza-Marinucci M, Chiorri M (2021) Farm efficiency related to animal welfare performance and management of sheep farms in marginal areas of central italy: a two-stage dea model. Ital J Anim Sci 20(1):955–969

Schefczyk M (1993) Operational performance of airlines: an extension of traditional measurement paradigms. Strateg Manag J 14(4):301–317

Oum TH, Yu C (1994) Economic efficiency of railways and implications for public policy: a comparative study of the oecd countries’ railways. J Trans Econ Policy 121–138

Cowie J, Riddington G (1996) Measuring the efficiency of european railways. Appl Econ 28(8):1027–1035

Adler N, Golany B (2001) Evaluation of deregulated airline networks using data envelopment analysis combined with principal component analysis with an application to western europe. Eur J Oper Res 132(2):260–273

Olfat L, Pishdar M (2017) Interval type-2 fuzzy dynamic network data envelopment analysis with undesirable outputs considering double frontiers: an application to iran airports’sustainability evaluation, Int J Indus Eng 24(6)

Sarmento J, Renneboog L, Matos PV (2017) Measuring highway efficiency by a dea approach and the malmquist index. Eur J Transp Infrastruct Res 17(4)

Song M, Jia G, Zhang P (2020) An evaluation of air transport sector operational efficiency in china based on a three-stage dea analysis. Sustainability 12(10):4220

Chen L, Gao Y, Li M-J, Wang Y-M, Liao L-H (2021) A new inverse data envelopment analysis approach to achieve china’s road transportation safety objectives. Saf Sci 142:105362

Charnes A (1979) Measuring efficiency of decision making units. Eur J Oper Res 3:339

Bessent AM, Bessent EW (1980) Determining the comparative efficiency of schools through data envelopment analysis. Educ Adm Q 16(2):57–75

Sarrico CS, Dyson RG (2000) Using dea for planning in uk universities-an institutional perspective. J Operat Res Soc 51(7):789–800

MATH   Google Scholar  

Casu B, Thanassoulis E (2006) Evaluating cost efficiency in central administrative services in uk universities. Omega 34(5):417–426

Kongar E, Sobh TM, Baral M (2009) Two-step data envelopment analysis approach for efficient engineering enrollment management. Int J Eng Educ 25(2):391

Miranda R, Gramani MC, Andrade E (2012) Technical efficiency of business administration courses: a simultaneous analysis using dea and sfa. Int Trans Oper Res 19(6):847–862

Si L-B, Qiao H-Y (2017) Performance of financial expenditure in china’s basic science and math education: panel data analysis based on ccr model and bbc model. EURASIA J Mathem Sci Technol Educ 13(8):5217–5224

Lita I (2018) Data envelopment analysis techniques-dea and malmquist indicators, in crs mode, for measuring the efficiency of romanian public higher education institutions. Econ Comput Econ Cybernet Stud Res 52(3)

Foladi S, Solimanpur M, Rezaee MJ (2020) Inverse dynamic data envelopment analysis for evaluating faculties of university with quasi-fixed inputs. Soc Indic Res 148(1):323–347

Chen S-P, Chang C-W (2021) Measuring the efficiency of university departments: an empirical study using data envelopment analysis and cluster analysis. Scientometrics 126(6):5263–5284

Giokas DI, Pentzaropoulos GC (2000) Evaluating productive efficiency in telecommunications: evidence from greece. Telecommun Policy 24(8–9):781–794

Uri ND (2001) Changing productive efficiency in telecommunications in the United States. Int J Prod Econ 72(2):121–137

Fernández-Menéndez AR-DJ, López-Sánchez JI, Sandulli FD (2009) Technical efficiency and use of information and communication technology in spanish firms. Telecomm. Policy 33(7):348–359

Goto M (2010) Financial performance analysis of us and world telecommunications companies: importance of information technology in the telecommunications industry after the at &t breakup and the ntt divestiture. Decis Support Syst 48(3):447–456

Liao C-H, Lien C-Y (2012) Measuring the technology gap of apec integrated telecommunications operators. Telecommun Policy 36(10–11):989–996

Lu H, Zhang Q, Cui Q, Luo Y, Pishdad-Bozorgi P, Hu X (2021) How can information technology use improve construction labor productivity? an empirical analysis from china. Sustainability 13(10):5401

Vestergaard N, Squires D, Kirkley J (2003) Measuring capacity and capacity utilization in fisheries: the case of the danish gill-net fleet. Fish Res 60(2–3):357–368

Maravelias CD, Tsitsika EV (2008) Economic efficiency analysis and fleet capacity assessment in mediterranean fisheries. Fish Res 93(1–2):85–91

Vázquez-Rowe MTMI, Iribarren D, Feijoo G (2010) Combined application of life cycle assessment and data envelopment analysis as a methodological approach for the assessment of fisheries. Int J Life Cycle Assess 15(3):272–283

Kim D-H, Lee K-H, Bae B-S, Park S-W (2011) Productive efficiency of the sandfish arctoscopus japonicus coastal gillnet fishery using stochastic frontier analysis. Fish Sci 77(1):35–40

Castilla-Espino D, García-del Hoyo J, Metreveli M, Bilashvili K (2014) Fishing capacity of the southeastern black sea anchovy fishery. J Marine Syst 135:160–169

Wang C-N, Nguyen T-L, Dang T-T, Bui T-H (2021) Performance evaluation of fishery enterprises using data envelopment analysis-a malmquist model. Mathematics 9(5):469

Önüt vnpypS, Soner S Energy and Buildings, Energy efficiency assessment for the antalya region hotels in Turkey

Sun S, Lu W-M (2005) Evaluating the performance of the taiwanese hotel industry using a weight slacks-based measure. Asia-Pacific J Oper Res 22(04):487–512

Chou J-R, Shieh C-J, Huang K-P (2012) A study of the performance on human resource management strategy in tourism industry with data envelopment analysis. Pak J Statist 28(5):735–741

Taheri H, Ansari S (2013) Measuring the relative efficiency of cultural-historical museums in tehran: Dea approach. J Cult Herit 14(5):431–438

Chiu Y-h, Wu M-F (2010) Performance evaluation of international tourism hotels in Taiwan-application of context-dependent dea. INFOR Inform Syst Operat Res 48(3):155–170

Shieh H-S (2012) The greener, the more cost efficient? an empirical study of international tourist hotels in Taiwan. Int J Sustain Dev World Ecol 19(6):536–545

Huang C-W, Ho FN, Chiu Y-H (2014) Measurement of tourist hotels productive efficiency, occupancy, and catering service effectiveness using a modified two-stage dea model in taiwan. Omega 48:49–59

Cuccia T, Guccio C, Rizzo I (2016) The effects of unesco world heritage list inscription on tourism destinations performance in Italian regions. Econ Model 53:494–508

Yang J, Wu Y, Wang J, Wan C, Wu Q (2021) A study on the efficiency of tourism poverty alleviation in ethnic regions based on the staged dea model. Front Psychol 12:970

Nunamaker TR (1983) Measuring routine nursing service efficiency: a comparison of cost per patient day and data envelopment analysis models. Health Serv Res 18(2 pt 1):183

Salinas-Jiménez J, Smith P (1996) Data envelopment analysis applied to quality in primary health care. Ann Oper Res 67(1):141–161

Johnston K, Gerard K (2001) Assessing efficiency in the uk breast screening programme: does size of screening unit make a difference? Health Policy 56(1):21–32

Kontodimopoulos N, Niakas D (2005) Efficiency measurement of hemodialysis units in greece with data envelopment analysis. Health Policy 71(2):195–204

Rouse P, Swales R (2006) Pricing public health care services using dea: methodology versus politics. Ann Oper Res 145(1):265–280

Ballestero E, Maldonado JA (2004) Objective measurement of efficiency: applying single price model to rank hospital activities. Comput Operat Res 31(4):515–532

Nayar P, Ozcan YA (2008) Data envelopment analysis comparison of hospital efficiency and quality. J Med Syst 32(3):193–199

Ram Jat T, San Sebastian M (2013) Technical efficiency of public district hospitals in madhya pradesh, India: a data envelopment analysis. Glob Health Action 6(1):21742

Arteaga FJS, Di Caprio D, Cucchiari D, Campistol JM, Oppenheimer F, Diekmann F, Revuelta I (2021) Modeling patients as decision making units: evaluating the efficiency of kidney transplantation through data envelopment analysis. Health Care Manag Sci 24(1):55–71

Cinaroglu S (2021) Changes in hospital efficiency and size: an integrated propensity score matching with data envelopment analysis. Socioecon Plann Sci 76:100960

Hamzah NM, Yu M-M, See KF (2021) Assessing the efficiency of malaysia health system in covid-19 prevention and treatment response. Health Care Manag Sci 1–13

Brey J, Contreras I, Carazo A, Brey R, Hernández-Díaz A, Castro A (2007) Evaluation of automobiles with alternative fuels utilizing multicriteria techniques. J Power Sour 169(1):213–219

Parameshwaran R, Srinivasan P, Punniyamoorthy M, Charunyanath S, Ashwin C (2009) Integrating fuzzy analytical hierarchy process and data envelopment analysis for performance management in automobile repair shops. Eur J Indus Eng 3(4):450–467

Hwang S-N, Chen C, Chen Y, Lee H-S, Shen P-D (2013) Sustainable design performance evaluation with applications in the automobile industry: focusing on inefficiency by undesirable factors. Omega 41(3):553–558

Wang C-N, Tibo H, Nguyen HA (2020) Malmquist productivity analysis of top global automobile manufacturers. Mathematics 8(4):580

Viitala E-J, Hänninen H (1998) Measuring the efficiency of public forestry organizations. For Sci 44(2):298–307

Bogetoft P, Thorsen BJ, Strange N (2003) Efficiency and merger gains in the danish forestry extension service. For Sci 49(4):585–595

Şafak MEAMGMKI, Gül AU, Portakal S (2014) Efficiency determination of the forest sub-districts by using fuzzy data envelopment analysis (case study: Denizli forest regional directorate). Int J Fuzzy Syst 16(3)

Limaei SM (2013) Efficiency of iranian forest industry based on dea models. J For Res 24(4):759–765

Li L, Hao T, Chi T (2017) Evaluation on china’s forestry resources efficiency based on big data. J Clean Prod 142:513–523

Lu C-C, Lin I-F, Wu D, Zhang X (2021) The effect of forestry on energy efficiency in eu countries: a non-oriented dynamic slack-based data envelopment analysis. Energy Sci Eng

Lambert DK, Dichev D, Raffiee K (1993) Ownership and sources of inefficiency in the provision of water services. Water Resour Res 29(6):1573–1578

Thanassoulis E (2000) Dea and its use in the regulation of water companies. Eur J Oper Res 127(1):1–13

Rodrguez-Daz EC-PJA, López-Luque R (2004) Application of data envelopment analysis to studies of irrigation efficiency in Andalusia. J Irrig Drain Eng 130(3):175–183

Lilienfeld A, Asmild M (2007) Estimation of excess water use in irrigated agriculture: a data envelopment analysis approach. Agric Water Manag 94(1–3):73–82

Alsharif K, Feroz EH, Klemer A, Raab R (2008) Governance of water supply systems in the palestinian territories: a data envelopment analysis approach to the management of water resources. J Environ Manage 87(1):80–94

Frija A, Chebil A, Speelman S, Buysse J, Van Huylenbroeck G (2009) Water use and technical efficiencies in horticultural greenhouses in Tunisia. Agric Water Manag 96(11):1509–1516

Ablanedo-Rosas EO-BJYS-GJH, Campanur AG, Nuñez-Ríos JE (2020) Operational efficiency of mexican water utilities: results of a double-bootstrap data envelopment analysis. Water 12(2):553

Soltani HBABAA, Oukil A, Boulassel MR, Soltani Aa, Oukil A, Boutaghane H, Bermad A, Boulassel MR (2021) A new methodology for assessing water quality, based on data envelopment analysis: application to algerian dams. Ecol Indic 121

Lins M. P. E., de Lyra Novaes L. F., Legey L. F. L. (2005) Real estate appraisal: a double perspective data envelopment analysis approach. Ann Oper Res 138(1):79–96

Xue X, Shen Q, Wang Y, Lu J (2008) Measuring the productivity of the construction industry in China by using dea-based malmquist productivity indices. J Constr Eng Manag 134(1):64–71

Chancellor W, Lu W (2016) A regional and provincial productivity analysis of the chinese construction industry: 1995 to 2012. J Constr Eng Manag 142(11):05016013

Li J, Chiang YH, Choi TN, Man KF (2013) Determinants of efficiency of contractors in Hong Kong and China: Panel data model analysis. J Constr Eng Manag 139(9):1211–1223

Li K, Ma Z, Zhang G (2019) Evaluation of the supply-side efficiency of china’s real estate market: a data envelopment analysis. Sustainability 11(1):288

Liu X-X, Liu H-H, Yang G-L, Pan J-F (2021) Productivity assessment of the real estate industry in China: a two-stage malmquist productivity index. Int J Strateg Prop Manag 25(2):146–168

Liu X-X, Song Y-Y, Liu H-H, Yang G-L (2021) Regional efficiency of the real estate industry in 35 large and medium-sized cities in china a meta-frontier sbm approach. Post-Communist Econo 1–33

Serrano-Cinca YF-CC, Mar-Molinero C (2005) Measuring DEA efficiency in Internet companies, vol 38. Elsevier

An Q, Meng F, Xiong B, Wang Z, Chen X (2020) Assessing the relative efficiency of Chinese high-tech industries: a dynamic network data envelopment analysis approach. Ann Oper Res 290(1):707–729

Zhu J, Paradi JC (2018) List of dea software about the authors

Barr RS (2004) Dea software tools and technology. In: Handbook on data envelopment analysis, Springer, pp 539–566

“Data Envelopment Analysis: Ali Emrouznejad’s DEA Homepage, The Most Comprehensive Source of Data Envelopment Analysis!!” Data Envelopment Analysis: Ali Emrouznejad’s DEA Homepage, The Most Comprehensive Source of Data Envelopment Analysis!!, https://www.deazone.com/ . Accessed 2 June 2022.

Download references

Acknowledgements

This work was supported by the Metaheuristics framework for combinatorial optimization problems (META-MO-COPS) under Grant DST/INT/Czech/P-12/2019.

Author information

Authors and affiliations.

Department of Applied Mathematics and Scientific Computing, Indian Institute of Technology Roorkee, Roorkee, Uttarakhand, India

Ankita Panwar & Millie Pant

Electrical Engineering and Computer Science, Department of Computer Science, Technical University of Ostrava, Ostrava, Czech Republic

Maryam Olfati & Vaclav Snasel

Mehta Family School for Data Science and Artificial Intelligence, Indian Institute of Technology Roorkee, Roorkee, Uttarakhand, India

Millie Pant

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Millie Pant .

Ethics declarations

Conflict of interest.

On behalf of all authors, the corresponding authors states that there is no conflict of interest.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix A: Important definitions in terms of DEA [ 266 ]:

Decision-making unit (DMU): A DMU is an entity useful to transport input variables into output variables. For instance: educational institutions, hospitals, banks, and any other decision-making firms.

Efficiency: A calculated of a unit’s maintaining to make outputs from its set of inputs. Since obtained efficiency is relative due to the efficiency of DMU is determined to all other DMUs.

Inefficiency: When the entity lies below and above its frontier line or production.

Reference set/peer group: A set of efficient units from which the inefficiency of an inefficient unit is determined.

Reference unit/peer unit: Any unit part of the peer group.

Technical efficiency (TE): When the efficiency is determined from the CCR/CRS model, is defined TE.

Pure technical efficiency (PTE): The efficiency examined from the BCC/VRS technique is defined as PTE.

Scale efficiency (SE): SE model depends on the TE and PTE score and is calculated by the ratio of the TE to PTE.

Appendix B: List of acronyms

Rights and permissions.

Reprints and permissions

About this article

Panwar, A., Olfati, M., Pant, M. et al. A Review on the 40 Years of Existence of Data Envelopment Analysis Models: Historic Development and Current Trends. Arch Computat Methods Eng 29 , 5397–5426 (2022). https://doi.org/10.1007/s11831-022-09770-3

Download citation

Received : 25 January 2022

Accepted : 10 May 2022

Published : 10 June 2022

Issue Date : November 2022

DOI : https://doi.org/10.1007/s11831-022-09770-3

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Find a journal
• Publish with us
• Track your research