homework section 3.2 statistics answers

Section 3.2: Measures of Dispersion

• 3.1 Measures of Central Tendency
• 3.2 Measures of Dispersion
• 3.3 Measures of Central Tendency and Dispersion from Grouped Data
• 3.4 Measures of Position and Outliers
• 3.5 The Five-Number Summary and Boxplots

By the end of this lesson, you will be able to...

• compute the range of a variable from raw data
• compute the variance of a variable from raw data
• compute the standard deviation of a variable from raw data
• use the empirical Rule to describe data that are bell-shaped

For a quick overview of this section, watch this short video summary:

Consider the following two sets of exam scores:

Often, we want to compare two data sets and look for differences. In this case, however, the sample mean for the first set is 78.3, with a median of 78, while the second set has a sample mean of 78.7, also with a median of 78.

We can see that the measures of center are not enough to distinguish between the two sets, so we'll need to somehow compare their "dispersion", or spread. The first statistic we'll learn about to help do that is called the range .

The range , R , of a variable is the difference between the largest and smallest data values.

Looking at our data from above, we see that the range for the first set of exam scores is 99-48 = 51, while the range for the second set is 91-58 = 33. As we can see from the histograms, the second set of exam scores has less dispersion .

Unfortunately, the range isn't always enough to distinguish between two sets of data, which we'll see on the next page.

Let's look at another two sets of exam scores.

In this case, we can see that the range is R = 95-48 = 47 for both sets, but they clearly don't have the same dispersion. The second set is much more condensed, with the bulk of the scores in the C range - 70-79.

To describe the dispersion in cases like these, we'll need to somehow describe how far a "typical" observation is from the mean, rather than looking at the extreme values.

An obvious choice would be to just look at the average distance from the mean. The figure below shows the heights of the 2008 US Men's Olympic Basketball team and each player's corresponding difference from the mean. (Source: USA Basketball )

If we try to take the average difference from the mean, we have a problem - we get 0!

Why is this? Well, it's because the mean acts as a balancing point, as we talked about earlier . In fact, this will always happen - the average difference from the mean will equal zero.

So what do we do? The obvious choice would be to take the average distance from the mean. That is, take the absolute value of each of the differences. It's a good thought, but anyone who's taken calculus will tell you that absolute values can be pretty difficult to work with, so instead, we square them.

This creates a new measure of dispersion, called the variance .

The population variance , σ 2 , of a variable is the sum of the squared deviations about the population mean divided by N.

This is pretty complex, but we'll have technology to do most of the work for us.

Like the mean, we also have a sample version of this calculation, but unlike the mean, it's actually different.

The sample variance , s 2 , is computed by determining the sum of the squared deviations about the sample mean and dividing the result by n-1.

The first thing most students ask when they see this (I did, too) is "Why n-1 instead of just n?" It's a good question, and a difficult to answer in plain English. The key is to look at the purpose of using the sample variance (or any sample statistics, for that matter). That purpose is to get an estimate for the true population variance.

Unless we have data for the entire population, our estimate will likely be incorrect. If we look at the average of all possible sample variances, though, that average should be the same as the population variance we're trying to estimate. In other words, we'll be wrong most of the time, but the average of all of our attempts will be correct.

The thing is, if we divide by N in the sample variance formula above, our estimate will, on average, be too low. (We can actually prove this mathematically, but it's pretty heady stuff. It's usually not covered until a graduate course in probability and statistics.) We call an estimate like this biased , since it consistently under-estimates the parameter it's trying to predict.

Interestingly enough, dividing by n-1 makes the estimate unbiased . (This can also be proven mathematically.) So it may seem like an odd thing to do, but there's very solid mathematical reasoning behind it.

Let's refer back to the heights of the players on the US Men's Olympic basketball team, and let's treat this as a sample of all the basketball players in the US.

So the sample variance is then:

You may notice that I rounded the variance to the tenths place.

Typically, we round the variance to one more digit than the data

When necessary, round the variance to one more digit than the original data . i.e. If the data are whole numbers, you should round the variance to the tenths place (as in the previous example). If the data are already to the tenths place, you should round to the hundredths place.

Here's a quick overview of the formulas for finding variance in StatCrunch.

One major problem with the variance is that the units don't really make sense. Take the previous example about the heights of the players on the 2008 US Men's Olympic Basketball team. If we look at the units for that variance, it's 10.64 inches squared . What does that have to do with the dispersion of the data? The data are in inches, not inches squared!

Standard Deviation

To remedy that, we need another measure of dispersion, called the standard deviation .

The population standard deviation , σ , is obtained by taking the square root of the population variance.

The sample standard deviation , s , is obtained by taking the square root of the sample variance.

Now that makes more sense!

When necessary, round the standard deviation to one more digit than the original data . i.e. If the data are whole numbers, you should round the standard deviation to the tenths place (as in the previous example). If the data are already to the tenths place, you should round to the hundredths place. You might also consider watching this video regarding rounding (in Quicktime or iPod format).

What Does It Mean?

So what can we tell from the standard deviation? Let's go back to those two sets of exam scores. Which one do you think has a higher standard deviation?

[ reveal answer ]

The first data set has a higher standard deviation.

It has a higher standard deviation because it is more spread out. That's the key:

The larger the standard deviation, the more dispersion the distribution has.

Here's a quick overview of the formulas for finding standard deviation in StatCrunch.

One nice benefit of understanding the relationship between the standard deviation and the shape of the distribution is it helps us get a sense of how much of the data should be within a certain number of standard deviations.

In particular, if the distribution is bell-shaped, we can be fairly precise about what percentage of the data should lie within 1, 2, or 3 standard deviations.

The Empirical Rule

If a distribution is roughly bell-shaped, then

• Approximately 68% of the data will lie within 1 standard deviation of the mean.
• Approximately 95% of the data will lie within 2 standard deviations of the mean.
• Approximately 99.7% of the data will lie within 3 standard deviations of the mean.

How do we know these percentages so accurately? Well, unfortunately we can't explain it until we get to Chapter 7 , but because it fits so well in here with standard deviations, you'll just have to accept it on faith at this point!

It does give us interesting information, though. Let's look at an example to illustrate.

IQ tests are generally designed to have a mean of 100 and a standard deviation of 15. It's also known that the distribution of EQ scores tends to follow a bell-curve.

With that in mind, approximately what percentage of individuals have IQs between 85 and 115?

About 68%. The mean is 100 and the standard deviation is 15, so 85 is one standard deviation below the mean (100-15=85) and 115 is one standard deviation above the mean (100+15=115).

It's difficult to characterize a "genius" explicitly, but some put it at an IQ of about 145+. About what percent of the population are "geniuses" by this criteria?

145 is 3 standard deviations above the mean. We also know that about 99.7% of all individuals have IQ scores within 3 standard deviations. That leaves 0.3% further than 3 standard deviations, so about half of that, or 0.15%, have IQs higher than 145.

<< previous section | next section >>

Chapter 2: Descriptive Statistics

Chapter 2 Homework

Homework from 2.1.

Student grades on a chemistry exam were: 77, 78, 76, 81, 86, 51, 79, 82, 84, 99

• Construct a stem-and-leaf plot of the data.
• Are there any potential outliers? If so, which scores are they? Why do you consider them outliers?

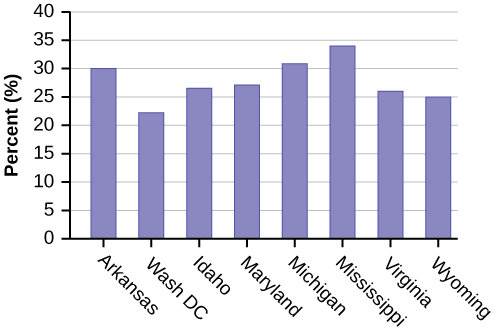
[link] contains the 2010 obesity rates in U.S. states and Washington, DC.

• Use a random number generator to randomly pick eight states. Construct a bar graph of the obesity rates of those eight states.
• Construct a bar graph for all the states beginning with the letter “A.”
• Construct a bar graph for all the states beginning with the letter “M.”
• Number the entries in the table 1–51 (Includes Washington, DC; Numbered vertically)
• Arrow over to PRB
• Press 5:randInt(
• Enter 51,1,8)

Eight numbers are generated (use the right arrow key to scroll through the numbers). The numbers correspond to the numbered states (for this example: {47 21 9 23 51 13 25 4}. If any numbers are repeated, generate a different number by using 5:randInt(51,1)). Here, the states (and Washington DC) are {Arkansas, Washington DC, Idaho, Maryland, Michigan, Mississippi, Virginia, Wyoming}.

Corresponding percentages are {30.1, 22.2, 26.5, 27.1, 30.9, 34.0, 26.0, 25.1}.

Homework from 2.2

Suppose that three book publishers were interested in the number of fiction paperbacks adult consumers purchase per month. Each publisher conducted a survey. In the survey, adult consumers were asked the number of fiction paperbacks they had purchased the previous month. The results are as follows:

• Find the relative frequencies for each survey. Write them in the charts.
• Using either a graphing calculator, computer, or by hand, use the frequency column to construct a histogram for each publisher’s survey. For Publishers A and B, make bar widths of one. For Publisher C, make bar widths of two.
• In complete sentences, give two reasons why the graphs for Publishers A and B are not identical.
• Would you have expected the graph for Publisher C to look like the other two graphs? Why or why not?
• Make new histograms for Publisher A and Publisher B. This time, make bar widths of two.
• Now, compare the graph for Publisher C to the new graphs for Publishers A and B. Are the graphs more similar or more different? Explain your answer.

Often, cruise ships conduct all on-board transactions, with the exception of gambling, on a cashless basis. At the end of the cruise, guests pay one bill that covers all onboard transactions. Suppose that 60 single travelers and 70 couples were surveyed as to their on-board bills for a seven-day cruise from Los Angeles to the Mexican Riviera. Following is a summary of the bills for each group.

• Fill in the relative frequency for each group.
• Construct a histogram for the singles group. Scale the x -axis by 💲50 widths. Use relative frequency on the y -axis.
• Construct a histogram for the couples group. Scale the x -axis by 💲50 widths. Use relative frequency on the y -axis.
• List two similarities between the graphs.
• List two differences between the graphs.
• Overall, are the graphs more similar or different?
• Construct a new graph for the couples by hand. Since each couple is paying for two individuals, instead of scaling the x -axis by 💲50, scale it by 💲100. Use relative frequency on the y -axis.
• How did scaling the couples graph differently change the way you compared it to the singles graph?
• Based on the graphs, do you think that individuals spend the same amount, more or less, as singles as they do person by person as a couple? Explain why in one or two complete sentences.
• See [link] and [link] .

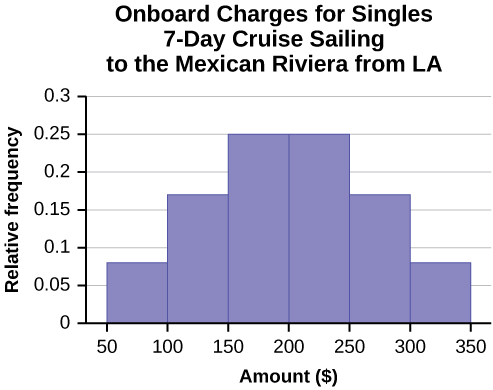
• Both graphs have a single peak.
• Both graphs use class intervals with width equal to 💲50.
• The couples graph has a class interval with no values.
• It takes almost twice as many class intervals to display the data for couples.
• Answers may vary. Possible answers include: The graphs are more similar than different because the overall patterns for the graphs are the same.
• Check student’s solution.
• Both graphs display 6 class intervals.
• Both graphs show the same general pattern.
• Answers may vary. Possible answers include: Although the width of the class intervals for couples is double that of the class intervals for singles, the graphs are more similar than they are different.
• Answers may vary. Possible answers include: You are able to compare the graphs interval by interval. It is easier to compare the overall patterns with the new scale on the Couples graph. Because a couple represents two individuals, the new scale leads to a more accurate comparison.
• Answers may vary. Possible answers include: Based on the histograms, it seems that spending does not vary much from singles to individuals who are part of a couple. The overall patterns are the same. The range of spending for couples is approximately double the range for individuals.

Twenty-five randomly selected students were asked the number of movies they watched the previous week. The results are as follows.

• Construct a histogram of the data.
• Complete the columns of the chart.

Use the following information to answer the next two exercises: Suppose one hundred eleven people who shopped in a special T-shirt store were asked the number of T-shirts they own costing more than 💲19 each.

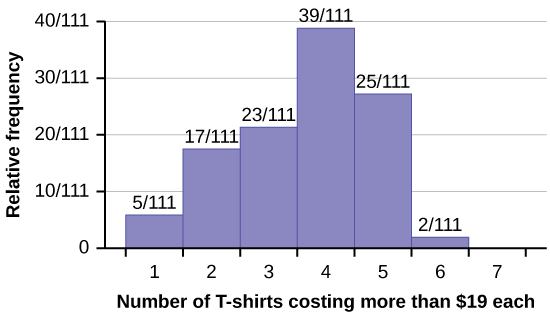
The percentage of people who own at most three T-shirts costing more than 💲19 each is approximately:

• Cannot be determined

If the data were collected by asking the first 111 people who entered the store, then the type of sampling is:

• simple random
• convenience

Following are the 2010 obesity rates by U.S. states and Washington, DC.

Construct a bar graph of obesity rates of your state and the four states closest to your state. Hint: Label the x -axis with the states.

Answers will vary.

Homework from 2.3

The median age for U.S. blacks currently is 30.9 years; for U.S. whites it is 42.3 years.

Six hundred adult Americans were asked by telephone poll, “What do you think constitutes a middle-class income?” The results are in [link] . Also, include left endpoint, but not the right endpoint.

• What percentage of the survey answered “not sure”?
• What percentage think that middle-class is from 💲25,000 to 💲50,000?
• Should all bars have the same width, based on the data? Why or why not?
• How should the <20,000 and the 100,000+ intervals be handled? Why?
• Find the 40 th and 80 th percentiles
• Construct a bar graph of the data
• 1 – (0.02+0.09+0.19+0.26+0.18+0.17+0.02+0.01) = 0.06
• 0.19+0.26+0.18 = 0.63

40 th percentile will fall between 30,000 and 40,000

80 th percentile will fall between 50,000 and 75,000

Given the following box plot:

• which quarter has the smallest spread of data? What is that spread?
• which quarter has the largest spread of data? What is that spread?
• find the interquartile range ( IQR ).
• are there more data in the interval 5–10 or in the interval 10–13? How do you know this?
• need more information

The following box plot shows the U.S. population for 1990, the latest available year.

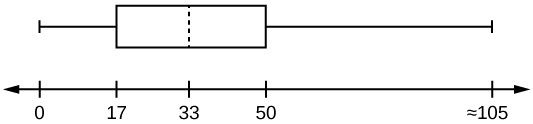
• Are there fewer or more children (age 17 and under) than senior citizens (age 65 and over)? How do you know?
• 12.6% are age 65 and over. Approximately what percentage of the population are working age adults (above age 17 to age 65)?
• more children; the left whisker shows that 25% of the population are children 17 and younger. The right whisker shows that 25% of the population are adults 50 and older, so adults 65 and over represent less than 25%.

Homework from 2.4

In a survey of 20-year-olds in China, Germany, and the United States, people were asked the number of foreign countries they had visited in their lifetime. The following box plots display the results.

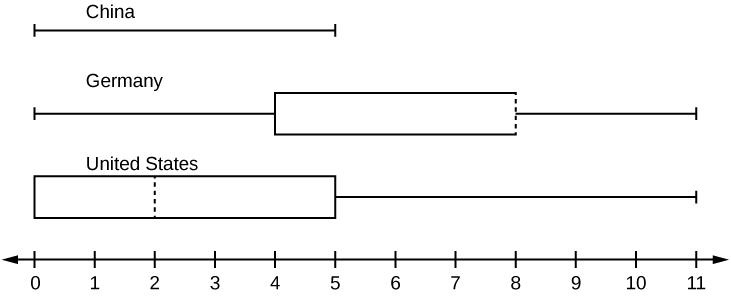
• In complete sentences, describe what the shape of each box plot implies about the distribution of the data collected.
• Have more Americans or more Germans surveyed been to over eight foreign countries?
• Compare the three box plots. What do they imply about the foreign travel of 20-year-old residents of the three countries when compared to each other?

Given the following box plot, answer the questions.

• Think of an example (in words) where the data might fit into the above box plot. In 2–5 sentences, write down the example.
• What does it mean to have the first and second quartiles so close together, while the second to third quartiles are far apart?
• Answers will vary. Possible answer: State University conducted a survey to see how involved its students are in community service. The box plot shows the number of community service hours logged by participants over the past year.
• Because the first and second quartiles are close, the data in this quarter is very similar. There is not much variation in the values. The data in the third quarter is much more variable or spread out. This is clear because the second quartile is so far away from the third quartile.

Given the following box plots, answer the questions.

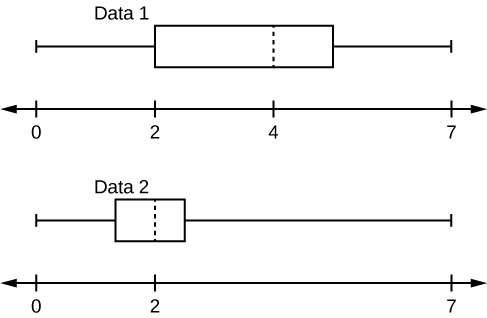
• Data 1 has more data values above two than Data 2 has above two.
• The data sets cannot have the same mode.
• For Data 1 , there are more data values below four than there are above four.
• For which group, Data 1 or Data 2, is the value of “7” more likely to be an outlier? Explain why in complete sentences.

A survey was conducted of 130 purchasers of new BMW 3 series cars, 130 purchasers of new BMW 5 series cars, and 130 purchasers of new BMW 7 series cars. In it, people were asked the age they were when they purchased their car. The following box plots display the results.

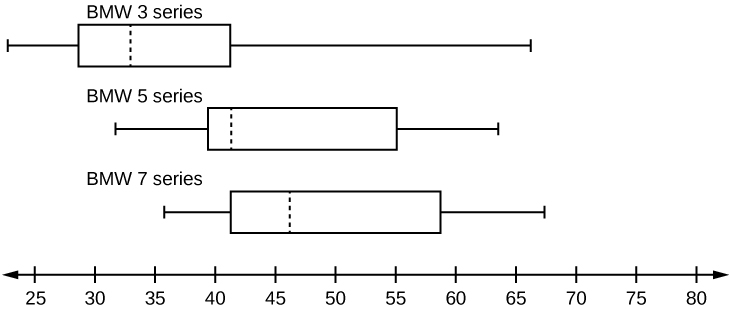
• In complete sentences, describe what the shape of each box plot implies about the distribution of the data collected for that car series.
• Which group is most likely to have an outlier? Explain how you determined that.
• Compare the three box plots. What do they imply about the age of purchasing a BMW from the series when compared to each other?
• Look at the BMW 5 series. Which quarter has the smallest spread of data? What is the spread?
• Look at the BMW 5 series. Which quarter has the largest spread of data? What is the spread?
• Look at the BMW 5 series. Estimate the interquartile range (IQR).
• Look at the BMW 5 series. Are there more data in the interval 31 to 38 or in the interval 45 to 55? How do you know this?
• Each box plot is spread out more in the greater values. Each plot is skewed to the right, so the ages of the top 50% of buyers are more variable than the ages of the lower 50%.
• The BMW 3 series is most likely to have an outlier. It has the longest whisker.
• Comparing the median ages, younger people tend to buy the BMW 3 series, while older people tend to buy the BMW 7 series. However, this is not a rule, because there is so much variability in each data set.
• The second quarter has the smallest spread. There seems to be only a three-year difference between the first quartile and the median.
• The third quarter has the largest spread. There seems to be approximately a 14-year difference between the median and the third quartile.
• IQR ~ 17 years
• There is not enough information to tell. Each interval lies within a quarter, so we cannot tell exactly where the data in that quarter is concentrated.
• The interval from 31 to 35 years has the fewest data values. Twenty-five percent of the values fall in the interval 38 to 41, and 25% fall between 41 and 64. Since 25% of values fall between 31 and 38, we know that fewer than 25% fall between 31 and 35.

Twenty-five randomly selected students were asked the number of movies they watched the previous week. The results are as follows:

Construct a box plot of the data.

Homework from 2.5

The most obese countries in the world have obesity rates that range from 11.4% to 74.6%. This data is summarized in the following table.

• What is the best estimate of the average obesity percentage for these countries?
• The United States has an average obesity rate of 33.9%. Is this rate above average or below?
• How does the United States compare to other countries?

[link] gives the percent of children under five considered to be underweight. What is the best estimate for the mean percentage of underweight children?

The mean percentage, [latex]\overline{x}=\frac{1328.65}{50}=26.75[/latex]

Homework from 2.6

The median age of the U.S. population in 1980 was 30.0 years. In 1991, the median age was 33.1 years.

• What does it mean for the median age to rise?
• Give two reasons why the median age could rise.
• For the median age to rise, is the actual number of children less in 1991 than it was in 1980? Why or why not?

Homework from 2.7

Use the following information to answer the next nine exercises: The population parameters below describe the full-time equivalent number of students (FTES) each year at Lake Tahoe Community College from 1976–1977 through 2004–2005.

• μ = 1000 FTES
• median = 1,014 FTES
• σ = 474 FTES
• first quartile = 528.5 FTES
• third quartile = 1,447.5 FTES
• n = 29 years

A sample of 11 years is taken. About how many are expected to have a FTES of 1014 or above? Explain how you determined your answer.

The median value is the middle value in the ordered list of data values. The median value of a set of 11 will be the 6th number in order. Six years will have totals at or below the median.

75% of all years have an FTES:

The population standard deviation = _____

What percentage of the FTES was from 528.5 to 1447.5? How do you know?

What is the IQR ? What does the IQR represent?

How many standard deviations away from the mean is the median?

Additional Information: The population FTES for 2005–2006 through 2010–2011 was given in an updated report. The data are reported here.

Calculate the mean, median, standard deviation, the first quartile, the third quartile and the IQR . Round to one decimal place.

• mean = 1,809.3
• median = 1,812.5
• standard deviation = 151.2
• first quartile = 1,690
• third quartile = 1,935

Construct a box plot for the FTES for 2005–2006 through 2010–2011 and a box plot for the FTES for 1976–1977 through 2004–2005.

Compare the IQR for the FTES for 1976–77 through 2004–2005 with the IQR for the FTES for 2005-2006 through 2010–2011. Why do you suppose the IQR s are so different?

Hint: Think about the number of years covered by each time period and what happened to higher education during those periods.

Three students were applying to the same graduate school. They came from schools with different grading systems. Which student had the best GPA when compared to other students at his school? Explain how you determined your answer.

A music school has budgeted to purchase three musical instruments. They plan to purchase a piano costing 💲3,000, a guitar costing 💲550, and a drum set costing 💲600. The mean cost for a piano is 💲4,000 with a standard deviation of 💲2,500. The mean cost for a guitar is 💲500 with a standard deviation of 💲200. The mean cost for drums is 💲700 with a standard deviation of 💲100. Which cost is the lowest, when compared to other instruments of the same type? Which cost is the highest when compared to other instruments of the same type. Justify your answer.

For pianos, the cost of the piano is 0.4 standard deviations BELOW the mean. For guitars, the cost of the guitar is 0.25 standard deviations ABOVE the mean. For drums, the cost of the drum set is 1.0 standard deviations BELOW the mean. Of the three, the drums cost the lowest in comparison to the cost of other instruments of the same type. The guitar costs the most in comparison to the cost of other instruments of the same type.

An elementary school class ran one mile with a mean of 11 minutes and a standard deviation of three minutes. Rachel, a student in the class, ran one mile in eight minutes. A junior high school class ran one mile with a mean of nine minutes and a standard deviation of two minutes. Kenji, a student in the class, ran 1 mile in 8.5 minutes. A high school class ran one mile with a mean of seven minutes and a standard deviation of four minutes. Nedda, a student in the class, ran one mile in eight minutes.

• Why is Kenji considered a better runner than Nedda, even though Nedda ran faster than him?
• Who is the fastest runner with respect to his or her class? Explain why.

The most obese countries in the world have obesity rates that range from 11.4% to 74.6%. This data is summarized in Table 14 .

What is the best estimate of the average obesity percentage for these countries? What is the standard deviation for the listed obesity rates? The United States has an average obesity rate of 33.9%. Is this rate above average or below? How “unusual” is the United States’ obesity rate compared to the average rate? Explain.

• [latex]\overline{x}=23.32[/latex]
• Using the TI 83/84, we obtain a standard deviation of: [latex]{s}_{x}=12.95.[/latex]
• The obesity rate of the United States is 10.58% higher than the average obesity rate.
• Since the standard deviation is 12.95, we see that 23.32 + 12.95 = 36.27 is the obesity percentage that is one standard deviation from the mean. The United States obesity rate is slightly less than one standard deviation from the mean. Therefore, we can assume that the United States, while 34% obese, does not have an unusually high percentage of obese people.

[link] gives the percent of children under five considered to be underweight.

What is the best estimate for the mean percentage of underweight children? What is the standard deviation? Which interval(s) could be considered unusual? Explain.

used to describe data that is not symmetrical; when the right side of a graph looks “chopped off” compared to the left side, we say it is “skewed to the left.” When the left side of the graph looks “chopped off” compared to the right side, we say the data is “skewed to the right.” Alternatively: when the lower values of the data are more spread out, we say the data are skewed to the left. When the greater values are more spread out, the data are skewed to the right.

Introductory Statistics Copyright © 2024 by LOUIS: The Louisiana Library Network is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

Bringing It Together: Homework

A certain small town in the United states has a population of 27,873 people. Their ages are as follows:

• Construct a histogram of the age distribution for this small town. The bars will not be the same width for this example. Why not? What impact does this have on the reliability of the graph?
• What percentage of the community is under age 35?
• Which box plot most resembles the information above?

Javier and Ercilia are supervisors at a shopping mall. Each was given the task of estimating the mean distance that shoppers live from the mall. They each randomly surveyed 100 shoppers. The samples yielded the following information.

• How can you determine which survey was correct ?
• Explain what the difference in the results of the surveys implies about the data.

Use the following information to answer the next three exercises : We are interested in the number of years students in a particular elementary statistics class have lived in California. The information in the following table is from the entire section.

What is the IQR ?

What is the mode?

Is this a sample or the entire population?

• entire population

Twenty-five randomly selected students were asked the number of movies they watched the previous week. The results are as follows:

• Find the sample mean x ¯ x ¯ .
• Find the approximate sample standard deviation, s .

Forty randomly selected students were asked the number of pairs of sneakers they owned. Let X = the number of pairs of sneakers owned. The results are as follows:

• Find the sample mean x – x –
• Find the sample standard deviation, s
• Construct a histogram of the data.
• Complete the columns of the chart.
• Find the first quartile.
• Find the median.
• Find the third quartile.
• Construct a box plot of the data.
• What percent of the students owned at least five pairs?
• Find the 40 th percentile.
• Find the 90 th percentile.
• Construct a line graph of the data
• Construct a stemplot of the data

Following are the published weights (in pounds) of all of the team members of the San Francisco 49ers from a previous year.

177; 205; 210; 210; 232; 205; 185; 185; 178; 210; 206; 212; 184; 174; 185; 242; 188; 212; 215; 247; 241; 223; 220; 260; 245; 259; 278; 270; 280; 295; 275; 285; 290; 272; 273; 280; 285; 286; 200; 215; 185; 230; 250; 241; 190; 260; 250; 302; 265; 290; 276; 228; 265

• Organize the data from smallest to largest value.
• The middle 50% of the weights are from _______ to _______.
• If our population were all professional football players, would the above data be a sample of weights or the population of weights? Why?
• the population mean, μ .
• the population standard deviation, σ .
• the weight that is two standard deviations below the mean.
• When Steve Young, quarterback, played football, he weighed 205 pounds. How many standard deviations above or below the mean was he?
• That same year, the mean weight for the Dallas Cowboys was 240.08 pounds with a standard deviation of 44.38 pounds. Emmit Smith weighed in at 209 pounds. With respect to his team, who was lighter, Smith or Young? How did you determine your answer?

One hundred teachers attended a seminar on mathematical problem solving. The attitudes of a representative sample of 12 of the teachers were measured before and after the seminar. A positive number for change in attitude indicates that a teacher's attitude toward math became more positive. The 12 change scores are as follows:

3 ; 8 ; –1 ; 2 ; 0 ; 5 ; –3 ; 1 ; –1 ; 6 ; 5 ; –2

• What is the mean change score?
• What is the standard deviation for this population?
• What is the median change score?
• Find the change score that is 2.2 standard deviations below the mean.

Refer to Figure 2.51 determine which of the following are true and which are false. Explain your solution to each part in complete sentences.

• The medians for all three graphs are the same.
• We cannot determine if any of the means for the three graphs is different.
• The standard deviation for graph b is larger than the standard deviation for graph a.
• We cannot determine if any of the third quartiles for the three graphs is different.

In a recent issue of the IEEE Spectrum , 84 engineering conferences were announced. Four conferences lasted two days. Thirty-six lasted three days. Eighteen lasted four days. Nineteen lasted five days. Four lasted six days. One lasted seven days. One lasted eight days. One lasted nine days. Let X = the length (in days) of an engineering conference.

• Organize the data in a chart.
• Find the median, the first quartile, and the third quartile.
• Find the 65 th percentile.
• Find the 10 th percentile.
• The middle 50% of the conferences last from _______ days to _______ days.
• Calculate the sample mean of days of engineering conferences.
• Calculate the sample standard deviation of days of engineering conferences.
• Find the mode.
• If you were planning an engineering conference, which would you choose as the length of the conference: mean; median; or mode? Explain why you made that choice.
• Give two reasons why you think that three to five days seem to be popular lengths of engineering conferences.

A survey of enrollment at 35 community colleges across the United States yielded the following figures:

6414; 1550; 2109; 9350; 21828; 4300; 5944; 5722; 2825; 2044; 5481; 5200; 5853; 2750; 10012; 6357; 27000; 9414; 7681; 3200; 17500; 9200; 7380; 18314; 6557; 13713; 17768; 7493; 2771; 2861; 1263; 7285; 28165; 5080; 11622

• Organize the data into a chart with five intervals of equal width. Label the two columns "Enrollment" and "Frequency."
• If you were to build a new community college, which piece of information would be more valuable: the mode or the mean?
• Calculate the sample mean.
• Calculate the sample standard deviation.
• A school with an enrollment of 8000 would be how many standard deviations away from the mean?

Use the following information to answer the next two exercises. X = the number of days per week that 100 clients use a particular exercise facility.

The 80 th percentile is _____

The number that is 1.5 standard deviations BELOW the mean is approximately _____

• Cannot be determined

Suppose that a publisher conducted a survey asking adult consumers the number of fiction paperback books they had purchased in the previous month. The results are summarized in the Table 2.84 .

• Are there any outliers in the data? Use an appropriate numerical test involving the IQR to identify outliers, if any, and clearly state your conclusion.
• If a data value is identified as an outlier, what should be done about it?
• Are any data values further than two standard deviations away from the mean? In some situations, statisticians may use this criteria to identify data values that are unusual, compared to the other data values. (Note that this criteria is most appropriate to use for data that is mound-shaped and symmetric, rather than for skewed data.)
• Do parts a and c of this problem give the same answer?
• Examine the shape of the data. Which part, a or c, of this question gives a more appropriate result for this data?
• Based on the shape of the data which is the most appropriate measure of center for this data: mean, median or mode?

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/introductory-statistics-2e/pages/1-introduction

• Authors: Barbara Illowsky, Susan Dean
• Publisher/website: OpenStax
• Book title: Introductory Statistics 2e
• Publication date: Dec 13, 2023
• Location: Houston, Texas
• Book URL: https://openstax.org/books/introductory-statistics-2e/pages/1-introduction
• Section URL: https://openstax.org/books/introductory-statistics-2e/pages/2-bringing-it-together-homework

© Dec 6, 2023 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.