problem solving algebra questions

Free Algebra Questions and Problems with Answers

Free intermediate and college algebra questions and problems are presented along with answers and explanations. Free worksheets to download are also included.

Intermediate Algebra Questions with Answers

• sample 1 .(student generated solutions). Also included are the solutions with full explanations .
• sample 2 .(True / False type). Also included are the solutions with full explanations .
• sample 3 .(student generated solutions). solutions with full explanations are included.
• sample 4 .(True / False type). solutions with full explanations included.
• sample 5 .(Multiple choice questions type). Also included are the solutions with full explanations .
• sample 6 .(True / False type). solutions with full explanations included.

Intermediate Algebra Problems with Detailed Solutions

• Algebra Problems .
• Intermediate Algebra Problems With Answers - sample 1 : equations, system of equations, percent problems, relations and functions.
• Intermediate Algebra Problems With Answers - sample 2 :Find equation of line, domain and range from graph, midpoint and distance of line segments, slopes of perpendicular and parallel lines.
• Intermediate Algebra Problems With Answers - sample 3 : equations and system of equations, quadratic equations, function given by a table, intersections of lines, problems.
• Intermediate Algebra Problems With Answers - sample 4 . Functions, domain, range, zeros.
• Intermediate Algebra Problems With Answers - sample 5 . Scientific Notation
• Intermediate Algebra Problems With Answers - sample 6 . Equations of Lines
• Intermediate Algebra Problems With Answers - sample 7 . Slopes of Lines
• Intermediate Algebra Problems With Answers - sample 8 . Absolute Value Expressions
• Intermediate Algebra Problems With Answers - sample 9 . Solve Absolute Value Equations
• Intermediate Algebra Problems With Answers - sample 10 . Solve Absolute Value Inequalities
• Intermediate Algebra Problems With Answers - sample 11 . Simplify Algebraic Expressions by Removing Brackets
• Intermediate Algebra Problems With Answers - sample 12 . Simplify Algebraic Expressions with Exponents

Intermediate Algebra Worksheets

• Worksheet (1) .
• Worksheet (2) .
• Worksheet (3) .
• Worksheet (4) .
• Worksheet (5) .
• Worksheet (6) .

College Algebra Questions with Answers

• sample 1 .(multiple choice questions). Also Detailed solutions with full explanations are included
• sample 2 . (multiple choice questions)

College Algebra Problems with Answers

• sample 1: Quadratic Functions .
• sample 2: Composite and Inverse Functions .
• sample 3: Exponential and Logarithmic Functions .
• sample 4: Graphs of Functions .
• sample 5: Find Domain and Range of Functions .
• sample 6: Problems on Polynomials : Graphs, Factoring, Finding, Multiplying, Dividing, Factor theorem, Zeros
• sample 7: Equation of Circle : Finding equations, center, radius of circles
• sample 8: Equation of Ellipse : Finding equations, foci, center, vertices of ellipses
• sample 9: Equation of Parabola : Finding equations, focus, vertex, axis, directrix of parabola.
• sample 10: Equation of Hyperbola : Finding equations, foci, center and vertices of hyperbola.

College Algebra Worksheets

• Worksheet (1): Graphs of Basic Functions .
• Worksheet (2): Exponential Growth and Decay Problems .
• Worksheet (3): Graphing Exponential Functions .
• Worksheet (4): Graphing Logarithmic Functions .
• Worksheet (5): Solve Exponential Equations .
• Worksheet (6): Solve Logarithmic Equations .
• Worksheet (7): Multiple Choice Questions on Polynomials and Solutions
• Worksheet (8): Multiple Choice Questions on Rational Functions and Solutions .
• Worksheet (9): Graphing Inverse Functions .

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

• Skip to main content
• Skip to primary sidebar
• Skip to footer

Additional menu

Khan Academy Blog

Free Math Worksheets — Over 100k free practice problems on Khan Academy

Looking for free math worksheets.

You’ve found something even better!

That’s because Khan Academy has over 100,000 free practice questions. And they’re even better than traditional math worksheets – more instantaneous, more interactive, and more fun!

Just choose your grade level or topic to get access to 100% free practice questions:

Kindergarten, basic geometry, pre-algebra, algebra basics, high school geometry.

• Trigonometry

Statistics and probability

High school statistics, ap®︎/college statistics, precalculus, differential calculus, integral calculus, ap®︎/college calculus ab, ap®︎/college calculus bc, multivariable calculus, differential equations, linear algebra.

• Addition and subtraction
• Place value (tens and hundreds)
• Addition and subtraction within 20
• Addition and subtraction within 100
• Addition and subtraction within 1000
• Measurement and data
• Counting and place value
• Measurement and geometry
• Place value
• Measurement, data, and geometry
• Add and subtract within 20
• Add and subtract within 100
• Add and subtract within 1,000
• Money and time
• Measurement
• Intro to multiplication
• 1-digit multiplication
• Addition, subtraction, and estimation
• Intro to division
• Understand fractions
• Equivalent fractions and comparing fractions
• More with multiplication and division
• Arithmetic patterns and problem solving
• Quadrilaterals
• Represent and interpret data
• Multiply by 1-digit numbers
• Multiply by 2-digit numbers
• Factors, multiples and patterns
• Add and subtract fractions
• Multiply fractions
• Understand decimals
• Plane figures
• Measuring angles
• Area and perimeter
• Units of measurement
• Decimal place value
• Add decimals
• Subtract decimals
• Multi-digit multiplication and division
• Divide fractions
• Multiply decimals
• Divide decimals
• Powers of ten
• Coordinate plane
• Algebraic thinking
• Converting units of measure
• Properties of shapes
• Ratios, rates, & percentages
• Arithmetic operations
• Negative numbers
• Properties of numbers
• Variables & expressions
• Equations & inequalities introduction
• Data and statistics
• Negative numbers: addition and subtraction
• Negative numbers: multiplication and division
• Fractions, decimals, & percentages
• Rates & proportional relationships
• Expressions, equations, & inequalities
• Numbers and operations
• Solving equations with one unknown
• Linear equations and functions
• Systems of equations
• Geometric transformations
• Data and modeling
• Volume and surface area
• Pythagorean theorem
• Transformations, congruence, and similarity
• Arithmetic properties
• Factors and multiples
• Reading and interpreting data
• Negative numbers and coordinate plane
• Ratios, rates, proportions
• Equations, expressions, and inequalities
• Exponents, radicals, and scientific notation
• Foundations
• Algebraic expressions
• Linear equations and inequalities
• Graphing lines and slope
• Expressions with exponents
• Quadratics and polynomials
• Equations and geometry
• Algebra foundations
• Solving equations & inequalities
• Working with units
• Linear equations & graphs
• Forms of linear equations
• Inequalities (systems & graphs)
• Absolute value & piecewise functions
• Exponents & radicals
• Exponential growth & decay
• Quadratics: Multiplying & factoring
• Quadratic functions & equations
• Irrational numbers
• Performing transformations
• Transformation properties and proofs
• Right triangles & trigonometry
• Non-right triangles & trigonometry (Advanced)
• Analytic geometry
• Conic sections
• Solid geometry
• Polynomial arithmetic
• Complex numbers
• Polynomial factorization
• Polynomial division
• Polynomial graphs
• Rational exponents and radicals
• Exponential models
• Transformations of functions
• Rational functions
• Trigonometric functions
• Non-right triangles & trigonometry
• Trigonometric equations and identities
• Analyzing categorical data
• Displaying and comparing quantitative data
• Summarizing quantitative data
• Modeling data distributions
• Exploring bivariate numerical data
• Study design
• Probability
• Counting, permutations, and combinations
• Random variables
• Sampling distributions
• Confidence intervals
• Significance tests (hypothesis testing)
• Two-sample inference for the difference between groups
• Inference for categorical data (chi-square tests)
• Advanced regression (inference and transforming)
• Analysis of variance (ANOVA)
• Scatterplots
• Data distributions
• Two-way tables
• Binomial probability
• Normal distributions
• Displaying and describing quantitative data
• Inference comparing two groups or populations
• Chi-square tests for categorical data
• More on regression
• Prepare for the 2020 AP®︎ Statistics Exam
• AP®︎ Statistics Standards mappings
• Polynomials
• Composite functions
• Probability and combinatorics
• Limits and continuity
• Derivatives: definition and basic rules
• Derivatives: chain rule and other advanced topics
• Applications of derivatives
• Analyzing functions
• Parametric equations, polar coordinates, and vector-valued functions
• Applications of integrals
• Differentiation: definition and basic derivative rules
• Differentiation: composite, implicit, and inverse functions
• Contextual applications of differentiation
• Applying derivatives to analyze functions
• Integration and accumulation of change
• Applications of integration
• AP Calculus AB solved free response questions from past exams
• AP®︎ Calculus AB Standards mappings
• Infinite sequences and series
• AP Calculus BC solved exams
• AP®︎ Calculus BC Standards mappings
• Integrals review
• Integration techniques
• Thinking about multivariable functions
• Derivatives of multivariable functions
• Applications of multivariable derivatives
• Integrating multivariable functions
• Green’s, Stokes’, and the divergence theorems
• First order differential equations
• Second order linear equations
• Laplace transform
• Vectors and spaces
• Matrix transformations
• Alternate coordinate systems (bases)

Frequently Asked Questions about Khan Academy and Math Worksheets

Why is khan academy even better than traditional math worksheets.

Khan Academy’s 100,000+ free practice questions give instant feedback, don’t need to be graded, and don’t require a printer.

What do Khan Academy’s interactive math worksheets look like?

Here’s an example:

What are teachers saying about Khan Academy’s interactive math worksheets?

“My students love Khan Academy because they can immediately learn from their mistakes, unlike traditional worksheets.”

Is Khan Academy free?

Khan Academy’s practice questions are 100% free—with no ads or subscriptions.

What do Khan Academy’s interactive math worksheets cover?

Our 100,000+ practice questions cover every math topic from arithmetic to calculus, as well as ELA, Science, Social Studies, and more.

Is Khan Academy a company?

Khan Academy is a nonprofit with a mission to provide a free, world-class education to anyone, anywhere.

Want to get even more out of Khan Academy?

Then be sure to check out our teacher tools . They’ll help you assign the perfect practice for each student from our full math curriculum and track your students’ progress across the year. Plus, they’re also 100% free — with no subscriptions and no ads.

Get Khanmigo

The best way to learn and teach with AI is here. Ace the school year with our AI-powered guide, Khanmigo. 

For learners     For teachers     For parents

Teacher-Trusted Tutoring

Personalised one to one tutoring that boosts confidence and doubles progress

FREE secondary maths resources

Here you can find all of our free secondary resources; explore the collections or navigate to each section to filter resources by topic

15 Algebra Questions And Practice Problems (KS3 & KS4): Harder GCSE Exam Style Questions Included

Beki Christian

Algebra questions involve using letters or symbols to represent unknown values or values that can change. Here you will find 15 algebra questions to test your knowledge and show you the different ways that algebra can be used to solve a problem to find an unknown value or to make generalisations.

FREE GCSE MATHS REVISION RESOURCES FOR SCHOOLS

As part of the Third Space Learning offer to schools, the personalised online GCSE maths tuition can be supplemented by hundreds of free GCSE maths revision resources from the secondary maths resources library including:

• GCSE maths past papers
• GCSE maths worksheets
• GCSE maths questions
• GCSE maths topic list

Algebra in KS3 and KS4

There are many topics and techniques within algebra . In KS3 we learn to write and manipulate basic algebraic expressions and linear equations. In KS4 we develop these techniques to allow us to deal with more complicated algebra problems such as ones that involve quadratic equations or a system of equations.

How to solve algebraic questions

When you are presented with an algebraic problem it is important to establish what you are being asked to do. Here are some of the key terms along with what they mean:

• Solve the equation – find out the value of the unknown
• Substitute – put the values you have been given into the algebraic expression
• Simplify – collect together like terms to make the expression or equation look simpler
• Expand brackets – multiply out the brackets
• Factorise – put into brackets
• Make x the subject – rewrite the equation in the form x =…..

Remember, when working with algebra, we must still apply BODMAS / BIDMAS. i.e. B rackets, I ndices (powers, exponents, square roots), D ivision, M ultiplication, A ddition, S ubtraction.

When working with algebraic expressions and equations we must consider carefully which operations to deal with first.

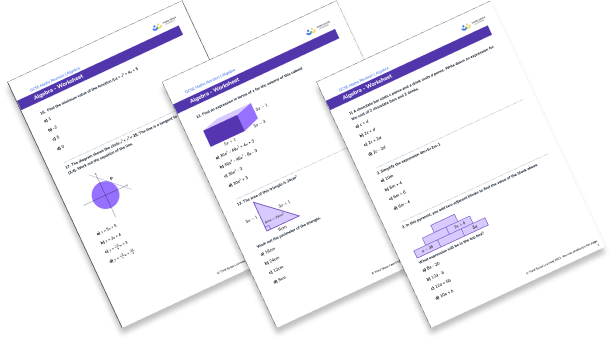
Download this 15 Algebra Questions And Practice Problems (KS3 & KS4) Worksheet

Help your students prepare for their Maths GCSE with this free Algebra worksheet of 15 multiple choice questions and answers.

Algebra in KS2

The ideas of writing and simplifying expressions, solving equations and substitution are introduced in KS2. Here are some example KS2 algebra questions:

Algebra questions KS2

1. A chocolate bar costs c pence and a drink costs d pence. Write down an expression for the cost of 2 chocolate bars and 2 drinks.

2 chocolate bars would cost 2 lots of c, or 2c, and 2 drinks would cost 2 lots of d, or 2d.

2. Simplify the expression 4m+5+2m-1

We need to collect together like terms here so 4m + 2m = 6m and 5 – 1 = 4 (watch out for the negative).

Algebra questions KS3

In KS3 we learn a variety of different algebra techniques to answer algebra questions and to practise problem solving with algebra. These include:

• Simplifying algebraic expressions
• Expanding brackets and factoring
• Forming algebraic equations from word problems
• Solving algebraic equations and inequalities
• Substituting into expressions
• Changing the subject of an equation
• Working with real life graphs and straight line graphs

You may also like:

• Year 6 Maths Test
• Year 7 Maths Test
• Year 8 Maths Test
• Year 9 Maths Test

Algebra questions KS3: basic algebra

1. In this pyramid, you add two adjacent blocks to find the value of the block above.

What expression will be in the top box?

2.  Brian is a window cleaner. He uses the following formula to calculate the amount to charge his customers:

Charge = £20 + 4n

Where n is the number of windows a house has.

If a house has 7 windows, how much would Brian charge?

In this question, n is 7 so we can substitute 7 into the formula.

Charge = £20 + 4 × 7

Charge = £48

3. The area of a rectangle is 4x-6.

Which of the following pairs could be the length and width of the rectangle?

2x and 2x-3

There are two ways of attempting this question. We know that area \;of \;a \;rectangle = length × width so we could multiply each pair together to see which pair makes 4x − 6.

Alternatively, if we factorise 4x − 6 we get 2(2x − 3) meaning the sides could be 2 and 2x − 3.

4.  The formula for changing degrees Celsius to degrees Fahrenheit is

F=\frac{9C}{5}+32

Rearrange this formula to make C the subject.

Algebra questions KS3: forming and solving equations

5. Work out the size of the smallest angle.

The angles in a triangle add up to 180^{\circ} therefore we can write

Now we have an equation we can solve.

The angles are :

The smallest angle is 34^{\circ} .

6.  Jamie’s dad is 4 times older than Jamie. In 14 years time, Jamie’s dad will be twice the age of Jamie.

What is the sum of Jamie’s age now and Jamie’s dad’s age now?

To solve this we need to write an equation.

Let Jamie’s age now be x . Then Jamie’s dad’s age is 4x .

In 14 years time Jamie’s age will be x + 14 and Jamie’s dad’s age will be 4x + 14 .

Since we know Jamie’s dad’s age will be two times Jamie’s age, we can write

4x+14=2(x+14)

Jamie is currently 7 years old meaning his dad is 28 years old. The sum of their ages is 35 .

Algebra questions KS3: graphs

7.  Which of the following lines passes through the point (2, 5)?

At the point (2, 5), x is 2 and y is 5. We can check which equation works when we substitute in these values:

Algebra questions KS4

Algebra is studied extensively in the GCSE and IGCSE curriculum.

In KS4 we build on the techniques learnt in KS3. Topics include:

• Expanding and factorising polynomials
• Solving quadratic equations
• Solving simultaneous equations
• Inequalities
• Algebraic fractions
• Further work on graphs

Algebra questions KS4: algebraic manipulation

8. Which of the following expressions has the smallest value when a=5 and b=-3?

9. Find an expression in terms of x for the volume of this cuboid

Volume = (5x+1)(2x-3)(3x-1)

Volume = (10x^2+2x-15x-3)(3x-1)

Volume = (10x^2-13x-3)(3x-1)

Volume = 30x^3-39x^2-9x-10x^2+13x+3

Volume = 30x^3-49x^2+4x+3

Algebra questions KS4: forming and solving equations

10. The area of this triangle is 24cm^2 .

Work out the perimeter of the triangle.

The area of a triangle is area = \frac{1}{2} × b × h.

If we fill in what we know we get:

Since x = 3 , the side lengths are 6m, 8cm and 10cm .

The perimeter is 6 + 8 + 10 = 24cm .

11.  Solve the equation x+2-\frac{15}{x}=0

x=-2 or x=15

x=-3 or x=5

x=-5 or x=3

x=-15 or x=2

We can make this a bit easier by getting rid of the fraction involving x. We do this by multiplying each term by x.

12. At a theme park the Jones family purchased 2 adult tickets and 3 child tickets for £48 .  The Evans family purchased 3 adult tickets and 1 child ticket for £44 . 

Calculate the cost of one child ticket.

We can write simultaneous equations to solve this.

2a+3c=48 (Equation 1) 3a+c=44 (Equation 2)

Multiply equation 2 by 3 to make the coefficients of c equal: 9a+3c=132 (Equation 3)

Subtract equation 1 from equation 3: 7a= 84 a=12

Substitute a into equation 3: 3×12+c=44 36+c=44 c=8

The cost of an adult ticket is £12 and a child ticket is £8 .

Algebra questions KS4: graphs

13.  Which of these lines is parallel to the line 2y = x + 7

For two lines to be parallel, their gradient must be equal.

If we rearrange 2y=x+7 to make y the subject we get y=\frac{1}{2}x+\frac{7}{2}.

The gradient is \frac{1}{2}

14. Find the minimum value of the function f(x) = x^2+4x+5 .

To find the minimum value we need to complete the square.

The minimum value is 1. This occurs when (x+2) is 0.

15. The diagram shows the circle x^2+y^2=25 . The line is a tangent to the circle at the point (3,4) . Work out the equation of the line.

To work out the gradient of the line we need to work out the gradient of the normal.

We know that the normal goes through the points (0, 0) and (3, 4) so we can calculate the gradient: \frac{4-0}{3-0}=\frac{4}{3}.

The gradient of the tangent will be \frac{-3}{4}.

We can now use y=mx+c . We know the tangent goes through the point (3, 4) and that it’s gradient is \frac{-3}{4} .

Looking for more algebra questions and resources?

Third Space Learning’s free GCSE maths resource library contains detailed lessons with step-by-step instructions on how to solve algebra problems, as well as worksheets with algebra practice questions and more GCSE exam questions.

Take a look at the Algebra lessons today – more are added every week.

Looking for more KS3 and KS4 maths questions?

• 15 Simultaneous equations questions
• 15 Trigonometry questions
• 15 Ratio questions
• 15 Probability questions
• 15 Venn diagram questions
• 15 Pythagoras theorem questions
• Long division questions

Read more: Question Level Analysis Of Edexcel Maths Past Papers (Foundation)

DO YOU HAVE STUDENTS WHO NEED MORE SUPPORT IN MATHS?

Every week Third Space Learning’s specialist online maths tutors support thousands of students across hundreds of schools with weekly online 1 to 1 maths lessons designed to plug gaps and boost progress.

Since 2013 these personalised one to one lessons have helped over 150,000 primary and secondary students become more confident, able mathematicians.

Learn how tutors develop pupils’ maths fluency or request a personalised quote for your school to speak to us about your school’s needs and how we can help.

Related articles

15 Pythagoras Theorem Questions And Practice Problems (KS3 & KS4)

Fluent In Five: A Daily Arithmetic Resource For Secondary

15 Venn Diagram Questions And Practice Problems (KS3 & KS4): Harder GCSE Exam Style Questions Included

15 Simultaneous Equations Questions And Practice Problems (KS3 & KS4): Harder GCSE Exam Style Questions Included

FREE GCSE Maths Practice Papers (Edexcel, AQA & OCR)

8 sets of free exam papers written by maths teachers and examiners.

Each set of exam papers contains the three papers that your students will expect to find in their GCSE mathematics exam.

Privacy Overview

Get step-by-step solutions to your math problems

Try Math Solver

Get step-by-step explanations

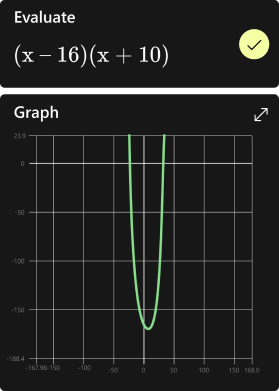
Graph your math problems

Practice, practice, practice

Get math help in your language

Math Solver

Geogebra math solver.

Get accurate solutions and step-by-step explanations for algebra and other math problems, while enhancing your problem-solving skills!

Algebraic Equations Questions

Algebraic equations questions with solutions are provided here to practice solving algebraic equations. An algebraic equation is a statement that equates two algebraic expressions .

The difference between an algebraic equation and an algebraic expression is:

A general form of an algebraic equation:

To learn the types of algebraic equations and how to solve them, click here .

Video Lesson on Solving Algebraic Equations

Algebraic Equations Questions with Solutions

Let us solve some questions on algebraic equations.

Question 1:

Solve for x: 2x + 22 = x + 1

2x + 22 = x + 1

⇒ 2x + 22 = x + 1

⇒ 2x – x = –22 + 1

Question 2:

Solve for x: x 2 – 8x – 33 = 0

x 2 – 8x – 33 = 0

⇒ x 2 – 11x + 3x – 33 = 0

⇒ (x – 11)(x + 3) = 0

⇒ x = 11 and x = 3

Refer: how to solve a quadratic equation ?

Question 3:

Solve: (5m – 3)/4 + (3m – 2)/5 = (m + 6)/7

\(\begin{array}{l}\frac{5m-3}{4}+\frac{3m-2}{5}=\frac{m+6}{7}\end{array} \)

\(\begin{array}{l}\Rightarrow\frac{25m-15}{20}+\frac{12m-8}{20}=\frac{m+6}{7}\end{array} \)

\(\begin{array}{l}\Rightarrow\frac{37m-23}{20}=\frac{m+6}{7}\end{array} \)

⇒ 259m – 161 = 20m + 120

⇒ 259m – 20m = 161 + 120

⇒ 239m = 281

⇒ m = 281/239.

Question 4:

The sum of two numbers is 82 and their product is 1456, find the two numbers.

Let the two numbers be x and y, then as per the question

⇒ y = 82 – x ………(i)

Again, x × y = 1456

Putting the value of y, we get

x × (82 – x) = 1456

⇒ 82x – x 2 = 1456

⇒ x 2 – 82x + 1456

⇒ x 2 – 26x – 56x + 1456

⇒ (x – 26)(x – 56) = 0

x = 26 and 56

∴ the two numbers are 26 and 56.

Question 5:

Solve: (y 2 – 4)/3 = 20.

(y 2 – 4)/3 = 20

⇒ y 2 – 4 = 60

⇒ y 2 = 60 + 4

⇒ y = –8 and 8

Question 6:

Solve the following system of algebraic equations:

3y = 4 + 4x

2x + y = 8 ….(i)

⇒ 4x – 3y = –4 ….(ii)

Multiply (i) by 2 on both sides, then subtracting (ii) from (i), we get

2y + 3y = 16 + 4

Putting the value of y in (i), we get x = 2.

∴ the solution of the given equations is x = 2 and y = 4

Question 7:

Find the values of x and y, if

\(\begin{array}{l}\frac{2}{x}+\frac{3}{y}=\frac{9}{xy}\:\:and\:\: \frac{4}{x}+\frac{9}{y}=\frac{21}{xy};x\neq0, y\neq0\end{array} \)

\(\begin{array}{l}\frac{2}{x}+\frac{3}{y}=\frac{9}{xy}\end{array} \)

= 3x + 2y = 9 ……..(i)

\(\begin{array}{l} \frac{4}{x}+\frac{9}{y}=\frac{21}{xy}\end{array} \)

= 9x + 4y = 21 ……..(ii)

Multiply (i) by 3 on both sides, then subtracting (ii) from (i), we get

6y – 4y = 27 – 21

Putting the value of y in (i), we get x = 1.

∴ the solution of the given equations is x = 1 and y = 3.

Question 8:

A man said, “Each of my sons has as many brothers as sisters and each of my daughters has twice as many brothers as sisters”. How many sons and daughters does the man have?

Let the man have x boys and y girls, then as per the question

⇒ x – y = 1 …..(i)

and 2(y – 1) = x

⇒ x – 2y = –1 …….(ii)

Subtracting (i) from (ii), we get

–2y + y = –1 –1

Putting the value of y in (i), we get x = 3.

∴ the man has 2 sons and 3 daughters.

Question 9:

A man bought 4 cows and 9 hens for ₹ 13400. If he sells the cows at 10% profit and hens at 20% profit, then he earns a total profit of ₹ 1880. What is the cost of a cow and a hen?

Let x be the cost of one cow and y be the cost of a hen.

Then 4x + 9y = 13400 ……(i)

Also, as there is 10% profit on selling cows and 20% profit on selling hens,

∴ 10/100 × 4x + 20/100 × 9y = 1880

⇒ 4x + 18y = 18800 ……(ii)

Subtracting equation (i) from (ii), we get

9y = 5400 ⇒ y = 600

Putting the value of y in (i), we get x = 2000

∴ the man bought a cow at ₹ 2000 and a hen at ₹ 600.

Question 10:

50 kg of an alloy of lead and tin contains 60% of lead. How much lead must be melted into it to make the alloy of 75% lead?

Let x kg lead is required to make the alloy contain 75% lead.

Now, the amount of lead in 50 kg of alloy = 50 × 60/100 = 30 kg

The weight of lead after melting x kg of lead = 30 + x

New weight of the alloy = 50 + x kg

Percentage of lead in the new alloy

(30 + x)/(50 + x) × 100% = 75%

⇒ (30 + x)/(50 + x) = 75/100

⇒ (30 + x)/(50 + x) = ¾

⇒ 4(30 + x) = 3(50 + x)

⇒ 120 + 4x = 150 + 3x

∴ 30 kg of lead is need to be melted into the alloy.

Recommended Videos

Practice Questions on Algebraic Equations

1. Solve the following:

(i) 1/(a + 2) + 3/(a + 23) = –4/(2a + 10)

(ii) (m + 2)/(m – 2) = 1

(iii) 4/x + 5y = 7 and 3/x + 4y = 5

(iv) 4√3x 2 + 5x – 2√3 = 0

2. If 2 a + 3 b = 17 and 2 a + 2 – 3 b + 1 = 5, then find the value of a and b.

3. The average of two numbers is 6 and four times the difference between them is 16. Find the numbers.

4. Find the area of a square whose perimeter is 240 cm.

Keep visiting BYJU’S to get more such Maths lessons in a simple, concise and easy to understand way. Also, register at BYJU’S – The Learning App to get complete assistance for Maths preparation with video lessons, notes, tips and other study materials.

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

• Algebra Test

Algebra Practice Test

• Algebra Test Guide
• Algebra Flash Cards

Test your knowledge of introductory Algebra with this Algebra practice exam. Whether you are studying for a school math test or looking to test your math skills, this free practice test will challenge your knowledge of algebra.

• Solve equations and inequalities
• Simplify expressions
• Factor polynomials
• Graph equations and inequalities
• Advanced solvers
• All solvers
• Arithmetics
• Determinant
• Percentages
• Scientific Notation
• Inequalities

What can QuickMath do?

QuickMath will automatically answer the most common problems in algebra, equations and calculus faced by high-school and college students.

• The algebra section allows you to expand, factor or simplify virtually any expression you choose. It also has commands for splitting fractions into partial fractions, combining several fractions into one and cancelling common factors within a fraction.
• The equations section lets you solve an equation or system of equations. You can usually find the exact answer or, if necessary, a numerical answer to almost any accuracy you require.
• The inequalities section lets you solve an inequality or a system of inequalities for a single variable. You can also plot inequalities in two variables.
• The calculus section will carry out differentiation as well as definite and indefinite integration.
• The matrices section contains commands for the arithmetic manipulation of matrices.
• The graphs section contains commands for plotting equations and inequalities.
• The numbers section has a percentages command for explaining the most common types of percentage problems and a section for dealing with scientific notation.

Math Topics

More solvers.

• Add Fractions
• Simplify Fractions

Solving Equations Practice Questions

Click here for questions, click here for answers.

equation, solve

GCSE Revision Cards

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2024

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Praxis Core Math

Course: praxis core math   >   unit 1.

• Algebraic properties | Lesson
• Algebraic properties | Worked example
• Solution procedures | Lesson
• Solution procedures | Worked example
• Equivalent expressions | Lesson
• Equivalent expressions | Worked example
• Creating expressions and equations | Lesson
• Creating expressions and equations | Worked example

Algebraic word problems | Lesson

• Algebraic word problems | Worked example
• Linear equations | Lesson
• Linear equations | Worked example
• Quadratic equations | Lesson
• Quadratic equations | Worked example

What are algebraic word problems?

What skills are needed.

• Translating sentences to equations
• Solving linear equations with one variable
• Evaluating algebraic expressions
• Solving problems using Venn diagrams

How do we solve algebraic word problems?

• Define a variable.
• Write an equation using the variable.
• Solve the equation.
• If the variable is not the answer to the word problem, use the variable to calculate the answer.

What's a Venn diagram?

• 7 + 10 − 13 = 4 ‍   brought both food and drinks.
• 7 − 4 = 3 ‍   brought only food.
• 10 − 4 = 6 ‍   brought only drinks.
• Your answer should be
• an integer, like 6 ‍  
• a simplified proper fraction, like 3 / 5 ‍  
• a simplified improper fraction, like 7 / 4 ‍  
• a mixed number, like 1   3 / 4 ‍  
• an exact decimal, like 0.75 ‍  
• a multiple of pi, like 12   pi ‍   or 2 / 3   pi ‍  
• (Choice A)   $ 4 ‍   A $ 4 ‍  
• (Choice B)   $ 5 ‍   B $ 5 ‍  
• (Choice C)   $ 9 ‍   C $ 9 ‍  
• (Choice D)   $ 14 ‍   D $ 14 ‍  
• (Choice E)   $ 20 ‍   E $ 20 ‍  
• (Choice A)   10 ‍   A 10 ‍  
• (Choice B)   12 ‍   B 12 ‍  
• (Choice C)   24 ‍   C 24 ‍  
• (Choice D)   30 ‍   D 30 ‍  
• (Choice E)   32 ‍   E 32 ‍  
• (Choice A)   4 ‍   A 4 ‍  
• (Choice B)   10 ‍   B 10 ‍  
• (Choice C)   14 ‍   C 14 ‍  
• (Choice D)   18 ‍   D 18 ‍  
• (Choice E)   22 ‍   E 22 ‍  

Things to remember

Want to join the conversation.

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

• Mathematicians
• Math Lessons
• Square Roots
• Math Calculators

Simple Algebra Problems – Easy Exercises with Solutions for Beginners

JUMP TO TOPIC

Understanding Algebraic Expressions

Breaking down algebra problems, solving algebraic equations, tackling algebra word problems, types of algebraic equations, algebra for different grades.

For instance, solving the equation (3x = 7) for (x) helps us understand how to isolate the variable to find its value.

I always find it fascinating how algebra serves as the foundation for more advanced topics in mathematics and science. Starting with basic problems such as ( $(x-1)^2 = [4\sqrt{(x-4)}]^2$ ) allows us to grasp key concepts and build the skills necessary for tackling more complex challenges.

So whether you’re refreshing your algebra skills or just beginning to explore this mathematical language, let’s dive into some examples and solutions to demystify the subject. Trust me, with a bit of practice, you’ll see algebra not just as a series of problems, but as a powerful tool that helps us solve everyday puzzles.

Simple Algebra Problems and Strategies

When I approach simple algebra problems, one of the first things I do is identify the variable.

The variable is like a placeholder for a number that I’m trying to find—a mystery I’m keen to solve. Typically represented by letters like ( x ) or ( y ), variables allow me to translate real-world situations into algebraic expressions and equations.

An algebraic expression is a mathematical phrase that can contain ordinary numbers, variables (like ( x ) or ( y )), and operators (like add, subtract, multiply, and divide). For example, ( 4x + 7 ) is an algebraic expression where ( x ) is the variable and the numbers ( 4 ) and ( 7 ) are terms. It’s important to manipulate these properly to maintain the equation’s balance.

Solving algebra problems often starts with simplifying expressions. Here’s a simple method to follow:

• Combine like terms : Terms that have the same variable can be combined. For instance, ( 3x + 4x = 7x ).
• Isolate the variable : Move the variable to one side of the equation. If the equation is ( 2x + 5 = 13 ), my job is to get ( x ) by itself by subtracting ( 5 ) from both sides, giving me ( 2x = 8 ).

With algebraic equations, the goal is to solve for the variable by performing the same operation on both sides. Here’s a table with an example:

Algebra word problems require translating sentences into equations. If a word problem says “I have six less than twice the number of apples than Bob,” and Bob has ( b ) apples, then I’d write the expression as ( 2b – 6 ).

Understanding these strategies helps me tackle basic algebra problems efficiently. Remember, practice makes perfect, and each problem is an opportunity to improve.

In algebra, we encounter a variety of equation types and each serves a unique role in problem-solving. Here, I’ll brief you about some typical forms.

Linear Equations : These are the simplest form, where the highest power of the variable is one. They take the general form ( ax + b = 0 ), where ( a ) and ( b ) are constants, and ( x ) is the variable. For example, ( 2x + 3 = 0 ) is a linear equation.

Polynomial Equations : Unlike for linear equations, polynomial equations can have variables raised to higher powers. The general form of a polynomial equation is ( $a_nx^n + a_{n-1}x^{n-1} + … + a_2x^2 + a_1x + a_0 = 0$ ). In this equation, ( n ) is the highest power, and ( $a_n$ ), ( $a_{n-1} $), …, ( $a_0$ ) represent the coefficients which can be any real number.

• Binomial Equations : They are a specific type of polynomial where there are exactly two terms. Like ($ x^2 – 4 $), which is also the difference of squares, a common format encountered in factoring.

To understand how equations can be solved by factoring, consider the quadratic equation ( $x^2$ – 5x + 6 = 0 ). I can factor this into ( (x-2)(x-3) = 0 ), which allows me to find the roots of the equation.

Here’s how some equations look when classified by degree:

Remember, identification and proper handling of these equations are essential in algebra as they form the basis for complex problem-solving.

In my experience with algebra, I’ve found that the journey begins as early as the 6th grade, where students get their first taste of this fascinating subject with the introduction of variables representing an unknown quantity.

I’ve created worksheets and activities aimed specifically at making this early transition engaging and educational.

6th Grade :

Moving forward, the complexity of algebraic problems increases:

7th and 8th Grades :

• Mastery of negative numbers: students practice operations like ( -3 – 4 ) or ( -5 $\times$ 2 ).
• Exploring the rules of basic arithmetic operations with negative numbers.
• Worksheets often contain numeric and literal expressions that help solidify their concepts.

Advanced topics like linear algebra are typically reserved for higher education. However, the solid foundation set in these early grades is crucial. I’ve developed materials to encourage students to understand and enjoy algebra’s logic and structure.

Remember, algebra is a tool that helps us quantify and solve problems, both numerical and abstract. My goal is to make learning these concepts, from numbers to numeric operations, as accessible as possible, while always maintaining a friendly approach to education.

I’ve walked through various simple algebra problems to help establish a foundational understanding of algebraic concepts. Through practice, you’ll find that these problems become more intuitive, allowing you to tackle more complex equations with confidence.

Remember, the key steps in solving any algebra problem include:

• Identifying variables and what they represent.
• Setting up the equation that reflects the problem statement.
• Applying algebraic rules such as the distributive property ($a(b + c) = ab + ac$), combining like terms, and inverse operations.
• Checking your solutions by substituting them back into the original equations to ensure they work.

As you continue to engage with algebra, consistently revisiting these steps will deepen your understanding and increase your proficiency. Don’t get discouraged by mistakes; they’re an important part of the learning process.

I hope that the straightforward problems I’ve presented have made algebra feel more manageable and a little less daunting. Happy solving!

• Pre Calculus
• Probability
• Sets & Set Theory
• Trigonometry

The resources on this page will hopefully help you teach AO2 and AO3 of the new GCSE specification - problem solving and reasoning.

This brief lesson is designed to lead students into thinking about how to solve mathematical problems. It features ideas of strategies to use, clear steps to follow and plenty of opportunities for discussion.

The PixiMaths problem solving booklets are aimed at "crossover" marks (questions that will be on both higher and foundation) so will be accessed by most students. The booklets are collated Edexcel exam questions; you may well recognise them from elsewhere. Each booklet has 70 marks worth of questions and will probably last two lessons, including time to go through answers with your students. There is one for each area of the new GCSE specification and they are designed to complement the PixiMaths year 11 SOL.

These problem solving starter packs are great to support students with problem solving skills. I've used them this year for two out of four lessons each week, then used Numeracy Ninjas as starters for the other two lessons.  When I first introduced the booklets, I encouraged my students to use scaffolds like those mentioned here , then gradually weaned them off the scaffolds. I give students some time to work independently, then time to discuss with their peers, then we go through it as a class. The levels correspond very roughly to the new GCSE grades.

Some of my favourite websites have plenty of other excellent resources to support you and your students in these assessment objectives.

@TessMaths has written some great stuff for BBC Bitesize.

There are some intersting though-provoking problems at Open Middle.

I'm sure you've seen it before, but if not, check it out now! Nrich is where it's at if your want to provide enrichment and problem solving in your lessons.

MathsBot  by @StudyMaths has everything, and if you scroll to the bottom of the homepage you'll find puzzles and problem solving too.

I may be a little biased because I love Edexcel, but these question packs are really useful.

The UKMT has a mentoring scheme that provides fantastic problem solving resources , all complete with answers.

I have only recently been shown Maths Problem Solving and it is awesome - there are links to problem solving resources for all areas of maths, as well as plenty of general problem solving too. Definitely worth exploring!

Solving Word Questions

With LOTS of examples!

In Algebra we often have word questions like:

Example: Sam and Alex play tennis.

On the weekend Sam played 4 more games than Alex did, and together they played 12 games.

How many games did Alex play?

How do we solve them?

The trick is to break the solution into two parts:

Turn the English into Algebra.

Then use Algebra to solve.

Turning English into Algebra

To turn the English into Algebra it helps to:

• Read the whole thing first
• Do a sketch if possible
• Assign letters for the values
• Find or work out formulas

You should also write down what is actually being asked for , so you know where you are going and when you have arrived!

Also look for key words:

Thinking Clearly

Some wording can be tricky, making it hard to think "the right way around", such as:

Example: Sam has 2 dollars less than Alex. How do we write this as an equation?

• Let S = dollars Sam has
• Let A = dollars Alex has

Now ... is that: S − 2 = A

or should it be: S = A − 2

or should it be: S = 2 − A

The correct answer is S = A − 2

( S − 2 = A is a common mistake, as the question is written "Sam ... 2 less ... Alex")

Example: on our street there are twice as many dogs as cats. How do we write this as an equation?

• Let D = number of dogs
• Let C = number of cats

Now ... is that: 2D = C

or should it be: D = 2C

Think carefully now!

The correct answer is D = 2C

( 2D = C is a common mistake, as the question is written "twice ... dogs ... cats")

Let's start with a really simple example so we see how it's done:

Example: A rectangular garden is 12m by 5m, what is its area ?

Turn the English into Algebra:

• Use w for width of rectangle: w = 12m
• Use h for height of rectangle: h = 5m

Formula for Area of a Rectangle : A = w × h

We are being asked for the Area.

A = w × h = 12 × 5 = 60 m 2

The area is 60 square meters .

Now let's try the example from the top of the page:

Example: Sam and Alex play Tennis. On the weekend Sam played 4 more games than Alex did, and together they played 12 games. How many games did Alex play?

• Use S for how many games Sam played
• Use A for how many games Alex played

We know that Sam played 4 more games than Alex, so: S = A + 4

And we know that together they played 12 games: S + A = 12

We are being asked for how many games Alex played: A

Which means that Alex played 4 games of tennis.

Check: Sam played 4 more games than Alex, so Sam played 8 games. Together they played 8 + 4 = 12 games. Yes!

A slightly harder example:

Example: Alex and Sam also build tables. Together they make 10 tables in 12 days. Alex working alone can make 10 in 30 days. How long would it take Sam working alone to make 10 tables?

• Use a for Alex's work rate
• Use s for Sam's work rate

12 days of Alex and Sam is 10 tables, so: 12a + 12s = 10

30 days of Alex alone is also 10 tables: 30a = 10

We are being asked how long it would take Sam to make 10 tables.

30a = 10 , so Alex's rate (tables per day) is: a = 10/30 = 1/3

Which means that Sam's rate is half a table a day (faster than Alex!)

So 10 tables would take Sam just 20 days.

Should Sam be paid more I wonder?

And another "substitution" example:

Example: Jenna is training hard to qualify for the National Games. She has a regular weekly routine, training for five hours a day on some days and 3 hours a day on the other days. She trains altogether 27 hours in a seven day week. On how many days does she train for five hours?

• The number of "5 hour" days: d
• The number of "3 hour" days: e

We know there are seven days in the week, so: d + e = 7

And she trains 27 hours in a week, with d 5 hour days and e 3 hour days: 5d + 3e = 27

We are being asked for how many days she trains for 5 hours: d

The number of "5 hour" days is 3

Check : She trains for 5 hours on 3 days a week, so she must train for 3 hours a day on the other 4 days of the week.

3 × 5 hours = 15 hours, plus 4 × 3 hours = 12 hours gives a total of 27 hours

Some examples from Geometry:

Example: A circle has an area of 12 mm 2 , what is its radius?

• Use A for Area: A = 12 mm 2
• Use r for radius

And the formula for Area is: A = π r 2

We are being asked for the radius.

We need to rearrange the formula to find the area

Example: A cube has a volume of 125 mm 3 , what is its surface area?

Make a quick sketch:

• Use V for Volume
• Use A for Area
• Use s for side length of cube
• Volume of a cube: V = s 3
• Surface area of a cube: A = 6s 2

We are being asked for the surface area.

First work out s using the volume formula:

Now we can calculate surface area:

An example about Money:

Example: Joel works at the local pizza parlor. When he works overtime he earns 1¼ times the normal rate. One week Joel worked for 40 hours at the normal rate of pay and also worked 12 hours overtime. If Joel earned $660 altogether in that week, what is his normal rate of pay?

• Joel's normal rate of pay: $N per hour
• Joel works for 40 hours at $N per hour = $40N
• When Joel does overtime he earns 1¼ times the normal rate = $1.25N per hour
• Joel works for 12 hours at $1.25N per hour = $(12 × 1¼N) = $15N
• And together he earned $660, so:

$40N + $(12 × 1¼N) = $660

We are being asked for Joel's normal rate of pay $N.

So Joel’s normal rate of pay is $12 per hour

Joel’s normal rate of pay is $12 per hour, so his overtime rate is 1¼ × $12 per hour = $15 per hour. So his normal pay of 40 × $12 = $480, plus his overtime pay of 12 × $15 = $180 gives us a total of $660

More about Money, with these two examples involving Compound Interest

Example: Alex puts $2000 in the bank at an annual compound interest of 11%. How much will it be worth in 3 years?

This is the compound interest formula:

So we will use these letters:

• Present Value PV = $2,000
• Interest Rate (as a decimal): r = 0.11
• Number of Periods: n = 3
• Future Value (the value we want): FV

We are being asked for the Future Value: FV

Example: Roger deposited $1,000 into a savings account. The money earned interest compounded annually at the same rate. After nine years Roger's deposit has grown to $1,551.33 What was the annual rate of interest for the savings account?

The compound interest formula:

• Present Value PV = $1,000
• Interest Rate (the value we want): r
• Number of Periods: n = 9
• Future Value: FV = $1,551.33

We are being asked for the Interest Rate: r

So the annual rate of interest is 5%

Check : $1,000 × (1.05) 9 = $1,000 × 1.55133 = $1,551.33

And an example of a Ratio question:

Example: At the start of the year the ratio of boys to girls in a class is 2 : 1 But now, half a year later, four boys have left the class and there are two new girls. The ratio of boys to girls is now 4 : 3 How many students are there altogether now?

• Number of boys now: b
• Number of girls now: g

The current ratio is 4 : 3

Which can be rearranged to 3b = 4g

At the start of the year there was (b + 4) boys and (g − 2) girls, and the ratio was 2 : 1

b + 4 g − 2 = 2 1

Which can be rearranged to b + 4 = 2(g − 2)

We are being asked for how many students there are altogether now: b + g

There are 12 girls !

And 3b = 4g , so b = 4g/3 = 4 × 12 / 3 = 16 , so there are 16 boys

So there are now 12 girls and 16 boys in the class, making 28 students altogether .

There are now 16 boys and 12 girls, so the ratio of boys to girls is 16 : 12 = 4 : 3 At the start of the year there were 20 boys and 10 girls, so the ratio was 20 : 10 = 2 : 1

And now for some Quadratic Equations :

Example: The product of two consecutive even integers is 168. What are the integers?

Consecutive means one after the other. And they are even , so they could be 2 and 4, or 4 and 6, etc.

We will call the smaller integer n , and so the larger integer must be n+2

And we are told the product (what we get after multiplying) is 168, so we know:

n(n + 2) = 168

We are being asked for the integers

That is a Quadratic Equation , and there are many ways to solve it. Using the Quadratic Equation Solver we get −14 and 12.

Check −14: −14(−14 + 2) = (−14)×(−12) = 168 YES

Check 12: 12(12 + 2) = 12×14 = 168 YES

So there are two solutions: −14 and −12 is one, 12 and 14 is the other.

Note: we could have also tried "guess and check":

• We could try, say, n=10: 10(12) = 120 NO (too small)
• Next we could try n=12: 12(14) = 168 YES

But unless we remember that multiplying two negatives make a positive we might overlook the other solution of (−14)×(−12).

Example: You are an Architect. Your client wants a room twice as long as it is wide. They also want a 3m wide veranda along the long side. Your client has 56 square meters of beautiful marble tiles to cover the whole area. What should the length of the room be?

Let's first make a sketch so we get things right!:

• the length of the room: L
• the width of the room: W
• the total Area including veranda: A
• the width of the room is half its length: W = ½L
• the total area is the (room width + 3) times the length: A = (W+3) × L = 56

We are being asked for the length of the room: L

This is a quadratic equation , there are many ways to solve it, this time let's use factoring :

And so L = 8 or −14

There are two solutions to the quadratic equation, but only one of them is possible since the length of the room cannot be negative!

So the length of the room is 8 m

L = 8, so W = ½L = 4

So the area of the rectangle = (W+3) × L = 7 × 8 = 56

There we are ...

... I hope these examples will help you get the idea of how to handle word questions. Now how about some practice?

• Share full article

Advertisement

Supported by

The Algebra Problem: How Middle School Math Became a National Flashpoint

Top students can benefit greatly by being offered the subject early. But many districts offer few Black and Latino eighth graders a chance to study it.

By Troy Closson

From suburbs in the Northeast to major cities on the West Coast, a surprising subject is prompting ballot measures, lawsuits and bitter fights among parents: algebra.

Students have been required for decades to learn to solve for the variable x, and to find the slope of a line. Most complete the course in their first year of high school. But top-achievers are sometimes allowed to enroll earlier, typically in eighth grade.

The dual pathways inspire some of the most fiery debates over equity and academic opportunity in American education.

Do bias and inequality keep Black and Latino children off the fast track? Should middle schools eliminate algebra to level the playing field? What if standout pupils lose the chance to challenge themselves?

The questions are so fraught because algebra functions as a crucial crossroads in the education system. Students who fail it are far less likely to graduate. Those who take it early can take calculus by 12th grade, giving them a potential edge when applying to elite universities and lifting them toward society’s most high-status and lucrative professions.

But racial and economic gaps in math achievement are wide in the United States, and grew wider during the pandemic. In some states, nearly four in five poor children do not meet math standards.

To close those gaps, New York City’s previous mayor, Bill de Blasio, adopted a goal embraced by many districts elsewhere. Every middle school would offer algebra, and principals could opt to enroll all of their eighth graders in the class. San Francisco took an opposite approach: If some children could not reach algebra by middle school, no one would be allowed to take it.

The central mission in both cities was to help disadvantaged students. But solving the algebra dilemma can be more complex than solving the quadratic formula.

New York’s dream of “algebra for all” was never fully realized, and Mayor Eric Adams’s administration changed the goal to improving outcomes for ninth graders taking algebra. In San Francisco, dismantling middle-school algebra did little to end racial inequities among students in advanced math classes. After a huge public outcry, the district decided to reverse course.

“You wouldn’t think that there could be a more boring topic in the world,” said Thurston Domina, a professor at the University of North Carolina. “And yet, it’s this place of incredibly high passions.”

“Things run hot,” he said.

In some cities, disputes over algebra have been so intense that parents have sued school districts, protested outside mayors’ offices and campaigned for the ouster of school board members.

Teaching math in middle school is a challenge for educators in part because that is when the material becomes more complex, with students moving from multiplication tables to equations and abstract concepts. Students who have not mastered the basic skills can quickly become lost, and it can be difficult for them to catch up.

Many school districts have traditionally responded to divergent achievement levels by simply separating children into distinct pathways, placing some in general math classes while offering others algebra as an accelerated option. Such sorting, known as tracking, appeals to parents who want their children to reach advanced math as quickly as possible.

But tracking has cast an uncomfortable spotlight on inequality. Around a quarter of all students in the United States take algebra in middle school. But only about 12 percent of Black and Latino eighth graders do, compared with roughly 24 percent of white pupils, a federal report found .

“That’s why middle school math is this flashpoint,” said Joshua Goodman, an associate professor of education and economics at Boston University. “It’s the first moment where you potentially make it very obvious and explicit that there are knowledge gaps opening up.”

In the decades-long war over math, San Francisco has emerged as a prominent battleground.

California once required that all eighth graders take algebra. But lower-performing middle school students often struggle when forced to enroll in the class, research shows. San Francisco later stopped offering the class in eighth grade. But the ban did little to close achievement gaps in more advanced math classes, recent research has found.

As the pendulum swung, the only constant was anger. Leading Bay Area academics disparaged one another’s research . A group of parents even sued the district last spring. “Denying students the opportunity to skip ahead in math when their intellectual ability clearly allows for it greatly harms their potential for future achievement,” their lawsuit said.

The city is now back to where it began: Middle school algebra — for some, not necessarily for all — will return in August. The experience underscored how every approach carries risks.

“Schools really don’t know what to do,” said Jon R. Star, an educational psychologist at Harvard who has studied algebra education. “And it’s just leading to a lot of tension.”

In Cambridge, Mass., the school district phased out middle school algebra before the pandemic. But some argued that the move had backfired: Families who could afford to simply paid for their children to take accelerated math outside of school.

“It’s the worst of all possible worlds for equity,” Jacob Barandes, a Cambridge parent, said at a school board meeting.

Elsewhere, many students lack options to take the class early: One of Philadelphia’s most prestigious high schools requires students to pass algebra before enrolling, preventing many low-income children from applying because they attend middle schools that do not offer the class.

In New York, Mr. de Blasio sought to tackle the disparities when he announced a plan in 2015 to offer algebra — but not require it — in all of the city’s middle schools. More than 15,000 eighth graders did not have the class at their schools at the time.

Since then, the number of middle schools that offer algebra has risen to about 80 percent from 60 percent. But white and Asian American students still pass state algebra tests at higher rates than their peers.

The city’s current schools chancellor, David Banks, also shifted the system’s algebra focus to high schools, requiring the same ninth-grade curriculum at many schools in a move that has won both support and backlash from educators.

And some New York City families are still worried about middle school. A group of parent leaders in Manhattan recently asked the district to create more accelerated math options before high school, saying that many young students must seek out higher-level instruction outside the public school system.

In a vast district like New York — where some schools are filled with children from well-off families and others mainly educate homeless children — the challenge in math education can be that “incredible diversity,” said Pedro A. Noguera, the dean of the University of Southern California’s Rossier School of Education.

“You have some kids who are ready for algebra in fourth grade, and they should not be denied it,” Mr. Noguera said. “Others are still struggling with arithmetic in high school, and they need support.”

Many schools are unequipped to teach children with disparate math skills in a single classroom. Some educators lack the training they need to help students who have fallen behind, while also challenging those working at grade level or beyond.

Some schools have tried to find ways to tackle the issue on their own. KIPP charter schools in New York have added an additional half-hour of math time to many students’ schedules, to give children more time for practice and support so they can be ready for algebra by eighth grade.

At Middle School 50 in Brooklyn, where all eighth graders take algebra, teachers rewrote lesson plans for sixth- and seventh-grade students to lay the groundwork for the class.

The school’s principal, Ben Honoroff, said he expected that some students would have to retake the class in high school. But after starting a small algebra pilot program a few years ago, he came to believe that exposing children early could benefit everyone — as long as students came into it well prepared.

Looking around at the students who were not enrolling in the class, Mr. Honoroff said, “we asked, ‘Are there other kids that would excel in this?’”

“The answer was 100 percent, yes,” he added. “That was not something that I could live with.”

Troy Closson reports on K-12 schools in New York City for The Times. More about Troy Closson

33 Math Puzzles (with Answers) to Test Your Smarts

M ath is not everyone's favorite, understandably. Hours of math homework and difficult equations can make anyone sour on the subject. But when math problems are outside of a school setting with no time limit, and there's a more whimsical concept than just finding x, they can be great activities for kids. (And adults, of course!) These math puzzles test your brain and critical-thinking skills and provide some constructive, educational fun.

Math riddles  and puzzles come in plenty of different varieties. Some more straightforward number puzzles require calculations to find the solution. Others are more like logic puzzles and challenge you to look for a pattern. Still, others present their brain teasers through pictures, making them great for visual learners. From Reader's Digest 's Mind Stretchers books, these math puzzles have a bit of everything!

Get  Reader's Digest' s  Read Up newsletter for more puzzles, pets, humor, travel, tech and fun facts all week long.

Math puzzles for kids

Symbol sums.

Can you make this equation correct using three of these four symbols?

+ – x  ÷

Order of operations doesn't apply, and no fractions or negative numbers are involved.

Number cube

Which number should replace the question mark?

Answer:  9

Which figure (1-6) is not colored correctly?

Answer : 6—it should be yellow.

Safe code 1

To open this safe, you have to replace the question marks with the correct figures. You can find this figure by determining the pattern behind the numbers shown.

Answer : 1 and 4. They're arranged in groups of two-digit numbers, all ending in 7 and ascending in both rows. Was this a hard math problem , or did you get the answer right?

Safe code 2

To open this safe, you have to replace the question marks with the correct figures. You can find these figures by determining the pattern behind the numbers shown.

Answer : 1 and 2. Every number in the bottom row is the number above it minus 3.

How many points does Archer B score knowing that the total score of Archer A is 55 and that different points are earned in the ten zones in ascending value toward the center?

Answer : 30 points. The outer zone is worth 1 point, then 2, 3, etc. The center is worth 10 points. 5 + 8 + 8 + 9 = 30.

Which pins must be knocked over to score exactly 100 points? (Hint: There are three!)

Answer : 13, 39 and 48.

Number puzzles

Pop numbers.

Answer: 4. The sum of the stamps of the same color combinations always equals 10. 1 + 9, 10 + 0, 3 + 7, and 6 + 4.

A bad year?

Which year does not belong on the chalkboard?

Answer: 1967. All the other years are formed with the same figures.

Each firework (A-F) contains 6 stars. Which firework has not been launched, knowing that each gives off 1, 2 or 3 stars of its corresponding color?

Answer : Firework C. There is a total of 9 yellow stars in the fireworks, but there are only 6 in the air. Do the firework math (9 – 6 = 3) and you'll find that 3 yellow stars have not been launched yet.

Which number should replace the question mark to form accurate equations, knowing that three numbers are shown per row (i.e. two of the numbers form a two-digit number)?

Answer : 6. Read every row as follows:

(3 + 2) x 2 = 10

(1 + 9) x 2 = 20

(0 + 8) x 2 = 16

(7 + 5) x 2 = 24

Which numbers should replace the question marks?

Answer : 563412. All the other ticket numbers are combinations of the numbers 12, 34 and 56, and 563412 is the last possible combination of these numbers.

Against the clock

The winner has run the distance in 15 seconds, the second in 21 seconds, etc. How many seconds will it take the sixth athlete to cross the line?

Answer : 39 seconds. This is the formula: 15 + (1 + 5) = 21; 21 + (2 + 1) = 24; 24 + (2 + 4) = 30; 30 + (3 + 0) = 33; 33 + (3 + 3) = 39.

Want to conquer some verbal trickery next? Try solving the viral numbers on a clock  riddle.

Credit rating

Which number is missing on the bottom credit card?

Answer : 8. The number formed by the two first digits is always doubled. 12, 24, 48, 96, 192 on the top card and 23, 46, 92, 184, 368 on the bottom card.

Missing script

Which number should replace the question mark, knowing that two-digit numbers are always shown?

Answer : 6. Read from left to right as a series of numbers that are always divided by four (or by two if you alternate between the top and bottom rows). 96 ÷ 4 = 24; 24 ÷ 4 = 6 (or 06); 48 ÷ 4 = 12.

Answer : 3. The numbers under the line are the average of the three numbers in the column above.

Math logic puzzles

Which team (A-E) will win the competition if the logic of this diagram is continued?

Answer: Team C. The order of the weakest to the strongest team is: D, A, E, B, C. The final match is played between C and B.

Safe code 3

To open this safe, you have to replace the question mark with the correct figure. You can find this figure by determining the logical method behind the numbers shown. These methods can include calculation, inversion, repetition, chronological succession or forming ascending and descending series.

Answer : 6. They're arranged in groups of two-digit numbers; you add 8 to the top two-digit number (75, 34, 68) to get the bottom number (83, 42, 76).

Keeping score

Which digit should replace the question mark in the score?

Answer : 6. The difference in the scores forms the following series: –2, +4, –6, +8. Alternating per column you also see the following two series: 7, 14, 21, 28; 9, 18, 27, 36.

Here's a challenging riddle : How much energy will the newest solar panel generate?

Answer : 04.96 V. The number before the decimal point is the same as the number of columns per panel, and the number after the decimal point is the same as the number of cells.

This is a number puzzle kind of like sudoku . Fill in the 5 x 5 grid with the numbers from 1 to 5 once per row and column, while following the greater than/less than symbols shown. There is only one valid solution that can be reached through logic and clear thinking alone!

Shooting hoops

A point is scored when the ball lands on an orange square. Give the coordinates of the last square that should be orange.

Answer : 6F. Points are scored on intersections where the number corresponds with the letter's place in the alphabet.

Which cream percentage should replace the question mark?

Answer : 54. The percentages consist of all numbers from 0 to 9, with the larger number first.

Knowing that there is a logical connection between the temperature and wind direction, which night temperature should replace the question mark? (Hint: It's "time" for some hard math puzzles.)

Answer : 11. Replace the compass rose with a clock on military time. The red tip of the compass needle points to the hour in the afternoon from 13 to 24 (midnight) and corresponds with the day temperature. The gray tip points to the hour in the morning from 1 to noon and is the night temperature.

Picture math puzzles

Do the math.

Enter numbers in each row and column to arrive at the end totals. Only numbers 1 through 9 are used, and each only once.

Answer: 

Tricky triangles

How many triangles can you see?

Answer : 23

If you got that right, see if you can correctly identify the number of triangles in this  puzzle .

How many spots should replace the question mark on the domino?

Answer : 6 spots. The dominoes are on an imaginary grid and the number of spots corresponds to the domino's spot on the grid. The grid contains alternating rows with numbers 4, 5, 4, 5, 4, 5, 4, 5 and the numbers 3, 6, 3, 6, 3, 6, 3, 6.

Which weight (A-D) should replace the question mark so that the scale is in balance?

Answer : B. A = B + C + D, C = B + D, A = 3D. So 3D = 2B + 2D, 3D – 2D = 2B, so D = 2B.

Berry puzzling

How many unripe berries are missing on the last branch?

Answer: 6 berries. The next branch always contains just as many unripe berries as ripe berries on the previous branch.

Here's a visual puzzle for you: Which flower branch (1-6) does not belong?

Answer : Flower branch 2. The top flower of all the other branches has just as many petals as flowers on the branch.

Losing marbles

Which marble (1-6) should replace the question mark?

Answer : Marble 3. All non-purple marbles are in groups of five and form an angle.

Which shape (1-6) contains more white than black?

Answer : Shape 3. All the others contain equal portions of each.

Symbol signs

Which symbol (1-6) is missing a line?

Answer : Symbol 4. From left to right, each symbol has one more line.

For more challenging puzzles…

Purchase your own copy of  Mind Stretchers  for crosswords, word searches, trivia, logic puzzles and more.

Why trust us

Reader’s Digest is known for our humor and brain games , including quizzes, puzzles, riddles, word games, trivia, math, pattern and logic puzzles, guessing games, crosswords, rebus, hidden objects and spot-the-difference challenges. We’ve earned prestigious ASME awards for our entertainment content and have produced dozens of brain-teaser books , including Word Searches , Word Power , Use Your Words , Fun Puzzles and Brain Ticklers , Mind Stretchers , Ultimate Christmas Puzzles and more. Our 10 published volumes of Mind Stretchers were edited by Allen D. Bragdon, founder of The Brainwaves Center and editor of Games  magazine. Read more about our team , our contributors and our editorial policies .

The post 33 Math Puzzles (with Answers) to Test Your Smarts appeared first on Reader's Digest .

• Today's news
• Reviews and deals
• Climate change
• 2024 election
• Fall allergies
• Health news
• Mental health
• Sexual health
• Family health
• So mini ways
• Unapologetically
• Buying guides

Entertainment

• How to Watch
• My watchlist
• Stock market
• Biden economy
• Personal finance
• Stocks: most active
• Stocks: gainers
• Stocks: losers
• Trending tickers
• World indices
• US Treasury bonds
• Top mutual funds
• Highest open interest
• Highest implied volatility
• Currency converter
• Basic materials
• Communication services
• Consumer cyclical
• Consumer defensive
• Financial services
• Industrials
• Real estate
• Mutual funds
• Credit cards
• Balance transfer cards
• Cash back cards
• Rewards cards
• Travel cards
• Online checking
• High-yield savings
• Money market
• Home equity loan
• Personal loans
• Student loans
• Options pit
• Fantasy football
• Pro Pick 'Em
• College Pick 'Em
• Fantasy baseball
• Fantasy hockey
• Fantasy basketball
• Download the app
• Daily fantasy
• Scores and schedules
• GameChannel
• World Baseball Classic
• Premier League
• CONCACAF League
• Champions League
• Motorsports
• Horse racing
• Newsletters

New on Yahoo

• Privacy Dashboard

The Algebra Problem: How Middle School Math Became a National Flashpoint

From suburbs in the Northeast to major cities on the West Coast, a surprising subject is prompting ballot measures, lawsuits and bitter fights among parents: algebra.

Students have been required for decades to learn to solve for the variable x, and to find the slope of a line. Most complete the course in their first year of high school. But top-achievers are sometimes allowed to enroll earlier, typically in eighth grade.

The dual pathways inspire some of the most fiery debates over equity and academic opportunity in American education.

Sign up for The Morning newsletter from the New York Times

Do bias and inequality keep Black and Latino children off the fast track? Should middle schools eliminate algebra to level the playing field? What if standout pupils lose the chance to challenge themselves?

The questions are so fraught because algebra functions as a crucial crossroads in the education system.

Students who fail it are far less likely to graduate. Those who take it early can take calculus by 12th grade, giving them a potential edge when applying to elite universities and lifting them toward society’s most high-status and lucrative professions.

But racial and economic gaps in math achievement are wide in the United States, and grew wider during the pandemic. In some states, nearly 4 in 5 poor children do not meet math standards.

To close those gaps, New York City’s previous mayor, Bill de Blasio, adopted a goal embraced by many districts elsewhere. Every middle school would offer algebra, and principals could opt to enroll all of their eighth graders in the class.

San Francisco took an opposite approach: If some children could not reach algebra by middle school, no one would be allowed to take it.

The central mission in both cities was to help disadvantaged students. But solving the algebra dilemma can be more complex than solving the quadratic formula.

New York’s dream of “algebra for all” was never fully realized, and Mayor Eric Adams’ administration changed the goal to improving outcomes for ninth graders taking algebra. In San Francisco, dismantling middle-school algebra did little to end racial inequities among students in advanced math classes. After a huge public outcry, the district decided to reverse course.

“You wouldn’t think that there could be a more boring topic in the world,” said Thurston Domina, a professor at the University of North Carolina. “And yet, it’s this place of incredibly high passions.”

“Things run hot,” he said.

In some cities, disputes over algebra have been so intense that parents have sued school districts, protested outside mayors’ offices and campaigned for the ouster of school board members.

Teaching math in middle school is a challenge for educators in part because that is when the material becomes more complex, with students moving from multiplication tables to equations and abstract concepts. Students who have not mastered the basic skills can quickly become lost, and it can be difficult for them to catch up.

Many school districts have traditionally responded to divergent achievement levels by simply separating children into distinct pathways, placing some in general math classes while offering others algebra as an accelerated option. Such sorting, known as tracking, appeals to parents who want their children to reach advanced math as quickly as possible.

But tracking has cast an uncomfortable spotlight on inequality. Around a quarter of all students in the United States take algebra in middle school. But only about 12% of Black and Latino eighth graders do, compared with roughly 24% of white pupils, a federal report found.

“That’s why middle school math is this flashpoint,” said Joshua Goodman, an associate professor of education and economics at Boston University. “It’s the first moment where you potentially make it very obvious and explicit that there are knowledge gaps opening up.”

In the decades-long war over math, San Francisco has emerged as a prominent battleground.

California once required that all eighth graders take algebra. But lower-performing middle school students often struggle when forced to enroll in the class, research shows. San Francisco later stopped offering the class in eighth grade. But the ban did little to close achievement gaps in more advanced math classes, recent research has found.

As the pendulum swung, the only constant was anger. Leading Bay Area academics disparaged one another’s research. A group of parents even sued the district last spring. “Denying students the opportunity to skip ahead in math when their intellectual ability clearly allows for it greatly harms their potential for future achievement,” their lawsuit said.

The city is now back to where it began: Middle school algebra — for some, not necessarily for all — will return in August. The experience underscored how every approach carries risks.

“Schools really don’t know what to do,” said Jon R. Star, an educational psychologist at Harvard who has studied algebra education. “And it’s just leading to a lot of tension.”

In Cambridge, Massachusetts, the school district phased out middle school algebra before the pandemic. But some argued that the move had backfired: Families who could afford to simply paid for their children to take accelerated math outside school.

“It’s the worst of all possible worlds for equity,” Jacob Barandes, a Cambridge parent, said at a school board meeting.

Elsewhere, many students lack options to take the class early: One of Philadelphia’s most prestigious high schools requires students to pass algebra before enrolling, preventing many low-income children from applying because they attend middle schools that do not offer the class.

In New York, de Blasio sought to tackle the disparities when he announced a plan in 2015 to offer algebra — but not require it — in all of the city’s middle schools. More than 15,000 eighth graders did not have the class at their schools at the time.

Since then, the number of middle schools that offer algebra has risen to about 80% from 60%. But white and Asian American students still pass state algebra tests at higher rates than their peers.

The city’s schools chancellor, David Banks, also shifted the system’s algebra focus to high schools, requiring the same ninth-grade curriculum at many schools in a move that has won support and backlash from educators.

And some New York City families are still worried about middle school. A group of parent leaders in Manhattan recently asked the district to create more accelerated math options before high school, saying that many young students must seek out higher-level instruction outside the public school system.

In a vast district like New York — where some schools are filled with children from well-off families and others mainly educate homeless children — the challenge in math education can be that “incredible diversity,” said Pedro A. Noguera, the dean of the University of Southern California’s Rossier School of Education.

“You have some kids who are ready for algebra in fourth grade, and they should not be denied it,” Noguera said. “Others are still struggling with arithmetic in high school, and they need support.”

Many schools are unequipped to teach children with disparate math skills in a single classroom. Some educators lack the training they need to help students who have fallen behind, while also challenging those working at grade level or beyond.

Some schools have tried to find ways to tackle the issue on their own. KIPP charter schools in New York have added an additional half-hour of math time to many students’ schedules, to give children more time for practice and support so they can be ready for algebra by eighth grade.

At Middle School 50 in Brooklyn, where all eighth graders take algebra, teachers rewrote lesson plans for sixth- and seventh-grade students to lay the groundwork for the class.

The school’s principal, Ben Honoroff, said he expected that some students would have to retake the class in high school. But after starting a small algebra pilot program a few years ago, he came to believe that exposing children early could benefit everyone — as long as students came into it well prepared.

Looking around at the students who were not enrolling in the class, Honoroff said, “we asked, ‘Are there other kids that would excel in this?’”

“The answer was 100%, yes,” he added. “That was not something that I could live with.”

c.2024 The New York Times Company

Recommended Stories

Mortgage rates today, may 28, 2024: it could be a good time to buy.

These are today's mortgage rates. Home inventory is up, and mortgage rates are down. This could be a good time to start house shopping. Lock in your rate today.

Savings interest rates today, May 28, 2024 (top rate at 5.15%)

Savings interest rates available today are well above historical norms. Find out where to get the best cd rates.

CD rates today, May 28, 2024 (top rate at 5.15% APY)

CD rates available today are well above historical norms. Find out where to get the best cd rates.

More neobanks are becoming mobile networks — and Nubank wants a piece of the action

Nubank is taking its first tentative steps into the mobile network realm, as the NYSE-traded Brazilian neobank rolls out an eSIM (embedded SIM) service for travelers. The service will give customers access to 10GB of free roaming internet in more than 40 countries without having to switch out their own existing physical SIM card or eSIM. The launch comes shortly after news first emerged that Brazil's National Telecommunications Agency (ANATEL) had quietly greenlit plans for Nubank to become a mobile virtual network operator (MVNO) in partnership with wireless giant Claro.

Jamie Dimon's retirement talk puts new spotlight on key JPMorgan deputies

Jamie Dimon made it clear that he sees an end to his time as boss of the biggest US bank, putting a new spotlight on key deputies considered front runners for his job. 'It's a two-woman race.'

Fixed vs. variable expenses: Key differences and how to budget for each

Understanding the difference between fixed expenses and variable expenses is key to proper budgeting. See examples of both and learn how to plan for them.

Adani looks to battle Reliance, Walmart in India's e-commerce, payments race, report says

India's energy and infrastructure giant Adani Group is plotting a move into digital payments and e-commerce, according to a Financial Times report, as the conglomerate seeks to diversify its portfolio and compete with Mukesh Ambani's Reliance, Amazon, and Walmart's Flipkart and PhonePe. Adani is considering applying for a license to operate on India's Unified Payments Interface (UPI) and is also finalizing plans for a co-branded credit card with banks, the report said. UPI is a public digital payments network that has become the most popular way Indians transact online.

'Millionaire Mission' author discusses wealth building: 'an incredibly optimistic time'

Becoming a millionaire is not an out-of-reach dream if you save automatically and consistently, author says.

The Dragon Quest 3 HD-2D remake is coming to Switch, Xbox Series X/S, PS5 and PC

After three years of largely staying silent about the Dragon Quest 3 HD-2D remake, Square Enix has revealed the platforms it's coming to. The publisher also suggested that the remake is coming soon.

Summer's calling! This comfy floating recliner is like a 'La-Z-Boy for the pool' — and it's just $30

Alright kids, outta the water — it's adult swim (er, lounge) time.

Ronald Acuña Jr. out for the year, Orioles mop the White Sox & Birmingham-Southern makes College World Series

Jake Mintz & Jordan Shusterman talk about the season-ending injury to Ronald Acuña Jr. and where the Braves go from here, the Orioles mopping the White Sox and Birmingham–Southern College Panthers making the College World Series despite their school shutting down.

How to write a standout cover letter

One way to grab the attention of hiring managers in a competitive job market is to write a captivating cover letter, according to top career coaches.

Junkyard Gem: Customized 1994 Chevrolet Caprice Classic LS Sedan

A 1994 Chevrolet Caprice sedan with custom paint and bodywork, found in a Colorado self-service wrecking yard.

Onyx Motorbikes was in trouble -- and then its 37-year-old owner died

James Khatiblou, the owner and CEO of Onyx Motorbikes, was watching his e-bike startup fall apart. Onyx was being evicted from its warehouse in El Segundo, Los Angeles. A shipment of around 100 CTY2 dirt bikes from Chinese supplier Suzhou Jindao was delayed, and customers were starting to demand refunds – a major problem considering Khatiblou already owed both lenders and shareholders a lot of money.

Amazon Memorial Day sale: We found the 40+ best deals on Apple, Bissell, Vizio and more

Save up to 80% on everything from vacuums and tech finds to outdoor essentials for summer.

Wall Street is getting even more bullish on stocks

Wall Street is growing increasingly optimistic as the stock market rally rolls on.

Genesis Neolun concept reportedly becoming GV90 electric SUV

Genesis will reportedly turn the Neolun concept into a GV90 flagship electric SUV due in 2026, just ahead of launching a second-gen GV80 Electrified.

Apple's 16-inch MacBook Pro M3 Max is $250 off

Amazon and B&H are running sales on Apple's 2023 MacBook Pro M3 Max.

CD rates today, May 27, 2024 (earn up to 5.15% APY)

Compare the best CD rates available today vs. the national average.

NBA playoffs: Luka Dončić, Mavericks power past Anthony Edwards to take a 3-0 lead over Timberwolves

The Mavericks are now just one win away from their first NBA Finals trip since 2011.