problem solving involving parabola

Parabola in Real Life

Real world applications and problems

Practice Problems

Below is a picture of a rainbow that makes a perfect parabola . What is the vertex of the parabola ?

Vertex of parabola is (0,40)

For the helicopter to fly above the rainbow parabola, how high must the copter fly? (In other words what is the maximum value of the parabola)

The helicopter must be above 40.

This real is simply a real world application of how to find the vertex of a parabola

Joseph threw a whiffle ball out of a window that is four units high. The position of the waffle ball is determined by the parabola y = -x² + 4. At how many feet from the building does the ball hit the ground?

The ball lands at the solution of this quadratic equation . There are two solutions. One at 2 and the other at − 2. This picture assumes that Joseph threw the ball to the right so that the whiffle balls lands at 2

You can solve this quadratic by factoring or by using the quadratic formula

Down in the street, Eric caught the ball and then he ran to 10 feet away from the base of the building. Eric throws the ball so that its highest point is where the x is on the first floor. What equation represents the path of the ball that Eric threw?

The ball lands at the solution of this quadratic equation . There are two solutions. One at 2 and the other at − 2. This picture assumes that Joseph threw the ball to the right so that the whiffle balls lands at 1.

A ball is dropped from a height of 36 feet. The quadratic equation d = -t² + 36 provides the distance, d, of the ball, after t seconds. After how many seconds, does the ball hit the ground?

The ball hits the ground at d = 0. To find the value of t at this point we must solve this quadratic equation.

0 = −t² + 36 t² = 36 t = 6

A ball is dropped from a height of 60 feet. The quadratic equation d = −5t² + 60 provides the distance, d, of the ball, after t seconds. After how many seconds, does the ball hit the ground?

We want to find when d=0, which represents the moment when the ball hits the ground.

d = 0, when 0 = -5t² +60 5t² = 60 t² = 60 ÷5 = 12

$$ \sqrt{12} \approx 3.5 $$

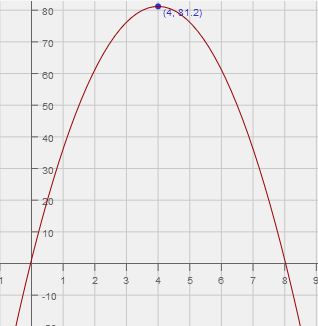
Find the height of the projectile 4 seconds after it is launched.

Identify all of the occurrences of 't' and substitute the input in

$$ h( {\color{blue} t} ) = -5 {\color{blue} t} ^2 + 41 {\color{blue}t} + 1.2 \\ h( {\color{blue}4} ) = -5 \cdot {\color{blue}4}^2 + 40 \cdot {\color{blue} 4} + 1.2 $$

Compute result

$$ h( {\color{blue} 4}) = -5 \cdot {\color{blue} 4}^2 + 40 \cdot {\color{blue} 4} + 1.2 \\ h( {\color{blue} 4}) = {\color{red} 81.2} $$

$$ h({\color{blue} input}) = {\color{red} output} \\ h({\color{blue} 4} ) = {\color{red} 81.2} $$

Here is a picture of graph of projectile's path with the point $$ ({\color{blue} t}, {\color{red} h(t)}) ({\color{blue} 4}, {\color{red} 81.2}) $$

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!

Popular pages @ mathwarehouse.com.

Free Mathematics Tutorials

Parabola Questions and Problems with Detailed Solutions

Parabola problems with answers and detailed solutions , in the bottom of the page, are presented.

Questions and Problems

• Find the x and y intercepts, the vertex and the axis of symmetry of the parabola with equation \( y = - x^2 + 2 x + 3 \)?
• What are the points of intersection of the line with equation \( 2x + 3y = 7 \) and the parabola with equation \( y = - 2 x^2 + 2 x + 5\)?
• Find the points of intersection of the two parabolas with equation \( y = -(x - 3)^2 + 2\) and \( y = x^2 - 4x + 1\).
• Find the equation of the parabola \( y = 2 x^2 + b x + c\) that passes through the points \( (-1,-5)\) and \( (2,10)\).
• What is the equation of the parabola with x intercepts at \( x = 2\) and \( x = -3\), and a y - intercept at \( y = 5\)?
• Find the equation of the parabola \( y = a x^2 + b x + c \) that passes through the points \( (0,3) \) , \( (1,-4)\) and \( (-1 , 4)\).
• Find the equation of the parabola, with vertical axis of symmetry, which is tangent to the line \( y = 3 \) at \( x = -2 \) and its graph passes through the point \((0,5) \ ).
• For what value of the slope m is the line, of equation \( y = m x - 3 \), tangent to the parabola of equation \( y = 3 x^2 - x \)?
• For what values of parameter b does the line of equation \( y = 2 x + b \) intersect the parabola of equation \( y = - x^2 - 2 x + 1\) in two points?
• Find the equation \( y = a x^2 + x\) of the tangent parabola to the line of equation \( y = 3 x + 1\).
• Shift the graph of the parabola \( y = x^2 \) to the left 3 units, then reflect the resulting graph in the x-axis, and then shift it up 4 units. What is the equation of the new parabola after these transformations?
• What transformations are needed to transform the graph of the parabola \( y = x^2 \) into the graph of the parabola \( y = - x^2 + 4 x + 6 \)?

Solutions to previous questions and problems

• The points \((-1,-5)\) and \((2,10) \) are on the graph of the parabola \( y = 2 x^2 + b x + c\), therefore. \( -5 = 2 (-1)^2 + b (-1) + c\) \( 10 = 2 (2)^2 + b (2) + c\) Rewrite the above system in b and c in standard form. \( - b + c = - 7\) \( 2b + c = 2\) Solve the above system of equations to obtain: \( c = - 4 \) and \( b = 3\) Equation of the parabola that passes through the points \( (-1,-5)\) and \( (2,10)\) is: \( y = 2 x^2 + b x + c = 2 x^2 + 3 x - 4\) Use a graph plotter to check your answer by graphing \( y = 2 x^2 + 3 x - 4 \)   and   Check that the graph passes through the points \( (-1,-5) \) and \((2,10)\).
• The equation of a parabola with x-intercepts at \( x = 2 \) and \( x = -3 \) can be written as the product of two factors whose zeros are the x-intercepts as follows: \( y = a(x - 2)(x + 3) \) We now use the y-intercept at (0, 5), which is a point through which the parabola passes, to write: \( 5 = a(0 - 2)(0 + 3) \) Solve for \(a\) \( a = - 5 / 6 \) Equation: \( y = (-5/6)(x - 2)(x + 3)\) Graph \( y = (-5/6)(x - 2)(x + 3)\) and verify that the graph has an x-intercept at \( x = 2 , x = -3 \) and an x-intercept at y in \( y = 5\).
• The points \( (0,3), (1,-4) \) and \( (-1,4) \) lie on the graph of the parabola \( y = a x^2 + b x + c \) and are therefore solutions to the equation of the parabola. Therefore, we write the system of 3 equations as follows: The point \( (0,3) \) gives the equation: \( 3 = a (0)^2 + b (0) + c \quad (I) \) The point \( (1,-4) \) gives the equation: \( - 4 = a (1)^2 + b (1) + c \quad (II) \) The point \( (-1,4) \) gives the equation: \( 4 = a (-1)^2 + b (-1) + c \quad (III) \) Equation (I) gives: \( c = 3 \) Substitute 3 for c in equations (II) and (III) \( a + b = -7 \) \( a - b = 1 \) Solve the system in a and b \( a = - 3 \) and \( b = - 4 \) Equation: \( y = a x^2 + b x + c = -3 x^2 - 4x + 3 \) Graph the graphs of \( y = -3 x^2 - 4x + 3 \) and verify that the graph passes through the points \( (0,3), (1,-4) \) and \( (-1 ,4) \).
• The equation of the parabola, with vertical axis of symmetry, has the form \( y = a x^2 + b x + c \) or in vertex form \( y = a(x - h)^2 + k \) where the vertex is at the point \( (h , k)\) . In this case it is tangent to a horizontal line \( y = 3 \) at \( x = -2 \) which means that its vertex is at the point \( (h , k) = (-2 , 3) \ ). Therefore, the equation of this parabola can be written as: \( y = a(x - h)^2 + k = a(x - (-2))^2 + 3 = a(x + 2)^2 + 3 \) Its graph passes through the point \( (0 , 5) \). That's why \( 5 = a(0 + 2)^2 + 3 = 4 a+ 3 \) Solve the above for \( a \) \( a = 1 / 2 \) Equation: \( y = (1/2)(x + 2)^2 + 3 \) Sketch the graphs of \( y = (1/2)(x + 2)^2 + 3 \) and verify that the graph is tangent to the horizontal line \( y = 3 \) at \( x = -2 \ ) and also the graph passes through the point \( (0 , 5) \).
• A line and a parabola are tangent if they have only one point of intersection, which is the point where they touch. The points of intersection are found by solving the system \( y = m x - 3 \) y \( y = 3 x^2 - x \) \( mx - 3 = 3 x^2 - x \) Write as a standard quadratic equation: \( 3 x^2 - x(1 + m) + 3 = 0 \) The discriminant of the above quadratic equation is given by: \( \Delta = (1 + m)^2 - 4(3)(3) \) The line is tangent to the parabola of the graphs of the two curves have a point of intersection if: \( \Delta = 0 \) (case of a solution of a quadratic equation) Hence the equation: \( (1 + m)^2 - 4(3)(3) = 0 \) solve for me \( (1 + m)^2 = 36 \) Solutions: \( m = 5 \) and \( m = -7 \) Use a graph plotter to check your answer by plotting the graphs of the lines: \( y = 5 x - 3 \) (m = 5 solution ), \( y = -7 x - 3 \) (m = 7 solution) and the parabola \( y = 3 x^2 - x\) and check that the two lines are tangent to the graph of the parabola \( y = 3 x^2 - x\).
• The points of intersection are found by solving the system \( y = 2 x + b \)   and   \( y = - x^2 - 2x + 1 \) \( 2x + b = - x^2 - 2x + 1 \) Write as a standard quadratic equation: \( - x^2 - 4x + 1 - b = 0 \) The discriminant of the above equation is given by: \( \Delta = (-4)^2 - 4(-1)(1 - b) = 20 - 4b \) The graphs of \( y = 2 x + b \) and \( y = - x^2 - 2 x + 1 \) have two points of intersection if \( \Delta \gt 0 \) (case of two real solutions of a quadratic equation) \( 20 - 4 b \gt 0 \) Solve for b \( b \lt 5 \) Use a graph plotter to check your answer by plotting graphs of \( y = - x^2 - 2 x + 1 \) and lines through equations \( y = 2 x + b \) for values of \( b \gt 5 \) , \( b \lt 5 \) and \( b = 5 \) to see how many points of intersection of the parabola and the line there are for each of these values of \( b \).
• The points of intersection are found by solving the system \( y = a x^2 + x \) y \( y = 3 x + 1 \) \( 3 x + 1 = a x^2 + x \) Write as a standard quadratic equation: \( a x^2 - 2 x - 1 = 0 \) Discriminant: \( \Delta = (-2)^2 - 4(a)(-1) = 4 + 4 a \) The graphs are tangent if they have a point of intersection (case for a solution of a quadratic equation) if \( \Delta = 0 \). That's why \( 4 + 4 a = 0 \) Solve for \(a\) \( a = -1 \) Parabola equation: \( y = -x^2 + x \) Graph \( y = - x^2 + x \) and \( y = 3 x + 1 \) to verify the answer above.
• Beginning: \( y = x^2 \) Shift 3 units to the left: \( y = (x + 3)^2 \) Reflect about the x-axis: \( y = -(x + 3)^2 \) Shift up 4 units: \( y = -(x + 3)^2 + 4 \)
• Given: \( y = - x^2 + 4 x + 6 \) Rewrite in vertex form by completing the square: \( y = - x^2 + 4 x + 6 = - (x - 2)^2 + 10\) Beginning: \( y = x^2\) Shift 2 units to the right: \( y = (x - 2)^2\) Reflect about the x-axis: \( y = -(x - 2)^2 \) Shift up 10 units: \( y = -(x - 2)^2 + 10\)
• Any point identified on the given graph can be used to find the equation of the parabola. However, using the x and y intercepts and the vertex are better ways to find the equation of the parabola whose graph is shown below. Two methods are presented to solve the problem: method 1: The graph has two x-intercepts: (-5, 0) and (-1, 0) Use the two x-intercepts at (-5, 0) and (-1, 0) to write the equation of the parabola as follows: \( y = a(x + 1)(x + 5)\) Use the y-intercept at (0, -5) to write \( - 5 = a(0 + 1)(0 + 5) = 5 a\) Solve for \(a \) \(a = -1\) Write the equation of the parabola: \( y = -(x + 1)(x + 5) = - x^2 -6 x - 5\) method 2: Use the vertex at \( ( h , k) = (-3 , 4) \) to write the equation of the parabola in vertex form as follows: \( y = a(x - h)^2 + k = a(x + 3)^2 + 4 \) Use the y-intercept (0, -5) to find \(a\). \( - 5 = a(0 + 3)^2 + 4 \) Solve the above for \(a\): \( a = -1 \) The equation of the parabola is given by \(y = -(x + 3)^2 + 4 = - x^2 -6 x - 5 \)

Study Guides > College Algebra

Solving applied problems involving parabolas.

Example 7: Solving Applied Problems Involving Parabolas

• Find the equation of the parabola that models the fire starter. Assume that the vertex of the parabolic mirror is the origin of the coordinate plane.
• Use the equation found in part (a) to find the depth of the fire starter.

• The vertex of the dish is the origin of the coordinate plane, so the parabola will take the standard form [latex]{x}^{2}=4py[/latex], where [latex]p>0[/latex]. The igniter, which is the focus, is 1.7 inches above the vertex of the dish. Thus we have [latex]p=1.7[/latex]. [latex]\begin{array}{ll}{x}^{2}=4py\hfill & \begin{array}{cccc}& & & \end{array}\text{Standard form of upward-facing parabola with vertex (0,0)}\hfill \\ {x}^{2}=4\left(1.7\right)y\hfill & \begin{array}{cccc}& & & \end{array}\text{Substitute 1}\text{.7 for }p.\hfill \\ {x}^{2}=6.8y\hfill & \begin{array}{cccc}& & & \end{array}\text{Multiply}.\hfill \end{array}[/latex]
• The dish extends [latex]\frac{4.5}{2}=2.25[/latex] inches on either side of the origin. We can substitute 2.25 for [latex]x[/latex] in the equation from part (a) to find the depth of the dish. [latex]\begin{array}{ll}\text{ }{x}^{2}=6.8y\hfill & \text{Equation found in part (a)}.\hfill \\ {\left(2.25\right)}^{2}=6.8y\hfill & \text{Substitute 2}\text{.25 for }x.\hfill \\ \text{ }y\approx 0.74 \hfill & \text{Solve for }y.\hfill \end{array}[/latex] The dish is about 0.74 inches deep.

a. Find an equation that models a cross-section of the solar cooker. Assume that the vertex of the parabolic mirror is the origin of the coordinate plane, and that the parabola opens to the right (i.e., has the x -axis as its axis of symmetry).

b. Use the equation found in part (a) to find the depth of the cooker.

Licenses & Attributions

Cc licensed content, specific attribution.

• Precalculus. Provided by: OpenStax Authored by: OpenStax College. Located at: https://cnx.org/contents/ [email protected] :1/Preface. License: CC BY: Attribution .

Please add a message.

Message received. Thanks for the feedback.

10.3 The Parabola

Learning objectives.

In this section, you will:

• Graph parabolas with vertices at the origin.
• Write equations of parabolas in standard form.
• Graph parabolas with vertices not at the origin.
• Solve applied problems involving parabolas.

Katherine Johnson is the pioneering NASA mathematician who was integral to the successful and safe flight and return of many human missions as well as satellites. Prior to the work featured in the movie Hidden Figures , she had already made major contributions to the space program. She provided trajectory analysis for the Mercury mission, in which Alan Shepard became the first American to reach space, and she and engineer Ted Sopinski authored a monumental paper regarding placing an object in a precise orbital position and having it return safely to Earth. Many of the orbits she determined were made up of parabolas, and her ability to combine different types of math enabled an unprecedented level of precision. Johnson said, "You tell me when you want it and where you want it to land, and I'll do it backwards and tell you when to take off."

Johnson's work on parabolic orbits and other complex mathematics resulted in successful orbits, Moon landings, and the development of the Space Shuttle program. Applications of parabolas are also critical to other areas of science. Parabolic mirrors (or reflectors) are able to capture energy and focus it to a single point. The advantages of this property are evidenced by the vast list of parabolic objects we use every day: satellite dishes, suspension bridges, telescopes, microphones, spotlights, and car headlights, to name a few. Parabolic reflectors are also used in alternative energy devices, such as solar cookers and water heaters, because they are inexpensive to manufacture and need little maintenance. In this section we will explore the parabola and its uses, including low-cost, energy-efficient solar designs.

Graphing Parabolas with Vertices at the Origin

In The Ellipse , we saw that an ellipse is formed when a plane cuts through a right circular cone. If the plane is parallel to the edge of the cone, an unbounded curve is formed. This curve is a parabola . See Figure 2 .

Like the ellipse and hyperbola , the parabola can also be defined by a set of points in the coordinate plane. A parabola is the set of all points ( x , y ) ( x , y ) in a plane that are the same distance from a fixed line, called the directrix , and a fixed point (the focus ) not on the directrix.

In Quadratic Functions , we learned about a parabola’s vertex and axis of symmetry. Now we extend the discussion to include other key features of the parabola. See Figure 3 . Notice that the axis of symmetry passes through the focus and vertex and is perpendicular to the directrix. The vertex is the midpoint between the directrix and the focus.

The line segment that passes through the focus and is parallel to the directrix is called the latus rectum . The endpoints of the latus rectum lie on the curve. By definition, the distance d d from the focus to any point P P on the parabola is equal to the distance from P P to the directrix.

To work with parabolas in the coordinate plane , we consider two cases: those with a vertex at the origin and those with a vertex at a point other than the origin. We begin with the former.

Let ( x , y ) ( x , y ) be a point on the parabola with vertex ( 0 , 0 ) , ( 0 , 0 ) , focus ( 0 , p ) , ( 0 , p ) , and directrix y = − p y = − p as shown in Figure 4 . The distance d d from point ( x , y ) ( x , y ) to point ( x , − p ) ( x , − p ) on the directrix is the difference of the y -values: d = y + p . d = y + p . The distance from the focus ( 0 , p ) ( 0 , p ) to the point ( x , y ) ( x , y ) is also equal to d d and can be expressed using the distance formula .

Set the two expressions for d d equal to each other and solve for y y to derive the equation of the parabola. We do this because the distance from ( x , y ) ( x , y ) to ( 0 , p ) ( 0 , p ) equals the distance from ( x , y ) ( x , y ) to ( x , − p ) . ( x , − p ) .

We then square both sides of the equation, expand the squared terms, and simplify by combining like terms.

The equations of parabolas with vertex ( 0 , 0 ) ( 0 , 0 ) are y 2 = 4 p x y 2 = 4 p x when the x -axis is the axis of symmetry and x 2 = 4 p y x 2 = 4 p y when the y -axis is the axis of symmetry. These standard forms are given below, along with their general graphs and key features.

Standard Forms of Parabolas with Vertex (0, 0)

Table 1 and Figure 5 summarize the standard features of parabolas with a vertex at the origin.

The key features of a parabola are its vertex, axis of symmetry, focus, directrix, and latus rectum. See Figure 5 . When given a standard equation for a parabola centered at the origin, we can easily identify the key features to graph the parabola.

A line is said to be tangent to a curve if it intersects the curve at exactly one point. If we sketch lines tangent to the parabola at the endpoints of the latus rectum, these lines intersect on the axis of symmetry, as shown in Figure 6 .

Given a standard form equation for a parabola centered at (0, 0), sketch the graph.

• Determine which of the standard forms applies to the given equation: y 2 = 4 p x y 2 = 4 p x or x 2 = 4 p y . x 2 = 4 p y .
• the axis of symmetry is the x -axis, y = 0 y = 0
• set 4 p 4 p equal to the coefficient of x in the given equation to solve for p . p . If p > 0 , p > 0 , the parabola opens right. If p < 0 , p < 0 , the parabola opens left.
• use p p to find the coordinates of the focus, ( p , 0 ) ( p , 0 )
• use p p to find the equation of the directrix, x = − p x = − p
• use p p to find the endpoints of the latus rectum, ( p , ± 2 p ) . ( p , ± 2 p ) . Alternately, substitute x = p x = p into the original equation.
• the axis of symmetry is the y -axis, x = 0 x = 0
• set 4 p 4 p equal to the coefficient of y in the given equation to solve for p . p . If p > 0 , p > 0 , the parabola opens up. If p < 0 , p < 0 , the parabola opens down.
• use p p to find the coordinates of the focus, ( 0 , p ) ( 0 , p )
• use p p to find equation of the directrix, y = − p y = − p
• use p p to find the endpoints of the latus rectum, ( ± 2 p , p ) ( ± 2 p , p )
• Plot the focus, directrix, and latus rectum, and draw a smooth curve to form the parabola.

Graphing a Parabola with Vertex (0, 0) and the x -axis as the Axis of Symmetry

Graph y 2 = 24 x . y 2 = 24 x . Identify and label the focus , directrix , and endpoints of the latus rectum .

The standard form that applies to the given equation is y 2 = 4 p x . y 2 = 4 p x . Thus, the axis of symmetry is the x -axis. It follows that:

• 24 = 4 p , 24 = 4 p , so p = 6. p = 6. Since p > 0 , p > 0 , the parabola opens right
• the coordinates of the focus are ( p , 0 ) = ( 6 , 0 ) ( p , 0 ) = ( 6 , 0 )
• the equation of the directrix is x = − p = − 6 x = − p = − 6
• the endpoints of the latus rectum have the same x -coordinate at the focus. To find the endpoints, substitute x = 6 x = 6 into the original equation: ( 6, ± 12 ) ( 6, ± 12 )

Next we plot the focus, directrix, and latus rectum, and draw a smooth curve to form the parabola . Figure 7

Graph y 2 = −16 x . y 2 = −16 x . Identify and label the focus, directrix, and endpoints of the latus rectum.

Graphing a Parabola with Vertex (0, 0) and the y -axis as the Axis of Symmetry

Graph x 2 = −6 y . x 2 = −6 y . Identify and label the focus , directrix , and endpoints of the latus rectum .

The standard form that applies to the given equation is x 2 = 4 p y . x 2 = 4 p y . Thus, the axis of symmetry is the y -axis. It follows that:

• − 6 = 4 p , − 6 = 4 p , so p = − 3 2 . p = − 3 2 . Since p < 0 , p < 0 , the parabola opens down.
• the coordinates of the focus are ( 0 , p ) = ( 0 , − 3 2 ) ( 0 , p ) = ( 0 , − 3 2 )
• the equation of the directrix is y = − p = 3 2 y = − p = 3 2
• the endpoints of the latus rectum can be found by substituting y = 3 2 y = 3 2 into the original equation, ( ± 3 , − 3 2 ) ( ± 3 , − 3 2 )

Next we plot the focus, directrix, and latus rectum, and draw a smooth curve to form the parabola .

Graph x 2 = 8 y . x 2 = 8 y . Identify and label the focus, directrix, and endpoints of the latus rectum.

Writing Equations of Parabolas in Standard Form

In the previous examples, we used the standard form equation of a parabola to calculate the locations of its key features. We can also use the calculations in reverse to write an equation for a parabola when given its key features.

Given its focus and directrix, write the equation for a parabola in standard form.

• If the given coordinates of the focus have the form ( p , 0 ) , ( p , 0 ) , then the axis of symmetry is the x -axis. Use the standard form y 2 = 4 p x . y 2 = 4 p x .
• If the given coordinates of the focus have the form ( 0 , p ) , ( 0 , p ) , then the axis of symmetry is the y -axis. Use the standard form x 2 = 4 p y . x 2 = 4 p y .
• Multiply 4 p . 4 p .
• Substitute the value from Step 2 into the equation determined in Step 1.

Writing the Equation of a Parabola in Standard Form Given its Focus and Directrix

What is the equation for the parabola with focus ( − 1 2 , 0 ) ( − 1 2 , 0 ) and directrix x = 1 2 ? x = 1 2 ?

The focus has the form ( p , 0 ) , ( p , 0 ) , so the equation will have the form y 2 = 4 p x . y 2 = 4 p x .

• Multiplying 4 p , 4 p , we have 4 p = 4 ( − 1 2 ) = −2. 4 p = 4 ( − 1 2 ) = −2.
• Substituting for 4 p , 4 p , we have y 2 = 4 p x = −2 x . y 2 = 4 p x = −2 x .

Therefore, the equation for the parabola is y 2 = −2 x . y 2 = −2 x .

What is the equation for the parabola with focus ( 0 , 7 2 ) ( 0 , 7 2 ) and directrix y = − 7 2 ? y = − 7 2 ?

Graphing Parabolas with Vertices Not at the Origin

Like other graphs we’ve worked with, the graph of a parabola can be translated. If a parabola is translated h h units horizontally and k k units vertically, the vertex will be ( h , k ) . ( h , k ) . This translation results in the standard form of the equation we saw previously with x x replaced by ( x − h ) ( x − h ) and y y replaced by ( y − k ) . ( y − k ) .

To graph parabolas with a vertex ( h , k ) ( h , k ) other than the origin, we use the standard form ( y − k ) 2 = 4 p ( x − h ) ( y − k ) 2 = 4 p ( x − h ) for parabolas that have an axis of symmetry parallel to the x -axis, and ( x − h ) 2 = 4 p ( y − k ) ( x − h ) 2 = 4 p ( y − k ) for parabolas that have an axis of symmetry parallel to the y -axis. These standard forms are given below, along with their general graphs and key features.

Standard Forms of Parabolas with Vertex ( h , k )

Table 2 and Figure 9 summarize the standard features of parabolas with a vertex at a point ( h , k ) . ( h , k ) .

Given a standard form equation for a parabola centered at ( h , k ), sketch the graph.

• Determine which of the standard forms applies to the given equation: ( y − k ) 2 = 4 p ( x − h ) ( y − k ) 2 = 4 p ( x − h ) or ( x − h ) 2 = 4 p ( y − k ) . ( x − h ) 2 = 4 p ( y − k ) .
• use the given equation to identify h h and k k for the vertex, ( h , k ) ( h , k )
• use the value of k k to determine the axis of symmetry, y = k y = k
• set 4 p 4 p equal to the coefficient of ( x − h ) ( x − h ) in the given equation to solve for p . p . If p > 0 , p > 0 , the parabola opens right. If p < 0 , p < 0 , the parabola opens left.
• use h , k , h , k , and p p to find the coordinates of the focus, ( h + p , k ) ( h + p , k )
• use h h and p p to find the equation of the directrix, x = h − p x = h − p
• use h , k , h , k , and p p to find the endpoints of the latus rectum, ( h + p , k ± 2 p ) ( h + p , k ± 2 p )
• use the value of h h to determine the axis of symmetry, x = h x = h
• set 4 p 4 p equal to the coefficient of ( y − k ) ( y − k ) in the given equation to solve for p . p . If p > 0 , p > 0 , the parabola opens up. If p < 0 , p < 0 , the parabola opens down.
• use h , k , h , k , and p p to find the coordinates of the focus, ( h , k + p ) ( h , k + p )
• use k k and p p to find the equation of the directrix, y = k − p y = k − p
• use h , k , h , k , and p p to find the endpoints of the latus rectum, ( h ± 2 p , k + p ) ( h ± 2 p , k + p )
• Plot the vertex, axis of symmetry, focus, directrix, and latus rectum, and draw a smooth curve to form the parabola.

Graphing a Parabola with Vertex ( h , k ) and Axis of Symmetry Parallel to the x -axis

Graph ( y − 1 ) 2 = −16 ( x + 3 ) . ( y − 1 ) 2 = −16 ( x + 3 ) . Identify and label the vertex , axis of symmetry , focus , directrix , and endpoints of the latus rectum .

The standard form that applies to the given equation is ( y − k ) 2 = 4 p ( x − h ) . ( y − k ) 2 = 4 p ( x − h ) . Thus, the axis of symmetry is parallel to the x -axis. It follows that:

• the vertex is ( h , k ) = ( − 3 , 1 ) ( h , k ) = ( − 3 , 1 )
• the axis of symmetry is y = k = 1 y = k = 1
• −16 = 4 p , −16 = 4 p , so p = −4. p = −4. Since p < 0 , p < 0 , the parabola opens left.
• the coordinates of the focus are ( h + p , k ) = ( −3 + ( −4 ) , 1 ) = ( −7 , 1 ) ( h + p , k ) = ( −3 + ( −4 ) , 1 ) = ( −7 , 1 )
• the equation of the directrix is x = h − p = −3 − ( −4 ) = 1 x = h − p = −3 − ( −4 ) = 1
• the endpoints of the latus rectum are ( h + p , k ± 2 p ) = ( −3 + ( −4 ) , 1 ± 2 ( −4 ) ) , ( h + p , k ± 2 p ) = ( −3 + ( −4 ) , 1 ± 2 ( −4 ) ) , or ( −7 , −7 ) ( −7 , −7 ) and ( −7 , 9 ) ( −7 , 9 )

Next we plot the vertex, axis of symmetry, focus, directrix, and latus rectum, and draw a smooth curve to form the parabola. See Figure 10 .

Graph ( y + 1 ) 2 = 4 ( x − 8 ) . ( y + 1 ) 2 = 4 ( x − 8 ) . Identify and label the vertex, axis of symmetry, focus, directrix, and endpoints of the latus rectum.

Graphing a Parabola from an Equation Given in General Form

Graph x 2 − 8 x − 28 y − 208 = 0. x 2 − 8 x − 28 y − 208 = 0. Identify and label the vertex, axis of symmetry, focus, directrix, and endpoints of the latus rectum.

Start by writing the equation of the parabola in standard form. The standard form that applies to the given equation is ( x − h ) 2 = 4 p ( y − k ) . ( x − h ) 2 = 4 p ( y − k ) . Thus, the axis of symmetry is parallel to the y -axis. To express the equation of the parabola in this form, we begin by isolating the terms that contain the variable x x in order to complete the square.

It follows that:

• the vertex is ( h , k ) = ( 4 , −8 ) ( h , k ) = ( 4 , −8 )
• the axis of symmetry is x = h = 4 x = h = 4
• since p = 7 , p > 0 p = 7 , p > 0 and so the parabola opens up
• the coordinates of the focus are ( h , k + p ) = ( 4 , −8 + 7 ) = ( 4 , −1 ) ( h , k + p ) = ( 4 , −8 + 7 ) = ( 4 , −1 )
• the equation of the directrix is y = k − p = −8 − 7 = −15 y = k − p = −8 − 7 = −15
• the endpoints of the latus rectum are ( h ± 2 p , k + p ) = ( 4 ± 2 ( 7 ) , −8 + 7 ) , ( h ± 2 p , k + p ) = ( 4 ± 2 ( 7 ) , −8 + 7 ) , or ( −10 , −1 ) ( −10 , −1 ) and ( 18 , −1 ) ( 18 , −1 )

Next we plot the vertex, axis of symmetry, focus, directrix, and latus rectum, and draw a smooth curve to form the parabola. See Figure 11 .

Graph ( x + 2 ) 2 = −20 ( y − 3 ) . ( x + 2 ) 2 = −20 ( y − 3 ) . Identify and label the vertex, axis of symmetry, focus, directrix, and endpoints of the latus rectum.

Solving Applied Problems Involving Parabolas

As we mentioned at the beginning of the section, parabolas are used to design many objects we use every day, such as telescopes, suspension bridges, microphones, and radar equipment. Parabolic mirrors, such as the one used to light the Olympic torch, have a very unique reflecting property. When rays of light parallel to the parabola’s axis of symmetry are directed toward any surface of the mirror, the light is reflected directly to the focus. See Figure 12 . This is why the Olympic torch is ignited when it is held at the focus of the parabolic mirror.

Parabolic mirrors have the ability to focus the sun’s energy to a single point, raising the temperature hundreds of degrees in a matter of seconds. Thus, parabolic mirrors are featured in many low-cost, energy efficient solar products, such as solar cookers, solar heaters, and even travel-sized fire starters.

A cross-section of a design for a travel-sized solar fire starter is shown in Figure 13 . The sun’s rays reflect off the parabolic mirror toward an object attached to the igniter. Because the igniter is located at the focus of the parabola, the reflected rays cause the object to burn in just seconds.

• ⓐ Find the equation of the parabola that models the fire starter. Assume that the vertex of the parabolic mirror is the origin of the coordinate plane.
• ⓑ Use the equation found in part ⓐ to find the depth of the fire starter.
• ⓐ The vertex of the dish is the origin of the coordinate plane, so the parabola will take the standard form x 2 = 4 p y , x 2 = 4 p y , where p > 0. p > 0. The igniter, which is the focus, is 1.7 inches above the vertex of the dish. Thus we have p = 1.7. p = 1.7. x 2 = 4 p y Standard form of upward-facing parabola with vertex (0,0) x 2 = 4 ( 1.7 ) y Substitute 1 .7 for  p . x 2 = 6.8 y Multiply . x 2 = 4 p y Standard form of upward-facing parabola with vertex (0,0) x 2 = 4 ( 1.7 ) y Substitute 1 .7 for  p . x 2 = 6.8 y Multiply .

The dish is about 0.74 inches deep.

Balcony-sized solar cookers have been designed for families living in India. The top of a dish has a diameter of 1600 mm. The sun’s rays reflect off the parabolic mirror toward the “cooker,” which is placed 320 mm from the base.

ⓐ Find an equation that models a cross-section of the solar cooker. Assume that the vertex of the parabolic mirror is the origin of the coordinate plane, and that the parabola opens to the right (i.e., has the x -axis as its axis of symmetry).

ⓑ Use the equation found in part ⓐ to find the depth of the cooker.

Access these online resources for additional instruction and practice with parabolas.

• Conic Sections: The Parabola Part 1 of 2
• Conic Sections: The Parabola Part 2 of 2
• Parabola with Vertical Axis
• Parabola with Horizontal Axis

10.3 Section Exercises

Define a parabola in terms of its focus and directrix.

If the equation of a parabola is written in standard form and p p is positive and the directrix is a vertical line, then what can we conclude about its graph?

If the equation of a parabola is written in standard form and p p is negative and the directrix is a horizontal line, then what can we conclude about its graph?

What is the effect on the graph of a parabola if its equation in standard form has increasing values of p ? p ?

As the graph of a parabola becomes wider, what will happen to the distance between the focus and directrix?

For the following exercises, determine whether the given equation is a parabola. If so, rewrite the equation in standard form.

y 2 = 4 − x 2 y 2 = 4 − x 2

y = 4 x 2 y = 4 x 2

3 x 2 − 6 y 2 = 12 3 x 2 − 6 y 2 = 12

( y − 3 ) 2 = 8 ( x − 2 ) ( y − 3 ) 2 = 8 ( x − 2 )

y 2 + 12 x − 6 y − 51 = 0 y 2 + 12 x − 6 y − 51 = 0

For the following exercises, rewrite the given equation in standard form, and then determine the vertex ( V ) , ( V ) , focus ( F ) , ( F ) , and directrix ( d ) ( d ) of the parabola.

x = 8 y 2 x = 8 y 2

y = 1 4 x 2 y = 1 4 x 2

y = −4 x 2 y = −4 x 2

x = 1 8 y 2 x = 1 8 y 2

x = 36 y 2 x = 36 y 2

x = 1 36 y 2 x = 1 36 y 2

( x − 1 ) 2 = 4 ( y − 1 ) ( x − 1 ) 2 = 4 ( y − 1 )

( y − 2 ) 2 = 4 5 ( x + 4 ) ( y − 2 ) 2 = 4 5 ( x + 4 )

( y − 4 ) 2 = 2 ( x + 3 ) ( y − 4 ) 2 = 2 ( x + 3 )

( x + 1 ) 2 = 2 ( y + 4 ) ( x + 1 ) 2 = 2 ( y + 4 )

( x + 4 ) 2 = 24 ( y + 1 ) ( x + 4 ) 2 = 24 ( y + 1 )

( y + 4 ) 2 = 16 ( x + 4 ) ( y + 4 ) 2 = 16 ( x + 4 )

y 2 + 12 x − 6 y + 21 = 0 y 2 + 12 x − 6 y + 21 = 0

x 2 − 4 x − 24 y + 28 = 0 x 2 − 4 x − 24 y + 28 = 0

5 x 2 − 50 x − 4 y + 113 = 0 5 x 2 − 50 x − 4 y + 113 = 0

y 2 − 24 x + 4 y − 68 = 0 y 2 − 24 x + 4 y − 68 = 0

x 2 − 4 x + 2 y − 6 = 0 x 2 − 4 x + 2 y − 6 = 0

y 2 − 6 y + 12 x − 3 = 0 y 2 − 6 y + 12 x − 3 = 0

3 y 2 − 4 x − 6 y + 23 = 0 3 y 2 − 4 x − 6 y + 23 = 0

x 2 + 4 x + 8 y − 4 = 0 x 2 + 4 x + 8 y − 4 = 0

For the following exercises, graph the parabola, labeling the focus and the directrix.

y = 36 x 2 y = 36 x 2

y = 1 36 x 2 y = 1 36 x 2

y = −9 x 2 y = −9 x 2

( y − 2 ) 2 = − 4 3 ( x + 2 ) ( y − 2 ) 2 = − 4 3 ( x + 2 )

−5 ( x + 5 ) 2 = 4 ( y + 5 ) −5 ( x + 5 ) 2 = 4 ( y + 5 )

−6 ( y + 5 ) 2 = 4 ( x − 4 ) −6 ( y + 5 ) 2 = 4 ( x − 4 )

y 2 − 6 y − 8 x + 1 = 0 y 2 − 6 y − 8 x + 1 = 0

x 2 + 8 x + 4 y + 20 = 0 x 2 + 8 x + 4 y + 20 = 0

3 x 2 + 30 x − 4 y + 95 = 0 3 x 2 + 30 x − 4 y + 95 = 0

y 2 − 8 x + 10 y + 9 = 0 y 2 − 8 x + 10 y + 9 = 0

x 2 + 4 x + 2 y + 2 = 0 x 2 + 4 x + 2 y + 2 = 0

y 2 + 2 y − 12 x + 61 = 0 y 2 + 2 y − 12 x + 61 = 0

− 2 x 2 + 8 x − 4 y − 24 = 0 − 2 x 2 + 8 x − 4 y − 24 = 0

For the following exercises, find the equation of the parabola given information about its graph.

Vertex is ( 0 , 0 ) ; ( 0 , 0 ) ; directrix is y = 4 , y = 4 , focus is ( 0 , −4 ) . ( 0 , −4 ) .

Vertex is ( 0 , 0 ) ; ( 0 , 0 ) ; directrix is x = 4 , x = 4 , focus is ( −4 , 0 ) . ( −4 , 0 ) .

Vertex is ( 2 , 2 ) ; ( 2 , 2 ) ; directrix is x = 2 − 2 , x = 2 − 2 , focus is ( 2 + 2 , 2 ) . ( 2 + 2 , 2 ) .

Vertex is ( −2 , 3 ) ; ( −2 , 3 ) ; directrix is x = − 7 2 , x = − 7 2 , focus is ( − 1 2 , 3 ) . ( − 1 2 , 3 ) .

Vertex is ( 2 , − 3 ) ; ( 2 , − 3 ) ; directrix is x = 2 2 , x = 2 2 , focus is ( 0 , − 3 ) . ( 0 , − 3 ) .

Vertex is ( 1 , 2 ) ; ( 1 , 2 ) ; directrix is y = 11 3 , y = 11 3 , focus is ( 1 , 1 3 ) . ( 1 , 1 3 ) .

For the following exercises, determine the equation for the parabola from its graph.

For the following exercises, the vertex and endpoints of the latus rectum of a parabola are given. Find the equation.

V ( 0 , 0 ) V ( 0 , 0 ) , Endpoints  ( 2 , 1 ) ( 2 , 1 ) , ( −2 , 1 ) ( −2 , 1 )

V ( 0 , 0 ) V ( 0 , 0 ) , Endpoints ( −2 , 4 ) ( −2 , 4 ) , ( −2 , −4 ) ( −2 , −4 )

V ( 1 , 2 ) V ( 1 , 2 ) , Endpoints ( −5 , 5 ) ( −5 , 5 ) , ( 7 , 5 ) ( 7 , 5 )

V ( −3 , −1 ) V ( −3 , −1 ) , Endpoints ( 0 , 5 ) ( 0 , 5 ) , ( 0 , −7 ) ( 0 , −7 )

V ( 4 , −3 ) V ( 4 , −3 ) , Endpoints ( 5 , − 7 2 ) ( 5 , − 7 2 ) , ( 3 , − 7 2 ) ( 3 , − 7 2 )

Real-World Applications

The mirror in an automobile headlight has a parabolic cross-section with the light bulb at the focus. On a schematic, the equation of the parabola is given as x 2 = 4 y . x 2 = 4 y . At what coordinates should you place the light bulb?

If we want to construct the mirror from the previous exercise such that the focus is located at ( 0 , 0.25 ) , ( 0 , 0.25 ) , what should the equation of the parabola be?

A satellite dish is shaped like a paraboloid of revolution. This means that it can be formed by rotating a parabola around its axis of symmetry. The receiver is to be located at the focus. If the dish is 12 feet across at its opening and 4 feet deep at its center, where should the receiver be placed?

Consider the satellite dish from the previous exercise. If the dish is 8 feet across at the opening and 2 feet deep, where should we place the receiver?

The reflector in a searchlight is shaped like a paraboloid of revolution. A light source is located 1 foot from the base along the axis of symmetry. If the opening of the searchlight is 3 feet across, find the depth.

If the reflector in the searchlight from the previous exercise has the light source located 6 inches from the base along the axis of symmetry and the opening is 4 feet, find the depth.

An arch is in the shape of a parabola. It has a span of 100 feet and a maximum height of 20 feet. Find the equation of the parabola, and determine the height of the arch 40 feet from the center.

If the arch from the previous exercise has a span of 160 feet and a maximum height of 40 feet, find the equation of the parabola, and determine the distance from the center at which the height is 20 feet.

An object is projected so as to follow a parabolic path given by y = − x 2 + 96 x , y = − x 2 + 96 x , where x x is the horizontal distance traveled in feet and y y is the height. Determine the maximum height the object reaches.

For the object from the previous exercise, assume the path followed is given by y = −0.5 x 2 + 80 x . y = −0.5 x 2 + 80 x . Determine how far along the horizontal the object traveled to reach maximum height.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/precalculus-2e/pages/1-introduction-to-functions

• Authors: Jay Abramson
• Publisher/website: OpenStax
• Book title: Precalculus 2e
• Publication date: Dec 21, 2021
• Location: Houston, Texas
• Book URL: https://openstax.org/books/precalculus-2e/pages/1-introduction-to-functions
• Section URL: https://openstax.org/books/precalculus-2e/pages/10-3-the-parabola

© Jan 9, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

9.6: Solve Applications of Quadratic Equations

• Last updated
• Save as PDF
• Page ID 5177

Learning Objectives

By the end of this section, you will be able to:

• Solve applications modeled by quadratic equations

Before you get started, take this readiness quiz.

• The sum of two consecutive odd numbers is \(−100\). Find the numbers. If you missed this problem, review Example 2.18.
• Solve: \(\frac{2}{x+1}+\frac{1}{x-1}=\frac{1}{x^{2}-1}\). If you missed this problem, review Example 7.35.
• Find the length of the hypotenuse of a right triangle with legs \(5\) inches and \(12\) inches. If you missed this problem, review Example 2.34.

Solve Applications Modeled by Quadratic Equations

We solved some applications that are modeled by quadratic equations earlier, when the only method we had to solve them was factoring. Now that we have more methods to solve quadratic equations, we will take another look at applications.

Let’s first summarize the methods we now have to solve quadratic equations.

Methods to Solve Quadratic Equations

• Square Root Property
• Completing the Square
• Quadratic Formula

As you solve each equation, choose the method that is most convenient for you to work the problem. As a reminder, we will copy our usual Problem-Solving Strategy here so we can follow the steps.

Use a Problem-Solving Strategy

• Read the problem. Make sure all the words and ideas are understood.
• Identify what we are looking for.
• Name what we are looking for. Choose a variable to represent that quantity.
• Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebraic equation.
• Solve the equation using algebra techniques.
• Check the answer in the problem and make sure it makes sense.
• Answer the question with a complete sentence.

We have solved number applications that involved consecutive even and odd integers, by modeling the situation with linear equations. Remember, we noticed each even integer is \(2\) more than the number preceding it. If we call the first one \(n\), then the next one is \(n+2\). The next one would be \(n+2+2\) or \(n+4\). This is also true when we use odd integers. One set of even integers and one set of odd integers are shown below.

\(\begin{array}{cl}{}&{\text{Consecutive even integers}}\\{}& {64,66,68}\\ {n} & {1^{\text { st }} \text { even integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive even integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive even integer }}\end{array}\)

\(\begin{array}{cl}{}&{\text{Consecutive odd integers}}\\{}& {77,79,81}\\ {n} & {1^{\text { st }} \text { odd integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive odd integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive odd integer }}\end{array}\)

Some applications of odd or even consecutive integers are modeled by quadratic equations. The notation above will be helpful as you name the variables.

Example \(\PageIndex{1}\)

The product of two consecutive odd integers is \(195\). Find the integers.

Step 1 : Read the problem

Step 2 : Identify what we are looking for.

We are looking for two consecutive odd integers.

Step 3 : Name what we are looking for.

Let \(n=\) the first odd integer.

\(n+2=\) the next odd integer.

Step 4 : Translate into an equation. State the problem in one sentence.

“The product of two consecutive odd integers is \(195\).” The product of the first odd integer and the second odd integer is \(195\).

Translate into an equation.

\(n(n+2)=195\)

Step 5 : Solve the equation. Distribute.

\(n^{2}+2 n=195\)

Write the equation in standard form.

\(n^{2}+2 n-195=0\)

\((n+15)(n-13)=0\)

Use the Zero Product Property.

\(n+15=0 \quad n-13=0\)

Solve each equation.

\(n=-15, \quad n=13\)

There are two values of \(n\) that are solutions. This will give us two pairs of consecutive odd integers for our solution.

\(\begin{array}{cc}{\text { First odd integer } n=13} & {\text { First odd integer } n=-15} \\ {\text { next odd integer } n+2} & {\text { next odd integer } n+2} \\ {13+2} & {-15+2} \\ {15} & {-13}\end{array}\)

Step 6 : Check the answer.

Do these pairs work? Are they consecutive odd integers?

\(\begin{aligned} 13,15 & \text { yes } \\-13,-15 & \text { yes } \end{aligned}\)

Is their product \(195\)?

\(\begin{aligned} 13 \cdot 15 &=195 &\text{yes} \\-13(-15) &=195 & \text { yes } \end{aligned}\)

Step 7 : Answer the question.

Two consecutive odd integers whose product is \(195\) are \(13,15\) and \(-13,-15\).

Exercise \(\PageIndex{1}\)

The product of two consecutive odd integers is \(99\). Find the integers.

The two consecutive odd integers whose product is \(99\) are \(9, 11\), and \(−9, −11\).

Exercise \(\PageIndex{2}\)

The product of two consecutive even integers is \(168\). Find the integers.

The two consecutive even integers whose product is \(128\) are \(12, 14\) and \(−12, −14\).

We will use the formula for the area of a triangle to solve the next example.

Definition \(\PageIndex{1}\)

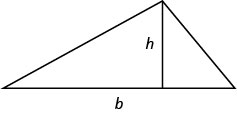
Area of a Triangle

For a triangle with base, \(b\), and height, \(h\), the area, \(A\), is given by the formula \(A=\frac{1}{2} b h\).

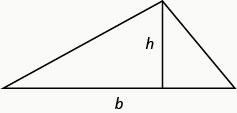
Recall that when we solve geometric applications, it is helpful to draw the figure.

Example \(\PageIndex{2}\)

An architect is designing the entryway of a restaurant. She wants to put a triangular window above the doorway. Due to energy restrictions, the window can only have an area of \(120\) square feet and the architect wants the base to be \(4\) feet more than twice the height. Find the base and height of the window.

Exercise \(\PageIndex{3}\)

Find the base and height of a triangle whose base is four inches more than six times its height and has an area of \(456\) square inches.

The height of the triangle is \(12\) inches and the base is \(76\) inches.

Exercise \(\PageIndex{4}\)

If a triangle that has an area of \(110\) square feet has a base that is two feet less than twice the height, what is the length of its base and height?

The height of the triangle is \(11\) feet and the base is \(20\) feet.

In the two preceding examples, the number in the radical in the Quadratic Formula was a perfect square and so the solutions were rational numbers. If we get an irrational number as a solution to an application problem, we will use a calculator to get an approximate value.

We will use the formula for the area of a rectangle to solve the next example.

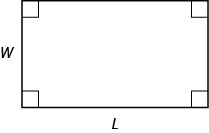
Definition \(\PageIndex{2}\)

Area of a Rectangle

For a rectangle with length, \(L\), and width, \(W\), the area, \(A\), is given by the formula \(A=LW\).

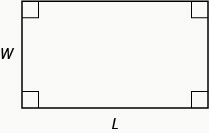
Example \(\PageIndex{3}\)

Mike wants to put \(150\) square feet of artificial turf in his front yard. This is the maximum area of artificial turf allowed by his homeowners association. He wants to have a rectangular area of turf with length one foot less than \(3\) times the width. Find the length and width. Round to the nearest tenth of a foot.

Exercise \(\PageIndex{5}\)

The length of a \(200\) square foot rectangular vegetable garden is four feet less than twice the width. Find the length and width of the garden, to the nearest tenth of a foot.

The length of the garden is approximately \(18\) feet and the width \(11\) feet.

Exercise \(\PageIndex{6}\)

A rectangular tablecloth has an area of \(80\) square feet. The width is \(5\) feet shorter than the length.What are the length and width of the tablecloth to the nearest tenth of a foot?

The length of the tablecloth is approximately \(11.8\) feet and the width \(6.8\) feet.

The Pythagorean Theorem gives the relation between the legs and hypotenuse of a right triangle. We will use the Pythagorean Theorem to solve the next example.

Definition \(\PageIndex{3}\)

Pythagorean Theorem

• In any right triangle, where \(a\) and \(b\) are the lengths of the legs, and \(c\) is the length of the hypotenuse, \(a^{2}+b^{2}=c^{2}\).

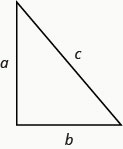
Example \(\PageIndex{4}\)

Rene is setting up a holiday light display. He wants to make a ‘tree’ in the shape of two right triangles, as shown below, and has two \(10\)-foot strings of lights to use for the sides. He will attach the lights to the top of a pole and to two stakes on the ground. He wants the height of the pole to be the same as the distance from the base of the pole to each stake. How tall should the pole be?

Exercise \(\PageIndex{7}\)

The sun casts a shadow from a flag pole. The height of the flag pole is three times the length of its shadow. The distance between the end of the shadow and the top of the flag pole is \(20\) feet. Find the length of the shadow and the length of the flag pole. Round to the nearest tenth.

The length of the flag pole’s shadow is approximately \(6.3\) feet and the height of the flag pole is \(18.9\) feet.

Exercise \(\PageIndex{8}\)

The distance between opposite corners of a rectangular field is four more than the width of the field. The length of the field is twice its width. Find the distance between the opposite corners. Round to the nearest tenth.

The distance between the opposite corners is approximately \(7.2\) feet.

The height of a projectile shot upward from the ground is modeled by a quadratic equation. The initial velocity, \(v_{0}\), propels the object up until gravity causes the object to fall back down.

Definition \(\PageIndex{4}\)

The height in feet, \(h\), of an object shot upwards into the air with initial velocity, \(v_{0}\), after \(t\) seconds is given by the formula

\(h=-16 t^{2}+v_{0} t\)

We can use this formula to find how many seconds it will take for a firework to reach a specific height.

Example \(\PageIndex{5}\)

A firework is shot upwards with initial velocity \(130\) feet per second. How many seconds will it take to reach a height of \(260\) feet? Round to the nearest tenth of a second.

Exercise \(\PageIndex{9}\)

An arrow is shot from the ground into the air at an initial speed of \(108\) ft/s. Use the formula \(h=-16 t^{2}+v_{0} t\) to determine when the arrow will be \(180\) feet from the ground. Round the nearest tenth.

The arrow will reach \(180\) feet on its way up after \(3\) seconds and again on its way down after approximately \(3.8\) seconds.

Exercise \(\PageIndex{10}\)

A man throws a ball into the air with a velocity of \(96\) ft/s. Use the formula \(h=-16 t^{2}+v_{0} t\) to determine when the height of the ball will be \(48\) feet. Round to the nearest tenth.

The ball will reach \(48\) feet on its way up after approximately \(.6\) second and again on its way down after approximately \(5.4\) seconds.

We have solved uniform motion problems using the formula \(D=rt\) in previous chapters. We used a table like the one below to organize the information and lead us to the equation.

The formula \(D=rt\) assumes we know \(r\) and \(t\) and use them to find \(D\). If we know \(D\) and \(r\) and need to find \(t\), we would solve the equation for \(t\) and get the formula \(t=\frac{D}{r}\).

Some uniform motion problems are also modeled by quadratic equations.

Example \(\PageIndex{6}\)

Professor Smith just returned from a conference that was \(2,000\) miles east of his home. His total time in the airplane for the round trip was \(9\) hours. If the plane was flying at a rate of \(450\) miles per hour, what was the speed of the jet stream?

This is a uniform motion situation. A diagram will help us visualize the situation.

We fill in the chart to organize the information.

We are looking for the speed of the jet stream. Let \(r=\) the speed of the jet stream.

When the plane flies with the wind, the wind increases its speed and so the rate is \(450 + r\).

When the plane flies against the wind, the wind decreases its speed and the rate is \(450 − r\).

The speed of the jet stream was \(50\) mph.

Exercise \(\PageIndex{11}\)

MaryAnne just returned from a visit with her grandchildren back east. The trip was \(2400\) miles from her home and her total time in the airplane for the round trip was \(10\) hours. If the plane was flying at a rate of \(500\) miles per hour, what was the speed of the jet stream?

The speed of the jet stream was \(100\) mph.

Exercise \(\PageIndex{12}\)

Gerry just returned from a cross country trip. The trip was \(3000\) miles from his home and his total time in the airplane for the round trip was \(11\) hours. If the plane was flying at a rate of \(550\) miles per hour, what was the speed of the jet stream?

Work applications can also be modeled by quadratic equations. We will set them up using the same methods we used when we solved them with rational equations.We’ll use a similar scenario now.

Example \(\PageIndex{7}\)

The weekly gossip magazine has a big story about the presidential election and the editor wants the magazine to be printed as soon as possible. She has asked the printer to run an extra printing press to get the printing done more quickly. Press #1 takes \(12\) hours more than Press #2 to do the job and when both presses are running they can print the job in \(8\) hours. How long does it take for each press to print the job alone?

This is a work problem. A chart will help us organize the information.

We are looking for how many hours it would take each press separately to complete the job.

Exercise \(\PageIndex{13}\)

The weekly news magazine has a big story naming the Person of the Year and the editor wants the magazine to be printed as soon as possible. She has asked the printer to run an extra printing press to get the printing done more quickly. Press #1 takes \(6\) hours more than Press #2 to do the job and when both presses are running they can print the job in \(4\) hours. How long does it take for each press to print the job alone?

Press #1 would take \(12\) hours, and Press #2 would take \(6\) hours to do the job alone.

Exercise \(\PageIndex{14}\)

Erlinda is having a party and wants to fill her hot tub. If she only uses the red hose it takes \(3\) hours more than if she only uses the green hose. If she uses both hoses together, the hot tub fills in \(2\) hours. How long does it take for each hose to fill the hot tub?

The red hose take \(6\) hours and the green hose take \(3\) hours alone.

Access these online resources for additional instruction and practice with solving applications modeled by quadratic equations.

• Word Problems Involving Quadratic Equations
• Quadratic Equation Word Problems
• Applying the Quadratic Formula

Key Concepts

• Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebra equation.
• Solve the equation using good algebra techniques.
• For a triangle with base, \(b\), and height, \(h\), the area, \(A\), is given by the formula \(A=\frac{1}{2}bh\).

• For a rectangle with length,\(L\), and width, \(W\), the area, \(A\), is given by the formula \(A=LW\).

• The height in feet, \(h\), of an object shot upwards into the air with initial velocity, \(v_{0}\), after \(t\) seconds is given by the formula \(h=-16 t^{2}+v_{0} t\).

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

14.4.2: The Parabola

• Last updated
• Save as PDF
• Page ID 67365

Learning Objectives

• Graph parabolas with vertices at the origin.
• Write equations of parabolas in standard form.
• Graph parabolas with vertices not at the origin.
• Solve applied problems involving parabolas.

Did you know that the Olympic torch is lit several months before the start of the games? The ceremonial method for lighting the flame is the same as in ancient times. The ceremony takes place at the Temple of Hera in Olympia, Greece, and is rooted in Greek mythology, paying tribute to Prometheus, who stole fire from Zeus to give to all humans. One of eleven acting priestesses places the torch at the focus of a parabolic mirror (Figure \(\PageIndex{1}\)), which focuses light rays from the sun to ignite the flame.

Parabolic mirrors (or reflectors) are able to capture energy and focus it to a single point. The advantages of this property are evidenced by the vast list of parabolic objects we use every day: satellite dishes, suspension bridges, telescopes, microphones, spotlights, and car headlights, to name a few. Parabolic reflectors are also used in alternative energy devices, such as solar cookers and water heaters, because they are inexpensive to manufacture and need little maintenance. In this section we will explore the parabola and its uses, including low-cost, energy-efficient solar designs.

Graphing Parabolas with Vertices at the Origin

Conic sections are formed when a plane cuts through a right circular cone as seen below. If the plane is parallel to the edge of the cone, an unbounded curve is formed. This curve is a parabola (Figure \(\PageIndex{2}\)).

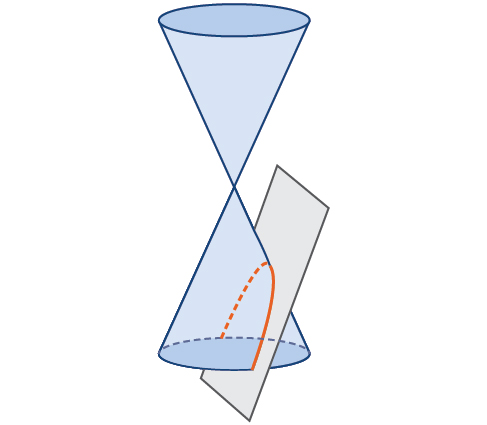
Figure \(\PageIndex{2}\): Parabola created by cutting a plane through a right circular cone.

Like the ellipse and hyperbola, the parabola can also be defined by a set of points in the coordinate plane. A parabola is the set of all points \((x,y)\) in a plane that are the same distance from a fixed line, called the directrix , and a fixed point (the focus ) not on the directrix.

Key features of the parabola are given in (Figure \(\PageIndex{3}\)). Notice that the axis of symmetry passes through the focus and vertex and is perpendicular to the directrix. The vertex is the midpoint between the directrix and the focus. The line segment that passes through the focus and is parallel to the directrix is called the latus rectum . The endpoints of the latus rectum lie on the curve. By definition, the distanced d from the focus to any point \(P\) on the parabola is equal to the distance from \(P\) to the directrix.

To work with parabolas in the coordinate plane , we consider two cases: those with a vertex at the origin and those with a vertex at a point other than the origin. We begin with the former.

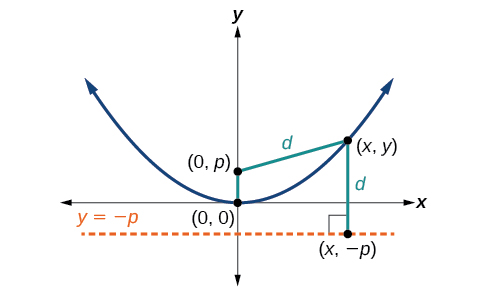
Let \((x,y)\) be a point on the parabola with vertex \((0,0)\), focus \((0,p)\),and directrix \(y=−p\)  as shown in Figure \(\PageIndex{4}\). The distanced d from point \((x,y)\) to point \((x,−p)\) on the directrix is the difference of the y -values: \(d=y+p\). The distance from the focus \((0,p)\) to the point \((x,y)\) is also equal to \(d\) and can be expressed using the distance formula.

\[ \begin{align*} d &=\sqrt{{(x−0)}^2+{(y−p)}^2} \\[4pt] &=\sqrt{x^2+{(y−p)}^2} \end{align*} \]

Set the two expressions for \(d\) equal to each other and solve for \(y\) to derive the equation of the parabola. We do this because the distance from \((x,y)\) to \((0,p)\) equals the distance from \((x,y)\) to \((x,−p)\).

\[\sqrt{x^2+{(y−p)}^2}=y+p \]

We then square both sides of the equation, expand the squared terms, and simplify by combining like terms.

\[ \begin{align*} x^2+{(y−p)}^2 &={(y+p)}^2 \\[4pt] x^2+y^2−2py+p^2 &=y^2+2py+p^2 \\[4pt] x^2−2py &=2py \\[4pt] x^2 &=4py \end{align*} \]

The equations of parabolas with vertex \((0,0)\) are \(y^2=4px\) when the x -axis is the axis of symmetry and \(x^2=4py\) when the y -axis is the axis of symmetry. These standard forms are given below, along with their general graphs and key features.

Standard Forms of Parabolas with Vertex at 0,0

STANDARD FORMS OF PARABOLAS WITH VERTEX \((0,0)\)

Table \(\PageIndex{1}\) and Figure \(\PageIndex{5}\) summarize the standard features of parabolas with a vertex at the origin.

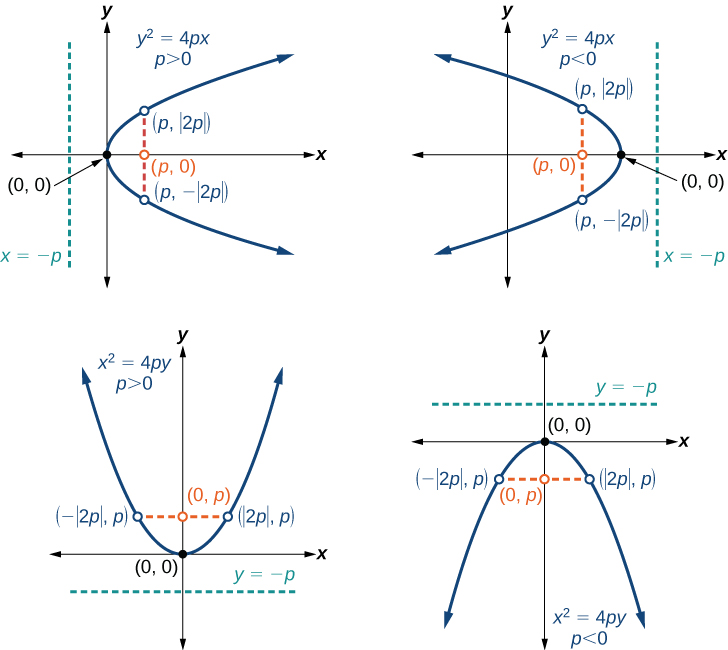
Figure \(\PageIndex{5}\): (a) When \(p>0\) and the axis of symmetry is the x-axis, the parabola opens right. (b) When \(p<0\) and the axis of symmetry is the x-axis, the parabola opens left. (c) When \(p>0\) and the axis of symmetry is the y-axis, the parabola opens up. (d) When \(p<0\) and the axis of symmetry is the y-axis, the parabola opens down.

The key features of a parabola are its vertex, axis of symmetry, focus, directrix, and latus rectum (Figure \(\PageIndex{5}\)). When given a standard equation for a parabola centered at the origin, we can easily identify the key features to graph the parabola. A line is said to be tangent to a curve if it intersects the curve at exactly one point. If we sketch lines tangent to the parabola at the endpoints of the latus rectum , these lines intersect on the axis of symmetry, as shown in Figure \(\PageIndex{6}\).

How to: Given a standard form equation for a parabola centered at \((0,0)\), sketch the graph

• Determine which of the standard forms applies to the given equation: \(y^2=4px\) or \(x^2=4py\).
• the axis of symmetry is the \(x\)-axis, \(y=0\)
• set \(4p\) equal to the coefficient of \(x\) in the given equation to solve for \(p\). If \(p>0\), the parabola opens right. If \(p<0\), the parabola opens left.
• use \(p\) to find the coordinates of the focus, \((p,0)\)
• use \(p\) to find the equation of the directrix, \(x=−p\)
• use \(p\) to find the endpoints of the latus rectum, \((p,\pm 2p)\). Alternately, substitute \(x=p\) into the original equation.
• the axis of symmetry is the \(y\)-axis, \(x=0\)
• set \(4p\) equal to the coefficient of \(y\) in the given equation to solve for \(p\). If \(p>0\), the parabola opens up. If \(p<0\), the parabola opens down.
• use \(p\) to find the coordinates of the focus, \((0,p)\)
• use \(p\) to find equation of the directrix, \(y=−p\)
• use \(p\) to find the endpoints of the latus rectum, \((\pm 2p,p)\)
• Plot the focus, directrix, and latus rectum, and draw a smooth curve to form the parabola.

x-axis as the Axis of Symmetry

Graph \(y^2=24x\). Identify and label the focus, directrix, and endpoints of the latus rectum .

The standard form that applies to the given equation is \(y^2=4px\). Thus, the axis of symmetry is the x -axis. It follows that:

• \(24=4p\), so \(p=6\). Since \(p>0\), the parabola opens right
• the coordinates of the focus are \((p,0)=(6,0)\)
• the equation of the directrix is \(x=−p=−6\)
• the endpoints of the latus rectum have the same x -coordinate at the focus. To find the endpoints, substitute \(x=6\) into the original equation: \((6,\pm 12)\)

Next we plot the focus, directrix, and latus rectum, and draw a smooth curve to form the parabola (Figure \(\PageIndex{7}\)).

Exercise \(\PageIndex{1}\)

Graph \(y^2=−16x\). Identify and label the focus, directrix, and endpoints of the latus rectum .

• Focus: \((−4,0)\)
• Directrix: \(x=4\)
• Endpoints of the latus rectum: \((−4,\pm 8)\)

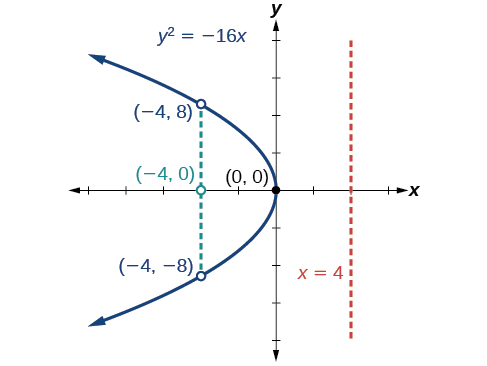
Figure \(\PageIndex{8}\): A graph of the solution to the problem presented herein.

y-axis as the Axis of Symmetry

Graph \(x^2=−6y\). Identify and label the focus, directrix, and endpoints of the latus rectum .

The standard form that applies to the given equation is \(x^2=4py\). Thus, the axis of symmetry is the \(y\)-axis. It follows that:

• \(−6=4p\),so \(p=−\dfrac{3}{2}\). Since \(p<0\), the parabola opens down.
• the coordinates of the focus are \((0,p)=(0,−\dfrac{3}{2})\)
• the equation of the directrix is \(y=−p=\dfrac{3}{2}\)
• the endpoints of the latus rectum can be found by substituting \(y=\dfrac{3}{2}\) into the original equation, \((\pm 3,−\dfrac{3}{2})\)

Next we plot the focus, directrix, and latus rectum , and draw a smooth curve to form the parabola.

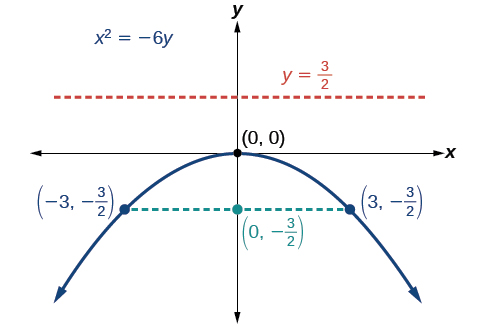
Figure \(\PageIndex{9}\): A graph of the solution to the problem presented herein.

Exercise \(\PageIndex{2}\)

Graph \(x^2=8y\). Identify and label the focus, directrix, and endpoints of the latus rectum .

• Focus: \((0,2)\)
• Directrix: \(y=−2\)
• Endpoints of the latus rectum: \((\pm 4,2)\).

Writing Equations of Parabolas in Standard Form

In the previous examples, we used the standard form equation of a parabola to calculate the locations of its key features. We can also use the calculations in reverse to write an equation for a parabola when given its key features.

How to: Given its focus and directrix, write the equation for a parabola in standard form

• If the given coordinates of the focus have the form \((p,0)\), then the axis of symmetry is the \(x\)-axis. Use the standard form \(y^2=4px\).
• If the given coordinates of the focus have the form \((0,p)\), then the axis of symmetry is the \(y\)-axis. Use the standard form \(x^2=4py\).
• Multiply \(4p\).
• Substitute the value from Step 2 into the equation determined in Step 1.

Example \(\PageIndex{3}\): Writing the Equation of a Parabola in Standard Form Given its Focus and Directrix

What is the equation for the parabola with focus \((−\dfrac{1}{2},0)\) and directrix \(x=\dfrac{1}{2}\)?

The focus has the form \((p,0)\), so the equation will have the form \(y^2=4px\).

• Multiplying \(4p\), we have \(4p=4(−\dfrac{1}{2})=−2\).
• Substituting for \(4p\), we have \(y^2=4px=−2x\).=

Therefore, the equation for the parabola is \(y^2=−2x\).

Exercise \(\PageIndex{3}\)

What is the equation for the parabola with focus \(\left(0,\dfrac{7}{2}\right)\) and directrix \(y=−\dfrac{7}{2}\)?

\(x^2=14y\).

Graphing Parabolas with Vertices Not at the Origin

Like other graphs we’ve worked with, the graph of a parabola can be translated. If a parabola is translated \(h\) units horizontally and \(k\) units vertically, the vertex will be \((h,k)\). This translation results in the standard form of the equation we saw previously with \(x\) replaced by \((x−h)\) and \(y\) replaced by \((y−k)\).

To graph parabolas with a vertex \((h,k)\) other than the origin, we use the standard form \({(y−k)}^2=4p(x−h)\) for parabolas that have an axis of symmetry parallel to the \(x\)-axis, and \({(x−h)}^2=4p(y−k)\) for parabolas that have an axis of symmetry parallel to the \(y\)-axis. These standard forms are given below, along with their general graphs and key features.

Standard Forms of Parabolas with Vertex at (h,k)

STANDARD FORMS OF PARABOLAS WITH VERTEX \((H, K)\)

Table \(\PageIndex{2}\) and Figure \(\PageIndex{11}\) summarize the standard features of parabolas with a vertex at a point \((h,k)\).

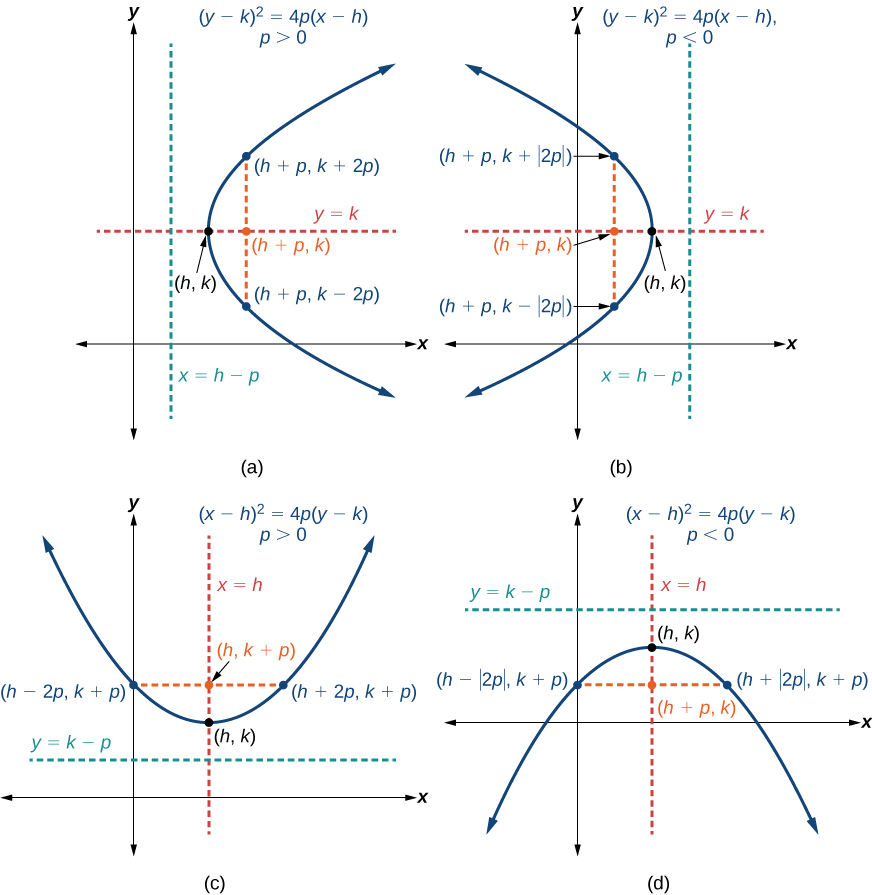
Figure \(\PageIndex{11}\): (a) When \(p > 0\), the parabola opens right. (b) When \(p < 0\), the parabola opens left. (c) When \(p > 0\), the parabola opens up. The equation to this becomes more familiar as \(y = ax^2 + bx + c\). (d) When \(p < 0\), the parabola opens down.

How to: Given a standard form equation for a parabola centered at \((h,k)\), sketch the graph

• Determine which of the standard forms applies to the given equation: \({(y−k)}^2=4p(x−h)\) or \({(x−h)}^2=4p(y−k)\).
• use the given equation to identify \(h\) and \(k\) for the vertex, \((h,k)\)
• use the value of \(k\) to determine the axis of symmetry, \(y=k\)
• set \(4p\) equal to the coefficient of \((x−h)\) in the given equation to solve for \(p\). If \(p>0\),the parabola opens right. If \(p<0\), the parabola opens left.
• use \(h\), \(k\), and \(p\) to find the coordinates of the focus, \((h+p, k)\)
• use \(h\)  andp p to find the equation of the directrix, \(x=h−p\)
• use \(h\), \(k\), and \(p\) to find the endpoints of the latus rectum, \((h+p,k\pm 2p)\)
• use the given equation to identify \(h\) and \(k\) for the vertex, \((h,k)\)
• use the value of \(h\) to determine the axis of symmetry, \(x=h\)
• set \(4p\) equal to the coefficient of \((y−k)\) in the given equation to solve for \(p\). If \(p>0\), the parabola opens up. If \(p<0\), the parabola opens down.
• use \(h\), \(k\), and \(p\) to find the coordinates of the focus, \((h, k+p)\)
• use \(k\) and \(p\) to find the equation of the directrix, \(y=k−p\)
• use \(h\), \(k\), and \(p\)  to find the endpoints of the latus rectum, \((h\pm 2p, k+p)\)
• Plot the vertex, axis of symmetry, focus, directrix, and latus rectum, and draw a smooth curve to form the parabola.

Example \(\PageIndex{4}\): Graphing a Parabola with Vertex \((h, k)\) and Axis of Symmetry Parallel to the \(x\)-axis

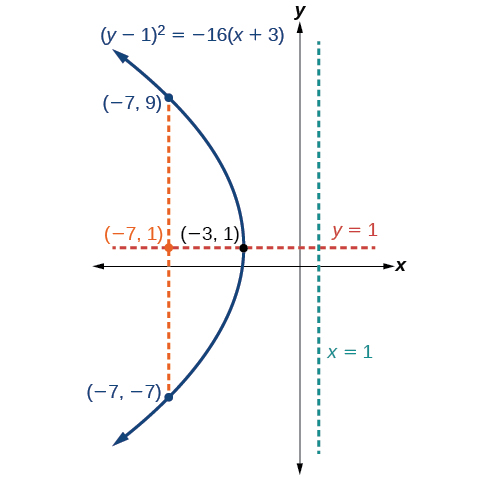
Graph \({(y−1)}^2=−16(x+3)\). Identify and label the vertex, axis of symmetry, focus, directrix, and endpoints of the latus rectum.

The standard form that applies to the given equation is \({(y−k)}^2=4p(x−h)\). Thus, the axis of symmetry is parallel to the \(x\)-axis. It follows that:

• the vertex is \((h,k)=(−3,1)\)
• the axis of symmetry is \(y=k=1\)
• \(−16=4p\),so \(p=−4\). Since \(p<0\), the parabola opens left.
• the coordinates of the focus are \((h+p,k)=(−3+(−4),1)=(−7,1)\)
• the equation of the directrix is \(x=h−p=−3−(−4)=1\)
• the endpoints of the latus rectum are \((h+p,k\pm 2p)=(−3+(−4),1\pm 2(−4))\), or \((−7,−7)\) and \((−7,9)\)

Next we plot the vertex, axis of symmetry, focus, directrix, and latus rectum, and draw a smooth curve to form the parabola (Figure \(\PageIndex{10}\)).

Exercise \(\PageIndex{4}\)

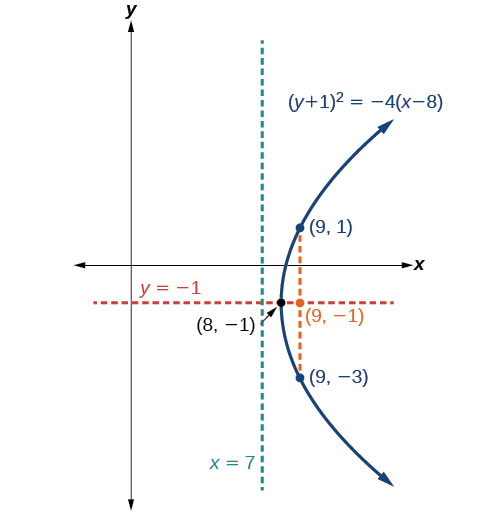
Graph \({(y+1)}^2=4(x−8)\). Identify and label the vertex, axis of symmetry, focus, directrix, and endpoints of the latus rectum .

• Vertex: \((8,−1)\)
• Axis of symmetry: \(y=−1\)
• Focus: \((9,−1)\)
• Directrix: \(x=7\)
•  Endpoints of the latus rectum : \((9,−3)\) and \((9,1)\).

Example \(\PageIndex{5}\): Graphing a Parabola from an Equation Given in General Form

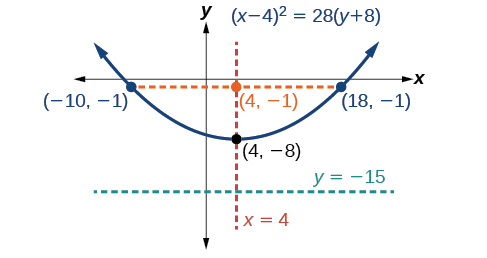
Graph \(x^2−8x−28y−208=0\). Identify and label the vertex, axis of symmetry, focus, directrix, and endpoints of the latus rectum .

Start by writing the equation of the parabola in standard form. The standard form that applies to the given equation is \({(x−h)}^2=4p(y−k)\). Thus, the axis of symmetry is parallel to the \(y\)-axis. To express the equation of the parabola in this form, we begin by isolating the terms that contain the variable \(x\) in order to complete the square.

\[ \begin{align*} x^2−8x−28y−208&=0 \\[4pt] x^2−8x &=28y+208 \\[4pt] x^2−8x+16 &=28y+208+16 \\[4pt] (x−4)^2 &=28y+224 \\[4pt] (x−4)^2 &=28(y+8) \\[4pt] (x−4)^2&= 4⋅7⋅(y+8) \end{align*}\]

It follows that:

• the vertex is \((h,k)=(4,−8)\)
• the axis of symmetry is \(x=h=4\)
• since \(p=7\), \(p>0\)  and so the parabola opens up
• the coordinates of the focus are \((h,k+p)=(4,−8+7)=(4,−1)\)
• the equation of the directrix is \(y=k−p=−8−7=−15\)
• the endpoints of the latus rectum are \((h\pm 2p,k+p)=(4\pm 2(7),−8+7)\), or \((−10,−1)\) and \((18,−1)\)

Next we plot the vertex, axis of symmetry, focus, directrix, and latus rectum, and draw a smooth curve to form the parabola (Figure \(\PageIndex{14}\)).

Exercise \(\PageIndex{5}\)

Graph \({(x+2)}^2=−20(y−3)\). Identify and label the vertex, axis of symmetry, focus, directrix, and endpoints of the latus rectum .

• Vertex: \((−2,3)\)
• Axis of symmetry: \(x=−2\)
• Focus: \((−2,−2)\)
• Directrix: \(y=8\)
• Endpoints of the latus rectum : \((−12,−2)\) and \((8,−2)\).

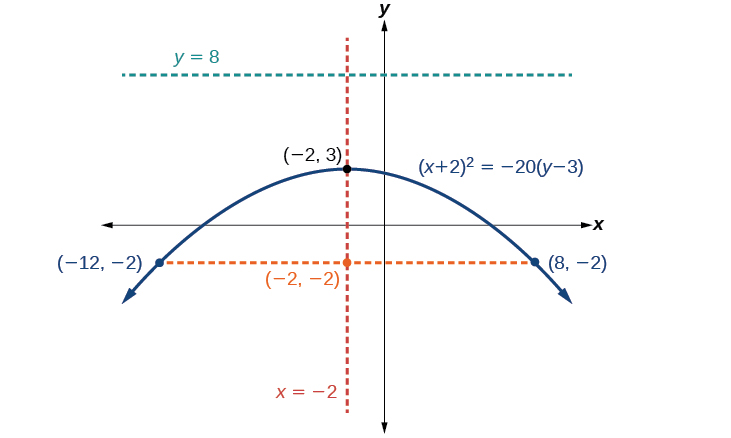
Figure \(\PageIndex{15}\): A graph of the solution to the problem presented herein.

Solving Applied Problems Involving Parabolas

As we mentioned at the beginning of the section, parabolas are used to design many objects we use every day, such as telescopes, suspension bridges, microphones, and radar equipment. Parabolic mirrors , such as the one used to light the Olympic torch, have a very unique reflecting property. When rays of light parallel to the parabola’s axis of symmetry are directed toward any surface of the mirror, the light is reflected directly to the focus (Figure \(\PageIndex{16}\)). This is why the Olympic torch is ignited when it is held at the focus of the parabolic mirror.

Solar Cookers

Parabolic mirrors have the ability to focus the sun’s energy to a single point, raising the temperature hundreds of degrees in a matter of seconds. Thus, parabolic mirrors are featured in many low-cost, energy efficient solar products, such as solar cookers, solar heaters, and even travel-sized fire starters.

Example \(\PageIndex{6}\): Solving Applied Problems Involving Parabolas

A cross-section of a design for a travel-sized solar fire starter is shown in Figure \(\PageIndex{17}\). The sun’s rays reflect off the parabolic mirror toward an object attached to the igniter. Because the igniter is located at the focus of the parabola, the reflected rays cause the object to burn in just seconds.

• Find the equation of the parabola that models the fire starter. Assume that the vertex of the parabolic mirror is the origin of the coordinate plane.
• Use the equation found in part (a) to find the depth of the fire starter.

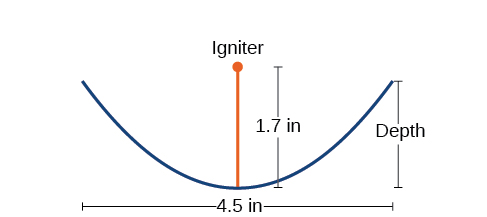
Figure \(\PageIndex{17}\) Cross-section of a travel-sized solar fire starter

• The vertex of the dish is the origin of the coordinate plane, so the parabola will take the standard form \(x^2=4py\),where \(p>0\).  The igniter, which is the focus, is \(1.7\) inches above the vertex of the dish. Thus we have \(p=1.7\). 

\[\begin{align*} x^2&=4py\qquad \text{Standard form of upward-facing parabola with vertex } (0,0)\\ x^2&=4(1.7)y\qquad \text{Substitute } 1.7 \text{ for } p\\ x^2&=6.8y\qquad \text{Multiply.} \end{align*}\]

• The dish extends \(\dfrac{4.5}{2}=2.25\) inches on either side of the origin. We can substitute \(2.25\) for \(x\) in the equation from part (a) to find the depth of the dish.

\[\begin{align*} x^2&=6.8y\qquad \text{ Equation found in part } (a)\\ {(2.25)}^2&=6.8y\qquad \text{Substitute } 2.25 \text{ for } x\\ y&\approx 0.74\qquad \text{Solve for } y \end{align*}\]

The dish is about \(0.74\) inches deep.

Exercise \(\PageIndex{6}\)

Balcony-sized solar cookers have been designed for families living in India. The top of a dish has a diameter of \(1600\) mm. The sun’s rays reflect off the parabolic mirror toward the “cooker,” which is placed \(320\) mm from the base.

• Find an equation that models a cross-section of the solar cooker. Assume that the vertex of the parabolic mirror is the origin of the coordinate plane, and that the parabola opens to the right (i.e., has the x -axis as its axis of symmetry).
• Use the equation found in part (a) to find the depth of the cooker.

\(y^2=1280x\)

The depth of the cooker is \(500\) mm

Key Equations

Key concepts.

• A parabola is the set of all points \((x,y)\) in a plane that are the same distance from a fixed line, called the directrix, and a fixed point (the focus) not on the directrix.
• The standard form of a parabola with vertex \((0,0)\) and the x -axis as its axis of symmetry can be used to graph the parabola. If \(p>0\), the parabola opens right. If \(p<0\), the parabola opens left. See Example \(\PageIndex{1}\).
• The standard form of a parabola with vertex \((0,0)\) and the y -axis as its axis of symmetry can be used to graph the parabola. If \(p>0\), the parabola opens up. If \(p<0\), the parabola opens down. See Example \(\PageIndex{2}\).
• When given the focus and directrix of a parabola, we can write its equation in standard form. See Example \(\PageIndex{3}\).
• The standard form of a parabola with vertex \((h,k)\) and axis of symmetry parallel to the \(x\)-axis can be used to graph the parabola. If \(p>0\), the parabola opens right. If \(p<0\), the parabola opens left. See Example \(\PageIndex{4}\).
• The standard form of a parabola with vertex \((h,k)\) and axis of symmetry parallel to the \(y\)-axis can be used to graph the parabola. If \(p>0\), the parabola opens up. If \(p<0\), the parabola opens down. See Example \(\PageIndex{5}\).
• Real-world situations can be modeled using the standard equations of parabolas. For instance, given the diameter and focus of a cross-section of a parabolic reflector, we can find an equation that models its sides. See Example \(\PageIndex{6}\).

Contributors and Attributions

• Template:ContribOpenStaxPreCalc

• HW Guidelines
• Study Skills Quiz
• Find Local Tutors
• Demo MathHelp.com
• Join MathHelp.com

Select a Course Below

• ACCUPLACER Math
• Math Placement Test
• PRAXIS Math
• + more tests
• 5th Grade Math
• 6th Grade Math
• Pre-Algebra
• College Pre-Algebra
• Introductory Algebra
• Intermediate Algebra
• College Algebra

Parabola Word Problems & Graphing Calculators

Introduction Getting Info from Equations Getting Equations from Info Word Problems & Calculators

What are some examples of parabolas in real life?

Because parabolas, by definition, collect information (signals, etc) at their foci, then they are useful in real life to things that collect signals. For instance, radio-antenna dishes are parabolic, as are parts of headlights and the parabolic dishes of lighthouses.

Content Continues Below

MathHelp.com

Also, "ballistic motion" is modelled by an arc based on parabolas.

What are some examples of things in real life that are *not* parabolas?

Many things are claimed to be in the shape of a parabola, but are not, such as:

• A chain hanging freely hanging between two attachment points forms a curve called a catenary ; a hanging chain (or rope) does not form a parabola.
• The St. Louis Arch is an upside-down catenary; it is not a parabola.
• Some part of some bananas *might* match a parabola, but not in general.
• Some parts of some bridges and roller coasters *might* match parabolas, but not in general.
• A Slinky toy does not form a parabola.
• A rainbow does not form a parabola; a rainbow is actually part of a circle.

Despite the ease of determining that rainbows, the St. Louis Arch, etc, are *not* parabolas, you should still expect to see some word problems that kind of assume that these things *are* parabolas. Just roll with it.

• An arch in a memorial park, having a parabolic shape, has a height of 25 feet and a base width of 30 feet. Find an equation which models this shape, using the x -axis to represent the ground. State the focus and directrix.

For simplicity, I'll center the curve for the arch on the y -axis, so the vertex will be at:

( h , k ) = (0, 25)

Advertisement

Since the width is thirty, then the x -intercepts must be at:

x = −15

Obviously, this is a regular (vertical) parabola, but it's upside-down so the x part is squared and I'll have a negative leading coefficient.

Working backwards from the x -intercepts, the equation has to be of the form:

y = a ( x − 15)( x + 15)

Plugging in the known vertex value, I get:

(25) = a ((0) − 15)((0) + 15) = −225 a

25 = −225 a

−(1/9) = a

With a being the leading coefficient from the regular quadratic equation y  =  ax 2  +  bx  +  c , I also know that the value of 1/ a is the same as the value of 4 p , so:

1/(−1/9) = −9 = 4 p

p = −9/4

Then my line equation is:

4 p ( y − k ) = ( x − h ) 2

4(−9/4)( y − 25) = ( x − 0) 2

−9( y − 25) = x 2

I placed the vertex at the point (0, 0) . The focus is 9/4 units below the vertex; the directrix is the horizontal line 9/4 units above the vertex. Therefore, my answer is:

equation: −9( y − 25) = x 2 focus: (0, 91/4) directrix: y = 109/4

Note: In the above exercise, I could also have worked directly from the conics form of the parabola equation, plugging in the vertex and an x -intercept, to find the value of p . This method would work as follows:

4 p ( y − 25) = ( x − 0) 2 4 p (0 − 25) = (15 − 0) 2 4 p (−25) = 225 4 p = −225/25 = −9 p = −9/4

You may encounter an exercise of this sort regarding the Gateway Arch in Saint Louis, Missouri, which is, in fact, an inverted catenary curve; in particular, a hyperbolic cosine curve. But its shape is close enough to that of a parabola for the purposes of the exercise.

(If you ever visit Saint Louis, you should definitely try to visit the Arch. You can watch a movie down in the basement describing the design and construction of the Arch, and then you ride the tram up to the top of the Arch. The view is fabulous!)

• A radio telescope has a parabolic dish with a diameter of 100 meters. The collected radio signals are reflected to one collection point, called the focal point, being the focus of the parabola. If the focal length is 45 meters, find the depth of the dish, rounded to one decimal place.

To simplify my computations, I'll put the vertex of my parabola (that is, the base of the dish) at the origin, so:

( h , k ) = (0, 0)

The focal length is the distance between the vertex and the focus. Since the focal length is 45 , then p  = 45 and the equation is:

4 py = x 2 4(45) y = x 2 180 y = x 2

This parabola extends forever in either direction, but I only care about the part of the curve that models the dish. Since the dish has a diameter of a hundred meters, then I only care about the part of the curve from x  = −50 to x  = +50 .

The height of the edge of the dish (and thus the depth of the dish) will be the y -value of the equation at the "ends" of the modelling curve. The height of the parabola will be the same at either x -value, since they're each the same distance from the vertex, so it doesn't matter which value I use. I prefer positive values, so I'll plug x  = 50 into my modelling equation:

180 y = (50) 2 180 y = 2500 y = 250/18 = 125/9

Plugging into my calculator and rounding to one decimal place (per instructions), my answer is:

depth: 13.9 meters

If you need to graph a sideways parabola in your graphing calculator (to check your work, for instance), you'll need to solve the equation for its two halves, and then graph the two halves as two separate functions. For instance, to view the graph of:

( y + 2) 2 = −4( x − 1)

...you'd solve and graph as:

Enter the "plus" and "minus" parts into your calculator as separate functions:

The calculator's graph will likely show a slight gap between the two halves of the parabola:

Don't expect the two halves of the graph to "meet in the middle" on your calculator screen; that's a higher degree of accuracy (and comprehension) than the calculator can handle.

In my experience, it is easier to remember the relationships between the vertex, focus, axis of symmetry, directrix, and the value of p , than to try to memorize the (often very long) list of formulas they give you. Do enough practice exercises that you have a good grasp of how these elements are related, and you should be successful with parabolas.

URL: https://www.purplemath.com/modules/parabola4.htm

Page 1 Page 2 Page 3 Page 4

Standardized Test Prep

College math, homeschool math, share this page.

• Terms of Use
• Privacy / Cookies
• About Purplemath
• About the Author
• Tutoring from PM
• Advertising
• Linking to PM
• Site licencing

Visit Our Profiles

Real World Examples of Quadratic Equations

A Quadratic Equation looks like this:

Quadratic equations pop up in many real world situations!

Here we have collected some examples for you, and solve each using different methods:

• Factoring Quadratics
• Completing the Square
• Graphing Quadratic Equations
• The Quadratic Formula
• Online Quadratic Equation Solver

Each example follows three general stages:

• Take the real world description and make some equations
• Use your common sense to interpret the results

Balls, Arrows, Missiles and Stones

When you throw a ball (or shoot an arrow, fire a missile or throw a stone) it goes up into the air, slowing as it travels, then comes down again faster and faster ...

... and a Quadratic Equation tells you its position at all times!

Example: Throwing a Ball

A ball is thrown straight up, from 3 m above the ground, with a velocity of 14 m/s. when does it hit the ground.

Ignoring air resistance, we can work out its height by adding up these three things: (Note: t is time in seconds)

Add them up and the height h at any time t is:

h = 3 + 14t − 5t 2

And the ball will hit the ground when the height is zero:

3 + 14t − 5t 2 = 0

Which is a Quadratic Equation !

In "Standard Form" it looks like:

−5t 2 + 14t + 3 = 0

It looks even better when we multiply all terms by −1 :

5t 2 − 14t − 3 = 0

Let us solve it ...

There are many ways to solve it, here we will factor it using the "Find two numbers that multiply to give ac , and add to give b " method in Factoring Quadratics :

ac = −15 , and b = −14 .

The factors of −15 are: −15, −5, −3, −1, 1, 3, 5, 15

By trying a few combinations we find that −15 and 1 work (−15×1 = −15, and −15+1 = −14)

The "t = −0.2" is a negative time, impossible in our case.

The "t = 3" is the answer we want:

The ball hits the ground after 3 seconds!

Here is the graph of the Parabola h = −5t 2 + 14t + 3

It shows you the height of the ball vs time

Some interesting points:

(0,3) When t=0 (at the start) the ball is at 3 m

(−0.2,0) says that −0.2 seconds BEFORE we threw the ball it was at ground level. This never happened! So our common sense says to ignore it.

(3,0) says that at 3 seconds the ball is at ground level.

Also notice that the ball goes nearly 13 meters high.

Note: You can find exactly where the top point is!

The method is explained in Graphing Quadratic Equations , and has two steps:

Find where (along the horizontal axis) the top occurs using −b/2a :

• t = −b/2a = −(−14)/(2 × 5) = 14/10 = 1.4 seconds

Then find the height using that value (1.4)

• h = −5t 2 + 14t + 3 = −5(1.4) 2 + 14 × 1.4 + 3 = 12.8 meters

So the ball reaches the highest point of 12.8 meters after 1.4 seconds.

Example: New Sports Bike

You have designed a new style of sports bicycle!

Now you want to make lots of them and sell them for profit.

Your costs are going to be:

• $700,000 for manufacturing set-up costs, advertising, etc
• $110 to make each bike

Based on similar bikes, you can expect sales to follow this "Demand Curve":

Where "P" is the price.

For example, if you set the price:

• at $0, you just give away 70,000 bikes
• at $350, you won't sell any bikes at all
• at $300 you might sell 70,000 − 200×300 = 10,000 bikes

So ... what is the best price? And how many should you make?

Let us make some equations!

How many you sell depends on price, so use "P" for Price as the variable

Profit = −200P 2 + 92,000P − 8,400,000

Yes, a Quadratic Equation. Let us solve this one by Completing the Square .

Solve: −200P 2 + 92,000P − 8,400,000 = 0

Step 1 Divide all terms by -200

Step 2 Move the number term to the right side of the equation:

Step 3 Complete the square on the left side of the equation and balance this by adding the same number to the right side of the equation:

(b/2) 2 = (−460/2) 2 = (−230) 2 = 52900

Step 4 Take the square root on both sides of the equation:

Step 5 Subtract (-230) from both sides (in other words, add 230):

What does that tell us? It says that the profit is ZERO when the Price is $126 or $334

But we want to know the maximum profit, don't we?

It is exactly half way in-between! At $230

And here is the graph:

The best sale price is $230 , and you can expect:

• Unit Sales = 70,000 − 200 x 230 = 24,000
• Sales in Dollars = $230 x 24,000 = $5,520,000
• Costs = 700,000 + $110 x 24,000 = $3,340,000
• Profit = $5,520,000 − $3,340,000 = $2,180,000

A very profitable venture.

Example: Small Steel Frame

Your company is going to make frames as part of a new product they are launching.

The frame will be cut out of a piece of steel, and to keep the weight down, the final area should be 28 cm 2

The inside of the frame has to be 11 cm by 6 cm

What should the width x of the metal be?

Area of steel before cutting:

Area of steel after cutting out the 11 × 6 middle:

Let us solve this one graphically !

Here is the graph of 4x 2 + 34x :

The desired area of 28 is shown as a horizontal line.

The area equals 28 cm 2 when:

x is about −9.3 or 0.8

The negative value of x make no sense, so the answer is:

x = 0.8 cm (approx.)

Example: River Cruise

A 3 hour river cruise goes 15 km upstream and then back again. the river has a current of 2 km an hour. what is the boat's speed and how long was the upstream journey.

There are two speeds to think about: the speed the boat makes in the water, and the speed relative to the land:

• Let x = the boat's speed in the water (km/h)
• Let v = the speed relative to the land (km/h)

Because the river flows downstream at 2 km/h:

• when going upstream, v = x−2 (its speed is reduced by 2 km/h)
• when going downstream, v = x+2 (its speed is increased by 2 km/h)

We can turn those speeds into times using:

time = distance / speed

(to travel 8 km at 4 km/h takes 8/4 = 2 hours, right?)

And we know the total time is 3 hours:

total time = time upstream + time downstream = 3 hours

Put all that together:

total time = 15/(x−2) + 15/(x+2) = 3 hours

Now we use our algebra skills to solve for "x".

First, get rid of the fractions by multiplying through by (x-2) (x+2) :

3(x-2)(x+2) = 15(x+2) + 15(x-2)

Expand everything:

3(x 2 −4) = 15x+30 + 15x−30

Bring everything to the left and simplify:

3x 2 − 30x − 12 = 0

It is a Quadratic Equation!

Let us solve it using the Quadratic Formula :

Where a , b and c are from the Quadratic Equation in "Standard Form": ax 2 + bx + c = 0

Solve 3x 2 - 30x - 12 = 0

Answer: x = −0.39 or 10.39 (to 2 decimal places)

x = −0.39 makes no sense for this real world question, but x = 10.39 is just perfect!

Answer: Boat's Speed = 10.39 km/h (to 2 decimal places)

And so the upstream journey = 15 / (10.39−2) = 1.79 hours = 1 hour 47min

And the downstream journey = 15 / (10.39+2) = 1.21 hours = 1 hour 13min

Example: Resistors In Parallel

Two resistors are in parallel, like in this diagram:

The total resistance has been measured at 2 Ohms, and one of the resistors is known to be 3 ohms more than the other.

What are the values of the two resistors?

The formula to work out total resistance "R T " is:

1 R T   =   1 R 1 + 1 R 2

In this case, we have R T = 2 and R 2 = R 1 + 3

1 2   =   1 R 1 + 1 R 1 +3

To get rid of the fractions we can multiply all terms by 2R 1 (R 1 + 3) and then simplify:

Yes! A Quadratic Equation!

Let us solve it using our Quadratic Equation Solver .

• Enter 1, −1 and −6
• And you should get the answers −2 and 3

R 1 cannot be negative, so R 1 = 3 Ohms is the answer.

The two resistors are 3 ohms and 6 ohms.

Quadratic Equations are useful in many other areas:

For a parabolic mirror, a reflecting telescope or a satellite dish, the shape is defined by a quadratic equation.

Quadratic equations are also needed when studying lenses and curved mirrors.

And many questions involving time, distance and speed need quadratic equations.

WORD PROBLEMS INVOLVING PARABOLA AND HYPERBOLA

Problem 1 :

An engineer designs a satellite dish with a parabolic cross section. The dish is 5 m wide at the opening, and the focus is placed 1 2 . m from the vertex

(a) Position a coordinate system with the origin at the vertex and the x -axis on the parabola’s axis of symmetry and find an equation of the parabola.

(b) Find the depth of the satellite dish at the vertex.

From the given information, the parabola is symmetric about x axis and open rightward.

y 2   =  4ax

here a = 1.2

y 2   =  4(1.2)x

y 2   =  4.8 x

The parabola is passing through the point (x, 2.5)

(2.5) 2   =  4.8 x

x  =  6.25/4.8

x  =  1.3 m

Hence the depth of the  satellite dish is 1.3 m.

Problem 2 :

Parabolic cable of a 60 m portion of the roadbed of a suspension bridge are positioned as shown below. Vertical Cables are to be spaced every 6 m along this portion of the roadbed. Calculate the lengths of first two of these vertical cables from the vertex.

(x - h) 2   =  4a(y - k)

(x - 0) 2   =  4a(y - 3)

x 2   =  4a(y - 3)

The parabola is passing through the point (30, 16)

30 2   =  4a(16 - 3)

900  =  4a(13)

a  =  900/42

a  =  225/13

x 2   =  4(225/13)(y - 3)

length of 1st cable :

6 2   =  4(225/13)(h 1 - 3)

36(13)/4(225)   =  (h 1  - 3)

0.52 + 3  =  h 1

h 1   =  3.52 m

length of 2nd cable :

12 2   =  4(225/13)(h 2  - 3)

144(13)/4(225)  =  (h 2  - 3)

2.08 + 3  =  h 2

h 2   =  5.08 m

Problem 3 :

Cross section of a Nuclear cooling tower is in the shape of a hyperbola with equation  (x 2 /30 2 ) - (y 2 /44 2 ) = 1 . The tower is 150 m tall and the distance from the top of the tower to the centre of the hyperbola is half the distance from the base of the tower to the centre of the hyperbola. Find the diameter of the top and base of the tower.

Since the distance from the top of the tower to the centre of the hyperbola is half the distance from the base of the tower to the centre of the hyperbola, let us consider 3y  =  150

 y  =  50

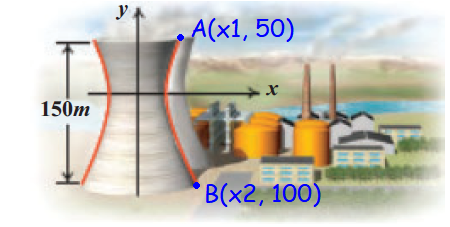
(x 2 /30 2 ) - (y 2 /44 2 ) = 1

By applying the point A in the general equation, we get

( x 1 2 /30 2 ) - (50 2 /44 2 ) = 1

( x 1 2 /30 2 )  =  1 +   (50 2 /44 2 ) 

( x 1 2 /30 2 )  =  (1936 + 2500)/1936

(x 1 2 /30 2 )  =  4436/1936

x 1 2   =  (4436) (900)/1936

x 1   =  45.41

By applying the point B in the equation, we get

( x 2 2 /30 2 ) - (100 2 /44 2 ) = 1

( x 2 2 /30 2 )  =  1 +   (100 2 /44 2 ) 

( x 2 2 /30 2 )  =  (1936 + 10000)/1936

( x 2 2 /30 2 )  =  11936/1936

x 2 2   =  (11936) (900)/1936

x 2   =  74.45 m

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to   [email protected]

We always appreciate your feedback.

© All rights reserved. onlinemath4all.com

• Sat Math Practice
• SAT Math Worksheets
• PEMDAS Rule
• BODMAS rule
• GEMDAS Order of Operations
• Math Calculators
• Transformations of Functions
• Order of rotational symmetry
• Lines of symmetry
• Compound Angles
• Quantitative Aptitude Tricks
• Trigonometric ratio table
• Word Problems
• Times Table Shortcuts
• 10th CBSE solution
• PSAT Math Preparation
• Privacy Policy
• Laws of Exponents

Recent Articles

Trigonometry Cofunction Identities

Apr 30, 24 09:01 PM

Worksheet on Unit Rates

Apr 30, 24 08:50 PM

Ratio Worksheet

Apr 29, 24 07:59 PM

Module 10: Quadratic Equations and Functions

10.3 – applications of quadratic functions, learning objectives, objects in free fall.

• Determining the width of a border

Finding the maximum and minimum values of a quadratic function

(10.3.1) – solve application problems involving quadratic functions.

Quadratic equations are widely used in science, business, and engineering. Quadratic equations are commonly used in situations where two things are multiplied together and they both depend on the same variable. For example, when working with area, if both dimensions are written in terms of the same variable, you use a quadratic equation. Because the quantity of a product sold often depends on the price, you sometimes use a quadratic equation to represent revenue as a product of the price and the quantity sold. Quadratic equations are also used when gravity is involved, such as the path of a ball or the shape of cables in a suspension bridge.

A very common and easy-to-understand application is the height of a ball thrown at the ground off a building. Because gravity will make the ball speed up as it falls, a quadratic equation can be used to estimate its height any time before it hits the ground. Note: The equation isn’t completely accurate, because friction from the air will slow the ball down a little. For our purposes, this is close enough.

A ball is thrown off a building from 200 feet above the ground. Its starting velocity (also called initial velocity ) is [latex]−10[/latex] feet per second. (The negative value means it’s heading toward the ground.)

The equation [latex]h=-16t^{2}-10t+200[/latex] can be used to model the height of the ball after [latex]t[/latex] seconds. About how long does it take for the ball to hit the ground?

When the ball hits the ground, the height is 0. Substitute 0 for [latex]h[/latex].

[latex]\begin{array}{c}h=-16t^{2}-10t+200\\0=-16t^{2}-10t+200\\-16t^{2}-10t+200=0\end{array}[/latex]

This equation is difficult to solve by factoring or by completing the square, so solve it by applying the Quadratic Formula, [latex] x=\frac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}[/latex]. In this case, the variable is [latex]t[/latex] rather than [latex]x[/latex]. [latex]a=−16,b=−10[/latex], and [latex]c=200[/latex].

[latex]\displaystyle t=\frac{-(-10)\pm \sqrt{{{(-10)}^{2}}-4(-16)(200)}}{2(-16)}[/latex]

Simplify. Be very careful with the signs.

[latex]\large \begin{array}{l}t=\frac{10\pm \sqrt{100+12800}}{-32}\\\,\,=\frac{10\pm \sqrt{12900}}{-32}\end{array}[/latex]

Use a calculator to find both roots.

[latex]t[/latex] is approximately [latex]−3.86[/latex] or [latex]3.24[/latex].

Consider the roots logically. One solution, [latex]−3.86[/latex], cannot be the time because it is a negative number. The other solution, [latex]3.24[/latex] seconds, must be when the ball hits the ground.

The ball hits the ground approximately [latex]3.24[/latex] seconds after being thrown.

In the next video we show another example of how the quadratic equation can be used to find the time it takes for an object in free fall to hit the ground.

Here are some more similar objects in free fall examples.

Example: Applying the Vertex and [latex] x[/latex] -Intercepts of a Parabola

A ball is thrown upward from the top of a 40 foot high building at a speed of 80 feet per second. The ball’s height above ground can be modeled by the equation [latex]H\left(t\right)=-16{t}^{2}+80t+40[/latex].

a. When does the ball reach the maximum height?

b. What is the maximum height of the ball?

c. When does the ball hit the ground?

[latex]\large \begin{array}{c} h=-\frac{80}{2\left(-16\right)} \text{ }=\frac{80}{32}\hfill \\ \text{ }=\frac{5}{2}\hfill \\ \text{ }=2.5\hfill \end{array}[/latex]

The ball reaches a maximum height after 2.5 seconds.

b. To find the maximum height, find the y  coordinate of the vertex of the parabola.

[latex]\large \begin{array}{c}k=H\left(-\frac{b}{2a}\right)\hfill \\ \text{ }=H\left(2.5\right)\hfill \\ \text{ }=-16{\left(2.5\right)}^{2}+80\left(2.5\right)+40\hfill \\ \text{ }=140\hfill \end{array}[/latex]

The ball reaches a maximum height of 140 feet.

c. To find when the ball hits the ground, we need to determine when the height is zero, [latex]H\left(t\right)=0[/latex].

We use the quadratic formula.

[latex]\large \begin{array}{c} t=\frac{-80\pm \sqrt{{80}^{2}-4\left(-16\right)\left(40\right)}}{2\left(-16\right)}\hfill \\ \text{ }=\frac{-80\pm \sqrt{8960}}{-32}\hfill \end{array}[/latex]

Because the square root does not simplify nicely, we can use a calculator to approximate the values of the solutions.

[latex]\large \begin{array}{c}t=\frac{-80-\sqrt{8960}}{-32}\approx 5.458\hfill & \text{or}\hfill & t=\frac{-80+\sqrt{8960}}{-32}\approx -0.458\hfill \end{array}[/latex]

The second answer is outside the reasonable domain of our model, so we conclude the ball will hit the ground after about 5.458 seconds.

A rock is thrown upward from the top of a 112-foot high cliff overlooking the ocean at a speed of 96 feet per second. The rock’s height above ocean can be modeled by the equation [latex]H\left(t\right)=-16{t}^{2}+96t+112[/latex].

a. When does the rock reach the maximum height?

b. What is the maximum height of the rock?

c. When does the rock hit the ocean?

a. 3 seconds

b. 256 feet

c. 7 seconds

Applications of quadratic functions: determining the width of a border

The area problem below does not look like it includes a Quadratic Formula of any type, and the problem seems to be something you have solved many times before by simply multiplying. But in order to solve it, you will need to use a quadratic equation.

Bob made a quilt that is 4 ft [latex]\times[/latex] 5 ft. He has 10 sq. ft. of fabric he can use to add a border around the quilt. How wide should he make the border to use all the fabric? (The border must be the same width on all four sides.)

Sketch the problem. Since you don’t know the width of the border, you will let the variable [latex]x[/latex] represent the width.

In the diagram, the original quilt is indicated by the red rectangle. The border is the area between the red and blue lines.

Since each side of the original 4 by 5 quilt has the border of width x added, the length of the quilt with the border will be [latex]5+2x[/latex], and the width will be [latex]4+2x[/latex].

(Both dimensions are written in terms of the same variable, and you will multiply them to get an area! This is where you might start to think that a quadratic equation might be used to solve this problem.)

You are only interested in the area of the border strips. Write an expression for the area of the border.

Area of border = Area of the blue rectangle minus the area of the red rectangle

Area of border[latex]=\left(4+2x\right)\left(5+2x\right)–\left(4\right)\left(5\right)[/latex]

There are 10 sq ft of fabric for the border, so set the area of border to be 10.

[latex]10=\left(4+2x\right)\left(5+2x\right)–20[/latex]

Multiply [latex]\left(4+2x\right)\left(5+2x\right)[/latex].

[latex]10=20+8x+10x+4x^{2}–20[/latex]

[latex]10=18x+4x^{2}[/latex]

Subtract 10 from both sides so that you have a quadratic equation in standard form and can apply the Quadratic Formula to find the roots of the equation.

[latex]\begin{array}{c}0=18x+4x^{2}-10\\\\\text{or}\\\\4x^{2}-10\\\\2\left(2x^{2}+9x-5\right)=0\end{array}[/latex]

Factor out the greatest common factor, 2, so that you can work with the simpler equivalent equation, [latex]2x^{2}+9x–5=0[/latex].

[latex]\large \begin{array}{r}2\left(2x^{2}+9x-5\right)=0\\\\\frac{2\left(2x^{2}+9x-5\right)}{2}=\frac{0}{2}\\\\2x^{2}+9x-5=0\end{array}[/latex]

Use the Quadratic Formula. In this case, [latex]a=2,b=9[/latex], and [latex]c=−5[/latex].

[latex]\large \begin{array}{l}x=\frac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}\\\\x=\frac{-9\pm \sqrt{{{9}^{2}}-4(2)(-5)}}{2(2)}\end{array}[/latex]

[latex]\displaystyle x=\frac{-9\pm \sqrt{121}}{4}=\frac{-9\pm 11}{4}[/latex]

Find the solutions, making sure that the [latex]\pm[/latex] is evaluated for both values.

[latex]\large \begin{array}{c}x=\frac{-9+11}{4}=\frac{2}{4}=\frac{1}{2}=0.5\\\\\text{or}\\\\x=\frac{-9-11}{4}=\frac{-20}{4}=-5\end{array}[/latex]

Ignore the solution [latex]x=−5[/latex], since the width could not be negative.

The width of the border should be 0.5 ft.

Here is a video which gives another example of using the quadratic formula for a geometry problem involving the border around a quilt.

There are many real-world scenarios that involve finding the maximum or minimum value of a quadratic function, such as applications involving area and revenue.

Find two numbers [latex]x[/latex] and [latex]y[/latex] whose difference is 100 and whose product is a minimum.

We are trying to find the minimum of the product [latex]P=xy[/latex] of two numbers, such that their difference is 100: [latex]y-x=100[/latex]. First, we rewrite one variable in terms of the other:

[latex]y-x=100 \rightarrow y=100+x[/latex]

Next, we plug in the above relationship between the variables into the first equation:

[latex]P=xy=x(100+x) = 100x+x^2 = x^2+100x[/latex]

As a result, we get a quadratic function [latex]P(x)=x^2+100x[/latex]. The graph of this quadratic function opens upwards, and its vertex is the minimum, So if we find the vertex of this parabola, we will find the minimum product. The vertex is:

[latex]\displaystyle \displaystyle \left(-\frac{b}{2a}, P\left(-\frac{b}{2a}\right)\right) = \left(-\frac{(100)}{2(1)}, P\left(-\frac{(100)}{2(1)}\right)\right) = (-50,-2,500)[/latex]

Thus the minimum of the parabola occurs at [latex]x=-50[/latex], and is [latex]-2,500[/latex]. So one of the numbers is [latex]x=-50[/latex], the other we obtain by plugging in [latex]x=-50[/latex] in to [latex]y-x=100[/latex]:

[latex]\begin{array}{cc}y-(-50)&=&100 \\ y+50 &=& 100 \\ y &=& 50\end{array}[/latex]

[latex]x=-50[/latex] and [latex]y=50[/latex]

Example: Finding the Maximum Value of a Quadratic Function

A backyard farmer wants to enclose a rectangular space for a new garden within her fenced backyard. She has purchased 80 feet of wire fencing to enclose three sides, and she will use a section of the backyard fence as the fourth side.

• Find a formula for the area enclosed by the fence if the sides of fencing perpendicular to the existing fence have length [latex]L[/latex].
• What dimensions should she make her garden to maximize the enclosed area?

Let’s use a diagram such as the one above to record the given information. It is also helpful to introduce a temporary variable, W , to represent the width of the garden and the length of the fence section parallel to the backyard fence.

1)  We know we have only 80 feet of fence available, and [latex]L+W+L=80[/latex], or more simply, [latex]2L+W=80[/latex]. This allows us to represent the width, [latex]W[/latex], in terms of [latex]L[/latex].

[latex]W=80 - 2L[/latex]

Now we are ready to write an equation for the area the fence encloses. We know the area of a rectangle is length multiplied by width, so

[latex]\begin{array}{l}\text{ }A&=&LW=L\left(80 - 2L\right)\hfill \\ A\left(L\right)&=&80L - 2{L}^{2}\hfill \end{array}[/latex]

This formula represents the area of the fence in terms of the variable length [latex]L[/latex]. The function, written in general form, is

[latex]A\left(L\right)=-2{L}^{2}+80L[/latex].

2) The quadratic has a negative leading coefficient, so the graph will open downward, and the vertex will be the maximum value for the area. In finding the vertex, we must be careful because the equation is not written in standard polynomial form with decreasing powers. This is why we rewrote the function in general form above. Since [latex]a[/latex] is the coefficient of the squared term, [latex]a=-2,b=80[/latex], and [latex]c=0[/latex].

To find the vertex:

[latex]\large \begin{array}{l}h=-\frac{80}{2\left(-2\right)}\hfill & \hfill & \hfill & \hfill & k=A\left(20\right)\hfill \\ \text{ }=20\hfill & \hfill & \text{and}\hfill & \hfill & \text{ }=80\left(20\right)-2{\left(20\right)}^{2}\hfill \\ \hfill & \hfill & \hfill & \hfill & \text{ }=800\hfill \end{array}[/latex]

The maximum value of the function is an area of 800 square feet, which occurs when [latex]L=20[/latex] feet. When the shorter sides are 20 feet, there is 40 feet of fencing left for the longer side. To maximize the area, she should enclose the garden so the two shorter sides have length 20 feet and the longer side parallel to the existing fence has length 40 feet.

Analysis of the Solution

This problem also could be solved by graphing the quadratic function. We can see where the maximum area occurs on a graph of the quadratic function below.

How To: Given an application involving revenue, use a quadratic equation to find the maximum.

• Write a quadratic equation for revenue.
• Find the vertex of the quadratic equation.
• Determine the [latex]y[/latex]-value of the vertex.

Example: Finding Maximum Revenue

The unit price of an item affects its supply and demand. That is, if the unit price goes up, the demand for the item will usually decrease. For example, a local newspaper currently has 84,000 subscribers at a quarterly charge of $30. Market research has suggested that if the owners raise the price to $32, they would lose 5,000 subscribers. Assuming that subscriptions are linearly related to the price, what price should the newspaper charge for a quarterly subscription to maximize their revenue?

Revenue is the amount of money a company brings in. In this case, the revenue can be found by multiplying the price per subscription times the number of subscribers, or quantity. We can introduce variables, [latex]p[/latex] for price per subscription and [latex]Q[/latex] for quantity, giving us the equation [latex]\text{Revenue}=pQ[/latex].

Because the number of subscribers changes with the price, we need to find a relationship between the variables. We know that currently [latex]p=30[/latex] and [latex]Q=84,000[/latex]. We also know that if the price rises to $32, the newspaper would lose 5,000 subscribers, giving a second pair of values, [latex]p=32[/latex] and [latex]Q=79,000[/latex]. From this we can find a linear equation relating the two quantities. The slope will be

[latex]\large \begin{array}{c}m=\frac{79,000 - 84,000}{32 - 30}\hfill \\ \text{ }=\frac{-5,000}{2}\hfill \\ \text{ }=-2,500\hfill \end{array}[/latex]

This tells us the paper will lose 2,500 subscribers for each dollar they raise the price. We can then solve for the y -intercept.

[latex]\begin{array}{c}\text{ }Q=-2500p+b\hfill & \text{Substitute in the point }Q=84,000\text{ and }p=30\hfill \\ 84,000=-2500\left(30\right)+b\hfill & \text{Solve for }b\hfill \\ \text{ }b=159,000\hfill & \hfill \end{array}[/latex]

This gives us the linear equation [latex]Q=-2,500p+159,000[/latex] relating cost and subscribers. We now return to our revenue equation.

[latex]\begin{array}{c}\text{Revenue}=pQ\hfill \\ \text{Revenue}=p\left(-2,500p+159,000\right)\hfill \\ \text{Revenue}=-2,500{p}^{2}+159,000p\hfill \end{array}[/latex]

We now have a quadratic function for revenue as a function of the subscription charge. To find the price that will maximize revenue for the newspaper, we can find the vertex.

[latex]\large \begin{array}{c}h=-\frac{159,000}{2\left(-2,500\right)}\hfill \\ \text{ }=31.8\hfill \end{array}[/latex]

The model tells us that the maximum revenue will occur if the newspaper charges $31.80 for a subscription. To find what the maximum revenue is, we evaluate the revenue function.

[latex]\begin{array}{c}\text{maximum revenue}&=&-2,500{\left(31.8\right)}^{2}+159,000\left(31.8\right)\hfill \\ \text{ }&=&2,528,100\hfill \end{array}[/latex]

This could also be solved by graphing the quadratic. We can see the maximum revenue on a graph of the quadratic function.

A coordinate grid has been superimposed over the quadratic path of a basketball in the picture below. Find an equation for the path of the ball. Does the shooter make the basket?

(credit: modification of work by Dan Meyer)

The path passes through the origin and has vertex at [latex]\left(-4,\text{ }7\right)[/latex], so [latex]\left(h\right)x=-\frac{7}{16}{\left(x+4\right)}^{2}+7[/latex]. To make the shot, [latex]h\left(-7.5\right)[/latex] would need to be about 4 but [latex]h\left(-7.5\right)\approx 1.64[/latex]; he doesn’t make it.

• Quadratic Formula Application - Time for an Object to Hit the Ground. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/RcVeuJhcuL0 . License : CC BY: Attribution
• Quadratic Formula Application - Determine the Width of a Border. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/Zxe-SdwutxA . License : CC BY: Attribution
• College Algebra. Authored by : Abramson, Jay, et al.. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected]:1/Preface . License : CC BY: Attribution . License Terms : Download for free at : http://cnx.org/contents/[email protected]:1/Preface
• Revision and Adaptation. Provided by : Lumen Learning. License : CC BY: Attribution

• Pre-Algebra Topics
• Algebra Topics
• Algebra Calculator
• Algebra Cheat Sheet
• Algebra Practice Test
• Algebra Readiness Test
• Algebra Formulas
• Want to Build Your Own Website?

Sign In / Register

Need Help Solving Those Dreaded Word Problems Involving Quadratic Equations?

Yes, I know it's tough. You've finally mastered factoring and using the quadratic formula and now you are asked to solve more problems!

Except these are even more tough. Now you have to figure out what the problem even means before trying to solve it. I completely understand and here's where I am going to try to help!

There are many types of problems that can easily be solved using your knowledge of quadratic equations. You may come across problems that deal with money and predicted incomes (financial) or problems that deal with physics such as projectiles. You may also come across construction type problems that deal with area or geometry problems that deal with right triangles.

Lucky for you, you can solve the quadratic equations, now you just have to learn how to apply this useful skill.

On this particular page, we are going to take a look at a physics "projectile problem".

Projectiles - Example 1

A ball is shot from a cannon into the air with an upward velocity of 40 ft/sec. The equation that gives the height (h) of the ball at any time (t) is: h(t)= -16t 2 + 40ft + 1.5. Find the maximum height attained by the ball.

Let's first take a minute to understand this problem and what it means. We know that a ball is being shot from a cannon. So, in your mind, imagine a cannon firing a ball. We know that the ball is going to shoot from the cannon, go into the air, and then fall to the ground.

So, here's a mathematical picture that I see in my head.

Now let's talk about what each part of this problem means. In our equation that we are given we must be given the value for the force of gravity (coefficient of t 2 ). We must also use our upward velocity (coefficient of t) and our original height of the cannon/ball (the constant or 1.5). Take a look...

Now that you have a mental picture of what's happening and you understand the formula given, we can go ahead and solve the problem.

• First, ask yourself, "What am I solving for?" "What do I need to find?" You are asked to find the maximum height (go back and take a look at the diagram). What part of the parabola is this? Yes, it's the vertex! We will need to use the vertex formula and I will need to know the y coordinate of the vertex because it's asking for the height.
• Next Step: Solve! Now that I know that I need to use the vertex formula, I can get to work.

Just as simple as that, this problem is solved.

Let's not stop here. Let's take this same problem and put a twist on it. There are many other things that we could find out about this ball!

Projectiles - Example 2

Same problem - different question. Take a look...

A ball is shot from a cannon into the air with an upward velocity of 40 ft/sec. The equation that gives the height (h) of the ball at any time (t) is: h(t)= -16t 2 + 40ft + 1.5. How long did it take for the ball to reach the ground?

Now, we've changed the question and we want to know how long did it take the ball to reach the ground.

What ground, you may ask. The problem didn't mention anything about a ground. Let's take a look at the picture "in our mind" again.

Do you see where the ball must fall to the ground. The x-axis is our "ground" in this problem. What do we know about points on the x-axis when we are dealing with quadratic equations and parabolas?

Yes, the points on the x-axis are our "zeros" or x-intercepts. This means that we must solve the quadratic equation in order to find the x-intercept.

Let's do it! Let's solve this equation. I'm thinking that this may not be a factorable equation. Do you agree? So, what's our solution?

Hopefully, you agree that we can use the quadratic formula to solve this equation.

The first time doesn't make sense because it's negative. This is the calculation for when the ball was on the ground initially before it was shot.

This actually never really occurred because the ball was shot from the cannon and was never shot from the ground. Therefore, we will disregard this answer.

The other answer was 2.54 seconds which is when the ball reached the ground (x-axis) after it was shot. Therefore, this is the only correct answer to this problem.

Ok, one more spin on this problem. What would you do in this case?

Projectiles - Example 3

A ball is shot from a cannon into the air with an upward velocity of 40 ft/sec. The equation that gives the height (h) of the ball at any time (t) is: h(t)= -16t 2 + 40ft + 1.5. How long does it take the ball to reach a height of 20 feet?

Yes, this problem is a little trickier because the question is not asking for the maximum height (vertex) or the time it takes to reach the ground (zeros), instead it it asking for the time it takes to reach a height of 20 feet.

Since the ball reaches a maximum height of 26.5 ft, we know that it will reach a height of 20 feet on the way up and on the way down.

Let's just estimate on our graph and also make sure that we get this visual in our head.

From looking at this graph, I would estimate the times to be about 0.7 sec and 1.9 sec. Do you see how the ball will reach 20 feet on the way up and on the way down?

Now, let's find the actual values. Where will we substitute 20 feet?

Yes, we must substitute 20 feet for h(t) because this is the given height. We will now be solving for t using the quadratic formula. Take a look.

Our actual times were pretty close to our estimates. Just don't forget that when you solve a quadratic equation, you must have the equation set equal to 0. Therefore, we had to subtract 20 from both sides in order to have the equation set to 0.

You've now seen it all when it comes to projectiles!

Great Job! Hopefully you've been able to understand how to solve problems involving quadratic equations. I also hope that you better understand these common velocity equations and how to think about what this problem looks like graphically in order to help you to understand which process or formula to use in order to solve the problem.

• Quadratic Equations
• Projectile Problems

Need More Help With Your Algebra Studies?

Get access to hundreds of video examples and practice problems with your subscription! 

Click here for more information on our affordable subscription options.

Not ready to subscribe?  Register for our FREE Pre-Algebra Refresher course.

ALGEBRA CLASS E-COURSE MEMBERS

Click here for more information on our Algebra Class e-courses.

Need Help? Try This Online Calculator!

Affiliate Products...

On this site, I recommend only one product that I use and love and that is Mathway   If you make a purchase on this site, I may receive a small commission at no cost to you. 

Privacy Policy

Let Us Know How we are doing!

  send us a message to give us more detail!

Would you prefer to share this page with others by linking to it?

• Click on the HTML link code below.
• Copy and paste it, adding a note of your own, into your blog, a Web page, forums, a blog comment, your Facebook account, or anywhere that someone would find this page valuable.

Copyright © 2009-2020   |   Karin Hutchinson   |   ALL RIGHTS RESERVED.

MyEngagement & Events

Help A Norse

Handshake (HireNKU)

Virtual OneStop

Change Password

• Steely Library
• Ways to Give
• Quick Links
• Search the NKU Site   Enter the search term or name
• Testing Services
• NKU Placement

Math Placement Test

• Testing Services Home
• NKU ACT On-Campus
• National ACT
• Accommodated Classroom Exams
• Avant STAMP
• American Institute of Constructors' Certification Exam
• Informatics Competency Testing
• Major Field Tests
• Nursing Classroom Make-Up Exams
• Free CLEP with Modern States
• Distance Learning
• Kryterion Network Testing
• Meazure Learning
• National Counselor Examination
• Pearson VUE
• Other Testing
• What To Expect When you Arrive
• Directions & Parking
• Meet Our Staff

Incoming first-time students will receive a link to a personalized survey that builds their mathematical history. The survey directs them to the most appropriate placement test based on this history and their major of interest.

Only a proctored attempt at the assessment may be used for placement.

Students have the option to take their proctored Math Placement Test in person at Testing Services for a $17 charge. Appointments can be made by clicking on the "Register Now" button below.

Register Now

Continuing and transfer students must consult their advisor for guidance on determining the appropriate placement test. Tests were constructed assuming a student had completed their high school mathematics curriculum, and they are not available to current high school students.

High school students seeking to enroll in dual-credit coursework should refer to the ACT and/or KYOTE tests for placement into quantitative coursework.

Topics covered on each exam can be found below.

The placement test has 25 questions, a mix of multiple-choice and open-response. A score of 17 or higher satisfies placement into Calculus (MAT 128 or MAT 129). Topics covered on the exam include:

• Simplify algebraic expressions involving roots and rational exponents.
• Add, subtract, and multiply polynomials.
• Factor a polynomial in one or more variables by factoring out its greatest common factor. Factor a trinomial. Factor the difference of squares.
• Add, subtract, multiply, divide, and simplify rational expressions.
• Solve linear and quadratic equations. Solve equations involving a radical, a rational, or an absolute value expression.
• Solve linear and nonlinear inequalities in one variable.
• Solve a system of two linear equations in two variables.
• Solve problems that can be modeled using a linear or quadratic equation or expression.
• Solve geometry problems using the Pythagorean theorem, the properties of similar triangles, and right-triangle trigonometry.
• Understand and apply the relationship between the properties of a graph of a line and its equation.
• Find the intercepts and the graph of a parabola given its equation. Find an equation of a parabola given its graph.
• Find the domain of a function. Evaluate a function at a point in its domain.
• Combine functions by composition, addition, subtraction, multiplication, and division. Find the inverse of a one-to-one function.
• Understand the relationship between radian measure and the arc length of a circle. 
• Know values of the sine, cosine, and tangent functions as functions on the unit circle that are multiples of  and . Sketch the graphs of these functions.
• Apply basic trigonometric identities to solve problems and verify more complex identities. Solve simple trigonometric equations.
• Understand and apply the properties of exponential and logarithmic functions.
• Know that the inverse of an exponential function is a logarithm and use this inverse relationship to solve simple logarithmic and exponential equations.

The test has 25 multiple-choice questions. A score of 17 or higher satisfies placement into pre-calculus (MAT 119). Topics on the placement test include:

• Evaluate algebraic expressions at specified values of their variables.
• Simplify algebraic expressions involving square roots and cube roots.
• Factor polynomials by factoring out the greatest common factor and factoring quadratic polynomials.
• Add, subtract, multiply, and simplify rational expressions.
• Solve linear equations and linear inequalities.
• Solve a multivariable equation for one of its variables.
• Solve quadratic equations by factoring and by using the quadratic formula.
• Solve an equation involving a radical, a rational, or an absolute value expression.
• Solve geometric problems using the Pythagorean theorem and the properties of similar triangles.
• Evaluate a function at a number in its domain.
• Find the domain of a rational function and the square root of a linear function.

The placement test has 25 multiple-choice questions. A score of 17 or higher satisfies placement into algebra (MAT 102). Topics on the placement test include:

• Evaluate numerical expressions with signed numbers, exponents, and parentheses using order of operations.
• Perform arithmetic operations with fractions, decimals, and percents.
• Order fractions and decimals on a number line.
• Solve applied problems using appropriate units, including problems involving percentage increase and decrease, rates, and proportions.
• Solve geometric problems about rectangles and triangles.
• Simplify algebraic expressions involving integer exponents and square roots.
• Factor polynomials by factoring out the greatest common factor and factoring quadratic polynomials (with a leading coefficient of 1).
• Use a linear equation to set up and solve a word problem.
• Find an equation of a line given two points on the line, one point and the slope, or the graph of the line.
• Given an equation of a line, find the slope and graph the line.

The placement test has 25 multiple-choice questions. A score of 17 or higher satisfies placement into general education coursework like STA 205 and MAT 115. Topics on the placement test include:

• Solve simple coordinate geometry problems.
• Solve a linear equation.
• Use a linear equation to solve a simple word problem.

For more information regarding math placement needs, students are encouraged to reach out to their Academic Advisor.

Nku uses cookies on this website.

Information is collected automatically by NKU as part of the software operation of our website. This data is not personally identifiable information. NKU uses this information for internal purposes, such as marketing and seeing what pages are most frequently visited. Click "Accept" to continue to use NKU website(s), and consent to our collection of cookies. For more information please see NKU's  Web Privacy Statement .