
- Exam Center
- Ticket Center
- Flash Cards
- Straight Line Motion

Grade 12: Physics Worksheet on Projectile Motion
Looking to master projectile motion in your physics class? Check out our comprehensive worksheet with detailed solutions to help you understand the concepts and excel in your studies!
There is also a pdf for worksheets with answers.
A summary of projectile motion:
Any motion having the following conditions is called a projectile motion. (i) Follows a parabolic path (trajectory). (ii) Moves under the influence of gravity.
The projectile motion formulas applied to solve two-dimensional projectile motion problems are as follows \begin{gather*} x=(v_0\cos\theta)t+x_0\\\\y=-\frac 12 gt^2+(v_0\sin\theta)t+y_0\\\\ v_y=v_0\sin\theta-gt\\\\v_y^2-(v_0\sin\theta)^2=-2g(y-y_0)\end{gather*}
Projectile motion problems and answers
Problem (1): A person kicks a ball with an initial velocity of 15 m/s at an angle of 37° above the horizontal (neglecting the air resistance). Find (a) the total time the ball is in the air. (b) the horizontal distance traveled by the ball
Solution : The initial step in answering any projectile motion questions is to establish a coordinate system and sketch the path of the projectile, including its initial and final positions and velocities.
By doing so, you will be able to solve the relevant projectile equations easily.
Hence, we choose the origin of the coordinate system to be at the throwing point, $x_0=0, y_0=0$.

(a) Here, we are seeking the time it takes for the projectile to travel from the point of release to the ground.
In reality, projectiles have two independent motions: one in the horizontal direction with uniform motion at a constant velocity (i.e., $a_x=0$), and the other in the vertical direction under the effect of gravity (with $a_y=-g$).
The kinematic equations that describe the horizontal and vertical distances are as follows: \begin{gather*} x=x_0+(\underbrace{v_0\cos \theta}_{v_{0x}})t \\ y=-\frac 12 gt^2+(\underbrace{v_0\sin \theta}_{v_{0y}})t+y_0\end{gather*} By substituting the coordinates of the initial and final points into the vertical equation, we can find the total time the ball is in the air.
Setting $y=0$ in the second equation (because the projectile lands at the same level as the throwing point.), we have: \begin{align*} y&=-\frac 12 gt^2+(v_0\sin \theta)t+y_0\\\\ 0&=-\frac 12 (9.8)t^2+(15)\sin 37^\circ\,t+0 \end{align*} By rearranging the above expression, we can obtain two solutions for $t$: \begin{gather*} t_1=0 \\\\ t_2=\frac{2\times 15\sin37^\circ}{9.8}=1.84\,{\rm s}\end{gather*} The first time represents the starting moment, and the second represents the total time the ball was in the air.
(b) As previously mentioned, projectile motion consists of two independent motions with different positions, velocities, and accelerations, each described by distinct kinematic equations.
The time it takes for the projectile to reach a specific point horizontally is equal to the time it takes to fall vertically to that point. Therefore, time is the common factor in both the horizontal and vertical motions of a projectile.
In this particular problem, the time calculated in part (a) can be used in the horizontal kinematic equation to determine the distance traveled.
Substituting the obtained time into the equation, we find that the projectile travels a distance of 22.08 meters. \begin{align*} x&=x_0+(v_0\cos \theta)t \\ &=0+(15)\cos 37^\circ\,(1.84) \\ &=22.08\quad {\rm m}\end{align*}
Be sure to check the following questions.
If you are getting ready for the AP Physics exam, these problems on the kinematics equation (or these AP Physics Kinematics Problems ) are probably also useful to you.
Problem (2): A ball is thrown into the air at an angle of 60° above the horizontal with an initial velocity of 40 m/s from a 50-m-high building. Find (a) The time to reach the top of its path. (b) The maximum height the ball reached from the base of the building.
Solution : In the previous question, we found that the motion of a projectile consists of two distinct vertical and horizontal movements.
We learned about how to find distances in both directions using relevant kinematic equations.
There is also another set of kinematic equations that discuss the velocities in vertical and horizontal directions as follows \begin{gather*} v_x=v_{0x}=v_0\cos\theta \\ v_y=v_{0y}-gt=v_0\sin\theta-gt\end{gather*} As you can see, the horizontal component of the velocity, $v_x$, is constant throughout the motion, but the vertical component varies with time.
As an important note, keep in mind that in the problems about projectile motions, at the highest point of the trajectory, the vertical component of the velocity is always zero, i.e., $v_y=0$.
To solve the first part of the problem, specify two points as the initial and final points, then solve the relevant kinematic equations between those points.
Here, setting $v_y=0$ in the second equation and solving for the unknown time $t$, we have \begin{align*} v_y&=v_{0y}-gt \\\\ &=v_0\sin\theta-gt \\\\ 0&=(40)(\sin 60^\circ)-(9.8)(t) \\\\ \Rightarrow t&=\boxed{3.53\, {\rm s}}\end{align*} Thus, the time taken to reach the maximum height of the trajectory (path) is 3.53 seconds from the moment of the launch. We call this maximum time $t_{max}$.
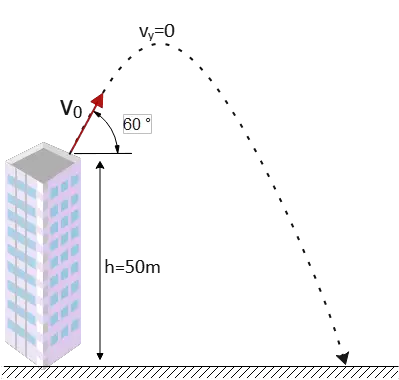
(b) Let the origin be at the throwing point, so $x_0=y_0=0$ in the kinematic equations. In this part, the vertical distance traveled to the maximum point is requested.
By substituting $t_{max}$ into the vertical distance projectile equation, we can find the maximum height as below \begin{align*} y-y_0&=-\frac 12 gt^2 +(v_0 \sin \theta)t\\ \\ y_{max}&=-\frac 12 (9.8)(3.53)^2+(40 \sin 60^\circ)(3.53)\\\\ &=61.22\quad {\rm m}\end{align*} Therefore, the maximum height at which the ball is reached from the base of the building is \[H=50+y_{max}=111.22\quad {\rm m}\]
For further reading about uniform motion along the horizontal direction, see speed, velocity, and acceleration problems .
Problem (3): A person standing on the edge of a 50-m-high cliff throws a stone horizontally at a speed of 18 m/s. (a) What is the initial position of the stone? (b) What are the components of the initial velocity? (c) What are the $x$- and $y$-components of the velocity of the stone at any arbitrary time $t$? (d) How long will it take the stone to strike the bottom of the cliff? (e) With what angle and speed does the stone strike the ground below the cliff?
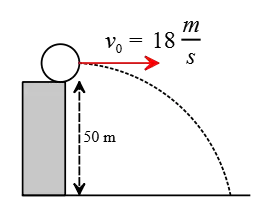
Solution : As mentioned repeatedly, as a first step to solving a projectile motion problem, choose a relevant coordinate system.
(a) Usually, we place the origin of the coordinate system at the point where the projectile is thrown. In this case, the coordinate of the initial position is $x_0=0\, , \, y_0=0$.
If we had chosen the coordinate at the base of the cliff and placed the origin at that point, the position of the initial point would have been $x_0=0\, , \, y_0=50\,\rm m$.
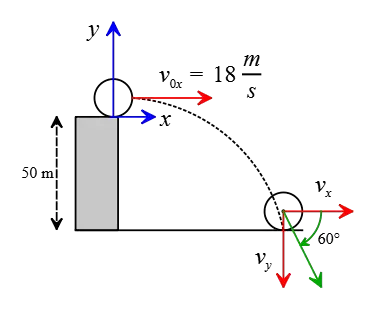
(b) The stone is thrown horizontally with $\theta=0$, so there is no vertical velocity component. Consequently, its initial speed components are $v_{0x}=18\,\rm m/s$ and $v_{0y}=0$.
(c) Remember that the velocity components of a projectile change over time according to the following formula. Substituting the given values into it, we get: \begin{align*} v_x&=v_{0x}=18\,\rm m/s \\\\ v_y&=v_{0y}-gt\\&=-9.8t \end{align*} (d) If we take the top of the cliff to be the origin of our coordinate system, with $x_0=y_0=0$, the stone hits the ground $50\,\rm m$ below our chosen origin. Therefore, the coordinates of that point would be $x_0=?\, ,\, y=-50\,\rm m$.
Use the vertical displacement kinematic equation below, substitute the numerical values into that, and solve for time $t$ get \begin{gather*} y-y_0=-\frac 12 gt^2+v_{0y}t \\\\ -50-0=-\frac 12 (9.8)t^2-0 \\\\ \Rightarrow \quad \boxed{t=3.2\,\rm s} \end{gather*} (e) First, find the velocity components just before the stone hits the ground. We know that it takes about $3.2\,\rm s$ for the stone to reach the bottom of the cliff. Thus, put this time value into the formulas of velocity components at any time $t$. \begin{align*} v_x&=v_{0x}=18\,\rm m/s \\\\ v_y&=v_{0y}-gt\\&=-9.8\times 3.2 \\&=-31.36\,\rm m/s \end{align*} Notice that the negative sign here indicates that the vertical velocity component just before hitting the ground points downward, as expected.
Recall from the section on vector practice problems that when we have the components of a vector, we can find its magnitude using the Pythagorean theorem. This gives us: \begin{align*} v&=\sqrt{v_x^2+v_y^2} \\\\ &=\sqrt{18^2+(-31.36)^2} \\ &=\boxed{36.15\,\rm m/s} \end{align*} We can also find the angle of impact with the ground using the velocity components: \begin{align*} \tan\theta&=\frac{v_y}{v_x} \\\\ &=\frac{-31.36}{18} \\\\ &=-1.74 \end{align*} Taking the inverse tangent of both sides gives: \[\theta=\tan^{-1}(-1.74)=\boxed{-60.1^\circ} \] Therefore, the stone hit the ground at an angle of about $60^\circ$ with a speed of $36.15\,\rm m/s$. The negative angle indicates that it is below horizontal, which is to be expected.
Problem (4): A book slides off a frictionless tabletop with a constant speed of 1.1 m/s, and 0.35 seconds later strikes the floor. (a) How high is the tabletop from the floor? (b) What is the horizontal distance to that point where the book strikes the floor? (c) How fast and at what angle does the book strike the floor?
Solution : The total time the book is in the air is $t=0.35\,\rm s$, and the initial speed with which the book leaves the table horizontally is $v_{0x}=1.1\,\rm m/s$, and $v_{0y}=0$.
Contrary to the earlier question, in this case, for practice, we place the origin at the bottom of the tabletop. Thus, the coordinates of the initial position would be $x_0=0\, ,\, y_0=h=?$ and the coordinates of the landing point would be $x=? \, , \, y=0$.
(a) If we substitute the given values into the vertical displacement kinematic equation, we will have \begin{gather*} y-y_0=-\frac 12 gt^2+v_{0y}t \\\\ 0-h=-\frac 12 (9.8)(1.1)^2+0 \\\\ \Rightarrow \quad \boxed{h=5.93\,\rm m} \end{gather*} Thus, the table is 3-m-high.
(b) Remember that projectile motion involves two motions that are uniformly accelerated in the horizontal and vertical directions. The time taken by the projectile in the vertical direction is equal to the horizontal time to the landing point.
Between the start and final points in the horizontal direction of the projectile path, we can write $\Delta x=v_{0x}t$. Substituting the given values into is get \begin{gather*} x-0=1.1\times (0.35) \\ \Rightarrow \quad \boxed{x=0.385\,\rm m} \end{gather*} where $\Delta x=x-x_0$. Therefore, the book strikes the floor about $39\,\rm cm$ ahead of the base of the table.
(c) This part is straightforward. Substitute the given numerical values into the velocity vector component formulas as below to find the velocity components just before the book strikes the floor. \begin{align*} v_x&=v_{0x}=1.1\,\rm m/s \\\\ v_y&=v_{0y}-gt \\\\ &=0-(9.8)(0.35) \\&=-3.43\,\rm m/s \end{align*} The square root of the sum of the velocity components squared gives the velocity of the book at the instant of hitting \begin{align*} v&=\sqrt{v_x^2+v_y^2} \\\\ &=\sqrt{1.1^2+(-3.43)^2} \\\\ &=\boxed{3.6\,\rm m/s} \end{align*} and angle of impact with the ground is found as below \begin{align*} \theta&=\tan^{-1}\left(\frac{v_y}{v_x}\right) \\\\ &=\tan^{-1}\left(\frac{-3.43}{1.1}\right) \\\\ &=\tan^{-1}(-3.11) \\\\&=\boxed{-72.17^\circ} \end{align*} Overall, the book hit the ground at an angle of about $72^\circ$ with a speed of nearly $3.6\,\rm m/s$.
Problem (5): A cannonball is fired from a cliff with a speed of 800 m/s at an angle of 30° below the horizontal. How long will it take to reach 150 m below the firing point?
Solution: First, choose the origin to be at the firing point, so $x_0=y_0=0$. Now, list the known values as follows (i) Projectile's initial velocity = $800\,{\rm m/s}$ (ii) Angle of projectile: $-30^\circ$, the negative sign is because the throw is below the horizontal. (iii) y-coordinate of the final point, 150 m below the origin, $y=-150\,{\rm m}$. In this problem, the time it takes for the cannonball to reach 100 m below the starting point is required.
Since the displacement to that point is known, we apply the vertical displacement projectile formula to find the needed time as below \begin{align*} y-y_0&=-\frac 12 gt^2+(v_0\sin\theta)t\\\\-150&=-\frac 12 (9.8)t^2+(800)\sin(-30^\circ)t\\\\ \Rightarrow & \ 4.9t^2+400t-150=0\end{align*} The above quadratic equation has two solutions, $t_1=0.37\,{\rm s}$ and $t_2=-82\,{\rm s}$. It is obvious that the second time is not acceptable.
Therefore, the cannonball takes 0.37 seconds to reach 150 meters below the firing point.
Problem (6): Someone throws a stone into the air from ground level. The horizontal component of velocity is 25 m/s and it takes 3 seconds for the stone to come back to the same height as before. Find (a) The range of the stone. (b) The initial vertical component of velocity (c) The angle of projection.
Solution: The known values are (i) The initial horizontal component of velocity, $v_{0x}=25\,{\rm m/s}$. (ii) The time between the initial and final points, which are at the same level, $t=3\,{\rm s}$.
(a) The range of projectile motion is defined as the horizontal distance between the launch point and impact at the same elevation.
Because the horizontal motion in projectiles is a motion with constant velocity, the distance traveled in this direction is obtained as $x=v_{0x}t$, where $v_{0x}$ is the initial component of the velocity.
If you put the total time the projectile is in the air into this formula, you get the range of the projectile.
In this problem, the stone is thrown from the ground level and, after 3 seconds, reaches the same height. Thus, this is the total time of the projectile.
Hence, the range of the stone is found as below \begin{align*} x&=v_{0x}t\\&=(25)(3)\\&=75\,{\rm m}\end{align*}
(b) The initial vertical component of the projectile's velocity appears in two equations, $v_y=v_{0y}-gt$ and $y-y_0=-\frac 12 gt^2+v_{0y}t$.
Using the second formula is more straightforward because the stone reaches the same height, so its vertical displacement between the initial and final points is zero, i.e., $y-y_0=0$. Setting this into the vertical distance projectile equation, we get \begin{align*} y-y_0&=-\frac 12 gt^2+v_{0y}t\\\\ 0&=-\frac 12 (9.8)(3)^2+v_{0y}(3) \\\\ \Rightarrow v_{0y}&=14.7\quad{\rm m/s}\end{align*} To use the first formula, we need some extra facts about projectile motion in the absence of air resistance, as below (i) The vertical velocity is zero at the highest point of the path of the projectile, i.e., $v_y=0$. (ii) If the projectile lands at the same elevation from which it was launched, then the time it takes to reach the highest point of the trajectory is half the total time between the initial and final points. The second note, in the absence of air resistance, is only valid.
In this problem, the total flight time is 3 s because air resistance is negligible, so 1.5 seconds are needed for the stone to reach the maximum height of its path.
Therefore, using the second equation, we can find $v_{0y}$ as below \begin{align*} v_y&=v_{0y}-gt\\0&=v_{0y}-(9.8)(1.5) \\\Rightarrow v_{0y}&=14.7\quad {\rm m/s}\end{align*} (c) The projection angle is the angle at which the projectile is thrown into the air and performs a two-dimensional motion.
Once the components of the initial velocity are available, using trigonometry, we can find the angle of projection as below \begin{align*} \theta&=\tan^{-1}\left(\frac{v_{0y}}{v_{0x}}\right)\\\\&=\tan^{-1}\left(\frac{14.7}{25}\right)\\\\&=+30.45^\circ\end{align*} Therefore, the stone is thrown into the air at an angle of about $30^\circ$ above the horizontal.
Problem (7): A ball is thrown at an angle of 60° with an initial speed of 200 m/s. (Neglect the air resistance.) (a) How long is the ball in the air? (b) Find the maximum horizontal distance traveled by the ball. (c) What is the maximum height reached by the ball?
Solution: We choose the origin to be the ball's initial position so that $x_0=y_0=0$. The given data is (i) The projection angle: $60^\circ$. (ii) Initial speed : $v_0=200\,{\rm m/s}$.
(a) The initial and final points of the ball are at the same level, i.e., $y-y_0=0$.
Thus, the total time the ball is in the air is found by setting $y=0$ in the projectile equation $y=-\frac 12 gt^2+v_{0y}t$ and solving for time $t$ as below \begin{align*} y&=-\frac 12 gt^2+(v_0\sin\theta)t\\\\0&=-\frac 12 (9.8)t^2+(200)(\sin 60^\circ)t\\\\\Rightarrow \quad & \boxed{(-4.9t+100\sqrt{3})t=0} \end{align*} The above expression has two solutions for $t$. One is the initial time, $t_1=0$, and the other is computed as $t_2=35.4\,{\rm s}$.
Hence, the ball has been in the air for about 35 s.
(b) The horizontal distance is called the range of the projectile. By inserting the above time (total flight time) into the horizontal distance projectile equation $x=v_{0x}t$, we can find the desired distance traveled. \begin{align*} x&=(v_0\cos\theta)t\\&=(200)(\cos 60^\circ)(35.4)\\&=3540 \quad {\rm m}\end{align*} Therefore, the ball hits the ground 3540 meters away from the throwing point.
(c) Using the projectile equation $v_y^2-v_{0y}^2=-2g(y-y_0)$, setting $v_y=0$ at the highest point of the path, and solving for the vertical distance $y$, the maximum height is found as follows \begin{align*} v_y^2-v_{0y}^2&=-2g(y-y_0)\\0-(200\sin 60^\circ)^2&=-2(9.8)y\\\Rightarrow y&=1531\quad {\rm m}\end{align*} Another method: As mentioned above, the ball hits the ground at the same level as before, so by knowing the total flight time and halving it, we can find the time it takes the ball to reach the highest point of its trajectory.
Therefore, by setting the half of the total flight time in the following projectile kinematic formula and solving for $y$, we can find the maximum height as \begin{align*} y-y_0&=-\frac 12 gt^2+(v_0\sin\theta)t\\\\y&=-\frac 12 (9.8)(17.7)^2+(200\sin60^\circ)(17.7)\\\\&=1531\quad {\rm m}\end{align*} Hence, the ball reaches 1531 meters above the launch point.
Problem (8): What are the horizontal range and maximum height of a bullet fired with a speed of 20 m/s at 30° above the horizontal?
Solution : first, find the total flight time, then insert it into the horizontal displacement projectile equation $x=v_{0x}t$ to find the range of the bullet.
Because the bullet lands at the same level as the original, its vertical displacement is zero, $y-y_0=0$, in the following projectile formula we can find the total flight time \begin{align*} y-y_0&=-\frac 12 gt^2+(v_0\sin\theta)t\\\\0&=-\frac 12 (9.8)t^2+(20)(\sin30^\circ)t\\\\ \Rightarrow & (-4.9t+10)t=0\end{align*} Solving for time $t$ gives two solutions: one is the initial time $t_1=0$, and the other is $t_2=1.02\,{\rm s}$. Thus the total time of flight is 2.04 s.
Therefore, the maximum horizontal distance traveled by the bullet, which is defined as the range of the projectile, is calculated as \begin{align*} x&=(v_0\cos\theta)t\\&=(20\cos 30^\circ)(2.04)\\&=35.3\quad {\rm m}\end{align*} Hence, the bullet lands about 17 m away from the launch point.
Because the air resistance is negligible and the bullet lands at the same height as the original, the time it takes to reach the highest point of its path is always half the total flight time.
On the other hand, recall that the vertical component of velocity at the maximum height is always zero, i.e., $v_y=0$. By inserting these two notes into the following projectile equation, we have \begin{align*} y&=-\frac 12 gt^2+(v_0\sin\theta)t\\\\&=-\frac 12 (9.8)(1.02)^2+(20\sin 30^\circ)(1.02)\\\\&=5.1\quad {\rm m}\end{align*} We could also use the kinematic equation $v_y^2-v_{0y}^2=-2g(y-y_0)$, to find the maximum height as below \begin{align*} v_y^2-(v_0 \sin \theta)^2 &=-2g(y-y_0) \\ 0-(20\sin 30^\circ)^2 &=-2(9.8)H\\ \Rightarrow H&= 5.1\quad {\rm m} \end{align*} I think the second method is much simpler.
Problem (9): A projectile is fired horizontally at a speed of 8 m/s from an 80-m-high cliff. Find (a) The velocity just before the projectile hits the ground. (b) The angle of impact.
Solution : In this problem, the angle of the projectile is zero because it is fired horizontally.
The velocity at each point of a projectile trajectory (path) is obtained by the following formula: \[v=\sqrt{v_x^2+v_y^2}\] where $v_x$ and $v_y$ are the horizontal and vertical components of the projectile's velocity at any instant of time.
(a) Recall that the horizontal component of the projectile's velocity is always constant and, for this problem, is found as \begin{align*} v_x&=v_0\cos\theta\\&=8\times \cos 0^\circ\\&=8\quad {\rm m/s}\end{align*} To find the vertical component of the projectile velocity at any moment, $v_y=v_0\sin\theta-gt$, we should find the time taken to reach that point.
In this problem, that point is located just before striking the ground, whose coordinates are $y=-80\,{\rm m}, x=?$.
Because it is below the origin, which is assumed to be at the firing point, we inserted a minus sign.
Because displacement in the vertical direction is known, we can use the projectile formula for vertical distance.
By setting $y=-80$ into it and solving for the time $t$ needed the projectile reaches the ground, we get \begin{align*} y&=-\frac 12 gt^2+(v_0\sin\theta)t\\\\-80&=-\frac 12 (9.8)t^2+(8\times \sin 0^\circ)t\\\\\Rightarrow t&=\sqrt{\frac{2(80)}{9.8}}\\\\&=2.86\quad {\rm s}\end{align*} Now insert this time into the $y$-component of the projectile's velocity to find $v_y$ just before hitting the ground \begin{align*} v_y&=v_0\sin\theta-gt\\ &=8\sin 0^\circ-(9.8)(2.86)\\&=-28\quad {\rm m/s}\end{align*} Now that both components of the velocity are available, we can compute its magnitude as below \begin{align*} v&=\sqrt{v_x^2+v_y^2}\\\\&=\sqrt{8^2+(-28)^2}\\\\&=29.1\quad {\rm m/s}\end{align*} Therefore, the projectile hits the ground at a speed of 29.1 m/s.
(b) At any instant of time, the velocity of the projectile makes some angle with the horizontal, whose magnitude is obtained as the follows: \[\alpha=\tan^{-1}\left(\frac{v_y}{v_x}\right)\] Substituting the above values into this formula, we get \[\alpha =\tan^{-1}\left(\frac{-28}{8}\right)=-74^\circ\] Therefore, the projectile hits the ground at an angle of 74° below the horizontal.
Problem (10): From a cliff 100 m high, a ball is kicked at $30^\circ$ above the horizontal with a speed of $20\,{\rm m/s}$. How far from the base of the cliff did the ball hit the ground? (Assume $g=10\,{\rm m/s^2}$).
Solution: Again, similar to any projectile motion problem, we first select a coordinate system and then draw the path of the projectile as shown in the figure below,
We choose the origin to be at the kicking point above the cliff, setting $x_0=y_0=0$ in the kinematic equations.
The coordinate of the hitting point to the ground is $y=-100\,{\rm m}, x = ?$. A negative is inserted because the final point is below the origin.
Now, we find the common quantity in projectile motions—that is, the time between the initial and final points, called total flight time.
To find the total time the ball was in the air, we can use the vertical equation and solve for the unknown $t$ as follows \begin{align*} y&=-\frac 12 gt^2 +(v_0\sin \theta)t \\\\ -100&=-\frac 12 (10) t^2+(20\sin 30^\circ)t\\\\&\Rightarrow \quad \boxed{t^2-2t-20=0} \end{align*} The solutions of a quadratic equation $at^2+bt+c=0$ are found by the formula below \[t=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\] By matching the above constant coefficients with the standard quadratic equation, we can find the total time as below \[t=\frac{-(-2)\pm\sqrt{(-2)^2-4(1)(-20)}}{2(1)}\] After simplifying, two solutions are obtained, $t_1=5.6\,{\rm s}$ and $t_2=-3.6\,{\rm s}$.
It is obvious that time cannot be negative in physics, so the acceptable answer is $t_1$.
It is the time it takes the ball to travel in the vertical direction. On the other hand, it is also the time it takes the ball to travel the horizontal distance between kicking and hitting points.
We insert this time into the horizontal equation to find the horizontal distance traveled, known as the projectile's range. \begin{align*} x&=(v_0\cos \theta)t\\ &=(20)(\cos 30^\circ)(5.6)\\&=97\quad {\rm m}\end{align*}
Problem (11): A cannonball is fired from the top of a $200\,{\rm m}$ cliff with a speed of $60\,{\rm m/s}$ at an angle of $60^\circ$ above the horizontal. Where does the ball land closest to which of the following choices? (Neglect air resistance.) (a) 90m (b) 402 m (c) 151 m (d) 200 m
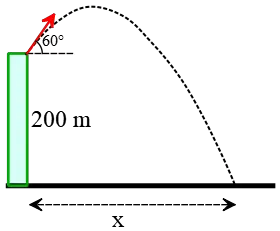
Solution : The horizontal distance from the point where the cannonball fired is wanted, $x=?$. The appropriate kinematic equation for this is \[x=(v_0\cos\theta)t\] The only thing we need is the total time the ball is in the air before landing.
If we take the firing point as the origin, then the cannonball lands $200\,{\rm m}$ below the origin. So, the ball's vertical displacement is $\Delta y=-200\,{\rm m}$. Set this in the vertical displacement equation, $\Delta y=-\frac 12 gt^2+(v_0\sin\theta)t$, and solve for $t$. \begin{gather*} \Delta y=-\frac 12 gt^2 +(v_0\sin\theta)t \\\\ -200=-\frac 12 (10)t^2 +(60\sin 60^\circ)t \\\\ \Rightarrow\quad 5t^2-30\sqrt{3}t-200=0 \\\\ \boxed{t^2-6\sqrt{3}t-40=0}\end{gather*} where we used $\sin 60^\circ=\frac{\sqrt{3}}2$. Using a graphing calculator plot this equation and find its intersections with the horizontal. Consequently, the total flight time is \[\boxed{t=13.4\,{\rm m}}\] Now, substitute this into the horizontal displacement projectile equation below \begin{align*} x&=(v_0\cos\theta)t \\\\ &=(60\,\cos 60^\circ)(13.4) \\\\ &=402\,{\rm m}\end{align*} Thus, the correct answer is (b).
Problem (12): During a kicking drill, a soccer player kicks two successive balls at different angles but with exactly the same speed. The paths that the balls follow are depicted in the figure shown. Which ball remains in the air for a longer time? Neglect air resistance.
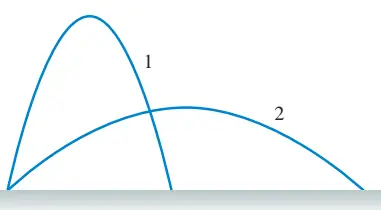
Solution : both balls land at the same level (or the ground), so the total vertical displacement of both is the same, $\Delta y_1=\Delta y_2=0$. The initial kicking speeds are equal $v_{01}=v_{02}$ and as seen from the figure, ball $1$ has greater kicking angle than ball $2$, i.e., $\theta_1>\theta_2$. Setting $\Delta y=0$ in the following equation and solving for $t$, gives us the total time the ball is in the air \begin{gather*} \Delta y=-\frac 12 gt^2+(v_0 \sin\theta)t \\\\ 0=-\frac 12 gt^2+(v_0 \sin\theta)t \\\\ \Rightarrow \boxed{t=\frac{2v_0 \sin\theta}{g}} \end{gather*} Now, substitute the given data into the equation to compare the flight time of both balls \begin{gather*} \theta_1>\theta_2 \\ \sin\theta_1 > \sin\theta_2 \\\\ \frac{2v_0 \sin\theta_1}{g} > \frac{2v_0 \sin\theta_2}{g} \\\\ \Rightarrow \boxed{t_1>t_2} \end{gather*} Thus, ball $1$ will be in the air for a longer time.
Author : Dr. Ali Nemati Date Published: 6/15/2021
Updated: Jun 22, 2023
© 2015 All rights reserved. by Physexams.com
4.3 Projectile Motion
Learning objectives.
By the end of this section, you will be able to:
- Use one-dimensional motion in perpendicular directions to analyze projectile motion.
- Calculate the range, time of flight, and maximum height of a projectile that is launched and impacts a flat, horizontal surface.
- Find the time of flight and impact velocity of a projectile that lands at a different height from that of launch.
- Calculate the trajectory of a projectile.
Projectile motion is the motion of an object thrown or projected into the air, subject only to acceleration as a result of gravity. The applications of projectile motion in physics and engineering are numerous. Some examples include meteors as they enter Earth’s atmosphere, fireworks, and the motion of any ball in sports. Such objects are called projectiles and their path is called a trajectory . The motion of falling objects as discussed in Motion Along a Straight Line is a simple one-dimensional type of projectile motion in which there is no horizontal movement. In this section, we consider two-dimensional projectile motion, and our treatment neglects the effects of air resistance.
The most important fact to remember here is that motions along perpendicular axes are independent and thus can be analyzed separately. We discussed this fact in Displacement and Velocity Vectors , where we saw that vertical and horizontal motions are independent. The key to analyzing two-dimensional projectile motion is to break it into two motions: one along the horizontal axis and the other along the vertical. (This choice of axes is the most sensible because acceleration resulting from gravity is vertical; thus, there is no acceleration along the horizontal axis when air resistance is negligible.) As is customary, we call the horizontal axis the x -axis and the vertical axis the y -axis. It is not required that we use this choice of axes; it is simply convenient in the case of gravitational acceleration. In other cases we may choose a different set of axes. Figure 4.11 illustrates the notation for displacement, where we define s → s → to be the total displacement, and x → x → and y → y → are its component vectors along the horizontal and vertical axes, respectively. The magnitudes of these vectors are s , x , and y .
To describe projectile motion completely, we must include velocity and acceleration, as well as displacement. We must find their components along the x- and y -axes. Let’s assume all forces except gravity (such as air resistance and friction, for example) are negligible. Defining the positive direction to be upward, the components of acceleration are then very simple:
Because gravity is vertical, a x = 0 . a x = 0 . If a x = 0 , a x = 0 , this means the initial velocity in the x direction is equal to the final velocity in the x direction, or v x = v 0 x . v x = v 0 x . With these conditions on acceleration and velocity, we can write the kinematic Equation 4.11 through Equation 4.18 for motion in a uniform gravitational field, including the rest of the kinematic equations for a constant acceleration from Motion with Constant Acceleration . The kinematic equations for motion in a uniform gravitational field become kinematic equations with a y = − g , a x = 0 : a y = − g , a x = 0 :
Horizontal Motion
Vertical Motion
Using this set of equations, we can analyze projectile motion, keeping in mind some important points.
Problem-Solving Strategy
Projectile motion.
- Resolve the motion into horizontal and vertical components along the x - and y -axes. The magnitudes of the components of displacement s → s → along these axes are x and y. The magnitudes of the components of velocity v → v → are v x = v cos θ and v y = v sin θ , v x = v cos θ and v y = v sin θ , where v is the magnitude of the velocity and θ is its direction relative to the horizontal, as shown in Figure 4.12 .
- Treat the motion as two independent one-dimensional motions: one horizontal and the other vertical. Use the kinematic equations for horizontal and vertical motion presented earlier.
- Solve for the unknowns in the two separate motions: one horizontal and one vertical. Note that the only common variable between the motions is time t . The problem-solving procedures here are the same as those for one-dimensional kinematics and are illustrated in the following solved examples.
- Recombine quantities in the horizontal and vertical directions to find the total displacement s → s → and velocity v → . v → . Solve for the magnitude and direction of the displacement and velocity using s = x 2 + y 2 , Φ = tan −1 ( y / x ) , v = v x 2 + v y 2 , s = x 2 + y 2 , Φ = tan −1 ( y / x ) , v = v x 2 + v y 2 , where Φ is the direction of the displacement s → . s → .
Example 4.7
A fireworks projectile explodes high and away.
Because y 0 y 0 and v y v y are both zero, the equation simplifies to
Solving for y gives
Now we must find v 0 y , v 0 y , the component of the initial velocity in the y direction. It is given by v 0 y = v 0 sin θ 0 , v 0 y = v 0 sin θ 0 , where v 0 v 0 is the initial velocity of 70.0 m/s and θ 0 = 75 ° θ 0 = 75 ° is the initial angle. Thus,
Thus, we have
Note that because up is positive, the initial vertical velocity is positive, as is the maximum height, but the acceleration resulting from gravity is negative. Note also that the maximum height depends only on the vertical component of the initial velocity, so that any projectile with a 67.6-m/s initial vertical component of velocity reaches a maximum height of 233 m (neglecting air resistance). The numbers in this example are reasonable for large fireworks displays, the shells of which do reach such heights before exploding. In practice, air resistance is not completely negligible, so the initial velocity would have to be somewhat larger than that given to reach the same height.
(b) As in many physics problems, there is more than one way to solve for the time the projectile reaches its highest point. In this case, the easiest method is to use v y = v 0 y − g t . v y = v 0 y − g t . Because v y = 0 v y = 0 at the apex, this equation reduces to simply
This time is also reasonable for large fireworks. If you are able to see the launch of fireworks, notice that several seconds pass before the shell explodes. Another way of finding the time is by using y = y 0 + 1 2 ( v 0 y + v y ) t . y = y 0 + 1 2 ( v 0 y + v y ) t . This is left for you as an exercise to complete.
(c) Because air resistance is negligible, a x = 0 a x = 0 and the horizontal velocity is constant, as discussed earlier. The horizontal displacement is the horizontal velocity multiplied by time as given by x = x 0 + v x t , x = x 0 + v x t , where x 0 x 0 is equal to zero. Thus,
where v x v x is the x -component of the velocity, which is given by
Time t for both motions is the same, so x is
Horizontal motion is a constant velocity in the absence of air resistance. The horizontal displacement found here could be useful in keeping the fireworks fragments from falling on spectators. When the shell explodes, air resistance has a major effect, and many fragments land directly below.
(d) The horizontal and vertical components of the displacement were just calculated, so all that is needed here is to find the magnitude and direction of the displacement at the highest point:
Note that the angle for the displacement vector is less than the initial angle of launch. To see why this is, review Figure 4.11 , which shows the curvature of the trajectory toward the ground level.
When solving Example 4.7 (a), the expression we found for y is valid for any projectile motion when air resistance is negligible. Call the maximum height y = h . Then,
This equation defines the maximum height of a projectile above its launch position and it depends only on the vertical component of the initial velocity.
Check Your Understanding 4.3
A rock is thrown horizontally off a cliff 100.0 m 100.0 m high with a velocity of 15.0 m/s. (a) Define the origin of the coordinate system. (b) Which equation describes the horizontal motion? (c) Which equations describe the vertical motion? (d) What is the rock’s velocity at the point of impact?
Example 4.8
Calculating projectile motion: tennis player.
If we take the initial position y 0 y 0 to be zero, then the final position is y = 10 m. The initial vertical velocity is the vertical component of the initial velocity:
Substituting into Equation 4.22 for y gives us
Rearranging terms gives a quadratic equation in t :
Use of the quadratic formula yields t = 3.79 s and t = 0.54 s. Since the ball is at a height of 10 m at two times during its trajectory—once on the way up and once on the way down—we take the longer solution for the time it takes the ball to reach the spectator:
The time for projectile motion is determined completely by the vertical motion. Thus, any projectile that has an initial vertical velocity of 21.2 m/s and lands 10.0 m above its starting altitude spends 3.79 s in the air.
(b) We can find the final horizontal and vertical velocities v x v x and v y v y with the use of the result from (a). Then, we can combine them to find the magnitude of the total velocity vector v → v → and the angle θ θ it makes with the horizontal. Since v x v x is constant, we can solve for it at any horizontal location. We choose the starting point because we know both the initial velocity and the initial angle. Therefore,
The final vertical velocity is given by Equation 4.21 :
Since v 0 y v 0 y was found in part (a) to be 21.2 m/s, we have
The magnitude of the final velocity v → v → is
The direction θ v θ v is found using the inverse tangent:
Significance
Time of flight, trajectory, and range.
Of interest are the time of flight, trajectory, and range for a projectile launched on a flat horizontal surface and impacting on the same surface. In this case, kinematic equations give useful expressions for these quantities, which are derived in the following sections.
Time of flight
We can solve for the time of flight of a projectile that is both launched and impacts on a flat horizontal surface by performing some manipulations of the kinematic equations. We note the position and displacement in y must be zero at launch and at impact on an even surface. Thus, we set the displacement in y equal to zero and find
Factoring, we have
Solving for t gives us
This is the time of flight for a projectile both launched and impacting on a flat horizontal surface. Equation 4.24 does not apply when the projectile lands at a different elevation than it was launched, as we saw in Example 4.8 of the tennis player hitting the ball into the stands. The other solution, t = 0, corresponds to the time at launch. The time of flight is linearly proportional to the initial velocity in the y direction and inversely proportional to g . Thus, on the Moon, where gravity is one-sixth that of Earth, a projectile launched with the same velocity as on Earth would be airborne six times as long.
The trajectory of a projectile can be found by eliminating the time variable t from the kinematic equations for arbitrary t and solving for y ( x ). We take x 0 = y 0 = 0 x 0 = y 0 = 0 so the projectile is launched from the origin. The kinematic equation for x gives
Substituting the expression for t into the equation for the position y = ( v 0 sin θ 0 ) t − 1 2 g t 2 y = ( v 0 sin θ 0 ) t − 1 2 g t 2 gives
Rearranging terms, we have
This trajectory equation is of the form y = a x + b x 2 , y = a x + b x 2 , which is an equation of a parabola with coefficients
From the trajectory equation we can also find the range , or the horizontal distance traveled by the projectile. Factoring Equation 4.25 , we have
The position y is zero for both the launch point and the impact point, since we are again considering only a flat horizontal surface. Setting y = 0 in this equation gives solutions x = 0, corresponding to the launch point, and
corresponding to the impact point. Using the trigonometric identity 2 sin θ cos θ = sin 2 θ 2 sin θ cos θ = sin 2 θ and setting x = R for range, we find
Note particularly that Equation 4.26 is valid only for launch and impact on a horizontal surface. We see the range is directly proportional to the square of the initial speed v 0 v 0 and sin 2 θ 0 sin 2 θ 0 , and it is inversely proportional to the acceleration of gravity. Thus, on the Moon, the range would be six times greater than on Earth for the same initial velocity. Furthermore, we see from the factor sin 2 θ 0 sin 2 θ 0 that the range is maximum at 45 ° . 45 ° . These results are shown in Figure 4.15 . In (a) we see that the greater the initial velocity, the greater the range. In (b), we see that the range is maximum at 45 ° . 45 ° . This is true only for conditions neglecting air resistance. If air resistance is considered, the maximum angle is somewhat smaller. It is interesting that the same range is found for two initial launch angles that sum to 90 ° . 90 ° . The projectile launched with the smaller angle has a lower apex than the higher angle, but they both have the same range.
Example 4.9
Comparing golf shots.
(a) What is the initial speed of the ball at the second hole?
(b) What is the initial speed of the ball at the fourth hole?
(c) Write the trajectory equation for both cases.
(d) Graph the trajectories.
(b) R = v 0 2 sin 2 θ 0 g ⇒ v 0 = R g sin 2 θ 0 = 90.0 m ( 9.8 m / s 2 ) sin ( 2 ( 70 ° ) ) = 37.0 m / s R = v 0 2 sin 2 θ 0 g ⇒ v 0 = R g sin 2 θ 0 = 90.0 m ( 9.8 m / s 2 ) sin ( 2 ( 70 ° ) ) = 37.0 m / s
(c) y = x [ tan θ 0 − g 2 ( v 0 cos θ 0 ) 2 x ] Second hole: y = x [ tan 30 ° − 9.8 m / s 2 2 [ ( 31.9 m / s)( cos 30 ° ) ] 2 x ] = 0.58 x − 0.0064 x 2 Fourth hole: y = x [ tan 70 ° − 9.8 m / s 2 2 [ ( 37.0 m / s)( cos 70 ° ) ] 2 x ] = 2.75 x − 0.0306 x 2 y = x [ tan θ 0 − g 2 ( v 0 cos θ 0 ) 2 x ] Second hole: y = x [ tan 30 ° − 9.8 m / s 2 2 [ ( 31.9 m / s)( cos 30 ° ) ] 2 x ] = 0.58 x − 0.0064 x 2 Fourth hole: y = x [ tan 70 ° − 9.8 m / s 2 2 [ ( 37.0 m / s)( cos 70 ° ) ] 2 x ] = 2.75 x − 0.0306 x 2
(d) Using a graphing utility, we can compare the two trajectories, which are shown in Figure 4.16 .
Check Your Understanding 4.4
If the two golf shots in Example 4.9 were launched at the same speed, which shot would have the greatest range?
When we speak of the range of a projectile on level ground, we assume R is very small compared with the circumference of Earth. If, however, the range is large, Earth curves away below the projectile and the acceleration resulting from gravity changes direction along the path. The range is larger than predicted by the range equation given earlier because the projectile has farther to fall than it would on level ground, as shown in Figure 4.17 , which is based on a drawing in Newton’s Principia. If the initial speed is great enough, the projectile goes into orbit. Earth’s surface drops 5 m every 8000 m. In 1 s an object falls 5 m without air resistance. Thus, if an object is given a horizontal velocity of 8000 m/s (or 18,000 mi/hr) near Earth’s surface, it will go into orbit around the planet because the surface continuously falls away from the object. This is roughly the speed of the Space Shuttle in a low Earth orbit when it was operational, or any satellite in a low Earth orbit. These and other aspects of orbital motion, such as Earth’s rotation, are covered in greater depth in Gravitation .
Interactive
At PhET Explorations: Projectile Motion , learn about projectile motion in terms of the launch angle and initial velocity.
As an Amazon Associate we earn from qualifying purchases.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/university-physics-volume-1/pages/1-introduction
- Authors: William Moebs, Samuel J. Ling, Jeff Sanny
- Publisher/website: OpenStax
- Book title: University Physics Volume 1
- Publication date: Sep 19, 2016
- Location: Houston, Texas
- Book URL: https://openstax.org/books/university-physics-volume-1/pages/1-introduction
- Section URL: https://openstax.org/books/university-physics-volume-1/pages/4-3-projectile-motion
© Jan 19, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

- Science Notes Posts
- Contact Science Notes
- Todd Helmenstine Biography
- Anne Helmenstine Biography
- Free Printable Periodic Tables (PDF and PNG)
- Periodic Table Wallpapers
- Interactive Periodic Table
- Periodic Table Posters
- How to Grow Crystals
- Chemistry Projects
- Fire and Flames Projects
- Holiday Science
- Chemistry Problems With Answers
- Physics Problems
- Unit Conversion Example Problems
- Chemistry Worksheets
- Biology Worksheets
- Periodic Table Worksheets
- Physical Science Worksheets
- Science Lab Worksheets
- My Amazon Books

Projectile Motion Example Problem – Physics Homework Help 1
Throwing or shooting a projectile follows a parabolic course. If you know the initial velocity and angle of elevation of the projectile, you can find its time aloft, maximum height or range. You can also its altitude and distance travelled if given a time. This example problem shows how to do all of these.
Projectile Motion Example Problem: A cannon is fired with muzzle velocity of 150 m/s at an angle of elevation = 45°. Gravity = 9.8 m/s 2 . a) What is the maximum height the projectile reaches? b) What is the total time aloft? c) How far away did the projectile land? (Range) d) Where is the projectile at 10 seconds after firing?

Let’s set up what we know. First, let’s define our variables.
V 0 = initial velocity = muzzle velocity = 150 m/s v x = horizontal velocity component v y = vertical velocity component θ = angle of elevation = 45° h = maximum height R = range x = horizontal position at t=10 s y = vertical position at t=10 s m = mass of projectile g = acceleration due to gravity = 9.8 m/s 2
Part a) Find h.
The formulas we will be using are:
d = v 0 t + ½at 2
v f – v 0 = at
In order to find the distance h, we need to know two things: the velocity at h and the amount of time it takes to get there. The first is easy. The vertical component of the velocity is equal to zero at point h. This is the point where the upward motion is stopped and the projectile begins to fall back to Earth.
The initial vertical velocity is v 0y = v 0 ·sinθ v 0y = 150 m/s · sin(45°) v 0y = 106.1 m/s
Now we know the beginning and final velocity. The next thing we need is the acceleration.
The only force acting on the projectile is the force of gravity. Gravity has a magnitude of g and a direction in the negative y direction.
F = ma = -mg
solve for a
Now we have enough information to find the time. We know the initial vertical velocity (V 0y ) and the final vertical velocity at h (v hy = 0)
v hy – v 0y = at 0 – v 0y = -9.8 m/s 2 ·t 0 – 106.1 m/s = -9.8 m/s 2 ·t
Solve for t
t = 10.8 s
Now solve the first equation for h
h = v 0y t + ½at 2 h = (106.1 m/s)(10.8 s) + ½(-9.8 m/s 2 )(10.8 s) 2 h = 1145.9 m – 571.5 m h = 574.4 m
The highest height the projectile reaches is 574.4 meters.
Part b: Find total time aloft.
We’ve already done most of the work to get this part of the question if you stop to think. The projectile’s trip can be broken into two parts: going up and coming down.
t total = t up + t down
The same acceleration force acts on the projectile in both directions. The time down takes the same amount of time it took to go up.
t up = t down
t total = 2 t up
we found t up in Part a of the problem: 10.8 seconds
t total = 2 (10.8 s) t total = 21.6 s
The total time aloft for the projectile is 21.6 seconds.
Part c: Find range R
To find the range, we need to know the initial velocity in the x direction.
v 0x = v 0 cosθ v 0x = 150 m/s·cos(45) v 0x = 106.1 m/s
To find the range R, use the equation:
R = v 0x t + ½at 2
There is no force acting along the x-axis. This means the acceleration in the x-direction is zero. The equation of motion is reduced to:
R = v 0x t + ½(0)t 2 R = v 0x t
The range is the point where the projectile strikes the ground which happens at the time we found in Part b of the problem.
R = 106.1 m/s · 21.6s R = 2291.8 m
The projectile landed 2291.8 meters from the canon.
Part d: Find the position at t = 10 seconds.
The position has two components: horizontal and vertical position. The horizontal position, x, is far downrange the projectile is after firing and the vertical component is the current altitude, y, of the projectile.
To find these positions, we will use the same equation:
First, let’s do the horizontal position. There is no acceleration in the horizontal direction so the second half of the equation is zero, just like in Part c.
We are given t = 10 seconds. V 0x was calculated in Part c of the problem.
x = 106.1 m/s · 10 s x = 1061 m
Now do the same thing for the vertical position.
y = v 0y t + ½at 2
We saw in Part b that v 0y = 109.6 m/s and a = -g = -9.8 m/s 2 . At t = 10 s:
y = 106.1 m/s · 10 s + ½(-9.8 m/s 2 )(10 s) 2 y = 1061 – 490 m y = 571 m
At t=10 seconds, the projectile is at (1061 m, 571 m) or 1061 m downrange and at an altitude of 571 meters.
If you need to know the velocity of the projectile at a specific time, you can use the formula
v – v 0 = at
and solve for v. Just remember velocity is a vector and will have both x and y components.
This specific example can be easily adapted for any initial velocity and any angle of elevation. If the cannon is fired on another planet with a different force of gravity, just change the value of g accordingly.
Related Posts
One thought on “ projectile motion example problem – physics homework help ”.
no you are not one who is correct
Comments are closed.
Your Physicist
I will answer anything from the world of physics.
Projectile Motion Problems
Introduction to projectile motion.
Projectile motion refers to the motion of an object that is propelled into the air and then moves in a curved path under the influence of gravity. It is a fundamental concept in physics, and many real-world applications rely on it. Understanding projectile motion is important because it can help predict the trajectory of objects in motion, such as a ball being kicked, a car moving over a hill, or a rocket launching into space. It is also essential for mastering physics at a high school or college level.
Solving Projectile Motion Problems
Solving projectile motion problems involves using equations of motion to calculate the trajectory of an object. There are several equations that can be used to solve these problems, including the kinematic equations, the quadratic formula, and the trigonometric ratios. To solve a projectile motion problem, one must first identify the initial velocity, the angle of launch, and any other relevant parameters, such as the height above the ground. Once these values are known, the equations of motion can be used to calculate the object’s trajectory and predict its landing point.
Examples of Projectile Motion Problems
Projectile motion problems can involve a wide variety of scenarios, from a ball being thrown from a balcony to a missile being launched from a military base. Here are some examples of common projectile motion problems:
- A baseball pitcher throws a ball at an angle of 45 degrees with an initial velocity of 30 m/s. What is the maximum height the ball reaches, and how far does it travel before landing?
- A cannon fires a cannonball at an angle of 60 degrees with an initial velocity of 100 m/s. How far away from the cannon does the cannonball land, and what is its maximum height?
- A skier jumps off a ramp at an angle of 30 degrees with an initial velocity of 20 m/s. How far does the skier travel before landing, and what is the maximum height the skier reaches?
Tips for Mastering Projectile Motion
To master projectile motion, it is important to practice solving problems using the equations of motion. Start with simple problems and gradually work your way up to more complex ones. It is also helpful to visualize the trajectory of an object in your mind, which can be done by drawing diagrams or using simulation software. Additionally, understanding the physics behind projectile motion, such as the effects of air resistance, can help you solve problems more effectively. Finally, don’t be afraid to ask for help or seek out additional resources, such as textbooks or online tutorials, to improve your understanding of the subject.
Projectile Problems with Solutions and Explanations
Projectile problems are presented along with detailed solutions . These problems may be better understood when projectile equations are first reviewed. An interactive html 5 applet may be used to better understand the projectile equations.
Problem 1: An object is launched at a velocity of 20 m/s in a direction making an angle of 25° upward with the horizontal. a) What is the maximum height reached by the object? b) What is the total flight time (between launch and touching the ground) of the object? c) What is the horizontal range (maximum x above ground) of the object? d) What is the magnitude of the velocity of the object just before it hits the ground? Solution to Problem 1
Problem 5: A ball kicked from ground level at an initial velocity of 60 m/s and an angle θ with ground reaches a horizontal distance of 200 meters. a) What is the size of angle θ? b) What is time of flight of the ball? Solution to Problem 5
Problem 6: A ball of 600 grams is kicked at an angle of 35° with the ground with an initial velocity V 0 . a) What is the initial velocity V 0 of the ball if its kinetic energy is 22 Joules when its height is maximum? b) What is the maximum height reached by the ball Solution to Problem 6
Problem 7: A projectile starting from ground hits a target on the ground located at a distance of 1000 meters after 40 seconds. a) What is the size of the angle θ? b) At what initial velocity was the projectile launched? Solution to Problem 7
Problem 8: The trajectory of a projectile launched from ground is given by the equation y = -0.025 x 2 + 0.5 x, where x and y are the coordinate of the projectile on a rectangular system of axes. a) Find the initial velocity and the angle at which the projectile is launched. Solution to Problem 8
Problem 9: Two balls A and B of masses 100 grams and 300 grams respectively are pushed horizontally from a table of height 3 meters. Ball has is pushed so that its initial velocity is 10 m/s and ball B is pushed so that its initial velocity is 15 m/s. a) Find the time it takes each ball to hit the ground. b) What is the difference in the distance between the points of impact of the two balls on the ground? Solution to Problem 9
More References and links
- Velocity and Speed: Tutorials with Examples
- Velocity and Speed: Problems with Solutions
- Acceleration: Tutorials with Examples
- Uniform Acceleration Motion: Problems with Solutions
- Uniform Acceleration Motion: Equations with Explanations
- Science & Math
- Sociology & Philosophy
- Law & Politics
Projectile Motion: Practice Problems & Solutions
- Projectile Motion: Practice Problems &…
- An object is projected horizontally at 8.0 m/s from the top of a 122.5 m cliff. How far from the base of the cliff will the object strike the ground?
- An arrow is shot at 30.0° angle with the horizontal. It has a velocity of 49 m/s.
a) How high will it go?
b) What horizontal distance will the arrow travel?
3. A person kicks a rock off a cliff horizontally with a speed of 20 m/s. It takes 7.0 seconds to hit the ground, find:
a) height of the cliff
b) final vertical velocity
- A ship fires its guns with a speed of 400 m/s at an angle of 35° with the horizontal. Find the range and maximum altitude.
- A basketball is held over head at a height of 2.4 m. The ball is lobbed to a teammate at 8 m/s at an angle of 40°. If the ball is caught at the same height it was tossed at, how far away is the teammate?
- Suppose the ball in #6 was missed, what would the range be?
- An athlete executing a long jump leaves the ground at angle of 30.0° and travels 7.80 m.
a) What is the takeoff speed?
b) If the takeoff speed was increased by 5.0%, how much longer would the jump be?
- A hunter aims directly at a target (on the same level) 140 m away. If the bullet leaves the gun at a speed of 280 m/s, by how much will the bullet miss the target?
- A ball is thrown horizontally from the roof of a building 50 m tall and lands 45 m from the base. What was the ball’s initial speed?
- A fire hose held near the ground shoots water at a speed of 7.5 m/s. At what angle should the nozzle point in order that the water land 2.0 m away? Why are there two different answers to this problem?
- A bullet traveling 800 m/s horizontally hits a target 180 m away. How far does the bullet fall before it hits the target?
- A student threw a ball horizontally out of a window 8.0 m above the ground. It was caught by another student who was 10.0 m away. What was the initial velocity of the ball?
13. A baseball was hit at 45 m/s at an angle of 45° above the horizontal.
a) How long did it remain in the air?
b) How far did it travel horizontally?
- A camper dives from the edge of a swimming pool at water level with a speed of 8.0 m/s at an angle of 30.0° above the horizontal.
a) How long is the diver in the air?
b) How high does the diver go?
c) How far out in the pool does the diver land?
b) 2.2 x 102 m
3) a) 2.4 x102 m
c) 1.4 x 102 m
4) a) 2.7 x 103 m
b) 1.5 x104 m
7) a) 9.4 m/s
12) 7.7 m/s, –>
13) a) 6.6 s
b) 2.1 x 102 m
14) a) 0.82 s
Related Posts
- Problems After the October Revolution
- Melody: Contour, Motion, Phrase
- Dihybrid Cross Practice Problems
- Phet Projectile Motion Lab: Lab Answers
- Projectile Motion Practice & Solutions
could you please post the solutions also?
Leave a Reply Cancel reply
Your email address will not be published. Required fields are marked *
Save my name, email, and website in this browser for the next time I comment.
Post comment
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
Mechanics (Essentials) - Class 11th
Course: mechanics (essentials) - class 11th > unit 5, how to solve a projectile motion problem.
- What is 2D projectile motion?
- Projectile at an angle
- Angled launch projectile vectors
- Comparing projectile trajectories
- Projectiles launched at an angle review
- Horizontally launched projectile
- Solving kinematic equations for horizontal projectiles
- Projectile motion graphs
- 2D projectile motion: Identifying graphs for projectiles
- 2D projectile motion: Vectors and comparing multiple trajectories
Want to join the conversation?
- Upvote Button navigates to signup page
- Downvote Button navigates to signup page
- Flag Button navigates to signup page
Video transcript

IMAGES
VIDEO
COMMENTS
Problem 8. The trajectory of a projectile launched from ground is given by the equation y = -0.025 x 2 + 0.5 x, where x and y are the coordinate of the projectile on a rectangular system of axes. a) Find the initial velocity and the angle at which the projectile is launched. Solution to Problem 8.
Projectile Motion: Practice Problems with Solutions Physexams.com Now, we use the horizontal displacement formula for projectile and set x= 2.5m. Thus, x= (v 0 cosθ)t 2.5 = (6cosθ)t ⇒6tcosθ= 2.5 Dividing these two boxed equations, we have 6sinθ 6tcosθ = 5t 2.5 tanθ= 2t2, (I) This is the only equation that we can find with the given ...
Figure 5.29 (a) We analyze two-dimensional projectile motion by breaking it into two independent one-dimensional motions along the vertical and horizontal axes. (b) The horizontal motion is simple, because a x = 0 a x = 0 and v x v x is thus constant. (c) The velocity in the vertical direction begins to decrease as the object rises; at its highest point, the vertical velocity is zero.
Problem (1): A person kicks a ball with an initial velocity of 15 m/s at an angle of 37° above the horizontal (neglecting the air resistance). Find. (a) the total time the ball is in the air. (b) the horizontal distance traveled by the ball. Solution: The initial step in answering any projectile motion questions is to establish a coordinate ...
Determine the initial horizontal velocity of the soccer ball. Problem Type 2: A projectile is launched at an angle to the horizontal and rises upwards to a peak while moving horizontally. Upon reaching the peak, the projectile falls with a motion that is symmetrical to its path upwards to the peak. Predictable unknowns include the time of ...
Learn how to analyze the motion of an object thrown or projected into the air, subject to only the acceleration of gravity, using kinematic equations and graphs. Explore the factors that affect the range and height of a projectile, and practice solving problems involving projectile motion.
To practice Problem-Solving Strategy 4.1 for projectile motion problems. A rock thrown with speed 9.50 and launch angle 30.0 (above the horizontal) travels a horizontal distance of = 18.0 before hitting the ground. ... PROBLEMSOLVING STRATEGY 4.1 Projectile motion problems M O D E L : Is it reasonable to ignore air resistance? If so, use the ...
Solving kinematic equations for horizontal projectiles. A volcano erupts, and a chunk of hot magma is launched horizontally with a speed of 208 m s from a height of 94 m . We can ignore air resistance. What is the magma's horizontal displacement from the launch to when it hits the ground?
Figure 4.12 (a) We analyze two-dimensional projectile motion by breaking it into two independent one-dimensional motions along the vertical and horizontal axes. (b) The horizontal motion is simple, because a x = 0 a x = 0 and v x v x is a constant. (c) The velocity in the vertical direction begins to decrease as the object rises. At its highest point, the vertical velocity is zero.
The equation of motion is reduced to: R = v 0x t + ½ (0)t 2. R = v 0x t. The range is the point where the projectile strikes the ground which happens at the time we found in Part b of the problem. R = 106.1 m/s · 21.6s. R = 2291.8 m. The projectile landed 2291.8 meters from the canon.
Angle-launched projectiles are objects projected at an angle to the horizontal. Their motion begins with both an x- and y-velocity component. • Projectiles have no horizontal acceleration and a vertical acceleration of 9.8 m/s/s, ↓. ax= 0 m/s/s ay= - 9.8 m/s/s. • At the highest point (the "peak"), the vertical velocity is 0 m/s.
Solving projectile motion problems involves using equations of motion to calculate the trajectory of an object. There are several equations that can be used to solve these problems, including the kinematic equations, the quadratic formula, and the trigonometric ratios. ... To master projectile motion, it is important to practice solving ...
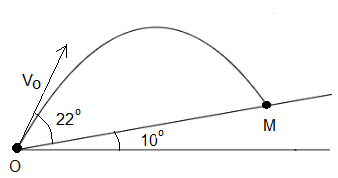
Solution to Problem 1. Problem 2: A projectile is launched from point O at an angle of 22° with an initial velocity of 15 m/s up an incline plane that makes an angle of 10° with the horizontal. The projectile hits the incline plane at point M. a) Find the time it takes for the projectile to hit the incline plane. b)Find the distance OM.
Learn how to solve problems involving projectile motion, such as finding the range, height, or velocity of a projectile. This lesson explains how to use the equations of motion in two dimensions and how to break a vector into its x and y components. You will also find examples and practice questions to test your understanding.
Are you struggling with projectile motion problems in physics? In this video, we'll show you how to solve them step-by-step!We'll start by explaining what pr...
5 PRACTICE PROBLEM. A missile is fired with a take-off speed of 120 m/s at an angle θ with respect to the ground. It experiences a horizontal acceleration of 50 m/s 2 along the x-axis in a direction opposite to the motion. Determine the value of θ so that the missile will cover the maximum distance. Hint: use the following expression d/dθ (A ...
5. Substitute known values; solve for unknown. Use of an X-Y Table. An "X-Y Table" is a useful means of organizing the given information in a projectile problem. It helps keep x- and y- variable values separate. Sample Problem: A ball is thrown horizontally at 12.8 m/s from the top of a 17.9-m high cliff.
3. A person kicks a rock off a cliff horizontally with a speed of 20 m/s. It takes 7.0 seconds to hit the ground, find: a) height of the cliff. b) final vertical velocity. c) range. A ship fires its guns with a speed of 400 m/s at an angle of 35° with the horizontal. Find the range and maximum altitude.
Video transcript. Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more. Khan Academy is a nonprofit with the mission of providing a free, world-class education for anyone, anywhere.
Solution: Using t = 2 v sin θ g, the time of flight is t ≈ 5.8 s. 12. A baseball is thrown at an angle of 60° with a velocity of 12 m/s. Find the horizontal range. Solution: Using R = v 2 sin 2 θ g, the range is R ≈ 14.0 m. 13. A projectile is launched with an initial velocity of 50 m/s at 37° above the horizontal.
Yes No. Students will learn how to use the equations of motion in two dimensions in order to solve problems for projectiles. It is necessary to understand how to break a vector into its x and y components.
A projectile is thrown from a point on the ground at an angle above the horizontal. It moves in such a way that its distance from P is always increasing from its launch until it falls back to the ground. Find all the possible values of with which the projectile could have been thrown. You can ignore air resistance.