hypothesis testing for correlation calculator

Correlation Calculator

Input your values with a space or comma between in the table below

Critical Value

Results shown here

Sample size, n

Sample correlation coefficient, r, standardized sample score.

Correlation Coefficient Significance Calculator using p-value

Instructions: Use this Correlation Coefficient Significance Calculator to enter the sample correlation \(r\), sample size \(n\) and the significance level \(\alpha\), and the solver will test whether or not the correlation coefficient is significantly different from zero using the critical correlation approach.

More About Significance of the Correlation Coefficient Significance Calculator

The sample correlation \(r\) is a statistic that estimates the population correlation, \(\rho\). On typical statistical test consists of assessing whether or not the correlation coefficient is significantly different from zero.

There are least two methods to assess the significance of the sample correlation coefficient: One of them is based on the critical correlation. Such approach is based upon on the idea that if the sample correlation \(r\) is large enough, then the population correlation \(\rho\) is different from zero.

In order to assess whether or not the sample correlation is significantly different from zero, the following t-statistic is obtained

So, this is the formula for the t test for correlation coefficient, which the calculator will provide for you showing all the steps of the calculation.

If the above t-statistic is significant, then we would reject the null hypothesis \(H_0\) (that the population correlation is zero). You can also the critical correlation approach , with the same purpose of assessing whether or not the sample correlation is significantly different from zero, but in that case by comparing the sample correlation with a critical correlation value.

Related Calculators

log in to your account

Reset password.

Testing the Significance of Correlations

• Comparison of correlations from independent samples
• Comparison of correlations from dependent samples
• Testing linear independence (Testing against 0)
• Testing correlations against a fixed value
• Calculation of confidence intervals of correlations
• Fisher-Z-Transformation
• Calculation of the Phi correlation coefficient r Phi for categorial data
• Calculation of the weighted mean of a list of correlations
• Transformation of the effect sizes r , d , f , Odds Ratio and eta square
• Calculation of Linear Correlations

1. Comparison of correlations from independent samples

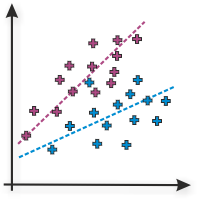
Correlations, which have been retrieved from different samples can be tested against each other. Example: Imagine, you want to test, if men increase their income considerably faster than women. You could f. e. collect the data on age and income from 1 200 men and 980 women. The correlation could amount to r = .38 in the male cohort and r = .31 in women. Is there a significant difference in the correlation of both cohorts?

(Calculation according to Eid, Gollwitzer & Schmidt, 2011 , pp. 547; single sided test)

2. Comparison of correlations from dependent samples

• 85 children from grade 3 have been tested with tests on intelligence (1), arithmetic abilities (2) and reading comprehension (3). The correlation between intelligence and arithmetic abilities amounts to r 12 = .53, intelligence and reading correlates with r 13 = .41 and arithmetic and reading with r 23 = .59. Is the correlation between intelligence an arithmetic abilities higher than the correlation between intelligence and reading comprehension?

(Calculation according to Eid et al., 2011 , S. 548 f.; single sided testing)

3. Testing linear independence (Testing against 0)

With the following calculator, you can test if correlations are different from zero. The test is based on the Student's t distribution with n - 2 degrees of freedom. An example: The length of the left foot and the nose of 18 men is quantified. The length correlates with r = .69. Is the correlation significantly different from 0?

(Calculation according to Eid et al., 2011 , S. 542; two sided test)

4. Testing correlations against a fixed value

With the following calculator, you can test if correlations are different from a fixed value. The test uses the Fisher-Z-transformation.

(Calculation according to Eid et al., 2011 , S. 543f.; two sided test)

5. Calculation of confidence intervals of correlations

The confidence interval specifies the range of values that includes a correlation with a given probability (confidence coefficient). The higher the confidence coefficient, the larger the confidence interval. Commonly, values around .9 are used.

based on Bonett & Wright (2000); cf. simulation of Gnambs (2022)

6. Fisher-Z-Transformation

The Fisher-Z-Transformation converts correlations into an almost normally distributed measure. It is necessary for many operations with correlations, f. e. when averaging a list of correlations. The following converter transforms the correlations and it computes the inverse operations as well. Please note, that the Fisher-Z is typed uppercase.

r Phi is a measure for binary data such as counts in different categories, e. g. pass/fail in an exam of males and females. It is also called contingency coefficent or Yule's Phi. Transformation to d Cohen is done via the effect size calculator .

8. Calculation of the weighted mean of a list of correlations

Due to the askew distribution of correlations(see Fisher-Z-Transformation ), the mean of a list of correlations cannot simply be calculated by building the arithmetic mean. Usually, correlations are transformed into Fisher-Z-values and weighted by the number of cases before averaging and retransforming with an inverse Fisher-Z. While this is the usual approach, Eid et al. (2011, pp. 544) suggest using the correction of Olkin & Pratt (1958) instead, as simulations showed it to estimate the mean correlation more precisely. The following calculator computes both for you, the "traditional Fisher-Z-approach" and the algorithm of Olkin and Pratt.

Please fill in the correlations into column A and the number of cases into column B. You can as well copy the values from tables of your spreadsheet program. Finally click on "OK" to start the calculation. Some values already filled in for demonstration purposes.

9. Transformation of the effect sizes r , d , f , Odds Ratio and eta square

Correlations are an effect size measure. They quantify the magnitude of an empirical effect. There are a number of other effect size measures as well, with d Cohen probably being the most prominent one. The different effect size measures can be converted into another. Please have a look at the online calculators on the page Computation of Effect Sizes .

10. Calculation of Linear Correlations

The Online-Calculator computes linear pearson or product moment correlations of two variables. Please fill in the values of variable 1 in column A and the values of variable 2 in column B and press 'OK'. As a demonstration, values for a high positive correlation are already filled in by default.

Many hypothesis tests on this page are based on Eid et al. (2011). jStat is used to generate the Student's t-distribution for testing correlations against each other. The spreadsheet element is based on Handsontable.

• Bonett, D. G., & Wright, T. A. (2000). Sample size requirements for estimating Pearson, Kendall, and Spearman correlations. Psychometrika, 65(1), 23-28. doi: 10.1007/BF0229418
• Eid, M., Gollwitzer, M., & Schmitt, M. (2011). Statistik und Forschungsmethoden Lehrbuch . Weinheim: Beltz.
• Gnambs, T. (2022, April 6). A brief note on the standard error of the Pearson correlation. https://doi.org/10.31234/osf.io/uts98

Please use the following citation: Lenhard, W. & Lenhard, A. (2014). Hypothesis Tests for Comparing Correlations . available: https://www.psychometrica.de/correlation.html. Psychometrica. DOI: 10.13140/RG.2.1.2954.1367

Copyright © 2017-2022; Drs. Wolfgang & Alexandra Lenhard

Correlation Coefficient Calculator

Reporting correlation in apa format, correlation test, residuals normality, correlation calculator, what is covariance, how to calculate the covariance, what is correlation, what is the pearson correlation coefficient, how to calculate the pearson correlation, population pearson correlation formula, sample pearson correlation formula, correlation effect size, assumptions, correlation tests, what is spearman's rank correlation coefficient, how to calculate the spearman's rank correlation, example - spearman's rank calculation, distribution, calculators.

Correlation Coefficient Calculator

What is the correlation coefficient, how to use this correlation calculator with steps, pearson correlation coefficient formula, spearman correlation coefficient, kendall rank correlation (tau), matthews correlation (pearson phi).

Welcome to Omni's correlation coefficient calculator! Here you can learn all there is about this important statistical concept. Apart from discussing the general definition of correlation and the intuition behind it, we will also cover in detail the formulas for the four most popular correlation coefficients :

• Pearson correlation;
• Spearman correlation;
• Kendall tau correlation (including the variants); and
• Matthews correlation (MCC, a.k.a. Pearson phi).

As a bonus, we will also explain how Pearson correlation is linked to simple linear regression . We will start, however, by explaining what the correlation coefficient is all about. Let's go!

Correlation coefficients are measures of the strength and direction of relation between two random variables. The type of relationship that is being measured varies depending on the coefficient. In general, however, they all describe the co-changeability between the variables in question – how increasing (or decreasing) the value of one variable affects the value of the other variable – does it tend to increase or decrease?

Importantly, correlation coefficients are all normalized , i.e., they assume values between -1 and +1. Values of ±1 indicate the strongest possible relationship between variables, and a value of 0 means there's no relationship at all.

And that's it when it comes to the general definition of correlation! If you wonder how to calculate correlation , the best answer is to... use Omni's correlation coefficient calculator 😊! It allows you to easily compute all of the different coefficients in no time. In the next section, we explain how to use this tool in the most effective way.

If you wonder how to calculate correlation by hand, you will find all the necessary formulas and definitions for several correlation coefficients in the following sections.

To use our correlation coefficient calculator:

• Kendall rank correlation; or
• Matthews correlation.
• Input your data into the rows. When at least three points (both an x and y coordinate) are in place, it will give you your result.
• Be aware that this is a correlation calculator with steps ! If you turn on the option Show calculation details? , our tool will show you the intermediate stages of calculations. This is very useful when you need to verify the correctness of your calculations.
• 0.8 ≤ |corr| ≤ 1.0 very strong ;
• 0.6 ≤ |corr| < 0.8 strong ;
• 0.4 ≤ |corr| < 0.6 moderate ;
• 0.2 ≤ |corr| < 0.4 weak ; and
• 0.0 ≤ |corr| < 0.2 very weak .

The Pearson correlation between two variables X and Y is defined as the covariance between these variables divided by the product of their respective standard deviations :

This translates into the following explicit formula:

where x ‾ \overline{x} x and y ‾ \overline{y} y ​ stand for the average of the sample, x 1 , . . . , x n x_1, ..., x_n x 1 ​ , ... , x n ​ and y 1 , . . . , y n y_1, ..., y_n y 1 ​ , ... , y n ​ , respectively.

Remember that the Pearson correlation detects only a linear relationship – a low value of Pearson correlation doesn't mean that there is no relationship at all! The two variables may be strongly related, yet their relationship may not be linear but of some other type.

In least squares regression Y = a X + b Y = aX + b Y = a X + b , the square of the Pearson correlation between X X X and Y Y Y is equal to the coefficient of determination, R² , which expresses the fraction of the variance in Y Y Y that is explained by X X X :

If you want to discover more about the Pearson correlation, visit our dedicated Pearson correlation calculator website .

The Spearman coefficient is closely related to the Pearson coefficient. Namely, the Spearman rank correlation between X X X and Y Y Y is defined as the Pearson correlation between the rank variables r ( X ) r(X) r ( X ) and r ( Y ) r(Y) r ( Y ) . That is, the formula for Spearman's rank correlation r h o rho r h o reads:

To obtain the rank variables, you just need to order the observations (in each sample separately) from lowest to highest. The smallest observation then gets rank 1 , the second-smallest rank 2 , and so on – the highest observation will have rank n . You only need to be careful when the same value appears in the data set more than once (we say there are ties ). If this happens, assign to all these identical observations the rank equal to the arithmetic mean of the ranks you would assign to these observations where they all had different values.

The Spearman correlation is sensitive to the monotonic relationship between the variables, so it is more general than the Pearson correlation – it can capture, e.g., quadratic or exponential relationships.

There is also a simpler and more explicit formula for Spearman correlation , but it holds only if there are no ties in either of our samples . More details await you in the Spearman's rank correlation calculator .

We most often denote Kendall's rank correlation by the Greek letter τ (tau), and that's why it's often referred to as Kendall tau.

Consider two samples, x and y , each of size n : x 1 , ..., x n and y 1 , ..., y n . Clearly, there are n(n+1)/2 possible pairs of x and y .

We have to go through all these pairs one by one and count the number of concordant and discordant pairs . Namely, for two pairs (x i , y i ) and (x j , y j ) we have the following rules:

• If x i < x j and y i < y j then this pair is concordant.
• If x i > x j and y i > y j then this pair is concordant.
• If x i < x j and y i > y j then this pair is discordant.
• If x i > x j and y i < y j then this pair is discordant.

The Kendall rank correlation coefficient formula reads:

• C C C – Number of concordant pairs; and
• D D D – Number of discordant pairs.

That is, τ \tau τ is the difference between the number of concordant and discordant pairs divided by the total number of all pairs.

Easy, don't you think? However, it is so only if there are no ties . That is, there are no repeating values in both sample x and sample y . If there are ties, there are two additional variants of Kendall tau. (Fortunately, our correlation coefficient calculator can calculate them all!) To define them, we need to distinguish different kinds of ties:

• If x i = x j and y i ≠ y j then we have a tie in x .
• If x i ≠ x j and y i = y j then we have a tie in y .
• If x i = x j and y i = y j then we have a double tie .

The Kendall rank tau-b correlation coefficient formula reads:

• T x T_x T x ​ – Number of ties in x x x ; and
• T y T_y T y ​ – Number of ties in y y y .

Use tau-b if the two variables have the same number of possible values (before ranking). In other words, if you can summarize the data in a square contingency table . An example of such a situation is when both variables use a 5-point Likert scale: strongly disagree, disagree, neither agree nor disagree, agree, or strongly agree .

If your data is assembled in a rectangular non-square contingency table , or, in other words, if the two variables have a different number of possible values , then use tau-c (sometimes called Stuart-Kendall tau-c ):

• m m m – m i n ( r , c ) {\rm min}(r,c) min ( r , c ) ;
• r r r – The number of rows in the contingency table; and
• c c c – The number of columns in the contingency table.

But where is tau-a , you may think? Fortunately, tau-a is defined in the same simple way as before (when we had no ties):

Kendall tau correlation coefficient is sensitive monotonic relationship between the variables.

The Matthews correlation (abbreviated as MCC, also known as Pearson phi) measures the quality of binary classifications . Most often, we can encounter it in machine learning and biology/medicine-related data.

To write down the formula for the Matthews correlation coefficient we need to assemble our data in a 2x2 contingency table, which in this context is also called the confusion matrix :

where we use the following quite standard abbreviations::

• TP – True positive;
• FP – False positive;
• TN – True negative; and
• FN – False negative.

Matthews correlation is given by the following formula:

The interpretation of this coefficient is a bit different now:

• +1 means we have a perfect prediction;
• 0 means we don't have any valid information; and
• -1 means we have a complete inconsistency between prediction and the actual outcome.

If you're interested, don't hesitate to visit our Matthews correlation coefficient calculator .

What does a positive correlation mean?

If the value of correlation is positive, then the two variables under consideration tend to change in the same direction : when the first one increases, the other tends to increase, and when the first one decreases, then the other one tends to decrease as well.

What does a negative correlation mean?

If the value of correlation is positive, then the two variables under consideration tend to change in the opposite directions : when the first one increases, the other tends to decrease, and when the first one decreases, then the other one tends to increase.

How to read a correlation matrix?

A correlation matrix is a table that shows the values of a correlation coefficient between all possible pairs of several variables . It always has ones at the main diagonal (this is the correlation of a variable with itself) and is symmetric (because the correlation between X and Y is the same as between Y and X). For these reasons, the redundant cells sometimes get trimmed . If there is some color-coding , make sure to check what it means: it may either illustrate the strength and direction of correlation or its statistical significance.

• VPD Calculator & Chart (Vapor Pressure Deficit)
• Sod Calculator
• Molar Mass Calculator
• Sum of Squares Calculator
• Midrange Calculator
• Coefficient of Variation Calculator

Binomial distribution

Roulette payout.

• Biology (100)
• Chemistry (100)
• Construction (144)
• Conversion (295)
• Ecology (30)
• Everyday life (262)
• Finance (570)
• Health (440)
• Physics (510)
• Sports (105)
• Statistics (184)
• Other (183)
• Discover Omni (40)

Calculator: p-Value for Correlation Coefficients

p-Value Calculator for Correlation Coefficients

This calculator will tell you the significance (both one-tailed and two-tailed probability values) of a Pearson correlation coefficient, given the correlation value r, and the sample size. Please enter the necessary parameter values, and then click 'Calculate'.

“extremely user friendly”

“truly amazing!”

“so easy to use!”

Statistics Calculator

You want to analyze your data effortlessly? DATAtab makes it easy and online.

Online Statistics Calculator

What do you want to calculate online? The online statistics calculator is simple and uncomplicated! Here you can find a list of all implemented methods!

Create charts online with DATAtab

Create your charts for your data directly online and uncomplicated. To do this, insert your data into the table under Charts and select which chart you want.

The advantages of DATAtab

Statistics, as simple as never before..

DATAtab is a modern statistics software, with unique user-friendliness. Statistical analyses are done with just a few clicks, so DATAtab is perfect for statistics beginners and for professionals who want more flow in the user experience.

Directly in the browser, fully flexible.

Directly in the browser, fully flexible. DATAtab works directly in your web browser. You have no installation and maintenance effort whatsoever. Wherever and whenever you want to use DATAtab, just go to the website and get started.

All the statistical methods you need.

DATAtab offers you a wide range of statistical methods. We have selected the most central and best known statistical methods for you and do not overwhelm you with special cases.

Data security is a top priority.

All data that you insert and evaluate on DATAtab always remain on your end device. The data is not sent to any server or stored by us (not even temporarily). Furthermore, we do not pass on your data to third parties in order to analyze your user behavior.

Many tutorials with simple examples.

In order to facilitate the introduction, DATAtab offers a large number of free tutorials with focused explanations in simple language. We explain the statistical background of the methods and give step-by-step explanations for performing the analyses in the statistics calculator.

Practical Auto-Assistant.

DATAtab takes you by the hand in the world of statistics. When making statistical decisions, such as the choice of scale or measurement level or the selection of suitable methods, Auto-Assistants ensure that you get correct results quickly.

Charts, simple and clear.

With DATAtab data visualization is fun! Here you can easily create meaningful charts that optimally illustrate your results.

New in the world of statistics?

DATAtab was primarily designed for people for whom statistics is new territory. Beginners are not overwhelmed with a lot of complicated options and checkboxes, but are encouraged to perform their analyses step by step.

Online survey very simple.

DATAtab offers you the possibility to easily create an online survey, which you can then evaluate immediately with DATAtab.

Our references

Alternative to statistical software like SPSS and STATA

DATAtab was designed for ease of use and is a compelling alternative to statistical programs such as SPSS and STATA. On datatab.net, data can be statistically evaluated directly online and very easily (e.g. t-test, regression, correlation etc.). DATAtab's goal is to make the world of statistical data analysis as simple as possible, no installation and easy to use. Of course, we would also be pleased if you take a look at our second project Statisty .

Extensive tutorials

Descriptive statistics.

Here you can find out everything about location parameters and dispersion parameters and how you can describe and clearly present your data using characteristic values.

Hypothesis Test

Here you will find everything about hypothesis testing: One sample t-test , Unpaired t-test , Paired t-test and Chi-square test . You will also find tutorials for non-parametric statistical procedures such as the Mann-Whitney u-Test and Wilcoxon-Test . mann-whitney-u-test and the Wilcoxon test

The regression provides information about the influence of one or more independent variables on the dependent variable. Here are simple explanations of linear regression and logistic regression .

Correlation

Correlation analyses allow you to analyze the linear association between variables. Learn when to use Pearson correlation or Spearman rank correlation . With partial correlation , you can calculate the correlation between two variables to the exclusion of a third variable.

Partial Correlation

The partial correlation shows you the correlation between two variables to the exclusion of a third variable.

Levene Test

The Levene Test checks your data for variance equality. Thus, the levene test is used as a prerequisite test for many hypothesis tests .

The p-value is needed for every hypothesis test to be able to make a statement whether the null hypothesis is accepted or rejected.

Distributions

DATAtab provides you with tables with distributions and helpful explanations of the distribution functions. These include the Table of t-distribution and the Table of chi-squared distribution

Contingency table

With a contingency table you can get an overview of two categorical variables in the statistics.

Equivalence and non-inferiority

In an equivalence trial, the statistical test aims at showing that two treatments are not too different in characteristics and a non-inferiority trial wants to show that an experimental treatment is not worse than an established treatment.

If there is a clear cause-effect relationship between two variables, then we can speak of causality. Learn more about causality in our tutorial.

Multicollinearity

Multicollinearity is when two or more independent variables have a high correlation.

Effect size for independent t-test

Learn how to calculate the effect size for the t-test for independent samples.

Reliability analysis calculator

On DATAtab, Cohen's Kappa can be easily calculated online in the Cohen’s Kappa Calculator . there is also the Fleiss Kappa Calculator . Of course, the Cronbach's alpha can also be calculated in the Cronbach's Alpha Calculator .

Analysis of variance with repeated measurement

Repeated measures ANOVA tests whether there are statistically significant differences in three or more dependent samples.

Cite DATAtab: DATAtab Team (2024). DATAtab: Online Statistics Calculator. DATAtab e.U. Graz, Austria. URL https://datatab.net

12.4 Testing the Significance of the Correlation Coefficient

The correlation coefficient, r , tells us about the strength and direction of the linear relationship between x and y . However, the reliability of the linear model also depends on how many observed data points are in the sample. We need to look at both the value of the correlation coefficient r and the sample size n , together.

We perform a hypothesis test of the "significance of the correlation coefficient" to decide whether the linear relationship in the sample data is strong enough to use to model the relationship in the population.

The sample data are used to compute r , the correlation coefficient for the sample. If we had data for the entire population, we could find the population correlation coefficient. But because we have only sample data, we cannot calculate the population correlation coefficient. The sample correlation coefficient, r , is our estimate of the unknown population correlation coefficient.

• The symbol for the population correlation coefficient is ρ , the Greek letter "rho."
• ρ = population correlation coefficient (unknown)
• r = sample correlation coefficient (known; calculated from sample data)

The hypothesis test lets us decide whether the value of the population correlation coefficient ρ is "close to zero" or "significantly different from zero". We decide this based on the sample correlation coefficient r and the sample size n .

If the test concludes that the correlation coefficient is significantly different from zero, we say that the correlation coefficient is "significant."

• Conclusion: There is sufficient evidence to conclude that there is a significant linear relationship between x and y because the correlation coefficient is significantly different from zero.
• What the conclusion means: There is a significant linear relationship between x and y . We can use the regression line to model the linear relationship between x and y in the population.

If the test concludes that the correlation coefficient is not significantly different from zero (it is close to zero), we say that correlation coefficient is "not significant".

• Conclusion: "There is insufficient evidence to conclude that there is a significant linear relationship between x and y because the correlation coefficient is not significantly different from zero."
• What the conclusion means: There is not a significant linear relationship between x and y . Therefore, we CANNOT use the regression line to model a linear relationship between x and y in the population.
• If r is significant and the scatter plot shows a linear trend, the line can be used to predict the value of y for values of x that are within the domain of observed x values.
• If r is not significant OR if the scatter plot does not show a linear trend, the line should not be used for prediction.
• If r is significant and if the scatter plot shows a linear trend, the line may NOT be appropriate or reliable for prediction OUTSIDE the domain of observed x values in the data.

PERFORMING THE HYPOTHESIS TEST

• Null Hypothesis: H 0 : ρ = 0
• Alternate Hypothesis: H a : ρ ≠ 0

WHAT THE HYPOTHESES MEAN IN WORDS:

• Null Hypothesis H 0 : The population correlation coefficient IS NOT significantly different from zero. There IS NOT a significant linear relationship (correlation) between x and y in the population.
• Alternate Hypothesis H a : The population correlation coefficient IS significantly DIFFERENT FROM zero. There IS A SIGNIFICANT LINEAR RELATIONSHIP (correlation) between x and y in the population.

DRAWING A CONCLUSION: There are two methods of making the decision. The two methods are equivalent and give the same result.

• Method 1: Using the p -value
• Method 2: Using a table of critical values

In this chapter of this textbook, we will always use a significance level of 5%, α = 0.05

Using the p -value method, you could choose any appropriate significance level you want; you are not limited to using α = 0.05. But the table of critical values provided in this textbook assumes that we are using a significance level of 5%, α = 0.05. (If we wanted to use a different significance level than 5% with the critical value method, we would need different tables of critical values that are not provided in this textbook.)

METHOD 1: Using a p -value to make a decision

Using the ti-83, 83+, 84, 84+ calculator.

To calculate the p -value using LinRegTTEST: On the LinRegTTEST input screen, on the line prompt for β or ρ , highlight " ≠ 0 " The output screen shows the p-value on the line that reads "p =". (Most computer statistical software can calculate the p -value.)

• Decision: Reject the null hypothesis.
• Conclusion: "There is sufficient evidence to conclude that there is a significant linear relationship between x and y because the correlation coefficient is significantly different from zero."
• Decision: DO NOT REJECT the null hypothesis.
• Conclusion: "There is insufficient evidence to conclude that there is a significant linear relationship between x and y because the correlation coefficient is NOT significantly different from zero."
• You will use technology to calculate the p -value. The following describes the calculations to compute the test statistics and the p -value:
• The p -value is calculated using a t -distribution with n - 2 degrees of freedom.
• The formula for the test statistic is t = r n − 2 1 − r 2 t = r n − 2 1 − r 2 . The value of the test statistic, t , is shown in the computer or calculator output along with the p -value. The test statistic t has the same sign as the correlation coefficient r .
• The p -value is the combined area in both tails.

An alternative way to calculate the p -value (p) given by LinRegTTest is the command 2*tcdf(abs(t),10^99, n-2) in 2nd DISTR.

• Consider the third exam/final exam example .
• The line of best fit is: ŷ = -173.51 + 4.83 x with r = 0.6631 and there are n = 11 data points.
• Can the regression line be used for prediction? Given a third exam score ( x value), can we use the line to predict the final exam score (predicted y value)?
• H 0 : ρ = 0
• H a : ρ ≠ 0
• The p -value is 0.026 (from LinRegTTest on your calculator or from computer software).
• The p -value, 0.026, is less than the significance level of α = 0.05.
• Decision: Reject the Null Hypothesis H 0
• Conclusion: There is sufficient evidence to conclude that there is a significant linear relationship between the third exam score ( x ) and the final exam score ( y ) because the correlation coefficient is significantly different from zero.

Because r is significant and the scatter plot shows a linear trend, the regression line can be used to predict final exam scores.

METHOD 2: Using a table of Critical Values to make a decision

The 95% Critical Values of the Sample Correlation Coefficient Table can be used to give you a good idea of whether the computed value of r r is significant or not . Compare r to the appropriate critical value in the table. If r is not between the positive and negative critical values, then the correlation coefficient is significant. If r is significant, then you may want to use the line for prediction.

Example 12.7

Suppose you computed r = 0.801 using n = 10 data points. df = n - 2 = 10 - 2 = 8. The critical values associated with df = 8 are -0.632 and + 0.632. If r < negative critical value or r > positive critical value, then r is significant. Since r = 0.801 and 0.801 > 0.632, r is significant and the line may be used for prediction. If you view this example on a number line, it will help you.

Try It 12.7

For a given line of best fit, you computed that r = 0.6501 using n = 12 data points and the critical value is 0.576. Can the line be used for prediction? Why or why not?

Example 12.8

Suppose you computed r = –0.624 with 14 data points. df = 14 – 2 = 12. The critical values are –0.532 and 0.532. Since –0.624 < –0.532, r is significant and the line can be used for prediction

Try It 12.8

For a given line of best fit, you compute that r = 0.5204 using n = 9 data points, and the critical value is 0.666. Can the line be used for prediction? Why or why not?

Example 12.9

Suppose you computed r = 0.776 and n = 6. df = 6 – 2 = 4. The critical values are –0.811 and 0.811. Since –0.811 < 0.776 < 0.811, r is not significant, and the line should not be used for prediction.

Try It 12.9

For a given line of best fit, you compute that r = –0.7204 using n = 8 data points, and the critical value is = 0.707. Can the line be used for prediction? Why or why not?

THIRD-EXAM vs FINAL-EXAM EXAMPLE: critical value method

Consider the third exam/final exam example . The line of best fit is: ŷ = –173.51+4.83 x with r = 0.6631 and there are n = 11 data points. Can the regression line be used for prediction? Given a third-exam score ( x value), can we use the line to predict the final exam score (predicted y value)?

• Use the "95% Critical Value" table for r with df = n – 2 = 11 – 2 = 9.
• The critical values are –0.602 and +0.602
• Since 0.6631 > 0.602, r is significant.
• Conclusion:There is sufficient evidence to conclude that there is a significant linear relationship between the third exam score ( x ) and the final exam score ( y ) because the correlation coefficient is significantly different from zero.

Example 12.10

Suppose you computed the following correlation coefficients. Using the table at the end of the chapter, determine if r is significant and the line of best fit associated with each r can be used to predict a y value. If it helps, draw a number line.

• r = –0.567 and the sample size, n , is 19. The df = n – 2 = 17. The critical value is –0.456. –0.567 < –0.456 so r is significant.
• r = 0.708 and the sample size, n , is nine. The df = n – 2 = 7. The critical value is 0.666. 0.708 > 0.666 so r is significant.
• r = 0.134 and the sample size, n , is 14. The df = 14 – 2 = 12. The critical value is 0.532. 0.134 is between –0.532 and 0.532 so r is not significant.
• r = 0 and the sample size, n , is five. No matter what the dfs are, r = 0 is between the two critical values so r is not significant.

Try It 12.10

For a given line of best fit, you compute that r = 0 using n = 100 data points. Can the line be used for prediction? Why or why not?

Assumptions in Testing the Significance of the Correlation Coefficient

Testing the significance of the correlation coefficient requires that certain assumptions about the data are satisfied. The premise of this test is that the data are a sample of observed points taken from a larger population. We have not examined the entire population because it is not possible or feasible to do so. We are examining the sample to draw a conclusion about whether the linear relationship that we see between x and y in the sample data provides strong enough evidence so that we can conclude that there is a linear relationship between x and y in the population.

The regression line equation that we calculate from the sample data gives the best-fit line for our particular sample. We want to use this best-fit line for the sample as an estimate of the best-fit line for the population. Examining the scatterplot and testing the significance of the correlation coefficient helps us determine if it is appropriate to do this.

• There is a linear relationship in the population that models the average value of y for varying values of x . In other words, the expected value of y for each particular value lies on a straight line in the population. (We do not know the equation for the line for the population. Our regression line from the sample is our best estimate of this line in the population.)
• The y values for any particular x value are normally distributed about the line. This implies that there are more y values scattered closer to the line than are scattered farther away. Assumption (1) implies that these normal distributions are centered on the line: the means of these normal distributions of y values lie on the line.
• The standard deviations of the population y values about the line are equal for each value of x . In other words, each of these normal distributions of y values has the same shape and spread about the line.
• The residual errors are mutually independent (no pattern).
• The data are produced from a well-designed, random sample or randomized experiment.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/introductory-statistics/pages/1-introduction

• Authors: Barbara Illowsky, Susan Dean
• Publisher/website: OpenStax
• Book title: Introductory Statistics
• Publication date: Sep 19, 2013
• Location: Houston, Texas
• Book URL: https://openstax.org/books/introductory-statistics/pages/1-introduction
• Section URL: https://openstax.org/books/introductory-statistics/pages/12-4-testing-the-significance-of-the-correlation-coefficient

© Jun 23, 2022 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• Calculators
• Descriptive Statistics
• Merchandise
• Which Statistics Test?

Pearson Correlation Coefficient Calculator

The Pearson correlation coefficient is used to measure the strength of a linear association between two variables, where the value r = 1 means a perfect positive correlation and the value r = -1 means a perfect negataive correlation. So, for example, you could use this test to find out whether people's height and weight are correlated (they will be - the taller people are, the heavier they're likely to be).

Requirements for Pearson's correlation coefficient

• Scale of measurement should be interval or ratio
• Variables should be approximately normally distributed
• The association should be linear
• There should be no outliers in the data

• Calculators
• Conversions

Statistics Calculator: Correlation Coefficient

Use this calculator to calculate the correlation coefficient from a set of bivariate data.

Correlation Coefficient Calculator

Instructions.

This calculator can be used to calculate the sample correlation coefficient .

• Each x i ,y i couple on separate lines: x 1 ,y 1 x 2 ,y 2 x 3 ,y 3 x 4 ,y 4 x 5 ,y 5
• All x i values in the first line and all y i values in the second line: x 1 ,x 2 ,x 3 ,x 4 ,x 5 y 1 ,y 2 ,y 3 ,y 4 ,y 5

Press the "Submit Data" button to perform the calculation. The correlation coefficient will be displayed if the calculation is successful. To clear the calculator and enter new data, press "Reset".

What is the correlation coefficient

The correlation coefficient , or Pearson product-moment correlation coefficient (PMCC) is a numerical value between -1 and 1 that expresses the strength of the linear relationship between two variables .When r is closer to 1 it indicates a strong positive relationship. A value of 0 indicates that there is no relationship. Values close to -1 signal a strong negative relationship between the two variables. You may use the linear regression calculator to visualize this relationship on a graph.

Correlation coefficient formula

There are many formulas to calculate the correlation coefficient (all yielding the same result). This calculator uses the following:

• Linear regression
• Scatter plot
• Central tendency and dispersion

Module 12: Linear Regression and Correlation

Hypothesis test for correlation, learning outcomes.

• Conduct a linear regression t-test using p-values and critical values and interpret the conclusion in context

The correlation coefficient,  r , tells us about the strength and direction of the linear relationship between x and y . However, the reliability of the linear model also depends on how many observed data points are in the sample. We need to look at both the value of the correlation coefficient r and the sample size n , together.

We perform a hypothesis test of the “ significance of the correlation coefficient ” to decide whether the linear relationship in the sample data is strong enough to use to model the relationship in the population.

The sample data are used to compute  r , the correlation coefficient for the sample. If we had data for the entire population, we could find the population correlation coefficient. But because we only have sample data, we cannot calculate the population correlation coefficient. The sample correlation coefficient, r , is our estimate of the unknown population correlation coefficient.

• The symbol for the population correlation coefficient is ρ , the Greek letter “rho.”
• ρ = population correlation coefficient (unknown)
• r = sample correlation coefficient (known; calculated from sample data)

The hypothesis test lets us decide whether the value of the population correlation coefficient  ρ is “close to zero” or “significantly different from zero.” We decide this based on the sample correlation coefficient r and the sample size n .

If the test concludes that the correlation coefficient is significantly different from zero, we say that the correlation coefficient is “significant.”

• Conclusion: There is sufficient evidence to conclude that there is a significant linear relationship between x and y because the correlation coefficient is significantly different from zero.
• What the conclusion means: There is a significant linear relationship between x and y . We can use the regression line to model the linear relationship between x and y in the population.

If the test concludes that the correlation coefficient is not significantly different from zero (it is close to zero), we say that the correlation coefficient is “not significant.”

• Conclusion: “There is insufficient evidence to conclude that there is a significant linear relationship between x and y because the correlation coefficient is not significantly different from zero.”
• What the conclusion means: There is not a significant linear relationship between x and y . Therefore, we CANNOT use the regression line to model a linear relationship between x and y in the population.
• If r is significant and the scatter plot shows a linear trend, the line can be used to predict the value of y for values of x that are within the domain of observed x values.
• If r is not significant OR if the scatter plot does not show a linear trend, the line should not be used for prediction.
• If r is significant and if the scatter plot shows a linear trend, the line may NOT be appropriate or reliable for prediction OUTSIDE the domain of observed x values in the data.

Performing the Hypothesis Test

• Null Hypothesis: H 0 : ρ = 0
• Alternate Hypothesis: H a : ρ ≠ 0

What the Hypotheses Mean in Words

• Null Hypothesis H 0 : The population correlation coefficient IS NOT significantly different from zero. There IS NOT a significant linear relationship (correlation) between x and y in the population.
• Alternate Hypothesis H a : The population correlation coefficient IS significantly DIFFERENT FROM zero. There IS A SIGNIFICANT LINEAR RELATIONSHIP (correlation) between x and y in the population.

Drawing a Conclusion

There are two methods of making the decision. The two methods are equivalent and give the same result.

• Method 1: Using the p -value
• Method 2: Using a table of critical values

In this chapter of this textbook, we will always use a significance level of 5%,  α = 0.05

Using the  p -value method, you could choose any appropriate significance level you want; you are not limited to using α = 0.05. But the table of critical values provided in this textbook assumes that we are using a significance level of 5%, α = 0.05. (If we wanted to use a different significance level than 5% with the critical value method, we would need different tables of critical values that are not provided in this textbook).

Method 1: Using a p -value to make a decision

Using the ti-83, 83+, 84, 84+ calculator.

To calculate the  p -value using LinRegTTEST:

• On the LinRegTTEST input screen, on the line prompt for β or ρ , highlight “≠ 0”
• The output screen shows the p-value on the line that reads “p =”.
• (Most computer statistical software can calculate the  p -value).

If the p -value is less than the significance level ( α = 0.05)

• Decision: Reject the null hypothesis.
• Conclusion: “There is sufficient evidence to conclude that there is a significant linear relationship between x and y because the correlation coefficient is significantly different from zero.”

If the p -value is NOT less than the significance level ( α = 0.05)

• Decision: DO NOT REJECT the null hypothesis.
• Conclusion: “There is insufficient evidence to conclude that there is a significant linear relationship between x and y because the correlation coefficient is NOT significantly different from zero.”

Calculation Notes:

• You will use technology to calculate the p -value. The following describes the calculations to compute the test statistics and the p -value:
• The p -value is calculated using a t -distribution with n – 2 degrees of freedom.
• The formula for the test statistic is [latex]\displaystyle{t}=\dfrac{{{r}\sqrt{{{n}-{2}}}}}{\sqrt{{{1}-{r}^{{2}}}}}[/latex]. The value of the test statistic, t , is shown in the computer or calculator output along with the p -value. The test statistic t has the same sign as the correlation coefficient r .
• The p -value is the combined area in both tails.

Recall: ORDER OF OPERATIONS

1st find the numerator:

Step 1: Find [latex]n-2[/latex], and then take the square root.

Step 2: Multiply the value in Step 1 by [latex]r[/latex].

2nd find the denominator: 

Step 3: Find the square of [latex]r[/latex], which is [latex]r[/latex] multiplied by [latex]r[/latex].

Step 4: Subtract this value from 1, [latex]1 -r^2[/latex].

Step 5: Find the square root of Step 4.

3rd take the numerator and divide by the denominator.

An alternative way to calculate the  p -value (p) given by LinRegTTest is the command 2*tcdf(abs(t),10^99, n-2) in 2nd DISTR.

THIRD-EXAM vs FINAL-EXAM EXAM:  p- value method

• Consider the  third exam/final exam example (example 2).
• The line of best fit is: [latex]\hat{y}[/latex] = -173.51 + 4.83 x  with  r  = 0.6631 and there are  n  = 11 data points.
• Can the regression line be used for prediction?  Given a third exam score ( x  value), can we use the line to predict the final exam score (predicted  y  value)?
• H 0 :  ρ  = 0
• H a :  ρ  ≠ 0
• The  p -value is 0.026 (from LinRegTTest on your calculator or from computer software).
• The  p -value, 0.026, is less than the significance level of  α  = 0.05.
• Decision: Reject the Null Hypothesis  H 0
• Conclusion: There is sufficient evidence to conclude that there is a significant linear relationship between the third exam score ( x ) and the final exam score ( y ) because the correlation coefficient is significantly different from zero.

Because  r  is significant and the scatter plot shows a linear trend, the regression line can be used to predict final exam scores.

Method 2: Using a table of Critical Values to make a decision

The 95% Critical Values of the Sample Correlation Coefficient Table can be used to give you a good idea of whether the computed value of r is significant or not . Compare  r to the appropriate critical value in the table. If r is not between the positive and negative critical values, then the correlation coefficient is significant. If  r is significant, then you may want to use the line for prediction.

Suppose you computed  r = 0.801 using n = 10 data points. df = n – 2 = 10 – 2 = 8. The critical values associated with df = 8 are -0.632 and + 0.632. If r < negative critical value or r > positive critical value, then r is significant. Since r = 0.801 and 0.801 > 0.632, r is significant and the line may be used for prediction. If you view this example on a number line, it will help you.

r is not significant between -0.632 and +0.632. r = 0.801 > +0.632. Therefore, r is significant.

For a given line of best fit, you computed that  r = 0.6501 using n = 12 data points and the critical value is 0.576. Can the line be used for prediction? Why or why not?

If the scatter plot looks linear then, yes, the line can be used for prediction, because  r > the positive critical value.

Suppose you computed  r = –0.624 with 14 data points. df = 14 – 2 = 12. The critical values are –0.532 and 0.532. Since –0.624 < –0.532, r is significant and the line can be used for prediction

r = –0.624-0.532. Therefore, r is significant.

For a given line of best fit, you compute that  r = 0.5204 using n = 9 data points, and the critical value is 0.666. Can the line be used for prediction? Why or why not?

No, the line cannot be used for prediction, because  r < the positive critical value.

Suppose you computed  r = 0.776 and n = 6. df = 6 – 2 = 4. The critical values are –0.811 and 0.811. Since –0.811 < 0.776 < 0.811, r is not significant, and the line should not be used for prediction.

–0.811 <  r = 0.776 < 0.811. Therefore, r is not significant.

For a given line of best fit, you compute that  r = –0.7204 using n = 8 data points, and the critical value is = 0.707. Can the line be used for prediction? Why or why not?

Yes, the line can be used for prediction, because  r < the negative critical value.

THIRD-EXAM vs FINAL-EXAM EXAMPLE: critical value method

Consider the  third exam/final exam example  again. The line of best fit is: [latex]\hat{y}[/latex] = –173.51+4.83 x  with  r  = 0.6631 and there are  n  = 11 data points. Can the regression line be used for prediction?  Given a third-exam score ( x  value), can we use the line to predict the final exam score (predicted  y  value)?

• Use the “95% Critical Value” table for  r  with  df  =  n  – 2 = 11 – 2 = 9.
• The critical values are –0.602 and +0.602
• Since 0.6631 > 0.602,  r  is significant.

Suppose you computed the following correlation coefficients. Using the table at the end of the chapter, determine if  r is significant and the line of best fit associated with each r can be used to predict a y value. If it helps, draw a number line.

• r = –0.567 and the sample size, n , is 19. The df = n – 2 = 17. The critical value is –0.456. –0.567 < –0.456 so r is significant.
• r = 0.708 and the sample size, n , is nine. The df = n – 2 = 7. The critical value is 0.666. 0.708 > 0.666 so r is significant.
• r = 0.134 and the sample size, n , is 14. The df = 14 – 2 = 12. The critical value is 0.532. 0.134 is between –0.532 and 0.532 so r is not significant.
• r = 0 and the sample size, n , is five. No matter what the dfs are, r = 0 is between the two critical values so r is not significant.

For a given line of best fit, you compute that  r = 0 using n = 100 data points. Can the line be used for prediction? Why or why not?

No, the line cannot be used for prediction no matter what the sample size is.

Assumptions in Testing the Significance of the Correlation Coefficient

Testing the significance of the correlation coefficient requires that certain assumptions about the data are satisfied. The premise of this test is that the data are a sample of observed points taken from a larger population. We have not examined the entire population because it is not possible or feasible to do so. We are examining the sample to draw a conclusion about whether the linear relationship that we see between  x and y in the sample data provides strong enough evidence so that we can conclude that there is a linear relationship between x and y in the population.

The regression line equation that we calculate from the sample data gives the best-fit line for our particular sample. We want to use this best-fit line for the sample as an estimate of the best-fit line for the population. Examining the scatterplot and testing the significance of the correlation coefficient helps us determine if it is appropriate to do this.

The assumptions underlying the test of significance are:

• There is a linear relationship in the population that models the average value of y for varying values of x . In other words, the expected value of y for each particular value lies on a straight line in the population. (We do not know the equation for the line for the population. Our regression line from the sample is our best estimate of this line in the population).
• The y values for any particular x value are normally distributed about the line. This implies that there are more y values scattered closer to the line than are scattered farther away. Assumption (1) implies that these normal distributions are centered on the line: the means of these normal distributions of y values lie on the line.
• The standard deviations of the population y values about the line are equal for each value of x . In other words, each of these normal distributions of y  values has the same shape and spread about the line.
• The residual errors are mutually independent (no pattern).
• The data are produced from a well-designed, random sample or randomized experiment.

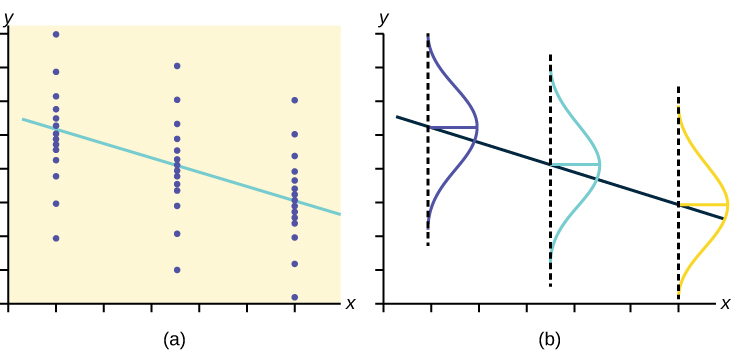
The  y values for each x value are normally distributed about the line with the same standard deviation. For each x value, the mean of the y values lies on the regression line. More y values lie near the line than are scattered further away from the line.

• Provided by : Lumen Learning. License : CC BY: Attribution
• Testing the Significance of the Correlation Coefficient. Provided by : OpenStax. Located at : https://openstax.org/books/introductory-statistics/pages/12-4-testing-the-significance-of-the-correlation-coefficient . License : CC BY: Attribution . License Terms : Access for free at https://openstax.org/books/introductory-statistics/pages/1-introduction
• Introductory Statistics. Authored by : Barbara Illowsky, Susan Dean. Provided by : OpenStax. Located at : https://openstax.org/books/introductory-statistics/pages/1-introduction . License : CC BY: Attribution . License Terms : Access for free at https://openstax.org/books/introductory-statistics/pages/1-introduction

Privacy Policy

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

12.5: Testing the Significance of the Correlation Coefficient

• Last updated
• Save as PDF
• Page ID 800

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

The correlation coefficient, \(r\), tells us about the strength and direction of the linear relationship between \(x\) and \(y\). However, the reliability of the linear model also depends on how many observed data points are in the sample. We need to look at both the value of the correlation coefficient \(r\) and the sample size \(n\), together. We perform a hypothesis test of the "significance of the correlation coefficient" to decide whether the linear relationship in the sample data is strong enough to use to model the relationship in the population.

The sample data are used to compute \(r\), the correlation coefficient for the sample. If we had data for the entire population, we could find the population correlation coefficient. But because we have only sample data, we cannot calculate the population correlation coefficient. The sample correlation coefficient, \(r\), is our estimate of the unknown population correlation coefficient.

• The symbol for the population correlation coefficient is \(\rho\), the Greek letter "rho."
• \(\rho =\) population correlation coefficient (unknown)
• \(r =\) sample correlation coefficient (known; calculated from sample data)

The hypothesis test lets us decide whether the value of the population correlation coefficient \(\rho\) is "close to zero" or "significantly different from zero". We decide this based on the sample correlation coefficient \(r\) and the sample size \(n\).

If the test concludes that the correlation coefficient is significantly different from zero, we say that the correlation coefficient is "significant."

• Conclusion: There is sufficient evidence to conclude that there is a significant linear relationship between \(x\) and \(y\) because the correlation coefficient is significantly different from zero.
• What the conclusion means: There is a significant linear relationship between \(x\) and \(y\). We can use the regression line to model the linear relationship between \(x\) and \(y\) in the population.

If the test concludes that the correlation coefficient is not significantly different from zero (it is close to zero), we say that correlation coefficient is "not significant".

• Conclusion: "There is insufficient evidence to conclude that there is a significant linear relationship between \(x\) and \(y\) because the correlation coefficient is not significantly different from zero."
• What the conclusion means: There is not a significant linear relationship between \(x\) and \(y\). Therefore, we CANNOT use the regression line to model a linear relationship between \(x\) and \(y\) in the population.
• If \(r\) is significant and the scatter plot shows a linear trend, the line can be used to predict the value of \(y\) for values of \(x\) that are within the domain of observed \(x\) values.
• If \(r\) is not significant OR if the scatter plot does not show a linear trend, the line should not be used for prediction.
• If \(r\) is significant and if the scatter plot shows a linear trend, the line may NOT be appropriate or reliable for prediction OUTSIDE the domain of observed \(x\) values in the data.

PERFORMING THE HYPOTHESIS TEST

• Null Hypothesis: \(H_{0}: \rho = 0\)
• Alternate Hypothesis: \(H_{a}: \rho \neq 0\)

WHAT THE HYPOTHESES MEAN IN WORDS:

• Null Hypothesis \(H_{0}\) : The population correlation coefficient IS NOT significantly different from zero. There IS NOT a significant linear relationship(correlation) between \(x\) and \(y\) in the population.
• Alternate Hypothesis \(H_{a}\) : The population correlation coefficient IS significantly DIFFERENT FROM zero. There IS A SIGNIFICANT LINEAR RELATIONSHIP (correlation) between \(x\) and \(y\) in the population.

DRAWING A CONCLUSION:There are two methods of making the decision. The two methods are equivalent and give the same result.

• Method 1: Using the \(p\text{-value}\)
• Method 2: Using a table of critical values

In this chapter of this textbook, we will always use a significance level of 5%, \(\alpha = 0.05\)

Using the \(p\text{-value}\) method, you could choose any appropriate significance level you want; you are not limited to using \(\alpha = 0.05\). But the table of critical values provided in this textbook assumes that we are using a significance level of 5%, \(\alpha = 0.05\). (If we wanted to use a different significance level than 5% with the critical value method, we would need different tables of critical values that are not provided in this textbook.)

METHOD 1: Using a \(p\text{-value}\) to make a decision

Using the ti83, 83+, 84, 84+ calculator.

To calculate the \(p\text{-value}\) using LinRegTTEST:

On the LinRegTTEST input screen, on the line prompt for \(\beta\) or \(\rho\), highlight "\(\neq 0\)"

The output screen shows the \(p\text{-value}\) on the line that reads "\(p =\)".

(Most computer statistical software can calculate the \(p\text{-value}\).)

If the \(p\text{-value}\) is less than the significance level ( \(\alpha = 0.05\) ):

• Decision: Reject the null hypothesis.
• Conclusion: "There is sufficient evidence to conclude that there is a significant linear relationship between \(x\) and \(y\) because the correlation coefficient is significantly different from zero."

If the \(p\text{-value}\) is NOT less than the significance level ( \(\alpha = 0.05\) )

• Decision: DO NOT REJECT the null hypothesis.
• Conclusion: "There is insufficient evidence to conclude that there is a significant linear relationship between \(x\) and \(y\) because the correlation coefficient is NOT significantly different from zero."

Calculation Notes:

• You will use technology to calculate the \(p\text{-value}\). The following describes the calculations to compute the test statistics and the \(p\text{-value}\):
• The \(p\text{-value}\) is calculated using a \(t\)-distribution with \(n - 2\) degrees of freedom.
• The formula for the test statistic is \(t = \frac{r\sqrt{n-2}}{\sqrt{1-r^{2}}}\). The value of the test statistic, \(t\), is shown in the computer or calculator output along with the \(p\text{-value}\). The test statistic \(t\) has the same sign as the correlation coefficient \(r\).
• The \(p\text{-value}\) is the combined area in both tails.

An alternative way to calculate the \(p\text{-value}\) ( \(p\) ) given by LinRegTTest is the command 2*tcdf(abs(t),10^99, n-2) in 2nd DISTR.

THIRD-EXAM vs FINAL-EXAM EXAMPLE: \(p\text{-value}\) method

• Consider the third exam/final exam example.
• The line of best fit is: \(\hat{y} = -173.51 + 4.83x\) with \(r = 0.6631\) and there are \(n = 11\) data points.
• Can the regression line be used for prediction? Given a third exam score ( \(x\) value), can we use the line to predict the final exam score (predicted \(y\) value)?
• \(H_{0}: \rho = 0\)
• \(H_{a}: \rho \neq 0\)
• \(\alpha = 0.05\)
• The \(p\text{-value}\) is 0.026 (from LinRegTTest on your calculator or from computer software).
• The \(p\text{-value}\), 0.026, is less than the significance level of \(\alpha = 0.05\).
• Decision: Reject the Null Hypothesis \(H_{0}\)
• Conclusion: There is sufficient evidence to conclude that there is a significant linear relationship between the third exam score (\(x\)) and the final exam score (\(y\)) because the correlation coefficient is significantly different from zero.

Because \(r\) is significant and the scatter plot shows a linear trend, the regression line can be used to predict final exam scores.

METHOD 2: Using a table of Critical Values to make a decision

The 95% Critical Values of the Sample Correlation Coefficient Table can be used to give you a good idea of whether the computed value of \(r\) is significant or not . Compare \(r\) to the appropriate critical value in the table. If \(r\) is not between the positive and negative critical values, then the correlation coefficient is significant. If \(r\) is significant, then you may want to use the line for prediction.

Example \(\PageIndex{1}\)

Suppose you computed \(r = 0.801\) using \(n = 10\) data points. \(df = n - 2 = 10 - 2 = 8\). The critical values associated with \(df = 8\) are \(-0.632\) and \(+0.632\). If \(r <\) negative critical value or \(r >\) positive critical value, then \(r\) is significant. Since \(r = 0.801\) and \(0.801 > 0.632\), \(r\) is significant and the line may be used for prediction. If you view this example on a number line, it will help you.

Exercise \(\PageIndex{1}\)

For a given line of best fit, you computed that \(r = 0.6501\) using \(n = 12\) data points and the critical value is 0.576. Can the line be used for prediction? Why or why not?

If the scatter plot looks linear then, yes, the line can be used for prediction, because \(r >\) the positive critical value.

Example \(\PageIndex{2}\)

Suppose you computed \(r = –0.624\) with 14 data points. \(df = 14 – 2 = 12\). The critical values are \(-0.532\) and \(0.532\). Since \(-0.624 < -0.532\), \(r\) is significant and the line can be used for prediction

Exercise \(\PageIndex{2}\)

For a given line of best fit, you compute that \(r = 0.5204\) using \(n = 9\) data points, and the critical value is \(0.666\). Can the line be used for prediction? Why or why not?

No, the line cannot be used for prediction, because \(r <\) the positive critical value.

Example \(\PageIndex{3}\)

Suppose you computed \(r = 0.776\) and \(n = 6\). \(df = 6 - 2 = 4\). The critical values are \(-0.811\) and \(0.811\). Since \(-0.811 < 0.776 < 0.811\), \(r\) is not significant, and the line should not be used for prediction.

Exercise \(\PageIndex{3}\)

For a given line of best fit, you compute that \(r = -0.7204\) using \(n = 8\) data points, and the critical value is \(= 0.707\). Can the line be used for prediction? Why or why not?

Yes, the line can be used for prediction, because \(r <\) the negative critical value.

THIRD-EXAM vs FINAL-EXAM EXAMPLE: critical value method

Consider the third exam/final exam example. The line of best fit is: \(\hat{y} = -173.51 + 4.83x\) with \(r = 0.6631\) and there are \(n = 11\) data points. Can the regression line be used for prediction? Given a third-exam score ( \(x\) value), can we use the line to predict the final exam score (predicted \(y\) value)?

• Use the "95% Critical Value" table for \(r\) with \(df = n - 2 = 11 - 2 = 9\).
• The critical values are \(-0.602\) and \(+0.602\)
• Since \(0.6631 > 0.602\), \(r\) is significant.
• Conclusion:There is sufficient evidence to conclude that there is a significant linear relationship between the third exam score (\(x\)) and the final exam score (\(y\)) because the correlation coefficient is significantly different from zero.

Example \(\PageIndex{4}\)

Suppose you computed the following correlation coefficients. Using the table at the end of the chapter, determine if \(r\) is significant and the line of best fit associated with each r can be used to predict a \(y\) value. If it helps, draw a number line.

• \(r = –0.567\) and the sample size, \(n\), is \(19\). The \(df = n - 2 = 17\). The critical value is \(-0.456\). \(-0.567 < -0.456\) so \(r\) is significant.
• \(r = 0.708\) and the sample size, \(n\), is \(9\). The \(df = n - 2 = 7\). The critical value is \(0.666\). \(0.708 > 0.666\) so \(r\) is significant.
• \(r = 0.134\) and the sample size, \(n\), is \(14\). The \(df = 14 - 2 = 12\). The critical value is \(0.532\). \(0.134\) is between \(-0.532\) and \(0.532\) so \(r\) is not significant.
• \(r = 0\) and the sample size, \(n\), is five. No matter what the \(dfs\) are, \(r = 0\) is between the two critical values so \(r\) is not significant.

Exercise \(\PageIndex{4}\)

For a given line of best fit, you compute that \(r = 0\) using \(n = 100\) data points. Can the line be used for prediction? Why or why not?

No, the line cannot be used for prediction no matter what the sample size is.

Assumptions in Testing the Significance of the Correlation Coefficient

Testing the significance of the correlation coefficient requires that certain assumptions about the data are satisfied. The premise of this test is that the data are a sample of observed points taken from a larger population. We have not examined the entire population because it is not possible or feasible to do so. We are examining the sample to draw a conclusion about whether the linear relationship that we see between \(x\) and \(y\) in the sample data provides strong enough evidence so that we can conclude that there is a linear relationship between \(x\) and \(y\) in the population.

The regression line equation that we calculate from the sample data gives the best-fit line for our particular sample. We want to use this best-fit line for the sample as an estimate of the best-fit line for the population. Examining the scatter plot and testing the significance of the correlation coefficient helps us determine if it is appropriate to do this.

The assumptions underlying the test of significance are:

• There is a linear relationship in the population that models the average value of \(y\) for varying values of \(x\). In other words, the expected value of \(y\) for each particular value lies on a straight line in the population. (We do not know the equation for the line for the population. Our regression line from the sample is our best estimate of this line in the population.)
• The \(y\) values for any particular \(x\) value are normally distributed about the line. This implies that there are more \(y\) values scattered closer to the line than are scattered farther away. Assumption (1) implies that these normal distributions are centered on the line: the means of these normal distributions of \(y\) values lie on the line.
• The standard deviations of the population \(y\) values about the line are equal for each value of \(x\). In other words, each of these normal distributions of \(y\) values has the same shape and spread about the line.
• The residual errors are mutually independent (no pattern).
• The data are produced from a well-designed, random sample or randomized experiment.

Linear regression is a procedure for fitting a straight line of the form \(\hat{y} = a + bx\) to data. The conditions for regression are:

• Linear In the population, there is a linear relationship that models the average value of \(y\) for different values of \(x\).
• Independent The residuals are assumed to be independent.
• Normal The \(y\) values are distributed normally for any value of \(x\).
• Equal variance The standard deviation of the \(y\) values is equal for each \(x\) value.
• Random The data are produced from a well-designed random sample or randomized experiment.

The slope \(b\) and intercept \(a\) of the least-squares line estimate the slope \(\beta\) and intercept \(\alpha\) of the population (true) regression line. To estimate the population standard deviation of \(y\), \(\sigma\), use the standard deviation of the residuals, \(s\). \(s = \sqrt{\frac{SEE}{n-2}}\). The variable \(\rho\) (rho) is the population correlation coefficient. To test the null hypothesis \(H_{0}: \rho =\) hypothesized value , use a linear regression t-test. The most common null hypothesis is \(H_{0}: \rho = 0\) which indicates there is no linear relationship between \(x\) and \(y\) in the population. The TI-83, 83+, 84, 84+ calculator function LinRegTTest can perform this test (STATS TESTS LinRegTTest).

Formula Review

Least Squares Line or Line of Best Fit:

\[\hat{y} = a + bx\]

\[a = y\text{-intercept}\]

\[b = \text{slope}\]

Standard deviation of the residuals:

\[s = \sqrt{\frac{SSE}{n-2}}\]

\[SSE = \text{sum of squared errors}\]

\[n = \text{the number of data points}\]