Your purchase has been completed. Your documents are now available to view.

Chapter 5: Transportation, Assignment, and Network Models

From the book managerial decision modeling.

Nagraj (Raju) Balakrishnan , Barry Render , Ralph Stair and Chuck Munson
X / Twitter

Supplementary Materials

Please login or register with De Gruyter to order this product.

Chapters in this book (21)

Quantitative Analysis for Management, 13/e by Barry Render, Ralph M. Stair, Michael E. Hanna, Trevor S. Hale

Get full access to Quantitative Analysis for Management, 13/e and 60K+ other titles, with a free 10-day trial of O'Reilly.

There are also live events, courses curated by job role, and more.

Chapter 9 Transportation, Assignment, and Network Models

Learning objectives.

After completing this chapter, students will be able to:

9.1 Construct LP problems for the transportation, assignment, and transshipment models.

9.2 Solve facility location and other application problems with transportation models.

9.3 Use LP to model and solve maximal-flow problems.

9.4 Use LP to model and solve shortest route problems.

9.5 Solve minimal-spanning tree problems.

Chapter 8 provided examples of a number of managerial problems that could be modeled using linear programming (LP), and this chapter will provide even more such examples. However, all of the problems in this chapter can be modeled as networks as well as linear programs. The use of networks ...

Get Quantitative Analysis for Management, 13/e now with the O’Reilly learning platform.

O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

Don’t leave empty-handed

Get Mark Richards’s Software Architecture Patterns ebook to better understand how to design components—and how they should interact.

It’s yours, free.

Check it out now on O’Reilly

Dive in for free with a 10-day trial of the O’Reilly learning platform—then explore all the other resources our members count on to build skills and solve problems every day.

transportation assignment and network models

Models for Traffic Assignment to Transportation Networks

Cite this chapter.

Ennio Cascetta 3

Part of the book series: Applied Optimization ((APOP,volume 49))

1074 Accesses

2 Citations

Models for traffic assignment to transportation networks simulate how demand and supply interact in transportation systems. These models allow the calculation of performance measures and user flows for each supply element (network link), resulting from origin-destination demand flows, path choice behavior, and the reciprocal interactions between supply and demand. Assignment models combine the supply and demand models described in the previous chapters; for this reason they are also referred to as demand-supply interaction models. In fact, as seen in Chapter 4, path choices and flows depend on path generalized costs, futhermore demand flows are generally influenced by path costs in choice dimensions such as mode and destination. Also, as seen in Chapter 2, link and path performance measures and costs may depend on flows due to congestion. There is therefore a circular dependence between demand, flows, and costs, which is represented in assignment models as can be seen in Fig. 5.1.1.

Giulio Erberto Cantarella is co-author of this Chapter.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Available as PDF
Read on any device
Instant download
Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Unable to display preview. Download preview PDF.

Reference Notes

Sheffi Y. (1985). Urban transportation networks . Prentice Hall, Englewood Cliff, NJ.

Google Scholar

Thomas R. (1991). Traffic Assignment Techniques . Avebury Technical, England.

Patriksson M. (1994). The Traffic Assignment Problem: Model and Methods . VSP, Utrecht, The Netherlands.

Cantarella G.E., and E. Cascetta (1998). Stochastic Assignment to Transportation Networks: Models and Algorithms . In Equilibrium and Advanced Transportation Modelling, P. Marcotte, S.Nguyen (editors): 87107. ( Proceedings of the International Colloquium, Montreal, Canada October, 1996 ).

Beckman M., C.B. McGuire, and Winsten C.B. (1956). Studies in the economics of transportation Yale University Press, New Haven, CT.

Wardrop J.G. (1952). Some Theoretical Aspects of Road Traffic Research Proc. Inst. Civ. Eng. 2: 325–378.

Dafermos S.C. (1971). An extended traffic assignment model with applications to two-way traffic Transportation Science 5: 366–389.

Dafermos S.C. (1972). The Traffic Assignment Problem for Multi-Class User Transportation Networks Transportation Science 6: 73–87.

Dafermos S.C. (1980). Traffic Equilibrium and Variational Inequalities Transportation Science 14: 42–54.

Dafermos S.C. (1982). The general multimodal network equilibrium problem with elastic demand Networks 12: 57–72.

Smith M.J. (1979). The Existence , Uniqueness and Stability of Traffic Equilibrium Transportation Research 13B: 295–304.

Hearn D.W., S. Lawphongpanich, and S. Nguyen (1984). Convex Programming Formulation of the Asymmetric Traffic Assignment Problem . Transportation Research 18B: 357–365.

Bernstein D. and Smith T. E. (1994). Equilibria for Networks with Lower Semicontinuous Costs: With an Application to Congestion Pricing. Transportation Science 28: 221–235.

Article MathSciNet MATH Google Scholar

Nguyen S., and S. Pallottino (1986). Assegnazione dei passeggeri ad un sistema di linee urbane: determinazione degli ipercammini minimi . Ricerca Operativa 39: 207–230.

M. Florian, and Spiess H. (1989). Optimal strategies: a new assignment model for transit networks . Transportation Research 23B: 82–102.

Nguyen S. and S. Pallottino (1988). Equilibrium Traffic Assignment for Large Scale Transit Networks . European Journal of Operational Research 37: 176–186.

Wu J. H., and M. Florian (1993). A Simplicial Decomposition Method for the Transit Equilibrium Assignment Problem ,Annals of Operations Research.

Bouzaiene-Ayari B., M. Gendreau, and S. Nguyen (1995). “On the Modelling of Bus Stops in Transit Networks”, Centre de recherche sur les transports, Université de Montréal.

Bouzaiene-Ayari B., Gendreau M., and Nguyen S. (1997). “Transit Equilibrium assignment Problem: A Fixed-Point Simplicial -Decomposition Solution Algorithm”, Operations Research.

Fisk C. (1980) Some Developments In Equilibrium Traffic Assignment Methodology Transportation Research B: 243–255.

Daganzo C.F., and Y. Sheffi (1982). Unconstrained Extremal formulation of Some Transportation Equilibrium Problems . Transportation Science 16: 332–360.

Bifulco G.N. (1993). A stochastic user equilibrium assignment model for the evaluation of parking policies EJOR 71: 269–287.

Nguyen S., S. Pallottino, and M. Gendreau (1993). Implicit Enumeration of Hyperpaths in a Logit Model for Transit Networks Publication CRT 84.

Daganzo C. (1983). Stochastic Network equilibrium problem with multiple vehicle types and asiymmetric , indefinite link cost jacobians Transportation Science 17: 282–300.

Cascetta E. (1987) Static and dynamic models of stochastic assignment to transportation networks in Flow control of congested networks (Szaego G., Bianco L., Odoni A. ed. ), Springer Verlag, Berlin.

Cantarella G.E. (1997). A General Fixed-Point Approach to Multi-Mode Multi-User Equilibrium Assignment with Elastic Demand Transportation Science 31: 107–128.

Mirchandani P., and H. Soroush (1987). Generalized Traffic Equilibrium with Probabilistic Travel Times and Perceptions . Transportation Science 21: 133–152.

Nielsen O. A. (1997). On The Distributions Of The Stochastic Components In SUE Traffic Assignment Models , In Proceedings of 25th European Transport Forum Annual Meeting, Seminar F On Transportation Planning Methods, Volume I I.

Cantarella G.E., and M. Binetti (2000). Stochastic Assignment with Gamma Distributed Perceived Costs . Proceedings of the 6th Meeting of the EURO Working Group on Transportation. Gothenburg, and Sweden, and September 1998, forthcoming.

Watling D.P. (1999). Stability of the stochastic equilibrium assignment problem: a dynamical systems approach Transportation Research 33B: 281312.

Ferrari P. (1997). The Meaning of Capacity Constraint Multipliers in The Theory of Road Network Equilibrium Rendiconti del circolo matematico di Palermo, Italy, 48: 107–120.

Bell M. (1995). Stochastic user equilibrium assignment in networks with queues Transportation Research 29B: 125–137.

Leurent F. (1993). Cost versus Time Equilibrium over a Network Eur. J. of Operations Research 71: 205–221.

Leurent, F. (1995). The practice of a dual criteria assignment model with continuously distributed values-of-time . In Proceedings of the 23`d European Transport Forum: Transportation Planning Methods, E, 117–128 PTRC, London.

Leurent, F. (1996). The Theory and Practice of a Dual Criteria Assignment Model with a Continuously Distributed Value-of-Time . In Transportation and Traffic Theory, J.B. Lesort ed., 455–477, Pergamon, Exeter, England.

Marcotte P. and D. Zhu (1996). An Efficient Algorithm for a Bicriterion Traffic Assignment Problem . In Advanced Methods in Transportation Analysis, L.Bianco, P.Toth eds., 63–73, Springer-Verlag, Berlin.

Dial R.B. (1996). Bicriterion Traffic Assignment: Basic Theory and Elementary Algorithms Transportation Science 30/2: 93–111.

Cantarella G.E., and M. Binetti (1998). Stochastic Equilibrium Traffic Assignment with Value-of-Time Distributed Among User In International Transactions of Operational Research 5: 541–553.

Daganzo C.F., and Y. Sheffi (1977) On stochastic models of traffic assignment Transportation Science 11: 253–274.

Horowitz J.L. (1984). The stability of stochastic equilibrium in a two link transportation network Transportation Research 18B: 13–28.

Cascetta E. (1989) A stochastic process approach to the analysis of temporal dynamics in transportation networks Transportation Research 23B: 1–17.

Davis G.A. N.L. Nihan (1993). Large population approximations of a general stochastic traffic assignment model Operations Research 41: 169178.

Watling D.P. (1996). Asymmetric problems and stochastic process models of traffic assignment Transportation Research 30B: 339–357.

Cantarella G.E., and E. Cascetta (1995). Dynamic Processes and Equilibrium in Transportation Networks: Towards a Undying Theory . Transportation Science 29: 305–329.

Download references

Author information

Authors and affiliations.

Dipartimento di Ingegneria dei Trasporti “Luigi Tocchetti”, Università degli Studi di Napoli “Federico II”, Napoli, Italy

Ennio Cascetta

You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

Copyright information

About this chapter

Cascetta, E. (2001). Models for Traffic Assignment to Transportation Networks. In: Transportation Systems Engineering: Theory and Methods. Applied Optimization, vol 49. Springer, Boston, MA. https://doi.org/10.1007/978-1-4757-6873-2_5

Download citation

DOI : https://doi.org/10.1007/978-1-4757-6873-2_5

Publisher Name : Springer, Boston, MA

Print ISBN : 978-1-4757-6875-6

Online ISBN : 978-1-4757-6873-2

eBook Packages : Springer Book Archive

Share this chapter

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

Publish with us

Policies and ethics

Find a journal
Track your research

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

9 Introduction to Transportation Modeling: Travel Demand Modeling and Data Collection

Chapter overview.

Chapter 9 serves as an introduction to travel demand modeling, a crucial aspect of transportation planning and policy analysis. As explained in previous chapters, the spatial distribution of activities such as employment centers, residential areas, and transportation systems mutually influence each other. The utilization of travel demand forecasting techniques leads to dynamic processes in urban areas. A comprehensive grasp of travel demand modeling is imperative for individuals involved in transportation planning and implementation.

This chapter covers the fundamentals of the traditional four-step travel demand modeling approach. It delves into the necessary procedures for applying the model, including establishing goals and criteria, defining scenarios, developing alternatives, collecting data, and conducting forecasting and evaluation.

Following this chapter, each of the four steps will be discussed in detail in Chapters 10 through 13.

Learning Objectives

Describe the need for travel demand modeling in urban transportation and relate it to the structure of the four-step model (FSM).
Summarize each step of FSM and the prerequisites for each in terms of data requirement and model calibration.
Summarize the available methods for each of the first three steps of FSM and compare their reliability.
Identify assumptions and limitations of each of the four steps and ways to improve the model.

Introduction

Transportation planning and policy analysis heavily rely on travel demand modeling to assess different policy scenarios and inform decision-making processes. Throughout our discussion, we have primarily explored the connection between urban activities, represented as land uses, and travel demands, represented by improvements and interventions in transportation infrastructure. Figure 9.1 provides a humorous yet insightful depiction of the transportation modeling process. In preceding chapters, we have delved into the relationship between land use and transportation systems, with the houses and factories in the figure symbolizing two crucial inputs into the transportation model: households and jobs. The output of this model comprises transportation plans, encompassing infrastructure enhancements and programs. Chapter 9 delves into a specific model—travel demand modeling. For further insights into transportation planning and programming, readers are encouraged to consult the UTA OERtransport book, “Transportation Planning, Policies, and History.”

A graphical representation of FSM input and outputs data in the process.

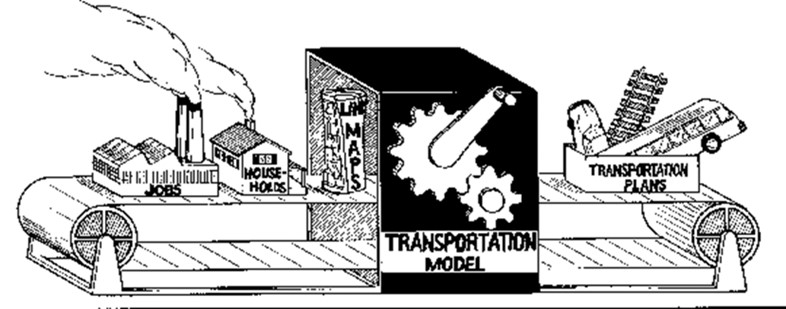
Travel demand models forecast how people will travel by processing thousands of individual travel decisions. These decisions are influenced by various factors, including living arrangements, the characteristics of the individual making the trip, available destination options, and choices regarding route and mode of transportation. Mathematical relationships are used to represent human behavior in these decisions based on existing data.

Through a sequential process, transportation modeling provides forecasts to address questions such as:

What will the future of the area look like?
What is the estimated population for the forecasting year?
How are job opportunities distributed by type and category?
What are the anticipated travel patterns in the future?
How many trips will people make? ( Trip Generation )
Where will these trips end? ( Trip Distribution )
Which transportation mode will be utilized? ( Mode Split )
What will be the demand for different corridors, highways, and streets? ( Traffic Assignment )
Lastly, what impact will this modeled travel demand have on our area? (Rahman, 2008).

9.2 Four-step Model

According to the questions above, Transportation modeling consists of two main stages, regarding the questions outlined above. Firstly, addressing the initial four questions involves demographic and land use analysis, which incorporates the community vision collected through citizen engagement and input. Secondly, the process moves on to the four-step travel demand modeling (FSM), which addresses questions 5 through 8. While FSM is generally accurate for aggregate calculations, it may occasionally falter in providing a reliable test for policy scenarios. The limitations of this model will be explored further in this chapter.

In the first stage, we develop an understanding of the study area from demographic information and urban form (land-use distribution pattern). These are important for all the reasons we discussed in this book. For instance, we must obtain the current age structure of the study area, based on which we can forecast future birth rates, death, and migrations (Beimborn & Kennedy, 1996).

Regarding economic forecasts, we must identify existing and future employment centers since they are the basis of work travel, shopping travel, or other travel purposes. Empirically speaking, employment often grows as the population grows, and the migration rate also depends on a region’s economic growth. A region should be able to generate new employment while sustaining the existing ones based upon past trends and form the basis for judgment for future trends (Mladenovic & Trifunovic, 2014).

After forecasting future population and employment, we must predict where people go (work, shop, school, or other locations). Land-use maps and plans are used in this stage to identify the activity concentrations in the study area. Future urban growth and land use can follow the same trend or change due to several factors, such as the availability of open land for development and local plans and zoning ordinances (Beimborn & Kennedy, 1996). Figure 9.3 shows different possible land-use patterns frequently seen in American cities.

This pictures shows 6 different land use patterns that are: (a) traditional grid, (b) post-war suburb, (c) traditional neighborhood design, (d) fused grid, (e) post-war suburb II, and (f) tranditional neighborhood design II.

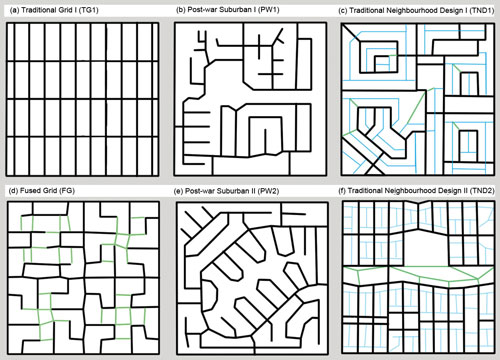
Land-use pattern can also be forecasted through the integration of land use and transportation as we explored in previous chapters.

Figure 9.3 above shows a simple structure of the second stage of FSM.

This picture shows the sequence of the fours steps of FSM.

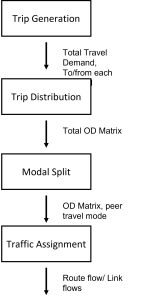
Once the number and types of trips are predicted, they are assigned to various destinations and modes. In the final step, these trips are allocated to the transportation network to compute the total demand for each road segment. During this second stage, additional choices such as the time of travel and whether to travel at all can be modeled using choice models (McNally, 2007). Travel forecasting involves simulating human behavior through mathematical series and calculations, capturing the sequence of decisions individuals make within an urban environment.

The first attempt at this type of analysis in the U.S. occurred during the post-war development period, driven by rapid economic growth. The influential study by Mitchell and Rapkin (1954) emphasized the need to establish a connection between travel and activities, highlighting the necessity for a comprehensive framework. Initial development models for trip generation, distribution, and diversion emerged in the 1950s, leading to the application of the four-step travel demand modeling (FSM) approach in a transportation study in the Chicago area. This model was primarily highway-oriented, aiming to compare new facility development and improved traffic engineering. In the 1960s, federal legislation mandated comprehensive and continuous transportation planning, formalizing the use of FSM. During the 1970s, scholars recognized the need to revise the model to address emerging concerns such as environmental issues and the rise of multimodal transportation systems. Consequently, enhancements were made, leading to the development of disaggregate travel demand forecasting and equilibrium assignment methods that complemented FSM. Today, FSM has been instrumental in forecasting travel demand for over 50 years (McNally, 2007; Weiner, 1997).

Initially outlined by Mannheim (1979), the basic structure of FSM was later expanded by Florian, Gaudry, and Lardinois (1988). Figure 9.3 illustrates various influential components of travel demand modeling. In this representation, “T” represents transportation, encompassing all elements related to the transportation system and its services. “A” denotes the activity system, defined according to land-use patterns and socio-demographic conditions. “P” refers to transportation network performance. “D,” which stands for demand, is generated based on the land-use pattern. According to Florian, Gaudry, and Lardinois (1988), “L” and “S” (location and supply procedures) are optional parts of FSM and are rarely integrated into the model.

This flowchart shows the relationship between various components of transportation network and their joint impact on traffic volume (flow) on the network.

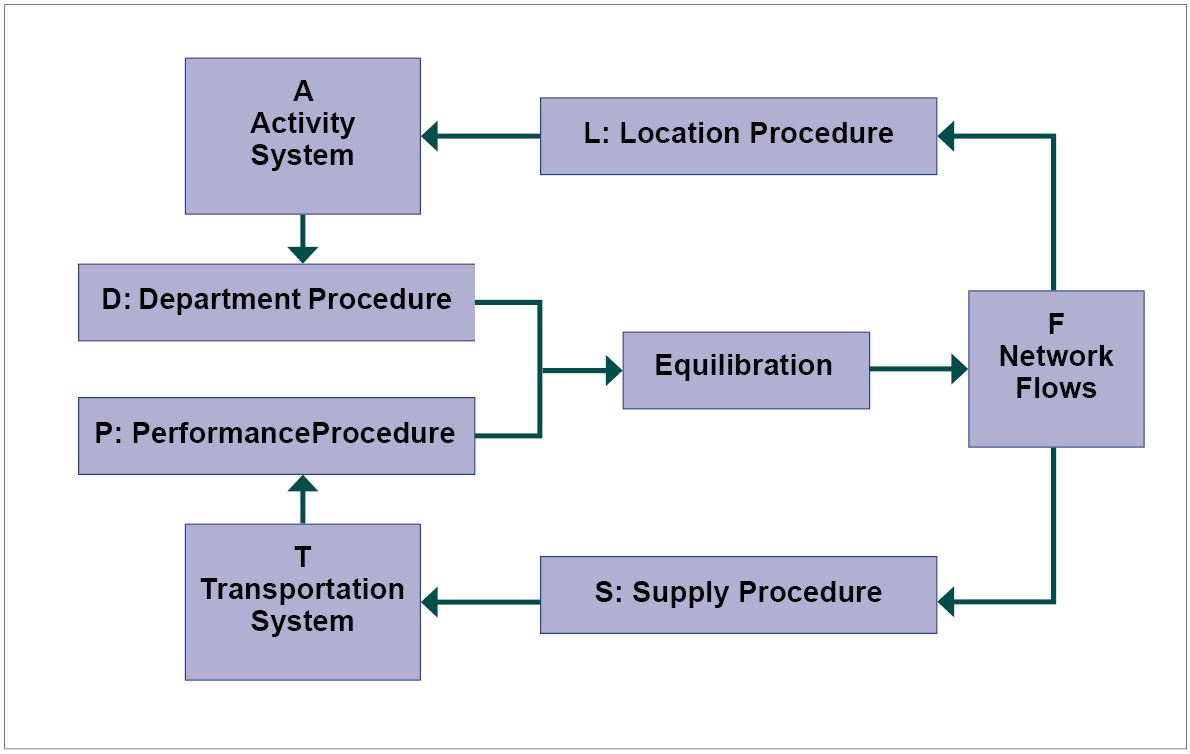
A crucial aspect of the process involves understanding the input units, which are defined both spatially and temporally. Demand generates person trips, which encompass both time and space (e.g., person trips per household or peak-hour person trips per zone). Performance typically yields a level of service, defined as a link volume capacity ratio (e.g., freeway vehicle trips per hour or boardings per hour for a specific transit route segment). Demand is primarily defined at the zonal level, whereas performance is evaluated at the link level.

It is essential to recognize that travel forecasting models like FSM are continuous processes. Model generation takes time, and changes may occur in the study area during the analysis period.

Before proceeding with the four steps of FSM, defining the study area is crucial. Like most models discussed, FSM uses traffic analysis zones (TAZs) as the geographic unit of analysis. However, a higher number of TAZs generally yield more accurate results. The number of TAZs in the model can vary based on its purpose, data availability, and vintage. These zones are characterized or categorized by factors such as population and employment. For modeling simplicity, FSM assumes that trip-making begins at the center of a zone (zone centroid) and excludes very short trips that start and end within a TAZ, such as those made by bike or on foot.

Furthermore, highway systems and transit systems are considered as networks in the model. Highway or transit line segments are coded as links, while intersections are represented as nodes. Data regarding network conditions, including travel times, speeds, capacity, and directions, are utilized in the travel simulation process. Trips originate from trip generation zones, traverse a network of links and nodes, and conclude at trip attraction zones.

Trip Generation

Trip generation is the first step in the FSM model. This step defines the magnitude of daily travel in the study area for different trip purposes. It will also provide us with an estimate of the total trips to and from each zone, creating a trip production and attraction matrix for each trip’s purpose. Trip purposes are typically categorized as follows:

Home-based work trips (work trips that begin or end at home),
Home-based shopping trips,
Home-based other trips,
School trips,
Non-home-based trips (trips that neitherbeginnorendathome),
Trucktrips,and
Taxitrips(Ahmed,2012).

Trip attractions are based on the level of employment in a zone. In the trip generation step, the assumptions and limitations are listed below:

Independent decisions: Travel behavior is affected by many factors generated within a household; the model ignores most of these factors. For example, childcare may force people to change their travel plans.
Limited trip purposes: This model consists of a limited number of trip purposes for simplicity, giving rise to some model limitations. Take shopping trips, for example; they are all considered in the same weather conditions. Similarly, we generate home-based trips for various purposes (banking, visiting friends, medical reasons, or other purposes), all of which are affected by factors ignored by the model.
Trip combinations: Travelers are often willing to combine various trips into a chain of short trips. While this behavior creates a complex process, the FSM model treats this complexity in a limited way.
Feedback, cause, and effect problems: Trip generation often uses factors that are a function of the number of trips. For instance, for shopping trip attractions in the FSM model, we assume they are a retail employment function. However, it is logical to assume how many customers these retail centers attract. Alternatively, we can assume that the number of trips a household makes is affected by the number of private cars they own. Nevertheless, the activity levels of families determine the total number of cars.

As mentioned, trip generation process estimations are done separately for each trip purpose. Equations 1 and 2 show the function of trip generation and attraction:

$O_i = f(x_{i1}, x_{i2}, x_{i3}, \ldots)$

where Oi and Dj trip are generated and attracted respectively, x refers to socio-economic characteristics, and y refers to land-use properties.

Generally, FSM aggregates different trip purposes previously listed into three categories: home-based work trips (HBW) , home-based other (or non-work) trips (HBO) , and non-home-based trips (NHB) . Trip ends are either the origin (generation) or destination (attraction), and home-end trips comprise most trips in a study area. We can also model trips at different levels, such as zones, households, or person levels (activity-based models). Household-level models are the most common scale for trip productions, and zonal-level models are appropriate for trip attractions (McNally, 2007).

There are three main methods for a trip generation or attraction.

The first method is multiple regression based on population, jobs, and income variables.
The second method in this step is experience-based analysis, which can show us the ratio of trips generated frequently.
The third method is cross-classification . Cross-classification is like the experience-based analysis in that it uses trip rates but in an extended format for different categories of trips (home-based trips or non-home-based trips) and different attributes of households, such as car ownership or income.

Elaborating on the differences between these methods, category analysis models are more common for the trip generation model, while regression models demonstrate better performance for trip attractions (Meyer, 2016). Production models are recognized to be influenced by a range of explanatory and policy-sensitive variables (e.g., car ownership, household income, household size, and the number of workers). However, estimation is more problematic for attraction models because regional travel surveys are at the household level (thus providing more accurate data for production models) and not for nonresidential land uses (which is important for trip attraction). Additionally, estimation can be problematic because explanatory trip attraction variables may usually underperform (McNally, 2007). For these reasons, survey data factoring is required prior to relating sample trips to population-level attraction variables, typically achieved via regression analysis. Table 9.1 shows the advantages and disadvantages of each of these two models.

Trip Distribution

Thus far, the number of trips beginning or ending in a particular zone have been calculated. The second step explores how trips are distributed between zones and how many trips are exchanged between two zones. Imagine a shopping trip. There are multiple options for accessible shopping malls accessible. However, in the end, only one will be selected for the destination. This information is modeled in the second step as a distribution of trips. The second step results are usually a very large Origin-Destination (O-D) matrix for each trip purpose. The O-D matrix can look like the table below (9.2), in which sum of Tij by j shows us the total number of trips attracted in zone J and the sum of Tij by I yield the total number of trips produced in zone I.

Up to this point, we have calculated the number of trips originating from or terminating in a specific zone. The next step involves examining how these trips are distributed across different zones and how many trips are exchanged between pairs of zones. To illustrate, consider a shopping trip: there are various options for reaching shopping malls, but ultimately, only one option is chosen as the destination. This process is modeled in the second step as the distribution of trips. The outcome of this step typically yields a large Origin-Destination (O-D) matrix for each trip purpose. An O-D matrix might resemble the table below (9.2), where the sum of Tij by j indicates the total number of trips attracted to zone J, and the sum of Tij by I represents the total number of trips originating from zone I.

$T_{ij} = \frac{P(A_i F_{ij}(K_{ij}))}{\sum(A_x F_{ij}(k_{ix}))}$

T ij = trips produced at I and attracted at j

P i = total trip production at I

A j = total trip attraction at j

F ij = a calibration term for interchange ij , (friction factor) or travel

time factor ( F ij =C/t ij n )

C= calibration factor for the friction factor

K ij = a socioeconomic adjustment factor for interchange ij

i = origin zone

n = number of zones

Different methods (units) in the gravity model can be used to perform distance measurements. For instance, distance can be represented by time, network distance, or travel costs. For travel costs, auto travel cost is the most common and straightforward way of monetizing distance. A combination of different costs, such as travel time, toll payments, parking payments, etc., can also be used. Alternatively, a composite cost of both car and transit costs can be used (McNally, 2007).

Generalized travel costs can be a function of time divided into different segments. For instance, public transit time can be divided into the following segments: in-vehicle time, walking time, waiting time, interchange time, fare, etc. Since travelers perceive time value differently for each segment (like in-vehicle time vs. waiting time), weights are assigned based on the perceived value of time (VOT). Similarly, car travel costs can be categorized into in-vehicle travel time or distance, parking charge, tolls, etc.

As with the first step in the FSM model, the second step has assumptions and limitations that are briefly explained below.

Constant trip times: In order to utilize the model for prediction, it assumes that the duration of trips remains constant. This means that travel distances are measured by travel time, and the assumption is that enhancements in the transportation system, which reduce travel times, are counterbalanced by the separation of origins and destinations.
Automobile travel times to represent distance: We utilize travel time as a proxy for travel distance. In the gravity model, this primarily relies on private car travel time and excludes travel times via other modes like public transit. This leads to a broader distribution of trips.
Limited consideration of socio-economic and cultural factors: Another drawback of the gravity model is its neglect of certain socio-economic or cultural factors. Essentially, this model relies on trip production and attraction rates along with travel times between them for predictions. Consequently, it may overestimate trip rates between high-income groups and nearby low-income Traffic Analysis Zones (TAZs). Therefore, incorporating more socio-economic factors into the model would enhance accuracy.
Feedback issues: The gravity model’s reliance on travel times is heavily influenced by congestion levels on roads. However, measuring congestion proves challenging, as discussed in subsequent sections. Typically, travel times are initially assumed and later verified. If the assumed values deviate from actual values, they require adjustment, and the calculations need to be rerun.

Mode choice

FSM model’s third step is a mode-choice estimation that helps identify what types of transportation travelers use for different trip purposes to offer information about users’ travel behavior. This usually results in generating the share of each transportation mode (in percentages) from the total number of trips in a study area using the utility function (Ahmed, 2012). Performing mode-choice estimations is crucial as it determines the relative attractiveness and usage of various transportation modes, such as public transit, carpooling, or private cars. Modal split analysis helps evaluate improvement programs or proposals (e.g., congestion pricing or parking charges) aimed at enhancing accessibility or service levels. It is essential to identify the factors contributing to the utility and disutility of different modes for different travel demands (Beimborn & Kennedy, 1996). Comparing the disutility of different modes between two points aids in determining mode share. Disutility typically refers to the burdens of making a trip, such as time, costs (fuel, parking, tolls, etc.). Once disutility is modeled for different trip purposes between two points, trips can be assigned to various modes based on their utility. As discussed in Chapter 12, a mode’s advantage in terms of utility over another can result in a higher share of trips using that mode.

The assumptions and limitations for this step are outlined as follows:

Choices are only affected by travel time and cost: This model assumes that changes in mode choices occur solely if transportation cost or travel time in the transportation network or transit system is altered. For instance, a more convenient transit mode with the same travel time and cost does not affect the model’s results.
Omitted factors: Certain factors like crime, safety, and security, which are not included in the model, are assumed to have no effect, despite being considered in the calibration process. However, modes with different attributes regarding these omitted factors yield no difference in the results.
Simplified access times: The model typically overlooks factors related to the quality of access, such as neighborhood safety, walkability, and weather conditions. Consequently, considerations like walkability and the impact of a bike-sharing program on the attractiveness of different modes are not factored into the model.
Constant weights: The model assumes that the significance of travel time and cost remains constant for all trip purposes. However, given the diverse nature of trip purposes, travelers may prioritize travel time and cost differently depending on the purpose of their trip.

The most common framework for mode choice models is the nested logit model, which can accommodate various explanatory variables. However, before the final step, results need to be aggregated for each zone (Koppelman & Bhat, 2006).

A generalized modal split chart is depicted in Figure 9.5.

a simple decision tree for transportation mode choice between car, train, and walking.

In our analysis, we can use binary logit models (dummy variable for dependent variable) if we have two modes of transportation (like private cars and public transit only). A binary logit model in the FSM model shows us if changes in travel costs would occur, such as what portion of trips changes by a specific mode of transport. The mathematical form of this model is:

$P_ij^1=\frac{T_ij^1}{T_{ij}}\ =\frac{e^-bcij^1 }{e^(-bc_ij^1 )+e^(-bc_ij^2 )}$

where: P_ij 1= The proportion of trips between i and j by mode 1 . Tij 1= Trips between i and j by mode 1.

Cij 1= Generalized cost of travel between i and j by mode 1 .

Cij^2= Generalized cost of travel between i and j by mode 2 .

b= Dispersion Parameter measuring sensitivity to cost.

It is also possible to have a hierarchy of transportation modes for using a binary logit model. For instance, we can first conduct the analysis for the private car and public transit and then use the result of public transit to conduct a binary analysis between rail and bus.

Trip assignment

After breaking down trip counts by mode of transportation, we analyze the routes commuters take from their starting point to their destination, especially for private car trips. This process is known as trip assignment and is the most intricate stage within the FSM model. Initially, the minimum path assigns trips for each origin-destination pair based on either travel costs or time. Subsequently, the assigned volume of trips is compared to the capacity of the route to determine if congestion would occur. If congestion does happen (meaning that traffic volume exceeds capacity), the speed of the route needs to be decreased, resulting in increased travel costs or time. When the Volume/Capacity ratio (v/c ratio) changes due to congestion, it can lead to alterations in both speed and the shortest path. This characteristic of the model necessitates an iterative process until equilibrium is achieved.

The process for public transit is similar, but with one distinction: instead of adjusting travel times, headways are adjusted. Headway refers to the time between successive arrivals of a vehicle at a stop. The duration of headways directly impacts the capacity and volume for each transit vehicle. Understanding the concept of equilibrium in the trip assignment step is crucial because it guides the iterative process of the model. The conclusion of this process is marked by equilibrium, a concept known as Wardrop equilibrium. In Wardrop equilibrium, traffic naturally organizes itself in congested networks so that individual commuters do not switch routes to reduce travel time or costs. Additionally, another crucial factor in this step is the time of day.

Like previous steps, the following assumptions and limitations are pertinent to the trip assignment step:

1. Delays on links: Most traffic assignment models assume that delays occur on the links, not the intersections. For highways with extensive intersections, this can be problematic because intersections involve highly complex movements. Intersections are excessively simplified if the assignment process does not modify control systems to reach an equilibrium.

2. Points and links are only for trips: This model assumes that all trips begin and finish at a single point in a zone (centroids), and commuters only use the links considered in the model network. However, these points and links can vary in the real world, and other arterials or streets might be used for commutes.

3. Roadway capacities: In this model, a simple assumption helps determine roadways’ capacity. Capacity is found based on the number of lanes a roadway provides and the type of road (highway or arterial).

4. Time of the day variations: Traffic volume varies greatly throughout the day and week. In this model, a typical workday of the week is considered and converted to peak hour conditions. A factor used for this step is called the hour adjustment factor. This value is critical because a small number can result in a massive difference in the congestion level forecasted on the model.

5. Emphasis on peak hour travel: The model forecasts for the peak hour but does not forecast for the rest of the day. The models make forecasts for a typical weekday but neglect specific conditions of that time of the year. After completing the fourth step, precise approximations of travel demand or traffic count on each road are achieved. Further models can be used to simulate transportation’s negative or positive externalities. These externalities include air pollution, updated travel times, delays, congestion, car accidents, toll revenues, etc. These need independent models such as emission rate models (Beimborn & Kennedy, 1996).

The basic equilibrium condition point calculation is an algorithm that involves the computation of minimum paths using an all-or-nothing (AON) assignment model to these paths. However, to reach equilibrium, multiple iterations are needed. In AON, it is assumed that the network is empty, and a free flow is possible. The first iteration of the AON assignment requires loading the traffic by finding the shortest path. Due to congestion and delayed travel times, the

previous shortest paths may no longer be the best minimum path for a pair of O-D. If we observe a notable decrease in travel time or cost in subsequent iterations, then it means the equilibrium point has not been reached, and we must continue the estimation. Typically, the following factors affect private car travel times: distance, free flow speed on links, link capacity, link speed capacity, and speed flow relationship .

The relationship between the traffic flow and travel time equation used in the fourth step is:

$t = t_0 + a v^n, \quad v < c$

t= link travel time per length unit

t 0 =free-flow travel time

v=link flow

c=link capacity

a, b, and n are model (calibrated) parameters

Model improvement

Improvements to FSM continue to generate more accurate results. Since transportation dynamics in urban and regional areas are under the complex influence of various factors, the existing models may not be able to incorporate all of them. These can be employer-based trip reduction programs, walking and biking improvement schemes, a shift in departure (time of the day), or more detailed information on socio-demographic and land-use-related factors. However, incorporating some of these variables is difficult and can require minor or even significant modifications to the model and/or computational capacities or software improvements. The following section identifies some areas believed to improve the FSM model performance and accuracy.

• Better data: An effective way of improving the model accuracy is to gather a complete dataset that represents the general characteristics of the population and travel pattern. If the data is out- of-date or incomplete, we will get poor results.

• Better modal split: As you saw in previous sections, the only modes incorporated into the model are private car and public transit trips, while in some cities, a considerable fraction of trips are made by bicycle or by walking. We can improve our models by producing methods to consider these trips in the first and third steps.

• Auto occupancy: In contemporary transportation planning practices, especially in the US, some new policies are emerging for carpooling. We can calculate auto occupancy rates using different mode types, such as carpooling, sensitive to private car trips’ disutility, parking costs, or introducing a new HOV lane.

• Time of the day: In this chapter, the FSM framework discussed is oriented toward peak hour (single time of the day) travel patterns. Nonetheless, understanding the nature of congestion in other hours of the day is also helpful for understanding how travelers choose their travel time.

• A broader trip purpose: Additional trip purposes may provide a better understanding of the

factors affecting different trip purposes and trip-chaining behaviors. We can improve accuracy by having more trip purposes (more disaggregate input and output for the model).

The concept of access: As discussed, land-use policies that encourage public transit use or create amenities for more convenient walking are not present in the model. Developing factors or indices that reflect such improvements in areas with high demand for non-private vehicles and incorporating them in choice models can be a good improvement.
Land use feedback: To better understand interactions between land use and travel demand, a land-use simulation model can be added to these steps to determine how a proposed transportation change will lead to a change in land use.
Intersection delays: As mentioned in the fourth step, intersections in major highways create significant delays. Incorporating models that calculate delays at these intersections, such as stop signs, could be another improvement to the model.

A Simple Example of the FSM model

An example of FSM is provided in this section to illustrate a typical application of this model in the U.S. In the first phase, the specifications about the transportation network and household data are needed. In this hypothetical example, 5 percent of households in each TAZ were sampled and surveyed, which generated 1,955 trips in 200 households. As a hypothetical case study, this sample falls below the standard required for statistical significance but is relevant to demonstrate FSM.

A home interview survey was carried out to gather data from a five percent sample of households in each TAZ. This survey resulted in 1,852 trips from 200 households. It is important to note that the sample size in this example falls below the minimum required for statistical significance, as it is intended for learning purposes only.

Table 9.3 provides network information such as speed limits, number of lanes, and capacity. Table 9.4 displays the total number of households and jobs in three industry sectors for each zone. Additionally, Table 9.5 breaks down the household data into three car ownership groups, which is one of the most significant factors influencing trip making.

In the first step (trip generation), a category model (i.e., cross-classification) helped estimate trips. The sampled population’s sociodemographic and trip data for different purposes helped calculate this estimate. Since research has shown the significant effect of auto ownership on private car trip- making (Ben-Akiva & Lerman, 1974), disaggregating the population based on the number of private cars generates accurate results. Table 9.7 shows the trip-making rate for different income and auto ownership groups.

Also, as mentioned in previous sections, multiple regression estimation analysis can be used to generate the results for the attraction model. Table 9.7 shows the equations for each of the trip purposes.

After estimating production and attraction, the models are used for population data to generate results for the first step. Next, comparing the results of trip production and attraction, we can observe that the total number of trips for each purpose is different. This can be due to using different methods for production and attraction. Since the production method is more reliable, attraction is typically normalized by production. Also, some external zones in our study area are either attracting trips from our zones or generating them. In this case, another alternative is to extend the boundary of the study area and include more zones.

As mentioned, the total number of trips produced and attracted are different in these results. To address this mismatch, we can use a balance factor to come up with the same trip generation and attraction numbers if we want to keep the number of zones within our study area. Alternatively, we can consider some external stations in addition to designated zones. In this example, using the latter seems more rational because, as we saw in Table 9.4, there are more jobs than the number of households aggregately, and our zone may attract trips from external locations.

For the trip distribution step, we use the gravity model. For internal trips, the gravity model is:

$T_{ij} = a_i b_j P_i A_j f(t_{ij})$

and f(tij) is some function of network level of service (LOS)

To apply the gravity model, we need to calculate the impedance function first, which is represented here by travel cost. Table 9.9 shows the minimum travel path between each pair of zones ( skim tree ) in a matrix format in which each cell represents travel time required to travel between the corresponding row and column of that cell.

Table 9.9-Travel cost table (skim tree)

Note. Table adapted from “The Four-Step Model” by M. McNally, In D. A. Hensher, & K. J. Button (Eds.), Handbook of transport modelling , Volume1, p. 5, Bingley, UK: Emerald Publishing. Copyright 2007 by Emerald Publishing.

With having minimum travel costs between each pair of zones, we can calculate the impedance function for each trip purpose using the formula

$f(t_{ij}) = a \cdot t_{ij} \cdot b \cdot e^{ct_{ij}}$

Table 9.10 shows the model parameters for calculating the impedance function for different trip purposes:

After calculating the impedance function , we can calculate the result of the trip distribution. This stage generates trip matrices since we calculate trips between each zone pair. These matrices are usually in “Origin-Destination” (OD) format and can be disaggregated by the time of day. Field surveys help us develop a base-year trip distribution for different periods and trip purposes. Later, these empirical results will help forecast trip distribution. When processing the surveys, the proportion of trips from the production zone to the attraction zone (P-A) is also generated. This example can be seen in Table 9.11. Looking at a specific example, the first row in table is for the 2-hour morning peak commute time period. The table documents that the production to attraction factor for the home-based work trip is 0.3. Unsurprisingly, the opposite direction, attraction to production zone is 0.0 for this time of day. Additionally, the table shows that the factor for HBO and NHB trips are low but do occur during this time period. This could represent shopping trips or trips to school. Table 9.11 table also contains the information for average occupancy levels of vehicles from surveys. This information can be used to convert person trips to vehicle trips or vice versa.

Table 9.11 Trip distribution rates for different time of the day and trip purposes

The O-D trip table is calculated by adding the multiplication of the P-to-A factor by corresponding cell of the P-A trip table and adding the corresponding cell of the transposed P-A trip table multiplied by the A-to-P factor. These results, which are the final output of second step, are shown in Table 9.12.

Once the Production-Attraction (P-A) table is transformed into Origin-Destination (O-D) format and the complete O-D matrix is computed, the outcomes will be aggregated for mode choice and traffic assignment modeling. Further elaboration on these two steps will be provided in Chapters 11 and 12.

In this chapter, we provided a comprehensive yet concise overview of four-step travel demand modeling including the process, the interrelationships and input data, modeling part and extraction of outputs. The complex nature of cities and regions in terms of travel behavior, the connection to the built environment and constantly growing nature of urban landscape, necessitate building models that are able to forecast travel patterns for better anticipate and prepare for future conditions from multiple perspectives such as environmental preservation, equitable distribution of benefits, safety, or efficiency planning. As we explored in this book, nearly all the land-use/transportation models embed a transportation demand module or sub model for translating magnitude of activities and interconnections into travel demand such as VMT, ridership, congestion, toll usage, etc. Four-step models can be categorized as gravity-based, equilibrium-based models from the traditional approaches. To improve these models, several new extensions has been developed such as simultaneous mode and destination choice, multimodality (more options for mode choice with utility), or microsimulation models that improve granularity of models by representing individuals or agents rather than zones or neighborhoods.

Travel demand modeling are models that predicts the flow of traffic or travel demand between zones in a city using a sequence of steps.

Intermodality refers to the concept of utilizing two or more travel modes for a trip such as biking to a transit station and riding the light rail.
Multimodality is a type of transportation network in which a variety of modes such as public transit, rail, biking networks, etc. are offered.

Zoning ordinances is legal categorization of land use policies that permits or prohibits certain built environment factors such as density.

Volume capacity ratio is ratio that divides the demand on a link by the capacity to determine the level of service.

Zone centroid is usually the geometric center of a zone in modeling process where all trips originate and end.

Home-based work trips (HBW) are the trips that originates from home location to work location usually in the AM peak.

Home-based other (or non-work) trips (HBO) are the trips that originates from home to destinations other than work like shopping or leisure.

Non-home-based trips (NHB) are the trips that neither origin nor the destination are home or they are part of a linked trip.

Cross-classification is a method for trip production estimation that disaggregates trip rates in an extended format for different categories of trips like home-based trips or non-home-based trips and different attributes of households such as car ownership or income.

Generalized travel costs is a function of time divided into sections such as in vehicle time vs. waiting time or transfer time in a transit trip.

Binary logit models is a type of logit model where the dependent variable can take only a value of 0 or 1.

Wardrop equilibrium is a state in traffic assignment model where are drivers are reluctant to change their path because the average travel time is at a minimum.

All-or-nothing (AON) assignment model is a model that assumes all trips between two zones uses the shortest path regardless of volume.

Speed flow relationship is a function that determines the speed based on the volume (flow)

skim tree is structure of travel time by defining minimum cost path for each section of a trip.

Key Takeaways

In this chapter, we covered:

What travel demand modeling is for and what the common methods are to do that.
How FSM is structured sequentially, what the relationships between different steps are, and what the outputs are.
What the advantages and disadvantages of different methods and assumptions in each step are.
What certain data collection and preparation for trip generation and distribution are needed through a hypothetical example.

Prep/quiz/assessments

What is the need for regular travel demand forecasting, and what are its two major components?
Describe what data we require for each of the four steps.
What are the advantages and disadvantages of regression and cross-classification methods for a trip generation?
What is the most common modeling framework for mode choice, and what result will it provide us?
What are the main limitations of FSM, and how can they be addressed? Describe the need for travel demand modeling in urban transportation and relate it to the structure of the four-step model (FSM).

Ahmed, B. (2012). The traditional four steps transportation modeling using a simplified transport network: A case study of Dhaka City, Bangladesh. International Journal of Advanced Scientific Engineering and Technological Research , 1 (1), 19–40. https://discovery.ucl.ac.uk/id/eprint/1418961/

ALMEC, C . (2015). The Project for capacity development on transportation planning and database management in the republic of the Philippines: MMUTIS update and enhancement project (MUCEP) : Project Completion Report . Japan International Cooperation Agency. (JICA) Department of Transportation and Communications (DOTC) . https://books.google.com/books?id=VajqswEACAAJ .

Beimborn, E., and Kennedy, R. (1996). Inside the black box: Making transportation models work for livable communities . Washington, DC: Citizens for a Better Environment and the Environmental Defense Fund. https://www.piercecountywa.gov/DocumentCenter/View/755/A-GuideToModeling?bidId

Ben-Akiva, M., & Lerman, S. R. (1974). Some estimation results of a simultaneous model of auto ownership and mode choice to work. Transportation , 3 (4), 357–376. https://doi.org/10.1007/bf00167966

Ewing, R., & Cervero, R. (2010). Travel and the built environment: A meta-analysis. Journal of the American Planning Association , 76 (3), 265–294. https://doi.org/10.1080/01944361003766766

Florian, M., Gaudry, M., & Lardinois, C. (1988). A two-dimensional framework for the understanding of transportation planning models. Transportation Research Part B: Methodological , 22 (6), 411–419. https://doi.org/10.1016/0191-2615(88)90022-7

Hadi, M., Ozen, H., & Shabanian, S. (2012). Use of dynamic traffic assignment in FSUTMS in support of transportation planning in Florida. Florida International University Lehman Center for Transportation Research. https://rosap.ntl.bts.gov/view/dot/24925

Hansen, W. (1959). How accessibility shapes land use.” Journal of the American Institute of Planners 25 (2): 73–76. https://doi.org/10.1080/01944365908978307

Gavu, E. K. (2010). Network based indicators for prioritising the location of a new urban transport connection: Case study Istanbul, Turkey (Master’s thesis, University of Twente). International Institute for Geo-Information Science and Earth Observation Enschede. http://essay.utwente.nl/90752/1/Emmanuel%20Kofi%20Gavu-22239.pdf

Karner, A., London, J., Rowangould, D., & Manaugh, K. (2020). From transportation equity to transportation justice: Within, through, and beyond the state. Journal of Planning Literature , 35 (4), 440–459. https://doi.org/10.1177/0885412220927691

Kneebone, E., & Berube, A. (2013). Confronting suburban poverty in America . Brookings Institution Press.

Koppelman, Frank S, and Chandra Bhat. (2006). A self instructing course in mode choice modeling: multinomial and nested logit models. U.S. Department of Transportation Federal Transit Administration https://www.caee.utexas.edu/prof/bhat/COURSES/LM_Draft_060131Final-060630.pdf

‌Manheim, M. L. (1979). Fundamentals of transportation systems analysis. Volume 1: Basic Concepts . The MIT Press https://mitpress.mit.edu/9780262632898/fundamentals-of-transportation-systems-analysis/

McNally, M. G. (2007). The four step model. In D. A. Hensher, & K. J. Button (Eds.), Handbook of transport modelling , Volume1 (pp.35–53). Bingley, UK: Emerald Publishing.

Meyer, M. D., & Institute Of Transportation Engineers. (2016). Transportation planning handbook . Wiley.

Mladenovic, M., & Trifunovic, A. (2014). The shortcomings of the conventional four step travel demand forecasting process. Journal of Road and Traffic Engineering , 60 (1), 5–12.

Mitchell, R. B., and C. Rapkin. (1954). Urban traffic: A function of land use . Columbia University Press. https://doi.org/10.7312/mitc94522

Rahman, M. S. (2008). “ Understanding the linkages of travel behavior with socioeconomic characteristics and spatial Environments in Dhaka City and urban transport policy applications .” Hiroshima: (Master’s thesis, Hiroshima University.) Graduate School for International Development and Cooperation. http://sr-milan.tripod.com/Master_Thesis.pdf

Rodrigue, J., Comtois, C., & Slack, B. (2020). The geography of transport systems . London ; New York Routledge.

Shen, Q. (1998). Location characteristics of inner-city neighborhoods and employment accessibility of low-wage workers. Environment and Planning B: Planning and Design , 25 (3), 345–365.

Sharifiasl, S., Kharel, S., & Pan, Q. (2023). Incorporating job competition and matching to an indicator-based transportation equity analysis for auto and transit in Dallas-Fort Worth Area. Transportation Research Record , 03611981231167424. https://doi.org/10.1177/03611981231167424

Weiner, Edward. 1997. Urban transportation planning in the United States: An historical overview . US Department of Transportation. https://rosap.ntl.bts.gov/view/dot/13691

Xiongbing, J, Grammenos, F. (2013, May, 21) . Taking the Guesswork out of Designing for Walkability. Planetizen . https://www.planetizen.com/node/63248

Home-based other (or non-work) trips (HBO) are the trips that originates from home to destinations other than work like shopping or leisure.

gravity model is a type of accessibility measurement in which the employment in destination and population in the origin defines thee degree of accessibility between the two zones.

Impedance function is a function that convert travel costs (usually time or distance) to the level of difficulty of getting from one location to the other.

Share This Book

Serving technical professionals globally for over 75 years. Learn more about us.

MIT Professional Education 700 Technology Square Building NE48-200 Cambridge, MA 02139 USA

Accessibility

Transportation Networks and Smart Mobility: Methods and Solutions

Moshe Ben-Akiva

Download the Course Schedule

Ready to design the transportation systems of the future? Acquire the cutting-edge strategies you need by exploring cutting-edge traffic simulation models, demand modeling methods, and related analytical techniques. Over the course of five days, you’ll delve into the latest research from MIT’s Intelligent Transportation Systems Lab and learn to translate real-time data into real-world results that mitigate traffic congestion and other transportation challenges.

Cities worldwide are undergoing radical changes in their transportation systems with the advent of advances in technology such as autonomous vehicles, electric vehicles, AI-enabled vehicles, vehicle-to-vehicle (V2V) communication, autopilot features and on-demand urban transportation services. Recent trends include the proliferation of on-demand and shared services and automation in public and private transportation systems. These trends have heightened interest in Intelligent Transportation Systems (ITS), Smart Mobility, and real-time network management as potential solutions to mitigate congestion issues and improve traffic network efficiency. ITS techniques traditionally include real-time traffic control measures and real-time traveler information and guidance systems whose purpose is to assist travelers in making travel decisions including departure time, mode, and route choice decisions. Transportation researchers have developed models and simulation tools for use in the planning, design, and operations of such systems. However, with the advent of new technologies and services, these techniques need to be modified and better leveraged to improve system performance.

This course presents theory of transportation modelling and simulation techniques, with a focus on Smart Mobility, AI and ML solutions and real-world applications. It provides an in-depth study of the most sophisticated traffic simulation models, demand modeling methods, and related discrete choice, machine learning analytical techniques. Some of the topics include: modeling and simulation approaches for future mobility; discrete choice models and their application to travel choices and driving behavior; predicting traffic congestion; traffic flow models and simulation methods (microscopic, mesoscopic, and macroscopic); automated and connective vehicles in mixed traffic; alternative dynamic traffic assignment methods; and calibration of large scale simulation systems. In addition, the course covers recent developments in modelling, simulation, operations of smart mobility services, and machine learning applications in transportation. The course also includes case studies to elucidate the concepts and showcase the potential applications.

This course draws heavily on the results of recent research and is sponsored by the ITS Lab of the Massachusetts Institute of Technology. It was previously titled "Modeling and Simulation of Transportation Networks."

Certificate of Completion from MIT Professional Education

Understand transportation network demand and supply models.
Distinguish among alternative approaches to dynamic traffic assignment and traffic simulation.
Assess the advantages and disadvantages of alternative network modeling and simulation methods.

Program Outline

Class runs 9:30 am - 5:00 pm every day.

Special events include a reception for course participants and faculty on Monday night and a dinner on Thursday evening. All evening activities are included in tuition.

The course consists of a series of lectures, including software demonstrations and case studies that develop the concepts and techniques.

The following lecture topics may be addressed as part of the course:

Traffic Performance

Modeling and Simulation Approaches for Future Mobility
Microscopic and Mesoscopic Traffic Simulation
Static and Dynamic Network Supply Models

Smart Mobility

Analyzing Smart Mobility
Automated and Connected Vehicles in Mixed Traffic
Bi-level Optimization Algorithms for Smart Mobility
Mobility of the Future Outlook

Demand and User Behavior

Overview of Discrete Choice Analysis
Machine Learning Concepts
Route and Time-of-Travel Choice

Traffic Assignment

Equilibrium and Day-to-Day Dynamics
DTA Algorithms and Applications
Pricing and Travel Time Reliability

Real-Time Systems

Public Transportation Models

Framework and Low Frequency Services
High Frequency Services

Freight Models

Freight Data and Economic Activity Models
Simulating Freight Flows and Logistics Choices
Evaluation of Traffic Predictions

Calibration and Validation

Calibrating Simulation Systems

Links & Resources

News/Articles:

MIT graduate transportation researchers reflect on work with Portugal
The Future of Urban Mobility
A Global Collaboration to Chart the Future of Urban Mobility
Transportation, transformed
The Taxi-Meter Effect - Why do consumers hate paying by the mile or the minute so much?

This program is intended for individuals interested in theory, research, and practice, including:

1. Professionals in the mobility industry: including car companies, all mobility business in the private sector, manufacturers, infrastructure, and Transportation Network Companies (TCNs) such as Uber, Lyft, and other car-rental and car-sharing companies

2. Individuals with experience in transportation consulting, planning, and related government agencies

3. PhD students in transportation systems, civil engineering, economics, planning, and/or urban mobility

Participants with backgrounds in diverse areas such as traffic engineering, systems engineering, transportation planning, operations management, operations research, and control systems are also welcome.

Computer requirements

This course will be taught on the Zoom platform.

Testimonials

Transportation Networks and Smart Mobility: Methods and Solutions - Brochure Image

One full scholarship will be awarded to an outstanding doctoral student. 50% scholarships are available for junior faculty, postdocs, and doctoral students. To apply for the scholarship, before submitting your registration for this program please email a CV and a letter stating the relevance of the course to your research to [email protected] . The deadline to apply for the scholarship is June 30 . You should wait for the scholarship decision before submitting your registration.

Please contact Katie Rosa at [email protected] with any questions.

Discounts for Faculty In addition, a limited number of 50% scholarships are available for teaching faculty, rank of instructor or higher, at other educational institutions. Decisions are made on a rolling basis after submitting a course registration form and a Scholarship Request Form . Please note that these scholarships are only for tuition and do not cover travel, lodging, or other expenses associated with the course.

If you have any questions please contact the Short Programs office .

The type of content you will learn in this course, whether it's a foundational understanding of the subject, the hottest trends and developments in the field, or suggested practical applications for industry.

How the course is taught, from traditional classroom lectures and riveting discussions to group projects to engaging and interactive simulations and exercises with your peers.

What level of expertise and familiarity the material in this course assumes you have. The greater the amount of introductory material taught in the course, the less you will need to be familiar with when you attend.

iUTS | intelligent Urban Transportation Systems

Dynamic Transportation Network Modeling, Analysis, Simulation, and Control (DTN-MASC)

DTN-MASC is to understand the behavior and interactions of major components/players in a multi-modal transportation network system, develop mathematical paradigms and tools to model such interactions and behavior, and design efficient solution methods. The main purpose is to develop novel management policies to manage the multi-modal transportation system more effectively and efficiently. Important applications include emergency evacuation planning and modeling, congestion pricing, urban traffic control, among others. This is particularly critical now in the era of connected / automated vehicles (CAVs), electric vehicles / buses, new mobility systems (ridehailing, ridesharing, carsharing, bike/scooter sharing) , and AI / big data analytics in transportation. The topics we are currently investigating include the network effect of new mobility services, the transit first-mile/last-mile problem using new mobility services, urban traffic control with CAVs, and optimizing the charging infrastructure of electric buses.

Below are some specific examples of DTN-MAS related research topics and results iUTS has conducted in the past.

Dynamic User Equilibrium (DUE) and applications

Our iUTS team has worked on developing dynamic user equilibrium (DUE) methods, models, and algorithms for both the continuous-time problems and the discrete-time problems. By collaborating with optimization experts and mathematicians, we were able to apply a new mathematical paradigm, called differential variational inequality (DVI) and its special form of differential complementarity systems (DCS), to model DUE to capture its two major and distinct components, i.e., (i) drivers’ choice behavior (such as departure time, route, and mode choices); and (ii) the network traffic flow dynamics. The former is usually formulated as an optimization problem or an equilibrium problem, while the latter is often formulated as an ordinary differential equation (ODE) or a partial differential equation (PDE). DVI and DCS integrates these two (mathematically very different) components into one consistent and coherent mathematical framework and gives them a formal treatment in terms of solution existence, uniqueness, stability, and solution methods. In particular, we reformulated the Vickrey-type point queue model as a DCS and applied/extended the double queue model for link level traffic flow dynamics. However, DUE problems are inherently more challenging than regular DVI and DCS, mainly due to the time-delayed terms in some of the major components (such as route choice and flow propagations). This requires new developments of the standard DVI/DCS theories, which are challenging yet very interesting problems both mathematically and practically.

Dynamic System Optimum (DSO) and Applications

Dynamic system optimum (DSO) describes and predicts the dynamic traffic network flow from the system perspective by assuming that all drivers are fully cooperative to minimize the total cost (e.g., travel time) of the system. It was widely believed in the past that DSO is less realistic than DUE, which however could provide a benchmark to develop and compare network-wide transportation management strategies such as congestion pricing. The iUTS team has developed continuous-time DSO models that integrates the link-based double queue model. In particular, we showed the solution properties and existence of free-flow DSO models in which all drivers would wait at the origins instead of in the network. Such free-flow DSO solutions are easier to compute and may play some important role in developing future dynamic traffic network management strategies especially when connected and automated vehicles (CAVs) are widely deployed. We also applied the DSO models to network-wide emission pricing and control, and the emergency evaluation planning for Lower Manhattan of the New York City.

Modeling the Network Effect of Shared Mobility

Emerging shared mobility services such as e-hailing, transportation network companies (TNCs), and ridesourcing and ridesharing, are rapidly changing the way how people travel in urban areas. There are however uncertainty regarding how these new services will impact congestion, energy use, and emissions at a network level, as well as how they will compete or complement the public transportation system. The iUTS team has worked on developing network models to capture and quantify those network effects of shared mobility services, including network-level congestion and how they may cooperate with transit to better solve the first-mile and last-mile transit problems.

Traffic Signal Control and Optimization with Connected and Automated Vehicles

The wide deployment of CAVs may profoundly change the look of urban traffic and the way how it is controlled. There are also uncertainties about how CAV technology may evolve and deployed, as well as challenges on understanding the dynamics/interactions of CAVs and human driven vehicles (HDVs). iUTS recently investigated the modeling of CAVs and HDVs on transportation networks, developed reinforcement-learning based eco-driving methods for a single CAV to save energy, and synthesized recent CAV-based urban traffic control studies and summarized the most critical gaps for future research.

By collaborating with vehicle control experts, iUTS developed CAV-based methods to optimize traffic signal timing plans by considering the driving and fuel consumption characteristics of individual vehicles. Some key features of the study include: (i) fixed cycle length so that signal coordination can be done readily for multiple intersection; (ii) different types of vehicles (such as gasoline cars and trucks, electric vehicles, buses, etc.) with their distinct fuel consumption characteristics; (iii) an optimization model that can be approximated as a dynamic programming (DP) problem, with a two-step method to guarantee the fixed-cycle-length solution.

When all vehicles are automated vehicles, the iUTS team, via collaborations with vehicle experts from Tsinghua University, worked on developing a cooperative method for the simultaneous optimization of traffic signal timing (macro level) and vehicle control (micro level), by considering two objectives: transportation efficiency and vehicle fuel consumption. We consider transportation efficiency at the macro signal timing control level and fuel economy at the micro vehicle control level. This also implies that the primary goal of the proposed method is to ensure the efficiency of all vehicles, while at the same time to minimize vehicle fuel consumption. Such consideration helps decompose the method into two interactive components, which makes the cooperative method easier to construct and solve. The results of this research received the Best Paper Award (2nd Prize) from the IEEE Intelligent Vehicles Symposium 2017. The paper is titled “V2I Based Cooperation between Traffic Signal and Approaching Automated Vehicles”, and is one of the two papers selected from over 300 papers submitted to the Symposium.

Publications

Guo, Q * , Ban, X. , Aziz, H.M.A., 2021. Mixed traffic flow of human driven vehicles and connected/automated vehicles on a dynamic transportation network. Transportation Research Part C 128, 103159 ( https://doi.org/10.1016/j.trc.2021.103159 ); To be presented at the International Symposium on Transportation and Traffic Theory (ISTTT) 2022.
Yang, X. , Ma, R., Yang. P., Ban, X. , 2021. Link Travel Time Estimation in Double-Queue-Based Traffic Models. Journal Promet – Traffic&Transportation , accepted.
Guo, Q. * , Angah, O. 1 , Liu, Z. 2 , Ban, X. , 2021. Hybrid deep reinforcement learning based eco-driving for low-level connected and automated vehicles. Transportation Research Part C 124, 102980.
Guo, Q. * , Ban, X. , 2020. Macroscopic fundamental diagram based perimeter control considering dynamic user equilibrium. Transportation Research Part B 136, 87-109.
Li, W. 1 , Ban, X . , Zheng, J., Liu, H., Cheng, G., Li, Y., 2020. A deep learning approach for real-time traffic volume prediction at signalized intersection. Journal of Transportation Engineering , 146(8): 04020081.
Li, W. * , Ban, X. , 2020. Connected vehicle based traffic signal coordination. Engineering 6(12), 1463-1472.
Li, W. * , Wang, J. * , Fan, R. * , Guo, Q. * , Zhang, Y. * , Siddique, N. * , Ban, X., 2020. Short-term traffic state prediction from latent structures: accuracy vs. efficiency. Transportation Research Part C 111, 72-90.
Ban, X. , Dessouky, M., Pang, J.S., Fan, R. * , 2019. A general equilibrium model for transportation systems with e-hailing services and flow congestion. Transportation Research Part B 129, 273-304.
Di, X. , Ban, X. , 2019. A mixed link-node and path formulation for equilibrium of new mobility systems. Transportation Research Part B 129, 50-78.
Wang, J.P. * , Huang, H.J. , Ban, X. , 2019. Optimal capacity allocation for high occupancy vehicle (HOV) lane in morning commute. Physica A 524, 354-361.
Guo, Q. * , Li, L. , Ban, X. , 2019. Urban traffic signal control with connected and automated vehicles: A survey. Transportation Research Part C 101, 313-334.
Wang, J.P.*, Ban, X. , Huang, H.J., 2019. Dynamic ridesharing with variable-ratio charging-compensation scheme for morning commute. Transportation Research Part B 122, 390-415.
Li, W. * , Ban, X. , 2019. Connected vehicle based traffic signal timing optimization. IEEE Transactions on Intelligent Transportation Systems 20(12), 4354-4366.
Xu, B.*, Li, S.E., Bian, Y., Li, S., Ban, X. , Wang, J., Li, K. , 2018. Distributed conflict-free cooperation for multiple connected vehicles at unsignalized intersections. Transportation Research Part C 93, 322-334 .
Xu, B. * , Ban, X. , Bian, Y., Li, W.*, Wang, J., Li, K. , 2018. Cooperative method of traffic signal optimization and speed control of connected vehicles at isolated intersections. I EEE Transactions on Intelligent Transportation Systems 20 (4), 1390-1403.
Di., X. , Ma, R., Liu, X., Ban, X. , Yang, H., 2018. Network design for ridesharing user equilibrium. Transportation Research Part B 112, 230-255.
Yang, X. * , Ban, X. , Mitchell, J., 2018. Modeling multimodal transportation network emergency evacuation considering evacuees’ cooperative behavior. Transportation Research Part A 114(B), 380-397.
Ma, R. * , Ban, X. , Pang, J.S., 2018. A link-based dynamic complementarity system formulation for continuous-time dynamic user equilibria with queue spillbacks. Transportation Science 52(3), 564-592.
Ji. X.F.*, Ban, X. , Zhang, J., Ran, B., 2017. Subjective-utility travel time budget modeling in the stochastic traffic network assignment. Journal of Intelligent Transportation Systems , Accepted.
Yang, X.*, Ban, X. , Mitchell, J., 2017. Modeling multimodal transportation network emergency evacuation considering evacuees’ cooperative behavior. Transportation Research, Part A , Accepted.
Ma, R.*, Ban, X. , Pang, J.S., 2017. A Link-Based Dynamic Complementarity System Formulation for Continuous-time Dynamic User Equilibria with Queue Spillbacks. Transportation Science , accepted.
Di, X., Liu, H, Ban, X. , Yang, H., 2017. Ridersharing user equilibrium and its implications for High-Occupancy-Toll lane pricing. Transportation Research Record , accepted.
Ji. X.F.*, Ban, X. , Li, M., Zhang, J., Ran, B., 2017. Non-expected route choice model under risk on stochastic traffic networks. Networks and Spatial Economics , in press. DOI: 10.1007/s11067-017-9344-3.
Yang, X.*, Ban, X. , Ma, R.*, 2017. Mixed equilibria with common constraints on transportation networks. Networks and Spatial Economics 17(2), 547-579.
Ma, R.*, Ban, X. , Szeto, W.Y., 2017. Emission modeling and pricing on single-destination dynamic traffic networks. Transportation Research Part B 100, 255-283.
Luo, L., Ge, Y., Zhang, F., Ban, X. , 2016. Real-Time Route Diversion Control in a Model Predictive Control Framework with Multiple Objectives: Traffic Efficiency, Emission Reduction and Fuel Economy. Transportation Research Part D 48, 332-356.
Di, X., Liu, H., Ban, X. , 2016. Second best toll pricing within the framework of bounded rationality. Transportation Research Part B 83, 74-90.
Zhao, J., Li, W.*, Wang, J., Ban, X. , 2016. Dynamic Traffic Signal Timing Optimization Strategy Incorporating Various Vehicle Fuel Consumption Characteristics. IEEE Transactions on Vehicular Technology 65 (6), 3874-3887.
Sánchez-Díaz, I., Holguin-Veras, J., Ban, X. , 2015. A time-dependent freight tour synthesis model. Transportation Research Part B , 78, 144-168.
Sun, Z.*, Ban, X. , Hao, P.*, Yang, D., 2015. Trajectory-based vehicle energy/emission estimation for signalized arterials using mobile sensing data. Transportation Research Part D 34, 27-40.
Ma, R.*, Ban, X. , Pang, J.S., Liu, X., 2015. Approximating time delays in solving continuous-time dynamic user equilibria. Networks and Spatial Economics 15(3), 443-463.
Ma, R.*, Ban, X. , Pang, J.S., Liu, X., 2015. Time discretization of continuous-time dynamic network loading models. Networks and Spatial Economics 15(3), 419-441.
Yushimito, W.*, Ban, X. , Holguin-Veras, J., 2015. Correcting the market failure in work trips with work rescheduling: an analysis using bi-level models for the firm-workers interplay, Networks and Spatial Economics 15(3), 883-915.
Ge, Y.E., Stewart, K., Sun, B., Ban, X. , Zhang, S., 2014. Investigating undesired spatial and temporal boundary effects of congestion charging. Transportmetrica B: Dynamics , in press.
Ma, R.*, Ban, X. , Pang, J.S., 2014. Continuous-time dynamic system optimal for single-destination traffic networks with queue spillbacks. Transportation Research Part B 68, 98-122.
Yushimito, W.*, Ban, X. , and Holguin-Veras, J., 2014. A two stage optimization model for staggered work hours. Journal of Intelligent Transportation Systems 18(4), 410-425.
Sanchez, I., Holguin-Veras, J., and Ban, X. , 2014. A time-dependent freight tour synthesis model. In Proceedings of the 93rd Annual Meeting of Transportation Research Board, Washington, DC.
Yushimito, W.*, Ban, X. , Holguin-Veras, J., 2013. Correcting the market failure in work trips with work rescheduling: an analysis using bi-level models for the firm-workers interplay, Networks and Spatial Economics , in press. DOI: 10.1007/s11067-013-9213-7.
Di, X., Liu, H., Ban, X ., and Yu, J.W., 2013. One the stability of a boundedly rational day to day dynamic. Networks and Spatial Economics , in press. DOI: 10.1007/s11067-014-9233-y.
Di, X., Liu, H., Pang, J.S., and Ban, X. , 2013. Boundedly rational user equilibria (BRUE): Mathematical formulation and solution sets. Transportation Research Part B 57, 300-313.
Ban, X. , Ferris, M.C., Tang, L., and Lu, S. , 2013. Risk-neutral second best toll pricing. Transportation Research Part B , 48(2), 67-87.
Ban, X. , Pang, J.S., Liu, X., and Ma, R.*, 2012. Continuous-time Point-Queue Models in Dynamic Network Loading. Transportation Research Part B , 46(3), 360-380.
Ban, X. , Pang, J.S ., Liu, X., and Ma, R.*, 2012. Modeling and Solution of Continuous-Time Instantaneous Dynamic User Equilibria: A Differential Complementarity Systems Approach. Transportation Research Part B , 46(3), 389-408.
Ban, X., Ferris, M., Liu, H., 2010. Numerical studies on reformulation techniques for continuous network design problems with asymmetric user equilibrium. International Journal of Operations Research and Information Systems , 1(1), 52-72.
Yushimito , W.F., Ban, X. , and Holguin-Veras, J. , 2010. Staggered work hours: a bi-level model and the role of incentives. In Proceedings of the 3rd International Symposium on Dynamic Traffic Assignment.
Ban, X. , and Liu, H., 2009. A link-node discrete-time dynamic second best toll pricing model with a relaxation solution algorithm. Networks and Spatial Economics 9(2), 243-267.
Ban, X., Liu, H., Ferris, M.C. , and Ran, B. , 2008. A link-node complementarity model and solution algorithm for dynamic user equilibria with exact flow propagations. Transportation Research, part B , 42(9), 823-842.
Ban, X. , and Liu, H., 2007. A link-node discrete-time dynamic second best toll pricing model with a relaxation solution algorithm. Presented at the 86th Transportation Research Board Annual Meeting and submitted for publication .
Ban, X. , Liu, H., and Ran, B., 2005. A link based quasi-variational inequality model for dynamic user equilibria, towards real time traffic operations. In Proceedings of the 8th IEEE International Conference on Intelligent Transportation Systems (CD-ROM) .
Yang, F., Liu, H., H, R., Ban, X , and Ran, B., 2003. Bi-level formulation for optimal traffic information dissemination. Transportation Research Record 1836, 21-28.
Liu, H., Ban, X. , Ran, B., and Mirchandani, P. , 2003. Formulation and solution algorithm for fuzzy dynamic traffic assignment model. Transportation Research Record 1854, 114-123.
Liu, H. , Ban, X. , Ran, B. , and Mirchandani , P., 2002. Analytical dynamic traffic assignment model with probabilistic network and travelers’ perceptions. Transportation Research Record 1783, 125-133.

Notes: * indicates graduate students Dr. Ban has advised or visiting students he has supervised.

NORTHWESTERN UNIVERSITY TRANSPORTATION CENTER

Core Topics

Transportation Network Modeling and Planning

Airspace congestion, flow relations, and 4-d fundamental diagrams for advanced urban air mobility.

Researcher(s): Christopher Cummings, Hani Mahmassani Year: 2023

This paper develops theoretical macroscopic air traffic flow models that relate vehicle density and spacing to traffic flow (throughput) measures under different operational parameters for unstructured airspace in the Advanced Air Mobility (AAM) context. Recognizing the role of conflicts in air traffic flow, we relate vehicle density to the frequency of conflict occurrence in airspace using a gas-kinetic analogy. The number of conflicts is then related to vehicle speeds using an average speed loss per conflict. The effects of the speed reductions are coupled with density to explore the fundamental diagram between flow rate and density. The theoretical models are tested and validated with simulated results for a number of parameter levels. The models can be applied for quick predictions of future traffic flow conditions, which will be especially useful for operators or air traffic flow management systems. The theoretical and simulated findings also provide operational and policy insights for AAM operators, planners, and modelers. Notable insights include the critical role of aircraft density in air traffic flow and the variable impact of that density on traffic flow behavior. AAM operators and planners will need to closely manage the airspace density to avoid large numbers of conflicts simultaneously and maintain acceptable travel times and throughputs. Key operational parameters such as aircraft spacing requirements and maximum aircraft speeds were also found to have significant impacts on traffic flow behavior, and offer policy avenues for managing air traffic.

Read the full publication

Highway Managed Lane Usage and Tolling for Mixed Traffic Flows with Connected Automated Vehicles and High-Occupancy Vehicles

Researcher(s): Max Ng, Hani Mahmassani Year: 2023

This paper investigates managed lane toll setting and its effect under mixed traffic of connected automated vehicles (CAVs), high-occupancy vehicles (HOVs), and human-driven vehicles (HDVs), with the goal of avoiding flow breakdown and minimizing total social cost. A mesoscopic finite difference traffic simulation model considers the flow–density relationship at different CAV market penetration rates, lane-changing behaviors, and multiple entries/exits, interacting with a reactive toll setting mechanism. The results of Monte Carlo simulation suggest an optimal policy of untolled HOV/CAV use with tolled HDVs in particular scenarios of limited CAV market penetration. Small and targeted tolling avoids flow breakdown in managed lanes while prioritizing HOVs and other vehicles with high values of time. Extensions of the formulation and sensitivity analysis quantify the benefits of converting high-occupancy HDVs to CAVs. The optimal tolling regime combines traffic science notions of flow stability and the economics of resource allocation.

Comparing Urban Air Mobility Network Airspaces: Experiments and Insights

Urban air mobility (UAM) systems include a network of (un)structured airspaces. The geometry and operations on these networks affect system performance across several goals including safety, efficiency, and externalities. The primary goal of this work is to find and illustrate the safety, efficiency, and externality trade-offs between different styles of network architecture. To do so, this paper uses a microscopic traffic simulator for UAM aircraft to experiment with different network architectures. Key performance measures reflecting the varied system goals are considered. Comparisons of network performance at varying demand levels illustrate the different behavior of traffic and congestion for each network architecture. The results indicate that there is no one-size-fits-all solution for network designs, rather there are trade-offs between designs. Fewer network restrictions and organization allow for routing efficiencies at the cost of a higher conflict rate and greater congestion at high demand levels. Greater network restrictions and organization can reduce the conflict rate and effectively manage high levels of demand but may suffer from locally concentrated conflicts and trajectories in addition to routing inefficiency. The insights will interest airspace researchers, regulators, and UAM operators as they consider appropriate future designs of airspace to accommodate UAM operations.

Reliable trajectory-adaptive routing strategies in stochastic, time-varying networks with generalized correlations

Researcher(s): Monika Filipovska, Hani Mahmassani Year: 2021

This paper focuses on the problem of finding optimal trajectory-adaptive routing strategies in stochastic time-varying networks with generalized spatio-temporal correlations. A representation for jointly distributed continuous link travel times across the entire network with time-varying distributions and correlation structures is presented, and the crucial characteristics and methodological difficulties of the problem are discussed. The paper presents a generalized 2-stage path and strategy finding solution approach that can serve for finding both exact and approximate solutions with the tuning of a risk-level tolerance parameter. The first stage of the solution approach generates eligible paths, where the risk-level parameter is used to eliminate paths that are likely to be inefficient. The second stage finds reliable trajectory-adaptive strategies, using the eligible paths only, based on one or multiple reliability-based optimality conditions. Thus, the approach allows the user to determine the optimal strategy for one or multiple groups of travelers with different reliability preferences. Numerical experiments show that the average running time of the algorithm reduces super-linearly with the increase of the risk-tolerance parameter ∊, while incurring some loss to the objective function relative to the exact solution. Thus, the heuristic can offer significant benefits in reducing the run time of the solution algorithm, while finding adaptive strategy solutions that consistently maintain better objective function values compared to the a priori (i.e., non-adaptive) solutions.

Anomalous Diffusion and the Structure of Human Transportation Networks

Researcher(s): Dirk Brockmann Year: 2008

The dispersal of individuals of a species is the key driving force of various spatiotemporal phenomena which occur on geographical scales. It can synchronise populations of interacting species, stabilise them, and diversify gene pools [1–3]. The geographic spread of human infectious diseases such as influenza, measles and the recent severe acute respiratory syndrome (SARS) is essentially promoted by human travel which occurs on many length scales and is sustained by a variety of means of transportation [4–8]. In the light of increasing international trade, intensified human traffic, and an imminent influenza A pandemic the knowledge of dynamical and statistical properties of human dispersal is of fundamental importance and acute [7,9,10]. A quantitative statistical theory for human travel and concomitant reliable forecasts would substantially improve and extend existing prevention strategies. Despite its crucial role, a quantitative assessment of human dispersal remains elusive and the opinion that humans disperse diffusively still prevails in many models [11]. In this chapter I will report on a recently developed technique which permits a solid and quantitative assessment of human dispersal on geographical scales [12]. The key idea is to infer the statistical properties of human travel by analysing the geographic circulation of individual bank notes for which comprehensive datasets are collected at the online bill-tracking website www.wheresgeorge.com. The analysis shows that the distribution of travelling distances decays as a power law, indicating that the movement of bank notes is reminiscent of superdiffusive, scale free random walks known as L`evy flights [13]. Secondly, the probability of remaining in a small, spatially confined region for a time T is dominated by heavy tails which attenuate superdiffusive dispersal. I will show that the dispersal of bank notes can be described on many spatiotemporal scales by a two parameter continuous time random walk (CTRW) model to a surprising accuracy. To this end, I will provide a brief introduction to continuous time random walk theory [14] and will show that human dispersal is an ambivalent, effectively superdiffusive process.

Crowdsourcing Service-level Network Event Monitoring

Researcher(s): David R. Choffnes, Fabián E. Bustamante, Zihui Ge Year: 2010

The user experience for networked applications is becoming a key benchmark for customers and network providers. Perceived user experience is largely determined by the frequency, duration and severity of network events that impact a service. While today’s networks implement sophisticated infrastructure that issues alarms for most failures, there remains a class of silent outages (e.g., caused by configuration errors) that are not detected. Further, existing alarms provide little information to help operators understand the impact of network events on services. Attempts to address this through infrastructure that monitors end-to-end performance for customers have been hampered by the cost of deployment and by the volume of data generated by these solutions. We present an alternative approach that pushes monitoring to applications on end systems and uses their collective view to detect network events and their impact on services - an approach we call Crowdsourcing Event Monitoring (CEM). This paper presents a general framework for CEM systems and demonstrates its effectiveness for a P2P application using a large dataset gathered from BitTorrent users and confirmed network events from two ISPs. We discuss how we designed and deployed a prototype CEM implementation as an extension to BitTorrent. This system performs online service-level network event detection through passive monitoring and correlation of performance in end-users’ applications.

Field Test of a Method for Finding Consistent Route Flows and Multiple-Class Link Flows in Road Traffic Assignments

Researcher(s): David Boyce, Yu (Marco) Nie, Hillel Bar-Gera, Yang Liu, and Yucong Hu Year: 2010

Road traffic assignment, or forecasting route and link flows corresponding to fixed matrices of origin-destination (OD) flows by vehicle class on a road network for a given time period, is commonly applied by transportation planning practitioners. The standard user-equilibrium traffic assignment method uniquely determines the total flow on each network link, subject to convergence errors. Multiple-class link flows and route flows, however, are indeterminate. To ensure that route and multiple-class link flows are uniquely determined, or consistent, an additional assumption is required. One option is that proportions of flow over alternative route segments with equal costs are the same for all drivers, regardless of origin or destination. Analyses based on the assigned link and route flows by vehicle class, such as select link, select zone and emissions analyses, are often performed without considering this issue. Although such analyses have become important in practice, no commercial software system currently considers the indeterminacy of these flows.

Traffic Assignment by Paired Alternative Segments (TAPAS) is a new algorithm offering the first practical way to address this issue. In this project six practitioners analyzed how route flows and/or multiple-class link flows generated by TAPAS compared with those found by the commercial software systems. A specialized tool VPAS was developed to compare the outputs of TAPAS and the practitioner software. The project team also undertook its own case study of the Chicago region with tools offered by four commercial software systems, which may be classified into two groups: link-based and quick-precision. Link-based tools applied in the project were CUBE, EMME, and TransCAD; quick precision tools applied were VISUM’s route-based method and TransCAD’s origin user-equilibrium (OUE) method. Findings of these applications may be summarized as follows:

Select link results for link-based tools were approximately similar to those found by TAPAS; differences in flows through a selected link by OD pair were relatively small. However, small flows were observed in link-based solutions on non-equilibrium routes not found in the more precise TAPAS solutions. As a result, the number of OD pairs using a select link was often much larger for link-based tools than for TAPAS. Analyses of flows on pairs of equal-cost segments showed that link-based solutions tended to satisfy approximately the proportionality condition. Slow convergence, however, is a costly limitation of link-based tools. Even so, the findings suggest that link-based tools do provide approximately proportional solutions, which was not realized before this project.
Select link results for quick-precision tools were very different from those produced by TAPAS. In particular, where TAPAS predicted positive flows, quick-precision tools often gave zero flow from an OD pair through a selected link. Analyses of flows on pairs of equal-cost segments showed that quick-precision tools produced solutions that violate the proportionality condition. In two-class assignments for pairs of alternative segments, the proportions of flow found by quick-precision solutions were also different by class.

Hub-and-Spoke Network Alliances and Mergers: Price-Location Competition in the Airline Industry

Researcher(s): Nicole Adler, Karen Smilowitz Year: 2007

This paper presents a framework to analyze global alliances and mergers in the airline industry under competition. The framework can help airlines identify partners and network structures, and help governments predict changes in social welfare before accepting or rejecting proposed mergers or alliances. The research combines profit-maximizing objectives to cost-based network design formulations within a game theoretic framework. The resulting analysis enables merging airlines to choose appropriate international hubs for their integrated network based on their own and their competitors’ costs and revenues in the form of best response functions. The results of an illustrative example suggest that some mergers may be more successful than others and optimal international gateway choices change according to the number of competitors remaining in the market. Furthermore, although the pressure on airlines would suggest a strong preference for mergers or alliances, perhaps surprisingly, the solution outcomes whereby all airlines merge or ally are not equilibria in the overall game.

Improving Our Understanding of How Pricing and Congestion Affect Travel Demand

Researcher(s): Hani Mahmassani Year: 2010

Dr. Mahmassani serves as co-PI on this study, awarded by the National Academy of Science to PB Americas, Inc. (with Northwestern University Transportation Center). The work plan can be conceptualized in three interconnected levels of behavioral rigor and practical application, with varying levels of sophistication:

Level 1 – Behavioral Foundations. The first level corresponds to behavioral models intended for a deep understanding and quantitative exploration of travel behavior. These models seek to address the full range of possible short and long‐term responses, but also may focus on select choice dimensions (for example, route and departure time choices, or usual workplace location choice).

Level 2 – Advanced Operational. The second level relates to relatively advanced, yet operational, Activity‐Based (AB) models, integrated with state of the art DTA (Dynamic Traffic Assignment) models. These models allows for the incorporation of a wide range of possible short‐ and long‐term responses that are embedded in the choice hierarchy. The integrity of operational models requires that each and every choice dimension should be allocated a proper “slot” in the hierarchy, with upward and downward linkages to related choices. Operational/computing time requirements often limit the total number of choice dimensions and alternatives, but this restriction is lessening with time.

Level 3 – Opportunities for Prevailing Practice. The third level relates to existing model systems used by most of MPOs and state DOTs, in the form of aggregate trip-based models (frequently referred to as 4-step models). Though rather restrictive in design, such models offer opportunities for meaningful and immediate contributions to the state of travel demand modeling practice. A serious restriction of 4‐step models is that these rely on static assignment procedures. Static assignments generate only crude average travel time and cost variables, and reliability can be incorporated only through certain proxies.

The SHRP 2 C04 project has completed an inventory of available datasets to support the research, and demonstrated an integrated application of user response models with a simulation-based DTA platform for the New York region Best Practice Model network.

Incorporating Reliability Performance Measures in Operations and Planning Modeling Tools

Researcher(s): Hani Mahmassani Year: 2009

Dr. Mahmassani is one of three principal investigators on the team led by Delcan, Inc. to undertake this project. Northwestern’s role focuses on the theoretical and methodological underpinnings of integrated supply-demand models that incorporate reliability. The objectives are to advance the state of the art in planning and operations models to produce measures of reliability performance of proposed system changes, and determine how travel demand forecasting models can use reliability measures to produce more realistic estimates of travel patterns. Project L04 draws on the quantitative measures of reliability as well as the impacts of reliability on route choice, time-of-day choice, and mode choice substantiated in “Improving Our Understanding of How Highway Congestion and Pricing Affect Travel Demand, SHRP2 C04”.

This project is developing approaches and tools to incorporate reliability as an input as well a key output in traffic models used for both operations and planning applications. A unifying framework for reliability analysis is proposed, applicable in conjunction with any particle-based micro- or meso- simulation model that produces trajectories. Vehicle trajectories are introduced and discussed as a central building block in this framework. The methodology is demonstrated using a simulation-based DTA platform.

In addition, to capture travel time variability introduced by random events, a repeatable framework is developed for modeling and evaluating incidents and events. A key variability-inducing phenomenon is traffic flow breakdown, which is modeled as an inherently stochastic phenomenon with structural dependence on state variables of the system. Reliability-improving measures highlighted in the report include information supply and dynamic pricing, whose effectiveness increases considerably when applied in real-time on the basis of predicted conditions.

Finally, possible applications of travel time reliability in operations-oriented models are presented.

Incorporating Weather Impacts in Traffic Estimation and Prediction Systems

Dr. Mahmassani served as PI for this study conducted for FHWA under a subcontract to SAIC, Inc. The objectives of the project are to develop weather-sensitive traffic prediction and estimation models and incorporate them in existing traffic estimation and prediction systems. This includes enhancement of the capabilities in mesoscopic DTA tools to model traffic behavior under inclement weather, and capture user responses to inclement weather with and without the presence of advisory and control strategies.

As a result of this project, The DYNASMART TrEPS can now capture the effects of adverse weather on traffic patterns through both supply and demand side modifications to the model. New weather‐related features in DYNASMART include:

Weather Scenario Specification : DYNASMART allows users to specify various weather scenarios for the study network. It can be represented as either the network-wide weather condition or the link‐specific weather condition.

Weather Adjustment Factor : Users can define the effect of weather on supply‐side traffic parameters such as free flow speed and capacity based on three weather condition parameters: visibility (mile), rain precipitation intensity (inch/hr) and snow precipitation intensity (inch/hr) by means of Weather Adjustment Factors (WAF). DYNASMART applies user‐specified WAF to 18 supply‐side traffic properties for links within the impacted region to simulate traffic conditions under the weather condition. WAF can be obtained based on calibrated weather‐traffic flow relation.

Modeling Traffic Advisory and Control via Variable Message Signs (VMS) : DYNASMART provides three weather‐related VMS operation functionalities: (1) Speed Reduction Warning – via a VMS warning sign indicating low visibility (e.g., fog) or slippery road (e.g. rain and snow), speed reduction behavior under adverse weather can be simulated; (2) Optional Detour – VMS suggests that travelers re-evaluate their current route based on the generalized cost that includes travel penalties of the added delays caused by adverse weather; and (3) Variable Speed Limit (VSL) – in DYNASMART, vehicle speed can be regulated through the speed limits posted on VMS in correspondence with prevailing weather conditions.

Methodology for Transportation System Redundancy Analysis in the Greater Baltimore Region

Researcher(s): Hani Mahmassani Year: 2007

Dr. Mahmassani served as PI of this study, funded by the Baltimore Metropolitan Council. This study developed a regional dynamic network model for simulation-assignment applications to examine the ability of the transportation network and services to withstand shocks and disruptions resulting from natural or man-made hazards and events, ascertain the extent to which the system would be able to meet the mobility needs of the Greater Baltimore Region residents and businesses, and develop contingency measures and strategies to cope with the resulting travel demand patterns under constrained supply conditions. The project provides an example of how to build a large scale simulation platform given existing planning network model.

Network Design for Code Sharing

Researcher(s): Diego Klabjan Year: 2010

An airline from an alliance faces the daunting task of code sharing its flights. The challenge mainly lies in the sheer size of the itineraries that can be sold on the entire network of all alliance partners. We developed a network design approach based on discrete choice modeling of passengers' utilities. The solution recommends flights to code share. In comparison to existing designs, our solution attains up to 2% improved profit, which was evaluated by a commercial profitability model.

Network Positioning from the Edge: An Empirical Study of the Effectiveness of Network Positioning in P2P Systems

Researcher(s): David R. Choffnes, Mario A. Sanchez, Fabian E. Bustamante Year: 2010

Network positioning systems provide an important service to large-scale P2P systems, potentially enabling clients to achieve higher performance, reduce cross-ISP traffic and improve the robustness of the system to failures. Because traces representative of this environment are generally unavailable, and there is no platform suited for experimentation at the appropriate scale, network positioning systems have been commonly implemented and evaluated in simulation and on research testbeds. The performance of network positioning remains an open question for large deployments at the edges of the network.

This paper evaluates how four key classes of network positioning systems fare when deployed at scale and measured in P2P systems where they are used. Using 2 billion network measurements gathered from more than 43,000 IP addresses probing over 8 million other IPs worldwide, we show that network positioning exhibits noticeably worse performance than previously reported in studies conducted on research testbeds. To explain this result, we identify several key properties of this environment that call into question fundamental assumptions driving network positioning research.

Optimal Short-Range Routing of Vessels in a Seaway

Researcher(s): I.S. Dolinskaya, M. Kotinis, M.G. Parsons, R.L. Smith, R. L Year: 2009

An investigation of the optimal short-range routing of a vessel in a stationary random seaway is presented. The calculations are performed not only in head seas but also in oblique waves. The evaluation of the added drag is performed by computing the time average wave force acting on the vessel in the longitudinal direction. Subsequently, the added drag is superimposed on the steady drag experienced by the ship as it advances in calm water. In this manner, the fastest path between the origin point A and the destination point B can be evaluated, taking into account operational constraints. To obtain the fastest path between two points, the underlying structure and properties of the maximum mean attainable speed are analyzed. This detailed analysis allows us to demonstrate the fastest path for the problem without any operational constraints to be a straight line. Subsequently, the solution is reevaluated for scenarios where the original optimal path violates at least one of the operability criteria considered. For that case, a fastest path is found to be a path consisting of one waypoint, that is, a two line segment path. In addition to providing a closed-form fastest-path solution for the case of no operational constraints, a bound is provided for travel time error for more general speed functions in the case where a straight line path is followed.

Providing Reliable Route Guidance Using Chicago Data

Researcher(s): Yu (Marco) Nie, Xing Wu Year: 2009

New techniques offer the potential to improve travel reliability for motorists, freight carriers and parcel delivery firms. This project confronts challenges to the implementation of these techniques, and demonstrated their feasibility and benefits using real data from the Chicago metropolitan area, one of the largest transportation hubs in the US. Conceptually, the most reliable routes can be found by solving the Dynamic Shortest Path problem with On-Time arrival reliability (DSPOT). DSPOT has recently been formulated and solved using the dynamic programming technique. The proposed research addresses two important issues that currently preclude its implementation: 1) development of solution algorithms fast enough for on-line application, and 2) validation using real data. In this project, historical traffic data from the Gary-Chicago-Milwaukee 9GCM) traveler information system will be used to prepare dynamic probability mass functions of travel times, which are the key inputs to DSPOT. Then a prototype path search tool will be developed, which implements DSPOT based on GCM data. This toll will be made available to the public through the Artificial Intelligence Laboratory at the University of Illinois at Chicago. The ultimate goal of this project is to provide motorists and carrier with commercialized DSPOT products that will allow them to make tradeoffs between reliability and other costs and constraints. With the benefits and market value demonstrated through this project and further implementation stages, we believe that the related industries will be interested in adding DSPOT to their product offerings. These firms include but are not limited to the manufacturers of in-vehicle navigation systems, web companies that provide internet-based driving directions and software vendors that produce logistics for freight carriers.

REORIENT: Implementing Change in the European Railway Area

Researcher(s): Hani Mahmassani Year: 2006

Dr. Mahmassani led, with Dr. Elise Miller-Hooks of the University of Maryland, a $1.06Million effort as part of a $7.2M multi-national multi-partner consortium project. The REORIENT project assessed the process of transforming the European railways from nationally fragmented into internationally integrated rail operating systems as a consequence of the EC interoperability legislation. By so doing, it supported the EU policy of balancing modal split between road and rail freight transport.

The team led by Dr. Mahmassani, jointly with Dr. E. Miller-Hooks at the University of Maryland, had lead responsibility for developing and validating strategies for identifying and removing technological, cultural, social and managerial barriers facing the implementation of competitive intermodal rail freight services across national boundaries. As such, the team was in charge of developing the key recommendations that arose from the entire research effort. The recommendations are necessarily based on a comprehensive understanding of the operational, institutional and political context surrounding freight service in Europe. Sophisticated quantitative and qualitative analyses of the operational and social aspects of the freight system likewise compose another essential basis for essential basis for any recommendations.

Dr. Mahmassani’s team also served as coordinator of all network modeling activities needed to support the project, and led the process of building the corresponding network models and associated freight flow processes through the rail network links and intermodal transfer points, as well as the demand models for short and long term freight flow in the study area. This resulted in development of a novel network modeling platform to support evaluation of different strategies and measures intended to improve the prospects of rail freight in the corridor, as well as improvement of capacity and service levels. As such, the network modeling effort plays a critical role in supporting the business case development. In addition, the project led to development of novel ways of calibrating and estimating demand models combining various data sources at both macroscopic and microscopic levels. These activities cut across several other work packages led by other entities. The project also involves coming up with a collaborative decision-making framework by which different entities in different countries, including private service providers, can jointly manage complex systems in real time.

Relationship between Proximity to Transit and Ridership for Journey-to-Work Trips in Chicago

Researcher(s): Lindsey Marshall, Joseph L. Schofer, Pablo Durango-Cohen, Kimberly A. Gray Year: 2010

This circular summarizes discussions at a peer exchange of state department of transportation officials and other professionals that focused on data and information uses, management strategies, needs, and gaps in their organizations. The peer exchange examined the role of data and information in transportation decision making; identified information resources, gaps, and opportunities; and explored data, access, and analysis improvements for information resource programs. In addition, participants discusses possible strategies that the transportation community might use to implement such improvements.

Solving the Dynamic User Optimal Assignment Problem Considering Queue Spillback

Researcher(s): Yu Nie, H.M. Zhang Year: 2007

This paper studies the dynamic user optimal (DUO) traffic assignment problem considering simultaneous route and departure time choice. The DUO problem is formulated as a discrete variational inequality (DVI), with an embedded LWR-consistent mesoscopic dynamic network loading (DNL) model to encapsulate traffic dynamics. The presented DNL model is capable of capturing realistic traffic phenomena such a queue spillback. Various VI solution algorithms, particularly those based on feasible directions and a line search, are applied to solve the formulated DUO problem. Two examples are constructed to check equilibrium solutions obtained from numerical algorithms, to compare the performance of the algorithms, and to study the impacts of traffic interacts across multiple links on equilibrium solutions.

Stability of User-equilibrium Route Flow Solutions for the Traffic Assignment Problem

Researcher(s): Shu Lu, Yu Nie Year: 2010

This paper studies stability of user-equilibrium (UE) route flow solutions with respect to inputs to a traffic assignment problem, namely the travel demand and parameters in the link cost function. It shows, under certain continuity and strict monotonicity assumptions on the link cost function, that the UE link flow is a continuous function of the inputs, that the set of UE route flows is a continuous multifunction of the inputs, and that the UE route flow selected to maximize an objective function with certain properties is a continuous function of the inputs. The maximum entropy UE route flow is an example of the last. On the other hand, a UE route flow arbitrarily generated in a standard traffic assignment procedure may not bear such continuity property, as demonstrated by an example in this paper.

Toward More Reliable Mobility: Improved Decision Support Tools for Transportation Systems

Researcher(s): Yu Nie Year: 2010

The overarching goal of the project is to enhance travel reliability of highway users by providing them with reliable route guidance produced from newly developed routing algorithms that are validated and implemented with real traffic data. Phase I of the project (funded by CCITT in 2008) focused on demonstrating the value of reliable route guidance through the development of dissemination of Chicago Testbed for Reliable Routing (CTR). Phase II aims at bringing the implementation of reliable-routing technology to the next stage through initial deployment of CTR.

The first objective in Phase II is to create a travel reliability inventory (TRI) of Northeastern Illinois using CTR, by collaborating with public agencies such as the Illinois Department of Transportation (IDOT), Chicago Transit Authority (CTA) and Chicago Traffic Management Authority (CTMA). TRI documents travel reliability indices (e.g., 95 percentile route travel times) between heavily-traveled origins-destination pairs in the region, which are of interest not only to individual travel decision-making, but also regional transportation planning and traffic operations/management. The second objective is to perform and initial market test in order to understand users’ need for and response to reliability information and reliable route guidance.

To these ends, the following research activities are proposed to further develop CTR:

Implement and test latest reliable routing algorithms that are suitable for large-scale applications.
Develop a web-based version of CTR and host the service at Northwestern University’s Translab Website. A web survey will be designed and posted along with CTR in order to collect user feedback.
Explore the possibility of achieving a greater degree of data coverage of the study area. Specifically, archived automatic vehicle location (AVL) data of CTA’s bus fleet is considered an important data source to supplement GCM data and will receive a focal study.

Using Simulation to Test Traffic Incident Management Strategies: The Benefits of Preplanning

Researcher(s): John J. Wirtz, Joseph L. Schofer, David F. Schulz Year: 2005

This study tested a dynamic traffic assignment model as a tool for pre-planning strategies for managing major freeway incidents. Incidents of various scales and durations were modeled in the northern Chicago, Illinois, highway network, and the impacts of incidents and response actions were measured in lane mile hours of highway links at Level of Service F and spread of congestion to alternate routes around the incident. It was found that the best response action to a given incident scenario was not necessarily intuitive and that implementing the wrong response could worsen congestion on the directly impacted freeway and its surrounding highway network. The simulation model showed that a full closure of the freeway caused congestion to spread to alternate parallel routes around the simulated incident. An event of this scale constitutes a major disruption that may warrant handing off traffic control authority from first responders to a corridor or regional traffic management center. Major arterials accessible from the impacted freeway sometimes need increased capacity to provide access to less congested parallel alternate routes during incidents. The simulation model showed that congestion increases with delayed response, underscoring the benefits of preplanning to speed the implementation of effective incident response actions. Regression analysis using data generated by the simulation demonstrates that incident scale and duration are statistically significant predictors of lane mile hours of congestion in the zone near the incident and on the expressway.

IMAGES

Transportation, Assignment and Network Models
transportation and assignment models
Representation of the Transportation Network Model The linear
Transportation Assignment And Network Models
Chapter 5 Transportation Assignment and Network Models
PPT

VIDEO

Transportation & assignment problem
MAXIMIZING TRANSPORTATION + ASSIGNMENT
Assignment Network Communication
Transportation Assignment and Sensitivity Analysis Review Pt3of3
TTE332 Lec7 S2021- 4Step Transportation Planning Process: Trip Assignment /Network Assignment
Video Assignment: Talking about transportation and location

COMMENTS

PDF Transportation and Assignment Models
The transportation model is only the most elementary kind of minimum-cost flow model. More general models are often best expressed as networks, in which nodes — some of which may be origins or destinations — are connected by arcs that carry flows of some kind. AMPL offers convenient features for describing network flow models, includ-
PDF Transportation Network Design
Therefore, currently the network designis thought of as supply demand problem or leader-follower game.The system designer leads, taking into account how the user follow. The core of all network design problems is how a user chooses his route of travel. The class of traffic assignment problem tries to model these behaviour.
Chapter 5: Transportation, Assignment, and Network Models
Chapter 5: Transportation, Assignment, and Network Models was published in Managerial Decision Modeling on page 239.
Transportation Assignment And Network Models
Videos for the book "Quantitative Analysis for Management (13th Edition)"by Barry Render, Ralph M. Stair Jr., Michael E. Hanna, Trevor S. HaleIntroduces Prob...
Traffic Assignments to Transportation Networks
Section 3.1 introduces the assignment problem in transportation as the distribution of traffic in a network considering the demand between locations and the transport supply of the network. Four trip assignment models relevant to transportation are presented and characterized. Section 3.2 covers traffic assignment to uncongested networks based ...
Large-scale multimodal transportation network models and algorithms
Yang et al. (2000) further develop an equilibrium network capacity model with combined trip distribution and trip assignment to consider the travelers' route choice and location choice behaviors. In order to assess the capacity of multimodal transportation network, many works have been done on this topic.
PDF Chapter 5 Basic Static Assignment to Transportation Networks
Basic Static Assignment to Transportation Networks 5.1 Introduction Trafﬁc assignment models simulate the interaction of demand and supply on a trans-portation network. These models allow calculation of performance measures and user ﬂows for each supply element (network link), resulting from origin-destination
PDF Chapter 5: Linear Programming: Transportation and Assignment Models
The basic assumption of the model is that the transportation cost on a given route is directly proportional to the number of units transported. The figure above depicts the transportation model as a network with m sources and n destinations. A source or a destination is represented by a node. The arc joining a source and a
Chapter 9 Transportation, Assignment, and Network Models
Chapter 9 Transportation, Assignment, and Network Models Learning Objectives. After completing this chapter, students will be able to: 9.1 Construct LP problems for the transportation, assignment, and transshipment models.. 9.2 Solve facility location and other application problems with transportation models.. 9.3 Use LP to model and solve maximal-flow problems.
Large-scale multimodal transportation network models and algorithms
Such models are more in line with the characteristics of bus travel in practice (De Cea and Fernández, 1993, Marcotte and Nguyen, 1998, Schmöcker et al., 2011), however, they are more complex than the transit assignment models based on simple paths (similar to car paths) and lead to a heavy computational burden especially for large-scale ...
Network flow problem
Classical models such as the assignment, transportation, maximal flow, and shortest path problem configurations have found their way into diverse settings, ranging from streamlining oil distribution networks along the gulf coast to arranging optimal scheduling assignments for college students amidst a global pandemic.
Models for Traffic Assignment to Transportation Networks
Abstract. Models for traffic assignment to transportation networks simulate how demand and supply interact in transportation systems. These models allow the calculation of performance measures and user flows for each supply element (network link), resulting from origin-destination demand flows, path choice behavior, and the reciprocal ...
Large-scale multimodal transportation network models and algorithms
A more comprehensive multimodal urban transportation network is built, which includes three basic travel modes and two P&R modes. • We develop ageneral fixed-point (FP) model to formulate the combined mode split and traffic assignment (CMSTA) problem.
Introduction to Transportation Modeling: Travel Demand Modeling and
Figure 9.2 Land use and transportation network different patterns. Adapted from "Taking the Guesswork out of Designing for Walkability" by Xiongbing, J, Grammenos, F., ... Wardrop equilibrium is a state in traffic assignment model where are drivers are reluctant to change their path because the average travel time is at a minimum.
CH5 Transportation, Assignment, and Network Models
3.0 (1 review) Network flow models. Click the card to flip 👆. Special LP models (there are 6): transportation, transshipment, assignment, maximal-flow, shortest-path, minimal-spanning tree models. Consists of nodes and arcs. Examples: roadways, telephone systems, etc. Click the card to flip 👆. 1 / 30.
Transportation Networks and Smart Mobility: Methods and Solutions
This course presents theory of transportation modelling and simulation techniques, with a focus on Smart Mobility, AI and ML solutions and real-world applications. It provides an in-depth study of the most sophisticated traffic simulation models, demand modeling methods, and related discrete choice, machine learning analytical techniques.
#3- Transportation, Assignment and network models
338 CHAPTER 9 • TRAnSPoRTATion, ASSignmEnT, And nETwoRk modELS. trucks, and so forth) that can go through a network of roads from one location to another. The shortest-route technique can find the shortest path through a network. For example, this tech- nique can find the shortest route from one city to another through a network of roads.
Chapter 5 Transportation, Assignment, and Network Models
1. in all network models, the decision variables represent the amount of flows that occur on the one-way arcs. 2. there will be a flow balance constraint written for each node in the network (calculates net flow) origin node. (supply) denotes a location such as a factory that creates goods. destination node. (demand) denotes a location such as ...
Ch 9 Discussion Questions
Transportation, Assignment, and Network Models SOLUTIONS TO DISCUSSION QUESTIONS 9-1. The transportation model is an example of decision making under certainty where a decision maker knows beforehand exactly what state of nature will occur (see Chapter 3). In transportation problems, this means that the costs of each shipping route, the demand ...
Dynamic Transportation Network Modeling, Analysis, Simulation, and
DTN-MASC is to understand the behavior and interactions of major components/players in a multi-modal transportation network system, develop mathematical paradigms and tools to model such interactions and behavior, and design efficient solution methods. ... Formulation and solution algorithm for fuzzy dynamic traffic assignment model ...
Chapter 9
C H A. P T E. R 9. T ransportation, Assignment, and Network Models. TEACHING SUGGESTIONS. T eaching Suggestion 9.1: Transportation and Assignment Models. The linear programming approach is used for both the transportation problem and the assignment. problem. Students should be told that the transportation and assignment models are very.
Transportation Network Modeling and Planning
This study developed a regional dynamic network model for simulation-assignment applications to examine the ability of the transportation network and services to withstand shocks and disruptions resulting from natural or man-made hazards and events, ascertain the extent to which the system would be able to meet the mobility needs of the Greater ...
After a string of safety issues, Boeing is about to release a plan to
Boeing is expected to release a plan this week to fix its endless string of safety issues that have been under federal investigation following a midflight fuselage blowout in January.
Large-scale multimodal transportation network models and algorithms
Yang et al. (2000) further develop an equilibrium network capacity model with combined trip distribution and trip assignment to consider the travelers' route choice and location choice behaviors. In order to assess the capacity of multimodal transportation network, many works have been done on this topic.