All Subjects

study guides for every class
That actually explain what's on your next test, polya's problem-solving steps, from class:, thinking like a mathematician.
Polya's Problem-Solving Steps are a systematic approach to tackling mathematical problems, consisting of four key phases: understanding the problem, devising a plan, carrying out the plan, and reviewing the solution. This method emphasizes the importance of breaking down complex problems into manageable parts, which enhances clarity and leads to more effective solutions. By following these steps, problem solvers can develop a structured way of thinking that not only aids in finding answers but also deepens their understanding of mathematical concepts.
congrats on reading the definition of Polya's Problem-Solving Steps . now let's actually learn it.
5 Must Know Facts For Your Next Test
- The first step of Polya's approach is crucial because it involves comprehending all aspects of the problem, which sets the foundation for effective problem-solving.
- In devising a plan, solvers may choose from various strategies like drawing diagrams, making a table, or identifying patterns based on similar problems they have solved before.
- Carrying out the plan requires executing the chosen strategy carefully while being open to adjustments if the initial approach doesn’t lead to a solution.
- The review step is vital as it allows solvers to verify their answer and reflect on the methods used, fostering better learning for future problems.
- Polya's steps not only apply to mathematics but can also be utilized in real-life situations where critical thinking and systematic approaches are beneficial.
Review Questions
- Understanding the problem is essential because it allows the solver to identify what is being asked and determine relevant information and constraints. This initial phase sets the stage for devising an effective strategy. If the solver doesn't grasp what the problem entails, subsequent steps may be misguided or ineffective. A clear understanding helps to avoid misinterpretations and ensures that the chosen methods align with the actual requirements of the problem.
- Polya's Problem-Solving Steps can be adapted to various disciplines such as science, engineering, and even everyday decision-making. The structured approach of understanding a challenge, planning solutions, executing them, and reviewing outcomes fosters critical thinking skills applicable in numerous contexts. For instance, scientists may use these steps when designing experiments by clearly defining hypotheses and evaluating results systematically, similar to how mathematicians solve equations.
- Using Polya's Problem-Solving Steps significantly enhances a student's problem-solving capabilities by promoting a systematic framework that encourages deeper engagement with mathematical concepts. By breaking down complex problems into manageable parts and emphasizing reflection on solutions, students develop resilience and adaptability when faced with challenges. This method fosters independent thinking and equips students with tools to tackle unfamiliar problems confidently, leading to improved performance and a stronger grasp of mathematical reasoning.
Related terms
Heuristic : A strategy or technique that aids in problem-solving, often through trial and error or educated guesses.
Algorithm : A step-by-step procedure or formula for solving a problem, often used in mathematics and computer science.
Problem-Solving Strategy : A systematic approach to tackling a problem that includes techniques such as working backward, looking for patterns, or simplifying the problem.
" Polya's Problem-Solving Steps " also found in:
© 2024 fiveable inc. all rights reserved., ap® and sat® are trademarks registered by the college board, which is not affiliated with, and does not endorse this website..
|
(1887-1985), a Hungarian mathematician, wrote "How to solve it." for high school students in 1957. Here is his four step method. Read the problem over carefully and ask yourself: Do I know the meaning of all the words? What is being asked for? What is given in the problem? Is the given information sufficient (for the solution to be unique)? Is there some inconsistent or superfluous information which is given? By way of checking your understanding, try restating the problem in a different way. In essence, decide how you are going to work on the problem. This involves making some choices about what strategies to use. Some possible strategies are: -- making a picture which relates the information given to what is asked for can often lead to a solution. -- this is a strategy which is especially useful in problems where you need to count the members of a set. -- almost any problem can be made simpler in some way. By working out simpler versions, you can often see patterns which help solve the original problem. -- Many problems can be broken into a series of smaller problems. This strategy can turn a problem which on first glance seems intractable into something more doable. -- the method of algebra. Very useful in a lot of problems. : Spend a reasonable amount of time trying to solve the problem using your plan. If you are not successful, go back to step 2. If you run out of strategies, go back to step 1. If you still don't have any luck, talk the problem over with a classmate. After you have a proposed solution, check your solution out. Is it reasonable? Is it unique? Can you see an easier way to solve the problem? Can you generalize the problem?
|

- Mathematics
- Reading and Writing
- Intervention
- Professional Learning
- Virtual Events
- What is Phonics?
- Teaching Grammar
- Vocabulary Games
- What is Virtual Learning?
- About Sadlier
- Find a Sales Representative
- International Distributors
- International Programs
- Online Catalogs
- Sadlier School Site Map
- Pricing & Ordering Information
- Sadlier’s W-9
- Sadlier’s Sole Source Letter
- Sadlier’s Credit Application
- Privacy Policy
- Return Policy
- Terms & Conditions
Sadlier's Math Blog

- Counting and Cardinality
- Operations and Algebraic Thinking
- Number and Operations in Base 10
- Measurement and Data
- Math Practices
- Number and Operations Fractions
- Statistics and Probability
- The Number System
- Ratios and Proportional Relationships
- Expressions and Equations
- MP1—Problem Solving
- MP2—Abstract <−>Quantitative
- MP3—Reasoning
- MP4—Modeling
- MP5—Using Tools
- MP6—Precision
- MP7—Structure
- MP8—Repeated Reasoning
- Kindergarten Math Activities
- First Grade Math Activities
- Second Grade Math Activities
- Third Grade Math Activities
- Fourth Grade Math Activities
- Fifth Grade Math Activities
- Sixth Grade Math Activities
- Seventh Grade Math Activities
- Eighth Grade Math Activities
- Professional Development
- Test-Taking Strategies
- Classroom Posters
- Writing In Mathematics
April 19, 2023 3-5-operations-and-algebraic-thinking , k-2-operations-and-algebraic-thinking , 6-8-expressions-and-equations
Polya’s problem-solving process: finding unknowns elementary & middle school, by: jeff todd.
In this article, we'll explore how a focus on finding “unknowns” in math will lead to active problem-solving strategies for Kindergarten to Grade 8 classrooms. Through the lens of George Polya and his four-step problem-solving heuristic, I will discuss how you can apply the concept of finding unknowns to your classroom. Plus, download my Finding Unknowns in Elementary and Middle School Math Classes Tip Sheet .

It is unfortunate that in the United States mathematics has a reputation for being dry and uninteresting. I hear this more from adults than I do from children—in fact, I find that children are naturally curious about how math works and how it relates to the world around them. It is from adults that they get the idea that math is dry, boring, and unrelated to their lives. Despite what children may or may not hear about math, I focus on making instruction exciting and showing my students that math applicable to their lives.
Problem solving is a fundamental means of developing students' mathematical knowledge and it also shows them that math concepts apply to real-world concepts.
Problem solving is one way I show my students that math relates to their lives! Problem solving is a fundamental means of developing students' mathematical knowledge and it also shows them that math concepts apply to real-world concepts.
Who Is George Polya?
George Polya was a European-born scholar and mathematician who moved to the U.S in 1940, to work at Stanford University. When considering the his classroom experience of teaching mathematics, he noticed that students were not presented with a view of mathematics that excited and energized them. I know that I have felt this way many times in my teaching career and have often asked: How can I make this more engaging and yet still maintain rigor?
Polya suggested that math should be presented in the light of being able to solve problems. His 1944 book, How to Solve It contains his famous four-step problem solving heuristic. Polya suggests that by presenting mathematical thinking as a way to find “unknowns,” it becomes more engaging for students.
He even goes as far as to say that his general four-step problem-solving heuristic can be applied to any field of human endeavor—to any opportunity where a problem exists.
Polya suggested that math should be presented in the light of being able to solve problems...that by presenting mathematical thinking as a way to find “unknowns,” it becomes more engaging for students.
Polya specifically wrote about problem-solving at the high school mathematics level. For those of us teaching students in the elementary and middle school levels, finding ways to apply Polya’s problem-solving process as he intended forces us to rethink the way we teach.
Particularly in the lower grade levels, finding “unknowns” can be relegated to prealgebra and algebra courses in the later grades. Nonetheless, today’s standards call for algebra and algebraic thinking at early grade levels. The download for today’s post presents one way you can find unknowns at each grade level.
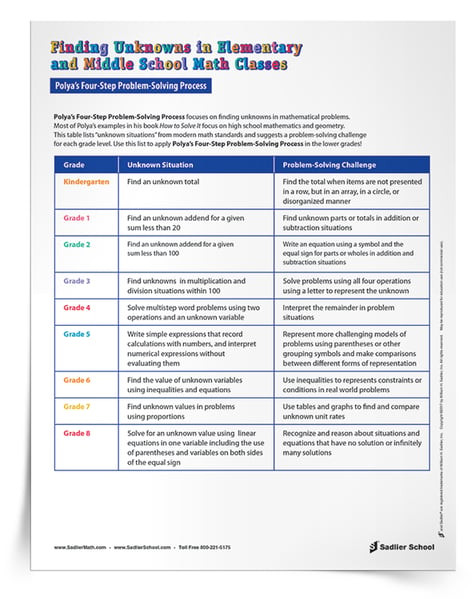
Presenting Mathematics As A Way To Find "Unknowns" In Real-Life Situations
I would like to share a conversation I had recently with my friend Stu. I have been spending my summers volunteering for a charitable organization in Central America that provides medical services for the poor, runs ESL classes, and operates a Pre-K to Grade 6 school. We were talking about the kind of professional development that I might provide the teachers, and he was intrigued by the thought that we could connect mathematical topics to real life. We specifically talked about the fact that he remembers little or nothing about how to find the area of a figure and never learned in school why it might be important to know about area. Math was presented to him as a set of rules and procedures rather than as a way to find unknowns in real-life situations.
That’s what I am talking about here, and it’s what I believe Polya was talking about. How can we create classrooms where students are able to use their mathematical knowledge to solve problems, whether real-life or purely mathematical?
As Polya noted, there are two ways that mathematics can be presented, either as deductive system of rules and procedures or as an inductive method of making mathematics. Both ways of thinking about mathematics have endured through the centuries, but at least in American education, there has been an emphasis on a procedural approach to math. Polya noticed this in the 1940s, and I think that although we have made progress, there is still an over-emphasis on skill and procedure at the expense of problem-solving and application.
I recently reread Polya’s book. I can’t say that it is an “easy” read, but I would say that it was valuable for me to revisit his own words in order to be sure I understood what he was advocating. As a result, I made the following outline of his problem-solving process and the questions he suggests we use with students.

Polya's Problem-Solving Process
1. understand the problem, and desiring the solution .
- Restate the problem
- Identify the principal parts of the problem
- Essential questions
- What is unknown?
- What data are available?
- What is the condition?
2. Devising a Problem-Solving Plan
- Look at the unknown and try to think of a familiar problem having the same or similar unknown
- Here is a problem related to yours and solved before. Can you use it?
- Can you restate the problem?
- Did you use all the data?
- Did you use the whole condition?
3. Carrying Out the Problem-Solving Plan
- Can you see that each step is correct?
- Can you prove that each step is correct?
4. Looking Back
- Can you check the result?
- Can you check the argument?
- Can you derive the result differently?
- Can you see the result in a glance?
- Can you use the result, or the method, for some other problem?
Polya's Suggestions For Helping Students Solve Problems
I also found four suggestions from Polya about what teachers can do to help students solve problems:
Suggestion One In order for students to understand the problem, the teacher must focus on fostering in students the desire to find a solution. Absent this motivation, it will always be a fight to get students to solve problems when they are not sure what to do.
Suggestion Two A second key feature of this first phase of problem-solving is giving students strategies forgetting acquainted with problems.
Suggestion Three Another suggestion is that teachers should help students learn strategies to be able to work toward a better understanding of any problem through experimentation.
Suggestion Four Finally, when students are not sure how to solve a problem, they need strategies to “hunt for the helpful idea.”
Whether you are thinking of problem-solving in a traditional sense (solving computational problems and geometric proofs, as illustrated in Polya’s book) or you are thinking of the kind of problem-solving students can do through STEAM activities, I can’t help but hear echoes of Polya in Standard for Math Practice 1: Make sense of problems and persevere in solving them.
Mathematically proficient students start by explaining to themselves the meaning of a problem and looking for entry points to its solution. They analyze givens, constraints, relationships, and goals. They make conjectures about the form and meaning of the solution and plan a solution pathway rather than simply jumping into a solution attempt. They consider analogous problems, and try special cases and simpler forms of the original problem in order to gain insight into its solution. They monitor and evaluate their progress and change course if necessary.
In Conclusion
We all know we should be fostering students’ problem-solving ability in our math classes. Polya’s focus on “finding unknowns” in math has wide applicability to problems whether they are purely mathematical or more general.
Grab my download and start applying Polya’s Four-Step Problem-Solving Process in the lower grades!
- My Dashboard

- Content: Polya’s Problem-Solving Method
Back to: Helping Students Do Math
The purpose of this tool for the field is to help paraprofessionals become more familiar with, and practice using, Polya’s four-step problem-solving method.

- Read the example below about Mrs. Byer’s class, and then look over the example of how Polya’s method was used to solve the problem.

Every person at a party of 12 people said hello to each of the other people at the party exactly once. How many “hellos” were said at the party?

A new burger restaurant offers two kinds of buns, three kinds of meats, and two types of condiments. How many different burger combinations are possible that have one type of bun, one type of meat, and one condiment type?
A family has five children. How many different gender combinations are possible, assuming that order matters? (For example, having four boys and then a girl is distinct from having a girl and then four boys.)
Hillary and Marco are both nurses at the city hospital. Hillary has every fifth day off, and Marco has off every Saturday (and only Saturdays). If both Hillary and Marco had today off, how many days will it be until the next day when they both have off?
Reflect on your experience.
- In which types of situations do you think students would find Polya’s method helpful?
- Are there types of problems for which students would find the method more cumbersome than it is helpful?
- Can you think of any students who would particularly benefit from a structured problem-solving approach such as Polya’s?
Background Information

Nearly 100 years ago, a man named George Polya designed a four-step method to solve all kinds of problems: Understand the problem, make a plan, execute the plan, and look back and reflect. Because the method is simple and generalizes well, it has become a classic method for solving problems. In fact, the method is applicable to all areas of our lives where we encounter problems—not just math. Although the method appears to be a straightforward method where you start at Step 1, and then go through Steps 2, 3, and 4, the reality is that you will often need to go back and forth through the four steps until you have solved and reflected on a problem.
Polya’s Problem-Solving Chart: An Example
A version of Polya’s problem-solving chart can be found below, complete with descriptions of each step and an illustration of how the method can be used systematically to solve the following problem:
Scenario
There are 22 students in Mrs. Byer’s third grade class. Every student is required to either play the recorder or sing in the choir, although students have the option of doing both. Eight of Mrs. Byer’s students chose to play the recorder, and 20 students sing in the choir. How many of Mrs. Byer’s students both play the recorder and sing in the choir?
|
|
|
|
| 1. Understand the problem. | Figure out what is being asked. What is known? What is not known? What type of answer is required? Is the problem similar to other problems you’ve seen? Are there any important terms for which you should look up definitions? | There are 22 total students. There are three groups of students: Students who only play recorder, students who only sing in choir, and students who do both. Initially, we do not know how many students are in any of these groups, but we know the total of the three groups adds up to 22. We also know that a total of 8 students play the recorder, and a total of 20 students sing in the choir. We must find the number of students who do both. |
| 2. Make a plan. | Come up with some strategies for solving the problem. Common strategies include making a list, drawing a picture, eliminating possibilities, using a formula, guessing and checking, and solving a simpler, related problem. | We could list out the 22 students and then assign to each either recorder, choir, or both until we got the right totals. We could draw a Venn Diagram that separates out the three types of groups. We could try solving a similar problem with a class of fewer students. |
| 3. Execute the plan. | Use the strategy chosen in Step 2 to solve the problem. If you encounter difficulties using the strategy, you may want to use resources such as the textbook to help. If the strategy itself appears not to be working, return to Step 2 and select a different strategy. | Let’s try solving a similar problem with a class of 6 students, 5 of whom play recorder and 3 of whom are in the choir. In this case, we know that there is only one student who doesn’t play recorder, and so this student must sing in the choir. That means the other two choir singers must play the recorder, so there are 2 students who do both. Now, let’s try that same method with the original problem. Since only 8 of the 22 students play recorder, the other 14 must sing in the choir and not play recorder. But there are 20 students in the choir, so 6 of these choir students also play the recorder. So the answer is 6. |
| 4. Look back and reflect. | Part of Step 4 is to find a way to check your answer, preferably using a different method than what you used to solve the problem. Another part of Step 4 is to evaluate the method you used to solve the problem. Was it effective? Are there ways you could have made it more effective? Are there other types of problems with which you might be able to use this type of solution method? |
Let’s check our answer with a Venn Diagram, which was one of the other strategies we considered in Step 2. We first fill in each region based on the results we found in Step 3. Now we check to see if the numbers match the original problem. Notice that 2 + 6 + 14 = 22 total students, 2 + 6 = 8 students playing the recorder, and 6 + 14 = 20 students in choir. So our answer checks out! Looking back on our answer, we now see that our process of subtracting from the total can be used in any similar situation, as long as all students must be in at least one of the two groups. In the future, we wouldn’t even have to use the simpler related problem since we’ve found a more general pattern! |
Helping Students Do Math
- Introductory Scenario and Pre-Test
- Content: Does Anyone Know What Math Is?
- Introductory Scenario
- Content: The Fennema-Sherman Attitude Scales
- Content: Past Experience with Math
- Content: Learning About Math
- Content: What is it like to teach math?
- Content: Using a Frayer Model
- Content: Helping a Child Learn from a Textbook
- Content: Using Online Math Resources
- Content: Helping a Student Learn to use a Calculator
- Links for More Information
- Content: Better Questions
- Content: Practice Asking Good Questions
- Content: Applying Poly’s Method to a Life Decision
- Content: Learning Progression Activities
- Content: Connecting Concepts and Procedures
- Content: Resources
- Activity: The Old Guy’s No-Math Test
- Take Notes and Post-Test
- Open All · Close All
Contact: [email protected]
The Ohio Partnership for Excellence in Paraprofessional Preparation is primarily supported through a grant with the Ohio Department of Education and Workforce, Office for Exceptional Children. Opinions expressed herein do not necessarily reflect those of the Ohio Department of Education or Offices within it, and you should not assume endorsement by the Ohio Department of Education and Workforce.


IMAGES
VIDEO
COMMENTS
Learn how to use Polya's four-step method to solve word problems in math. See examples, definitions, and tips for each step: understand the problem, devise a plan, carry out the plan, and look back.
Polya's Problem-Solving Steps are a systematic approach to tackling mathematical problems, consisting of four key phases: understanding the problem, devising a plan, carrying out the plan, and reviewing the solution. This method emphasizes the importance of breaking down complex problems into manageable parts, which enhances clarity and leads to more effective solutions.
Learn how to use Polya's four-step problem-solving method and some basic strategies to solve mathematical problems. The first step is to understand the problem, which involves reading the conditions carefully and drawing pictures if needed.
Learn how to use Polya's four-step approach to problem solving: preparation, thinking time, insight, and verification. See examples of problems and strategies for each step, and tips for becoming a better problem solver.
A teacher shares how she taught Polya's problem-solving process to her Year Six class and the impact it had on their skills and confidence. Polya's process is a four-step framework that helps students understand, plan, try, and revisit problems in various domains.
Learn how to use Polya's four-step method to solve mathematical problems effectively. See examples of guess and test, make a table, and check strategies with solutions and exercises.
10: Problem Solving Logic Packet 10.1: George Polya's Four Step Problem Solving Process Expand/collapse global location
Welcome! In this video, we explore Polya's four-step approach to problem-solving. From understanding the problem to reflecting on the solution, these steps t...
Learn how to solve problems using George Polya's four-step method: understanding the problem, devising a plan, carrying out the plan, and looking back. The second step is to find the connection between the data and the unknown, or to restate the problem in a useful way.
Learn how to use Polya's four-step method to solve mathematical problems: understand, devise, carry out, and look back. See examples of problems and strategies from the textbook and the handout.
Learn how to solve problems using Polya's four step method: understand, design, carry out, and look back. The third step is to design a plan for solving the problem, which involves choosing strategies such as drawing a picture, making a list, or using variables.
Polya's four-step plan for problem solving 1. Understand the problem. 2. Devise a plan. 3. Execute the plan. 4. Look back. Understand the problem. § What definitions, notation, etc. do you need to know before you start? § Do some work, and make a guess. § Is there a smaller, similar problem that might give you some intuition?
Learn how George Polya, a mathematician and scholar, developed a four-step problem-solving heuristic that can be applied to any field of human endeavor. Find out how to use Polya's process to teach and engage students in elementary and middle school math classrooms.
Learn how to use Polya's four-step method to solve problems in math and other areas of life. See examples, practice problems, and reflect on your experience.
•A problemis a situation, condition, person, or thing that needs attention and needs to be dealt with or solved. •Not solving a problem leads to undesirable consequences. "The solution to any problem lies in asking the right questions" Polya'sfour step method: A systematic way to answer/attack questions
Can you restate the problem in your own words? Do you know what is given? Do you know what the goal is? Is there enough information? Is there extraneous information? Is this problem similar to another problem you have solved? Step 2: Devise a Plan: Below are some strategies one might use to solve a problem. Can one (or more) of the following ...