- En español – ExME
- Em português – EME

Multivariate analysis: an overview
Posted on 9th September 2021 by Vighnesh D
Data analysis is one of the most useful tools when one tries to understand the vast amount of information presented to them and synthesise evidence from it. There are usually multiple factors influencing a phenomenon.
Of these, some can be observed, documented and interpreted thoroughly while others cannot. For example, in order to estimate the burden of a disease in society there may be a lot of factors which can be readily recorded, and a whole lot of others which are unreliable and, therefore, require proper scrutiny. Factors like incidence, age distribution, sex distribution and financial loss owing to the disease can be accounted for more easily when compared to contact tracing, prevalence and institutional support for the same. Therefore, it is of paramount importance that the data which is collected and interpreted must be done thoroughly in order to avoid common pitfalls.
Image from: https://imgs.xkcd.com/comics/useful_geometry_formulas.png under Creative Commons License 2.5 Randall Munroe. xkcd.com.
Why does it sound so important?
Data collection and analysis is emphasised upon in academia because the very same findings determine the policy of a governing body and, therefore, the implications that follow it are the direct product of the information that is fed into the system.
Introduction
In this blog, we will discuss types of data analysis in general and multivariate analysis in particular. It aims to introduce the concept to investigators inclined towards this discipline by attempting to reduce the complexity around the subject.
Analysis of data based on the types of variables in consideration is broadly divided into three categories:
- Univariate analysis: The simplest of all data analysis models, univariate analysis considers only one variable in calculation. Thus, although it is quite simple in application, it has limited use in analysing big data. E.g. incidence of a disease.
- Bivariate analysis: As the name suggests, bivariate analysis takes two variables into consideration. It has a slightly expanded area of application but is nevertheless limited when it comes to large sets of data. E.g. incidence of a disease and the season of the year.
- Multivariate analysis: Multivariate analysis takes a whole host of variables into consideration. This makes it a complicated as well as essential tool. The greatest virtue of such a model is that it considers as many factors into consideration as possible. This results in tremendous reduction of bias and gives a result closest to reality. For example, kindly refer to the factors discussed in the “overview” section of this article.
Multivariate analysis is defined as:
The statistical study of data where multiple measurements are made on each experimental unit and where the relationships among multivariate measurements and their structure are important
Multivariate statistical methods incorporate several techniques depending on the situation and the question in focus. Some of these methods are listed below:
- Regression analysis: Used to determine the relationship between a dependent variable and one or more independent variable.
- Analysis of Variance (ANOVA) : Used to determine the relationship between collections of data by analyzing the difference in the means.
- Interdependent analysis: Used to determine the relationship between a set of variables among themselves.
- Discriminant analysis: Used to classify observations in two or more distinct set of categories.
- Classification and cluster analysis: Used to find similarity in a group of observations.
- Principal component analysis: Used to interpret data in its simplest form by introducing new uncorrelated variables.
- Factor analysis: Similar to principal component analysis, this too is used to crunch big data into small, interpretable forms.
- Canonical correlation analysis: Perhaps one of the most complex models among all of the above, canonical correlation attempts to interpret data by analysing relationships between cross-covariance matrices.
ANOVA remains one of the most widely used statistical models in academia. Of the several types of ANOVA models, there is one subtype that is frequently used because of the factors involved in the studies. Traditionally, it has found its application in behavioural research, i.e. Psychology, Psychiatry and allied disciplines. This model is called the Multivariate Analysis of Variance (MANOVA). It is widely described as the multivariate analogue of ANOVA, used in interpreting univariate data.

Image from: https://imgs.xkcd.com/comics/t_distribution.png under Creative Commons License 2.5 Randall Munroe. xkcd.com.
Interpretation of results
Interpretation of results is probably the most difficult part in the technique. The relevant results are generally summarized in a table with an associated text. Appropriate information must be highlighted regarding:
- Multivariate test statistics used
- Degrees of freedom
- Appropriate test statistics used
- Calculated p-value (p < x)
Reliability and validity of the test are the most important determining factors in such techniques.
Applications
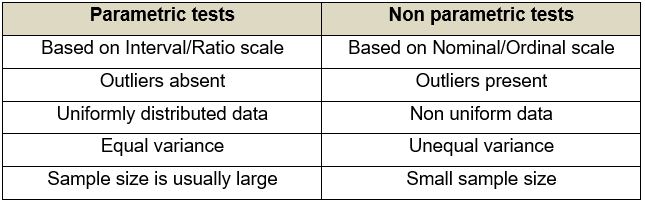
Multivariate analysis is used in several disciplines. One of its most distinguishing features is that it can be used in parametric as well as non-parametric tests.
Quick question: What are parametric and non-parametric tests?
- Parametric tests: Tests which make certain assumptions regarding the distribution of data, i.e. within a fixed parameter.
- Non-parametric tests: Tests which do not make assumptions with respect to distribution. On the contrary, the distribution of data is assumed to be free of distribution.
Uses of Multivariate analysis: Multivariate analyses are used principally for four reasons, i.e. to see patterns of data, to make clear comparisons, to discard unwanted information and to study multiple factors at once. Applications of multivariate analysis are found in almost all the disciplines which make up the bulk of policy-making, e.g. economics, healthcare, pharmaceutical industries, applied sciences, sociology, and so on. Multivariate analysis has particularly enjoyed a traditional stronghold in the field of behavioural sciences like psychology, psychiatry and allied fields because of the complex nature of the discipline.
Multivariate analysis is one of the most useful methods to determine relationships and analyse patterns among large sets of data. It is particularly effective in minimizing bias if a structured study design is employed. However, the complexity of the technique makes it a less sought-out model for novice research enthusiasts. Therefore, although the process of designing the study and interpretation of results is a tedious one, the techniques stand out in finding the relationships in complex situations.
References (pdf)
Leave a Reply Cancel reply
Your email address will not be published. Required fields are marked *
Save my name, email, and website in this browser for the next time I comment.
No Comments on Multivariate analysis: an overview
I got good information on multivariate data analysis and using mult variat analysis advantages and patterns.
Great summary. I found this very useful for starters
Thank you so much for the dscussion on multivariate design in research. However, i want to know more about multiple regression analysis. Hope for more learnings to gain from you.
Thank you for letting the author know this was useful, and I will see if there are any students wanting to blog about multiple regression analysis next!
When you want to know what contributed to an outcome what study is done?
Dear Philip, Thank you for bringing this to our notice. Your input regarding the discussion is highly appreciated. However, since this particular blog was meant to be an overview, I consciously avoided the nuances to prevent complicated explanations at an early stage. I am planning to expand on the matter in subsequent blogs and will keep your suggestion in mind while drafting for the same. Many thanks, Vighnesh.
Sorry, I don’t want to be pedantic, but shouldn’t we differentiate between ‘multivariate’ and ‘multivariable’ regression? https://stats.stackexchange.com/questions/447455/multivariable-vs-multivariate-regression https://www.ajgponline.org/article/S1064-7481(18)30579-7/fulltext
Subscribe to our newsletter
You will receive our monthly newsletter and free access to Trip Premium.
Related Articles

Data mining or data dredging?
Advances in technology now allow huge amounts of data to be handled simultaneously. Katherine takes a look at how this can be used in healthcare and how it can be exploited.

Nominal, ordinal, or numerical variables?
How can you tell if a variable is nominal, ordinal, or numerical? Why does it even matter? Determining the appropriate variable type used in a study is essential to determining the correct statistical method to use when obtaining your results. It is important not to take the variables out of context because more often than not, the same variable that can be ordinal can also be numerical, depending on how the data was recorded and analyzed. This post will give you a specific example that may help you better grasp this concept.

Data analysis methods
A description of the two types of data analysis – “As Treated” and “Intention to Treat” – using a hypothetical trial as an example
An Introduction to Multivariate Analysis
Data analytics is all about looking at various factors to see how they impact certain situations and outcomes. When dealing with data that contains more than two variables, you’ll use multivariate analysis.
Multivariate analysis isn’t just one specific method—rather, it encompasses a whole range of statistical techniques. These techniques allow you to gain a deeper understanding of your data in relation to specific business or real-world scenarios.
So, if you’re an aspiring data analyst or data scientist, multivariate analysis is an important concept to get to grips with.
In this post, we’ll provide a complete introduction to multivariate analysis. We’ll delve deeper into defining what multivariate analysis actually is, and we’ll introduce some key techniques you can use when analyzing your data. We’ll also give some examples of multivariate analysis in action.
Want to skip ahead to a particular section? Just use the clickable menu.
- What is multivariate analysis?
- Multivariate data analysis techniques (with examples)
- What are the advantages of multivariate analysis?
- Key takeaways and further reading
Ready to demystify multivariate analysis? Let’s do it.
1. What is multivariate analysis?
In data analytics, we look at different variables (or factors) and how they might impact certain situations or outcomes.
For example, in marketing, you might look at how the variable “money spent on advertising” impacts the variable “number of sales.” In the healthcare sector, you might want to explore whether there’s a correlation between “weekly hours of exercise” and “cholesterol level.” This helps us to understand why certain outcomes occur, which in turn allows us to make informed predictions and decisions for the future.
There are three categories of analysis to be aware of:
- Univariate analysis , which looks at just one variable
- Bivariate analysis , which analyzes two variables
- Multivariate analysis , which looks at more than two variables
As you can see, multivariate analysis encompasses all statistical techniques that are used to analyze more than two variables at once. The aim is to find patterns and correlations between several variables simultaneously—allowing for a much deeper, more complex understanding of a given scenario than you’ll get with bivariate analysis.
An example of multivariate analysis
Let’s imagine you’re interested in the relationship between a person’s social media habits and their self-esteem. You could carry out a bivariate analysis, comparing the following two variables:
- How many hours a day a person spends on Instagram
- Their self-esteem score (measured using a self-esteem scale)
You may or may not find a relationship between the two variables; however, you know that, in reality, self-esteem is a complex concept. It’s likely impacted by many different factors—not just how many hours a person spends on Instagram. You might also want to consider factors such as age, employment status, how often a person exercises, and relationship status (for example). In order to deduce the extent to which each of these variables correlates with self-esteem, and with each other, you’d need to run a multivariate analysis.
So we know that multivariate analysis is used when you want to explore more than two variables at once. Now let’s consider some of the different techniques you might use to do this.
2. Multivariate data analysis techniques and examples
There are many different techniques for multivariate analysis, and they can be divided into two categories:
- Dependence techniques
- Interdependence techniques
So what’s the difference? Let’s take a look.
Multivariate analysis techniques: Dependence vs. interdependence
When we use the terms “dependence” and “interdependence,” we’re referring to different types of relationships within the data. To give a brief explanation:
Dependence methods
Dependence methods are used when one or some of the variables are dependent on others. Dependence looks at cause and effect; in other words, can the values of two or more independent variables be used to explain, describe, or predict the value of another, dependent variable? To give a simple example, the dependent variable of “weight” might be predicted by independent variables such as “height” and “age.”
In machine learning, dependence techniques are used to build predictive models. The analyst enters input data into the model, specifying which variables are independent and which ones are dependent—in other words, which variables they want the model to predict, and which variables they want the model to use to make those predictions.
Interdependence methods
Interdependence methods are used to understand the structural makeup and underlying patterns within a dataset. In this case, no variables are dependent on others, so you’re not looking for causal relationships. Rather, interdependence methods seek to give meaning to a set of variables or to group them together in meaningful ways.
So: One is about the effect of certain variables on others, while the other is all about the structure of the dataset.
With that in mind, let’s consider some useful multivariate analysis techniques. We’ll look at:
Multiple linear regression
Multiple logistic regression, multivariate analysis of variance (manova), factor analysis, cluster analysis.
Multiple linear regression is a dependence method which looks at the relationship between one dependent variable and two or more independent variables. A multiple regression model will tell you the extent to which each independent variable has a linear relationship with the dependent variable. This is useful as it helps you to understand which factors are likely to influence a certain outcome, allowing you to estimate future outcomes.
Example of multiple regression:
As a data analyst, you could use multiple regression to predict crop growth. In this example, crop growth is your dependent variable and you want to see how different factors affect it. Your independent variables could be rainfall, temperature, amount of sunlight, and amount of fertilizer added to the soil. A multiple regression model would show you the proportion of variance in crop growth that each independent variable accounts for.
Source: Public domain via Wikimedia Commons
Logistic regression analysis is used to calculate (and predict) the probability of a binary event occurring. A binary outcome is one where there are only two possible outcomes; either the event occurs (1) or it doesn’t (0). So, based on a set of independent variables, logistic regression can predict how likely it is that a certain scenario will arise. It is also used for classification. You can learn about the difference between regression and classification here .
Example of logistic regression:
Let’s imagine you work as an analyst within the insurance sector and you need to predict how likely it is that each potential customer will make a claim. You might enter a range of independent variables into your model, such as age, whether or not they have a serious health condition, their occupation, and so on. Using these variables, a logistic regression analysis will calculate the probability of the event (making a claim) occurring. Another oft-cited example is the filters used to classify email as “spam” or “not spam.” You’ll find a more detailed explanation in this complete guide to logistic regression .
Multivariate analysis of variance (MANOVA) is used to measure the effect of multiple independent variables on two or more dependent variables. With MANOVA, it’s important to note that the independent variables are categorical, while the dependent variables are metric in nature. A categorical variable is a variable that belongs to a distinct category—for example, the variable “employment status” could be categorized into certain units, such as “employed full-time,” “employed part-time,” “unemployed,” and so on. A metric variable is measured quantitatively and takes on a numerical value.
In MANOVA analysis, you’re looking at various combinations of the independent variables to compare how they differ in their effects on the dependent variable.
Example of MANOVA:
Let’s imagine you work for an engineering company that is on a mission to build a super-fast, eco-friendly rocket. You could use MANOVA to measure the effect that various design combinations have on both the speed of the rocket and the amount of carbon dioxide it emits. In this scenario, your categorical independent variables could be:
- Engine type, categorized as E1, E2, or E3
- Material used for the rocket exterior, categorized as M1, M2, or M3
- Type of fuel used to power the rocket, categorized as F1, F2, or F3
Your metric dependent variables are speed in kilometers per hour, and carbon dioxide measured in parts per million. Using MANOVA, you’d test different combinations (e.g. E1, M1, and F1 vs. E1, M2, and F1, vs. E1, M3, and F1, and so on) to calculate the effect of all the independent variables. This should help you to find the optimal design solution for your rocket.
Factor analysis is an interdependence technique which seeks to reduce the number of variables in a dataset. If you have too many variables, it can be difficult to find patterns in your data. At the same time, models created using datasets with too many variables are susceptible to overfitting. Overfitting is a modeling error that occurs when a model fits too closely and specifically to a certain dataset, making it less generalizable to future datasets, and thus potentially less accurate in the predictions it makes.
Factor analysis works by detecting sets of variables which correlate highly with each other. These variables may then be condensed into a single variable. Data analysts will often carry out factor analysis to prepare the data for subsequent analyses.
Factor analysis example:
Let’s imagine you have a dataset containing data pertaining to a person’s income, education level, and occupation. You might find a high degree of correlation among each of these variables, and thus reduce them to the single factor “socioeconomic status.” You might also have data on how happy they were with customer service, how much they like a certain product, and how likely they are to recommend the product to a friend. Each of these variables could be grouped into the single factor “customer satisfaction” (as long as they are found to correlate strongly with one another). Even though you’ve reduced several data points to just one factor, you’re not really losing any information—these factors adequately capture and represent the individual variables concerned. With your “streamlined” dataset, you’re now ready to carry out further analyses.
Another interdependence technique, cluster analysis is used to group similar items within a dataset into clusters.
When grouping data into clusters, the aim is for the variables in one cluster to be more similar to each other than they are to variables in other clusters. This is measured in terms of intracluster and intercluster distance. Intracluster distance looks at the distance between data points within one cluster. This should be small. Intercluster distance looks at the distance between data points in different clusters. This should ideally be large. Cluster analysis helps you to understand how data in your sample is distributed, and to find patterns.
Learn more: What is Cluster Analysis? A Complete Beginner’s Guide
Cluster analysis example:
A prime example of cluster analysis is audience segmentation. If you were working in marketing, you might use cluster analysis to define different customer groups which could benefit from more targeted campaigns. As a healthcare analyst , you might use cluster analysis to explore whether certain lifestyle factors or geographical locations are associated with higher or lower cases of certain illnesses. Because it’s an interdependence technique, cluster analysis is often carried out in the early stages of data analysis.
Source: Chire, CC BY-SA 3.0 via Wikimedia Commons
More multivariate analysis techniques
This is just a handful of multivariate analysis techniques used by data analysts and data scientists to understand complex datasets. If you’re keen to explore further, check out discriminant analysis, conjoint analysis, canonical correlation analysis, structural equation modeling, and multidimensional scaling.
3. What are the advantages of multivariate analysis?
The one major advantage of multivariate analysis is the depth of insight it provides. In exploring multiple variables, you’re painting a much more detailed picture of what’s occurring—and, as a result, the insights you uncover are much more applicable to the real world.
Remember our self-esteem example back in section one? We could carry out a bivariate analysis, looking at the relationship between self-esteem and just one other factor; and, if we found a strong correlation between the two variables, we might be inclined to conclude that this particular variable is a strong determinant of self-esteem. However, in reality, we know that self-esteem can’t be attributed to one single factor. It’s a complex concept; in order to create a model that we could really trust to be accurate, we’d need to take many more factors into account. That’s where multivariate analysis really shines; it allows us to analyze many different factors and get closer to the reality of a given situation.
4. Key takeaways and further reading
In this post, we’ve learned that multivariate analysis is used to analyze data containing more than two variables. To recap, here are some key takeaways:
- The aim of multivariate analysis is to find patterns and correlations between several variables simultaneously
- Multivariate analysis is especially useful for analyzing complex datasets, allowing you to gain a deeper understanding of your data and how it relates to real-world scenarios
- There are two types of multivariate analysis techniques: Dependence techniques, which look at cause-and-effect relationships between variables, and interdependence techniques, which explore the structure of a dataset
- Key multivariate analysis techniques include multiple linear regression, multiple logistic regression, MANOVA, factor analysis, and cluster analysis—to name just a few
So what now? For a hands-on introduction to data analytics, try this free five-day data analytics short course . And, if you’d like to learn more about the different methods used by data analysts, check out the following:
- What is data cleaning and why does it matter?
- SQL cheatsheet: Learn your first 8 commands
- A step-by-step guide to the data analysis process
- +1 415-349-0105 +44 800-088-5450 +1 844-822-8378 +61 1-800-614-417
- VWO Engage Login

- EN DE ES BR
Multivariate Testing
What is multivariate testing.
Multivariate testing (MVT) is a form of A/B testing wherein a combination of multiple page elements are modified and tested against the original version (called the control) to determine which permutation leaves the highest impact on the business metrics you’re tracking. This form of testing is recommended if you want to test the impact of radical changes on a webpage as compared to analyzing the impact of one particular element.
Unlike a traditional A/B test, MVT is more complex and best suited for advanced marketing, product, and development professionals. Let’s consider an example to give you a more comprehensive explanation of this testing methodology and see how it aids in conversion rate optimization .
Let’s say you have an online business of homemade chocolates. Your product landing page typically has three important elements to attract visitors and push them down the conversion funnel – product images, call-to-action button color, and product headline. You decide to test 2 versions of all the 3 elements to understand which combination performs the best and increases your conversion rate. This would make your test a Multivariate Test (MVT).
A set of 2 variations for 3 page elements means a total of 8 variation combinations. The formula to calculate the total number of versions in MVT is as follows:
[No. of variations of element A] x [No. of variations of element B] x [No. of variations of element C]… = [Total No. of variations]
Now, variation combinations would be:
2 (Product image) x 2 (CTA button color) x 2 (Product headline) = 8
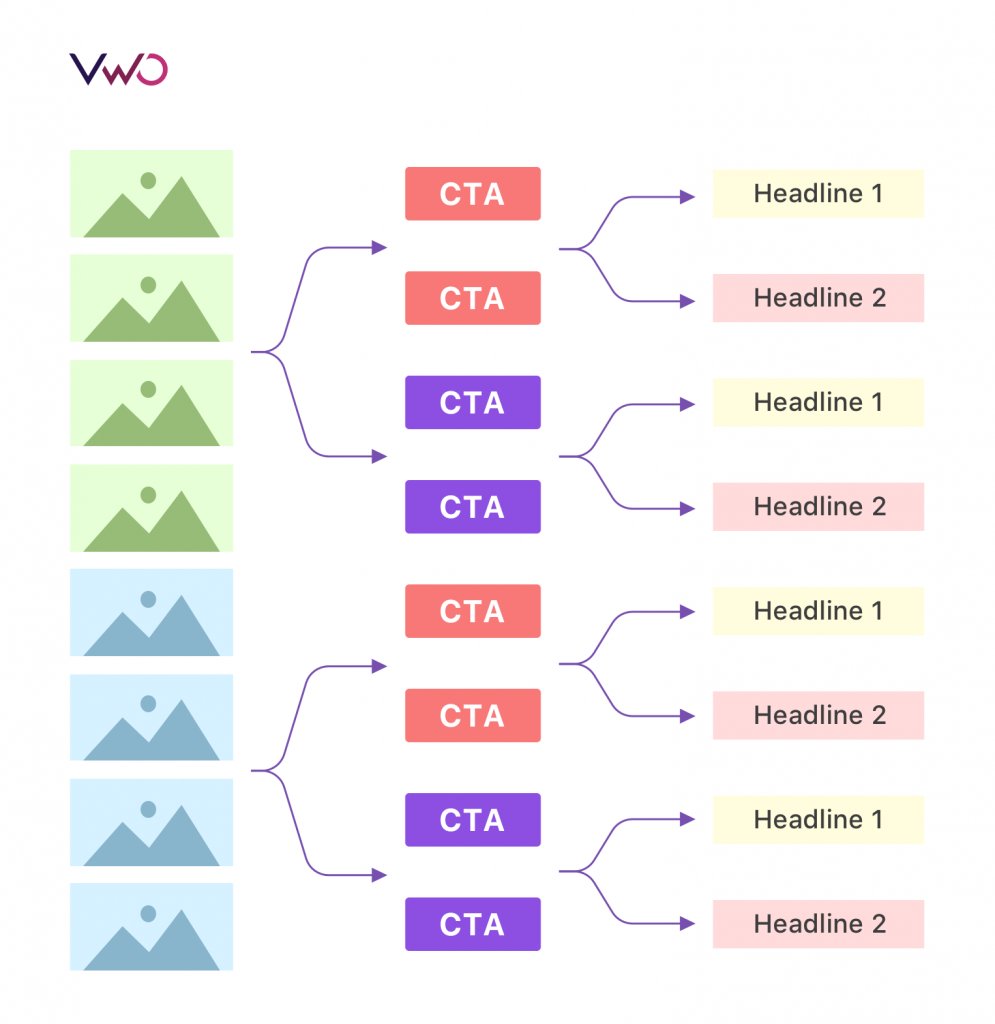
Each of these combinations will now be concurrently tested to analyze which combination helps get maximum conversions on your product landing page .
Note, a multivariate test eliminates the need to run multiple A/B tests and subsequent A/B tests to find the winning variation. Running concurrent tests with greater variation combinations not only helps you save time, money, and effort, but also draw conclusions in the shortest possible time.
Here’s a real-life example of multivariate testing to testify the benefits of this experimentation methodology.
Hyundai.io found that while the traffic on its car model landing pages was significant, not many people were requesting a test drive or downloading car brochures. Using VWO’s qualitative and quantitative tools, they analyzed that each of their landing pages has many different elements, including car headline, car visuals, car specifications, testimonials, and so on which might be causing friction. They decided to run a multivariate test to understand which elements were influencing a visitor’s decision to request a test drive or download a car brochure.
They created variations of the following sections of the car landing page:
- New SEO friendly text vs old text: They hypothesized that by making the text more SEO friendly, they could reap more SEO benefits.
- Extra CTA buttons vs no extra CTA buttons: They hypothesized that by adding extra and more prominent CTA buttons on the page, they’ll be able to nudge visitors in the right direction.
- Large photo of the car versus thumbnails: They hypothesized that it’s better to have larger photographs on the page than thumbnails to create better visitor traction
Hyundai.io tested a total of 8 combinations (3 sections, 2 variations each = 2*2*2) on their website.
Here’s a screenshot of the original page and the winning variation:
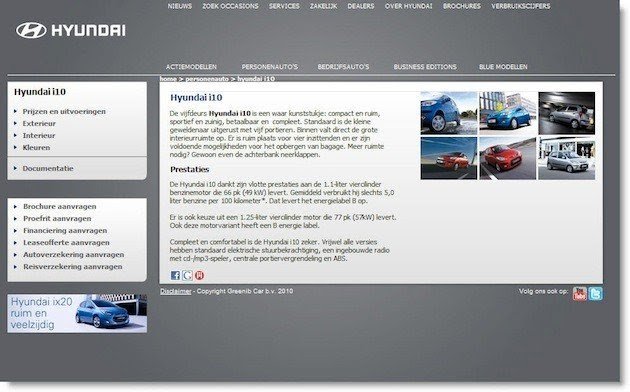
The variation with more SEO-friendly, extra CTA buttons and larger images increased Hyundai.io’s conversion rates for both, request for test drive and download brochure, by a total of 62%. They also saw a 208% increase in their click-through rate .
MVT is not just restricted to testing the performance of your webpages. You can use it across a range of fields. For instance, you can test your PPC ads, server-side codes, and so on. But, MVT should only be used on sufficiently sized visitor segments. More in-depth analysis means longer completion time. You must also not test too many variables at once as the test will take a longer time to complete and may or may not achieve statistical significance.

Understanding some basic multivariate testing terminologies
Although an integral part of A/B testing, there are a couple of terminologies specific to multivariate testing that anyone getting into this experimentation arena should know.
- Combination: It refers to a number of possible arrangements or unions you can create to test a collection of variable options in multiple locations. The order of selection or permutation does not matter. For instance, if you’re testing three elements on your home page, each with three variable options, then there are a total of 27 possible combinations (3x3x3) that you’ll test. When a visitor becomes a part of your test, they’ll see one combination, also referred to as an experience, when they visit your website.
- Content: Text, image, or any element that becomes a part of an experiment. In multivariate testing, several content options spread across a web page are compared in tandem to analyze which combination shows the best results. Content is also sometimes referred to as a level in MVT..
- Location: Ideally, a location refers to a page on the website or a specific area where you run optimizations. It’s essential to website activities and experiences, and display content to visitors or track visitor behavior.
- Control: Ideally, control refers to the original page, element, or content against which you’re planning to run a test. It also represents the “A” in the A/B testing scenario. For instance, if you want to test the performance of your homepage’s banner image, the original or existing banner image will be the “control.” Control is often also referred to as “Champion” by many seasoned optimizers.
- Goal: An event or a combination of events that help measure the success of a test or an experiment. For instance, a content writer’s goal is to increase visitor engagement on their content pieces and even generate content leads.
- Confidence Level: How positive or assertive you are about the success of your experiment.
- Conversion Rate: The percentage of unique visitors entering your conversion funnel and converting it into paying customers.
- Element: A discrete page component such as a form, block of text, an image, call-to-action button, etc.
- Experiment: It’s another way of assessing or evaluating the performance of one or more page elements.
- Hypothesis: A tentative assumption made to draft and test a logical or empirical consequence of a particular problem. An example of a hypothesis could be: Based on the previously run experiments and qualitative data gathered through heatmap and scrollmap analysis, I expect that adding banner and text CTAs on the guide page at regular intervals will help generate more content leads and MQLs.
- Non-Conclusive Results: Not deriving any solid conclusion from the experiment(s) you’ve run. Non-conclusive results do not point to a test’s failure—instead, just the failure of deriving a learning curve.
- Qualitative Research: A technique of gathering and analyzing non-numerical data from existing and potential customers to understand a concept, opinion, or experience.
- Quantitative Research: Digging through numerical data derived from analytics to find insights around the behavior of your website visitors and draw statistical analysis.
- Visitors: A person or a unique entity visiting your site or landing pages. They’re termed unique because no matter how many times a person visits your site or page, they’re counted only once.

What are the different types of multivariate testing methods?
MVT is in itself an umbrella methodology. There are several different types of multivariate tests that you can choose to run. We’ve defined each of these in detail below.
1. Full factorial testing
This is the most basic and frequently used MVT method. Using this testing methodology, you basically distribute your website traffic equally among all testing combinations. For instance, if you’re planning to test 8 different types of combinations on your homepage, each testing variation will receive one-eighth of all the website traffic.
Since each variation gets the same amount of traffic, the full factorial testing method offers all the necessary data you’d need to determine which testing variation and page elements perform the best. You’ll be able to discover which element had no effect on your targeted business metrics and which ones influenced them the most.
Because this MVT methodology makes no assumptions with respect to statistics or testing mathematics used in the background, our seasoned optimizers highly recommend it for people running or planning to run multivariate tests.
Increase your recurring revenue by optimizing your website using VWO’s Multivariate testing methodology. Sign up and start your 1-month free trial today !
2. Partial or fractional factorial testing
Partial or fractional factorial MVT methodology exposes only a fraction of all testing variations to the website’s total traffic. The conversion rate of the unexposed testing variations is interpreted from the ones that were included in the test.
Say you want to test 16 variations or combinations of your website’s homepage. In a regular test (or full factorial test), traffic is split equally between all variations. However, in the case of fractional factorial testing, traffic is divided between only 8 variations. The conversion rate of the remaining 8 variations is calculated or statistically deduced based on those actually tested.
This method involves the use of advanced mathematical techniques and the use of multiple assumptions to gather insights, and has many disadvantages. One pro point of this MVT methodology is that it requires less traffic. It’s a good option for websites or pages with low traffic.
However, regardless of how advanced mathematics techniques you use to draw statistically significant results using fractional factorial testing, hard data is any day better than speculation.
3. Taguchi testing
This is an old and esoteric MVT method. If you run a Google search, you’ll find that most tools on the market today claim to cut down on your testing time and traffic requirement by using the Taguchi testing technique. It’s more of an “off-line quality control” technique as it helps test and ensure good performance of products or processes in their design stage.
While some optimizers consider this a good MVT methodology, we at VWO believe that this is an old-school practice which is not theoretically sound. It was initially used in the manufacturing industry to reduce the number of combinations required to be tested for QA and other experiments.
Taguchi testing is not applicable or suitable for online testing and hence, not recommended. Use the full factorial or partial factorial MVT approach.

How is multivariate testing different?
A/b testing vs multivariate testing.
Ask an experience optimizer and they’ll say the ideal use of A/B testing is to analyze the performance of two or more radically different website elements. Meanwhile, MVT is a perfect technique to test which combination of page element(s) gets maximum conversions.
In testing terms, it’s often recommended to use A/B testing to find what’s called the “global maximum,” and MVT to refine your way towards the “local maximum.”
Let’s take an example to understand the concept of global maximum and local maximum.
Imagine for a second that you’ve never tasted even a single piece of chocolate in your life, and you’re standing in a chocolate shop looking at 25 different types of chocolates, confused about which one to purchase.
There are probably 5 different kinds of caramel chocolates, 10 different varieties of truffles, 6 different variations of lollipops, and 4 different types of exotic fruit chocolates. Are you going to taste all these 25 flavors before deciding which one to buy?
You may try one kind of chocolate from each of the above-mentioned categories, but surely not all. If you find that you like truffles the most over lollipops, caramel chocolates and exotic fruit chocolates, you’ll start tasting more truffle flavors like “coconut truffles,” “Oreo truffles,” “chocolate-fudge truffles,” and so on to decide which among the truffle flavors you like the most.
In statistical terms, we’d say that the category of chocolates you like the most will become the global maximum. This is the type of chocolate that spoke to your taste buds and tasted the best among the lot. When you get down to the specific flavors of truffles, i.e., coconut truffle, Oreo truffle, chocolate fudge, and more, you’ll discover the local maximum – the best version of the variety that you chose.
As an experience optimizer, you must approach testing in a similar manner. Find the webpage that gives you maximum conversions (global maximum), and then test combinations of specific elements on that webpage to understand which one improves your page’s performance and makes the highest-converting page (local maximum). What you’re looking for, global maximum or local maximum will define which testing methodology you must use.
Here’s a list of pros and cons of using A/B testing and multivariate testing .
| A/B testing | Multivariate testing |
| : 1. A comparatively simple method to design and execute. 2. Helps conclude debates around campaign tactics when there’s one hypothesis in question. 3. Helps generate statistically significant results even with lesser traffic samples. 4. Provides clear and detailed result reports which are easy for even non-technical teams to interpret and implement. 1. Limited to testing a single element with a few variations, typically 2 to 3. 2. Not possible to analyze the interaction between various page elements within the same testing campaign. | 1. Gives insights regarding the interaction between multiple page elements. 2. Provides a granular picture around which element poses impact on the performance of a page. 3. Enables optimizers to compare many versions of a campaign and conclude which one has the maximum impact. 1. A comparatively complex experimentation methodology to design and execute. 2. It requires more traffic than an A/B test to show statistically significant results. 3. Too many combinations make result interpretation difficult. 4. Can serve as an overkill when an A/B test could have been sufficient to show results. |

Split URL testing vs multivariate testing
Assuming you’re fairly clear with the definition and concept of MVT, we’ll begin by breaking down the concept of Split URL testing . Rather than testing page elements at a granular level such as in the case of MVT, a split URL test enables you to run a test on a page level. Meaning, variations in the case of Split URL test are dramatically different and hosted on separate URLs but have the same end goal.
Let’s continue on the example of you running an online business of homemade chocolates. Imagine your current homepage has a banner that shows different offers running on your website along with a section displaying your featured products, another section highlighting different chocolate categories, brand story, and related recipes. According to your gut feeling, the page looks attractive and has the potential to convert.
However, after looking at the qualitative results, viewing heatmaps , session recording, etc. you find that many elements on your homepage are not showing the results they should.
If you decide to run a Split URL test, you can create an entirely new page design with elements placed in a different manner and compare the performance of this variation with the control to analyze which one’s generating more conversions.
Meanwhile, if you decide to run a multivariate test, you can create permutations of different page elements that you want to examine, maybe test different colors of your homepage’s CTA button, banner image, sub headings, and so on, and check which combination generates maximum conversion. There can be ‘n’ number of permutations that you can test with MVT.

One of the primary reasons MVT is better than split URL testing is that the latter demands a lot of design and development team’s bandwidth and is a lengthy process. MVT, on the other hand, is comparatively less complex to run and demands lesser bandwidth as well.
Here’s a comparison table between Split URL testing and MVT:
| Split URL testing | Multivariate testing |
| : 1. Sizeable changes such as completely new page designs are tested to check which gets maximum traction and conversions. 2. Variations are created on separate URLs to maintain distinction and clarity. 3. Helps examine different page flows and complex changes such as a complete redesign of your website’s homepage, product page, etc. 4. With Split URL testing, you test a completely new webpage. : 1. A comparatively complex test to design and execute. 2. Requires a lot of design and development team bandwidth. 3. Assess the performance of a website as a whole while ignoring the performance of individual page elements. | : 1. A combination of web page elements are modified and tested to check which permutation gets maximum conversions. 2. Runs on a granular level to understand the performance of each page element. 3. Comparatively test more variations.Requires less changes in terms of design and layout. : 1. Usually requires more traffic to reach statistical significance. 2. Demands more variable combinations to run and show results. 3. The traffic spread across variations is too thin. This sometimes makes the test results unreliable. 4. Since more subtle changes are tested, the impact on conversion rate may not be significant or dramatic. |
Multipage testing vs multivariate testing
As the name suggests, multipage testing is a form of experimentation method wherein changes in particular elements are tested across multiple pages . For instance, you can modify your homemade chocolate eCommerce website’s primary CTA buttons (Add to Cart and Become a Member) on the homepage, replicate the change across the entire site, and run a multipage test to analyze results.
Compared to MVT, optimizers suggest it’s best to use multipage testing when you want to provide a consistent experience to your traffic, when you’re redesigning your website, or you want to improve your conversion funnel . Meanwhile, if you want to map the performance of certain elements on one particular web page, go with A/B testing or MVT.
Here’s a clear distinction between multipage testing and multivariate testing.
| Multipage testing | Multivariate testing |
| 1. Create one test to map the performance of a particular element, say site-wide navigation, across the entire website. 2. Run funnel tests to examine different voices and tones on web pages. 3. Experiment different design theories and analyze which one’s the best. 4. Helps map site-wide conversion rate. 1. Requires huge traffic to show statistically significant results. 2. Can take longer than usual to conclude.Gaining results from this form of experimentation method can be tricky. | 1. 2. You can validate even the minutest of choices, such as the color of a CTA button. 3. Gives in-depth insights about how different page elements play together. 4. Determine the contribution of individual page elements. 5. Eliminates the need to run multiple A/B tests. 1. More permutations or variations means longer time for a test to reach the stage of statistical significance. 2. Unlike multipage testing, you can test changes only on one particular page at a time in MVT. |
How to run a multivariate test?
The process of setting up and running MVT is not very different from a regular A/B test, except for a couple of steps in between. But we’ll start from the beginning so that the process stays afresh. Let’s deep dive.
1. Identify a problem
The first step to running MVT and improving the performance of your web page is to dig into data and identify all the loopholes causing visitors to drop off. For instance, the link attached to your “download guide” button may be broken or the form on your product page may be asking for information more than necessary. To spot these points of ambiguities, take the following steps.
- Conduct informal research: Take a look at customer support feedback and examine product reviews to understand how people are reacting to your products and services. Speak to your sales, support, and design teams to get honest feedback about your website from a customer’s point of view.
- Quantitative tools such Google Analytics to analyze bounce rate, page time spent, exit percentage, and similar metrics.
- Qualitative tools such as heatmaps to see where the majority of your website visitors are concentrating their attention, scrollmaps to analyze how far they’re scrolling down the page, and session recordings to visually see their entire journey.
- Explore the option of usability testing: This tool offers an insight into how people are actually using or navigating through your website. With usability testing you can gather direct feedback about visitor issues and draft necessary solutions.
VWO Insights offers you a full suite of qualitative and quantitative tools such as heatmaps, scroll maps, click maps, session recordings, form analytics, etc. for quick and thorough analysis.
2. Define your goals and formulate a hypothesis
Successful experimentation begins by clearly defining goals. It is these goals or metrics that help prepare smart testing strategies around element selection and their variations. For example, if you’re trying to increase your average order value (AOV) or revenue per visitor (RPV) , you may select elements that directly aid these metrics and create different variations.
Once you’ve defined your goals and selected your page elements to test, it’s time to formulate a hypothesis. A hypothesis is basically a suggested solution to a problem. For instance, after looking at the heatmap of your product page you analyze that your “Add to Cart” button is not prominently visible, you’ll perhaps form a hypothesis that “ based on observations gathered through heatmap and other qualitative tools, I expect that if we put the “Add to Cart” button in a colored box, we will see high visitor interaction with the button and more conversions.
Here’s a hypothesis format that we at VWO use:
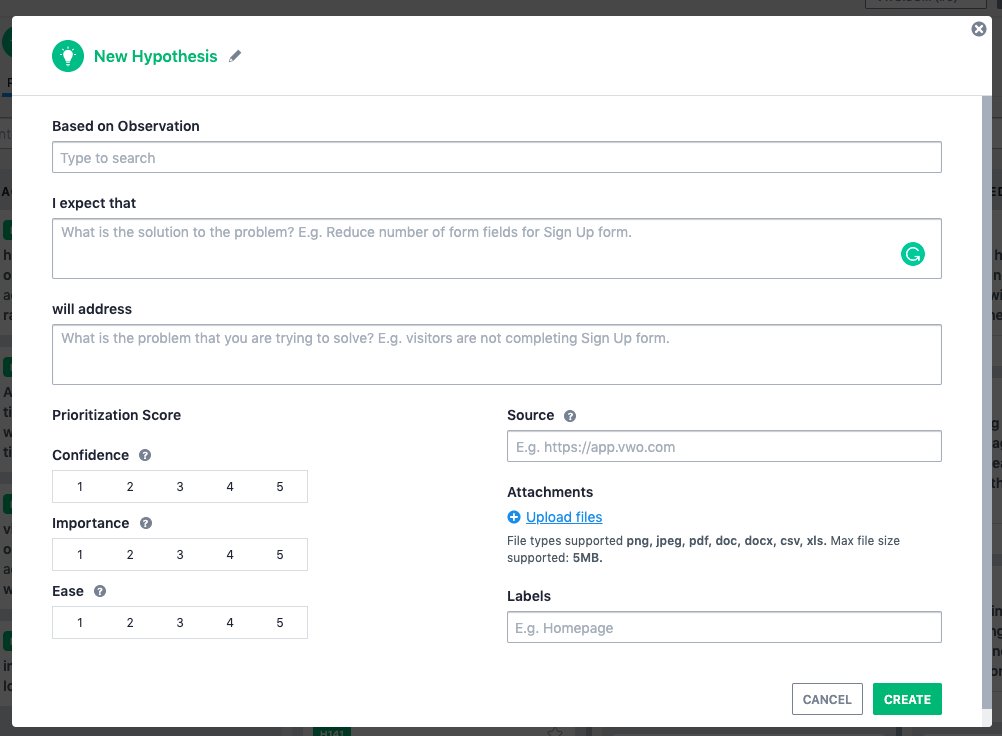
If you don’t have a good heatmap tool in your arsenal, use VWO’s AI-powered free heatmap generator to know how visitors are likely to engage on your webpage. You can also invest in VWO Insights to generate actual visitor behavior data and use it to your leverage.
3. Create variations
Post forming a hypothesis and having a good idea around which page elements you want to test, the next step is to create variations. Infuse your site with the new web elements or variations such as clearer and more prominently visible call-to-action buttons, enhanced images, text that’s more factual and resonates with what visitors expect, and so on.
VWO provides an excellent and highly user-friendly platform to run a multivariate test. Using VWO’s Visual Editor , you can play with your website and its elements and create as many variations as you want without the help of a developer. Do watch this video on ‘Introduction to VWO Visual Editor’ to learn more.
4. Determine your sample size
As stated in the above sections, it’s best to run MVT on a page with high traffic volume. If you choose to run it on a small traffic volume, your test is most likely to fail or take longer than usual to reach its statistically significant stage. The higher the traffic volume, the better will be the traffic split between variations, and hence, the better shall be the test results.
You can use our A/B and multivariate test duration calculator to find out how much traffic, and how long you need to run MVT based on your website’s current traffic volume, number of variations including control, and your statistical significance.
5. Review your test setup
The next step to running an effective and successful MVT is to review your test setup in your testing app. You may be confident that you’ve taken all the necessary steps and added the variations correctly in your testing app, but there’s no harm thoroughly reviewing it one or two times more.
One of the clearest advantages of conducting a review is that it gives you an opportunity to ensure every element has been added correctly and all the necessary test selections have been made. Taking the time to quality check your test is a critical step to ensure its success.
6. Start driving traffic
If you think your webpage doesn’t have enough traffic to support the MVT experiment, it’s time to look for ways to do so. Your job is to ensure your page has as much traffic as possible to make sure your testing efforts don’t fail. Use paid advertising, social media promotion, and other traffic generation methods to prove or disprove the hypothesis you’re currently playing with.
7. Analyze your results
Once your test has run its due course and reached its statistically significant stage, it’s time to access it’s results and see if your hypothesis was right or wrong.
Since you’ve tested multiple page elements at once, take some time to interpret your results. Examine each variation and analyze their performance. Note that it’s not necessary a variation that won which may be the best one to implement on your website permanently. Sometimes, these results can be inconclusive. Use qualitative tools such as heatmaps, clickmaps, session recordings, form analytics, etc. to examine the performance of each variation and draw a conclusion.
After all, it’s important to ensure the validity of your test and implement changes on your webpage as per the preference of your audience and deliver the experience they want.
How to run a multivariate test on a low-traffic website?
We’ve concluded time and again that MVT requires more traffic than an A/B test to show statistically significant results. But, does that mean websites with low traffic volume cannot do multivariate testing? Absolutely not!
The theory behind MVT asking for high traffic is pretty obvious. The higher the number of variations, the higher shall be the traffic split between the variations, and hence, the longer it will take to draw conclusive results. If you’re planning to run MVT on a website with low traffic volume, all you need to do is make some modifications.
1. Only test high-impact changes
Let’s say, there are 6 elements on your product page which you believe have the potential to improve the performance of your page and even increase conversions. Do all of these have equal potential? Probably not. Some may be more impactful and have more noticeable effects than others.
When you’re planning to run MVT on a low traffic website, focus your energies on testing those site elements that can have a significant impact on your page’s performance and goals rather than testing small modifications with low impact intensity.
Although it may be intimidating to test radical changes, when you do, the likelihood of them showing a dramatic difference in conversion rate is also high. No matter the outcome, the learnings and valuable insights about your customer’s behavior and perception of your brand, can help run informed future tests and business decisions.
2. Use fewer variations
Needless to say, low traffic volume means testing less number of variations. We understand that it’s tempting to test different optimization ideas to solve visitor problems. But, with every added variation in your test, the time to achieve statistical significance also increases . Don’t take that risk. Go small and go slow. This may cost you some extra efforts and resources, it will surely save you much time compared to running MVT with more number of variations.
Use tools like heatmaps, scrollmaps, session recordings, usability testing , etc. to find high-impact page elements. Use the ICE model (impact, confidence, ease) to create a testing pipeline and follow it.
3. Focus on micro-conversions
Your primary goal may be to increase page sign-ups, click-through rate or overall conversions, but does it make sense to use these as your primary metrics when you know it would take you much longer to gather enough conversions and even verify the test results? Surely not.
The better thing to do is test conversions on a micro-level . A level at which conversions are plentiful and can help you optimize your page quickly. For instance, focus your efforts on increasing your page engagement rate, clicks on add to cart button, clicks on images, etc.
Other goals could be setting up a conversion goal that fires when a visitor fills up an exit-intent pop-up form, stays on your website for more than 30 minutes, or scrolls down a certain depth/folds through your long-copy page. You can also use a quantitative tool like Google Analytics to analyze which conversions to map or use as goals to optimize your website .
4. Consider lowering down your statistical significance setting
When you don’t have the leverage to run a test on a large sample size , resort to using other methods to measure the performance of your control and variation. Do not wait for your test to reach its statistically significant level. If your testing tool allows, you can also lower your statistical significance levels. So, for instance, if you set your significance level to 70%, any version that reaches this mark will become the winner. In this case, you would also require a much smaller sample size than going for 99% significance.
Optimizers across the industry recommend many ways to measure the performance of a test version, but the ones we recommend are as follows:
- The 2-sample t-test: Also known as the independent sample t-test, it’s a method used to examine whether the means of two or more unknown samples are equal or not. If your sample distribution is unequal, you can use a different estimate of the standard deviation to check results.
- B. The Chi-Squared Test: The primary objective of this test is to examine the statistical significance of the observed relationship between two variants with respect to the expected outcome. In other words, it helps you analyze which version of your test is most likely to reach statistical significance and has better chances of winning.
- Confidence Interval : This method simply measures the degree of certainty or uncertainty of a variation to reach its statistical significance by observing the data at hand.
- Measuring sessions : This is another way to test the statistical significance of a variation. Rather than measuring your test’s performance by counting users, take into account sessions. This means that your test treats each individual as a participant in an experiment only once.
5. Avoid niche testing
Avoid testing those sections or elements of your site that get very few hits. Instead, target page elements that get more traction. Site-wide CTA tests, landing page tests , and the like will help you take advantage of your site’s incoming traffic . Such tests are also likely to show statistically significant results in a shorter time span.
What are the advantages and disadvantages of multivariate testing?
Instances in which multivariate testing is valuable, 1. mvt helps measure the interaction between multiple page elements .
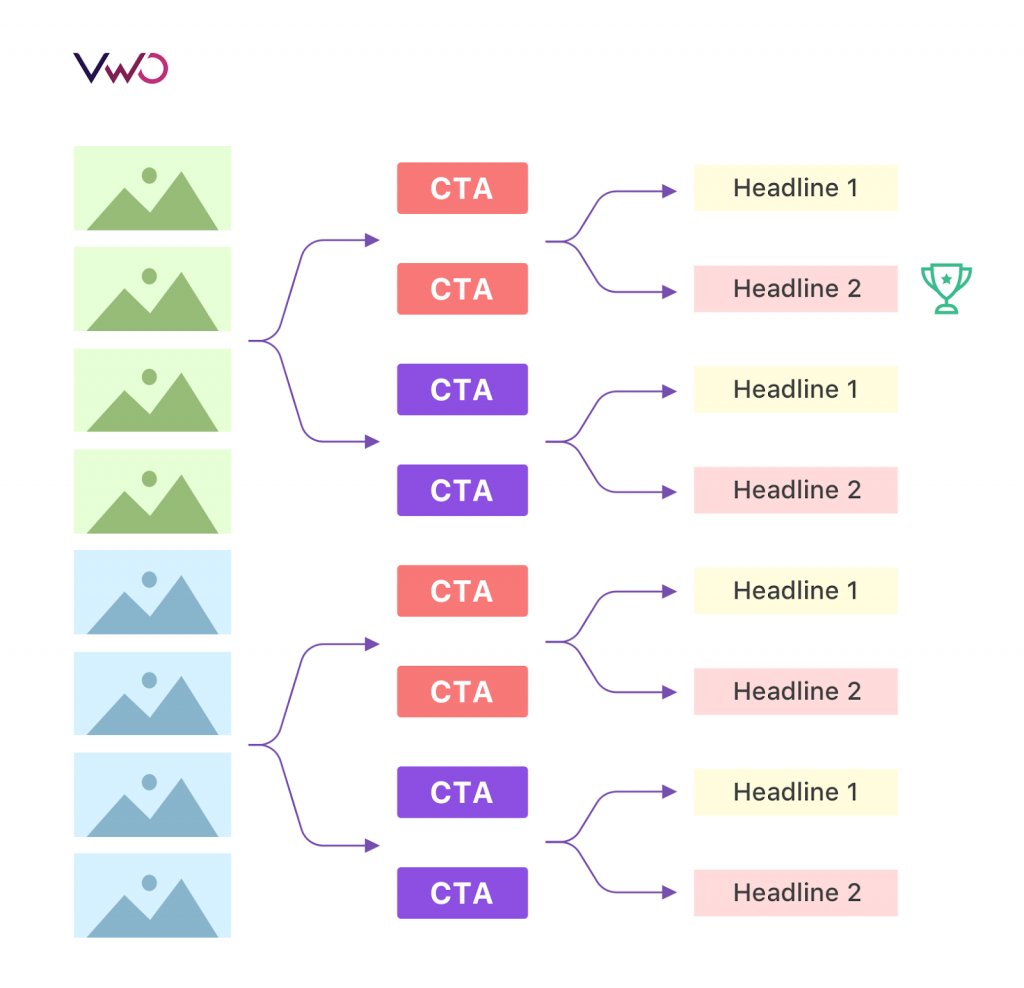
Let’s come back to evaluating the performance of your homemade chocolate eCommerce website. You’re confident that two sequential A/B tests can produce the same results as an MVT. So, you decide to first run an A/B test to compare a static banner image with a video banner, and the latter wins. Next, on the winning variation, i.e., the video banner, you do another A/B test between two possible CTAs, ‘Explore More’ and ‘Buy Now,’ and the former proved better. Don’t you think you could’ve come to the same conclusion with an MVT test?
Unlike an A/B test, a multivariate test gives you the leverage to test and measure how multiple page elements interact with each other. Just by testing a combination of various elements (let’s say your product page’s hero image, a CTA, and headline) you can not only figure out which variation performs better than others and helps increase conversions but also discover the best possible combinations of the tested page elements.
2. Provides an in-depth visitor behavior analysis
MVT enables you to conduct an in-depth analysis on visitor behavior and their preference patterns. It provides you with statistics on the performance of the variations vs their conversion effects. This helps re-orienting the visitor connection of your website. The better the re-orientation as per a visitor’s intent, the more are the chances of high conversions.
3. Sheds light on dead or least contributing page elements.
A multivariate test doesn’t just help you find the right combination of page elements that will help increase your conversions. It also sheds light on those that are contributing least or nothing to your site’s conversions and occupying huge page space. These elements can be anything, textual content, images, banner, etc.
Relocate or replace them with elements that catch the attention of your visitors and channelize some conversions as well. It’s always better to have your page elements contribute something to your goals than absolutely nothing.
4. Guides you through page structurization
The importance of placing elements at the right location can be understood from the fact that visitors today have a short view span. They devote maximum time reading and taking in information mentioned in the first fold of your web page. So, if you’re not placing the relevant content at the top, you’re reducing the chances of getting conversions by a great margin. MVT allows you to study the placement of various page elements and locate them at their right place in order to facilitate conversions for your business and make it easy for visitors to find what they came to look for on your page.
5. Test a wide range of combinations
Unlike a regular A/B test that gives you the leverage to test one or more variations of a particular element in singularity, MVT allows you to test multiple elements at the same time by applying the concept of permutations and combinations. Such an experimentation method not only increases your testing options that you can use to tap on conversions but helps save time by avoiding running sequential A/B tests.
Instances where multivariate testing is not valuable
MVT is a highly sophisticated testing methodology. A single MVT test helps answer multiple questions at once. But, just because it’s a complicated testing technique doesn’t mean it’s better than other techniques or that the data it generates is more useful. Every coin has two sides. We listed the pros of using a multivariate test in the above section. It’s time to know the cons as well.
1. Requires more traffic to show statistically significant results
Unlike a traditional A/B test, MVT demands high traffic inflow. This means that it only works or shows statistically significant results for sites which have a ton of traffic. Even if you do run it on a site with low traffic, you’ll have to compromise on something or the other such as test fewer combinations, use other methods to calculate a winner, etc. Read the section above on ‘How to run a multivariate test on low traffic websites’ for better clarity.
2. They’re comparatively tricky to set up
One thing that makes people opt for an A/B test over MVT is that the former is comparatively very simple to set up. After all, you just need to change one or two elements and add variations while keeping the rest of the page design the same. Anyone who has an understanding of web design can easily set up an A/B test, and even complex A/B tests today rarely require more than a couple of minutes of a developer’s time. Tools like VWO enable even non-technical folks to set up an A/B test within a matter of minutes .
On the contrary, MVT requires more efforts even if you’re creating a basic one, and it’s also very easy for them to go off the rails. A minute mistake in the design or while creating the variations can hamper the test results. MVT is a good option for optimizers who have a lot of experience in the arena of experimentation.
3. There’s a hidden opportunity cost
Time is always of the essence and a valuable commodity for any business. When you run a test on your website, you’re investing time and playing with your conversion rate. There’s a hidden cost that you put on the line. Multivariate tests are comparatively complex and slow to set up, and slower to run. All the time lost during its setup phase and course of running creates an opportunity cost.
Amidst the time MVT takes to show meaningful results, you could have run dozens of A/B tests and drawn conclusions. A/B tests are quick to set up and also provide definite answers to many specific problems.
4. The chances of failure are comparatively high
Needless to say that testing allows you to move fast and break things to optimize your website and make it more user friendly. You get the leverage to try crazy ideas and even fail spectacularly without facing any real risk or consequences. While this approach seems effective in the case of an A/B test, we can’t say the same for multivariate testing.
While each A/B test, despite its success or failure, provides a series of learning points to refer back, the same fails in the case of a multivariate test. It’s comparatively difficult to draw meaningful learnings as you play with a lot of elements that too in combination. More so, MVT is so slow and tedious that it doesn’t really make any sense to take such a risk in the first place and fail in the end.
5. MVT is biased towards design
Another MVT con that most optimizers have realized over the years is that the testing method often provides answers to problems related to design. Some of the strongest advocates or supporters of MVT are also UI and UX professionals.
Design is obviously important, but it’s surely not everything. UI and UX elements represent only a small part of all the total variables you use to enhance the performance of your website. Copy, promotional offers, and even site functionality are essential to ensure your website is liked by your target audience. These elements are often underestimated and overlooked in the case of MVT despite the fact that they have a huge impact on the conversion rate of your site.
Machine learning and multivariate testing
The advancement in the field of technology, especially artificial intelligence, is now prominently visible in the testing arena as well. For many years, a program called a neural network was enabling computers to learn as they gather data and take necessary actions that were more accurate than humans while using less data and time. However, neural networks were able to help humans solve some specific problems only.
Looking at the capabilities of these neural networks, many software companies thought to use their potential to develop solutions which could enhance the entire multivariate testing process. This solution is called the evolutionary neural network or a generic neural network.
The approach uses the capabilities of machine learning to select which website elements to test and creates all possible variations on its own. It restricts the need to test all combinations and enables \ optimizers to test only those which have the ability to show highest conversions.
The algorithms behind the solution prune the poor performing combinations to pave the way for more likely winners to participate in the test. Over time, the highest performing combination emerges as the winner and then becomes the new control.
Once that happens, these algorithms then introduce variables called mutations in the test. Variants that were previously pruned are reintroduced as new combinations to analyze whether any one of these might turn successful amidst the better-performing combinations.
This approach has proved to show better and faster results even with less traffic.
Evolutionary neural networks enable testing tools to learn which set of combinations will show positive results without testing all possible multivariate combinations. With machine learning, websites that have too little traffic to opt for MVT can also consider this option now without making compromises.
Best practices to follow when running a multivariate test
MVT has the ability to empower optimizers to discover effective content that helps drive KPIs and enhance the performance of a website, but only when they follow best practices.
1. Create a learning agenda
Before getting started, be sure that MVT is the best testing approach to your identified problems or whether a simple A/B test would best suit your needs. We, at VWO, believe that it’s important to first draft a learning agenda. This will help you define what exactly you want to test and what you hope to learn from this experiment.
The agenda basically acts as a blueprint, helping you establish a hypothesis, define the page elements you want to test and for which audience segment, and prioritize learning objectives accordingly. It also comes in handy when you begin to set up your test and ensures that all adjustments have been made correctly.
2. Avoid testing all possible combinations
For most people, running a multivariate test means testing everything that comes under their radar. That should not be the case. Restrict yourself and test only those variables that you believe can have a high impact on your conversion rate. Also, the more the number of elements, the more shall be the number of permutations, the more it will be to run and gauge the final results.
Say for example, you want to test the performance of your display ad. You decide to test four possible images, two possible CTA button colors, and three possible headlines. This totals up to 24 variations of your display ad. When you test all the variations at once, each gets 1/24th traffic of the total incoming traffic.
With such a high traffic split, the chances of any variation reaching its statistical significance is quite low. And, even if one or some of them do, the time they take will make the test insignificant.
Furthermore, it’s not necessary that all combinations may sense from a design standpoint. For instance, an image with a blue background and blue CTA button color will make it hard for visitors to identify the CTA, especially on a mobile screen. Use good judgment and select only those variations which can show some results.
3. Generate ideas from data for greater experimental variety and relevancy
While it’s a great practice to limit yourself from testing every possible idea that pops in your head, it’s also important to not ignore possibilities that could impact your conversion rate. To know if a variation is worth sampling, generate ideas from various data sources . These could include:
- First-hand data collected on the basis of visitor behavior, segment demographics, and interests.
- Third-party data extracted from multiple data providers for additional visitor information such as purchase behavior, transactional data, or industry-specific data.
- Historical performance data extracted from previously run campaigns targeting similar traffic.
4. Start eliminating low performers once your test reaches minimum sample size
It’s not necessary to end your multivariate test the moment it achieves adequate sample size . Rather, you should begin eliminating the non-performing variations. Shut down variations that have negligible movement compared to control once they’ve achieved the needed representative sample size. This means that more traffic will flow towards variations that are performing well, enabling you to optimize your test for higher quality results, faster.
5. Use high-performing combinations for further testing
Once you’ve discovered a few potential variations, restructure your test and fine-tune the variable elements. If a certain headline on a product page is outperforming others, come up with a fresh set of variations around that headline.
You can even opt to run a discrete A/B/n test with limited experimental groups to analyze the performance of the new variations in a shorter time. Most experience optimizers suggest that when you learn something from an experiment, use the knowledge to enhance the performance of other page elements. Testing is not just about increasing revenue, but about understanding visitor behavior and serving to their needs.
Best multivariate testing tools
The market today is swamping with A/B testing tools . Not all have the required capabilities to help you run successful experiments without a hassle. Neither can you take the risk of developing an in-house experimentation suite. Here’s a list of the top 5 multivariate testing tools for experience optimizers who have a passion for testing:
VWO is an all-in-one, cloud-based experimentation tool that helps optimizers run multiple tests on their website and optimize it to ensure better conversions. Besides laying an easy-to-use experimentation platform, the tool allows you to conduct qualitative and quantitative research work, create test variations, and even analyze the performance of your tests via its robust dashboard.
VWO also offers the SmartStats feature that runs on Bayesian statistics. It gives you more control of your tests and helps derive conclusions sooner. Sign up today for a free trial and get into the habit of experimentation.
2. Optimizely
Optimizely platform offers a comprehensive suite of CRO tools and generally entertain enterprise-level customers only.

Essentially, Optimizely primarily provides web experimentation and personalization services. However, you can use its capabilities to run experiments on mobile apps and messaging platforms as well. You can even opt to run multiple tests on the same page and rest assured of accurate results.
3. A/B Tasty
A/B Tasty is another experimentation platform that offers a holistic range of testing features. Besides the usual A/B and Split URL testing option, it also allows you to run multivariate tests. It has an integrated platform that’s easy-to-use and offers a real-time view of your tests and their respective confidence levels.
4. Oracle Maxymiser
An advanced A/B testing and personalization tool, Oracle Maxymiser enables you to design and run sophisticated experiments. The platform offers many powerful features and capabilities such as multivariate testing, funnel optimization, advanced targeting and segmentation, and predictive analytics. Such features make it a perfect match for data-driven optimizers with an in-house IT support team.
5. Google Optimize 360
Google Optimize 360 is a Google product that offers a broad range of services besides experimentation. Some of these include native Google Analytics integration, URL targeting, and Geo-targeting. If you opt for Google Optimize 360’s premium version, you get to explore the tool in-depth. With Google Optimize 360 you can:
- test up to 36 combinations when running MVT
- run 100+ test simultaneously
- make 100+ personalizations at a time
- get access to Google Analytics 360 Suite administration
Multivariate testing is an arm of A/B testing that uses the same experimentation mechanics, but compares more than one variable on a website in a live environment. It opposes the traditional scientific notion and enables you to, in a way, run multiple A/B/n tests on the same page simultaneously. At the core, it’s a highly complex process that requires more time and effort, but provides comprehensive information around how different page elements interact with each other and which combinations work the best magic on your site.
If you still have questions around what is multivariate testing or how it can benefit your website, request a demo today ! Or, get into the habit of experimentation and start A/B testing today! Sign up for VWO’s free trial .

Download this Guide
Deliver great experiences. grow faster, starting today..
Talk to a sales representative
Get in touch
Thank you for writing to us.
One of our representatives will get in touch with you shortly.
Signup for a full-featured trial
Free for 30 days. No credit card required
Set up your password to get started
Awesome! Your meeting is confirmed for at
Thank you, for sharing your details.
Hi 👋 Let's schedule your demo
To begin, tell us a bit about yourself
While we will deliver a demo that covers the entire VWO platform, please share a few details for us to personalize the demo for you.
Select the capabilities that you would like us to emphasise on during the demo., which of these sounds like you, please share the use cases, goals or needs that you are trying to solve., please share the url of your website..
We will come prepared with a demo environment for this specific website.
I can't wait to meet you on at
, thank you for sharing the details. Your dedicated VWO representative, will be in touch shortly to set up a time for this demo.
We're satisfied and glad we picked VWO. We're getting the ROI from our experiments. Christoffer Kjellberg CRO Manager
VWO has been so helpful in our optimization efforts. Testing opportunities are endless and it has allowed us to easily identify, set up, and run multiple tests at a time. Elizabeth Levitan Digital Optimization Specialist
As the project manager for our experimentation process, I love how the functionality of VWO allows us to get up and going quickly but also gives us the flexibility to be more complex with our testing. Tara Rowe Marketing Technology Manager
You don't need a website development background to make VWO work for you. The VWO support team is amazing Elizabeth Romanski Consumer Marketing & Analytics Manager
Trusted by thousands of leading brands

A Guide on Data Analysis
22 multivariate methods.
\(y_1,...,y_p\) are possibly correlated random variables with means \(\mu_1,...,\mu_p\)
\[ \mathbf{y} = \left( \begin{array} {c} y_1 \\ . \\ y_p \\ \end{array} \right) \]
\[ E(\mathbf{y}) = \left( \begin{array} {c} \mu_1 \\ . \\ \mu_p \\ \end{array} \right) \]
Let \(\sigma_{ij} = cov(y_i, y_j)\) for \(i,j = 1,…,p\)
\[ \mathbf{\Sigma} = (\sigma_{ij}) = \left( \begin{array} {cccc} \sigma_{11} & \sigma_{22} & ... & \sigma_{1p} \\ \sigma_{21} & \sigma_{22} & ... & \sigma_{2p} \\ . & . & . & . \\ \sigma_{p1} & \sigma_{p2} & ... & \sigma_{pp} \end{array} \right) \]
where \(\mathbf{\Sigma}\) (symmetric) is the variance-covariance or dispersion matrix
Let \(\mathbf{u}_{p \times 1}\) and \(\mathbf{v}_{q \times 1}\) be random vectors with means \(\mu_u\) and \(\mu_v\) . Then
\[ \mathbf{\Sigma}_{uv} = cov(\mathbf{u,v}) = E[(\mathbf{u} - \mu_u)(\mathbf{v} - \mu_v)'] \]
in which \(\mathbf{\Sigma}_{uv} \neq \mathbf{\Sigma}_{vu}\) and \(\mathbf{\Sigma}_{uv} = \mathbf{\Sigma}_{vu}'\)
Properties of Covariance Matrices
- Symmetric \(\mathbf{\Sigma}' = \mathbf{\Sigma}\)
- Non-negative definite \(\mathbf{a'\Sigma a} \ge 0\) for any \(\mathbf{a} \in R^p\) , which is equivalent to eigenvalues of \(\mathbf{\Sigma}\) , \(\lambda_1 \ge \lambda_2 \ge ... \ge \lambda_p \ge 0\)
- \(|\mathbf{\Sigma}| = \lambda_1 \lambda_2 ... \lambda_p \ge 0\) ( generalized variance ) (the bigger this number is, the more variation there is
- \(trace(\mathbf{\Sigma}) = tr(\mathbf{\Sigma}) = \lambda_1 + ... + \lambda_p = \sigma_{11} + ... + \sigma_{pp} =\) sum of variance ( total variance )
- \(\mathbf{\Sigma}\) is typically required to be positive definite, which means all eigenvalues are positive, and \(\mathbf{\Sigma}\) has an inverse \(\mathbf{\Sigma}^{-1}\) such that \(\mathbf{\Sigma}^{-1}\mathbf{\Sigma} = \mathbf{I}_{p \times p} = \mathbf{\Sigma \Sigma}^{-1}\)
Correlation Matrices
\[ \rho_{ij} = \frac{\sigma_{ij}}{\sqrt{\sigma_{ii} \sigma_{jj}}} \]
\[ \mathbf{R} = \left( \begin{array} {cccc} \rho_{11} & \rho_{12} & ... & \rho_{1p} \\ \rho_{21} & \rho_{22} & ... & \rho_{2p} \\ . & . & . &. \\ \rho_{p1} & \rho_{p2} & ... & \rho_{pp} \\ \end{array} \right) \]
where \(\rho_{ij}\) is the correlation, and \(\rho_{ii} = 1\) for all i
Alternatively,
\[ \mathbf{R} = [diag(\mathbf{\Sigma})]^{-1/2}\mathbf{\Sigma}[diag(\mathbf{\Sigma})]^{-1/2} \]
where \(diag(\mathbf{\Sigma})\) is the matrix which has the \(\sigma_{ii}\) ’s on the diagonal and 0’s elsewhere
and \(\mathbf{A}^{1/2}\) (the square root of a symmetric matrix) is a symmetric matrix such as \(\mathbf{A} = \mathbf{A}^{1/2}\mathbf{A}^{1/2}\)
\(\mathbf{x}\) and \(\mathbf{y}\) be random vectors with means \(\mu_x\) and \(\mu_y\) and variance -variance matrices \(\mathbf{\Sigma}_x\) and \(\mathbf{\Sigma}_y\) .
\(\mathbf{A}\) and \(\mathbf{B}\) be matrices of constants and \(\mathbf{c}\) and \(\mathbf{d}\) be vectors of constants
\(E(\mathbf{Ay + c} ) = \mathbf{A} \mu_y + c\)
\(var(\mathbf{Ay + c}) = \mathbf{A} var(\mathbf{y})\mathbf{A}' = \mathbf{A \Sigma_y A}'\)
\(cov(\mathbf{Ay + c, By+ d}) = \mathbf{A\Sigma_y B}'\)
\(E(\mathbf{Ay + Bx + c}) = \mathbf{A \mu_y + B \mu_x + c}\)
\(var(\mathbf{Ay + Bx + c}) = \mathbf{A \Sigma_y A' + B \Sigma_x B' + A \Sigma_{yx}B' + B\Sigma'_{yx}A'}\)
Multivariate Normal Distribution
Let \(\mathbf{y}\) be a multivariate normal (MVN) random variable with mean \(\mu\) and variance \(\mathbf{\Sigma}\) . Then the density of \(\mathbf{y}\) is
\[ f(\mathbf{y}) = \frac{1}{(2\pi)^{p/2}|\mathbf{\Sigma}|^{1/2}} \exp(-\frac{1}{2} \mathbf{(y-\mu)'\Sigma^{-1}(y-\mu)} ) \]
\(\mathbf{y} \sim N_p(\mu, \mathbf{\Sigma})\)
22.0.1 Properties of MVN
Let \(\mathbf{A}_{r \times p}\) be a fixed matrix. Then \(\mathbf{Ay} \sim N_r (\mathbf{A \mu, A \Sigma A'})\) . \(r \le p\) and all rows of \(\mathbf{A}\) must be linearly independent to guarantee that \(\mathbf{A \Sigma A}'\) is non-singular.
Let \(\mathbf{G}\) be a matrix such that \(\mathbf{\Sigma}^{-1} = \mathbf{GG}'\) . Then \(\mathbf{G'y} \sim N_p(\mathbf{G' \mu, I})\) and \(\mathbf{G'(y-\mu)} \sim N_p (0,\mathbf{I})\)
Any fixed linear combination of \(y_1,...,y_p\) (say \(\mathbf{c'y}\) ) follows \(\mathbf{c'y} \sim N_1 (\mathbf{c' \mu, c' \Sigma c})\)
Define a partition, \([\mathbf{y}'_1,\mathbf{y}_2']'\) where
\(\mathbf{y}_1\) is \(p_1 \times 1\)
\(\mathbf{y}_2\) is \(p_2 \times 1\) ,
\(p_1 + p_2 = p\)
\(p_1,p_2 \ge 1\) Then
\[ \left( \begin{array} {c} \mathbf{y}_1 \\ \mathbf{y}_2 \\ \end{array} \right) \sim N \left( \left( \begin{array} {c} \mu_1 \\ \mu_2 \\ \end{array} \right), \left( \begin{array} {cc} \mathbf{\Sigma}_{11} & \mathbf{\Sigma}_{12} \\ \mathbf{\Sigma}_{21} & \mathbf{\Sigma}_{22}\\ \end{array} \right) \right) \]
The marginal distributions of \(\mathbf{y}_1\) and \(\mathbf{y}_2\) are \(\mathbf{y}_1 \sim N_{p1}(\mathbf{\mu_1, \Sigma_{11}})\) and \(\mathbf{y}_2 \sim N_{p2}(\mathbf{\mu_2, \Sigma_{22}})\)
Individual components \(y_1,...,y_p\) are all normally distributed \(y_i \sim N_1(\mu_i, \sigma_{ii})\)
The conditional distribution of \(\mathbf{y}_1\) and \(\mathbf{y}_2\) is normal
\(\mathbf{y}_1 | \mathbf{y}_2 \sim N_{p1}(\mathbf{\mu_1 + \Sigma_{12} \Sigma_{22}^{-1}(y_2 - \mu_2),\Sigma_{11} - \Sigma_{12} \Sigma_{22}^{-1} \sigma_{21}})\)
- In this formula, we see if we know (have info about) \(\mathbf{y}_2\) , we can re-weight \(\mathbf{y}_1\) ’s mean, and the variance is reduced because we know more about \(\mathbf{y}_1\) because we know \(\mathbf{y}_2\)
which is analogous to \(\mathbf{y}_2 | \mathbf{y}_1\) . And \(\mathbf{y}_1\) and \(\mathbf{y}_2\) are independently distrusted only if \(\mathbf{\Sigma}_{12} = 0\)
If \(\mathbf{y} \sim N(\mathbf{\mu, \Sigma})\) and \(\mathbf{\Sigma}\) is positive definite, then \(\mathbf{(y-\mu)' \Sigma^{-1} (y - \mu)} \sim \chi^2_{(p)}\)
If \(\mathbf{y}_i\) are independent \(N_p (\mathbf{\mu}_i , \mathbf{\Sigma}_i)\) random variables, then for fixed matrices \(\mathbf{A}_{i(m \times p)}\) , \(\sum_{i=1}^k \mathbf{A}_i \mathbf{y}_i \sim N_m (\sum_{i=1}^{k} \mathbf{A}_i \mathbf{\mu}_i, \sum_{i=1}^k \mathbf{A}_i \mathbf{\Sigma}_i \mathbf{A}_i)\)
Multiple Regression
\[ \left( \begin{array} {c} Y \\ \mathbf{x} \end{array} \right) \sim N_{p+1} \left( \left[ \begin{array} {c} \mu_y \\ \mathbf{\mu}_x \end{array} \right] , \left[ \begin{array} {cc} \sigma^2_Y & \mathbf{\Sigma}_{yx} \\ \mathbf{\Sigma}_{yx} & \mathbf{\Sigma}_{xx} \end{array} \right] \right) \]
The conditional distribution of Y given x follows a univariate normal distribution with
\[ \begin{aligned} E(Y| \mathbf{x}) &= \mu_y + \mathbf{\Sigma}_{yx} \Sigma_{xx}^{-1} (\mathbf{x}- \mu_x) \\ &= \mu_y - \Sigma_{yx} \Sigma_{xx}^{-1}\mu_x + \Sigma_{yx} \Sigma_{xx}^{-1}\mathbf{x} \\ &= \beta_0 + \mathbf{\beta'x} \end{aligned} \]
where \(\beta = (\beta_1,...,\beta_p)' = \mathbf{\Sigma}_{xx}^{-1} \mathbf{\Sigma}_{yx}'\) (e.g., analogous to \(\mathbf{(x'x)^{-1}x'y}\) but not the same if we consider \(Y_i\) and \(\mathbf{x}_i\) , \(i = 1,..,n\) and use the empirical covariance formula: \(var(Y|\mathbf{x}) = \sigma^2_Y - \mathbf{\Sigma_{yx}\Sigma^{-1}_{xx} \Sigma'_{yx}}\) )
Samples from Multivariate Normal Populations
A random sample of size n, \(\mathbf{y}_1,.., \mathbf{y}_n\) from \(N_p (\mathbf{\mu}, \mathbf{\Sigma})\) . Then
Since \(\mathbf{y}_1,..., \mathbf{y}_n\) are iid, their sample mean, \(\bar{\mathbf{y}} = \sum_{i=1}^n \mathbf{y}_i/n \sim N_p (\mathbf{\mu}, \mathbf{\Sigma}/n)\) . that is, \(\bar{\mathbf{y}}\) is an unbiased estimator of \(\mathbf{\mu}\)
The \(p \times p\) sample variance-covariance matrix, \(\mathbf{S}\) is \(\mathbf{S} = \frac{1}{n-1}\sum_{i=1}^n (\mathbf{y}_i - \bar{\mathbf{y}})(\mathbf{y}_i - \bar{\mathbf{y}})' = \frac{1}{n-1} (\sum_{i=1}^n \mathbf{y}_i \mathbf{y}_i' - n \bar{\mathbf{y}}\bar{\mathbf{y}}')\)
- where \(\mathbf{S}\) is symmetric, unbiased estimator of \(\mathbf{\Sigma}\) and has \(p(p+1)/2\) random variables.
\((n-1)\mathbf{S} \sim W_p (n-1, \mathbf{\Sigma})\) is a Wishart distribution with n-1 degrees of freedom and expectation \((n-1) \mathbf{\Sigma}\) . The Wishart distribution is a multivariate extension of the Chi-squared distribution.
\(\bar{\mathbf{y}}\) and \(\mathbf{S}\) are independent
\(\bar{\mathbf{y}}\) and \(\mathbf{S}\) are sufficient statistics. (All of the info in the data about \(\mathbf{\mu}\) and \(\mathbf{\Sigma}\) is contained in \(\bar{\mathbf{y}}\) and \(\mathbf{S}\) , regardless of sample size).
Large Sample Properties
\(\mathbf{y}_1,..., \mathbf{y}_n\) are a random sample from some population with mean \(\mathbf{\mu}\) and variance-covariance matrix \(\mathbf{\Sigma}\)
\(\bar{\mathbf{y}}\) is a consistent estimator for \(\mu\)
\(\mathbf{S}\) is a consistent estimator for \(\mathbf{\Sigma}\)
Multivariate Central Limit Theorem : Similar to the univariate case, \(\sqrt{n}(\bar{\mathbf{y}} - \mu) \dot{\sim} N_p (\mathbf{0,\Sigma})\) where n is large relative to p ( \(n \ge 25p\) ), which is equivalent to \(\bar{\mathbf{y}} \dot{\sim} N_p (\mu, \mathbf{\Sigma}/n)\)
Wald’s Theorem : \(n(\bar{\mathbf{y}} - \mu)' \mathbf{S}^{-1} (\bar{\mathbf{y}} - \mu)\) when n is large relative to p.
Maximum Likelihood Estimation for MVN
Suppose iid \(\mathbf{y}_1 ,... \mathbf{y}_n \sim N_p (\mu, \mathbf{\Sigma})\) , the likelihood function for the data is
\[ \begin{aligned} L(\mu, \mathbf{\Sigma}) &= \prod_{j=1}^n (\frac{1}{(2\pi)^{p/2}|\mathbf{\Sigma}|^{1/2}} \exp(-\frac{1}{2}(\mathbf{y}_j -\mu)'\mathbf{\Sigma}^{-1})(\mathbf{y}_j -\mu)) \\ &= \frac{1}{(2\pi)^{np/2}|\mathbf{\Sigma}|^{n/2}} \exp(-\frac{1}{2} \sum_{j=1}^n(\mathbf{y}_j -\mu)'\mathbf{\Sigma}^{-1})(\mathbf{y}_j -\mu) \end{aligned} \]
Then, the MLEs are
\[ \hat{\mu} = \bar{\mathbf{y}} \]
\[ \hat{\mathbf{\Sigma}} = \frac{n-1}{n} \mathbf{S} \]
using derivatives of the log of the likelihood function with respect to \(\mu\) and \(\mathbf{\Sigma}\)
Properties of MLEs
Invariance: If \(\hat{\theta}\) is the MLE of \(\theta\) , then the MLE of \(h(\theta)\) is \(h(\hat{\theta})\) for any function h(.)
Consistency: MLEs are consistent estimators, but they are usually biased
Efficiency: MLEs are efficient estimators (no other estimator has a smaller variance for large samples)
Asymptotic normality: Suppose that \(\hat{\theta}_n\) is the MLE for \(\theta\) based upon n independent observations. Then \(\hat{\theta}_n \dot{\sim} N(\theta, \mathbf{H}^{-1})\)
\(\mathbf{H}\) is the Fisher Information Matrix, which contains the expected values of the second partial derivatives fo the log-likelihood function. the (i,j)th element of \(\mathbf{H}\) is \(-E(\frac{\partial^2 l(\mathbf{\theta})}{\partial \theta_i \partial \theta_j})\)
we can estimate \(\mathbf{H}\) by finding the form determined above, and evaluate it at \(\theta = \hat{\theta}_n\)
Likelihood ratio testing: for some null hypothesis, \(H_0\) we can form a likelihood ratio test
The statistic is: \(\Lambda = \frac{\max_{H_0}l(\mathbf{\mu}, \mathbf{\Sigma|Y})}{\max l(\mu, \mathbf{\Sigma | Y})}\)
For large n, \(-2 \log \Lambda \sim \chi^2_{(v)}\) where v is the number of parameters in the unrestricted space minus the number of parameters under \(H_0\)
Test of Multivariate Normality
Check univariate normality for each trait (X) separately
Can check \[Normality Assessment\]
The good thing is that if any of the univariate trait is not normal, then the joint distribution is not normal (see again [m]). If a joint multivariate distribution is normal, then the marginal distribution has to be normal.
However, marginal normality of all traits does not imply joint MVN
Easily rule out multivariate normality, but not easy to prove it
Mardia’s tests for multivariate normality
Multivariate skewness is \[ \beta_{1,p} = E[(\mathbf{y}- \mathbf{\mu})' \mathbf{\Sigma}^{-1} (\mathbf{x} - \mathbf{\mu})]^3 \]
where \(\mathbf{x}\) and \(\mathbf{y}\) are independent, but have the same distribution (note: \(\beta\) here is not regression coefficient)
Multivariate kurtosis is defined as
\[ \beta_{2,p} - E[(\mathbf{y}- \mathbf{\mu})' \mathbf{\Sigma}^{-1} (\mathbf{x} - \mathbf{\mu})]^2 \]
For the MVN distribution, we have \(\beta_{1,p} = 0\) and \(\beta_{2,p} = p(p+2)\)
For a sample of size n, we can estimate
\[ \hat{\beta}_{1,p} = \frac{1}{n^2}\sum_{i=1}^n \sum_{j=1}^n g^2_{ij} \]
\[ \hat{\beta}_{2,p} = \frac{1}{n} \sum_{i=1}^n g^2_{ii} \]
- where \(g_{ij} = (\mathbf{y}_i - \bar{\mathbf{y}})' \mathbf{S}^{-1} (\mathbf{y}_j - \bar{\mathbf{y}})\) . Note: \(g_{ii} = d^2_i\) where \(d^2_i\) is the Mahalanobis distance
( Mardia 1970 ) shows for large n
\[ \kappa_1 = \frac{n \hat{\beta}_{1,p}}{6} \dot{\sim} \chi^2_{p(p+1)(p+2)/6} \]
\[ \kappa_2 = \frac{\hat{\beta}_{2,p} - p(p+2)}{\sqrt{8p(p+2)/n}} \sim N(0,1) \]
Hence, we can use \(\kappa_1\) and \(\kappa_2\) to test the null hypothesis of MVN.
When the data are non-normal, normal theory tests on the mean are sensitive to \(\beta_{1,p}\) , while tests on the covariance are sensitive to \(\beta_{2,p}\)
Alternatively, Doornik-Hansen test for multivariate normality ( Doornik and Hansen 2008 )
Chi-square Q-Q plot
Let \(\mathbf{y}_i, i = 1,...,n\) be a random sample sample from \(N_p(\mathbf{\mu}, \mathbf{\Sigma})\)
Then \(\mathbf{z}_i = \mathbf{\Sigma}^{-1/2}(\mathbf{y}_i - \mathbf{\mu}), i = 1,...,n\) are iid \(N_p (\mathbf{0}, \mathbf{I})\) . Thus, \(d_i^2 = \mathbf{z}_i' \mathbf{z}_i \sim \chi^2_p , i = 1,...,n\)
plot the ordered \(d_i^2\) values against the qualities of the \(\chi^2_p\) distribution. When normality holds, the plot should approximately resemble a straight lien passing through the origin at a 45 degree
it requires large sample size (i.e., sensitive to sample size). Even if we generate data from a MVN, the tail of the Chi-square Q-Q plot can still be out of line.
If the data are not normal, we can
use nonparametric methods
use models based upon an approximate distribution (e.g., GLMM)
try performing a transformation

22.0.2 Mean Vector Inference
In the univariate normal distribution, we test \(H_0: \mu =\mu_0\) by using
\[ T = \frac{\bar{y}- \mu_0}{s/\sqrt{n}} \sim t_{n-1} \]
under the null hypothesis. And reject the null if \(|T|\) is large relative to \(t_{(1-\alpha/2,n-1)}\) because it means that seeing a value as large as what we observed is rare if the null is true
Equivalently,
\[ T^2 = \frac{(\bar{y}- \mu_0)^2}{s^2/n} = n(\bar{y}- \mu_0)(s^2)^{-1}(\bar{y}- \mu_0) \sim f_{(1,n-1)} \]
22.0.2.1 Natural Multivariate Generalization
\[ \begin{aligned} &H_0: \mathbf{\mu} = \mathbf{\mu}_0 \\ &H_a: \mathbf{\mu} \neq \mathbf{\mu}_0 \end{aligned} \]
Define Hotelling’s \(T^2\) by
\[ T^2 = n(\bar{\mathbf{y}} - \mathbf{\mu}_0)'\mathbf{S}^{-1}(\bar{\mathbf{y}} - \mathbf{\mu}_0) \]
which can be viewed as a generalized distance between \(\bar{\mathbf{y}}\) and \(\mathbf{\mu}_0\)
Under the assumption of normality,
\[ F = \frac{n-p}{(n-1)p} T^2 \sim f_{(p,n-p)} \]
and reject the null hypothesis when \(F > f_{(1-\alpha, p, n-p)}\)
The \(T^2\) test is invariant to changes in measurement units.
- If \(\mathbf{z = Cy + d}\) where \(\mathbf{C}\) and \(\mathbf{d}\) do not depend on \(\mathbf{y}\) , then \(T^2(\mathbf{z}) - T^2(\mathbf{y})\)
The \(T^2\) test can be derived as a likelihood ratio test of \(H_0: \mu = \mu_0\)
22.0.2.2 Confidence Intervals
22.0.2.2.1 confidence region.
An “exact” \(100(1-\alpha)\%\) confidence region for \(\mathbf{\mu}\) is the set of all vectors, \(\mathbf{v}\) , which are “close enough” to the observed mean vector, \(\bar{\mathbf{y}}\) to satisfy
\[ n(\bar{\mathbf{y}} - \mathbf{\mu}_0)'\mathbf{S}^{-1}(\bar{\mathbf{y}} - \mathbf{\mu}_0) \le \frac{(n-1)p}{n-p} f_{(1-\alpha, p, n-p)} \]
- \(\mathbf{v}\) are just the mean vectors that are not rejected by the \(T^2\) test when \(\mathbf{\bar{y}}\) is observed.
In case that you have 2 parameters, the confidence region is a “hyper-ellipsoid”.
In this region, it consists of all \(\mathbf{\mu}_0\) vectors for which the \(T^2\) test would not reject \(H_0\) at significance level \(\alpha\)
Even though the confidence region better assesses the joint knowledge concerning plausible values of \(\mathbf{\mu}\) , people typically include confidence statement about the individual component means. We’d like all of the separate confidence statements to hold simultaneously with a specified high probability. Simultaneous confidence intervals: intervals against any statement being incorrect
22.0.2.2.1.1 Simultaneous Confidence Statements
- Intervals based on a rectangular confidence region by projecting the previous region onto the coordinate axes:
\[ \bar{y}_{i} \pm \sqrt{\frac{(n-1)p}{n-p}f_{(1-\alpha, p,n-p)}\frac{s_{ii}}{n}} \]
for all \(i = 1,..,p\)
which implied confidence region is conservative; it has at least \(100(1- \alpha)\%\)
Generally, simultaneous \(100(1-\alpha) \%\) confidence intervals for all linear combinations , \(\mathbf{a}\) of the elements of the mean vector are given by
\[ \mathbf{a'\bar{y}} \pm \sqrt{\frac{(n-1)p}{n-p}f_{(1-\alpha, p,n-p)}\frac{\mathbf{a'Sa}}{n}} \]
works for any arbitrary linear combination \(\mathbf{a'\mu} = a_1 \mu_1 + ... + a_p \mu_p\) , which is a projection onto the axis in the direction of \(\mathbf{a}\)
These intervals have the property that the probability that at least one such interval does not contain the appropriate \(\mathbf{a' \mu}\) is no more than \(\alpha\)
These types of intervals can be used for “data snooping” (like \[Scheffe\] )
22.0.2.2.1.2 One \(\mu\) at a time
- One at a time confidence intervals:
\[ \bar{y}_i \pm t_{(1 - \alpha/2, n-1} \sqrt{\frac{s_{ii}}{n}} \]
Each of these intervals has a probability of \(1-\alpha\) of covering the appropriate \(\mu_i\)
But they ignore the covariance structure of the \(p\) variables
If we only care about \(k\) simultaneous intervals, we can use “one at a time” method with the \[Bonferroni\] correction.
This method gets more conservative as the number of intervals \(k\) increases.
22.0.3 General Hypothesis Testing
22.0.3.1 one-sample tests.
\[ H_0: \mathbf{C \mu= 0} \]
- \(\mathbf{C}\) is a \(c \times p\) matrix of rank c where \(c \le p\)
We can test this hypothesis using the following statistic
\[ F = \frac{n - c}{(n-1)c} T^2 \]
where \(T^2 = n(\mathbf{C\bar{y}})' (\mathbf{CSC'})^{-1} (\mathbf{C\bar{y}})\)
\[ H_0: \mu_1 = \mu_2 = ... = \mu_p \]
\[ \begin{aligned} \mu_1 - \mu_2 &= 0 \\ &\vdots \\ \mu_{p-1} - \mu_p &= 0 \end{aligned} \]
a total of \(p-1\) tests. Hence, we have \(\mathbf{C}\) as the \(p - 1 \times p\) matrix
\[ \mathbf{C} = \left( \begin{array} {ccccc} 1 & -1 & 0 & \ldots & 0 \\ 0 & 1 & -1 & \ldots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & 1 & -1 \end{array} \right) \]
number of rows = \(c = p -1\)
Equivalently, we can also compare all of the other means to the first mean. Then, we test \(\mu_1 - \mu_2 = 0, \mu_1 - \mu_3 = 0,..., \mu_1 - \mu_p = 0\) , the \((p-1) \times p\) matrix \(\mathbf{C}\) is
\[ \mathbf{C} = \left( \begin{array} {ccccc} -1 & 1 & 0 & \ldots & 0 \\ -1 & 0 & 1 & \ldots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ -1 & 0 & \ldots & 0 & 1 \end{array} \right) \]
The value of \(T^2\) is invariant to these equivalent choices of \(\mathbf{C}\)
This is often used for repeated measures designs , where each subject receives each treatment once over successive periods of time (all treatments are administered to each unit).
Let \(y_{ij}\) be the response from subject i at time j for \(i = 1,..,n, j = 1,...,T\) . In this case, \(\mathbf{y}_i = (y_{i1}, ..., y_{iT})', i = 1,...,n\) are a random sample from \(N_T (\mathbf{\mu}, \mathbf{\Sigma})\)
Let \(n=8\) subjects, \(T = 6\) . We are interested in \(\mu_1, .., \mu_6\)
\[ H_0: \mu_1 = \mu_2 = ... = \mu_6 \]
\[ \begin{aligned} \mu_1 - \mu_2 &= 0 \\ \mu_2 - \mu_3 &= 0 \\ &... \\ \mu_5 - \mu_6 &= 0 \end{aligned} \]
We can test orthogonal polynomials for 4 equally spaced time points. To test for example the null hypothesis that quadratic and cubic effects are jointly equal to 0, we would define \(\mathbf{C}\)
\[ \mathbf{C} = \left( \begin{array} {cccc} 1 & -1 & -1 & 1 \\ -1 & 3 & -3 & 1 \end{array} \right) \]
22.0.3.2 Two-Sample Tests
Consider the analogous two sample multivariate tests.
Example: we have data on two independent random samples, one sample from each of two populations
\[ \begin{aligned} \mathbf{y}_{1i} &\sim N_p (\mathbf{\mu_1, \Sigma}) \\ \mathbf{y}_{2j} &\sim N_p (\mathbf{\mu_2, \Sigma}) \end{aligned} \]
equal variance-covariance matrices
independent random samples
We can summarize our data using the sufficient statistics \(\mathbf{\bar{y}}_1, \mathbf{S}_1, \mathbf{\bar{y}}_2, \mathbf{S}_2\) with respective sample sizes, \(n_1,n_2\)
Since we assume that \(\mathbf{\Sigma}_1 = \mathbf{\Sigma}_2 = \mathbf{\Sigma}\) , compute a pooled estimate of the variance-covariance matrix on \(n_1 + n_2 - 2\) df
\[ \mathbf{S} = \frac{(n_1 - 1)\mathbf{S}_1 + (n_2-1) \mathbf{S}_2}{(n_1 -1) + (n_2 - 1)} \]
\[ \begin{aligned} &H_0: \mathbf{\mu}_1 = \mathbf{\mu}_2 \\ &H_a: \mathbf{\mu}_1 \neq \mathbf{\mu}_2 \end{aligned} \]
At least one element of the mean vectors is different
\(\mathbf{\bar{y}}_1 - \mathbf{\bar{y}}_2\) to estimate \(\mu_1 - \mu_2\)
\(\mathbf{S}\) to estimate \(\mathbf{\Sigma}\)
Note: because we assume the two populations are independent, there is no covariance
\(cov(\mathbf{\bar{y}}_1 - \mathbf{\bar{y}}_2) = var(\mathbf{\bar{y}}_1) + var(\mathbf{\bar{y}}_2) = \frac{\mathbf{\Sigma_1}}{n_1} + \frac{\mathbf{\Sigma_2}}{n_2} = \mathbf{\Sigma}(\frac{1}{n_1} + \frac{1}{n_2})\)
Reject \(H_0\) if
\[ \begin{aligned} T^2 &= (\mathbf{\bar{y}}_1 - \mathbf{\bar{y}}_2)'\{ \mathbf{S} (\frac{1}{n_1} + \frac{1}{n_2})\}^{-1} (\mathbf{\bar{y}}_1 - \mathbf{\bar{y}}_2)\\ &= \frac{n_1 n_2}{n_1 +n_2} (\mathbf{\bar{y}}_1 - \mathbf{\bar{y}}_2)'\{ \mathbf{S} \}^{-1} (\mathbf{\bar{y}}_1 - \mathbf{\bar{y}}_2)\\ & \ge \frac{(n_1 + n_2 -2)p}{n_1 + n_2 - p - 1} f_{(1- \alpha,n_1 + n_2 - p -1)} \end{aligned} \]
or equivalently, if
\[ F = \frac{n_1 + n_2 - p -1}{(n_1 + n_2 -2)p} T^2 \ge f_{(1- \alpha, p , n_1 + n_2 -p -1)} \]
A \(100(1-\alpha) \%\) confidence region for \(\mu_1 - \mu_2\) consists of all vector \(\delta\) which satisfy
\[ \frac{n_1 n_2}{n_1 + n_2} (\mathbf{\bar{y}}_1 - \mathbf{\bar{y}}_2 - \mathbf{\delta})' \mathbf{S}^{-1}(\mathbf{\bar{y}}_1 - \mathbf{\bar{y}}_2 - \mathbf{\delta}) \le \frac{(n_1 + n_2 - 2)p}{n_1 + n_2 -p - 1}f_{(1-\alpha, p , n_1 + n_2 - p -1)} \]
The simultaneous confidence intervals for all linear combinations of \(\mu_1 - \mu_2\) have the form
\[ \mathbf{a'}(\mathbf{\bar{y}}_1 - \mathbf{\bar{y}}_2) \pm \sqrt{\frac{(n_1 + n_2 -2)p}{n_1 + n_2 - p -1}}f_{(1-\alpha, p, n_1 + n_2 -p -1)} \times \sqrt{\mathbf{a'Sa}(\frac{1}{n_1} + \frac{1}{n_2})} \]
Bonferroni intervals, for k combinations
\[ (\bar{y}_{1i} - \bar{y}_{2i}) \pm t_{(1-\alpha/2k, n_1 + n_2 - 2)}\sqrt{(\frac{1}{n_1} + \frac{1}{n_2})s_{ii}} \]
22.0.3.3 Model Assumptions
If model assumption are not met
Unequal Covariance Matrices
If \(n_1 = n_2\) (large samples) there is little effect on the Type I error rate and power fo the two sample test
If \(n_1 > n_2\) and the eigenvalues of \(\mathbf{\Sigma}_1 \mathbf{\Sigma}^{-1}_2\) are less than 1, the Type I error level is inflated
If \(n_1 > n_2\) and some eigenvalues of \(\mathbf{\Sigma}_1 \mathbf{\Sigma}_2^{-1}\) are greater than 1, the Type I error rate is too small, leading to a reduction in power
Sample Not Normal
Type I error level of the two sample \(T^2\) test isn’t much affect by moderate departures from normality if the two populations being sampled have similar distributions
One sample \(T^2\) test is much more sensitive to lack of normality, especially when the distribution is skewed.
Intuitively, you can think that in one sample your distribution will be sensitive, but the distribution of the difference between two similar distributions will not be as sensitive.
Transform to make the data more normal
Large large samples, use the \(\chi^2\) (Wald) test, in which populations don’t need to be normal, or equal sample sizes, or equal variance-covariance matrices
- \(H_0: \mu_1 - \mu_2 =0\) use \((\mathbf{\bar{y}}_1 - \mathbf{\bar{y}}_2)'( \frac{1}{n_1} \mathbf{S}_1 + \frac{1}{n_2}\mathbf{S}_2)^{-1}(\mathbf{\bar{y}}_1 - \mathbf{\bar{y}}_2) \dot{\sim} \chi^2_{(p)}\)
22.0.3.3.1 Equal Covariance Matrices Tests
With independent random samples from k populations of \(p\) -dimensional vectors. We compute the sample covariance matrix for each, \(\mathbf{S}_i\) , where \(i = 1,...,k\)
\[ \begin{aligned} &H_0: \mathbf{\Sigma}_1 = \mathbf{\Sigma}_2 = \ldots = \mathbf{\Sigma}_k = \mathbf{\Sigma} \\ &H_a: \text{at least 2 are different} \end{aligned} \]
Assume \(H_0\) is true, we would use a pooled estimate of the common covariance matrix, \(\mathbf{\Sigma}\)
\[ \mathbf{S} = \frac{\sum_{i=1}^k (n_i -1)\mathbf{S}_i}{\sum_{i=1}^k (n_i - 1)} \]
with \(\sum_{i=1}^k (n_i -1)\)
22.0.3.3.1.1 Bartlett’s Test
(a modification of the likelihood ratio test). Define
\[ N = \sum_{i=1}^k n_i \]
and (note: \(| |\) are determinants here, not absolute value)
\[ M = (N - k) \log|\mathbf{S}| - \sum_{i=1}^k (n_i - 1) \log|\mathbf{S}_i| \]
\[ C^{-1} = 1 - \frac{2p^2 + 3p - 1}{6(p+1)(k-1)} \{\sum_{i=1}^k (\frac{1}{n_i - 1}) - \frac{1}{N-k} \} \]
Reject \(H_0\) when \(MC^{-1} > \chi^2_{1- \alpha, (k-1)p(p+1)/2}\)
If not all samples are from normal populations, \(MC^{-1}\) has a distribution which is often shifted to the right of the nominal \(\chi^2\) distribution, which means \(H_0\) is often rejected even when it is true (the Type I error level is inflated). Hence, it is better to test individual normality first, or then multivariate normality before you do Bartlett’s test.
22.0.3.4 Two-Sample Repeated Measurements
Define \(\mathbf{y}_{hi} = (y_{hi1}, ..., y_{hit})'\) to be the observations from the i-th subject in the h-th group for times 1 through T
Assume that \(\mathbf{y}_{11}, ..., \mathbf{y}_{1n_1}\) are iid \(N_t(\mathbf{\mu}_1, \mathbf{\Sigma})\) and that \(\mathbf{y}_{21},...,\mathbf{y}_{2n_2}\) are iid \(N_t(\mathbf{\mu}_2, \mathbf{\Sigma})\)
\(H_0: \mathbf{C}(\mathbf{\mu}_1 - \mathbf{\mu}_2) = \mathbf{0}_c\) where \(\mathbf{C}\) is a \(c \times t\) matrix of rank \(c\) where \(c \le t\)
The test statistic has the form
\[ T^2 = \frac{n_1 n_2}{n_1 + n_2} (\mathbf{\bar{y}}_1 - \mathbf{\bar{y}}_2)' \mathbf{C}'(\mathbf{CSC}')^{-1}\mathbf{C} (\mathbf{\bar{y}}_1 - \mathbf{\bar{y}}_2) \]
where \(\mathbf{S}\) is the pooled covariance estimate. Then,
\[ F = \frac{n_1 + n_2 - c -1}{(n_1 + n_2-2)c} T^2 \sim f_{(c, n_1 + n_2 - c-1)} \]
when \(H_0\) is true
If the null hypothesis \(H_0: \mu_1 = \mu_2\) is rejected. A weaker hypothesis is that the profiles for the two groups are parallel.
\[ \begin{aligned} \mu_{11} - \mu_{21} &= \mu_{12} - \mu_{22} \\ &\vdots \\ \mu_{1t-1} - \mu_{2t-1} &= \mu_{1t} - \mu_{2t} \end{aligned} \]
The null hypothesis matrix term is then
\(H_0: \mathbf{C}(\mu_1 - \mu_2) = \mathbf{0}_c\) , where \(c = t - 1\) and
\[ \mathbf{C} = \left( \begin{array} {ccccc} 1 & -1 & 0 & \ldots & 0 \\ 0 & 1 & -1 & \ldots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \ldots & -1 \end{array} \right)_{(t-1) \times t} \]
can’t reject the null of hypothesized vector of means
reject the null that the two labs’ measurements are equal

reject null. Hence, there is a difference in the means of the bivariate normal distributions
22.1 MANOVA
Multivariate Analysis of Variance
One-way MANOVA
Compare treatment means for h different populations
Population 1: \(\mathbf{y}_{11}, \mathbf{y}_{12}, \dots, \mathbf{y}_{1n_1} \sim idd N_p (\mathbf{\mu}_1, \mathbf{\Sigma})\)
Population h: \(\mathbf{y}_{h1}, \mathbf{y}_{h2}, \dots, \mathbf{y}_{hn_h} \sim idd N_p (\mathbf{\mu}_h, \mathbf{\Sigma})\)
Assumptions
- Independent random samples from \(h\) different populations
- Common covariance matrices
- Each population is multivariate normal
Calculate the summary statistics \(\mathbf{\bar{y}}_i, \mathbf{S}\) and the pooled estimate of the covariance matrix \(\mathbf{S}\)
Similar to the univariate one-way ANVOA, we can use the effects model formulation \(\mathbf{\mu}_i = \mathbf{\mu} + \mathbf{\tau}_i\) , where
\(\mathbf{\mu}_i\) is the population mean for population i
\(\mathbf{\mu}\) is the overall mean effect
\(\mathbf{\tau}_i\) is the treatment effect of the i-th treatment.
For the one-way model: \(\mathbf{y}_{ij} = \mu + \tau_i + \epsilon_{ij}\) for \(i = 1,..,h; j = 1,..., n_i\) and \(\epsilon_{ij} \sim N_p(\mathbf{0, \Sigma})\)
However, the above model is over-parameterized (i.e., infinite number of ways to define \(\mathbf{\mu}\) and the \(\mathbf{\tau}_i\) ’s such that they add up to \(\mu_i\) . Thus we can constrain by having
\[ \sum_{i=1}^h n_i \tau_i = 0 \]
\[ \mathbf{\tau}_h = 0 \]
The observational equivalent of the effects model is
\[ \begin{aligned} \mathbf{y}_{ij} &= \mathbf{\bar{y}} + (\mathbf{\bar{y}}_i - \mathbf{\bar{y}}) + (\mathbf{y}_{ij} - \mathbf{\bar{y}}_i) \\ &= \text{overall sample mean} + \text{treatement effect} + \text{residual} \text{ (under univariate ANOVA)} \end{aligned} \]
After manipulation
\[ \sum_{i = 1}^h \sum_{j = 1}^{n_i} (\mathbf{\bar{y}}_{ij} - \mathbf{\bar{y}})(\mathbf{\bar{y}}_{ij} - \mathbf{\bar{y}})' = \sum_{i = 1}^h n_i (\mathbf{\bar{y}}_i - \mathbf{\bar{y}})(\mathbf{\bar{y}}_i - \mathbf{\bar{y}})' + \sum_{i=1}^h \sum_{j = 1}^{n_i} (\mathbf{\bar{y}}_{ij} - \mathbf{\bar{y}})(\mathbf{\bar{y}}_{ij} - \mathbf{\bar{y}}_i)' \]
LHS = Total corrected sums of squares and cross products (SSCP) matrix
1st term = Treatment (or between subjects) sum of squares and cross product matrix (denoted H;B)
2nd term = residual (or within subject) SSCP matrix denoted (E;W)
\[ \mathbf{E} = (n_1 - 1)\mathbf{S}_1 + ... + (n_h -1) \mathbf{S}_h = (n-h) \mathbf{S} \]
MANOVA table
| Source | SSCP | df |
|---|---|---|
| Treatment | \(\mathbf{H}\) | \(h -1\) |
| Residual (error) | \(\mathbf{E}\) | \(\sum_{i= 1}^h n_i - h\) |
| Total Corrected | \(\mathbf{H + E}\) | \(\sum_{i=1}^h n_i -1\) |
\[ H_0: \tau_1 = \tau_2 = \dots = \tau_h = \mathbf{0} \]
We consider the relative “sizes” of \(\mathbf{E}\) and \(\mathbf{H+E}\)
Wilk’s Lambda
Define Wilk’s Lambda
\[ \Lambda^* = \frac{|\mathbf{E}|}{|\mathbf{H+E}|} \]
Properties:
Wilk’s Lambda is equivalent to the F-statistic in the univariate case
The exact distribution of \(\Lambda^*\) can be determined for especial cases.
For large sample sizes, reject \(H_0\) if
\[ -(\sum_{i=1}^h n_i - 1 - \frac{p+h}{2}) \log(\Lambda^*) > \chi^2_{(1-\alpha, p(h-1))} \]
22.1.1 Testing General Hypotheses
\(h\) different treatments
with the i-th treatment
applied to \(n_i\) subjects that
are observed for \(p\) repeated measures.
Consider this a \(p\) dimensional obs on a random sample from each of \(h\) different treatment populations.
\[ \mathbf{y}_{ij} = \mathbf{\mu} + \mathbf{\tau}_i + \mathbf{\epsilon}_{ij} \]
for \(i = 1,..,h\) and \(j = 1,..,n_i\)
\[ \mathbf{Y} = \mathbf{XB} + \mathbf{\epsilon} \]
where \(n = \sum_{i = 1}^h n_i\) and with restriction \(\mathbf{\tau}_h = 0\)
\[ \mathbf{Y}_{(n \times p)} = \left[ \begin{array} {c} \mathbf{y}_{11}' \\ \vdots \\ \mathbf{y}_{1n_1}' \\ \vdots \\ \mathbf{y}_{hn_h}' \end{array} \right], \mathbf{B}_{(h \times p)} = \left[ \begin{array} {c} \mathbf{\mu}' \\ \mathbf{\tau}_1' \\ \vdots \\ \mathbf{\tau}_{h-1}' \end{array} \right], \mathbf{\epsilon}_{(n \times p)} = \left[ \begin{array} {c} \epsilon_{11}' \\ \vdots \\ \epsilon_{1n_1}' \\ \vdots \\ \epsilon_{hn_h}' \end{array} \right] \]
\[ \mathbf{X}_{(n \times h)} = \left[ \begin{array} {ccccc} 1 & 1 & 0 & \ldots & 0 \\ \vdots & \vdots & \vdots & & \vdots \\ 1 & 1 & 0 & \ldots & 0 \\ \vdots & \vdots & \vdots & \ldots & \vdots \\ 1 & 0 & 0 & \ldots & 0 \\ \vdots & \vdots & \vdots & & \vdots \\ 1 & 0 & 0 & \ldots & 0 \end{array} \right] \]
\[ \mathbf{\hat{B}} = (\mathbf{X'X})^{-1} \mathbf{X'Y} \]
Rows of \(\mathbf{Y}\) are independent (i.e., \(var(\mathbf{Y}) = \mathbf{I}_n \otimes \mathbf{\Sigma}\) , an \(np \times np\) matrix, where \(\otimes\) is the Kronecker product).
\[ \begin{aligned} &H_0: \mathbf{LBM} = 0 \\ &H_a: \mathbf{LBM} \neq 0 \end{aligned} \]
\(\mathbf{L}\) is a \(g \times h\) matrix of full row rank ( \(g \le h\) ) = comparisons across groups
\(\mathbf{M}\) is a \(p \times u\) matrix of full column rank ( \(u \le p\) ) = comparisons across traits
The general treatment corrected sums of squares and cross product is
\[ \mathbf{H} = \mathbf{M'Y'X(X'X)^{-1}L'[L(X'X)^{-1}L']^{-1}L(X'X)^{-1}X'YM} \]
or for the null hypothesis \(H_0: \mathbf{LBM} = \mathbf{D}\)
\[ \mathbf{H} = (\mathbf{\hat{LBM}} - \mathbf{D})'[\mathbf{X(X'X)^{-1}L}]^{-1}(\mathbf{\hat{LBM}} - \mathbf{D}) \]
The general matrix of residual sums of squares and cross product
\[ \mathbf{E} = \mathbf{M'Y'[I-X(X'X)^{-1}X']YM} = \mathbf{M'[Y'Y - \hat{B}'(X'X)^{-1}\hat{B}]M} \]
We can compute the following statistic eigenvalues of \(\mathbf{HE}^{-1}\)
Wilk’s Criterion: \(\Lambda^* = \frac{|\mathbf{E}|}{|\mathbf{H} + \mathbf{E}|}\) . The df depend on the rank of \(\mathbf{L}, \mathbf{M}, \mathbf{X}\)
Lawley-Hotelling Trace: \(U = tr(\mathbf{HE}^{-1})\)
Pillai Trace: \(V = tr(\mathbf{H}(\mathbf{H}+ \mathbf{E}^{-1})\)
Roy’s Maximum Root: largest eigenvalue of \(\mathbf{HE}^{-1}\)
If \(H_0\) is true and n is large, \(-(n-1- \frac{p+h}{2})\ln \Lambda^* \sim \chi^2_{p(h-1)}\) . Some special values of p and h can give exact F-dist under \(H_0\)
reject the null of equal multivariate mean vectors between the three admmission groups
- If independent = time with 3 levels -> univariate ANOVA (require sphericity assumption (i.e., the variances for all differences are equal))
- If each level of independent time as a separate variable -> MANOVA (does not require sphericity assumption)
can’t reject the null hypothesis of sphericity, hence univariate ANOVA is also appropriate.We also see linear significant time effect, but no quadratic time effect

reject the null hypothesis of no difference in means between treatments
there is no significant difference in means between the control and bww9 drug
there is a significant difference in means between ax23 drug treatment and the rest of the treatments
22.1.2 Profile Analysis
Examine similarities between the treatment effects (between subjects), which is useful for longitudinal analysis. Null is that all treatments have the same average effect.
\[ H_0: \mu_1 = \mu_2 = \dots = \mu_h \]
\[ H_0: \tau_1 = \tau_2 = \dots = \tau_h \]
The exact nature of the similarities and differences between the treatments can be examined under this analysis.
Sequential steps in profile analysis:
- Are the profiles parallel ? (i.e., is there no interaction between treatment and time)
- Are the profiles coincidental ? (i.e., are the profiles identical?)
- Are the profiles horizontal ? (i.e., are there no differences between any time points?)
If we reject the null hypothesis that the profiles are parallel, we can test
Are there differences among groups within some subset of the total time points?
Are there differences among time points in a particular group (or groups)?
Are there differences within some subset of the total time points in a particular group (or groups)?
4 times (p = 4)
3 treatments (h=3)
22.1.2.1 Parallel Profile
Are the profiles for each population identical expect for a mean shift?
\[ \begin{aligned} H_0: \mu_{11} - \mu_{21} - \mu_{12} - \mu_{22} = &\dots = \mu_{1t} - \mu_{2t} \\ \mu_{11} - \mu_{31} - \mu_{12} - \mu_{32} = &\dots = \mu_{1t} - \mu_{3t} \\ &\dots \end{aligned} \]
for \(h-1\) equations
\[ H_0: \mathbf{LBM = 0} \]
\[ \mathbf{LBM} = \left[ \begin{array} {ccc} 1 & -1 & 0 \\ 1 & 0 & -1 \end{array} \right] \left[ \begin{array} {ccc} \mu_{11} & \dots & \mu_{14} \\ \mu_{21} & \dots & \mu_{24} \\ \mu_{31} & \dots & \mu_{34} \end{array} \right] \left[ \begin{array} {ccc} 1 & 1 & 1 \\ -1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & -1 \end{array} \right] = \mathbf{0} \]
where this is the cell means parameterization of \(\mathbf{B}\)
The multiplication of the first 2 matrices \(\mathbf{LB}\) is
\[ \left[ \begin{array} {cccc} \mu_{11} - \mu_{21} & \mu_{12} - \mu_{22} & \mu_{13} - \mu_{23} & \mu_{14} - \mu_{24}\\ \mu_{11} - \mu_{31} & \mu_{12} - \mu_{32} & \mu_{13} - \mu_{33} & \mu_{14} - \mu_{34} \end{array} \right] \]
which is the differences in treatment means at the same time
Multiplying by \(\mathbf{M}\) , we get the comparison across time
\[ \left[ \begin{array} {ccc} (\mu_{11} - \mu_{21}) - (\mu_{12} - \mu_{22}) & (\mu_{11} - \mu_{21}) -(\mu_{13} - \mu_{23}) & (\mu_{11} - \mu_{21}) - (\mu_{14} - \mu_{24}) \\ (\mu_{11} - \mu_{31}) - (\mu_{12} - \mu_{32}) & (\mu_{11} - \mu_{31}) - (\mu_{13} - \mu_{33}) & (\mu_{11} - \mu_{31}) -(\mu_{14} - \mu_{34}) \end{array} \right] \]
Alternatively, we can also use the effects parameterization
\[ \mathbf{LBM} = \left[ \begin{array} {cccc} 0 & 1 & -1 & 0 \\ 0 & 1 & 0 & -1 \end{array} \right] \left[ \begin{array} {c} \mu' \\ \tau'_1 \\ \tau_2' \\ \tau_3' \end{array} \right] \left[ \begin{array} {ccc} 1 & 1 & 1 \\ -1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & -1 \end{array} \right] = \mathbf{0} \]
In both parameterizations, \(rank(\mathbf{L}) = h-1\) and \(rank(\mathbf{M}) = p-1\)
We could also choose \(\mathbf{L}\) and \(\mathbf{M}\) in other forms
\[ \mathbf{L} = \left[ \begin{array} {cccc} 0 & 1 & 0 & -1 \\ 0 & 0 & 1 & -1 \end{array} \right] \]
\[ \mathbf{M} = \left[ \begin{array} {ccc} 1 & 0 & 0 \\ -1 & 1 & 0 \\ 0 & -1 & 1 \\ 0 & 0 & -1 \end{array} \right] \]
and still obtain the same result.
22.1.2.2 Coincidental Profiles
After we have evidence that the profiles are parallel (i.e., fail to reject the parallel profile test), we can ask whether they are identical?
Given profiles are parallel , then if the sums of the components of \(\mu_i\) are identical for all the treatments, then the profiles are identical .
\[ H_0: \mathbf{1'}_p \mu_1 = \mathbf{1'}_p \mu_2 = \dots = \mathbf{1'}_p \mu_h \]
\[ H_0: \mathbf{LBM} = \mathbf{0} \]
where for the cell means parameterization
\[ \mathbf{L} = \left[ \begin{array} {ccc} 1 & 0 & -1 \\ 0 & 1 & -1 \end{array} \right] \]
\[ \mathbf{M} = \left[ \begin{array} {cccc} 1 & 1 & 1 & 1 \end{array} \right]' \]
multiplication yields
\[ \left[ \begin{array} {c} (\mu_{11} + \mu_{12} + \mu_{13} + \mu_{14}) - (\mu_{31} + \mu_{32} + \mu_{33} + \mu_{34}) \\ (\mu_{21} + \mu_{22} + \mu_{23} + \mu_{24}) - (\mu_{31} + \mu_{32} + \mu_{33} + \mu_{34}) \end{array} \right] = \left[ \begin{array} {c} 0 \\ 0 \end{array} \right] \]
Different choices of \(\mathbf{L}\) and \(\mathbf{M}\) can yield the same result
22.1.2.3 Horizontal Profiles
Given that we can’t reject the null hypothesis that all \(h\) profiles are the same, we can ask whether all of the elements of the common profile equal? (i.e., horizontal)
\[ \mathbf{L} = \left[ \begin{array} {ccc} 1 & 0 & 0 \end{array} \right] \]
\[ \left[ \begin{array} {ccc} (\mu_{11} - \mu_{12}) & (\mu_{12} - \mu_{13}) & (\mu_{13} + \mu_{14}) \end{array} \right] = \left[ \begin{array} {ccc} 0 & 0 & 0 \end{array} \right] \]
- If we fail to reject all 3 hypotheses, then we fail to reject the null hypotheses of both no difference between treatments and no differences between traits.
| Test | Equivalent test for |
|---|---|
| Parallel profile | Interaction |
| Coincidental profile | main effect of between-subjects factor |
| Horizontal profile | main effect of repeated measures factor |
22.1.3 Summary

22.2 Principal Components
- Unsupervised learning
- find important features
- reduce the dimensions of the data set
- “decorrelate” multivariate vectors that have dependence.
- uses eigenvector/eigvenvalue decomposition of covariance (correlation) matrices.
According to the “spectral decomposition theorem”, if \(\mathbf{\Sigma}_{p \times p}\) i s a positive semi-definite, symmetric, real matrix, then there exists an orthogonal matrix \(\mathbf{A}\) such that \(\mathbf{A'\Sigma A} = \Lambda\) where \(\Lambda\) is a diagonal matrix containing the eigenvalues \(\mathbf{\Sigma}\)
\[ \mathbf{\Lambda} = \left( \begin{array} {cccc} \lambda_1 & 0 & \ldots & 0 \\ 0 & \lambda_2 & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & \lambda_p \end{array} \right) \]
\[ \mathbf{A} = \left( \begin{array} {cccc} \mathbf{a}_1 & \mathbf{a}_2 & \ldots & \mathbf{a}_p \end{array} \right) \]
the i-th column of \(\mathbf{A}\) , \(\mathbf{a}_i\) , is the i-th \(p \times 1\) eigenvector of \(\mathbf{\Sigma}\) that corresponds to the eigenvalue, \(\lambda_i\) , where \(\lambda_1 \ge \lambda_2 \ge \ldots \ge \lambda_p\) . Alternatively, express in matrix decomposition:
\[ \mathbf{\Sigma} = \mathbf{A \Lambda A}' \]
\[ \mathbf{\Sigma} = \mathbf{A} \left( \begin{array} {cccc} \lambda_1 & 0 & \ldots & 0 \\ 0 & \lambda_2 & \ldots & 0 \\ \vdots & \vdots& \ddots & \vdots \\ 0 & 0 & \ldots & \lambda_p \end{array} \right) \mathbf{A}' = \sum_{i=1}^p \lambda_i \mathbf{a}_i \mathbf{a}_i' \]
where the outer product \(\mathbf{a}_i \mathbf{a}_i'\) is a \(p \times p\) matrix of rank 1.
For example,
\(\mathbf{x} \sim N_2(\mathbf{\mu}, \mathbf{\Sigma})\)
\[ \mathbf{\mu} = \left( \begin{array} {c} 5 \\ 12 \end{array} \right); \mathbf{\Sigma} = \left( \begin{array} {cc} 4 & 1 \\ 1 & 2 \end{array} \right) \]

\[ \mathbf{A} = \left( \begin{array} {cc} 0.9239 & -0.3827 \\ 0.3827 & 0.9239 \\ \end{array} \right) \]
Columns of \(\mathbf{A}\) are the eigenvectors for the decomposition
Under matrix multiplication ( \(\mathbf{A'\Sigma A}\) or \(\mathbf{A'A}\) ), the off-diagonal elements equal to 0
Multiplying data by this matrix (i.e., projecting the data onto the orthogonal axes); the distribution of the resulting data (i.e., “scores”) is
\[ N_2 (\mathbf{A'\mu,A'\Sigma A}) = N_2 (\mathbf{A'\mu, \Lambda}) \]
\[ \mathbf{y} = \mathbf{A'x} \sim N \left[ \left( \begin{array} {c} 9.2119 \\ 9.1733 \end{array} \right), \left( \begin{array} {cc} 4.4144 & 0 \\ 0 & 1.5859 \end{array} \right) \right] \]

No more dependence in the data structure, plot
The i-th eigenvalue is the variance of a linear combination of the elements of \(\mathbf{x}\) ; \(var(y_i) = var(\mathbf{a'_i x}) = \lambda_i\)
The values on the transformed set of axes (i.e., the \(y_i\) ’s) are called the scores. These are the orthogonal projections of the data onto the “new principal component axes
Variances of \(y_1\) are greater than those for any other possible projection
Covariance matrix decomposition and projection onto orthogonal axes = PCA
22.2.1 Population Principal Components
\(p \times 1\) vectors \(\mathbf{x}_1, \dots , \mathbf{x}_n\) which are iid with \(var(\mathbf{x}_i) = \mathbf{\Sigma}\)
The first PC is the linear combination \(y_1 = \mathbf{a}_1' \mathbf{x} = a_{11}x_1 + \dots + a_{1p}x_p\) with \(\mathbf{a}_1' \mathbf{a}_1 = 1\) such that \(var(y_1)\) is the maximum of all linear combinations of \(\mathbf{x}\) which have unit length
The second PC is the linear combination \(y_1 = \mathbf{a}_2' \mathbf{x} = a_{21}x_1 + \dots + a_{2p}x_p\) with \(\mathbf{a}_2' \mathbf{a}_2 = 1\) such that \(var(y_1)\) is the maximum of all linear combinations of \(\mathbf{x}\) which have unit length and uncorrelated with \(y_1\) (i.e., \(cov(\mathbf{a}_1' \mathbf{x}, \mathbf{a}'_2 \mathbf{x}) =0\)
continues for all \(y_i\) to \(y_p\)
\(\mathbf{a}_i\) ’s are those that make up the matrix \(\mathbf{A}\) in the symmetric decomposition \(\mathbf{A'\Sigma A} = \mathbf{\Lambda}\) , where \(var(y_1) = \lambda_1, \dots , var(y_p) = \lambda_p\) And the total variance of \(\mathbf{x}\) is
\[ \begin{aligned} var(x_1) + \dots + var(x_p) &= tr(\Sigma) = \lambda_1 + \dots + \lambda_p \\ &= var(y_1) + \dots + var(y_p) \end{aligned} \]
Data Reduction
To reduce the dimension of data from p (original) to k dimensions without much “loss of information”, we can use properties of the population principal components
Suppose \(\mathbf{\Sigma} \approx \sum_{i=1}^k \lambda_i \mathbf{a}_i \mathbf{a}_i'\) . Even thought the true variance-covariance matrix has rank \(p\) , it can be be well approximate by a matrix of rank k (k <p)
New “traits” are linear combinations of the measured traits. We can attempt to make meaningful interpretation fo the combinations (with orthogonality constraints).
The proportion of the total variance accounted for by the j-th principal component is
\[ \frac{var(y_j)}{\sum_{i=1}^p var(y_i)} = \frac{\lambda_j}{\sum_{i=1}^p \lambda_i} \]
The proportion of the total variation accounted for by the first k principal components is \(\frac{\sum_{i=1}^k \lambda_i}{\sum_{i=1}^p \lambda_i}\)
Above example , we have \(4.4144/(4+2) = .735\) of the total variability can be explained by the first principal component
22.2.2 Sample Principal Components
Since \(\mathbf{\Sigma}\) is unknown, we use
\[ \mathbf{S} = \frac{1}{n-1}\sum_{i=1}^n (\mathbf{x}_i - \bar{\mathbf{x}})(\mathbf{x}_i - \bar{\mathbf{x}})' \]
Let \(\hat{\lambda}_1 \ge \hat{\lambda}_2 \ge \dots \ge \hat{\lambda}_p \ge 0\) be the eigenvalues of \(\mathbf{S}\) and \(\hat{\mathbf{a}}_1, \hat{\mathbf{a}}_2, \dots, \hat{\mathbf{a}}_p\) denote the eigenvectors of \(\mathbf{S}\)
Then, the i-th sample principal component score (or principal component or score) is
\[ \hat{y}_{ij} = \sum_{k=1}^p \hat{a}_{ik}x_{kj} = \hat{\mathbf{a}}_i'\mathbf{x}_j \]
Properties of Sample Principal Components
The estimated variance of \(y_i = \hat{\mathbf{a}}_i'\mathbf{x}_j\) is \(\hat{\lambda}_i\)
The sample covariance between \(\hat{y}_i\) and \(\hat{y}_{i'}\) is 0 when \(i \neq i'\)
The proportion of the total sample variance accounted for by the i-th sample principal component is \(\frac{\hat{\lambda}_i}{\sum_{k=1}^p \hat{\lambda}_k}\)
The estimated correlation between the \(i\) -th principal component score and the \(l\) -th attribute of \(\mathbf{x}\) is
\[ r_{x_l , \hat{y}_i} = \frac{\hat{a}_{il}\sqrt{\lambda_i}}{\sqrt{s_{ll}}} \]
The correlation coefficient is typically used to interpret the components (i.e., if this correlation is high then it suggests that the l-th original trait is important in the i-th principle component). According to R. A. Johnson, Wichern, et al. ( 2002 ) , pp.433-434, \(r_{x_l, \hat{y}_i}\) only measures the univariate contribution of an individual X to a component Y without taking into account the presence of the other X’s. Hence, some prefer \(\hat{a}_{il}\) coefficient to interpret the principal component.
\(r_{x_l, \hat{y}_i} ; \hat{a}_{il}\) are referred to as “loadings”
To use k principal components, we must calculate the scores for each data vector in the sample
\[ \mathbf{y}_j = \left( \begin{array} {c} y_{1j} \\ y_{2j} \\ \vdots \\ y_{kj} \end{array} \right) = \left( \begin{array} {c} \hat{\mathbf{a}}_1' \mathbf{x}_j \\ \hat{\mathbf{a}}_2' \mathbf{x}_j \\ \vdots \\ \hat{\mathbf{a}}_k' \mathbf{x}_j \end{array} \right) = \left( \begin{array} {c} \hat{\mathbf{a}}_1' \\ \hat{\mathbf{a}}_2' \\ \vdots \\ \hat{\mathbf{a}}_k' \end{array} \right) \mathbf{x}_j \]
Large sample theory exists for eigenvalues and eigenvectors of sample covariance matrices if inference is necessary. But we do not do inference with PCA, we only use it as exploratory or descriptive analysis.
PC is not invariant to changes in scale (Exception: if all trait are rescaled by multiplying by the same constant, such as feet to inches).
PCA based on the correlation matrix \(\mathbf{R}\) is different than that based on the covariance matrix \(\mathbf{\Sigma}\)
PCA for the correlation matrix is just rescaling each trait to have unit variance
Transform \(\mathbf{x}\) to \(\mathbf{z}\) where \(z_{ij} = (x_{ij} - \bar{x}_i)/\sqrt{s_{ii}}\) where the denominator affects the PCA
After transformation, \(cov(\mathbf{z}) = \mathbf{R}\)
PCA on \(\mathbf{R}\) is calculated in the same way as that on \(\mathbf{S}\) (where \(\hat{\lambda}{}_1 + \dots + \hat{\lambda}{}_p = p\) )
The use of \(\mathbf{R}, \mathbf{S}\) depends on the purpose of PCA.
- If the scale of the observations if different, covariance matrix is more preferable. but if they are dramatically different, analysis can still be dominated by the large variance traits.
How many PCs to use can be guided by
Scree Graphs: plot the eigenvalues against their indices. Look for the “elbow” where the steep decline in the graph suddenly flattens out; or big gaps.
minimum Percent of total variation (e.g., choose enough components to have 50% or 90%). can be used for interpretations.
Kaiser’s rule: use only those PC with eigenvalues larger than 1 (applied to PCA on the correlation matrix) - ad hoc
Compare to the eigenvalue scree plot of data to the scree plot when the data are randomized.
22.2.3 Application
PCA on the covariance matrix is usually not preferred due to the fact that PCA is not invariant to changes in scale. Hence, PCA on the correlation matrix is more preferred
This also addresses the problem of multicollinearity
The eigvenvectors may differ by a multiplication of -1 for different implementation, but same interpretation.
Covid Example
To reduce collinearity problem in this dataset, we can use principal components as regressors.

MSE for the PC-based model is larger than regular regression, because models with a large degree of collinearity can still perform well.
pcr function in pls can be used for fitting PC regression (it will select the optimal number of components in the model).
22.3 Factor Analysis
Using a few linear combinations of underlying unobservable (latent) traits, we try to describe the covariance relationship among a large number of measured traits
Similar to PCA , but factor analysis is model based
More details can be found on PSU stat or UMN stat
Let \(\mathbf{y}\) be the set of \(p\) measured variables
\(E(\mathbf{y}) = \mathbf{\mu}\)
\(var(\mathbf{y}) = \mathbf{\Sigma}\)
\[ \begin{aligned} \mathbf{y} - \mathbf{\mu} &= \mathbf{Lf} + \epsilon \\ &= \left( \begin{array} {c} l_{11}f_1 + l_{12}f_2 + \dots + l_{tm}f_m \\ \vdots \\ l_{p1}f_1 + l_{p2}f_2 + \dots + l_{pm} f_m \end{array} \right) + \left( \begin{array} {c} \epsilon_1 \\ \vdots \\ \epsilon_p \end{array} \right) \end{aligned} \]
\(\mathbf{y} - \mathbf{\mu}\) = the p centered measurements
\(\mathbf{L}\) = \(p \times m\) matrix of factor loadings
\(\mathbf{f}\) = unobserved common factors for the population
\(\mathbf{\epsilon}\) = random errors (i.e., variation that is not accounted for by the common factors).
We want \(m\) (the number of factors) to be much smaller than \(p\) (the number of measured attributes)
Restrictions on the model
\(E(\epsilon) = \mathbf{0}\)
\(var(\epsilon) = \Psi_{p \times p} = diag( \psi_1, \dots, \psi_p)\)
\(\mathbf{\epsilon}, \mathbf{f}\) are independent
Additional assumption could be \(E(\mathbf{f}) = \mathbf{0}, var(\mathbf{f}) = \mathbf{I}_{m \times m}\) (known as the orthogonal factor model) , which imposes the following covariance structure on \(\mathbf{y}\)
\[ \begin{aligned} var(\mathbf{y}) = \mathbf{\Sigma} &= var(\mathbf{Lf} + \mathbf{\epsilon}) \\ &= var(\mathbf{Lf}) + var(\epsilon) \\ &= \mathbf{L} var(\mathbf{f}) \mathbf{L}' + \mathbf{\Psi} \\ &= \mathbf{LIL}' + \mathbf{\Psi} \\ &= \mathbf{LL}' + \mathbf{\Psi} \end{aligned} \]
Since \(\mathbf{\Psi}\) is diagonal, the off-diagonal elements of \(\mathbf{LL}'\) are \(\sigma_{ij}\) , the co variances in \(\mathbf{\Sigma}\) , which means \(cov(y_i, y_j) = \sum_{k=1}^m l_{ik}l_{jk}\) and the covariance of \(\mathbf{y}\) is completely determined by the m factors ( \(m <<p\) )
\(var(y_i) = \sum_{k=1}^m l_{ik}^2 + \psi_i\) where \(\psi_i\) is the specific variance and the summation term is the i-th communality (i.e., portion of the variance of the i-th variable contributed by the \(m\) common factors ( \(h_i^2 = \sum_{k=1}^m l_{ik}^2\) )
The factor model is only uniquely determined up to an orthogonal transformation of the factors.
Let \(\mathbf{T}_{m \times m}\) be an orthogonal matrix \(\mathbf{TT}' = \mathbf{T'T} = \mathbf{I}\) then
\[ \begin{aligned} \mathbf{y} - \mathbf{\mu} &= \mathbf{Lf} + \epsilon \\ &= \mathbf{LTT'f} + \epsilon \\ &= \mathbf{L}^*(\mathbf{T'f}) + \epsilon & \text{where } \mathbf{L}^* = \mathbf{LT} \end{aligned} \]
\[ \begin{aligned} \mathbf{\Sigma} &= \mathbf{LL}' + \mathbf{\Psi} \\ &= \mathbf{LTT'L} + \mathbf{\Psi} \\ &= (\mathbf{L}^*)(\mathbf{L}^*)' + \mathbf{\Psi} \end{aligned} \]
Hence, any orthogonal transformation of the factors is an equally good description of the correlations among the observed traits.
Let \(\mathbf{y} = \mathbf{Cx}\) , where \(\mathbf{C}\) is any diagonal matrix, then \(\mathbf{L}_y = \mathbf{CL}_x\) and \(\mathbf{\Psi}_y = \mathbf{C\Psi}_x\mathbf{C}\)
Hence, we can see that factor analysis is also invariant to changes in scale
22.3.1 Methods of Estimation
To estimate \(\mathbf{L}\)
- Principal Component Method
- Principal Factor Method
22.3.1.1 Principal Component Method
Spectral decomposition
\[ \begin{aligned} \mathbf{\Sigma} &= \lambda_1 \mathbf{a}_1 \mathbf{a}_1' + \dots + \lambda_p \mathbf{a}_p \mathbf{a}_p' \\ &= \mathbf{A\Lambda A}' \\ &= \sum_{k=1}^m \lambda+k \mathbf{a}_k \mathbf{a}_k' + \sum_{k= m+1}^p \lambda_k \mathbf{a}_k \mathbf{a}_k' \\ &= \sum_{k=1}^m l_k l_k' + \sum_{k=m+1}^p \lambda_k \mathbf{a}_k \mathbf{a}_k' \end{aligned} \]
where \(l_k = \mathbf{a}_k \sqrt{\lambda_k}\) and the second term is not diagonal in general.
\[ \psi_i = \sigma_{ii} - \sum_{k=1}^m l_{ik}^2 = \sigma_{ii} - \sum_{k=1}^m \lambda_i a_{ik}^2 \]
\[ \mathbf{\Sigma} \approx \mathbf{LL}' + \mathbf{\Psi} \]
To estimate \(\mathbf{L}\) and \(\Psi\) , we use the expected eigenvalues and eigenvectors from \(\mathbf{S}\) or \(\mathbf{R}\)
The estimated factor loadings don’t change as the number of actors increases
The diagonal elements of \(\hat{\mathbf{L}}\hat{\mathbf{L}}' + \hat{\mathbf{\Psi}}\) are equal to the diagonal elements of \(\mathbf{S}\) and \(\mathbf{R}\) , but the covariances may not be exactly reproduced
We select \(m\) so that the off-diagonal elements close to the values in \(\mathbf{S}\) (or to make the off-diagonal elements of \(\mathbf{S} - \hat{\mathbf{L}} \hat{\mathbf{L}}' + \hat{\mathbf{\Psi}}\) small)
22.3.1.2 Principal Factor Method
Consider modeling the correlation matrix, \(\mathbf{R} = \mathbf{L} \mathbf{L}' + \mathbf{\Psi}\) . Then
\[ \mathbf{L} \mathbf{L}' = \mathbf{R} - \mathbf{\Psi} = \left( \begin{array} {cccc} h_1^2 & r_{12} & \dots & r_{1p} \\ r_{21} & h_2^2 & \dots & r_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ r_{p1} & r_{p2} & \dots & h_p^2 \end{array} \right) \]
where \(h_i^2 = 1- \psi_i\) (the communality)
Suppose that initial estimates are available for the communalities, \((h_1^*)^2,(h_2^*)^2, \dots , (h_p^*)^2\) , then we can regress each trait on all the others, and then use the \(r^2\) as \(h^2\)
The estimate of \(\mathbf{R} - \mathbf{\Psi}\) at step k is
\[ (\mathbf{R} - \mathbf{\Psi})_k = \left( \begin{array} {cccc} (h_1^*)^2 & r_{12} & \dots & r_{1p} \\ r_{21} & (h_2^*)^2 & \dots & r_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ r_{p1} & r_{p2} & \dots & (h_p^*)^2 \end{array} \right) = \mathbf{L}_k^*(\mathbf{L}_k^*)' \]
\[ \mathbf{L}_k^* = (\sqrt{\hat{\lambda}_1^*\hat{\mathbf{a}}_1^* , \dots \hat{\lambda}_m^*\hat{\mathbf{a}}_m^*}) \]
\[ \hat{\psi}_{i,k}^* = 1 - \sum_{j=1}^m \hat{\lambda}_i^* (\hat{a}_{ij}^*)^2 \]
we used the spectral decomposition on the estimated matrix \((\mathbf{R}- \mathbf{\Psi})\) to calculate the \(\hat{\lambda}_i^* s\) and the \(\mathbf{\hat{a}}_i^* s\)
After updating the values of \((\hat{h}_i^*)^2 = 1 - \hat{\psi}_{i,k}^*\) we will use them to form a new \(\mathbf{L}_{k+1}^*\) via another spectral decomposition. Repeat the process
The matrix \((\mathbf{R} - \mathbf{\Psi})_k\) is not necessarily positive definite
The principal component method is similar to principal factor if one considers the initial communalities are \(h^2 = 1\)
if \(m\) is too large, some communalities may become larger than 1, causing the iterations to terminate. To combat, we can
fix any communality that is greater than 1 at 1 and then continues.
continue iterations regardless of the size of the communalities. However, results can be outside fo the parameter space.
22.3.1.3 Maximum Likelihood Method
Since we need the likelihood function, we make the additional (critical) assumption that
\(\mathbf{y}_j \sim N(\mathbf{\mu},\mathbf{\Sigma})\) for \(j = 1,..,n\)
\(\mathbf{f} \sim N(\mathbf{0}, \mathbf{I})\)
\(\epsilon_j \sim N(\mathbf{0}, \mathbf{\Psi})\)
and restriction
- \(\mathbf{L}' \mathbf{\Psi}^{-1}\mathbf{L} = \mathbf{\Delta}\) where \(\mathbf{\Delta}\) is a diagonal matrix. (since the factor loading matrix is not unique, we need this restriction).
Finding MLE can be computationally expensive
we typically use other methods for exploratory data analysis
Likelihood ratio tests could be used for testing hypotheses in this framework (i.e., Confirmatory Factor Analysis)
22.3.2 Factor Rotation
\(\mathbf{T}_{m \times m}\) is an orthogonal matrix that has the property that
\[ \hat{\mathbf{L}} \hat{\mathbf{L}}' + \hat{\mathbf{\Psi}} = \hat{\mathbf{L}}^*(\hat{\mathbf{L}}^*)' + \hat{\mathbf{\Psi}} \]
where \(\mathbf{L}^* = \mathbf{LT}\)
This means that estimated specific variances and communalities are not altered by the orthogonal transformation.
Since there are an infinite number of choices for \(\mathbf{T}\) , some selection criterion is necessary
For example, we can find the orthogonal transformation that maximizes the objective function
\[ \sum_{j = 1}^m [\frac{1}{p}\sum_{i=1}^p (\frac{l_{ij}^{*2}}{h_i})^2 - \{\frac{\gamma}{p} \sum_{i=1}^p (\frac{l_{ij}^{*2}}{h_i})^2 \}^2] \]
where \(\frac{l_{ij}^{*2}}{h_i}\) are “scaled loadings”, which gives variables with small communalities more influence.
Different choices of \(\gamma\) in the objective function correspond to different orthogonal rotation found in the literature;
Varimax \(\gamma = 1\) (rotate the factors so that each of the \(p\) variables should have a high loading on only one factor, but this is not always possible).
Quartimax \(\gamma = 0\)
Equimax \(\gamma = m/2\)
Parsimax \(\gamma = \frac{p(m-1)}{p+m-2}\)
Promax: non-orthogonal or olique transformations
Harris-Kaiser (HK): non-orthogonal or oblique transformations
22.3.3 Estimation of Factor Scores
\[ (\mathbf{y}_j - \mathbf{\mu}) = \mathbf{L}_{p \times m}\mathbf{f}_j + \epsilon_j \]
If the factor model is correct then
\[ var(\epsilon_j) = \mathbf{\Psi} = diag (\psi_1, \dots , \psi_p) \]
Thus we could consider using weighted least squares to estimate \(\mathbf{f}_j\) , the vector of factor scores for the j-th sampled unit by
\[ \begin{aligned} \hat{\mathbf{f}} &= (\mathbf{L}'\mathbf{\Psi}^{-1} \mathbf{L})^{-1} \mathbf{L}' \mathbf{\Psi}^{-1}(\mathbf{y}_j - \mathbf{\mu}) \\ & \approx (\mathbf{L}'\mathbf{\Psi}^{-1} \mathbf{L})^{-1} \mathbf{L}' \mathbf{\Psi}^{-1}(\mathbf{y}_j - \mathbf{\bar{y}}) \end{aligned} \]
22.3.3.1 The Regression Method
Alternatively, we can use the regression method to estimate the factor scores
Consider the joint distribution of \((\mathbf{y}_j - \mathbf{\mu})\) and \(\mathbf{f}_j\) assuming multivariate normality, as in the maximum likelihood approach. then,
\[ \left( \begin{array} {c} \mathbf{y}_j - \mathbf{\mu} \\ \mathbf{f}_j \end{array} \right) \sim N_{p + m} \left( \left[ \begin{array} {cc} \mathbf{LL}' + \mathbf{\Psi} & \mathbf{L} \\ \mathbf{L}' & \mathbf{I}_{m\times m} \end{array} \right] \right) \]
when the \(m\) factor model is correct
\[ E(\mathbf{f}_j | \mathbf{y}_j - \mathbf{\mu}) = \mathbf{L}' (\mathbf{LL}' + \mathbf{\Psi})^{-1}(\mathbf{y}_j - \mathbf{\mu}) \]
notice that \(\mathbf{L}' (\mathbf{LL}' + \mathbf{\Psi})^{-1}\) is an \(m \times p\) matrix of regression coefficients
Then, we use the estimated conditional mean vector to estimate the factor scores
\[ \mathbf{\hat{f}}_j = \mathbf{\hat{L}}'(\mathbf{\hat{L}}\mathbf{\hat{L}}' + \mathbf{\hat{\Psi}})^{-1}(\mathbf{y}_j - \mathbf{\bar{y}}) \]
Alternatively, we could reduce the effect of possible incorrect determination fo the number of factors \(m\) by using \(\mathbf{S}\) as a substitute for \(\mathbf{\hat{L}}\mathbf{\hat{L}}' + \mathbf{\hat{\Psi}}\) then
\[ \mathbf{\hat{f}}_j = \mathbf{\hat{L}}'\mathbf{S}^{-1}(\mathbf{y}_j - \mathbf{\bar{y}}) \]
where \(j = 1,\dots,n\)
22.3.4 Model Diagnostic
Check for outliers (recall that \(\mathbf{f}_j \sim iid N(\mathbf{0}, \mathbf{I}_{m \times m})\) )
Check for multivariate normality assumption
Use univariate tests for normality to check the factor scores
Confirmatory Factor Analysis : formal testing of hypotheses about loadings, use MLE and full/reduced model testing paradigm and measures of model fit
22.3.5 Application
In the psych package,
h2 = the communalities
u2 = the uniqueness
com = the complexity

The output info for the null hypothesis of no common factors is in the statement “The degrees of freedom for the null model ..”
The output info for the null hypothesis that number of factors is sufficient is in the statement “The total number of observations was …”
One factor is not enough, two is sufficient, and not enough data for 3 factors (df of -2 and NA for p-value). Hence, we should use 2-factor model.
22.4 Discriminant Analysis
Suppose we have two or more different populations from which observations could come from. Discriminant analysis seeks to determine which of the possible population an observation comes from while making as few mistakes as possible
This is an alternative to logistic approaches with the following advantages:
when there is clear separation between classes, the parameter estimates for the logic regression model can be surprisingly unstable, while discriminant approaches do not suffer
If X is normal in each of the classes and the sample size is small, then discriminant approaches can be more accurate
Similar to MANOVA, let \(\mathbf{y}_{j1},\mathbf{y}_{j2},\dots, \mathbf{y}_{in_j} \sim iid f_j (\mathbf{y})\) for \(j = 1,\dots, h\)
Let \(f_j(\mathbf{y})\) be the density function for population j . Note that each vector \(\mathbf{y}\) contain measurements on all \(p\) traits
- Assume that each observation is from one of \(h\) possible populations.
- We want to form a discriminant rule that will allocate an observation \(\mathbf{y}\) to population j when \(\mathbf{y}\) is in fact from this population
22.4.1 Known Populations
The maximum likelihood discriminant rule for assigning an observation \(\mathbf{y}\) to one of the \(h\) populations allocates \(\mathbf{y}\) to the population that gives the largest likelihood to \(\mathbf{y}\)
Consider the likelihood for a single observation \(\mathbf{y}\) , which has the form \(f_j (\mathbf{y})\) where j is the true population.
Since \(j\) is unknown, to make the likelihood as large as possible, we should choose the value j which causes \(f_j (\mathbf{y})\) to be as large as possible
Consider a simple univariate example. Suppose we have data from one of two binomial populations.
The first population has \(n= 10\) trials with success probability \(p = .5\)
The second population has \(n= 10\) trials with success probability \(p = .7\)
to which population would we assign an observation of \(y = 7\)
\(f(y = 7|n = 10, p = .5) = .117\)
\(f(y = 7|n = 10, p = .7) = .267\) where \(f(.)\) is the binomial likelihood.
Hence, we choose the second population
Another example
We have 2 populations, where
First population: \(N(\mu_1, \sigma^2_1)\)
Second population: \(N(\mu_2, \sigma^2_2)\)
The likelihood for a single observation is
\[ f_j (y) = (2\pi \sigma^2_j)^{-1/2} \exp\{ -\frac{1}{2}(\frac{y - \mu_j}{\sigma_j})^2\} \]
Consider a likelihood ratio rule
\[ \begin{aligned} \Lambda &= \frac{\text{likelihood of y from pop 1}}{\text{likelihood of y from pop 2}} \\ &= \frac{f_1(y)}{f_2(y)} \\ &= \frac{\sigma_2}{\sigma_1} \exp\{-\frac{1}{2}[(\frac{y - \mu_1}{\sigma_1})^2- (\frac{y - \mu_2}{\sigma_2})^2] \} \end{aligned} \]
Hence, we classify into
pop 1 if \(\Lambda >1\)
pop 2 if \(\Lambda <1\)
for ties, flip a coin
Another way to think:
we classify into population 1 if the “standardized distance” of y from \(\mu_1\) is less than the “standardized distance” of y from \(\mu_2\) which is referred to as a quadratic discriminant rule .
(Significant simplification occurs in th special case where \(\sigma_1 = \sigma_2 = \sigma^2\) )
Thus, we classify into population 1 if
\[ (y - \mu_2)^2 > (y - \mu_1)^2 \]
\[ |y- \mu_2| > |y - \mu_1| \]
\[ -2 \log (\Lambda) = -2y \frac{(\mu_1 - \mu_2)}{\sigma^2} + \frac{(\mu_1^2 - \mu_2^2)}{\sigma^2} = \beta y + \alpha \]
Thus, we classify into population 1 if this is less than 0.
Discriminant classification rule is linear in y in this case.
22.4.1.1 Multivariate Expansion
Suppose that there are 2 populations
\(N_p(\mathbf{\mu}_1, \mathbf{\Sigma}_1)\)
\(N_p(\mathbf{\mu}_2, \mathbf{\Sigma}_2)\)
\[ \begin{aligned} -2 \log(\frac{f_1 (\mathbf{x})}{f_2 (\mathbf{x})}) &= \log|\mathbf{\Sigma}_1| + (\mathbf{x} - \mathbf{\mu}_1)' \mathbf{\Sigma}^{-1}_1 (\mathbf{x} - \mathbf{\mu}_1) \\ &- [\log|\mathbf{\Sigma}_2|+ (\mathbf{x} - \mathbf{\mu}_2)' \mathbf{\Sigma}^{-1}_2 (\mathbf{x} - \mathbf{\mu}_2) ] \end{aligned} \]
Again, we classify into population 1 if this is less than 0, otherwise, population 2. And like the univariate case with non-equal variances, this is a quadratic discriminant rule.
And if the covariance matrices are equal: \(\mathbf{\Sigma}_1 = \mathbf{\Sigma}_2 = \mathbf{\Sigma}_1\) classify into population 1 if
\[ (\mathbf{\mu}_1 - \mathbf{\mu}_2)' \mathbf{\Sigma}^{-1}\mathbf{x} - \frac{1}{2} (\mathbf{\mu}_1 - \mathbf{\mu}_2)' \mathbf{\Sigma}^{-1} (\mathbf{\mu}_1 - \mathbf{\mu}_2) \ge 0 \]
This linear discriminant rule is also referred to as Fisher’s linear discriminant function
By assuming the covariance matrices are equal, we assume that the shape and orientation fo the two populations must be the same (which can be a strong restriction)
In other words, for each variable, it can have different mean but the same variance.
- Note: LDA Bayes decision boundary is linear. Hence, quadratic decision boundary might lead to better classification. Moreover, the assumption of same variance/covariance matrix across all classes for Gaussian densities imposes the linear rule, if we allow the predictors in each class to follow MVN distribution with class-specific mean vectors and variance/covariance matrices, then it is Quadratic Discriminant Analysis. But then, you will have more parameters to estimate (which gives more flexibility than LDA) at the cost of more variance (bias -variance tradeoff).
When \(\mathbf{\mu}_1, \mathbf{\mu}_2, \mathbf{\Sigma}\) are known, the probability of misclassification can be determined:
\[ \begin{aligned} P(2|1) &= P(\text{calssify into pop 2| x is from pop 1}) \\ &= P((\mathbf{\mu}_1 - \mathbf{\mu}_2)' \mathbf{\Sigma}^{-1} \mathbf{x} \le \frac{1}{2} (\mathbf{\mu}_1 - \mathbf{\mu}_2)' \mathbf{\Sigma}^{-1} (\mathbf{\mu}_1 - \mathbf{\mu}_2)|\mathbf{x} \sim N(\mu_1, \mathbf{\Sigma}) \\ &= \Phi(-\frac{1}{2} \delta) \end{aligned} \]
\(\delta^2 = (\mathbf{\mu}_1 - \mathbf{\mu}_2)' \mathbf{\Sigma}^{-1} (\mathbf{\mu}_1 - \mathbf{\mu}_2)\)
\(\Phi\) is the standard normal CDF
Suppose there are \(h\) possible populations, which are distributed as \(N_p (\mathbf{\mu}_p, \mathbf{\Sigma})\) . Then, the maximum likelihood (linear) discriminant rule allocates \(\mathbf{y}\) to population j where j minimizes the squared Mahalanobis distance
\[ (\mathbf{y} - \mathbf{\mu}_j)' \mathbf{\Sigma}^{-1} (\mathbf{y} - \mathbf{\mu}_j) \]
22.4.1.2 Bayes Discriminant Rules
If we know that population j has prior probabilities \(\pi_j\) (assume \(\pi_j >0\) ) we can form the Bayes discriminant rule.
This rule allocates an observation \(\mathbf{y}\) to the population for which \(\pi_j f_j (\mathbf{y})\) is maximized.
- Maximum likelihood discriminant rule is a special case of the Bayes discriminant rule , where it sets all the \(\pi_j = 1/h\)
Optimal Properties of Bayes Discriminant Rules
let \(p_{ii}\) be the probability of correctly assigning an observation from population i
then one rule (with probabilities \(p_{ii}\) ) is as good as another rule (with probabilities \(p_{ii}'\) ) if \(p_{ii} \ge p_{ii}'\) for all \(i = 1,\dots, h\)
The first rule is better than the alternative if \(p_{ii} > p_{ii}'\) for at least one i.
A rule for which there is no better alternative is called admissible
Bayes Discriminant Rules are admissible
If we utilized prior probabilities, then we can form the posterior probability of a correct allocation, \(\sum_{i=1}^h \pi_i p_{ii}\)
Bayes Discriminant Rules have the largest possible posterior probability of correct allocation with respect to the prior
These properties show that Bayes Discriminant rule is our best approach .
Unequal Cost
We want to consider the cost misallocation
- Define \(c_{ij}\) to be the cost associated with allocation a member of population j to population i.
Assume that
\(c_{ij} >0\) for all \(i \neq j\)
\(c_{ij} = 0\) if \(i = j\)
We could determine the expected amount of loss for an observation allocated to population i as \(\sum_j c_{ij} p_{ij}\) where the \(p_{ij}s\) are the probabilities of allocating an observation from population j into population i
We want to minimize the amount of loss expected for our rule. Using a Bayes Discrimination, allocate \(\mathbf{y}\) to the population j which minimizes \(\sum_{k \neq j} c_{ij} \pi_k f_k(\mathbf{y})\)
We could assign equal probabilities to each group and get a maximum likelihood type rule. here, we would allocate \(\mathbf{y}\) to population j which minimizes \(\sum_{k \neq j}c_{jk} f_k(\mathbf{y})\)
Two binomial populations, each of size 10, with probabilities \(p_1 = .5\) and \(p_2 = .7\)
And the probability of being in the first population is .9
However, suppose the cost of inappropriately allocating into the first population is 1 and the cost of incorrectly allocating into the second population is 5.
In this case, we pick population 1 over population 2
In general, we consider two regions, \(R_1\) and \(R_2\) associated with population 1 and 2:
\[ R_1: \frac{f_1 (\mathbf{x})}{f_2 (\mathbf{x})} \ge \frac{c_{12} \pi_2}{c_{21} \pi_1} \]
\[ R_2: \frac{f_1 (\mathbf{x})}{f_2 (\mathbf{x})} < \frac{c_{12} \pi_2}{c_{21} \pi_1} \]
where \(c_{12}\) is the cost of assigning a member of population 2 to population 1.
22.4.1.3 Discrimination Under Estimation
Suppose we know the form of the distributions for populations of interests, but we still have to estimate the parameters.
we know the distributions are multivariate normal, but we have to estimate the means and variances
The maximum likelihood discriminant rule allocates an observation \(\mathbf{y}\) to population j when j maximizes the function
\[ f_j (\mathbf{y} |\hat{\theta}) \]
where \(\hat{\theta}\) are the maximum likelihood estimates of the unknown parameters
For instance, we have 2 multivariate normal populations with distinct means, but common variance covariance matrix
MLEs for \(\mathbf{\mu}_1\) and \(\mathbf{\mu}_2\) are \(\mathbf{\bar{y}}_1\) and \(\mathbf{\bar{y}}_2\) and common \(\mathbf{\Sigma}\) is \(\mathbf{S}\) .
Thus, an estimated discriminant rule could be formed by substituting these sample values for the population values
22.4.1.4 Native Bayes
The challenge with classification using Bayes’ is that we don’t know the (true) densities, \(f_k, k = 1, \dots, K\) , while LDA and QDA make strong multivariate normality assumptions to deal with this.
Naive Bayes makes only one assumption: within the k-th class, the p predictors are independent (i.e,, for \(k = 1,\dots, K\)
\[ f_k(x) = f_{k1}(x_1) \times f_{k2}(x_2) \times \dots \times f_{kp}(x_p) \]
where \(f_{kj}\) is the density function of the j-th predictor among observation in the k-th class.
This assumption allows the use of joint distribution without the need to account for dependence between observations. However, this (native) assumption can be unrealistic, but still works well in cases where the number of sample (n) is not large relative to the number of features (p).
With this assumption, we have
\[ P(Y=k|X=x) = \frac{\pi_k \times f_{k1}(x_1) \times \dots \times f_{kp}(x_p)}{\sum_{l=1}^K \pi_l \times f_{l1}(x_1)\times \dots f_{lp}(x_p)} \]
we only need to estimate the one-dimensional density function \(f_{kj}\) with either of these approaches:
When \(X_j\) is quantitative, assume it has a univariate normal distribution (with independence): \(X_j | Y = k \sim N(\mu_{jk}, \sigma^2_{jk})\) which is more restrictive than QDA because it assumes predictors are independent (e.g., a diagonal covariance matrix)
When \(X_j\) is quantitative, use a kernel density estimator Kernel Methods ; which is a smoothed histogram
When \(X_j\) is qualitative, we count the promotion of training observations for the j-th predictor corresponding to each class.
22.4.1.5 Comparison of Classification Methods
Assuming we have K classes and K is the baseline from (James , Witten, Hastie, and Tibshirani book)
Comparing the log odds relative to the K class
22.4.1.5.1 Logistic Regression
\[ \log(\frac{P(Y=k|X = x)}{P(Y = K| X = x)}) = \beta_{k0} + \sum_{j=1}^p \beta_{kj}x_j \]
22.4.1.5.2 LDA
\[ \log(\frac{P(Y = k | X = x)}{P(Y = K | X = x)} = a_k + \sum_{j=1}^p b_{kj} x_j \]
where \(a_k\) and \(b_{kj}\) are functions of \(\pi_k, \pi_K, \mu_k , \mu_K, \mathbf{\Sigma}\)
Similar to logistic regression, LDA assumes the log odds is linear in \(x\)
Even though they look like having the same form, the parameters in logistic regression are estimated by MLE, where as LDA linear parameters are specified by the prior and normal distributions
We expect LDA to outperform logistic regression when the normality assumption (approximately) holds, and logistic regression to perform better when it does not
22.4.1.5.3 QDA
\[ \log(\frac{P(Y=k|X=x}{P(Y=K | X = x}) = a_k + \sum_{j=1}^{p}b_{kj}x_{j} + \sum_{j=1}^p \sum_{l=1}^p c_{kjl}x_j x_l \]
where \(a_k, b_{kj}, c_{kjl}\) are functions \(\pi_k , \pi_K, \mu_k, \mu_K ,\mathbf{\Sigma}_k, \mathbf{\Sigma}_K\)
22.4.1.5.4 Naive Bayes
\[ \log (\frac{P(Y = k | X = x)}{P(Y = K | X = x}) = a_k + \sum_{j=1}^p g_{kj} (x_j) \]
where \(a_k = \log (\pi_k / \pi_K)\) and \(g_{kj}(x_j) = \log(\frac{f_{kj}(x_j)}{f_{Kj}(x_j)})\) which is the form of generalized additive model
22.4.1.5.5 Summary
LDA is a special case of QDA
LDA is robust when it comes to high dimensions
Any classifier with a linear decision boundary is a special case of naive Bayes with \(g_{kj}(x_j) = b_{kj} x_j\) , which means LDA is a special case of naive Bayes. LDA assumes that the features are normally distributed with a common within-class covariance matrix, and naive Bayes assumes independence of the features.
Naive bayes is also a special case of LDA with \(\mathbf{\Sigma}\) restricted to a diagonal matrix with diagonals, \(\sigma^2\) (another notation \(diag (\mathbf{\Sigma})\) ) assuming \(f_{kj}(x_j) = N(\mu_{kj}, \sigma^2_j)\)
QDA and naive Bayes are not special case of each other. In principal,e naive Bayes can produce a more flexible fit by the choice of \(g_{kj}(x_j)\) , but it’s restricted to only purely additive fit, but QDA includes multiplicative terms of the form \(c_{kjl}x_j x_l\)
None of these methods uniformly dominates the others: the choice of method depends on the true distribution of the predictors in each of the K classes, n and p (i.e., related to the bias-variance tradeoff).
Compare to the non-parametric method (KNN)
KNN would outperform both LDA and logistic regression when the decision boundary is highly nonlinear, but can’t say which predictors are most important, and requires many observations
KNN is also limited in high-dimensions due to the curse of dimensionality
Since QDA is a special type of nonlinear decision boundary (quadratic), it can be considered as a compromise between the linear methods and KNN classification. QDA can have fewer training observations than KNN but not as flexible.
From simulation:
| True decision boundary | Best performance |
|---|---|
| Linear | LDA + Logistic regression |
| Moderately nonlinear | QDA + Naive Bayes |
| Highly nonlinear (many training, p is not large) | KNN |
- like linear regression, we can also introduce flexibility by including transformed features \(\sqrt{X}, X^2, X^3\)
22.4.2 Probabilities of Misclassification
When the distribution are exactly known, we can determine the misclassification probabilities exactly. however, when we need to estimate the population parameters, we have to estimate the probability of misclassification
Naive method
Plugging the parameters estimates into the form for the misclassification probabilities results to derive at the estimates of the misclassification probability.
But this will tend to be optimistic when the number of samples in one or more populations is small.
Resubstitution method
Use the proportion of the samples from population i that would be allocated to another population as an estimate of the misclassification probability
But also optimistic when the number of samples is small
Jack-knife estimates:
The above two methods use observation to estimate both parameters and also misclassification probabilities based upon the discriminant rule
Alternatively, we determine the discriminant rule based upon all of the data except the k-th observation from the j-th population
then, determine if the k-th observation would be misclassified under this rule
perform this process for all \(n_j\) observation in population j . An estimate fo the misclassification probability would be the fraction of \(n_j\) observations which were misclassified
repeat the process for other \(i \neq j\) populations
This method is more reliable than the others, but also computationally intensive
Cross-Validation
Consider the group-specific densities \(f_j (\mathbf{x})\) for multivariate vector \(\mathbf{x}\) .
Assume equal misclassifications costs, the Bayes classification probability of \(\mathbf{x}\) belonging to the j-th population is
\[ p(j |\mathbf{x}) = \frac{\pi_j f_j (\mathbf{x})}{\sum_{k=1}^h \pi_k f_k (\mathbf{x})} \]
\(j = 1,\dots, h\)
where there are \(h\) possible groups.
We then classify into the group for which this probability of membership is largest
Alternatively, we can write this in terms of a generalized squared distance formation
\[ D_j^2 (\mathbf{x}) = d_j^2 (\mathbf{x})+ g_1(j) + g_2 (j) \]
\(d_j^2(\mathbf{x}) = (\mathbf{x} - \mathbf{\mu}_j)' \mathbf{V}_j^{-1} (\mathbf{x} - \mathbf{\mu}_j)\) is the squared Mahalanobis distance from \(\mathbf{x}\) to the centroid of group j, and
\(\mathbf{V}_j = \mathbf{S}_j\) if the within group covariance matrices are not equal
\(\mathbf{V}_j = \mathbf{S}_p\) if a pooled covariance estimate is appropriate
\[ g_1(j) = \begin{cases} \ln |\mathbf{S}_j| & \text{within group covariances are not equal} \\ 0 & \text{pooled covariance} \end{cases} \]
\[ g_2(j) = \begin{cases} -2 \ln \pi_j & \text{prior probabilities are not equal} \\ 0 & \text{prior probabilities are equal} \end{cases} \]
then, the posterior probability of belonging to group j is
\[ p(j| \mathbf{x}) = \frac{\exp(-.5 D_j^2(\mathbf{x}))}{\sum_{k=1}^h \exp(-.5 D^2_k (\mathbf{x}))} \]
where \(j = 1,\dots , h\)
and \(\mathbf{x}\) is classified into group j if \(p(j | \mathbf{x})\) is largest for \(j = 1,\dots,h\) (or, \(D_j^2(\mathbf{x})\) is smallest).
22.4.2.1 Assessing Classification Performance
For binary classification, confusion matrix
| Predicted class | ||||
|---|---|---|---|---|
| - or Null | + or Null | Total | ||
| True Class | - or Null | True Neg (TN) | False Pos (FP) | N |
| + or Null | False Neg (FN) | True Pos (TP) | P | |
| Total | N* | P* |
and table 4.6 from ( James et al. 2013 )
| Name | Definition | Synonyms |
|---|---|---|
| False Pos rate | FP/N | Type I error, 1 0 Specificity |
| True Pos. rate | TP/P | 1 - Type II error, power, sensitivity, recall |
| Pos Pred. value | TP/P* | Precision, 1 - false discovery promotion |
| Neg. Pred. value | TN/N* |
ROC curve (receiver Operating Characteristics) is a graphical comparison between sensitivity (true positive) and specificity ( = 1 - false positive)
y-axis = true positive rate
x-axis = false positive rate
as we change the threshold rate for classifying an observation as from 0 to 1
AUC (area under the ROC) ideally would equal to 1, a bad classifier would have AUC = 0.5 (pure chance)
22.4.3 Unknown Populations/ Nonparametric Discrimination
When your multivariate data are not Gaussian, or known distributional form at all, we can use the following methods
22.4.3.1 Kernel Methods
We approximate \(f_j (\mathbf{x})\) by a kernel density estimate
\[ \hat{f}_j(\mathbf{x}) = \frac{1}{n_j} \sum_{i = 1}^{n_j} K_j (\mathbf{x} - \mathbf{x}_i) \]
\(K_j (.)\) is a kernel function satisfying \(\int K_j(\mathbf{z})d\mathbf{z} =1\)
\(\mathbf{x}_i\) , \(i = 1,\dots , n_j\) is a random sample from the j-th population.
Thus, after finding \(\hat{f}_j (\mathbf{x})\) for each of the \(h\) populations, the posterior probability of group membership is
\[ p(j |\mathbf{x}) = \frac{\pi_j \hat{f}_j (\mathbf{x})}{\sum_{k-1}^h \pi_k \hat{f}_k (\mathbf{x})} \]
where \(j = 1,\dots, h\)
There are different choices for the kernel function:
Epanechnikov
We these kernels, we have to pick the “radius” (or variance, width, window width, bandwidth) of the kernel, which is a smoothing parameter (the larger the radius, the more smooth the kernel estimate of the density).
To select the smoothness parameter, we can use the following method
If we believe the populations were close to multivariate normal, then
\[ R = (\frac{4/(2p+1)}{n_j})^{1/(p+1} \]
But since we do not know for sure, we might choose several different values and select one that vies the best out of sample or cross-validation discrimination.
Moreover, you also have to decide whether to use different kernel smoothness for different populations, which is similar to the individual and pooled covariances in the classical methodology.
22.4.3.2 Nearest Neighbor Methods
The nearest neighbor (also known as k-nearest neighbor) method performs the classification of a new observation vector based on the group membership of its nearest neighbors. In practice, we find
\[ d_{ij}^2 (\mathbf{x}, \mathbf{x}_i) = (\mathbf{x}, \mathbf{x}_i) V_j^{-1}(\mathbf{x}, \mathbf{x}_i) \]
which is the distance between the vector \(\mathbf{x}\) and the \(i\) -th observation in group \(j\)
We consider different choices for \(\mathbf{V}_j\)
\[ \begin{aligned} \mathbf{V}_j &= \mathbf{S}_p \\ \mathbf{V}_j &= \mathbf{S}_j \\ \mathbf{V}_j &= \mathbf{I} \\ \mathbf{V}_j &= diag (\mathbf{S}_p) \end{aligned} \]
We find the \(k\) observations that are closest to \(\mathbf{x}\) (where users pick \(k\) ). Then we classify into the most common population, weighted by the prior.

22.4.3.3 Modern Discriminant Methods
Logistic regression (with or without random effects) is a flexible model-based procedure for classification between two populations.
The extension of logistic regression to the multi-group setting is polychotomous logistic regression (or, mulinomial regression).
The machine learning and pattern recognition are growing with strong focus on nonlinear discriminant analysis methods such as:
radial basis function networks
support vector machines
multiplayer perceptrons (neural networks)
The general framework
\[ g_j (\mathbf{x}) = \sum_{l = 1}^m w_{jl}\phi_l (\mathbf{x}; \mathbf{\theta}_l) + w_{j0} \]
\(m\) nonlinear basis functions \(\phi_l\) , each of which has \(n_m\) parameters given by \(\theta_l = \{ \theta_{lk}: k = 1, \dots , n_m \}\)
We assign \(\mathbf{x}\) to the \(j\) -th population if \(g_j(\mathbf{x})\) is the maximum for all \(j = 1,\dots, h\)
Development usually focuses on the choice and estimation of the basis functions, \(\phi_l\) and the estimation of the weights \(w_{jl}\)
More details can be found ( Webb, Copsey, and Cawley 2011 )
22.4.4 Application
22.4.4.1 lda.
Default prior is proportional to sample size and lda and qda do not fit a constant or intercept term
LDA didn’t do well on both within sample and out-of-sample data.
22.4.4.2 QDA
22.4.4.3 knn.
knn uses design matrices of the features.
22.4.4.4 Stepwise
Stepwise discriminant analysis using the stepclass in function in the klaR package.

22.4.4.5 PCA with Discriminant Analysis
we can use both PCA for dimension reduction in discriminant analysis


- > Machine Learning
What is Multivariate Data Analysis?
- Bhumika Dutta
- Aug 23, 2021

Introduction
We have access to huge amounts of data in today’s world and it is very important to analyze and manage the data in order to use it for something important. The words data and analysis go hand in hand, as they depend on each other.
Data analysis and research are also related as they both involve several tools and techniques that are used to predict the outcome of specific tasks for the benefit of any company. The majority of business issues include several factors.
When making choices, managers use a variety of performance indicators and associated metrics. When selecting which items or services to buy, consumers consider a variety of factors. The equities that a broker suggests are influenced by a variety of variables.
When choosing a restaurant, diners evaluate a variety of things. More elements affect managers' and customers' decisions as the world grows more complicated. As a result, business researchers, managers, and consumers must increasingly rely on more sophisticated techniques for data analysis and comprehension.
One of those analytical techniques that are used to read huge amounts of data is known as Multivariate Data Analysis.
(Also read: Binary and multiclass classification in ML )
In statistics, one might have heard of variates, which is a particular combination of different variables. Two of the common variate analysis approaches are univariate and bivariate approaches.
A single variable is statistically tested in univariate analysis, whereas two variables are statistically tested in bivariate analysis. When three or more variables are involved, the problem is intrinsically multidimensional, necessitating the use of multivariate data analysis. In this article, we are going to discuss:
What is multivariate data analysis? Objectives of MVA.
Types of multivariate data analysis.
Advantages of multivariate data analysis.
Disadvantages of multivariate data analysis.
(Recommended read: What is Hypothesis Testing? Types and Methods )
Multivariate data analysis
Multivariate data analysis is a type of statistical analysis that involves more than two dependent variables, resulting in a single outcome. Many problems in the world can be practical examples of multivariate equations as whatever happens in the world happens due to multiple reasons.
One such example of the real world is the weather. The weather at any particular place does not solely depend on the ongoing season, instead many other factors play their specific roles, like humidity, pollution, etc. Just like this, the variables in the analysis are prototypes of real-time situations, products, services, or decision-making involving more variables.
Wishart presented the first article on multivariate data analysis (MVA) in 1928. The topic of the study was the covariance matrix distribution of a normal population with numerous variables.
Hotelling, R. A. Fischer, and others published theoretical work on MVA in the 1930s. multivariate data analysis was widely used in the disciplines of education, psychology, and biology at the time.
As time advanced, MVA was extended to the fields of meteorology, geology, science, and medicine in the mid-1950s. Today, it focuses on two types of statistics: descriptive statistics and inferential statistics. We frequently find the best linear combination of variables that are mathematically docile in the descriptive region, but an inference is an informed estimate that is meant to save analysts time from diving too deeply into the data.
Till now we have talked about the definition and history of multivariate data analysis. Let us learn about the objectives as well.
Objectives of multivariate data analysis:
Multivariate data analysis helps in the reduction and simplification of data as much as possible without losing any important details.
As MVA has multiple variables, the variables are grouped and sorted on the basis of their unique features.
The variables in multivariate data analysis could be dependent or independent. It is important to verify the collected data and analyze the state of the variables.
In multivariate data analysis, it is very important to understand the relationship between all the variables and predict the behavior of the variables based on observations.
It is tested to create a statistical hypothesis based on the parameters of multivariate data. This testing is carried out to determine whether or not the assumptions are true.
(Must read: Hypothesis testing )
Advantages of multivariate data analysis:
The following are the advantages of multivariate data analysis:
As multivariate data analysis deals with multiple variables, all the variables can either be independent or dependent on each other. This helps the analysis to search for factors that can help in drawing accurate conclusions.
Since the analysis is tested, the drawn conclusions are closer to real-life situations.
Disadvantages of multivariate data analysis:
The following are the disadvantages of multivariate data analysis:
Multivariate data analysis includes many complex computations and hence can be laborious.
The analysis necessitates the collection and tabulation of a large number of observations for various variables. This process of observation takes a long time.
(Also read: 15 Statistical Terms for Machine Learning )
7 Types of Multivariate Data Analysis
According to this source , the following types of multivariate data analysis are there in research analysis:
Structural Equation Modelling:
SEM or Structural Equation Modelling is a type of statistical multivariate data analysis technique that analyzes the structural relationships between variables. This is a versatile and extensive data analysis network.
SEM evaluates the dependent and independent variables. In addition, latent variable metrics and model measurement verification are obtained. SEM is a hybrid of metric analysis and structural modeling.
For multivariate data analysis, this takes into account measurement errors and factors observed. The factors are evaluated using multivariate analytic techniques. This is an important component of the SEM model.
(Look also: Statistical data analysis )
Interdependence technique:
The relationships between the variables are studied in this approach to have a better understanding of them. This aids in determining the data's pattern and the variables' assumptions.
Canonical Correlation Analysis:
The canonical correlation analysis deals with the relations of straight lines between two types of variables. It has two main purposes- reduction of data and interpretation of data. Between the two categories of variables, all probability correlations are calculated.
When the two types of correlations are large, interpreting them might be difficult, but canonical correlation analysis can assist to highlight the link between the two variables.
Factor Analysis:
Factor analysis reduces data from a large number of variables to a small number of variables. Dimension reduction is another name for it. Before proceeding with the analysis, this approach is utilized to decrease the data. The patterns are apparent and much easier to examine when factor analysis is completed.
Cluster Analysis:
Cluster analysis is a collection of approaches for categorizing instances or objects into groupings called clusters. The data is divided based on similarity and then labeled to the group throughout the analysis. This is a data mining function that allows them to acquire insight into the data distribution based on each group's distinct characteristics.
Correspondence Analysis:
A table with a two-way array of non-negative values is used in a correspondence analysis approach. This array represents the relationship between the table's row and column entries. A table of contingency, in which the column and row entries relate to the two variables and the numbers in the table cells refer to frequencies, is a popular multivariate data analysis example.
Multidimensional Scaling:
MDS, or multidimensional scaling, is a technique that involves creating a map with the locations of the variables in a table, as well as the distances between them. There can be one or more dimensions to the map.
A metric or non-metric answer can be provided by the software. The proximity matrix is a table that shows the distances in tabular form. The findings of the trials or a correlation matrix are used to update this tabular column.
From the rows and columns of a database table to meaningful data, multivariate data analysis may be used to read and analyze data contained in various databases. This approach, also known as factor analysis, is used to gain an overview of a table in a database by reading strong patterns in the data such as trends, groupings, outliers, and their repetitions, producing a pattern. This is used by huge organizations and companies.
(Must read: Feature engineering in ML )
The output of this applied multivariate statistical analysis is the basis for the sales plan. Multivariate data analysis approaches are often utilized in companies to define objectives.
Share Blog :
Be a part of our Instagram community
Trending blogs
5 Factors Influencing Consumer Behavior
Elasticity of Demand and its Types
An Overview of Descriptive Analysis
What is PESTLE Analysis? Everything you need to know about it
What is Managerial Economics? Definition, Types, Nature, Principles, and Scope
5 Factors Affecting the Price Elasticity of Demand (PED)
6 Major Branches of Artificial Intelligence (AI)
Scope of Managerial Economics
Dijkstra’s Algorithm: The Shortest Path Algorithm
Different Types of Research Methods
Latest Comments

Really this is an informative post, thanks so much for this. I look forward to more posts. Here students can study all the subjects of the school. (Standard 8 to 12) CBSE, ICSE can learn the previous year's solved papers and other entrance exams like JEE, NEET, SSC etc. for free. Click to know: - https://www.zigya.com
R (BGU course)
Chapter 9 multivariate data analysis.
The term “multivariate data analysis” is so broad and so overloaded, that we start by clarifying what is discussed and what is not discussed in this chapter. Broadly speaking, we will discuss statistical inference , and leave more “exploratory flavored” matters like clustering, and visualization, to the Unsupervised Learning Chapter 11 .
We start with an example.
Formally, let \(y\) be single (random) measurement of a \(p\) -variate random vector. Denote \(\mu:=E[y]\) . Here is the set of problems we will discuss, in order of their statistical difficulty.
Signal Detection : a.k.a. multivariate test , or global test , or omnibus test . Where we test whether \(\mu\) differs than some \(\mu_0\) .
Signal Counting : a.k.a. prevalence estimation , or \(\pi_0\) estimation . Where we count the number of entries in \(\mu\) that differ from \(\mu_0\) .
Signal Identification : a.k.a. selection , or multiple testing . Where we infer which of the entries in \(\mu\) differ from \(\mu_0\) . In the ANOVA literature, this is known as a post-hoc analysis, which follows an omnibus test .
Estimation : Estimating the magnitudes of entries in \(\mu\) , and their departure from \(\mu_0\) . If estimation follows a signal detection or signal identification stage, this is known as selective estimation .
9.1 Signal Detection
Signal detection deals with the detection of the departure of \(\mu\) from some \(\mu_0\) , and especially, \(\mu_0=0\) . This problem can be thought of as the multivariate counterpart of the univariate hypothesis t-test.
9.1.1 Hotelling’s T2 Test
The most fundamental approach to signal detection is a mere generalization of the t-test, known as Hotelling’s \(T^2\) test .
Recall the univariate t-statistic of a data vector \(x\) of length \(n\) : \[\begin{align} t^2(x):= \frac{(\bar{x}-\mu_0)^2}{Var[\bar{x}]}= (\bar{x}-\mu_0)Var[\bar{x}]^{-1}(\bar{x}-\mu_0), \tag{9.1} \end{align}\] where \(Var[\bar{x}]=S^2(x)/n\) , and \(S^2(x)\) is the unbiased variance estimator \(S^2(x):=(n-1)^{-1}\sum (x_i-\bar x)^2\) .
Generalizing Eq (9.1) to the multivariate case: \(\mu_0\) is a \(p\) -vector, \(\bar x\) is a \(p\) -vector, and \(Var[\bar x]\) is a \(p \times p\) matrix of the covariance between the \(p\) coordinated of \(\bar x\) . When operating with vectors, the squaring becomes a quadratic form, and the division becomes a matrix inverse. We thus have \[\begin{align} T^2(x):= (\bar{x}-\mu_0)' Var[\bar{x}]^{-1} (\bar{x}-\mu_0), \tag{9.2} \end{align}\] which is the definition of Hotelling’s \(T^2\) one-sample test statistic. We typically denote the covariance between coordinates in \(x\) with \(\hat \Sigma(x)\) , so that \(\widehat \Sigma_{k,l}:=\widehat {Cov}[x_k,x_l]=(n-1)^{-1} \sum (x_{k,i}-\bar x_k)(x_{l,i}-\bar x_l)\) . Using the \(\Sigma\) notation, Eq. (9.2) becomes \[\begin{align} T^2(x):= n (\bar{x}-\mu_0)' \hat \Sigma(x)^{-1} (\bar{x}-\mu_0), \end{align}\] which is the standard notation of Hotelling’s test statistic.
For inference, we need the null distribution of Hotelling’s test statistic. For this we introduce some vocabulary 17 :
- Low Dimension : We call a problem low dimensional if \(n \gg p\) , i.e. \(p/n \approx 0\) . This means there are many observations per estimated parameter.
- High Dimension : We call a problem high dimensional if \(p/n \to c\) , where \(c\in (0,1)\) . This means there are more observations than parameters, but not many.
- Very High Dimension : We call a problem very high dimensional if \(p/n \to c\) , where \(1<c<\infty\) . This means there are less observations than parameters.
Hotelling’s \(T^2\) test can only be used in the low dimensional regime. For some intuition on this statement, think of taking \(n=20\) measurements of \(p=100\) physiological variables. We seemingly have \(20\) observations, but there are \(100\) unknown quantities in \(\mu\) . Say you decide that \(\mu\) differs from \(\mu_0\) based on the coordinate with maximal difference between your data and \(\mu_0\) . Do you know how much variability to expect of this maximum? Try comparing your intuition with a quick simulation. Did the variabilty of the maximum surprise you? Hotelling’s \(T^2\) is not the same as the maxiumum, but the same intuition applies. This criticism is formalized in Bai and Saranadasa ( 1996 ) . In modern applications, Hotelling’s \(T^2\) is rarely recommended. Luckily, many modern alternatives are available. See J. Rosenblatt, Gilron, and Mukamel ( 2016 ) for a review.
9.1.2 Various Types of Signal to Detect
In the previous, we assumed that the signal is a departure of \(\mu\) from some \(\mu_0\) . For vactor-valued data \(y\) , that is distributed \(\mathcal F\) , we may define “signal” as any departure from some \(\mathcal F_0\) . This is the multivaraite counterpart of goodness-of-fit (GOF) tests.
Even when restricting “signal” to departures of \(\mu\) from \(\mu_0\) , “signal” may come in various forms:
- Dense Signal : when the departure is in a large number of coordinates of \(\mu\) .
- Sparse Signal : when the departure is in a small number of coordinates of \(\mu\) .
Process control in a manufactoring plant, for instance, is consistent with a dense signal: if a manufacturing process has failed, we expect a change in many measurements (i.e. coordinates of \(\mu\) ). Detection of activation in brain imaging is consistent with a dense signal: if a region encodes cognitive function, we expect a change in many brain locations (i.e. coordinates of \(\mu\) .) Detection of disease encodig regions in the genome is consistent with a sparse signal: if susceptibility of disease is genetic, only a small subset of locations in the genome will encode it.
Hotelling’s \(T^2\) statistic is best for dense signal. The next test, is a simple (and forgotten) test best with sparse signal.
9.1.3 Simes’ Test
Hotelling’s \(T^2\) statistic has currently two limitations: It is designed for dense signals, and it requires estimating the covariance, which is a very difficult problem.
An algorithm, that is sensitive to sparse signal and allows statistically valid detection under a wide range of covariances (even if we don’t know the covariance) is known as Simes’ Test . The statistic is defined vie the following algorithm:
- Compute \(p\) variable-wise p-values: \(p_1,\dots,p_j\) .
- Denote \(p_{(1)},\dots,p_{(j)}\) the sorted p-values.
- Simes’ statistic is \(p_{Simes}:=min_j\{p_{(j)} \times p/j\}\) .
- Reject the “no signal” null hypothesis at significance \(\alpha\) if \(p_{Simes}<\alpha\) .
9.1.4 Signal Detection with R
We start with simulating some data with no signal. We will convince ourselves that Hotelling’s and Simes’ tests detect nothing, when nothing is present. We will then generate new data, after injecting some signal, i.e., making \(\mu\) depart from \(\mu_0=0\) . We then convince ourselves, that both Hotelling’s and Simes’ tests, are indeed capable of detecting signal, when present.
Generating null data:
Now making our own Hotelling one-sample \(T^2\) test using Eq.( (9.2) ).
Things to note:
- stopifnot(n > 5 * p) is a little verification to check that the problem is indeed low dimensional. Otherwise, the \(\chi^2\) approximation cannot be trusted.
- solve returns a matrix inverse.
- %*% is the matrix product operator (see also crossprod() ).
- A function may return only a single object, so we wrap the statistic and its p-value in a list object.
Just for verification, we compare our home made Hotelling’s test, to the implementation in the rrcov package. The statistic is clearly OK, but our \(\chi^2\) approximation of the distribution leaves room to desire. Personally, I would never trust a Hotelling test if \(n\) is not much greater than \(p\) , in which case I would use a high-dimensional adaptation (see Bibliography).
Let’s do the same with Simes’:
And now we verify that both tests can indeed detect signal when present. Are p-values small enough to reject the “no signal” null hypothesis?
… yes. All p-values are very small, so that all statistics can detect the non-null distribution.
9.2 Signal Counting
There are many ways to approach the signal counting problem. For the purposes of this book, however, we will not discuss them directly, and solve the signal counting problem as a signal identification problem: if we know where \(\mu\) departs from \(\mu_0\) , we only need to count coordinates to solve the signal counting problem.
9.3 Signal Identification
The problem of signal identification is also known as selective testing , or more commonly as multiple testing .
In the ANOVA literature, an identification stage will typically follow a detection stage. These are known as the omnibus F test , and post-hoc tests, respectively. In the multiple testing literature there will typically be no preliminary detection stage. It is typically assumed that signal is present, and the only question is “where?”
The first question when approaching a multiple testing problem is “what is an error”? Is an error declaring a coordinate in \(\mu\) to be different than \(\mu_0\) when it is actually not? Is an error an overly high proportion of falsely identified coordinates? The former is known as the family wise error rate (FWER), and the latter as the false discovery rate (FDR).
9.3.1 Signal Identification in R
One (of many) ways to do signal identification involves the stats::p.adjust function. The function takes as inputs a \(p\) -vector of the variable-wise p-values . Why do we start with variable-wise p-values, and not the full data set?
- Because we want to make inference variable-wise, so it is natural to start with variable-wise statistics.
- Because we want to avoid dealing with covariances if possible. Computing variable-wise p-values does not require estimating covariances.
- So that the identification problem is decoupled from the variable-wise inference problem, and may be applied much more generally than in the setup we presented.
We start be generating some high-dimensional multivariate data and computing the coordinate-wise (i.e. hypothesis-wise) p-value.
We now compute the pvalues of each coordinate. We use a coordinate-wise t-test. Why a t-test? Because for the purpose of demonstration we want a simple test. In reality, you may use any test that returns valid p-values.
- t.pval is a function that merely returns the p-value of a t.test.
- We used the apply function to apply the same function to each column of x .
- MARGIN=2 tells apply to compute over columns and not rows.
- The output, p.values , is a vector of 100 p-values.
We are now ready to do the identification, i.e., find which coordinate of \(\mu\) is different than \(\mu_0=0\) . The workflow for identification has the same structure, regardless of the desired error guarantees:
- Compute an adjusted p-value .
- Compare the adjusted p-value to the desired error level.
If we want \(FWER \leq 0.05\) , meaning that we allow a \(5\%\) probability of making any mistake, we will use the method="holm" argument of p.adjust .
If we want \(FDR \leq 0.05\) , meaning that we allow the proportion of false discoveries to be no larger than \(5\%\) , we use the method="BH" argument of p.adjust .
We now inject some strong signal in \(\mu\) just to see that the process works. We will artificially inject signal in the first 10 coordinates.
Indeed- we are now able to detect that the first coordinates carry signal, because their respective coordinate-wise null hypotheses have been rejected.
9.4 Signal Estimation (*)
The estimation of the elements of \(\mu\) is a seemingly straightforward task. This is not the case, however, if we estimate only the elements that were selected because they were significant (or any other data-dependent criterion). Clearly, estimating only significant entries will introduce a bias in the estimation. In the statistical literature, this is known as selection bias . Selection bias also occurs when you perform inference on regression coefficients after some model selection, say, with a lasso, or a forward search 18 .
Selective inference is a complicated and active research topic so we will not offer any off-the-shelf solution to the matter. The curious reader is invited to read Rosenblatt and Benjamini ( 2014 ) , Javanmard and Montanari ( 2014 ) , or Will Fithian’s PhD thesis (Fithian 2015 ) for more on the topic.
9.5 Bibliographic Notes
For a general introduction to multivariate data analysis see Anderson-Cook ( 2004 ) . For an R oriented introduction, see Everitt and Hothorn ( 2011 ) . For more on the difficulties with high dimensional problems, see Bai and Saranadasa ( 1996 ) . For some cutting edge solutions for testing in high-dimension, see J. Rosenblatt, Gilron, and Mukamel ( 2016 ) and references therein. Simes’ test is not very well known. It is introduced in Simes ( 1986 ) , and proven to control the type I error of detection under a PRDS type of dependence in Benjamini and Yekutieli ( 2001 ) . For more on multiple testing, and signal identification, see Efron ( 2012 ) . For more on the choice of your error rate see Rosenblatt ( 2013 ) . For an excellent review on graphical models see Kalisch and Bühlmann ( 2014 ) . Everything you need on graphical models, Bayesian belief networks, and structure learning in R, is collected in the Task View .
9.6 Practice Yourself
Generate multivariate data with:
- Use Hotelling’s test to determine if \(\mu\) equals \(\mu_0=0\) . Can you detect the signal?
- Perform t.test on each variable and extract the p-value. Try to identify visually the variables which depart from \(\mu_0\) .
- Use p.adjust to identify in which variables there are any departures from \(\mu_0=0\) . Allow 5% probability of making any false identification.
- Use p.adjust to identify in which variables there are any departures from \(\mu_0=0\) . Allow a 5% proportion of errors within identifications.
- Do we agree the groups differ?
- Implement the two-group Hotelling test described in Wikipedia: ( https://en.wikipedia.org/wiki/Hotelling%27s_T-squared_distribution#Two-sample_statistic ).
- Verify that you are able to detect that the groups differ.
- Perform a two-group t-test on each coordinate. On which coordinates can you detect signal while controlling the FWER? On which while controlling the FDR? Use p.adjust .
Return to the previous problem, but set n=9 . Verify that you cannot compute your Hotelling statistic.
Anderson-Cook, Christine M. 2004. “An Introduction to Multivariate Statistical Analysis.” Journal of the American Statistical Association 99 (467). American Statistical Association: 907–9.
Bai, Zhidong, and Hewa Saranadasa. 1996. “Effect of High Dimension: By an Example of a Two Sample Problem.” Statistica Sinica . JSTOR, 311–29.
Benjamini, Yoav, and Daniel Yekutieli. 2001. “The Control of the False Discovery Rate in Multiple Testing Under Dependency.” Annals of Statistics . JSTOR, 1165–88.
Efron, Bradley. 2012. Large-Scale Inference: Empirical Bayes Methods for Estimation, Testing, and Prediction . Vol. 1. Cambridge University Press.
Everitt, Brian, and Torsten Hothorn. 2011. An Introduction to Applied Multivariate Analysis with R . Springer Science & Business Media.
Fithian, William. 2015. “Topics in Adaptive Inference.” PhD thesis, STANFORD UNIVERSITY.
Javanmard, Adel, and Andrea Montanari. 2014. “Confidence Intervals and Hypothesis Testing for High-Dimensional Regression.” Journal of Machine Learning Research 15 (1): 2869–2909.
Kalisch, Markus, and Peter Bühlmann. 2014. “Causal Structure Learning and Inference: A Selective Review.” Quality Technology & Quantitative Management 11 (1). Taylor & Francis: 3–21.
Rosenblatt, Jonathan. 2013. “A Practitioner’s Guide to Multiple Testing Error Rates.” arXiv Preprint arXiv:1304.4920 .
Rosenblatt, Jonathan D, and Yoav Benjamini. 2014. “Selective Correlations; Not Voodoo.” NeuroImage 103. Elsevier: 401–10.
Rosenblatt, Jonathan, Roee Gilron, and Roy Mukamel. 2016. “Better-Than-Chance Classification for Signal Detection.” arXiv Preprint arXiv:1608.08873 .
Simes, R John. 1986. “An Improved Bonferroni Procedure for Multiple Tests of Significance.” Biometrika 73 (3). Oxford University Press: 751–54.
This vocabulary is not standard in the literature, so when you read a text, you will need to verify yourself what the author means. ↩
You might find this shocking, but it does mean that you cannot trust the summary table of a model that was selected from a multitude of models. ↩
An official website of the United States government
The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.
The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.
- Publications
- Account settings
The PMC website is updating on October 15, 2024. Learn More or Try it out now .
- Advanced Search
- Journal List
- Hippokratia
- v.14(Suppl 1); 2010 Dec
Introduction to Multivariate Regression Analysis
Statistics are used in medicine for data description and inference. Inferential statistics are used to answer questions about the data, to test hypotheses (formulating the alternative or null hypotheses), to generate a measure of effect, typically a ratio of rates or risks, to describe associations (correlations) or to model relationships (regression) within the data and, in many other functions. Usually point estimates are the measures of associations or of the magnitude of effects. Confounding, measurement errors, selection bias and random errors make unlikely the point estimates to equal the true ones. In the estimation process, the random error is not avoidable. One way to account for is to compute p-values for a range of possible parameter values (including the null). The range of values, for which the p-value exceeds a specified alpha level (typically 0.05) is called confidence interval. An interval estimation procedure will, in 95% of repetitions (identical studies in all respects except for random error), produce limits that contain the true parameters. It is argued that the question if the pair of limits produced from a study contains the true parameter could not be answered by the ordinary (frequentist) theory of confidence intervals 1 . Frequentist approaches derive estimates by using probabilities of data (either p-values or likelihoods) as measures of compatibility between data and hypotheses, or as measures of the relative support that data provide hypotheses. Another approach, the Bayesian, uses data to improve existing (prior) estimates in light of new data. Proper use of any approach requires careful interpretation of statistics 1 , 2 .
The goal in any data analysis is to extract from raw information the accurate estimation. One of the most important and common question concerning if there is statistical relationship between a response variable (Y) and explanatory variables (Xi). An option to answer this question is to employ regression analysis in order to model its relationship. There are various types of regression analysis. The type of the regression model depends on the type of the distribution of Y; if it is continuous and approximately normal we use linear regression model; if dichotomous we use logistic regression; if Poisson or multinomial we use log-linear analysis; if time-to-event data in the presence of censored cases (survival-type) we use Cox regression as a method for modeling. By modeling we try to predict the outcome (Y) based on values of a set of predictor variables (Xi). These methods allow us to assess the impact of multiple variables (covariates and factors) in the same model 3 , 4 .
In this article we focus in linear regression. Linear regression is the procedure that estimates the coefficients of the linear equation, involving one or more independent variables that best predict the value of the dependent variable which should be quantitative. Logistic regression is similar to a linear regression but is suited to models where the dependent variable is dichotomous. Logistic regression coefficients can be used to estimate odds ratios for each of the independent variables in the model.
Linear equation
In most statistical packages, a curve estimation procedure produces curve estimation regression statistics and related plots for many different models (linear, logarithmic, inverse, quadratic, cubic, power, S-curve, logistic, exponential etc.). It is essential to plot the data in order to determine which model to use for each depedent variable. If the variables appear to be related linearly, a simple linear regression model can be used but in the case that the variables are not linearly related, data transformation might help. If the transformation does not help then a more complicated model may be needed. It is strongly advised to view early a scatterplot of your data; if the plot resembles a mathematical function you recognize, fit the data to that type of model. For example, if the data resemble an exponential function, an exponential model is to be used. Alternatively, if it is not obvious which model best fits the data, an option is to try several models and select among them. It is strongly recommended to screen the data graphically (e.g. by a scatterplot) in order to determine how the independent and dependent variables are related (linearly, exponentially etc.) 4 – 6 .
The most appropriate model could be a straight line, a higher degree polynomial, a logarithmic or exponential. The strategies to find an appropriate model include the forward method in which we start by assuming the very simple model i.e. a straight line (Y = a + bX or Y = b 0 + b 1 X ). Then we find the best estimate of the assumed model. If this model does not fit the data satisfactory, then we assume a more complicated model e.g. a 2nd degree polynomial (Y=a+bX+cX 2 ) and so on. In a backward method we assume a complicated model e.g. a high degree polynomial, we fit the model and we try to simplify it. We might also use a model suggested by theory or experience. Often a straight line relationship fits the data satisfactory and this is the case of simple linear regression. The simplest case of linear regression analysis is that with one predictor variable 6 , 7 .
Linear regression equation
The purpose of regression is to predict Y on the basis of X or to describe how Y depends on X (regression line or curve)

The Xi (X 1 , X 2 , , X k ) is defined as "predictor", "explanatory" or "independent" variable, while Y is defined as "dependent", "response" or "outcome" variable.
Assuming a linear relation in population, mean of Y for given X equals α+βX i.e. the "population regression line".
If Y = a + bX is the estimated line, then the fitted
Ŷi = a + bXi is called the fitted (or predicted) value, and Yi Ŷi is called the residual.
The estimated regression line is determined in such way that (residuals) 2 to be the minimal i.e. the standard deviation of the residuals to be minimized (residuals are on average zero). This is called the "least squares" method. In the equation

b is the slope (the average increase of outcome per unit increase of predictor)
a is the intercept (often has no direct practical meaning)
A more detailed (higher precision of the estimates a and b) regression equation line can also be written as

Further inference about regression line could be made by the estimation of confidence interval (95%CI for the slope b). The calculation is based on the standard error of b:

so, 95% CI for β is b ± t0.975*se(b) [t-distr. with df = n-2]
and the test for H0: β=0, is t = b / se(b) [p-value derived from t-distr. with df = n-2].
If the p value lies above 0.05 then the null hypothesis is not rejected which means that a straight line model in X does not help predicting Y. There is the possibility that the straight line model holds (slope = 0) or there is a curved relation with zero linear component. On the other hand, if the null hypothesis is rejected either the straight line model holds or in a curved relationship the straight line model helps, but is not the best model. Of course there is the possibility for a type II or type I error in the first and second option, respectively. The standard deviation of residual (σ res ) is estimated by

The standard deviation of residual (σ res ) characterizes the variability around the regression line i.e. the smaller the σ res , the better the fit. It has a number of degrees of freedom. This is the number to divide by in order to have an unbiased estimate of the variance. In this case df = n-2, because two parameters, α and β, are estimated 7 .
Multiple linear regression analysis
As an example in a sample of 50 individuals we measured: Y = toluene personal exposure concentration (a widespread aromatic hydrocarbon); X1 = hours spent outdoors; X2 = wind speed (m/sec); X3 = toluene home levels. Y is the continuous response variable ("dependent") while X1, X2, , Xp as the predictor variables ("independent") [7]. Usually the questions of interest are how to predict Y on the basis of the X's and what is the "independent" influence of wind speed, i.e. corrected for home levels and other related variables? These questions can in principle be answered by multiple linear regression analysis.
In the multiple linear regression model, Y has normal distribution with mean

The model parameters β 0 + β 1 + +β ρ and σ must be estimated from data.
β 0 = intercept
β 1 β ρ = regression coefficients
σ = σ res = residual standard deviation
Interpretation of regression coefficients
In the equation Y = β 0 + β 1 1 + +βρXρ
β 1 equals the mean increase in Y per unit increase in Xi , while other Xi's are kept fixed. In other words βi is influence of Xi corrected (adjusted) for the other X's. The estimation method follows the least squares criterion.
If b 0 , b 1 , , bρ are the estimates of β 0 , β 1 , , βρ then the "fitted" value of Y is

In our example, the statistical packages give the following estimates or regression coefficients (bi) and standard errors (se) for toluene personal exposure levels.

Then the regression equation for toluene personal exposure levels would be:

The estimated coefficient for time spent outdoors (0.582) means that the estimated mean increase in toluene personal levels is 0.582 g/m 3 if time spent outdoors increases 1 hour, while home levels and wind speed remain constant. More precisely one could say that individuals differing one hour in the time that spent outdoors, but having the same values on the other predictors, will have a mean difference in toluene xposure levels equal to 0.582 µg/m 3 8 .
Be aware that this interpretation does not imply any causal relation.
Confidence interval (CI) and test for regression coefficients
95% CI for i is given by bi ± t0.975*se(bi) for df= n-1-p (df: degrees of freedom)
In our example that means that the 95% CI for the coefficient of time spent outdoors is 95%CI: - 0.19 to 0.49

As in example if we test the H0: β humidity = 0 and find P = 0.40, which is not significant, we assumed that the association between between toluene personal exposure and humidity could be explained by the correlation between humididty and wind speed 8 .
In order to estimate the standard deviation of the residual (Y Yfit), i.e. the estimated standard deviation of a given set of variable values in a population sample, we have to estimate σ

The number of degrees of freedom is df = n (p + 1), since p + 1 parameters are estimated.
The ANOVA table gives the total variability in Y which can be partitioned in a part due to regression and a part due to residual variation:

With degrees of freedom (n 1) = p + (n p 1)
In statistical packages the ANOVA table in which the partition is given usually has the following format [6]:

SS: "sums of squares"; df: Degrees of freedom; MS: "mean squares" (SS/dfs); F: F statistics (see below)
As a measure of the strength of the linear relation one can use R. R is called the multiple correlation coefficient between Y, predictors (X1, Xp ) and Yfit and R square is the proportion of total variation explained by regression (R 2 =SSreg / SStot).
Test on overall or reduced model

In our example Tpers = β 0 + β 1 time outdoors + β 2 Thome +β 3 wind speed + residual
The null hypothesis (H 0 ) is that there is no regression overall i.e. β 1 = β 2 =+βρ = 0
The test is based on the proportion of the SS explained by the regression relative to the residual SS. The test statistic (F= MSreg / MSres) has F-distribution with df1 = p and df2 = n p 1 (F- distribution table). In our example F= 5.49 (P<0.01)
If now we want to test the hypothesis Ho: β 1 = β 2 = β 5 = 0 (k = 3)
In general k of p regression coefficients are set to zero under H0. The model that is valid if H 0 =0 is true is called the "reduced model". The Idea is to compare the explained variability of the model at hand with that of the reduced model.
The test statistic (F):

follows a F-distribution with df 1 = k and df 2 = n p 1.
If one or two variables are left out and we calculate SS reg (the statistical package does) and we find that the test statistic for F lies between 0.05 < P < 0.10, that means that there is some evidence, although not strong, that these variables together, independently of the others, contribute to the prediction of the outcome.
Assumptions
If a linear model is used, the following assumptions should be met. For each value of the independent variable, the distribution of the dependent variable must be normal. The variance of the distribution of the dependent variable should be constant for all values of the independent variable. The relationship between the dependent variable and the independent variables should be linear, and all observations should be independent. So the assumptions are: independence; linearity; normality; homoscedasticity. In other words the residuals of a good model should be normally and randomly distributed i.e. the unknown does not depend on X ("homoscedasticity") 2 , 4 , 6 , 9 .
Checking for violations of model assumptions
To check model assumptions we used residual analysis. There are several kinds of residuals most commonly used are the standardized residuals (ZRESID) and the studentized residuals (SRESID) [6]. If the model is correct, the residuals should have a normal distribution with mean zero and constant sd (i.e. not depending on X). In order to check this we can plot residuals against X. If the variation alters with increasing X, then there is violation of homoscedasticity. We can also use the Durbin-Watson test for serial correlation of the residuals and casewise diagnostics for the cases meeting the selection criterion (outliers above n standard deviations). The residuals are (zero mean) independent, normally distributed with constant standard deviation (homogeneity of variances) 4 , 6 .
To discover deviations form linearity and homogeneity of variables we can plot residuals against each predictor or against predicted values. Alternatively by using the PARTIAL plot we can assess linearity of a predictor variable. The partial plot for a predictor X 1 is a plot of residuals of Y regressed on other Xs and against residuals of Xi regressed on other X's. The plot should be linear. To check the normality of residuals we can use an histogram (with normal curve) or a normal probability plot 6 , 7 .
The goodness-of-fit of the model is assessed by studying the behavior of the residuals, looking for "special observations / individuals" like outliers, observations with high "leverage" and influential points. Observations deserving extra attention are outliers i.e. observations with unusually large residual; high leverage points: unusual x - pattern, i.e. outliers in predictor space; influential points: individuals with high influence on estimate or standard error of one or more β's. An observation could be all three. It is recommended to inspect individuals with large residual, for outliers; to use distances for high leverage points i.e. measures to identify cases with unusual combinations of values for the independent variables and cases that may have a large impact on the regression model. For influential points use influence statistics i.e. the change in the regression coefficients (DfBeta(s)) and predicted values (DfFit) that results from the exclusion of a particular case. Overall measure for influence on all β's jointly is "Cook's distance" (COOK). Analogously for standard errors overall measure is COVRATIO 6 .
Deviations from model assumptions
We can use some tips to correct some deviation from model assumptions. In case of curvilinearity in one or more plots we could add quadratic term(s). In case of non homogeneity of residual sd, we can try some transformation: log Y if Sres is proportional to predicted Y; square root of Y if Y distribution is Poisson-like; 1/Y if Sres 2 is proportional to predicted Y; Y 2 if Sres 2 decreases with Y. If linearity and homogeneity hold then non-normality does not matter if the sample size is big enough (n≥50- 100). If linearity but not homogeneity hold then estimates of β's are correct, but not the standard errors. They can be corrected by computing the "robust" se's (sandwich, Huber's estimate) 4 , 6 , 9 .
Selection methods for Linear Regression modeling
There are various selection methods for linear regression modeling in order to specify how independent variables are entered into the analysis. By using different methods, a variety of regression models from the same set of variables could be constructed. Forward variable selection enters the variables in the block one at a time based on entry criteria. Backward variable elimination enters all of the variables in the block in a single step and then removes them one at a time based on removal criteria. Stepwise variable entry and removal examines the variables in the block at each step for entry or removal. All variables must pass the tolerance criterion to be entered in the equation, regardless of the entry method specified. A variable is not entered if it would cause the tolerance of another variable already in the model to drop below the tolerance criterion 6 . In a model fitting the variables entered and removed from the model and various goodness-of-fit statistics are displayed such as R2, R squared change, standard error of the estimate, and an analysis-of-variance table.
Relative issues
Binary logistic regression models can be fitted using either the logistic regression procedure or the multinomial logistic regression procedure. An important theoretical distinction is that the logistic regression procedure produces all statistics and tests using data at the individual cases while the multinomial logistic regression procedure internally aggregates cases to form subpopulations with identical covariate patterns for the predictors based on these subpopulations. If all predictors are categorical or any continuous predictors take on only a limited number of values the mutinomial procedure is preferred. As previously mentioned, use the Scatterplot procedure to screen data for multicollinearity. As with other forms of regression, multicollinearity among the predictors can lead to biased estimates and inflated standard errors. If all of your predictor variables are categorical, you can also use the loglinear procedure.
In order to explore correlation between variables, Pearson or Spearman correlation for a pair of variables r (Xi, Xj) is commonly used. For each pair of variables (Xi, Xj) Pearson's correlation coefficient (r) can be computed. Pearsons r (Xi; Xj) is a measure of linear association between two (ideally normally distributed) variables. R 2 is the proportion of total variation of the one explained by the other (R 2 = b * Sx/Sy), identical with regression. Each correlation coefficient gives measure for association between two variables without taking other variables into account. But there are several useful correlation concepts involving more variables. The partial correlation coefficient between Xi and Xj, adjusted for other X's e.g. r (X1; X2 / X3). The partial correlation coefficient can be viewed as an adjustment of the simple correlation taking into account the effect of a control variable: r(X ; Y / Z ) i.e. correlation between X and Y controlled for Z. The multiple correlation coefficient between one X and several other X's e.g. r (X1 ; X2 , X3 , X4) is a measure of association between one variable and several other variables r (Y ; X1, X2, , Xk). The multiple correlation coefficient between Y and X1, X2,, Xk is defined as the simple Pearson correlation coefficient r (Y ; Yfit) between Y and its fitted value in the regression model: Y = β0 + β1X1+ βkXk + residual. The square of r (Y; X1, , Xk ) is interpreted as the proportion of variability in Y that can be explained by X1, , Xk. The null hypothesis [H 0 : ρ ( : X1, , Xk) = 0] is tested with the F-test for overall regression as it is in the multivariate regression model (see above) 6 , 7 . The multiple-partial correlation coefficient between one X and several other X`s adjusted for some other X's e.g. r (X1 ; X2 , X3 , X4 / X5 , X6 ). The multiple partial correlation coefficient equal the relative increase in % explained variability in Y by adding X1,, Xk to a model already containing Z1, , Zρ as predictors 6 , 7 .
Other interesting cases of multiple linear regression analysis include: the comparison of two group means. If for example we wish to answer the question if mean HEIGHT differs between men and women? In the simple linear regression model:

Testing β1 = 0 is equivalent with testing
HEIGHT MEN sub> = HEIGHT WOMEN by means of Student's t-test
The linear regression model assumes a normal distribution of HEIGHT in both groups, with equal . This is exactly the model of the two-sample t-test. In the case of comparison of several group means, we wish to answer the question if mean HEIGHT differ between different SES classes?
SES: 1 (low); 2 (middle) and 3 (high) (socioeconomic status)
We can use the following linear regression model:

Then β 1 and β 2 are interpreted as:
β 1 = difference in mean HEIGHT between low and high class
β 2 = difference in mean HEIGHT between middle and high class
Testing β 1 = β 2 = 0 is equivalent with the one-way ANalysis Of VAriance F-test . The statistical model in both cases is in fact the same 4 , 6 , 7 , 9 .
Analysis of covariance (ANCOVA)
If we wish to compare a continuous variable Y (e.g. HEIGHT) between groups (e.g. men and women) corrected (adjusted or controlled) for one or more covariables X (confounders) (e.g. X = age or weight) then the question is formulated: Are means of HEIGHT of men and women different, if men and women of equal weight are compared? Be aware that this question is different from that if there is a difference between the means of HEIGHT for men and women? And the answers can be quite different! The difference between men and women could be opposite, larger or smaller than the crude if corrected. In order to estimate the corrected difference the following multiple regression model is used:

where Y: response variable (for example HEIGHT); Z: grouping variable (for example Z = 0 for men and Z = 1 for women); X: covariable (confounder) (for example weight).
So, for men the regression line is y = β 0 + β 2 and for women is y = (β 0 + β 1 ) + β 2 .
This model assumes that regression lines are parallel. Therefore β 1 is the vertical difference, and can be interpreted as the: for X corrected difference between the mean response Y of the groups. If the regression lines are not parallel, then difference in mean Y depends on value of X. This is called "interaction" or "effect modification" .
A more complicated model, in which interaction is admitted, is:

regression line men: y = β 0 + β 2
regression line women: y = (β 0 + β 1 )+ (β 2 + β 3 )X
The hypothesis of the absence of "effect modification" is tested by H 0 : 3 = 0
As an example, we are interested to answer what is - the corrected for body weight - difference in HEIGHT between men and women in a population sample?
We check the model with interaction:

By testing β 3 =0, a p-value much larger than 0.05 was calculated. We assume therefore that there is no interaction i.e. regression lines are parallel. Further Analysis of Covariance for ≥ 3 groups could be used if we ask the difference in mean HEIGHT between people with different level of education (primary, medium, high), corrected for body weight. In a model where the three lines may be not parallel we have to check for interaction (effect modification) 7. Testing the hypothesis that coefficient of interactions terms equal 0, it is reasonable to assume a model without interaction. Testing the hypothesis H 0 : β 1 = β 2 = 0, i.e. no differences between education level when corrected for weight, gives the result of fitting the model, for which the P-values for Z 1 and Z 2 depend on your choice of the reference group. The purposes of ANCOVA are to correct for confounding and increase of precision of an estimated difference.
In a general ANCOVA model as:

where Y the response variable; k groups (dummy variables Z 1 , Z 2 , , Z k-1 ) and X 1 , , X p confounders
there is a straightforward extension to arbitrary number of groups and covariables.
Coding categorical predictors in regression
One always has to figure out which way of coding categorical factors is used, in order to be able to interpret the parameter estimates. In "reference cell" coding, one of the categories plays the role of the reference category ("reference cell"), while the other categories are indicated by dummy variables. The β's corresponding to the dummies that are interpreted as the difference of corresponding category with the reference category. In "difference with overall mean" coding in the model of the previous example: [Y = β 0 + β 1 1 + β 2 2 ++ residual], the β 0 is interpreted as the overall mean of the three levels of education while β 1 and β 2 are interpreted as the deviation of mean of primary and medium from overall mean, respectively. The deviation of the mean of high level from overall mean is given by (- β 1 - β 2 ). In "cell means" coding in the previous model (without intercept): [Y = β 0 + β 1 1 + β 2 2 + β 3 3 + residual], β 1 is the mean of primary, β 2 the middle and β 3 of the high level education 6 , 7 , 9 .
Conclusions
It is apparent to anyone who reads the medical literature today that some knowledge of biostatistics and epidemiology is a necessity. The goal in any data analysis is to extract from raw information the accurate estimation. But before any testing or estimation, a careful data editing, is essential to review for errors, followed by data summarization. One of the most important and common question is if there is statistical relationship between a response variable (Y) and explanatory variables (Xi). An option to answer this question is to employ regression analysis. There are various types of regression analysis. All these methods allow us to assess the impact of multiple variables on the response variable.
JABSTB: Statistical Design and Analysis of Experiments with R
Chapter 38 multivariate analysis of variance (manova).
MANOVA is a procedure to analyze experimental data involving simultaneous measurements of two or more dependent variables in response to two or more predictor groups.
The basic MANOVA designs are no different than the various t-test or ANOVA designs. Paired, unpaired, one-way (one-factor), two-way (two-factor) and even three-way (three-factor) (or more way) MANOVA experiments are possible. They can be structured either as independent (completely randomized) or intrinsically-linked (related/repeated measures) or a mixture of the two.
What differs is MANOVA designs collect measurements for more than one dependent variable from each replicate.
The statistical jargon for such experiments is they are “multivariate,” whereas ANOVA is “univariate.” This term is owed to a mathematical feature of underlying MANOVA which involves calculating linear combinations of these dependent variables to uncover latent “variates.” The statistical test is actually performed on these latent variates.
Statistical jargon is very confusing most of the time. When we have experiments that involve more than one treatment variable (each at many levels) and only one outcome variable, such as a two-way ANOVA, we call these “multivariable” experiments. But they are also known as “univariate” tests because there is only one dependent variable. When we have experiments that have one or more treatment variables and multiple outcome variables, such as one- or two-way MANOVA, we call these multivariate tests. I’m sorry.
38.1 What does MANOVA test?
Exactly what is that null hypothesis?
Like ANOVA, MANOVA experiments involve groups of factorial predictor variables (it is possible to run MANOVA on only two groups). The null hypothesis addresses whether there are any differences between groups of means. As in ANOVA, this is accomplished by partitioning variance. Therefore, as for ANOVA, the test is whether the variance in the MANOVA model exceeds the residual variance.
However, in MANOVA this operates on the basis of statistical parameters for a composite dependent variable, which is calculated from the array of dependent variables in the experiment.
You’ll see that the MANOVA test output per se generates an F statistic. In that regard the inferential procedure is very much like ANOVA. If the F value is extreme, the model variance exceeds the residual variance, and it has a low p-value. A p-value falling below a preset type1 error threshold favors a rejection of null hypotheses.
However, this is a funny F statistic.
First it is an approximated F, which is mapped to the F test statistic distribution.
MANOVA data sets have one column for each dependent variable, which creates a matrix when there are multiple dependent variables.
The MANOVA test statistic operates on a matrix parameter called the eigenvalue. Eigenvalues are scaling factors for eigenvectors, which are also matrix parameters. Eigenvectors are ways of reducing the complexity of matrix data. Eigenvectors represent latent variates within these multivariate datasets. Note the plural. There can be more than one eigenvector in a multivariate dataset, the number for which is related to the number of dependent and independent variables.
There are four different MANOVA test statistics: Wilks’ Lambda, Hotelling-Lawley Trace, Pillai’s Trace, and Roy’s Largest Root. Each are calculated differently. Given the same input data, each test statistic is then used to generate an F statistic.
Like a lot of things in statistics, they represent different ways to achieve the same objective, but generate different results in the process. Their eponymous inventors believe their’s offers a better mousetrap.
Choosing which of the MANOVA test statistics to use for inference is not unlike choosing which multiple correction method to use following ANOVA. It can be confusing.
It is not uncommon for the test statistics to yield conflicting outcomes. Therefore, it is imperative for the test statistic to be chosen in advance.
38.2 Types of experiments
We imagine a gene expression study that measures the transcripts for several different genes simultaneously within every replicate. Each transcript represents a unique dependent variable since they come from different genes, each with its own network of transcription factors. But we can also imagine underlying latent relationships between some of the genes. For example, some of the genes may be regulated by a common transcript. We might be interested in how different genes are expressed over time and in the absence or presence of certain stimuli. Time and stimuli are each predictor variables. The sample source informs whether the design is completely randomized or related/repeated measure.
Or we are interested in quantifying several different proteins simultaneously by western blot technique. We might be interested in testing how different groups of stimuli or certain mutations affects each of their levels. Or we are able to measure multiple proteins simultaneously in cells using differentially colored fluorescent tags. Each protein (each color) is a unique dependent variable.
Or we’ve placed a set of animals through some protocol comparing three or more groups of treatments. The animals are run through some behavioral assay, such as a latency test. Afterwards, specimens are collected for bloodwork, and also for quantitative histochemical and gene expression analysis. The latency test, the various measures from the blood, and the markers and genes assayed post -mortum are each a unique dependent variable. There might be a dozen or more of these outcome variables measured in each replicate!
38.3 MANOVA is not many ANOVAs
In one respect, you can think of experiments involving multiple dependent variables as running a bunch of ANOVA experiments.
In fact, that’s the mistake most researchers make. They treat each dependent variable as if it came from a distinct experiment involving separate replicates, when in fact they all come from just one experiment. They subsequently run a series of ANOVAs in parallel, one each for all of the dependent variables.
The most common mistake is holding each ANOVA at the standard 5% error threshold, following each with multiple post hoc comparisons. The family-wise error rate (FWER) for this single experiment explodes. A cacophony of undeserved asterisks are splattered all over the chart. It doesn’t help that the data are plotted in a way to make the dependent variables look like they are predictor variables. Maybe they have been treated as predictors?! What a mess!
Minimally, MANOVA provides a handy way to manage the FWER when probing several different dependent variables simultaneously. As an omnibus test MANOVA provides fairly strong type1 error protection in cases where many dependent variables are assessed simultaneously.
But it is important to recall what was mentioned above. MANOVA is not really testing for the signal-to-noise for the effects of the independent variables on each of the dependent variables. MANOVA tests whether there are treatment effects on a combination of the outcome variables. The advantage is that this is performed in a way that maximizes the treatment group differences.
38.3.1 Why MANOVA?
For experiments that measure multiple dependent variables the main alternative to MANOVA is to run separate ANOVAs, each with a multiple comparison correction to limit the FWER. For example, if there are five dependent variables, use the Bonferroni correction to run the ANOVA for each under at type1 error threshold of 1%, meaning we only reject the null when the F p-value < 0.01.
There are good reasons to run MANOVA instead.
The first is as an omnibus test offering protection against inflated type1 error, as when running a series of ANOVA’s for each dependent variable. Particularly when the latter are uncorrected for multiple comparison.
The second is testing more dependent variables increases the chances of identifying treatment effects. For example, a given stimulus condition may not affect the expression of three genes, but it does affect that for a fourth. Had the fourth gene not been added to the analysis we might have concluded that stimulus condition is ineffective.
Third, because it operates on a composite variable, sometimes MANOVA detects effects that ANOVA misses. Imagine studying the effect of diet on growth. We could measure just the weight (or length) of a critter and be done with it. However, with only a little extra effort measuring both weight and height, we have measures in two dimensions instead of just one. In some cases the effects of diet on weight alone or on height alone may be weak, but stronger when assessed in combination.
Select variable to measure judiciously. MANOVA works best when dependent variables are negatively correlated or modestly correlated, and does not work well when they are uncorrelated or strongly positively correlated.
38.4 Assumptions
Some of these should look very familiar by now:
All replicates are independent of each other (of course, repeated/related measurements of one variable my be collected from a single replicate, but this must be accounted for). Data collection must involve some random process.
Here are some proscriptions unique to MANOVA but with univariate congeners:
The dependent variables are linearly related. The distribution of residuals are multivariate normal. *The residual variance-covariance matrices of all groups are approximately equal or homogeneous.
As a general rule MANOVA is thought to be more sensitive to violations of these latter three assumptions than is ANOVA.
Several adjustments can help prevent this:
Strive for balanced data (have equal or near-equal sample sizes in each group). Transform variables with outliers or that have nonlinearity to lessen their impact (or establish other a priori rules to deal with them if they arise). *Avoid multicolinearity.
38.4.1 Multicolinearity
Multicolinearity occurs in a couple of ways. When one dependent variable is derived from other variables in the set (or if they represent two ways to measure the same response) they may have a very high \(R^2\) value. More rarely, dependent variables may be highly correlated naturally. In these cases one of the offending variables should be removed. For example, multicolinearity is likely to happen if including a body mass index (BMI) as a dependent variable along with variables for height and weight, since the BMI is calculated from the others.
Multicolinearity collapse will also occur when the number of replicates are fewer than the number of dependent variables being assessed.
Don’t skimp on replicates and avoid the urge to be too ambitious in terms of the numbers of dependent variables collected and the number of treatment groups. As a general rule, if the dataset rows are replicates and the columns are dependent variables, we want the dataset to be longer than it is wide.
38.5 Calculating variation
There are many parallels between ANOVA and MANOVA.
Both are based upon the general linear model \[Y=\beta X+\epsilon\]
However, for MANOVA, \(Y\) is an \(n \times m\) matrix of dependent variables, \(X\) is an \(n \times p\) matrix of predictor variables, \(\beta\) is an \(p \times m\) matrix of regression coefficients and \(\epsilon\) is a \(n \times m\) matrix of residuals.
Least squares regression for calculating the \(SS\) for each dependent variable is performed in MANOVA as for ANOVA. In addition, variation is also tabulated from cross products between all possible combinations of dependent variables. As for ANOVA, the conservation of variation law applies for cross products just as it does for \(SS\) ,
\[CP_{total}=CP_{model}\ +CP_{residual}\]
For illustration, consider the simplest MANOVA experiment with only two dependent variables ( \(dv1, dv2\) ). The cross product for total variation is:
\[CP_{total}= \sum_{i=1}^n(y_{i,dv1}-\bar y_{grand, dv1})(y_{i,dv2}-\bar y_{grand, dv2}) \]
The cross product for variation associated with the model (group means) is:
\[CP_{model}= \sum_{j=1}^kn\times(\bar y_{group_j,dv1}-\bar y_{grand, dv1})(\bar y_{group_j,dv2}-\bar y_{grand, dv2}) \]
And the cross product, \(CP\) , for residual variation is:
\[CP_{residual}= \sum_{i=1}^n(y_{i,dv1}-\bar y_{group_j, dv1})(y_{i,dv2}-\bar y_{group_j, dv2}) \]
For partitioning of the overall variation, these cross products, along with their related \(SS\) are assembled into \(T\) , \(H\) and \(E\) matrices. These letters reflect a historical MANOVA jargon representing total, hypothesis and error variation. These correspond to the total, model and residual terms we’ve adopted in this course for discussing ANOVA.
\[T = \begin{pmatrix} SS_{total,dv1} & CP_{total} \\ CP_{total} & SS_{total,dv2} \end{pmatrix}\]
\[H = \begin{pmatrix} SS_{model,dv1} & CP_{model} \\ CP_{model} & SS_{model,dv2} \end{pmatrix}\]
\[E = \begin{pmatrix} SS_{residual,dv1} & CP_{residual} \\ CP_{residual} & SS_{residual,dv2} \end{pmatrix}\]
The most important take away is that MANOVA not only accounts for the variation within each dependent variable via \(SS\) in the usual way, the \(CP\) computes the variation associated with all possible relationships between each of the dependent variables.
Note: When experiments have even more dependent variables, there is more variation to track. For example an experiment with three independent variables has a T matrix of 9 cells with 3 unique cross-product values, each duplicated:
\[T = \begin{pmatrix} SS_{total,dv1} & CP_{total,dv1\times dv2} & CP_{total,dv1\times dv3} \\ CP_{total, dv2\times dv1} & SS_{total,dv2} & CP_{total,dv2\times dv3}\\ CP_{total,dv3\times d1} & CP_{total,dv3\times dv2} & SS_{total, dv3} \end{pmatrix}\]
The conservation of variation rule applies to these matrices just as in univariate ANOVA. The total variation is equal to the sum of the model and the residual variation. The same applies in MANOVA, which is expressed by the simple matrix algebraic relationship: \(T=H+E\) .
38.5.1 Eigenvectors and eigenvalues
To deal with this mathematically all of the computations necessary to sort out whether anything is meaningful involve matrix algebra, where the focus is upon “decomposing” these matrices into their eigenvectors and eigenvalues.
What is an eigenvector? The best way I’ve been able to answer this is an eigenvector represents a base dimension in multivariate data, and the eigenvalues serve as the magnitude of that dimension.
MANOVA datasets have multiple response variables, \(p\) , and also multiple predictor groups, \(k\) . How many dimensions can these datasets possess? They will have either \(p\) or \(k-1\) dimensions, whichever is smaller.
The mathematics of these are beyond where I want to go on this topic. If interested in learning more the Kahn Academy has a nice primer . Here is a good place to start for an introduction to R applications . Here’s a graphical approach that explains this further .
It is not necessary to fully understand these fundamentals of matrix algebra in order to operate MANOVA for experimental data. However, it is worth understanding that the MANOVA test statistics operate on something that represents a dimension of the original data set.
38.5.2 MANOVA test statistics
Recall in ANOVA the F statistic is derived from the ratio of the model variance with \(df1\) degrees of freedom to residual variance with \(df2\) degrees of freedom. In MANOVA these variances are essentially replaced by matrix determinants.
The congeners to ANOVA’s model and residual variances in MANOVA are the hypothesis \(H\) and error \(E\) matrices, which have \(h\) and \(e\) degrees of freedom, respectively. There are \(p\) dependent variables. Let the eigenvalues for the matrices \(HE^{-1}\) , \(H(H+E)^{-1}\) , and \(E(H+E)^{-1}\) be \(\phi\) , \(\theta\) , and \(\lambda\) , respectively.
From these let’s catch a glimpse of the four test statistic options available to the researcher when using MANOVA. When we read a MANOVA table in R the test stat column will have values calculated from the parameters below.
38.5.2.1 Pillai
\[V^{(s)}=\sum_{j=1}^s\theta_j \] where \(s=min(p,h)\) $V^{(s)} is then used in the calculation of an adjusted F statistic, from which p-values are derived. Calculation not shown^.
38.5.2.2 Wilks
\[\Lambda = \prod_{j=1}^p(1-\theta_j) \] \(\Lambda\) is then used to calculate an adjusted F statistic, from which p-values are derived. Calculation not shown.
38.5.2.3 Hotelling-Lawley
\[T_g^s = e\sum_{j=1}^s\theta_j \] where \(g=\frac{ph-2}{2}\)
\(T_g^s\) is then used to calculate an adjusted F statistic, from which p-values are derived. Calculation not shown.
38.5.2.4 Roy
\[F_{(2v_1+2, 2v_2+2)}=\frac{2v_1+2}{2v_2+2}\phi_{max} \] where \(v1=(|p-h|-1)/2\) and \(v2=(|e-p|-1)/2\)
Unlike the other MANOVA test statistics, Roy’s greatest root ( \(\phi_max\) ) is used in a fairly direct calculation of an adjusted F statistic, so that is shown here. Note how the degrees of freedom are calculated.
One purpose of showing these test statistics is to illustrate that each are calculated differently. Why? The statisticians who created these worked from different assumptions and objectives, believing their statistic would perform well under certain conditions.
A second reason to show these is so the researcher avoids freeze when looking at MANOVA output: “OMG! What the heck??!”
Yes, the numbers in the MANOVA table can be intimidating at first, even if when we have a pretty good idea of what we are up to. There are three columns for degrees of freedom and two for test statistics. Then there is the p-value. And then there is a MANOVA table for each independent variable. And if we don’t argue a specific test, we might get all four!! Yikes.
38.5.3 Which MANOVA test statistic is best?
That’s actually very difficult to answer.
In practice, the researcher should go into a MANOVA analysis with one test in mind, declared in a planning note, ideally based upon some simulation runs. This is no different than running a Monte Carlo before a t-test experiment, or an ANOVA experiment. Knowing in advance how to conduct the statistical analysis is always the most unbiased approach.
Otherwise, the temptation will be to produce output with all four tests and choose the one that yields the lowest p-value. In most instances the four tests should lead to the same conclusion, though they will not always generate the same p-values.
The most commonly used test seems to be Wilk’s lambda. The Pillai test is held to be more robust against violations of testing conditions assumptions listed above and is a reasonable choice.
38.6 Drug clearance example
Mimche and colleagues developed a mouse model to test how drug metabolism is influenced by a malaria-like infection (Plasmodium chaubadi chaubadi AS, or PccAS).
On the day of peak parisitaemia an experiment was performed to derive values for clearance (in units of volume/time) of four drugs. Clearance values are derived from a regression procedure on data for repeated measurements of drug levels in plasma at various time points following an injection. Any factor causing lower clearance indicates drug metabolism is reduced.
Thus, the clearance values for each drug are the dependent variables in the study. All four drugs were assessed simultaneously within each replicate. The independent variable is treatment, which is at two levels, naive or infection with PccAS, a murine plasmodium parasite. Ten mice were randomly assigned to either of these two treatments.
38.6.1 Rationale for MANOVA
The overarching scientific hypothesis is that parasite infection alters drug metabolism.
The drug panel tested here surveys a range of drug metabolizing enzymes. Limiting the clearance study to only a single drug would preclude an opportunity to gain insight into the broader group of drug metabolizing systems that might be affected by malaria.
Thus, there is good scientific reason to test multiple dependent variables. Together, they answer one question: Is drug metabolism influenced by the parasite? Clearance values are also collected in one experiment in which all four drugs are injected as a cocktail and measured simultaneously. This cannot be treated as four separate experiments statistically.
The main reason to use MANOVA in this case is as an omnibus test to protect type1 error while considering all of the information for the experiment simultaneously.
38.6.2 Data structure
Read in the data. Note that each dependent variable is it’s own column, just as for the predictor variable. An ID variable is good data hygiene.
38.6.3 MANOVA procedure
The Manova function in the car package can take several types of models as an argument. In this case, we have a two group treatment variable so a linear model is defined using the base R lm .
Recall the linear model, \[Y=\beta_o+\beta_1X+\epsilon\] Here we have one model for each of the four dependent variables.
In this experiment we have four \(Y\) variables, each corresponding to one of the drugs. The same \(X\) variable (at two levels) applies to all four dependent variables.
\(\beta_0\) is the y-intercept, and \(\beta_1\) is the coefficient. Each dependent variable will have an intercept and a coefficient. \(\epsilon\) is the residual error, accounting for the variation in the data unexplained by the model parameters for that dependent variable.
By including each of the dependent variable names as arguments within a cbind function we effectively instruct lm to treat these columns as a matrix and run a linear model on each.
Here is the omnibus test. The Pillai test statistic is chosen because it is more robust than the others to violations of the uniform variance assumptions:
The approximated F statistic of 11.943 is extreme on a null distribution of 4 and 5 degrees of freedom with a p-value of 0.009017. Reject the null hypothesis that the variance associated with the combination of linear models is less than or equal to the combined residual error variance.
Since this is a linear model for independent group means this result indicates that there are difference between group means.
Additional information about the Manova test can be obtained using the summary function. Note the matrices for the error and hypothesis, which are as described above.
Also not the output for the four different test statistics. In this simple case of one independent variable with two groups, they all produce an identical approximate F and the p-values that flows from it. The test values do differ, however, although the Hotelling-Lawley and the Roy generate the same values. More complex experimental designs tend to shatter this uniform agreement between the tests.
38.6.3.1 Now what?
Here are the data visualized. The red lines connect group means. This is presented as a way to illustrate the linear model output.

Figure 38.1: Drug clearance in a mouse model for malaria.
Print the linear model results to view the effect sizes as regression coefficients:
Considering the graph above it should be clear what the intercept values represent. They are the means for the naive treatment groups. The ‘treatmentpccas’ values are the differences between the naive and pccas group means. Their values are equivalent to the slopes of the red lines in the graph. In other words, the ‘treatmentpccas’ values are the means of the pccas groups subtracted from the means of the naive groups.
Intercept and treatmentpccas correspond respectively to the general linear model parameters \(\beta_0\) and \(\beta_1\) .
Another way to think about this is the intercept ( \(\beta_0\) ) is an estimate for the value of the dependent variable when the independent variable is without any effect, or \(X=0\) . In this example, if pccas has no influence on metabolism, then drug clearance is simply \(Y= \beta_0\)
In regression the intercept can cause confusion. In part, this happens because R operates alphanumerically by default. It will always subtract the second group from the first. Scientifically, we want the pccas means to be subtracted from naive….because our hypothesis is that malaria will lower clearance. Fortunately, n comes before p in the alphabet, so the group means for p will be subtracted from group means for n and this happens automagically. For simplicity, it is always a good idea to name your variables with this default alphanumeric behavior in mind.
38.6.3.2 MANOVA post hoc
In this the data passes and omnibus MANOVA. It tells us that somewhere among the four dependent variables there are differences between the naive and pccas group means. The question is which ones?
As a follow on procedure we want to know which of the downward slopes are truly negative, and which are no different than zero.
We answer that in the summary of the linear model. There is a lot of information here, but two things are most important. First, the estimate values for the treatmentpccas term. These are differences in group means between naive and pccas. Second, statistics and p-values associated with the ‘treatmentpccas’ effect. These are a one-sample t-test.
These each ask, “Is the Estimate value, given its standard error, equal to zero?” For example, the estimate for caffeine is -0.07269, which is the slope of the red line above. The t-statistic value is -2.344 and it has a p-value just under 0.05.
We’re usually not interested in the information on the intercept term or the statistical test for it. It is the group mean for the control condition, in this case, demonstrating the background level of clearance. Whether that differs from zero not important to know.
Therefore to make the p-value adjustment we should only be interested in the estimates for the ‘treatmentpccas’ terms. We shouldn’t waste precious alpha on the intercept values.
Here’s how we do that:
Given a family-wise type1 error threshold of 5%, we can conclude that PccAS infection changes tolbutamide and buproprion clearance relative to naive animals. There is no statistical difference for caffeine and midazolam clearance between PccAS-infected and naive animals.
It should be noted that this is a very conservative adjustment. In fact, were the Holm adjustment used instead all four drugs would have shown statistical differences.
38.6.3.3 Write up
The drug clearance experiment evaluates the effect of PccAS infection on the metabolism of caffeine, tolbutamide, buproprion and midazolam simultaneously in two treatment groups, naive and PccAS-infected, with five independent replicates within each group. Clearance data were analyzed by a multiple linear model using MANOVA as an omnibus test (Pillai test statistic = 0.905 with 1 df, F(4,5)=11.943, p=0.009). Posthoc analysis usig t-tests indicates PccAS the reductions in clearance relative to naive for tolbutamide (-0.006 clearance units) and buproprion (-0.654 clearance units) are statistically different than zero (Bonferroni adjusted p-values are 0.0199 and 0.0009, respectively).
38.7 Planning MANOVA experiments
Collecting several types of measurements from every replicate in one experiment is a lot of work. In these cases, front end statistical planning can really pay off.
We need to put some thought into choosing the dependent variables.
MANOVA doesn’t work well when too many dependent variables in the dataset are too highly correlated and all are pointing in the same general direction. For example, when several different mRNAs increase in the same way in response to a treatment. They will be statistically redundant, which can cause computational difficulties and the regression fails to converge to a solution. The only recovery from that is to add the variables back to a model one at a time until the offending variable is found. Which invariably causes the creepy bias feeling.
Besides, it seems wasteful to measure the same thing many different ways.
Therefore, omit some redundant variables. Be sure to offset positively correlated variables with negatively correlated variables in the dataset. Similarly, MANOVA uncorrelated dependent variables should be avoided.
Use pilot studies, other information, or intuition to understand relationships between the variables. How are they correlated? Once we have that we can calculate covariances?
38.7.1 MANOVA Monte Carlo Power Analysis
The Monte Carlo procedure is the same as for any other test: 1)Simulate a set of expected data. 2)Run an MANOVA analysis, defining and counting “hits.” 3)Repeat many times to get a long run performance average. 4)Change conditions (sample size, add/remove variables, remodel, etc) 5)Iterate through step 1 again.
38.7.1.1 Design an MVME
Let’s simulate a minimally viable MANOVA experiment (MVME) involving three dependent variables. For each there are a negative and positive control and a test group, for a total of 3 treatment groups.
For all three dependent variables we have decent pilot data for the negative and positive controls. We have a general idea of what we would consider minimally meaningful scientific responses for the test group.
One of our dependent variables represents a molecular measurement (ie, an mRNA), the second DV represents a biochemical measurement (ie, an enzyme activity), and the third DV represents a measurement at the organism level (ie, a behavior). We’ll make the organism measurement decrease with treatment so that it is negatively correlated with the other two.
We must assume each of these dependent variables in normally distributed, \(N(\mu, \sigma^2)\) . We have a decent idea of the values of these parameters. We have a decent idea of how correlated they may be.
All three of the measurements are taken from each replicate. Replicates are randomized to receiving one and only one of the three treatment groups.
The model is essentially one-way completely randomized MANOVA; in other words, one factorial independent variable at three levels, with three dependent variables.
38.7.1.2 Simulate multivariate normal data
The rmvtnorm function in the mvtnorm package provides a nice way to simulate several vectors of correlated data simultaneously, the kind of data you’d expect to generate and then analyze with MANOVA.
But it takes a willingness to wrestle with effect size predictions, correlations, variances and covariances, and matrices to take full advantage.
rmvtnorm takes as arguments the expected means of each variable, and sigma, which is a covariance matrix.
First, estimate some expected means and then their standard deviations. Then simply square the latter to calculate variances.
To predict standard deviations, it is easiest to think in terms of coefficient of variation: What is the noise to signal for the measurement? What is the typical ratio of standard deviation to mean that you see for that variable? 10%, 20%, more, less?
For this example, we’re assuming homoscedasticity, which means that the variance is about the same no matter the treatment level. But when we know there will be heterscedasticity, we should code it in here.
| treat | param | molec | bioch | organ |
|---|---|---|---|---|
| neg | mean | 270 | 900 | 0 |
| neg | sd | 60 | 100 | 5 |
| neg | var | 3600 | 10000 | 25 |
| pos | mean | 400 | 300 | -20 |
| pos | sd | 60 | 100 | 5 |
| pos | var | 3600 | 10000 | 25 |
| test | mean | 350 | 450 | -10 |
| test | sd | 60 | 100 | 5 |
| test | var | 3600 | 10000 | 25 |
38.7.1.2.1 Building a covariance matrix
For the next step we estimate the correlation coefficients between the dependent variables. We predict the biochem measurements and the organ will be reduced by the positive control and test treatments. That means they will be negatively correlated with the molec variables, where the positive and test are predicted to increase the response.
Where do these correlation coefficients come from? They are estimates based upon pilot data. But they can be from some other source. Or they can be based upon scientific intuition. Estimating these coefficients is no different than estimating means, standard deviations and effect sizes. We use imagination and scientific judgment to make these predictions.
We pop them into a matrix here. We’ll need this in a matrix form to create our covariance matrix.
Next we can build out a variance product matrix, using the variances estimated in the table above. The value in each cell in this matrix is the square root of the product of the corresponding variance estimates ( \(\sqrt {var(Y_1)var(Y_2)}\) . We do this for every combination of variances, which should yield a symmetrical matrix.
Here’s why we’ve done this. The relationship between any two dependent variables, \(Y_1\) and \(Y_2\) is
\[cor(Y_1, Y_2) = \frac{cov(Y_1, Y_2)}{\sqrt {var(Y_1)var(Y_2)}}]\]
Therefore, the covariance matrix we want for the sigma argument in the rmvnorm function is calculated by multiplying the variance product matrix by the correlation matrix.
Since we assume homescedasticity we can use sigmas for each of the three treatment groups. Now it is just a matter of simulating the dataset with that one sigma and the means for each of the variables and groups.
Parenthetically, if we are expecting heteroscedasticity, we would need to calculate a different sigma for each of the groups.
Pop it into a data frame and summarise by groups to see how well the simulation meets our plans. Keep in mind this is a small random sample. Increase the sample size, \(n\) , to get a more accurate picture.
Now we run a the “sample” through a manova. We’re switching to base R’s manova here because it plays nicer than Manova with Monte Carlo
Assuming this Manova test gives a positive response, we follow up with look post hoc at the key comparison, because we’d want to power up an experiment to ensure this one is detected.
Our scientific strategy is to assure the organ effect of the test group. Because one has nothig without the animal model, right?
So out of all the posthoc comparisons we could make, we’ll focus in on that.
The comparison in the 9th row is between the test and the negative control for the organ variable. The estimate means its value is -11.46 units less than the negative control. The unadjusted p-value for that difference is 0.0041. Assuming we’d also compare the test to negative controls for the other two variables, were’s how we can collect that p-value while adjusting it for multiple comparisons simultaneously.
The code below comes from finding a workable way to create test output so the parameter of interest is easy to grab. Unfortunately, output from the Manova function is more difficult to handle.
38.7.2 An MANOVA Monte Carlo Power function
The purpose of this function is to determine the sample size of suitable power for an MANOVA experiment.
This function pulls all of the above together into a single script. The input of this script is a putative sample size. The output is the power of the MANOVA, and the power of the most important posthoc comparison: that between the test group and negative control for the organ variable.
Here’s how to run manpwr . It’s a check to see the power for a sample size of 5 replicates per group.
The output is interesting. Although the MANOVA test is overpowered, the critical finding of interest is underpowered at this sample size. Repeat the function at higher values of n until the posthoc power is sufficient.
It is crucial to understand that powering up for the posthoc results can be so important.
38.8 Summary
MANOVA is an option for statistical testing of multivariate experiments. The dependent variables are random normal The test is more senstive than other parametrics to violations of normality and homogeneity of variance. MANOVA tests whether independent variables affect an abstract combination of dependent variables. For most, use MANOVA as an omnibus test followed by post hoc comparisons of interest to control FWER. Care should be taken in selecting the dependent variables of interest.

A/B Testing Vs. Multivariate Testing: Which One Is Better
- March 5, 2024
- AB Vs. Multivariate Testing
- Analyzing AB Tests
- AB Testing Tools
- AB Testing Best Practices
- AB Testing Process

Khalid Saleh
Khalid Saleh is CEO and co-founder of Invesp. He is the co-author of Amazon.com bestselling book: "Conversion Optimization: The Art and Science of...

Join 25,000+ Marketing Professionals!
Subscribe to Invesp's blog feed for future articles delivered to your feed reader or receive weekly updates by email.
A/B testing vs. multivariate testing? This question plagues every CRO professional every once in a while.
When optimizing your digital assets, knowing whether to use A/B or multivariate testing is critical.
Are you looking to quickly determine the superior version of a webpage for low-traffic sites?A/B testing is your go-to.
Or do you aim to dissect complex interactions between various elements on a high-traffic page? Then, A/B and multivariate testing will provide your in-depth analysis.
This guide breaks down each method and offers strategic insights into deploying them for maximum conversion optimization.
TL; DR? Here are some quick takeaways:
- A/B vs. Multivariate: A Quick Comparison: A/B testing is ideal for testing two versions of a single variable and requires less traffic. Conversely, multivariate testing involves testing multiple variables and their interactions but needs a higher traffic volume to provide significant results.
- Formulating a SMART Hypothesis: Both methods require a clear, evidence-based hypothesis following the SMART framework to predict the outcome and define the changes, expected impact, and metrics for measurement.
- Analyzing Test Results for Actionable Insights: Analyzing results involves tools like heat maps and session recordings. A/B testing emphasizes statistical significance, while multivariate testing focuses on element interactions.
Decoding A/B and Multivariate Testing: The Essentials
A/B Testing : also known as split testing, compares two versions of a digital element to determine which performs better with the target audience.

It effectively optimizes various marketing efforts, including emails, newsletters, ads, and website elements. A/B testing is particularly useful when you need quick feedback on two distinct designs or for websites with lower traffic.
Key aspects of A/B testing:
- Controlled Comparison: Craft two different versions and evaluate them side by side while keeping all other variables constant.
- Sample Size: Utilizing an adequate sample size to ensure reliable and accurate findings.
- Qualitative Evaluation: Use tools like heat maps and session recordings to gain insights into user interactions with different variations.
Multivariate Testing:
Multivariate testing takes it up a notch by evaluating multiple page elements simultaneously to uncover the most effective combination that maximizes conversion rates.

By using multivariate testing, you can gain valuable insights into how different elements or variables impact user experience and optimize your website or product accordingly.
Key aspects of multivariate testing:
- Multiple Element Testing: Running tests to evaluate different combinations of elements.
- Interaction Analysis: Understanding how variables interact with each other.
- Comprehensive View: Providing insights into visitor behavior and preference patterns.
- High Traffic Requirement: Demanding substantial web traffic due to increased variations.
- Potential Bias: Focusing excessively on design-related problems and underestimating UI/UX elements’ impact.
Unlike A/B testing, which compares two variations, MVT changes more than one variable to test all resulting combinations simultaneously. It provides a comprehensive view of visitor behavior and preference patterns, making it ideal for testing different combinations of elements or variables.
A/B Testing vs. Multivariate Testing: Choosing the Right Method
Deciding between multivariate and A/B testing depends on the complexity of the tested elements and the ease of implementation.
A/B testing is more straightforward and suitable for quick comparisons, while multivariate testing offers more comprehensive insights but requires more traffic and careful consideration of potential biases.
Designing Your Experiment: A/B vs. Multivariate
Choosing between A/B and multivariate testing depends on traffic, complexity, and goals.
A/B testing is ideal for limited traffic due to its simplicity and clear outcomes. Multivariate testing offers detailed insights but requires more effort and time.
However, before you set up either of the testing types, you’ll have to form a hypothesis. In the case of multivariate testing, you’ll also need to identify a number of variables you intend to test.
Crafting a Hypothesis for Effective Testing
Prior to commencing your A/B or multivariate testing, it’s imperative to construct a hypothesis. This conjecture about the potential influence of alterations on user behavior is crucial for executing substantive tests.
An articulate hypothesis will include:
- The specific modification under examination
- The anticipated effect of this modification
- The measurement that will be employed to evaluate said effect
- It must be evidence-based and provide justification.
A compelling hypothesis also embraces the SMART criteria: Specificity, Measurability, Actionability, Relevance, and Testability.
It integrates quantitative data and qualitative insights to guarantee that the supposition is grounded in reality, predicated upon hard facts, and pertinent to the variables being examined.
A/B testing vs. Multivariate testing hypothesis example:
For example, if you’re running an A/B test, your hypothesis could be:
Changing the CTA button of the existing landing page from blue to orange will increase the click-through rate by 10% within one month, based on previous test results and user feedback favoring brighter colors.
If you’re running a multivariate test, your hypothesis could be:
Testing different combinations of headline, hero image, and CTA button style on the homepage will result in a winning combination that increases the conversion rate by 15% within two weeks, supported by prior test results and user preferences.
Identifying Variables for Your Test
Selecting the correct multiple variables to assess in a multivariate experiment is crucial. Each variable should have solid backing based on business objectives and expected influence on outcomes. When testing involving multiple variables, it’s essential to rigorously evaluate their possible effect and likelihood of affecting targeted results.
Variation ideas for inclusion in multivariate testing ought to stem from an analysis grounded in data, which bolsters their potential ability to positively affect conversion rates. Adopting this strategy ensures that the selected variables are significant and poised to yield insightful findings.
Setting Up A/B Tests
To implement an A/B testing protocol, one must:
- Formulate a Hypothesis: Clearly define the problem you want to address and create a testable hypothesis (we’ve already done it in the above section).
- Identify the Variable: Select the single element you want to test. This could be a headline, button color, image placement, or any other modifiable aspect.
- Create Variations: Develop two versions of the element: the control (original) and the variant (modified). Ensure the change is significant enough to measure a potential impact.
- Random Assignment: Distribute your sample randomly into two segments to assess the performance of the control version relative to that of its counterpart. By doing so, you minimize any distortion in outcomes due to external influences.
- Determine Sample Size: Calculate the required sample size to achieve statistical significance. This depends on factors like desired confidence level, expected effect size, and existing conversion rate.
- Run the Test: Finally, implement the test and allow it to run for a predetermined duration or until the desired sample size is reached.
- Analyze Results: Collect and analyze data on relevant metrics (click-through rates, conversions, etc.). Use statistical analysis to determine if the observed differences are significant.
For a more detailed overview of how to run and set up A/B tests, check out our ultimate guide to A/B testing .
Setting up Multivariate Tests
To set up multivariate tests:
- Identify Multiple Variables: Select multiple elements you want to test simultaneously. This could involve testing variations of headlines, images, button colors, and other factors.
- Create Combinations: Generate all possible combinations of the selected elements. For example, if you’re testing two headlines and two button colors, you’ll have four combinations to test.
After this, all the steps remain the same as in the A/B test implementation, including randomly assigning audience to different combinations, determining sample size, and then finally running the test.
Pro Tip: Implement trigger settings to specify when variations appear to users, and use fractional factorial testing to manage traffic distribution among variations. During the multivariate test, systematically evaluate the impact of variations and consider eliminating low-performing ones after reaching the minimum sample size.
Analyzing Test Outcomes for Data-Driven Decisions
Finally, it’s time to analyze your results.
For a thorough assessment of user interactions post-A/B and multivariate testing sessions:
- Session recordings
- Form Analytics
They serve as indispensable tools by allowing you to observe real-time engagement metrics and dissect and comprehend findings after reaching statistical significance in an A/B test.
Making Sense of Multivariate Test Data
Interpreting multivariate test data calls for a distinct methodology. In multivariate testing, it is essential to evaluate the collective impact of various landing page elements on user behavior and conversion rates rather than examining aspects in isolation.
This testing method provides comprehensive insights into how different elements interact, allowing teams to discover effects between variables that could lead to further optimization.
When assessing multivariate test data, it’s necessary to:
- Identify the combinations of page elements that lead to the highest conversions
- Recognize elements that contribute least to the site’s conversions
- Discover the best possible combinations of tested page elements
- Increase conversions
- Identify the right combination of components that produces the highest conversion rate.
This process helps optimize your website’s performance and improve your conversion rate through conversion rate optimization.
Common Pitfalls in A/B and Multivariate Testing
Both testing methods offer valuable insights, but they also share some pitfalls to avoid.
Here are some common mistakes to avoid when setting up your A/B or multivariate tests:
- Insufficient Traffic: Not gathering enough traffic can lead to statistically insignificant results and unreliable conclusions.
- Ignoring External Factors: Overlooking seasonal trends, market shifts, or other external influences can skew results and lead to inaccurate interpretations.
- Technical Issues: Testing tools can sometimes impact website speed, affecting user behavior and compromising test results. Ensure your tools don’t interfere with the natural user experience.
A/B Testing vs. Multivariate Testing: Final Verdict
A/B and multivariate testing are potent methods that can transform how you approach digital marketing. By comparing different variations, whether it’s two in A/B testing or multiple in multivariate testing, you can gain valuable insights into what resonates with your audience.
The key is to embrace a culture of experimentation, value data over opinions, and constantly learn from your tests. This approach can optimize your strategy, boost your results, and ultimately drive your business forward.
Frequently Asked Questions
What is the main difference between a/b and multivariate testing.
Multivariate testing distinguishes itself from A/B testing by evaluating various elements at the same time in order to determine which combination yields the most favorable results, as opposed to A/B testing which only contrasts two variations.
Recognizing this distinction will assist you in determining the appropriate method for your particular experimentation requirements.
When should I use A/B testing over multivariate testing?
When swift outcomes are needed from evaluating two distinct designs, or when your website experiences low traffic volumes, A/B testing is the method to employ.
On the other hand, if your intention is to examine several variations at once, multivariate testing could be a better fit for such purposes.
What factors should I consider when setting up an A/B test?
When setting up an A/B test, it’s crucial to consider the sample size for reliable results and precision, control the testing environment, and use tools for qualitative insights like session recordings. These factors will ensure the accuracy and effectiveness of your test.
How can I effectively analyze multivariate test data?
To thoroughly assess data from multivariate tests, consider how different combinations of page elements together influence user behavior and ultimately conversion rates. Determine which specific sets of page elements result in the most significant increase in conversions, while also noting which individual components contribute the least to overall site conversions.
What common mistakes should I avoid when conducting A/B and multivariate tests?
Ensure that you allow sufficient traffic to accumulate in order to reach statistical significance. It’s important to factor in external variables such as seasonal variations or shifts in the marketplace, and also be mindful of technical elements like how testing instruments might affect website performance. Overlooking these considerations may result in deceptive test outcomes and false interpretations, which could squander both time and investment.
Bivariate Analysis: Associations, Hypotheses, and Causal Stories
- Open Access
- First Online: 04 October 2022
Cite this chapter
You have full access to this open access chapter

- Mark Tessler 2
Part of the book series: SpringerBriefs in Sociology ((BRIEFSSOCY))
3547 Accesses
Every day, we encounter various phenomena that make us question how, why, and with what implications they vary. In responding to these questions, we often begin by considering bivariate relationships, meaning the way that two variables relate to one another. Such relationships are the focus of this chapter.
You have full access to this open access chapter, Download chapter PDF
3.1 Description, Explanation, and Causal Stories
There are many reasons why we might be interested in the relationship between two variables. Suppose we observe that some of the respondents interviewed in Arab Barometer surveys and other surveys report that they have thought about emigrating, and we are interested in this variable. We may want to know how individuals’ consideration of emigration varies in relation to certain attributes or attitudes. In this case, our goal would be descriptive , sometimes described as the mapping of variance. Our goal may also or instead be explanation , such as when we want to know why individuals have thought about emigrating.
Description
Description means that we seek to increase our knowledge and refine our understanding of a single variable by looking at whether and how it varies in relation to one or more other variables. Descriptive information makes a valuable contribution when the structure and variance of an important phenomenon are not well known, or not well known in relation to other important variables.
Returning to the example about emigration, suppose you notice that among Jordanians interviewed in 2018, 39.5 percent of the 2400 men and women interviewed reported that they have considered the possibility of emigrating.
Our objective may be to discover what these might-be migrants look like and what they are thinking. We do this by mapping the variance of emigration across attributes and orientations that provide some of this descriptive information, with the descriptions themselves each expressed as bivariate relationships. These relationships are also sometimes labeled “associations” or “correlations” since they are not considered causal relationships and are not concerned with explanation.
Of the 39.5 percent of Jordanians who told interviewers that they have considered emigrating, 57.3 percent are men and 42.7 percent are women. With respect to age, 34 percent are age 29 or younger and 19.2 percent are age 50 or older. It might have been expected that a higher percentage of respondents age 29 or younger would have considered emigrating. In fact, however, 56 percent of the 575 men and women in this age category have considered emigrating. And with respect to destination, the Arab country most frequently mentioned by those who have considered emigration is the UAE, named by 17 percent, followed by Qatar at 10 percent and Saudi Arabia at 9.8 percent. Non-Arab destinations were mentioned more frequently, with Turkey named by 18.1 percent, Canada by 21.1 percent, and the U.S. by 24.2 percent.
With the variables sex, age, and prospective destination added to the original variable, which is consideration of emigration, there are clearly more than two variables under consideration. But the variables are described two at a time and so each relationship is bivariate.
These bivariate relationships, between having considered emigration on the one hand and sex, age, and prospective destination on the other, provide descriptive information that is likely to be useful to analysts, policymakers, and others concerned with emigration. They tell, or begin to tell, as noted above, what might-be migrants look like and what they are thinking. Still additional insight may be gained by adding descriptive bivariate relationships for Jordanians interviewed in a different year to those interviewed in 2018. In addition, of course, still more information and possibly a more refined understanding, may be gained by examining the attributes and orientations of prospective emigrants who are citizens of other Arab (and perhaps also non-Arab) countries.
With a focus on description, these bivariate relationships are not constructed to shed light on explanation, that is to contribute to causal stories that seek to account for variance and tell why some individuals but not others have considered the possibility of emigrating. In fact, however, as useful as bivariate relationships that provide descriptive information may be, researchers usually are interested as much if not more in bivariate relationships that express causal stories and purport to provide explanations.
Explanation and Causal Stories
There is a difference in the origins of bivariate relationships that seek to provide descriptive information and those that seek to provide explanatory information. The former can be thought to be responding to what questions: What characterizes potential emigrants? What do they look like? What are their thoughts about this or that subject? If the objective is description, a researcher collects and uses her data to investigate the relationship between two variables without a specific and firm prediction about the relationship between them. Rather, she simply wonders about the “what” questions listed above and believes that finding out the answers will be instructive. In this case, therefore, she selects the bivariate relationships to be considered based on what she thinks it will be useful to know, and not based on assessing the accuracy of a previously articulated causal story that specifies the strength and structure of the effect that one variable has on the other.
A researcher is often interested in causal stories and explanation, however, and this does usually begin with thinking about the relationship between two variables, one of which is the presumed cause and the other the presumed effect. The presumed cause is the independent variable, and the presumed effect is the dependent variable . Offering evidence that there is a strong relationship between two variables is not sufficient to demonstrate that the variables are likely to be causally related, but it is a necessary first step. In this respect it is a point of departure for the fuller, probably multivariate analysis, required to persuasively argue that a relationship is likely to be causal. In addition, as discussed in Chap. 4 , multivariate analysis often not only strengthens the case for inferring that a relationship is causal, but also provides a more elaborate and more instructive causal story. The foundation, however, on which a multivariate analysis aimed at causal inference is built, is a bivariate relationship composed of a presumed independent variable and a presumed dependent variable.
A hypothesis that posits a causal relationship between two variables is not the same as a causal story, although the two are of course closely connected. The former specifies a presumed cause, a presumed determinant of variance on the dependent variable. It probably also specifies the structure of the relationship, such as linear as opposed to non-linear, or positive (also called direct) as opposed to negative (also called inverse).
On the other hand, a causal story describes in more detail what the researcher believes is actually taking place in the relationship between the variables in her hypothesis; and accordingly, why she thinks this involves causality. A causal story provides a fuller account of operative processes, processes that the hypothesis references but does not spell out. These processes may, for example, involve a pathway or a mechanism that tells how it is that the independent variable causes and thus accounts for some of the variance on the dependent variable. Expressed yet another way, the causal story describes the researcher’s understandings, or best guesses, about the real world, understandings that have led her to believe, and then propose for testing, that there is a causal connection between her variables that deserves investigation. The hypothesis itself does not tell this story; it is rather a short formulation that references and calls attention to the existence, or hypothesized existence, of a causal story. Research reports present the causal story as well as the hypothesis, as the hypothesis is often of limited interpretability without the causal story.
A causal story is necessary for causal inference. It enables the researcher to formulate propositions that purport to explain rather than merely describe or predict. There may be a strong relationship between two variables, and if this is the case, it will be possible to predict with relative accuracy the value, or score, of one variable from knowledge of the value, or score, of the other variable. Prediction is not explanation, however. To explain, or attribute causality, there must be a causal story to which a hypothesized causal relationship is calling attention.
An instructive illustration is provided by a recent study of Palestinian participation in protest activities that express opposition to Israeli occupation. Footnote 1 There is plenty of variance on the dependent variable: There are many young Palestinians who take part in these activities, and there are many others who do not take part. Education is one of the independent variables that the researcher thought would be an important determinant of participation, and so she hypothesized that individuals with more education would be more likely to participate in protest activities than individuals with less education.
But why would the researcher think this? The answer is provided by the causal story. To the extent that this as yet untested story is plausible, or preferably, persuasive, at least in the eyes of the investigator, it gives the researcher a reason to believe that education is indeed a determinant of participation in protest activities in Palestine. By spelling out in some detail how and why the hypothesized independent variable, education in this case, very likely impacts a person’s decision about whether or not to protest, the causal story provides a rationale for the researcher’s hypothesis.
In the case of Palestinian participation in protest activities, another investigator offered an insightful causal story about the ways that education pushes toward greater participation, with emphasis on its role in communication and coordination. Footnote 2 Schooling, as the researcher theorizes and subsequently tests, integrates young Palestinians into a broader institutional environment that facilitates mass mobilizations and lowers informational and organizational barriers to collective action. More specifically, she proposes that those individuals who have had at least a middle school education, compared to those who have not finished middle school, have access to better and more reliable sources of information, which, among other things, enables would-be protesters to assess risks. More schooling also makes would-be protesters better able to forge inter-personal relationships and establish networks that share information about needs, opportunities, and risks, and that in this way facilitate engaging in protest activities in groups, rather than on an individual basis. This study offers some additional insights to be discussed later.
The variance motivating the investigation of a causal story may be thought of as the “variable of interest,” and it may be either an independent variable or a dependent variable. It is a variable of interest because the way that it varies poses a question, or puzzle, that a researcher seeks to investigate. It is the dependent variable in a bivariate relationship if the researcher seeks to know why this variable behaves, or varies, as it does, and in pursuit of this objective, she will seek to identify the determinants and drivers that account for this variance. The variable of interest is an independent variable in a particular research project if the researcher seeks to know what difference it makes—on what does its variance have an impact, of what other variable or variables is it a driver or determinant.
The variable in which a researcher is initially interested, that is to say the variable of interest, can also be both a dependent variable and an independent variable. Returning to the variable pertaining to consideration of emigration, but this time with country as the unit of analysis, the variance depicted in Table 3.1 provides an instructive example. The data are based on Arab Barometer surveys conducted in 2018–2019, and the table shows that there is substantial variation across twelve countries. Taking the countries together, the mean percentage of citizens that have thought about relocating to another country is 30.25 percent. But in fact, there is very substantial variation around this mean. Kuwait is an outlier, with only 8 percent having considered emigration. There are also countries in which only 21 percent or 22 percent of the adult population have thought about this, figures that may be high in absolute terms but are low relative to other Arab countries. At the other end of the spectrum are countries in which 45 percent or even 50 percent of the citizens report having considered leaving their country and relocating elsewhere.
The very substantial variance shown in Table 3.1 invites reflection on both the causes and the consequences of this country-level variable, aggregate thinking about emigration. As a dependent variable, the cross-country variance brings the question of why the proportion of citizens that have thought about emigrating is higher in some countries than in others; and the search for an answer begins with the specification of one or more bivariate relationships, each of which links this dependent variable to a possible cause or determinant. As an independent variable, the cross-country variance brings the question of what difference does it make—of what is it a determinant or driver and what are the consequences for a country if more of its citizens, rather than fewer, have thought about moving to another country.
3.2 Hypotheses and Formulating Hypotheses
Hypotheses emerge from the research questions to which a study is devoted. Accordingly, a researcher interested in explanation will have something specific in mind when she decides to hypothesize and then evaluate a bivariate relationship in order to determine whether, and if so how, her variable of interest is related to another variable. For example, if the researcher’s variable of interest is attitude toward gender equality and one of her research questions asks why some people support gender equality and others do not, she might formulate the hypothesis below to see if education provides part of the answer.
Hypothesis 1. Individuals who are better educated are more likely to support gender equality than are individuals who are less well-educated.
The usual case, and the preferred case, is for an investigator to be specific about the research questions she seeks to answer, and then to formulate hypotheses that propose for testing part of the answer to one or more of these questions. Sometimes, however, a researcher will proceed without formulating specific hypotheses based on her research questions. Sometimes she will simply look at whatever relationships between her variable of interest and a second variable her data permit her to identify and examine, and she will then follow up and incorporate into her study any findings that turn out to be significant and potentially instructive. This is sometimes described as allowing the data to “speak.” When this hit or miss strategy of trial and error is used in bivariate and multivariate analysis, findings that are significant and potentially instructive are sometimes described as “grounded theory.” Some researchers also describe the latter process as “inductive” and the former as “deductive.”
Although the inductive, atheoretical approach to data analysis might yield some worthwhile findings that would otherwise have been missed, it can sometimes prove misleading, as you may discover relationships between variables that happened by pure chance and are not instructive about the variable of interest or research question. Data analysis in research aimed at explanation should be, in most cases, preceded by the formulation of one or more hypotheses. In this context, when the focus is on bivariate relationships and the objective is explanation rather than description, each hypothesis will include a dependent variable and an independent variable and make explicit the way the researcher thinks the two are, or probably are, related. As discussed, the dependent variable is the presumed effect; its variance is what a hypothesis seeks to explain. The independent variable is the presumed cause; its impact on the variance of another variable is what the hypothesis seeks to determine.
Hypotheses are usually in the form of if-then, or cause-and-effect, propositions. They posit that if there is variance on the independent variable, the presumed cause, there will then be variance on the dependent variable, the presumed effect. This is because the former impacts the latter and causes it to vary.
An illustration of formulating hypotheses is provided by a study of voting behavior in seven Arab countries: Algeria, Bahrain, Jordan, Lebanon, Morocco, Palestine, and Yemen. Footnote 3 The variable of interest in this individual-level study is electoral turnout, and prominent among the research questions is why some citizens vote and others do not. The dependent variable in the hypotheses proposed in response to this question is whether a person did or did not vote in the country’s most recent parliamentary election. The study initially proposed a number of hypotheses, which include the two listed here and which would later be tested with data from Arab Barometer surveys in the seven countries in 2006–2007. We will return to this illustration later in this chapter.
Hypothesis 1: Individuals who have used clientelist networks in the past are more likely to turn out to vote than are individuals who have not used clientelist networks in the past.
Hypothesis 2: Individuals with a positive evaluation of the economy are more likely to vote than are individuals with a negative evaluation of the economy.
Another example pertaining to voting, which this time is hypothetical but might be instructively tested with Arab Barometer data, considers the relationship between perceived corruption and turning out to vote at the individual level of analysis.
The normal expectation in this case would be that perceptions of corruption influence the likelihood of voting. Even here, however, competing causal relationships are plausible. More perceived corruption might increase the likelihood of voting, presumably to register discontent with those in power. But greater perceived corruption might also actually reduce the likelihood of voting, presumably in this case because the would-be voter sees no chance that her vote will make a difference. But in this hypothetical case, even the direction of the causal connection might be ambiguous. If voting is complicated, cumbersome, and overly bureaucratic, it might be that the experience of voting plays a role in shaping perceptions of corruption. In cases like this, certain variables might be both independent and dependent variables, with causal influence pushing in both directions (often called “endogeneity”), and the researcher will need to carefully think through and be particularly clear about the causal story to which her hypothesis is designed to call attention.
The need to assess the accuracy of these hypotheses, or any others proposed to account for variance on a dependent variable, will guide and shape the researcher’s subsequent decisions about data collection and data analysis. Moreover, in most cases, the finding produced by data analysis is not a statement that the hypothesis is true or that the hypothesis is false. It is rather a statement that the hypothesis is probably true or it is probably false. And more specifically still, when testing a hypothesis with quantitative data, it is often a statement about the odds, or probability, that the researcher will be wrong if she concludes that the hypothesis is correct—if she concludes that the independent variable in the hypothesis is indeed a significant determinant of the variance on the dependent variable. The lower the probability of being wrong, of course, the more confident a researcher can be in concluding, and reporting, that her data and analysis confirm her hypothesis.
Exercise 3.1
Hypotheses emerge from the research questions to which a study is devoted. Thinking about one or more countries with which you are familiar: (a) Identify the independent and dependent variables in each of the example research questions below. (b) Formulate at least one hypothesis for each question. Make sure to include your expectations about the directionality of the relationship between the two variables; is it positive/direct or negative/inverse? (c) In two or three sentences, describe a plausible causal story to which each of your hypotheses might call attention.
Does religiosity affect people’s preference for democracy?
Does preference for democracy affect the likelihood that a person will vote? Footnote 4
Exercise 3.2
Since its establishment in 2006, the Arab Barometer has, as of spring 2022, conducted 68 social and political attitude surveys in the Middle East and North Africa. It has conducted one or more surveys in 16 different Arab countries, and it has recorded the attitudes, values, and preferences of more than 100,000 ordinary citizens.
The Arab Barometer website ( arabbarometer.org ) provides detailed information about the Barometer itself and about the scope, methodology, and conduct of its surveys. Data from the Barometer’s surveys can be downloaded in either SPSS, Stata, or csv format. The website also contains numerous reports, articles, and summaries of findings.
In addition, the Arab Barometer website contains an Online Data Analysis Tool that makes it possible, without downloading any data, to find the distribution of responses to any question asked in any country in any wave. The tool is found in the “Survey Data” menu. After selecting the country and wave of interest, click the “See Results” tab to select the question(s) for which you want to see the response distributions. Click the “Cross by” tab to see the distributions of respondents who differ on one of the available demographic attributes.
The charts below present, in percentages, the response distributions of Jordanians interviewed in 2018 to two questions about gender equality. Below the charts are questions that you are asked to answer. These questions pertain to formulating hypotheses and to the relationship between hypotheses and causal stories.
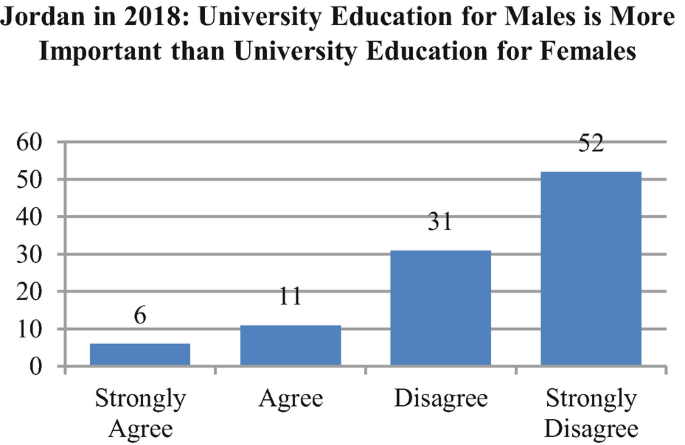
For each of the two distributions, do you think (hypothesize) that the attitudes of Jordanian women are:
About the same as those of Jordanian men
More favorable toward gender equality than those of Jordanian men
Less favorable toward gender equality than those of Jordanian men
For each of the two distributions, do you think (hypothesize) that the attitudes of younger Jordanians are:
About the same as those of older Jordanians
More favorable toward gender equality than those of older Jordanians
Less favorable toward gender equality than those of older Jordanians
Restate your answers to Questions 1 and 2 as hypotheses.
Give the reasons for your answers to Questions 1 and 2. In two or three sentences, make explicit the presumed causal story on which your hypotheses are based.
Using the Arab Barometer’s Online Analysis Tool, check to see whether your answers to Questions 1 and 2 are correct. For those instances in which an answer is incorrect, suggest in a sentence or two a causal story on which the correct relationship might be based.
In which other country surveyed by the Arab Barometer in 2018 do you think the distributions of responses to the questions about gender equality are very similar to the distributions in Jordan? What attributes of Jordan and the other country informed your selection of the other country?
In which other country surveyed by the Arab Barometer in 2018 do you think the distributions of responses to the questions about gender equality are very different from the distributions in Jordan? What attributes of Jordan and the other country informed your selection of the other country?
Using the Arab Barometer’s Online Analysis Tool, check to see whether your answers to Questions 6 and 7 are correct. For those instances in which an answer is incorrect, suggest in a sentence or two a causal story on which the correct relationship might be based.
We will shortly return to and expand the discussion of probabilities and of hypothesis testing more generally. First, however, some additional discussion of hypothesis formulation is in order. Three important topics will be briefly considered. The first concerns the origins of hypotheses; the second concerns the criteria by which the value of a particular hypothesis or set of hypotheses should be evaluated; and the third, requiring a bit more discussion, concerns the structure of the hypothesized relationship between an independent variable and a dependent variable, or between any two variables that are hypothesized to be related.
Origins of Hypotheses
Where do hypotheses come from? How should an investigator identify independent variables that may account for much, or at least some, of the variance on a dependent variable that she has observed and in which she is interested? Or, how should an investigator identify dependent variables whose variance has been determined, presumably only in part, by an independent variable whose impact she deems it important to assess.
Previous research is one place the investigator may look for ideas that will shape her hypotheses and the associated causal stories. This may include previous hypothesis-testing research, and this can be particularly instructive, but it may also include less systematic and structured observations, reports, and testimonies. The point, very simply, is that the investigator almost certainly is not the first person to think about, and offer information and insight about, the topic and questions in which the researcher herself is interested. Accordingly, attention to what is already known will very likely give the researcher some guidance and ideas as she strives for originality and significance in delineating the relationship between the variables in which she is interested.
Consulting previous research will also enable the researcher to determine what her study will add to what is already known—what it will contribute to the collective and cumulative work of researchers and others who seek to reduce uncertainty about a topic in which they share an interest. Perhaps the researcher’s study will fill an important gap in the scientific literature. Perhaps it will challenge and refine, or perhaps even place in doubt, distributions and explanations of variance that have thus far been accepted. Or perhaps her study will produce findings that shed light on the generalizability or scope conditions of previously accepted variable relationships. It need not do any of these things, but that will be for the researcher to decide, and her decision will be informed by knowledge of what is already known and reflection on whether and in what ways her study should seek to add to that body of knowledge.
Personal experience will also inform the researcher’s search for meaningful and informative hypotheses. It is almost certainly the case that a researcher’s interest in a topic in general, and in questions pertaining to this topic in particular, have been shaped by her own experience. The experience itself may involve many different kinds of connections or interactions, some more professional and work-related and some flowing simply and perhaps unintentionally from lived experience. The hypotheses about voting mentioned earlier, for example, might be informed by elections the researcher has witnessed and/or discussions with friends and colleagues about elections, their turnout, and their fairness. Or perhaps the researcher’s experience in her home country has planted questions about the generalizability of what she has witnessed at home.
All of this is to some extent obvious. But the take-away is that an investigator should not endeavor to set aside what she has learned about a topic in the name of objectivity, but rather, she should embrace whatever personal experience has taught her as she selects and refines the puzzles and propositions she will investigate. Should it happen that her experience leads her to incorrect or perhaps distorted understandings, this will be brought to light when her hypotheses are tested. It is in the testing that objectivity is paramount. In hypothesis formation, by contrast, subjectivity is permissible, and, in fact, it may often be unavoidable.
A final arena in which an investigator may look for ideas that will shape her hypotheses overlaps with personal experience and is also to some extent obvious. This is referenced by terms like creativity and originality and is perhaps best captured by the term “sociological imagination.” The take-away here is that hypotheses that deserve attention and, if confirmed, will provide important insights, may not all be somewhere out in the environment waiting to be found, either in the relevant scholarly literature or in recollections about relevant personal experience. They can and sometimes will be the product of imagination and wondering, of discernments that a researcher may come upon during moments of reflection and deliberation.
As in the case of personal experience, the point to be retained is that hypothesis formation may not only be a process of discovery, of finding the previous research that contains the right information. Hypothesis formation may also be a creative process, a process whereby new insights and proposed original understandings are the product of an investigator’s intellect and sociological imagination.
Crafting Valuable Hypotheses
What are the criteria by which the value of a hypothesis or set of hypotheses should be evaluated? What elements define a good hypothesis? Some of the answers to these questions that come immediately to mind pertain to hypothesis testing rather than hypothesis formation. A good hypothesis, it might be argued, is one that is subsequently confirmed. But whether or not a confirmed hypothesis makes a positive contribution depends on the nature of the hypothesis and goals of the research. It is possible that a researcher will learn as much, and possibly even more, from findings that lead to rejection of a hypothesis. In any event, findings, whatever they may be, are valuable only to the extent that the hypothesis being tested is itself worthy of study.
Two important considerations, albeit somewhat obvious ones, are that a hypothesis should be non-trivial and non-obvious. If a proposition is trivial, suggesting a variable relationship with little or no significance, discovering whether and how the variables it brings together are related will not make a meaningful contribution to knowledge about the determinants and/or impact of the variance at the heart of the researcher’s concern. Few will be interested in findings, however rigorously derived, about a trivial proposition. The same is true of an obvious hypothesis, obvious being an attribute that makes a proposition trivial. As stated, these considerations are themselves somewhat obvious, barely deserving mention. Nevertheless, an investigator should self-consciously reflect on these criteria when formulating hypotheses. She should be sure that she is proposing variable relationships that are neither trivial nor obvious.
A third criterion, also somewhat obvious but nonetheless essential, has to do with the significance and salience of the variables being considered. Will findings from research about these variables be important and valuable, and perhaps also useful? If the primary variable of interest is a dependent variable, meaning that the primary goal of the research is to account for variance, then the significance and salience of the dependent variable will determine the value of the research. Similarly, if the primary variable of interest is an independent variable, meaning that the primary goal of the research is to determine and assess impact, then the significance and salience of the independent variable will determine the value of the research.
These three criteria—non-trivial, non-obvious, and variable importance and salience—are not very different from one another. They collectively mean that the researcher must be able to specify why and how the testing of her hypothesis, or hypotheses, will make a contribution of value. Perhaps her propositions are original or innovative; perhaps knowing whether they are true or false makes a difference or will be of practical benefit; perhaps her findings add something specific and identifiable to the body of existing scholarly literature on the subject. While calling attention to these three connected and overlapping criteria might seem unnecessary since they are indeed somewhat obvious, it remains the case that the value of a hypothesis, regardless of whether or not it is eventually confirmed, is itself important to consider, and an investigator should, therefore, know and be able to articulate the reasons and ways that consideration of her hypothesis, or hypotheses, will indeed be of value.
Hypothesizing the Structure of a Relationship
Relevant in the process of hypothesis formation are, as discussed, questions about the origins of hypotheses and the criteria by which the value of any particular hypothesis or set of hypotheses will be evaluated. Relevant, too, is consideration of the structure of a hypothesized variable relationship and the causal story to which that relationship is believed to call attention.
The point of departure in considering the structure of a hypothesized variable relationship is an understanding that such a relationship may or may not be linear. In a direct, or positive, linear relationship, each increase in the independent variable brings a constant increase in the dependent variable. In an inverse, or negative, linear relationship, each increase in the independent variable brings a constant decrease in the dependent variable. But these are only two of the many ways that an independent variable and a dependent variable may be related, or hypothesized to be related. This is easily illustrated by hypotheses in which level of education or age is the independent variable, and this is relevant in hypothesis formation because the investigator must be alert to and consider the possibility that the variables in which she is interested are in fact related in a non-linear way.
Consider, for example, the relationship between age and support for gender equality, the latter measured by an index based on several questions about the rights and behavior of women that are asked in Arab Barometer surveys. A researcher might expect, and might therefore want to hypothesize, that an increase in age brings increased support for, or alternatively increased opposition to, gender equality. But these are not the only possibilities. Likely, perhaps, is the possibility of a curvilinear relationship, in which case increases in age bring increases in support for gender equality until a person reaches a certain age, maybe 40, 45, or 50, after which additional increases in age bring decreases in support for gender equality. Or the researcher might hypothesize that the curve is in the opposite direction, that support for gender equality initially decreases as a function of age until a particular age is reached, after which additional increases in age bring an increase in support.
Of course, there are also other possibilities. In the case of education and gender equality, for example, increased education may initially have no impact on attitudes toward gender equality. Individuals who have not finished primary school, those who have finished primary school, and those who have gone somewhat beyond primary school and completed a middle school program may all have roughly the same attitudes toward gender equality. Thus, increases in education, within a certain range of educational levels, are not expected to bring an increase or a decrease in support for gender equality. But the level of support for gender equality among high school graduates may be higher and among university graduates may be higher still. Accordingly, in this hypothetical illustration, an increase in education does bring increased support for gender equality but only beginning after middle school.
A middle school level of education is a “floor” in this example. Education does not begin to make a difference until this floor is reached, and thereafter it does make a difference, with increases in education beyond middle school bringing increases in support for gender equality. Another possibility might be for middle school to be a “ceiling.” This would mean that increases in education through middle school would bring increases in support for gender equality, but the trend would not continue beyond middle school. In other words, level of education makes a difference and appears to have explanatory power only until, and so not after, this ceiling is reached. This latter pattern was found in the study of education and Palestinian protest activity discussed earlier. Increases in education through middle school brought increases in the likelihood that an individual would participate in demonstrations and protests of Israeli occupation. However, additional education beyond middle school was not associated with greater likelihood of taking part in protest activities.
This discussion of variation in the structure of a hypothesized relationship between two variables is certainly not exhaustive, and the examples themselves are straightforward and not very complicated. The purpose of the discussion is, therefore, to emphasize that an investigator must be open to and think through the possibility and plausibility of different kinds of relationships between her two variables, that is to say, relationships with different structures. Bivariate relationships with several different kinds of structures are depicted visually by the scatter plots in Fig. 3.4 .
These possibilities with respect to structure do not determine the value of a proposed hypothesis. As discussed earlier, the value of a proposed relationship depends first and foremost on the importance and salience of the variable of interest. Accordingly, a researcher should not assume that the value of a hypothesis varies as a function of the degree to which it posits a complicated variable relationship. More complicated hypotheses are not necessarily better or more correct. But while she should not strive for or give preference to variable relationships that are more complicated simply because they are more complicated, she should, again, be alert to the possibility that a more complicated pattern does a better job of describing the causal connection between the two variables in the place and time in which she is interested.
This brings the discussion of formulating hypotheses back to our earlier account of causal stories. In research concerned with explanation and causality, a hypothesis for the most part is a simplified stand-in for a causal story. It represents the causal story, as it were. Expressing this differently, the hypothesis states the causal story’s “bottom line;” it posits that the independent variable is a determinant of variance on the dependent variable, and it identifies the structure of the presumed relationship between the independent variable and the dependent variable. But it does not describe the interaction between the two variables in a way that tells consumers of the study why the researcher believes that the relationship involves causality rather than an association with no causal implications. This is left to the causal story, which will offer a fuller account of the way the presumed cause impacts the presumed effect.
3.3 Describing and Visually Representing Bivariate Relationships
Once a researcher has collected or otherwise obtained data on the variables in a bivariate relationship she wishes to examine, her first step will be to describe the variance on each of the variables using the univariate statistics described in Chap. 2 . She will need to understand the distribution on each variable before she can understand how these variables vary in relation to one another. This is important whether she is interested in description or wishes to explore a bivariate causal story.
Once she has described each one of the variables, she can turn to the relationship between them. She can prepare and present a visual representation of this relationship, which is the subject of the present section. She can also use bivariate statistical tests to assess the strength and significance of the relationship, which is the subject of the next section of this chapter.
Contingency Tables
Contingency tables are used to display the relationship between two categorical variables. They are similar to the univariate frequency distributions described in Chap. 2 , the difference being that they juxtapose the two univariate distributions and display the interaction between them. Also called cross-tabulation tables, the cells of the table may present frequencies, row percentages, column percentages, and/or total percentages. Total frequencies and/or percentages are displayed in a total row and a total column, each one of which is the same as the univariate distribution of one of the variables taken alone.
Table 3.2 , based on Palestinian data from Wave V of the Arab Barometer, crosses gender and the average number of hours watching television each day. Frequencies are presented in the cells of the table. In the cell showing the number of Palestinian men who do not watch television at all, row percentage, column percentage, and total percentage are also presented. Note that total percentage is based on the 10 cells showing the two variables taken together, which are summed in the lower right-hand cell. Thus, total percent for this cell is 342/2488 = 13.7. Only frequencies are given in the other cells of the table; but in a full table, these four figures – frequency, row percent, column percent and total percent – would be given in every cell.
Exercise 3.3
Compute the row percentage, the column percentage, and the total percentage in the cell showing the number of Palestinian women who do not watch television at all.
Describe the relationship between gender and watching television among Palestinians that is shown in the table. Do the television watching habits of Palestinian men and women appear to be generally similar or fairly different? You might find it helpful to convert the frequencies in other cells to row or column percentages.
Stacked Column Charts and Grouped Bar Charts
Stacked column charts and grouped bar charts are used to visually describe how two categorical variables, or one categorical and one continuous variable, relate to one another. Much like contingency tables, they show the percentage or count of each category of one variable within each category of the second variable. This information is presented in columns stacked on each other or next to each other. The charts below show the number of male Palestinians and the number of female Palestinians who watch television for a given number of hours each day. Each chart presents the same information as the other chart and as the contingency table shown above (Fig. 3.1 ).
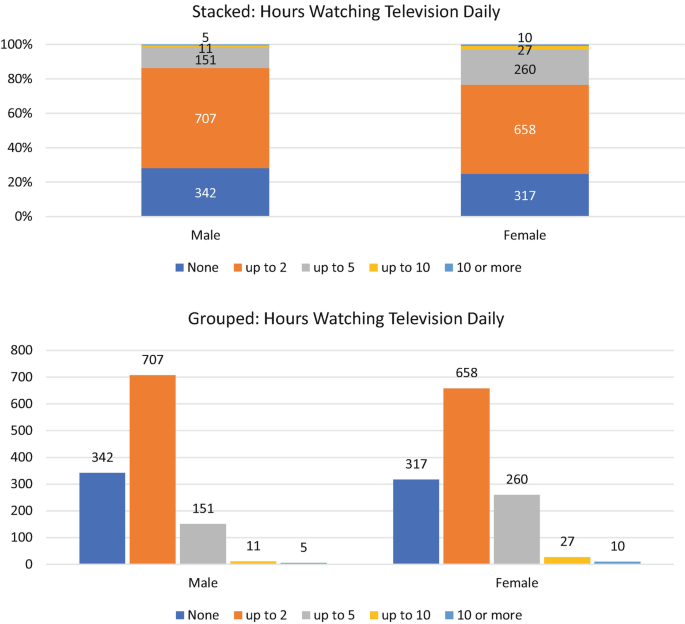
Stacked column charts and grouped bar charts comparing Palestinian men and Palestinian women on hours watching television
Box Plots and Box and Whisker Plots
Box plots, box and whisker plots, and other types of plots can also be used to show the relationship between one categorical variable and one continuous variable. They are particularly useful for showing how spread out the data are. Box plots show five important numbers in a variable’s distribution: the minimum value; the median; the maximum value; and the first and third quartiles (Q1 and Q2), which represent, respectively, the number below which are 25 percent of the distribution’s values and the number below which are 75 percent of the distribution’s values. The minimum value is sometimes called the lower extreme, the lower bound, or the lower hinge. The maximum value is sometimes called the upper extreme, the upper bound, or the upper hinge. The middle 50 percent of the distribution, the range between Q1 and Q3 that represents the “box,” constitutes the interquartile range (IQR). In box and whisker plots, the “whiskers” are the short perpendicular lines extending outside the upper and lower quartiles. They are included to indicate variability below Q1 and above Q3. Values are usually categorized as outliers if they are less than Q1 − IQR*1.5 or greater than Q3 + IQR*1.5. A visual explanation of a box and whisker plot is shown in Fig. 3.2a and an example of a box plot that uses actual data is shown in Fig. 3.2b .
The box plot in Fig. 3.2b uses Wave V Arab Barometer data from Tunisia and shows the relationship between age, a continuous variable, and interpersonal trust, a dichotomous categorical variable. The line representing the median value is shown in bold. Interpersonal trust, sometimes known as generalized trust, is an important personal value. Previous research has shown that social harmony and prospects for democracy are greater in societies in which most citizens believe that their fellow citizens for the most part are trustworthy. Although the interpersonal trust variable is dichotomous in Fig. 3.2b , the variance in interpersonal trust can also be measured by a set of ordered categories or a scale that yields a continuous measure, the latter not being suitable for presentation by a box plot. Figure 3.2b shows that the median age of Tunisians who are trusting is slightly higher than the median age of Tunisians who are mistrustful of other people. Notice also that the box plot for the mistrustful group has an outlier.
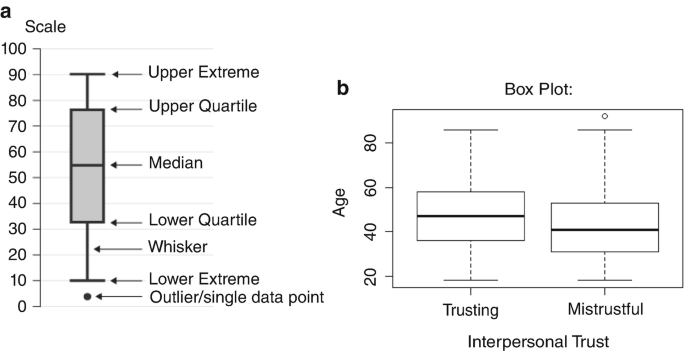
( a ) A box and whisker plot. ( b ) Box plot comparing the ages of trusting and mistrustful Tunisians in 2018
Line plots may be used to visualize the relationship between two continuous variables or a continuous variable and a categorical variable. They are often used when time, or a variable related to time, is one of the two variables. If a researcher wants to show whether and how a variable changes over time for more than one subgroup of the units about which she has data (looking at men and women separately, for example), she can include multiple lines on the same plot, with each line showing the pattern over time for a different subgroup. These lines will generally be distinguished from each other by color or pattern, with a legend provided for readers.
Line plots are a particularly good way to visualize a relationship if an investigator thinks that important events over time may have had a significant impact. The line plot in Fig. 3.3 shows the average support for gender equality among men and among women in Tunisia from 2013 to 2018. Support for gender equality is a scale based on four questions related to gender equality in the three waves of the Arab Barometer. An answer supportive of gender equality on a question adds +.5 to the scale and an answer unfavorable to gender equality adds −.5 to the scale. Accordingly, a scale score of 2 indicates maximum support for gender equality and a scale score of −2 indicates maximum opposition to gender equality.
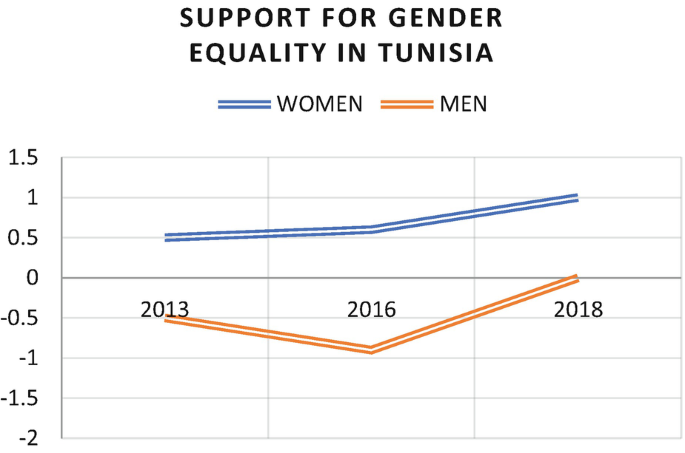
Line plot showing level of support for gender equality among Tunisian women and men in 2013, 2016, and 2018
Scatter Plots
Scatter plots are used to visualize a bivariate relationship when both variables are numerical. The independent variable is put on the x-axis, the horizontal axis, and the dependent variable is put on the y-axis, the vertical axis. Each data point becomes a dot in the scatter plot’s two-dimensional field, with its precise location being the point at which its value on the x-axis intersects with its value on the y-axis. The scatter plot shows how the variables are related to one another, including with respect to linearity, direction, and other aspects of structure. The scatter plots in Fig. 3.4 illustrate a strong positive linear relationship, a moderately strong negative linear relationship, a strong non-linear relationship, and a pattern showing no relationship. Footnote 5 If the scatter plot displays no visible and clear pattern, as in the lower left hand plot shown in Fig. 3.4 , the scatter plot would indicate that the independent variable, by itself, has no meaningful impact on the dependent variable.
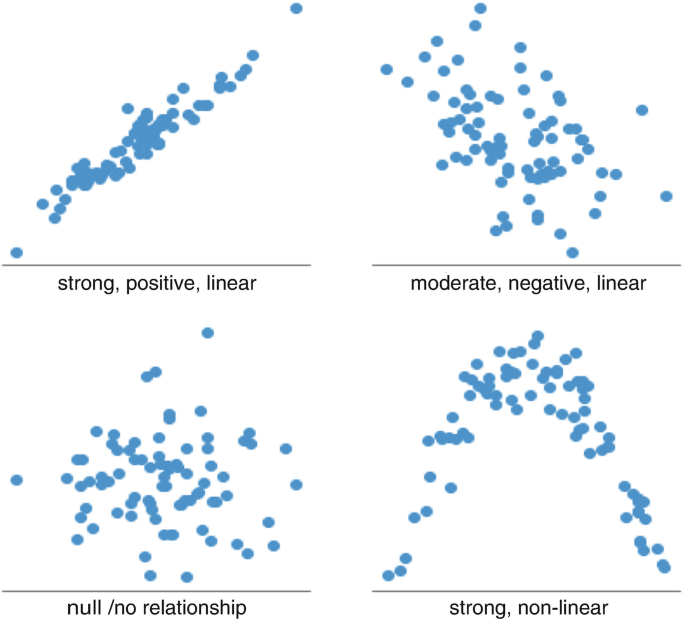
Scatter plots showing bivariate relationships with different structures
Scatter plots are also a good way to identify outliers—data points that do not follow a pattern that characterizes most of the data. These are also called non-scalar types. Figure 3.5 shows a scatter plot with outliers.
Outliers can be informative, making it possible, for example, to identify the attributes of cases for which the measures of one or both variables are unreliable and/or invalid. Nevertheless, the inclusion of outliers may not only distort the assessment of measures, raising unwarranted doubts about measures that are actually reliable and valid for the vast majority of cases, they may also bias bivariate statistics and make relationships seem weaker than they really are for most cases. For this reason, researchers sometimes remove outliers prior to testing a hypothesis. If one does this, it is important to have a clear definition of what is an outlier and to justify the removal of the outlier, both using the definition and perhaps through substantive analysis. There are several mathematical formulas for identifying outliers, and researchers should be aware of these formulas and their pros and cons if they plan to remove outliers.
If there are relatively few outliers, perhaps no more than 5–10 percent of the cases, it may be justifiable to remove them in order to better discern the relationship between the independent variable and the dependent variable. If outliers are much more numerous, however, it is probably because there is not a significant relationship between the two variables being considered. The researcher might in this case find it instructive to introduce a third variable and disaggregate the data. Disaggregation will be discussed in Chap. 4 .
A scatter plot with outliers marked in red
Exercise 3.4 Exploring Hypotheses through Visualizing Data: Exercise with the Arab Barometer Online Analysis Tool
Go to the Arab Barometer Online Analysis Tool ( https://www.arabbarometer.org/survey-data/data-analysis-tool/ )
Select Wave V and a country that interests you
Select “See Results”
Select “Social, Cultural and Religious topics”
Select “Religion: frequency: pray”
Questions: What does the distribution of this variable look like? How would you describe the variance?
Click on “Cross by,” then
Select “Show all variables”
Select “Kind of government preferable” and click
Select “Options,” then “Show % over Row total,” then “Apply”
Questions: Does there seem to be a relationship between religiosity and preference for democracy? If so, what might explain the relationship you observe—what is a plausible causal story? Is it consistent with the hypothesis you wrote for Exercise 3.1?
What other variables could be used to measure religiosity and preference for democracy? Explore your hypothesis using different items from the list of Arab Barometer variables
Do these distributions support the previous results you found? Do you learn anything additional about the relationship between religiosity and preference for democracy?
Now it is your turn to explore variables and variable relationships that interest you!
Pick two variables that interest you from the list of Arab Barometer variables. Are they continuous or categorical? Ordinal or nominal? (Hint: Most Arab Barometer variables are categorical, even if you might be tempted to think of them as continuous. For example, age is divided into the ordinal categories 18–29, 30–49, and 50 and more.)
Do you expect there to be a relationship between the two variables? If so, what do you think will be the structure of that relationship, and why?
Select the wave (year) and the country that interest you
Select one of your two variables of interest
Click on “Cross by,” and then select your second variable of interest.
On the left side of the page, you’ll see a contingency table. On the right side at the top, you’ll see several options to graphically display the relationship between your two variables. Which type of graph best represents the relationship between your two variables of interest?
Do the two variables seem to be independent of each other, or do you think there might be a relationship between them? Is the relationship you see similar to what you had expected
3.4 Probabilities and Type I and Type II Errors
As in visual presentations of bivariate relationships, selecting the appropriate measure of association or bivariate statistical test depends on the types of the two variables. The data on both variables may be categorical; the data on both may be continuous; or the data may be categorical on one variable and continuous on the other variable. These characteristics of the data will guide the way in which our presentation of these measures and tests is organized. Before briefly describing some specific measures of association and bivariate statistical tests, however, it is necessary to lay a foundation by introducing a number of terms and concepts. Relevant here are the distinction between population and sample and the notions of the null hypothesis, of Type I and Type II errors, and of probabilities and confidence intervals. As concepts, or abstractions, these notions may influence the way a researcher thinks about drawing conclusions about a hypothesis from qualitative data, as was discussed in Chap. 2 . In their precise meaning and application, however, these terms and concepts come into play when hypothesis testing involves the statistical analysis of quantitative data.
To begin, it is important to distinguish between, on the one hand, the population of units—individuals, countries, ethnic groups, political movements, or any other unit of analysis—in which the researcher is interested and about which she aspires to advance conclusions and, on the other hand, the units on which she has actually acquired the data to be analyzed. The latter, the units on which she actually has data, is her sample. In cases where the researcher has collected or obtained data on all of the units in which she is interested, there is no difference between the sample and the population, and drawing conclusions about the population based on the sample is straightforward. Most often, however, a researcher does not possess data on all of the units that make up the population in which she is interested, and so the possibility of error when making inferences about the population based on the analysis of data in the sample requires careful and deliberate consideration.
This concern for error is present regardless of the size of the sample and the way it was constructed. The likelihood of error declines as the size of the sample increases and thus comes closer to representing the full population. It also declines if the sample was constructed in accordance with random or other sampling procedures designed to maximize representation. It is useful to keep these criteria in mind when looking at, and perhaps downloading and using, Arab Barometer data. The Barometer’s website gives information about the construction of each sample. But while it is possible to reduce the likelihood of error when characterizing the population from findings based on the sample, it is not possible to eliminate entirely the possibility of erroneous inference. Accordingly, a researcher must endeavor to make the likelihood of this kind of error as small as possible and then decide if it is small enough to advance conclusions that apply to the population as well as the sample.
The null hypothesis, frequently designated as H0, is a statement to the effect that there is no meaningful and significant relationship between the independent variable and the dependent variable in a hypothesis, or indeed between two variables even if the relationship between them has not been formally specified in a hypothesis and does not purport to be causal or explanatory. The null hypothesis may or may not be stated explicitly by an investigator, but it is nonetheless present in her thinking; it stands in opposition to the hypothesized variable relationship. In a point and counterpoint fashion, the hypothesis, H1, posits that the variables are significantly related, and the null hypothesis, H0, replies and says no, they are not significantly related. It further says that they are not related in any meaningful way, neither in the way proposed in H1 nor in any other way that could be proposed.
Based on her analysis, the researcher needs to determine whether her findings permit rejecting the null hypothesis and concluding that there is indeed a significant relationship between the variables in her hypothesis, concluding in effect that the research hypothesis, H1, has been confirmed. This is most relevant and important when the investigator is basing her analysis on some but not all of the units to which her hypothesis purports to apply—when she is analyzing the data in her sample but seeks to advance conclusions that apply to the population in which she is interested. The logic here is that the findings produced by an analysis of some of the data, the data she actually possesses, may be different than the findings her analysis would hypothetically produce were she able to use data from very many more, or ideally even all, of the units that make up her population of interest.
This means, of course, that there will be uncertainty as the researcher adjudicates between H0 and H1 on the basis of her data. An analysis of these data may suggest that there is a strong and significant relationship between the variables in H1. And the stronger the relationship, the more unlikely it is that the researcher’s sample is a subset of a population characterized by H0 and that, therefore, the researcher may consider H1 to have been confirmed. Yet, it remains at least possible that the researcher’s sample, although it provides strong support for H1, is actually a subset of a population characterized by the null hypothesis. This may be unlikely, but it is not impossible, and so, therefore, to consider H1 to have been confirmed is to run the risk, at least a small risk, of what is known as a Type I error. A Type I error is made when a researcher accepts a research hypothesis that is actually false, when she judges to be true a hypothesis that does not characterize the population of which her sample is a subset. Because of the possibility of a Type I error, even if quite unlikely, researchers will often write something like “We can reject the null hypothesis,” rather than “We can confirm our hypothesis.”
Another analysis related to voter turnout provides a ready illustration. In the Arab Barometer Wave V surveys in 12 Arab countries, Footnote 6 13,899 respondents answered a question about voting in the most recent parliamentary election. Of these, 46.6 percent said they had voted, and the remainder, 53.4 percent, said they had not voted in the last parliamentary election. Footnote 7 Seeking to identify some of the determinants of voting—the attitudes and experiences of an individual that increase the likelihood that she will vote, the researcher might hypothesize that a judgment that the country is going in the right direction will push toward voting. More formally:
H1. An individual who believes that her country is going in the right direction is more likely to vote in a national election than is an individual who believes her country is going in the wrong direction.
Arab Barometer surveys provide data with which to test this proposition, and in fact there is a difference associated with views about the direction in which the country is going. Among those who judged that their country is going in the right direction, 52.4 percent voted in the last parliamentary election. By contrast, among those who judged that their country is going in the wrong direction, only 43.8 percent voted in the last parliamentary election.
This illustrates the choice a researcher faces when deciding what to conclude from a study. Does the analysis of her data from a subset of her population of interest confirm or not confirm her hypothesis? In this example, based on Arab Barometer data, the findings are in the direction of her hypothesis, and differences in voting associated with views about the direction the country is going do not appear to be trivial. But are these differences big enough to justify the conclusion that judgements about the country’s path going forward are a determinant of voting, one among others of course, in the population from which her sample was drawn? In other words, although this relationship clearly characterizes the sample, it is unclear whether it characterizes the researcher’s population of interest, the population from which the sample was drawn.
Unless the researcher can gather data on the entire population of eligible voters, or at least almost all of this population, it is not possible to entirely eliminate uncertainty when the researcher makes inferences about the population of voters based on findings from the subset, or sample, of voters on which she has data. She can either conclude that her findings are sufficiently strong and clear to propose that the pattern she has observed characterizes the population as well, and that H1 is therefore confirmed; or she can conclude that her findings are not strong enough to make such an inference about the population, and that H1, therefore, is not confirmed. Either conclusion could be wrong, and so there is a chance of error no matter which conclusion the researcher advances.
The terms Type I error and Type II error are often used to designate the possible error associated with each of these inferences about the population based on the sample. Type I error refers to the rejection of a true null hypothesis. This means, in other words, that the investigator could be wrong if she concludes that her finding of a strong, or at least fairly strong, relationship between her variables characterizes Arab voters in the 12 countries in general, and if she thus judges H1 to have been confirmed when the population from which her sample was drawn is in fact characterized by H0. Type II error refers to acceptance of a false null hypothesis. This means, in other words, that the investigator could be wrong if she concludes that her finding of a somewhat weak relationship, or no relationship at all, between her variables characterizes Arab voters in the 12 countries in general, and that she thus judges H0 to be true when the population from which her sample was drawn is in fact characterized by H1.
In statistical analyses of quantitative data, decisions about whether to risk a Type I error or a Type II error are usually based on probabilities. More specifically, they are based on the probability of a researcher being wrong if she concludes that the variable relationship—or hypothesis in most cases—that characterizes her data, meaning her sample, also characterizes the population on which the researcher hopes her sample and data will shed light. To say this in yet another way, she computes the odds that her sample does not represent the population of which it is a subset; or more specifically still, she computes the odds that from a population that is characterized by the null hypothesis she could have obtained, by chance alone, a subset of the population, her sample, that is not characterized by the null hypothesis. The lower the odds, or probability, the more willing the researcher will be to risk a Type I error.
There are numerous statistical tests that are used to compute such probabilities. The nature of the data and the goals of the analysis will determine the specific test to be used in a particular situation. Most of these tests, frequently called tests of significance or tests of statistical significance, provide output in the form of probabilities, which always range from 0 to 1. The lower the value, meaning the closer to 0, the less likely it is that a researcher has collected and is working with data that produce findings that differ from what she would find were she to somehow have data on the entire population. Another way to think about this is the following:
If the researcher provisionally assumes that the population is characterized by the null hypothesis with respect to the variable relationship under study, what is the probability of obtaining from that population, by chance alone, a subset or sample that is not characterized by the null hypothesis but instead shows a strong relationship between the two variables;
The lower the probability value, meaning the closer to 0, the less likely it is that the researcher’s data, which support H1, have come from a population that is characterized by H0;
The lower the probability that her sample could have come from a population characterized by H0, the lower the possibility that the researcher will be wrong, that she will make a Type I error, if she rejects the null hypothesis and accepts that the population, as well as her sample, is characterized by H1;
When the probability value is low, the chance of actually making a Type I error is small. But while small, the possibility of an error cannot be entirely eliminated.
If it helps you to think about probability and Type I and Type II error, imagine that you will be flipping a coin 100 times and your goal is to determine whether the coin is unbiased, H0, or biased in favor of either heads or tails, H1. How many times more than 50 would heads have to come up before you would be comfortable concluding that the coin is in fact biased in favor of heads? Would 60 be enough? What about 65? To begin to answer these questions, you would want to know the odds of getting 60 or 65 heads from a coin that is actually unbiased, a coin that would come up heads and come up tails roughly the same number of times if it were flipped many more than 100 times, maybe 1000 times, maybe 10,000. With this many flips, would the ratio of heads to tails even out. The lower the odds, the less likely it is that the coin is unbiased. In this analogy, you can think of the mathematical calculations about an unbiased coin’s odds of getting heads as the population, and your actual flips of the coin as the sample.
But exactly how low does the probability of a Type I error have to be for a researcher to run the risk of rejecting H0 and accepting that her variables are indeed related? This depends, of course, on the implications of being wrong. If there are serious and harmful consequences of being wrong, of accepting a research hypothesis that is actually false, the researcher will reject H0 and accept H1 only if the odds of being wrong, of making a Type I error, are very low.
There are some widely used probability values, which define what are known as “confidence intervals,” that help researchers and those who read their reports to think about the likelihood that a Type I error is being made. In the social sciences, rejecting H0 and running the risk of a Type I error is usually thought to require a probability value of less than .05, written as p < .05. The less stringent value of p < .10 is sometimes accepted as sufficient for rejecting H0, although such a conclusion would be advanced with caution and when the consequences of a Type I error are not very harmful. Frequently considered safer, meaning that the likelihood of accepting a false hypothesis is lower, are p < .01 and p < .001. The next section introduces and briefly describes some of the bivariate statistics that may be used to calculate these probabilities.
3.5 Measures of Association and Bivariate Statistical Tests
The following section introduces some of the bivariate statistical tests that can be used to compute probabilities and test hypotheses. The accounts are not very detailed. They will provide only a general overview and refresher for readers who are already fairly familiar with bivariate statistics. Readers without this familiarity are encouraged to consult a statistics textbook, for which the accounts presented here will provide a useful guide. While the account below will emphasize calculating these test statistics by hand, it is also important to remember that they can be calculated with the assistance of statistical software as well. A discussion of statistical software is available in Appendix 4.
Parametric and Nonparametric Statistics
Parametric and nonparametric are two broad classifications of statistical procedures. A parameter in statistics refers to an attribute of a population. For example, the mean of a population is a parameter. Parametric statistical tests make certain assumptions about the shape of the distribution of values in a population from which a sample is drawn, generally that it is normally distributed, and about its parameters, that is to say the means and standard deviations of the assumed distributions. Nonparametric statistical procedures rely on no or very few assumptions about the shape or parameters of the distribution of the population from which the sample was drawn. Chi-squared is the only nonparametric statistical test among the tests described below.
Degrees of Freedom
Degrees of freedom (df) is the number of values in the calculation of a statistic that are free to vary. Statistical software programs usually give degrees of freedom in the output, so it is generally unnecessary to know the number of the degrees of freedom in advance. It is nonetheless useful to understand what degrees of freedom represent. Consistent with the definition above, it is the number of values that are not predetermined, and thus are free to vary, within the variables used in a statistical test.
This is illustrated by the contingency tables below, which are constructed to examine the relationship between two categorical variables. The marginal row and column totals are known since these are just the univariate distributions of each variable. df = 1 for Table 3.3a , which is a 4-cell table. You can enter any one value in any one cell, but thereafter the values of all the other three cells are determined. Only one number is not free to vary and thus not predetermined. df = 2 for Table 3.3b , which is a 6-cell table. You can enter any two values in any two cells, but thereafter the values of all the other cells are determined. Only two numbers are free to vary and thus not predetermined. For contingency tables, the formula for calculating df is:
Chi-Squared
Chi-squared, frequently written X 2 , is a statistical test used to determine whether two categorical variables are significantly related. As noted, it is a nonparametric test. The most common version of the chi-squared test is the Pearson chi-squared test, which gives a value for the chi-squared statistic and permits determining as well a probability value, or p-value. The magnitude of the statistic and of the probability value are inversely correlated; the higher the value of the chi-squared statistic, the lower the probability value, and thus the lower the risk of making a Type I error—of rejecting a true null hypothesis—when asserting that the two variables are strongly and significantly related.
The simplicity of the chi-squared statistic permits giving a little more detail in order to illustrate several points that apply to bivariate statistical tests in general. The formula for computing chi-squared is given below, with O being the observed (actual) frequency in each cell of a contingency table for two categorical variables and E being the frequency that would be expected in each cell if the two variables are not related. Put differently, the distribution of E values across the cells of the two-variable table constitutes the null hypothesis, and chi-squared provides a number that expresses the magnitude of the difference between an investigator’s actual observed values and the values of E.
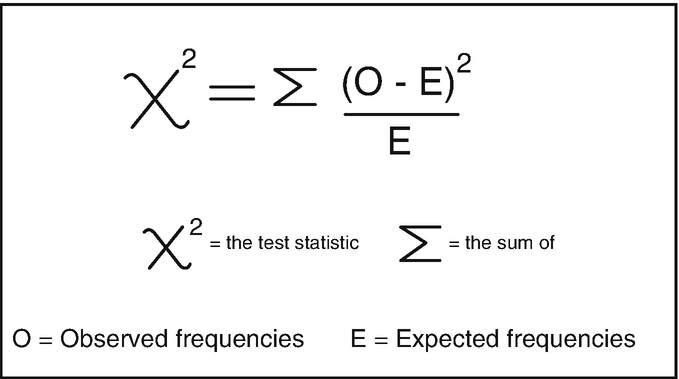
The computation of chi-squared involves the following procedures, which are illustrated using the data in Table 3.4 .
The values of O in the cells of the table are based on the data collected by the investigator. For example, Table 3.4 shows that of the 200 women on whom she collected information, 85 are majoring in social science.
The value of E for each cell is computed by multiplying the marginal total of the column in which the cell is located by the marginal total of the row in which the cell is located divided by N, N being the total number of cases. For the female students majoring in social science in Table 3.4 , this is: 200 * 150/400 = 30,000/400 = 75. For the female students majoring in math and natural science in Table 3.4 , this is: 200 * 100/400 = 20,000/400 = 50.
The difference between the value of O and the value of E is computed for each cell using the formula for chi-squared. For the female students majoring in social science in Table 3.4 , this is: (85–75) 2 /75 = 10 2 /75 = 100/75 = 1.33. For the female students majoring in math and natural science, the value resulting from the application of the chi-squared is: (45–50) 2 /50 = 5 2 /75 = 25/75 = .33.
The values in each cell of the table resulting from the application of the chi-squared formula are summed (Σ). This chi-squared value expresses the magnitude of the difference between a distribution of values indicative of the null hypothesis and what the investigator actually found about the relationship between gender and field of study. In Table 3.4 , the cell for female students majoring in social science adds 1.33 to the sum of the values in the eight cells, the cell for female students majoring in math and natural science adds .33 to the sum, and so forth for the remaining six cells.
A final point to be noted, which applies to many other statistical tests as well, is that the application of chi-squared and other bivariate (and multivariate) statistical tests yields a value with which can be computed the probability that an observed pattern does not differ from the null hypothesis and that a Type I error will be made if the null hypothesis is rejected and the research hypothesis is judged to be true. The lower the probability, of course, the lower the likelihood of an error if the null hypothesis is rejected.
Prior to the advent of computer assisted statistical analysis, the value of the statistic and the number of degrees of freedom were used to find the probability value in a table of probability values in an appendix in most statistics books. At present, however, the probability value, or p-value, and also the degrees of freedom, are routinely given as part of the output when analysis is done by one of the available statistical software packages.
Table 3.5 shows the relationship between economic circumstance and trust in the government among 400 ordinary citizens in a hypothetical country. The observed data were collected to test the hypothesis that greater wealth pushes people toward greater trust and less wealth pushes people toward lesser trust. In the case of all three patterns, the probability that the null hypothesis is true is very low. All three patterns have the same high chi-squared value and low probability value. Thus, the chi-squared and p-values show only that the patterns all differ significantly from what would be expected were the null hypothesis true. They do not show whether the data support the hypothesized variable relationship or any other particular relationship.
As the three patterns in Table 3.5 show, variable relationships with very different structures can yield similar or even identical statistical test and probability values, and thus these tests provide only some of the information a researcher needs to draw conclusions about her hypothesis. To draw the right conclusion, it may also be necessary for the investigator to “look at” her data. For example, as Table 3.5 suggests, looking at a tabular or visual presentation of the data may also be needed to draw the proper conclusion about how two variables are related.
How would you describe the three patterns shown in the table, each of which differs significantly from the null hypothesis? Which pattern is consistent with the research hypothesis? How would you describe the other two patterns? Try to visualize a plot of each pattern.
Pearson Correlation Coefficient
The Pearson correlation coefficient, more formally known as the Pearson product-moment correlation, is a parametric measure of linear association. It gives a numerical representation of the strength and direction of the relationship between two continuous numerical variables. The coefficient, which is commonly represented as r , will have a value between −1 and 1. A value of 1 means that there is a perfect positive, or direct, linear relationship between the two variables; as one variable increases, the other variable consistently increases by some amount. A value of −1 means that there is a perfect negative, or inverse, linear relationship; as one variable increases, the other variable consistently decreases by some amount. A value of 0 means that there is no linear relationship; as one variable increases, the other variable neither consistently increases nor consistently decreases.
It is easy to think of relationships that might be assessed by a Pearson correlation coefficient. Consider, for example, the relationship between age and income and the proposition that as age increases, income consistently increases or consistently decreases as well. The closer a coefficient is to 1 or −1, the greater the likelihood that the data on which it is based are not the subset of a population in which age and income are unrelated, meaning that the population of interest is not characterized by the null hypothesis. Coefficients very close to 1 or −1 are rare; although it depends on the number of units on which the researcher has data and also on the nature of the variables. Coefficients higher than .3 or lower than −.03 are frequently high enough, in absolute terms, to yield a low probability value and justify rejecting the null hypothesis. The relationship in this case would be described as “statistically significant.”
Exercise 3.5
Estimating Correlation Coefficients from scatter plots
Look at the scatter plots in Fig. 3.4 and estimate the correlation coefficient that the bivariate relationship shown in each scatter plot would yield.
Explain the basis for each of your estimates of the correlation coefficient.
Spearman’s Rank-Order Correlation Coefficient
The Spearman’s rank-order correlation coefficient is a nonparametric version of the Pearson product-moment correlation . Spearman’s correlation coefficient, (ρ, also signified by r s ) measures the strength and direction of the association between two ranked variables.
Bivariate Regression
Bivariate regression is a parametric measure of association that, like correlation analysis, assesses the strength and direction of the relationship between two variables. Also, like correlation analysis, regression assumes linearity. It may give misleading results if used with variable relationships that are not linear.
Regression is a powerful statistic that is widely used in multivariate analyses. This includes ordinary least squares (OLS) regression, which requires that the dependent variable be continuous and assumes linearity; binary logistic regression, which may be used when the dependent variable is dichotomous; and ordinal logistic regression, which is used with ordinal dependent variables. The use of regression in multivariate analysis will be discussed in the next chapter. In bivariate analysis, regression analysis yields coefficients that indicate the strength and direction of the relationship between two variables. Researchers may opt to “standardize” these coefficients. Standardized coefficients from a bivariate regression are the same as the coefficients produced by Pearson product-moment correlation analysis.
The t-test, also sometimes called a “difference of means” test, is a parametric statistical test that compares the means of two variables and determines whether they are different enough from each other to reject the null hypothesis and risk a Type I error. The dependent variable in a t-test must be continuous or ordinal—otherwise the investigator cannot calculate a mean. The independent variable must be categorical since t-tests are used to compare two groups.
An example, drawing again on Arab Barometer data, tests the relationship between voting and support for democracy. The hypothesis might be that men and women who voted in the last parliamentary election are more likely than men and women who did not vote to believe that democracy is suitable for their country. Whether a person did or did not vote would be the categorical independent variable, and the dependent variable would be the response to a question like, “To what extent do you think democracy is suitable for your country?” The question about democracy asked respondents to situate their views on a 11-point scale, with 0 indicating completely unsuitable and 10 indicating completely suitable.
Focusing on Tunisia in 2018, Arab Barometer Wave V data show that the mean response on the 11-point suitability question is 5.11 for those who voted and 4.77 for those who did not vote. Is this difference of .34 large enough to be statistically significant? A t-test will determine the probability of getting a difference of this magnitude from a population of interest, most likely all Tunisians of voting age, in which there is no difference between voters and non-voters in views about the suitability of democracy for Tunisia. In this example, the t-test showed p < .086. With this p-value, which is higher than the generally accepted standard of .05, a researcher cannot with confidence reject the null hypotheses, and she is unable, therefore, to assert that the proposed relationship has been confirmed.
This question can also be explored at the country level of analysis with, for example, regime type as the independent variable. In this illustration, the hypothesis is that citizens of monarchies are more likely than citizens of republics to believe that democracy is suitable for their country. Of course, a researcher proposing this hypothesis would also advance an associated causal story that provides the rationale for the hypothesis and specifies what is really being tested. To test this proposition, an investigator might merge data from surveys in, say, three monarchies, perhaps Morocco, Jordan, and Kuwait, and then also merge data from surveys in three republics, perhaps Algeria, Egypt, and Iraq. A t-test would then be used to compare the means of people in republics and people in monarchies and give the p-value.
A similar test, the Wilcoxon-Mann-Whitney test, is a nonparametric test that does not require that the dependent variable be normally distributed.
Analysis of variance, or ANOVA, is closely related to the t-test. It may be used when the dependent variable is continuous and the independent variable is categorical. A one-way ANOVA compares the mean and variance values of a continuous dependent variable in two or more categories of a categorical independent variable in order to determine if the latter affects the former.
ANOVA calculates the F-ratio based on the variance between the groups and the variance within each group. The F-ratio can then be used to calculate a p-value. However, if there are more than two categories of the independent variable, the ANOVA test will not indicate which pairs of categories differ enough to be statistically significant, making it necessary, again, to look at the data in order to draw correct conclusions about the structure of the bivariate relationships. Two-way ANOVA is used when an investigator has more than two variables.
Table 3.6 presents a summary list of the visual representations and bivariate statistical tests that have been discussed. It reminds readers of the procedures that can be used when both variables are categorical, when both variables are numerical/continuous, and when one variable is categorical and one variable is numerical/continuous.
Bivariate Statistics and Causal Inference
It is important to remember that bivariate statistical tests only assess the association or correlation between two variables. The tests described above can help a researcher estimate how much confidence her hypothesis deserves and, more specifically, the probability that any significant variable relationships she has found characterize the larger population from which her data were drawn and about which she seeks to offer information and insight.
The finding that two variables in a hypothesized relationship are related to a statistically significant degree is not evidence that the relationship is causal, only that the independent variable is related to the dependent variable. The finding is consistent with the causal story that the hypothesis represents, and to that extent, it offers support for this story. Nevertheless, there are many reasons why an observed statistically significant relationship might be spurious. The correlation might, for example, reflect the influence of one or more other and uncontrolled variables. This will be discussed more fully in the next chapter. The point here is simply that bivariate statistics do not, by themselves, address the question of whether a statistically significant relationship between two variables is or is not a causal relationship.
Only an Introductory Overview
As has been emphasized throughout, this chapter seeks only to offer an introductory overview of the bivariate statistical tests that may be employed when an investigator seeks to assess the relationship between two variables. Additional information will be presented in Chap. 4 . The focus in Chap. 4 will be on multivariate analysis, on analyses involving three or more variables. In this case again, however, the chapter will provide only an introductory overview. The overviews in the present chapter and the next provide a foundation for understanding social statistics, for understanding what statistical analyses involve and what they seek to accomplish. This is important and valuable in and of itself. Nevertheless, researchers and would-be researchers who intend to incorporate statistical analyses into their investigations, perhaps to test hypotheses and decide whether to risk a Type I error or a Type II error, will need to build on this foundation and become familiar with the contents of texts on social statistics. If this guide offers a bird’s eye view, researchers who implement these techniques will also need to expose themselves to the view of the worm at least once.
Chapter 2 makes clear that the concept of variance is central and foundational for much and probably most data-based and quantitative social science research. Bivariate relationships, which are the focus of the present chapter, are building blocks that rest on this foundation. The goal of this kind of research is very often the discovery of causal relationships, relationships that explain rather than merely describe or predict. Such relationships are also frequently described as accounting for variance. This is the focus of Chap. 4 , and it means that there will be, first, a dependent variable, a variable that expresses and captures the variance to be explained, and then, second, an independent variable, and possibly more than one independent variable, that impacts the dependent variable and causes it to vary.
Bivariate relationships are at the center of this enterprise, establishing the empirical pathway leading from the variance discussed in Chap. 2 to the causality discussed in Chap. 4 . Finding that there is a significant relationship between two variables, a statistically significant relationship, is not sufficient to establish causality, to conclude with confidence that one of the variables impacts the other and causes it to vary. But such a finding is necessary.
The goal of social science inquiry that investigates the relationship between two variables is not always explanation. It might be simply to describe and map the way two variables interact with one another. And there is no reason to question the value of such research. But the goal of data-based social science research is very often explanation; and while the inter-relationships between more than two variables will almost always be needed to establish that a relationship is very likely to be causal, these inter-relationships can only be examined by empirics that begin with consideration of a bivariate relationship, a relationship with one variable that is a presumed cause and one variable that is a presumed effect.
Against this background, with the importance of two-variable relationships in mind, the present chapter offers a comprehensive overview of bivariate relationships, including but not only those that are hypothesized to be causally related. The chapter considers the origin and nature of hypotheses that posit a particular relationship between two variables, a causal relationship if the larger goal of the research is explanation and the delineation of a causal story to which the hypothesis calls attention. This chapter then considers how a bivariate relationship might be described and visually represented, and thereafter it discusses how to think about and determine whether the two variables actually are related.
Presenting tables and graphs to show how two variables are related and using bivariate statistics to assess the likelihood that an observed relationship differs significantly from the null hypothesis, the hypothesis of no relationship, will be sufficient if the goal of the research is to learn as much as possible about whether and how two variables are related. And there is plenty of excellent research that has this kind of description as its primary objective, that makes use for purposes of description of the concepts and procedures introduced in this chapter. But there is also plenty of research that seeks to explain, to account for variance, and for this research, use of these concepts and procedures is necessary but not sufficient. For this research, consideration of a two-variable relationship, the focus of the present chapter, is a necessary intermediate step on a pathway that leads from the observation of variance to explaining how and why that variance looks and behaves as it does.
Dana El Kurd. 2019. “Who Protests in Palestine? Mobilization Across Class Under the Palestinian Authority.” In Alaa Tartir and Timothy Seidel, eds. Palestine and Rule of Power: Local Dissent vs. International Governance . New York: Palgrave Macmillan.
Yael Zeira. 2019. The Revolution Within: State Institutions and Unarmed Resistance in Palestine . New York: Cambridge University Press.
Carolina de Miguel, Amaney A. Jamal, and Mark Tessler. 2015. “Elections in the Arab World: Why do citizens turn out?” Comparative Political Studies 48, (11): 1355–1388.
Question 1: Independent variable is religiosity; dependent variable is preference for democracy. Example of hypothesis for Question 1: H1. More religious individuals are more likely than less religious individuals to prefer democracy to other political systems. Question 2: Independent variable is preference for democracy; dependent variable is turning out to vote. Example of hypothesis for Question 2: H2. Individuals who prefer democracy to other political systems are more likely than individuals who do not prefer democracy to other political systems to turn out to vote.
Mike Yi. “A complete Guide to Scatter Plots,” posted October 16, 2019 and seen at https://chartio.com/learn/charts/what-is-a-scatter-plot/
The countries are Algeria, Egypt, Iraq, Jordan, Kuwait, Lebanon, Libya, Morocco, Palestine, Sudan, Tunisia, and Yemen. The Wave V surveys were conducted in 2018–2019.
Not considered in this illustration are the substantial cross-country differences in voter turnout. For example, 63.6 of the Lebanese respondents reported voting, whereas in Algeria the proportion who reported voting was only 20.3 percent. In addition to testing hypotheses about voting in which the individual is the unit of analysis, country could also be the unit of analysis, and hypotheses seeking to account for country-level variance in voting could be formulated and tested.
Author information
Authors and affiliations.
Department of Political Science, University of Michigan, Ann Arbor, MI, USA
Mark Tessler
You can also search for this author in PubMed Google Scholar
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License ( http://creativecommons.org/licenses/by/4.0/ ), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Reprints and permissions
Copyright information
© 2023 The Author(s)
About this chapter
Tessler, M. (2023). Bivariate Analysis: Associations, Hypotheses, and Causal Stories. In: Social Science Research in the Arab World and Beyond. SpringerBriefs in Sociology. Springer, Cham. https://doi.org/10.1007/978-3-031-13838-6_3
Download citation
DOI : https://doi.org/10.1007/978-3-031-13838-6_3
Published : 04 October 2022
Publisher Name : Springer, Cham
Print ISBN : 978-3-031-13837-9
Online ISBN : 978-3-031-13838-6
eBook Packages : Social Sciences Social Sciences (R0)
Share this chapter
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Publish with us
Policies and ethics
- Find a journal
- Track your research

IMAGES
VIDEO
COMMENTS
Multivariate analysis (MVA) is based on the principles of multivariate statistics.Typically, MVA is used to address situations where multiple measurements are made on each experimental unit and the relations among these measurements and their structures are important. [1] A modern, overlapping categorization of MVA includes: [1] Normal and general multivariate models and distribution theory
Spring 2021. Lecture 11: Multiple hypothesis testInstructor: Yen-Chi Chen11.1 IntroductionThe multiple hypothesis testing. s the scenario that we are conducting several hyp. thesis tests at the same time. Suppose we have n tests, each leads to a p-value. So we ca. view the `data' as P1; ; Pn 2 [0; 1], where Pi is the p-value of the i-th test. We c.
Conclusion. Multivariate analysis is one of the most useful methods to determine relationships and analyse patterns among large sets of data. It is particularly effective in minimizing bias if a structured study design is employed. However, the complexity of the technique makes it a less sought-out model for novice research enthusiasts.
Multivariate Z -test (MZ; Wald test) For examinee i, the null hypothesis, H0:θi2 = θi1, is tested against the alternative hypothesis, Ha:θi2 ≠ θi1. This is an overall test; hence, the change can occur in any direction or pattern (i.e., a two-tailed test) and involve one or more dimensions.
1. What is multivariate analysis? In data analytics, we look at different variables (or factors) and how they might impact certain situations or outcomes. For example, in marketing, you might look at how the variable "money spent on advertising" impacts the variable "number of sales.". In the healthcare sector, you might want to explore ...
Multivariate testing helps examine the performance of multiple page elements in various combinations to analyze the impact of each element. Learn more. ... Hypothesis: A tentative ... Also known as the independent sample t-test, it's a method used to examine whether the means of two or more unknown samples are equal or not. If your sample ...
Abstract. Multivariate analysis is appropriate whenever more than one variable is measured on each sample individual, and overall conclusions about the whole system are sought. Many different multivariate techniques now exist for addressing a variety of objectives. This brief review outlines, in broad terms, some of the more common objectives ...
Multivariate data analysis is therefore an extension of univariate (analysis of a single variable) and bivariate analysis (cross-classification, correlation, and simple regression used to examine two variables). Figure 1 displays a useful classification of statistical techniques. Multivariate as well as univariate and bivariate techniques are ...
The table also gives the value of the constant, also known as the intercept. This is the value of the dependent variable when the independent variable has a value of zero. As will be shown, a formula that includes both the constant and the regression coefficient can be used to estimate, or predict, hypothetical values of the dependent variable.
4.1 Multinomial Test Statistics. In this section we consider three well-known test statistics, namely the likelihood ratio test, the Wald test, and the Score test. We show that all three test statistics are asymptotically equivalent, and the score statistic is the same as Pearson's goodness of fit test statistic.
Introduction. Multivariate analysis refers to statistical techniques that simultaneously look at three or more variables in relation to the subject under investigation with the aim of identifying or clarifying the relationships between them. The real world is always multivariate. Anything happening is the result of many different inputs and ...
Test of Multivariate Normality. Check univariate normality for each trait (X) separately. Can check \[Normality Assessment\] The good thing is that if any of the univariate trait is not normal, then the joint distribution is not normal (see again [m]). If a joint multivariate distribution is normal, then the marginal distribution has to be normal.
One of those analytical techniques that are used to read huge amounts of data is known as Multivariate Data Analysis. (Also read: Binary and multiclass classification in ML) ... It is tested to create a statistical hypothesis based on the parameters of multivariate data. This testing is carried out to determine whether or not the assumptions ...
This problem can be thought of as the multivariate counterpart of the univariate hypothesis t-test. 9.1.1 Hotelling's T2 Test The most fundamental approach to signal detection is a mere generalization of the t-test, known as Hotelling's \(T^2\) test .
We might also use a model suggested by theory or experience. Often a straight line relationship fits the data satisfactory and this is the case of simple linear regression. ... The null hypothesis [H 0: ρ ( : X1, , Xk) = 0] is tested with the F-test for overall regression as it is in the multivariate regression model (see above) 6, 7. The ...
The multivariate general linear model is a straightforward generalization of the univariate case in Equation (5.3). Instead of having one dependent variable in one column of the vector y, we have a set of p dependent variables in the several columns of the matrix Y. The model is therefore. ⎡ yˆ L yˆ.
The statistical jargon for such experiments is they are "multivariate," whereas ANOVA is "univariate." ... But they are also known as "univariate" tests because there is only one dependent variable. When we have experiments that have one or more treatment variables and multiple outcome variables, such as one- or two-way MANOVA, we ...
Given multivariate random samples originating from several Gaussian populations sharing the same covariance matrix, the one-way multivariate analysis of variation (also known as multivariate analysis of variance) technique enables one to test whether or not the population mean value vectors are equal. When a second set of treatments is also ...
A/B Testing: also known as split testing, compares two versions of a digital element to determine which performs better with the target audience. ... If you're running a multivariate test, your hypothesis could be: Testing different combinations of headline, hero image, and CTA button style on the homepage will result in a winning combination ...
Mathematically, a general k-sample problem, also known as one-way multivariate analy-sis of variance for functional data (FMANOVA) can be described as follows. Let SP p(η,Γ) denote a p-dimensional stochastic process with vector of mean functions η(t),t∈T, and
A/B testing (also known as bucket testing, split-run testing, or split testing) is a user experience research method. [1] A/B tests consist of a randomized experiment that usually involves two variants (A and B), [ 2 ] [ 3 ] [ 4 ] although the concept can be also extended to multiple variants of the same variable.
3.1 Description, Explanation, and Causal Stories. Every day, we encounter various phenomena that make us question how, why, and with what implications they vary. In responding to these questions, we often begin by considering bivariate relationships, meaning the way that two variables relate to one another. Such relationships are the focus of ...