problem solving in momentum and impulse

• Exam Center
• Ticket Center
• Flash Cards
• Momentum and Conservation laws

Momentum and Impulse Example Problems and Solutions AP Physics

Some impulse and momentum practice problems in one dimension are presented and solved. All these problems are helpful for your homework and/or the AP Physics 1 test. 

For better practice, all subjects are broken down into sections.

Linear momentum and its conservation

Problem (1): What is the momentum of a $0.057-\rm kg$ small object moving with a constant speed of $30\,\rm m/s$?

Solution : Linear momentum in physics is defined as the product of mass times the velocity, i.e., $p=mv$. Thus, we have \[p=0.057\times 30=1.71\,\rm \frac{kg\cdot m}{s}\] 

Problem (2): Suppose you are kicking a $410-\rm g$ soccer ball against a wall. The ball, traveling at $25\,\rm m/s$ strikes the wall and rebounds at the same speed.  (a) Find the direction and magnitude of the ball's momentum before and after striking. (b) What is the change in momentum of the ball?

Solution : According to the definition of momentum, it is the product of mass and velocity. Hence, momentum is a definition of a vector quantity in physics . 

(a) To find the direction of the momentum of a moving object, first, choose a reference coordinate. In all momentum and impulse problems, it is better and simpler to take the positive $x$ axis as the reference. 

Here, we assume that the ball initially is kicking toward the positive $x$ axis, so its original momentum just before striking the wall is \begin{align*} \vec{p}_b&=m\vec{v}\\ &=0.410 \times 25\,(\hat{i}) \\ &=10.25\,(\hat{i}) \quad {\rm kg\cdot m/s}\end{align*} where $b$ stands for '' before''. The ball, after rebounding, moves in the negative $x$ direction. So, the ball's momentum just after rebounding is \begin{align*} \vec{p}_a &=m\vec{v}\\ &=0.410 \times 25\,(-\hat{i}) \\ &=10.25\,(-\hat{i}) \quad {\rm kg\cdot m/s}\end{align*}  (b) The change in momentum is the difference between after and before momenta, i.e., $\Delta \vec{p}=\vec{p}_a-\vec{p}_b$. Thus, \begin{align*} \Delta\vec{p}&=(-10.25\,\hat{i})-(10.25\,\hat{i}) \\ &=20.5\,(-\hat{i}) \quad {\rm kg\cdot m/s}\end{align*} where $-\hat{i}$ indicates the direction of the vector of momentum change, which is to the left. 

Problem (3): A $0.025-\rm kg$ tennis ball traveling at a speed of $34\,\rm m/s$ hits a wall at a $45^\circ$ angle, as shown in the figure below.  (a) What is the direction and magnitude of the change in the ball's momentum? (b) Find the direction of the force exerted on the wall by the ball.

Solution : As in all momentum and impulse problems, take the positive $x$ axis as the reference of the coordinate system. Momentum is a vector quantity with components. In this problem, the ball is hit at an angle to the horizontal. 

As shown in the figure below, resolve the velocity vector into its components: \begin{align*} \vec{v}_i&=v\cos\theta\,\hat{i}+v\sin\theta\,(-\hat{j}) \\ &=34\,\left(\cos 45^\circ\,\hat{i}+\sin 45^\circ\,(-\hat{j})\right) \\&=17\sqrt{2}\,(\hat{i}-\hat{j}) \end{align*} where we used the fact that the sine and cosine of $45^\circ$ are $\frac{\sqrt{2}}{2}$. After rebounding from the wall, the ball moves at the same angle as before. Now, the velocity just after hitting the wall is found as below \begin{align*} \vec{v}_f&=v\cos\theta\,(-\hat{i})+v\sin\theta\,(-\hat{j}) \\ &=34\,\left(\cos 45^\circ\,(-\hat{i})+\sin 45^\circ\,(-\hat{j})\right) \\&=17\sqrt{2}\,(-\hat{i}-\hat{j}) \\&=-17\sqrt{2}\,(\hat{i}+\hat{j}) \end{align*} Its corresponding momentum is \[\vec{p}_f=m\vec{v}_f\] The subtraction of final momentum from initial momentum is defined as the change in momentum of a moving object. Thus, we will have \begin{align*} \Delta \vec{p}&=\vec{p}_f-\vec{p}_i \\\\ &=m(\vec{v}_f-\vec{v}_i) \\\\ &=0.025(-34\sqrt{2}\,\hat{i}) \\\\ &=0.85\sqrt{2}\,(-\hat{i}) \end{align*}

(b) According to Newton's second law, the net force applied to an object is equal to the rate of change of its momentum \[\vec{F}=\frac{\Delta\vec{p}}{\Delta t}\] This formula tells us that the direction of the applied force is in the same direction as the change in momentum. In this case, the change in momentum is toward the negative $x$ axis, so the force exerted on the ball due to the wall is also in the same direction.

Problem (4): The velocity of a $2-\rm kg$ object is given as $(3\,\hat{i}-4\,\hat{j}) \,\rm m/s$. Find: (a) The $x$ and $y$ components of its momentum. (b) The magnitude of the direction of its momentum.

Solution : Momentum is defined as the scalar multiplication of mass and velocity vector, i.e., $\vec{p}=m\vec{v}$. As you know, momentum is a vector quantity with some components. This problem is nothing but a vector problem in physics.

(a) The components of momentum are: \begin{align*} p_x&=mv_x \\ &=2(3\,\hat{i}) \\&=6\,\hat{i}\quad \rm kg\cdot m/s \\\\ p_y&=mv_y \\ &=2(-4\,\hat{j}) \\&=-8\,\hat{j}\quad \rm kg\cdot m/s \end{align*} Note that $\hat{i}$ and $\hat{j}$ are the unit vectors along the $x$ and $y$ directions. Recall that unit vectors are defined as ones with a magnitude of unity. 

(b) The magnitude of a given vector with its components is found by following the Pythagorean equation \begin{align*} p&=\sqrt{p_x^2+p_y^2} \\\\&=\sqrt{6^2+8^2}\\\\&=10\quad \rm kg\cdot m/s\end{align*} The direction of a vector is also found as below \begin{align*} \theta &=\tan^{-1}\left(\frac{p_y}{p_x}\right) \\\\ &=\tan^{-1}\left(\frac{-8}{6}\right) \\\\ &=-53^\circ \end{align*} The negative indicates that the angle is below the horizontal.

Problem (5): A $8000-\rm kg$ car moving at a constant speed of $14\,\rm m/s$ strikes a barrier. The two stick together and move for a while at a speed of $5\,\rm m/s$. What is the mass of the barrier? 

Solution : According to the law of conservation of linear momentum, the sum of momenta before any collision equals the sum of momenta after the collision, provided that there is no external force involved in the collision. In this case, the sum of momenta before the collision is \begin{align*} \vec{p}_i &=m_1 \vec{v}_1+m_2\vec{v}_2\\ &=(8000)(14)+m_2(0) \\ &=114000 \quad \rm kg\cdot m/s \end{align*} where we set the velocity of the barrier zero. After the collision, the two stick together and have a common velocity, say $V_f$, so \[ p_f=(m_1+m_2)V_f\] Equating these two momenta and solving for the unknown mass $m_2$, we will have \begin{gather*} p_i=p_f \\ 114000=(8000+m_2)(5) \\ \Rightarrow \quad \boxed{m_2=14800\,\rm kg} \end{gather*} To have a better understanding of this fundamental law in physics, refer to the solved problems of conservation of momentum .

Problem (6): A car of mass $m$ traveling at a speed of $v$ to the right collides with an identical car moving right at half the speed. As a result, the two stick together. Find their combined speed after the collision. 

Solution : Again, there is a collision, and we should apply the principle of conservation of momentum. Before the collision, the sum of momenta is \begin{align*} \vec{p}_i&=m_1 \vec{v}_1+m_2\vec{v}_2 \\\\ &=m(v+\frac v2) \end{align*} Similarly, after the collision, we have \[ \vec{p}_f=(m_1+m_2)\vec{V}_f \] Applying the principle of the conservation of linear momentum, and solving for the common velocity $V_f$, we get \begin{gather*} \vec{p}_i=\vec{p}_f \\\\ \frac 32 mv= (2m)V_f \\\\ \Rightarrow \quad \boxed{V_f= \frac{3}{4}v} \end{gather*} Hence, after the collision, the two cars move at three-fourths of the initial speed of the faster car. 

Impulse and Momentum Problems:

Problem (7): As a result of a force exerted on a ball lasting for about $2\,\rm s$, its momentum increases by $20\,\rm N\cdot s$. What is the average force on the ball? 

Solution : Applying Newton's second law of motion in its momentum form, we get \begin{align*} F_{av}&=\frac{\Delta p}{\Delta t} \\\\ &=\frac{20}{2}\\\\&= 10\,\rm N \end{align*}

Problem (8): Consider a car standing at rest behind the traffic light. After the light turns green, the car accelerates and increases its speed from zero to $6\,\rm m/s$ in $0.6\,\rm s$. What impulse and average force does a $75-\rm kg$ person in the car experience? 

Solution : Impulse and average force are related together by the following formula \[\text{Impulse}=\vec{F}_{av}\Delta t =\Delta \vec{p}\] Thus, if we could find the change in momentum of the passenger, then the impulse and average force on it would also be found. 

The change in the passenger's momentum is \begin{align*} \Delta \vec{p}&=m(\vec{v}_2-\vec{v}_1) \\ &=75(6-0) \\ &=450\,\rm kg \cdot m/s \end{align*} This is also equal to the impulse delivered to the person, so \[\text{impulse}=450\,\rm kg \cdot m/s\] The average force that exerted on the person in the car is also found as below \begin{align*} F_{av}&=\frac{\Delta p}{\Delta t} \\\\ &=\frac{450}{0.6}\\\\ &= 750\,\rm N \end{align*} 

Problem (9): Assume you kick a baseball of mass $0.145-\rm kg$ traveling at a speed of $30\,\rm m/s$. As a result of the collision, it leaves the bat with a speed of $45\,\rm m/s$. If the contact of time between them is $5\times 10^{-3}\,\rm s$,  (a) what is the direction and magnitude of the net force exerted on the ball? (b) how about the force on the bat?  (c) What work do you do on the ball?

Before and after the collision, velocities are given and we are asked about the net force between the bat and baseball. In such problems, we should use the definition of impulse since it relates the average external force exerted during a short time interval of a collision to the change in momentum of the object as below \[\text{Impulse}=\vec{F}\Delta t=\Delta \vec{p}\] (a) According to this definition, the net force on the ball is found as the change in the ball's momentum divided by that short time interval. But there is a subtle point to this problem. 

Assume the baseball originally travels to the right, and we set this direction as the positive direction of our system. After the collision, the ball rebounds in the opposite direction, namely in the negative direction ($-\hat{i}$). With these assumptions, the change in momentum of the ball is written as \begin{align*} \Delta\vec{p} &=m(\vec{v}_2-\vec{v}_1) \\\\ &=(0.145) \left(45\,(-\hat{i})-30\,\hat{i}\right) \\\\ &=10.875(-\hat{i}) \quad \rm kg\cdot m/s \end{align*} Now, using the definition of impulse, we get \begin{align*} \vec{F}&=\frac{\Delta \vec{p}}{\Delta t}\\\\ &= \frac{10.875(-\hat{i})}{5\times 10^{-3}} \\\\ &=2175\,(-\hat{i}) \quad \rm N \end{align*} Impulse is a vector quantity pointing in the same direction as the force. Thus, a net force of $2175\,\rm N$ toward the negative $x$-axis is applied to the ball. 

(b) According to Newton's third law of motion, the force that the bat exerts on the ball is the same force that the ball exerts on the bat but in the opposite direction.

(c) By definition, the work done by a constant force on an object over a displacement $\Delta x$ is \[W=F\Delta x \cos\theta\] where $\theta$ is the angle between $F$ and $\Delta x$ but in this case, the displacement is not known. But there is another method to solve work problems in physics. 

According to the work-kinetic energy theorem, the change in kinetic energy of a moving body is just the work done on it. \[W=\Delta \rm K.E.\] Thus, this part is converted to a work-kinetic energy theorem problem ! \begin{align*} W&=\Delta K \\\\ &=\frac 12 m(v_a^2-v_b^2) \\\\ &=\frac 12 (0.06)\left((-45)^2-30^2\right) \\\\ &=33.75\quad \rm J \end{align*}

Problem (10): A hammer of mass $m=15\,\rm kg$ strikes a nail with a speed of $8\,\rm m/s$ and comes to a stop in a time interval of $5\,\rm ms$.  (a) What impulse is imparted to the nail? (b) What is the average net force exerted on the nail?

Solution : Impulse, which is denoted by $\vec{J}$, is defined as the product of the average net external force applied to an object during a time interval $\Delta t$ and that short time interval, i.e., $\vec{J}=\vec{F}_{av}\Delta t$. Keep in mind that in all momentum and impulse problems, the impulse is also equal to the change in momentum of the object. \[\text{impulse}=\Delta \vec{p}\] Impulse and momentum are vector quantities, meaning they have direction. Hence, in all such problems, you should choose a positive direction and compare all velocities with that. Consider up as positive, in this case. 

(a) The initial and final velocities of the hammer are $v_i=-8\,\rm m/s$ and $v_f=0$, so the change in momentum of the hammer is \begin{align*} \Delta p&=m(v_2-v_1) \\ &=15(0-(-8))=+120\quad \rm kg\cdot m/s \end{align*} The initial velocity is to the down, so we put an extra negative in front of it. Therefore, the impulse imparted to the nail is \[\text{impulse}=+120\quad \rm kg\cdot m/s\]  (b) According to Newton's second law in momentum form, the force exerted on the nail by the hammer is equal to the change in momentum of the nail divided by the contact time between them, \[F_{av}=\frac{\Delta p}{\Delta t}=\frac{120}{5\times 10^{-3}}=24000\,\rm N\] 

Problem (11): A $0.06-\rm kg$ golf ball strikes a wall at an angle of $37^\circ$ with a speed of $28\,\rm m/s$ and rebounds at the same angle and speed.  Determine the magnitude and direction of the impulse given to the ball. (Take $\cos 37^\circ=0.8$ and $\sin 37^\circ=0.6$)

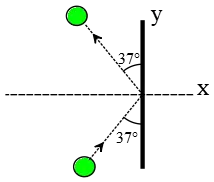
Solution : Take right and up as positive directions. Impulse is the change in momentum of an object. On the other side, momentum is defined as $\vec{p}=m\vec{v}$. 

The velocity vectors before ($b$) and after ($a$) strike make a $37^\circ$ angle with the wall, so resolve them into their components as below \begin{align*} v_{by}&=v_b \cos 37^\circ \\ &=28\times 0.8\\ &=22.4\,\rm m/s \\\\ v_{bx}&=v_b \sin 37^\circ \\&=28\times 0.6 \\&=16.8\,\rm m/s \\\\ v_{ay}&=v_a \cos 37^\circ \\&=28\times 0.8 \\ &=22.4\,\rm m/s \\\\  v_{ax}&=v_b \sin 37^\circ \\&=28\times 0.6 \\&=-16.8\,\rm m/s \end{align*} As you can see in the figure, the component $v_{ax}$ is to the left in the negative $x$ direction, so we put a negative in front of it.

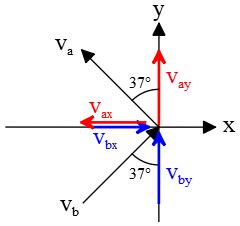
Now, it's time to find the change in momentum of the golf ball. The $y$ components (or vertical ones) are in the same direction, so their subtraction gets zero, but the horizontal ones are in the opposite direction, and their subtraction is written as below \begin{align*} \Delta \vec{p}&=m\Delta\vec{v} \\ &=m(\vec{v}_{after-x}-\vec{v}_{before-x}) \\ &=m(v_{ax}-v_{bx}) \\&=(0.06)(-16.8-16.8) \\&=-2.016 \,\rm kg\cdot m/s \end{align*} The minus sign indicates that the direction of the change in momentum (or impulse) is to the left in the $x$ direction. Therefore, the total impulse imparted to the ball is equal to the change in the ball's momentum, \[\text{Impulse}=\Delta \vec{p}=-2.016\,\rm kg\cdot m/s\] The absolute value of this is the magnitude of the impulse. 

For more problems on resolving vectors into their components, go here .

Problem (12): A ball of mass $0.150\,\rm kg$, initially at rest, is dropped from a height of $1.25\,\rm m$ and rebounds from the floor to a height of $0.96\,\rm m$. Assume the ball was in contact with the floor for $0.2\,\rm s$.  (a) What impulse was delivered to the ball by the floor? (b) What is the average force given to the ball by the floor?

Solution: As before, the impulse in physics equals the change in momentum of a moving body. After the ball strikes the floor, its momentum changes both in direction and magnitude. We should find the value of this change. 

In this problem, the ball's velocities immediately before and after striking the floor are not given. In this case, we must use the law of conservation of mechanical energy. 

Initially, the ball is at rest at a height of $h_1=1.25\,\rm m$ and hits the floor with a speed of, say, $v_b$, so in this part of the motion, the sum of its kinetic ($K=\frac 12 mv^2$) and potential ($U=mgh$) energies (or mechanical energy $E$) is written as below \begin{align*}  E_i&= E_f \\\\ K_i+U_i&=K_f+U_f \\ 0+mgh_1&=\frac 12 mv_b^2 + 0 \\ \Rightarrow \quad v_b&=\sqrt{2gh_1} \end{align*} Just after the ball strikes the floor, its velocity is, say, $v_a$ and it reaches a height of $h_2$. Thus, for this part, the law of conservation of energy tells us again that the velocity just after rebounding from the floor is $v_a=\sqrt{2gh_2}$. Substituting the numerical values of heights into the above expressions, we get \begin{gather*} v_b=\sqrt{2(9.8)(1.25)}=-5\,\rm m/s \quad \downarrow \\\\ v_a=\sqrt{2(9.8)(0.96)}=+4.3\,\rm m/s \quad \uparrow \end{gather*} But keep in mind that velocity is a vector quantity with a direction. If we assume up as the positive direction, then we must choose the minus sign for $v_b$. 

(a) Now that we have the velocities before and after striking, we can construct the change in momentum of the ball, which is equal to the impulse ($\vec{J}$). \begin{align*} \vec{J}&=\Delta \vec{p} \\ &=m(\vec{v}_a-\vec{v}_b) \\&= (0.15)(4.3-(-5)) \\ &=1.25 \quad\rm N\cdot s\end{align*} (b) Using Newton's second law the average force exerted on an object during a short time interval of a collision is related to the change in momentum of that object as below \begin{align*} F_{av}&=\frac{\Delta p}{\Delta t} \\\\ &=\frac{1.25}{0.2} \\\\&=6.25 \quad \rm N \end{align*}

Impulse and force-time graphs problems

One of the most important problems in the momentum and impulse sections is related to the force-time graphs. 

Problem (13): In the graph below, a time-varying force on an object of mass $3\,\rm kg$ is plotted against time.  (a) What impulse is delivered to the object from $t=0$ to $t=15\,\rm s$?  (b) What is the final speed of the object, assuming its initial speed was zero? (c) Now suppose we want the final speed of the object to be zero. In this case, what should be the initial speed?

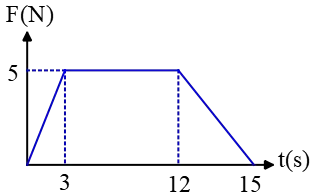
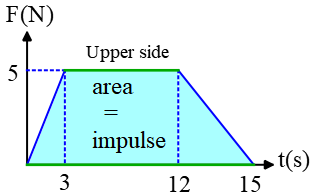
Solution : (a) The area under the force-time graph shows the impulse delivered to an object. In this problem, the area is a trapezoid whose value is one-second times the sum of the lengths of the parallel sides times the perpendicular distance between parallel sides, or \[\text{area}=\frac{(\text{lower side+upper side})\times height}{2}\] Therefore, the impulse equals to \[J=\frac{(9+15)\times 5}{2}=60\,\rm N\cdot s \]

Problem (14): The net force on a $4-\rm kg$ object varies in time as shown in the figure below. Find: (a) The initial acceleration of the object.  (b) The total impulse of the force delivered to the object over the entire time interval. (c) The final velocity of the object, assuming its initial velocity is $-3\,\hat{i}$. 

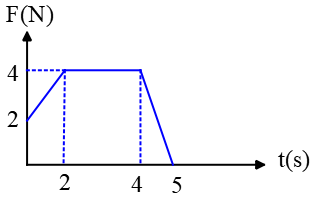
Solution : Here, the force vs. time graph exerted on an object is given.  (a) The initial acceleration is the force at time zero $t=0$ divided by the object's mass \[a=\frac{F}{m}=\frac{2}{4}=0.5\,\rm m/s^2\] (b) By definition, impulse ($J$) is the area under the force-time graph. In this case, the area is a trapezoid whose area is obtained as below \begin{align*} J&=\frac{(\text{lower side+upper side})\times height}{2} \\\\ &=\frac{(5+2)\times 4}{2} \\\\ &=14\,\rm N\cdot s \end{align*}  (c) In this part, it is assumed that the object initially traveled to the negative $x$ axis so a negative sign was added. Keep in mind that the area under the force vs. time graph represents the impulse or the change in momentum of the object. \[\text{area=impulse}=\Delta \vec{p}\] In the previous part, the impulse over the entire time period was computed. Now, equate that with the change in the object's momentum and solve for the final velocity \begin{gather*} \vec{J}=m(\vec{v}_f-\vec{v}_i) \\\\ 14\,\hat{i}=4(v_f-(-3) \,\hat{i}) \\\\ 14\,\hat{i}=4\vec{v}_f +12\,\hat{i} \\\\ \rightarrow \quad 4\vec{v}_f=14\,\hat{i}-12\,\hat{i} \\\\ \Rightarrow \quad \boxed{\vec{v}_f=0.5\,\hat{i}\quad \rm m/s} \end{gather*} Hence, after applying such a force varying in time, the object finally has a speed of $2\,\rm m/s$ in the positive $x$ direction. 

Problem (15): A varying force in time is applied to a body of mass $2\,\rm kg$ initially at rest. Below, the force-versus-time graph is shown. Find the speed of the object at $7\,\rm s$ and $12\,\rm s$. 

Solution : The object is initially at rest, so its initial momentum is zero, i.e., $p_0=0$. The momentum of the object at a later time $t=7\,\rm s$ is $p_7=mv_7$. Hence, the momentum change of the object in this time interval is \[\Delta p=m(v_7-v_0)=2v_7\] Recall that the area under the force-time graph gives us the impulse ($J$) of the force, which, on the other hand, is equal to the momentum change. The area between $0\,\rm s$ and $7\,\rm s$ is a triangle whose magnitude is half the product of base and height. \[J=\frac 12 \times 7\times 12 =42\,\rm N\cdot s\] Equating these two above expressions and solving for the speed at time $7\,\rm s$, we will get \begin{gather*} J=\Delta p \\\\ 42=2v_7 \\\\ \Rightarrow \quad v_7=21\,\rm m/s \end{gather*} Again, the impulse from $0\,\rm s$ to $12\,\rm s$ is the area under the graph, but notice that here the total area is composed of two areas: one is below the axis and the other is above the axis. That part below the axis always has a negative area!

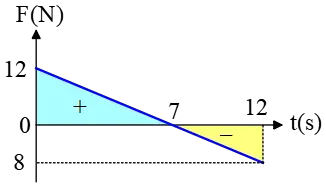
Thus, the impulse or area in this time interval is found as \begin{align*}Area &= area \uparrow + area \downarrow \\\\ &=\frac 12 (7)(12)+\frac 12 (5)(-8) \\\\ &=22\quad \rm N\cdot s \end{align*} Equating this with the momentum change in the whole time interval and solving for the speed at the instant of $t=12\,\rm s$, we will get \begin{gather*} J=\Delta p=m(v_{12}-v_0) \\\\ 22=2(v_{12}-0) \\\\ \Rightarrow \quad v_{12}=11\,\rm m/s \end{gather*}  

Elastic Collisions in one Dimension: 

Problem (16): Two $4-\rm kg$ and $12-\rm kg$ balls traveling at speeds of $24\,\rm m/s$ and $-2\,\rm m/s$, respectively, collide head-on with each other. After the collision, the lighter ball moves at $-3\,\rm m/s$ in the opposite direction. What is the velocity (magnitude and direction) of the heavier object after the collision? 

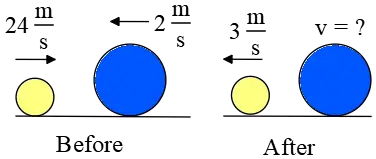
Solution : Assume the positive direction to be rightward and label the after-collision velocities with a prime. The given information are $m_1=4\,\rm kg$, $m_2=12\,\rm kg$, $v_1=24\,\rm m/s$, $v_2=-2\,\rm m/s$, and $v'_1=-3\,\rm m/s$. Keep in mind that in all collisions, first of all, apply the conservation law of momentum as below  \begin{gather*} \vec{p}_{before}=\vec{p}_{after} \\\\ m_1v_1+m_2 v_2 =m_1 v'_1+m_2 v'_2 \\\\ (4)(24)+(12)(-2)=(4)(-3)+(12)v'_2 \\\\ \Rightarrow \boxed{v'_2=+7\quad \rm m/s} \end{gather*} Therefore, the heavier ball moves at a speed of $7\,\rm m/s$ to the right in the positive $x$ direction.

Problem (17): A $0.44-\rm kg$ golf ball moving to the right with a speed of $3.8\,\rm m/s$ collides head-on with another golf ball of mass $0.22\,\rm kg$ initially at rest. Assume the collision to be perfectly elastic. What are the magnitude and direction of each ball's velocity after the collision? 

Solution : Since the collision is perfectly elastic, we must apply the conservation of kinetic energy and momentum. Let $v'_1$ and $v'_2$ be the velocities after the collision. We are given $m_1=0.44\,\rm kg$, $m_2=0.22\,\rm kg$, $v_1=3.8\,\rm m/s$, and $v_2=0$. The law of conservation of momentum tells us that the sum of the momenta before the collision must be equal to the sum of the momenta after the collision. \begin{gather*} \vec{p}_{before}=\vec{p}_{after} \\\\ m_1v_1+m_2 v_2 =m_1 v'_1+m_2 v'_2 \\\\ (0.44)(3.8)+0=(0.44)v'_1+(0.22)v'_2 \\\\ \Rightarrow \boxed{v'_2+2v'_1=7.6} \end{gather*} where in the last step we divided both sides by the common factor of $0.22$. 

Since the collision is assumed to be perfectly elastic, kinetic energy is also conserved \begin{gather*} K.E._{before}=K.E._{after} \\\\ \frac 12 m_1 v_1^2+\frac 12 m_2 v_2^2 = \frac 12 m_1 {v'_1}^2 +\frac 12 m_2 v'_2 \\\\ \frac 12 (0.44)(3.8)^2+0=\frac 12 (0.44){v'_1}^2+\frac 12 (0.22){v'_2}^2 \\\\ \Rightarrow \boxed{{v'_2}^2 +2{v'_1}^2=2(3.8)^2} \end{gather*} Consider the right as a positive direction. Now, we have two equations and two unknowns. Solve for $v'_2$ from the first equation, put it into the second one, and solve for $v'_1$ using a quadratic equation online solver. For this equation we get two solutions, $\boxed{v'_1=+1.27\,\rm m/s}$ or $v'_1=+3.8\,\rm m/s$. It is obvious that the second cannot be true since it tells us that the velocity of the incoming object after the collision must be equal to its initial velocity in the same direction, which does not make sense. Now substitute this value into the first equation again and solve for $v'_2$ which gets $\boxed{v'_2=+5.06\,\rm m/s}$. Thus, the second ball moves in the same direction as the incoming ball, which is in the positive $x$ direction. 

In order to help students prepare for the AP Physics 1 exam, this page includes several practice problems on impulse and momentum that are solved. 

As you learned, an impulse is a change in the momentum of an object or the product of the average force exerted on the object times the short interval of time that force exerted.

You can also check this out for solving simple problems on Momentum .

Author : Dr. Ali Nemati Published : 2/1/2022 

© 2015 All rights reserved. by Physexams.com

9.2 Impulse and Collisions

Learning objectives.

By the end of this section, you will be able to:

• Explain what an impulse is, physically
• Describe what an impulse does
• Relate impulses to collisions
• Apply the impulse-momentum theorem to solve problems

We have defined momentum to be the product of mass and velocity. Therefore, if an object’s velocity should change (due to the application of a force on the object), then necessarily, its momentum changes as well. This indicates a connection between momentum and force. The purpose of this section is to explore and describe that connection.

Suppose you apply a force on a free object for some amount of time. Clearly, the larger the force, the larger the object’s change of momentum will be. Alternatively, the more time you spend applying this force, again the larger the change of momentum will be, as depicted in Figure 9.5 . The amount by which the object’s motion changes is therefore proportional to the magnitude of the force, and also to the time interval over which the force is applied.

Mathematically, if a quantity is proportional to two (or more) things, then it is proportional to the product of those things. The product of a force and a time interval (over which that force acts) is called impulse , and is given the symbol J → . J → .

Let F → ( t ) F → ( t ) be the force applied to an object over some differential time interval dt ( Figure 9.6 ). The resulting impulse on the object is defined as

The total impulse over the interval t f − t i t f − t i is

Equation 9.2 and Equation 9.3 together say that when a force is applied for an infinitesimal time interval dt , it causes an infinitesimal impulse d J → d J → , and the total impulse given to the object is defined to be the sum (integral) of all these infinitesimal impulses.

To calculate the impulse using Equation 9.3 , we need to know the force function F ( t ), which we often don’t. However, a result from calculus is useful here: Recall that the average value of a function over some interval is calculated by

where Δ x = x f − x i Δ x = x f − x i . Applying this to the time-dependent force function, we obtain

Therefore, from Equation 9.3 ,

The idea here is that you can calculate the impulse on the object even if you don’t know the details of the force as a function of time; you only need the average force. In fact, though, the process is usually reversed: You determine the impulse (by measurement or calculation) and then calculate the average force that caused that impulse.

To calculate the impulse, a useful result follows from writing the force in Equation 9.3 as F → ( t ) = m a → ( t ) F → ( t ) = m a → ( t ) :

For a constant force F → ave = F → = m a → F → ave = F → = m a → , this simplifies to

Note that the integral form, Equation 9.3 , applies to constant forces as well; in that case, since the force is independent of time, it comes out of the integral, which can then be trivially evaluated.

Example 9.1

The arizona meteor crater.

Using the given data about the meteor, and making reasonable guesses about the shape of the meteor and impact time, we first calculate the impulse using Equation 9.6 . We then use the relationship between force and impulse Equation 9.5 to estimate the average force during impact. Next, we choose a reasonable force function for the impact event, calculate the average value of that function Equation 9.4 , and set the resulting expression equal to the calculated average force. This enables us to solve for the maximum force.

The average force during the impact is related to the impulse by

From Equation 9.6 , J → = m Δ v → J → = m Δ v → , so we have

The mass is equal to the product of the meteor’s density and its volume:

If we assume (guess) that the meteor was roughly spherical, we have

Thus we obtain

The problem says the velocity at impact was −1.28 × 10 4 m/s j ^ −1.28 × 10 4 m/s j ^ (the final velocity is zero); also, we guess that the primary impact lasted about t max = 2 s t max = 2 s . Substituting these values gives

This is the average force applied during the collision. Notice that this force vector points in the same direction as the change of velocity vector Δ v → Δ v → .

Next, we calculate the maximum force. The impulse is related to the force function by

We need to make a reasonable choice for the force as a function of time. We define t = 0 t = 0 to be the moment the meteor first touches the ground. Then we assume the force is a maximum at impact, and rapidly drops to zero. A function that does this is

(The parameter τ τ represents how rapidly the force decreases to zero.) The average force is

where Δ t = t max − 0 s Δ t = t max − 0 s . Since we already have a numeric value for F ave F ave , we can use the result of the integral to obtain F max F max .

Choosing τ = 1 e t max τ = 1 e t max (this is a common choice, as you will see in later chapters), and guessing that t max = 2 s t max = 2 s , this integral evaluates to

Thus, the maximum force has a magnitude of

The complete force function, including the direction, is

This is the force Earth applied to the meteor; by Newton’s third law, the force the meteor applied to Earth is

which is the answer to the original question.

Significance

Notice that the area under each plot has been filled in. For the plot of the (constant) force F ave F ave , the area is a rectangle, corresponding to F ave Δ t = J F ave Δ t = J . As for the plot of F ( t ), recall from calculus that the area under the plot of a function is numerically equal to the integral of that function, over the specified interval; so here, that is ∫ 0 t max F ( t ) d t = J ∫ 0 t max F ( t ) d t = J . Thus, the areas are equal, and both represent the impulse that the meteor applied to Earth during the two-second impact. The average force on Earth sounds like a huge force, and it is. Nevertheless, Earth barely noticed it. The acceleration Earth obtained was just

which is completely immeasurable. That said, the impact created seismic waves that nowadays could be detected by modern monitoring equipment.

Example 9.2

The benefits of impulse.

• What average force does the driver experience during the collision?
• Without the seatbelt and airbag, his collision time (with the steering wheel) would have been approximately 0.20 s. What force would he experience in this case?
• Define the + x -direction to be the direction the car is initially moving. We know J → = F → Δ t J → = F → Δ t and J → = m Δ v → . J → = m Δ v → . Since J is equal to both those things, they must be equal to each other: F → Δ t = m Δ v → . F → Δ t = m Δ v → . We need to convert this weight to the equivalent mass, expressed in SI units: 860 N 9.8 m/s 2 = 87.8 kg . 860 N 9.8 m/s 2 = 87.8 kg . Remembering that Δ v → = v → f − v → i Δ v → = v → f − v → i , and noting that the final velocity is zero, we solve for the force: F → = m 0 − v i i ^ Δ t = ( 87.8 kg ) ( − ( 27 m / s ) i ^ 2.5 s ) = − ( 948 N ) i ^ . F → = m 0 − v i i ^ Δ t = ( 87.8 kg ) ( − ( 27 m / s ) i ^ 2.5 s ) = − ( 948 N ) i ^ . The negative sign implies that the force slows him down. For perspective, this is about 1.1 times his own weight.
• Same calculation, just the different time interval: F → = ( 87.8 kg ) ( − ( 27 m / s ) i ^ 0.20 s ) = − ( 11,853 N ) i ^ F → = ( 87.8 kg ) ( − ( 27 m / s ) i ^ 0.20 s ) = − ( 11,853 N ) i ^ which is about 14 times his own weight. Big difference!

Effect of Impulse

Since an impulse is a force acting for some amount of time, it causes an object’s motion to change. Recall Equation 9.6 :

Because m v → m v → is the momentum of a system, m Δ v → m Δ v → is the change of momentum Δ p → Δ p → . This gives us the following relation, called the impulse-momentum theorem (or relation).

Impulse-Momentum Theorem

An impulse applied to a system changes the system’s momentum, and that change of momentum is exactly equal to the impulse that was applied:

The impulse-momentum theorem is depicted graphically in Figure 9.10 .

There are two crucial concepts in the impulse-momentum theorem:

• Impulse is a vector quantity; an impulse of, say, − ( 10 N · s ) i ^ − ( 10 N · s ) i ^ is very different from an impulse of + ( 10 N · s ) i ^ + ( 10 N · s ) i ^ ; they cause completely opposite changes of momentum.
• An impulse does not cause momentum; rather, it causes a change in the momentum of an object. Thus, you must subtract the initial momentum from the final momentum, and—since momentum is also a vector quantity—you must take careful account of the signs of the momentum vectors.

The most common questions asked in relation to impulse are to calculate the applied force, or the change of velocity that occurs as a result of applying an impulse. The general approach is the same.

Problem-Solving Strategy

• Express the impulse as force times the relevant time interval.
• Express the impulse as the change of momentum, usually m Δ v m Δ v .
• Equate these and solve for the desired quantity.

Example 9.3

Moving the enterprise.

When Captain Picard commands, “Take us out,” the starship Enterprise ( Figure 9.11 ) starts from rest to a final speed of v f = 7.5 × 10 7 m/s v f = 7.5 × 10 7 m/s . Assuming this maneuver is completed in 60 s, what average force did the impulse engines apply to the ship?

Equating these expressions gives

Solving for the magnitude of the force and inserting the given values leads to

Check Your Understanding 9.1

The U.S. Air Force uses “10 g s” (an acceleration equal to 10 × 9.8 m/s 2 10 × 9.8 m/s 2 ) as the maximum acceleration a human can withstand (but only for several seconds) and survive. How much time must the Enterprise spend accelerating if the humans on board are to experience an average of at most 10 g s of acceleration? (Assume the inertial dampeners are offline.)

Example 9.4

The iphone drop.

We need to make a couple of reasonable estimates, as well as find technical data on the phone itself. First, let’s suppose that the phone is most often dropped from about chest height on an average-height person. Second, assume that it is dropped from rest, that is, with an initial vertical velocity of zero. Finally, we assume that the phone bounces very little—the height of its bounce is assumed to be negligible.

The impulse J → J → equals the change in momentum,

Next, the change of momentum is

We need to be careful with the velocities here; this is the change of velocity due to the collision with the floor. But the phone also has an initial drop velocity [ v → i = ( 0 m/s ) j ^ v → i = ( 0 m/s ) j ^ ], so we label our velocities. Let:

• v → i = v → i = the initial velocity with which the phone was dropped (zero, in this example)
• v → 1 = v → 1 = the velocity the phone had the instant just before it hit the floor
• v → 2 = v → 2 = the final velocity of the phone as a result of hitting the floor

Figure 9.12 shows the velocities at each of these points in the phone’s trajectory.

With these definitions, the change of momentum of the phone during the collision with the floor is

Since we assume the phone doesn’t bounce at all when it hits the floor (or at least, the bounce height is negligible), then v → 2 v → 2 is zero, so

We can get the speed of the phone just before it hits the floor using either kinematics or conservation of energy. We’ll use conservation of energy here; you should re-do this part of the problem using kinematics and prove that you get the same answer.

First, define the zero of potential energy to be located at the floor. Conservation of energy then gives us:

Defining h floor = 0 h floor = 0 and using v → i = ( 0 m/s ) j ^ v → i = ( 0 m/s ) j ^ gives

Because v 1 v 1 is a vector magnitude, it must be positive. Thus, m Δ v = m v 1 = m 2 g h drop m Δ v = m v 1 = m 2 g h drop . Inserting this result into the expression for force gives

Finally, we need to estimate the collision time. One common way to estimate a collision time is to calculate how long the object would take to travel its own length. The phone is moving at 5.4 m/s just before it hits the floor, and it is 0.14 m long, giving an estimated collision time of 0.026 s. Inserting the given numbers, we obtain

Check Your Understanding 9.2

What if we had assumed the phone did bounce on impact? Would this have increased the force on the iPhone, decreased it, or made no difference?

Momentum and Force

In Example 9.3 , we obtained an important relationship:

In words, the average force applied to an object is equal to the change of the momentum that the force causes, divided by the time interval over which this change of momentum occurs. This relationship is very useful in situations where the collision time Δ t Δ t is small, but measureable; typical values would be 1/10th of a second, or even one thousandth of a second. Car crashes, punting a football, or collisions of subatomic particles would meet this criterion.

For a continuously changing momentum—due to a continuously changing force—this becomes a powerful conceptual tool. In the limit Δ t → d t Δ t → d t , Equation 9.2 becomes

This says that the rate of change of the system’s momentum (implying that momentum is a function of time) is exactly equal to the net applied force (also, in general, a function of time). This is, in fact, Newton’s second law, written in terms of momentum rather than acceleration. This is the relationship Newton himself presented in his Principia Mathematica (although he called it “quantity of motion” rather than “momentum”).

If the mass of the system remains constant, Equation 9.3 reduces to the more familiar form of Newton’s second law. We can see this by substituting the definition of momentum:

The assumption of constant mass allowed us to pull m out of the derivative. If the mass is not constant, we cannot use this form of the second law, but instead must start from Equation 9.3 . Thus, one advantage to expressing force in terms of changing momentum is that it allows for the mass of the system to change, as well as the velocity; this is a concept we’ll explore when we study the motion of rockets.

Newton’s Second Law of Motion in Terms of Momentum

The net external force on a system is equal to the rate of change of the momentum of that system caused by the force:

Although Equation 9.3 allows for changing mass, as we will see in Rocket Propulsion , the relationship between momentum and force remains useful when the mass of the system is constant, as in the following example.

Example 9.5

Calculating force: venus williams’ tennis serve.

As noted above, when mass is constant, the change in momentum is given by

where we have used scalars because this problem involves only one dimension. In this example, the velocity just after impact and the time interval are given; thus, once Δ p Δ p is calculated, we can use F = Δ p Δ t F = Δ p Δ t to find the force.

Now the magnitude of the net external force can be determined by using

where we have retained only two significant figures in the final step.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/university-physics-volume-1/pages/1-introduction

• Authors: William Moebs, Samuel J. Ling, Jeff Sanny
• Publisher/website: OpenStax
• Book title: University Physics Volume 1
• Publication date: Sep 19, 2016
• Location: Houston, Texas
• Book URL: https://openstax.org/books/university-physics-volume-1/pages/1-introduction
• Section URL: https://openstax.org/books/university-physics-volume-1/pages/9-2-impulse-and-collisions

© Jan 19, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

HIGH SCHOOL

• ACT Tutoring
• SAT Tutoring
• PSAT Tutoring
• ASPIRE Tutoring
• SHSAT Tutoring
• STAAR Tutoring

GRADUATE SCHOOL

• MCAT Tutoring
• GRE Tutoring
• LSAT Tutoring
• GMAT Tutoring
• AIMS Tutoring
• HSPT Tutoring
• ISAT Tutoring
• SSAT Tutoring

Search 50+ Tests

Loading Page

math tutoring

• Elementary Math
• Pre-Calculus
• Trigonometry

science tutoring

Foreign languages.

• Mandarin Chinese

elementary tutoring

• Computer Science

Search 350+ Subjects

• Video Overview
• Tutor Selection Process
• Online Tutoring
• Mobile Tutoring
• Instant Tutoring
• How We Operate
• Our Guarantee
• Impact of Tutoring
• Reviews & Testimonials
• Media Coverage
• About Varsity Tutors

AP Physics 1 : Impulse and Momentum

Study concepts, example questions & explanations for ap physics 1, all ap physics 1 resources, example questions, example question #1 : impulse and momentum.

Since the collision is completely elastic, we know that both momentum and kinetic energy are conserved. We can write the following equations (initial momentum and energy of the second ball are neglected since it is not moving:

We can rewrite the second equation as:

Rearranging, we get:

Plug in our values for the initial and final velocities:

Example Question #2 : Impulse And Momentum

It does not matter whether the collision is elastic or inelastic (although it would be best to assume that it's inelastic). Momentum is conserved in either type of collision, and is the only value needed for our calculation. Since they come to a standstill, their momentums at the moment of collision are equal and opposite:

Plug in the given values from the question and solve:

Example Question #3 : Impulse And Momentum

Since the collision is completely inelastic, momentum is conserved but energy is not. Furthermore, the two cars stick to each other and travel as one. The equation for conservation of momentum is as follows:

There are two inital masses with different velocities and one final mass with a single velocity. Therefore, we can write:

Rearranging for final velocity, we get:

At this point, we can denote which direction is positive and which is negative. Since the car traveling west has more momentum, we will consider west to be positive. Substituting our values into the equation, we get:

Example Question #4 : Impulse And Momentum

Impulse can be written as either of two popular expressions:

From the problem statement, we can determine the velocity of the marble as it hits the floor, allowing us to use the latter expression. To determining the velocity of the marble, we can use the equation for conservation of energy:

Assuming the final height is zero, we can eliminate initial kinetic energy and final potential energy. Therefore, we can write:

Canceling out mass and rearranging for final velocity, we get:

We know these variables, allowing us to solve for the velocity:

Plugging this value into the expression for impulse, we get:

Example Question #5 : Impulse And Momentum

Consider the following system:

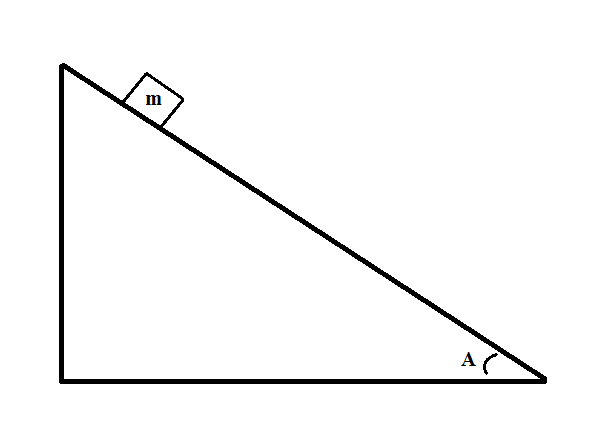
To calculate the momentum of the block, we first need to know the velocity of the block. This can be found using the equation for the conservation of momentum:

If we assume that the final height is zero, we can eliminate initial kinetic energy and final potential energy, getting:

Substituting expressions for each term, we get:

Cancel out mass and rearrange to solve for velocity:

We can use the horizontal distance traveled and the angle of the slope to determine the initial height:

Now that we have the initial height, we can solve for final velocity:

Finally, we can now use the equation for momentum to solve the problem:

Example Question #6 : Impulse And Momentum

Momentum is always conserved. Equation for conservation of momentum: 

There is only one velocity on the right since the two astronauts grab onto each other, thus they move together at the same velocity. Solve.

The equation for momentum is:

To maintain conservation of momentum, a new state must have the same momentum as a previous state:

Plug in known values and solve.

To solve this problem, we need to consider the change in the ball's momentum. To do so, we'll use the following equation.

Rearrange the above equation to solve for the average force.

Example Question #9 : Impulse And Momentum

Joe, of mass 90kg, jumps straight up. To do so, he bends his knees and produces an upwards force that results in a constant upward net force of 100N. If Joe experiences this force for 0.9s before leaving the ground, what is Joe's velocity immediately after he leaves the ground? 

To solve this problem we need to use the relationship between force and impulse, which is given by the following equation:

This equation represents that the rate of change of momentum with respect to time is equal to the net force that causes said change in momentum. Thus:

Which of the following explains why when we land on our feet, we instinctively bend our knees? Hint: think about the relationship between force, impulse, and time.

When we bend our knees we extend the time in which we apply the force that stops us, so our impulse is greater

When we bend our knees we extend the time in which we apply the force that stops us, so our impulse is smaller

By bending our knees we use a greater force to stop, which makes the impulse smaller

By bending our knees we extend the time it takes us to stop, which increases the impact force

By bending our knees we extend the time it takes us to stop, which diminishes the impact force

Note that the initial momentum does not depend on the impact force nor on how much time it takes to stop. The initial momentum depends on the velocity we have when we first hit the ground. This velocity is given by whatever happened before we hit the ground, which no longer concerns us since we only care about what happens from the moment we first hit the ground till the moment we stop. Yes, the time that passes for you to stop is very small, but it is impossible for it to be zero. So we have that the change in momentum (impulse) is a constant:

Remember that any change in momentum for a given mass occurs because its velocity changes. The velocity of the mass changes due to an acceleration and an acceleration is caused by a force. This gives us a relationship between force and impulse:

Report an issue with this question

If you've found an issue with this question, please let us know. With the help of the community we can continue to improve our educational resources.

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC 101 S. Hanley Rd, Suite 300 St. Louis, MO 63105

Or fill out the form below:

Contact Information

Complaint details.

Impulse and Momentum

Now, the bears I live with average, the males, eight to twelve hundred pounds [360 to 540 kg]. They're the largest bears in the world…. They've been clocked at 41 [mph] and they've run a hundred meter dash in 5.85 seconds, which a human on steroids doesn't even approach. Timothy Treadwell, 2001

• Compute the speed of a grizzly bear using Mr. Treadwell's hundred meter statement.
• Compute the momentum of a grizzly bear using the speed you calculated in part a. and the average mass stated by Mr. Treadwell.
• How fast would a 250 lb man have to run to have the same momentum you calculated in part b? (Do not use a calculator to compute your answer.)
• How fast would a 4000 lb car have to drive to have the same momentum you calculated in part b? (Do not use a calculator to compute your answer.)

For the first month of its journey, the Mars Orbiter Spacecraft actually orbited the Earth. After a series of orbit raising maneuvers, the tiny main engine gave the spacecraft enough speed in the right direction to escape. For the next nine months the main engine was only used twice and only very briefly (less than a minute of total burn time) to correct the spacecraft's trajectory.

Nine months after leaving Earth orbit, the spacecraft arrived at Mars. To enter orbit around Mars, the spacecraft needed to slow down — a maneuver called orbit insertion. Since the main engine hadn't been used much in nine months, a quick little test was needed.

Press Release: September 22, 2014 Mars Orbiter Spacecraft's Main Liquid Engine Successfully Test Fired The 440 newton Liquid Apogee Motor (LAM) of India's Mars Orbiter Spacecraft, last fired on December 01, 2013, was successfully fired for a duration of 3.968 seconds at 1430 hrs IST today (September 22, 2014). This operation of the spacecraft's main liquid engine was also used for the spacecraft's trajectory correction and changed its velocity by 2.18 metre/second. With this successful test firing, Mars Orbiter Insertion (MOI) operation of the spacecraft is scheduled to be performed on the morning of September 24, 2014 at 07:17:32 hrs IST by firing the LAM along with eight smaller liquid engines for a duration of about 24 minutes. ISRO, 2014

• Using the press release, determine the mass of the Mars Orbiter Spacecraft at the time of this test firing.
• Why was the qualifying phrase "at the time of this test firing" added to the end of the previous question? Why does the mass of the spacecraft vary with time?

After all, the faster we go, the more difficult it is to avoid collisions with small objects and the more damage such a collision will wreak. Even if we are fortunate enough to miss all sizable objects, we can scarcely expect to miss the dust and individual atoms that are scattered throughout space. At two-tenths of the speed of light, dust and atoms might not do significant damage even in a voyage of 40 years, but the faster you go, the worse it is — space begins to become abrasive. When you begin to approach the speed of light, each hydrogen atom becomes a cosmic ray particle and will fry the crew. (A hydrogen atom or its nucleus striking the ship at nearly the speed of light is a cosmic ray particle, and there is no difference if the ship strikes the hydrogen atom or nucleus at nearly the speed of light. As Sancho Panza: "Whether the stone strikes the pitcher, or the pitcher strikes the stone, it is bad for the pitcher.") So 60,000 kilometers per second may be the practical speed limit for space travel. Isaac Asimov, 1987

The density of the interstellar medium is about one hydrogen atom per cubic centimeter. Imagine a 1,000 tonne, 4 by 6 meter, classroom-sized interstellar spacecraft traveling at 60,000 km/s on its way to Proxima Centauri (the nearest solar system to our own) 4.243 light years away.

Kinematics:

• How long would it take our hypothetical spacecraft to complete its hypothetical journey?

Impulse-Momentum:

• Determine the momentum of our spacecraft.
• What mass of interstellar medium is swept up during the journey?
• What impulse does the interstellar medium deliver to the spacecraft?
• How does this impulse compare to the momentum of the spacecraft?

Work-Energy:

• Determine the kinetic energy of our spacecraft.
• What is the effective drag force of the interstellar medium during the journey?
• How much work does the interstellar medium do on the spacecraft?
• How does this work compare to the kinetic energy of the spacecraft?
• Write something.
• In older passenger cars, body panels were attached to a single frame around the perimeter, making them very rigid. This is known as body-over-frame construction. In newer cars, different body parts have stress-bearing elements within them and these parts are then welded to each other. This is known as unitized body construction. Repairing "unibody" cars after collision is comparatively difficult as stress (and thus damage) are distributed throughout the different parts. Why then are cars now built this way
• To escape from a horrible fire, two people are forced to jump from the third story of a burning building on to solid concrete. Which person is more likely to sustain serious injuries: the jumper who comes to an abrupt halt when he lands or the jumper who bounces after impact?
• What is the basic idea behind crash safety features in cars like seatbelts, airbags, crumple zones, etc. What quantities in the impulse-momentum theorem ( F ∆ t  =  m ∆ v ) change as a result of these features, how are they changed, and how does this result in increased safety during a crash?
• The phrase "roll with the punches" has its origin in boxing. What does it mean to roll with a punch (or ride a punch)? How does rolling reduce the severity of a punch?
• Is it possible for a motorcycle to have more momentum (that is, a momentum with a larger magnitude) than a train?
• When hit, the velocity of a 0.145 kg baseball changes from +20 m/s to −20 m/s. What is the magnitude of the impulse delivered by the bat to the ball?
• the ground is soft and the ball stops dead
• the ground is hard and the ball bounces straight up at 2.0 m/s
• Draw a free body diagram showing all the forces acting on the model rocket.
• the weight of the rocket
• the net force on the rocket while the engine was running
• the net impulse on the rocket while the engine was running
• the speed of the rocket when the engine stopped
• the height of the rocket above the ground when the engine stopped
• What is the acceleration of the rocket after the engine shut down?
• What maximum height above the ground did the rocket reach?
• What does the area under this curve represent?
• Calculate its cumulative value at 2 s intervals. Compile your results in a table like the one below.
• Sketch a graph of this quantity with respect to time.

statistical

• Use the given data to create a force-time graph.
• Determine the impulse acting on the projectile as a function of time.
• Compute the launch speed of the projectile.

Data adapted from Kampen, Kaczmarczik, and Rath; 2006 .

investigative

• Which plate have you chosen to work with?
• What is the speed of this plate ?
• What is the area of this plate?
• Is the plate you've chosen continental or oceanic?
• What is a typical density of this kind of crust?
• What is a typical thickness of this type of crust?
• Compute the momentum of the tectonic plate you've chosen from the data you've found. State your answer to the nearest order of magnitude (the nearest power of ten). Don't forget the unit.
• the thrust-time data used to generate the graph on the data sheet
• the propellant mass
• the mass after firing (i.e., the mass of the empty rocket)
• impulse provided by the motor
• fractional propellant mass loss (You need to determine the initial and final mass of the rocket. Assume that the loss of mass is directly proportional to the cumulative impulse. When the impulse is zero at the beginning, the mass loss is zero. When the impulse reaches its final value, the mass loss is 100%.)
• mass of the rocket
• speed of the rocket (Don't forget to include the force of gravity in your calculations.)
• acceleration of the rocket
• altitude of the rocket

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

9.3: Impulse and Collisions (Part 1)

• Last updated
• Save as PDF
• Page ID 4021

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Explain what an impulse is, physically
• Describe what an impulse does
• Relate impulses to collisions
• Apply the impulse-momentum theorem to solve problems

We have defined momentum to be the product of mass and velocity. Therefore, if an object’s velocity should change (due to the application of a force on the object), then necessarily, its momentum changes as well. This indicates a connection between momentum and force. The purpose of this section is to explore and describe that connection.

Suppose you apply a force on a free object for some amount of time. Clearly, the larger the force, the larger the object’s change of momentum will be. Alternatively, the more time you spend applying this force, again the larger the change of momentum will be, as depicted in Figure \(\PageIndex{1}\). The amount by which the object’s motion changes is therefore proportional to the magnitude of the force, and also to the time interval over which the force is applied.

Mathematically, if a quantity is proportional to two (or more) things, then it is proportional to the product of those things. The product of a force and a time interval (over which that force acts) is called impulse, and is given the symbol \(\vec{J}\).

Definition: Impulse

Let \(\vec{F}\)(t) be the force applied to an object over some differential time interval \(dt\) (Figure \(\PageIndex{2}\)). The resulting impulse on the object is defined as

\[d \vec{J} \equiv \vec{F} (t) dt \ldotp \label{9.2}\]

The total impulse over the interval t f − t i is

\[\vec{J} = \int_{t_{i}}^{t_{f}} d \vec{J}\]

\[\vec{J} \equiv \int_{t_{i}}^{t_{f}} \vec{F} (t) dt \ldotp \label{9.3}\]

Equations \ref{9.2} and \ref{9.3} together say that when a force is applied for an infinitesimal time interval dt, it causes an infinitesimal impulse d\(\vec{J}\), and the total impulse given to the object is defined to be the sum (integral) of all these infinitesimal impulses.

To calculate the impulse using Equation \ref{9.3}, we need to know the force function F(t), which we often don’t. However, a result from calculus is useful here: Recall that the average value of a function over some interval is calculated by

\[f(x)_{ave} = \frac{1}{\Delta x} \int_{x_{i}}^{x_{f}} f(x)dx\]

where \(\Delta\)x = x f − x i . Applying this to the time-dependent force function, we obtain

\[\vec{F}_{ave} = \frac{1}{\Delta t} \int_{t_{i}}^{t_{f}} \vec{F} (t)dt \ldotp \label{9.4}\]

Therefore, from Equation \ref{9.3},

\[\vec{J} = \vec{F}_{ave} \Delta t \ldotp \label{9.5}\]

The idea here is that you can calculate the impulse on the object even if you don’t know the details of the force as a function of time; you only need the average force. In fact, though, the process is usually reversed: You determine the impulse (by measurement or calculation) and then calculate the average force that caused that impulse.

To calculate the impulse, a useful result follows from writing the force in Equation \ref{9.3} as \(\vec{F}\)(t) = m \(\vec{a}\)(t):

\[\vec{J} = \int_{t_{i}}^{t_{f}} \vec{F} (t)dt = m \int_{t_{i}}^{t_{f}} \vec{a} (t)dt = m \big[ \vec{v} (t_{f}) - \vec{v} (t_{i}) \big] \ldotp\]

For a constant force \(\vec{F}_{ave}\) = \(\vec{F}\) = m\(\vec{a}\), this simplifies to

\[\vec{J} = m \vec{a} \Delta t = m \vec{v}_{f} - m \vec{v}_{i} = m (\vec{v}_{f} - \vec{v}_{i}) \ldotp\]

\[\vec{J} = m \Delta \vec{v} \ldotp \label{9.6}\]

Note that the integral form, Equation \ref{9.3}, applies to constant forces as well; in that case, since the force is independent of time, it comes out of the integral, which can then be trivially evaluated.

Example \(\PageIndex{1}\): The Arizona Meteor Crater

Approximately 50,000 years ago, a large (radius of 25 m) iron-nickel meteorite collided with Earth at an estimated speed of 1.28 x 10 4 m/s in what is now the northern Arizona desert, in the United States. The impact produced a crater that is still visible today (Figure \(\PageIndex{3}\)); it is approximately 1200 m (three-quarters of a mile) in diameter, 170 m deep, and has a rim that rises 45 m above the surrounding desert plain. Iron-nickel meteorites typically have a density of \(\rho\) = 7970 kg/m 3 . Use impulse considerations to estimate the average force and the maximum force that the meteor applied to Earth during the impact.

It is conceptually easier to reverse the question and calculate the force that Earth applied on the meteor in order to stop it. Therefore, we’ll calculate the force on the meteor and then use Newton’s third law to argue that the force from the meteor on Earth was equal in magnitude and opposite in direction.

Using the given data about the meteor, and making reasonable guesses about the shape of the meteor and impact time, we first calculate the impulse using Equation \ref{9.6}. We then use the relationship between force and impulse Equation \ref{9.5} to estimate the average force during impact. Next, we choose a reasonable force function for the impact event, calculate the average value of that function Equation \ref{9.4}, and set the resulting expression equal to the calculated average force. This enables us to solve for the maximum force.

Define upward to be the +y-direction. For simplicity, assume the meteor is traveling vertically downward prior to impact. In that case, its initial velocity is \(\vec{v}_{i}\) = −v i \(\hat{j}\), and the force Earth exerts on the meteor points upward, \(\vec{F}\)(t) = + F(t) \(\hat{j}\). The situation at t = 0 is depicted below.

The average force during the impact is related to the impulse by

\[\vec{F}_{ave} = \frac{\vec{J}}{\Delta t} \ldotp\]

From Equation \ref{9.6}, \(\vec{J}\) = m\(\Delta \vec{v}\), so we have

\[\vec{F}_{ave} = \frac{m \Delta \vec{v}}{\Delta t} \ldotp\]

The mass is equal to the product of the meteor’s density and its volume:

\[m = \rho V \ldotp\]

If we assume (guess) that the meteor was roughly spherical, we have

\[V = \frac{4}{3} \pi R^{3} \ldotp\]

Thus we obtain

\[\vec{F}_{ave} = \frac{\rho V \Delta \vec{v}}{\Delta t} = \frac{\rho \left(\dfrac{4}{3} \pi R^{3}\right) (\vec{v}_{f} - \vec{v}_{i})}{\Delta t} \ldotp\]

The problem says the velocity at impact was −1.28 x 10 4 m/s \(\hat{j}\) (the final velocity is zero); also, we guess that the primary impact lasted about t max = 2 s. Substituting these values gives

\[\begin{split} \vec{F}_{ave} & = \frac{(7970\; kg/m^{3}) \big[ \frac{4}{3} \pi (25\; m)^{3} \big] \big[ 0\; m/s - (-1.28 \times 10^{4}\; m/s\; \hat{j}) \big]}{2\; s} \\ & = + (3.33 \times 10^{12}\; N) \hat{j} \end{split}\]

This is the average force applied during the collision. Notice that this force vector points in the same direction as the change of velocity vector \(\Delta \vec{v}\).

Next, we calculate the maximum force. The impulse is related to the force function by

\[\vec{J} = \int_{t_{i}}^{t_{max}} \vec{F} (t)dt \ldotp\]

We need to make a reasonable choice for the force as a function of time. We define t = 0 to be the moment the meteor first touches the ground. Then we assume the force is a maximum at impact, and rapidly drops to zero. A function that does this is

\[F(t) = F_{max} e^{\frac{-t^{2}}{2 \tau^{2}}} \ldotp\]

The parameter \(\tau\) represents how rapidly the force decreases to zero.) The average force is

\[F_{ave} = \frac{1}{\Delta t} \int_{0}^{t_{max}} F_{max} e^{\frac{-t^{2}}{2 \tau^{2}}} dt\]

where \(\Delta\)t = t max − 0 s. Since we already have a numeric value for F ave , we can use the result of the integral to obtain F max . Choosing \(\tau\) = \(\frac{1}{e}\)t max (this is a common choice, as you will see in later chapters), and guessing that t max = 2 s, this integral evaluates to

\[F_{avg} = 0.458\; F_{max} \ldotp\]

Thus, the maximum force has a magnitude of

\[\begin{split} 0.458\; F_{max} & = 3.33 \times 10^{12}\; N \\ F_{max} & = 7.27 \times 10^{12}\; N \ldotp \end{split}\]

The complete force function, including the direction, is

\[\vec{F} (t) = (7.27 \times 10^{12}\; N) e^{\frac{-t^{2}}{8\; s^{2}}} \hat{y} \ldotp\]

This is the force Earth applied to the meteor; by Newton’s third law, the force the meteor applied to Earth is

\[\vec{F} (t) = - (7.27 \times 10^{12}\; N) e^{\frac{-t^{2}}{8\; s^{2}}} \hat{y}\]

which is the answer to the original question.

Significance

The graph of this function contains important information. Let’s graph (the magnitude of) both this function and the average force together (Figure \(\PageIndex{4}\)).

Notice that the area under each plot has been filled in. For the plot of the (constant) force F ave , the area is a rectangle, corresponding to F ave \(\Delta\)t = J. As for the plot of F(t), recall from calculus that the area under the plot of a function is numerically equal to the integral of that function, over the specified interval; so here, that is \(\int_{0}^{t_{max}}\)F(t)dt = J. Thus, the areas are equal, and both represent the impulse that the meteor applied to Earth during the two-second impact. The average force on Earth sounds like a huge force, and it is. Nevertheless, Earth barely noticed it. The acceleration Earth obtained was just

\[\vec{a} = \frac{- \vec{F}_{ave}}{M_{Earth}} = \frac{- (3.33 \times 10^{12}\; N) \hat{j}}{5.97 \times 10^{24}\; kg} = - (5.6 \times 10^{-13} m/s^{2}) \hat{j}\]

which is completely immeasurable. That said, the impact created seismic waves that nowadays could be detected by modern monitoring equipment.

Example \(\PageIndex{2}\): The Benefits of Impulse

A car traveling at 27 m/s collides with a building. The collision with the building causes the car to come to a stop in approximately 1 second. The driver, who weighs 860 N, is protected by a combination of a variable-tension seatbelt and an airbag (Figure \(\PageIndex{5}\)). (In effect, the driver collides with the seatbelt and airbag and not with the building.) The airbag and seatbelt slow his velocity, such that he comes to a stop in approximately 2.5 s.

• What average force does the driver experience during the collision?
• Without the seatbelt and airbag, his collision time (with the steering wheel) would have been approximately 0.20 s. What force would he experience in this case?

We are given the driver’s weight, his initial and final velocities, and the time of collision; we are asked to calculate a force. Impulse seems the right way to tackle this; we can combine Equation \ref{9.5} and Equation \ref{9.6}.

• Define the +x-direction to be the direction the car is initially moving. We know $$\vec{J} = \vec{F} \Delta t$$and $$\vec{J} = m \Delta \vec{v} \ldotp$$Since J is equal to both those things, they must be equal to each other: $$\vec{F} \Delta t = m \Delta \vec{v} \ldotp$$We need to convert this weight to the equivalent mass, expressed in SI units: $$\frac{860\; N}{9.8\; m/s^{2}} = 87.8\; kg \ldotp$$Remembering that \(\Delta \vec{v} = \vec{v}_{f} − \vec{v}_{i}\), and noting that the final velocity is zero, we solve for the force: $$\vec{F} = m \frac{0 - v_{i}\; \hat{i}}{\Delta t} = (87.8\; kg) \left(\dfrac{-(27\; m/s) \hat{i}}{2.5\; s}\right) = - (948\; N) \hat{i} \ldotp$$The negative sign implies that the force slows him down. For perspective, this is about 1.1 times his own weight.
• Same calculation, just the different time interval: $$\vec{F} = (87.8\; kg) \left(\dfrac{-(27\; m/s) \hat{i}}{0.20\; s}\right) = - (11,853\; N) \hat{i} \ldotp$$which is about 14 times his own weight. Big difference!

You see that the value of an airbag is how greatly it reduces the force on the vehicle occupants. For this reason, they have been required on all passenger vehicles in the United States since 1991, and have been commonplace throughout Europe and Asia since the mid-1990s. The change of momentum in a crash is the same, with or without an airbag; the force, however, is vastly different.

About me and why I created this physics website.

Impulse And Momentum

• Search Website

Real World Applications — for high school level and above

• Amusement Parks
• Battle & Weapons
• Engineering
• Miscellaneous

Education & Theory — for high school level and above

• Useful Formulas
• Physics Questions
• Example Mechanics Problems
• Learn Physics Compendium

Kids Section

• Physics For Kids
• Science Experiments
• Science Fair Ideas
• Science Quiz
• Science Toys
• Teacher Resources
• Commercial Disclosure
• Privacy Policy

© Copyright 2009-2024 real-world-physics-problems.com

Gurumuda Networks

Momentum and impulse – problems and solutions

1. A small ball is thrown horizontally with a constant speed of 10 m/s. The ball hits the wall and reflected with the same speed. What is the change in linear momentum of the ball?

Mass (m) = 0.2 kg

Initial speed (v o ) = -10 m/s

Final speed (v t ) = 10 m/s

The plus and minus sign indicates that the objects moves in opposite direction.

Wanted : the change in linear momentum (Δp)

Formula of the change in linear momentum :

Δp = m v t – m v o = m (v t – v o )

The change in linear momentum :

Δp = 0.2 (10 – (-10)) = 0.2 (10 + 10)

Δp = 0.2 (20)

Δp = 4 kg m/s

2. A 10-gram ball falls freely from a height, hits the floor at 15 m/s, then reflected upward at 10 m/s. Determine the impulse!

Mass (m) = 10 gram = 0.01 kg

Initial velocity (v o ) = -15 m/s

Final velocity (v t ) = 10 m/s

Wanted : Impulse (I)

The impulse (I) equals the change in momentum (Δp)

I = m v t – m v o = m (v t – v o )

I = 0.01 (10 – (-15)) = 0.01 (10 + 15)

I = 0.01 (25)

I = 0.25 kg m/s

3. A 200-gram ball thrown horizontally with a speed of 4 m/s, then the ball was hit in the same direction. The duration of the ball in contact with the bat is 2 mi l liseconds and the ball speed after leaving the bat is 12 m/s. The magnitude of force exerted by the batter on the ball is …

Mass (m) = 200 gram = 0.2 kg

Initial velocity (v o ) = 4 m/s

Final velocity (v t ) = 12 m/s

Time interval (t) = 2 milliseconds = (2/1000) seconds = 0.002 seconds

Wanted : The magnitude of the force (F)

Formula of impulse :

Formula of the change in momentum :

m v t – m v o = m (v t – v o )

F t = m (v t – v o )

F (0.002) = (0.2)(12 – 4)

F (0.002) = (0.2)(8)

F (0.002) = 1.6

F = 1.6 / 0.002

F = 800 Newton

[wpdm_package id=’1155′]

• Linear momentum problems and solutions
• Momentum and impulse problems and solutions
• Perfectly elastic collisions in one dimension problems and solutions
• Perfectly inelastic collisions in one dimension problems and solutions
• Inelastic collisions in one dimension problems and solutions

Leave a Comment Cancel reply

You must be logged in to post a comment.

This site uses Akismet to reduce spam. Learn how your comment data is processed .

Impulse and Momentum

by Gary Gende and Owen "O-Dog" Zahorcak, January 1998

Table of Contents

New quantities.

• General Problem Solving Strategy
• Example Problem #1
• Example Problem #2

Sample Problems

Solutions to sample problems.

• Go back to Tutorial Page

Here's the quantities you can know:

• /\ Delta (aka the change)
• /\ p Impulse

These quantities are defined and explained on other pages execept Impulse and momentum. They are defined below.

Momentum is defined as the product of an object's mass and velocity This means p(momentum)=m(mass)*V(velocity) by the definition of momentum Momentum is measured in N(Newton)m(meters)/s(per second)

Impulse is the product of force and time. As this suggests the unit for measuring impulse is N(Newton)s(seconds) A formula for finding impulse is shown and explained below.

From other chapters we know that

We can use these formulas to show that /\ p(Impulse)=Ft

• F = ma....it just does
• F = m( /\ V/t) ....a= /\ a/t
• F = (m(V-V o ))/t = (mV-mV o )/t.... /\ V = V-V o and The Distributive Property
• F = (p-p o )/ /\ t = /\ p/t....p=mv and /\ p = p-p o
• /\ p = Ft....multiply both sides by t

*Several of the formula in the work above become important*

F= /\ p/t is Newton's Second Law of Motion.

So now we have all the formulas we need for solving impulse and momentum problems:

• F = m( /\ V/t)....(From above)

Go back to: Table of Contents

General Problem Solving Strategy:

• Read the problem.
• Go through the problem and figure out what is given or implied Make a list, and identify the quantities you know.
• Find any formula that will allow you to calculate anything that you don't know, and apply it.
• Add what you just found in the last step to your list of knowns.
• Check to see if you have found the answer. If not, repeat the previous two steps until you are done.

Mother of all Example Problems

Joe the alien fires a 20 Kg photon torpedo at 200 m/s from his stationary UFO in deep space. The torpedo has special no fuel engines that can give 650 N of force. What is the momentum of the torpedo? How long must Joe fire the engines to get 3000 Ns of impulse. What speed is Joe attempting to get the torpedo to go? If Joe is firing at you and your UFO can accelerate at a rate of 30 m/s/s, will you be able to out accellerate the torpedo?

a. Momentum is just p=mv so plug in the known m (20) and V (200) 20 * 200 = 4000 Kgm/s

b. The needed formula is /\ p = Ft. F (650) and /\ p (1500) are given. divide both sides of the equation by F to get /\ p/F = t then plug in the known values to get 3000/650 = t = 4.62 Ns

c. The needed formula now is F = m( /\ V/t). F is still 650 N, the torpedo still has a mass of 20 Kg and time can be found from part b. When you plug them in you get 650 = 20( /\ V/2.31). Multiplying both sides by 2.31/20 gives you (4.62 * 650)/20 = /\ V = 150 m/s. Since this is the change in speed (hence the /\ ), 150 needs to be added to the original 200. The final speed is 350 m/s.

d. F = ma is the importanr equation now. You know F (650 N) and m (20 Kg) so just divide both sides of the equation by m to solve it for a and plug in the numbers to get 650/20 = a = 32.5 m/s/s. So you better hope you have a big enough head start.

The answers to each problem follow it in parentheses. They also link to a solution to the problem. Try the problem, check your answer, and go to the solution if you do not understand.

What is the momentum of a 23 Kg cannon shell going 530 m/s?

Impulse Momentum Exam 1 and Problem Solutions

where ΔV=V₂-V₁=-3-4=-7m/s

I=m.ΔV=3.(-7)=-21kg.m/s

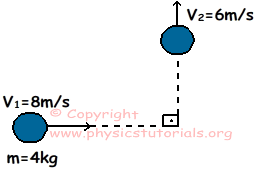
P₂=m.V₂=4kg.6m/s=24kg.m/s

ΔP=P₂+P₁ (vector addition)

ΔP²=P₂²+P₁²=m²(v₂²+v₁²)

ΔP=40kg.m/s

Impulse=change in momentum

I=ΔP=40kg.m/s

3. Find the impulse and force which make 12m/s change in the velocity of object having 16kg mass in 4 s.

F.Δt=ΔP=m.ΔV

F.4s=16kg.12m/s

F.Δt=Impulse=192kg.m/s

F.Δt=20.2/2+20.(6-2)+20.(10-6)/2

F.Δt=140kg.m/s

5. A ball having mass 500g hits wall with a10m/s velocity. Wall applies 4000 N force to the ball and it turns back with 8m/s velocity. Find the time of ball-wall contact.

F.Δt=ΔP=m.ΔV=m.(V₂-V₁)

-4000.Δt=0,5kg.(8-10)

Δt=0,00025s