what is an assignment problem give two applications

Assignment Problem: Meaning, Methods and Variations | Operations Research

After reading this article you will learn about:- 1. Meaning of Assignment Problem 2. Definition of Assignment Problem 3. Mathematical Formulation 4. Hungarian Method 5. Variations.

Meaning of Assignment Problem:

An assignment problem is a particular case of transportation problem where the objective is to assign a number of resources to an equal number of activities so as to minimise total cost or maximize total profit of allocation.

The problem of assignment arises because available resources such as men, machines etc. have varying degrees of efficiency for performing different activities, therefore, cost, profit or loss of performing the different activities is different.

Thus, the problem is “How should the assignments be made so as to optimize the given objective”. Some of the problem where the assignment technique may be useful are assignment of workers to machines, salesman to different sales areas.

Definition of Assignment Problem:

ADVERTISEMENTS:

Suppose there are n jobs to be performed and n persons are available for doing these jobs. Assume that each person can do each job at a term, though with varying degree of efficiency, let c ij be the cost if the i-th person is assigned to the j-th job. The problem is to find an assignment (which job should be assigned to which person one on-one basis) So that the total cost of performing all jobs is minimum, problem of this kind are known as assignment problem.

The assignment problem can be stated in the form of n x n cost matrix C real members as given in the following table:

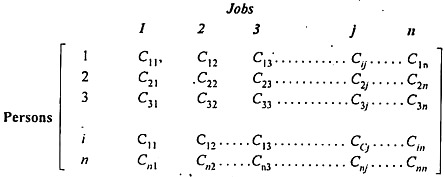
How to Solve the Assignment Problem: A Complete Guide

Table of Contents

Assignment problem is a special type of linear programming problem that deals with assigning a number of resources to an equal number of tasks in the most efficient way. The goal is to minimize the total cost of assignments while ensuring that each task is assigned to only one resource and each resource is assigned to only one task. In this blog, we will discuss the solution of the assignment problem using the Hungarian method, which is a popular algorithm for solving the problem.

Understanding the Assignment Problem

Before we dive into the solution, it is important to understand the problem itself. In the assignment problem, we have a matrix of costs, where each row represents a resource and each column represents a task. The objective is to assign each resource to a task in such a way that the total cost of assignments is minimized. However, there are certain constraints that need to be satisfied – each resource can be assigned to only one task and each task can be assigned to only one resource.

Solving the Assignment Problem

There are various methods for solving the assignment problem, including the Hungarian method, the brute force method, and the auction algorithm. Here, we will focus on the steps involved in solving the assignment problem using the Hungarian method, which is the most commonly used and efficient method.

Step 1: Set up the cost matrix

The first step in solving the assignment problem is to set up the cost matrix, which represents the cost of assigning a task to an agent. The matrix should be square and have the same number of rows and columns as the number of tasks and agents, respectively.

Step 2: Subtract the smallest element from each row and column

To simplify the calculations, we need to reduce the size of the cost matrix by subtracting the smallest element from each row and column. This step is called matrix reduction.

Step 3: Cover all zeros with the minimum number of lines

The next step is to cover all zeros in the matrix with the minimum number of horizontal and vertical lines. This step is called matrix covering.

Step 4: Test for optimality and adjust the matrix

To test for optimality, we need to calculate the minimum number of lines required to cover all zeros in the matrix. If the number of lines equals the number of rows or columns, the solution is optimal. If not, we need to adjust the matrix and repeat steps 3 and 4 until we get an optimal solution.

Step 5: Assign the tasks to the agents

The final step is to assign the tasks to the agents based on the optimal solution obtained in step 4. This will give us the most cost-effective or profit-maximizing assignment.

Solution of the Assignment Problem using the Hungarian Method

The Hungarian method is an algorithm that uses a step-by-step approach to find the optimal assignment. The algorithm consists of the following steps:

• Subtract the smallest entry in each row from all the entries of the row.
• Subtract the smallest entry in each column from all the entries of the column.
• Draw the minimum number of lines to cover all zeros in the matrix. If the number of lines drawn is equal to the number of rows, we have an optimal solution. If not, go to step 4.
• Determine the smallest entry not covered by any line. Subtract it from all uncovered entries and add it to all entries covered by two lines. Go to step 3.

The above steps are repeated until an optimal solution is obtained. The optimal solution will have all zeros covered by the minimum number of lines. The assignments can be made by selecting the rows and columns with a single zero in the final matrix.

Applications of the Assignment Problem

The assignment problem has various applications in different fields, including computer science, economics, logistics, and management. In this section, we will provide some examples of how the assignment problem is used in real-life situations.

Applications in Computer Science

The assignment problem can be used in computer science to allocate resources to different tasks, such as allocating memory to processes or assigning threads to processors.

Applications in Economics

The assignment problem can be used in economics to allocate resources to different agents, such as allocating workers to jobs or assigning projects to contractors.

Applications in Logistics

The assignment problem can be used in logistics to allocate resources to different activities, such as allocating vehicles to routes or assigning warehouses to customers.

Applications in Management

The assignment problem can be used in management to allocate resources to different projects, such as allocating employees to tasks or assigning budgets to departments.

Let’s consider the following scenario: a manager needs to assign three employees to three different tasks. Each employee has different skills, and each task requires specific skills. The manager wants to minimize the total time it takes to complete all the tasks. The skills and the time required for each task are given in the table below:

The assignment problem is to determine which employee should be assigned to which task to minimize the total time required. To solve this problem, we can use the Hungarian method, which we discussed in the previous blog.

Using the Hungarian method, we first subtract the smallest entry in each row from all the entries of the row:

Next, we subtract the smallest entry in each column from all the entries of the column:

We draw the minimum number of lines to cover all the zeros in the matrix, which in this case is three:

Since the number of lines is equal to the number of rows, we have an optimal solution. The assignments can be made by selecting the rows and columns with a single zero in the final matrix. In this case, the optimal assignments are:

• Emp 1 to Task 3
• Emp 2 to Task 2
• Emp 3 to Task 1

This assignment results in a total time of 9 units.

I hope this example helps you better understand the assignment problem and how to solve it using the Hungarian method.

Solving the assignment problem may seem daunting, but with the right approach, it can be a straightforward process. By following the steps outlined in this guide, you can confidently tackle any assignment problem that comes your way.

How useful was this post?

Click on a star to rate it!

Average rating 0 / 5. Vote count: 0

No votes so far! Be the first to rate this post.

We are sorry that this post was not useful for you! 😔

Let us improve this post!

Tell us how we can improve this post?

Operations Research

1 Operations Research-An Overview

• History of O.R.
• Approach, Techniques and Tools
• Phases and Processes of O.R. Study
• Typical Applications of O.R
• Limitations of Operations Research
• Models in Operations Research
• O.R. in real world

2 Linear Programming: Formulation and Graphical Method

• General formulation of Linear Programming Problem
• Optimisation Models
• Basics of Graphic Method
• Important steps to draw graph
• Multiple, Unbounded Solution and Infeasible Problems
• Solving Linear Programming Graphically Using Computer
• Application of Linear Programming in Business and Industry

3 Linear Programming-Simplex Method

• Principle of Simplex Method
• Computational aspect of Simplex Method
• Simplex Method with several Decision Variables
• Two Phase and M-method
• Multiple Solution, Unbounded Solution and Infeasible Problem
• Sensitivity Analysis
• Dual Linear Programming Problem

4 Transportation Problem

• Basic Feasible Solution of a Transportation Problem
• Modified Distribution Method
• Stepping Stone Method
• Unbalanced Transportation Problem
• Degenerate Transportation Problem
• Transhipment Problem
• Maximisation in a Transportation Problem

5 Assignment Problem

• Solution of the Assignment Problem
• Unbalanced Assignment Problem
• Problem with some Infeasible Assignments
• Maximisation in an Assignment Problem
• Crew Assignment Problem

6 Application of Excel Solver to Solve LPP

• Building Excel model for solving LP: An Illustrative Example

7 Goal Programming

• Concepts of goal programming
• Goal programming model formulation
• Graphical method of goal programming
• The simplex method of goal programming
• Using Excel Solver to Solve Goal Programming Models
• Application areas of goal programming

8 Integer Programming

• Some Integer Programming Formulation Techniques
• Binary Representation of General Integer Variables
• Unimodularity
• Cutting Plane Method
• Branch and Bound Method
• Solver Solution

9 Dynamic Programming

• Dynamic Programming Methodology: An Example
• Definitions and Notations
• Dynamic Programming Applications

10 Non-Linear Programming

• Solution of a Non-linear Programming Problem
• Convex and Concave Functions
• Kuhn-Tucker Conditions for Constrained Optimisation
• Quadratic Programming
• Separable Programming
• NLP Models with Solver

11 Introduction to game theory and its Applications

• Important terms in Game Theory
• Saddle points
• Mixed strategies: Games without saddle points
• 2 x n games
• Exploiting an opponent’s mistakes

12 Monte Carlo Simulation

• Reasons for using simulation
• Monte Carlo simulation
• Limitations of simulation
• Steps in the simulation process
• Some practical applications of simulation
• Two typical examples of hand-computed simulation
• Computer simulation

13 Queueing Models

• Characteristics of a queueing model
• Notations and Symbols
• Statistical methods in queueing
• The M/M/I System
• The M/M/C System
• The M/Ek/I System
• Decision problems in queueing

www.springer.com The European Mathematical Society

• StatProb Collection
• Recent changes
• Current events
• Random page
• Project talk
• Request account
• What links here
• Related changes
• Special pages
• Printable version
• Permanent link
• Page information
• View source

Assignment problem

The problem of optimally assigning $ m $ individuals to $ m $ jobs. It can be formulated as a linear programming problem that is a special case of the transport problem :

maximize $ \sum _ {i,j } c _ {ij } x _ {ij } $

$$ \sum _ { j } x _ {ij } = a _ {i} , i = 1 \dots m $$

(origins or supply),

$$ \sum _ { i } x _ {ij } = b _ {j} , j = 1 \dots n $$

(destinations or demand), where $ x _ {ij } \geq 0 $ and $ \sum a _ {i} = \sum b _ {j} $, which is called the balance condition. The assignment problem arises when $ m = n $ and all $ a _ {i} $ and $ b _ {j} $ are $ 1 $.

If all $ a _ {i} $ and $ b _ {j} $ in the transposed problem are integers, then there is an optimal solution for which all $ x _ {ij } $ are integers (Dantzig's theorem on integral solutions of the transport problem).

In the assignment problem, for such a solution $ x _ {ij } $ is either zero or one; $ x _ {ij } = 1 $ means that person $ i $ is assigned to job $ j $; the weight $ c _ {ij } $ is the utility of person $ i $ assigned to job $ j $.

The special structure of the transport problem and the assignment problem makes it possible to use algorithms that are more efficient than the simplex method . Some of these use the Hungarian method (see, e.g., [a5] , [a1] , Chapt. 7), which is based on the König–Egervary theorem (see König theorem ), the method of potentials (see [a1] , [a2] ), the out-of-kilter algorithm (see, e.g., [a3] ) or the transportation simplex method.

In turn, the transportation problem is a special case of the network optimization problem.

A totally different assignment problem is the pole assignment problem in control theory.

• This page was last edited on 5 April 2020, at 18:48.
• Privacy policy
• About Encyclopedia of Mathematics
• Disclaimers
• Impressum-Legal

Quantitative Techniques: Theory and Problems by P. C. Tulsian, Vishal Pandey

Get full access to Quantitative Techniques: Theory and Problems and 60K+ other titles, with a free 10-day trial of O'Reilly.

There are also live events, courses curated by job role, and more.

WHAT IS ASSIGNMENT PROBLEM

Assignment Problem is a special type of linear programming problem where the objective is to minimise the cost or time of completing a number of jobs by a number of persons.

The assignment problem in the general form can be stated as follows:

“Given n facilities, n jobs and the effectiveness of each facility for each job, the problem is to assign each facility to one and only one job in such a way that the measure of effectiveness is optimised (Maximised or Minimised).”

Several problems of management has a structure identical with the assignment problem.

Example I A manager has four persons (i.e. facilities) available for four separate jobs (i.e. jobs) and the cost of assigning (i.e. effectiveness) each job to each ...

Get Quantitative Techniques: Theory and Problems now with the O’Reilly learning platform.

O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

Don’t leave empty-handed

Get Mark Richards’s Software Architecture Patterns ebook to better understand how to design components—and how they should interact.

It’s yours, free.

Check it out now on O’Reilly

Dive in for free with a 10-day trial of the O’Reilly learning platform—then explore all the other resources our members count on to build skills and solve problems every day.

International Symposium on Combinatorial Optimization

ISCO 2022: Combinatorial Optimization pp 172–186 Cite as

Nash Balanced Assignment Problem

• Minh Hieu Nguyen 11 ,
• Mourad Baiou 11 &
• Viet Hung Nguyen 11  
• Conference paper
• First Online: 21 November 2022

339 Accesses

2 Citations

Part of the book series: Lecture Notes in Computer Science ((LNCS,volume 13526))

In this paper, we consider a variant of the classic Assignment Problem (AP), called the Balanced Assignment Problem (BAP) [ 2 ]. The BAP seeks to find an assignment solution which has the smallest value of max-min distance : the difference between the maximum assignment cost and the minimum one. However, by minimizing only the max-min distance, the total cost of the BAP solution is neglected and it may lead to an inefficient solution in terms of total cost. Hence, we propose a fair way based on Nash equilibrium [ 1 , 3 , 4 ] to inject the total cost into the objective function of the BAP for finding assignment solutions having a better trade-off between the two objectives: the first aims at minimizing the total cost and the second aims at minimizing the max-min distance. For this purpose, we introduce the concept of Nash Fairness (NF) solutions based on the definition of proportional-fair scheduling adapted in the context of the AP: a transfer of utilities between the total cost and the max-min distance is considered to be fair if the percentage increase in the total cost is smaller than the percentage decrease in the max-min distance and vice versa.

We first show the existence of a NF solution for the AP which is exactly the optimal solution minimizing the product of the total cost and the max-min distance. However, finding such a solution may be difficult as it requires to minimize a concave function. The main result of this paper is to show that finding all NF solutions can be done in polynomial time. For that, we propose a Newton-based iterative algorithm converging to NF solutions in polynomial time. It consists in optimizing a sequence of linear combinations of the two objective based on Weighted Sum Method [ 5 ]. Computational results on various instances of the AP are presented and commented.

This is a preview of subscription content, log in via an institution .

Buying options

• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Available as EPUB and PDF
• Compact, lightweight edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Bertsimas, D., Farias, V.F., Trichakis, N.: The price of fairness. Oper. Res. January–February 59 (1), 17–31 (2011)

MathSciNet   MATH   Google Scholar  

Martello, S., Pulleyblank, W.R., Toth, P., De Werra, D.: Balanced optimization problems. Oper. Res. Lett. 3 (5), 275–278 (1984)

Article   MathSciNet   MATH   Google Scholar  

Kelly, F.P., Maullo, A.K., Tan, D.K.H.: Rate control for communication networks: shadow prices, proportional fairness and stability. J. Oper. Res. Soc. 49 (3), 237–252 (1997). https://doi.org/10.1057/palgrave.jors.2600523

Article   Google Scholar  

Ogryczak, W., Luss, H., Pioro, M., Nace, D., Tomaszewski, A.: Fair optimization and networks: a survey. J. Appl. Math. 2014 , 1–26 (2014)

Marler, R.T., Arora, J.S.: The weighted sum method for multi-objective optimization: new insights. Struct. Multi. Optim. 41 (6), 853–862 (2010)

Heller, I., Tompkins, C.B.: An extension of a theorem of Dantzig’s. Ann. Math. Stud. (38), 247–254 (1956)

Google Scholar  

Kuhn, H.W.: The Hungarian method for assignment problem. Naval Res. Logist. Q. 2 (1–2), 83–97 (1955)

Martello, S.: Most and least uniform spanning trees. Discrete Appl. Math. 15 (2), 181–197 (1986)

Beasley, J.E.: Linear programming on Clay supercomputer. J. Oper. Res. Soc. 41 , 133–139 (1990)

Nguyen, M.H, Baiou, M., Nguyen, V.H., Vo, T.Q.T.: Nash fairness solutions for balanced TSP. In: International Network Optimization Conference (INOC2022) (2022)

Download references

Author information

Authors and affiliations.

INP Clermont Auvergne, Univ Clermont Auvergne, Mines Saint-Etienne, CNRS, UMR 6158 LIMOS, 1 Rue de la Chebarde, Aubiere Cedex, France

Minh Hieu Nguyen, Mourad Baiou & Viet Hung Nguyen

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Viet Hung Nguyen .

Editor information

Editors and affiliations.

ESSEC Business School of Paris, Cergy Pontoise Cedex, France

Ivana Ljubić

IBM TJ Watson Research Center, Yorktown Heights, NY, USA

Francisco Barahona

Georgia Institute of Technology, Atlanta, GA, USA

Santanu S. Dey

Université Paris-Dauphine, Paris, France

A. Ridha Mahjoub

Proposition 1 . There may be more than one NF solution for the AP.

Let us illustrate this by an instance of the AP having the following cost matrix

By verifying all feasible assignment solutions in this instance, we obtain easily three assignment solutions \((1-1, 2-2, 3-3), (1-2, 2-3, 3-1)\) , \((1-3, 2-2, 3-1)\) and \((1-3, 2-1, 3-2)\) corresponding to 4 NF solutions (280, 36), (320, 32), (340, 30) and (364, 28). Note that \(i-j\) where \(1 \le i,j \le 3\) represents the assignment between worker i and job j in the solution of this instance.     \(\square \)

We recall below the proofs of some recent results that we have published in [ 10 ]. They are needed to prove the new results presented in this paper.

Theorem 2 [ 10 ] . \((P^{*},Q^{*}) = {{\,\mathrm{arg\,min}\,}}_{(P,Q) \in \mathcal {S}} PQ\) is a NF solution.

Obviously, there always exists a solution \((P^{*},Q^{*}) \in \mathcal {S}\) such that

Now \(\forall (P',Q') \in \mathcal {S}\) we have \(P'Q' \ge P^{*}Q^{*}\) . Then

The first inequality holds by the Cauchy-Schwarz inequality.

Hence, \((P^{*},Q^{*})\) is a NF solution.     \(\square \)

Theorem 3 [ 10 ] . \((P^{*},Q^{*}) \in \mathcal {S}\) is a NF solution if and only if \((P^{*},Q^{*})\) is an optimal solution of \(\mathcal {P(\alpha ^{*})}\) where \(\alpha ^{*} = \frac{Q^{*}}{P^{*}}\) .

Firstly, let \((P^{*},Q^{*})\) be a NF solution and \(\alpha ^{*} = \frac{Q^{*}}{P^{*}}\) . We will show that \((P^{*},Q^{*})\) is an optimal solution of \(\mathcal {P(\alpha ^{*})}\) .

Since \((P^{*},Q^{*})\) is a NF solution, we have

Since \(\alpha ^{*} = \frac{Q^{*}}{P^{*}}\) , we have \(\alpha ^{*}P^{*}+Q^{*} = 2Q^{*}\) .

Dividing two sides of ( 6 ) by \(P^{*} > 0\) we obtain

So we deduce from ( 7 )

Hence, \((P^{*},Q^{*})\) is an optimal solution of \(\mathcal {P}(\alpha ^{*})\) .

Now suppose \(\alpha ^{*} = \frac{Q^{*}}{P^{*}}\) and \((P^{*},Q^{*})\) is an optimal solution of \(\mathcal {P}(\alpha ^{*})\) , we show that \((P^{*},Q^{*})\) is a NF solution.

If \((P^{*},Q^{*})\) is not a NF solution, there exists a solution \((P',Q') \in \mathcal {S}\) such that

We have then

which contradicts the optimality of \((P^{*},Q^{*})\) .     \(\square \)

Lemma 3 [ 10 ] . Let \(\alpha , \alpha ' \in \mathbb {R}_+\) and \((P_{\alpha }, Q_{\alpha })\) , \((P_{\alpha '}, Q_{\alpha '})\) be the optimal solutions of \(\mathcal {P(\alpha )}\) and \(\mathcal {P(\alpha ')}\) respectively, if \(\alpha \le \alpha '\) then \(P_{\alpha } \ge P_{\alpha '}\) and \(Q_{\alpha } \le Q_{\alpha '}\) .

The optimality of \((P_{\alpha }, Q_{\alpha })\) and \((P_{\alpha '}, Q_{\alpha '})\) gives

By adding both sides of ( 8a ) and ( 8b ), we obtain \((\alpha - \alpha ') (P_{\alpha } - P_{\alpha '}) \le 0\) . Since \(\alpha \le \alpha '\) , it follows that \(P_{\alpha } \ge P_{\alpha '}\) .

On the other hand, inequality ( 8a ) implies \(Q_{\alpha '} - Q_{\alpha } \ge \alpha (P_{\alpha } - P_{\alpha '}) \ge 0\) that leads to \(Q_{\alpha } \le Q_{\alpha '}\) .     \(\square \)

Lemma 4 [ 10 ] . During the execution of Procedure Find ( \(\alpha _{0})\) in Algorithm 1 , \(\alpha _{i} \in [0,1], \, \forall i \ge 1\) . Moreover, if \(T_{0} \ge 0\) then the sequence \(\{\alpha _i\}\) is non-increasing and \(T_{i} \ge 0, \, \forall i \ge 0\) . Otherwise, if \(T_{0} \le 0\) then the sequence \(\{\alpha _i\}\) is non-decreasing and \(T_{i} \le 0, \, \forall i \ge 0\) .

Since \(P \ge Q \ge 0, \, \forall (P, Q) \in \mathcal {S}\) , it follows that \(\alpha _{i+1} = \frac{Q_i}{P_i} \in [0,1], \, \forall i \ge 0\) .

We first consider \(T_{0} \ge 0\) . We proof \(\alpha _i \ge \alpha _{i+1}, \, \forall i \ge 0\) by induction on i . For \(i = 0\) , we have \(T_{0} = \alpha _{0} P_{0} - Q_{0} = P_{0}(\alpha _{0}-\alpha _{1}) \ge 0\) , it follows that \(\alpha _{0} \ge \alpha _{1}\) . Suppose that our hypothesis is true until \(i = k \ge 0\) , we will prove that it is also true with \(i = k+1\) .

Indeed, we have

The inductive hypothesis gives \(\alpha _k \ge \alpha _{k+1}\) that implies \(P_{k+1} \ge P_k > 0\) and \(Q_{k} \ge Q_{k+1} \ge 0\) according to Lemma 3 . It leads to \(Q_{k}P_{k+1} - P_{k}Q_{k+1} \ge 0\) and then \(\alpha _{k+1} - \alpha _{k+2} \ge 0\) .

Hence, we have \(\alpha _{i} \ge \alpha _{i+1}, \, \forall i \ge 0\) .

Consequently, \(T_{i} = \alpha _{i}P_{i} - Q_{i} = P_{i}(\alpha _{i}-\alpha _{i+1}) \ge 0, \, \forall i \ge 0\) .

Similarly, if \(T_{0} \le 0\) we obtain that the sequence \(\{\alpha _i\}\) is non-decreasing and \(T_{i} \le 0, \, \forall i \ge 0\) . That concludes the proof.     \(\square \)

Lemma 5 [ 10 ] . From each \(\alpha _{0} \in [0,1]\) , Procedure Find \((\alpha _{0})\) converges to a coefficient \(\alpha _{k} \in \mathcal {C}_{0}\) satisfying \(\alpha _{k}\) is the unique element \(\in \mathcal {C}_{0}\) between \(\alpha _{0}\) and \(\alpha _{k}\) .

As a consequence of Lemma 4 , Procedure \(\textit{Find}(\alpha _{0})\) converges to a coefficient \(\alpha _{k} \in [0,1], \forall \alpha _{0} \in [0,1]\) .

By the stopping criteria of Procedure Find \((\alpha _{0})\) , when \(T_{k} = \alpha _{k} P_{k} - Q_{k} = 0\) we obtain \(\alpha _{k} \in C_{0}\) and \((P_{k},Q_{k})\) is a NF solution. (Theorem 3 )

If \(T_{0} = 0\) then obviously \(\alpha _{k} = \alpha _{0}\) . We consider \(T_{0} > 0\) and the sequence \(\{\alpha _i\}\) is now non-negative, non-increasing. We will show that \([\alpha _{k},\alpha _{0}] \cap \mathcal {C}_{0} = \alpha _{k}\) .

Suppose that we have \(\alpha \in (\alpha _{k},\alpha _{0}]\) and \(\alpha \in \mathcal {C}_{0}\) corresponding to a NF solution ( P ,  Q ). Then there exists \(1 \le i \le k\) such that \(\alpha \in (\alpha _{i}, \alpha _{i-1}]\) . Since \(\alpha \le \alpha _{i-1}\) , \(P \ge P_{i-1}\) and \(Q \le Q_{i-1}\) due to Lemma 3 . Thus, we get

By the definitions of \(\alpha \) and \(\alpha _{i}\) , inequality ( 9 ) is equivalent to \(\alpha \le \alpha _{i}\) which leads to a contradiction.

By repeating the same argument for \(T_{0} < 0\) , we also have a contradiction.     \(\square \)

Rights and permissions

Reprints and permissions

Copyright information

© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG

About this paper

Cite this paper.

Nguyen, M.H., Baiou, M., Nguyen, V.H. (2022). Nash Balanced Assignment Problem. In: Ljubić, I., Barahona, F., Dey, S.S., Mahjoub, A.R. (eds) Combinatorial Optimization. ISCO 2022. Lecture Notes in Computer Science, vol 13526. Springer, Cham. https://doi.org/10.1007/978-3-031-18530-4_13

Download citation

DOI : https://doi.org/10.1007/978-3-031-18530-4_13

Published : 21 November 2022

Publisher Name : Springer, Cham

Print ISBN : 978-3-031-18529-8

Online ISBN : 978-3-031-18530-4

eBook Packages : Computer Science Computer Science (R0)

Share this paper

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

Assignment Model | Linear Programming Problem (LPP) | Introduction

What is assignment model.

→ Assignment model is a special application of Linear Programming Problem (LPP) , in which the main objective is to assign the work or task to a group of individuals such that;

i) There is only one assignment.

ii) All the assignments should be done in such a way that the overall cost is minimized (or profit is maximized, incase of maximization).

→ In assignment problem, the cost of performing each task by each individual is known. → It is desired to find out the best assignments, such that overall cost of assigning the work is minimized.

For example:

Suppose there are 'n' tasks, which are required to be performed using 'n' resources.

The cost of performing each task by each resource is also known (shown in cells of matrix)

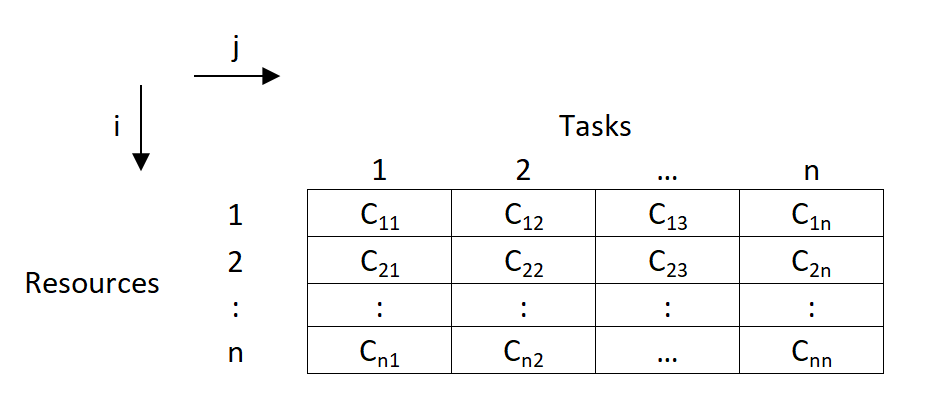
• In the above asignment problem, we have to provide assignments such that there is one to one assignments and the overall cost is minimized.

How Assignment Problem is related to LPP? OR Write mathematical formulation of Assignment Model.

→ Assignment Model is a special application of Linear Programming (LP).

→ The mathematical formulation for Assignment Model is given below:

→ Let, C i j \text {C}_{ij} C ij ​ denotes the cost of resources 'i' to the task 'j' ; such that

→ Now assignment problems are of the Minimization type. So, our objective function is to minimize the overall cost.

→ Subjected to constraint;

(i) For all j t h j^{th} j t h task, only one i t h i^{th} i t h resource is possible:

(ii) For all i t h i^{th} i t h resource, there is only one j t h j^{th} j t h task possible;

(iii) x i j x_{ij} x ij ​ is '0' or '1'.

Types of Assignment Problem:

(i) balanced assignment problem.

• It consist of a suqare matrix (n x n).
• Number of rows = Number of columns

(ii) Unbalanced Assignment Problem

• It consist of a Non-square matrix.
• Number of rows ≠ \not=  = Number of columns

Methods to solve Assignment Model:

(i) integer programming method:.

In assignment problem, either allocation is done to the cell or not.

So this can be formulated using 0 or 1 integer.

While using this method, we will have n x n decision varables, and n+n equalities.

So even for 4 x 4 matrix problem, it will have 16 decision variables and 8 equalities.

So this method becomes very lengthy and difficult to solve.

(ii) Transportation Methods:

As assignment problem is a special case of transportation problem, it can also be solved using transportation methods.

In transportation methods ( NWCM , LCM & VAM), the total number of allocations will be (m+n-1) and the solution is known as non-degenerated. (For eg: for 3 x 3 matrix, there will be 3+3-1 = 5 allocations)

But, here in assignment problems, the matrix is a square matrix (m=n).

So total allocations should be (n+n-1), i.e. for 3 x 3 matrix, it should be (3+3-1) = 5

But, we know that in 3 x 3 assignment problem, maximum possible possible assignments are 3 only.

So, if are we will use transportation methods, then the solution will be degenerated as it does not satisfy the condition of (m+n-1) allocations.

So, the method becomes lengthy and time consuming.

(iii) Enumeration Method:

It is a simple trail and error type method.

Consider a 3 x 3 assignment problem. Here the assignments are done randomly and the total cost is found out.

For 3 x 3 matrix, the total possible trails are 3! So total 3! = 3 x 2 x 1 = 6 trails are possible.

The assignments which gives minimum cost is selected as optimal solution.

But, such trail and error becomes very difficult and lengthy.

If there are more number of rows and columns, ( For eg: For 6 x 6 matrix, there will be 6! trails. So 6! = 6 x 5 x 4 x 3 x 2 x 1 = 720 trails possible) then such methods can't be applied for solving assignments problems.

(iv) Hungarian Method:

It was developed by two mathematicians of Hungary. So, it is known as Hungarian Method.

It is also know as Reduced matrix method or Flood's technique.

There are two main conditions for applying Hungarian Method:

(1) Square Matrix (n x n). (2) Problem should be of minimization type.

Suggested Notes:

Modified Distribution Method (MODI) | Transportation Problem | Transportation Model

Stepping Stone | Transportation Problem | Transportation Model

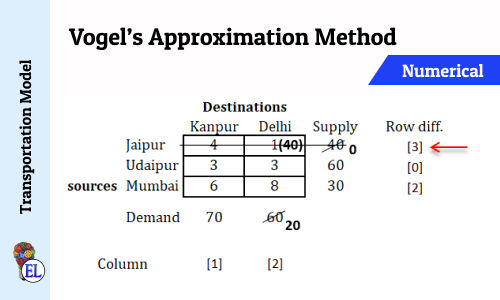
Vogel’s Approximation Method (VAM) | Method to Solve Transportation Problem | Transportation Model

Transportation Model - Introduction

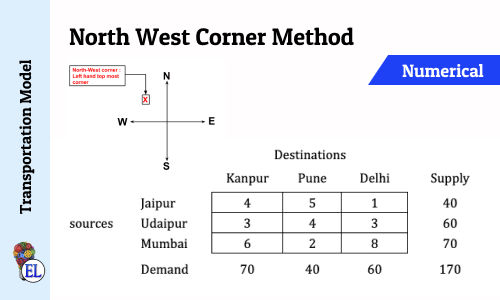
North West Corner Method | Method to Solve Transportation Problem | Transportation Model

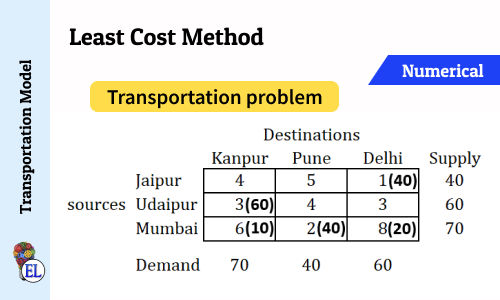
Least Cost Method | Method to Solve Transportation Problem | Transportation Model

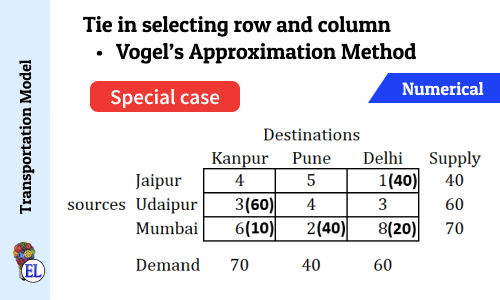
Tie in selecting row and column (Vogel's Approximation Method - VAM) | Numerical | Solving Transportation Problem | Transportation Model

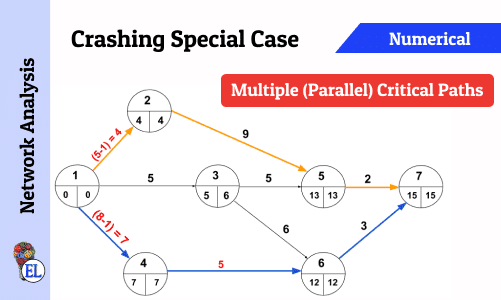
Crashing Special Case - Multiple (Parallel) Critical Paths

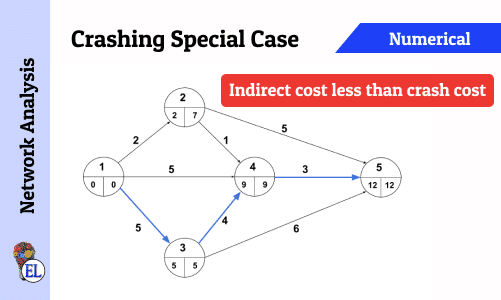
Crashing Special Case - Indirect cost less than Crash Cost

Basics of Program Evaluation and Review Technique (PERT)

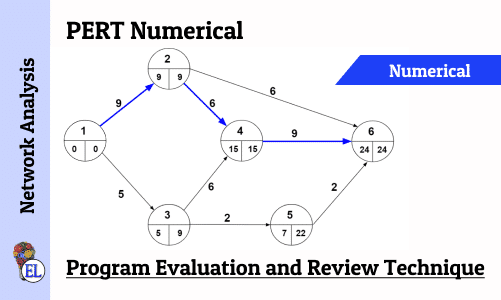
Numerical on PERT (Program Evaluation and Review Technique)

Network Analysis - Dealing with Network Construction Basics

Construct a project network with predecessor relationship | Operation Research | Numerical

Graphical Method | Methods to solve LPP | Linear Programming

Basics of Linear Programming

Linear Programming Problem (LPP) Formulation with Numericals

All comments that you add will await moderation. We'll publish all comments that are topic related, and adhere to our Code of Conduct .

Want to tell us something privately? Contact Us

Post comment

Education Lessons

Stay in touch, [notes] operation research, [notes] dynamics of machinery, [notes] maths, [notes] science, [notes] computer aided design.

• Analysis of Algorithms
• Backtracking
• Dynamic Programming
• Divide and Conquer
• Geometric Algorithms
• Mathematical Algorithms
• Pattern Searching
• Bitwise Algorithms
• Branch & Bound
• Randomized Algorithms
• Art Gallery Problem
• Transform and Conquer Technique
• Implementation of Exact Cover Problem and Algorithm X using DLX
• Preemptive Priority CPU Scheduling Algorithm
• Introduction to Exact Cover Problem and Algorithm X
• Introduction to Grover's Algorithm
• Approximation Algorithms
• What Does Big O(N^2) Complexity Mean?
• How to develop an Algorithm from Scratch | Develop Algorithmic Thinking
• Algorithm definition and meaning
• Representation Change in Transform and Conquer Technique
• How to write a Pseudo Code?
• Print numbers 1 to N using Indirect recursion
• Genetic Algorithms
• The Role of Algorithms in Computing
• Trial division Algorithm for Prime Factorization
• Mo's Algo with update and without update
• Instance Simplification Method in Transform and Conquer Technique
• Make n using 1s and 2s with minimum number of terms multiple of k

Quadratic Assignment Problem (QAP)

The Quadratic Assignment Problem (QAP) is an optimization problem that deals with assigning a set of facilities to a set of locations, considering the pairwise distances and flows between them.

The problem is to find the assignment that minimizes the total cost or distance, taking into account both the distances and the flows.

The distance matrix and flow matrix, as well as restrictions to ensure each facility is assigned to exactly one location and each location is assigned to exactly one facility, can be used to formulate the QAP as a quadratic objective function.

The QAP is a well-known example of an NP-hard problem , which means that for larger cases, computing the best solution might be difficult. As a result, many algorithms and heuristics have been created to quickly identify approximations of answers.

There are various types of algorithms for different problem structures, such as:

• Precise algorithms
• Approximation algorithms
• Metaheuristics like genetic algorithms and simulated annealing
• Specialized algorithms

Example: Given four facilities (F1, F2, F3, F4) and four locations (L1, L2, L3, L4). We have a cost matrix that represents the pairwise distances or costs between facilities. Additionally, we have a flow matrix that represents the interaction or flow between locations. Find the assignment that minimizes the total cost based on the interactions between facilities and locations. Each facility must be assigned to exactly one location, and each location can only accommodate one facility.

Facilities cost matrix:

Flow matrix:

To solve the QAP, various optimization techniques can be used, such as mathematical programming, heuristics, or metaheuristics. These techniques aim to explore the search space and find the optimal or near-optimal solution.

The solution to the QAP will provide an assignment of facilities to locations that minimizes the overall cost.

The solution generates all possible permutations of the assignment and calculates the total cost for each assignment. The optimal assignment is the one that results in the minimum total cost.

To calculate the total cost, we look at each pair of facilities in (i, j) and their respective locations (location1, location2). We then multiply the cost of assigning facility1 to facility2 (facilities[facility1][facility2]) with the flow from location1 to location2 (locations[location1][location2]). This process is done for all pairs of facilities in the assignment, and the costs are summed up.

Overall, the output tells us that assigning facilities to locations as F1->L1, F3->L2, F2->L3, and F4->L4 results in the minimum total cost of 44. This means that Facility 1 is assigned to Location 1, Facility 3 is assigned to Location 2, Facility 2 is assigned to Location 3, and Facility 4 is assigned to Location 4, yielding the lowest cost based on the given cost and flow matrices.This example demonstrates the process of finding the optimal assignment by considering the costs and flows associated with each facility and location. The objective is to find the assignment that minimizes the total cost, taking into account the interactions between facilities and locations.

Applications of the QAP include facility location, logistics, scheduling, and network architecture, all of which require effective resource allocation and arrangement.

Please Login to comment...

Similar reads.

• What are Tiktok AI Avatars?
• Poe Introduces A Price-per-message Revenue Model For AI Bot Creators
• Truecaller For Web Now Available For Android Users In India
• Google Introduces New AI-powered Vids App
• 30 OOPs Interview Questions and Answers (2024)

Improve your Coding Skills with Practice

What kind of Experience do you want to share?