what type of learning involves problem solving

Insight Learning Theory: Definition, Stages, and Examples

Categories Learning

Insight learning theory is all about those “lightbulb moments” we experience when we suddenly understand something. Instead of slowly figuring things out through trial and error, insight theory says we can suddenly see the solution to a problem in our minds. 

This theory is super important because it helps us understand how our brains work when we learn and solve problems. It can help teachers find better ways to teach and improve our problem-solving skills and creativity. It’s not just useful in school—insight theory also greatly impacts science, technology, and business.

Table of Contents

What Is Insight Learning?

Insight learning is like having a lightbulb moment in your brain. It’s when you suddenly understand something without needing to go through a step-by-step process. Instead of slowly figuring things out by trial and error, insight learning happens in a flash. One moment, you’re stuck, and the next, you have the solution. 

This type of learning is all about those “aha” experiences that feel like magic. The key principles of insight learning involve recognizing patterns, making connections, and restructuring our thoughts. It’s as if our brains suddenly rearrange the pieces of a puzzle, revealing the big picture. So, next time you have a brilliant idea pop into your head out of nowhere, you might just be experiencing insight learning in action!

Three Components of Insight Learning Theory

Insight learning, a concept rooted in psychology, comprises three distinct properties that characterize its unique nature:

1. Sudden Realization

Unlike gradual problem-solving methods, insight learning involves sudden and profound understanding. Individuals may be stuck on a problem for a while, but then, seemingly out of nowhere, the solution becomes clear. This sudden “aha” moment marks the culmination of mental processes that have been working behind the scenes to reorganize information and generate a new perspective .

2. Restructuring of Problem-Solving Strategies

Insight learning often involves a restructuring of mental representations or problem-solving strategies . Instead of simply trying different approaches until stumbling upon the correct one, individuals experience a shift in how they perceive and approach the problem. This restructuring allows for a more efficient and direct path to the solution once insight occurs.

3. Aha Moments

A hallmark of insight learning is the experience of “aha” moments. These moments are characterized by a sudden sense of clarity and understanding, often accompanied by a feeling of satisfaction or excitement. It’s as if a mental lightbulb turns on, illuminating the solution to a previously perplexing problem. 

These moments of insight can be deeply rewarding and serve as powerful motivators for further learning and problem-solving endeavors.

Four Stages of Insight Learning Theory

Insight learning unfolds in a series of distinct stages, each contributing to the journey from problem recognition to the sudden realization of a solution. These stages are as follows:

1. Problem Recognition

The first stage of insight learning involves recognizing and defining the problem at hand. This may entail identifying obstacles, discrepancies, or gaps in understanding that need to be addressed. Problem recognition sets the stage for the subsequent stages of insight learning by framing the problem and guiding the individual’s cognitive processes toward finding a solution.

2. Incubation

After recognizing the problem, individuals often enter a period of incubation where the mind continues to work on the problem unconsciously. During this stage, the brain engages in background processing, making connections, and reorganizing information without the individual’s conscious awareness. 

While it may seem like a period of inactivity on the surface, incubation is a crucial phase where ideas gestate, and creative solutions take shape beneath the surface of conscious thought.

3. Illumination

The illumination stage marks the sudden emergence of insight or understanding. It is characterized by a moment of clarity and realization, where the solution to the problem becomes apparent in a flash of insight. 

This “aha” moment often feels spontaneous and surprising, as if the solution has been waiting just below the surface of conscious awareness to be revealed. Illumination is the culmination of the cognitive processes initiated during problem recognition and incubation, resulting in a breakthrough in understanding.

4. Verification

Following the illumination stage, individuals verify the validity and feasibility of their insights by testing the proposed solution. This may involve applying the solution in practice, checking it against existing knowledge or expertise, or seeking feedback from others. 

Verification serves to confirm the efficacy of the newfound understanding and ensure its practical applicability in solving the problem at hand. It also provides an opportunity to refine and iterate on the solution based on real-world feedback and experience.

Famous Examples of Insight Learning

Examples of insight learning can be observed in various contexts, ranging from everyday problem-solving to scientific discoveries and creative breakthroughs. Some well-known examples of how insight learning theory works include the following:

Archimedes’ Principle

According to legend, the ancient Greek mathematician Archimedes experienced a moment of insight while taking a bath. He noticed that the water level rose as he immersed his body, leading him to realize that the volume of water displaced was equal to the volume of the submerged object. This insight led to the formulation of Archimedes’ principle, a fundamental concept in fluid mechanics.

Köhler’s Chimpanzee Experiments

In Wolfgang Köhler’s experiments with chimpanzees on Tenerife in the 1920s, the primates demonstrated insight learning in solving novel problems. One famous example involved a chimpanzee named Sultan, who used sticks to reach bananas placed outside his cage. After unsuccessful attempts at using a single stick, Sultan suddenly combined two sticks to create a longer tool, demonstrating insight into the problem and the ability to use tools creatively.

Eureka Moments in Science

Many scientific discoveries are the result of insight learning. For instance, the famed naturalist Charles Darwin had many eureka moments where he gained sudden insights that led to the formation of his influential theories.

Everyday Examples of Insight Learning Theory

You can probably think of some good examples of the role that insight learning theory plays in your everyday life. A few common real-life examples include:

• Finding a lost item : You might spend a lot of time searching for a lost item, like your keys or phone, but suddenly remember exactly where you left them when you’re doing something completely unrelated. This sudden recollection is an example of insight learning.
• Untangling knots : When trying to untangle a particularly tricky knot, you might struggle with it for a while without making progress. Then, suddenly, you realize a new approach or see a pattern that helps you quickly unravel the knot.
• Cooking improvisation : If you’re cooking and run out of a particular ingredient, you might suddenly come up with a creative substitution or alteration to the recipe that works surprisingly well. This moment of improvisation demonstrates insight learning in action.
• Solving riddles or brain teasers : You might initially be stumped when trying to solve a riddle or a brain teaser. However, after some time pondering the problem, you suddenly grasp the solution in a moment of insight.
• Learning a new skill : Learning to ride a bike or play a musical instrument often involves moments of insight. You might struggle with a certain technique or concept but then suddenly “get it” and experience a significant improvement in your performance.
• Navigating a maze : While navigating through a maze, you might encounter dead ends and wrong turns. However, after some exploration, you suddenly realize the correct path to take and reach the exit efficiently.
• Remembering information : When studying for a test, you might find yourself unable to recall a particular piece of information. Then, when you least expect it, the answer suddenly comes to you in a moment of insight.

These everyday examples illustrate how insight learning is a common and natural part of problem-solving and learning in our daily lives.

Exploring the Uses of Insight Learning

Insight learning isn’t an interesting explanation for how we suddenly come up with a solution to a problem—it also has many practical applications. Here are just a few ways that people can use insight learning in real life:

Problem-Solving

Insight learning helps us solve all sorts of problems, from finding lost items to untangling knots. When we’re stuck, our brains might suddenly come up with a genius idea or a new approach that saves the day. It’s like having a mental superhero swoop in to rescue us when we least expect it!

Ever had a brilliant idea pop into your head out of nowhere? That’s insight learning at work! Whether you’re writing a story, composing music, or designing something new, insight can spark creativity and help you come up with fresh, innovative ideas.

Learning New Skills

Learning isn’t always about memorizing facts or following step-by-step instructions. Sometimes, it’s about having those “aha” moments that make everything click into place. Insight learning can help us grasp tricky concepts, master difficult skills, and become better learners overall.

Insight learning isn’t just for individuals—it’s also crucial for innovation and progress in society. Scientists, inventors, and entrepreneurs rely on insight to make groundbreaking discoveries and develop new technologies that improve our lives. Who knows? The next big invention could start with someone having a brilliant idea in the shower!

Overcoming Challenges

Life is full of challenges, but insight learning can help us tackle them with confidence. Whether it’s navigating a maze, solving a puzzle, or facing a tough decision, insight can provide the clarity and creativity we need to overcome obstacles and achieve our goals.

The next time you’re feeling stuck or uninspired, remember: the solution might be just one “aha” moment away!

Alternatives to Insight Learning Theory

While insight learning theory emphasizes sudden understanding and restructuring of problem-solving strategies, several alternative theories offer different perspectives on how learning and problem-solving occur. Here are some of the key alternative theories:

Behaviorism

Behaviorism is a theory that focuses on observable, overt behaviors and the external factors that influence them. According to behaviorists like B.F. Skinner, learning is a result of conditioning, where behaviors are reinforced or punished based on their consequences. 

In contrast to insight learning theory, behaviorism suggests that learning occurs gradually through repeated associations between stimuli and responses rather than sudden insights or realizations.

Cognitive Learning Theory

Cognitive learning theory, influenced by psychologists such as Jean Piaget and Lev Vygotsky , emphasizes the role of mental processes in learning. This theory suggests that individuals actively construct knowledge and understanding through processes like perception, memory, and problem-solving. 

Cognitive learning theory acknowledges the importance of insight and problem-solving strategies but places greater emphasis on cognitive structures and processes underlying learning.

Gestalt Psychology

Gestalt psychology, which influenced insight learning theory, proposes that learning and problem-solving involve the organization of perceptions into meaningful wholes or “gestalts.” 

Gestalt psychologists like Max Wertheimer emphasized the role of insight and restructuring in problem-solving, but their theories also consider other factors, such as perceptual organization, pattern recognition, and the influence of context.

Information Processing Theory

Information processing theory views the mind as a computer-like system that processes information through various stages, including input, processing, storage, and output. This theory emphasizes the role of attention, memory, and problem-solving strategies in learning and problem-solving. 

While insight learning theory focuses on sudden insights and restructuring, information processing theory considers how individuals encode, manipulate, and retrieve information to solve problems.

Related reading:

• What Is Kolb’s Learning Cycle?
• What Is Latent Learning?
• What Is Scaffolding in Psychology?
• What Is Observational Learning?

Kizilirmak, J. M., Fischer, L., Krause, J., Soch, J., Richter, A., & Schott, B. H. (2021). Learning by insight-like sudden comprehension as a potential strategy to improve memory encoding in older adults .  Frontiers in Aging Neuroscience ,  13 , 661346. https://doi.org/10.3389/fnagi.2021.661346

Lind, J., Enquist, M. (2012). Insight learning and shaping . In: Seel, N.M. (eds) Encyclopedia of the Sciences of Learning . Springer, Boston, MA. https://doi.org/10.1007/978-1-4419-1428-6_851

Osuna-Mascaró, A. J., & Auersperg, A. M. I. (2021). Current understanding of the “insight” phenomenon across disciplines . Frontiers in Psychology , 12, 791398. https://doi.org/10.3389/fpsyg.2021.791398

Salmon-Mordekovich, N., & Leikin, M. (2023). Insight problem solving is not that special, but business is not quite ‘as usual’: typical versus exceptional problem-solving strategies .  Psychological Research ,  87 (6), 1995–2009. https://doi.org/10.1007/s00426-022-01786-5

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Evan Glazer (University of Georgia)

Editor’s Note: Dr. Glazer chose to use the term Problem-based Instruction and Inquiry, but my reading and other references to this chapter also use the term Problem-based Learning. The reader can assume the terms are equivalent.

Description

• Problem-based inquiry is an effort to challenge students to address real-world problems and resolve realistic dilemmas.

Such problems create opportunities for meaningful activities that engage students in problem solving and higher-ordered thinking in authentic settings. Many textbooks attempt to promote these skills through contrived settings without relevance to students’ lives or interests. A notorious algebra problem concerns the time at which two railway trains will pass each other:

Two trains leave different stations headed toward each other. Station A is 500 miles west of Station B. Train A leaves station A at 12:00 pm traveling toward Station B at a rate of 60 miles per hour. Train B leaves Station B at 2:30 pm for Station A at a rate of 45 miles per hour. At what time will the trains meet?

Reading this question, one might respond, “Who cares?”, or, “Why do we need to know this?” Such questions have created substantial anxiety among students and have, perhaps, even been the cause of nightmares. Critics would argue that classic “story problems” leave a lasting impression of meaningless efforts to confuse and torment students, as if they have come from hell’s library. Problem-based inquiry, on the other hand, intends to engage students in relevant, realistic problems.

Several changes would need to be made in the above problem to promote problem-based inquiry. It would first have to be acknowledged that the trains are not, in fact, traveling at constant rates when they are in motion; negotiating curves or changing tracks at high speeds can result in accidents.

Further, all of the information about the problem cannot be presented to the learner at the outset; that is, some ambiguity must exist in the context so that students have an opportunity to engage in a problem-solving activity. In addition, the situation should involve a meaningful scenario. Suppose that a person intends to catch a connecting train at the second station and requires a time-efficient itinerary? What if we are not given data about the trains, but instead, the outcome of a particular event, such as an accident?

Why should we use problem-based inquiry to help students learn?

The American educational system has been criticized for having an underachieving curriculum that leads students to memorize and regurgitate facts that do not apply to their lives (Martin, 1987; Paul, 1993). Many claim that the traditional classroom environment, with its orderly conduct and didactic teaching methods in which the teacher dispenses information, has greatly inhibited students’ opportunities to think critically (Dossey et al., 1988; Goodlad, 1984; Wood, 1987). Problem-based inquiry is an attempt to overcome these obstacles and confront the concerns presented by the National Assessment of Educational Progress:

If an unfriendly foreign power had attempted to impose on America the mediocre educational performance that exists today, we might well have viewed it as an act of war. We have, in effect, been committing an act of unthinking, unilateral educational disarmament. (A Nation at Risk, 1983)

Problem-based inquiry emphasizes learning as a process that involves problem solving and critical thinking in situated contexts. It provides opportunities to address broader learning goals that focus on preparing students for active and responsible citizenship. Students gain experience in tackling realistic problems, and emphasis is placed on using communication, cooperation, and resources to formulate ideas and develop reasoning skills.

What is a framework for a problem-based inquiry?

Situated cognition, constructivism, social learning, and communities of practice are assumed theories of learning and cognition in problem-based inquiry environments. These theories have common themes about the context and the process of learning and are often associated.

Characteristics

Some common characteristics in problem-based learning models:

Activity is grounded in a general question about a problem that has multiple possible answers and methods for addressing the question. Each problem has a general question that guides the overall task followed by ill-structured problems or questions that are generated throughout the problem-solving process. That is, to address the larger question, students must derive and investigate smaller problems or questions that relate to the findings and implications of the broader goal. The problems or questions thus created are most likely new to the students and lack known definitive methods or answers that have been predetermined by the teacher.

Learning is student-centered; the teacher acts as facilitator. In essence, the teacher creates an environment where students take ownership in the direction and content of their learning.

Students work collaboratively towards addressing the general question . All of the students work together to attain the shared goal of producing a solution to the problem. Consequently, the groups co-depend on each other’s performance and contributions in order to make their own advances in reasoning toward answering the research questions and the overall problem.

Learning is driven by the context of the problem and is not bound by an established curriculum. In this environment, students determine what and how much they need to learn in order to accomplish a specific task. Consequently, acquired information and learned concepts and strategies are tied directly to the context of the learning situation. Learning is not confined to a preset curriculum. Creation of a final product is not a necessary requirement of all problem-based inquiry models.

Project-based learning models most often include this type of product as an integral part of the learning process, because learning is expected to occur primarily in the act of creating something. Unlike problem based inquiry models, project-based learning does not necessarily address a real-world problem, nor does it focus on providing argumentation for resolution of an issue.

In a problem-based inquiry setting, there is greater emphasis on problem-solving, analysis, resolution, and explanation of an authentic dilemma. Sometimes this analysis and explanation is represented in the form of a project, but it can also take the form of verbal debate and written summary.

Instructional models and applications

• There is no single method for designing problem-based inquiry learning environments.

Various techniques have been used to generate the problem and stimulate learning. Promoting student-ownership, using a particular medium to focus attention, telling stories, simulating and recreating events, and utilizing resources and data on the Internet are among them. The instructional model, problem based learning will be discussed next with attention to instructional strategies and practical examples.

Problem-Based Learning

• Problem-based learning (PBL) is an instructional strategy in which students actively resolve complex problems in realistic situations.

It can be used to teach individual lessons, units, or even entire curricula. PBL is often approached in a team environment with emphasis on building skills related to consensual decision making, dialogue and discussion, team maintenance, conflict management, and team leadership. While the fundamental approach of problem solving in situated environments has been used throughout the history of schooling, the term PBL did not appear until the 1970s and was devised as an alternative approach to medical education.

In most medical programs, students initially take a series of fact intensive courses in biology and anatomy and then participate in a field experience as a medical resident in a hospital or clinic. However, Barrows reported that, unfortunately, medical residents frequently had difficulty applying knowledge from their classroom experiences in work-related, problem-solving situations. He argued that the classical framework of learning medical knowledge first in classrooms through studying and testing was too passive and removed from context to take on meaning.

Consequently, PBL was first seen as a medical field immersion experience whereby students learned about their medical specialty through direct engagement in realistic problems and gradual apprenticeship in natural or simulated settings. Problem solving is emphasized as an initial area of learning and development in PBL medical programs more so than memorizing a series of facts outside their natural context.

In addition to the field of medicine, PBL is used in many areas of education and training. In academic courses, PBL is used as a tool to help students understand the utility of a particular concept or study. For example, students may learn about recycling and materials as they determine methods that will reduce the county landfill problem.

In addition, alternative education programs have been created with a PBL emphasis to help at-risk students learn in a different way through partnerships with local businesses and government. In vocational education, PBL experiences often emphasize participation in natural settings.

For example, students in architecture address the problem of designing homes for impoverished areas. Many of the residents need safe housing and cannot afford to purchase typical homes. Consequently, students learn about architectural design and resolving the problem as they construct homes made from recycled materials. In business and the military, simulations are used as a means of instruction in PBL. The affective and physiological stress associated with warfare can influence strategic planning, so PBL in military settings promotes the use of “war games” as a tactic for facing authentic crises.

In business settings, simulations of “what if” scenarios are used to train managers in various strategies and problem-solving approaches to conflict resolution. In both military and business settings, the simulation is a tool that provides an opportunity to not only address realistic problems but to learn from mistakes in a more forgiving way than in an authentic context.

Designing the learning environment

The following elements are commonly associated with PBL activities.

Problem generation: The problems must address concepts and principles relevant to the content domain. Problems are not investigated by students solely for problem solving experiences but as a means of understanding the subject area. Some PBL activities incorporate multidisciplinary approaches, assuming the teacher can provide and coordinate needed resources such as additional content, instructional support, and other teachers. In addition, the problems must relate to real issues that are present in society or students’ lives. Contrived scenarios detract from the perceived usefulness of a concept.

Problem presentation: Students must “own” the problem, either by creating or selecting it. Ownership also implies that their contributions affect the outcome of solving the problem. Thus, more than one solution and more than one method of achieving a solution to the problem are often possible. Furthermore, ownership means that students take responsibility for representing and communicating their work in a unique way.

Predetermined formats of problem structure and analysis towards resolution are not recommended; however, the problem should be presented such that the information in the problem does not call attention to critical factors in the case that will lead to immediate resolution. Ownership also suggests that students will ask further questions, reveal further information, and synthesize critical factors throughout the problem-solving process.

Teacher role: Teachers act primarily as cognitive coaches by facilitating learning and modeling higher order thinking and meta cognitive skills. As facilitators, teachers give students control over how they learn and provide support and structure in the direction of their learning. They help the class create a common framework of expectations using tools such as general guidelines and time lines.

As cognitive modelers, teachers think aloud about strategies and questions that influence how students manage the progress of their learning and accomplish group tasks. In addition, teachers continually question students about the concepts they are learning in the context of the problem in order to probe their understanding, challenge their thinking, and help them deepen or extend their ideas.

Student role: Students first define or select an ill-structured problem that has no obvious solution. They develop alternative hypotheses to resolve the problem and discuss and negotiate their conjectures in a group. Next, they access, evaluate, and utilize data from a variety of available sources to support or refute their hypotheses. They may alter, develop, or synthesize hypotheses in light of new information. Finally, they develop clearly stated solutions that fit the problem and its inherent conditions, based upon information and reasoning to support their arguments. Solutions can be in the form of essays, presentations, or projects.

Maine School Engages Kids With Problem-Solving Challenges (11:37)

https://youtu.be/i17F-b5GG94

[PBS NewsHour].(2013, May 6). Maine School Engages Kids with Problem Solving Challenges. [Video File]. Retrieve from https://youtu.be/i17F-b5GG94

Special correspondent John Tulenko of Leaning Matters reports on a public middle school in Portland, Maine that is taking a different approach to teaching students. Teachers have swapped traditional curriculum for an unusually comprehensive science curriculum that emphasizes problem-solving, with a little help from some robots.

Effectiveness of Problem and Inquiry-based learning.

Why does inquiry-based learning only have an effect size of 0.31 when it is an approach to learning that seems to engage students and teachers so readily in the process of learning?

When is the right and wrong time to introduce inquiry and problem based learning?

Watch video from John Hattie on inquiry and problem-based learning, (2:11 minutes).

[Corwin]. (2015, Nov. 9). John Hattie on inquiry-based learning. [Video File]. Retrieved from https://youtu.be/YUooOYbgSUg.

Glazer, E. (2010) Emerging Perspectives on Learning, Teaching, and Technology, Global Text, Michael Orey. (Chapter 14) Attribution CC 3.0. Retrieved from https://textbookequity.org/Textbooks/Orey_Emerging_Perspectives_Learning.pdf

Instructional Methods, Strategies and Technologies to Meet the Needs of All Learners Copyright © 2017 by Evan Glazer (University of Georgia) is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

Center for Teaching Innovation

Resource library.

• Establishing Community Agreements and Classroom Norms
• Sample group work rubric
• Problem-Based Learning Clearinghouse of Activities, University of Delaware

Problem-Based Learning

Problem-based learning  (PBL) is a student-centered approach in which students learn about a subject by working in groups to solve an open-ended problem. This problem is what drives the motivation and the learning. 

Why Use Problem-Based Learning?

Nilson (2010) lists the following learning outcomes that are associated with PBL. A well-designed PBL project provides students with the opportunity to develop skills related to:

• Working in teams.
• Managing projects and holding leadership roles.
• Oral and written communication.
• Self-awareness and evaluation of group processes.
• Working independently.
• Critical thinking and analysis.
• Explaining concepts.
• Self-directed learning.
• Applying course content to real-world examples.
• Researching and information literacy.
• Problem solving across disciplines.

Considerations for Using Problem-Based Learning

Rather than teaching relevant material and subsequently having students apply the knowledge to solve problems, the problem is presented first. PBL assignments can be short, or they can be more involved and take a whole semester. PBL is often group-oriented, so it is beneficial to set aside classroom time to prepare students to   work in groups  and to allow them to engage in their PBL project.

Students generally must:

• Examine and define the problem.
• Explore what they already know about underlying issues related to it.
• Determine what they need to learn and where they can acquire the information and tools necessary to solve the problem.
• Evaluate possible ways to solve the problem.
• Solve the problem.
• Report on their findings.

Getting Started with Problem-Based Learning

• Articulate the learning outcomes of the project. What do you want students to know or be able to do as a result of participating in the assignment?
• Create the problem. Ideally, this will be a real-world situation that resembles something students may encounter in their future careers or lives. Cases are often the basis of PBL activities. Previously developed PBL activities can be found online through the University of Delaware’s PBL Clearinghouse of Activities .
• Establish ground rules at the beginning to prepare students to work effectively in groups.
• Introduce students to group processes and do some warm up exercises to allow them to practice assessing both their own work and that of their peers.
• Consider having students take on different roles or divide up the work up amongst themselves. Alternatively, the project might require students to assume various perspectives, such as those of government officials, local business owners, etc.
• Establish how you will evaluate and assess the assignment. Consider making the self and peer assessments a part of the assignment grade.

Nilson, L. B. (2010).  Teaching at its best: A research-based resource for college instructors  (2nd ed.).  San Francisco, CA: Jossey-Bass. 

Problem-Based Learning (PBL)

What is Problem-Based Learning (PBL)? PBL is a student-centered approach to learning that involves groups of students working to solve a real-world problem, quite different from the direct teaching method of a teacher presenting facts and concepts about a specific subject to a classroom of students. Through PBL, students not only strengthen their teamwork, communication, and research skills, but they also sharpen their critical thinking and problem-solving abilities essential for life-long learning.

See also: Just-in-Time Teaching

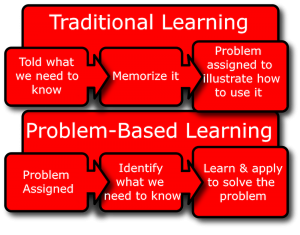
In implementing PBL, the teaching role shifts from that of the more traditional model that follows a linear, sequential pattern where the teacher presents relevant material, informs the class what needs to be done, and provides details and information for students to apply their knowledge to a given problem. With PBL, the teacher acts as a facilitator; the learning is student-driven with the aim of solving the given problem (note: the problem is established at the onset of learning opposed to being presented last in the traditional model). Also, the assignments vary in length from relatively short to an entire semester with daily instructional time structured for group work.

By working with PBL, students will:

• Become engaged with open-ended situations that assimilate the world of work
• Participate in groups to pinpoint what is known/ not known and the methods of finding information to help solve the given problem.
• Investigate a problem; through critical thinking and problem solving, brainstorm a list of unique solutions.
• Analyze the situation to see if the real problem is framed or if there are other problems that need to be solved.

How to Begin PBL

• Establish the learning outcomes (i.e., what is it that you want your students to really learn and to be able to do after completing the learning project).
• Find a real-world problem that is relevant to the students; often the problems are ones that students may encounter in their own life or future career.
• Discuss pertinent rules for working in groups to maximize learning success.
• Practice group processes: listening, involving others, assessing their work/peers.
• Explore different roles for students to accomplish the work that needs to be done and/or to see the problem from various perspectives depending on the problem (e.g., for a problem about pollution, different roles may be a mayor, business owner, parent, child, neighboring city government officials, etc.).
• Determine how the project will be evaluated and assessed. Most likely, both self-assessment and peer-assessment will factor into the assignment grade.

Designing Classroom Instruction

See also: Inclusive Teaching Strategies

• Take the curriculum and divide it into various units. Decide on the types of problems that your students will solve. These will be your objectives.
• Determine the specific problems that most likely have several answers; consider student interest.
• Arrange appropriate resources available to students; utilize other teaching personnel to support students where needed (e.g., media specialists to orientate students to electronic references).
• Decide on presentation formats to communicate learning (e.g., individual paper, group PowerPoint, an online blog, etc.) and appropriate grading mechanisms (e.g., rubric).
• Decide how to incorporate group participation (e.g., what percent, possible peer evaluation, etc.).

How to Orchestrate a PBL Activity

• Explain Problem-Based Learning to students: its rationale, daily instruction, class expectations, grading.
• Serve as a model and resource to the PBL process; work in-tandem through the first problem
• Help students secure various resources when needed.
• Supply ample class time for collaborative group work.
• Give feedback to each group after they share via the established format; critique the solution in quality and thoroughness. Reinforce to the students that the prior thinking and reasoning process in addition to the solution are important as well.

Teacher’s Role in PBL

See also: Flipped teaching

As previously mentioned, the teacher determines a problem that is interesting, relevant, and novel for the students. It also must be multi-faceted enough to engage students in doing research and finding several solutions. The problems stem from the unit curriculum and reflect possible use in future work situations.

• Determine a problem aligned with the course and your students. The problem needs to be demanding enough that the students most likely cannot solve it on their own. It also needs to teach them new skills. When sharing the problem with students, state it in a narrative complete with pertinent background information without excessive information. Allow the students to find out more details as they work on the problem.
• Place students in groups, well-mixed in diversity and skill levels, to strengthen the groups. Help students work successfully. One way is to have the students take on various roles in the group process after they self-assess their strengths and weaknesses.
• Support the students with understanding the content on a deeper level and in ways to best orchestrate the various stages of the problem-solving process.

The Role of the Students

See also: ADDIE model

The students work collaboratively on all facets of the problem to determine the best possible solution.

• Analyze the problem and the issues it presents. Break the problem down into various parts. Continue to read, discuss, and think about the problem.
• Construct a list of what is known about the problem. What do your fellow students know about the problem? Do they have any experiences related to the problem? Discuss the contributions expected from the team members. What are their strengths and weaknesses? Follow the rules of brainstorming (i.e., accept all answers without passing judgment) to generate possible solutions for the problem.
• Get agreement from the team members regarding the problem statement.
• Put the problem statement in written form.
• Solicit feedback from the teacher.
• Be open to changing the written statement based on any new learning that is found or feedback provided.
• Generate a list of possible solutions. Include relevant thoughts, ideas, and educated guesses as well as causes and possible ways to solve it. Then rank the solutions and select the solution that your group is most likely to perceive as the best in terms of meeting success.
• Include what needs to be known and done to solve the identified problems.
• Prioritize the various action steps.
• Consider how the steps impact the possible solutions.
• See if the group is in agreement with the timeline; if not, decide how to reach agreement.
• What resources are available to help (e.g., textbooks, primary/secondary sources, Internet).
• Determine research assignments per team members.
• Establish due dates.
• Determine how your group will present the problem solution and also identify the audience. Usually, in PBL, each group presents their solutions via a team presentation either to the class of other students or to those who are related to the problem.
• Both the process and the results of the learning activity need to be covered. Include the following: problem statement, questions, data gathered, data analysis, reasons for the solution(s) and/or any recommendations reflective of the data analysis.
• A well-stated problem and conclusion.
• The process undertaken by the group in solving the problem, the various options discussed, and the resources used.
• Your solution’s supporting documents, guests, interviews and their purpose to be convincing to your audience.
• In addition, be prepared for any audience comments and questions. Determine who will respond and if your team doesn’t know the answer, admit this and be open to looking into the question at a later date.
• Reflective thinking and transfer of knowledge are important components of PBL. This helps the students be more cognizant of their own learning and teaches them how to ask appropriate questions to address problems that need to be solved. It is important to look at both the individual student and the group effort/delivery throughout the entire process. From here, you can better determine what was learned and how to improve. The students should be asked how they can apply what was learned to a different situation, to their own lives, and to other course projects.

See also: Kirkpatrick Model: Four Levels of Learning Evaluation

I am a professor of Educational Technology. I have worked at several elite universities. I hold a PhD degree from the University of Illinois and a master's degree from Purdue University.

Similar Posts

How can we align learning objectives, instructional strategies, and assessments.

What is course alignment When a course is being designed, it is important to ensure that ensure that these three components of your course are aligned. In order to align various components of…

Concept Maps and How To Use Them

Concept maps help our brains take in information, mostly when there is visual information. The maps help us to see the big picture along with the connected and related data. They also help…

Definitions of Educational Technology

Educational Technology What is educational technology? There are a variety of definitions of educational technology. What is instructional design and technology? The Association for Educational Communications and Technology (AECT): Educational technology is the study…

Open Source Learning Management Systems (LMS)

Learning Management Systems (LMSs) are becoming a vital part of classrooms in the 21th Century. This is a list of open source learning management systems. By open source we mean that source code of…

SAMR Model: Substitution, Augmentation, Modification, and Redefinition

When integrating technology into education, the SAMR model serves as a foundational guide. Crafted by Ruben R. Puentedura, SAMR offers educators a structured way to think about incorporating technology effectively. It stands for…

How To Design A Course

This article includes tips on designing and building a course. Allow enough time to carefully plan and revise content for a new course. Careful planning will make teaching easier and more enjoyable. Talk…

7.3 Problem-Solving

Learning objectives.

By the end of this section, you will be able to:

• Describe problem solving strategies
• Define algorithm and heuristic
• Explain some common roadblocks to effective problem solving

   People face problems every day—usually, multiple problems throughout the day. Sometimes these problems are straightforward: To double a recipe for pizza dough, for example, all that is required is that each ingredient in the recipe be doubled. Sometimes, however, the problems we encounter are more complex. For example, say you have a work deadline, and you must mail a printed copy of a report to your supervisor by the end of the business day. The report is time-sensitive and must be sent overnight. You finished the report last night, but your printer will not work today. What should you do? First, you need to identify the problem and then apply a strategy for solving the problem.

The study of human and animal problem solving processes has provided much insight toward the understanding of our conscious experience and led to advancements in computer science and artificial intelligence. Essentially much of cognitive science today represents studies of how we consciously and unconsciously make decisions and solve problems. For instance, when encountered with a large amount of information, how do we go about making decisions about the most efficient way of sorting and analyzing all the information in order to find what you are looking for as in visual search paradigms in cognitive psychology. Or in a situation where a piece of machinery is not working properly, how do we go about organizing how to address the issue and understand what the cause of the problem might be. How do we sort the procedures that will be needed and focus attention on what is important in order to solve problems efficiently. Within this section we will discuss some of these issues and examine processes related to human, animal and computer problem solving.

PROBLEM-SOLVING STRATEGIES

   When people are presented with a problem—whether it is a complex mathematical problem or a broken printer, how do you solve it? Before finding a solution to the problem, the problem must first be clearly identified. After that, one of many problem solving strategies can be applied, hopefully resulting in a solution.

Problems themselves can be classified into two different categories known as ill-defined and well-defined problems (Schacter, 2009). Ill-defined problems represent issues that do not have clear goals, solution paths, or expected solutions whereas well-defined problems have specific goals, clearly defined solutions, and clear expected solutions. Problem solving often incorporates pragmatics (logical reasoning) and semantics (interpretation of meanings behind the problem), and also in many cases require abstract thinking and creativity in order to find novel solutions. Within psychology, problem solving refers to a motivational drive for reading a definite “goal” from a present situation or condition that is either not moving toward that goal, is distant from it, or requires more complex logical analysis for finding a missing description of conditions or steps toward that goal. Processes relating to problem solving include problem finding also known as problem analysis, problem shaping where the organization of the problem occurs, generating alternative strategies, implementation of attempted solutions, and verification of the selected solution. Various methods of studying problem solving exist within the field of psychology including introspection, behavior analysis and behaviorism, simulation, computer modeling, and experimentation.

A problem-solving strategy is a plan of action used to find a solution. Different strategies have different action plans associated with them (table below). For example, a well-known strategy is trial and error. The old adage, “If at first you don’t succeed, try, try again” describes trial and error. In terms of your broken printer, you could try checking the ink levels, and if that doesn’t work, you could check to make sure the paper tray isn’t jammed. Or maybe the printer isn’t actually connected to your laptop. When using trial and error, you would continue to try different solutions until you solved your problem. Although trial and error is not typically one of the most time-efficient strategies, it is a commonly used one.

   Another type of strategy is an algorithm. An algorithm is a problem-solving formula that provides you with step-by-step instructions used to achieve a desired outcome (Kahneman, 2011). You can think of an algorithm as a recipe with highly detailed instructions that produce the same result every time they are performed. Algorithms are used frequently in our everyday lives, especially in computer science. When you run a search on the Internet, search engines like Google use algorithms to decide which entries will appear first in your list of results. Facebook also uses algorithms to decide which posts to display on your newsfeed. Can you identify other situations in which algorithms are used?

A heuristic is another type of problem solving strategy. While an algorithm must be followed exactly to produce a correct result, a heuristic is a general problem-solving framework (Tversky & Kahneman, 1974). You can think of these as mental shortcuts that are used to solve problems. A “rule of thumb” is an example of a heuristic. Such a rule saves the person time and energy when making a decision, but despite its time-saving characteristics, it is not always the best method for making a rational decision. Different types of heuristics are used in different types of situations, but the impulse to use a heuristic occurs when one of five conditions is met (Pratkanis, 1989):

• When one is faced with too much information
• When the time to make a decision is limited
• When the decision to be made is unimportant
• When there is access to very little information to use in making the decision
• When an appropriate heuristic happens to come to mind in the same moment

Working backwards is a useful heuristic in which you begin solving the problem by focusing on the end result. Consider this example: You live in Washington, D.C. and have been invited to a wedding at 4 PM on Saturday in Philadelphia. Knowing that Interstate 95 tends to back up any day of the week, you need to plan your route and time your departure accordingly. If you want to be at the wedding service by 3:30 PM, and it takes 2.5 hours to get to Philadelphia without traffic, what time should you leave your house? You use the working backwards heuristic to plan the events of your day on a regular basis, probably without even thinking about it.

Another useful heuristic is the practice of accomplishing a large goal or task by breaking it into a series of smaller steps. Students often use this common method to complete a large research project or long essay for school. For example, students typically brainstorm, develop a thesis or main topic, research the chosen topic, organize their information into an outline, write a rough draft, revise and edit the rough draft, develop a final draft, organize the references list, and proofread their work before turning in the project. The large task becomes less overwhelming when it is broken down into a series of small steps.

Further problem solving strategies have been identified (listed below) that incorporate flexible and creative thinking in order to reach solutions efficiently.

Additional Problem Solving Strategies :

• Abstraction – refers to solving the problem within a model of the situation before applying it to reality.
• Analogy – is using a solution that solves a similar problem.
• Brainstorming – refers to collecting an analyzing a large amount of solutions, especially within a group of people, to combine the solutions and developing them until an optimal solution is reached.
• Divide and conquer – breaking down large complex problems into smaller more manageable problems.
• Hypothesis testing – method used in experimentation where an assumption about what would happen in response to manipulating an independent variable is made, and analysis of the affects of the manipulation are made and compared to the original hypothesis.
• Lateral thinking – approaching problems indirectly and creatively by viewing the problem in a new and unusual light.
• Means-ends analysis – choosing and analyzing an action at a series of smaller steps to move closer to the goal.
• Method of focal objects – putting seemingly non-matching characteristics of different procedures together to make something new that will get you closer to the goal.
• Morphological analysis – analyzing the outputs of and interactions of many pieces that together make up a whole system.
• Proof – trying to prove that a problem cannot be solved. Where the proof fails becomes the starting point or solving the problem.
• Reduction – adapting the problem to be as similar problems where a solution exists.
• Research – using existing knowledge or solutions to similar problems to solve the problem.
• Root cause analysis – trying to identify the cause of the problem.

The strategies listed above outline a short summary of methods we use in working toward solutions and also demonstrate how the mind works when being faced with barriers preventing goals to be reached.

One example of means-end analysis can be found by using the Tower of Hanoi paradigm . This paradigm can be modeled as a word problems as demonstrated by the Missionary-Cannibal Problem :

Missionary-Cannibal Problem

Three missionaries and three cannibals are on one side of a river and need to cross to the other side. The only means of crossing is a boat, and the boat can only hold two people at a time. Your goal is to devise a set of moves that will transport all six of the people across the river, being in mind the following constraint: The number of cannibals can never exceed the number of missionaries in any location. Remember that someone will have to also row that boat back across each time.

Hint : At one point in your solution, you will have to send more people back to the original side than you just sent to the destination.

The actual Tower of Hanoi problem consists of three rods sitting vertically on a base with a number of disks of different sizes that can slide onto any rod. The puzzle starts with the disks in a neat stack in ascending order of size on one rod, the smallest at the top making a conical shape. The objective of the puzzle is to move the entire stack to another rod obeying the following rules:

• 1. Only one disk can be moved at a time.
• 2. Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack or on an empty rod.
• 3. No disc may be placed on top of a smaller disk.

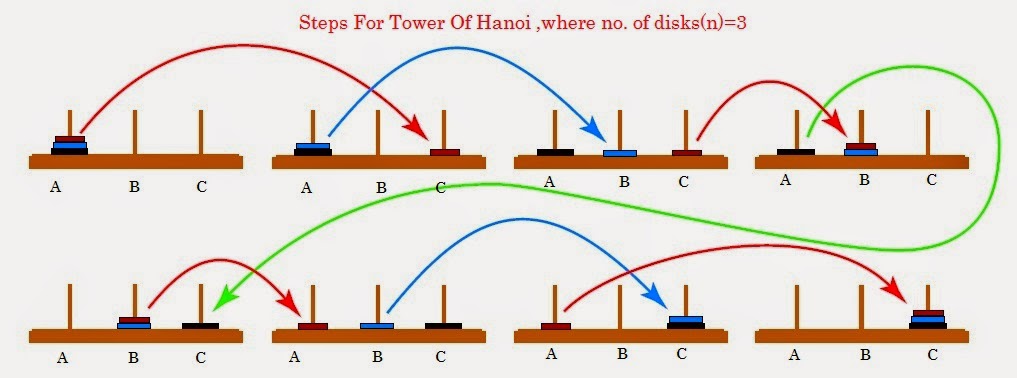
  Figure 7.02. Steps for solving the Tower of Hanoi in the minimum number of moves when there are 3 disks.

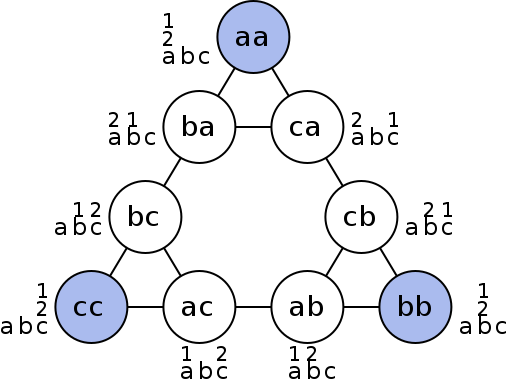
Figure 7.03. Graphical representation of nodes (circles) and moves (lines) of Tower of Hanoi.

The Tower of Hanoi is a frequently used psychological technique to study problem solving and procedure analysis. A variation of the Tower of Hanoi known as the Tower of London has been developed which has been an important tool in the neuropsychological diagnosis of executive function disorders and their treatment.

GESTALT PSYCHOLOGY AND PROBLEM SOLVING

As you may recall from the sensation and perception chapter, Gestalt psychology describes whole patterns, forms and configurations of perception and cognition such as closure, good continuation, and figure-ground. In addition to patterns of perception, Wolfgang Kohler, a German Gestalt psychologist traveled to the Spanish island of Tenerife in order to study animals behavior and problem solving in the anthropoid ape.

As an interesting side note to Kohler’s studies of chimp problem solving, Dr. Ronald Ley, professor of psychology at State University of New York provides evidence in his book A Whisper of Espionage  (1990) suggesting that while collecting data for what would later be his book  The Mentality of Apes (1925) on Tenerife in the Canary Islands between 1914 and 1920, Kohler was additionally an active spy for the German government alerting Germany to ships that were sailing around the Canary Islands. Ley suggests his investigations in England, Germany and elsewhere in Europe confirm that Kohler had served in the German military by building, maintaining and operating a concealed radio that contributed to Germany’s war effort acting as a strategic outpost in the Canary Islands that could monitor naval military activity approaching the north African coast.

While trapped on the island over the course of World War 1, Kohler applied Gestalt principles to animal perception in order to understand how they solve problems. He recognized that the apes on the islands also perceive relations between stimuli and the environment in Gestalt patterns and understand these patterns as wholes as opposed to pieces that make up a whole. Kohler based his theories of animal intelligence on the ability to understand relations between stimuli, and spent much of his time while trapped on the island investigation what he described as  insight , the sudden perception of useful or proper relations. In order to study insight in animals, Kohler would present problems to chimpanzee’s by hanging some banana’s or some kind of food so it was suspended higher than the apes could reach. Within the room, Kohler would arrange a variety of boxes, sticks or other tools the chimpanzees could use by combining in patterns or organizing in a way that would allow them to obtain the food (Kohler & Winter, 1925).

While viewing the chimpanzee’s, Kohler noticed one chimp that was more efficient at solving problems than some of the others. The chimp, named Sultan, was able to use long poles to reach through bars and organize objects in specific patterns to obtain food or other desirables that were originally out of reach. In order to study insight within these chimps, Kohler would remove objects from the room to systematically make the food more difficult to obtain. As the story goes, after removing many of the objects Sultan was used to using to obtain the food, he sat down ad sulked for a while, and then suddenly got up going over to two poles lying on the ground. Without hesitation Sultan put one pole inside the end of the other creating a longer pole that he could use to obtain the food demonstrating an ideal example of what Kohler described as insight. In another situation, Sultan discovered how to stand on a box to reach a banana that was suspended from the rafters illustrating Sultan’s perception of relations and the importance of insight in problem solving.

Grande (another chimp in the group studied by Kohler) builds a three-box structure to reach the bananas, while Sultan watches from the ground.  Insight , sometimes referred to as an “Ah-ha” experience, was the term Kohler used for the sudden perception of useful relations among objects during problem solving (Kohler, 1927; Radvansky & Ashcraft, 2013).

Solving puzzles.

   Problem-solving abilities can improve with practice. Many people challenge themselves every day with puzzles and other mental exercises to sharpen their problem-solving skills. Sudoku puzzles appear daily in most newspapers. Typically, a sudoku puzzle is a 9×9 grid. The simple sudoku below (see figure) is a 4×4 grid. To solve the puzzle, fill in the empty boxes with a single digit: 1, 2, 3, or 4. Here are the rules: The numbers must total 10 in each bolded box, each row, and each column; however, each digit can only appear once in a bolded box, row, and column. Time yourself as you solve this puzzle and compare your time with a classmate.

How long did it take you to solve this sudoku puzzle? (You can see the answer at the end of this section.)

   Here is another popular type of puzzle (figure below) that challenges your spatial reasoning skills. Connect all nine dots with four connecting straight lines without lifting your pencil from the paper:

Did you figure it out? (The answer is at the end of this section.) Once you understand how to crack this puzzle, you won’t forget.

   Take a look at the “Puzzling Scales” logic puzzle below (figure below). Sam Loyd, a well-known puzzle master, created and refined countless puzzles throughout his lifetime (Cyclopedia of Puzzles, n.d.).

What steps did you take to solve this puzzle? You can read the solution at the end of this section.

Pitfalls to problem solving.

   Not all problems are successfully solved, however. What challenges stop us from successfully solving a problem? Albert Einstein once said, “Insanity is doing the same thing over and over again and expecting a different result.” Imagine a person in a room that has four doorways. One doorway that has always been open in the past is now locked. The person, accustomed to exiting the room by that particular doorway, keeps trying to get out through the same doorway even though the other three doorways are open. The person is stuck—but she just needs to go to another doorway, instead of trying to get out through the locked doorway. A mental set is where you persist in approaching a problem in a way that has worked in the past but is clearly not working now.

Functional fixedness is a type of mental set where you cannot perceive an object being used for something other than what it was designed for. During the Apollo 13 mission to the moon, NASA engineers at Mission Control had to overcome functional fixedness to save the lives of the astronauts aboard the spacecraft. An explosion in a module of the spacecraft damaged multiple systems. The astronauts were in danger of being poisoned by rising levels of carbon dioxide because of problems with the carbon dioxide filters. The engineers found a way for the astronauts to use spare plastic bags, tape, and air hoses to create a makeshift air filter, which saved the lives of the astronauts.

   Researchers have investigated whether functional fixedness is affected by culture. In one experiment, individuals from the Shuar group in Ecuador were asked to use an object for a purpose other than that for which the object was originally intended. For example, the participants were told a story about a bear and a rabbit that were separated by a river and asked to select among various objects, including a spoon, a cup, erasers, and so on, to help the animals. The spoon was the only object long enough to span the imaginary river, but if the spoon was presented in a way that reflected its normal usage, it took participants longer to choose the spoon to solve the problem. (German & Barrett, 2005). The researchers wanted to know if exposure to highly specialized tools, as occurs with individuals in industrialized nations, affects their ability to transcend functional fixedness. It was determined that functional fixedness is experienced in both industrialized and nonindustrialized cultures (German & Barrett, 2005).

In order to make good decisions, we use our knowledge and our reasoning. Often, this knowledge and reasoning is sound and solid. Sometimes, however, we are swayed by biases or by others manipulating a situation. For example, let’s say you and three friends wanted to rent a house and had a combined target budget of $1,600. The realtor shows you only very run-down houses for $1,600 and then shows you a very nice house for $2,000. Might you ask each person to pay more in rent to get the $2,000 home? Why would the realtor show you the run-down houses and the nice house? The realtor may be challenging your anchoring bias. An anchoring bias occurs when you focus on one piece of information when making a decision or solving a problem. In this case, you’re so focused on the amount of money you are willing to spend that you may not recognize what kinds of houses are available at that price point.

The confirmation bias is the tendency to focus on information that confirms your existing beliefs. For example, if you think that your professor is not very nice, you notice all of the instances of rude behavior exhibited by the professor while ignoring the countless pleasant interactions he is involved in on a daily basis. Hindsight bias leads you to believe that the event you just experienced was predictable, even though it really wasn’t. In other words, you knew all along that things would turn out the way they did. Representative bias describes a faulty way of thinking, in which you unintentionally stereotype someone or something; for example, you may assume that your professors spend their free time reading books and engaging in intellectual conversation, because the idea of them spending their time playing volleyball or visiting an amusement park does not fit in with your stereotypes of professors.

Finally, the availability heuristic is a heuristic in which you make a decision based on an example, information, or recent experience that is that readily available to you, even though it may not be the best example to inform your decision . Biases tend to “preserve that which is already established—to maintain our preexisting knowledge, beliefs, attitudes, and hypotheses” (Aronson, 1995; Kahneman, 2011). These biases are summarized in the table below.

Were you able to determine how many marbles are needed to balance the scales in the figure below? You need nine. Were you able to solve the problems in the figures above? Here are the answers.

   Many different strategies exist for solving problems. Typical strategies include trial and error, applying algorithms, and using heuristics. To solve a large, complicated problem, it often helps to break the problem into smaller steps that can be accomplished individually, leading to an overall solution. Roadblocks to problem solving include a mental set, functional fixedness, and various biases that can cloud decision making skills.

References:

Openstax Psychology text by Kathryn Dumper, William Jenkins, Arlene Lacombe, Marilyn Lovett and Marion Perlmutter licensed under CC BY v4.0. https://openstax.org/details/books/psychology

Review Questions:

1. A specific formula for solving a problem is called ________.

a. an algorithm

b. a heuristic

c. a mental set

d. trial and error

2. Solving the Tower of Hanoi problem tends to utilize a  ________ strategy of problem solving.

a. divide and conquer

b. means-end analysis

d. experiment

3. A mental shortcut in the form of a general problem-solving framework is called ________.

4. Which type of bias involves becoming fixated on a single trait of a problem?

a. anchoring bias

b. confirmation bias

c. representative bias

d. availability bias

5. Which type of bias involves relying on a false stereotype to make a decision?

6. Wolfgang Kohler analyzed behavior of chimpanzees by applying Gestalt principles to describe ________.

a. social adjustment

b. student load payment options

c. emotional learning

d. insight learning

7. ________ is a type of mental set where you cannot perceive an object being used for something other than what it was designed for.

a. functional fixedness

c. working memory

Critical Thinking Questions:

1. What is functional fixedness and how can overcoming it help you solve problems?

2. How does an algorithm save you time and energy when solving a problem?

Personal Application Question:

1. Which type of bias do you recognize in your own decision making processes? How has this bias affected how you’ve made decisions in the past and how can you use your awareness of it to improve your decisions making skills in the future?

anchoring bias

availability heuristic

confirmation bias

functional fixedness

hindsight bias

problem-solving strategy

representative bias

trial and error

working backwards

Answers to Exercises

algorithm:  problem-solving strategy characterized by a specific set of instructions

anchoring bias:  faulty heuristic in which you fixate on a single aspect of a problem to find a solution

availability heuristic:  faulty heuristic in which you make a decision based on information readily available to you

confirmation bias:  faulty heuristic in which you focus on information that confirms your beliefs

functional fixedness:  inability to see an object as useful for any other use other than the one for which it was intended

heuristic:  mental shortcut that saves time when solving a problem

hindsight bias:  belief that the event just experienced was predictable, even though it really wasn’t

mental set:  continually using an old solution to a problem without results

problem-solving strategy:  method for solving problems

representative bias:  faulty heuristic in which you stereotype someone or something without a valid basis for your judgment

trial and error:  problem-solving strategy in which multiple solutions are attempted until the correct one is found

working backwards:  heuristic in which you begin to solve a problem by focusing on the end result

Share This Book

• Increase Font Size

• Search Menu
• Browse content in Arts and Humanities
• Browse content in Archaeology
• Anglo-Saxon and Medieval Archaeology
• Archaeological Methodology and Techniques
• Archaeology by Region
• Archaeology of Religion
• Archaeology of Trade and Exchange
• Biblical Archaeology
• Contemporary and Public Archaeology
• Environmental Archaeology
• Historical Archaeology
• History and Theory of Archaeology
• Industrial Archaeology
• Landscape Archaeology
• Mortuary Archaeology
• Prehistoric Archaeology
• Underwater Archaeology
• Urban Archaeology
• Zooarchaeology
• Browse content in Architecture
• Architectural Structure and Design
• History of Architecture
• Residential and Domestic Buildings
• Theory of Architecture
• Browse content in Art
• Art Subjects and Themes
• History of Art
• Industrial and Commercial Art
• Theory of Art
• Biographical Studies
• Byzantine Studies
• Browse content in Classical Studies
• Classical Literature
• Classical Reception
• Classical History
• Classical Philosophy
• Classical Mythology
• Classical Art and Architecture
• Classical Oratory and Rhetoric
• Greek and Roman Archaeology
• Greek and Roman Papyrology
• Greek and Roman Epigraphy
• Greek and Roman Law
• Late Antiquity
• Religion in the Ancient World
• Digital Humanities
• Browse content in History
• Colonialism and Imperialism
• Diplomatic History
• Environmental History
• Genealogy, Heraldry, Names, and Honours
• Genocide and Ethnic Cleansing
• Historical Geography
• History by Period
• History of Agriculture
• History of Education
• History of Emotions
• History of Gender and Sexuality
• Industrial History
• Intellectual History
• International History
• Labour History
• Legal and Constitutional History
• Local and Family History
• Maritime History
• Military History
• National Liberation and Post-Colonialism
• Oral History
• Political History
• Public History
• Regional and National History
• Revolutions and Rebellions
• Slavery and Abolition of Slavery
• Social and Cultural History
• Theory, Methods, and Historiography
• Urban History
• World History
• Browse content in Language Teaching and Learning
• Language Learning (Specific Skills)
• Language Teaching Theory and Methods
• Browse content in Linguistics
• Applied Linguistics
• Cognitive Linguistics
• Computational Linguistics
• Forensic Linguistics
• Grammar, Syntax and Morphology
• Historical and Diachronic Linguistics
• History of English
• Language Variation
• Language Families
• Language Evolution
• Language Reference
• Language Acquisition
• Lexicography
• Linguistic Theories
• Linguistic Typology
• Linguistic Anthropology
• Phonetics and Phonology
• Psycholinguistics
• Sociolinguistics
• Translation and Interpretation
• Writing Systems
• Browse content in Literature
• Bibliography
• Children's Literature Studies
• Literary Studies (Modernism)
• Literary Studies (Romanticism)
• Literary Studies (American)
• Literary Studies (Asian)
• Literary Studies (European)
• Literary Studies (Eco-criticism)
• Literary Studies - World
• Literary Studies (1500 to 1800)
• Literary Studies (19th Century)
• Literary Studies (20th Century onwards)
• Literary Studies (African American Literature)
• Literary Studies (British and Irish)
• Literary Studies (Early and Medieval)
• Literary Studies (Fiction, Novelists, and Prose Writers)
• Literary Studies (Gender Studies)
• Literary Studies (Graphic Novels)
• Literary Studies (History of the Book)
• Literary Studies (Plays and Playwrights)
• Literary Studies (Poetry and Poets)
• Literary Studies (Postcolonial Literature)
• Literary Studies (Queer Studies)
• Literary Studies (Science Fiction)
• Literary Studies (Travel Literature)
• Literary Studies (War Literature)
• Literary Studies (Women's Writing)
• Literary Theory and Cultural Studies
• Mythology and Folklore
• Shakespeare Studies and Criticism
• Browse content in Media Studies
• Browse content in Music
• Applied Music
• Dance and Music
• Ethics in Music
• Ethnomusicology
• Gender and Sexuality in Music
• Medicine and Music
• Music Cultures
• Music and Culture
• Music and Media
• Music and Religion
• Music Education and Pedagogy
• Music Theory and Analysis
• Musical Scores, Lyrics, and Libretti
• Musical Structures, Styles, and Techniques
• Musicology and Music History
• Performance Practice and Studies
• Race and Ethnicity in Music
• Sound Studies
• Browse content in Performing Arts
• Browse content in Philosophy
• Aesthetics and Philosophy of Art
• Epistemology
• Feminist Philosophy
• History of Western Philosophy
• Metaphysics
• Moral Philosophy
• Non-Western Philosophy
• Philosophy of Action
• Philosophy of Law
• Philosophy of Religion
• Philosophy of Language
• Philosophy of Mind
• Philosophy of Perception
• Philosophy of Science
• Philosophy of Mathematics and Logic
• Practical Ethics
• Social and Political Philosophy
• Browse content in Religion
• Biblical Studies
• Christianity
• East Asian Religions
• History of Religion
• Judaism and Jewish Studies
• Qumran Studies
• Religion and Education
• Religion and Health
• Religion and Politics
• Religion and Science
• Religion and Law
• Religion and Art, Literature, and Music
• Religious Studies
• Browse content in Society and Culture
• Cookery, Food, and Drink
• Cultural Studies
• Customs and Traditions
• Ethical Issues and Debates
• Hobbies, Games, Arts and Crafts
• Lifestyle, Home, and Garden
• Natural world, Country Life, and Pets
• Popular Beliefs and Controversial Knowledge
• Sports and Outdoor Recreation
• Technology and Society
• Travel and Holiday
• Visual Culture
• Browse content in Law
• Arbitration
• Browse content in Company and Commercial Law
• Commercial Law
• Company Law
• Browse content in Comparative Law
• Systems of Law
• Competition Law
• Browse content in Constitutional and Administrative Law
• Government Powers
• Judicial Review
• Local Government Law
• Military and Defence Law
• Parliamentary and Legislative Practice
• Construction Law
• Contract Law
• Browse content in Criminal Law
• Criminal Procedure
• Criminal Evidence Law
• Sentencing and Punishment
• Employment and Labour Law
• Environment and Energy Law
• Browse content in Financial Law
• Banking Law
• Insolvency Law
• History of Law
• Human Rights and Immigration
• Intellectual Property Law
• Browse content in International Law
• Private International Law and Conflict of Laws
• Public International Law
• IT and Communications Law
• Jurisprudence and Philosophy of Law
• Law and Society
• Law and Politics
• Browse content in Legal System and Practice
• Courts and Procedure
• Legal Skills and Practice
• Primary Sources of Law
• Regulation of Legal Profession
• Medical and Healthcare Law
• Browse content in Policing
• Criminal Investigation and Detection
• Police and Security Services
• Police Procedure and Law
• Police Regional Planning
• Browse content in Property Law
• Personal Property Law
• Study and Revision
• Terrorism and National Security Law
• Browse content in Trusts Law
• Wills and Probate or Succession
• Browse content in Medicine and Health
• Browse content in Allied Health Professions
• Arts Therapies
• Clinical Science
• Dietetics and Nutrition
• Occupational Therapy
• Operating Department Practice
• Physiotherapy
• Radiography
• Speech and Language Therapy
• Browse content in Anaesthetics
• General Anaesthesia
• Neuroanaesthesia
• Clinical Neuroscience
• Browse content in Clinical Medicine
• Acute Medicine
• Cardiovascular Medicine
• Clinical Genetics
• Clinical Pharmacology and Therapeutics
• Dermatology
• Endocrinology and Diabetes
• Gastroenterology
• Genito-urinary Medicine
• Geriatric Medicine
• Infectious Diseases
• Medical Oncology
• Medical Toxicology
• Pain Medicine
• Palliative Medicine
• Rehabilitation Medicine
• Respiratory Medicine and Pulmonology
• Rheumatology
• Sleep Medicine
• Sports and Exercise Medicine
• Community Medical Services
• Critical Care
• Emergency Medicine
• Forensic Medicine
• Haematology
• History of Medicine
• Medical Ethics
• Browse content in Medical Skills
• Clinical Skills
• Communication Skills
• Nursing Skills
• Surgical Skills
• Browse content in Medical Dentistry
• Oral and Maxillofacial Surgery
• Paediatric Dentistry
• Restorative Dentistry and Orthodontics
• Surgical Dentistry
• Medical Statistics and Methodology
• Browse content in Neurology
• Clinical Neurophysiology

Problem based learning: a teacher's guide

December 10, 2021

Find out how teachers use problem-based learning models to improve engagement and drive attainment.

Main, P (2021, December 10). Problem based learning: a teacher's guide. Retrieved from https://www.structural-learning.com/post/problem-based-learning-a-teachers-guide

What is problem-based learning?

Problem-based learning (PBL) is a style of teaching that encourages students to become the drivers of their learning process . Problem-based learning involves complex learning issues from real-world problems and makes them the classroom's topic of discussion ; encouraging students to understand concepts through problem-solving skills rather than simply learning facts. When schools find time in the curriculum for this style of teaching it offers students an authentic vehicle for the integration of knowledge .

Embracing this pedagogical approach enables schools to balance subject knowledge acquisition with a skills agenda . Often used in medical education, this approach has equal significance in mainstream education where pupils can apply their knowledge to real-life problems. 

PBL is not only helpful in learning course content , but it can also promote the development of problem-solving abilities , critical thinking skills , and communication skills while providing opportunities to work in groups , find and analyse research materials , and take part in life-long learning .

PBL is a student-centred teaching method in which students understand a topic by working in groups. They work out an open-ended problem , which drives the motivation to learn. These sorts of theories of teaching do require schools to invest time and resources into supporting self-directed learning. Not all curriculum knowledge is best acquired through this process, rote learning still has its place in certain situations. In this article, we will look at how we can equip our students to take more ownership of the learning process and utilise more sophisticated ways for the integration of knowledge .

Philosophical Underpinnings of PBL

Problem-Based Learning (PBL), with its roots in the philosophies of John Dewey, Maria Montessori, and Jerome Bruner, aligns closely with the social constructionist view of learning. This approach positions learners as active participants in the construction of knowledge, contrasting with traditional models of instruction where learners are seen as passive recipients of information.

Dewey, a seminal figure in progressive education, advocated for active learning and real-world problem-solving, asserting that learning is grounded in experience and interaction. In PBL, learners tackle complex, real-world problems, which mirrors Dewey's belief in the interconnectedness of education and practical life.

Montessori also endorsed learner-centric, self-directed learning, emphasizing the child's potential to construct their own learning experiences. This parallels with PBL’s emphasis on self-directed learning, where students take ownership of their learning process.

Jerome Bruner’s theories underscored the idea of learning as an active, social process. His concept of a 'spiral curriculum' – where learning is revisited in increasing complexity – can be seen reflected in the iterative problem-solving process in PBL.

Webb’s Depth of Knowledge (DOK) framework aligns with PBL as it encourages higher-order cognitive skills. The complex tasks in PBL often demand analytical and evaluative skills (Webb's DOK levels 3 and 4) as students engage with the problem, devise a solution, and reflect on their work.

The effectiveness of PBL is supported by psychological theories like the information processing theory, which highlights the role of active engagement in enhancing memory and recall. A study by Strobel and Van Barneveld (2009) found that PBL students show improved retention of knowledge, possibly due to the deep cognitive processing involved.

As cognitive scientist Daniel Willingham aptly puts it, "Memory is the residue of thought." PBL encourages learners to think critically and deeply, enhancing both learning and retention.

Here's a quick overview:

• John Dewey : Emphasized learning through experience and the importance of problem-solving.
• Maria Montessori : Advocated for child-centered, self-directed learning.
• Jerome Bruner : Underlined learning as a social process and proposed the spiral curriculum.
• Webb’s DOK : Supports PBL's encouragement of higher-order thinking skills.
• Information Processing Theory : Reinforces the notion that active engagement in PBL enhances memory and recall.

This deep-rooted philosophical and psychological framework strengthens the validity of the problem-based learning approach, confirming its beneficial role in promoting valuable cognitive skills and fostering positive student learning outcomes.

What are the characteristics of problem-based learning?

Adding a little creativity can change a topic into a problem-based learning activity. The following are some of the characteristics of a good PBL model:

• The problem encourages students to search for a deeper understanding of content knowledge;
• Students are responsible for their learning. PBL has a student-centred learning approach . Students' motivation increases when responsibility for the process and solution to the problem rests with the learner;
• The problem motivates pupils to gain desirable learning skills and to defend well-informed decisions ;
• The problem connects the content learning goals with the previous knowledge. PBL allows students to access, integrate and study information from multiple disciplines that might relate to understanding and resolving a specific problem—just as persons in the real world recollect and use the application of knowledge that they have gained from diverse sources in their life.
• In a multistage project, the first stage of the problem must be engaging and open-ended to make students interested in the problem. In the real world, problems are poorly-structured. Research suggests that well-structured problems make students less invested and less motivated in the development of the solution. The problem simulations used in problem-based contextual learning are less structured to enable students to make a free inquiry.

• In a group project, the problem must have some level of complexity that motivates students towards knowledge acquisition and to work together for finding the solution. PBL involves collaboration between learners. In professional life, most people will find themselves in employment where they would work productively and share information with others. PBL leads to the development of such essential skills . In a PBL session, the teacher would ask questions to make sure that knowledge has been shared between pupils;
• At the end of each problem or PBL, self and peer assessments are performed. The main purpose of assessments is to sharpen a variety of metacognitive processing skills and to reinforce self-reflective learning.
• Student assessments would evaluate student progress towards the objectives of problem-based learning. The learning goals of PBL are both process-based and knowledge-based. Students must be assessed on both these dimensions to ensure that they are prospering as intended from the PBL approach. Students must be able to identify and articulate what they understood and what they learned.

Why is Problem-based learning a significant skill?

Using Problem-Based Learning across a school promotes critical competence, inquiry , and knowledge application in social, behavioural and biological sciences. Practice-based learning holds a strong track record of successful learning outcomes in higher education settings such as graduates of Medical Schools.

Educational models using PBL can improve learning outcomes by teaching students how to implement theory into practice and build problem-solving skills. For example, within the field of health sciences education, PBL makes the learning process for nurses and medical students self-centred and promotes their teamwork and leadership skills. Within primary and secondary education settings, this model of teaching, with the right sort of collaborative tools , can advance the wider skills development valued in society.

At Structural Learning, we have been developing a self-assessment tool designed to monitor the progress of children. Utilising these types of teaching theories curriculum wide can help a school develop the learning behaviours our students will need in the workplace.

Curriculum wide collaborative tools include Writers Block and the Universal Thinking Framework . Along with graphic organisers, these tools enable children to collaborate and entertain different perspectives that they might not otherwise see. Putting learning in action by using the block building methodology enables children to reach their learning goals by experimenting and iterating. 

How is problem-based learning different from inquiry-based learning?

The major difference between inquiry-based learning and PBL relates to the role of the teacher . In the case of inquiry-based learning, the teacher is both a provider of classroom knowledge and a facilitator of student learning (expecting/encouraging higher-order thinking). On the other hand, PBL is a deep learning approach, in which the teacher is the supporter of the learning process and expects students to have clear thinking, but the teacher is not the provider of classroom knowledge about the problem—the responsibility of providing information belongs to the learners themselves.

As well as being used systematically in medical education, this approach has significant implications for integrating learning skills into mainstream classrooms .

Using a critical thinking disposition inventory, schools can monitor the wider progress of their students as they apply their learning skills across the traditional curriculum. Authentic problems call students to apply their critical thinking abilities in new and purposeful ways. As students explain their ideas to one another, they develop communication skills that might not otherwise be nurtured.

Depending on the curriculum being delivered by a school, there may well be an emphasis on building critical thinking abilities in the classroom. Within the International Baccalaureate programs, these life-long skills are often cited in the IB learner profile . Critical thinking dispositions are highly valued in the workplace and this pedagogical approach can be used to harness these essential 21st-century skills.

What are the Benefits of Problem-Based Learning?

Student-led Problem-Based Learning is one of the most useful ways to make students drivers of their learning experience. It makes students creative, innovative, logical and open-minded. The educational practice of Problem-Based Learning also provides opportunities for self-directed and collaborative learning with others in an active learning and hands-on process. Below are the most significant benefits of problem-based learning processes:

• Self-learning: As a self-directed learning method, problem-based learning encourages children to take responsibility and initiative for their learning processes . As children use creativity and research, they develop skills that will help them in their adulthood.
• Engaging : Students don't just listen to the teacher, sit back and take notes. Problem-based learning processes encourages students to take part in learning activities, use learning resources , stay active , think outside the box and apply critical thinking skills to solve problems.
• Teamwork : Most of the problem-based learning issues involve students collaborative learning to find a solution. The educational practice of PBL builds interpersonal skills, listening and communication skills and improves the skills of collaboration and compromise.
• Intrinsic Rewards: In most problem-based learning projects, the reward is much bigger than good grades. Students gain the pride and satisfaction of finding an innovative solution, solving a riddle, or creating a tangible product.
• Transferable Skills: The acquisition of knowledge through problem-based learning strategies don't just help learners in one class or a single subject area. Students can apply these skills to a plethora of subject matter as well as in real life.
• Multiple Learning Opportunities : A PBL model offers an open-ended problem-based acquisition of knowledge, which presents a real-world problem and asks learners to come up with well-constructed responses. Students can use multiple sources such as they can access online resources, using their prior knowledge, and asking momentous questions to brainstorm and come up with solid learning outcomes. Unlike traditional approaches , there might be more than a single right way to do something, but this process motivates learners to explore potential solutions whilst staying active.

Embracing problem-based learning

Problem-based learning can be seen as a deep learning approach and when implemented effectively as part of a broad and balanced curriculum , a successful teaching strategy in education. PBL has a solid epistemological and philosophical foundation and a strong track record of success in multiple areas of study. Learners must experience problem-based learning methods and engage in positive solution-finding activities. PBL models allow learners to gain knowledge through real-world problems, which offers more strength to their understanding and helps them find the connection between classroom learning and the real world at large.

As they solve problems, students can evolve as individuals and team-mates. One word of caution, not all classroom tasks will lend themselves to this learning theory. Take spellings , for example, this is usually delivered with low-stakes quizzing through a practice-based learning model. PBL allows students to apply their knowledge creatively but they need to have a certain level of background knowledge to do this, rote learning might still have its place after all.

Key Concepts and considerations for school leaders

1. Problem Based Learning (PBL)

Problem-based learning (PBL) is an educational method that involves active student participation in solving authentic problems. Students are given a task or question that they must answer using their prior knowledge and resources. They then collaborate with each other to come up with solutions to the problem. This collaborative effort leads to deeper learning than traditional lectures or classroom instruction .

Key question: Inside a traditional curriculum , what opportunities across subject areas do you immediately see?

2. Deep Learning

Deep learning is a term used to describe the ability to learn concepts deeply. For example, if you were asked to memorize a list of numbers, you would probably remember the first five numbers easily, but the last number would be difficult to recall. However, if you were taught to understand the concept behind the numbers, you would be able to remember the last number too.

Key question: How will you make sure that students use a full range of learning styles and learning skills ?

3. Epistemology

Epistemology is the branch of philosophy that deals with the nature of knowledge . It examines the conditions under which something counts as knowledge.

Key question:  As well as focusing on critical thinking dispositions, what subject knowledge should the students understand?

4. Philosophy

Philosophy is the study of general truths about human life. Philosophers examine questions such as “What makes us happy?”, “How should we live our lives?”, and “Why does anything exist?”

Key question: Are there any opportunities for embracing philosophical enquiry into the project to develop critical thinking abilities ?

5. Curriculum

A curriculum is a set of courses designed to teach specific subjects. These courses may include mathematics , science, social studies, language arts, etc.

Key question: How will subject leaders ensure that the integrity of the curriculum is maintained?

6. Broad and Balanced Curriculum

Broad and balanced curricula are those that cover a wide range of topics. Some examples of these types of curriculums include AP Biology, AP Chemistry, AP English Language, AP Physics 1, AP Psychology , AP Spanish Literature, AP Statistics, AP US History, AP World History, IB Diploma Programme, IB Primary Years Program, IB Middle Years Program, IB Diploma Programme .

Key question: Are the teachers who have identified opportunities for a problem-based curriculum?

7. Successful Teaching Strategy

Successful teaching strategies involve effective communication techniques, clear objectives, and appropriate assessments. Teachers must ensure that their lessons are well-planned and organized. They must also provide opportunities for students to interact with one another and share information.

Key question: What pedagogical approaches and teaching strategies will you use?

8. Positive Solution Finding

Positive solution finding is a type of problem-solving where students actively seek out answers rather than passively accept what others tell them.

Key question: How will you ensure your problem-based curriculum is met with a positive mindset from students and teachers?

9. Real World Application

Real-world application refers to applying what students have learned in class to situations that occur in everyday life.

Key question: Within your local school community , are there any opportunities to apply knowledge and skills to real-life problems?

10. Creativity

Creativity is the ability to think of ideas that no one else has thought of yet. Creative thinking requires divergent thinking, which means thinking in different directions.

Key question: What teaching techniques will you use to enable children to generate their own ideas ?

11. Teamwork

Teamwork is the act of working together towards a common goal. Teams often consist of two or more people who work together to achieve a shared objective.

Key question: What opportunities are there to engage students in dialogic teaching methods where they talk their way through the problem?

12. Knowledge Transfer

Knowledge transfer occurs when teachers use their expertise to help students develop skills and abilities .

Key question: Can teachers be able to track the success of the project using improvement scores?

13. Active Learning

Active learning is any form of instruction that engages students in the learning process. Examples of active learning include group discussions, role-playing, debates, presentations, and simulations .

Key question: Will there be an emphasis on learning to learn and developing independent learning skills ?

14. Student Engagement

Student engagement is the degree to which students feel motivated to participate in academic activities.

Key question: Are there any tools available to monitor student engagement during the problem-based curriculum ?

Enhance Learner Outcomes Across Your School

Download an Overview of our Support and Resources

We'll send it over now.

Please fill in the details so we can send over the resources.

What type of school are you?

We'll get you the right resource

Is your school involved in any staff development projects?

Are your colleagues running any research projects or courses?

Do you have any immediate school priorities?

Please check the ones that apply.

Download your resource

Thanks for taking the time to complete this form, submit the form to get the tool.

Classroom Practice

Problem-Based Learning

• 1 Understand
• 2 Get Started
• 3 Train Your Peers
• 4 Related Links

What is Problem-Based Learning

Problem-based learning & the classroom, the problem-based learning process, problem-based learning & the common core, project example: a better community, project example: preserving appalachia, project example: make an impact.

All Toolkits

A Learning is Open toolkit written by the New Learning Institute.

Problem-based learning (PBL) challenges students to identify and examine real problems, then work together to address and solve those problems through advocacy and by mobilizing resources. Importantly, every aspect of the problem solving process involves students in real work—work that is a reflection of the range of expertise required to solve issues in the world outside of school.

While problem-based learning can use any type of problem as its basis, the approach described here is deliberately focused on local ones. Local problems allow students to have a meaningful voice, and be instrumental in a process where real, recognizable change results. It also gives students opportunities to source and interact with a variety of local experts.

In many classrooms teachers give students information and then ask them to solve problems at the culmination of a unit. Problem-based learning turns this on its head by challenging students to define the problem before finding the resources necessary to address or solve it. In this approach, teachers are facilitators: they set the context for the problem, ask questions to propel students’ interests and learning forward, help students locate necessary resources and experts, and provide multiple opportunities to critique students’ process and progress. In some cases, the teacher may identify a problem that is connected to existing curriculum; in others the teacher may assign a larger topic and challenge the students to identify a specific problem they are interested in addressing.

This approach is interdisciplinary and provides natural opportunities for integrating a variety of required content areas. Because recognizing and making relationships between content areas is a necessary part of the problem-solving process—as it is in the real world—students are building skills to prepare them for life, work, and civic participation. Problem-based learning gives students a variety of ways to address and tackle a problem. It encourages everyone to contribute and rewards different kinds of success. This builds confidence in students who have not always been successful in school. With the changing needs of today’s world, there is a growing urgency for people who are competent in a range of areas including the ability to apply critical thinking to complex problems, collaborate, network and gather resources, and communicate and persuade others to actively take up a cause.

Problem-based learning builds agency & independence

Although students work collaboratively throughout the process, applying a wide range of skills to new tasks requires them to develop their own specialties that lead to greater confidence and competency. And because the process is student-driven, students are challenged to define the problem, conduct comprehensive research, sort through multiple solutions and present the one that allows them best move forward. This reinforces a sense of self-agency and independence.

Problem-based learning promotes adaptability & flexibility

Investigating and solving problems requires students to work with many different types of people and encounter many unknowns throughout the process. These experiences help students learn to be adaptable and flexible during periods of uncertainty. From an academic standpoint, this flexible mindset is an opportunity for students to develop a range of communication aptitudes and styles. For example, in the beginning research phases, students must gather multiple perspectives and gain a clear understanding of their various audiences. As they move into the later project phases they must develop more nuanced ways to communicate with each audience, from clearly presenting information to persuasion to defending the merits of a new idea.

Problem-based learning is persistent

Educators recognize that when students are working towards a real goal they care about, they show increased investment and willingness to persist through challenges. Problem-based learning requires students to navigate many variables including the diverse personalities on a project team, the decisions and perspectives of stakeholders, challenging and rigorous content, and real world deadlines. Students will experience frustration and failure, but they will learn that working though that by trying new things will be its own reward. And this is a critical lesson that will be carried on into life and work.

Problem-based learning is civically engaged

Because problem-based learning focuses on using local issues as jumping off points it gives students a meaningful context in which to voice their opinions and take the initiative to find solutions. Problems within schools and communities also provide opportunities for students to work directly with stakeholders (i.e. the school principal or a town council member) and experts (i.e. local residents, professionals, and business owners). These local connections make it more likely that students will successfully implement some aspect of their plan and gives students firsthand experience with civic processes.

A problem well put is half solved. – John Dewey

The problem-based learning process described in this toolkit has been refined and tested through the Model Classroom Program, a project of the New Learning Institute. Educators throughout the United States participated in this program by designing, implementing, and documenting projects. The resulting problem-based learning approach provides a clear process and diverse set of tools to support problem-based learning.

The problem-based learning process can help students define problems in new ways, explore multiple perspectives, challenge their thinking, and develop the real-world skills needed for planning and carrying out a project. Beyond this, because the approach emphasizes local and community-based issues, this process develops student drive and motivation as they work towards a tangible end result with the potential to impact their community.

Make it Real

The world is full of unsolved problems and opportunities just waiting to be addressed. The Make It Real phase is about identifying a real problem within the local community, then conducting further investigation to define the problem.

Identify what you do and don’t know about the problem Brainstorm what is known about the problem. What do you know about it at the local level? Is this problem globally relevant? How? What questions would you investigate further?

Discover the problem’s root causes and impacts on the community While it’s easy to find a problem, it’s much harder to understand it. Investigate how the problem impacts different people and places. As a result of these investigations, students will gain a clearer understanding of the problem.

Make it Relevant

Problems are everywhere, but it can often be difficult to convince people that a specific problem should matter to them. The word relevant is from the Latin root meaning “to raise” or “to lift up.” To Make It Relevant, elevate the problem so that people in the community and beyond will take interest and become invested in its resolution. Make important connections in order to begin a plan to address the problem.

Field Studies

Collect as much information as possible on the problem. Conduct the kind of research experts in the field—scientists and historians—conduct. While online and library research is a good starting point, it’s important that students get out into the real world to conduct their own original research! This includes using methods such as surveys, interviews, photo and video documentation, collection of evidence (such as science related activities), and working with a variety of experts and viewpoints.

Develop an action-plan Have students analyze their field studies data and create charts, graphs, and other visual representations to understand their findings. After analyzing, students will have the information needed to develop a plan of action. Importantly, they’ll need to consider how best to meet the needs of all stakeholders, which will include a diverse community such as local businesses, community members, experts, and even the natural world.

Make an Impact

Make An Impact with a creative implementation based on the best research-supported ideas. In many cases, making an impact is about solving the problem. Sometimes it’s about addressing it, making representations to stakeholders, or presenting a possible solution for future implementation. At the most rigorous level, students will implement a project that has lasting impact on their community.

Put your plan into action See the hard work of researching and analyzing the problem pay off as students begin implementing their plans. In so doing, they’ll act as part of a team creating a product to share. Depending on the problem, purpose, and audience, their products might be anything from a website to an art installation to the planning of a community-wide event.

Share your findings and make an impact Share results with important stakeholders and the larger community. Depending on the project, this effort may include awareness campaigns, a persuasive presentation to stakeholders, an action-oriented campaign, a community-wide event, or a re-designed program. In many cases this “final” act leads to the beginning of another project!

With the Common Core implementation, teachers have found different strategies and resources to help align their practice to the standards. Indeed, many schools and districts have discovered a variety of solutions. When considering Common Core alignment, the opportunity presented by methods like problem-based learning hinges on a belief in the art of teaching and the importance of developing students’ passion and love of learning. In short, with the ultimate goal of making students college-, career-, and life-ready, it’s essential that educators put students in the driver’s seat to collaboratively solve real problems.

The Common Core ELA standards draw a portrait of a college- and career-ready student. This portrait includes characteristics such as independence, the ability to adapt communication to different audiences and purposes, the ability to comprehend and critique, appreciation for the value of evidence (when reading and when creating their own work), and the capability to make strategic use of digital media. Developing creative solutions to complex problems provides students with multiple opportunities to develop all of these skills.

Independence

Students are challenged to define the problem and conduct comprehensive research, then present solutions. This student-driven process requires students to find multiple answers and think critically about the best way to act, ultimately building confidence and independence.

Adapting Communication to Different Audiences and Purposes

In the initial research phases, students must gather multiple perspectives and gain a clear understanding of who those audiences are. As they move into the later project phases, they must communicate in a variety of ways (including informative and persuasive methods) to reach diverse audiences.

Comprehending and Critiquing

In examining multiple perspectives, students must summarize various viewpoints, addressing their strengths and critiquing their weaknesses. Furthermore, as students develop solutions they must analyze each idea for its potential success, which compels them to critique their own work in addition to the work of others.

Valuing Evidence

Collecting evidence is essential to the process, whether through visual documentation of a problem, uncovering key facts, or collecting narratives from the community.

Strategic Use of Digital Media

The use of digital media is naturally integrated throughout the entire process. The problem-based learning approach not only builds the specific 21st century skills called for by the Common Core, it also embraces practices supported by hundreds of years of educational theory. This is not the next new thing – problem-based learning is one example of how vetted best educational practices will meet the needs of a future economy and society; and, more immediately, the new Common Core Standards.

Language Arts

The Key Design Considerations for the English Language Arts standards describe an integrated literacy model in which all communication processes are closely connected. Likewise, the problem-based learning approach expects students to read, write, and speak about the issue (whether through interviews or speeches) in a variety of ways (expository, persuasive). In addition, the Key Design Considerations describe how literacy is a shared responsibility across subject areas. Because problem-based learning is rooted in real issues, these naturally connect to science content areas (environmental sciences, engineering and design, innovation and invention), social studies (community history, geography/land forms), math (including operations such as graphing, statistics, economics, and mathematical modeling), and art. As part of this interdisciplinary model, problem-based learning follows a process that touches on key ELA skill areas including research, a variety of writing styles and formats (both reading and writing in these formats), publishing, and integration of digital media.

It’s also important to note that the Common Core calls for an increase in informational and nonfiction text. This objective is easily met through examining real problems. Quite simply, informational and nonfiction text is everywhere – in newspaper articles, public surveys, government documents, etc. Very often, when reading out of context, many students struggle to work through and comprehend these types of complex texts. Because problem-based learning authentically integrates a real purpose with reading informational text, students work harder to comprehend and apply their reading.

Note: Each project has the potential to meet many additional standards. The standards outlined here are only a sampling of those addressed by this approach.

Reading Standards

CCSS.ELA-Literacy.CCRA.R.6 Assess how point of view or purpose shapes the content and style of a text. In the early phases of problem-based learning, students investigate the topic by reading a range of informational and persuasive texts, and by talking to a variety of experts and community members. As an essential component to these investigations on multiple perspectives, students must be able to understand the purpose of the text, the intended audience, and the individual’s position on the issue (if applicable).

CCSS.ELA-Literacy.CCRA.R.7 Integrate and evaluate content presented in diverse media and formats, including visually and quantitatively, as well as in words. As students consider multiple perspectives on their identified problem, they naturally will seek a wide range of print materials, media resources (videos, presentations), and formats (research studies, opinion pieces). Comparing and contrasting the viewpoints of these various texts will help students shape a more holistic view of the problem.

Writing Standards

CCSS.ELA-Literacy.CCRA.W.1 Write arguments to support claims in an analysis of substantive topics or texts using valid reasoning and relevant and sufficient evidence. As students analyze the problem, multiple opportunities for persuasive writing emerge. In the early project phases, students might summarize their perspective on the problem using key evidence from a variety of research (online, community polling, and discussions with experts). In the later project phases, students might develop a proposal or presentation to persuade others to change personal habits or consider a larger change in the community.

Speaking & Listening Standards

CCSS.ELA-Literacy.CCRA.SL.1 Prepare for and participate effectively in a range of conversations and collaborations with diverse partners, building on others’ ideas and expressing their own clearly and persuasively. Multiple perspectives are an essential component to any problem-based project. As students investigate, they must seek a wide range of opinions and personal stories on the issues. Furthermore, this process is collaborative. Students must trust and work with each other, they must trust and work with key experts, and, in some cases, they must convince others to collaborate with them around a shared purpose or cause.

CCSS.ELA-Literacy.CCRA.SL.5 Make strategic use of digital media and visual displays of data to express information and enhance understanding of presentations. Because each problem-based project requires students to analyze information, share their findings with others, and collaborate on a variety of levels, digital media is naturally integrated into these tasks. Students might create charts, graphs, or other illustrative/photo/video displays to communicate their research results. Students might use a variety of digital formats including graphic posters, video public service announcements (PSAs), and digital presentations to mobilize the community to their cause. Inherent to these processes is special consideration of how images, videos, and other media support key ideas and key evidence and further the effectiveness of their presentation on the intended audience.

Mathematics

Simply put, math is problem solving. Problem-based learning provides multiple opportunities for students to apply and develop their understanding of various mathematical concepts within real contexts. Through the various stages of problem-based learning, students engage in the same dispositions encouraged by the Standards for Mathematical Practice

CCSS.Math.Practice.MP1 Make sense of problems and persevere in solving them. Problem-based learning is all about problem solving. An essential first step is understanding the problem as deeply as possible, rather than rushing to solve it. This is a process that takes time and perseverance, both individually and in collaborative student groups.

CCSS.Math.Practice.MP3 Construct viable arguments and critique the reasoning of others. As students understand and deconstruct a problem, they must begin to form solutions. As part of this process, they must have evidence (including visual and mathematical evidence) to support their position. They must also understand other perspectives to solving the problem, and they must be prepared to critique those other perspectives based on verbal and mathematical reasoning.

CCSS.Math.Practice.MP4 Model with mathematics. Throughout the process, students must analyze information and data using a variety of mathematical models. These range from charts and graphs to 3-D modeling used in science or engineering projects.

CCSS.Math.Practice.MP5 Use appropriate tools strategically. According to the Common Core Math Practices standard, “Mathematically proficient students consider the available tools when solving a mathematical problem. These tools might include pencil and paper, concrete models, a ruler, a protractor, a calculator, a spreadsheet, a computer algebra system, a statistical package, or dynamic geometry software.” In addition to providing opportunities to use these tools, problem-based learning asks students to make effective use of digital and mobile media as they collect information, document the issue, share their findings, and mobilize others to their cause.

School Name | Big Horn Elementary Location | Big Horn, Wyoming Total Time | 1 year Subjects | English Language Arts, Social Studies, Math, Science Grade Level | 3rd Grade Number of Participants | 40 students in two classrooms

Students informed the school about the importance of recycling, developed systems to improve recycling options and implemented a school-wide recycling program that involved all students, other teachers, school principals, school custodians, and the county recycling center.

While investigating their local county history, students were challenged to recognize their role in the community and ultimately realize the importance of stewardship for the county’s land, history and culture. Students began by researching their local history through many first hand experiences including museum visits, local resident interviews and visits to places representing the current culture.

Challenged to find ways to make “A Better Community”, students chose to investigate recycling.

They conducted hands-on research to determine the need for a recycling program through a school survey, town trash pickup and visit to the local Landfill and Recycling Center.

Students then developed a proposal for a school-wide recycling program, interviewed the principal to address their concerns and began to carry out their plan.

Students designed recycling bins for each classroom and worked with school janitors to develop a plan for collection.

Students visited each classroom to distribute the recycling bins and describe how to use them. Students developed a schedule for collecting bins and sorting materials. The program continues beyond the initial school-year; students continue to expand their efforts.

School Name | Bates Middle School Location | Danville, Kentucky Total Time | 8 weeks Subjects | English Language Arts Grade Level | 6th Grade Number of Participants |25 students

Students created Project Playhouse, a live production for the local community. Audience members included community members, parents, and other students. In addition, students designed a quilt sharing Appalachian history, and recorded their work on a community website.

Appalachia has a rich culture full of unique traditions and an impressive heritage, yet many negative stereotypes persist. 6th grade students brainstormed existing stereotypes and their consequences on the community.

Students discussions led them to realize that, in their region, stereotypes were preventing people from overcoming adversity. They set about to conduct further research demonstrating the strengths of Appalachian heritage.

Students investigated Appalachian culture by working with local experts like Tammy Horn, professor at Eastern Kentucky University and specialist in Appalachian cultural traditions; taking a field trip to Logan Hubble Park to explore the natural region; talking with a “coon” hunter and other local Appalachians including quilters, cooks, artists, and writers.

Students developed a plan to curate an exhibition and live production for the local community. Finally, students connected virtually with museum expert Rebecca Kasemeyer, Associate Director of Education at the Smithsonian National Portrait Gallery to discuss exhibition design.

For their final projects students produced a series of works exhibiting Appalachian life, work, play and community structure including a quilt, a theatrical performance and a website.

Students invited the community to view their exhibit and theatrical performance.

School Name | Northwestern High School Location | Rock Hill, South Carolina Total Time | One Semester Subjects | Engineering Grade Level | High School Number of Participants | 20 students

Engineering teacher Bryan Coburn presented a scenario to his students inspired by the community’s very real drought, a drought so bad that cars could only be washed on specific days. Students identified and examined environmental issues related to water scarcity in their community.

Based on initial brainstorming, students divided into teams based on specific problems related to a water shortage. These included topics like watering gardens and lawns, watering cars, drinking water to name a few.

Based on their topic, students conducted online research on existing solutions to their specific problem.

Students analyzed their research to develop their own prototypes and plans for addressing the problem. Throughout the planning phase students received peer and teacher feedback on the viability of their prototypes, resulting in many edits before final designs were selected for creation.

Students created online portfolios showcasing their research, 3D designs, and multimedia presentations marketing their designs. Student portfolios included documentation of each stage of the design process, a design brief, decision matrix, a prototype using Autodesk Inventor 3D professional modeling tool, and a final presentation.

Students shared their presentations and portfolios in a public forum, pitching their proposed solution to a review committee consisting of local engineers from the community, the city water manager and the school principal.

Plan Your PBL Experience

Resources to help you plan.

Problem-based learning projects are inspired by students’ real world experiences and the pressing issues and concerns they want to address. Problem-based learning projects benefit teachers by increasing student motivation and engagement, while deepening knowledge and improving essential skills. In spite of the inherent value problem-based learning brings to any educational setting, planning a large project can be an overwhelming task.

Through the New Learning Institute’s Model Classroom, a range of problem-based learning planning tools have been developed and tested in a variety of educational settings. These tools make the planning process more manageable by supporting teachers in establishing the context and/or problem for a project, planning for and procuring the necessary resources for a real-world project (including community organizations, expert involvement, and tools needed for communicating, creating and sharing), and facilitating students through the project phases.

Here are some initial considerations when planning a problem-based learning project. (More detailed tips and planning tools follow.) These questions can help you determine where to begin your project planning. Once you have a clear idea, the problem-based learning planning tools will guide you through the process.

Are you starting from the curriculum? It’s probably tempting to jump in and define a problem for students based on the unit of study. And time constraints may make a teacher-defined problem necessary. If time permits, a problem-based learning project will be more successful if time is built-in for students to define a problem they’d like to address. Do this by building in topic exploration time, and then challenging students to define a problem based on their findings. Including this extra time will allow students to develop their own interests and questions about the topic, deepening engagement and ensuring that students are investigating a problem they’re invested in—all while covering curriculum requirements.

Are you starting from student interest? Perhaps your students want to solve a problem in the school, such as bullying or lack of recycling. Perhaps they’re concerned about a larger community problem, such as a contested piece of parkland that is up for development or a pollution problem in your local waterways. Starting with student interest can help ensure students’ investment and motivation. However, this starting point provides less direct navigation than existing projects or curriculum materials. When taking on a project of this nature, be sure to identify natural intersections with your curriculum. It also helps to enlist community or expert support.

Start Small – Focus on Practices as Entry Points

If you’re new to problem-based learning it makes sense to start small. Many teachers new to this approach report that starting with the smaller practices—such as integrating research methods or having students define a specific problem within a unit of study—ultimately sets the stage for larger projects and more easily leads them to implement a problem-based learning project.

Opportunities to address and solve problems are everywhere. Just look in your own backyard or schoolyard. Better yet, ask students to identify problems within the school community or based on a topic of interest within a unit of study. As you progress through the project, find natural opportunities for research and problem solving by working with the people who are affected by the issue and invested in solving it. Finally, make sure students share their work with an authentic audience who cares about the problem and its resolution.

Be Honest About Project Constraints

When you’re new to problem-based learning, the most important consideration is your project constraints. For example, perhaps you’re required to cover a designated set of standards and content. Or perhaps you have limited time for this project experience. Whatever the constraints, determine them in advance then plan backwards to determine the length and depth of your project.

Identify Intersections With Your Curriculum

Problem-based learning projects are interdisciplinary and have the ability to meet a range of standards. Identify where these intersections naturally occur with the topic students have selected, then design some activities or project requirements to ensure these content areas are covered.

Turn Limitations Into Opportunities

Many educators work in schools with pre-defined curriculum or schedule constraints that make implementing larger projects difficult. In these cases, it may help to find small windows of opportunity during the school day or after school to implement problem-based learning. For example, some teachers implement problem-based learning in special subject courses which have a more flexible curriculum. Others host afterschool “Genius Hour” programs that challenge students to explore and investigate their interests. Whatever opportunity you find, make the work highly visible to staff and parents. Make it an intention to get the school community exploring and designing possibilities of integrating these practices more holistically.

Take Risks and Model Perseverance

The problem-based learning process is messy and full of opportunities to fail, just like real life and real jobs. Many educators share that this is incredibly difficult for their students and themselves. Despite the initial letdown that comes with small failures, it’s important that students see the value in learning from failure and persevering through these challenges. Model risk taking for your students and when you make a mistake or face a challenge, welcome it with open arms by demonstrating what you’ve learned and what you’ll do differently next time around. Let students know that it’s okay to make mistakes; that mistakes are a welcome opportunity to learn and try something new.

Be Less Helpful

A key to building problem-solving and critical thinking capacities is to be less helpful. Let students figure things out on their own. In classroom implementation, teachers repeatedly share that handing over control to the students and “being less helpful” makes for a big mindshift. This shift is often described as becoming a facilitator, which means knowing when to stand back and knowing when to step-in and offer extra support.

Be Flexible

Recognize that there is no one-size-fits-all answer to any problem. Understanding this and being able to identify unique challenges will help students understand that an initial failure is just a bump in the road. Being flexible also helps students focus on the importance of process over product.

Experts are Everywhere

Experts are everywhere; their differing perspectives and expertise help bring learning to life. But think outside the box about who experts are and integrate multiple opportunities for their involvement. Parents and community members who are not often thought of as experts can speak to life, work, and lived historical experiences. Beyond that, the people usually thought of as experts—researchers, scientists, museum professionals, business professionals, university professors—are more available than many teachers think. It’s often just a matter of asking. And don’t take sole responsibility for finding experts! Seek your students’ help in identifying and securing expert or community support. And when trying to locate experts, don’t forget: students can also be experts.

Maintain a List of Your Support Networks

Some schools have brought the practice of working with the community and outside experts to scale by building databases of parent and community expertise and their interest in working with students. See if a school administrative assistant, student intern, or parent helper can take the lead in developing and maintaining this list for your school community.

Encourage Original Research

Online research is often a great starting point. It can be a way to identify a knowledge base, locate experts, and even find interest-based communities for the topic being approached. While online research is literally right at students’ fingertips, make sure your students spend time offline as well. Original research methods include student-conducted surveys, interviewing experts, and working alongside experts in the field.

This Learning is Open toolkit includes a number of tools and resources that may be helpful as you plan and reflect on your project.

Brainstorming Project Details (Google Presentation) This tool is designed to aid teachers as they brainstorm a project from a variety of starting-points. It’s a helpful tool for independent brainstorming, and would also make a useful workshop tool for teachers who are designing problem-based learning experiences.

Guide to Writing a Problem Statement (PDF) You’ve got to start somewhere. Finding—and defining—a problem is a great place to begin. This guide is a useful tool for teachers and students alike. It will walk you through the process of identifying a problem by providing inspiration on where to look. Then it will support you through the process of defining that problem clearly.

Project Planning Templates (PDF) Need a place to plan out each project phase? Use this project planner to record your ideas in one place. This template is great used alone or in tandem with the other problem-based learning tools.

Ladder of Real World Learning Experiences (PDF) Want to determine if your project is “real” enough? This ladder can be used to help teachers assess their project design based on the real world nature of the project’s learning context, type of activities, and the application of digital tools.

Digital Toolkit (Google Doc) This toolkit was developed in collaboration with teachers and continues to be a community-edited document. The toolkit provides extensive information on digital tools that can be used for planning, brainstorming, collaborating, creating, and sharing work.

Assessing student learning is a crucial part of any dynamic, nonlinear problem-based learning project. Problem-based projects have many parts to them. It’s important to understand each project as a whole as well as each individual component. This section of the toolkit will help you understand problem-based learning assessments and help you develop assessment tools for your problem-based learning experiences.

Because the subject of assessments is so complex, it may be helpful to define how it is approached here.

Portfolio-based Assessment

Each phase of problem-based learning has important tasks and outcomes associated with it. Assessing each phase of the process allows students to receive on-time feedback about their process and associated products and gives them the opportunity to refine and revise their work throughout the process.

Feedback-based Assessment

Problem-based learning emphasizes collaboration with classmates and a range of experts. Assessment should include multiple opportunities for peer feedback, teacher feedback, and expert feedback.

Assessment as a System of Interrelated Feedback Tools

These tools may include rubrics, checklists, observation, portfolios, or quizzes. Whatever the matrix of carefully selected tools, they should optimize the feedback that students receive about what and how they are learning and growing.

Assessment Tools

One way to approach developing assessment tools for your students’ specific problem-based learning project is to deconstruct the learning experience into various categories. Together, these categories make up a simple system through which students may receive feedback on their learning.

Assessing Process

Many students and teachers alike have been conditioned to emphasize and evaluate the end product. While problem-based learning projects often result in impressive end products, it’s important to emphasize each stage of the process with students.

Each phase of problem-based learning process emphasizes important skills, from research and data gathering in the early phases to problem solving, collaboration, and persuasion in the later phases. There are many opportunities to assess student understanding and skill throughout the process. The tools here provide many methods for students to self-assess their process, get feedback from peers, and get feedback from their teachers and other adults.

The Process Portfolio Tool (PDF) provides a place for students to collect their work, define their problem and goals, and reflect throughout the process. Use this as a self-assessment tool, as well as a place to organize the materials for student portfolios.

Driving & Reflection Questioning Guidelines (PDF) is a simple tool for teachers who are integrating problem-based learning into the learning process. The tool highlights the two types of questions teachers/facilitators should consider with students: driving questions and reflection questions. Driving questions push students in their thinking, challenging them to build upon ideas and try new ways to solve problems. Reflection questions ask students to reflect on a process phase once it’s complete, challenging them to think about how they think.

The Peer Feedback Guidelines (PDF) will help students frame how they provide feedback to their peers. The guide includes tips on how and when to use these guidelines in different types of forums (i.e. whole group, gallery-style, and peer-to-peer).

The Buck Institute has also developed a series of rubrics that address various project phases. Their Collaboration Rubric (PDF) can help students be better teammates. (Being an effective teammate is critical to the problem-based learning process.) Their Presentation Rubric (PDF) can help students, adult mentors, and outside experts evaluate final presentations. Final presentations are often one of the most exciting parts of a project.

Assessing Subject Matter and Content

A common concern that emerges in any problem-based learning design is whether projects are able to meet all required subject matter content targets. Because many students are required to learn specific content, there is often tension around the student-directed nature of problem-based learning. While teachers acknowledge that students go deeper into specific content during problem-based learning experiences, teachers also want to ensure that their students are meeting all content goals.

Many teachers in the New Learning Institute’s Model Classroom Program addressed this issue directly by carefully examining their curriculum requirements throughout the planning and implementation phases. Begin by planning activities and real world explorations that address core content. As the project evolves, revisit content standards to mark off and record additional standards met and create a contingency plan for those that have not been addressed.

The Buck Institute’s Rubric for Rubrics (DOC) is an excellent source for designing a rubric to fit your needs. Developing a rubric can be the most simple and effective tool for planning a project around required content targets.

Blended learning is another emerging trend that educators are moving towards as a way to both address individualized skill needs and to create space for real world project strategies, like problem-based learning. In these learning environments, students address skill acquisition through blended experiences and then apply their skills through projects and other real world applications. To learn more about blended models, visit Blend My Learning .

Assessing Mindsets and Skills

In addition to assessing process and subject matter content, it may be helpful to consider the other important mindsets and skills that the problem-based learning project experience fosters. These include persistence, problem solving, collaboration, and adaptability. While problem-based learning supports the development of a large suite of 21st century mindsets and skills, it may be helpful to focus assessments on one or two issues that are most relevant. Some helpful tools may include:

The Buck Institute offers rubrics for Critical Thinking (PDF), Collaboration (PDF), and Creativity and Innovation (PDF) that are aligned to the Common Core State Standards. These can be used as is or tailored to your specific needs.

The Character Growth Card (PDF) from the CharacterLab at Kipp is designed for school assessments more than it is for project assessment, but the list of skills and character traits are relevant to design thinking. With the inclusion of a more relevant, effective scale, these can easily be turned into a rubric, especially when paired with the Buck Institute’s Rubric for Rubrics tool.

Host a Teacher Workshop

Teachers are instrumental in sharing and spreading best practices and innovative strategies to other teachers. Once you’re confident in your conceptual and practical grasp of problem-based learning, share your knowledge and expertise with others.

The downloadable presentation decks below (PowerPoint) are adaptable tools for helping you spread the word to other educators. The presentations vary in length and depth. A 90-minute presentation introduces problem-based learning and provides a hands-on opportunity to complete an activity. The half-day and full day presentations provide in-depth opportunities to explore projects and consider their classroom applications. While this series is structured in a way that each presentation builds on the previous one, each one can also be used individually as appropriate. Each is designed to be interactive and participatory.

Getting Started with Problem-based Learning (PPT) A presentation deck for introducing educators to the Learning is Open problem-based learning process during a 90-minute peer workshop.

Dig Deeper with Problem-based Learning – Half-day (PPT) A presentation deck for training educators on the Learning is Open problem-based learning process during a half-day peer workshop.

Dig Deeper with Problem-based Learning – Full day (PPT) A presentation deck for training educators on the Learning is Open problem-based learning process during a full day peer workshop.

Related Links

Problem-based learning: detailed case studies from the model classroom.

For three years, the New Learning Institute’s Model Classroom program worked with teachers to design and implement projects. This report details the work and provides extensive case studies.

Title: Model Classroom: 3-Year Report (PDF) Type: PDF Source: New Learning Institute

Setting up Learning Experiences Using Real Problems

This New York Times Learning Blog article explores how projects can be set-up with real problems, providing many examples and suggestions for this approach.

Title: “ Guest Lesson | For Authentic Learning Start with Real Problems ” Type: Article Source: Suzie Boss. New York Times Learning Blog

Guest Lesson: Recycling as a Focus for Project-based Learning

There are many ways to set-up a project with a real world problem. This article describes the problem of recycling, providing multiple examples of student projects addressing the issue.

Title: “ Guest Lesson | Recycling as a Focus for Project-Based Learning ” Type: Article Source: Suzie Boss. New York Times Learning Blog

Problem-based Learning: Professional Development Inspires Classroom Project

This video features how the Model Classroom professional development workshop model worked in practice, challenging teachers to collaboratively problem-solve using real world places and experts. It also shows how one workshop participant used her experience to design a yearlong problem-based learning project for first-graders called the “Streamkeepers Project.”

Title: Mission Possible: the Model Classroom Type: Video Source: New Learning Institute

Problem-based Learning in an Engineering Class: Solutions to a Water Shortage

Engineering teacher Bryan Coburn used the problem of a local water shortage to inspire his students to conduct research and design solutions.

Title: “ National Project Aims to Inspire the Model Classroom ” Type: Article Source: eSchool News

Making Project-based Learning More Meaningful

This article provides great tips on how to design projects to be relevant and purposeful for students. While it addresses the larger umbrella of project-based learning, the suggestions and tips provided apply to problem-based learning.

Title: “ How to Reinvent Project-Based Learning to Make it More Meaningful ” Type: Article Source: KQED Mindshift

PBL Downloads

Guide to Writing a Problem Statement (PDF)

A walk-through guide for identifying and defining a problem.

Project Planning Templates (PDF)

A planning template for standalone use or to be used along with other problem-based learning tools.

Process Portfolio Tool (PDF)

A self-assessment tool to support students as they collect their work, define their problem and goals, and make reflections throughout the process.

More PBL Downloads

Getting Started with Problem-based Learning (PPT)

A presentation deck for introducing educators to the Project MASH problem-based learning process during a 90-minute peer workshop.

Dig Deeper with Problem-based Learning – Half-day (PPT)

A presentation deck for training educators on the PBL process during a half-day peer workshop.

Dig Deeper with Problem-based Learning – Full day (PPT)

A presentation deck for training educators on the PBL process during a full day peer workshop.

• Youth Cardio Equipment
• Challenge Courses and Climbing
• School Spotlights
• Research & Data
• Grants & Funding
• State Vendor No. & Contracts

Problem Solving

Problem Solving, what is it and why is it important?

Problem Solving takes information from what we already know and adds it together to make a sequence of events to solve a specific task.

Problem solving is a skill that must be taught, and practiced in order to develop the skills necessary for success throughout grade school, into adulthood. 

We practice problem solving from a very young age. Learning how to problem solve applies to both academics, and real world situations. Students need problem solving skills to learn to navigate through different situations which will impact their ability to preform tasks, especially later on in life. 

Problem solving involves much of the brain to help focus and attend to the information necessary to overcome challenges....... The prefrontal cortex controls executive functions like decision-making, problem solving, memory, language, emotions and attention. The cerebellum initiates putting patterns into a sequence, like letters into words, words into a sentences and numbers into order. Activities that activate the cerebellum while performing challenging cognitive skills strengthens areas in the brain for focus and attention. 

If a child is lacking problem solving skills........ A prominent sign children are struggling with problem solving skills is their inability to understand a concept such as putting patterns into a sequence, how to handle a difficult situation, or having trouble working with others to solve a problem. If a child can't figure out how to put patterns into a sequence, they might struggle with where to start with steps to a task and how to stay on track with steps. Another situation might be them having trouble with classmates and not knowing how to handle it appropriately. 

We can practice and strengthen problem solving skills through embodied cognition........... Embodied cognitions is using gestures, actions and emotions to help understand a concept.

-------------------

What's new at abl.

ACTION BASED LEARNING CERTIFICATIONS

ABL-LF Certified Action Based Learning Lab Faciliator

ABL-ST Certified Action Based Learning School Trainer

ABL-DT Certified Action Based Learning District Trainer

What is the difference between each certification?

The Lab facilitator certification is a specialized certification specifically for implementing, managing, and enhancing the effectiveness of your ABL Lab. This certification is designed for Lab Facilitators, or educators and administrators involved in creating and maintaining a successful lab in your school.  The school and district certification on the other hand, extend well beyond the lab, to help you become an expert on all things movement and learning, including creating active classrooms and active schools, and overall culture of healthy, happy, engaged, using movement!

ABL PRODUCT TOP PICKS

NEW! ABL Academic Card Set Boxes include complete collections of Elementary Academic Station Cards for Math, ELAR, SS, Health and Wellness, and more!

VIEW ALL ACADEMIC BOXES

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

7 Module 7: Thinking, Reasoning, and Problem-Solving

This module is about how a solid working knowledge of psychological principles can help you to think more effectively, so you can succeed in school and life. You might be inclined to believe that—because you have been thinking for as long as you can remember, because you are able to figure out the solution to many problems, because you feel capable of using logic to argue a point, because you can evaluate whether the things you read and hear make sense—you do not need any special training in thinking. But this, of course, is one of the key barriers to helping people think better. If you do not believe that there is anything wrong, why try to fix it?

The human brain is indeed a remarkable thinking machine, capable of amazing, complex, creative, logical thoughts. Why, then, are we telling you that you need to learn how to think? Mainly because one major lesson from cognitive psychology is that these capabilities of the human brain are relatively infrequently realized. Many psychologists believe that people are essentially “cognitive misers.” It is not that we are lazy, but that we have a tendency to expend the least amount of mental effort necessary. Although you may not realize it, it actually takes a great deal of energy to think. Careful, deliberative reasoning and critical thinking are very difficult. Because we seem to be successful without going to the trouble of using these skills well, it feels unnecessary to develop them. As you shall see, however, there are many pitfalls in the cognitive processes described in this module. When people do not devote extra effort to learning and improving reasoning, problem solving, and critical thinking skills, they make many errors.

As is true for memory, if you develop the cognitive skills presented in this module, you will be more successful in school. It is important that you realize, however, that these skills will help you far beyond school, even more so than a good memory will. Although it is somewhat useful to have a good memory, ten years from now no potential employer will care how many questions you got right on multiple choice exams during college. All of them will, however, recognize whether you are a logical, analytical, critical thinker. With these thinking skills, you will be an effective, persuasive communicator and an excellent problem solver.

The module begins by describing different kinds of thought and knowledge, especially conceptual knowledge and critical thinking. An understanding of these differences will be valuable as you progress through school and encounter different assignments that require you to tap into different kinds of knowledge. The second section covers deductive and inductive reasoning, which are processes we use to construct and evaluate strong arguments. They are essential skills to have whenever you are trying to persuade someone (including yourself) of some point, or to respond to someone’s efforts to persuade you. The module ends with a section about problem solving. A solid understanding of the key processes involved in problem solving will help you to handle many daily challenges.

7.1. Different kinds of thought

7.2. Reasoning and Judgment

7.3. Problem Solving

READING WITH PURPOSE

Remember and understand.

By reading and studying Module 7, you should be able to remember and describe:

• Concepts and inferences (7.1)
• Procedural knowledge (7.1)
• Metacognition (7.1)
• Characteristics of critical thinking:  skepticism; identify biases, distortions, omissions, and assumptions; reasoning and problem solving skills  (7.1)
• Reasoning:  deductive reasoning, deductively valid argument, inductive reasoning, inductively strong argument, availability heuristic, representativeness heuristic  (7.2)
• Fixation:  functional fixedness, mental set  (7.3)
• Algorithms, heuristics, and the role of confirmation bias (7.3)
• Effective problem solving sequence (7.3)

By reading and thinking about how the concepts in Module 6 apply to real life, you should be able to:

• Identify which type of knowledge a piece of information is (7.1)
• Recognize examples of deductive and inductive reasoning (7.2)
• Recognize judgments that have probably been influenced by the availability heuristic (7.2)
• Recognize examples of problem solving heuristics and algorithms (7.3)

Analyze, Evaluate, and Create

By reading and thinking about Module 6, participating in classroom activities, and completing out-of-class assignments, you should be able to:

• Use the principles of critical thinking to evaluate information (7.1)
• Explain whether examples of reasoning arguments are deductively valid or inductively strong (7.2)
• Outline how you could try to solve a problem from your life using the effective problem solving sequence (7.3)

7.1. Different kinds of thought and knowledge

• Take a few minutes to write down everything that you know about dogs.
• Do you believe that:
• Psychic ability exists?
• Hypnosis is an altered state of consciousness?
• Magnet therapy is effective for relieving pain?
• Aerobic exercise is an effective treatment for depression?
• UFO’s from outer space have visited earth?

On what do you base your belief or disbelief for the questions above?

Of course, we all know what is meant by the words  think  and  knowledge . You probably also realize that they are not unitary concepts; there are different kinds of thought and knowledge. In this section, let us look at some of these differences. If you are familiar with these different kinds of thought and pay attention to them in your classes, it will help you to focus on the right goals, learn more effectively, and succeed in school. Different assignments and requirements in school call on you to use different kinds of knowledge or thought, so it will be very helpful for you to learn to recognize them (Anderson, et al. 2001).

Factual and conceptual knowledge

Module 5 introduced the idea of declarative memory, which is composed of facts and episodes. If you have ever played a trivia game or watched Jeopardy on TV, you realize that the human brain is able to hold an extraordinary number of facts. Likewise, you realize that each of us has an enormous store of episodes, essentially facts about events that happened in our own lives. It may be difficult to keep that in mind when we are struggling to retrieve one of those facts while taking an exam, however. Part of the problem is that, in contradiction to the advice from Module 5, many students continue to try to memorize course material as a series of unrelated facts (picture a history student simply trying to memorize history as a set of unrelated dates without any coherent story tying them together). Facts in the real world are not random and unorganized, however. It is the way that they are organized that constitutes a second key kind of knowledge, conceptual.

Concepts are nothing more than our mental representations of categories of things in the world. For example, think about dogs. When you do this, you might remember specific facts about dogs, such as they have fur and they bark. You may also recall dogs that you have encountered and picture them in your mind. All of this information (and more) makes up your concept of dog. You can have concepts of simple categories (e.g., triangle), complex categories (e.g., small dogs that sleep all day, eat out of the garbage, and bark at leaves), kinds of people (e.g., psychology professors), events (e.g., birthday parties), and abstract ideas (e.g., justice). Gregory Murphy (2002) refers to concepts as the “glue that holds our mental life together” (p. 1). Very simply, summarizing the world by using concepts is one of the most important cognitive tasks that we do. Our conceptual knowledge  is  our knowledge about the world. Individual concepts are related to each other to form a rich interconnected network of knowledge. For example, think about how the following concepts might be related to each other: dog, pet, play, Frisbee, chew toy, shoe. Or, of more obvious use to you now, how these concepts are related: working memory, long-term memory, declarative memory, procedural memory, and rehearsal? Because our minds have a natural tendency to organize information conceptually, when students try to remember course material as isolated facts, they are working against their strengths.

One last important point about concepts is that they allow you to instantly know a great deal of information about something. For example, if someone hands you a small red object and says, “here is an apple,” they do not have to tell you, “it is something you can eat.” You already know that you can eat it because it is true by virtue of the fact that the object is an apple; this is called drawing an  inference , assuming that something is true on the basis of your previous knowledge (for example, of category membership or of how the world works) or logical reasoning.

Procedural knowledge

Physical skills, such as tying your shoes, doing a cartwheel, and driving a car (or doing all three at the same time, but don’t try this at home) are certainly a kind of knowledge. They are procedural knowledge, the same idea as procedural memory that you saw in Module 5. Mental skills, such as reading, debating, and planning a psychology experiment, are procedural knowledge, as well. In short, procedural knowledge is the knowledge how to do something (Cohen & Eichenbaum, 1993).

Metacognitive knowledge

Floyd used to think that he had a great memory. Now, he has a better memory. Why? Because he finally realized that his memory was not as great as he once thought it was. Because Floyd eventually learned that he often forgets where he put things, he finally developed the habit of putting things in the same place. (Unfortunately, he did not learn this lesson before losing at least 5 watches and a wedding ring.) Because he finally realized that he often forgets to do things, he finally started using the To Do list app on his phone. And so on. Floyd’s insights about the real limitations of his memory have allowed him to remember things that he used to forget.

All of us have knowledge about the way our own minds work. You may know that you have a good memory for people’s names and a poor memory for math formulas. Someone else might realize that they have difficulty remembering to do things, like stopping at the store on the way home. Others still know that they tend to overlook details. This knowledge about our own thinking is actually quite important; it is called metacognitive knowledge, or  metacognition . Like other kinds of thinking skills, it is subject to error. For example, in unpublished research, one of the authors surveyed about 120 General Psychology students on the first day of the term. Among other questions, the students were asked them to predict their grade in the class and report their current Grade Point Average. Two-thirds of the students predicted that their grade in the course would be higher than their GPA. (The reality is that at our college, students tend to earn lower grades in psychology than their overall GPA.) Another example: Students routinely report that they thought they had done well on an exam, only to discover, to their dismay, that they were wrong (more on that important problem in a moment). Both errors reveal a breakdown in metacognition.

The Dunning-Kruger Effect

In general, most college students probably do not study enough. For example, using data from the National Survey of Student Engagement, Fosnacht, McCormack, and Lerma (2018) reported that first-year students at 4-year colleges in the U.S. averaged less than 14 hours per week preparing for classes. The typical suggestion is that you should spend two hours outside of class for every hour in class, or 24 – 30 hours per week for a full-time student. Clearly, students in general are nowhere near that recommended mark. Many observers, including some faculty, believe that this shortfall is a result of students being too busy or lazy. Now, it may be true that many students are too busy, with work and family obligations, for example. Others, are not particularly motivated in school, and therefore might correctly be labeled lazy. A third possible explanation, however, is that some students might not think they need to spend this much time. And this is a matter of metacognition. Consider the scenario that we mentioned above, students thinking they had done well on an exam only to discover that they did not. Justin Kruger and David Dunning examined scenarios very much like this in 1999. Kruger and Dunning gave research participants tests measuring humor, logic, and grammar. Then, they asked the participants to assess their own abilities and test performance in these areas. They found that participants in general tended to overestimate their abilities, already a problem with metacognition. Importantly, the participants who scored the lowest overestimated their abilities the most. Specifically, students who scored in the bottom quarter (averaging in the 12th percentile) thought they had scored in the 62nd percentile. This has become known as the  Dunning-Kruger effect . Many individual faculty members have replicated these results with their own student on their course exams, including the authors of this book. Think about it. Some students who just took an exam and performed poorly believe that they did well before seeing their score. It seems very likely that these are the very same students who stopped studying the night before because they thought they were “done.” Quite simply, it is not just that they did not know the material. They did not know that they did not know the material. That is poor metacognition.

In order to develop good metacognitive skills, you should continually monitor your thinking and seek frequent feedback on the accuracy of your thinking (Medina, Castleberry, & Persky 2017). For example, in classes get in the habit of predicting your exam grades. As soon as possible after taking an exam, try to find out which questions you missed and try to figure out why. If you do this soon enough, you may be able to recall the way it felt when you originally answered the question. Did you feel confident that you had answered the question correctly? Then you have just discovered an opportunity to improve your metacognition. Be on the lookout for that feeling and respond with caution.

concept :  a mental representation of a category of things in the world

Dunning-Kruger effect : individuals who are less competent tend to overestimate their abilities more than individuals who are more competent do

inference : an assumption about the truth of something that is not stated. Inferences come from our prior knowledge and experience, and from logical reasoning

metacognition :  knowledge about one’s own cognitive processes; thinking about your thinking

Critical thinking

One particular kind of knowledge or thinking skill that is related to metacognition is  critical thinking (Chew, 2020). You may have noticed that critical thinking is an objective in many college courses, and thus it could be a legitimate topic to cover in nearly any college course. It is particularly appropriate in psychology, however. As the science of (behavior and) mental processes, psychology is obviously well suited to be the discipline through which you should be introduced to this important way of thinking.

More importantly, there is a particular need to use critical thinking in psychology. We are all, in a way, experts in human behavior and mental processes, having engaged in them literally since birth. Thus, perhaps more than in any other class, students typically approach psychology with very clear ideas and opinions about its subject matter. That is, students already “know” a lot about psychology. The problem is, “it ain’t so much the things we don’t know that get us into trouble. It’s the things we know that just ain’t so” (Ward, quoted in Gilovich 1991). Indeed, many of students’ preconceptions about psychology are just plain wrong. Randolph Smith (2002) wrote a book about critical thinking in psychology called  Challenging Your Preconceptions,  highlighting this fact. On the other hand, many of students’ preconceptions about psychology are just plain right! But wait, how do you know which of your preconceptions are right and which are wrong? And when you come across a research finding or theory in this class that contradicts your preconceptions, what will you do? Will you stick to your original idea, discounting the information from the class? Will you immediately change your mind? Critical thinking can help us sort through this confusing mess.

But what is critical thinking? The goal of critical thinking is simple to state (but extraordinarily difficult to achieve): it is to be right, to draw the correct conclusions, to believe in things that are true and to disbelieve things that are false. We will provide two definitions of critical thinking (or, if you like, one large definition with two distinct parts). First, a more conceptual one: Critical thinking is thinking like a scientist in your everyday life (Schmaltz, Jansen, & Wenckowski, 2017).  Our second definition is more operational; it is simply a list of skills that are essential to be a critical thinker. Critical thinking entails solid reasoning and problem solving skills; skepticism; and an ability to identify biases, distortions, omissions, and assumptions. Excellent deductive and inductive reasoning, and problem solving skills contribute to critical thinking. So, you can consider the subject matter of sections 7.2 and 7.3 to be part of critical thinking. Because we will be devoting considerable time to these concepts in the rest of the module, let us begin with a discussion about the other aspects of critical thinking.

Let’s address that first part of the definition. Scientists form hypotheses, or predictions about some possible future observations. Then, they collect data, or information (think of this as making those future observations). They do their best to make unbiased observations using reliable techniques that have been verified by others. Then, and only then, they draw a conclusion about what those observations mean. Oh, and do not forget the most important part. “Conclusion” is probably not the most appropriate word because this conclusion is only tentative. A scientist is always prepared that someone else might come along and produce new observations that would require a new conclusion be drawn. Wow! If you like to be right, you could do a lot worse than using a process like this.

A Critical Thinker’s Toolkit 

Now for the second part of the definition. Good critical thinkers (and scientists) rely on a variety of tools to evaluate information. Perhaps the most recognizable tool for critical thinking is  skepticism (and this term provides the clearest link to the thinking like a scientist definition, as you are about to see). Some people intend it as an insult when they call someone a skeptic. But if someone calls you a skeptic, if they are using the term correctly, you should consider it a great compliment. Simply put, skepticism is a way of thinking in which you refrain from drawing a conclusion or changing your mind until good evidence has been provided. People from Missouri should recognize this principle, as Missouri is known as the Show-Me State. As a skeptic, you are not inclined to believe something just because someone said so, because someone else believes it, or because it sounds reasonable. You must be persuaded by high quality evidence.

Of course, if that evidence is produced, you have a responsibility as a skeptic to change your belief. Failure to change a belief in the face of good evidence is not skepticism; skepticism has open mindedness at its core. M. Neil Browne and Stuart Keeley (2018) use the term weak sense critical thinking to describe critical thinking behaviors that are used only to strengthen a prior belief. Strong sense critical thinking, on the other hand, has as its goal reaching the best conclusion. Sometimes that means strengthening your prior belief, but sometimes it means changing your belief to accommodate the better evidence.

Many times, a failure to think critically or weak sense critical thinking is related to a  bias , an inclination, tendency, leaning, or prejudice. Everybody has biases, but many people are unaware of them. Awareness of your own biases gives you the opportunity to control or counteract them. Unfortunately, however, many people are happy to let their biases creep into their attempts to persuade others; indeed, it is a key part of their persuasive strategy. To see how these biases influence messages, just look at the different descriptions and explanations of the same events given by people of different ages or income brackets, or conservative versus liberal commentators, or by commentators from different parts of the world. Of course, to be successful, these people who are consciously using their biases must disguise them. Even undisguised biases can be difficult to identify, so disguised ones can be nearly impossible.

Here are some common sources of biases:

• Personal values and beliefs.  Some people believe that human beings are basically driven to seek power and that they are typically in competition with one another over scarce resources. These beliefs are similar to the world-view that political scientists call “realism.” Other people believe that human beings prefer to cooperate and that, given the chance, they will do so. These beliefs are similar to the world-view known as “idealism.” For many people, these deeply held beliefs can influence, or bias, their interpretations of such wide ranging situations as the behavior of nations and their leaders or the behavior of the driver in the car ahead of you. For example, if your worldview is that people are typically in competition and someone cuts you off on the highway, you may assume that the driver did it purposely to get ahead of you. Other types of beliefs about the way the world is or the way the world should be, for example, political beliefs, can similarly become a significant source of bias.
• Racism, sexism, ageism and other forms of prejudice and bigotry.  These are, sadly, a common source of bias in many people. They are essentially a special kind of “belief about the way the world is.” These beliefs—for example, that women do not make effective leaders—lead people to ignore contradictory evidence (examples of effective women leaders, or research that disputes the belief) and to interpret ambiguous evidence in a way consistent with the belief.
• Self-interest.  When particular people benefit from things turning out a certain way, they can sometimes be very susceptible to letting that interest bias them. For example, a company that will earn a profit if they sell their product may have a bias in the way that they give information about their product. A union that will benefit if its members get a generous contract might have a bias in the way it presents information about salaries at competing organizations. (Note that our inclusion of examples describing both companies and unions is an explicit attempt to control for our own personal biases). Home buyers are often dismayed to discover that they purchased their dream house from someone whose self-interest led them to lie about flooding problems in the basement or back yard. This principle, the biasing power of self-interest, is likely what led to the famous phrase  Caveat Emptor  (let the buyer beware) .  

Knowing that these types of biases exist will help you evaluate evidence more critically. Do not forget, though, that people are not always keen to let you discover the sources of biases in their arguments. For example, companies or political organizations can sometimes disguise their support of a research study by contracting with a university professor, who comes complete with a seemingly unbiased institutional affiliation, to conduct the study.

People’s biases, conscious or unconscious, can lead them to make omissions, distortions, and assumptions that undermine our ability to correctly evaluate evidence. It is essential that you look for these elements. Always ask, what is missing, what is not as it appears, and what is being assumed here? For example, consider this (fictional) chart from an ad reporting customer satisfaction at 4 local health clubs.

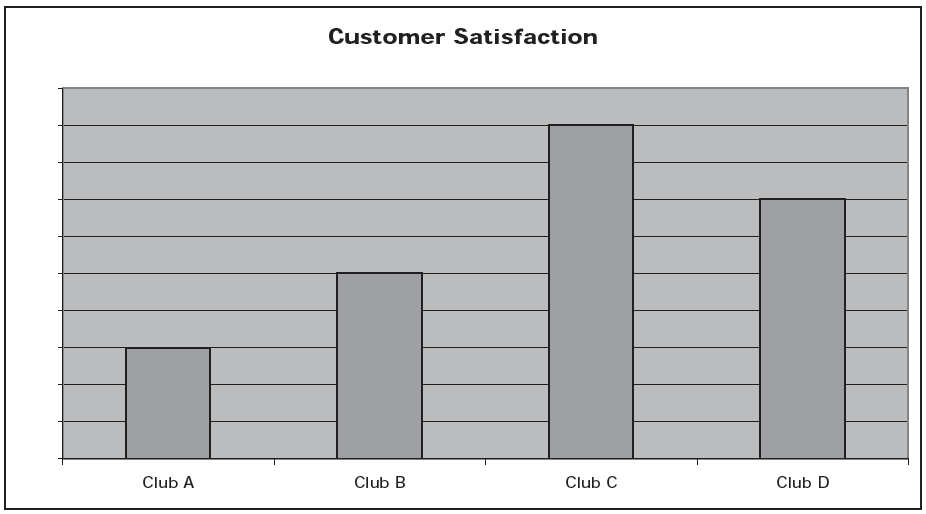
Clearly, from the results of the chart, one would be tempted to give Club C a try, as customer satisfaction is much higher than for the other 3 clubs.

There are so many distortions and omissions in this chart, however, that it is actually quite meaningless. First, how was satisfaction measured? Do the bars represent responses to a survey? If so, how were the questions asked? Most importantly, where is the missing scale for the chart? Although the differences look quite large, are they really?

Well, here is the same chart, with a different scale, this time labeled:

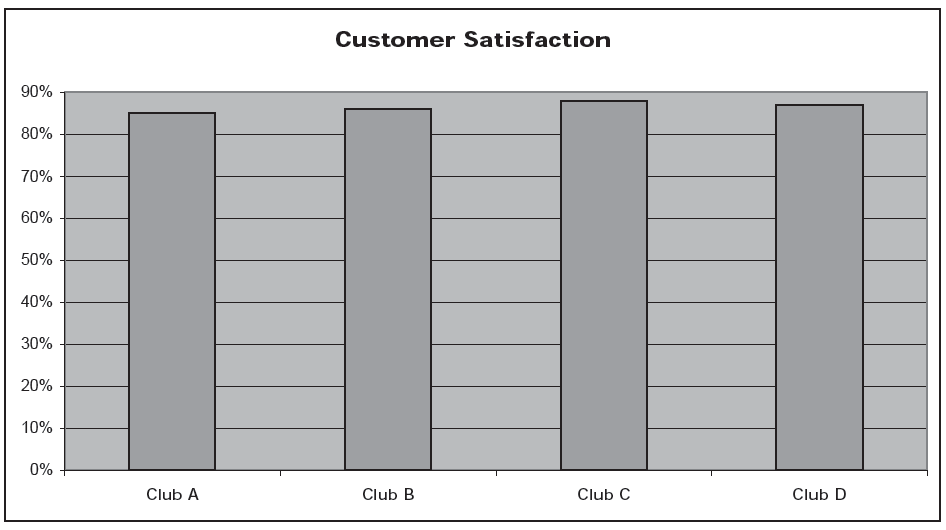
Club C is not so impressive any more, is it? In fact, all of the health clubs have customer satisfaction ratings (whatever that means) between 85% and 88%. In the first chart, the entire scale of the graph included only the percentages between 83 and 89. This “judicious” choice of scale—some would call it a distortion—and omission of that scale from the chart make the tiny differences among the clubs seem important, however.

Also, in order to be a critical thinker, you need to learn to pay attention to the assumptions that underlie a message. Let us briefly illustrate the role of assumptions by touching on some people’s beliefs about the criminal justice system in the US. Some believe that a major problem with our judicial system is that many criminals go free because of legal technicalities. Others believe that a major problem is that many innocent people are convicted of crimes. The simple fact is, both types of errors occur. A person’s conclusion about which flaw in our judicial system is the greater tragedy is based on an assumption about which of these is the more serious error (letting the guilty go free or convicting the innocent). This type of assumption is called a value assumption (Browne and Keeley, 2018). It reflects the differences in values that people develop, differences that may lead us to disregard valid evidence that does not fit in with our particular values.

Oh, by the way, some students probably noticed this, but the seven tips for evaluating information that we shared in Module 1 are related to this. Actually, they are part of this section. The tips are, to a very large degree, set of ideas you can use to help you identify biases, distortions, omissions, and assumptions. If you do not remember this section, we strongly recommend you take a few minutes to review it.

skepticism :  a way of thinking in which you refrain from drawing a conclusion or changing your mind until good evidence has been provided

bias : an inclination, tendency, leaning, or prejudice

• Which of your beliefs (or disbeliefs) from the Activate exercise for this section were derived from a process of critical thinking? If some of your beliefs were not based on critical thinking, are you willing to reassess these beliefs? If the answer is no, why do you think that is? If the answer is yes, what concrete steps will you take?

7.2 Reasoning and Judgment

• What percentage of kidnappings are committed by strangers?
• Which area of the house is riskiest: kitchen, bathroom, or stairs?
• What is the most common cancer in the US?
• What percentage of workplace homicides are committed by co-workers?

An essential set of procedural thinking skills is  reasoning , the ability to generate and evaluate solid conclusions from a set of statements or evidence. You should note that these conclusions (when they are generated instead of being evaluated) are one key type of inference that we described in Section 7.1. There are two main types of reasoning, deductive and inductive.

Deductive reasoning

Suppose your teacher tells you that if you get an A on the final exam in a course, you will get an A for the whole course. Then, you get an A on the final exam. What will your final course grade be? Most people can see instantly that you can conclude with certainty that you will get an A for the course. This is a type of reasoning called  deductive reasoning , which is defined as reasoning in which a conclusion is guaranteed to be true as long as the statements leading to it are true. The three statements can be listed as an  argument , with two beginning statements and a conclusion:

Statement 1: If you get an A on the final exam, you will get an A for the course

Statement 2: You get an A on the final exam

Conclusion: You will get an A for the course

This particular arrangement, in which true beginning statements lead to a guaranteed true conclusion, is known as a  deductively valid argument . Although deductive reasoning is often the subject of abstract, brain-teasing, puzzle-like word problems, it is actually an extremely important type of everyday reasoning. It is just hard to recognize sometimes. For example, imagine that you are looking for your car keys and you realize that they are either in the kitchen drawer or in your book bag. After looking in the kitchen drawer, you instantly know that they must be in your book bag. That conclusion results from a simple deductive reasoning argument. In addition, solid deductive reasoning skills are necessary for you to succeed in the sciences, philosophy, math, computer programming, and any endeavor involving the use of logic to persuade others to your point of view or to evaluate others’ arguments.

Cognitive psychologists, and before them philosophers, have been quite interested in deductive reasoning, not so much for its practical applications, but for the insights it can offer them about the ways that human beings think. One of the early ideas to emerge from the examination of deductive reasoning is that people learn (or develop) mental versions of rules that allow them to solve these types of reasoning problems (Braine, 1978; Braine, Reiser, & Rumain, 1984). The best way to see this point of view is to realize that there are different possible rules, and some of them are very simple. For example, consider this rule of logic:

therefore q

Logical rules are often presented abstractly, as letters, in order to imply that they can be used in very many specific situations. Here is a concrete version of the of the same rule:

I’ll either have pizza or a hamburger for dinner tonight (p or q)

I won’t have pizza (not p)

Therefore, I’ll have a hamburger (therefore q)

This kind of reasoning seems so natural, so easy, that it is quite plausible that we would use a version of this rule in our daily lives. At least, it seems more plausible than some of the alternative possibilities—for example, that we need to have experience with the specific situation (pizza or hamburger, in this case) in order to solve this type of problem easily. So perhaps there is a form of natural logic (Rips, 1990) that contains very simple versions of logical rules. When we are faced with a reasoning problem that maps onto one of these rules, we use the rule.

But be very careful; things are not always as easy as they seem. Even these simple rules are not so simple. For example, consider the following rule. Many people fail to realize that this rule is just as valid as the pizza or hamburger rule above.

if p, then q

therefore, not p

Concrete version:

If I eat dinner, then I will have dessert

I did not have dessert

Therefore, I did not eat dinner

The simple fact is, it can be very difficult for people to apply rules of deductive logic correctly; as a result, they make many errors when trying to do so. Is this a deductively valid argument or not?

Students who like school study a lot

Students who study a lot get good grades

Jane does not like school

Therefore, Jane does not get good grades

Many people are surprised to discover that this is not a logically valid argument; the conclusion is not guaranteed to be true from the beginning statements. Although the first statement says that students who like school study a lot, it does NOT say that students who do not like school do not study a lot. In other words, it may very well be possible to study a lot without liking school. Even people who sometimes get problems like this right might not be using the rules of deductive reasoning. Instead, they might just be making judgments for examples they know, in this case, remembering instances of people who get good grades despite not liking school.

Making deductive reasoning even more difficult is the fact that there are two important properties that an argument may have. One, it can be valid or invalid (meaning that the conclusion does or does not follow logically from the statements leading up to it). Two, an argument (or more correctly, its conclusion) can be true or false. Here is an example of an argument that is logically valid, but has a false conclusion (at least we think it is false).

Either you are eleven feet tall or the Grand Canyon was created by a spaceship crashing into the earth.

You are not eleven feet tall

Therefore the Grand Canyon was created by a spaceship crashing into the earth

This argument has the exact same form as the pizza or hamburger argument above, making it is deductively valid. The conclusion is so false, however, that it is absurd (of course, the reason the conclusion is false is that the first statement is false). When people are judging arguments, they tend to not observe the difference between deductive validity and the empirical truth of statements or conclusions. If the elements of an argument happen to be true, people are likely to judge the argument logically valid; if the elements are false, they will very likely judge it invalid (Markovits & Bouffard-Bouchard, 1992; Moshman & Franks, 1986). Thus, it seems a stretch to say that people are using these logical rules to judge the validity of arguments. Many psychologists believe that most people actually have very limited deductive reasoning skills (Johnson-Laird, 1999). They argue that when faced with a problem for which deductive logic is required, people resort to some simpler technique, such as matching terms that appear in the statements and the conclusion (Evans, 1982). This might not seem like a problem, but what if reasoners believe that the elements are true and they happen to be wrong; they will would believe that they are using a form of reasoning that guarantees they are correct and yet be wrong.

deductive reasoning :  a type of reasoning in which the conclusion is guaranteed to be true any time the statements leading up to it are true

argument :  a set of statements in which the beginning statements lead to a conclusion

deductively valid argument :  an argument for which true beginning statements guarantee that the conclusion is true

Inductive reasoning and judgment

Every day, you make many judgments about the likelihood of one thing or another. Whether you realize it or not, you are practicing  inductive reasoning   on a daily basis. In inductive reasoning arguments, a conclusion is likely whenever the statements preceding it are true. The first thing to notice about inductive reasoning is that, by definition, you can never be sure about your conclusion; you can only estimate how likely the conclusion is. Inductive reasoning may lead you to focus on Memory Encoding and Recoding when you study for the exam, but it is possible the instructor will ask more questions about Memory Retrieval instead. Unlike deductive reasoning, the conclusions you reach through inductive reasoning are only probable, not certain. That is why scientists consider inductive reasoning weaker than deductive reasoning. But imagine how hard it would be for us to function if we could not act unless we were certain about the outcome.

Inductive reasoning can be represented as logical arguments consisting of statements and a conclusion, just as deductive reasoning can be. In an inductive argument, you are given some statements and a conclusion (or you are given some statements and must draw a conclusion). An argument is  inductively strong   if the conclusion would be very probable whenever the statements are true. So, for example, here is an inductively strong argument:

• Statement #1: The forecaster on Channel 2 said it is going to rain today.
• Statement #2: The forecaster on Channel 5 said it is going to rain today.
• Statement #3: It is very cloudy and humid.
• Statement #4: You just heard thunder.
• Conclusion (or judgment): It is going to rain today.

Think of the statements as evidence, on the basis of which you will draw a conclusion. So, based on the evidence presented in the four statements, it is very likely that it will rain today. Will it definitely rain today? Certainly not. We can all think of times that the weather forecaster was wrong.

A true story: Some years ago psychology student was watching a baseball playoff game between the St. Louis Cardinals and the Los Angeles Dodgers. A graphic on the screen had just informed the audience that the Cardinal at bat, (Hall of Fame shortstop) Ozzie Smith, a switch hitter batting left-handed for this plate appearance, had never, in nearly 3000 career at-bats, hit a home run left-handed. The student, who had just learned about inductive reasoning in his psychology class, turned to his companion (a Cardinals fan) and smugly said, “It is an inductively strong argument that Ozzie Smith will not hit a home run.” He turned back to face the television just in time to watch the ball sail over the right field fence for a home run. Although the student felt foolish at the time, he was not wrong. It was an inductively strong argument; 3000 at-bats is an awful lot of evidence suggesting that the Wizard of Ozz (as he was known) would not be hitting one out of the park (think of each at-bat without a home run as a statement in an inductive argument). Sadly (for the die-hard Cubs fan and Cardinals-hating student), despite the strength of the argument, the conclusion was wrong.

Given the possibility that we might draw an incorrect conclusion even with an inductively strong argument, we really want to be sure that we do, in fact, make inductively strong arguments. If we judge something probable, it had better be probable. If we judge something nearly impossible, it had better not happen. Think of inductive reasoning, then, as making reasonably accurate judgments of the probability of some conclusion given a set of evidence.

We base many decisions in our lives on inductive reasoning. For example:

Statement #1: Psychology is not my best subject

Statement #2: My psychology instructor has a reputation for giving difficult exams

Statement #3: My first psychology exam was much harder than I expected

Judgment: The next exam will probably be very difficult.

Decision: I will study tonight instead of watching Netflix.

Some other examples of judgments that people commonly make in a school context include judgments of the likelihood that:

• A particular class will be interesting/useful/difficult
• You will be able to finish writing a paper by next week if you go out tonight
• Your laptop’s battery will last through the next trip to the library
• You will not miss anything important if you skip class tomorrow
• Your instructor will not notice if you skip class tomorrow
• You will be able to find a book that you will need for a paper
• There will be an essay question about Memory Encoding on the next exam

Tversky and Kahneman (1983) recognized that there are two general ways that we might make these judgments; they termed them extensional (i.e., following the laws of probability) and intuitive (i.e., using shortcuts or heuristics, see below). We will use a similar distinction between Type 1 and Type 2 thinking, as described by Keith Stanovich and his colleagues (Evans and Stanovich, 2013; Stanovich and West, 2000). Type 1 thinking is fast, automatic, effortful, and emotional. In fact, it is hardly fair to call it reasoning at all, as judgments just seem to pop into one’s head. Type 2 thinking , on the other hand, is slow, effortful, and logical. So obviously, it is more likely to lead to a correct judgment, or an optimal decision. The problem is, we tend to over-rely on Type 1. Now, we are not saying that Type 2 is the right way to go for every decision or judgment we make. It seems a bit much, for example, to engage in a step-by-step logical reasoning procedure to decide whether we will have chicken or fish for dinner tonight.

Many bad decisions in some very important contexts, however, can be traced back to poor judgments of the likelihood of certain risks or outcomes that result from the use of Type 1 when a more logical reasoning process would have been more appropriate. For example:

Statement #1: It is late at night.

Statement #2: Albert has been drinking beer for the past five hours at a party.

Statement #3: Albert is not exactly sure where he is or how far away home is.

Judgment: Albert will have no difficulty walking home.

Decision: He walks home alone.

As you can see in this example, the three statements backing up the judgment do not really support it. In other words, this argument is not inductively strong because it is based on judgments that ignore the laws of probability. What are the chances that someone facing these conditions will be able to walk home alone easily? And one need not be drunk to make poor decisions based on judgments that just pop into our heads.

The truth is that many of our probability judgments do not come very close to what the laws of probability say they should be. Think about it. In order for us to reason in accordance with these laws, we would need to know the laws of probability, which would allow us to calculate the relationship between particular pieces of evidence and the probability of some outcome (i.e., how much likelihood should change given a piece of evidence), and we would have to do these heavy math calculations in our heads. After all, that is what Type 2 requires. Needless to say, even if we were motivated, we often do not even know how to apply Type 2 reasoning in many cases.

So what do we do when we don’t have the knowledge, skills, or time required to make the correct mathematical judgment? Do we hold off and wait until we can get better evidence? Do we read up on probability and fire up our calculator app so we can compute the correct probability? Of course not. We rely on Type 1 thinking. We “wing it.” That is, we come up with a likelihood estimate using some means at our disposal. Psychologists use the term heuristic to describe the type of “winging it” we are talking about. A  heuristic   is a shortcut strategy that we use to make some judgment or solve some problem (see Section 7.3). Heuristics are easy and quick, think of them as the basic procedures that are characteristic of Type 1.  They can absolutely lead to reasonably good judgments and decisions in some situations (like choosing between chicken and fish for dinner). They are, however, far from foolproof. There are, in fact, quite a lot of situations in which heuristics can lead us to make incorrect judgments, and in many cases the decisions based on those judgments can have serious consequences.

Let us return to the activity that begins this section. You were asked to judge the likelihood (or frequency) of certain events and risks. You were free to come up with your own evidence (or statements) to make these judgments. This is where a heuristic crops up. As a judgment shortcut, we tend to generate specific examples of those very events to help us decide their likelihood or frequency. For example, if we are asked to judge how common, frequent, or likely a particular type of cancer is, many of our statements would be examples of specific cancer cases:

Statement #1: Andy Kaufman (comedian) had lung cancer.

Statement #2: Colin Powell (US Secretary of State) had prostate cancer.

Statement #3: Bob Marley (musician) had skin and brain cancer

Statement #4: Sandra Day O’Connor (Supreme Court Justice) had breast cancer.

Statement #5: Fred Rogers (children’s entertainer) had stomach cancer.

Statement #6: Robin Roberts (news anchor) had breast cancer.

Statement #7: Bette Davis (actress) had breast cancer.

Judgment: Breast cancer is the most common type.

Your own experience or memory may also tell you that breast cancer is the most common type. But it is not (although it is common). Actually, skin cancer is the most common type in the US. We make the same types of misjudgments all the time because we do not generate the examples or evidence according to their actual frequencies or probabilities. Instead, we have a tendency (or bias) to search for the examples in memory; if they are easy to retrieve, we assume that they are common. To rephrase this in the language of the heuristic, events seem more likely to the extent that they are available to memory. This bias has been termed the  availability heuristic   (Kahneman and Tversky, 1974).

The fact that we use the availability heuristic does not automatically mean that our judgment is wrong. The reason we use heuristics in the first place is that they work fairly well in many cases (and, of course that they are easy to use). So, the easiest examples to think of sometimes are the most common ones. Is it more likely that a member of the U.S. Senate is a man or a woman? Most people have a much easier time generating examples of male senators. And as it turns out, the U.S. Senate has many more men than women (74 to 26 in 2020). In this case, then, the availability heuristic would lead you to make the correct judgment; it is far more likely that a senator would be a man.

In many other cases, however, the availability heuristic will lead us astray. This is because events can be memorable for many reasons other than their frequency. Section 5.2, Encoding Meaning, suggested that one good way to encode the meaning of some information is to form a mental image of it. Thus, information that has been pictured mentally will be more available to memory. Indeed, an event that is vivid and easily pictured will trick many people into supposing that type of event is more common than it actually is. Repetition of information will also make it more memorable. So, if the same event is described to you in a magazine, on the evening news, on a podcast that you listen to, and in your Facebook feed; it will be very available to memory. Again, the availability heuristic will cause you to misperceive the frequency of these types of events.

Most interestingly, information that is unusual is more memorable. Suppose we give you the following list of words to remember: box, flower, letter, platypus, oven, boat, newspaper, purse, drum, car. Very likely, the easiest word to remember would be platypus, the unusual one. The same thing occurs with memories of events. An event may be available to memory because it is unusual, yet the availability heuristic leads us to judge that the event is common. Did you catch that? In these cases, the availability heuristic makes us think the exact opposite of the true frequency. We end up thinking something is common because it is unusual (and therefore memorable). Yikes.

The misapplication of the availability heuristic sometimes has unfortunate results. For example, if you went to K-12 school in the US over the past 10 years, it is extremely likely that you have participated in lockdown and active shooter drills. Of course, everyone is trying to prevent the tragedy of another school shooting. And believe us, we are not trying to minimize how terrible the tragedy is. But the truth of the matter is, school shootings are extremely rare. Because the federal government does not keep a database of school shootings, the Washington Post has maintained their own running tally. Between 1999 and January 2020 (the date of the most recent school shooting with a death in the US at of the time this paragraph was written), the Post reported a total of 254 people died in school shootings in the US. Not 254 per year, 254 total. That is an average of 12 per year. Of course, that is 254 people who should not have died (particularly because many were children), but in a country with approximately 60,000,000 students and teachers, this is a very small risk.

But many students and teachers are terrified that they will be victims of school shootings because of the availability heuristic. It is so easy to think of examples (they are very available to memory) that people believe the event is very common. It is not. And there is a downside to this. We happen to believe that there is an enormous gun violence problem in the United States. According the the Centers for Disease Control and Prevention, there were 39,773 firearm deaths in the US in 2017. Fifteen of those deaths were in school shootings, according to the Post. 60% of those deaths were suicides. When people pay attention to the school shooting risk (low), they often fail to notice the much larger risk.

And examples like this are by no means unique. The authors of this book have been teaching psychology since the 1990’s. We have been able to make the exact same arguments about the misapplication of the availability heuristics and keep them current by simply swapping out for the “fear of the day.” In the 1990’s it was children being kidnapped by strangers (it was known as “stranger danger”) despite the facts that kidnappings accounted for only 2% of the violent crimes committed against children, and only 24% of kidnappings are committed by strangers (US Department of Justice, 2007). This fear overlapped with the fear of terrorism that gripped the country after the 2001 terrorist attacks on the World Trade Center and US Pentagon and still plagues the population of the US somewhat in 2020. After a well-publicized, sensational act of violence, people are extremely likely to increase their estimates of the chances that they, too, will be victims of terror. Think about the reality, however. In October of 2001, a terrorist mailed anthrax spores to members of the US government and a number of media companies. A total of five people died as a result of this attack. The nation was nearly paralyzed by the fear of dying from the attack; in reality the probability of an individual person dying was 0.00000002.

The availability heuristic can lead you to make incorrect judgments in a school setting as well. For example, suppose you are trying to decide if you should take a class from a particular math professor. You might try to make a judgment of how good a teacher she is by recalling instances of friends and acquaintances making comments about her teaching skill. You may have some examples that suggest that she is a poor teacher very available to memory, so on the basis of the availability heuristic you judge her a poor teacher and decide to take the class from someone else. What if, however, the instances you recalled were all from the same person, and this person happens to be a very colorful storyteller? The subsequent ease of remembering the instances might not indicate that the professor is a poor teacher after all.

Although the availability heuristic is obviously important, it is not the only judgment heuristic we use. Amos Tversky and Daniel Kahneman examined the role of heuristics in inductive reasoning in a long series of studies. Kahneman received a Nobel Prize in Economics for this research in 2002, and Tversky would have certainly received one as well if he had not died of melanoma at age 59 in 1996 (Nobel Prizes are not awarded posthumously). Kahneman and Tversky demonstrated repeatedly that people do not reason in ways that are consistent with the laws of probability. They identified several heuristic strategies that people use instead to make judgments about likelihood. The importance of this work for economics (and the reason that Kahneman was awarded the Nobel Prize) is that earlier economic theories had assumed that people do make judgments rationally, that is, in agreement with the laws of probability.

Another common heuristic that people use for making judgments is the  representativeness heuristic (Kahneman & Tversky 1973). Suppose we describe a person to you. He is quiet and shy, has an unassuming personality, and likes to work with numbers. Is this person more likely to be an accountant or an attorney? If you said accountant, you were probably using the representativeness heuristic. Our imaginary person is judged likely to be an accountant because he resembles, or is representative of the concept of, an accountant. When research participants are asked to make judgments such as these, the only thing that seems to matter is the representativeness of the description. For example, if told that the person described is in a room that contains 70 attorneys and 30 accountants, participants will still assume that he is an accountant.

inductive reasoning :  a type of reasoning in which we make judgments about likelihood from sets of evidence

inductively strong argument :  an inductive argument in which the beginning statements lead to a conclusion that is probably true

heuristic :  a shortcut strategy that we use to make judgments and solve problems. Although they are easy to use, they do not guarantee correct judgments and solutions

availability heuristic :  judging the frequency or likelihood of some event type according to how easily examples of the event can be called to mind (i.e., how available they are to memory)

representativeness heuristic:   judging the likelihood that something is a member of a category on the basis of how much it resembles a typical category member (i.e., how representative it is of the category)

Type 1 thinking : fast, automatic, and emotional thinking.

Type 2 thinking : slow, effortful, and logical thinking.

• What percentage of workplace homicides are co-worker violence?

Many people get these questions wrong. The answers are 10%; stairs; skin; 6%. How close were your answers? Explain how the availability heuristic might have led you to make the incorrect judgments.

• Can you think of some other judgments that you have made (or beliefs that you have) that might have been influenced by the availability heuristic?

7.3 Problem Solving

• Please take a few minutes to list a number of problems that you are facing right now.
• Now write about a problem that you recently solved.
• What is your definition of a problem?

Mary has a problem. Her daughter, ordinarily quite eager to please, appears to delight in being the last person to do anything. Whether getting ready for school, going to piano lessons or karate class, or even going out with her friends, she seems unwilling or unable to get ready on time. Other people have different kinds of problems. For example, many students work at jobs, have numerous family commitments, and are facing a course schedule full of difficult exams, assignments, papers, and speeches. How can they find enough time to devote to their studies and still fulfill their other obligations? Speaking of students and their problems: Show that a ball thrown vertically upward with initial velocity v0 takes twice as much time to return as to reach the highest point (from Spiegel, 1981).

These are three very different situations, but we have called them all problems. What makes them all the same, despite the differences? A psychologist might define a  problem   as a situation with an initial state, a goal state, and a set of possible intermediate states. Somewhat more meaningfully, we might consider a problem a situation in which you are in here one state (e.g., daughter is always late), you want to be there in another state (e.g., daughter is not always late), and with no obvious way to get from here to there. Defined this way, each of the three situations we outlined can now be seen as an example of the same general concept, a problem. At this point, you might begin to wonder what is not a problem, given such a general definition. It seems that nearly every non-routine task we engage in could qualify as a problem. As long as you realize that problems are not necessarily bad (it can be quite fun and satisfying to rise to the challenge and solve a problem), this may be a useful way to think about it.

Can we identify a set of problem-solving skills that would apply to these very different kinds of situations? That task, in a nutshell, is a major goal of this section. Let us try to begin to make sense of the wide variety of ways that problems can be solved with an important observation: the process of solving problems can be divided into two key parts. First, people have to notice, comprehend, and represent the problem properly in their minds (called  problem representation ). Second, they have to apply some kind of solution strategy to the problem. Psychologists have studied both of these key parts of the process in detail.

When you first think about the problem-solving process, you might guess that most of our difficulties would occur because we are failing in the second step, the application of strategies. Although this can be a significant difficulty much of the time, the more important source of difficulty is probably problem representation. In short, we often fail to solve a problem because we are looking at it, or thinking about it, the wrong way.

problem :  a situation in which we are in an initial state, have a desired goal state, and there is a number of possible intermediate states (i.e., there is no obvious way to get from the initial to the goal state)

problem representation :  noticing, comprehending and forming a mental conception of a problem

Defining and Mentally Representing Problems in Order to Solve Them

So, the main obstacle to solving a problem is that we do not clearly understand exactly what the problem is. Recall the problem with Mary’s daughter always being late. One way to represent, or to think about, this problem is that she is being defiant. She refuses to get ready in time. This type of representation or definition suggests a particular type of solution. Another way to think about the problem, however, is to consider the possibility that she is simply being sidetracked by interesting diversions. This different conception of what the problem is (i.e., different representation) suggests a very different solution strategy. For example, if Mary defines the problem as defiance, she may be tempted to solve the problem using some kind of coercive tactics, that is, to assert her authority as her mother and force her to listen. On the other hand, if Mary defines the problem as distraction, she may try to solve it by simply removing the distracting objects.

As you might guess, when a problem is represented one way, the solution may seem very difficult, or even impossible. Seen another way, the solution might be very easy. For example, consider the following problem (from Nasar, 1998):

Two bicyclists start 20 miles apart and head toward each other, each going at a steady rate of 10 miles per hour. At the same time, a fly that travels at a steady 15 miles per hour starts from the front wheel of the southbound bicycle and flies to the front wheel of the northbound one, then turns around and flies to the front wheel of the southbound one again, and continues in this manner until he is crushed between the two front wheels. Question: what total distance did the fly cover?

Please take a few minutes to try to solve this problem.

Most people represent this problem as a question about a fly because, well, that is how the question is asked. The solution, using this representation, is to figure out how far the fly travels on the first leg of its journey, then add this total to how far it travels on the second leg of its journey (when it turns around and returns to the first bicycle), then continue to add the smaller distance from each leg of the journey until you converge on the correct answer. You would have to be quite skilled at math to solve this problem, and you would probably need some time and pencil and paper to do it.

If you consider a different representation, however, you can solve this problem in your head. Instead of thinking about it as a question about a fly, think about it as a question about the bicycles. They are 20 miles apart, and each is traveling 10 miles per hour. How long will it take for the bicycles to reach each other? Right, one hour. The fly is traveling 15 miles per hour; therefore, it will travel a total of 15 miles back and forth in the hour before the bicycles meet. Represented one way (as a problem about a fly), the problem is quite difficult. Represented another way (as a problem about two bicycles), it is easy. Changing your representation of a problem is sometimes the best—sometimes the only—way to solve it.

Unfortunately, however, changing a problem’s representation is not the easiest thing in the world to do. Often, problem solvers get stuck looking at a problem one way. This is called  fixation . Most people who represent the preceding problem as a problem about a fly probably do not pause to reconsider, and consequently change, their representation. A parent who thinks her daughter is being defiant is unlikely to consider the possibility that her behavior is far less purposeful.

Problem-solving fixation was examined by a group of German psychologists called Gestalt psychologists during the 1930’s and 1940’s. Karl Dunker, for example, discovered an important type of failure to take a different perspective called  functional fixedness . Imagine being a participant in one of his experiments. You are asked to figure out how to mount two candles on a door and are given an assortment of odds and ends, including a small empty cardboard box and some thumbtacks. Perhaps you have already figured out a solution: tack the box to the door so it forms a platform, then put the candles on top of the box. Most people are able to arrive at this solution. Imagine a slight variation of the procedure, however. What if, instead of being empty, the box had matches in it? Most people given this version of the problem do not arrive at the solution given above. Why? Because it seems to people that when the box contains matches, it already has a function; it is a matchbox. People are unlikely to consider a new function for an object that already has a function. This is functional fixedness.

Mental set is a type of fixation in which the problem solver gets stuck using the same solution strategy that has been successful in the past, even though the solution may no longer be useful. It is commonly seen when students do math problems for homework. Often, several problems in a row require the reapplication of the same solution strategy. Then, without warning, the next problem in the set requires a new strategy. Many students attempt to apply the formerly successful strategy on the new problem and therefore cannot come up with a correct answer.

The thing to remember is that you cannot solve a problem unless you correctly identify what it is to begin with (initial state) and what you want the end result to be (goal state). That may mean looking at the problem from a different angle and representing it in a new way. The correct representation does not guarantee a successful solution, but it certainly puts you on the right track.

A bit more optimistically, the Gestalt psychologists discovered what may be considered the opposite of fixation, namely  insight . Sometimes the solution to a problem just seems to pop into your head. Wolfgang Kohler examined insight by posing many different problems to chimpanzees, principally problems pertaining to their acquisition of out-of-reach food. In one version, a banana was placed outside of a chimpanzee’s cage and a short stick inside the cage. The stick was too short to retrieve the banana, but was long enough to retrieve a longer stick also located outside of the cage. This second stick was long enough to retrieve the banana. After trying, and failing, to reach the banana with the shorter stick, the chimpanzee would try a couple of random-seeming attempts, react with some apparent frustration or anger, then suddenly rush to the longer stick, the correct solution fully realized at this point. This sudden appearance of the solution, observed many times with many different problems, was termed insight by Kohler.

Lest you think it pertains to chimpanzees only, Karl Dunker demonstrated that children also solve problems through insight in the 1930s. More importantly, you have probably experienced insight yourself. Think back to a time when you were trying to solve a difficult problem. After struggling for a while, you gave up. Hours later, the solution just popped into your head, perhaps when you were taking a walk, eating dinner, or lying in bed.

fixation :  when a problem solver gets stuck looking at a problem a particular way and cannot change his or her representation of it (or his or her intended solution strategy)

functional fixedness :  a specific type of fixation in which a problem solver cannot think of a new use for an object that already has a function

mental set :  a specific type of fixation in which a problem solver gets stuck using the same solution strategy that has been successful in the past

insight :  a sudden realization of a solution to a problem

Solving Problems by Trial and Error

Correctly identifying the problem and your goal for a solution is a good start, but recall the psychologist’s definition of a problem: it includes a set of possible intermediate states. Viewed this way, a problem can be solved satisfactorily only if one can find a path through some of these intermediate states to the goal. Imagine a fairly routine problem, finding a new route to school when your ordinary route is blocked (by road construction, for example). At each intersection, you may turn left, turn right, or go straight. A satisfactory solution to the problem (of getting to school) is a sequence of selections at each intersection that allows you to wind up at school.

If you had all the time in the world to get to school, you might try choosing intermediate states randomly. At one corner you turn left, the next you go straight, then you go left again, then right, then right, then straight. Unfortunately, trial and error will not necessarily get you where you want to go, and even if it does, it is not the fastest way to get there. For example, when a friend of ours was in college, he got lost on the way to a concert and attempted to find the venue by choosing streets to turn onto randomly (this was long before the use of GPS). Amazingly enough, the strategy worked, although he did end up missing two out of the three bands who played that night.

Trial and error is not all bad, however. B.F. Skinner, a prominent behaviorist psychologist, suggested that people often behave randomly in order to see what effect the behavior has on the environment and what subsequent effect this environmental change has on them. This seems particularly true for the very young person. Picture a child filling a household’s fish tank with toilet paper, for example. To a child trying to develop a repertoire of creative problem-solving strategies, an odd and random behavior might be just the ticket. Eventually, the exasperated parent hopes, the child will discover that many of these random behaviors do not successfully solve problems; in fact, in many cases they create problems. Thus, one would expect a decrease in this random behavior as a child matures. You should realize, however, that the opposite extreme is equally counterproductive. If the children become too rigid, never trying something unexpected and new, their problem solving skills can become too limited.

Effective problem solving seems to call for a happy medium that strikes a balance between using well-founded old strategies and trying new ground and territory. The individual who recognizes a situation in which an old problem-solving strategy would work best, and who can also recognize a situation in which a new untested strategy is necessary is halfway to success.

Solving Problems with Algorithms and Heuristics

For many problems there is a possible strategy available that will guarantee a correct solution. For example, think about math problems. Math lessons often consist of step-by-step procedures that can be used to solve the problems. If you apply the strategy without error, you are guaranteed to arrive at the correct solution to the problem. This approach is called using an  algorithm , a term that denotes the step-by-step procedure that guarantees a correct solution. Because algorithms are sometimes available and come with a guarantee, you might think that most people use them frequently. Unfortunately, however, they do not. As the experience of many students who have struggled through math classes can attest, algorithms can be extremely difficult to use, even when the problem solver knows which algorithm is supposed to work in solving the problem. In problems outside of math class, we often do not even know if an algorithm is available. It is probably fair to say, then, that algorithms are rarely used when people try to solve problems.

Because algorithms are so difficult to use, people often pass up the opportunity to guarantee a correct solution in favor of a strategy that is much easier to use and yields a reasonable chance of coming up with a correct solution. These strategies are called  problem solving heuristics . Similar to what you saw in section 6.2 with reasoning heuristics, a problem solving heuristic is a shortcut strategy that people use when trying to solve problems. It usually works pretty well, but does not guarantee a correct solution to the problem. For example, one problem solving heuristic might be “always move toward the goal” (so when trying to get to school when your regular route is blocked, you would always turn in the direction you think the school is). A heuristic that people might use when doing math homework is “use the same solution strategy that you just used for the previous problem.”

By the way, we hope these last two paragraphs feel familiar to you. They seem to parallel a distinction that you recently learned. Indeed, algorithms and problem-solving heuristics are another example of the distinction between Type 1 thinking and Type 2 thinking.

Although it is probably not worth describing a large number of specific heuristics, two observations about heuristics are worth mentioning. First, heuristics can be very general or they can be very specific, pertaining to a particular type of problem only. For example, “always move toward the goal” is a general strategy that you can apply to countless problem situations. On the other hand, “when you are lost without a functioning gps, pick the most expensive car you can see and follow it” is specific to the problem of being lost. Second, all heuristics are not equally useful. One heuristic that many students know is “when in doubt, choose c for a question on a multiple-choice exam.” This is a dreadful strategy because many instructors intentionally randomize the order of answer choices. Another test-taking heuristic, somewhat more useful, is “look for the answer to one question somewhere else on the exam.”

You really should pay attention to the application of heuristics to test taking. Imagine that while reviewing your answers for a multiple-choice exam before turning it in, you come across a question for which you originally thought the answer was c. Upon reflection, you now think that the answer might be b. Should you change the answer to b, or should you stick with your first impression? Most people will apply the heuristic strategy to “stick with your first impression.” What they do not realize, of course, is that this is a very poor strategy (Lilienfeld et al, 2009). Most of the errors on exams come on questions that were answered wrong originally and were not changed (so they remain wrong). There are many fewer errors where we change a correct answer to an incorrect answer. And, of course, sometimes we change an incorrect answer to a correct answer. In fact, research has shown that it is more common to change a wrong answer to a right answer than vice versa (Bruno, 2001).

The belief in this poor test-taking strategy (stick with your first impression) is based on the  confirmation bias   (Nickerson, 1998; Wason, 1960). You first saw the confirmation bias in Module 1, but because it is so important, we will repeat the information here. People have a bias, or tendency, to notice information that confirms what they already believe. Somebody at one time told you to stick with your first impression, so when you look at the results of an exam you have taken, you will tend to notice the cases that are consistent with that belief. That is, you will notice the cases in which you originally had an answer correct and changed it to the wrong answer. You tend not to notice the other two important (and more common) cases, changing an answer from wrong to right, and leaving a wrong answer unchanged.

Because heuristics by definition do not guarantee a correct solution to a problem, mistakes are bound to occur when we employ them. A poor choice of a specific heuristic will lead to an even higher likelihood of making an error.

algorithm :  a step-by-step procedure that guarantees a correct solution to a problem

problem solving heuristic :  a shortcut strategy that we use to solve problems. Although they are easy to use, they do not guarantee correct judgments and solutions

confirmation bias :  people’s tendency to notice information that confirms what they already believe

An Effective Problem-Solving Sequence

You may be left with a big question: If algorithms are hard to use and heuristics often don’t work, how am I supposed to solve problems? Robert Sternberg (1996), as part of his theory of what makes people successfully intelligent (Module 8) described a problem-solving sequence that has been shown to work rather well:

• Identify the existence of a problem.  In school, problem identification is often easy; problems that you encounter in math classes, for example, are conveniently labeled as problems for you. Outside of school, however, realizing that you have a problem is a key difficulty that you must get past in order to begin solving it. You must be very sensitive to the symptoms that indicate a problem.
• Define the problem.  Suppose you realize that you have been having many headaches recently. Very likely, you would identify this as a problem. If you define the problem as “headaches,” the solution would probably be to take aspirin or ibuprofen or some other anti-inflammatory medication. If the headaches keep returning, however, you have not really solved the problem—likely because you have mistaken a symptom for the problem itself. Instead, you must find the root cause of the headaches. Stress might be the real problem. For you to successfully solve many problems it may be necessary for you to overcome your fixations and represent the problems differently. One specific strategy that you might find useful is to try to define the problem from someone else’s perspective. How would your parents, spouse, significant other, doctor, etc. define the problem? Somewhere in these different perspectives may lurk the key definition that will allow you to find an easier and permanent solution.
• Formulate strategy.  Now it is time to begin planning exactly how the problem will be solved. Is there an algorithm or heuristic available for you to use? Remember, heuristics by their very nature guarantee that occasionally you will not be able to solve the problem. One point to keep in mind is that you should look for long-range solutions, which are more likely to address the root cause of a problem than short-range solutions.
• Represent and organize information.  Similar to the way that the problem itself can be defined, or represented in multiple ways, information within the problem is open to different interpretations. Suppose you are studying for a big exam. You have chapters from a textbook and from a supplemental reader, along with lecture notes that all need to be studied. How should you (represent and) organize these materials? Should you separate them by type of material (text versus reader versus lecture notes), or should you separate them by topic? To solve problems effectively, you must learn to find the most useful representation and organization of information.
• Allocate resources.  This is perhaps the simplest principle of the problem solving sequence, but it is extremely difficult for many people. First, you must decide whether time, money, skills, effort, goodwill, or some other resource would help to solve the problem Then, you must make the hard choice of deciding which resources to use, realizing that you cannot devote maximum resources to every problem. Very often, the solution to problem is simply to change how resources are allocated (for example, spending more time studying in order to improve grades).
• Monitor and evaluate solutions.  Pay attention to the solution strategy while you are applying it. If it is not working, you may be able to select another strategy. Another fact you should realize about problem solving is that it never does end. Solving one problem frequently brings up new ones. Good monitoring and evaluation of your problem solutions can help you to anticipate and get a jump on solving the inevitable new problems that will arise.

Please note that this as  an  effective problem-solving sequence, not  the  effective problem solving sequence. Just as you can become fixated and end up representing the problem incorrectly or trying an inefficient solution, you can become stuck applying the problem-solving sequence in an inflexible way. Clearly there are problem situations that can be solved without using these skills in this order.

Additionally, many real-world problems may require that you go back and redefine a problem several times as the situation changes (Sternberg et al. 2000). For example, consider the problem with Mary’s daughter one last time. At first, Mary did represent the problem as one of defiance. When her early strategy of pleading and threatening punishment was unsuccessful, Mary began to observe her daughter more carefully. She noticed that, indeed, her daughter’s attention would be drawn by an irresistible distraction or book. Fresh with a re-representation of the problem, she began a new solution strategy. She began to remind her daughter every few minutes to stay on task and remind her that if she is ready before it is time to leave, she may return to the book or other distracting object at that time. Fortunately, this strategy was successful, so Mary did not have to go back and redefine the problem again.

Pick one or two of the problems that you listed when you first started studying this section and try to work out the steps of Sternberg’s problem solving sequence for each one.

a mental representation of a category of things in the world

an assumption about the truth of something that is not stated. Inferences come from our prior knowledge and experience, and from logical reasoning

knowledge about one’s own cognitive processes; thinking about your thinking

individuals who are less competent tend to overestimate their abilities more than individuals who are more competent do

Thinking like a scientist in your everyday life for the purpose of drawing correct conclusions. It entails skepticism; an ability to identify biases, distortions, omissions, and assumptions; and excellent deductive and inductive reasoning, and problem solving skills.

a way of thinking in which you refrain from drawing a conclusion or changing your mind until good evidence has been provided

an inclination, tendency, leaning, or prejudice

a type of reasoning in which the conclusion is guaranteed to be true any time the statements leading up to it are true

a set of statements in which the beginning statements lead to a conclusion

an argument for which true beginning statements guarantee that the conclusion is true

a type of reasoning in which we make judgments about likelihood from sets of evidence

an inductive argument in which the beginning statements lead to a conclusion that is probably true

fast, automatic, and emotional thinking

slow, effortful, and logical thinking

a shortcut strategy that we use to make judgments and solve problems. Although they are easy to use, they do not guarantee correct judgments and solutions

udging the frequency or likelihood of some event type according to how easily examples of the event can be called to mind (i.e., how available they are to memory)

judging the likelihood that something is a member of a category on the basis of how much it resembles a typical category member (i.e., how representative it is of the category)

a situation in which we are in an initial state, have a desired goal state, and there is a number of possible intermediate states (i.e., there is no obvious way to get from the initial to the goal state)

noticing, comprehending and forming a mental conception of a problem

when a problem solver gets stuck looking at a problem a particular way and cannot change his or her representation of it (or his or her intended solution strategy)

a specific type of fixation in which a problem solver cannot think of a new use for an object that already has a function

a specific type of fixation in which a problem solver gets stuck using the same solution strategy that has been successful in the past

a sudden realization of a solution to a problem

a step-by-step procedure that guarantees a correct solution to a problem

The tendency to notice and pay attention to information that confirms your prior beliefs and to ignore information that disconfirms them.

a shortcut strategy that we use to solve problems. Although they are easy to use, they do not guarantee correct judgments and solutions

Introduction to Psychology Copyright © 2020 by Ken Gray; Elizabeth Arnott-Hill; and Or'Shaundra Benson is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Free ready-to-use math resources

Hundreds of free math resources created by experienced math teachers to save time, build engagement and accelerate growth

20 Effective Math Strategies To Approach Problem-Solving 

Katie Keeton

Math strategies for problem-solving help students use a range of approaches to solve many different types of problems. It involves identifying the problem and carrying out a plan of action to find the answer to mathematical problems.  

Problem-solving skills are essential to math in the general classroom and real-life. They require logical reasoning and critical thinking skills. Students must be equipped with strategies to help them find solutions to problems.

This article explores mathematical problem solving strategies, logical reasoning and critical thinking skills to help learners with solving math word problems independently in real-life situations. 

What are problem-solving strategies?

Problem-solving strategies in math are methods students can use to figure out solutions to math problems. Some problem-solving strategies: 

• Draw a model
• Use different approaches
• Check the inverse to make sure the answer is correct

Students need to have a toolkit of math problem-solving strategies at their disposal to provide different ways to approach math problems. This makes it easier to find solutions and understand math better. 

Strategies can help guide students to the solution when it is difficult ot know when to start.

The ultimate guide to problem solving techniques

Download these ready-to-go problem solving techniques that every student should know. Includes printable tasks for students including challenges, short explanations for teachers with questioning prompts.

20 Math Strategies For Problem-Solving

Different problem-solving math strategies are required for different parts of the problem. It is unlikely that students will use the same strategy to understand and solve the problem. 

Here are 20 strategies to help students develop their problem-solving skills. 

Strategies to understand the problem

Strategies that help students understand the problem before solving it helps ensure they understand: 

• The context
• What the key information is
• How to form a plan to solve it

Following these steps leads students to the correct solution and makes the math word problem easier .

Here are five strategies to help students understand the content of the problem and identify key information. 

1. Read the problem aloud

Read a word problem aloud to help understand it. Hearing the words engages auditory processing. This can make it easier to process and comprehend the context of the situation.

2. Highlight keywords 

When keywords are highlighted in a word problem, it helps the student focus on the essential information needed to solve it. Some important keywords help determine which operation is needed.  For example, if the word problem asks how many are left, the problem likely requires subtraction.  Ensure students highlight the keywords carefully and do not highlight every number or keyword. There is likely irrelevant information in the word problem.

3. Summarize the information

Read the problem aloud, highlight the key information and then summarize the information. Students can do this in their heads or write down a quick summary.  Summaries should include only the important information and be in simple terms that help contextualize the problem.

4. Determine the unknown

A common problem that students have when solving a word problem is misunderstanding what they are solving. Determine what the unknown information is before finding the answer.  Often, a word problem contains a question where you can find the unknown information you need to solve. For example, in the question ‘How many apples are left?’ students need to find the number of apples left over.

5. Make a plan

Once students understand the context of the word problem, have dentified the important information and determined the unknown, they can make a plan to solve it.  The plan will depend on the type of problem. Some problems involve more than one step to solve them as some require more than one answer.  Encourage students to make a list of each step they need to take to solve the problem before getting started.

Strategies for solving the problem 

1. draw a model or diagram.

Students may find it useful to draw a model, picture, diagram, or other visual aid to help with the problem solving process.  It can help to visualize the problem to understand the relationships between the numbers in the problem. In turn, this helps students see the solution.

Similarly, you could draw a model to represent the objects in the problem:

2. Act it out

This particular strategy is applicable at any grade level but is especially helpful in math investigation in elementary school . It involves a physical demonstration or students acting out the problem using movements, concrete resources and math manipulatives .  When students act out a problem, they can visualize and contectualize the word problem in another way and secure an understanding of the math concepts.  The examples below show how 1st-grade students could “act out” an addition and subtraction problem:

3. Work backwards

Working backwards is a popular problem-solving strategy. It involves starting with a possible solution and deciding what steps to take to arrive at that solution.  This strategy can be particularly helpful when students solve math word problems involving multiple steps. They can start at the end and think carefully about each step taken as opposed to jumping to the end of the problem and missing steps in between.

For example,

To solve this problem working backwards, start with the final condition, which is Sam’s grandmother’s age (71) and work backwards to find Sam’s age. Subtract 20 from the grandmother’s age, which is 71.  Then, divide the result by 3 to get Sam’s age. 71 – 20 = 51 51 ÷ 3 = 17 Sam is 17 years old.

4. Write a number sentence

When faced with a word problem, encourage students to write a number sentence based on the information. This helps translate the information in the word problem into a math equation or expression, which is more easily solved.  It is important to fully understand the context of the word problem and what students need to solve before writing an equation to represent it.

5. Use a formula

Specific formulas help solve many math problems. For example, if a problem asks students to find the area of a rug, they would use the area formula (area = length × width) to solve.   Make sure students know the important mathematical formulas they will need in tests and real-life. It can help to display these around the classroom or, for those who need more support, on students’ desks.

Strategies for checking the solution 

Once the problem is solved using an appropriate strategy, it is equally important to check the solution to ensure it is correct and makes sense. 

There are many strategies to check the solution. The strategy for a specific problem is dependent on the problem type and math content involved.

Here are five strategies to help students check their solutions. 

1. Use the Inverse Operation

For simpler problems, a quick and easy problem solving strategy is to use the inverse operation. For example, if the operation to solve a word problem is 56 ÷ 8 = 7 students can check the answer is correct by multiplying 8 × 7. As good practice, encourage students to use the inverse operation routinely to check their work. 

2. Estimate to check for reasonableness

Once students reach an answer, they can use estimation or rounding to see if the answer is reasonable.  Round each number in the equation to a number that’s close and easy to work with, usually a multiple of ten.  For example, if the question was 216 ÷ 18 and the quotient was 12, students might round 216 to 200 and round 18 to 20. Then use mental math to solve 200 ÷ 20, which is 10.  When the estimate is clear the two numbers are close. This means your answer is reasonable. 

3. Plug-In Method

This method is particularly useful for algebraic equations. Specifically when working with variables.  To use the plug-in method, students solve the problem as asked and arrive at an answer. They can then plug the answer into the original equation to see if it works. If it does, the answer is correct.

If students use the equation 20m+80=300 to solve this problem and find that m = 11, they can plug that value back into the equation to see if it is correct. 20m + 80 = 300 20 (11) + 80 = 300 220 + 80 = 300 300 = 300 ✓

4. Peer Review

Peer review is a great tool to use at any grade level as it promotes critical thinking and collaboration between students. The reviewers can look at the problem from a different view as they check to see if the problem was solved correctly.   Problem solvers receive immediate feedback and the opportunity to discuss their thinking with their peers. This strategy is effective with mixed-ability partners or similar-ability partners. In mixed-ability groups, the partner with stronger skills provides guidance and support to the partner with weaker skills, while reinforcing their own understanding of the content and communication skills.  If partners have comparable ability levels and problem-solving skills, they may find that they approach problems differently or have unique insights to offer each other about the problem-solving process.

5. Use a Calculator

A calculator can be introduced at any grade level but may be best for older students who already have a foundational understanding of basic math operations. Provide students with a calculator to allow them to check their solutions independently, accurately, and quickly. Since calculators are so readily available on smartphones and tablets, they allow students to develop practical skills that apply to real-world situations.  

Step-by-step problem-solving processes for your classroom

In his book, How to Solve It , published in 1945, mathematician George Polya introduced a 4-step process to solve problems. 

Polya’s 4 steps include:

• Understand the problem
• Devise a plan
• Carry out the plan

Today, in the style of George Polya, many problem-solving strategies use various acronyms and steps to help students recall. 

Many teachers create posters and anchor charts of their chosen process to display in their classrooms. They can be implemented in any elementary, middle school or high school classroom. 

Here are 5 problem-solving strategies to introduce to students and use in the classroom.

How Third Space Learning improves problem-solving 

Resources .

Third Space Learning offers a free resource library is filled with hundreds of high-quality resources. A team of experienced math experts carefully created each resource to develop students mental arithmetic, problem solving and critical thinking. 

Explore the range of problem solving resources for 2nd to 8th grade students. 

One-on-one tutoring 

Third Space Learning offers one-on-one math tutoring to help students improve their math skills. Highly qualified tutors deliver high-quality lessons aligned to state standards. 

Former teachers and math experts write all of Third Space Learning’s tutoring lessons. Expertly designed lessons follow a “my turn, follow me, your turn” pedagogy to help students move from guided instruction and problem-solving to independent practice. 

Throughout each lesson, tutors ask higher-level thinking questions to promote critical thinking and ensure students are developing a deep understanding of the content and problem-solving skills.

Problem-solving

Educators can use many different strategies to teach problem-solving and help students develop and carry out a plan when solving math problems. Incorporate these math strategies into any math program and use them with a variety of math concepts, from whole numbers and fractions to algebra. 

Teaching students how to choose and implement problem-solving strategies helps them develop mathematical reasoning skills and critical thinking they can apply to real-life problem-solving.

READ MORE : 8 Common Core math examples

There are many different strategies for problem-solving; Here are 5 problem-solving strategies: • draw a model  • act it out  • work backwards  • write a number sentence • use a formula

Here are 10 strategies of problem-solving: • Read the problem aloud • Highlight keywords • Summarize the information • Determine the unknown • Make a plan • Draw a model  • Act it out  • Work backwards  • Write a number sentence • Use a formula

1. Understand the problem 2. Devise a plan 3. Carry out the plan 4. Look back

Some strategies you can use to solve challenging math problems are: breaking the problem into smaller parts, using diagrams or models, applying logical reasoning, and trying different approaches.

Related articles

Why Student Centered Learning Is Important: A Guide For Educators

13 Effective Learning Strategies: A Guide to Using them in your Math Classroom

Differentiated Instruction: 9 Differentiated Curriculum And Instruction Strategies For Teachers 

5 Math Mastery Strategies To Incorporate Into Your 4th and 5th Grade Classrooms

Ultimate Guide to Metacognition [FREE]

Looking for a summary on metacognition in relation to math teaching and learning?

Check out this guide featuring practical examples, tips and strategies to successfully embed metacognition across your school to accelerate math growth.

Privacy Overview

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List

Cognitive control, intentions, and problem solving in skill learning

Wayne christensen.

1 Philosophy, University of Barcelona, Barcelona, Spain

Kath Bicknell

2 School of Social Sciences and School of Psychological Sciences, Macquarie University, Sydney, Australia

We investigate flexibility and problem solving in skilled action. We conducted a field study of mountain bike riding that required a learner rider to cope with major changes in technique and equipment. Our results indicate that relatively inexperienced individuals can be capable of fairly complex 'on-the-fly' problem solving which allows them to cope with new conditions. This problem solving is hard to explain for classical theories of skill because the adjustments are too large to be achieved by automatic mechanisms and too complex and rapid to be achieved by cognitive processes as they are usually understood. A recent theory, Mesh, can explain these results because it posits that skill-specific cognitive abilities develop during skill learning and that control typically involves an interplay between cognitive and automatic mechanisms. Here we develop Mesh further, providing a detailed explanation for these problem solving abilities. We argue that causal representation, metacognitive awareness and other forms of performance awareness combine in the formulation and control of action strategies. We also argue that the structure of control present in this case is inconsistent with Bratman's model of intentions, and that, in the face of high uncertainty and risk, intentions can be much more labile than Bratman recognises. In addition, we found limitations and flaws in problem solving which illuminate the representations involved. Finally, we highlight the crucial role of social and cultural learning in the development of complex skills.

Introduction

What is learned during skill learning? What role does cognitive control—the form of control involved in flexible, goal-directed thought and action—play in the learning process? Classical skill theories, such as those of Fitts and Posner ( 1967 ) and Anderson ( 1982 ), treat cognitive control as responsible for discovering the structure of the actions that the skill requires, and for their initial implementation, but as being supplanted by more efficient automatic processes as learning progresses. Most work on skill focuses on the development of automaticity and the abilities and mechanisms that automatically-produced skills might involve. But humans show an exceptionally high degree of flexibility in skilled action, including forms of flexibility that rely on problem solving to construct solutions, as opposed to the deployment of pre-learned solutions. This kind of flexibility has not received much attention, even though it is arguably the critical ability underlying the richness and diversity of human skill.

The classical view sees skill as automating because it regards cognitive control as fundamentally unsuited to the demands of skilled action control. Cognitive control is thought to be slow, serial, and as having limited capacity, whereas automatic processes are fast, parallel, and have high capacity (Shiffrin & Schneider, 1977 ; Evans & Stanovich, 2013 ). Cognitive control uses highly generalised representations and problem solving methods which are an inefficient means for producing the specialised responses of skill (Anderson, 1982 ). In other words, cognitive control is specialised for reasoning, not action control, and it is a clumsy tool to use for action control. But it's questionable whether cognitive control is really fundamentally unsuited to skilled action control, as assumed by the classical view. Certainly, early cognitively-driven efforts to perform a skill are clumsy, and working memory is often overloaded by task demands. But significant degrees of fluency emerge long before strong automaticity could be in place. Skill research tends to focus on motor skill in particular, but if we consider expertise research more generally it is clear that experts can acquire domain-specific cognitive skills which can allow them to rapidly process large amounts of information (Ericsson & Kintsch, 1995 ) and engage in powerful, domain-specific forms of problem solving (Chi et al., 1982 ). There is no obvious reason why skills that involve a strong motor component might not also incorporate cognitive abilities involved in control and problem solving.

A recent skill theory called Mesh proposes just this (Christensen & Sutton, 2018 ; Christensen et al., 2016 , 2019 ). It claims that almost all skills incorporate an important cognitive component, including those which are paradigmatically motoric like golf putting. Skilled performance is produced by meshed cognitive and automatic processes which are generated by the cooperative operation of many neural systems. Cognitive processes provide flexibility by shaping action to the context and by solving the problems that complex, variable environments and tasks present. This paper extends Mesh by investigating the nature of skilled problem solving more closely. We conducted a field study investigating adjustments to major task changes by a rider with several years mountain bike riding experience (and many years of road riding experience) but beginner-level mountain bike technique. This was one of the authors, Wayne. Kath, who is a highly experienced rider, provided instruction. Guidance from Kath prompted major changes in Wayne's riding technique. A change in bike during the field study also encouraged significant adjustments in Wayne’s riding.

Because Wayne was not a raw novice he possessed mountain-biking-specific problem solving abilities which allowed him to cope with these large changes more fluently than might be expected based on the classical view. His experiences navigating rocky descents and ascents, and challenging log roll-overs, help to illuminate the nature of the control involved in this kind of problem solving. These problems involve high uncertainty and significant risk, and control processes flexibly adjust action to manage this risk and uncertainty. The learner is learning the structure of the problem as they try out solutions, and the strategy is monitored, modified and sometimes abandoned during execution. Evaluation is complex, employing a rich set of criteria and flexible holistic assessment. To understand these features of control we need a more expansive concept of control and a more labile picture of intentions than the standard picture recognises (Bratman, 1987 ).

The problem solving that Wayne engaged in also helps to illuminate the nature of the representations involved. Recently there has been considerable interest in characterising the type of the representations that are required for the ability to perform actions (Pacherie, 2011 ). Most accounts have focused on representations of action form , with an emphasis on schemas (e.g. Mylopoulos & Pacherie, 2018 ; Fridland, 2021 ). In contrast, some accounts have focused on the representation of causal structure (Christensen et al., 2015 ; Goldenberg, 2013 ).

Here we endorse the view that causal representation plays an important role, and show how this kind of representation supports flexibility. We suggest that Wayne employed causal representation to identify the structure of the problems he faced and formulate solutions. Because he could understand the causal significance of some of the features of the altered technique and equipment he could rapidly formulate new strategies to cope with and exploit the changes. But Wayne's problem solving abilities showed strong limitations which are also revealing. Wayne failed to properly implement a key riding technique even though he understood the technique abstractly and thought he was implementing it. The problem was diagnosed by Kath, who corrected his implementation. His difficulty involved a failure to properly map between an abstract representation of the technique and the representations used in the control of execution. The latter have particular a type of content, in particular a systematic representation of the state space of execution control . They also have a characteristic perspective that we call the perspective of execution control . This perspective is related to, though distinct from, the type of perspective described by (Pavese, 2019 ) in her concept of practical modes of presentation.

In Sect.  2 we present the theoretical context for the study and describe its conception. In Sect.  3 we give an overview of the activities we conducted. Section  4 then analyses these experiences in close detail using the theoretical ideas developed in Sect.  2 .

Context and approach

This paper centers on a field study which is analysed for its theoretical implications. In both philosophy and psychology this is an unusual method which requires some explanation and defense. In a separate paper, Christensen (in preparation) develops a general argument that cognitive ecology should be a central discipline in psychology, that ecological methods should be incorporated into philosophy just as experimental methods have been, and that the present lack of attention to cognitive ecology is a serious limitation on the development of deep theory in both psychology and philosophy of mind (see also Bicknell & Sutton, 2022 ). Here we focus on a more restricted argument which highlights some of the ways that the theoretical issues we are concerned with in this paper are sensitive to ecological data.

As noted, we are concerned with skill learning, and with the role of cognitive control, intentions, and action strategies in skill learning. These are evolved adaptive traits whose structure and function are shaped by a complex mixture of evolutionary adaptation and learning. It follows that understanding the nature of the adaptive functions and mechanisms depends critically on understanding the ecological problems they respond to. Consequently, we need to investigate these phenomena in the context of the ecological problems they are adapted to solve. This requires the use of ecological methods to investigate the nature of these problems. We currently lack a detailed understanding of these ecological problems.

Bratman's ( 1987 ) theory of intentions is an especially relevant case where theory is sensitive to the details of these ecological problems. 1 Bratman’s account is widely accepted and is used as a framework by numerous contemporary researchers. Mylopoulos and Pacherie’s ( 2018 ) account of intentional action control is an example which we will compare with our own model. Bratman characterises intentions based on an analysis of human planning behavior. In developing his theory Bratman focuses primarily on "ordinary, humdrum cases in which future-directed intentions and partial plans lead without great difficulty from prior deliberation to later conduct" (p. 12). He sees these kinds of cases as contrasting with more complex cases that involve difficulties of self-control. He writes,

Such examples are quite fascinating. But I think we get a distorted view of future-directed intention if we take them as paradigmatic of intention. It is best, I think, to begin with ordinary, garden-variety cases in which, without major psychological resistance, future-directed intentions and partial plans support coordination in the lives of limited agents like us. It is here that we need to look to get at the major regularities, roles, and norms in terms of which we can understand intention and its associated commitment . (p. 12, emphasis added.)

In this passage Bratman shows an awareness of the importance of the ecological representativeness of types of cases. However, Bratman's ecological picture is itself flawed. Bratman appears to assume that ordinary humdrum cases “without great difficulty” are ecologically typical or predominant while cases with major psychological conflict are exceptional. He also assumes that these are the only significant variations to be considered. Bratman's examples are indeed, for the most part, mundane, such as going to the library to borrow a book, or deciding whether to have a milkshake for lunch. These cases involve low stakes, high information, low complexity, context stability, and low time pressure. Only one of his examples, a presidential TV debate, involves high stakes, high complexity and high time pressure. Bratman uses the complexity and time pressure of the case in his analysis but he doesn't systematically examine these features as such or consider the significance of variation in them for his theory. All these features vary greatly across naturally occurring human ecological contexts. And crucially, these variations have important theoretical implications. The basic structure of Bratman’s model of intention involves a phase of deliberation in which an intention is formed, followed by a phase in which evaluation of the intention has ceased and cognitive processes are devoted to implementation. Intentions serve as fixed anchor points which structure cognition and behavior after they have been adopted. But this model may be best suited to cases that involve low stakes and high information. In cases with significant uncertainty and high stakes we might expect evaluation of the intention to be ongoing during execution as information comes in. In some kinds of cases it is possible to abort an action part way through or change its fundamental nature. Accordingly, in these kinds of contexts intentions may be relatively labile, being evaluated, modified, and sometimes abandoned during execution as information about the action is acquired. Skill learning is an important context in which this kind of pattern is likely.

Lack of ecological data is also a problem for skill theory. Classical skill theories, such as those of Fitts and Posner ( 1967 ) and Dreyfus and Dreyfus ( 1986 ), propose that skill acquisition has a well-defined stage structure culminating in a final stage of full automaticity. Fitts and Posner's model has just three stages, while Dreyfus and Dreyfus's account has five. Yet skills are extremely diverse, ranging from the ability to play tic-tac-toe to being a concert pianist or astrophysicist. It is unlikely that a simple three or five stage model provides a satisfactory fit to all the skill acquisition pathways involved in developing such diverse expert abilities. In athletics, high jumping has a standardised, invariant task structure, and a single action strategy, the Fosbury Flop, has dominated since the late 1960s. In contrast, in competition bouldering route setters set highly diverse novel climbing problems at each competition. Climbers are allowed only four minutes to inspect the wall and formulate strategies. Climbers try out varied strategies, often employing strategies which suit their individual abilities and physical characteristics, such as explosive strength, limb and hand size, or flexibility and balance. 2 Multiple strategies may succeed on a given problem, including strategies not anticipated by the route setters. 3 At odds with classical skill theories, climbers and commentators often describe bouldering at elite levels as highly cognitive. This is less often said about high jump. To get a better understanding of skill we need a fuller picture of this diversity.

In this paper we take a small step towards filling out this picture. Our objective is to bring detailed theoretical analysis into a close engagement with detailed empirical ecological reporting and analysis. While our sample is a tiny slice of the big picture, close analysis reveals that it has features with wide-ranging theoretical significance.

Ecological context

The ecological context we have focused on is that of socially-guided learning of a complex, fast-paced skill in a variable, physically demanding environment. Specifically, we have focused on the problems of coping with major changes in mountain biking technique and equipment in an individual at a relatively early stage of skill development, with some experience but beginner-level technique. The ability to acquire complex, fast-paced sensorimotor skills is highly developed in primates, with arboreal lifestyle being a primary ecological basis for this. Primates show high levels of behavioral flexibility, manifested in foraging strategies, communication, social behavior and tool use. Amongst primates, humans are exceptional in showing an extremely highly developed capacity for flexible skill acquisition. This plays a fundamental role in human lifestyles. Human skills tend to be highly social, often acquired through social learning and exercised in social contexts.

Cognitive control plays a central role in learning complex novel skills. It is accordingly likely that in human evolution there has been selection on the capacity for cognitive control for functions that contribute to complex skill learning. Some contributions of cognitive control are probably not specific adaptations for skill learning, but rather more general abilities that contribute to skill learning amongst other important adaptive human capacities. Conversely, skill learning is likely to shape the mechanisms of cognitive control generally, both via selection and activity-dependent plasticity. During skill learning, new capacities for cognitive control are acquired, so some of the capacities and mechanisms involved in cognitive control may be more apparent (see for example, Bicknell, 2021 ; Bicknell & Brümmer, 2022 ; Downey, 2022 ).

Our rationale for focusing on the ability to cope with major changes in technique and equipment is that this is a demanding context which should illuminate mechanisms for control of performance and skill learning.

Testing the classical procedural-cognitive contrast

We can make an initial framing in terms of the standard distinction between implicit and explicit processes. Broadly, the kind of procedural or implicit learning usually associated with skill acquisition occurs slowly and incrementally, and the abilities which result are relatively inflexible (Reber et al., 2019 ). These mechanisms should hence be unable to respond to large, rapid changes. In addition, the classical view of skill claims that cognitive processes are ill-suited to the control of skilled action. Cognitive control processes should therefore struggle to cope with major novel changes to the way a task is performed. In contrast, Mesh theory claims that cognitive control of action improves with skill learning and incorporates several features which allow relatively efficient control, including representation of the causal structure of action problems and metacognitive and other kinds of performance awareness (Christensen et al., 2015 , 2019 ). It is consequently better placed to explain relatively fluent adjustments to major novel changes if, as we expected, these do occur.

Forms of flexibility

We also need a more fine-grained framing of the rationale for looking at large changes in technique and equipment. This is because numerous motor control mechanisms have been proposed which are capable of flexibility in various forms. In the situations we're concerned with it is plausible that multiple forms of flexibility play important roles.

One of the simplest forms of flexible control is feedback control. Here, feedback corrects deviation from a reference. The goal can be achieved from any point in a state space 'basin' defined by the abilities to detect deviations and produce control inputs which drive the system towards the goal state. Trace theory (Adams, 1971 ) and the control law model (Fajen, 2005 ; Gibson, 1979 ) are theories of skilled action production based on feedback. Another class of control system achieves greater flexibility by means of generalised sensorimotor mappings. Theories of this type include Schmidt's ( 1975 ) schema theory , the internal models approach (Daniel M. Wolpert & Kawato, 1998 ; Wolpert et al., 1995 ), Optimal Feedback Control theory (Todorov, 2004 ), and the coordinative structures of dynamical systems theory (e.g. Kelso & Zanone, 2002), which generate high order patterns in movement. The perception-motor mappings are generalised in the sense that they generalise from practiced to unpracticed contexts based on similarity.

Calibration is a form of flexibility in which the parameters of a control function are adjusted to suit the context. A different kind of flexibility is achieved by restricting regulation only to variables that affect goal-achievement (Todorov, 2004 ; Tseng et al., 2003 ). Restricting control only to variables that affect goal-achievement is resource-efficient and can have the effect of decoupling variables important for the goal from those which aren't, which buffers performance against variations in unimportant variables. Yet another kind of flexibility involves control of the way a strategy is executed. Impedance control , or the control of the stiffness of the motor system, is an example (Franklin et al., 2008 ). Thus, a given action type can be performed while maintaining varying degrees and forms of stiffness. Control of stiffness can have a variety of functional benefits. For instance, increasing stiffness can reduce the degrees of freedom present in a movement and hence simplify the movement problem, while reducing stiffness can reduce the negative consequences of impacts that arise as a result of errors.

A key form of flexibility, sometimes called equivalence , involves the ability to achieve a given goal using multiple qualitatively distinct movement patterns. Ranganathan et al. ( 2020 ) identify two kinds of mechanism capable of this kind of flexibility. The first type involve high order task-specific coordination functions which constrain the dynamics of the system in a way that allows multiple coordination modes, or synergies . The second consist of explicit strategies (Christensen & Bicknell, 2019 ; Christensen et al., 2015 , 2019 ; Shepherd, 2017 ; Taylor & Ivry, 2012 ). Ranganathan et al. ( 2020 ) suggest that flexibility is likely to be based on synergies when the variations in movement pattern are relatively small and the task constraints can be learned over a long period of time. Explicit strategies are likely to be used when the variations in movement patterns are large and the task constraints change over short time scales. The situation we are examining has these features so it should evoke the use of strategies.

Problem solving

The key question that then arises with regard to action strategies is how they are formulated and controlled using cognitive processes. As we saw, according to the classical view (e.g. Anderson, 1982 ) cognitive control includes no specialisations for action control. An alternative view, adopted in Mesh, is that control of action is one of the primary functions performed by cognitive control, and it incorporates mechanisms acquired through evolution and learning that are specialised for this role. These mechanisms engage in problem solving processes which represent the structure of action problems and construct solution strategies. Cognitive control then governs the implementation of these strategies.

Problem solving is a relatively understudied issue in motor control research, which is surprising on ecological grounds given the high degree of diversity and flexibility of human motor abilities, and the importance of flexible motor abilities in human evolution. Bernstein's ( 1996 ) concept of dexterity is an exception to this neglect. Bernstein characterises dexterity as the ability to find solutions to novel motor problems, and he regards it as central to human motor ability. Dexterity in this sense is likely to have fairly deep evolutionary roots, being important for locomotion in arboreal primates, for example. A recent study of squirrels illuminates some of the kinds of motor problem solving that an arboreal lifestyle involves, including adjusting to the flexibility of branches, distances, and the three-dimensional configuration of space and surfaces. 4 Human dexterity shows greatly enhanced range and depth, in the sense that humans are able to solve a much wider variety of motor problems and much more complex problems (Gibson 1979 ).

Causal representation and problem solving

Mesh treats the capacity for flexible problem solving as central to human skill and proposes that it incorporates three key ingredients. Firstly, there is the ability to flexibly represent problems as causally structured wholes by means of causal models . These represent problems as structured wholes incorporating constituents and relations. At least some constituents must be represented as able to vary in state, requiring a distinction between variables and the values that variables can take. We will refer to some variables as parameters , where by this we mean key features of a type, such as an action type. The representation of causal relations requires that parameters are represented as related by production relations, such that, in the simplest case, a change in the of state of a particular parameter produces a change in the state of a second parameter.

Most accounts of action representation have focused on the representation of action form , such as motor patterns, schemas and automated procedures (Anderson, 1982 ; Buxbaum, 2001 ; Fridland, 2021 ; Pacherie & Mylopoulos, 2020 ; Schmidt, 1975 ; Wolpert et al., 1995 ). These theories propose that, when provided with a goal in a particular context, the motor system predicts what action structure will achieve the goal and then produces that structure. Crucially, there is no representation of the causal relation between the action structure and the goal, or between components of the action structure. In contrast, causal theories claim that action control incorporates explicit representation of causal relations. For instance, the individual might use awareness of the weight of an object in order to estimate how much force to use in picking it up, or awareness of the mechanical properties of a knife blade to control its manipulation when using it as a prying lever. Thus, Goldenberg ( 2013 ) proposes that action control employs a mechanical problem-solving system that represents objects and the body in terms of parts and properties relevant to action problems. Pavese ( 2021 ) argues that these representations of causal principles are practical concepts, or concepts used for intentional control of action. Somewhat similarly to Goldenberg, we suggest that causal control models are employed in action control which explicitly represent causal structure involved in action and help to identify control acts that can achieve goal states (Christensen & Bicknell, 2019 ; Christensen et al., 2015 ).

It is plausible that cognitive action representations include representations of both action forms and causal structure, but causal representation is crucial for intentional control and flexible problem solving. Intentional control of action characteristically involves producing an action with particular features because an action with these features will bring about a goal. The representation of instrumental relations is based on the representation of causal relations. Flexible problem solving involves representing the causal structure of novel problems and finding a means to produce a causal intervention which will bring about a goal state. 5

We can further illustrate the role of causal control models in action control using the example of braking. A causal control model involved in the control of braking will represent key causal factors such as braking strength , grip , speed , and braking distance as distinct, interrelated components of braking. This allows the individual to formulate a wide range of braking strategies, and adopt strategies appropriate to the conditions and their goals. Some of the possible strategies include early braking , in which gentle braking is applied far from the point at which halting or a desired speed is attained, and late braking , in which a high speed is maintained until relatively close proximity to the target point and speed is rapidly reduced by means of hard braking. A much more advanced example of the use of causal representation in formulating action strategies can be seen in a video lesson by the climber Tomoa Narasaki. 6 Narasaki is one of the best boulderers in the world, and has a dramatic style which involves frequent use of leaps between climbing positions that are far apart. These moves are called 'dynos'. In this video Narasaki explains his technique for performing a particular kind of dyno. What is of most relevance here is that he gives a detailed rationale for each component of the technique that is based on a deep causal understanding of the technique. This causal representation includes principles that can be used, not just for this particular technique, but for refining other techniques and formulating new strategies.

Our notion of causal control models is related to Pacherie's (Mylopoulos & Pacherie, 2017 ; Pacherie, 2011 ) concept of executable action concepts . Pacherie ( 2011 ) illustrated the idea of executable action concepts by contrasting them with observational action concepts which may not be executable. Thus, a spectator at an ice-skating competition may acquire the concept of a triple-axel by watching it being performed, but is unlikely to be able to perform it themselves. Pacherie argues that, since possession of the observational concept doesn't guarantee the ability to perform the action, in order to possess an executable action concept the individual must already possess motor representations capable of producing the movement. Mylopoulos and Pacherie ( 2017 ) argue that executable action concepts are executable in virtue of being linked to motor schemas which are acquired through bottom-up learning processes.

A difficulty with this account, however, is that bottom-up motor learning in most cases depends on the action being first produced intentionally. Indeed, it has been a standard assumption that skill learning involves an initial phase in which the action is produced intentionally (Anderson, 1983 ; Fitts & Posner, 1967 ). There are possible exceptions in which the structure of the movement is produced incidentally as part a larger action and consolidated by bottom-up learning (Sun et al., 2001 ). Sequence learning tasks such as the serial reaction time task (SRTT) are designed to exploit this possibility as a means for studying implicit learning. In the SRTT the participant presses buttons in response to cues (Robertson, 2007 ). They are not informed that the sequence of cues/button presses contains a pattern. On subsequent tests participants are faster at the task, indicating they have some learning of the sequence. It was hoped that tasks like this would reveal purely implicit learning, operationally measured as speeded response combined with lack of explicit awareness of the sequence. However, participants do learn some of the sequence structure explicitly while performing the task and this appears to fully explain speed improvements (Krakauer et al., 2019 ). Thus, even in tasks specifically designed to elicit implicit, bottom-up learning it has proven difficult to do so. Masters and colleagues have attempted to develop training methods which allow the movement patterns of a skill to be learned largely or entirely implicitly (Masters, 2000; Poolton et al., 2006). However, it has proved difficult to apply these methods to complex skills (e.g. Poolton & Zachry, 2007). For most complex real-world skills like performing a dance step or changing gear in a manual car there is no other practical way to initially generate the action than by intentional control.

Thus, for the most part, the individual must already be able to intentionally produce the action before bottom-up motor learning can start to occur. Bottom-up motor learning refines and consolidates movement patterns that are intentionally produced. It doesn't construct novel movement patterns. Pacherie is right that to develop an executable action concept the individual must already possess motor representations capable of producing (at least an approximation of) the reference movement pattern. But in the initial stages of motor skill acquisition the individual does not have an integrated motor representation that is specific to the movement pattern being learned. The individual usually needs to construct a cognitive representation of the desired movement as an integrated structure assembled from intentionally controllable motor components.

This brings us to a crucial phenomenon that any theory of action and skill must accommodate, namely the ability to intentionally produce novel movement patterns. The basic level of control in intentional action is not the ability to produce 'basic actions', in the philosophical sense, it is the ability to intentionally control movement parameters such as postural parameters, direction, distance, speed, force, and so on. To intentionally produce novel movement patterns as functionally integrated wholes it is necessary to represent causal interdependencies amongst at least some of these parameters, such as between position, distance, speed, time, and force. 7 Thus, causal control models of the same kind as we described for braking are used in the fundamental control of movement.

Infants and young children learn a repertoire of basic coordinated actions, including pointing, reaching, grasping, manipulating, stepping, and so on. These actions are basic in the sense that they come to function as units which will be employed in the construction of more complex actions. They incorporate stereotyped movement patterns and their control is likely to incorporate linked conceptual and motor schema representations in the way that the Mylopoulos and Pacherie model describes. But they are intentionally controllable , in the sense that their parameters can be intentionally adjusted to achieve a variety of goals. To explain this we need to supplement the Mylopoulos and Pacherie model of executable action concepts with the account of causal control models that we are proposing. Typically, in skill acquisition, such as when learning to play a musical instrument, more basic intentionally controlled movement capacities are adapted for the specific demands of the skill. During skill learning cognition leads in the construction of new actions to suit the task demands. Once a novel action structure has been constructed, consolidation and refinement will occur across the whole control system, including the formation of integrated motor schemas and the formation of integrated causal control models.

Translation between representational systems

Theories of action control face the problem of understanding translation between and within representational systems during action control, including multiple perceptual modalities, visual and verbal linguistic representations, emotion experience, gestures, computer and web interface 'languages', the iconography and signaling conventions of driving on roads, maps, music representational systems such as notation and tab, and so on. 8 Hierarchical models of intentional control, such as that of Mylopoulos and Pacherie ( 2018 ), must explain translation across different levels of abstraction. Translation across all these representational systems and levels plays a central role in problem solving and flexibility. Abstract goals and plans must be interpreted in more concrete situational terms. Flexibility hinges on being able to vary the way actions are performed in relation to features of the situation while realising the features of action critical to achieving the goals. Learning involves abstracting action features from instances in a way that allows varied concrete implementations. Recent philosophical theories of the architecture of action control, such as the DPM and Mesh models, have not so far addressed these issues but there is a long tradition of work on them in other fields (Fitch & Martins, 2014; Lashley, 1951; MacKay, 1982; Ondobaka & Bekkering, 2012). 9

A connected issue that has received recent attention in philosophy is that of the perspective of the representations involved in action control. Pavese ( 2019 ) develops the idea that some representations have a distinctive practical mode of presentation or practical perspective . She argues that these are imperative representations which specify a method of performing a task in terms of the abilities of a system that can implement the method. She claims that motor commands and motor schemas are examples of this kind of representation. We agree this is an important form of practical perspective, but we need to also understand the form of practical perspective of the representations used in the problem solving by which schemas and motor commands are formulated and evaluated. We'll call this the perspective of control . The perspective of control encompasses all of the phases, levels and aspects of control, many of which have their own perspectival characters, including those of distal decision-making and proximal control of execution.

The structure of control

In addition to causal control models, previous explications of Mesh have identified two further components of action control: forms of higher order performance and metacognitive awareness. Before describing these in detail, however, it will help to clarify the structure of control. Mesh is similar to the DPM model of Mylopoulos and Pacherie ( 2018 ) in depicting action control as involving a hierarchical structure. Mesh has not yet been very specific about the details of the nature of the control involved in the hierarchy, whereas the DPM model, based on Bratman's account of intentions (along with Searle ( 1983 ), Brand ( 1984 ), and Mele ( 1992 )), specifies a control organisation that involves multiple levels of intentions which are responsible for specific aspects of action control. In particular, a distal intention, commonly formed outside the action context, represents the overarching goal of the action. Proximal intentions are formed which specify how the distal intention is to be implemented in the context of performance. Motor intentions specify the motoric means by which proximal intentions are implemented. Here we extend Mesh by specifying the structure of control in more detail. This account shares with the DPM model the idea that intentional action often involves a hierachical goal structure, but departs from it in certain respects which in part stem from a departure from Bratman's model of intentions. 10

One way to conceptualise control is as the ability of the agent to achieve its goals. We'll call this the goal-based conception of control. Mylopoulos and Pacherie ( 2018 ) and Shepherd ( 2021 ) employ this conception. 11 A different way to conceptualise control is as the ability of an agent to solve the problems that it faces. We'll call this the problem-based conception of control. Both concepts of control are useful but the problem-based concept is important for understanding adaptive control systems and the structure of control in skill learning. Thus, when we perform a full analysis of a biological control system we need to determine both the proximal goals (the represented goals) and the ultimate goals, which are solutions to adaptive problems faced by the biological agent. These problems are to a significant degree independent of and prior to the explicit goals of the control system. Solving them is often obligatory or very difficult to avoid. The relationship between proximal goals and adaptive problems will often be imperfect, and evolution will generally tend to bring the represented goals of organisms into alignment with their adaptive problems. Proximal criteria used in the control of eating include satisfying hunger and enjoyment of the experiences of eating. The primary adaptive goal is nutrition. Humans can adopt conceptualised nutrition as an explicit goal of eating but they need not. The proximal control criteria for eating can be satisfied while the adaptive problem is not. In cases where conceptualised nutrition is a goal of eating it may correspond imperfectly to objective nutrition. Thus, goal-based and problem-based control can be dissociated.

Humans are a highly social species and are exceptionally flexible in developing varied lifestyles and technologies which have allowed the colonisation of almost every kind of terrestrial environment on earth. This flexibility in lifestyles is founded on an exceptional capacity for flexible skill learning. Human evolution has thus endowed us with skill learning capacities which are extremely good at solving the ecological and social problems we face. Uncertainty plays a central role in this flexibility. Humans face a fundamental and pervasive uncertainty concerning their goals. Their goals correspond imperfectly to their problems and they must learn about the structure of the problems that they have. Problem discovery thus plays a central role in skill learning. Skill learners typically begin with poor representations of their problems. Their goals correspond imperfectly to their problems and they must learn about the structure of the problems that they have, and learn to form better goals. This learning occurs at every level, from the specific problems involved in performing particular actions up to and including self-conception, whether to engage in the skilled activity at all, and to what degree.

More specifically, uncertainty and problem discovery play a key role in the structure of action evaluation. On a goal-based hierarchical model of control, such as the DPM model, performance at a given level of control is evaluated with respect to the goal at that level and to higher level goals. Thus, the success of motor performance is evaluated with respect to whether it achieves the goal specified by the M-intention, and whether this satisfies the goal specified by the P-intention. However, there are certain phenomena which arise quite commonly during skill learning which don't fit this model very well. An action can go according to plan yet be assessed negatively. For example, an inexperienced guitarist might perform with a band at a gig in a way that they have planned to, and which they consider to be aligned with their norms for playing well, yet later evaluate their performance negatively when they review a recording. This later evaluation may be based on performance norms they had not previously considered, but which are highlighted when they assess their performance from the perspective of a listener and compare it to performances of more advanced players they admire. For example, they might realise that their playing was overly busy, failing to complement the song, and too loud, overshadowing the rest of the band. 12

An action can also go contrary to plan yet be assessed positively; a mistake which proves to be a 'happy accident'. For instance, you might accidentally shake out more hotsauce on your eggs than intended, yet regard the outcome as superior to the intended quantity of hotsauce.

These possibilities can't be explained if the only evaluative criteria are the goals specified by the intentions.

The action evaluation system

To understand these phenomena we need to recognise a broader set of evaluative criteria. While it is often the case that a specific explicit goal operates as a primary focus of action selection and regulation processes, this goal is only one item amongst a complex set of criteria used to evaluate the action. Some criteria are low level and generalised. Thus, all actions are evaluated for efficiency, regardless of whether efficiency is an explicit constituent of the content of the goal of the action. Other criteria are higher level and also generalised. A bluegrass musician will evaluate their playing according to their internalised aesthetic norms for bluegrass music. Some norms are specific to the action type, such as technique criteria. Some norms are specific to an individual, such as a personal playing style. In the performance of any given action an ensemble of criteria will be operative in evaluation processes. Criteria other than the primary goal can be used to evaluate the primary goal and its implementation. These additional criteria are themselves imperfect and subject to learning. A novice has evaluative criteria for the skill which are impoverished and poorly reflect the norms of the skill domain. Experts often have very rich, articulated evaluative criteria. For this reason, instruction and other forms of social feedback can play a vital role in guiding learners. Techniques for self-assessment which use an external perspective, such as recording and analysing performances, are also very valuable because they allow the individual to better apply performance norms they have acquired from an observer's perspective to their own performances.

Thus, we add to Mesh the proposal that skilled action evaluation is based on an action evaluation system (AES) which develops during skill learning. 13 The AES plays a role in the cognitive processes of intention formation and in the control of action execution. Action evaluation is holistic: no single criterion has strict dominance (e.g., there is no strict master goal) and the weighting of criteria can vary across contexts. The breadth and depth of evaluation will vary across contexts, but a complex set of criteria are often operative in the control of action execution. 14

In this respect the account departs from Bratman's model of intentions. As described above, Bratman's model has a strongly punctate structure in which there is a phase of deliberation which culminates in commitment to an intention, followed by a phase in which cognitive processes are focused on implementation of the intention and evaluation of it is bracketed. Bratman's rationale for the bracketing of intention evaluation is based on cognitive resource limitations: he claims that it is not possible to continuously determine the best course of action at each point in time. But while it is true that it isn't possible to perform a comprehensive analysis of the best course of action at each point in time, this doesn't imply that intention evaluation must have the punctate structure of his model. Bratman recognises that intentions may be reconsidered when stakes are high and 'new information comes in', but he regards this as exceptional. He says that it is reasonable to have a default presumption in favour of plan stability rather than reconsideration. Concerning the circumstances in which reconsideration is reasonable, he writes:

Sometimes the stakes are quite high, and there is an opportunity for calm and careful reconsideration of one's prior plan. It seems plausible to suppose that it is in the long-run interests of an agent occasionally to reconsider what he is up to, given such opportunities for reflection and given that the stakes are high, as long as the resources used in the process of such reconsideration are themselves modest ( 1987 , p. 67).

Our model is very different. It is common to have highly imperfect information and it is hence adaptive to continue to evaluate intentions after they have been adopted, including during action execution. This allows them to be flexibly modified and abandoned as more information is gained and as circumstances change. Here we need to distinguish between evaluation of implementation intentions involved in carrying out a plan and evaluation of the overarching intention. We claim that evaluation occurs at every level. The breadth and depth of evaluation varies, and it is certainly true that there is greater opportunity for deep and wide evaluation before and after performance compared with during, but nevertheless, higher levels of control can be 'in play' during performance. Thus a professional bike rider might, during a race, re-evaluate their ability, re-evaluate their strategy for a particular obstacle, re-evaluate their race strategy, or pacing plan (Christensen & Bicknell, 2019 ; Sutton & Bicknell, 2020 ). More broadly, an athlete may re-evaluate their strategy for the season, and might even re-evaluate their commitment to racing at this level. For instance, an older rider near the end of their career might switch during a race from assessing themselves as still being competitive at the highest level to no longer being competitive, and decide on this basis to retire. At the other end of the skill career time line, we can expect that evaluation of commitment to the skill to commonly occur during performance during early phases of acquisition and at key career stages.

The basis for such evaluation is the individual's AES. A well-developed, adaptive AES represents relevant evaluative criteria at various stages of intention formation and action performance.

This model of control differs from the DPM model. In keeping with Bratman's model, on the DPM model distal intentions are ascribed the function of terminating practical reasoning about what to do. Evaluation of success is goal-based and top-down. In contrast, our model places more weight on bottom-up processes in which higher-level goals are revised in response to information gained during action execution. Evaluation of intentions does not necessarily terminate with their adoption. Evaluation of success is not only with respect to achieving the goals specified by intentions. We think the DPM model can be readily amended to accommodate the phenomena we're describing, but these are nonetheless features of control that have high significance because they play important roles in learning and flexibility.

Performance and metacognitive awareness

Performance and metacognitive forms of awareness play a key role in action evaluation. In contrast, on Bratman's account reconsideration is based on habits and dispositions, deliberation, or by policies. He thus fails to recognise the importance of such forms of awareness. Confidence, for example, can have performance and metacognitive forms. Performance confidence is awareness of the likelihood of action success. Metacognitive confidence is awareness of the extent to which sufficient information is available for effective decision-making and control. When both kinds of confidence are high, as they are likely to be when a philosophy professor makes a plan to go to the library to borrow a book, depth of evaluation can be low during decision making and performance. When these forms of confidence are much lower, as they will be when learning a new mountain bike riding technique, depth of evaluation will tend to be higher in all stages of action.

According to Mesh, causal representation contributes to performance and metacognitive awareness. A causal control model represents the causal features of the situation relevant to action decisions and control. In the case of braking this will include causal features such as the nature of the surface, the amount of grip, and the amount of braking force that can be applied. Thus, the causal control model is the basis for awareness of the performance envelope , or range of performance states that are available. In this case, awareness of the performance envelope includes awareness of the range of braking forces that can be applied without losing grip. Awareness of the performance envelope serves as a basis for evaluating whether to continue with an action during performance. If a breakdown is likely it may be best to abandon the action. At a more finegrained level, awareness of the performance envelope allows the formulation and modification of action strategies. If grip proves to be unexpectedly high, for instance when using a new type of tire, braking strategies can be modified accordingly. When the individual is uncertain they may adopt a conservative strategy and attempt to gather more information (Christensen & Bicknell, 2019 ). Thus, if they are unsure of how powerful their brakes are, for example if they are on a new or recently serviced bike, they might use early braking or ride at a slower speed as they assess the performance of the brakes. If the individual is confident they may operate closer to the edges of the envelope.

Social and cultural learning and the degrees of freedom problem

The standard approach to skill is individualistic. When seeking to understand advanced skills the focus is on the autonomous abilities of individual experts. When seeking to understand skill learning the focus is on the processes by which an individual's abilities are transformed from novice to expert. Of course, it is understood that teaching and other forms of social learning play a role in skill learning. It's understood that some skills, such as theatre, dance, music, and team sports, involve collective action. Indeed, there is burgeoning transdisciplinary interest in collaborative experiences of, and influences on, skilled performance (Bicknell & Sutton, 2022 ). Nevertheless, skill theories treat social phenomena as secondary, or subtopics of skill. Mesh has followed this individualistic orientation (but see Christensen & Sutton, 2018 ).

Attention to the larger evolutionary and ecological context indicates that we should see individual and social aspects of skill as fundamentally interwoven. Human skills are exceptionally flexible, complex, and are generally acquired and practiced in highly social ways. These associations are not accidental. The flexibility of human skill is founded on a sensorimotor system capable of many 'degrees of freedom', being able to adopt an extremely large number of configurations that can be structured in many ways over time. The diversity and complexity of human skills, in comparison with other species, is possible only because of this underlying potential. But the high dimensionality of the human sensorimotor system, combined with the complexity of many skills, presents difficult problems for learning and control. The learner confronts an extremely large problem space in which solutions must be found. The degrees of freedom of the sensorimotor system must be steered in ways that realise solutions (Bernstein, 1996 ). Learning thus presents extremely difficult search and control problems.

One way that learning is made tractable is to acquire skill progressively, beginning with basic abilities that present relatively simple problems and moving to progressively more complex abilities that build on the simpler abilities (Bryan & Harter, 1899 ). Another way that learning is made tractable is by making it social. Experts and peers provide models of high quality solutions. Teachers can guide learners through the extended pathways to complex solutions. A skill community is able to explore the space of possibilities and solutions far more effectively than a lone individual. When a member of a community discovers a superior solution or other form of valuable skill knowledge, this can be propagated through the community (Goodwin, 1994 ). Many discoveries can be combined into complex, sophisticated methods.

Rival expectations

Based on the preceding discussion we can distinguish between two main contrasting sets of expectations for the situation we are investigating. Based on the classical view we should expect major changes to technique and equipment to be highly disruptive for two reasons. Firstly, automated forms of flexibility should be unable to cope with these kinds of changes because they require qualitatively new sensorimotor patterns. Secondly, cognitive processes should also struggle to cope because they employ general purpose representations and problem solving methods. They are hence poorly suited to skilled action control, and should be overwhelmed by the alterations to the complex relations involved in action production. Mesh yields a different set of expectations. An individual with a significant amount of experience will have developed mechanisms for the cognitive control of action which allow relatively fluent coping based on problem solving. This problem solving will be based on causal representation and an action evaluation system employing a complex set of criteria. Control will be more flexible than depicted by Bratman's model, with continuous evaluation even at higher intentional levels. This problem solving will be imperfect, however, especially in an individual whose technical abilities are fairly basic. Social guidance from an expert can supplement individual problem solving by directing the learner to better solutions.

The nature of our study

We conducted a field study investigating responses to major changes in a rider with several years mountain biking experience but beginner-level technique.

We employed a researcher-practitioner approach, in which the authors served the dual roles of investigators and participants (see Bicknell, 2021 ; Downey, 2022 ; Downey et al., 2015 ; McIlwain & Sutton, 2014 , 2015 ; Nemani & Thorpe 2016 ; Olive et al. 2016 ; Ravn, 2022 ; Samudra, 2008 ; Spinney, 2006 ; Sutton & Bicknell, 2020 ). This approach brings attention to theoretically and ecologically significant aspects of skilled action in contexts that are difficult to capture in the laboratory, from the armchair, or when the researcher is unfamiliar with the nuances of a particular community of practice. Our experiences were undoubtedly shaped by our theoretical interests, and the evidence should be viewed as exploratory and tentative. Validation of the kinds of phenomena we describe is needed using other methods. These include broader ecological sampling and laboratory investigation. It is especially important that ecological methods be employed which use structured data gathering in close temporal proximity to performance with theoretically naïve participants. But it must be emphasized that all methods have strengths and limitations. The best overall research strategy is to use a large methodological toolkit and seek to buttress each investigative mode with convergent evidence from others.

The two authors of this paper have differing levels of mountain bike expertise. Kath has been a mountain bike rider for over twenty years. She has worked for global cycling media for more than ten years, taught skills clinics, raced domestically and internationally, and has written academic papers and a PhD on the sport. Wayne, in contrast, has very limited mountain bike riding experience. He is not a raw novice; he has extensive experience of recreational and commuting riding on roads and about fifteen years previously he spent about a year mountain biking regularly, riding once or twice a week. This experience included twisty 'singletrails', tracks roughly the width of a foot trail, with rutting and differences in grip due to the type of dirt underneath his wheels (eg. loose and skatey or smoother ‘hardpack’). He had largely avoided more 'technical' trails including features like ‘rock gardens’ and logs. With respect to mountain bike riding he was self-taught and as a result had not acquired some important basic mountain bike riding techniques. As part of research for a previous paper (Christensen et al., 2015 ), he read a mountain bike instruction book and gained some familiarity with basic mountain bike techniques this way. Kath had also given him some instruction during the study. He had not, however, spent a significant amount of time practicing these techniques or received any further ‘live’ riding instruction.

The fieldwork session was designed to explore and document Wayne’s experience of the trails through an initial ride with no input from Kath, followed by two major changes. After observing Wayne ride an initial series of beginner-intermediate singletrails, Kath provided instruction on core mountain bike riding techniques, which Wayne then attempted to employ. Secondly, after riding the track on his own bike, Wayne then switched to Kath’s bike, which was a more modern and capable design.

In more detail, at the time of the study Wayne’s bike was approximately ten years old, an aluminium ‘cross country’-style hardtail (meaning no rear suspension), with 26″ wheels, hydraulic disc brakes, and basic front suspension in need of a service. Kath’s ‘trail’-style bike was a few months old. The design reflected substantial changes in bike technology, trends and manufacturing materials. These included: larger 29″ wheels with wide 2.4″ tubeless tyres, which roll over obstacles with more ease and traction compared to Wayne’s smaller wheels with narrower tyres; a more stable and relaxed geometry, which adds traction and confidence on climbs and descents; far more sophisticated front and rear suspension for better traction and compliance, and other modern features such as a 1 × 12 drive train (so no shifting is needed with the left hand) and a dropper seat post which allows the rider to press a lever on the handlebars and move the seat downwards so it doesn’t catch on their thighs when they move their body toward the rear of the bike while descending. The brakes were far more powerful, the frame material (carbon) more compliant, and the handlebars substantially wider, again providing enhanced stability and control. Kath and Wayne are a similar height, meaning they both ‘fit’ the same size frame. However, when Wayne switched to Kath’s bike the contact points were adjusted for Wayne, with the seat height being modified and his own pedals used.

The trail used for this investigation, a popular cross-country loop at the Ourimbah trail network in New South Wales, Australia, was chosen on the basis that Wayne could tackle it with reasonable safety, with guidance from Kath, but which contained obstacles that were more challenging than Wayne's prior experience made him comfortable with. During the ride, Kath gave Wayne the kind of instruction and induction into the mountain bike subculture that would be characteristic of an experienced rider taking a friend on a ride for the first or second time. For example, when Wayne was concerned about riding over a log obstacle she explained and demonstrated key body movements and the amount of speed needed to do it safely, but also encouraged him to walk the obstacle and try it again later if he preferred.

We took photos and recorded video of Wayne’s successive attempts at challenging obstacles on both bikes, and recorded video of Wayne describing his immediate responses to these experiences. We met the next day to write notes on the experience.

Riding the Ourimbah cross-country track

There were two aspects that stood out as especially noteworthy in Wayne’s experience: a change in technique that dramatically improved descending steeper trails, and adaptations to the increased performance capabilities provided by the second bike, particularly due to its stability over rough terrain.

At the beginning of our fieldwork session, Wayne rode a short loop of ‘singletrails’ without instruction or interference from Kath, who rode behind him, watching and observing. These trails included several relatively steep descending sections of trail, linked together by narrow, winding, rocky connections and the occasional smooth section for the rider to relax and catch their breath. (Understandably) Wayne was riding somewhat nervously and cautiously. He felt that his approach to riding these trails was reasonable given his limited overall experience and that he had not ridden a mountain bike trail in a number of years. Riding behind him, however, Kath could identify specific technical problems. She could see and hear the rear wheel skidding and noticed that Wayne’s body position (and centre of gravity) was quite far forward on the bike. This puts a lot of pressure on the front wheel, which causes several problems while descending, the most severe of which is that it increases the risk of flipping over the front of the bike. In the mountain biking subculture this is referred to as an ‘OTB’ (over the bars)—the standardization of the term suggesting it is a fairly common experience but one to be wary of.

We paused on a long flat section of fire road to discuss the experience of the first section of trails. Worried that Wayne was going to injure himself, Kath provided instructions that would help him ride the section more smoothly and safely on the next attempt. She explained a technique for descending steep obstacles, which involves keeping the feet balanced evenly on the pedals while the rider moves their bodyweight rearward on the bike to maintain balance and stability. She explained this to Wayne verbally, along with an arm gesture showing the effect of weight on the bike in relation to the terrain. She used the cue words ‘butt back’ and ‘weight back’ as a shorthand way to emphasize and direct this technique after the initial description of what to do. Taking advantage of the less threatening and challenging terrain provided by the wide, flat fire road, Kath showed Wayne an exercise which encouraged him to experiment with how far he could move his body rearwards while maintaining momentum on the bike. This involved riding in a straight line at a moderate speed, moving his butt behind the saddle and allowing it to graze the rear tyre. This exercise was designed to increase his awareness of how much space he had to move rearward on the bike, what this felt like in practice, and how this sensation differed to what Wayne thought was the near-maximum amount he could get his bodyweight behind the bike. 15 The sound and feel of grazing the tire provide aural and kinaesthetic cues that signify the rider has succeeded in the task when it is not possible to see, visually, how far back they have reached.

We then rode the same short sequence of trails again. Wayne now focused on getting behind the saddle during any steep downward sections of trail. The result was a dramatic improvement in the controllability of the bike. This transformed the experience of sustained descents and short, sharp drops or ‘rolldowns’. Rather than feeling threatening, the experience of riding these obstacles felt relatively comfortable—it felt less steep, less rough, less like he was about to have a crash. After applying the technique cautiously to a rocky ‘stepdown’, Wayne immediately began to apply the same technique to other steep, downward sections of the trails: log rolls, steep downward corners, rocky rolldowns, anything where the front of the bike is much lower than the rear of the bike while riding a trail obstacle.

After a longer lap of the trail on Wayne’s bike, Kath gave him her own bike to use for the second lap. She had another bike waiting in the car to facilitate this exercise. The technological differences described above between Kath’s bike and Wayne’s older model bike indicate that Kath’s bike would be more stable, compliant, absorbent and confidence inspiring. While this makes sense on paper, Wayne was nevertheless astonished at how much more capable the bike was in practice. The most immediately striking feature of the bike to him was its greater stability, and the fact that this allowed much better low speed control than his own bike. In comparison, the relative instability of Wayne’s own bike meant it would often feel like it was going to tip over at slow speeds.

The combination of greatly enhanced stability and compliance had a dramatic effect on Wayne’s experience riding the trail. He was able to ride faster on bumpier sections, with the bike soaking up rocks and gaps between them that would produce strong jarring on his own bike. Within 10–20 min of riding this bike his confidence greatly increased. Many descents and ascents he had struggled on while riding a lap of the trails on his own bike—rooty straights, rocky windy uphills, small rocky step-ups, uphill corners, rutted entries into corners, descents littered with a messy array of small obstacles—were experienced as being much more ‘ridable’ than they had been earlier that same day. The bike maintained traction more easily allowing Wayne to pedal and guide it through the obstacle with more control, confidence and ease. He continued to approach some obstacles cautiously, however, and Kath spent some time teaching him to ride over a log, which looked difficult to him but in fact was not. His main difficulty was simply overcoming his fear of the obstacle so that his approach was fast enough to carry him over the rocky ramp that led to the log itself. We make no claims that Wayne was able to ride all sections of the trail, or ride flawlessly ever after. He subsequently crashed when he misjudged a rocky section later in the day, bruising his ankle and wrist and acquiring some grazing.

Finding theory in action

In this section we use the theoretical concepts introduced in Sect.  2.2 to characterise the processes by which Wayne adjusted to the new technique and the new bike. Wayne was familiar with these concepts, which makes it easy for him to describe his riding experiences in these terms. This familiarity also undoubtedly influenced Wayne's experiences during our field study. However, based on Kath’s extensive experience teaching skills clinics, and riding with mountain bikers at a diverse range of skillsets, we think that the kinds of problem solving Wayne engaged in are not unusual. In particular, his experiences of identifying control problems and experimenting with solutions were in many respects fairly typical for a beginner rider.

Simple forms of adaptation

Wayne adapted rapidly to the new technique and new bike. Some of this adaptation involved relatively simple forms of flexibility. Simple calibration changes in important parameters, such as braking forces and braking timing, played a role. Both of the major changes improved stability, which had the effect of making feedback control more tolerant or less 'twitchy'. Feedback control processes quickly recalibrated for the new tolerances. As riding became more manageable Wayne could relax more, and reduced bodily stiffness is likely to have made control easier; bumps and other perturbations which might have been jarring and disruptive would now be absorbed more effectively through his limbs. Experience selectively highlighted key parameters, allowing control to be more focused.

Problem solving using causal knowledge and metacognition

Nevertheless, the changes in technique and bike were large enough to require adjustments by means of strategies formulated using problem solving. Wayne's ability to adapt to large changes hinged critically on an ability to formulate and implement new action strategies 'on the fly'. We can illustrate this by describing in detail a change in riding strategy associated with the technique change of getting behind the saddle. Although Kath wasn’t aware of it, the rear wheel skidding that she observed during Wayne’s initial ride was partly the result of a deliberate braking strategy that he thinks of as ‘tail dragging’, which involves using primarily the rear brake. After adopting the behind-the-saddle technique Wayne switched to an equalized front-rear braking strategy. Wayne was familiar with rear-wheel-based braking from riding as a child, with this experience including riding ‘back pedal’ brake bikes and with using the rear brake to skid out the back wheel on loose surfaces when coming to a halt, a satisfying and popular maneuver. He knew, however, that equalized braking is regarded as the superior technique and he had generally used it in his previous mountain bike riding. He nevertheless initially used rear-biased braking as an improvised strategy in response to control problems that he was experiencing. Wayne wasn’t aware that his weight was too far forward, but he was aware of some of the consequences of this. The load on the front wheel caused instability and had the potential to cause the front wheel to lose grip and slide out, resulting in a crash (which Wayne thought of as a ‘washout’). 16 Wayne felt that the wheel was most likely to lose grip under braking and using a rear-biased braking strategy helped to reduce this risk.

Thus, causal awareness played a key role in the adoption of the tail-dragging strategy and the later switch to equalized braking. Here we should note that Wayne's perception of the most immediate and important risk that he faced differed from Kath's assessment. Wayne was preoccupied with the danger of a washout due to heavy front braking, whereas Kath viewed the primary risk in Wayne's riding during this phase as being a front wheel washout or OTB crash caused by insufficient rearward weight. Other riders in a similar situation might have interpreted their risks differently and adopted different strategies. Other strategies which reduce the risk of loss of control when riding a difficult descent include putting one or both feet on the ground and scooting down, using both brakes fairly heavily and ‘inching’ down the obstacle (generally ill-advised), avoiding braking all together and focusing on body position, balance and looking ahead to the exit of the obstacle, or getting off the bike and walking (or sliding) the bike down the obstacle.

Metacognition can also be seen in this example. While Wayne thought there was a danger of the front wheel sliding out, he didn’t know in detail in what conditions this could occur. He was still adjusting to the ‘feel’ of the bike on the terrain and was uncertain about the amount of grip available and the braking forces that could be used. That is to say, Wayne was aware that he lacked sufficient information for good control. Estimating these action parameters is complicated by the fact that they are strongly affected by the nature of the surface, which was variable, and by the fact that in a washout the loss of grip tends to be abrupt. In the face of this uncertainty, tail dragging combined with low speed was a relatively safe, conservative strategy. And it worked! Wayne did manage to ride these difficult sections of trail without crashing. Kath’s intervention was to help Wayne ride them more smoothly, more safely and, ultimately, more enjoyably.

Metacognition also influenced Wayne’s use of tail dragging in another way. Tail dragging is a simple strategy to employ because there is no need to precisely coordinate front and rear braking pressures. Wayne was experiencing high cognitive load because he needed to pick a line with care over the deep rutting of the trail to ensure that the front wheel did not glance off the side of a rut and get channeled down it, resulting in a crash. In addition, Wayne was experiencing significant jarring through the handlebars, and he was concerned that if he hit a bump while braking he might accidentally grab the front brake too hard. Tail dragging simplified the cognitive demands of braking and allowed him to direct more attention to line choice. That is, the choice of strategy was based in part on awareness of excessive cognitive load and the need to reduce this load.

One of the main problems with tail dragging is that it reduces effective braking power because braking force is provided by only one wheel, and because it often results in the rear wheel skidding. This in turn means that speed must be kept low. Partly for this reason Wayne maintained a fairly low speed during the descents, but he preferred to ride at a relatively low speed in any case to allow more time for line choice and to minimize the consequences of a crash. He thus didn’t regard the speed limitations of tail dragging as a reason to avoid it in this context.

However, after Wayne began getting fully behind the seat while descending he switched to equalized braking. This was because the control problems that prompted the tail dragging strategy had been largely eliminated. Independently of any detailed causal understanding, the rearward riding posture leads to several changes in the feel and handling of the bike which provide greater sense of control on steep sections of trail. Cues indicating instability are reduced and handling is improved. The arms are more extended, which reduces unwanted side-to-side rotation of the handlebars and, consequently, the front wheel (compared to the freedom of movement that comes with a larger bend at the elbows). But Wayne was more specifically aware that with his weight now towards the rear there was a greatly reduced risk that the front wheel would lock up under braking. The risk of an over-the-bars crash was also much lower. As noted, this danger had not been at the forefront of Wayne's mind but he was aware of it (he had experienced such a crash previously). Now that his weight was positioned rearwards, and the bike could rotate forwards without pitching him forwards, he became aware that an OTB crash was a lot less likely.

Indeed, the front wheel could now rise and fall much more easily as it tracked over obstacles. This made line choice less critical because there was less chance that the front wheel would glance sideways when it struck the side of a rut. This reduced cognitive load. There was less jarring through the handlebars, making it easier to judge and execute braking pressures. With braking distributed between front and rear, overall grip was increased and there was less chance of either wheel skidding. Wayne became more confident about applying much stronger braking pressures than he had previously. And since the improved handling made similar riding problems more tractable, he became more generally confident about tackling various kinds of descent obstacles. There were distinct limits to these improvements, however, and there were some descents that he still regarded as too challenging. For these he would dismount and walk.

We can illustrate changes in strategy in response to the new bike with the example of a decision to tackle a particular ascent. It was short, relatively steep and had a somewhat loose surface. Wayne tackled it several times on his own bike and once on Kath’s. On his own bike Wayne found the ascent challenging because he needed to begin with high momentum in order to climb it. There were two problems that contributed to this. One was that he had relatively little grip because of the geometry of his bike and the tires. Specifically, on this slope, with its loose surface, if his speed became too slow while using high power pedal strokes the rear wheel could lose traction and 'spin out'. The other was that his riding position on this bike had a relatively high and forward center of gravity, which meant that the bike felt unstable and 'tippy' when riding at slow speeds. If Wayne was going too slow he needed to come to a complete halt and dismount, or he would fall over. The approach to the ascent was downhill, and each time he made the approach he needed to quickly decide whether he had the right line and was going fast enough to make the ascent successfully. He made it up the first time on his bike but stopped on the second attempt because he didn’t think he was going fast enough.

On Kath’s bike Wayne decided to tackle the ascent even though his approach was slow. This point is worth emphasizing because it highlights the way that the different capacities of the new bike led him to use altered riding strategies for obstacles that he had not yet experienced on the bike. Had Wayne been on his own bike he would not have attempted the ascent with the approach that he had at this point. He did attempt the climb because he was confident that the low speed stability of the bike and its grip would allow him to ride it slowly, with less risk of falling over and less risk of losing traction. This proved to be the case. He found that he could come to a near halt during the climb without falling over, and the increased grip of the tires meant that he could use slow, high power pedal strokes without the rear wheel spinning out.

To sum up, Wayne was able to construct riding strategies ‘on the fly’ based on causal and metacognitive awareness. He could form, evaluate and modify strategies based on awareness of factors such as instability and threatened loss of grip. The strategies could take into account multiple factors, reflecting an awareness of how causal factors interrelate in riding. Wayne also selected and adjusted strategies based on sensed uncertainty and risk. This problem solving ability extended to large changes in causal relations associated with major changes in technique and equipment, and hence allowed him to cope with these changes.

It's important to note that Wayne's adaptations went beyond the formulation of specific strategies for particular problems. Wayne showed generalised learning in the sense that each major change allowed him to solve new classes of control problems. As he formulated and implemented new strategies he was also learning about the underlying causal structure of control. He was, thus, extending his causal control model as well as refining it.

Difficulties in adaptation

Difficulties and limitations in Wayne's adjustments are also revealing.

The new bike had only a rear derailleur rather than front and rear. This simplified changing gears but Wayne had well-entrenched gear changing methods which involved coordinated shifting of front and rear derailleurs. It's worth emphasising just how important gear changing is in mountain bike riding. With frequent, rapid changes in gradient and other trail features, it's necessary to change gears often. Smooth, fast riding depends on anticipative gear shifts, especially when the change in gear is large. When encountering a steep slope, for instance, the rider may need to shift from a high to a low gear, and be in the right gear to effectively apply power as speed slows. It's desirable to maintain as much speed and momentum as possible. Wayne's technique for such a situation involved making several shifts in sequence. An initial anticipative shift selects the middle or small front chain ring (lower range gears) and a rear gear that is medium-to-low but high enough to 'catch' the initial phase of slow-down and extend the speed and momentum. Multiple subsequent shifts downward are then made, using the rear derailleur, as slow-down continues, until the right gear for sustained climb is reached. Selecting the wrong gear for a shift disrupts the smooth progression. When the gear is too high or too low the rider will 'bog down' or spin, and either way lose speed and momentum. A further consideration on Wayne's bike was that his gears would sometimes not shift under heavy load, making it important to shift before high power output was required. This was not the case with Kath's bike, which shifted smoothly during high-power pedaling on climbs.

On Kath's bike Wayne had to inhibit his urge to operate the front gear system and reorganise the way that he made anticipative gear shifts. This required heightened attention. An especially attention-drawing feature of the alteration was that in the location where Wayne would operate his front derailleur there was a lever to activate the 'dropper' post. This, in combination with pressure (or lack of) on the saddle, lowered and raised the seat. Lowering the seat during descents gives more freedom to move backwards and forwards as needed. But having the seat drop is not something which the rider will want to happen unexpectedly when trying to change gears or pedal up a hill. When raised the seat would spring upwards to its normal position, and was, in effect, a spring-loaded piston driving towards the rider's crotch. This bike feature was unlike any that Wayne had previously experienced and he found it somewhat disconcerting.

Wayne was able to modify his gear change method and learn to use the dropper post, but these adjustments were more effortful and less smooth than those described in the previous section. Why this should be so raises interesting questions. In general, it's reasonable to expect that some modifications to control are easier to make than others because the control system is better prepared to handle some kinds of change than others. Piaget's ( 2015 ) distinction between assimilation and accommodation is one expression of this idea. In the Piagetian picture increasingly powerful/flexible forms of problem solving ability develop in a progressive sequence as more abstract/deep concepts are learned. The Einstellung (Luchins, 1942 ) and functional fixedness effects (Duncker, 1945 ) are manifestations of the somewhat contrary-seeming phenomenon of increases in rigidity with learning. There is no deep conflict, however. Learning can involve increases in rigidity with respect to some aspects of control together with increases in flexibility with respect to others.

We can develop a preliminary explanation for differences in difficulty in this case which draws on the resources developed in Sect.  2.2 . With respect to the new bike, changes in attributes such as stability and grip were relatively easy for Wayne to incorporate into his riding in at least an initial, basic way. This may be because, although the parameter values were substantially different to his own bike, the parameters themselves, and their role in control, were reasonably familiar. He could therefore adjust his existing methods relatively smoothly. But other differences involved more substantial changes in causal relations and more extensive changes in control operations. Thus, a familiar operation needed to be 'remapped' to a different mechanism with drastically different causal effects, along lines such as {[L-LEVER-OP → F-GEAR-OP] ⇒ [L-LEVER-OP → SEAT-OP]}. Since the operations involved considerable novel structure, the structure needed to be composed in working memory, with implementation and monitoring requiring greater attention than more familiar control operations.

More generally, based on the causal control model account we could expect that skill learning will often exhibit a somewhat Piagetian pattern of increases in generalisation and flexibility which arise as the learner learns to solve varied causal problems. More generalised causal representations develop which capture deeper structure, and more powerful and flexible forms of control develop in order to efficiently manage varied problems.

An even stronger limitation in Wayne's ability to solve the riding problems he was facing is evident in the fact that he needed instruction on the correct implementation of the behind-the-seat technique. During the initial ride he was aware that he was experiencing control problems and rode cautiously for this reason. But he was unable to diagnose the source of these problems to specific technical flaws. At this point he assumed that he simply needed more experience in order to improve calibration and refinement, as opposed to making large technical changes.

This failure in problem solving is all the more striking because he understood the technique abstractly and believed he was implementing it. When Kath explained verbally the technique of getting behind the saddle during descents, the information was already familiar. He had not known of the technique when he was mountain bike riding by himself many years previously, but he had since learned of it from a mountain bike instruction book. He knew that good riding technique involves shifting one’s weight backwards during a descent to maintain even weight distribution across both wheels. What he didn’t realize is that he was implementing this technique incorrectly. More specifically, he didn’t realize that he wasn’t moving nearly as far backwards as he could and should. From his perspective it seemed like he was moving backwards to about the limits of rearward movement for his body. This was far from being the case.

To understand how Wayne could be as mistaken as he was about this it will help to note that in riding on roads—which was the bulk of his riding experience—there is relatively little need for front-rear body movement. Consequently, a relatively small amount of rearwards movement felt like a lot. Moreover, although Wayne knew that it was important to maintain even weight distribution across the front and rear wheels, he was not used to maintaining this form of awareness and had been preoccupied by line choice. There is a distinctive ‘feel’ to a weight distribution that is too far forward in a descent, which notably involves pressure on the hands and wrists. Wayne had not yet learned to efficiently identify this and respond appropriately.

Thus, although Wayne was able to detect the front wheel instability and formulate a compensatory strategy, he failed to autonomously find a much more effective strategy. This stemmed from a poor representation of weight and balance and a poor awareness of his ability to adjust balance. He failed to properly relate the instability to a forward weight distribution and solve this by moving far enough rearwards. This is despite the fact that he knew the correct technique abstractly. A poor on-the-bike representation of balance contributed to a failure to properly interpret the abstract instructions.

We can interpret these points in terms of the concepts of causal control models, action evaluation systems, and problem discovery. Wayne experienced cues to poor control in his initial ride which prompted him to ride cautiously. But his ability to represent the causes of these problems was underdeveloped and so, while he found a solution that achieved the goal of riding the obstacle, he failed to find a more optimal (smoother, safer, speedier) solution. Once he had learned the superior technique his causal control model was altered and his capacity for action evaluation improved. He became aware of an expanded range of body movements and as he experimented with this range he gained new information about the interrelations between weight distribution, stability and handling. He could now interpret high pressure through the wrists as a sign of weight being too far forward. He could better interpret perceptual cues related to balance and perform bodily adjustments to modify weight distribution more appropriately. Putting this in more general terms, he had acquired a revised understanding of balance control on the bike which yielded a generalised improvement in his ability to solve riding problems.

The problem of translating between representational systems

The difficulties Wayne experienced involved a failure to properly translate between abstract and situated representational systems. As such, they help to reveal how these mappings are constructed. In the earliest stages of skill learning the individual must laboriously construct concrete interpretations of abstract action descriptions. This is hampered by two factors. Firstly, the individual lacks systematic representations of skill-specific phenomena at the level of concrete control of execution. Secondly, the individual lacks well-developed systematic mappings from abstract to concrete representations. In this case Wayne lacked a fully-developed systematic representation of the range of positions he could take on the bike and their relations to balance. Once he had learned to move his body backwards, and experienced the technique in an approximation of its correct form, he developed an awareness of balance and stability which he could relate to his abstract knowledge of the structure of the technique. He had thus developed a representation of the structure of the technique from the perspective of control which he could use for control. One way to describe this is that he had now acquired a relatively well-structured executable action concept for the technique. However, much more practice would be needed to consolidate this concept in relation to a well-developed causal control model for implementation.

Improvements in the structure of control

Wayne experienced a significant degree of uncertainty throughout the ride. His intentions, in particular the riding strategies he adopted, involved commitment that was always qualified and evaluated during performance. He maintained awareness of opportunities to abort actions and he did so on several occasions, such as the one described above where he initiated an ascent but stopped part way for fear of losing traction at a higher section of the ascent and falling over. He modified strategies both prior to and during execution to reduce problems, increase the chances of success, and, later, to exploit improved capabilities. His intentions were thus much more labile than Bratman's model recognises. This lability was based on an action evaluation system which could evaluate intentions against a complex ensemble of further criteria represented by the AES. Indeed, the learning process hinged on this.

Wayne's uncertainty was especially high in the initial stages of the ride. He was unsure of which trail sections he could and could not ride safely and he was unsure of whether his riding strategies would be effective in negotiating obstacles and avoiding crashes. His ability to evaluate his performance was also limited, as evident in his flawed diagnosis of the stability problems he was experiencing. Thus, his control ability was relatively poor in both the goal-based and problem-based senses. His ability to achieve the goals that he had was modest and not reliable enough to provide reasonable confidence. But he was also uncertain about his goals, and not able to form all of the right goals, because he lacked a good understanding of his riding problems.

Wayne’s control ability improved over the course of the ride in both the goal-based and problem-based senses. He became better able to achieve the goals that he had, and he became better able to solve the riding problems that he faced. This was based in part on improvements in his understanding of his riding problems, which included greater ability to evaluate action strategies and performance, and form appropriate goals. Improvements in evaluation ability, with enhanced ability to manage uncertainty, are critical to mountain biking, which routinely involves riding unfamiliar, challenging trails.

The technical improvements in particular involved a relatively deep form of problem discovery. As Wayne learned how to properly implement the behind-the-seat technique he was learning both technique-specific and more generalised representations. He was refining a technique-specific concept linked to a causal control model for the technique. These representations incorporated more generalised representations, such as of body position on the bike, balance state, terrain, grip, speed, and so on. These more generalised representations allowed improved representation of a larger set of riding problems. This enabled the formulation of an expanded range of riding strategies which were more effective. These representations also improved the ability to interrelate techniques and strategies by means of common features. Thus, when one strategy is succeeded by another, such as a descent followed by the negotiation of a corner, features of each can be related to each other and adjusted to provide good fit. The speed and line of the descent can be shaped to set up a good entry to the corner and an efficient cornering line, for instance. Action-specific representations are thus integrated into a global state-space of control which represents the situation, performance state, and action possibilities. This state-space can be more or less well integrated, and the more integrated it is, the better able the individual will be to produce coherent complex action.

Social and cultural influences

Wayne's prior mountain bike riding experience was not insignificant, involving about a year of riding one or more times a week on a mixed set of singletrack and fire trails. This provided him with enough skill to engage in the problem-solving described above. But his learning was based largely on solo discovery, adapting skills from road riding and casual BMX-style riding in childhood. The kind of flaws in we’ve described in Wayne's technique, and the limitations in his problem solving ability, are common in individuals who attempt to teach themselves complex skills. Rich engagement with teachers and a skill community can scaffold skill development, allowing the individual to develop solutions and an expanded sense of what is possible (Aggerholm & Hølbjerre-Larsen, 2017 ).

One of the most important ways that a skill community can guide individual learning is by furnishing skill norms. As we described above, during the initial ride Wayne was aware that he was experiencing control problems but thought his riding was reasonable given his experience and the context. This is an example of a general phenomenon: learners tend to possess impoverished norms for the skill domain, and this hampers their ability to evaluate and improve their performance. In this case, Wayne did not have a good grasp of what kind of performance he should be able to achieve, given his base skill level. In fact, at that point he could relatively easily achieve a much higher level of performance. In general, it is difficult for learners to know what performance standards could be expected for their level and experience. This in turn limits their ability to diagnose problems in their methods.

Skill communities often have highly developed performance norms which orient individuals. In mountain biking, speed is a highly valued performance norm. Wayne was not especially concerned with speed at this point, and Kath found it amusing that Wayne’s initial reactions to the new bike were primarily focused on its improved low speed handling. Speed, though, is only one element of a set of norms for assessing quality of performance. Smoothness and efficiency are also valued. These attributes are integrated into an umbrella concept of flow , 17 which serves as a goal for riders and trail builders (Bicknell, 2016 ). Other norms concern safety and risk management. In this respect, a feature of the risk norms for mountain biking that is striking to Wayne is the acceptance that there is a fairly high level of risk that is ineliminable and must simply be accepted. Crashes and injuries are simply part of mountain biking. Thus, through social interaction learners acquire concepts for normatively characterising performance which help them to evaluate their own performances and set goals. Group riding, both social and competition, exposes the individual directly to the performance abilities and conventions of others, providing further information for self-evaluation and goal setting.

The ability to use social information is itself skill-dependent. For example, in riding with Kath, Wayne was aware that she was a more capable rider. However, from this he gained little information that was useful for his own riding. Because Kath was so much more advanced, her performance ability did not serve as a useful benchmark for him and he was unable to identify the structure of her methods in a way that would allow him to copy them. Individuals with more advanced skill are often much better at identifying the structure of methods used by others (Bicknell, 2010 , 2011 ). This can allow them to copy and adapt them for themselves, or identify problems which should be avoided or corrected. Teaching can scaffold learners through this limitation. The learner's limited action evaluation system is supplemented by the much more sophisticated action evaluation system of the teacher. In such situations, the causal control model of the more experienced rider can help to develop the causal control model of the learner.

The mountain bike community routinely scaffolds the experiences of the individual in other ways, too. The difficulty and type of experience that riders have is shaped by trail and bike design. Trail grading gives riders information about the difficulty of particular trails which allows riders to decide in advance whether a trail will be within their ability. Grading systems like this also provide individuals with benchmarks for assessing performance. If an individual finds an intermediate trail difficult they are able to locate themselves within the spectrum of abilities within the community. This can in turn guide goal setting for learning and performance. An individual having difficulties at a particular level can seek to identify technical limitations that are holding them back, and work on those, for example. At a more immediate level, signage on trails alerts riders to the required skill level needed to ride specific, upcoming obstacles. Double- or triple-downward arrows before a particularly steep section of trail that isn’t clearly visible on approach serve this function on some trails, alerting the rider to challenging terrain they typically cannot see until they are already riding it. In other trail communities a sign saying ‘warning’ may be used. An alternative convention is signs pointing to A-, B- or C-lines, indicating the technical difficulty of upcoming sections of trail and encouraging riders to make a decision about which line to take (Fig. ​ (Fig.1 1 ).

Trail sign, Ourimbah cross-country mountain bike track. This sign prompts riders to prepare for the jump line on the right, or to veer left to avoid it. Importantly, it is placed on an unremarkable section of track, at eye height, to catch the rider’s attention with enough time to make a decision about how to approach the upcoming section of trail, without having to stop riding in order to do so. Photo by Kath Bicknell.

Indeed, the mountain bike community has a rich set of community-specific caretaking practices which manage awareness, decision making and problem solving. Additional practices include:

• ‘Pre-riding’ (looking at a trail slowly, with an explorative mindset, before riding it at speed);
• ‘Sessioning an obstacle’ (stopping to look at and practice an obstacle before riding it at speed);
• ‘Riding and scoping’ (eg. riding around a jump while looking at it sideways during the first run of a trail and deciding whether it is safe to attempt on the next lap of that section of trail);
• Building up ‘reserve techniques’ (which can help to regain control if the speed, shape or pitch of the bike mid-obstacle indicates a crash is imminent).

Communication methods are also used to manage problem solving. For example, the question, ‘Is it rollable?’ is one that a skilled rider may ask another before attempting a trail for the first time. If a trail is ‘rollable’ it means there are no gaps that need to be jumped—as long as balance and momentum are maintained everything is ‘rideable’. The trail may well be frighteningly steep and require a high skillset in a number of other areas, but it will be manageable for a rider with a particular set of abilities.

To sum up, skill communities scaffold learning and performance in many ways, allowing higher levels of performance to be achieved and a better, safer quality of experience. The practices which achieve this do so to a significant degree by enhancing the decision-making and problem solving of the individual. Indeed, the engaging nature of sports like mountain biking rests on achieving a complex balance between approachability, challenge, and safety. Mountain biking has been very successful in this respect, and is a fast-growing sport (eg. Latz, 2020 ). This point is worth emphasising because it helps make the case that the phenomena we’ve been describing are not marginal or unimportant—they’re integral to many skills and can be crucial to their success.

The ability to formulate action strategies and control their execution is a central issue for understanding action and skill, yet there is very little work on it. Here we found that even an individual with relatively modest skill experience can be capable of fairly complex, fast-paced construction and control of action strategies. Our results need to be validated by further ecological and laboratory-based investigation but we are confident that the core phenomena we've described are real, and that the use of strategies and problem solving is very common in skilled action. The kind of problem solving we found, together with its flaws, is likely to be fairly typical for individuals in relatively early stages of skill learning. But in skills which require significant levels of flexibility—such as mountain biking and climbing—problem solving is also likely to be central to the most advanced levels of skill. It is consequently of high importance that we develop a better understanding of the mechanisms which support these abilities and the way they develop during skill learning. We've argued that causal representation, performance awareness, metacognitive awareness and action evaluation all play important roles and operate together in a complex, integrated action control system. Our account of these mechanisms goes beyond previous work and adds to the Mesh theory of skill a more detailed model of action control.

Acknowledgements

We thank John Sutton, John Michael, Josh Shepherd, Chiara Brozzo, Cynthia Siew, Gaye Camm, Tom McClelland, Doris McIlwain, and the generosity of colleagues and students in the Cognitive Ecologies and Microethnography Labs at Macquarie University, Sydney, Australia. An earlier version of this paper was presented as a keynote at the ‘Actions: The Mental and the Bodily’ conference at the University of Warwick, UK, and in a shorter form at the ‘Cognitive Futures in the Arts and Humanities: Paradigms of Understanding—Sharing Cognitive Worlds’ conference in Mainz, Germany. We thank the audiences for their questions, provocations and enthusiasm for this work.

Open Access funding provided thanks to the CRUE-CSIC agreement with Springer Nature. This research was funded by European Research Council starting Grant 757698, awarded under the Horizon 2020 program for research and innovation, and the Australian Research Council Discovery Project grants DP130100756 ‘Mindful Bodies in Action: a philosophical study of skilled movement’, awarded to Doris McIlwain and John Sutton (2013–2015) and DP180100107 ‘The Cognitive Ecologies of Collaborative Embodied Skills’, awarded to John Sutton (2018–2020).

Declarations

The authors report no conflict of interest.

1 See Preston ( 2013 ) for a related discussion of Bratman’s account.

2 See Chisholm ( 2008 ) for an in-depth exploration of the relationship between bodily characteristics, technique and environment in climbing.

3 This video shows six different strategies used to solve a particular problem at the 2021 World Championships: https://www.instagram.com/p/CT9pAfTpMmm/ .

4 A video of squirrels engaging in this kind of problem solving can be seen here: https://theconversation.com/we-used-peanuts-and-a-climbing-wall-to-learn-how-squirrels-judge-their-leaps-so-successfully-and-how-their-skills-could-inspire-more-nimble-robots-165524 .

5 Nanay (2020) and Fridland ( 2021 ) argue that action control is based on imagistic representation, drawing on evidence that practice using mental imagery can be highly beneficial. Causal control models should be differentiated from mental images. Imagistic representations do not represent causal relations per se, although causal representation can be incorporated into imagistic representations. Nor is causal representation necessarily imagistic. It is the representation of causal relations specifically that plays a foundational enabling role in the intentional control of action.

6 https://www.youtube.com/watch?v=IqsNJv2VROs .

7 Not all parameter relations need be represented as causally related since the motor system can sometimes ‘fill-in’ some parameters when given others as explicit goals. Indeed, because of the limits of attention capacity learners must often rely on some degree of ‘filling-in’ because they can’t continuously attend to the full structure of the technique for a novel action while performing it. For instance, when learning a new chord the learner might initially attend primarily to landing finger locations then switch to correcting overall hand posture, while largely ignoring timing. But these kinds of cases illustrate limitations of automated ‘filling-in’ because the filled-in parameters will often not correspond to good technique. Focusing on finger locations while neglecting hand posture when learning a new chord is likely to result in poor posture. Once an individual has developed a high level of skill automated filling-in will tend to better correspond to good technique, but this is because the techniques have already been intentionally learned. We thank a referee for prompting this clarification.

8 We’re using the term ‘translation’ in a broad sense which involves the construction of alternative representations of the same, similar or related content (see Christensen, 2020). This includes translation between alternative expressions within a representational system such as a language. An alternative approach would be to restrict ‘translation’ to content re-representations and interpretations across representational systems with distinct formats and use an alternative concept such as ‘mapping’ for such content relating processes within a representational system, such as between levels of abstraction (we thank a reviewer for this suggestion). This raises a complex set of issues. We agree that there may be reasons to adopt a more restricted concept of translation but we think it is unclear how this should be done. In general, we think that philosophers and cognitive scientists have been overly focused on the idea that mental representational systems are discrete, static systems defined by a distinct, unchanging format Evidence from cognitive neuroscience suggests that the brain has an extremely flexible ability to construct representational systems, that representational systems with different formats can overlap (auditory, visual, and haptic representational systems use shared spatial representations), that multiple formats can be encompassed in an integrated representational system (working memory is an integrated workspace which includes auditory, visual and other subcomponents), and so on (see Author 2020 for an extended discussion). Consequently, we doubt that it will be possible to draw a clear distinction between within-system and between-system content-relating processes. More specifically, it’s likely that content-relating and construction processes that operate within cognitive representational systems also play a role in constructing new representational systems and building relations across existing systems when this becomes functionally beneficial. These points have strong implications for understanding skill learning, which, we suggest, involves the construction of multiple interlinked domain-specific representational systems. In future work we’ll develop the idea that the processes we described here as translating between levels of abstraction play a key role in the formation of new representational systems for skill control.

9 Recent philosophical discussion has been preoccupied with a narrower 'interface problem' formulated by Butterfill and Sinigaglia (2014). The idea is that there is a special difficulty understanding how cognitive and motor representations can interact which stems from the supposed impossibility of translation between their formats. However, Christensen (2020) argues that the theoretical rationale for rejecting translation is unsound and that there is extensive empirical evidence that the brain translates across many representational formats, including motor and cognitive.

10 We won't engage in a comprehensive analysis of the DPM model here. Brozzo (2021) criticises the distinction between present- and future-directed intentions. Christensen (2020) gives an alternative account of motor representations and their interface with higher level intentions.

11 Although it should be noted that Shepherd's account includes a discussion of the role of domain norms in action evaluation which brings it closer to the problem-based conception.

12 This example reflects common advice to, and complaints about, inexperienced musicians. The following article provides a fairly typical illustration: https://www.premierguitar.com/articles/print/28953-last-call-space-is-music-too .

13 Our use of the term ‘system’ here may suggest that we have in mind a Fodorian module. However, we are adopting a different, non-Fodorian conception of modules and systems which is based in a biological framework. By ‘system’ we mean a network of structures and processes that show a degree of somewhat specific functional integration and perform one or more somewhat specific functional roles (in this case, action evaluation). A cognitive system in this sense can integrate with, and overlap with, other cognitive systems. The AES will be a ‘system of systems’ which encompasses multiple lower and higher level evaluative systems, for instance including both reward and efficiency evaluation systems.

14 In this respect our account can be contrasted with that of the predictive processing framework, which claims that behaviour is governed by a single dominant goal, namely predictive error minimization. Our account thus avoids the ‘dark room’ problem facing the predictive coding approach, which is that predictive error minimization can be achieved by placing oneself in a highly predictable environment (Sun & Firestone, 2020). We thank a referee for this point.

15 Drawing on Kath’s experience of teaching this exercise to beginner riders at skills clinics, many riders think they are almost about the graze the tyre when they are still approximately 20 cm away from reaching it. This was also true of Wayne. Kath communicated this to him verbally during the exercise, showed the gap with a hand gesture, and demonstrated the correct vs incorrect technique. In response, Wayne exaggerated his attempt at the task and was able to graze the rear tyre. Both riders were delighted!

16 Also called a ‘front wheel washout’. There are some differences in the way that ‘washout’ is conceptualised in the mountain bike community. The version of the concept Wayne was using treats it as any case in which the front wheel loses traction and slides out from underneath the rider, causing a crash.

17 This folk concept of flow should be differentiated from the concept used in psychology (Csikszentmihalyi 1990 ).

S.I.: Minds in Skilled Performance.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Contributor Information

Wayne Christensen, Email: [email protected] .

Kath Bicknell, Email: moc.llenkcibhtak@liame .

• Adams JA. A closed-loop theory of motor learning. Journal of Motor Behavior. 1971; 3 (2):111–150. doi: 10.1080/00222895.1971.10734898. [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Aggerholm K, Hølbjerre Larsen S. Parkour as acrobatics: An existential phenomenological study of movement in parkour. Qualitative Research in Sport, Exercise and Health. 2017; 9 (1):69–86. doi: 10.1080/2159676X.2016.1196387. [ CrossRef ] [ Google Scholar ]
• Anderson J. Acquisition of cognitive skill. Psychological Review. 1982; 89 (4):369–406. doi: 10.1037/0033-295X.89.4.369. [ CrossRef ] [ Google Scholar ]
• Anderson J. The architecture of cognition. Harvard University Press; 1983. [ Google Scholar ]
• Bernstein, N. A. (1996). Dexterity and its development (Ed. M. L. Latash & M. T. Turvey). Lawrence Erlbaum Associates, Inc.
• Bicknell K. Feeling them ride: Corporeal exchange in cross-country mountain bike racing. About Performance. 2010; 10 :81–91. [ Google Scholar ]
• Bicknell K. Sport, entertainment and the Live(d) experience of cheering. Popular Entertainment Studies. 2011; 2 (1):96–111. [ Google Scholar ]
• Bicknell, K. (2016). Glen Jacobs – Building trails for the 78%. Australian Mountain Bike . June 2 2016. Retrieved August 3, 2022, from https://www.ambmag.com.au/feature/glen-jacobs---building-trails-for-the-78-429797
• Bicknell K. Embodied intelligence and self-regulation in skilled performance: Or, two anxious moments on the static trapeze. Review of Philosophy and Psychology. 2021; 12 :595–614. doi: 10.1007/s13164-021-00528-7. [ CrossRef ] [ Google Scholar ]
• Bicknell K, Brümmer K. ‘No elephants today!’ Recurrent experiences of failure while learning a movement practice. In: Bicknell K, Sutton J, editors. Collaborative embodied performance: Ecologies of skill. Bloomsbury; 2022. pp. 77–92. [ Google Scholar ]
• Bicknell K, Sutton J, editors. Collaborative embodied performance: Ecologies of skill. Bloomsbury; 2022. [ Google Scholar ]
• Brand M. Intending and acting: Toward a naturalized action theory. MIT Press; 1984. [ Google Scholar ]
• Bratman M. Intention, plans, and practical reason. Harvard University Press; 1987. [ Google Scholar ]
• Bryan WL, Harter N. Studies on the telegraphic language: The acquisition of a hierarchy of habits. Psychological Review. 1899; 6 (4):345–375. doi: 10.1037/h0073117. [ CrossRef ] [ Google Scholar ]
• Buxbaum LJ. Ideomotor apraxia: A call to action. Neurocase. 2001; 7 (6):445–458. doi: 10.1093/neucas/7.6.445. [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Chi MTH, Glaser R, Rees E. Expertise in problem solving. In: Sternberg RJ, editor. Advances in the psychology of human intelligence. Erlbaum; 1982. [ Google Scholar ]
• Chisholm D. Climbing like a girl: An exemplary adventure in feminist phenomenology. Hypatia. 2008 doi: 10.2979/hyp.2008.23.1.9. [ CrossRef ] [ Google Scholar ]
• Christensen W, Bicknell K. Affordances and the anticipatory control of action. In: Cappuccio M, editor. Handbook of embodied cognition and sport. The MIT Press; 2019. [ Google Scholar ]
• Christensen W, Bicknell K, McIlwain DJF, Sutton J. The sense of agency and its role in strategic control for expert mountain bikers. Psychology of Consciousness: Theory, Research, and Practice. 2015; 2 (3):340–353. doi: 10.1037/cns0000066. [ CrossRef ] [ Google Scholar ]
• Christensen, W., & Sutton, J. (2018). Mesh: Cognition, body and environment in skilled action. In M. Cappuccio (Ed.), Handbook of embodied cognition and sport psychology (pp.157–164).
• Christensen W, Sutton J, Bicknell K. Memory systems and the control of skilled action. Philosophical Psychology. 2019; 32 (5):692–718. doi: 10.1080/09515089.2019.1607279. [ CrossRef ] [ Google Scholar ]
• Christensen W, Sutton J, McIlwain DJF. Cognition in skilled action: Meshed control and the varieties of skill experience. Mind & Language. 2016; 31 (1):37–66. doi: 10.1111/mila.12094. [ CrossRef ] [ Google Scholar ]
• Csikszentmihalyi, M. (1990). Flow: The psychology of optimal experience . New York: Harper and Row.
• Downey G. Not breathing together: The collaborative development of expert apnoea. In: Bicknell K, Sutton J, editors. Collaborative embodied performance: Ecologies of skill. Bloomsbury; 2022. pp. 93–108. [ Google Scholar ]
• Downey G, Dalidowicz M, Mason PH. Apprenticeship as method: Embodied learning in ethnographic practice. Qualitative Research. 2015 doi: 10.1177/1468794114543400. [ CrossRef ] [ Google Scholar ]
• Dreyfus HL, Dreyfus SE, Athanasiou T. Mind over machine: The power of human intuition and expertise in the era of the computer. Free Press; 1986. [ Google Scholar ]
• Duncker K, Lees LS. On problem-solving. Psychological Monographs. 1945; 58 (5):1–113. doi: 10.1037/h0093599. [ CrossRef ] [ Google Scholar ]
• Ericsson KA, Kintsch W. Long-term working memory. Psychological Review. 1995; 102 (2):211–244. doi: 10.1037/0033-295X.102.2.211. [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Evans JBT, Stanovich KE. Dual-process theories of higher cognition advancing the debate. Perspectives on Psychological Science. 2013; 8 (3):223–241. doi: 10.1177/1745691612460685. [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Fajen BR. Calibration, information, and control strategies for braking to avoid a collision. Journal of Experimental Psychology: Human Perception and Performance. 2005; 31 (3):480–501. doi: 10.1037/0096-1523.31.3.480. [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Fitts PM, Posner MI. Human performance. Wadsworth; 1967. [ Google Scholar ]
• Franklin DW, Burdet E, Tee KP, Osu R, Chew C-M, Milner TE, Kawato M. CNS learns stable, accurate, and efficient movements using a simple algorithm. Journal of Neuroscience. 2008; 28 (44):11165–11173. doi: 10.1523/JNEUROSCI.3099-08.2008. [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Fridland E. Skill and strategic control. Synthese. 2021 doi: 10.1007/s11229-021-03053-3. [ CrossRef ] [ Google Scholar ]
• Gibson JJ. The ecological approach to visual perception. Houghton Mifflin; 1979. [ Google Scholar ]
• Goldenberg G. Apraxia: The cognitive side of motor control. Oxford University Press; 2013. [ Google Scholar ]
• Goodwin C. Professional vision. American Anthropologist. 1994; 96 :606–633. doi: 10.1525/aa.1994.96.3.02a00100. [ CrossRef ] [ Google Scholar ]
• Krakauer JW, Hadjiosif AM, Xu J, Wong AL, Haith AM. Motor learning. Comprehensive Physiology. 2019 doi: 10.1002/cphy.c170043. [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Latz, P. (2020). Mountain Biking’s $100 Million Jump!. The Latz Report . February 28, Retrieved August 3, 2022, from https://thelatzreport.com.au/news/trade/mountain-bikings-100-million-jump/
• Luchins AS. Mechanization in problem solving: The effect of Einstellung. Psychological Monographs. 1942; 54 (6):i–95. doi: 10.1037/h0093502. [ CrossRef ] [ Google Scholar ]
• McIlwain D, Sutton J. Yoga from the mat up: How words alight on bodies. Educational Philosophy and Theory. 2014; 46 (6):655–673. doi: 10.1080/00131857.2013.779216. [ CrossRef ] [ Google Scholar ]
• McIlwain DJF, Sutton J. Methods for measuring breadth and depth of knowledge. In: Baker J, Farrow D, editors. Routledge handbook of sport expertise. Routledge; 2015. pp. 221–231. [ Google Scholar ]
• Mele AR. Springs of action: Understanding intentional behavior. Oxford University Press; 1992. [ Google Scholar ]
• Mylopoulos M, Pacherie E. Intentions and motor representations: The interface challenge. Review of Philosophy and Psychology. 2017; 8 (2):317–336. doi: 10.1007/s13164-016-0311-6. [ CrossRef ] [ Google Scholar ]
• Mylopoulos M, Pacherie E. Intentions: The dynamic hierarchical model revisited. Wiley Interdisciplinary Reviews Cognitive Science. 2018 doi: 10.1002/wcs.1481. [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Nemani M, Thorpe H. The experiences of ‘brown’ female bodyboarders: Negotiating multiple axes of marginality. In: Thorpe H, Olive R, editors. Women in action sport cultures: Identity, politics and experience. Palgrave Macmillan; 2016. pp. 213–233. [ Google Scholar ]
• Olive R, Thorpe H, Roy G, Nemani M, lisahunter, Wheaton B, Humberstone B. Surfing together: Exploring the potential of a collaborative ethnographic moment. In: Thorpe H, Olive R, editors. Women in action sport cultures: identity, politics and experience. Palgrave Macmillan; 2016. pp. 45–68. [ Google Scholar ]
• Pacherie E. Nonconceptual representations for action and the limits of intentional control. Social Psychology. 2011; 42 (1):67–73. doi: 10.1027/1864-9335/a000044. [ CrossRef ] [ Google Scholar ]
• Pacherie E, Mylopoulos M. Beyond automaticity: The psychological complexity of skill. Topoi. 2020 doi: 10.1007/s11245-020-09715-0. [ CrossRef ] [ Google Scholar ]
• Pavese C. The psychological reality of practical representation. Philosophical Psychology. 2019; 32 (5):784–821. doi: 10.1080/09515089.2019.1612214. [ CrossRef ] [ Google Scholar ]
• Pavese, C. (2021). Practical concepts and productive reasoning. Synthese .
• Piaget J. Structuralism. Psychology Press; 2015. [ Google Scholar ]
• Preston B. A philosophy of material culture: action, function, and mind. Routledge; 2013. [ Google Scholar ]
• Ranganathan R, Lee M-H, Newell KM. Repetition without repetition: Challenges in understanding behavioral flexibility in motor skill. Frontiers in Psychology. 2020 doi: 10.3389/fpsyg.2020.02018. [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Ravn S. Cultivating one’s skills through the experienced other in aikido. In: Bicknell K, Sutton J, editors. Collaborative embodied performance: Ecologies of skill. Bloomsbury; 2022. pp. 109–123. [ Google Scholar ]
• Reber PJ, Batterink LJ, Thompson KR, Reuveni B. Implicit learning: History and applications. Routledge; 2019. [ Google Scholar ]
• Robertson EM. The serial reaction time task: Implicit motor skill learning? The Journal of Neuroscience. 2007; 27 (38):10073–10075. doi: 10.1523/JNEUROSCI.2747-07.2007. [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Samudra J. Memory in our body: Thick participation and the translation of kinesthetic experience. American Ethnologist. 2008; 35 (4):665–681. doi: 10.1111/j.1548-1425.2008.00104.x. [ CrossRef ] [ Google Scholar ]
• Schmidt RA. a schema theory of discrete motor skill learning. Psychological Review. 1975; 82 (4):225–260. doi: 10.1037/h0076770. [ CrossRef ] [ Google Scholar ]
• Searle, J. R., Willi, S. and Marion Slusser Professor of Philosophy John R. Searle. (1983). Intentionality: An essay in the philosophy of mind . Cambridge University Press.
• Shepherd J. Skilled action and the double life of intention. Philosophy and Phenomenological Research. 2017; 98 (2):286–305. doi: 10.1111/phpr.12433. [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Shepherd J. The shape of agency: Control, action, skill. Oxford University Press; 2021. [ Google Scholar ]
• Shiffrin RM, Schneider W. Controlled and automatic human information processing: II. Perceptual learning, automatic attending, and a general theory. Psychological Review. 1977; 84 (2):127–190. doi: 10.1037/0033-295X.84.2.127. [ CrossRef ] [ Google Scholar ]
• Spinney J. A place of sense: A kinaesthetic ethnography of cyclists on Mont Ventoux. Environment and Planning d: Society and Space. 2006; 24 :709–732. doi: 10.1068/d66j. [ CrossRef ] [ Google Scholar ]
• Sun R, Merrill E, Peterson T. From implicit skills to explicit knowledge: A bottom-up model of skill learning. Cognitive Science. 2001; 25 (2):203–244. doi: 10.1207/s15516709cog2502_2. [ CrossRef ] [ Google Scholar ]
• Sutton J, Bicknell K. Embodied experience in the cognitive ecologies of skilled performance. In: Fridland E, Pavese C, editors. The Routledge handbook of philosophy of skill and expertise. London: Routledge; 2020. pp. 194–206. [ Google Scholar ]
• Taylor JA, Ivry RB. The role of strategies in motor learning. Annals of the New York Academy of Sciences. 2012; 1251 (1):1–12. doi: 10.1111/j.1749-6632.2011.06430.x. [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Todorov E. Optimality principles in sensorimotor control. Nature Neuroscience. 2004; 7 (9):907–915. doi: 10.1038/nn1309. [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Tseng Y-W, Scholz JP, Schöner G, Hotchkiss L. Effect of accuracy constraint on joint coordination during pointing movements. Experimental Brain Research. 2003; 149 (3):276–288. doi: 10.1007/s00221-002-1357-5. [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Wolpert DM, Ghahramani Z, Jordan MI. An internal model for sensorimotor integration. Science. 1995; 269 (5232):1880–1882. doi: 10.1126/science.7569931. [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Wolpert DM, Kawato M. Multiple paired forward and inverse models for motor control. Neural Networks. 1998; 11 (7–8):1317–1329. doi: 10.1016/S0893-6080(98)00066-5. [ PubMed ] [ CrossRef ] [ Google Scholar ]

• Bipolar Disorder
• Therapy Center
• When To See a Therapist
• Types of Therapy
• Best Online Therapy
• Best Couples Therapy
• Best Family Therapy
• Managing Stress
• Sleep and Dreaming
• Understanding Emotions
• Self-Improvement
• Healthy Relationships
• Student Resources
• Personality Types
• Guided Meditations
• Verywell Mind Insights
• 2024 Verywell Mind 25
• Mental Health in the Classroom
• Editorial Process
• Meet Our Review Board
• Crisis Support

What Does 'Cognitive' Mean in Psychology?

How People Think and What's Involved in Cognitive Processes

Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

Daniel B. Block, MD, is an award-winning, board-certified psychiatrist who operates a private practice in Pennsylvania.

Verywell / Laura Porter

• Improving Cognitive Skills

Frequently Asked Questions

'Cognitive' is a term used in psychology to describe anything related to thinking, learning, and understanding. So when you hear people talk about cognitive skills or processes, they are referring to different aspects of how the brain works—things like remembering information, learning new things, paying attention, and processing all of the information you encounter each day. 

Cognitive abilities are something you use each and every day. For example, when you are learning a new instrument, you are using your cognitive skills to learn the basics of music theory, pick up melodies, learn the notes, and put that information together to produce music.

'Cognitive' refers to the mental processes involved in gaining knowledge and comprehension. Some of the many different cognitive processes include thinking, knowing, remembering, judging, and problem-solving .

These are higher-level brain functions that encompass language, imagination, perception, and planning. Cognitive psychology is the field of psychology that investigates how people think and the processes involved in cognition. 

At a Glance

Cognitive psychology seeks to understand all of the mental processes involved in human thought and behavior. It focuses on cognitive processes such as decision-making, problem-solving, attention, memory, learning, and more. Keep reading to learn more about different types of cognitive processes, factors that can affect cognition, and the different uses for these cognitive processes.

Types of Cognitive Processes

There are many different types of cognitive processes. They include:

Attention is a cognitive process that allows people to focus on a specific environmental stimulus. Attention is an important cognitive ability because it allows us to focus on the information we need, while also filtering out irrelevant distractions.

Language and language development are cognitive processes that involve the ability to understand and express thoughts through spoken and written words. This allows us to communicate with others, including conveying our own thoughts and learning about others. It also plays an important role in thought.

Learning requires cognitive processes involved in taking in new things, synthesizing information, and integrating it with prior knowledge. Cognitive psychologists often study the mental processes that involved in processing, comprehending, and remembering information.

Memory is an important cognitive process that allows people to encode, store, and retrieve information. It is a critical component in the learning process and allows people to retain knowledge about the world and their personal histories.

Perception is a cognitive process that allows people to take in information through their senses, then utilize this information to respond and interact with the world.

Thought is an essential part of every cognitive process. It allows people to engage in decision-making , problem-solving, and higher reasoning.

Hot Cognition vs. Cold Cognition

Some split cognition into two categories: hot and cold. Hot cognition refers to mental processes in which emotion plays a role, such as reward-based learning . Conversely, cold cognition refers to mental processes that don't involve feelings or emotions, such as working memory .

What is an example of cognition?

Cognition includes all of the conscious and unconscious processes involved in thinking, perceiving, and reasoning. Examples of cognition include paying attention to something in the environment, learning something new, making decisions, processing language, sensing and perceiving environmental stimuli, solving problems, and using memory. 

History of the Study of Cognition

The study of how humans think dates back to the time of ancient Greek philosophers Plato and Aristotle.

Philosophical Origins

Plato's approach to the study of the mind suggested that people understand the world by first identifying basic principles buried deep inside themselves, then using rational thought to create knowledge. This viewpoint was later advocated by philosophers such as Rene Descartes and linguist Noam Chomsky. It is often referred to as rationalism.

Aristotle, on the other hand, believed that people acquire knowledge through their observations of the world around them. Later thinkers such as John Locke and B.F. Skinner also advocated this point of view, which is often referred to as empiricism.

Early Psychology

During the earliest days of psychology—and for the first half of the 20th century—psychology was largely dominated by psychoanalysis , behaviorism , and humanism .

Eventually, a formal field of study devoted solely to the study of cognition emerged as part of the "cognitive revolution" of the 1960s. This field is known as cognitive psychology.

The Emergence of Cognitive Psychology

One of the earliest definitions of cognition was presented in the first textbook on cognitive psychology, which was published in 1967. According to Ulric Neisser, a psychologist and the book's author, cognition is "those processes by which the sensory input is transformed, reduced, elaborated, stored, recovered, and used."

What Can Affect Cognitive Processes?

It is important to remember that these cognitive processes are complex and often imperfect. Some of the factors that can affect or influence cognition include:

Research indicates that as we age, our cognitive function tends to decline. Age-related cognitive changes include processing things more slowly, finding it harder to recall past events, and a failure to remember information that was once known (such as how to solve a particular math equation or historical information).

Attention Issues

Selective attention is a limited resource, so there are a number of things that can make it difficult to focus on everything in your environment. Attentional blink , for example, happens when you are so focused on one thing that you completely miss something else happening right in front of you.

Cognitive Biases

Cognitive biases are systematic errors in thinking related to how people process and interpret information about the world. Confirmation bias is one common example that involves only paying attention to information that aligns with your existing beliefs while ignoring evidence that doesn't support your views. 

Some studies have connected cognitive function with certain genes. For example, a 2020 study published in Brain Communications found that a person's level of brain-derived neurotrophic factor (BDNF), which is 30% determined by heritability, can impact the rate of brain neurodegeneration, a condition that ultimately impacts cognitive function.

Memory Limitations

Short-term memory is surprisingly brief, typically lasting just 20 to 30 seconds, whereas long-term memory can be stable and enduring, with memories lasting years and even decades. Memory can also be fragile and fallible. Sometimes we forget and other times we are subject to misinformation effects that may even lead to the formation of false memories .

Uses for Cognitive Processes

Cognitive processes affect every aspect of life, from school to work to relationships. Some specific uses for these processes include the following.

Learning New Things

Learning requires being able to take in new information, form new memories, and make connections with other things that you already know. Researchers and educators use their knowledge of these cognitive processes to create instructive materials to help people learn new concepts .

Forming Memories

Memory is a major topic of interest in the field of cognitive psychology. How we remember, what we remember, and what we forget reveal a great deal about how cognitive processes operate.

While people often think of memory as being much like a video camera—carefully recording, cataloging, and storing life events away for later recall—research has found that memory is much more complex.

Making Decisions

Whenever people make any type of a decision, it involves making judgments about things they have processed. This might involve comparing new information to prior knowledge, integrating new information into existing ideas, or even replacing old knowledge with new knowledge before making a choice.

Impact of Cognition

Our cognitive processes have a wide-ranging impact that influences everything from our daily life to our overall health.

Perceiving the World

As you take in sensations from the world around you, the information that you see, hear, taste, touch, and smell must first be transformed into signals that the brain can understand. The perceptual process allows you to take in this sensory information and convert it into a signal that your brain can recognize and act upon.

Forming Impressions

The world is full of an endless number of sensory experiences . To make meaning out of all this incoming information, it is important for the brain to be able to capture the fundamentals. Events are reduced to only the critical concepts and ideas that we need.

Filling in the Gaps

In addition to reducing information to make it more memorable and understandable, people also elaborate on these memories as they reconstruct them. In some cases, this elaboration happens when people are struggling to remember something . When the information cannot be recalled, the brain sometimes fills in the missing data with whatever seems to fit.

Interacting With the World

Cognition involves not only the things that go on inside our heads but also how these thoughts and mental processes influence our actions. Our attention to the world around us, memories of past events, understanding of language, judgments about how the world works, and abilities to solve problems all contribute to how we behave and interact with our surrounding environment.

Tips for Improving Cognitive Skills

Cognitive processes are influenced by a range of factors, including genetics and experiences. While you cannot change your genes or age, there are things that you can do to protect and maximize your cognitive abilities:

• Stay healthy . Lifestyle factors such as eating a nutritious diet and getting regular exercise can have a positive effect on cognitive functioning.  
• Think critically . Question your assumptions and ask questions about your thoughts, beliefs, and conclusions.
• Stay curious and keep learning . A great way to flex your cognitive abilities is to keep challenging yourself to learn more about the world.
• Skip multitasking . While it might seem like doing several things at once would help you get done faster, research has shown it actually decreases both productivity and work quality.

In psychology, the term 'cognitive' refers to all of the different mental events involved in thinking, learning, and comprehending. Cognitive processes such as learning, attention, perception, and memory are important parts of the human experience. Understanding how they function can provide insight into normal human thought and behavior and how different cognitive conditions might create problems and impairments. 

Thinking is an important component, but cognition also encompasses unconscious and perceptual processes as well. In addition to thinking, cognition involves language, attention, learning, memory, and perception.

People utilize cognitive skills to think, learn, recall, and reason. Five important cognitive skills include short-term memory, logic, processing speed, attention, and spatial recognition.

American Psychological Association. Cognition .

Ezebuilo HC. Descartes, Leibniz and Spinoza: A brief survey of rationalism . J App Philos . 2020;18(6):95-118. doi:10.13140/RG.2.2.19692.39043

Sgarbi M.  The Aristotelian Tradition and the Rise of British Empiricism: Logic and Epistemology in the British Isles (1570–1689) .

Lachman R, Lachman J L, Butterfield EC.  Cognitive Psychology and Information Processing: An Introduction .

Neisser U.  Cognitive Psychology: Classic edition .

Murman D. The impact of age on cognition . Semin Hear . 2015;36(3):111-121. doi:10.1055/s-0035-1555115

Li S, Weinstein G, Zare H, et al. The genetics of circulating BDNF: Towards understanding the role of BDNF in brain structure and function in middle and old ages . Brain Commun . 2020;2(2):fcaa176. doi:10.1093/braincomms/fcaa176

Weinsten Y. How long is short-term memory: Shorter than you might think . Duke Undergraduate Education.

Leding J, Antonio L. Need for cognition and discrepancy detection in the misinformation effect . J Cognitive Psychol . 2019;31(4):409-415. doi:10.1080/20445911.2019.1626400

Scheiter K, Schubert C, Schuler A. Self-regulated learning from illustrated text: Eye movement modelling to support use and regulation of cognitive processes during learning from multimedia . Brit J Educ Psychol . 2017;88(1):80-94. doi:10.1111/bjep.12175

Toppi J, Astolfi L, Risetti M, et al. Different topological properties of EEG-derived networks describe working memory phases as revealed by graph theoretical analysis . Front Hum Neurosci . 2018;11:637. doi:10.3389/fnhum.2017.00637

Mather G. Foundations of sensation and perception .

Sousa D.  How the brain learns .

Houben S, Otgaar H, Roelofs J, Merckelbach H. EMDR and false memories: A response to Lee, de Jongh, and Hase (2019) . Clin Psycholog Sci . 2019;7(3):405-6. doi:10.1177/2167702619830392

Schwarzer R. Self-efficacy: Thought control of action .

Imaoka M, Nakao H, Nakamura M, et al. Effect of multicomponent exercise and nutrition support on the cognitive function of older adults: A randomized controlled trial . Clin Interv Aging . 2019;14:2145-53. doi:10.2147/CIA.S229034

Petroutsatou K, Sifiniadis A. Exploring the consequences of human multitasking in industrial automation projects: A tool to mitigate impacts - Part II . Organiz Techn Manage Construct . 2018;10(1):1770-1777. doi:10.2478/otmcj-2016-0031

Mullis CE, Hatfield RC. The effects of multitasking on auditors' judgment quality . Contemp Account Res . 2017;35(1):314-333. doi:10.1111/1911-3846.12392

Revlin R. Cognition: Theory and Practice .

By Kendra Cherry, MSEd Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

• Book a Demo

Struggling to overcome challenges in your life? We all face problems, big and small, on a regular basis.

So how do you tackle them effectively? What are some key problem-solving strategies and skills that can guide you?

Effective problem-solving requires breaking issues down logically, generating solutions creatively, weighing choices critically, and adapting plans flexibly based on outcomes. Useful strategies range from leveraging past solutions that have worked to visualizing problems through diagrams. Core skills include analytical abilities, innovative thinking, and collaboration.

Want to improve your problem-solving skills? Keep reading to find out 17 effective problem-solving strategies, key skills, common obstacles to watch for, and tips on improving your overall problem-solving skills.

Key Takeaways:

• Effective problem-solving requires breaking down issues logically, generating multiple solutions creatively, weighing choices critically, and adapting plans based on outcomes.
• Useful problem-solving strategies range from leveraging past solutions to brainstorming with groups to visualizing problems through diagrams and models.
• Core skills include analytical abilities, innovative thinking, decision-making, and team collaboration to solve problems.
• Common obstacles include fear of failure, information gaps, fixed mindsets, confirmation bias, and groupthink.
• Boosting problem-solving skills involves learning from experts, actively practicing, soliciting feedback, and analyzing others’ success.
• Onethread’s project management capabilities align with effective problem-solving tenets – facilitating structured solutions, tracking progress, and capturing lessons learned.

What Is Problem-Solving?

Problem-solving is the process of understanding an issue, situation, or challenge that needs to be addressed and then systematically working through possible solutions to arrive at the best outcome.

It involves critical thinking, analysis, logic, creativity, research, planning, reflection, and patience in order to overcome obstacles and find effective answers to complex questions or problems.

The ultimate goal is to implement the chosen solution successfully.

What Are Problem-Solving Strategies?

Problem-solving strategies are like frameworks or methodologies that help us solve tricky puzzles or problems we face in the workplace, at home, or with friends.

Imagine you have a big jigsaw puzzle. One strategy might be to start with the corner pieces. Another could be looking for pieces with the same colors. 

Just like in puzzles, in real life, we use different plans or steps to find solutions to problems. These strategies help us think clearly, make good choices, and find the best answers without getting too stressed or giving up.

Why Is It Important To Know Different Problem-Solving Strategies?

Knowing different problem-solving strategies is important because different types of problems often require different approaches to solve them effectively. Having a variety of strategies to choose from allows you to select the best method for the specific problem you are trying to solve.

This improves your ability to analyze issues thoroughly, develop solutions creatively, and tackle problems from multiple angles. Knowing multiple strategies also aids in overcoming roadblocks if your initial approach is not working.

Here are some reasons why you need to know different problem-solving strategies:

• Different Problems Require Different Tools: Just like you can’t use a hammer to fix everything, some problems need specific strategies to solve them.
• Improves Creativity: Knowing various strategies helps you think outside the box and come up with creative solutions.
• Saves Time: With the right strategy, you can solve problems faster instead of trying things that don’t work.
• Reduces Stress: When you know how to tackle a problem, it feels less scary and you feel more confident.
• Better Outcomes: Using the right strategy can lead to better solutions, making things work out better in the end.
• Learning and Growth: Each time you solve a problem, you learn something new, which makes you smarter and better at solving future problems.

Knowing different ways to solve problems helps you tackle anything that comes your way, making life a bit easier and more fun!

17 Effective Problem-Solving Strategies

Effective problem-solving strategies include breaking the problem into smaller parts, brainstorming multiple solutions, evaluating the pros and cons of each, and choosing the most viable option. 

Critical thinking and creativity are essential in developing innovative solutions. Collaboration with others can also provide diverse perspectives and ideas. 

By applying these strategies, you can tackle complex issues more effectively.

Now, consider a challenge you’re dealing with. Which strategy could help you find a solution? Here we will discuss key problem strategies in detail.

1. Use a Past Solution That Worked

This strategy involves looking back at previous similar problems you have faced and the solutions that were effective in solving them.

It is useful when you are facing a problem that is very similar to something you have already solved. The main benefit is that you don’t have to come up with a brand new solution – you already know the method that worked before will likely work again.

However, the limitation is that the current problem may have some unique aspects or differences that mean your old solution is not fully applicable.

The ideal process is to thoroughly analyze the new challenge, identify the key similarities and differences versus the past case, adapt the old solution as needed to align with the current context, and then pilot it carefully before full implementation.

An example is using the same negotiation tactics from purchasing your previous home when putting in an offer on a new house. Key terms would be adjusted but overall it can save significant time versus developing a brand new strategy.

2. Brainstorm Solutions

This involves gathering a group of people together to generate as many potential solutions to a problem as possible.

It is effective when you need creative ideas to solve a complex or challenging issue. By getting input from multiple people with diverse perspectives, you increase the likelihood of finding an innovative solution.

The main limitation is that brainstorming sessions can sometimes turn into unproductive gripe sessions or discussions rather than focusing on productive ideation —so they need to be properly facilitated.

The key to an effective brainstorming session is setting some basic ground rules upfront and having an experienced facilitator guide the discussion. Rules often include encouraging wild ideas, avoiding criticism of ideas during the ideation phase, and building on others’ ideas.

For instance, a struggling startup might hold a session where ideas for turnaround plans are generated and then formalized with financials and metrics.

3. Work Backward from the Solution

This technique involves envisioning that the problem has already been solved and then working step-by-step backward toward the current state.

This strategy is particularly helpful for long-term, multi-step problems. By starting from the imagined solution and identifying all the steps required to reach it, you can systematically determine the actions needed. It lets you tackle a big hairy problem through smaller, reversible steps.

A limitation is that this approach may not be possible if you cannot accurately envision the solution state to start with.

The approach helps drive logical systematic thinking for complex problem-solving, but should still be combined with creative brainstorming of alternative scenarios and solutions.

An example is planning for an event – you would imagine the successful event occurring, then determine the tasks needed the week before, two weeks before, etc. all the way back to the present.

4. Use the Kipling Method

This method, named after author Rudyard Kipling, provides a framework for thoroughly analyzing a problem before jumping into solutions.

It consists of answering six fundamental questions: What, Where, When, How, Who, and Why about the challenge. Clearly defining these core elements of the problem sets the stage for generating targeted solutions.

The Kipling method enables a deep understanding of problem parameters and root causes before solution identification. By jumping to brainstorm solutions too early, critical information can be missed or the problem is loosely defined, reducing solution quality.

Answering the six fundamental questions illuminates all angles of the issue. This takes time but pays dividends in generating optimal solutions later tuned precisely to the true underlying problem.

The limitation is that meticulously working through numerous questions before addressing solutions can slow progress.

The best approach blends structured problem decomposition techniques like the Kipling method with spurring innovative solution ideation from a diverse team. 

An example is using this technique after a technical process failure – the team would systematically detail What failed, Where/When did it fail, How it failed (sequence of events), Who was involved, and Why it likely failed before exploring preventative solutions.

5. Try Different Solutions Until One Works (Trial and Error)

This technique involves attempting various potential solutions sequentially until finding one that successfully solves the problem.

Trial and error works best when facing a concrete, bounded challenge with clear solution criteria and a small number of discrete options to try. By methodically testing solutions, you can determine the faulty component.

A limitation is that it can be time-intensive if the working solution set is large.

The key is limiting the variable set first. For technical problems, this boundary is inherent and each element can be iteratively tested. But for business issues, artificial constraints may be required – setting decision rules upfront to reduce options before testing.

Furthermore, hypothesis-driven experimentation is far superior to blind trial and error – have logic for why Option A may outperform Option B.

Examples include fixing printer jams by testing different paper tray and cable configurations or resolving website errors by tweaking CSS/HTML line-by-line until the code functions properly.

6. Use Proven Formulas or Frameworks (Heuristics)

Heuristics refers to applying existing problem-solving formulas or frameworks rather than addressing issues completely from scratch.

This allows leveraging established best practices rather than reinventing the wheel each time.

It is effective when facing recurrent, common challenges where proven structured approaches exist.

However, heuristics may force-fit solutions to non-standard problems.

For example, a cost-benefit analysis can be used instead of custom weighting schemes to analyze potential process improvements.

Onethread allows teams to define, save, and replicate configurable project templates so proven workflows can be reliably applied across problems with some consistency rather than fully custom one-off approaches each time.

Try One thread

Experience One thread full potential, with all its features unlocked. Sign up now to start your 14-day free trial!

7. Trust Your Instincts (Insight Problem-Solving)

Insight is a problem-solving technique that involves waiting patiently for an unexpected “aha moment” when the solution pops into your mind.

It works well for personal challenges that require intuitive realizations over calculated logic. The unconscious mind makes connections leading to flashes of insight when relaxing or doing mundane tasks unrelated to the actual problem.

Benefits include out-of-the-box creative solutions. However, the limitations are that insights can’t be forced and may never come at all if too complex. Critical analysis is still required after initial insights.

A real-life example would be a writer struggling with how to end a novel. Despite extensive brainstorming, they feel stuck. Eventually while gardening one day, a perfect unexpected plot twist sparks an ideal conclusion. However, once written they still carefully review if the ending flows logically from the rest of the story.

8. Reverse Engineer the Problem

This approach involves deconstructing a problem in reverse sequential order from the current undesirable outcome back to the initial root causes.

By mapping the chain of events backward, you can identify the origin of where things went wrong and establish the critical junctures for solving it moving ahead. Reverse engineering provides diagnostic clarity on multi-step problems.

However, the limitation is that it focuses heavily on autopsying the past versus innovating improved future solutions.

An example is tracing back from a server outage, through the cascade of infrastructure failures that led to it finally terminating at the initial script error that triggered the crisis. This root cause would then inform the preventative measure.

9. Break Down Obstacles Between Current and Goal State (Means-End Analysis)

This technique defines the current problem state and the desired end goal state, then systematically identifies obstacles in the way of getting from one to the other.

By mapping the barriers or gaps, you can then develop solutions to address each one. This methodically connects the problem to solutions.

A limitation is that some obstacles may be unknown upfront and only emerge later.

For example, you can list down all the steps required for a new product launch – current state through production, marketing, sales, distribution, etc. to full launch (goal state) – to highlight where resource constraints or other blocks exist so they can be addressed.

Onethread allows dividing big-picture projects into discrete, manageable phases, milestones, and tasks to simplify execution just as problems can be decomposed into more achievable components. Features like dependency mapping further reinforce interconnections.

Using Onethread’s issues and subtasks feature, messy problems can be decomposed into manageable chunks.

10. Ask “Why” Five Times to Identify the Root Cause (The 5 Whys)

This technique involves asking “Why did this problem occur?” and then responding with an answer that is again met with asking “Why?” This process repeats five times until the root cause is revealed.

Continually asking why digs deeper from surface symptoms to underlying systemic issues.

It is effective for getting to the source of problems originating from human error or process breakdowns.

However, some complex issues may have multiple tangled root causes not solvable through this approach alone.

An example is a retail store experiencing a sudden decline in customers. Successively asking why five times may trace an initial drop to parking challenges, stemming from a city construction project – the true starting point to address.

11. Evaluate Strengths, Weaknesses, Opportunities, and Threats (SWOT Analysis)

This involves analyzing a problem or proposed solution by categorizing internal and external factors into a 2×2 matrix: Strengths, Weaknesses as the internal rows; Opportunities and Threats as the external columns.

Systematically identifying these elements provides balanced insight to evaluate options and risks. It is impactful when evaluating alternative solutions or developing strategy amid complexity or uncertainty.

The key benefit of SWOT analysis is enabling multi-dimensional thinking when rationally evaluating options. Rather than getting anchored on just the upsides or the existing way of operating, it urges a systematic assessment through four different lenses:

• Internal Strengths: Our core competencies/advantages able to deliver success
• Internal Weaknesses: Gaps/vulnerabilities we need to manage
• External Opportunities: Ways we can differentiate/drive additional value
• External Threats: Risks we must navigate or mitigate

Multiperspective analysis provides the needed holistic view of the balanced risk vs. reward equation for strategic decision making amid uncertainty.

However, SWOT can feel restrictive if not tailored and evolved for different issue types.

Teams should view SWOT analysis as a starting point, augmenting it further for distinct scenarios.

An example is performing a SWOT analysis on whether a small business should expand into a new market – evaluating internal capabilities to execute vs. risks in the external competitive and demand environment to inform the growth decision with eyes wide open.

12. Compare Current vs Expected Performance (Gap Analysis)

This technique involves comparing the current state of performance, output, or results to the desired or expected levels to highlight shortfalls.

By quantifying the gaps, you can identify problem areas and prioritize address solutions.

Gap analysis is based on the simple principle – “you can’t improve what you don’t measure.” It enables facts-driven problem diagnosis by highlighting delta to goals, not just vague dissatisfaction that something seems wrong. And measurement immediately suggests improvement opportunities – address the biggest gaps first.

This data orientation also supports ROI analysis on fixing issues – the return from closing larger gaps outweighs narrowly targeting smaller performance deficiencies.

However, the approach is only effective if robust standards and metrics exist as the benchmark to evaluate against. Organizations should invest upfront in establishing performance frameworks.

Furthermore, while numbers are invaluable, the human context behind problems should not be ignored – quantitative versus qualitative gap assessment is optimally blended.

For example, if usage declines are noted during software gap analysis, this could be used as a signal to improve user experience through design.

13. Observe Processes from the Frontline (Gemba Walk)

A Gemba walk involves going to the actual place where work is done, directly observing the process, engaging with employees, and finding areas for improvement.

By experiencing firsthand rather than solely reviewing abstract reports, practical problems and ideas emerge.

The limitation is Gemba walks provide anecdotes not statistically significant data. It complements but does not replace comprehensive performance measurement.

An example is a factory manager inspecting the production line to spot jam areas based on direct reality rather than relying on throughput dashboards alone back in her office. Frontline insights prove invaluable.

14. Analyze Competitive Forces (Porter’s Five Forces)

This involves assessing the marketplace around a problem or business situation via five key factors: competitors, new entrants, substitute offerings, suppliers, and customer power.

Evaluating these forces illuminates risks and opportunities for strategy development and issue resolution. It is effective for understanding dynamic external threats and opportunities when operating in a contested space.

However, over-indexing on only external factors can overlook the internal capabilities needed to execute solutions.

A startup CEO, for example, may analyze market entry barriers, whitespace opportunities, and disruption risks across these five forces to shape new product rollout strategies and marketing approaches.

15. Think from Different Perspectives (Six Thinking Hats)

The Six Thinking Hats is a technique developed by Edward de Bono that encourages people to think about a problem from six different perspectives, each represented by a colored “thinking hat.”

The key benefit of this strategy is that it pushes team members to move outside their usual thinking style and consider new angles. This brings more diverse ideas and solutions to the table.

It works best for complex problems that require innovative solutions and when a team is stuck in an unproductive debate. The structured framework keeps the conversation flowing in a positive direction.

Limitations are that it requires training on the method itself and may feel unnatural at first. Team dynamics can also influence success – some members may dominate certain “hats” while others remain quiet.

A real-life example is a software company debating whether to build a new feature. The white hat focuses on facts, red on gut feelings, black on potential risks, yellow on benefits, green on new ideas, and blue on process. This exposes more balanced perspectives before deciding.

Onethread centralizes diverse stakeholder communication onto one platform, ensuring all voices are incorporated when evaluating project tradeoffs, just as problem-solving should consider multifaceted solutions.

16. Visualize the Problem (Draw it Out)

Drawing out a problem involves creating visual representations like diagrams, flowcharts, and maps to work through challenging issues.

This strategy is helpful when dealing with complex situations with lots of interconnected components. The visuals simplify the complexity so you can thoroughly understand the problem and all its nuances.

Key benefits are that it allows more stakeholders to get on the same page regarding root causes and it sparks new creative solutions as connections are made visually.

However, simple problems with few variables don’t require extensive diagrams. Additionally, some challenges are so multidimensional that fully capturing every aspect is difficult.

A real-life example would be mapping out all the possible causes leading to decreased client satisfaction at a law firm. An intricate fishbone diagram with branches for issues like service delivery, technology, facilities, culture, and vendor partnerships allows the team to trace problems back to their origins and brainstorm targeted fixes.

17. Follow a Step-by-Step Procedure (Algorithms)

An algorithm is a predefined step-by-step process that is guaranteed to produce the correct solution if implemented properly.

Using algorithms is effective when facing problems that have clear, binary right and wrong answers. Algorithms work for mathematical calculations, computer code, manufacturing assembly lines, and scientific experiments.

Key benefits are consistency, accuracy, and efficiency. However, they require extensive upfront development and only apply to scenarios with strict parameters. Additionally, human error can lead to mistakes.

For example, crew members of fast food chains like McDonald’s follow specific algorithms for food prep – from grill times to ingredient amounts in sandwiches, to order fulfillment procedures. This ensures uniform quality and service across all locations. However, if a step is missed, errors occur.

The Problem-Solving Process

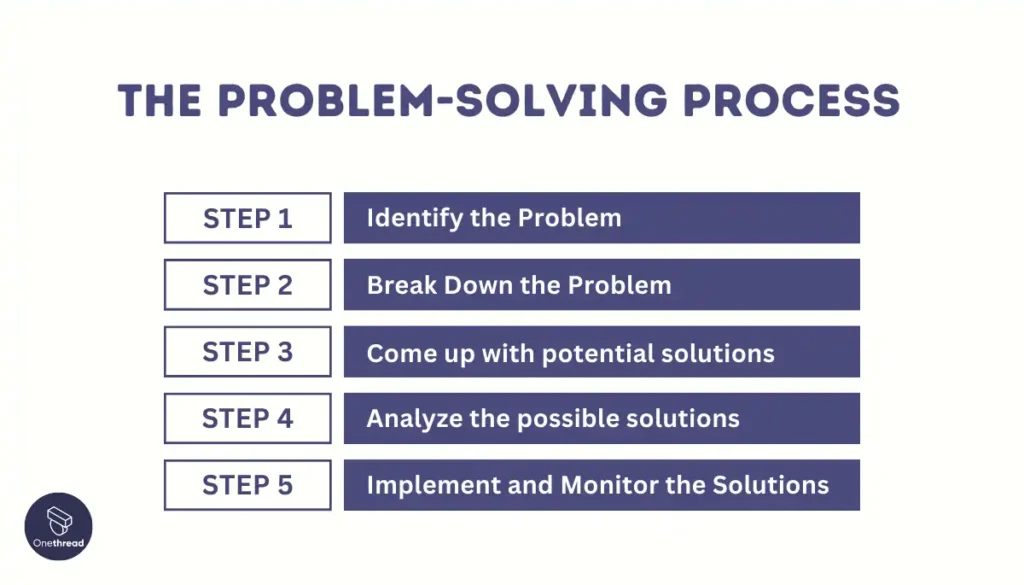
The problem-solving process typically includes defining the issue, analyzing details, creating solutions, weighing choices, acting, and reviewing results.

In the above, we have discussed several problem-solving strategies. For every problem-solving strategy, you have to follow these processes. Here’s a detailed step-by-step process of effective problem-solving:

Step 1: Identify the Problem

The problem-solving process starts with identifying the problem. This step involves understanding the issue’s nature, its scope, and its impact. Once the problem is clearly defined, it sets the foundation for finding effective solutions.

Identifying the problem is crucial. It means figuring out exactly what needs fixing. This involves looking at the situation closely, understanding what’s wrong, and knowing how it affects things. It’s about asking the right questions to get a clear picture of the issue. 

This step is important because it guides the rest of the problem-solving process. Without a clear understanding of the problem, finding a solution is much harder. It’s like diagnosing an illness before treating it. Once the problem is identified accurately, you can move on to exploring possible solutions and deciding on the best course of action.

Step 2: Break Down the Problem

Breaking down the problem is a key step in the problem-solving process. It involves dividing the main issue into smaller, more manageable parts. This makes it easier to understand and tackle each component one by one.

After identifying the problem, the next step is to break it down. This means splitting the big issue into smaller pieces. It’s like solving a puzzle by handling one piece at a time. 

By doing this, you can focus on each part without feeling overwhelmed. It also helps in identifying the root causes of the problem. Breaking down the problem allows for a clearer analysis and makes finding solutions more straightforward. 

Each smaller problem can be addressed individually, leading to an effective resolution of the overall issue. This approach not only simplifies complex problems but also aids in developing a systematic plan to solve them.

Step 3: Come up with potential solutions

Coming up with potential solutions is the third step in the problem-solving process. It involves brainstorming various options to address the problem, considering creativity and feasibility to find the best approach.

After breaking down the problem, it’s time to think of ways to solve it. This stage is about brainstorming different solutions. You look at the smaller issues you’ve identified and start thinking of ways to fix them. This is where creativity comes in. 

You want to come up with as many ideas as possible, no matter how out-of-the-box they seem. It’s important to consider all options and evaluate their pros and cons. This process allows you to gather a range of possible solutions. 

Later, you can narrow these down to the most practical and effective ones. This step is crucial because it sets the stage for deciding on the best solution to implement. It’s about being open-minded and innovative to tackle the problem effectively.

Step 4: Analyze the possible solutions

Analyzing the possible solutions is the fourth step in the problem-solving process. It involves evaluating each proposed solution’s advantages and disadvantages to determine the most effective and feasible option.

After coming up with potential solutions, the next step is to analyze them. This means looking closely at each idea to see how well it solves the problem. You weigh the pros and cons of every solution.

Consider factors like cost, time, resources, and potential outcomes. This analysis helps in understanding the implications of each option. It’s about being critical and objective, ensuring that the chosen solution is not only effective but also practical.

This step is vital because it guides you towards making an informed decision. It involves comparing the solutions against each other and selecting the one that best addresses the problem.

By thoroughly analyzing the options, you can move forward with confidence, knowing you’ve chosen the best path to solve the issue.

Step 5: Implement and Monitor the Solutions

Implementing and monitoring the solutions is the final step in the problem-solving process. It involves putting the chosen solution into action and observing its effectiveness, making adjustments as necessary.

Once you’ve selected the best solution, it’s time to put it into practice. This step is about action. You implement the chosen solution and then keep an eye on how it works. Monitoring is crucial because it tells you if the solution is solving the problem as expected. 

If things don’t go as planned, you may need to make some changes. This could mean tweaking the current solution or trying a different one. The goal is to ensure the problem is fully resolved. 

This step is critical because it involves real-world application. It’s not just about planning; it’s about doing and adjusting based on results. By effectively implementing and monitoring the solutions, you can achieve the desired outcome and solve the problem successfully.

Why This Process is Important

Following a defined process to solve problems is important because it provides a systematic, structured approach instead of a haphazard one. Having clear steps guides logical thinking, analysis, and decision-making to increase effectiveness. Key reasons it helps are:

• Clear Direction: This process gives you a clear path to follow, which can make solving problems less overwhelming.
• Better Solutions: Thoughtful analysis of root causes, iterative testing of solutions, and learning orientation lead to addressing the heart of issues rather than just symptoms.
• Saves Time and Energy: Instead of guessing or trying random things, this process helps you find a solution more efficiently.
• Improves Skills: The more you use this process, the better you get at solving problems. It’s like practicing a sport. The more you practice, the better you play.
• Maximizes collaboration: Involving various stakeholders in the process enables broader inputs. Their communication and coordination are streamlined through organized brainstorming and evaluation.
• Provides consistency: Standard methodology across problems enables building institutional problem-solving capabilities over time. Patterns emerge on effective techniques to apply to different situations.

The problem-solving process is a powerful tool that can help us tackle any challenge we face. By following these steps, we can find solutions that work and learn important skills along the way.

Key Skills for Efficient Problem Solving

Efficient problem-solving requires breaking down issues logically, evaluating options, and implementing practical solutions.

Key skills include critical thinking to understand root causes, creativity to brainstorm innovative ideas, communication abilities to collaborate with others, and decision-making to select the best way forward. Staying adaptable, reflecting on outcomes, and applying lessons learned are also essential.

With practice, these capacities will lead to increased personal and team effectiveness in systematically addressing any problem.

 Let’s explore the powers you need to become a problem-solving hero!

Critical Thinking and Analytical Skills

Critical thinking and analytical skills are vital for efficient problem-solving as they enable individuals to objectively evaluate information, identify key issues, and generate effective solutions. 

These skills facilitate a deeper understanding of problems, leading to logical, well-reasoned decisions. By systematically breaking down complex issues and considering various perspectives, individuals can develop more innovative and practical solutions, enhancing their problem-solving effectiveness.

Communication Skills

Effective communication skills are essential for efficient problem-solving as they facilitate clear sharing of information, ensuring all team members understand the problem and proposed solutions. 

These skills enable individuals to articulate issues, listen actively, and collaborate effectively, fostering a productive environment where diverse ideas can be exchanged and refined. By enhancing mutual understanding, communication skills contribute significantly to identifying and implementing the most viable solutions.

Decision-Making

Strong decision-making skills are crucial for efficient problem-solving, as they enable individuals to choose the best course of action from multiple alternatives. 

These skills involve evaluating the potential outcomes of different solutions, considering the risks and benefits, and making informed choices. Effective decision-making leads to the implementation of solutions that are likely to resolve problems effectively, ensuring resources are used efficiently and goals are achieved.

Planning and Prioritization

Planning and prioritization are key for efficient problem-solving, ensuring resources are allocated effectively to address the most critical issues first. This approach helps in organizing tasks according to their urgency and impact, streamlining efforts towards achieving the desired outcome efficiently.

Emotional Intelligence

Emotional intelligence enhances problem-solving by allowing individuals to manage emotions, understand others, and navigate social complexities. It fosters a positive, collaborative environment, essential for generating creative solutions and making informed, empathetic decisions.

Leadership skills drive efficient problem-solving by inspiring and guiding teams toward common goals. Effective leaders motivate their teams, foster innovation, and navigate challenges, ensuring collective efforts are focused and productive in addressing problems.

Time Management

Time management is crucial in problem-solving, enabling individuals to allocate appropriate time to each task. By efficiently managing time, one can ensure that critical problems are addressed promptly without neglecting other responsibilities.

Data Analysis

Data analysis skills are essential for problem-solving, as they enable individuals to sift through data, identify trends, and extract actionable insights. This analytical approach supports evidence-based decision-making, leading to more accurate and effective solutions.

Research Skills

Research skills are vital for efficient problem-solving, allowing individuals to gather relevant information, explore various solutions, and understand the problem’s context. This thorough exploration aids in developing well-informed, innovative solutions.

Becoming a great problem solver takes practice, but with these skills, you’re on your way to becoming a problem-solving hero. 

How to Improve Your Problem-Solving Skills?

Improving your problem-solving skills can make you a master at overcoming challenges. Learn from experts, practice regularly, welcome feedback, try new methods, experiment, and study others’ success to become better.

Learning from Experts

Improving problem-solving skills by learning from experts involves seeking mentorship, attending workshops, and studying case studies. Experts provide insights and techniques that refine your approach, enhancing your ability to tackle complex problems effectively.

To enhance your problem-solving skills, learning from experts can be incredibly beneficial. Engaging with mentors, participating in specialized workshops, and analyzing case studies from seasoned professionals can offer valuable perspectives and strategies. 

Experts share their experiences, mistakes, and successes, providing practical knowledge that can be applied to your own problem-solving process. This exposure not only broadens your understanding but also introduces you to diverse methods and approaches, enabling you to tackle challenges more efficiently and creatively.

Improving problem-solving skills through practice involves tackling a variety of challenges regularly. This hands-on approach helps in refining techniques and strategies, making you more adept at identifying and solving problems efficiently.

One of the most effective ways to enhance your problem-solving skills is through consistent practice. By engaging with different types of problems on a regular basis, you develop a deeper understanding of various strategies and how they can be applied. 

This hands-on experience allows you to experiment with different approaches, learn from mistakes, and build confidence in your ability to tackle challenges.

Regular practice not only sharpens your analytical and critical thinking skills but also encourages adaptability and innovation, key components of effective problem-solving.

Openness to Feedback

Being open to feedback is like unlocking a secret level in a game. It helps you boost your problem-solving skills. Improving problem-solving skills through openness to feedback involves actively seeking and constructively responding to critiques. 

This receptivity enables you to refine your strategies and approaches based on insights from others, leading to more effective solutions. 

Learning New Approaches and Methodologies

Learning new approaches and methodologies is like adding new tools to your toolbox. It makes you a smarter problem-solver. Enhancing problem-solving skills by learning new approaches and methodologies involves staying updated with the latest trends and techniques in your field. 

This continuous learning expands your toolkit, enabling innovative solutions and a fresh perspective on challenges.

Experimentation

Experimentation is like being a scientist of your own problems. It’s a powerful way to improve your problem-solving skills. Boosting problem-solving skills through experimentation means trying out different solutions to see what works best. This trial-and-error approach fosters creativity and can lead to unique solutions that wouldn’t have been considered otherwise.

Analyzing Competitors’ Success

Analyzing competitors’ success is like being a detective. It’s a smart way to boost your problem-solving skills. Improving problem-solving skills by analyzing competitors’ success involves studying their strategies and outcomes. Understanding what worked for them can provide valuable insights and inspire effective solutions for your own challenges. 

Challenges in Problem-Solving

Facing obstacles when solving problems is common. Recognizing these barriers, like fear of failure or lack of information, helps us find ways around them for better solutions.

Fear of Failure

Fear of failure is like a big, scary monster that stops us from solving problems. It’s a challenge many face. Because being afraid of making mistakes can make us too scared to try new solutions. 

How can we overcome this? First, understand that it’s okay to fail. Failure is not the opposite of success; it’s part of learning. Every time we fail, we discover one more way not to solve a problem, getting us closer to the right solution. Treat each attempt like an experiment. It’s not about failing; it’s about testing and learning.

Lack of Information

Lack of information is like trying to solve a puzzle with missing pieces. It’s a big challenge in problem-solving. Because without all the necessary details, finding a solution is much harder. 

How can we fix this? Start by gathering as much information as you can. Ask questions, do research, or talk to experts. Think of yourself as a detective looking for clues. The more information you collect, the clearer the picture becomes. Then, use what you’ve learned to think of solutions. 

Fixed Mindset

A fixed mindset is like being stuck in quicksand; it makes solving problems harder. It means thinking you can’t improve or learn new ways to solve issues. 

How can we change this? First, believe that you can grow and learn from challenges. Think of your brain as a muscle that gets stronger every time you use it. When you face a problem, instead of saying “I can’t do this,” try thinking, “I can’t do this yet.” Look for lessons in every challenge and celebrate small wins. 

Everyone starts somewhere, and mistakes are just steps on the path to getting better. By shifting to a growth mindset, you’ll see problems as opportunities to grow. Keep trying, keep learning, and your problem-solving skills will soar!

Jumping to Conclusions

Jumping to conclusions is like trying to finish a race before it starts. It’s a challenge in problem-solving. That means making a decision too quickly without looking at all the facts. 

How can we avoid this? First, take a deep breath and slow down. Think about the problem like a puzzle. You need to see all the pieces before you know where they go. Ask questions, gather information, and consider different possibilities. Don’t choose the first solution that comes to mind. Instead, compare a few options. 

Feeling Overwhelmed

Feeling overwhelmed is like being buried under a mountain of puzzles. It’s a big challenge in problem-solving. When we’re overwhelmed, everything seems too hard to handle. 

How can we deal with this? Start by taking a step back. Breathe deeply and focus on one thing at a time. Break the big problem into smaller pieces, like sorting puzzle pieces by color. Tackle each small piece one by one. It’s also okay to ask for help. Sometimes, talking to someone else can give you a new perspective. 

Confirmation Bias

Confirmation bias is like wearing glasses that only let you see what you want to see. It’s a challenge in problem-solving. Because it makes us focus only on information that agrees with what we already believe, ignoring anything that doesn’t. 

How can we overcome this? First, be aware that you might be doing it. It’s like checking if your glasses are on right. Then, purposely look for information that challenges your views. It’s like trying on a different pair of glasses to see a new perspective. Ask questions and listen to answers, even if they don’t fit what you thought before.

Groupthink is like everyone in a group deciding to wear the same outfit without asking why. It’s a challenge in problem-solving. It means making decisions just because everyone else agrees, without really thinking it through. 

How can we avoid this? First, encourage everyone in the group to share their ideas, even if they’re different. It’s like inviting everyone to show their unique style of clothes. 

Listen to all opinions and discuss them. It’s okay to disagree; it helps us think of better solutions. Also, sometimes, ask someone outside the group for their thoughts. They might see something everyone in the group missed.

Overcoming obstacles in problem-solving requires patience, openness, and a willingness to learn from mistakes. By recognizing these barriers, we can develop strategies to navigate around them, leading to more effective and creative solutions.

What are the most common problem-solving techniques?

The most common techniques include brainstorming, the 5 Whys, mind mapping, SWOT analysis, and using algorithms or heuristics. Each approach has its strengths, suitable for different types of problems.

What’s the best problem-solving strategy for every situation?

There’s no one-size-fits-all strategy. The best approach depends on the problem’s complexity, available resources, and time constraints. Combining multiple techniques often yields the best results.

How can I improve my problem-solving skills?

Improve your problem-solving skills by practicing regularly, learning from experts, staying open to feedback, and continuously updating your knowledge on new approaches and methodologies.

Are there any tools or resources to help with problem-solving?

Yes, tools like mind mapping software, online courses on critical thinking, and books on problem-solving techniques can be very helpful. Joining forums or groups focused on problem-solving can also provide support and insights.

What are some common mistakes people make when solving problems?

Common mistakes include jumping to conclusions without fully understanding the problem, ignoring valuable feedback, sticking to familiar solutions without considering alternatives, and not breaking down complex problems into manageable parts.

Final Words

Mastering problem-solving strategies equips us with the tools to tackle challenges across all areas of life. By understanding and applying these techniques, embracing a growth mindset, and learning from both successes and obstacles, we can transform problems into opportunities for growth. Continuously improving these skills ensures we’re prepared to face and solve future challenges more effectively.

Let's Get Started with Onethread

Onethread empowers you to plan, organise, and track projects with ease, ensuring you meet deadlines, allocate resources efficiently, and keep progress transparent.

By subscribing you agree to our  Privacy Policy .

Giving modern marketing teams superpowers with short links that stand out.

• Live Product Demo

© Copyright 2023 Onethread, Inc

35 problem-solving techniques and methods for solving complex problems

Design your next session with SessionLab

Join the 150,000+ facilitators 
using SessionLab.

Recommended Articles

A step-by-step guide to planning a workshop, how to create an unforgettable training session in 8 simple steps, 47 useful online tools for workshop planning and meeting facilitation.

All teams and organizations encounter challenges as they grow. There are problems that might occur for teams when it comes to miscommunication or resolving business-critical issues . You may face challenges around growth , design , user engagement, and even team culture and happiness. In short, problem-solving techniques should be part of every team’s skillset.

Problem-solving methods are primarily designed to help a group or team through a process of first identifying problems and challenges , ideating possible solutions , and then evaluating the most suitable .

Finding effective solutions to complex problems isn’t easy, but by using the right process and techniques, you can help your team be more efficient in the process.

So how do you develop strategies that are engaging, and empower your team to solve problems effectively?

In this blog post, we share a series of problem-solving tools you can use in your next workshop or team meeting. You’ll also find some tips for facilitating the process and how to enable others to solve complex problems.

Let’s get started! 

How do you identify problems?

How do you identify the right solution.

• Tips for more effective problem-solving

Complete problem-solving methods

• Problem-solving techniques to identify and analyze problems
• Problem-solving techniques for developing solutions

Problem-solving warm-up activities

Closing activities for a problem-solving process.

Before you can move towards finding the right solution for a given problem, you first need to identify and define the problem you wish to solve. 

Here, you want to clearly articulate what the problem is and allow your group to do the same. Remember that everyone in a group is likely to have differing perspectives and alignment is necessary in order to help the group move forward. 

Identifying a problem accurately also requires that all members of a group are able to contribute their views in an open and safe manner. It can be scary for people to stand up and contribute, especially if the problems or challenges are emotive or personal in nature. Be sure to try and create a psychologically safe space for these kinds of discussions.

Remember that problem analysis and further discussion are also important. Not taking the time to fully analyze and discuss a challenge can result in the development of solutions that are not fit for purpose or do not address the underlying issue.

Successfully identifying and then analyzing a problem means facilitating a group through activities designed to help them clearly and honestly articulate their thoughts and produce usable insight.

With this data, you might then produce a problem statement that clearly describes the problem you wish to be addressed and also state the goal of any process you undertake to tackle this issue.  

Finding solutions is the end goal of any process. Complex organizational challenges can only be solved with an appropriate solution but discovering them requires using the right problem-solving tool.

After you’ve explored a problem and discussed ideas, you need to help a team discuss and choose the right solution. Consensus tools and methods such as those below help a group explore possible solutions before then voting for the best. They’re a great way to tap into the collective intelligence of the group for great results!

Remember that the process is often iterative. Great problem solvers often roadtest a viable solution in a measured way to see what works too. While you might not get the right solution on your first try, the methods below help teams land on the most likely to succeed solution while also holding space for improvement.

Every effective problem solving process begins with an agenda . A well-structured workshop is one of the best methods for successfully guiding a group from exploring a problem to implementing a solution.

In SessionLab, it’s easy to go from an idea to a complete agenda . Start by dragging and dropping your core problem solving activities into place . Add timings, breaks and necessary materials before sharing your agenda with your colleagues.

The resulting agenda will be your guide to an effective and productive problem solving session that will also help you stay organized on the day!

Tips for more effective problem solving

Problem-solving activities are only one part of the puzzle. While a great method can help unlock your team’s ability to solve problems, without a thoughtful approach and strong facilitation the solutions may not be fit for purpose.

Let’s take a look at some problem-solving tips you can apply to any process to help it be a success!

Clearly define the problem

Jumping straight to solutions can be tempting, though without first clearly articulating a problem, the solution might not be the right one. Many of the problem-solving activities below include sections where the problem is explored and clearly defined before moving on.

This is a vital part of the problem-solving process and taking the time to fully define an issue can save time and effort later. A clear definition helps identify irrelevant information and it also ensures that your team sets off on the right track.

Don’t jump to conclusions

It’s easy for groups to exhibit cognitive bias or have preconceived ideas about both problems and potential solutions. Be sure to back up any problem statements or potential solutions with facts, research, and adequate forethought.

The best techniques ask participants to be methodical and challenge preconceived notions. Make sure you give the group enough time and space to collect relevant information and consider the problem in a new way. By approaching the process with a clear, rational mindset, you’ll often find that better solutions are more forthcoming.  

Try different approaches  

Problems come in all shapes and sizes and so too should the methods you use to solve them. If you find that one approach isn’t yielding results and your team isn’t finding different solutions, try mixing it up. You’ll be surprised at how using a new creative activity can unblock your team and generate great solutions.

Don’t take it personally 

Depending on the nature of your team or organizational problems, it’s easy for conversations to get heated. While it’s good for participants to be engaged in the discussions, ensure that emotions don’t run too high and that blame isn’t thrown around while finding solutions.

You’re all in it together, and even if your team or area is seeing problems, that isn’t necessarily a disparagement of you personally. Using facilitation skills to manage group dynamics is one effective method of helping conversations be more constructive.

Get the right people in the room

Your problem-solving method is often only as effective as the group using it. Getting the right people on the job and managing the number of people present is important too!

If the group is too small, you may not get enough different perspectives to effectively solve a problem. If the group is too large, you can go round and round during the ideation stages.

Creating the right group makeup is also important in ensuring you have the necessary expertise and skillset to both identify and follow up on potential solutions. Carefully consider who to include at each stage to help ensure your problem-solving method is followed and positioned for success.

Document everything

The best solutions can take refinement, iteration, and reflection to come out. Get into a habit of documenting your process in order to keep all the learnings from the session and to allow ideas to mature and develop. Many of the methods below involve the creation of documents or shared resources. Be sure to keep and share these so everyone can benefit from the work done!

Bring a facilitator 

Facilitation is all about making group processes easier. With a subject as potentially emotive and important as problem-solving, having an impartial third party in the form of a facilitator can make all the difference in finding great solutions and keeping the process moving. Consider bringing a facilitator to your problem-solving session to get better results and generate meaningful solutions!

Develop your problem-solving skills

It takes time and practice to be an effective problem solver. While some roles or participants might more naturally gravitate towards problem-solving, it can take development and planning to help everyone create better solutions.

You might develop a training program, run a problem-solving workshop or simply ask your team to practice using the techniques below. Check out our post on problem-solving skills to see how you and your group can develop the right mental process and be more resilient to issues too!

Design a great agenda

Workshops are a great format for solving problems. With the right approach, you can focus a group and help them find the solutions to their own problems. But designing a process can be time-consuming and finding the right activities can be difficult.

Check out our workshop planning guide to level-up your agenda design and start running more effective workshops. Need inspiration? Check out templates designed by expert facilitators to help you kickstart your process!

In this section, we’ll look at in-depth problem-solving methods that provide a complete end-to-end process for developing effective solutions. These will help guide your team from the discovery and definition of a problem through to delivering the right solution.

If you’re looking for an all-encompassing method or problem-solving model, these processes are a great place to start. They’ll ask your team to challenge preconceived ideas and adopt a mindset for solving problems more effectively.

• Six Thinking Hats
• Lightning Decision Jam
• Problem Definition Process
• Discovery & Action Dialogue

Design Sprint 2.0

• Open Space Technology

1. Six Thinking Hats

Individual approaches to solving a problem can be very different based on what team or role an individual holds. It can be easy for existing biases or perspectives to find their way into the mix, or for internal politics to direct a conversation.

Six Thinking Hats is a classic method for identifying the problems that need to be solved and enables your team to consider them from different angles, whether that is by focusing on facts and data, creative solutions, or by considering why a particular solution might not work.

Like all problem-solving frameworks, Six Thinking Hats is effective at helping teams remove roadblocks from a conversation or discussion and come to terms with all the aspects necessary to solve complex problems.

2. Lightning Decision Jam

Featured courtesy of Jonathan Courtney of AJ&Smart Berlin, Lightning Decision Jam is one of those strategies that should be in every facilitation toolbox. Exploring problems and finding solutions is often creative in nature, though as with any creative process, there is the potential to lose focus and get lost.

Unstructured discussions might get you there in the end, but it’s much more effective to use a method that creates a clear process and team focus.

In Lightning Decision Jam, participants are invited to begin by writing challenges, concerns, or mistakes on post-its without discussing them before then being invited by the moderator to present them to the group.

From there, the team vote on which problems to solve and are guided through steps that will allow them to reframe those problems, create solutions and then decide what to execute on. 

By deciding the problems that need to be solved as a team before moving on, this group process is great for ensuring the whole team is aligned and can take ownership over the next stages. 

Lightning Decision Jam (LDJ)   #action   #decision making   #problem solving   #issue analysis   #innovation   #design   #remote-friendly   The problem with anything that requires creative thinking is that it’s easy to get lost—lose focus and fall into the trap of having useless, open-ended, unstructured discussions. Here’s the most effective solution I’ve found: Replace all open, unstructured discussion with a clear process. What to use this exercise for: Anything which requires a group of people to make decisions, solve problems or discuss challenges. It’s always good to frame an LDJ session with a broad topic, here are some examples: The conversion flow of our checkout Our internal design process How we organise events Keeping up with our competition Improving sales flow

3. Problem Definition Process

While problems can be complex, the problem-solving methods you use to identify and solve those problems can often be simple in design. 

By taking the time to truly identify and define a problem before asking the group to reframe the challenge as an opportunity, this method is a great way to enable change.

Begin by identifying a focus question and exploring the ways in which it manifests before splitting into five teams who will each consider the problem using a different method: escape, reversal, exaggeration, distortion or wishful. Teams develop a problem objective and create ideas in line with their method before then feeding them back to the group.

This method is great for enabling in-depth discussions while also creating space for finding creative solutions too!

Problem Definition   #problem solving   #idea generation   #creativity   #online   #remote-friendly   A problem solving technique to define a problem, challenge or opportunity and to generate ideas.

4. The 5 Whys 

Sometimes, a group needs to go further with their strategies and analyze the root cause at the heart of organizational issues. An RCA or root cause analysis is the process of identifying what is at the heart of business problems or recurring challenges. 

The 5 Whys is a simple and effective method of helping a group go find the root cause of any problem or challenge and conduct analysis that will deliver results. 

By beginning with the creation of a problem statement and going through five stages to refine it, The 5 Whys provides everything you need to truly discover the cause of an issue.

The 5 Whys   #hyperisland   #innovation   This simple and powerful method is useful for getting to the core of a problem or challenge. As the title suggests, the group defines a problems, then asks the question “why” five times, often using the resulting explanation as a starting point for creative problem solving.

5. World Cafe

World Cafe is a simple but powerful facilitation technique to help bigger groups to focus their energy and attention on solving complex problems.

World Cafe enables this approach by creating a relaxed atmosphere where participants are able to self-organize and explore topics relevant and important to them which are themed around a central problem-solving purpose. Create the right atmosphere by modeling your space after a cafe and after guiding the group through the method, let them take the lead!

Making problem-solving a part of your organization’s culture in the long term can be a difficult undertaking. More approachable formats like World Cafe can be especially effective in bringing people unfamiliar with workshops into the fold. 

World Cafe   #hyperisland   #innovation   #issue analysis   World Café is a simple yet powerful method, originated by Juanita Brown, for enabling meaningful conversations driven completely by participants and the topics that are relevant and important to them. Facilitators create a cafe-style space and provide simple guidelines. Participants then self-organize and explore a set of relevant topics or questions for conversation.

6. Discovery & Action Dialogue (DAD)

One of the best approaches is to create a safe space for a group to share and discover practices and behaviors that can help them find their own solutions.

With DAD, you can help a group choose which problems they wish to solve and which approaches they will take to do so. It’s great at helping remove resistance to change and can help get buy-in at every level too!

This process of enabling frontline ownership is great in ensuring follow-through and is one of the methods you will want in your toolbox as a facilitator.

Discovery & Action Dialogue (DAD)   #idea generation   #liberating structures   #action   #issue analysis   #remote-friendly   DADs make it easy for a group or community to discover practices and behaviors that enable some individuals (without access to special resources and facing the same constraints) to find better solutions than their peers to common problems. These are called positive deviant (PD) behaviors and practices. DADs make it possible for people in the group, unit, or community to discover by themselves these PD practices. DADs also create favorable conditions for stimulating participants’ creativity in spaces where they can feel safe to invent new and more effective practices. Resistance to change evaporates as participants are unleashed to choose freely which practices they will adopt or try and which problems they will tackle. DADs make it possible to achieve frontline ownership of solutions.

7. Design Sprint 2.0

Want to see how a team can solve big problems and move forward with prototyping and testing solutions in a few days? The Design Sprint 2.0 template from Jake Knapp, author of Sprint, is a complete agenda for a with proven results.

Developing the right agenda can involve difficult but necessary planning. Ensuring all the correct steps are followed can also be stressful or time-consuming depending on your level of experience.

Use this complete 4-day workshop template if you are finding there is no obvious solution to your challenge and want to focus your team around a specific problem that might require a shortcut to launching a minimum viable product or waiting for the organization-wide implementation of a solution.

8. Open space technology

Open space technology- developed by Harrison Owen – creates a space where large groups are invited to take ownership of their problem solving and lead individual sessions. Open space technology is a great format when you have a great deal of expertise and insight in the room and want to allow for different takes and approaches on a particular theme or problem you need to be solved.

Start by bringing your participants together to align around a central theme and focus their efforts. Explain the ground rules to help guide the problem-solving process and then invite members to identify any issue connecting to the central theme that they are interested in and are prepared to take responsibility for.

Once participants have decided on their approach to the core theme, they write their issue on a piece of paper, announce it to the group, pick a session time and place, and post the paper on the wall. As the wall fills up with sessions, the group is then invited to join the sessions that interest them the most and which they can contribute to, then you’re ready to begin!

Everyone joins the problem-solving group they’ve signed up to, record the discussion and if appropriate, findings can then be shared with the rest of the group afterward.

Open Space Technology   #action plan   #idea generation   #problem solving   #issue analysis   #large group   #online   #remote-friendly   Open Space is a methodology for large groups to create their agenda discerning important topics for discussion, suitable for conferences, community gatherings and whole system facilitation

Techniques to identify and analyze problems

Using a problem-solving method to help a team identify and analyze a problem can be a quick and effective addition to any workshop or meeting.

While further actions are always necessary, you can generate momentum and alignment easily, and these activities are a great place to get started.

We’ve put together this list of techniques to help you and your team with problem identification, analysis, and discussion that sets the foundation for developing effective solutions.

Let’s take a look!

• The Creativity Dice
• Fishbone Analysis
• Problem Tree
• SWOT Analysis
• Agreement-Certainty Matrix
• The Journalistic Six
• LEGO Challenge
• What, So What, Now What?
• Journalists

Individual and group perspectives are incredibly important, but what happens if people are set in their minds and need a change of perspective in order to approach a problem more effectively?

Flip It is a method we love because it is both simple to understand and run, and allows groups to understand how their perspectives and biases are formed. 

Participants in Flip It are first invited to consider concerns, issues, or problems from a perspective of fear and write them on a flip chart. Then, the group is asked to consider those same issues from a perspective of hope and flip their understanding.  

No problem and solution is free from existing bias and by changing perspectives with Flip It, you can then develop a problem solving model quickly and effectively.

Flip It!   #gamestorming   #problem solving   #action   Often, a change in a problem or situation comes simply from a change in our perspectives. Flip It! is a quick game designed to show players that perspectives are made, not born.

10. The Creativity Dice

One of the most useful problem solving skills you can teach your team is of approaching challenges with creativity, flexibility, and openness. Games like The Creativity Dice allow teams to overcome the potential hurdle of too much linear thinking and approach the process with a sense of fun and speed. 

In The Creativity Dice, participants are organized around a topic and roll a dice to determine what they will work on for a period of 3 minutes at a time. They might roll a 3 and work on investigating factual information on the chosen topic. They might roll a 1 and work on identifying the specific goals, standards, or criteria for the session.

Encouraging rapid work and iteration while asking participants to be flexible are great skills to cultivate. Having a stage for idea incubation in this game is also important. Moments of pause can help ensure the ideas that are put forward are the most suitable. 

The Creativity Dice   #creativity   #problem solving   #thiagi   #issue analysis   Too much linear thinking is hazardous to creative problem solving. To be creative, you should approach the problem (or the opportunity) from different points of view. You should leave a thought hanging in mid-air and move to another. This skipping around prevents premature closure and lets your brain incubate one line of thought while you consciously pursue another.

11. Fishbone Analysis

Organizational or team challenges are rarely simple, and it’s important to remember that one problem can be an indication of something that goes deeper and may require further consideration to be solved.

Fishbone Analysis helps groups to dig deeper and understand the origins of a problem. It’s a great example of a root cause analysis method that is simple for everyone on a team to get their head around. 

Participants in this activity are asked to annotate a diagram of a fish, first adding the problem or issue to be worked on at the head of a fish before then brainstorming the root causes of the problem and adding them as bones on the fish. 

Using abstractions such as a diagram of a fish can really help a team break out of their regular thinking and develop a creative approach.

Fishbone Analysis   #problem solving   ##root cause analysis   #decision making   #online facilitation   A process to help identify and understand the origins of problems, issues or observations.

12. Problem Tree 

Encouraging visual thinking can be an essential part of many strategies. By simply reframing and clarifying problems, a group can move towards developing a problem solving model that works for them. 

In Problem Tree, groups are asked to first brainstorm a list of problems – these can be design problems, team problems or larger business problems – and then organize them into a hierarchy. The hierarchy could be from most important to least important or abstract to practical, though the key thing with problem solving games that involve this aspect is that your group has some way of managing and sorting all the issues that are raised.

Once you have a list of problems that need to be solved and have organized them accordingly, you’re then well-positioned for the next problem solving steps.

Problem tree   #define intentions   #create   #design   #issue analysis   A problem tree is a tool to clarify the hierarchy of problems addressed by the team within a design project; it represents high level problems or related sublevel problems.

13. SWOT Analysis

Chances are you’ve heard of the SWOT Analysis before. This problem-solving method focuses on identifying strengths, weaknesses, opportunities, and threats is a tried and tested method for both individuals and teams.

Start by creating a desired end state or outcome and bare this in mind – any process solving model is made more effective by knowing what you are moving towards. Create a quadrant made up of the four categories of a SWOT analysis and ask participants to generate ideas based on each of those quadrants.

Once you have those ideas assembled in their quadrants, cluster them together based on their affinity with other ideas. These clusters are then used to facilitate group conversations and move things forward. 

SWOT analysis   #gamestorming   #problem solving   #action   #meeting facilitation   The SWOT Analysis is a long-standing technique of looking at what we have, with respect to the desired end state, as well as what we could improve on. It gives us an opportunity to gauge approaching opportunities and dangers, and assess the seriousness of the conditions that affect our future. When we understand those conditions, we can influence what comes next.

14. Agreement-Certainty Matrix

Not every problem-solving approach is right for every challenge, and deciding on the right method for the challenge at hand is a key part of being an effective team.

The Agreement Certainty matrix helps teams align on the nature of the challenges facing them. By sorting problems from simple to chaotic, your team can understand what methods are suitable for each problem and what they can do to ensure effective results. 

If you are already using Liberating Structures techniques as part of your problem-solving strategy, the Agreement-Certainty Matrix can be an invaluable addition to your process. We’ve found it particularly if you are having issues with recurring problems in your organization and want to go deeper in understanding the root cause. 

Agreement-Certainty Matrix   #issue analysis   #liberating structures   #problem solving   You can help individuals or groups avoid the frequent mistake of trying to solve a problem with methods that are not adapted to the nature of their challenge. The combination of two questions makes it possible to easily sort challenges into four categories: simple, complicated, complex , and chaotic .  A problem is simple when it can be solved reliably with practices that are easy to duplicate.  It is complicated when experts are required to devise a sophisticated solution that will yield the desired results predictably.  A problem is complex when there are several valid ways to proceed but outcomes are not predictable in detail.  Chaotic is when the context is too turbulent to identify a path forward.  A loose analogy may be used to describe these differences: simple is like following a recipe, complicated like sending a rocket to the moon, complex like raising a child, and chaotic is like the game “Pin the Tail on the Donkey.”  The Liberating Structures Matching Matrix in Chapter 5 can be used as the first step to clarify the nature of a challenge and avoid the mismatches between problems and solutions that are frequently at the root of chronic, recurring problems.

Organizing and charting a team’s progress can be important in ensuring its success. SQUID (Sequential Question and Insight Diagram) is a great model that allows a team to effectively switch between giving questions and answers and develop the skills they need to stay on track throughout the process. 

Begin with two different colored sticky notes – one for questions and one for answers – and with your central topic (the head of the squid) on the board. Ask the group to first come up with a series of questions connected to their best guess of how to approach the topic. Ask the group to come up with answers to those questions, fix them to the board and connect them with a line. After some discussion, go back to question mode by responding to the generated answers or other points on the board.

It’s rewarding to see a diagram grow throughout the exercise, and a completed SQUID can provide a visual resource for future effort and as an example for other teams.

SQUID   #gamestorming   #project planning   #issue analysis   #problem solving   When exploring an information space, it’s important for a group to know where they are at any given time. By using SQUID, a group charts out the territory as they go and can navigate accordingly. SQUID stands for Sequential Question and Insight Diagram.

16. Speed Boat

To continue with our nautical theme, Speed Boat is a short and sweet activity that can help a team quickly identify what employees, clients or service users might have a problem with and analyze what might be standing in the way of achieving a solution.

Methods that allow for a group to make observations, have insights and obtain those eureka moments quickly are invaluable when trying to solve complex problems.

In Speed Boat, the approach is to first consider what anchors and challenges might be holding an organization (or boat) back. Bonus points if you are able to identify any sharks in the water and develop ideas that can also deal with competitors!   

Speed Boat   #gamestorming   #problem solving   #action   Speedboat is a short and sweet way to identify what your employees or clients don’t like about your product/service or what’s standing in the way of a desired goal.

17. The Journalistic Six

Some of the most effective ways of solving problems is by encouraging teams to be more inclusive and diverse in their thinking.

Based on the six key questions journalism students are taught to answer in articles and news stories, The Journalistic Six helps create teams to see the whole picture. By using who, what, when, where, why, and how to facilitate the conversation and encourage creative thinking, your team can make sure that the problem identification and problem analysis stages of the are covered exhaustively and thoughtfully. Reporter’s notebook and dictaphone optional.

The Journalistic Six – Who What When Where Why How   #idea generation   #issue analysis   #problem solving   #online   #creative thinking   #remote-friendly   A questioning method for generating, explaining, investigating ideas.

18. LEGO Challenge

Now for an activity that is a little out of the (toy) box. LEGO Serious Play is a facilitation methodology that can be used to improve creative thinking and problem-solving skills. 

The LEGO Challenge includes giving each member of the team an assignment that is hidden from the rest of the group while they create a structure without speaking.

What the LEGO challenge brings to the table is a fun working example of working with stakeholders who might not be on the same page to solve problems. Also, it’s LEGO! Who doesn’t love LEGO! 

LEGO Challenge   #hyperisland   #team   A team-building activity in which groups must work together to build a structure out of LEGO, but each individual has a secret “assignment” which makes the collaborative process more challenging. It emphasizes group communication, leadership dynamics, conflict, cooperation, patience and problem solving strategy.

19. What, So What, Now What?

If not carefully managed, the problem identification and problem analysis stages of the problem-solving process can actually create more problems and misunderstandings.

The What, So What, Now What? problem-solving activity is designed to help collect insights and move forward while also eliminating the possibility of disagreement when it comes to identifying, clarifying, and analyzing organizational or work problems. 

Facilitation is all about bringing groups together so that might work on a shared goal and the best problem-solving strategies ensure that teams are aligned in purpose, if not initially in opinion or insight.

Throughout the three steps of this game, you give everyone on a team to reflect on a problem by asking what happened, why it is important, and what actions should then be taken. 

This can be a great activity for bringing our individual perceptions about a problem or challenge and contextualizing it in a larger group setting. This is one of the most important problem-solving skills you can bring to your organization.

W³ – What, So What, Now What?   #issue analysis   #innovation   #liberating structures   You can help groups reflect on a shared experience in a way that builds understanding and spurs coordinated action while avoiding unproductive conflict. It is possible for every voice to be heard while simultaneously sifting for insights and shaping new direction. Progressing in stages makes this practical—from collecting facts about What Happened to making sense of these facts with So What and finally to what actions logically follow with Now What . The shared progression eliminates most of the misunderstandings that otherwise fuel disagreements about what to do. Voila!

20. Journalists  

Problem analysis can be one of the most important and decisive stages of all problem-solving tools. Sometimes, a team can become bogged down in the details and are unable to move forward.

Journalists is an activity that can avoid a group from getting stuck in the problem identification or problem analysis stages of the process.

In Journalists, the group is invited to draft the front page of a fictional newspaper and figure out what stories deserve to be on the cover and what headlines those stories will have. By reframing how your problems and challenges are approached, you can help a team move productively through the process and be better prepared for the steps to follow.

Journalists   #vision   #big picture   #issue analysis   #remote-friendly   This is an exercise to use when the group gets stuck in details and struggles to see the big picture. Also good for defining a vision.

Problem-solving techniques for developing solutions 

The success of any problem-solving process can be measured by the solutions it produces. After you’ve defined the issue, explored existing ideas, and ideated, it’s time to narrow down to the correct solution.

Use these problem-solving techniques when you want to help your team find consensus, compare possible solutions, and move towards taking action on a particular problem.

• Improved Solutions
• Four-Step Sketch
• 15% Solutions
• How-Now-Wow matrix
• Impact Effort Matrix

21. Mindspin  

Brainstorming is part of the bread and butter of the problem-solving process and all problem-solving strategies benefit from getting ideas out and challenging a team to generate solutions quickly. 

With Mindspin, participants are encouraged not only to generate ideas but to do so under time constraints and by slamming down cards and passing them on. By doing multiple rounds, your team can begin with a free generation of possible solutions before moving on to developing those solutions and encouraging further ideation. 

This is one of our favorite problem-solving activities and can be great for keeping the energy up throughout the workshop. Remember the importance of helping people become engaged in the process – energizing problem-solving techniques like Mindspin can help ensure your team stays engaged and happy, even when the problems they’re coming together to solve are complex. 

MindSpin   #teampedia   #idea generation   #problem solving   #action   A fast and loud method to enhance brainstorming within a team. Since this activity has more than round ideas that are repetitive can be ruled out leaving more creative and innovative answers to the challenge.

22. Improved Solutions

After a team has successfully identified a problem and come up with a few solutions, it can be tempting to call the work of the problem-solving process complete. That said, the first solution is not necessarily the best, and by including a further review and reflection activity into your problem-solving model, you can ensure your group reaches the best possible result. 

One of a number of problem-solving games from Thiagi Group, Improved Solutions helps you go the extra mile and develop suggested solutions with close consideration and peer review. By supporting the discussion of several problems at once and by shifting team roles throughout, this problem-solving technique is a dynamic way of finding the best solution. 

Improved Solutions   #creativity   #thiagi   #problem solving   #action   #team   You can improve any solution by objectively reviewing its strengths and weaknesses and making suitable adjustments. In this creativity framegame, you improve the solutions to several problems. To maintain objective detachment, you deal with a different problem during each of six rounds and assume different roles (problem owner, consultant, basher, booster, enhancer, and evaluator) during each round. At the conclusion of the activity, each player ends up with two solutions to her problem.

23. Four Step Sketch

Creative thinking and visual ideation does not need to be confined to the opening stages of your problem-solving strategies. Exercises that include sketching and prototyping on paper can be effective at the solution finding and development stage of the process, and can be great for keeping a team engaged. 

By going from simple notes to a crazy 8s round that involves rapidly sketching 8 variations on their ideas before then producing a final solution sketch, the group is able to iterate quickly and visually. Problem-solving techniques like Four-Step Sketch are great if you have a group of different thinkers and want to change things up from a more textual or discussion-based approach.

Four-Step Sketch   #design sprint   #innovation   #idea generation   #remote-friendly   The four-step sketch is an exercise that helps people to create well-formed concepts through a structured process that includes: Review key information Start design work on paper,  Consider multiple variations , Create a detailed solution . This exercise is preceded by a set of other activities allowing the group to clarify the challenge they want to solve. See how the Four Step Sketch exercise fits into a Design Sprint

24. 15% Solutions

Some problems are simpler than others and with the right problem-solving activities, you can empower people to take immediate actions that can help create organizational change. 

Part of the liberating structures toolkit, 15% solutions is a problem-solving technique that focuses on finding and implementing solutions quickly. A process of iterating and making small changes quickly can help generate momentum and an appetite for solving complex problems.

Problem-solving strategies can live and die on whether people are onboard. Getting some quick wins is a great way of getting people behind the process.   

It can be extremely empowering for a team to realize that problem-solving techniques can be deployed quickly and easily and delineate between things they can positively impact and those things they cannot change. 

15% Solutions   #action   #liberating structures   #remote-friendly   You can reveal the actions, however small, that everyone can do immediately. At a minimum, these will create momentum, and that may make a BIG difference.  15% Solutions show that there is no reason to wait around, feel powerless, or fearful. They help people pick it up a level. They get individuals and the group to focus on what is within their discretion instead of what they cannot change.  With a very simple question, you can flip the conversation to what can be done and find solutions to big problems that are often distributed widely in places not known in advance. Shifting a few grains of sand may trigger a landslide and change the whole landscape.

25. How-Now-Wow Matrix

The problem-solving process is often creative, as complex problems usually require a change of thinking and creative response in order to find the best solutions. While it’s common for the first stages to encourage creative thinking, groups can often gravitate to familiar solutions when it comes to the end of the process. 

When selecting solutions, you don’t want to lose your creative energy! The How-Now-Wow Matrix from Gamestorming is a great problem-solving activity that enables a group to stay creative and think out of the box when it comes to selecting the right solution for a given problem.

Problem-solving techniques that encourage creative thinking and the ideation and selection of new solutions can be the most effective in organisational change. Give the How-Now-Wow Matrix a go, and not just for how pleasant it is to say out loud. 

How-Now-Wow Matrix   #gamestorming   #idea generation   #remote-friendly   When people want to develop new ideas, they most often think out of the box in the brainstorming or divergent phase. However, when it comes to convergence, people often end up picking ideas that are most familiar to them. This is called a ‘creative paradox’ or a ‘creadox’. The How-Now-Wow matrix is an idea selection tool that breaks the creadox by forcing people to weigh each idea on 2 parameters.

26. Impact and Effort Matrix

All problem-solving techniques hope to not only find solutions to a given problem or challenge but to find the best solution. When it comes to finding a solution, groups are invited to put on their decision-making hats and really think about how a proposed idea would work in practice. 

The Impact and Effort Matrix is one of the problem-solving techniques that fall into this camp, empowering participants to first generate ideas and then categorize them into a 2×2 matrix based on impact and effort.

Activities that invite critical thinking while remaining simple are invaluable. Use the Impact and Effort Matrix to move from ideation and towards evaluating potential solutions before then committing to them. 

Impact and Effort Matrix   #gamestorming   #decision making   #action   #remote-friendly   In this decision-making exercise, possible actions are mapped based on two factors: effort required to implement and potential impact. Categorizing ideas along these lines is a useful technique in decision making, as it obliges contributors to balance and evaluate suggested actions before committing to them.

27. Dotmocracy

If you’ve followed each of the problem-solving steps with your group successfully, you should move towards the end of your process with heaps of possible solutions developed with a specific problem in mind. But how do you help a group go from ideation to putting a solution into action? 

Dotmocracy – or Dot Voting -is a tried and tested method of helping a team in the problem-solving process make decisions and put actions in place with a degree of oversight and consensus. 

One of the problem-solving techniques that should be in every facilitator’s toolbox, Dot Voting is fast and effective and can help identify the most popular and best solutions and help bring a group to a decision effectively. 

Dotmocracy   #action   #decision making   #group prioritization   #hyperisland   #remote-friendly   Dotmocracy is a simple method for group prioritization or decision-making. It is not an activity on its own, but a method to use in processes where prioritization or decision-making is the aim. The method supports a group to quickly see which options are most popular or relevant. The options or ideas are written on post-its and stuck up on a wall for the whole group to see. Each person votes for the options they think are the strongest, and that information is used to inform a decision.

All facilitators know that warm-ups and icebreakers are useful for any workshop or group process. Problem-solving workshops are no different.

Use these problem-solving techniques to warm up a group and prepare them for the rest of the process. Activating your group by tapping into some of the top problem-solving skills can be one of the best ways to see great outcomes from your session.

• Check-in/Check-out
• Doodling Together
• Show and Tell
• Constellations
• Draw a Tree

28. Check-in / Check-out

Solid processes are planned from beginning to end, and the best facilitators know that setting the tone and establishing a safe, open environment can be integral to a successful problem-solving process.

Check-in / Check-out is a great way to begin and/or bookend a problem-solving workshop. Checking in to a session emphasizes that everyone will be seen, heard, and expected to contribute. 

If you are running a series of meetings, setting a consistent pattern of checking in and checking out can really help your team get into a groove. We recommend this opening-closing activity for small to medium-sized groups though it can work with large groups if they’re disciplined!

Check-in / Check-out   #team   #opening   #closing   #hyperisland   #remote-friendly   Either checking-in or checking-out is a simple way for a team to open or close a process, symbolically and in a collaborative way. Checking-in/out invites each member in a group to be present, seen and heard, and to express a reflection or a feeling. Checking-in emphasizes presence, focus and group commitment; checking-out emphasizes reflection and symbolic closure.

29. Doodling Together  

Thinking creatively and not being afraid to make suggestions are important problem-solving skills for any group or team, and warming up by encouraging these behaviors is a great way to start. 

Doodling Together is one of our favorite creative ice breaker games – it’s quick, effective, and fun and can make all following problem-solving steps easier by encouraging a group to collaborate visually. By passing cards and adding additional items as they go, the workshop group gets into a groove of co-creation and idea development that is crucial to finding solutions to problems. 

Doodling Together   #collaboration   #creativity   #teamwork   #fun   #team   #visual methods   #energiser   #icebreaker   #remote-friendly   Create wild, weird and often funny postcards together & establish a group’s creative confidence.

30. Show and Tell

You might remember some version of Show and Tell from being a kid in school and it’s a great problem-solving activity to kick off a session.

Asking participants to prepare a little something before a workshop by bringing an object for show and tell can help them warm up before the session has even begun! Games that include a physical object can also help encourage early engagement before moving onto more big-picture thinking.

By asking your participants to tell stories about why they chose to bring a particular item to the group, you can help teams see things from new perspectives and see both differences and similarities in the way they approach a topic. Great groundwork for approaching a problem-solving process as a team! 

Show and Tell   #gamestorming   #action   #opening   #meeting facilitation   Show and Tell taps into the power of metaphors to reveal players’ underlying assumptions and associations around a topic The aim of the game is to get a deeper understanding of stakeholders’ perspectives on anything—a new project, an organizational restructuring, a shift in the company’s vision or team dynamic.

31. Constellations

Who doesn’t love stars? Constellations is a great warm-up activity for any workshop as it gets people up off their feet, energized, and ready to engage in new ways with established topics. It’s also great for showing existing beliefs, biases, and patterns that can come into play as part of your session.

Using warm-up games that help build trust and connection while also allowing for non-verbal responses can be great for easing people into the problem-solving process and encouraging engagement from everyone in the group. Constellations is great in large spaces that allow for movement and is definitely a practical exercise to allow the group to see patterns that are otherwise invisible. 

Constellations   #trust   #connection   #opening   #coaching   #patterns   #system   Individuals express their response to a statement or idea by standing closer or further from a central object. Used with teams to reveal system, hidden patterns, perspectives.

32. Draw a Tree

Problem-solving games that help raise group awareness through a central, unifying metaphor can be effective ways to warm-up a group in any problem-solving model.

Draw a Tree is a simple warm-up activity you can use in any group and which can provide a quick jolt of energy. Start by asking your participants to draw a tree in just 45 seconds – they can choose whether it will be abstract or realistic. 

Once the timer is up, ask the group how many people included the roots of the tree and use this as a means to discuss how we can ignore important parts of any system simply because they are not visible.

All problem-solving strategies are made more effective by thinking of problems critically and by exposing things that may not normally come to light. Warm-up games like Draw a Tree are great in that they quickly demonstrate some key problem-solving skills in an accessible and effective way.

Draw a Tree   #thiagi   #opening   #perspectives   #remote-friendly   With this game you can raise awarness about being more mindful, and aware of the environment we live in.

Each step of the problem-solving workshop benefits from an intelligent deployment of activities, games, and techniques. Bringing your session to an effective close helps ensure that solutions are followed through on and that you also celebrate what has been achieved.

Here are some problem-solving activities you can use to effectively close a workshop or meeting and ensure the great work you’ve done can continue afterward.

• One Breath Feedback
• Who What When Matrix
• Response Cards

How do I conclude a problem-solving process?

All good things must come to an end. With the bulk of the work done, it can be tempting to conclude your workshop swiftly and without a moment to debrief and align. This can be problematic in that it doesn’t allow your team to fully process the results or reflect on the process.

At the end of an effective session, your team will have gone through a process that, while productive, can be exhausting. It’s important to give your group a moment to take a breath, ensure that they are clear on future actions, and provide short feedback before leaving the space. 

The primary purpose of any problem-solving method is to generate solutions and then implement them. Be sure to take the opportunity to ensure everyone is aligned and ready to effectively implement the solutions you produced in the workshop.

Remember that every process can be improved and by giving a short moment to collect feedback in the session, you can further refine your problem-solving methods and see further success in the future too.

33. One Breath Feedback

Maintaining attention and focus during the closing stages of a problem-solving workshop can be tricky and so being concise when giving feedback can be important. It’s easy to incur “death by feedback” should some team members go on for too long sharing their perspectives in a quick feedback round. 

One Breath Feedback is a great closing activity for workshops. You give everyone an opportunity to provide feedback on what they’ve done but only in the space of a single breath. This keeps feedback short and to the point and means that everyone is encouraged to provide the most important piece of feedback to them. 

One breath feedback   #closing   #feedback   #action   This is a feedback round in just one breath that excels in maintaining attention: each participants is able to speak during just one breath … for most people that’s around 20 to 25 seconds … unless of course you’ve been a deep sea diver in which case you’ll be able to do it for longer.

34. Who What When Matrix 

Matrices feature as part of many effective problem-solving strategies and with good reason. They are easily recognizable, simple to use, and generate results.

The Who What When Matrix is a great tool to use when closing your problem-solving session by attributing a who, what and when to the actions and solutions you have decided upon. The resulting matrix is a simple, easy-to-follow way of ensuring your team can move forward. 

Great solutions can’t be enacted without action and ownership. Your problem-solving process should include a stage for allocating tasks to individuals or teams and creating a realistic timeframe for those solutions to be implemented or checked out. Use this method to keep the solution implementation process clear and simple for all involved. 

Who/What/When Matrix   #gamestorming   #action   #project planning   With Who/What/When matrix, you can connect people with clear actions they have defined and have committed to.

35. Response cards

Group discussion can comprise the bulk of most problem-solving activities and by the end of the process, you might find that your team is talked out! 

Providing a means for your team to give feedback with short written notes can ensure everyone is head and can contribute without the need to stand up and talk. Depending on the needs of the group, giving an alternative can help ensure everyone can contribute to your problem-solving model in the way that makes the most sense for them.

Response Cards is a great way to close a workshop if you are looking for a gentle warm-down and want to get some swift discussion around some of the feedback that is raised. 

Response Cards   #debriefing   #closing   #structured sharing   #questions and answers   #thiagi   #action   It can be hard to involve everyone during a closing of a session. Some might stay in the background or get unheard because of louder participants. However, with the use of Response Cards, everyone will be involved in providing feedback or clarify questions at the end of a session.

Save time and effort discovering the right solutions

A structured problem solving process is a surefire way of solving tough problems, discovering creative solutions and driving organizational change. But how can you design for successful outcomes?

With SessionLab, it’s easy to design engaging workshops that deliver results. Drag, drop and reorder blocks  to build your agenda. When you make changes or update your agenda, your session  timing   adjusts automatically , saving you time on manual adjustments.

Collaborating with stakeholders or clients? Share your agenda with a single click and collaborate in real-time. No more sending documents back and forth over email.

Explore  how to use SessionLab  to design effective problem solving workshops or  watch this five minute video  to see the planner in action!

Over to you

The problem-solving process can often be as complicated and multifaceted as the problems they are set-up to solve. With the right problem-solving techniques and a mix of creative exercises designed to guide discussion and generate purposeful ideas, we hope we’ve given you the tools to find the best solutions as simply and easily as possible.

Is there a problem-solving technique that you are missing here? Do you have a favorite activity or method you use when facilitating? Let us know in the comments below, we’d love to hear from you! 

thank you very much for these excellent techniques

Certainly wonderful article, very detailed. Shared!

Your list of techniques for problem solving can be helpfully extended by adding TRIZ to the list of techniques. TRIZ has 40 problem solving techniques derived from methods inventros and patent holders used to get new patents. About 10-12 are general approaches. many organization sponsor classes in TRIZ that are used to solve business problems or general organiztational problems. You can take a look at TRIZ and dwonload a free internet booklet to see if you feel it shound be included per your selection process.

Leave a Comment Cancel reply

Your email address will not be published. Required fields are marked *

Going from a mere idea to a workshop that delivers results for your clients can feel like a daunting task. In this piece, we will shine a light on all the work behind the scenes and help you learn how to plan a workshop from start to finish. On a good day, facilitation can feel like effortless magic, but that is mostly the result of backstage work, foresight, and a lot of careful planning. Read on to learn a step-by-step approach to breaking the process of planning a workshop into small, manageable chunks.  The flow starts with the first meeting with a client to define the purposes of a workshop.…

How does learning work? A clever 9-year-old once told me: “I know I am learning something new when I am surprised.” The science of adult learning tells us that, in order to learn new skills (which, unsurprisingly, is harder for adults to do than kids) grown-ups need to first get into a specific headspace.  In a business, this approach is often employed in a training session where employees learn new skills or work on professional development. But how do you ensure your training is effective? In this guide, we'll explore how to create an effective training session plan and run engaging training sessions. As team leader, project manager, or consultant,…

Effective online tools are a necessity for smooth and engaging virtual workshops and meetings. But how do you choose the right ones? Do you sometimes feel that the good old pen and paper or MS Office toolkit and email leaves you struggling to stay on top of managing and delivering your workshop? Fortunately, there are plenty of online tools to make your life easier when you need to facilitate a meeting and lead workshops. In this post, we’ll share our favorite online tools you can use to make your job as a facilitator easier. In fact, there are plenty of free online workshop tools and meeting facilitation software you can…

Design your next workshop with SessionLab

Join the 150,000 facilitators using SessionLab

Sign up for free