hypothesis testing excel one sample

• DNA/RNA Analysis
• Lab Recipes
• GraphPad Prism
• Calculators

How To Perform A One-Sample T-Test In Excel

In this tutorial, I will show you how to perform a one-sample T-test by using Microsoft Excel.

What is a one-sample T-test?

A one-sample T-test is a statistical test to determine if a sample mean is significantly different from a hypothesized mean.

Example data

For this tutorial, I have a sample of 12 young female adults (18 years old). I measured their height in inches and entered the data into a single column in Excel.

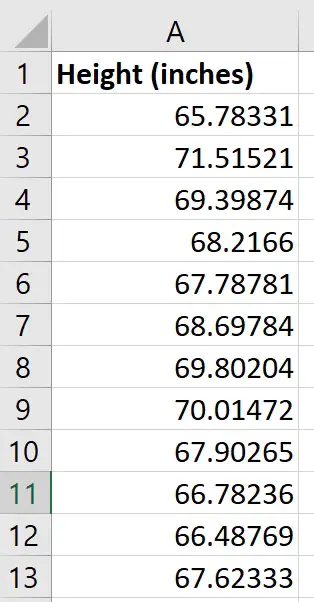
For the purpose of this example, I will pretend the national average height of 18-year-old girls is 66.5 inches.

I want to perform a one-sample T-test in Excel to determine if there is any significant difference between the heights of my sample compared with the national average height (66.5 inches).

The null and alternative hypothesis are:

• Null hypothesis – There is no significant difference between the heights of the sample, compared with the national average
• Alternative hypothesis – There is a significant difference between the heights of the sample, compared with the national average

How to perform a one-sample T-test in Excel

There is no function in Excel to perform a one-sample T-test. Instead, I will show you a step-by-step process on how to achieve this.

Firstly, calculate the mean, standard deviation (SD) and standard error of the mean (SEM) in Excel. Then, use this information to determine the t-statistic and ultimately the p-value.

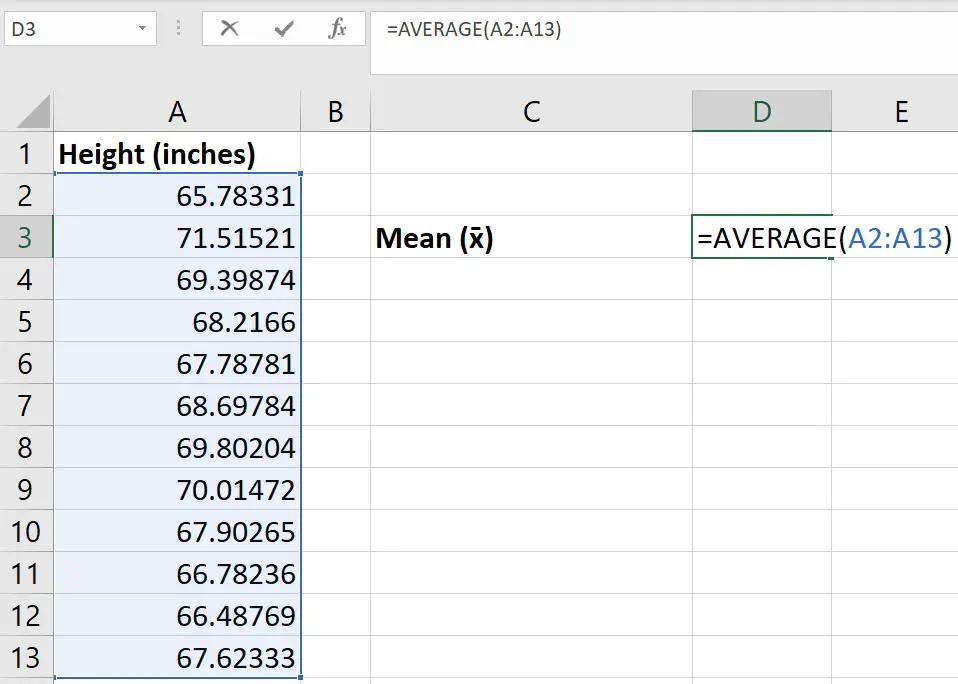
Step 1: Calculate the average

The first thing you should do is to calculate the average value of the sample data.

This can be easily calculated by using the AVERAGE function in Excel.

In Excel, click on an empty cell and enter the following…

Replace cell1 in the equation with the cell containing the first data point and replace cell2 with the cell containing the last data point.

Below is a screenshot of what my example looks like.

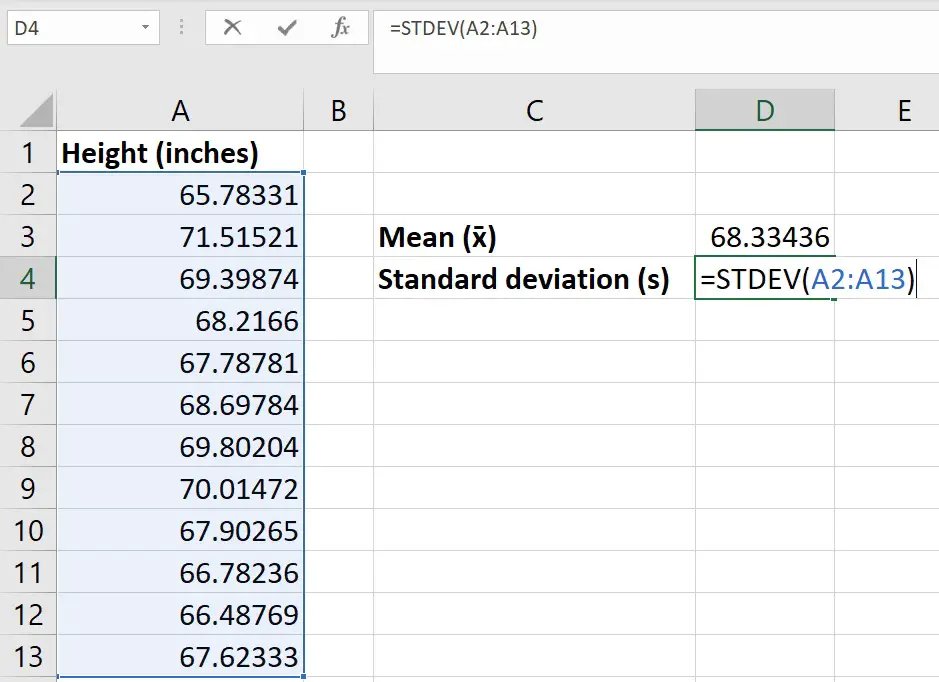
Step 2: Calculate the standard deviation

The next step is the calculate the SD of the sample data.

To do this, use the STDEV function.

In an empty cell, enter the following…

Again, replace cell1 and cell 2 in the equation with the cell containing the first and last data points, respectively.

Note, you can also use the STDEV.S function to achieve the same result.

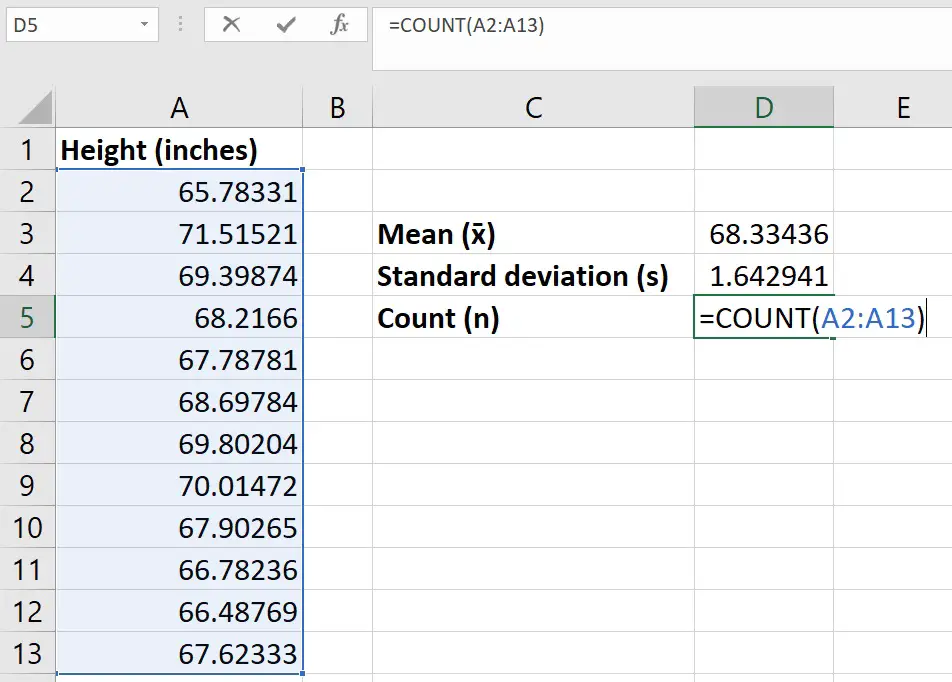
Step 3: Calculate the number of observations

For the next step, simply count the number of observations in the sample.

This can be easily done if you have relatively small numbers. Otherwise, use the COUNT function to get Excel to count them for you.

As before, replace the cell1 and cell2 with the respected first and last cells.

Step 4: Calculate the standard error of the mean

Now we have the mean and n, we can now work out the standard error of the mean (SEM) .

To manually calculate the SEM, simply divide the SD by the square root of n.

Replace the following:

• SD – With the cell containing the SD
• n – With the cell containing the n

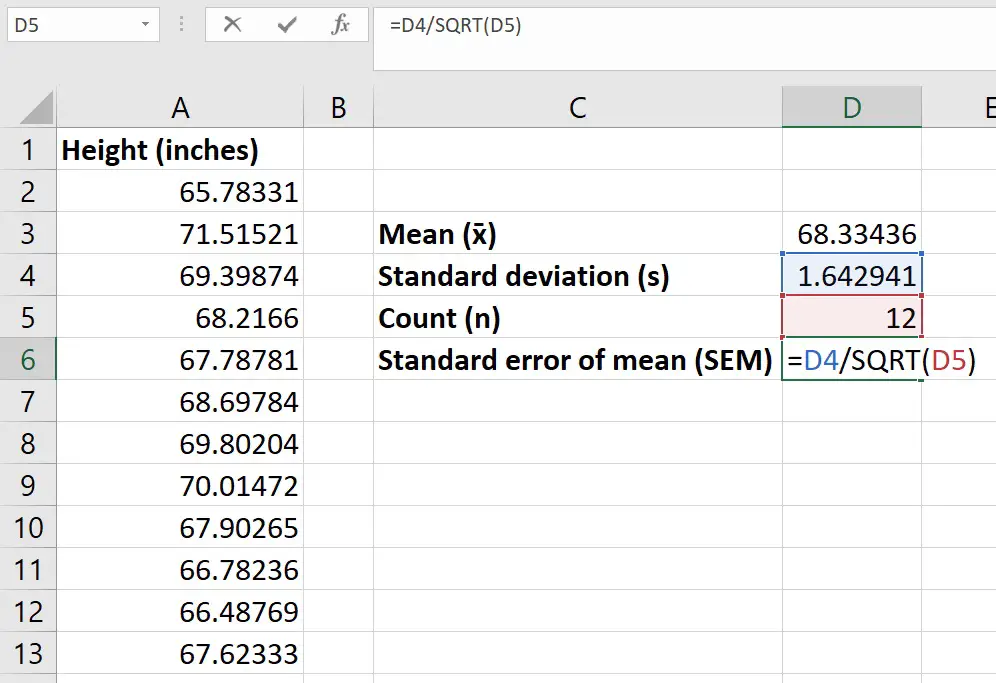
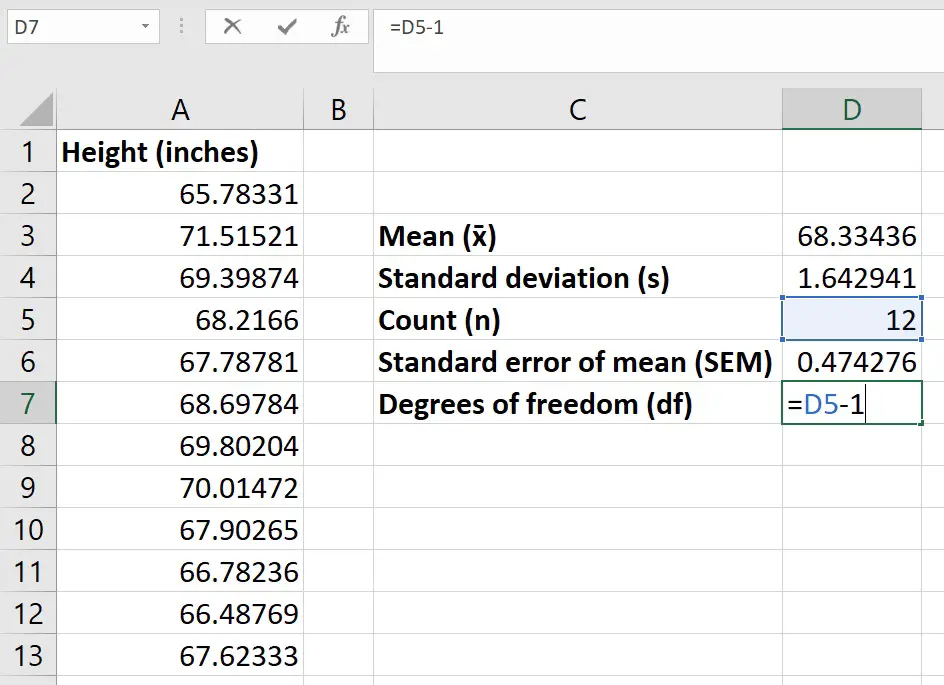
Step 5: Calculate the degrees of freedom

To calculate the degrees of freedom (df) in this case, simply subtract 1 from the n.

In a new cell, enter the following…

Replace n with the cell containing the n.

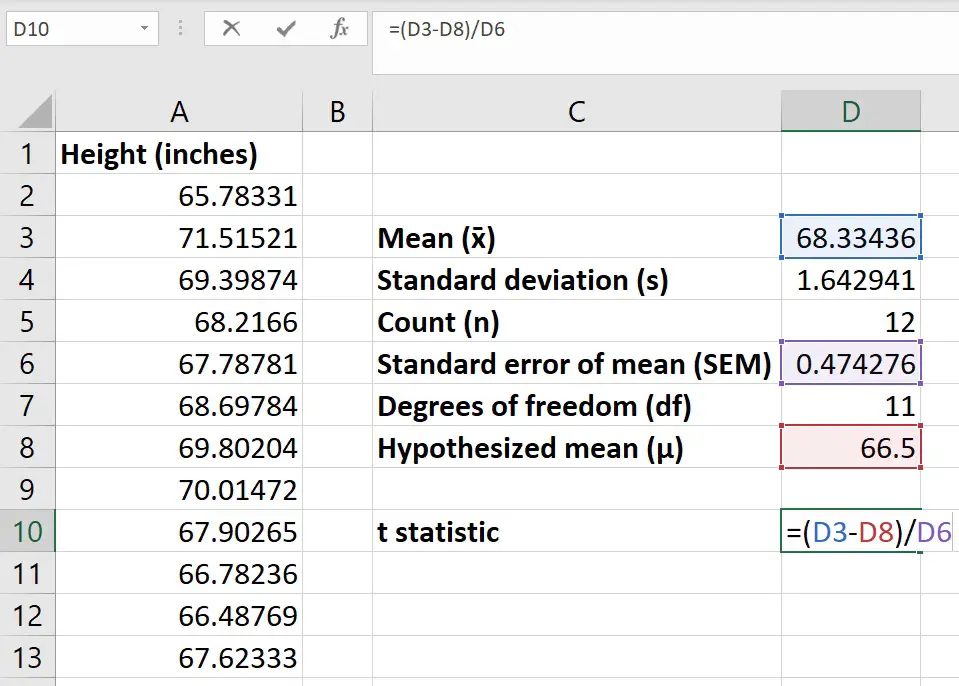
Step 6: Calculate the t-statistic

Before calculating the t-statistic, enter the hypothesized mean into a new cell in Excel.

The hypothesized mean is the value you want to compare your sample data to. So, in my example, this will be the national average height of 18-year-old girls – 66.5.

The formula to calculate the t-statistic for a one-sample T-test is shown below.

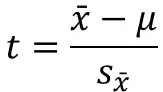
• x̄ – The sample mean
• μ – The hypothesized mean; in this case, the population mean
• s x̄ – The SEM

So, to work this out in Excel, click on an empty cell and enter the following…

Replace each component of the formula with the cell containing the corresponding value.

Step 7: Calculate the p-value

The last step is to calculate the p-value by using the t-statistic and the df. This is achieved by using the TDIST function.

Replace the following components of the function with…

• t – The cell containing the t-statistic
• df – The cell containing the df
• tails – Enter 1 if you want to perform a one-tailed analysis, or a 2 if you want to do a two-tailed analysis

For my example, I did not hypothesize if my sample data was greater or lower than the national average. Therefore, I will perform a two-tailed analysis.

If I hypothesized the sample data will be greater than the national average, then I would select to do a one-tailed analysis instead.

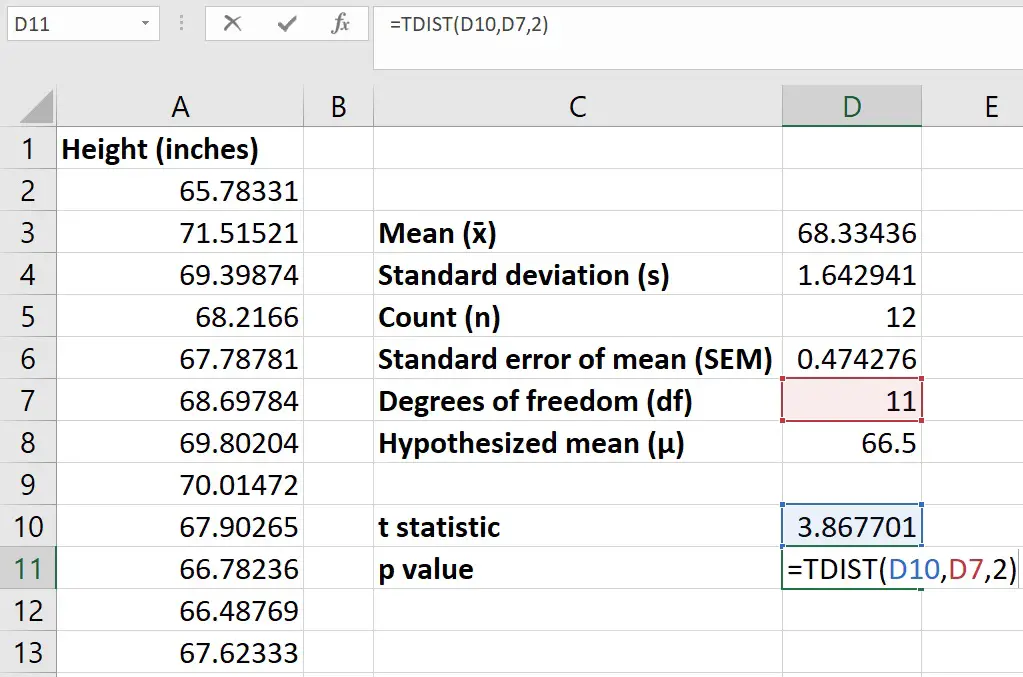
So, the p-value for my example is 0.0026.

If my alpha level was set at 0.05, then since the p-value is below the alpha level, I will reject the null hypothesis and accept the alternative hypothesis.

In other words, there is a significant difference between the heights of the sample, compared with the national average.

Wrapping up

In this tutorial, I have shown you how to perform a one-sample T-test in Excel. There is no function to perform a one-sample T-test in Excel. However, you can still perform this by using a stepwise approach.

Microsoft Excel version used: 365 ProPlus

RELATED ARTICLES MORE FROM AUTHOR

How To Perform Descriptive Statistics In Microsoft Excel

How To Do Basic Math In Excel (Add, Subtract, Multiply & Divide)

How To Calculate A Weighted Average In Microsoft Excel

OMG!. Thank you sooooo much! I’ve been in statistics hell and this is exactly what I was looking for. The process is explained well and had all of the formulas I needed to do both the test statistic and p value.

LEAVE A REPLY Cancel reply

Save my name, email, and website in this browser for the next time I comment.

Other Excel tutorials

How to perform random sampling in microsoft excel, how to perform a chi-square test of independence in excel, stay connected.

• Skip to secondary menu
• Skip to main content
• Skip to primary sidebar

Statistics By Jim

Making statistics intuitive

One Sample T Test: Definition, Using & Example

By Jim Frost Leave a Comment

What is a One Sample T Test?

Use a one sample t test to evaluate a population mean using a single sample. Usually, you conduct this hypothesis test to determine whether a population mean differs from a hypothesized value you specify. The hypothesized value can be theoretically important in the study area, a reference value, or a target.

For example, a beverage company claims its soda cans contain 12 ounces. A researcher randomly samples their cans and measures the amount of fluid in each one. A one-sample t-test can use the sample data to determine whether the entire population of soda cans differs from the hypothesized value of 12 ounces.

In this post, learn about the one-sample t-test, its hypotheses and assumptions, and how to interpret the results.

Related post : Difference between Descriptive and Inferential Statistics

One Sample T Test Hypotheses

A one sample t test has the following hypotheses:

• Null hypothesis (H 0 ): The population mean equals the hypothesized value (µ = H 0 ).
• Alternative hypothesis (H A ): The population mean does not equal the hypothesized value (µ ≠ H 0 ).

If the p-value is less than your significance level (e.g., 0.05), you can reject the null hypothesis. The difference between the sample mean and the hypothesized value is statistically significant. Your sample provides strong enough evidence to conclude that the population mean does not equal the hypothesized value.

Learn how this analysis compares to the Z Test .

Related posts : How to Interpret P Values and Null Hypothesis: Definition, Rejecting & Examples .

One Sample T Test Assumptions

For reliable one sample t test results, your data should satisfy the following assumptions:

Random Sample

Drawing a random sample from your target population helps ensure your data represent the population. Samples that don’t reflect that population tend to produce invalid results.

Related posts : Populations, Parameters, and Samples in Inferential Statistics and Representative Samples: Definition, Uses & Examples .

Continuous Data

One-sample t-tests require continuous data . These variables can take on any numeric value, and the scale can be split meaningfully into smaller increments. For example, temperature, height, weight, and volume are continuous data.

Read  Comparing Hypothesis Tests for Continuous, Binary, and Count Data  for more information. .

Normally distributed data or your sample has more than 20 observations

This hypothesis test assumes your data follow the normal distribution . However, your data can be mildly skewed when the distribution is unimodal and your sample size is greater than 20 because of the central limit theorem.

Be sure to check for outliers because they can throw off the results.

Related posts : Central Limit Theorem , Skewed Distributions , and 5 Ways to Find Outliers .

Independent Observations

The one-sample t-test assumes that observations are independent of each other, meaning that the value of one observation does not influence or depend on another observation’s value. Violating this assumption can lead to inaccurate results because the test relies on the premise that each data point provides unique and separate information.

Example One Sample T Test

Let’s return to the 12-ounce soda can example and perform a one-sample t-test on the data. Imagine we randomly collected 30 cans of soda and measured their contents.

We want to determine whether the difference between the sample mean and the hypothesized value (12) is statistically significant. Download the CSV file that contains the example data: OneSampleTTest .

Here is how a portion of the data appear in the worksheet.

The histogram shows the data are not skewed , and no outliers are present.

Interpreting the Results

Here’s how to read and report the results for a one sample t test.

The statistical output indicates that the sample mean (A) is 11.8013. Because the p-value (B) of 0.000 is less than our significance level of 0.05, the results are statistically significant. We reject the null hypothesis and conclude that the population mean does not equal 12 ounces. Specifically, it is less than that target value. The beverage company is underfilling the cans.

Learn more about Statistical Significance: Definition & Meaning .

The confidence interval (C) indicates the population mean for all cans is likely between 11.7358 and 11.8668 ounces. This range excludes our hypothesized value of 12 ounces, reaffirming the statistical significance. Learn more about confidence intervals .

To learn more about performing t-tests and how they work, read the following posts:

• T Test Overview
• Independent Samples T Test
• Paired T Test
• Running T Tests in Excel
• T-Values and T-Distributions

Share this:

Reader Interactions

Comments and questions cancel reply.

• Mastering Hypothesis Testing in Excel: A Practical Guide for Students

Excel for Hypothesis Testing: A Practical Approach for Students

Hypothesis testing lies at the heart of statistical inference, serving as a cornerstone for drawing meaningful conclusions from data. It's a methodical process used to evaluate assumptions about a population parameter, typically based on sample data. The fundamental idea behind hypothesis testing is to assess whether observed differences or relationships in the sample are statistically significant enough to warrant generalizations to the larger population. This process involves formulating null and alternative hypotheses, selecting an appropriate statistical test, collecting sample data, and interpreting the results to make informed decisions. In the realm of statistical software, SAS stands out as a robust and widely used tool for data analysis in various fields such as academia, industry, and research. Its extensive capabilities make it particularly favored for complex analyses, large datasets, and advanced modeling techniques. However, despite its versatility and power, SAS can have a steep learning curve, especially for students who are just beginning their journey into statistics. The intricacies of programming syntax, data manipulation, and interpreting output may pose challenges for novice users, potentially hindering their understanding of statistical concepts like hypothesis testing. Understanding hypothesis testing is essential for performing statistical analyses and drawing meaningful conclusions from data using Excel 's built-in functions and tools.

Enter Excel, a ubiquitous spreadsheet software that most students are already familiar with to some extent. While Excel may not offer the same level of sophistication as SAS in terms of advanced statistical procedures, it remains a valuable tool, particularly for introductory and intermediate-level analyses. Its intuitive interface, user-friendly features, and widespread accessibility make it an attractive option for students seeking a practical approach to learning statistics. By leveraging Excel's built-in functions, data visualization tools, and straightforward formulas, students can gain hands-on experience with hypothesis testing in a familiar environment. In this blog post, we aim to bridge the gap between theoretical concepts and practical application by demonstrating how Excel can serve as a valuable companion for students tackling hypothesis testing problems, including those typically encountered in SAS assignments. We will focus on demystifying the process of hypothesis testing, breaking it down into manageable steps, and showcasing Excel's capabilities for conducting various tests commonly encountered in introductory statistics courses.

Understanding the Basics

Hypothesis testing is a fundamental concept in statistics that allows researchers to draw conclusions about a population based on sample data. At its core, hypothesis testing involves making a decision about whether a statement regarding a population parameter is likely to be true. This decision is based on the analysis of sample data and is guided by two competing hypotheses: the null hypothesis (H0) and the alternative hypothesis (Ha). The null hypothesis represents the status quo or the absence of an effect. It suggests that any observed differences or relationships in the sample data are due to random variation or chance. On the other hand, the alternative hypothesis contradicts the null hypothesis and suggests the presence of an effect or difference in the population. It reflects the researcher's belief or the hypothesis they aim to support with their analysis.

Formulating Hypotheses

In Excel, students can easily formulate hypotheses using simple formulas and logical operators. For instance, suppose a researcher wants to test whether the mean of a sample is equal to a specified value. They can use the AVERAGE function in Excel to calculate the sample mean and then compare it to the specified value using logical operators like "=" for equality. If the calculated mean is equal to the specified value, it supports the null hypothesis; otherwise, it supports the alternative hypothesis.

Excel's flexibility allows students to customize their hypotheses based on the specific parameters they are testing. Whether it's comparing means, proportions, variances, or other population parameters, Excel provides a user-friendly interface for formulating hypotheses and conducting statistical analysis.

Selecting the Appropriate Test

Excel offers a plethora of functions and tools for conducting various types of hypothesis tests, including t-tests, z-tests, chi-square tests, and ANOVA (analysis of variance). However, selecting the appropriate test requires careful consideration of the assumptions and conditions associated with each test. Students should familiarize themselves with the assumptions underlying each hypothesis test and assess whether their data meets those assumptions. For example, t-tests assume that the data follow a normal distribution, while chi-square tests require categorical data and independence between observations.

Furthermore, students should consider the nature of their research question and the type of data they are analyzing. Are they comparing means of two independent groups or assessing the association between categorical variables? By understanding the characteristics of their data and the requirements of each test, students can confidently choose the appropriate hypothesis test in Excel.

T-tests are statistical tests commonly used to compare the means of two independent samples or to compare the mean of a single sample to a known value. These tests are valuable in various fields, including psychology, biology, economics, and more. In Excel, students can employ the T.TEST function to conduct t-tests, providing them with a practical and accessible way to analyze their data and draw conclusions about population parameters based on sample statistics.

Independent Samples T-Test

The independent samples t-test, also known as the unpaired t-test, is utilized when comparing the means of two independent groups. This test is often employed in experimental and observational studies to assess whether there is a significant difference between the means of the two groups. In Excel, students can easily organize their data into separate columns representing the two groups, calculate the sample means and standard deviations for each group, and then use the T.TEST function to obtain the p-value. The p-value obtained from the T.TEST function represents the probability of observing the sample data if the null hypothesis, which typically states that there is no difference between the means of the two groups, is true.

A small p-value (typically less than the chosen significance level, commonly 0.05) indicates that there is sufficient evidence to reject the null hypothesis in favor of the alternative hypothesis, suggesting a significant difference between the group means. By conducting an independent samples t-test in Excel, students can not only assess the significance of differences between two groups but also gain valuable experience in data analysis and hypothesis testing, which are essential skills in various academic and professional settings.

Paired Samples T-Test

The paired samples t-test, also known as the dependent t-test or matched pairs t-test, is employed when comparing the means of two related groups. This test is often used in studies where participants are measured before and after an intervention or when each observation in one group is matched or paired with a specific observation in the other group. Examples include comparing pre-test and post-test scores, analyzing the performance of individuals under different conditions, and assessing the effectiveness of a treatment or intervention. In Excel, students can perform a paired samples t-test by first calculating the differences between paired observations (e.g., subtracting the before-measurement from the after-measurement). Next, they can use the one-sample t-test function, specifying the calculated differences as the sample data. This approach allows students to determine whether the mean difference between paired observations is statistically significant, indicating whether there is a meaningful change or effect between the two related groups.

Interpreting the results of a paired samples t-test involves assessing the obtained p-value in relation to the chosen significance level. A small p-value suggests that there is sufficient evidence to reject the null hypothesis, indicating a significant difference between the paired observations. This information can help students draw meaningful conclusions from their data and make informed decisions based on statistical evidence. By conducting paired samples t-tests in Excel, students can not only analyze the relationship between related groups but also develop critical thinking skills and gain practical experience in hypothesis testing, which are valuable assets in both academic and professional contexts. Additionally, mastering the application of statistical tests in Excel can enhance students' data analysis skills and prepare them for future research endeavors and real-world challenges.

Chi-Square Test

The chi-square test is a versatile statistical tool used to assess the association between two categorical variables. In essence, it helps determine whether the observed frequencies in a dataset significantly deviate from what would be expected under certain assumptions. Excel provides a straightforward means to perform chi-square tests using the CHISQ.TEST function, which calculates the probability associated with the chi-square statistic.

Goodness-of-Fit Test

One application of the chi-square test is the goodness-of-fit test, which evaluates how well the observed frequencies in a single categorical variable align with the expected frequencies dictated by a theoretical distribution. This test is particularly useful when researchers wish to ascertain whether their data conforms to a specific probability distribution. In Excel, students can organize their data into a frequency table, listing the categories of the variable of interest along with their corresponding observed frequencies. They can then specify the expected frequencies based on the theoretical distribution they are testing against. For example, if analyzing the outcomes of a six-sided die roll, where each face is expected to occur with equal probability, the expected frequency for each category would be the total number of observations divided by six.

Once the observed and expected frequencies are determined, students can employ the CHISQ.TEST function in Excel to calculate the chi-square statistic and its associated p-value. The p-value represents the probability of obtaining a chi-square statistic as extreme or more extreme than the observed value under the assumption that the null hypothesis is true (i.e., the observed frequencies match the expected frequencies). Interpreting the results of the goodness-of-fit test involves comparing the calculated p-value to a predetermined significance level (commonly denoted as α). If the p-value is less than α (e.g., α = 0.05), there is sufficient evidence to reject the null hypothesis, indicating that the observed frequencies significantly differ from the expected frequencies specified by the theoretical distribution. Conversely, if the p-value is greater than α, there is insufficient evidence to reject the null hypothesis, suggesting that the observed frequencies align well with the expected frequencies.

Test of Independence

Another important application of the chi-square test in Excel is the test of independence, which evaluates whether there is a significant association between two categorical variables in a contingency table. This test is employed when researchers seek to determine whether the occurrence of one variable is related to the occurrence of another. To conduct a test of independence in Excel, students first create a contingency table that cross-tabulates the two categorical variables of interest. Each cell in the table represents the frequency of occurrences for a specific combination of categories from the two variables.

Similar to the goodness-of-fit test, students then calculate the expected frequencies for each cell under the assumption of independence between the variables. Using the CHISQ.TEST function in Excel, students can calculate the chi-square statistic and its associated p-value based on the observed and expected frequencies in the contingency table. The interpretation of the test results follows a similar procedure to that of the goodness-of-fit test, with the p-value indicating whether there is sufficient evidence to reject the null hypothesis of independence between the two variables.

Excel, despite being commonly associated with spreadsheet tasks, offers a plethora of features that make it a versatile and powerful tool for statistical analysis, especially for students diving into the intricacies of hypothesis testing. Its widespread availability and user-friendly interface make it accessible to students at various levels of statistical proficiency. However, the true value of Excel lies not just in its accessibility but also in its ability to facilitate a hands-on learning experience that reinforces theoretical concepts.

At the core of utilizing Excel for hypothesis testing is a solid understanding of the fundamental principles of statistical inference. Students need to grasp concepts such as the null and alternative hypotheses, significance levels, p-values, and test statistics. Excel provides a practical platform for students to apply these concepts in a real-world context. Through hands-on experimentation with sample datasets, students can observe how changes in data inputs and statistical parameters affect the outcome of hypothesis tests, thus deepening their understanding of statistical theory.

Post a comment...

Mastering hypothesis testing in excel: a practical guide for students submit your homework, attached files.

Hypothesis Test in Excel for the Population Mean (Large Sample)

Microsoft Excel for statistics > Hypothesis Test in Excel #1

Note : This article covers z-tests in Excel. If you have a small sample (under 30), or don’t know the population standard deviation , run a T Test in Excel instead.

Hypothesis Test in Excel: Overview

Hypothesis Test in Excel: Two Sample for Means

Hypothesis test in excel: manual steps.

Step 1: Type your data into a single column in Excel. For example, type your data into cells A1:A40.

Step 2: Click the “Data” tab and then click “Data Analysis.” If you don’t see the Data Analysis button then you may need to load the Data Analysis Toolpak .

Step 3: Click “ Descriptive Statistics “ and then click “OK.” When the Descriptive Statistics dialog box opens, click “Summary Statistics” and then type the location for a cell where you want your result to appear. For example, type”B1.”

Step 4: Click “OK. ” A variety of descriptive statistics, like the median and mode , will appear starting in cell B1.

Step 5: Find the cells that have the mean and the standard error results in it. If you typed in cell B1 in Step 3, your mean will be in cell C3 and your standard error will be in cell C4. Take a note of those cell locations.

Step 6: Type the following formula into cell D1 (assuming your mean is in cell C3 and your SE is in cell C4 — if they are not, you’ll need to adjust the formula): (C3-0)/C4

Change the “zero” to reflect the mean in your null hypothesis . For example, if your null hypothesis states that the mean is $7 per hour, then change the 0 to “7.”

Step 7: Press “Enter” to get the value of the test statistic. Compare the value to the accepted value for your mean from the z-table*. If the test statistic falls into the accepted range, then you will fail to reject the null hypothesis .

Subscribe to our YouTube channel for more Microsoft Excel for Statistics help and tips!

Comments are closed.

Click through the PLOS taxonomy to find articles in your field.

For more information about PLOS Subject Areas, click here .

Loading metrics

Open Access

Peer-reviewed

Research Article

Fast & furious: Rejecting the hypothesis that secondary psychopathy improves reaction time-based concealed information detection

Roles Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Software, Visualization, Writing – original draft

* E-mail: [email protected]

Affiliation Department of Criminology, Bar-Ilan University, Ramat Gan, Israel

Roles Conceptualization, Formal analysis, Investigation, Methodology, Writing – original draft, Writing – review & editing

Affiliations Department of Criminology, Bar-Ilan University, Ramat Gan, Israel, The Leslie and Susan Gonda (Goldschmied) Multidisciplinary Brain Research Center, Bar-Ilan University, Ramat Gan, Israel

• Imbar Mizrahi, 
• Nathalie klein Selle

• Published: October 15, 2024
• https://doi.org/10.1371/journal.pone.0311948
• Reader Comments

Deception, a complex aspect of human behavior, is inherently difficult to detect directly. A valid alternative involves memory detection, particularly through methods such as the Reaction-Time based Concealed Information Test (RT-CIT). The RT-CIT assesses whether an individual possesses specific knowledge by presenting various probe (familiar) items amidst irrelevant (unfamiliar) items. The task-required "unfamiliar" response to probes may induce a response conflict. Resolving this conflict, by inhibiting the automatic "familiar" response, takes time and slows probe RTs–a phenomenon known as the RT-CIT effect. Notably, secondary psychopathy is characterized by disinhibition and impulsivity, traits which may hinder the ability to effectively manage experienced conflict. Therefore, we hypothesized that secondary psychopathy would be associated with an elevated RT-CIT effect. To investigate this hypothesized relation, we conducted a pre-registered study ( n = 86, student sample), employing a novel CIT paradigm that incorporates no-go trials to assess response inhibition capacity. Psychopathic traits were measured using the Levenson Self-Report Psychopathy (LSRP) scale, while the Barratt Impulsiveness Scale (BIS-11) assessed impulsivity. The novel CIT paradigm revealed impressive detection efficiency. However, contrary to our expectations, we observed no significant correlation between the RT-CIT effect and secondary psychopathic traits (BF 01 = 6.98). This cautiously suggests that while secondary psychopathic tendencies do not improve RT-CIT validity, they also do not compromise it. Although future investigations should explore more diverse contexts and populations, this tentative finding is reassuring and underscores the robustness of the CIT paradigm.

Citation: Mizrahi I, klein Selle N (2024) Fast & furious: Rejecting the hypothesis that secondary psychopathy improves reaction time-based concealed information detection. PLoS ONE 19(10): e0311948. https://doi.org/10.1371/journal.pone.0311948

Editor: Vilfredo De Pascalis, Sapienza University of Rome: Universita degli Studi di Roma La Sapienza, ITALY

Received: April 17, 2024; Accepted: September 28, 2024; Published: October 15, 2024

Copyright: © 2024 Mizrahi, klein Selle. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

Data Availability: The data, analysis scripts and results were published at OSF: https://osf.io/s5mrn/ .

Funding: The author(s) received no specific funding for this work.

Competing interests: The authors (we) have declared that no competing interests exist.

Introduction

Lying is an intrinsic feature of human behavior [ 1 ]. We all lie and we have all been lied to [ 2 – 4 ]. When people are asked to discriminate between truth and lie based on their perceptions, they correctly notice lies in about 47% of cases and classify truths as nondeceptive in about 61% of cases–which is close to chance level [ 5 , 6 ]. Hence, it’s not surprising that throughout history humans have sought for techniques and methods that can distinguish between truth and lie [ 2 , 7 , 8 ]. In ancient Israel, for instance, a woman accused of adultery was considered guilty if her belly swelled after drinking "bitter water" [ 7 ]. In ancient China, those accused of fraud had to hold dry rice in their mouths–if the rice stayed dry, they were deemed guilty [ 9 ].

These historical methods, though lacking scientific validation, hint at a connection between physiological changes and deception. Building upon this understanding, psychophysiological methods for lie detection, popularly known as "polygraphs", emerged in the early twentieth century [ 10 ]. Such lie detection tools generally rely on physiological reactivity [ 11 – 13 ]. Importantly, the difference between the various lie detection methods lies in the adopted paradigm and the way its questions are formulated [see 12 ]. The classical, and probably most influential method, is the Control Question Test [CQT; 14 ]. This test assumes that guilty examinees will show stronger physiological responses to relevant, e.g., crime-related, questions, whereas innocents will show stronger physiological responses to control questions [ 15 ].

However, in real police investigations, both guilty (liars) and innocent (truth tellers) suspects may quickly identify the relevant questions and become emotionally aroused by them [ 11 ]. As a result, both types of subjects (guilty and innocent) may show enhanced physiological responses to the relevant questions, making accurate classification difficult [ 11 , 16 – 19 ]. Consequently, it is not surprising that the scientific community has criticized this method for being biased against the innocent in addition to lacking a theoretical basis [ 15 – 17 , 20 ]. Indeed, many criminal investigations have been hindered by the unreliable results of the CQT. For instance, consider the infamous Green River Killer case, which began in 1982 with the discovery of five bodies in the Green River, Washington. In this case, Melvin Foster, a taxi driver, failed a CQT despite his innocence. It wasn’t until 2001 that DNA evidence implicated Gary Ridgway, who was ultimately convicted of 49 murders. Remarkably, Ridgway passed a CQT in 1984 [ 19 , 21 – 24 ].

Lykken (1959) was one of the first to question the existence of specific deception reactions and, hence, he developed the Guilty Knowledge Test [GKT; 25 ]. Today, the GKT is called the Concealed Information Test [CIT; 25 ] and is considered a well-validated diagnostic test that aims to detect concealed knowledge [ 11 ]. In this test, examinees are faced with several multiple-choice questions, each followed by one probe (e.g., crime-related) item and several irrelevant alternatives, which are similar to the probe [ 26 ]. For instance, in the Green River Killer case, the body of the first victim, Wendy Lee Coffield, was pulled from the river with a pair of blue jeans knotted around her neck [ 21 , 22 , 24 ]. An appropriate CIT question could have been: "What article of clothing was tied around the victim’s neck?" (a) black sweater; (b) purple shirt; (c) blue jeans; (d) red scarf; (e) green jacket. Importantly, knowledgeable suspects recognize the significant probes, leading to differential physiological and behavioral responses. Unknowledgeable suspects, on the other hand, cannot distinguish between probe and irrelevant items and respond uniformly to all items [ 12 , 13 , 27 , 28 ]. Interestingly, while CIT researchers traditionally relied on autonomic physiological measures like heart rate, skin conductance, and brain responses, recent studies have incorporated behavioral measures such as reaction time [ 29 , 30 ].

The RT-based CIT is designed according to the 3-stimulus protocol and includes, in addition to probe and irrelevant items, a third item type known as the “target stimulus” [ 31 , 32 ]. These targets ensure stimulus-processing as they require a unique response [ 33 , 34 ]. Specifically, participants are typically asked to judge the stimuli on familiarity and are instructed to press buttons with the captions "familiar" (for targets) versus "unfamiliar” [for probe and irrelevant items 35 , 36 ]. The task-required "unfamiliar" response to probe items is presumed to create a response conflict [ 37 , 38 ]. Such response conflict may be resolved by inhibiting the automatic “familiar” response, which requires time [ 39 – 41 ]. Hence, response conflict has been theorized to underlie the longer RTs for probe versus irrelevant items–i.e., the RT-CIT effect [ 28 , 42 , 43 ].

Several studies provide direct support for the role of response conflict. Suchotzki et al . (2018), for instance, reasoned that since conflict arises when one denies familiarity with the known probe items, conflict should be stronger when one relies more heavily on familiarity. To explore this hypothesis, the authors manipulated familiarity-based responding by: (1) increasing the number of different targets (4 instead of 2 newly learned targets); and (2) using more familiar targets (2 personally relevant instead of 2 newly learned targets). Both manipulations increased the RT-CIT effect, supporting the response conflict account. Moreover, Suchotzki et al . (2015) instructed participants to admit knowledge of half the probes and deny knowledge of the remaining half. Their findings showed that overt deception, which generates response conflict, was essential for both the RT-CIT effect and the activation of the right inferior frontal gyrus, a brain region associated with inhibition [ 44 , 45 ]. Interestingly, a recent study has provided support for the crucial role of conflict, however, also suggests that additional factors such as orientation to significant information contribute to the RT-CIT effect [ 46 ].

Beyond theoretical considerations, meta-analytic research [ 29 ] has demonstrated that the RT-CIT is a highly valid method for detecting concealed information. Nevertheless, it remains to be assessed how the RT-CIT is affected by different personality traits, such as the constellation of traits associated with psychopathy [ 47 , 48 ]. This is especially relevant considering that psychopathic individuals constitute a significant proportion of the incarcerated population, with prevalence ranging from 20% to 30% [ 49 , 50 ]. Notably, classical dual-factor models of psychopathy distinguish between primary and secondary variants [ 51 – 54 ]. Secondary psychopathy, which is characterized by disinhibition and impulsivity, holds particular relevance in the context of the RT-CIT [ 55 – 59 ]. Specifically, a diminished ability to inhibit responses and manage response conflict should lead to an elevated RT-CIT effect.

Only a few studies have examined the influence of psychopathy on the CIT and found a significant CIT effect for psychopaths, which did not differ from that of non-psychopaths. However, these studies relied on physiological responses rather than RT [ 60 – 62 ]. RT serves as a behavioral measure and is assumed to reflect a different cognitive mechanism. Specifically, while the autonomic CIT effects have been tied to either orienting or arousal inhibition [see 63 – 66 ], the RT-CIT effect has primarily been associated with response conflict [ 28 , 46 ]. As outlined above, efficient conflict resolution requires adept inhibition capacities, which may be compromised by secondary psychopathic tendencies [ 55 , 57 , 59 ]. Therefore, the objective of the present study was to examine whether the RT-based CIT is sensitive to secondary psychopathic traits in a student sample. To get a fuller comprehension of this relationship, we used a novel CIT protocol which features no-go trials to assess disinhibition (see Method).

This study was approved by the Ethics Review Board of the Criminology department of Bar-Ilan University (BIU; January 26 th , 2023; see Ethics Review Board approval on https://osf.io/s5mrn/ ) and was performed in accordance with the relevant guidelines and regulations. The methods of this study, including sample size determination and exclusion criteria, were pre-registered on: https://osf.io/hz58u .

Participants

A total of 100 BIU students (79% female) were recruited through BIU’s online research portal (i.e., SONA). Participants’ average age was 23.88 years ( SD = 2.3, range = 20–37). All participants signed an informed consent form. At the end of the experiment, each participant received one credit point. All data of fourteen participants were excluded: thirteen participants were excluded because they made more than 50% errors to either target, probe or irrelevant items, and one participant was excluded because s/he did not complete the entire CIT (< 336 trials). Accordingly, the final sample included 86 participants (81.4% female, average age = 23.83, SD = 2.3, range = 20–37).

As indicated in the pre-registration, we stopped data collection when we reached N = 100, since the Bayes Factor (BF) provided substantial evidence for the null hypothesis (i.e., BF 01 > 5; there is no linear association between the RT-CIT effect and secondary psychopathic traits).

The present study included (1) the Levenson’s Self-Report Psychopathy (LSRP) scale, which provided the psychopathy scores; (2) a Go/No-go RT-CIT, which provided the RT-CIT effect as well as a behavioral measure of response inhibition (i.e., the no-go error rate; as explained below); and (3) the Barratt Impulsiveness Scale (BIS-11), which provided the impulsivity scores.

Psychopathic traits within our student sample were assessed using the LSRP [ 67 ]. The LSRP contains a total of 26 items, rated on a four-point Likert scale from “disagree strongly” to “agree strongly", resulting in a total score range from 26 to 104. Developed specifically for non-forensic populations, the LSRP distinguishes between primary and secondary psychopathy, aligning with the original Psychopathy Checklist–Revised (PCL-R) factors [ 67 – 71 ]. The primary psychopathy subscale (16-items; range: 16–64) evaluates interpersonal and affective features of psychopathy, while the secondary psychopathy subscale (10-items; range: 10–40) assesses impulsivity and antisocial lifestyle [ 60 , 67 , 72 ].

The overall scale’s reliability typically falls within the range of 0.59 to 0.87; for the primary subscale Cronbach’s alpha ranges from 0.74 to 0.86, and for the secondary subscale, it ranges from 0.61 to 0.71 [ 67 , 72 – 75 ]. In the current study, Cronbach’s alpha values were 0.79 for the overall LSRP, 0.8 for the primary subscale, and 0.63 for the secondary subscale. This study used a Hebrew translated version of the LSRP [ 76 ].

Go/No-go RT-CIT.

The Go/No-go task is widely used in psychology as a measure of inhibition and impulsivity [ 77 ]. Therefore, the present experiment integrated this task within the RT-CIT–i.e., this study relied on a Go/No-go RT-CIT with both go and no-go trials. The regular CIT items–probes, irrelevants and targets–played the role of ’go’ items, to which participants had to respond by pressing a button. Specifically, a “unfamiliar” button for probes and irrelevants, but a “familiar” button for targets (as is common in the RT-CIT). When seeing the no-go items, participants were asked not to respond. Importantly, these no-go items were used to measure participants’ capacity for response inhibition, which is assumed to be compromised in secondary psychopathy [ 78 , 79 ].

In addition to measuring response inhibition capacity with the novel no-go trials, we assessed impulsivity using the Barratt Impulsiveness Scale [BIS-11; 80 ]. The BIS-11 is a self-report questionnaire which contains a total of 30 items that are rated on a four-point Likert scale ranging from “rarely/never” to “almost always" [ 81 ]. Cronbach’s alpha for the BIS-11 typically falls within the range of 0.69 to 0.83 [ 80 , 82 , 83 ]. In the current study, Cronbach’s alpha was 0.84. This study used a Hebrew translated version of the BIS-11 [ 84 ].

The experiment was built in PsychoPy [ 85 ] and performed online in ’Pavlovia’ (see script on https://osf.io/s5mrn/ ). Participants received a link to the experiment through SONA (i.e., BIU’s online research portal). Importantly, once participants finished the experiment, SONA prevented them from performing the experiment again. The experiment contained three main stages: (1) the LSRP questionnaire, (2) the RT-CIT, and (3) the BIS-11 and subjective ratings. Before starting the experiment, participants read and approved an informed consent form (by pressing a button).

The LSRP questionnaire was completed after signing the informed consent form. All items (a total of 26) were presented one by one, and participants were asked to rate their agreement for each item, on a scale from 1 (“disagree strongly”) to 4 (“agree strongly").

Before starting the actual CIT, participants were presented with two item-lists, one of last names, and one of first names (female names for women and male names for men). Each list contained 16 items (i.e., names). Participants were asked to mark a maximum of 12 names, from each list, that have a special meaning for them. The irrelevant items (for the CIT) were chosen randomly from the words that were not marked.

Then, participants were explained about the upcoming CIT and motivated to conceal their autobiographical items (i.e., the probe items). To increase motivation, participants read a short paragraph which states that the upcoming task is difficult, and that only highly intelligent people with a strong willpower can successfully conceal. In addition, to become familiar with the no-go items, Tiger and Zebra, participants read a short paragraph about these items (i.e., Two animals with spectacularly beautiful stripes patterns are the Tiger (part of the Felidae family) with black-orange stripes, and of course, the Zebra (part of the Equidae family) with black-and-white stripes). Similarly, to become familiar with the target items, Caesarea and Milan, participants read a short paragraph about these cities (i.e., Who has not heard about the city of Milan, which is located in northern Italy and known for its great wealth? And of course, there is no one who does not know the city of Caesarea that was established 2000 years ago by the Roman Empire!). Thus, the CIT items were divided into three semantic categories, names for probes and irrelevants, cities for targets, and animals for no-go items. In total, there were 14 distinct items: 2 probes (participants first name and participants last name), 8 irrelevants (4 other first names and 4 other last names), 2 targets (Caesarea and Milan), and 2 no-go items (Tiger and Zebra).

The RT-CIT was operated according to the multiple-probes-protocol (MPP), which means that all 14 items were intermixed in each block of the CIT (there were 4 blocks in total). Per block, each item was presented 6 times, and thus, each block contained 84 items (14 x 6 = 84). The entire experiment contained 336 items (84 items x 4 blocks = 336). The order of items’ presentation was determined randomly, with the following restriction: two consecutive presentations of the same item were not allowed. All stimuli were displayed in a serial manner, in the middle of the screen, for 1500ms. Between each two items, a symbol of a plus was presented; this inter stimulus interval (ISI) was either 250ms, 500ms, or 750ms [similar to 28 , 46 , 86 , 87 ]. On top of the items, participants also saw the question: "Is this word familiar to you"? Participants were requested to respond using one of two buttons: unfamiliar (i.e., “I”) for probes and irrelevant items, familiar (i.e., “E”) for targets [ 34 , 88 ]. In addition, when seeing a no-go item, participants were requested not to respond. During ’go’ trials only, two feedback messages in the form of red words could briefly appear above the item for 200ms: (1) "WRONG" if participants pressed the wrong button, and (2) "TOO SLOW", if 800ms passed since the item appeared and no button was pressed [similar to 28 , 38 , 46 , 86 , 87 , 89 – 91 ]. For a visual presentation, please see Fig 1 .

• PPT PowerPoint slide
• PNG larger image
• TIFF original image

On “go” trials, which included irrelevant, probe and target items, participants had to respond by pressing a button. During “no-go” trials, participants were instructed not to respond.

https://doi.org/10.1371/journal.pone.0311948.g001

Importantly, the actual RT-CIT was also preceded by three successive practice phases that familiarized participants with the test procedure. These practice phases were repeated until certain criteria were met (as detailed below). In the first practice phase, which included solely “go” trials, items remained on the screen until one of the two available buttons (“E” or “I”) was pressed. If participants pressed the wrong button, they received "WRONG" feedback. In the second practice phase, which included both “go” and “no-go” trials, items remained on the screen until a button was pressed or until 1500ms had elapsed. Similar to the first practice phase, participants received "WRONG" feedback in case of an incorrect response. In the last practice phase, participants also received "TOO SLOW" feedback if they failed to press any button within 800ms during “go” trials. Please note that participants were able to advance through each phase if they met the following three criteria: (1) a maximum of 50% errors (i.e., incorrect button presses), (2) a maximum of 20% of RTs falling under 150ms, and (3) a mean reaction time that did not exceed 800ms. If participants did not meet these criteria, they received feedback about their performance (i.e., "Sorry, you failed this practice phase. Please repeat the training") and had to perform the practice phase again (up to a maximum of two attempts).

After the CIT, participants were asked to complete the BIS-11 questionnaire. All items (a total of 30) were presented one by one, and participants were asked to rate their agreement for each item, on a scale from 1 (“rarely/never”) to 4 (“almost always"). Finally, after the BIS-11, participants were asked to complete four parts to summarize their experience in the experiment. First, they were asked to rate the significance level of the 2 probes, 2 targets, 8 irrelevants, and 2 no-go items on a scale from 1 ("not significant at all") to 9 ("extremely significant"). These ratings were obtained to examine (and ensure) that the selected probes were more significant than the irrelevant items. Second, participants were asked to rate how motivated they were to succeed in the test, on a scale from 1 ("not motivated at all") to 10 ("very motivated"). Third, participants were asked to rate how impulsive they think they were during the CIT, on a scale from 1 ("not impulsive at all") to 10 ("very impulsive"). Fourth, participants were presented with a list of countermeasures, and were asked to mark the options they used. If they didn’t use any countermeasures, they could mark the option "No countermeasures were used". At the end of the experiment, participants were thanked for their participation and granted their credit points.

Outliers and exclusions.

Single items were excluded according to the following criteria: (1) Each button press under 150ms; (2) Each button press above 800ms; (3) Each error of pressing the wrong button.

Moreover, the data of an entire participant were excluded when: (1) The participant made at least 50% errors (in go trials of the CIT) to any of the 3 stimulus types (probe, irrelevant, target); (2) The participant did not complete the entire CIT (< 336 trials). Accordingly, all data of fourteen participants were excluded (see Participants).

All data were pre-processed using Matlab R2022b (The MathWorks, Natick, MA). Thereafter, data analyses were performed using JASP statistical program [ 92 , version 0.17.2.]. The analysis plan was pre-registered on: https://osf.io/hz58u , and the data along with analysis scripts can be accessed at: https://osf.io/s5mrn/ .

Subjective ratings

Prior to testing the main hypothesis (i.e., correlation between the RT-CIT effect and secondary psychopathic traits), we analyzed the subjective ratings which were obtained after the CIT (these analyses were not pre-registered). First, we analyzed (1) participants self-reported motivation to conceal their identity during the CIT, and (2) participants self-reported impulsivity during the CIT (in both cases, scale ranged from 1–10). Both the motivation to conceal ( M = 7.71, SD = 2.2) and experienced impulsivity ( M = 6.22, SD = 2.16) were high.

Second, we analyzed the self-reported significance of probe and irrelevant items (scale ranged from 1–9). As expected, the significance of probes ( M = 8.58, SD = 1.21) was higher than the significance of irrelevants ( M = 1.94, SD = 1.1); t (85) = 36.01, p < .001, d = 3.88, BF 10 = 9.440 × 10 +49 .

Third, we analyzed the reported countermeasures: 9% of participants reported that they tried to distract themselves; 14% reported that they tried to answer faster to the probe items (i.e., their own name); 1% reported that they tried to answer more slowly to probes; 2% reported that they tried to answer without looking at the screen; and 70% reported that they did not use any countermeasures.

Main analyses

For the main analysis, we computed for each participant the RT-CIT effect, which is defined as the mean RT of probes minus the mean RT of irrelevants. As we relied on a modified RT-CIT with ‘no-go’ trials, we first compared the mean RT-CIT effect across participants (i.e., 55 ms; see also Table 1 ) to 0. A statistically significant difference was observed, t (85) = 15.7, p < .001, d = 1.69 (95% CI = [1.36, 2.02]), which was very strongly supported by the BF 10 = 9.527×10 +23 .

https://doi.org/10.1371/journal.pone.0311948.t001

To test the main hypothesis, we correlated the individual RT-CIT effects with the secondary LSRP scores. Contrary to the research hypothesis, no significant correlation was observed: r = 0.04, p = 0.725, BF₀₁ = 6.98 (see Table 2 ).

All values below the diagonal are correlations (r), while all values above the diagonal are BFs.

https://doi.org/10.1371/journal.pone.0311948.t002

This result suggests that there is no linear association between the RT-CIT effect and secondary psychopathy (the null hypothesis is ~7 times more likely than the alternative hypothesis). Please note that similar results are obtained when including the data of the fourteen excluded participants: r = 0.03, p = 0.74, BF₀₁ = 7.5. Moreover, as can be seen in Fig 2 , support for the null hypothesis increased as data accumulated.

https://doi.org/10.1371/journal.pone.0311948.g002

To further examine the relationship between the RT-CIT effect, psychopathy, inhibition and impulsivity, we also correlated the RT-CIT effect with the total LSRP score, primary LSRP score, No-go error rate, and the BIS-11 score. Consistent with the main results reported above, which support the null hypothesis, no significant correlations were found with the RT-CIT effect (see Tables 1 and 2 ).

Notably, in a non-preregistered exploratory analysis, we performed a Bayesian Analysis of Covariance with Primary LSRP, Secondary LSRP, BIS-11, No-go errors, and Gender as predictors, and the RT-CIT effect as dependent variable. Using the BF Inclusion metric, we compared all models including a particular predictor to those without the predictor [see 93 ]. The Inclusion BF for Secondary LSRP was 0.134 (note that similar values were observed for other predictors). This analysis further supports our main conclusion: there is no discernible linear relationship between secondary psychopathic traits and the RT-CIT effect (full results are available on the OSF at https://osf.io/s5mrn/ ).

ROC analysis

In sum, the novel CIT paradigm demonstrated impressive detection efficiency. However, contrary to our expectations, we observed no significant correlation between the RT-CIT effect and secondary psychopathic traits (BF 01 = 6.98). This finding is further corroborated by the absence of significant correlations between the RT-CIT effect and both impulsivity (as measured by the BIS-11; BF₀₁ = 3.14) and response inhibition capacity (assessed by the no-go error rate; BF₀₁ = 3.08).

The present study examined the relation between the RT-CIT effect and secondary psychopathy in a student sample. The RT-CIT effect has been suggested to be largely driven by response conflict [ 28 , 42 , 46 , 81 ]. Specifically, the need to classify familiar probes as “unfamiliar” induces a conflict. This conflict may be resolved by inhibiting the automatic “familiar” response, a process that consumes time and consequently slows down RT. Hence, it was hypothesized that individuals with higher secondary psychopathic traits, marked by impulsivity and impaired inhibition capacity, would produce larger RT-CIT effects compared to individuals with lower levels of secondary psychopathic traits.

Secondary psychopathic traits were measured using the LSRP questionnaire and correlated with the RT-CIT effect. Notably, both the mean score and reliability of the different LSRP scales were consistent with other reports in the literature [ 95 – 97 ]. Moreover, the mean RT-CIT effect was large and significantly different from 0 (Cohen’s d = 1.69; BF 10 = 9.527×10 +23 ). However, contrary to our hypothesis, no significant correlation between secondary psychopathy and the CIT effect was observed, as supported by the Bayesian analysis that revealed substantial evidence for the null hypothesis (BF 01 = 6.98).

These findings are in line with those of Verschuere and in ´t Hout (2016), who examined the cognitive cost of lying among psychopaths using a Sheffield lie test (which measures deception, not concealed information). Similar to the present study, no significant correlation was found between psychopathy and the RT effect (RT LIE minus RT TRUTH ). Moreover, the current findings are in accordance with findings of CIT studies that used physiological measures and revealed no effect of psychopathy on the CIT [ 60 , 62 ].

To delve deeper into our primary research question, we included two additional measures: impulsivity and response inhibition capacity. Impulsivity was assessed using the BIS-11 questionnaire, and although we found a significant correlation between impulsivity and secondary psychopathy, no significant correlation was observed between impulsivity and the RT-CIT effect [consistent with 81 ]. It is noteworthy that self-reports and behavioral measures (like the RT-CIT) typically yield weak correlations [ 97 – 101 ). Hence, to measure response inhibition capacity, we integrated a Go/No-go task within the CIT. However, consistent with our main findings, response inhibition capacity (as indicated by the no-go error rate) did not correlate with secondary psychopathy or the RT-CIT effect (please see Table 2 ).

Thus, the present study suggests that secondary psychopathy does not influence the RT-CIT effect. This conclusion should, however, be approached with caution for two primary reasons. Firstly, while our hypothesis was built on the premise that secondary psychopathy is marked by impulsivity and impaired response inhibition capacity, our measures of inhibition and secondary psychopathy did not correlate. This may be due to our non-forensic student sample. While studies utilizing non-forensic samples have generally shown no correlation between psychopathy and response inhibition capacity, studies involving forensic samples have demonstrated such a correlation [e.g., 102 vs. 103 ]. Secondly, our inhibition and CIT effect measures did not correlate. Although the integration of the Go/No-go task within the RT-CIT is unique to our study, few previous CIT studies have used “secondary response inhibition tasks”. For example, Ambach et al . (2008) included the Go/No-go task alongside the CIT (with different stimuli for each task, unlike the present study) and Suchotzki et al . (2019) introduced a Stroop task after the CIT. Both studies showed similar results to the present one–no significant correlation between response inhibition capacity and the RT-CIT effect. Ultimately, this raises the question of whether response conflict is the only mechanism underlying the RT-CIT.

Accordingly, as indicated previously, a recent study of klein Selle et al . (2023) has provided support for the idea that additional factors may contribute to the RT-CIT effect. These authors compared a conflict condition (where the response buttons emphasized familiarity) with a no conflict condition (where the response buttons emphasized categorical membership). Although conflict strengthened the RT-CIT effect, the effect was significant even in the no conflict condition. Therefore, it was suggested that conflict theory alone is not a sufficient account of the RT-CIT effect and that other mechanisms such as orientation may play a role. The orienting response entails reflexive behavioral and physiological responses to changes in the environment [ 104 – 106 ]. This response is primarily modulated by two key factors: the novelty of the stimulus and its perceived significance [ 70 , 107 , 108 ]. In the context of the CIT, probe items are both significant and novel (i.e., presented less frequently) for knowledgeable individuals. Hence, these items should elicit an enhanced orienting response. Such enhanced responses [ 103 , 105 ] to significant probe items [see 63 – 66 ] may briefly interrupt ongoing behavior and consequently lengthen RTs. This notion is supported by a limited number of CIT studies. For instance, Lukács et al . (2019) categorized stimuli into three salience levels [forename, birthday, and favorite animal, from highest to lowest; 109 ] and found a larger RT-CIT effect for more significant items [ 91 , 110 ]. Suchotzki et al . (2015) manipulated the proportion of probe versus irrelevant items and found a stronger RT-CIT effect for more novel probes [ 42 ].

Interestingly, when comparing our RT-CIT effect to that of a classical CIT study [ 46 ], which used a similar design, stimuli and was also performed online, a significant difference was observed. Specifically, the RT-CIT effect of our novel Go/No-go CIT, Cohen’s d = 1.69 (95% CI = [1.36, 2.02]), was significantly larger than that of the classical CIT study, Cohen’s d = 1.24 (95% CI [0.90; 1.57]). Although the BF (BF 10 = 1.64) provides only weak evidence for this difference, a Bayesian sequential analysis showed increasing evidence for the alternative hypothesis as data accumulates (suggesting that more data should be obtained). Similarly, the Cohen’s d (1.69, 95% CI = [1.36, 2.02]) observed in the present study is higher than the mean Cohen’s d (1.30, 95% CI [1.06; 1.54]) reported in the meta-analysis of Suchotzki et al . (2017). Moreover, the current AUC value (0.92), which indicates detection efficiency of knowledgeable and unknowledgeable individuals, exceeds the mean AUC value (0.82) reported in the review paper by Meijer et al . (2016). Together this suggests that the additional “no-go” trials in our novel Go/No-go CIT may have increased CIT detection efficiency.

The observed increase in CIT detection efficiency may be the result of heightened cognitive load, a factor previously shown to enhance the RT-CIT effect [ 111 – 115 ]. For example, Visu-Petra et al . (2013) compared three CIT conditions: a classical RT-CIT, a RT-CIT with a concurrent memory task, and a RT-CIT with a concurrent set-shifting task. In line with the idea that additional cognitive load increases CIT detection efficiency, the RT-CIT effect was higher in the conditions that included an additional task (as evidenced by a larger increase in probe RTs than irrelevant RTs). Similarly, the no-go trials of our Go/No-go RT-CIT likely raised cognitive load, thereby reducing the capacity for inhibitory control and conflict resolution. Moreover, the additional no-go items may have also (1) made it harder to correctly respond to the different types of stimuli, thereby increasing conflict, and (2) diminished the relative frequency of probes, thereby amplifying the orienting response. As both conflict and orienting have been suggested to underlie the RT-CIT effect [see 46 ], it can explain how our modified format increased detection efficiency. Future investigations should aim to directly compare this novel format with a classical RT-CIT.

Additionally, while we strictly adhered to our preregistered protocol, future studies should aim to address several methodological limitations of the present study. First, as previously mentioned, the use of a non-forensic student sample may have influenced our findings. Therefore, investigating how more diverse samples could yield different results is essential. Moreover, conducting the experiment online may have influenced the RT-CT effect and, consequently, potentially affected the observed relationship between the RT-CIT effect and secondary psychopathy. Hence, replication studies conducted in a controlled laboratory setting are crucial [see 116 ]. Furthermore, while the use of highly salient autobiographical details ensured a strong CIT effect, it may not reflect real-world scenarios accurately. Thus, future studies should also examine the relationship between psychopathy and CIT using less salient crime-related stimuli, for instance. Lastly, it might be more appropriate to use the Single-Probe Protocol (SPP) of the CIT, where each block detects a single piece of information pertinent to the issue under investigation. This method is often the sole feasible interviewing approach in real-life contexts [ 117 – 120 ].

Furthermore, we would like to suggest that future examinations of psychopathy within the CIT incorporate both RT and neural measures. Notably, psychopaths exhibit distinct neural responses during tasks assessing conflict and orientation–i.e., the mechanisms assumed to underlie the RT-CT effect [ 121 – 128 ]. As such, methods such as fMRI, capable of monitoring conflict-related neural activity [see 42 , 129 – 131 ], and EEG, capable of examining the P300 component of the event-related potential associated with attentional orientation [e.g., 132 ], hold particular promise. Integrating these neuroimaging methods would not only deepen our understanding of the RT-CIT effect but also further elucidate the neurobiological underpinnings of psychopathy, thereby advancing both fields of study.

In summary, previous studies have provided scientific evidence indicating that psychopathy does not affect the physiological response-based CIT [ 60 , 62 ]. The present study provides preliminary evidence that psychopathic tendencies similarly do not affect the response time-based CIT. This is reassuring, as it suggests that although such tendencies do not improve CIT detection efficiency, they do not impede it. To expand and confirm these findings, future research is crucial. This should include conceptual replication studies using more diverse participant samples, CIT stimuli, and alternative protocols such as the SPP. Moreover, given the theoretical insight that orientation, alongside conflict, may drive the RT-CIT effect, it is imperative to thoroughly investigate the underlying mechanisms of this effect. Such exploration will not only advance theory but also deepen our understanding of practical aspects, such as susceptibility to countermeasures and potential influences from different clinical conditions. Ultimately, these investigations will bolster the validity and practical application of the RT-CIT across diverse settings and populations.

Supporting information

S1 graphical abstract..

https://doi.org/10.1371/journal.pone.0311948.s001

• View Article
• Google Scholar
• PubMed/NCBI
• 10. Granhag PA, Vrij A, Verschuere B. Detecting deception: current challenges and cognitive approaches. Malden (Mass.): Wiley Blackwell; 2015. (Wiley series in the psychology of crime, policing and law).
• 16. Ben-Shakhar G. A Critical Review of the Control Questions Test (CQT). In: Kleiner M, editor. Handbook of Polygraph Testing. Academic Press; 2002. p. 103–26.
• 17. Committee to Review the Scientific Evidence on the Polygraph (National Research Council (U.S.)), National Research Council (U.S.), National Research Council (U.S.), National Research Council (U.S.), editors. The polygraph and lie detection. Washington, D.C: National Academies Press; 2003. 398 p.
• 18. Bull R, Baron H, Gudjonsson G, Hampson S, Rippon G, Vrij A. A review of the current scientific status and fields of application of polygraphic deception detection. London, UK: British Psychological Society. 2004;
• 21. Chan HC. Case 13—The Washington Green River Killer: The Case of Gary Leon Ridgway (1982–2001; U.S.A.). In: A Global Casebook of Sexual Homicide [Internet]. Singapore: Springer Singapore; 2019 [cited 2024 Jun 8]. p. 211–31. Available from: http://link.springer.com/10.1007/978-981-13-8859-0_14
• 22. Rule A. Green River, running red: the real story of the Green River killer, America’s deadliest serial murderer. Gallery Books trade paperback edition. New York, NY: Gallery Books; 2004. 525 p.
• 23. NITV Federal Services. NITV Federal Services. 2010 [cited 2024 Jun 8]. Killer passes polygraph, innocent man fails, killer goes on to kill again. Available from: https://www.cvsa1.com/press-releases/killer-passes-polygraph-innocent-man-fails-killer-goes-on-to-kill-again/
• 33. Rosenfeld JP. P300 in detecting concealed information. In: Verschuere B, Ben-Shakhar G, Meijer E, editors. Memory Detection [Internet]. 1st ed. Cambridge University Press; 2011 [cited 2022 Jun 29]. p. 63–89. Available from: https://www.cambridge.org/core/product/identifier/CBO9780511975196A017/type/book_part
• 36. Verschuere B, De Houwer J. Detecting concealed information in less than a second: response latency-based measures. In: Verschuere B, Ben-Shakhar G, Meijer E, editors. Memory Detection [Internet]. 1st ed. Cambridge University Press; 2011 [cited 2022 Jun 29]. p. 46–62. Available from: https://www.cambridge.org/core/product/identifier/CBO9780511975196A016/type/book_part
• 57. Hare RD. The Hare Psychopathy Checklist Revised (2nd ed.). Toronto: Multi-Health Systems; 2003.
• 85. Peirce J, MacAskill M, Hirst B. Building experiments in psychopy. 2nd ed. Thousand Oaks: SAGE Publishing; 2022.
• 94. Schmidt FL, Hunter JE. Methods of Meta-Analysis: Correcting Error and Bias in Research Findings [Internet]. 1 Oliver’s Yard, 55 City Road London EC1Y 1SP: SAGE Publications, Ltd; 2015 [cited 2023 Mar 12]. Available from: https://methods.sagepub.com/book/methods-of-meta-analysis-3e
• 105. Sokolov EN. Orienting reflex as information regulator. In: Leontyev A, Luria A, Smirnov A, editors. Psychological Research in USSR. Moscow: Progress Publishers; 1966. p. 334–60.
• 106. Verschuere B, Ben-Shakhar G. Theory of the Concealed Information Test. In: Verschuere B, Ben-Shakhar G, Meijer E, editors. Memory Detection [Internet]. 1st ed. Cambridge University Press; 2011 [cited 2023 Aug 5]. p. 128–48. Available from: https://www.cambridge.org/core/product/identifier/CBO9780511975196A020/type/book_part
• 126. Anderson NE. Functional neuroimaging and psychopathy. In: Kiehl KA, Sinnott-Armstrong WP, editors. Handbook on Psychopathy and Law. Oxford University Press; 2013. p. 131–49.