

Strategy: Write a Number Sentence

Math Problem Solving Strategy: Write a Number Sentence to Solve a Problem

This is another free resource for teachers from The Curriculum Corner.
Looking to help your students learn to write a number sentence to solve a problem?
This math problem solving strategy can be practiced with this set of resources.
Math Problem Solving Strategies
This is one in a series of resources to help you focus on specific problem solving strategies in the classroom.
Within this download, we are offering you a range of word problems for practice.
Each page provided contains a single problem solving word problem.
Below each story problem you will find a set of four steps for students to follow when finding the answer.
This set will focus on the write a number sentence strategy for math problem solving.
What are the 4 problem solving steps?
After carefully reading the problem, students will:
- Step 1: Circle the math words.
- Step 2: Ask yourself: Do I understand the problem?
- Step 3: Solve the problem using words and pictures below.
- Step 4: Share the answer along with explaining why the answer makes sense.

Write a Number Sentence to Solve a Problem Word Work Questions
The problems within this post are meant to help students solve problems by writing a number sentence. These problems are designed to be used with first, second or third grade math students.
Within this collection you will find two variations of each problem.
You will easily be able to create additional problems using the wording below as a base.
The problems include the following selections:
- Cookies – easy addition
- Coin Collection – addition with regrouping
- Jewelry – addition with regrouping
- Making Cards – easy subtraction
- Beads for Bracelets – subtraction without regrouping
- Toy Cards – subtraction with regrouping
- Hot Chocolate – easy multiplication
- Pencils – one-digit times two-digit multiplication
- Legos – two-digit times two-digit multiplication
You can download this set of Write a Number Sentence to Solve a Problem here:
Problem Solving
You might also be interested in the following problem solving resources:
- Drawing Pictures to Solve Problems
- Addition & Subtraction Word Problem Strategies
- Fall Problem Solving
- Winter Problem Solving
- Spring Problem Solving
- Summer Problem Solving
As with all of our resources, The Curriculum Corner creates these for free classroom use. Our products may not be sold. You may print and copy for your personal classroom use. These are also great for home school families!
You may not modify and resell in any form. Please let us know if you have any questions.
Strategy: Make a Table - The Curriculum Corner 123
Monday 27th of January 2020
[…] Write a Number Sentence to Solve a Problem […]
Travelling Stem Teacher
Thursday 7th of June 2018
Thank you for sharing.
Wednesday 2nd of January 2013
Great activities for understanding how to solve word problems.
Question: Sam put 18 pencils in 3 equal groups. How many pencils are in each group? Strategy: 1) UNDERSTAND: What do you need to know? You need to know that there are 18 pencils and they are divided into 3 equal groups 2) PLAN: How can you solve the problem? You can write a number sentence to solve the problem. Write a division sentence to divide the pencils in 3 equal groups. 3) SOLVE: 18 ÷ 3 = 6 There are 6 pencils in each group.
High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
Free ready-to-use math resources
Hundreds of free math resources created by experienced math teachers to save time, build engagement and accelerate growth

20 Effective Math Strategies To Approach Problem-Solving
Katie Keeton
Math strategies for problem-solving help students use a range of approaches to solve many different types of problems. It involves identifying the problem and carrying out a plan of action to find the answer to mathematical problems.
Problem-solving skills are essential to math in the general classroom and real-life. They require logical reasoning and critical thinking skills. Students must be equipped with strategies to help them find solutions to problems.
This article explores mathematical problem solving strategies, logical reasoning and critical thinking skills to help learners with solving math word problems independently in real-life situations.
What are problem-solving strategies?
Problem-solving strategies in math are methods students can use to figure out solutions to math problems. Some problem-solving strategies:
- Draw a model
- Use different approaches
- Check the inverse to make sure the answer is correct
Students need to have a toolkit of math problem-solving strategies at their disposal to provide different ways to approach math problems. This makes it easier to find solutions and understand math better.
Strategies can help guide students to the solution when it is difficult ot know when to start.

The ultimate guide to problem solving techniques
Download these ready-to-go problem solving techniques that every student should know. Includes printable tasks for students including challenges, short explanations for teachers with questioning prompts.
20 Math Strategies For Problem-Solving
Different problem-solving math strategies are required for different parts of the problem. It is unlikely that students will use the same strategy to understand and solve the problem.
Here are 20 strategies to help students develop their problem-solving skills.
Strategies to understand the problem
Strategies that help students understand the problem before solving it helps ensure they understand:
- The context
- What the key information is
- How to form a plan to solve it
Following these steps leads students to the correct solution and makes the math word problem easier .
Here are five strategies to help students understand the content of the problem and identify key information.
1. Read the problem aloud
Read a word problem aloud to help understand it. Hearing the words engages auditory processing. This can make it easier to process and comprehend the context of the situation.
2. Highlight keywords
When keywords are highlighted in a word problem, it helps the student focus on the essential information needed to solve it. Some important keywords help determine which operation is needed. For example, if the word problem asks how many are left, the problem likely requires subtraction. Ensure students highlight the keywords carefully and do not highlight every number or keyword. There is likely irrelevant information in the word problem.
3. Summarize the information
Read the problem aloud, highlight the key information and then summarize the information. Students can do this in their heads or write down a quick summary. Summaries should include only the important information and be in simple terms that help contextualize the problem.
4. Determine the unknown
A common problem that students have when solving a word problem is misunderstanding what they are solving. Determine what the unknown information is before finding the answer. Often, a word problem contains a question where you can find the unknown information you need to solve. For example, in the question ‘How many apples are left?’ students need to find the number of apples left over.
5. Make a plan
Once students understand the context of the word problem, have dentified the important information and determined the unknown, they can make a plan to solve it. The plan will depend on the type of problem. Some problems involve more than one step to solve them as some require more than one answer. Encourage students to make a list of each step they need to take to solve the problem before getting started.
Strategies for solving the problem
1. draw a model or diagram.
Students may find it useful to draw a model, picture, diagram, or other visual aid to help with the problem solving process. It can help to visualize the problem to understand the relationships between the numbers in the problem. In turn, this helps students see the solution.

Similarly, you could draw a model to represent the objects in the problem:

2. Act it out
This particular strategy is applicable at any grade level but is especially helpful in math investigation in elementary school . It involves a physical demonstration or students acting out the problem using movements, concrete resources and math manipulatives . When students act out a problem, they can visualize and contectualize the word problem in another way and secure an understanding of the math concepts. The examples below show how 1st-grade students could “act out” an addition and subtraction problem:
3. Work backwards
Working backwards is a popular problem-solving strategy. It involves starting with a possible solution and deciding what steps to take to arrive at that solution. This strategy can be particularly helpful when students solve math word problems involving multiple steps. They can start at the end and think carefully about each step taken as opposed to jumping to the end of the problem and missing steps in between.
For example,

To solve this problem working backwards, start with the final condition, which is Sam’s grandmother’s age (71) and work backwards to find Sam’s age. Subtract 20 from the grandmother’s age, which is 71. Then, divide the result by 3 to get Sam’s age. 71 – 20 = 51 51 ÷ 3 = 17 Sam is 17 years old.
4. Write a number sentence
When faced with a word problem, encourage students to write a number sentence based on the information. This helps translate the information in the word problem into a math equation or expression, which is more easily solved. It is important to fully understand the context of the word problem and what students need to solve before writing an equation to represent it.
5. Use a formula
Specific formulas help solve many math problems. For example, if a problem asks students to find the area of a rug, they would use the area formula (area = length × width) to solve. Make sure students know the important mathematical formulas they will need in tests and real-life. It can help to display these around the classroom or, for those who need more support, on students’ desks.
Strategies for checking the solution
Once the problem is solved using an appropriate strategy, it is equally important to check the solution to ensure it is correct and makes sense.
There are many strategies to check the solution. The strategy for a specific problem is dependent on the problem type and math content involved.
Here are five strategies to help students check their solutions.
1. Use the Inverse Operation
For simpler problems, a quick and easy problem solving strategy is to use the inverse operation. For example, if the operation to solve a word problem is 56 ÷ 8 = 7 students can check the answer is correct by multiplying 8 × 7. As good practice, encourage students to use the inverse operation routinely to check their work.
2. Estimate to check for reasonableness
Once students reach an answer, they can use estimation or rounding to see if the answer is reasonable. Round each number in the equation to a number that’s close and easy to work with, usually a multiple of ten. For example, if the question was 216 ÷ 18 and the quotient was 12, students might round 216 to 200 and round 18 to 20. Then use mental math to solve 200 ÷ 20, which is 10. When the estimate is clear the two numbers are close. This means your answer is reasonable.
3. Plug-In Method
This method is particularly useful for algebraic equations. Specifically when working with variables. To use the plug-in method, students solve the problem as asked and arrive at an answer. They can then plug the answer into the original equation to see if it works. If it does, the answer is correct.

If students use the equation 20m+80=300 to solve this problem and find that m = 11, they can plug that value back into the equation to see if it is correct. 20m + 80 = 300 20 (11) + 80 = 300 220 + 80 = 300 300 = 300 ✓
4. Peer Review
Peer review is a great tool to use at any grade level as it promotes critical thinking and collaboration between students. The reviewers can look at the problem from a different view as they check to see if the problem was solved correctly. Problem solvers receive immediate feedback and the opportunity to discuss their thinking with their peers. This strategy is effective with mixed-ability partners or similar-ability partners. In mixed-ability groups, the partner with stronger skills provides guidance and support to the partner with weaker skills, while reinforcing their own understanding of the content and communication skills. If partners have comparable ability levels and problem-solving skills, they may find that they approach problems differently or have unique insights to offer each other about the problem-solving process.
5. Use a Calculator
A calculator can be introduced at any grade level but may be best for older students who already have a foundational understanding of basic math operations. Provide students with a calculator to allow them to check their solutions independently, accurately, and quickly. Since calculators are so readily available on smartphones and tablets, they allow students to develop practical skills that apply to real-world situations.
Step-by-step problem-solving processes for your classroom
In his book, How to Solve It , published in 1945, mathematician George Polya introduced a 4-step process to solve problems.
Polya’s 4 steps include:
- Understand the problem
- Devise a plan
- Carry out the plan
Today, in the style of George Polya, many problem-solving strategies use various acronyms and steps to help students recall.
Many teachers create posters and anchor charts of their chosen process to display in their classrooms. They can be implemented in any elementary, middle school or high school classroom.
Here are 5 problem-solving strategies to introduce to students and use in the classroom.

How Third Space Learning improves problem-solving
Resources .
Third Space Learning offers a free resource library is filled with hundreds of high-quality resources. A team of experienced math experts carefully created each resource to develop students mental arithmetic, problem solving and critical thinking.
Explore the range of problem solving resources for 2nd to 8th grade students.
One-on-one tutoring
Third Space Learning offers one-on-one math tutoring to help students improve their math skills. Highly qualified tutors deliver high-quality lessons aligned to state standards.
Former teachers and math experts write all of Third Space Learning’s tutoring lessons. Expertly designed lessons follow a “my turn, follow me, your turn” pedagogy to help students move from guided instruction and problem-solving to independent practice.
Throughout each lesson, tutors ask higher-level thinking questions to promote critical thinking and ensure students are developing a deep understanding of the content and problem-solving skills.

Problem-solving
Educators can use many different strategies to teach problem-solving and help students develop and carry out a plan when solving math problems. Incorporate these math strategies into any math program and use them with a variety of math concepts, from whole numbers and fractions to algebra.
Teaching students how to choose and implement problem-solving strategies helps them develop mathematical reasoning skills and critical thinking they can apply to real-life problem-solving.
READ MORE : 8 Common Core math examples
There are many different strategies for problem-solving; Here are 5 problem-solving strategies: • draw a model • act it out • work backwards • write a number sentence • use a formula
Here are 10 strategies of problem-solving: • Read the problem aloud • Highlight keywords • Summarize the information • Determine the unknown • Make a plan • Draw a model • Act it out • Work backwards • Write a number sentence • Use a formula
1. Understand the problem 2. Devise a plan 3. Carry out the plan 4. Look back
Some strategies you can use to solve challenging math problems are: breaking the problem into smaller parts, using diagrams or models, applying logical reasoning, and trying different approaches.
Related articles

Why Student Centered Learning Is Important: A Guide For Educators

13 Effective Learning Strategies: A Guide to Using them in your Math Classroom

Differentiated Instruction: 9 Differentiated Curriculum And Instruction Strategies For Teachers

5 Math Mastery Strategies To Incorporate Into Your 4th and 5th Grade Classrooms
Ultimate Guide to Metacognition [FREE]
Looking for a summary on metacognition in relation to math teaching and learning?
Check out this guide featuring practical examples, tips and strategies to successfully embed metacognition across your school to accelerate math growth.
Privacy Overview

Number sentence – Definition, Application, FAQs, Examples
What is a number sentence, application of number sentences, solved examples on number sentence, practice problems on number sentence, frequently asked questions on number sentence.
A number sentence is a mathematical sentence made up of numbers and symbols, as shown below.

The term “number sentence” is introduced at the elementary school level. However, the application of these sentences extends beyond elementary school because it includes equations and inequalities . These sentences can also be described as the language of mathematics. As shown below, a sentence combines two expressions with a relational symbol $(=, \gt, \lt, \text{etc.})$.

These sentences show the equality or inequality relations using different mathematical operations like addition , subtraction , multiplication , and division .
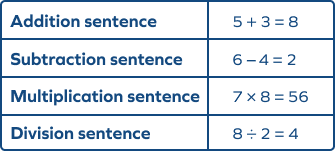
The sign of equality and inequality is significant as the sentence is incomplete and makes no sense without them.
$10 + 8 \gt 15$, is an example of a number sentence. However, if we write $10 + 8$ $15$, it does not make any sense.
A math sentence can be true or false depending on the information provided.
A mathematical sentence that gives all the information and is known to be either true or false, as shown in the example below.
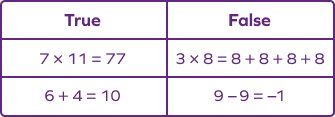
Mathematical sentence problems can appear in the form of word problems, asking students how to write a number sentence.
For example: Mary has 10 strawberries. If Dan gives her 15 strawberries, how many strawberries does Mary have in total?
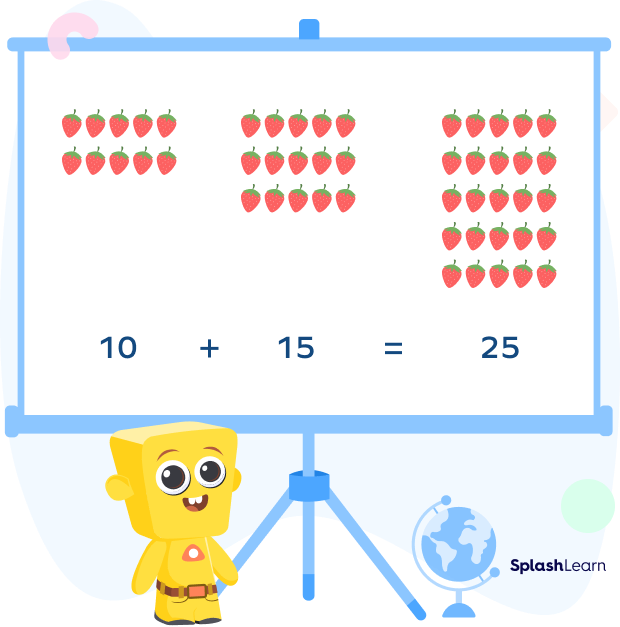
So, Mary has $10 + 15 = 25$ strawberries.
Related Worksheets

Why Do Students Need to Be Fluent in Math Sentences?
- Mathematical sentences help students understand algebra. This involves weaving algebraic thinking into elementary and middle-school math.
- Math sentences provide flexibility to solve a problem as compared to basic algorithms. Using sentences, students can break the numbers out to see the value of each digit. They can compose and decompose numbers by place value or use other strategies, building their reasoning and mental math skills as shown in the example below.

Number sentences are simply the numerical expression of a word problem.
Example 1: Determine whether the following sentence is true or false.
$12 + 12 + 12 \lt 4 \times 12$
The expression on the right side of the inequality (less than) sign is $12 + 12 + 12$, which is equal to 36.
Solving expressions on the right side of the inequality (less than) sign, we get $4 \times 12$ or 48.
Since $36 \lt 48$, we can say the given sentence $12 + 12 + 12 \lt 4 \times 12$ is true.
Example 2: Complete the math sentence so that it is true.
$6 + 7 = 9$ $+$ $\underline{}$
$6 + 7 = 13$
So, to make the sentence true, $9$ $+$ $\underline{}$ must be equal to 13. Therefore, the missing number must be $13$ $–$ $9$ or 4.
Example 3: Substitute the value into the variable (x) and state whether the resulting sentence is true or false.
$12 –$ x $= 9$ , substitute 4 for x
If we substitute x as 4 in the given sentence, we $12$ $–$ $4 = 9$, which is false, as $12$ $–$ $4 = 8 ≠ 9$.
Example 4: Find the value of the x so that the following sentence is true.
$\text{x}$ $–$ $24 = 10$
Adding the same number to both sides of the equal sign will keep the sentence true.
To find the value of x, we can add 24 to both sides of the equal sign.
$\text{x}$ $–$ $24 + 24 = 10 + 24$
Therefore, $\text{x}$ $= 34$
Number sentence - Definition With Examples
Attend this quiz & Test your knowledge.
Which of the following is not a number sentence?
Select the correct statement for the sentences given below. $40 + 30 = 70$ $90 + 1000 = 1900$, identify the symbol that can fill the blank to make the sentence true 90 ◯ 20 = 70.
Is it important for a number sentence to be true?
A math sentence does not necessarily have to be true. However, every sentence gives us information, and based on the information provided, it is possible to change the statement from false to true.
What is the difference between equations and inequalities?
An equation is a mathematical sentence that shows the equal value of two expressions while an inequality is a sentence that shows an expression is lesser than or more than the other.
Can fractional numbers be written in the form of a number sentence?
Yes, fractional numbers can be written in the form of a sentence. For instance,
$\frac{3}{4}+\frac{5}{4} = \frac{8}{4}$
RELATED POSTS
- Area in Math – Definition, Composite Figures, FAQs, Examples
- Equal – Definition with Examples
- Repeated Addition – Definition, Examples, Practice Problems, FAQs
- Row in Math
- Multiplication Chart – Definition with Examples

Math & ELA | PreK To Grade 5
Kids see fun., you see real learning outcomes..
Make study-time fun with 14,000+ games & activities, 450+ lesson plans, and more—free forever.
Parents, Try for Free Teachers, Use for Free
Learning Coach —
Students will:
Skills Needed
Students must be able to:
Materials Needed
Students will need:
Learning Coach Notes
Problem-solving strategy: write an number sentence video, let’s watch a video about writing a number sentence..

Goal: Learn how to choose an addition strategy.
Can you fix Elias' costume? Click the video to use your addition strategies to help!
Elias and Hudson are best friends. It is Halloween and they are just about to go trick-or-treating. Oh no! Elias’s costume has fallen apart. We need to help Elias and Hudson fix the costume.
There are 20 white buttons and 10 white and blue circles on the ground. These buttons and circles belong on the bottom part of Elias’s costume. How many buttons and circles are there altogether?
Hmmm, we need to add these buttons and circles together, but what should our number sentence be? There are 20 buttons and 10 circles. We can use the addition sentence 20 + 10. Solving addition sentences is simple when we use an addition strategy! Let’s see, we could solve this problem using base ten blocks, a number line, or ten frames.
Let’s use base ten blocks! This is a good idea since 10 and 20 can both be easily represented by base ten blocks.
Here are two groups of ten to represent the number 20, and here is one group of ten to represent the number 10. When we add these base ten blocks, we can think of adding 2 and 1. 2+1=3 groups of ten. We know that 3 groups of ten equals 30.
Great job! Hudson will glue 30 buttons and circles onto Elias’s costume.
These white lines fell off of Elias’s arms. Let’s find out how many lines there are all together so that Hudson can glue them back on.
How many thin, white lines do you see?
Yes! There are 17 thin lines. How many thick, white lines do you see?
Very good! There are 6 thick lines. We can use these numbers to create an addition sentence. Do you know what it is?
That’s right! This is the addition sentence 17 + 6. What addition strategy should we use do solve this equation? Base ten blocks, a number line, or ten frames?
Let’s use the number line! Since 6 is a single-digit number, a number line will be a quick and easy way to add 6 to 17.
Number lines help us see and understand the addends we add together. Begin by circling the largest addend, 17. Now count on by jumping to the right 6 times. This shows 17+6. We landed on the number 23. Great job!
Now Hudson will glue 17 thin lines on Elias’s left arm and 6 thick lines on his right. They are almost ready to go trick-or-treating!
These buttons and levers fell off of Elias’s torso. Let’s find out how many buttons and levers Hudson will glue back on Elias.
Can you create the addition sentence?
Great job! There are 36 buttons and 6 levers. This is the addition sentence 36+6. There is only one addition strategy that we haven’t used today! Let’s add using ten frames!
Ten frames help us add to ten quickly because we can easily group numbers together. Let’s use 36 red dots to represent the 36 buttons and 6 blue dots to represent the 6 levers. First, place the 36 red dots in the ten frames. Then, place the 6 blue dots in the ten frames.
A ten frame holds 10 dots, so if a ten frame is full, we can simply look at it as the number “10”. 40 + 2 = 42. There are 42 buttons and levers all together.
Hudson will glue 42 buttons and levers onto Elias’s costume.
Hooray! Elias’s costume is fixed and now the boys are ready to go trick-or-treating! Thank you for helping them write number sentences and use addition strategies!
Choose an addition sentence that matches this picture.

- 12 + 13 = 25
- 10 + 10 = 20
- 15 + 12 = 27
Great job! 12 + 13 = 25 matches this picture.
Sorry, that is not right. 12 + 13 = 25 matches this picture.
Questions answered correctly:
Questions answered incorrectly:
Appendix A: Applications
Using a problem-solving strategy to solve number problems, learning outcomes.
- Apply the general problem-solving strategy to number problems
- Identify how many numbers you are solving for given a number problem
- Solve consecutive integer problems
Now we will translate and solve number problems. In number problems, you are given some clues about one or more numbers, and you use these clues to build an equation. Number problems don’t usually arise on an everyday basis, but they provide a good introduction to practicing the Problem-Solving Strategy. Remember to look for clue words such as difference , of , and and .
The difference of a number and six is [latex]13[/latex]. Find the number.
https://ohm.lumenlearning.com/multiembedq.php?id=142763&theme=oea&iframe_resize_id=mom50
The sum of twice a number and seven is [latex]15[/latex]. Find the number.
Show Solution
https://ohm.lumenlearning.com/multiembedq.php?id=142770&theme=oea&iframe_resize_id=mom60
Watch the following video to see another example of how to solve a number problem.
Solving for Two or More Numbers
Some number word problems ask you to find two or more numbers. It may be tempting to name them all with different variables, but so far we have only solved equations with one variable. We will define the numbers in terms of the same variable. Be sure to read the problem carefully to discover how all the numbers relate to each other.
One number is five more than another. The sum of the numbers is twenty-one. Find the numbers.
https://ohm.lumenlearning.com/multiembedq.php?id=142775&theme=oea&iframe_resize_id=mom70
Watch the following video to see another example of how to find two numbers given the relationship between the two.
The sum of two numbers is negative fourteen. One number is four less than the other. Find the numbers.
https://ohm.lumenlearning.com/multiembedq.php?id=142806&theme=oea&iframe_resize_id=mom80
One number is ten more than twice another. Their sum is one. Find the numbers.
https://ohm.lumenlearning.com/multiembedq.php?id=142811&theme=oea&iframe_resize_id=mom90
Solving for Consecutive Integers
Consecutive integers are integers that immediately follow each other. Some examples of consecutive integers are:
[latex]\begin{array}{c}\phantom{\rule{0.2em}{0ex}}\\ \phantom{\rule{0.2em}{0ex}}\\ \phantom{\rule{0.2em}{0ex}}\\ \phantom{\rule{0.2em}{0ex}}\\ \hfill \text{…}1,2,3,4\text{,…}\hfill \end{array}[/latex] [latex]\text{…}-10,-9,-8,-7\text{,…}[/latex] [latex]\text{…}150,151,152,153\text{,…}[/latex]
Notice that each number is one more than the number preceding it. So if we define the first integer as [latex]n[/latex], the next consecutive integer is [latex]n+1[/latex]. The one after that is one more than [latex]n+1[/latex], so it is [latex]n+1+1[/latex], or [latex]n+2[/latex].
[latex]\begin{array}{cccc}n\hfill & & & \text{1st integer}\hfill \\ n+1\hfill & & & \text{2nd consecutive integer}\hfill \\ n+2\hfill & & & \text{3rd consecutive integer}\hfill \end{array}[/latex]
The sum of two consecutive integers is [latex]47[/latex]. Find the numbers.
Find three consecutive integers whose sum is [latex]42[/latex].
Watch this video for another example of how to find three consecutive integers given their sum.
- Ex: Linear Equation Application with One Variable - Number Problem. Authored by : James Sousa (Mathispower4u.com). Located at : https://youtu.be/juslHscrh8s . License : CC BY: Attribution
- Ex: Write and Solve an Equation for Consecutive Natural Numbers with a Given Sum. Authored by : James Sousa (Mathispower4u.com). Located at : https://youtu.be/Bo67B0L9hGs . License : CC BY: Attribution
- Write and Solve a Linear Equations to Solve a Number Problem (1) Mathispower4u . Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/izIIqOztUyI . License : CC BY: Attribution
- Question ID 142763, 142770, 142775, 142806, 142811, 142816, 142817. Authored by : Lumen Learning. License : CC BY: Attribution . License Terms : IMathAS Community License, CC-BY + GPL
- Prealgebra. Provided by : OpenStax. License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]

Privacy Policy
3.1 Use a Problem-Solving Strategy
Learning objectives.
By the end of this section, you will be able to:
- Approach word problems with a positive attitude
- Use a problem-solving strategy for word problems
- Solve number problems
Be Prepared 3.1
Before you get started, take this readiness quiz.
- Translate “6 less than twice x ” into an algebraic expression. If you missed this problem, review Example 1.26 .
- Solve: 2 3 x = 24 . 2 3 x = 24 . If you missed this problem, review Example 2.16 .
- Solve: 3 x + 8 = 14 . 3 x + 8 = 14 . If you missed this problem, review Example 2.27 .
Approach Word Problems with a Positive Attitude
“If you think you can… or think you can’t… you’re right.”—Henry Ford
The world is full of word problems! Will my income qualify me to rent that apartment? How much punch do I need to make for the party? What size diamond can I afford to buy my girlfriend? Should I fly or drive to my family reunion?
How much money do I need to fill the car with gas? How much tip should I leave at a restaurant? How many socks should I pack for vacation? What size turkey do I need to buy for Thanksgiving dinner, and then what time do I need to put it in the oven? If my sister and I buy our mother a present, how much does each of us pay?
Now that we can solve equations, we are ready to apply our new skills to word problems. Do you know anyone who has had negative experiences in the past with word problems? Have you ever had thoughts like the student below?
When we feel we have no control, and continue repeating negative thoughts, we set up barriers to success. We need to calm our fears and change our negative feelings.
Start with a fresh slate and begin to think positive thoughts. If we take control and believe we can be successful, we will be able to master word problems! Read the positive thoughts in Figure 3.3 and say them out loud.
Think of something, outside of school, that you can do now but couldn’t do 3 years ago. Is it driving a car? Snowboarding? Cooking a gourmet meal? Speaking a new language? Your past experiences with word problems happened when you were younger—now you’re older and ready to succeed!
Use a Problem-Solving Strategy for Word Problems
We have reviewed translating English phrases into algebraic expressions, using some basic mathematical vocabulary and symbols. We have also translated English sentences into algebraic equations and solved some word problems. The word problems applied math to everyday situations. We restated the situation in one sentence, assigned a variable, and then wrote an equation to solve the problem. This method works as long as the situation is familiar and the math is not too complicated.
Now, we’ll expand our strategy so we can use it to successfully solve any word problem. We’ll list the strategy here, and then we’ll use it to solve some problems. We summarize below an effective strategy for problem solving.
Use a Problem-Solving Strategy to Solve Word Problems.
- Step 1. Read the problem. Make sure all the words and ideas are understood.
- Step 2. Identify what we are looking for.
- Step 3. Name what we are looking for. Choose a variable to represent that quantity.
- Step 4. Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebraic equation.
- Step 5. Solve the equation using good algebra techniques.
- Step 6. Check the answer in the problem and make sure it makes sense.
- Step 7. Answer the question with a complete sentence.
Example 3.1
Pilar bought a purse on sale for $18, which is one-half of the original price. What was the original price of the purse?
Step 1. Read the problem. Read the problem two or more times if necessary. Look up any unfamiliar words in a dictionary or on the internet.
- In this problem, is it clear what is being discussed? Is every word familiar?
Step 2. Identify what you are looking for. Did you ever go into your bedroom to get something and then forget what you were looking for? It’s hard to find something if you are not sure what it is! Read the problem again and look for words that tell you what you are looking for!
- In this problem, the words “what was the original price of the purse” tell us what we need to find.
Step 3. Name what we are looking for. Choose a variable to represent that quantity. We can use any letter for the variable, but choose one that makes it easy to remember what it represents.
- Let p = p = the original price of the purse.
Step 4. Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Translate the English sentence into an algebraic equation.
Reread the problem carefully to see how the given information is related. Often, there is one sentence that gives this information, or it may help to write one sentence with all the important information. Look for clue words to help translate the sentence into algebra. Translate the sentence into an equation.
Step 5. Solve the equation using good algebraic techniques. Even if you know the solution right away, using good algebraic techniques here will better prepare you to solve problems that do not have obvious answers.
Step 6. Check the answer in the problem to make sure it makes sense. We solved the equation and found that p = 36 , p = 36 , which means “the original price” was $36.
- Does $36 make sense in the problem? Yes, because 18 is one-half of 36, and the purse was on sale at half the original price.
Step 7. Answer the question with a complete sentence. The problem asked “What was the original price of the purse?”
- The answer to the question is: “The original price of the purse was $36.”
If this were a homework exercise, our work might look like this:
Pilar bought a purse on sale for $18, which is one-half the original price. What was the original price of the purse?
Joaquin bought a bookcase on sale for $120, which was two-thirds of the original price. What was the original price of the bookcase?
Two-fifths of the songs in Mariel’s playlist are country. If there are 16 country songs, what is the total number of songs in the playlist?
Let’s try this approach with another example.
Example 3.2
Ginny and her classmates formed a study group. The number of girls in the study group was three more than twice the number of boys. There were 11 girls in the study group. How many boys were in the study group?
Guillermo bought textbooks and notebooks at the bookstore. The number of textbooks was 3 more than twice the number of notebooks. He bought 7 textbooks. How many notebooks did he buy?
Gerry worked Sudoku puzzles and crossword puzzles this week. The number of Sudoku puzzles he completed is eight more than twice the number of crossword puzzles. He completed 22 Sudoku puzzles. How many crossword puzzles did he do?
Solve Number Problems
Now that we have a problem solving strategy, we will use it on several different types of word problems. The first type we will work on is “number problems.” Number problems give some clues about one or more numbers. We use these clues to write an equation. Number problems don’t usually arise on an everyday basis, but they provide a good introduction to practicing the problem solving strategy outlined above.
Example 3.3
The difference of a number and six is 13. Find the number.
The difference of a number and eight is 17. Find the number.
The difference of a number and eleven is −7 . −7 . Find the number.
Example 3.4
The sum of twice a number and seven is 15. Find the number.
Did you notice that we left out some of the steps as we solved this equation? If you’re not yet ready to leave out these steps, write down as many as you need.
The sum of four times a number and two is 14. Find the number.
The sum of three times a number and seven is 25. Find the number.
Some number word problems ask us to find two or more numbers. It may be tempting to name them all with different variables, but so far we have only solved equations with one variable. In order to avoid using more than one variable, we will define the numbers in terms of the same variable. Be sure to read the problem carefully to discover how all the numbers relate to each other.
Example 3.5
One number is five more than another. The sum of the numbers is 21. Find the numbers.
One number is six more than another. The sum of the numbers is twenty-four. Find the numbers.
Try It 3.10
The sum of two numbers is fifty-eight. One number is four more than the other. Find the numbers.
Example 3.6
The sum of two numbers is negative fourteen. One number is four less than the other. Find the numbers.
Try It 3.11
The sum of two numbers is negative twenty-three. One number is seven less than the other. Find the numbers.
Try It 3.12
The sum of two numbers is −18 . −18 . One number is 40 more than the other. Find the numbers.
Example 3.7
One number is ten more than twice another. Their sum is one. Find the numbers.

Try It 3.13
One number is eight more than twice another. Their sum is negative four. Find the numbers.
Try It 3.14
One number is three more than three times another. Their sum is −5 . −5 . Find the numbers.
Some number problems involve consecutive integers. Consecutive integers are integers that immediately follow each other. Examples of consecutive integers are:
Notice that each number is one more than the number preceding it. So if we define the first integer as n , the next consecutive integer is n + 1 . n + 1 . The one after that is one more than n + 1 , n + 1 , so it is n + 1 + 1 , n + 1 + 1 , which is n + 2 . n + 2 .
Example 3.8
The sum of two consecutive integers is 47. Find the numbers.
Try It 3.15
The sum of two consecutive integers is 95 . 95 . Find the numbers.
Try It 3.16
The sum of two consecutive integers is −31 . −31 . Find the numbers.
Example 3.9
Find three consecutive integers whose sum is −42 . −42 .
Try It 3.17
Find three consecutive integers whose sum is −96 . −96 .
Try It 3.18
Find three consecutive integers whose sum is −36 . −36 .
Now that we have worked with consecutive integers, we will expand our work to include consecutive even integers and consecutive odd integers. Consecutive even integers are even integers that immediately follow one another. Examples of consecutive even integers are:
Notice each integer is 2 more than the number preceding it. If we call the first one n , then the next one is n + 2 . n + 2 . The next one would be n + 2 + 2 n + 2 + 2 or n + 4 . n + 4 .
Consecutive odd integers are odd integers that immediately follow one another. Consider the consecutive odd integers 77, 79, and 81.
Does it seem strange to add 2 (an even number) to get from one odd integer to the next? Do you get an odd number or an even number when we add 2 to 3? to 11? to 47?
Whether the problem asks for consecutive even numbers or odd numbers, you don’t have to do anything different. The pattern is still the same—to get from one odd or one even integer to the next, add 2.
Example 3.10
Find three consecutive even integers whose sum is 84.
Try It 3.19
Find three consecutive even integers whose sum is 102.
Try It 3.20
Find three consecutive even integers whose sum is −24 . −24 .
Example 3.11
A married couple together earns $110,000 a year. The wife earns $16,000 less than twice what her husband earns. What does the husband earn?
Try It 3.21
According to the National Automobile Dealers Association, the average cost of a car in 2014 was $28,500. This was $1,500 less than 6 times the cost in 1975. What was the average cost of a car in 1975?
Try It 3.22
U.S. Census data shows that the median price of new home in the United States in November 2014 was $280,900. This was $10,700 more than 14 times the price in November 1964. What was the median price of a new home in November 1964?
Section 3.1 Exercises
Practice makes perfect.
Use the Approach Word Problems with a Positive Attitude
In the following exercises, prepare the lists described.
List five positive thoughts you can say to yourself that will help you approach word problems with a positive attitude. You may want to copy them on a sheet of paper and put it in the front of your notebook, where you can read them often.
List five negative thoughts that you have said to yourself in the past that will hinder your progress on word problems. You may want to write each one on a small piece of paper and rip it up to symbolically destroy the negative thoughts.
In the following exercises, solve using the problem solving strategy for word problems. Remember to write a complete sentence to answer each question.
Two-thirds of the children in the fourth-grade class are girls. If there are 20 girls, what is the total number of children in the class?
Three-fifths of the members of the school choir are women. If there are 24 women, what is the total number of choir members?
Zachary has 25 country music CDs, which is one-fifth of his CD collection. How many CDs does Zachary have?
One-fourth of the candies in a bag of M&M’s are red. If there are 23 red candies, how many candies are in the bag?
There are 16 girls in a school club. The number of girls is four more than twice the number of boys. Find the number of boys.
There are 18 Cub Scouts in Pack 645. The number of scouts is three more than five times the number of adult leaders. Find the number of adult leaders.
Huong is organizing paperback and hardback books for her club’s used book sale. The number of paperbacks is 12 less than three times the number of hardbacks. Huong had 162 paperbacks. How many hardback books were there?
Jeff is lining up children’s and adult bicycles at the bike shop where he works. The number of children’s bicycles is nine less than three times the number of adult bicycles. There are 42 adult bicycles. How many children’s bicycles are there?
Philip pays $1,620 in rent every month. This amount is $120 more than twice what his brother Paul pays for rent. How much does Paul pay for rent?
Marc just bought an SUV for $54,000. This is $7,400 less than twice what his wife paid for her car last year. How much did his wife pay for her car?
Laurie has $46,000 invested in stocks and bonds. The amount invested in stocks is $8,000 less than three times the amount invested in bonds. How much does Laurie have invested in bonds?
Erica earned a total of $50,450 last year from her two jobs. The amount she earned from her job at the store was $1,250 more than three times the amount she earned from her job at the college. How much did she earn from her job at the college?
In the following exercises, solve each number word problem.
The sum of a number and eight is 12. Find the number.
The sum of a number and nine is 17. Find the number.
The difference of a number and 12 is three. Find the number.
The difference of a number and eight is four. Find the number.
The sum of three times a number and eight is 23. Find the number.
The sum of twice a number and six is 14. Find the number.
The difference of twice a number and seven is 17. Find the number.
The difference of four times a number and seven is 21. Find the number.
Three times the sum of a number and nine is 12. Find the number.
Six times the sum of a number and eight is 30. Find the number.
One number is six more than the other. Their sum is 42. Find the numbers.
One number is five more than the other. Their sum is 33. Find the numbers.
The sum of two numbers is 20. One number is four less than the other. Find the numbers.
The sum of two numbers is 27. One number is seven less than the other. Find the numbers.
The sum of two numbers is −45 . −45 . One number is nine more than the other. Find the numbers.
The sum of two numbers is −61 . −61 . One number is 35 more than the other. Find the numbers.
The sum of two numbers is −316 . −316 . One number is 94 less than the other. Find the numbers.
The sum of two numbers is −284 . −284 . One number is 62 less than the other. Find the numbers.
One number is 14 less than another. If their sum is increased by seven, the result is 85. Find the numbers.
One number is 11 less than another. If their sum is increased by eight, the result is 71. Find the numbers.
One number is five more than another. If their sum is increased by nine, the result is 60. Find the numbers.
One number is eight more than another. If their sum is increased by 17, the result is 95. Find the numbers.
One number is one more than twice another. Their sum is −5 . −5 . Find the numbers.
One number is six more than five times another. Their sum is six. Find the numbers.
The sum of two numbers is 14. One number is two less than three times the other. Find the numbers.
The sum of two numbers is zero. One number is nine less than twice the other. Find the numbers.
The sum of two consecutive integers is 77. Find the integers.
The sum of two consecutive integers is 89. Find the integers.
The sum of two consecutive integers is −23 . −23 . Find the integers.
The sum of two consecutive integers is −37 . −37 . Find the integers.
The sum of three consecutive integers is 78. Find the integers.
The sum of three consecutive integers is 60. Find the integers.
Find three consecutive integers whose sum is −3 . −3 .
Find three consecutive even integers whose sum is 258.
Find three consecutive even integers whose sum is 222.
Find three consecutive odd integers whose sum is 171.
Find three consecutive odd integers whose sum is 291.
Find three consecutive even integers whose sum is −36 . −36 .
Find three consecutive even integers whose sum is −84 . −84 .
Find three consecutive odd integers whose sum is −213 . −213 .
Find three consecutive odd integers whose sum is −267 . −267 .
Everyday Math
Sale Price Patty paid $35 for a purse on sale for $10 off the original price. What was the original price of the purse?
Sale Price Travis bought a pair of boots on sale for $25 off the original price. He paid $60 for the boots. What was the original price of the boots?
Buying in Bulk Minh spent $6.25 on five sticker books to give his nephews. Find the cost of each sticker book.
Buying in Bulk Alicia bought a package of eight peaches for $3.20. Find the cost of each peach.
Price before Sales Tax Tom paid $1,166.40 for a new refrigerator, including $86.40 tax. What was the price of the refrigerator?
Price before Sales Tax Kenji paid $2,279 for a new living room set, including $129 tax. What was the price of the living room set?
Writing Exercises
What has been your past experience solving word problems?
When you start to solve a word problem, how do you decide what to let the variable represent?
What are consecutive odd integers? Name three consecutive odd integers between 50 and 60.
What are consecutive even integers? Name three consecutive even integers between −50 −50 and −40 . −40 .
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
ⓑ If most of your checks were:
…confidently. Congratulations! You have achieved your goals in this section! Reflect on the study skills you used so that you can continue to use them. What did you do to become confident of your ability to do these things? Be specific!
…with some help. This must be addressed quickly as topics you do not master become potholes in your road to success. Math is sequential—every topic builds upon previous work. It is important to make sure you have a strong foundation before you move on. Who can you ask for help? Your fellow classmates and instructor are good resources. Is there a place on campus where math tutors are available? Can your study skills be improved?
…no—I don’t get it! This is critical and you must not ignore it. You need to get help immediately or you will quickly be overwhelmed. See your instructor as soon as possible to discuss your situation. Together you can come up with a plan to get you the help you need.
As an Amazon Associate we earn from qualifying purchases.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/elementary-algebra/pages/1-introduction
- Authors: Lynn Marecek, MaryAnne Anthony-Smith
- Publisher/website: OpenStax
- Book title: Elementary Algebra
- Publication date: Feb 22, 2017
- Location: Houston, Texas
- Book URL: https://openstax.org/books/elementary-algebra/pages/1-introduction
- Section URL: https://openstax.org/books/elementary-algebra/pages/3-1-use-a-problem-solving-strategy
© Feb 9, 2022 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
CHAPTER 5 Solving First Degree Equations in One Variable
5.7 Use a Problem-Solving Strategy
Learning Objectives
By the end of this section, you will be able to:
- Approach word problems with a positive attitude
- Use a problem-solving strategy for word problems
- Solve number problems
Approach Word Problems with a Positive Attitude
“If you think you can… or think you can’t… you’re right.”—Henry Ford
The world is full of word problems! Will my income qualify me to rent that apartment? How much punch do I need to make for the party? What size diamond can I afford to buy my girlfriend? Should I fly or drive to my family reunion?
How much money do I need to fill the car with gas? How much tip should I leave at a restaurant? How many socks should I pack for vacation? What size turkey do I need to buy for Thanksgiving dinner, and then what time do I need to put it in the oven? If my sister and I buy our mother a present, how much does each of us pay?
Now that we can solve equations, we are ready to apply our new skills to word problems. Do you know anyone who has had negative experiences in the past with word problems? Have you ever had thoughts like the student below?

When we feel we have no control, and continue repeating negative thoughts, we set up barriers to success. We need to calm our fears and change our negative feelings.
Start with a fresh slate and begin to think positive thoughts. If we take control and believe we can be successful, we will be able to master word problems! Read the positive thoughts in (Figure 2) and say them out loud.

Think of something, outside of school, that you can do now but couldn’t do 3 years ago. Is it driving a car? Snowboarding? Cooking a gourmet meal? Speaking a new language? Your past experiences with word problems happened when you were younger—now you’re older and ready to succeed!
Use a Problem-Solving Strategy for Word Problems
We have reviewed translating English phrases into algebraic expressions, using some basic mathematical vocabulary and symbols. We have also translated English sentences into algebraic equations and solved some word problems. The word problems applied math to everyday situations. We restated the situation in one sentence, assigned a variable, and then wrote an equation to solve the problem. This method works as long as the situation is familiar and the math is not too complicated.
Now, we’ll expand our strategy so we can use it to successfully solve any word problem. We’ll list the strategy here, and then we’ll use it to solve some problems. We summarize below an effective strategy for problem solving.
Use a Problem-Solving Strategy to Solve Word Problems.
- Read the problem. Make sure all the words and ideas are understood.
- Identify what we are looking for.
- Name what we are looking for. Choose a variable to represent that quantity.
- Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebraic equation.
- Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
Pilar bought a purse on sale for $18, which is one-half of the original price. What was the original price of the purse?
Step 1. Read the problem. Read the problem two or more times if necessary. Look up any unfamiliar words in a dictionary or on the internet.
- In this problem, is it clear what is being discussed? Is every word familiar?
Step 2. Identify what you are looking for. Did you ever go into your bedroom to get something and then forget what you were looking for? It’s hard to find something if you are not sure what it is! Read the problem again and look for words that tell you what you are looking for!
- In this problem, the words “what was the original price of the purse” tell us what we need to find.
Step 3. Name what we are looking for. Choose a variable to represent that quantity. We can use any letter for the variable, but choose one that makes it easy to remember what it represents.
Step 4. Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Translate the English sentence into an algebraic equation.
Reread the problem carefully to see how the given information is related. Often, there is one sentence that gives this information, or it may help to write one sentence with all the important information. Look for clue words to help translate the sentence into algebra. Translate the sentence into an equation.
Step 5. Solve the equation using good algebraic techniques. Even if you know the solution right away, using good algebraic techniques here will better prepare you to solve problems that do not have obvious answers.
- Does $36 make sense in the problem? Yes, because 18 is one-half of 36, and the purse was on sale at half the original price.
Step 7. Answer the question with a complete sentence. The problem asked “What was the original price of the purse?”
- The answer to the question is: “The original price of the purse was $36.”
If this were a homework exercise, our work might look like this:
Pilar bought a purse on sale for $18, which is one-half the original price. What was the original price of the purse?
Joaquin bought a bookcase on sale for $120, which was two-thirds of the original price. What was the original price of the bookcase?
Two-fifths of the songs in Mariel’s playlist are country. If there are 16 country songs, what is the total number of songs in the playlist?
Let’s try this approach with another example.
Ginny and her classmates formed a study group. The number of girls in the study group was three more than twice the number of boys. There were 11 girls in the study group. How many boys were in the study group?
Guillermo bought textbooks and notebooks at the bookstore. The number of textbooks was 3 more than twice the number of notebooks. He bought 7 textbooks. How many notebooks did he buy?
Gerry worked Sudoku puzzles and crossword puzzles this week. The number of Sudoku puzzles he completed is eight more than twice the number of crossword puzzles. He completed 22 Sudoku puzzles. How many crossword puzzles did he do?
Solve Number Problems
Now that we have a problem solving strategy, we will use it on several different types of word problems. The first type we will work on is “number problems.” Number problems give some clues about one or more numbers. We use these clues to write an equation. Number problems don’t usually arise on an everyday basis, but they provide a good introduction to practicing the problem solving strategy outlined above.
The difference of a number and six is 13. Find the number.
The difference of a number and eight is 17. Find the number.
The sum of twice a number and seven is 15. Find the number.
Did you notice that we left out some of the steps as we solved this equation? If you’re not yet ready to leave out these steps, write down as many as you need.
The sum of four times a number and two is 14. Find the number.
The sum of three times a number and seven is 25. Find the number.
Some number word problems ask us to find two or more numbers. It may be tempting to name them all with different variables, but so far we have only solved equations with one variable. In order to avoid using more than one variable, we will define the numbers in terms of the same variable. Be sure to read the problem carefully to discover how all the numbers relate to each other.
One number is five more than another. The sum of the numbers is 21. Find the numbers.
One number is six more than another. The sum of the numbers is twenty-four. Find the numbers.
The sum of two numbers is fifty-eight. One number is four more than the other. Find the numbers.
The sum of two numbers is negative fourteen. One number is four less than the other. Find the numbers.
The sum of two numbers is negative twenty-three. One number is seven less than the other. Find the numbers.
One number is ten more than twice another. Their sum is one. Find the numbers.
One number is eight more than twice another. Their sum is negative four. Find the numbers.
Some number problems involve consecutive integers. Consecutive integers are integers that immediately follow each other.
Examples of consecutive integers are:
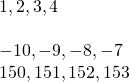
The sum of two consecutive integers is 47. Find the numbers.
Now that we have worked with consecutive integers, we will expand our work to include consecutive even integers and consecutive odd integers. Consecutive even integers are even integers that immediately follow one another. Examples of consecutive even integers are:
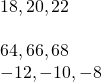
Consecutive odd integers are odd integers that immediately follow one another. Consider the consecutive odd integers 77, 79, and 81
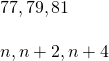
Does it seem strange to add 2 (an even number) to get from one odd integer to the next? Do you get an odd number or an even number when we add 2 to 3? to 11? to 47?
Whether the problem asks for consecutive even numbers or odd numbers, you don’t have to do anything different. The pattern is still the same—to get from one odd or one even integer to the next, add 2
Find three consecutive even integers whose sum is 84
TRY IT 10.1
Find three consecutive even integers whose sum is 102
TRY IT 10.2
A married couple together earns $110,000 a year. The wife earns $16,000 less than twice what her husband earns. What does the husband earn?
TRY IT 11.1
According to the National Automobile Dealers Association, the average cost of a car in 2014 was 28,500. This was 1,500 less than 6 times the cost in 1975. What was the average cost of a car in 1975?
TRY IT 11.2
The Canadian Real Estate Association (CREA) data shows that the median price of new home in the Canada in December 2018 was $470,000. This was $14,000 more than 19 times the price in December 1967. What was the median price of a new home in December 1967?
$24,000
Key Concepts
- Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebra equation.
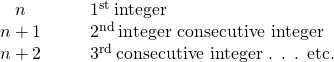
Consecutive even integers are even integers that immediately follow one another.
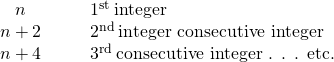
Consecutive odd integers are odd integers that immediately follow one another.
Practice Makes Perfect
Use the approach word problems with a positive attitude.
In the following exercises, prepare the lists described.
In the following exercises, solve using the problem solving strategy for word problems. Remember to write a complete sentence to answer each question.
In the following exercises, solve each number word problem.
Everyday Math
Writing exercises, attributions.
This chapter has been adapted from “Use a Problem-Solving Strategy” in Elementary Algebra (OpenStax) by Lynn Marecek and MaryAnne Anthony-Smith, which is under a CC BY 4.0 Licence . Adapted by Izabela Mazur. See the Copyright page for more information.
Introductory Algebra Copyright © 2021 by Izabela Mazur is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.
Share This Book

- Share on Facebook
- Tweet This Resource
- Pin This Resource

Problem-Solving Strategy: Write a Number Sentence: Problem Solving
In this number sentence worksheet, students use the problem solving strategy of understand, plan, solve, and look back to help them write number sentences to solve the word problem.
Start Your Free Trial
Save time and discover engaging curriculum for your classroom. Reviewed and rated by trusted, credentialed teachers.

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

9.2: Use a Problem Solving Strategy
- Last updated
- Save as PDF
- Page ID 114974

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
Learning Objectives
By the end of this section, you will be able to:
- Approach word problems with a positive attitude
- Use a problem solving strategy for word problems
- Solve number problems
Be Prepared 9.1
Before you get started, take this readiness quiz.
Translate “6 “6 less than twice x ” x ” into an algebraic expression. If you missed this problem, review Example 2.25.
Be Prepared 9.2
Solve: 2 3 x = 24 . 2 3 x = 24 . If you missed this problem, review Example 8.16.
Be Prepared 9.3
Solve: 3 x + 8 = 14 . 3 x + 8 = 14 . If you missed this problem, review Example 8.20.
Approach Word Problems with a Positive Attitude
The world is full of word problems. How much money do I need to fill the car with gas? How much should I tip the server at a restaurant? How many socks should I pack for vacation? How big a turkey do I need to buy for Thanksgiving dinner, and what time do I need to put it in the oven? If my sister and I buy our mother a present, how much will each of us pay?
Now that we can solve equations, we are ready to apply our new skills to word problems. Do you know anyone who has had negative experiences in the past with word problems? Have you ever had thoughts like the student in Figure 9.2?
When we feel we have no control, and continue repeating negative thoughts, we set up barriers to success. We need to calm our fears and change our negative feelings.
Start with a fresh slate and begin to think positive thoughts like the student in Figure 9.3. Read the positive thoughts and say them out loud.
If we take control and believe we can be successful, we will be able to master word problems.
Think of something that you can do now but couldn't do three years ago. Whether it's driving a car, snowboarding, cooking a gourmet meal, or speaking a new language, you have been able to learn and master a new skill. Word problems are no different. Even if you have struggled with word problems in the past, you have acquired many new math skills that will help you succeed now!
Use a Problem-solving Strategy for Word Problems
In earlier chapters, you translated word phrases into algebraic expressions, using some basic mathematical vocabulary and symbols. Since then you've increased your math vocabulary as you learned about more algebraic procedures, and you've had more practice translating from words into algebra.
You have also translated word sentences into algebraic equations and solved some word problems. The word problems applied math to everyday situations. You had to restate the situation in one sentence, assign a variable, and then write an equation to solve. This method works as long as the situation is familiar to you and the math is not too complicated.
Now we'll develop a strategy you can use to solve any word problem. This strategy will help you become successful with word problems. We'll demonstrate the strategy as we solve the following problem.
Example 9.1
Pete bought a shirt on sale for $18 , $18 , which is one-half the original price. What was the original price of the shirt?
Step 1. Read the problem. Make sure you understand all the words and ideas. You may need to read the problem two or more times. If there are words you don't understand, look them up in a dictionary or on the Internet.
- In this problem, do you understand what is being discussed? Do you understand every word?
Step 2. Identify what you are looking for. It's hard to find something if you are not sure what it is! Read the problem again and look for words that tell you what you are looking for!
- In this problem, the words “what was the original price of the shirt” tell you that what you are looking for: the original price of the shirt.
Step 3. Name what you are looking for. Choose a variable to represent that quantity. You can use any letter for the variable, but it may help to choose one that helps you remember what it represents.
- Let p = p = the original price of the shirt
Step 4. Translate into an equation. It may help to first restate the problem in one sentence, with all the important information. Then translate the sentence into an equation.
Step 5. Solve the equation using good algebra techniques. Even if you know the answer right away, using algebra will better prepare you to solve problems that do not have obvious answers.
Step 6. Check the answer in the problem and make sure it makes sense.
- We found that p = 36 , p = 36 , which means the original price was $36 . $36 . Does $36 $36 make sense in the problem? Yes, because 18 18 is one-half of 36 , 36 , and the shirt was on sale at half the original price.
- Step 7. Answer the question with a complete sentence.
- The problem asked “What was the original price of the shirt?” The answer to the question is: “The original price of the shirt was $36 .” $36 .”
If this were a homework exercise, our work might look like this:
Joaquin bought a bookcase on sale for $120 , $120 , which was two-thirds the original price. What was the original price of the bookcase?
Two-fifths of the people in the senior center dining room are men. If there are 16 16 men, what is the total number of people in the dining room?
We list the steps we took to solve the previous example.
Problem-Solving Strategy
- Step 1. Read the word problem. Make sure you understand all the words and ideas. You may need to read the problem two or more times. If there are words you don't understand, look them up in a dictionary or on the internet.
- Step 2. Identify what you are looking for.
- Step 3. Name what you are looking for. Choose a variable to represent that quantity.
- Step 4. Translate into an equation. It may be helpful to first restate the problem in one sentence before translating.
- Step 5. Solve the equation using good algebra techniques.
- Step 6. Check the answer in the problem. Make sure it makes sense.
Let's use this approach with another example.
Example 9.2
Yash brought apples and bananas to a picnic. The number of apples was three more than twice the number of bananas. Yash brought 11 11 apples to the picnic. How many bananas did he bring?
Guillermo bought textbooks and notebooks at the bookstore. The number of textbooks was 3 3 more than the number of notebooks. He bought 5 5 textbooks. How many notebooks did he buy?
Gerry worked Sudoku puzzles and crossword puzzles this week. The number of Sudoku puzzles he completed is seven more than the number of crossword puzzles. He completed 14 14 Sudoku puzzles. How many crossword puzzles did he complete?
In Solve Sales Tax, Commission, and Discount Applications, we learned how to translate and solve basic percent equations and used them to solve sales tax and commission applications. In the next example, we will apply our Problem Solving Strategy to more applications of percent.
Example 9.3
Nga's car insurance premium increased by $60 , $60 , which was 8% 8% of the original cost. What was the original cost of the premium?
Pilar's rent increased by 4% . 4% . The increase was $38 . $38 . What was the original amount of Pilar's rent?
Steve saves 12% 12% of his paycheck each month. If he saved $504 $504 last month, how much was his paycheck?
Solve Number Problems
Now we will translate and solve number problems . In number problems, you are given some clues about one or more numbers, and you use these clues to build an equation. Number problems don't usually arise on an everyday basis, but they provide a good introduction to practicing the Problem Solving Strategy . Remember to look for clue words such as difference , of , and and .
Example 9.4
The difference of a number and six is 13 . 13 . Find the number.
The difference of a number and eight is 17 . 17 . Find the number.
The difference of a number and eleven is −7 . −7 . Find the number.
Example 9.5
The sum of twice a number and seven is 15 . 15 . Find the number.
The sum of four times a number and two is 14 . 14 . Find the number.
Try It 9.10
The sum of three times a number and seven is 25 . 25 . Find the number.
Some number word problems ask you to find two or more numbers. It may be tempting to name them all with different variables, but so far we have only solved equations with one variable. We will define the numbers in terms of the same variable. Be sure to read the problem carefully to discover how all the numbers relate to each other.
Example 9.6
One number is five more than another. The sum of the numbers is twenty-one. Find the numbers.
Try It 9.11
One number is six more than another. The sum of the numbers is twenty-four. Find the numbers.
Try It 9.12
The sum of two numbers is fifty-eight. One number is four more than the other. Find the numbers.
Example 9.7
The sum of two numbers is negative fourteen. One number is four less than the other. Find the numbers.
Try It 9.13
The sum of two numbers is negative twenty-three. One number is 7 7 less than the other. Find the numbers.
Try It 9.14
The sum of two numbers is negative eighteen. One number is 40 40 more than the other. Find the numbers.
Example 9.8
One number is ten more than twice another. Their sum is one. Find the numbers.
Try It 9.15
One number is eight more than twice another. Their sum is negative four. Find the numbers.
Try It 9.16
One number is three more than three times another. Their sum is negative five. Find the numbers.
Consecutive integers are integers that immediately follow each other. Some examples of consecutive integers are:
... 1 , 2 , 3 , 4 ,... ... 1 , 2 , 3 , 4 ,...
... −10 , −9 , −8 , −7 ,... ... −10 , −9 , −8 , −7 ,...
... 150 , 151 , 152 , 153 ,... ... 150 , 151 , 152 , 153 ,...
Notice that each number is one more than the number preceding it. So if we define the first integer as n , n , the next consecutive integer is n + 1 . n + 1 . The one after that is one more than n + 1 , n + 1 , so it is n + 1 + 1 , n + 1 + 1 , or n + 2 . n + 2 .
n 1st integer n + 1 2nd consecutive integer n + 2 3rd consecutive integer n 1st integer n + 1 2nd consecutive integer n + 2 3rd consecutive integer
Example 9.9
The sum of two consecutive integers is 47 . 47 . Find the numbers.
Try It 9.17
The sum of two consecutive integers is 95 . 95 . Find the numbers.
Try It 9.18
The sum of two consecutive integers is −31 . −31 . Find the numbers.
Example 9.10
Find three consecutive integers whose sum is 42 . 42 .
Try It 9.19
Find three consecutive integers whose sum is 96 . 96 .
Try It 9.20
Find three consecutive integers whose sum is −36 . −36 .
Links To Literacy
The Links to Literacy activities Math Curse , Missing Mittens and Among the Odds and Evens will provide you with another view of the topics covered in this section.
Section 9.1 Exercises
Practice makes perfect.
In the following exercises, use the problem-solving strategy for word problems to solve. Answer in complete sentences.
Two-thirds of the children in the fourth-grade class are girls. If there are 20 20 girls, what is the total number of children in the class?
Three-fifths of the members of the school choir are women. If there are 24 24 women, what is the total number of choir members?
Zachary has 25 25 country music CDs, which is one-fifth of his CD collection. How many CDs does Zachary have?
One-fourth of the candies in a bag of are red. If there are 23 23 red candies, how many candies are in the bag?
There are 16 16 girls in a school club. The number of girls is 4 4 more than twice the number of boys. Find the number of boys in the club.
There are 18 18 Cub Scouts in Troop 645 . 645 . The number of scouts is 3 3 more than five times the number of adult leaders. Find the number of adult leaders.
Lee is emptying dishes and glasses from the dishwasher. The number of dishes is 8 8 less than the number of glasses. If there are 9 9 dishes, what is the number of glasses?
The number of puppies in the pet store window is twelve less than the number of dogs in the store. If there are 6 6 puppies in the window, what is the number of dogs in the store?
After 3 3 months on a diet, Lisa had lost 12% 12% of her original weight. She lost 21 21 pounds. What was Lisa's original weight?
Tricia got a 6% 6% raise on her weekly salary. The raise was $30 $30 per week. What was her original weekly salary?
Tim left a $9 $9 tip for a $50 $50 restaurant bill. What percent tip did he leave?
Rashid left a $15 $15 tip for a $75 $75 restaurant bill. What percent tip did he leave?
Yuki bought a dress on sale for $72 . $72 . The sale price was 60% 60% of the original price. What was the original price of the dress?
Kim bought a pair of shoes on sale for $40.50 . $40.50 . The sale price was 45% 45% of the original price. What was the original price of the shoes?
In the following exercises, solve each number word problem.
The sum of a number and eight is 12 . 12 . Find the number.
The sum of a number and nine is 17 . 17 . Find the number.
The difference of a number and twelve is 3 . 3 . Find the number.
The difference of a number and eight is 4 . 4 . Find the number.
The sum of three times a number and eight is 23 . 23 . Find the number.
The sum of twice a number and six is 14 . 14 . Find the number.
The difference of twice a number and seven is 17 . 17 . Find the number.
The difference of four times a number and seven is 21 . 21 . Find the number.
Three times the sum of a number and nine is 12 . 12 . Find the number.
Six times the sum of a number and eight is 30 . 30 . Find the number.
One number is six more than the other. Their sum is forty-two. Find the numbers.
One number is five more than the other. Their sum is thirty-three. Find the numbers.
The sum of two numbers is twenty. One number is four less than the other. Find the numbers.
The sum of two numbers is twenty-seven. One number is seven less than the other. Find the numbers.
A number is one more than twice another number. Their sum is negative five. Find the numbers.
One number is six more than five times another. Their sum is six. Find the numbers.
The sum of two numbers is fourteen. One number is two less than three times the other. Find the numbers.
The sum of two numbers is zero. One number is nine less than twice the other. Find the numbers.
One number is fourteen less than another. If their sum is increased by seven, the result is 85 . 85 . Find the numbers.
One number is eleven less than another. If their sum is increased by eight, the result is 71 . 71 . Find the numbers.
The sum of two consecutive integers is 77 . 77 . Find the integers.
The sum of two consecutive integers is 89 . 89 . Find the integers.
The sum of two consecutive integers is −23 . −23 . Find the integers.
The sum of two consecutive integers is −37 . −37 . Find the integers.
The sum of three consecutive integers is 78 . 78 . Find the integers.
The sum of three consecutive integers is 60 . 60 . Find the integers.
Find three consecutive integers whose sum is −3 . −3 .
Everyday Math
Shopping Patty paid $35 $35 for a purse on sale for $10 $10 off the original price. What was the original price of the purse?
Shopping Travis bought a pair of boots on sale for $25 $25 off the original price. He paid $60 $60 for the boots. What was the original price of the boots?
Shopping Minh spent $6.25 $6.25 on 5 5 sticker books to give his nephews. Find the cost of each sticker book.
Shopping Alicia bought a package of 8 8 peaches for $3.20 . $3.20 . Find the cost of each peach.
Shopping Tom paid $1,166.40 $1,166.40 for a new refrigerator, including $86.40 $86.40 tax. What was the price of the refrigerator before tax?
Shopping Kenji paid $2,279 $2,279 for a new living room set, including $129 $129 tax. What was the price of the living room set before tax?
Study Guides > ALGEBRA / TRIG I
Using a problem-solving strategy to solve number problems, learning outcomes.
- Solve number problems
- Solve consecutive integer problems
Solving Number Problems
Solving for two or more numbers, solving for consecutive integers.
[latex]\begin{array}{c} \hfill \text{...}1, 2, 3, 4, 5, 6\text{,...}\hfill \end{array}[/latex] [latex-display]\text{...}-10,-9,-8,-7\text{,...}[/latex-display] [latex]\text{...}150,151,152,153\text{,...}[/latex]
[latex]\begin{array}{cccc}n\hfill & & & \text{1st integer}\hfill \\ n+1\hfill & & & \text{2nd consecutive integer}\hfill \\ n+2\hfill & & & \text{3rd consecutive integer}\hfill \end{array}[/latex]
- Read and understand: We are looking for three numbers, and we know they are consecutive integers.
- Constants and Variables: [latex]93[/latex] is a constant. The first integer we will call [latex]x[/latex]. Second integer: [latex]x+1[/latex] Third integer: [latex]x+2[/latex]
- Translate: The sum of three consecutive integers translates to [latex]x+\left(x+1\right)+\left(x+2\right)[/latex], based on how we defined the first, second, and third integers. Notice how we placed parentheses around the second and third integers. This is just to make each integer more distinct. " is 93 " translates to "[latex]=93[/latex]" since " is " is associated with equals.
- Write an equation: [latex]x+\left(x+1\right)+\left(x+2\right)=93[/latex]
[latex]x+x+1+x+2=93[/latex]
[latex]\begin{array}{r}x+x+1+x+2=93\\3x+3 = 93\\\underline{-3\,\,\,\,\,-3}\\3x=90\\\frac{3x}{3}=\frac{90}{3}\\x=30\end{array}[/latex]
- Check and Interpret: Okay, we have found a value for [latex]x[/latex]. We were asked to find the value of three consecutive integers, so we need to do a couple more steps. Remember how we defined our variables:
The first integer we will call [latex]x[/latex], [latex]x=30[/latex] Second integer: [latex]x+1[/latex] so [latex]30+1=31[/latex] Third integer: [latex]x+2[/latex] so [latex]30+2=32[/latex] The three consecutive integers whose sum is [latex]93[/latex] are [latex]30\text{, }31\text{, and }32[/latex]
Contribute!
Licenses & attributions, cc licensed content, shared previously.
- Ex: Linear Equation Application with One Variable - Number Problem. Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution .
- Ex: Write and Solve an Equation for Consecutive Natural Numbers with a Given Sum. Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution .
- Write and Solve a Linear Equations to Solve a Number Problem (1) Mathispower4u . Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution .
- Question ID 142763, 142770, 142775, 142806, 142811, 142816, 142817. Authored by: Lumen Learning. License: CC BY: Attribution . License terms: IMathAS Community License, CC-BY + GPL.
CC licensed content, Specific attribution
- Prealgebra. Provided by: OpenStax License: CC BY: Attribution . License terms: Download for free at http://cnx.org/contents/ [email protected] .
Please add a message.
Message received. Thanks for the feedback.

IMAGES
VIDEO
COMMENTS
Within this download, we are offering you a range of word problems for practice. Each page provided contains a single problem solving word problem. Below each story problem you will find a set of four steps for students to follow when finding the answer. This set will focus on the write a number sentence strategy for math problem solving.
This video explains the Number Sentence Strategy for solving word problems. This strategy is most commonly used. It helps us identify the mathematical operat...
Strategy: Write a Number Sentence. Word problems can become numbers and math symbols (+ − ÷ × = < >). Write a number sentence. This strategy helps you decide which numbers and math operations will solve the problem. Example: Ollie spent $24 shopping for summer camp. He bought 6 snack bars and 3 packages of trail mix. The snack bars were $2 ...
You need to know that there are 18 pencils and they are divided into 3 equal groups. 2) PLAN: How can you solve the problem? You can write a number sentence to solve the problem. Write a division sentence to divide the pencils in 3 equal groups. 3) SOLVE: 18 ÷ 3 = 6. There are 6 pencils in each group.
Here are five strategies to help students check their solutions. 1. Use the Inverse Operation. For simpler problems, a quick and easy problem solving strategy is to use the inverse operation. For example, if the operation to solve a word problem is 56 ÷ 8 = 7 students can check the answer is correct by multiplying 8 × 7.
A teaching and learning video about using number sentences as a problem solving strategy. See also my video on Drawing a Diagram at https://youtu.be/7_5iYyy0...
Grade 1 - Unit 1 - Lesson 6G1 - 1-6 Problem-Solving Strategy Write a Number SentenceWatch on YouTube: https://youtu.be/XttfT9io8t4 Download The Application: ...
Read each word problem below, and find the answer by writing the equation. Remember to follow these steps: Problem Solving Strategy: Write a Number Sentence Step 1: What are the numbers? Step 2: What is the question? Step 3: What is the key word? Step 4: What is the equation? Walter ran 44 minutes on Saturday and 25 minutes on Sunday.
Example 2: Complete the math sentence so that it is true. 6 + 7 = 9 + ―. Solution: 6 + 7 = 13. So, to make the sentence true, 9 + ― must be equal to 13. Therefore, the missing number must be 13 - 9 or 4. Example 3: Substitute the value into the variable (x) and state whether the resulting sentence is true or false.
There are 20 buttons and 10 circles. We can use the addition sentence 20 + 10. Solving addition sentences is simple when we use an addition strategy! Let's see, we could solve this problem using base ten blocks, a number line, or ten frames.
We will now apply the problem solving strategy to "number word problems." Number word problems give some clues about one or more numbers and we use these clues to write an equation. Number word problems provide good practice for using the Problem Solving Strategy. ... Write a sentence that gives the information to find it. Translate into an ...
Choose a variable to represent the number. Step 4. Translate. Restate as one sentence.Translate into an equation. Step 5. Solve the equation.Add 6 to both sides. Simplify. Step 6. Check: The difference of [Math Processing Error] 19 and [Math Processing Error] 6 is [Math Processing Error] 13.
The first type we will work on is "number problems." Number problems give some clues about one or more numbers. We use these clues to write an equation. Number problems don't usually arise on an everyday basis, but they provide a good introduction to practicing the problem solving strategy outlined above.
Learn how to use number sentences to solve a word problem.We hope you are enjoying this video! For more in-depth learning, check out Miacademy.co (https://ww...
The first type we will work on is "number problems." Number problems give some clues about one or more numbers. We use these clues to write an equation. Number problems don't usually arise on an everyday basis, but they provide a good introduction to practicing the problem solving strategy outlined above.
We will now apply the problem solving strategy to "number word problems." Number word problems give some clues about one or more numbers and we use these clues to write an equation. ... Write a sentence that gives the information to find it. Translate the sentence into an equation. Multiply. Divide both sides by 240. Put in percent form ...
5.7 Use a Problem-Solving Strategy. Learning Objectives. By the end of this section, you will be able to: Approach word problems with a positive attitude. Use a problem-solving strategy for word problems. Solve number problems.
This Problem-Solving Strategy: Write a Number Sentence: Problem Solving Worksheet is suitable for 4th - 5th Grade. In this number sentence activity, students use the problem solving strategy of understand, plan, solve, and look back to help them write number sentences to solve the word problem.
Problem-Solving Strategy. Step 1. Read the word problem. Make sure you understand all the words and ideas. You may need to read the problem two or more times. If there are words you don't understand, look them up in a dictionary or on the internet. Step 2. Identify what you are looking for. Step 3.
Grade 2Chapter 7 - Subtract Three-Digit NumbersLesson 8 - Problem-Solving Strategy Write a Number Sentencewww.eslamacademy.com
n+5= {2}^ {\text {nd}}\text {number} n+5 = 2ndnumber. Step 4. Translate. Restate the problem as one sentence with all the important information. Translate into an equation. Substitute the variable expressions. The sum of the numbers is. 2 1. 21 21 .The sum of the 1st number and the 2nd number is.
Problem Solving Strategy Write a Number Sentence